Diagonalt snitt av et rektangulært parallellepiped. Diagonale snitt av et parallellepiped

Utsnitt av geometriske figurer har forskjellige former. Tverrsnittet av et parallellepiped er alltid et rektangel eller kvadrat. Den har en rekke parametere som kan oppdages med en analysemetode.

Bruksanvisning

1. Det er mulig å tegne fire seksjoner gjennom parallellepipedet, som er firkanter eller rektangler. Hver den har to diagonale og to veikryss. Som vanlig har de forskjellige størrelser. Unntaket er kuben, der de er identiske. Før du konstruerer en del av et parallellepiped, få en ide om hva denne figuren representerer. Det er to typer parallellepipeder - vanlige og rektangulære. I et vanlig parallellepiped er flatene plassert i en viss vinkel til basen, mens de i en rektangulær er vinkelrett på den. Alle ansikter rektangulært parallellepipedum er rektangler eller firkanter. Det følger av dette at en kube er spesielt tilfelle rektangulært parallellepipedum.

2. Hver del av et parallellepiped har visse sammenstillinger. De viktigste er areal, omkrets og lengder på diagonaler. Hvis sidene av seksjonen eller noen av dens andre parametere er kjent fra disse problemene, er dette nok til å bestemme omkretsen eller området. Diagonalene til seksjonene bestemmes også langs sidene. Den første av disse parameterne er arealet av diagonalseksjonen. For å bestemme arealet av diagonalseksjonen, er det nødvendig å kjenne høyden og sidene til bunnen av parallellepipedet. Hvis lengden og bredden til bunnen av parallellepipedet er gitt, finn diagonalen ved å bruke Pythagoras teorem: d=?a^2+b^2. Etter å ha funnet diagonalen og vite høyden på parallellepipedet, regn ut kryss- snittareal av parallellepipedet: S=d*h.

3. Omkretsen til diagonalseksjonen kan også beregnes ved å bruke to verdier - diagonalen til basen og høyden på parallellepipedet. I dette tilfellet, finn først to diagonaler (øvre og nedre baser) ved å bruke Pythagoras teorem, og legg dem deretter til med to ganger høyden.

4. Hvis du tegner et fly, parallelt med ribbeina parallellepiped, er det mulig å oppnå en rektangulær seksjon, hvis sider er en av sidene av bunnen av parallellepipedet og høyden. Finn arealet til denne seksjonen på følgende måte: S = a * h. Finn omkretsen til denne seksjonen på lignende måte ved å bruke følgende formel: p = 2 * (a + h).

5. Det siste tilfellet oppstår når seksjonen løper parallelt med de to basene til parallellepipedet. Da er dens areal og omkrets lik verdien av arealet og omkretsen til basene, dvs.: S=a*b - tverrsnittsareal; p=2*(a+b).

Før du går videre til å finne høyden på et parallellepiped, er det nødvendig å avklare hva en høyde er og hva et parallellepiped er. I geometri er høyde en vinkelrett fra toppen av en figur til basen, eller et segment som forbinder øvre og nedre baser ved å bruke den korteste metoden. Et parallellepiped er et polyeder som har to parallelle og lik polygon som baser hvis hjørner er forenet av segmenter. Parallepipedet er bygd opp av seks parallellogrammer, parallelle i par og like med hverandre.

Bruksanvisning

1. Det kan være tre høyder i et parallellogram, avhengig av plasseringen til figuren i rommet; ved å snu parallellepipedet på siden, vil du bytte base og ansikter. De øvre og nedre parallellogrammene er alltid baser. Hvis sidekantene på figuren er vinkelrette på basene, er parallellepipedet rett, og hver av kantene er en klar høyde. Tillatt å måle.

2. For å få et rett parallellepiped av samme størrelse fra et skrånende parallellepiped, må du forlenge sideflatene i én retning. Etter dette, bygg vinkelrett snitt, fra hjørnene som, sett til side lengden på kanten av parallellepipedet, og på denne avstanden konstruer en andre vinkelrett seksjon. De to parallellogrammene du konstruerte vil binde det nye parallellepipedet, som har samme areal som det første. For fremtiden bør det bemerkes at volumene like store figurer identisk.

3. Ofte stilte spørsmål Vi møter høyder i problemer. Vi får alltid data som gjør at vi kan beregne det. Dette kan være volumet, lineære dimensjoner til parallellepipedet, lengdene på diagonalene. Altså volumet til parallellepipedet lik produktet basen etter høyden, det vil si å vite volumet og størrelsen på basen, er det lett å finne ut høyden ved å dele den første på den andre. Hvis du har å gjøre med et rektangulært parallellepiped, det vil si en hvis base er et rektangel, kan de prøve å komplisere oppgaven din på grunn av dens spesielle egenskaper. Så i et rektangulært parallellepiped, hvert kvadrat av diagonalen lik summen kvadrater med 3 dimensjoner av et parallellepiped. Hvis "gitt" for problemet med et rektangulært parallellepiped indikerer lengden på diagonalen og lengden på sidene av basen, er denne informasjonen nok til å finne ut størrelsen på ønsket høyde.

Et parallellepiped er et spesielt tilfelle av et prisme, der alle seks flatene er parallellogrammer eller rektangler. Parallellepiped med rektangulære kanter også kalt rektangulær. Et parallellepiped har fire kryssende diagonaler. Hvis tre kanter a, b, c er gitt, kan du finne alle diagonalene til et rektangulært parallellepiped ved å utføre tilleggskonstruksjoner.

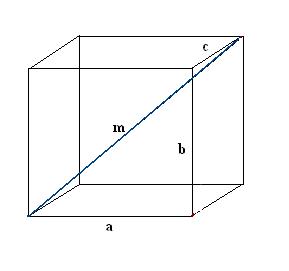
Bruksanvisning

1. Tegn et rektangulært parallellepiped. Skriv ned de kjente dataene: tre kanter a, b, c. Konstruer først en diagonal m. For å bestemme det, bruker vi kvaliteten til et rektangulært parallellepiped, ifølge hvilken alle vinklene er rette.

2. Konstruer diagonalen n til en av flatene til parallellepipedet. Utfør konstruksjonen slik at ønsket kant, ønsket diagonal på parallellepipedet og diagonalen på ansiktet til sammen danner en rettvinklet trekant a, n, m.

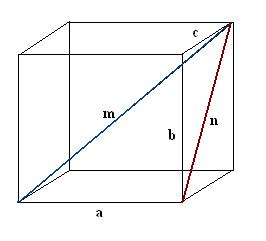
3. Finn den konstruerte diagonalen til ansiktet. Hun er hypotenusen til en annen høyre trekant b, c, n. I følge Pythagoras teorem er n² = c² + b². Regne ut dette uttrykket og ta kvadratroten av den resulterende verdien - dette vil være diagonalen til ansikt n.

4. Finn diagonalen til parallellepipedet m. For å gjøre dette, i den rette trekanten a, n, m, finn den ukjente hypotenusen: m² = n² + a². Bytt ut de kjente verdiene, og beregn deretter kvadratroten. Det resulterende resultatet vil være den første diagonalen av parallellepipedet m.

5. Tegn på samme måte alle de tre andre diagonalene til parallellepipedet i trinn. Utfør også ytterligere konstruksjon av diagonaler til tilstøtende ansikter for dem alle. Ved å se på de rette trekantene som er dannet og bruke Pythagoras teorem, oppdag verdiene til de gjenværende diagonalene til kuboiden.

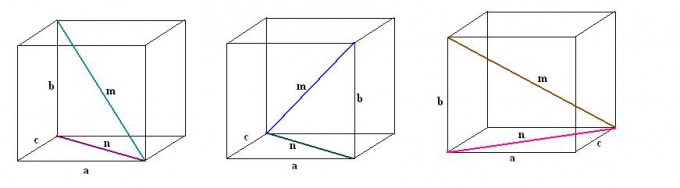
Video om emnet

Mange virkelige gjenstander har en parallellepipedform. Eksempler er rommet og bassenget. Deler med denne formen er ikke uvanlig i industrien. Av denne grunn oppstår ofte oppgaven med å finne volumet til en gitt figur.

Bruksanvisning

1. Et parallellepiped er et prisme hvis base er et parallellogram. Et parallellepiped har ansikter - alle planene som dannes denne figuren. Hver av dem har seks ansikter, og alle er parallellogrammer. Dens motsatte sider er like og parallelle med hverandre. I tillegg har den diagonaler som skjærer hverandre på ett punkt og halverer i det.

2. Det finnes 2 typer parallellepiped. For den første er alle ansikter parallellogrammer, og for den andre er de rektangler. Den siste kalles et rektangulært parallellepiped. Alle dens flater er rektangulære, og sideflatene er vinkelrette på basen. Hvis et rektangulært parallellepiped har flater hvis base er kvadrater, kalles det en terning. I dette tilfellet er ansiktene og kantene like. En kant er en side av et hvilket som helst polyeder, som inkluderer et parallellepiped.

3. For å finne volumet til et parallellepiped, må du vite arealet av basen og høyden. Volumet er funnet basert på hvilket spesielt parallellepiped som opptrer i forholdene til problemet. Et vanlig parallellepiped har et parallellogram ved bunnen, mens et rektangulært har et rektangel eller et kvadrat, som alltid har rette vinkler. Hvis det er et parallellogram ved bunnen av et parallellepiped, blir volumet funnet som følger: V = S * H, der S er arealet av basen, H er høyden til parallellepipedet. Høyden til et parallellepiped er vanligvis dens sideribbe. Ved bunnen av et parallellepiped kan det også være et parallellogram som ikke er et rektangel. Fra løpet av planimetri er det kjent at arealet til et parallellogram er lik: S = a*h, der h er høyden på parallellogrammet, a er lengden på basen, dvs. :V=a*hk*H

4. Hvis det andre tilfellet oppstår, når bunnen av parallellepipedet er et rektangel, beregnes volumet ved hjelp av samme formel, men arealet av basen er funnet på en litt annen måte: V = S * H, S = a * b, hvor a og b er sidene, henholdsvis rektangel og parallellepipedum.V=a*b*H

5. For å finne volumet til en kube bør man ledes av primitiv logiske metoder. Siden alle flatene og kantene på kuben er like, og ved bunnen av kuben er det en firkant, ledet av formlene angitt ovenfor, kan vi utlede følgende formel: V = a^3

I mange lærebøker er det oppgaver knyttet til konstruksjon av utsnitt av ulike geometriske figurer, inkludert parallellepipeder. For å takle en slik oppgave, bør du bevæpne deg med litt kunnskap.

Du vil trenge

- papir;
- penn;
- Hersker.

Bruksanvisning

1. Tegn et parallellepipedum på et stykke papir. Hvis problemet ditt sier at parallellepipedet skal være rektangulært, gjør hjørnene riktige. Husk at motsatte kanter må være parallelle med hverandre. Navngi hjørnene, si S1, T1, T, R, P, R1, P1 (som vist på bildet).

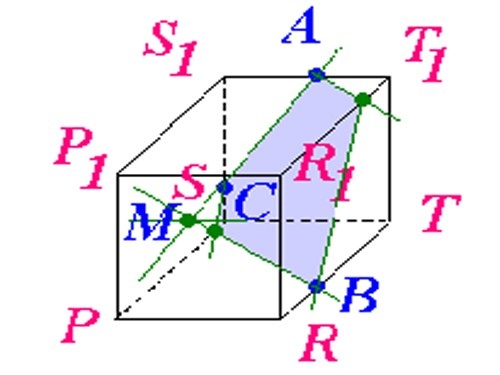
2. På kanten av SS1TT1 setter du 2 punkter: A og C, la punkt A være på segmentet S1T1, og punkt C på segmentet S1S. Hvis problemet ditt ikke sier hvor nøyaktig disse punktene må være, og avstanden fra toppunktene ikke er angitt, plasser dem vilkårlig. Tegn en rett linje gjennom punktene A og C. Fortsett denne linjen til den skjærer linjestykket ST. Merk skjæringsstedet, la det være punkt M.

3. Plasser et punkt på stykket RT, angi det som punkt B. Tegn en rett linje gjennom punktene M og B. Angi skjæringspunktet for denne linjen med kanten SP som punkt K.

4. Kombiner punktene K og C. De må ligge på samme side PP1SS1. Tegn senere en rett linje gjennom punkt B, parallelt med segmentet KS, fortsett linjen til den skjærer kant R1T1. Angi skjæringspunktet som punkt E.

5. Kombiner punktene A og E. Senere markerer du det resulterende polygonet ACKBE med en annen farge - dette vil være seksjonen bak av dette parallellepipedet.

Merk!
Husk at når du konstruerer en seksjon av et parallellepiped, har du bare lov til å koble sammen de punktene som ligger i samme plan; hvis punktene du har ikke er tilstrekkelige for å konstruere seksjonen, fullfør dem ved å forlenge segmentene til de krysser ansiktet hvor punktet er nødvendig.

Nyttige råd
Hvert parallellepiped kan ha 4 seksjoner: 2 diagonale og 2 tverrgående. For større klarhet, velg den resulterende polygon-seksjonen; for dette kan du ganske enkelt skissere den eller skyggelegge den med en annen farge.

Tips 6: Hvordan finne lengden på diagonalene til et parallellepiped

Et parallellepiped er et prisme hvis base er et parallellogram. Parallelogrammene som utgjør et parallellepiped kalles dets flater, sidene deres kalles kanter, og toppunktene til parallellepipedet kalles toppunktene til parallellepipedet.

Bruksanvisning

1. U parallellepipedum det er lov å konstruere fire kryssende diagonaler. Hvis de gitte 3 kantene a, b og c er kjent, finn lengdene diagonaler rektangulær parallellepipedum Det vil ikke være vanskelig å utføre ytterligere formasjoner.

2. Tegn først et rektangulært parallellepiped. Signer alle dataene du kjenner, det skal være tre av dem: kantene a, b og c. Tegn den første diagonalen m. For å konstruere den, bruk egenskapen til rektangulære parallellepipeder, i henhold til hvilke alle vinkler av lignende figurer er rette.

3. Konstruer diagonalen n av en av flatene parallellepipedum. Gjør konstruksjonen på en slik måte at den kjente kanten(e), den ukjente diagonalen parallellepipedum og diagonalen til den tilstøtende flaten (n) dannet en rettvinklet trekant a, n, m.

4. Se på den konstruerte diagonalen til ansiktet (n). Det er hypotenusen til en annen rettvinklet trekant b, c, n. Følg Pythagoras teorem, som sier at kvadratet av hypotenusen er lik summen av kvadratene til bena (n? = c? + b?), finn kvadratet av hypotenusen, og ta kvadratroten av den resulterende verdi - dette vil være lengden på diagonalen til ansiktet n.

5. Finn diagonalen til parallellepipedum m. For å finne verdien, i en rettvinklet trekant a, n, m, beregne hypotenusen med samme formel: m? = n? + a?. Regn ut kvadratroten. Den oppdagede summen vil være den første diagonalen av din parallellepipedum. Diagonal m.

6. Riktig, tegn alle de andre diagonalene i trinn også. parallellepipedum, for alle som utfører tilleggskonstruksjoner diagonaler tilstøtende kanter. Ved å bruke Pythagoras teorem, oppdag verdiene til de gjenværende diagonaler gitt parallellepipedum .

7. Det er en annen metode som kan brukes til å bestemme lengden på diagonalen. I følge en av egenskapene til et parallellogram, er kvadratet på diagonalen lik summen av kvadratene på dens 3 sider. Det følger av dette at lengden kan finnes ved å legge til kvadratene på sidene parallellepipedum og trekke ut kvadratet fra den resulterende verdien.

Nyttige råd
Egenskaper til et parallellepiped: - et parallellepiped er symmetrisk rundt midten av diagonalen; - ethvert segment med ender som tilhører overflaten av et parallellepiped og som går gjennom midten av dets diagonal, deles i to av det, spesielt alle diagonaler av et parallellepiped skjærer hverandre i ett punkt og er delt i to av det; - motsatte flater av en parallellepiped som er parallelle og like; - kvadratet på diagonallengden til et rektangulært parallellepiped er lik summen av kvadratene av dets tre dimensjoner.

Et parallellepiped er en tredimensjonal geometrisk figur med tre måledimensjoner: lengde, bredde og høyde. Alle er involvert i å finne arealet til begge overflatene parallellepipedum: full og side.

Bruksanvisning

1. Et parallellepiped er et polyeder bygget på grunnlag av et parallellogram. Den har seks ansikter, som også er disse todimensjonale formene. Avhengig av hvordan de befinner seg i rommet, skilles det mellom rett og skrånende parallellepipedum. Denne forskjellen kommer til uttrykk i likheten mellom vinkelen mellom basen og sidekanten på 90°.

2. Basert på hvilket spesielt tilfelle av et parallellogram basen tilhører, kan vi skille et rektangulært parallellepiped og dets spesielt vanlige variant - kuben. Disse formene er spesielt vanlige i Hverdagen og kalles standard. De er iboende i husholdningsapparater, møbler, elektroniske enheter, etc., så vel som i selve menneskelige boliger, hvis dimensjoner er av vesentlig betydning for beboere og eiendomsmeglere.

3. Vanligvis blir det trodd torget begge overflater parallellepipedum, side og full. Den første numeriske sammenstillingen representerer det vanlige området av ansiktene, den andre er den samme verdien pluss arealene til begge basene, dvs. summen av alle todimensjonale figurer som utgjør et parallellepiped. Følgende formler ha navnet på de viktigste sammen med volumet: Sb = P h, der P er omkretsen av basen, h er høyden; Sp = Sb + 2 S, hvor So er torget begrunnelse.

4. For spesielle tilfeller, kube og figur med rektangulære baser, er formlene forenklet. Nå er det ikke lenger nødvendig å bestemme høyden, som er lik lengden på den vertikale kanten, men torget og omkretsen er mye lettere å oppdage på grunn av tilstedeværelsen av rette vinkler; bare lengde og bredde er involvert i deres bestemmelse. Det viser seg at for en rektangulær parallellepipedum:Sb = 2 c (a + b), hvor 2 (a + b) er den doble summen av sidene av basen (omkretsen), c er lengden på sidekanten; Sp = Sb + 2 a b = 2 a c + 2 b c + 2 a b = 2 (a c + b c + a b).

5. Alle kanter på en kube har identiske lengder, derfor: Sb = 4 a a = 4 a?; Sp = Sb + 2 a? = 6 a?.

Spørsmålet gjelder analytisk geometri. Det løses ved å bruke ligningene til romlige linjer og plan, representasjonen av kuben og dens geometriske egenskaper, samt å bruke vektoralgebra. Metoder for å løse systemer med lineære ligninger kan være nødvendig.

Bruksanvisning

1. Velg disse oppgavene slik at de er omfattende, men ikke overflødige. Kutte fly? skal gis ved en generell ligning på formen Ax+By+Cz+D=0, som den beste måten i samsvar med hans vilkårlige valg. For å definere en kube er koordinatene til alle tre av dens toppunkter absolutt nok. Ta for eksempel punktene M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3), i henhold til figur 1. Denne figuren illustrerer et tverrsnitt av en kube. Den skjærer to sideribber og tre baseribber.

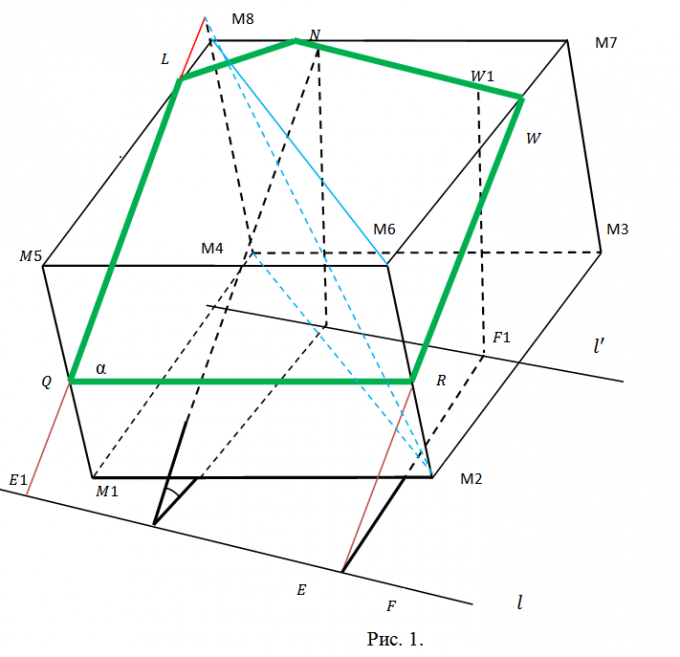
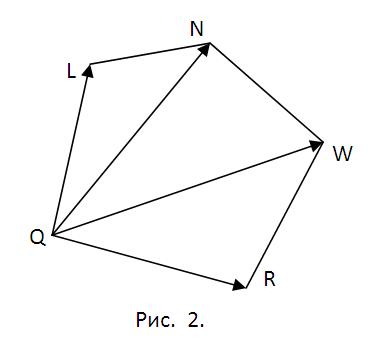
2. Bestem en plan for påfølgende arbeid. Vi må se etter koordinatene til punktene Q, L, N, W, R der snittet skjærer de tilsvarende kantene på kuben. For å gjøre dette, må du finne ligningene til linjene som inneholder disse kantene og se etter skjæringspunktene mellom kantene og planet?. Senere vil dette bli fulgt ved å dele opp femkanten QLNWR i trekanter (se fig. 2) og beregne arealet til alle av dem ved å bruke egenskapene til vektorproduktet. Metodikken er den samme hver gang. Følgelig kan vi begrense oss til punktene Q og L og arealet av trekanten?QLN.

3. Retningsvektoren h til den rette linjen, som inneholder kanten M1M5 (og punktet Q), finnes som vektorproduktet M1M2=(x2-x1, y2-y1, z2-z1) og M2M3=(x3-x2, y3- y2, z3-z2), h=(ml, n1, p1)=. Den resulterende vektoren er en guide for alle andre sidekanter. Finn lengden på kanten av kuben som for eksempel ?=?((x2-x1)^2+(y2-y1)^2+(z2-z1)^2). Hvis modulen til vektoren h |h|??, erstatt den med den tilsvarende kollineær vektor s=(m, n, p)=(h/|h|)?. Skriv nå ned ligningen til den rette linjen som inneholder M1M5 parametrisk (se fig. 3). Etter å ha erstattet de tilsvarende uttrykkene i ligningen til skjæreplanet, får du A(x1+mt)+B(y1+nt)+C(z1+pt)+D=0. Bestem t, sett den inn i ligningene for M1M5 og skriv ned koordinatene til punktet Q(qx, qy, qz) (fig. 3).

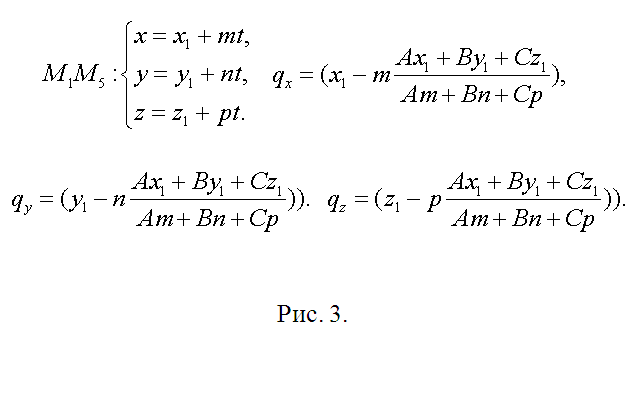
4. Tilsynelatende har punkt M5 koordinatene M5(x1+m, y1+n, z1+p). Retningsvektoren for den rette linjen som inneholder kanten M5M8 faller sammen med M2M3=(x3-x2, y3-y2,z3-z2). Etter dette gjentar du det forrige resonnementet angående punktet L(lx, ly, lz) (se fig. 4). Alt som følger for N(nx, ny, nz) er en nøyaktig kopi av dette trinnet.

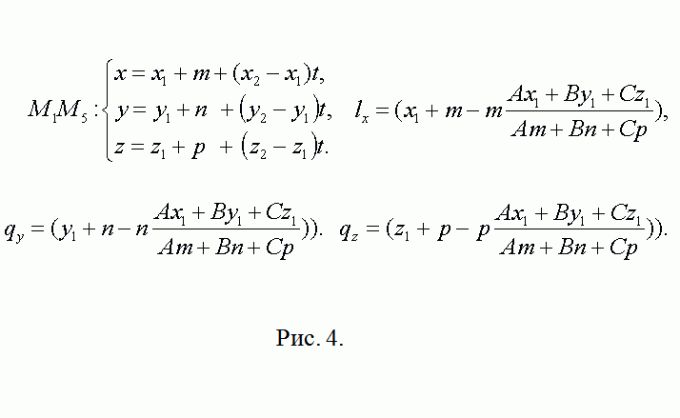
5. Skriv ned vektorene QL=(lx-qx, ly-qy, lz-qz) og QN=(nx-qx, ny-qy, nz-qz). Den geometriske betydningen av deres vektorprodukt er at dets modul lik areal parallellogram bygget på vektorer. Følgelig vil området?QLN S1=(1/2)||. Følg den foreslåtte metoden og beregn arealene til trekantene ?QNW og ?QWR - S1 og S2. Vektor kunstverk Det er mer behagelig å finne alle med støtte fra determinantvektoren (se fig. 5). Skriv ned det endelige resultatet S=S1+S2+S3.

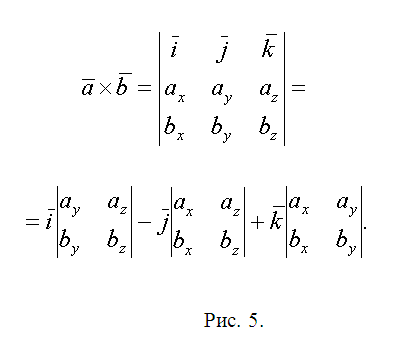
Tips 9: Hvordan finne det diagonale tverrsnittsarealet til et prisme

Et prisme er et polyeder med to parallelle baser og sideflater i form av et parallellogram og i antall, lik tallet sider av grunnpolygonet.

Bruksanvisning

1. I et vilkårlig prisme er sideribbene plassert i en vinkel til basens plan. Et spesielt tilfelle er et rett prisme. I det sider ligge i plan vinkelrett på basene. I et rett prisme er sideflatene rektangler, og sidekantene er lik høyden på prismet.

2. Den diagonale seksjonen av et prisme er en del av planet som er helt inneholdt i det indre rommet til polyederet. Diagonalsnittet kan begrenses av to sideribber geometrisk kropp og diagonaler til basene. Tilsynelatende er antall tillatte diagonale seksjoner bestemt av antall diagonaler i basispolygonen.

3. Eller grensene til diagonalsnittet kan være diagonalene til sideflatene og motsatte sider prismebaser. Det diagonale tverrsnittet av et rektangulært prisme har form som et rektangel. I det generelle tilfellet med et vilkårlig prisme, er formen på diagonalsnittet et parallellogram.

4. I rektangulært prisme Arealet av diagonalseksjonen S bestemmes av formlene: S=d*H hvor d er diagonalen til basen, H er høyden på prismet. Eller S=a*D hvor a er siden av basen som hører samtidig til snittplanet, D er diagonalen til sideflaten.

5. I et vilkårlig indirekte prisme er diagonalseksjonen et parallellogram, hvor den ene siden er lik sidekanten av prismet, den andre er lik diagonalen til basen. Eller sidene av diagonalsnittet kan være diagonalene til sideflatene og sidene til basene mellom hjørnene til prismet, hvorfra diagonalene til sideflatene er trukket. Arealet til et parallellogram S bestemmes av formelen: S=d*hhvor d er diagonalen til bunnen av prismet, h er høyden på parallellogrammet - den diagonale delen av prismet. Eller S=a* hder a er siden av prismets basis, som også er grensen til diagonalsnittet, h er høyden til parallellogrammet.

6. For å bestemme høyden på diagonalsnittet er det utilfredsstillende å kjenne prismets lineære dimensjoner. Vi trenger data om prismets helning til grunnplanet. Det påfølgende problemet kommer ned til en trinnvis løsning av flere trekanter avhengig av de første dataene om vinklene mellom elementene i prismet.

"Golden Section" - Hensikten med studien: Å utlede loven om skjønnhet i verden fra et matematikksynspunkt. Admiralitet. Vindu. Fullført av 10. klasses elev Yulia Smetanina. Forbønnskatedralen (St. Basil's Cathedral). Gyldent snitt i arkitektur. I matematikk er en proporsjon likheten mellom to forhold: a: b = c: d. egyptiske pyramider.

"Konstruksjon av seksjoner" - Snitt utføres i samme skala som bildet det gjelder. Funksjoner ved å lage seksjoner. Bruk av dimensjoner. Betegnelse på seksjoner. Omrisset av de eksponerte seksjonene utføres solid linje. Regler for å lage seksjoner. Seksjoner. Snitt i tegningene er delt inn i utvidede og overliggende.

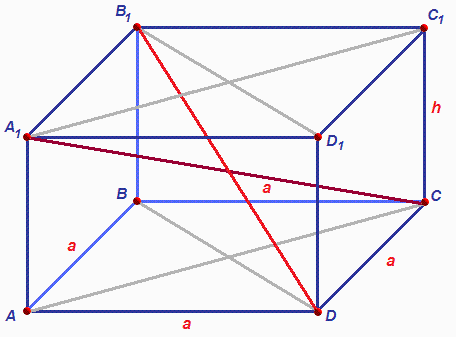
"Parallelepiped grade 10" - Vinkelen er 60?. 3. Fire, hvis parallellepipedet er en terning. Vinkelen er 60?. 3.Like kvadrater, vinkler 90?. Islands sparkrystaller har en romboederform. Alternativ 2. Gitt parallellepiped ABCDA1B1C1D1. Diagonaler til et parallellepiped. Bevis at linjene B1C og A1D er parallelle. 2. Diagonalene til parallellepipedet er like. Parallelepiped.

"Volum av et parallellepiped" - Vi gjør det samme nå. I Det gamle Babylon Volumenhetene var kuber. La oss nå definere hva volumenheter er? Dette betyr, i henhold til regelen for beregning av volum, får vi: 3x3x3=27 (cm3). Oppgave nr. 2. Finn volumet til en kube hvis kant er 3 cm En volumenhet lik 1 dm3 kalles en liter. Oppgave nr. 1.

"Leksjon rektangulært parallellepiped" - Leksjonsmål: Lengde. Speilbilde. Finn arealet av bunnen av det rektangulære parallellepipedet. Konstruer et rektangel gitt lengde(a) og høyde (h). Skann. Kanter. Ribb. Kroppsøvingsminutt. Algoritme for å konstruere et rektangulært parallellepiped. Tre ganger lengden mindre høyde, og bredden er 6 ganger mindre enn høyden.

"Volum av et rektangulært parallellepiped" - T e s t. ( Geometrisk figur). 6. Alle flater av et parallellepiped er rektangler. 3. Alle flater av en terning er firkanter. Svare på neste spørsmål: Firkanter. Navngi kantene som har toppunkt E. Øk. Volumetrisk. Oppgave 2: Dimensjonene til et rektangulært parallellepiped er 3cm, 6cm og 6cm.

Med. 1

Leksjonsbasert utvikling 11. klasse ved hjelp av læreboken "Geometry" L. S. Atanasyan

LEKSJON nr. 1. REKTANGULÆRT KOORDINATSYSTEM B SPACES !:

hovedmål : introduser konseptet med et rektangulært koordinatsystem, lær hvordan du konstruerer et punkt, kjenner dets koordinater og bestemmer det. koordinater til et punkt konstruert i et rektangulært koordinatsystem.

Jeg . Muntlig arbeid .

II bygg inn i samsvar med s. 42 lærebøker.

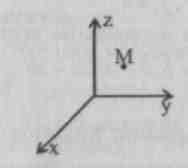Problemet er om posisjonen til punktet er satt M. V rom? Nei. Det er nødvendig å konstruere projeksjoner av punktet M per fly (åh), (Oxz) (Ozy).

TIL 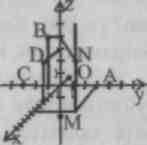test spørsmål

Bruk bildet til å finne koordinatene til punktene A, B, C,D, M, N.
Tegn et koordinatsystem Oxyz og plott punktene

A (0;0;7), B(0;2;-3), C(-1;2;4).

Løse problemer: nr. 400 (muntlig), 401 (muntlig), 402.
Hjemmelekser: teori (klausul 42), nr. 501.

LEKSJON nr. 2. VEKTORKOORDINATER

hovedmål : introduser begrepet vektorkoordinater

Jeg . Forklaring av nytt materiale bygge i samsvar med paragraf 43 i læreboken.

II . Problemløsning : nr. 403, 404,407(a, b, g, i, j, l) 410, 408, 412.

III . Hjemmelekser : teori (element 13), gjenta (element 38, 39), nr. 405, 407 (d, e, f, g, h), 409 (c, d, e, f, h, m), 411.

LEKSJON nr. 3. FORHOLD MELLOM VEKTORKOORDINATER OG PUNKTKOORDINATER

Hovedmål: bevise at koordinatene til ethvert punkt er lik de tilsvarende koordinatene til radiusvektoren; lære hvordan du finner koordinatene til en vektor, og kjenne koordinatene til begynnelsen og slutten.

Jeg . Forklaring av nytt materiale bygge i samsvar med paragraf 44 i læreboken.

II. Problemløsning : nr. 416.417, 418 (a), 419.420.

III. Hjemmelekser : teori (sak 44), nr. 418 (b, c), 421.

LEKSJON nr. 4. DE ENKLE PROBLEMENE I KOORDINATER

Hovedmål: utlede formler for å finne koordinatene til midten av et segment, lengden på en vektor fra dens koordinater og avstanden mellom to punkter.

Sjekker lekser. nr. 421. Løs nr. 422.

nr. 422(a).

III. Forklaring av nytt materiale bygge i samsvar med paragraf 45 i læreboken.

IV. Løse problemer: Nei. 424, 426, 427, 430.

V. Hjemmelekser: teori (sak 45), nr. 425, 429, 431.

LEKSJON nr. 5.6 VINKEL MELLOM VEKTORER

Hovedmål: generaliser konseptet "vinkel mellom vektorer", lær deg å finne vinkelen mellom vektorer i rommet.

Sh. Forklaring av nytt materiale konstruer i samsvar med avsnitt 46. Vis et eksempel på å finne vinkler mellom vektorer på stereometriske modeller (vær oppmerksom på vektorene som ligger på kryssende rette linjer).

IV. Problemløsning № 442,507,508

V. Hjemmelekser: teori (klausul 46), nr. 441, for repetisjon - nr. 490, 491 (muntlig), 492, 501.

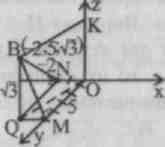№501. Finne VM,BN, VH.

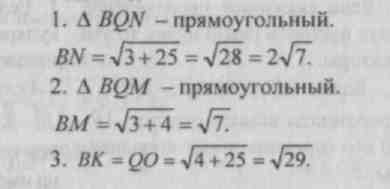Løsning.

Forklaring av nytt materiale.

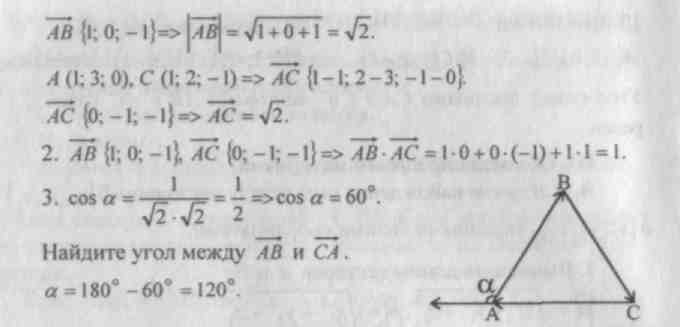
Hjemmelekser: teori (klausul 48), nr. 451, 453, 464 (b, c, d), 469 (b, c).

Diktat

LEKSJON nr. 7 SKALAR PRODUKT AV VEKTORER

Hovedmål: utvikle ferdigheten til å løse problemer med å finne en vinkel med vektorer, rette linjer, en rett linje og et plan.

Jeg. Sjekker lekser ( ved styret): nr. 451 (b, d), nr. 464 (c; d).

II. Problemløsning(etter ferdige tegninger).

Algoritme for å løse problemer:

Tast inn rektangulært system koordinere"1
Skriv ned koordinatene til alle punktene.

Bruk en algoritme for å finne vinkelen mellom rette linjer, mellom en rett linje og et plan.

III. Problemløsning.

(vektormetode)

III. (Vektorkoordinatmetode).

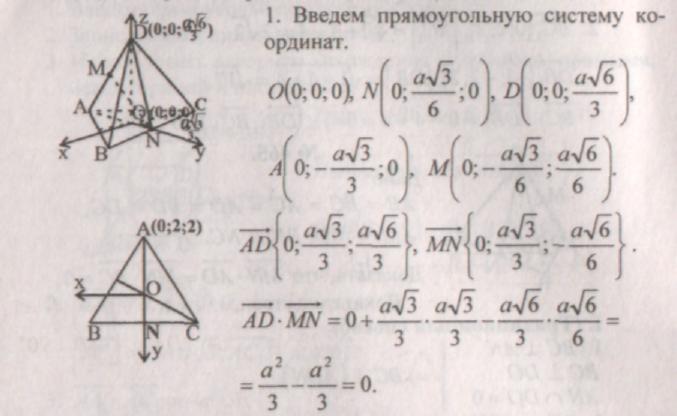
Hjemmelekser:№ 455, 457, 462.

LEKSJON nr. 8 SKALAR PRODUKT AV VEKTORER

Hovedmål: utvikle ferdigheten til å finne vinkler mellom rette linjer, mellom en rett linje og et plan.

№ 455.

(Tegningen er utarbeidet på forhånd. Elevene sier fra eller noen skriver svarene på tavla.)

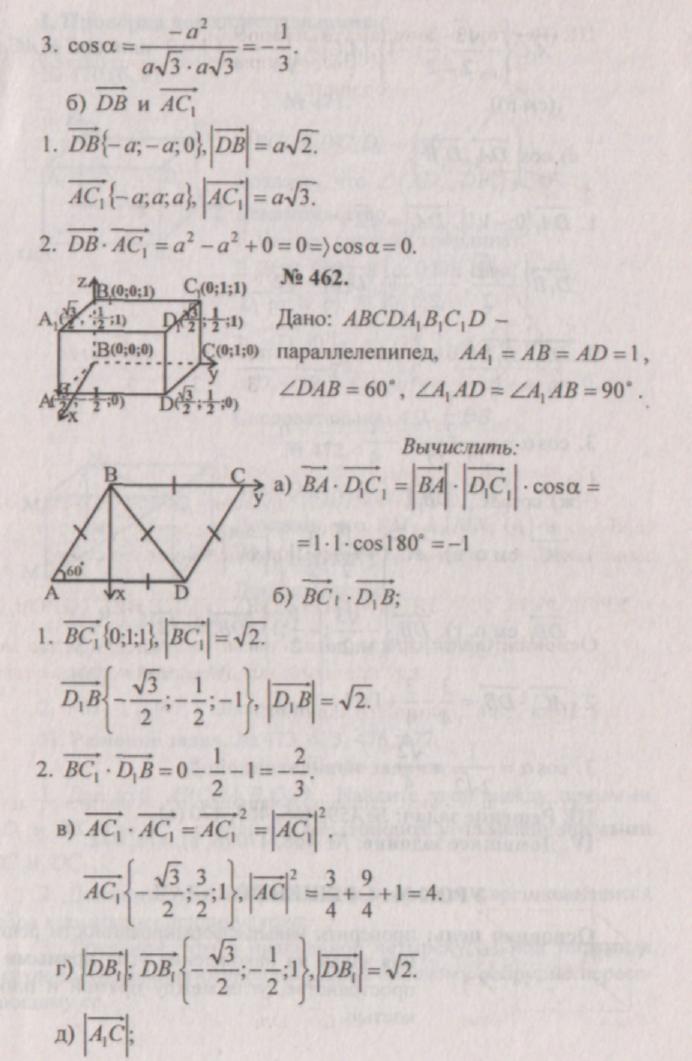
III. Problemløsning: nr. 459, 466, 467, 470 (a).

IV. Hjemmelekser: nr. 468, 470 (b, c), 471, 472.

LEKSJON nr. 9 PRØVE nr. 1
Tester for egentesting og korrigering av elevenes kunnskaper

Alternativ	1	2	3	4	5	6	7	8
Jeg	V	G	V	b	EN	b	G	V
II	b	EN	V	G	V	b	G	G

Alternativ	1	2	3	4	5	6	7	8
Jeg	b	G	b	V	V	G	V	b
II	b	EN	G	V	G	EN	V	b

LEKSJON #10. SYLINDER

Hovedmål: introdusere begrepet en sylinder, elementer av en sylinder.

Jeg. Forklaring av nytt materiale bygge etter planen:

1. Konsept sylindrisk overflate, sylinder.

Ta i betraktning ulike gjenstander omgivelsene, noe som gir en ide om sylinderen - en sirkulær blyant, et glass, en penny, en panne, et stykke rør, etc. (De viste sylindrene må ha forskjellige forhold mellom høyde og diameter.) Gi et bilde av en sylinder, vis på tegningen - akse, høyde, radius, generatorer, sylinderbaser.

2. Gå inn konseptet med aksial seksjon av en sylinder, angi egenskapene:

a) den aksiale seksjonen av sylinderen er et rektangel;

b) to aksiale seksjoner av sylinderen er like med hverandre.

Introduser konseptet med en likesidet sylinder med et aksialsnitt

som er en firkant.

3. Betrakt snittet av en firkant ved et plan

EN) parallell akse sylinder;

b) vinkelrett på sylinderaksen.

4. Introduser konseptet med et tangentplan til en sylinder som et plan som går gjennom generatrisen til sylinderen og vinkelrett på det aksiale snittet trukket gjennom denne generatrisen. (En analogi med en tangent til en sirkel).

II. Problemløsning:№ 521, 522, 526, 529.

III. Hjemmelekser:№ 523, 525, 530.

LEKSJON #11. SYLINDER

Hovedmål:å formulere ferdigheten til å løse problemer med å finne elementene i en sylinder.

Jeg. Sjekker lekser(ved tavlen).

II. Muntlig arbeid.

Identifiser objekter i naturen, teknologien, arkitekturen og blant objektene rundt deg som har en sylindrisk form.
Forklar hva som kalles en sylinder, en sirkulær sylinder. Nevn hovedelementene og gi dem en definisjon.

Gi definisjonen av en rett sylinder.
Hvor mange aksiale seksjoner av sylinderen går gjennom hver av dens generatriser?

Bestem typen aksial seksjon av sylinderen. Begrunn svaret ditt.
Kan den aksiale seksjonen av en sylinder være: a) et rektangel; b) kvadratisk; c) trapes?
Har sylinderen: a) et symmetrisenter; b) symmetriakse; c) symmetriplan? Vennligst angi dem i hvert enkelt tilfelle. Hvor mange er det? Vises på modellen.
La AA 1 I 1 I Og MM1 N 1 N - to aksiale seksjoner av sylinderen. Sammenlign områdene deres.

En sylinder ruller langs et fly. Hvilken figur får man når dens akse beveger seg?
Hvilke av følgende påstander er sanne:

a) enhver seksjon av en sylinder med et plan vinkelrett på aksen er en sirkel, lik en sirkel begrunnelse;

b) enhver seksjon av en sylinder ved et plan er en sirkel lik omkretsen av basen;

c) et plan vinkelrett på sylinderens akse skjærer den i en sirkel, likt grunnlag sylinder;

d) snittet av en sylinder etter plan kan være en sirkel, et rektangel og en ellipse?

12. Formuler og bevis et teorem om snittet av en sylinder i et plan vinkelrett på dens akse.

III. Problemløsning: nr. 527 (b), 532, 534.

IV. Hjemmelekser: nr. 527 (a), 531, 535.

LEKSJON #12. KJEGLE

Hovedmål: sjekk formuleringsnivået til problemløsningsferdigheten for å finne elementene i en sylinder. Introduser begrepene en kjegle og elementene i en kjegle.

Selvstendig arbeid (15 min).

Alternativ I

Seksjonen av sylinderen med et plan parallelt med aksen er en firkant, hvis areal er 20 dm. Finn det aksiale tverrsnittsarealet til sylinderen hvis diagonalen er 10 dm.

Sylinderens sideflate folder seg ut kvadrat med diagonal lik cm Finn området full overflate sylinder.

Alternativ II

Høyden på sylinderen er 16 cm, basens radius er 10 cm Sylinderen krysses av et plan parallelt med aksen slik at tverrsnittet blir kvadratisk. Finn avstanden fra sylinderaksen til denne delen.
Utviklingen av sylinderens sideflate er et rektangel, hvis diagonal, lik 12l, gir en vinkel på 30° på den ene siden. Finn det totale overflatearealet til sylinderen hvis høyden er lik den korte siden av utviklingen.

II. Forklaring av nytt materiale bygge etter planen:

1. Konsepter for en kjegle, dens elementer (topp, akse, generatorer, base, sideflate Kjegle). Kjeglebilde

N 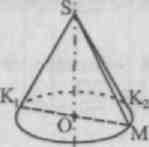i figuren tegner vi tangenter fra punktet S til ellipsen som representerer bunnen av kjeglen. La oss betegne med TIL 1 Og TIL 2 berøringspunkter. En vanlig feil er at elevene antar trekanten S.K. 1 K 2 for bildet av den aksiale delen av kjeglen. Imidlertid akkorden TIL 1 TIL 2 går ikke gjennom sentrum OM bunnen av kjeglen. Å konstruere et bilde av et aksialsnitt som går gjennom generatrisen S.K. 1 det er nok å konstruere et bilde av diameteren TIL 1 M og koble det resulterende punktet M med topp S Kjegle S.K. 1 Og S.K. 2 - bilder av ekstreme generatorer, dvs. de skiller de synlige generatorene (bildene deres oppnås ved å koble til vilkårlig poeng buer TIL 1 MK 2 ellipse med toppunkt S) fra usynlig.

2. Vurder tverrsnittet av en kjegle med forskjellige plan, og fremhev to tilfeller:

Skjæreplan gjennom toppunktet til en kjegle;
Kutteplanet er parallelt med bunnen av kjeglen.

Ved skjæringspunktet mellom skjæreplanet og sirkelen til kjeglens base.

1(a). Hvis de krysser hverandre i to punkter, får vi i tverrsnittet av kjeglen likebent trekant, hvis basis er et segment med ender på disse punktene. Fra aksialsnitt. Det oppnås hvis skjæringspunktene som vurderes er endene av diameteren til kjeglens base. Blant kjeglene skiller en likesidet seg ut (den aksiale seksjonen er likesidet trekant). Hvis R er radiusen til basen, så er generatrisen til en likesidet kjegle lik 2 R .

1(b). Hvis de bare har en felles poeng, så er planet under vurdering tangent til kjeglen.

Tangentplanet til en kjegle kan defineres på forskjellige måter.

Definisjon 1. Planet som går gjennom generatrisen til kjeglen er vinkelrett på det aksiale snittet trukket gjennom denne generatrisen.

Definisjon 2. Et plan som bare har én felles generatrise med en kjegle.

Tolkningen av et plan tangent til en kjegle og et plan tangent til en sylinder bør være den samme i samme lærebok. Det skal bemerkes at ved å godta en av proposisjonene 1 eller 2 in som en definisjon, er det nødvendig å gjøre elevene kjent med den andre som en egenskap ved et tangentplan til en kjegle.

1 (c). Ved å fortsette vår vurdering av planet som går gjennom kjeglens toppunkt, kommer vi til tilfellet: hvis planet og sirkelen til basen ikke har felles punkter, har det aktuelle planet med kjeglen bare ett felles punkt - toppunktet til kjeglen.

2. Når du skal bevise teoremet om seksjonen av en kjegle med et plan parallelt med basen (nr. 556), er det tilrådelig å oppnå følgende konklusjoner:

1. Seksjonen som vurderes er en sirkel.

2. Utpekt av R Og r - henholdsvis radius av kjeglen og seksjonen under vurdering og gjennom N Og h høyden til den gitte og avskårne kjeglen, får vi det, ,hvor k er likhetskoeffisienten til de gitte og avskårne kjeglene. Bevis det

Generaliser ved å løse oppgave nr. 557.

Betraktning av seksjonen, vinkelrett på aksen kjegle, tillater effektiv bruk homotetisk metode som ligner på tverrsnitt av pyramiden etter plan, parallelt med basen. Etter å ha etablert formen og plasseringen av seksjonen, introduseres konseptet med en avkortet kjegle.

Når du viser en avkortet kjegle, er det praktisk å først tegne kjeglen som den avkortede kjeglen er oppnådd fra.

Problemløsning: nr. 548 (a), 549.
Hjemmelekser: teori (s. 55, 56), nr. 547, 548 (b, c), 550.

LEKSJON #13. KEGLE

Hovedmål: introduser konseptet med området til sideoverflaten til en kjegle som området for dens utvikling.

Jeg. Sjekker lekser(ved tavlen).

Introduser konseptet med sideoverflate ved å bruke utviklingen av en kjegle.
Det totale overflatearealet til en kjegle.
Utled en formel for å beregne arealet av sideoverflaten til en avkortet kjegle.

IV. Problemløsning: nr. 558, 559, 560 (a), 562, 567.

V. Hjemmelekser: nr. 560 (b, c), 561, 563, 568.

LEKSJON nr. 14. KULE OG BALL. Sfærelikning. RELATIV POSISJON AV KULE OG FLY. TANGENT FLY TIL KULEN. OMRÅDE AV Sfæren

Hovedmål: Tast inn begreper sfære og ball, utled sfærens ligning, vurder den relative posisjonen til sfæren og planet, definer tangentplanet til sfæren, skriv ned formelen for å beregne arealet av sfæren.

Jeg. Forklaring av nytt materiale konstruere på en forelesningsmåte i samsvar med paragrafene 58 - 62 i læreboken.

For eksempler, bruk problemer: nr. 575 for å forstå definisjonene av sfæren; nr. 576, 578 for å utarbeide sfærens ligning; nr. 586 for illustrasjon relativ posisjon kuler og fly; nr. 593 (a), 594 for å praktisere formelen for arealet av en kule.

Problemløsning:

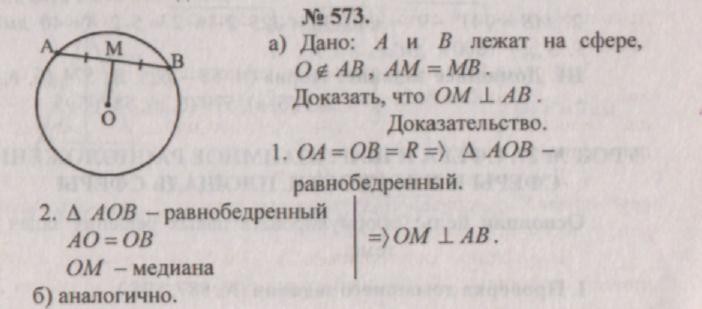
III. Hjemmelekser: teori (s. 58 - 62), nr. 574 (b, c, d).

577 (b, c), 579 (6, c), 587, 595.

LEKSJON nr. 15. KULE OG BALL. RELATIV POSISJON AV KULE OG FLY. OMRÅDE AV Sfæren

Hovedmål: formulere ferdigheten til å løse problemer om et emne.

Undersøkelse hjem oppgaver (nr. 587, 595.)
Problemløsning

III. Lekser: Nei. 582, 584, 585, 592, 597.

LEKSJON nr. 16. FORBEREDELSE TIL PRØVEN

Hovedmål: gjenta, systematisere, generalisere det studerte materialet.

Jeg. Sjekker lekser(ved tavlen): nr. 582, 584, 585.

II. Muntlig arbeid- på spørsmål til kapittel VI.

III. Problemløsning.

Leksjon #17 Test № 2

LEKSJON nr. 18. VOLUM AV ET REKTANGULÆRT PARALLELEPIPED

Hovedmål: introdusere begrepet kroppsvolum.

I. Forklaring av nytt materiale.

EN. Begrepet volum av en kropp introduseres i analogi med begrepet område flat figur. Mulig sammen med studenter fylle ut andre halvdel tabeller.

Kontrollspørsmål.

Hva er volumet til en kropp?
Hva vil det si å måle kroppsvolum?

3. Hva betyr det: «Volumet på dette rommet er 60 m 3 "; "Volum fyrstikkeske 10 cm 2 "; "Vanntønnevolum 200 m 3 ».

4. Hvordan få enhetskube?

5. Enhetskuben passer inn i den delen av rommet som oktaederet okkuperer, 2 ganger og 2 ganger - brøkdelen av enhetskuben, hvilket tall er karakterisert V oktaeder?

B. Volum av en kube lik kube ribbeina hans. V= a 3 .

Utled formelen for beregning V kube, hvis diagonalen er kjent

II. Problemløsning.

1. Det totale overflatearealet til en kube er 6 m 2 . Finn volumet. (1 m 3)

Volumet av kuben er 8 m. Finn det totale overflatearealet.
Hvis hver kant av en kube økes med 1 m, vil volumet øke 125 ganger. Finn kanten på kuben.

Tre kuber laget av bly har kanter på 3, 4 og 5 cm.De smeltes til én kube. Finn ribben hans
Volumet til en kube er A. Finn arealet av dens diagonal

8. Rundt en kule med radius G et rektangulært parallellepiped er beskrevet. Bestem dens type. Finn volumet.

III. To kropper hvis volumer er like kalles like store.

(Når du skal bevise følgende teorem, bruk en modell eller en tidligere utarbeidet tegning.)

Teorem. Et skrånende prisme er lik størrelse med et rett prisme, hvis basis er vinkelrett på den skrånende seksjonen, og sidekanten er lik sidekanten skrå prisme.

Kontrollspørsmål.

Hvilke to kropper kalles like store?
To kropper er like. Er de like store?
De to kroppene er like store. Er de likeverdige?

IV. Hjemmelekser: teori (pkt. 63), nr. 647, 649.

LEKSJON nr. 19. VOLUM AV ET REKTANGULÆRT PARALLELEPIPED

Hovedmål: utvikle ferdigheten til å løse problemer for å finne volumet til et parallellepiped.

I. Muntlig arbeid.

Hva er volumet til en kropp?
Hva er volumet til en kube? En tidel av det?
Kuben er krysset av to diagonale seksjoner. Hva er volumet til hver del?
I en kube med en kant på 2 cm diagonalt snitt laget. Hva er volumet til hver av de resulterende delene?
Det totale overflatearealet til kuben er 24 cm2. Hva er volumet til en kube?
Diagonalen til kuben er EN. Finn volumet.
Volum av en kube V. Finn diagonalen.
Diagonalen til en terningflate er 8. Hva er volumet til kuben?

9. Volumet til en kube er 8 cm3. Hva er arealet av diagonalsnittet?

Volumet til det skråstilte prismet er 27 cm 3 . Hva er størrelsen på kanten av en terning av lik størrelse?

Forklaring av nytt materiale.

En kube er et spesialtilfelle av et rektangulært parallellepiped. Hva er volumet til et rektangulært parallellepiped?

Volumet til et rektangulært parallellepiped er lik produktet av dets tre dimensjoner. V = abc . Eller volumet til et rektangulært parallellepiped er lik produktet av arealet av basen og høyden. V= S grunnleggende H

III. Problemløsning.

Hjemmelekser: teori (vol. 64), nr. 648.650.651.652

IV. Selvstendig arbeid.

ALTERNATIV I

1. Volumet til et rektangulært parallellepiped er 96 cm, sidekanten er 8 cm. Hva er arealet av basen?

Basen til et rektangulært parallellepiped er en firkant med side EN. Diagonalen til sideflaten danner en vinkel α med basens plan.
I et rektangulært parallellepiped danner diagonalene til tilstøtende sideflater som kommer fra samme toppunkt vinklene α og β med felles sideribbe som kommer fra samme toppunkt. Sidekanten av parallellepipedet er lik b . Finn volumet til parallellepipedet.

ALTERNATIV II

Volumet til et rektangulært parallellepiped er 100 cm 3, grunnflaten er 25 cm 2. Finn høyden på parallellepipedet.
I et rektangulært parallellepiped er basen en firkant. Diagonalen til parallellepipedet er d og danner en vinkel α med sidekanten som har generell begynnelse. Finn volumet til parallellepipedet.

3. ABCDA 1 B 1 C 1 D 1 - rektangulært parallellepipedum. Diagonal D.A. 1 lager en vinkel α med grunnplan, og diagonalen DC 1 lager en vinkel β med planet til grunnflaten. Kant AD er lik EN. Finn volumet til parallellepipedet.

LEKSJON nr. 20. VOLUMEN AV ET DIREKTE PRISM

Hovedmål: utlede en formel for å beregne volumet til et rett prisme.

I. Sjekke lekser.

P. Forklaring av nytt materiale.

Grunnlaget til et rett prisme er en rettvinklet trekant. Volumet er lik produktet av arealet av basen og høyden.

Basen til et rett prisme - vilkårlig trekant. Volumet er lik produktet av arealet av basen og høyden.

Vilkårlig rett prisme. Bevis at volumet er lik produktet av arealet av basen og høyden.

AT. Volumet til et rett prisme er lik produktet av arealet av basen og høyden.

Sh. Problemløsning.№ 659, 661, 662, 729.

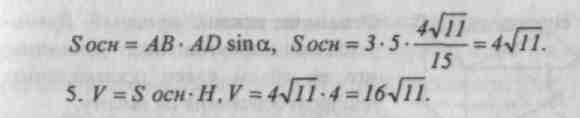
Hjemmelekser: teori (artikkel 65), nr. 660, 728, 730, 731.

LEKSJON nr. 21. SYLINDERVOLUM

Hovedmål: utlede en formel for å beregne volumet til en sylinder.

Jeg . Forklaring av det nye bygge i samsvar med paragraf 66 i læreboken.

II. Problemløsning. Nei. 671, 672.

Sh. Lekser: teori (punkt 66), nr. 666, 667, 668, 699, 670.

Tilleggsoppgaver.

En seksjon av sylinderen med et plan parallelt med aksen avskjærer en bue på 60° fra bunnomkretsen. Tverrsnittsarealet er S, og diagonalen til seksjonen danner en vinkel α med planet til bunnen av sylinderen. Finn volumet til sylinderen.
En seksjon av en sylinder ved et plan parallelt med aksen avskjærer en bue på 90° fra basisomkretsen. Tverrsnittsarealet er S, og diagonalen til seksjonen lager en vinkel α med generatrisen til sylinderen. Finn volumet til sylinderen.

En kube er innskrevet i en sylinder. Volumet til kuben er F. Finn volumet til sylinderen.

LEKSJON nr. 22. VOLUMEN AV EN PYRAMID

Hovedmål: utvikle ferdighetene til å finne volumet til en pyramide, hvis toppunkt er projisert til midten innskrevet i bunnen av en sirkel eller omskrevet rundt bunnen av en sirkel.

I. Sjekke lekser.

Fortsett med setningene.

Hvis alle sidekantene av pyramiden er like, projiseres toppunktet på basen i ...
Hvis alle apotemene til pyramiden er like, projiseres toppen på basen i ...
Jeg faller dihedrale vinkler når basen er lik, projiseres toppunktet på basen i...
Hvis alle sideribbene er på linje med underlagets plan like vinkler, så projiseres toppunktet på basen i...

Jeg . Forklaring av det nye bygge i samsvar med avsnittet i læreboka

Sh. Problemløsning.№ 691, 693, 695, 740.

IV. Hjemmelekser:№ 692, 694.

P. Diktat.

LEKSJON nr. 23,24. FORBEREDELSE TIL TEST TEST TEST nr. 4

Hovedmål: sjekk utviklingsnivået for problemløsningsferdigheter for å finne volumet til en sylinder, skrå prisme, pyramide og kjegle.

LEKSJON nr. 25 BOLUM AV BALLEN OG DELER

Hovedmål: utlede formelen for volumet til en kule og dens deler.

I. Forklaring av nytt materiale.

1. Volum av en kule med radius R er lik

For bevis, se avsnitt 71.
2. Et sfærisk segment er den delen av kulen som er avskåret fra den av et plan (fig. a, c).

OM volum ballsegment bestemmes av formelen , hvor H er høyden på det sfæriske segmentet

3. Det sfæriske laget er den delen av ballen som ligger mellom to parallelle plan, kryssende ballen (fig. 323, b).
4. En sfærisk sektor er et legeme som er hentet fra et sfærisk segment og en kjegle. Volumet av den sfæriske sektoren bestemmes av formelen, hvor H er høyden på det tilsvarende sfæriske segmentet

II. Problemløsning.

Oppgave 1. Hva er volumet til en sfærisk sektor hvis radiusen til grunnsirkelen er 60 cm og kulens radius er 75 cm?

Løsning. 1. Under bunnen av sektoren i oppgaven forstås som grunnlaget segment som tilsvarer sektoren. La R - ballens radius, r - radius av segmentbasen.

2. Vår oppgave går ut på å finne høyden på dette segmentet: N – RO 1 . ELLER - radiusen til kulen vinkelrett på bunnen av segmentet.

3. Fra en rettvinklet trekant O.O. l M(˂ M.O. 1 O= 90°) la oss finne: OO 1 = √OM 2 - O 1 M 2 = √75 2 +60 2 =40, derfor H = P.O. l = OP- O.O. l = R-00 ] =75-45 = 30.

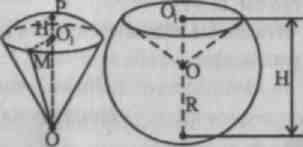
4. Volum av den sfæriske sektoren. =112500π

5. Merk. Problemet har to løsninger:

1) Den sfæriske sektoren som vi vurderte kalles konveks, og dens høyde er lik R – OO 1 , kalles ikke-konveks.

La oss finne volumet.

6. Tenk på det andre tilfellet, hvor sektorhøyden N =R + O.O. 1 = 120, så det resulterende volumet vil være 4 ganger større enn det beregnede volumet: V = π45 10 4 cm 3

7. Dermed er det nødvendige volumet enten 112 500 π cm eller 450 000 π cm 3.

III. Hjemmelaget oppgave: teori (s. 71, 72), nr. 710, 711, 717.

LEKSE№ 26 . VOLUM AV BALLEN OG DELER

Hovedmål: formulere ferdigheten til å finne volumet til en ball og dens deler.

I. Sjekke lekser.

Sh. Problemløsning.

EN. 1. Den ytre diameteren på en hul kule er 18 cm, veggtykkelsen er 3 cm Finn volumet på materialet som kulen er laget av.

[b84πcm 3.]

Diameteren på en blykule er 30 cm Hvor mange kuler med en diameter på 3 cm kan lages av dette blyet?
Radiene til de tre kulene er 3, 4, 5 cm. Finn radiusen til en kule hvis volum er lik summen av volumene deres,
Den største ballen er skåret ut av en kube. Hvor mange prosent av materialet fjernes? [≈ 47,6 %]
Kulesektorradius R, vinkel inn aksialt snitt 120°. Finn volumet.

B. 1. Hvilken del av volumet til ballen er volumet til det sfæriske segmentet, hvis høyde er lik 0,1 kule diameter?

Bevis at hvis radiene til tre kuler er i forholdet 1:2:3, så er volumet til den større kulen 3 ganger mer enn beløpet volumer av mindre kuler.
Høyden på kulesegmentet er 0,4 ganger radiusen til ballen. Hvilken del er volumet av dette segmentet fra volumet til en sylinder med samme base og høyde? 13\24

To lik ball arrangert slik at midten av den ene ligger på overflaten av den andre. Hvordan forholder volumet av den totale delen av kulene seg til volumet av hele ballen?
Diameteren på ballen, lik 30 cm, fungerer som aksen til en sylinder hvis basisradius er 12 cm. Finn volumet til delen av ballen,

innelukket inne i sylinderen.

Hvilken figur har et større volum: en kule med en radius på 1 dm eller en vanlig? trekantet prisme, hvor hver kant er lik 2 dm? [Volumet på ballen er større.]

En seksjon av en kule med et plan vinkelrett på dens radius deler radiusen i to. Finn forholdet mellom volumene til delene av ballen.
En seksjon av en kule med et plan vinkelrett på diameteren deler diameteren i forholdet 1:2. Finn forholdet mellom volumene til delene av ballen.

LEKSJON nr. 27. OMRÅDE AV EN SFER

Hovedmål: utlede en formel for å beregne overflaten til en ball.

Jeg. Forklaring av nytt materiale bygge i samsvar med paragraf 73 i læreboken.

II. Problemløsning: nr. 722, 723, 724; for repetisjon - nr. 761, 762, 763.

III. Lekser: kort.

LEKSJON nr. 28. FORBEREDELSE TIL PRØVEN

I. Spørsmål for å gjennomgå emnet.

Ball og dens elementer.
Volum av ballen og dens deler.
Rotasjonslegemer og deres volumer.
Polyedre og deres volumer.
Ballens overflateareal.
Overflateareal av polyeder.

P. Muntlig arbeid med spørsmål til kapittel VH.

III. Problemløsning.

Volum av en kuleradius R er lik V. Finn volumet til en kule med radius: 2 R; 0,5R.
Flateareal vanlig tetraeder lik overflatearealet til kulen. Finn forholdet mellom volumene til tetraederet og kulen.
Diameteren til en kule med radius 12 cm er delt inn i 3 deler, hvor lengdene er i forholdet 3:3:2. Plan vinkelrett på diameteren trekkes gjennom delingspunktene. Finn volumet av hver dannet deler av ballen.

4. En vanlig firkantet pyramide er innskrevet i en ball ABCDM. Arealet av en trekant AMS lik S, sidekanten av pyramiden er lik diagonalen til basen. Finn volumet til kulen.

5. Til den høyre firkantet pyramide en ball er innskrevet slik at sideflatene til pyramiden berører ballens overflate, og dens stor sirkel ligger ved bunnen av pyramiden. Sideflater pyramider er skråstilt til planet til basen i en vinkel EN, og volumet av ballen er lik V . Finn volumet til pyramiden.

Hjemmeprøve

valg 1

Ballens volum er 400 cm3. En annen kule er bygget på radiusen som på diameteren. Finn volumet til den lille kulen.

2. Overflatearealet til en kube er lik overflatearealet til en kule. Finn forholdet mellom volumene til en kube og en kule.

3. Diagonalsnittet til et rektangulært parallellepiped innskrevet i en kule er en firkant med areal S. Finn volumet til kulen.

4. Diameteren til en ball med en radius på 12 cm er delt inn i 3 deler, hvor lengdene er i forholdet 1:3:4. Plan vinkelrett på diameteren trekkes gjennom delingspunktene. Finn volumet til det resulterende sfæriske laget.

MO "Senkinskaya Secondary School"

Med. 1