Pyramidekonsept

Definisjon 1

En geometrisk figur dannet av en polygon og et punkt som ikke ligger i planet som inneholder denne polygonen, forbundet med alle toppunktene i polygonen, kalles en pyramide (fig. 1).

Polygonen som pyramiden er laget av kalles bunnen av pyramiden, når de er koblet til et punkt, er sideflatene til pyramiden, sidene til trekantene er sidene til pyramiden, og punktet felles; til alle trekanter er toppen av pyramiden.

Typer pyramider

Avhengig av antall vinkler ved bunnen av pyramiden, kan den kalles trekantet, firkantet, og så videre (fig. 2).

Figur 2.

En annen type pyramide er den vanlige pyramiden.

La oss introdusere og bevise egenskapen til en vanlig pyramide.

Teorem 1

Alle sideflater av en vanlig pyramide er likebente trekanter som er like hverandre.

Bevis.

Tenk på en vanlig $n-$gonal pyramide med toppunktet $S$ av høyden $h=SO$. La oss tegne en sirkel rundt basen (fig. 4).

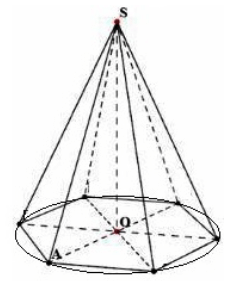
Figur 4.

Tenk på trekanten $SOA$. I følge Pythagoras teorem får vi

Selvfølgelig vil enhver sidekant bli definert på denne måten. Følgelig er alle sidekanter like med hverandre, det vil si at alle sideflater er likebente trekanter. La oss bevise at de er like med hverandre. Siden basen er en vanlig polygon, er grunnflatene til alle sideflater lik hverandre. Følgelig er alle sideflater like i henhold til III-kriteriet om trekanters likhet.

Teoremet er bevist.

La oss nå introdusere følgende definisjon relatert til begrepet en vanlig pyramide.

Definisjon 3

Apotemet til en vanlig pyramide er høyden på sideflaten.

Åpenbart, ved setning 1, er alle apotemer like hverandre.

Teorem 2

Det laterale overflatearealet til en vanlig pyramide bestemmes som produktet av halvperimeteren til basen og apotemet.

Bevis.

La oss betegne siden av bunnen av $n-$gonalpyramiden med $a$, og apotemet med $d$. Derfor er arealet av sideflaten lik

Siden, ifølge setning 1, er alle sider like, altså

Teoremet er bevist.

En annen type pyramide er en avkortet pyramide.

Definisjon 4

Hvis et plan parallelt med basen trekkes gjennom en vanlig pyramide, kalles figuren som dannes mellom dette planet og basens plan en avkortet pyramide (fig. 5).

Figur 5. Avkuttet pyramide

Sideflatene til den avkortede pyramiden er trapeser.

Teorem 3

Det laterale overflatearealet til en vanlig avkortet pyramide bestemmes som produktet av summen av halvperimetrene til basene og apotemet.

Bevis.

La oss betegne sidene av basene til $n-$gonalpyramiden med henholdsvis $a\ og\ b$, og apotemet med $d$. Derfor er arealet av sideflaten lik

Siden alle sider er like, altså

Teoremet er bevist.

Eksempeloppgave

Eksempel 1

Finn arealet av sideoverflaten til en avkortet trekantet pyramide hvis den er hentet fra en vanlig pyramide med baseside 4 og apotem 5 ved å kutte av et plan som går gjennom midtlinjen til sideflatene.

Løsning.

Ved å bruke midtlinjeteoremet finner vi at den øvre basen til den avkortede pyramiden er lik $4\cdot \frac(1)(2)=2$, og apotemet er lik $5\cdot \frac(1)(2) =2,5$.

Så, ved teorem 3, får vi

Pyramide. Avkuttet pyramide

Pyramide er et polyeder, hvor en av ansiktene er en polygon ( utgangspunkt ), og alle andre flater er trekanter med et felles toppunkt ( sideflater ) (Fig. 15). Pyramiden kalles riktig , hvis basen er en vanlig polygon og toppen av pyramiden projiseres inn i midten av basen (fig. 16). En trekantet pyramide med alle kanter like kalles tetraeder .

Sideribbe av en pyramide er siden av sideflaten som ikke tilhører basen Høyde pyramiden er avstanden fra toppen til grunnplanet. Alle sidekanter av en vanlig pyramide er like med hverandre, alle sideflater er like likebente trekanter. Høyden på sideflaten til en vanlig pyramide trukket fra toppunktet kalles apotem . Diagonalt snitt kalles en del av en pyramide av et plan som går gjennom to sidekanter som ikke tilhører samme flate.

Sideoverflateareal pyramide er summen av arealene til alle sideflater. Totalt overflateareal kalles summen av arealene til alle sideflatene og grunnflaten.

Teoremer

1. Hvis alle sidekantene i en pyramide er like skråstilt til basens plan, projiseres toppen av pyramiden inn i midten av sirkelen som er omskrevet nær basen.

2. Hvis alle sidekantene til en pyramide har like lengder, projiseres toppen av pyramiden inn i midten av en sirkel som er omskrevet nær basen.

3. Hvis alle flatene i en pyramide er likt skråstilt til basens plan, så projiseres toppen av pyramiden i midten av sirkelen som er innskrevet i basen.

For å beregne volumet til en vilkårlig pyramide, er den riktige formelen:

Hvor V- volum;

S base– basisareal;

H– høyden på pyramiden.

For en vanlig pyramide er følgende formler riktige:

Hvor s– baseomkrets;

h a– apotem;

H- høyde;

S full

S-siden

S base– basisareal;

V– volum av en vanlig pyramide.

Avkuttet pyramide kalt den delen av pyramiden som er innelukket mellom bunnen og et skjæreplan parallelt med bunnen av pyramiden (fig. 17). Vanlig avkortet pyramide er den delen av en vanlig pyramide som er innelukket mellom bunnen og et skjæreplan parallelt med bunnen av pyramiden.

Begrunnelse avkortet pyramide - lignende polygoner. Sideflater – trapeser. Høyde av en avkortet pyramide er avstanden mellom dens baser. Diagonal en avkortet pyramide er et segment som forbinder toppene som ikke ligger på samme side. Diagonalt snitt er en del av en avkortet pyramide av et plan som går gjennom to sidekanter som ikke tilhører samme flate.

For en avkortet pyramide er følgende formler gyldige:

(4)

Hvor S 1 , S 2 - områder av øvre og nedre baser;

S full– totalt overflateareal;

S-siden– sideoverflateareal;

H- høyde;

V– volum av en avkortet pyramide.

For en vanlig avkortet pyramide er formelen riktig:

Hvor s 1 , s 2 - omkretsene til basene;

h a– apotem av en vanlig avkortet pyramide.

Eksempel 1. I en vanlig trekantet pyramide er den dihedrale vinkelen ved basen 60º. Finn tangenten til helningsvinkelen til sidekanten til basens plan.

Løsning. La oss lage en tegning (fig. 18).

Pyramiden er regelmessig, noe som betyr at ved basen er det en likesidet trekant og alle sideflatene er like likebente trekanter. Den dihedriske vinkelen ved basen er helningsvinkelen til pyramidens sideflate til basens plan. Den lineære vinkelen er vinkelen en mellom to perpendikulære: osv. Toppen av pyramiden projiseres i midten av trekanten (senteret av den omskrevne sirkelen og den innskrevne sirkelen til trekanten ABC). Helningsvinkelen til sidekanten (for eksempel S.B.) er vinkelen mellom selve kanten og dens projeksjon på basens plan. For ribben S.B. denne vinkelen vil være vinkelen SBD. For å finne tangenten må du kjenne beina SÅ Og O.B.. La lengden på segmentet BD tilsvarer 3 EN. Punktum OM linjestykke BD er delt inn i deler: og Fra finner vi SÅ: Fra finner vi:

Svar:

Eksempel 2. Finn volumet til en vanlig avkortet firkantet pyramide hvis diagonalene til basene er lik cm og cm, og høyden er 4 cm.

Løsning. For å finne volumet til en avkortet pyramide bruker vi formel (4). For å finne arealet til basene, må du finne sidene til basefirkantene, og kjenne diagonalene deres. Sidene av basene er lik henholdsvis 2 cm og 8 cm. Dette betyr at arealene til basene og erstatter alle dataene i formelen, beregner vi volumet til den avkortede pyramiden:

Svar: 112 cm 3.

Eksempel 3. Finn arealet av sideflaten til en vanlig trekantet avkortet pyramide, hvis sider er 10 cm og 4 cm, og pyramidens høyde er 2 cm.

Løsning. La oss lage en tegning (fig. 19).

Sideflaten til denne pyramiden er en likebenet trapes. For å beregne arealet til en trapes, må du vite basen og høyden. Basene er gitt i henhold til tilstanden, bare høyden forblir ukjent. Vi finner henne hvorfra EN 1 E vinkelrett fra et punkt EN 1 på planet til den nedre basen, EN 1 D– vinkelrett fra EN 1 pr AC. EN 1 E= 2 cm, siden dette er høyden på pyramiden. Å finne DE La oss lage en ekstra tegning som viser toppvisningen (fig. 20). Punktum OM– projeksjon av sentrene til øvre og nedre baser. siden (se fig. 20) og På den annen side OK– radius innskrevet i sirkelen og OM– radius innskrevet i en sirkel:

MK = DE.

I følge Pythagoras teorem fra

Sideflateområde:

Svar:

Eksempel 4. Ved bunnen av pyramiden ligger en likebenet trapes, hvis baser EN Og b (en> b). Hver sideflate danner en vinkel som er lik planet til bunnen av pyramiden j. Finn det totale overflatearealet til pyramiden.

Løsning. La oss lage en tegning (fig. 21). Totalt overflateareal av pyramiden SABCD lik summen av arealene og arealet av trapesen ABCD.

La oss bruke utsagnet om at hvis alle flatene til pyramiden er like tilbøyelige til basens plan, så projiseres toppunktet inn i midten av sirkelen som er innskrevet i basen. Punktum OM– toppunktprojeksjon S ved bunnen av pyramiden. Triangel SOD er den ortogonale projeksjonen av trekanten CSD til basens plan. Ved å bruke teoremet om arealet av den ortogonale projeksjonen av en plan figur, får vi:

På samme måte betyr det Dermed ble problemet redusert til å finne området til trapesen ABCD. La oss tegne en trapes ABCD separat (fig. 22). Punktum OM– midten av en sirkel innskrevet i en trapes.

Siden en sirkel kan skrives inn i en trapes, har vi eller Fra Pythagoras teorem

Denne videoopplæringen vil hjelpe brukere med å få en ide om Pyramid-temaet. Riktig pyramide. I denne leksjonen skal vi bli kjent med begrepet en pyramide og gi det en definisjon. La oss vurdere hva en vanlig pyramide er og hvilke egenskaper den har. Deretter beviser vi teoremet om sideflaten til en vanlig pyramide.

I denne leksjonen skal vi bli kjent med begrepet en pyramide og gi det en definisjon.

Tenk på en polygon A 1 A 2...A n, som ligger i α-planet, og punktet P, som ikke ligger i α-planet (fig. 1). La oss koble sammen prikkene P med hjørner A 1, A 2, A 3, … A n. Vi får n trekanter: A 1 A 2 R, A 2 A 3 R og så videre.

Definisjon. Polyeder RA 1 A 2 ...A n, består av n-torget A 1 A 2...A n Og n trekanter RA 1 A 2, RA 2 A 3 …RA n A n-1 kalles n-kullpyramide. Ris. 1.

Ris. 1

Tenk på en firkantet pyramide PABCD(Fig. 2).

R- toppen av pyramiden.

ABCD- bunnen av pyramiden.

RA- sideribbe.

AB- bunnribb.

Fra poenget R la oss slippe perpendikulæren RN til grunnplanet ABCD. Den tegnede perpendikulæren er høyden på pyramiden.

Ris. 2

Hele overflaten av pyramiden består av sideflaten, det vil si arealet til alle sideflatene, og arealet av basen:

S full = S side + S hoved

En pyramide kalles riktig hvis:

• basen er en vanlig polygon;
• segmentet som forbinder toppen av pyramiden til midten av basen er høyden.

Forklaring ved å bruke eksempelet på en vanlig firkantet pyramide

Tenk på en vanlig firkantet pyramide PABCD(Fig. 3).

R- toppen av pyramiden. Basen av pyramiden ABCD- en vanlig firkant, det vil si en firkant. Punktum OM, skjæringspunktet mellom diagonalene, er midten av kvadratet. Midler, RO er høyden på pyramiden.

Ris. 3

Forklaring: i riktig n I en trekant faller midten av den innskrevne sirkelen og midten av den omskrevne sirkelen sammen. Dette senteret kalles polygonens senter. Noen ganger sier de at toppunktet er projisert inn i midten.

Høyden på sideflaten til en vanlig pyramide trukket fra toppunktet kalles apotem og er utpekt h a.

1. alle sidekanter av en vanlig pyramide er like;

2. Sideflatene er like likebenede trekanter.

Vi vil gi et bevis på disse egenskapene ved å bruke eksemplet med en vanlig firkantet pyramide.

Gitt: PABCD- vanlig firkantet pyramide,

ABCD- torget,

RO- høyden på pyramiden.

Bevise:

1. RA = PB = RS = PD

2.∆ABP = ∆BCP =∆CDP =∆DAP Se fig. 4.

Ris. 4

Bevis.

RO- høyden på pyramiden. Det vil si rett RO vinkelrett på planet ABC, og derfor direkte JSC, VO, SO Og GJØRE ligger i den. Så trekanter ROA, ROV, ROS, ROD- rektangulær.

Tenk på en firkant ABCD. Av egenskapene til et kvadrat følger det at AO = VO = CO = GJØRE.

Deretter rette trekanter ROA, ROV, ROS, ROD bein RO- generelt og ben JSC, VO, SO Og GJØRE er like, som betyr at disse trekantene er like på to sider. Fra likheten av trekanter følger likheten av segmenter, RA = PB = RS = PD. Punkt 1 er bevist.

Segmenter AB Og Sol er like fordi de er sider av samme kvadrat, RA = PB = RS. Så trekanter AVR Og VSR - likebenet og like på tre sider.

På lignende måte finner vi at trekanter ABP, VCP, CDP, DAP er likebente og like, som kreves for å være bevist i paragraf 2.

Det laterale overflatearealet til en vanlig pyramide er lik halvparten av produktet av omkretsen av basen og apotemet:

For å bevise dette, la oss velge en vanlig trekantet pyramide.

Gitt: RAVS- vanlig trekantet pyramide.

AB = BC = AC.

RO- høyde.

Bevise: . Se fig. 5.

Ris. 5

Bevis.

RAVS- vanlig trekantet pyramide. Det er AB= AC = BC. La OM- midten av trekanten ABC, Deretter RO er høyden på pyramiden. Ved bunnen av pyramiden ligger en likesidet trekant ABC. Legg merke til det .

Trekanter RAV, RVS, RSA- like likebente trekanter (etter egenskap). En trekantet pyramide har tre sideflater: RAV, RVS, RSA. Dette betyr at området til pyramidens sideoverflate er:

S side = 3S RAW

Teoremet er bevist.

Radiusen til en sirkel innskrevet ved bunnen av en vanlig firkantet pyramide er 3 m, høyden på pyramiden er 4 m Finn arealet av sideoverflaten til pyramiden.

Gitt: vanlig firkantet pyramide ABCD,

ABCD- torget,

r= 3 m,

RO- høyden på pyramiden,

RO= 4 m.

Finne: S-siden. Se fig. 6.

Ris. 6

Løsning.

I følge det beviste teoremet, .

La oss først finne siden av basen AB. Vi vet at radiusen til en sirkel innskrevet ved bunnen av en vanlig firkantet pyramide er 3 m.

Så, m.

Finn omkretsen av firkanten ABCD med en side på 6 m:

Tenk på en trekant BCD. La M- midt på siden DC. Fordi OM- midten BD, Det (m).

Triangel DPC- likebent. M- midten DC. Det er, RM- median, og derfor høyden i trekanten DPC. Deretter RM- apotem av pyramiden.

RO- høyden på pyramiden. Så rett RO vinkelrett på planet ABC, og derfor direkte OM, ligger i den. La oss finne apotemet RM fra en rettvinklet trekant rom.

Nå kan vi finne sideoverflaten til pyramiden:

Svar: 60 m2.

Radiusen til sirkelen omskrevet rundt bunnen av en vanlig trekantet pyramide er lik m. Sideoverflaten er 18 m 2. Finn lengden på apotemet.

Gitt: ABCP- vanlig trekantet pyramide,

AB = BC = SA,

R= m,

S side = 18 m2.

Finne: . Se fig. 7.

Ris. 7

Løsning.

I en rettvinklet trekant ABC Radiusen til den omskrevne sirkelen er gitt. La oss finne en side AB denne trekanten ved å bruke sinussetningen.

Når vi kjenner siden til en vanlig trekant (m), finner vi dens omkrets.

Ved teoremet om det laterale overflatearealet til en vanlig pyramide, hvor h a- apotem av pyramiden. Deretter:

Svar: 4 m.

Så vi så på hva en pyramide er, hva en vanlig pyramide er, og vi beviste teoremet om sideoverflaten til en vanlig pyramide. I neste leksjon skal vi bli kjent med den avkortede pyramiden.

Bibliografi

1. Geometri. Karakterer 10-11: lærebok for studenter ved generelle utdanningsinstitusjoner (grunnleggende og spesialiserte nivåer) / I. M. Smirnova, V. A. Smirnov. - 5. utgave, rev. og tillegg - M.: Mnemosyne, 2008. - 288 s.: ill.
2. Geometri. 10-11 klassetrinn: Lærebok for allmenne utdanningsinstitusjoner / Sharygin I.F. - M.: Bustard, 1999. - 208 s.: ill.
3. Geometri. Karakter 10: Lærebok for allmenne utdanningsinstitusjoner med fordypning og spesialisering i matematikk /E. V. Potoskuev, L. I. Zvalich. - 6. utgave, stereotypi. - M.: Bustard, 008. - 233 s.: ill.

1. Internettportal "Yaklass" ()
2. Internettportal "Festival for pedagogiske ideer "Første september" ()
3. Internettportal «Slideshare.net» ()

Hjemmelekser

1. Kan en regulær polygon være bunnen av en uregelmessig pyramide?
2. Bevis at usammenhengende kanter på en vanlig pyramide er vinkelrette.
3. Finn verdien av den dihedriske vinkelen ved siden av basen til en vanlig firkantet pyramide hvis apotemet til pyramiden er lik siden av basen.
4. RAVS- vanlig trekantet pyramide. Konstruer den lineære vinkelen til den dihedrale vinkelen ved bunnen av pyramiden.

I hvilken en av sideribbene er vinkelrett på basen.

I dette tilfellet vil denne kanten være høyden på pyramiden.

Egenskaper til pyramiden.

1. Når alle sidekanter er av samme størrelse:

• det er lett å beskrive en sirkel nær bunnen av pyramiden, og toppen av pyramiden vil bli projisert inn i midten av denne sirkelen;
• sideribbene danner like vinkler med basens plan;
• Dessuten er det motsatte også sant, dvs. når sideribbene danner like vinkler med bunnplanet, eller når en sirkel kan beskrives rundt bunnen av pyramiden og toppen av pyramiden vil projiseres inn i midten av denne sirkelen, betyr det at alle sidekantene av pyramiden er like store.

2. Når sideflatene har en helningsvinkel til bunnplanet med samme verdi, da:

• det er lett å beskrive en sirkel nær bunnen av pyramiden, og toppen av pyramiden vil bli projisert inn i midten av denne sirkelen;
• høydene på sideflatene er like lange;
• arealet av sideflaten er lik ½ produktet av omkretsen av basen og høyden på sideflaten.

3. En kule kan beskrives rundt en pyramide hvis det ved bunnen av pyramiden er en polygon som en sirkel kan beskrives rundt (en nødvendig og tilstrekkelig betingelse). Sentrum av sfæren vil være skjæringspunktet mellom flyene som går gjennom midten av kantene på pyramiden vinkelrett på dem. Fra denne teoremet konkluderer vi med at en kule kan beskrives både rundt en hvilken som helst trekantet og rundt en hvilken som helst vanlig pyramide;

4. En kule kan skrives inn i en pyramide hvis halveringslinjene til de indre dihedrale vinklene til pyramiden skjærer hverandre i 1. punkt (en nødvendig og tilstrekkelig betingelse). Dette punktet vil bli sentrum av sfæren.

5. Kjeglen vil bli skrevet inn i pyramiden når toppunktene deres faller sammen, og kjeglens base vil bli skrevet inn i bunnen av pyramiden. I dette tilfellet er det mulig å passe en kjegle inn i en pyramide bare hvis apotemene til pyramiden har like størrelser (en nødvendig og tilstrekkelig betingelse);

6. Kjeglen vil bli beskrevet nær pyramiden hvis toppunktene deres sammenfaller, og kjeglens base vil bli beskrevet nær pyramidens basis. I dette tilfellet er det mulig å beskrive en kjegle nær en pyramide bare hvis alle sidekantene av pyramiden har de samme verdiene (en nødvendig og tilstrekkelig betingelse). Høydene på disse kjeglene og pyramidene er de samme.

7. En sylinder vil bli innskrevet i en pyramide hvis en av dens baser faller sammen med en sirkel som er innskrevet i seksjonen av pyramiden av et plan parallelt med basen, og den andre basen tilhører basen av pyramiden.

8. Sylinderen vil bli beskrevet nær pyramiden når toppen av pyramiden tilhører en av dens baser, og den andre bunnen av sylinderen vil bli beskrevet nær bunnen av pyramiden. I dette tilfellet er det mulig å beskrive en sylinder nær en pyramide bare hvis bunnen av pyramiden er en innskrevet polygon (en nødvendig og tilstrekkelig betingelse).

Formler for å bestemme volumet og arealet til en rektangulær pyramide.

V- volum av pyramiden,

S- området av bunnen av pyramiden,

h- høyden på pyramiden,

Sb- området av sideoverflaten av pyramiden,

en- apotem (ikke å forveksle med α ) pyramider,

P- omkretsen av bunnen av pyramiden,

n- antall sider av bunnen av pyramiden,

b- lengden på sidekanten av pyramiden,

α - flat vinkel på toppen av pyramiden.

Her kan du finne grunnleggende informasjon om pyramider og relaterte formler og konsepter. Alle blir studert med en matematikkveileder som forberedelse til Unified State Exam.

Tenk på et plan, en polygon , liggende i den og et punkt S, ikke liggende i den. La oss koble S til alle toppunktene i polygonet. Det resulterende polyederet kalles en pyramide. Segmentene kalles sideribber. Polygonet kalles grunnflaten, og punktet S er toppen av pyramiden. Avhengig av tallet n, kalles pyramiden trekantet (n=3), firkantet (n=4), femkantet (n=5) og så videre. Et alternativt navn for en trekantet pyramide er tetraeder. Høyden på en pyramide er vinkelrett som går ned fra toppen til basens plan.

En pyramide kalles vanlig if en vanlig polygon, og bunnen av pyramidens høyde (grunnen til perpendikulæren) er dens sentrum.

Lærerens kommentar:
Ikke forveksle begrepene "vanlig pyramide" og "vanlig tetraeder". I en vanlig pyramide er sidekantene ikke nødvendigvis like kantene på basen, men i en vanlig tetraeder er alle 6 kantene like. Dette er hans definisjon. Det er lett å bevise at likheten innebærer sammenfall av sentrum P av polygonet med en grunnhøyde, så et vanlig tetraeder er en vanlig pyramide.

Hva er et apotem?
Apotemet til en pyramide er høyden på sideflaten. Hvis pyramiden er vanlig, er alle dens apotemer like. Det motsatte er ikke sant.

En matematikklærer om terminologien hans: 80 % av arbeidet med pyramider er bygget gjennom to typer trekanter:
1) Inneholder apotem SK og høyde SP
2) Inneholder sidekanten SA og dens projeksjon PA

For å forenkle referanser til disse trekantene, er det mer praktisk for en matteveileder å ringe den første av dem apotek, og andre costal. Dessverre finner du ikke denne terminologien i noen av lærebøkene, og læreren må introdusere den ensidig.

Formel for pyramidevolum:
1) , hvor er arealet av bunnen av pyramiden, og er høyden på pyramiden
2) , hvor er radien til den innskrevne sfæren, og er arealet av den totale overflaten av pyramiden.
3) , der MN er avstanden mellom to kryssende kanter, og er arealet av parallellogrammet dannet av midtpunktene til de fire gjenværende kantene.

Egenskapen til bunnen av høyden til en pyramide:

Punkt P (se figur) faller sammen med sentrum av den innskrevne sirkelen ved bunnen av pyramiden hvis en av følgende betingelser er oppfylt:
1) Alle apotemer er like
2) Alle sideflater er likt skråstilt mot basen
3) Alle apotemer er like tilbøyelige til pyramidens høyde
4) Høyden på pyramiden er likt skråstilt til alle sideflater

Mattelærerens kommentar: Vær oppmerksom på at alle punkter er forent av en felles eiendom: på en eller annen måte er sideflater involvert overalt (apotemer er deres elementer). Derfor kan veilederen tilby en mindre presis, men mer praktisk for læring, formulering: punkt P faller sammen med sentrum av den innskrevne sirkelen, bunnen av pyramiden, hvis det er lik informasjon om sideflatene. For å bevise det er det nok å vise at alle apotemtrekanter er like.

Punkt P faller sammen med sentrum av en sirkel omskrevet nær bunnen av pyramiden hvis en av tre betingelser er sann:
1) Alle sidekanter er like
2) Alle sideribber er likt skråstilt mot basen
3) Alle sideribber er likt skråstilt til høyden