Rektangulært (andre navn - flatt, todimensjonalt) koordinatsystem, oppkalt etter den franske vitenskapsmannen Descartes (1596-1650) " Kartesisk system koordinater på planet" dannes av skjæringspunktet på planet i rette vinkler (vinkelrett) av to numeriske akser slik at den positive halvaksen til den ene er rettet mot høyre (x-aksen eller abscisseaksen), og den andre er rettet oppover (y-aksen eller ordinataksen).
Skjæringspunktet for aksene faller sammen med 0-punktet til hver av dem og kalles opprinnelsen til koordinatene.
For hver av aksene velges en vilkårlig skala (et enkelt lengdesegment). Hvert punkt på planet tilsvarer ett tallpar, kalt koordinatene til dette punktet på planet. Omvendt tilsvarer et hvilket som helst ordnet tallpar til ett punkt på planet som disse tallene er koordinater for.
Den første koordinaten til et punkt kalles abscissen til det punktet, og den andre koordinaten kalles ordinaten.
Hele koordinatplanet er delt inn i 4 kvadranter (kvartaler). Kvadranter er plassert fra den første til den fjerde mot klokken (se figur).
For å bestemme koordinatene til et punkt, må du finne avstanden til abscissen og ordinataksen. Siden avstanden (korteste) bestemmes av perpendikulæren, senkes fra punktet to perpendikulære (hjelpelinjer på koordinatplanet) ned på aksen slik at punktet for deres skjæringspunkt er plasseringen gitt poeng i koordinatplanet. Skjæringspunktene for perpendikulære med akser kalles projeksjoner av punktet på koordinataksene.
Den første kvadranten er begrenset av de positive halvaksene til abscisse og ordinat. Derfor vil koordinatene til punktene i denne fjerdedelen av flyet være positive
(tegn "+" og
For eksempel punkt M (2; 4) i figuren over.
Den andre kvadranten er begrenset av den negative x-aksen og den positive y-aksen. Følgelig vil koordinatene til punktene langs abscisseaksen være negative (tegn "-"), og langs ordinataksen vil de være positive (tegn "+").
For eksempel punkt C (-4; 1) i figuren over.
Den tredje kvadranten er begrenset av den negative x-aksen og den negative y-aksen. Følgelig vil koordinatene til punktene langs abscissen og ordinataksen være negative (tegn "-" og "-").
For eksempel punkt D (-6; -2) i figuren over.
Fjerde kvadrant er begrenset av den positive x-aksen og den negative y-aksen. Følgelig vil koordinatene til punktene langs abscisseaksen være positive (“+”-tegnet). og langs ordinataksen - negativ (tegn "-").
For eksempel punkt R (3; -3) i figuren over.
Konstruere et punkt ved å bruke dets spesifiserte koordinater
vi finner den første koordinaten til punktet på x-aksen og trekker en hjelpelinje gjennom den - en vinkelrett;
vi finner den andre koordinaten til punktet på ordinataksen og tegner en hjelpelinje gjennom den - en vinkelrett;
skjæringspunktet mellom to perpendikulære (hjelpelinjer) vil tilsvare punktet med de gitte koordinatene.
yrkesfaglig grunnskoleutdanning
"Fagskole nr. 5" Belgorod
Leksjonssammendrag
i matematikk om emnet:
Rektangulært system koordinater i rommet
for elever i 11. klasse
lærer i informatikk og matematikk
GOU NPO PU nr. 5
Belgorod 2010
Leksjonens tema
: Rektangulært koordinatsystem i rommet. Vektorkoordinater
Leksjonens mål: - utvikle logisk og romlig tenker
Introduser konseptet med et koordinatsystem i rommet, vektorkoordinater
Litteratur: Geometri 10-11 klasse L. S. Atanasyan, M.: Education, 2006
I løpet av timene:
Org. Øyeblikk
Forklaring av nytt materiale
Hvis tre parvise vinkelrette linjer trekkes gjennom et punkt i rommet, velges en retning på hver av dem (det er indikert med en pil) og måleenheten for segmenter er valgt, så sier de at rektangulært koordinatsystem i rommet (fig. 121). Rette linjer med retninger valgt på dem kalles koordinatakser, og deres felles poeng - opprinnelse. Det er vanligvis betegnet med bokstaven O. Koordinataksene er betegnet som følger: Ox, Oy, Oz - og har navn: abscisseakse, ordinatakse, applikatakse. Hele koordinatsystemet er betegnet Oxyz. Flyene som går gjennom koordinataksene Ox og Oy, Oy og Oz, Oz og Ox, henholdsvis, kalles koordinere fly og er betegnet Oxy, Oyz, Ozx.
Punkt O deler hver av koordinataksene i to stråler. En stråle hvis retning sammenfaller med aksens retning kalles positiv halvakse, og den andre strålen negativ halvakse.
I 
I det rektangulære koordinatsystemet er hvert punkt M i rommet assosiert med en trippel av tall, som kalles dens koordinater. De bestemmes på samme måte som koordinatene til punktene på planet. La oss tegne tre plan gjennom punktet M, vinkelrett på koordinataksene, og betegne med M 1, M 2 og M 3 skjæringspunktene til henholdsvis disse planene med abscisse-, ordinat- og applikataksene (fig. 122). Den første koordinaten til punktet M (kalles abscisse og er vanligvis betegnet med bokstaven x) er definert som følger: x = OM 1, hvis M 1 er punktet til den positive halvaksen; x = - OM 1, hvis M 1 er punktet til den negative halvaksen; x = 0 hvis M 1 sammenfaller med punktet O. På samme måte bruker du punkt M 2 den andre koordinaten ( ordinere) y punkt M, og ved å bruke punkt M 3 den tredje koordinaten ( søknad) z punkt M. Koordinatene til punkt M er skrevet i parentes etter betegnelsen av punktet: M (x; y; z), med abscissen angitt først, ordinaten angitt som andre, og den aktuelle tredje angitt. Figur 123 viser seks punkter A (9; 5; 10), B (4; -3; 6), C (9; 0; 0), E (4; 0; 5), E (0; 3; 0 ) , F (0; 0; -3).
E 
hvis punktet M (x; y; z) ligger på koordinatplan eller på koordinataksen, så er noen av dens koordinater lik null. Så, hvis M € Oxy, så er applikatet til punktet M lik null: z = 0. På samme måte, hvis M med Oxz, så er y = 0, og hvis M € Oyz, så er x = 0. Hvis M € Ox , da er ordinaten og applikatet til punktet M lik null: y = 0 og z = 0 (for eksempel ved punktet C i figur 123). Hvis M € Oy, så er x = 0 og z = 0; hvis M € Oz, så er x = 0 og y = 0. Alle tre koordinatene til origo er lik null: 0 (0; 0; 0).
Vektorkoordinater
Z 
La oss definere et rektangulært koordinatsystem Oxyz i rommet. På hver av de positive halvaksene plotter vi fra opprinnelsen til koordinatene enhetsvektor
, dvs. en vektor hvis lengde er lik én. Jeg enhetsvektor for x-aksen, gjennom j- enhetsvektor for ordinataksen og gjennom k enhetsvektor for applikataksen (fig. 124). La oss kalle vektorene i, j, k koordinatvektorer. Åpenbart er disse vektorene ikke koplanære. Derfor hvilken som helst vektorenog kan dekomponeres til koordinatvektorer, dvs. representere det i formen
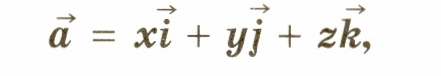
og ekspansjonskoeffisientene x, y,z er bestemt på en unik måte.
TIL 
koeffisientene x, y og z i ekspansjonen av vektor a i koordinatvektorer kalles vektorkoordinatereni dette koordinatsystemet. Vi vil skrive koordinatene til vektoren a i krøllede parenteser etter vektorbetegnelsen: a (x; y; z). Figur 125 viser kuboid, med følgende dimensjoner: OA 1 = 2, OA 2 = 2, OA 3 = 4. Koordinatene til vektorene vist i denne figuren er: a (2; 2; 4), b(2; 2; -1), A 3 A (2; 2; 0), i(1; 0; 0), j (0; 1; 0), k(0; 0; 1).
Siden nullvektoren kan representeres som 0 = oi+ oj+ 0k, så er alle koordinatene til nullvektoren lik null. Lengre, koordinater like vektorer henholdsvis like, dvs. hvis vektorene a(x 1, y 1, z 1) og b(x 2, y 2, z 2) er like, så er x 1 = x 2, y 1 = y 2 og z 1 = z 2 ( Forklar hvorfor).
La oss vurdere regler, som gjør det mulig å bruke koordinatene til disse vektorene for å finne koordinatene til summen og differansen deres, samt koordinatene til produktet gitt vektor for dette nummeret.
1 0 . Hver koordinat av summen av to eller flere vektorer er lik summen av de tilsvarende koordinatene til disse vektorene. Med andre ord, hvis a (x 1, y 1, z 1) og b(x 2, y 2, z 2) er gitt vektorer, så har vektoren a + b koordinater (x 1 + x 2, y 1 + y2, z1 + z2).
2 0 . Hver koordinat av forskjellen mellom to vektorer er lik forskjellen til de tilsvarende koordinatene til disse vektorene. Med andre ord, hvis a (x 1, y 1, z 1) og b(x 2 y 2; z 2) er gitt vektorer, så har vektoren a- b koordinater (x 1 - x 2, y 1 - y 2, z1 - z2).
3 OM. Hver koordinat av produktet av en vektor og et tall er lik produktet av den tilsvarende koordinaten til vektoren og dette tallet. Med andre ord, hvis a(x;y;x) -
For å bestemme posisjonen til et punkt i rommet vil vi bruke kartesisk rektangulære koordinater(Fig. 2).
Det kartesiske rektangulære koordinatsystemet i rommet er dannet av tre innbyrdes perpendikulære koordinatakser OX, OY, OZ. Koordinataksene skjærer hverandre i punktet O, som kalles origo, på hver akse velges en positiv retning, angitt med piler, og en måleenhet for segmentene på aksene. Måleenhetene er vanligvis (ikke nødvendigvis) de samme for alle akser. OX-aksen kalles abscisse-aksen (eller ganske enkelt abscisse), OY-aksen er ordinataksen, og OZ-aksen er applikataksen.
Posisjonen til punktet A i rommet bestemmes av tre koordinater x, y og z. X-koordinaten er lik lengden på segmentet OB, y-koordinaten er lengden på segmentet OC, z-koordinaten er lengden på segmentet OD i de valgte måleenhetene. Segmentene OB, OC og OD er definert av plan trukket fra et punkt parallelt med henholdsvis planene YOZ, XOZ og XOY.
X-koordinaten kalles abscissen til punkt A, y-koordinaten kalles ordinaten til punkt A, og z-koordinaten kalles applikatet til punkt A.
Symbolsk er det skrevet slik:
eller koble en koordinatpost til et spesifikt punkt ved hjelp av en indeks:
x A , y A , z A ,
Hver akse betraktes som en talllinje, dvs. har en positiv retning, og punkter som ligger på den negative strålen er tildelt negative verdier koordinater (avstand tas med minustegn). Det vil si, hvis for eksempel punkt B ikke lå som på figuren - på strålen OX, men på dens fortsettelse i motsatt side fra punkt O (på den negative delen av aksen OX), så ville x-abscissen til punkt A være negativ (minus avstanden OB). Likeså for de to andre aksene.
Koordinatakser OX, OY, OZ, vist i fig. 2, danner et høyrehendt koordinatsystem. Dette betyr at hvis du ser på YOZ-planet langs den positive retningen til OX-aksen, så vil bevegelsen til OY-aksen mot OZ-aksen være med klokken. Denne situasjonen kan beskrives ved hjelp av gimlet-regelen: hvis gimlet (skrue med en høyregjenge) roteres i retningen fra OY-aksen til OZ-aksen, vil den bevege seg langs den positive retningen til OX-aksen.
Vektorer av lengdeenhet rettet langs koordinatakser, kalles koordinatenhetsvektorer. De er vanligvis betegnet som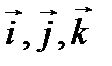 
(Fig. 3). Det er også betegnelsen 
Enhetsvektorene danner grunnlaget for koordinatsystemet.
Ved høyrehendt koordinatsystem, gyldig følgende formler Med vektor fungerer ortov:
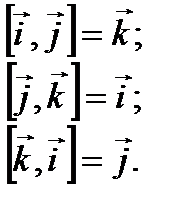
Et rektangulært koordinatsystem i rommet er en trippel gjensidig vinkelrette akser, kryssende ved ett punkt O, kalt origo.
Koordinatakser er vanligvis betegnet med bokstaver og kalles henholdsvis abscisseaksen, ordinataksen, applikataksen eller Oy-aksen (fig. 33).
Enhetsvektorene til koordinataksene Ox, Oy, Oz er utpekt henholdsvis eller. Vi vil hovedsakelig bruke sistnevnte betegnelse.
Det er høyre og venstre koordinatsystem.
Koordinatsystemet kalles rett hvis fra slutten av tredje ort til svingen fra første ort til andre ort sees å skje mot klokken (fig. 34, a).
Koordinatsystemet kalles venstrehendt hvis, fra slutten av tredje ort, rotasjonen fra første ort til andre ort er synlig som skjer med klokken (fig. 34, b).
Så hvis du skruer inn skruen i retning av vektor k, roterer den bort, så i tilfelle av et høyrehendt system, bør gjengen være høyrehendt, og i tilfelle av et venstrehendt system, venstre -hendt (fig. 35).
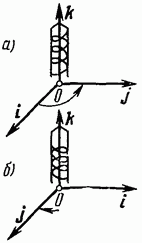
Mange bestemmelser i vektoralgebra avhenger ikke av om vi bruker et høyrehendt eller venstrehendt koordinatsystem. Noen ganger er imidlertid denne omstendigheten viktig. I det følgende vil vi alltid bruke det høyrehendte koordinatsystemet, slik det er vanlig i fysikk.