TEKSTTRANSKRIPT AV LEKSJONEN:
Hvis tre parvise perpendikulære linjer trekkes gjennom et punkt i rommet, på hver av dem er valgt en retning og et enhetssegment, så sier de at et rektangulært koordinatsystem i rommet er spesifisert.
Rette linjer med retninger valgt på dem kalles koordinatakser og er utpekt som følger: Ox, Oy, Oz, har sine egne navn: abscisse-akse, ordinatakse og applikatakse, og deres felles poeng- opprinnelse til koordinater. Det er vanligvis betegnet med bokstaven O.
Hele koordinatsystemet er betegnet Oxyz.
Hvis fly trekkes gjennom koordinataksene Ox og Oy, Oy og Oz, Oz og Ox, vil slike plan bli kalt koordinatplan og betegnet henholdsvis Oxy, Oyz, Ozx.
Punkt O deler hver av koordinataksene i to stråler. Strålen hvis retning faller sammen med retningen til aksen kalles den positive halvaksen, og den andre strålen kalles den negative halvaksen.
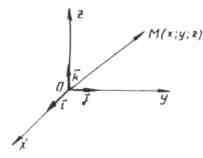
I et rektangulært koordinatsystem er hvert punkt M i rommet assosiert med en trippel av tall, som kalles dets koordinater. De bestemmes på samme måte som koordinatene til punktene på planet.
La oss se hvordan det gjøres.
La oss tegne tre plan gjennom punkt M, vinkelrett på aksene koordinater, og angir med M1, M2 og M3 skjæringspunktene til henholdsvis disse planene med abscissen, ordinaten og applikataksene.
Den første koordinaten til punktet M (den kalles abscissen og er vanligvis betegnet med bokstaven x) er definert som følger: x = OM₁, hvis M1 er punktet til den positive halvaksen;
x= - OM1, hvis M1 er punktet til den negative halvaksen; x =0 hvis M₁ sammenfaller med punkt O.
På samme måte, ved å bruke punktet M₂, bestemmes den andre koordinaten (ordinaten) i punktet M,
og ved å bruke punktet M₃ - den tredje koordinaten (applikat) z til punktet M.
Koordinatene til punktet M er skrevet i parentes etter betegnelsen til punktet M (x; y; z).
Husk at abscissen er indikert først, ordinaten er andre, og applikasjonen er tredje.
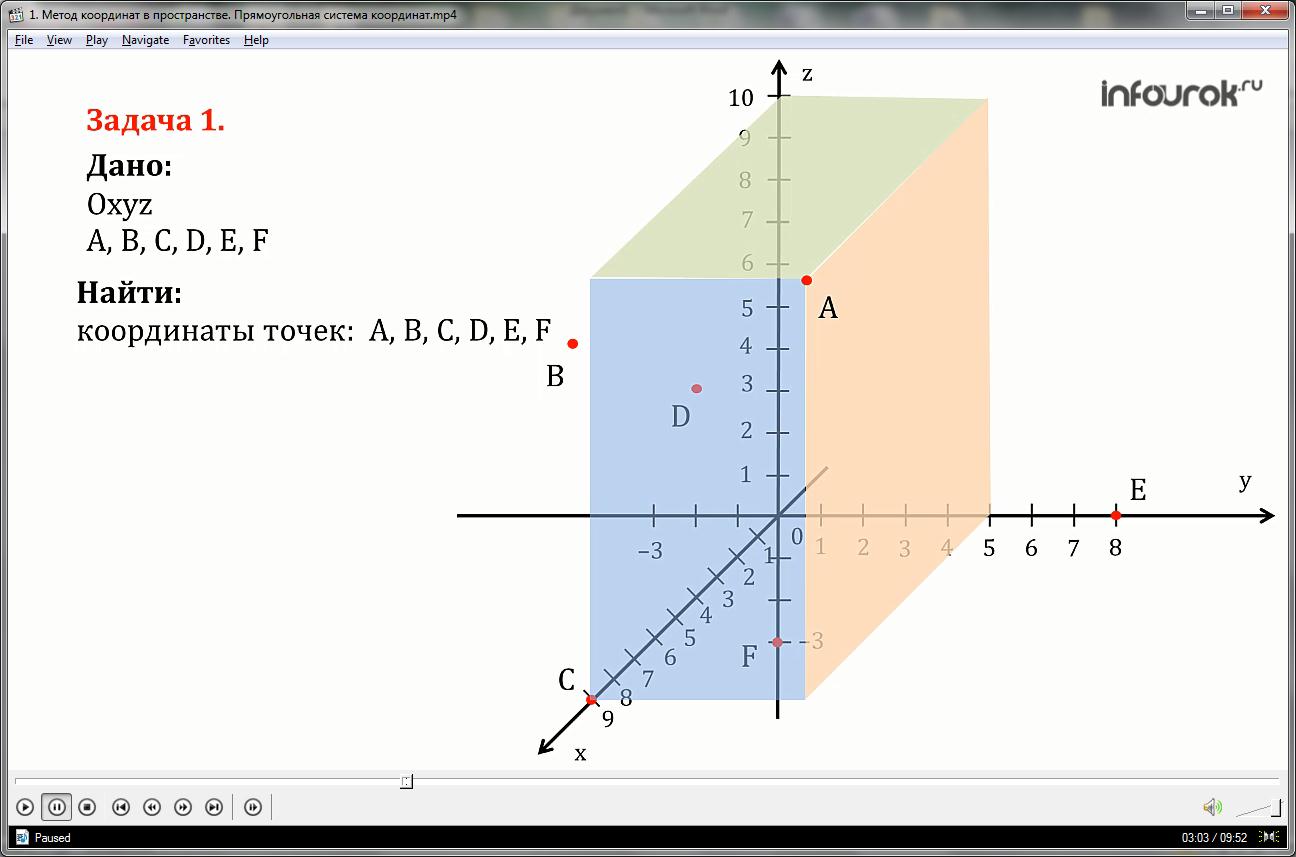
La oss finne koordinatene til punktene A, B, C, D, E, F, vist i figuren.
La oss tegne tre plan gjennom punkt A, vinkelrett på koordinataksene, da vil skjæringspunktene til disse planene med henholdsvis abscissen, ordinataksen og applikataksen være koordinatene til punkt A. Punkt A har koordinatene: abscisse = 9, ordinat = 5, applikat = 10 og det er skrevet slik: A (9; 5; 10).
Koordinatene til følgende punkter er skrevet på samme måte:
Punkt B har koordinater: abscisse = 4, ordinat = -3, applikat = 6
Punkt C har koordinater: abscisse = 9, ordinat = 0, applikat = 0
Punktet har D-koordinater: abscisse = 4, ordinat = 0, applikat = 5
Punkt E har koordinater: abscisse = 0, ordinat = 8, applikat = 0
Punkt F har koordinater: abscisse = 0, ordinat = 0, applikat = -3
Hvis et punkt M (x; y; z) ligger på koordinatplanet på koordinataksen, så er noen av dets koordinater lik null.
Hvis MЄОху (punkt M tilhører oksyplanet), så er applikatet til punktet M lik null: z=0.
Tilsvarende, hvis МЄОхz (punkt M tilhører Oxz-planet), så er y = 0, og hvis МЄОуz (punkt M tilhører Oyz-planet), så er x = 0.
Hvis МЄОх (punkt M ligger på abscisseaksen), er ordinaten og applikatet til punktet M lik null: y=o og z=0. I vårt eksempel er dette punkt C.
Hvis MЄОу (punkt M ligger på ordinaten), så er x=0 og z=0. I vårt eksempel er dette punkt E.
Hvis МЄОz (punkt M ligger på applikataksen), så er x = 0 og y = 0. I vårt eksempel er dette punktet F.
Hvis alle tre koordinatene til punktet M er lik null, betyr dette at M=O (0; 0; 0) er opprinnelsen til koordinatene.
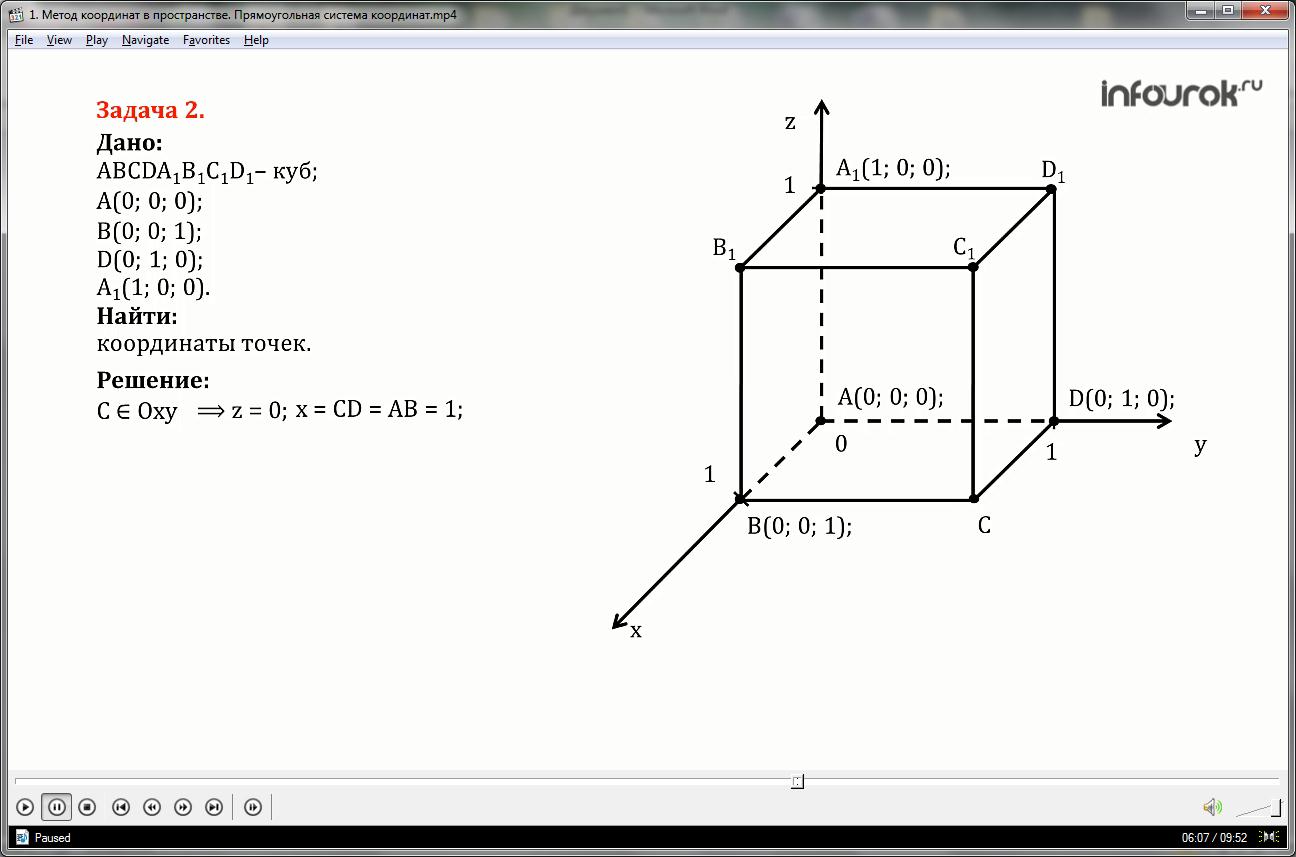
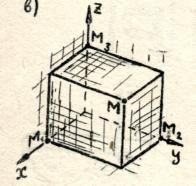
Gitt koordinatene til de fire toppunktene til kuben ABCDA 1 B 1 C 1 D 1: A(0; 0; 0); B(0; 0; 1); D(0; 1; 0); A 1 (1; 0; 0). Finn koordinatene til de gjenværende toppunktene i kuben.
Siden figuren er en kube, er alle sider lik én, alle flater er firkanter.
Punkt C tilhører oksyplanet, det vil si at z-koordinaten er lik null, x-koordinaten er lik siden CD og er lik AB, noe som betyr at den er lik én, koordinaten Y er lik siden av kuben CB, som betyr at den er lik AD og er lik en.
Tilsvarende hører punkt B 1 til Oxz-planet, det vil si at dens y-koordinat er lik null, x-koordinaten er lik siden, x-koordinaten er lik siden A1B1 og er lik AB, som betyr lik med en, z-koordinaten er lik siden av kuben B B1, som betyr lik AA1 og lik en.
Punkt D 1 tilhører Oyz-planet, det vil si at x-koordinaten er lik null, y-koordinaten er lik side A 1 D 1 og er lik AD, som betyr at den er lik én, z-koordinaten er lik. til siden av kuben A 1 B 1, som betyr at den er lik AB og er lik én.
Punkt C 1 tilhører ikke noe plan, det vil si at alle koordinater er forskjellige fra null, x-koordinaten er lik siden C 1 D 1 og er lik AB, som betyr at den er lik en, koordinaten y er lik siden av kuben B 1 C 1, som betyr at den er lik AD og er lik én, og z-koordinaten er lik siden CC 1, det vil si AA 1 og er også lik én.
Finn koordinatene til projeksjonene til punkt C(; ;) på koordinatplanene Oxy, Oxz, Oyz og koordinataksene Ox, Oy, Oz.
1) la oss slippe perpendikulære til Oxy-planet - dette er CN, til Oxz-planet - CL, og til Oyz-planet - linjen CR.
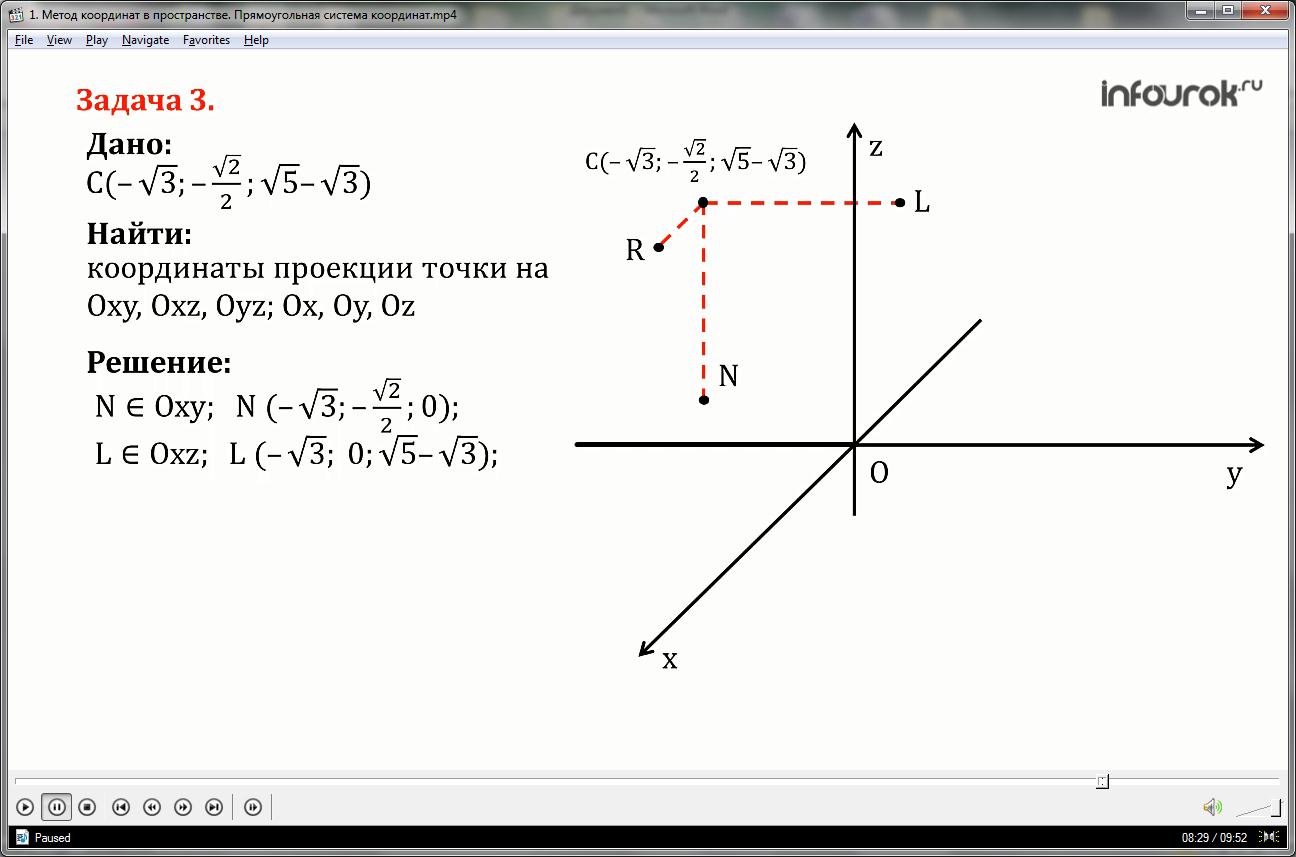
Dermed er projeksjonen av punkt C på Oxy-planet punkt N og det har koordinater x lik minusroten av tre, y lik minusroten av to og to, z lik null.
Projeksjonen av punkt C på Oxz-planet er punkt L og det har koordinater x lik minus roten av tre, i lik null, z lik roten på fem minus roten av tre.
Projeksjonen av punktet C på planet Oyz er punktet R og det har koordinater x er lik null, y er lik minus roten av to og to, z er lik roten av fem minus roten av tre.
2) Fra punkt N tegner vi perpendikulærer til Ox-aksen - rett linje NK, og til Oy - rett linje NG, og til Oz-aksen tegner vi en perpendikulær fra punkt R - dette er rett linje RP.
Projeksjonen av punktet C på Ox-aksen - punktet K har koordinater x lik minus roten av tre, og y og z lik null.
Projeksjonen av punktet C på Oy-aksen - punkt G har koordinatene x og z lik null, i er lik minus roten av to og to.
Projeksjonen av punktet C på Oz-aksen - punktet P har koordinatene x og y lik null, z lik rot på fem minus roten av tre.
Kunnskapsdepartementet Den russiske føderasjonen
Kommunal utdanningsinstitusjon"Gjennomsnitt ungdomsskolen nr. 18"
ABSTRAKT
VED GEOMETRI
TEMA: METODE FOR KOORDINATER I ROMMET
Fullført av elev "C" i 11. klasse
Melnik Roman
Veileder
matematikklærer Baksheeva I.K.
Biysk - 2008
Innhold
Introduksjon……………………………………………………………..… 3.
Kapittel 1.
Koordinatmetode: utviklingshistorie…………………………………………4
Koordinater til et punkt i rommet……………………………….…...5
Definere figurer i rommet……………………………………….……...8
Kapittel 2.
Dekomponering av en vektor til koordinatvektorer. Koordinater
vektor………………………………………………………………………..……..10
Lineære operasjoner over vektorer i koordinater…………..………12
Betingelse for kollinearitet av to vektorer i koordinater…………………..13
De enkleste problemene i koordinater………………………………………….....14
Skalært produkt vektorer og beregning av vinkelen mellom vektorer gjennom deres koordinater………………………………………….………15
Beregning av vinkler mellom rette linjer og plan…………………..16
4. Kapittel 3.
4.1. applikasjon koordinere metodeå løse stereometri
oppgaver ………………………………………………………..…………….. 19
Konklusjon. …………………………………………………………………..26
Bibliografi……………………………………………………... 27
Introduksjon
Emnet for arbeidet mitt er "Method of coordinates in space." Dette emnet relevant i dag for alle nyutdannede videregående skole fordi:
Målet med arbeidet: systematisere kunnskap om dette emnet og vurdere søknad denne metoden når du løser ulike stereometriske problemer.
For å nå målet ble følgende satt oppgaver:
tillater mange eksamener geometriske problemer løse analytisk, noe som krever mindre kunnskap om geometri og reduserer utførelsestiden betydelig;
Denne metoden ligger til grunn for analytisk geometri, som studeres i løpet av høyere matematikk.
studere teoretisk materiale om emnet;
systematisere og oppsummere det studerte materialet;
identifisere funksjonene ved bruk av metoden;
vurdere bruken av koordinatmetoden for å løse stereometriske problemer;
sammenligne anvendelsen av koordinatmetoden med andre metoder for å løse stereometriske problemer.
Metoder som brukes :
metode for analyse og syntese,
sammenligningsmetode.
Kapittel 1
1. Koordinatmetode: utviklingshistorie.
Koordinatmetoden er en måte å bestemme posisjonen til et punkt eller en kropp ved hjelp av tall eller andre symboler.
Tallene som brukes til å bestemme posisjonen til et punkt kalles punktkoordinater.
Godt kjent for oss geografiske koordinater bestemme posisjonen til et punkt på jordens overflate - hvert punkt på jordens overflate har to koordinater: breddegrad og lengdegrad.
For å bestemme posisjonen til et punkt i rommet, trengs tre tall. For å bestemme posisjonen til en satellitt kan du for eksempel spesifisere høyden over jordens overflate, samt breddegrad og lengdegrad til punktet den befinner seg over.
Ved hjelp av koordinatmetoden kan du presentere nesten hele skolegeometrikurset uten en eneste tegning, med kun tall og algebraiske operasjoner. For eksempel kan en sirkel defineres som et sett med punkter som tilfredsstiller ligningen, og en rett linje kan defineres som et sett med punkter som tilfredsstiller ligningen  . Dermed var det ved hjelp av denne metoden mulig å koble sammen tilsynelatende fullstendig ulike vitenskaper algebra og geometri. Denne forbindelsen var i hovedsak en revolusjon innen matematikk. Det gjenopprettet matematikk som en enhetlig vitenskap.
. Dermed var det ved hjelp av denne metoden mulig å koble sammen tilsynelatende fullstendig ulike vitenskaper algebra og geometri. Denne forbindelsen var i hovedsak en revolusjon innen matematikk. Det gjenopprettet matematikk som en enhetlig vitenskap.
Skaperen av koordinatmetoden anses å være den franske filosofen og matematikeren Rene Descartes (1596-1650), som i siste del av Descartes’ store filosofiske avhandling, publisert i 1637, beskrev koordinatmetoden og dens anvendelse for å løse geometriske problemer.
Utviklingen av Descartes ideer førte til fremveksten av en spesiell gren av matematikken, som nå kalles analytisk geometri.
Dette navnet i seg selv uttrykker den grunnleggende ideen om teorien. Analytisk geometri er den delen av matematikken som løser geometriske problemer analytisk (dvs. algebraisk) ved hjelp av midler.
Sammen med Descartes er grunnleggeren av analytisk geometri den bemerkelsesverdige franske matematikeren P. Fermat. Ved å bruke koordinatmetoden studerte Fermat rette linjer og andreordens kurver. Studiet av analytisk geometri i tredimensjonalt rom ble betydelig avansert på 1700-tallet av A. Clairaut. Eksplisitt og konsekvent analytisk geometri på planet og i tredimensjonalt rom skissert av L. Euler i 1748 i læreboken "Introduction to the Analysis of Infinites".
I XIXårhundre ble det tatt et nytt skritt i utviklingen av geometri - flerdimensjonale rom ble studert. Hovedideen for skaperne av teorien var analogien med Descartes "Geometri". Poenget hans på flyet er et par tall 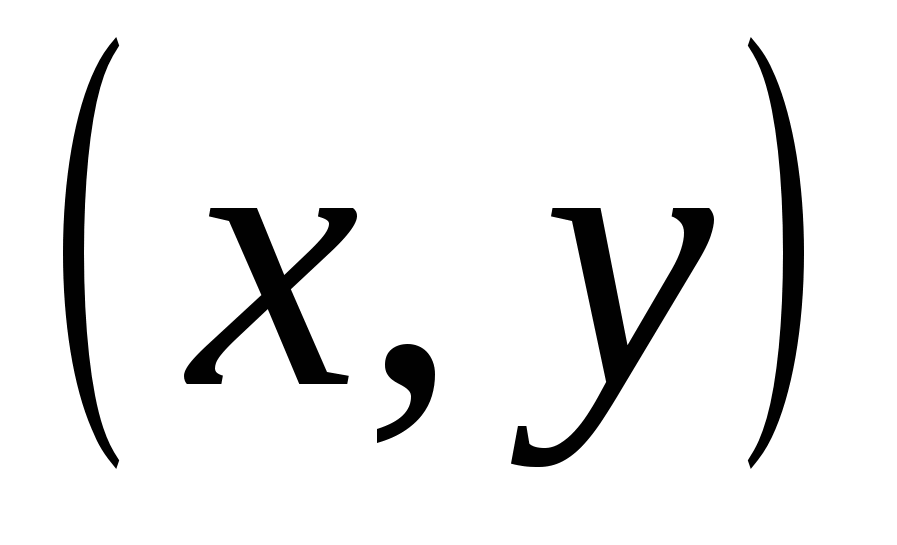 , et punkt i tredimensjonalt rom – en trippel av tall
, et punkt i tredimensjonalt rom – en trippel av tall 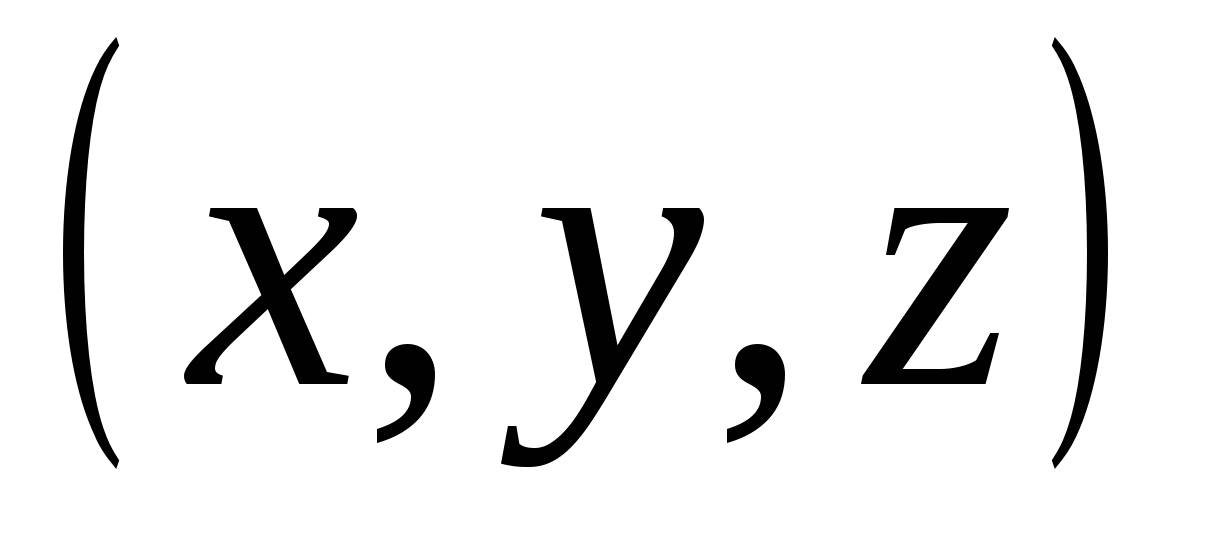 ; V ny teori et punkt i firedimensjonalt rom er en firedobbel av tall
; V ny teori et punkt i firedimensjonalt rom er en firedobbel av tall 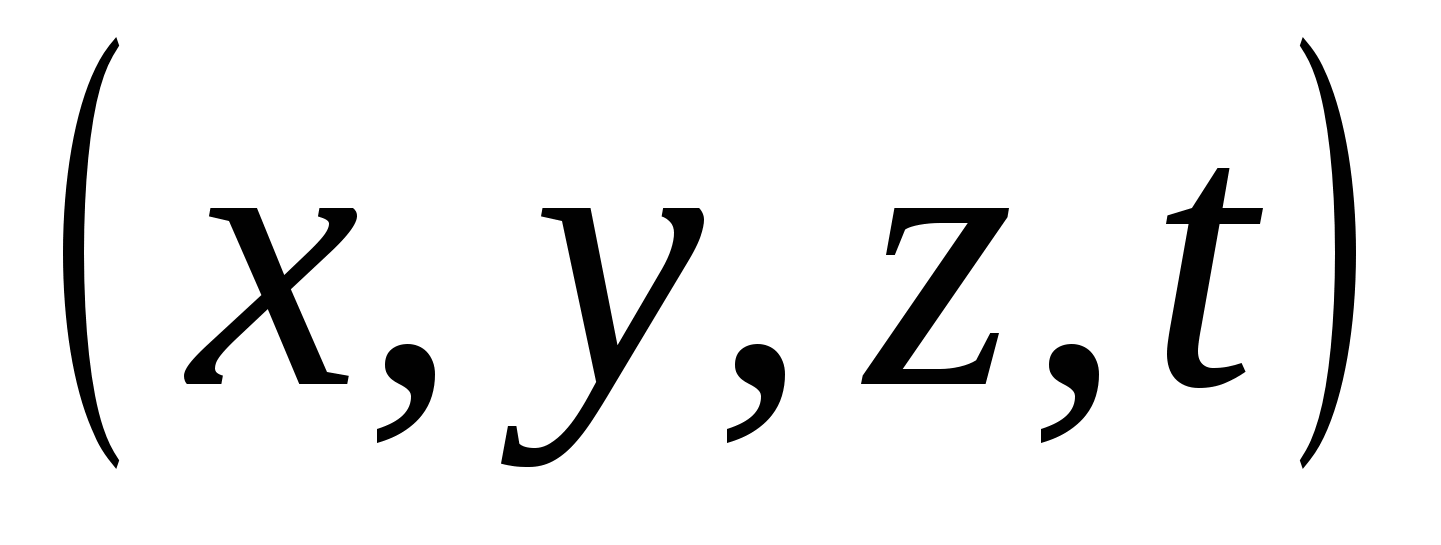 . I Descartes
. I Descartes 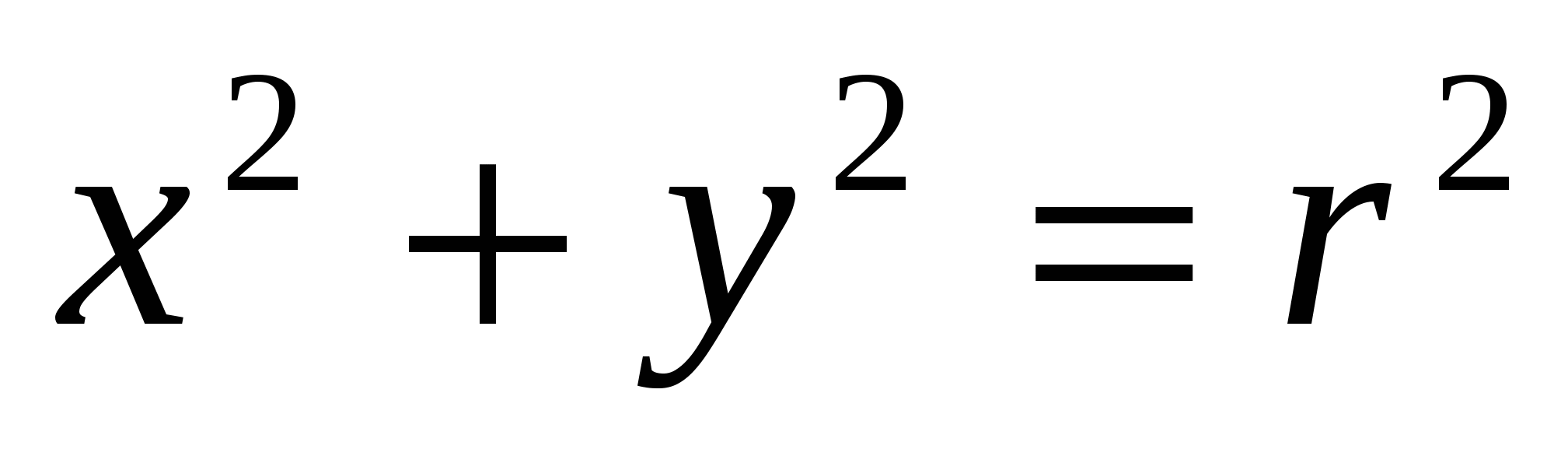 - ligning av en sirkel på et plan,
- ligning av en sirkel på et plan,  - ligning av overflaten til en ball i tredimensjonalt rom; i den nye teorien
- ligning av overflaten til en ball i tredimensjonalt rom; i den nye teorien 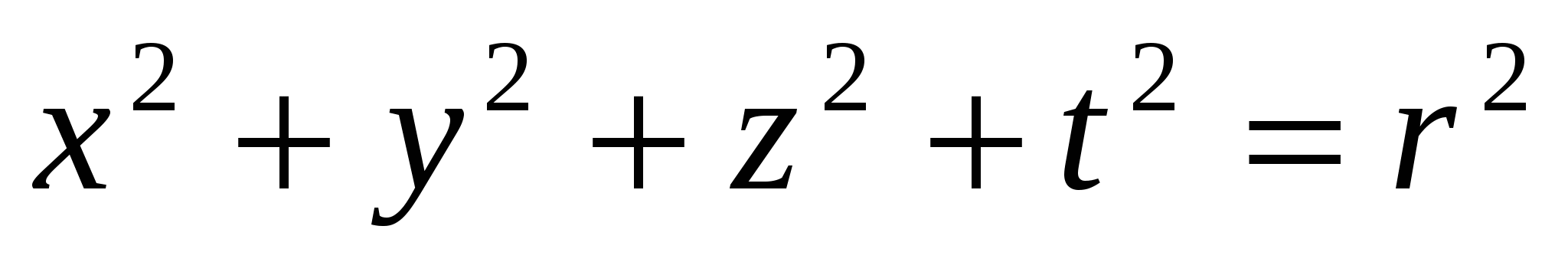 overflaten av en kule i firedimensjonalt rom. Tilsvarende in
-
dimensjonal geometri vurderer plan, rette linjer, avstander mellom punkter, vinkler mellom rette linjer, etc.
overflaten av en kule i firedimensjonalt rom. Tilsvarende in
-
dimensjonal geometri vurderer plan, rette linjer, avstander mellom punkter, vinkler mellom rette linjer, etc.
Ideene om flerdimensjonal geometri ble solid etablert i matematikken på sluttenXIXårhundrer, og helt i begynnelsenXXårhundrer har de funnet anvendelse i spesiell teori relativitet, hvor til tre romlige koordinater en fjerde legges til – tid. Dermed ligger ideene til Descartes 'geometri, utviklet av forskere fra påfølgende generasjoner, til grunnlaget for moderne vitenskap.
2. Koordinater til et punkt i rommet .
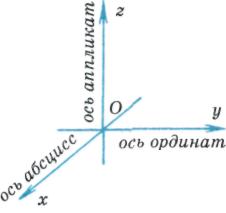 De sier at et rektangulært (kartesisk) koordinatsystem er gitt hvis tre parvise perpendikulære linjer trekkes gjennom et punkt i rommet, en retning velges på hver av dem, og en måleenhet for segmentene velges. Plan som går gjennom henholdsvis koordinataksene
De sier at et rektangulært (kartesisk) koordinatsystem er gitt hvis tre parvise perpendikulære linjer trekkes gjennom et punkt i rommet, en retning velges på hver av dem, og en måleenhet for segmentene velges. Plan som går gjennom henholdsvis koordinataksene 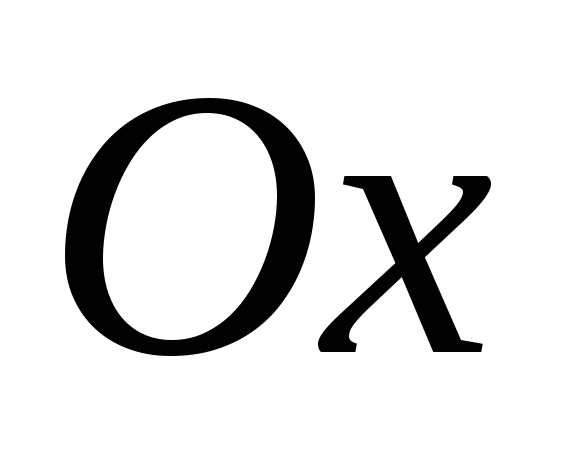 Og
Og 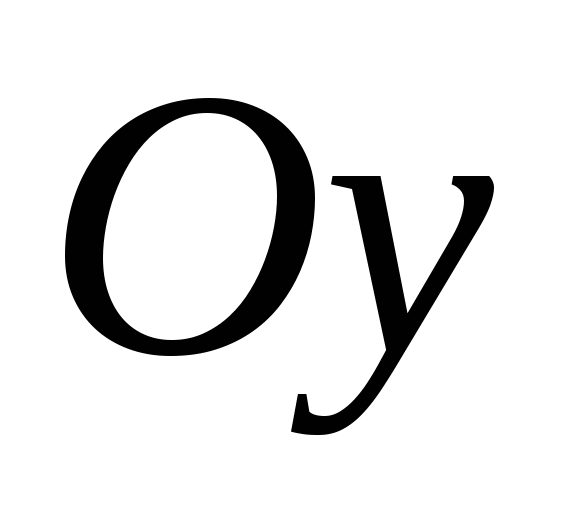 ,
, 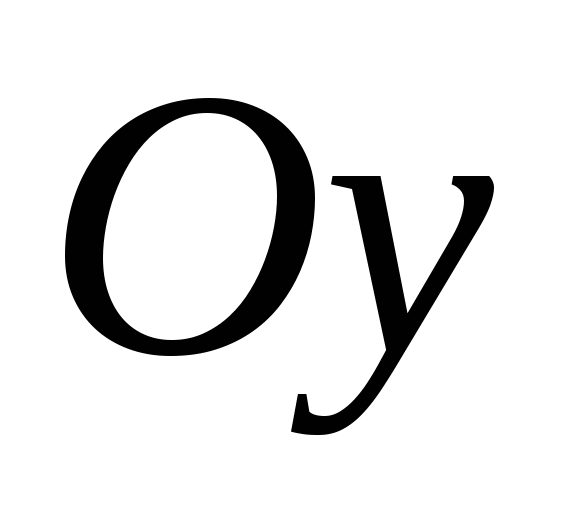 Og
Og  ,
,  Og
Og 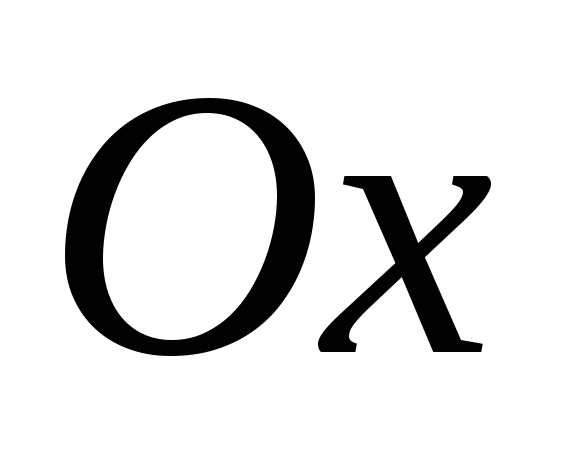 , er kaltkoordinere fly
og er utpekt
, er kaltkoordinere fly
og er utpekt 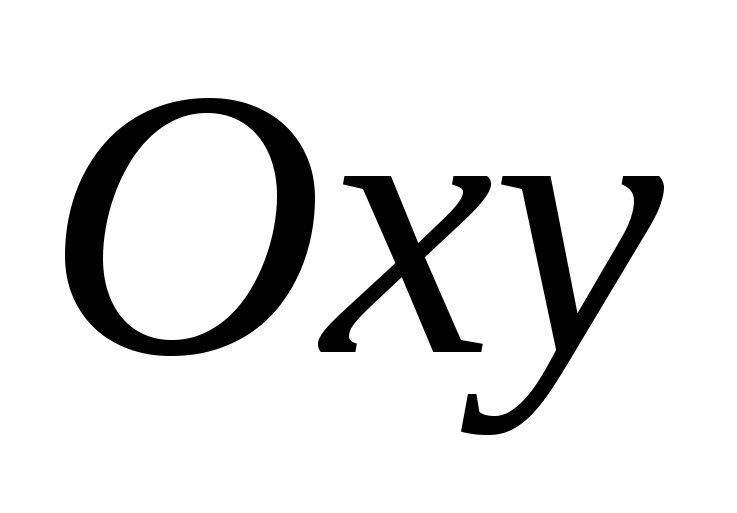 ,
, 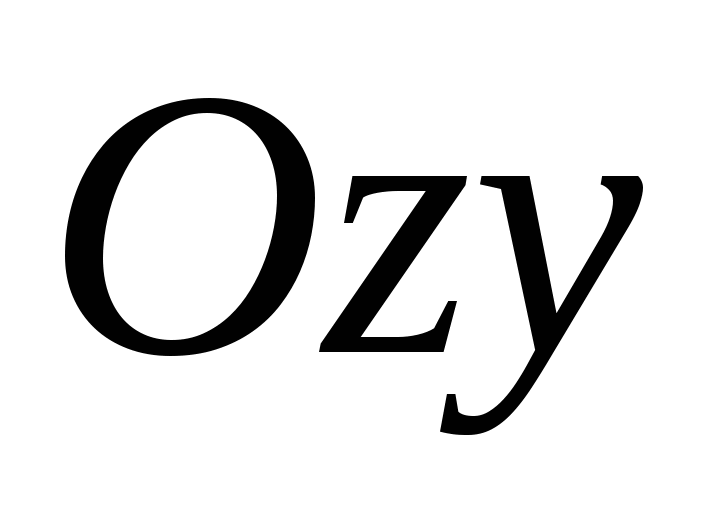 ,
,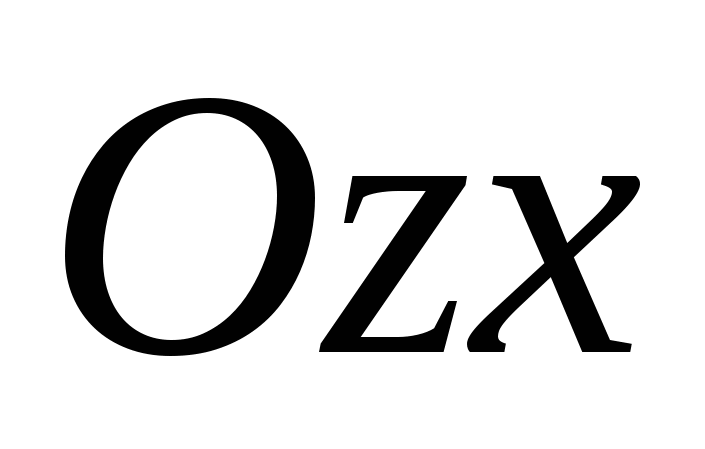 .
.
TIL  Koordinatene til et punkt i rommet er koordinatene til projeksjonene av dette punktet på koordinataksene.
Koordinatene til et punkt i rommet er koordinatene til projeksjonene av dette punktet på koordinataksene.
Punktkoordinater: 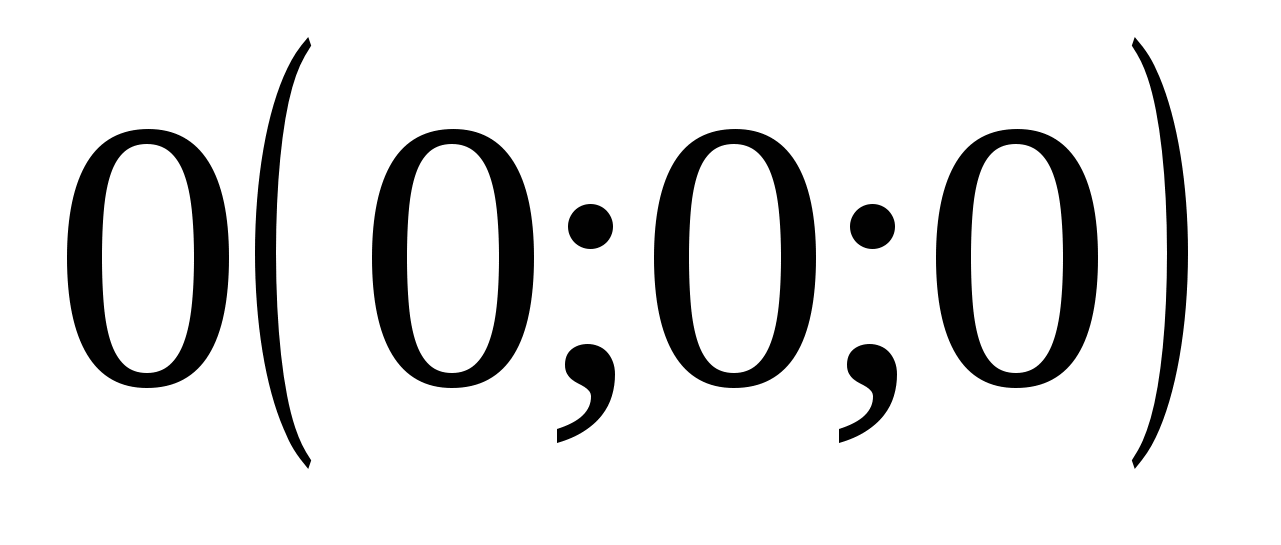 ,
, 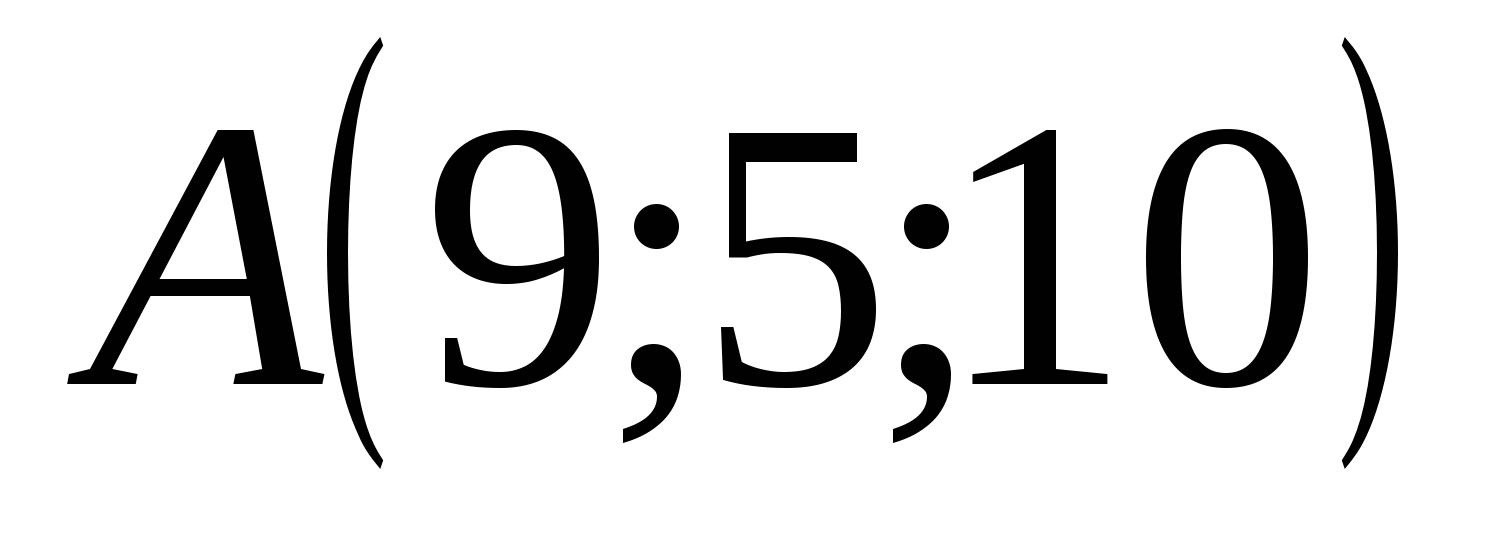 ,
, 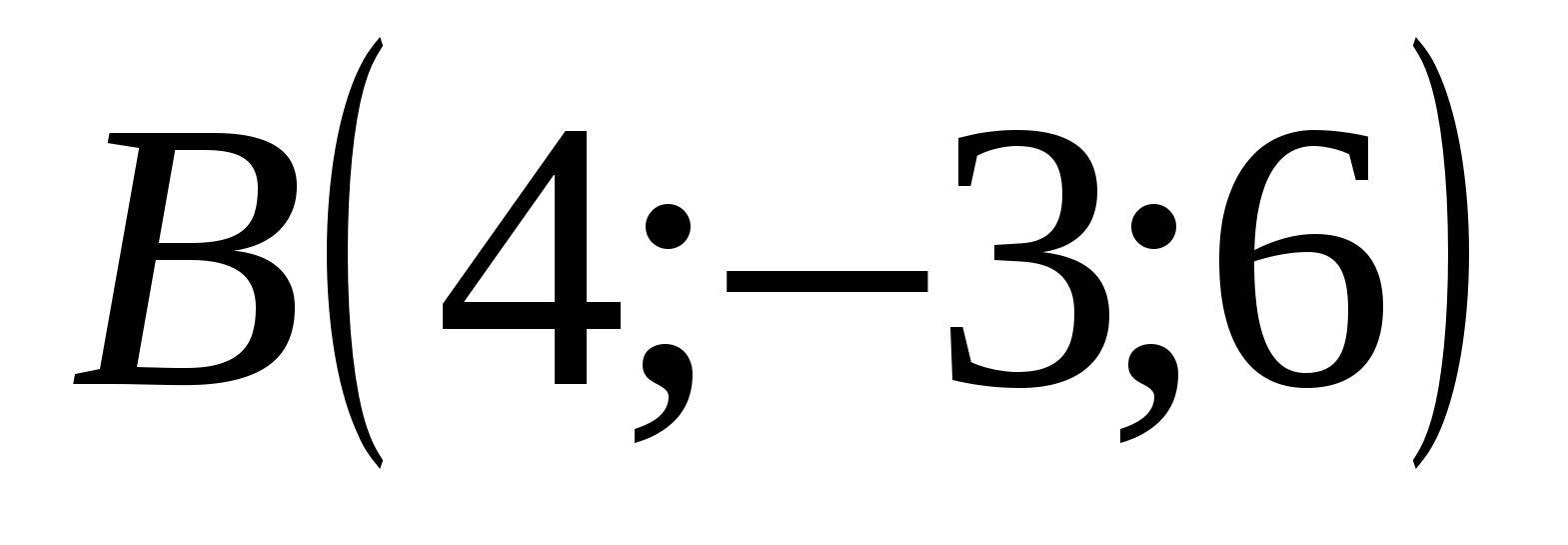 ,
, 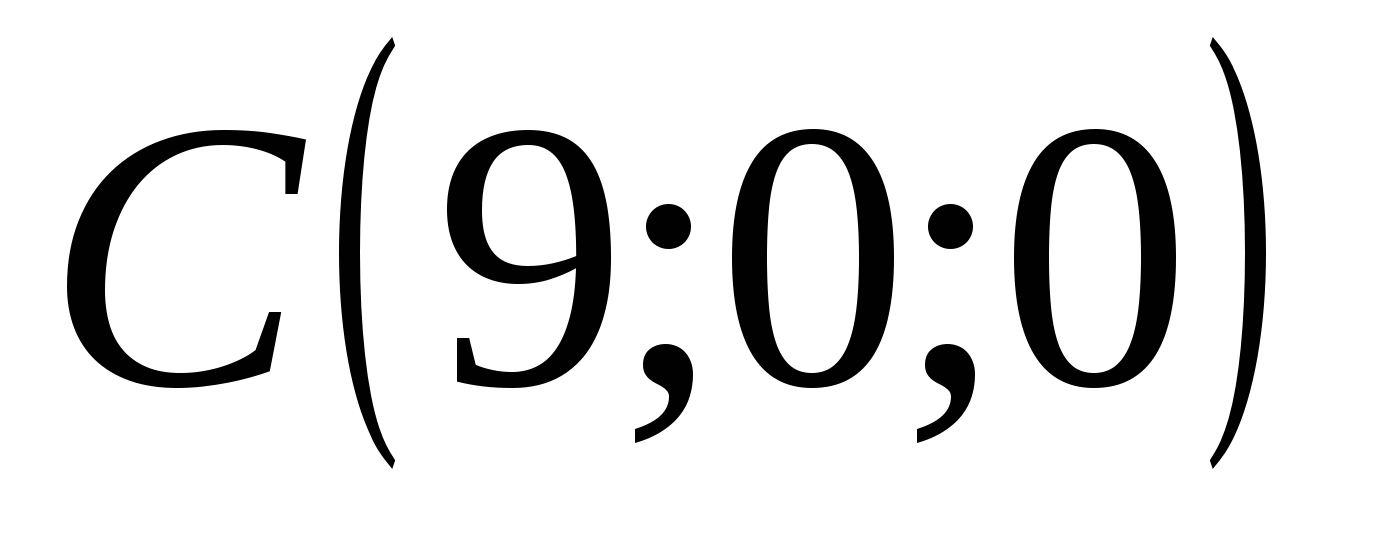 ,
, 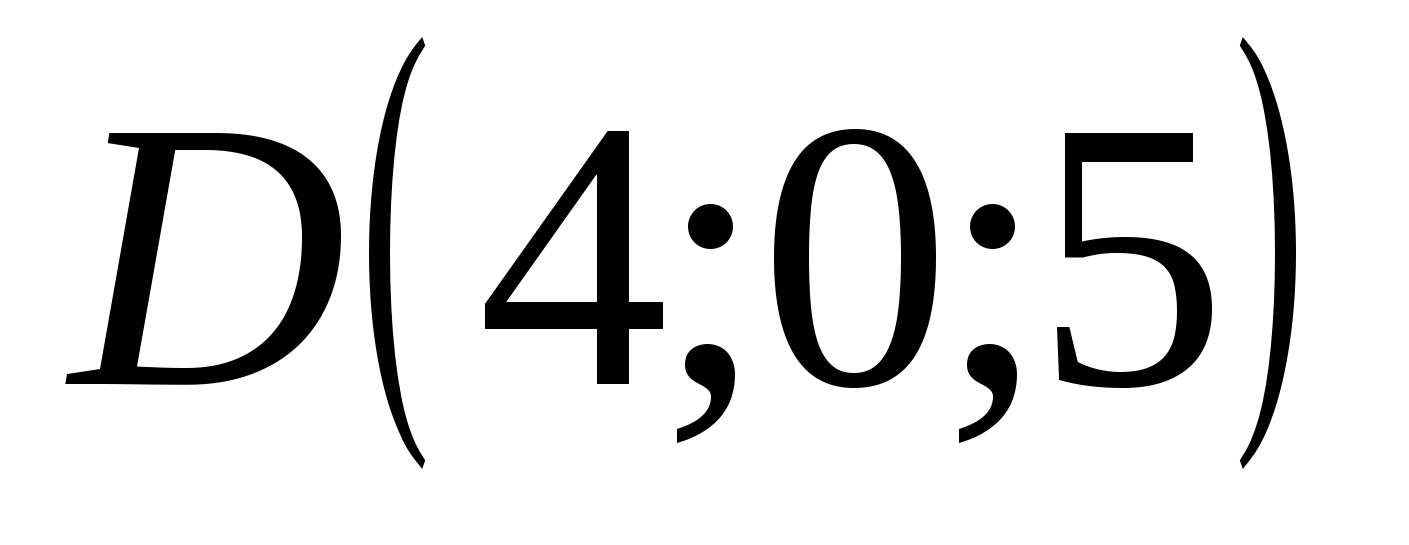 ,
, 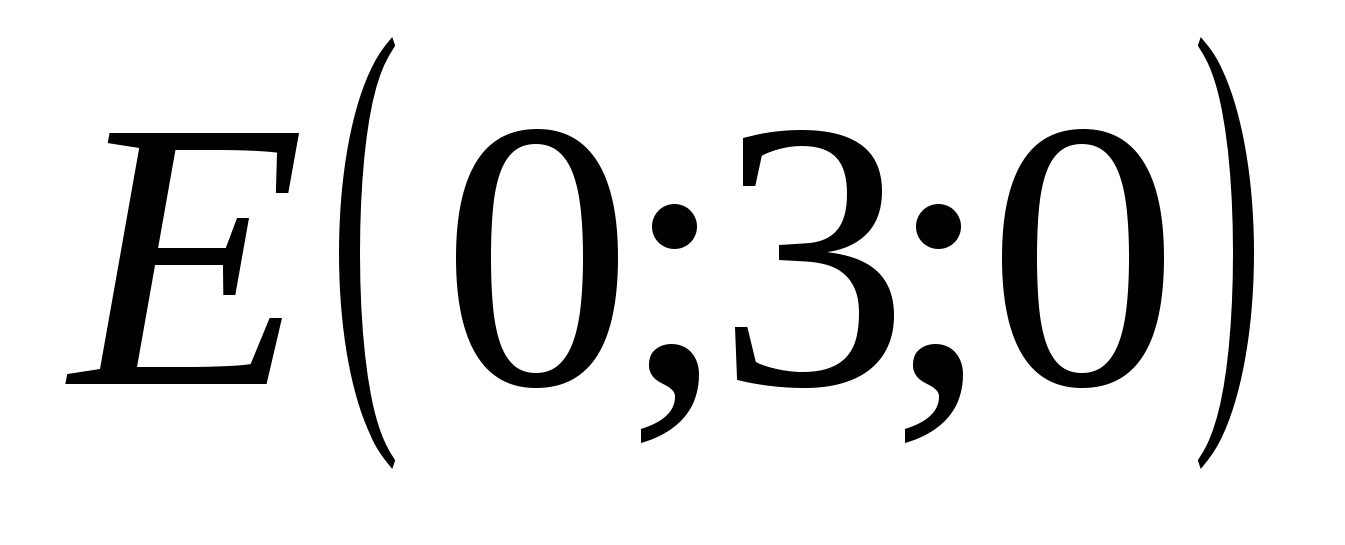 ,
, 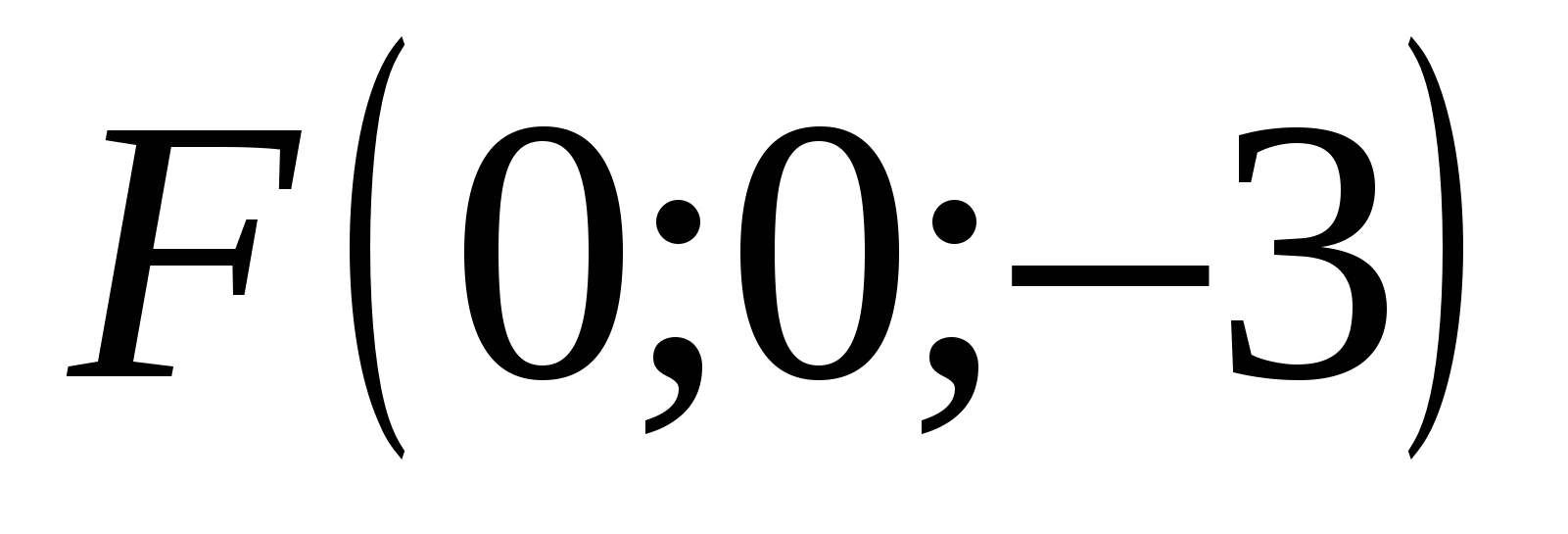 .
.
I verdensrommet, bortsett fra koordinatakser, er det praktisk å også vurdere koordinatplan, dvs. fly som passerer gjennom to akser. Det er tre slike fly:
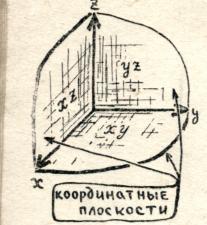
Fly ![]() (passer gjennom aksene
(passer gjennom aksene  Og
Og 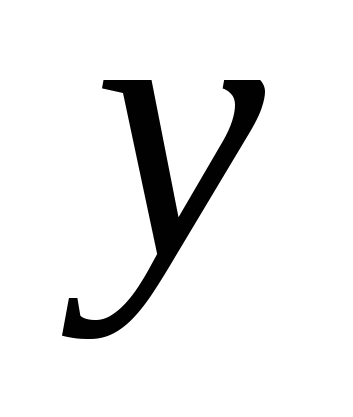 ) - et sett med punkter i skjemaet
) - et sett med punkter i skjemaet  , Hvor
, Hvor  Og
Og 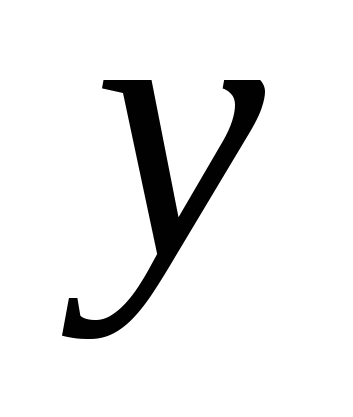 - eventuelle tall;
- eventuelle tall;
Fly 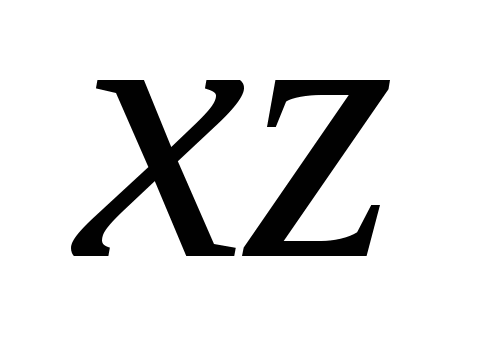 (passer gjennom aksene
(passer gjennom aksene  Og
Og  ) - et sett med punkter i skjemaet
) - et sett med punkter i skjemaet 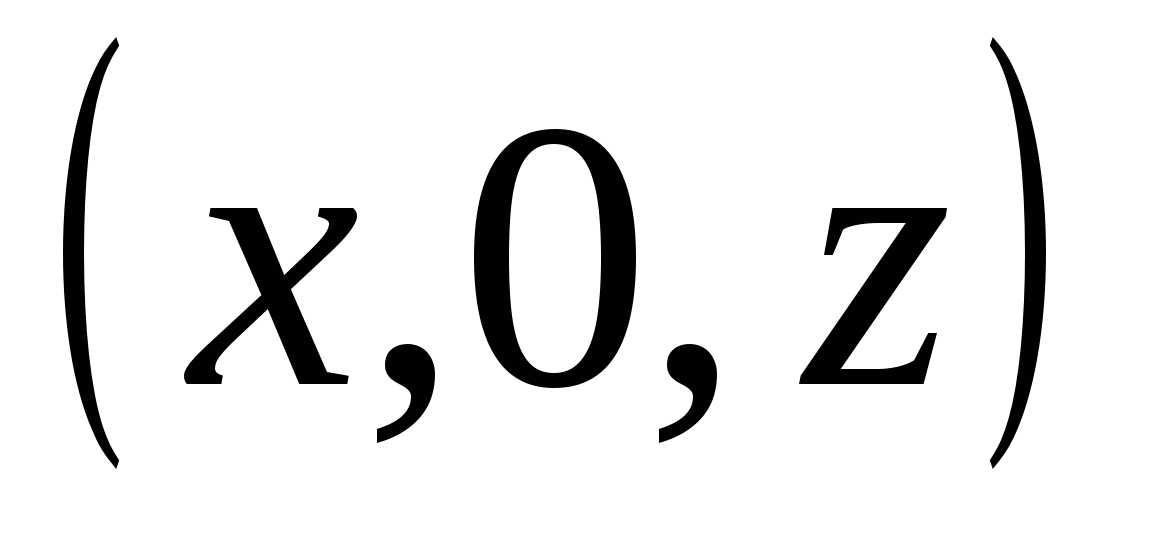 , Hvor
, Hvor  Og
Og  - eventuelle tall;
- eventuelle tall;
Fly  (passer gjennom aksene
(passer gjennom aksene 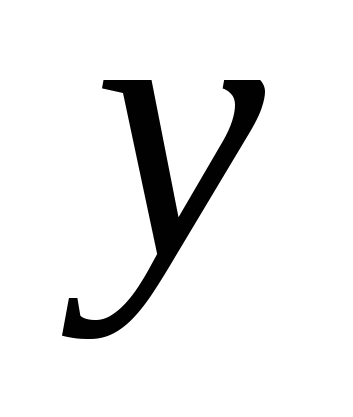 Og
Og  ) - et sett med punkter i skjemaet
) - et sett med punkter i skjemaet 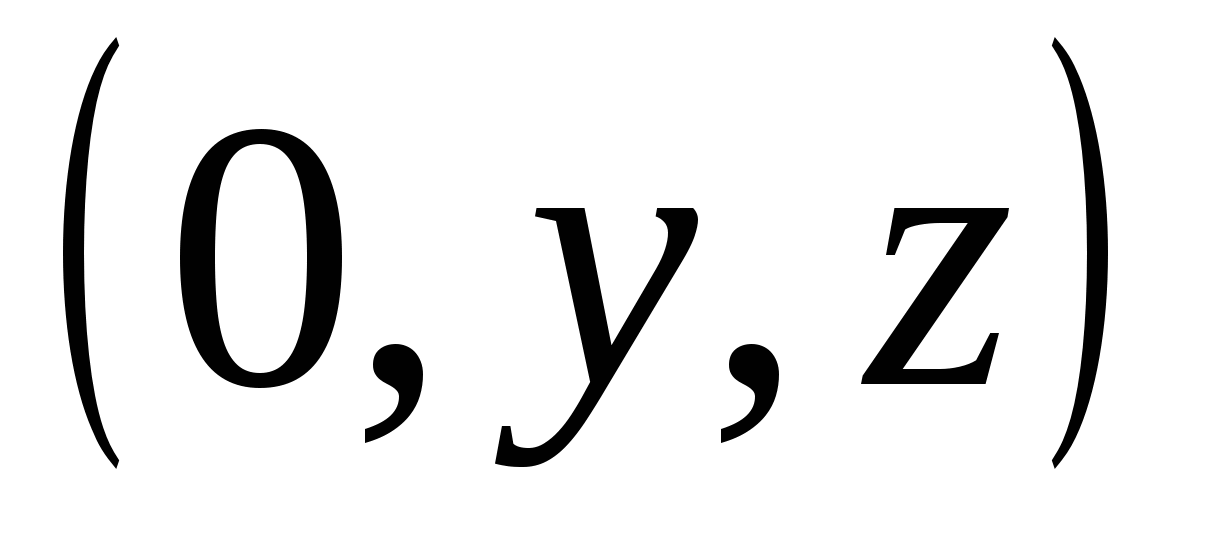 , Hvor
, Hvor 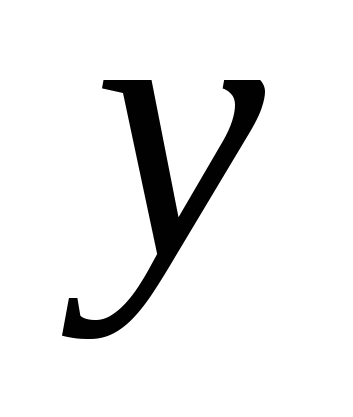 Og
Og  - alle tall.
- alle tall.
For ethvert punkt M i rommet kan du finne tre tall 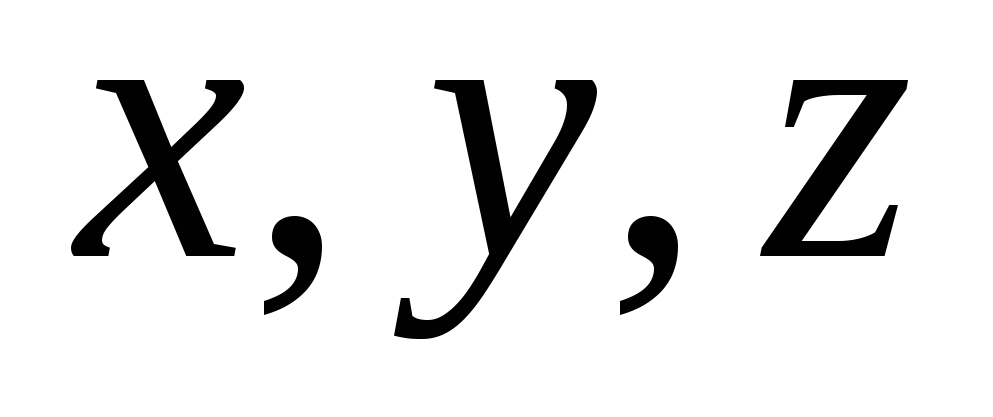 , som vil tjene som dens koordinater.
, som vil tjene som dens koordinater.
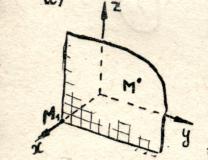 For å finne det første tallet
For å finne det første tallet  , la oss tegne et plan parallelt med punktet M koordinatplan
, la oss tegne et plan parallelt med punktet M koordinatplan  (vinkelrett på aksenx).Skjæringspunktet for dette planet med aksen
(vinkelrett på aksenx).Skjæringspunktet for dette planet med aksen  (punkt M 1
) har en koordinat på denne aksen
(punkt M 1
) har en koordinat på denne aksen  .Dette er nummeret
.Dette er nummeret  - Koordinaten til punkt M 1
på aksen
- Koordinaten til punkt M 1
på aksen  - kaltabscisse poeng M.
- kaltabscisse poeng M.
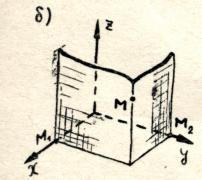 For å finne den andre koordinaten, tegn et plan gjennom punktet M parallelt med flyet
For å finne den andre koordinaten, tegn et plan gjennom punktet M parallelt med flyet 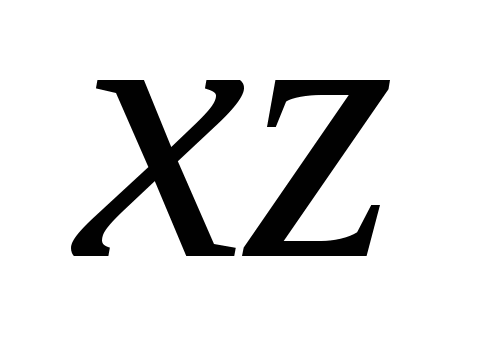 (vinkelrett på akseny), funnet på aksen y punkt M 2. Antall y– koordinaten til punkt M 2 per akse y- kalt ordinere poeng M.
(vinkelrett på akseny), funnet på aksen y punkt M 2. Antall y– koordinaten til punkt M 2 per akse y- kalt ordinere poeng M.
 Vi finner den tredje koordinaten til punktet M ved å utføre lignende konstruksjoner, men vinkelrett på z-aksen. La oss kalle det resulterende nummeret z søknad poeng M.
Vi finner den tredje koordinaten til punktet M ved å utføre lignende konstruksjoner, men vinkelrett på z-aksen. La oss kalle det resulterende nummeret z søknad poeng M.
3. Definere figurer i rommet.
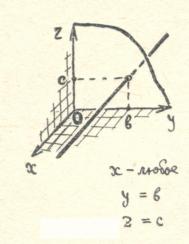
Akkurat som på et fly, gjør koordinater i rommet det mulig å spesifisere ved hjelp av tall og numeriske forhold ikke bare punkter, men også linjer, flater og andre sett med punkter. La oss for eksempel se hvilket sett med punkter som vil bli oppnådd hvis vi spesifiserer bare to koordinater og anser den tredje som vilkårlig.
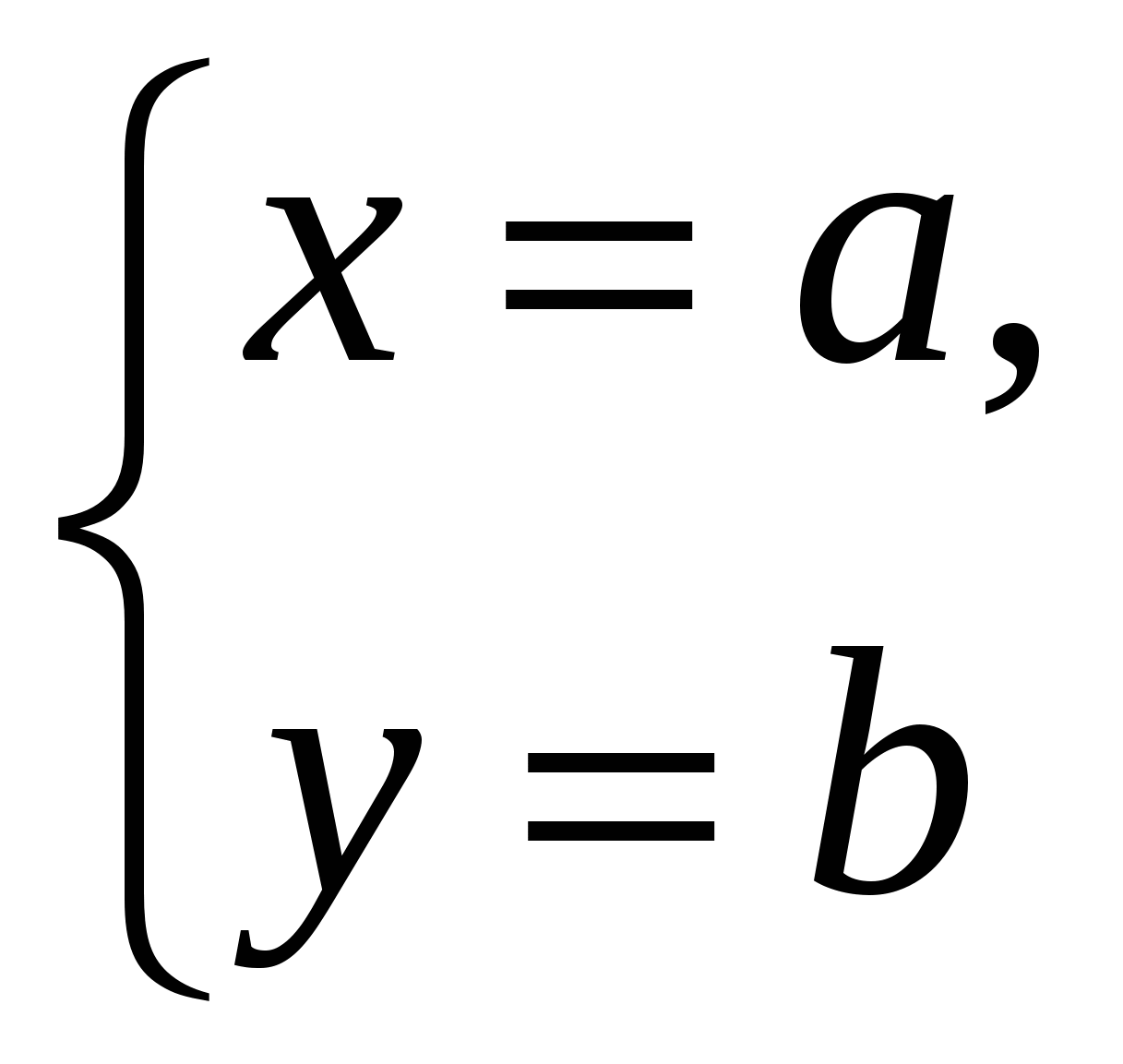
(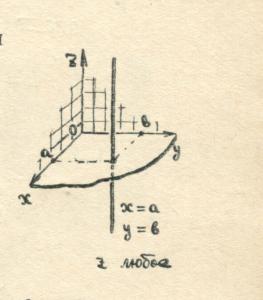 For eksempel,
For eksempel, 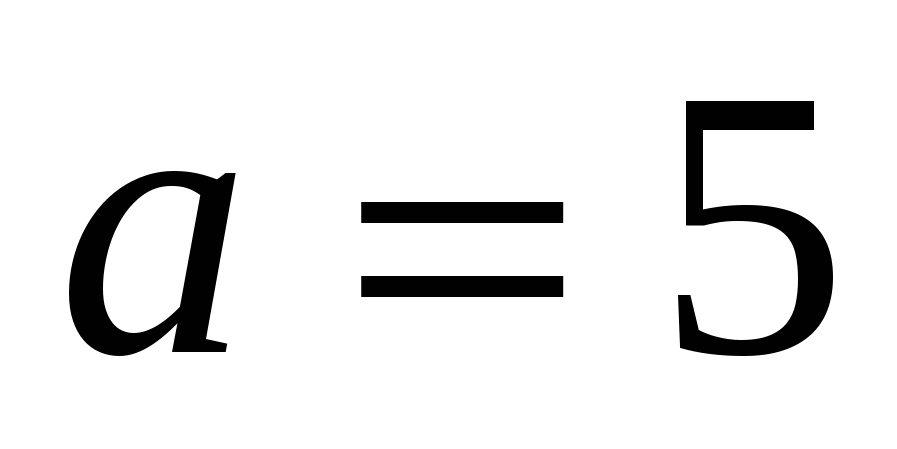
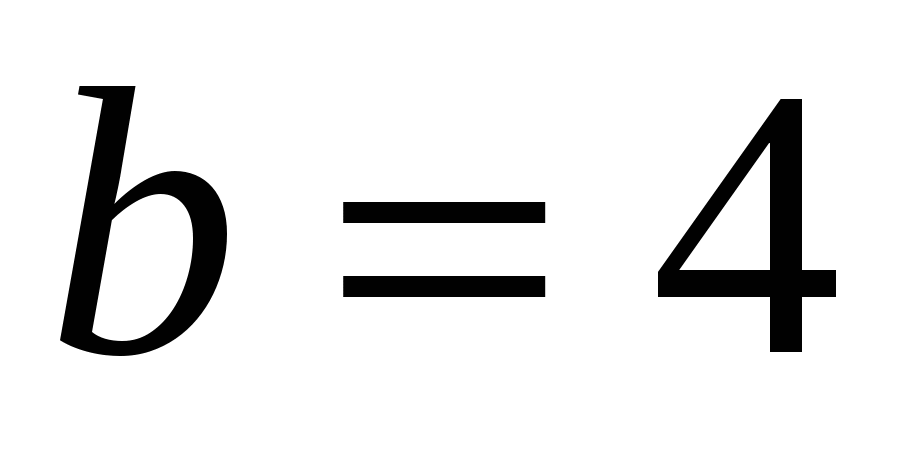 ), definere en rett linje i rommet, parallelt med aksen
), definere en rett linje i rommet, parallelt med aksen  .
.
Alle punkter på en slik linje har samme abscisse og samme ordinat. Koordinere  kan ta hvilken som helst verdi.
kan ta hvilken som helst verdi.


La oss se på noen flere eksempler som viser hvordan du kan sette inn
rom ulike sett ved hjelp av ligninger og andre sammenhenger mellom koordinater.
1). Tenk på ligningen.
Siden avstanden til punktet 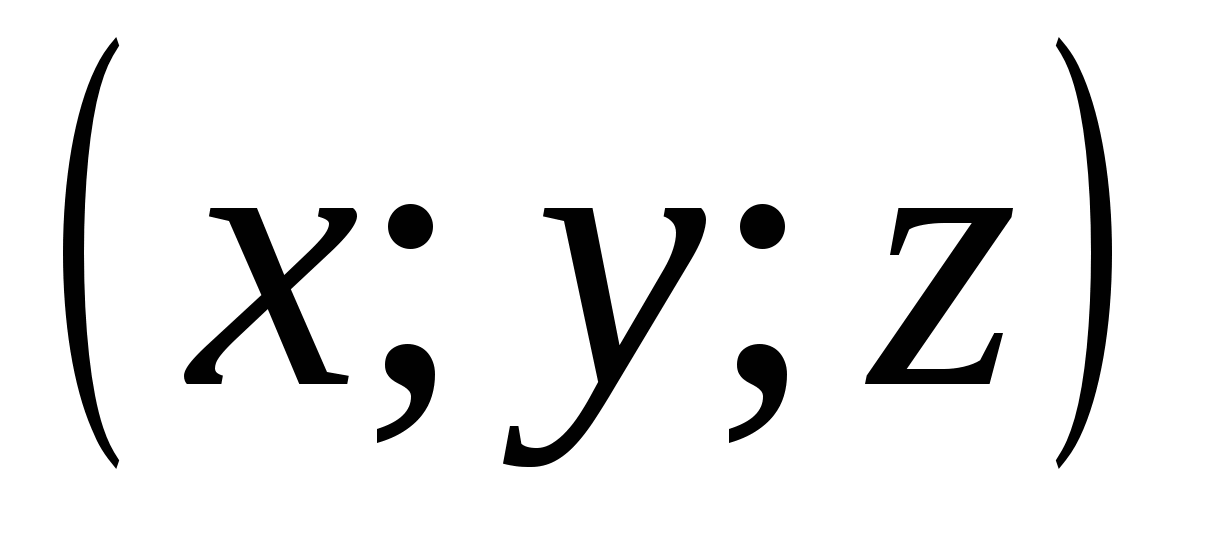 fra opprinnelsen er gitt av uttrykket
fra opprinnelsen er gitt av uttrykket 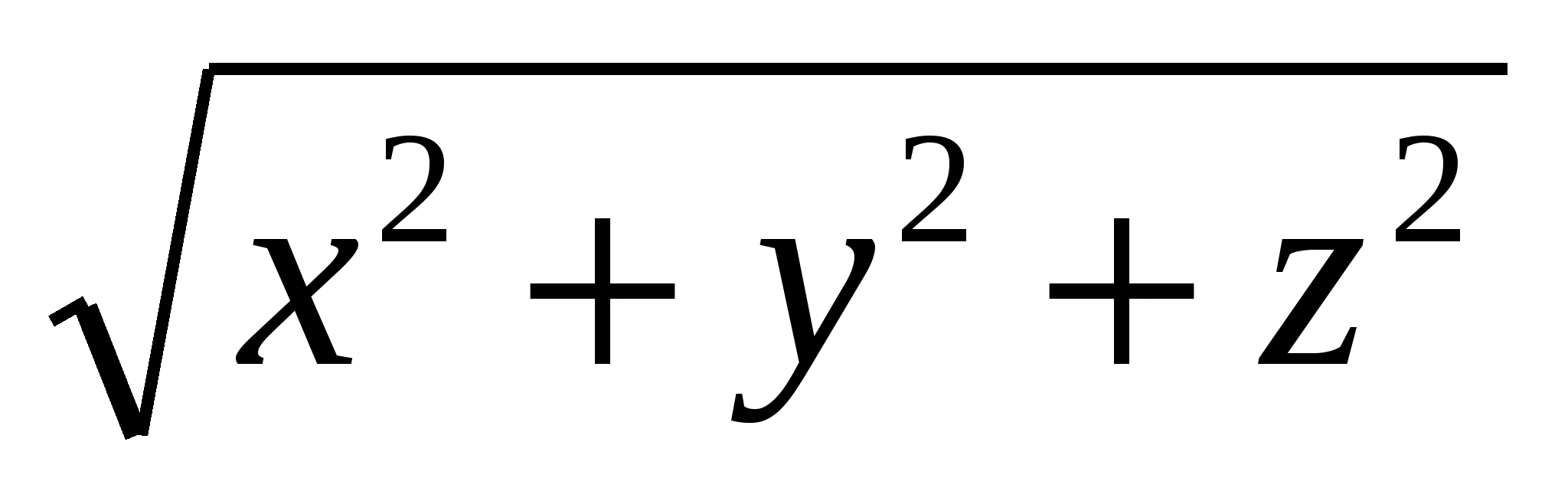 , så er det klart at oversatt til geometrisk språk forholdet
, så er det klart at oversatt til geometrisk språk forholdet 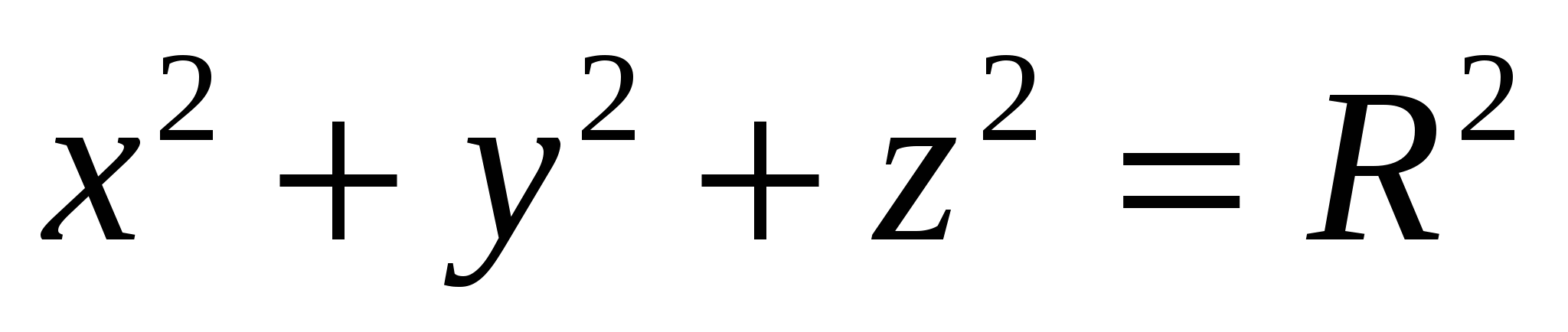 betyr at punktet med koordinater
betyr at punktet med koordinater 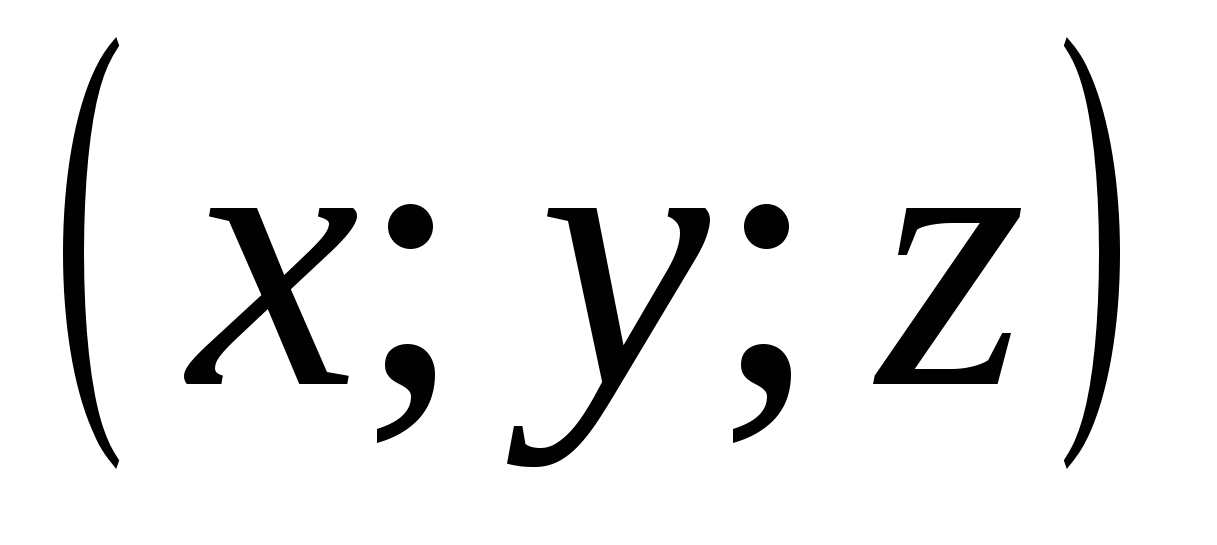 , er på avstandR
fra opprinnelsen. Dette betyr at settet av alle punkter som relasjonen gjelder
, er på avstandR
fra opprinnelsen. Dette betyr at settet av alle punkter som relasjonen gjelder 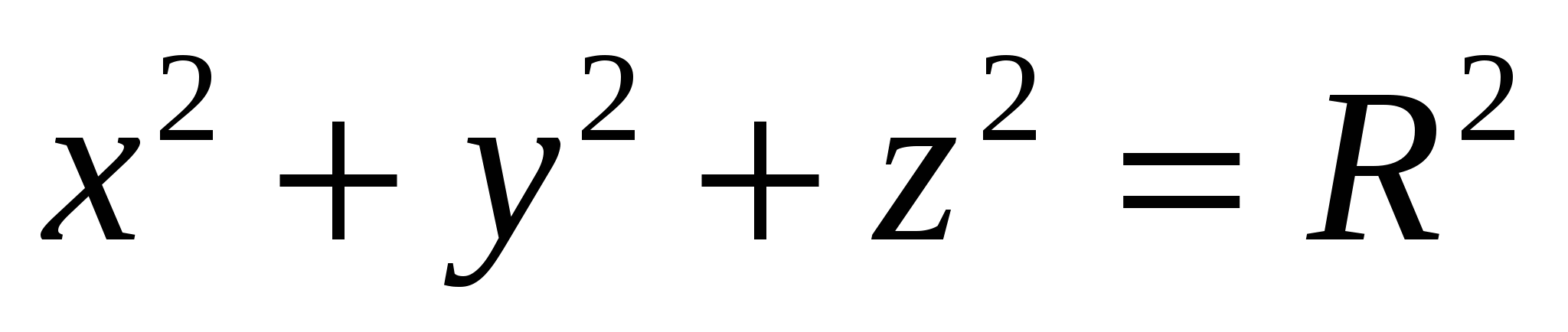 , er overflaten til en kule - en kule med sentrum ved origo og radiusR
.
, er overflaten til en kule - en kule med sentrum ved origo og radiusR
.
2). La oss vurdere hvor punktene er plassert hvis koordinater tilfredsstiller forholdet  .
.
Siden dette forholdet betyr at avstanden til punktet 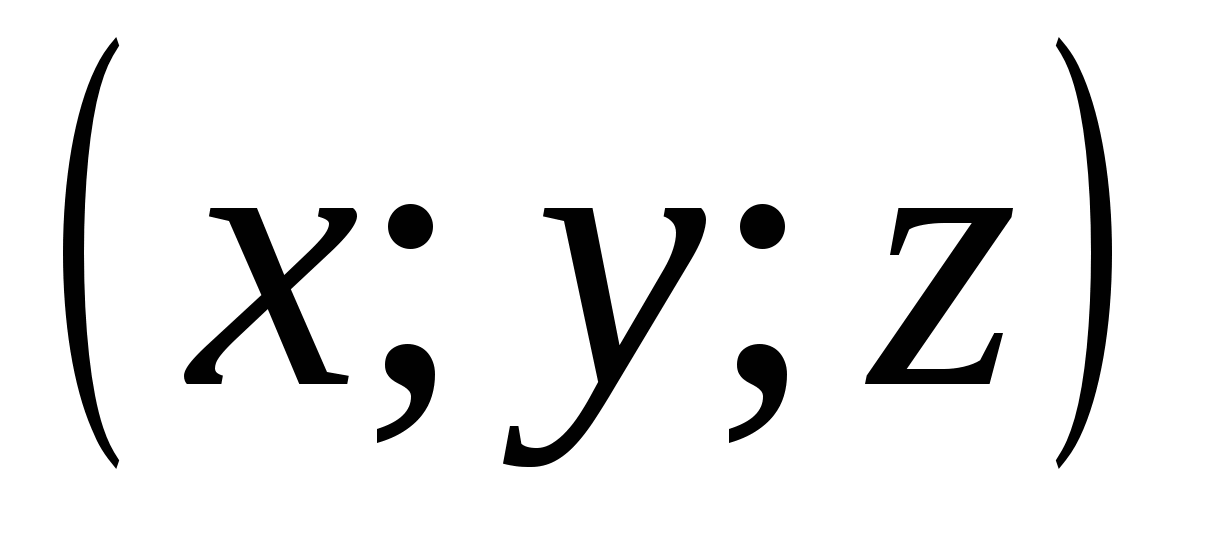 fra opprinnelsen til koordinatene er mindre enn én, så er det nødvendige settet settet med punkter som ligger inne i en ball med et senter ved opprinnelsen til koordinatene og en radius lik én.
fra opprinnelsen til koordinatene er mindre enn én, så er det nødvendige settet settet med punkter som ligger inne i en ball med et senter ved opprinnelsen til koordinatene og en radius lik én.
Kapittel 2
1. Dekomponering av en vektor til koordinatvektorer. Vektorkoordinater.
Grunnlaget for et rom er en hvilken som helst ordnet trippel av ikke-koplanare vektorer 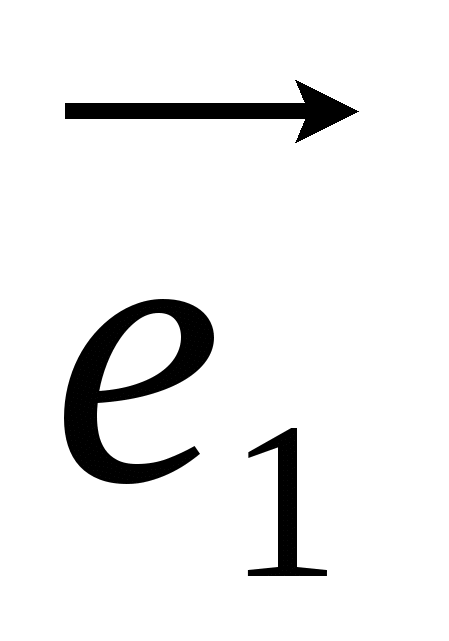 ,
, 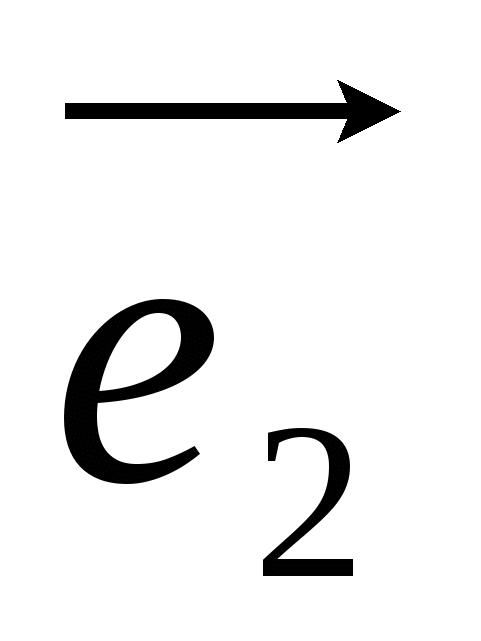 ,
, 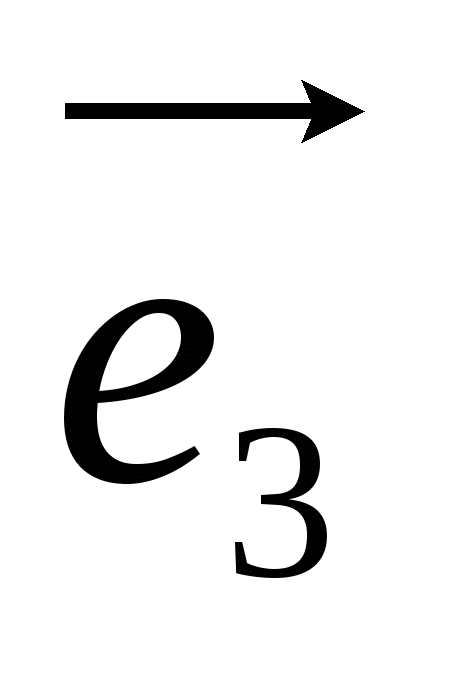 , angitt med symbolet
, angitt med symbolet 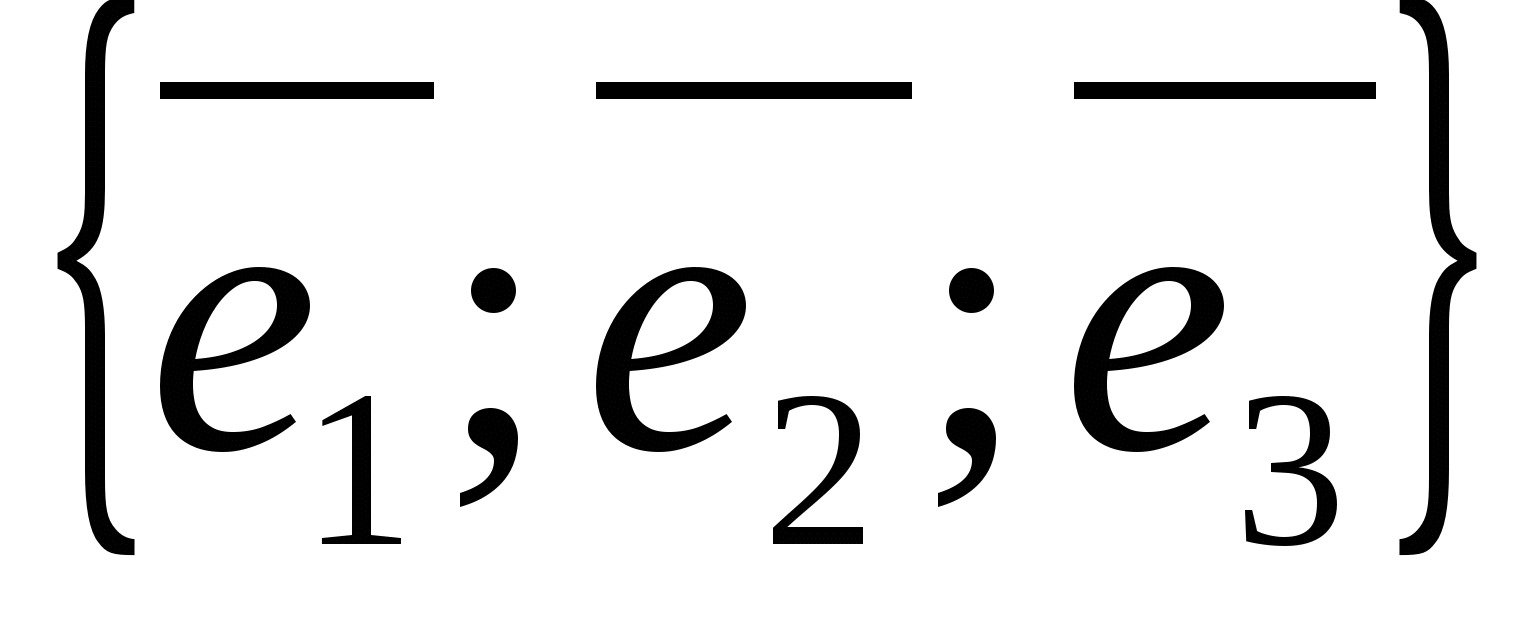 .
.
Et spesielt tilfelle er den rektangulære ortonormale basis  , Hvor
, Hvor 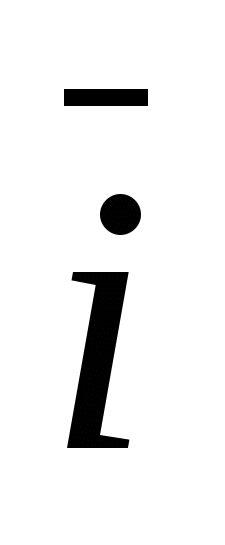 - enhetsvektor for x-aksen, gjennom -
- enhetsvektor for x-aksen, gjennom -  enhetsvektor for ordinataksen og gjennom
enhetsvektor for ordinataksen og gjennom 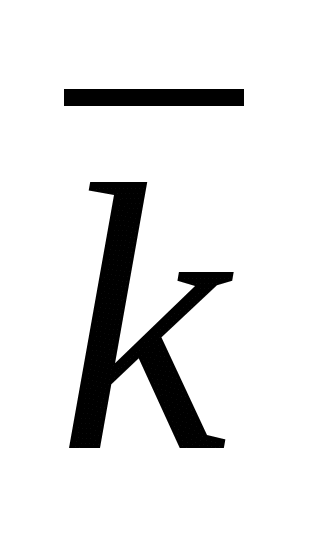 -enhetsvektor akseapplikasjon, dvs.
-enhetsvektor akseapplikasjon, dvs. 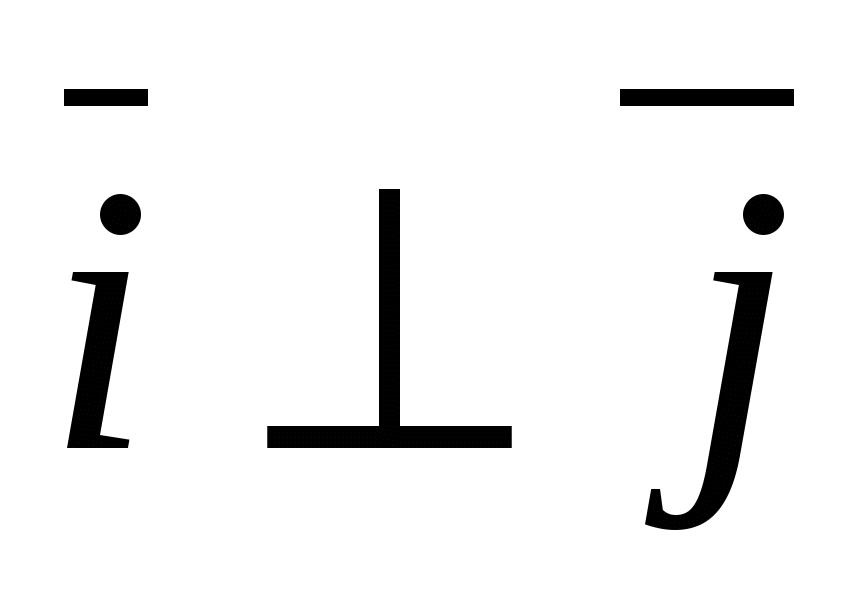 ,
, 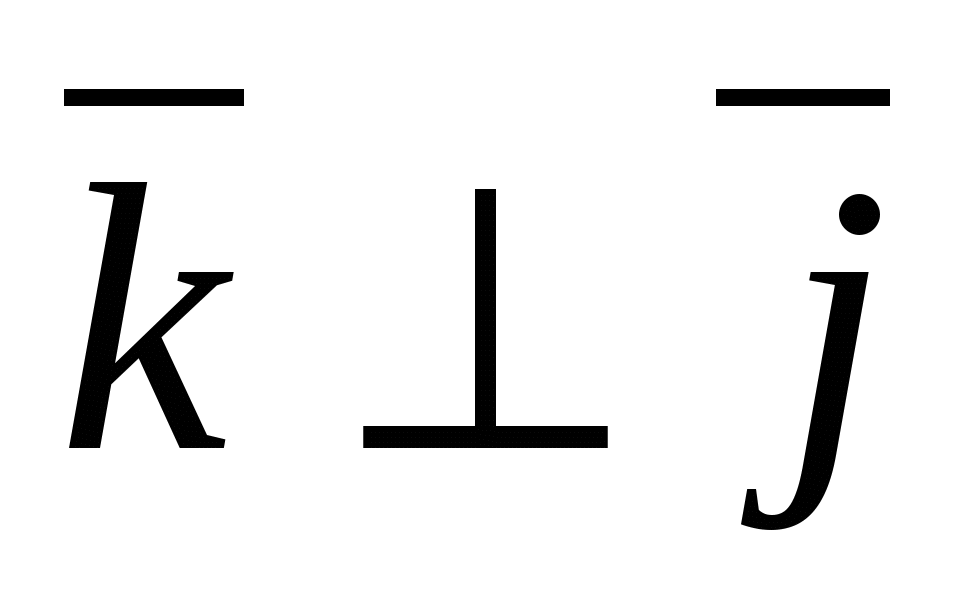 ,
, 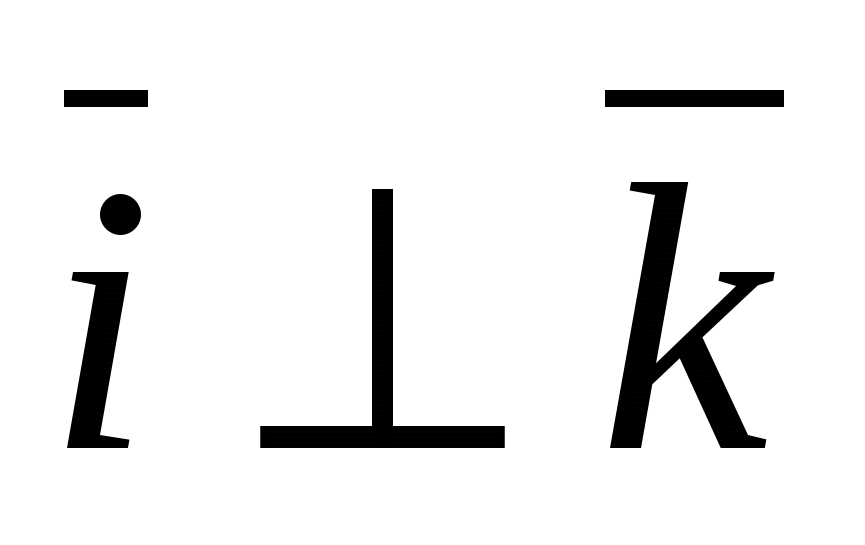 ,
,  .
.
Dette grunnlaget 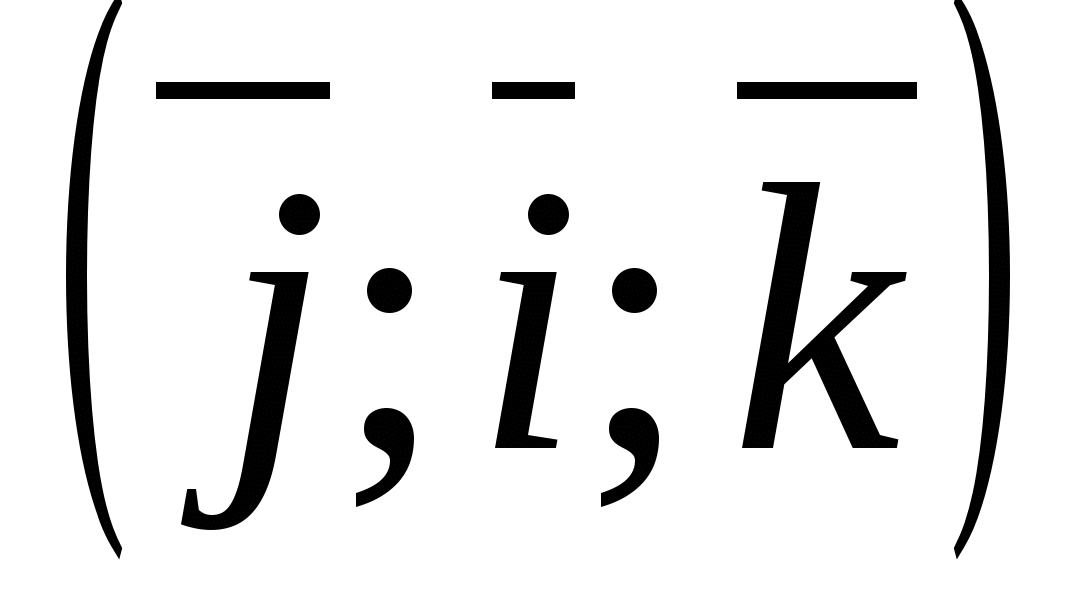 og begynnelsen av nedtellingen OM definere et rektangulært kartesisk koordinatsystem
og begynnelsen av nedtellingen OM definere et rektangulært kartesisk koordinatsystem  i verdensrommet.
i verdensrommet.
Teorem 1
Enhver romvektor
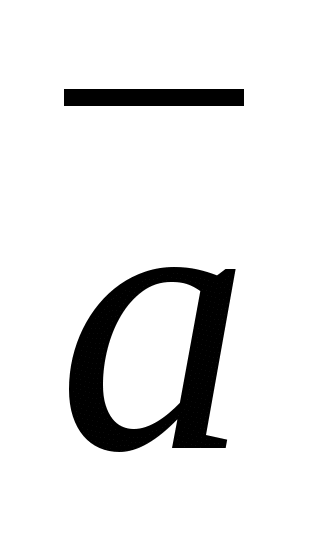 kan utvides til koordinatvektorer, dvs. tilstede i form -
kan utvides til koordinatvektorer, dvs. tilstede i form -
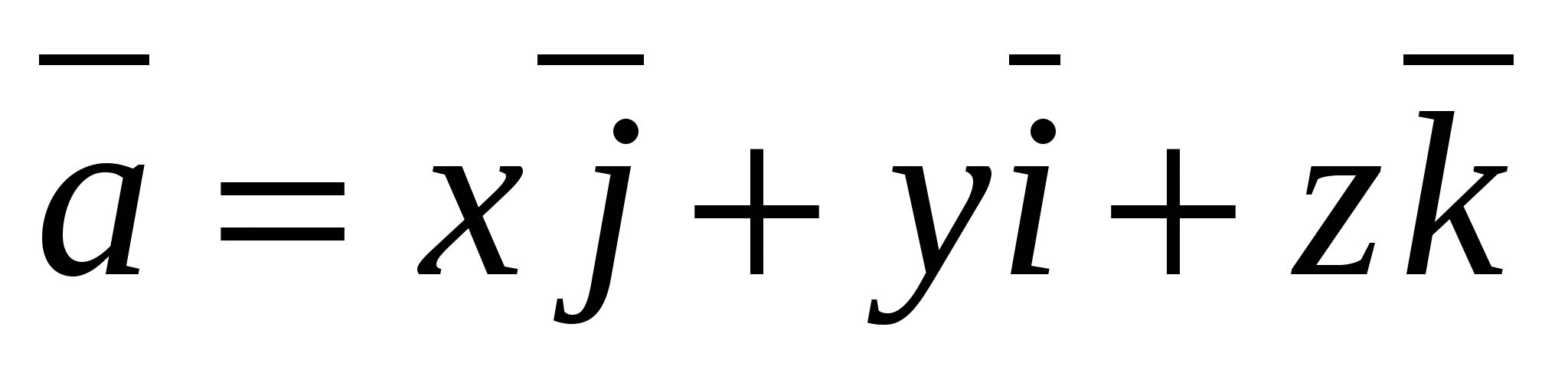 ,
,
og ekspansjonskoeffisientene  er bestemt på en unik måte.
er bestemt på en unik måte.
H 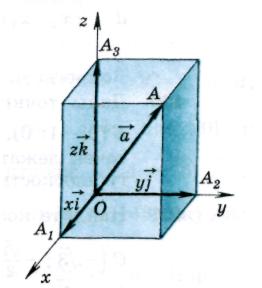 isla
isla  kalles vektorkoordinater
kalles vektorkoordinater 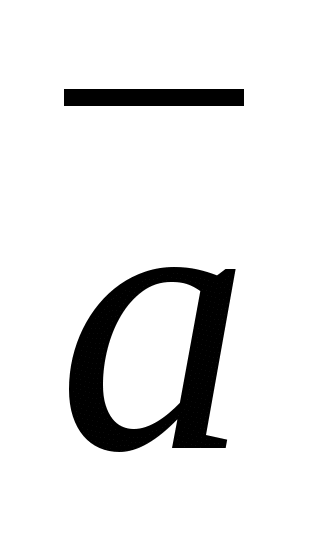 , dvs.
, dvs. 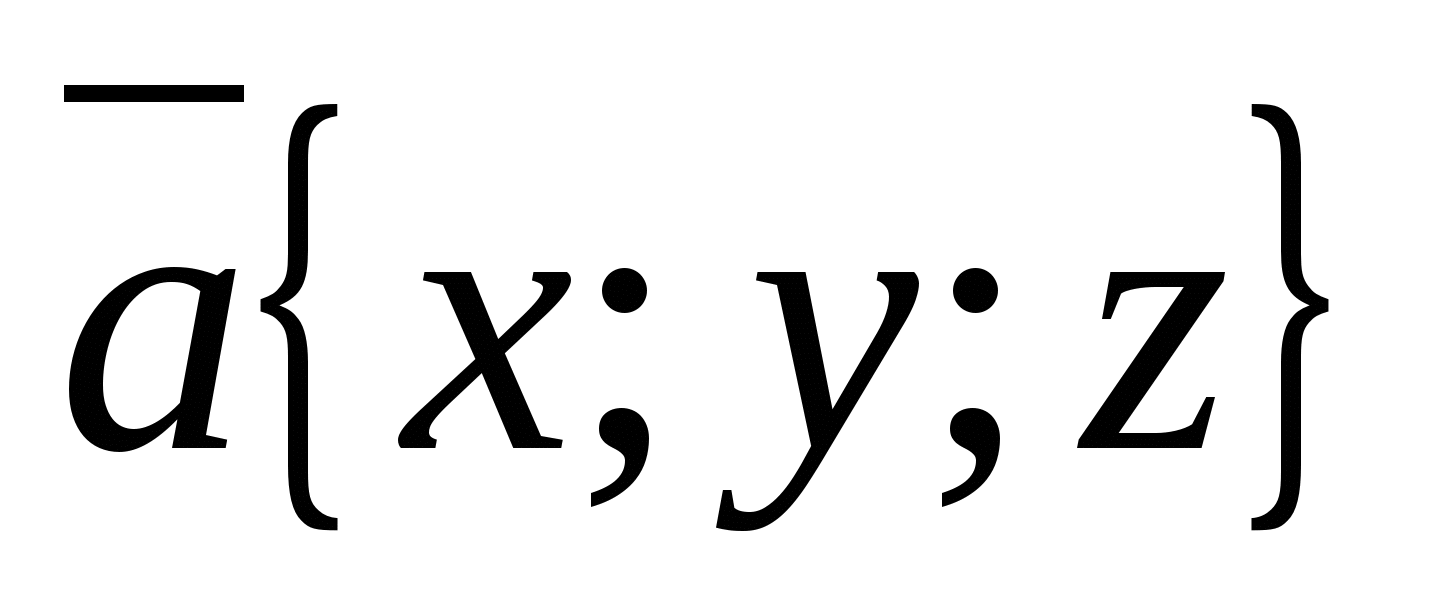 . Siden nullvektoren kan representeres som
. Siden nullvektoren kan representeres som  , da er alle koordinatene til nullvektoren lik null,
, da er alle koordinatene til nullvektoren lik null, 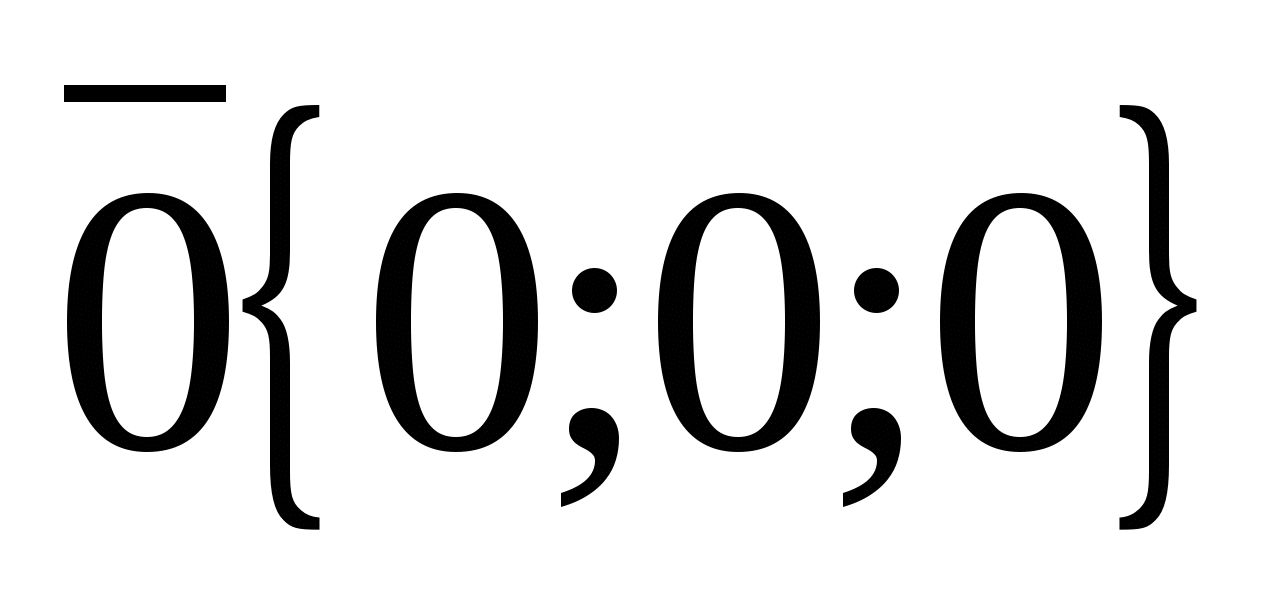 .
.
2. Lineære operasjoner på vektorer i koordinater.
Regel 1.
Koordinater av like
vektorer er henholdsvis like,
de. hvis vektorer 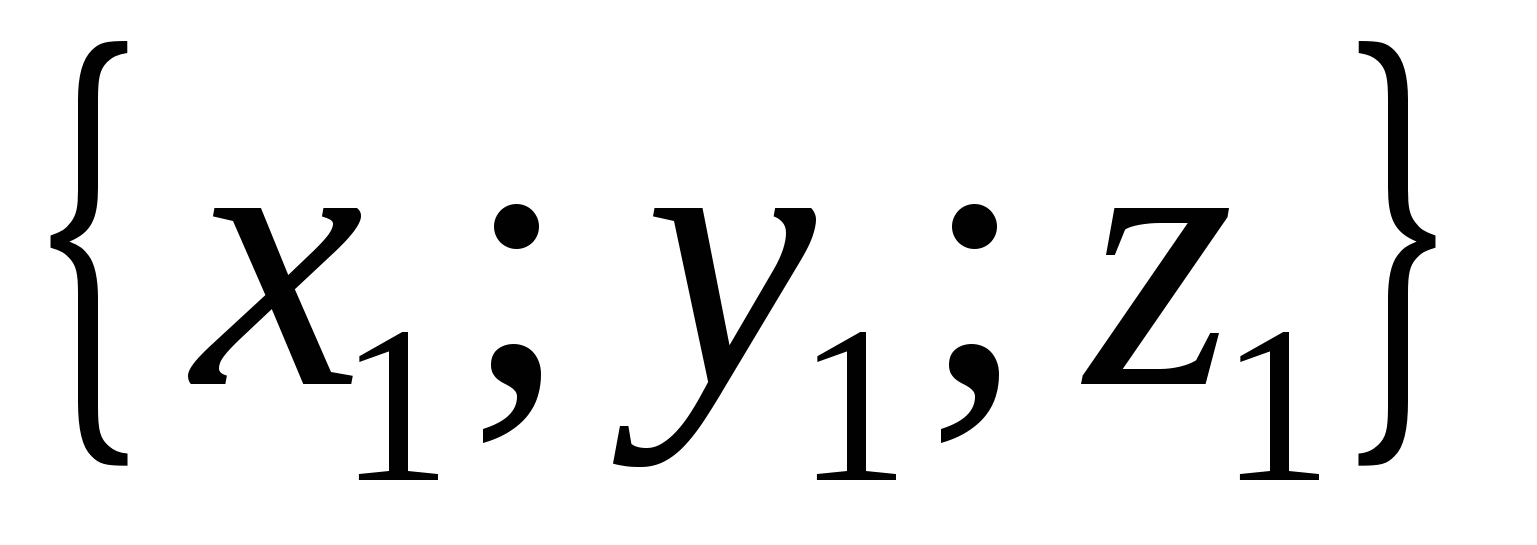 Og
Og 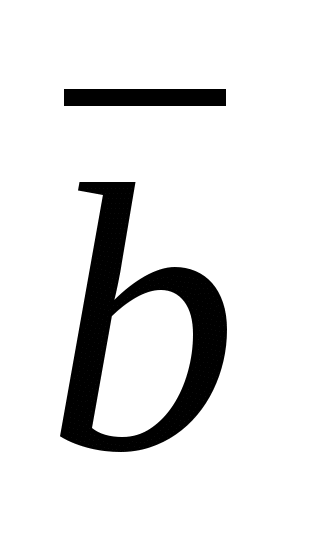
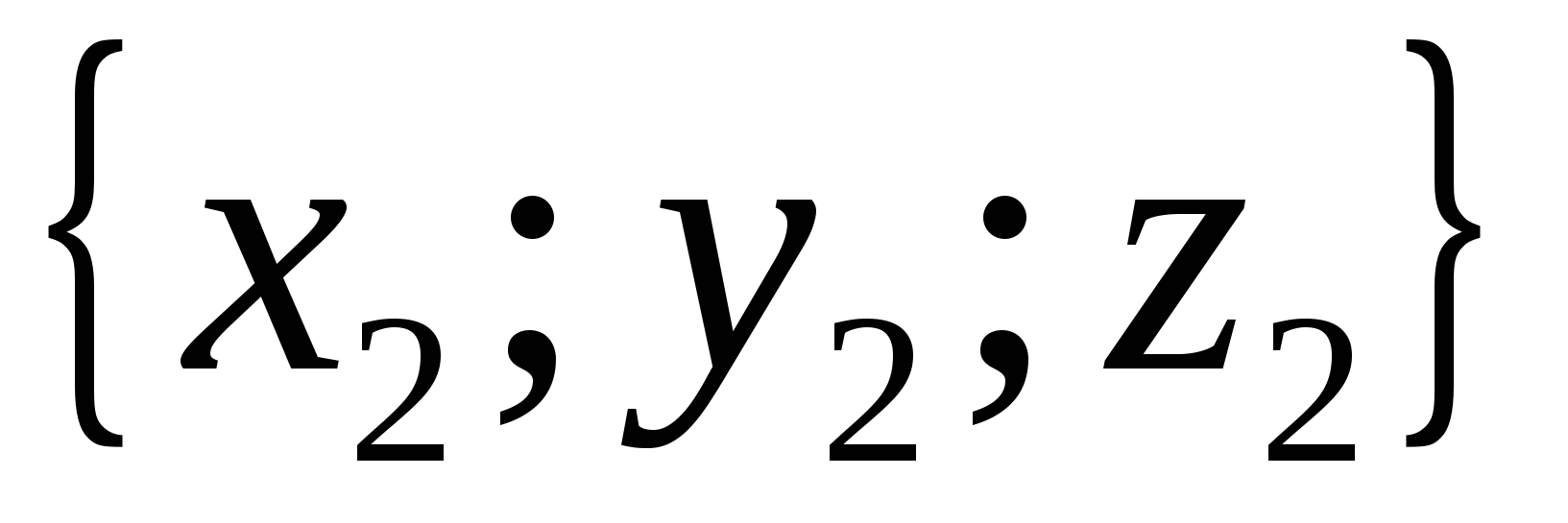 er like, da
er like, da 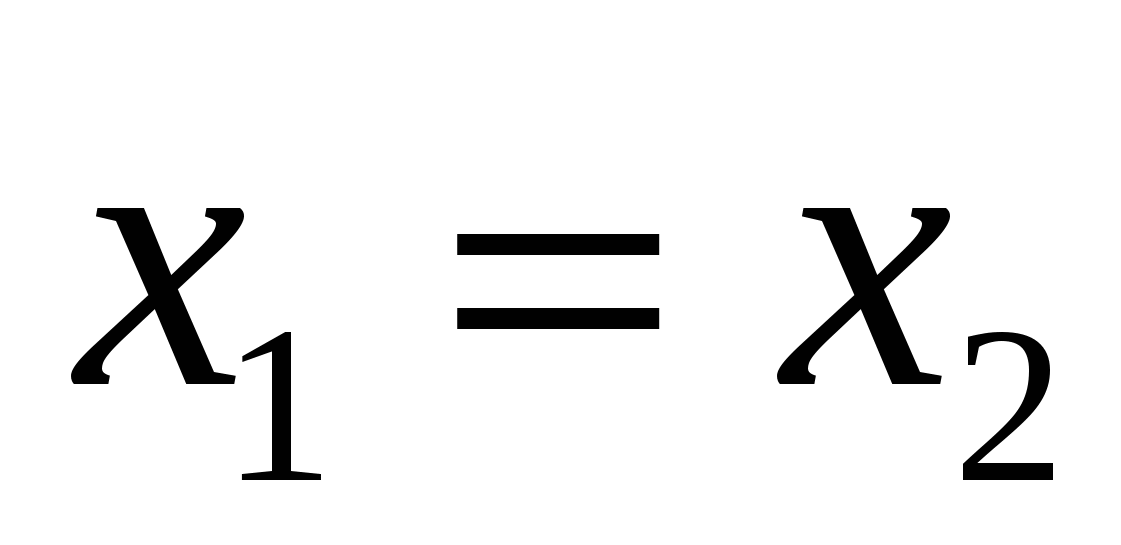 ,
,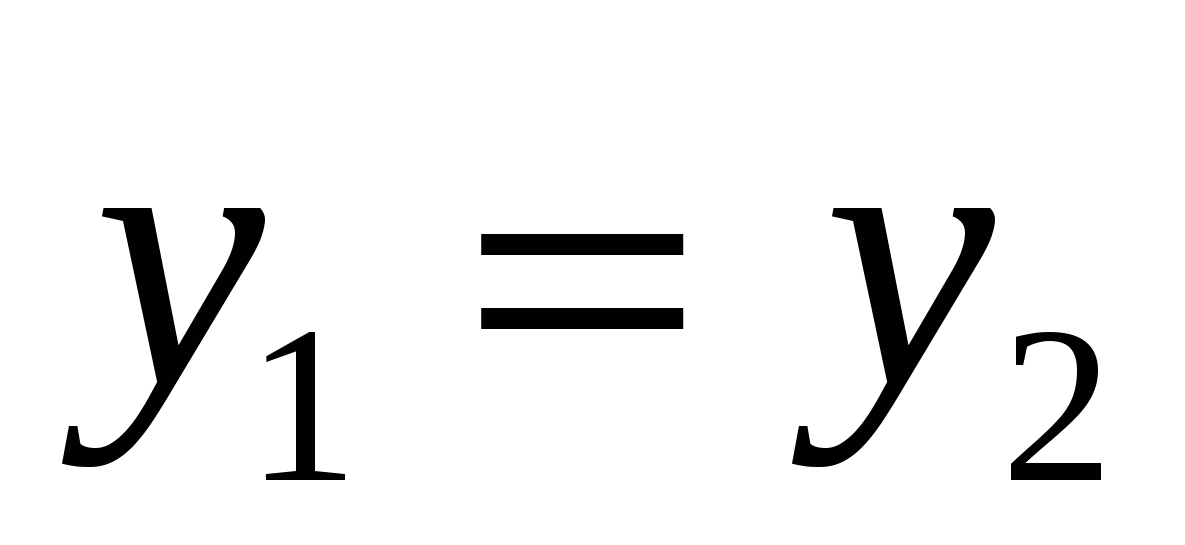 Og
Og 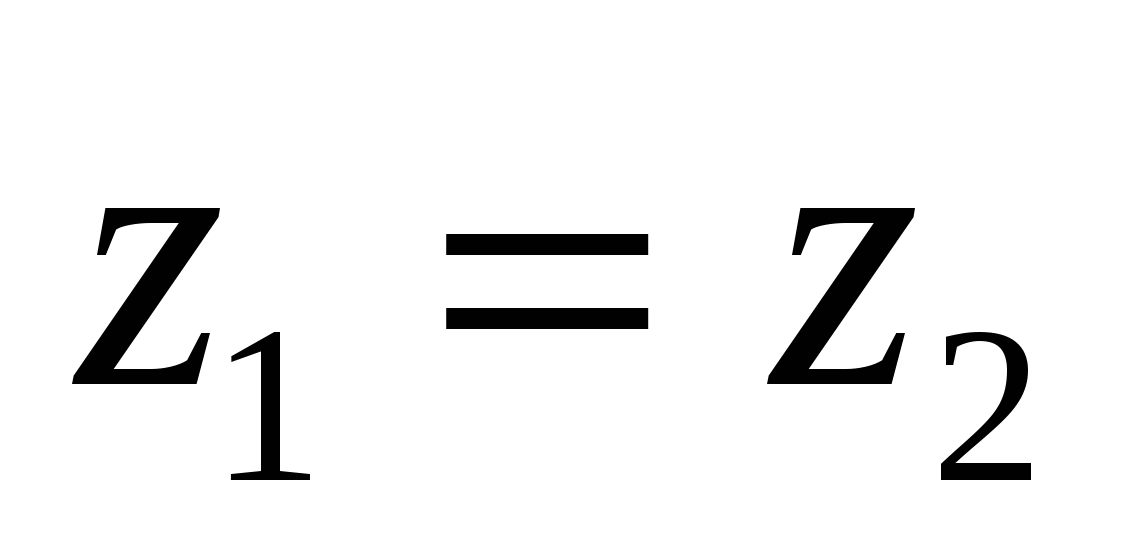 .
.
Regel 2.
Hver koordinat av summen av to eller flere vektorer er lik summen av de tilsvarende koordinatene til disse vektorene.
Med andre ord, hvis 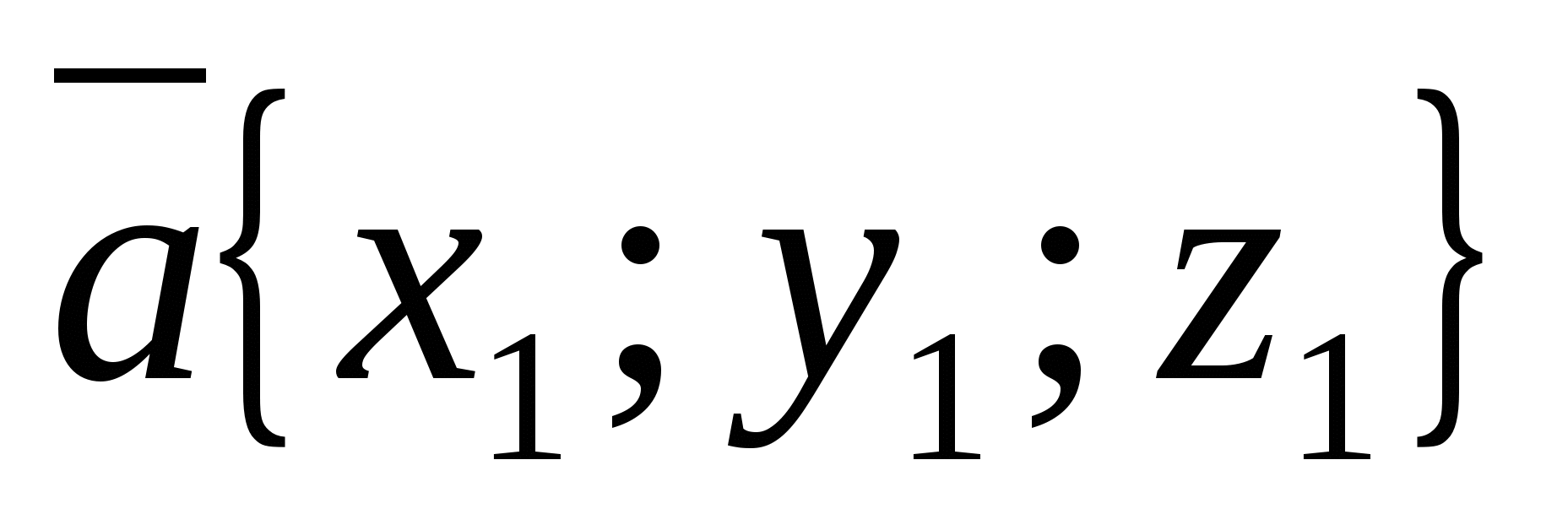 Og
Og 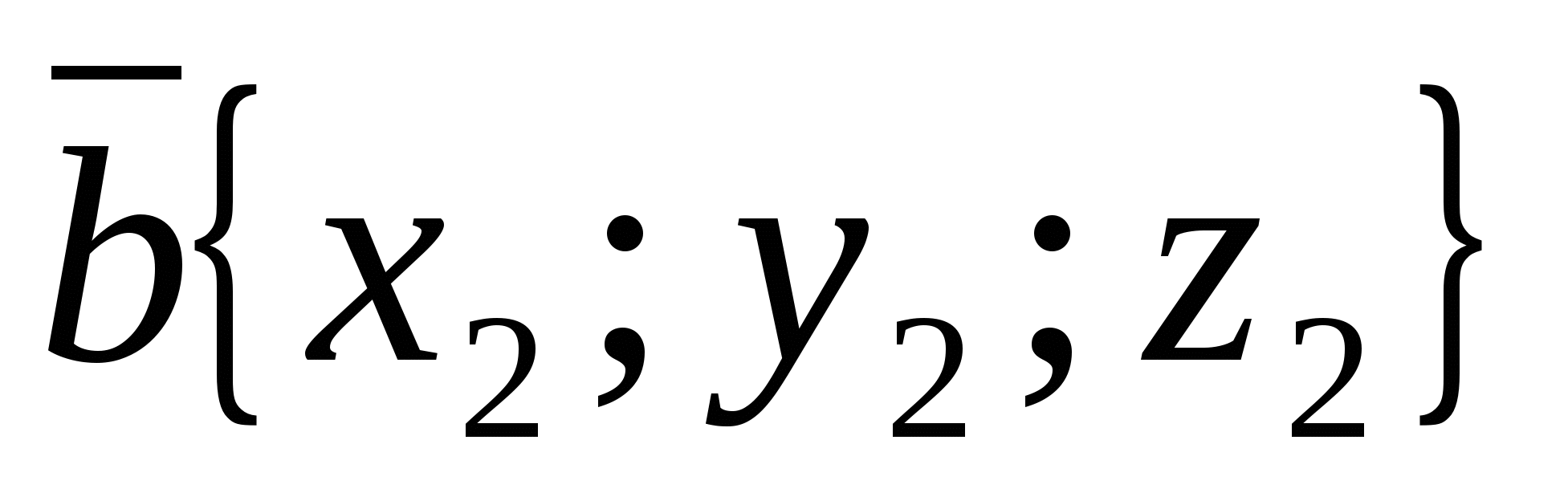 -gitte vektorer, deretter vektor
-gitte vektorer, deretter vektor 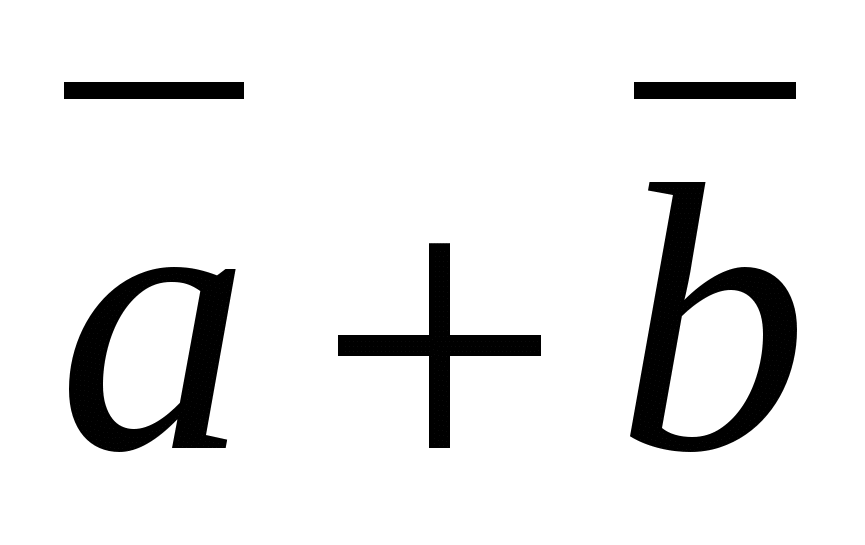 har koordinater.
har koordinater.
Regel 3.
Hver koordinat av forskjellen mellom to vektorer er lik forskjellen til de tilsvarende koordinatene til disse vektorene.
Med andre ord, hvis 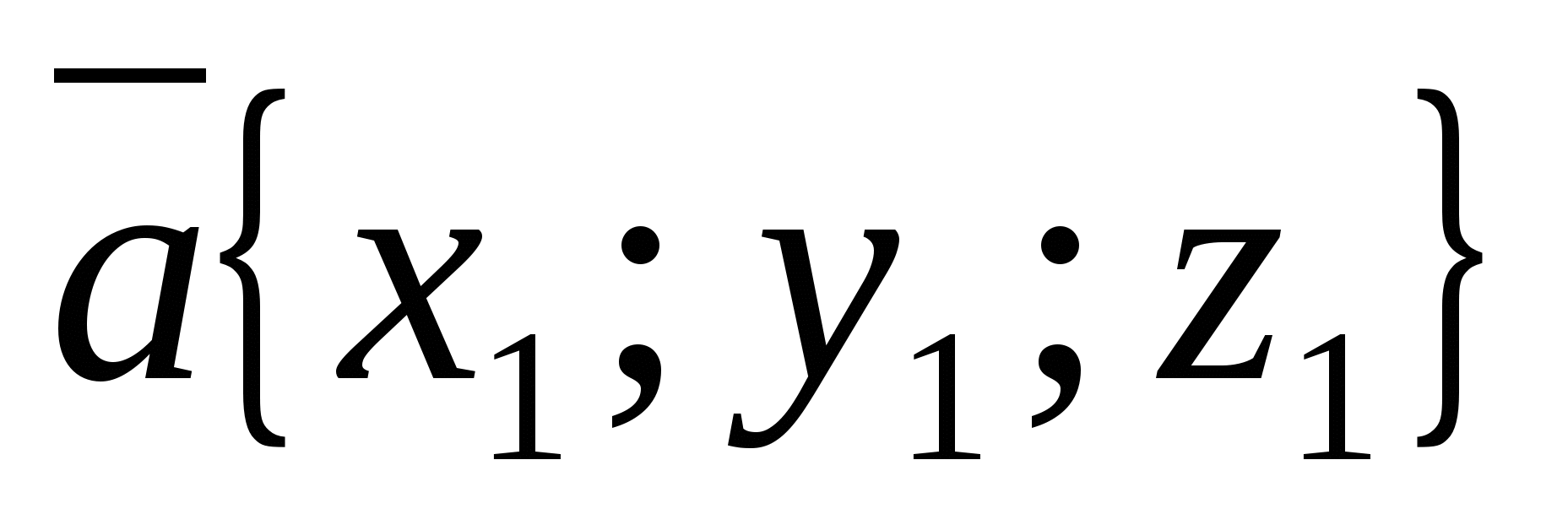 Og
Og 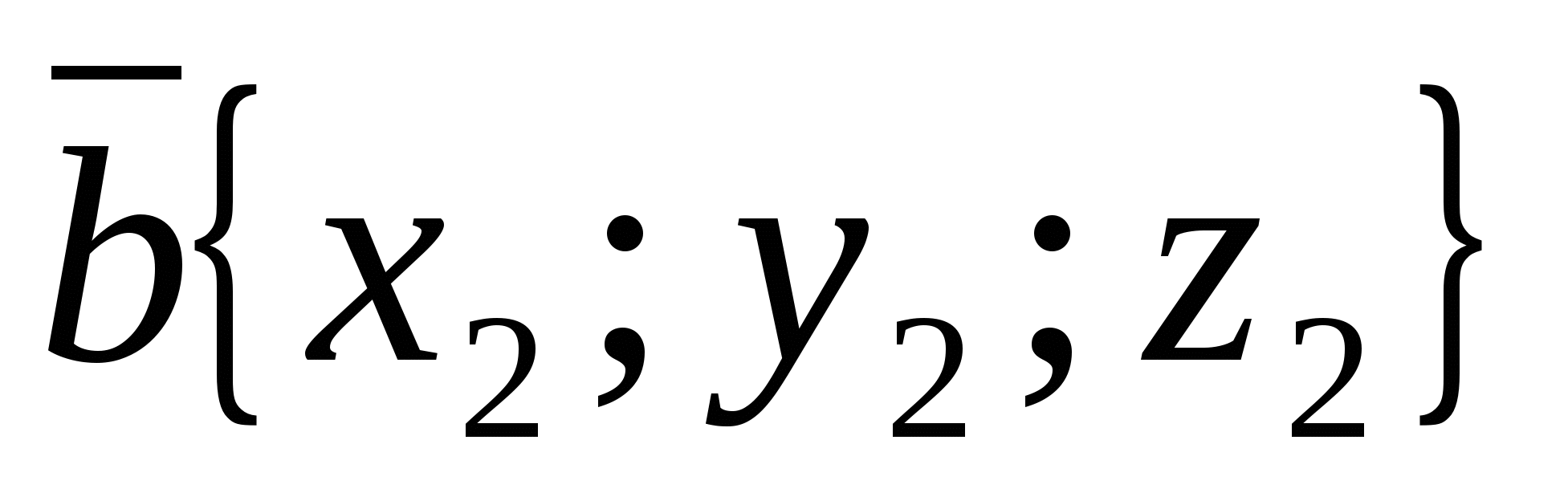 -gitte vektorer, deretter vektor
-gitte vektorer, deretter vektor 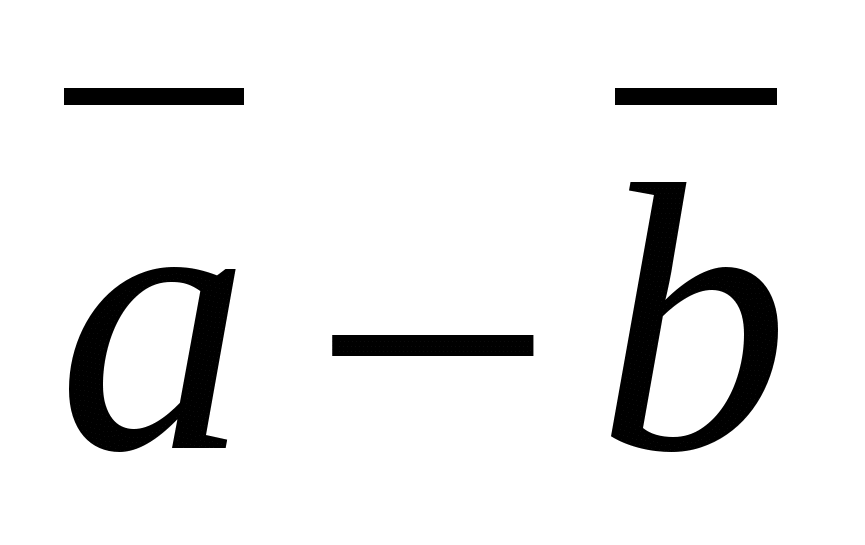 har koordinater
har koordinater
Regel 4.
Hver koordinat av produktet av en vektor og et tall er lik produktet av de tilsvarende koordinatene til vektoren og dette tallet.
Med andre ord, hvis 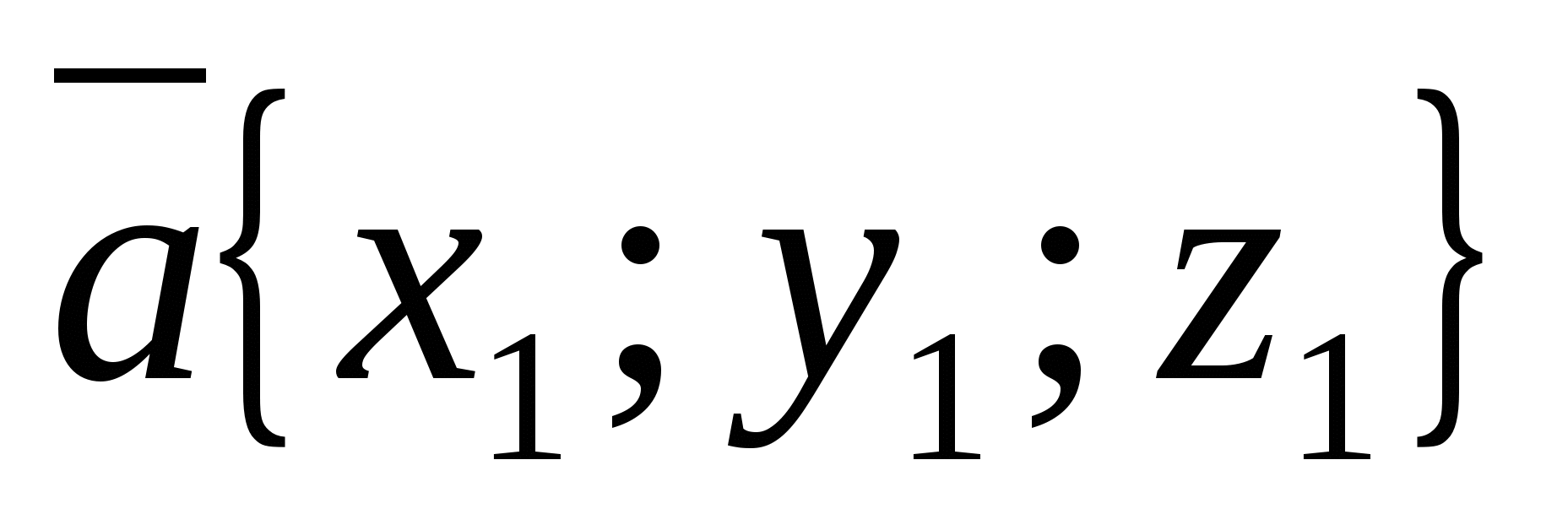 -gitt vektor,
-gitt vektor, ![]() -gitt nummer, deretter vektoren
-gitt nummer, deretter vektoren 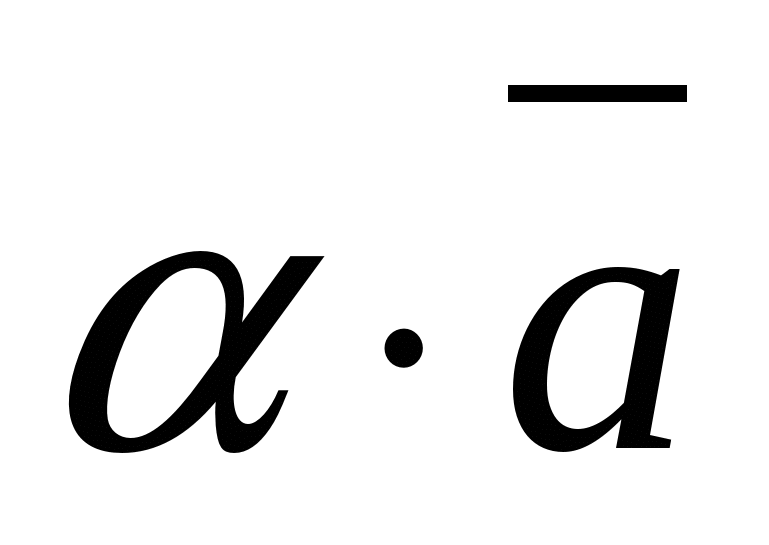 har koordinater.
har koordinater. 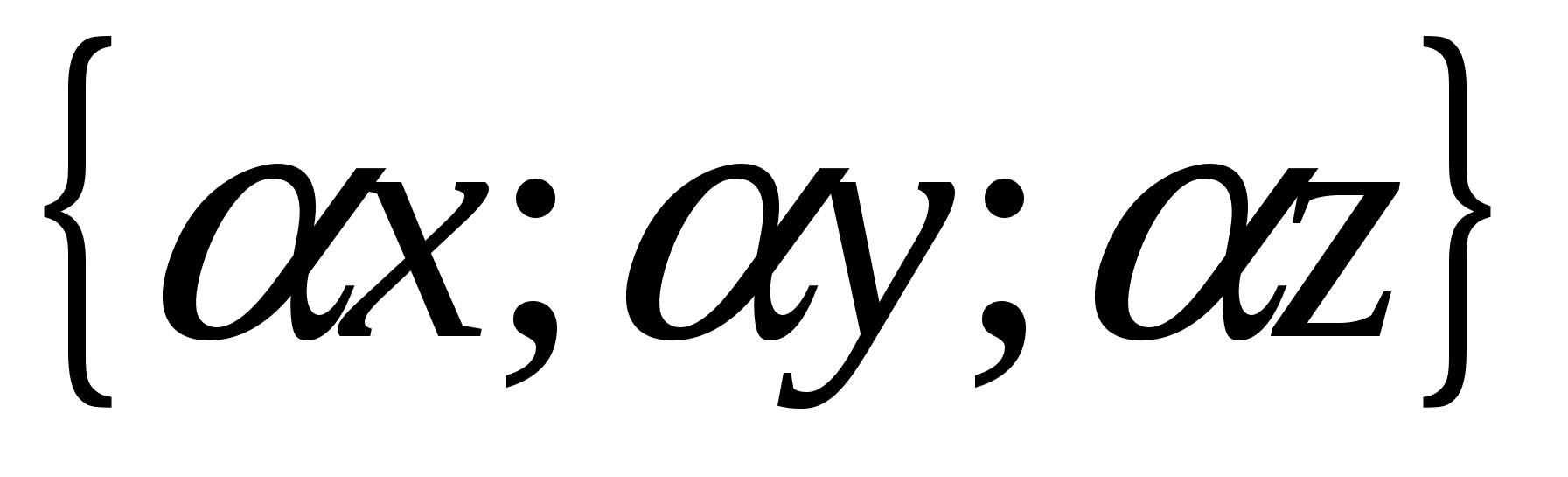 .
.
Eksempel.
Finn vektorkoordinater  , Hvis
, Hvis 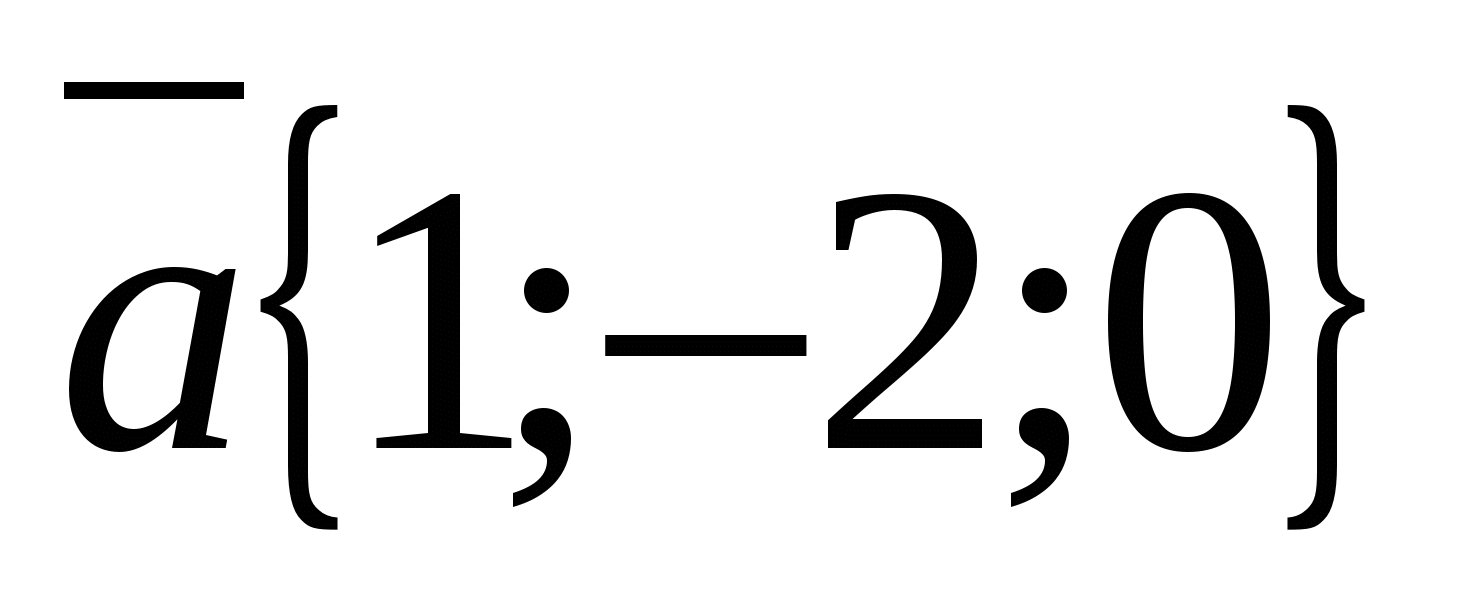 ,
, 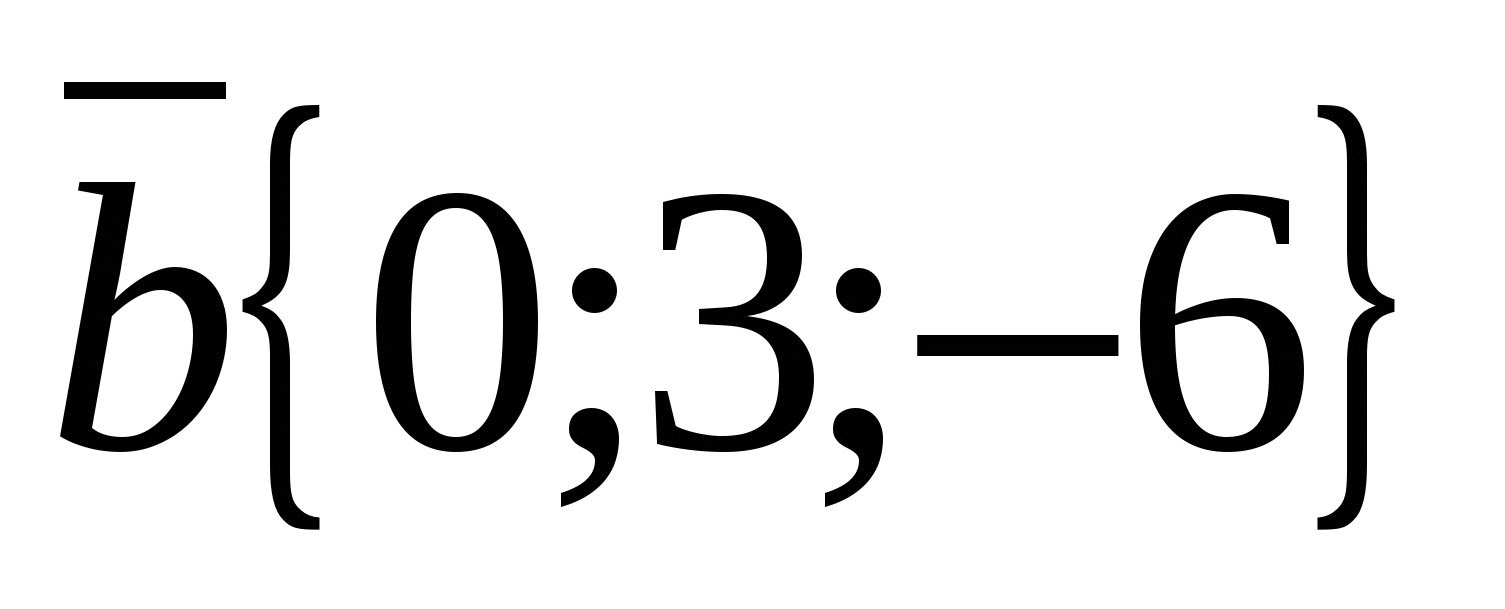 ,
, 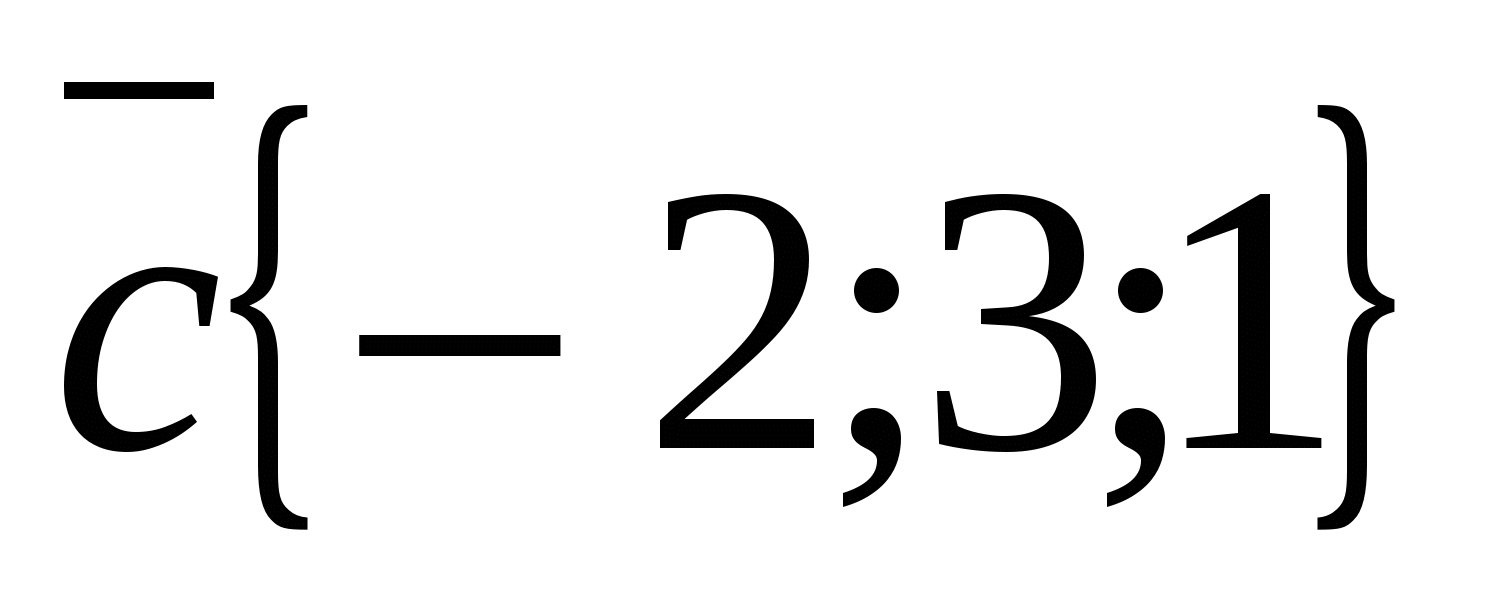 .
.
Løsning.
Vektor 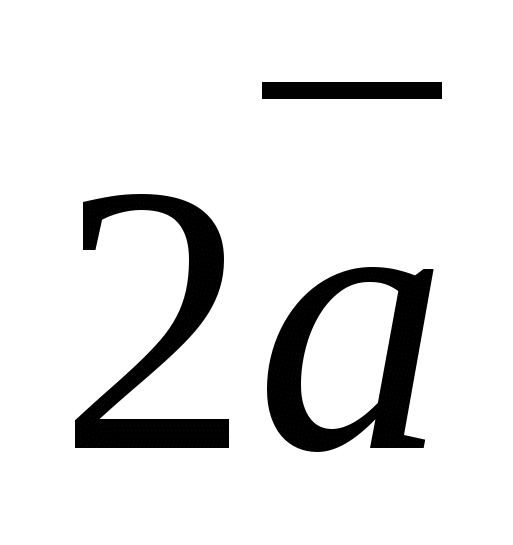 har koordinater
har koordinater 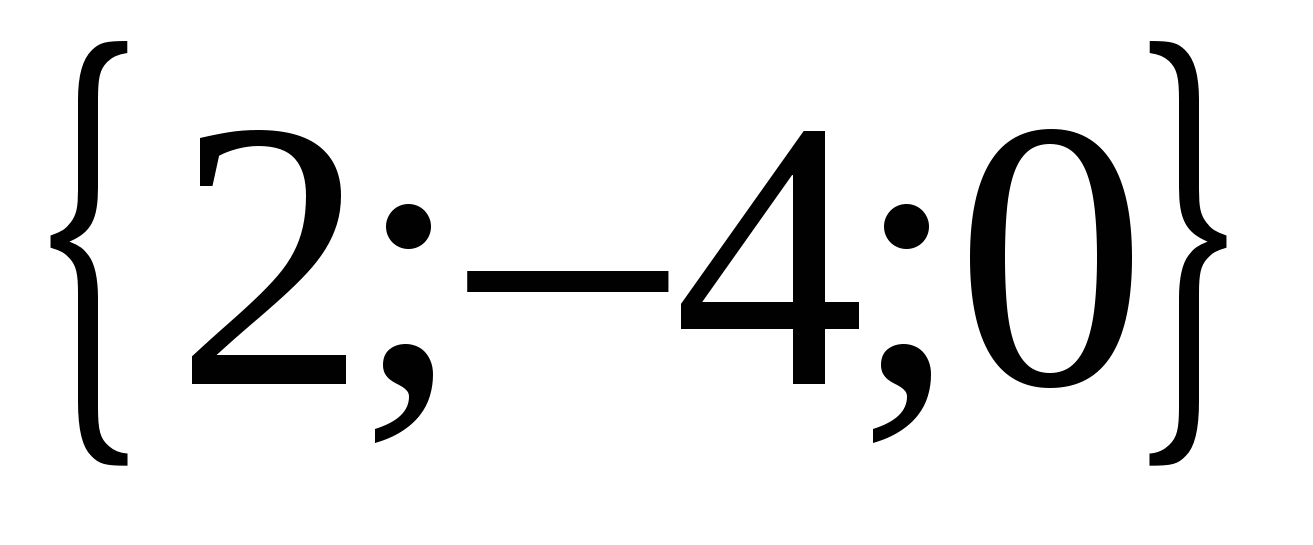 , og vektoren
, og vektoren  - koordinater
- koordinater 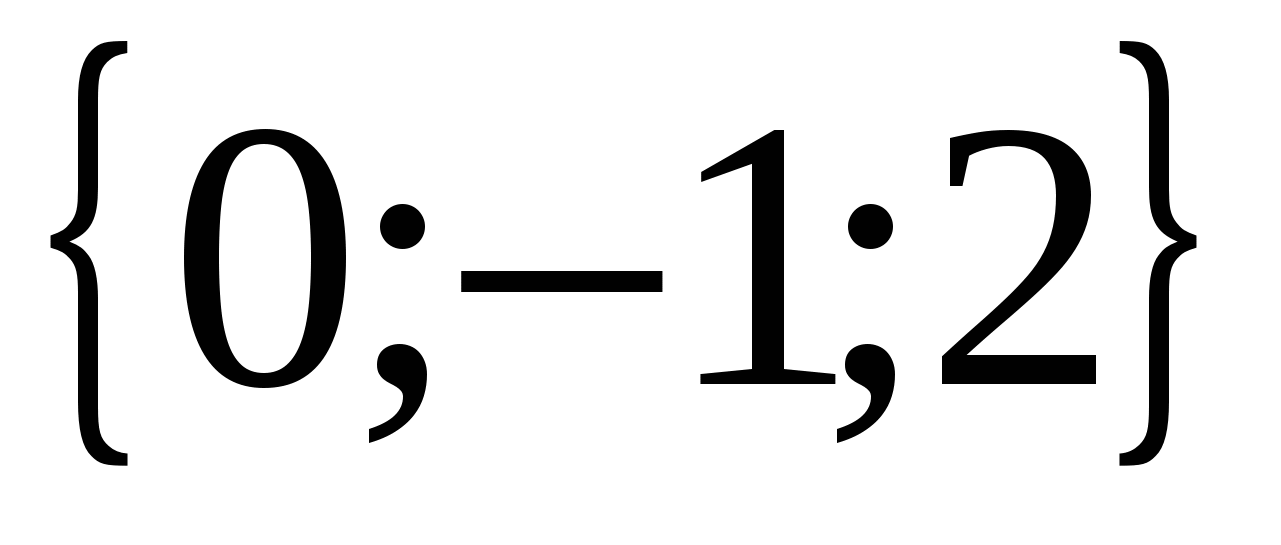 .
.
Fordi 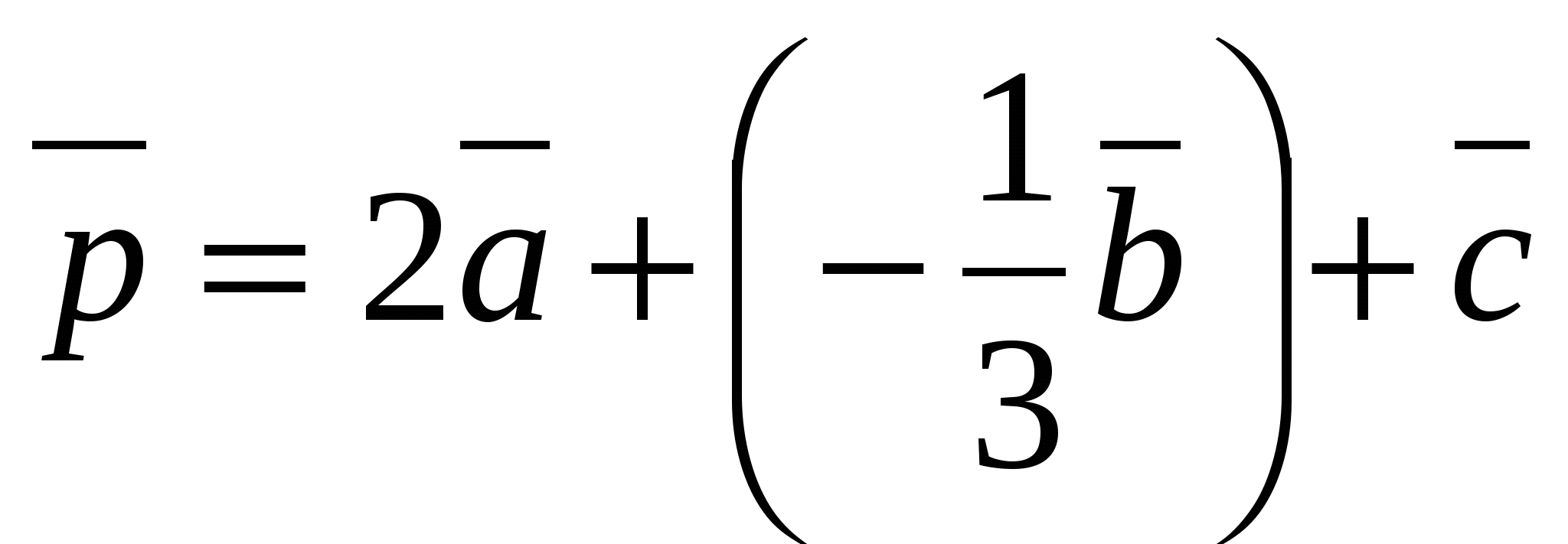 , deretter koordinatene
, deretter koordinatene  kan beregnes som:
kan beregnes som:  ,
, 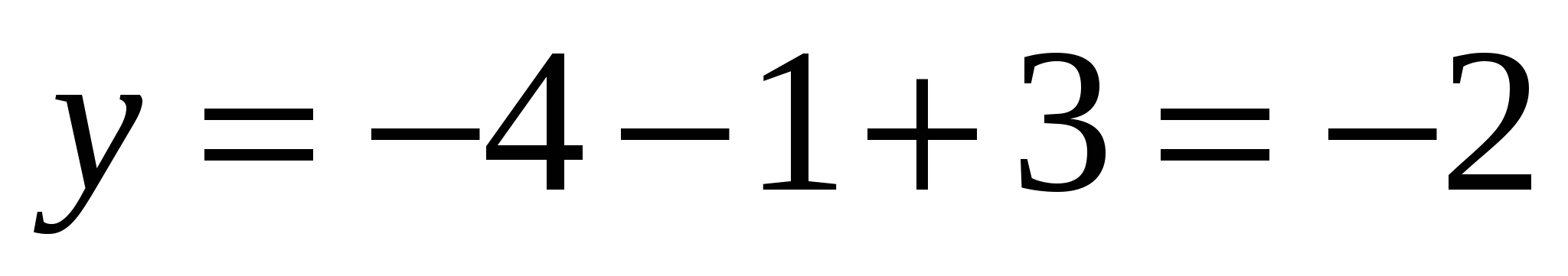 ,
, 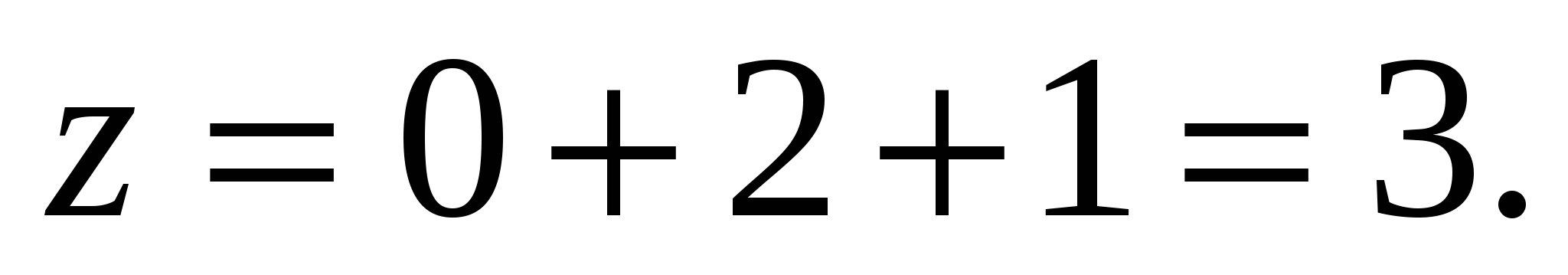 Så det er en vektor
Så det er en vektor 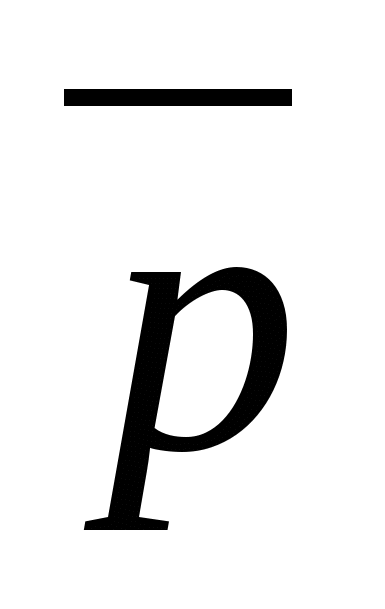 har koordinater
har koordinater 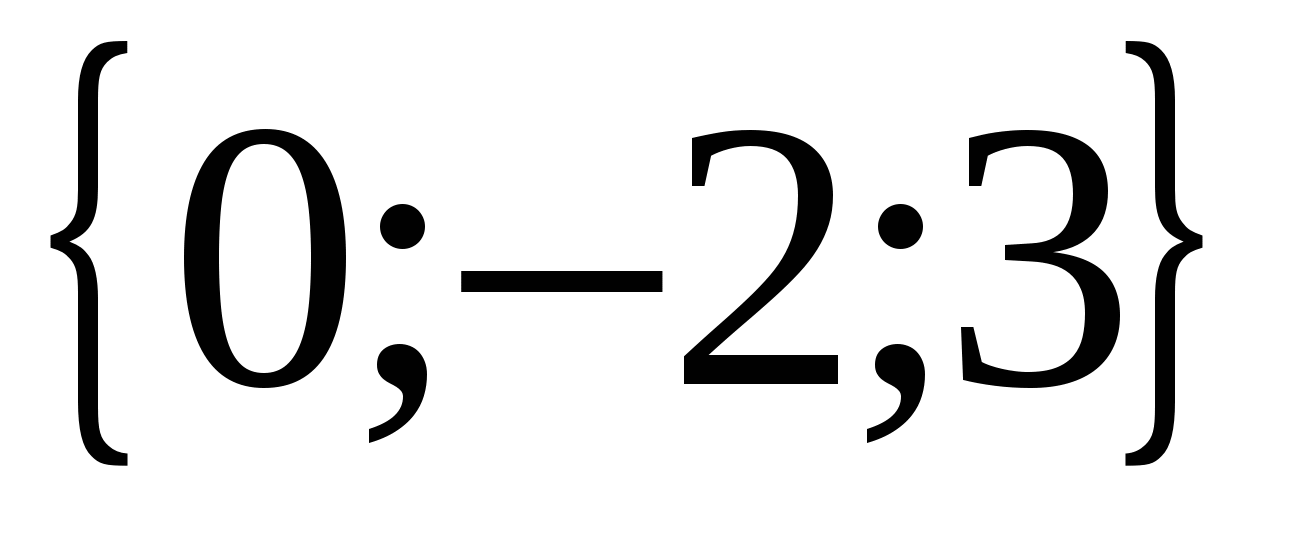 .
.
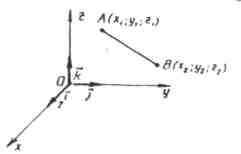
3. Sammenheng mellom vektorkoordinater og punktkoordinater.
Definisjon.
En vektor hvis ende sammenfaller med et gitt punkt, og hvis begynnelse sammenfaller med opprinnelsen til koordinatene, kalles radius vektor dette punktet.
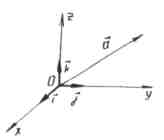
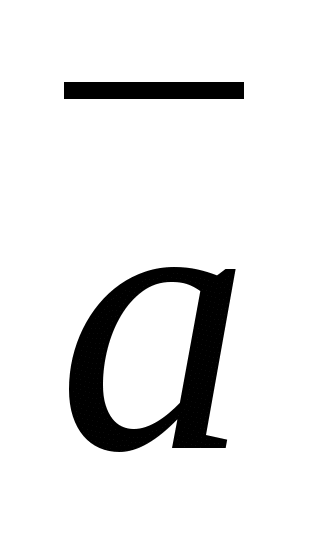
 - radiusvektor
- radiusvektor
 ,
,
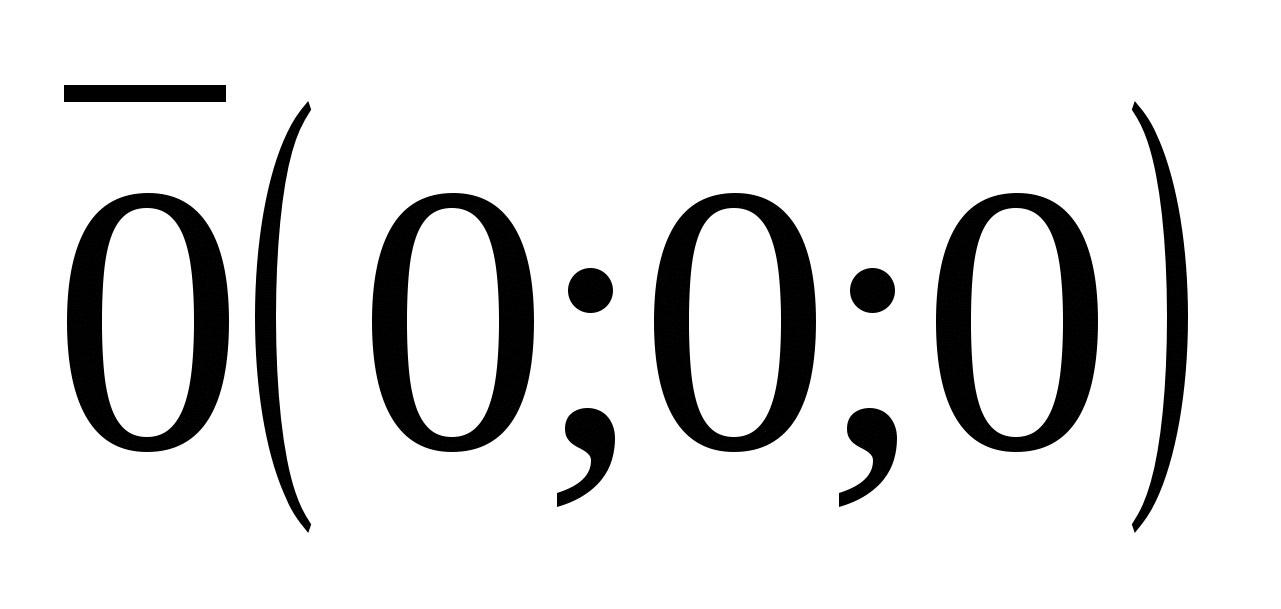 ;
;
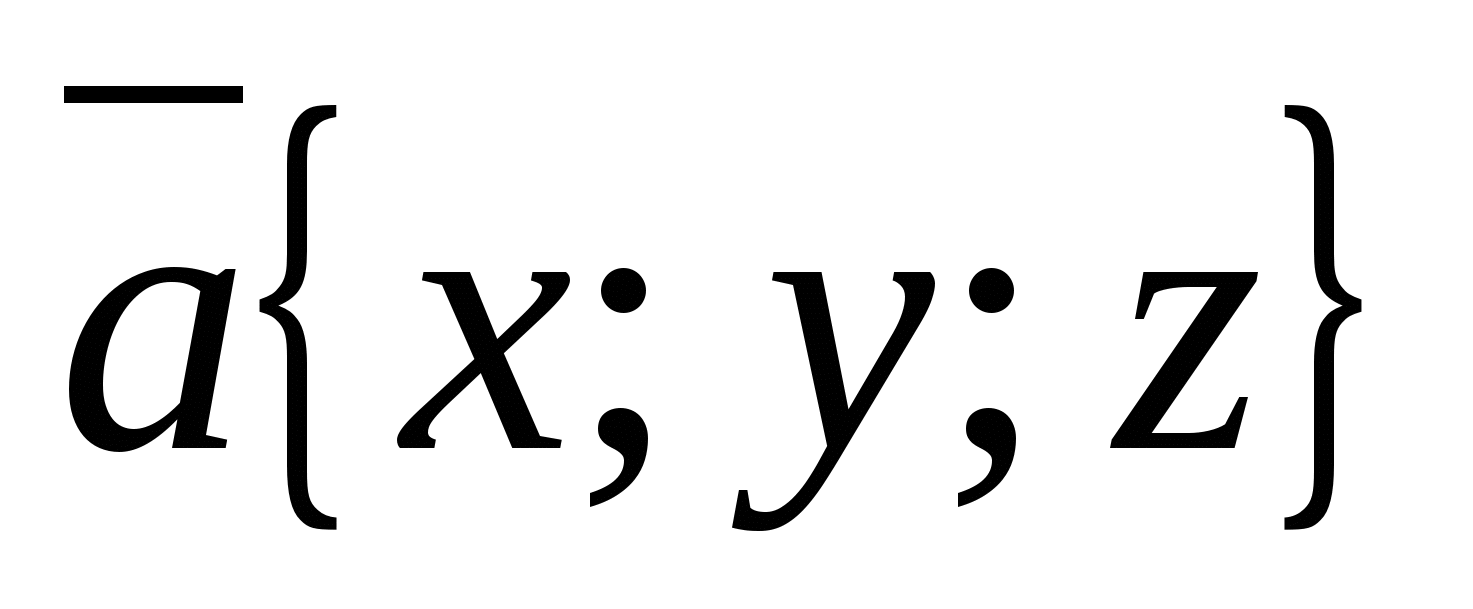
Regel 5.
Koordinatene til ethvert punkt er lik de tilsvarende koordinatene til radiusvektoren. ,.

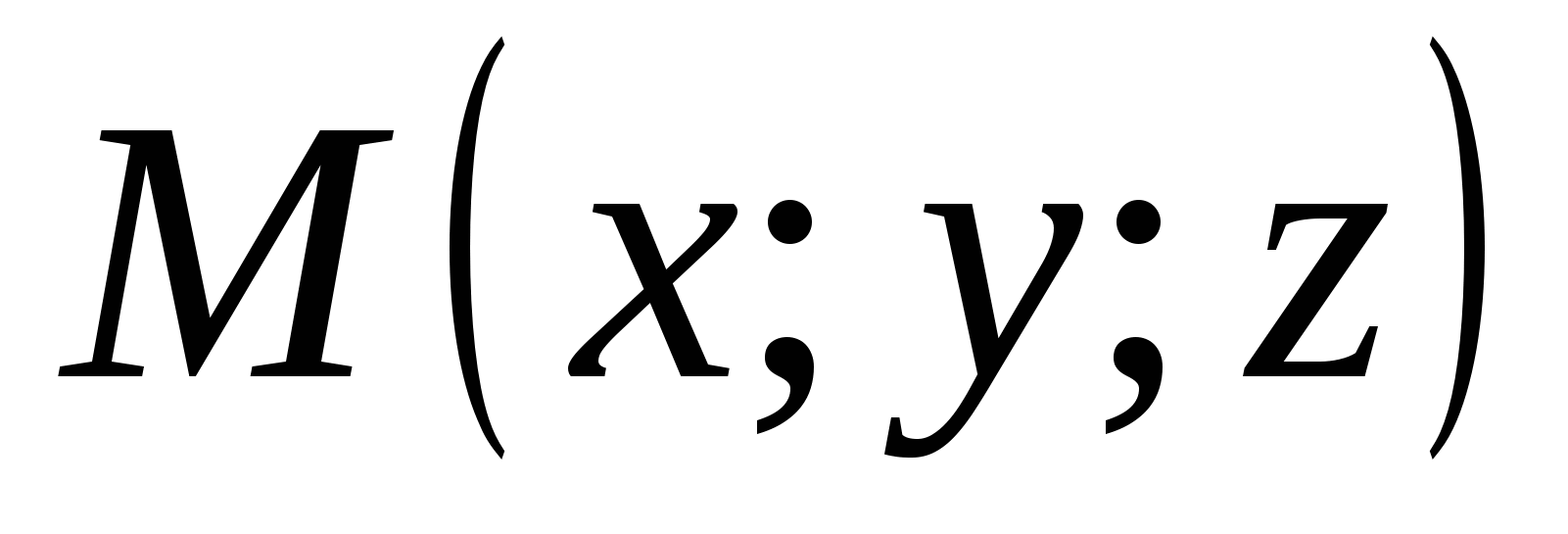
Regel 6.
Hver vektorkoordinat er lik forskjellen mellom de tilsvarende koordinatene til slutten og begynnelsen.
 .
.
4. Betingelse for kollinearitet av to vektorer i koordinater.
Slipp inn koordinatsystemet  to vektorer får sine koordinater
to vektorer får sine koordinater  Og
Og 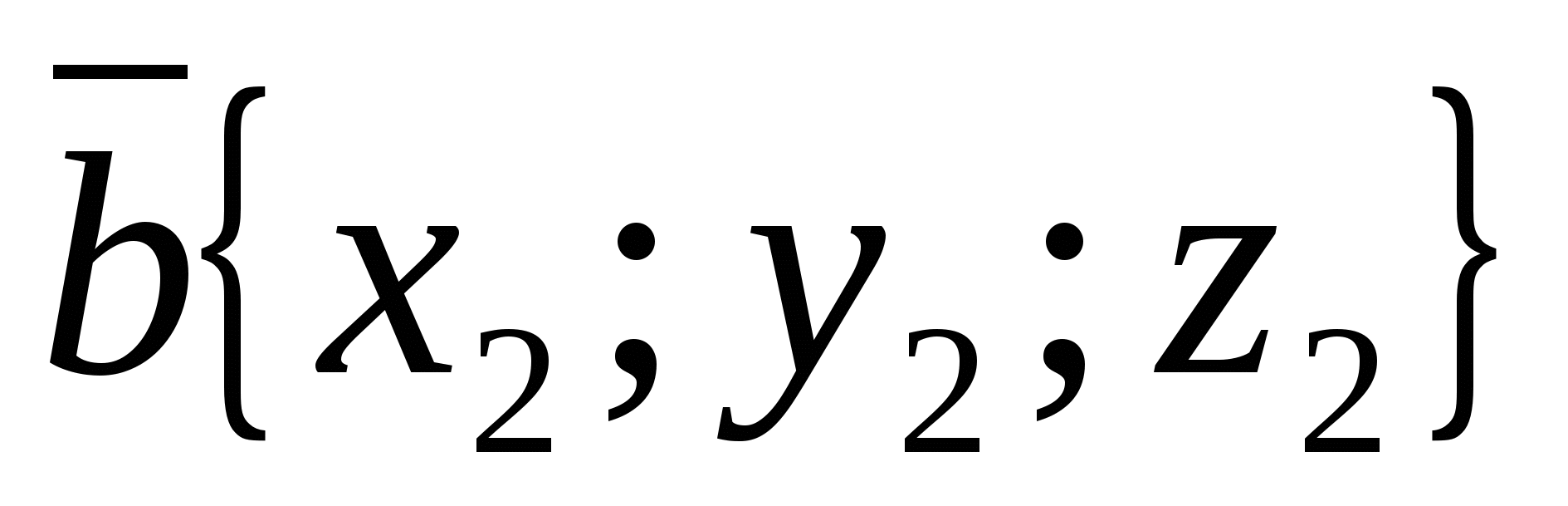 .
.
Regel 7.
Vektorer
 Og
Og 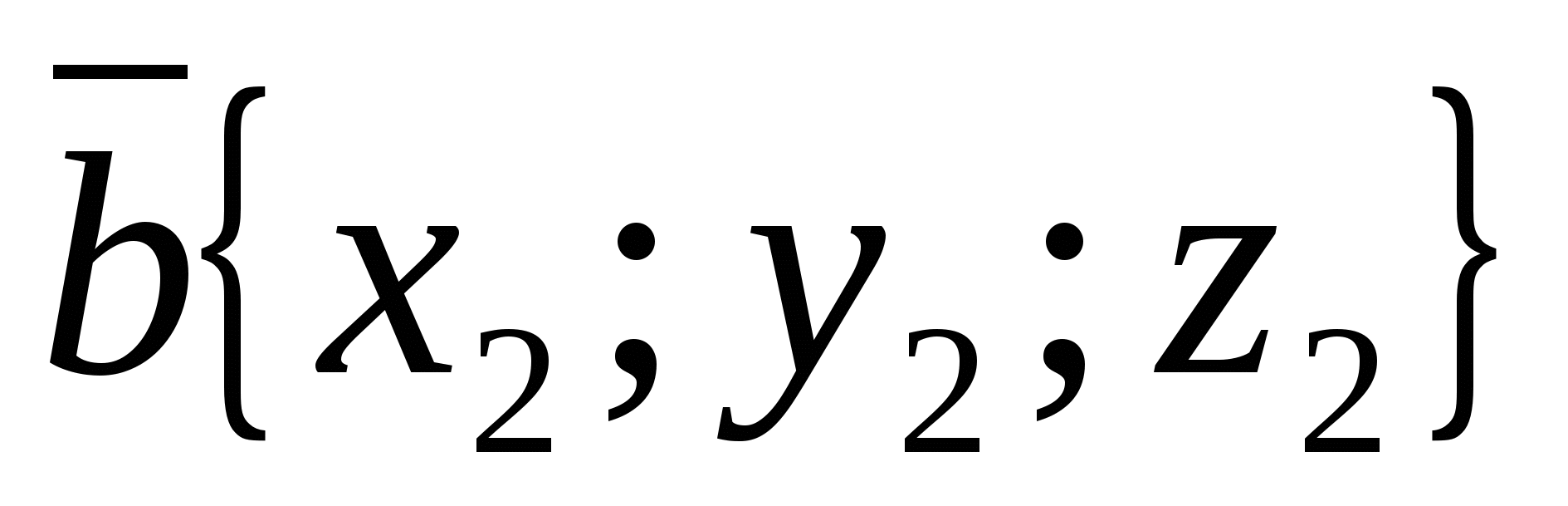 er kollineære hvis og bare hvis deres korresponderende koordinater er proporsjonale,
er kollineære hvis og bare hvis deres korresponderende koordinater er proporsjonale, 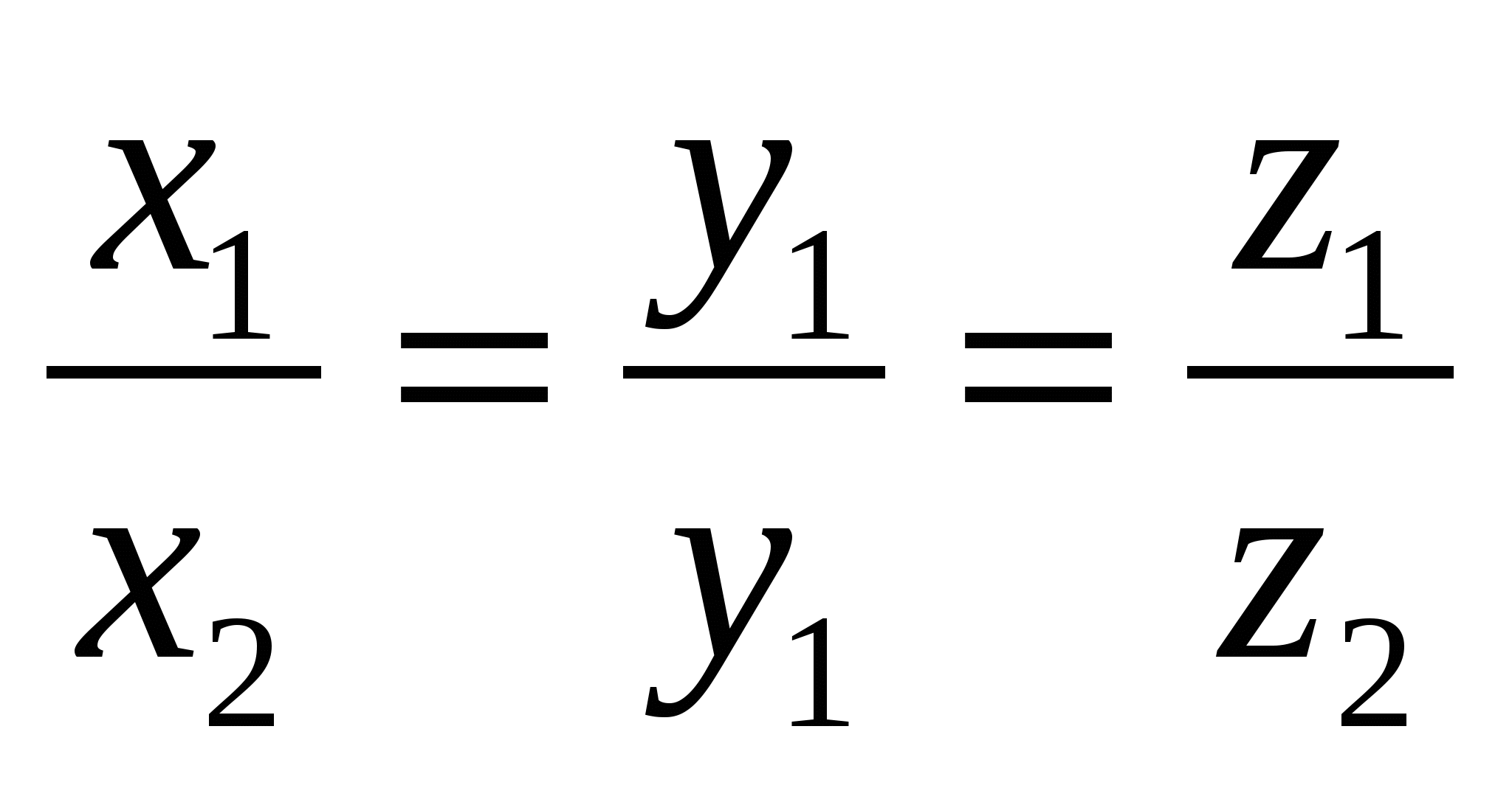 .
.
Eksempel.
a) Tenk på vektorene 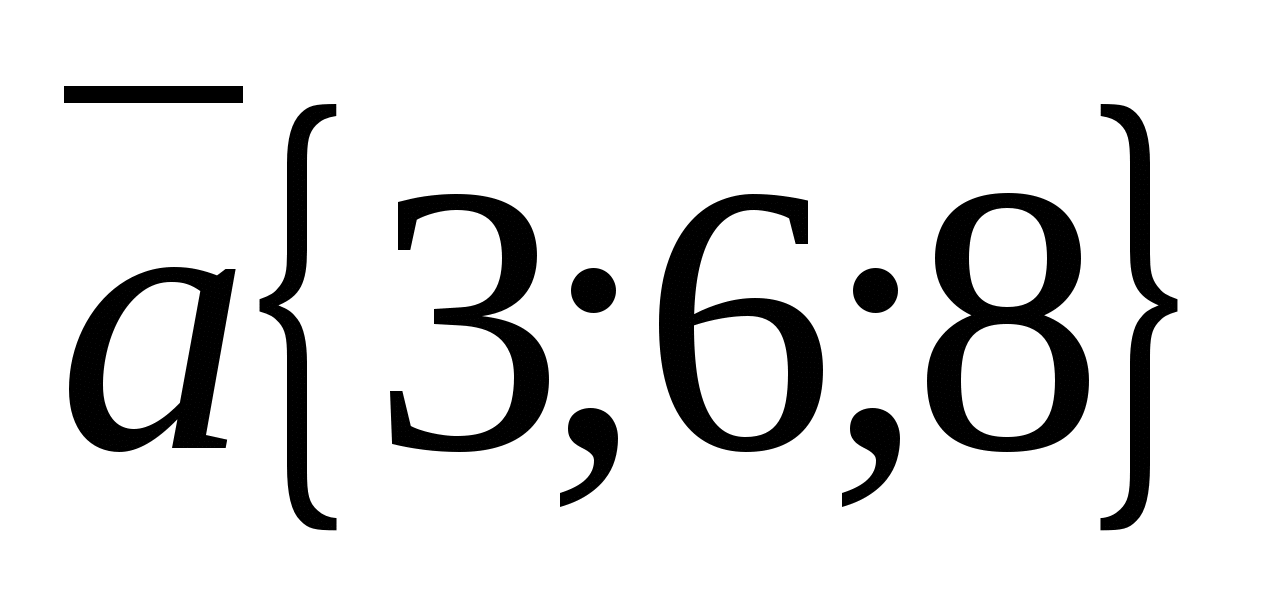 Og
Og 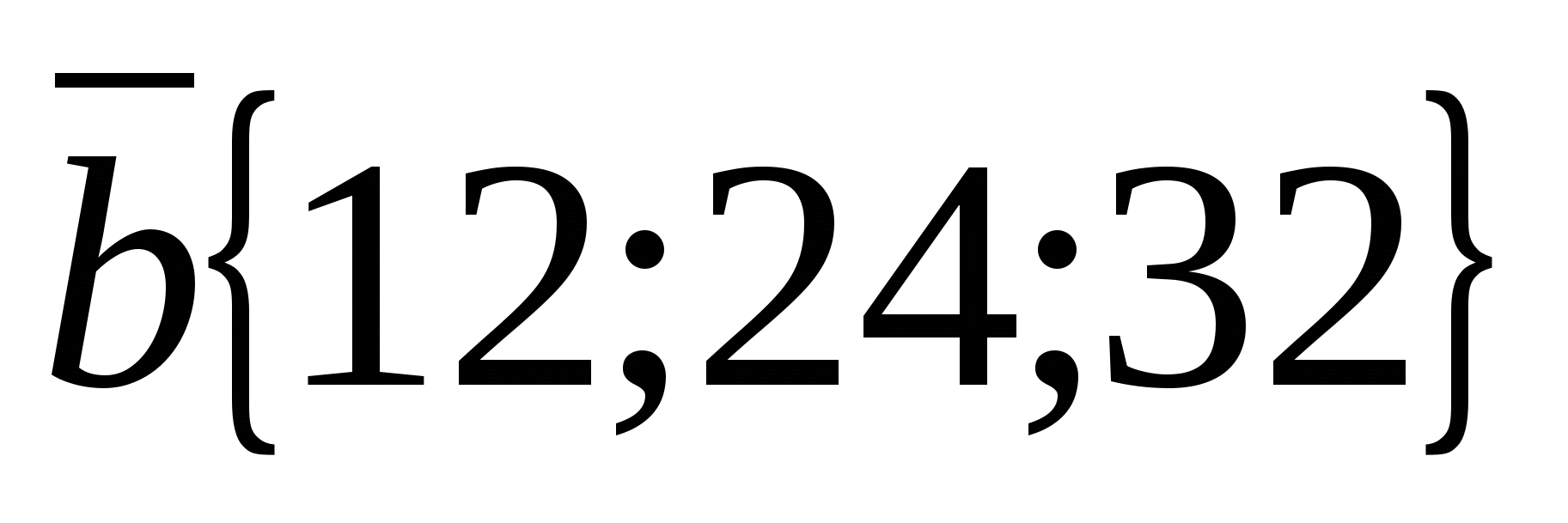 .
.
Vektorkoordinater 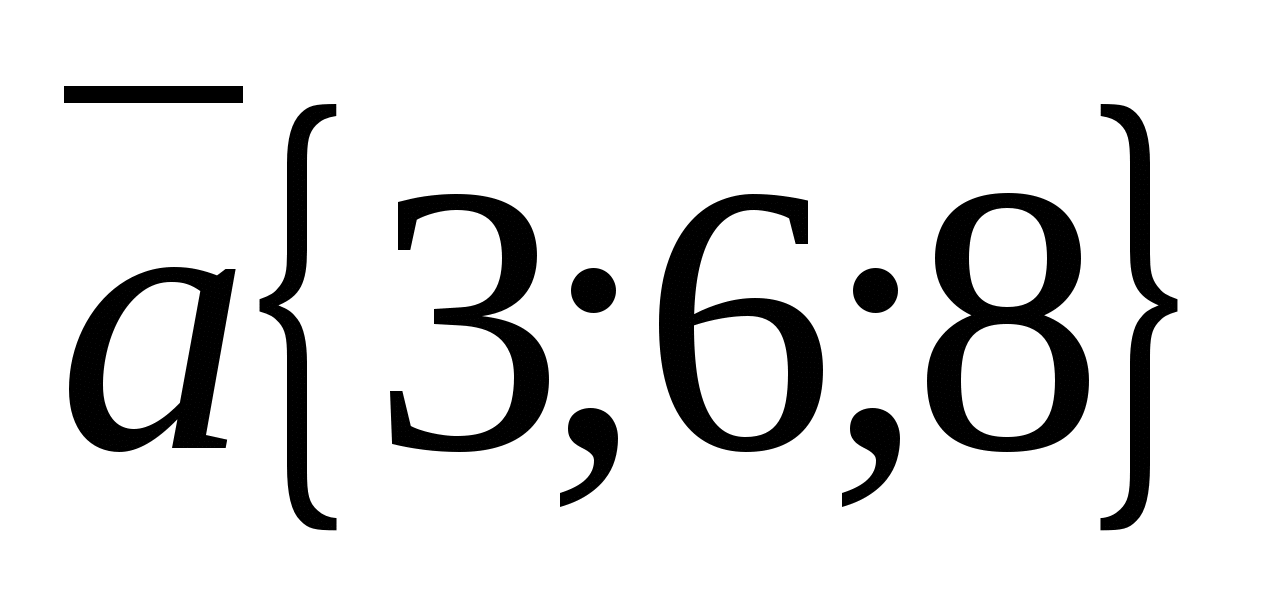 er proporsjonale med de tilsvarende vektorkoordinatene
er proporsjonale med de tilsvarende vektorkoordinatene 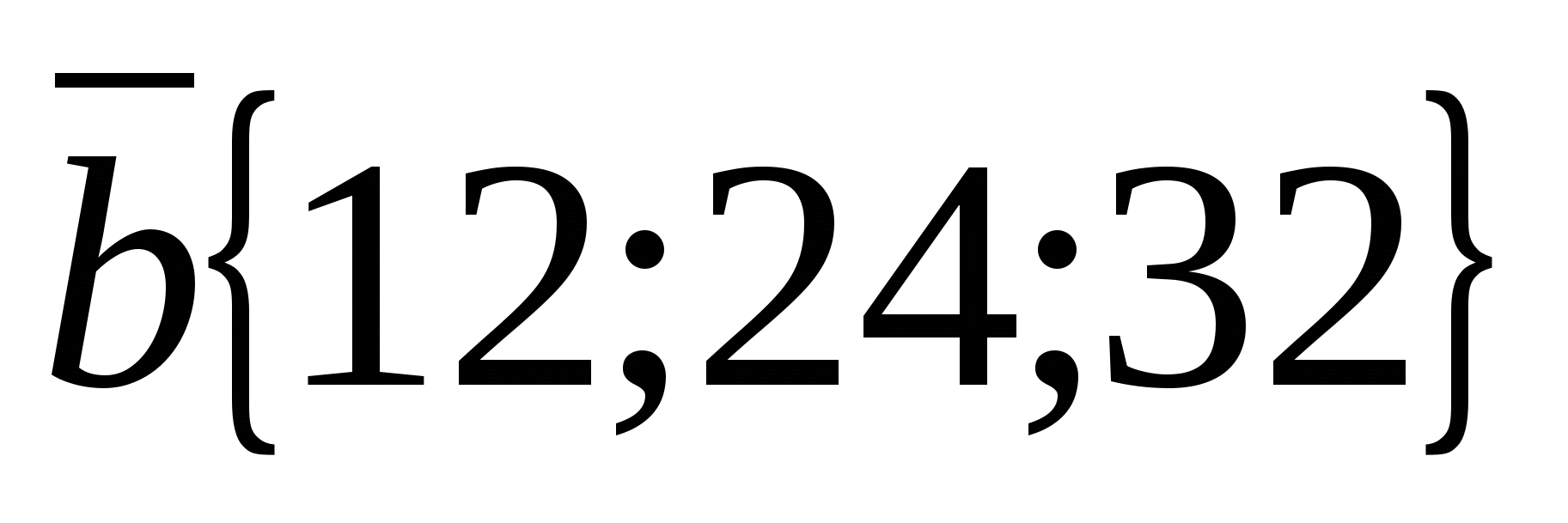 :
: 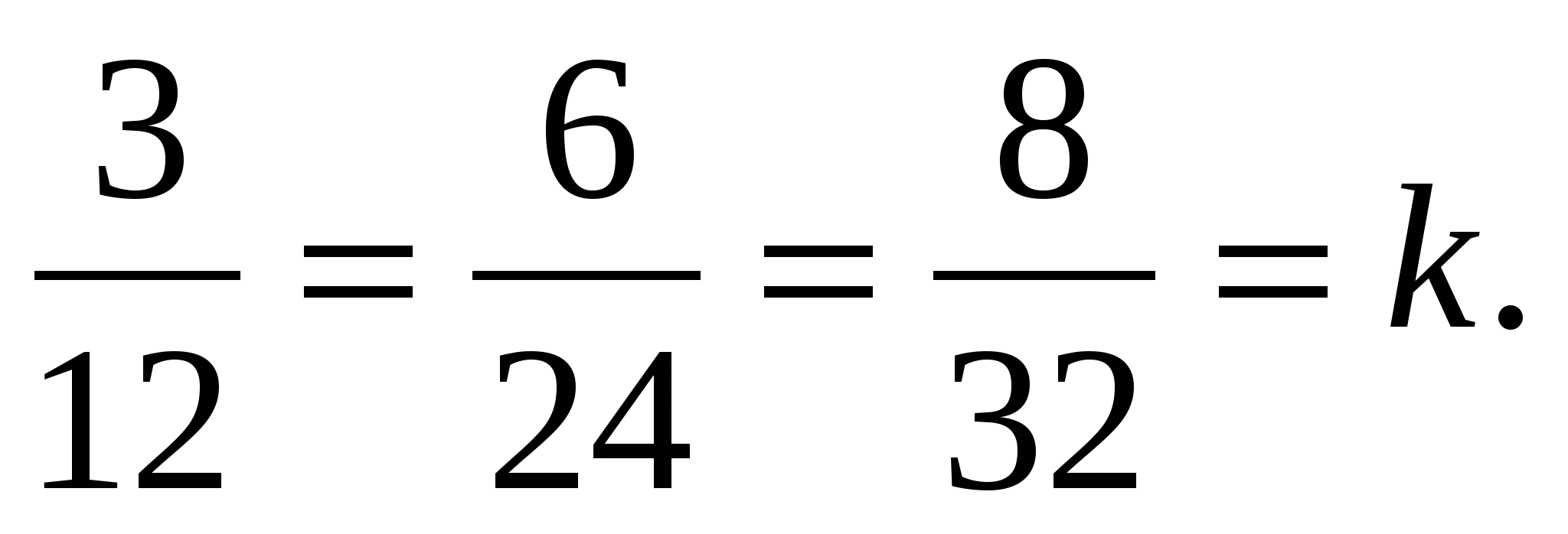 Derfor
Derfor 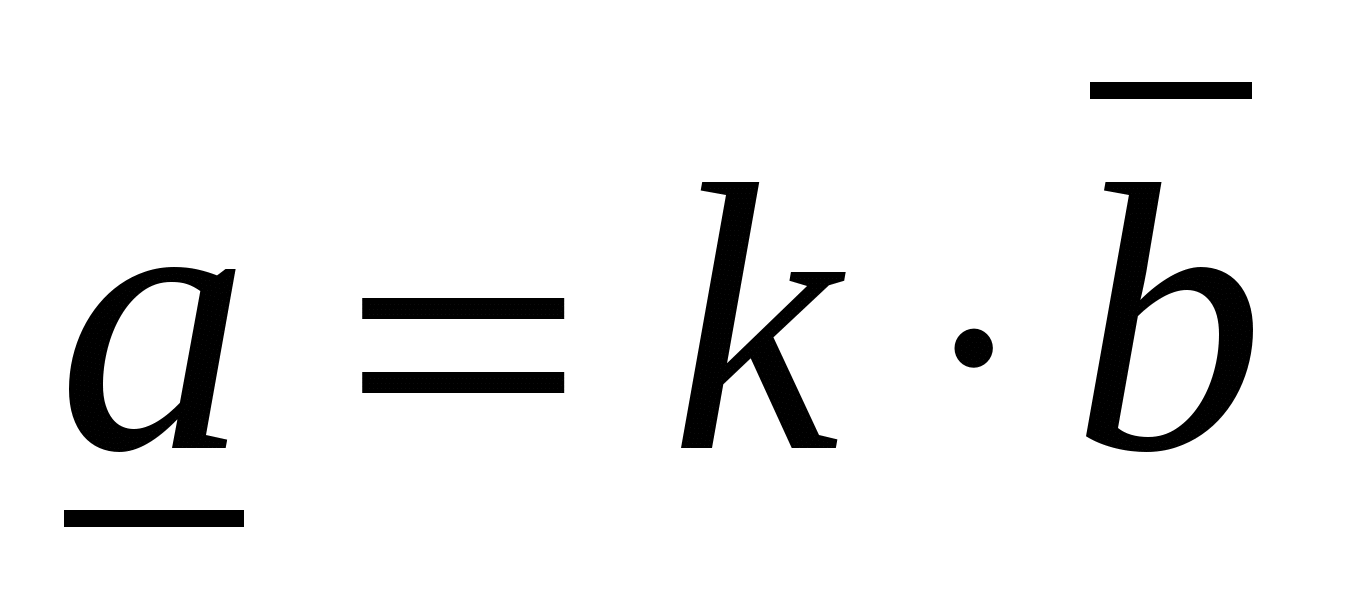 , og derfor er vektorene kollineære.
, og derfor er vektorene kollineære.
b) Betrakt vektorene 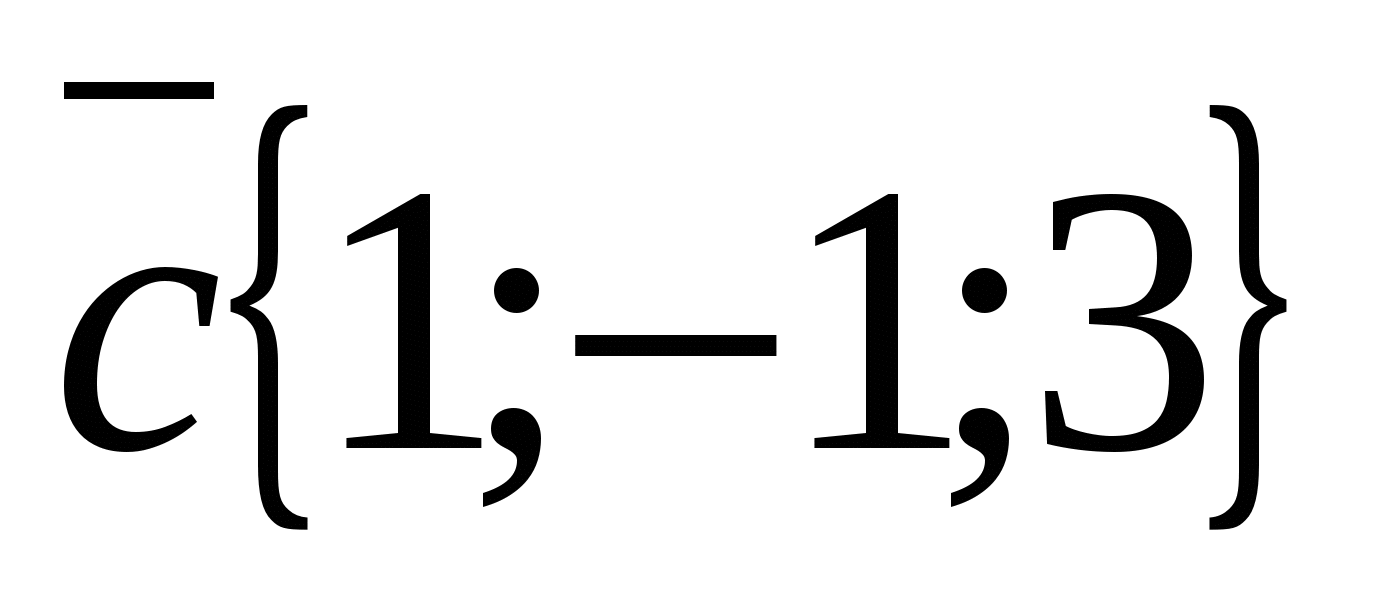 Og
Og 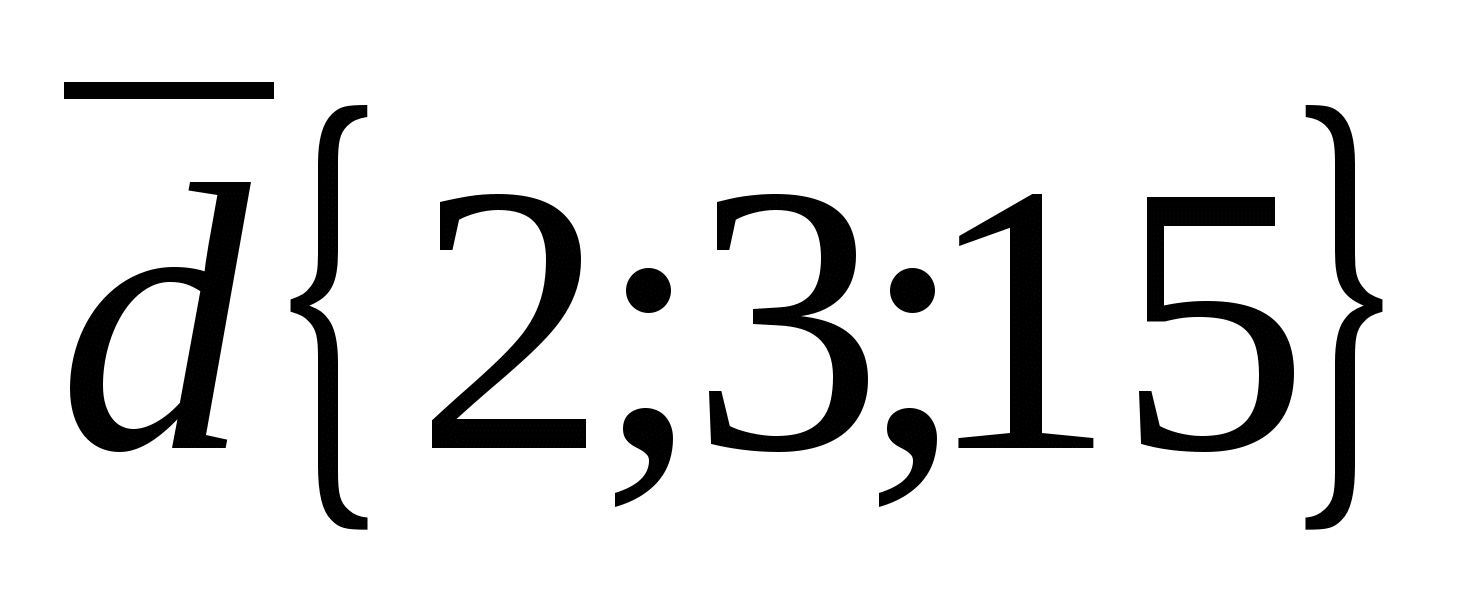 .
.
Vektorkoordinater 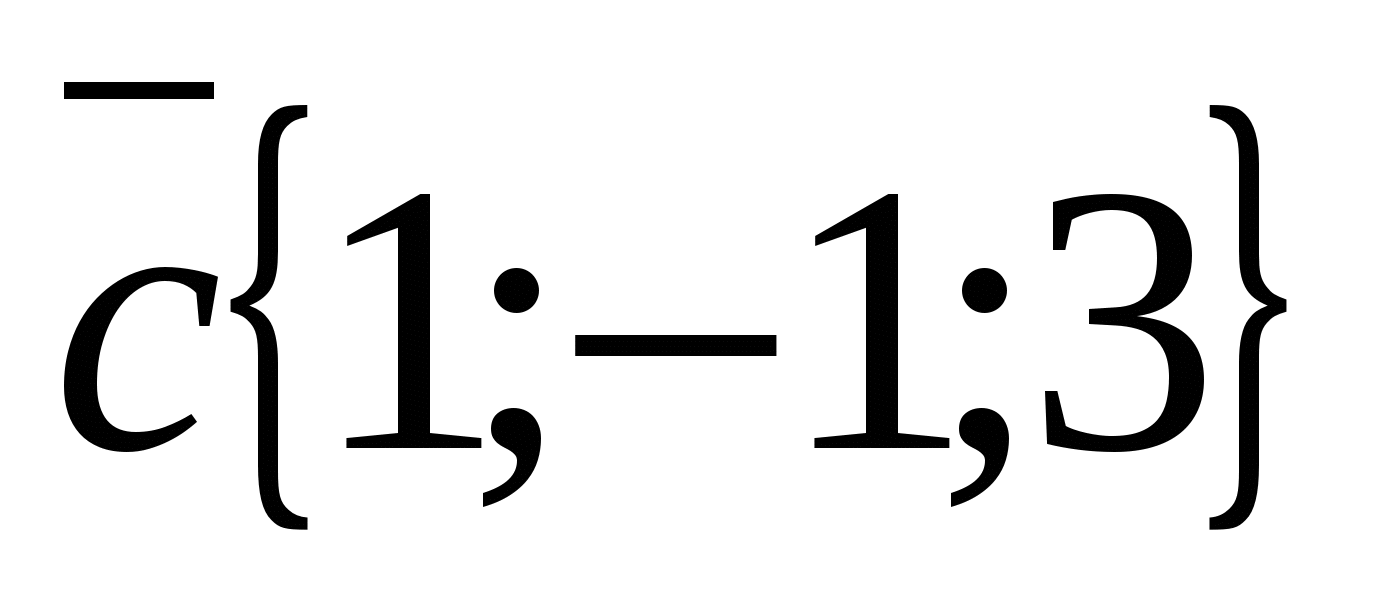 er ikke proporsjonale med de tilsvarende vektorkoordinatene
er ikke proporsjonale med de tilsvarende vektorkoordinatene 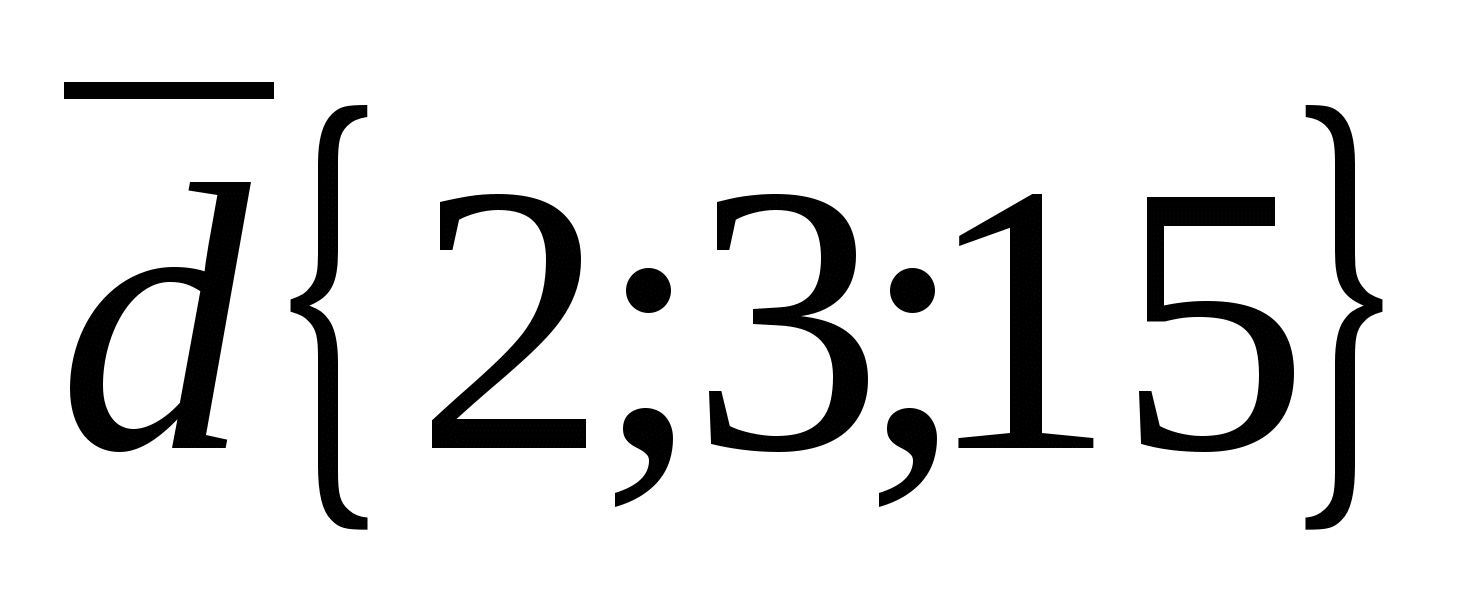 , For eksempel
, For eksempel 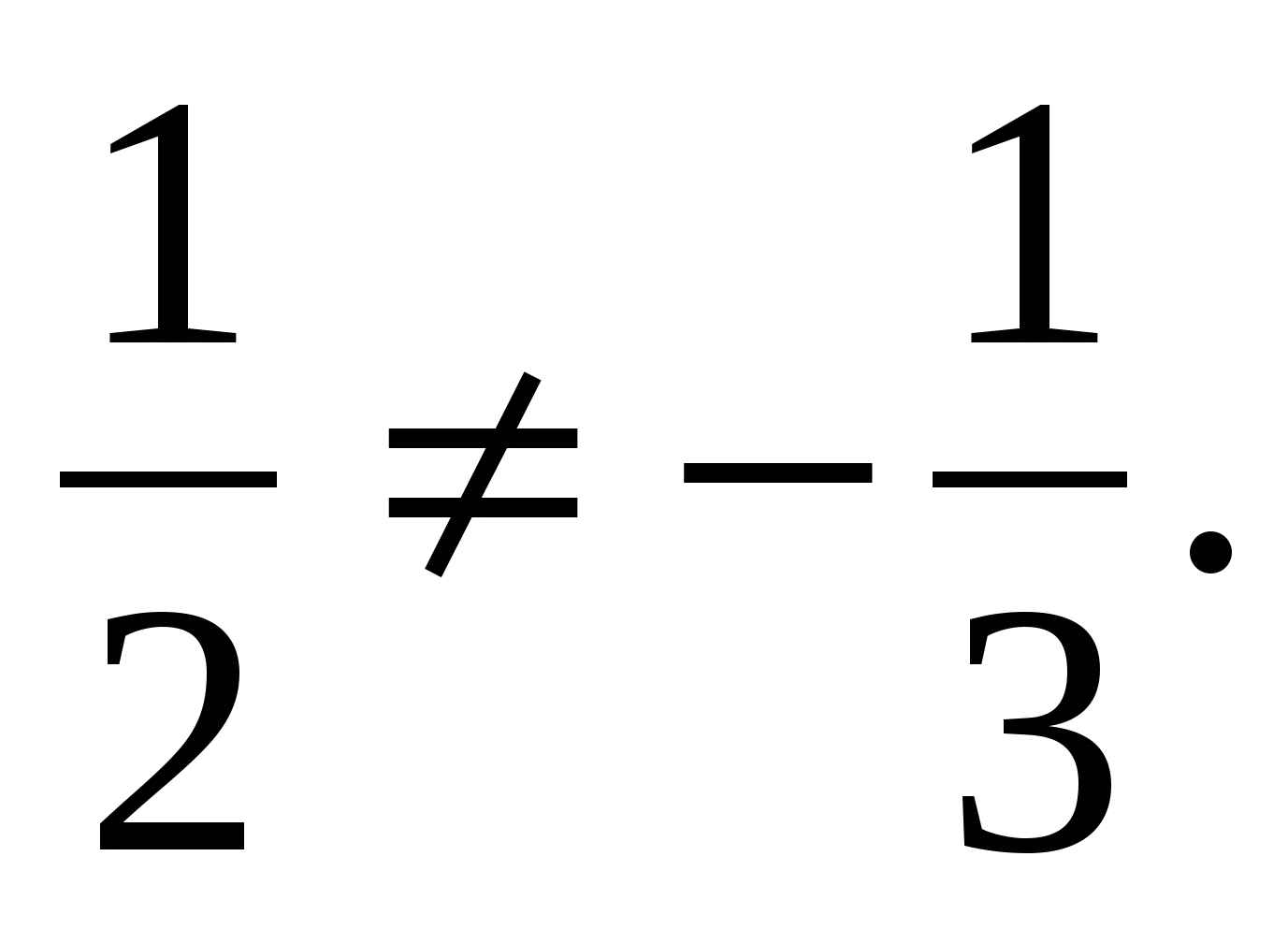 Dette betyr at vektorene ikke er kollineære.
Dette betyr at vektorene ikke er kollineære.
5. De enkleste problemene i koordinater.
Oppgave 1.
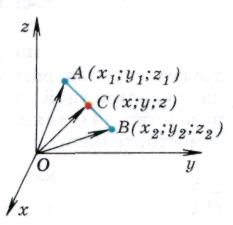 Hver koordinat i midten av et segment er lik halvparten av summen av de tilsvarende koordinatene til endene.
Hver koordinat i midten av et segment er lik halvparten av summen av de tilsvarende koordinatene til endene.
 , Hvor
, Hvor 
 ,
, 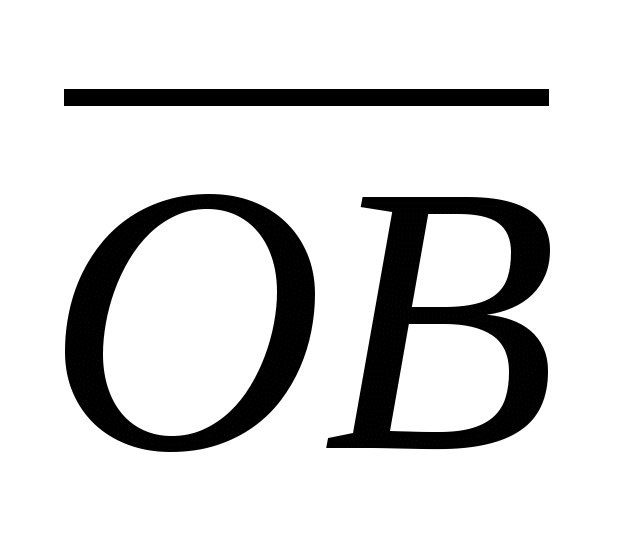
 Og
Og 
 .
.
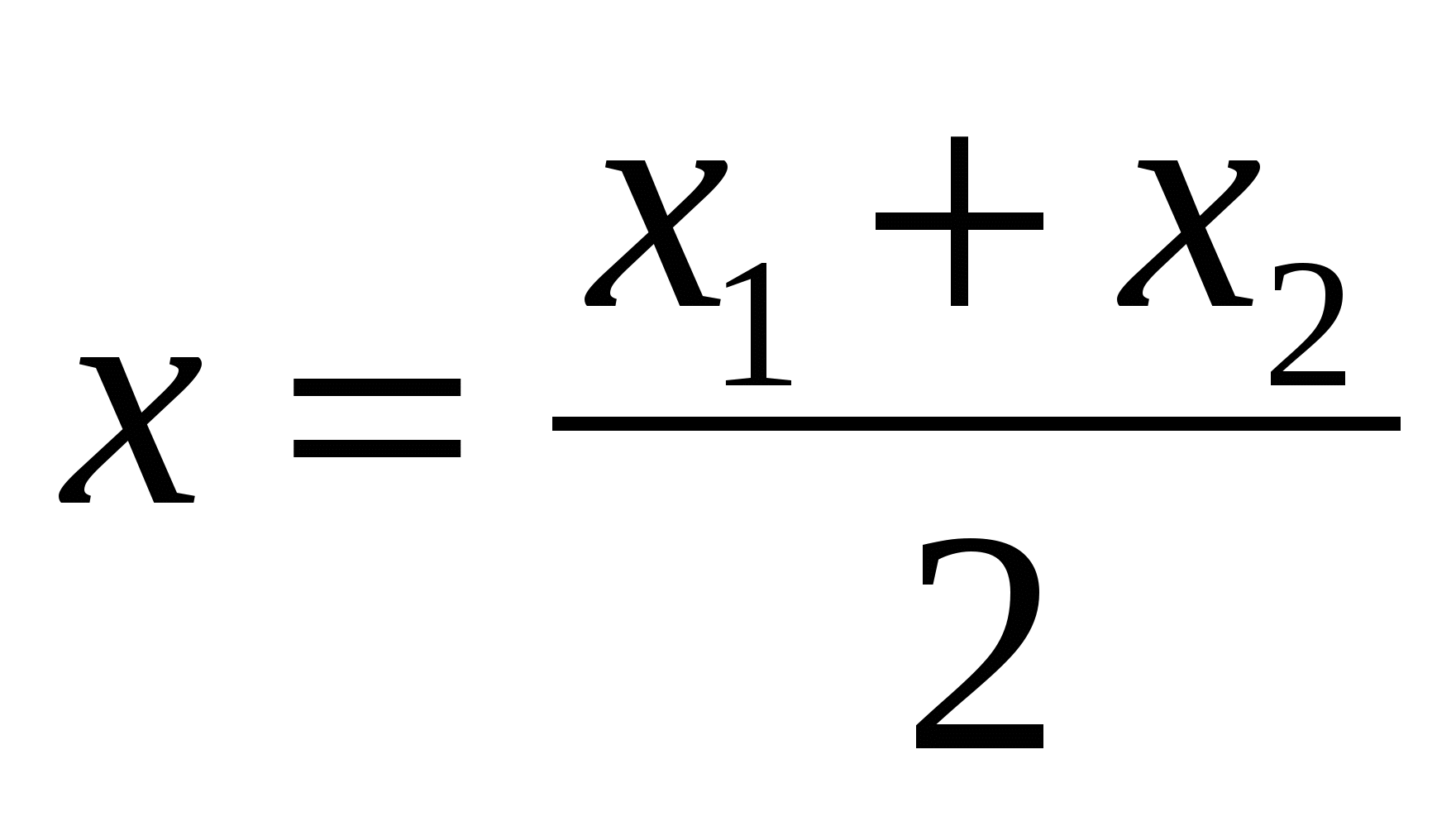 ,
,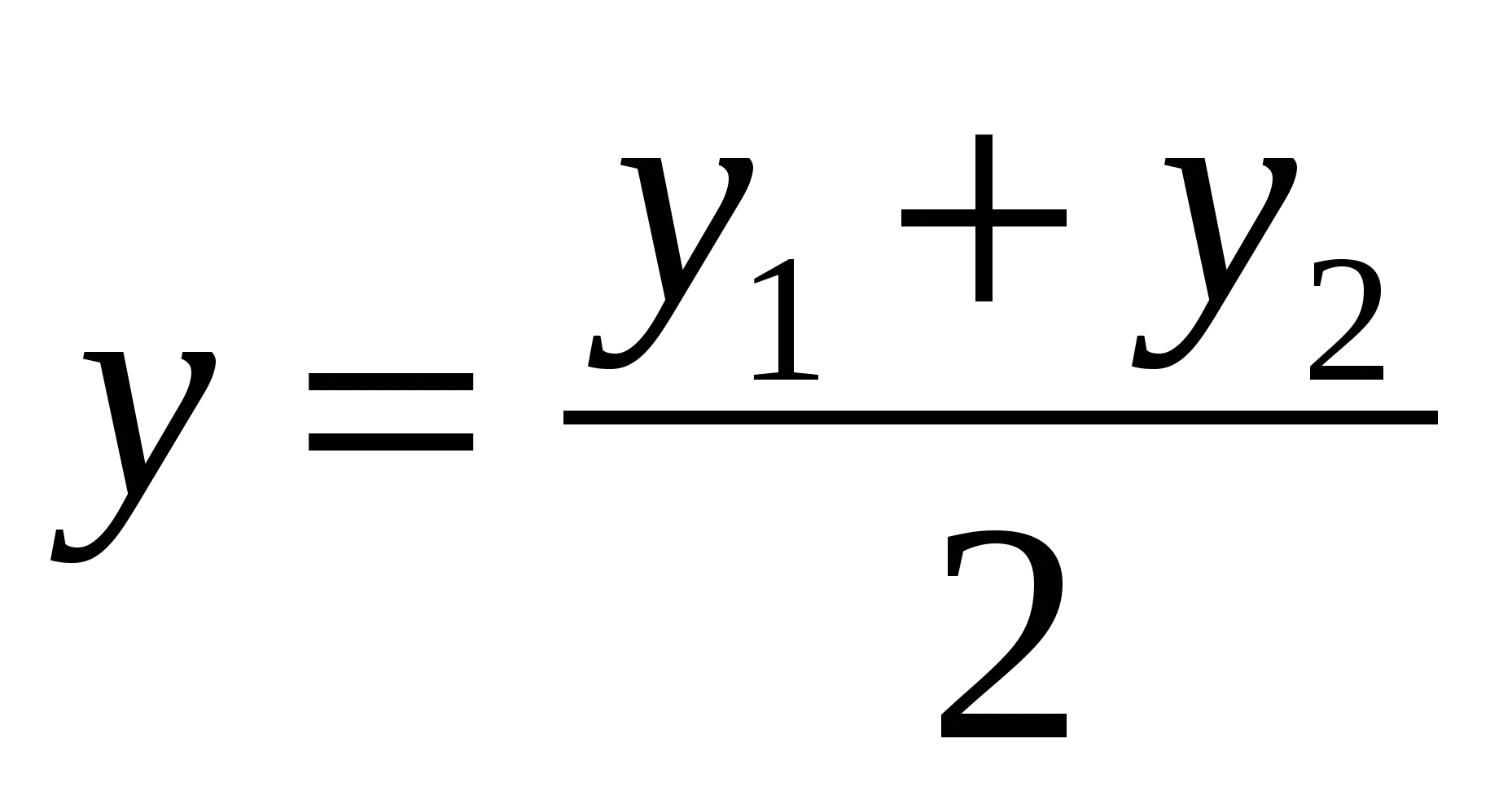 ,
, 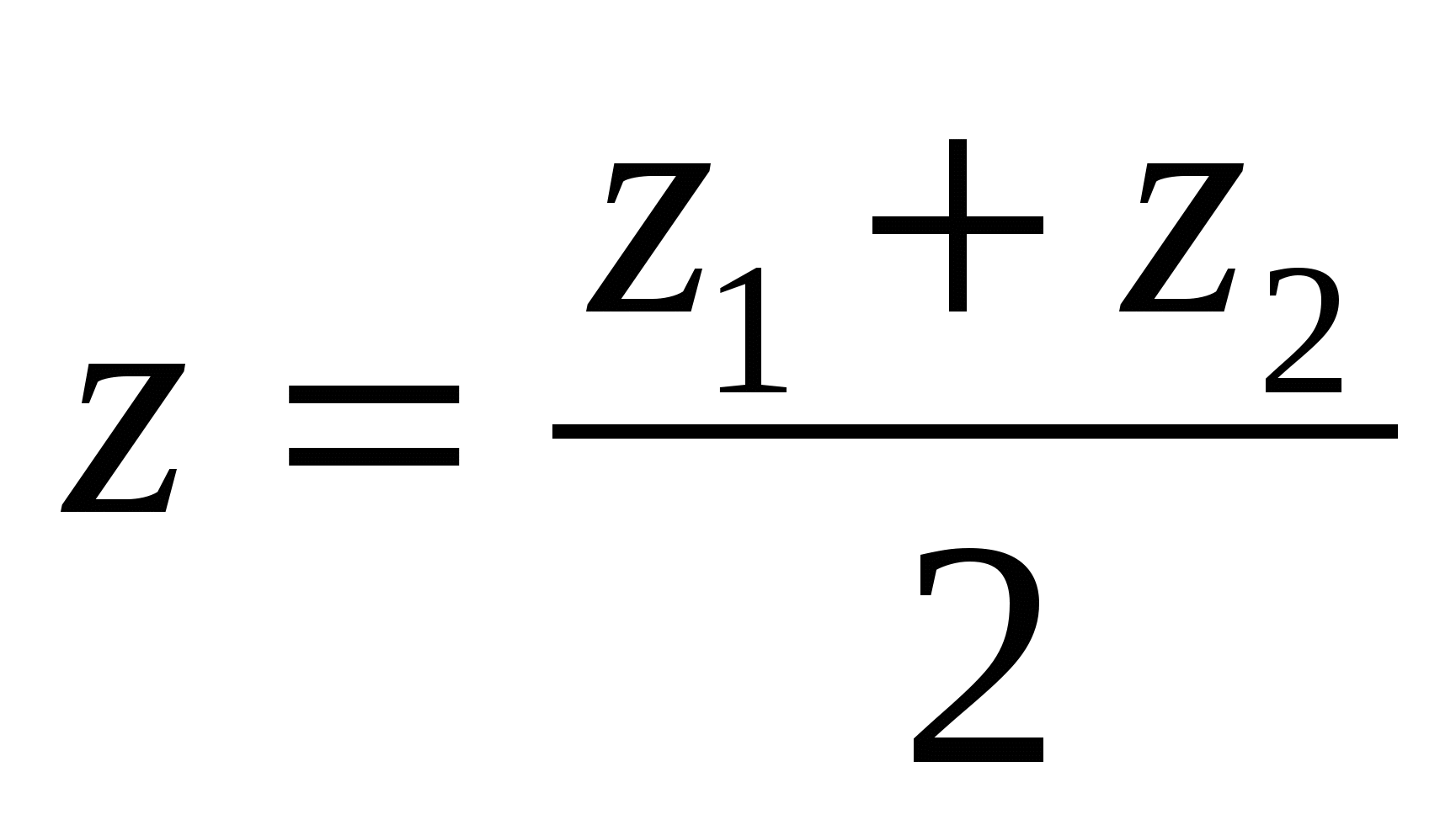 ,
,
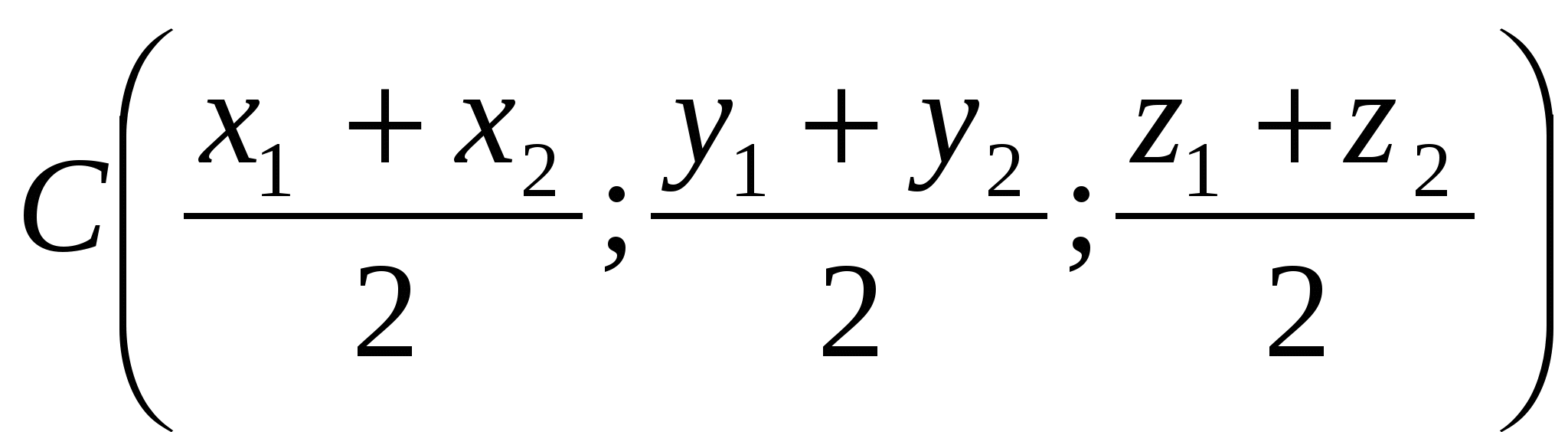
b) Beregning av lengden til en vektor fra dens koordinater.
Tenk på en vektor  ,
,
vektorlengden beregnes av formelen
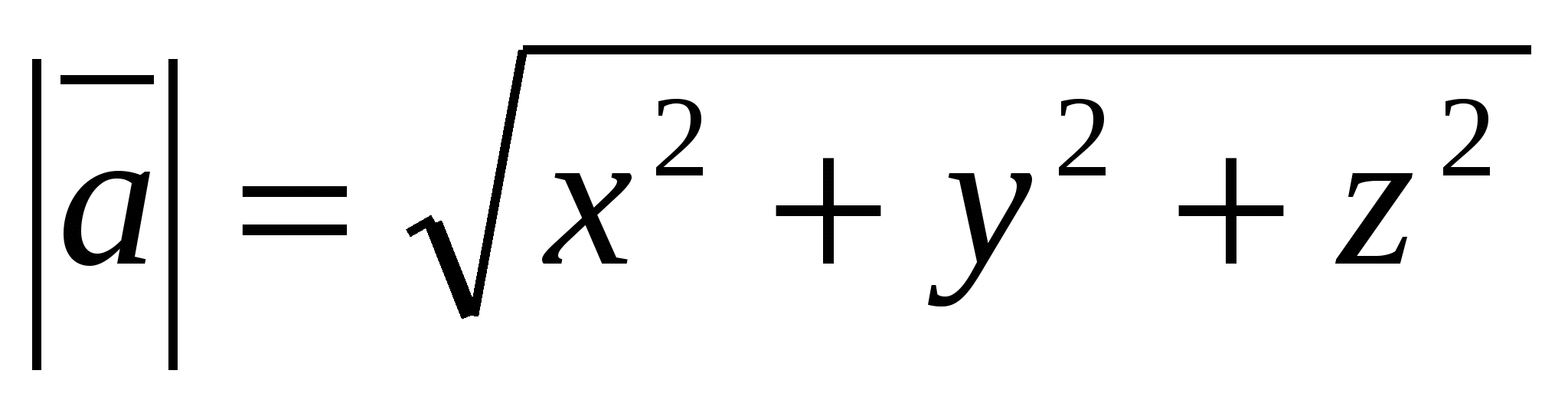 .
.
Fordi  =
=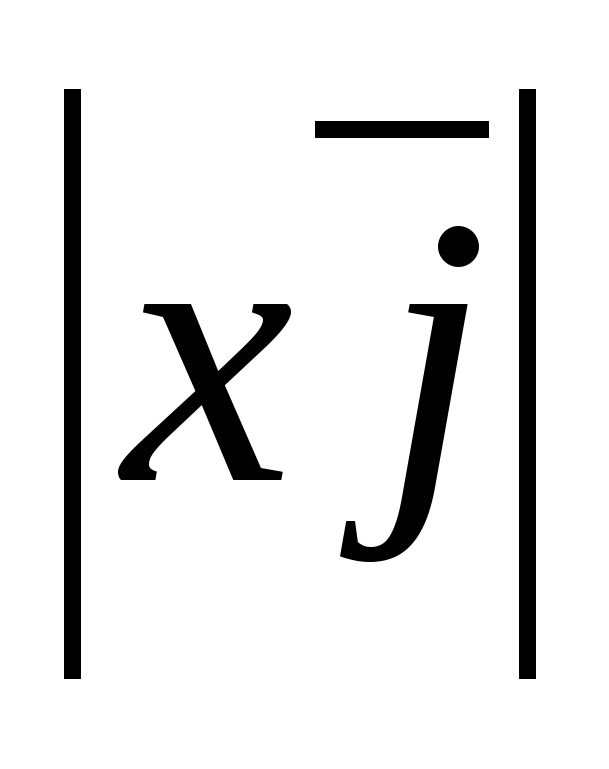 =
=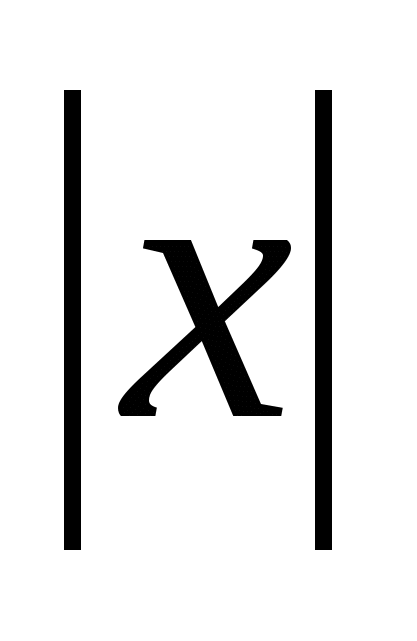 ,
,
 =
= =
=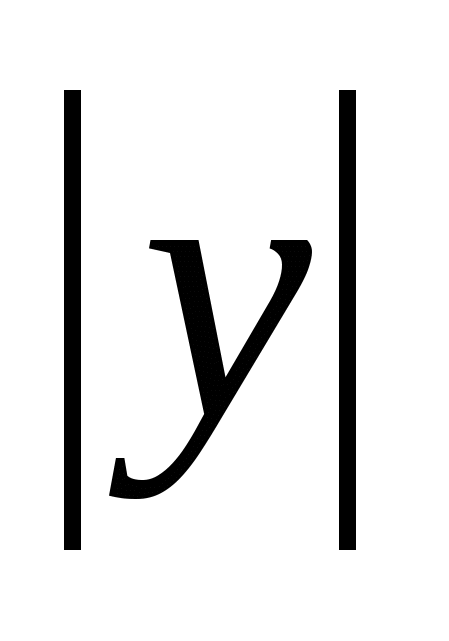 ,
,
 =
= =
= , Og
, Og 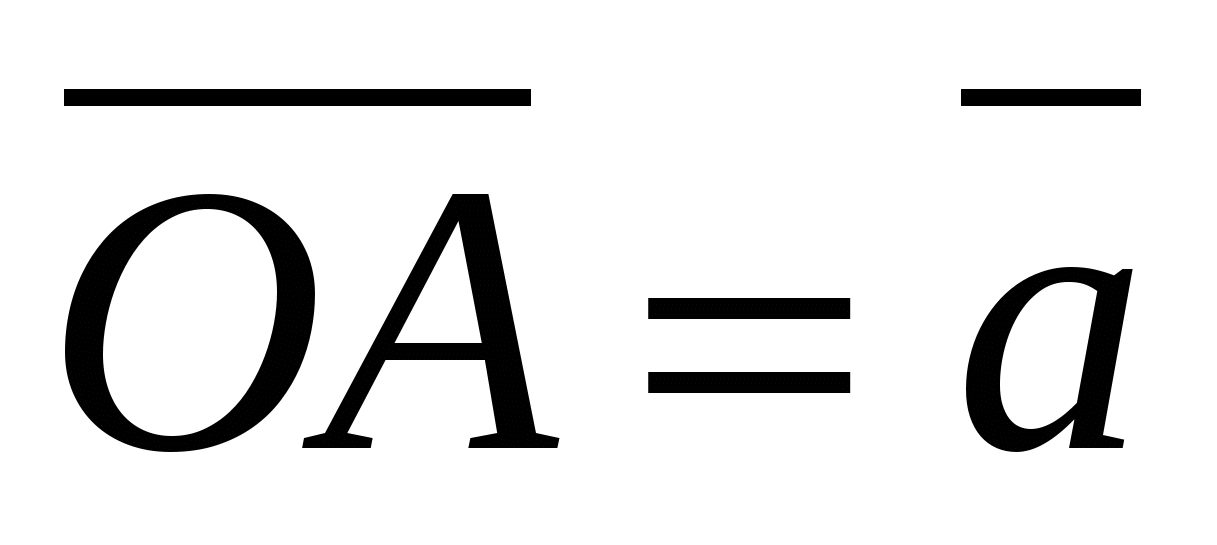 , da fra likestillingen
, da fra likestillingen 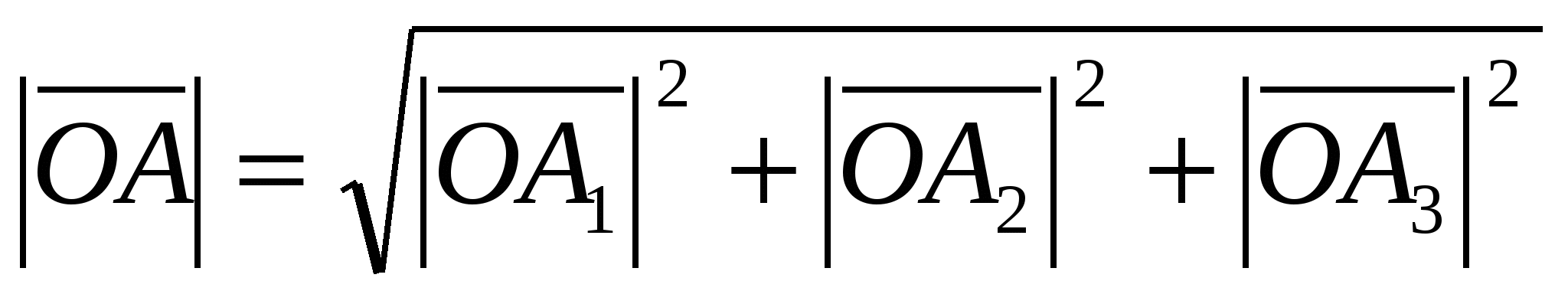 vi får formelen:.
vi får formelen:.
V) Avstanden mellom to punkter.
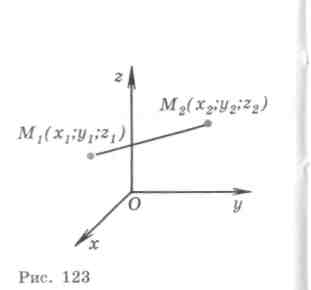 La oss vurdere to vilkårlige poeng: punkt
La oss vurdere to vilkårlige poeng: punkt  og periode
og periode 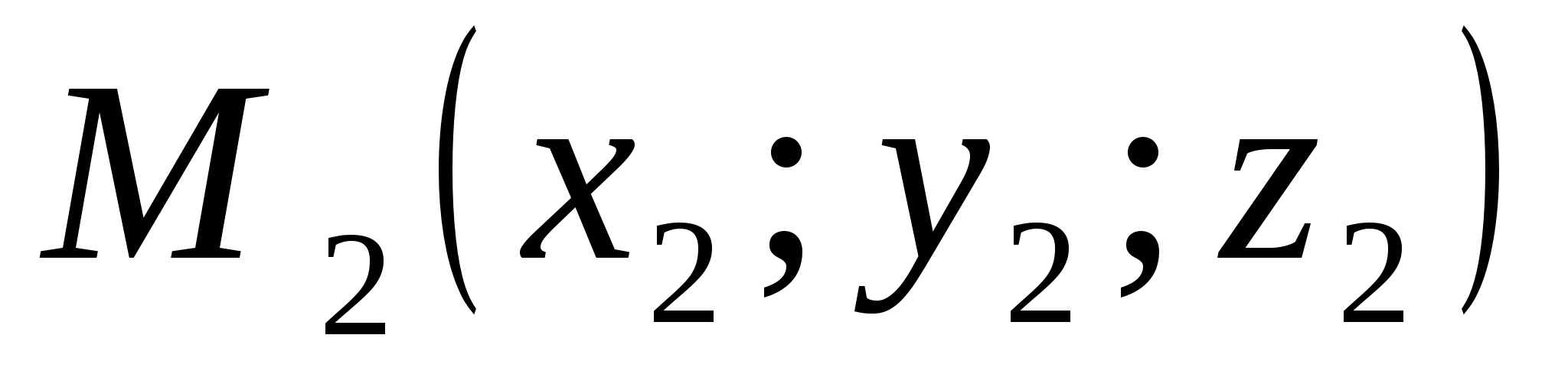 . La oss uttrykke avstandend
mellom punktene
. La oss uttrykke avstandend
mellom punktene 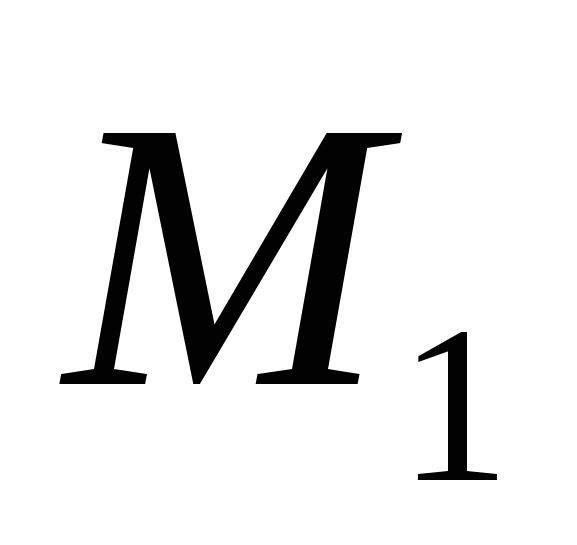 Og
Og 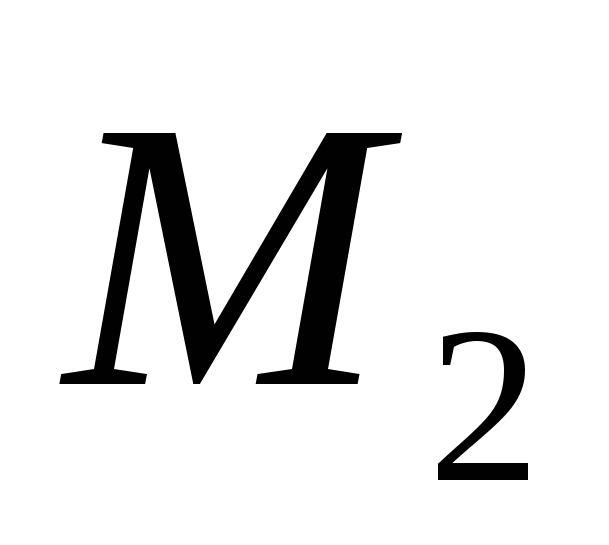 gjennom deres koordinater.
gjennom deres koordinater.
Tenk på vektoren hvor .
Men 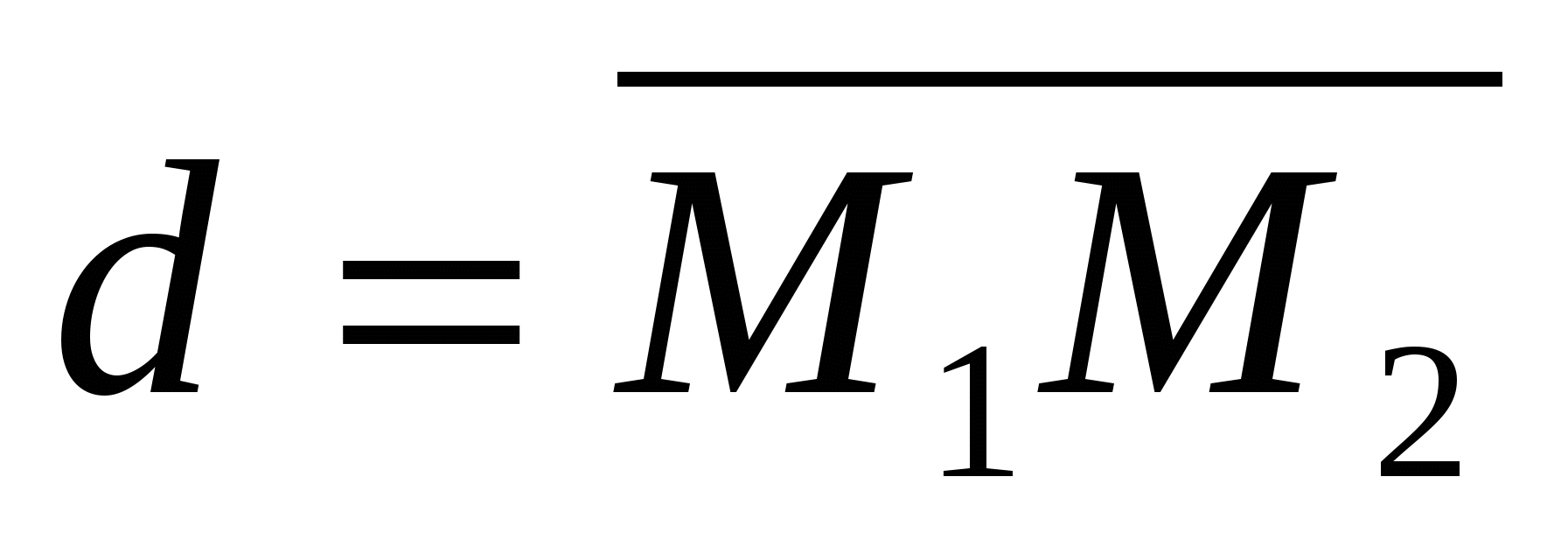 . Dermed,avstand mellom punktene
. Dermed,avstand mellom punktene 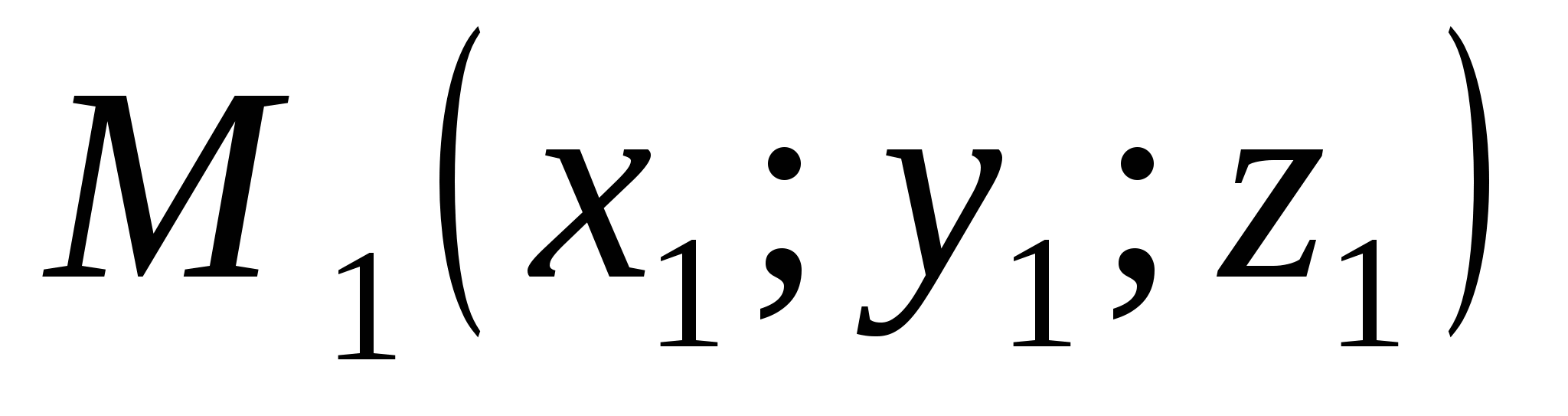 Og
Og 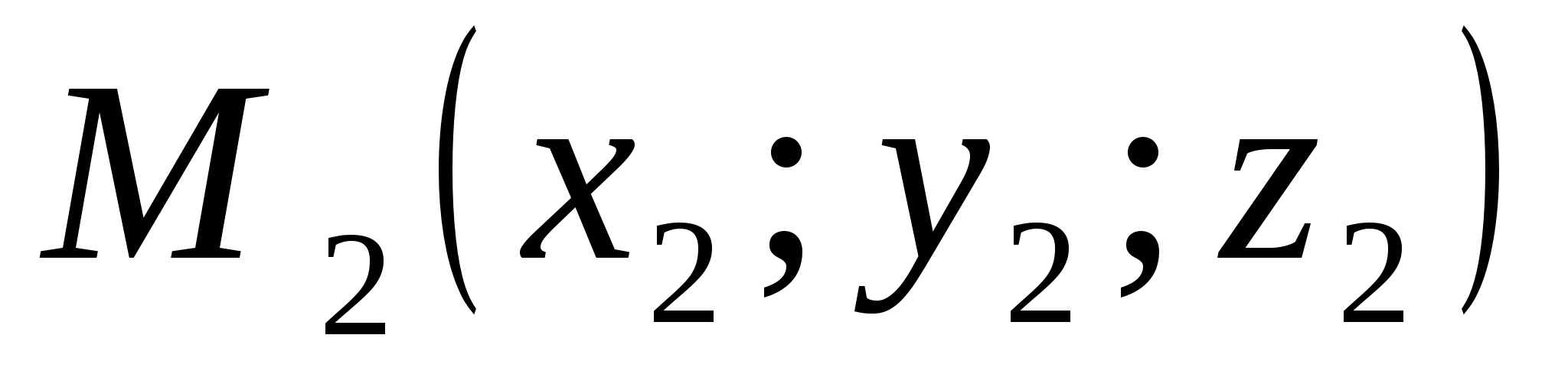
beregnet med formelen .
6. Punktprodukt av vektorer og beregning av vinkelen mellom vektorer gjennom deres koordinater.
1) Punktprodukt av vektorer
Skalarproduktet av to vektorer er produktet av deres lengder og cosinus til vinkelen mellom dem.
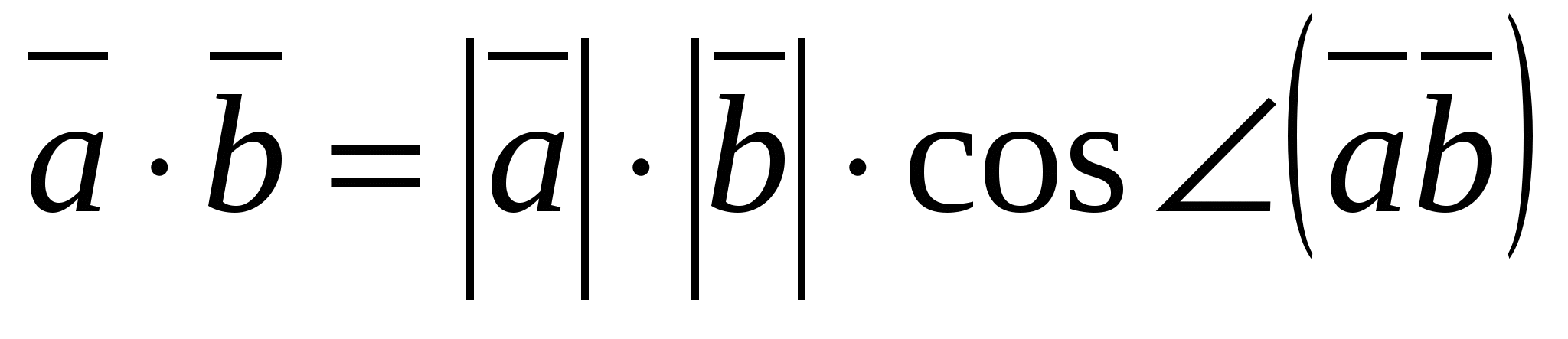
de.
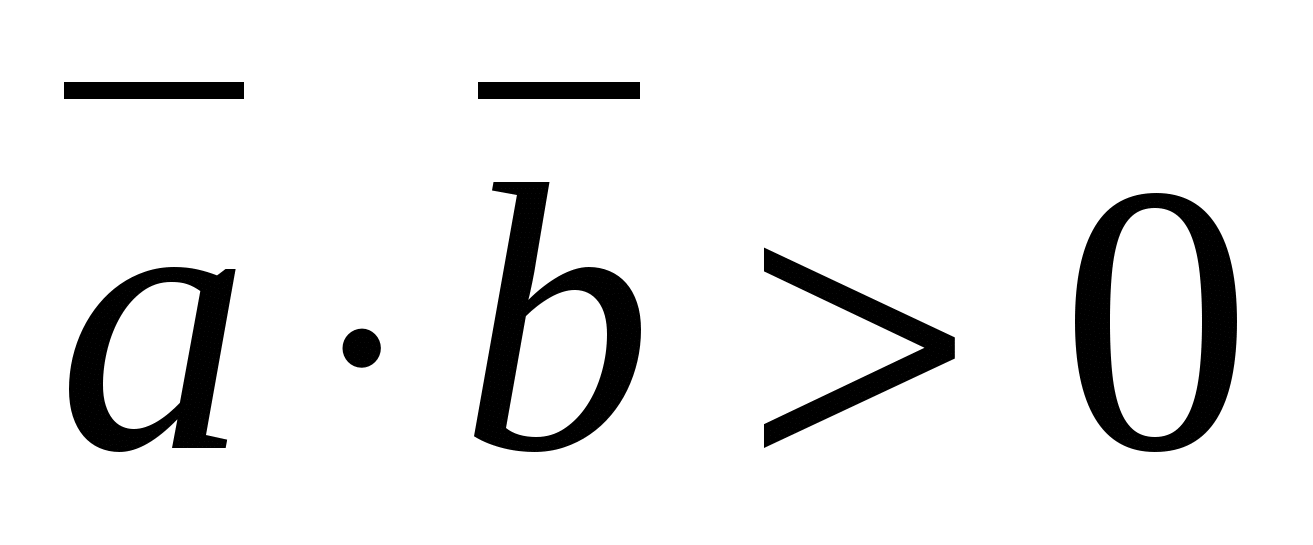

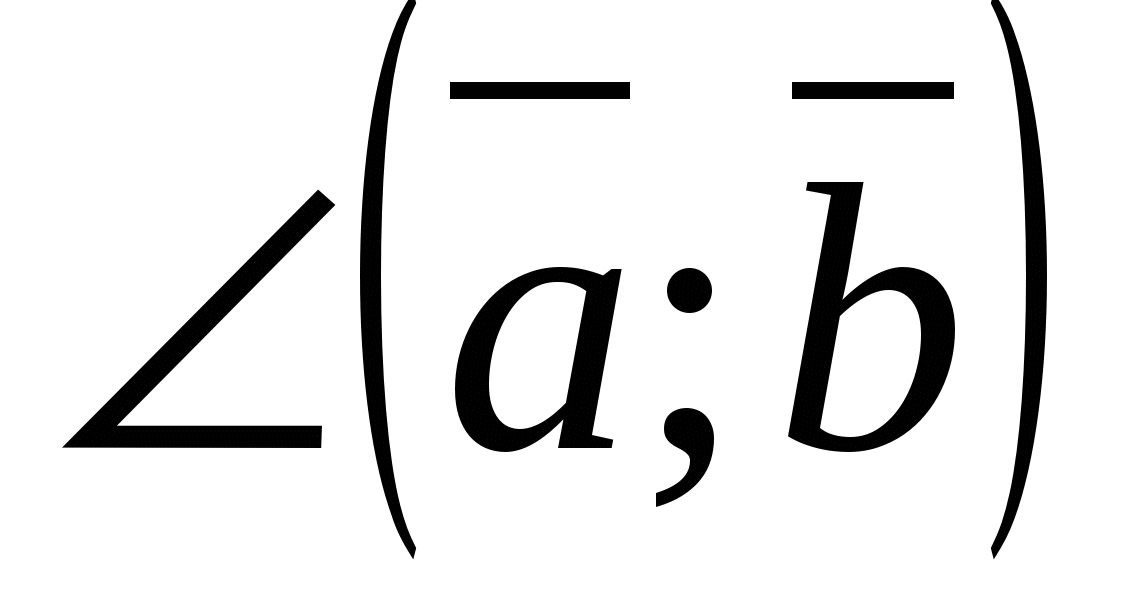 - krydret.
- krydret.
Skalarproduktet av vektorer som ikke er null er negativt hvis og bare hvis vinkelen mellom vektorene er stump,
de.
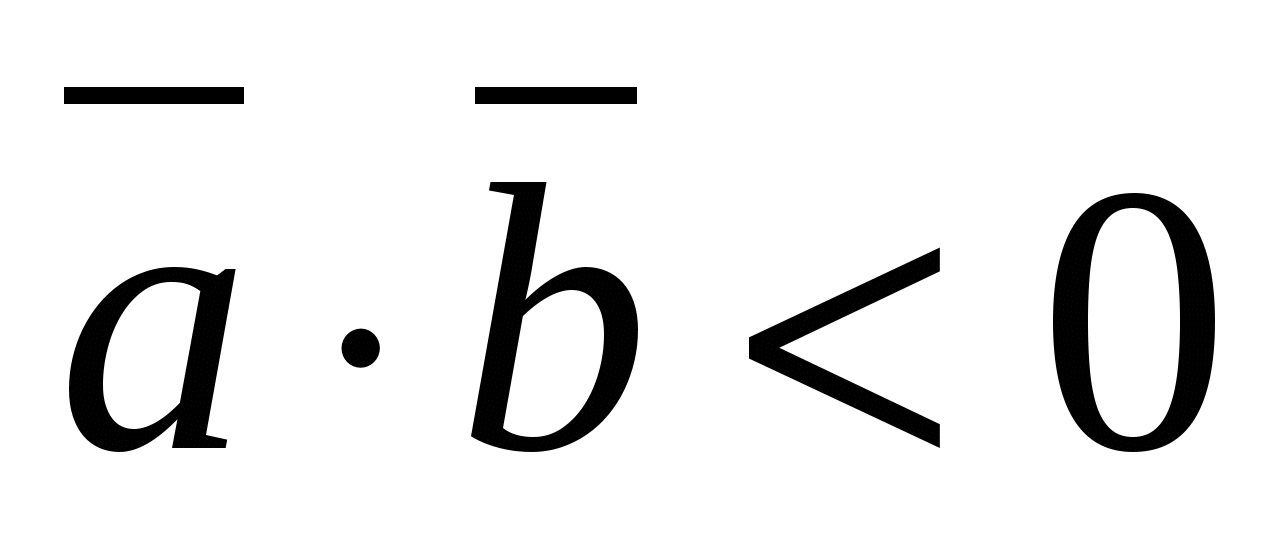

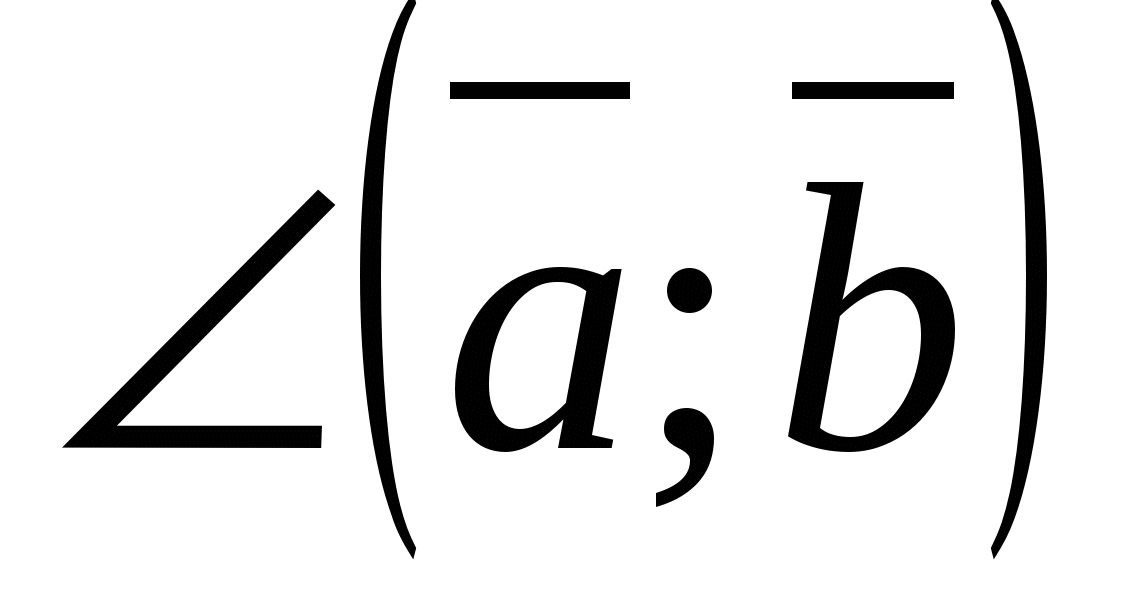 - sløv.
- sløv.
For alle vektorer,  ,
, 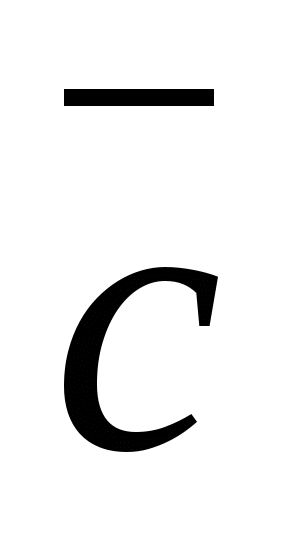 , og et hvilket som helst nummerk
likhetene er gyldige:
, og et hvilket som helst nummerk
likhetene er gyldige:
1. 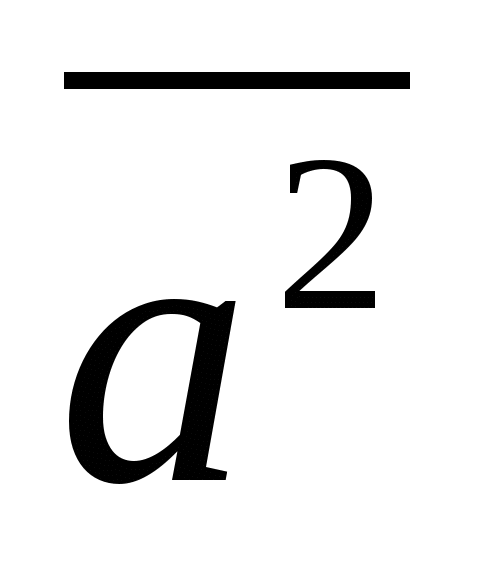
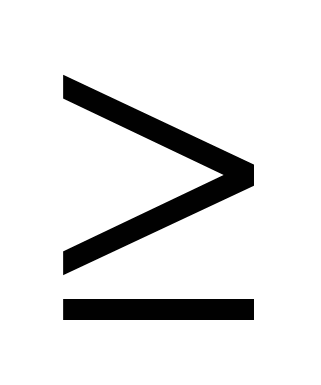 0, og
0, og 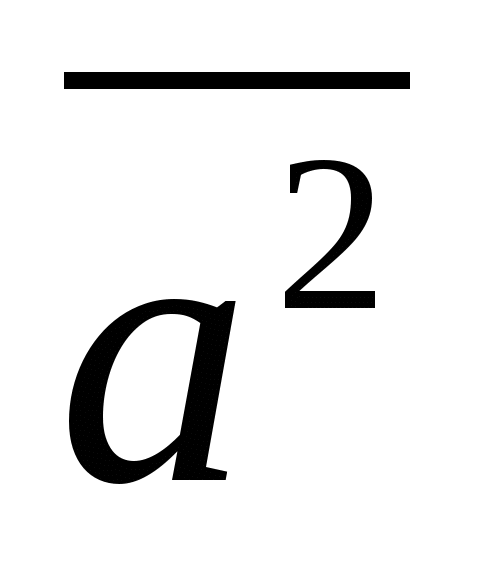 >0 kl
>0 kl 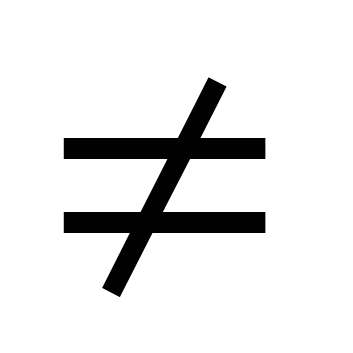 0.
0.
2. 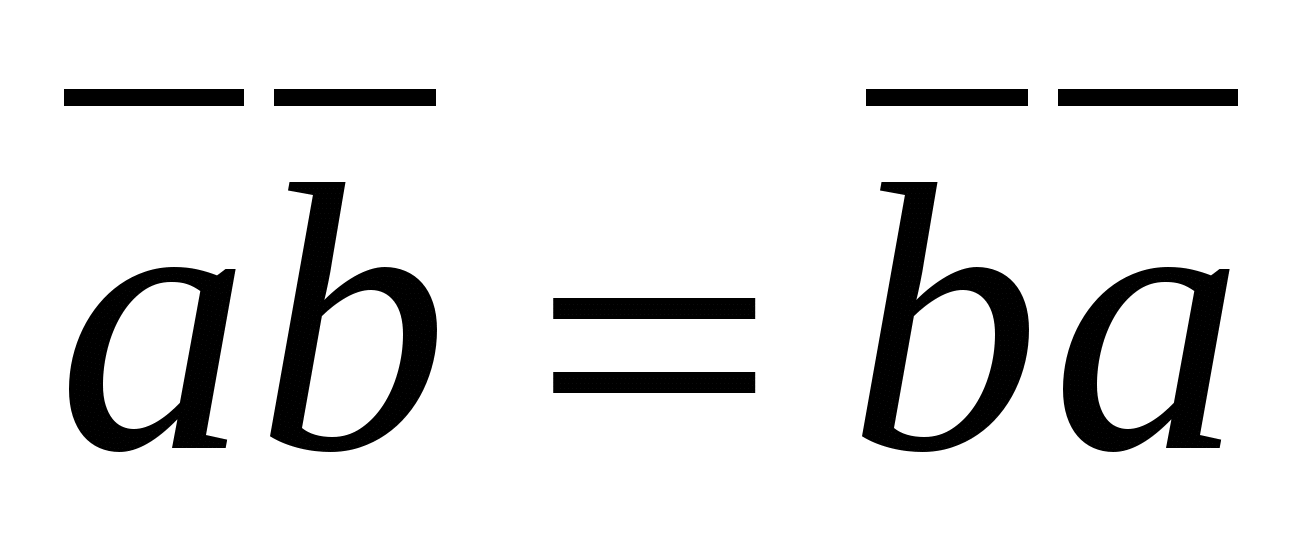 (overdragelsesloven).
(overdragelsesloven).
3.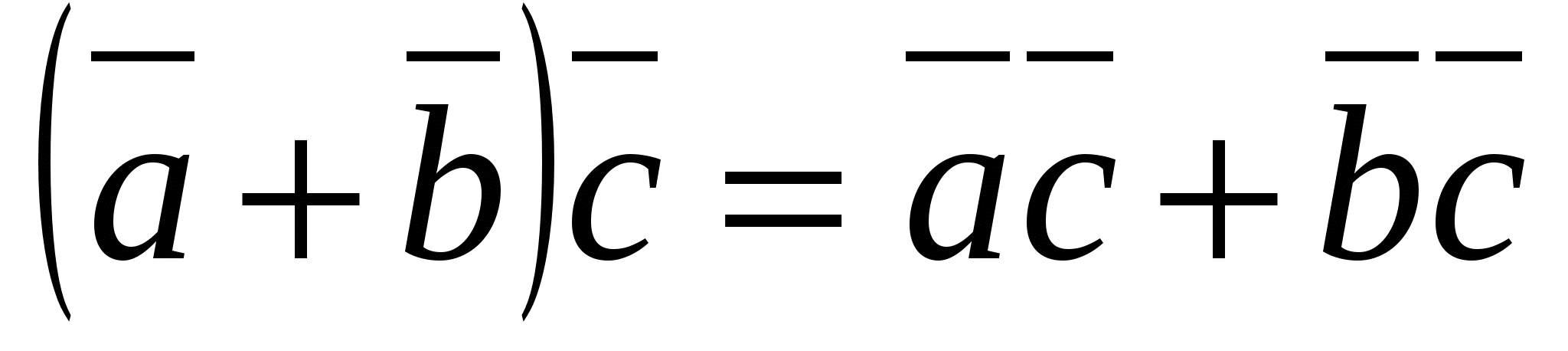 (fordelingslov).
(fordelingslov).
4. 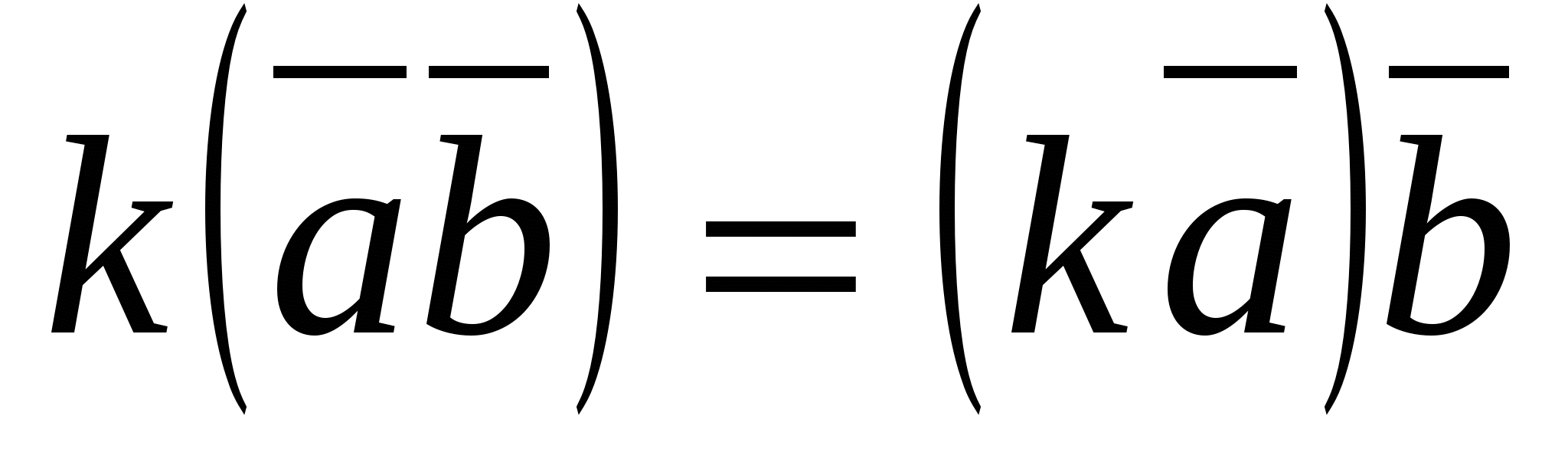 (kombinasjonsrett).
(kombinasjonsrett).
2) Beregning av vinkelen mellom vektorer ved hjelp av deres koordinater.
Cosinus av vinkel  mellom vektorer som ikke er null
mellom vektorer som ikke er null 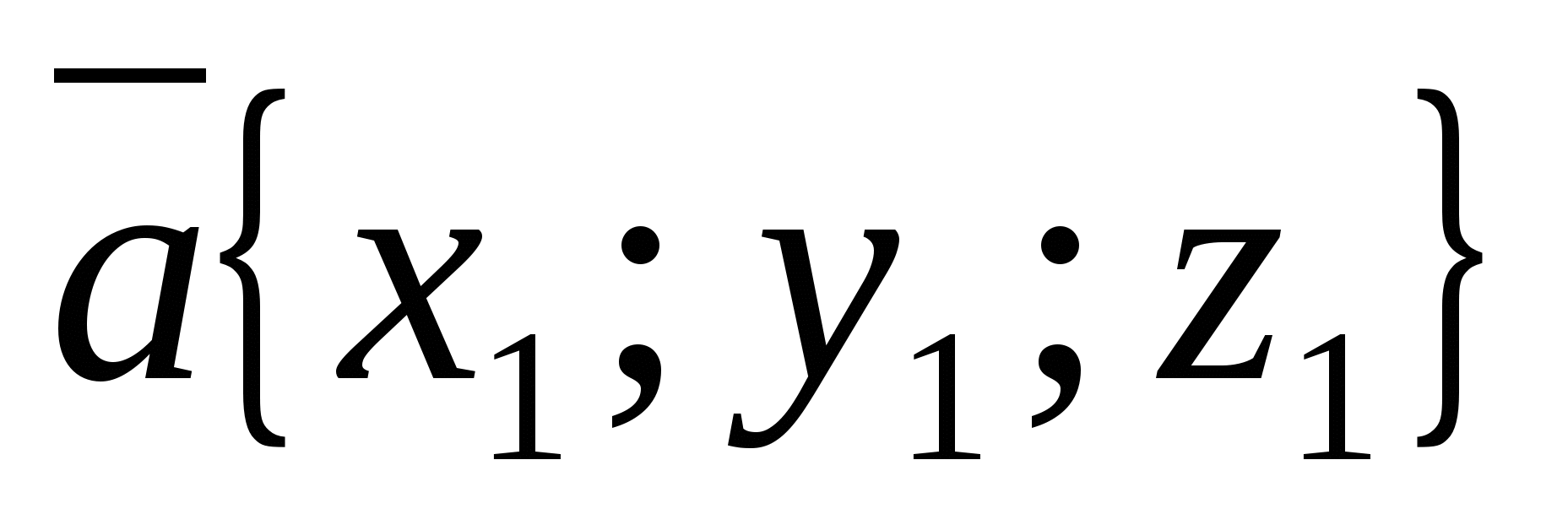 Og
Og 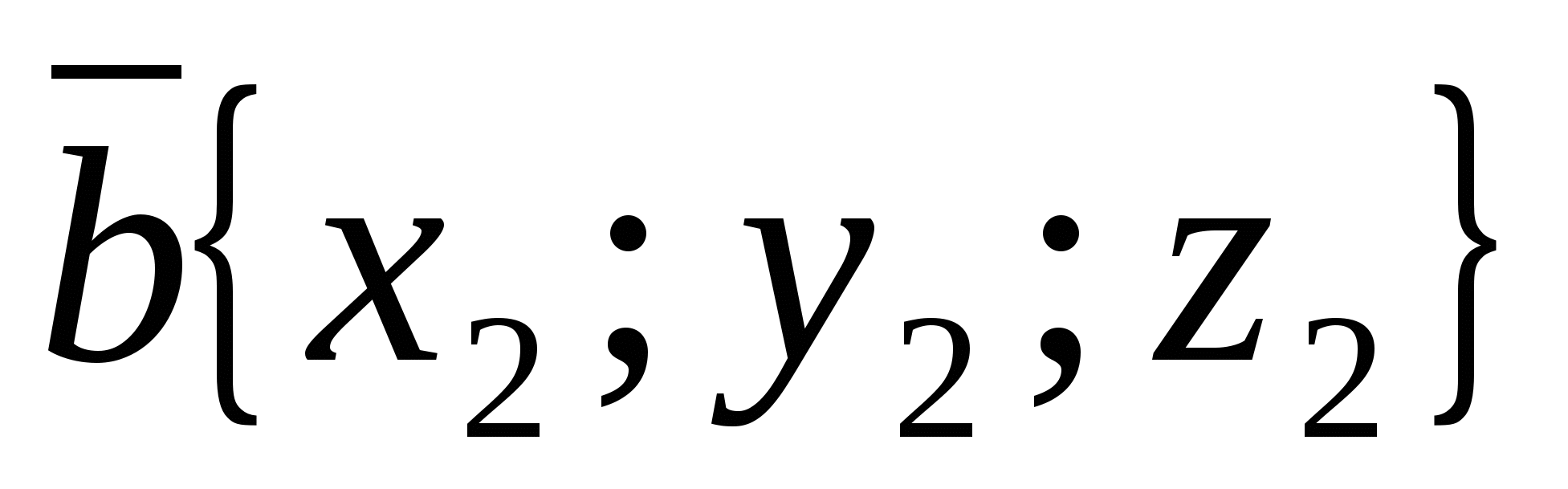 beregnet med formelen
beregnet med formelen
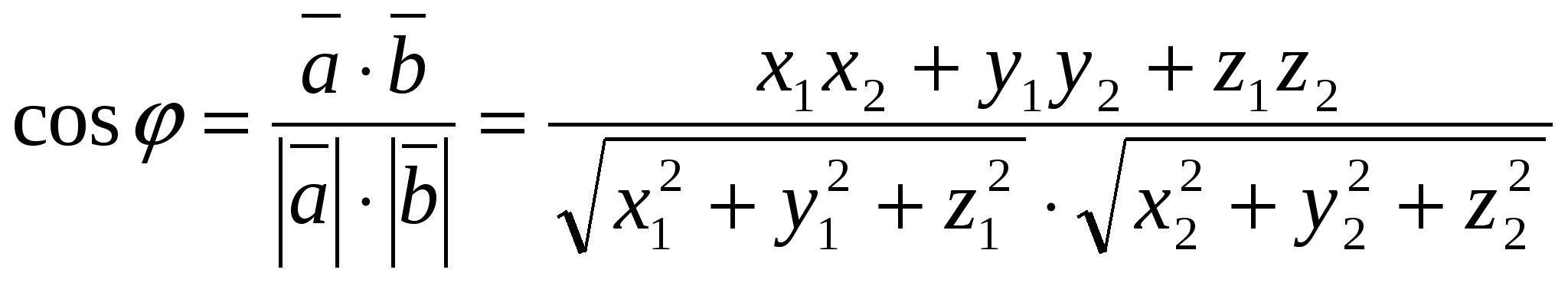 ,
,
Hvor 
7. Beregning av vinkler mellom rette linjer og plan.
1) Vinkel mellom rette linjer.
For å løse dette problemet introduserer vi konseptet med en retningsvektor av en rett linje.
Definisjon.
En vektor som ikke er null kalles en retningsvektor for en linje a hvis den ligger enten på en linje a eller på en linje parallelt med a.
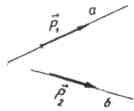 Eksempel
Eksempel
Vektorer 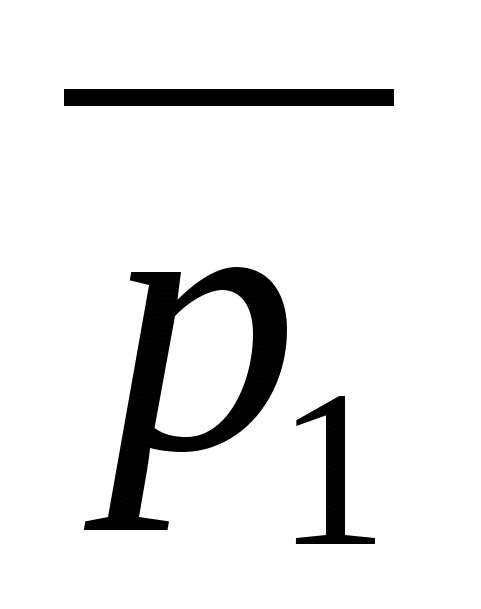 Og
Og  rette føringeren
Og b
, henholdsvis.
rette føringeren
Og b
, henholdsvis.
Definisjon.
Vinkelen mellom linjer er vinkelen mellom retningsvektorene til disse linjene.
Vinkel mellom rette linjeren
Og b
lik vinkel mellom retningsvektorene til de rette linjene, 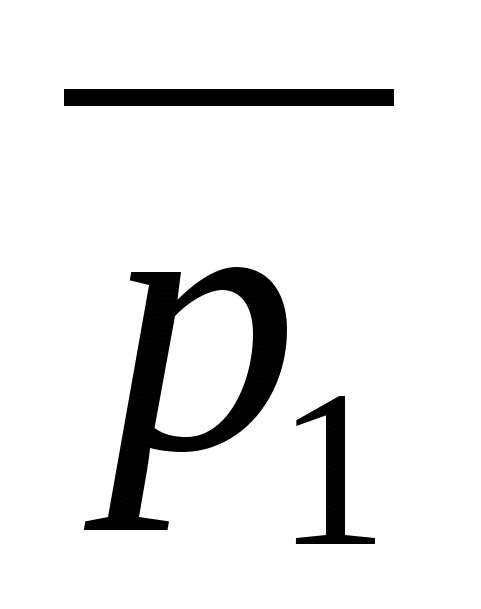 Og
Og 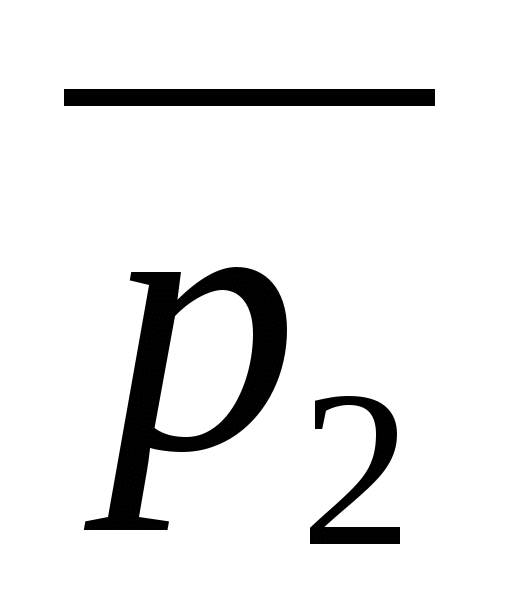 .
.
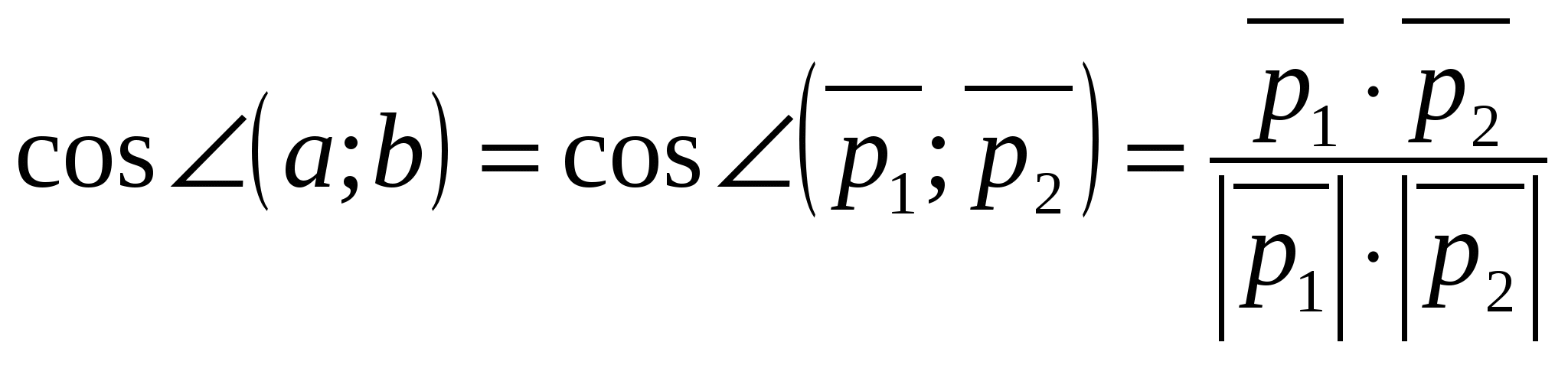 .
.
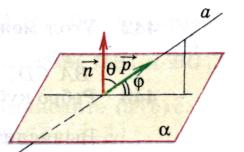
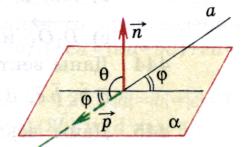
2). Vinkel mellom en rett linje og et plan.
Definisjon.
Vinkelen mellom en linje og et plan er vinkelen mellom retningsvektoren til en gitt linje og en vektor som ikke er null vinkelrett på planet(normal).
La 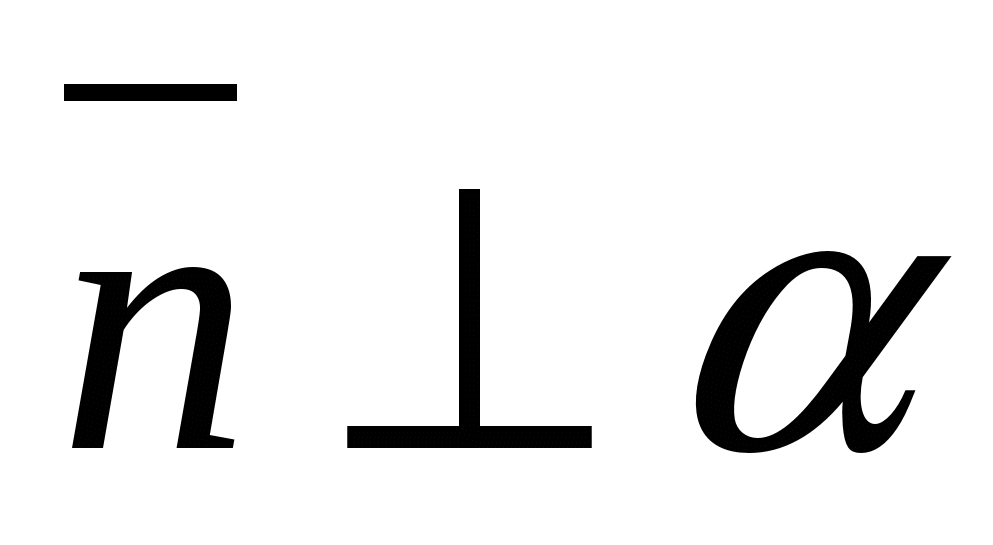 , (
, (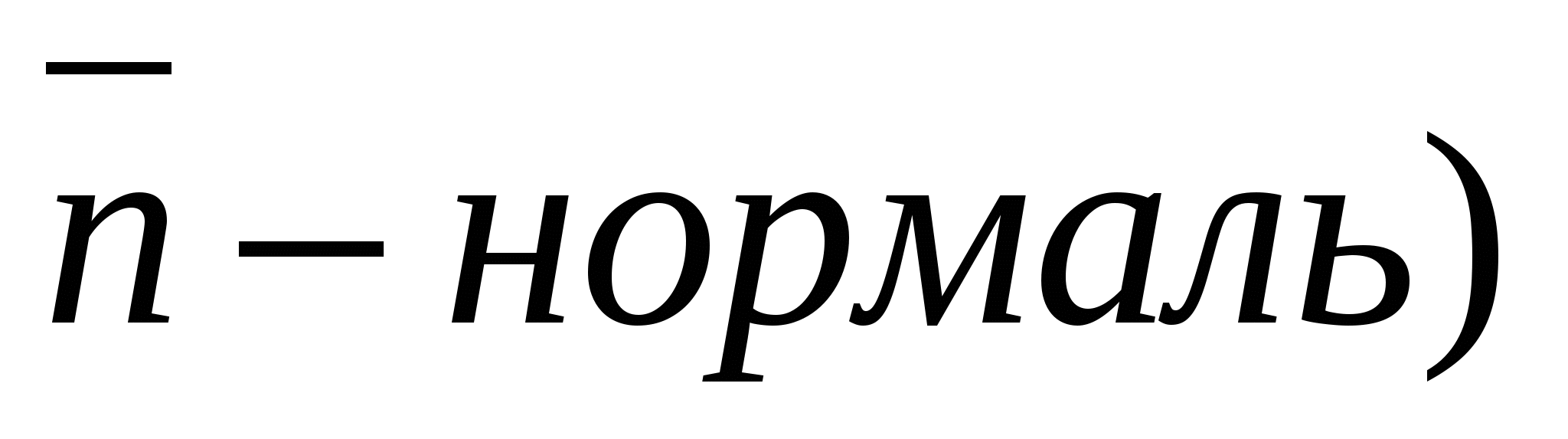
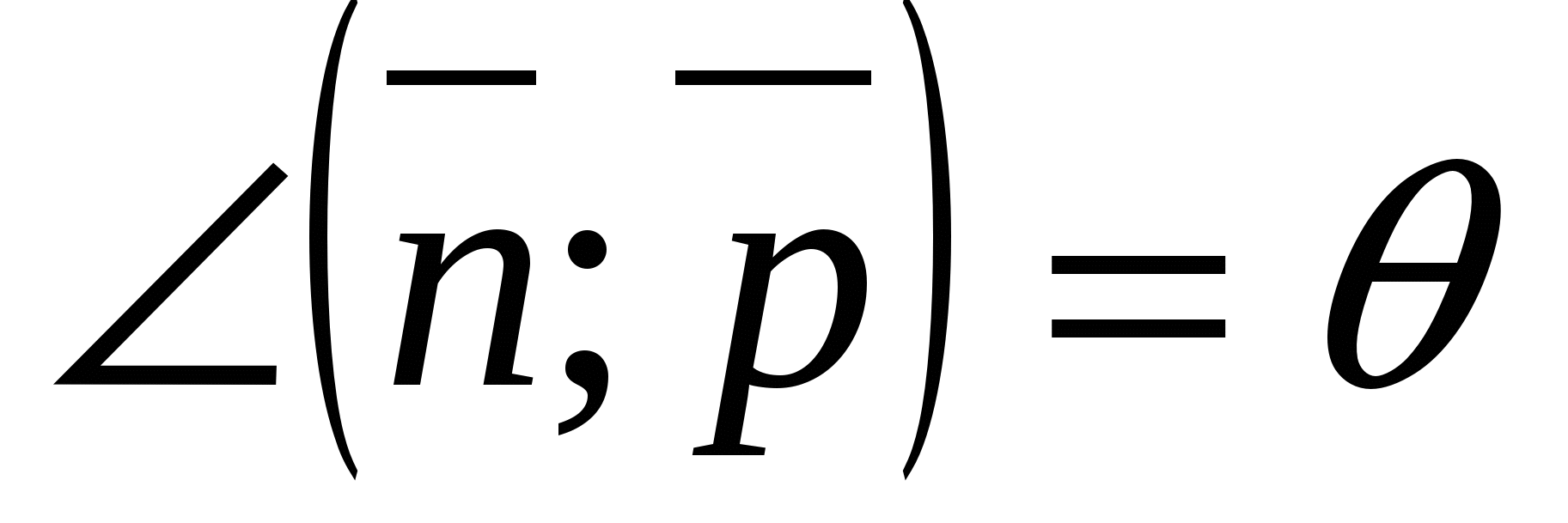 , A
, A 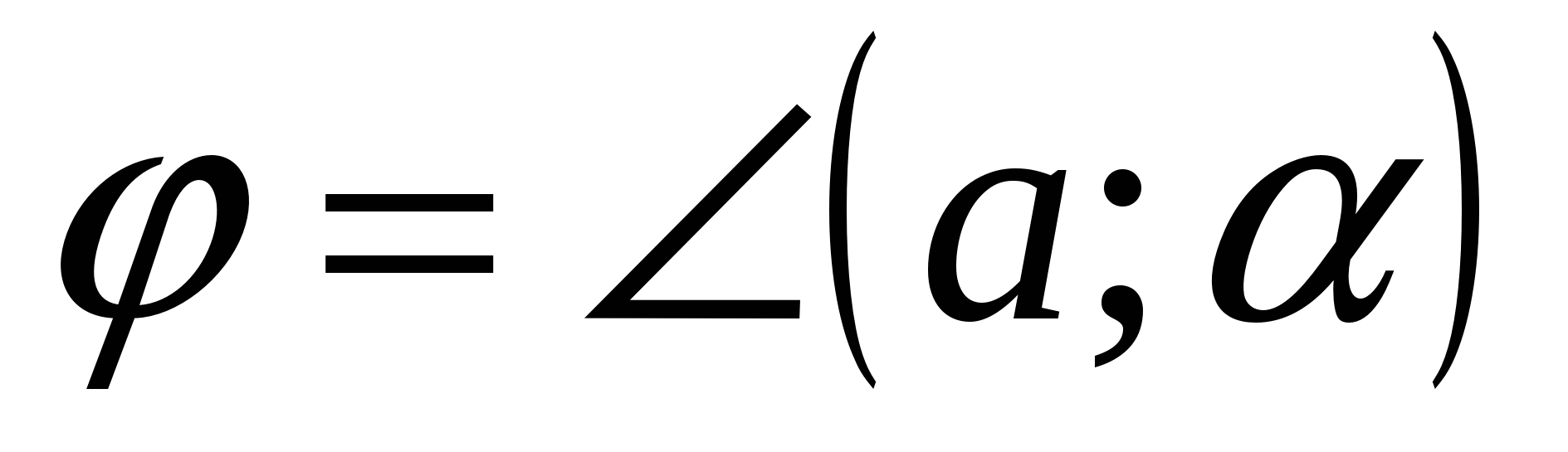 - ønsket vinkel (
- ønsket vinkel ( 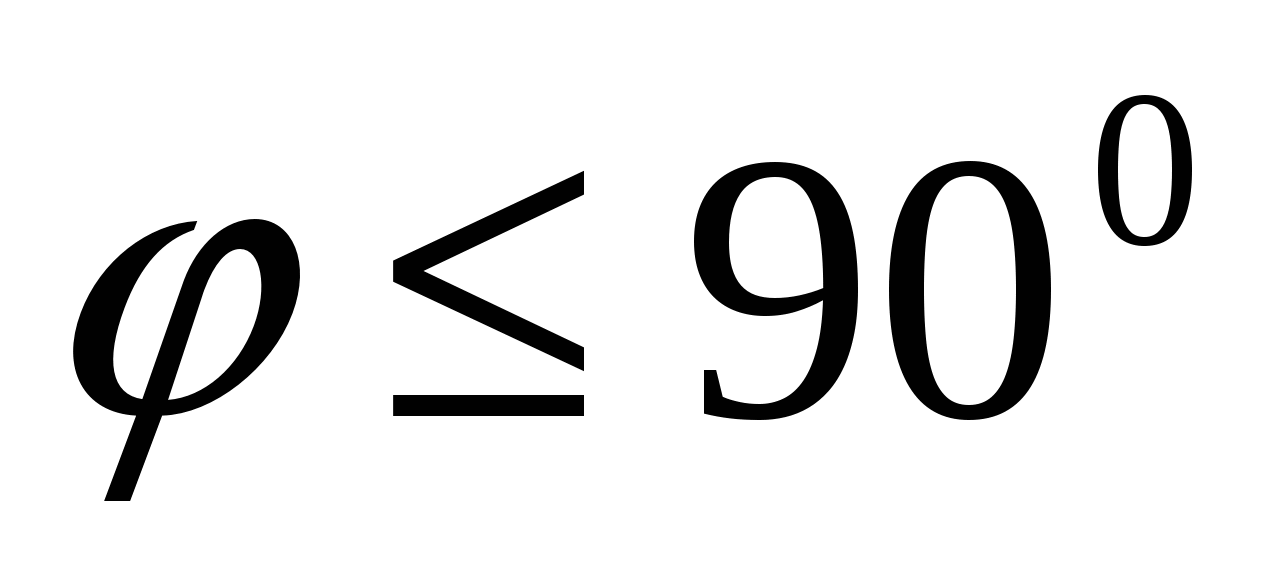 ).
).
Deretter

Midler  .
.
Kapittel 3.
Anvendelse av koordinatmetoden for å løse stereometriske problemer.
Problem.1
Ved bunnen av MABC-pyramiden ligger høyre trekant ABC. 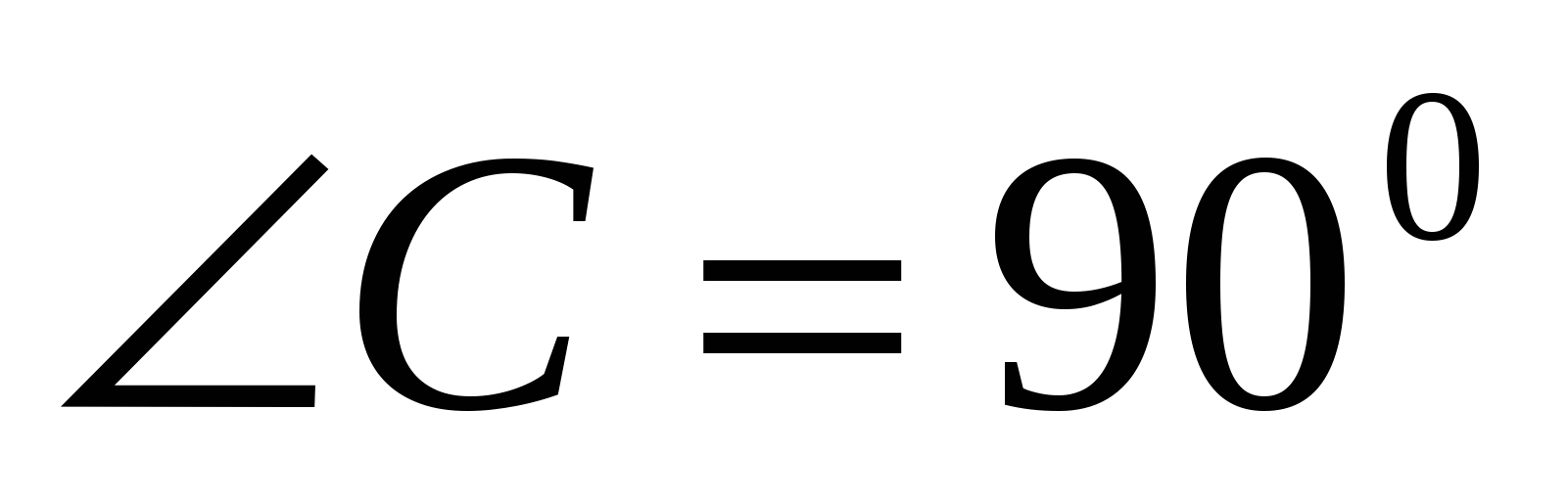 ,
A.C.=3,
B.C.=5. Edge AM er vinkelrett på AC, AM=4,
,
A.C.=3,
B.C.=5. Edge AM er vinkelrett på AC, AM=4, 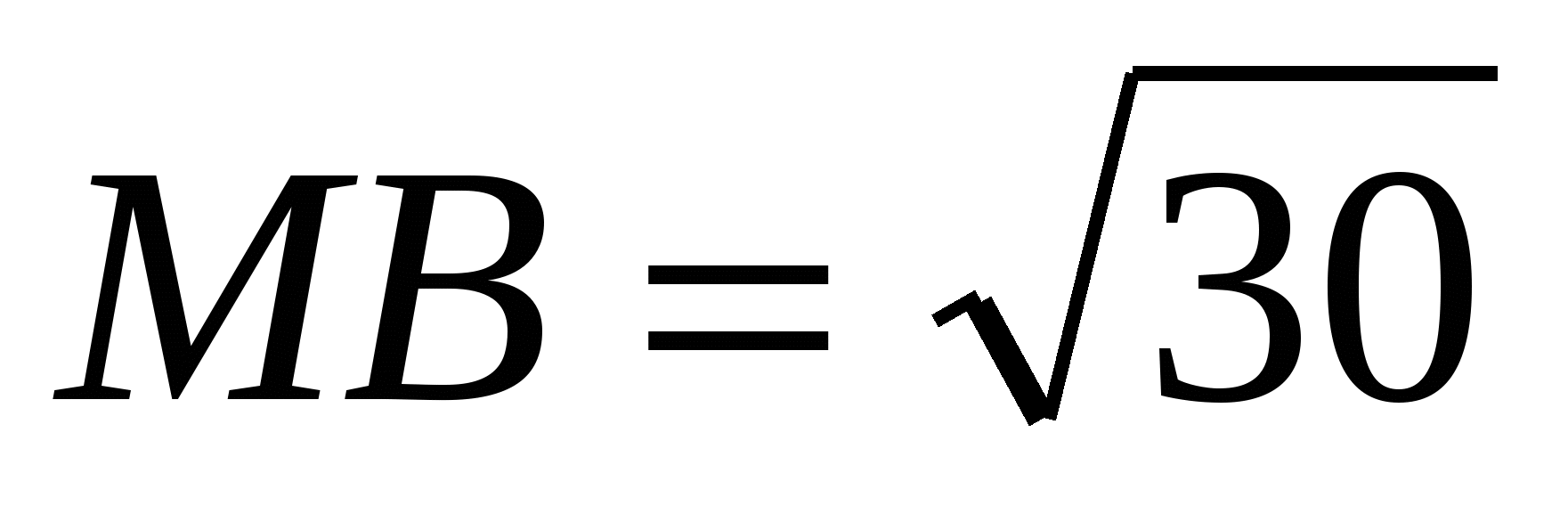 . Finn volumet til pyramiden.
. Finn volumet til pyramiden.
R 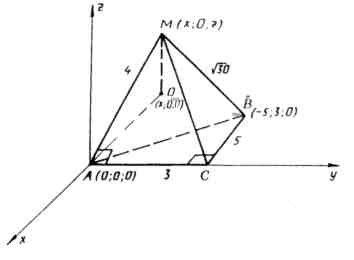 beslutning.
beslutning.
1) La oss introdusere et rektangulært koordinatsystem med origo i punktet  . Akser
. Akser  la oss lede langs kantenAC, og flyet Åh
y
langs bunnen av pyramidenABC.
la oss lede langs kantenAC, og flyet Åh
y
langs bunnen av pyramidenABC.
I dette koordinatsystemet: 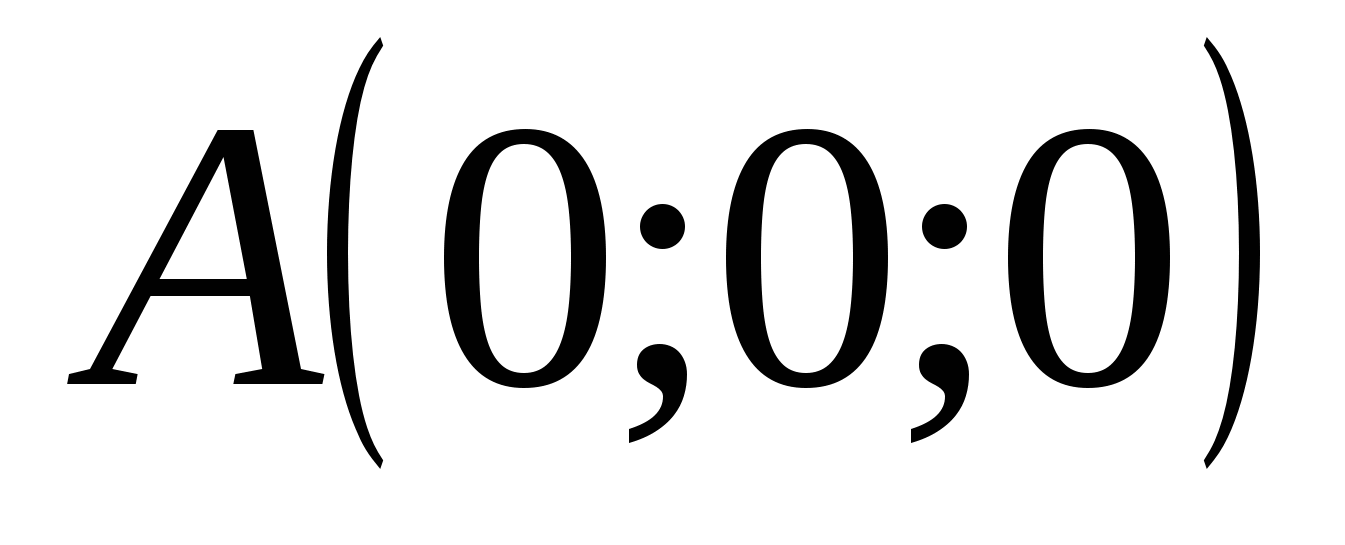 ,
, 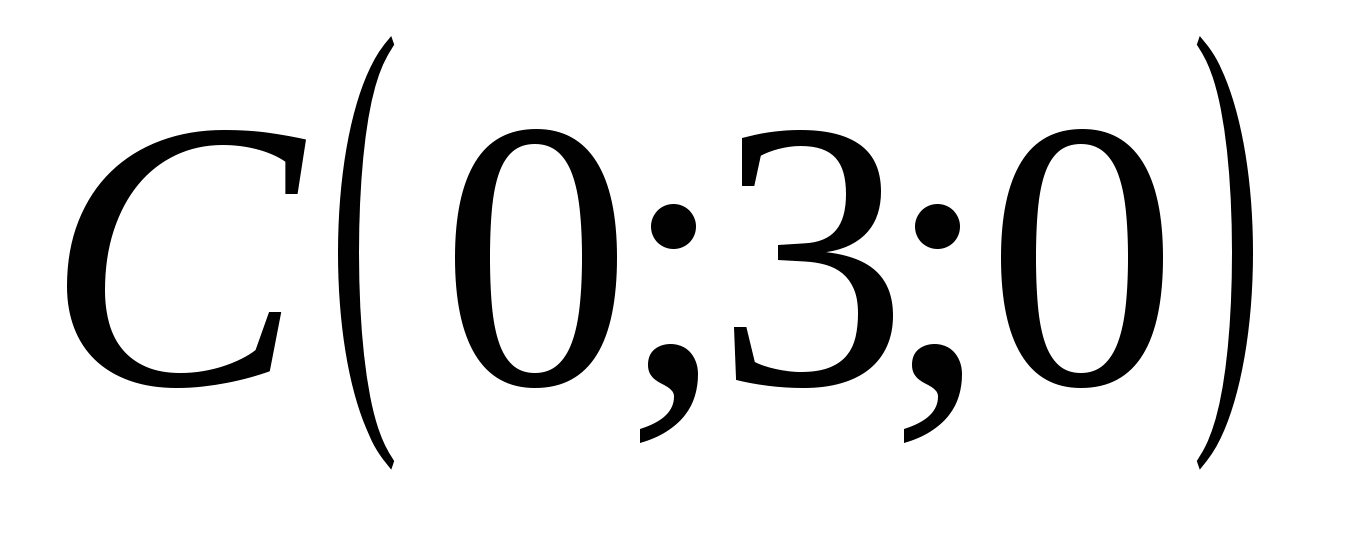 ,
, 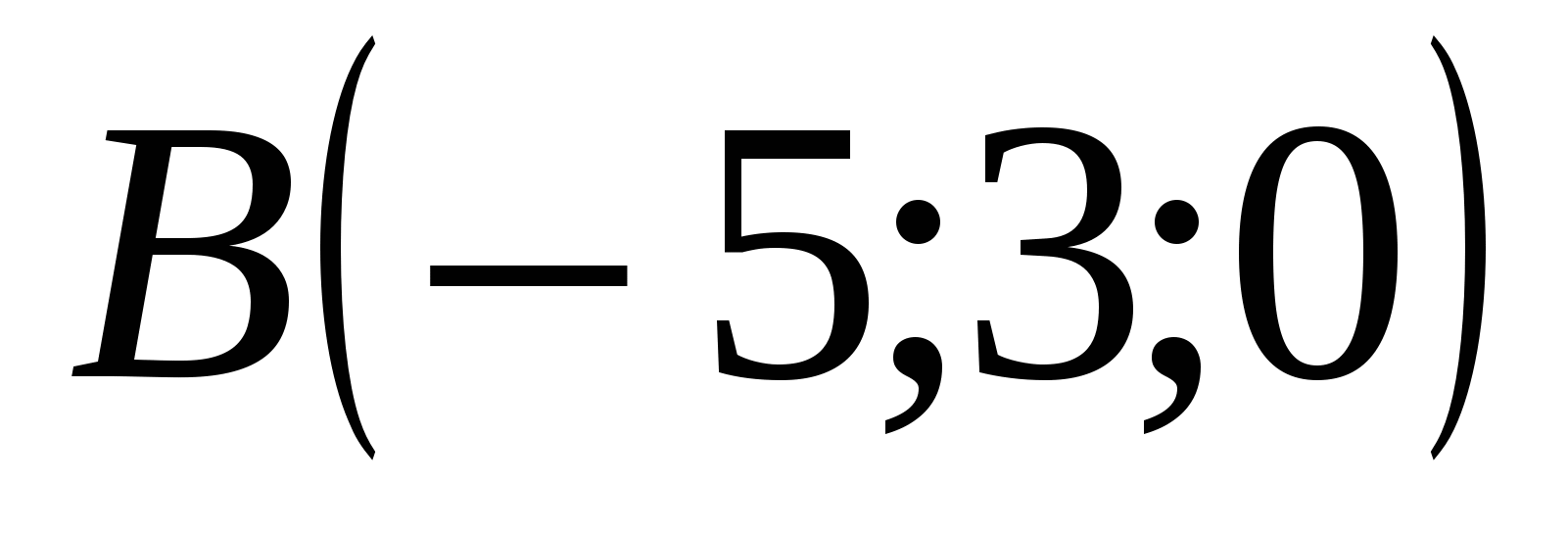 . Siden etter tilstand
. Siden etter tilstand 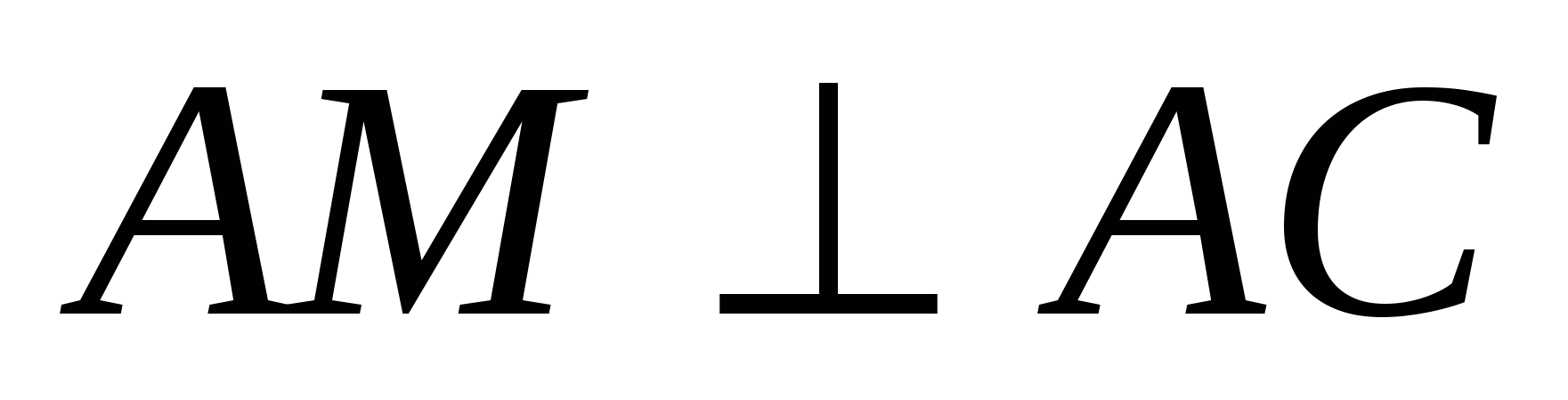 , da ligger punktet M i planetxz
og har koordinater
, da ligger punktet M i planetxz
og har koordinater
 .
.
2) 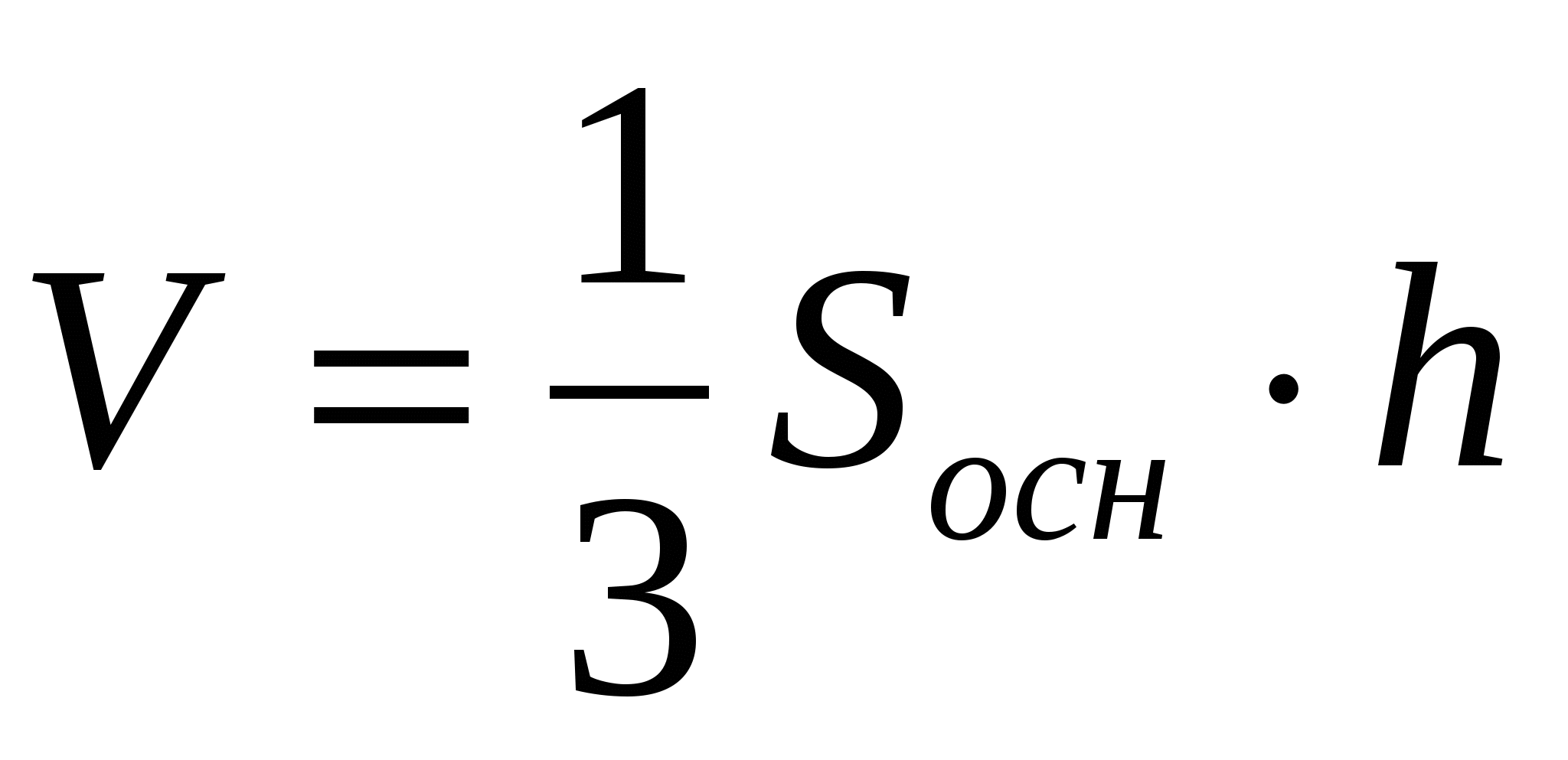 ,
, 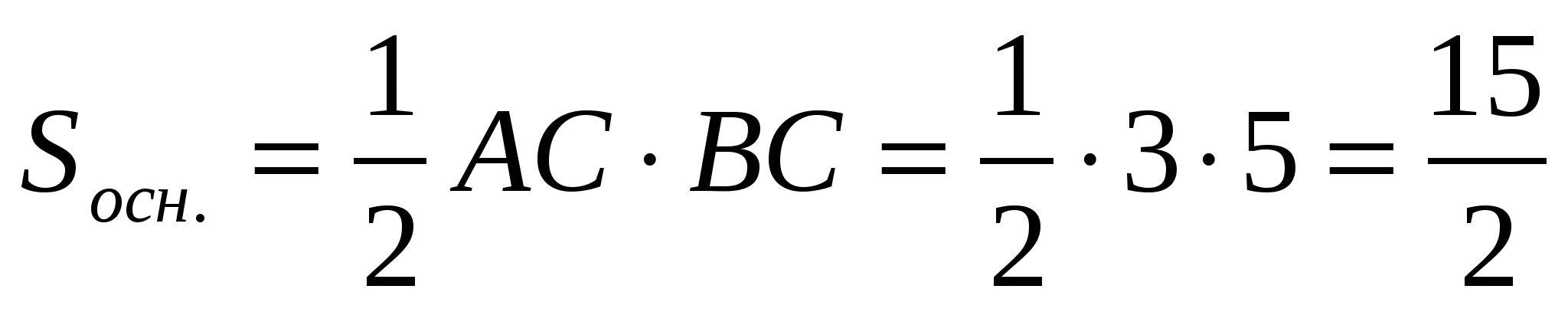 .
.
La oss finne høyden på pyramiden. La oss gå fra poengetM vinkelrett M
D
til flyet (ABC),
Deretter  , fordi
, fordi 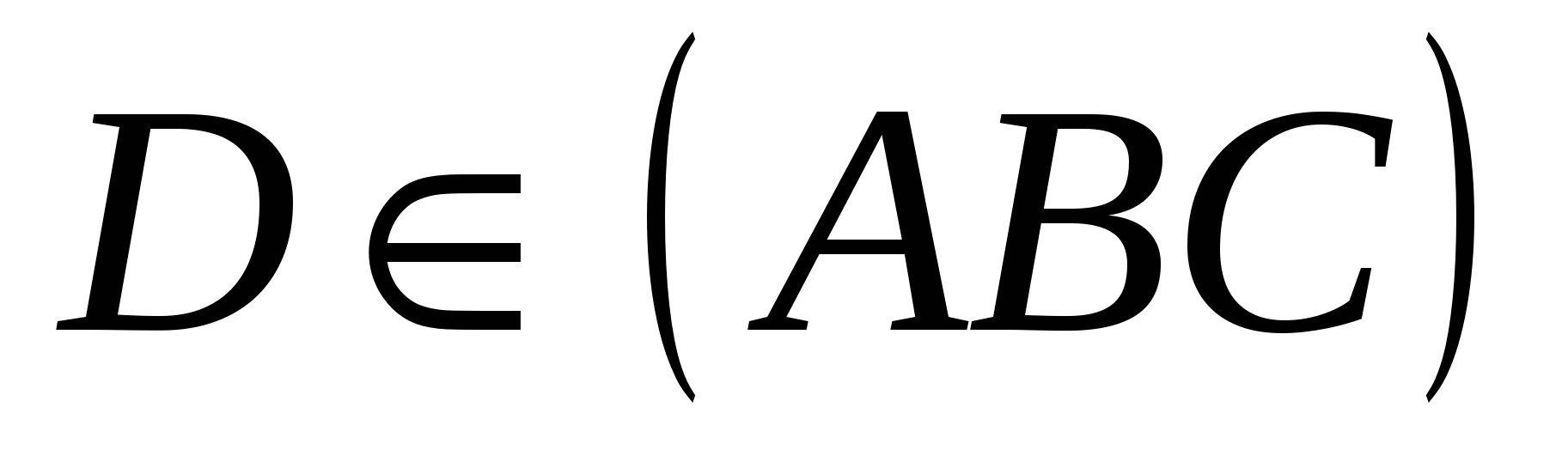 . Derfor,
. Derfor,  og avstand mellom punkteneM Og Dlik , fordi
og avstand mellom punkteneM Og Dlik , fordi 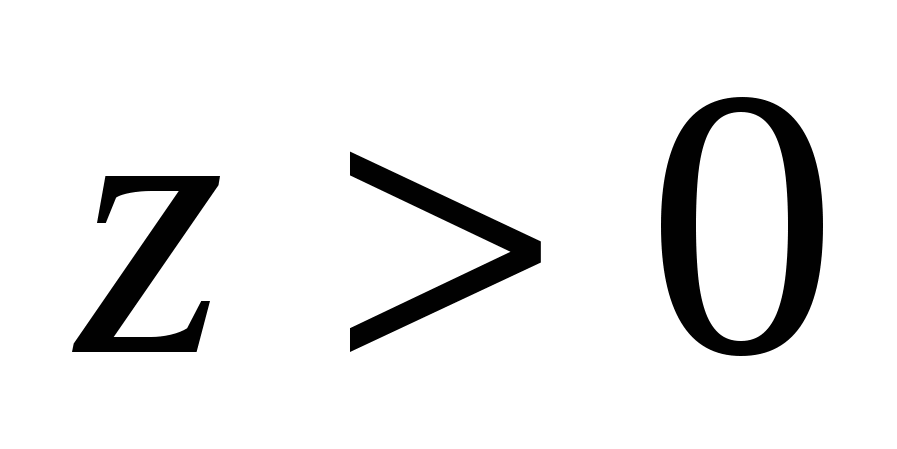 .
.
La oss finne koordinatverdienz
ved å bruke avstandene mellom punkter som inneholder gitt koordinat: 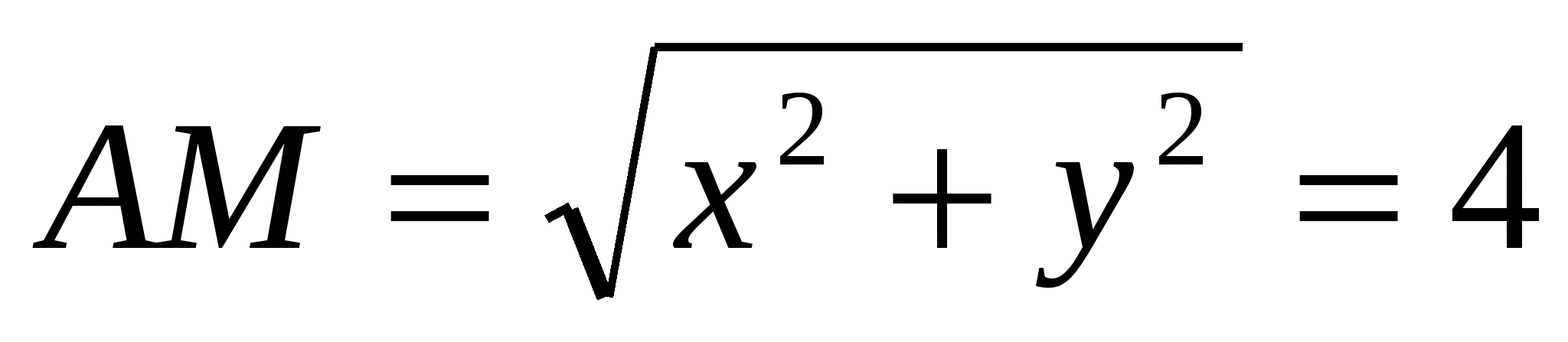 ,
,  . , dvs.
. , dvs. 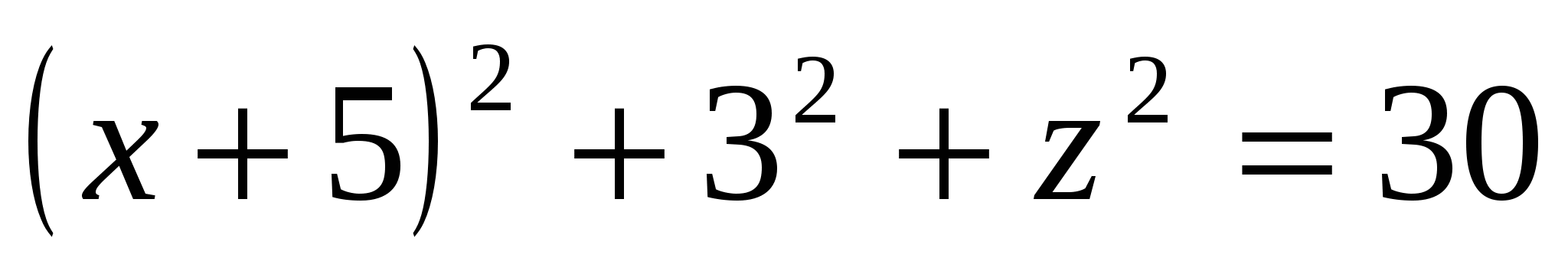 .
.
Vi har: 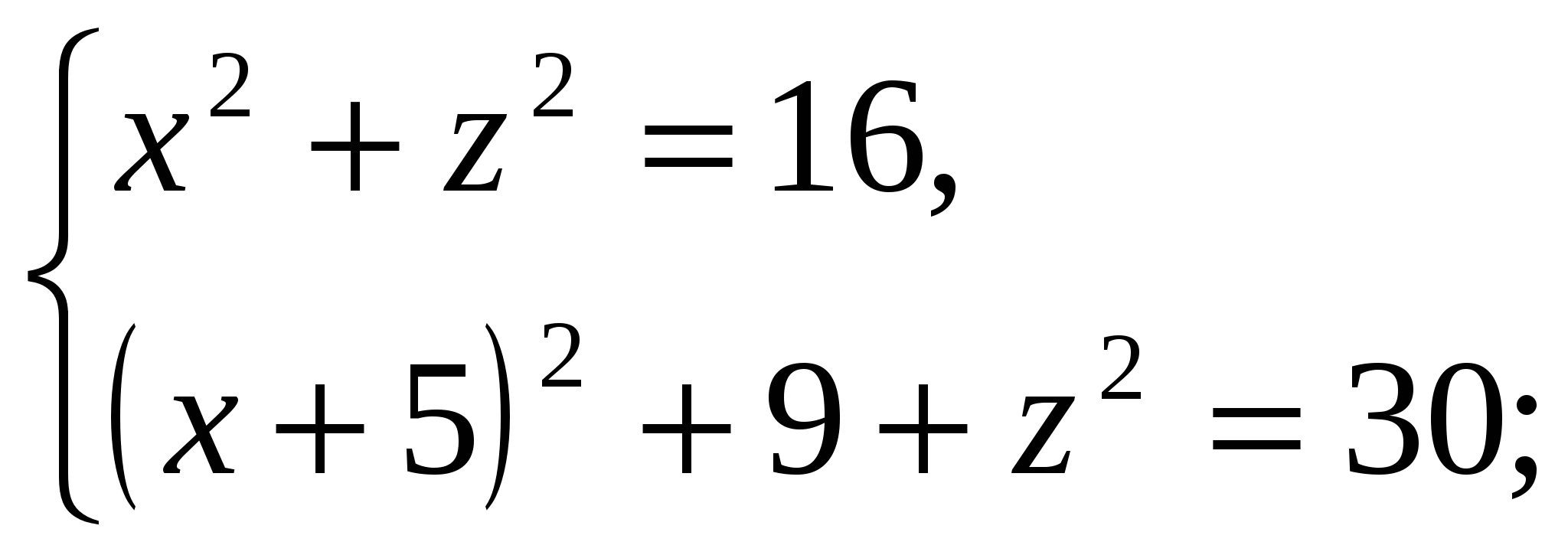
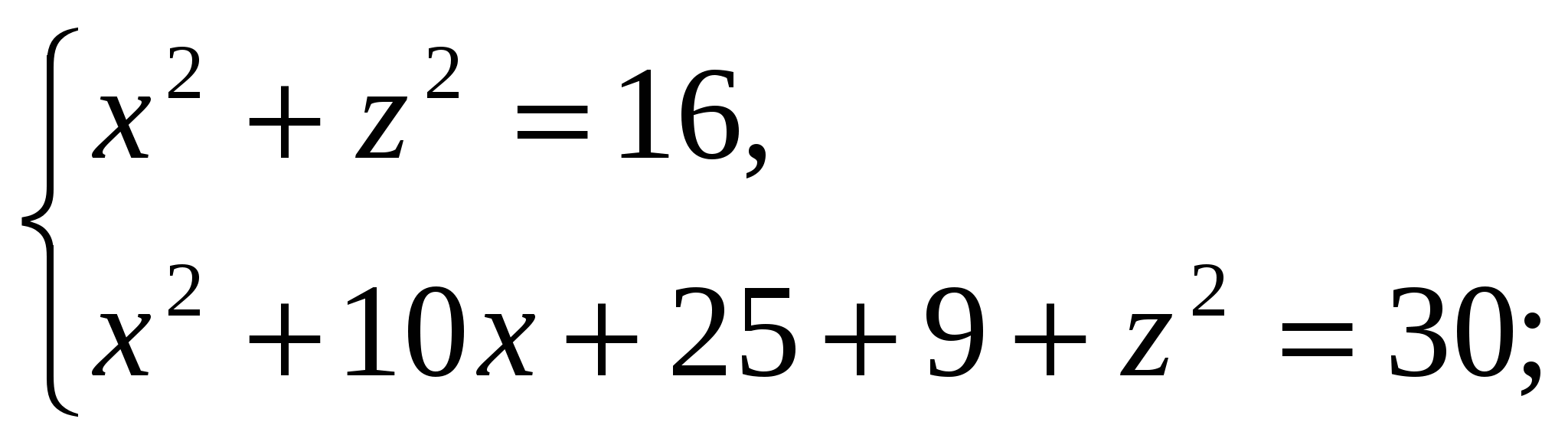
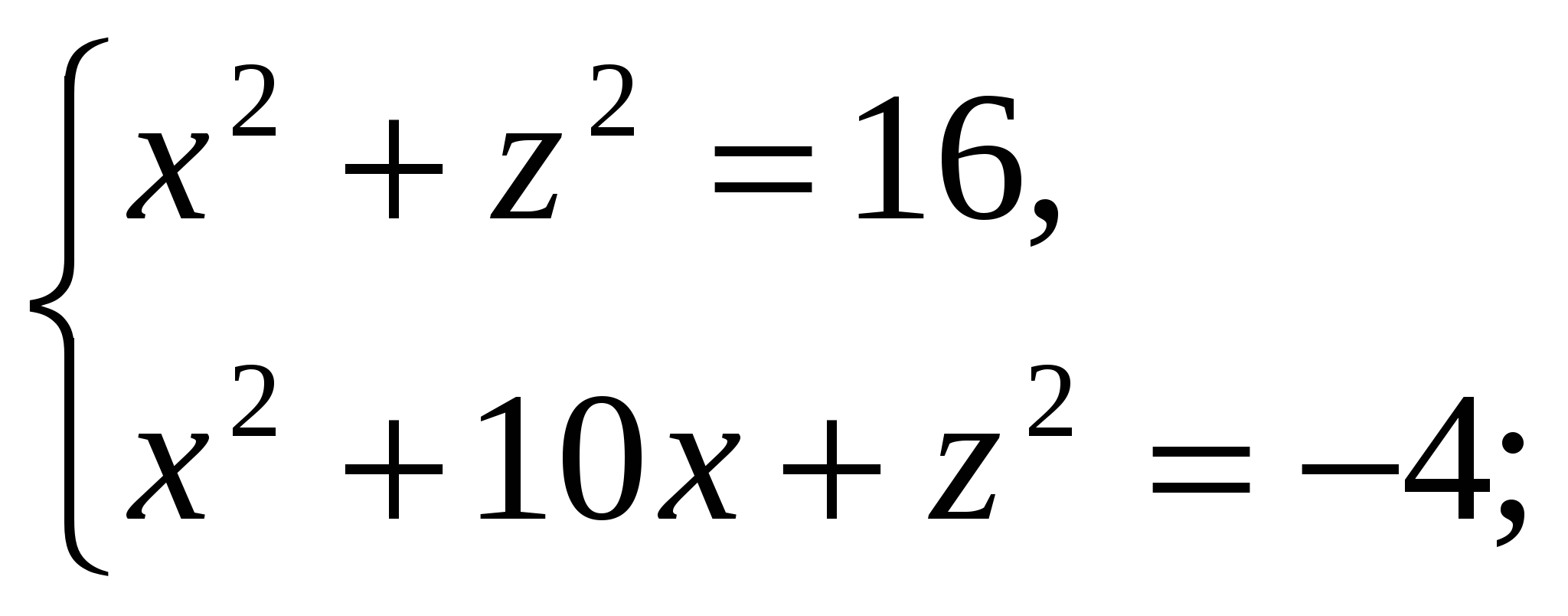
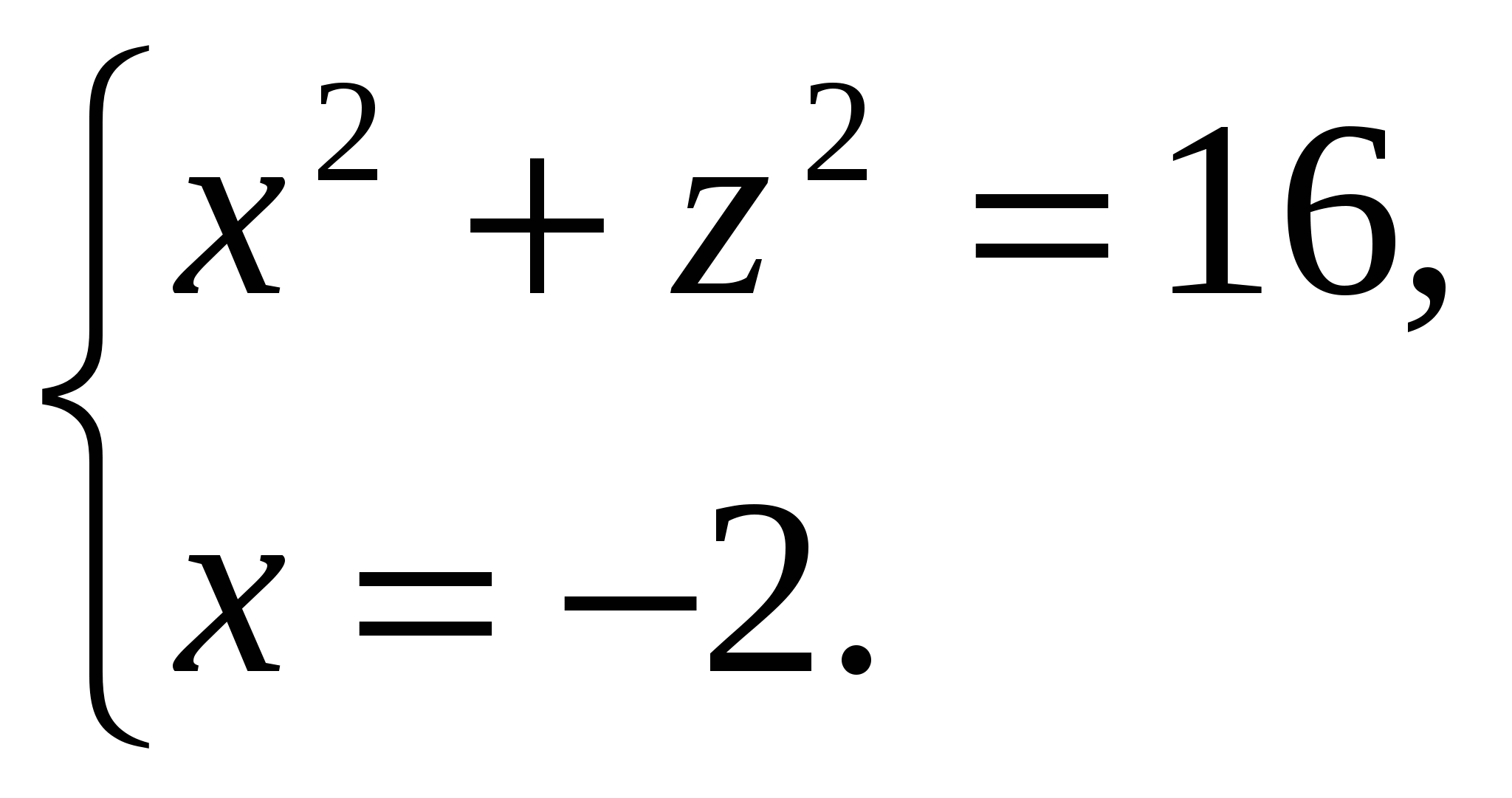
Fordi 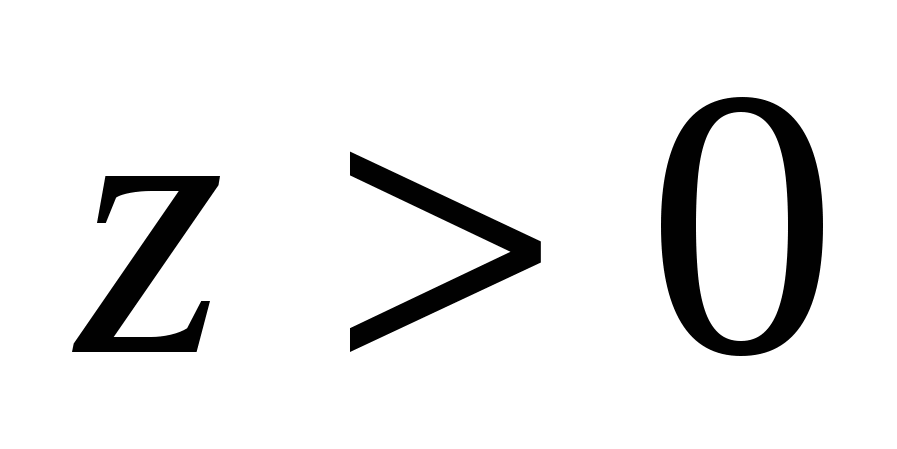 , da er høyden på pyramiden lik
, da er høyden på pyramiden lik 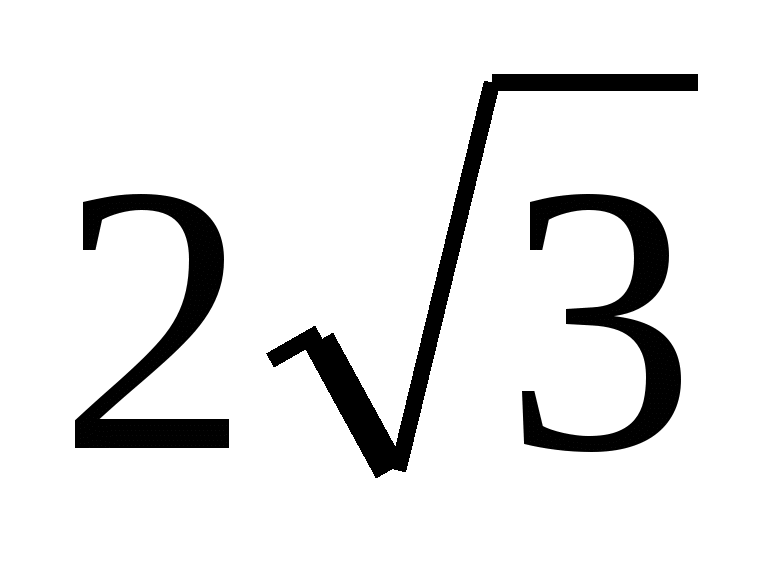 . Derfor
. Derfor 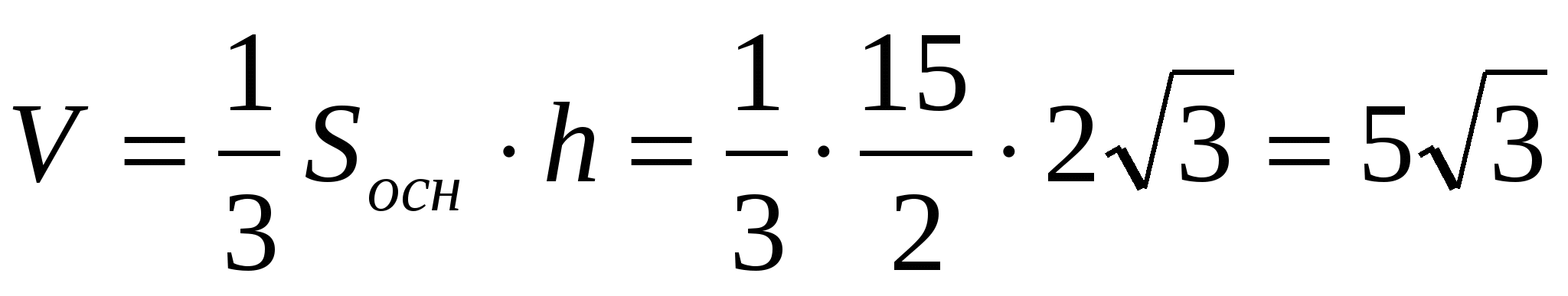 .
.
Svar: 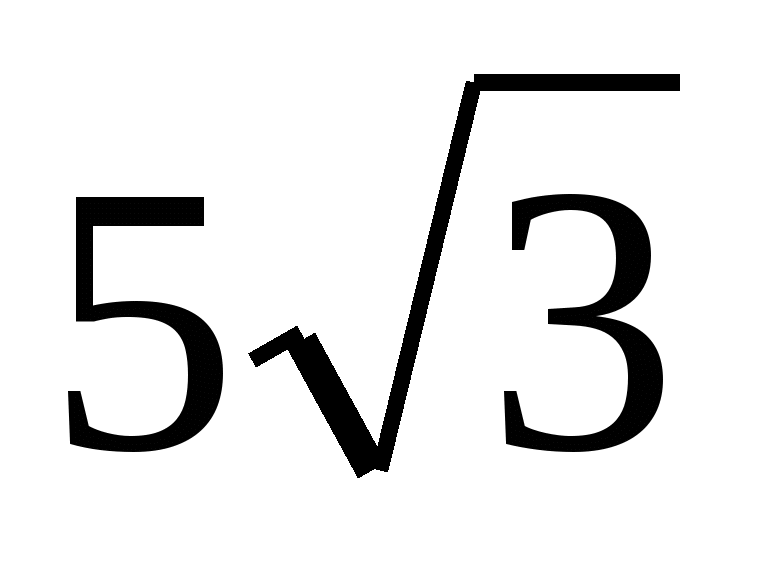 .
.
Problem.2.
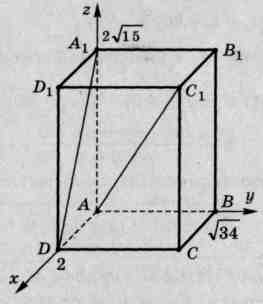
I et rektangulært parallellepiped 
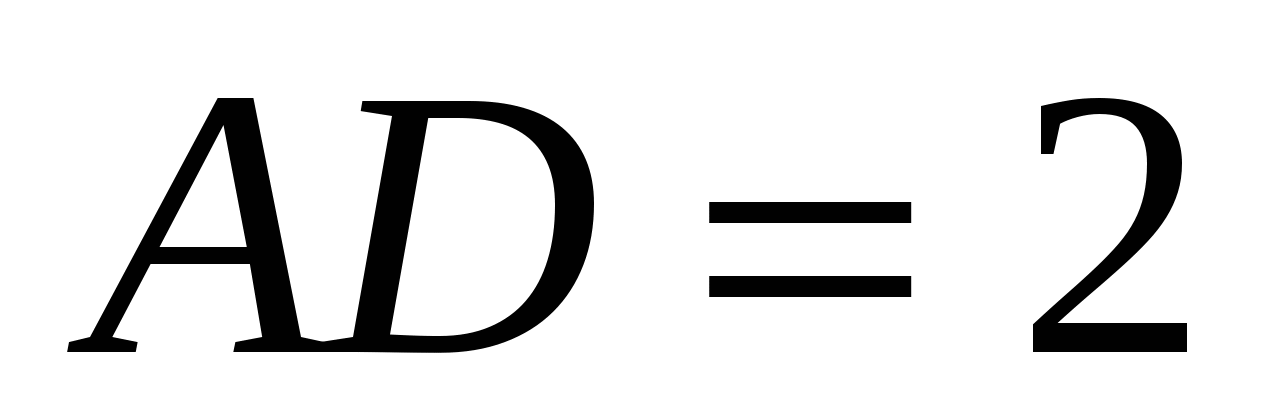 ,
, 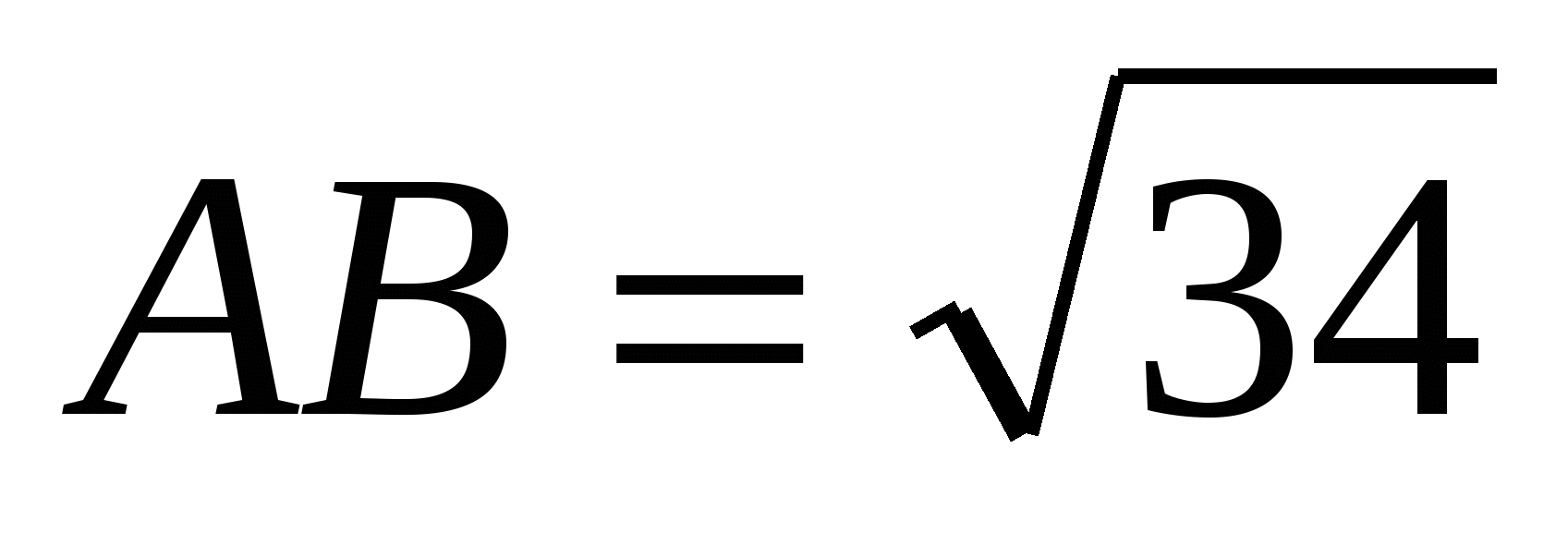 ,
,  . Finne:
vinkel mellom rette linjer
. Finne:
vinkel mellom rette linjer  Og
Og  .
.
 Løsning.
Løsning.
1) La oss introdusere et koordinatsystem med origo i punktet 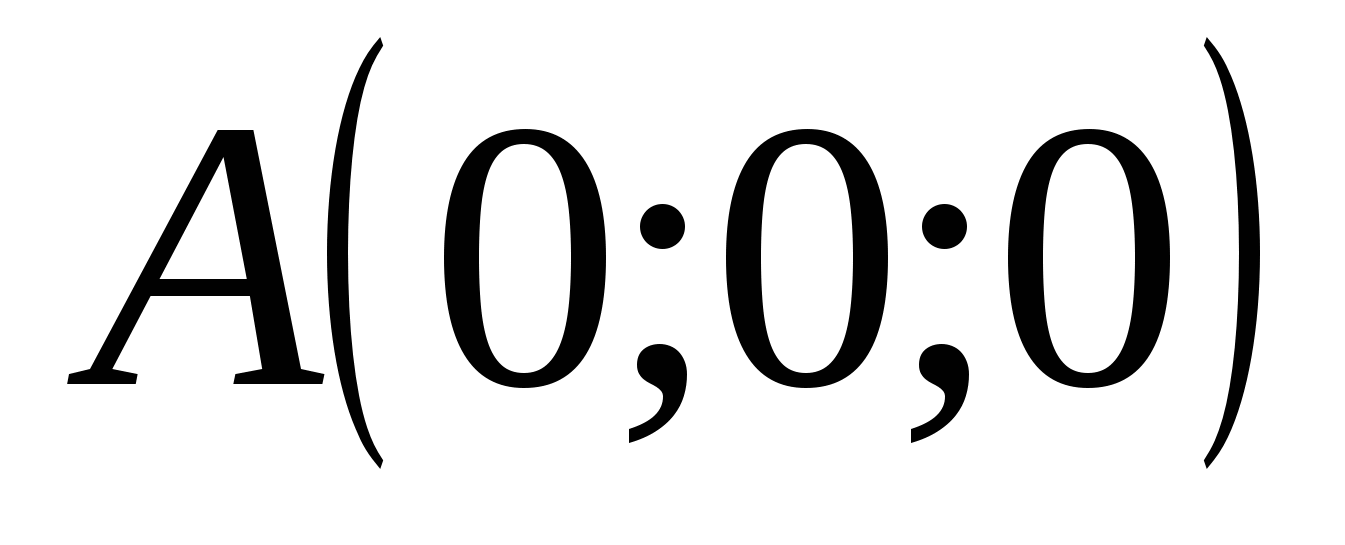 . Aksler
. Aksler 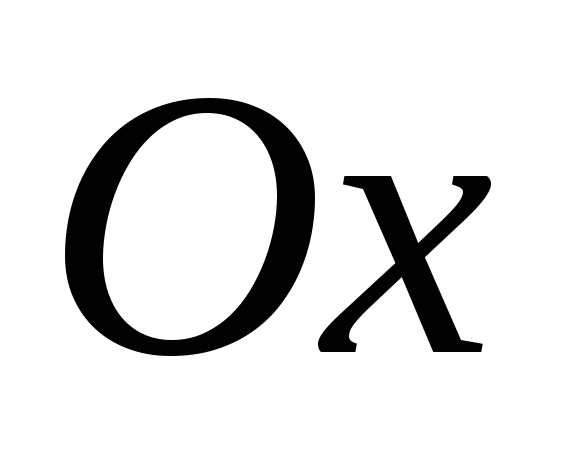 ,
,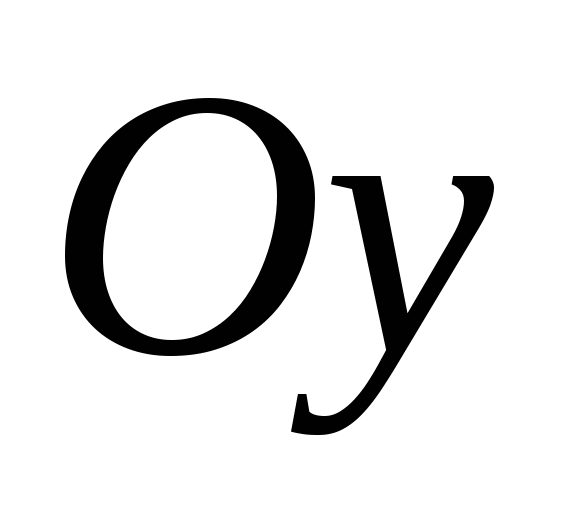 Og
Og  la oss lede langs ribbeina
la oss lede langs ribbeina  ,
, 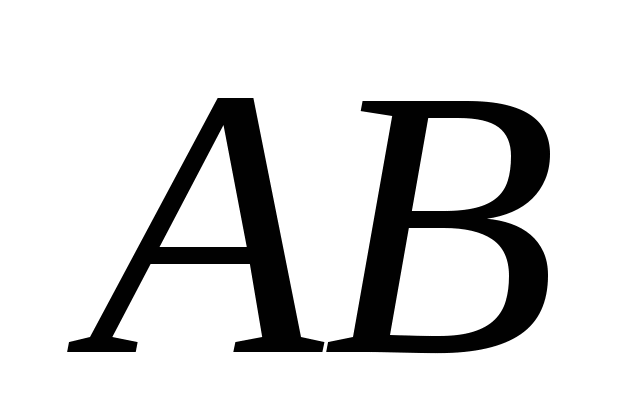 Og
Og 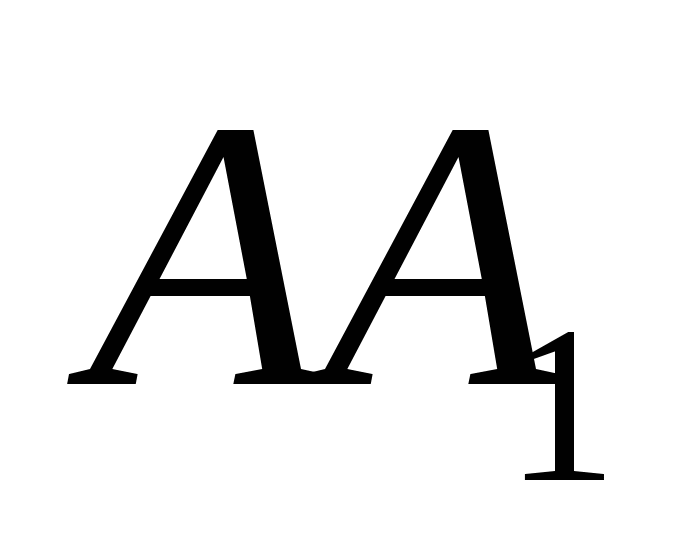 hhv. Siden vinkelen mellom rette linjer varierer fra
hhv. Siden vinkelen mellom rette linjer varierer fra  før
før  , og vinkelen mellom vektorene fra
, og vinkelen mellom vektorene fra  før
før 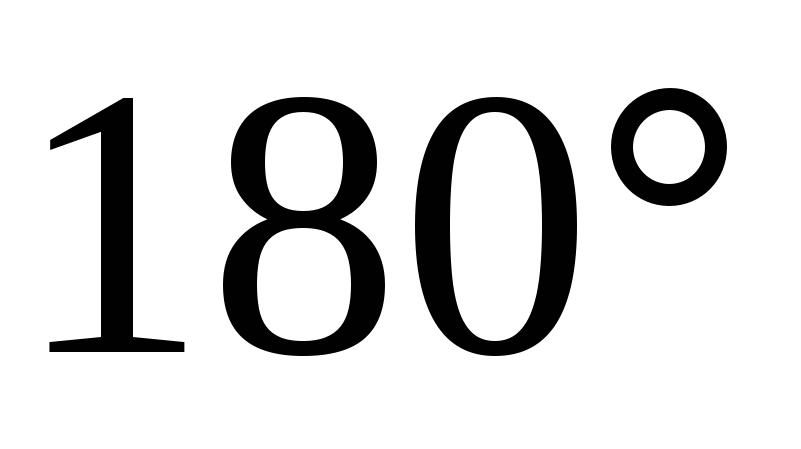 , deretter vinkelen mellom linjene
, deretter vinkelen mellom linjene  Og
Og  lik vinkelen mellom vektorene
lik vinkelen mellom vektorene 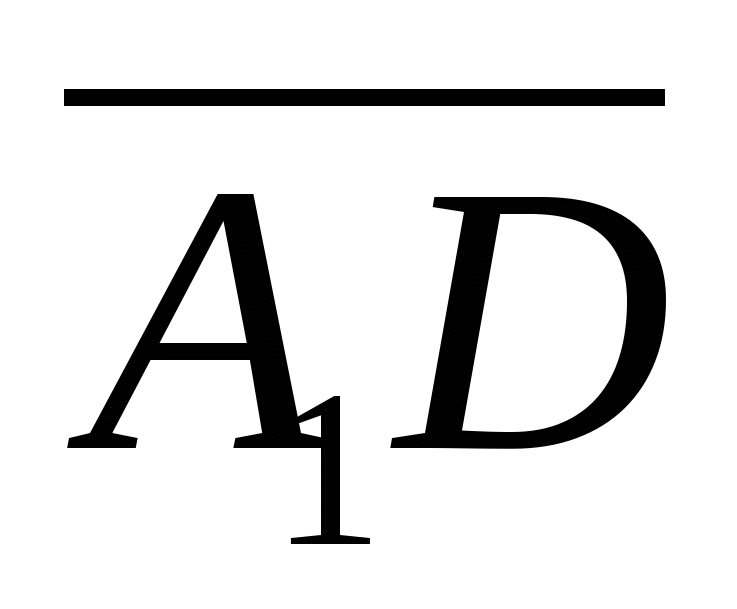 Og
Og 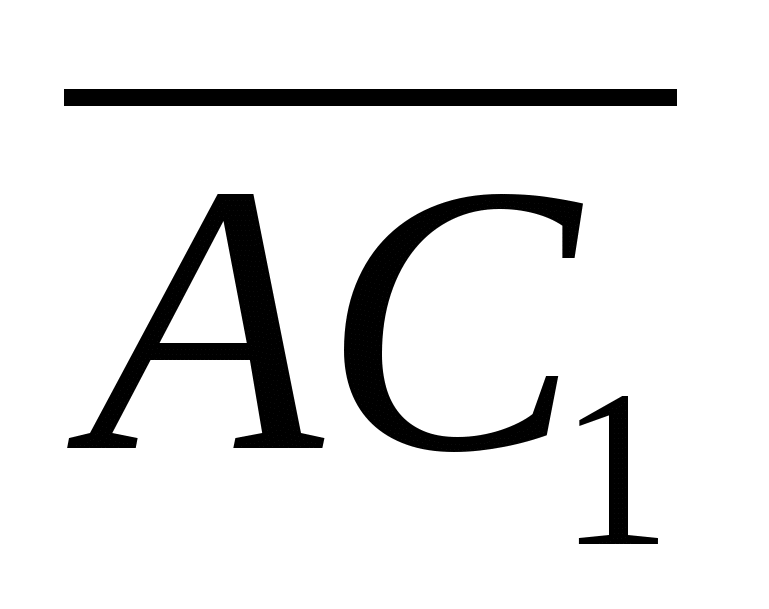 , hvis den er spiss, eller ved siden av den, hvis vinkelen mellom vektorene er stump.
, hvis den er spiss, eller ved siden av den, hvis vinkelen mellom vektorene er stump.
Dermed,
2).Regn ut vinkelen mellom vektorene 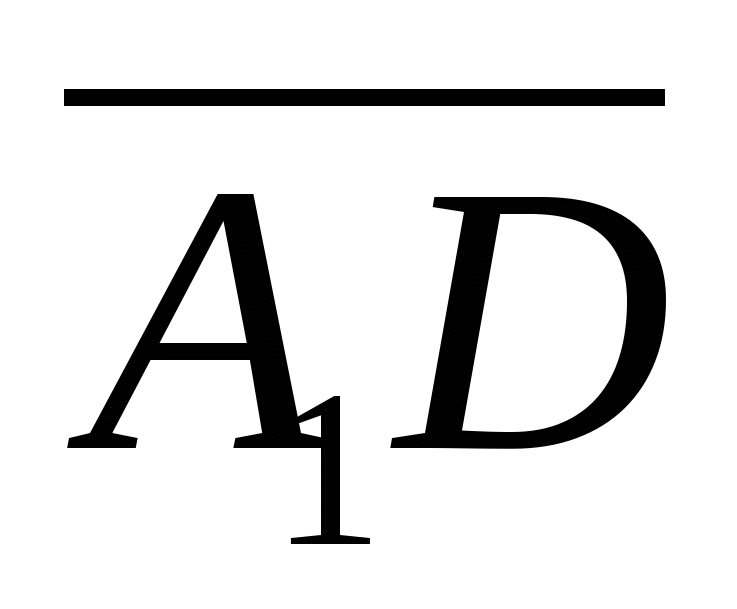 Og
Og 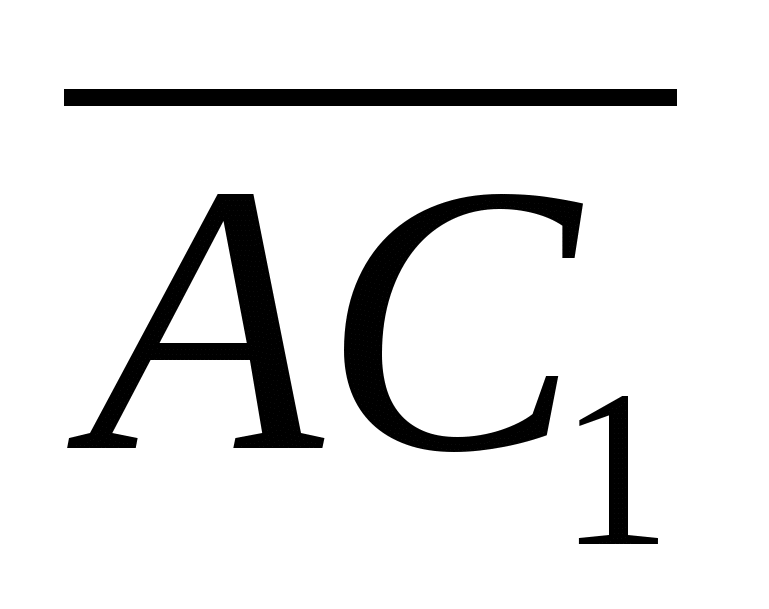 .
.
Finn koordinatene til vektorene ved å bruke koordinatene til punktene 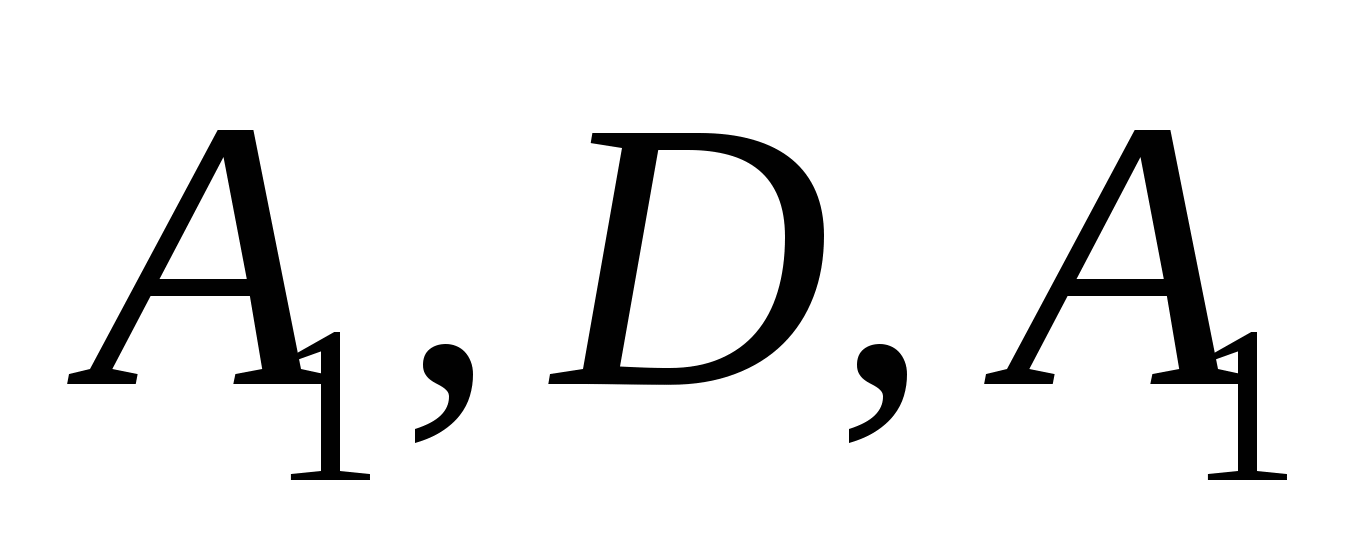 Og
Og  :
:
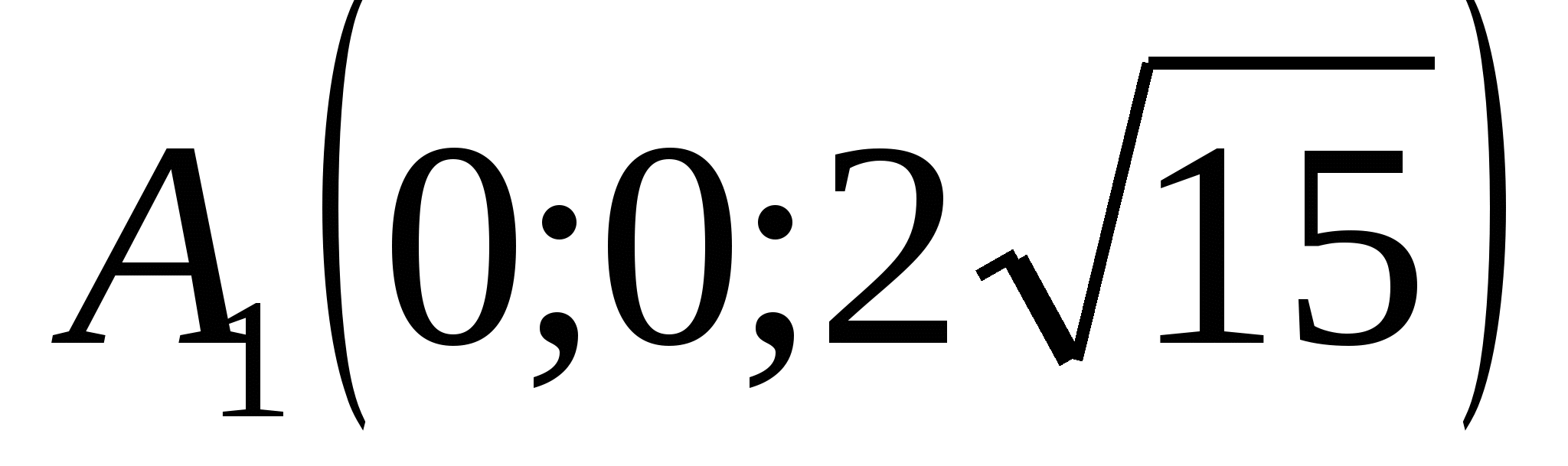 ,
, 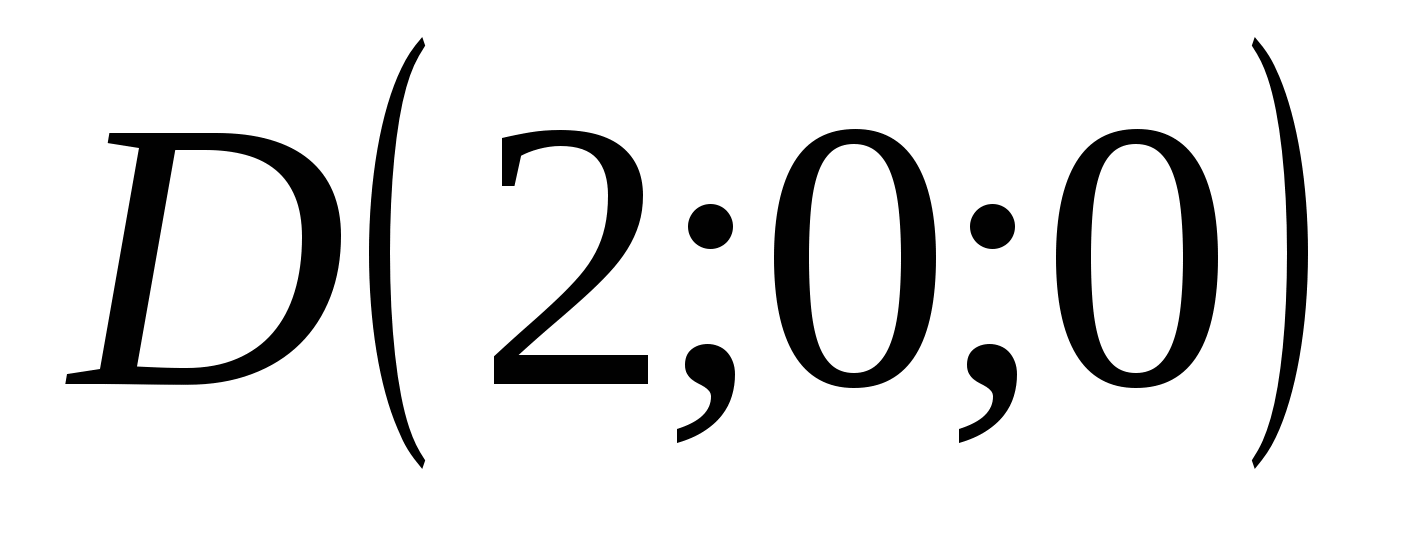 ,
,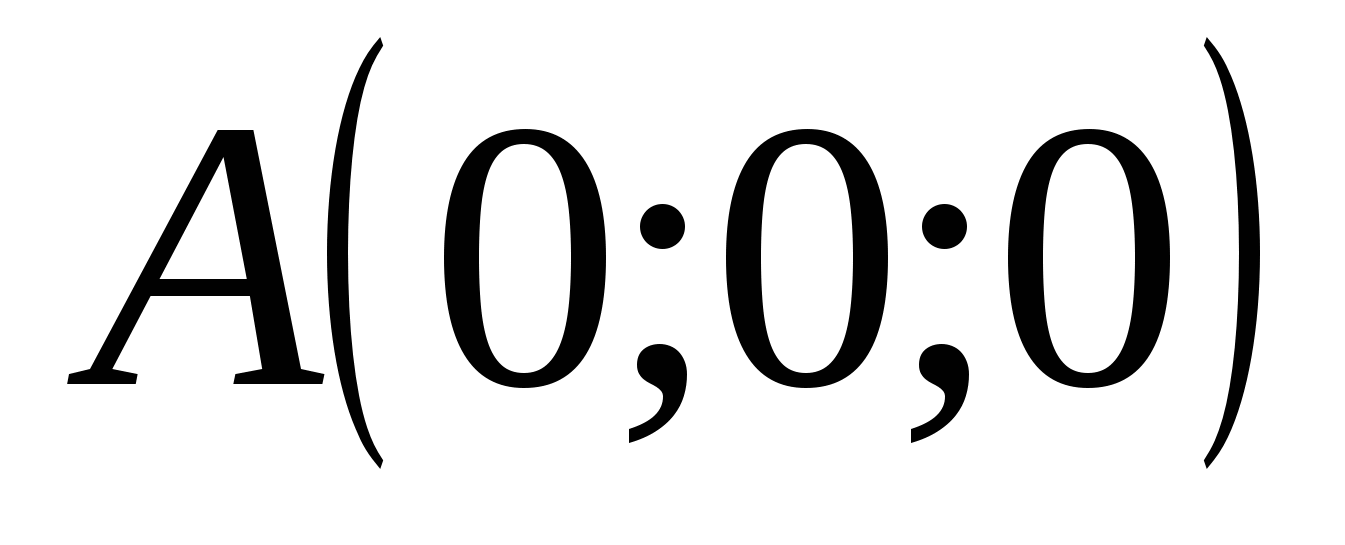 ,
,  .
.
Deretter koordinatene til vektorene 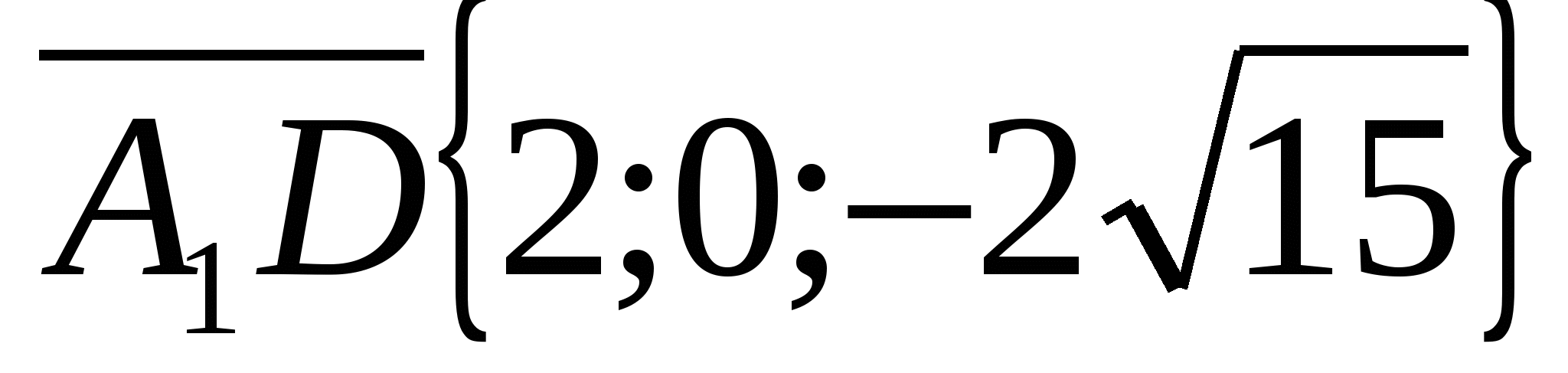 Og
Og 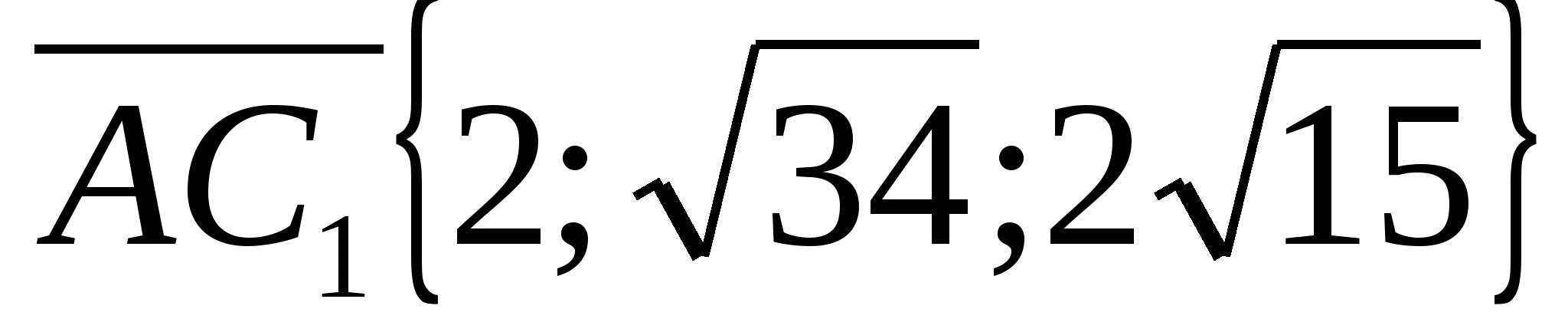 .
.
=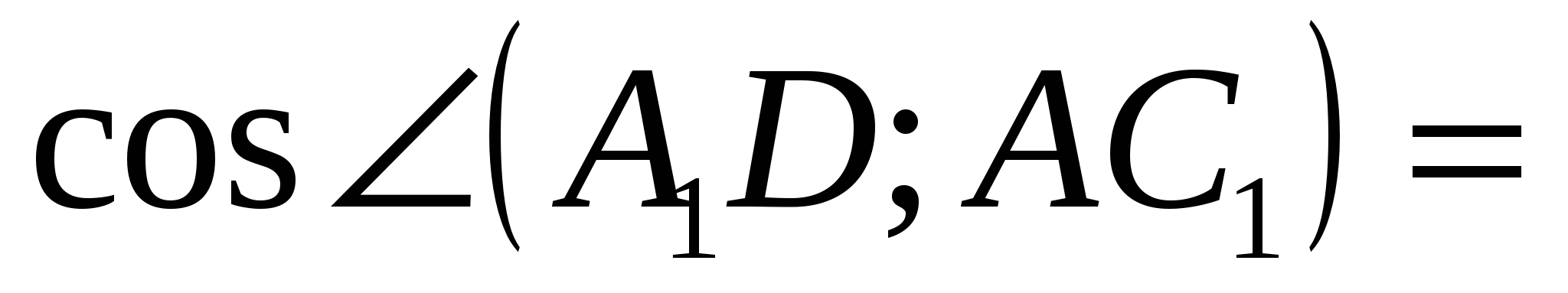
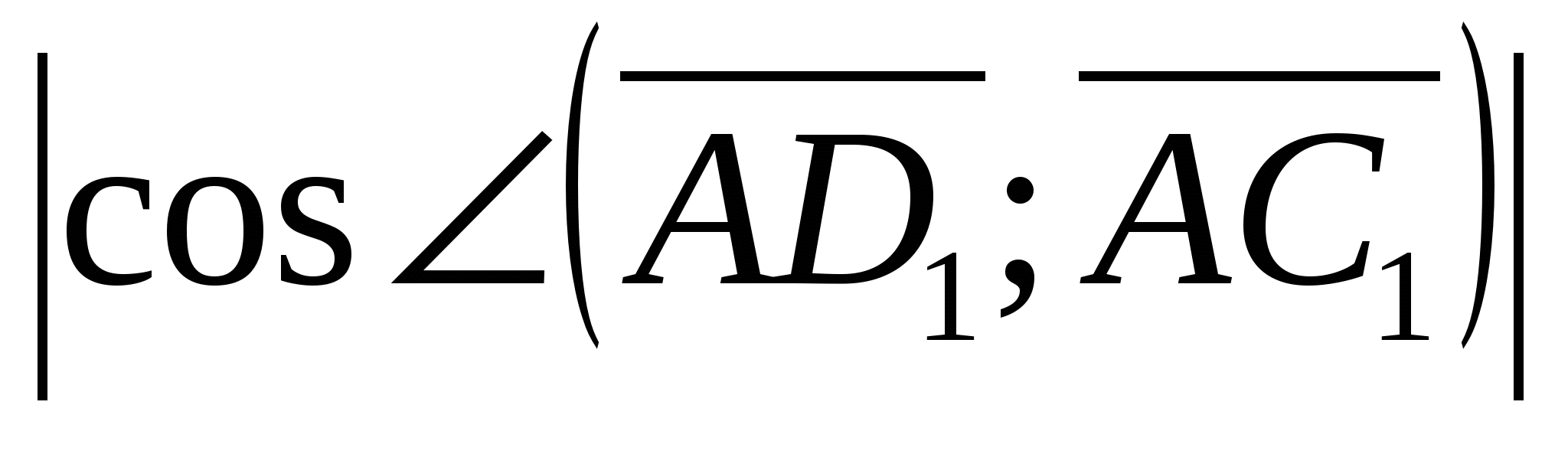 =
= =
=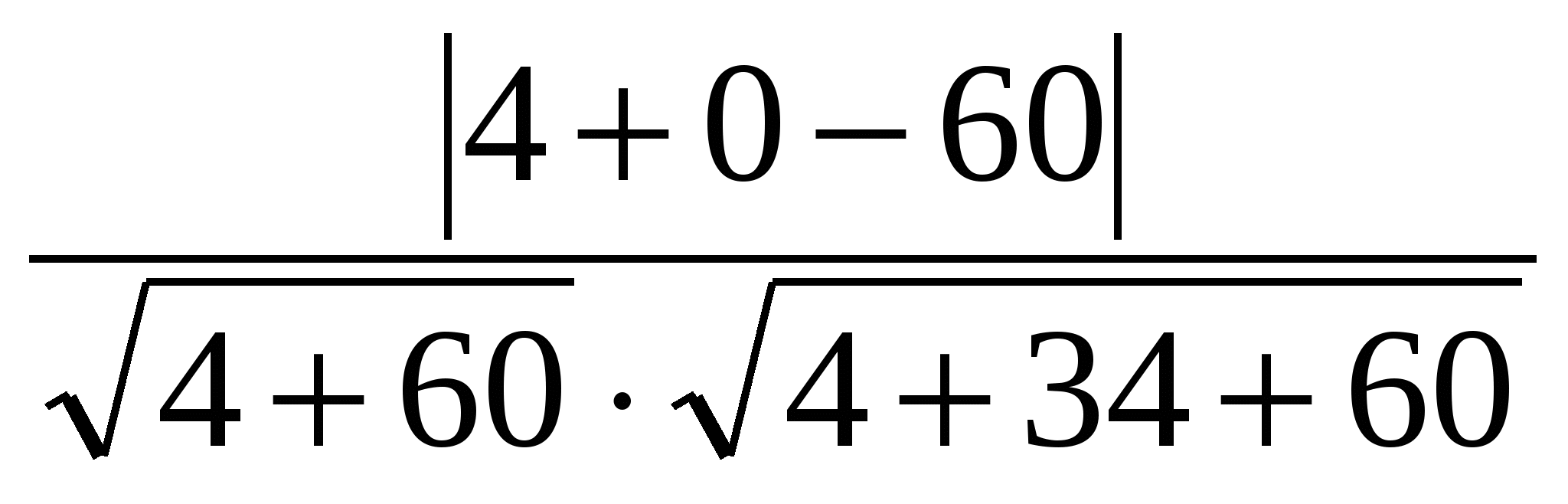
=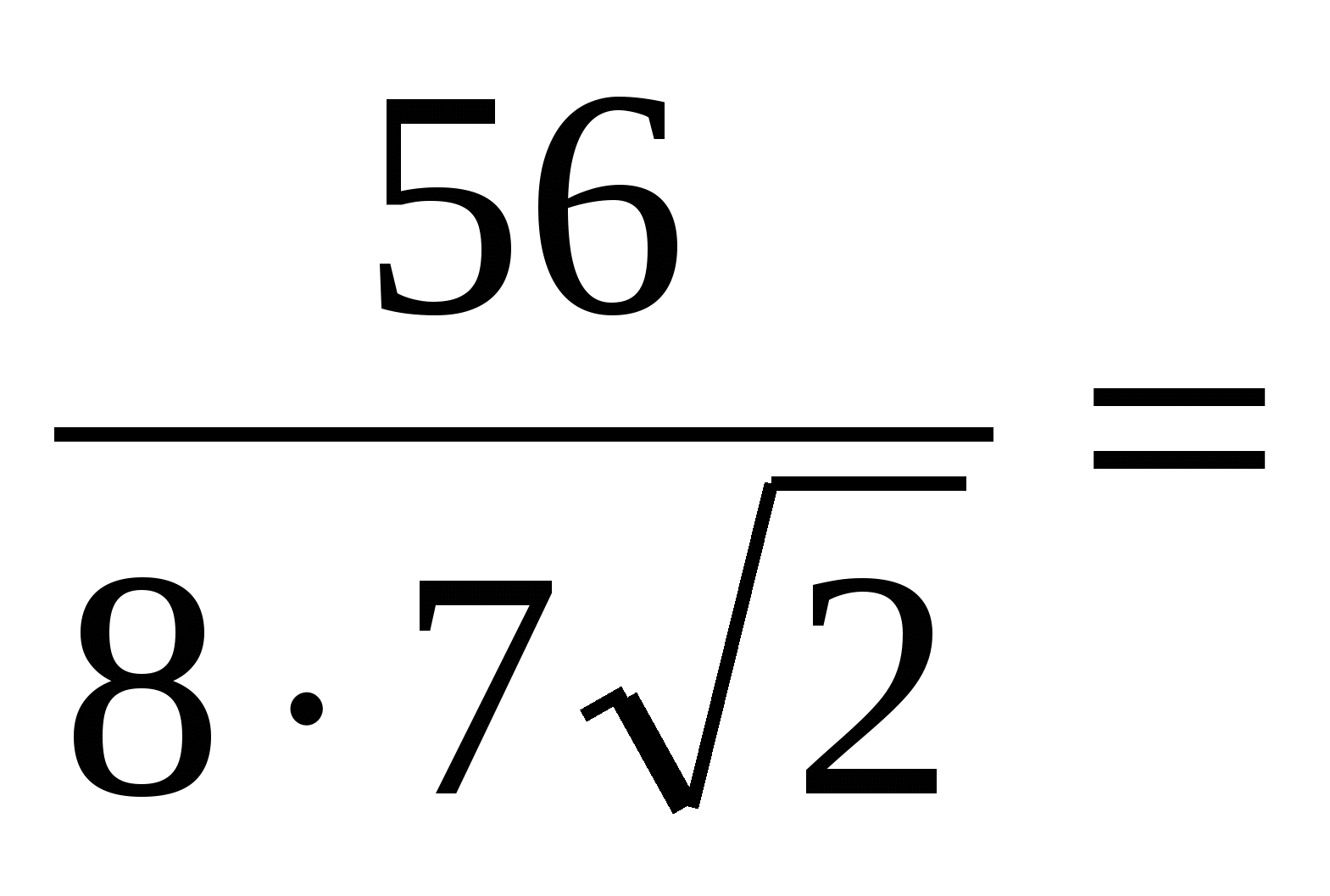
 .
.
Derfor, 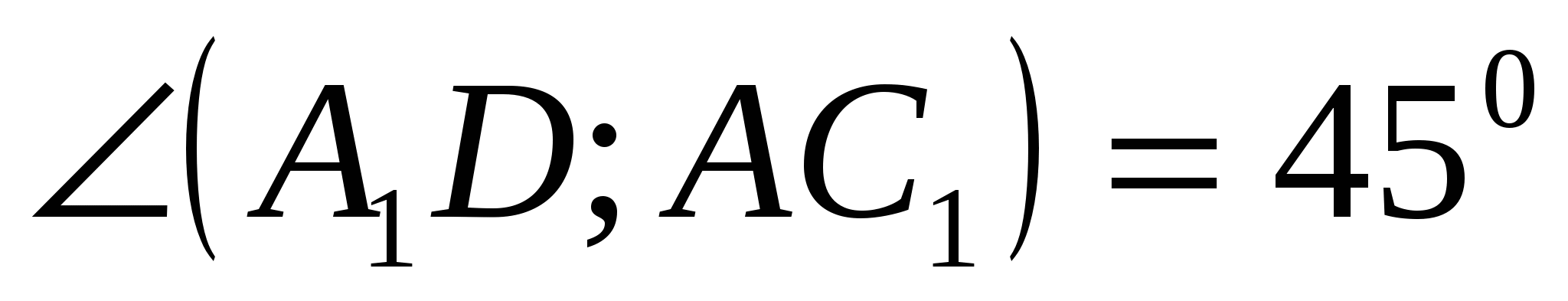
Svar:
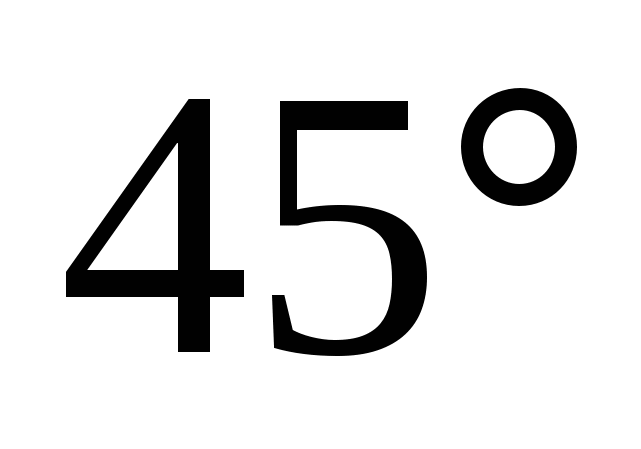 .
.
Oppgave 3.
Dan kuboid  . Finn vinkelen mellom en rett linje
. Finn vinkelen mellom en rett linje 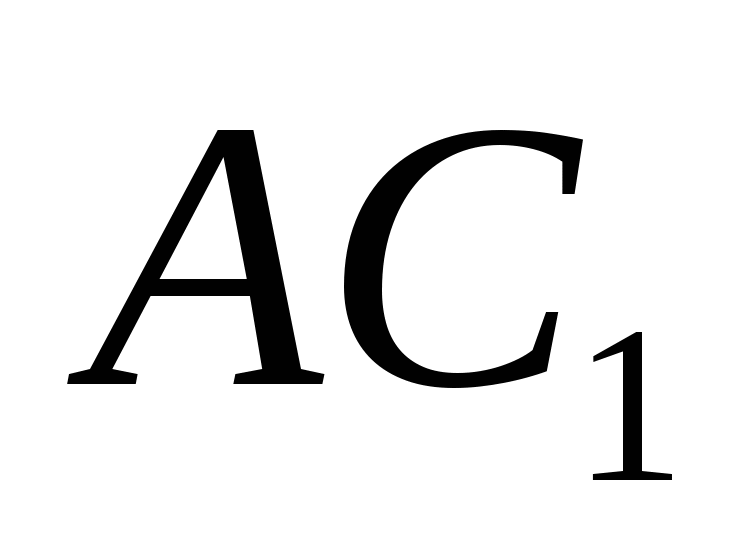 og basens plan
og basens plan  .
.
Løsning.
1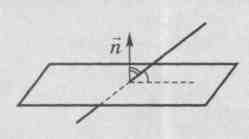 ) Vinkel mellom rett linje
) Vinkel mellom rett linje 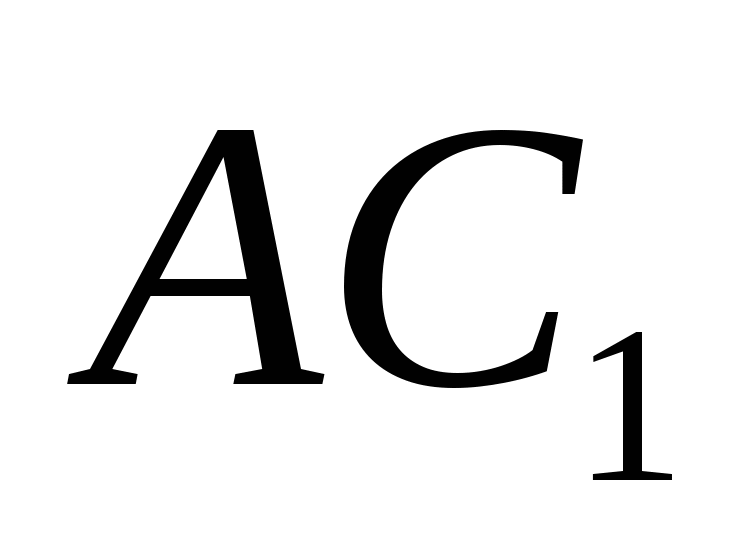 og flyAB
1
MED- Dette
vinkelen mellom en rett linje og dens projeksjon på et plan. Vinkel mellom normal
og flyAB
1
MED- Dette
vinkelen mellom en rett linje og dens projeksjon på et plan. Vinkel mellom normal 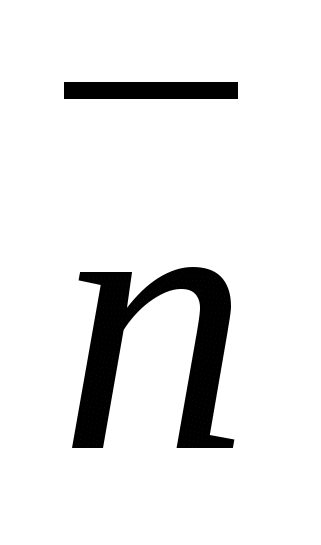 til et plan og en rett linje
til et plan og en rett linje 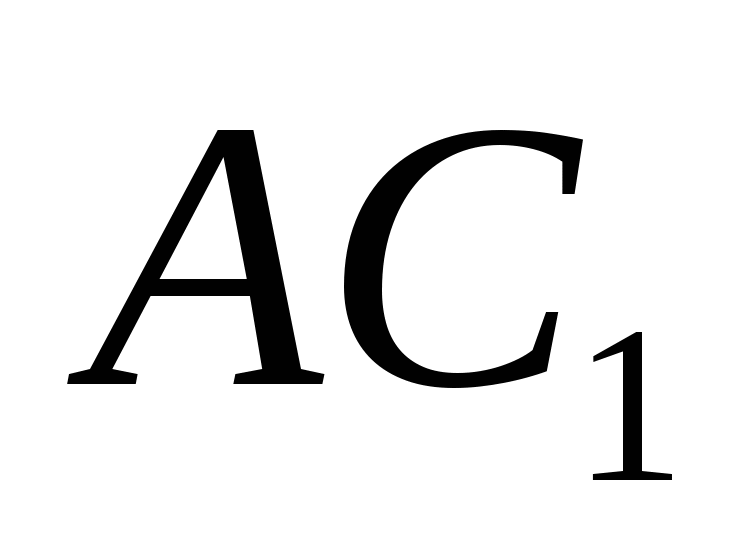 utfyller den til 90 0, derfor.
utfyller den til 90 0, derfor.
Så, for å finne vinkelen mellom en rett linje 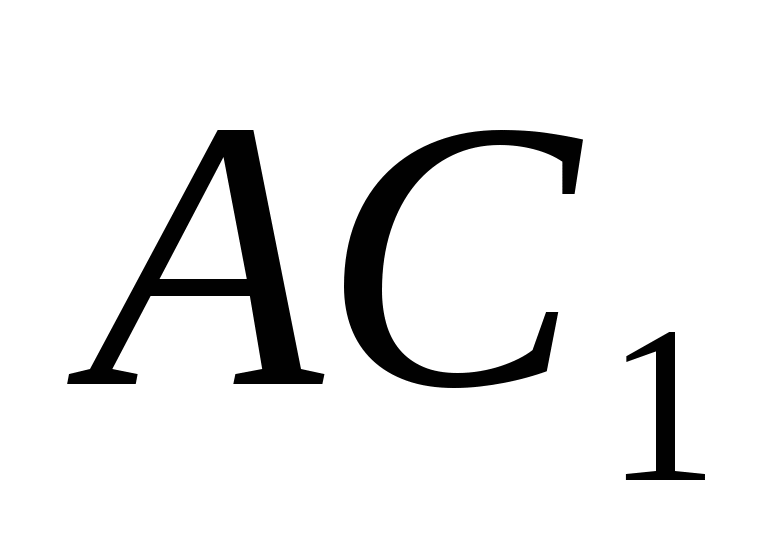 og fly (
og fly (  ), bør du finne vinkelen mellom den rette linjen
), bør du finne vinkelen mellom den rette linjen 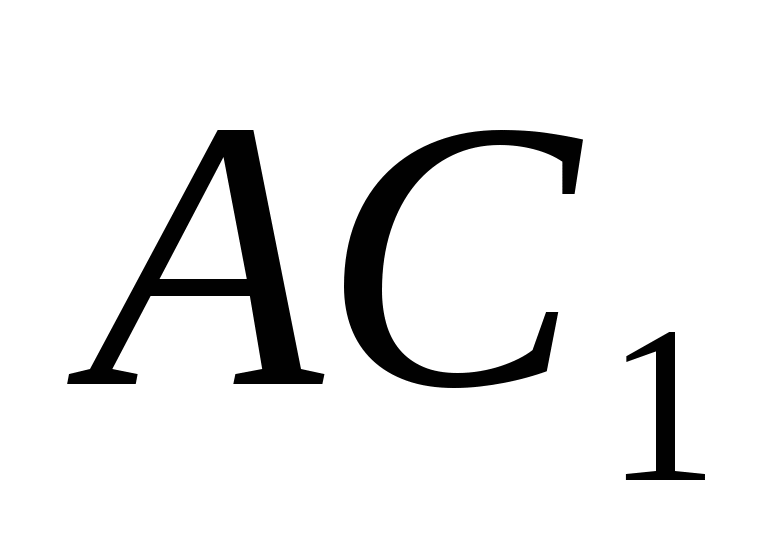 og normalt
og normalt 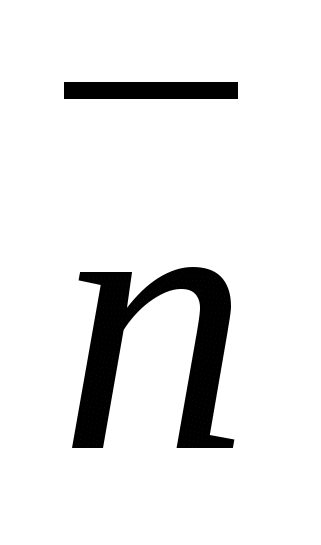 til flyet (
til flyet (  )
.
)
.
2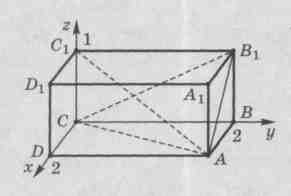 ) La oss introdusere et koordinatsystem med origo i punktet
) La oss introdusere et koordinatsystem med origo i punktet 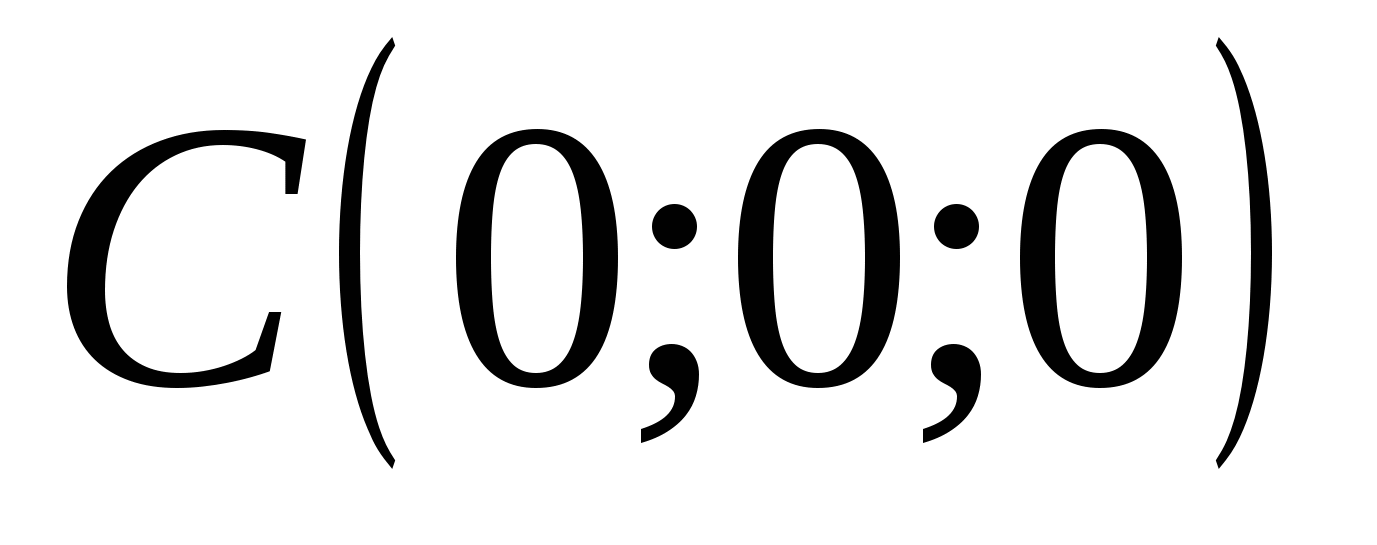 . Aksler
. Aksler 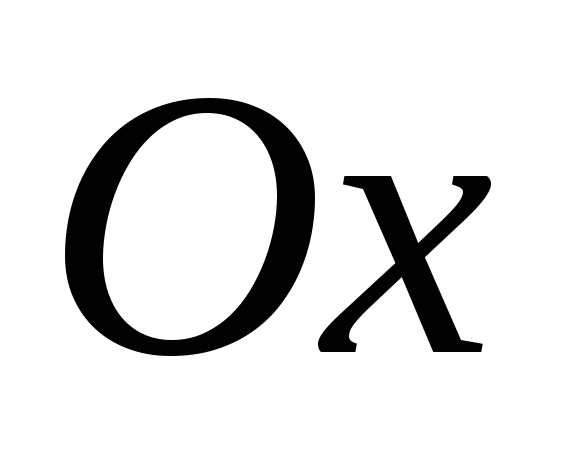 ,
,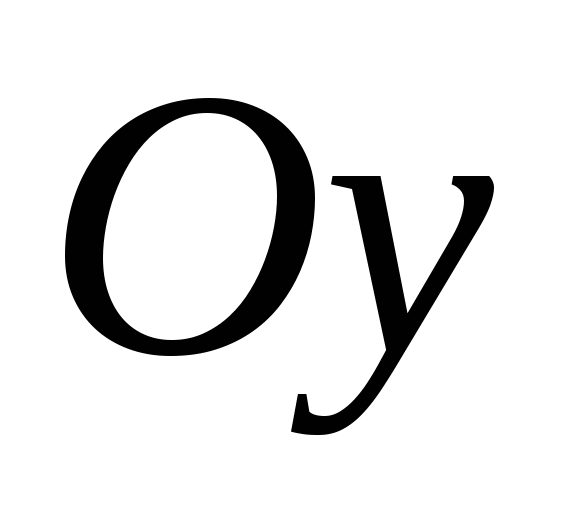 Og
Og  la oss lede langs ribbeina
la oss lede langs ribbeina  ,
, 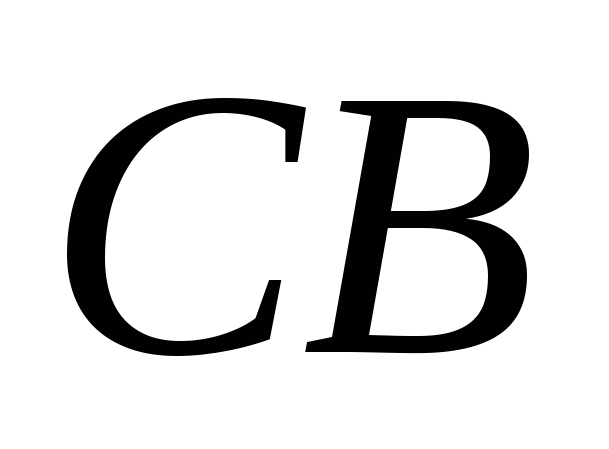 Og
Og 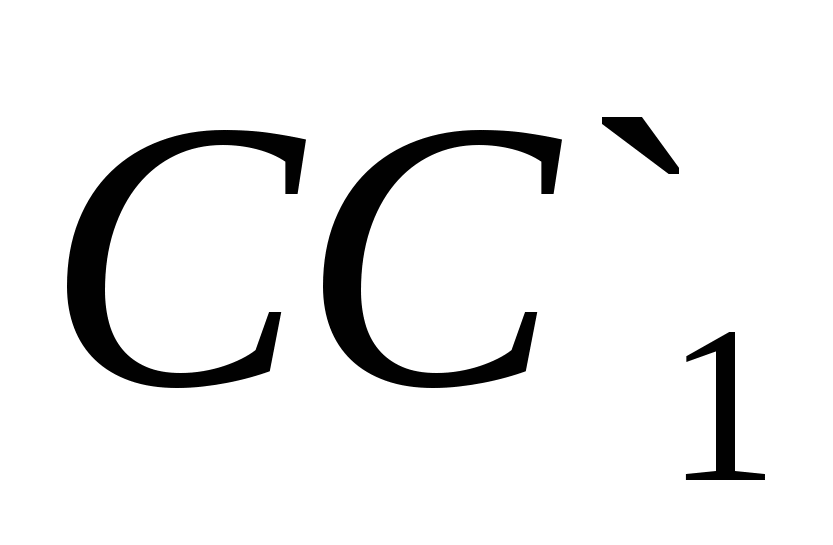 hhv.
hhv.
Punktkoordinater:
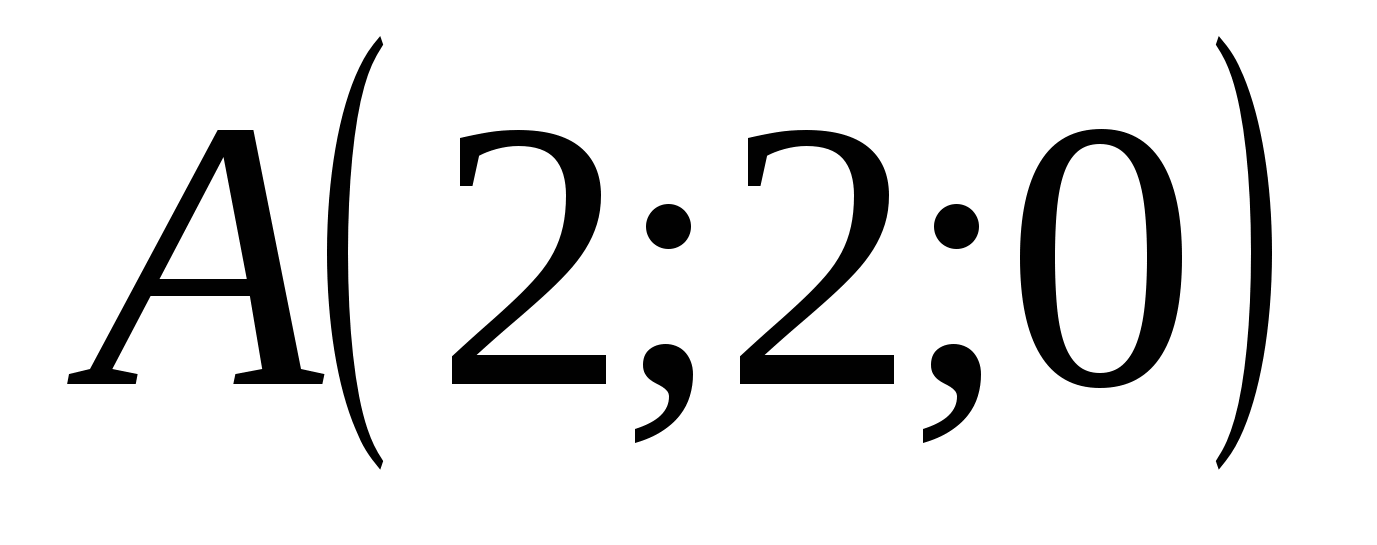 ,
, 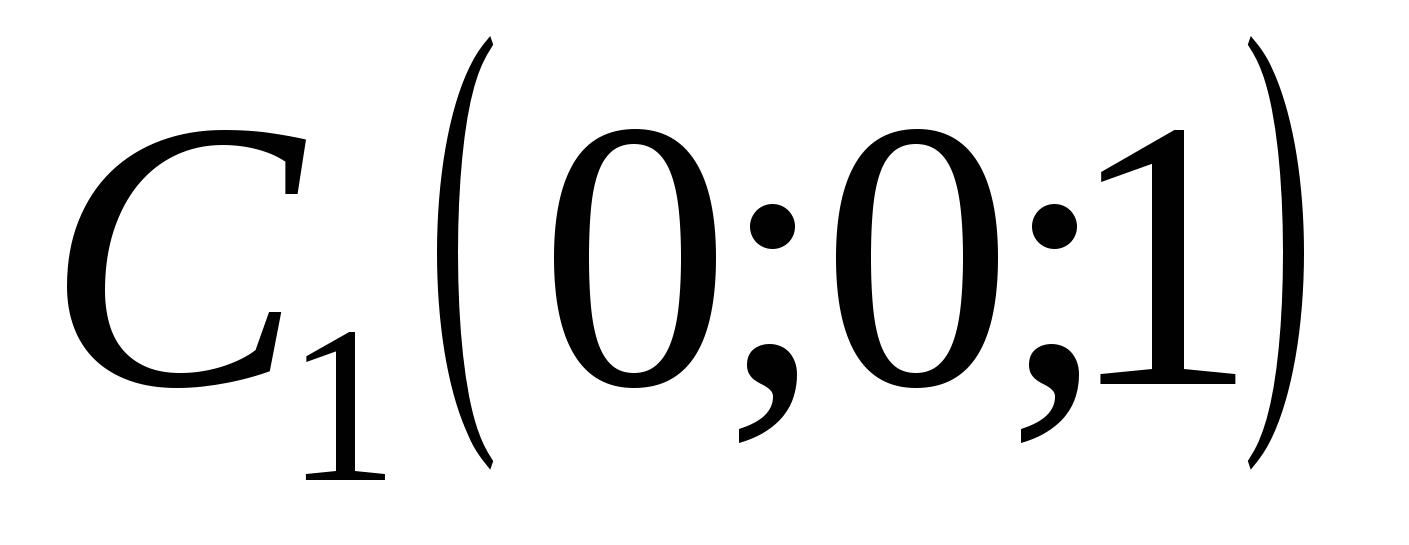 ,
, 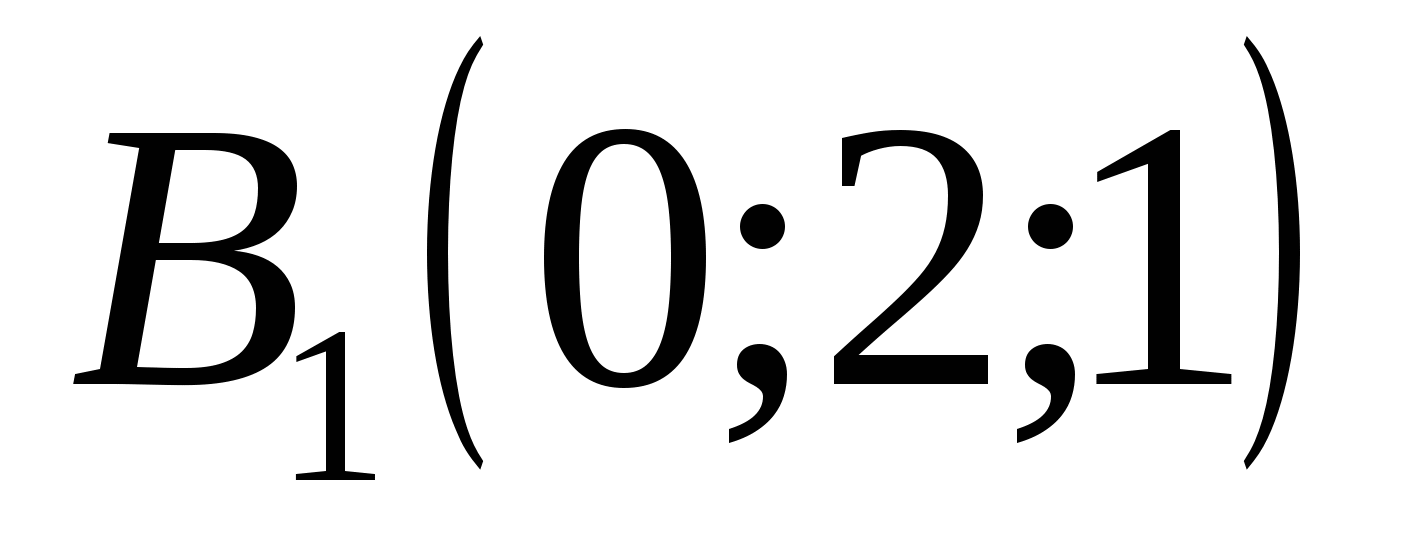 ,
,
EN 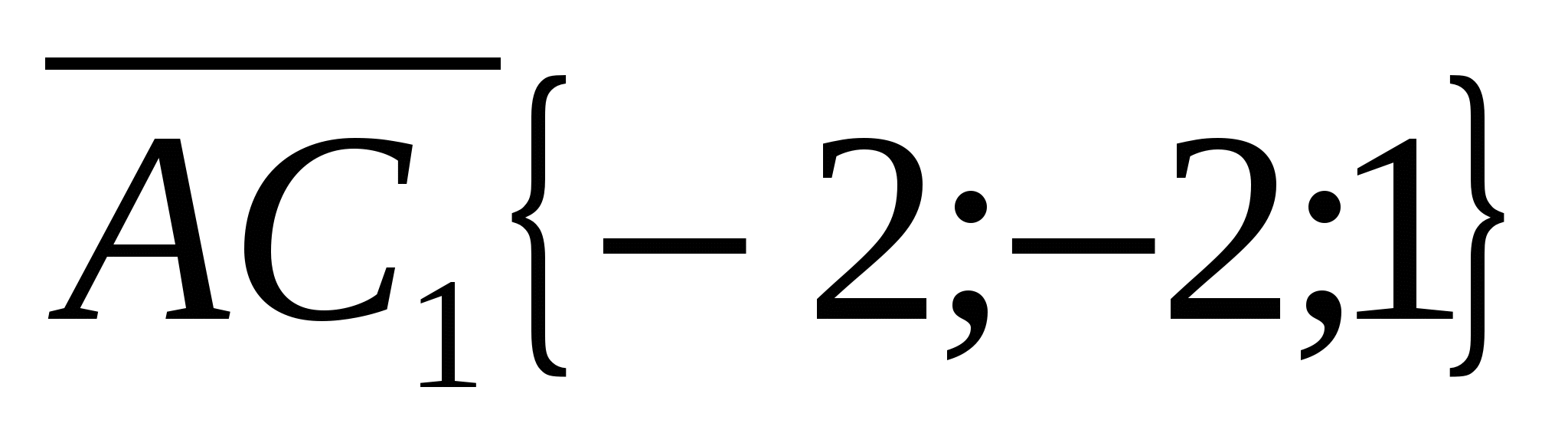 .
.
3) Finn koordinatene til normalplanet (  ). La oss skrive likningen til planet (
). La oss skrive likningen til planet (  ), erstatter koordinatene til punkteneEN
,
B
1
Og MED V
plan ligning
.
), erstatter koordinatene til punkteneEN
,
B
1
Og MED V
plan ligning
.
Vi får et system med lineære ligninger:
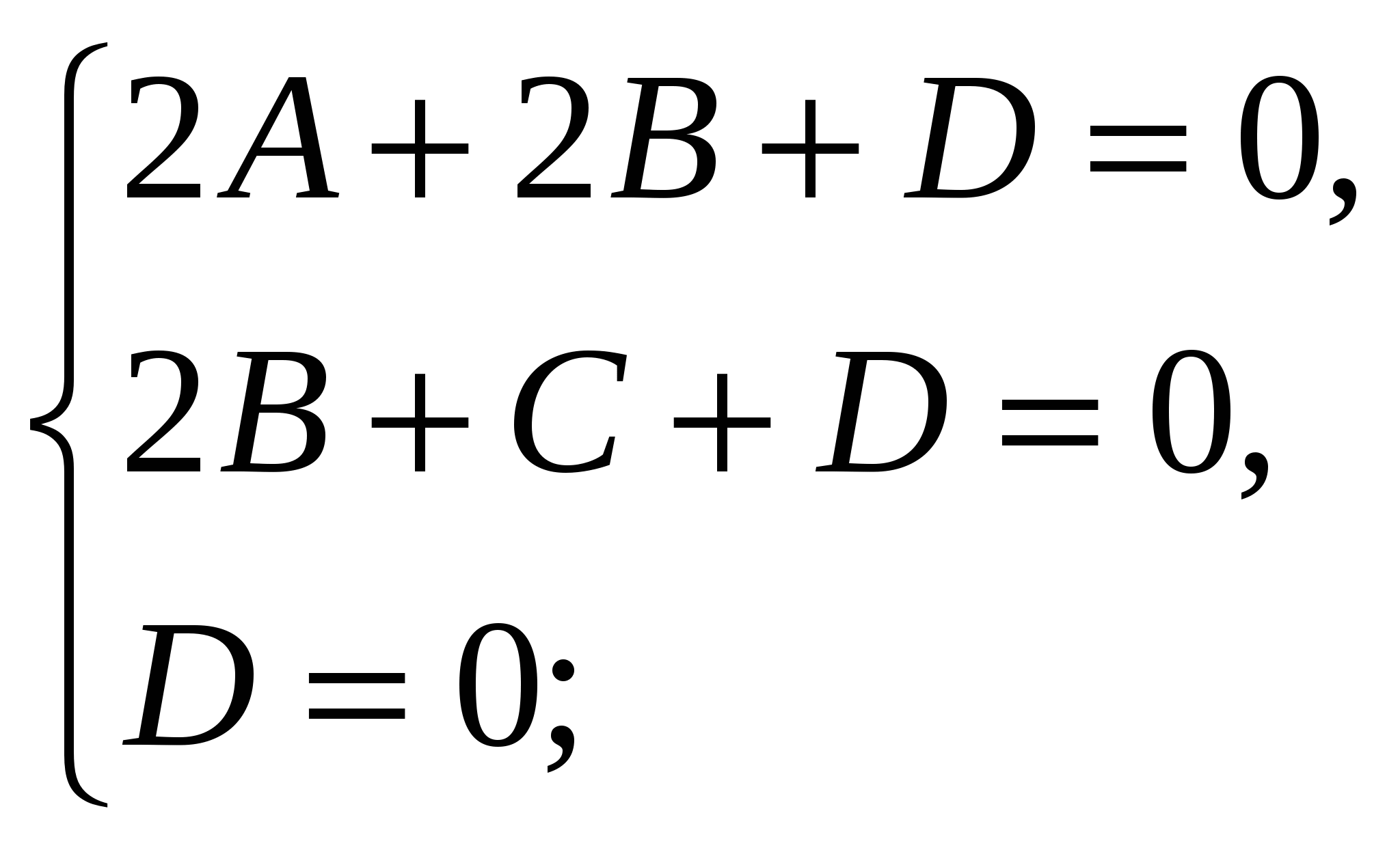
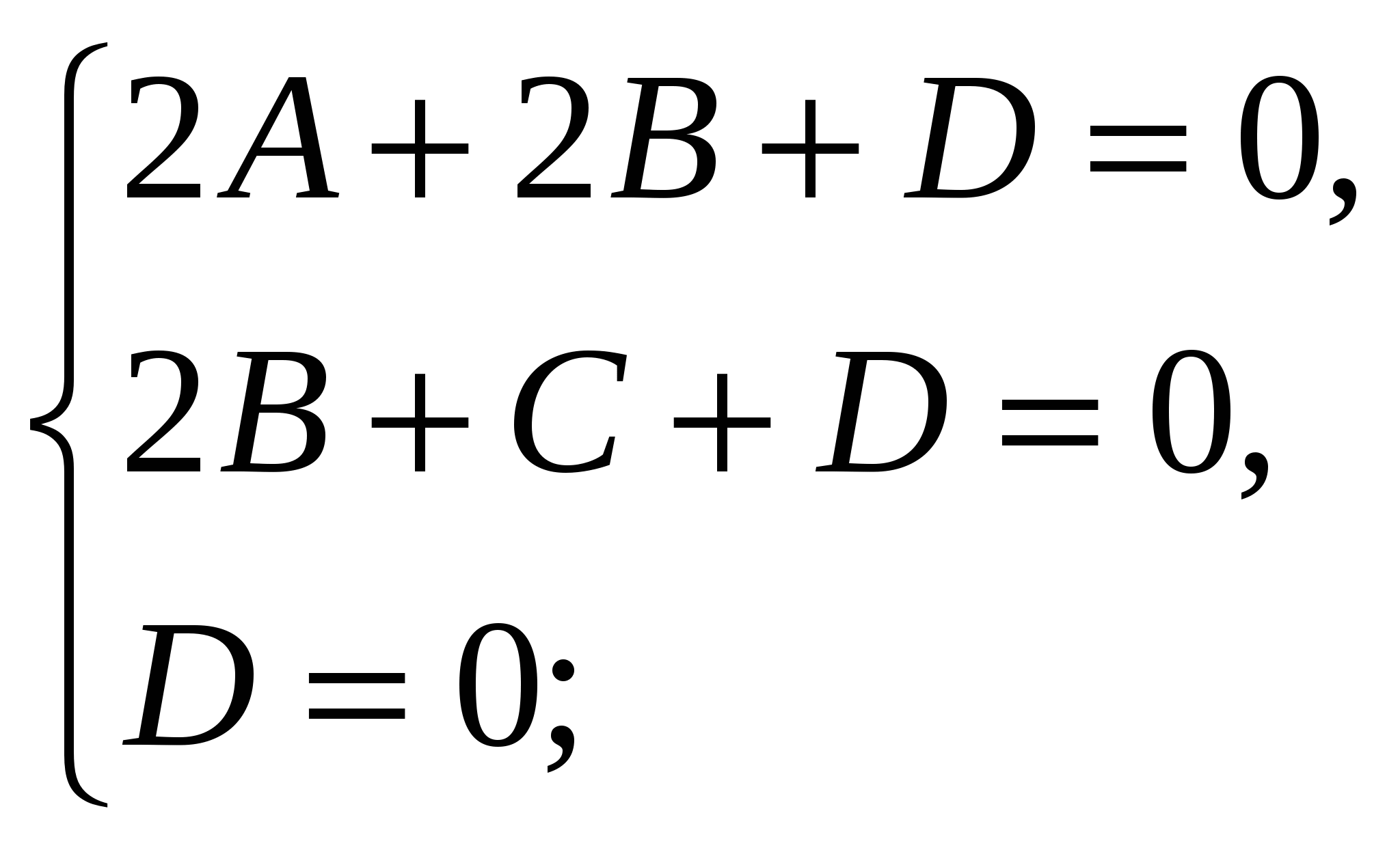
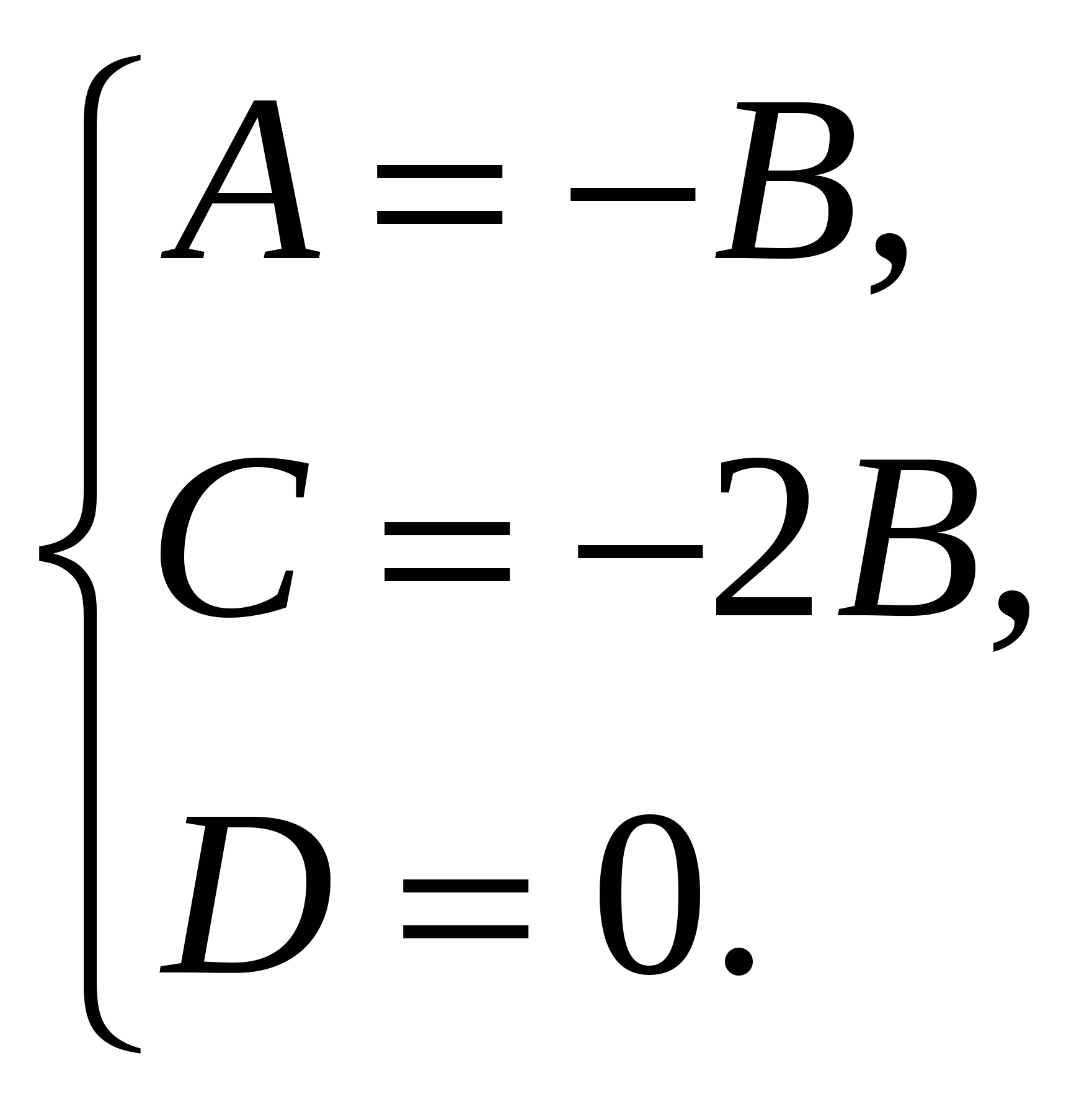
Derfor, ligningen til planet (  ) har formen , eller
) har formen , eller  , og normalvektoren har koordinater
, og normalvektoren har koordinater  .
.
Midler
OG 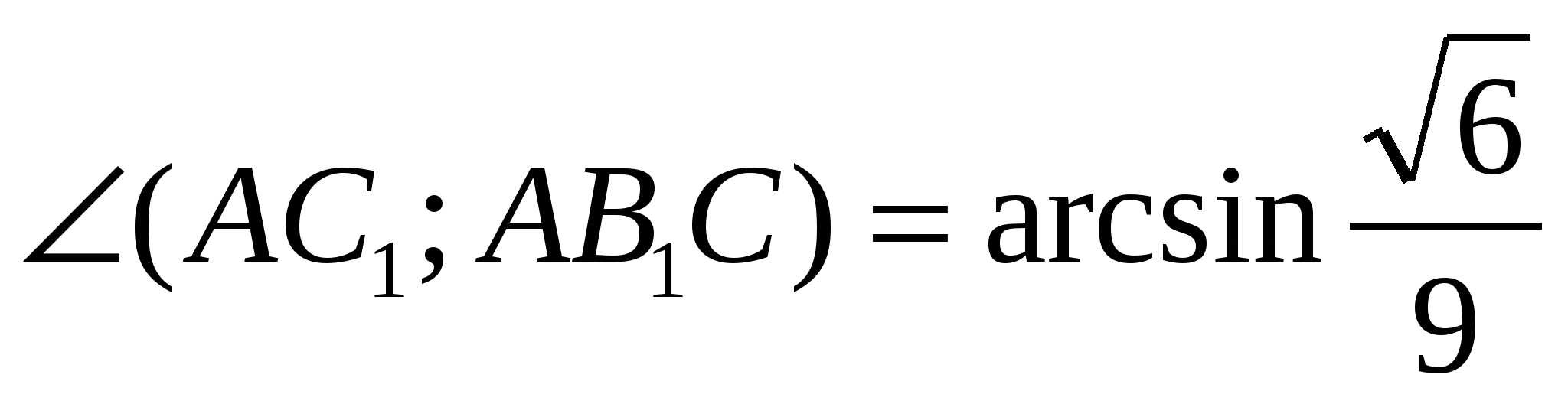 .
.
Svar:
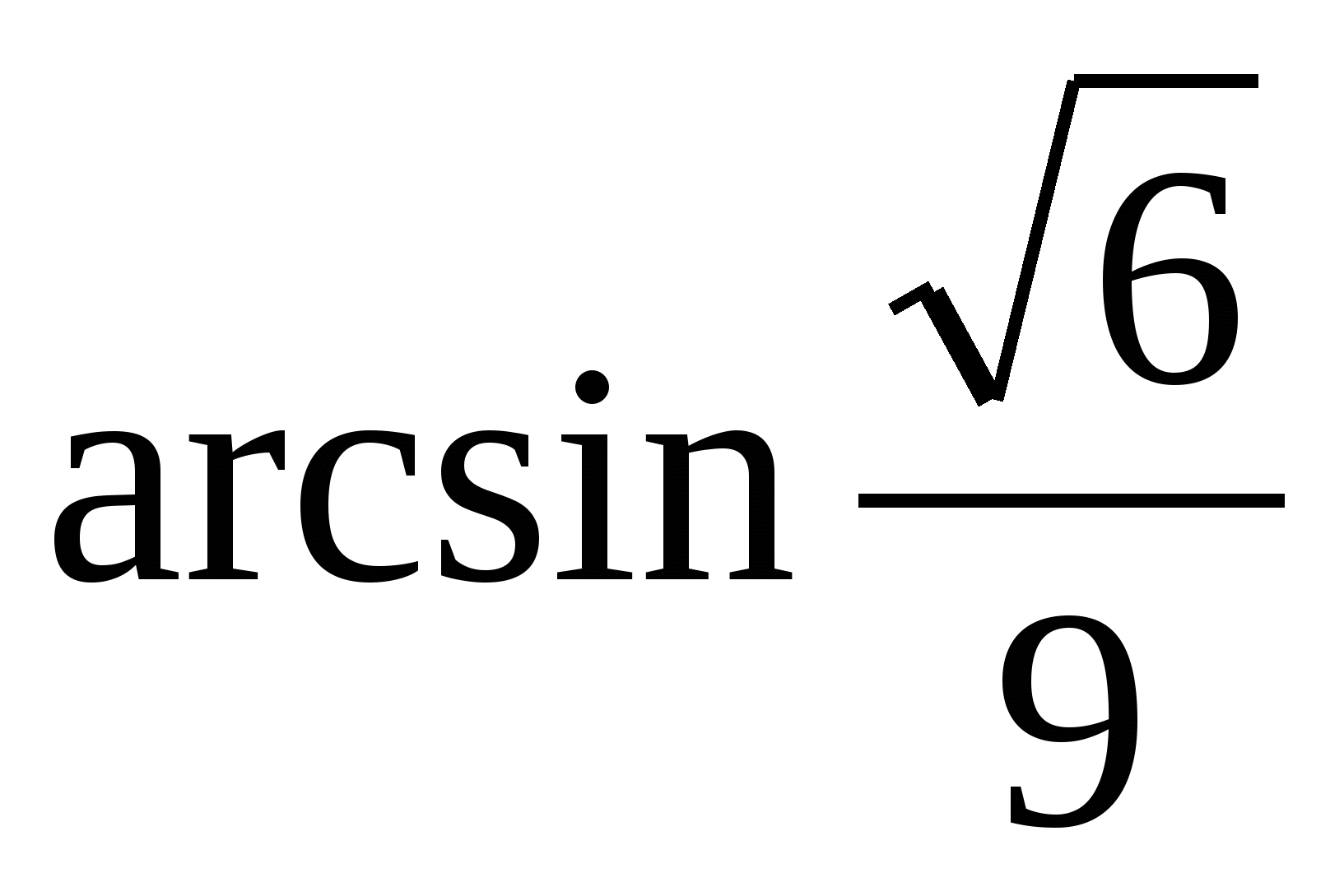 .
.
La oss vurdere å løse problemet på to måter.
Oppgave 4. Metode 1: geometrisk.
På ribbeina  ,
,  Og. . La oss gå rett - midtlinje trekant og, dvs. Og,
Og. . La oss gå rett - midtlinje trekant og, dvs. Og,
Det studerte teoretiske materialet ble systematisert.
Ved bruk av metoden for å løse problemer, ble følgende funksjoner ved metoden identifisert:
ferdighet riktig administrasjon koordinatsystemer,
korrekt bestemmelse av punktkoordinater,
kunnskap om metodens analyseapparat.
Anvendelsen av metoden ble vurdert som en løsning forskjellige typer oppgaver, og i sammenligning med andre metoder.
Jeg møtte noen vanskeligheter mens jeg utførte arbeidet:
når du setter mål og mål;
utilstrekkelig volum teoretisk materiale i en skolebok;
når du identifiserer særegenhetene ved bruk av metoden,
ved valg av materiale for presentasjon av et abstrakt.
Bibliografi.
L S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev, L. S. Kiseleva, E. G. Poznyak. Geometry, 10-11.M., Education, 2003.
V.N.Litvinenko. Workshop på elementær matematikk. Stereometri: Opplæringen.-M.: Verbum-M, 2000.
DEM.Gelfand, E.G. Glagoleva, A.A. Koordinatmetode - M.: Nauka, 1968.
S.G. Grigoriev. Vektoralgebra og analytisk geometri. Lærebok i høyere matematikk.-M.: Informasjons- og implementeringssenter “Markedsføring”, 2000.
I. Ivanova, Z. Ilchenkova. applikasjon koordinatvektor til å løse stereometriske problemer.//Matematikk, 2007, nr. 2.
A.V. Dorofeev. Descartes og hans geometri.//Matematikk, 1992, nr. 4.
