Kuidas kasutada Pythagorase teoreemi. Probleemid Pythagorase teoreemi kasutamisel

Erinevad viisid Pythagorase teoreemi tõestamiseks

9. "A" klassi õpilane

Munitsipaalharidusasutus keskkool nr 8

Teadusnõustaja:

matemaatika õpetaja,

Munitsipaalharidusasutus keskkool nr 8

Art. Novoroždestvenskaja

Krasnodari piirkond.

Art. Novoroždestvenskaja

MÄRKUS.

Pythagorase teoreemi peetakse geomeetria käigus õigustatult kõige olulisemaks ja see väärib suurt tähelepanu. See on komplekti lahendamise aluseks geomeetrilised probleemid, õppimise aluseks teoreetilised ja praktiline kursus geomeetria hiljem. Teoreemi ümbritseb rikas ajalooline materjal seotud selle välimuse ja tõendamismeetoditega. Geomeetria arenguloo uurimine sisendab armastust selle aine vastu, soodustab kognitiivse huvi, üldise kultuuri ja loovuse arengut ning arendab ka uurimisoskusi.

Otsingutegevuse tulemusena saavutati töö eesmärk, milleks oli teadmiste täiendamine ja üldistamine Pythagorase teoreemi tõestuse kohta. Õnnestus leida ja üle vaadata erinevaid viise tõendeid ja süvendada teadmisi sellel teemal, ulatudes kooliõpiku lehekülgedest kaugemale.

Kogutud materjal veenab veelgi enam, et Pythagorase teoreem on suurepärane geomeetria teoreem, sellel on tohutult teoreetilisi ja praktiline tähtsus.

Sissejuhatus. Ajalooline taust 5 Põhiosa 8

3. Järeldus 19

4. Kasutatud kirjandus 20
1. SISSEJUHATUS. AJALOOLINE VIIDE.

Tõe olemus on see, et see on meie jaoks igavesti,

Kui me vähemalt korra tema nägemuses valgust näeme,

Ja Pythagorase teoreem nii paljude aastate pärast

Meie jaoks, nagu ka tema jaoks, on see vaieldamatu, laitmatu.

Rõõmustamiseks andis Pythagoras jumalatele tõotuse:

Lõpmatu tarkuse puudutamise eest,

Ta tappis sada pulli, tänu igavestele;

Ta palvetas ja kiitis pärast ohvrit.

Sellest ajast peale suruvad pullid seda haistma,

Mida teha uus tõde inimesi juhatab jälle rada,

Nad möirgavad raevukalt, nii et pole mõtet kuulata,

Selline Pythagoras sisendas neisse igaveseks hirmu.

Sõnnidele, jõuetud uus tõde vastu panna,

Mis jääb alles? - Lihtsalt sulgege silmad, möirgate, värisevad.

Pole teada, kuidas Pythagoras oma teoreemi tõestas. Kindel on see, et ta avastas selle Egiptuse teaduse tugeval mõjul. Pythagorase teoreemi erijuhtum - kolmnurga küljega 3, 4 ja 5 omadused - oli püramiidide ehitajatele teada juba ammu enne Pythagorase sündi ning ta ise õppis Egiptuse preestritega üle 20 aasta. Säilinud on legend, mis ütleb, et Pythagoras ohverdas oma kuulsa teoreemi tõestades jumalatele härja ja teistel andmetel isegi 100 pulli. See aga on vastuolus teabega Pythagorase moraalsete ja religioossete vaadete kohta. Kirjandusallikatest võib lugeda, et ta "keelas isegi loomade tapmise, veel vähem neist toitmise, sest loomadel on hing nagu meilgi". Pythagoras sõi ainult mett, leiba, köögivilju ja aeg-ajalt kala. Selle kõigega seoses võib usutavamaks pidada järgmist kirjet: “... ja isegi siis, kui ta avastas, et täisnurkses kolmnurgas vastab hüpotenuus jalgadele, ohverdas ta nisutainast valmistatud pulli.

Pythagorase teoreemi populaarsus on nii suur, et selle tõestust leiab isegi ilukirjandusest, näiteks kuulsa inglise kirjaniku Huxley jutustuses “Noor Archimedes”. Sama tõestus, kuid võrdhaarse täisnurkse kolmnurga erijuhtumi jaoks, on esitatud Platoni dialoogis "Meno".

Muinasjutt "Kodu".

"Kaugel, kaugel, kus isegi lennukid ei lenda, on geomeetria riik. Selles ebatavaline riik Seal oli üks hämmastav linn – Teoremi linn. Ühel päeval tulin sellesse linna ilus tüdruk nimega Hüpotenuus. Ta püüdis tuba üürida, kuid olenemata sellest, kuhu ta kandideeris, lükati ta tagasi. Lõpuks lähenes ta raputavale majale ja koputas. Mees, kes nimetas end Õigenurgaks, avas talle ukse ja ta kutsus Hüpotenuse enda juurde elama. Hüpotenuus jäi majja, kus elasid Right Angle ja tema kaks väikest poega nimega Katetes. Sellest ajast peale on elu Right Angle majas muutunud uutmoodi. Hüpotenuus istutas aknale lilled ja eesaeda punased roosid. Maja võttis täisnurkse kolmnurga kuju. Mõlemale jalale meeldis väga hüpotenuus ja nad palusid tal jääda igaveseks nende majja. Õhtuti koguneb see sõbralik perekond pere laua taha. Mõnikord mängib Right Angle oma lastega peitust. Kõige sagedamini peab ta vaatama ja hüpotenuus peidab end nii osavalt, et seda võib olla väga raske leida. Ühel päeval märkas Right Angle mängides huvitavat omadust: kui tal õnnestub jalad leida, pole hüpotenuusi leidmine keeruline. Nii et Right Angle kasutab seda mustrit, pean ütlema, väga edukalt. Pythagorase teoreem põhineb selle täisnurkse kolmnurga omadusel.

(A. Okunevi raamatust “Aitäh õppetunni eest, lapsed”).

Teoreemi humoorikas sõnastus:

Kui meile antakse kolmnurk

Ja pealegi täisnurgaga,

See on hüpotenuusi ruut

Meil on alati lihtne leida:

Me teeme jalad sirgeks,

Leiame jõudude summa -

Ja nii lihtsal viisil

Jõuame tulemuseni.

10. klassis algebrat ning analüüsi ja geomeetria algust õppides veendusin, et lisaks 8. klassis käsitletud Pythagorase teoreemi tõestamismeetodile on ka teisi tõestusmeetodeid. Esitan need teie tähelepanuks.
2. PÕHIOSA.

Teoreem. Täisnurkses kolmnurgas on ruut

hüpotenuus võrdne summaga jalgade ruudud.

1 MEETOD.

Kasutades hulknurkade pindalade omadusi, loome märkimisväärse seose täisnurkse kolmnurga hüpotenuusi ja jalgade vahel.

Tõestus.

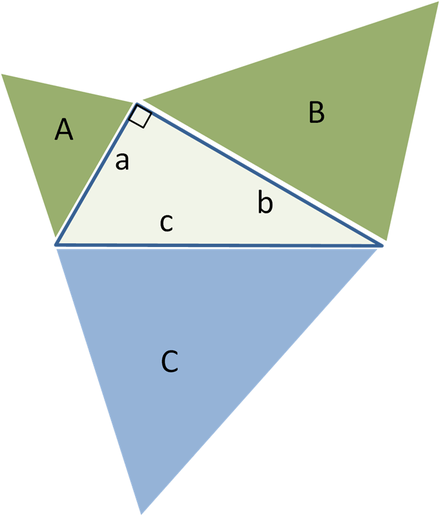
a, c ja hüpotenuus Koos(Joonis 1, a).

Tõestame seda c²=a²+b².

Tõestus.

Lõpetame kolmnurga küljega ruuduks a + b nagu on näidatud joonisel fig. 1, b. Selle ruudu pindala S on (a + b)². Teisest küljest koosneb see ruut neljast võrdsest täisnurksest kolmnurgast, millest igaühe pindala on ½ ah ja küljega ruut koos, seetõttu S = 4 * ½ aw + c² = 2aw + c².

Seega

(a + b)² = 2 aw + c²,

c²=a²+b².

Teoreem on tõestatud.
2 MEETOD.

Uurides teemat “Sarnased kolmnurgad”, sain teada, et kolmnurkade sarnasust saab rakendada Pythagorase teoreemi tõestuses. Nimelt kasutasin väidet, et täisnurkse kolmnurga jalg on jala ja täisnurga tipust tõmmatud kõrguse vahele jääva hüpotenuusi ja hüpotenuusi lõiguga võrdeline keskmine.

Vaatleme täisnurkset kolmnurka täisnurgaga C, CD – kõrgus (joon. 2). Tõestame seda AC² +NE² = AB² .

Tõestus.

Põhineb väide täisnurkse kolmnurga jala kohta:

AC = , SV = .

Teeme ruudu ja lisame saadud võrrandid:

AC² = AB * AD, CB² = AB * DB;

AC² + CB² = AB * (AD + DB), kus AD+DB=AB, siis

AC² + CB² = AB * AB,

AC² + CB² = AB².

Tõestus on täielik.
3 MEETOD.

Pythagorase teoreemi tõestamiseks saate kasutada täisnurkse kolmnurga teravnurga koosinuse määratlust. Vaatame joonist fig. 3.

Tõestus:

Olgu ABC antud täisnurkne kolmnurk täisnurgaga C. Joonestame kõrguse CD täisnurga C tipust.

Nurga koosinuse määratluse järgi:

cos A = AD/AC = AC/AB. Seega AB * AD = AC²

Samamoodi

cos B = ВD/ВС = ВС/АВ.

Seega AB * BD = BC².

Lisades saadud võrdsused termini haaval ja märkides, et AD + DB = AB, saame:

AC² + päike² = AB (AD + DB) = AB²

Tõestus on täielik.
4 MEETOD.

Olles uurinud teemat “Täisnurkse kolmnurga külgede ja nurkade vahelised seosed”, arvan, et Pythagorase teoreemi saab tõestada ka muul viisil.

Mõelge jalgadega täisnurksele kolmnurgale a, c ja hüpotenuus Koos. (joonis 4).

Tõestame seda c²=a²+b².

Tõestus.

patt B= kõrge kvaliteet ; cos B= a/c , siis saadud võrrandite ruudustamisel saame:

sin² B= in²/s²; cos² IN= a²/c².

Kui need kokku liita, saame:

sin² IN+cos² B=в²/с²+ а²/с², kus sin² IN+cos² B=1,

1= (в²+ а²) / с², seega

c²= a² + b².

Tõestus on täielik.

5 MEETOD.

See tõestus põhineb jalgadele ehitatud ruutude lõikamisel (joonis 5) ja saadud osade asetamisel hüpotenuusile ehitatud ruudule.

6 MEETOD.

Tõestuseks küljelt Päike me ehitame BCD ABC(joonis 6). Me teame, et piirkond sarnased arvud on seotud nende sarnaste lineaarsete mõõtmetega ruutudena:

Lahutades esimesest võrdsusest teise, saame

c2 = a2 + b2.

Tõestus on täielik.

7 MEETOD.

Antud(Joonis 7):

ABC,= 90° , päike= a, AC=b, AB = c.

Tõesta:c2 = a2 +b2.

Tõestus.

Lase jalga b A. Jätkame lõiku NE punkti kohta IN ja ehitada kolmnurk BMD nii et punktid M Ja A lamada sirgjoone ühel küljel CD ja pealegi, BD =b, BDM= 90°, DM= a, siis BMD= ABC kahel küljel ja nendevahelise nurga all. Punktid A ja Mühendage segmentidega OLEN. Meil on M.D. CD Ja A.C. CD, see tähendab, et see on sirge AC joonega paralleelne M.D. Sest M.D.< АС, siis otse CD Ja OLEN. mitte paralleelne. Seetõttu AMDC- ristkülikukujuline trapets.

Täisnurksetes kolmnurkades ABC ja BMD 1 + 2 = 90° ja 3 + 4 = 90°, kuid kuna = =, siis 3 + 2 = 90°; Siis AVM=180° - 90° = 90°. Selgus, et trapets AMDC on jagatud kolmeks mittekattuvad täisnurkseks kolmnurgaks, seejärel pindala aksioomide järgi

(a+b)(a+b)

Jagades kõik ebavõrdsuse liikmed arvuga , saame

Ab + c2 + ab = (a +b) , 2 ab+ c2 = a2+ 2ab+ b2,

c2 = a2 + b2.

Tõestus on täielik.

8 MEETOD.

See meetod põhineb täisnurkse kolmnurga hüpotenuusil ja jalgadel ABC. Ta konstrueerib vastavad ruudud ja tõestab, et hüpotenuusile ehitatud ruut on võrdne jalgadele ehitatud ruutude summaga (joon. 8).

Tõestus.

1) DBC= FBA= 90°;

DBC+ ABC= FBA+ ABC, Tähendab, FBC = DBA.

Seega FBC=ABD(kahele küljele ja nende vahelisele nurgale).

2) , kus AL DE, alates BD - ühisosa, DL- kogukõrgus.

3) , kuna FB on sihtasutus, AB- kogukõrgus.

4)

5) Samamoodi saab tõestada, et

6) Termini kaupa lisades saame:

, eKr2 = AB2 + AC2 . Tõestus on täielik.

9 MEETOD.

Tõestus.

1) Lase ABDE- ruut (joon. 9), mille külg on võrdne täisnurkse kolmnurga hüpotenuusiga ABC= s, BC = a, AC =b).

2) Lase DK B.C. Ja DK = päike, kuna 1 + 2 = 90° (nagu täisnurkse kolmnurga teravnurk), 3 + 2 = 90° (nagu ruudu nurk), AB= BD(väljaku küljed).

Tähendab, ABC= BDK(hüpotenuusi ja teravnurga järgi).

3) Lase EL D.K., A.M. E.L. Seda saab kergesti tõestada, et ABC = BDK = DEL = EAM (jalgadega A Ja b). Siis KS= CM= M.L.= L.K.= A -b.

4) SKB = 4S+SKLMC= 2ab+ (a–b),Koos2 = 2ab + a2 - 2ab + b2,c2 = a2 + b2.

Tõestus on täielik.

10 MEETOD.

Tõestust saab teha kujuga, mida naljatamisi kutsutakse "Pütagorase püksid" (joon. 10). Selle idee on muuta külgedele ehitatud ruudud võrdseteks kolmnurkadeks, mis koos moodustavad hüpotenuusi ruudu.

ABC liigutage seda noolega näidatud viisil ja see võtab positsiooni KDN.Ülejäänud joonis AKDCB ruudu võrdne pindala AKDC see on rööpkülik AKNB.

Valmistatud on rööpküliku mudel AKNB. Paigutame rööpküliku ümber nii, nagu töö sisus visandatud. Rööpküliku teisenduse näitamiseks võrdse pindalaga kolmnurgaks lõikame õpilaste ees mudelil ära kolmnurga ja liigutame selle alla. Seega väljaku pindala AKDC osutus võrdseks ristküliku pindalaga. Samamoodi teisendame ruudu pindala ristküliku pindalaks.

Teeme teisenduse küljele ehitatud ruudu jaoks A(Joonis 11,a):

a) ruut teisendatakse võrdseks rööpkülikuks (joonis 11.6):

b) rööpkülik pöörleb veerand pööret (joonis 12):

c) rööpkülik muudetakse võrdseks ristkülikuks (joon. 13): 11 MEETOD.

Tõestus:

PCL - sirge (joon. 14);

KLOA= ACPF= ACED= a2;

LGBO= SVMR =CBNQ= b 2;

AKGB= AKLO +LGBO= c2;

c2 = a2 + b2.

Tõestus on läbi .

12 MEETOD.

Riis. Joonis 15 illustreerib Pythagorase teoreemi teist originaalset tõestust.

Siin: kolmnurk ABC täisnurgaga C; joonelõik B.F. risti NE ja sellega võrdne segment OLE risti AB ja sellega võrdne segment AD risti AC ja sellega võrdne; punktid F, C,D kuuluvad samasse ritta; nelinurgad ADFB Ja ASVE suuruselt võrdsed, kuna ABF = EKP; kolmnurgad ADF Ja ACE võrdse suurusega; lahutage mõlemast võrdsest nelinurgast kolmnurk, mida nad jagavad ABC, saame

, c2 = a2 + b2.

Tõestus on täielik.

13 MEETOD.

Antud täisnurkse kolmnurga pindala ühel küljel on võrdne , teisega, ,

3. KOKKUVÕTE.

Otsingutegevuse tulemusena saavutati töö eesmärk, milleks oli teadmiste täiendamine ja üldistamine Pythagorase teoreemi tõestuse kohta. Selle tõestamiseks ja teemakohaste teadmiste süvendamiseks oli võimalik leida ja kaaluda erinevaid võimalusi, väljudes kooliõpiku lehekülgedest.

Kogutud materjal veenab mind veelgi enam, et Pythagorase teoreem on suurepärane geomeetria teoreem ning sellel on tohutu teoreetiline ja praktiline tähendus. Kokkuvõtteks tahaksin öelda: Pythagorase kolmikteoreemi populaarsuse põhjuseks on selle ilu, lihtsus ja tähendus!

4. KASUTATUD KIRJANDUS.

1. Meelelahutuslik algebra. . Moskva "Teadus", 1978.

2. Iganädalane hariduslik rakendus ajalehele “Esimene september”, 24/2001.

3. Geomeetria 7-9. ja jne.

4. Geomeetria 7-9. ja jne.

(Berliini muuseumi papüüruse 6619 järgi). Cantori sõnul ehitasid harpedonaptes ehk "köietõmbajad" täisnurki, kasutades täisnurkseid kolmnurki, mille küljed on 3, 4 ja 5.

Nende ehitusmeetodit on väga lihtne reprodutseerida. Võtame 12 m pikkuse köie ja seome selle külge värvilise riba ühest otsast 3 m ja teisest 4 meetri kaugusel. Täisnurk jääb 3–4 meetri pikkuste külgede vahele. Harpedonaptlastele võib vastu vaielda, et nende ehitusmeetod muutub üleliigseks, kui kasutada näiteks puidust ruutu, mida kasutavad kõik puusepad. Tõepoolest, on teada Egiptuse joonised, millelt selline tööriist on leitud, näiteks puusepatöökoda kujutavad joonised.

Babüloonlaste seas on Pythagorase teoreemi kohta mõnevõrra rohkem teada. Ühes tekstis, mis pärineb Hammurapi ajast, see tähendab aastast 2000 eKr. e. , on antud täisnurkse kolmnurga hüpotenuusi ligikaudne arvutus. Sellest võime järeldada, et Mesopotaamias suudeti vähemalt mõnel juhul teha arvutusi täisnurksete kolmnurkadega. Tuginedes ühelt poolt Egiptuse ja Babüloonia matemaatika teadmiste praegusele tasemele ning teiselt poolt kreeka allikate kriitilisele uurimisele, jõudis Van der Waerden (Hollandi matemaatik) järeldusele, et suure tõenäosusega et teoreem hüpotenuusi ruudu kohta oli Indias tuntud juba umbes 18. sajandil eKr. e.

Umbes 400 eKr. eKr, Proklose sõnul andis Platon meetodi Pythagorase kolmikute leidmiseks, ühendades algebra ja geomeetria. Umbes 300 eKr. e. Pythagorase teoreemi vanim aksiomaatiline tõestus ilmus Eukleidese elementides.

Preparaadid

Geomeetriline koostis:

Teoreem oli algselt sõnastatud järgmisel viisil:

Algebraline formuleering:

See tähendab, et tähistab kolmnurga hüpotenuusi pikkust ja jalgade pikkust ja :

Teoreemi mõlemad sõnastused on samaväärsed, kuid teine ​​formuleering on elementaarsem, see ei nõua pindala mõistet. See tähendab, et teist väidet saab kontrollida pindala kohta midagi teadmata ja mõõtes ainult täisnurkse kolmnurga külgede pikkusi.

Pythagorase vastupidine teoreem:

Tõestus

Peal Sel hetkel Selle teoreemi tõestust on teaduskirjanduses registreeritud 367. Tõenäoliselt on Pythagorase teoreem ainus teoreem, millel on nii muljetavaldav hulk tõestusi. Sellist mitmekesisust saab seletada ainult teoreemi fundamentaalse tähtsusega geomeetria jaoks.

Mõistagi võib neid kõiki jagada väheseks arvuks klassideks. Tuntuimad neist: tõestused pindalameetodil, aksiomaatilised ja eksootilised tõestused (näiteks diferentsiaalvõrrandite abil).

Läbi sarnaste kolmnurkade

Järgmine algebralise formuleeringu tõestus on kõige lihtsam tõestus, mis on konstrueeritud otse aksioomidest. Eelkõige ei kasuta see figuuri pindala mõistet.

Lase ABC on täisnurkne kolmnurk täisnurgaga C. Joonistame kõrguse C ja tähistage selle alust H. Kolmnurk ACH sarnane kolmnurgaga ABC kahes nurgas. Samamoodi kolmnurk CBH sarnased ABC. Noodi sisseviimisega

saame

Mis on samaväärne

Selle kokku liitmisel saame

, mida oli vaja tõestada

Tõestused pindalameetodil

Vaatamata sellele on järgmised tõendid näiline lihtsus, pole üldse nii lihtsad. Kõik nad kasutavad ala omadusi, mille tõendid raskem tõestus Pythagorase teoreem ise.

Tõestus võrdväärse täienduse kaudu

1. Järjestame neli võrdset täisnurkset kolmnurka, nagu on näidatud joonisel 1.
2. Nelinurk külgedega c on ruut, kuna kahe summa teravad nurgad 90° ja voldimata nurk on 180°.
3. Kogu joonise pindala on ühelt poolt võrdne ruudu pindalaga, mille külg on (a + b), ja teiselt poolt nelja kolmnurga pindalade summaga ja sisemise väljaku pindala.

Q.E.D.

Eukleidese tõestus

Eukleidese tõestuse idee on järgmine: proovime tõestada, et pool hüpotenuusile ehitatud ruudu pindalast võrdub jalgadele ehitatud ruutude poolte pindalade summaga ja seejärel suur ja kaks väikest ruutu on võrdsed.

Vaatame vasakpoolset joonist. Sellele konstrueerisime täisnurkse kolmnurga külgedele ruudud ja joonistasime hüpotenuusiga AB risti oleva täisnurga C tipust kiiri s, mis lõikab hüpotenuusile ehitatud ruudu ABIK kaheks ristkülikuks - BHJI ja HAKJ, vastavalt. Selgub, et nende ristkülikute pindalad on täpselt võrdsed vastavatele jalgadele ehitatud ruutude pindaladega.

Proovime tõestada, et ruudu DECA pindala on võrdne ristküliku AHJK pindalaga. Selleks kasutame abivaatlust: kolmnurga pindala, mille kõrgus ja alus on sama antud ristkülik, võrdne poolega antud ristküliku pindalast. See tuleneb sellest, et kolmnurga pindala on pool aluse ja kõrguse korrutisest. Sellest tähelepanekust järeldub, et kolmnurga ACK pindala on võrdne kolmnurga AHK pindalaga (joonisel pole näidatud), mis omakorda võrdub poolega ristküliku AHJK pindalast.

Tõestame nüüd, et kolmnurga ACK pindala on samuti võrdne poolega DECA ruudu pindalast. Ainus asi, mida selleks tuleb teha, on tõestada kolmnurkade ACK ja BDA võrdsust (kuna kolmnurga BDA pindala on ülaltoodud omaduse järgi võrdne poole ruudu pindalaga). See võrdsus on ilmne: kolmnurgad on mõlemal küljel võrdsed ja nendevaheline nurk. Nimelt - AB=AK, AD=AC - nurkade CAK ja BAD võrdsust on lihtne tõestada liikumismeetodiga: pöörame kolmnurka CAK 90° vastupäeva, siis on ilmne, et kahe kolmnurga vastavad küljed küsimus langeb kokku (tänu asjaolule, et nurga ruudu tipus on 90°).

Ruudu BCFG ja ristküliku BHJI pindalade võrdsuse põhjendus on täiesti sarnane.

Seega tõestasime, et hüpotenuusile ehitatud ruudu pindala koosneb jalgadele ehitatud ruutude pindaladest. Selle tõestuse idee on veelgi illustreeritud ülaltoodud animatsiooniga.

Leonardo da Vinci tõend

Tõestuse põhielemendid on sümmeetria ja liikumine.

Vaatleme joonist, nagu sümmeetriast näha, lõikab segment ruudu kaheks identseks osaks (kuna kolmnurgad on ehituselt võrdsed).

Kasutades 90-kraadist vastupäeva pööramist ümber punkti, näeme varjutatud kujundite võrdsust ja.

Nüüd on selge, et meie poolt varjutatud joonise pindala on võrdne väikeste (jalgadele ehitatud) ruutude pindala ja algse kolmnurga pindala summaga. Teisest küljest on see võrdne poole suure ruudu pindalast (ehitatud hüpotenuusile) pluss algse kolmnurga pindala. Seega on pool väikeste ruutude pindalade summast võrdne poolega suure ruudu pindalast ja seetõttu võrdub jalgadele ehitatud ruutude pindalade summa ruudule ehitatud ruudu pindalaga. hüpotenuus.

Tõestus lõpmatu väikese meetodiga

Järgnev diferentsiaalvõrrandeid kasutav tõestus on sageli omistatud kuulsale inglise matemaatikule Hardyle, kes elas 20. sajandi esimesel poolel.

Vaadates joonisel näidatud joonist ja jälgides külje muutust a, saame kirjutada järgmise seose lõpmatute külgmiste juurdekasvude jaoks Koos Ja a(kasutades kolmnurga sarnasust):

Kasutades muutujate eraldamise meetodit, leiame

Rohkem üldine väljendus hüpotenuusi muutmiseks mõlema jala juurdekasvu korral

Integreerides selle võrrandi ja kasutades esialgsed tingimused, saame

Nii jõuame soovitud vastuseni

Kui lihtne on seda näha ruutsõltuvus ilmub lõplikus valemis tänu lineaarne proportsionaalsus kolmnurga külgede ja juurdekasvu vahel, samas kui summa on seotud erinevate jalgade juurdekasvu sõltumatute panustega.

Lihtsama tõestuse saab, kui eeldame, et üks jalg ei suurene (in sel juhul jalg). Seejärel saame integratsioonikonstandi jaoks

Variatsioonid ja üldistused

Sarnased geomeetrilised kujundid kolmel küljel

Üldistus jaoks sarnased kolmnurgad, roheliste kujundite pindala A + B = sinise C pindala

Pythagorase teoreem, kasutades sarnaseid täisnurkseid kolmnurki

Euclid üldistas oma töös Pythagorase teoreemi Algused, laiendades külgedel olevate ruutude alasid sarnaste geomeetriliste kujundite aladeks:

Kui konstrueerida sarnased geomeetrilised kujundid (vt Eukleidiline geomeetria) täisnurkse kolmnurga külgedele, on kahe väiksema kujundi summa võrdne suurema kujundi pindalaga.

Selle üldistuse põhiidee seisneb selles, et sellise ala geomeetriline kujund on võrdeline selle mis tahes lineaarmõõtme ruuduga ja eelkõige mis tahes külje pikkuse ruuduga. Seetõttu pindaladega sarnaste näitajate puhul A, B Ja C ehitatud külgedele pikkusega a, b Ja c, meil on:

Kuid Pythagorase teoreemi kohaselt a 2 + b 2 = c 2 siis A + B = C.

Ja vastupidi, kui suudame seda tõestada A + B = C kolme sarnase geomeetrilise kujundi puhul ilma Pythagorase teoreemi kasutamata saame teoreemi ennast tõestada liikudes vastupidine suund. Näiteks saab alustavat keskkolmnurka kolmnurgana uuesti kasutada C hüpotenuusil ja kaks sarnast täisnurkset kolmnurka ( A Ja B), mis on ehitatud kahele teisele küljele, mis moodustatakse keskse kolmnurga jagamisel selle kõrgusega. Kahe väiksema kolmnurga pindalade summa on siis ilmselgelt võrdne kolmanda pindalaga, seega A + B = C ja täites eelmise tõendi vastupidises järjekorras, saame Pythagorase teoreemi a 2 + b 2 = c 2 .

Koosinusteoreem

Pythagorase teoreem on erijuhtum rohkem üldine teoreem koosinused, mis seostab suvalise kolmnurga külgede pikkusi:

kus θ on külgede vaheline nurk a Ja b.

Kui θ on 90 kraadi, siis cos θ = 0 ja valem lihtsustub tavalise Pythagorase teoreemiga.

Tasuta kolmnurk

Suvalise külgedega kolmnurga mis tahes valitud nurka a, b, c Kirjutame võrdhaarse kolmnurga nii, et selle aluse θ võrdsed nurgad on võrdsed valitud nurgaga. Oletame, et valitud nurk θ asub määratud külje vastas c. Selle tulemusena saime kolmnurga ABD nurgaga θ, mis asub külje vastas a ja peod r. Teise kolmnurga moodustab nurk θ, mis asub külje vastas b ja peod Koos pikkus s, nagu pildil näidatud. Thabit Ibn Qurra väitis, et nende kolme kolmnurga küljed on seotud järgmiselt:

Kui nurk θ läheneb π/2-le, on alus võrdhaarne kolmnurk väheneb ning kaks külge r ja s kattuvad üha vähem. Kui θ = π/2, muutub ADB täisnurkseks kolmnurgaks, r + s = c ja saame esialgse Pythagorase teoreemi.

Vaatleme üht argumenti. Kolmnurga ABC nurgad on samad, mis kolmnurgal ABD, kuid vastupidises järjekorras. (Kaks kolmnurka on ühine nurk tipus B on mõlemal nurk θ ja neil on ka sama kolmas nurk, kolmnurga nurkade summa võrra) Seega on ABC sarnane kolmnurga DBA peegeldusega ABD, nagu on näidatud alumisel joonisel. Paneme kirja suhted vastasküljed ja nurga θ kõrval,

Ka teise kolmnurga peegeldus,

Korrutame murrud ja liidame need kaks suhet:

Q.E.D.

Üldistus suvaliste kolmnurkade jaoks rööpküliku abil

Üldistus jaoks suvalised kolmnurgad,
haljasala krunt = pindala sinine

Tõestus väitekirjale, mis on ülaltoodud joonisel

Teeme mittetäisnurksete kolmnurkade jaoks täiendava üldistuse, kasutades ruutude asemel rööpkülikuid kolmel küljel. (ruudud on erijuht.) Ülemine joonis näitab, et jaoks terav kolmnurk Rööpküliku pindala pikal küljel on võrdne kahe teise külje rööpküliku summaga eeldusel, et pika külje rööpkülik on konstrueeritud nii, nagu joonisel näidatud (nooltega tähistatud mõõtmed on samad ja määrata alumise rööpküliku küljed). Sellel ruutude asendamisel rööpkülikutega on selge sarnasus Pythagorase algse teoreemiga, mille arvatavasti sõnastas Pappus Aleksandriast aastal 4 pKr. e.

Alumine joonis näitab tõestuse edenemist. Vaatame kolmnurga vasakut külge. Vasakpoolse rohelise rööpküliku pindala on sama mis vasak pool sinine rööpkülik, kuna neil on sama alus b ja kõrgus h. Samuti on vasakpoolsel rohelisel rööpkülikul sama ala mis ülemisel pildil vasakul rohelisel rööpkülikul, kuna neil on ühine alus (ülemine vasakul pool kolmnurk) ja kogukõrgus, mis on risti kolmnurga selle küljega. Kasutades sarnast põhjendust kolmnurga parema külje kohta, tõestame, et alumisel rööpkülikul on sama pindala kui kahel rohelisel rööpkülikul.

Keerulised numbrid

Pythagorase teoreemi kasutatakse kahe punkti vahelise kauguse leidmiseks Descartes'i koordinaatsüsteemis ja see teoreem kehtib kõigi tõeliste koordinaatide kohta: kaugus. s kahe punkti vahel ( a, b) ja ( c, d) võrdub

Valemiga probleeme ei teki, kui kompleksarve käsitletakse reaalkomponentidega vektoritena x + mina y = (x, y). . Näiteks kaugus s vahemikus 0 + 1 i ja 1 + 0 i arvutatakse vektori moodulina (0, 1) − (1, 0) = (−1, 1), või

Keeruliste koordinaatidega vektoritega tehtavate toimingute jaoks on aga vaja Pythagorase valemit teha mõned parandused. Punktide vaheline kaugus koos kompleksarvud (a, b) ja ( c, d); a, b, c, Ja d kõik keerulised, sõnastagem kasutades absoluutväärtused. Kaugus s põhineb vektorite erinevusel (a − c, b − d) V järgmine vorm: lase vahet teha a − c = lk+i q, Kus lk- tegelik osa erinevusest, q on imaginaarne osa ja i = √(−1). Samamoodi lase b − d = r+i s. Seejärel:

kus on komplekskonjugaadi arv . Näiteks punktide vaheline kaugus (a, b) = (0, 1) Ja (c, d) = (i, 0) , arvutame vahe välja (a − c, b − d) = (−i, 1) ja tulemus oleks 0, kui komplekskonjugaate ei kasutata. Seega, kasutades täiustatud valemit, saame

Moodul on määratletud järgmiselt:

Stereomeetria

Pythagorase teoreemi oluline üldistus kolmemõõtmelise ruumi jaoks on de Goy teoreem, mis sai nime J.-P. de Gois: kui tetraeedril on täisnurk (nagu kuubil), siis on täisnurga vastas oleva tahu pindala ruut võrdne ülejäänud kolme tahu pindalade ruutude summaga. Selle järelduse võib kokku võtta järgmiselt: n-mõõtmeline Pythagorase teoreem":

Pythagorase teoreem kolmemõõtmeline ruumühendab diagonaali AD kolme küljega.

Veel üks üldistus: Pythagorase teoreemi saab stereomeetriale rakendada järgmisel kujul. Vaatleme ristkülikukujulist rööptahukat, nagu on näidatud joonisel. Leiame Pythagorase teoreemi abil diagonaali BD pikkuse:

kus kolm külge moodustavad täisnurkse kolmnurga. Diagonaali AD pikkuse leidmiseks kasutame horisontaalset diagonaali BD ja vertikaalset serva AB, selleks kasutame taas Pythagorase teoreemi:

või kui me kirjutame kõik ühte võrrandisse:

See tulemus on kolmemõõtmeline avaldis vektori suuruse määramiseks v(diagonaal AD), väljendatuna selle risti olevate komponentidena ( v k ) (kolm üksteisega risti olevat külge):

Seda võrrandit võib pidada Pythagorase teoreemi üldistuseks mitmemõõtmelise ruumi kohta. Tulemuseks pole aga tegelikult midagi muud kui Pythagorase teoreemi korduv rakendamine täisnurksete kolmnurkade jadale järjestikku risti asetsevatel tasapindadel.

Vektorruum

Millal ortogonaalne süsteem vektorites on võrdsus, mida nimetatakse ka Pythagorase teoreemiks:

Kui on vektori projektsioon koordinaatteljed, siis langeb see valem kokku eukleidilise kaugusega - ja tähendab, et vektori pikkus on võrdne selle komponentide ruutude summa ruutjuurega.

Selle võrdsuse analoogi lõpmatu vektorite süsteemi korral nimetatakse Parsevali võrduseks.

Mitteeukleidiline geomeetria

Pythagorase teoreem on tuletatud Eukleidilise geomeetria aksioomidest ja tegelikult ei kehti mitteeukleidilise geomeetria puhul sellisel kujul, nagu see on ülalpool kirjutatud. (See tähendab, et Pythagorase teoreem osutub omamoodi ekvivalendiks Eukleidese parallelismipostulaadile) Teisisõnu, mitte-eukleidilises geomeetrias on kolmnurga külgede vaheline suhe paratamatult Pythagorase teoreemist erineval kujul. Näiteks sfäärilises geomeetrias on täisnurkse kolmnurga kõik kolm külge (näiteks a, b Ja c), mis piiravad ühikkera oktanti (kaheksandat osa), on pikkusega π/2, mis on vastuolus Pythagorase teoreemiga, sest a 2 + b 2 ≠ c 2 .

Vaatleme siin kahte mitteeukleidilise geomeetria juhtumit – sfäärilist ja hüperboolset geomeetriat; mõlemal juhul, nagu ka täisnurksete kolmnurkade eukleidilise ruumi puhul, tuleneb Pythagorase teoreemi asendav tulemus koosinusteoreemist.

Siiski jääb Pythagorase teoreem kehtima hüperboolse ja elliptilise geomeetria puhul, kui kolmnurga ristkülikukujulisuse nõue asendatakse tingimusega, et kolmnurga kahe nurga summa peab olema võrdne kolmandaga, ütleme A+B = C. Siis näeb külgede suhe välja selline: läbimõõduga ringide pindalade summa a Ja b võrdne läbimõõduga ringi pindalaga c.

Sfääriline geomeetria

Mis tahes täisnurkse kolmnurga jaoks raadiusega sfääril R(näiteks kui nurk γ kolmnurgas on täisnurkne) külgedega a, b, c Osapoolte vaheline suhe näeb välja selline:

Seda võrdsust saab tuletada järgmiselt erijuhtum sfäärilise koosinuse teoreem, mis kehtib kõigi sfääriliste kolmnurkade puhul:

kus cosh on hüperboolne koosinus. See valem on hüperboolse koosinusteoreemi erijuhtum, mis kehtib kõigi kolmnurkade puhul:

kus γ on nurk, mille tipp on külje vastas c.

Kus g ij nimetatakse meetriliseks tenoriks. See võib olla asendi funktsioon. Sellised kõverjoonelised ruumid hõlmavad Riemanni geomeetriat nagu üldine näide. See formulatsioon sobib ka Eukleidilise ruumi jaoks, kui kasutatakse kõverjoonelisi koordinaate. Näiteks polaarkoordinaatide jaoks:

Vektorkunstiteos

Pythagorase teoreem ühendab kaks vektorkorrutise suuruse avaldist. Üks lähenemisviis ristkorrutise määratlemiseks nõuab, et see vastaks võrrandile:

see valem kasutab punktkorrutist. Parem pool võrrandit nimetatakse grammi determinandiks a Ja b, mis on võrdne nende kahe vektori moodustatud rööpküliku pindalaga. Lähtudes sellest nõudest, samuti nõudest, et vektorkorrutis on selle komponentidega risti a Ja b sellest järeldub, et välja arvatud triviaalsed juhud 0- ja 1-mõõtmelisest ruumist, on ristkorrutis defineeritud ainult kolme- ja seitsmemõõtmelisena. Kasutame nurga määratlust in n- mõõtmete ruum:

See ristkorrutise omadus annab selle suuruse järgmiselt:

Fundamentaalse kaudu trigonomeetriline identiteet Pythagoras saame selle väärtuse kirjutamiseks veel ühe vormi:

Alternatiivne lähenemisviis ristkorrutise määratlemiseks on kasutada selle suurusjärgu avaldist. Seejärel, arutledes vastupidises järjekorras, saame seose skalaarkorrutis:

Vaata ka

Märkmed

1. Ajaloo teema: Pythagorase teoreem Babüloonia matemaatikas
2. ( , lk 351) lk 351
3. ( , I köide, lk 144)
4. Arutelu ajaloolised faktid antud (, lk 351) lk 351
5. Kurt Von Fritz (apr., 1945). "Metapontumi Hippasuse poolt võrreldamatuse avastus". Matemaatika aastaraamatud, teine ​​seeria(Matemaatika aastaraamatud) 46 (2): 242–264.
6. Lewis Carroll, “Lugu sõlmedega”, M., Mir, 1985, lk. 7
7. Asger Aaboe Episoodid matemaatika varasest ajaloost. - Mathematical Association of America, 1997. - Lk 51. - ISBN 0883856131
8. Pythoni ettepanek autor Elisha Scott Loomis
9. Eukleidese oma Elemendid: VI raamat, VI väide 31: "Täisnurksete kolmnurkade korral on täisnurka kallutaval küljel olev kujund võrdne sarnaste ja sarnaselt kirjeldatud kujunditega täisnurka sisaldavatel külgedel."
10. Lawrence S. Leff viidatud töö. - Barroni õppesari. - Lk 326. - ISBN 0764128922
11. Howard Whitley Eves§4.8:...Pythagorase teoreemi üldistus // Matemaatika suurhetked (enne 1650. aastat). - Ameerika Matemaatikaliit, 1983. - Lk 41. - ISBN 0883853108
12. Tâbit ibn Qorra (täisnimi Thābit ibn Qurra ibn Marwan Al-Ṣābiʾ al-Ḥarrānī) (826–901 pKr) oli Bagdadis elanud arst, kes kirjutas põhjalikult Eukleidese elementidest ja muudest matemaatilistest ainetest.
13. Aydin Sayili (märts 1960). "Thâbit ibn Qurra" Pythagorase teoreemi üldistus. Isis 51 (1): 35–37. DOI: 10.1086/348837.
14. Judith D. Sally, Paul Sally Harjutus 2.10 (ii) // Viidatud töö. - Lk 62. - ISBN 0821844032
15. Jaoks sellise konstruktsiooni üksikasju vt George Jennings Joonis 1.32: Üldistatud Pythagorase teoreem // Kaasaegne geomeetria rakendustega: 150 joonisega. - 3. - Springer, 1997. - Lk 23. - ISBN 038794222X
16. Arlen Brown, Carl M. PearcyÜksus C: Norm suvalise jaoks n-tuple ... // Sissejuhatus analüüsi . - Springer, 1995. - Lk 124. - ISBN 0387943692 Vaata ka lk 47-50.
17. Alfred Gray, Elsa Abbena, Simon Salamon Moodne kõverate ja pindade diferentsiaalgeomeetria Mathematicaga. - 3. - CRC Press, 2006. - Lk 194. - ISBN 1584884487
18. Rajendra Bhatia Maatriksanalüüs. - Springer, 1997. - Lk 21. - ISBN 0387948465
19. Stephen W. Hawking viidatud töö. - 2005. - Lk 4. - ISBN 0762419229
20. Eric W. Weisstein CRC lühike matemaatika entsüklopeedia. - 2. - 2003. - Lk 2147. - ISBN 1584883472
21. Aleksander R. Pruss

Pythagorase teoreemi ajalugu ulatub mitu tuhat aastat tagasi. Avaldus, mis väidab, et see oli teada juba ammu enne kreeka matemaatiku sündi. Kuid Pythagorase teoreem, selle loomise ajalugu ja selle tõestamine on enamuse jaoks seotud selle teadlasega. Mõnede allikate kohaselt oli selle põhjuseks teoreemi esimene tõestus, mille esitas Pythagoras. Mõned teadlased aga eitavad seda fakti.

Muusika ja loogika

Enne kui räägime Pythagorase teoreemi ajaloo kujunemisest, vaatame lühidalt matemaatiku elulugu. Ta elas 6. sajandil eKr. Pythagorase sünniajaks loetakse aastat 570 eKr. e., koht on Samose saar. Teadlase elust on usaldusväärselt vähe teada. Biograafilised andmed sisse Vana-Kreeka allikad läbi põimunud ilmse ilukirjandusega. Traktaatide lehekülgedel esineb ta suure targana, kellel on suurepärane sõnaoskus ja veenmisvõime. Muide, sellepärast sai kreeka matemaatik hüüdnime Pythagoras, see tähendab "veenv kõne". Teise versiooni kohaselt ennustas tulevase targa sündi Pythia. Isa pani poisile tema auks nimeks Pythagoras.

Tark õppis oma aja suurtelt mõistustelt. Noorte Pythagorase õpetajate hulgas on Hermodamantus ja Syrose Pherecydes. Esimene sisendas temasse armastuse muusika vastu, teine ​​õpetas filosoofiat. Mõlemad teadused jäävad teadlase tähelepanu keskmesse kogu tema elu jooksul.

30 aastat koolitust

Ühe versiooni kohaselt lahkus Pythagoras, olles uudishimulik noormees, kodumaalt. Ta läks teadmisi otsima Egiptusesse, kus ta viibis erinevatel andmetel 11–22 aastat, seejärel tabati ja saadeti Babüloni. Pythagoras sai oma positsioonist kasu. 12 aastat õppis ta aastal matemaatikat, geomeetriat ja maagiat iidne riik. Pythagoras naasis Samosele alles 56-aastaselt. Sel ajal valitses siin türann Polycrates. Pythagoras ei saanud sellise poliitilise süsteemiga leppida ja läks peagi Lõuna-Itaaliasse, kus see asus Kreeka koloonia Croton.

Tänapäeval on võimatu kindlalt öelda, kas Pythagoras oli Egiptuses ja Babülonis. Võib-olla lahkus ta hiljem Samosest ja läks otse Crotonisse.

Pythagoraslased

Pythagorase teoreemi ajalugu on seotud kreeka filosoofi loodud koolkonna arenguga. See usuline ja eetiline vennaskond jutlustas erilise eluviisi järgimist, õppis aritmeetikat, geomeetriat ja astronoomiat ning tegeles arvude filosoofilise ja müstilise poole uurimisega.

Kõik Kreeka matemaatiku õpilaste avastused omistati talle. Pythagorase teoreemi tekkimise ajalugu seostavad iidsed biograafid aga ainult filosoofi endaga. Eeldatakse, et ta andis kreeklastele edasi Babülonis ja Egiptuses omandatud teadmised. On ka versioon, et ta avastas tegelikult teoreemi jalgade ja hüpotenuusi vahelise seose kohta, teadmata teiste rahvaste saavutustest.

Pythagorase teoreem: avastamise ajalugu

Mõned Vana-Kreeka allikad kirjeldavad Pythagorase rõõmu, kui tal õnnestus teoreem tõestada. Selle sündmuse auks käskis ta jumalatele ohverdada sadade härgade kujul ja pidas pidu. Mõned teadlased aga osutavad sellise teo võimatusele pütagoorlaste vaadete iseärasuste tõttu.

Arvatakse, et Eukleidese loodud traktaadis “Elements” esitab autor tõestuse teoreemile, mille autor oli suur Kreeka matemaatik. Kuid mitte kõik ei toetanud seda seisukohta. Nii juhtis isegi antiikneoplatonistlik filosoof Proclus tähelepanu sellele, et Elementides antud tõestuse autor oli Eukleides ise.

Olgu kuidas on, aga esimene inimene, kes teoreemi sõnastas, polnud Pythagoras.

Vana-Egiptus ja Babülon

Pythagorase teoreem, mille ajalugu artiklis käsitletakse, oli saksa matemaatiku Cantori sõnul teada juba 2300 eKr. e. Egiptuses. Niiluse oru iidsed elanikud vaarao Amenemhat I valitsemisajal teadsid võrdsust 3 2 + 4 ² = 5 ². Eeldatakse, et 3, 4 ja 5 külgedega kolmnurkade abil ehitasid Egiptuse “köietõmbajad” täisnurki.

Nad teadsid Babülonis ka Pythagorase teoreemi. Aastast 2000 eKr pärinevatel savitahvlitel. ja valitsemisajast pärit, avastati täisnurkse kolmnurga hüpotenuusi ligikaudne arvutus.

India ja Hiina

Pythagorase teoreemi ajalugu on seotud ka India ja Hiina iidsete tsivilisatsioonidega. Traktaat “Zhou-bi suan jin” sisaldab viiteid sellele, et (selle küljed on omavahel seotud kui 3:4:5) tunti Hiinas juba 12. sajandil. eKr e. ja 6. sajandiks. eKr e. selle osariigi matemaatikud teadsid üldine vorm teoreemid.

Täisnurga konstrueerimine kasutades Egiptuse kolmnurk seda väideti ka India traktaadis “Sulva Sutra”, mis pärineb 7.-5. eKr e.

Seega oli Pythagorase teoreemi ajalugu Kreeka matemaatiku ja filosoofi sünni ajaks juba mitusada aastat vana.

Tõestus

Oma eksisteerimise ajal sai teoreem üheks geomeetria põhialuseks. Tõenäoliselt sai Pythagorase teoreemi tõestuse ajalugu alguse võrdkülgse ruudu käsitlemisest, mille hüpotenuusile ja jalgadele konstrueeritakse ruudud. See, mis hüpotenuusil "kasvas", koosneb neljast kolmnurgast, võrdne esimesega. Külgedel olevad ruudud koosnevad kahest sellisest kolmnurgast. Lihtne graafiline pilt näitab selgelt kuulsa teoreemi vormis sõnastatud väite paikapidavust.

Teine lihtne tõestus ühendab geomeetria algebraga. Neli identset täisnurkset kolmnurka külgedega a, b, c tõmmatakse nii, et need moodustavad kaks ruutu: välimise küljega (a + b) ja sisemise küljega c. Sel juhul on väiksema ruudu pindala võrdne c 2-ga. Suure pindala arvutatakse pindalade summast väike ruut ja kõik kolmnurgad (täisnurkse kolmnurga pindala, meenutamine, arvutatakse valemiga (a * b) / 2), see tähendab c 2 + 4 * ((a * b) / 2), mis on võrdne kuni c 2 + 2ab. Suure ruudu pindala saab arvutada ka muul viisil - kahe külje korrutisena, see tähendab (a + b) 2, mis võrdub a 2 + 2ab + b 2. Selgub:

a 2 + 2ab + b 2 = c 2 + 2ab,

a 2 + b 2 = c 2.

Selle teoreemi tõestuseks on palju versioone. Nende kallal töötasid Euclid, India teadlased ja Leonardo da Vinci. Sageli viitasid muistsed targad joonistele, mille näited on ülalpool, ega lisanud neile muid selgitusi peale märkuse "Vaata!" Geomeetrilise tõestuse lihtsus, eeldusel, et teadmised olid olemas, ei vajanud kommentaare.

Artiklis lühidalt kirjeldatud Pythagorase teoreemi ajalugu lükkab ümber müüdi selle päritolu kohta. Siiski on raske isegi ette kujutada, et suure kreeka matemaatiku ja filosoofi nimi lakkab kunagi sellega seostamast.

Pythagorase teoreem - põhiteoreem Eukleidiline geomeetria, mis postuleerib täisnurkse kolmnurga jalgade ja hüpotenuusi suhet. See on võib-olla kõige populaarsem teoreem maailmas, mida kõik koolist teavad.

Teoreemi ajalugu

Tegelikult oli täisnurkse kolmnurga külgede suhte teooria tuntud juba ammu enne Pythagorast Samose saarelt. Seega leitakse kuvasuhtega seotud probleeme iidsetest tekstidest alates Babüloonia kuninga Hammurapi valitsusajast, see tähendab 1500 aastat enne Sami matemaatiku sündi. Märkmeid kolmnurga külgede kohta ei salvestatud mitte ainult Babüloonias, vaid ka Vana-Egiptuses ja Hiinas. Üks tuntumaid jalgade ja hüpotenuusi täisarvude suhet näeb välja nagu 3, 4 ja 5. Neid numbreid kasutasid iidsed maamõõtjad ja arhitektid täisnurkade konstrueerimiseks.

Niisiis, Pythagoras ei leiutanud teoreemi jalgade ja hüpotenuusi vahelise seose kohta. Ta oli esimene ajaloos, kes seda tõestas. Selles on aga kahtlusi, kuna saami matemaatiku tõestus, kui see registreeriti, kadus sajandeid. Arvatakse, et Eukleidese elementides antud teoreemi tõestus kuulub konkreetselt Pythagorasele. Matemaatika ajaloolastel on selles aga suured kahtlused.

Pythagoras oli esimene, kuid pärast teda tõestati teoreem täisnurkse kolmnurga külgede kohta umbes 400 korda, kasutades erinevaid tehnikaid: alates klassikaline geomeetria enne diferentsiaalarvutus. Pythagorase teoreem on uudishimulikke meeli alati hõivanud, nii et tõestuste autoritest võib meenutada USA presidenti James Garfieldi.

Tõestus

IN matemaatiline kirjandus Pythagorase teoreemi tõestust on registreeritud vähemalt nelisada. Sellist mõistusevastast numbrit seletab teoreemi fundamentaalne tähtsus teadusele ja tulemuse elementaarne olemus. Põhimõtteliselt tõestatakse Pythagorase teoreem geomeetriliste meetoditega, millest populaarseimad on alade meetod ja sarnasuste meetod.

Kõige lihtne meetod teoreemi tõestus, mis ei nõua kohustuslikku geomeetrilised konstruktsioonid, on ala meetod. Pythagoras väitis, et hüpotenuusi ruut võrdub jalgade ruutude summaga:

Proovime seda julget väidet tõestada. Teame, et iga kujundi pindala määratakse joone segmendi ruudustamisel. Joonelõik võib olla ükskõik milline, kuid enamasti on see kujundi külg või selle raadius. Sõltuvalt segmendi valikust ja geomeetrilise kujundi tüübist on ruudul erinevad koefitsiendid:

• ühtsus ruudu puhul – S = a 2;
• puhul ligikaudu 0,43 Võrdkülgne kolmnurk– S = (sqrt(3)/4)a 2 ;
• Pi ringi puhul – S = pi × R 2.

Seega saame väljendada mis tahes kolmnurga pindala kujul S = F × a 2, kus F on teatud koefitsient.

Täisnurkne kolmnurk - hämmastav figuur, mida saab hõlpsasti jagada kaheks sarnaseks täisnurkseks kolmnurgaks, jättes lihtsalt risti ükskõik millisest tipust. See jagamine muudab täisnurkse kolmnurga kahe väiksema täisnurkse kolmnurga summaks. Kuna kolmnurgad on sarnased, arvutatakse nende pindala sama valemiga, mis näeb välja järgmine:

S = F × hüpotenuus 2

Jagamise tulemusena suur kolmnurk külgedega a, b ja c (hüpotenuus) saime kolm kolmnurka ning väiksemate kujundite hüpotenuusid osutusid algse kolmnurga a ja b külgedeks. Seega arvutatakse sarnaste kolmnurkade pindalad järgmiselt:

• S1 = F × c 2 – algne kolmnurk;
• S2 = F × a 2 – esimene sarnane kolmnurk;
• S3 = F × b 2 – teine ​​sarnane kolmnurk.

Ilmselt on suure kolmnurga pindala võrdne sarnaste pindalade summaga:

F × c 2 = F × a2 + F × b 2

F faktorit on lihtne vähendada. Selle tulemusena saame:

c 2 = a 2 + b 2,

Q.E.D.

Pythagorase kolmikud

Eespool on juba mainitud populaarset jalgade ja hüpotenuuste suhet 3, 4 ja 5. Pythagorase kolmikud on komplekt kolmest vastastikku algarvud, mis rahuldavad tingimust a 2 + b 2 = c 2 . Sellised kombinatsioonid on olemas lõpmatu arv, ja esimesi neist kasutati iidsetel aegadel täisnurkade konstrueerimiseks. Sidudes nöörile võrdsete ajavahemike järel teatud arvu sõlmi ja voltides selle kolmnurgaks, saavutasid muistsed teadlased täisnurga. Selleks oli vaja kolmnurga mõlemale küljele siduda sõlmed koguses, mis vastas Pythagorase kolmikutele:

• 3, 4 ja 5;
• 5, 12 ja 13;
• 7, 24 ja 25;
• 8, 15 ja 17.

Sel juhul saab mis tahes Pythagorase kolmikut suurendada täisarvu võrra ja saada Pythagorase teoreemi tingimustele vastava proportsionaalse seose. Näiteks kolmikutest 5, 12, 13 saate külgväärtused 10, 24, 26 lihtne korrutamine poolt 2. Tänapäeval kasutatakse Pythagorase kolmikuid kiire lahendus geomeetrilised probleemid.

Pythagorase teoreemi rakendamine

Sami matemaatiku teoreemi ei kasutata mitte ainult kooligeomeetrias. Pythagorase teoreem leiab rakendust arhitektuuris, astronoomias, füüsikas, kirjanduses, infotehnoloogia ja isegi tulemuslikkuse hindamisel sotsiaalsed võrgustikud. Teoreem kehtib ka päriselus.

Pitsa valik

Pizzeriates seisavad kliendid sageli küsimuse ees: kas võtta üks suur pitsa või kaks väiksemat? Oletame, et saad osta ühe 50 cm läbimõõduga pitsa või kaks väiksemat 30 cm läbimõõduga pitsat.Esmapilgul on kaks väiksemat pitsat suuremad ja tulusamad, kuid see pole nii. Kuidas kiiresti võrrelda teile meeldivate pitsade pinda?

Meenub saami matemaatiku ja Pythagorase kolmikute teoreem. Ringi pindala on läbimõõdu ruut koefitsiendiga F = pi/4. Ja esimene Pythagorase kolmik on 3, 4 ja 5, mille saame kergesti muuta kolmikuks 30, 40, 50. Seega 50 2 = 30 2 + 40 2. Ilmselt on 50 cm läbimõõduga pitsa pindala suurem kui 30 cm läbimõõduga pitsade summa. Näib, et teoreem on rakendatav ainult geomeetria ja ainult kolmnurkade puhul, kuid see näide näitab et seost c 2 = a 2 + b 2 saab kasutada ka teiste arvude ja nende tunnuste võrdlemiseks.

Meie veebikalkulaator võimaldab teil arvutada mis tahes väärtuse, mis vastab ruutude summa põhivõrrandile. Arvutamiseks sisestage lihtsalt 2 väärtust, mille järel programm arvutab puuduva koefitsiendi. Kalkulaator ei tööta mitte ainult täisarvude, vaid ka murdosa väärtustega, nii et saate arvutamiseks kasutada mis tahes numbreid, mitte ainult Pythagorase kolmikuid.

Järeldus

Pythagorase teoreem on fundamentaalne asi, mida kasutatakse laialdaselt paljudes teaduslikud rakendused. Kasutage meie veebikalkulaatorit väärtuste suuruste arvutamiseks, mis on seotud c 2 = a 2 + b 2 .

GEOMEETRILISTE KUJUDE ALA MÕÕTMINE.

§ 58. PÜTAGOROE TEOREEM 1.

__________
1 Pythagoras on kreeka teadlane, kes elas umbes 2500 aastat tagasi (564-473 eKr).
_________

Olgu meile antud täisnurkne kolmnurk, mille küljed A, b Ja Koos(joonis 267).

Ehitame selle külgedele ruudud. Nende ruutude pindalad on vastavalt võrdsed A 2 , b 2 ja Koos 2. Tõestame seda Koos 2 = a 2 +b 2 .

Ehitame kaks ruutu MKOR ja M"K"O"R (joonised 268, 269), võttes mõlema küljeks lõigu, mis on võrdne täisnurkse kolmnurga ABC jalgade summaga.

Pärast joonistel 268 ja 269 näidatud konstruktsioonide valmimist nendes ruutudes näeme, et MCOR ruut on jagatud kaheks pindalaga ruuduks A 2 ja b 2 ja neli võrdset täisnurkset kolmnurka, millest igaüks on võrdne täisnurkse kolmnurgaga ABC. Ruut M"K"O"R jagati nelinurgaks (joonisel 269 on varjutatud) ja neljaks täisnurkseks kolmnurgaks, millest igaüks on samuti võrdne kolmnurgaga ABC. Varjutatud nelinurk on ruut, kuna selle küljed on võrdsed (igaüks võrdub kolmnurga ABC hüpotenuusiga, st. Koos) ja nurgad on õiged / 1 + / 2 = 90°, kust / 3 = 90°).

Seega võrdub jalgadele ehitatud ruutude pindalade summa (joonisel 268 on need ruudud varjutatud) ruudu pindalaga MCOR ilma nelja võrdse kolmnurga pindalade summata ja . hüpotenuusile ehitatud ruut (joonisel 269 on ka see ruut varjutatud) on võrdne ruudu M"K"O"R pindalaga, võrdne ruuduga MCOR, ilma nelja sarnase kolmnurga pindalade summata. Seetõttu on täisnurkse kolmnurga hüpotenuusile ehitatud ruudu pindala võrdne jalgadele ehitatud ruutude pindalade summaga.

Saame valemi Koos 2 = a 2 +b 2 kus Koos- hüpotenuus, A Ja b- täisnurkse kolmnurga jalad.

Pythagorase teoreem sõnastatakse tavaliselt lühidalt järgmiselt:

Täisnurkse kolmnurga hüpotenuusi ruut võrdub jalgade ruutude summaga.

Valemist Koos 2 = a 2 +b 2 saate järgmised valemid:

A 2 = Koos 2 - b 2 ;
b 2 = Koos 2 - A 2 .

Neid valemeid saab kasutada leidmiseks tundmatu pool täisnurkne kolmnurk piki selle kahte etteantud külge.
Näiteks:

a) kui jalad on antud A= 4 cm, b=3 cm, siis leiad hüpotenuusi ( Koos):
Koos 2 = a 2 +b 2, st. Koos 2 = 4 2 + 3 2; kus 2 = 25, kust Koos= √25 =5 (cm);

b) kui hüpotenuus on antud Koos= 17 cm ja jalg A= 8 cm, siis leiad teise jala ( b):

b 2 = Koos 2 - A 2, st. b 2 = 17 2 - 8 2 ; b 2 = 225, kust b= √225 = 15 (cm).

Tagajärg: Kui kahel täisnurksel kolmnurgal ABC ja A on 1 B 1 C 1 hüpotenuus Koos Ja Koos 1 on võrdsed ja jalg b kolmnurk ABC on pikem kui jalg b 1 kolmnurk A 1 B 1 C 1,
siis jalg A kolmnurk ABC vähem jalga A 1 kolmnurk A 1 B 1 C 1. (Tehke seda tagajärge illustreeriv joonis.)

Tegelikult saame Pythagorase teoreemi põhjal:

A 2 = Koos 2 - b 2 ,
A 1 2 = Koos 1 2 - b 1 2

Kirjutatud valemites on minuendid võrdsed ja esimese valemi alamlahend on suurem kui teise valemi alamosa, seega on esimene erinevus väiksem kui teine,
st. A 2 < A 12 . Kus A< A 1 .

Harjutused.

1. Tõesta joonise 270 abil Pythagorase teoreem võrdhaarse täisnurkse kolmnurga kohta.

2. Täisnurkse kolmnurga üks jalg on 12 cm, teine ​​5 cm Arvutage selle kolmnurga hüpotenuusi pikkus.

3. Täisnurkse kolmnurga hüpotenuus on 10 cm, üks jalg on 8 cm Arvuta selle kolmnurga teise jala pikkus.

4. Täisnurkse kolmnurga hüpotenuus on 37 cm, selle üks jalg on 35 cm Arvuta selle kolmnurga teise jala pikkus.

5. Ehitage ruut, mille pindala on kaks korda suurem etteantud ruut.

6. Ehitage ruut, mille pindala on etteantust poole väiksem. Märge. Viige sisse antud ruut diagonaalid. Nende diagonaalide pooltele konstrueeritud ruudud on need, mida me otsime.

7. Täisnurkse kolmnurga jalad on vastavalt 12 cm ja 15 cm Arvutage selle kolmnurga hüpotenuusi pikkus 0,1 cm täpsusega.

8. Täisnurkse kolmnurga hüpotenuus on 20 cm, selle üks jalg on 15 cm Arvuta teise jala pikkus 0,1 cm täpsusega.

9. Kui pikk peab redel olema, et seda saaks kinnitada 6 m kõrgusel asuva akna külge, kui redeli alumine ots peab asuma hoonest 2,5 m kaugusel? (diagramm 271.)