Przekroje figur geometrycznych mają różne kształty. Przekrój równoległościanu jest niezmiennie prostokątem lub kwadratem. Posiada szereg parametrów, które można wykryć metodą analityczną.
Instrukcje
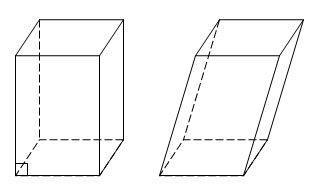
1. Możliwe jest narysowanie czterech odcinków równoległościanu, które są kwadratami lub prostokątami. Każdy ma dwie przekątne i dwie przekroje. Jak zwykle mają różne rozmiary. Wyjątkiem jest sześcian, w którym są identyczne.Przed zbudowaniem odcinka równoległościanu zastanów się, co reprezentuje ta figura. Istnieją dwa rodzaje równoległościanów - zwykłe i prostokątne. W zwykłym równoległościanie ściany znajdują się pod pewnym kątem do podstawy, natomiast w prostokątnym są do niej prostopadłe. Wszystkie twarze prostokątny równoległościan są prostokątami lub kwadratami. Wynika z tego, że sześcian jest szczególny przypadek prostokątny równoległościan.
2. Każdy odcinek równoległościanu ma pewne zestawienia. Najważniejsze z nich to powierzchnia, obwód i długość przekątnych. Jeśli z tych problemów znane są boki przekroju lub inne jego parametry, wystarczy określić jego obwód lub powierzchnię. Przekątne sekcji są również określane wzdłuż boków. Pierwszym z tych parametrów jest pole przekroju ukośnego.Aby wyznaczyć pole przekroju ukośnego, konieczna jest znajomość wysokości i boków podstawy równoległościanu. Jeżeli podana jest długość i szerokość podstawy równoległościanu, to znajdź przekątną korzystając z twierdzenia Pitagorasa: d=?a^2+b^2.Po znalezieniu przekątnej i znając wysokość równoległościanu oblicz przekątną- pole przekroju równoległościanu: S=d*h.
3. Obwód przekroju ukośnego można również obliczyć za pomocą dwóch wartości - przekątnej podstawy i wysokości równoległościanu. W takim przypadku najpierw znajdź dwie przekątne (górną i dolną podstawę) korzystając z twierdzenia Pitagorasa, a następnie dodaj je o podwójnej wysokości.
4. Jeśli narysujesz samolot, równolegle do żeber równoległościan, możliwe jest uzyskanie przekroju prostokątnego, którego boki są jednym z boków podstawy równoległościanu i wysokości. Pole tego przekroju znajdź w następujący sposób: S = a * h. W podobny sposób znajdź obwód tego przekroju, korzystając ze wzoru: p = 2 * (a + h).
5. Ostatni przypadek ma miejsce, gdy odcinek przebiega równolegle do dwóch podstaw równoległościanu. Wtedy jego pole i obwód są równe wartości pola i obwodu podstaw, czyli: S=a*b - pole przekroju poprzecznego, p=2*(a+b).
Zanim przejdziemy do znalezienia wysokości równoległościanu, należy wyjaśnić, czym jest wysokość i czym jest równoległościan. W geometrii wysokość jest prostopadłą od góry figury do jej podstawy lub odcinkiem łączącym górną i dolną podstawę najkrótszą metodą. Równoległościan to wielościan, który ma dwa równoległe i równy wielokąt jako podstawy, których narożniki są połączone segmentami. Równoległościan składa się z sześciu równoległoboków, równoległych parami i równych sobie.
Instrukcje
1. W równoległoboku mogą znajdować się trzy wysokości, w zależności od położenia figury w przestrzeni; obracając równoległościan na bok, zamienisz jego podstawy i ściany. Górny i dolny równoległobok są niezmiennie podstawami. Jeżeli boczne krawędzie figury są prostopadłe do podstaw, to równoległościan jest prosty, a każda z jego krawędzi ma gotową wysokość. Pozwolono zmierzyć.
2. Aby uzyskać prosty równoległościan tego samego rozmiaru z nachylonego równoległościanu, należy przedłużyć ściany boczne w jednym kierunku. Następnie zbuduj przekrój prostopadły, z którego narożników odłóż długość krawędzi równoległościanu i w tej odległości zbuduj drugi prostopadły odcinek. Dwa skonstruowane równoległoboki ograniczą nowy równoległościan o polu równym pierwszemu. Na przyszłość należy zauważyć, że woluminy figury o jednakowej wielkości identyczny.
3. Często zadawane pytanie W problemach napotykamy wyżyny. Zawsze otrzymujemy dane, które pozwalają nam to obliczyć. Może to być objętość, wymiary liniowe równoległościanu, długości jego przekątnych. Zatem objętość równoległościanu równy produktowi jego podstawę na podstawie jej wysokości, to znaczy znając objętość i rozmiar podstawy, łatwo jest obliczyć wysokość, dzieląc pierwszą przez drugą. Jeśli masz do czynienia z równoległościanem prostokątnym, czyli takim, którego podstawą jest prostokąt, mogą próbować skomplikować Twoje zadanie ze względu na jego szczególne właściwości. Zatem w równoległościanie prostokątnym każdy kwadrat jego przekątnej równa sumie kwadraty o 3 wymiarach równoległościanu. Jeśli „podane” dla problemu prostokątnego równoległościanu wskazuje długość jego przekątnej i długości boków podstawy, wówczas ta informacja wystarczy, aby określić rozmiar pożądanej wysokości.
Równoległościan to szczególny przypadek pryzmatu, w którym wszystkie sześć ścian jest równoległobokami lub prostokątami. Równoległościan z prostokątne krawędzie zwany także prostokątnym. Równoległościan ma cztery przecinające się przekątne. Jeśli dane są trzy krawędzie a, b, c, wszystkie przekątne równoległościanu prostokątnego można znaleźć, wykonując dodatkowe konstrukcje.
Instrukcje
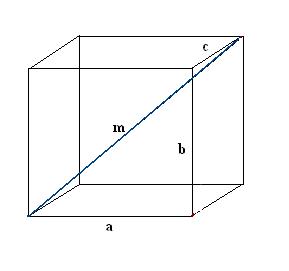
1. Narysuj prostokątny równoległościan. Zapisz znane dane: trzy krawędzie a, b, c. Najpierw zbuduj jedną przekątną m. Aby to określić, używamy jakości prostokątnego równoległościanu, zgodnie z którym wszystkie jego kąty są proste.
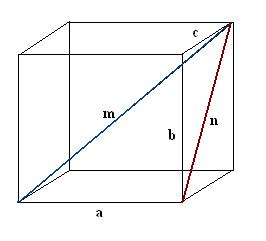
2.
Skonstruuj przekątną n jednej ze ścian równoległościanu. Wykonaj konstrukcję tak, aby pożądana krawędź, pożądana przekątna równoległościanu i przekątna twarzy razem tworzyły trójkąt prostokątny a, n, m.
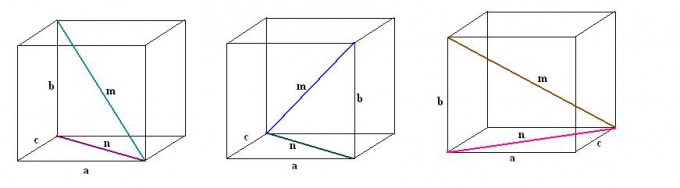
3. Znajdź zbudowaną przekątną twarzy. Ona jest przeciwprostokątną innego trójkąt prostokątny b, c, rz. Zgodnie z twierdzeniem Pitagorasa n² = c² + b². Oblicz to wyrażenie i weź pierwiastek kwadratowy z otrzymanej wartości - będzie to przekątna ściany n.
4. Znajdź przekątną równoległościanu m. Aby to zrobić, w prawym trójkącie a, n, m znajdź nieznaną przeciwprostokątną: m² = n² + a². Zastąp znane wartości i oblicz pierwiastek kwadratowy. Wynikowy wynik będzie pierwszą przekątną równoległościanu m.
5. Podobnie narysuj stopniowo wszystkie pozostałe trzy przekątne równoległościanu. Ponadto dla wszystkich wykonaj dodatkową konstrukcję przekątnych sąsiednich ścian. Patrząc na powstałe trójkąty prostokątne i stosując twierdzenie Pitagorasa, odkryj wartości pozostałych przekątnych prostopadłościanu.
Wideo na ten temat
Wiele rzeczywistych obiektów ma kształt równoległościanu. Przykładami są pokój i basen. Części o tym kształcie nie są rzadkością w przemyśle. Z tego powodu często pojawia się zadanie znalezienia objętości danej figury.
Instrukcje
1. Równoległościan to pryzmat, którego podstawą jest równoległobok. Równoległościan ma ściany – wszystkie tworzące się płaszczyzny tę figurę. Każdy z nich ma sześć ścian i wszystkie są równoległobokami. Jego przeciwne strony są równe i równoległe do siebie. Ponadto ma przekątne, które przecinają się w jednym punkcie i przecinają się w nim na pół.
2. Istnieją 2 rodzaje równoległościanów. W pierwszym przypadku wszystkie ściany są równoległobokami, a w drugim prostokątami. Ostatni nazywa się prostokątnym równoległościanem. Wszystkie jego ściany są prostokątne, a ściany boczne są prostopadłe do podstawy. Jeśli prostokątny równoległościan ma ściany, których podstawy są kwadratami, wówczas nazywa się go sześcianem. W tym przypadku jego ściany i krawędzie są równe. Krawędź to bok dowolnego wielościanu, który zawiera równoległościan.
3. Aby znaleźć objętość równoległościanu, musisz znać obszar jego podstawy i wysokość. Objętość wyznacza się na podstawie tego, który konkretny równoległościan pojawia się w warunkach zadania. Zwykły równoległościan ma u podstawy równoległobok, natomiast prostokątny ma prostokąt lub kwadrat, który niezmiennie ma kąty proste. Jeśli u podstawy równoległościanu znajduje się równoległobok, wówczas jego objętość określa się w następujący sposób: V = S * H, gdzie S jest polem podstawy, H jest wysokością równoległościanu. Wysokość równoległościanu zwykle jest boczne żebro. U podstawy równoległościanu może znajdować się również równoległobok, który nie jest prostokątem. Z przebiegu planimetrii wiadomo, że pole równoległoboku jest równe: S = a*h, gdzie h jest wysokością równoległoboku, a jest długością podstawy, tj. :V=a*hp*H
4. Jeżeli zachodzi drugi przypadek, gdy podstawą równoległościanu jest prostokąt, wówczas objętość oblicza się według tego samego wzoru, ale pole podstawy oblicza się w nieco inny sposób: V = S * H, S = a * b, gdzie aib to boki odpowiednio prostokąta i krawędzi równoległościanu.V=a*b*H
5. Aby znaleźć objętość sześcianu, należy kierować się prymitywem metody logiczne. Ponieważ wszystkie ściany i krawędzie sześcianu są równe, a u podstawy sześcianu znajduje się kwadrat, kierując się powyższymi wzorami, możemy wyprowadzić następujący wzór: V = a^3
W wielu podręcznikach znajdują się zadania związane z konstruowaniem przekrojów różnych figur geometrycznych, w tym równoległościanów. Aby podołać takiemu zadaniu, należy uzbroić się w pewną wiedzę.
Będziesz potrzebować
- - papier;
- - długopis;
- - linijka.
Instrukcje
1. Narysuj równoległościan na kartce papieru. Jeśli Twój problem mówi, że równoległościan powinien być prostokątny, popraw jego rogi. Pamiętaj, że przeciwległe krawędzie muszą być do siebie równoległe. Nazwij jego wierzchołki, powiedzmy S1, T1, T, R, P, R1, P1 (jak pokazano na rysunku).
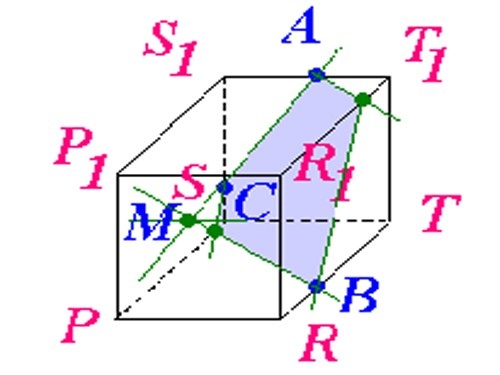
2. Na krawędzi SS1TT1 umieść 2 punkty: A i C, niech punkt A będzie na odcinku S1T1, a punkt C na odcinku S1S. Jeśli w Twoim zadaniu nie jest określone, gdzie dokładnie te punkty mają się znajdować, a odległość od wierzchołków nie jest wskazana, rozmieść je dowolnie. Narysuj linię prostą przez punkty A i C. Kontynuuj tę linię, aż przetnie się z odcinkiem ST. Zaznacz miejsce przecięcia, niech będzie to punkt M.
3. Umieść punkt na odcinku RT, oznacz go jako punkt B. Poprowadź linię prostą przez punkty M i B. Punkt przecięcia tej prostej z krawędzią SP oznacz jako punkt K.
4. Połącz punkty K i C. Muszą leżeć na tej samej powierzchni PP1SS1. Później narysuj linię prostą przez punkt B, równolegle do odcinka KS, kontynuuj linię, aż przetnie się z krawędzią R1T1. Oznacz punkt przecięcia jako punkt E.
5. Połącz punkty A i E. Później podświetl powstały wielokąt ACKBE innym kolorem - to będzie sekcja z tyłu tego równoległościanu.
Notatka!
Pamiętaj, że konstruując odcinek równoległościanu, możesz łączyć tylko te punkty, które leżą na tej samej płaszczyźnie; jeśli posiadanych punktów nie wystarczy do zbudowania przekroju, uzupełnij je wydłużając odcinki, aż przetną się z ścianą w którym potrzebny jest ten punkt.
Pomocna rada
Każdy równoległościan może mieć 4 sekcje: 2 ukośne i 2 poprzeczne. Dla większej przejrzystości wybierz powstały przekrój wielokąta, w tym celu możesz po prostu go obrysować lub przyciemnić innym kolorem.
Wskazówka 6: Jak znaleźć długość przekątnych równoległościanu
Równoległościan to pryzmat, którego podstawą jest równoległobok. Równoległoboki tworzące równoległościan nazywane są jego ścianami, boki nazywane są krawędziami, a wierzchołki równoległościanu nazywane są wierzchołkami równoległościanu.
Instrukcje
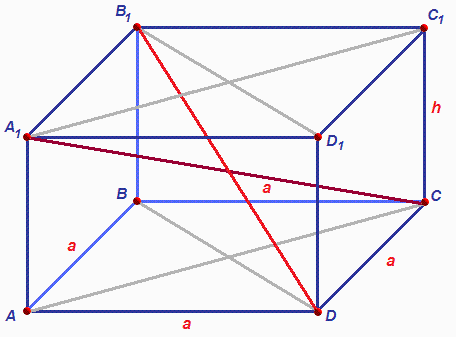
1. U równoległościan można skonstruować cztery przecinające się przekątne. Jeśli znane są dane 3 krawędzie a, b i c, znajdź ich długości przekątne prostokątny równoległościan Wykonanie dodatkowych formacji nie będzie trudne.
2. Najpierw narysuj prostokątny równoległościan. Podpisz wszystkie znane Ci dane, powinny być trzy: krawędzie a, b i c. Narysuj pierwszą przekątną m. Aby go skonstruować, skorzystaj z własności równoległościanów prostokątnych, zgodnie z którą wszystkie kąty figur podobnych są proste.
3. Skonstruuj przekątną n jednej ze ścian równoległościan. Skonstruuj konstrukcję w taki sposób, aby słynna krawędź (krawędzie) była nieznaną przekątną równoległościan a przekątna sąsiedniej ściany (n) utworzyła trójkąt prostokątny a, n, m.
4. Spójrz na zbudowaną przekątną twarzy (n). Jest przeciwprostokątną innego trójkąta prostokątnego b, c, n. Kierując się twierdzeniem Pitagorasa, które stwierdza, że kwadrat przeciwprostokątnej jest równy sumie kwadratów nóg (n? = c? + b?), znajdź kwadrat przeciwprostokątnej, a następnie oblicz pierwiastek kwadratowy otrzymanej wartość - będzie to długość przekątnej ściany n.
5. Znajdź przekątną równoległościan M. Aby znaleźć jej wartość, w trójkącie prostokątnym a, n, m oblicz przeciwprostokątną, korzystając z tego samego wzoru: m? = n? + a?. Oblicz pierwiastek kwadratowy. Odkryta suma będzie pierwszą przekątną twojej równoległościan. Przekątna m.
6. Poprawnie, narysuj także wszystkie pozostałe przekątne krok po kroku. równoległościan, dla których wszystkie wykonują dodatkowe konstrukcje przekątne sąsiadujące krawędzie. Korzystając z twierdzenia Pitagorasa, odkryj wartości pozostałych przekątne dany równoległościan .
7. Istnieje inna metoda, którą można zastosować do określenia długości przekątnej. Zgodnie z jedną z właściwości równoległoboku, kwadrat przekątnej jest równy sumie kwadratów jego 3 boków. Wynika z tego, że długość można obliczyć, dodając kwadraty boków równoległościan i wyodrębnij kwadrat z wynikowej wartości.
Pomocna rada
Właściwości równoległościanu: - równoległościan jest symetryczny względem środka swojej przekątnej, - każdy odcinek, którego końce należą do powierzchni równoległościanu i przechodzący przez środek jego przekątnej, dzieli się przez niego na pół, w szczególności wszystkie przekątne równoległościan przecina się w jednym punkcie i jest przez niego podzielony na pół, - przeciwległe ściany równoległościanu są równoległe i równe, - kwadrat długości przekątnej równoległościanu prostokątnego jest równy sumie kwadratów jego trzech wymiarów.
Równoległościan to trójwymiarowa figura geometryczna posiadająca trzy wymiary pomiarowe: długość, szerokość i wysokość. Wszyscy zajmują się wyznaczaniem pól obu powierzchni równoległościan: pełne i boczne.
Instrukcje
1. Równoległościan to wielościan zbudowany na podstawie równoległoboku. Ma sześć twarzy, które są jednocześnie tymi dwuwymiarowymi kształtami. W zależności od ich umiejscowienia w przestrzeni rozróżnia się proste i nachylony równoległościan. Różnica ta wyraża się w równości kąta między podstawą a krawędzią boczną wynoszącej 90°.
2. Na podstawie tego, do jakiego konkretnego przypadku równoległoboku należy podstawa, możemy rozróżnić równoległościan prostokątny i jego szczególnie powszechną odmianę - sześcian. Formy te są szczególnie powszechne w Życie codzienne i nazywane są standardowymi. Są nieodłącznym elementem sprzętu gospodarstwa domowego, mebli, urządzeń elektronicznych itp., A także samych mieszkań ludzkich, których wymiary mają istotne znaczenie dla mieszkańców i pośredników w handlu nieruchomościami.
3. Zwykle się w to wierzy kwadrat obie powierzchnie równoległościan, boczne i pełne. Pierwsze zestawienie liczbowe reprezentuje wspólny obszar jego ścian, drugie to ta sama wartość plus pola obu podstaw, tj. suma wszystkich dwuwymiarowych figur tworzących równoległościan. Poniższe formuły noszą nazwy głównych wraz z objętością: Sb = P h, gdzie P to obwód podstawy, h to wysokość, Sp = Sb + 2 S, gdzie So to kwadrat fusy.
4. W szczególnych przypadkach kostka i figura z podstawy prostokątne, wzory są uproszczone. Teraz nie jest już konieczne określanie wysokości, która jest równa długości pionowej krawędzi, ale kwadrat a obwód jest znacznie łatwiejszy do wykrycia ze względu na obecność kątów prostych, przy ich wyznaczaniu bierze się pod uwagę tylko długość i szerokość. Okazuje się, że dla prostokąta równoległościan:Sb = 2 c (a + b), gdzie 2 (a + b) to podwójna suma boków podstawy (obwodu), c to długość krawędzi bocznej, Sp = Sb + 2 a b = 2 a c + 2 b do + 2 za b = 2 (za do + b do + za b).
5. Wszystkie krawędzie sześcianu mają jednakową długość, zatem: Sb = 4 a a = 4 a?; Sp = Sb + 2 a? = 6 a?.
Pytanie dotyczy geometria analityczna. Rozwiązuje się to za pomocą równań linii i płaszczyzn przestrzennych, reprezentacji sześcianu i jego właściwości geometryczne, a także przy użyciu algebry wektorowej. Mogą być wymagane metody rozwiązywania układów równań liniowych.
Instrukcje
1. Wybierz te zadania tak, aby były kompleksowe, ale nie zbędne. Samolot do cięcia? należy podać ogólnym równaniem w postaci Ax+By+Cz+D=0, które Najlepszym sposobem zgodny z jego arbitralnym wyborem. Do zdefiniowania sześcianu wystarczą współrzędne dowolnych 3 jego wierzchołków. Weźmy, powiedzmy, punkty M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3), zgodnie z rysunkiem 1. Rysunek ten ilustruje przekrój sześcianu. Przecina dwa żebra boczne i trzy żebra podstawowe.
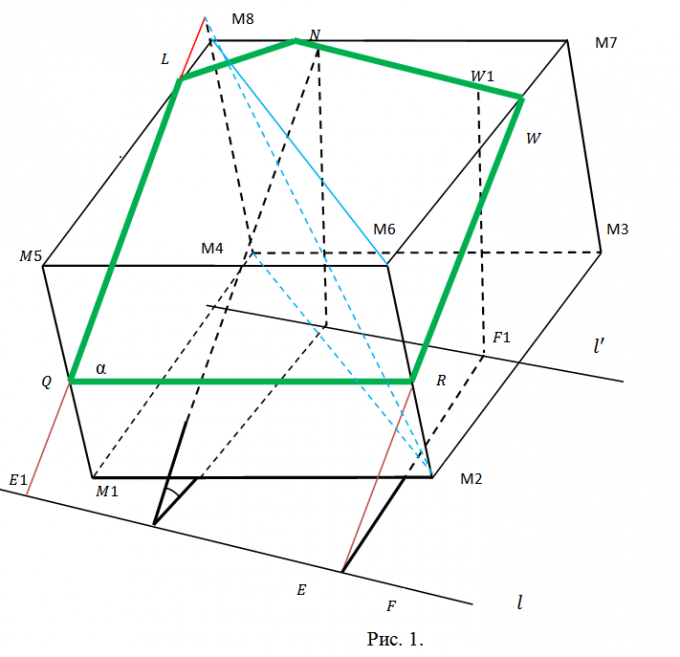
2. Zdecyduj o planie dalszej pracy. Musimy poszukać współrzędnych punktów Q, L, N, W, R, w których przekrój przecina się z odpowiednimi krawędziami sześcianu. Aby to zrobić, będziesz musiał znaleźć równania prostych zawierających te krawędzie i poszukać punktów przecięcia krawędzi z płaszczyzną?. Później nastąpi podzielenie pięciokąta QLNWR na trójkąty (patrz ryc. 2) i obliczenie pola każdego z nich przy użyciu właściwości iloczynu wektorowego. Metodologia jest za każdym razem taka sama. W konsekwencji możemy ograniczyć się do punktów Q i L oraz pola trójkąta?QLN.
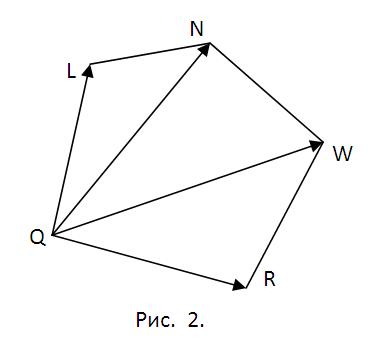
3. Wektor kierunkowy h prostej, zawierającej krawędź M1M5 (i punkt Q), wyznaczamy jako iloczyn wektorowy M1M2=(x2-x1, y2-y1, z2-z1) i M2M3=(x3-x2, y3- y2, z3-z2), h=(m1, n1, p1)=. Powstały wektor jest wskazówką dla wszystkich pozostałych krawędzi bocznych. Znajdź długość krawędzi sześcianu jako, powiedzmy, ?=?((x2-x1)^2+(y2-y1)^2+(z2-z1)^2). Jeżeli moduł wektora h |h|??, to zamień go na odpowiedni wektor współliniowy s=(m, n, p)=(h/|h|)?. Teraz zapisz parametrycznie równanie prostej zawierającej M1M5 (patrz rys. 3). Po podstawieniu odpowiednich wyrażeń do równania płaszczyzny cięcia otrzymujemy A(x1+mt)+B(y1+nt)+C(z1+pt)+D=0. Wyznacz t, podstaw je do równań M1M5 i zapisz współrzędne punktu Q(qx, qy, qz) (rys. 3).
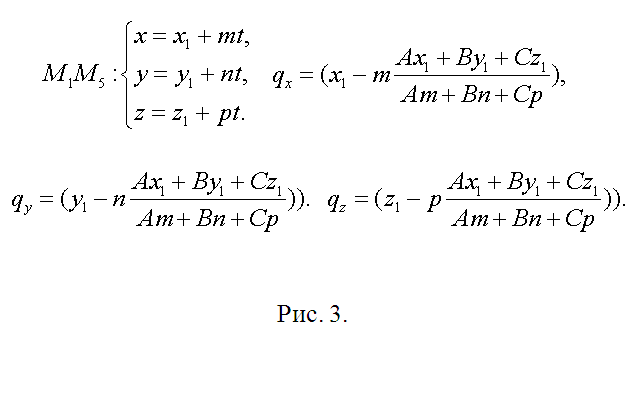
4. Najwyraźniej punkt M5 ma współrzędne M5(x1+m, y1+n, z1+p). Wektor kierunkowy prostej zawierającej krawędź M5M8 pokrywa się z M2M3=(x3-x2, y3-y2,z3-z2). Następnie powtórz poprzednie rozumowanie dotyczące punktu L(lx, ly, lz) (patrz rys. 4). Wszystko, co następuje dla N(nx, ny, nz) jest dokładną kopią tego kroku.
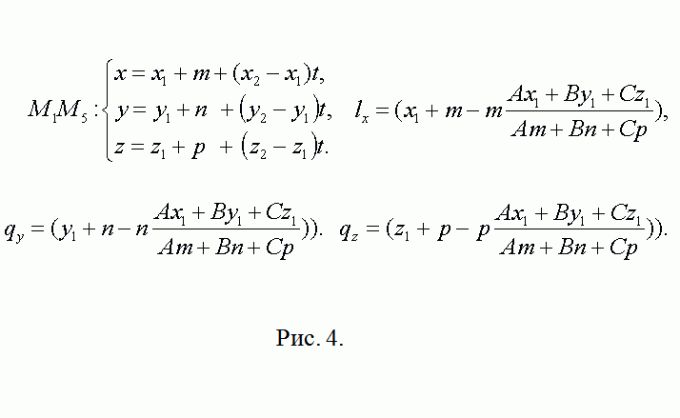
5. Zapisz wektory QL=(lx-qx, ly-qy, lz-qz) i QN=(nx-qx, ny-qy, nz-qz). Geometryczne znaczenie ich iloczynu wektorowego polega na tym, że jest to jego moduł równa powierzchni równoległobok zbudowany na wektorach. W konsekwencji obszar?QLN S1=(1/2)||. Postępuj zgodnie z sugerowaną metodą i oblicz pola trójkątów ?QNW i ?QWR - S1 i S2. Grafika wektorowa Wygodniej jest znaleźć wszystkich przy pomocy wektora determinującego (patrz ryc. 5). Zapisz wynik końcowy S=S1+S2+S3.
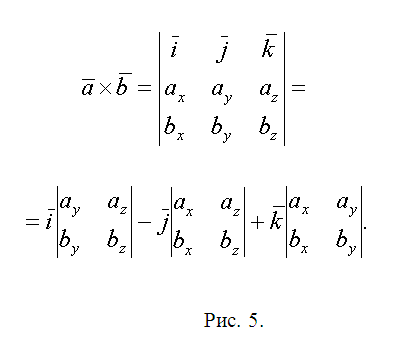
Wskazówka 9: Jak znaleźć ukośne pole przekroju poprzecznego pryzmatu
Pryzmat to wielościan o dwóch równoległych podstawach i ścianach bocznych w kształcie równoległoboku i liczbie, równa liczbie boki wielokąta bazowego.
Instrukcje
1. W dowolnym pryzmacie żebra boczne są umieszczone pod kątem do płaszczyzny podstawy. Szczególnym przypadkiem jest prosty pryzmat. W tym boki leżą w płaszczyznach prostopadłych do podstaw. W prostym pryzmacie ściany boczne są prostokątami, a krawędzie boczne są równe wysokości pryzmatu.
2. Przekątna pryzmatu jest częścią płaszczyzny całkowicie zawartej w wewnętrznej przestrzeni wielościanu. Przekrój ukośny można ograniczyć dwoma bocznymi żebrami geometryczne ciało i przekątne podstaw. Najwyraźniej liczba dopuszczalnych przekątnych jest określona przez liczbę przekątnych w wielokącie podstawowym.
3. Lub granice przekroju ukośnego mogą być przekątnymi ścian bocznych i przeciwne strony podstawy pryzmatu. Przekrój poprzeczny prostopadłościanu ma kształt prostokąta. W ogólnym przypadku dowolnego pryzmatu kształt przekroju przekątnej jest równoległobokiem.
4. W prostopadłościan Pole przekroju przekątnej S określa się za pomocą wzorów: S=d*Hgdzie d jest przekątną podstawy, H jest wysokością pryzmatu Lub S=a*Dgdzie a jest bokiem podstawy jednocześnie należy do płaszczyzny przekroju, D jest przekątną powierzchni bocznej.
5. W dowolnym pryzmacie pośrednim przekrój przekątny jest równoległobokiem, którego jedna strona jest równa bocznej krawędzi pryzmatu, druga jest równa przekątnej podstawy. Lub boki przekroju ukośnego mogą być przekątnymi ścian bocznych i bokami podstaw między wierzchołkami pryzmatu, skąd rysowane są przekątne powierzchni bocznych. Pole równoległoboku S określa się wzorem: S=d*hgdzie d jest przekątną podstawy pryzmatu, h jest wysokością równoległoboku - przekątną pryzmatu Lub S=a* hgdzie a jest bokiem podstawy pryzmatu, który jest jednocześnie granicą przekroju przekątnej, h jest wysokością równoległoboku.
6. Aby określić wysokość przekroju ukośnego, niezadowalająca jest znajomość wymiarów liniowych pryzmatu. Potrzebujemy danych o nachyleniu pryzmatu do płaszczyzny bazowej. Kolejne zadanie sprowadza się do stopniowego rozwiązania kilku trójkątów w zależności od początkowych danych o kątach pomiędzy elementami pryzmatu.
„Złota Sekcja” - Cel pracy: Wyprowadzenie prawa piękna świata z punktu widzenia matematyki. Admiralicja. Okno. Ukończyła uczennica 10. klasy Julia Smetanina. Katedra wstawiennicza (katedra św. Bazylego). Złoty podział w architekturze. W matematyce proporcja to równość dwóch stosunków: a: b = c: d. Piramidy egipskie.
„Konstrukcja przekrojów” - przekroje wykonywane są w tej samej skali, co obraz, do którego się odnoszą. Funkcje tworzenia sekcji. Stosowanie wymiarów. Oznaczenie sekcji. Wykonywany jest obrys odsłoniętych odcinków linia ciągła. Zasady tworzenia przekrojów. Sekcje. Przekroje na rysunkach są podzielone na rozszerzone i nałożone.
„Równoległościan klasy 10” - Kąt wynosi 60?. 3.Cztery, jeśli równoległościan jest sześcianem. Kąt ma miarę 60°. 3.Równe kwadraty, kąty 90°. Islandzkie kryształy dźwigarów mają kształt romboedru. Opcja 2. Biorąc pod uwagę równoległościan ABCDA1B1C1D1. Przekątne równoległościanu. Udowodnić, że proste B1C i A1D są równoległe. 2. Przekątne równoległościanu są równe. Równoległościan.
„Objętość równoległościanu” - Teraz robimy to samo. W Starożytny Babilon Jednostką objętości były sześciany. Zdefiniujmy teraz, jakie są jednostki objętości? Oznacza to, że zgodnie z zasadą obliczania objętości otrzymujemy: 3x3x3=27 (cm3). Zadanie nr 2. Znajdź objętość sześcianu, którego krawędź wynosi 3 cm.Jednostka objętości równa 1 dm3 nazywa się litrem. Zadanie nr 1.
„Lekcja Równoległościan prostokątny” - Cel lekcji: Długość. Odbicie. Znajdź obszar podstawy prostokątnego równoległościanu. Zbuduj prostokąt podana długość(a) i wysokość (h). Skanowanie. Krawędzie. Żeberka. Minuta wychowania fizycznego. Algorytm konstruowania równoległościanu prostokątnego. Trzykrotna długość mniejsza wysokość, a szerokość jest 6 razy mniejsza niż wysokość.
„Objętość prostokątnego równoległościanu” - T e s t. ( Figura geometryczna). 6. Wszystkie ściany równoległościanu są prostokątami. 3. Wszystkie ściany sześcianu są kwadratami. Odpowiedzieć do kolejne pytania: Kwadraty. Nazwij krawędzie, które mają wierzchołek E. Zwiększ. Wolumetryczny. Zadanie 2: Wymiary prostokątnego równoległościanu wynoszą 3 cm, 6 cm i 6 cm.
Z. 1
Rozwój oparty na lekcjach Klasa 11 korzystająca z podręcznika „Geometria” L. S. Atanasyan
LEKCJA nr 1. PROSTOKĄTNY UKŁAD WSPÓŁRZĘDNYCH B PRZESTRZENI !:
główny cel : wprowadzić pojęcie prostokątnego układu współrzędnych, nauczyć konstruowania punktu, znając jego współrzędne, i wyznaczać go. współrzędne punktu zbudowanego w prostokątnym układzie współrzędnych.
I . Praca ustna .
II zamurować zgodnie ze str. 42 podręczniki.
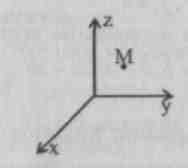Problem polega na tym, czy położenie punktu jest ustawione M.
V przestrzeń? NIE. Konieczne jest skonstruowanie rzutów punktu M na samolot (Och), (Oxz) (Ozy).
DO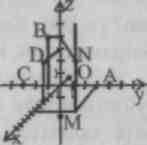 
pytania testowe
Korzystając z rysunku, znajdź współrzędne punktów A, B, C,D, M, N.
Narysuj układ współrzędnych Oksyz i narysuj punkty
Rozwiązywanie problemów: nr 400 (ustnie), 401 (ustnie), 402.
Praca domowa: teoria (klauzula 42), nr 501.
LEKCJA nr 2. WSPÓŁRZĘDNE WEKTORY
główny cel : wprowadzenie pojęcia współrzędnych wektorowych
I . Wyjaśnienie nowego materiału zbudować zgodnie z paragrafem 43 podręcznika.
II . Rozwiązywanie problemów : Nr 403, 404,407(a, b, g, i, j, l) 410, 408, 412.
III
. Praca domowa
: teoria (poz. 13), powtórzenie (poz. 38, 39), nr 405, 407 (d, e, f, g, h), 409 (c, d, e, f, h, m), 411.
LEKCJA nr 3. ZWIĄZEK MIĘDZY WSPÓŁRZĘDNYMI WEKTORAMI A WSPÓŁRZĘDNYMI PUNKTAMI
Główny cel: udowodnić, że współrzędne dowolnego punktu są równe odpowiednim współrzędnym jego wektora promienia; uczyć, jak znaleźć współrzędne wektora, znając współrzędne jego początku i końca.
I . Wyjaśnienie nowego materiału zbudować zgodnie z paragrafem 44 podręcznika.
II. Rozwiązywanie problemów : Nr 416.417, 418 (a), 419.420.
III. Praca domowa : teoria (poz. 44), nr 418 (b, c), 421.
LEKCJA nr 4. PROSTE PROBLEMY ZE WSPÓŁRZĘDNYMI
Główny cel: wyprowadzać wzory na znalezienie współrzędnych środka odcinka, długości wektora na podstawie jego współrzędnych oraz odległości między dwoma punktami.
Sprawdzanie pracy domowej. Nr 421. Rozwiąż nr 422.
III. Wyjaśnienie nowego materiału zbudować zgodnie z paragrafem 45 podręcznika.
IV. Rozwiązywanie problemów: Nie. 424, 426, 427, 430.
V. Praca domowa: teoria (poz. 45), nr 425, 429, 431.
LEKCJA nr 5.6 KĄT MIĘDZY WEKTORAMI
Główny cel: uogólnić pojęcie „kąta między wektorami”, nauczyć znaleźć kąt między wektorami w przestrzeni.
Sh. Wyjaśnienie nowego materiału skonstruuj zgodnie z paragrafem 46. Pokaż przykład znajdowania kątów między wektorami na modelach stereometrycznych (zwróć uwagę na wektory leżące na przecinających się prostych).
IV. Rozwiązywanie problemów № 442,507,508
V. Praca domowa: teoria (klauzula 46), nr 441, do powtórzenia - nr 490, 491 (ustnie), 492, 501.
№
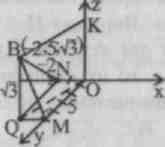501.
Znajdować maszyna wirtualna,BN, VH.
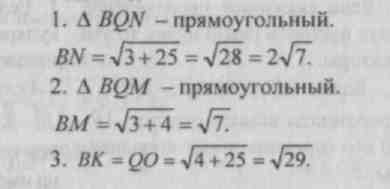Rozwiązanie.
Wyjaśnienie nowego materiału.
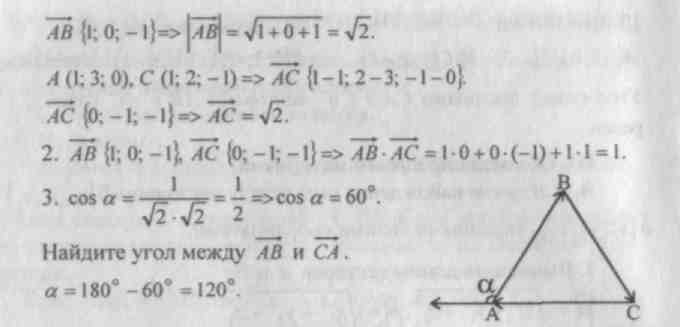
Praca domowa: teoria (klauzula 48), nr 451, 453, 464 (b, c, d), 469 (b, c).
Dyktando
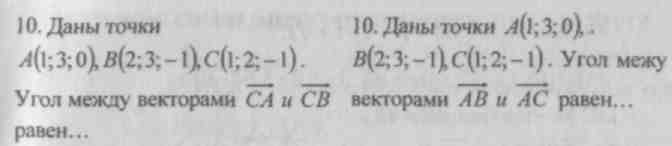
LEKCJA nr 7 ILOCZYN SKALARNY WEKTORÓW
Główny cel: rozwinąć umiejętność rozwiązywania problemów ze znalezieniem kąta za pomocą wektorów, linii prostych, prostej i płaszczyzny.
I. Sprawdzanie pracy domowej ( na tablicy): nr 451 (b, d), nr 464 (c; d).
II. Rozwiązywanie problemów(wg gotowych rysunków).
Algorytm rozwiązywania problemów:
Wchodzić układ prostokątny współrzędna”1
Zapisz współrzędne wszystkich punktów.
Zastosuj algorytm znajdowania kąta między liniami prostymi, między linią prostą a płaszczyzną.
III. Rozwiązywanie problemów.
(metoda wektorowa)
III. (Metoda współrzędnych wektorowych).
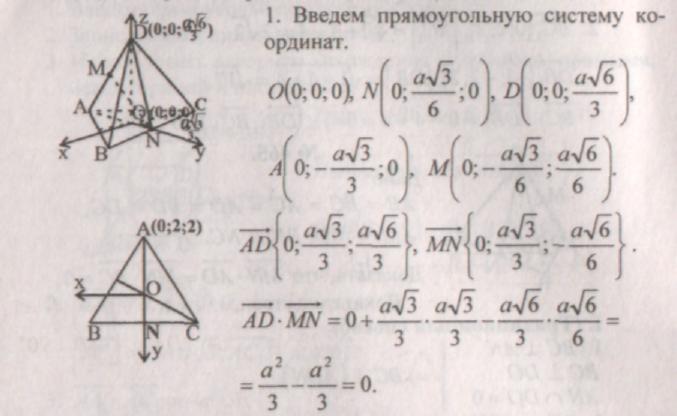
Praca domowa:№ 455, 457, 462.
LEKCJA nr 8 Iloczyn skalarny wektorów
Główny cel: rozwinąć umiejętność znajdowania kątów pomiędzy liniami prostymi, pomiędzy linią prostą a płaszczyzną.
№ 455.
(Rysunek jest przygotowany wcześniej. Uczniowie wypowiadają się lub ktoś zapisuje odpowiedzi na tablicy.) 
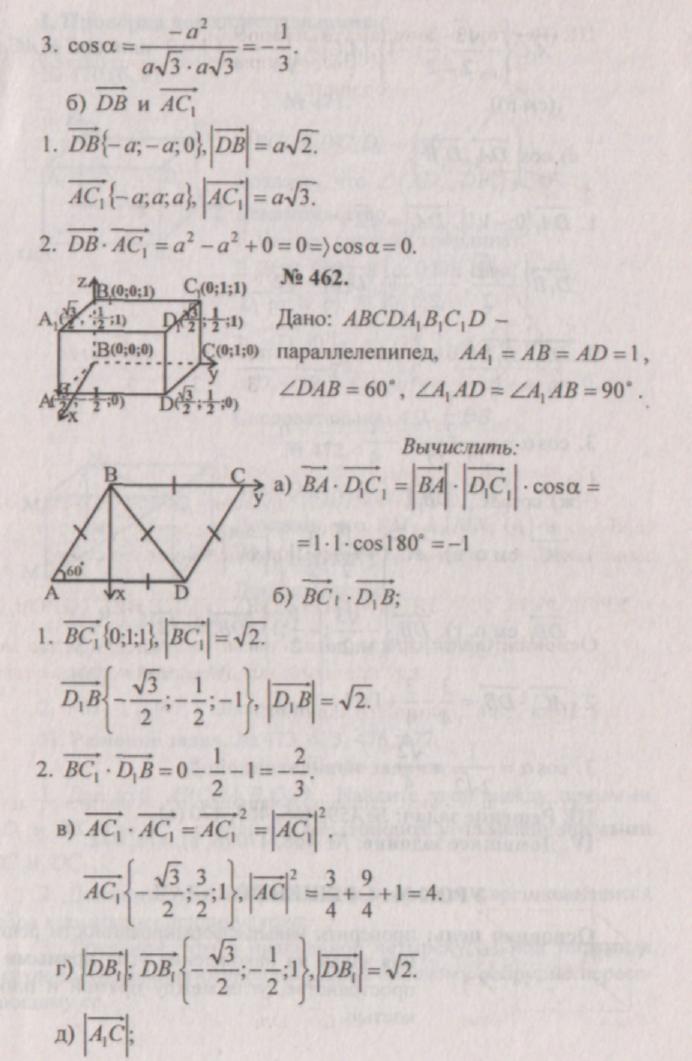
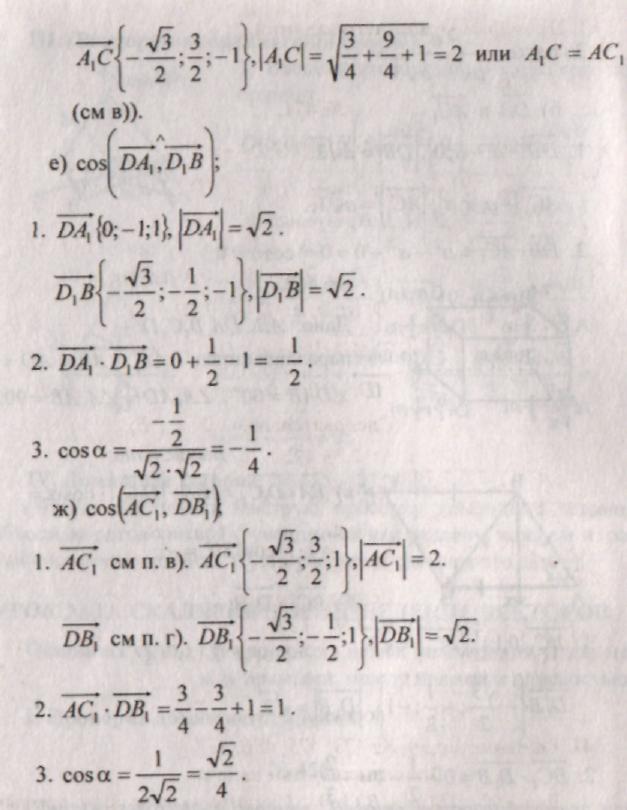
III. Rozwiązywanie problemów: nr 459, 466, 467, 470 (a).
IV. Praca domowa: nr 468, 470 (b, c), 471, 472.
LEKCJA nr 9 TEST nr 1
Testy służące do samodzielnego sprawdzenia i sprawdzenia wiedzy uczniów
|
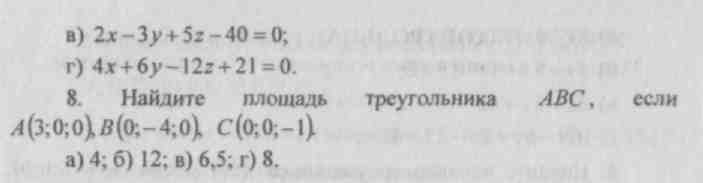
Opcja |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
I |
V |
G |
V |
B |
A |
B |
G |
V |
|
II |
B |
A |
V |
G |
V |
B |
G |
G |
|
Opcja |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
I |
B |
G |
B |
V |
V |
G |
V |
B |
|
II |
B |
A |
G |
V |
G |
A |
V |
B |
LEKCJA nr 10. CYLINDER
Główny cel: przedstawić pojęcie cylindra, elementy cylindra.
I. Wyjaśnienie nowego materiału zbuduj według planu:
1. Koncepcja powierzchnia cylindryczna, cylinder.
Rozważać różne przedmioty otaczające środowisko, dające wyobrażenie o cylindrze - okrągłym ołówku, szklance, groszu, patelni, kawałku fajki itp. (Pokazane cylindry muszą mieć różne proporcje wysokości i średnicy.) Podaj obraz cylindra, pokaż na rysunku - oś, wysokość, promień, generatory, podstawy cylindra.
2. Wejdź koncepcja przekroju osiowego cylindra, ustaw jego właściwości:
a) przekrój osiowy cylindra jest prostokątem;
b) dowolne dwa przekroje osiowe cylindra są sobie równe.
Przedstaw koncepcję walca równobocznego o przekroju osiowym
który jest kwadratem.
3. Rozważmy przekrój kwadratu przez płaszczyznę
A) oś równoległa cylinder;
b) prostopadle do osi cylindra.
4. Wprowadzić pojęcie płaszczyzny stycznej walca jako płaszczyzny przechodzącej przez tworzącą walca i prostopadłej do przekroju osiowego przechodzącego przez tę tworzącą. (Analogia ze styczną do okręgu).
II. Rozwiązywanie problemów:№ 521, 522, 526, 529.
III. Praca domowa:№ 523, 525, 530.
LEKCJA 11. CYLINDER
Główny cel: sformułować umiejętność rozwiązywania problemów znalezienia elementów walca.
I. Sprawdzanie pracy domowej(przy tablicy).
II. Praca ustna.
Zidentyfikuj obiekty w przyrodzie, technologii, architekturze i wśród obiektów wokół ciebie, które mają kształt cylindryczny.
Wyjaśnij, co nazywa się cylindrem, okrągłym cylindrem. Nazwij jego główne elementy i podaj definicję.
Podaj definicję walca prostego.
Ile odcinków osiowych cylindra przechodzi przez każdą z jego tworzących?
Określ rodzaj przekroju osiowego cylindra. Uzasadnij swoją odpowiedź.
Czy przekrój osiowy walca może być: a) prostokątem; b) kwadratowy; c) trapez?
Czy cylinder ma: a) środek symetrii; b) oś symetrii; c) płaszczyzna symetrii? Prosimy o ich wskazanie w każdym przypadku. Ile tu tego jest? Pokaż na modelu.
Pozwalać AA 1 W 1 W I MM1 N 1 N - dwie sekcje osiowe cylindra. Porównaj ich obszary.
Walec toczy się po płaszczyźnie. Jaką figurę uzyskuje się, gdy porusza się jej oś?
Które z poniższych stwierdzeń jest prawdziwe:
b) dowolny przekrój walca przez płaszczyznę jest okręgiem równym obwodowi podstawy;
c) płaszczyzna prostopadła do osi walca przecina go po okręgu, równa podstawa cylinder;
d) przekrój walca przez płaszczyznę może być okręgiem, prostokątem i elipsą?
12. Sformułuj i udowodnij twierdzenie o przekroju walca przez płaszczyznę prostopadłą do jego osi.
III. Rozwiązywanie problemów: nr 527 (b), 532, 534.
IV. Praca domowa: nr 527 (a), 531, 535.
LEKCJA #12. STOŻEK
Główny cel: sprawdzić poziom sformułowania umiejętności rozwiązywania problemów związanych ze znalezieniem elementów cylindra. Wprowadź pojęcia stożka i elementy stożka.
Samodzielna praca (15 min).
Przekrój walca z płaszczyzną równoległą do osi jest kwadratem, którego powierzchnia wynosi 20 dm. Znajdź osiowe pole przekroju poprzecznego cylindra, jeśli jego przekątna wynosi 10 dm.
Opcja II
Wysokość walca wynosi 16 cm, promień podstawy 10 cm, cylinder przecina płaszczyzna równoległa do osi, tak że przekrój jest kwadratowy. Znajdź odległość od osi cylindra do tego odcinka.
Rozwinięcie powierzchni bocznej walca ma kształt prostokąta, którego przekątna równa 12l tworzy z jednej strony kąt 30°. Znajdź całkowitą powierzchnię walca, jeśli jego wysokość jest równa krótszemu bokowi zabudowy.
1. Pojęcia stożka, jego elementów (góra, oś, generatory, podstawa, powierzchnia boczna stożek). Obraz stożka
N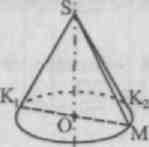 
na rysunku rysujemy styczne od punktu S
do elipsy reprezentującej podstawę stożka. Oznaczmy przez DO 1
I DO 2
punkty dotykowe. Częstym błędem jest zakładanie przez uczniów trójkąta SK 1
K 2
dla obrazu osiowego przekroju stożka. Jednak akord DO 1
DO 2
nie przechodzi przez środek O podstawa stożka. Aby skonstruować obraz przekroju osiowego przechodzącego przez tworzącą SK 1
wystarczy skonstruować obraz średnicy DO 1
M i połącz powstały punkt M z górą S
stożek SK 1
I SK 2
- obrazy generatorów ekstremalnych, tj. oddzielają widoczne generatory (ich obrazy uzyskuje się poprzez połączenie dowolny punktłuki DO 1
MK 2
elipsa z wierzchołkiem S) od niewidzialnego.
2. Rozważ przekrój stożka o różnych płaszczyznach, podkreślając dwa przypadki:
Płaszczyzna tnąca przez wierzchołek stożka;
Płaszczyzna cięcia jest równoległa do podstawy stożka.
1 lit. a). Jeśli przecinają się w dwóch punktach, to w przekroju stożka otrzymamy Trójkąt równoramienny, którego podstawą jest odcinek z końcami w tych punktach. Z przekroju osiowego. Uzyskuje się je, jeśli rozważane punkty przecięcia są końcami średnicy podstawy stożka. Wśród stożków wyróżnia się równoboczny (jego przekrój osiowy wynosi trójkąt równoboczny). Jeśli R jest promieniem jego podstawy, wówczas tworząca stożka równobocznego jest równa 2 R .
1 lit. b). Jeśli mają tylko jednego wspólny punkt, wówczas rozważana płaszczyzna jest styczna do stożka.
Płaszczyznę styczną do stożka można zdefiniować na różne sposoby.
Definicja 1. Płaszczyzna przechodząca przez tworzącą stożka jest prostopadła do przekroju osiowego przechodzącego przez tę tworzącą.
Definicja 2. Płaszczyzna, która ma tylko jedną wspólną tworzącą ze stożkiem.
Interpretacja płaszczyzny stycznej do stożka i płaszczyzny stycznej do walca powinna być taka sama w tym samym podręczniku. Należy zaznaczyć, że przyjmując jedną z propozycji 1 lub 2 in jako definicja, należy zapoznać uczniów z drugą jako właściwością płaszczyzny stycznej do stożka.
1 lit. c). Kontynuując rozpatrywanie płaszczyzny przechodzącej przez wierzchołek stożka, dochodzimy do przypadku: jeśli płaszczyzna i okrąg podstawy nie mają punktów wspólnych, to płaszczyzna, o której mowa, ze stożkiem, ma tylko jeden punkt wspólny – wierzchołek stożka.
2. Dowodząc twierdzenia o przekroju stożka przez płaszczyznę równoległą do jego podstawy (nr 556), warto wyciągnąć następujące wnioski:
1. Rozważany odcinek to okrąg.
2. Wyznaczony przez R I R - odpowiednio promień stożka i rozważany przekrój i przelot N I H wysokość danego i odciętego stożka, otrzymujemy, że ,gdzie k jest współczynnikiem podobieństwa danego i odciętego stożka. Udowodnij to
Uogólnij, rozwiązując zadanie nr 557.
Rozpatrzenie sekcji, prostopadle do osi stożek, pozwala na efektywne wykorzystanie metoda jednorodności podobna do przekrój piramidy przez płaszczyznę, równolegle do podstawy. Po ustaleniu kształtu i położenia przekroju wprowadza się pojęcie stożka ściętego.
Przedstawiając ścięty stożek, wygodnie jest najpierw narysować stożek, z którego uzyskany jest stożek ścięty.
Rozwiązywanie problemów: nr 548(a), 549.
Praca domowa: teoria (s. 55, 56), nr 547, 548 (b, c), 550.
LEKCJA 13. STOŻEK
Główny cel: wprowadzić koncepcję pola powierzchni bocznej stożka jako obszaru jego rozwoju.
I. Sprawdzanie pracy domowej(przy tablicy).
II
Wprowadź pojęcie pola powierzchni bocznej wykorzystując rozwinięcie stożka.
Całkowita powierzchnia stożka.
Wyprowadź wzór na obliczenie pola powierzchni bocznej stożka ściętego.
V. Praca domowa: nr 560 (b, c), 561, 563, 568.
LEKCJA nr 14. KULA I PIŁKA. RÓWNANIE KULI. Względne położenie kuli i płaszczyzny. PŁASZCZYZNA STYCZNA DO KULI. POWIERZCHNIA KULI
Główny cel: Wchodzić pojęcia kuli i kuli, wyprowadź równanie kuli, rozważ względne położenie kuli i płaszczyzny, zdefiniuj płaszczyznę styczną do kuli, zapisz wzór na obliczenie pola kuli.
I. Wyjaśnienie nowego materiału konstruować w sposób wykładowy zgodnie z paragrafami 58 - 62 podręcznika.
Dla przykładów użyj zadań: nr 575, aby zrozumieć definicje kuli; nr 576, 578 do obliczenia równania kuli; Nr 586 dla ilustracji względne położenie kule i płaszczyzny; nr 593 (a), 594, aby przećwiczyć wzór na pole kuli.
Rozwiązywanie problemów:
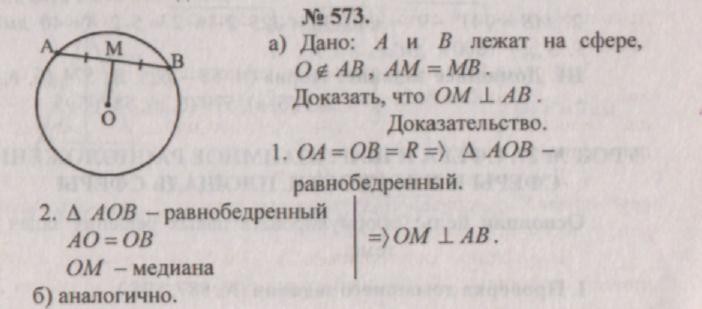
III. Praca domowa: teoria (s. 58 - 62), nr 574 (b, c, d).
577 (b, c), 579 (6, c), 587, 595.
LEKCJA nr 15. KULA I PIŁKA. Względne położenie kuli i płaszczyzny. POWIERZCHNIA KULI
Główny cel: formułować umiejętność rozwiązywania problemów na zadany temat.
Badanie dom zadania (nr. 587, 595.)
Rozwiązywanie problemów
III. Praca domowa: Nie. 582, 584, 585, 592, 597.
LEKCJA nr 16. PRZYGOTOWANIE DO TESTU
Główny cel: powtarzaj, systematyzuj, uogólniaj badany materiał.
I. Sprawdzanie pracy domowej(przy tablicy): Nr 582, 584, 585.
II. Praca ustna- w sprawie pytań do rozdziału VI.
III. Rozwiązywanie problemów.
Lekcja nr 17 Test № 2
LEKCJA nr 18. OBJĘTOŚĆ PROSTOKĄTNEGO RÓWNOLEGŁEGO
Główny cel: wprowadzić pojęcie objętości ciała.
I. Wyjaśnienie nowego materiału.
A. Pojęcie objętości ciała wprowadza się przez analogię z pojęciem pola płaska figura. Możliwe razem ze studentami wypełnij drugą połowę stoły.
Pytania kontrolne.
Jaka jest objętość ciała?
Co to znaczy mierzyć objętość ciała?
4. Jak zdobyć 
sześcian jednostkowy?
5. Kostka jednostkowa mieści się w części przestrzeni zajmowanej przez ośmiościan, 2 razy i 2 razy - ułamek sześcianu jednostkowego, którego liczbą charakteryzuje się V oktaedr?
B. Objętość sześcianu równy sześcianowi jego żebra. V= za 3 .
Wyprowadź wzór do obliczeń V sześcian, jeśli znana jest jego przekątna
II. Rozwiązywanie problemów.
1. Całkowita powierzchnia sześcianu wynosi 6 M 2 . Znajdź jego objętość (1 m 3)
Objętość sześcianu wynosi 8 m. Znajdź całkowite pole powierzchni.
Jeśli każdą krawędź sześcianu powiększymy o 1 m, wówczas jego objętość wzrośnie 125 razy. Znajdź krawędź sześcianu.
Trzy sześciany wykonane z ołowiu mają krawędzie 3, 4 i 5 cm i zostały przetopione w jedną kostkę. Znajdź jego żebro
Objętość sześcianu wynosi A. Znajdź pole jego przekątnej
III. Dwa ciała których objętości są równe, nazywane są równą wielkością.
(Dowodząc poniższego twierdzenia należy posłużyć się modelem lub wcześniej przygotowanym rysunkiem.)
Twierdzenie. Nachylony pryzmat ma wielkość równą prostemu pryzmatowi, którego podstawa jest prostopadła do nachylonej części, a krawędź boczna jest równa krawędzi bocznej nachylony pryzmat.
Pytania kontrolne.
Które dwa ciała nazywamy równymi rozmiarami?
Dwa ciała są równe. Czy są tego samego rozmiaru?
Obydwa ciała są równej wielkości. Czy są równi?
LEKCJA nr 19. OBJĘTOŚĆ PROSTOKĄTNEJ RÓWNOLEGLINY
Główny cel: rozwinąć umiejętność rozwiązywania problemów w celu znalezienia objętości równoległościanu.
I. Praca ustna.
Jaka jest objętość ciała?
Jaka jest objętość sześcianu? Jedna dziesiąta tego?
Sześcian przecinają dwie przekątne. Jaka jest objętość każdej części?
W sześcianie o krawędzi 2 cm wykonany przekrój ukośny. Jaka jest objętość każdej z powstałych części?
Całkowita powierzchnia sześcianu wynosi 24 cm2. Jaka jest objętość sześcianu?
Przekątna sześcianu wynosi A. Znajdź jego objętość.
Objętość sześcianu V. Znajdź jego przekątną.
Przekątna ściany sześcianu wynosi 8. Jaka jest objętość sześcianu?
Objętość nachylonego pryzmatu wynosi 27 cm 3 . Jaki jest rozmiar krawędzi sześcianu o tej samej wielkości?
Wyjaśnienie nowego materiału.
Objętość prostokątnego równoległościanu jest równa iloczynowi jego trzech wymiarów. V = ABC . Lub objętość prostokątnego równoległościanu jest równa iloczynowi pola podstawy i wysokości. V= S podstawowy H
III. Rozwiązywanie problemów.
Praca domowa: teoria (t. 64), nr 648 650 651 652
IV. Niezależna praca.
OPCJA I
1. Objętość prostokątnego równoległościanu wynosi 96 cm, krawędź boczna wynosi 8 cm Jakie jest pole podstawy?
Podstawą równoległościanu prostokątnego jest kwadrat o boku A. Przekątna ściany bocznej tworzy kąt α z płaszczyzną podstawy.
W równoległościanie prostokątnym przekątne sąsiednich ścian bocznych wychodzących z tego samego wierzchołka tworzą kąty α i β ze wspólnym żebrem bocznym wychodzące z tego samego wierzchołka. Boczna krawędź równoległościanu jest równa b . Znajdź objętość równoległościanu.
Objętość prostokątnego równoległościanu wynosi 100 cm 3, a pole podstawy wynosi 25 cm 2. Znajdź wysokość równoległościanu.
W równoległościanie prostokątnym podstawą jest kwadrat. Przekątna równoległościanu wynosi D i tworzy kąt α z boczną krawędzią mającą ogólny początek. Znajdź objętość równoległościanu.
LEKCJA nr 20. OBJĘTOŚĆ PRASTY PROSTEJ
Główny cel: wyprowadź wzór na obliczenie objętości prostego pryzmatu.
I. Sprawdzanie pracy domowej.
P. Wyjaśnienie nowego materiału.
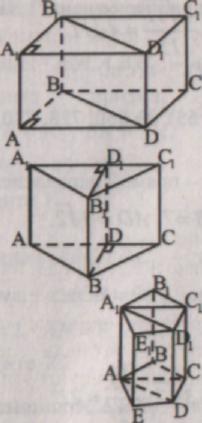
Podstawą prostego graniastosłupa jest trójkąt prostokątny. Jego objętość jest równa iloczynowi pola podstawy i wysokości.
Podstawa prostego pryzmatu - dowolny trójkąt. Jego objętość jest równa iloczynowi pola podstawy i wysokości.
Dowolny prosty pryzmat. Udowodnij, że jego objętość jest równa iloczynowi pola podstawy i wysokości.
TO. Objętość prostego pryzmatu jest równa iloczynowi pola podstawy i wysokości. 
Sh. Rozwiązywanie problemów.№ 659, 661, 662, 729.
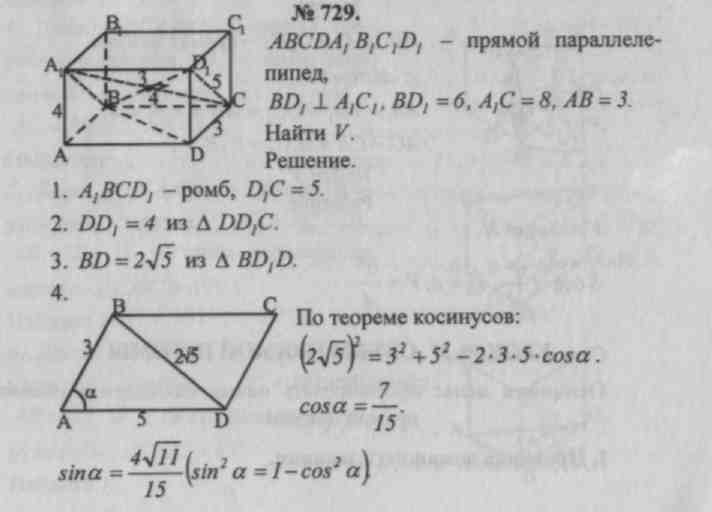
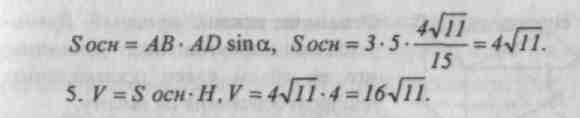
Praca domowa: teoria (poz. 65), nr 660, 728, 730, 731.
LEKCJA nr 21. OBJĘTOŚĆ CYLINDRA
Główny cel: wyprowadzić wzór na obliczenie objętości walca.
I . Wyjaśnienie nowego zbudować zgodnie z paragrafem 66 podręcznika.
II. Rozwiązywanie problemów. NIE. 671, 672.
Sh. Praca domowa: teoria (poz. 66), nr 666, 667, 668, 699, 670.
Dodatkowe zadania.
Odcinek walca o płaszczyźnie równoległej do osi odcina od obwodu podstawy łuk o wartości 60°. Pole przekroju wynosi S, a przekątna przekroju tworzy kąt α z płaszczyzną podstawy walca. Znajdź objętość cylindra.
Przekrój walca przez płaszczyznę równoległą do osi odcina od obwodu podstawy łuk o 90°. Pole przekroju wynosi S, a przekątna przekroju tworzy kąt α z tworzącą walca. Znajdź objętość cylindra.
Sześcian jest wpisany w cylinder. Objętość sześcianu wynosi F. Znajdź objętość walca.
LEKCJA nr 22. OBJĘTOŚĆ PIRAMIDY
Głównycel: rozwinąć umiejętność wyznaczania objętości piramidy, którego wierzchołek jest rzutowany na środek wpisany w podstawę koła lub opisany wokół podstawy koła.
I. Sprawdzanie pracy domowej.
Kontynuuj zdania.
Jeśli wszystkie boczne krawędzie piramidy są równe, wówczas wierzchołek zostanie rzutowany na podstawę w...
Jeśli wszystkie apotemy piramidy są równe, wówczas wierzchołek zostanie rzutowany na podstawę w...
Spadam kąty dwuścienne gdy podstawa jest równa, wierzchołek jest rzutowany na podstawę w...
Jeśli wszystkie żebra boczne są wyrównane z płaszczyzną podstawy równe kąty, następnie wierzchołek jest rzutowany na podstawę w...
Sh. Rozwiązywanie problemów.№ 691, 693, 695, 740.
IV. Praca domowa:№ 692, 694.
P. Dyktando.
LEKCJA nr 23,24. PRZYGOTOWANIE DO TESTU TEST TEST nr 4
Główny cel: sprawdź poziom rozwoju umiejętności rozwiązywania problemów, aby znaleźć objętość walca, nachylonego pryzmatu, piramidy i stożka.
LEKCJA nr 25 OBJĘTOŚĆ PIŁKI I JEJ CZĘŚCI
Głównycel: wyprowadź wzór na objętość kuli i jej części.
I. Wyjaśnienie nowego materiału.
1. Objętość kuli o promieniu R równa się
Dowód można znaleźć w paragrafie 71.
2. Segment kulisty to część kuli odcięta od niej płaszczyzną (ryc. a, c).
O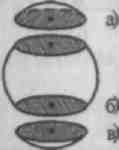 
tom segment piłki określa się na podstawie wzoru 
, gdzie H jest wysokością odcinka kuli
3. Warstwa kulista to część kuli znajdująca się pomiędzy dwoma płaszczyzny równoległe, przecinając piłkę (ryc. 323, b).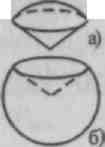 
4. Sektor kulisty to bryła otrzymana z odcinka kuli i stożka. Objętość sektora kulistego określa wzór, gdzie H jest wysokością odpowiedniego odcinka kuli
II. Rozwiązywanie problemów.
Zadanie 1. Jaka jest objętość wycinka kuli, jeśli promień jego okręgu podstawowego wynosi 60 cm, a promień kuli 75 cm?
Rozwiązanie. 1. Pod podstawą sektora w zadanie jest rozumiane jako podstawa segment odpowiadający sektorowi. Pozwalać R - promień kuli, r - promień podstawy segmentu.
2. Nasze zadanie sprowadza się do znalezienia wysokości tego odcinka: N – RO 1 . LUB - promień kuli prostopadły do podstawy segmentu.
3. Z trójkąta prostokątnego O.O. l M(˂ MO 1 O= 90°) znajdźmy: OO 1 = √OM 2 - O 1 M 2 = √75 2 +60 2 =40 zatem H = PO l = OP- O.O. l = R-00 ] =75-45 = 30.
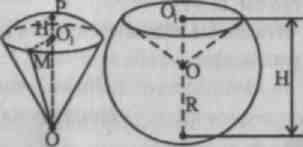
4. Objętość sektora kulistego. =112500π
5. Uwaga. Problem ma dwa rozwiązania:
1) Rozważany przez nas sektor kulisty nazywa się wypukłym, a jego wysokość jest równa R – OO 1 , nazywa się niewypukłym.
Znajdźmy jego objętość.
6. Rozważmy drugi przypadek, w którym wysokość sektora N =R + O.O. 1 = 120, więc wynikowa objętość będzie 4 razy większa od obliczonej objętości: V = π45 10 4 cm 3
7. Zatem wymagana objętość wynosi 112 500 π cm lub 450 000 π cm 3.
III. Domowej roboty zadanie: teoria (s. 71, 72), nr 710, 711, 717.
LEKCJA№ 26 . OBJĘTOŚĆ PIŁKI I JEJ CZĘŚCI
Główny cel: formułować umiejętność wyznaczania objętości kuli i jej części.
I. Sprawdzanie pracy domowej.
Sh. Rozwiązywanie problemów.
A. 1. Zewnętrzna średnica wydrążonej kuli wynosi 18 cm, grubość ścianki 3 cm Znajdź objętość materiału, z którego wykonana jest kula.
[b84πcm 3.]
Średnica kulki ołowianej wynosi 30 cm. Ile kulek o średnicy 3 cm można ułożyć z tej kulki?
Promienie trzech kul wynoszą 3, 4, 5 cm Znajdź promień kuli, której objętość jest równa sumie ich objętości,
Największa kula jest wyrzeźbiona z sześcianu. Jaki procent materiału został usunięty? [≈ 47,6%]
Promień sektora piłki R, kąt w przekrój osiowy 120°. Znajdź głośność.
Udowodnić, że jeśli promienie trzech kul są w stosunku 1:2:3, to objętość większej kuli jest 3 razy większa więcej niż kwota objętości mniejszych kulek.
Wysokość segmentu kuli jest 0,4 razy większa od promienia kuli. Jaką część objętości tego odcinka stanowi objętość walca o tej samej podstawie i wysokości? 13\24
Dwa równa piłka ułożone tak, że środek jednego leży na powierzchni drugiego. Jak objętość całkowitej części kul ma się do objętości całej kuli?
Średnica kuli równa 30 cm służy jako oś walca, którego promień podstawy wynosi 12 cm. Znajdź objętość części kuli,
Która figura ma większą objętość: kula o promieniu 1 dm czy zwykła? trójkątny pryzmat, którego każda krawędź jest równa 2 dm? [Objętość piłki jest większa.]
Przekrój kuli przez płaszczyznę prostopadłą do jej promienia dzieli promień na pół. Znajdź stosunek objętości części kuli.
Przekrój kuli przez płaszczyznę prostopadłą do jej średnicy dzieli średnicę w stosunku 1:2. Znajdź stosunek objętości części kuli.
LEKCJA nr 27. POWIERZCHNIA KULI
Główny cel: wyprowadź wzór na obliczenie pola powierzchni kuli.
I. Wyjaśnienie nowego materiału zbudować zgodnie z paragrafem 73 podręcznika.
II. Rozwiązywanie problemów: nr 722, 723, 724; do powtórzenia - nr 761, 762, 763.
III. Praca domowa: karty.
LEKCJA nr 28. PRZYGOTOWANIE DO TESTU
I. Pytania w celu przeglądu tematu.
Piłka i jej elementy.
Objętość piłki i jej części.
Ciała wirujące i ich objętości.
Wielościany i ich objętości.
Powierzchnia kuli.
Pole powierzchni wielościanów.
III. Rozwiązywanie problemów.
Objętość promienia kuli R równa się V. Znajdź objętość kuli o promieniu: 2 R; 0,5R.
Powierzchnia regularny czworościan równa powierzchni kuli. Znajdź stosunek objętości czworościanu i kuli.
Średnicę kuli o promieniu 12 cm podzielono na 3 części, których długości są w stosunku 3:3:2. Przez punkty podziału poprowadzono płaszczyzny prostopadłe do średnicy. Znajdź objętość każdego z nich uformowane części piłki.
5. W prawo czworokątna piramida kula jest wpisana w taki sposób, że boczne ściany piramidy dotykają powierzchni kuli i jej duże koło leży u podstawy piramidy. Boczne twarze piramidy są nachylone do płaszczyzny podstawy pod pewnym kątem A, a objętość piłki jest równa V . Znajdź objętość piramidy.
Próba domowa
opcja 1
Objętość kuli wynosi 400 cm3. Kolejna kula jest zbudowana na promieniu, podobnie jak na średnicy. Znajdź objętość małej kuli.
3. Przekrój równoległościanu prostokątnego wpisanego w kulę jest kwadratem o polu S. Znajdź objętość kuli.
4. Średnicę kuli o promieniu 12 cm podzielono na 3 części, których długości są w stosunku 1:3:4. Przez punkty podziału poprowadzono płaszczyzny prostopadłe do średnicy. Znajdź objętość powstałej warstwy kulistej.
MO „Szkoła średnia Senkinskaya”
Z. 1