Definicja
Piramida jest wielościanem złożonym z wielokąta \(A_1A_2...A_n\) i \(n\) trójkątów o wspólnym wierzchołku \(P\) (nie leżącym w płaszczyźnie wielokąta) i przeciwległych mu bokach, pokrywających się z boki wielokąta.
Oznaczenie: \(PA_1A_2...A_n\) .
Przykład: piramida pięciokątna \(PA_1A_2A_3A_4A_5\) .
Trójkąty \(PA_1A_2, \PA_2A_3\) itp. są nazywane boczne twarze piramidy, segmenty \(PA_1, PA_2\) itp. – żebra boczne, wielokąt \(A_1A_2A_3A_4A_5\) – podstawa, punkt \(P\) – szczyt.
Wysokość piramidy to prostopadła schodząca ze szczytu piramidy do płaszczyzny podstawy.
Nazywa się piramidą mającą u podstawy trójkąt czworościan.
Piramida nazywa się prawidłowy, jeżeli jego podstawą jest wielokąt foremny i spełniony jest jeden z poniższych warunków:
\((a)\) boczne krawędzie piramidy równy;
\((b)\) wysokość piramidy przechodzi przez środek okręgu opisanego w pobliżu podstawy;
\((c)\) żebra boczne są nachylone do płaszczyzny podstawy pod tym samym kątem.
\((D)\) boczne twarze nachylona do płaszczyzny podstawy pod tym samym kątem.
Regularny czworościan jest trójkątną piramidą, której wszystkie ściany są równymi trójkątami równobocznymi.
Twierdzenie
Warunki \(a), (b), (c), (d)\) są równoważne.
Dowód
Znajdźmy wysokość piramidy \(PH\) . Niech \(\alpha\) będzie płaszczyzną podstawy piramidy.

1) Udowodnijmy, że z \((a)\) wynika \((b)\) . Niech \(PA_1=PA_2=PA_3=...=PA_n\) .
Ponieważ \(PH\perp \alpha\), wówczas \(PH\) jest prostopadła do dowolnej prostej leżącej w tej płaszczyźnie, co oznacza, że trójkąty są prostokątne. Oznacza to, że te trójkąty mają wspólną nogę \(PH\) i przeciwprostokątną \(PA_1=PA_2=PA_3=...=PA_n\) . Oznacza to \(A_1H=A_2H=...=A_nH\) . Oznacza to, że punkty \(A_1, A_2, ..., A_n\) znajdują się w tej samej odległości od punktu \(H\), zatem leżą na tym samym okręgu o promieniu \(A_1H\) . Okrąg ten z definicji jest opisany na wielokącie \(A_1A_2...A_n\) .
2) Udowodnijmy, że \((b)\) implikuje \((c)\) .
\(PA_1H, PA_2H, PA_3H,..., PA_nH\) prostokątny i równy na dwóch nogach. Oznacza to, że ich kąty są również równe, zatem \(\kąt PA_1H=\kąt PA_2H=...=\kąt PA_nH\).
3) Udowodnijmy, że \((c)\) implikuje \((a)\) .
Podobnie jak w przypadku pierwszego punktu, trójkąty \(PA_1H, PA_2H, PA_3H,..., PA_nH\) prostokątne i wzdłuż nogi i ostry róg. Oznacza to, że ich przeciwprostokątne są również równe, czyli \(PA_1=PA_2=PA_3=...=PA_n\) .
4) Udowodnijmy, że \((b)\) implikuje \((d)\) .
Ponieważ w wielokącie foremnym środki okręgu opisanego i wpisanego pokrywają się (ogólnie punkt ten nazywany jest środkiem wielokąta foremnego), wówczas \(H\) jest środkiem okręgu wpisanego. Narysujmy prostopadłe z punktu \(H\) do boków podstawy: \(HK_1, HK_2\) itd. Są to promienie okręgu wpisanego (z definicji). Wtedy zgodnie z TTP (\(PH\) jest prostopadłą do płaszczyzny, \(HK_1, HK_2\), itd. są rzutami prostopadłymi do boków) ukośną \(PK_1, PK_2\), itd. prostopadle do boków \(A_1A_2, A_2A_3\) itd. odpowiednio. Tak z definicji \(\kąt PK_1H, \kąt PK_2H\) równy kątom między ścianami bocznymi a podstawą. Ponieważ trójkąty \(PK_1H, PK_2H, ...\) są równe (z dwóch stron prostokątne), to kąty \(\kąt PK_1H, \kąt PK_2H, ...\) są równe.
5) Udowodnijmy, że \((d)\) implikuje \((b)\) .
Podobnie jak w punkcie czwartym, trójkąty \(PK_1H, PK_2H, ...\) są równe (jako prostokąt wzdłuż ramienia i kąt ostry), co oznacza, że odcinki \(HK_1=HK_2=...=HK_n\) są równy. Oznacza to z definicji, że \(H\) jest środkiem okręgu wpisanego w podstawę. Ale ponieważ Na regularne wielokątyśrodki okręgów wpisanego i opisanego pokrywają się, wówczas \(H\) jest środkiem okręgu opisanego. czt.
Konsekwencja
Boczne ściany regularnej piramidy są równymi trójkątami równoramiennymi.
Definicja
Nazywa się wysokość bocznej ściany regularnej piramidy narysowanej od jej wierzchołka apotem.
Apotemy wszystkich bocznych ścian regularnej piramidy są sobie równe i są także środkowymi i dwusiecznymi.
Ważne notatki
1. Wzrost jest prawidłowy trójkątna piramida przypada w punkcie przecięcia wysokości (lub dwusiecznych lub środkowych) podstawy (podstawa jest regularnym trójkątem).
2. Wzrost jest prawidłowy czworokątna piramida przypada w miejscu przecięcia przekątnych podstawy (podstawa jest kwadratem).
3. Wzrost jest prawidłowy sześciokątna piramida przypada na przecięcie przekątnych podstawy (podstawa jest sześciokątem foremnym).
4. Wysokość piramidy jest prostopadła do dowolnej linii prostej leżącej u podstawy.
Definicja
Piramida nazywa się prostokątny, jeżeli jedna z jego krawędzi bocznych jest prostopadła do płaszczyzny podstawy.

Ważne notatki
1. W piramidzie prostokątnej krawędź prostopadła do podstawy jest wysokością piramidy. Oznacza to, że \(SR\) jest wysokością.
2. Ponieważ \(SR\) jest zatem prostopadła do dowolnej linii wychodzącej z podstawy \(\trójkąt SRM, \trójkąt SRP\) – trójkąty prostokątne.
3. Trójkąty \(\trójkąt SRN, \trójkąt SRK\)- również prostokątne.
Oznacza to, że dowolny trójkąt utworzony przez tę krawędź i przekątną wychodzącą z wierzchołka tej krawędzi leżącą u podstawy będzie prostokątny.
\[(\Large(\text(Objętość i powierzchnia piramidy)))\]
Twierdzenie
Objętość piramidy jest równa jednej trzeciej iloczynu pola podstawy i wysokości piramidy: \
Konsekwencje
Niech \(a\) będzie bokiem podstawy, \(h\) będzie wysokością piramidy.
1. Objętość regularnej trójkątnej piramidy wynosi \(V_(\text(trójkąt prawy.pir.))=\dfrac(\sqrt3)(12)a^2h\),
2. Objętość regularnej czworokątnej piramidy wynosi \(V_(\text(right.four.pir.))=\dfrac13a^2h\).
3. Objętość regularnej sześciokątnej piramidy wynosi \(V_(\text(right.six.pir.))=\dfrac(\sqrt3)(2)a^2h\).
4. Objętość regularny czworościan równa się \(V_(\text(prawy tetr.))=\dfrac(\sqrt3)(12)a^3\).
Twierdzenie
Pole powierzchni bocznej regularnej piramidy jest równe połowie iloczynu obwodu podstawy i apothemu.
\[(\Duży(\text(Frustum)))\]
Definicja
Rozważmy dowolną piramidę \(PA_1A_2A_3...A_n\) . Narysujmy płaszczyznę równoległą do podstawy piramidy przez pewien punkt leżący na bocznej krawędzi piramidy. Ten samolot podzieli piramidę na dwa wielościany, z których jeden jest piramidą (\(PB_1B_2...B_n\) ), a drugi nazywa się ścięta piramida(\(A_1A_2...A_nB_1B_2...B_n\) ).
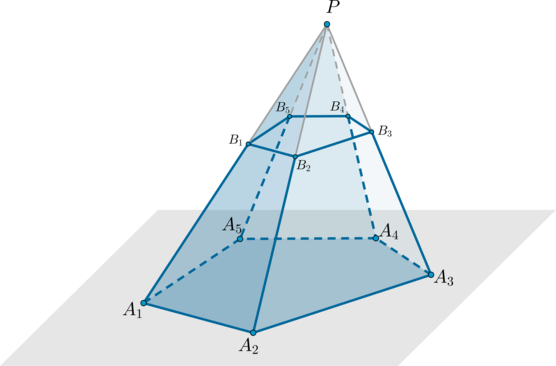
Ścięta piramida ma dwie podstawy - wielokąty \(A_1A_2...A_n\) i \(B_1B_2...B_n\), które są do siebie podobne.
Wysokość ściętej piramidy jest prostopadłą poprowadzoną od pewnego punktu górnej podstawy do płaszczyzny dolnej podstawy.
Ważne notatki
1. Wszystkie boczne ściany ściętej piramidy są trapezami.
2. Odcinek łączący środki podstaw regularnej piramidy ściętej (to znaczy piramidy uzyskanej przez przekrój regularnej piramidy) to wysokość.
Zastanówmy się, jakie właściwości mają piramidy, w których ściany boczne są prostopadłe do podstawy.
Jeśli dwie sąsiednie boczne ściany piramidy są prostopadłe do podstawy, To wspólna boczna krawędź tych ścian to wysokość piramidy. Jeśli problem tak mówi krawędź piramidy to jej wysokość, To mówimy o szczególnie na temat tego typu piramidy.
Ściany piramidy prostopadłe do podstawy są trójkątami prostokątnymi.
Jeśli podstawą piramidy jest trójkąt
Powierzchnia boczna takiej piramidy w przypadek ogólny szukamy go jako sumy pól wszystkich ścian bocznych.
Podstawa piramidy to rzut ortogonalny powierzchnia nie prostopadła do podstawy (w w tym przypadku, SBC). Oznacza to, że zgodnie z twierdzeniem o obszarze rzutu ortogonalnego pole podstawy jest równe iloczynowi pola tej ściany i cosinusa kąta między nią a płaszczyzną podstawy .
Jeśli podstawą piramidy jest trójkąt prostokątny

W tym przypadku wszystkie ściany piramidy są trójkątami prostokątnymi.
Trójkąty SAB i SAC są prostokątne, ponieważ SA jest wysokością piramidy. Trójkąt ABC prostokątny według warunku.
To, że trójkąt SBC jest prostokątny, wynika z twierdzenia o trzech prostopadłych (AB jest rzutem nachylonej SB na płaszczyznę podstawy. Ponieważ AB jest prostopadłe do BC zgodnie z warunkiem, to SB jest prostopadłe do BC).
Kąt pomiędzy boczną powierzchnią SBC a podstawą w tym przypadku jest kątem ABS.
Pole powierzchni bocznej jest równe sumie pól trójkątów prostokątnych:
Ponieważ w tym przypadku
![]()
Jeśli podstawą piramidy jest trójkąt równoramienny
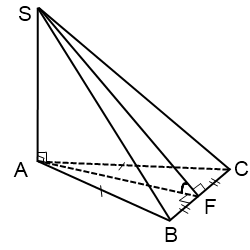
W tym przypadku kąt pomiędzy płaszczyzną ściany bocznej BCS a płaszczyzną podstawy to kąt AFS, gdzie AF to wysokość, mediana i dwusieczna Trójkąt równoramienny ABC.
Podobnie, jeśli u podstawy piramidy leży trójkąt równoboczny ABC.
Jeśli podstawą piramidy jest równoległobok
 W tym przypadku podstawa piramidy jest rzutem prostopadłym ścian bocznych, które nie są prostopadłe do podstawy.
W tym przypadku podstawa piramidy jest rzutem prostopadłym ścian bocznych, które nie są prostopadłe do podstawy.
Jeśli podzielimy podstawę na dwa trójkąty, to
gdzie α i β są kątami odpowiednio pomiędzy płaszczyznami ADS i CDS a płaszczyzną bazową.

Jeżeli BF i BK są wysokościami równoległoboku, to kąt BFS jest kątem nachylenia ściany bocznej CDS do płaszczyzny podstawy, a kąt BKS jest kątem nachylenia boku ADS.
(rysunek wykonano dla przypadku, gdy B jest kątem rozwartym).
Jeżeli podstawą ostrosłupa jest romb ABCD, to kąty BFS i BKS są sobie równe. Trójkąty ABS i CBS, a także ADS i CDS są w tym przypadku również równe.
Jeśli podstawą piramidy jest prostokąt
 W tym przypadku kąt pomiędzy płaszczyzną ściany bocznej SAD i płaszczyzną podstawy jest kątem SAB,
W tym przypadku kąt pomiędzy płaszczyzną ściany bocznej SAD i płaszczyzną podstawy jest kątem SAB,
zaś kąt pomiędzy płaszczyzną boku SCD i płaszczyzną podstawy jest kątem SCB
(na podstawie twierdzenia o trzech prostopadłych).
Odpowiednio,
Stąd powierzchnia boczna można znaleźć jako
Tutaj wszystkie boczne ściany piramidy są trójkątami prostokątnymi(kąty SAD i SCD są kątami prostymi zgodnie z twierdzeniem o trzech prostopadłych). Dlatego powierzchnię boczną można przeszukiwać bezpośrednio:
Jeżeli podstawą piramidy jest kwadrat ABCD, to problem jest uproszczony: trójkąty ABS i BCS, a także trójkąty ADS i CDS są w tym przypadku równe.
15 grudnia 2012 r
Recenzje (12) na temat “Piramidy, w których krawędzie są prostopadłe do podstawy”
-
Jeśli wpiszesz w Google „prostokątna piramida” po rosyjsku, Twój materiał znajdzie się w pierwszej piątce. Widzę, że na tej stronie jest tylko jedna piramida prostokątna, ostatnia i oznaczenia nie są do końca poprawne. Google wraz z Wikipedią wymyśliło dziwną definicję - krawędź prostopadła i taka sama jak u podstawy piramidy. Swoją drogą, dalej język angielski Ogólnie rzecz biorąc, piramida prostokątna to piramida, u podstawy której znajduje się prostokąt i nie ma w ogóle znaczenia, gdzie jest wysokość.
W tekście nie ma ani słowa o piramidzie prostokątnej. Bardzo często w zagadnieniach dotyczących ostrosłupów, w których występują dwie ściany boczne prostopadłe do podstawy, mówimy o kącie pomiędzy płaszczyzną ściany bocznej a płaszczyzną podstawy.
W ten materiał zastanów się, jak wyznaczyć ten kąt w zależności od wielokąta u podstawy. Jeśli podstawa zawiera równoległobok (w tym romb), musisz narysować wysokości równoległoboku od podstawy piramidy do przeciwne strony(lub linia prosta zawierająca te boki). Jeśli podstawą jest prostokąt (w tym kwadrat), nie ma potrzeby rysowania wysokości, ponieważ boki prostokąta są do siebie prostopadłe. W tym przypadku określa się kąt między podstawą a krawędzią boczną kąt liniowy, utworzony przez krawędzie piramidy; ściany boczne są trójkątami prostokątnymi.
Podświetlone są kąty proste u podstawy, aby podkreślić tę różnicę w stosunku do przypadku, gdy podstawą jest równoległobok, który nie jest prostokątem.Ponieważ usunąłeś „prostokątną piramidę”, ale techników, którzy znają i rozumieją, jak działają wyszukiwarki, raczej nie przekonają twoje argumenty. Ucz się informatyki, nie tylko matematyki.
Drogi Natashoku! Zarzucasz mi kłamstwo? Mówiłam Wam, że w swojej pracy nie używam określenia „piramida prostokątna”.
P.S. Niestety nie jestem informatykiem. Zgadzam się, umiejętność czytania i pisania jest potrzebna we wszystkich dziedzinach: zarówno w matematyce, jak i w technologia informacyjna i w ortografii.
Rysunek ilustruje przypadek, gdy u podstawy piramidy znajduje się prostokąt. W projektowaniu równoległym kąty nie są zachowywane, dlatego prostokąt jest rysowany jako równoległobok. Drugi kąt prosty na rysunku zanotowano w związku z twierdzeniem o trzech prostopadłych.
Po pierwsze, nie rysunek, ale rysunek. Rysujesz rysunki na rysunku, ale w matematyce są to nadal rysunki. Po drugie, spójrz na ostatni rysunek. Nie ma twierdzeń o trzech prostopadłych. Powtarzam, podstawa na ostatnim rysunku nie jest prostokątem. Nie ma znaczenia, jak to przedstawisz. Kieruję się zapisami. Chociaż zauważyłem, że trzeci rysunek poniżej też jest dla mnie nieczytelny. Równoległobok nie jest zaznaczony na rysunku. Po prostu czworokąt! Jego wygląd przypomina równoległobok, ale oznaczenia pozostawiają wiele do życzenia.
1) Tak, w geometrii wykonujemy rysunek, ale ilustracją do tekstu jest rysunek. W każdym podręczniku do geometrii piszą „na rysunku 1”, a nie „na rysunku 1”.
2) Prostokąt w stereometrii jest przedstawiany jako równoległobok, ponieważ podczas projektowania równoległego kąty nie są zachowywane. Ale równoległość linii zostaje zachowana. Przeciwległe boki czworoboku są przedstawione jako leżące na równoległych liniach. Wynika z tego, że ten czworokąt jest równoległobokiem.Przeciwległe boki czworoboku są przedstawione jako leżące na równoległych liniach. Nie widzę żadnej przesłanki wskazującej, że linie te są równoległe, a w tekście nie wskazano na równoległość. Więc dla mnie podstawą jest nadal ostatni rysunek dowolny czworokąt
Kochana Natasza! Obraz figury przestrzenne w samolocie odbywa się zgodnie z przepisami projekt równoległy. Oznacza to, że linie równoległe na rysunku są przedstawiane jako linie równoległe, a linie nierównoległe nie są równoległe.
Nie zgadzam się z definicją piramidy prostokątnej. Prostokątna piramida jest ostrosłupem, którego jeden wierzchołek ma trzy kąty proste. Napisz mi dlaczego rozpowszechniasz błędny materiał na poziomie nieświadomej Wikipedii.
Jeśli podstawą piramidy jest prostokąt, to dlaczego na rysunku zaznaczono dwa przeciwległe rogi, aby to zaznaczyć? Na ostatnim rysunku podstawa ta może być rombem i innym czworobokiem.
W którym jedno z żeber bocznych jest prostopadłe do podstawy.
W tym przypadku ta krawędź będzie wysokością piramidy.
Właściwości piramidy.
1. Gdy wszystkie krawędzie boczne mają ten sam rozmiar, to:
- w pobliżu podstawy piramidy jest łatwe do opisania koło, podczas gdy wierzchołek piramidy będzie rzutowany na środek tego okręgu;
- żebra boczne tworzą się identycznie kąty ;
- Co więcej, prawdą jest również coś odwrotnego, tj. kiedy boczne żebra tworzą się z płaszczyzną podstawy równe kąty, lub gdy w pobliżu podstawy piramidy można opisać okrąg, a wierzchołek piramidy zostanie rzucony na środek tego okręgu, co oznacza, że wszystkie boczne krawędzie piramidy są tej samej wielkości.
2. Gdy ściany boczne mają kąt nachylenia do płaszczyzny podstawy o tej samej wartości, to:
- łatwo jest opisać okrąg w pobliżu podstawy piramidy, a wierzchołek piramidy będzie rzutowany na środek tego okręgu;
- wysokość ścian bocznych wynosi jednakowa długość;
- powierzchnia powierzchni bocznej jest równa ½ iloczynu obwodu podstawy i wysokości ściany bocznej.
3. Można opisać piramidę kula w przypadku, gdy u podstawy piramidy leży wielokąt, wokół którego można opisać okrąg (konieczne i warunek wystarczający). Środek kuli będzie kropka przecięcia płaszczyzn przechodzących przez środki prostopadłych do nich krawędzi piramidy. Z tego twierdzenia wnioskujemy, że kulę można opisać zarówno wokół dowolnego trójkąta, jak i wokół dowolnej regularnej piramidy;
4. W ostrosłup można wpisać kulę, jeżeli jej płaszczyzny są dwusieczne kąty dwuścienne piramidy przecinają się w pierwszym punkcie (warunek konieczny i wystarczający). Ten punkt stanie się środkiem kuli.
5. Stożek zostanie wpisany w piramidę, gdy ich wierzchołki zbiegną się, a podstawa stożka zostanie wpisana w podstawę piramidy. W takim przypadku stożek w piramidę można zmieścić tylko wtedy, gdy apotemy piramidy mają jednakową wielkość (warunek konieczny i wystarczający);
6. Stożek zostaną opisane w pobliżu piramidy, jeśli ich wierzchołki się pokrywają, a podstawa stożka zostanie opisana w pobliżu podstawy piramidy. W tym przypadku stożek w pobliżu piramidy można opisać tylko wtedy, gdy wszystkie boczne krawędzie piramidy mają te same wartości(warunek konieczny i wystarczający). Wysokości tych stożków i piramid są takie same.
7. Cylinder zostanie wpisany w piramidę, jeżeli jedna z jej podstaw pokrywa się z okręgiem wpisanym w przekroju piramidy płaszczyzną równoległą do podstawy, a druga podstawa należy do podstawy piramidy.
8. Walec zostanie opisany w pobliżu piramidy, gdy wierzchołek piramidy będzie należał do jednej z jej podstaw, a druga podstawa walca zostanie opisana w pobliżu podstawy piramidy. W tym przypadku walec w pobliżu piramidy można opisać tylko wtedy, gdy podstawą piramidy jest wielokąt wpisany (warunek konieczny i wystarczający).
Wzory do określania objętości i powierzchni prostokątnej piramidy.
V- objętość piramidy,
S- powierzchnia podstawy piramidy,
H- wysokość piramidy,
Sb- powierzchnia bocznej powierzchni piramidy,
A- apotem (nie mylić z α ) piramidy,
P- obwód podstawy piramidy,
N- liczba boków podstawy piramidy,
B- długość żebro boczne piramidy,
α - kąt płaski na szczycie piramidy.
