Jak zbudować przekrój sześcianu za pomocą trzech punktów. Budowa sekcji

Temat lekcji: Zadania dotyczące konstruowania przekrojów.

Cel lekcji:

Rozwijanie umiejętności rozwiązywania problemów polegających na konstruowaniu odcinków czworościanu i równoległoboku.

Podczas zajęć

I. Moment organizacyjny.

II. Badanie Praca domowa

Odpowiedzi na pytania 14, 15.

14. Czy istnieje czworościan, który ma pięć kątów prostych na swoich ścianach?

(Odpowiedź: nie, ponieważ są tylko 4 ściany, są to trójkąty, a trójkąt z dwoma kątami prostymi nie istnieje.)

15. Czy istnieje równoległościan, który ma: a) tylko jedną ścianę - prostokąt;

b) tylko dwie sąsiednie ściany rombu; c) wszystkie rogi twarzy są ostre; d) wszystkie kąty ścian są proste; e) liczba wszystkich ostrych krawędzi nie jest równa liczbie wszystkich kątów rozwartych ścian?

(Odpowiedź: a) nie (przeciwne strony są równe); b) nie (z tego samego powodu); c) nie (takie równoległoboki nie istnieją); d) tak ( prostopadłościan); e) nie (każda twarz ma dwie ostre i dwie kąty rozwarte lub wszystkie linie proste).

III. Nauka nowego materiału

Część teoretyczna. Część praktyczna. Część teoretyczna.

Aby rozwiązać wiele problemy geometryczne kojarzone z czworościanem i równoległościanem, przydatna jest możliwość narysowania ich przekrojów w różnych płaszczyznach na rysunku. Przez przekrój rozumiemy dowolną płaszczyznę (nazwijmy ją płaszczyzną przecięcia), po obu stronach której znajdują się punkty danej figury (czyli czworościanu lub równoległościanu). Płaszczyzna cięcia przecina czworościan (równoległościan) wzdłuż segmentów. Wielokąt, który zostanie utworzony przez te segmenty, jest przekrojem figury. Ponieważ czworościan ma cztery ściany, jego przekrój może składać się z trójkątów i czworokątów. Równoległościan ma sześć ścian. Jego przekrój może mieć kształt trójkątów, czworokątów, pięciokątów, sześciokątów.

Konstruując odcinek równoległościanu, bierzemy pod uwagę fakt, że jeśli płaszczyzna przecięcia przecina dwie przeciwległe ściany na niektórych odcinkach, to odcinki te są równoległe (właściwość 1, akapit 11: Jeśli dwie równoległe płaszczyzny przecinają się przez trzecią, to linie ich przecięcia są równoległe).

Aby skonstruować przekrój, wystarczy skonstruować punkty przecięcia płaszczyzny przecięcia z krawędziami czworościanu (równoległościanu), a następnie narysować odcinki łączące każde dwa skonstruowane punkty leżące na tej samej ścianie.

Czy czworościan można przeciąć płaszczyzną w czworokąt pokazany na rysunku?

https://pandia.ru/text/78/630/images/image002_130.gif" szerokość="626" wysokość="287 src=">

2.2. Skonstruuj wycinek sześcianu z płaszczyzną przechodzącą przez punkty mi, F, G, leżące na krawędziach sześcianu.

mi, F, G,

zróbmy bezpośredni E.F. i oznaczać P jego punkt przecięcia z OGŁOSZENIE.

Oznaczmy Q punkt przecięcia linii PG I AB.

Połączmy kropki mi I Q, F I G.

Powstały trapez EFGQ będzie żądaną sekcją.

https://pandia.ru/text/78/630/images/image004_91.gif" szerokość="624" wysokość="287">

2.4. Skonstruuj wycinek sześcianu z płaszczyzną przechodzącą przez punkty mi, F, leżące na krawędziach sześcianu i wierzchołku B.

Rozwiązanie. Konstruowanie przekroju sześcianu przechodzącego przez punkty mi, F i góra B,

Połączmy punkty odcinkami mi I B, F I B.

Przez kropki mi I F narysujmy linie równoległe B.F. I BYĆ odpowiednio.

Wynikowy równoległobok BFGE będzie żądaną sekcją.

2.5. Skonstruuj wycinek sześcianu z płaszczyzną przechodzącą przez punkty mi, F, G, leżące na krawędziach sześcianu.

Rozwiązanie. Konstruowanie przekroju sześcianu przechodzącego przez punkty mi, F, G,

zróbmy bezpośredni E.F. i oznaczać P jego punkt przecięcia z OGŁOSZENIE.

Oznaczmy Q,R punkty przecięcia linii PG Z AB I DC.

Oznaczmy S punkt przecięcia FR C SS 1.

Połączmy kropki mi I Q, G I S.

Powstały pięciokąt EFSGQ będzie żądaną sekcją.

2.6. Skonstruuj wycinek sześcianu z płaszczyzną przechodzącą przez punkty mi, F, G, leżące na krawędziach sześcianu.

Rozwiązanie. Konstruowanie przekroju sześcianu przechodzącego przez punkty mi, F, G,

znajdźmy punkt P przecięcie linii prostej E.F. i płaszczyzna czołowa ABCD.

Oznaczmy Q, R punkty przecięcia linii PG Z AB I płyta CD.

Zróbmy bezpośredni RF i oznaczać S, T jego punkty przecięcia z CC 1 i DD 1.

Zróbmy bezpośredni TE i oznaczać U jego punkt przecięcia z A 1D 1.

Połączmy kropki mi I Q, G I S, F i U.

Powstały sześciokąt EUFSGQ będzie żądaną sekcją.

2.7. Skonstruuj przekrój czworościanu ABCD OGŁOSZENIE i przechodząc przez punkty mi, F.

Rozwiązanie. Połączmy kropki mi I F. Przez punktF narysujmy linię prostąFG, równolegleOGŁOSZENIE.

Połączmy kropki G I mi.

Powstały trójkąt EFG będzie żądaną sekcją.

2.8. Skonstruuj przekrój czworościanu ABCD płaski, równolegle do krawędzi płyta CD i przechodząc przez punkty mi, F .

Rozwiązanie. Przez kropki mi I F narysujmy linie proste NP. I FH, równoległy PŁYTA CD.

Połączmy kropki G I F, mi I H.

Powstały trójkąt EFG będzie żądaną sekcją.

2.9. Skonstruuj przekrój czworościanu ABCD płaszczyzna przechodząca przez te punkty mi, F, G.

Rozwiązanie. Konstruowanie przekroju czworościanu przechodzącego przez punkty mi, F, G,

zróbmy bezpośredni E.F. i oznaczać P jego punkt przecięcia z BD.

Oznaczmy Q punkt przecięcia linii PG I płyta CD.

Połączmy kropki F I Q, mi I G.

Powstały czworokąt EFQG będzie żądaną sekcją.

IV. Podsumowanie lekcji.

V. Praca domowa s. 14, s. 27 nr 000 – opcja 1, 2.

Cele Lekcji

Kształtowanie umiejętności studentów w rozwiązywaniu problemów związanych z budową sekcji.
Kształcenie i rozwój wyobraźni przestrzennej uczniów.
Rozwój kultury graficznej i mowy matematycznej.
Rozwijanie umiejętności pracy indywidualnej i zespołowej.

Typ lekcji: lekcja kształtowania i doskonalenia wiedzy.

Formy organizacji zajęć edukacyjnych: grupowy, indywidualny, zbiorowy.

Wsparcie techniczne lekcji: komputer, rzutnik multimedialny, ekran, zbiór brył geometrycznych (sześcian, równoległościan, czworościan).

PODCZAS ZAJĘĆ

1. Moment organizacyjny

Klasa podzielona jest na 3 grupy po 5-6 osób. Na każdym stole znajdują się indywidualne i grupowe zadania polegające na zbudowaniu sekcji, zestawu brył. Zapoznanie uczniów z tematem i celami lekcji.

2. Aktualizuj wiedza podstawowa

Teoria sondażu:

– Aksjomaty stereometrii.
– Pojęcie linii równoległych w przestrzeni.
– Twierdzenie o prostych równoległych.
– Równoległość trzech prostych.
– Względne położenie prostej i płaszczyzny w przestrzeni.
– Znak równoległości linii i płaszczyzny.
– Wyznaczanie równoległości płaszczyzn.
– Znak równoległości dwóch płaszczyzn.
- Nieruchomości płaszczyzny równoległe.
- Czworościan. Równoległościan. Właściwości równoległościanu.

3. Nauka nowego materiału

Słowo nauczyciela: Przy rozwiązywaniu wielu problemów stereometrycznych wykorzystuje się przekrój wielościanu przez płaszczyznę. Sieczną płaszczyzną wielościanu nazwiemy dowolną płaszczyznę, po obu stronach której znajdują się punkty danego wielościanu.
Płaszczyzna cięcia przecina ściany wzdłuż segmentów. Wielokąt, którego bokami są te segmenty, nazywany jest odcinkiem wielościanu.
Korzystając z rysunków 38-39, przekonajmy się: Ile boków może mieć przekrój czworościanu i równoległościanu?

Studenci analizuj zdjęcia i wyciągaj wnioski. Nauczyciel poprawia odpowiedzi uczniów, zwracając uwagę, że jeśli płaszczyzna przecięcia przecina na niektórych odcinkach dwie przeciwległe ściany równoległościanu, to odcinki te są równoległe.

Analiza rozwiązywanie zadań 1, 2, 3 podanych w podręczniku (ustna praca w grupach).

4. Utrwalenie badanego materiału(według grup)

1 grupa: wyjaśnić, jak skonstruować przekrój czworościanu z płaszczyzną przechodzącą przez dane punkty M, N, K i w zadaniach 1-3 znaleźć obwód przekroju, jeśli M, N, K są środkami krawędzi i każdej krawędzi czworościan jest równy A.

Grupa 2: wyjaśnić, jak skonstruować przekrój sześcianu z płaszczyzną przechodzącą przez trzy dane punkty, które są albo wierzchołkami sześcianu, albo środkami jego krawędzi (trzy podane punkty są zaznaczone na rysunkach); w zadaniach 1-4 i 6, znajdź obwód przekroju, jeśli krawędź sześcianu jest równa A. w zadaniu 5 udowodnij, że AE = A/3

Grupa 3: skonstruuj przekrój równoległościanu ABCDA 1 B 1 Do 1 D 1 płaszczyzna przechodząca przez punkty:

Grupa broni wszystkich wykonanych zadań na tablicy za pomocą slajdów.

5. Niezależna praca № 85, № 105.

6. Podsumowanie lekcji

Ocena pracy uczniów na zajęciach.

7. Praca domowa: poszczególne karty.

Definicja

Sekcja jest płaska figura, który powstaje w wyniku przecięcia figury przestrzennej z płaszczyzną i którego granica leży na powierzchni figury przestrzennej.

Komentarz

Do konstruowania różnych sekcji figury przestrzenne należy pamiętać o podstawowych definicjach i twierdzeniach dotyczących równoległości i prostopadłości prostych i płaszczyzn oraz własności figur przestrzennych. Przypomnijmy podstawowe fakty.
Aby uzyskać więcej szczegółowe badanie Zalecane jest zapoznanie się z tematami „Wprowadzenie do stereometrii. Równoległość” i „Prostopadłość. Kąty i odległości w przestrzeni”.

Ważne definicje

1. Dwie linie w przestrzeni są równoległe, jeśli leżą w tej samej płaszczyźnie i nie przecinają się.

2. Dwie proste w przestrzeni przecinają się, jeśli nie można przez nie poprowadzić płaszczyzny.

4. Dwie płaszczyzny są równoległe, jeśli nie mają punktów wspólnych.

5. Dwie linie w przestrzeni nazywamy prostopadłymi, jeśli kąt między nimi jest równy \(90^\circ\) .

6. Nazywa się linię prostą prostopadle do płaszczyzny, jeśli jest prostopadła do dowolnej linii leżącej w tej płaszczyźnie.

7. Dwie płaszczyzny nazywamy prostopadłymi, jeśli kąt między nimi wynosi \(90^\circ\) .

Ważne aksjomaty

1. Przez trzy punkty, które nie leżą na tej samej linii, przechodzi płaszczyzna i tylko jeden.

2. Płaszczyzna i tylko jedna przechodzi przez linię prostą i punkt na niej nie leżący.

3. Samolot przechodzi przez dwie przecinające się linie i tylko jedną.

Ważne twierdzenia

1. Jeżeli prosta \(a\) nie leżąca na płaszczyźnie \(\pi\) jest równoległa do jakiejś prostej \(p\) leżącej na płaszczyźnie \(\pi\) to jest równoległa do tej samolot.

2. Niech prosta \(p\) będzie równoległa do płaszczyzny \(\mu\) . Jeżeli płaszczyzna \(\pi\) przechodzi przez prostą \(p\) i przecina płaszczyznę \(\mu\) , to linia przecięcia płaszczyzn \(\pi\) i \(\mu\) jest linią \(m\) - równoległą do linii prostej \(p\) .

3. Jeżeli dwie przecinające się linie z jednej płaszczyzny są równoległe do dwóch przecinających się linii z innej płaszczyzny, to takie płaszczyzny będą równoległe.

4. Jeżeli dwie równoległe płaszczyzny \(\alpha\) i \(\beta\) przecina trzecia płaszczyzna \(\gamma\), to linie przecięcia płaszczyzn również są równoległe:

\[\alpha\parallel \beta, \ \alpha\cap \gamma=a, \ \beta\cap\gamma=b \Longrightarrow a\parallel b\]

5. Niech prosta \(l\) leży na płaszczyźnie \(\lambda\) . Jeżeli prosta \(s\) przecina płaszczyznę \(\lambda\) w punkcie \(S\) nie leżącym na prostej \(l\), to proste \(l\) i \(s\) przecinać.

6. Jeżeli prosta jest prostopadła do dwóch przecinających się linii leżących na danej płaszczyźnie, to jest prostopadła do tej płaszczyzny.

7. Twierdzenie o trzech prostopadłych.

Niech \(AH\) będzie prostopadła do płaszczyzny \(\beta\) . Niech \(AB, BH\) będzie płaszczyzną nachyloną i jej rzutem na płaszczyznę \(\beta\) . Wtedy prosta \(x\) w płaszczyźnie \(\beta\) będzie prostopadła do nachylonej wtedy i tylko wtedy, gdy jest prostopadła do rzutu.

8. Jeżeli płaszczyzna przechodzi przez linię prostopadłą do innej płaszczyzny, to jest prostopadła do tej płaszczyzny.

Komentarz

Inny ważny fakt, często używane do konstruowania sekcji:

aby znaleźć punkt przecięcia prostej i płaszczyzny, wystarczy znaleźć punkt przecięcia danej prostej i jej rzut na tę płaszczyznę.

Do tego dwa dowolne punkty\(A\) i \(B\) linia \(a\) rysują prostopadłe do płaszczyzny \(\mu\) – \(AA"\) i \(BB"\) (punkty \(A", B " \) nazywane są rzutami punktów \(A,B\) na płaszczyznę). Wtedy prosta \(A"B"\) jest rzutem prostej \(a\) na płaszczyznę \(\mu\) . Punkt \(M=a\cap A"B"\) jest punktem przecięcia prostej \(a\) i płaszczyzny \(\mu\) .

Ponadto zauważamy, że wszystkie punkty \(A, B, A", B", M\) leżą w tej samej płaszczyźnie.

Przykład 1.

Biorąc pod uwagę sześcian \(ABCDA"B"C"D"\) . \(A"P=\dfrac 14AA", \KC=\dfrac15 CC"\). Znajdź punkt przecięcia prostej \(PK\) i płaszczyzny \(ABC\) .

Rozwiązanie

1) Ponieważ krawędzie sześcianu \(AA", CC"\) są prostopadłe do \((ABC)\), wówczas punkty \(A\) i \(C\) są rzutami punktów \(P\) i \(K\). Wtedy prosta \(AC\) jest rzutem prostej \(PK\) na płaszczyznę \(ABC\) . Wydłużmy odcinki \(PK\) i \(AC\) poza punkty odpowiednio \(K\) i \(C\) i uzyskajmy punkt przecięcia prostych - punkt \(E\) .

2) Znajdź stosunek \(AC:EC\) . \(\trójkąt PAE\sim \trójkąt KCE\) w dwóch rogach ( \(\kąt A=\kąt C=90^\circ, \kąt E\)- ogólnie), tzn \[\dfrac(PA)(KC)=\dfrac(EA)(EC)\]

Jeśli oznaczymy krawędź sześcianu jako \(a\) , to \(PA=\dfrac34a, \KC=\dfrac15a, \AC=a\sqrt2\). Następnie:

\[\dfrac(\frac34a)(\frac15a)=\dfrac(a\sqrt2+EC)(EC) \Rightarrow EC=\dfrac(4\sqrt2)(11)a \Rightarrow AC:EC=4:11\ ]

Przykład 2.

Dana ma rację trójkątna piramida\(DABC\) o podstawie \(ABC\), której wysokość jest równa bokowi podstawy. Niech punkt \(M\) się podzieli boczne żebro piramida w stosunku \(1:4\), licząc od wierzchołka piramidy, a \(N\) to wysokość piramidy w stosunku \(1:2\), licząc od wierzchołka piramidy . Znajdź punkt przecięcia prostej \(MN\) z płaszczyzną \(ABC\) .

Rozwiązanie

1) Niech \(DM:MA=1:4, \DN:NO=1:2\) (patrz rysunek). Ponieważ piramida jest regularna, wówczas wysokość przypada na punkt \(O\) przecięcia środkowych podstawy. Znajdźmy rzut prostej \(MN\) na płaszczyznę \(ABC\) . Ponieważ \(DO\perp (ABC)\) , następnie \(NIE\perp (ABC)\) . Oznacza to, że \(O\) jest punktem należącym do tego rzutu. Znajdźmy drugi punkt. Spuśćmy prostopadłą \(MQ\) z punktu \(M\) na płaszczyznę \(ABC\) . Punkt \(Q\) będzie leżał na środkowej \(AK\) .
Rzeczywiście, ponieważ \(MQ\) i \(NO\) są prostopadłe do \((ABC)\), to są równoległe (co oznacza, że leżą w tej samej płaszczyźnie). Dlatego od punkty \(M, N, O\) leżą w tej samej płaszczyźnie \(ADK\), to punkt \(Q\) będzie leżeć w tej płaszczyźnie. Ale także (konstrukcyjnie) punkt \(Q\) musi leżeć na płaszczyźnie \(ABC\), zatem leży na linii przecięcia tych płaszczyzn, a to jest \(AK\) .

Oznacza to, że prosta \(AK\) jest rzutem prostej \(MN\) na płaszczyznę \(ABC\) . \(L\) jest punktem przecięcia tych linii.

2) Zauważ, że aby poprawnie narysować rysunek, konieczne jest znalezienie dokładnej pozycji punktu \(L\) (przykładowo na naszym rysunku punkt \(L\) leży poza odcinkiem \(OK\ ), chociaż mógłby w nim leżeć; co jest poprawne?).

Ponieważ zgodnie z warunkiem bok podstawy jest równy wysokości ostrosłupa, wówczas oznaczamy \(AB=DO=a\) . Wtedy mediana wynosi \(AK=\dfrac(\sqrt3)2a\) . Oznacza, \(OK=\dfrac13AK=\dfrac 1(2\sqrt3)a\). Znajdźmy długość odcinka \(OL\) (wtedy możemy zrozumieć, czy punkt \(L\) znajduje się wewnątrz, czy na zewnątrz odcinka \(OK\): jeśli \(OL>OK\) to jest na zewnątrz, w przeciwnym razie jest w środku).

A) \(\trójkąt AMQ\sim \trójkąt ADO\) w dwóch rogach ( \(\kąt Q=\kąt O=90^\circ, \\kąt A\)- ogólny). Oznacza,

\[\dfrac(MQ)(DO)=\dfrac(AQ)(AO)=\dfrac(MA)(DA)=\dfrac 45 \Rightarrow MQ=\dfrac 45a, \AQ=\dfrac 45\cdot \dfrac 1(\sqrt3)a\]

Oznacza, \(QK=\dfrac(\sqrt3)2a-\dfrac 45\cdot \dfrac 1(\sqrt3)a=\dfrac7(10\sqrt3)a\).

b) Oznaczmy \(KL=x\) .
\(\trójkąt LMQ\sim \trójkąt LNO\) w dwóch rogach ( \(\kąt Q=\kąt O=90^\circ, \\kąt L\)- ogólny). Oznacza,

\[\dfrac(MQ)(NO)=\dfrac(QL)(OL) \Rightarrow \dfrac(\frac45 a)(\frac 23a) =\dfrac(\frac(7)(10\sqrt3)a+x )(\frac1(2\sqrt3)a+x) \Rightarrow x=\dfrac a(2\sqrt3) \Rightarrow OL=\dfrac a(\sqrt3)\]

Zatem \(OL>OK\) oznacza, że punkt \(L\) rzeczywiście leży poza odcinkiem \(AK\) .

Komentarz

Nie przejmuj się, jeśli podejmiesz decyzję podobne zadanie przekonasz się, że długość odcinka jest ujemna. Jeżeli w warunkach poprzedniego zadania otrzymaliśmy, że \(x\) jest ujemne, oznaczałoby to, że błędnie wybraliśmy położenie punktu \(L\) (czyli że znajduje się on wewnątrz odcinka \(AK \)) .

Przykład 3

Dana ma rację czworokątna piramida\(SABCD\) . Znajdź przekrój piramidy przez płaszczyznę \(\alpha\) przechodzącą przez punkt \(C\) i środek krawędzi \(SA\) i równoległą do prostej \(BD\) .

Rozwiązanie

1) Oznaczmy środek krawędzi \(SA\) przez \(M\) . Ponieważ piramida jest regularna, wówczas wysokość \(SH\) piramidy spada do punktu przecięcia przekątnych podstawy. Rozważmy płaszczyznę \(SAC\) . Odcinki \(CM\) i \(SH\) leżą na tej płaszczyźnie, niech przecinają się w punkcie \(O\) .

Aby płaszczyzna \(\alfa\) była równoległa do prostej \(BD\) , musi zawierać jakąś prostą równoległą do \(BD\) . Punkt \(O\) znajduje się wraz z prostą \(BD\) w tej samej płaszczyźnie - w płaszczyźnie \(BSD\) . Narysujmy w tej płaszczyźnie przez punkt \(O\) prostą \(KP\równoległą BD\) (\(K\in SB, P\in SD\) ). Następnie łącząc punkty \(C, P, M, K\) otrzymujemy przekrój piramidy przez płaszczyznę \(\alpha\) .

2) Znajdźmy relację, w której punkty \(K\) i \(P\) są podzielone przez krawędzie \(SB\) i \(SD\) . W ten sposób całkowicie zdefiniujemy konstruowaną sekcję.

Zauważ, że ponieważ \(KP\parallel BD\) , to według twierdzenia Talesa \(\dfrac(SB)(SK)=\dfrac(SD)(SP)\). Ale \(SB=SD\) oznacza \(SK=SP\) . Zatem można znaleźć tylko \(SP:PD\).

Rozważ \(\trójkąt ASC\) . \(CM, SH\) są środkowymi w tym trójkącie, dlatego punkt przecięcia dzieli się w stosunku \(2:1\), licząc od wierzchołka, czyli \(SO:OH=2:1\ ) .

Teraz zgodnie z twierdzeniem Talesa z \(\triangle BSD\) : \(\dfrac(SP)(PD)=\dfrac(SO)(OH)=\dfrac21\).

3) Zauważ, że zgodnie z twierdzeniem o trzech prostopadłych \(CO\perp BD\) jest jak ukośna (\(OH\) jest prostopadłą do płaszczyzny \(ABC\), \(CH\perp BD\) jest projekcją). Zatem \(CO\perp KP\) . Zatem przekrój jest czworobokiem \(CPMK\), którego przekątne są wzajemnie prostopadłe.

Przykład 4

Dana prostokątna piramida\(DABC\) z krawędzią \(DB\) prostopadłą do płaszczyzny \(ABC\) . U podstawy leży trójkąt prostokątny z \(\kąt B=90^\circ\) i \(AB=DB=CB\) . Narysuj płaszczyznę przechodzącą przez prostą \(AB\) prostopadłą do ściany \(DAC\) i znajdź przekrój piramidy przez tę płaszczyznę.

Rozwiązanie

1) Płaszczyzna \(\alfa\) będzie prostopadła do ściany \(DAC\), jeśli zawiera linię prostopadłą do \(DAC\) . Narysujmy prostopadłą z punktu \(B\) do płaszczyzny \(DAC\) - \(BH\) , \(H\in DAC\) .

Narysujmy pomocniczą \(BK\) – medianę w \(\trójkącie ABC\) i \(DK\) – medianę w \(\trójkąt DAC\) .
Ponieważ \(AB=BC\) , to \(\trójkąt ABC\) jest równoramiennym, co oznacza, że \(BK\) jest wysokością, czyli \(BK\perp AC\) .
Ponieważ \(AB=DB=CB\) i \(\kąt ABD=\kąt CBD=90^\circ\), To \(\trójkąt ABD=\trójkąt CBD\), zatem \(AD=CD\) , zatem \(\trójkąt DAC\) jest także równoramiennym i \(DK\perp AC\) .

Zastosujmy twierdzenie o trzech prostopadłych: \(BH\) – prostopadłe do \(DAC\) ; ukośny \(BK\perp AC\) , co oznacza rzutowanie \(HK\perp AC\) . Ale już to ustaliliśmy \(DK\perp AC\) . Zatem punkt \(H\) leży na odcinku \(DK\) .

Łącząc punkty \(A\) i \(H\) otrzymujemy odcinek \(AN\), wzdłuż którego płaszczyzna \(\alpha\) przecina ścianę \(DAC\) . Wtedy \(\trójkąt ABN\) jest pożądanym przekrojem piramidy przez płaszczyznę \(\alpha\) .

2) Określ dokładne położenie punktu \(N\) na krawędzi \(DC\) .

Oznaczmy \(AB=CB=DB=x\) . Następnie \(BK\), gdy mediana spadła z wierzchołka prosty kąt w \(\trójkąt ABC\) jest równy \(\frac12 AC\) , zatem \(BK=\frac12 \cdot \sqrt2 x\) .

Rozważmy \(\trójkąt BKD\) . Znajdźmy stosunek \(DH:HK\) .

Zauważ, że od \(BH\perp (DAC)\), wówczas \(BH\) jest prostopadła do dowolnej linii prostej wychodzącej z tej płaszczyzny, co oznacza, że \(BH\) jest wysokością w \(\trójkącie DBK\) . Następnie \(\trójkąt DBH\sim \trójkąt DBK\), stąd

\[\dfrac(DH)(DB)=\dfrac(DB)(DK) \Rightarrow DH=\dfrac(\sqrt6)3x \Rightarrow HK=\dfrac(\sqrt6)6x \Rightarrow DH:HK=2:1 \]

Rozważmy teraz \(\trójkąt ADC\) . Mediany dokładnego trójkąta przecięcia są podzielone w stosunku \(2:1\), licząc od wierzchołka. Oznacza to, że \(H\) jest punktem przecięcia środkowych w \(\trójkącie ADC\) (ponieważ \(DK\) jest medianą). Oznacza to, że \(AN\) jest także medianą, co oznacza \(DN=NC\) .

Szkoła ogólnokształcąca poziomów І-ІІІ nr 2

Departament Edukacji Administracji Miasta Kirowskie

„Przekrój sześcianu płaszczyzną

i ich praktyczne zastosowanie w problematyce.”

Przygotowane przez nauczyciela matematyki

nauczyciel-metodolog

Chumakova G.V.

2015

Wstęp:

Zagadnienia konstruowania przekrojów wielościanów zajmują istotne miejsce zarówno na lekcjach geometrii w szkołach średnich, jak i na egzaminach różne poziomy. Rozwiązanie tego typu problemów przyczynia się do przyswojenia aksjomatów stereometrii, usystematyzowania wiedzy i umiejętności, rozwoju zrozumienia przestrzennego i umiejętności konstruktywnych. Trudności, jakie pojawiają się przy rozwiązywaniu problemów związanych z budową odcinków, są powszechnie znane.

Główne działania składające się na metodę konstruowania odcinków to: znalezienie punktu przecięcia prostej z płaszczyzną, zbudowanie linii przecięcia dwóch płaszczyzn, zbudowanie prostej równoległej do płaszczyzny oraz zbudowanie prostej prostopadłej do samolot.

Zilustruję konstrukcję sekcji za pomocą jednego problemu z kurs szkolny matematyka:

№1. Zbuduj co najmniej dwie części sześcianuABCDA 1 B 1 C 1 D 1 samolot AM 1 C, jeśli punkt M 1 porusza się po odcinku BB 1 od B do B 1 . Znajdź granice pomiaru wysokości przekroju narysowanego z punktu M 1 .

Rozwiązanie: Zbudujmy dwa wymagane sekcje, biorąc punkt M 1 bliżej punktu B i punktu M 2 bliżej B 1 . Obie sekcje pokazano na rysunku. Na początku ruchu, gdy punkt M 1 właśnie oddaliłem się od punktu B 1 , przekrój jest trójkątem o podstawie AC i wysokości M 1 O, który jest nieco większy od odcinka BO, tj.
Jeżeli punkt M 1 zajmie stanowisko M 2 położony bardzo blisko punktu B 1 , To JESTEM 2 C prawie się zbiegnie AB 1 C, a jego wysokość to M 1 O – z odcinkiem B 1 O, którego długość wynosi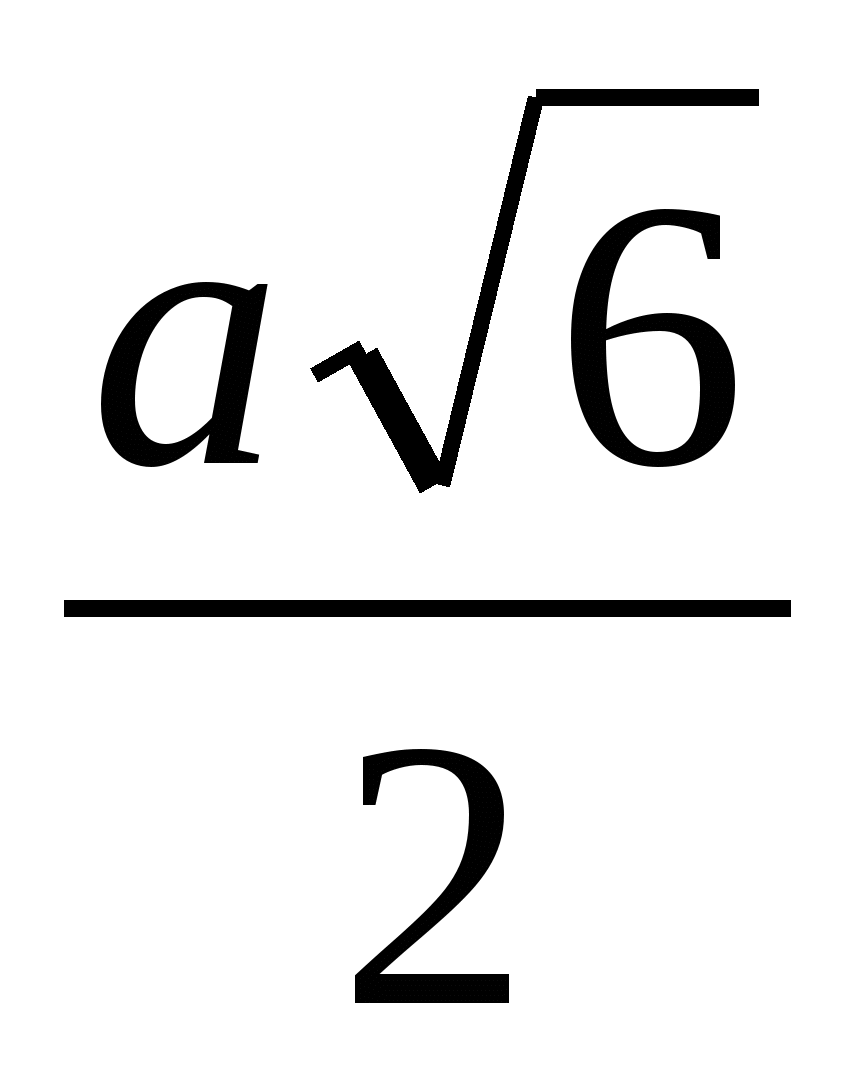
(OB 1 =
=
).

Stąd, ze względu na ciągłość, stwierdzamy: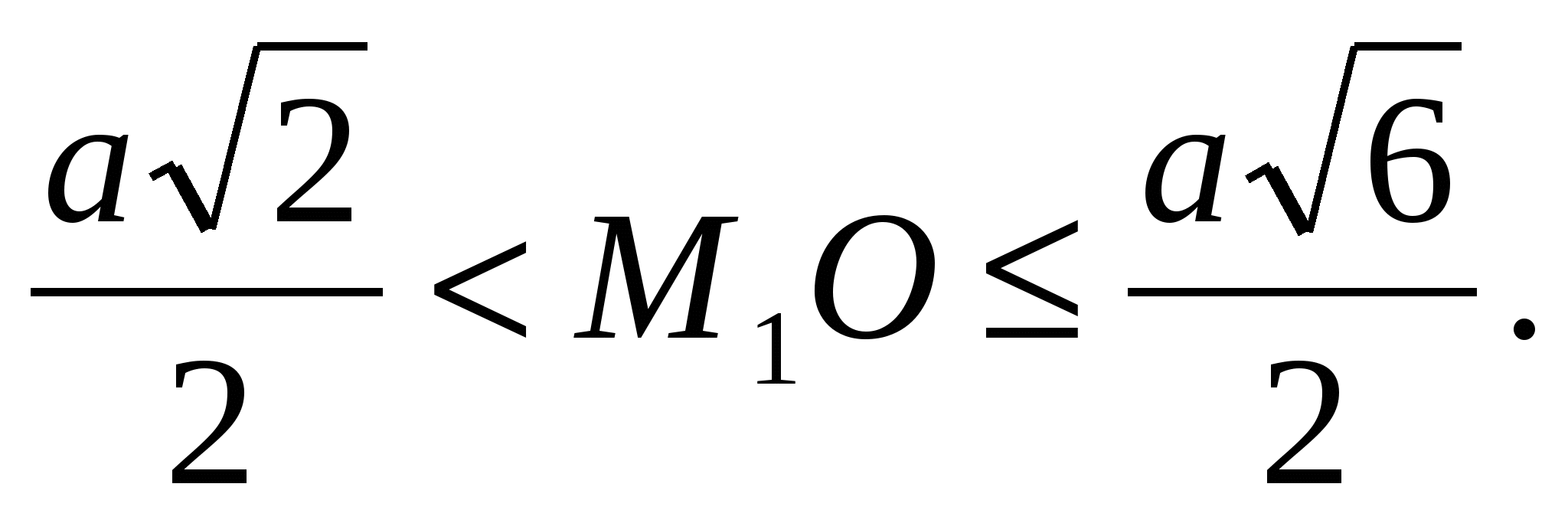

Powinieneś szczególnie przyjrzeć się temu, co się stanie, jeśli punkt M 1 zajmie pozycję wierzchołka B.

№2. Skonstruuj odcinek sześcianu z płaszczyzną przechodzącą przez trzy punkty A 1, E i L leżące na krawędziach sześcianu.

Płaszczyzny ścian A 1 ADD 1 i DD 1 C 1 C przecinają się na prostej DD 1 , a płaszczyzny ścian A 1 B 1 C 1 D 1 u DD 1 C 1 C przecinają się na prostej D 1 C 1 . Łącząc punkty A i E, otrzymujemy prostą linię przecięcia płaszczyzny cięcia z płaszczyzną ściany AA 1 D 1 D i kontynuując ją, znajdujemy punkt N, należący do trzech płaszczyzn: płaszczyzny cięcia i płaszczyzny płaszczyzny ścian AA 1 D 1 D u DD 1 C 1 C.

Podobnie znajdujemy punkt M wspólny dla trzech płaszczyzn: płaszczyzny przekroju i płaszczyzn ścian A 1 B 1 C 1 D 1 u DD 1 C 1 C . Zatem punkty N u M należą do płaszczyzny cięcia i płaszczyzny DD 1 C 1 C; linia prosta MN jest linią przecięcia płaszczyzny przekroju z płaszczyzną ściany DD 1 C 1 C, a F i K są punktami jej przecięcia z krawędziami sześcianu CD u CC 1. Łącząc konsekwentnie punkty A 1 , E , F , K u L liniami prostymi otrzymujemy pięciokąt A ! EFKL, który da nam żądaną sekcję.

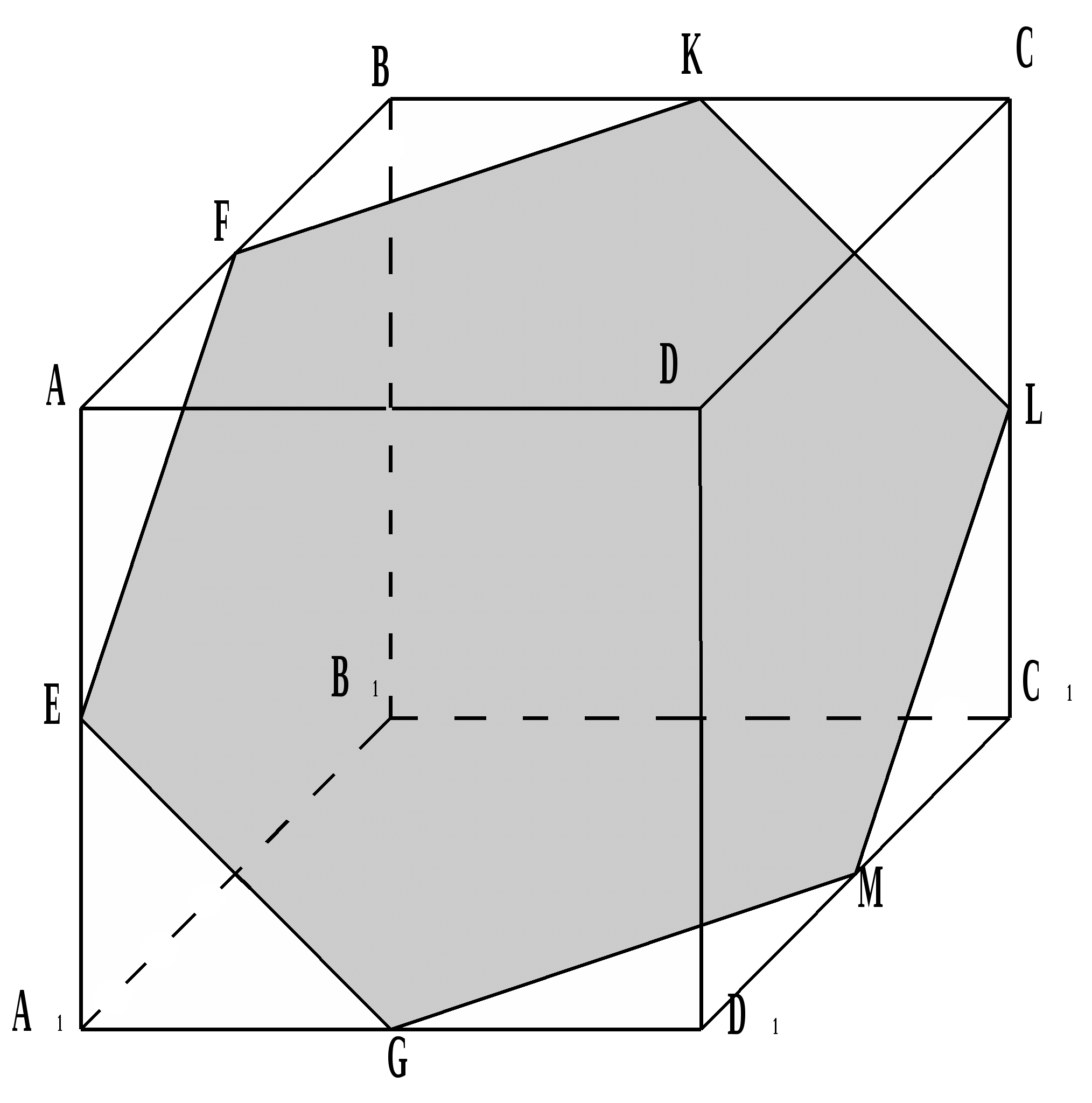
Podczas konstruowania odcinka sześcianu za pomocą płaszczyzny X przy dowolnym rozmieszczeniu punktów w przekroju otrzymujemy: trójkąt, trapez, prostokąt, pięciokąt lub sześciokąt. Naturalnie pojawiło się pytanie, w jaki sposób rodzaj przekroju zależy od rodzaju położenia punktów wyznaczających ten przekrój

Aby się tego dowiedzieć, postanowiłem przeprowadzić badanie.

Konstruuj przekroje sześcianu na płaszczyźnie, gdy dane są trzy punkty należące do krawędzi o jednym wierzchołku.

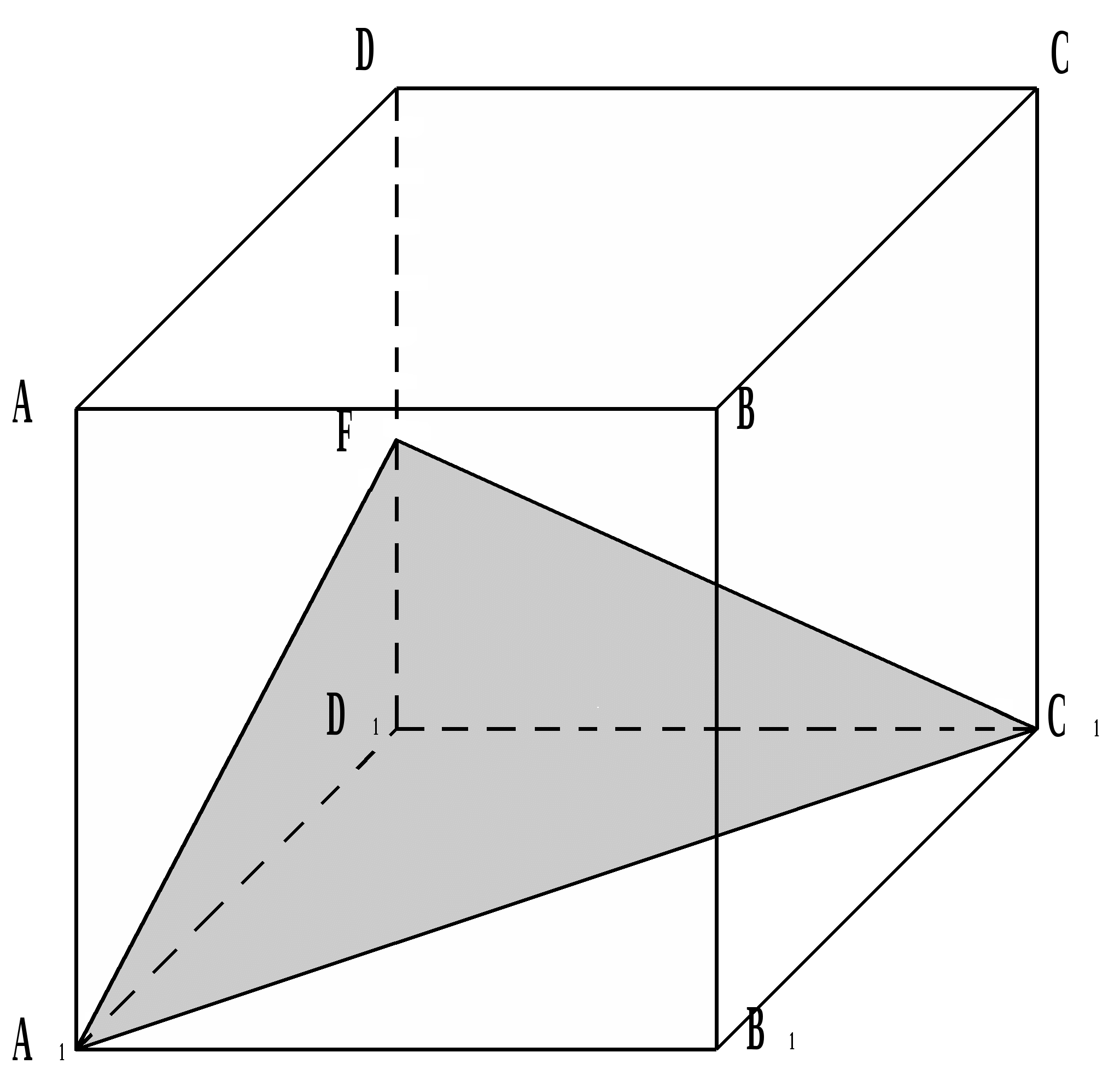
Bierze się trzy punkty A 1 , D , C 1, które należą do wierzchołka D 1 i same są wierzchołkami sześcianu.

W przekroju okazało się trójkąt równoboczny, ponieważ A 1 C 1 , A 1 D u DC 1 są przekątnymi ścian tego sześcianu.

Trzy kropki: A 1 u C 1 to wierzchołki sześcianu, a punkt F należy do krawędzi sześcianu DD 1. Punkty należą do prostych wychodzących z wierzchołka D 1 .

Z przekroju powstaje trójkąt równoramienny, ponieważ F jest w jednakowej odległości od punktów A 1 u C 1 .

Trzy kropki: A 1 u C 1 to wierzchołki sześcianu, a punkt F należy do prostej krawędzi sześcianu DD 1. Punkty należą do linii prostych wychodzących z jednego wierzchołka D 1 .

W przekroju okazuje się trapez równoramienny, ponieważ F jest w równej odległości od punktów A 1 u C 1, to znaczy LA 1 = KC 1.

Trzy punkty należące do krawędzi z jednym wierzchołkiem D 1. Punkty F u M należą odpowiednio do kontynuacji krawędzi D 1 D u D 1 C, a punkt A 1 jest wierzchołkiem sześcianu.

Z przekroju powstaje pięciokąt A 1 KLNG.

Trzy punkty F, M i Q są brane tak, że leżą odpowiednio na kontynuacji krawędzi D 1 D, D 1 C 1 i D 1 A 1.

Z przekroju powstaje sześciokąt KLNGJH.

Trzy punkty leżą na krawędziach z jednym wierzchołkiem D 1.

W wyniku przekroju powstaje dowolny trójkąt, ale jeśli punkty są ułożone w taki sposób, że D 1 Q = D 1 M = D 1 F , to znaczy, jeśli są w równej odległości od wierzchołka D 1, to przekrój będzie wynikał w trójkącie równobocznym.

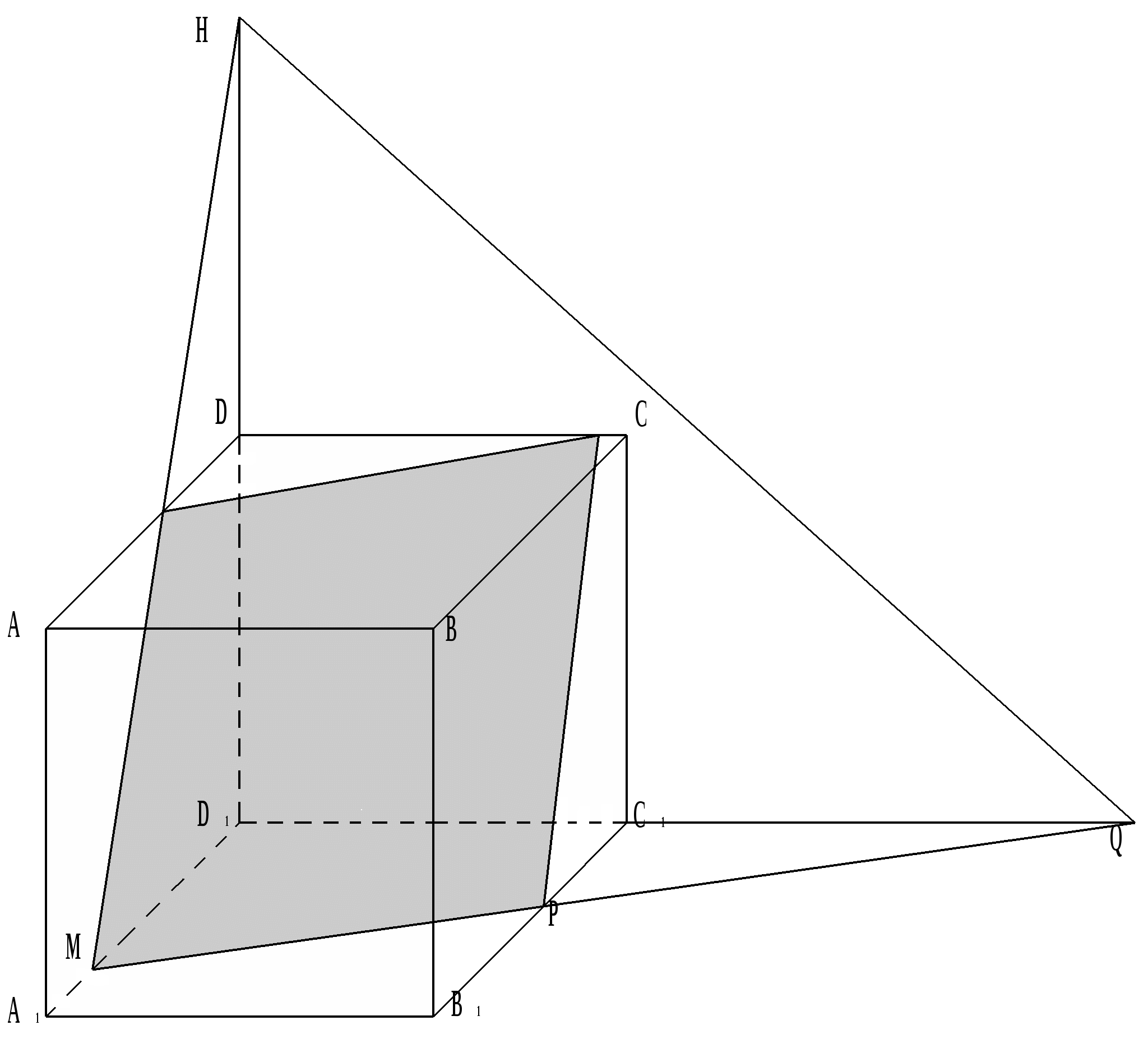
Płaszczyznę cięcia wyznaczają punkty H, Q i M. Przekrój tworzy równoległobok, ponieważ KC ││ MP i MK ││ PC na podstawie twierdzenia o przecięciu dwóch równoległych płaszczyzn z trzecią.

Jeśli punkty H, Q i M, definiują płaszczyznę cięcia odległą od D, w odległości 2a, gdzie a oznacza krawędź sześcianu, to w przekroju okazuje się zwykły trójkąt ACB 1.

Wniosek: trzy punkty wyznaczające przekrój należą do trzech krawędzi sześcianu o wspólnym wierzchołku lub są ich kontynuacją, wówczas z przekroju powstają: trójkąt, pięciokąt, sześciokąt, trapez, równoległobok.

Konstruowanie przekroju sześcianu przez płaszczyznę przy danych trzech punktach, z których dwa leżą na sąsiednich krawędziach, a trzeci punkt na krawędzi do nich nie sąsiadującej.

Trzy kropki M, K u F, przyjmuje się tak, że M u F należą do krawędzi z jednym wierzchołkiem A 1, a punkt K leży na krawędzi do nich nie sąsiadującej.

Z przekroju wynika prostokąt, ponieważ A 1 M = D 1 K i korzystając z twierdzenia o trzech prostopadłych można udowodnić, że MKLF jest prostokątem, a jeśli A 1 M D 1 K, wtedy możesz otrzymać trapez lub pięciokąt.

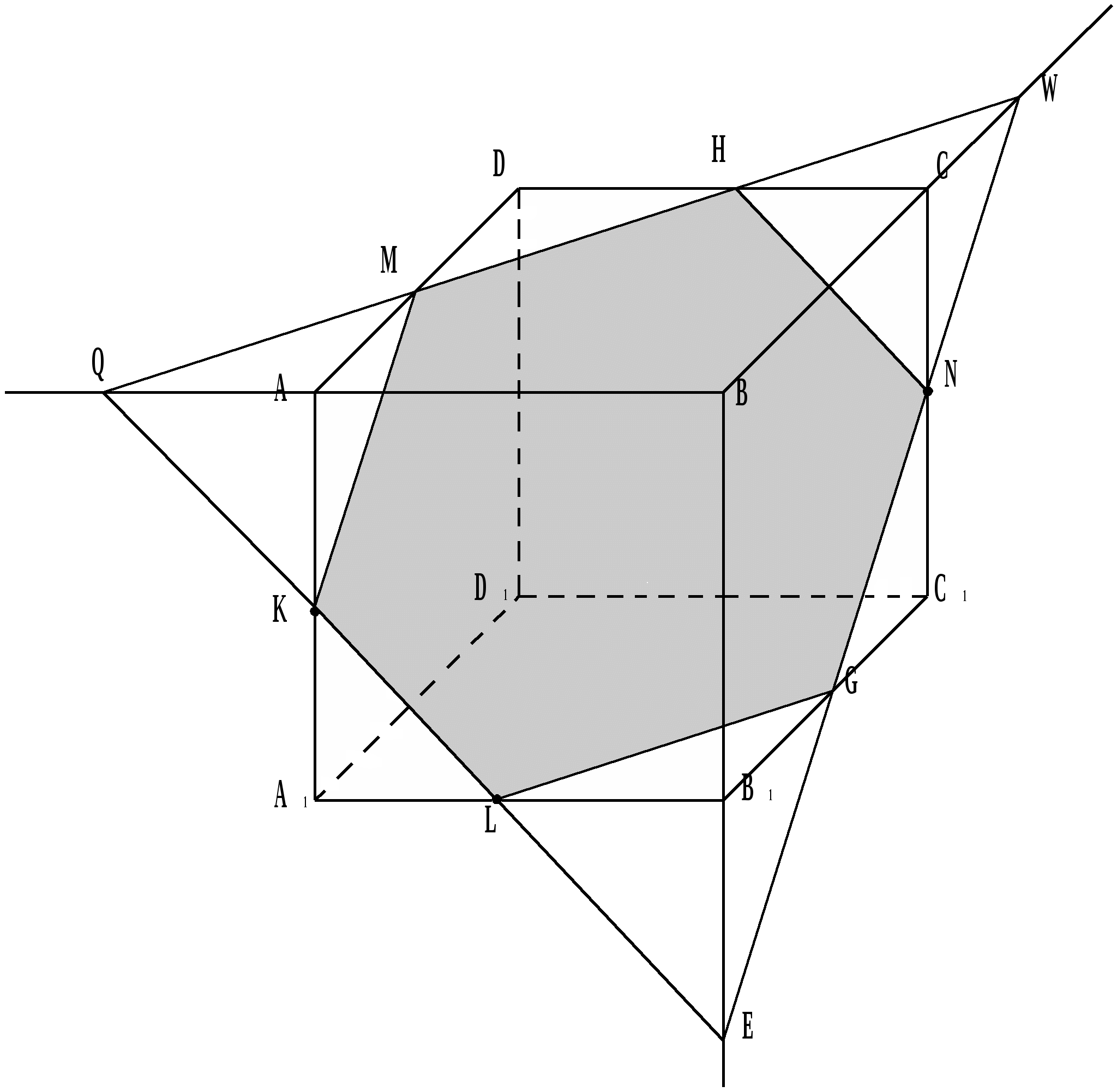
Bierze się trzy punkty tak, że K u L należy do krawędzi wychodzących z jednego wierzchołka A 1, a punkt N należy do krawędzi CC 1, która do nich nie przylega. K, L u N środków krawędzi A 1 A, A 1 B 1 u CC 1 – odpowiednio.

W przekroju okazuje się zwykły sześciokąt KLGNHM

Bierze się trzy punkty tak, że K u L należy do krawędzi wychodzących z jednego wierzchołka A 1, a punkt T należy do krawędzi DC.

Z przekroju powstaje sześciokąt KLFRTZ.

Bierze się trzy punkty tak, że K u L należy do krawędzi sześcianu z jednego wierzchołka A 1, a punkt M należy do krawędzi DD 1.

Z przekroju powstaje trapez LKQM.

Trzy kropki K u L należące do krawędzi mających jeden wierzchołek A 1 i punkt R leżący na krawędzi BC.

Z przekroju powstaje pięciokąt KLFRT.

Wniosek: Jeżeli płaszczyznę przekroju wyznaczają trzy punkty, z czego dwa leżą na sąsiednich krawędziach, a trzeci na krawędzi do nich nie sąsiadującej, to z przekroju może powstać prostokąt, pięciokąt, sześciokąt, trapez.

W przekroju sześcianu i jego szczególnych przypadków występuje równoległobok.

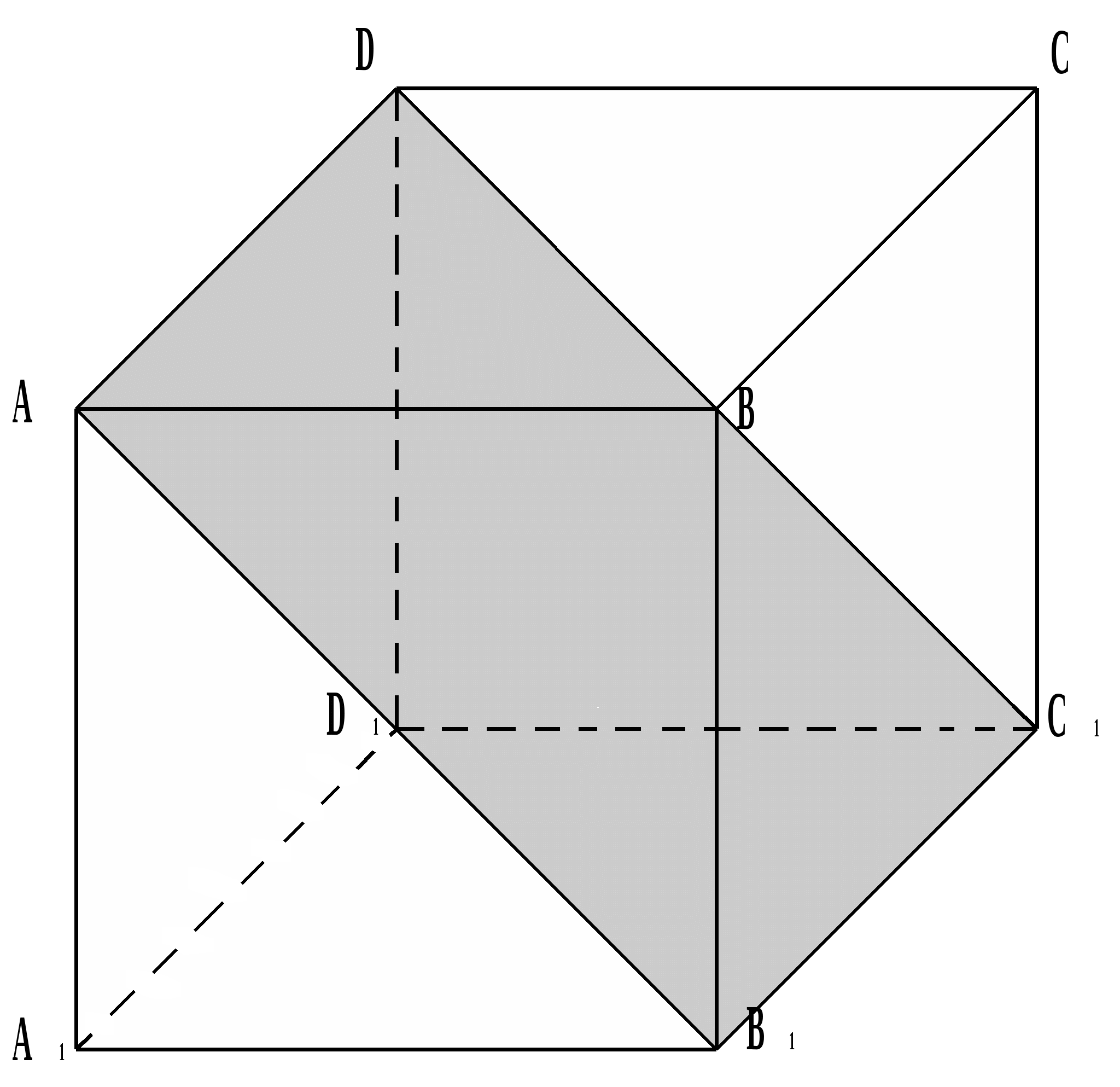
Zwrotnica T, H, J określające przekrój są umieszczone tak, że T.H. OGŁOSZENIE, H.J. OGŁOSZENIE. Przekrój daje kwadratowy HTKJ.

Przekrój wyznaczają punkty C, F, L, gdzie DF = FD 1, BL = LB 1. Przekrój tworzy romb AFCL.

Przekrój wyznaczają punkty C, G, H. B1H =DG. W przekroju równoległobok A 1 GCH.

Punktami wyznaczającymi przekrój są wierzchołki sześcianu A, D, C 1. Przekrój poprzeczny daje prostokąt

Przekrój sześcianu regularne wielokąty

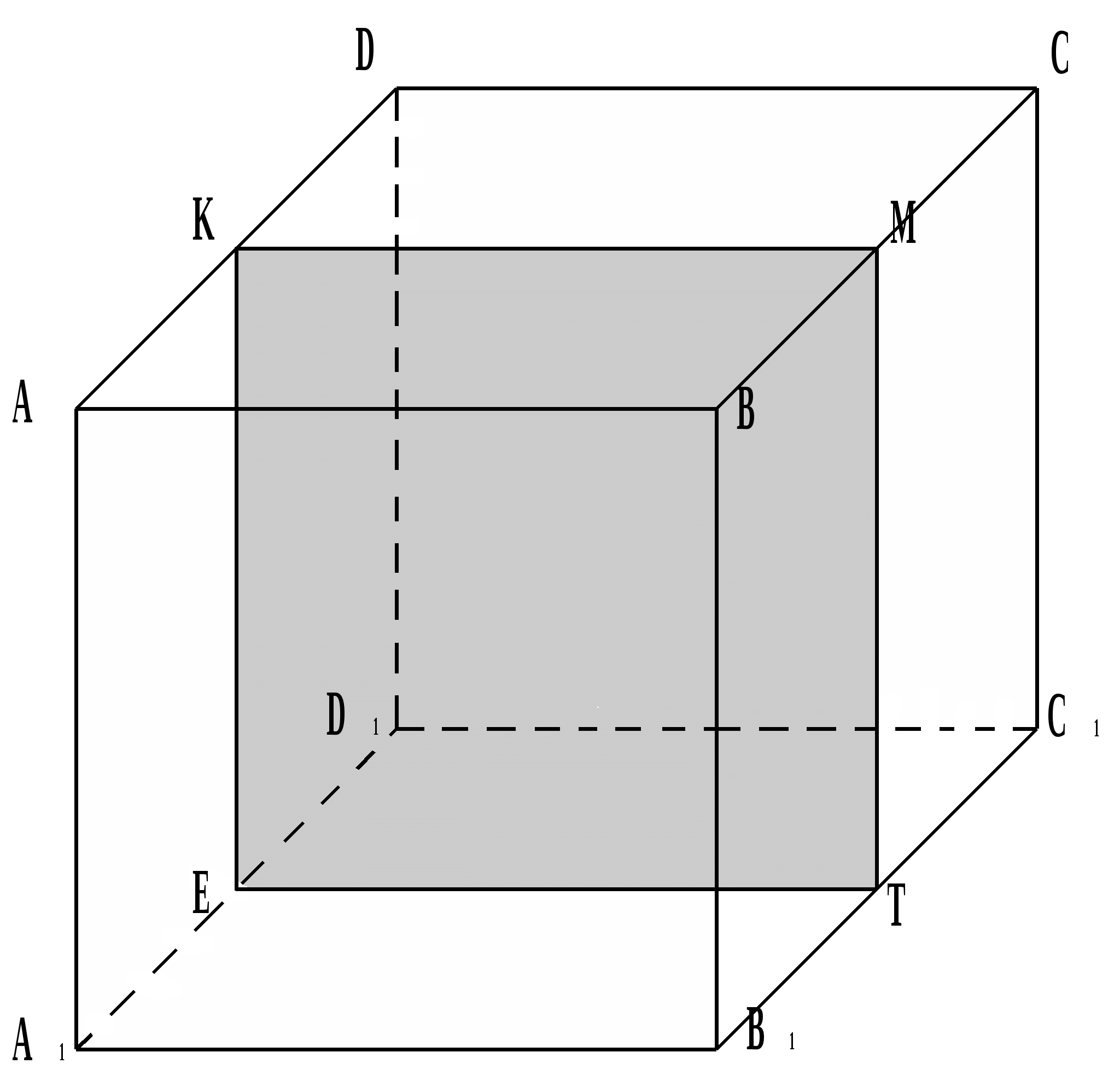
Trójkąt ABC 1 jest równoboczny, ponieważ jego boki są przekątnymi ścian sześcianu.

Trójkąt KMT jest równoboczny, ponieważ KV = MV = TV.

KMTE jest kwadratem, ponieważ przekrój wyznaczają punkty M, K, E i MK OGŁOSZENIE, E.K. OGŁOSZENIE.

Przekrój ma regularny sześciokąt KMTNEO, ponieważ punkty H, E, K definiujące przekrój są środkami odpowiednio krawędzi CC 1, DC, AA 1.

Cube i kilka problemów ze stereometrii z egzaminu Unified State Exam.

W podręczniku „Ujednolicony egzamin państwowy 2005. Matematyka. Typowy problemy testowe” (Kornikova T. A. i in.) Zawiera 10 problemów (C4) w stereometrii, połączonych wspólną ideą: podany jest trójkątny pryzmat ABCA 1 W 1 Z 1 boki podstawy AB i BC są wzajemnie prostopadłe i prostopadłe do krawędzi BB 1 , AB=BC=BB 1 , wierzchołek A jest wierzchołkiem stożka (lub środkiem jednej z podstaw walca lub środkiem kuli), podstawa stożka (kula lub druga podstawa walca) przechodzi przez środek jednej krawędzi pryzmatu, znana jest jego długość. Musimy znaleźć objętość lub powierzchnię stożka (kuli, cylindra).

Ogólny przykład rozwiązania:

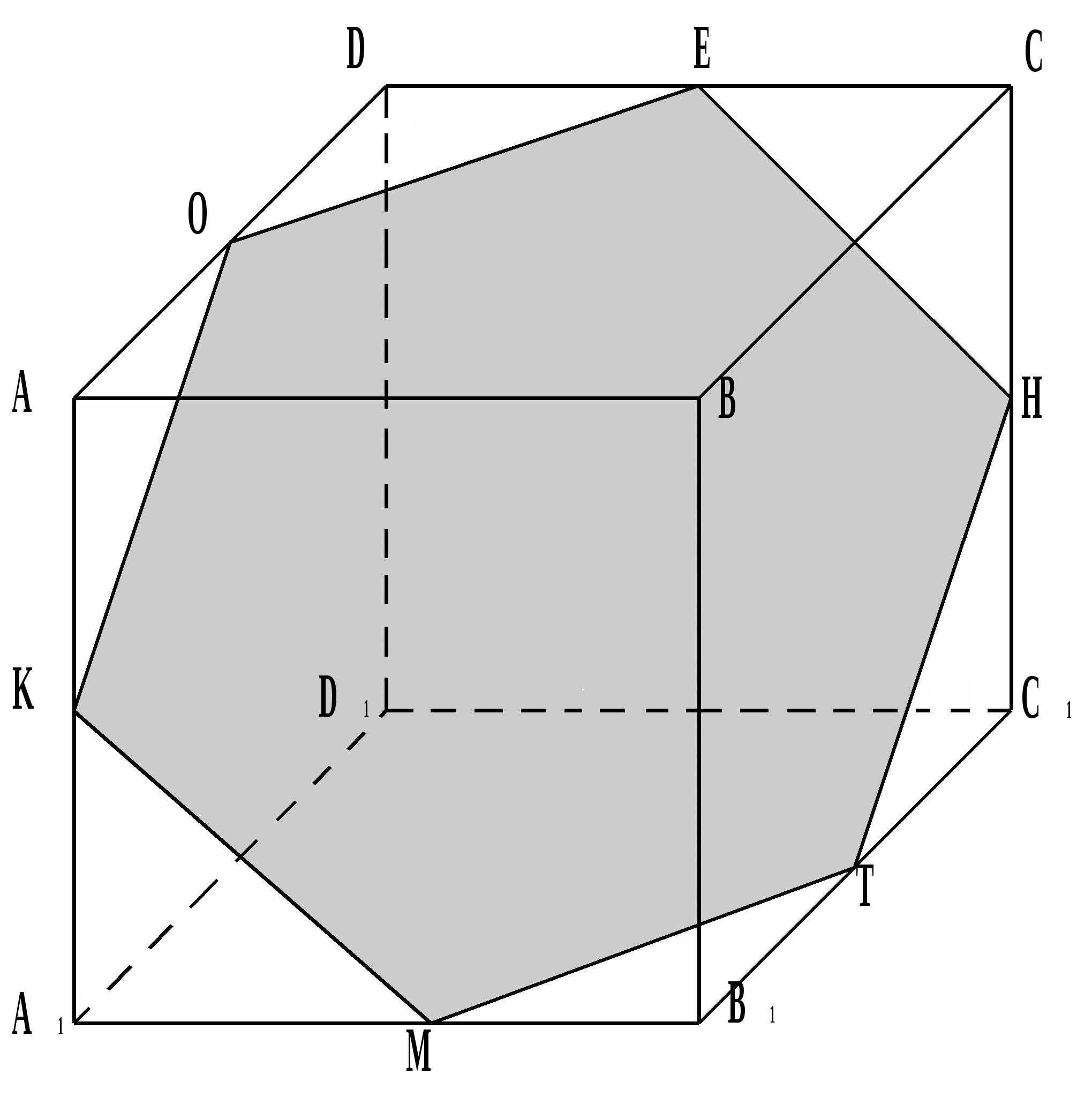
Dodaj ten pryzmat do sześcianu. Sześciokąt DEFKLM - przekrój sześcianu przez płaszczyznę podstawy stożka, którego okrąg przechodzi przez środek A 1 B 1, A jest wierzchołkiem stożka lub

DEFKLM to przekrój sześcianu przez płaszczyznę podstawy walca, którego okrąg przechodzi przez środek A 1 B 1, A jest środkiem drugiej podstawy walca, lub jest to przekrój sześcian samolotem wielkie koło kule o środku A, których kula przechodzi przez środek A 1 B 1.

SześciokątDEFKLM– przekrój sześcianu przez płaszczyznę przechodzącą przez środki krawędzi A 1 W 1 , BB 1 , VSZh przy uzyskiwaniu punktów konstrukcyjnychK, L, M, które są środkami odpowiednich krawędzi. Boki tego sześciokąta są przeciwprostokątnymi trójkątówD.B. 1 mi, EBF, FCK, KQL, LRM, MAMA. 1 D, którego ramiona są równe połowie krawędzi sześcianu. Wówczas środkiem tego sześciokąta jest środek okręgu wokół niego opisanego, który przecina krawędzie sześcianu w punktachD, mi, F, K, Li M, promień tego okręgu
, gdzie 1 W 1 = A .

AO E.L. T. Do. EAL – równoramienne:glin = AE .

( ABE ty EAL– prostokątne,AB= AQ= A, BYĆ = L.Q. = )

EO =OL jako środek przekątnej EL sześciokąta DEFKLM, tj. AO jest medianą i zgodnie z jej właściwościami Trójkąt równoramienny i wysokość. AO dowodzi się w podobny sposób DK. Ponieważ AO jest prostopadłe do dwóch przecinających się prostych płaszczyzny sześciokąta, to AO jest prostopadłe do całej płaszczyzny.

Jeśli A jest wierzchołkiem stożka, to AO jest jego wysokością, jeśli A jest środkiem drugiej podstawy walca, to AO jest wysokością walca.

ABC: AC=
, P – punkty przecięcia przekątnych podstawy sześcianu, AP=
, RR 1 =AA 1 = A . LUB=RR 1 = , a następnie z prostokąta ROA SA=
. I tak AO=
.

Zatem jeśli mówimy o stożku:

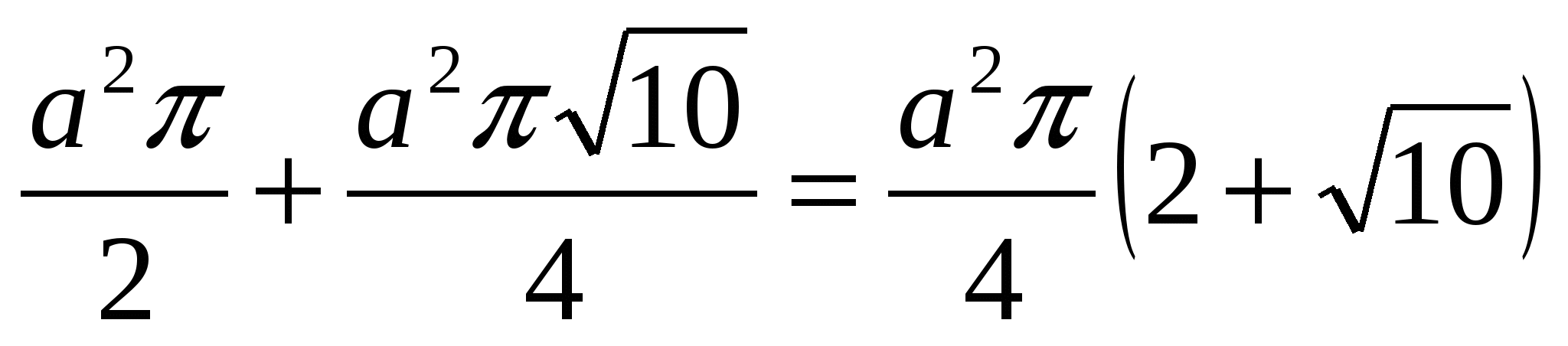
(z
).

Odpowiedź:

Jeśli mówimy o cylindrze:

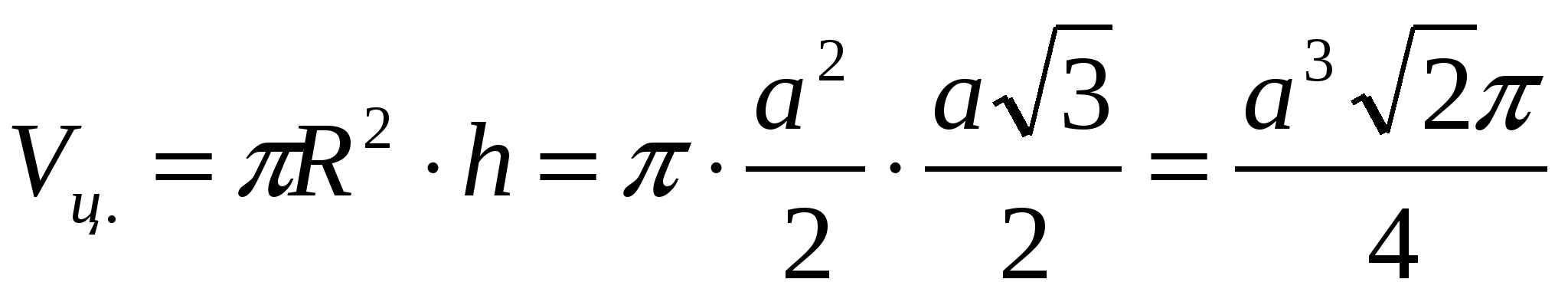
Odpowiedź:

Jeśli mówimy o kuli:

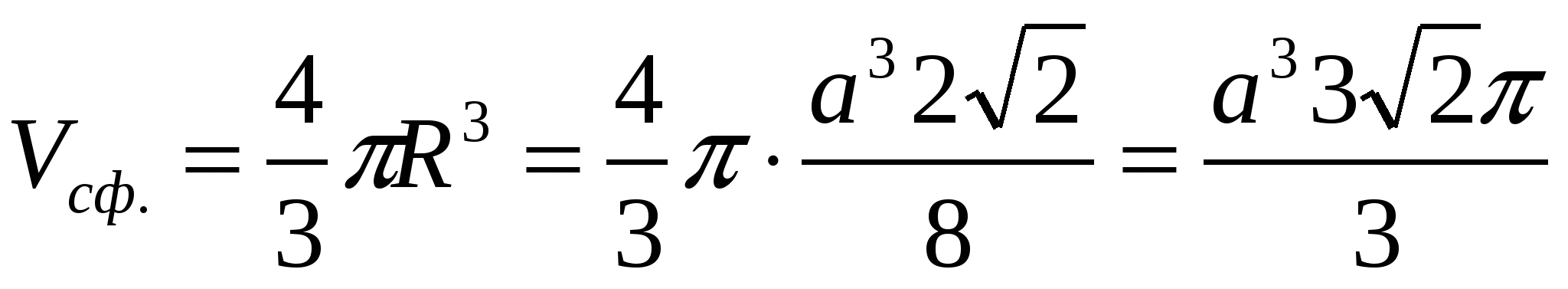
Odpowiedź: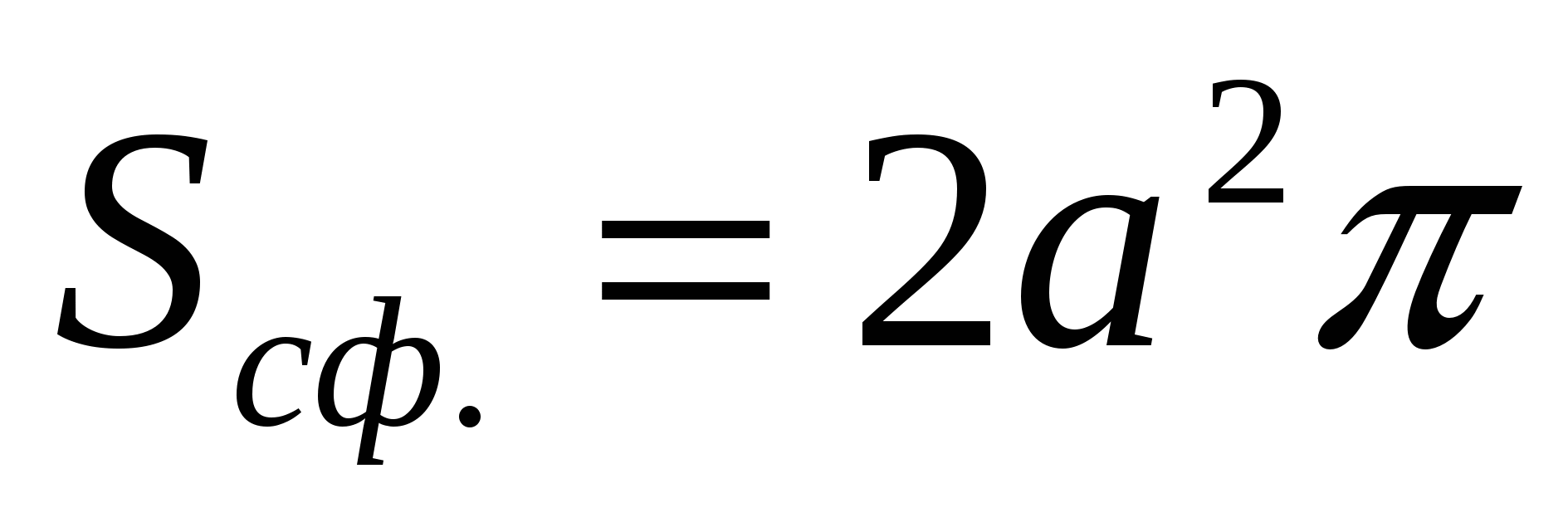

Kornikova T. A. i inne typowe zadania testowe. Jednolity egzamin państwowy - 2005

Opcja 6.

Zadanie. Dany jest pryzmat ABCA 1 B 1 C 1 i walec. Boki AB i BC podstawy graniastosłupa są prostopadłe do krawędzi BB 1 i wzajemnie prostopadłe. Środek podstawy walca to punkt A 1, okrąg drugiej podstawy przechodzi przez środek krawędzi A 1 B 1.

Znajdź obszar pełna powierzchnia cylinder, jeśli BB 1 =AB=BC=10. Znajdź jego objętość.

Rozwiązanie:

.
.

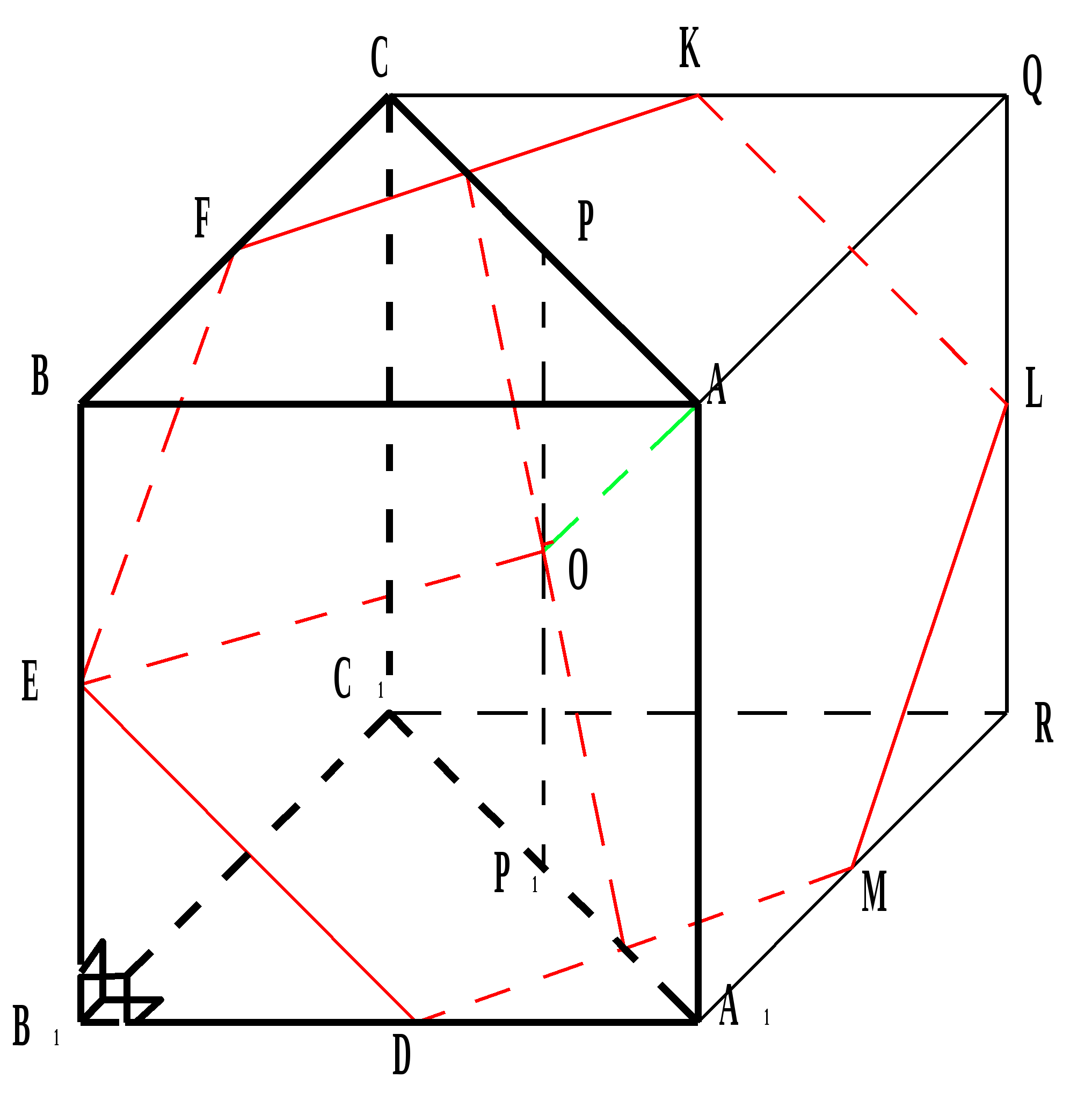
Typ lekcji: Lekcja łączona.

Cele i zadania:

edukacyjny – kształtowanie i rozwój koncepcji przestrzennych u studentów; rozwijanie umiejętności rozwiązywania problemów polegających na konstruowaniu przekrojów najprostszych wielościanów;
edukacyjny - pielęgnuj wolę i wytrwałość w osiąganiu końcowych rezultatów przy konstruowaniu odcinków najprostszych wielościanów; Rozwijaj miłość i zainteresowanie nauką matematyki.
rozwijający się – rozwój uczniów logiczne myślenie, reprezentacje przestrzenne, rozwój umiejętności samokontroli.

Sprzęt: komputery ze specjalnie opracowanym programem, ulotki w formie gotowe rysunki z zadaniami, bryłami wielościanów, indywidualnymi kartami z zadaniami domowymi.

Struktura lekcji:

Podaj temat i cel lekcji (2 min).
Instrukcja wykonywania zadań na komputerze (2 min).
Aktualizacja podstawowej wiedzy i umiejętności uczniów (4 min).
Autotest (3 min).
Rozwiązywanie problemów z wyjaśnieniem rozwiązania przez nauczyciela (15 min).
Samodzielna praca z autotestem (10 min).
Zadawanie zadań domowych (2 min).
Podsumowanie (2 min).

Podczas zajęć

1. Przekazanie tematu i celu lekcji

Po sprawdzeniu gotowości klasy do lekcji nauczyciel melduje, że dzisiaj odbędzie się lekcja na temat „Konstruowanie przekrojów wielościanów”; będą rozpatrywane problemy przy konstruowaniu przekrojów jakiegoś prostego wielościanu z płaszczyznami przechodzącymi przez trzy punkty należące do krawędzi wielościany. Lekcja prowadzona będzie z wykorzystaniem prezentacji komputerowej wykonanej w programie Power Point.

2. Zasady bezpieczeństwa podczas pracy w pracowni komputerowej

Nauczyciel. Zwracam uwagę na fakt, że rozpoczynasz pracę na zajęciach komputerowych i musisz przestrzegać zasad postępowania i pracy przy komputerze. Zabezpiecz wysuwane blaty i upewnij się, że są prawidłowo dopasowane.

3. Aktualizowanie podstawowej wiedzy i umiejętności uczniów

Nauczyciel. Do rozwiązania wielu problemów geometrycznych związanych z wielościanami przydatna jest umiejętność skonstruowania ich przekrojów na rysunku z wykorzystaniem różnych płaszczyzn, znalezienie punktu przecięcia danej prostej z daną płaszczyzną oraz znalezienie linii przecięcia dwóch danych płaszczyzn . Na poprzednich lekcjach przyglądaliśmy się przekrojom wielościanów w płaszczyznach równoległych do krawędzi i ścian wielościanów. Na tej lekcji przyjrzymy się zagadnieniom konstruowania odcinków z płaszczyzną przechodzącą przez trzy punkty znajdujące się na krawędziach wielościanów. Aby to zrobić, rozważ najprostszy wielościan. Co to są za wielościany? (Modele sześcianu, czworościanu, ostrosłupa czworokątnego foremnego, proste trójkątny pryzmat).

Uczniowie muszą określić typ wielościanu.

Nauczyciel. Zobaczmy, jak wyglądają na ekranie monitora. Poruszamy się od obrazka do obrazka wciskając lewy przycisk myszki.

Obrazy nazwanych wielościanów pojawiają się na ekranie jeden po drugim.

Nauczyciel. Przypomnijmy sobie tak zwany przekrój wielościanu.

Student. Wielokąt, którego boki są odcinkami należącymi do ścian wielościanu, mającymi końce na krawędziach wielościanu, uzyskany przez przecięcie wielościanu dowolną płaszczyzną przecięcia.

Nauczyciel. Jakie wielokąty mogą być przekrojami tych wielościanów.

Student. Przekroje sześcianu: trzy - sześciokąty. Przekroje czworościanu: trójkąty, czworokąty. Przekroje czworokątnej piramidy i trójkątnego pryzmatu: trzy - pięciokąty.

4. Samotestowanie

Nauczyciel. Zgodnie z koncepcją przekrojów wielościanów, znajomością aksjomatów stereometrii oraz względnego położenia linii i płaszczyzn w przestrzeni, prosimy o udzielenie odpowiedzi na pytania testowe. Komputer Cię doceni. Maksymalny wynik 3 punkty – za 3 poprawne odpowiedzi. Na każdym slajdzie należy kliknąć przycisk z numerem prawidłowej odpowiedzi. Pracujecie w parach, więc każdy z Was otrzyma taką samą, określoną przez komputer liczbę punktów. Kliknij następny wskaźnik slajdu. Na wykonanie zadania masz 3 minuty.

I. Który rysunek przedstawia przekrój sześcianu przez płaszczyznę ABC?

II. Który rysunek przedstawia przekrój piramidy z płaszczyzną przechodzącą przez przekątną podstawy? BD równolegle do krawędzi SA?

III. Który rysunek przedstawia przekrój czworościanu przechodzącego przez punkt M równolegle do płaszczyzny ABS?

5. Rozwiązywanie problemów z wyjaśnieniem rozwiązania przez nauczyciela

Nauczyciel. Przejdźmy bezpośrednio do rozwiązywania problemów. Kliknij następny wskaźnik slajdu.

Problem 1 To zadanie Przyjrzyjmy się temu ustnie z demonstracją krok po kroku konstrukcji na ekranie monitora. Przejście odbywa się poprzez kliknięcie myszką.

Biorąc pod uwagę sześcian ABCDAA 1 B 1 C 1 D 1. Na jego krawędzi nocleg ze śniadaniem 1 dany punkt M. Znajdź punkt przecięcia linii C 1 M z płaszczyzną ściany sześcianu ABCD.

Rozważmy obraz sześcianu ABCDAA 1 B 1 C 1 D 1 z kropką M na krawędzi nocleg ze śniadaniem 1 punkty M I Z 1 należą do samolotu nocleg ze śniadaniem 1 Z 1 Co można powiedzieć o linii prostej C 1 M ?

Student. Prosty C 1 M należy do samolotu nocleg ze śniadaniem 1 Z 1

Nauczyciel. Szukany punkt X należy do linii C 1 M, a co za tym idzie samoloty nocleg ze śniadaniem 1 Z 1. Jakie to jest wzajemne porozumienie samoloty nocleg ze śniadaniem 1 Z 1 i ABC?

Student. Płaszczyzny te przecinają się w linii prostej PNE..

Nauczyciel. To znaczy wszystko punkty wspólne samoloty nocleg ze śniadaniem 1 Z 1 i ABC należą do linii PNE.. Szukany punkt X musi jednocześnie należeć do płaszczyzn dwóch ścian: ABCD I nocleg ze śniadaniem 1 C 1 C; wynika z tego, że punkt X musi leżeć na linii ich przecięcia, czyli na prostej Słońce. Oznacza to, że punkt X musi leżeć jednocześnie na dwóch prostych: Z 1 M I Słońce i dlatego jest ich punktem przecięcia. Budowa żądany punkt spójrz na to na ekranie monitora. Po naciśnięciu lewego przycisku myszy zobaczysz sekwencję budowy: kontynuuj Z 1 M I Słońce do skrzyżowania w tym punkcie X, który jest pożądanym punktem przecięcia linii Z 1 M z płaszczyzną czołową ABCD.

Nauczyciel. Aby przejść do kolejnego zadania użyj wskaźnika następnego slajdu. Rozważmy ten problem z krótkim opisem konstrukcji.

A) Skonstruuj wycinek sześcianu z płaszczyzną przechodzącą przez punkty A 1 , MD 1 C 1 i NDD 1 i B) Znajdź linię przecięcia płaszczyzny cięcia z płaszczyzną dolnej podstawy sześcianu.

Rozwiązanie. I. Płaszczyzna cięcia ma twarz A 1 B 1 C 1 D 1 dwa punkty wspólne A 1 i M i dlatego przecina się z nim wzdłuż linii prostej przechodzącej przez te punkty. Łączenie kropek A 1 i M odcinek linii prostej, znajdujemy linię przecięcia płaszczyzny przyszłego odcinka i płaszczyzny górna krawędź. Będziemy ten fakt rejestrować w następujący sposób: A 1 M. Naciśnij lewy przycisk myszy, ponowne naciśnięcie spowoduje utworzenie tej linii prostej.

Podobnie znajdujemy linie przecięcia płaszczyzny cięcia z powierzchniami AA 1 D 1 D I DD 1 Z 1 Z. Klikając przyciskiem myszy, zobaczysz krótkie nagranie i postęp budowy.

Zatem, A 1 NM? żądaną sekcję.

Przejdźmy do drugiej części problemu. Znajdźmy linię przecięcia płaszczyzny cięcia z płaszczyzną dolnej podstawy sześcianu.

II. Płaszczyzna cięcia przecina się z płaszczyzną podstawy sześcianu po linii prostej. Aby zobrazować tę prostą, wystarczy znaleźć dwa punkty należące do tej prostej, tj. punkty wspólne płaszczyzny cięcia i płaszczyzny czołowej ABCD. Polegając na poprzednie zadanie takimi punktami będą: pkt X=. Naciśnij klawisz, zobaczysz krótkie nagranie i konstrukcję. I okres Y Jak myślicie, jak to zdobyć?

Student. Y =

Nauczyciel. Przyjrzyjmy się jego budowie na ekranie. Kliknij przycisk myszy. Łączenie kropek X I Y(Nagrywać X-Y), otrzymujemy pożądaną linię prostą - linię przecięcia płaszczyzny cięcia z płaszczyzną dolnej podstawy sześcianu. Naciśnij lewy przycisk myszy - krótkie nagranie i konstrukcja.

Problem 3 Skonstruuj odcinek sześcianu z płaszczyzną przechodzącą przez punkty:

Ponadto, naciskając przycisk myszy, zobaczysz na ekranie monitora postęp budowy i krótkie nagranie. Opierając się na koncepcji przekroju, wystarczy znaleźć dwa punkty na płaszczyźnie każdej ściany, aby skonstruować linię przecięcia płaszczyzny przecięcia z płaszczyzną każdej ściany sześcianu. Zwrotnica M I N należą do samolotu A 1 W 1 Z 1. Łącząc je otrzymujemy linię przecięcia płaszczyzny cięcia z płaszczyzną górnej powierzchni sześcianu (wciśnij klawisz myszki). Kontynuujmy linie proste MN I D 1 C 1 przed skrzyżowaniem. Zdobądźmy punkt X, należące do obu samolotów A 1 W 1 Z 1 i samolot DD 1 C 1 (kliknięcie myszką). Zwrotnica N I DO należą do samolotu nocleg ze śniadaniem 1 Z 1. Łącząc je, otrzymujemy linię przecięcia płaszczyzny cięcia i powierzchni nocleg ze śniadaniem 1 Z 1 Z. (Kliknięcie myszką). Łączenie kropek X I DO, i jedź dalej prosto HC do przecięcia z linią DC. Zdobądźmy punkt R i segment KR – linia przecięcia płaszczyzny cięcia i powierzchni DD 1 C 1 C. (Kliknięcie myszką). Jedź dalej prosto KR I DD 1 przed przecięciem, zdobywamy punkt Y, należący do samolotu AA 1 D 1. (Kliknięcie myszką). W płaszczyźnie tej ściany potrzebny jest jeszcze jeden punkt, który uzyskujemy w wyniku przecięcia linii MN I A 1 D 1. O to chodzi . (Kliknięcie myszką). Łączenie kropek Y I Z, otrzymujemy I . (Kliknięcie myszką). Złączony Q I R, R I M, dostaniemy to? żądaną sekcję.

Krótki opis konstrukcji:

2) ;

6) ;

7) ;

13) ? żądaną sekcję.