حدد الزوايا ثنائية السطوح التي تكونت من تقاطع أزواج المستويات. المشكلة: المستوى يتقاطع مع الخط

تتناول هذه المقالة الزاوية بين المستويات وكيفية العثور عليها. أولاً، تم تقديم تعريف الزاوية بين مستويين وتم تقديم رسم توضيحي. بعد ذلك، يتم تحليل مبدأ إيجاد الزاوية بين مستويين متقاطعين باستخدام طريقة الإحداثيات، ويتم الحصول على صيغة تسمح لك بحساب الزاوية بين المستويين المتقاطعين باستخدام الإحداثيات المعروفة للمتجهات العادية لهذه المستويات. وفي الختام يظهر حلول مفصلةالمهام المميزة.

التنقل في الصفحة.

الزاوية بين الطائرات - التعريف.

دعونا نقدم الحجج التي ستسمح لنا بالاقتراب تدريجيًا من تحديد الزاوية بين طائرتين متقاطعتين.

دعونا نعطي طائرتين متقاطعتين و . وتتقاطع هذه المستويات على طول خط مستقيم نشير إليه بالحرف ج. لنقم ببناء مستوى يمر عبر النقطة M من الخط c وعموديًا على الخط c. في هذه الحالة، سوف تتقاطع الطائرة مع الطائرات و. دعونا نشير إلى الخط المستقيم الذي تتقاطع عليه المستويات بـ a، والخط المستقيم الذي تتقاطع به المستويات بـ b. من الواضح أن الخطين a وb يتقاطعان عند النقطة M.

من السهل توضيح أن الزاوية بين الخطين المتقاطعين a وb لا تعتمد على موقع النقطة M على الخط c الذي يمر عبره المستوى.

لنقم ببناء مستوى عمودي على الخط c ومختلف عن المستوى. يتقاطع المستوى مع مستويات وعلى طول خطوط مستقيمة، والتي نشير إليها بـ 1 وb 1، على التوالي.

ويترتب على طريقة بناء المستويات أن الخطين a و b متعامدان مع الخط c، والخطان a 1 و b 1 متعامدان مع الخط c. بما أن الخطين a و 1 يقعان في نفس المستوى ومتعامدان على الخط c، فإنهما متوازيان. وبالمثل، فإن الخطين b وb 1 يقعان في نفس المستوى ومتعامدان على الخط c، وبالتالي فإنهما متوازيان. لذلك يمكنك أن تفعل نقل موازيمن مستوى إلى مستوى، حيث يتطابق الخط المستقيم أ 1 مع الخط المستقيم أ، والخط المستقيم ب مع الخط المستقيم ب 1. وبالتالي فإن الزاوية بين خطين متقاطعين أ 1 و ب 1 يساوي الزاويةبين الخطين المتقاطعين أ و ب.

وهذا يثبت أن الزاوية بين الخطين المتقاطعين a و b تقع في مستويات متقاطعة ولا تعتمد على اختيار النقطة M التي يمر عبرها المستوى. ولذلك فمن المنطقي اعتبار هذه الزاوية هي الزاوية بين مستويين متقاطعين.

يمكنك الآن التعبير عن تعريف الزاوية بين طائرتين متقاطعتين و.

تعريف.

الزاوية بين طائرتين متقاطعتين في خط مستقيم و- هذه هي الزاوية بين خطين متقاطعين a و b، والتي تتقاطع على طولها المستويات وتتقاطع مع المستوى المتعامد مع الخط c.

يمكن إعطاء تعريف الزاوية بين طائرتين بشكل مختلف قليلاً. إذا كان على الخط المستقيم c الذي تتقاطع فيه الطائرات، قم بتمييز نقطة M وارسم خطوطًا مستقيمة a و b من خلالها، متعامدة مع الخط المستقيم c وتقع في المستويات، وعلى التوالي، ثم الزاوية بين الخطوط المستقيمة a و b هي الزاوية بين الطائرات و. عادة في الممارسة العملية، يتم تنفيذ مثل هذه الإنشاءات من أجل الحصول على الزاوية بين الطائرات.

وبما أن الزاوية بين الخطوط المتقاطعة لا تزيد عن ، فيترتب على التعريف المذكور أن قياس درجةيتم التعبير عن الزاوية بين طائرتين متقاطعتين رقم حقيقيمن الفاصل . في هذه الحالة، يتم استدعاء الطائرات المتقاطعة عموديإذا كانت الزاوية بينهما تسعين درجة. الزاوية بين المستويين المتوازيين إما لم يتم تحديدها على الإطلاق أو تعتبر تساوي الصفر.

إيجاد الزاوية بين مستويين متقاطعين.

عادة، عند إيجاد زاوية بين مستويين متقاطعين، عليك أولاً إجراء إنشاءات إضافية لرؤية الخطوط المستقيمة المتقاطعة، والزاوية بينهما تساوي الزاوية المطلوبة، ثم ربط هذه الزاوية بالبيانات الأصلية باستخدام اختبارات المساواة والتشابه الاختبارات، ونظرية جيب التمام أو تعريفات الجيب وجيب التمام والظل للزاوية. في سياق الهندسة مدرسة ثانويةتحدث مشاكل مماثلة.

كمثال، لنعطي حل المشكلة C2 من امتحان الدولة الموحد في الرياضيات لعام 2012 (تم تغيير الشرط عمدا، ولكن هذا لا يؤثر على مبدأ الحل). في ذلك، كان عليك فقط العثور على الزاوية بين طائرتين متقاطعتين.

مثال.

حل.

أولا، دعونا نجعل الرسم.

لنقم بإجراء إنشاءات إضافية من أجل "رؤية" الزاوية بين الطائرات.

أولاً، دعونا نحدد الخط المستقيم الذي يتقاطع على طوله المستويان ABC وBED 1. النقطة B هي إحدى النقاط المشتركة بينهما. دعونا نجد الثاني نقطة مشتركةهذه الطائرات. يقع الخطان DA وD 1 E في نفس المستوى ADD 1، وهما ليسا متوازيين، وبالتالي يتقاطعان. من ناحية أخرى، يقع الخط DA في المستوى ABC، والخط D 1 E - في المستوى BED 1، وبالتالي فإن نقطة تقاطع الخطين DA و D 1 E ستكون نقطة مشتركة طائرات اي بي سيوالسرير 1. لذا، فلنواصل الخطين DA وD 1 E حتى تقاطعهما، للإشارة إلى نقطة تقاطعهما مع الحرف F. إذن BF هو الخط المستقيم الذي تتقاطع فيه المستويتان ABC وBED 1.

يبقى بناء خطين يقعان في المستويين ABC وBED 1، على التوالي، ويمران عبر نقطة واحدة على الخط BF وعموديين على الخط BF - الزاوية بين هذه الخطوط، بحكم التعريف، ستكون مساوية للزاوية المطلوبة بين الخطين. الطائرات ABC وBED 1. دعونا نفعل هذا.

نقطة A هو إسقاط النقطة E على المستوى ABC. لنرسم خطًا مستقيمًا يتقاطع مع الخط BF بزاوية قائمة عند النقطة M. ثم الخط المستقيم AM هو إسقاط الخط المستقيم EM على المستوى ABC، وبنظرية الثلاثة المتعامدين.

وبالتالي، فإن الزاوية المطلوبة بين المستويين ABC وBED 1 تساوي .

يمكننا تحديد جيب أو جيب التمام أو ظل هذه الزاوية (وبالتالي الزاوية نفسها) من المثلث القائم AEM إذا عرفنا طولي ضلعيه. من السهل العثور على طول AE من الشرط: بما أن النقطة E تقسم الضلع AA 1 بنسبة 4 إلى 3، عد من النقطة A، وطول الضلع AA 1 هو 7، إذن AE = 4. لنجد الطول AM.

للقيام بذلك، النظر في المثلث الأيمن ABF مع الزاوية القائمة A، حيث AM هو الارتفاع. حسب الشرط AB = 2. يمكننا إيجاد طول الضلع AF من تشابه المثلثين القائمين DD 1 F و AEF:

وباستخدام نظرية فيثاغورس نجد من المثلث ABF. نجد الطول AM من خلال مساحة المثلث ABF: من أحد الجانبين مساحة المثلث ABF تساوي ، على الجانب الآخر ، أين .

وهكذا، من المثلث الأيمن AEM لدينا .

إذن الزاوية المطلوبة بين المستويين ABC و BED 1 متساوية (لاحظ أن ).

إجابة:

في بعض الحالات، للعثور على الزاوية بين مستويين متقاطعين، يكون من المناسب ضبط Oxyz واستخدام طريقة الإحداثيات. دعونا نتوقف عند هذا الحد.

دعونا نحدد المهمة: العثور على الزاوية بين طائرتين متقاطعتين و . دعونا نشير إلى الزاوية المطلوبة .

سنفترض أنه في نظام إحداثيات مستطيل معين أوكسيز، نعرف إحداثيات المتجهات العادية للمستويات المتقاطعة و/أو لدينا الفرصة للعثور عليها. يترك هو المتجه الطبيعي للطائرة، و هو المتجه الطبيعي للطائرة. سنوضح كيفية إيجاد الزاوية بين المستويات المتقاطعة ومن خلال إحداثيات المتجهات العمودية لهذه المستويات.

دعونا نشير إلى الخط المستقيم الذي تتقاطع معه الطائرات ويرمز له بـ c. من خلال النقطة M على الخط c نرسم مستوى عموديًا على الخط c. يتقاطع المستوى مع المستويين وعلى طول الخطين a وb، على التوالي، يتقاطع الخطان a وb عند النقطة M. بحكم التعريف، الزاوية بين الطائرات المتقاطعة وتساوي الزاوية بين الخطوط المتقاطعة أ و ب.

دعونا نرسم المتجهات والمستويات العادية ومن النقطة M في المستوى. في هذه الحالة، يقع المتجه على خط عمودي على الخط أ، ويقع المتجه على خط عمودي على الخط ب. وهكذا، في المستوى المتجه هو المتجه الطبيعي للخط أ، هو المتجه العادي للخط ب.

في مقالة إيجاد الزاوية بين الخطوط المتقاطعة، تلقينا صيغة تسمح لك بحساب جيب تمام الزاوية بين الخطوط المتقاطعة باستخدام إحداثيات المتجهات العادية. وبالتالي جيب تمام الزاوية بين الخطين a و b، وبالتالي، جيب تمام الزاوية بين الطائرات المتقاطعةوتم العثور عليه بواسطة الصيغة، أين و هي المتجهات العادية للطائرات، وعلى التوالي. ثم يتم حسابه على النحو .

دعونا نحل المثال السابق باستخدام الطريقة الإحداثية.

مثال.

دان مكعبة ABCDA 1 B 1 C 1 D 1، حيث AB=2، AD=3، AA 1 =7 والنقطة E تقسم الضلع AA 1 بنسبة 4 إلى 3، بدءًا من النقطة A. أوجد الزاوية بين المستويين ABC وBED 1.

حل.

نظرًا لأن جوانب متوازي السطوح المستطيل عند قمة واحدة تكون متعامدة بشكل زوجي، فمن المناسب تقديمها نظام مستطيلإحداثيات Oxyz كالتالي: قم بمحاذاة البداية مع الرأس C، وقم بتوجيه محاور الإحداثيات Ox وOy وOz على طول الجوانب CD وCB وCC 1، على التوالي.

يمكن العثور على الزاوية بين المستويين ABC وBED 1 من خلال إحداثيات المتجهات العادية لهذه المستويات باستخدام الصيغة حيث، و هي المتجهات العادية للطائرات ABC و BED 1، على التوالي. دعونا نحدد إحداثيات المتجهات العادية.

قياس الزاوية بين الطائرات هو زاوية حادةيتكون من خطين مستقيمين يقعان في هذه المستويات ومرسومان بشكل متعامد على خط تقاطعهما.

خوارزمية البناء

1. من النقطة العشوائية K، يتم رسم خطوط عمودية على كل مستوى من المستويات المعطاة.
2. من خلال الدوران حول خط المستوى، يتم تحديد الزاوية γ° مع قمة الرأس عند النقطة K.
3. احسب الزاوية بين المستويين ϕ° = 180 – γ°، بشرط أن تكون γ° > 90°. إذا γ°< 90°, то ∠ϕ° = ∠γ°.

يوضح الشكل الحالة التي يتم فيها إعطاء المستويين α و β بواسطة الآثار. تم تنفيذ جميع الإنشاءات اللازمة وفقًا للخوارزمية والموضحة أدناه.

حل

1. في مكان تعسفي في الرسم، ضع علامة على النقطة K. ومنه نخفض العمودين m و n، على التوالي، إلى المستويين α و β. اتجاه الإسقاطات m و n هو كما يلي: m""⊥f 0α , m"⊥h 0α , n""⊥f 0β , n"⊥h 0β .
2. نحدد الحجم الفعلي ∠γ° بين الخطين m و n. للقيام بذلك، حول الجزء الأمامي f نقوم بتدوير مستوى الزاوية مع قمة الرأس K إلى موضع موازٍ للمستوى الأمامي للإسقاط. نصف قطر الدوران R للنقطة K يساوي القيمةوتر المثلث القائم الزاوية O""K""K 0، وضلعه K""K 0 = y K – y O.
3. الزاوية المطلوبة هي ϕ° = ∠γ°، لأن ∠γ° حادة.

يوضح الشكل أدناه حل مشكلة تتطلب إيجاد الزاوية γ° بين المستويين α و β، المعطاة بخطوط متوازية ومتقاطعة، على التوالي.

حل

1. نحدد اتجاه إسقاطات الأفقية h 1، h 2 والجبهات f 1، f 2، تابعة للطائراتα و β، بالترتيب المشار إليه بواسطة الأسهم. من نقطة تعسفية K على الساحة. α و β نحذف العمودين e و k. في هذه الحالة، e""⊥f"" 1 , e"⊥h" 1 و k""⊥f"" 2 , k"⊥h" 2 .
2. نحدد ∠γ° بين الخطين e و k. للقيام بذلك، ارسم خطًا أفقيًا h 3 وحوله نقوم بتدوير النقطة K إلى الموضع K 1، حيث يصبح △CKD موازيًا للمستوى الأفقي وسينعكس عليه بالحجم الطبيعي - △C"K" 1 D ". يقع إسقاط مركز الدوران O" على الخط المرسوم على h" 3 عموديًا على K"O". يتم تحديد نصف القطر R من المثلث القائم O"K"K 0، الذي جانبه K"K 0 = زد أو – زد ك.
3. قيمة القيمة المطلوبة هي ∠ϕ° = ∠γ°، لأن الزاوية γ° حادة.

تتحدث المقالة عن إيجاد الزاوية بين الطائرات. بعد إعطاء التعريف، سنقدم رسمًا توضيحيًا وننظر في طريقة تفصيلية للعثور على الإحداثيات باستخدام الطريقة. نحصل على صيغة للمستويات المتقاطعة، والتي تتضمن إحداثيات المتجهات العادية.

Yandex.RTB RA-A-339285-1

ستستخدم المادة البيانات والمفاهيم التي تمت دراستها مسبقًا في مقالات حول المستوى والخط في الفضاء. أولًا، علينا الانتقال إلى المنطق الذي يسمح لنا باتباع طريقة معينة لتحديد الزاوية بين مستويين متقاطعين.

يتم إعطاء طائرتين متقاطعتين γ 1 و γ 2. سوف يأخذ تقاطعهم التسمية ج. يرتبط بناء المستوى χ بتقاطع هذه المستويات. يمر المستوى χ عبر النقطة M كخط مستقيم c. سيتم إجراء تقاطع المستويين γ 1 و γ 2 باستخدام المستوى χ. نحن نأخذ تسمية الخط المتقاطع γ 1 و χ بالخط a، والخط المتقاطع γ 2 و χ بالخط b. نجد أن تقاطع الخطين a وb يعطي النقطة M.

موقع النقطة M لا يؤثر على الزاوية بين الخطين المتقاطعين a و b، وتقع النقطة M على الخط c، الذي يمر عبره المستوى χ.

من الضروري بناء مستوى χ 1 عمودي على الخط c ومختلف عن المستوى χ. تقاطع المستويين γ 1 و γ 2 بمساعدة χ 1 سيأخذ تعيين الخطين a 1 و b 1.

يمكن أن نرى أنه عند بناء χ و χ 1، يكون الخطان a و b متعامدين على الخط c، ثم يقع a 1، b 1 بشكل عمودي على الخط c. العثور على الخطوط المستقيمة a و 1 في المستوى γ 1 متعامدة مع الخط المستقيم c، فيمكن اعتبارها متوازية. وبنفس الطريقة، يشير موقع b وb 1 في المستوى γ 2 بشكل عمودي على الخط المستقيم c إلى توازيهما. هذا يعني أنه من الضروري إجراء نقل موازي للمستوى χ 1 إلى χ، حيث نحصل على خطين مستقيمين متطابقين a و a 1، b و b 1. نجد أن الزاوية بين الخطين المتقاطعين a و b 1 تساوي زاوية تقاطع الخطين a و b.

دعونا ننظر إلى الشكل أدناه.

ويدل على هذا الطرح أن بين الخطين المتقاطعين a وb زاوية لا تعتمد على موقع النقطة M، أي نقطة التقاطع. تقع هذه الخطوط في المستويين γ 1 و γ 2. في الواقع، يمكن اعتبار الزاوية الناتجة هي الزاوية بين طائرتين متقاطعتين.

دعنا ننتقل إلى تحديد الزاوية بين المستويين المتقاطعين الموجودين γ 1 و γ 2.

التعريف 1

الزاوية بين طائرتين متقاطعتين γ 1 و γ 2تسمى الزاوية التي تتكون من تقاطع الخطين a و b، حيث يتقاطع المستويان γ 1 و γ 2 مع المستوى χ المتعامد مع الخط c.

النظر في الشكل أدناه.

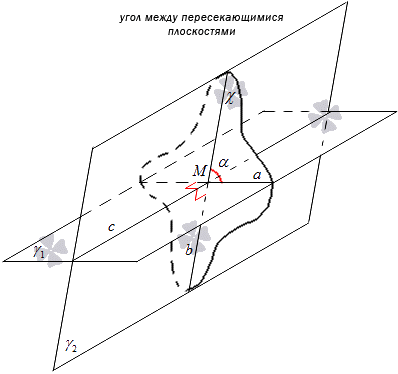
ويجوز تقديم القرار بصيغة أخرى. عندما يتقاطع المستويان γ 1 و γ 2، حيث c هو الخط الذي يتقاطعان عليه، حدد نقطة M يتم من خلالها رسم الخطين a و b المتعامدين على الخط c ويقعان في المستويين γ 1 و γ 2، ثم الزاوية بينهما الخطوط a و b ستكون الزاوية بين الطائرات. عمليًا، هذا ينطبق على بناء الزاوية بين المستويات.

عند التقاطع تتشكل زاوية قيمتها أقل من 90 درجة، أي أن قياس درجة الزاوية صالح على فترة من هذا النوع (0، 90).وفي الوقت نفسه، تسمى هذه المستويات متعامدة إذا تتشكل زاوية قائمة عند التقاطع وتعتبر الزاوية بين المستويين المتوازيين تساوي الصفر.

الطريقة المعتادة للعثور على الزاوية بين المستويات المتقاطعة هي إجراء إنشاءات إضافية. يساعد ذلك في تحديدها بدقة، ويمكن القيام بذلك باستخدام علامات المساواة أو التشابه للمثلث وجيب التمام وجيب التمام للزاوية.

دعونا نفكر في حل المشكلات باستخدام مثال من مشاكل امتحان الدولة الموحدةالكتلة ج 2.

مثال 1

نظرًا لمتوازي السطوح المستطيل A B C D A 1 B 1 C 1 D 1، حيث الضلع A B = 2، A D = 3، A A 1 = 7، فإن النقطة E تقسم الضلع A A 1 بنسبة 4: 3. أوجد الزاوية المحصورة بين المستويين A B C و B E D 1.

حل

من أجل الوضوح، من الضروري إجراء رسم. لقد حصلنا على ذلك

يعد التمثيل المرئي ضروريًا لجعل العمل بالزاوية بين المستويات أكثر ملاءمة.

نحدد الخط المستقيم الذي يحدث على طوله تقاطع المستويين ABC و B E D 1. النقطة B هي نقطة مشتركة. ينبغي إيجاد نقطة تقاطع مشتركة أخرى. لنتأمل الخطين المستقيمين D A و D 1 E، اللذين يقعان في نفس المستوى A D D 1. موقعهم لا يشير إلى التوازي، بل يعني أن لديهم نقطة تقاطع مشتركة.

ومع ذلك، يقع الخط المستقيم D A في المستوى ABC، ويقع D 1 E في المستوى B E D 1. ومن هذا نحصل على الخطوط المستقيمة د أو د1 هلها نقطة تقاطع مشتركة، وهي مشتركة بين المستويين ABC و B E D 1. يشير إلى نقطة تقاطع الخطوط د أو د 1 ه حرف ف ومن هذا نستنتج أن B F هو الخط المستقيم الذي يتقاطع على طوله المستويان A B C و B E D 1.

دعونا ننظر إلى الشكل أدناه.

للحصول على الإجابة، من الضروري إنشاء خطوط مستقيمة تقع في المستويين A B C و B E D 1 مروراً بنقطة تقع على الخط B F ومتعامدة معها. ثم تعتبر الزاوية الناتجة بين هذه الخطوط المستقيمة هي الزاوية المطلوبة بين المستويين ABC و B E D 1.

من هذا يمكننا أن نرى أن النقطة A هي إسقاط النقطة E على المستوى A B C. ومن الضروري رسم خط مستقيم يتقاطع مع الخط B F بزاوية قائمة عند النقطة M. ويمكن ملاحظة أن الخط المستقيم A M هو الإسقاط من الخط المستقيم E M على المستوى A B C، بناءً على نظرية تلك المتعامدة A M ⊥ B F . النظر في الشكل أدناه.

∠ A M E هي الزاوية المطلوبة التي تشكلها المستويات ABC و B E D 1. من المثلث الناتج A E M يمكننا إيجاد جيب الزاوية أو جيب تمامها أو ظلها، ثم الزاوية نفسها، فقط إذا كان ضلعاها معروفين. بشرط أن يكون الطول A E موجودًا بهذه الطريقة: الخط المستقيم A A 1 مقسوم على النقطة E بنسبة 4: 3، مما يعني أن الطول الإجمالي للخط المستقيم هو 7 أجزاء، إذن A E = 4 أجزاء. نجد أ م .

من الضروري النظر في المثلث القائم A B F. لدينا زاوية قائمة A مع الارتفاع A M. ومن الشرط A B = 2، يمكننا إيجاد الطول A F من خلال تشابه المثلثات D D 1 F و A E F. نحصل على A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

من الضروري إيجاد طول الضلع B F للمثلث A B F باستخدام نظرية فيثاغورس. نحصل على B F  = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . تم العثور على طول الضلع A M من خلال مساحة المثلث A B F. لدينا أن المساحة يمكن أن تكون مساوية لكل من S A B C = 1 2 · A B · A F و S A B C = 1 2 · B F · A M .

نحصل على أن A M = A B A F B F = 2 4 2 5 = 4 5 5

ثم يمكننا إيجاد قيمة ظل زاوية المثلث A E M. ونحصل على:

t g ∠ A M E = A E A M = 4 4 5 5 = 5

الزاوية المطلوبة التي يتم الحصول عليها من تقاطع المستويين A B C و B E D 1 تساوي a r c t g 5، ثم بالتبسيط نحصل على a r c t g 5 = a r c sin 30 6 = a r c cos 6 6.

إجابة: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

يتم تحديد بعض حالات إيجاد الزاوية بين الخطوط المتقاطعة باستخدام مستوى الإحداثيات O x y z وطريقة الإحداثيات. دعونا نلقي نظرة فاحصة.

إذا تم تقديم مشكلة حيث يكون من الضروري العثور على الزاوية بين المستويات المتقاطعة γ 1 و γ 2، فإننا نشير إلى الزاوية المطلوبة بـ α.

ثم نظام معينتوضح الإحداثيات أن لدينا إحداثيات المتجهات العادية للطائرات المتقاطعة γ 1 و γ 2. ثم نشير إلى أن n 1 → = n 1 x، n 1 y، n 1 z هو المتجه الطبيعي للمستوى γ 1، و n 2 → = (n 2 x، n 2 y، n 2 z) - بالنسبة إلى الطائرة γ 2. دعونا نفكر اكتشاف مفصلالزاوية الواقعة بين هذه المستويات على طول إحداثيات المتجهات.

من الضروري تحديد الخط المستقيم الذي تتقاطع فيه المستويتان γ 1 و γ 2 مع الحرف c. على الخط c لدينا نقطة M نرسم من خلالها المستوى χ المتعامد على c. المستوى χ على طول الخطين a و b يتقاطع مع المستويين γ 1 و γ 2 عند النقطة M. ويترتب على التعريف أن الزاوية بين المستويين المتقاطعين γ 1 و γ 2 تساوي زاوية الخطين المتقاطعين a و b التابعين لهذه المستويات، على التوالي.

في المستوى χ نرسم المتجهات العادية من النقطة M ونشير إليها n 1 → و n 2 → . يقع المتجه n 1 → على خط عمودي على الخط a، ويقع المتجه n 2 → على خط عمودي على الخط b. من هنا حصلنا على ذلك طائرة معينةχ لديه متجه عادي للخط يساوي n 1 → وللخط b يساوي n 2 →. النظر في الشكل أدناه.

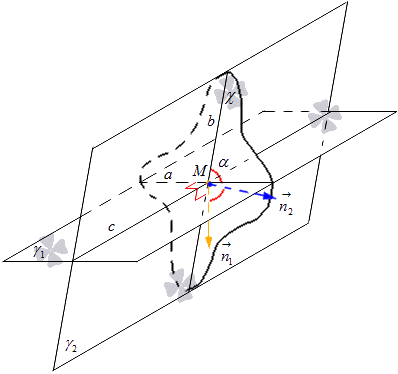
من هنا نحصل على صيغة يمكننا من خلالها حساب جيب زاوية الخطوط المتقاطعة باستخدام إحداثيات المتجهات. لقد وجدنا أن جيب تمام الزاوية بين الخطين المستقيمين a وb هو نفس جيب التمام بين المستويين المتقاطعين γ 1 و γ 2، وهو مشتق من صيغ كوسα = cos n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2، حيث لدينا أن n 1 → = (n 1 x, n 1 y, n 1 z) و n 2 → = (n 2 x, n 2 y, n 2 z) هي إحداثيات ناقلات الطائرات الممثلة.

يتم حساب الزاوية بين الخطوط المتقاطعة باستخدام الصيغة

α = أ r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2

مثال 2

وفقا للشرط، يتم إعطاء متوازي السطوح A B C D A 1 B 1 C 1 D 1 , حيث أ ب = 2، أ د = 3، أ أ 1 = 7، والنقطة هـ تقسم الضلع أ أ 1 4: 3. أوجد الزاوية المحصورة بين المستويين A B C و B E D 1.

حل

ويتبين من الشرط أن أضلاعها متعامدة بشكل زوجي. وهذا يعني أنه من الضروري إدخال نظام الإحداثيات O x y z مع قمة الرأس عند النقطة C ومحاور الإحداثيات O x، O y، O z. من الضروري ضبط الاتجاه على الجوانب المناسبة. النظر في الشكل أدناه.

طائرات متقاطعة أ ب جو ب ه د 1قم بتكوين زاوية يمكن إيجادها بالصيغة α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2، حيث n 1 → = (n 1 x, n 1 y, n 1 z) و n 2 → = (n 2 x, n 2 y, n 2 z ) هي ناقلات عادية لـ هذه الطائرات. من الضروري تحديد الإحداثيات. ومن الشكل نرى ذلك محور الإحداثيات O x y يتزامن مع المستوى ABC، وهذا يعني أن إحداثيات المتجه العادي k → تساوي القيمة n 1 → = k → = (0، 0، 1).

يتم أخذ المتجه الطبيعي للمستوى B E D 1 منتج ناقل B E → و B D 1 → حيث يتم العثور على إحداثياتهم عن طريق الإحداثيات النقاط المتطرفة B,E,D1 والتي يتم تحديدها بناء على ظروف المشكلة.

نحصل على ذلك ب (0، 3، 0)، د 1 (2، 0، 7). لأن A E E A 1 = 4 3، من إحداثيات النقاط A 2، 3، 0، A 1 2، 3، 7 نجد E 2، 3، 4. نجد أن B E → = (2 , 0 , 4) , B D 1 → = 2 , - 3 , 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 - 3 7 = 12 · أنا → - 6 ي → - 6 ك → ⇔ ن 2 → = (12 , - 6 , - 6)

من الضروري استبدال الإحداثيات الموجودة في صيغة حساب الزاوية من خلال قوس جيب التمام. نحصل على

α = أ r c cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = a r c cos 6 6 6 = a r c cos 6 6

تعطي طريقة الإحداثيات نتيجة مماثلة.

إجابة:أ ر ج كوس 6 6 .

أما المسألة الأخيرة فهي بهدف إيجاد الزاوية بين المستويات المتقاطعة بمعلومية المعادلات المعروفة للمستويات.

مثال 3

احسب جيب الزاوية وجيب تمام الزاوية وقيمة الزاوية المتكونة من خطين متقاطعين، والتي تم تعريفها في نظام الإحداثيات O x y z والمعطى بواسطة المعادلتين 2 x - 4 y + z + 1 = 0 و3 y - z - 1 = 0.

حل

عند دراسة موضوع ما المعادلة العامةكشف الخط المستقيم من الشكل A x + B y + C z + D = 0 أن A، B، C هي معاملات مساوية لإحداثيات المتجه العادي. هذا يعني أن n 1 → = 2, - 4, 1 و n 2 → = 0, 3, - 1 هي متجهات عادية للخطوط المحددة.

من الضروري استبدال إحداثيات المتجهات العادية للمستويات في صيغة حساب الزاوية المطلوبة للمستويات المتقاطعة. ثم حصلنا على ذلك

α = أ r c cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210

من هنا نحصل على جيب تمام الزاوية عرض كوسα = 13,210. إذن زاوية المستقيمين المتقاطعين ليست منفرجة. الاستبدال في الهوية المثلثيةنجد أن قيمة جيب الزاوية تساوي التعبير. دعونا نحسب ونجد ذلك

الخطيئة α = 1 - جتا 2 α = 1 - 13,210 = 41,210

إجابة: sin α = 41,210، cos α = 13,210، α = a r c cos 13,210 = a r c sin 41,210.

إذا لاحظت وجود خطأ في النص، فيرجى تحديده والضغط على Ctrl+Enter

نوع الوظيفة: 14
الموضوع: الزوايا بين المستويات

حالة

دانا المنشور الصحيح ABCDA_1B_1C_1D_1، M وN هما نقطتا منتصف الحافتين AB وBC، على التوالي، والنقطة K هي نقطة منتصف MN.

أ)أثبت أن الخطين KD_1 وMN متعامدان.

ب)أوجد الزاوية بين المستويين MND_1 وABC إذا أب = 8، AA_1=6\sqrt 2.

عرض الحل

حل

أ)في \triangle DCN و\triangle MAD لدينا: \الزاوية C=\الزاوية A=90^(\circ), CN=AM=\frac12AB, مؤتمر نزع السلاح = دا.

وبالتالي \triangle DCN =\triangle MAD على قدمين. ثم مد = الاسم المميز، \مثلث DMNمتساوي الساقين. وهذا يعني أن متوسط ​​DK هو أيضًا الارتفاع. ولذلك، DK \perp MN.

DD_1 \perp MND حسب الحالة، D_1K - مائل، KD - إسقاط، DK \perp MN.

وبالتالي، من خلال نظرية حول ثلاثة متعامدين MN\perp D_1K.

ب)كما ثبت في أ)، DK \perp MN و MN \perp D_1K، لكن MN هو خط تقاطع المستويين MND_1 و ABC، مما يعني \angle DKD_1 - زاوية خطيةزاوية ثنائية السطوح بين المستويين MND_1 وABC.

في \triangle DAM حسب نظرية فيثاغورس مارك ألماني= \sqrt (DA^2+AM^2)= \sqrt (64+16)= 4\sqrt 5, مينيسوتا = \sqrt (MB^2+BN^2)= \sqrt (16+16)= 4\sqrt 2.لذلك، في \المثلث DKM بواسطة نظرية فيثاغورس لا أعرف = \sqrt (DM^2-KM^2)= \sqrt (80-8)= 6\sqrt 2.ثم في \المثلث DKD_1، tg\angle DKD_1=\frac(DD_1)(DK)=\frac(6\sqrt 2)(6\sqrt 2)=1.

وهذا يعني \الزاوية DKD_1=45^(\circ).

إجابة

45 ^ (\ سيرك).

نوع الوظيفة: 14
الموضوع: الزوايا بين المستويات

حالة

في اليمين المنشور الرباعي ABCDA_1B_1C_1D_1 جوانب القاعدة هي 4، الأضلاع الجانبيةتساوي 6. النقطة M هي منتصف الحافة CC_1، ويتم وضع علامة على النقطة N على الحافة BB_1، بحيث يكون BN:NB_1=1:2.

أ)ما هي النسبة التي يقسم بها مستوى AMN الحافة DD_1؟

ب)أوجد الزاوية بين المستويين ABC وAMN.

عرض الحل

حل

أ)يتقاطع المستوى AMN مع الحافة DD_1 عند النقطة K، وهي الرأس الرابع لقسم المنشور المعطى بهذا المستوى. المقطع العرضي هو متوازي الأضلاع ANMK لأن الأوجه المتقابلة لمنشور معين متوازية.

بن =\frac13BB_1=2.لنرسم KL \parallel CD، إذن المثلثان ABN وKLM متساويان، مما يعني مل = BN = 2، لك = ماك-مل = 3-2 = 1، دينار كويتي=LC=1.ثم KD_1=6-1=5.

ب)يمكنك الآن العثور على النسبة KD:KD_1=1:5.

F هي نقطة تقاطع الخطوط المستقيمة CD و KM. يتقاطع المستويان ABC وAMN على طول الخط المستقيم AF. Angle \angle KHD =\alpha هي الزاوية الخطية لزاوية ثنائية السطوح (HD\perp AF، ثم عن طريق النظرية العكسية لنظرية الثلاثة المتعامدين، KH \perp AF)، وهي زاوية حادة للمثلث القائم KHD، الساق دينار كويتي = 1. المثلثان FKD وFMC متشابهان (KD \parallel MC)، وبالتالي FD:FC=KD:MC، وبحل النسبة FD:(FD+4)=1:3، نحصل على FD=2. في المثلث القائم AFD (\angle D=90^(\circ)) ذو الأرجل 2 و4، نحسب الوتر AF=\sqrt (4^2+2^2)=2\sqrt 5, درهم= AD\cdot FD:AF=

\frac(4\cdot 2)(2\sqrt 5)= \frac4(\sqrt 5).في المثلث القائم KHD نجد تيراغرام \alpha =\frac(KD)(DH)=\frac(\sqrt 5)4,

إجابة

أ) 1:5;

ب) وهذا يعني الزاوية المطلوبة

\alpha =arctg\frac(\sqrt 5)4. أركتج\فارك(\sqrt 5)4.المصدر: "الرياضيات. التحضير لامتحان الدولة الموحدة 2017.

نوع الوظيفة: 14
الموضوع: الزوايا بين المستويات

حالة

مستوى الملف الشخصي " إد. F. F. ليسينكو، S. Yu.

أ)أنشئ قسمًا من الهرم بمستوى يمر عبر الخط NF الموازي للقطر MP، إذا كانت النقطة F هي منتصف الحافة MK.

ب)أوجد الزاوية بين مستوى القسم ومستوى KMP.

عرض الحل

حل

أ)دع KO يكون ارتفاع الهرم، F نقطة منتصف MK ؛ FE\parallel MP (في مستوى PKM) . منذ FE خط الوسط\ مثلث PKM، إذن FE=\frac(MP)2.

دعونا نبني قسمًا من الهرم بمستوى يمر عبر NF وموازٍ للمستوى MP، أي المستوى NFE. L هي نقطة تقاطع EF وKO. نظرًا لأن النقطتين L و N تنتميان إلى القسم المطلوب وتقعان في مستوى KQN، فإن النقطة T، التي تم الحصول عليها كتقاطع LN وKQ، هي أيضًا نقطة تقاطع القسم المطلوب والحافة KQ. NETF هو القسم المطلوب.

ب)تتقاطع الطائرات NFE وMPK على طول الخط المستقيم FE. هذا يعني أن الزاوية بين هذه المستويات تساوي الزاوية الخطية للزاوية ثنائية السطوح OFEN، فلنبنيها: لو\بيرمب، النائب \ الموازي FE،لذلك، LO\perpFE;\triangle NFE - متساوي الساقين (NE=NF كالمتوسطات المقابلة مثلثات متساوية KPN وKMN)، NL هو متوسطها (EL=LF، منذ PO=OM، و \مثلث KEF \sim \triangle KPM) . ومن ثم فإن NL \perp FE و \angle NLO هو المطلوب.

ON=\frac12QN=\frac12MN\sqrt 2=3\sqrt 2.

\مثلث KON - مستطيل.

الساق KO حسب نظرية فيثاغورس تساوي كو=\sqrt (KN^2-ON^2).

OL= \frac12KO= \frac12\sqrt(KN^2-ON^2)= \frac12\sqrt (9\cdot 26-9\cdot 2)= \frac12\sqrt(9(26-2))= \frac32\sqrt (24)= \frac32\cdot 2\sqrt 6= 3\sqrt 6.

tg\angle NLO =\frac(ON)(OL)=\frac(3\sqrt 2)(3\sqrt 6)=\frac1(\sqrt 3)،

\زاوية NLO=30^(\circ).

إجابة

المصدر: "الرياضيات. التحضير لامتحان الدولة الموحدة 2017. مستوى الملف الشخصي." إد. F. F. ليسينكو، S. Yu.

نوع الوظيفة: 14
الموضوع: الزوايا بين المستويات

حالة

جميع أحرف المنشور الثلاثي المنتظم ABCA_(1)B_(1)C_(1) تساوي 6. يتم رسم مستوى القطع من خلال نقاط المنتصف للحواف AC وBB_(1) والقمة A_(1).

أ)أثبت أن الحافة BC مقسومة على مستوى القطع بنسبة 2:1، بدءًا من الرأس C.

ب)أوجد الزاوية بين مستوى القطع والمستوى الأساسي.

عرض الحل

حل

أ)اجعل D وE هما نقطتا المنتصف للحافتين AC وBB_(1)، على التوالي.

في المستوى AA_(1)C_(1) نرسم خطًا مستقيمًا A_(1)D، الذي يتقاطع مع الخط المستقيم CC_(1) عند النقطة K، في المستوى BB_(1)C_(1) - خط مستقيم KE، الذي يتقاطع مع الحافة BC عند النقطة F . عند توصيل النقطتين A_(1) وE، الواقعتين في المستوى AA_(1)B_(1)، وكذلك D وF، الواقعتين في المستوى ABC، نحصل على القسم A_(1)EFD.

\bigtriangleup AA_(1)D=\bigtriangleup CDKعلى طول الساق AD=DC والزاوية الحادة.

\angle ADA_(1)=\angle CDK - مثل الزوايا الرأسية، يتبع ذلك AA_(1)=CK=6. \bigtriangleup CKF و\bigtriangleup BFE متشابهان في زاويتين\زاوية FBE=\زاوية KCF=90^\circ,

\angle BFE=\angle CFK - مثل تلك الرأسية.\frac(CK)(BE)=\frac(6)(3)=2,

ب)أي أن معامل التشابه هو 2، مما يعني أن CF:FB=2:1. دعونا ننفذ AH\perp DF.الزاوية بين مستوى القسم والمستوى الأساسي تساوي الزاوية AHA_(1).

في الواقع، المقطع AH \perp DF (DF هو خط تقاطع هذه المستويات) هو إسقاط المقطع A_(1)H على المستوى الأساسي، وبالتالي، وفقًا لنظرية الخطوط المتعامدة الثلاثة، A_(1)H \perp مدافع.

\الزاوية AHA_(1)=arctg\frac(AA_(1))(AH).

أ_(1)=6. دعونا نجد آه. \angle ADH =\angle FDC (مثل العمودي).

بواسطة نظرية جيب التمام في \bigtriangleup DFC:

مدافع^2=FC^2+DC^2- 2FC \cdot DC \cdot \cos 60^\circ,

DF^2=4^2+3^2-2 \cdot 4 \cdot 3 \cdot \frac(1)(2)=13.

FC^2=DF^2+DC^2-

2DF\cdot DC\cdot\cos\زاوية FDC،

4^2=13+9-2\sqrt(13) \cdot 3 \cdot \cos \angle FDC،\cos \angle FDC=\frac(6)(2\sqrt(13) \cdot 3)=\frac(1)(\sqrt(13)).

كنتيجة طبيعية للهوية المثلثية الأساسية \sin \angle FDC=\sqrt(1-\left (\frac(1)(\sqrt(13))\right)^2)=\frac(2\sqrt(3))(\sqrt(13)) .

من \bigtriangleup ADH نجد AH : AH=AD \cdot \sin \angle ADH، (\angle FDC=\angle ADH). AH=3 \cdot \frac(2\sqrt(3))(\sqrt(13))=\frac(6\sqrt(13))(\sqrt(13)). \الزاوية AHA_(1)=

إجابة

arctg\frac(AA_(1))(AH)=

المصدر: "الرياضيات. التحضير لامتحان الدولة الموحدة 2017. مستوى الملف الشخصي." إد. F. F. ليسينكو، S. Yu.

نوع الوظيفة: 14
الموضوع: الزوايا بين المستويات

حالة

arctg\frac(6 \cdot \sqrt(13))(6\sqrt(3))= أركتج\فارك(\sqrt(39))(3).أركتج\فارك(\sqrt(39))(3).

أ)قاعدة المنشور الأيمن ABCDA_(1)B_(1)C_(1)D_(1) عبارة عن مُعين به

ب)زاوية منفرجة

عرض الحل

حل

أ)ب يساوي 120^\circ. جميع حواف هذا المنشور تساوي 10. النقطتان P وK هما نقطتا المنتصف للحواف CC_(1) وCD، على التوالي.أثبت أن الخطين PK وPB_(1) متعامدان.

أوجد الزاوية بين المستويين PKB_(1) وC_(1)B_(1)B. سوف نستخدم طريقة الإحداثيات. دعونا نجدمنتج نقطة المتجهات \vec(PK) و \vec(PB_(1)) ثم جيب تمام الزاوية بين هذه المتجهات. دعونا نوجه محور Oy على طول CD، ومحور Oz على طول CC_(1)، ومحور Ox \perp CD. ج هو الأصل. ثم ج (0;0;0);

C_(1)(0;0;10); ف(0;0;5);

ك(0;5;0);

ب(BC \cos 30^\circ; BC\sin 30^\circ; 0), إنه ب(5\sqrt(3); 5;0),

\cos \alpha =0، \vec(PK) \perp \vec(PB_(1)) والخطان PK وPB_(1) متعامدان.

ب)الزاوية بين المستويات تساوي الزاوية بين المتجهات غير الصفرية المتعامدة مع هذه المستويات (أو، إذا كانت الزاوية منفرجة، الزاوية المجاورة لها). تسمى هذه المتجهات بالمستويات الطبيعية. دعونا نجدهم.

اجعل \vec(n_(1))=\(x; y; z\) عموديًا على المستوى PKB_(1). دعونا نجد ذلك عن طريق حل النظام

\begin(cases) \vec(n_(1)) \perp \vec(PK)، \\ \vec(n_(1)) \perp \vec(PB_(1)). \end(الحالات)

\begin(cases) \vec(n_(1)) \cdot \vec(PK)=0, \\ \vec(n_(1)) \cdot \vec(PB_(1))=0; \end(الحالات)

\begin(cases) 0x+5y-5z=0, \\ 5\sqrt(3)x+5y+5z=0; \end(الحالات)

\begin(cases)y=z, \\ x=\frac(-y-z)(\sqrt(3)). \end(الحالات) دعونا نأخذ ص=1; ض=1; س=\فارك(-2)(\sqrt(3)))،

\vec(n_(1))=\left \( \frac(-2)(\sqrt(3)); 1;1 \right \). اجعل \vec(n_(2))=\(x; y; z\) عموديًا على المستوى C_(1)B_(1)B.

دعونا نجد ذلك عن طريق حل النظام

\begin(cases) \vec(n_(2)) \perp \vec(CC_(1)), \\ \vec(n_(2)) \perp \vec(CB). \end(الحالات)

\vec(CC_(1))=\(0;0;10\), \vec(CB)=\(5\sqrt(3); 5; 0\).

\begin(cases) \vec(n_(2)) \cdot \vec(CC_(1))=0, \\ \vec(n_(2)) \cdot \vec(CB)=0; \end(الحالات)

\begin(cases)y=z, \\ x=\frac(-y-z)(\sqrt(3)). \end(الحالات) \begin(cases) 0x+0y+10z=0, \\ 5\sqrt(3)x+5y+0z=0; \end(الحالات) \begin(cases)z=0, \\ y=-\sqrt(3)x. \end(الحالات)

س=1; y=-\sqrt(3); ض = 0، \vec(n_(2))=\(1; -\sqrt(3);0\).دعونا نجد جيب التمام للزاوية المطلوبة \beta (it

يساوي المعامل جيب تمام الزاوية بين \vec(n_(1)) و \vec(n_(2)) ). \كوس \بيتا= \frac(|\vec(n_(1)) \cdot \vec(n_(2))|)(|\vec(n_(1))| \cdot |\vec(n_(2))|)= \frac(\left |-\dfrac(2)(\sqrt(3))\cdot 1+1 \cdot (-\sqrt(3))+1 \cdot 0 \right |)(\sqrt(\dfrac( 4)(3)+1+1) \cdot \sqrt(1+3+0))=

\frac(\dfrac(5)(\sqrt(3)))(2\sqrt(\dfrac(10)(3)))= \frac(\sqrt(10))(4).

إجابة

\cos \beta =\frac(\sqrt(10))(4),

المصدر: "الرياضيات. التحضير لامتحان الدولة الموحدة 2017. مستوى الملف الشخصي." إد. F. F. ليسينكو، S. Yu.

\beta=\arccos\frac(\sqrt(10))(4). \arccos\frac(\sqrt(10))(4) ABCD هو مربع و

وجوه جانبية

- مستطيلات متساوية. بما أن مستوى القسم يمر عبر النقطتين M و D الموازيتين للقطري AC، إذن لبناءه في المستوى A_(1)AC عبر النقطة M، نرسم قطعة MN موازية للAC. نحصل على AC \parallel (MDN) بناءً على توازي الخط والمستوى.المستوى MDN يتقاطع مع المستويين المتوازيين A_(1)AD و B_(1)BC ، إذن بالخاصية

طائرات متوازية

، خطوط تقاطع الوجوه A_(1)ADD_(1) وB_(1)BCC_(1) مع مستوى MDN متوازية.

ب)دعونا نجد الزاوية بين مستوى القسم والمستوى الأساسي. دع مستوى المقطع يتقاطع مع المستوى الأساسي على طول خط مستقيم p يمر عبر النقطة D. AC \parallel MN، وبالتالي، AC \parallel p (إذا مر مستوى عبر خط موازٍ لمستوى آخر ويتقاطع مع هذا المستوى، فإن خط تقاطع المستويات يكون موازيًا لهذا الخط). BD \perp AC كأقطار المربع، وهو ما يعني BD \perp p.

BD هو إسقاط ED على المستوى ABC، ثم وفقًا لنظرية الخطوط المتعامدة الثلاثة ED \perp p، وبالتالي، \angle EDB هي الزاوية الخطية للزاوية ثنائية السطوح بين مستوى القسم والمستوى الأساسي.

قم بتعيين نوع DMEN الرباعي. MD \parallel EN، مشابه لـ ME \parallel DN، وهو ما يعني أن DMEN هو متوازي أضلاع، وبما أن MD=DN (المثلثات القائمة MAD وNCD متساوية على قدمين: AD=DC كأضلاع المربع، AM=CN كـ المسافات بين الخطوط المتوازية AC وMN)، وبالتالي فإن DMEN عبارة عن معين. ومن ثم، F هي نقطة المنتصف لـ MN. حسب الشرط AM:MA_(1)=2:3، إذن

AM=\frac(2)(5)AA_(1)=\frac(2)(5) \cdot 5\sqrt(6)=2\sqrt(6). AMNC مستطيل، F هو منتصف MN، O هو منتصف AC. وسائل، FO \ الموازي MA، FO \ بيرب أس،

FO=MA=2\sqrt(6). مع العلم أن قطر المربع هوأ\sqrt(2)، حيث a هو جانب المربع، نحصل عليه دينار بحريني=4\sqrt(2).

OD=\frac(1)(2)BD=\frac(1)(2) \cdot 4\sqrt(2)=2\sqrt(2). في المثلث الأيمن FOD\enspace tg \angle FDO=\frac(FO)(OD)=\frac(2\sqrt(6))(2\sqrt(2))=\sqrt(3).

لذلك، \الزاوية FDO=60^\circ.

\(\blacktriangleright\) الزاوية ثنائية السطوح هي زاوية مكونة من نصفي مستويين وخط مستقيم \(a\)، وهو الحد المشترك بينهما. \(\blacktriangleright\) للعثور على الزاوية بين المستويين \(\xi\) و \(\pi\) ، تحتاج إلى إيجاد الزاوية الخطية (وحار أومباشر

) زاوية ثنائية السطوح مكونة من المستويين \(\xi\) و \(\pi\) : الخطوة 1: دع \(\xi\cap\pi=a\) (خط تقاطع المستويات). في المستوى \(\xi\) نلاحظنقطة تعسفية

\(F\) وتنفيذ \(FA\perp a\) ;

الخطوة 2: تنفيذ \(FG\perp \pi\) ؛

الخطوة 3: وفقًا لـ TTP (\(FG\) - عمودي، \(FA\) - مائل، \(AG\) - إسقاط) لدينا: \(AG\perp a\) ؛

الخطوة 4: الزاوية \(\angle FAG\) تسمى الزاوية الخطية للزاوية ثنائية السطوح التي شكلتها المستويتان \(\xi\) و \(\pi\) .
لاحظ أن المثلث \(AG\) قائم الزاوية. لاحظ أيضًا أن المستوى \(AFG\) الذي تم إنشاؤه بهذه الطريقة عمودي على كلا المستويين \(\xi\) و \(\pi\) . ولذلك يمكننا أن نقول ذلك بشكل مختلف:\(\xi\) و \(\pi\) هي الزاوية بين خطين متقاطعين \(c\in \xi\) و \(b\in\pi\) يشكلان مستوى متعامدًا مع و \(\xi\ ) و \(\pi\) .

المهمة 1 #2875

مستوى المهمة: أصعب من امتحان الدولة الموحدة

دانا الهرم الرباعي، وجميع أحرفها متساوية، وقاعدتها مربعة. أوجد \(6\cos \alpha\) حيث \(\alpha\) هي الزاوية بين وجوهها الجانبية المجاورة.

دع \(SABCD\) – هذا الهرم(\(S\) هو قمة) حوافها تساوي \(a\) . وبالتالي فإن جميع الأوجه الجانبية هي مثلثات متساوية الأضلاع. دعونا نجد الزاوية بين الوجوه \(SAD\) و \(SCD\) .

لنفعل \(CH\perp SD\) . لأن \(\مثلث SAD=\مثلث SCD\)، فإن \(AH\) سيكون أيضًا ارتفاع \(\triangle SAD\) . لذلك، بحكم التعريف، \(\angle AHC=\alpha\) هي الزاوية الخطية للزاوية ثنائية السطوح بين الوجوه \(\angle AHC=\alpha\) و \(SCD\) .
بما أن القاعدة مربعة، إذن \(AC=a\sqrt2\) . لاحظ أيضًا أن \(CH=AH\) هو الارتفاع مثلث متساوي الأضلاعمع الجانب \(a\) ، \(CH=AH=\frac(\sqrt3)2a\) .
ثم، من خلال نظرية جيب التمام من \(\triangle AHC\) : \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]

الجواب: -2

المهمة 2 #2876

مستوى المهمة: أصعب من امتحان الدولة الموحدة

تتقاطع المستويتان \(\pi_1\) و\(\pi_2\) بزاوية جيب تمامها يساوي \(0.2\). يتقاطع المستويان \(\pi_2\) و \(\pi_3\) بزوايا قائمة، ويكون خط تقاطع المستويين \(\pi_1\) و \(\pi_2\) موازيًا لخط تقاطع المستويين \(\pi_2\) و \(\pi_2\) الطائرات \(\pi_2\) و \(\ pi_3\) . أوجد جيب الزاوية بين المستويين \(\pi_1\) و \(\pi_3\) .

اجعل خط تقاطع \(\pi_1\) و \(\pi_2\) خطًا مستقيمًا \(a\)، وخط تقاطع \(\pi_2\) و \(\pi_3\) خطًا مستقيمًا الخط \(\b\)، وخط التقاطع \(\pi_3\) و \(\pi_1\) – الخط المستقيم \(c\) . منذ \(a\parallel b\) ، ثم \(c\parallel a\parallel b\) (وفقًا للنظرية من قسم المرجع النظري "الهندسة في الفضاء" \(\rightarrow\) "مقدمة في القياس المجسم، التوازي").

لنضع علامة على النقاط \(A\in a, B\in b\) بحيث يكون \(AB\perp a, AB\perp b\) (وهذا ممكن منذ \(a\parallel b\) ). دعونا نضع علامة \(C\in c\) بحيث يكون \(BC\perp c\) \(BC\perp b\) . ثم \(AC\perp c\) و \(AC\perp a\) .
في الواقع، نظرًا لأن \(AB\perp b, BC\perp b\) ، فإن \(b\) عمودي على المستوى \(ABC\) . بما أن \(c\parallel a\parallel b\)، فإن الخطين \(a\) و \(c\) متعامدان أيضًا على المستوى \(ABC\)، وبالتالي على أي خط من هذا المستوى، على وجه الخصوص , السطر \ (AC\) .

ويترتب على ذلك \(\زاوية BAC=\زاوية (\pi_1, \pi_2)\), \(\الزاوية ABC=\الزاوية (\pi_2, \pi_3)=90^\circ\), \(\زاوية BCA=\زاوية (\pi_3, \pi_1)\). اتضح أن \(\المثلث ABC\) مستطيل، مما يعني \[\sin \angle BCA=\cos \angle BAC=0.2.\]

الجواب: 0.2

المهمة 3 #2877

مستوى المهمة: أصعب من امتحان الدولة الموحدة

إذا كانت الخطوط المستقيمة \(a, b, c\) متقاطعة عند نقطة واحدة، والزاوية المحصورة بين أي خطين منها تساوي \(60^\circ\) . ابحث عن \(\cos^(-1)\alpha\) حيث \(\alpha\) هي الزاوية بين المستوى الذي يتكون من الخطوط \(a\) و \(c\) والمستوى الذي يشكله الخطوط \( ب\ ) و \(ج\) . اكتب إجابتك بالدرجات.

دع الخطوط تتقاطع عند النقطة \(O\) . بما أن الزاوية بين أي اثنين منها تساوي \(60^\circ\)، فلا يمكن للخطوط الثلاثة المستقيمة أن تقع في نفس المستوى. دعونا نحدد النقطة \(A\) على السطر \(a\) ونرسم \(AB\perp b\) و \(AC\perp c\) . ثم \(\مثلث AOB=\مثلث AOC\)مستطيلة على طول الوتر والزاوية الحادة. ولذلك، \(OB=OC\) و \(AB=AC\) .
لنفعل \(AH\perp (BOC)\) . ثم من خلال نظرية ثلاثة خطوط متعامدة \(HC\perp c\) , \(HB\perp b\) . منذ \(AB=AC\) إذن \(\مثلث AHB=\مثلث AHC\)مستطيلة على طول الوتر والساق. ولذلك، \(HB=HC\) . هذا يعني أن \(OH\) ​​​​هو منصف الزاوية \(BOC\) (نظرًا لأن النقطة \(H\) متساوية البعد من جانبي الزاوية).

لاحظ أنه بهذه الطريقة قمنا أيضًا ببناء الزاوية الخطية للزاوية ثنائية السطوح التي يشكلها المستوى الذي يشكله الخطان \(a\) و\(c\) والمستوى الذي يشكله الخطان \(b\) و\(c) \) . هذه هي الزاوية \(ACH\) .

دعونا نجد هذه الزاوية. وبما أننا اخترنا النقطة \(A\) بشكل عشوائي، فلنختارها بحيث \(OA=2\) . ثم في شكل مستطيل \(\triangle AOC\) : \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ]بما أن \(OH\) ​​​​منصف، إذن \(\angle HOC=30^\circ\) ، في \(\triangle HOC\) مستطيل : \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\]ثم من المستطيل \(\triangle ACH\) : \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]

الجواب: 3

المهمة 4 #2910

مستوى المهمة: أصعب من امتحان الدولة الموحدة

يتقاطع المستويان \(\pi_1\) و\(\pi_2\) على طول الخط المستقيم \(l\) الذي تقع عليه النقطتان \(M\) و\(N\). المقطعان \(MA\) و \(MB\) متعامدان مع الخط المستقيم \(l\) ويقعان في المستويين \(\pi_1\) و \(\pi_2\) على التوالي، و \(MN = 15 \) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) . ابحث عن \(3\cos\alpha\) حيث \(\alpha\) هي الزاوية بين المستويين \(\pi_1\) و \(\pi_2\) .

المثلث \(AMN\) قائم الزاوية، \(AN^2 = AM^2 + MN^2\)، ومن هنا \ المثلث \(BMN\) مستطيل، \(BN^2 = BM^2 + MN^2\)، ومنه \نكتب نظرية جيب التمام للمثلث \(AMB\): \ ثم \ نظرًا لأن الزاوية \(\alpha\) بين الطائرات هي زاوية حادة، وتبين أن \(\angle AMB\) منفرجة، إذن \(\cos\alpha=\dfrac5(12)\) . ثم \

الجواب: 1.25

المهمة 5 #2911

مستوى المهمة: أصعب من امتحان الدولة الموحدة

\(ABCDA_1B_1C_1D_1\) هو متوازي سطوح، \(ABCD\) مربع ذو ضلع \(a\)، النقطة \(M\) هي قاعدة العمود العمودي المسقط من النقطة \(A_1\) إلى المستوى \ ((ABCD)\) بالإضافة إلى ذلك، \(M\) هي نقطة تقاطع قطري المربع \(ABCD\) . ومن المعروف أن \(A_1M = \dfrac(\sqrt(3))(2)أ\). أوجد الزاوية بين المستويين \((ABCD)\) و \((AA_1B_1B)\) . اكتب إجابتك بالدرجات.

لنقم بإنشاء \(MN\) عموديًا على \(AB\) كما هو موضح في الشكل.

بما أن \(ABCD\) مربع ذو ضلع \(a\) و \(MN\perp AB\) و \(BC\perp AB\) ، إذن \(MN\parallel BC\) . بما أن \(M\) هي نقطة تقاطع قطري المربع، فإن \(M\) هو منتصف \(AC\)، وبالتالي فإن \(MN\) هو الخط الأوسط و \(MN =\frac12BC= \frac(1)(2)أ\).
\(MN\) هو إسقاط \(A_1N\) على المستوى \((ABCD)\)، و\(MN\) عمودي على \(AB\)، إذن، وفقًا لنظرية الثلاثة المتعامدين، \ (A_1N\) عمودي على \(AB \) والزاوية بين المستويين \((ABCD)\) و \((AA_1B_1B)\) هي \(\angle A_1NM\) .
\[\mathrm(tg)\, \الزاوية A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\angle A_1NM = 60^(\circ)\]

الجواب: 60

المهمة 6 #1854

مستوى المهمة: أصعب من امتحان الدولة الموحدة

في المربع \(ABCD\) : \(O\) – نقطة تقاطع الأقطار؛ \(S\) – لا يقع في مستوى المربع، \(SO \perp ABC\) . أوجد الزاوية بين المستويين \(ASD\) و \(ABC\) إذا كان \(SO = 5\) و \(AB = 10\) .

المثلثان القائمان \(\triangle SAO\) و \(\triangle SDO\) متساويان في الجانبين والزاوية بينهما (\(SO \perp ABC\) \(\Rightarrow\) \(\زاوية SOA = \زاوية SOD = 90^\دائرة\); \(AO = DO\) لأن \(O\) – نقطة تقاطع أقطار المربع، \(SO\) – الجانب المشترك) \(\Rightarrow\) \(AS = SD\) \(\Rightarrow\) \(\مثلث ASD\) – متساوي الساقين. النقطة \(K\) هي منتصف \(AD\)، ثم \(SK\) هو الارتفاع في المثلث \(\triangle ASD\)، و\(OK\) هو الارتفاع في المثلث \( AOD\) \(\ Rightarrow\) المستوى \(SOK\) متعامد مع المستويين \(ASD\) و \(ABC\) \(\Rightarrow\) \(\angle SKO\) – الزاوية الخطية المساوية للمطلوب زاوية ثنائي السطوح.

في \(\مثلث SKO\): \(OK = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\Rightarrow\) \(\triangle SOK\) – مثلث متساوي الساقين قائم الزاوية \(\Rightarrow\) \(\angle SKO = 45^\circ\) .

الجواب: 45

المهمة 7 #1855

مستوى المهمة: أصعب من امتحان الدولة الموحدة

في المربع \(ABCD\) : \(O\) – نقطة تقاطع الأقطار؛ \(S\) – لا يقع في مستوى المربع، \(SO \perp ABC\) . أوجد الزاوية بين المستويين \(ASD\) و \(BSC\) إذا كان \(SO = 5\) و \(AB = 10\) .

المثلثات القائمة \(\triangle SAO\) و \(\triangle SDO\) و \(\triangle SOB\) و \(\triangle SOC\) متساوية في الجانبين والزاوية بينهما (\(SO \perp ABC \) \(\السهم الأيمن\) \(\زاوية SOA = \زاوية SOD = \زاوية SOB = \زاوية SOC = 90^\circ\); \(AO = OD = OB = OC\)، لأن \(O\) – نقطة تقاطع قطري المربع، \(SO\) – الضلع المشترك) \(\Rightarrow\) \(AS = DS = BS = CS\) \(\Rightarrow\) \( \triangle ASD\) و \(\triangle BSC\) متساوي الساقين. النقطة \(K\) هي منتصف \(AD\)، ثم \(SK\) هو الارتفاع في المثلث \(\triangle ASD\)، و\(OK\) هو الارتفاع في المثلث \( AOD\) \(\ Rightarrow\) المستوى \(SOK\) متعامد مع المستوى \(ASD\) . النقطة \(L\) هي منتصف \(BC\)، ثم \(SL\) هو الارتفاع في المثلث \(\triangle BSC\)، و\(OL\) هو الارتفاع في المثلث \( BOC\) \(\ Rightarrow\) المستوى \(SOL\) (المعروف أيضًا باسم المستوى \(SOK\)) عمودي على المستوى \(BSC\) . وبالتالي، نحصل على أن \(\angle KSL\) هي زاوية خطية تساوي زاوية ثنائي السطوح المطلوبة.

\(KL = KO + OL = 2\cdot OL = AB = 10\)\(\Rightarrow\) \(OL = 5\) ; \(SK = SL\) – ارتفاعات متساوية مثلثات متساوية الساقينوالتي يمكن العثور عليها باستخدام نظرية فيثاغورس: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). ويمكن ملاحظة ذلك \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)\(\Rightarrow\) بالنسبة للمثلث \(\triangle KSL\) فإن نظرية فيثاغورس العكسية تنص على \(\Rightarrow\) \(\triangle KSL\) – المثلث القائم \(\Rightarrow\) \(\angle KSL = 90 ^\الدائرة\) .

الجواب: 90

يبدأ إعداد الطلاب لامتحان الدولة الموحدة في الرياضيات، كقاعدة عامة، بتكرار الصيغ الأساسية، بما في ذلك تلك التي تسمح لك بتحديد الزاوية بين المستويات. على الرغم من أن هذا القسم من الهندسة مغطى بتفاصيل كافية في الداخل المنهج المدرسييحتاج العديد من الخريجين إلى تكرار المواد الأساسية. من خلال فهم كيفية العثور على الزاوية بين الطائرات، سيتمكن طلاب المدارس الثانوية من حساب الإجابة الصحيحة بسرعة عند حل المشكلة والاعتماد على الحصول على درجات لائقة في نتائج اجتياز اختبار الدولة الموحدة.

الفروق الدقيقة الرئيسية

للتأكد من أن مسألة كيفية العثور على زاوية ثنائية السطوح لا تسبب صعوبات، نوصي باتباع خوارزمية حل ستساعدك على التعامل مع مهام امتحان الدولة الموحدة.

تحتاج أولاً إلى تحديد الخط المستقيم الذي تتقاطع به الطائرات.

ثم تحتاج إلى تحديد نقطة على هذا الخط ورسم خطين متعامدين عليها.

الخطوة التالية- العثور على وظيفة المثلثيةزاوية ثنائية السطوح تشكلت من المتعامدين. الطريقة الأكثر ملاءمة للقيام بذلك هي بمساعدة المثلث الناتج، والذي تكون الزاوية جزءًا منه.

ستكون الإجابة هي قيمة الزاوية أو دالتها المثلثية.

التحضير للاختبار مع شكولكوفو هو مفتاح نجاحك

خلال الفصول الدراسية في اليوم السابق اجتياز امتحان الدولة الموحدةيواجه العديد من تلاميذ المدارس مشكلة العثور على تعريفات وصيغ تسمح لهم بحساب الزاوية بين طائرتين. الكتاب المدرسيإنه ليس في متناول اليد دائمًا عندما تحتاج إليه بالضبط. وأن تجد الصيغ اللازمةوأمثلة على استخدامها الصحيح، بما في ذلك العثور على الزاوية بين المستويات على الإنترنت عبر الإنترنت، الأمر الذي يتطلب أحيانًا قضاء الكثير من الوقت.

تقدم البوابة الرياضية "شكولكوفو". نهج جديدللتحضير لامتحان الدولة. ستساعد الفصول الدراسية الموجودة على موقعنا الطلاب على تحديد الأقسام الأكثر صعوبة لأنفسهم وسد الفجوات في المعرفة.

لقد قمنا بإعداد وتقديم جميع المواد اللازمة بشكل واضح. التعاريف الأساسيةويتم عرض الصيغ في قسم "المعلومات النظرية".

ومن أجل فهم المادة بشكل أفضل، نقترح أيضًا ممارسة التمارين المناسبة. مجموعة كبيرة من المهام بدرجات متفاوتةالتعقيد، على سبيل المثال، معروض في قسم "الكتالوج". تحتوي جميع المهام على خوارزمية مفصلة للعثور على الإجابة الصحيحة. يتم استكمال وتحديث قائمة التمارين الموجودة على الموقع باستمرار.

أثناء التدرب على حل المشكلات التي تتطلب إيجاد الزاوية بين مستويين، تتاح للطلاب الفرصة لحفظ أي مهمة عبر الإنترنت باعتبارها "المفضلة". بفضل هذا سيكونون قادرين على العودة إليه الكمية المطلوبةالوقت ومناقشة التقدم المحرز في قرارها مع معلم المدرسةأو المعلم.