Süsteem materiaalsed punktid nimetatakse nende hulka, milles iga punkti asukoht ja liikumine sõltub antud süsteemi kõikide punktide asukohast ja liikumisest. Materiaalsete punktide süsteemi nimetatakse sageli mehaaniliseks süsteemiks.
Materiaalsete punktide süsteemi massikese. Massikeskme raadiusvektori määramine. Massikeskme omadused. Massikeskme kiirus. Massikeskme liikumisvõrrandi tuletamine. Materiaalsete punktide süsteemi massikeskme koordinaatide jäävuse seadus.
massikese (või inertskese)
nimetatakse materiaalsete punktide süsteeme
Xia kujuteldav punkt C, asukoht
mis iseloomustab jaotust
selle süsteemi mass. Selle raadiuse vektor

Suletud süsteemi massikese kas liigub sirgjooneliselt ja ühtlaselt või jääb paigale.
Massi kiiruse kese
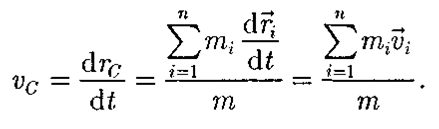
Pideva massijaotuse jaoks tihedusega r  . Kui süsteemi igale osakesele rakenduvad gravitatsioonijõud on suunatud üks viis, siis langeb massikese kokku raskuskeskmega. Aga kui mitte paralleelne, siis massikese ja raskuskese ei lange kokku.
. Kui süsteemi igale osakesele rakenduvad gravitatsioonijõud on suunatud üks viis, siis langeb massikese kokku raskuskeskmega. Aga kui mitte paralleelne, siis massikese ja raskuskese ei lange kokku.
Võttes ajatuletise , saame: 
need. täielik impulss süsteemid võrdne tootega selle mass massikeskme kiiruse järgi.
Asendades selle avaldise kogu impulsi muutumise seadusega, leiame: 
Süsteemi massikese liigub nagu osake, millesse on koondunud kogu süsteemi mass ja millele kantakse saadud mass välised tugevus
Kell progressiivne liigutada kõiki punkte tahke liikuda samamoodi nagu massikese (mööda samu trajektoore), seega kirjeldada edasi liikumine piisab massikeskme liikumisvõrrandi üleskirjutamisest ja lahendamisest.
Sest  , siis massikese suletud süsteem peab säilitama puhkeoleku või vormiriietuse sirgjooneline liikumine, st. =konst. Kuid samal ajal võib kogu süsteem pöörata, laiali lennata, plahvatada jne. tegevuse tulemusena sisemised jõud
.
, siis massikese suletud süsteem peab säilitama puhkeoleku või vormiriietuse sirgjooneline liikumine, st. =konst. Kuid samal ajal võib kogu süsteem pöörata, laiali lennata, plahvatada jne. tegevuse tulemusena sisemised jõud
.
Rс(t1) = Rc(t2) massikeskme koordinaatide jäävuse seadus
Potentsiaalsete (konservatiivsete) jõudude töö, kasutades näitena gravitatsiooni. Potentsiaalsete (konservatiivsete) jõuväljade määramine. Kontseptsiooni tutvustus potentsiaalne energia jõutöö kaudu. Jõu ja potentsiaalse energia suhe
Potentsiaalne jõud on jõud, mille töö sõltub ainult selle rakenduspunkti alg- ja lõppasendist ning ei sõltu ei trajektoori tüübist ega selle punkti liikumisseadusest. Konservatiivsed jõud on need jõud, mille töö mis tahes suletud teel on 0.
Potentsiaalne (konservatiivne) jõuväli: potentsiaal on väli, mille töö ühest välja punktist teise liikumisel ei sõltu trajektoori kujust. Potentsiaalseteks väljadeks on gravitatsiooniväli ja elektrostaatiline väli.
Potentsiaalsuse mõiste tutvustus. Energia läbi jõudude töö – Potentsiaalne energia – skalaar füüsiline kogus, iseloomustab teatud potentsiaalses jõuväljas paikneva keha (või materiaalse punkti) energiavaru, mida kasutatakse väljajõudude töö tõttu keha kineetilise energia omandamiseks (muutmiseks).
Jõu ja potentsiaalse energia suhe – iga punkt potentsiaalne väli vastab teatud kehale mõjuva jõu väärtusele ja teatud potentsiaalse energia väärtusele U. See tähendab, et jõu ja U vahel peab olema seos, seevastu dA = –dU,
Matemaatiliste punktide kogum, mille liikumine ja asukoht on ette määratud (näiteks jalgratas, päikesesüsteem).
Süsteemi mass on määratletud kui aritmeetiline summa süsteemi kaasatud punktide massid.
CMS on punkt, mille asukoht ruumis määratakse raadiusvektori abil.
2. Materiaalse punkti süsteemi välis- ja sisejõud. Sisejõudude omadused.
Sideme reaktsioonijõud jagunevad täpsustatud ja reaktsioonijõududeks.
Välisjõud (F e) on jõud, mis mõjuvad vaadeldava süsteemi kehadele kehadest, mis ei kuulu vaadeldavasse süsteemi.
Sisejõud (F i) on jõud, mis toimivad vaadeldavas süsteemis kehade vahel.
3. Materiaalse süsteemi sisejõudude töö.
Muutumatu süsteemi sisejõudude tehtud töö summa mis tahes liikumise korral on võrdne nulliga.
Olgu A ja B süsteemi kaks punkti.
RA ja R B – mooduli poolest võrdsed ja in
nende punktide vastastikuse jõu suund.
Liikumisel saavad punktid A ja B elementaarsed liigutused ds A ja ds B.
Jõudude toimejoontega risti olevatel liikumistel ds A II ja ds B II ei tekita jõud tööd. Kuna muutumatu süsteemi punktide A ja B vaheline kaugus tema liikumise ajal muutuda ei saa, peavad liikumised ds A I ja ds B I olema võrdsed ja suunatud samas suunas. Sellest järeldub.
4. Teoreem süsteemi massikeskme liikumise kohta. Massikeskme liikumise jäävuse seadus.
Kus c on massipunkti keskpunkt
A c – massikeskme kiirendus
M – kogu süsteemi mass
Massikeskme liikumise jäävuse seadus: kui summa, siis kehtib massikeskme liikumise jäävuse seadus.
=>
5. Jäiga keha translatsioonilise liikumise diferentsiaalvõrrand.
Translatsiooniline m*a c =∑F e i
a i =m i *V i mehhaansüsteemi liikumiste arv
m i – i-nda punkti mass
F e i – kõige tulemus välised jõud
Q i =m i *V i i-nda punkti liikumiste arv
Liidame kõik süsteemi võrrandid (1).
…………
________
∑Q i = ∑ (m i *V i)
Q=M*V c (3) kogu süsteemi liikumise hulk
M*r c = ∑(m i * r i) (2)
Diferentseerime võrrandit (2) aja suhtes:
M*v c =∑(m i * r i)
6. Materiaalse süsteemi impulsi muutumise teoreem.
Diferentsiaalne vorm
Integraalne vorm
kus on liikumise hulk mehaaniline süsteem lõpp- ja algasendis
Impulsside summa lõpp- ja lähteasendis
7. Kindla telje ümber pöörleva jäiga keha impulss.
Jäiga keha nurkimpulsi projektsiooni mis tahes keskpunkti suhtes seda keskpunkti läbivale teljele z nimetatakse keha nurkimpulssiks l z selle telje suhtes:
8. Materiaalse süsteemi nurkimpulsi muutumise teoreem.
(1) Kui summa (1)=0, siis L 0 =konst L 0 x =konst.
Punkti impulsi momendi l z ajatuletis mis tahes fikseeritud telje z suhtes on võrdne punktile sama telje suhtes mõjuva jõumomendiga F.
Järeldus punktist (1): kui punktile mõjuv jõumoment on mõnda aega mis tahes telje suhtes võrdne nulliga, siis jääb antud punkti nurkimpulss selle telje suhtes kogu selle aja konstantseks.
9. Keha inertsmomendi mõiste. Inertsiraadius.
Jäiga keha inertsmoment mis tahes telje z suhtes (teljeline inertsimoment) on skalaarsuurus, võrdne summaga, mis koosneb keha iga punkti massi m k korrutisest selle kauguse r k ruudust antud teljega.
Lõpmatult õhukese rõnga inertsmoment ( materjali ring) on tema pöörlemistelje suhtes võrdne tema massi korrutisega selle raadiuse ruuduga:
Keha inertsimomenti telje suhtes esitatakse keha massi korrutisena teatud segmendi pikkuse ruuduga, mida nimetatakse keha inertsiraadiuseks vastava telje suhtes:
Keha inertsiraadiuse järgi mis tahes telje suhtes saame mõista sellise lõpmata õhukese rõnga raadiust, millesse on vaja koondada kogu keha mass M, et saada rõnga inertsmoment. võrdne hetkega keha inerts selle telje suhtes.
10. Inertsmomendi suhteline paralleelsed teljed(Huygensi-Steini teoreem).
Keha inertsmoment mis tahes telje suhtes võrdne hetkega selle keha suhteline inerts kesktelg, paralleelselt antud teljega, mis liidetakse kehamassi ja nende telgede vahelise kauguse ruudu korrutisele.
Huygensi-Steini teoreem.
11. Homogeensete kehade aksiaalsed inertsmomendid: varras, õõnes- ja täissilindrid, kuul.
Konstantse ristlõikega õhukese sirge varda inertsimoment
Homogeense sirge peenikese varda inertsimoment kesksümmeetriatelje suhtes on võrdne 1/12 varda massi korrutisega selle pikkuse ruuduga.
Tahke aine inertsmoment
ümmargune silinder.
Homogeense tahke ringsilindri inertsmoment oma pöörlemistelje ümber võrdne poolega silindri massi ja selle raadiuse ruudu korrutis.
Õõnes ümmarguse silindri inertsimoment.
Homogeense õõnsa ümmarguse silindri inertsmoment selle pöörlemistelje suhtes on võrdne poolega silindri massi korrutisest selle välimise ja sisemise raadiuse ruutude summaga.
12. Jäiga keha pöörlemise dünaamiline võrrand ümber fikseeritud telje.
Keha pöörlemistelje suhtes inertsmomendi ja keha nurkkiirenduse korrutis on võrdne kõigi kehale mõjutavate välisjõudude peamomendiga sama telje suhtes.
Võrrandit (1) nimetatakse dünaamiliseks võrrandiks pöörlev liikumine tahke keha.
13. Materiaalse süsteemi kineetilise energia muutumise teoreem.
Mehaanilise süsteemi kineetilise energia muutus teatud nihke korral võrdub sellel nihkel süsteemi materiaalsetele punktidele mõjuvate välis- ja sisejõudude töö summaga.
Kus T on kineetiline energia aja viimasel hetkel
T 0 - kineetiline energia sisse algushetk aega
∑А i e +∑А i j – välis- ja sisejõudude töö summa
Seisukord: Alg- ja lõppasendid on nõutavad.
14. Materiaalse süsteemi kineetiline energia. Koenigi teoreem.
Mehaaniline süsteem on kehade kogum, mis on omavahel ühendatud erinevate ühendustega.
Iga keha asendid ja liigutused on vastastikku määratud. Mehaanilise süsteemi kineetiline energia on defineeritud kui süsteemi kaasatud i-nda keha kineetiliste energiate aritmeetiline summa.
Koenigi teoreem:
Mehaanilise süsteemi kineetiline energia on võrdne süsteemi massikeskme kineetilise energia summaga, mille mass on võrdne kogu süsteemi massiga, ja selle süsteemi kineetilise energia summaga. suhteline liikumine massikeskme suhtes.
15. Tahke keha kineetiline energia juures erinevad tüübid tema liigutusi.
Keha kineetiline energia määratakse sõltuvalt sellest, millist liigutust tehakse.
1) edasiliikumine
2) pöörlev liikumine
3) tasapinnaline paralleelne liikumine
16. Jäiga keha dünaamiline tasapinnaline paralleelne liikumine.
17. D'Alemberti põhimõte materiaalse punkti jaoks.
Kõigi punktile rakendatavate jõudude ja selle punkti inertsjõu geomeetriline summa on võrdne nulliga. , Kus
18. D'Alemberti põhimõte materiaalse süsteemi jaoks.
(i=1,2,…,n), kus on punktile rakendatud kindlaksmääratud jõudude resultant; -sellele punktile rakendatud sidemete reaktsioonide tulemus; -materiaalse punkti inertsjõud.
Võrrand näitab, et mittevaba mehaanilise süsteemi iga materiaalse punkti korral on määratud jõudude resultantide, ühenduste resultantreaktsiooni ja inertsiaaljõu geomeetriline summa igal ajahetkel nulliga.
19. Absoluutselt jäiga keha peavektor ja peamine inertsimoment.
Edasi liikumine
Peavektoriks on põhimoment, kus J z on keha inertsimoment pöörlemistelje suhtes, ε on keha nurkkiirenduse algebraline väärtus.
20. Mehaanilised ühendused, hoidvad ja mittekinnitavad ühendused, statsionaarsed ja mittestatsionaarsed, pea- ja mittepealised.
Ühendused on kehad, mis piiravad teise keha liikumisvabadust.
OA=l – painduv keerme – jäik ühendusvõrrand
Ühenduste klassifikatsioon:
1) pea – ühendused, mille võrrandid ei sisalda
koordinaatide diferentsiaalid.
2) mittepealised – seosed, mille võrrandid sisaldavad
koordinaatide diferentsiaalid.
Statsionaarne (mille võrrandid ei sisalda
parameeter t.)
Mittestatsionaarne (mille võrrandid sisaldavad
parameeter t.)
Säilitamine (võrrand määratakse
võrdsus).
Mittesäilitav (võrrand määratakse ebavõrdsusega).
21. Võimalikud liigutused.
Võimalik liikumine on keha liikumine, mida võimaldavad süsteemile peale pandud ühendused.
Punkti võimalikku liikumist tähistatakse tavaliselt sümboliga, erinevalt selle tegelikust elementaarsest liikumisest.
22. Elementaarne jõutöö võimalikule nihkele. Ideaalsed ühendused.
Ideaalsed ühendused on sellised ühendused, mille elementaarreaktsioonide summa süsteemi mis tahes võimalike punktide nihke korral on võrdne nulliga. Ideaalsed ühendused hõlmavad kõiki statsionaarseid ühendusi geomeetrilised ühendused ilma hõõrdumiseta.
Sile pind (reaktsioon on suunatud pinna suhtes normaalselt, sellise sideme liikumine on võimalik ainult puutujatasandil, st alati risti sideme reaktsiooni ja töö suunaga = 0)
Fikseeritud liigend (selle reaktsiooni rakenduspunkt
ühendus jääb liikumatuks olenemata sellest, kuidas süsteem liigub
ja reaktsiooni töö on null).
Liigutatav liigend, mis ühendab kahte keha (reaktsioon R 1 ja R 2
need kehad on üksteisega võrdsed ja on suunatud ühes suunas
otse vastasküljed, mis tahes algklasside jaoks
liigutades selle seose reaktsioonide rakenduspunkti, nende summat
algtöö on 0).
23. Võimalike liigutuste põhimõte. Lagrange'i põhimõte.
Süsteemi tasakaalustamiseks ideaalsed ühendused On vajalik ja piisav, et kõigi sellele rakendatud aktiivjõudude elementaartööde summa oleks võrdne nulliga süsteemi võimalikuks tasakaaluasendist välja nihutamiseks.
Põhieeldus: kõik nihked on lõpmata väikesed (δS, δφ).
Eeldatakse, et punktide liikumine on sirgjooneline.
24. D’Alembert – Lagrange’i põhimõte ( üldvõrrand dünaamiline süsteem).
Kõigi aktiivsete või antud jõudude elementaartööde summa ja kõigi inertsiaalsete jõudude elementaartööde summa on null.
Dünaamika üldvõrrand.
25. Üldkoordinaat, kiirus ja kiirendus.
Sõltumatuid suurusi, mille spetsifikatsioon määrab üheselt mehaanilise süsteemi kõigi punktide asukoha, nimetatakse selle süsteemi üldistatud koordinaatideks. Holonoomiliste süsteemide puhul on mehaanilise süsteemi sõltumatute üldistatud koordinaatide arv võrdne selle süsteemi vabadusastmete arvuga.
Üldistatud koordinaatide ajatuletisi nimetatakse üldistatud kiirusteks.
Üldistatud kiiruste ajatuletisi nimetatakse üldistatud kiirendusteks.
26. Üldised jõud ja nende arvutamise meetodid.
Nimetatakse üldistatud koordinaadile vastavat üldistatud jõudu skalaarne suurus, mille määrab seos põhitöö aktiivsed jõud mehaanilise süsteemi liikumise kohta, mis on põhjustatud koordinaadi elementaarsest juurdekasvust selle juurdekasvu väärtuseni.
Üldised jõud jagunevad üldistatud välis- ja sisejõududeks.
27. Mehaanilise süsteemi tasakaalutingimus üldistatud koordinaatides.
Mis tahes jõudude süsteemi jaoks on tasakaalutingimustel vorm
Konservatiivse jõudude süsteemi tasakaalutingimustel on vorm
28. Teist tüüpi Lagrange'i võrrand.
(j = 1, 2, …, s)
Need võrrandid on diferentsiaalvõrrandid teist järku süsteemi q 1, q 2, ..., q s üldistatud koordinaatide suhtes.
29. Potentsiaalses jõuväljas liikuv teist tüüpi Lagrange'i võrrand.
Kui materiaalne süsteem liigub potentsiaalses jõuväljas ainult väljajõudude mõjul (kõik süsteemile peale pandud ühendused on ideaalsed), siis saab üldistatud jõud määrata valemiga
Q i = - dP/dq i
Võtame arvesse funktsiooni L=T-P (kineetiline potentsiaal).
Seda funktsiooni nimetatakse Lagrange'i funktsiooniks. Seejärel asendage see teist tüüpi Lagrange'i võrrandiga:
süsteem s diff. võrrandid nn 2. tüüpi Lagrange'i võrrandid. Need võrrandid on esitatud. on erinevus. teist järku suhte võrrandid. üldistatud koordinaadid süsteemid, ..., Nende võrrandite integreerimine ja määramine alguse järgi. Tingimused pidevaks integratsiooniks saame s ekv. karusnaha liigutused süsteemid üldistatud koordinaatides:
30. Vaba vibratsioonühe massiga süsteem ühe vabadusastmega.
Vabade vibratsioonide diferentsiaalvõrrand.
Vaba võnkeperiood
Lasti liikumise võrrand
Vaba vibratsiooni sagedus
31. Sunnitud vibratsioon.
Taastavate ja häirivate jõudude samaaegsel toimel täidab materiaalne punkt kompleksi võnkuv liikumine, mis on vabade ja sunnitud võnkumised punktid.
Sundvõnkumised ei sõltu esialgsed tingimused punkti liikumine.
Madala sagedusega sundvõnkumiste võrrand.
Madala sagedusega võnkeamplituud
Kõrgsageduslike sundvõnkumiste võrrand
Kõrgsagedusliku võnke amplituud
Sundvõnkumiste amplituudi A B suhet η väärtusesse A 0 nimetatakse dünaamilisuse koefitsiendiks.
32. Kahe või enama vabadusastmega süsteemide võnkumised. Vabad ja loomulikud vibratsioonid.
Kutsutakse võnkumisi, mis vastavad ainult ühe üldistatud koordinaadi muutumisele. Omad. Vaba vibratsioon on nende endi lisamise tulemus. Ühe vabadusastmega süsteemidel on ainult üks vibratsioonisagedus. Seetõttu langevad nende jaoks vabad ja loomulikud vibratsioonid kokku. Kahe vabadusastme süsteemil on kaks sagedust loomulikud vibratsioonid. Samamoodi saab näidata, et n-vabadusastmega süsteemil on n-sagedused omavõnkumised, st. Vabadusastmete arv on võrdne sageduste arvuga.
33. Löögi nähtus punktides. Löögijõud ja löögiimpulss.
Löök on nähtus, mille puhul kehade vastasmõju tulemusena muutub nende kiirus väga lühikese aja jooksul lõplikult. Reeglina kaasneb lööknähtusega kokkupuutuvate kehade plastiline deformatsioon, mille tulemusena mehaaniline energia muundub soojusenergiaks. Seetõttu ei saa kehade mõju probleemide lahendamisel kasutada teoreemi kineetilise energia muutumise kohta. Nendel juhtudel rakendatakse teoreem impulsi ja nurkimpulsi muutumise kohta, mis on kirjutatud integraalvormis.
Lööginähtus on nähtus, mille puhul tühise aja jooksul muutuvad keha punktide kiirused lõplikult (pall lööb vastu seina jne).
Televisioonide arvu lõplik muutus. keha ebaoluliselt lühikese löögiaja jooksul tekib seetõttu, et löögi ajal tekkivate jõudude suurused on väga suured, mistõttu nende jõudude impulsid löögi ajal on lõplikud väärtused. Selliseid jõude nimetatakse. - kohene või šokk.
1) mittehetkeliste jõudude mõju löögi ajal võib tähelepanuta jätta.
2) liikuda mater. kokkupõrke ajal võib punkte eirata.
3) materjalile mõjuva löögijõu tulemus. punkt on väljendatud lõpliku muutusega kiirusvektori mõjul, mis on määratud võrrandiga - b
34. Teoreem materiaalse punkti impulsi muutumise kohta kokkupõrkel.
Mehaanilise süsteemi impulsi muutus löögi ajal on võrdne geomeetriline summa kõik välised šokiimpulsid, rakendatakse süsteemi punktidele.
(1)
Võrrand väljendab teoreemi karusnaha liigutuste arvu muutumise kohta. lööksüsteemid:
Karusnaha liigutuste arvu muutmine. süsteemid kokkupõrke ajal TO= kõigi väliste löögiimpulsside geomeetriline summa S süsteemi külge kinnitatud.
Liikumiste arv saab väljendada kogu süsteemi massina m ja süsteemi massikeskme kiirust ja valemite järgi
Asendame need võrrandid väärtusega (1) ja saame selle võrrandi, mis määrab massikeskme kiiruse muutuse kokkupõrkel.
Väliste löögiimpulsside puudumisel on meil:
Karusnahale tegutsedes. ainult sisemiste šokiimpulsside süsteem, süsteemi liikumise hulk ei muutu.
1. lehekülg
Kui me ei lahutaks, vaid liidaksime võrrandid (6.1), saaksime lihtsalt impulsi jäävuse seaduse
Seda saab puhtformaalselt ümber kirjutada ajas püsivuse seaduseks
mingi kiirus Vc:
Liigume kiirusega liikuva võrdlussüsteemi juurde (6.4). Kiirused
osakesed 1 ja 2 muunduvad järgmisel viisil:
st uues tugisüsteemis väljenduvad need suhtelise kiiruse kaudu
liigutused. Seome kiiruse Vc kindla punkti raadiusevektoriga r Koos:
Pange tähele, et definitsioon (6.6) langeb kokku definitsiooniga, mis on teada koolikursus
raskuskeskme füüsika mõiste. Tõestuseks liigume algusesse
punkti koordinaadid r Koos. Siis täiesti analoogselt (6.5) saame
Seega
(raskuskese määrab massi ja “õla” korrutiste võrdsus). Kuid definitsioonid (6.4) ja (6.6) on õigemad ja universaalsemad, kuna neid saab probleemideta üldistada suvalisele hulgale materiaalsetele punktidele ja seega
makroskoopilised kehad. Punkti C mehaanikas – ja üldse füüsikas – nimetatakse tavaliselt
materiaalsete punktide süsteemi massikese või inertskese.
Laske mõned sisse inertsiaalsüsteem Interakteeruvate materjalide punktide asukohakoordinaadid massidega m 1, m 2, ... m N määratakse igal ajahetkel t raadiusvektorite abil r 1(t), r 2 (t), ... r N(t)
(vt joonis 6.3 a). Siis on vaadeldava materiaalsete punktide süsteemi massikeseks selline punkt, mille raadiuse vektor R r 1(t), r 2 (t), ... r N (t) materjalipunktid vastavalt
Rõhutagem seda sisse üldine juhtum massikeskme asend ei lange kokku
süsteemi mis tahes materiaalse punkti asukoht (vt joonis 6.3 b),
kuigi mõnikord võib see juhtuda.

Riis. 6.3, on materiaalsete punktide süsteemi massikeseks selline punkt, mille raadiuse vektor R c(t) väljendatakse raadiusvektorites r 1(t), r 2 (t), ... r N(t) materiaalseid punkte
Eristame võrdsuse (6.7) vasakut ja paremat poolt aja suhtes.
Raadiusvektori tuletis aja suhtes on definitsiooni järgi kiirus, seega
mida me selle tulemusena saame
kus Vc on massikeskme kiirus, v 1, v 2,... v N on materiaalsete punktide kiirused. Suurus m 1 v 1 in (6.8) on esimese materiaalse punkti impulss, m 2 V 2 on teise punkti impulss ja
jne. Seega on avaldise (6.8) lokkis sulgudes vaadeldava materiaalsete punktide süsteemi impulsside summa, st kogu süsteemi impulss P. Järelikult saab võrdsuse (6.8) vormis ümber kirjutada
P = (m 1 + m 2 + .... + m N )V c. (6.9)
Võrdlusraamistikus, kus massikese on puhkeasendis,
Kui meid ei huvita materiaalsete punktide suhteline liikumine, vaid meid huvitab kogu süsteemi liikumine, siis võib kogu süsteemi vaadelda kui üht materiaalset punkti, mis liigub kiirusega Vc ja millel on impulss P. Tuletame meelde, et mass Materiaalne punkt on definitsiooni järgi impulsi ja kiiruse vaheline proportsionaalsustegur. Seetõttu võrduse (6.9) proportsionaalsuskoefitsient, mis on suletud sulgudes, on vaadeldava süsteemi mass M:
M = m 1 + m 2 + …. + m N , (6,10)
see tähendab, et materiaalsete punktide süsteemi mass on võrdne nende punktide masside summaga. Seos (6.10), mille järgi mass keeruline keha võrdne selle osade masside summaga, tundub meile tuttav ja ilmne. Kuid nagu hiljem näeme, on relativistlikus mehaanikas (s.o üldisemal juhul) olukord hoopis teistsugune. Newtoni mehaanika piiraval juhul on võrdsus (6.10). erijuhtum teatud
füüsiline seadus- massi jäävuse seadus.
Väliste jõudude puudumisel, s.o suletud süsteemi korral, ei sõltu süsteemi kõigi kehade impulsside summa ajast; siis (6.9) järgneb materiaalsete punktide suletud süsteemi massikeskme liikumise oluline omadus:
st. materiaalsete punktide suletud süsteemi massikese on liikumatu või
liigub ühtlaselt ja lineaarselt, kuigi iga materiaalne punkt võib toimida keeruline liikumine. Ülaltoodud väidet nimetatakse mõnikord massikeskme liikumise teoreemiks.
Nüüd tõestame kineetilise energia järgmist olulist omadust:
materiaalsete punktide süsteemi kineetiline energia T võrdub kogu selle massikeskmesse vaimselt koondunud ja sellega koos liikuva süsteemi massi kineetilise energia ja sama süsteemi kineetilise energia T summaga selle süsteemis. suhteline liikumine võrdlussüsteemi suhtes, mis liigub koos massikeskmega:
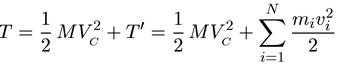
kus M = m 1 + m 2 + ... + m N. Vc on massikeskme kiirus algses võrdlusraamis, v i on i-nda materjali punkti kiirus võrdlusraami suhtes, mis liigub koos punktiga C. Sellist süsteemi nimetatakse tavaliselt massikeskme süsteemiks. , "inertsikeskus" või lihtsalt "c-süsteem" . (Referentssüsteemi, milles probleem püstitatakse, kui see süsteem ei kattu c-süsteemiga, nimetatakse tavaliselt laboratoorseks referentssüsteemiks või l-süsteemiks).
Selle tõestamiseks saame esmalt üldisema seose, mis ühendab kineetilist energiat kahes võrdlussüsteemis (vt joonis 6.4). Vana süsteemi R i, V i ja uue süsteemi r i, v i punktide koordinaatide ja kiiruste jaoks kirjutame üles Galilei teisendused:
kus R on vanast süsteemist uude ülemineku raadiuse vektor ja V on vastavalt uue süsteemi liikumiskiirus vana süsteemi suhtes.
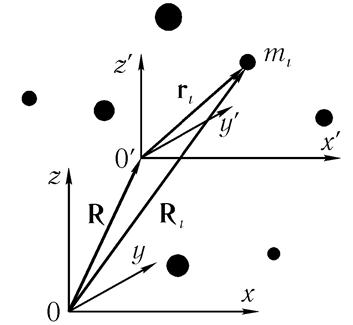
Riis. 6.4 koordinaatide ühendamine kahes referentssüsteemis
Siis saab kineetilist energiat vanas võrdlusraamistikus esitada kui
 (6.12)
(6.12)
(6.12) paremat poolt saab esitada kolme summana:
kus P on materiaalsete punktide süsteemi koguimpulss uues võrdlusraamis. Seost (6.13) nimetatakse tavaliselt Koenigi teoreemiks. Kui uus süsteem langeb kokku q-süsteemiga, siis kogumoment selles on null, V = Vc, mis tähendab, et seos (6.11) kehtib.
Selle lõigu lõpetuseks märgime kahte olulised omadused, mis tuleneb massikeskme määratlusest. Esiteks saab punktis (6.7) olevad osakesed ühendada mis tahes rühmadesse, näiteks:
Siit, nagu on lihtne mõista, järeldub, et mis tahes makroskoopiliste kehade süsteemi massikeskpunkti võib leida materiaalsete punktide süsteemi massikeskmena, eeldusel, et iga keha mass on koondunud sellesse oma massikese.
Ja teiseks, summeerimisest punktis (6.7) on lihtne üle minna integreerimisele,
kui arvutame pideva ainetiheduse ρ(t) jaotusega keha massikeskme asukoha:

