Bare noget kompliceret: komplekse tal. Mulighed for at bruge komplekse tal i et matematikkursus i gymnasiet

Tekstdel af publikationen

Indhold
Indledning………………………………………………………………………………………..3 Kapitel I. Fra historien komplekse tal…………………………………………………………4 Kapitel II. Grundlæggende om metoden med komplekse tal…………………………………………6 Kapitel III. Geometri af en trekant i komplekse tal………………………………12 Kapitel IV. Løsning Unified State Exam problemer og forskellige olympiader ved hjælp af metoden med komplekse tal…………………………………………………………………………....20 Konklusion………………………………… ………………………………………………….24 Bibliografi………………………………………………………………………..25

Introduktion
Den store betydning af komplekse tal i matematik og dens anvendelser er almindeligt kendt. Algebraen af ​​komplekse tal kan med succes bruges i elementær geometri, trigonometri, teorien om bevægelser og ligheder, såvel som i elektroteknik, forskellige mekaniske og fysiske problemer. I planimetri giver metoden med komplekse tal dig mulighed for at løse problemer ved direkte beregning ved hjælp af færdige formler. Dette er enkelheden ved denne metode sammenlignet med vektor og koordinere metoder, ved metoden med geometriske transformationer, hvilket kræver, at eleverne har betydelig intelligens og lange søgninger. I flere årtusinder har trekanten været et symbol på geometri. Du kan endda sige, at en trekant er et atom med geometri. Enhver polygon kan opdeles i trekanter, og undersøgelsen af ​​dens egenskaber kommer ned til at studere egenskaberne for trekanter af dens komponenter. Lad os se på, hvordan metoden med komplekse tal fungerer, når man beviser egenskaberne for en trekant fra skoleforløb planimetri, samt til at løse problemer C-4 i Unified State Exam. 2

Kapitel I. Fra historien om komplekse tal,,
For første gang blev tilsyneladende imaginære mængder nævnt i det berømte værk "Great Art, or About. algebraiske regler»Cardano (1545), som en del af en formel løsning på problemet med at beregne to tal, der lægger sammen til 10, og når ganget giver 40. Til denne opgave fik han en andengradsligning for et af vilkårene og fandt dens rødder: 5 + √ − 15 og 5 − √ − 15 . I en kommentar til beslutningen skrev han: "disse de mest komplekse mængder ubrugelige, selv om de er meget smarte" og "Aritmetiske overvejelser bliver mere og mere uhåndgribelige og når en grænse så subtil som den er ubrugelig." Muligheden for at bruge imaginære størrelser ved løsning af en kubisk ligning, i det såkaldte irreducible tilfælde (når polynomiets reelle rødder udtrykkes gennem terningrødder af imaginære mængder), blev først beskrevet af Bombelli (1572). Han var den første til at beskrive reglerne for addition, subtraktion, multiplikation og division af komplekse tal, men betragtede dem stadig som en ubrugelig og snedig "opfindelse". Udtryk, der er repræsenteret i formen a + b √ − 1, der opstår ved løsning af kvadratisk og kubiske ligninger, begyndte at blive kaldt "imaginær" i XVI-XVII århundreder på foranledning af Descartes, som kaldte dem det, og forkastede deres virkelighed, og for mange andre store videnskabsmænd XVIIårhundreder, virkede naturen og retten til eksistensen af ​​imaginære mængder meget tvivlsom, ligesom de anså for tvivlsom på det tidspunkt irrationelle tal og endda negative værdier. På trods af dette ansøgte matematikere modigt formelle metoder algebraer af reelle størrelser og til komplekse, opnåede korrekte reelle resultater selv fra mellemliggende komplekse, og dette kunne ikke andet end at begynde at indgyde tillid. I lang tid var det uklart, om alle operationer på komplekse tal fører til komplekse eller reelle resultater, eller om for eksempel at udtrække en rod kunne føre til opdagelsen af ​​en anden ny type tal. Problemet med at udtrykke rødder af grad n fra givet nummer blev løst i værker af Moivre (1707) og Cotes (1722). Symbolet for at betegne den imaginære enhed blev foreslået af Euler (1777, udgivet 1794), som tog det første bogstav i det latinske ord for dette. imaginarius - imaginær. Han udvidede også alle standardfunktioner, inklusive logaritmen, til det komplekse domæne. Euler udtrykte også ideen i 1751, at feltet for komplekse tal er algebraisk lukket. D'Alembert (1747) kom til samme konklusion, men det første strenge bevis for dette faktum tilhører Gauss (1799). Det var Gauss, der opfandt udtrykket "komplekst tal" til udbredt brug i 1831, selvom udtrykket tidligere var blevet brugt i samme betydning af den franske matematiker Lazare Carnot i 1803. 3
Den aritmetiske (standard) model af komplekse tal som par af reelle tal blev konstrueret af Hamilton (1837); dette beviste konsistensen af ​​deres egenskaber. Meget tidligere, i 1685, i sit værk "Algebra", viste Wallis (England), at komplekse rødder en andengradsligning med reelle koefficienter kan repræsenteres geometrisk ved punkter på en plan. Men det gik ubemærket hen. Næste gang dukkede en geometrisk fortolkning af komplekse tal og operationer på dem op i Wessel's arbejde (1799). Den moderne geometriske repræsentation, undertiden kaldet "Argand-diagrammet", kom i brug efter udgivelsen af ​​J. R. Argands værk i 1806 og 1814, som uafhængigt gentog Wessels konklusioner. Udtrykkene "modul", "argument" og "konjugeret antal" blev introduceret af Cauchy. Således blev det opdaget, at komplekse tal også egner sig til ren udførelse. algebraiske operationer addition, subtraktion, multiplikation og division af vektorer på planet, hvilket i høj grad ændrede vektoralgebra. 4

Kapitel II. Grundlæggende om den komplekse talmetode
[ 1 ]
,
[2], [3] [4] Geometrisk fortolkning af komplekse tal Længde af et segment Givet en rektangulær Kartesisk system koordinater på planen, kan det komplekse tal z = x+iy (i 2 = -1) være en-til-en knyttet til punktet M i planen med koordinaterne x, y (fig. 1): z = x + iy ↔M (x, y) ↔M (z) . Tallet z kaldes så den komplekse koordinat af punktet M. Da det euklidiske plans punkter er i en-til-en overensstemmelse med mængden af ​​komplekse tal, kaldes denne plan også for de komplekse tals plan. Oprindelsen O for det kartesiske koordinatsystem kaldes begyndelses- eller nulpunktet af planet af komplekse tal. Når = 0, er tallet z reelt. Reelle tal er repræsenteret ved punkter på x-aksen, hvorfor det kaldes den reelle akse. Ved x=0 er tallet z rent imaginært: z=iy. Imaginære tal er repræsenteret ved punkter på y-aksen, hvorfor det kaldes den imaginære akse. Nul er både et reelt og rent imaginært tal. Afstanden fra begyndelsen af ​​O-planet til punktet M(z) kaldes modulet af det komplekse tal z og betegnes med |z| eller r: | z | = r = | OM | = √ x 2 + y 2 Hvis φ er den orienterede vinkel dannet af vektoren ⃗ OM med x-aksen, så ved definition af sinus- og cosinusfunktionen sin φ = y r, cos φ = x r 5
hvorfra x = r cos φ, y = r sin φ, og derfor z = r (cos φ + sin φ). Denne repræsentation af et komplekst tal z kaldes dens
trigonometri

cheskoe
form. Den oprindelige repræsentation z=x+iy kaldes
algebraisk
form af dette nummer. På trigonometrisk repræsentation vinklen  kaldes argumentet for et komplekst tal og betegnes også med arg z: φ = arg z Hvis der er givet et komplekst tal z = x + iy, så kaldes tallet ´ z = x − iy
komplekst konjugat
(eller simpelthen
konjugat
) til dette nummer z. Så er tallet z naturligvis også konjugeret med tallet ´ z. Punkterne M(z) og M 1 (´ z) er symmetriske om x-aksen Af ligheden z = ´ z følger, at y = 0 og omvendt. Det betyder at
et tal lig med

til dets konjugat er ægte og omvendt.
Punkter med komplekse koordinater z og -z er symmetriske i forhold til startpunktet O. Punkter med komplekse koordinater z og − ´z er symmetriske i forhold til y-aksen. Af ligheden z = ´ z følger det, at x = 0 og omvendt. Derfor er betingelsen z =− ´ z et kriterium for et rent imaginært tal. For ethvert tal z, naturligvis | z | = | ´z | =¿− z ∨¿∨−´ z ∨¿ .
Sum og produkt
to konjugerede komplekse tal er reelle tal: z + ´ z = 2 z, z ´ z = x 2 + y 2 =¿ z 2 ∨¿. Et tal konjugeret til en sum, et produkt eller en kvotient af kompleks 6
tal er henholdsvis summen, produktet eller kvotienten af ​​tal konjugeret til givne komplekse tal: ´ z 1 + z 2 = ´ z 1 + ´ z 2 ; ´ z 1 z 2 = ´ z 1 ´ z 2 ; ´ z 1: z 2 = ´ z 1: ´ z 2 Disse ligheder kan let verificeres ved hjælp af formler for operationer på komplekse tal. Hvis a og b er de komplekse koordinater for henholdsvis punkt A og B, så er tallet c = a + b koordinaten for punkt C, således at ⃗ OC = ⃗ OA + ⃗ OB (fig. 3). Et komplekst tal d = a − b svarer til et punkt D, således at ⃗ OD = ⃗ OA − ⃗ OB . Afstanden mellem punkt A og B er | ⃗BA | = | ⃗ OD | =¿ a − b ∨¿: ¿ AB ∨¿∨ a − b ∨¿ (1) Da ¿ z ∨ 2 = z ´ z , så ¿ AB ∨ 2 =(a − b) (´ a − ´ b) . (2)
Ligningen
z ´ z = r 2
definerer en cirkel med centrum

Om radius

r.
Relationen AC CB = λ, (λ ≠ − 1), hvori punkt C deler sig dette segment AB, udtrykkes gennem de komplekse koordinater for disse punkter som følger: λ = c − a b − c, λ = ´ λ, hvorfra c = a + λb 1 + λ (3) For λ = 1 er punkt C midtpunktet af segmentet AB og omvendt. Så: c = 1 2 (a + b) (4) Multiplikation af komplekse tal Multiplikation af komplekse tal udføres efter formlen, Det vil sige | a b | = | en || b | , og 7
Parallelisme og perpendikularitet Kollinearitet af tre punkter Lad punkterne A(a) og B(b) være givet på planet af komplekse tal. Vektorerne ⃗ OA og ⃗ OB er co-dirigeret, hvis og kun hvis arg a = arg b, dvs. når arg a – arg b=arg a b =0 (når der divideres komplekse tal, trækkes divisors argument fra argumentet for udbytte). Det er også indlysende, at disse vektorer er rettet i modsatte retninger, hvis og kun hvis arg a - arg b= arg a b = ± π. Komplekse tal med argumenterne 0, π, - π er reelle.
Kolinearitetskriterium for punkt O, A, B:
For at punkterne A(a) og B(b) skal være kollineære med startpunktet O, er det nødvendigt og tilstrækkeligt, at kvotienten a b er et reelt tal, dvs. a b = ´ a ´ b eller a ´ b = ´ a b (6 ) Tag nu punkterne A(a), B(b), C(c), D(d). Vektorer ⃗ BA og ⃗ DC collie er ikke-ære, hvis og kun hvis punkterne defineret ved kompleks numrene a-b og с-d, er kolineære med begyndelsen O. Bemærk: 1. Baseret på (6) har vi: ⃗ AB ∨¿ ⃗ CD↔ (a − b) (´ c − ´ d) =(´ a − ´ b ) (c - d); (8) 2. Hvis punkterne A, B, C, D hører til enhedscirklen z ´ z = 1, så er ´ a = 1 a; 'b = 1 b; 'c = 1 c; ´ d = 1 d og derfor har betingelse (8) formen: ⃗ AB ∨¿ ⃗ CD↔ ab = cd ; (9) 3. Kollineariteten af ​​punkterne A, B, C er karakteriseret ved kollineariteten af ​​vektorerne ⃗AB og ⃗AC. Ved hjælp af (8) får vi: (a − b) (´ a −´ c) =(´ a − ´ b) (a − c) (10) Dette er kriteriet for, at punkterne A, B, C hører til til samme lige linje. Det kan repræsenteres i den symmetriske form a (´ b −´ c) + b (´ c −´ a) + c (´ a − ´ b) = 0 (11) 8
Hvis punkterne A og B hører til enhedscirklen z ´ z = 1, så er ´ a = 1 a; ´ b = 1 b og derfor transformeres hver af relationerne (10) og (11) (efter reduktion med (a-b) til følgende: c + ab ´ c = a + b (12) Punkterne A og B er faste, og punktet Vi vil betragte C som en variabel, der omdesigner dens koordinat til z. Så vil hver af de opnåede relationer (10), (11), (12) være en ligning for den rette linje AB: (´ a − ´ b). z + (b − a) ´ z + a ´ b − b ´ a = 0 , (10a) z + ab ´ z = a + b (12a) Især den direkte OA har ligningen a ´ z = ´ a z er rent imaginære Derfor er OA ⊥ OB↔ a b = − ´ a ´ b eller OA ⊥ OB↔a ´ b + ´ a b = 0 (13) Vinkelværdien af ​​segmenterne AB og CD bestemmes af ligheden (a. − b) (´ c − ´ d) + (´ a − ´ b) (c − d) = 0 (14) Især når punkterne A, B, C, D hører til enhedscirklen z ´ z = 1 , så simplificeres afhængighed (14): ab + cd = 0 (15) Det skalære produkt af vektorer udtrykkes. skalært produkt vektorer ⃗ OA og ⃗ OB gennem de komplekse koordinater a og b for punkt A og B. Lad a=x 1 +iy 1, b=x 2 +iy 2 . Derefter a b + a b=(x 1 +iy 1)(x 2 −iy 2)+(x 1 −iy 1)(x 2 +iy 2)=2(x 1 x 2 +y 1 y 2)= 2 ⃗ OA∙⃗OB. Så ⃗ OA ∙ ⃗ OB = 1 2 (a b + ab) (16) 9
Lad nu fire blive givet vilkårlige punkter A(a), B(b), C(c), D(d) ved deres komplekse koordinater. Så 2 ⃗ AB ∙ ⃗ CB = 1 2 (a-b)(c - d)+(a - b)(c-d) (17) Vinkler Lad os blive enige om at betegne den positivt orienterede vinkel med symbolet ∠ (AB ,CD) hvor vektoren ⃗ skal drejes AB, så den bliver co-dirigeret med vektoren ⃗ CD. Derefter, cos ∠ (AB, CD)= (d − c) (´ b − ´ a) +(´ d −´ c)(b − a) 2 | d − c || b − a | (18) sin ∠ (AB ,CD)= (d − c) (´ b −´ a) +(´ d −´ c)(b − a) 2 i | d − c || b − a | (19) Skæringspunkt for sekanter til en cirkel Hvis punkterne A, B, C og D ligger på cirklen z ´ z = 1, så findes den komplekse koordinat for skæringspunktet ved formlen ´ z = (a + b) − (c + d) ab − cd (20) Hvis AB er vinkelret på CD, så er z= 1 2 (a+b+c+d) (21) Skæringspunkt for tangenterne til cirklen 10
Den komplekse koordinat for skæringspunktet for tangenterne til cirklen z ´ z =1 i punkterne A(a) og B(b) findes ved formlen z= 2ab a + b (22) Ortogonal projektion af et punkt på en ret linje Ortogonal projektion af et punkt M(m) på en ret linje AB, hvor A(a) og B(b) findes ved formlen I det tilfælde hvor A og B hører til enhedscirklen z= 1 2 (a + b + m - cb m).
Kapitel III.

Trekantgeometri i komplekse tal
På planet af komplekse tal er en trekant defineret af tre komplekse tal, der svarer til dens hjørner. Centroid og orthocenter af en trekant. [ 2 ] Det er kendt, at for tyngdepunktet G (skæringspunktet for medianerne) af trekanten ABC og ethvert punkt O er følgende lighed sand: ⃗ OG = 1 3 (⃗ OA + ⃗ OB + ⃗ OC). Derfor beregnes den komplekse koordinat g for tyngdepunktet G ved formlen g = 1 3 (a + b + c) (23) Lad os udtrykke h den komplekse koordinat for orthocentret H i trekanten ABC gennem koordinaterne a, b, c af dets hjørner. Lad linjerne AH, BH, CH skære trekantens omskrevne cirkel i henholdsvis punkterne A1, B1, C1. Lad denne cirkel have ligningen z ´ z =1, så har vi ifølge (15): a 1 = − bc a , b 1 = − ca b , c 1 = − ab c Ved formel (20) h = (a + a 1 ) −(b + b 1) a a 1 − bb 1 = ab + bc + ca abc = 1 a + 1 b + 1 c 11
Hvor h=a+b+c kommer fra. (24) Det resulterende udtryk inkluderer koordinaterne for trekantens hjørner symmetrisk, derfor passerer trekantens tredje højde gennem skæringspunktet for de to første Lignende trekanter [2,1] trekanter ABC og A 1 B 1 C 1 er ens og identisk orienterede (lighed af den første slags), hvis B 1 =kAB, A 1 B 1 =kAC og vinkler B 1 A 1 C 1 og BAC er ens (vinkler er orienteret). Ved hjælp af komplekse tal kan disse ligheder skrives som følger: |a 1 −b 1 |=k|a−b|, |a 1 −c 1 |=k|a−c|,arg c 1 − a 1 b 1 − a 1 =arg c − a b − a . De to ligheder svarer til én med 1 − a 1 c − a = b 1 − a 1 b − a = σ , (25) hvor σ er et komplekst tal, |σ|=k-lighedskoefficient. Hvis σ er reel, så er c 1 − a 1 c − a = ´ c 1 − ´ a 1 ´ c − ´ a , hvor AC║A 1 C 1. Følgelig er trekanter ABC og A 1 B 1 C 1 homotetiske. Relation (25) er nødvendig og tilstrækkelig stand således at trekanter ABC og A 1 B 1 C 1 er ens og lige orienterede. Det kan gives en symmetrisk form ab 1 +bc 1 +ca 1 =ba 1 +cb 1 +ac 1 (25a) Lige trekanter Hvis | σ | = 1, så er trekanter ABC og A 1 B 1 C 1 lige store. Så er relation (25) et tegn på lighed af identisk orienterede trekanter, og relation (26) er et tegn på lighed af modsat orienterede trekanter. Regelmæssige trekanter Hvis du kræver, at en orienteret trekant ABC lignede orienteret trekant BCA, så vil trekant ABC være regulær. 12
Derfor får vi fra (25) en nødvendig og tilstrækkelig betingelse for, at trekant ABC er regulær (a−b) 2 +(b−c) 2 +(c−a) 2 =0 (27) Trekantens areal (bevist af forfatteren) Vi udleder formel for arealet S af en positivt orienteret trekant ABC: S = 1 2 | AB || AC | sin ∠ (AB , AC)= 1 4i ((c − a) (´ b − ´ a) − (b − a) (´ c − ´ a)) = − 1 4i (a (´ b − ´ c) + b (´ c − ´ a) + c (´ a − ´ b)) eller S = i 4 (a (´ b − ´ c) + b (´ c − ´ a) + c (´ a − ´ b )) (28) Hvis trekant ABC indskrevet i cirklen z ´ z = 1, så transformeres formlen (28) til formen: S = i 4 (a − b)(b − c)(c − a) abc (29) Sætning om midtlinjen af ​​en trekant (bevist af forfatteren)
Sætning
. midterste linje af trekanten er parallel med grundfladen og lig med halvdelen af ​​den. Bevis. Lad punkterne M og N være midtpunkterne på siderne AB og BC, så er m = b 2 ; n = b + c2. Da z 2 =z ´ z, så er MN 2 =(m-n)(´ m - ´ n)=(b 2 - b + c 2)(´ b 2 – ´ b + ´ c 2)= b ´ b 4 − b ´ b + b ´ c 4 − b ´ b + ´ b c 4 + b ´ b + b ´ c + ´ b c + c ´ c 4 = c ´ c 4 13
4MN2 =c ´c, AC 2 =(c-0)(c-0)=c ´c, derfor er 4MN2 = AC 2 eller 2MN=AC Betingelse (8) for vektorerne MN og AC opfyldt , og derfor MN ║AC. Thales' sætning (bevist af forfatteren)
Sætning
. Hvis parallelle linjer på den ene side af en vinkel skærer lige store segmenter af, så skærer de lige store segmenter af på den anden side af vinklen. Bevis Lad os antage, at c=kb. Så hvis BD||CE, så har vi (b-d)(´ c − 2 ´ d ¿= (´ b − ´ d) (c − 2d) Åbning af parenteserne og bringe lignende vilkår, får vi ligningen b ´ c − 2 b ´ d −´ c d = ´ b c − 2 ´ b d − c ´ d Ved at erstatte c med kb og ´ c med k ´ b , får vi bk ´ b -2b ´ d -dk ´ b = ´ b kb-2 ´ b d-kb ´ d . Hvis man bringer lignende udtryk igen og flytter alt til den ene side, får vi 2b ´ d + dk ´ b − 2 ´ b d − kb ´ d =0. Vi tager den ud fælles multiplikator og vi får 2(b ´ d − ´ b d ¿+ k (´ b d − b ´ d) = 0. Derfor k=2, dvs. c=2b. På samme måde er det bevist, at f=3b osv. Pythagoras sætning ( bevist af forfatteren) B retvinklet trekant kvadratet af hypotenusen lig med summen firkantede ben 14
Bevis. Afstanden mellem punkt B og C er lig med BC=|b-c|=b, BC 2 =b ´ b. Siden |z| 2 = z ´ z , så AC 2 =(a-c)(c ´ a − ´ ¿ ¿=(a − 0) (´ a - 0)=a ´ a . AB 2 =(a-b)(´ a − ´ b) ¿= a ´ a − a ´ b - ´ a b+b ´ b. Da b er et reelt tal, dvs. b= ´ b , så er -a ´ b =− ab , så a = - ´ a, det vil sige - ´ ab = ab Således er AB 2 = a ´ a -a ´ b - ´ ab +b ´ b = a ´ a +b ´ b = AC 2 +BC 2. Sætningen er bevist ret linje (bevist af forfatteren) Lad os bevise, at trekantens ortocenter, tyngdepunkt og omkredscenter ligger på den samme rette linje (denne rette linje kaldes Eulers rette linje), og OG = 1/2GH 15.
Bevis: Punkt G(g) er tyngdepunktet i trekanten ABC, H(h) er orthocenteret, og O(o) er midten af ​​trekantens omskrevne cirkel. For at disse punkter kan være kollineære, skal lighed (10) være opfyldt: (g-о)(´ g - ´ h ¿ -(´ g − ´ o ¿ (g − h) =0 Lad os tage punkt O som oprindelsen, derefter g(´ g - ´ h ¿ - ´ g (g − h) =g 2 -g ´ h −¿ (g 2 - h ´ g ¿ =-g ´ h + h ´ g (30) komplekse koordinater for ortocentret beregnes i henhold til formel (24) h=a+b+c, (30a) og tyngdepunktet i henhold til formel (23) g = 1 3 (a + b + c) (30c) Erstat til ( 30), får vi 1 3 (a+b +c)(´ a + b + c)-(a+b+c)(´ a + b + c 1 3 ¿))=0 Ligestilling (10) er opfyldt, derfor ligger tyngdepunktet, ortocentret og midten af ​​den omskrevne trekant på samme linje OG=g= 1 3 (a+b+c) GH=h-g=a+b+c- 1 3 (a. +b+c)= 2 3 (a+b+c) Vi fik, at OG= 1 2 GH Sætningen er bevist 16.
Eulers cirkel (ni punkts cirkel). Bevist af forfatteren Overvej trekant ABC. Lad os blive enige om, at‌ | OA | = | OB | = | OC | =1, dvs. alle hjørner i trekanten hører til enhedscirklen z ´ z = 1 (midten af ​​den omskårne cirkel O er origo, og radius er længdeenheden). Lad os bevise, at baserne for de tre højder af en vilkårlig trekant, midtpunkterne på dens tre sider og midtpunkterne af de tre segmenter, der forbinder dens toppunkter med ortocentret, ligger på den samme cirkel, og dens centrum er midtpunktet af segmentet OH , hvor H, husker, er orthocenteret af trekanten ABC. Sådan en cirkel kaldes
Euler cirkel
. Lad punkterne K, L og M være midtpunkterne på siderne af trekanten ABC, punkterne Q, N, P grundene for dens højder, punkterne F, E, D midtpunkterne af tre segmenter, der forbinder dens toppunkter med ortocentret. Lad os bevise, at punkterne D, E, F, K, L, M, N, P, Q tilhører den samme cirkel. Tildel de tilsvarende komplekse koordinater til punkterne: k = a + b 2 , l = b + c 2 ; m = a + c2,o1 = h2 = a + b + c2d = 2a + b + c2; e = 2c + a + b2; f = 2 b + a + c 2 n = 1 2 (a + b + c − ab c), q = 1 2 (a + c + b − ac b), p = 1 2 (c + b + a − cb a) O 1 K = | o 1 − k | = | c 2 | ,O1L = | o 1 − l | = | en 2 | 01M = | o 1 − m | = | b 2 | O1D = | o 1 − d | = | en 2 | ,OiE = | o 1 − e | = | c 2 | ,O1F = | o 1 − f | = | b 2 | O1N= | o 1 − n | = 1 2 | ab c | = 1 2 | en || b | | c | 01Q= 12 | en || c | | b | 01F= 12 | b || c | | en | . 17
Fordi trekant ABC er indskrevet i cirklen z ´ z = 1, derefter | en | = | b | = | c | = 1,→ | en 2 | = | b 2 | = | c 2 | = 1 2 | en || b | | c | = 1 2 | en || c | | b | = 1 2 | b || c | | en | = 1 2 Altså, punkterne D, E, F, K, L, M, N, Q, F tilhører samme cirkel Gauss' sætning Hvis en linje skærer linjerne, der indeholder siderne BC, CA, AB i henholdsvis trekant ABC, kl. punkterne A 1, B 1 , C 1, så er midtpunkterne af segmenterne AA 1, BB 1, СС 1 kollineære. Ved hjælp af (11) skriver vi betingelserne for kollineariteten af ​​tripletter af punkterne AB 1 C, CA 1 B, BC 1 A, A 1 B 1 C 1: 0,) b - a (c) a - c () c - b (a 0 ,) c - b a() b - a () a - c b(0,) a - c b() c - b () b - a c(0,) b - a (c) a - c () c - b a (1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1              s i midten af ​​M c a b (3, P er midtpunktet af M a b (3) segmenterne AA 1, BB 1, CC 1, så skal vi vise, at 0) () () (      n m p m p n p n m (32) Siden), (2 1), (2 1), (2 1 1 1 1 c c p b b n a a m       så svarer ligheden, der bliver bevist (31), til dette: 0))(())(())((1 1 1 1 1 1 1 1 1                b b a c c a c c b b c c b b a a eller efter multiplikation: 0) () () () () () () () () () () () (1 1 1 1 1) 1 1 1 1 1 1 1                                                b a med b a c b a c a c b a med b a c b a c b c b a c b a c b a c a (33) Nu er det let at se, at ( 33) opnås ved termisk tilføjelse af ligheder (31) Beviset er fuldstændigt

Kapitel IV.

Løsning af USE-problemer og forskellige olympiader ved hjælp af den komplekse talmetode.
Opgave 1. Unified State Examination -2012, P-4 På en linje, der indeholder medianen AD af en retvinklet ABC med ret vinkel C, tages et punkt E, fjernt fra toppunktet A i en afstand lig med 4. Find arealet af trekant BCE hvis BC=6, AC=4. Første løsning. Ifølge Pythagoras sætning AD=5. Så ED=1 Lad punkt E ligge på stråle AD. Medianen AD er længere end AE, og punktet E ligger inde i trekant ABC (Fig. 1) Lad os slippe den vinkelrette EF fra punkt E til linje BC og betragte lignende retvinklede trekanter DEF og DAC. Ud fra ligheden mellem disse trekanter finder vi: EF = AC ∙ ED AD = 4 5 19
Derfor er S BCE = 1 2 ∙ 6 ∙ 4 5 = 2,4. Lad nu punkt A ligge mellem E og D (fig. 2). I dette tilfælde ED=9 og EF = AC ∙ ED AD = 36 5 . Så S BCE = 1 2 ∙ 6 ∙ 36 5 = 21,6. Svar: 2,4; 21.6. Løsning af problemet ved hjælp af komplekse tal. Case I: punkt E ligger på stråle AD. Da D er midten af ​​CB, så er CD=3. Og da CA=4, er det klart, at AD=5, dvs. DE=1. Lad os tage punkt C som startpunktet og linjerne CA og CB som de reelle og imaginære akser. Derefter A(4), C(0), B(6i), D(3i), E(e). Punkterne A, E og D er kollineære, så e − 4 3i − e = 4 dvs. e= 12i + 4 5 . Ifølge formel (25) S CBE =│ ´ i 4 (e6 ´ i +6i(− ´ e)│= e e − ´ ¿ 6 i 2 4 ¿ ¿ =2.4 Tilfælde II: punkt A ligger mellem punkterne D og E, derefter 4 − e 3i − 4 = 4 5 , dvs. e= 36 − 12 i 5 S CBE = | den første måde, er det nødvendigt at have en række gæt, som måske ikke vises med det samme, men efter ret mange ræsonnementer, selvom den studerende er godt forberedt, så dannes selve løsningen med det samme den anden måde, vi bruger færdige formler, hvilket sparer tid på at søge. Men vi forstår, at uden at kende formlerne, kan problemer ikke løses ved hjælp af komplekse tal-metoden .
Opgave 2 (MIOO, 2011):
"Punkt M ligger på segment AB. På en cirkel med diameter AB tages punktet C, fjernt fra punkterne A, M og B i afstande på henholdsvis 20, 14 og 15. Find arealet af trekanten BMC." 20
Løsning: Da AB er diameteren af ​​en cirkel, så er ∆ ABC rektangulær, ∠ C = 90 ° Lad os tage C som nulpunkt plan, derefter A(20i), B(15), M(z). Da CM=14, er ligheden z ´ z = 196 sand, dvs. punktet M ∈ en cirkel med centrum i punktet C og r=14. Lad os finde skæringspunkterne for denne cirkel med linjen AB: Ligning for linjen AB (10a): 20 i (15 −´ z) + 15 (´ z + 20 i) + z (− 20 i − 15) = 0 Erstatter ´ z med 196 z og gange hele ligningen med (4 i − 3), får vi en andengradsligning for z: 25 z 2 + 120 i (4 i − 3) z + 196 (4 i − 3) 2 = 0 z 1,2 = 2 (3 − 4 i) (6 i± √ 13) 5 Ved hjælp af formel (28) finder vi arealet ∆ MBC: S = i 4 (z (´ b − ´ c) + b (´ c − ´ z) + c (´ z − ´ b)) Hvor c = 0, ´ c = 0, b = 15, ´ b = 15, ´ z = 196 ∗ 5 2 (3 − 4 i) (6 i ± √ 13) Efter at have gennemført tilsvarende transformationer, får vi S = 54 ± 12 √ 13 sq. enheder Svar. 54 ± 12 √ 13 kvm. enheder Hvis du løser problemet geometriske metoder, så er det nødvendigt at overveje to forskellige tilfælde: 1. punkt M ligger mellem A og D; 2. - mellem D og B. 21

Når du løser et problem ved hjælp af metoden med komplekse tal, opnås dualiteten af ​​løsningen på grund af tilstedeværelsen af ​​to skæringspunkter mellem en cirkel og en linje. Denne omstændighed giver os mulighed for at undgå en almindelig fejl.
Opgave 3
Medianerne AA 1, BB 1 og CC 1 i trekant ABC skærer hinanden i punktet M. Det er kendt, at AB=6MC 1. Bevis at trekant ABC er retvinklet. Løsning: Lad C være nulpunktet i planet, og tildel en reel enhed til punkt A. Problemet reduceres derefter til at bevise, at b er et rent imaginært tal. AB 2 = (b − 1) (´ b − 1) . M er tyngdepunktet, dens koordinat er 1 3 b + 1 3 MC 1 2 = (1 3 b + 1 3 − 1 2 b − 1 2)(1 3 ´ b + 1 3 − 1 2 ´ b − 1 2) = 1 3 b (b + 1) (´ b + 1) Da AB=6MC 1, så (b − 1) (´ b − 1) = (b + 1) (´ b + 1) . Efter at have udført transformationerne får vi b =− ´ b, dvs. b er et rent imaginært tal, dvs. vinklen C er en ret linje.
Opgave 4.
22
Som et resultat af en 90° rotation omkring punkt O, blev segment AB til segment A "B". Bevis at medianen OM for trekanten OAB " er vinkelret på linjen A " B . Løsning: Lad koordinaterne O, A, B være lig med henholdsvis 0,1, b. Så vil punkt A " og B " have koordinaterne a" = i og b" = bi, og det midterste M af segmentet AB " vil have koordinaterne m = 1 2 (1 + bi). Vi finder: a " − b m − 0 = i − b 1 2 (1 + bi) = 2 i (i − b) i − b = 2i tal er rent imaginært. Baseret på perpendikularitetskriteriet (segmenterne AB og CD er vinkelrette, hvis og kun hvis tallet a − b c − d er rent imaginært), er linjerne OM og A ’ B vinkelrette.
Opgave 5
. 23
Fra bunden af ​​trekantens højde falder vinkelrette sider på to sider, der ikke svarer til denne højde. Bevis, at afstanden mellem baserne af disse perpendikulære ikke afhænger af valget af trekantens højde. Løsning: Lad trekant ABC være givet, og cirklen, der er omskrevet omkring den, har ligningen z ´ z = 1. Hvis CD er højden af ​​trekanten, så er d = 1 2 (a + b + c − ab c) De komplekse koordinater for baserne M og N af perpendikulærerne faldet fra punkt D til henholdsvis AC og BC er lig med m = 1 2 (a + c + d − ac ´ d 2) n = 1 2 (b + c + d − bc ´ d 2) Vi finder: m − n = 1 2 (a − b + c ´ d ( b − a)) = 1 2 ( a − b) (1 − c ´ d) = (a − b) (a − c) (b − c) 4 ab Siden | en | = | b | = 1, derefter | m − n | = | (a − b) × (b − c) (c − a) | 4 . Dette udtryk er symmetrisk med hensyn til a, b, c, dvs. afstanden MN afhænger ikke af valg af trekanthøjde.
Konklusion
24
"Sikkert! Alle problemer kan løses uden komplekse tal. Men sagen er, at algebraen af ​​komplekse tal er en anden effektiv metode løsning af planimetriske problemer. Vi kan kun tale om at vælge en metode, der er mere effektiv til en given opgave. Tvister om fordelene ved en bestemt metode er meningsløse, hvis vi betragter disse metoder generelt, uden anvendelse på et specifikt problem” [2]. En stor plads i studiet af metoden er optaget af et sæt formler. Dette er
største ulempe
metode og på samme tid
værdighed
, da det giver dig mulighed for at løse nok komplekse opgaver efter færdige formler med elementære beregninger. Derudover mener jeg, at når man løser planimetriske problemer denne metode er universel.
Bibliografi
1. Markushevich A.I. Komplekse tal og konforme kortlægninger - M.: State Publishing House of Technical and Theoretical Literature, 1954. - 52 s. 25
2. Ponarin Ya P. Algebra af komplekse tal i geometriske problemer: En bog for studerende i matematiske klasser i skoler, lærere og studerende på pædagogiske universiteter - M.: MTsNMO, 2004. - 160 s. 3. Shvetsov D. Fra Simsons linje til Droz-Farny-sætningen, Kvant. - nr. 6, 2009. – s. 44-48 4. Yaglom I. M. Geometriske transformationer. Lineære og cirkulære transformationer. - Statens Forlag for Teknisk og Teoretisk Litteratur, 1956. – 612 s. 5. Yaglom I.M. Komplekse tal og deres anvendelse i geometri - M.: Fizmatgiz, 1963. - 192 s. 6. Morkovich A.G. og andre, Algebra og begyndelsen af ​​matematisk analyse 10. klasse. Om 2 timer Del 1. Lærebog for studerende på almene uddannelsesinstitutioner (profilniveau) - M.: Mnemosyne, 2012. - 343 s. 7. Andronov I.K. Matematik af reelle og komplekse tal - M.: Prosveshchenie, 1975. - 158 s. 26

Ansøgning

Klassiske sætninger om elementær geometri

Newtons sætning.
I en firkant, der er afgrænset omkring en cirkel, er diagonalernes midtpunkter kolineære med cirklens centrum. 27
Bevis. Lad os tage centrum af cirklen som udgangspunkt og sætte dens radius lig med én. Lad os betegne kontaktpunkterne for siderne af denne firkantede trekant A o B o C o D o med A, B, C, D (i en cirkulær rækkefølge) (fig. 4). Lad M og N være midtpunkterne for henholdsvis diagonalerne A o C o og B o D o. I henhold til formlen for skæringspunkterne for tangenter til en cirkel z = 2ab a + b vil punkterne A o , B o , C o , D o have komplekse koordinater, henholdsvis: , 2 , 2 , 2 , 2 0 0 0 0 d c cd d c b bc c b a ab b d a ad a         hvor a, b, c, d er de komplekse koordinater for punkterne A, B, C, D. Derfor.) (2 1 ,) (2 1 0 0 0 0 d c cd b a ab d b n c b bc d a ad ca m             Beregn.))( b )(a d c   Siden, 1 , 1 b b a a   , 1 , 1 d d c c   så er det direkte klart, at n m n m  Baseret på (6) er punkterne O, M, N kollineære.
Pascals sætning

.
Skæringspunkterne for linjer, der indeholder modsatte sider af en indskrevet sekskant, ligger på samme linje. 28
Bevis. Lad sekskanten ABCDEF og P FA CD N EF BC M DE AB   ) () (,) () (,) () (   (Fig. 6) indskrives i en cirkel (Fig. 6). Lad os tage midten af ​​cirklen som planets nulpunkt, og dens radius er pr. længdeenhed. Så har vi ifølge (17): ,) (,) (,) (fa cd a f d c p ef bc f e c b n. de ab e d b a m                Beregn) )(())((ef bc de ab fa ef de cd bc        og lignende .))(())((fa cd ef bc bc ab fa ef de cd f c p n           Dernæst finder vi: .))(())((de ab c f fa cd e b p n .       Da tallene f e d c b a er ens henholdsvis f e d c b a 1 , 1 , 1 , 1, 1, 1, så afslører en mundtlig kontrol, at det fundne udtryk falder sammen med dets konjugat, dvs. det er et reelt tal. Det betyder, at punkterne M, N, P er kollineære.
Monges sætning.
I en firkant indskrevet i en cirkel går linjerne gennem midtpunkterne på siderne og. Hver diagonal er vinkelret på de modsatte sider, og følgelig skærer den anden diagonal et punkt. Det kaldes Monge-punktet for en cyklisk firkant. Bevis. De vinkelrette halveringslinjer på siderne af firkanten ABCD skærer i midten af ​​den omskrevne cirkel, som vi tager udgangspunkt i. For hvert punkt M(z) i den vinkelrette halveringslinje til [AB] tallet b a b a z   ) (2 1 rent imaginært. 29
Især for z=0 er det lig med) (2) (b a b a    . For hvert punkt N(z) på linjen, der går gennem midten af ​​siden CD vinkelret på (AB), tallet b a d c z   ) (2 1 skal være rent imaginært og omvendt. Men for z=) (2 1 d c b a    er det ens) (2 b a b a   dvs. rent imaginært. Derfor punkt E med en kompleks koordinat) ( 2 1 d c b a    ligger på den angivne linje Og dette udtryk er symmetrisk i forhold til bogstaverne a, b, c, d. Derfor indeholder de andre fem ens opbyggede linjer punkt E. 30

MULIGHED FOR ANVENDELSE AF KOMPLEKSE TAL

I LØSET I MATEMATIK PÅ ALMINDELIG UDDANNELSE SKOLEN

Videnskabelig rådgiver:

Kommunal uddannelsesinstitution

Pervomaiskaya gymnasiet

Med. Kichmengsky by

St. Zarechnaya 38

Det præsenterede arbejde er afsat til studiet af komplekse tal. Relevans: løse mange problemer inden for fysik og teknologi fører til andengradsligninger med negativ diskriminant. Disse ligninger har ingen løsning i regionen reelle tal. Men løsningen af ​​mange sådanne problemer har en meget bestemt fysisk betydning.

Praktisk betydning: komplekse tal og funktioner af komplekse variabler bruges i mange spørgsmål om videnskab og teknologi, de kan bruges i skolen til at løse andengradsligninger.

Objektområde: matematik. Genstand for forskning: algebraiske begreber og handlinger. Genstand for forskning- komplekse tal. Problem: komplekse tal undervises ikke i matematikkurser folkeskole, selvom de kan bruges til at løse andengradsligninger. Muligheden for at indføre komplekse tal i Unified State Exam-opgaver i fremtiden. Hypotese: Du kan bruge komplekse tal til at løse andengradsligninger i gymnasiet. Mål: at undersøge muligheden for at bruge komplekse tal, når man læser matematik i 10. klasse på en gymnasieskole. Opgaver: 1. Studer teorien om komplekse tal 2. Overvej muligheden for at bruge komplekse tal i et 10. klasses matematikkursus. 3. Udvikle og afprøve opgaver med komplekse tal.

For løsninger algebraiske ligninger Der er ikke nok reelle tal. Derfor er det naturligt at stræbe efter at gøre disse ligninger løselige, hvilket igen fører til en udvidelse af talbegrebet..gif" width="10" height="65 src=">

https://pandia.ru/text/78/027/images/image005_18.gif" width="10" height="62">.gif" width="97" height="28 src=">

du skal bare acceptere at handle på sådanne udtryk i henhold til reglerne for almindelig algebra og antage det

I 1572 blev der udgivet en bog af den italienske algebraist R. Bombelli, hvori de første regler for aritmetiske operationer på sådanne tal blev fastlagt, indtil udtrækket fra dem kubikrødder. Navnet "imaginære tal" blev introduceret i 1637. fransk matematiker og filosof R. Descartes, og i 1777 en af ​​de største matematikere VIIIårhundrede X..gif" width="58" height="19"> som et eksempel på brugen af ​​komplekse tal, når man studerer matematik i 10. klasse. Derfor. Tallet x, hvis kvadrat er lig med –1, kaldes den imaginære enhed og betegnes således i, hvorfra ..gif" width="120" height="27 src=">.gif" width="100" height="27 src=">8. klasse. " href="/text/category/8_klass/" rel ="bogmærke">8. klasse i algebra.- M.: Uddannelse, 1994.-P.134-139.

2. encyklopædisk ordbog ung matematiker / Komp. E-68. - M.: Pædagogik, 19с

• Vi vil være baseret på forbindelser, ikke på mekaniske formler.
• Lad os betragte komplekse tal som et supplement til vores talsystem, det samme som nul-, brøk- eller negative tal.
• Vi visualiserer ideer i grafik for bedre at forstå essensen, og ikke blot præsentere dem i tør tekst.

Og vores hemmeligt våben: læring ved analogi. Vi kommer til komplekse tal ved at starte med deres forfædre, negative tal. Her er en lille guide til dig:

For nu giver dette bord ikke meget mening, men lad det være der. Ved slutningen af ​​artiklen vil alt falde på plads.

Lad os virkelig forstå, hvad negative tal er

Negative tal er ikke så enkle. Forestil dig, at du er en europæisk matematiker i det 18. århundrede. Du har 3 og 4, og du kan skrive 4 – 3 = 1. Det er enkelt.

Men hvad er 3-4? Hvad betyder det helt præcist? Hvordan kan du tage 4 køer væk fra 3? Hvordan kan du have mindre end ingenting?

Negative tal blev betragtet som fuldstændig nonsens, noget der "kastede en skygge over hele teorien om ligninger" (Francis Maceres, 1759). I dag ville det være fuldstændig nonsens at tænke på negative tal som noget ulogisk og uhensigtsmæssigt. Spørg din lærer, om negative tal overtræder grundlæggende matematik.

Hvad skete der? Vi opfandt et teoretisk tal, der havde nyttige egenskaber. Negative tal kan ikke røres eller mærkes, men de er gode til at beskrive visse forhold (som f.eks. gæld). Dette er en meget nyttig idé.

I stedet for at sige: "Jeg skylder dig 30" og læse ordene for at se, om jeg er i sort eller i sort, kan jeg bare skrive "-30" ned og vide, hvad det betyder. Hvis jeg tjener penge og betaler af på min gæld (-30 + 100 = 70), kan jeg nemt skrive denne transaktion med et par tegn. Jeg står tilbage med +70.

Plus- og minustegnet fanger automatisk retningen - du behøver ikke en hel sætning for at beskrive ændringerne efter hver transaktion. Matematik er blevet enklere, mere elegant. Det var ikke længere ligegyldigt, om negative tal var "håndgribelige" - de havde nyttige egenskaber, og vi brugte dem, indtil de blev solidt etableret i vores hverdag. Hvis nogen du kender endnu ikke har forstået essensen af ​​negative tal, nu vil du hjælpe dem.

Men lad os ikke forklejne menneskelig lidelse: Negative tal var et reelt skift i bevidstheden. Selv Euler, geniet, der opdagede tallet e og meget mere, forstod ikke negative tal så godt, som vi gør i dag. De blev set som "meningsløse" resultater af beregninger.

Det er mærkeligt at forvente, at børn roligt forstår ideer, der engang forvirrede selv de bedste matematikere.

Indtastning af imaginære tal

Det er den samme historie med imaginære tal. Vi kan løse ligninger som denne hele dagen lang:

Svarene bliver 3 og -3. Men lad os forestille os, at en eller anden smart fyr tilføjede et minus her:

Nå nå. Det er den slags spørgsmål, der får folk til at ryste sig, når de ser det for første gang. Vil du beregne kvadratroden af ​​et tal mindre end nul? Dette er utænkeligt! (Historisk var der virkelig lignende spørgsmål, men det er mere bekvemt for mig at forestille mig en vis ansigtsløs fyr, for ikke at genere fortidens videnskabsmænd).

Det ser skørt ud, ligesom negative tal, nul og irrationelle tal (ikke-gentagende tal) så tilbage på dagen. Der er ingen "rigtig" mening med dette spørgsmål, vel?

Nej det er ikke sandt. Såkaldte "imaginære tal" er lige så normale som alle andre (eller lige så unormale): de er et værktøj til at beskrive verden. I samme ånd, som vi forestiller os, at -1, 0,3 og 0 "eksisterer", lad os antage, at der er et tal i, hvor:

Med andre ord gange du i med sig selv for at få -1. Hvad sker der nu?

Nå, først har vi helt sikkert hovedpine. Men ved at spille spillet "Lad os som om, at jeg eksisterer" gør vi faktisk matematikken enklere og mere elegant. Der opstår nye forbindelser, som vi nemt kan beskrive.

Du vil ikke tro på i, ligesom de gamle sure matematikere ikke troede på eksistensen af ​​-1. Alle nye begreber, der vrider hjernen til et rør, er svære at opfatte, og deres betydning kommer ikke umiddelbart frem, selv for den geniale Euler. Men som negative tal har vist os, kan mærkelige nye ideer være yderst nyttige.

Jeg kan ikke lide selve udtrykket "imaginære tal" - det føles som om det er valgt specifikt for at støde følelserne hos bl.a. Tallet i er lige så normalt som de andre, men kaldenavnet "imaginært" har holdt sig til det, så vi vil også bruge det.

Visuel forståelse af negative og komplekse tal

Ligningen x^2 = 9 betyder faktisk dette:

Hvilken transformation af x, anvendt to gange, gør 1 til 9?

Der er to svar: "x = 3" og "x = -3". Det vil sige, du kan "skalere med" 3 gange eller "skalere med 3 og vende" (at vende eller tage det gensidige af resultatet er alle fortolkninger af at gange med negativ).

Lad os nu tænke på ligningen x^2 = -1, som kan skrives sådan:

Hvilken transformation af x, anvendt to gange, gør 1 til -1? Hm.

• Vi kan ikke gange to gange positivt tal fordi resultatet bliver positivt.
• Vi kan ikke gange et negativt tal to gange, fordi resultatet igen bliver positivt.

Hvad med... rotation! Det lyder selvfølgelig usædvanligt, men hvad nu hvis vi tænker på x som en "90 graders rotation", så ved at anvende x to gange vil vi lave en 180 graders rotation ved at koordinatakse, og 1 bliver til -1!

Wow! Og hvis vi tænker os lidt mere om, kan vi lave to omdrejninger ind modsatte retning, og gå også fra 1 til -1. Dette er en "negativ" rotation eller multiplikation med -i:

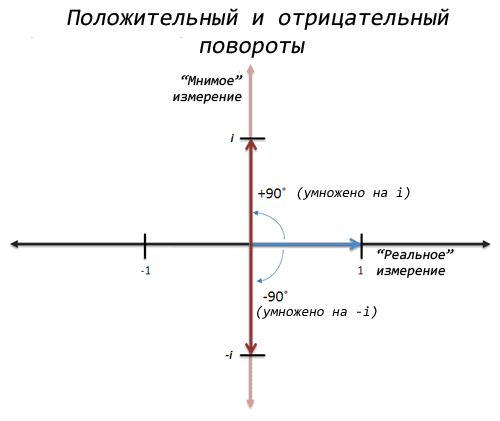
Hvis vi gange med -i to gange, så får vi ved den første multiplikation -i fra 1, og på den anden -1 fra -i. Så der er faktisk to kvadratrødder-1: i og -i.

Det her er ret fedt! Vi har noget i retning af en løsning, men hvad betyder det?

• i er den "nye imaginære dimension" til måling af tal
• i (eller -i) er, hvad tallene "bliver", når de roteres
• Multiplikation med i roterer 90 grader mod uret
• Multiplikation med -i er en 90 graders rotation med uret.
• At rotere to gange i begge retninger giver -1: det tager os tilbage til den "normale" dimension af positive og negative tal (x-aksen).

Alle tal er 2-dimensionelle. Ja, det er svært at acceptere, men det ville have været lige så svært for de gamle romere at acceptere. decimaler eller lang division. (Hvordan er det, at der er flere tal mellem 1 og 2?). Ser mærkeligt ud som nogen ny vej tænke i matematik.

Vi spurgte "Hvordan gør man 1 til -1 i to handlinger?" og fandt svaret: drej 1 90 grader to gange. En ret mærkelig, ny måde at tænke på i matematik. Men meget nyttigt. (Denne geometriske fortolkning af komplekse tal optrådte i øvrigt kun årtier efter opdagelsen af ​​selve tallet i).

Glem heller ikke, at det er at tage en omdrejning mod uret positivt resultat- det er en rent menneskelig konvention, og alt kunne have været helt anderledes.

Søg efter sæt

Lad os gå lidt dybere ned i detaljerne. Når du multiplicerer negative tal (som -1), får du et sæt:

• 1, -1, 1, -1, 1, -1, 1, -1

Da -1 ikke ændrer størrelsen på tallet, kun tegnet, får du det samme tal enten med et "+" tegn eller med et "-" tegn. For tallet x får du:

• x, -x, x, -x, x, -x...

Dette er en meget nyttig idé. Tallet "x" kan repræsentere gode og dårlige uger. Lad os forestille os det god uge erstatter den dårlige; Det er en god uge; Hvordan bliver den 47. uge?

X betyder, at det bliver en dårlig uge. Se hvordan negative tal "følger tegnet" - vi kan blot indtaste (-1)^47 i lommeregneren i stedet for at tælle ("Uge 1 god, uge ​​2 dårlig... uge 3 god..."). Ting, der konstant veksler, kan perfekt modelleres ved hjælp af negative tal.

Okay, hvad sker der, hvis vi fortsætter med at gange med i?

Meget sjovt, lad os forenkle dette lidt:

Her er det samme præsenteret grafisk:

Vi gentager cyklussen hver 4. omgang. Det giver bestemt mening, ikke? Ethvert barn vil fortælle dig, at 4 drejninger til venstre er det samme som slet ikke at dreje. Tag nu en pause fra de imaginære tal (i, i^2) og se på det samlede sæt:

• X, Y, -X, -Y, X, Y, -X, -Y...

Præcis hvordan negative tal modelleres spejlrefleksion tal, imaginære tal kan modellere alt, der roterer mellem to dimensioner "X" og "Y". Eller noget med en cyklisk, cirkulær afhængighed - har du noget i tankerne?

Forstå komplekse tal

Der er endnu en detalje at overveje: kan et tal være både "rigtigt" og "imaginært"?

Tvivl ikke engang på det. Hvem sagde, at vi skal dreje præcis 90 grader? Hvis vi står med den ene fod på den "rigtige" dimension og den anden på den "imaginære", vil det se sådan ud:

Vi er ved 45 graders mærket, hvor de reelle og imaginære dele er de samme, og selve tallet er "1 + i". Det er ligesom en hotdog, hvor der både er ketchup og sennep – hvem har sagt, at man skal vælge det ene eller det andet?

Grundlæggende kan vi vælge enhver kombination af ægte og imaginære dele og lave en trekant ud af det hele. Vinklen bliver "drejningsvinklen". Et komplekst tal er et fancy navn for tal, der har en reel og en imaginær del. De er skrevet som "a + bi", hvor:

• en - reel del
• b - imaginær del

Ikke dårligt. Men der er kun én tilbage sidste spørgsmål: Hvor "stort" er et komplekst tal? Vi kan ikke måle den virkelige del eller den imaginære del separat, fordi vi vil gå glip af det store billede.

Lad os tage et skridt tilbage. Størrelse negativt tal er afstanden fra nul:

Dette er en anden måde at finde absolut værdi. Men hvordan måler man begge komponenter ved 90 grader for komplekse tal?

Er det en fugl på himlen... eller et fly... Pythagoras kommer til undsætning!

Denne sætning dukker op, hvor det er muligt, selv i antal opfundet 2000 år efter selve sætningen. Ja, vi laver en trekant, og dens hypotenus vil være lig med afstanden fra nul:

Selvom det ikke er så simpelt at måle et komplekst tal som "bare at udelade tegnet -", har komplekse tal meget nyttige applikationer. Lad os se på nogle af dem.

Reelt eksempel: Rotationer

Vi vil ikke vente til universitetets fysik med at øve komplekse tal. Det gør vi i dag. Der kan siges meget om emnet multiplikation af komplekse tal, men for nu skal du forstå det vigtigste:

• Multiplikation med et komplekst tal roterer med dets vinkel

Lad os se, hvordan det virker. Forestil dig, at jeg er på en båd og bevæger mig på en kurs på 3 enheder mod øst hver 4. enheder mod nord. Jeg vil ændre min kurs 45 grader mod uret. Hvad bliver mit nye kursus?

Nogen vil måske sige "Det er nemt! Beregn sinus, cosinus, google tangentværdien... og så..." Jeg tror, ​​jeg knækkede min lommeregner...

Lad os gå over på en enkel måde: vi er på en kurs på 3 + 4i (det er ligegyldigt hvad vinklen er, vi er ligeglade nu) og vi vil dreje 45 grader. Nå, 45 grader er 1 + i (ideel diagonal). Så vi kan gange vores sats med dette tal!

Her er kernen:

• Indledende overskrift: 3 enheder øst, 4 enheder nord = 3 + 4i
• Roter 45 grader mod uret = gang med 1 + i

Når vi ganges får vi:

Vores nyt vartegn- 1 enhed mod vest (-1 mod øst) og 7 enheder mod nord, du kan tegne koordinaterne på grafen og følge dem.

Men! Vi fandt svaret på 10 sekunder uden nogen sinus og cosinus. Der var ingen vektorer, ingen matricer, ingen sporing af hvilken kvadrant vi var i. Det var simpelt regnestykke og lidt algebra at regne ud ligningen. Imaginære tal er gode til rotation!

Desuden er resultatet af en sådan beregning meget nyttigt. Vi har kurs (-1, 7) i stedet for vinkel (atan(7/-1) = 98,13, og det er umiddelbart tydeligt, at vi er i anden kvadrant. Hvordan havde du helt præcist planer om at tegne og følge den angivne vinkel ? bruge en vinkelmåler ved hånden?

Nej, du ville konvertere vinklen til cosinus og sinus (-0,14 og 0,99), finde det omtrentlige forhold mellem dem (ca. 1 til 7) og skitsere en trekant. Og her vinder komplekse tal uden tvivl - præcist, lynhurtigt og uden lommeregner!

Hvis du er ligesom mig, vil du finde denne opdagelse forbløffende. Hvis ikke, er jeg bange for, at matematik slet ikke ophidser dig. Undskyld!

Trigonometri er godt, men komplekse tal gør beregninger meget nemmere (som at finde cos(a + b)). Dette er blot en lille meddelelse; i de følgende artikler vil jeg give dig den komplette menu.

Lyrisk digression: nogle mennesker tænker sådan her: "Hey, det er ikke praktisk at have en nord/øst-bane i stedet for simpel vinkel for skibets passage!

Er det sandt? Okay, se på din højre hånd. Hvad er vinklen mellem bunden af ​​din lillefinger og spidsen pegefinger? Held og lykke med din beregningsmetode.

Eller du kan blot svare: "Tja, spidsen er X tommer til højre og Y tommer op", og du kan gøre noget ved det.

Kommer komplekse tal tættere på?

Vi gennemgik mine grundlæggende opdagelser inden for komplekse tal som en tornado. Se på den allerførste illustration, den skulle nu blive mere tydelig.

Der er så meget mere at opdage i disse smukke, vidunderlige numre, men min hjerne er allerede træt. Mit mål var enkelt:

• Overbevise dig om, at komplekse tal kun blev set som "skøre", men faktisk kan de være meget nyttige (ligesom negative tal)
• Vis, hvordan komplekse tal kan forenkle nogle problemer som rotation.

Hvis jeg virker overdrevent bekymret over dette emne, er der en grund til det. Fantasifulde tal har været en besættelse af mig i årevis – den manglende forståelse irriterede mig.

Men at tænde et stearinlys er bedre end at vade gennem buldmørket: det er mine tanker, og jeg er sikker på, at lyset vil lyse i mine læseres sind.

Epilog: Men de er stadig ret underlige!

Jeg ved, at de stadig ser mærkelige ud for mig. Jeg prøver at tænke som den første person, der opdagede nul tanke.

Nul er sådan en mærkelig idé, "noget" repræsenterer "intet", og dette kunne ikke forstås på nogen måde i Det gamle Rom. Det er det samme med komplekse tal – det er en ny måde at tænke på. Men både nul og komplekse tal forenkler i høj grad matematikken. Hvis vi aldrig havde indført mærkelige ting som nye talsystemer, ville vi stadig tælle alt på fingrene.

Jeg gentager denne analogi, fordi det er så nemt at begynde at tro, at komplekse tal er "ikke normale." Lad os være åbne over for innovation: I fremtiden vil folk kun spøge med, hvordan nogen indtil det 21. århundrede ikke troede på komplekse tal.

23. oktober 2015