يعد العثور على إحداثيات المتجه حالة شائعة إلى حد ما في العديد من المسائل في الرياضيات. ستساعدك القدرة على العثور على إحداثيات المتجهات في أمور أخرى المهام المعقدةمع مواضيع مماثلة. في هذه المقالة سوف نلقي نظرة على صيغة إيجاد إحداثيات المتجهات والعديد من المشاكل.
إيجاد إحداثيات المتجه في المستوى
ما هي الطائرة؟ يعتبر المستوى بمثابة فضاء ثنائي الأبعاد، وهو فضاء ذو بعدين (البعد x والبعد y). على سبيل المثال، الورق مسطح. سطح الطاولة مسطح. أي شكل غير حجمي (مربع، مثلث، شبه منحرف) هو أيضًا مستوى. وبالتالي، إذا كنت بحاجة في بيان المشكلة إلى العثور على إحداثيات المتجه الذي يقع على المستوى، فإننا نتذكر على الفور x و y. يمكنك العثور على إحداثيات هذا المتجه بالطريقة الآتية: إحداثيات المتجهات AB = (xB - xA؛ yB - xA). من الصيغة يتضح أنه من الإحداثيات نقطة النهايةتحتاج إلى طرح إحداثيات نقطة البداية.
مثال:
- يحتوي القرص المضغوط المتجه على إحداثيات أولية (5؛ 6) ونهائية (7؛ 8).
- أوجد إحداثيات المتجه نفسه.
- باستخدام الصيغة أعلاه، نحصل على التعبير التالي: CD = (7-5؛ 8-6) = (2؛ 2).
- وبالتالي فإن إحداثيات المتجه CD = (2; 2).
- وبناءً على ذلك، فإن الإحداثي x يساوي اثنين، والإحداثي y أيضًا اثنان.
إيجاد إحداثيات المتجه في الفضاء
ما هو الفضاء؟ الفضاء هو بالفعل بعد ثلاثي الأبعاد، حيث يتم إعطاء 3 إحداثيات: x، y، z. إذا كنت بحاجة إلى العثور على متجه يقع في الفضاء، فإن الصيغة لا تتغير عمليا. تتم إضافة إحداثي واحد فقط. للعثور على متجه، تحتاج إلى طرح إحداثيات البداية من إحداثيات النهاية. AB = (xB - xA؛ yB - yA؛ zB - zA)
مثال:
- يحتوي Vector DF على أولي (2؛ 3؛ 1) ونهائي (1؛ 5؛ 2).
- بتطبيق الصيغة أعلاه، نحصل على: إحداثيات المتجهات DF = (1-2؛ 5-3؛ 2-1) = (-1؛ 2؛ 1).
- تذكر أن قيمة الإحداثيات يمكن أن تكون سالبة، فلا توجد مشكلة.
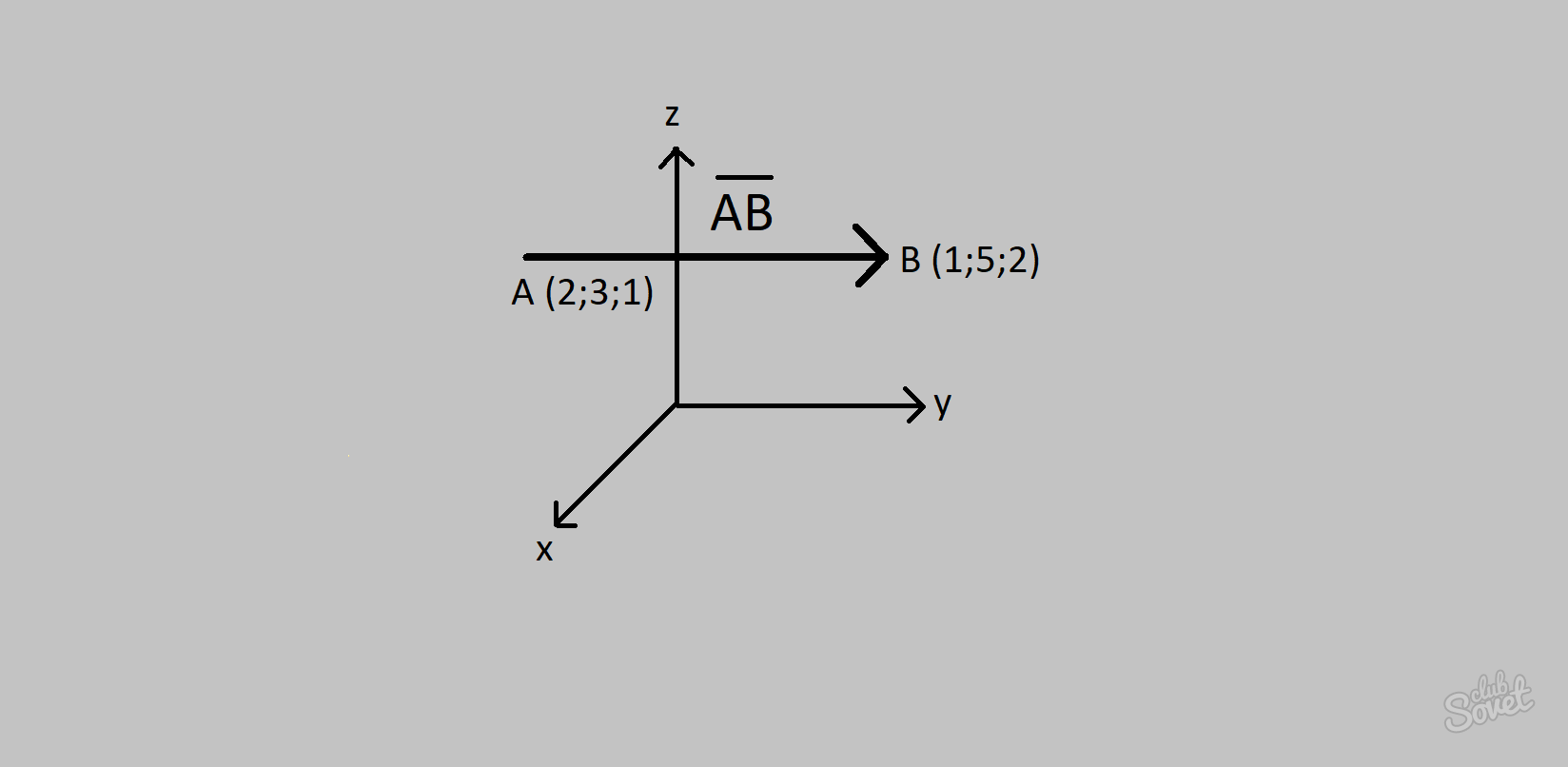
كيفية العثور على إحداثيات المتجهات على الإنترنت؟
إذا كنت لا ترغب لسبب ما في العثور على الإحداثيات بنفسك، فيمكنك استخدام الآلة الحاسبة عبر الإنترنت. للبدء، حدد البعد المتجه. البعد المتجه هو المسؤول عن أبعاده. البعد 3 يعني أن المتجه موجود في الفضاء، والبعد 2 يعني أنه موجود في المستوى. بعد ذلك، أدخل إحداثيات النقاط في الحقول المناسبة وسيحدد لك البرنامج إحداثيات المتجه نفسه. كل شيء بسيط جدا.
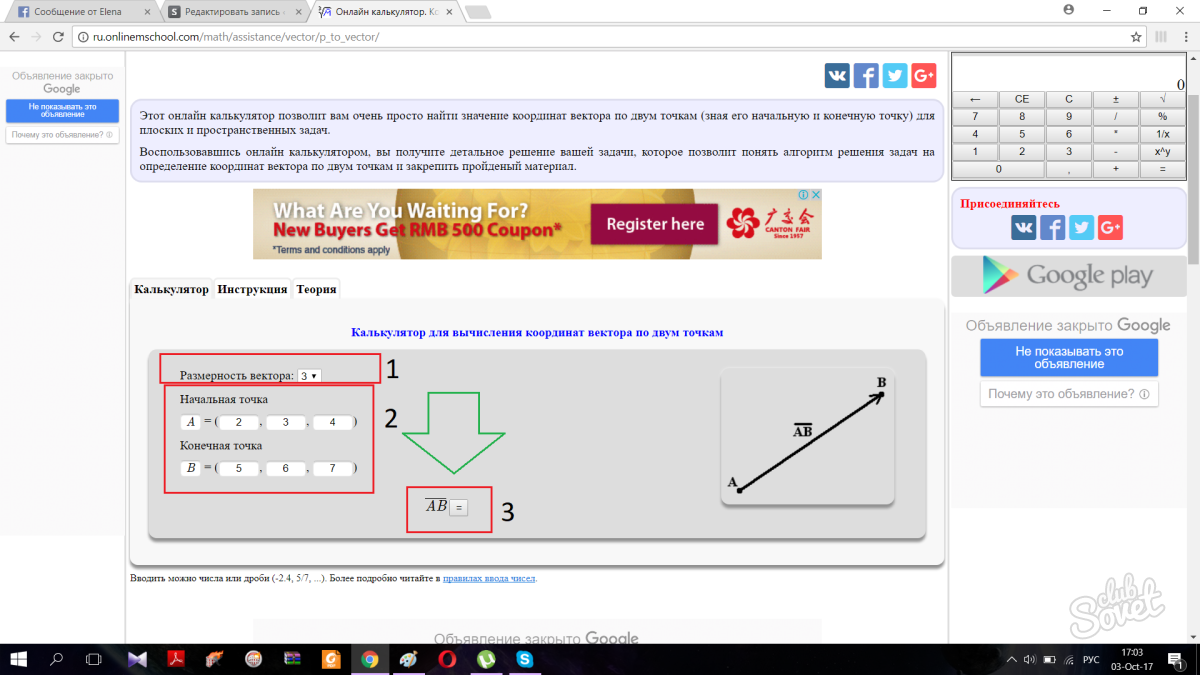
بالضغط على الزر، ستنتقل الصفحة تلقائيًا إلى الأسفل وتعطيك الإجابة الصحيحة مع خطوات الحل.
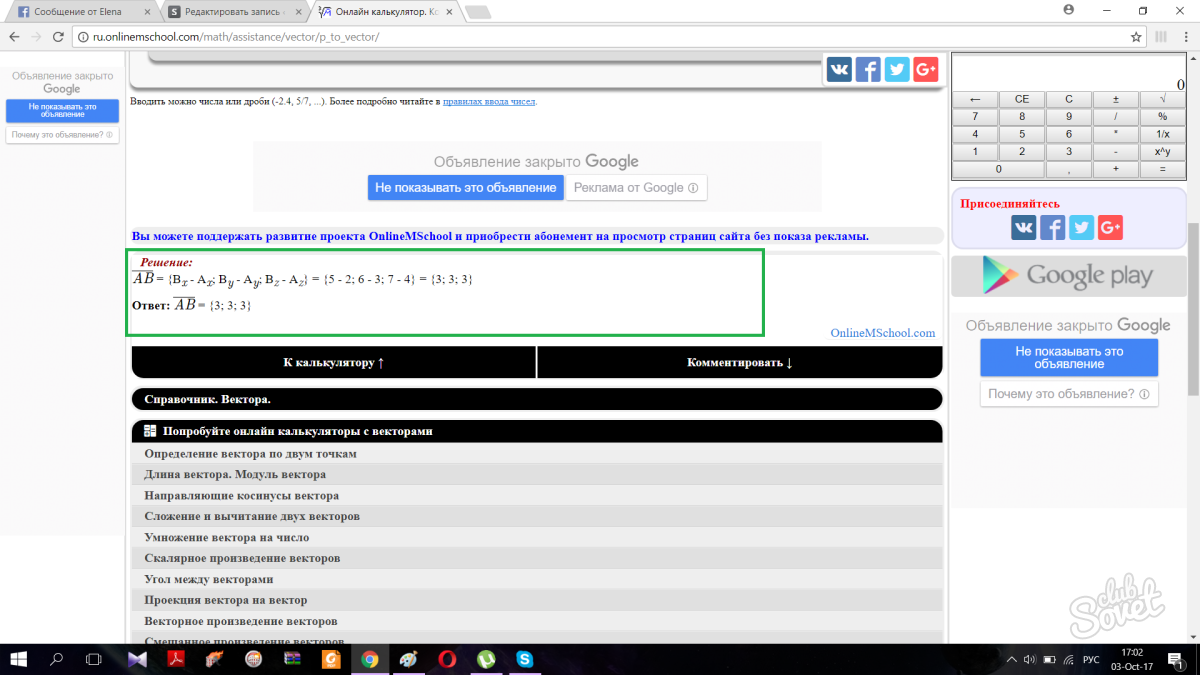
ينصح بالدراسة الجيدة هذا الموضوعلأن مفهوم المتجه لا يوجد في الرياضيات فحسب، بل في الفيزياء أيضًا. طلاب الكلية تقنيات المعلوماتكما أنهم يدرسون موضوع المتجهات، ولكن على مستوى أكثر تعقيدًا.
إذا تم إعطاء نقطتين من المستوى، فإن المتجه يكون له الإحداثيات التالية:
إذا كانت هناك نقطتان في الفضاء، فإن المتجه يكون له الإحداثيات التالية:
إنه، من إحداثيات نهاية المتجهتحتاج إلى طرح الإحداثيات المقابلة بداية المتجه.
يمارس:لنفس النقاط، اكتب الصيغ لإيجاد إحداثيات المتجه. الصيغ في نهاية الدرس.
مثال 1
نظرا لنقطتين من الطائرة و . البحث عن إحداثيات المتجهات
حل:وفقا للصيغة المناسبة:
وبدلاً من ذلك، يمكن استخدام الإدخال التالي:
سوف يقرر الجماليات هذا:
أنا شخصياً اعتدت على الإصدار الأول من التسجيل.
إجابة:
وفقًا للحالة، لم يكن من الضروري إنشاء رسم (وهو أمر نموذجي للمهام الهندسة التحليلية)، ولكن من أجل توضيح بعض النقاط للدمى، لن أكون كسولًا جدًا:
أنت بالتأكيد بحاجة إلى أن تفهم الفرق بين إحداثيات النقطة وإحداثيات المتجهات:
إحداثيات النقطة- هذه إحداثيات عادية في نظام إحداثيات مستطيل. ضع النقاط على خطة تنسيقأعتقد أن الجميع يمكنهم القيام بذلك من الصف الخامس إلى السادس. كل نقطة لها مكان محدد على المستوى، ولا يمكن نقلها إلى أي مكان.
إحداثيات المتجههو توسعها من حيث الأساس، في في هذه الحالة. أي متجه هو حر، لذا إذا لزم الأمر، يمكننا بسهولة نقله بعيدًا عن نقطة أخرى في المستوى. ومن المثير للاهتمام أنه بالنسبة للمتجهات، لا يتعين عليك بناء محاور على الإطلاق، نظام مستطيلالإحداثيات، ما عليك سوى أساس، وهو في هذه الحالة أساس متعامد للمستوى.
يبدو أن سجلات إحداثيات النقاط وإحداثيات المتجهات متشابهة: و معنى الإحداثياتقطعاً مختلف، ويجب أن تعي هذا الفرق جيدًا. وهذا الاختلاف، بالطبع، ينطبق أيضًا على الفضاء.
أيها السيدات والسادة، دعونا نملأ أيدينا:
مثال 2
أ) النقاط وتعطى. البحث عن المتجهات و .
ب) النقاط وتعطى. البحث عن المتجهات و .
ج) النقاط وتعطى. البحث عن المتجهات و .
د) يتم إعطاء النقاط. البحث عن المتجهات.
ربما هذا يكفي. هذه أمثلة ل قرار مستقل، حاول ألا تهملهم، فهذا سيؤتي ثماره ؛-). ليست هناك حاجة لعمل الرسومات. الحلول والأجوبة في نهاية الدرس.
ما هو المهم عند حل مشاكل الهندسة التحليلية؟من المهم أن تكون حذرًا للغاية لتجنب الوقوع في الخطأ البارع "اثنان زائد اثنان يساوي صفرًا". أعتذر على الفور إذا ارتكبت خطأ في مكان ما =)
كيفية العثور على طول الجزء؟
الطول، كما ذكرنا سابقًا، يُشار إليه بعلامة المعامل.
إذا تم إعطاء نقطتين من المستوى و، فيمكن حساب طول المقطع باستخدام الصيغة
إذا تم إعطاء نقطتين في الفضاء، فيمكن حساب طول المقطع باستخدام الصيغة
ملحوظة: ستظل الصيغ صحيحة إذا تم تبديل الإحداثيات المقابلة: و ، ولكن الخيار الأول هو أكثر القياسية
مثال 3
حل:وفقا للصيغة المناسبة:
إجابة:
من أجل الوضوح، سأقوم بالرسم 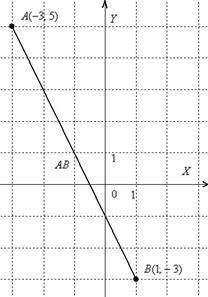
القطعة المستقيمة - هذا ليس ناقلوبالطبع لا يمكنك نقله إلى أي مكان. بالإضافة إلى ذلك، إذا قمت بالرسم على نطاق واسع: 1 وحدة. = 1 سم (خليتان دفتريتان)، ثم يمكن التحقق من الإجابة الناتجة باستخدام مسطرة عادية عن طريق قياس طول القطعة مباشرة.
نعم الحل قصير، لكن هناك حلين آخرين فيه نقاط مهمةالذي أود توضيحه:
أولاً، نضع في الجواب البعد: "الوحدات". الشرط لا يذكر ما هو، ملليمتر، سنتيمتر، متر أو كيلومتر. لذلك، فإن الحل الصحيح رياضيًا هو الصيغة العامة: "الوحدات" - والمختصرة بـ "الوحدات".
ثانيا، دعونا نكرر المواد المدرسية، وهو مفيد ليس فقط للمشكلة قيد النظر:
انتبه على مهم تقنية فنية – إزالة المضاعف من تحت الجذر. نتيجة للحسابات، حصلنا على نتيجة وأسلوب رياضي جيد يتضمن إزالة العامل من تحت الجذر (إن أمكن). وبمزيد من التفاصيل تبدو العملية كما يلي: . وبطبيعة الحال، فإن ترك الإجابة كما هي لن يكون خطأ - ولكنه سيكون بالتأكيد قصورًا وحجة قوية للمراوغة من جانب المعلم.
فيما يلي حالات شائعة أخرى: 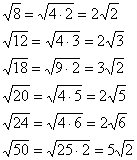
في كثير من الأحيان يكون هناك ما يكفي في الجذر رقم ضخم، على سبيل المثال . ماذا تفعل في مثل هذه الحالات؟ باستخدام الآلة الحاسبة، نتحقق مما إذا كان الرقم قابلاً للقسمة على 4: . نعم تم تقسيمها بالكامل كالتالي: ![]() . أو ربما يمكن تقسيم الرقم على 4 مرة أخرى؟ . هكذا:
. أو ربما يمكن تقسيم الرقم على 4 مرة أخرى؟ . هكذا: ![]() . الرقم الأخير من الرقم فردي، لذا من الواضح أن القسمة على 4 للمرة الثالثة لن تنجح. دعونا نحاول القسمة على تسعة: . نتيجة ل:
. الرقم الأخير من الرقم فردي، لذا من الواضح أن القسمة على 4 للمرة الثالثة لن تنجح. دعونا نحاول القسمة على تسعة: . نتيجة ل:
مستعد.
خاتمة:إذا حصلنا تحت الجذر على رقم لا يمكن استخراجه ككل، فإننا نحاول إزالة العامل من تحت الجذر - باستخدام الآلة الحاسبة نتحقق مما إذا كان الرقم قابلاً للقسمة على: 4، 9، 16، 25، 36، 49، الخ.
خلال القرار المهام المختلفةالجذور شائعة، حاول دائمًا استخراج العوامل من تحت الجذر لتجنب الحصول على درجة أقل ومشاكل غير ضرورية في إنهاء حلولك بناءً على تعليقات المعلم.
لنكرر أيضًا الجذور التربيعية والقوى الأخرى:
قواعد الإجراءات مع درجات في منظر عاميمكن العثور عليها في الكتاب المدرسيفي الجبر، ولكن أعتقد أنه من خلال الأمثلة المقدمة، كل شيء أو كل شيء تقريبًا واضح بالفعل.
مهمة الحل المستقل مع قطعة في الفضاء:
مثال 4
النقاط وتعطى. أوجد طول القطعة.
الحل والجواب في نهاية الدرس .
كيفية العثور على طول المتجه؟
إذا تم إعطاء متجه مستوي، فسيتم حساب طوله بواسطة الصيغة.
إذا تم إعطاء متجه الفضاء، فسيتم حساب طوله بواسطة الصيغة ![]() .
.
يمكن بسهولة اشتقاق هذه الصيغ (وكذلك الصيغ الخاصة بطول المقطع) باستخدام نظرية فيثاغورس المعروفة.
مثال 5
النقاط وتعطى. أوجد طول المتجه.
أخذت نفس النقاط كما في المثال 3.
حل:أولاً، دعونا نجد المتجه:
باستخدام الصيغة، نحسب طول المتجه:
إجابة:
لا تنس الإشارة إلى البعد – "الوحدات"! بالمناسبة، هل من الضروري دائمًا حساب قيمة تقريبية (في في هذا المثال 8.94)، إذا لم يكن هذا مطلوبا في الشرط؟ من وجهة نظري، لن يكون الأمر غير ضروري؛ فعدم وجود قيمة تقريبية يؤدي إلى التصيد. يُنصح بالتقريب إلى 2-3 منازل عشرية.
لنقم بعمل رسم للمهمة:
ما هو الفرق الأساسي عن المثال 3؟ الفرق هو أننا هنا نتحدث عن متجه، وليس قطعة. يمكن نقل المتجه إلى أي نقطة في المستوى.
ما هي أوجه التشابه بين المثال 3 والمثال 5؟ ومن الواضح هندسيًا أن طول القطعة يساوي طول المتجه. ومن الواضح أيضًا أن طول المتجه سيكون هو نفسه. نتيجة ل: ![]() .
.
ب) بالنظر إلى المتجهات و و . أوجد أطوالهم.
الحلول والأجوبة في نهاية الدرس.
في هذه المقالة، سنبدأ بمناقشة "العصا السحرية" التي ستسمح لك بتقليل العديد من المسائل الهندسية إلى عمليات حسابية بسيطة. يمكن لهذه "العصا" أن تجعل حياتك أسهل كثيرًا، خاصة عندما تشعر بعدم اليقين بشأن البناء الأرقام المكانيةوالأقسام وما إلى ذلك. كل هذا يتطلب خيالًا معينًا ومهارات عملية. الطريقة التي سنبدأ في النظر فيها هنا ستسمح لك بالتجريد الكامل تقريبًا من أي نوع الانشاءات الهندسيةوالتفكير. تسمى الطريقة "طريقة الإحداثيات". في هذه المقالة سننظر في الأسئلة التالية:
- خطة تنسيق
- النقاط والمتجهات على المستوى
- بناء متجه من نقطتين
- طول المتجه (المسافة بين نقطتين).
- إحداثيات منتصف القطعة
- المنتج النقطي للمتجهات
- الزاوية بين متجهين
أعتقد أنك خمنت بالفعل سبب تسمية طريقة الإحداثيات بهذا الاسم؟ هذا صحيح، لقد حصل على هذا الاسم لأنه لا يعمل به كائنات هندسية، ومعهم الخصائص العددية(الإحداثيات). والتحويل نفسه، الذي يسمح لنا بالانتقال من الهندسة إلى الجبر، يتكون من إدخال نظام الإحداثيات. إذا كان الشكل الأصلي مسطحاً فإن الإحداثيات تكون ثنائية الأبعاد، وإذا كان الشكل ثلاثي الأبعاد فإن الإحداثيات ثلاثية الأبعاد. في هذه المقالة سننظر فقط في الحالة ثنائية الأبعاد. والهدف الرئيسي من المقال هو تعليمك كيفية استخدام البعض التقنيات الأساسيةطريقة الإحداثيات (في بعض الأحيان تكون مفيدة عند حل المشكلات المتعلقة بقياس التخطيط في الجزء ب من امتحان الدولة الموحدة). القسمان التاليان حول هذا الموضوع مخصصان لمناقشة طرق حل المشكلات C2 (مشكلة القياس المجسم).
أين سيكون من المنطقي البدء بمناقشة طريقة الإحداثيات؟ ربما من مفهوم نظام الإحداثيات. تذكر عندما واجهتها لأول مرة. يبدو لي أنه في الصف السابع، عندما تعلمت عن الوجود دالة خطية، على سبيل المثال. دعني أذكرك أنك قمت ببنائها نقطة نقطة. هل تذكر؟ اخترت عدد التعسفي، استبدلها في الصيغة وحسابها بهذه الطريقة. على سبيل المثال، إذا، ثم، إذا، ثم، وما إلى ذلك. ما الذي حصلت عليه في النهاية؟ وحصلت على نقاط مع الإحداثيات: و. بعد ذلك، قمت برسم "تقاطع" (نظام الإحداثيات)، واخترت مقياسًا عليه (كم عدد الخلايا التي ستحصل عليها كقطعة وحدة) ووضعت علامة على النقاط التي حصلت عليها، والتي قمت بعد ذلك بتوصيلها بخط مستقيم الناتج؛ الخط هو الرسم البياني للوظيفة.
هناك بعض النقاط هنا التي ينبغي شرحها لك بمزيد من التفصيل:
1. اخترت مقطعًا واحدًا لأسباب الراحة، بحيث يتناسب كل شيء بشكل جميل ومضغوط في الرسم
2. من المقبول أن ينتقل المحور من اليسار إلى اليمين، والمحور من الأسفل إلى الأعلى
3. يتقاطعان بزاوية قائمة، ونقطة تقاطعهما تسمى نقطة الأصل. ويشار إليه بحرف.
4. عند كتابة إحداثيات نقطة ما، على سبيل المثال، على اليسار بين قوسين يوجد إحداثيات النقطة على طول المحور، وعلى اليمين على طول المحور. على وجه الخصوص، فهذا يعني ببساطة أنه عند هذه النقطة
5. من أجل تحديد أي نقطة محور الإحداثيات، تحتاج إلى الإشارة إلى إحداثياتها (رقمان)
6. لأي نقطة تقع على المحور،
7. لأي نقطة تقع على المحور،
8. يسمى المحور بالمحور السيني
9. يسمى المحور بالمحور الصادي
الآن دعونا نفعل ذلك معك الخطوة التالية: دعونا نحتفل بنقطتين. دعونا نربط هاتين النقطتين بقطعة. وسنضع السهم كما لو أننا نرسم قطعة من نقطة إلى أخرى: أي أننا سنجعل قطعتنا موجهة!

هل تتذكر ما يسمى الجزء الاتجاهي الآخر؟ هذا صحيح، ويسمى ناقل!
فإذا قمنا بربط نقطة بنقطة، والبداية ستكون النقطة أ، والنهاية ستكون النقطة ب،ثم نحصل على ناقلات. لقد قمت أيضًا بهذا البناء في الصف الثامن، هل تتذكر؟
اتضح أن المتجهات، مثل النقاط، يمكن الإشارة إليها برقمين: تسمى هذه الأرقام بإحداثيات المتجهات. سؤال: هل تعتقد أنه يكفي أن نعرف إحداثيات بداية ونهاية المتجه لإيجاد إحداثياته؟ اتضح أن نعم! ويتم ذلك بكل بساطة:
وبالتالي، بما أن النقطة في المتجه هي البداية والنهاية هي النهاية، فإن المتجه له الإحداثيات التالية:
على سبيل المثال، إذا، فإن إحداثيات المتجه
والآن لنفعل العكس، لنجد إحداثيات المتجه. ماذا نحتاج للتغيير لهذا؟ نعم، أنت بحاجة إلى تبديل البداية والنهاية: الآن ستكون بداية المتجه عند النقطة، وستكون النهاية عند النقطة. ثم:
انظر بعناية، ما هو الفرق بين المتجهات و؟ الفرق الوحيد بينهما هو العلامات الموجودة في الإحداثيات. هم الأضداد. عادة ما يتم كتابة هذه الحقيقة على النحو التالي:
في بعض الأحيان، إذا لم يتم تحديد النقطة التي هي بداية المتجه وأيها هي النهاية، فسيتم الإشارة إلى المتجهات بأكثر من نقطتين بالحروف الكبيرة، وحرف صغير واحد، على سبيل المثال: ، إلخ.
الآن قليلا يمارسنفسك وابحث عن إحداثيات المتجهات التالية:
فحص:
الآن قم بحل مشكلة أكثر صعوبة قليلاً:
المتجه الذي يبدأ عند نقطة ما له co-or-di-na-you. ابحث عن نقاط abs-cis-su.
كل هذا أمر مبتذل تمامًا: دع إحداثيات النقطة. ثم
لقد قمت بتجميع النظام بناءً على تعريف الإحداثيات المتجهة. ثم النقطة لها إحداثيات. نحن مهتمون بالإحداثي. ثم
إجابة:
ماذا يمكنك أن تفعل مع المتجهات؟ نعم، كل شيء تقريبا هو نفسه كما هو الحال مع أرقام عادية(باستثناء أنه لا يمكنك القسمة، ولكن يمكنك الضرب بطريقتين، سنناقش إحداهما هنا بعد قليل)
- يمكن إضافة المتجهات لبعضها البعض
- يمكن طرح المتجهات من بعضها البعض
- يمكن ضرب المتجهات (أو قسمتها) برقم عشوائي غير الصفر
- يمكن ضرب المتجهات ببعضها البعض
كل هذه العمليات لها تمثيل هندسي واضح جدا. على سبيل المثال، قاعدة المثلث (أو متوازي الأضلاع) للجمع والطرح:
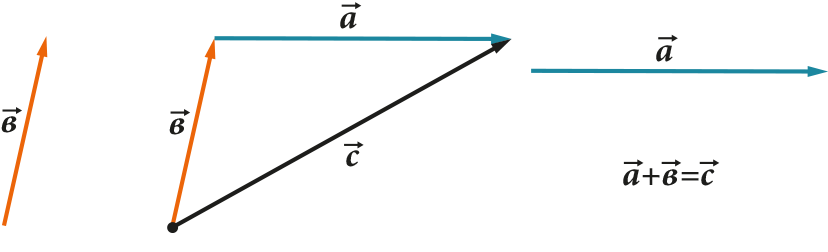
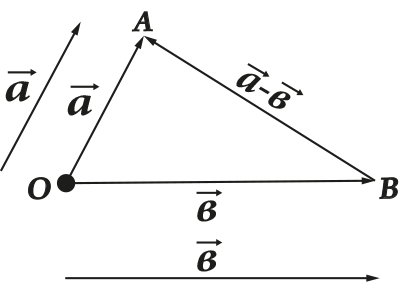
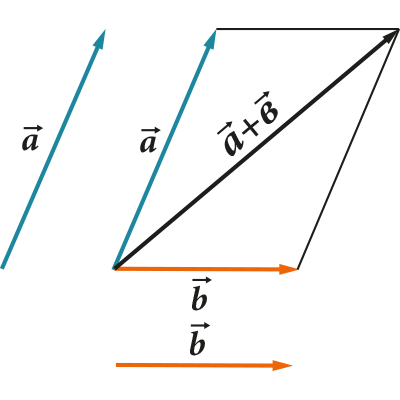
يمتد المتجه أو يتقلص أو يغير اتجاهه عند ضربه أو قسمته على رقم:

ومع ذلك، سنكون هنا مهتمين بمسألة ما يحدث للإحداثيات.
1. عند إضافة (طرح) متجهين، فإننا نضيف (طرح) إحداثياتهما عنصرًا تلو الآخر. إنه:
2. عند ضرب (قسمة) متجه بعدد، يتم ضرب (قسمة) جميع إحداثياته على هذا الرقم:
على سبيل المثال:
· العثور على مقدار co-or-di-nat من القرن إلى ra.
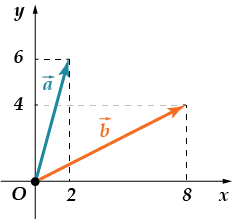
دعونا أولًا نوجد إحداثيات كل متجه. كلاهما لهما نفس الأصل - نقطة الأصل. نهاياتهم مختلفة. ثم، . الآن دعونا نحسب إحداثيات المتجه، ثم يكون مجموع إحداثيات المتجه الناتج متساويًا.
إجابة:
الآن قم بحل المشكلة التالية بنفسك:
· العثور على مجموع إحداثيات المتجهات
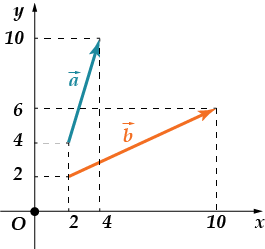
نحن نفحص:
لنفكر الآن في المشكلة التالية: لدينا نقطتان على المستوى الإحداثي. كيف تجد المسافة بينهما؟ فلتكن النقطة الأولى، والثانية. دعونا نشير إلى المسافة بينهما بواسطة. لنقم بعمل الرسم التالي من أجل الوضوح:
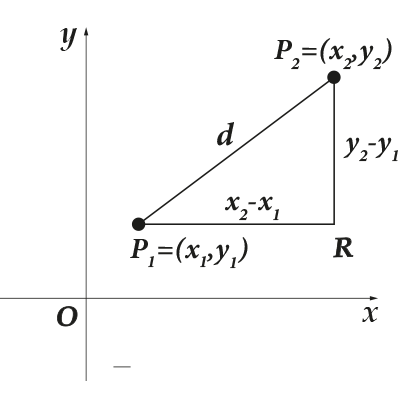
ما الذي فعلته؟ أولا وقبل كل شيء، لقد قمت بالاتصال النقاط و، أكما رسم خطًا من النقطة، موازية للمحورومن النقطة رسمت خطاً موازياً للمحور. هل تقاطعا عند نقطة معينة لتشكلا شكلا مميزا؟ ما الذي يميزها؟ نعم، أنت وأنا نعرف كل شيء تقريبًا عن المثلث القائم الزاوية. حسنا، نظرية فيثاغورس بالتأكيد. القطعة المطلوبة هي الوتر في هذا المثلث، والأجزاء هي الأرجل. ما هي إحداثيات النقطة؟ نعم، من السهل العثور عليها من الصورة: نظرًا لأن المقاطع متوازية مع المحاور، وعلى التوالي، فمن السهل العثور على أطوالها: إذا أشرنا إلى أطوال المقاطع بواسطة، على التوالي، إذن
الآن دعونا نستخدم نظرية فيثاغورس. نحن نعرف أطوال الساقين، وسوف نجد الوتر:
وبالتالي، فإن المسافة بين نقطتين هي جذر مجموع مربعات الفروق من الإحداثيات. أو - المسافة بين نقطتين هي طول القطعة التي تربط بينهما. من السهل أن نرى أن المسافة بين النقاط لا تعتمد على الاتجاه. ثم:
ومن هنا نستخلص ثلاث استنتاجات:
دعونا نتدرب قليلًا على حساب المسافة بين نقطتين:
على سبيل المثال، إذا، فإن المسافة بين وتساوي
أو دعنا نتبع طريقة أخرى: ابحث عن إحداثيات المتجه
وأوجد طول المتجه:
كما ترون، إنه نفس الشيء!
الآن تدرب بنفسك قليلاً:
المهمة: العثور على المسافة بين النقاط المشار إليها:
نحن نفحص:
فيما يلي بعض المشاكل الأخرى التي تستخدم نفس الصيغة، على الرغم من أنها تبدو مختلفة قليلاً:
1. أوجد مربع طول الجفن.

2. أوجد مربع طول الجفن

أعتقد أنك تعاملت معهم دون صعوبة؟ نحن نفحص:
1. وهذا من أجل الانتباه) لقد وجدنا بالفعل إحداثيات المتجهات سابقًا: . ثم المتجه له إحداثيات. مربع طوله سيكون مساوياً لـ:
2. أوجد إحداثيات المتجه
ثم مربع طوله هو
لا شيء معقد، أليس كذلك؟ عملية حسابية بسيطة، لا أكثر.
لا يمكن تصنيف المشكلات التالية بشكل لا لبس فيه، فهي تتعلق أكثر بسعة الاطلاع العامة والقدرة على رسم صور بسيطة.
1. أوجد جيب الزاوية عند القطع الذي يربط النقطة بمحور الإحداثي السيني.
 و
و
كيف سنمضي قدما هنا؟ علينا إيجاد جيب الزاوية الواقعة بين المحور والمحور. أين يمكننا أن نبحث عن جيب؟ هذا صحيح، في مثلث قائم. إذن ماذا علينا أن نفعل؟ بناء هذا المثلث!
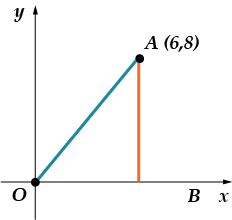
بما أن إحداثيات النقطة هي و، فإن القطعة تساوي القطعة. علينا إيجاد جيب الزاوية. اسمحوا لي أن أذكرك أن جيب الجيب هو نسبة الجانب المعاكسإلى الوتر إذن
ماذا بقي لنا لنفعله؟ أوجد الوتر. يمكنك القيام بذلك بطريقتين: استخدام نظرية فيثاغورس (الأرجل معروفة!) أو استخدام صيغة المسافة بين نقطتين (في الواقع، نفس الطريقة الأولى!). سأذهب في الاتجاه الثاني:
إجابة:
سوف تبدو المهمة التالية أسهل بالنسبة لك. وهي على إحداثيات النقطة.
المهمة 2.من النقطة يتم إنزال كل قلم-دي-كو-ليار على محور ab-ciss. Nai-di-te abs-cis-su os-no-va-niya per-pen-di-ku-la-ra.
لنقم بعمل رسم:
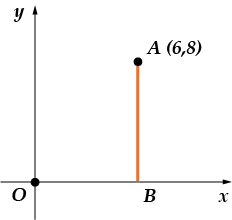
قاعدة العمودي هي النقطة التي يتقاطع عندها مع المحور السيني، وهذه نقطة بالنسبة لي. يوضح الشكل أن له إحداثيات: . نحن مهتمون بالإحداثي السيني - أي المكون "x". إنها متساوية.
إجابة: .
المهمة 3.في الظروف المهمة السابقةأوجد مجموع المسافات من النقطة إلى محاور الإحداثيات.
تكون المهمة أساسية بشكل عام إذا كنت تعرف المسافة من نقطة إلى المحاور. أنت تعرف؟ أتمنى ذلك، لكني سأذكرك:
إذن، في الرسم أعلاه، هل رسمت بالفعل واحدًا من هذا النوع المتعامد؟ على أي محور هو؟ الى المحور. وما هو طوله إذن؟ إنها متساوية. الآن ارسم عموديًا على المحور بنفسك وأوجد طوله. سوف تكون متساوية، أليس كذلك؟ إذن مجموعهما متساوي.
إجابة: .
المهمة 4.في شروط المهمة 2، أوجد إحداثية النقطة، نقطة متناظرةنسبة إلى محور الإحداثي.
أعتقد أنه من الواضح بالنسبة لك ما هو التناظر؟ العديد من الأشياء تمتلكها: العديد من المباني، والطاولات، والطائرات، والعديد منها أشكال هندسية: الكرة، الاسطوانة، المربع، المعين، إلخ. بشكل تقريبي، يمكن فهم التناظر على النحو التالي: يتكون الشكل من نصفين متطابقين (أو أكثر). ويسمى هذا التماثل التماثل المحوري. ما هو المحور إذن؟ هذا هو بالضبط الخط الذي يمكن "قطع" الشكل على طوله نسبيًا إلى نصفين متساويين (في هذه الصورة يكون محور التماثل مستقيمًا):

الآن دعونا نعود إلى مهمتنا. نحن نعلم أننا نبحث عن نقطة متناظرة حول المحور. إذن هذا المحور هو محور التماثل. هذا يعني أننا بحاجة إلى تحديد نقطة بحيث يقطع المحور القطعة إلى جزأين متساويين. حاول تحديد هذه النقطة بنفسك. قارن الآن مع الحل الخاص بي:
![]()
هل نجح الأمر بنفس الطريقة بالنسبة لك؟ بخير! نحن مهتمون بإحداثيات النقطة التي تم العثور عليها. إنه متساوي
إجابة:
الآن أخبرني، بعد التفكير لبضع ثوان، ما هو الإحداثي الإحداثي لنقطة متناظرة مع النقطة A بالنسبة إلى الإحداثي؟ ما هو جوابك؟ اجابة صحيحة: .
في الحالة العامةيمكن كتابة القاعدة هكذا:
النقطة المتناظرة لنقطة نسبة إلى محور الإحداثي السيني لها الإحداثيات:
النقطة المتناظرة لنقطة نسبة إلى المحور الإحداثي لها إحداثيات:
حسنًا، الآن أصبح الأمر مخيفًا تمامًا مهمة: العثور على إحداثيات نقطة متناظرة مع النقطة بالنسبة إلى الأصل. فكر أولاً بنفسك، ثم انظر إلى رسمتي!
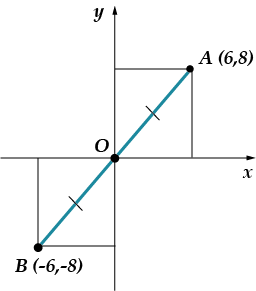
إجابة:
الآن مشكلة متوازي الأضلاع:
المهمة 5: تظهر النقاط ver-shi-na-mi pa-ral-le-lo-gram-ma. البحث عن أو دي على تلك النقطة.
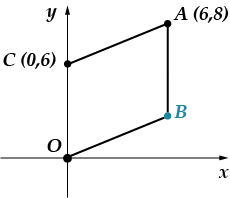
يمكنك حل هذه المشكلة بطريقتين: المنطق وطريقة الإحداثيات. سأستخدم طريقة الإحداثيات أولاً، وبعد ذلك سأخبرك كيف يمكنك حلها بشكل مختلف.
ومن الواضح تماما أن حدود النقطة متساوية. (يقع على الخط المتعامد المرسوم من النقطة على محور الإحداثي السيني). نحن بحاجة إلى العثور على الإحداثيات. دعونا نستفيد من حقيقة أن الشكل الذي لدينا هو متوازي الأضلاع، وهذا يعني ذلك. دعنا نوجد طول المقطع باستخدام صيغة المسافة بين نقطتين:
نخفض العمودي الذي يربط النقطة بالمحور. سأشير إلى نقطة التقاطع بحرف.
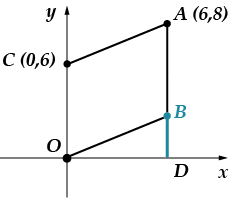
طول القطعة متساوي. (ابحث بنفسك عن المشكلة حيث ناقشنا هذه النقطة)، ثم سنوجد طول القطعة باستخدام نظرية فيثاغورس:
يتطابق طول القطعة تمامًا مع إحداثيتها.
إجابة: .
حل آخر (سأقدم صورة توضح ذلك فقط)
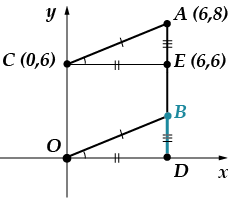
تقدم الحل:
1. السلوك
2. أوجد إحداثيات النقطة والطول
3. أثبت ذلك.
واحدة أخرى مشكلة طول المقطع:
تظهر النقاط أعلى المثلث. أوجد طول خط المنتصف الموازي له.

هل تتذكر ما هو عليه خط الوسطمثلث؟ إذن هذه المهمة أساسية بالنسبة لك. إذا كنت لا تتذكر، فسأذكرك: الخط الأوسط للمثلث هو الخط الذي يصل بين نقاط المنتصف الأطراف المقابلة. وهو موازي للقاعدة ويساوي نصفها.
القاعدة هي قطعة. كان علينا أن نبحث عن طوله سابقًا، فهو متساوٍ. ثم يكون طول الخط الأوسط نصف كبير ومتساوي.
إجابة: .
تعليق: يمكن حل هذه المشكلة بطريقة أخرى سنتطرق إليها بعد قليل.
في هذه الأثناء، إليك بعض المسائل التي يمكنك التدرب عليها، فهي بسيطة جدًا، ولكنها تساعدك على تحسين استخدام الطريقة الإحداثية!
1. النقط هي قمة النقائص. أوجد طول خط وسطه.

2. النقاط والمظاهر ver-shi-na-mi pa-ral-le-lo-gram-ma. البحث عن أو دي على تلك النقطة.

3. ابحث عن الطول من القطع، وربط النقطة و

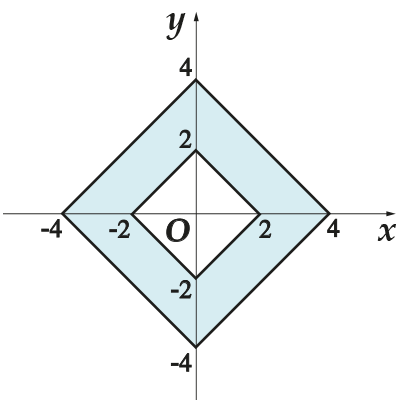
4. أوجد المساحة خلف الشكل الملون على المستوى الإحداثي.
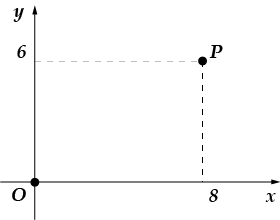
5. دائرة مركزها في na-cha-le ko-or-di-nat تمر عبر النقطة. ابحث عنها ra-di-us.
6. ابحث عن-di-te ra-di-us للدائرة، وصف-san-noy حول الزاوية اليمنى-no-ka، قمم شيء ما لها مشاركة أو -di-na-أنت مسؤول جدًا

حلول:
1. من المعلوم أن خط الوسط لشبه المنحرف يساوي نصف مجموع قواعده. القاعدة متساوية، والقاعدة. ثم
إجابة:
2. أسهل طريقة لحل هذه المشكلة هي ملاحظة (قاعدة متوازي الأضلاع). حساب إحداثيات المتجهات ليس بالأمر الصعب: . عند إضافة المتجهات، تتم إضافة الإحداثيات. ثم لديه الإحداثيات. وللنقطة أيضًا هذه الإحداثيات، لأن أصل المتجه هو النقطة ذات الإحداثيات. نحن مهتمون بالإحداثيات. إنها متساوية.
إجابة:
3. نتصرف على الفور وفقًا لصيغة المسافة بين نقطتين:
إجابة:
4. انظر إلى الصورة وأخبرني أي الشكلين تقع المنطقة المظللة بينهما؟ وهي محصورة بين مربعين. ثم مساحة الشكل المطلوب تساوي مساحة المربع الكبير ناقص مساحة المربع الصغير. جانب مربع صغيرهو قطعة تربط النقاط وطولها
ثم مساحة المربع الصغير هي
نحن نفعل الشيء نفسه مع مربع كبير: جانبه عبارة عن قطعة تربط النقاط وطوله
ثم مساحة المربع الكبير هي
نجد مساحة الشكل المطلوب باستخدام الصيغة:
إجابة:
5. إذا كان مركز الدائرة هو الأصل وتمر بنقطة، فإن نصف قطرها سيكون بالضبط يساوي الطولالمقطع (ارسم رسمًا وسوف تفهم سبب وضوح ذلك). دعونا نجد طول هذا الجزء:
إجابة:
6. من المعلوم أن نصف قطر الدائرة يحدها مستطيل يساوي النصفأقطارها. دعونا نوجد طول أي من القطرين (بعد كل شيء، في المستطيل متساويان!)
إجابة:
حسنًا ، هل تعاملت مع كل شيء؟ لم يكن من الصعب جدًا معرفة ذلك، أليس كذلك؟ هناك قاعدة واحدة فقط هنا - أن تكون قادرًا على إنشاء صورة مرئية و"قراءة" جميع البيانات منها ببساطة.
لم يبق لدينا سوى القليل جدا. هناك حرفيًا نقطتان أخريان أود مناقشتهما.
دعونا نحاول حل هذه المشكلة البسيطة. دع نقطتين وتعطى. أوجد إحداثيات منتصف القطعة. الحل لهذه المشكلة هو كما يلي: لتكن النقطة هي الوسط المطلوب، فيكون لها إحداثيات:
إنه: إحداثيات منتصف القطعة = الوسط الحسابي للإحداثيات المقابلة لأطراف القطعة.
هذه القاعدة بسيطة جدًا وعادةً لا تسبب صعوبات للطلاب. دعونا نرى ما هي المشاكل وكيف يتم استخدامها:
1. ابحث عن-di-te أو-di-na-tu se-re-di-ny من القطع، وقم بتوصيل النقطة و

2. النقاط تبدو وكأنها قمة العالم. ابحث عن نقاط-di-te أو-di-na-tu لكل إعادة-se-che-niya من dia-go-na-ley.

3. ابحث عن مركز di-te abs-cis-su للدائرة، وصف-san-noy حول no-ka المستطيل، وقمم شيء ما شاركت فيه أو di-na-you بمسؤولية كبيرة ولكن.

حلول:
1. المشكلة الأولى هي ببساطة مشكلة كلاسيكية. ننتقل على الفور إلى تحديد منتصف الجزء. لديها إحداثيات. الإحداثي متساوي.
إجابة:
2. من السهل أن نرى أن هذا الشكل الرباعي هو متوازي أضلاع (حتى المعين!). يمكنك إثبات ذلك بنفسك عن طريق حساب أطوال الجوانب ومقارنتها مع بعضها البعض. ماذا أعرف عن متوازي الأضلاع؟ أقطارها مقسمة إلى نصفين عند نقطة التقاطع! نعم! إذن ما هي نقطة تقاطع القطرين؟ هذا هو منتصف أي من الأقطار! سأختار القطر على وجه الخصوص. ثم النقطة لها إحداثيات إحداثيات النقطة يساوي.
إجابة:
3. ما الذي يتطابق معه مركز الدائرة المحيطة بالمستطيل؟ ويتزامن مع نقطة تقاطع قطريه. ماذا تعرف عن أقطار المستطيل؟ إنهما متساويان ونقطة التقاطع تقسمهما إلى نصفين. تم تقليص المهمة إلى المهمة السابقة. لنأخذ، على سبيل المثال، القطر. فإذا كان مركز الدائرة المحيطة، فهو نقطة المنتصف. أبحث عن الإحداثيات: الإحداثيات متساوية.
إجابة:
الآن تدرب قليلًا بمفردك، وسأقدم لك الإجابات لكل مشكلة حتى تتمكن من اختبار نفسك.
1. ابحث عن-di-te ra-di-us للدائرة، وصف-san-noy حول الزاوية الثلاثية-no-ka، قمم شيء ما بها رفاق مشتركون أو-di-no

2. ابحث عن-di-te أو-di-on-مركز الدائرة، وصف-san-noy حول المثلث-no-ka، الذي تحتوي قممه على إحداثيات
3. ما هو نوع ra-di-u-sa الذي يجب أن تكون فيه دائرة مركزها عند نقطة بحيث تلامس محور ab-ciss؟
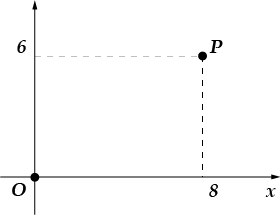
4. ابحث عن تلك النقطة أو نقطة إعادة انفصال المحور ومن القطع وقم بتوصيل النقطة و

الإجابات:
هل كان كل شيء ناجحا؟ آمل حقا لذلك! الآن - الدفعة الأخيرة. الآن كن حذرًا بشكل خاص. المادة التي سأشرحها الآن لا ترتبط ارتباطًا مباشرًا بها فقط مهام بسيطةإلى طريقة الإحداثيات من الجزء B، ولكنها موجودة أيضًا في كل مكان في المشكلة C2.
أي من وعودي لم أفي بها بعد؟ هل تتذكر ما هي العمليات التي أجريت على المتجهات التي وعدت بتقديمها وأي منها قدمتها في النهاية؟ هل أنت متأكد من أنني لم أنس أي شيء؟ نسيت! لقد نسيت أن أشرح ما يعنيه ضرب المتجهات.
هناك طريقتان لضرب المتجه بالمتجه. اعتمادًا على الطريقة المختارة، سنحصل على أشياء ذات طبيعة مختلفة:
يتم تنفيذ المنتج المتقاطع بذكاء تام. سنناقش كيفية القيام بذلك وسبب الحاجة إليه في المقالة التالية. وفي هذا سوف نركز على المنتج القياسي.
هناك طريقتان تسمحان لنا بحسابه:
كما خمنت، يجب أن تكون النتيجة هي نفسها! لذلك دعونا ننظر إلى الطريقة الأولى أولاً:
نقطة المنتج عبر الإحداثيات
البحث عن: - التدوين المقبول عمومًا للمنتج العددي
صيغة الحساب هي كما يلي:
إنه المنتج العددي= مجموع منتجات إحداثيات المتجهات!
مثال:
البحث عن الشركة المصرية للاتصالات
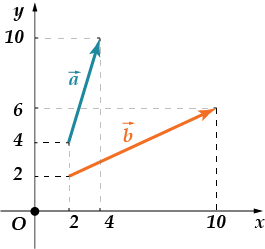
حل:
دعونا نجد إحداثيات كل من المتجهات:
نحسب المنتج العددي باستخدام الصيغة:
إجابة:
انظر، لا شيء معقد على الإطلاق!
حسنًا، جرب الآن بنفسك:
· ابحث عن عددي مؤيد لقرون و
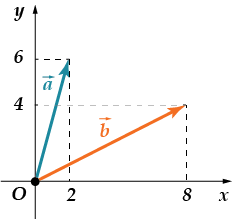
هل تستطيع فعلها؟ ربما لاحظت صيدًا صغيرًا؟ دعونا تحقق:
إحداثيات المتجهات كما في اخر مهمة! إجابة: .
بالإضافة إلى الإحداثيات، هناك طريقة أخرى لحساب حاصل الضرب القياسي، وهي من خلال أطوال المتجهات وجيب تمام الزاوية بينهما:
يدل على الزاوية بين المتجهات و.
أي أن حاصل الضرب القياسي يساوي حاصل ضرب أطوال المتجهات وجيب تمام الزاوية بينهما.
لماذا نحتاج إلى هذه الصيغة الثانية، إذا كان لدينا الصيغة الأولى، وهي أبسط بكثير، على الأقل لا يوجد جيب التمام فيها. وهو ضروري حتى نتمكن أنا وأنت من الصيغتين الأولى والثانية من استنتاج كيفية العثور على الزاوية بين المتجهات!
دعونا ثم نتذكر صيغة طول المتجه!
ثم إذا قمت باستبدال هذه البيانات في صيغة المنتج العددية، أحصل على:
ولكن بطريقة أخرى:
إذن ماذا حصلنا أنا وأنت؟ لدينا الآن صيغة تسمح لنا بحساب الزاوية بين متجهين! في بعض الأحيان يتم كتابته أيضًا على هذا النحو للإيجاز:
أي أن خوارزمية حساب الزاوية بين المتجهات هي كما يلي:
- حساب المنتج العددي من خلال الإحداثيات
- أوجد أطوال المتجهات واضربها
- اقسم نتيجة النقطة 1 على نتيجة النقطة 2
دعونا نتدرب مع الأمثلة:
1. أوجد الزاوية بين الجفون و. إعطاء الجواب في غراد دو ساه.
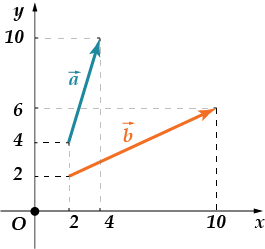
2. في شروط المشكلة السابقة، أوجد جيب التمام بين المتجهات
فلنفعل هذا: سأساعدك على حل المشكلة الأولى، وحاول حل المشكلة الثانية بنفسك! يوافق؟ ثم دعونا نبدأ!
1. هذه المتجهات هي أصدقائنا القدامى. لقد حسبنا بالفعل حاصل ضربهم القياسي وكان متساويًا. إحداثياتهم هي : . ثم نجد أطوالها:
ثم نبحث عن جيب التمام بين المتجهات:
ما هو جيب تمام الزاوية؟ هذه هي الزاوية.
إجابة:
حسنًا، قم الآن بحل المشكلة الثانية بنفسك، ثم قارن! سأقدم حلاً قصيرًا جدًا:
2. له إحداثيات، له إحداثيات.
اسمحوا أن تكون الزاوية بين المتجهات و، ثم
إجابة:
وتجدر الإشارة إلى أن المشاكل مباشرة على المتجهات وطريقة الإحداثيات في الجزء ب ورقة الامتحاننادرة جدا. ومع ذلك، فإن الغالبية العظمى من مشاكل C2 يمكن حلها بسهولة عن طريق إدخال نظام الإحداثيات. لذلك يمكنك اعتبار هذه المقالة الأساس الذي سنبني على أساسه إنشاءات ذكية للغاية سنحتاجها لحل المشكلات المعقدة.
