Ten artykuł dotyczy kąta między płaszczyznami i sposobu jego znalezienia. Najpierw podano definicję kąta między dwiema płaszczyznami i podano ilustrację graficzną. Następnie przeanalizowano zasadę wyznaczania kąta pomiędzy dwiema przecinającymi się płaszczyznami metodą współrzędnych i uzyskano wzór pozwalający obliczyć kąt pomiędzy przecinającymi się płaszczyznami przy wykorzystaniu znanych współrzędnych wektorów normalnych tych płaszczyzn. Podsumowując, zostało to pokazane szczegółowe rozwiązania charakterystyczne zadania.
Nawigacja strony.
Kąt między płaszczyznami - definicja.
Przedstawmy argumenty, które pozwolą nam stopniowo zbliżać się do wyznaczania kąta pomiędzy dwiema przecinającymi się płaszczyznami.
Daj nam mieć dwie przecinające się płaszczyzny i . Płaszczyzny te przecinają się na linii prostej, którą oznaczamy literą c. Skonstruujmy płaszczyznę przechodzącą przez punkt M prostej c i prostopadłą do prostej c. W tym przypadku płaszczyzna przetnie płaszczyzny i. Oznaczmy linię prostą, wzdłuż której płaszczyzny przecinają się, jako a, a linię prostą, wzdłuż której przecinają się płaszczyzny jako b. Oczywiście proste aib przecinają się w punkcie M.

Łatwo pokazać, że kąt pomiędzy przecinającymi się prostymi a i b nie zależy od położenia punktu M na prostej c, przez którą przechodzi płaszczyzna.
Skonstruujmy płaszczyznę prostopadłą do prostej c i różną od płaszczyzny. Płaszczyzna przecina się płaszczyznami i liniami prostymi, które oznaczamy odpowiednio jako 1 i b 1.
Z sposobu konstruowania płaszczyzn wynika, że linie a i b są prostopadłe do linii c, a linie a 1 i b 1 są prostopadłe do linii c. Ponieważ linie a i a 1 leżą w tej samej płaszczyźnie i są prostopadłe do linii c, to są one równoległe. Podobnie linie b i b 1 leżą w tej samej płaszczyźnie i są prostopadłe do linii c, a zatem są równoległe. Więc możesz to zrobić transfer równoległy płaszczyzna do płaszczyzny, w której prosta a 1 pokrywa się z prostą a, a prosta b z prostą b 1. Dlatego kąt między dwiema przecinającymi się liniami a 1 i b 1 równy kątowi pomiędzy przecinającymi się liniami a i b.

Dowodzi to, że kąt pomiędzy przecinającymi się prostymi a i b leżącymi w przecinających się płaszczyznach nie zależy od wyboru punktu M, przez który przechodzi płaszczyzna. Dlatego logiczne jest przyjęcie tego kąta jako kąta między dwiema przecinającymi się płaszczyznami.
Teraz możesz wyrazić definicję kąta między dwiema przecinającymi się płaszczyznami i.
Definicja.
Kąt między dwiema płaszczyznami przecinającymi się na linii prostej i- jest to kąt pomiędzy dwiema przecinającymi się liniami a i b, wzdłuż których płaszczyzny i przecinają się z płaszczyzną prostopadłą do prostej c.

Definicję kąta między dwiema płaszczyznami można podać nieco inaczej. Jeżeli na prostej c, wzdłuż której przecinają się płaszczyzny i, zaznacz punkt M i poprowadź przez niego proste a i b, prostopadłe do prostej c i leżące w płaszczyznach, i odpowiednio kąt między prostymi a oraz b jest kątem pomiędzy płaszczyznami i. Zwykle w praktyce właśnie takie konstrukcje wykonuje się w celu uzyskania kąta pomiędzy płaszczyznami.
Ponieważ kąt pomiędzy przecinającymi się prostymi nie przekracza , z podanej definicji wynika, że miara stopnia wyrażany jest kąt między dwiema przecinającymi się płaszczyznami prawdziwy numer z interwału. W tym przypadku nazywane są przecinające się płaszczyzny prostopadły, jeśli kąt między nimi wynosi dziewięćdziesiąt stopni. Kąt między równoległymi płaszczyznami albo w ogóle nie jest określony, albo uważa się go za równy zeru.
Znalezienie kąta między dwiema przecinającymi się płaszczyznami.
Zwykle, szukając kąta pomiędzy dwiema przecinającymi się płaszczyznami, należy najpierw wykonać dodatkowe konstrukcje, aby zobaczyć przecinające się proste, których kąt jest równy żądanemu kątowi, a następnie połączyć ten kąt z danymi pierwotnymi za pomocą testów równości, podobieństwa testy, twierdzenie cosinus czy definicje sinusa, cosinusa i tangensa kąta. W trakcie geometrii Liceum występują podobne problemy.
Jako przykład podamy rozwiązanie Zadania C2 z Unified State Exam in Mathematics za rok 2012 (warunek został celowo zmieniony, ale nie wpływa to na zasadę rozwiązania). W nim wystarczyło znaleźć kąt między dwiema przecinającymi się płaszczyznami.
Przykład.
Rozwiązanie.
Najpierw zróbmy rysunek.

Wykonajmy dodatkowe konstrukcje, żeby „zobaczyć” kąt pomiędzy płaszczyznami.
Najpierw zdefiniujmy linię prostą, wzdłuż której przecinają się płaszczyzny ABC i BED 1. Punkt B jest jednym z ich punktów wspólnych. Znajdźmy to drugie wspólny punkt te samoloty. Proste DA i D 1 E leżą w tej samej płaszczyźnie ADD 1 i nie są równoległe, więc się przecinają. Natomiast prosta DA leży w płaszczyźnie ABC, a prosta D 1 E - w płaszczyźnie BED 1, zatem punkt przecięcia prostych DA i D 1 E będzie punktem wspólnym Samoloty ABC i ŁÓŻKO 1. Kontynuujmy więc linie DA i D 1 E do ich przecięcia, oznaczając punkt ich przecięcia literą F. Wtedy BF jest prostą, wzdłuż której przecinają się płaszczyzny ABC i BED 1.

Pozostaje skonstruować dwie proste leżące odpowiednio w płaszczyznach ABC i BED 1, przechodzące przez jeden punkt na prostej BF i prostopadłe do prostej BF - kąt pomiędzy tymi prostymi z definicji będzie równy pożądanemu kątowi pomiędzy samoloty ABC i BED 1. Zróbmy to.
Kropka A jest rzutem punktu E na płaszczyznę ABC. Narysujmy prostą przecinającą linię BF pod kątem prostym w punkcie M. Wtedy prosta AM jest rzutem prostej EM na płaszczyznę ABC i na podstawie twierdzenia o trzech prostopadłych.

Zatem wymagany kąt pomiędzy płaszczyznami ABC i BED 1 wynosi .
Możemy wyznaczyć sinus, cosinus lub tangens tego kąta (a tym samym i sam kąt) z trójkąta prostokątnego AEM, jeśli znamy długości jego dwóch boków. Z warunku łatwo wyznaczyć długość AE: skoro punkt E dzieli bok AA 1 w stosunku 4 do 3, licząc od punktu A, a długość boku AA 1 wynosi 7, to AE = 4. Znajdźmy długość AM.
Aby to zrobić, rozważ trójkąt prostokątny ABF z kątem prostym A, gdzie AM jest wysokością. Według warunku AB = 2. Długość boku AF możemy wyznaczyć z podobieństwa trójkątów prostokątnych DD 1 F i AEF: 
Korzystając z twierdzenia Pitagorasa, znajdujemy z trójkąta ABF. Znajdujemy długość AM przez obszar trójkąta ABF: z jednej strony pole trójkąta ABF jest równe ![]() , z drugiej strony
, z drugiej strony ![]() , Gdzie
, Gdzie  .
.
Zatem z trójkąta prostokątnego AEM mamy  .
.
Wtedy wymagany kąt pomiędzy płaszczyznami ABC i BED 1 jest równy (zwróć uwagę, że  ).
).
Odpowiedź:

W niektórych przypadkach, aby znaleźć kąt między dwiema przecinającymi się płaszczyznami, wygodnie jest ustawić Oxyz i zastosować metodę współrzędnych. Zatrzymajmy się na tym.
Ustalmy zadanie: znaleźć kąt pomiędzy dwiema przecinającymi się płaszczyznami i . Oznaczmy żądany kąt jako .
Zakładamy, że w danym prostokątnym układzie współrzędnych Oxyz znamy współrzędne wektorów normalnych przecinających się płaszczyzn i/lub mamy możliwość ich znalezienia. Pozwalać ![]() jest wektorem normalnym płaszczyzny, oraz
jest wektorem normalnym płaszczyzny, oraz ![]() jest wektorem normalnym płaszczyzny. Pokażemy, jak znaleźć kąt między przecinającymi się płaszczyznami i poprzez współrzędne wektorów normalnych tych płaszczyzn.
jest wektorem normalnym płaszczyzny. Pokażemy, jak znaleźć kąt między przecinającymi się płaszczyznami i poprzez współrzędne wektorów normalnych tych płaszczyzn.
Oznaczmy linię prostą, wzdłuż której płaszczyzny i przecinają się jako c. Przez punkt M na prostej c rysujemy płaszczyznę prostopadłą do prostej c. Płaszczyzna przecina płaszczyzny i odpowiednio linie a i b przecinają się w punkcie M. Z definicji kąt między przecinającymi się płaszczyznami i jest równy kątowi między przecinającymi się liniami a i b.
Narysujmy wektory i płaszczyzny normalne oraz z punktu M na płaszczyźnie. W tym przypadku wektor leży na prostej prostopadłej do prostej a, a wektor leży na prostej prostopadłej do prostej b. Zatem w płaszczyźnie wektor jest wektorem normalnym linii a, jest wektorem normalnym linii b.

W artykule o znalezieniu kąta między przecinającymi się prostymi otrzymaliśmy wzór, który pozwala nam obliczyć cosinus kąta między przecinającymi się prostymi przy użyciu współrzędnych wektorów normalnych. Zatem cosinus kąta między liniami a i b, a co za tym idzie, cosinus kąta pomiędzy przecinającymi się płaszczyznami i można go znaleźć za pomocą wzoru gdzie ![]() I
I ![]() są wektorami normalnymi płaszczyzn i, odpowiednio. Następnie oblicza się to jako
są wektorami normalnymi płaszczyzn i, odpowiednio. Następnie oblicza się to jako  .
.
Rozwiążmy poprzedni przykład za pomocą metody współrzędnych.
Przykład.
Dan prostopadłościan ABCDA 1 B 1 C 1 D 1, w którym AB=2, AD=3, AA 1 =7 i punkt E dzieli bok AA 1 w stosunku 4 do 3, licząc od punktu A. Znajdź kąt pomiędzy płaszczyznami ABC i BED 1.
Rozwiązanie.
Ponieważ boki prostokątnego równoległościanu w jednym wierzchołku są prostopadłe parami, wygodnie jest to wprowadzić układ prostokątny współrzędne Oxyz w ten sposób: zrównaj początek z wierzchołkiem C i skieruj osie współrzędnych Ox, Oy i Oz odpowiednio wzdłuż boków CD, CB i CC 1.

Kąt pomiędzy płaszczyznami ABC i BED 1 można znaleźć poprzez współrzędne wektorów normalnych tych płaszczyzn, korzystając ze wzoru , gdzie i są wektorami normalnymi odpowiednio płaszczyzn ABC i BED 1. Wyznaczmy współrzędne wektorów normalnych.
Miarą kąta między płaszczyznami jest ostry róg, utworzony przez dwie linie proste leżące w tych płaszczyznach i poprowadzone prostopadle do linii ich przecięcia.
Algorytm konstrukcji
- Z dowolnego punktu K poprowadzono prostopadłe do każdej z podanych płaszczyzn.
- Obracając się wokół linii poziomu, wyznacza się kąt γ° z wierzchołkiem w punkcie K.
- Oblicz kąt pomiędzy płaszczyznami ϕ° = 180 – γ°, pod warunkiem, że γ° > 90°. Jeśli γ°< 90°, то ∠ϕ° = ∠γ°.
Na rysunku przedstawiono przypadek, gdy płaszczyzny α i β są podane śladami. Wszystkie niezbędne konstrukcje zostały wykonane zgodnie z algorytmem i zostały opisane poniżej.
Rozwiązanie
- W dowolnym miejscu na rysunku zaznacz punkt K. Z niego obniżamy odpowiednio prostopadłe m i n do płaszczyzn α i β. Kierunek występów m i n jest następujący: m""⊥f 0α , m"⊥h 0α , n""⊥f 0β , n"⊥h 0β .
- Rzeczywisty rozmiar ∠γ° wyznaczamy pomiędzy liniami m i n. W tym celu wokół czoła f obracamy płaszczyznę kąta z wierzchołkiem K do położenia równoległego do przedniej płaszczyzny rzutu. Promień skrętu R punktu K równa wartości przeciwprostokątna trójkąta prostokątnego O""K""K 0, którego bok to K""K 0 = y K – y O.
- Pożądany kąt to ϕ° = ∠γ°, ponieważ ∠γ° jest ostry.
Poniższy rysunek przedstawia rozwiązanie zadania polegającego na znalezieniu kąta γ° pomiędzy płaszczyznami α i β, wyznaczonego odpowiednio przez proste równoległe i przecinające się.

Rozwiązanie
- Określamy kierunek rzutów poziomych h 1, h 2 i frontów f 1, f 2, należące do samolotówα i β, w kolejności wskazanej strzałkami. Z dowolnego punktu K na kwadracie. α i β pomijamy prostopadłe e i k. W tym przypadku e""⊥f"" 1 , e"⊥h" 1 i k""⊥f"" 2 , k"⊥h" 2 .
- Definiujemy ∠γ° pomiędzy liniami e i k. Aby to zrobić, narysuj poziomą linię h 3 i wokół niej obracamy punkt K do pozycji K 1, w której △CKD stanie się równoległe do płaszczyzny poziomej i odbije się na niej w naturalnym rozmiarze - △C"K" 1 D „. Rzut środka obrotu O” znajduje się na narysowanym do h” 3 prostopadle do K”O”. Promień R wyznacza się z trójkąta prostokątnego O”K”K 0, którego bok K”K 0 = Z O – Z K.
- Wartość pożądanej wartości wynosi ∠ϕ° = ∠γ°, ponieważ kąt γ° jest ostry.
W artykule mowa o znajdowaniu kąta pomiędzy płaszczyznami. Po podaniu definicji podamy ilustrację graficzną i rozważymy szczegółowy sposób znajdowania współrzędnych tą metodą. Otrzymujemy wzór na przecinające się płaszczyzny, który zawiera współrzędne wektorów normalnych.
Yandex.RTB R-A-339285-1
W materiale zostaną wykorzystane dane i koncepcje, które były wcześniej badane w artykułach na temat płaszczyzny i linii w przestrzeni. Najpierw należy przejść do rozumowania, które pozwala nam mieć pewne podejście do wyznaczania kąta między dwiema przecinającymi się płaszczyznami.
Dane są dwie przecinające się płaszczyzny γ 1 i γ 2. Ich przecięcie otrzyma oznaczenie c. Konstrukcja płaszczyzny χ związana jest z przecięciem tych płaszczyzn. Płaszczyzna χ przechodzi przez punkt M jako linia prosta c. Przecięcie płaszczyzn γ 1 i γ 2 zostanie wykonane za pomocą płaszczyzny χ. Oznaczenie prostej przecinającej γ 1 i χ przyjmujemy jako linię a, a prostą przecinającą γ 2 i χ jako linię b. Stwierdzamy, że przecięcie prostych aib daje punkt M.
Położenie punktu M nie ma wpływu na kąt pomiędzy przecinającymi się liniami a i b, a punkt M leży na prostej c, przez którą przechodzi płaszczyzna χ.
Należy skonstruować płaszczyznę χ 1 prostopadłą do prostej c i różną od płaszczyzny χ. Przecięcie płaszczyzn γ 1 i γ 2 za pomocą χ 1 przyjmie oznaczenie linii a 1 i b 1.
Można zauważyć, że przy konstruowaniu χ i χ 1 linie aib są prostopadłe do linii c, wówczas a 1, b 1 leżą prostopadle do linii c. Znajdując proste a i a 1 w płaszczyźnie γ 1 prostopadle do prostej c, wówczas można je uznać za równoległe. W ten sam sposób położenie b i b 1 w płaszczyźnie γ 2 prostopadle do prostej c wskazuje na ich równoległość. Oznacza to, że konieczne jest równoległe przeniesienie płaszczyzny χ 1 do χ, gdzie otrzymamy dwie pokrywające się linie proste a i a 1, b i b 1. Stwierdzamy, że kąt między przecinającymi się liniami a i b 1 jest równy kątowi przecinających się linii a i b.
Spójrzmy na poniższy rysunek.

Twierdzenie to potwierdza fakt, że pomiędzy przecinającymi się liniami a i b istnieje kąt niezależny od położenia punktu M, czyli punktu przecięcia. Linie te znajdują się w płaszczyznach γ 1 i γ 2. W rzeczywistości powstały kąt można uznać za kąt między dwiema przecinającymi się płaszczyznami.
Przejdźmy do określenia kąta pomiędzy istniejącymi przecinającymi się płaszczyznami γ 1 i γ 2.
Definicja 1
Kąt między dwiema przecinającymi się płaszczyznami γ 1 i γ 2 nazywany kątem utworzonym przez przecięcie linii a i b, w którym płaszczyzny γ 1 i γ 2 przecinają się z płaszczyzną χ prostopadłą do linii c.
Rozważ poniższy rysunek.
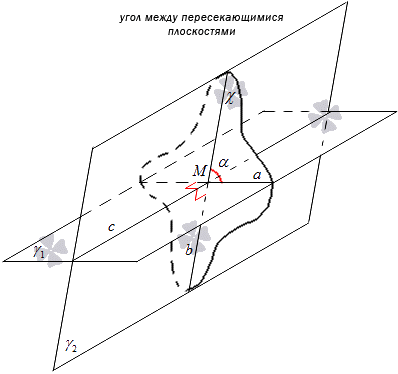
Orzeczenie może zostać złożone w innej formie. Kiedy płaszczyzny γ 1 i γ 2 przecinają się, gdzie c jest prostą, na której się przecinają, zaznacz punkt M, przez który poprowadź linie a i b prostopadłe do prostej c i leżące w płaszczyznach γ 1 i γ 2, wówczas kąt między linie aib będą kątem pomiędzy płaszczyznami. W praktyce ma to zastosowanie przy konstruowaniu kąta między płaszczyznami.
Podczas przecięcia powstaje kąt o wartości mniejszej niż 90 stopni, to znaczy miara kąta w stopniach obowiązuje w przedziale tego typu (0, 90). Jednocześnie płaszczyzny te nazywane są prostopadłymi, jeśli na przecięciu powstaje kąt prosty.Kąt między równoległymi płaszczyznami uważa się za równy zeru.
Typowym sposobem znalezienia kąta między przecinającymi się płaszczyznami jest wykonanie dodatkowych konstrukcji. Pomaga to określić to z dokładnością, a można to zrobić za pomocą znaków równości lub podobieństwa trójkąta, sinusów i cosinusów kąta.
Rozważmy rozwiązanie problemów na przykładzie z Problemy z egzaminem jednolitym blok C 2.
Przykład 1
Biorąc pod uwagę prostokątny równoległościan A B C D A 1 B 1 C 1 D 1, gdzie bok A B = 2, A D = 3, A A 1 = 7, punkt E dzieli bok A A 1 w stosunku 4: 3. Znajdź kąt pomiędzy płaszczyznami A B C i B E D 1.
Rozwiązanie
Dla jasności konieczne jest wykonanie rysunku. Rozumiemy to

Aby praca z kątem między płaszczyznami była wygodniejsza, konieczna jest reprezentacja wizualna.
Wyznaczamy linię prostą, wzdłuż której następuje przecięcie płaszczyzn A B C i B E D 1. Punkt B jest punktem wspólnym. Należy znaleźć inny wspólny punkt przecięcia. Rozważmy linie proste D A i D 1 E, które znajdują się w tej samej płaszczyźnie A D D 1. Ich położenie nie wskazuje na równoległość, oznacza to, że mają wspólny punkt przecięcia.
Natomiast prosta D A leży w płaszczyźnie A B C, a D 1 E w B E D 1. Z tego otrzymujemy linie proste DA I D 1 E mają wspólny punkt przecięcia, który jest wspólny dla płaszczyzn A B C i B E D 1. Wskazuje punkt przecięcia linii DA i D1E litera F. Z tego wynika, że B F jest linią prostą, wzdłuż której przecinają się płaszczyzny A B C i B E D 1.
Spójrzmy na poniższy rysunek.

Aby uzyskać odpowiedź należy skonstruować proste leżące w płaszczyznach A B C i B E D 1 przechodzące przez punkt leżący na prostej B F i prostopadły do niej. Następnie powstały kąt między tymi prostymi jest uważany za pożądany kąt między płaszczyznami A B C i B E D 1.
Widzimy z tego, że punkt A jest rzutem punktu E na płaszczyznę A B C. Należy narysować linię prostą przecinającą linię B F pod kątem prostym w punkcie M. Można zauważyć, że prosta A M jest rzutem prostej E M na płaszczyznę A B C, w oparciu o twierdzenie o tych prostopadłych A M ⊥ B F . Rozważ poniższy obrazek.

∠ A M E to pożądany kąt utworzony przez płaszczyzny A B C i B E D 1. Z powstałego trójkąta A E M możemy znaleźć sinus, cosinus lub tangens kąta, a następnie sam kąt, tylko jeśli znane są jego dwa boki. Pod warunkiem mamy, że długość A E wyznacza się w następujący sposób: linia prosta A A 1 jest dzielona przez punkt E w stosunku 4:3, co oznacza, że całkowita długość prostej wynosi 7 części, wówczas A E = 4 części. Znajdujemy A M.
Konieczne jest rozważenie trójkąta prostokątnego A B F. Mamy kąt prosty A o wysokości A M. Z warunku A B = 2 możemy znaleźć długość A F z podobieństwa trójkątów D D 1 F i A E F. Otrzymujemy, że A E D D 1 = ZA F D F ⇔ A E D D 1 = A F D A + ZA F ⇒ 4 7 = ZA F 3 + ZA F ⇔ ZA F = 4
Należy obliczyć długość boku B F trójkąta A B F korzystając z twierdzenia Pitagorasa. Otrzymujemy, że B fa = ZA B 2 + ZA F 2 = 2 2 + 4 2 = 2 5 . Długość boku A M oblicza się przez obszar trójkąta A B F. Mamy, że pole może być równe zarówno S A B C = 1 2 · A B · A F i S A B C = 1 2 · B F · A M .
Otrzymujemy, że A M = A B A F B F = 2 4 2 5 = 4 5 5
Następnie możemy znaleźć wartość tangensa kąta trójkąta A E M. Otrzymujemy:
t sol ∠ ZA M mi = ZA E ZA M = 4 4 5 5 = 5
Pożądany kąt uzyskany przez przecięcie płaszczyzn A B C i B E D 1 jest równy a r c t g 5, wówczas po uproszczeniu otrzymujemy a r c t g 5 = a r c sin 30 6 = a r c cos 6 6.
Odpowiedź: za r do t sol 5 = za r do grzech 30 6 = za r do sałata 6 6 .
Niektóre przypadki znalezienia kąta między przecinającymi się liniami są określone za pomocą płaszczyzna współrzędnych O x y z i metoda współrzędnych. Przyjrzyjmy się bliżej.
Jeżeli pojawia się problem polegający na konieczności znalezienia kąta pomiędzy przecinającymi się płaszczyznami γ 1 i γ 2, pożądany kąt oznaczamy jako α.
Następnie danego systemu współrzędne pokazują, że mamy współrzędne wektorów normalnych przecinających się płaszczyzn γ 1 i γ 2. Następnie oznaczamy, że n 1 → = n 1 x, n 1 y, n 1 z jest wektorem normalnym płaszczyzny γ 1, a n 2 → = (n 2 x, n 2 y, n 2 z) - dla płaszczyzna γ2. Rozważmy szczegółowe ustalenia kąt znajdujący się pomiędzy tymi płaszczyznami wzdłuż współrzędnych wektorów.
Konieczne jest wyznaczenie linii prostej, wzdłuż której płaszczyzny γ 1 i γ 2 przecinają się z literą c. Na prostej c mamy punkt M, przez który rysujemy płaszczyznę χ prostopadłą do c. Płaszczyzna χ wzdłuż linii aib przecina płaszczyzny γ 1 i γ 2 w punkcie M. z definicji wynika, że kąt pomiędzy przecinającymi się płaszczyznami γ 1 i γ 2 jest równy kątowi przecinających się linii a i b należących odpowiednio do tych płaszczyzn.
W płaszczyźnie χ wykreślamy wektory normalne z punktu M i oznaczamy je n 1 → i n 2 → . Wektor n 1 → leży na prostej prostopadłej do prostej a, a wektor n 2 → leży na prostej prostopadłej do prostej b. Stąd to rozumiemy dany samolotχ ma wektor normalny linii a równy n 1 → i dla linii b równy n 2 →. Rozważ poniższy rysunek.
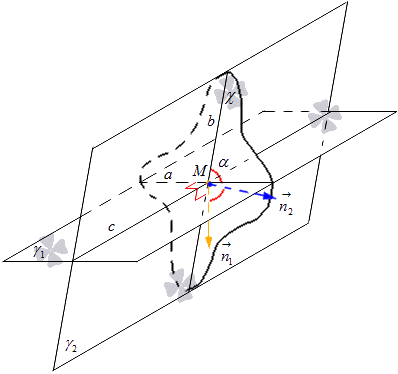
Stąd otrzymujemy wzór, dzięki któremu możemy obliczyć sinus kąta przecinających się prostych, korzystając ze współrzędnych wektorów. Ustaliliśmy, że cosinus kąta pomiędzy prostymi a i b jest taki sam, jak cosinus między przecinającymi się płaszczyznami γ 1 i γ 2, co wynika z formuły cosα = sałata n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2, gdzie mamy, że n 1 → = (n 1 x, n 1 y, n 1 z) i n 2 → = (n 2 x, n 2 y, n 2 z) są współrzędnymi wektory reprezentowanych płaszczyzn.
Kąt między przecinającymi się liniami oblicza się za pomocą wzoru
α = za r do cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2
Przykład 2
Zgodnie z warunkiem dany jest równoległościan A B C D A 1 B 1 C 1 D 1 , gdzie A B = 2, A D = 3, A A 1 = 7, a punkt E dzieli bok A A 1 4: 3. Znajdź kąt pomiędzy płaszczyznami A B C i B E D 1.
Rozwiązanie
Z warunku jasno wynika, że jego boki są prostopadłe parami. Oznacza to, że konieczne jest wprowadzenie układu współrzędnych O x y z z wierzchołkiem w punkcie C i osiami współrzędnych O x, O y, O z. Konieczne jest ustawienie kierunku w odpowiednie strony. Rozważ poniższy rysunek.

Przecinające się płaszczyzny A B C I B E D 1 utwórz kąt, który można znaleźć według wzoru α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2, w którym n 1 → = (n 1 x, n 1 y, n 1 z) i n 2 → = (n 2 x, n 2 y, n 2 z ) są wektorami normalnymi te samoloty. Konieczne jest określenie współrzędnych. Z rysunku to widzimy oś współrzędnych O x y pokrywa się z płaszczyzną A B C, co oznacza, że współrzędne wektora normalnego k → są równe wartości n 1 → = k → = (0, 0, 1).
Przyjmuje się wektor normalny płaszczyzny B E D 1 produkt wektorowy B E → i B D 1 → , gdzie ich współrzędne można znaleźć za pomocą współrzędnych skrajne punkty B, E, D 1, które są określane na podstawie warunków problemu.
Otrzymujemy, że B (0, 3, 0), D 1 (2, 0, 7). Ponieważ A E E A 1 = 4 3, ze współrzędnych punktów A 2, 3, 0, A 1 2, 3, 7 znajdujemy E 2, 3, 4. Stwierdzamy, że B E → = (2 , 0 , 4) , B D 1 → = 2 , - 3 , 7 n 2 → = B E → × B D 1 = i → jot → k → 2 0 4 2 - 3 7 = 12 · ja → - 6 jot → - 6 k → ⇔ n 2 → = (12 , - 6 , - 6)
Konieczne jest podstawienie znalezionych współrzędnych do wzoru na obliczenie kąta przechodzącego przez łuk cosinus. Dostajemy
α = za r do cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = za r do cos 6 6 6 = za r do cos 6 6
Metoda współrzędnych daje podobny wynik.
Odpowiedź: a r do cos 6 6 .
Ostatni problem jest rozpatrywany w celu znalezienia kąta między przecinającymi się płaszczyznami przy użyciu istniejących znanych równań płaszczyzn.
Przykład 3
Oblicz sinus, cosinus kąta oraz wartość kąta utworzonego przez dwie przecinające się proste, które są określone w układzie współrzędnych O x y z i określone równaniami 2 x - 4 y + z + 1 = 0 i 3 y - z - 1 = 0.
Rozwiązanie
Podczas studiowania tematu równanie ogólne prosta postaci A x + B y + C z + D = 0 ujawniła, że A, B, C są współczynnikami równymi współrzędnym wektora normalnego. Oznacza to, że n 1 → = 2, - 4, 1 i n 2 → = 0, 3, - 1 są wektorami normalnymi danych prostych.
Konieczne jest podstawienie współrzędnych wektorów normalnych płaszczyzn do wzoru na obliczenie pożądanego kąta przecinających się płaszczyzn. Wtedy to zrozumiemy
α = za r do cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = za r do cos 13 210
Stąd mamy cosinus kąta bo widokα = 13210. Wtedy kąt przecinających się linii nie jest rozwarty. Zastępowanie w tożsamość trygonometryczna, stwierdzamy, że wartość sinusa kąta jest równa wyrażeniu. Obliczmy i znajdźmy to
grzech α = 1 - cos 2 α = 1 - 13 210 = 41 210
Odpowiedź: sin α = 41 210, cos α = 13 210, α = a r do cos 13 210 = a r do sin 41 210.
Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter
Rodzaj pracy: 14
Temat: Kąt między płaszczyznami
Stan
Dana prawidłowy pryzmat ABCDA_1B_1C_1D_1, M i N są środkami odpowiednio krawędzi AB i BC, punkt K jest środkiem MN.
A) Udowodnij, że proste KD_1 i MN są prostopadłe.
B) Znajdź kąt pomiędzy płaszczyznami MND_1 i ABC jeżeli AB=8, AA_1=6\kwadrat 2.
Pokaż rozwiązanieRozwiązanie
A) W \triangle DCN i \triangle MAD mamy: \angle C=\angle A=90^(\circ), CN=AM=\frac12AB, CD=DA.
Stąd \triangle DCN=\triangle MAD na dwóch nogach. Następnie MD=DN, \trójkąt DMN równoramienny. Oznacza to, że mediana DK jest również wysokością. Dlatego DK \perp MN.
DD_1 \perp MND według warunku, D_1K - ukośne, KD - rzutowanie, DK \perp MN.
Stąd z twierdzenia o trzech prostopadłych MN\perp D_1K.
B) Jak udowodniono w A), DK \perp MN i MN \perp D_1K, ale MN jest linią przecięcia płaszczyzn MND_1 i ABC, co oznacza \angle DKD_1 - kąt liniowy kąt dwuścienny pomiędzy płaszczyznami MND_1 i ABC.
W \triangle DAM zgodnie z twierdzeniem Pitagorasa DM= \sqrt (DA^2+AM^2)= \sqrt (64+16)= 4 \ kwadrat 5, MN= \sqrt (MB^2+BN^2)= \sqrt (16+16)= 4\kwadrat 2. Dlatego w \triangle DKM według twierdzenia Pitagorasa DK= \sqrt (DM^2-KM^2)= \sqrt (80-8)= 6\kwadrat 2. Następnie w \triangle DKD_1, tg\kąt DKD_1=\frac(DD_1)(DK)=\frac(6\sqrt 2)(6\sqrt 2)=1.
Oznacza to \angle DKD_1=45^(\circ).
Odpowiedź
45^(\circ).
Rodzaj pracy: 14
Temat: Kąt między płaszczyznami
Stan
Po prawej czworokątny pryzmat ABCDA_1B_1C_1D_1 boków podstawy jest 4, żebra boczne są równe 6. Punkt M jest środkiem krawędzi CC_1, punkt N jest zaznaczony na krawędzi BB_1 tak, że BN:NB_1=1:2.
A) W jakim stosunku płaszczyzna AMN dzieli krawędź DD_1?
B) Znajdź kąt pomiędzy płaszczyznami ABC i AMN.
Pokaż rozwiązanieRozwiązanie
A) Płaszczyzna AMN przecina krawędź DD_1 w punkcie K, który jest czwartym wierzchołkiem przekroju danego pryzmatu przez tę płaszczyznę. Przekrój jest równoległobokiem ANMK, ponieważ przeciwległe ściany danego pryzmatu są równoległe.
.png)
BN =\frac13BB_1=2. Narysujmy KL \parallel CD, wówczas trójkąty ABN i KLM są równe, co oznacza ML=BN=2, LC=MC-ML=3-2=1, KD=LC=1. Wtedy KD_1=6-1=5. Teraz możesz znaleźć stosunek KD:KD_1 = 1:5.
B) F jest punktem przecięcia prostych CD i KM. Płaszczyzny ABC i AMN przecinają się wzdłuż prostej AF. Kąt \angle KHD =\alpha jest kątem liniowym kąta dwuściennego (HD\perp AF, następnie zgodnie z twierdzeniem odwrotnym do twierdzenia o trzech prostopadłych, KH \perp AF) i jest kątem ostrym trójkąta prostokątnego KHD, noga KD=1.
Trójkąty FKD i FMC są podobne (KD \parallel MC), zatem FD:FC=KD:MC rozwiązując proporcję FD:(FD+4)=1:3 otrzymujemy FD=2. W trójkącie prostokątnym AFD (\angle D=90^(\circ)) o nogach 2 i 4 obliczamy przeciwprostokątną AF=\sqrt (4^2+2^2)=2\sqrt 5, DH= AD\cdot FD:AF= \frac(4\cdot 2)(2\sqrt 5)= \frac4(\sqrt 5).
W trójkącie prostokątnym KHD znajdujemy tg \alpha =\frac(KD)(DH)=\frac(\sqrt 5)4, oznacza to pożądany kąt \alfa =arctg\frac(\sqrt 5)4.
Odpowiedź
A) 1:5;
B) arctg\frac(\sqrt 5)4.
Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu" wyd. F. F. Łysenko, S. Yu Kulabukhova.
Rodzaj pracy: 14
Temat: Kąt między płaszczyznami
Stan
Biorąc pod uwagę regularną czworokątną piramidę KMNPQ z podstawą MNPQ równą 6 i krawędzią boczną 3 \ kwadrat (26).
A) Skonstruuj odcinek ostrosłupa z płaszczyzną przechodzącą przez prostą NF równoległą do przekątnej MP, jeśli punkt F jest środkiem krawędzi MK.
B) Znajdź kąt pomiędzy płaszczyzną przekroju a płaszczyzną KMP.
Pokaż rozwiązanieRozwiązanie
A) Niech KO będzie wysokością piramidy, F środkiem MK ; FE \parallel MP (w płaszczyźnie PKM) . Ponieważ FE jest Środkowa linia\triangle PKM, zatem FE=\frac(MP)2.

Skonstruujmy odcinek piramidy z płaszczyzną przechodzącą przez NF i równoległą do MP, czyli płaszczyzną NFE. L jest punktem przecięcia EF i KO. Ponieważ punkty L i N należą do żądanego przekroju i leżą na płaszczyźnie KQN, to punkt T, otrzymany jako przecięcie LN i KQ, jest jednocześnie punktem przecięcia żądanego przekroju i krawędzi KQ. NETF jest wymaganą sekcją.
B) Płaszczyzny NFE i MPK przecinają się na prostej FE. Oznacza to, że kąt pomiędzy tymi płaszczyznami jest równy kątowi liniowemu kąta dwuściennego OFEN, skonstruujmy go: LO\perpMP, MP\równoległy FE, stąd, LO\perpFE;\triangle NFE - równoramienne (NE=NF jako odpowiadające im mediany równe trójkąty KPN i KMN ), NL jest jej medianą (EL=LF, ponieważ PO=OM i \triangle KEF \sim \triangle KPM) . Zatem pożądane jest NL \perp FE i \angle NLO.
WŁ=\frac12QN=\frac12MN\sqrt 2=3\sqrt 2.
\triangle KON - prostokątny.
Noga KO zgodnie z twierdzeniem Pitagorasa jest równa KO=\sqrt (KN^2-ON^2).
OL= \frac12KO= \frac12\sqrt(KN^2-ON^2)= \frac12\sqrt (9\cdot 26-9\cdot 2)= \frac12\sqrt(9(26-2))= \frac32\sqrt (24)= \frac32\cdot 2\sqrt 6= 3\kwadrat 6.
tg\kąt NLO =\frac(ON)(OL)=\frac(3\sqrt 2)(3\sqrt 6)=\frac1(\sqrt 3),
\angle NLO=30^(\circ).
Odpowiedź
Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu.” wyd. F. F. Łysenko, S. Yu Kulabukhova.
Rodzaj pracy: 14
Temat: Kąt między płaszczyznami
Stan
Wszystkie krawędzie foremnego trójkątnego pryzmatu ABCA_(1)B_(1)C_(1) są równe 6. Przez środki krawędzi AC i BB_(1) oraz wierzchołek A_(1) rysuje się płaszczyzna cięcia.
A) Udowodnij, że krawędź BC jest podzielona przez płaszczyznę cięcia w stosunku 2:1, licząc od wierzchołka C.
B) Znajdź kąt pomiędzy płaszczyzną cięcia a płaszczyzną bazową.
Pokaż rozwiązanieRozwiązanie
A) Niech D i E będą środkami odpowiednio krawędzi AC i BB_(1).

W płaszczyźnie AA_(1)C_(1) rysujemy prostą A_(1)D, która przecina prostą CC_(1) w punkcie K, w płaszczyźnie BB_(1)C_(1) - prostą KE, który przecina krawędź BC w punkcie F . Łącząc punkty A_(1) i E leżące na płaszczyźnie AA_(1)B_(1) oraz D i F leżące na płaszczyźnie ABC otrzymujemy przekrój A_(1)EFD.
\bigtriangleup AA_(1)D=\bigtriangleup CDK wzdłuż ramienia AD=DC i kąta ostrego.
\angle ADA_(1)=\angle CDK - podobnie jak pionowe, wynika z tego, że AA_(1)=CK=6. \bigtriangleup CKF i \bigtriangleup BFE są podobne pod dwoma kątami \angle FBE=\angle KCF=90^\circ,\angle BFE=\angle CFK - jak pionowe.
\frac(CK)(BE)=\frac(6)(3)=2, oznacza to, że współczynnik podobieństwa wynosi 2, co oznacza, że CF:FB=2:1.
B) Wykonajmy AH \perp DF. Kąt pomiędzy płaszczyzną przekroju a płaszczyzną bazową jest równy kątowi AHA_(1). Rzeczywiście odcinek AH \perp DF (DF jest linią przecięcia tych płaszczyzn) jest rzutem odcinka A_(1)H na płaszczyznę bazową, zatem zgodnie z twierdzeniem o trzech prostopadłych A_(1)H \perp DF. \angle AHA_(1)=arctg\frac(AA_(1))(AH). AA_(1)=6.
Znajdźmy AH. \angle ADH =\angle FDC (tak samo jak w pionie).

Z twierdzenia cosinus w \bigtriangleup DFC:
DF^2=FC^2+DC^2- 2FC \cdot DC \cdot \cos 60^\circ,
DF^2=4^2+3^2-2 \cdot 4 \cdot 3 \cdot \frac(1)(2)=13.
FC^2=DF^2+DC^2- 2DF\cdot DC\cdot\cos\kąt FDC,
4^2=13+9-2\sqrt(13) \cdot 3 \cdot \cos \angle FDC,
\cos \angle FDC=\frac(6)(2\sqrt(13) \cdot 3)=\frac(1)(\sqrt(13)).
W następstwie podstawowej tożsamości trygonometrycznej
\sin \angle FDC=\sqrt(1-\left (\frac(1)(\sqrt(13))\right)^2)=\frac(2\sqrt(3))(\sqrt(13)) . Z \bigtriangleup ADH znajdujemy AH :
AH=AD \cdot \sin \angle ADH, (\angle FDC=\kąt ADH). AH=3 \cdot \frac(2\sqrt(3))(\sqrt(13))=\frac(6\sqrt(13))(\sqrt(13)).
\angle AHA_(1)= arctg\frac(AA_(1))(AH)= arctg\frac(6 \cdot \sqrt(13))(6\sqrt(3))= arctg\frac(\sqrt(39))(3).
Odpowiedź
arctg\frac(\sqrt(39))(3).
Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu.” wyd. F. F. Łysenko, S. Yu Kulabukhova.
Rodzaj pracy: 14
Temat: Kąt między płaszczyznami
Stan
Podstawą prawego pryzmatu ABCDA_(1)B_(1)C_(1)D_(1) jest romb o kąt rozwarty B równe 120^\circ. Wszystkie krawędzie tego pryzmatu są równe 10. Punkty P i K są środkami odpowiednio krawędzi CC_(1) i CD.
A) Udowodnij, że proste PK i PB_(1) są prostopadłe.
B) Znajdź kąt pomiędzy płaszczyznami PKB_(1) i C_(1)B_(1)B.
Pokaż rozwiązanieRozwiązanie
A) Zastosujemy metodę współrzędnych. Znajdźmy produkt skalarny wektory \vec(PK) i \vec(PB_(1)), a następnie cosinus kąta między tymi wektorami. Skierujmy oś Oy wzdłuż CD, oś Oz wzdłuż CC_(1), a oś Ox \perp CD. C jest początkiem.

Następnie C (0;0;0); C_(1)(0;0;10); P(0;0;5); K(0;5;0); B(BC \cos 30^\circ; BC\sin 30^\circ; 0), to jest B(5\sqrt(3); 5;0), B_(1)(5\sqrt(3); 5;10).
Znajdźmy współrzędne wektorów: \vec(PK)=\(0;5;-5\); \vec(PB_(1))=\(5\sqrt(3); 5;5\).
Niech kąt pomiędzy \vec(PK) i \vec(PB_(1)) będzie równy \alpha.
Dostajemy \cos \alpha=\frac(\vec(PK) \cdot \vec(PB_(1)))(|\vec(PK)| \cdot |\vec(PB_(1))|)= \frac(0 \cdot 5\sqrt(3) + 5 \cdot 5-5 \cdot 5)(|\vec(PK)| \cdot |\vec(PB_(1))|)=0.
\cos \alpha =0, co oznacza \vec(PK) \perp \vec(PB_(1)) a proste PK i PB_(1) są prostopadłe.
B) Kąt między płaszczyznami jest równy kątowi między niezerowymi wektorami prostopadłymi do tych płaszczyzn (lub, jeśli kąt jest rozwarty, kątowi do niego przylegającemu). Takie wektory nazywane są normalnymi do płaszczyzn. Znajdźmy je.
Niech \vec(n_(1))=\(x; y; z\) będzie prostopadłe do płaszczyzny PKB_(1). Znajdźmy to rozwiązując układ \begin(cases) \vec(n_(1)) \perp \vec(PK), \\ \vec(n_(1)) \perp \vec(PB_(1)). \end(przypadki)
\begin(cases) \vec(n_(1)) \cdot \vec(PK)=0, \\ \vec(n_(1)) \cdot \vec(PB_(1))=0; \end(przypadki)
\begin(przypadki) 0x+5y-5z=0, \\ 5\sqrt(3)x+5y+5z=0; \end(przypadki)
\begin(cases)y=z, \\ x=\frac(-y-z)(\sqrt(3)). \end(przypadki)
Weźmy y=1; z=1; x=\frac(-2)(\sqrt(3)), \vec(n_(1))=\lewo \( \frac(-2)(\sqrt(3)); 1;1 \prawo \).
Niech \vec(n_(2))=\(x; y; z\) będzie prostopadłe do płaszczyzny C_(1)B_(1)B. Znajdźmy to rozwiązując układ \begin(cases) \vec(n_(2)) \perp \vec(CC_(1)), \\ \vec(n_(2)) \perp \vec(CB). \end(przypadki)
\vec(CC_(1))=\(0;0;10\), \vec(CB)=\(5\sqrt(3); 5; 0\).
\begin(cases) \vec(n_(2)) \cdot \vec(CC_(1))=0, \\ \vec(n_(2)) \cdot \vec(CB)=0; \end(przypadki)
\begin(przypadki) 0x+0y+10z=0, \\ 5\sqrt(3)x+5y+0z=0; \end(przypadki)
\begin(cases)z=0, \\ y=-\sqrt(3)x. \end(przypadki)
Weźmy x=1; y=-\sqrt(3); z=0, \vec(n_(2))=\(1; -\sqrt(3);0\).
Znajdźmy cosinus żądanego kąta \beta (it równy modułowi cosinus kąta pomiędzy \vec(n_(1)) i \vec(n_(2)) ).
\cos\beta= \frac(|\vec(n_(1)) \cdot \vec(n_(2))|)(|\vec(n_(1))| \cdot |\vec(n_(2))|)= \frac(\left |-\dfrac(2)(\sqrt(3))\cdot 1+1 \cdot (-\sqrt(3))+1 \cdot 0 \right |)(\sqrt(\dfrac( 4)(3)+1+1) \cdot \sqrt(1+3+0))= \frac(\dfrac(5)(\sqrt(3)))(2\sqrt(\dfrac(10)(3)))= \frac(\sqrt(10))(4).
\cos \beta =\frac(\sqrt(10))(4), \beta=\arccos\frac(\sqrt(10))(4).
Odpowiedź
\arccos\frac(\sqrt(10))(4)
Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu.” wyd. F. F. Łysenko, S. Yu Kulabukhova.
ABCD jest kwadratem i boczne twarze- równe prostokąty.

Ponieważ płaszczyzna przekroju przechodzi przez punkty M i D równolegle do przekątnej AC, to konstruując ją na płaszczyźnie A_(1)AC przez punkt M rysujemy odcinek MN równoległy do AC. Otrzymujemy AC \parallel (MDN) na podstawie równoległości prostej i płaszczyzny.
Płaszczyzna MDN przecina równoległe płaszczyzny A_(1)AD i B_(1)BC, zatem według właściwości płaszczyzny równoległe, linie przecięcia ścian A_(1)ADD_(1) i B_(1)BCC_(1) z płaszczyzną MDN są równoległe.
Narysujmy odcinek NE równolegle do odcinka MD.
Wymaganym przekrojem jest czworokąt DMEN.
B) Znajdźmy kąt między płaszczyzną przekroju a płaszczyzną bazową. Niech płaszczyzna przekroju przecina płaszczyznę bazową wzdłuż prostej p przechodzącej przez punkt D. AC \parallel MN zatem AC \parallel p (jeżeli płaszczyzna przechodzi przez prostą równoległą do innej płaszczyzny i przecina tę płaszczyznę, to linia przecięcia płaszczyzn jest równoległa do tej prostej). BD \perp AC jako przekątne kwadratu, co oznacza BD \perp p. BD jest rzutem ED na płaszczyznę ABC, a następnie z twierdzenia o trzech prostopadłych ED \perp p, zatem \angle EDB jest kątem liniowym kąta dwuściennego pomiędzy płaszczyzną przekroju a płaszczyzną podstawy.
Ustaw typ czworoboku DMEN. MD \parallel EN, podobnie jak ME \parallel DN, co oznacza, że DMEN jest równoległobokiem, a ponieważ MD=DN (trójkąty prostokątne MAD i NCD są równe na dwóch nogach: AD=DC jako boki kwadratu, AM=CN jako odległości między równoległymi liniami AC i MN), zatem DMEN jest rombem. Zatem F jest środkiem MN.
Zatem według warunku AM:MA_(1)=2:3 AM=\frac(2)(5)AA_(1)=\frac(2)(5) \cdot 5\sqrt(6)=2\sqrt(6).
AMNC jest prostokątem, F jest środkiem MN, O jest środkiem AC. Oznacza, FO\równoległe MA, FO\perp AC, FO=MA=2\sqrt(6).
Wiedząc, że przekątna kwadratu wynosi a\sqrt(2), gdzie a jest bokiem kwadratu, otrzymujemy BD=4\sqrt(2). OD=\frac(1)(2)BD=\frac(1)(2) \cdot 4\sqrt(2)=2\sqrt(2).
W trójkącie prostokątnym FOD\enspace tg \angle FDO=\frac(FO)(OD)=\frac(2\sqrt(6))(2\sqrt(2))=\sqrt(3). Dlatego \angle FDO=60^\circ.
\(\blacktriangleright\) Kąt dwuścienny to kąt utworzony przez dwie półpłaszczyzny i linię prostą \(a\), która jest ich wspólną granicą.
\(\blacktriangleright\) Aby znaleźć kąt pomiędzy płaszczyznami \(\xi\) i \(\pi\) , musisz znaleźć kąt liniowy (i pikantny Lub prosty) kąt dwuścienny utworzony przez płaszczyzny \(\xi\) i \(\pi\) :
Krok 1: niech \(\xi\cap\pi=a\) (linia przecięcia płaszczyzn). W płaszczyźnie \(\xi\) zauważamy dowolny punkt\(F\) i wykonaj \(FA\perp a\) ;
Krok 2: wykonaj \(FG\perp \pi\) ;
Krok 3: zgodnie z TTP (\(FG\) – prostopadła, \(FA\) – ukośna, \(AG\) – rzut) mamy: \(AG\perp a\) ;
Krok 4: Kąt \(\angle FAG\) nazywany jest kątem liniowym kąta dwuściennego utworzonego przez płaszczyzny \(\xi\) i \(\pi\) .
Zauważ, że trójkąt \(AG\) jest prostokątny.
Należy również zauważyć, że tak skonstruowana płaszczyzna \(AFG\) jest prostopadła do obu płaszczyzn \(\xi\) i \(\pi\) . Dlatego możemy to powiedzieć inaczej: kąt między płaszczyznami\(\xi\) i \(\pi\) to kąt pomiędzy dwiema przecinającymi się liniami \(c\in \xi\) i \(b\in\pi\) tworzącymi płaszczyznę prostopadłą do i \(\xi\ ) i \(\pi\) .
Zadanie 1 #2875
Poziom zadania: Trudniejszy niż ujednolicony egzamin państwowy
Dana czworokątna piramida, którego wszystkie krawędzie są równe, a podstawą jest kwadrat. Znajdź \(6\cos \alpha\) , gdzie \(\alpha\) jest kątem pomiędzy sąsiednimi ścianami bocznymi.
Niech \(SABCD\) – tę piramidę(\(S\) to wierzchołek), którego krawędzie są równe \(a\) . W związku z tym wszystkie ściany boczne są równymi trójkątami równobocznymi. Znajdźmy kąt pomiędzy ścianami \(SAD\) i \(SCD\) .

Zróbmy \(CH\perp SD\) . Ponieważ \(\trójkąt SAD=\trójkąt SCD\), wówczas \(AH\) będzie także wysokością \(\triangle SAD\) . Dlatego z definicji \(\angle AHC=\alpha\) jest kątem liniowym kąta dwuściennego pomiędzy ścianami \(SAD\) i \(SCD\) .
Ponieważ podstawą jest kwadrat, wówczas \(AC=a\sqrt2\) . Zauważ również, że \(CH=AH\) to wysokość trójkąt równoboczny z bokiem \(a\) , zatem \(CH=AH=\frac(\sqrt3)2a\) .
Następnie, zgodnie z twierdzeniem cosinus z \(\triangle AHC\) : \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]
Odpowiedź: -2
Zadanie 2 #2876
Poziom zadania: Trudniejszy niż ujednolicony egzamin państwowy
Płaszczyzny \(\pi_1\) i \(\pi_2\) przecinają się pod kątem, którego cosinus jest równy \(0,2\). Płaszczyzny \(\pi_2\) i \(\pi_3\) przecinają się pod kątem prostym, a linia przecięcia płaszczyzn \(\pi_1\) i \(\pi_2\) jest równoległa do linii przecięcia płaszczyzny \(\pi_2\) i \(\ pi_3\) . Znajdź sinus kąta pomiędzy płaszczyznami \(\pi_1\) i \(\pi_3\) .
Niech linia przecięcia \(\pi_1\) i \(\pi_2\) będzie linią prostą \(a\), linia przecięcia \(\pi_2\) i \(\pi_3\) będzie prostą linia \(b\), oraz linia przecięcia \(\pi_3\) i \(\pi_1\) – prosta \(c\) . Ponieważ \(a\równoległy b\) , to \(c\równoległy a\równoległy b\) (zgodnie z twierdzeniem z części podręcznika teoretycznego „Geometria w przestrzeni” \(\rightarrow\) „Wprowadzenie do stereometrii, równoległość").

Zaznaczmy punkty \(A\in a, B\in b\) tak, aby \(AB\perp a, AB\perp b\) (jest to możliwe, ponieważ \(a\równoległe b\) ). Zaznaczmy \(C\in c\) tak, że \(BC\perp c\) , zatem \(BC\perp b\) . Następnie \(AC\perp c\) i \(AC\perp a\) .
Rzeczywiście, ponieważ \(AB\perp b, BC\perp b\) , to \(b\) jest prostopadłe do płaszczyzny \(ABC\) . Ponieważ \(c\równoległy a\równoległy b\), to proste \(a\) i \(c\) są również prostopadłe do płaszczyzny \(ABC\), a zatem do dowolnej prostej z tej płaszczyzny, w szczególności , linia \ (AC\) .
Wynika, że \(\kąt BAC=\kąt (\pi_1, \pi_2)\), \(\kąt ABC=\kąt (\pi_2, \pi_3)=90^\circ\), \(\kąt BCA=\kąt (\pi_3, \pi_1)\). Okazuje się, że \(\trójkąt ABC\) jest prostokątny, co oznacza \[\sin \angle BCA=\cos \angle BAC=0.2.\]
Odpowiedź: 0,2
Zadanie 3 #2877
Poziom zadania: Trudniejszy niż ujednolicony egzamin państwowy
Dane proste \(a, b, c\) przecinają się w jednym punkcie, a kąt między dowolnymi dwoma z nich jest równy \(60^\circ\) . Znajdź \(\cos^(-1)\alpha\) , gdzie \(\alpha\) jest kątem pomiędzy płaszczyzną utworzoną przez linie \(a\) i \(c\) a płaszczyzną utworzoną przez linie \( b\ ) i \(c\) . Podaj odpowiedź w stopniach.
Niech linie przecinają się w punkcie \(O\) . Ponieważ kąt między dowolnymi dwoma jest równy \(60^\circ\), to wszystkie trzy proste nie mogą leżeć w tej samej płaszczyźnie. Zaznaczmy punkt \(A\) na prostej \(a\) i narysujmy \(AB\perp b\) i \(AC\perp c\) . Następnie \(\trójkąt AOB=\trójkąt AOC\) jako prostokątny wzdłuż przeciwprostokątnej i kąta ostrego. Dlatego \(OB=OC\) i \(AB=AC\) .
Zróbmy \(AH\perp (BOC)\) . Następnie z twierdzenia o trzech prostopadłych \(HC\perp c\) , \(HB\perp b\) . Ponieważ \(AB=AC\) , zatem \(\trójkąt AHB=\trójkąt AHC\) jako prostokątny wzdłuż przeciwprostokątnej i nogi. Dlatego \(HB=HC\) . Oznacza to, że \(OH\) jest dwusieczną kąta \(BOC\) (ponieważ punkt \(H\) jest w równej odległości od boków kąta).

Zauważ, że w ten sposób skonstruowaliśmy również kąt liniowy kąta dwuściennego utworzonego przez płaszczyznę utworzoną przez linie \(a\) i \(c\) oraz płaszczyznę utworzoną przez linie \(b\) i \(c \) . To jest kąt \(ACH\) .
Znajdźmy ten kąt. Ponieważ wybraliśmy punkt \(A\) arbitralnie, wybierzmy go tak, aby \(OA=2\) . Następnie w prostokącie \(\trójkąt AOC\): \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ] Ponieważ \(OH\) jest dwusieczną, to \(\angle HOC=30^\circ\) , zatem w prostokącie \(\triangle HOC\) : \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\] Następnie z prostokąta \(\trójkąt ACH\) : \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]
Odpowiedź: 3
Zadanie 4 #2910
Poziom zadania: Trudniejszy niż ujednolicony egzamin państwowy
Płaszczyzny \(\pi_1\) i \(\pi_2\) przecinają się wzdłuż linii prostej \(l\), na której leżą punkty \(M\) i \(N\). Odcinki \(MA\) i \(MB\) są prostopadłe do prostej \(l\) i leżą odpowiednio w płaszczyznach \(\pi_1\) i \(\pi_2\), a \(MN = 15 \) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) . Znajdź \(3\cos\alpha\) , gdzie \(\alpha\) jest kątem pomiędzy płaszczyznami \(\pi_1\) i \(\pi_2\) .

Trójkąt \(AMN\) jest prostokątny, \(AN^2 = AM^2 + MN^2\), skąd \ Trójkąt \(BMN\) jest prostokątny, \(BN^2 = BM^2 + MN^2\), z czego \Zapisujemy twierdzenie cosinus dla trójkąta \(AMB\): \ Następnie \ Ponieważ kąt \(\alpha\) pomiędzy płaszczyznami jest kątem ostrym, a \(\angle AMB\) okazał się rozwarty, to \(\cos\alpha=\dfrac5(12)\) . Następnie \
Odpowiedź: 1,25
Zadanie 5 #2911
Poziom zadania: Trudniejszy niż ujednolicony egzamin państwowy
\(ABCDA_1B_1C_1D_1\) jest równoległościanem, \(ABCD\) jest kwadratem o boku \(a\), punkt \(M\) jest podstawą prostopadłej spuszczonej z punktu \(A_1\) na płaszczyznę \ ((ABCD)\) , dodatkowo \(M\) jest punktem przecięcia przekątnych kwadratu \(ABCD\) . Wiadomo, że \(A_1M = \dfrac(\sqrt(3))(2)a\). Znajdź kąt pomiędzy płaszczyznami \((ABCD)\) i \((AA_1B_1B)\) . Podaj odpowiedź w stopniach.
Skonstruujmy \(MN\) prostopadle do \(AB\), jak pokazano na rysunku.

Ponieważ \(ABCD\) jest kwadratem o boku \(a\) i \(MN\perp AB\) i \(BC\perp AB\) , to \(MN\równoległy BC\) . Ponieważ \(M\) jest punktem przecięcia przekątnych kwadratu, to \(M\) jest środkiem \(AC\), zatem \(MN\) jest linią środkową i \(MN =\frac12BC= \frac(1)(2)a\).
\(MN\) jest rzutem \(A_1N\) na płaszczyznę \((ABCD)\), a \(MN\) jest prostopadłe do \(AB\), wówczas, zgodnie z twierdzeniem o trzech prostopadłych, \ (A_1N\) jest prostopadła do \(AB \) i kąt pomiędzy płaszczyznami \((ABCD)\) i \((AA_1B_1B)\) wynosi \(\kąt A_1NM\) .
\[\mathrm(tg)\, \angle A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\kąt A_1NM = 60^(\circ)\]
Odpowiedź: 60
Zadanie 6 #1854
Poziom zadania: Trudniejszy niż ujednolicony egzamin państwowy
W kwadracie \(ABCD\): \(O\) – punkt przecięcia przekątnych; \(S\) – nie leży w płaszczyźnie kwadratu, \(SO \perp ABC\) . Znajdź kąt pomiędzy płaszczyznami \(ASD\) i \(ABC\) jeśli \(SO = 5\) i \(AB = 10\) .

Trójkąty prostokątne \(\triangle SAO\) i \(\triangle SDO\) są równe w dwóch bokach i kącie między nimi (\(SO \perp ABC\) \(\Rightarrow\) \(\kąt SOA = \kąt SOD = 90^\circ\); \(AO = DO\) , ponieważ \(O\) – punkt przecięcia przekątnych kwadratu, \(SO\) – wspólna strona) \(\Strzałka w prawo\) \(AS = SD\) \(\Strzałka w prawo\) \(\trójkąt ASD\) – równoramienny. Punkt \(K\) jest środkiem \(AD\), wówczas \(SK\) jest wysokością w trójkącie \(\trójkąt ASD\), a \(OK\) jest wysokością w trójkącie \( AOD\) \(\ Rightarrow\) płaszczyzna \(SOK\) jest prostopadła do płaszczyzn \(ASD\) i \(ABC\) \(\Rightarrow\) \(\angle SKO\) – kąt liniowy równy żądanemu kąt dwuścienny.

W \(\trójkąt SKO\): \(OK = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\Rightarrow\) \(\trójkąt SOK\) – trójkąt równoramienny \(\Rightarrow\) \(\kąt SKO = 45^\circ\) .
Odpowiedź: 45
Zadanie 7 #1855
Poziom zadania: Trudniejszy niż ujednolicony egzamin państwowy
W kwadracie \(ABCD\): \(O\) – punkt przecięcia przekątnych; \(S\) – nie leży w płaszczyźnie kwadratu, \(SO \perp ABC\) . Znajdź kąt pomiędzy płaszczyznami \(ASD\) i \(BSC\) jeśli \(SO = 5\) i \(AB = 10\) .
Trójkąty prostokątne \(\triangle SAO\) , \(\triangle SDO\) , \(\triangle SOB\) i \(\triangle SOC\) są równe po dwóch bokach i kąt między nimi (\(SO \perp ABC \) \(\Prawa strzałka\) \(\angle SOA = \angle SOD = \angle SOB = \angle SOC = 90^\circ\); \(AO = OD = OB = OC\), ponieważ \(O\) – punkt przecięcia przekątnych kwadratu, \(SO\) – wspólny bok) \(\Rightarrow\) \(AS = DS = BS = CS\) \(\Rightarrow\) \( \triangle ASD\) i \(\triangle BSC\) są równoramiennymi. Punkt \(K\) jest środkiem \(AD\), wówczas \(SK\) jest wysokością w trójkącie \(\trójkąt ASD\), a \(OK\) jest wysokością w trójkącie \( AOD\) \(\ Strzałka w prawo\) płaszczyzna \(SOK\) jest prostopadła do płaszczyzny \(ASD\) . Punkt \(L\) jest środkiem \(BC\), wówczas \(SL\) jest wysokością w trójkącie \(\trójkąt BSC\), a \(OL\) jest wysokością w trójkącie \( BOC\) \(\ Rightarrow\) płaszczyzna \(SOL\) (inaczej płaszczyzna \(SOK\)) jest prostopadła do płaszczyzny \(BSC\) . W ten sposób otrzymujemy, że \(\kąt KSL\) jest kątem liniowym równym żądanemu kątowi dwuściennemu.

\(KL = KO + OL = 2\cdot OL = AB = 10\)\(\Strzałka w prawo\) \(OL = 5\) ; \(SK = SL\) – równe wysokości trójkąty równoramienne, które można znaleźć korzystając z twierdzenia Pitagorasa: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). Można to zauważyć \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)\(\Strzałka w prawo\) dla trójkąta \(\trójkąt KSL\) odwrotne twierdzenie Pitagorasa zachodzi w \(\Strzałka w prawo\) \(\trójkąt KSL\) – trójkąt prostokątny \(\Strzałka w prawo\) \(\kąt KSL = 90 ^\około\) .
Odpowiedź: 90
Przygotowanie uczniów do zdania Unified State Exam z matematyki rozpoczyna się z reguły od powtórzenia podstawowych wzorów, w tym tych, które pozwalają wyznaczyć kąt między płaszczyznami. Pomimo tego, że ta sekcja geometrii jest omówiona wystarczająco szczegółowo program nauczania wielu absolwentów musi powtarzać podstawowy materiał. Rozumiejąc, jak znaleźć kąt między płaszczyznami, uczniowie szkół średnich będą mogli szybko obliczyć poprawną odpowiedź przy rozwiązywaniu problemu i liczyć na uzyskanie przyzwoitych wyników w wynikach zdania ujednoliconego egzaminu państwowego.
Główne niuanse
Aby mieć pewność, że pytanie o znalezienie kąta dwuściennego nie sprawi trudności, zalecamy skorzystanie z algorytmu rozwiązania, który pomoże Ci poradzić sobie z zadaniami Unified State Examination.
Najpierw musisz określić linię prostą, wzdłuż której przecinają się płaszczyzny.
Następnie musisz wybrać punkt na tej linii i narysować do niego dwie prostopadłe.
Następny krok- znalezienie funkcja trygonometryczna kąt dwuścienny utworzony przez prostopadłe. Najwygodniej to zrobić za pomocą powstałego trójkąta, którego częścią jest kąt.
Odpowiedzią będzie wartość kąta lub jego funkcja trygonometryczna.
Przygotowanie do egzaminu testowego z Shkolkovo to klucz do Twojego sukcesu
Dzień wcześniej podczas zajęć zdanie jednolitego egzaminu państwowego Wiele uczniów staje przed problemem znalezienia definicji i wzorów, które pozwolą im obliczyć kąt między 2 płaszczyznami. Podręcznik szkolny Nie zawsze jest pod ręką dokładnie wtedy, gdy jest potrzebny. I znaleźć niezbędne formuły oraz przykłady ich prawidłowego wykorzystania, w tym do wyszukiwania kąta między płaszczyznami w Internecie, co czasami wymaga poświęcenia dużej ilości czasu.
Portal matematyczny „Shkolkovo” oferuje nowe podejście przygotować się do egzaminu państwowego. Zajęcia na naszej stronie pomogą uczniom zidentyfikować dla siebie najtrudniejsze fragmenty i uzupełnić braki wiedzy.
Przygotowaliśmy i przejrzyście przedstawiliśmy cały niezbędny materiał. Podstawowe definicje i wzory przedstawiono w części „Informacje teoretyczne”.
Aby lepiej zrozumieć materiał, sugerujemy również przećwiczenie odpowiednich ćwiczeń. Duży wybór zadań różnym stopniu na przykład złożoność jest przedstawiona w sekcji „Katalog”. Wszystkie zadania zawierają szczegółowy algorytm znajdowania prawidłowej odpowiedzi. Lista ćwiczeń na stronie jest na bieżąco uzupełniana i aktualizowana.
Ćwicząc rozwiązywanie problemów wymagających znalezienia kąta między dwiema płaszczyznami, uczniowie mają możliwość zapisania dowolnego zadania online jako „Ulubionych”. Dzięki temu będą mogli do niego wrócić wymagana ilość czas i omówić z nim postęp w podejmowaniu decyzji nauczyciel szkoły lub korepetytor.
