Vektori koordinaatide leidmine on matemaatika paljude ülesannete puhul üsna tavaline tingimus. Võimalus leida vektorkoordinaate aitab teid muus, enamas keerulised ülesanded koos sarnased teemad. Selles artiklis vaatleme vektori koordinaatide leidmise valemit ja mitmeid probleeme.
Vektori koordinaatide leidmine tasapinnal
Mis on lennuk? Tasapinda peetakse kahemõõtmeliseks ruumiks, kahemõõtmeliseks ruumiks (x-mõõde ja y-mõõde). Näiteks paber on tasane. Laua pind on tasane. Iga mittemahuline kujund (ruut, kolmnurk, trapets) on samuti tasapind. Seega, kui ülesandepüstituses on vaja leida tasapinnal paikneva vektori koordinaadid, meenume kohe x ja y kohta. Sellise vektori koordinaadid leiate järgmisel viisil: AB vektori koordinaadid = (xB - xA; yB - xA). Valemist selgub, et koordinaatidest lõpp-punkt peate lahutama lähtepunkti koordinaadid.
Näide:
- Vektor-CD-l on algsed (5; 6) ja lõplikud (7; 8) koordinaadid.
- Leidke vektori enda koordinaadid.
- Kasutades ülaltoodud valemit, saame järgmise avaldise: CD = (7-5; 8-6) = (2; 2).
- Seega CD vektori koordinaadid = (2; 2).
- Vastavalt sellele on x-koordinaat võrdne kahega, y-koordinaat on samuti kaks.
Vektori koordinaatide leidmine ruumis
Mis on ruum? Ruum on juba kolmemõõtmeline mõõde, kus on antud 3 koordinaati: x, y, z. Kui teil on vaja leida vektor, mis asub ruumis, siis valem praktiliselt ei muutu. Lisatakse ainult üks koordinaat. Vektori leidmiseks tuleb lõppkoordinaatidest lahutada alguse koordinaadid. AB = (xB - xA; yB - yA; zB - zA)
Näide:
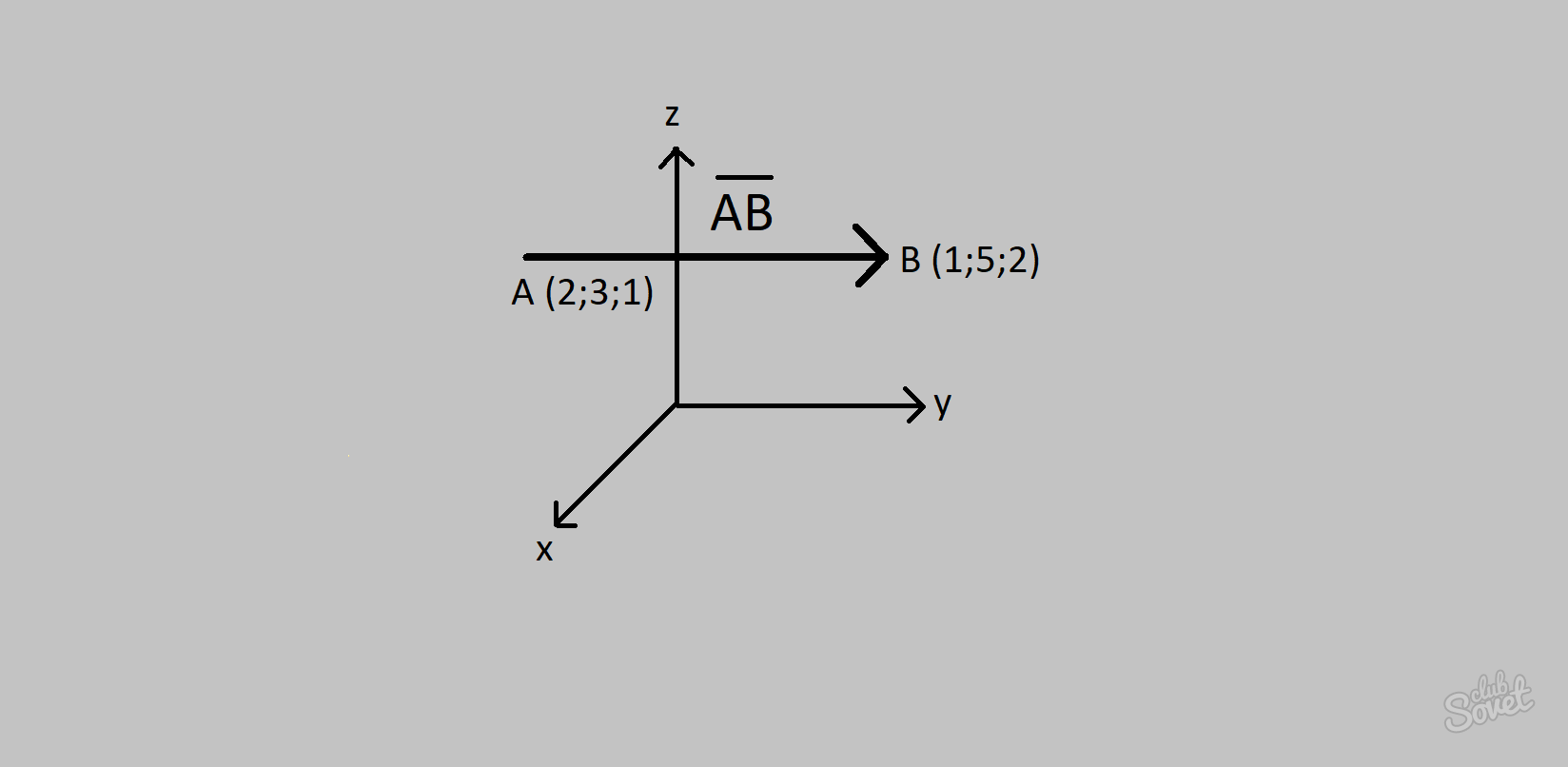
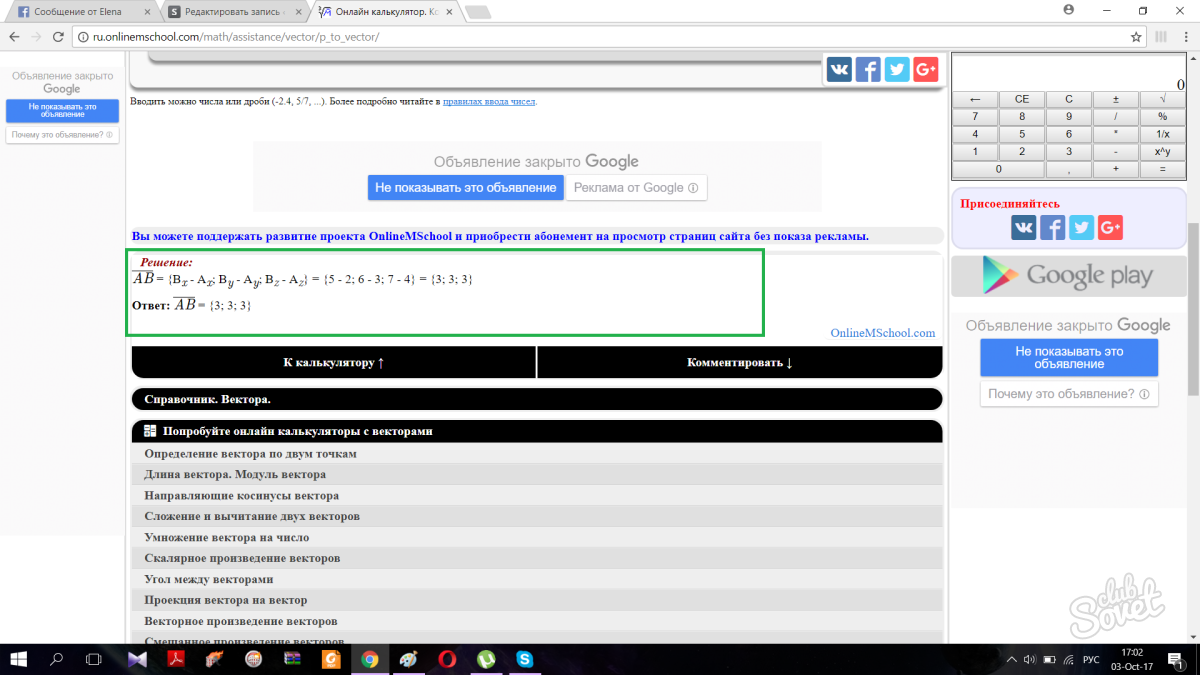
- Vektoril DF on algus (2; 3; 1) ja lõpp (1; 5; 2).
- Rakendades ülaltoodud valemit, saame: Vektori koordinaadid DF = (1-2; 5-3; 2-1) = (-1; 2; 1).
- Pidage meeles, et koordinaatide väärtus võib olla negatiivne, probleemi pole.
Kuidas leida veebist vektorkoordinaate?
Kui te mingil põhjusel ei soovi koordinaate ise leida, võite kasutada veebikalkulaatorit. Alustuseks valige vektori mõõde. Vektori mõõde vastutab selle mõõtmete eest. Mõõde 3 tähendab, et vektor on ruumis, mõõde 2 tähendab, et see asub tasapinnal. Järgmisena sisesta punktide koordinaadid vastavatesse väljadesse ja programm määrab sinu eest ise vektori koordinaadid. Kõik on väga lihtne.
Nupule klõpsates kerib leht automaatselt alla ja annab teile õige vastuse koos lahendusetappidega.
Soovitatav on hästi õppida see teema, sest vektori mõistet ei leia mitte ainult matemaatikas, vaid ka füüsikas. Teaduskonna üliõpilased Infotehnoloogiad Nad uurivad ka vektorite teemat, kuid keerulisemal tasemel.
Kui on antud kaks tasandi punkti ja, siis on vektoril järgmised koordinaadid:
Kui on antud kaks punkti ruumis ja, siis on vektoril järgmised koordinaadid:
See on, vektori lõpu koordinaatidest peate lahutama vastavad koordinaadid vektori algus.
Harjutus: Samade punktide jaoks kirjuta üles valemid vektori koordinaatide leidmiseks. Valemid tunni lõpus.
Näide 1
Arvestades kaks punkti lennuk ja . Leidke vektori koordinaadid
Lahendus: vastavalt sobivale valemile:
Teise võimalusena võib kasutada järgmist kirjet:
Esteetid otsustavad selle:
Isiklikult olen salvestuse esimese versiooniga harjunud.
Vastus:
Tingimuse kohaselt ei olnud vaja joonist ehitada (mis on tüüpiline ülesannete jaoks analüütiline geomeetria), kuid mannekeenide jaoks mõne punkti selgitamiseks ei ole ma liiga laisk:
Peate kindlasti aru saama erinevus punktikoordinaatide ja vektorkoordinaatide vahel:
Punktide koordinaadid– need on tavalised koordinaadid ristkülikukujulises koordinaatsüsteemis. Pange punktid peale koordinaattasand Arvan, et kõik saavad hakkama 5.-6. Igal punktil on lennukis range koht ja neid ei saa kuhugi teisaldada.
Vektori koordinaadid on selle laienemine aluse poolest, sisse sel juhul. Iga vektor on vaba, nii et vajadusel saame selle hõlpsalt mõnest teisest tasandi punktist eemale nihutada. Huvitav on see, et vektorite jaoks ei pea te üldse telgi ehitama, ristkülikukujuline süsteem koordinaadid, vajate ainult alust, antud juhul tasandi ortonormaalset baasi.
Punktide koordinaatide ja vektorite koordinaatide kirjed näivad olevat sarnased: , ja koordinaatide tähendus absoluutselt erinev, ja peaksite sellest erinevusest hästi teadlik olema. See erinevus kehtib loomulikult ka ruumi kohta.
Daamid ja härrad, täidame oma käed:
Näide 2
a) Punkte ja antakse. Leia vektorid ja .
b) Punkte ja antakse. Leia vektorid ja .
c) Punkte ja antakse. Leia vektorid ja .
d) Punkte antakse. Otsige vektoreid.
Võib-olla sellest piisab. Need on näited sõltumatu otsus, proovi neid mitte hooletusse jätta, see tasub end ära ;-). Jooniseid pole vaja teha. Lahendused ja vastused tunni lõpus.
Mis on oluline analüütilise geomeetria ülesannete lahendamisel? Oluline on olla ERITI ETTEVAATLIK, et vältida meisterlikku viga “kaks pluss kaks võrdub null”. Vabandan kohe, kui kuskil vea tegin =)
Kuidas leida lõigu pikkust?
Pikkus, nagu juba märgitud, on näidatud mooduli märgiga.
Kui on antud kaks tasandi punkti ja , siis saab segmendi pikkuse arvutada valemiga
Kui on antud kaks punkti ruumis ja, siis saab segmendi pikkuse arvutada valemi abil
Märge: Valemid jäävad õigeks, kui vastavad koordinaadid vahetatakse: Ja , kuid esimene variant on standardsem
Näide 3
Lahendus: vastavalt sobivale valemile:
Vastus:
Selguse huvides teen joonise 
Joonelõik – see ei ole vektor, ja loomulikult ei saa te seda kuhugi liigutada. Lisaks, kui joonistate mõõtkavas: 1 ühik. = 1 cm (kaks märkmiku lahtrit), siis saab saadud vastust kontrollida tavalise joonlauaga, mõõtes vahetult lõigu pikkust.
Jah, lahendus on lühike, kuid selles on veel paar olulised punktid mida ma tahaksin selgitada:
Esiteks paneme vastusesse mõõtme: "ühikud". Seisundis pole kirjas, MIS see on, millimeetrites, sentimeetrites, meetrites või kilomeetrites. Seetõttu oleks matemaatiliselt õige lahendus üldine sõnastus: "ühikud" - lühendatult "ühikud".
Teiseks kordame koolimaterjal, mis on kasulik mitte ainult vaadeldava probleemi korral:
pööra tähelepanu oluline tehniline tehnika – kordaja eemaldamine juure alt. Arvutuste tulemusena saame tulemuse ja hea matemaatiline stiil hõlmab teguri eemaldamist juure alt (kui võimalik). Täpsemalt näeb protsess välja järgmine: . Vastuse jätmine niisama poleks muidugi viga – aga kindlasti oleks see puudujääk ja kaalukas argument õpetaja näägutamiseks.
Siin on muud levinud juhtumid: 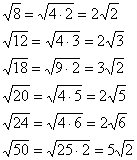
Sageli on juure juures piisavalt suur number, Näiteks . Mida sellistel juhtudel teha? Kalkulaatori abil kontrollime, kas arv jagub 4-ga: . Jah, see oli täielikult jagatud, nii: ![]() . Või äkki saab arvu jälle 4-ga jagada? . Seega:
. Või äkki saab arvu jälle 4-ga jagada? . Seega: ![]() . Arvu viimane number on paaritu, seega kolmandat korda 4-ga jagamine ilmselgelt ei toimi. Proovime jagada üheksaga: . Tulemusena:
. Arvu viimane number on paaritu, seega kolmandat korda 4-ga jagamine ilmselgelt ei toimi. Proovime jagada üheksaga: . Tulemusena:
Valmis.
Järeldus: kui juure alla saame arvu, mida ei saa tervikuna välja võtta, siis proovime teguri juure alt eemaldada - kalkulaatori abil kontrollime, kas arv jagub arvuga: 4, 9, 16, 25, 36, 49 jne.
Otsuse tegemise ajal erinevaid ülesandeid juured on levinud, proovige alati juure alt välja tuua tegurid, et vältida madalama hinde langemist ja tarbetuid probleeme oma lahenduste viimistlemisel õpetaja kommentaaride põhjal.
Kordame ka juurte ruudustamist ja muid võimeid:
Kraadidega toimingute reeglid üldine vaade võib leida kooliõpik algebras, aga arvan, et toodud näidete põhjal on kõik või peaaegu kõik juba selge.
Iseseisva lahenduse ülesanne ruumisegmendiga:
Näide 4
Punkte ja antakse. Leidke lõigu pikkus.
Lahendus ja vastus on tunni lõpus.
Kuidas leida vektori pikkust?
Kui on antud tasapinnaline vektor, siis arvutatakse selle pikkus valemiga.
Kui ruumivektor on antud, arvutatakse selle pikkus valemiga ![]() .
.
Neid valemeid (nagu ka lõigu pikkuse valemeid) on lihtne tuletada tuntud Pythagorase teoreemi abil.
Näide 5
Punkte ja antakse. Leia vektori pikkus.
Võtsin samad punktid nagu näites 3.
Lahendus: Esiteks leiame vektori:
Valemi abil arvutame vektori pikkuse:
Vastus:
Ärge unustage märkida mõõdet – "ühikud"! Muide, kas on alati vaja arvutada ligikaudne väärtus (in selles näites 8.94), kui tingimuses seda nõuta pole? Minu vaatevinklist pole see üleliigne, ligikaudse väärtuse puudumine toob kaasa nipet-näpet. Soovitatav on ümardada 2–3 kümnendkohani.
Teeme ülesande jaoks joonise:
Mis on põhimõtteline erinevus näitest 3? Erinevus seisneb selles, et siin räägime vektorist, mitte segmendist. Vektorit saab liigutada tasapinna mis tahes punkti.
Millised on näite 3 ja näite 5 sarnasused? Geomeetriliselt on ilmne, et lõigu pikkus on võrdne vektori pikkusega. Samuti on ilmne, et vektori pikkus on sama. Tulemusena: ![]() .
.
b) Arvestades vektorid , Ja . Leidke nende pikkus.
Lahendused ja vastused tunni lõpus.
Selles artiklis hakkame arutama ühte "võlukeppi", mis võimaldab teil taandada paljud geomeetriaprobleemid lihtsaks aritmeetikaks. See "pulk" võib teie elu palju lihtsamaks muuta, eriti kui te ei ole ehitamises kindel ruumikujud, sektsioonid jne. Kõik see nõuab teatud kujutlusvõimet ja praktilisi oskusi. Meetod, mida me siin kaaluma hakkame, võimaldab teil peaaegu täielikult loobuda igasugusest geomeetrilised konstruktsioonid ja arutluskäiku. Meetodit nimetatakse "koordinaatide meetod". Selles artiklis käsitleme järgmisi küsimusi:
- Koordinaatide tasapind
- Punktid ja vektorid tasapinnal
- Vektori konstrueerimine kahest punktist
- Vektori pikkus (kahe punkti vaheline kaugus).
- Lõigu keskkoha koordinaadid
- Vektorite punktkorrutis
- Nurk kahe vektori vahel
Arvan, et olete juba arvanud, miks koordinaatmeetodit nii nimetatakse? See on õige, see sai selle nime, kuna see ei tööta geomeetrilised objektid, ja nendega numbrilised omadused(koordinaadid). Ja teisendus ise, mis võimaldab meil liikuda geomeetriast algebrasse, seisneb koordinaatide süsteemi sisseviimises. Kui algne kujund oli tasane, siis on koordinaadid kahemõõtmelised ja kui kujund on kolmemõõtmelised, siis on koordinaadid kolmemõõtmelised. Selles artiklis käsitleme ainult kahemõõtmelist juhtumit. Ja artikli peamine eesmärk on õpetada teile mõnda kasutamist põhilised tehnikad koordinaatide meetod (need osutuvad mõnikord kasulikuks ühtse riigieksami B osas planimeetria ülesannete lahendamisel). Selle teema kaks järgmist osa on pühendatud probleemide C2 (stereomeetria probleem) lahendamise meetodite arutelule.
Kust oleks loogiline alustada arutelu koordinaatmeetodi üle? Ilmselt koordinaatsüsteemi mõistest. Pidage meeles, kui temaga esimest korda kohtusite. Mulle tundub, et 7. klassis, kui sa olemasolust teada said lineaarne funktsioon, Näiteks. Tuletan teile meelde, et ehitasite selle punkt-punktilt üles. Kas sa mäletad? Sina valisid suvaline arv, asendas selle valemiga ja arvutas selle nii. Näiteks kui, siis, kui, siis jne. Mis sa lõpuks said? Ja saite punkte koordinaatidega: ja. Järgmiseks joonistasite "risti" (koordinaatsüsteem), valisite sellele skaala (mitu lahtrit teil ühikulise segmendina on) ja märkisite sellele saadud punktid, mille seejärel sirgjoonega ühendasite. joon on funktsiooni graafik.
Siin on mõned punktid, mida tuleks teile veidi üksikasjalikumalt selgitada:
1. Valite mugavuse huvides ühe segmendi, et kõik mahuks ilusti ja kompaktselt joonisele.
2. On aktsepteeritud, et telg läheb vasakult paremale ja telg läheb alt üles
3. Nad lõikuvad täisnurga all ja nende lõikepunkti nimetatakse alguspunktiks. Seda tähistab kiri.
4. Punkti koordinaatide kirjutamisel on näiteks vasakul sulgudes punkti koordinaat piki telge ja paremal pool piki telge. Eelkõige tähendab see lihtsalt seda, et hetkel
5. Mis tahes punkti sisselülitamiseks koordinaatide telg, peate märkima selle koordinaadid (2 numbrit)
6. Iga teljel paikneva punkti puhul
7. Iga teljel paikneva punkti puhul
8. Telge nimetatakse x-teljeks
9. Telge nimetatakse y-teljeks
Nüüd teeme seda teiega järgmine samm: Märgime kaks punkti. Ühendame need kaks punkti segmendiga. Ja me paneme noole nii, nagu joonistaksime lõigu punktist punkti: see tähendab, et me muudame oma lõigu suunatud!

Pea meeles, kuidas nimetatakse teist suunalist segmenti? Täpselt nii, seda nimetatakse vektoriks!
Nii et kui ühendame punkti punktiga, ja algus on punkt A ja lõpp on punkt B, siis saame vektori. Sa tegid seda ehitust ka 8. klassis, mäletad?
Selgub, et vektoreid, nagu ka punkte, saab tähistada kahe numbriga: neid arve nimetatakse vektorkoordinaatideks. Küsimus: Kas teie arvates piisab, kui me teame vektori alguse ja lõpu koordinaate, et leida selle koordinaadid? Tuleb välja, et jah! Ja seda tehakse väga lihtsalt:
Seega, kuna vektoris on punkt algus ja punkt lõpp, on vektoril järgmised koordinaadid:
Näiteks kui, siis vektori koordinaadid
Nüüd teeme vastupidi, leiame vektori koordinaadid. Mida me selleks muutma peame? Jah, peate algust ja lõppu vahetama: nüüd on vektori algus punktis ja lõpp punktis. Seejärel:
Vaadake hoolikalt, mis vahe on vektorite ja? Nende ainus erinevus on koordinaatides olevad märgid. Nad on vastandid. See fakt on tavaliselt kirjutatud järgmiselt:
Mõnikord, kui pole konkreetselt öeldud, milline punkt on vektori algus ja milline lõpp, tähistatakse vektoreid rohkem kui kahega. suurte tähtedega, ja üks väiketäht, näiteks: , jne.
Nüüd natuke harjutada ise ja leidke järgmiste vektorite koordinaadid:
Eksam:
Nüüd lahendage veidi keerulisem ülesanne:
Punktis algusega vektoril on ko-or-di-na-you. Leidke abs-cis-su punktid.
Kõik sama on üsna proosaline: Olgu punkti koordinaadid. Siis
Süsteemi koostasin lähtuvalt definitsioonist, mis on vektori koordinaadid. Siis on punktil koordinaadid. Oleme huvitatud abstsissist. Siis
Vastus:
Mida saab veel vektoritega teha? Jah, peaaegu kõik on sama, mis on tavalised numbrid(välja arvatud see, et jagada ei saa, aga korrutada saab kahel viisil, millest üht räägime siin veidi hiljem)
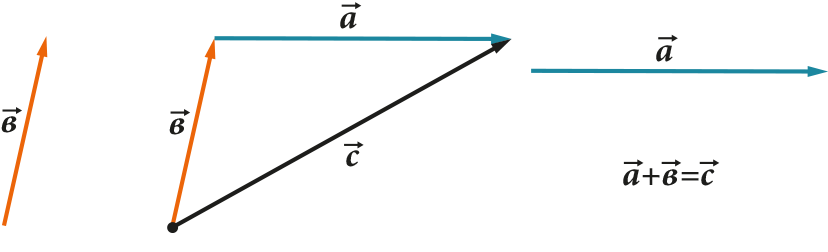
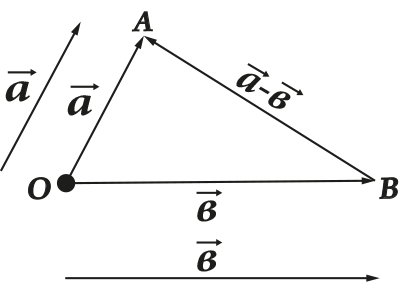
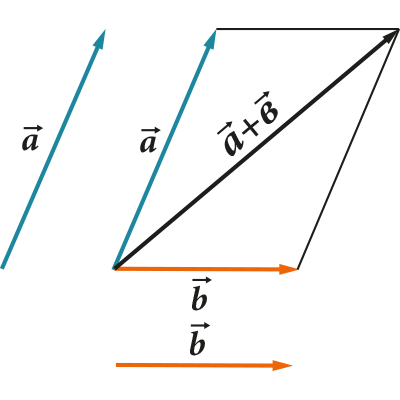
- Vektoreid saab üksteisele lisada
- Vektoreid saab üksteisest lahutada
- Vektoreid saab korrutada (või jagada) suvalise nullist erineva arvuga
- Vektoreid saab üksteisega korrutada
Kõigil neil toimingutel on väga selge geomeetriline kujutis. Näiteks kolmnurga (või rööpküliku) reegel liitmiseks ja lahutamiseks:
Vektor venib, tõmbub kokku või muudab suunda, kui seda arvuga korrutada või jagada:

Siinkohal huvitab meid aga küsimus, mis juhtub koordinaatidega.
1. Kahe vektori liitmisel (lahutamisel) liidame (lahutame) nende koordinaadid elemendi haaval. See on:
2. Vektori arvuga korrutamisel (jagamisel) korrutatakse (jagatakse) selle arvuga kõik selle koordinaadid:
Näiteks:
· Leia summa co-or-di-nat sajandist-ra.
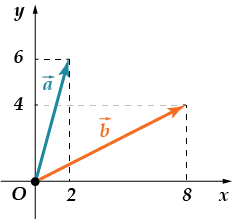
Leiame esmalt iga vektori koordinaadid. Neil mõlemal on sama päritolu – lähtepunkt. Nende otsad on erinevad. Siis,. Nüüd arvutame vektori koordinaadid Siis on saadud vektori koordinaatide summa võrdne.
Vastus:
Nüüd lahendage järgmine probleem ise:
· Leia vektori koordinaatide summa
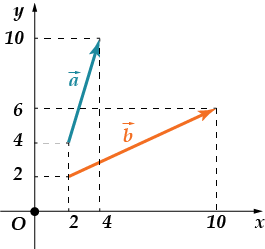
Kontrollime:
Vaatleme nüüd järgmist ülesannet: meil on koordinaattasandil kaks punkti. Kuidas nende vahelist kaugust leida? Olgu esimene punkt ja teine. Tähistagem nende vahelist kaugust. Selguse huvides teeme järgmise joonise:
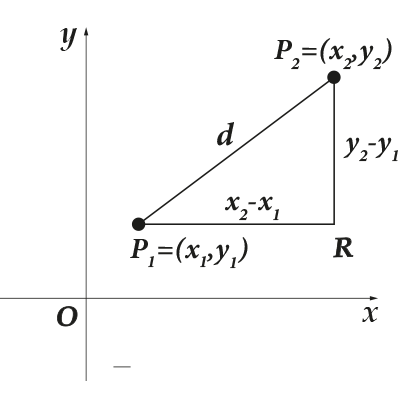
Mis ma teinud olen? Esiteks ühendasin punktid ja,a tõmbas ka punktist joone, teljega paralleelne, ja punktist tõmbasin teljega paralleelse sirge. Kas need lõikuvad mingis punktis, moodustades tähelepanuväärse kuju? Mis on temas nii erilist? Jah, sina ja mina teame täisnurksest kolmnurgast peaaegu kõike. Noh, Pythagorase teoreem kindlasti. Vajalik segment on selle kolmnurga hüpotenuus ja segmendid on jalad. Mis on punkti koordinaadid? Jah, neid on pildilt lihtne leida: Kuna lõigud on paralleelsed telgedega ja vastavalt, on nende pikkused kergesti leitavad: kui tähistame lõikude pikkused vastavalt, siis
Nüüd kasutame Pythagorase teoreemi. Me teame jalgade pikkust, leiame hüpotenuusi:
Seega on kahe punkti vaheline kaugus koordinaatide ruudu erinevuste summa juur. Või - kahe punkti vaheline kaugus on neid ühendava lõigu pikkus. On hästi näha, et punktide vaheline kaugus ei sõltu suunast. Seejärel:
Siit teeme kolm järeldust:
Harjutame veidi kahe punkti vahelise kauguse arvutamist:
Näiteks kui, siis kaugus ja vahel on võrdne
Või lähme teist teed: leiame vektori koordinaadid
Ja leidke vektori pikkus:
Nagu näete, on see sama asi!
Nüüd harjutage natuke ise:
Ülesanne: leidke näidatud punktide vaheline kaugus:
Kontrollime:
Siin on veel paar probleemi, mis kasutavad sama valemit, kuigi need kõlavad veidi erinevalt:
1. Leia silmalau pikkuse ruut.

2. Leia silmalau pikkuse ruut

Arvan, et saite nendega raskusteta hakkama? Kontrollime:
1. Ja see on tähelepanelikkuseks) Oleme vektorite koordinaadid juba varem leidnud: . Siis on vektoril koordinaadid. Selle pikkuse ruut on võrdne:
2. Leidke vektori koordinaadid
Siis on selle pikkuse ruut
Pole midagi keerulist, eks? Lihtne aritmeetika, ei midagi muud.
Järgmisi probleeme ei saa üheselt liigitada, need puudutavad pigem üldist eruditsiooni ja lihtsate piltide joonistamise oskust.
1. Leidke lõikest nurga siinus, mis ühendab punkti abstsissteljega.
 Ja
Ja
Kuidas me siin edasi läheme? Peame leidma siinuse nurga ja telje vahel. Kust siinust otsida? See on õige, sisse täisnurkne kolmnurk. Mida me siis tegema peame? Ehitage see kolmnurk!
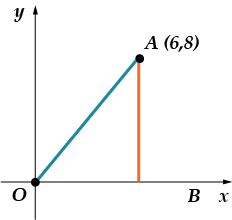
Kuna punkti koordinaadid on ja, siis on lõik võrdne ja lõiguga. Peame leidma nurga siinuse. Lubage mul teile meelde tuletada, et siinus on suhe vastasjalg hüpotenuusile, siis
Mis meil teha jääb? Leidke hüpotenuus. Seda saab teha kahel viisil: kasutades Pythagorase teoreemi (jalad on teada!) või kasutades kahe punkti vahelise kauguse valemit (tegelikult sama, mis esimene meetod!). Ma lähen teist teed:
Vastus:
Järgmine ülesanne tundub teile veelgi lihtsam. Ta on punkti koordinaatidel.
2. ülesanne. Alates punktist langetatakse per-pen-di-ku-lyar ab-cissi teljele. Nai-di-te abs-cis-su os-no-va-niya per-pen-di-ku-la-ra.
Teeme joonise:
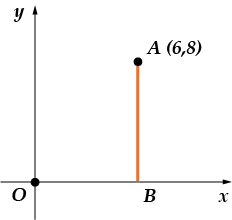
Perpendikulaari alus on punkt, kus see lõikub x-teljega (teljega), minu jaoks on see punkt. Joonisel on näha, et sellel on koordinaadid: . Oleme huvitatud abstsissist - see tähendab "x" komponendist. Ta on võrdne.
Vastus: .
3. ülesanne. Tingimustes eelmine ülesanne leida punktist koordinaattelgede kauguste summa.
Ülesanne on üldiselt elementaarne, kui tead, milline on kaugus punktist telgedeni. Sa tead? Loodan, aga tuletan siiski meelde:
Niisiis, kas ma olen juba joonistanud oma ülaltoodud joonisel ühe sellise risti? Millisel teljel see on? Teljele. Ja mis selle pikkus siis on? Ta on võrdne. Nüüd joonistage ise teljega risti ja leidke selle pikkus. See saab olema võrdne, eks? Siis on nende summa võrdne.
Vastus: .
4. ülesanne.Ülesande 2 tingimustes leidke punkti ordinaat, sümmeetriline punkt abstsisstelje suhtes.
Ma arvan, et teile on intuitiivselt selge, mis on sümmeetria? Paljudel objektidel on see olemas: palju hooneid, laudu, lennukeid, palju geomeetrilised kujundid: pall, silinder, ruut, romb jne. Jämedalt võib sümmeetriat mõista järgmiselt: kujund koosneb kahest (või enamast) identsest poolest. Seda sümmeetriat nimetatakse aksiaalseks sümmeetriaks. Mis on siis telg? Täpselt seda joont mööda saab figuuri suhteliselt võrdseteks pooleks lõigata (sellel pildil on sümmeetriatelg sirge):

Nüüd pöördume tagasi oma ülesande juurde. Teame, et otsime punkti, mis on telje suhtes sümmeetriline. Siis on see telg sümmeetriatelg. See tähendab, et peame märkima punkti nii, et telg lõikab segmendi kaheks võrdseks osaks. Proovige ise selline punkt ära märkida. Võrrelge nüüd minu lahendusega:
![]()
Kas see läks teil samamoodi? Hästi! Meid huvitab leitud punkti ordinaat. See on võrdne
Vastus:
Nüüd öelge mulle pärast mõnesekundilist mõtlemist, milline on punkti A suhtes sümmeetrilise punkti abstsiss ordinaadi suhtes? Mis on teie vastus? Õige vastus:.
IN üldine juhtum reegli võib kirjutada nii:
Abstsisstelje suhtes punktiga sümmeetrilisel punktil on koordinaadid:
Ordinaattelje suhtes punktiga sümmeetrilisel punktil on koordinaadid:
No nüüd on täitsa hirmus ülesanne: otsib lähtepunkti suhtes sümmeetrilise punkti koordinaadid. Kõigepealt mõtle ise ja siis vaata minu joonistust!
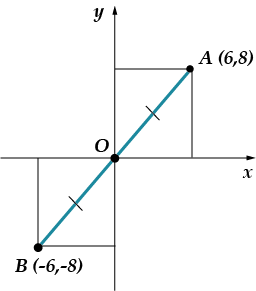
Vastus:
Nüüd rööpküliku probleem:
Ülesanne 5: Punktid ilmuvad ver-shi-na-mi pa-ral-le-lo-gram-ma. Otsige üles see punkt.
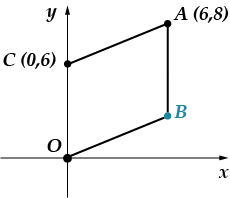
Saate selle probleemi lahendada kahel viisil: loogika ja koordinaatide meetod. Ma kasutan kõigepealt koordinaatide meetodit ja siis räägin teile, kuidas saate seda teisiti lahendada.
On täiesti selge, et punkti abstsiss on võrdne. (see asub punktist abstsissteljele tõmmatud ristil). Peame leidma ordinaat. Kasutame ära asjaolu, et meie joonis on rööpkülik, see tähendab seda. Leiame lõigu pikkuse kahe punkti vahelise kauguse valemi abil:
Langetame punkti, mis ühendab punkti teljega. Tähistan ristumispunkti tähega.
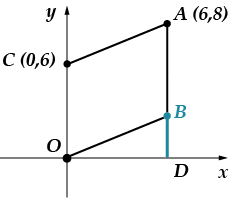
Segmendi pikkus on võrdne. (leidke probleem ise sealt, kus me seda punkti arutasime), siis leiame Pythagorase teoreemi abil segmendi pikkuse:
Lõigu pikkus langeb täpselt kokku selle ordinaadiga.
Vastus: .
Teine lahendus (ma annan lihtsalt pildi, mis seda illustreerib)
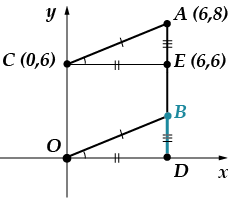
Lahenduse edenemine:
1. Käitumine
2. Leia punkti ja pikkuse koordinaadid
3. Tõesta seda.
Veel üks segmendi pikkuse probleem:
Punktid ilmuvad kolmnurga kohale. Leidke selle paralleelse keskjoone pikkus.

Kas mäletate, mis see on keskmine joon kolmnurk? Siis on see ülesanne teie jaoks elementaarne. Kui te ei mäleta, tuletan teile meelde: kolmnurga keskjoon on joon, mis ühendab keskpunkte vastasküljed. See on alusega paralleelne ja võrdne poolega sellest.
Alus on segment. Selle pikkust pidime varem otsima, see on võrdne. Siis on keskmise joone pikkus poole suurem ja võrdne.
Vastus: .
Kommentaar: seda probleemi saab lahendada muul viisil, mille juurde pöördume veidi hiljem.
Seniks aga siin on teile mõned probleemid, harjutage nende kallal, need on väga lihtsad, kuid aitavad teil koordinaatide meetodit paremini kasutada!
1. Punktid on tra-pe-tsioonide tipud. Leidke selle keskjoone pikkus.

2. Punktid ja esinemised ver-shi-na-mi pa-ral-le-lo-gram-ma. Otsige üles see punkt.

3. Leia pikkus lõikest, ühendades punkti ja

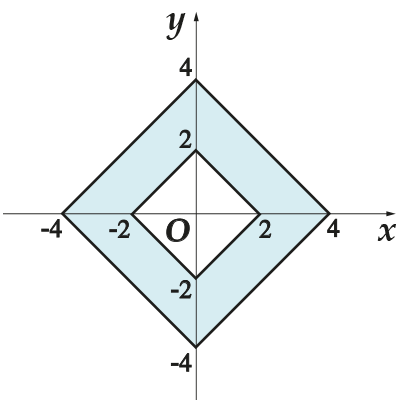
4. Leia koordinaattasandil värvilise kujundi taga olev ala.
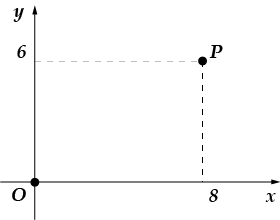
5. Punkti läbib ring, mille keskpunkt on na-cha-le ko-or-di-nat. Otsige üles tema raadio.
6. Otsi-di-te ra-di-us ringist, kirjelda-san-noy umbes täisnurk-no-ka, millegi tippudel on kaas-või -di-na-sa oled nii-vastutav

Lahendused:
1. On teada, et trapetsi keskjoon on võrdne poolega selle aluste summast. Alus on võrdne ja alus. Siis
Vastus:
2. Lihtsaim viis selle probleemi lahendamiseks on märkida see (parallelogrammi reegel). Vektorite koordinaatide arvutamine pole keeruline: . Vektorite lisamisel liidetakse koordinaadid. Siis on koordinaadid. Punktil on ka need koordinaadid, kuna vektori alguspunkt on koordinaatidega punkt. Oleme huvitatud ordinaatidest. Ta on võrdne.
Vastus:
3. Toimime kohe kahe punkti vahelise kauguse valemi järgi:
Vastus:
4. Vaata pilti ja öelge, millise kahe kuju vahele on varjutatud ala “vajutud”? See asetseb kahe ruudu vahele. Seejärel võrdub soovitud kujundi pindala suure ruudu pindalaga, millest on lahutatud väikese ruudu pindala. Külg väike ruut on punkte ühendav segment ja selle pikkus on
Siis on väikese ruudu pindala
Teeme sama suure ruuduga: selle külg on punkte ühendav segment ja pikkus on
Siis on suure ruudu pindala
Leiame soovitud kujundi pindala järgmise valemi abil:
Vastus:
5. Kui ringi keskpunkt on alguspunkt ja see läbib punkti, siis on selle raadius täpselt sama pikkusega võrdne segment (koostage joonis ja saate aru, miks see on ilmne). Leiame selle segmendi pikkuse:
Vastus:
6. On teada, et ristküliku ümber piiratud ringi raadius võrdne poolega selle diagonaalid. Leiame ükskõik millise kahe diagonaali pikkuse (ristkülikus on need ju võrdsed!)
Vastus:
No kas sa tulid kõigega toime? Ei olnud väga raske aru saada, eks? Siin on ainult üks reegel - suutma teha visuaalset pilti ja lihtsalt sellest kõik andmed “lugeda”.
Meil on jäänud väga vähe. Sõna otseses mõttes on veel kaks punkti, mida tahaksin arutada.
Proovime seda lihtsat probleemi lahendada. Olgu kaks punkti ja antakse. Leidke lõigu keskpunkti koordinaadid. Selle ülesande lahendus on järgmine: olgu punkt soovitud keskpunkt, siis on sellel koordinaadid:
See on: lõigu keskkoha koordinaadid = lõigu otste vastavate koordinaatide aritmeetiline keskmine.
See reegel on väga lihtne ega tekita õpilastele tavaliselt raskusi. Vaatame, millistes probleemides ja kuidas seda kasutatakse:
1. Otsi-di-te või-di-na-tu se-re-di-ny alates-lõigatud, ühenda-punkt ja

2. Punktid näivad olevat maailma tipud. Leia-di-te või-di-na-tu punkte per-re-se-che-niya tema dia-go-na-ley.

3. Otsi-di-te abs-cis-su ringi keskpunkt, kirjelda-san-noy ristkülikukujulise-no-ka kohta, millegi tippudel on co-or-di-na-you nii-vastutustundlikult-aga.

Lahendused:
1. Esimene probleem on lihtsalt klassikaline. Jätkame kohe segmendi keskkoha määramiseks. Sellel on koordinaadid. Ordinaat on võrdne.
Vastus:
2. On hästi näha, et see nelinurk on rööpkülik (isegi romb!). Saate seda ise tõestada, arvutades külgede pikkused ja võrreldes neid omavahel. Mida ma tean rööpkülikutest? Selle diagonaalid jagatakse lõikepunktiga pooleks! Jah! Mis on siis diagonaalide lõikepunkt? See on ükskõik millise diagonaali keskpunkt! Eelkõige valin diagonaali. Siis on punktil koordinaadid Punkti ordinaat on võrdne.
Vastus:
3. Millega ühtib ristküliku ümber piiritletud ringi keskpunkt? See langeb kokku selle diagonaalide lõikepunktiga. Mida teate ristküliku diagonaalide kohta? Need on võrdsed ja lõikepunkt jagab need pooleks. Ülesanne taandati eelmisele. Võtame näiteks diagonaali. Siis, kui on ümbermõõdu keskpunkt, siis on keskpunkt. Otsin koordinaate: Abstsiss on võrdne.
Vastus:
Nüüd harjutage veidi omaette, ma annan lihtsalt vastused igale probleemile, et saaksite end proovile panna.
1. Otsi-di-te ra-di-us ringist, kirjelda-san-noy kolmnurga-no-ka kohta, millegi tippudel on co-or-di -no misters

2. Otsi-di-te või-di-sellel ringi keskpunktil, kirjelda-san-noy kolmnurga-no-ka kohta, mille tippudel on koordinaadid
3. Missugune ra-di-u-sa peaks olema ring, mille keskpunkt on ühes punktis nii, et see puudutab ab-cissi telge?
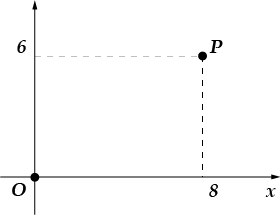
4. Otsige üles need või-di-selles punktis, kus telje taas-se-ase-mine ja alates lõikest, ühendage-punkt ja

Vastused:
Kas kõik õnnestus? Ma väga loodan seda! Nüüd – viimane tõuge. Ole nüüd eriti ettevaatlik. Materjal, mida ma nüüd selgitan, on otseselt seotud mitte ainult lihtsaid ülesandeid koordinaatmeetodile osast B, kuid seda leidub kõikjal ka ülesandes C2.
Milliseid lubadusi ma pole veel täitnud? Kas mäletate, milliseid vektorite tehteid lubasin kasutusele võtta ja millised lõpuks kasutusele võtsin? Oled sa kindel, et ma pole midagi unustanud? Unustasin! Unustasin selgitada, mida tähendab vektorkorrutis.
Vektori korrutamiseks vektoriga on kaks võimalust. Sõltuvalt valitud meetodist saame erineva iseloomuga objekte:
Risttoode on tehtud üsna nutikalt. Kuidas seda teha ja miks seda vaja on, arutame järgmises artiklis. Ja selles keskendume skalaarkorrutisele.
Selle arvutamiseks on kaks võimalust:
Nagu arvasite, peaks tulemus olema sama! Nii et vaatame kõigepealt esimest meetodit:
Punkttoode koordinaatide kaudu
Leidke: - skalaarkorrutise üldtunnustatud tähistus
Arvutamise valem on järgmine:
See on skalaarkorrutis= vektori koordinaatide korrutiste summa!
Näide:
Find-di-te
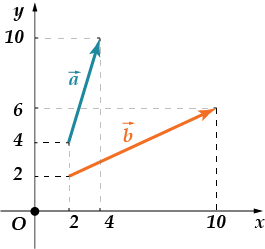
Lahendus:
Leiame iga vektori koordinaadid:
Arvutame skalaarkorrutise järgmise valemi abil:
Vastus:
Vaata, absoluutselt ei midagi keerulist!
Noh, proovige nüüd ise:
· Leia skalaarne pro-iz-ve-de-nie sajandite ja
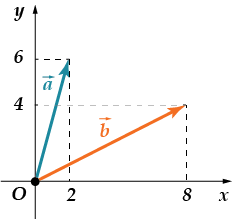
Kas said hakkama? Võib-olla märkasite väikest saaki? Kontrollime:
Vektori koordinaadid nagu näidatud viimane ülesanne! Vastus:.
Lisaks koordinaadile on skalaarkorrutise arvutamiseks veel üks viis, nimelt vektorite pikkuste ja nendevahelise nurga koosinuse kaudu:
Tähistab nurka vektorite ja vahel.
See tähendab, et skalaarkorrutis on võrdne vektorite pikkuste ja nendevahelise nurga koosinuse korrutisega.
Milleks meile seda teist valemit vaja, kui meil on esimene, mis on palju lihtsam, selles pole vähemalt koosinusi. Ja seda on vaja selleks, et esimesest ja teisest valemist saaksime teiega järeldada, kuidas vektorite vahelist nurka leida!
Olgu Siis jäta meelde vektori pikkuse valem!
Siis kui ma asendan need andmed skalaarkorrutise valemiga, saan:
Aga muul viisil:
Mida sina ja mina siis saime? Meil on nüüd valem, mis võimaldab meil arvutada kahe vektori vahelise nurga! Mõnikord on see lühiduse mõttes kirjutatud ka nii:
See tähendab, et vektorite vahelise nurga arvutamise algoritm on järgmine:
- Arvutage skalaarkorrutis koordinaatide kaudu
- Leidke vektorite pikkused ja korrutage need
- Jagage punkti 1 tulemus punkti 2 tulemusega
Harjutame näidetega:
1. Leia silmalaugude vaheline nurk ja. Andke vastus keeles grad-du-sah.
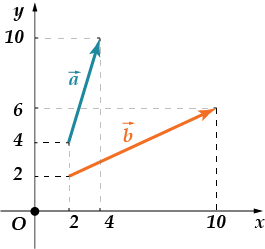
2. Leia eelmise ülesande tingimustes koosinus vektorite vahel
Teeme nii: aitan teil esimese probleemi lahendada ja proovige teist ise teha! Nõus? Alustame siis!
1. Need vektorid on meie vanad sõbrad. Oleme nende skalaarkorrutise juba välja arvutanud ja see oli võrdne. Nende koordinaadid on: , . Seejärel leiame nende pikkused:
Seejärel otsime vektorite vahel koosinust:
Mis on nurga koosinus? See on nurk.
Vastus:
Noh, nüüd lahendage teine probleem ise ja seejärel võrrelge! Ma annan väga lühikese lahenduse:
2. omab koordinaate, omab koordinaate.
Laskma olema nurk vektorite ja, siis
Vastus:
Tuleb märkida, et probleemid otse vektoritel ja koordinaatide meetodil B osas eksamitööüsna haruldane. Valdav enamus C2 ülesandeid on aga kergesti lahendatavad koordinaatsüsteemi kasutuselevõtuga. Nii et võite pidada seda artiklit vundamendiks, mille põhjal teeme üsna nutikaid konstruktsioone, mida vajame keerukate probleemide lahendamiseks.
