BẢNG BẢN VĂN BẢN CỦA BÀI HỌC:
Nếu ba đường thẳng vuông góc từng cặp được vẽ qua một điểm trong không gian, trên đó mỗi đường thẳng được chọn một hướng và một đoạn đơn vị, thì chúng ta nói rằng một hệ tọa độ hình chữ nhật trong không gian được chỉ định.
Các đường thẳng với các hướng được chọn trên chúng được gọi là trục tọa độ và được ký hiệu như sau: Ox, Oy, Oz, có tên riêng: trục abscissa, trục tọa độ và trục ứng dụng tương ứng, và trục ứng dụng của chúng. điểm chung- gốc tọa độ. Nó thường được ký hiệu bằng chữ O.
Toàn bộ hệ tọa độ được chỉ định là Oxyz.
Nếu vẽ các mặt phẳng đi qua các trục tọa độ Ox và Oy, Oy và Oz, Oz và Ox thì các mặt phẳng đó gọi là mặt phẳng tọa độ và ký hiệu lần lượt là: Oxy, Oyz, Ozx.
Điểm O chia mỗi trục tọa độ thành hai tia. Tia có hướng trùng với hướng của trục gọi là bán trục dương, tia còn lại gọi là bán trục âm.
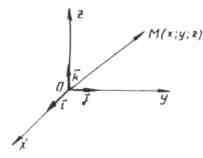
Trong hệ tọa độ hình chữ nhật, mỗi điểm M trong không gian được liên kết với một bộ ba số, được gọi là tọa độ của nó. Chúng được xác định tương tự như tọa độ các điểm trên mặt phẳng.
Hãy xem nó được thực hiện như thế nào.
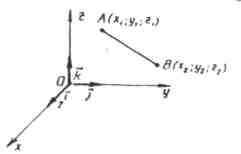
Vẽ ba mặt phẳng đi qua điểm M vuông góc với các trục tọa độ và biểu thị bằng M₁, M₂ và M₃ các điểm giao nhau của các mặt phẳng này tương ứng với trục hoành, trục tọa độ và trục ứng dụng.
Tọa độ đầu tiên của điểm M (gọi là hoành độ và thường được ký hiệu bằng chữ x) được xác định như sau: x = OM₁, nếu M₁ là điểm của bán trục dương;
x= - OM₁, nếu M₁ là điểm của bán trục âm; x =0 nếu M₁ trùng với điểm O.
Tương tự, sử dụng điểm M₂, tọa độ thứ hai (thứ cấp) tại điểm M được xác định,
và sử dụng điểm M₃ - tọa độ thứ ba (áp dụng) z của điểm M.
Tọa độ điểm M được viết trong ngoặc đơn sau ký hiệu điểm M (x; y; z).
Hãy nhớ rằng hoành độ được chỉ định đầu tiên, thứ tự là thứ hai và ứng dụng là thứ ba.
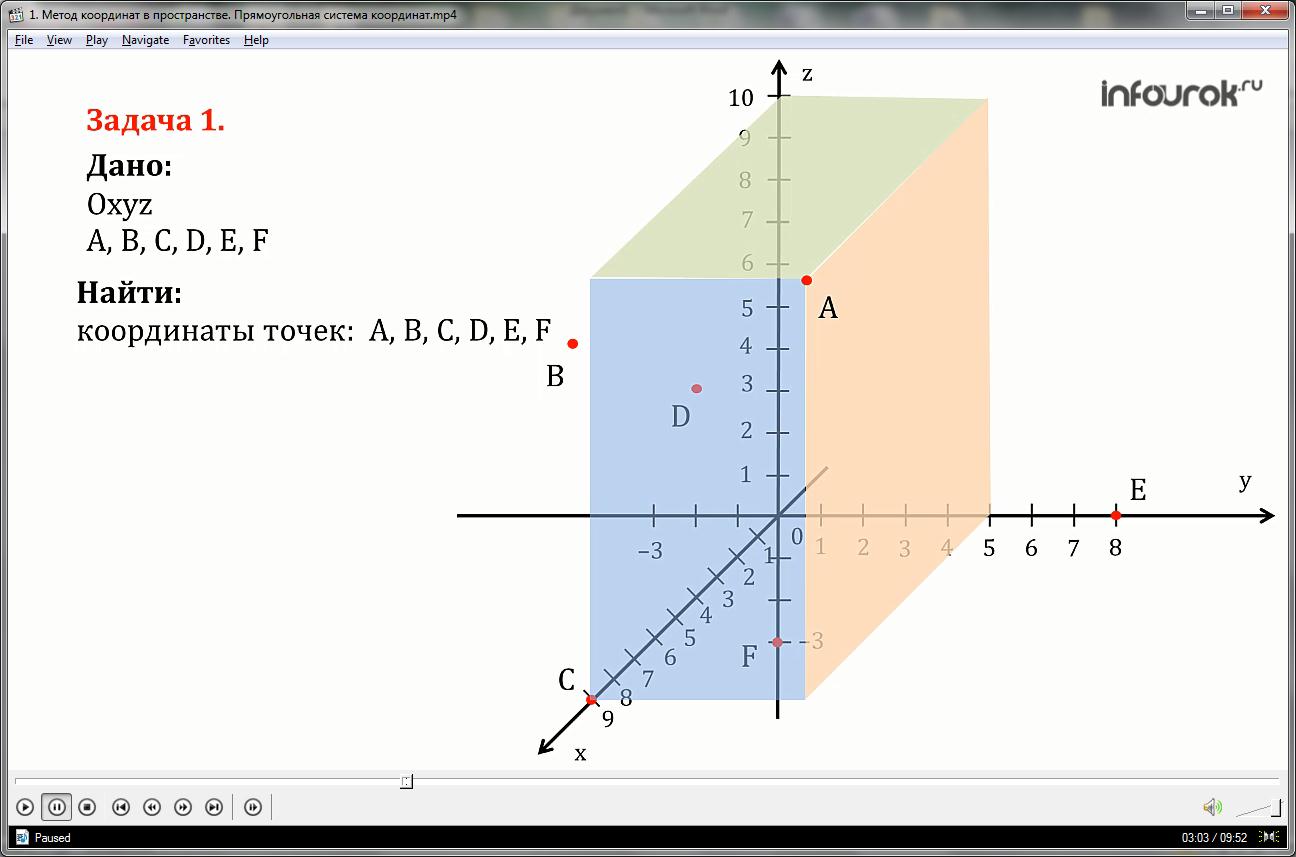
Hãy tìm tọa độ các điểm A, B, C, D, E, F như hình vẽ.
Ta vẽ ba mặt phẳng đi qua điểm A, vuông góc với các trục tọa độ, khi đó giao điểm của các mặt phẳng này với trục hoành, trục hoành và trục ứng dụng lần lượt sẽ là tọa độ của điểm A. Điểm A có tọa độ: abscissa = 9, thứ tự = 5, áp dụng = 10 và nó được viết như sau: A(9; 5; 10).
Tọa độ các điểm sau được viết tương tự:
Điểm B có tọa độ: hoành độ = 4, tọa độ = -3, ứng dụng = 6
Điểm C có tọa độ: hoành độ = 9, tọa độ = 0, ứng dụng = 0
Điểm có tọa độ D: abscissa = 4, tọa độ = 0, ứng dụng = 5
Điểm E có tọa độ: hoành độ = 0, tọa độ = 8, ứng dụng = 0
Điểm F có tọa độ: hoành độ = 0, tọa độ = 0, ứng dụng = -3
Nếu một điểm M (x; y; z) nằm trên mặt phẳng tọa độ trên trục tọa độ thì một số tọa độ của nó bằng 0.
Nếu MЄОху (điểm M thuộc mặt phẳng Oxy), thì ứng dụng của điểm M bằng 0: z=0.
Tương tự, nếu МЄОхz (điểm M thuộc mặt phẳng Oxz) thì y = 0, và nếu МЄОуz (điểm M thuộc mặt phẳng Oyz) thì x = 0.
Nếu МЄОх (điểm M nằm trên trục hoành) thì tọa độ và ứng dụng của điểm M bằng 0: y=o và z=0. Trong ví dụ của chúng tôi, đây là điểm C.
Nếu MЄОу (điểm M nằm trên tọa độ) thì x=0 và z=0. Trong ví dụ của chúng tôi, đây là điểm E.
Nếu МЄОz (điểm M nằm trên trục ứng dụng), thì x = 0 và y = 0. Trong ví dụ của chúng ta, đây là điểm F.
Nếu cả ba tọa độ của điểm M đều bằng 0 thì điều này có nghĩa là M=O (0; 0; 0) là gốc tọa độ.
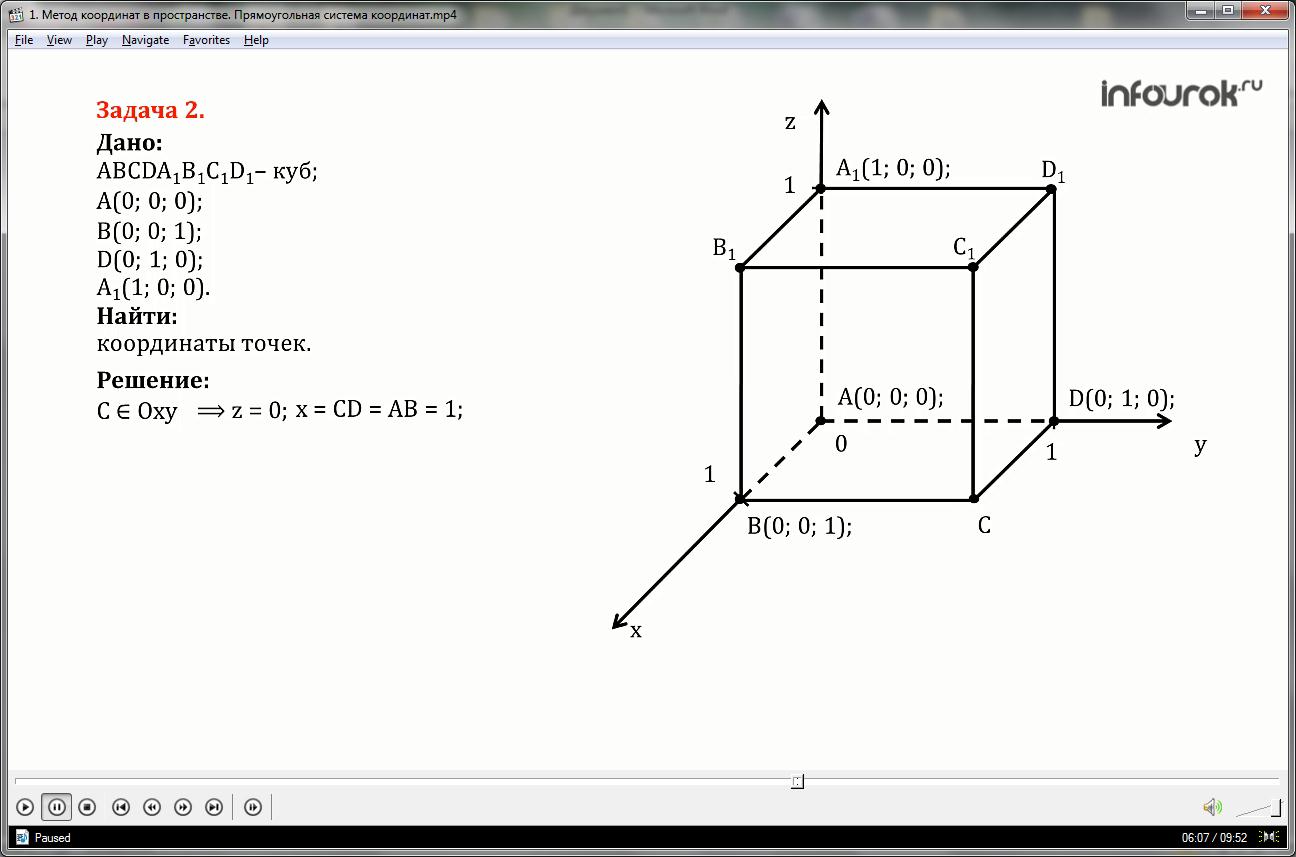
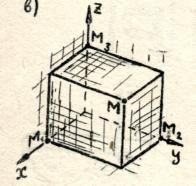
Cho tọa độ bốn đỉnh của hình lập phương ABCDA 1 B 1 C 1 D 1: A(0; 0; 0); B(0; 0; 1); D(0; 1; 0); A 1 (1; 0; 0). Tìm tọa độ các đỉnh còn lại của hình lập phương.
Vì hình này là hình lập phương nên các cạnh đều bằng một, mọi mặt đều là hình vuông.
Điểm C thuộc mặt phẳng Oxy, nghĩa là tọa độ z của nó bằng 0, tọa độ x bằng cạnh CD và bằng AB tức là bằng 1, tọa độ Y bằng cạnh của khối CB, nghĩa là nó bằng AD và bằng 1.
Tương tự, Điểm B 1 thuộc mặt phẳng Oxz, tức là tọa độ y bằng 0, tọa độ x bằng cạnh, tọa độ x bằng cạnh A1B1 và bằng AB, nghĩa là bằng một, tọa độ z bằng cạnh của hình lập phương B B1, nghĩa là bằng AA1 và bằng một.
Điểm D 1 thuộc mặt phẳng Oyz, tức là tọa độ x của nó bằng 0, tọa độ y bằng cạnh A 1 D 1 và bằng AD, nghĩa là bằng 1, tọa độ z bằng cạnh của hình lập phương A 1 B 1, nghĩa là nó bằng AB và bằng 1.
Điểm C 1 không thuộc mặt phẳng nào, tức là mọi tọa độ đều khác 0, tọa độ x bằng cạnh C 1 D 1 và bằng AB, nghĩa là nó bằng 1, tọa độ y là bằng cạnh của hình lập phương B 1 C 1, nghĩa là nó bằng AD và bằng 1, tọa độ z bằng cạnh CC 1, tức là AA 1 và cũng bằng 1.
Tìm tọa độ các hình chiếu của điểm C(;;) lên các mặt phẳng tọa độ Oxy, Oxz, Oyz và các trục tọa độ Ox, Oy, Oz.
1) vuông góc với mặt phẳng Oxy - đây là CN, với mặt phẳng Oxz - CL và với mặt phẳng Oyz - đường thẳng CR.
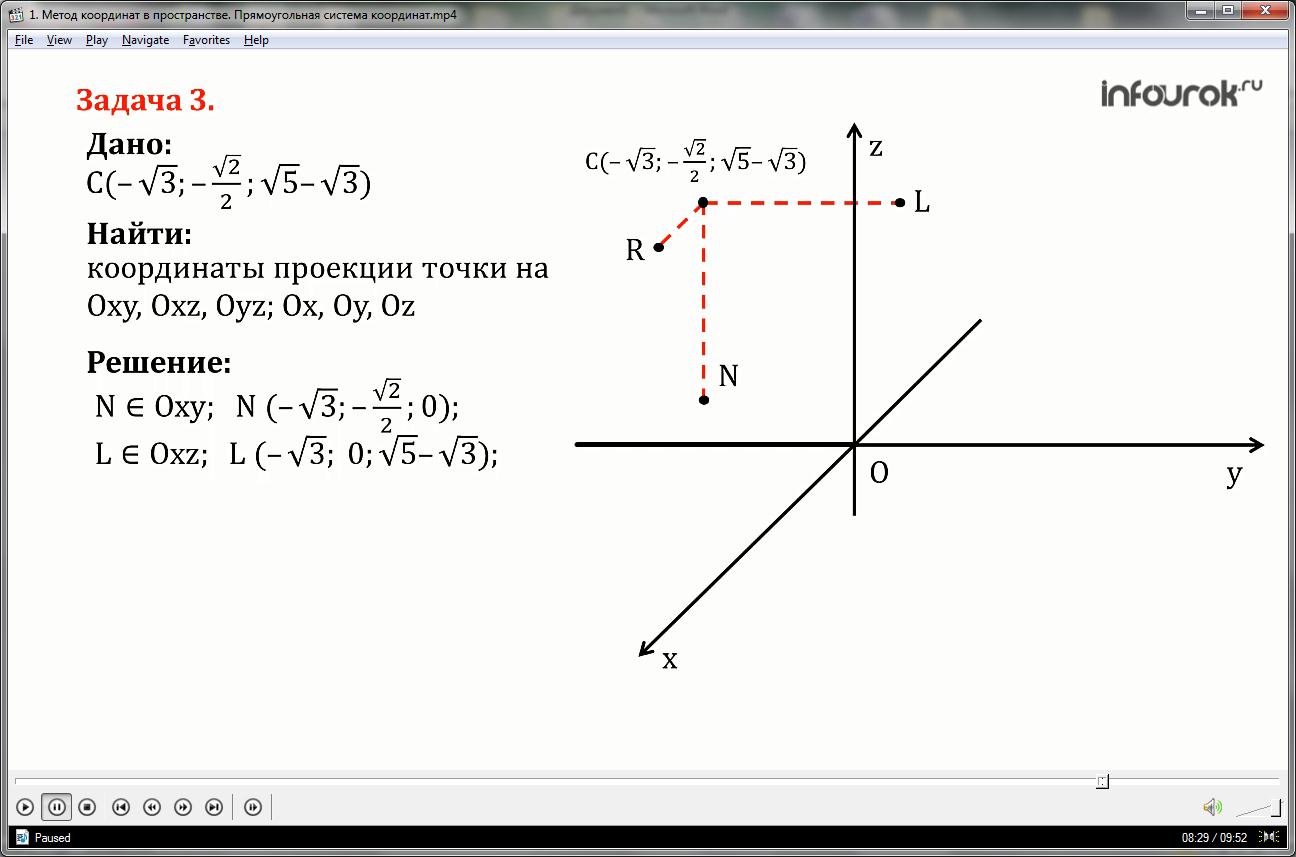
Như vậy, hình chiếu của điểm C lên mặt phẳng Oxy là điểm N và có tọa độ x bằng trừ căn ba, y bằng trừ căn hai nhân hai, z bằng 0.
Hình chiếu của điểm C lên mặt phẳng Oxz là điểm L và có tọa độ x bằng trừ căn ba, i bằng 0, z bằng với gốc của năm trừ căn của ba.
Hình chiếu của điểm C lên mặt phẳng Oyz là điểm R và có tọa độ x bằng 0, y bằng trừ căn hai nhân hai, z bằng căn năm trừ căn ba.
2) Từ điểm N vẽ đường vuông góc với trục Ox - đường thẳng NK, và với Oy - đường thẳng NG, và đến trục Oz vẽ đường vuông góc từ điểm R - đây là đường thẳng RP.
Hình chiếu của điểm C lên trục Ox - điểm K có tọa độ x bằng trừ căn ba, y và z bằng 0.
Hình chiếu của điểm C lên trục Oy - điểm G có tọa độ x và z bằng 0, i bằng trừ căn hai nhân hai.
Hình chiếu của điểm C lên trục Oz - điểm P có tọa độ x và y bằng 0, z gốc bằng nhau của năm trừ căn của ba.
Bộ Giáo dục Liên Bang Nga
thành phố cơ sở giáo dục"Trung bình trường trung học Số 18"
TÓM TẮT
THEO HÌNH HỌC
ĐỀ TÀI: PHƯƠNG PHÁP Tọa độ trong KHÔNG GIAN
Hoàn thành bởi học sinh lớp 11 “C”
La Mã Melnik
Người giám sát
giáo viên toán Baksheeva I.K.
Biysk - 2008
Nội dung
Giới thiệu……………………………………………………………..… 3.
Chương 1.
Phương pháp phối hợp: lịch sử phát triển…………………………4
Tọa độ của một điểm trong không gian……………………….……5
Xác định các hình trong không gian………………….…….8
Chương 2.
Phân tích một vectơ thành các vectơ tọa độ. tọa độ
vectơ……………………………..……..10
Hoạt động tuyến tính trên các vectơ trong tọa độ…………..………12
Điều kiện cộng tuyến của hai vectơ trong tọa độ……..13
Các bài toán đơn giản nhất về tọa độ……………………….14
Sản phẩm chấm vectơ và tính góc giữa các vectơ thông qua tọa độ của chúng……………………………….………15
Tính góc giữa đường thẳng và mặt phẳng………..16
4. Chương 3.
4.1. Ứng dụng phương pháp tọa độđể giải quyết lập thể
nhiệm vụ ………………………………………………………..…………….. 19
Phần kết luận. ……………………………..26
Danh sách tài liệu tham khảo……………………….. 27
Giới thiệu
Đề tài công việc của tôi là “Phương pháp tọa độ trong không gian”. chủ đề này có liên quan ngày hôm nay cho bất kỳ sinh viên tốt nghiệp trường trung học bởi vì:
Mục đích của công việc: hệ thống hóa kiến thức về chủ đề này và xem xét áp dụng phương pháp này khi giải các bài toán lập thể khác nhau.
Để đạt được mục tiêu, những điều sau đây đã được đặt ra nhiệm vụ:
cho phép nhiều kỳ thi bài toán hình học giải theo phương pháp phân tích, đòi hỏi ít kiến thức về hình học hơn và giảm đáng kể thời gian thực hiện;
Phương pháp này làm nền tảng cho hình học giải tích, được nghiên cứu trong quá trình toán học cao hơn.
nghiên cứu tài liệu lý thuyết về chủ đề này;
hệ thống hóa và tóm tắt tài liệu đã học;
xác định các tính năng của việc sử dụng phương pháp;
xét việc áp dụng phương pháp tọa độ để giải các bài toán lập thể;
so sánh việc áp dụng phương pháp tọa độ với các phương pháp khác để giải các bài toán lập thể.
Phương pháp được sử dụng :
phương pháp phân tích và tổng hợp,
phương pháp so sánh.
Chương 1
1. Phương pháp phối hợp: lịch sử phát triển.
Phương pháp tọa độ là một cách để xác định vị trí của một điểm hoặc vật bằng cách sử dụng các con số hoặc các ký hiệu khác.
Các số dùng để xác định vị trí của một điểm được gọi là tọa độ điểm.
Được chúng tôi biết đến tọa độ địa lý xác định vị trí của một điểm trên bề mặt Trái Đất - mỗi điểm trên bề mặt trái đất có hai tọa độ: vĩ độ và kinh độ.
Để xác định vị trí của một điểm trong không gian, cần có ba số. Ví dụ: để xác định vị trí của vệ tinh, bạn có thể chỉ định độ cao của nó so với bề mặt Trái đất, cũng như vĩ độ và kinh độ của điểm mà nó nằm trên đó.
Sử dụng phương pháp tọa độ, bạn có thể trình bày gần như toàn bộ khóa học hình học ở trường mà không cần một bức vẽ nào, chỉ sử dụng số và phép toán đại số. Ví dụ: đường tròn có thể được định nghĩa là tập hợp các điểm thỏa mãn phương trình và đường thẳng có thể được định nghĩa là tập hợp các điểm thỏa mãn phương trình.  . Vì vậy, với sự trợ giúp của phương pháp này, có thể kết nối với nhau dường như hoàn toàn khoa học khác nhauđại số và hình học. Về bản chất, mối liên hệ này là một cuộc cách mạng trong toán học. Nó khôi phục toán học như một khoa học thống nhất.
. Vì vậy, với sự trợ giúp của phương pháp này, có thể kết nối với nhau dường như hoàn toàn khoa học khác nhauđại số và hình học. Về bản chất, mối liên hệ này là một cuộc cách mạng trong toán học. Nó khôi phục toán học như một khoa học thống nhất.
Người tạo ra phương pháp tọa độ được coi là nhà triết học và toán học người Pháp Rene Descartes (1596-1650), người trong phần cuối của chuyên luận triết học lớn của Descartes, xuất bản năm 1637, đã mô tả phương pháp tọa độ và ứng dụng của nó để giải các bài toán hình học.
Sự phát triển các ý tưởng của Descartes đã dẫn đến sự xuất hiện của một nhánh toán học đặc biệt, ngày nay được gọi là hình học giải tích.
Bản thân cái tên này đã thể hiện ý tưởng cơ bản của lý thuyết. Hình học giải tích là một phần của toán học giải quyết các vấn đề hình học bằng phương pháp phân tích (tức là đại số).
Cùng với Descartes, người sáng lập ra hình học giải tích là nhà toán học nổi tiếng người Pháp P. Fermat. Sử dụng phương pháp tọa độ, Fermat đã nghiên cứu các đường thẳng và đường cong bậc hai. Nghiên cứu về hình học giải tích trong không gian ba chiều đã được A. Clairaut tiến bộ đáng kể vào thế kỷ 18. Hình học phân tích rõ ràng và nhất quán trên mặt phẳng và trong không gian ba chiềuđược L. Euler phác thảo vào năm 1748 trong sách giáo khoa “Giới thiệu về phân tích các số vô hạn”.
TRONG XIXthế kỷ này, một bước nữa đã được thực hiện trong sự phát triển của hình học - các không gian đa chiều đã được nghiên cứu. Ý tưởng chính của những người tạo ra lý thuyết này là sự tương tự với “Hình học” của Descartes. Điểm của anh ta trên mặt phẳng là một cặp số 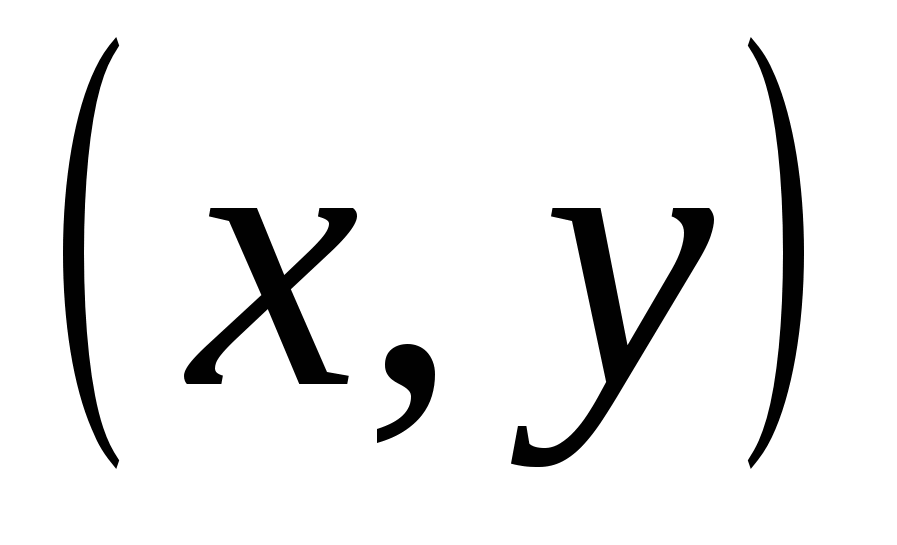 , một điểm trong không gian ba chiều – bộ ba số
, một điểm trong không gian ba chiều – bộ ba số 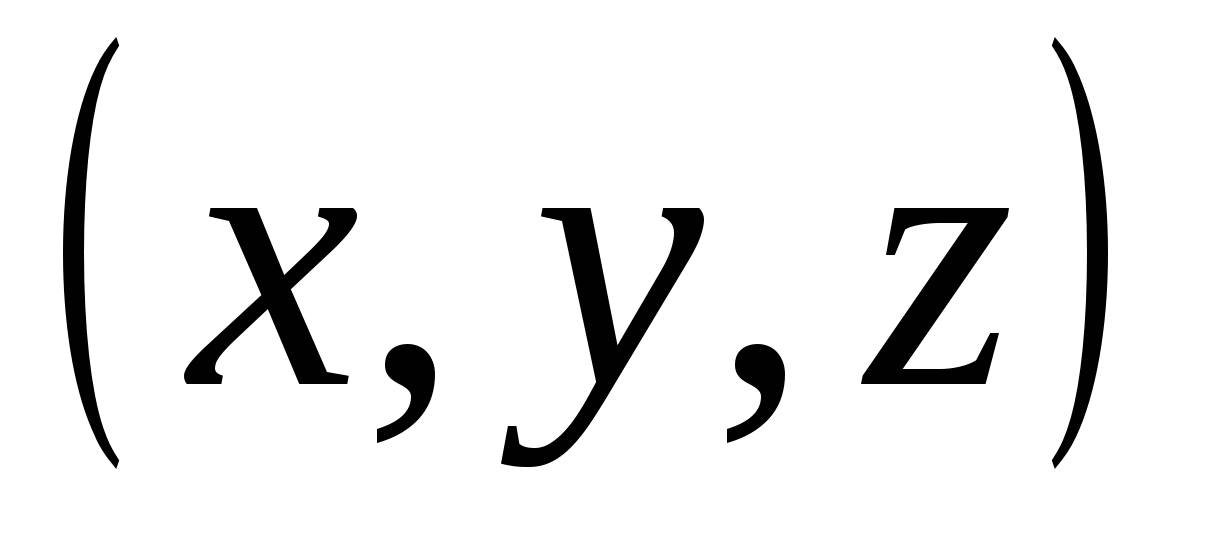 ; V. lý thuyết mới một điểm trong không gian bốn chiều là một bộ bốn số
; V. lý thuyết mới một điểm trong không gian bốn chiều là một bộ bốn số 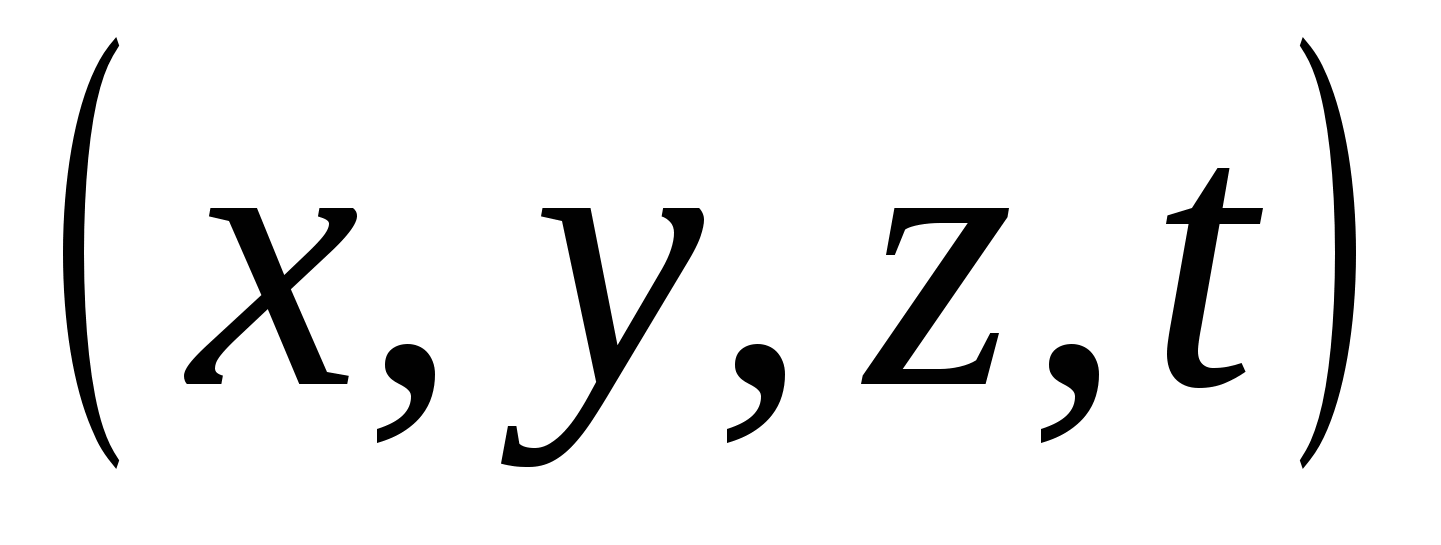 . Trong Descartes
. Trong Descartes 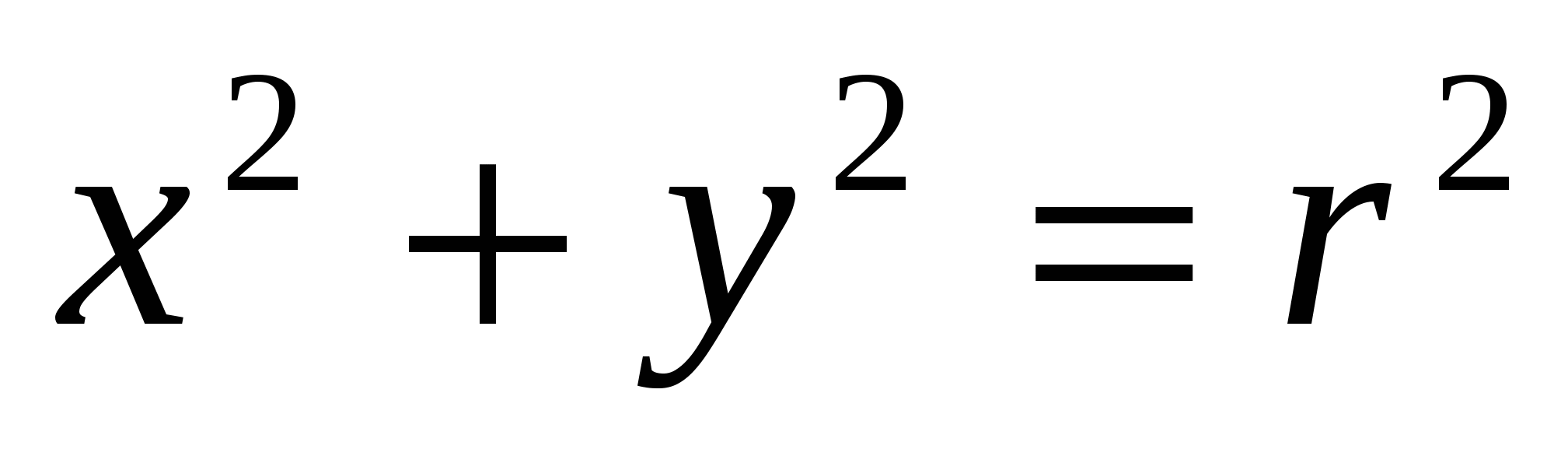 - phương trình đường tròn trên mặt phẳng,
- phương trình đường tròn trên mặt phẳng,  - phương trình bề mặt của quả bóng trong không gian ba chiều; trong lý thuyết mới
- phương trình bề mặt của quả bóng trong không gian ba chiều; trong lý thuyết mới 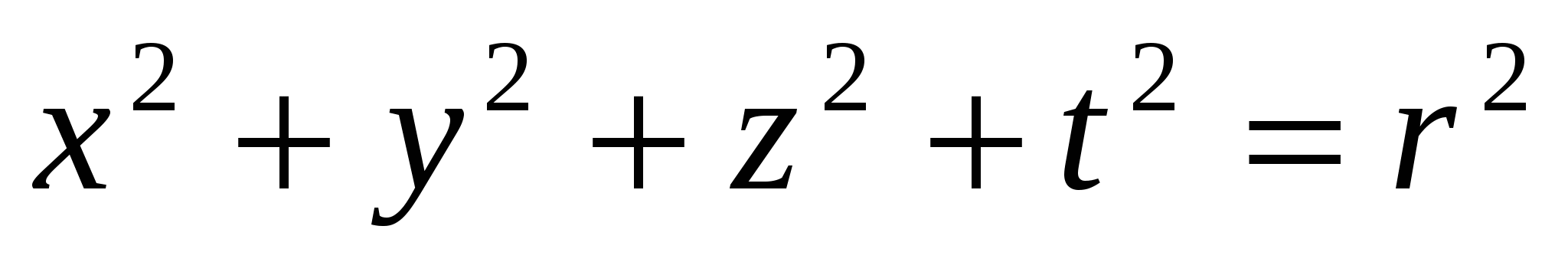 bề mặt của một hình cầu trong không gian bốn chiều. Tương tự ởN
-
hình học chiều xem xét các mặt phẳng, đường thẳng, khoảng cách giữa các điểm, góc giữa các đường thẳng, v.v.
bề mặt của một hình cầu trong không gian bốn chiều. Tương tự ởN
-
hình học chiều xem xét các mặt phẳng, đường thẳng, khoảng cách giữa các điểm, góc giữa các đường thẳng, v.v.
Những ý tưởng về hình học đa chiều đã được thiết lập vững chắc trong toán học vào cuốiXIXnhiều thế kỷ, và ngay từ đầuXXnhiều thế kỷ, họ đã tìm thấy ứng dụng trong lý thuyết đặc biệt thuyết tương đối, nơi đến ba tọa độ không gian thứ tư được thêm vào - thời gian. Vì vậy, những ý tưởng về hình học Descartes, được phát triển bởi các nhà khoa học thuộc thế hệ tiếp theo, là nền tảng của khoa học hiện đại.
2. Tọa độ của một điểm trong không gian .
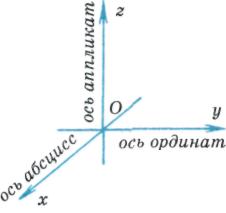 Họ nói rằng một hệ tọa độ hình chữ nhật (Cartesian) được đưa ra nếu ba đường vuông góc theo cặp được vẽ qua một điểm trong không gian, một hướng được chọn trên mỗi đường thẳng đó và một đơn vị đo cho các đoạn được chọn. Các mặt phẳng lần lượt đi qua các trục tọa độ
Họ nói rằng một hệ tọa độ hình chữ nhật (Cartesian) được đưa ra nếu ba đường vuông góc theo cặp được vẽ qua một điểm trong không gian, một hướng được chọn trên mỗi đường thẳng đó và một đơn vị đo cho các đoạn được chọn. Các mặt phẳng lần lượt đi qua các trục tọa độ 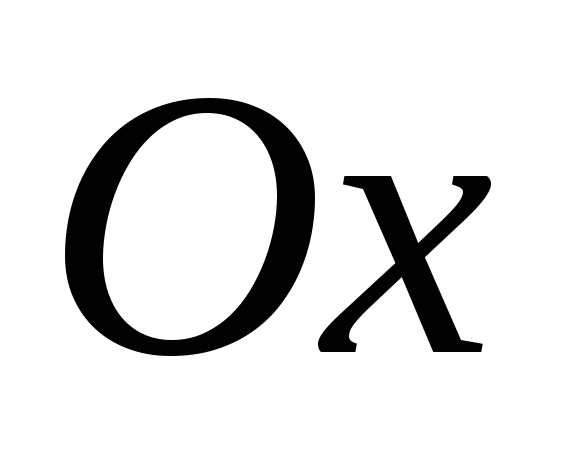 Và
Và 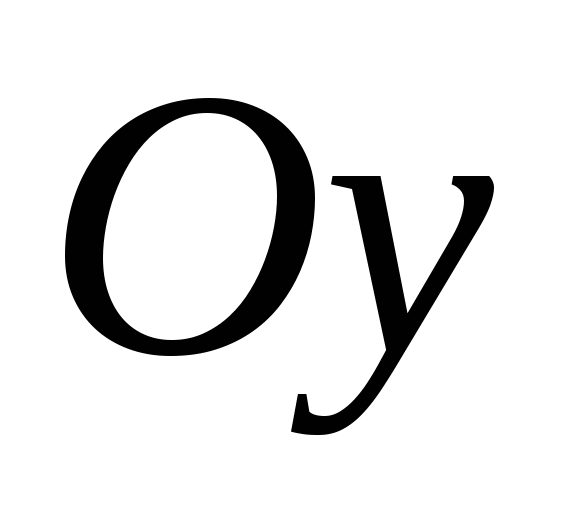 ,
, 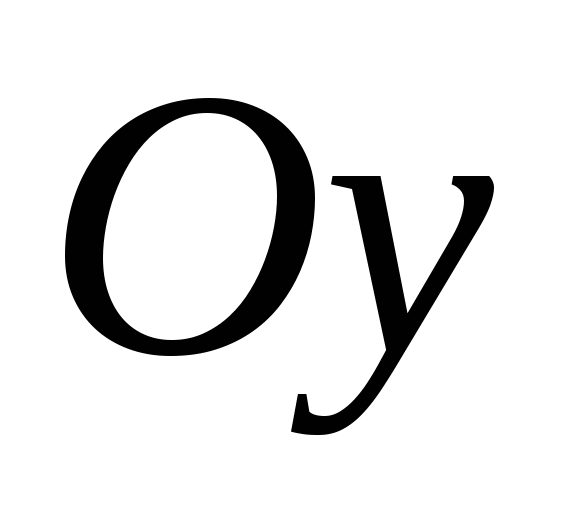 Và
Và  ,
,  Và
Và 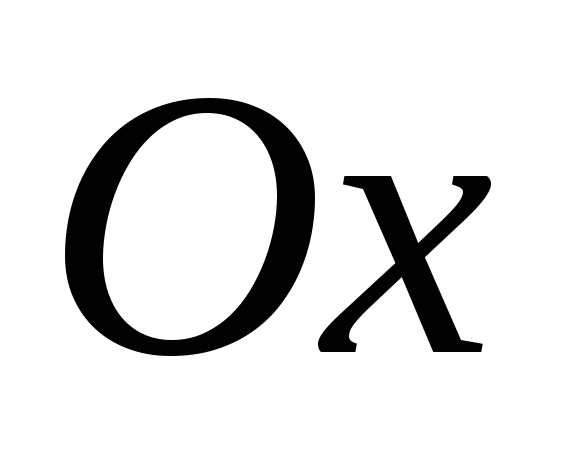 , được gọi làmặt phẳng tọa độ
và được chỉ định
, được gọi làmặt phẳng tọa độ
và được chỉ định 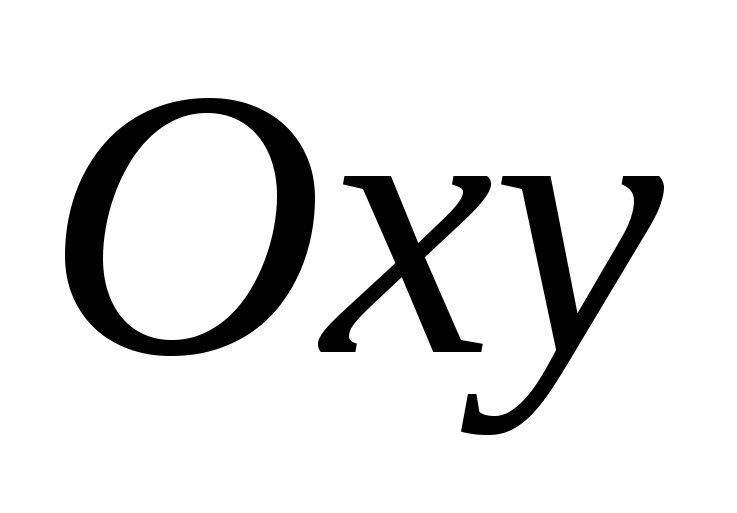 ,
, 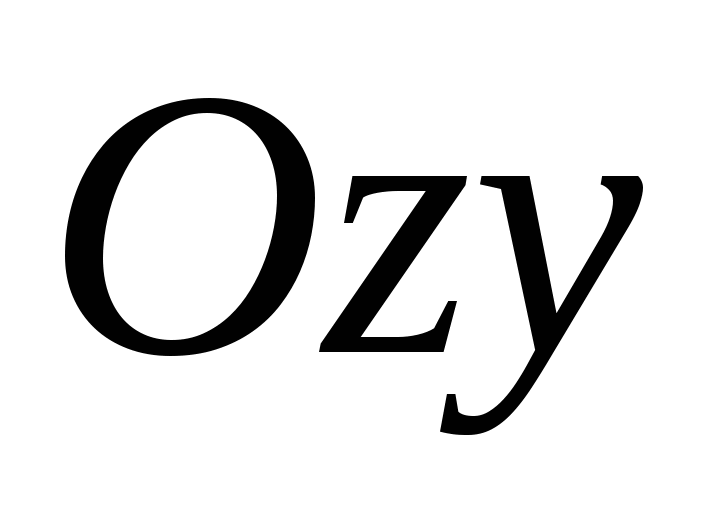 ,
,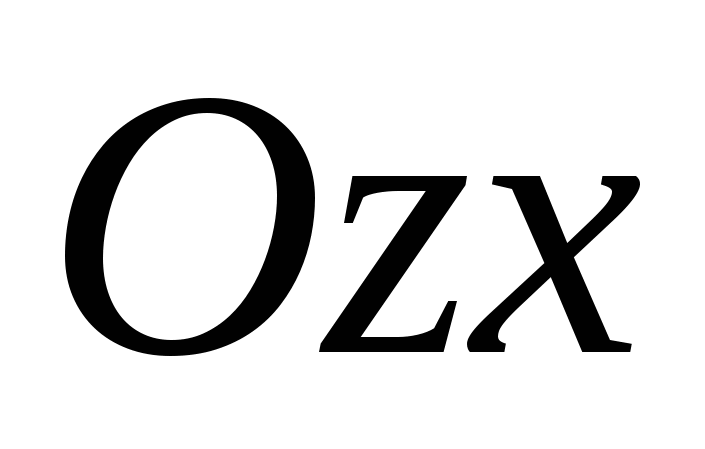 .
.
ĐẾN  Tọa độ của một điểm trong không gian là tọa độ hình chiếu của điểm này lên các trục tọa độ.
Tọa độ của một điểm trong không gian là tọa độ hình chiếu của điểm này lên các trục tọa độ.
tọa độ điểm: 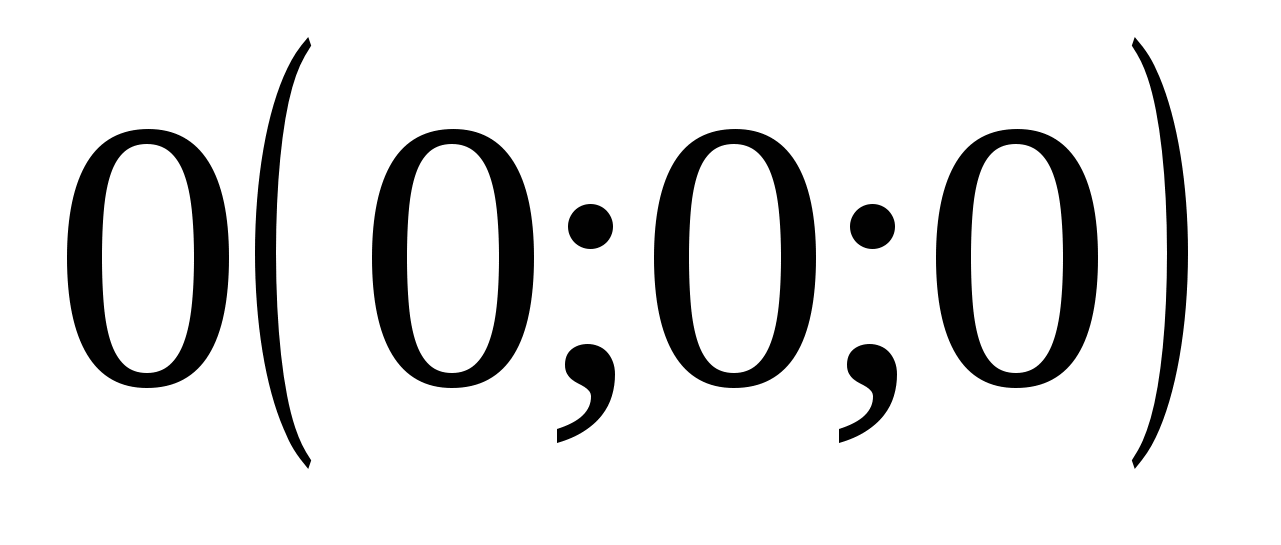 ,
, 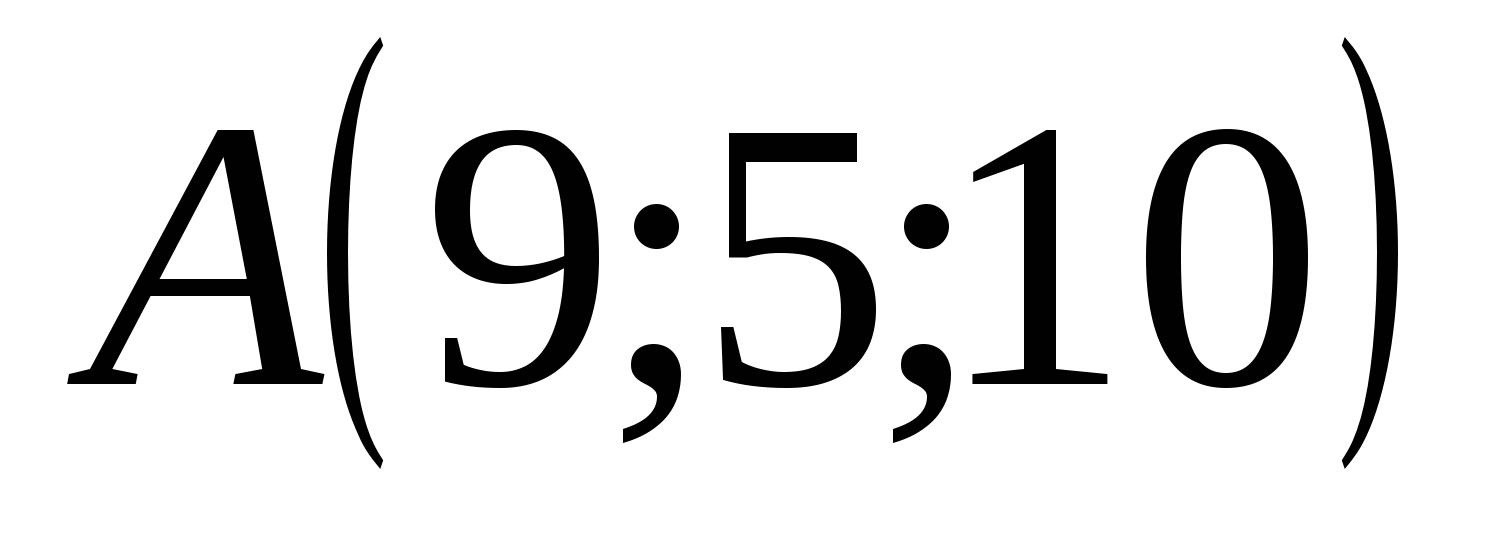 ,
, 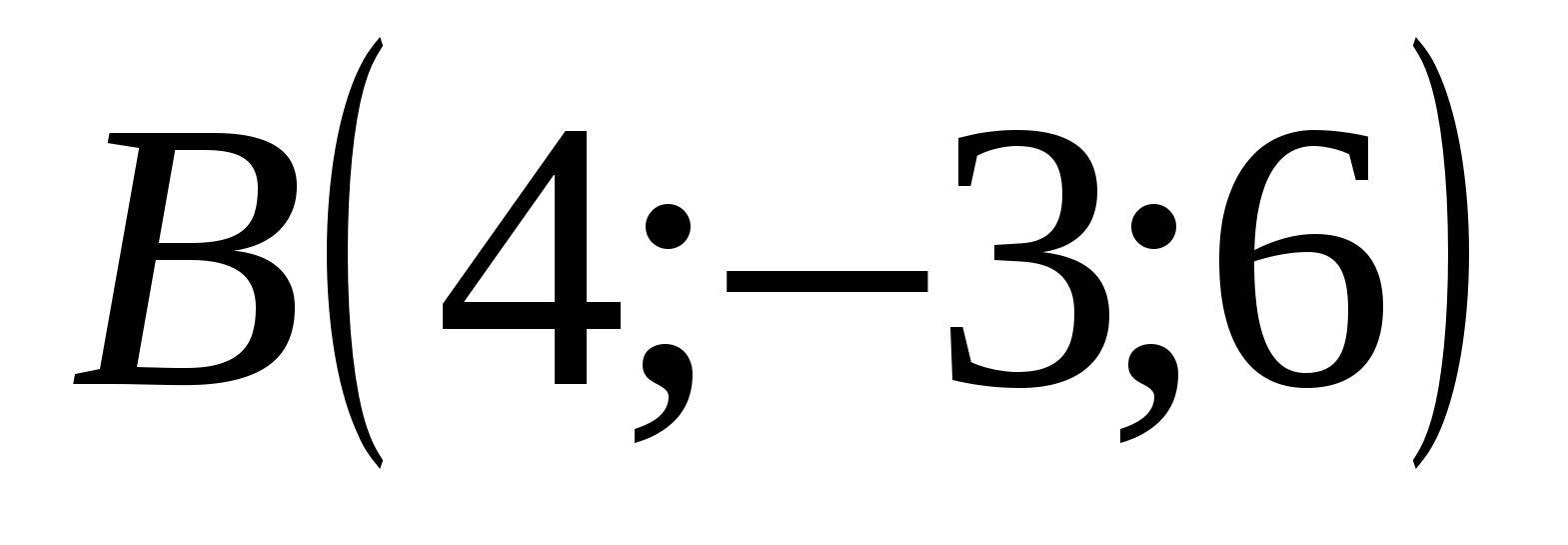 ,
, 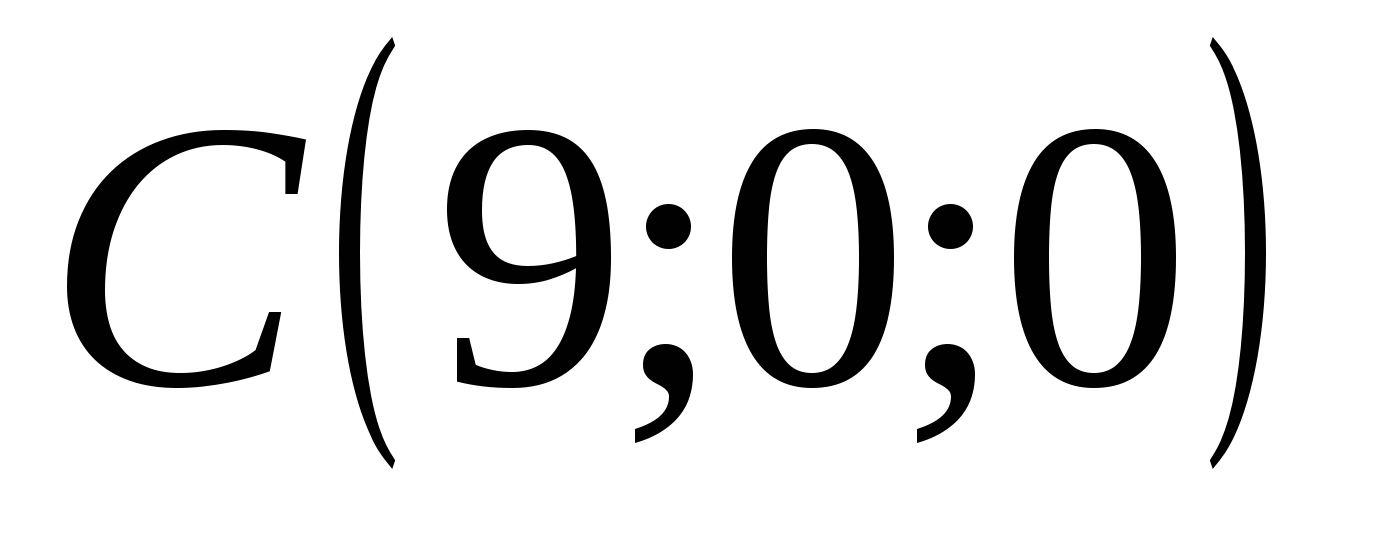 ,
, 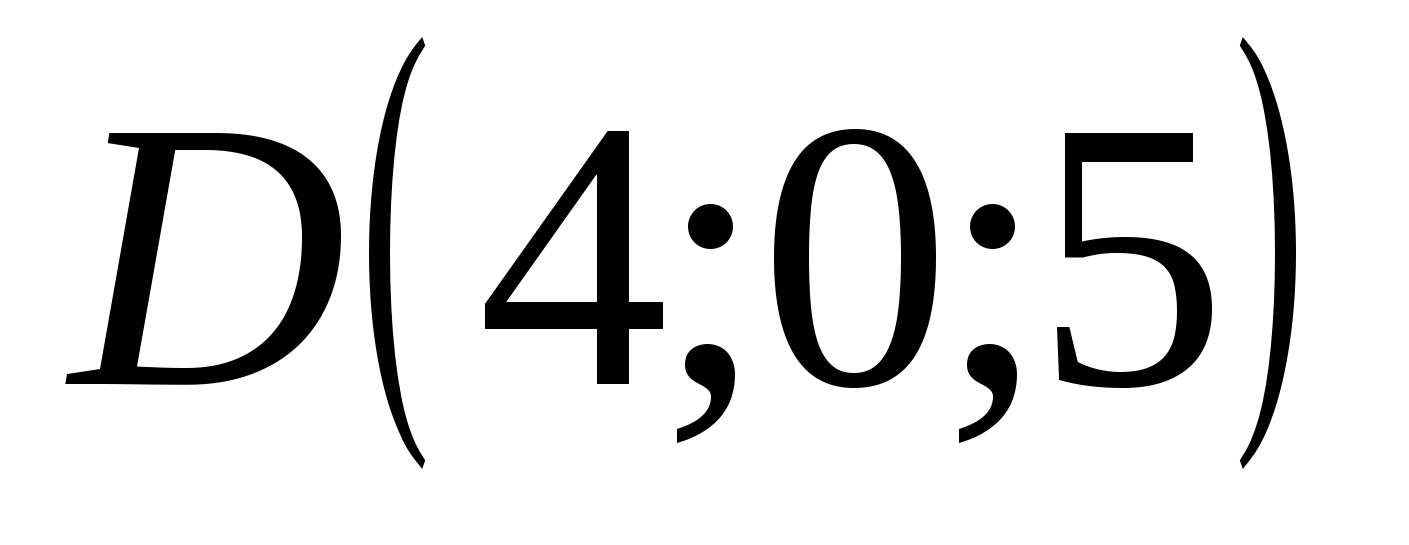 ,
, 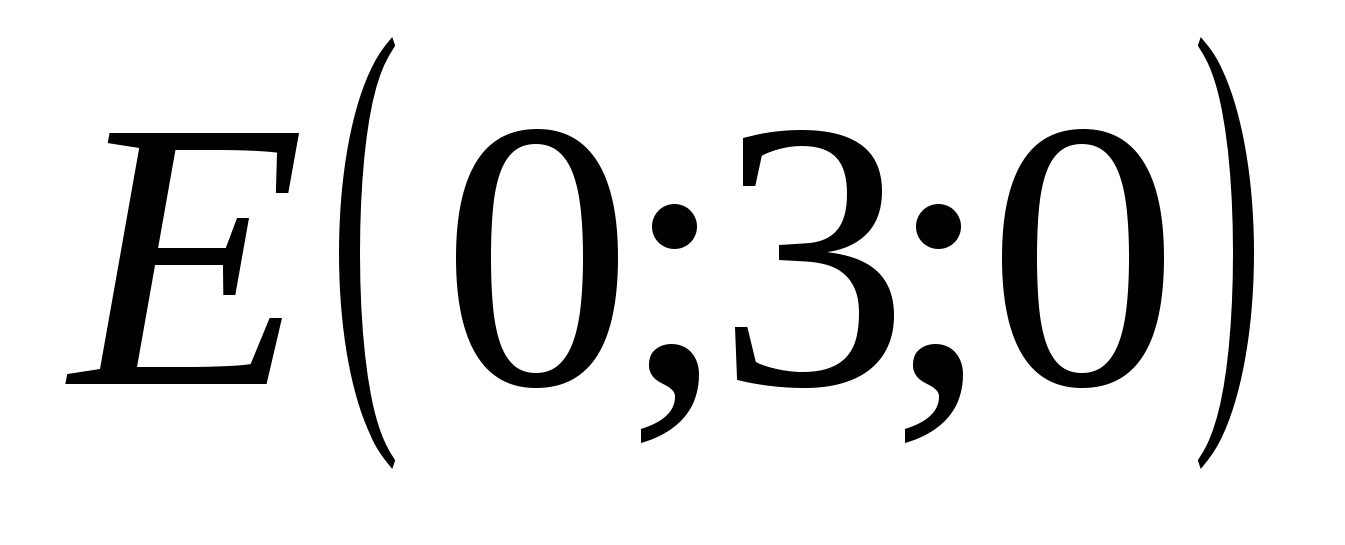 ,
, 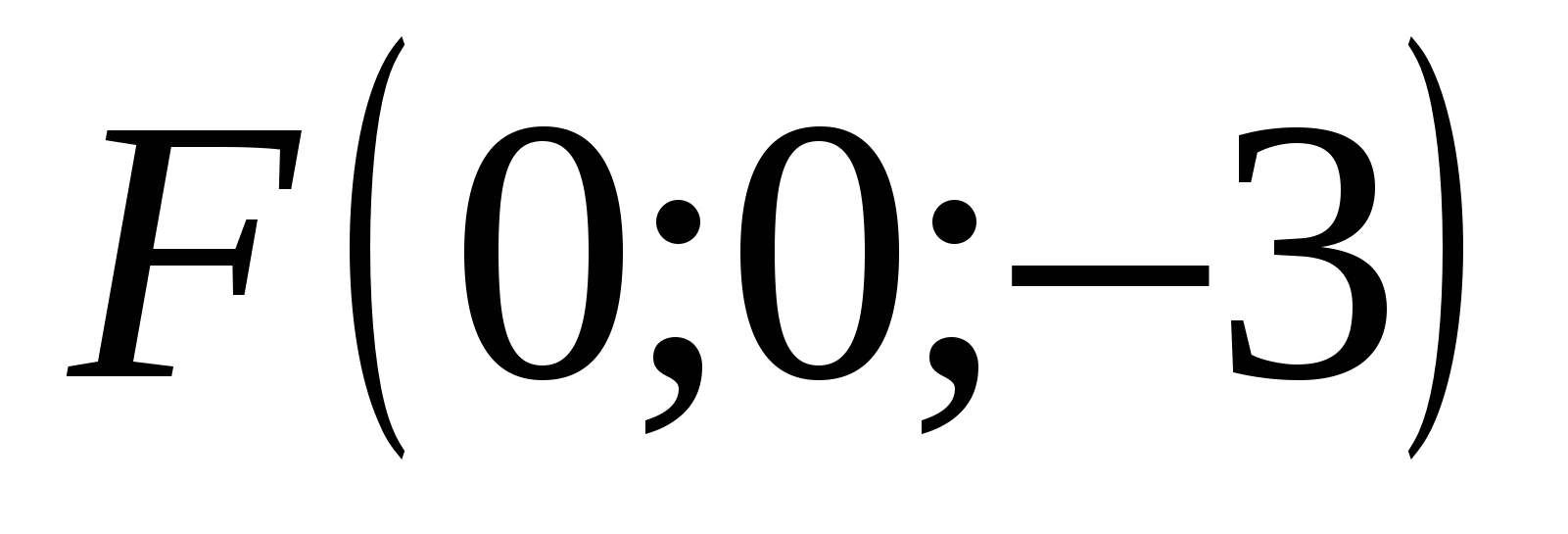 .
.
Trong không gian, ngoại trừ trục tọa độ, thật thuận tiện khi xem xét các mặt phẳng tọa độ, tức là mặt phẳng đi qua hai trục bất kỳ. Có ba mặt phẳng như vậy:
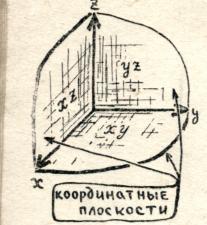
Máy bay ![]() (đi qua trục
(đi qua trục  Và
Và 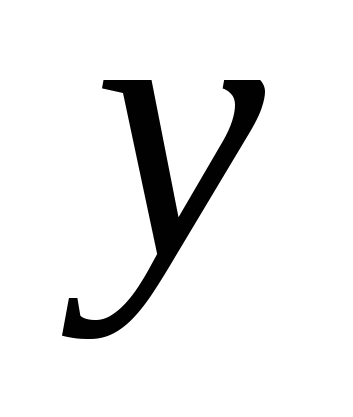 ) - tập hợp các điểm có dạng
) - tập hợp các điểm có dạng  , Ở đâu
, Ở đâu  Và
Và 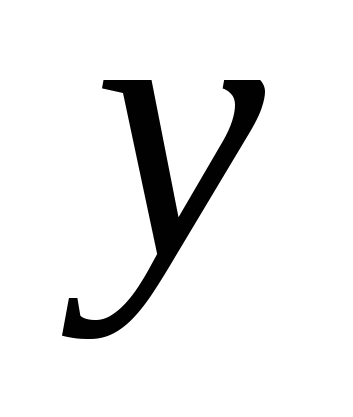 - bất kỳ số nào;
- bất kỳ số nào;
Máy bay 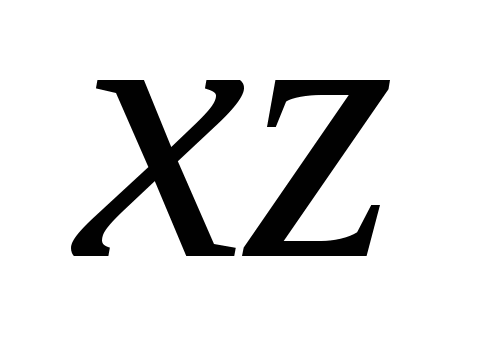 (đi qua trục
(đi qua trục  Và
Và  ) - tập hợp các điểm có dạng
) - tập hợp các điểm có dạng 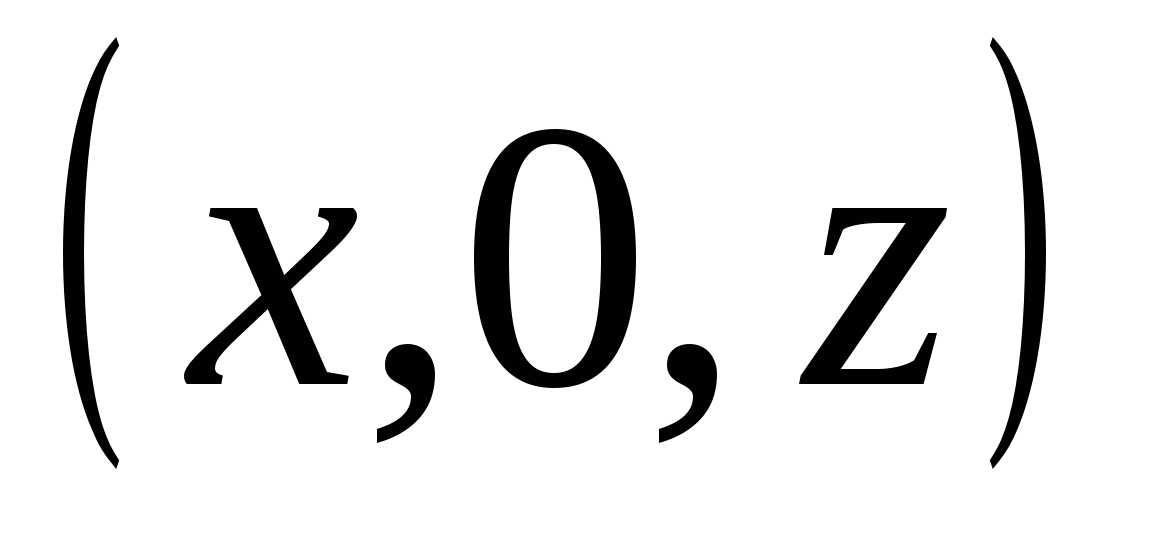 , Ở đâu
, Ở đâu  Và
Và  - bất kỳ số nào;
- bất kỳ số nào;
Máy bay  (đi qua trục
(đi qua trục 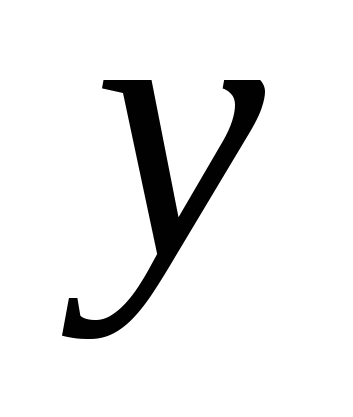 Và
Và  ) - tập hợp các điểm có dạng
) - tập hợp các điểm có dạng 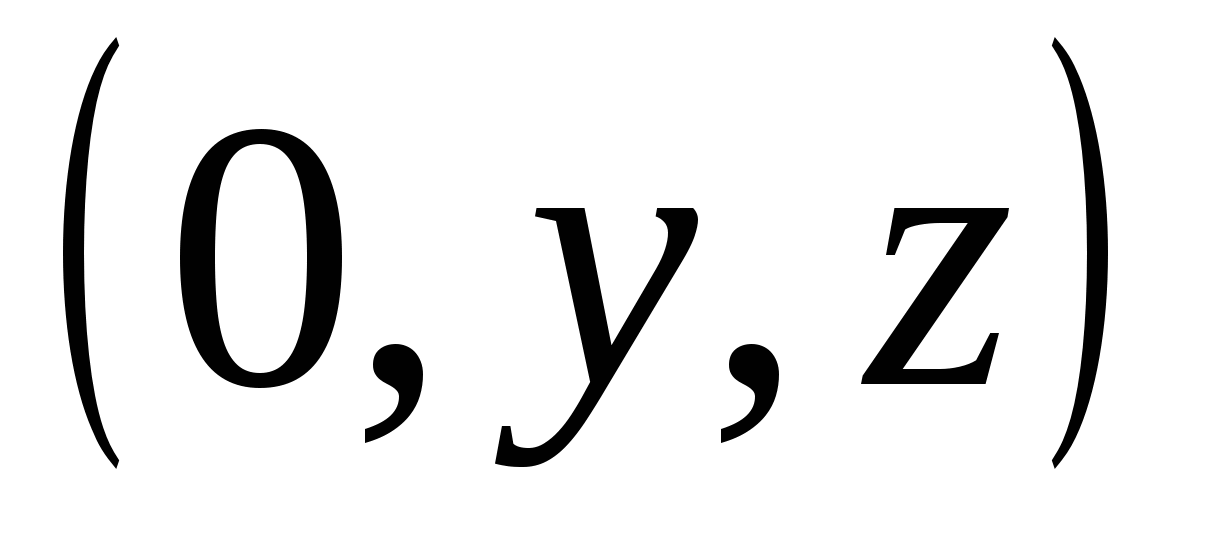 , Ở đâu
, Ở đâu 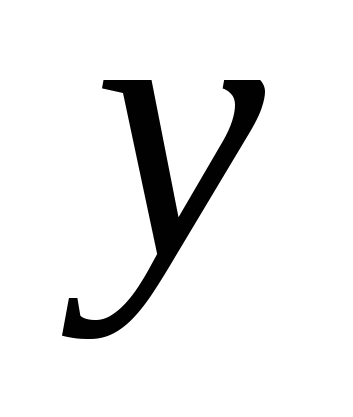 Và
Và  - bất kỳ số nào.
- bất kỳ số nào.
Đối với bất kỳ điểm M nào trong không gian, bạn có thể tìm thấy ba số 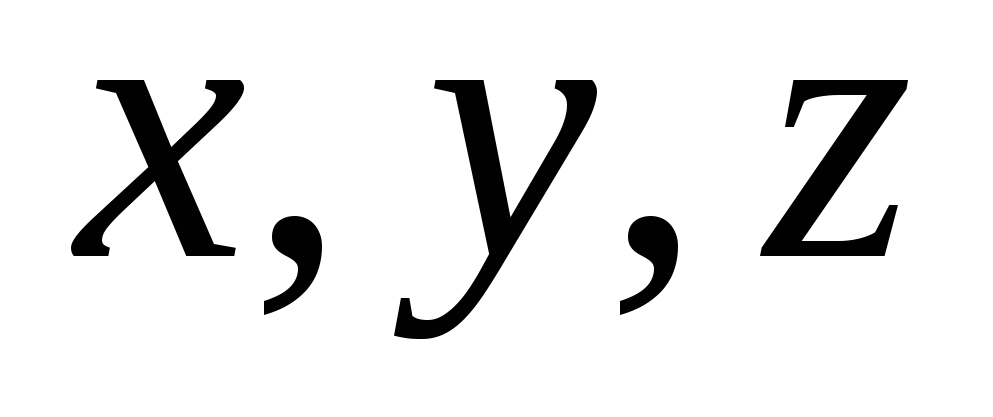 , sẽ đóng vai trò là tọa độ của nó.
, sẽ đóng vai trò là tọa độ của nó.
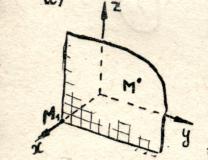 Để tìm số đầu tiên
Để tìm số đầu tiên  , vẽ mặt phẳng song song với điểm M mặt phẳng tọa độ
, vẽ mặt phẳng song song với điểm M mặt phẳng tọa độ  (vuông góc với trụcx).Giao điểm của mặt phẳng này với trục
(vuông góc với trụcx).Giao điểm của mặt phẳng này với trục  (điểm M 1
) có tọa độ trên trục này
(điểm M 1
) có tọa độ trên trục này  .Đây là số
.Đây là số  - tọa độ điểm M 1
trên trục
- tọa độ điểm M 1
trên trục  - gọi điệncơ bụngđiểm M
- gọi điệncơ bụngđiểm M
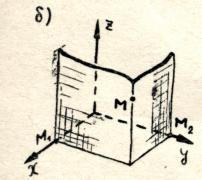 Để tìm tọa độ thứ hai, vẽ mặt phẳng đi qua điểm M song song với mặt phẳng
Để tìm tọa độ thứ hai, vẽ mặt phẳng đi qua điểm M song song với mặt phẳng 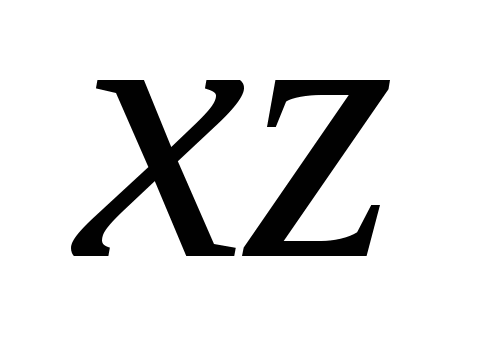 (vuông góc với trụcy), tìm thấy trên trục yđiểm M2. Con số y– tọa độ điểm M 2 mỗi trục y- gọi điện điều hànhđiểm M
(vuông góc với trụcy), tìm thấy trên trục yđiểm M2. Con số y– tọa độ điểm M 2 mỗi trục y- gọi điện điều hànhđiểm M
 Chúng ta sẽ tìm tọa độ thứ ba của điểm M bằng cách thực hiện cách dựng tương tự nhưng vuông góc với trục z. Hãy gọi số kết quả là z áp dụngđiểm M
Chúng ta sẽ tìm tọa độ thứ ba của điểm M bằng cách thực hiện cách dựng tương tự nhưng vuông góc với trục z. Hãy gọi số kết quả là z áp dụngđiểm M
3. Xác định các hình trong không gian.
Cũng giống như trên mặt phẳng, tọa độ trong không gian cho phép xác định bằng cách sử dụng các con số và tỷ lệ số không chỉ các điểm mà còn cả các đường, bề mặt và các tập hợp điểm khác. Ví dụ, chúng ta hãy xem tập hợp điểm nào sẽ thu được nếu chúng ta chỉ xác định hai tọa độ và coi tọa độ thứ ba là tùy ý.
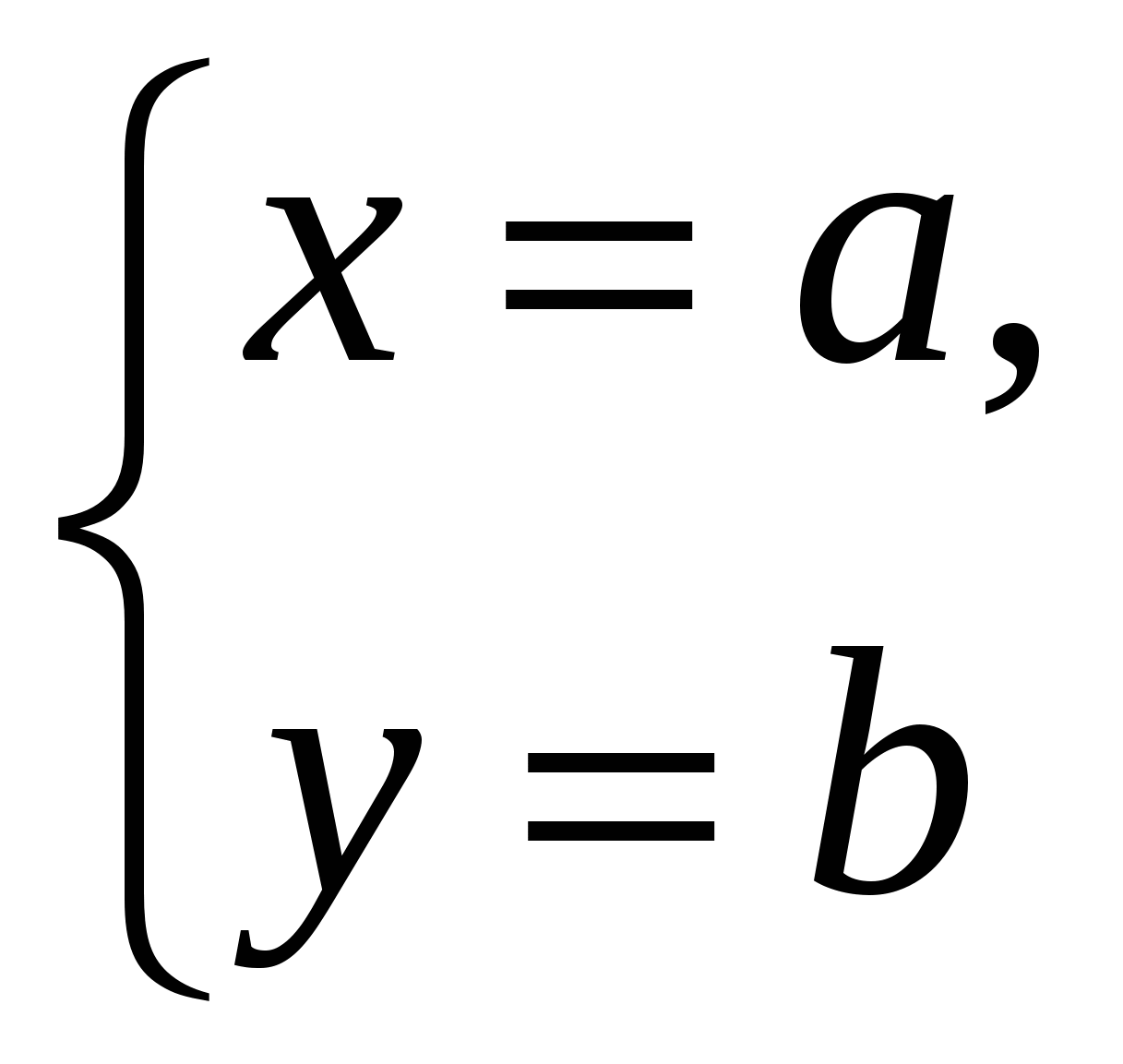
(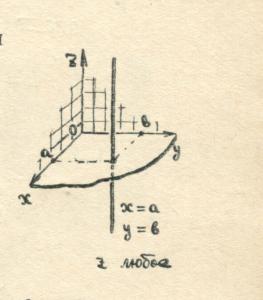 Ví dụ,
Ví dụ, 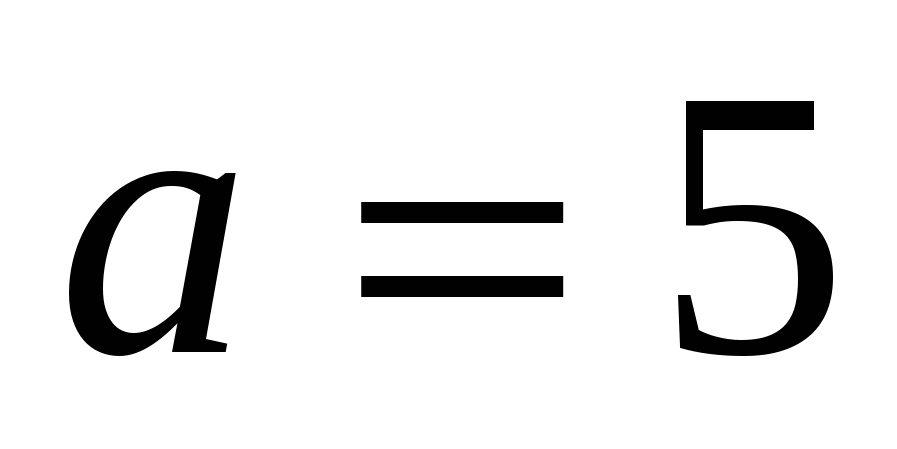
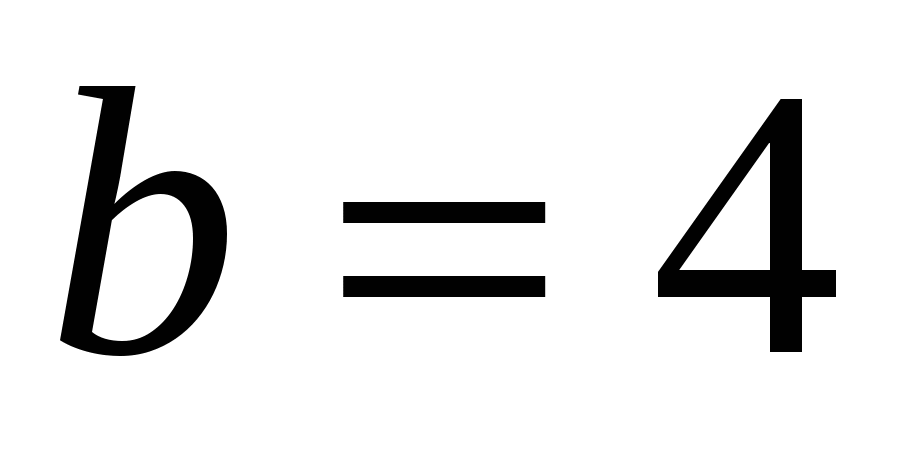 ), xác định một đường thẳng trong không gian, song song với trục
), xác định một đường thẳng trong không gian, song song với trục  .
.
Tất cả các điểm trên một đường thẳng như vậy đều có cùng hoành độ và cùng tọa độ. Điều phối  có thể nhận bất kỳ giá trị nào.
có thể nhận bất kỳ giá trị nào.
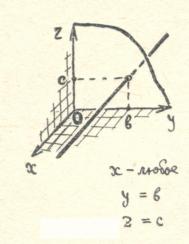


Hãy xem xét thêm một vài ví dụ cho thấy cách bạn có thể thiết lập
không gian bộ khác nhau sử dụng các phương trình và các mối quan hệ khác giữa các tọa độ.
1). Hãy xem xét phương trình.
Vì khoảng cách của điểm 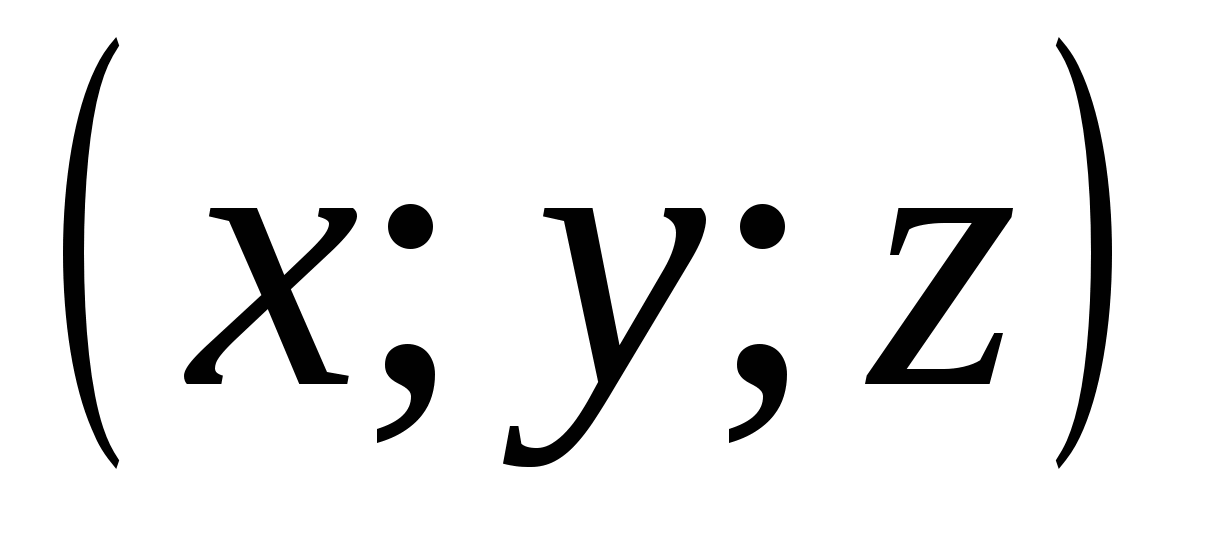 từ gốc được cho bởi biểu thức
từ gốc được cho bởi biểu thức 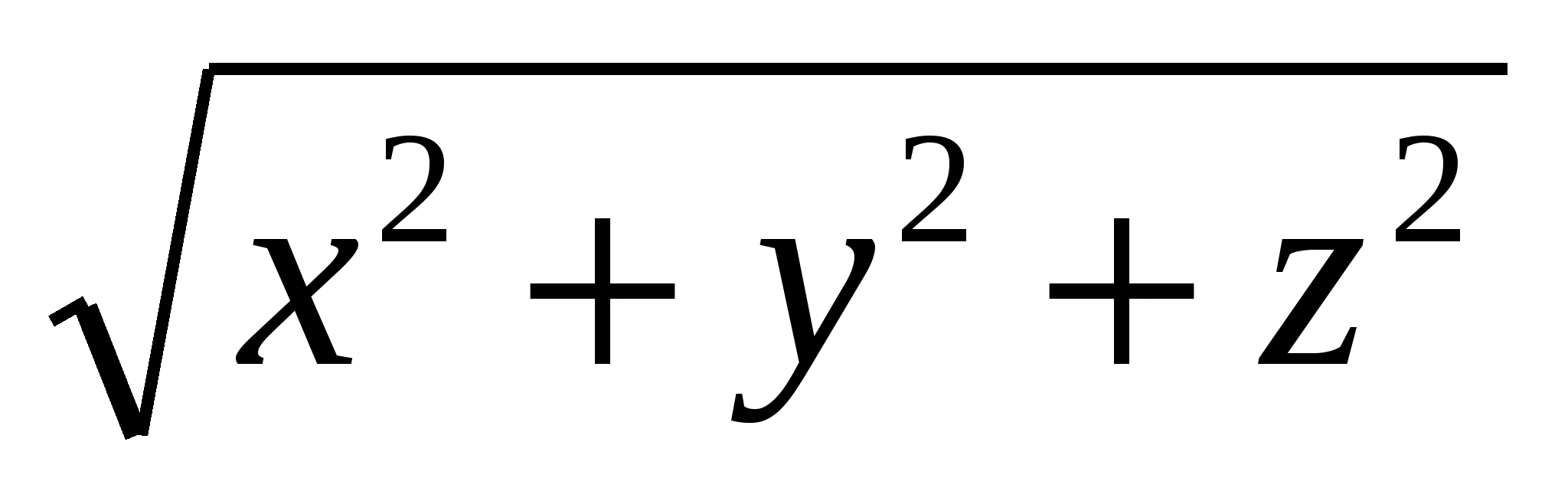 , thì rõ ràng là được dịch sang ngôn ngữ hình học mối quan hệ
, thì rõ ràng là được dịch sang ngôn ngữ hình học mối quan hệ 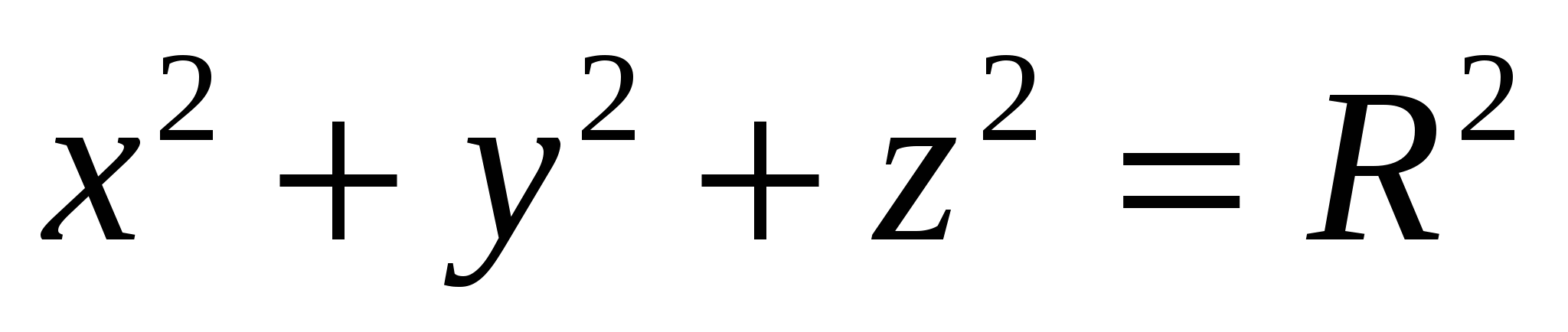 có nghĩa là điểm có tọa độ
có nghĩa là điểm có tọa độ 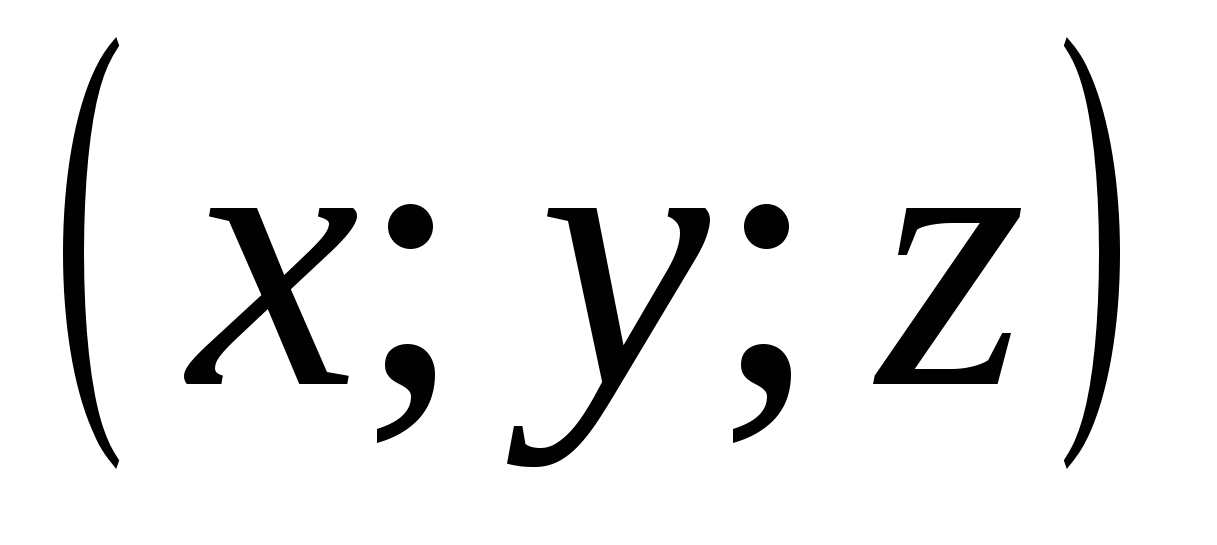 , đang ở một khoảng cáchR
từ nguồn gốc. Điều này có nghĩa là tập hợp tất cả các điểm chứa mối quan hệ
, đang ở một khoảng cáchR
từ nguồn gốc. Điều này có nghĩa là tập hợp tất cả các điểm chứa mối quan hệ 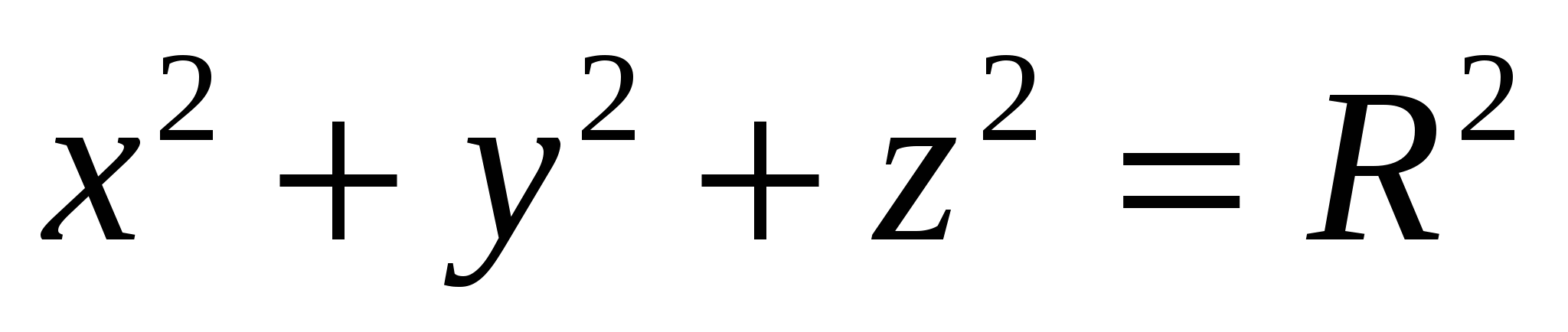 , là bề mặt của một quả cầu - một hình cầu có tâm tại gốc và bán kínhR
.
, là bề mặt của một quả cầu - một hình cầu có tâm tại gốc và bán kínhR
.
2). Chúng ta hãy xem xét vị trí của các điểm có tọa độ thỏa mãn mối quan hệ  .
.
Vì mối quan hệ này có nghĩa là khoảng cách của điểm 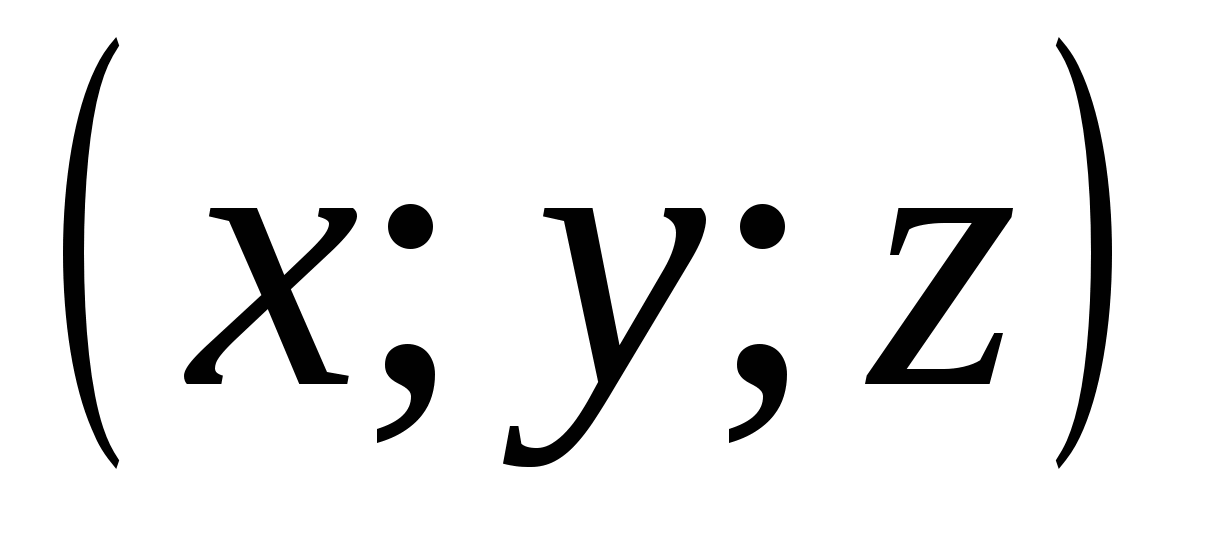 từ gốc tọa độ nhỏ hơn một thì tập hợp bắt buộc là tập hợp các điểm nằm bên trong một quả cầu có tâm tại gốc tọa độ và bán kính bằng 1.
từ gốc tọa độ nhỏ hơn một thì tập hợp bắt buộc là tập hợp các điểm nằm bên trong một quả cầu có tâm tại gốc tọa độ và bán kính bằng 1.
Chương 2
1. Phân tích vectơ thành vectơ tọa độ. Tọa độ vectơ.
Cơ sở của không gian là bộ ba vectơ không đồng phẳng bất kỳ có thứ tự 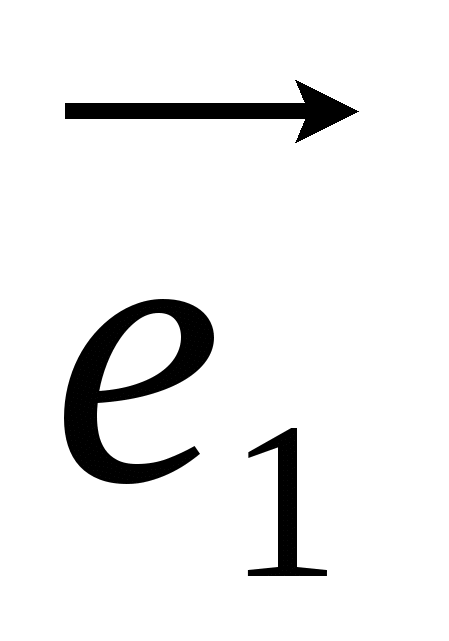 ,
, 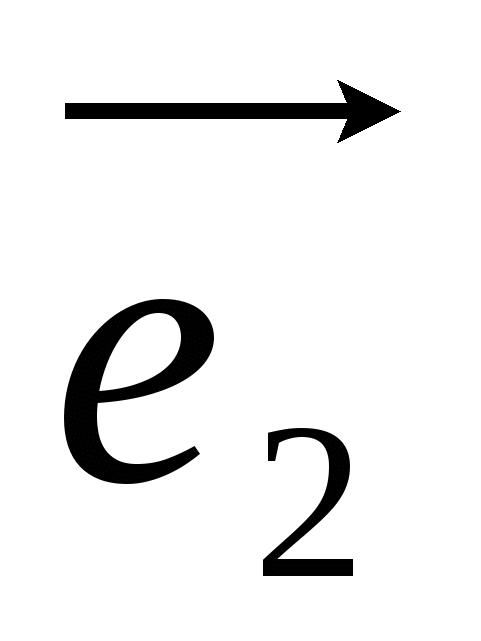 ,
, 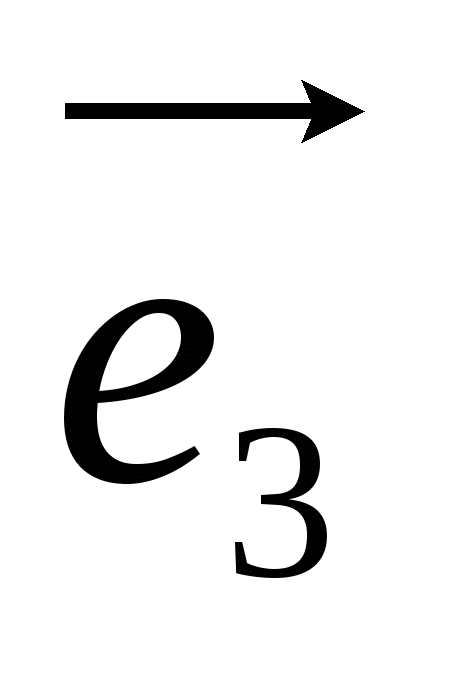 , ký hiệu là ký hiệu
, ký hiệu là ký hiệu 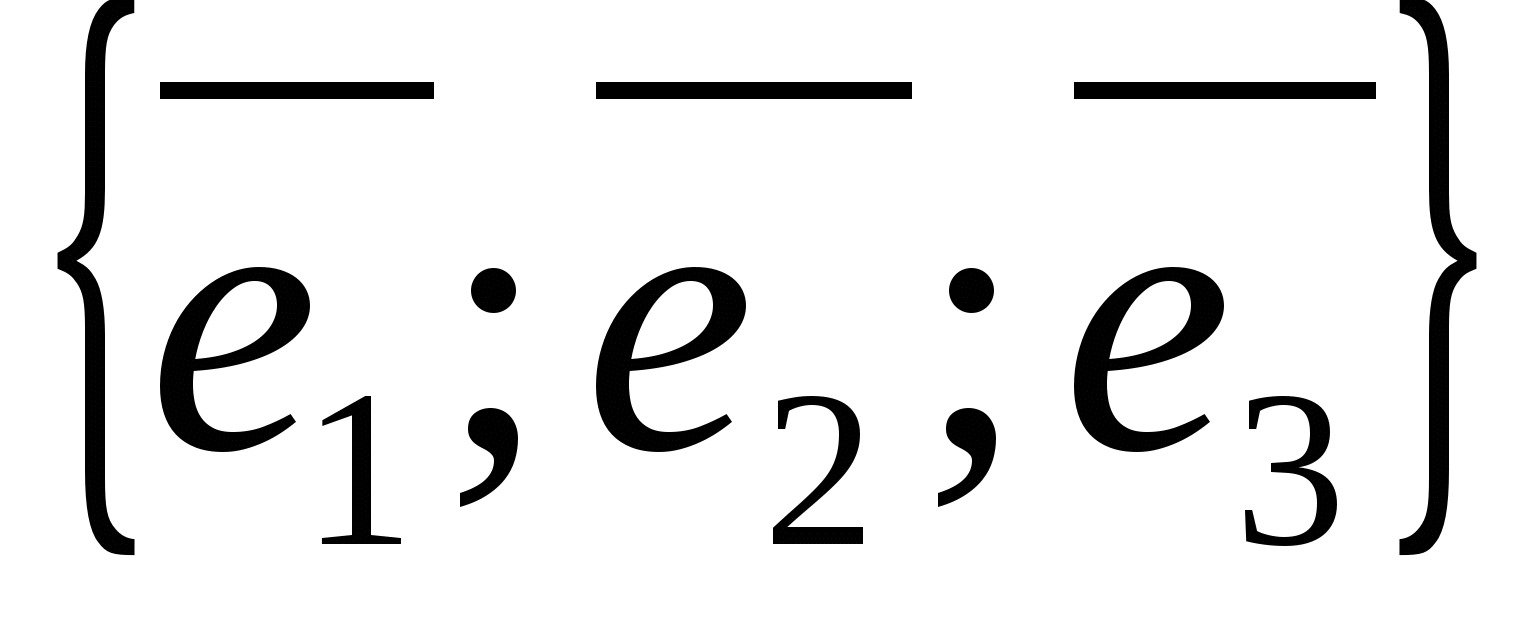 .
.
Trường hợp đặc biệt là cơ sở trực chuẩn hình chữ nhật  , Ở đâu
, Ở đâu 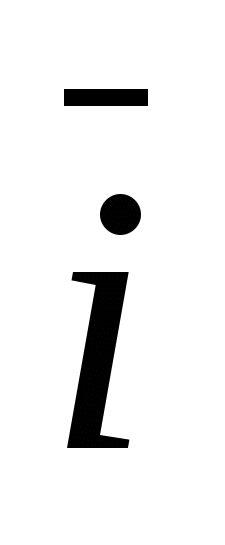 - vectơ đơn vị của trục x, thông qua -
- vectơ đơn vị của trục x, thông qua -  vectơ đơn vị của trục tọa độ và thông qua
vectơ đơn vị của trục tọa độ và thông qua 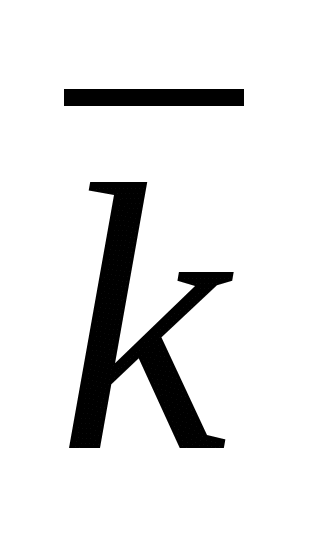 -vectơ đơn vị trục áp dụng, tức là
-vectơ đơn vị trục áp dụng, tức là  ,
,  ,
, 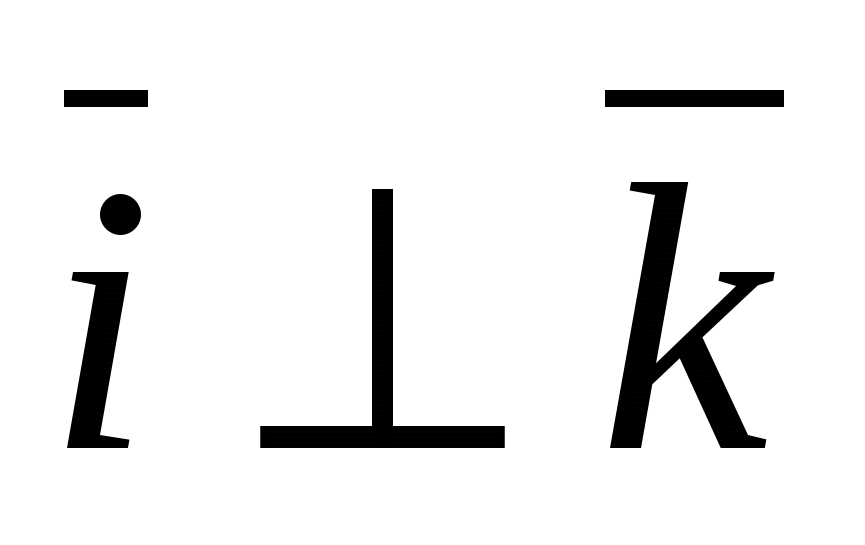 ,
,  .
.
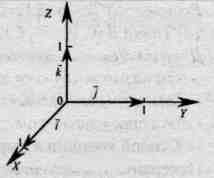
Cơ sở này  và sự bắt đầu đếm ngược VỀ định nghĩa hệ tọa độ Descartes hình chữ nhật
và sự bắt đầu đếm ngược VỀ định nghĩa hệ tọa độ Descartes hình chữ nhật  trong không gian.
trong không gian.
Định lý 1
Bất kỳ vectơ không gian nào
 có thể được mở rộng thành các vectơ tọa độ, tức là hiện diện dưới dạng -
có thể được mở rộng thành các vectơ tọa độ, tức là hiện diện dưới dạng -
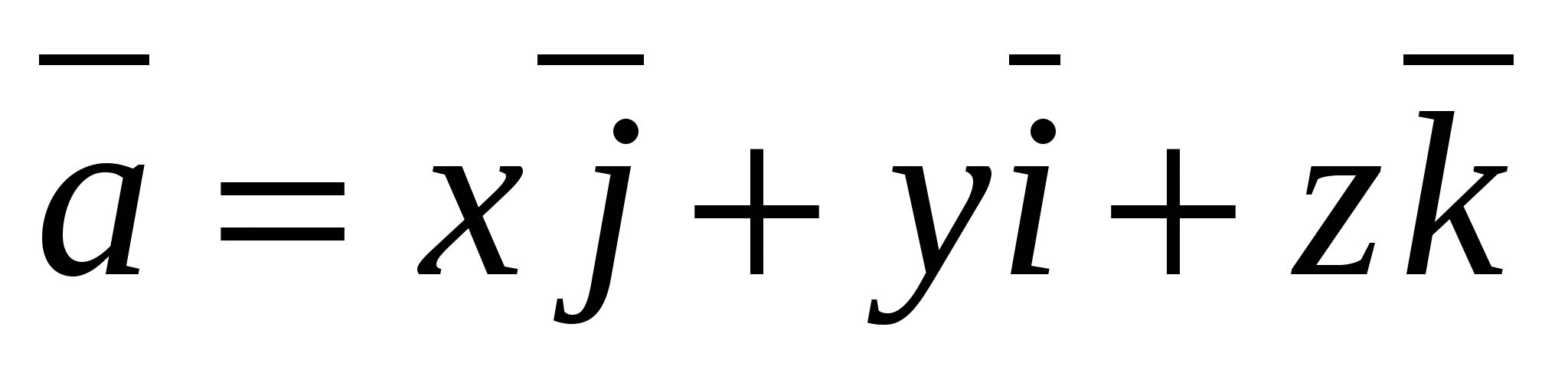 ,
,
và các hệ số giãn nở  được xác định một cách độc đáo.
được xác định một cách độc đáo.
H 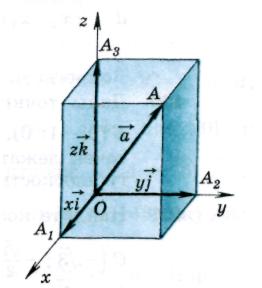 isla
isla  được gọi là tọa độ vectơ
được gọi là tọa độ vectơ 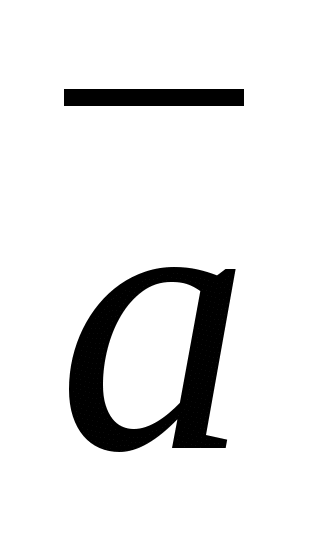 , tức là
, tức là 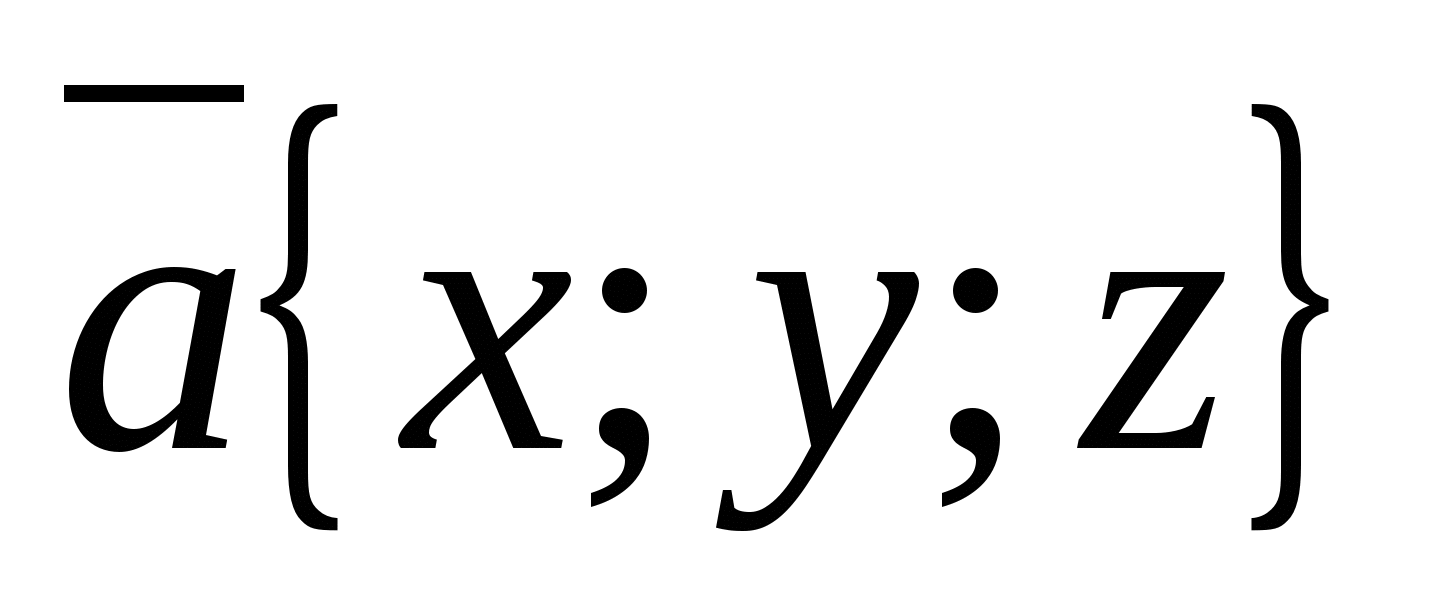 . Vì vectơ 0 có thể được biểu diễn dưới dạng
. Vì vectơ 0 có thể được biểu diễn dưới dạng 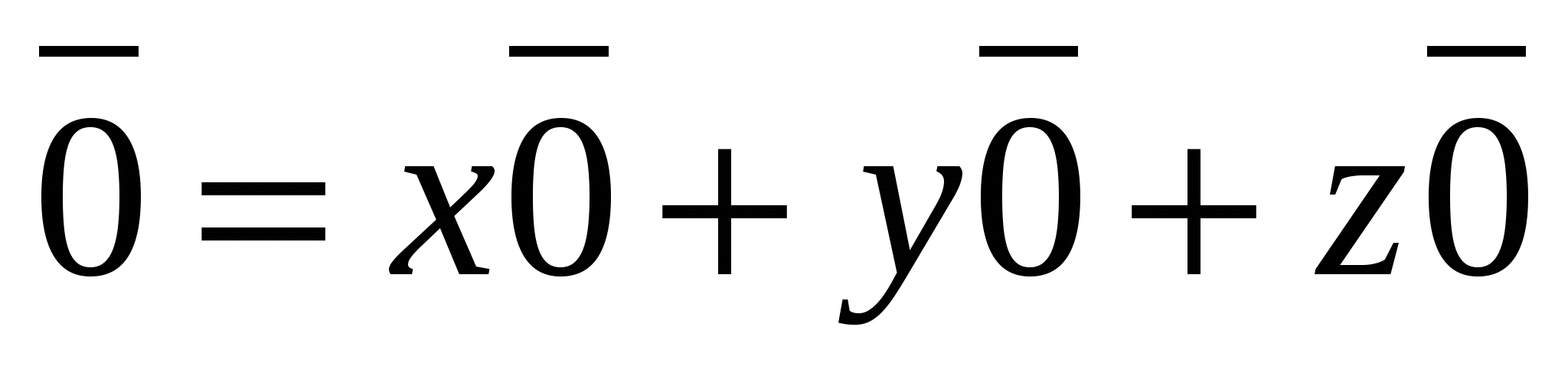 , thì mọi tọa độ của vectơ 0 đều bằng 0,
, thì mọi tọa độ của vectơ 0 đều bằng 0, 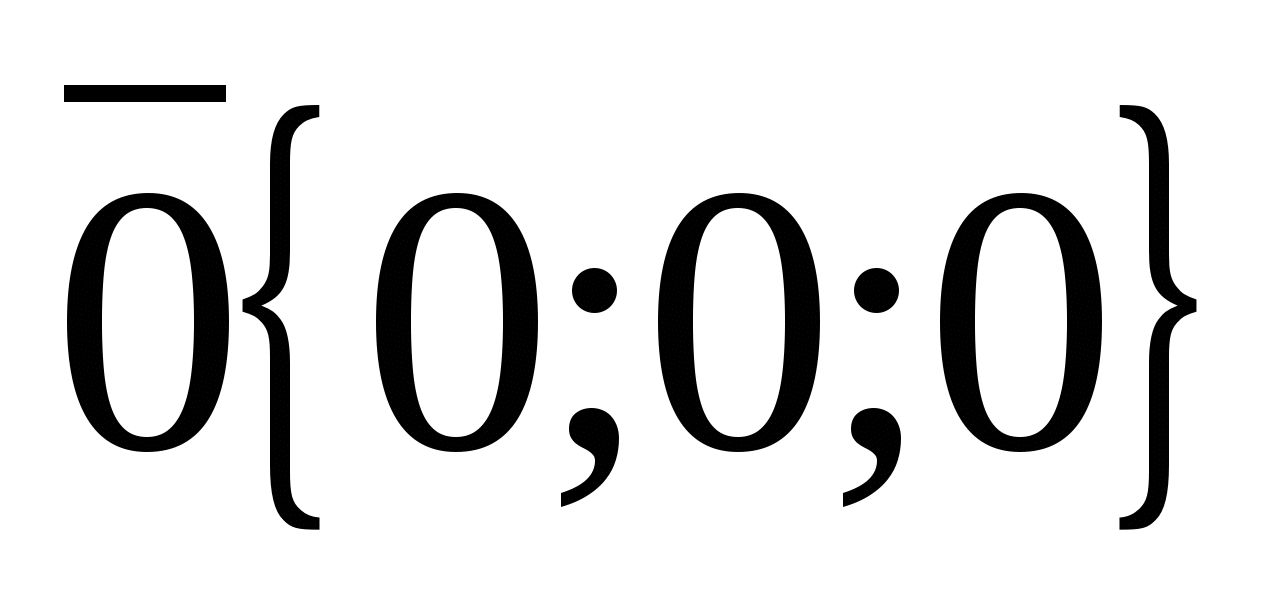 .
.
2. Các phép toán tuyến tính trên vectơ trong tọa độ.
Quy tắc 1.
Tọa độ bằng nhau
các vectơ tương ứng bằng nhau,
những thứ kia. nếu vectơ 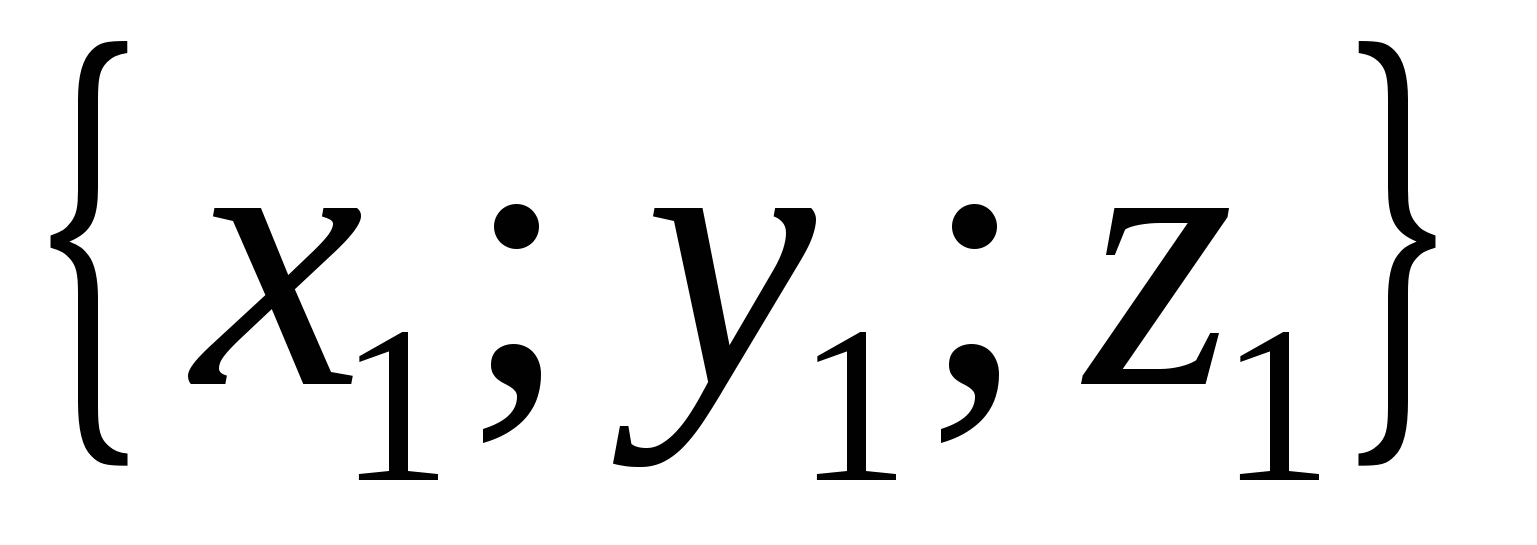 Và
Và 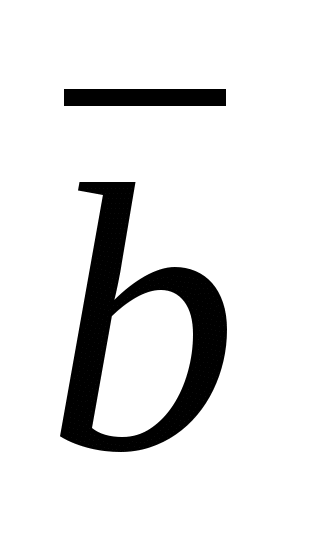
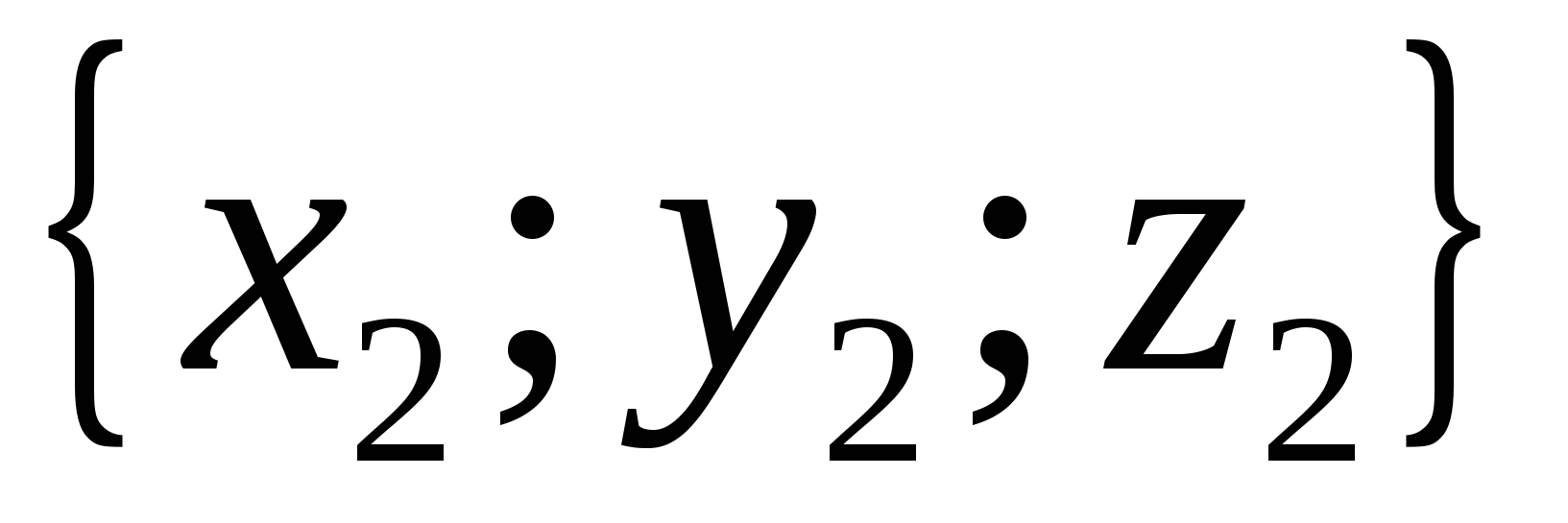 thì bằng nhau
thì bằng nhau 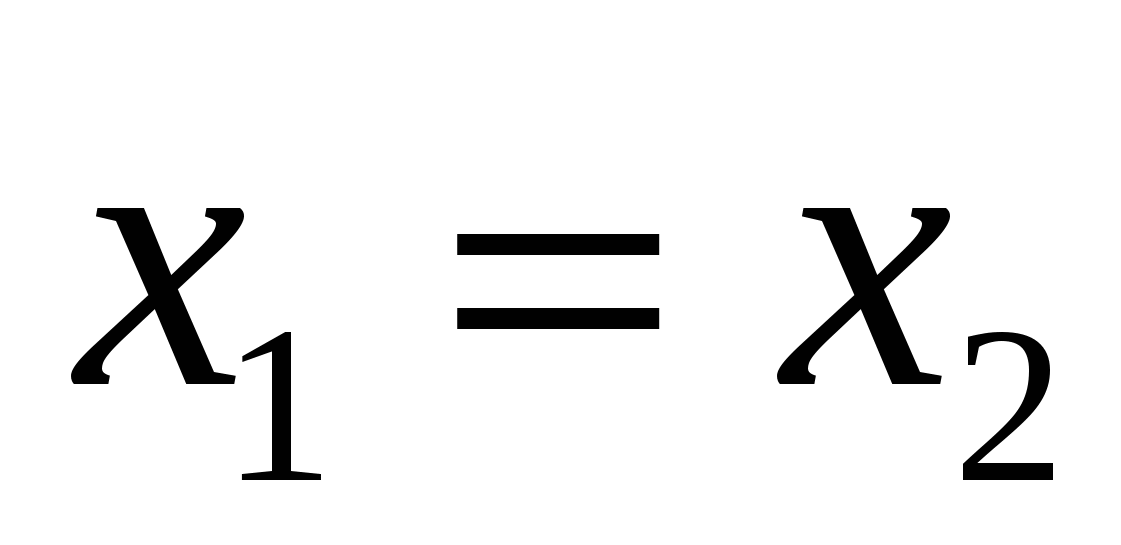 ,
,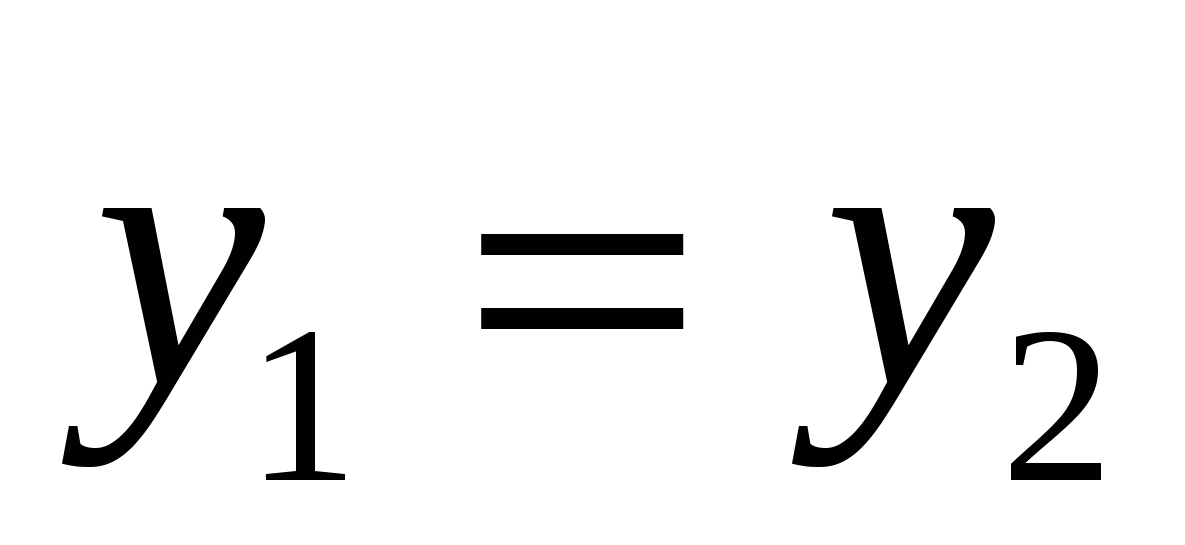 Và
Và 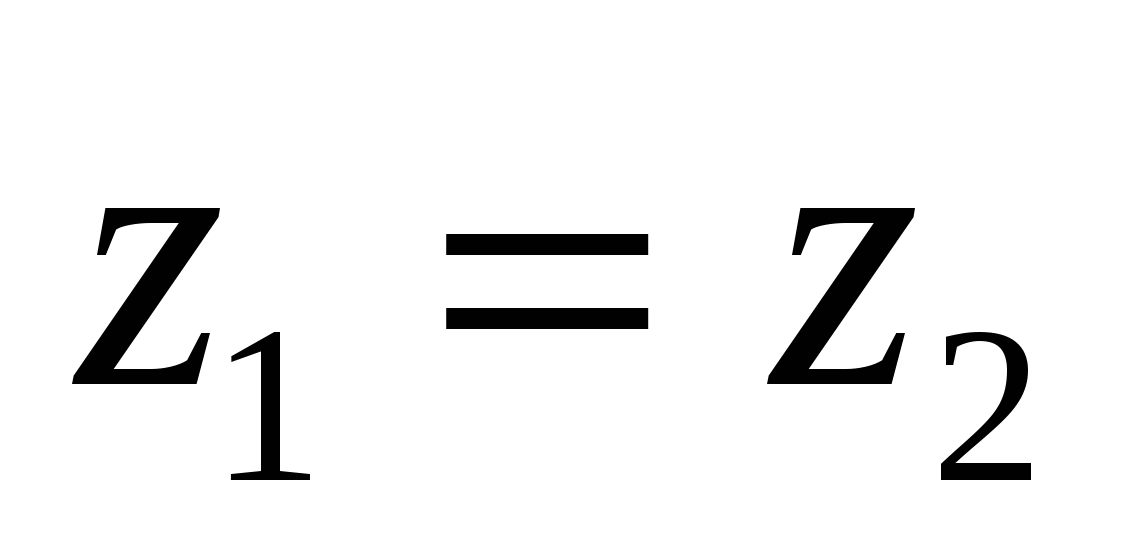 .
.
Quy tắc 2.
Mỗi tọa độ của tổng của hai hoặc nhiều vectơ bằng tổng tọa độ tương ứng của các vectơ này.
Nói cách khác, nếu 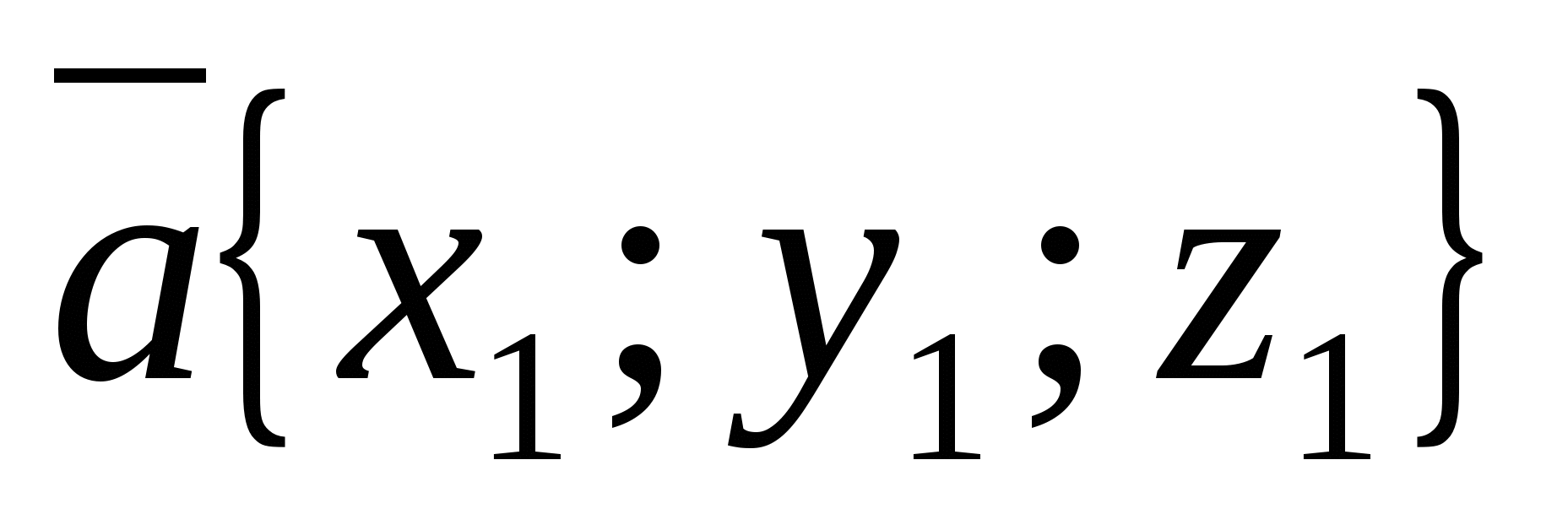 Và
Và 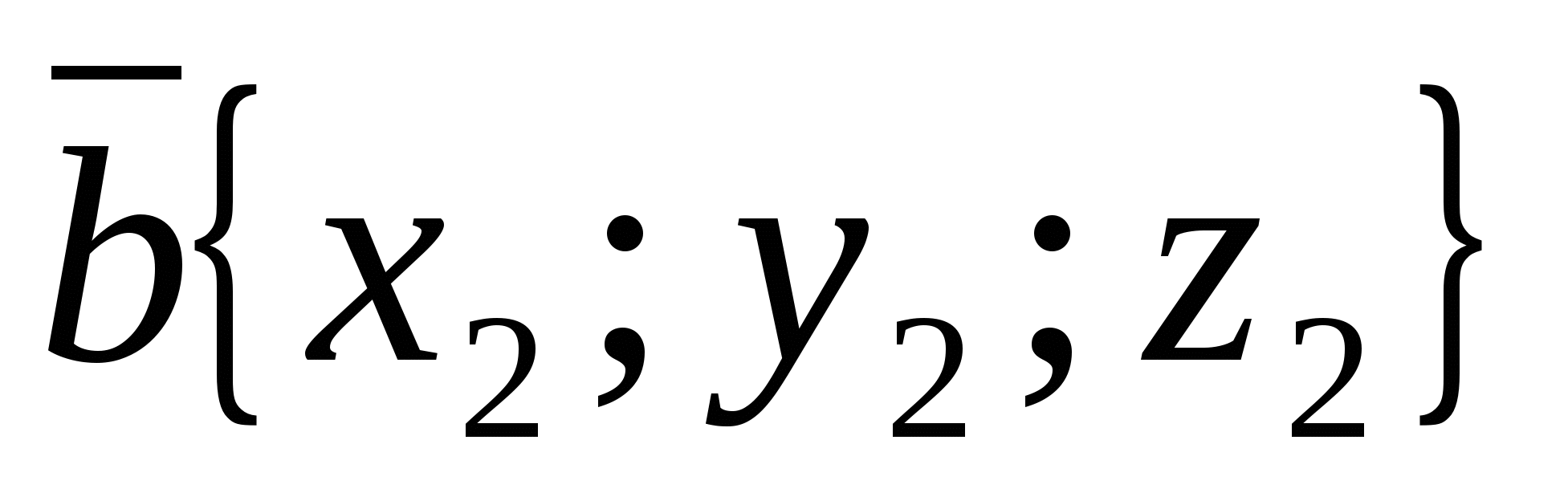 -cho vectơ, rồi vectơ
-cho vectơ, rồi vectơ 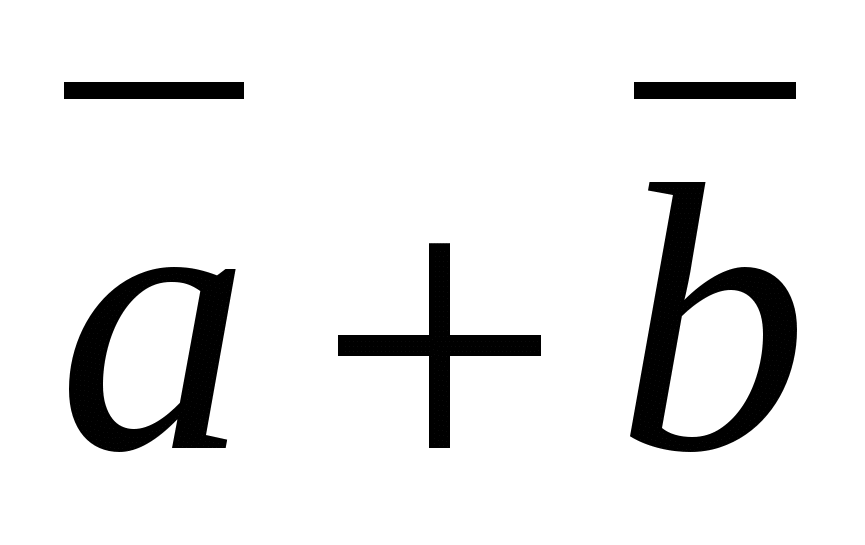 có tọa độ.
có tọa độ.
Quy tắc 3.
Mỗi tọa độ hiệu của hai vectơ bằng hiệu tọa độ tương ứng của các vectơ này.
Nói cách khác, nếu 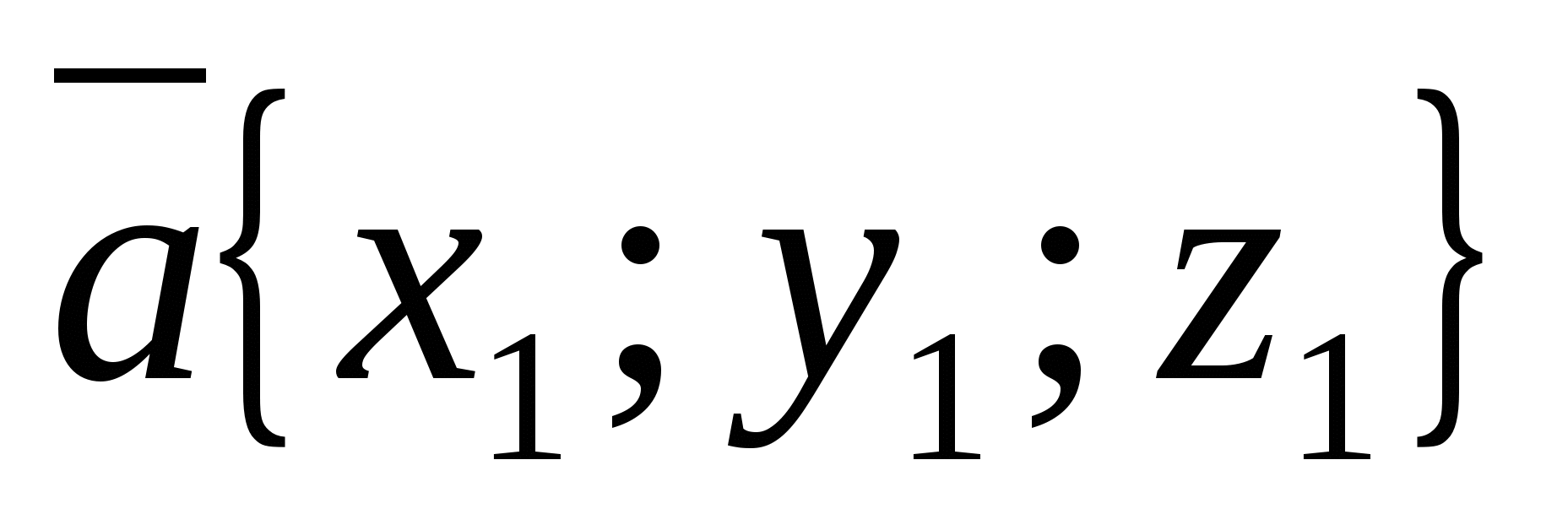 Và
Và 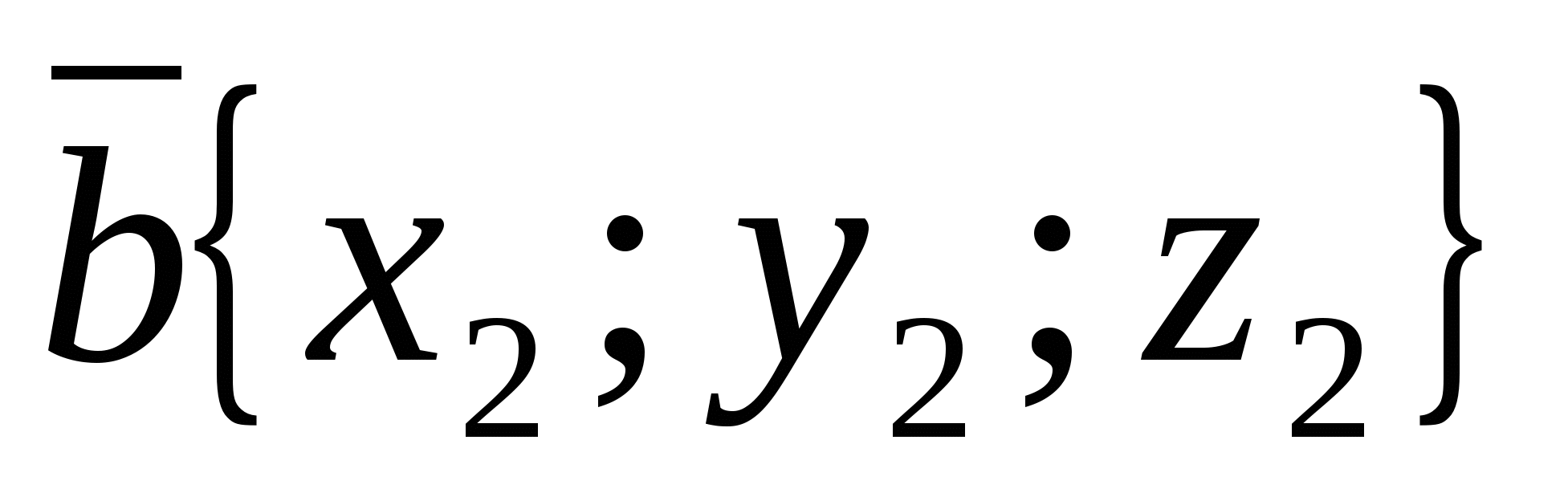 -cho vectơ, rồi vectơ
-cho vectơ, rồi vectơ 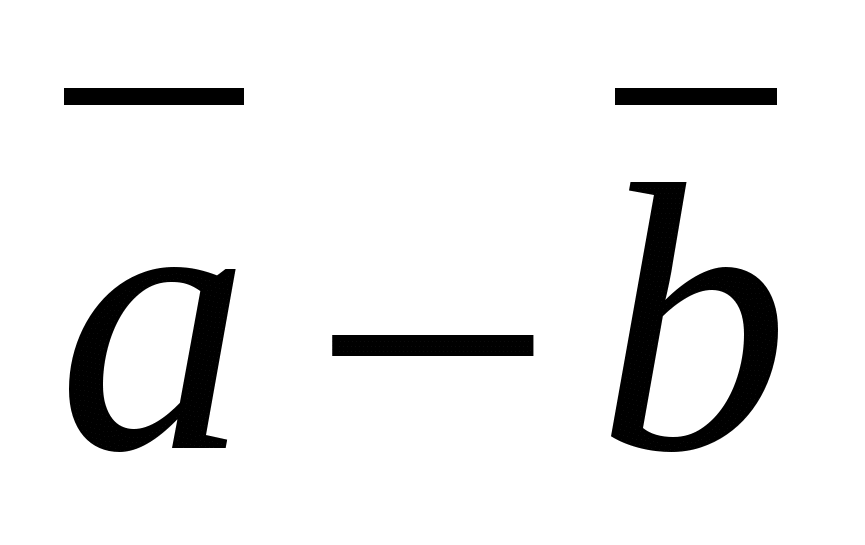 có tọa độ
có tọa độ
Quy tắc 4.
Mỗi tọa độ của tích của vectơ và một số bằng tích của tọa độ tương ứng của vectơ và số này.
Nói cách khác, nếu 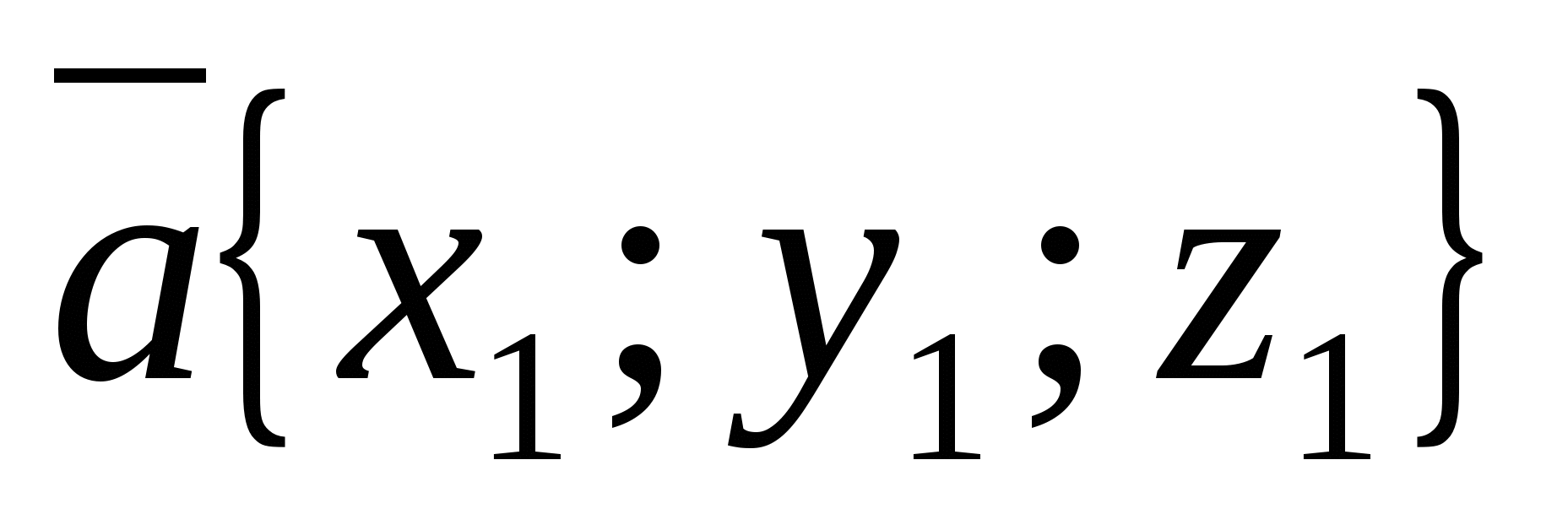 -vectơ đã cho,
-vectơ đã cho, ![]() -số đã cho, thì vectơ
-số đã cho, thì vectơ 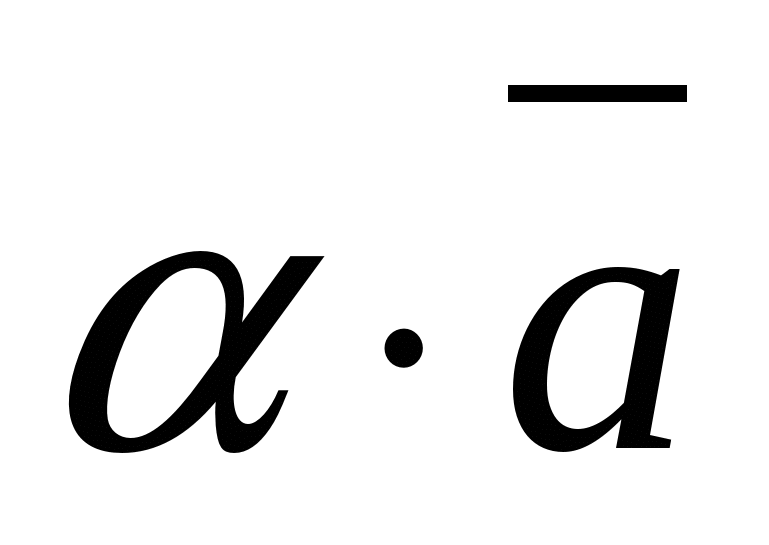 có tọa độ.
có tọa độ. 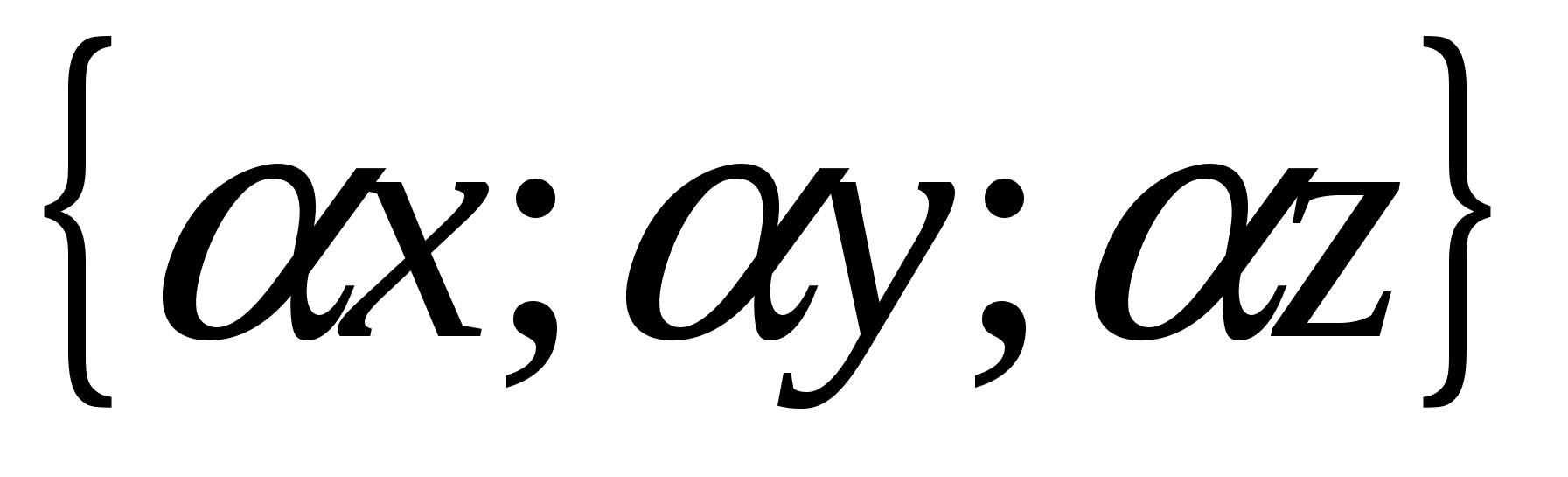 .
.
Ví dụ.
Tìm tọa độ vectơ  , Nếu như
, Nếu như 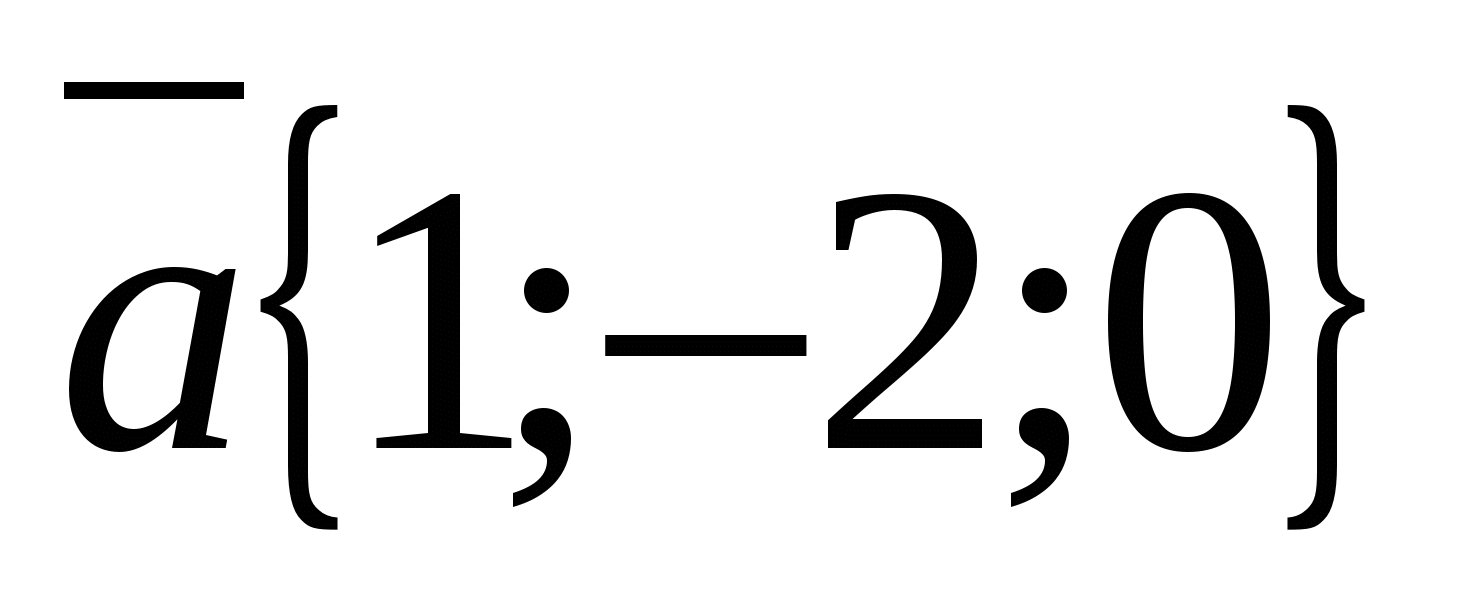 ,
, 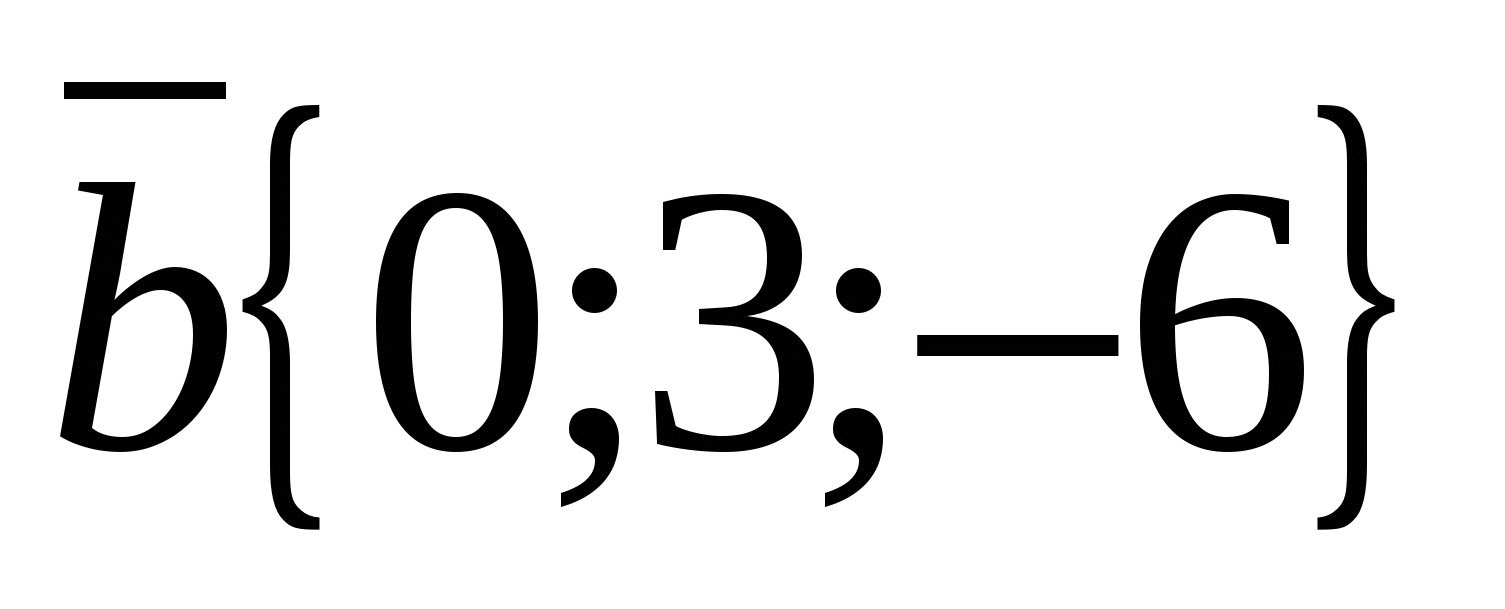 ,
, 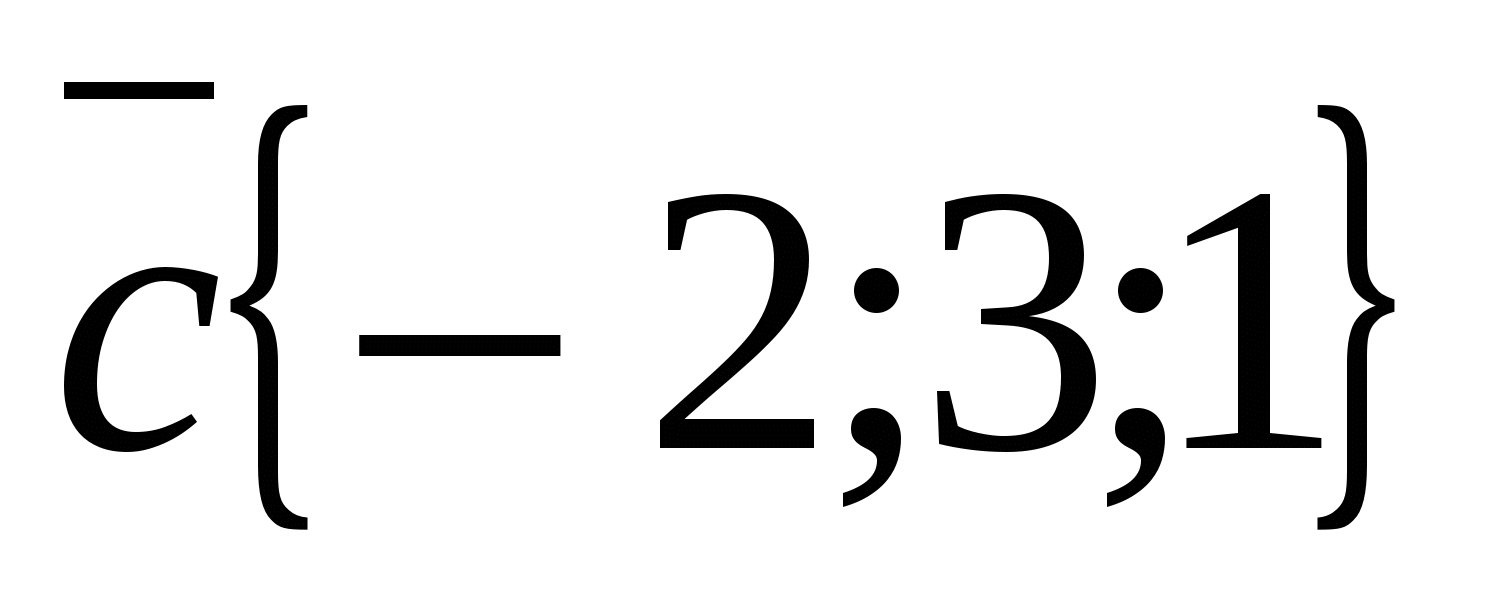 .
.
Giải pháp.
Vectơ 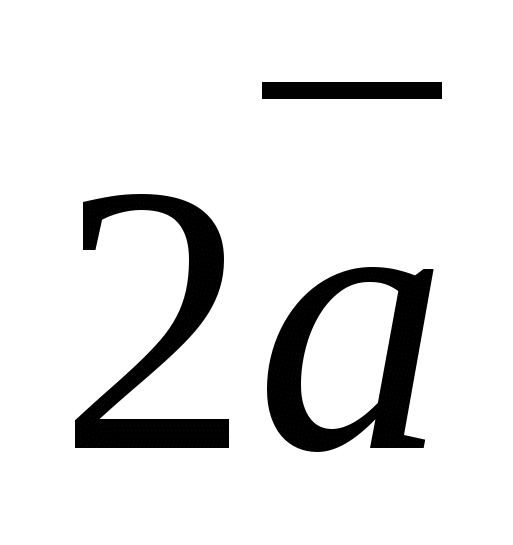 có tọa độ
có tọa độ 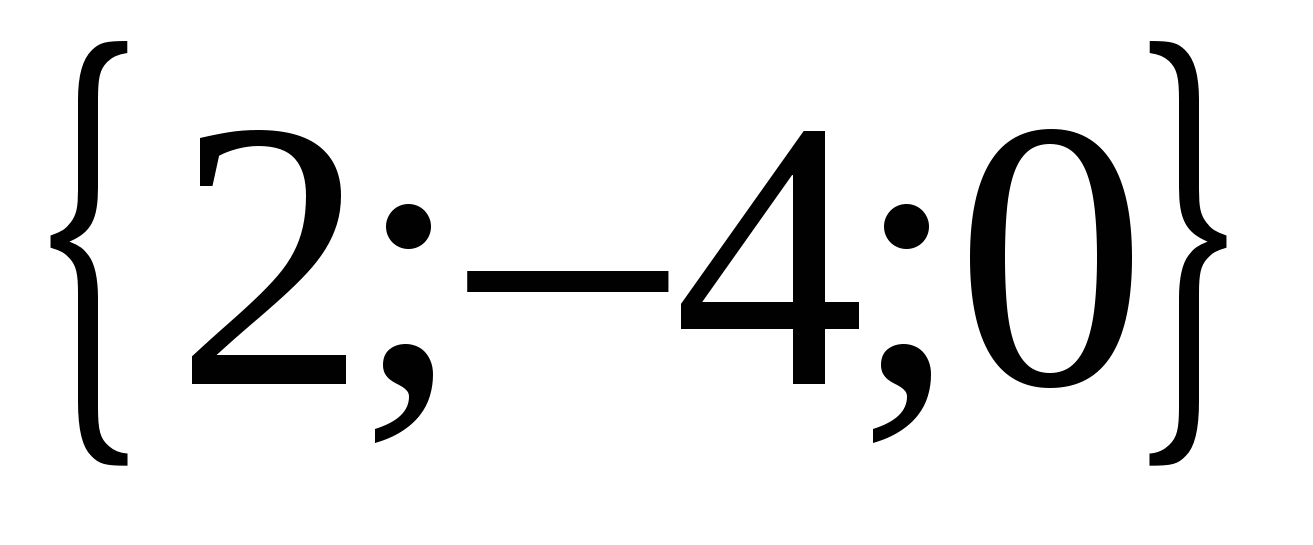 , và vectơ
, và vectơ  - tọa độ
- tọa độ 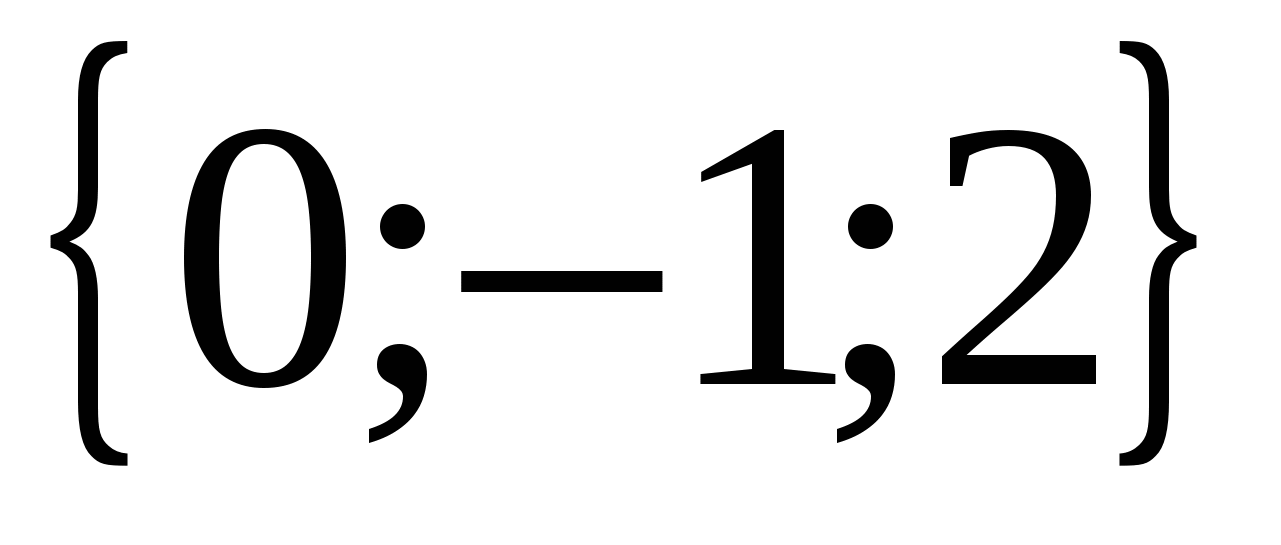 .
.
Bởi vì 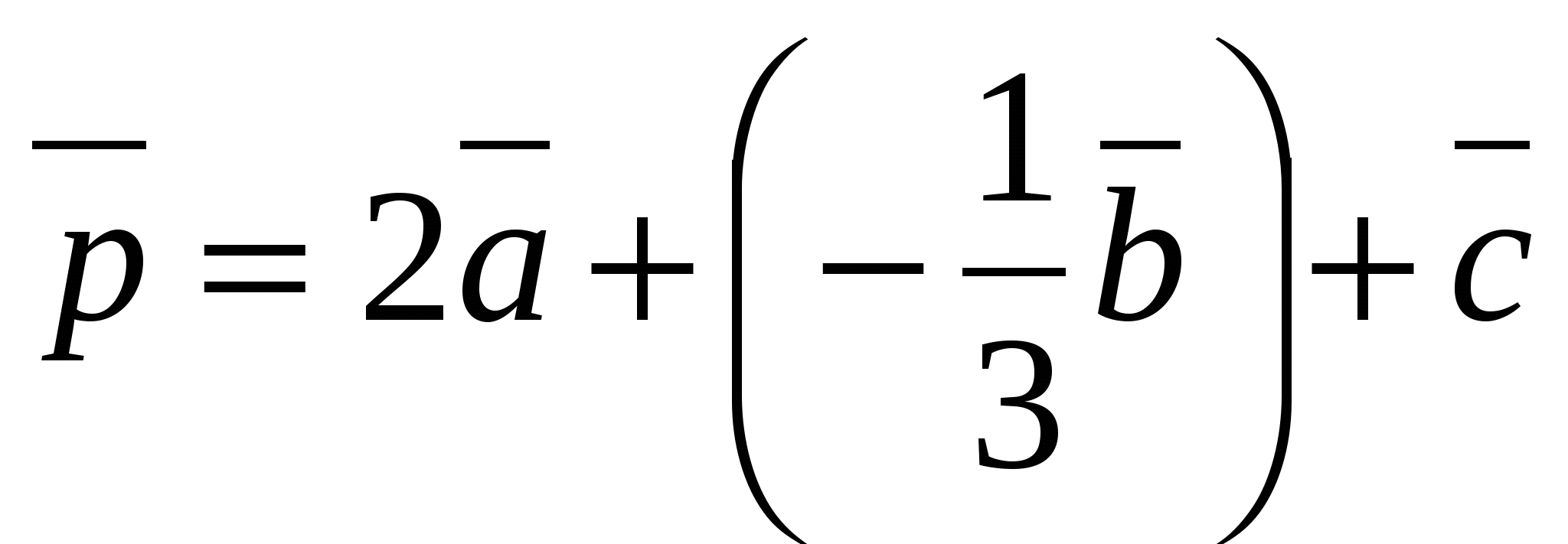 , thì tọa độ của nó
, thì tọa độ của nó  có thể được tính như sau:
có thể được tính như sau:  ,
,  ,
, 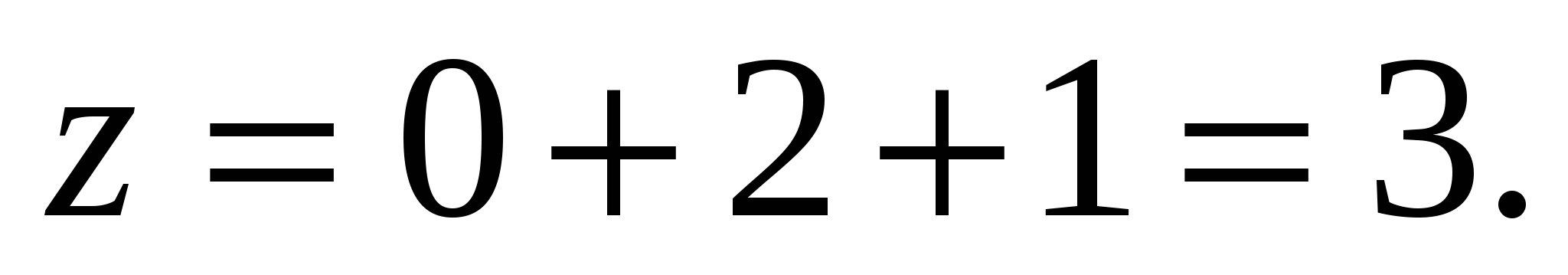 Vậy nó là một vectơ
Vậy nó là một vectơ 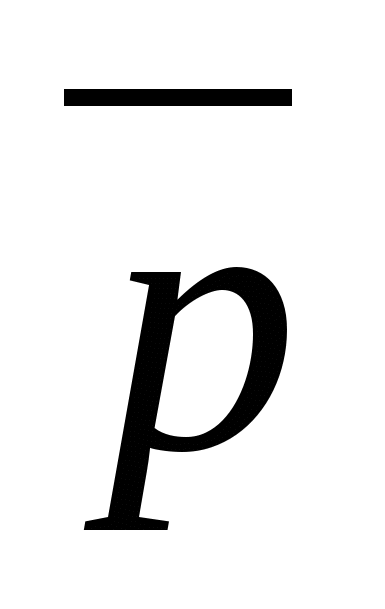 có tọa độ
có tọa độ  .
.
3. Mối liên hệ giữa tọa độ vectơ và tọa độ điểm.
Sự định nghĩa.
Một vectơ có điểm cuối trùng với một điểm cho trước và điểm đầu trùng với gốc tọa độ được gọi là vectơ bán kínhđiểm này.
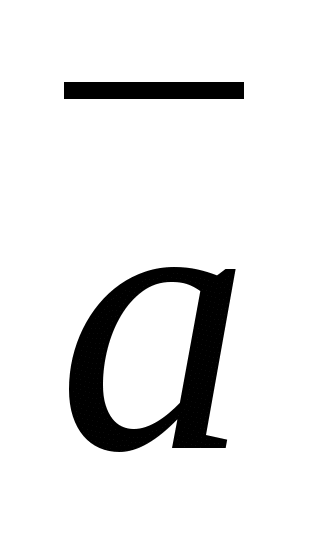
 - vectơ bán kính
- vectơ bán kính
 ,
,
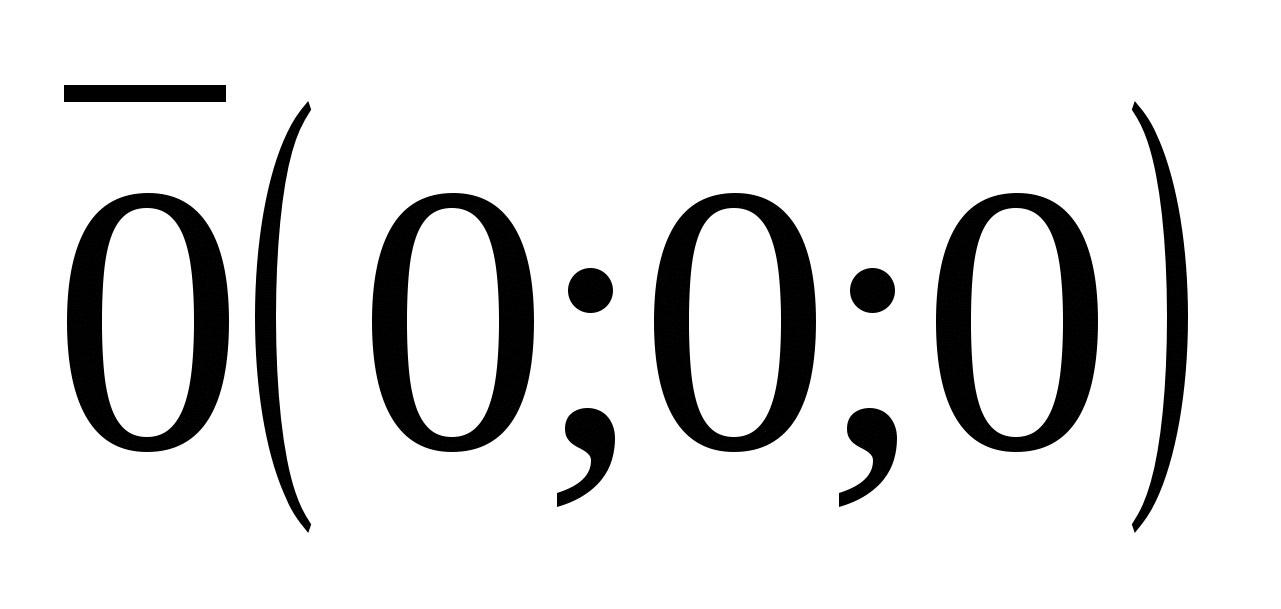 ;
;
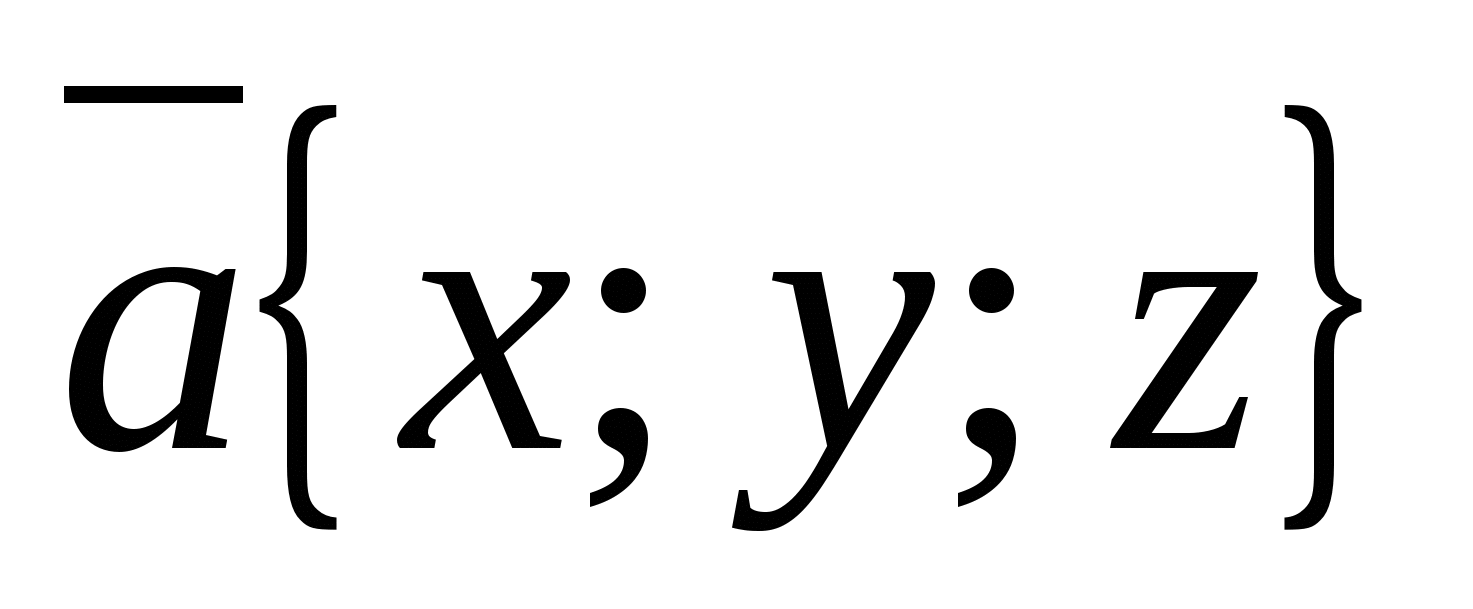
Quy tắc 5.
Tọa độ của bất kỳ điểm nào đều bằng tọa độ tương ứng của vectơ bán kính của nó. ,.

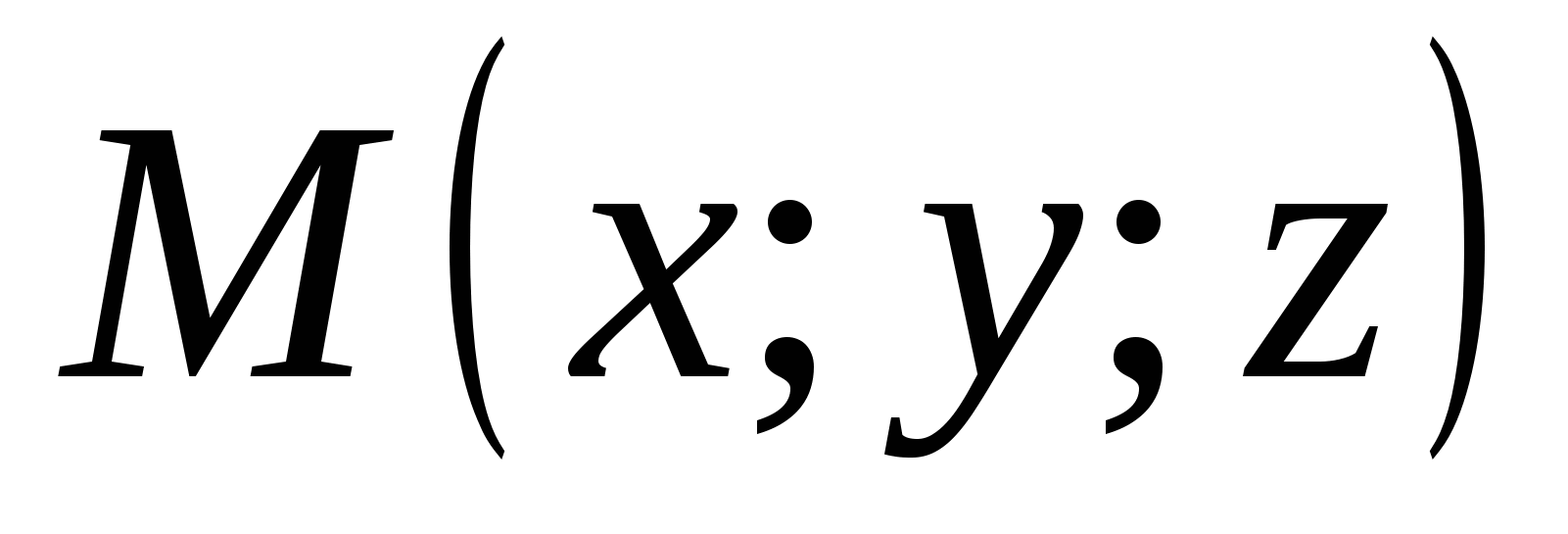
Quy tắc 6.
Mỗi tọa độ vectơ bằng hiệu giữa tọa độ tương ứng của điểm cuối và điểm đầu của nó.
 .
.
4. Điều kiện cộng tuyến của hai vectơ trong tọa độ.
Cho vào hệ tọa độ  hai vectơ được cho tọa độ của chúng
hai vectơ được cho tọa độ của chúng  Và
Và 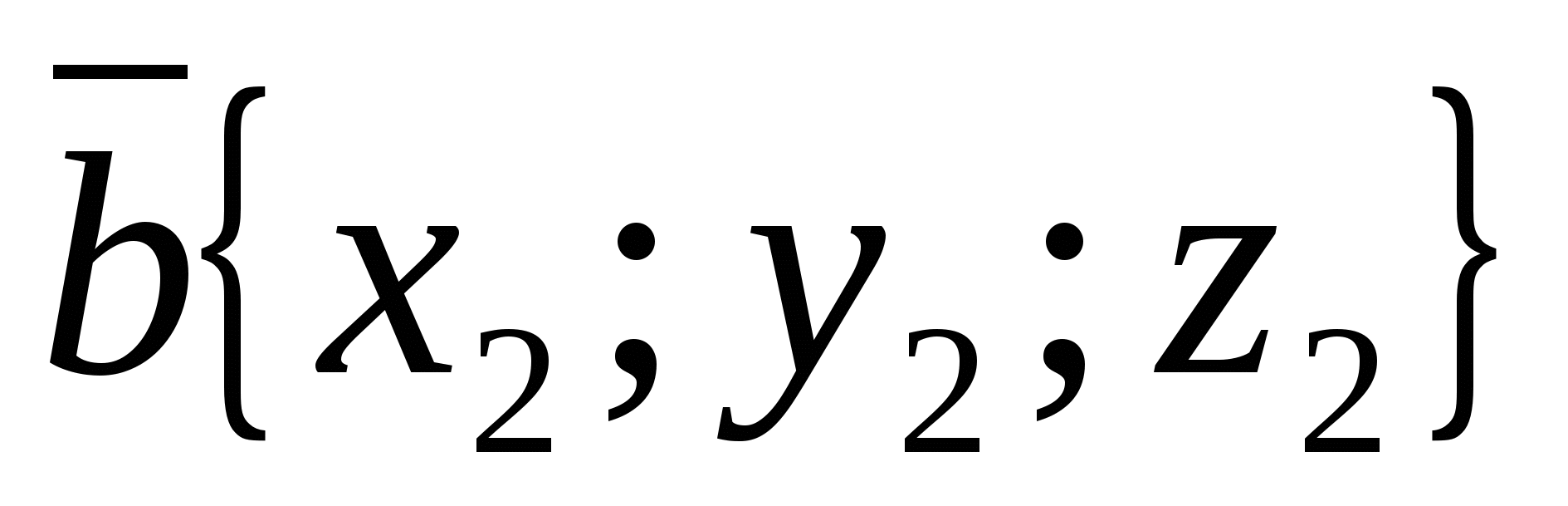 .
.
Quy tắc 7.
Vectơ
 Và
Và 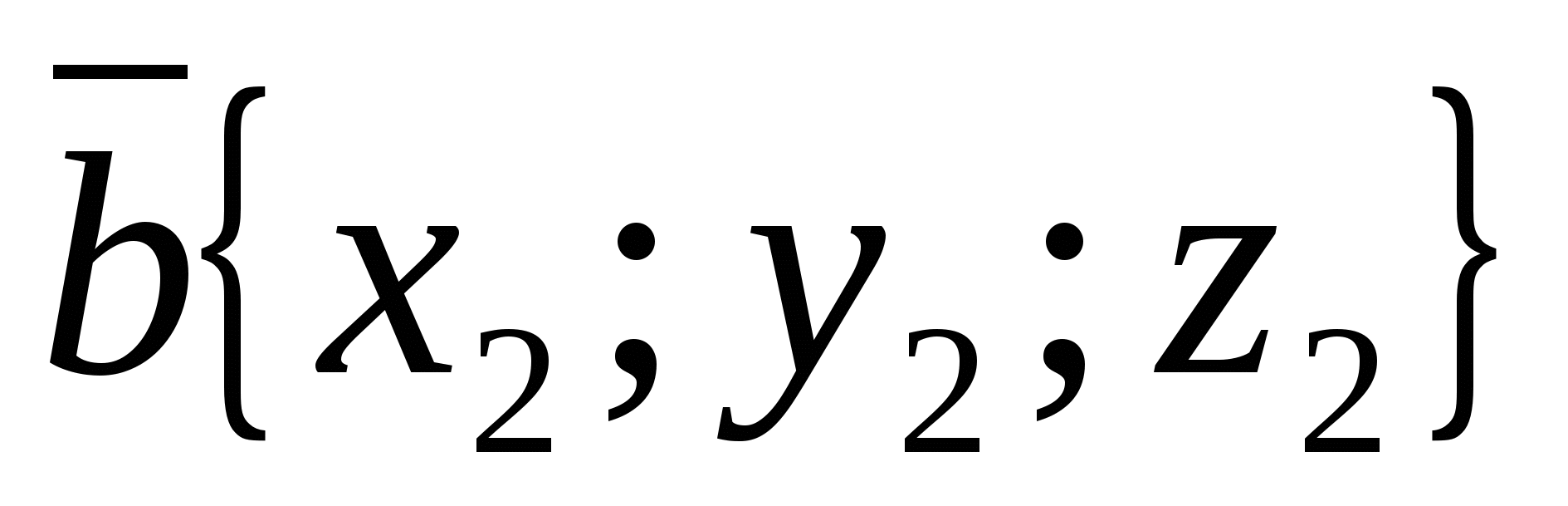 thẳng hàng khi và chỉ khi tọa độ tương ứng của chúng tỉ lệ với nhau,
thẳng hàng khi và chỉ khi tọa độ tương ứng của chúng tỉ lệ với nhau, 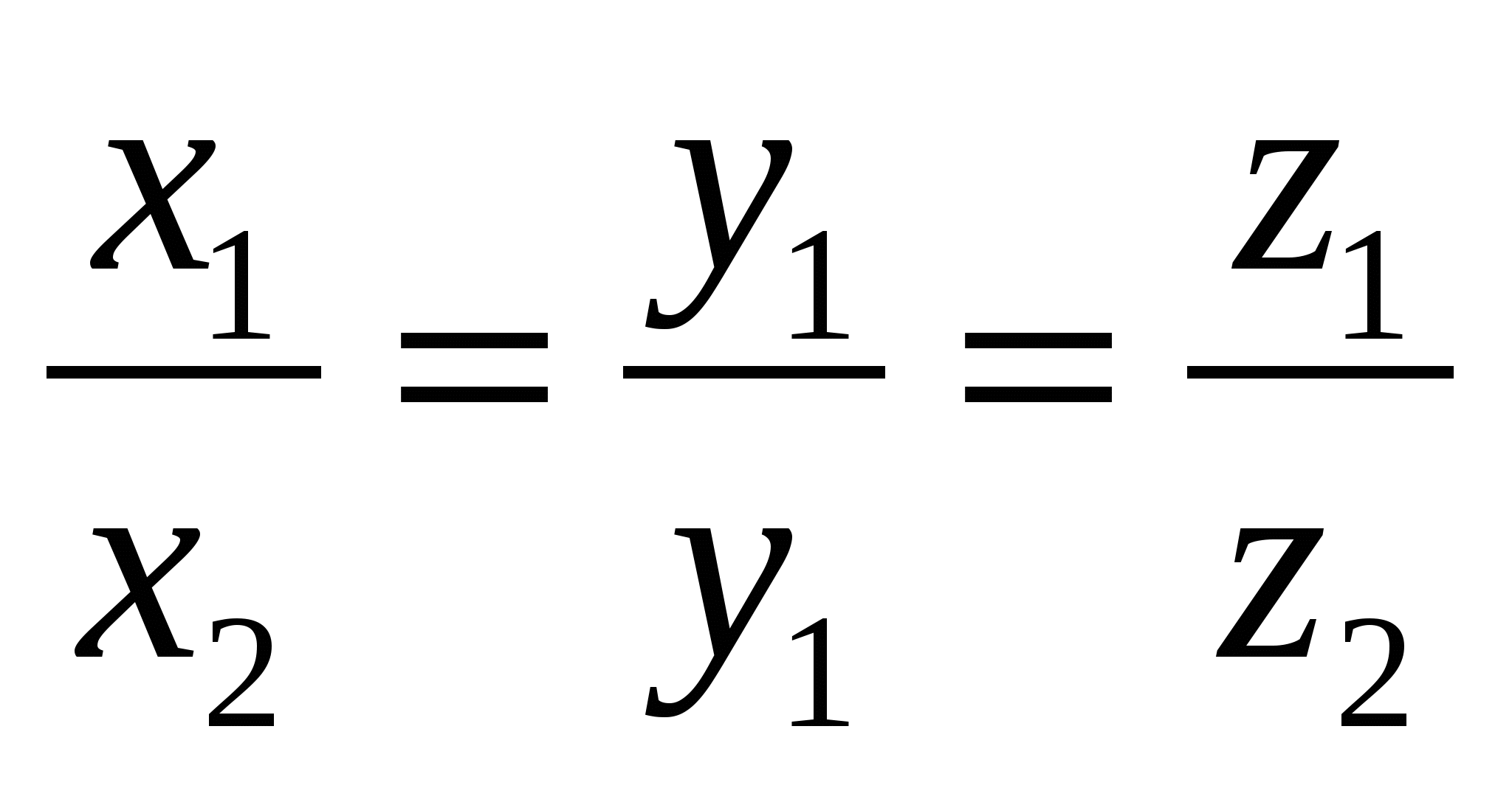 .
.
Ví dụ.
a) Xét các vectơ 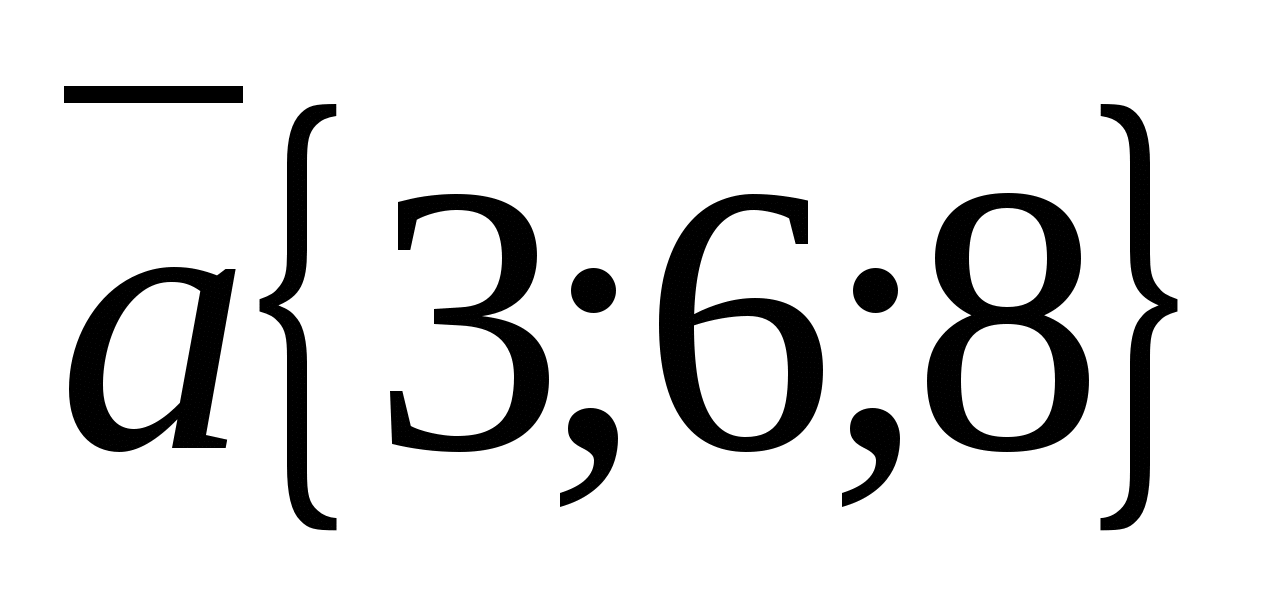 Và
Và 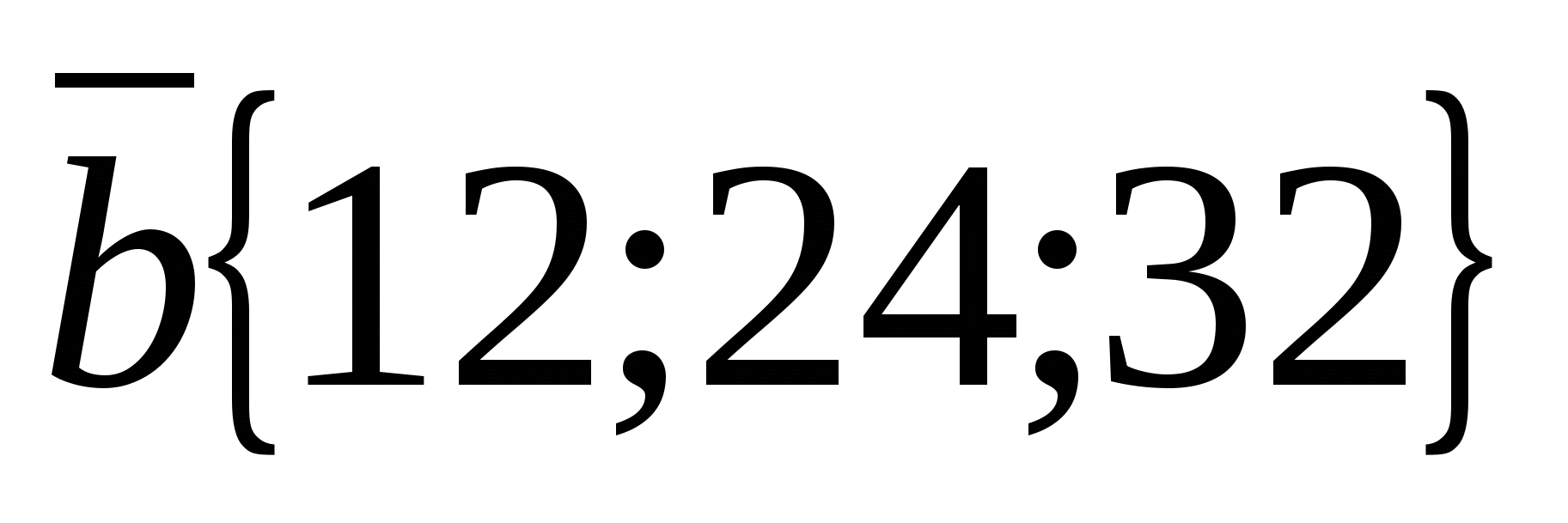 .
.
Tọa độ vectơ 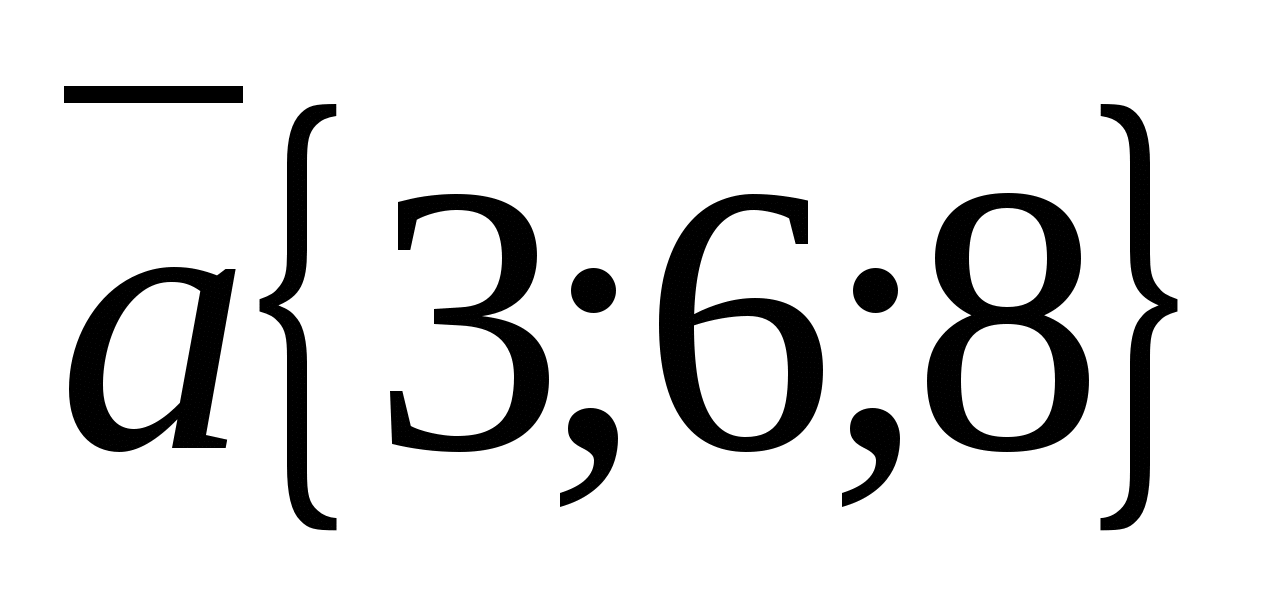 tỉ lệ thuận với tọa độ vectơ tương ứng
tỉ lệ thuận với tọa độ vectơ tương ứng 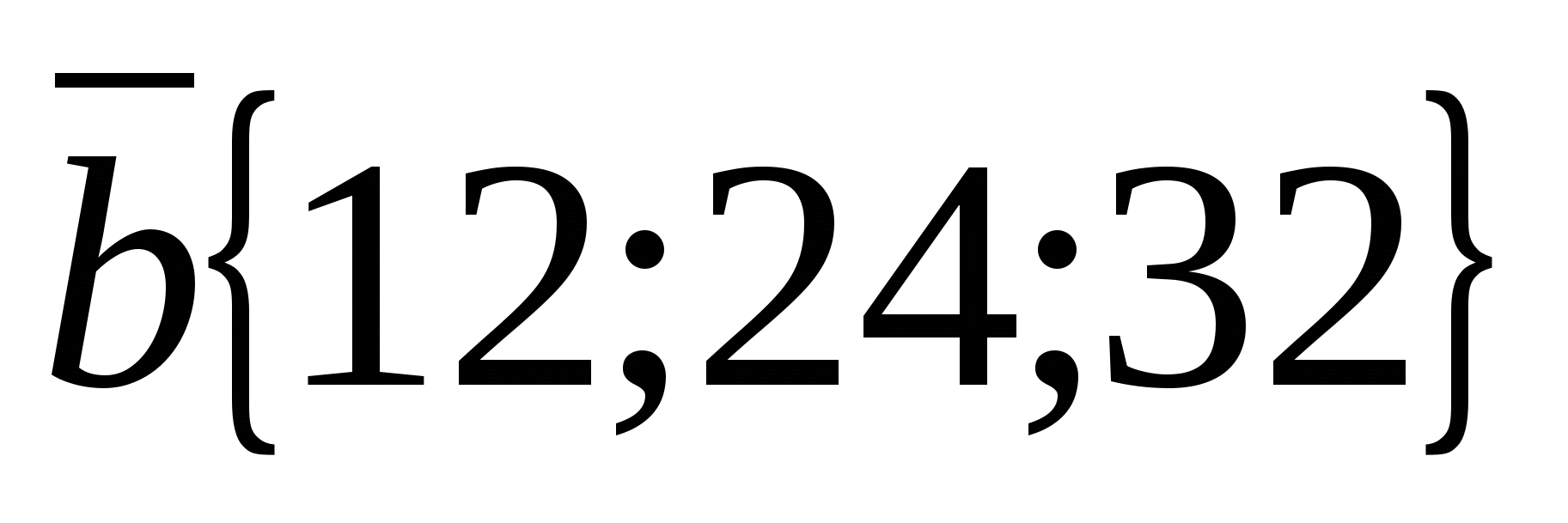 :
: 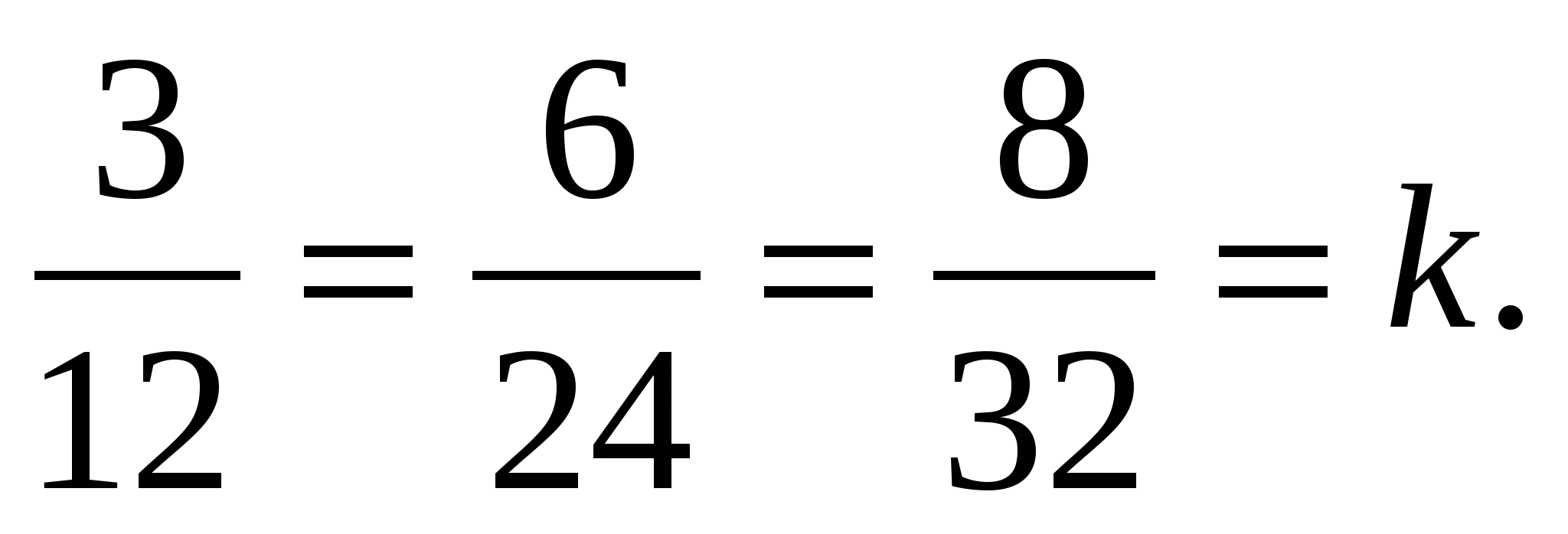 Đó là lý do tại sao
Đó là lý do tại sao 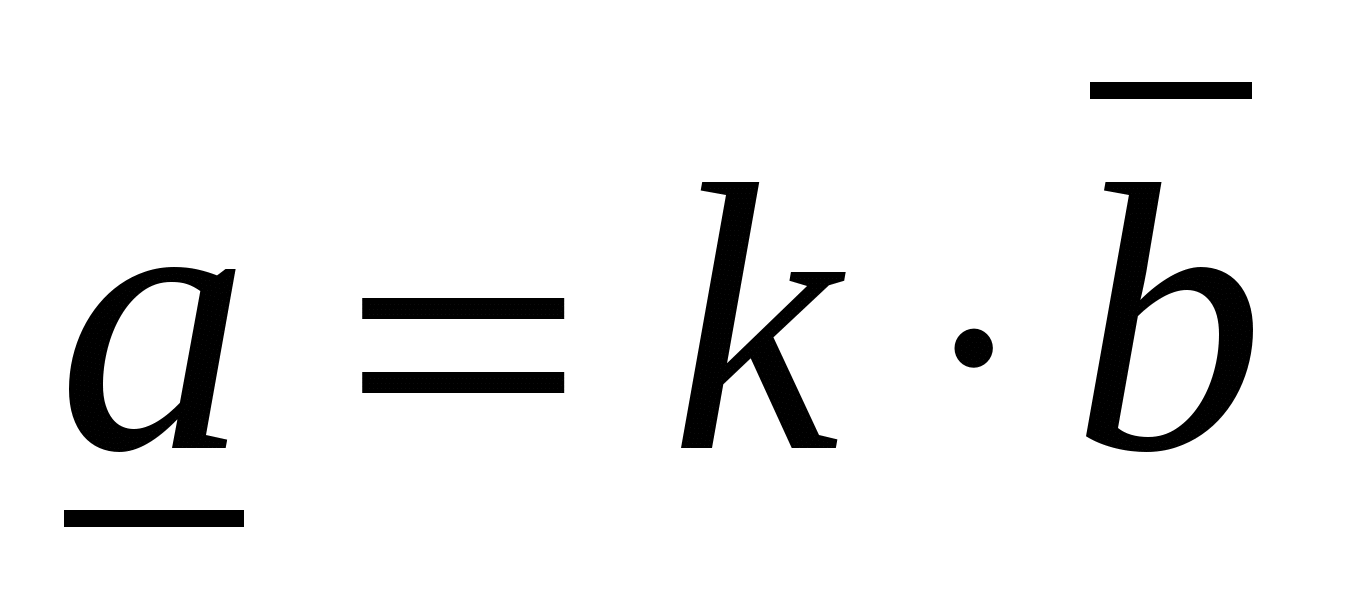 , và do đó các vectơ thẳng hàng.
, và do đó các vectơ thẳng hàng.
b) Xét các vectơ 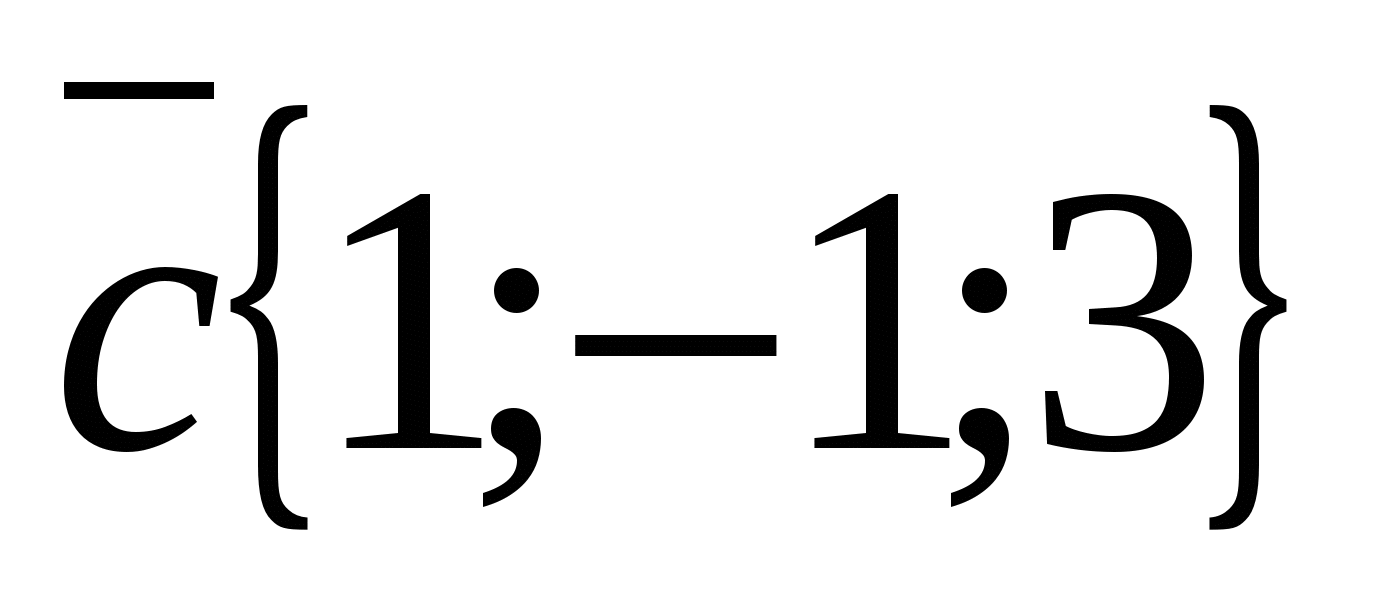 Và
Và 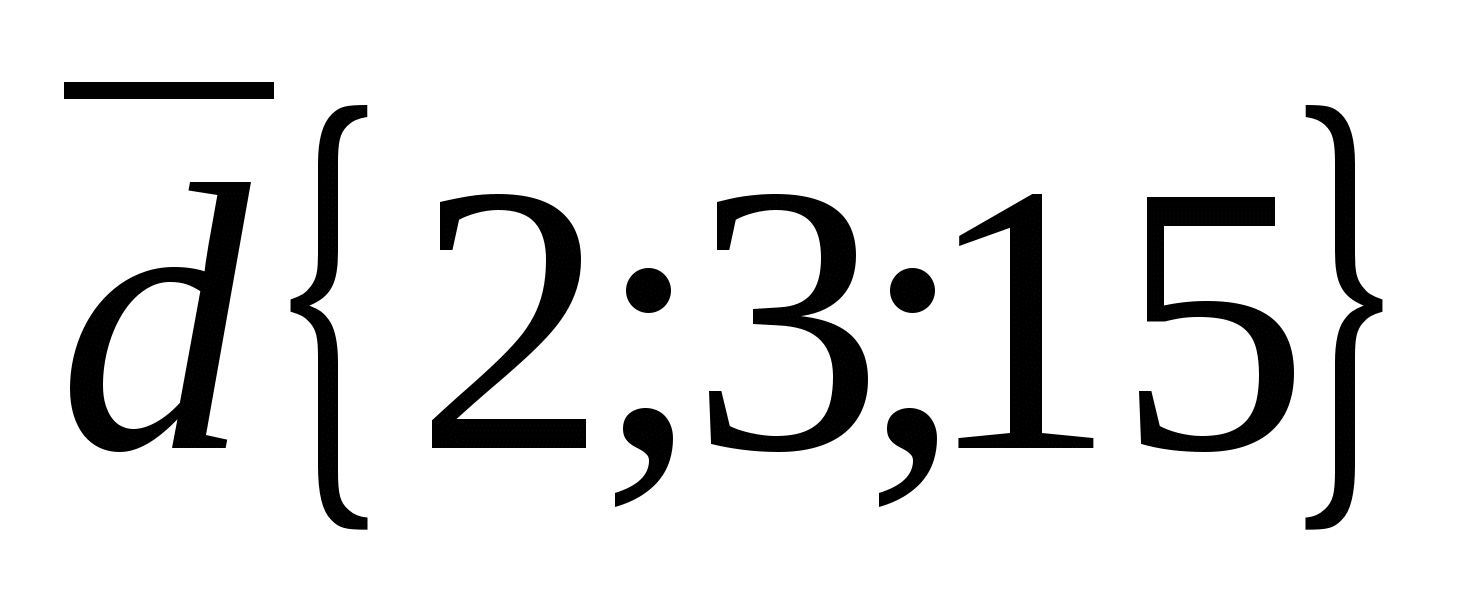 .
.
Tọa độ vectơ 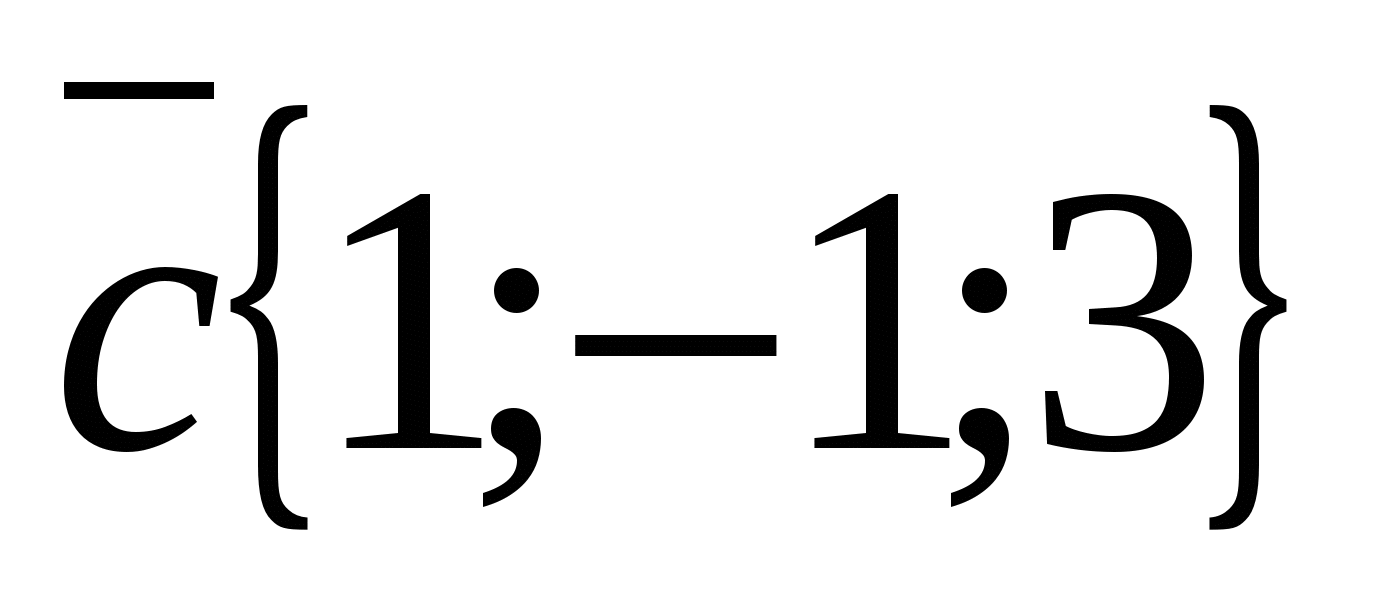 không tỷ lệ thuận với tọa độ vectơ tương ứng
không tỷ lệ thuận với tọa độ vectơ tương ứng 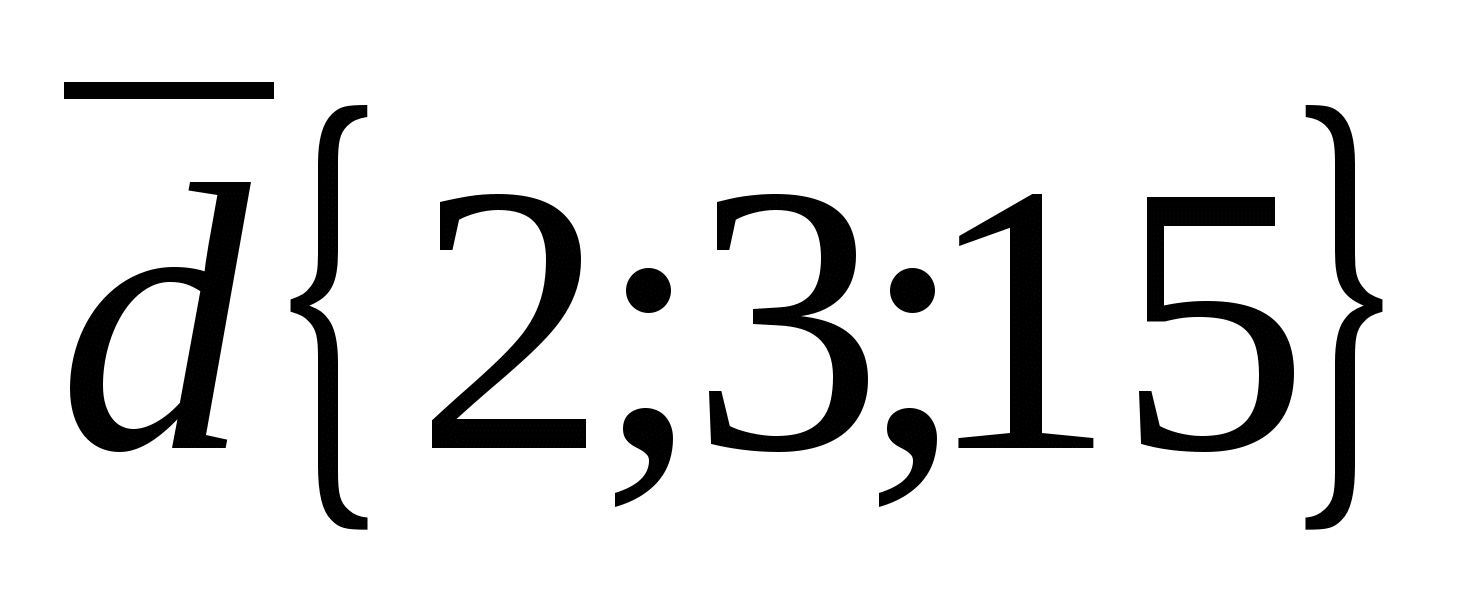 , Ví dụ
, Ví dụ 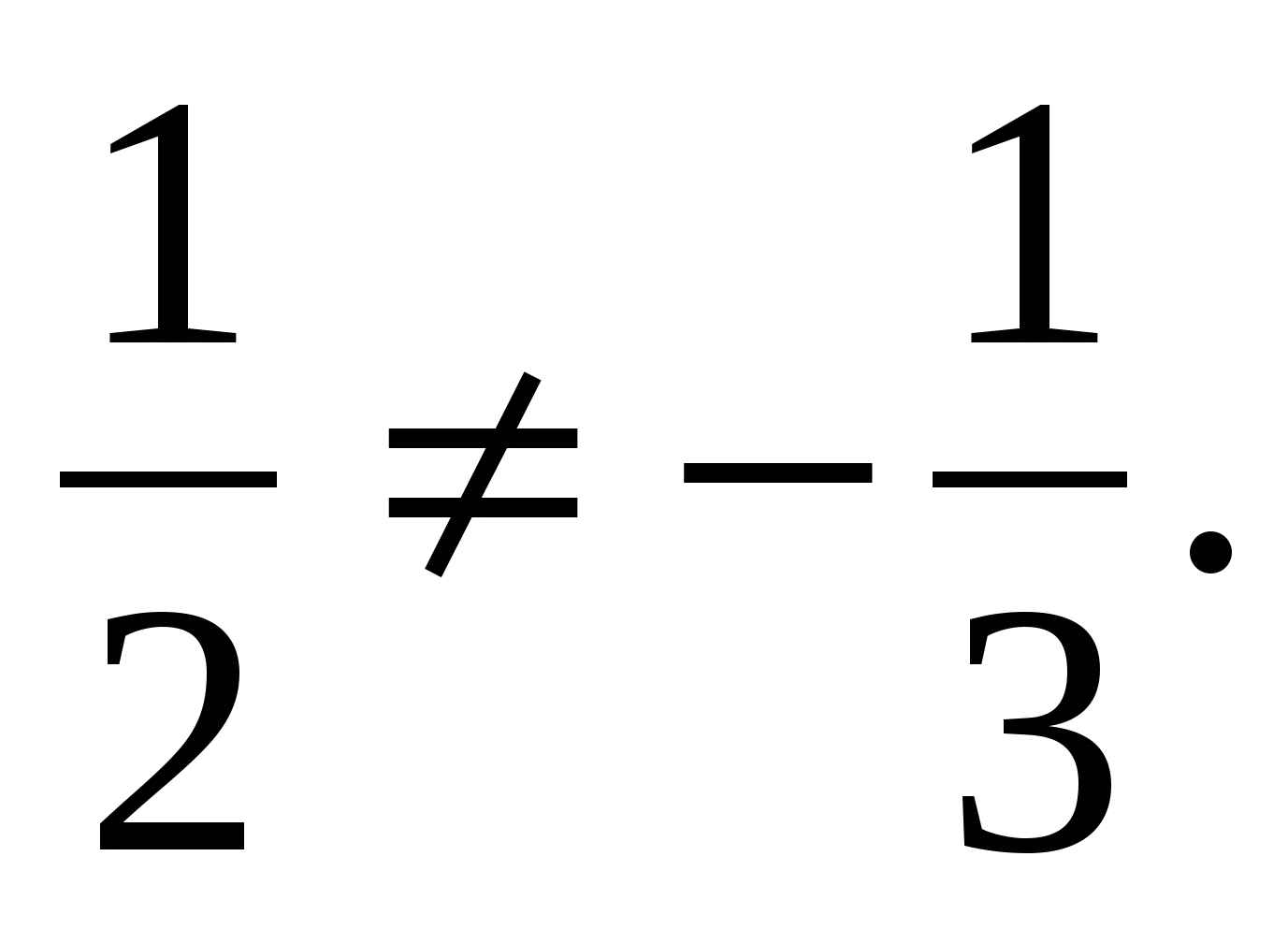 Điều này có nghĩa là các vectơ không thẳng hàng.
Điều này có nghĩa là các vectơ không thẳng hàng.
5. Các bài toán đơn giản nhất về tọa độ.
Nhiệm vụ 1.
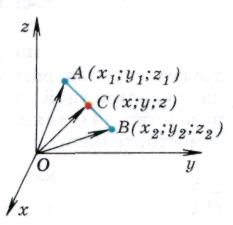 Mỗi tọa độ của phần giữa của một đoạn bằng một nửa tổng tọa độ tương ứng của các đầu của nó.
Mỗi tọa độ của phần giữa của một đoạn bằng một nửa tổng tọa độ tương ứng của các đầu của nó.
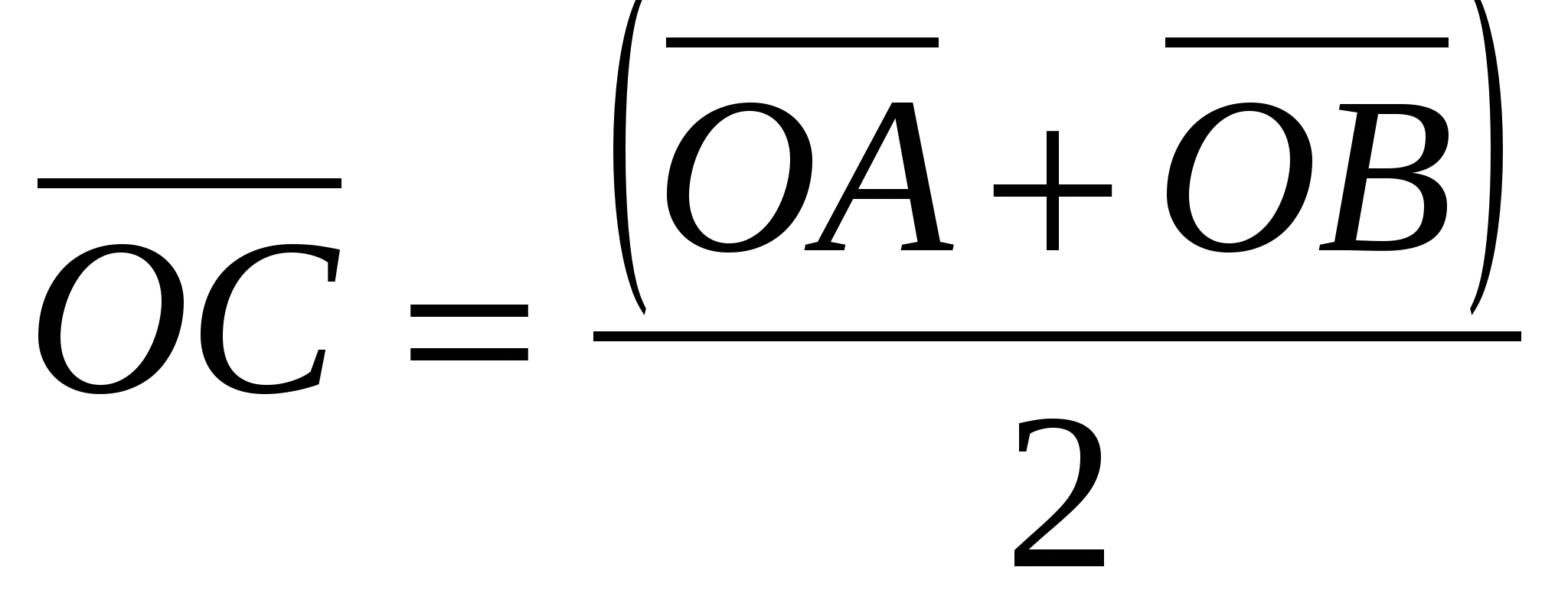 , Ở đâu
, Ở đâu 
 ,
, 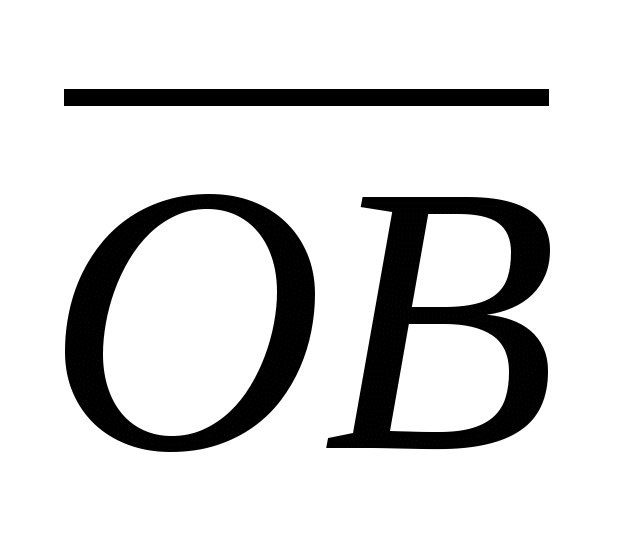
 Và
Và 
 .
.
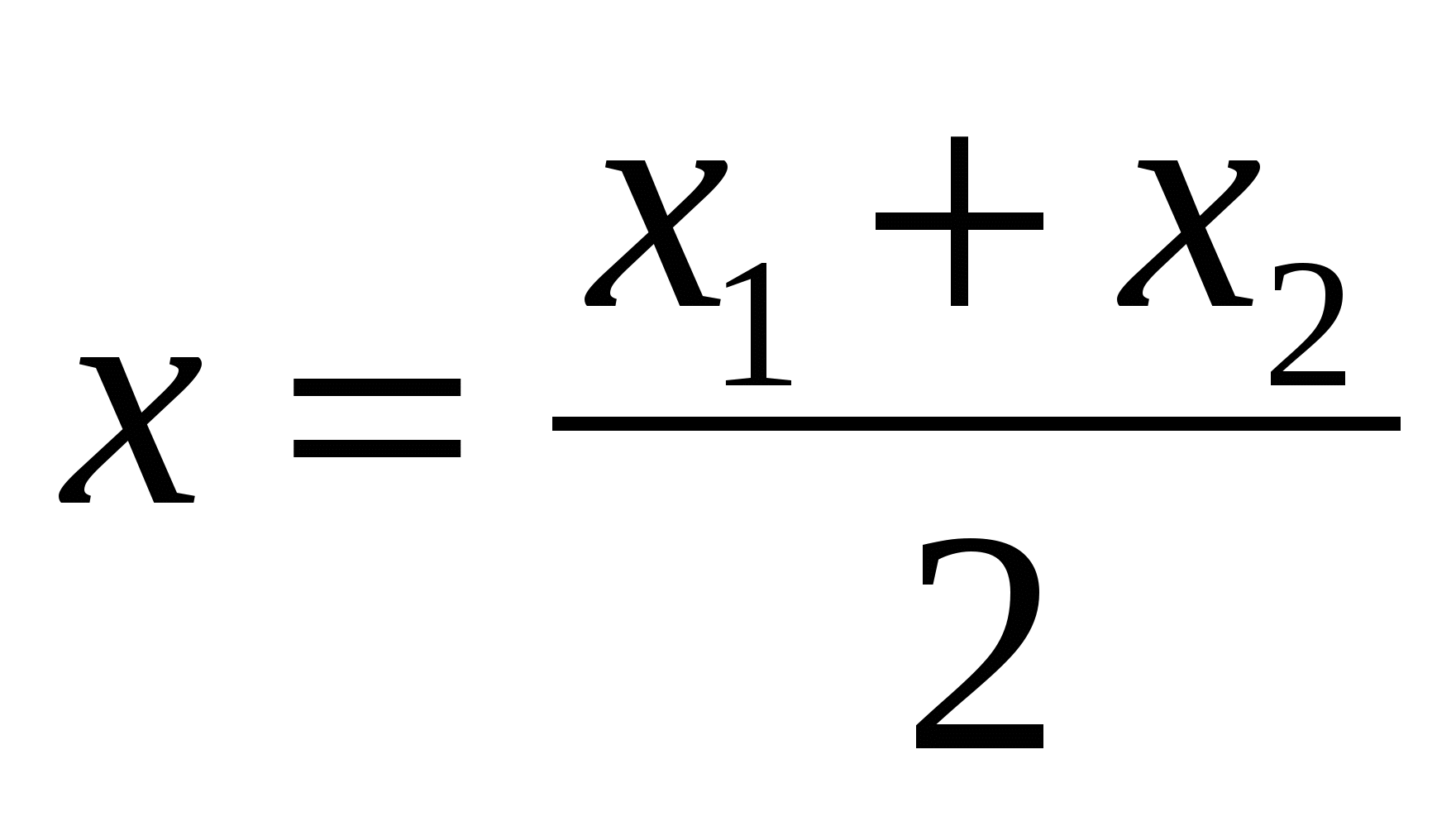 ,
,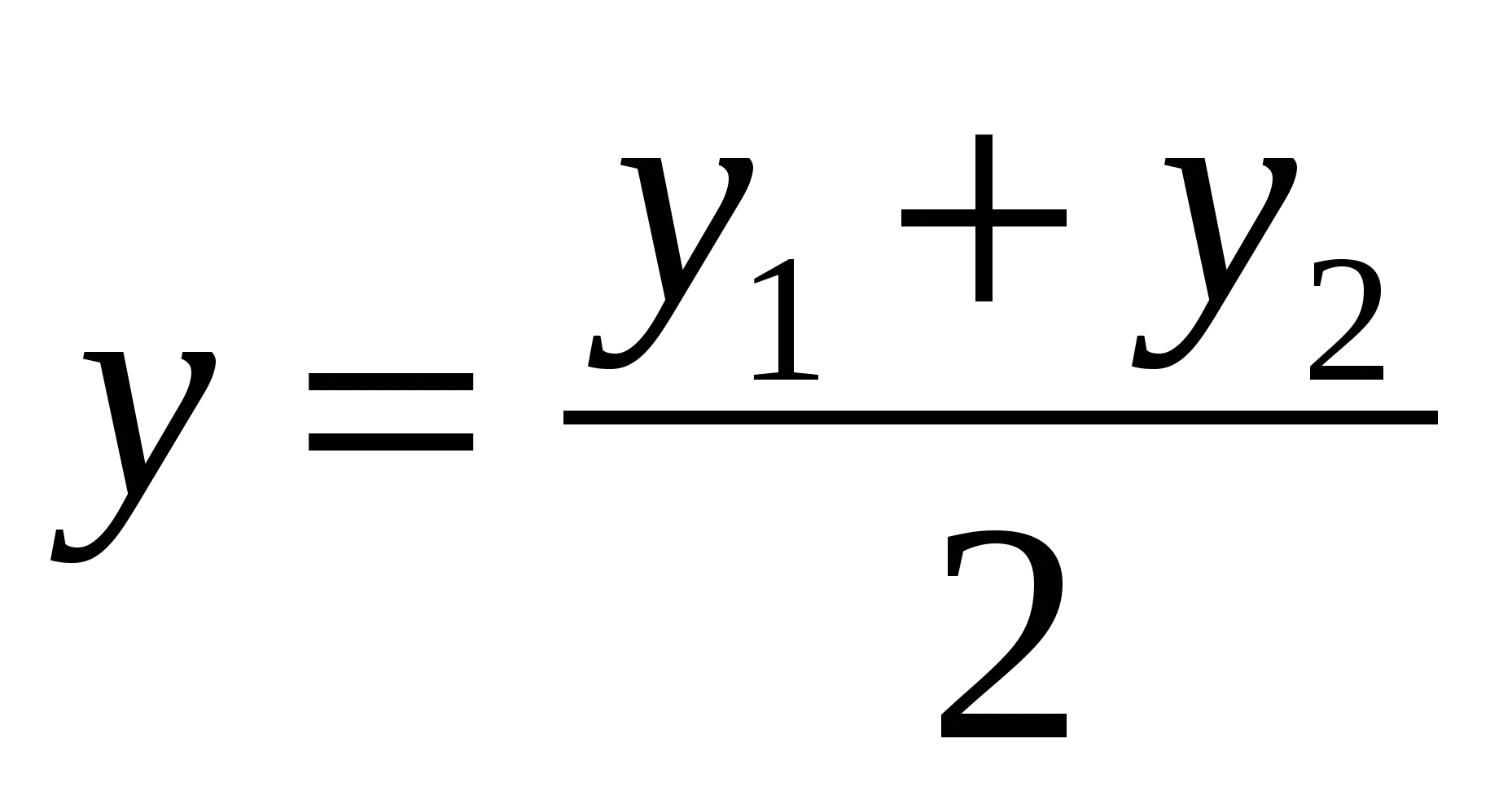 ,
, 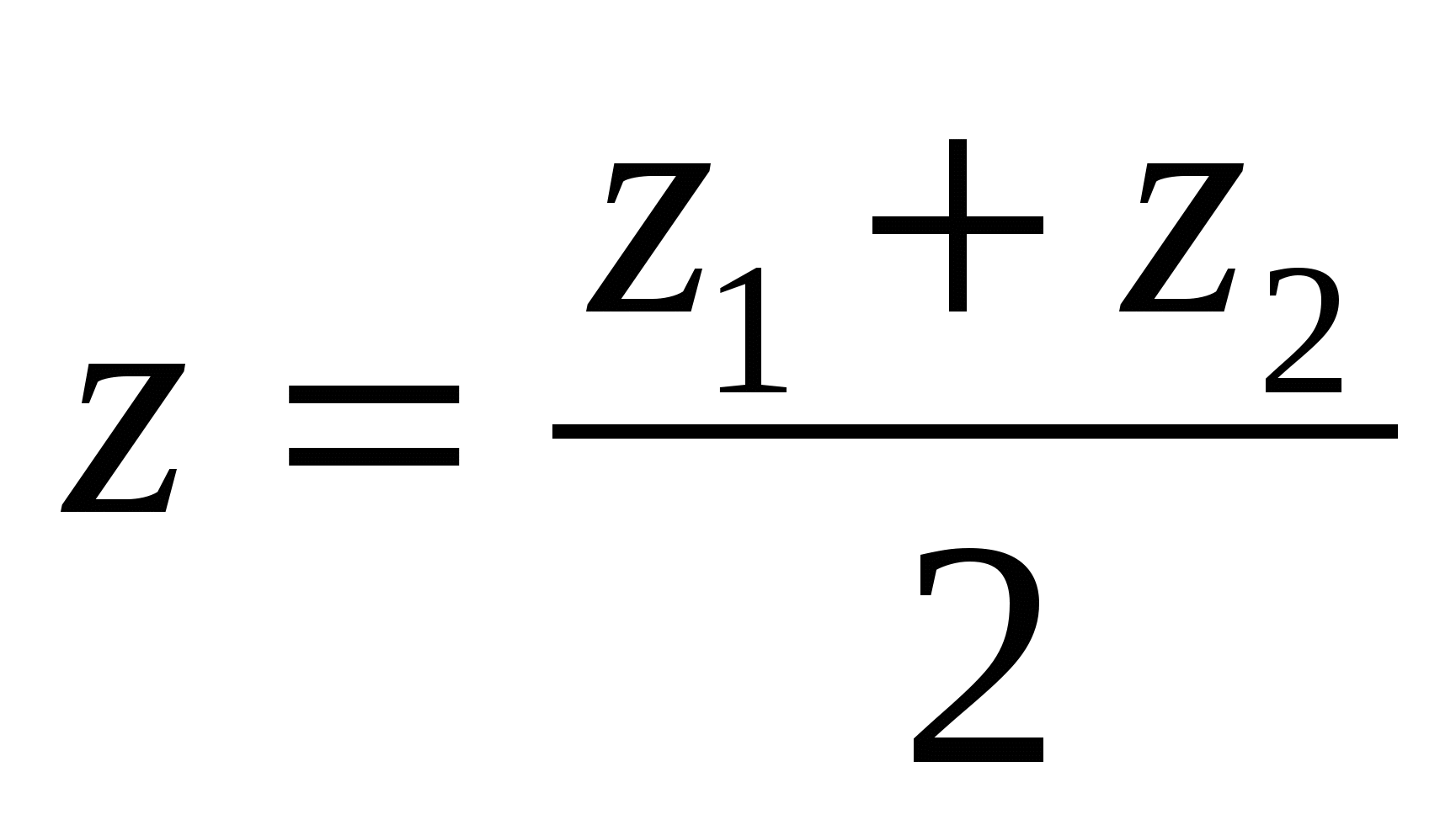 ,
,
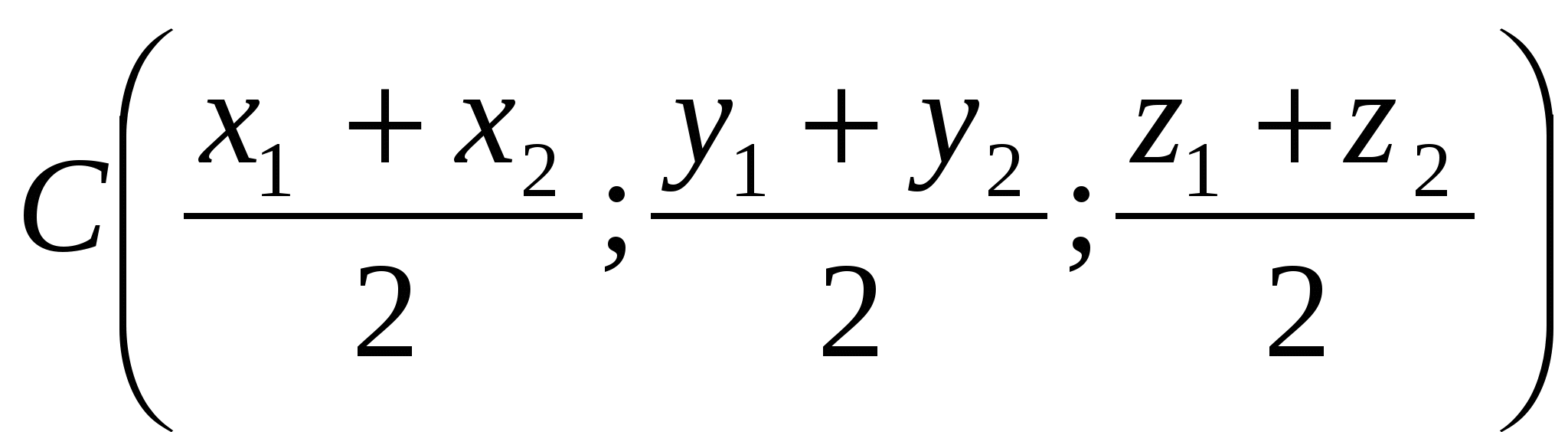
b) Tính độ dài của vectơ từ tọa độ của nó.
Xét một vectơ  ,
,
chiều dài vectơ được tính theo công thức
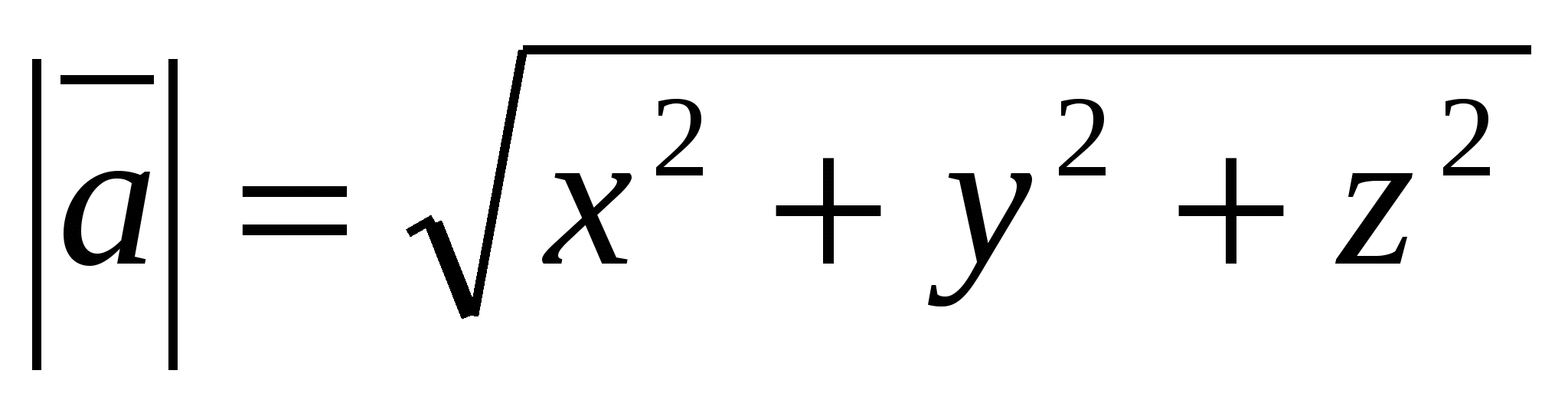 .
.
Bởi vì  =
=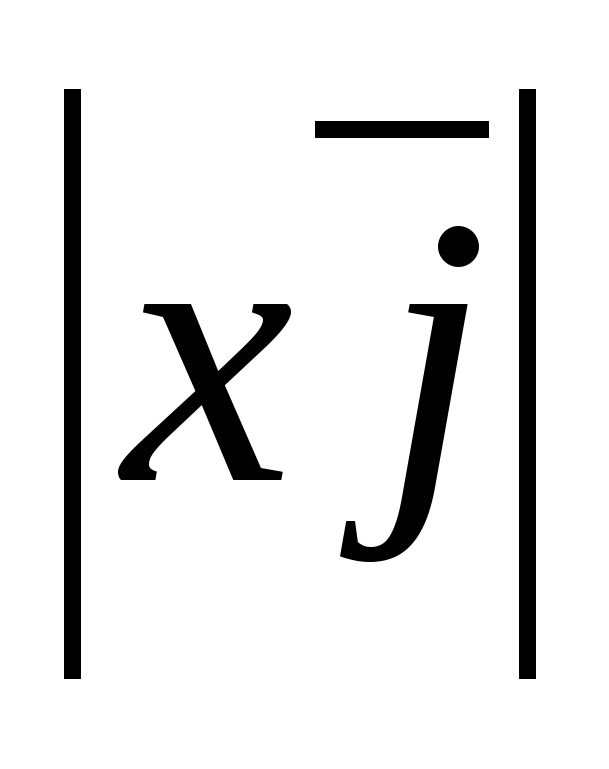 =
= ,
,
 =
= =
= ,
,
 =
= =
= , Và
, Và 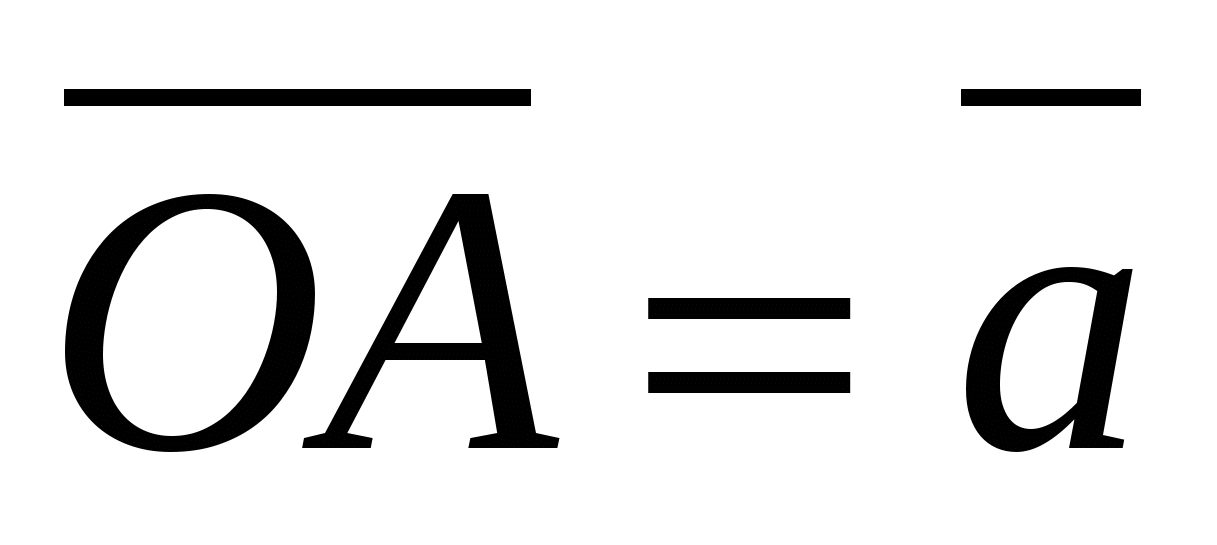 , thì từ đẳng thức
, thì từ đẳng thức 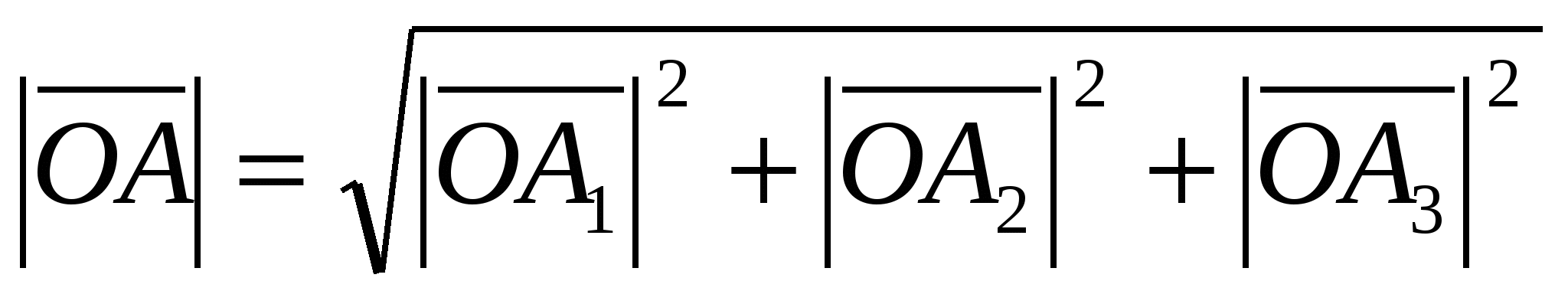 ta thu được công thức: .
ta thu được công thức: .
V) Khoảng cách giữa hai điểm.
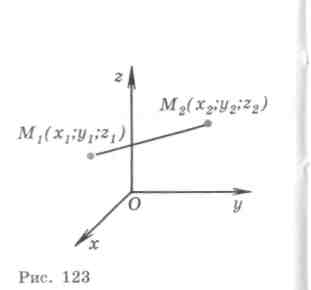 Chúng ta hãy xem xét hai điểm tùy ý: điểm
Chúng ta hãy xem xét hai điểm tùy ý: điểm  và thời kỳ
và thời kỳ 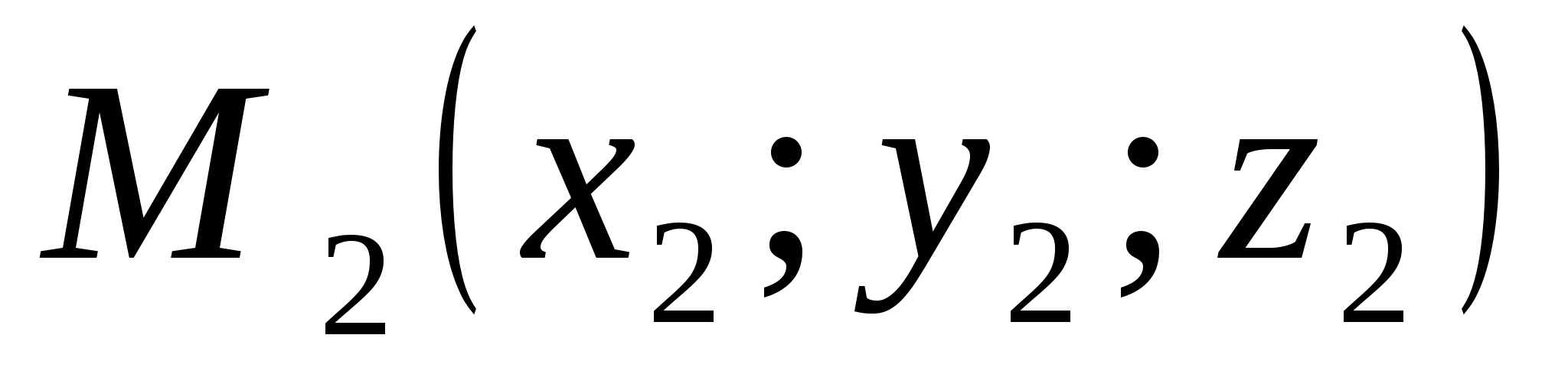 . Hãy thể hiện khoảng cáchd
giữa các điểm
. Hãy thể hiện khoảng cáchd
giữa các điểm 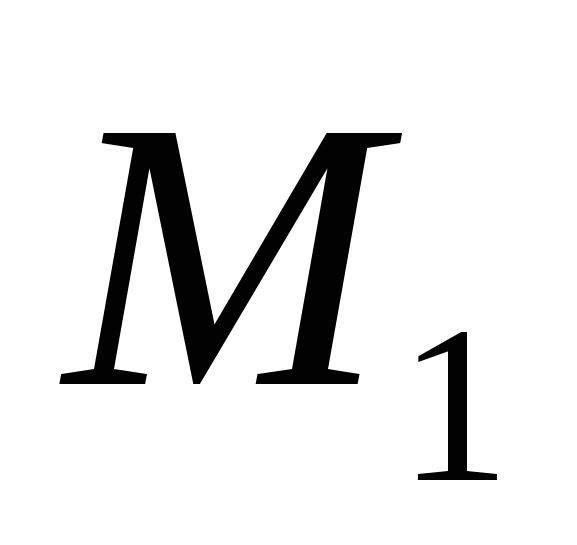 Và
Và 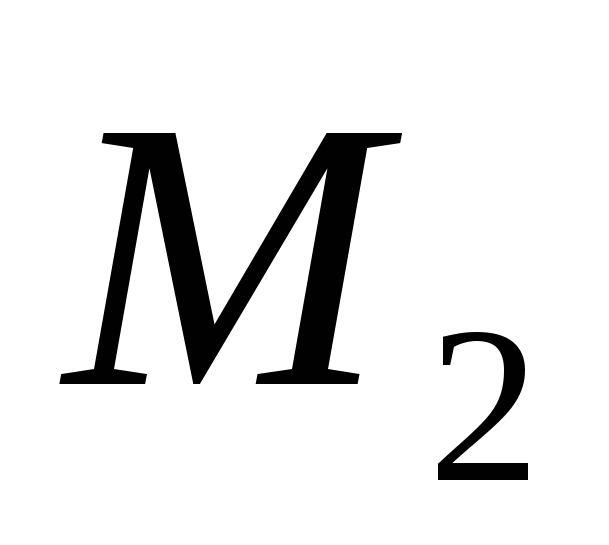 thông qua tọa độ của chúng.
thông qua tọa độ của chúng.
Xét vectơ ở đó .
Nhưng 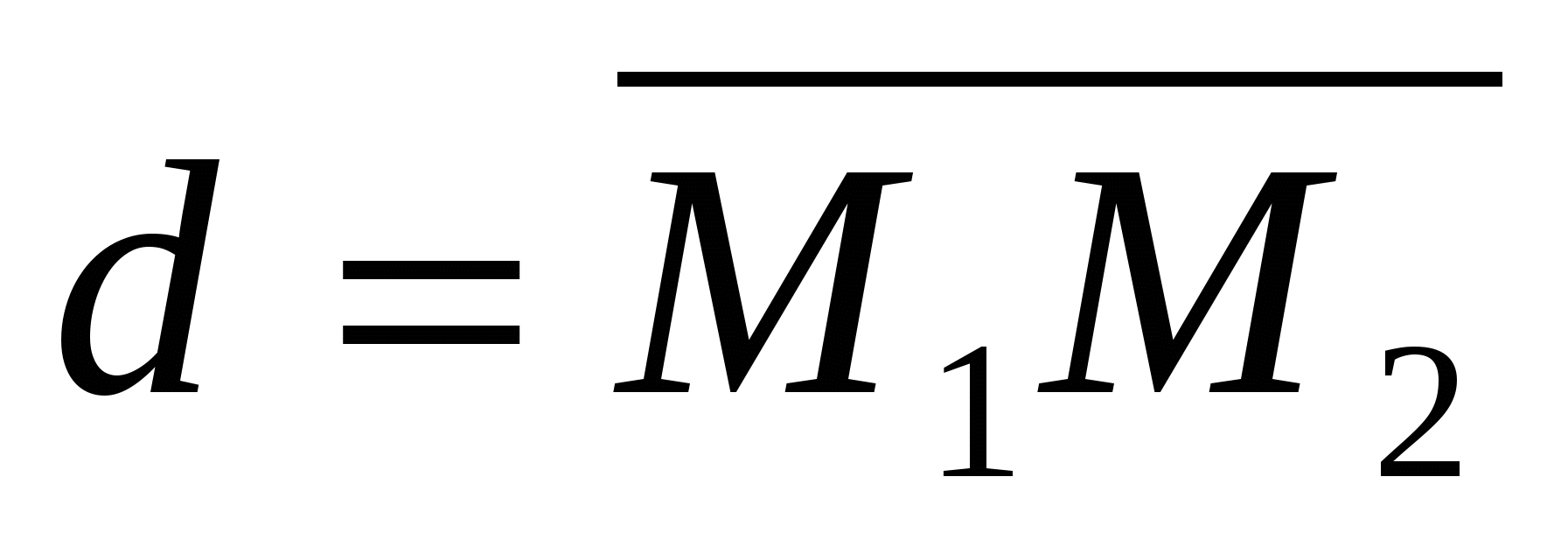 . Như vậy,khoảng cách giữa các điểm
. Như vậy,khoảng cách giữa các điểm 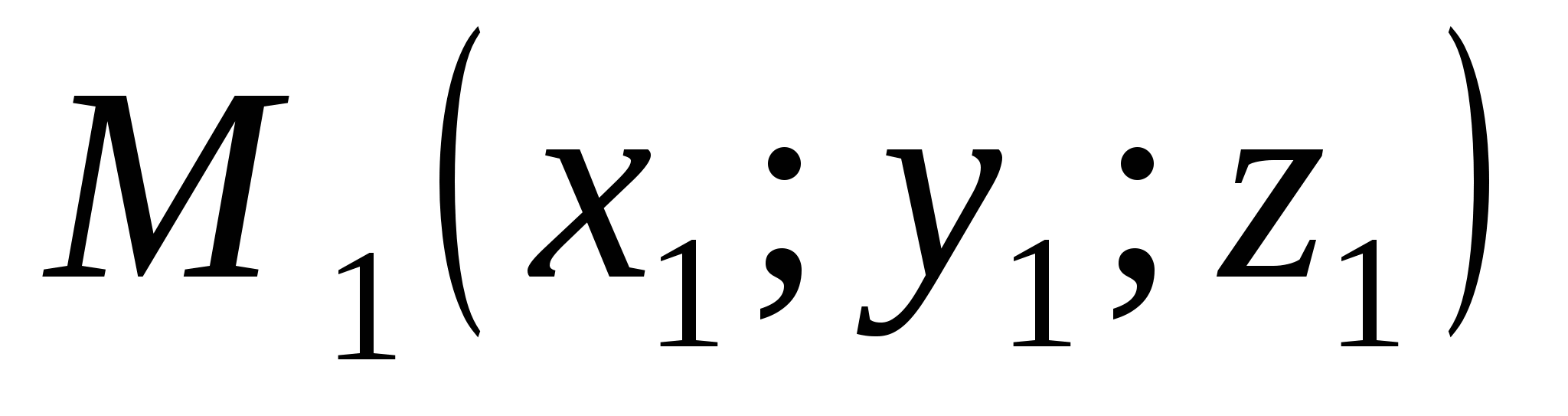 Và
Và 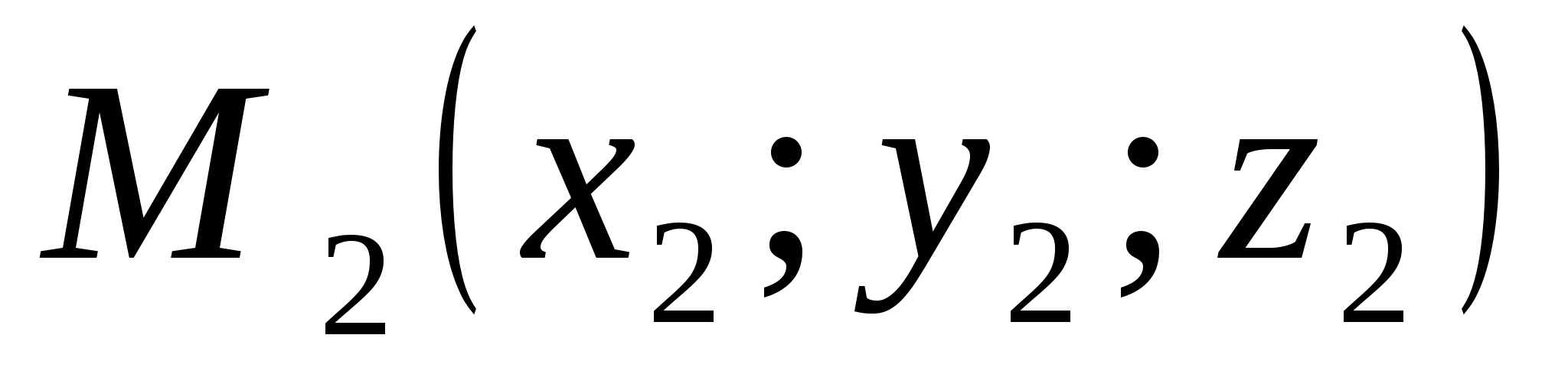
tính theo công thức .
6. Tích vô hướng các vectơ và tính góc giữa các vectơ qua tọa độ của chúng.
1) Tích vô hướng của vectơ
Tích vô hướng của hai vectơ là tích độ dài của chúng và cosin của góc giữa chúng.
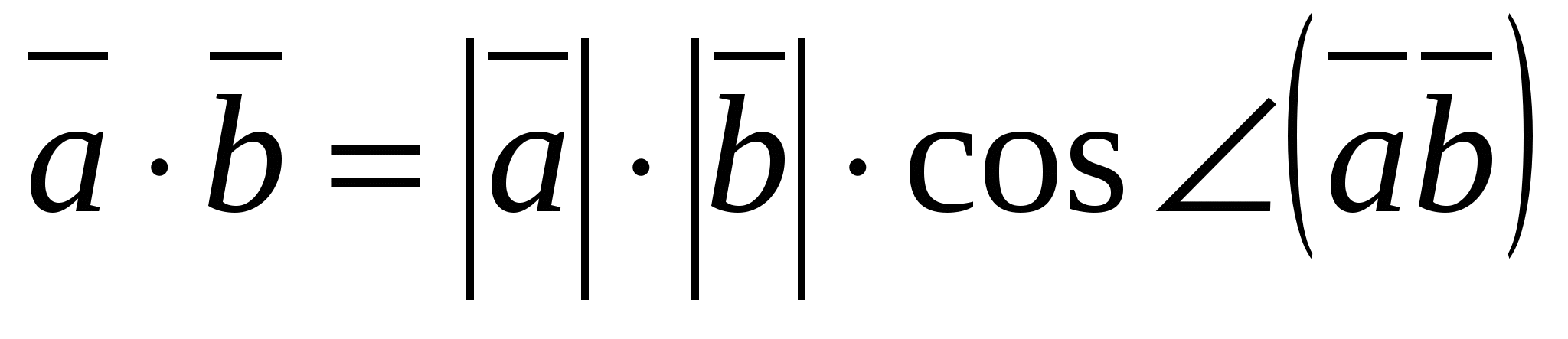
những thứ kia.

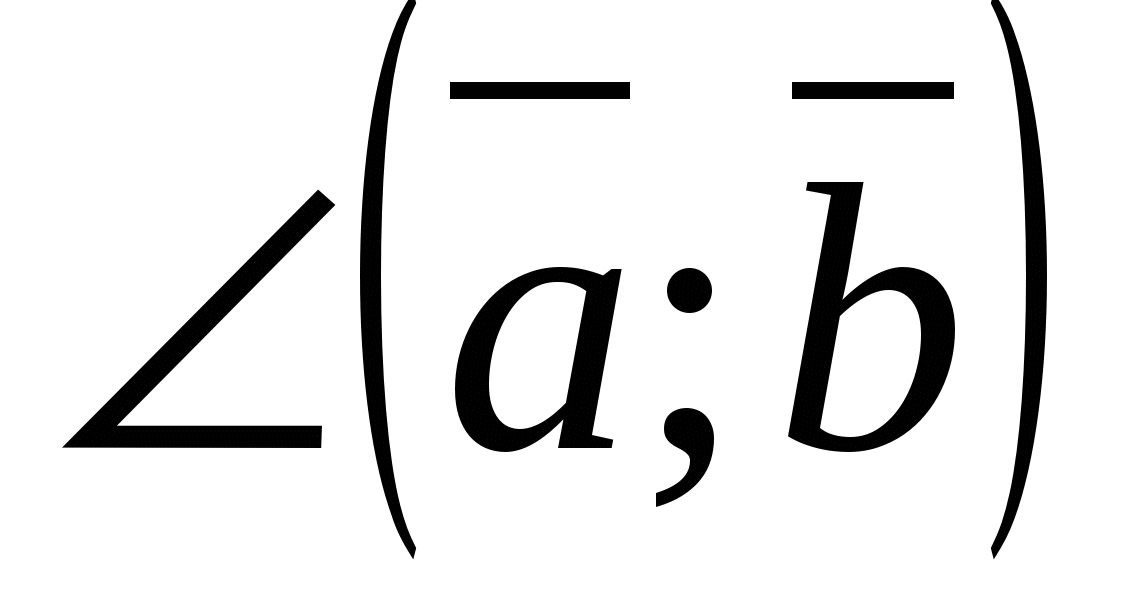 - cay.
- cay.
Tích vô hướng của các vectơ khác 0 là âm khi và chỉ khi góc giữa các vectơ là tù,
những thứ kia.
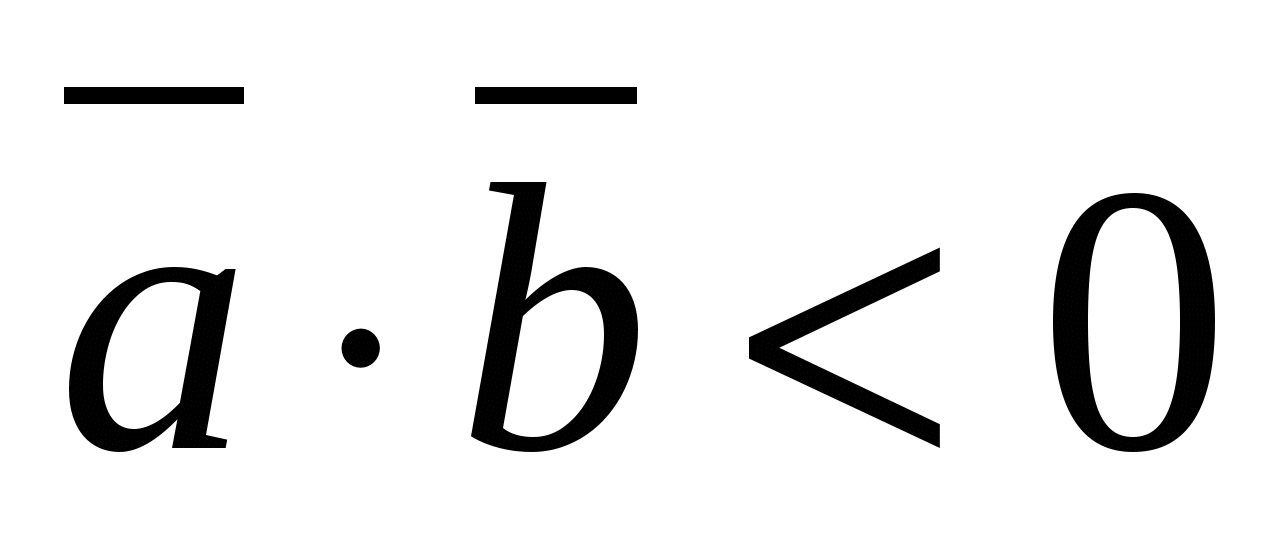

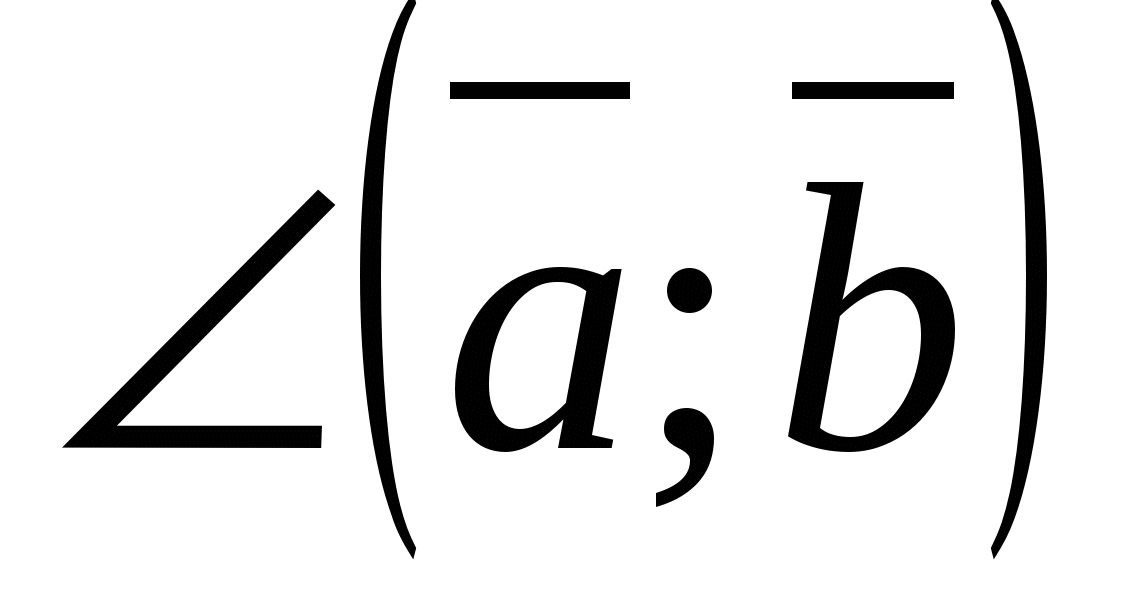 - thẳng thừng.
- thẳng thừng.
Đối với mọi vectơ, 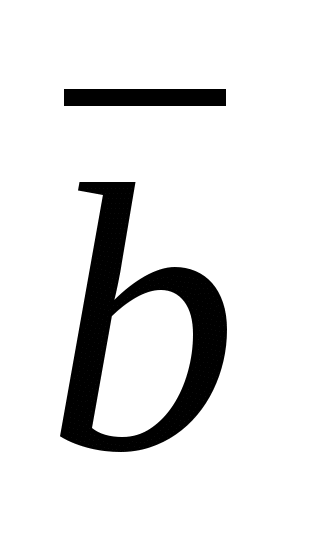 ,
, 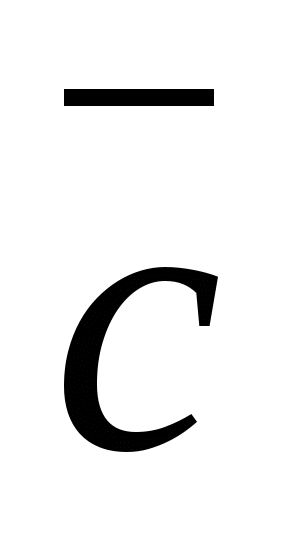 , và bất kỳ số nàok
các đẳng thức có giá trị:
, và bất kỳ số nàok
các đẳng thức có giá trị:
1. 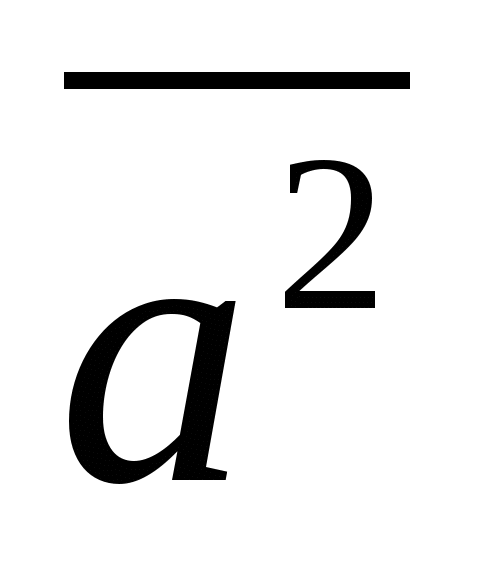
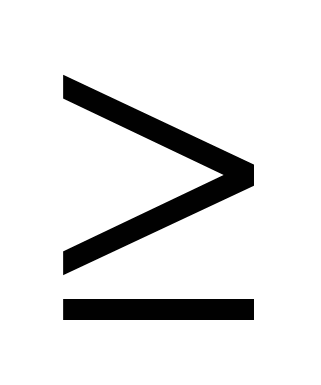 0 và
0 và 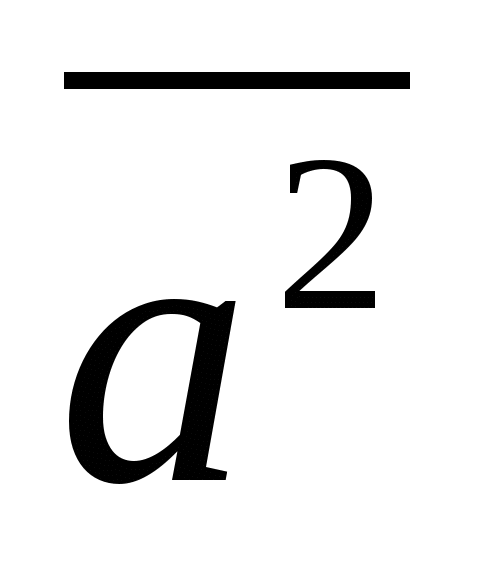 > 0 lúc
> 0 lúc 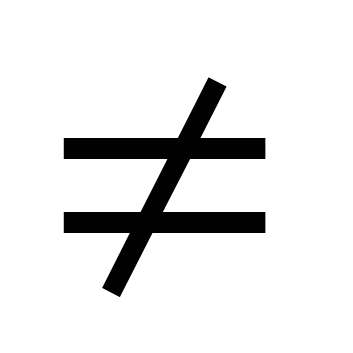 0.
0.
2. 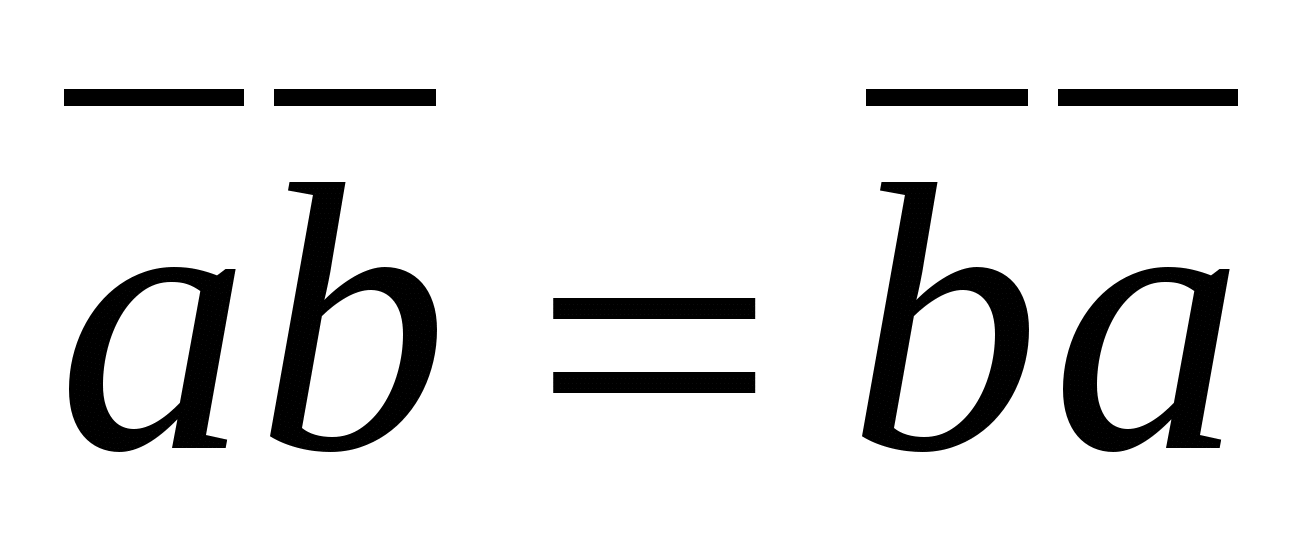 (luật chuyển nhượng).
(luật chuyển nhượng).
3.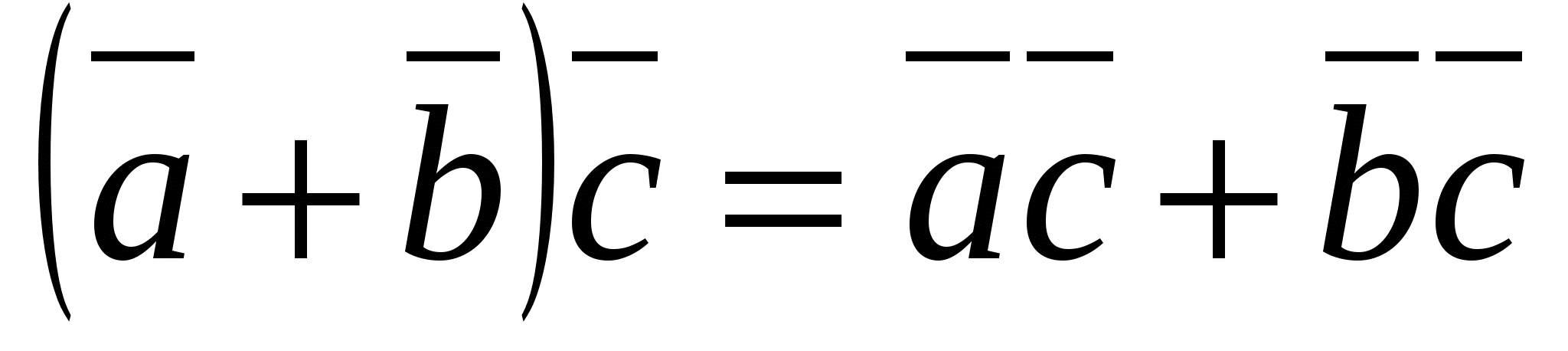 (luật phân phối).
(luật phân phối).
4. 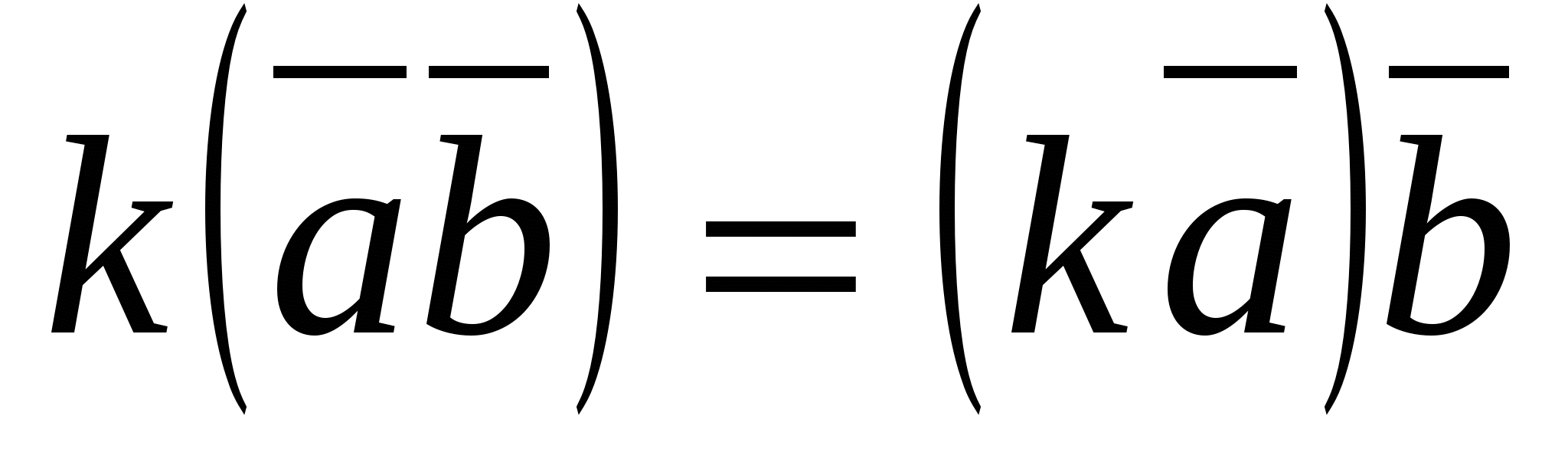 (luật kết hợp).
(luật kết hợp).
2) Tính góc giữa các vectơ bằng tọa độ của chúng.
Cosin của góc  giữa các vectơ khác 0
giữa các vectơ khác 0 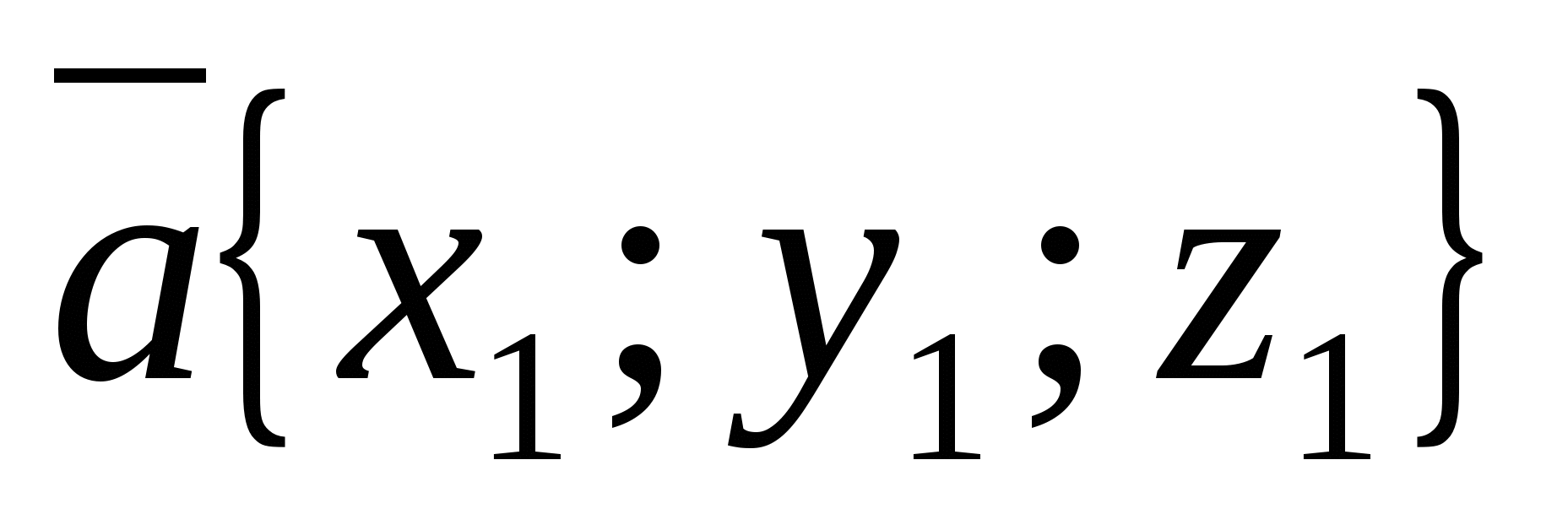 Và
Và 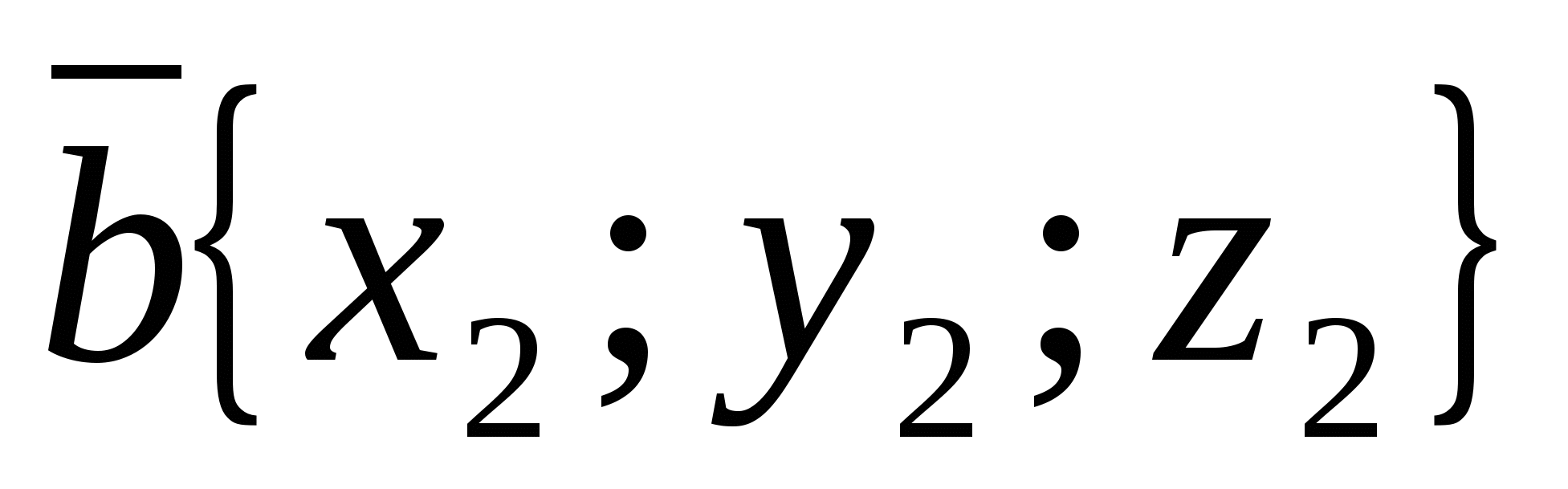 tính theo công thức
tính theo công thức
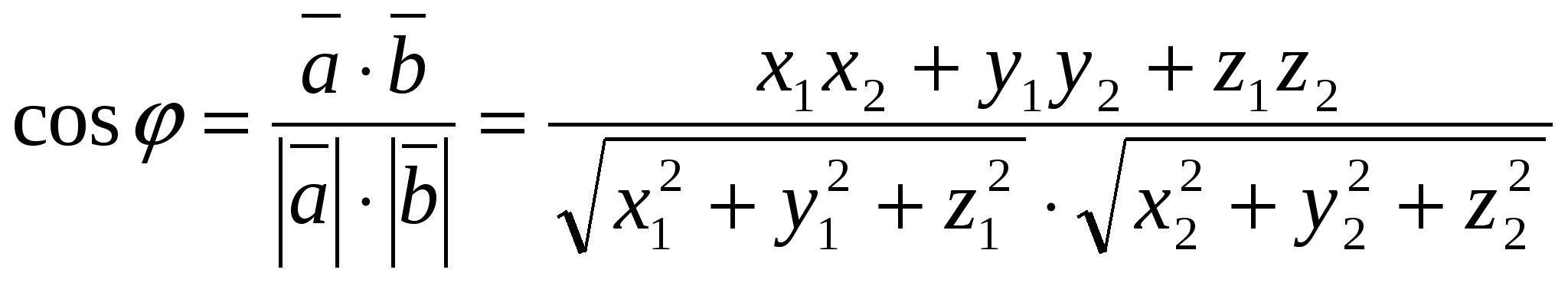 ,
,
Ở đâu 
7. Tính góc giữa đường thẳng và mặt phẳng.
1) Góc giữa các đường thẳng.
Để giải quyết vấn đề này, chúng tôi đưa ra khái niệm vectơ chỉ hướng của đường thẳng.
Sự định nghĩa.
Một vectơ khác 0 được gọi là vectơ chỉ phương của đường thẳng a nếu nó nằm trên đường thẳng a hoặc trên đường thẳng song song với a.
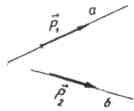 Ví dụ
Ví dụ
Vectơ 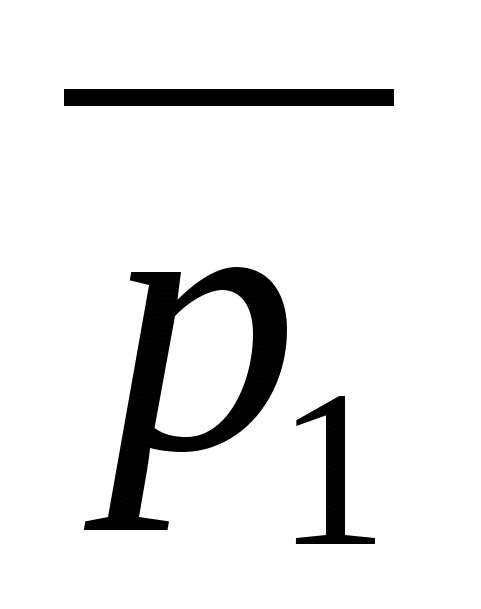 Và
Và  hướng dẫn thẳngMột
Và b
, tương ứng.
hướng dẫn thẳngMột
Và b
, tương ứng.
Sự định nghĩa.
Góc giữa các đường thẳng là góc giữa các vectơ chỉ phương của các đường thẳng đó.
Góc giữa các đường thẳngMột
Và b
bằng góc giữa các vectơ chỉ phương của đường thẳng 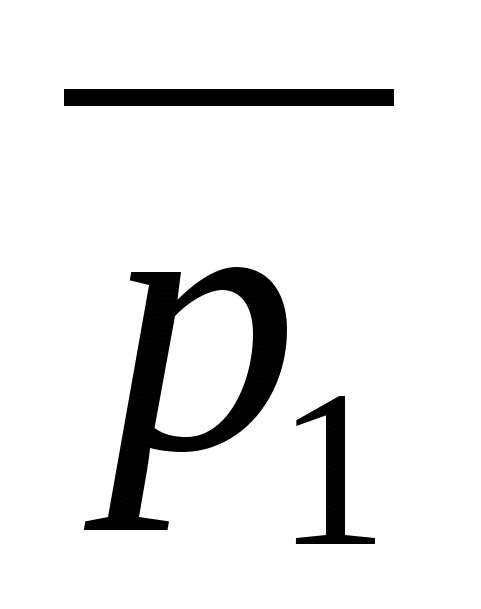 Và
Và 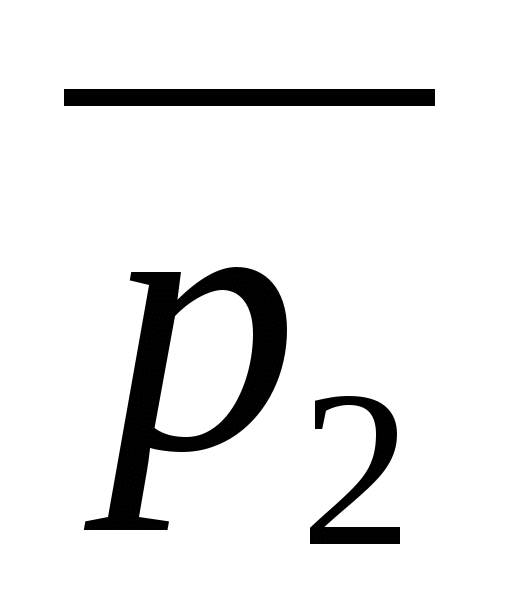 .
.
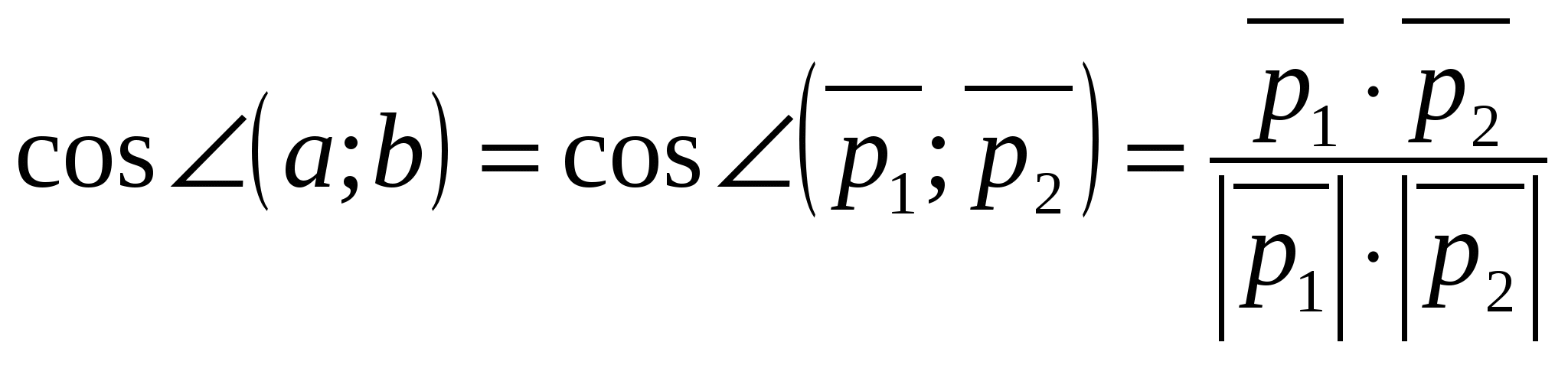 .
.
2) Góc giữa đường thẳng và mặt phẳng.
Sự định nghĩa.
Góc giữa một đường thẳng và một mặt phẳng là góc giữa vectơ chỉ phương của một đường thẳng cho trước và một vectơ khác 0 vuông góc với mặt phẳng(Bình thường).
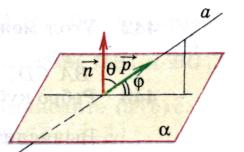
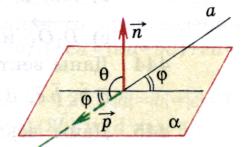
Cho phép 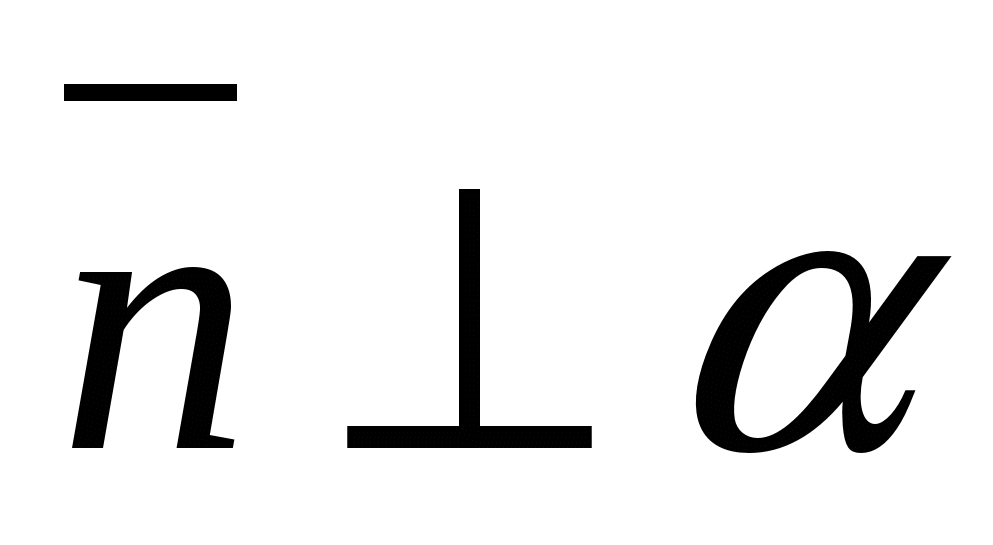 , (
, (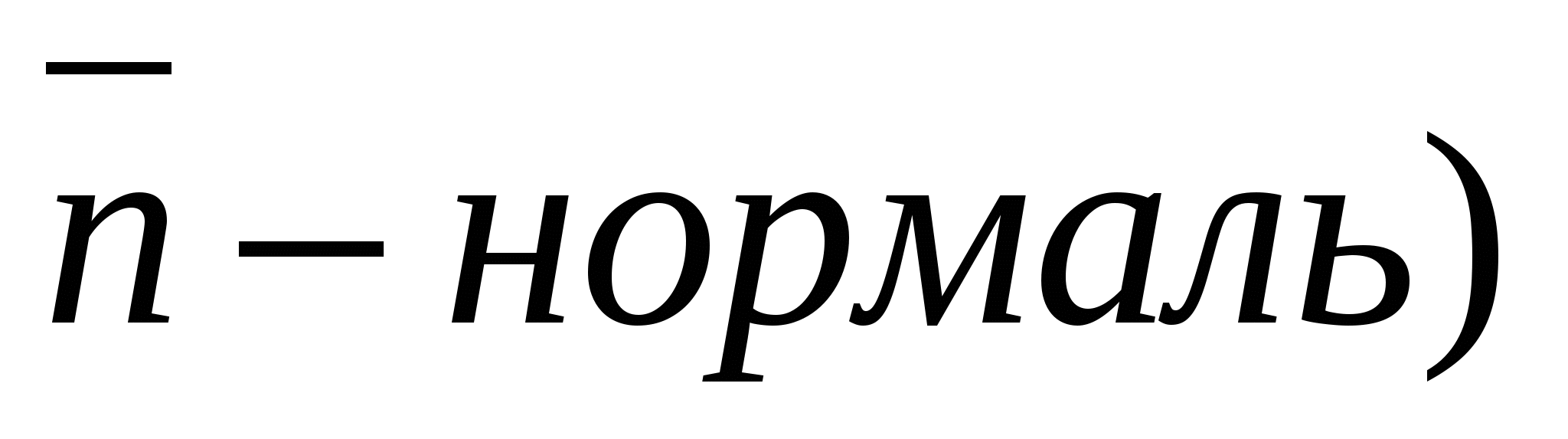
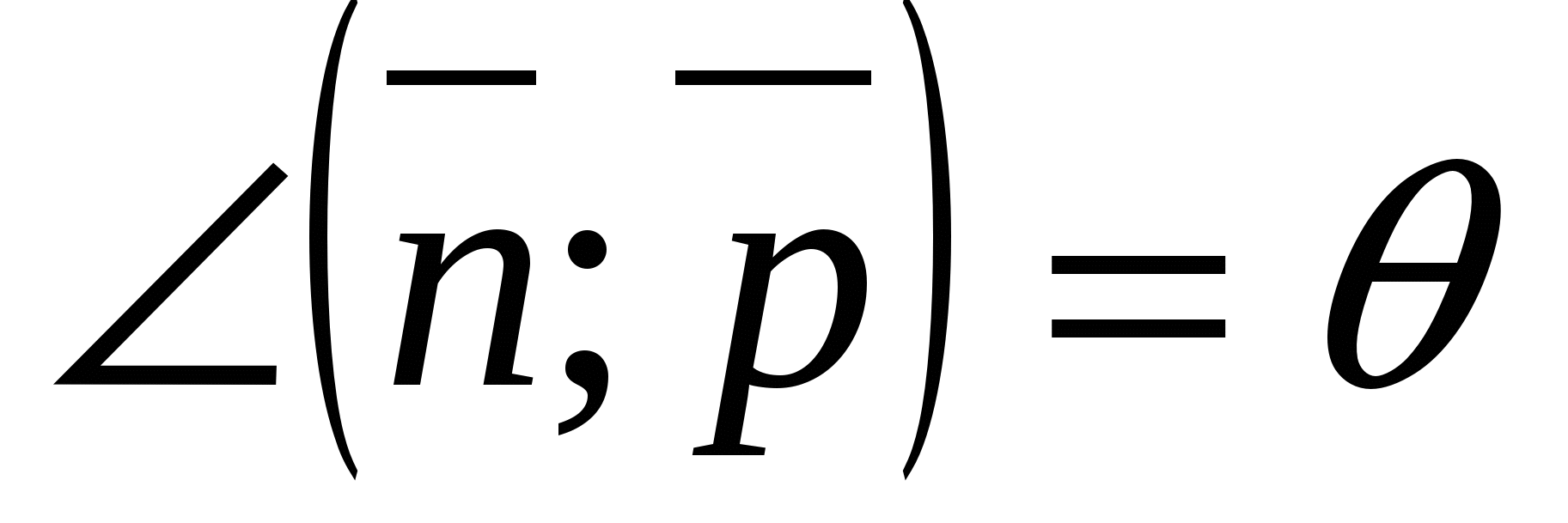 , MỘT
, MỘT  - góc mong muốn (
- góc mong muốn (  ).
).
Sau đó

Có nghĩa  .
.
Chương 3.
Ứng dụng phương pháp tọa độ để giải các bài toán lập thể.
Vấn đề.1
Dưới chân kim tự tháp MABC nằm tam giác vuông ABC. 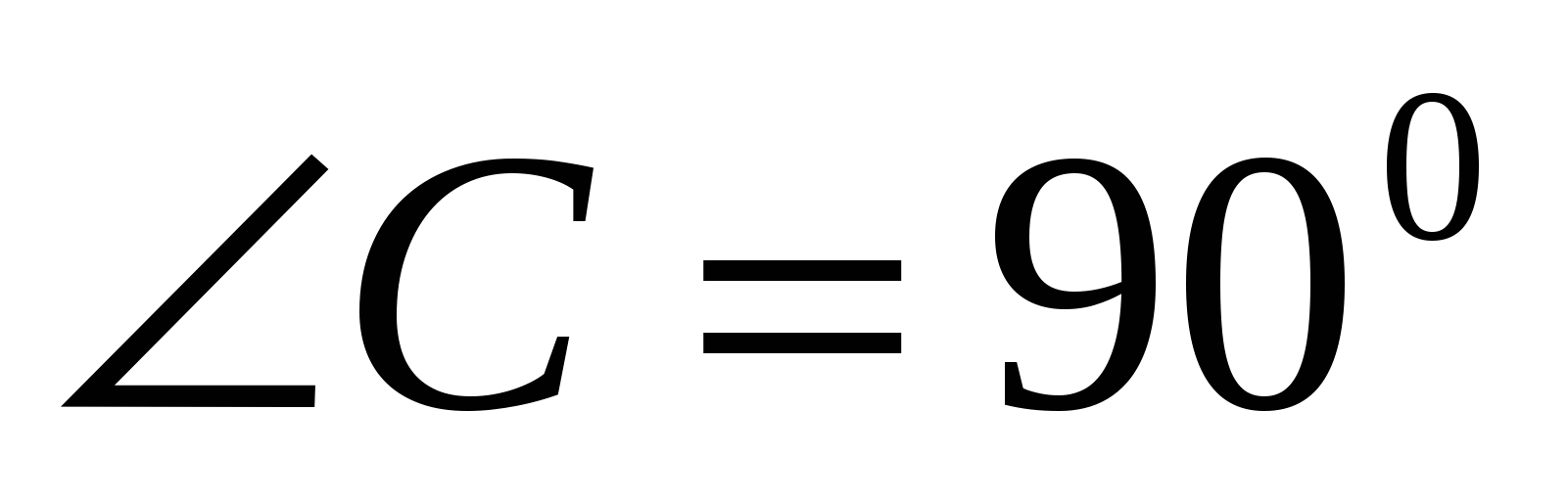 ,
A.C.=3,
BC=5. Cạnh AM vuông góc với AC, AM=4,
,
A.C.=3,
BC=5. Cạnh AM vuông góc với AC, AM=4, 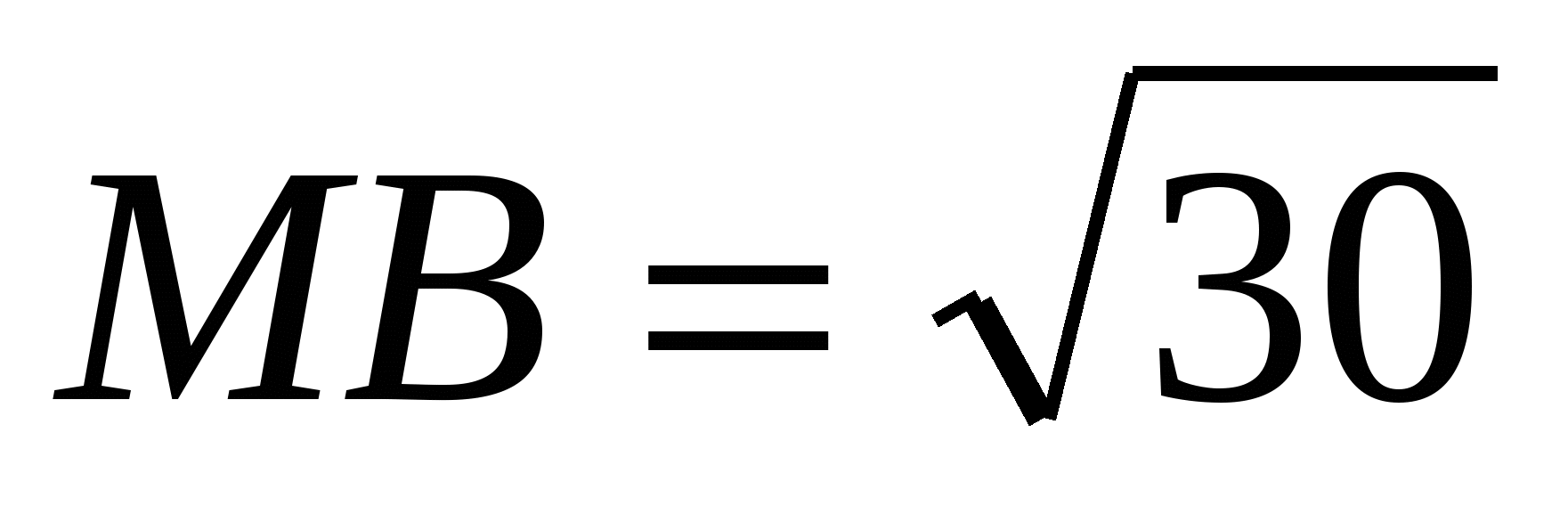 . Tìm khối lượng của kim tự tháp.
. Tìm khối lượng của kim tự tháp.
R 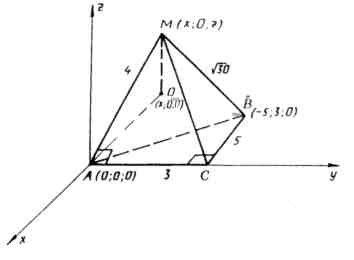 phán quyết.
phán quyết.
1) Hãy giới thiệu hệ tọa độ chữ nhật có gốc tọa độ tại điểm  . Trục
. Trục 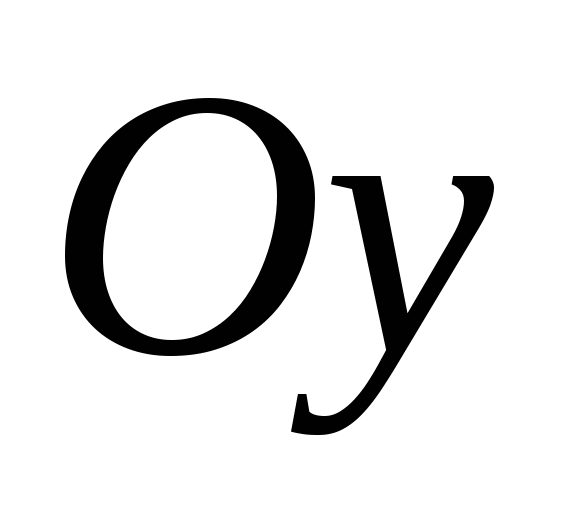 hãy hướng dọc theo rìaAC, và máy bay Ồ
y
dọc theo đáy của kim tự thápABC.
hãy hướng dọc theo rìaAC, và máy bay Ồ
y
dọc theo đáy của kim tự thápABC.
Trong hệ tọa độ này: 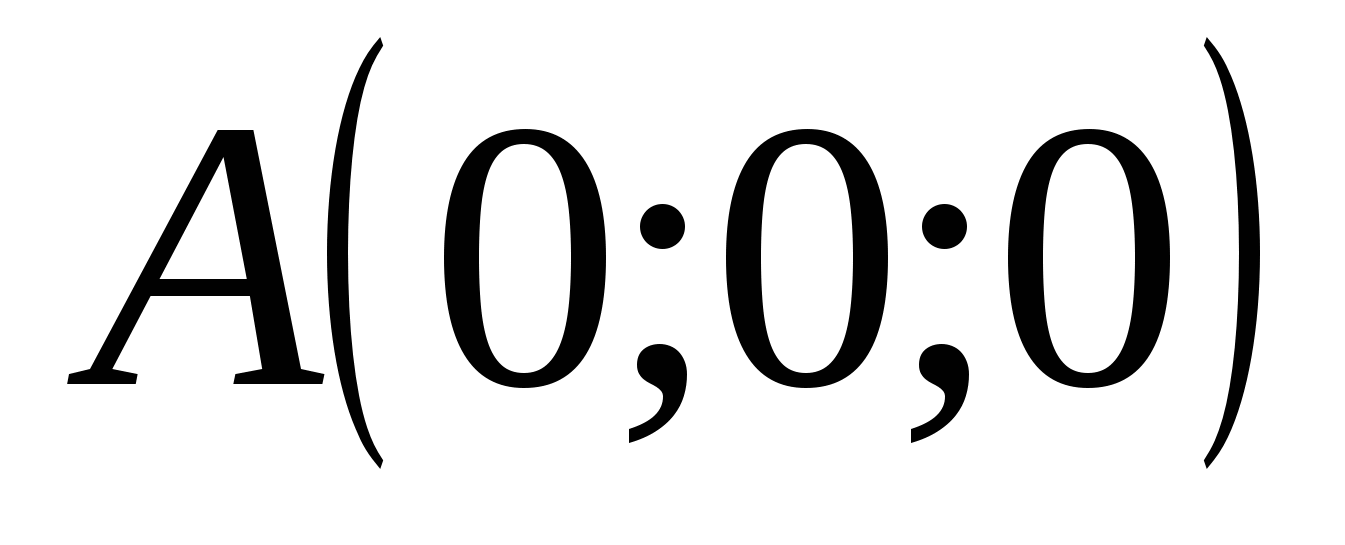 ,
, 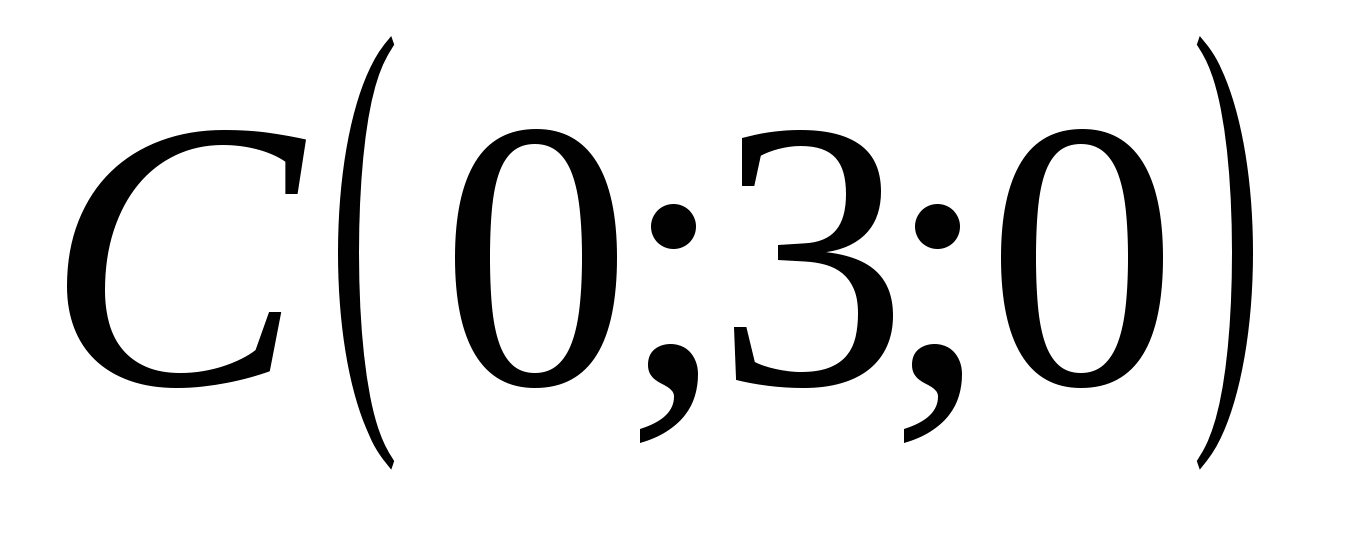 ,
, 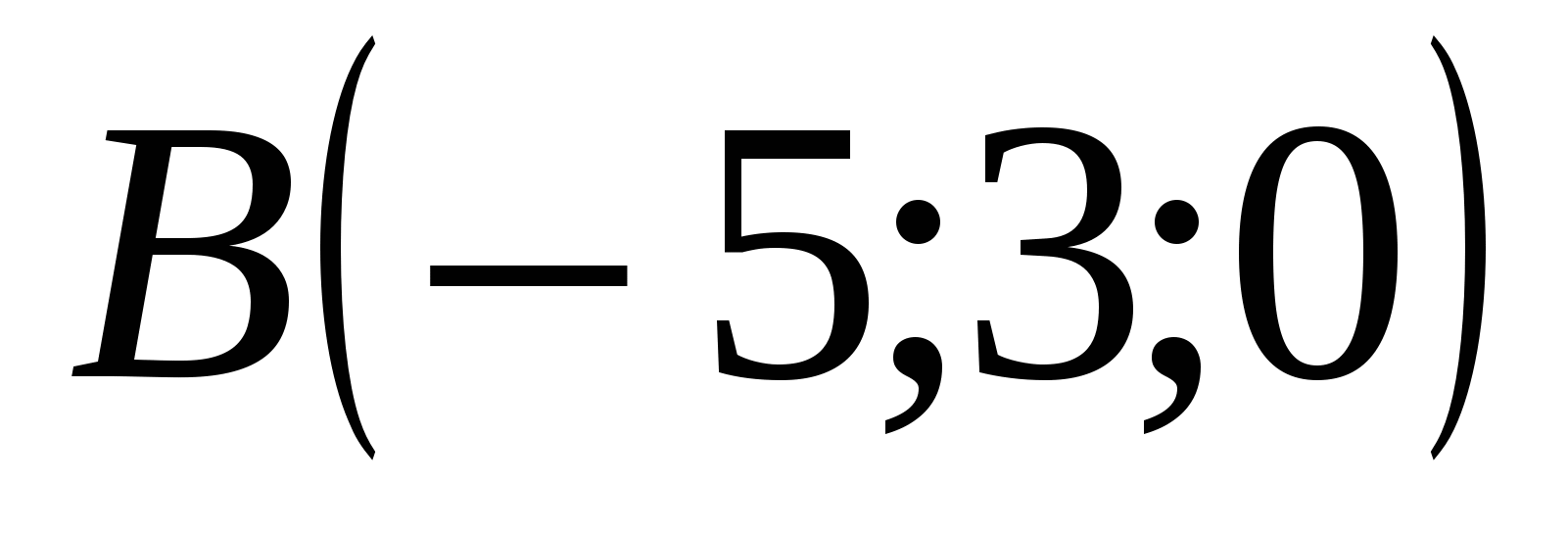 . Vì theo điều kiện
. Vì theo điều kiện 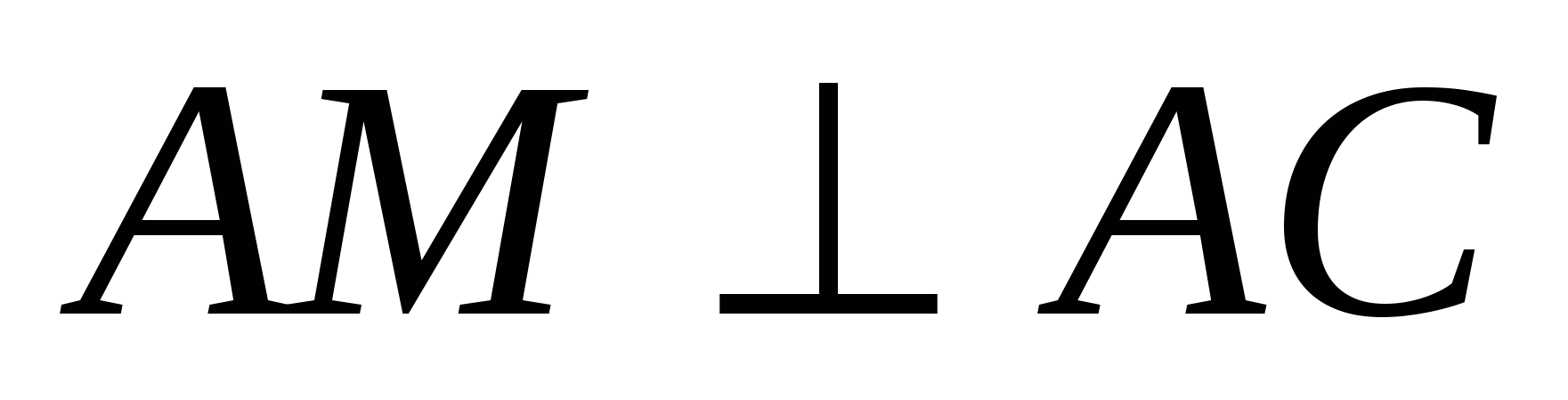 , thì điểm M nằm trong mặt phẳngxz
và có tọa độ
, thì điểm M nằm trong mặt phẳngxz
và có tọa độ
 .
.
2) 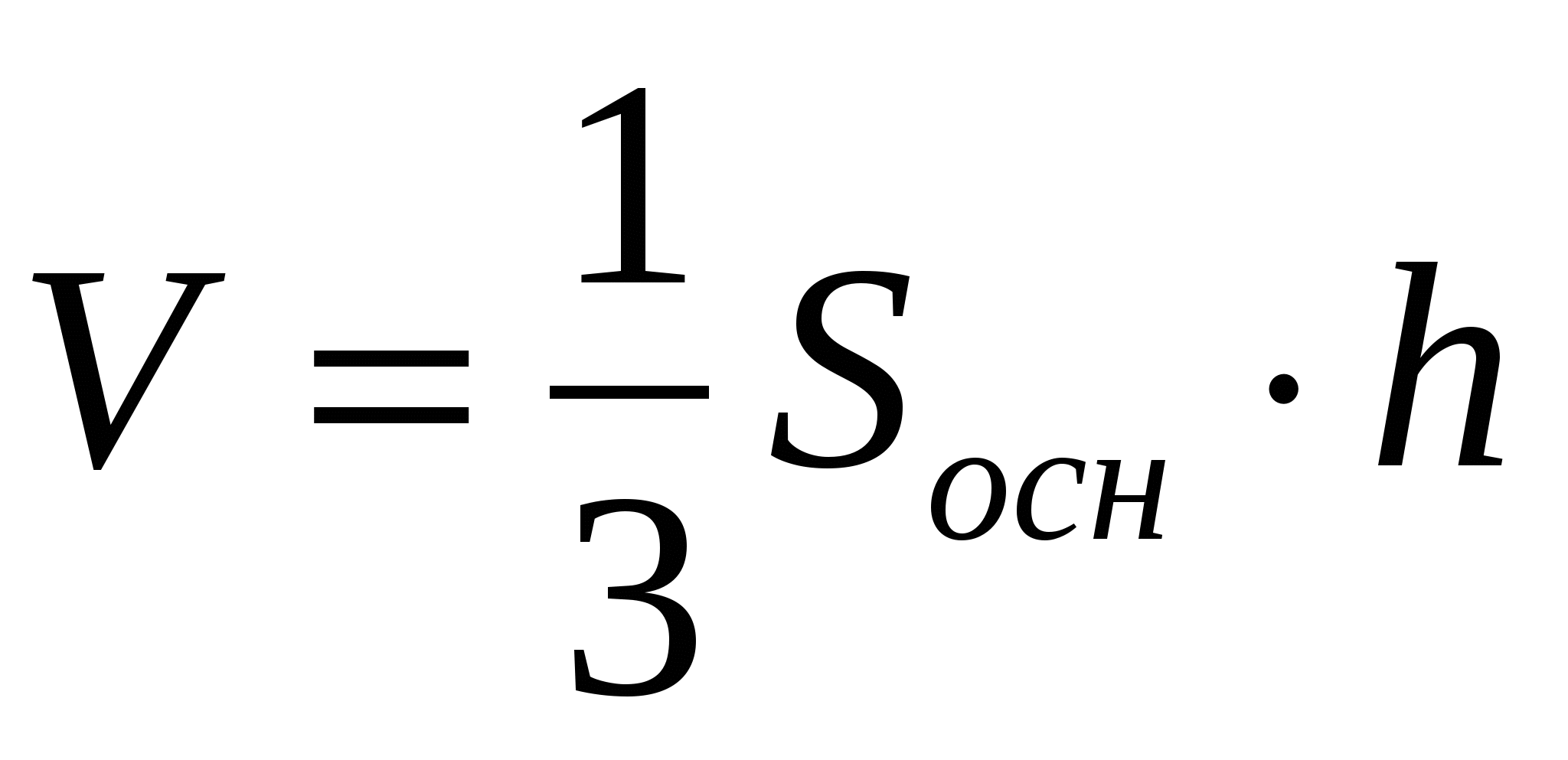 ,
, 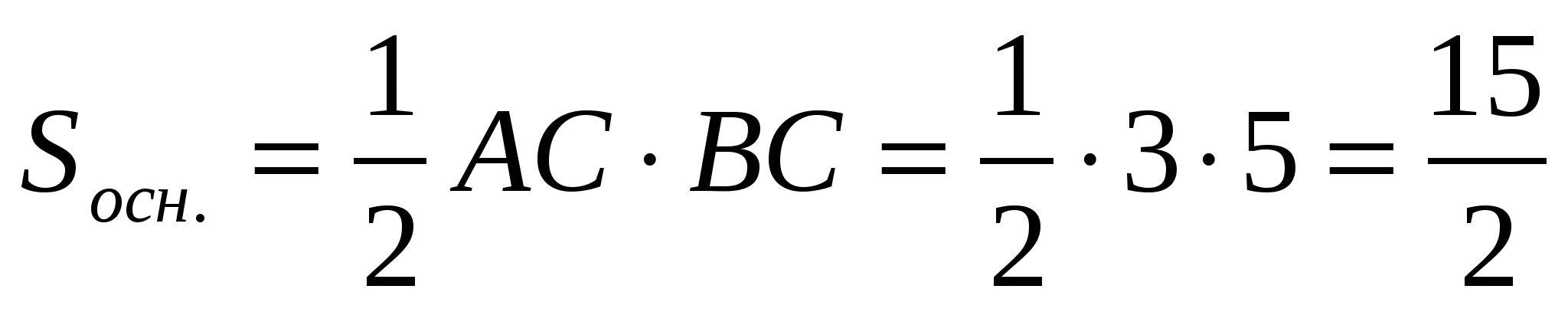 .
.
Hãy tìm chiều cao của kim tự tháp. Hãy thả từ điểmM vuông góc M
D
lên máy bay (ABC),
Sau đó  , bởi vì
, bởi vì 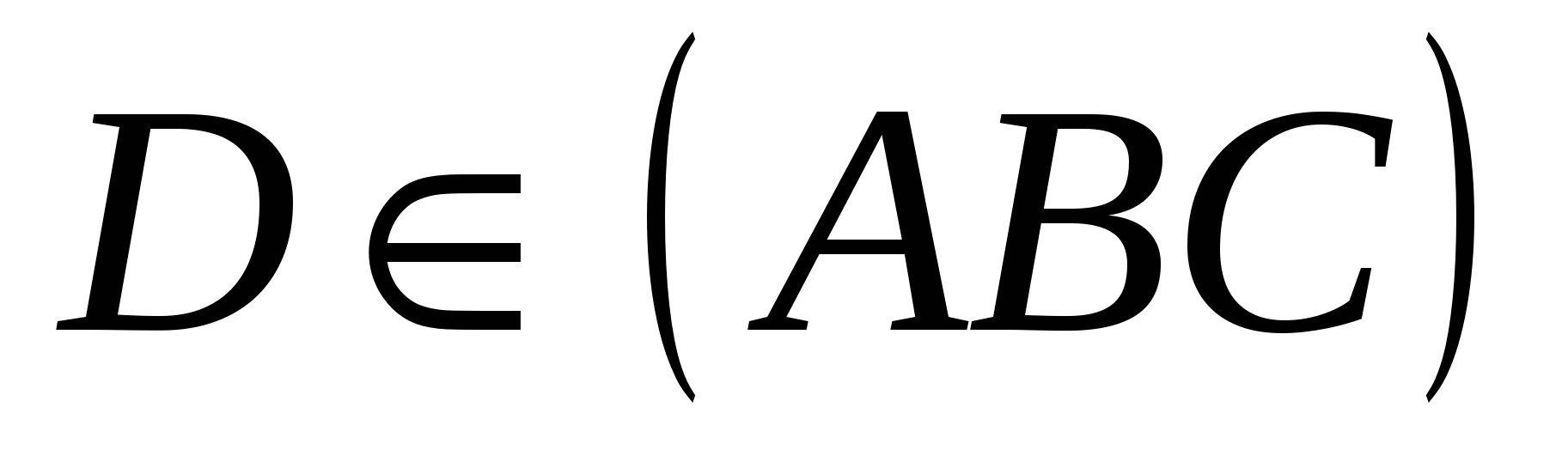 . Kể từ đây,
. Kể từ đây,  và khoảng cách giữa các điểmM Và Dbằng , bởi vì
và khoảng cách giữa các điểmM Và Dbằng , bởi vì 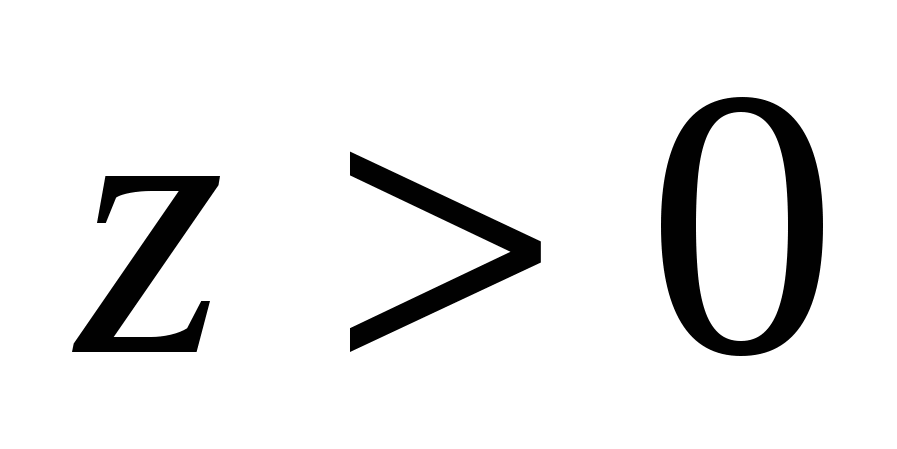 .
.
Hãy tìm giá trị tọa độz
sử dụng khoảng cách giữa các điểm chứa tọa độ đã cho: 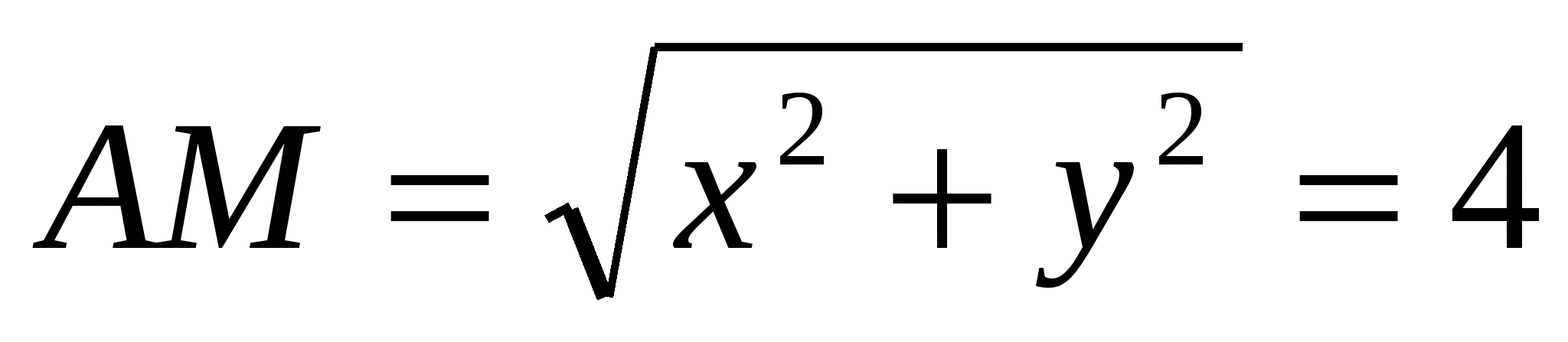 ,
,  . , tức là
. , tức là 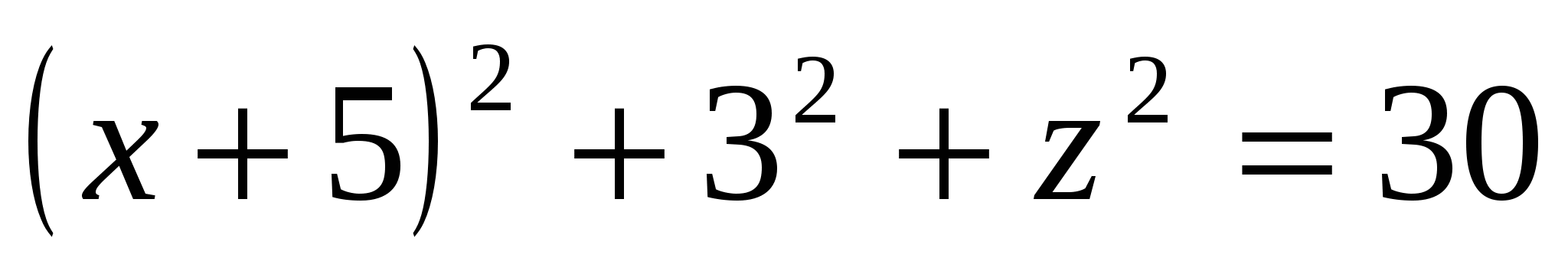 .
.
Chúng tôi có: 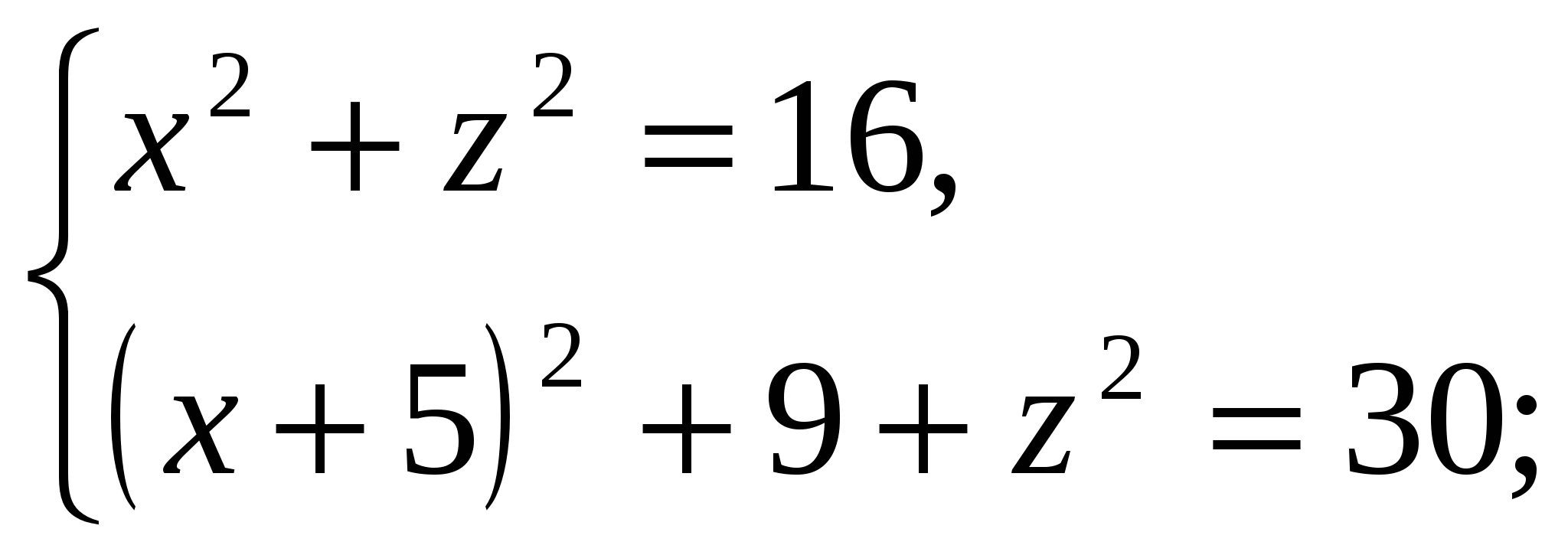
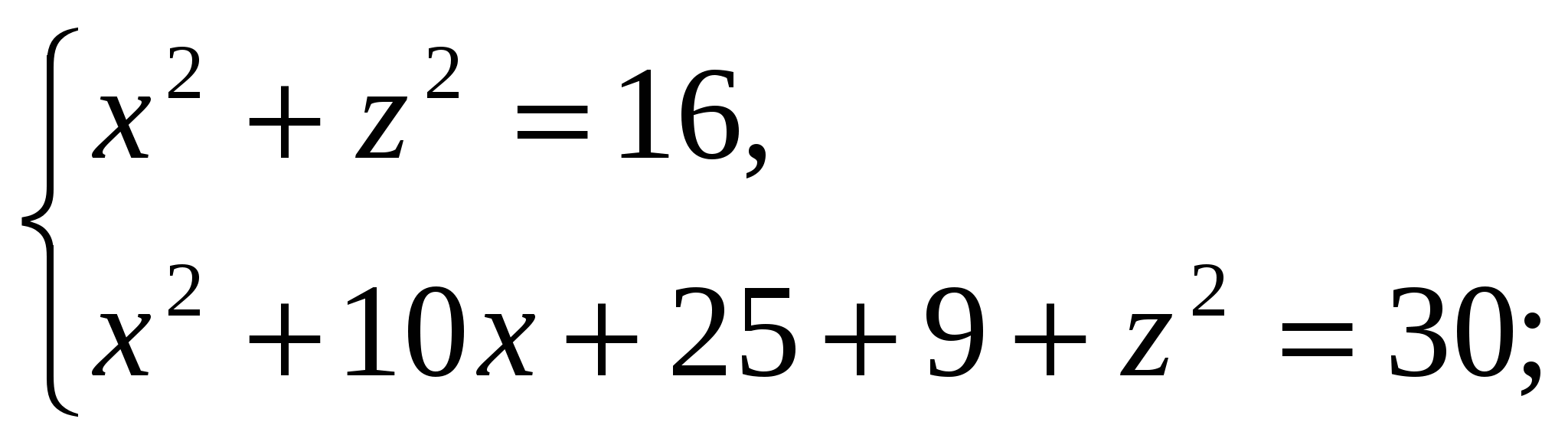
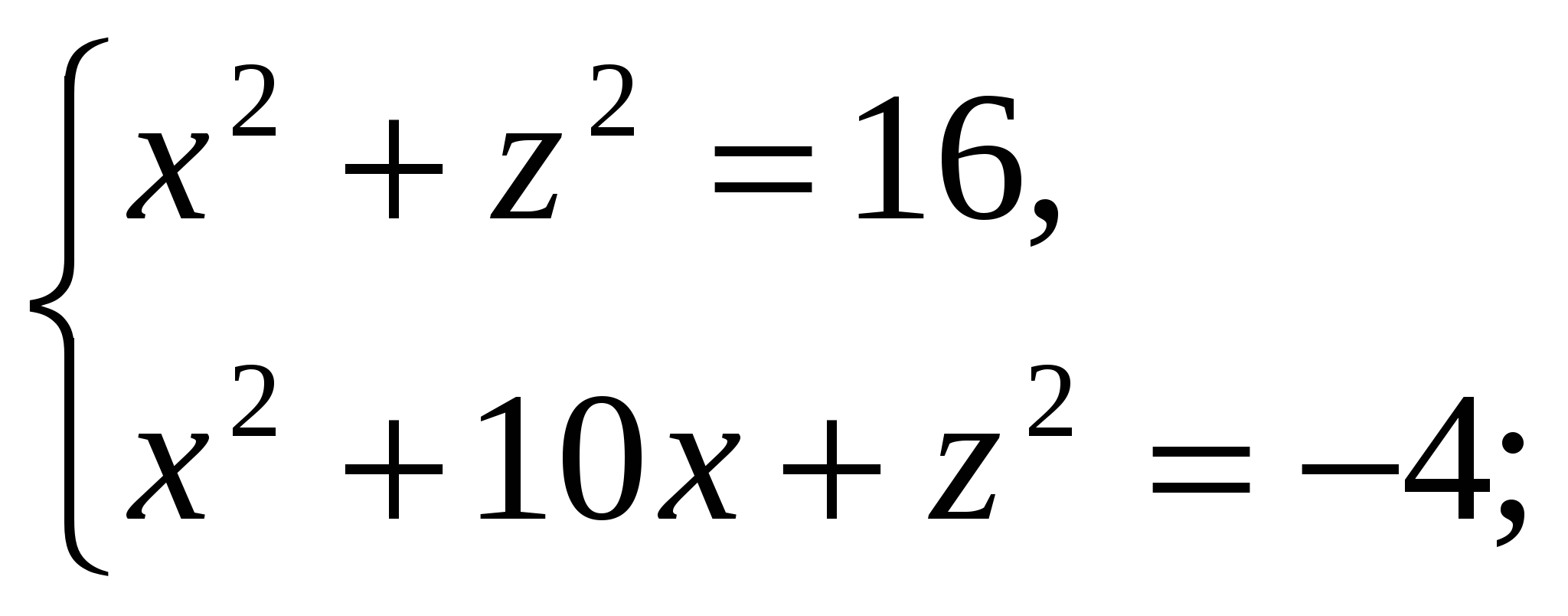
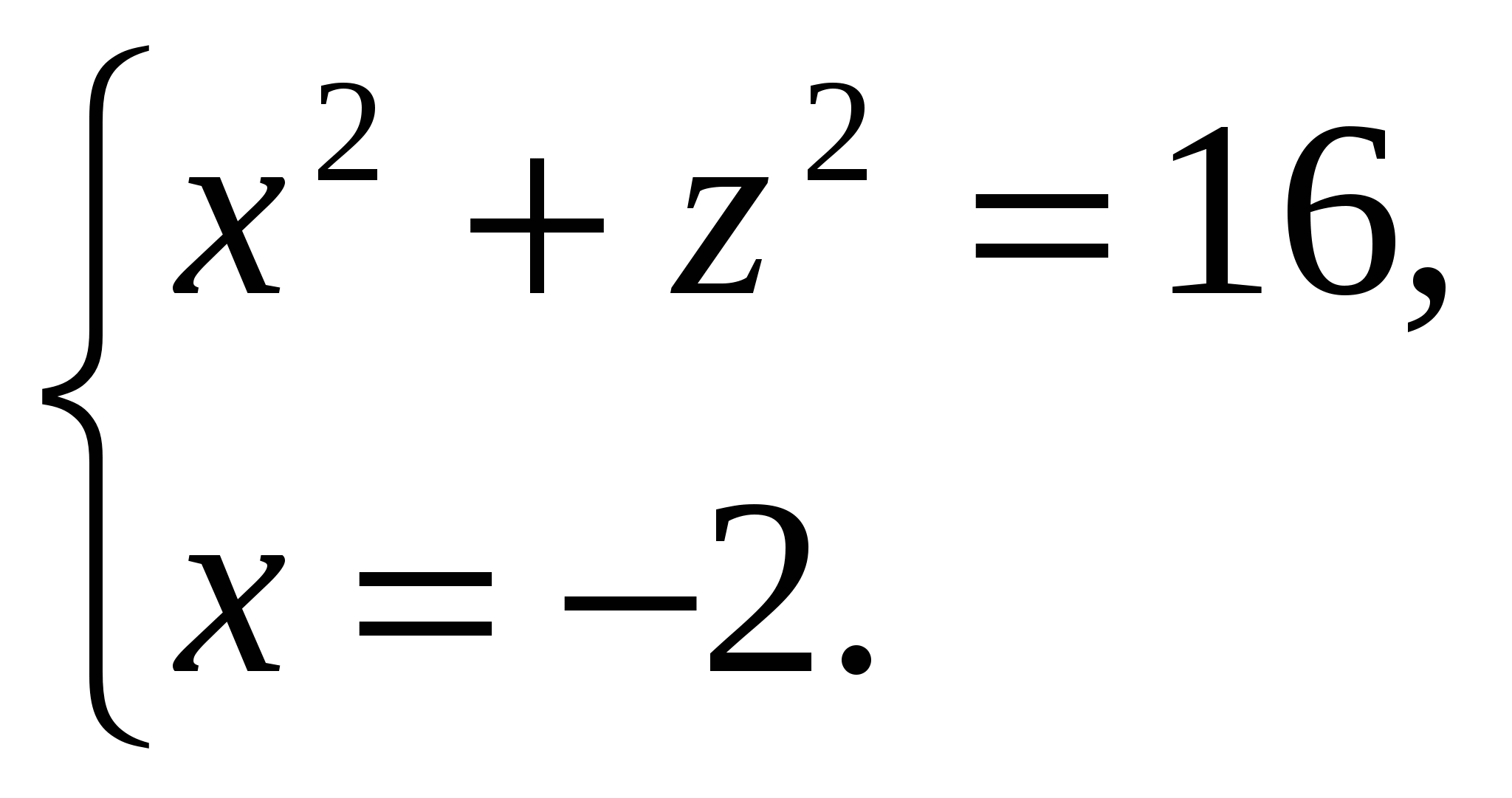
Bởi vì 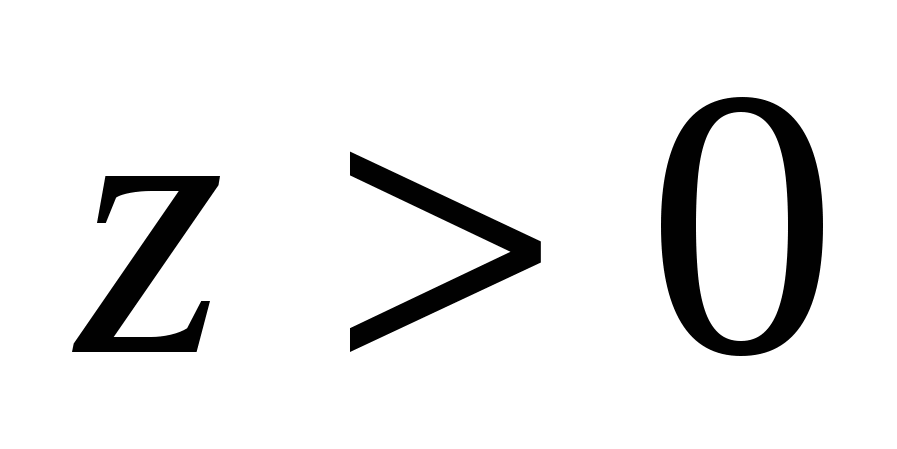 , thì chiều cao của kim tự tháp bằng
, thì chiều cao của kim tự tháp bằng 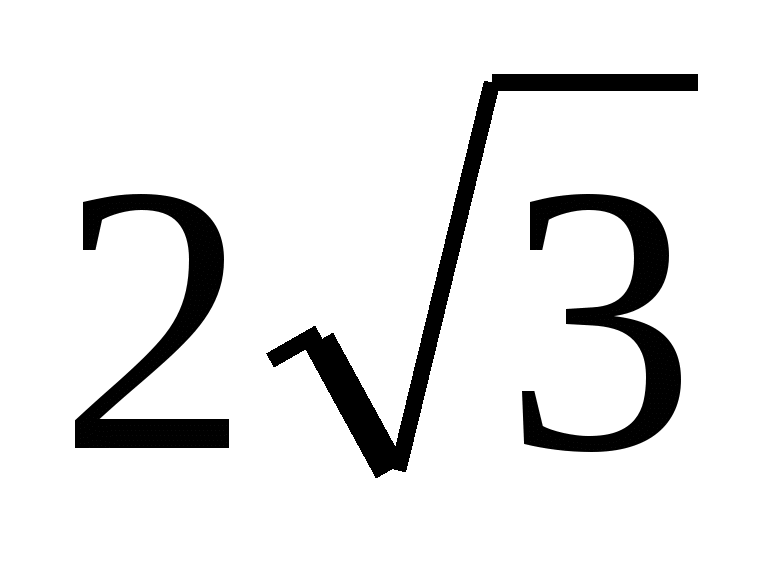 . Kể từ đây
. Kể từ đây 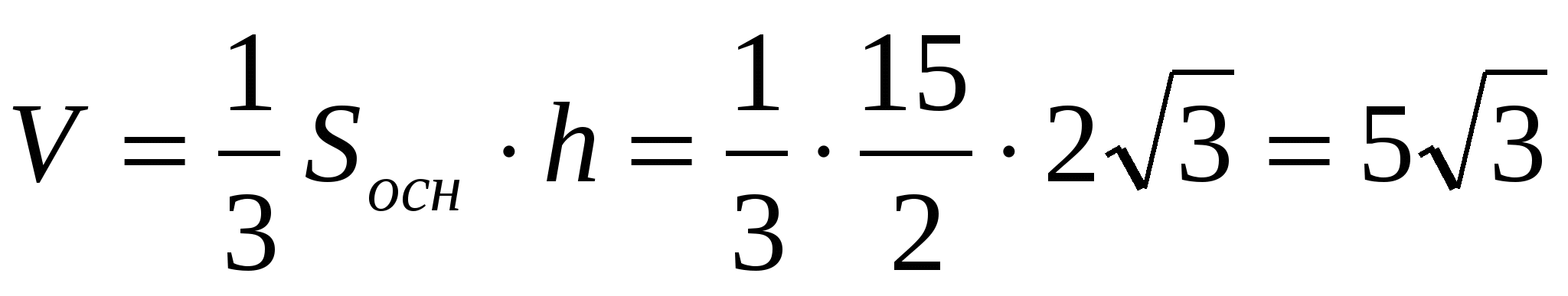 .
.
Trả lời: 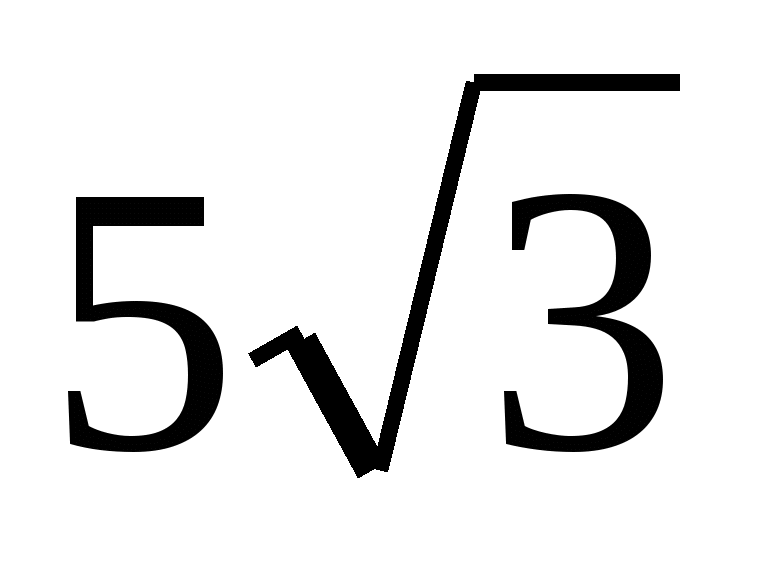 .
.
Vấn đề.2.
Trong hình chữ nhật có hình song song 
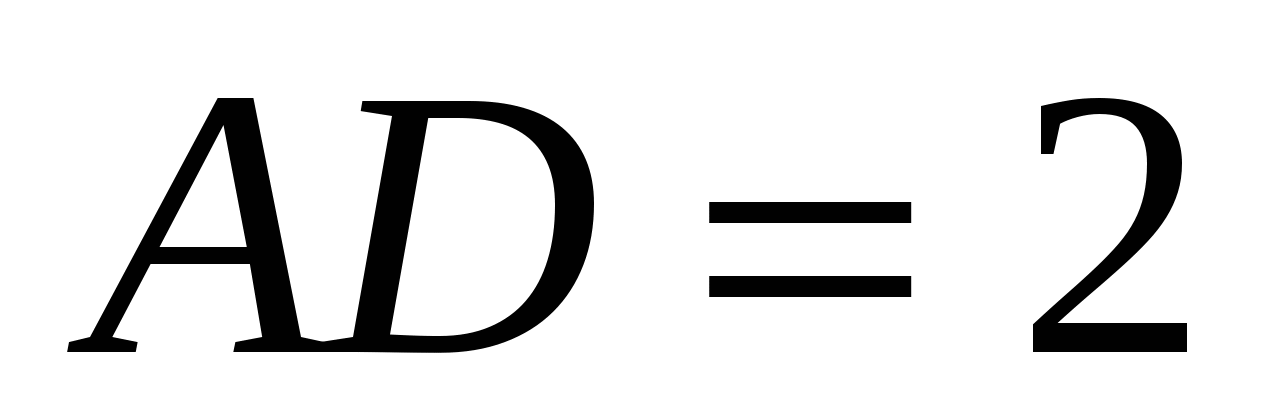 ,
, 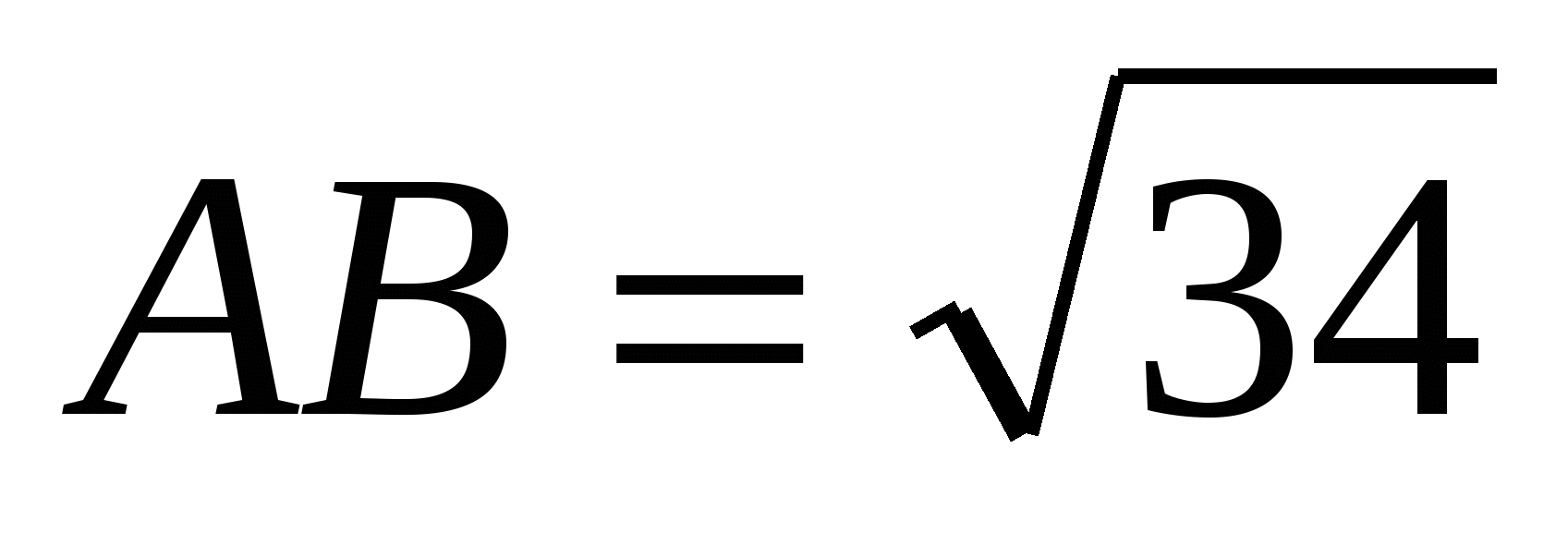 ,
,  . Tìm thấy:
góc giữa các đường thẳng
. Tìm thấy:
góc giữa các đường thẳng  Và
Và  .
.
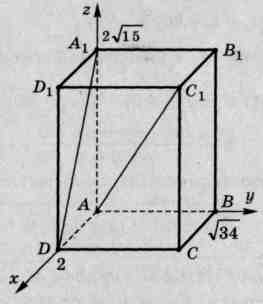 Giải pháp.
Giải pháp.
1). Hãy giới thiệu hệ tọa độ có gốc tọa độ tại điểm. 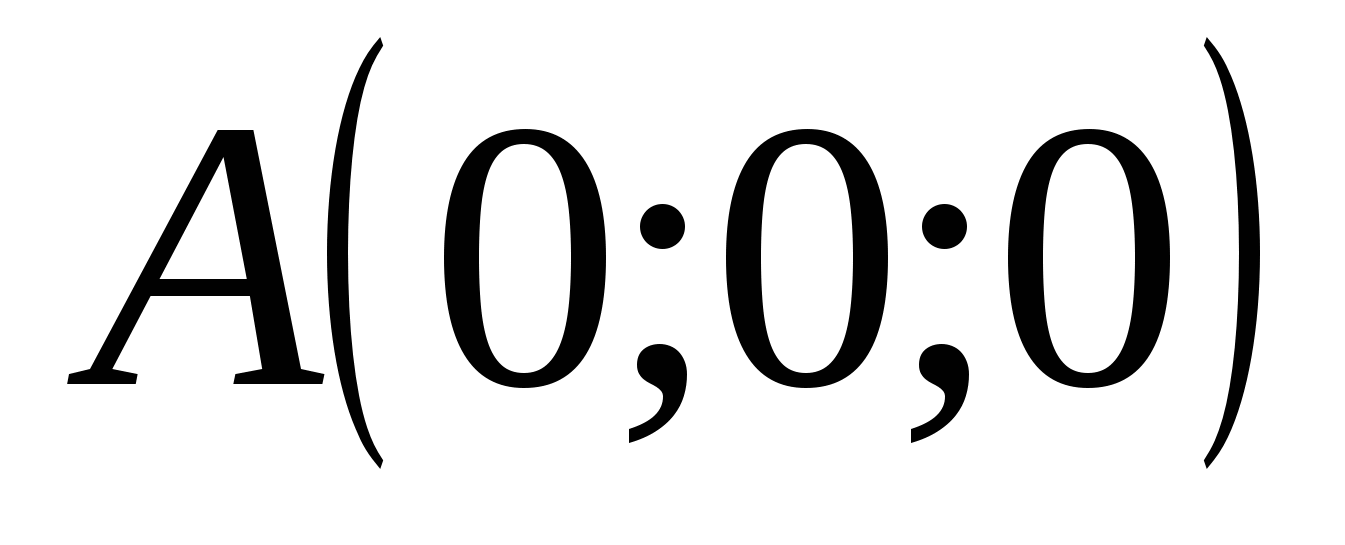 . Trục
. Trục 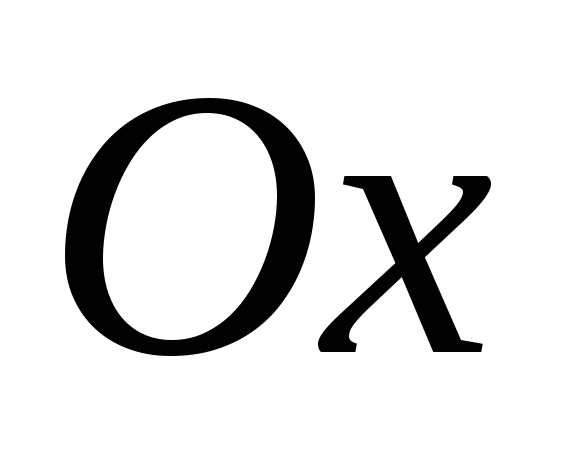 ,
,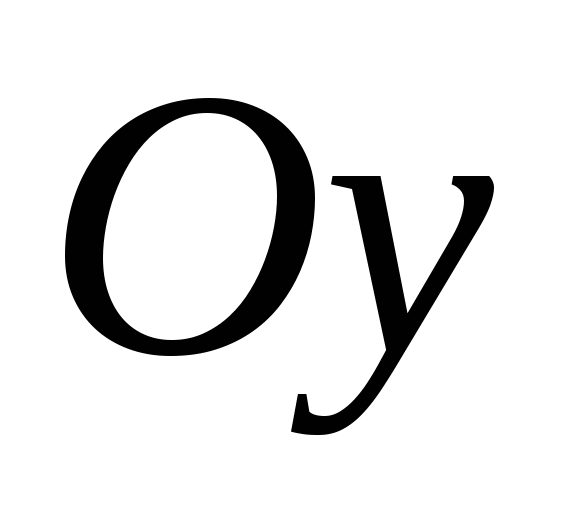 Và
Và  hãy hướng dọc theo xương sườn
hãy hướng dọc theo xương sườn  ,
, 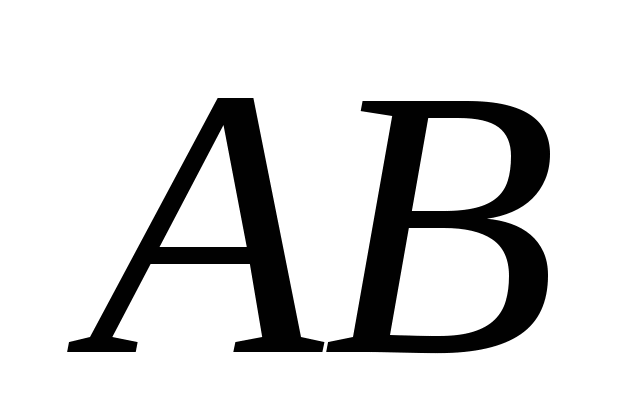 Và
Và 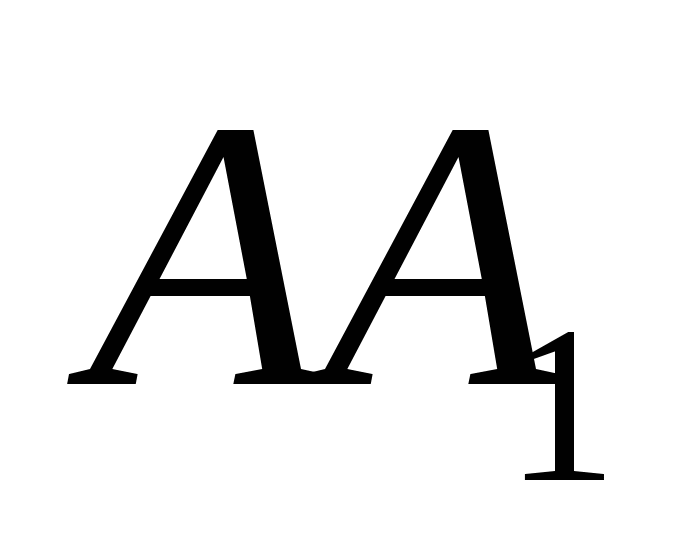 tương ứng. Vì góc giữa các đường thẳng thay đổi từ
tương ứng. Vì góc giữa các đường thẳng thay đổi từ  ĐẾN
ĐẾN  và góc giữa các vectơ từ
và góc giữa các vectơ từ  ĐẾN
ĐẾN 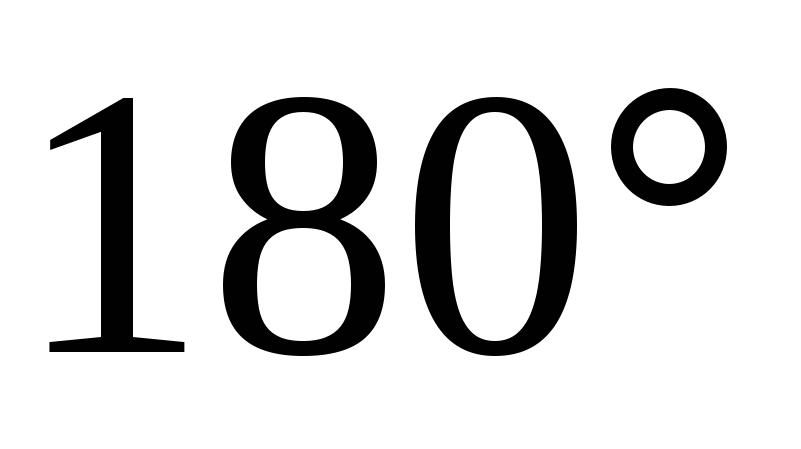 , khi đó góc giữa các đường thẳng
, khi đó góc giữa các đường thẳng  Và
Và  bằng góc giữa các vectơ
bằng góc giữa các vectơ  Và
Và  , nếu nó nhọn hoặc liền kề với nó, nếu góc giữa các vectơ là tù.
, nếu nó nhọn hoặc liền kề với nó, nếu góc giữa các vectơ là tù.
Như vậy,
2).Tính góc giữa các vectơ  Và
Và 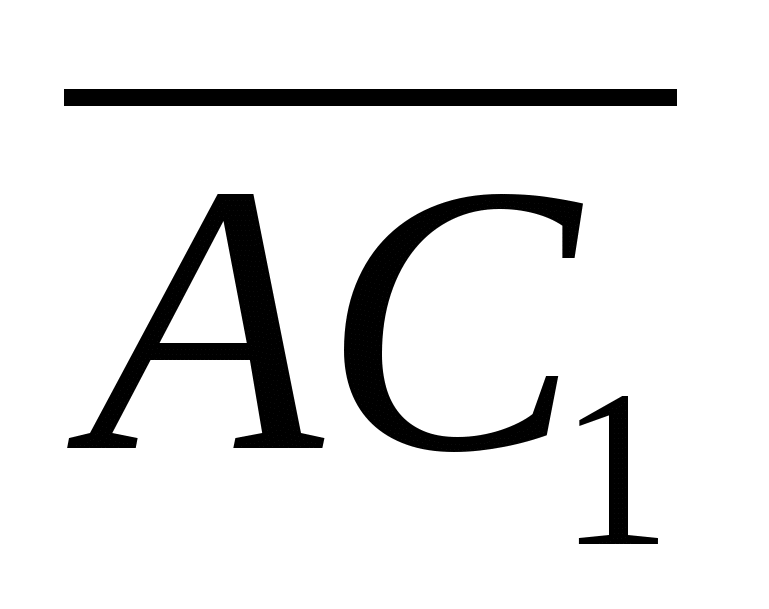 .
.
Tìm tọa độ của vectơ bằng cách sử dụng tọa độ của các điểm 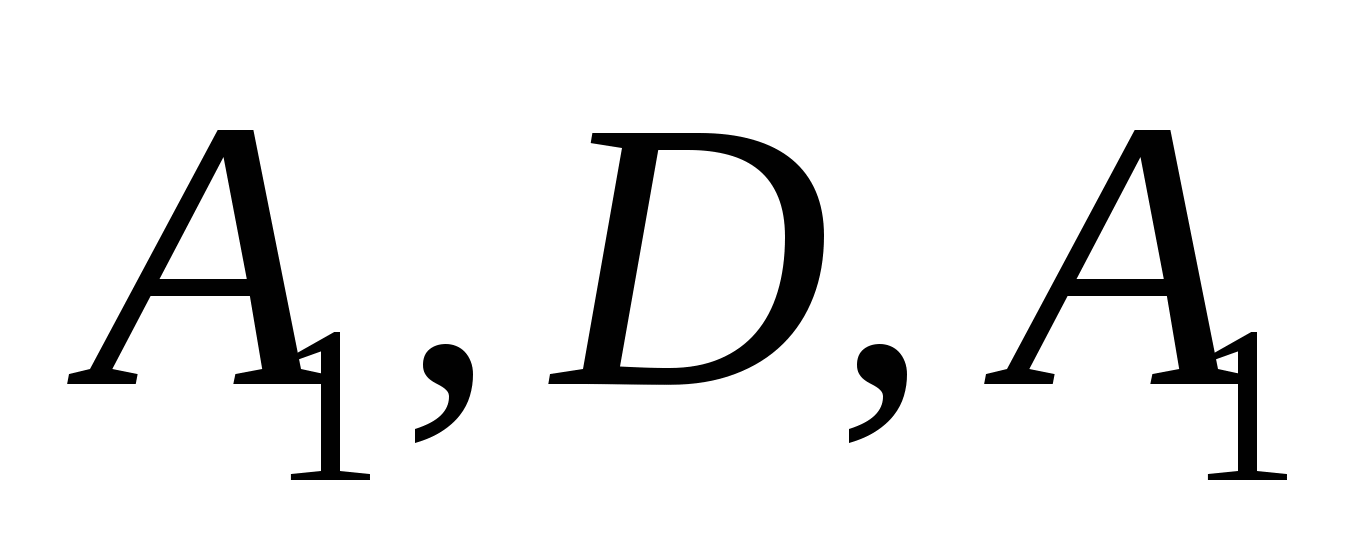 Và
Và  :
:
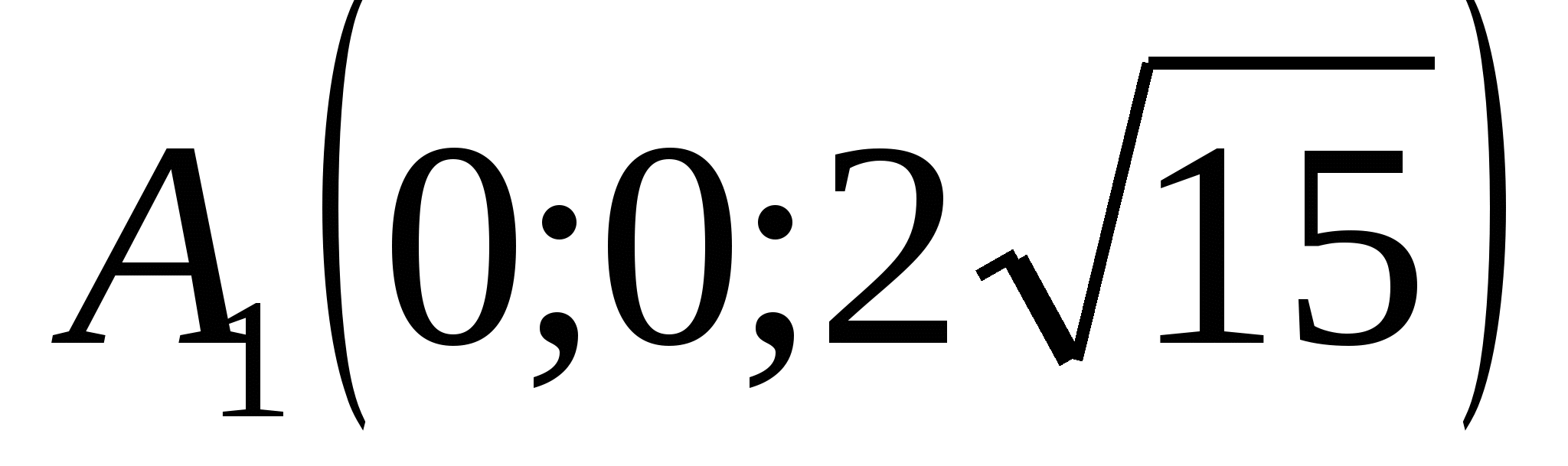 ,
, 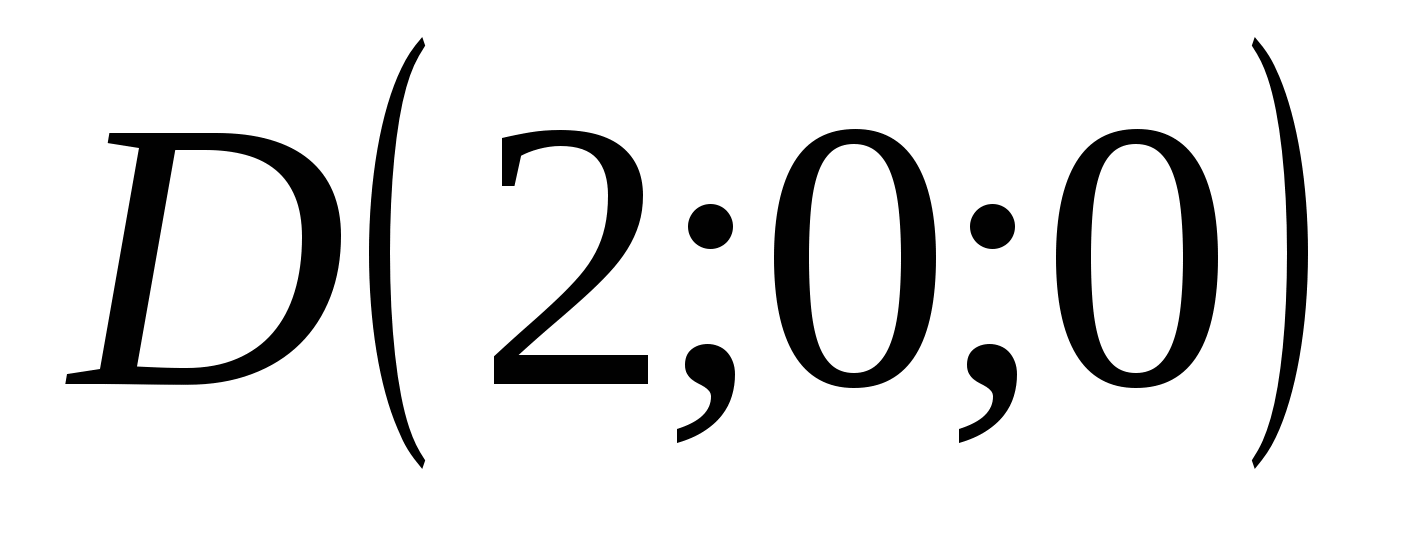 ,
,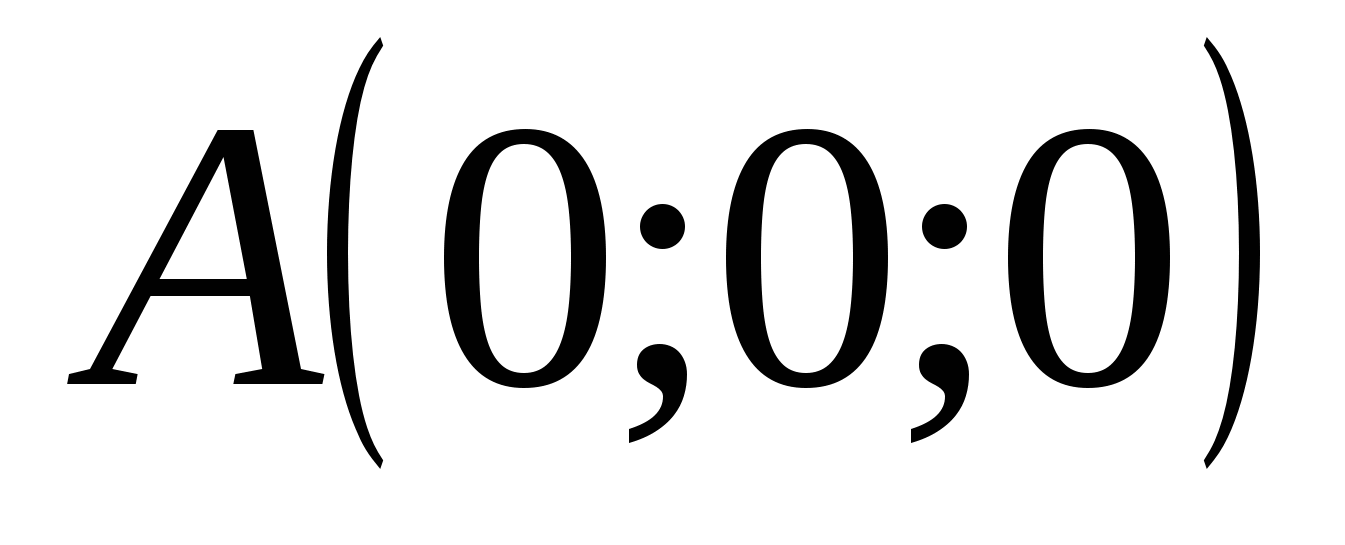 ,
,  .
.
Khi đó tọa độ của các vectơ 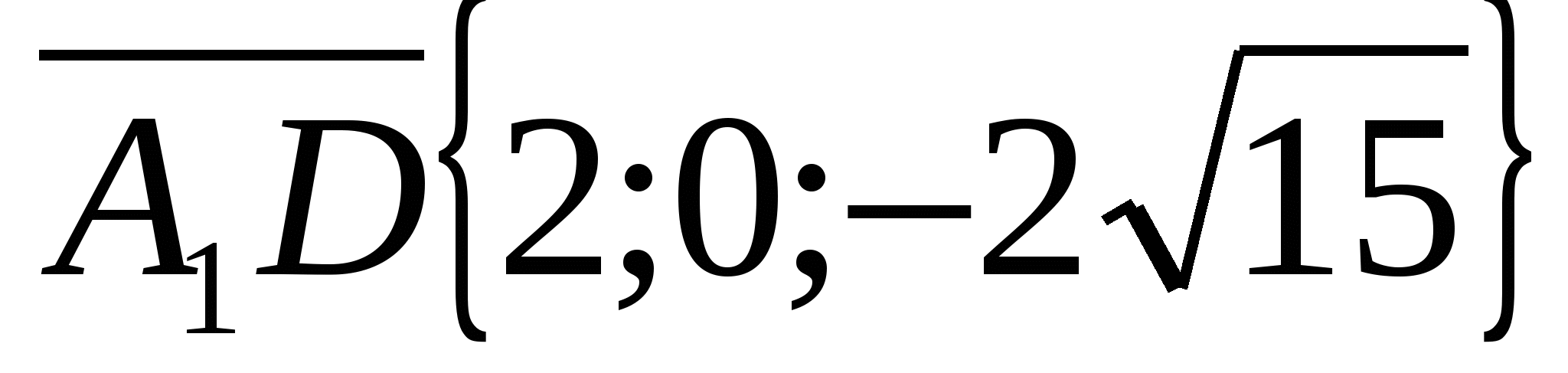 Và
Và 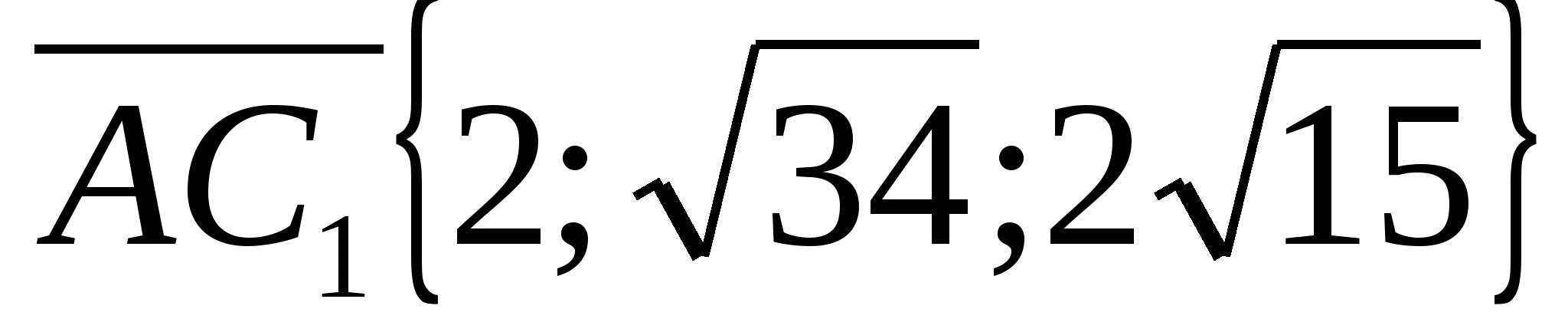 .
.
=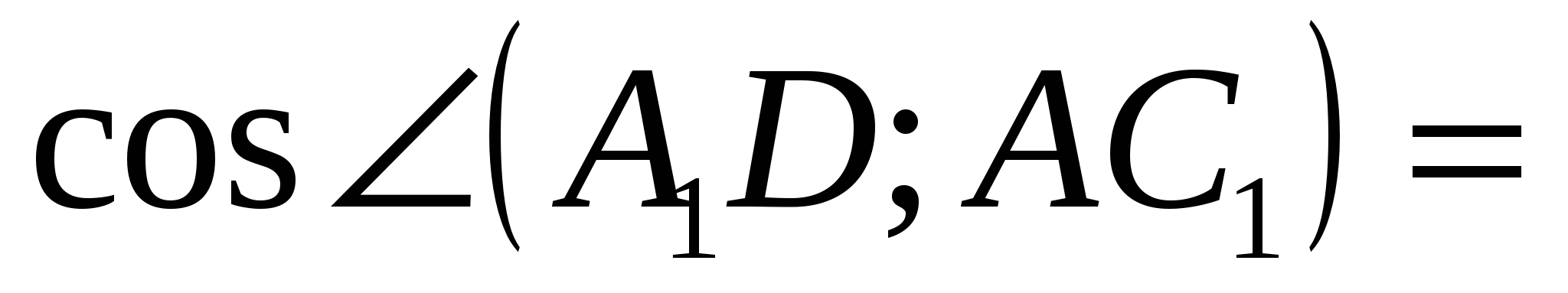
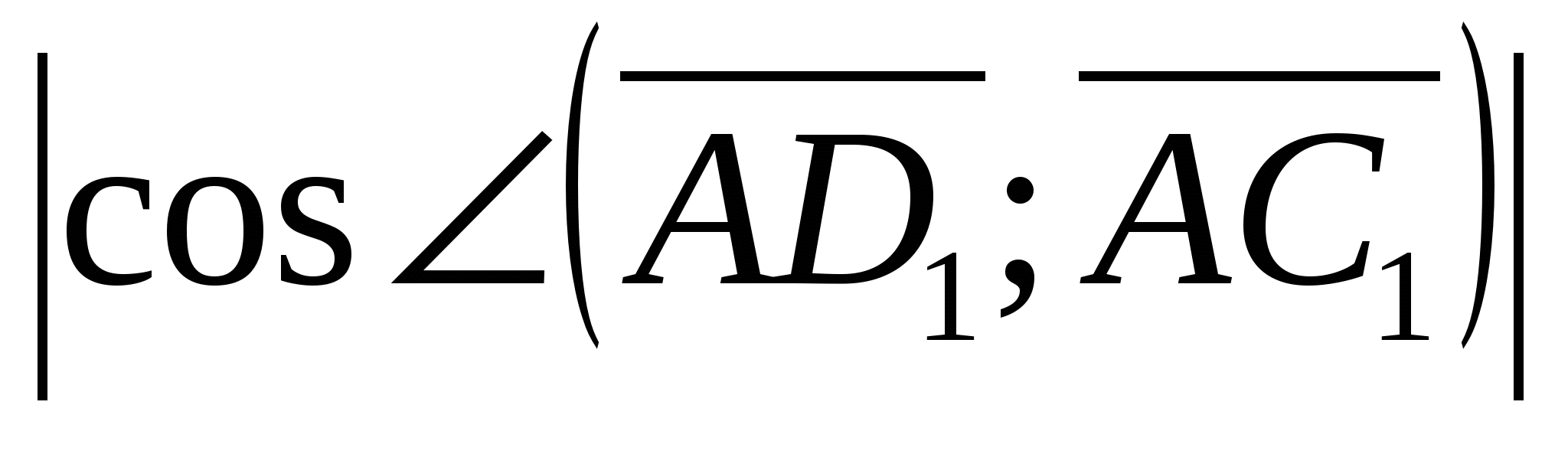 =
= =
=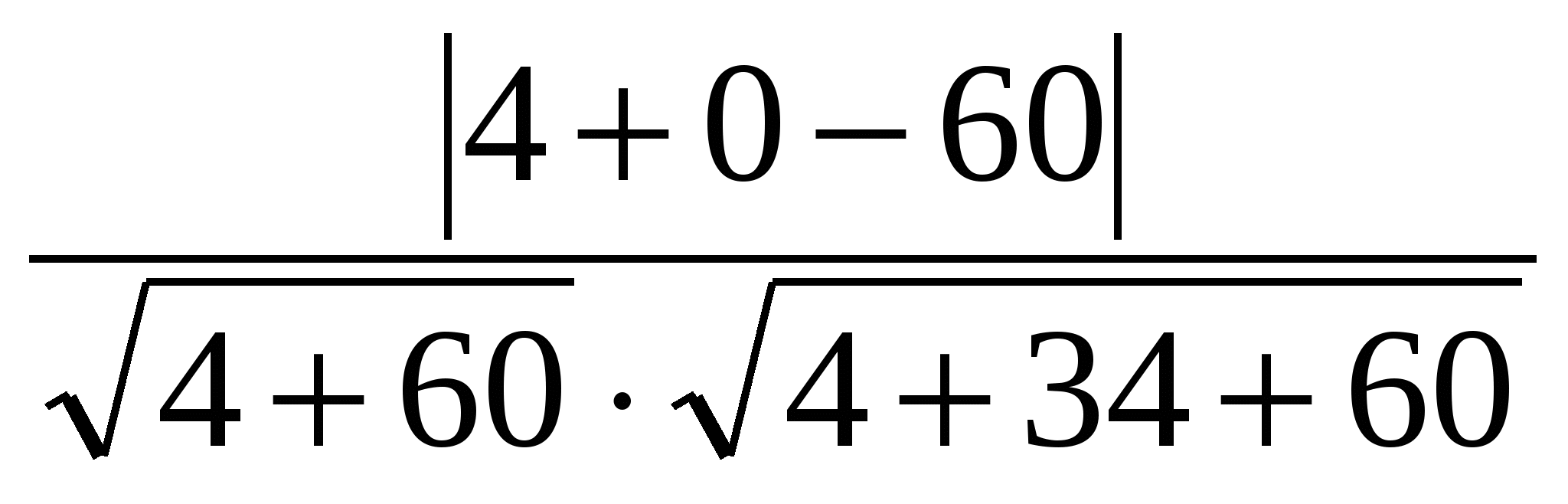
=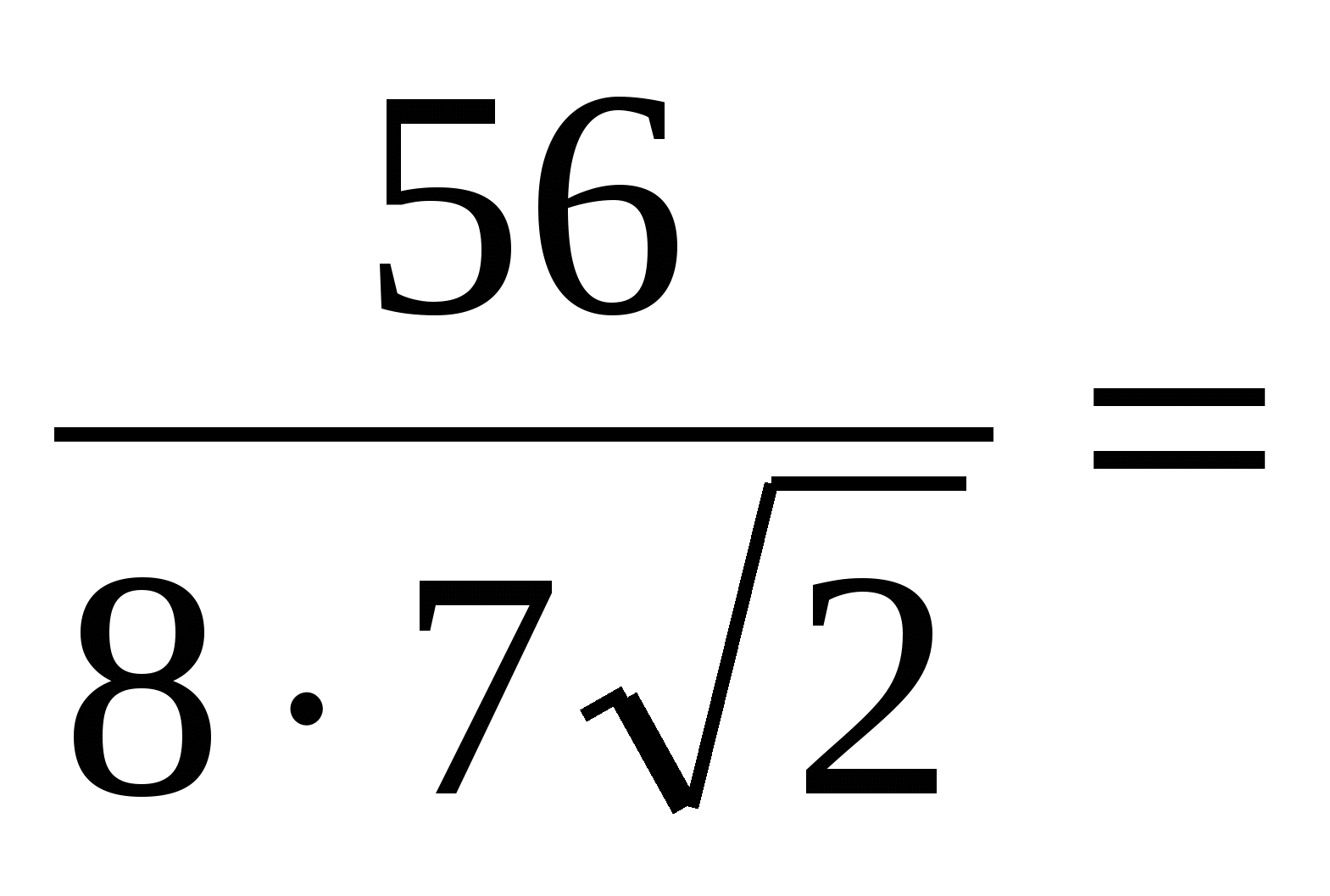
 .
.
Kể từ đây, 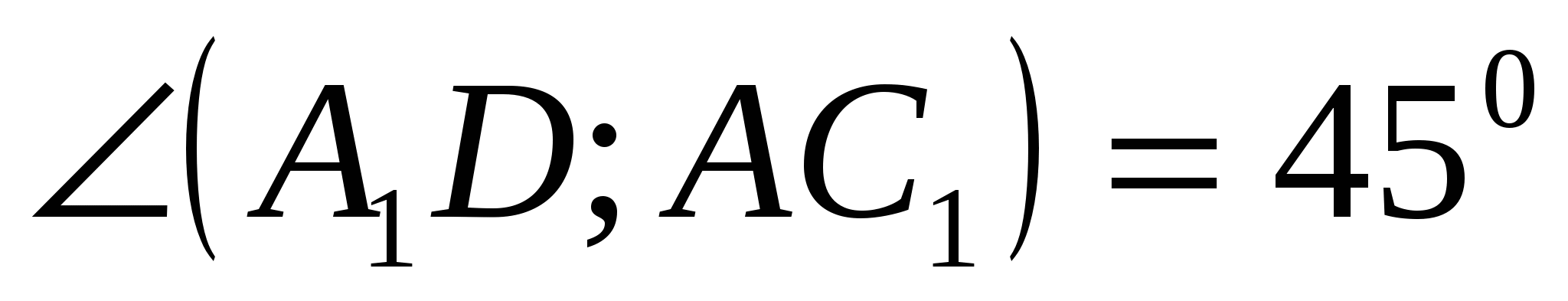
Trả lời:
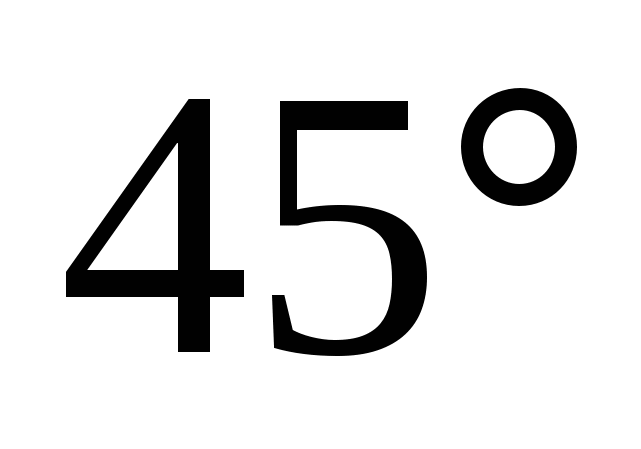 .
.
Nhiệm vụ 3.
Dân hình khối  . Tìm góc giữa một đường thẳng
. Tìm góc giữa một đường thẳng 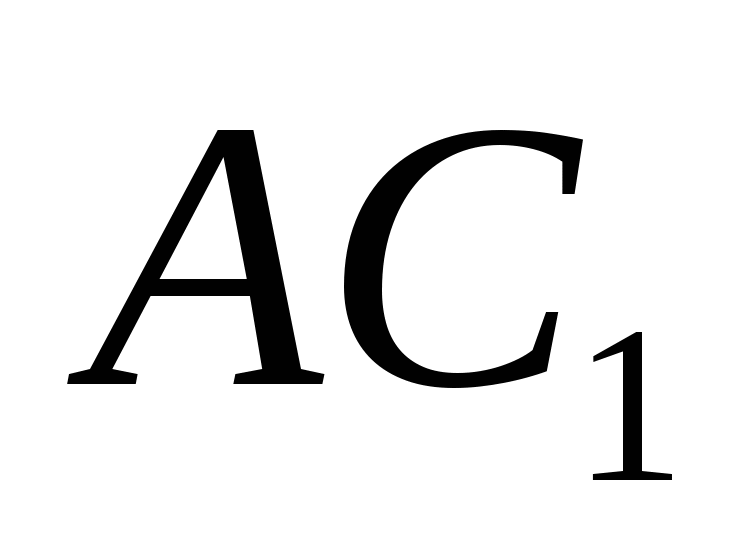 và mặt phẳng đáy
và mặt phẳng đáy  .
.
Giải pháp.
1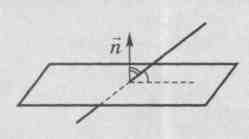 ) Góc giữa đường thẳng
) Góc giữa đường thẳng 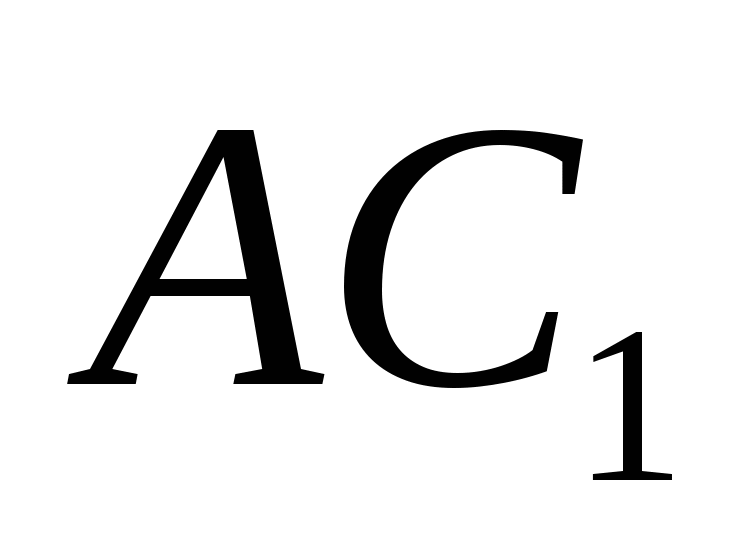 và máy bayAB
1
VỚI- Cái này
góc giữa đường thẳng và hình chiếu của nó lên mặt phẳng. Góc giữa bình thường
và máy bayAB
1
VỚI- Cái này
góc giữa đường thẳng và hình chiếu của nó lên mặt phẳng. Góc giữa bình thường 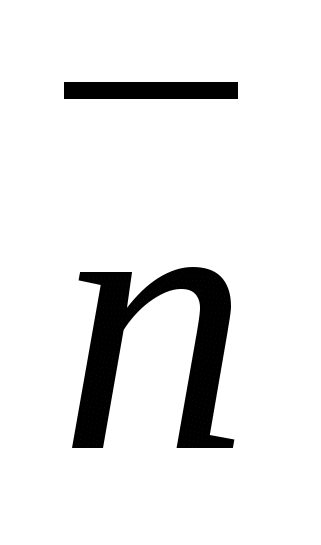 đến một mặt phẳng và một đường thẳng
đến một mặt phẳng và một đường thẳng 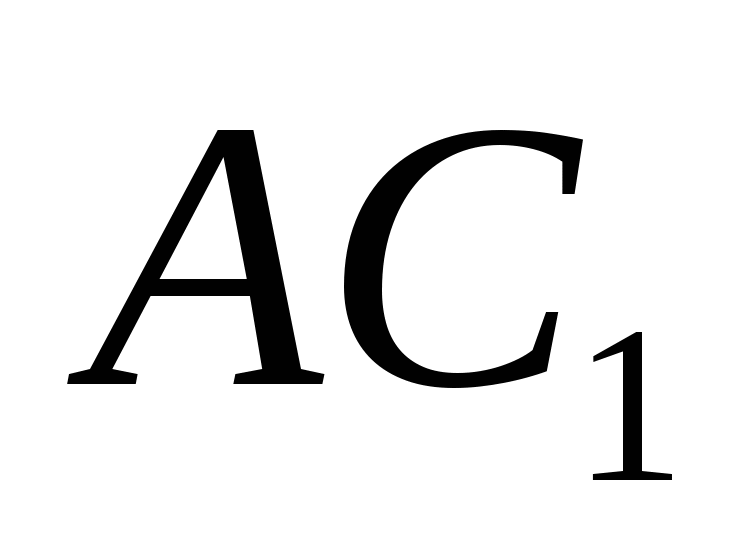 bổ sung cho nó tới 90 0, do đó.
bổ sung cho nó tới 90 0, do đó.
Vì vậy, để tìm góc giữa một đường thẳng 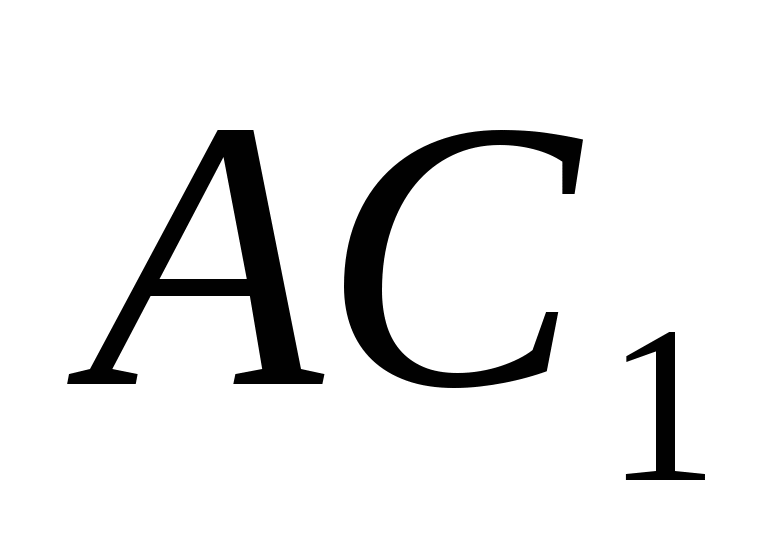 và mặt phẳng (
và mặt phẳng (  ), bạn hãy tìm góc giữa đường thẳng
), bạn hãy tìm góc giữa đường thẳng 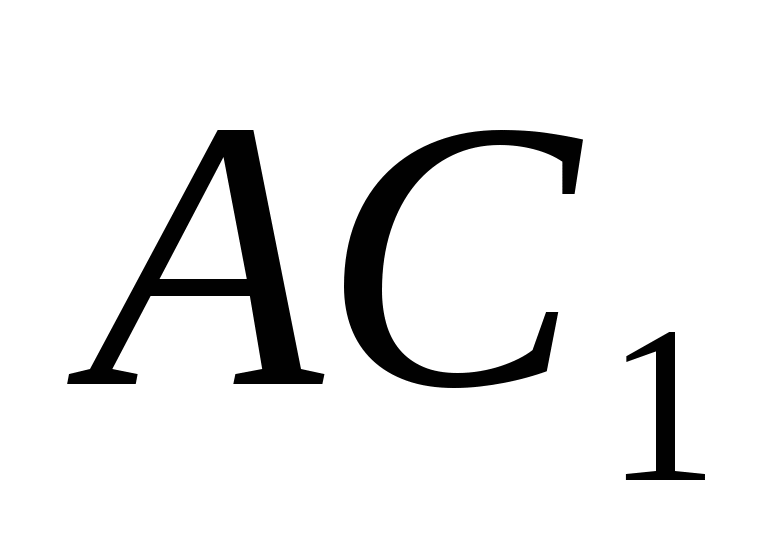 và bình thường
và bình thường 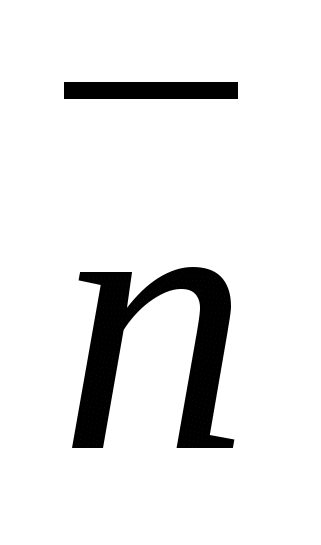 lên máy bay (
lên máy bay (  )
.
)
.
2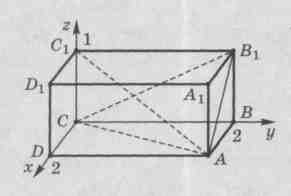 ) Hãy giới thiệu hệ tọa độ có gốc tọa độ tại điểm
) Hãy giới thiệu hệ tọa độ có gốc tọa độ tại điểm 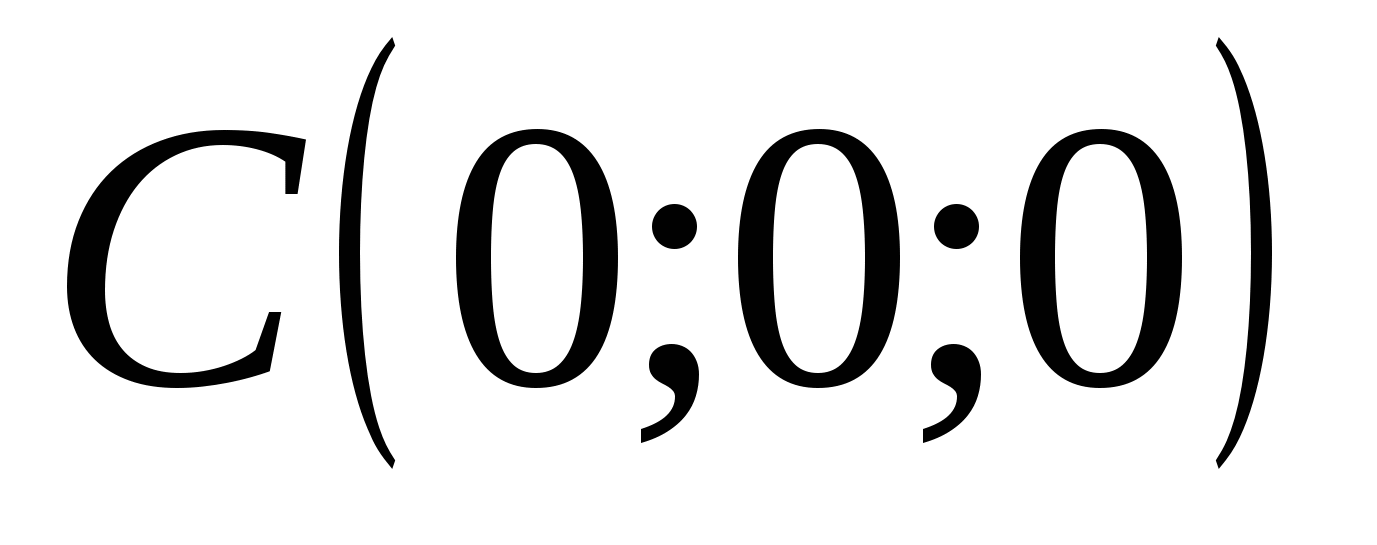 . Trục
. Trục 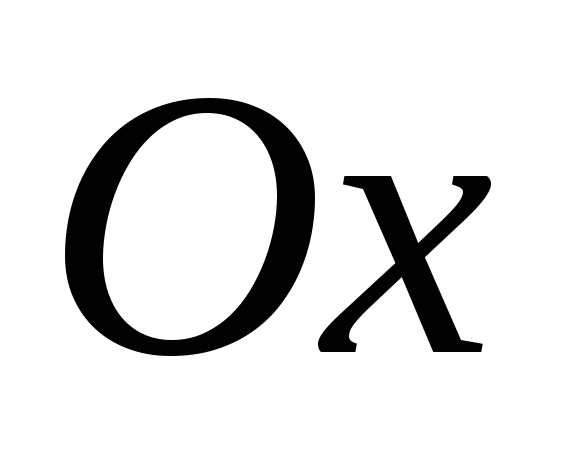 ,
,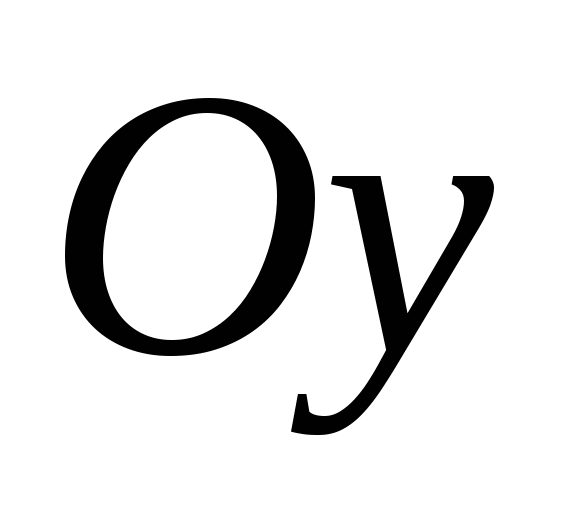 Và
Và  hãy hướng dọc theo xương sườn
hãy hướng dọc theo xương sườn  ,
, 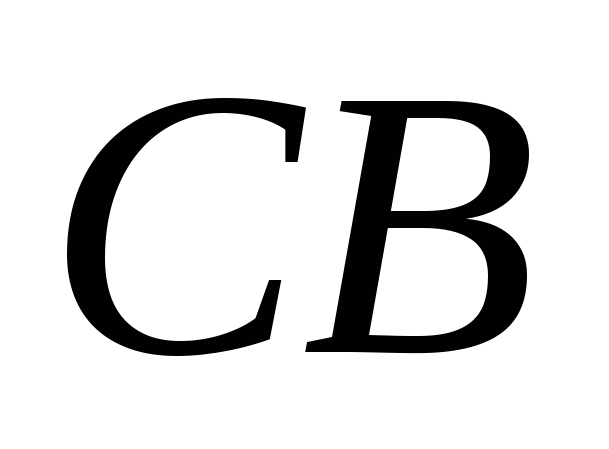 Và
Và 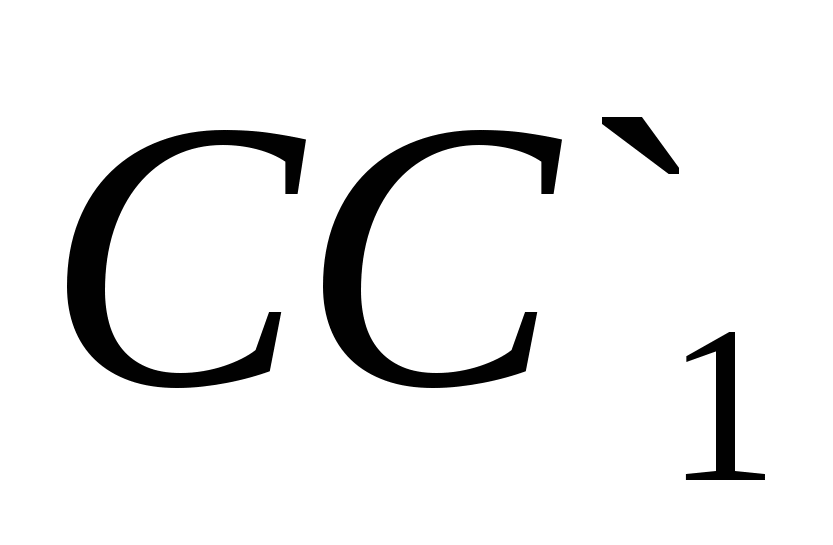 tương ứng.
tương ứng.
tọa độ điểm:
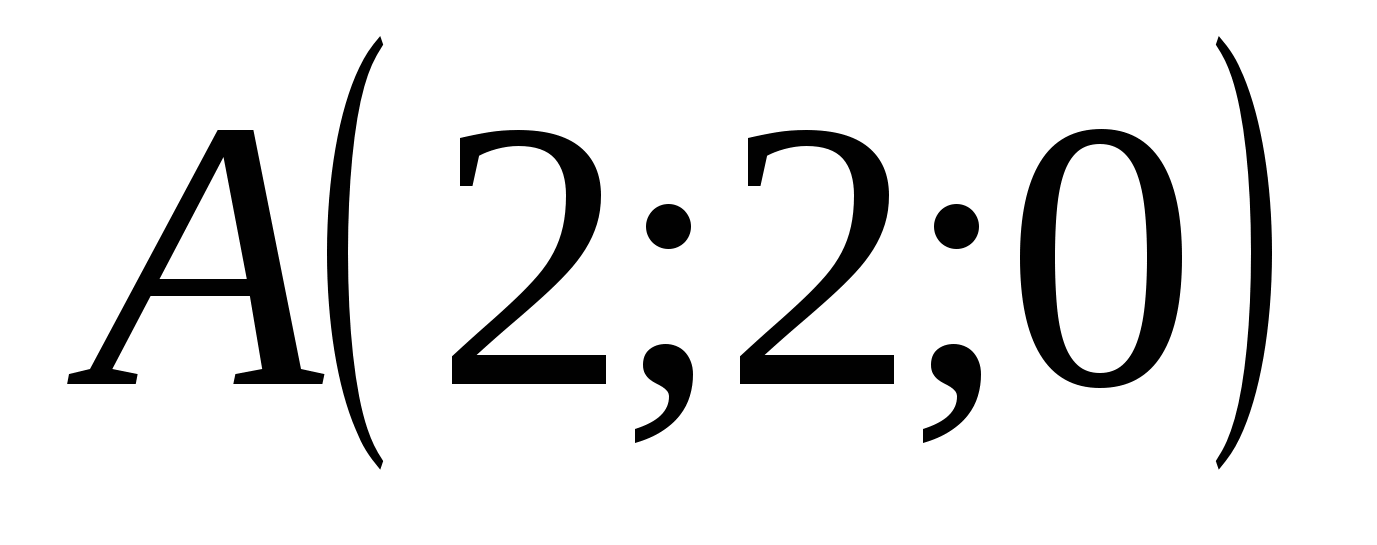 ,
, 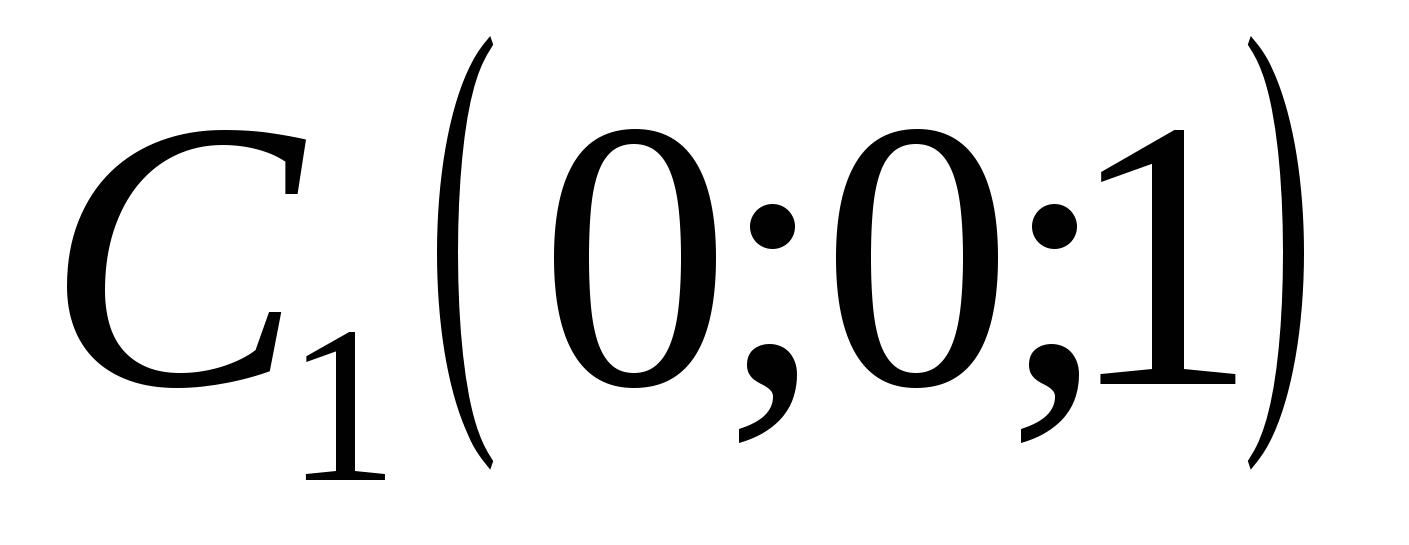 ,
, 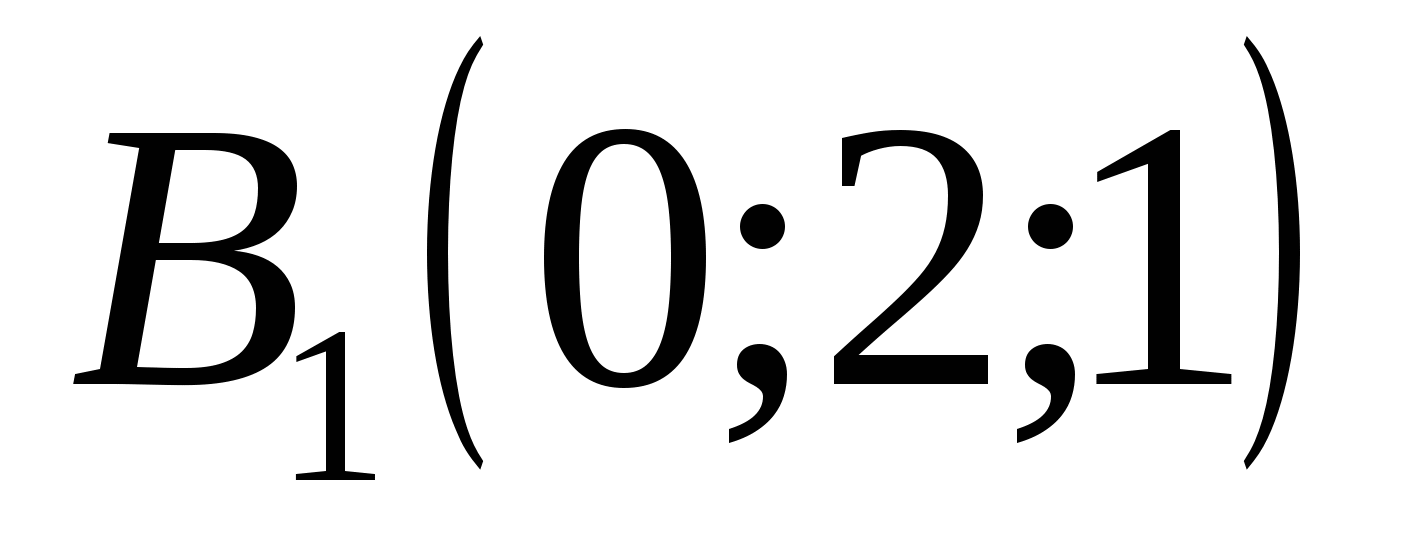 ,
,
MỘT 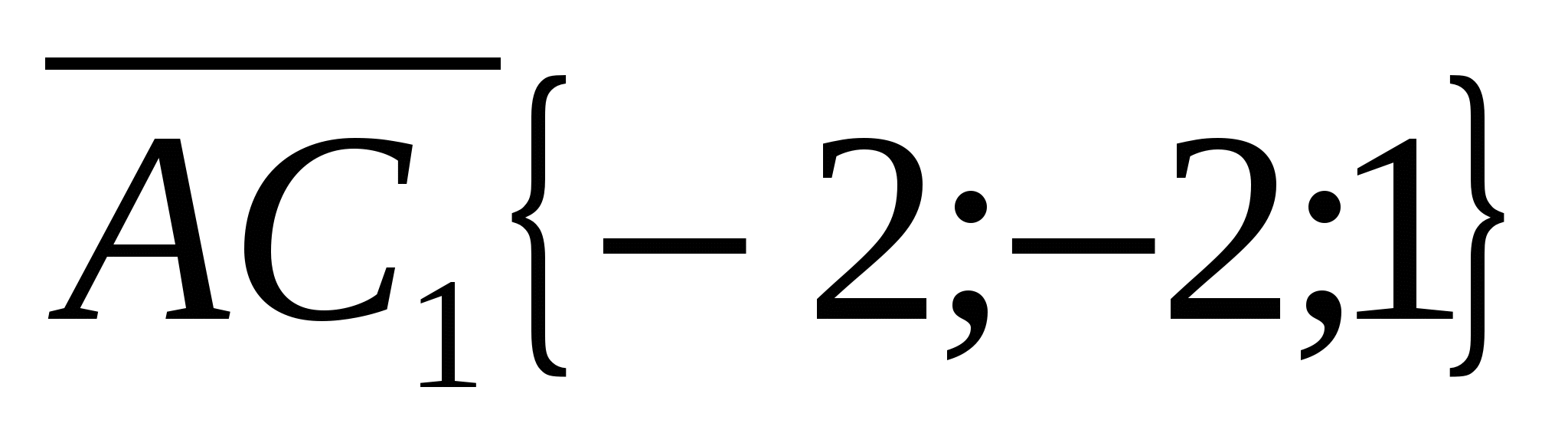 .
.
3) Tìm tọa độ của mặt phẳng pháp tuyến (  ). Hãy viết phương trình mặt phẳng (
). Hãy viết phương trình mặt phẳng (  ), thay tọa độ của các điểmMỘT
,
B
1
Và VỚI V.
phương trình mặt phẳng
.
), thay tọa độ của các điểmMỘT
,
B
1
Và VỚI V.
phương trình mặt phẳng
.
Ta thu được hệ phương trình tuyến tính:
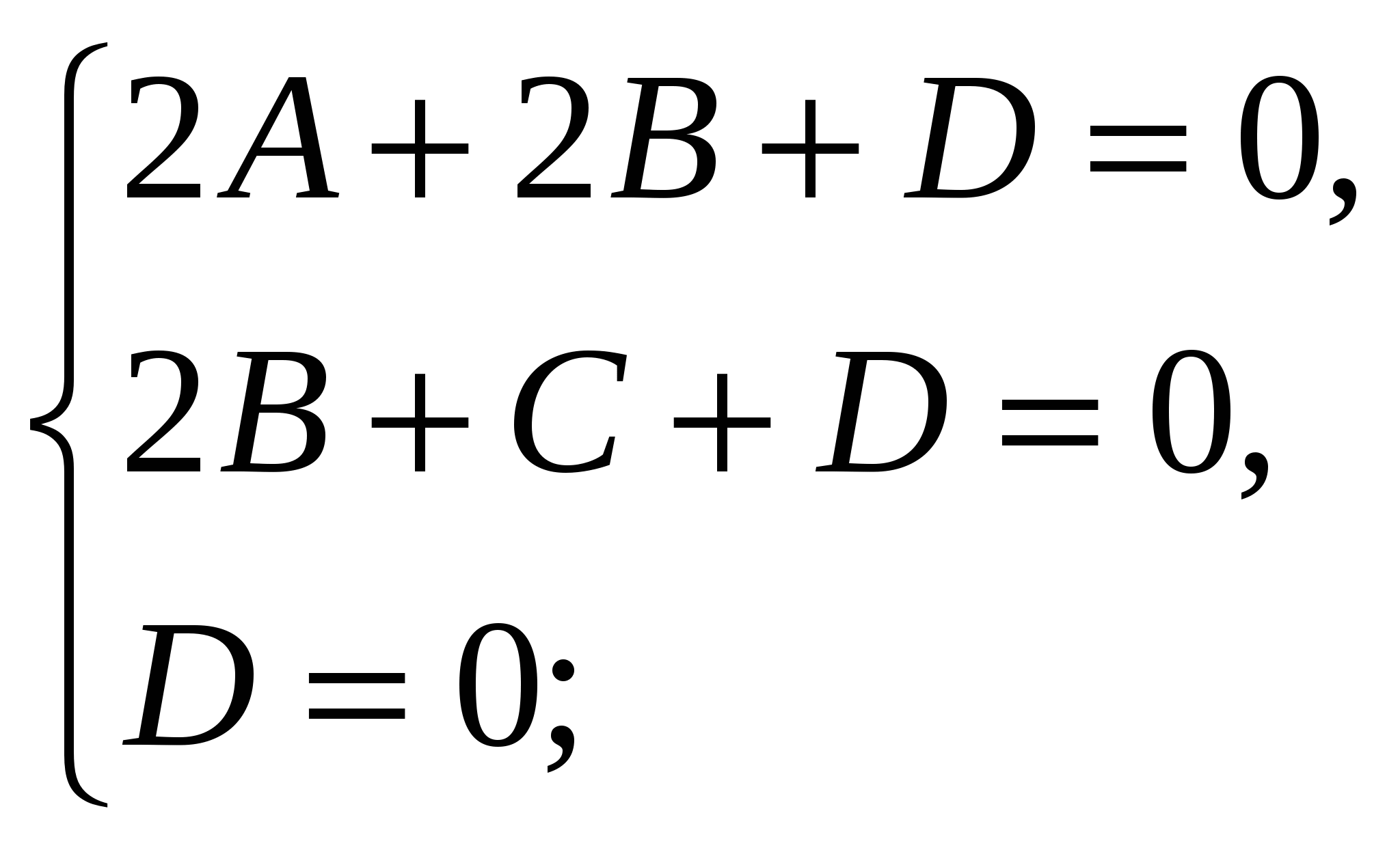
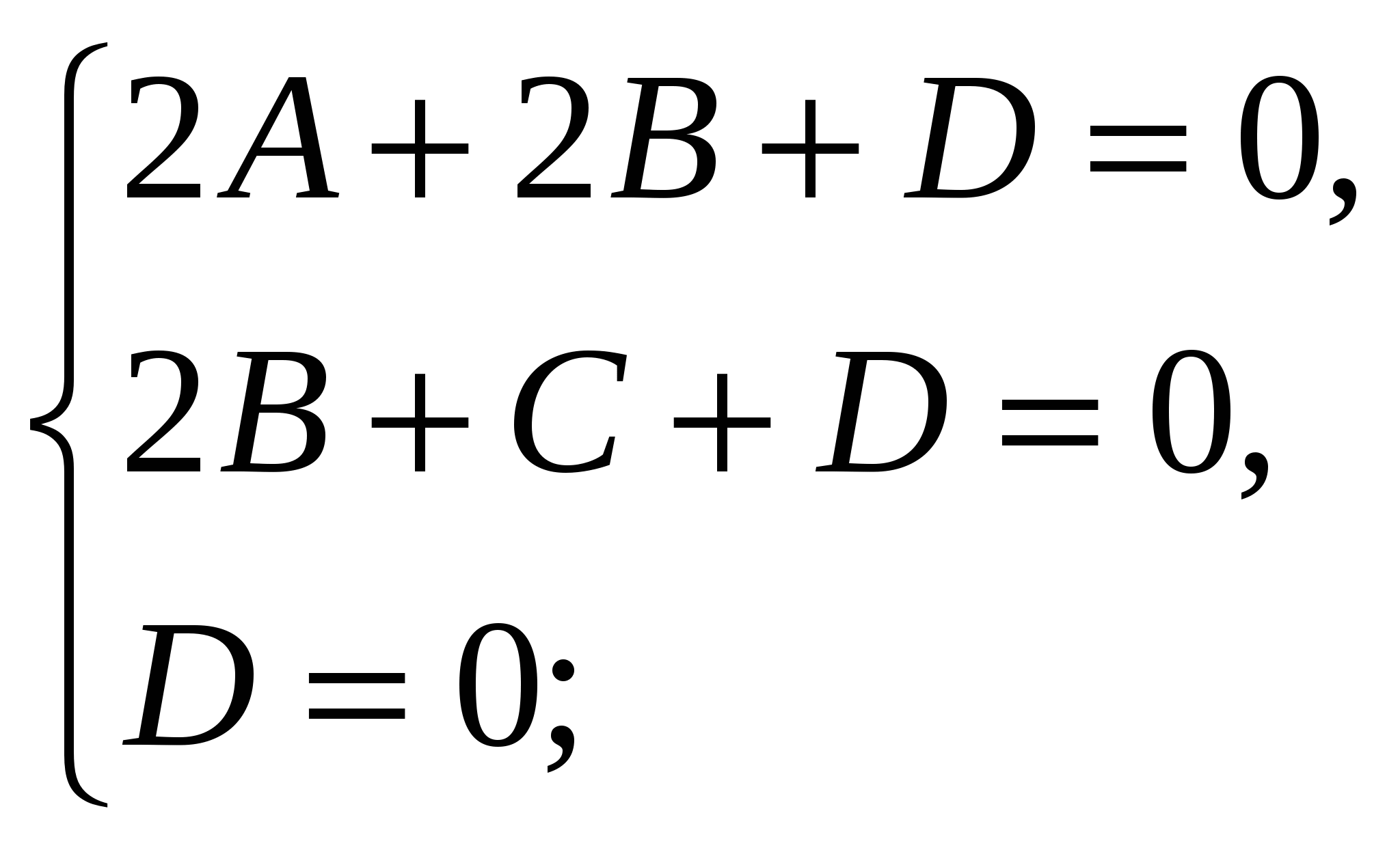
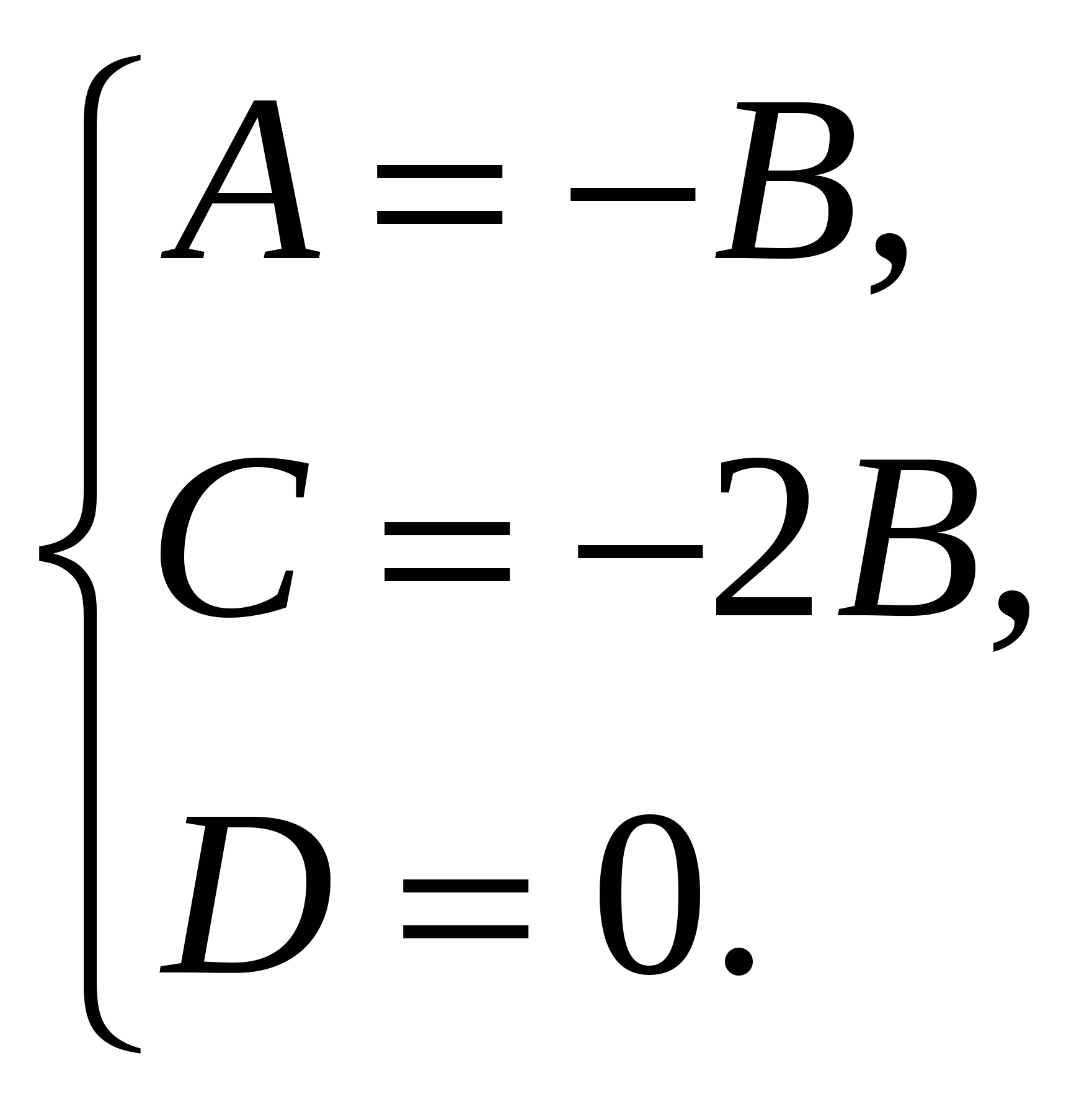
Do đó, phương trình của mặt phẳng (  ) có dạng , hoặc
) có dạng , hoặc  và vectơ pháp tuyến có tọa độ
và vectơ pháp tuyến có tọa độ 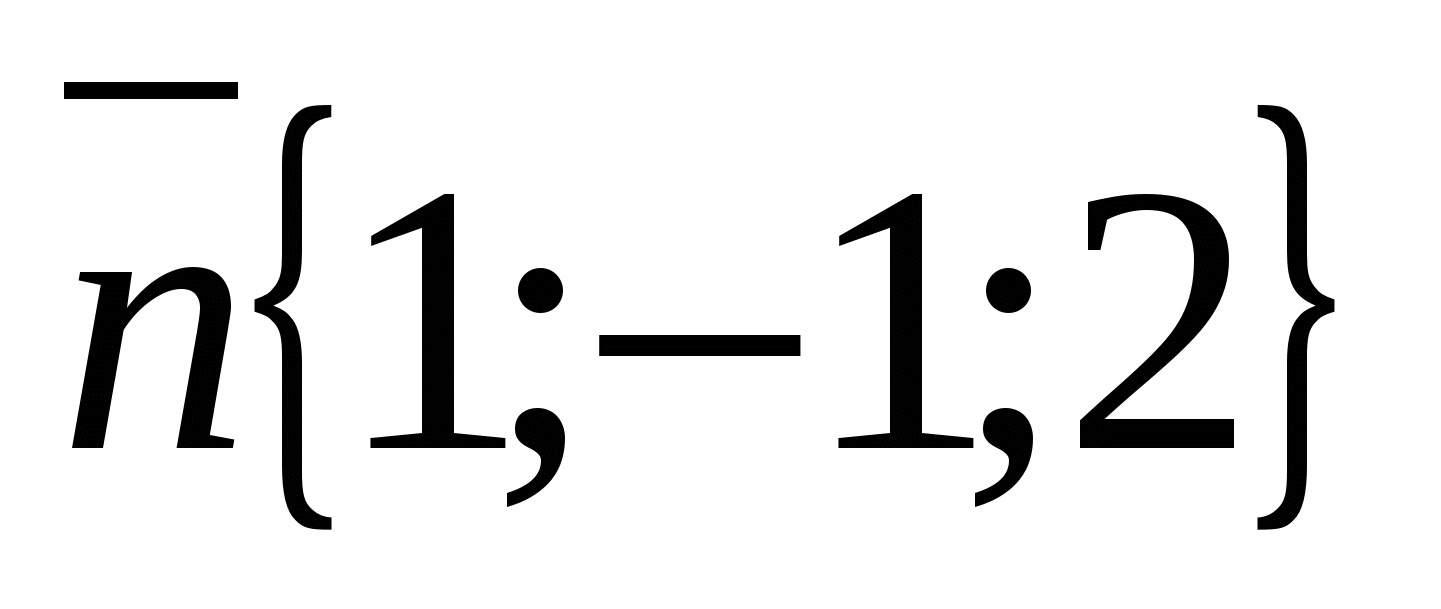 .
.
Có nghĩa
VÀ 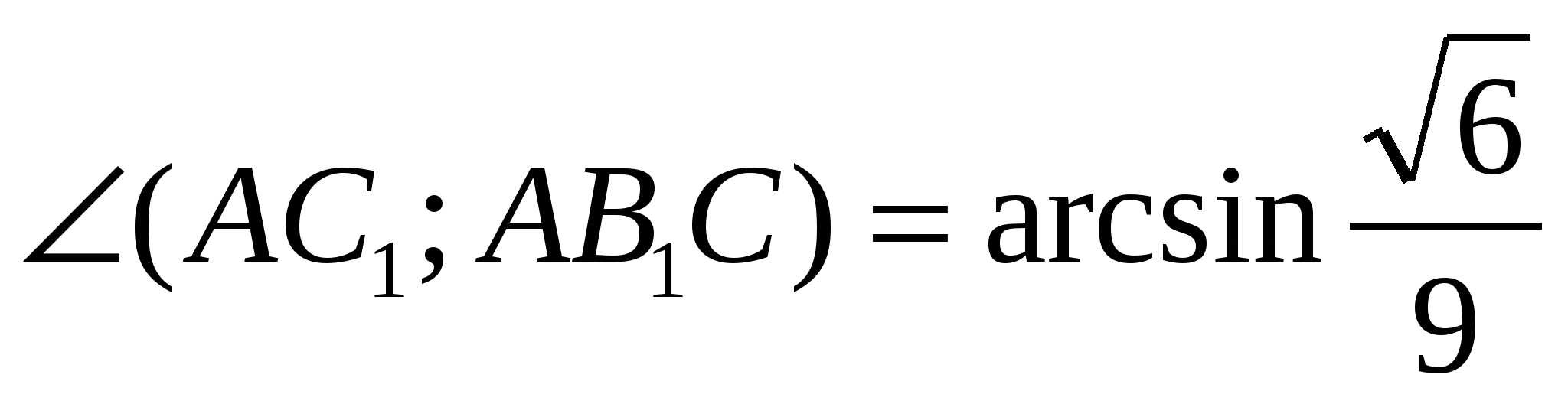 .
.
Trả lời:
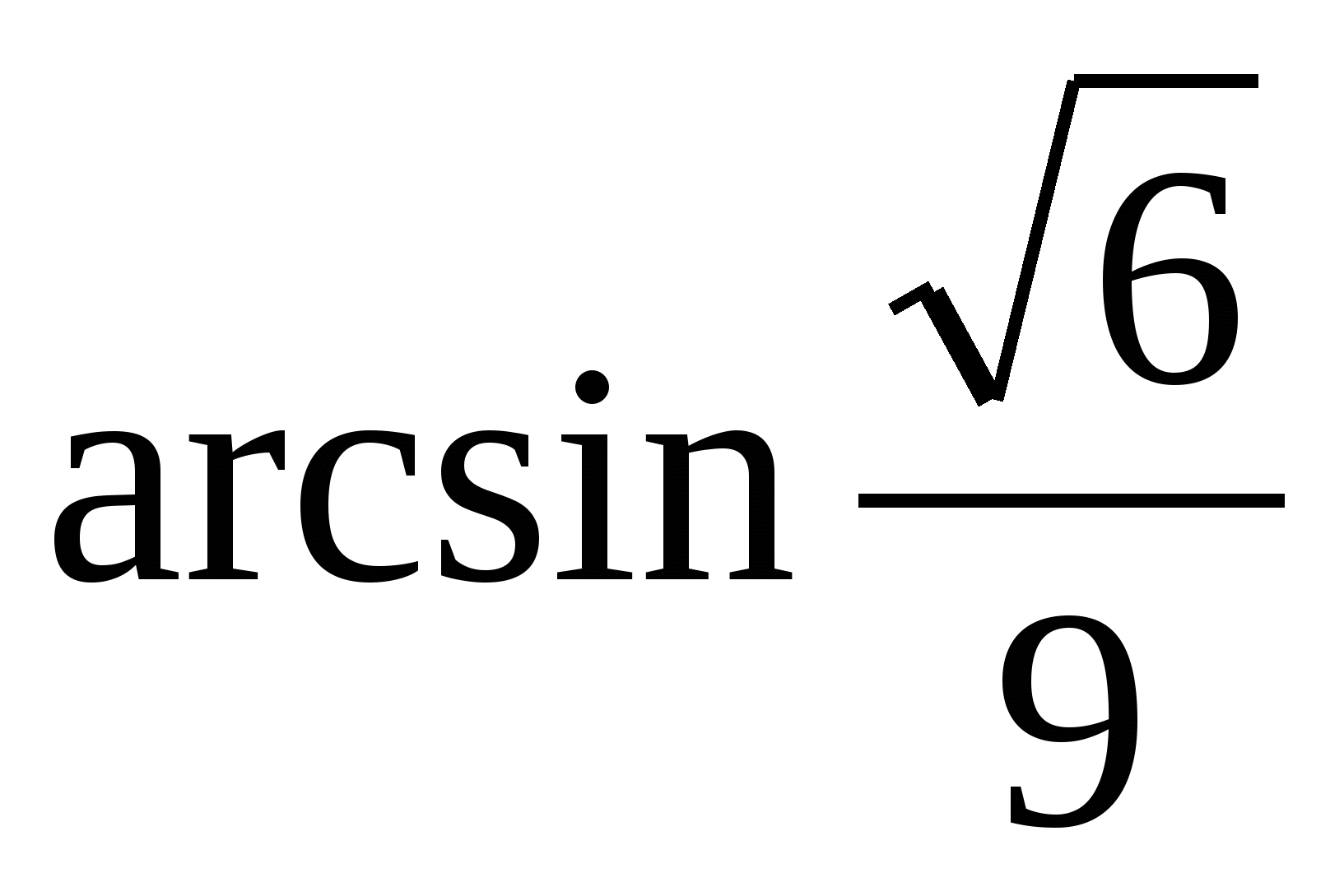 .
.
Hãy xem xét việc giải quyết vấn đề theo hai cách.
Nhiệm vụ 4. Cách 1: hình học.
Trên sườn  ,
,  Và. . Hãy đi thẳng - đường giữa tam giác và, tức là Và,
Và. . Hãy đi thẳng - đường giữa tam giác và, tức là Và,
Tài liệu lý luận nghiên cứu đã được hệ thống hóa.
Khi sử dụng phương pháp để giải quyết vấn đề, các đặc điểm sau của phương pháp được xác định:
kỹ năng quản trị đúng hệ tọa độ,
xác định chính xác tọa độ điểm,
kiến thức về thiết bị phân tích của phương pháp.
Việc áp dụng phương pháp này được coi là một giải pháp nhiều loại nhiệm vụ và so sánh với các phương pháp khác.
Tôi gặp một số khó khăn trong quá trình thực hiện công việc:
khi thiết lập mục tiêu và mục tiêu;
khối lượng không đủ tài liệu lý thuyết trong sách giáo khoa ở trường;
khi xác định đặc thù của việc sử dụng phương pháp,
khi lựa chọn tài liệu để trình bày một bản tóm tắt.
Tài liệu tham khảo.
L S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev, L. S. Kiseleva, E. G. Poznyak. Hình học, 10-11.M., Giáo dục, 2003.
V.N.Litvinenko. Hội thảo về toán tiểu học. Lập thể: Hướng dẫn.-M.: Verbum-M, 2000.
HỌ.Gelfand, E.G. Glagoleva, A.A. Kirillov. Phương pháp tọa độ - M.: Nauka, 1968.
S.G. Grigoriev.đại số vectơ và hình học giải tích. Sách giáo khoa về toán cao cấp.-M.: Trung tâm Thông tin và Triển khai “Tiếp thị”, 2000.
I. Ivanova, Z. Ilchenkova.Ứng dụng vectơ tọa độđể giải các bài toán lập thể.//Toán học, 2007, số 2.
A.V. Dorofeev. Descartes và hình học của ông.//Toán học, 1992, số 4.
