Bir vektörün koordinatlarını bulmak matematikteki birçok problem için oldukça yaygın bir durumdur. Vektör koordinatlarını bulma yeteneği size diğer konularda da yardımcı olacaktır. karmaşık görevler ile benzer konular. Bu yazıda vektör koordinatlarını bulma formülüne ve çeşitli problemlere bakacağız.
Düzlemdeki bir vektörün koordinatlarını bulma
Uçak nedir? Düzlem, iki boyutlu bir uzay, iki boyutlu (x boyutu ve y boyutu) bir uzay olarak kabul edilir. Örneğin kağıt düzdür. Masanın yüzeyi düzdür. Hacimsel olmayan herhangi bir şekil (kare, üçgen, yamuk) aynı zamanda bir düzlemdir. Bu nedenle, eğer problem ifadesinde bir düzlem üzerinde bulunan bir vektörün koordinatlarını bulmanız gerekiyorsa, hemen x ve y'yi hatırlarız. Böyle bir vektörün koordinatlarını bulabilirsiniz. Aşağıdaki şekilde: AB vektör koordinatları = (xB - xA; yB - xA). Formülden koordinatlardan açıkça anlaşılıyor bitiş noktası başlangıç noktasının koordinatlarını çıkarmanız gerekir.
Örnek:
- Vektör CD'sinin başlangıç (5; 6) ve son (7; 8) koordinatları vardır.
- Vektörün kendisinin koordinatlarını bulun.
- Yukarıdaki formülü kullanarak şu ifadeyi elde ederiz: CD = (7-5; 8-6) = (2; 2).
- Böylece CD vektörünün koordinatları = (2; 2).
- Buna göre x koordinatı ikiye eşit, y koordinatı da ikidir.
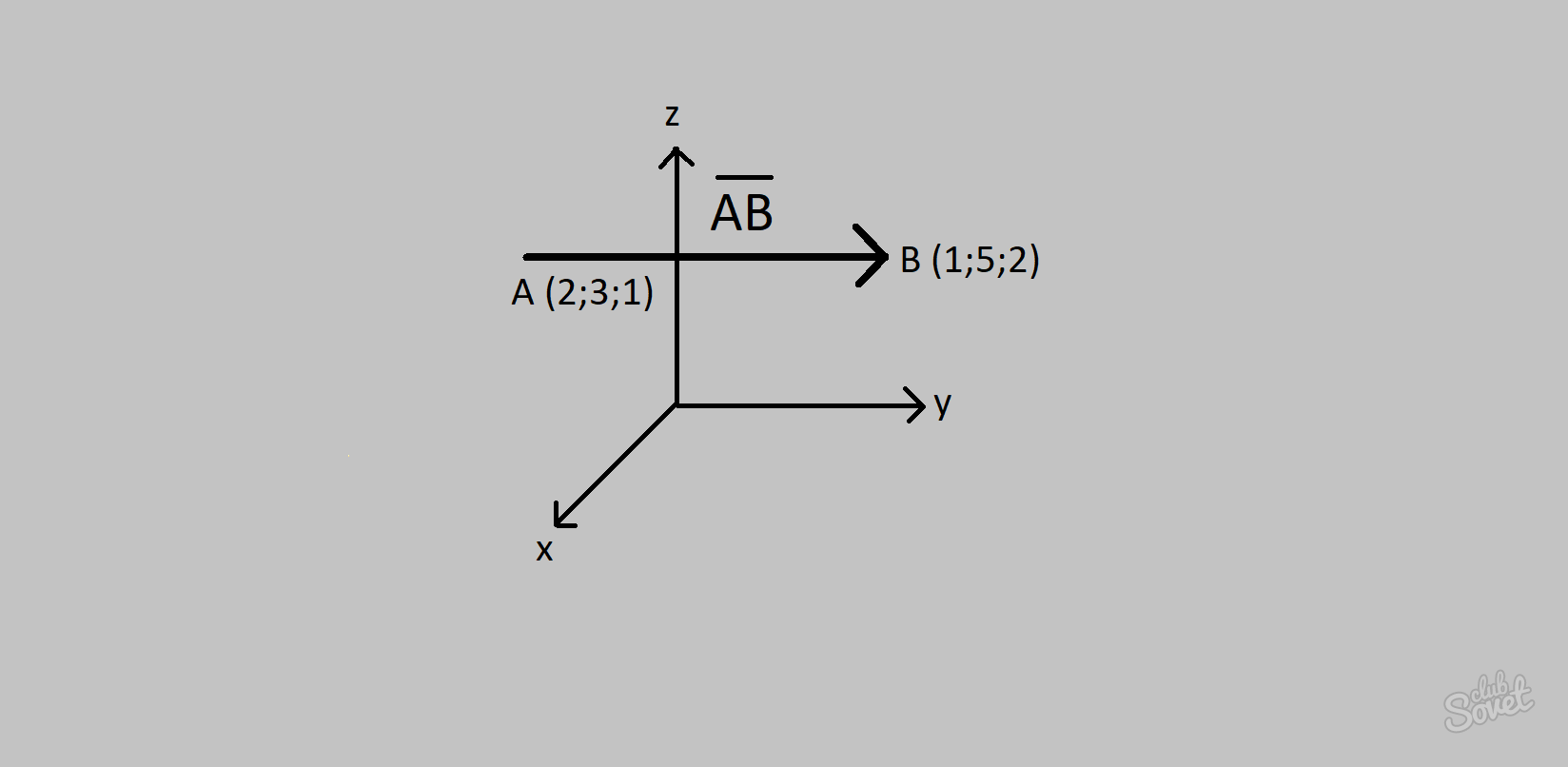
Uzaydaki bir vektörün koordinatlarını bulma
Uzay nedir? Uzay zaten üç koordinatın verildiği üç boyutlu bir boyuttur: x, y, z. Uzayda bulunan bir vektör bulmanız gerekiyorsa formül pratikte değişmez. Yalnızca bir koordinat eklenir. Bir vektör bulmak için başlangıç koordinatlarını bitiş koordinatlarından çıkarmanız gerekir. AB = (xB - xA; yB - yA; zB - zA)
Örnek:
- DF vektörünün başlangıcı (2; 3; 1) ve sonu (1; 5; 2) vardır.
- Yukarıdaki formülü uygulayarak şunu elde ederiz: Vektör koordinatları DF = (1-2; 5-3; 2-1) = (-1; 2; 1).
- Unutmayın koordinat değeri negatif olabilir, sorun olmaz.
Vektör koordinatları çevrimiçi olarak nasıl bulunur?
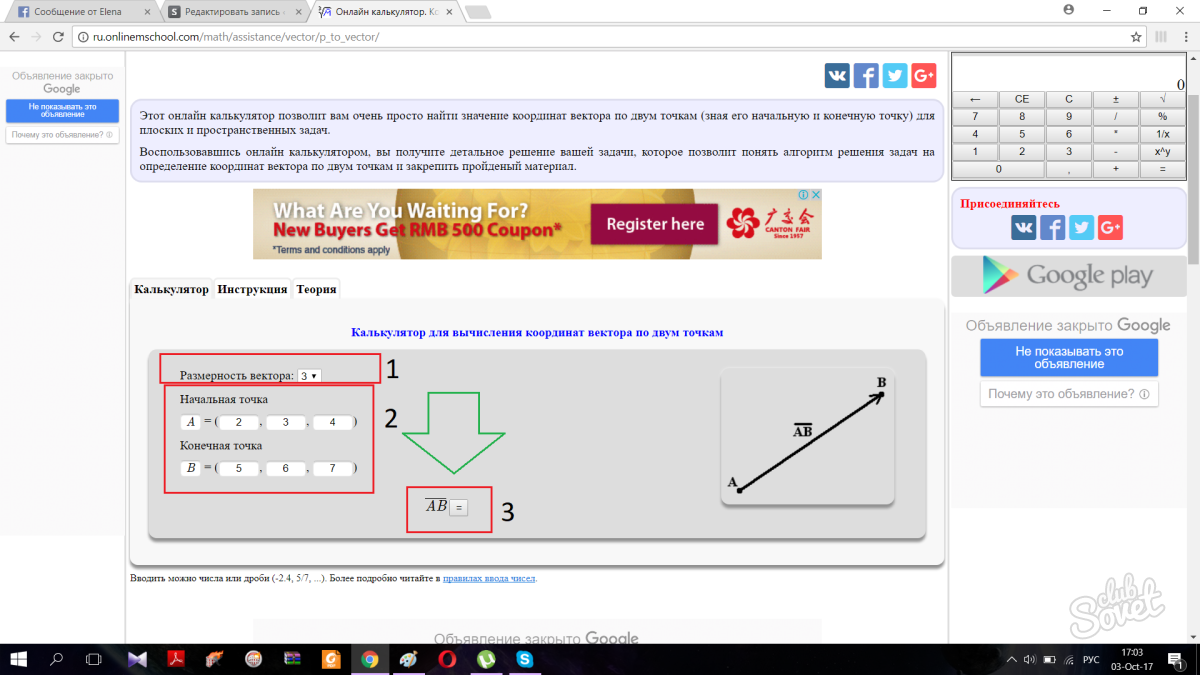
Herhangi bir nedenle koordinatları kendiniz bulmak istemiyorsanız çevrimiçi hesap makinesini kullanabilirsiniz. Başlamak için vektör boyutunu seçin. Bir vektörün boyutu onun boyutlarından sorumludur. Boyut 3, vektörün uzayda olduğu, boyut 2 ise düzlemde olduğu anlamına gelir. Daha sonra, noktaların koordinatlarını uygun alanlara girin; program sizin için vektörün koordinatlarını belirleyecektir. Her şey çok basit.
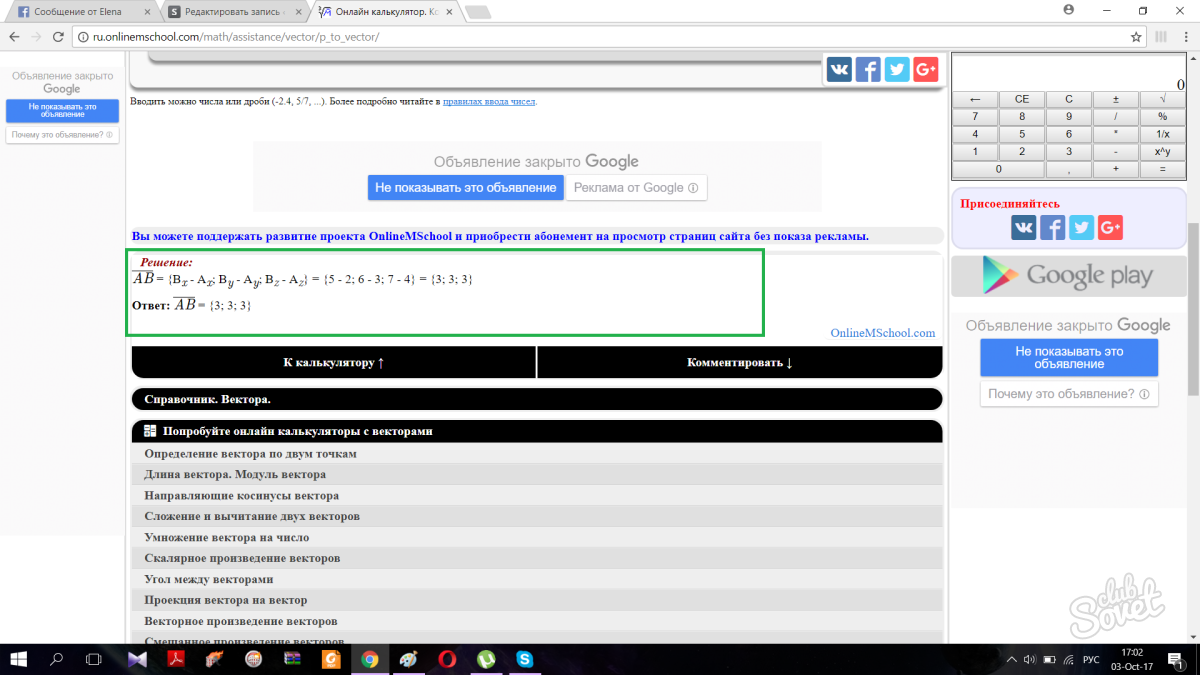
Butona tıkladığınızda sayfa otomatik olarak aşağıya doğru kaydırılacak ve çözüm adımlarıyla birlikte size doğru cevabı verecektir.
İyi çalışmanız tavsiye edilir bu konuÇünkü vektör kavramı sadece matematikte değil fizikte de bulunur. Fakülte öğrencileri Bilişim Teknolojileri Ayrıca vektörler konusunu da inceliyorlar, ancak daha karmaşık bir düzeyde.
Düzlemin iki noktası verilirse, vektör aşağıdaki koordinatlara sahiptir:
Uzayda iki nokta verilirse, vektör aşağıdaki koordinatlara sahiptir:
Yani, vektörün sonunun koordinatlarından karşılık gelen koordinatları çıkarmanız gerekir vektörün başlangıcı.
Egzersiz yapmak: Aynı noktalar için vektörün koordinatlarını bulma formüllerini yazın. Dersin sonunda formüller.
örnek 1
Düzlemin iki noktası verildiğinde ve . Vektör koordinatlarını bulun
Çözüm: ilgili formüle göre:
Alternatif olarak aşağıdaki giriş kullanılabilir:
Buna estetik karar verecek:
Şahsen ben kaydın ilk versiyonuna alışkınım.
Cevap:
Koşula göre, bir çizim oluşturmak gerekli değildi (bu, görevler için tipiktir) analitik geometri), ancak aptallar için bazı noktaları açıklığa kavuşturmak için fazla tembel olmayacağım:
Kesinlikle anlamalısın nokta koordinatları ve vektör koordinatları arasındaki fark:
Nokta koordinatları– bunlar dikdörtgen koordinat sistemindeki sıradan koordinatlardır. Puanları koy koordinat uçağı 5-6. sınıftan itibaren herkesin yapabileceğini düşünüyorum. Her noktanın düzlemde kesin bir yeri vardır ve hiçbir yere taşınamazlar.
Vektörün koordinatları temel açısından genişlemesidir, bu durumda. Herhangi bir vektör serbesttir, dolayısıyla gerekirse onu düzlemdeki başka bir noktadan kolaylıkla uzaklaştırabiliriz. İlginçtir ki vektörler için eksen oluşturmanıza hiç gerek yok, dikdörtgen sistem Koordinatlar için yalnızca bir tabana, bu durumda düzlemin ortonormal tabanına ihtiyacınız vardır.
Noktaların koordinatları ile vektörlerin koordinatlarının kayıtları benzer görünmektedir: , ve koordinatların anlamı kesinlikle farklı ve bu farkın çok iyi farkında olmalısınız. Bu fark elbette uzay için de geçerli.
Bayanlar ve baylar, ellerimizi dolduralım:
Örnek 2
a) Puan ve verilir. Vektörleri bulun ve .
b) Puan ve verilir. Vektörleri bulun ve .
c) Puan ve verilir. Vektörleri bulun ve .
d) Puan verilir. Vektörleri bulun.
Belki bu yeterlidir. Bunlar için örnekler bağımsız karar, onları ihmal etmemeye çalışın, karşılığını alacaktır ;-). Çizim yapmaya gerek yoktur. Dersin sonunda çözümler ve cevaplar.
Analitik geometri problemlerini çözerken önemli olan nedir? Ustaca yapılan “iki artı iki eşittir sıfır” hatasını yapmamak için SON DERECE DİKKATLİ olmak önemlidir. Bir yerde hata yaptıysam hemen özür dilerim =)
Bir segmentin uzunluğu nasıl bulunur?
Uzunluk, daha önce belirtildiği gibi modül işaretiyle gösterilir.
Düzlemin iki noktası verilirse ve o zaman parçanın uzunluğu formül kullanılarak hesaplanabilir.
Uzayda iki nokta verilirse, parçanın uzunluğu formül kullanılarak hesaplanabilir.
Not: İlgili koordinatlar değiştirilirse formüller doğru kalacaktır: Ve , ancak ilk seçenek daha standarttır
Örnek 3
Çözüm: ilgili formüle göre:
Cevap:
Netlik sağlamak için bir çizim yapacağım 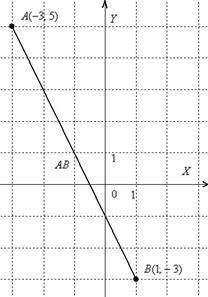
Çizgi segmenti - bu bir vektör değil ve tabii ki onu hiçbir yere taşıyamazsınız. Ayrıca ölçekli çizim yaparsanız: 1 birim. = 1 cm (iki dizüstü bilgisayar hücresi), o zaman ortaya çıkan cevap, parçanın uzunluğu doğrudan ölçülerek normal bir cetvelle kontrol edilebilir.
Evet çözüm kısa ama içinde birkaç tane daha var önemli noktalarşunu açıklığa kavuşturmak isterim:
İlk olarak cevaba boyutu koyuyoruz: “birimler”. Koşul ne olduğunu söylemiyor; milimetre, santimetre, metre veya kilometre. Bu nedenle, matematiksel olarak doğru bir çözüm, genel formülasyon olacaktır: "birimler" - "birimler" olarak kısaltılır.
İkinci olarak tekrarlayalım okul materyali, bu yalnızca ele alınan sorun için yararlı değildir:
dikkat et önemli teknik teknik – çarpanı kökün altından kaldırmak. Hesaplamalar sonucunda bir sonuç elde ediyoruz ve iyi bir matematik stili, faktörün (mümkünse) kökün altından çıkarılmasını içerir. Daha ayrıntılı olarak süreç şöyle görünür: . Elbette cevabı olduğu gibi bırakmak bir hata olmayacaktır; ancak bu kesinlikle bir eksiklik ve öğretmen açısından saçma sapan bir tartışma olacaktır.
İşte diğer yaygın durumlar: 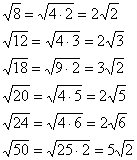
Çoğunlukla kökte yeterli miktarda bulunur Büyük sayı, Örneğin . Bu gibi durumlarda ne yapmalı? Hesap makinesini kullanarak sayının 4'e bölünüp bölünmediğini kontrol ederiz: . Evet, tamamen bölünmüştü, dolayısıyla: ![]() . Ya da belki sayı tekrar 4'e bölünebilir? . Böylece:
. Ya da belki sayı tekrar 4'e bölünebilir? . Böylece: ![]() . Sayının son rakamı tek olduğundan üçüncü kez 4'e bölmek elbette işe yaramayacaktır. Dokuza bölmeye çalışalım: . Sonuç olarak:
. Sayının son rakamı tek olduğundan üçüncü kez 4'e bölmek elbette işe yaramayacaktır. Dokuza bölmeye çalışalım: . Sonuç olarak:
Hazır.
Çözüm: kökün altında bir bütün olarak çıkarılamayan bir sayı alırsak, o zaman faktörü kökün altından kaldırmaya çalışırız - bir hesap makinesi kullanarak sayının şu şekilde bölünebilir olup olmadığını kontrol ederiz: 4, 9, 16, 25, 36, 49 vb.
Karar sırasında çeşitli görevler Kökler yaygındır, öğretmenin yorumlarına göre çözümlerinizi sonuçlandırırken daha düşük not almaktan ve gereksiz sorunlardan kaçınmak için her zaman faktörleri kökün altından çıkarmaya çalışın.
Köklerin karesini almayı ve diğer kuvvetleri de tekrarlayalım:
Derecesi olan eylemler için kurallar Genel görünüm Içinde bulunabilir okul ders kitabı cebirde, ancak verilen örneklerden her şeyin veya hemen hemen her şeyin zaten açık olduğunu düşünüyorum.
Uzayda bir segmentle bağımsız çözüm görevi:
Örnek 4
Puanlar ve verilir. Segmentin uzunluğunu bulun.
Çözüm ve cevap dersin sonundadır.
Bir vektörün uzunluğu nasıl bulunur?
Bir düzlem vektörü verilirse uzunluğu formülle hesaplanır.
Bir uzay vektörü verilirse uzunluğu formülle hesaplanır. ![]() .
.
Bu formüller (bir parçanın uzunluğuna ilişkin formüllerin yanı sıra) iyi bilinen Pisagor teoremi kullanılarak kolayca türetilir.
Örnek 5
Puanlar ve verilir. Vektörün uzunluğunu bulun.
Örnek 3'teki puanların aynısını aldım.
Çözüm:İlk önce vektörü bulalım:
Formülü kullanarak vektörün uzunluğunu hesaplıyoruz:
Cevap:
Boyutunu “birimler” olarak belirtmeyi unutmayın! Bu arada, yaklaşık bir değerin hesaplanması her zaman gerekli midir? bu örnekte 8.94), eğer bu durumda gerekli değilse? Benim açımdan gereksiz olmayacak; yaklaşık bir değerin olmaması, kusurlara yol açıyor. 2-3 ondalık basamağa yuvarlamanız tavsiye edilir.
Görev için bir çizim yapalım:
Örnek 3'ten temel fark nedir? Aradaki fark, burada bir segmentten değil, bir vektörden bahsediyor olmamızdır. Vektör düzlemdeki herhangi bir noktaya taşınabilir.
Örnek 3 ile Örnek 5 arasındaki benzerlikler nelerdir? Segmentin uzunluğunun vektörün uzunluğuna eşit olduğu geometrik olarak açıktır. Vektör uzunluğunun aynı olacağı da açıktır. Sonuç olarak: ![]() .
.
b) , , ve vektörleri verildiğinde. Uzunluklarını bulun.
Dersin sonunda çözümler ve cevaplar.
Bu makalede, birçok geometri problemini basit aritmetiğe indirgemenizi sağlayacak bir "sihirli değnek"i tartışmaya başlayacağız. Bu "çubuk", özellikle de inşa etme konusunda emin olmadığınızda hayatınızı çok daha kolaylaştırabilir. mekansal figürler, bölümler vb. Bütün bunlar belirli bir hayal gücü ve pratik beceriler gerektirir. Burada ele almaya başlayacağımız yöntem, her türden neredeyse tamamen soyutlama yapmanızı sağlayacaktır. geometrik yapılar ve muhakeme. Yöntem denir "koordinat yöntemi". Bu yazıda aşağıdaki soruları ele alacağız:
- Koordinat uçağı
- Düzlemdeki noktalar ve vektörler
- İki noktadan bir vektör oluşturma
- Vektör uzunluğu (iki nokta arasındaki mesafe)
- Segmentin ortasının koordinatları
- Vektörlerin nokta çarpımı
- İki vektör arasındaki açı
Koordinat yöntemine neden böyle denildiğini zaten tahmin ettiğinizi düşünüyorum. Doğru, bu ismi aldı çünkü çalışmıyor geometrik nesneler ve onlarla sayısal özellikler(koordinatlar). Geometriden cebire geçmemizi sağlayan dönüşümün kendisi de bir koordinat sisteminin tanıtılmasından ibarettir. Orijinal şekil düzse koordinatlar iki boyutludur, şekil üç boyutluysa koordinatlar üç boyutludur. Bu yazıda sadece iki boyutlu durumu ele alacağız. Ve makalenin asıl amacı size bazılarının nasıl kullanılacağını öğretmektir. temel teknikler koordinat yöntemi (bazen Birleşik Devlet Sınavının B Bölümündeki planimetri ile ilgili problemleri çözerken yararlı oldukları ortaya çıkar). Bu konuyla ilgili sonraki iki bölüm, C2 problemlerini (stereometri problemi) çözme yöntemlerinin tartışılmasına ayrılmıştır.
Koordinat yöntemini tartışmaya nereden başlamak mantıklı olur? Muhtemelen koordinat sistemi kavramından. Onunla ilk karşılaştığınız zamanı hatırlayın. Bana öyle geliyor ki 7. sınıfta varoluşu öğrendiğinde doğrusal fonksiyon, Örneğin. Bunu nokta nokta inşa ettiğinizi hatırlatmama izin verin. Hatırlıyor musun? Sen seçtin Rasgele sayı, bunu formülde yerine koydum ve bu şekilde hesapladım. Örneğin, eğer, o zaman, eğer, o zaman vb. Sonunda ne elde ettiniz? Ve koordinatları olan puanlar aldınız: ve. Daha sonra bir “çapraz” (koordinat sistemi) çizdiniz, üzerinde bir ölçek seçtiniz (birim segment olarak kaç hücreye sahip olacağınız) ve elde ettiğiniz noktaları üzerinde işaretleyip bunları düz bir çizgiyle birleştirdiniz; ortaya çıkan sonuç çizgi fonksiyonun grafiğidir.
Burada size biraz daha ayrıntılı olarak anlatılması gereken birkaç nokta var:
1. Kolaylık olması açısından tek bir segment seçersiniz, böylece her şey çizime güzel ve kompakt bir şekilde sığar.
2. Eksenin soldan sağa, eksenin aşağıdan yukarıya doğru gittiği kabul edilir.
3. Dik açılarda kesişirler ve kesiştikleri noktaya orijin denir. Bir harfle belirtilir.
4. Bir noktanın koordinatlarını yazarken, örneğin, parantez içinde solda noktanın eksen boyunca ve sağda eksen boyunca koordinatları vardır. Özellikle, bu şu anlama gelir:
5. Herhangi bir noktayı belirlemek için koordinat ekseni koordinatlarını belirtmeniz gerekir (2 sayı)
6. Eksen üzerinde yer alan herhangi bir nokta için,
7. Eksen üzerinde yer alan herhangi bir nokta için,
8. Eksene x ekseni denir
9. Eksen y ekseni olarak adlandırılır
Şimdi bunu seninle yapalım Sonraki adım: İki noktayı işaretleyelim. Bu iki noktayı bir doğru parçasıyla birleştirelim. Ve sanki noktadan noktaya bir doğru parçası çiziyormuşuz gibi oku koyacağız: yani parçamızın yönlendirilmesini sağlayacağız!

Başka bir yönlü segmentin ne dendiğini hatırlıyor musunuz? Doğru, buna vektör deniyor!
Yani noktayı noktaya bağlarsak, ve başlangıç A noktası olacak ve son B noktası olacak, sonra bir vektör elde ederiz. Bu inşaatı 8. sınıfta da yapmıştın, hatırladın mı?
Noktalar gibi vektörlerin de iki sayı ile gösterilebileceği ortaya çıktı: bu sayılara vektör koordinatları denir. Soru: Bir vektörün koordinatlarını bulmak için başlangıç ve bitiş koordinatlarını bilmemiz sizce yeterli midir? Görünüşe göre evet! Ve bu çok basit bir şekilde yapılır:
Böylece, bir vektörde nokta başlangıç ve nokta son olduğundan, vektör aşağıdaki koordinatlara sahiptir:
Örneğin, eğer öyleyse vektörün koordinatları
Şimdi bunun tersini yapalım, vektörün koordinatlarını bulalım. Bunun için neyi değiştirmemiz gerekiyor? Evet, başlangıcı ve bitişi değiştirmeniz gerekiyor: şimdi vektörün başlangıcı noktada olacak ve sonu da noktada olacak. Daha sonra:
Dikkatlice bakın, vektörler arasındaki fark nedir? Tek farkları koordinatlardaki işaretlerdir. Onlar birbirine zıttır. Bu gerçek genellikle şu şekilde yazılır:
Bazen hangi noktanın vektörün başlangıcı, hangisinin sonu olduğu açıkça belirtilmezse, vektörler ikiden fazla sayı ile gösterilir. büyük harflerle ve bir küçük harf, örneğin: , vb.
Şimdi biraz pratik kendiniz ve aşağıdaki vektörlerin koordinatlarını bulun:
Muayene:
Şimdi biraz daha zor bir problemi çözün:
Bir noktada başlangıcı olan bir vektörün co-or-di-na-you'su vardır. Abs-cis-su noktalarını bulun.
Yine de oldukça sıradan: Noktanın koordinatları olsun. Daha sonra
Sistemi vektör koordinatlarının ne olduğunun tanımına göre derledim. O halde noktanın koordinatları vardır. Apsisle ilgileniyoruz. Daha sonra
Cevap:
Vektörlerle başka neler yapabilirsiniz? Evet hemen hemen her şey aynı sıradan sayılar(Bölme yapamazsınız ancak iki şekilde çarpabilirsiniz; bunlardan birini biraz sonra burada tartışacağız)
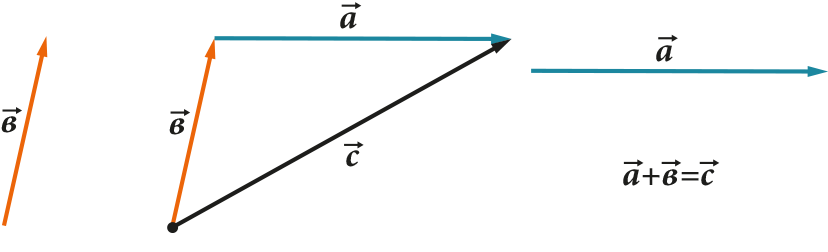
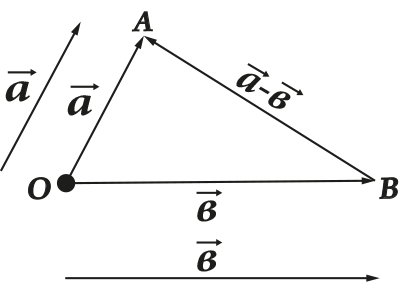
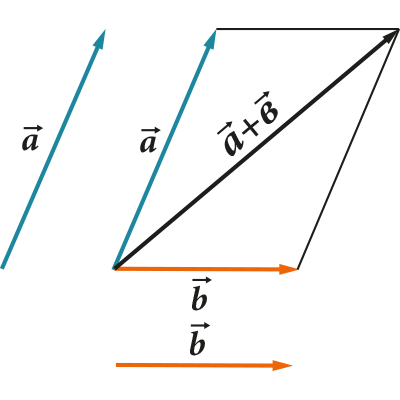
- Vektörler birbirine eklenebilir
- Vektörler birbirinden çıkarılabilir
- Vektörler sıfırdan farklı bir sayıyla çarpılabilir (veya bölünebilir)
- Vektörler birbirleriyle çarpılabilir
Tüm bu işlemlerin çok net bir geometrik temsili vardır. Örneğin, toplama ve çıkarma için üçgen (veya paralelkenar) kuralı:
Bir vektör bir sayıyla çarpıldığında veya bölündüğünde uzar, daralır veya yön değiştirir:

Ancak burada koordinatlara ne olacağı sorusuyla ilgileneceğiz.
1. İki vektörü toplarken (çıkarırken), koordinatlarını öğe öğe ekleriz (çıkarırız). Yani:
2. Bir vektörü bir sayıyla çarparken (bölerken), tüm koordinatları bu sayıyla çarpılır (bölülür):
Örneğin:
· Yüzyıldan raya eş-or-di-nat miktarını bulun.
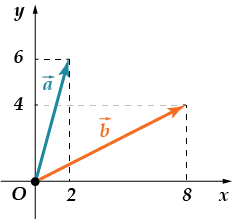
Önce vektörlerin her birinin koordinatlarını bulalım. İkisi de aynı kökene sahiptir; başlangıç noktası. Bunların sonu farklıdır. Daha sonra, . Şimdi vektörün koordinatlarını hesaplayalım, sonra ortaya çıkan vektörün koordinatlarının toplamı eşit olur.
Cevap:
Şimdi aşağıdaki sorunu kendiniz çözün:
· Vektör koordinatlarının toplamını bulun
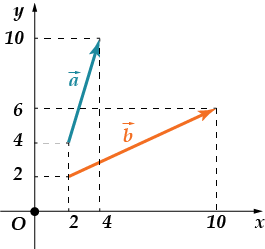
Kontrol ediyoruz:
Şimdi şu problemi ele alalım: Koordinat düzleminde iki noktamız var. Aralarındaki mesafe nasıl bulunur? Birinci nokta ve ikincisi olsun. Aralarındaki mesafeyi ile gösterelim. Açıklık sağlamak için aşağıdaki çizimi yapalım:
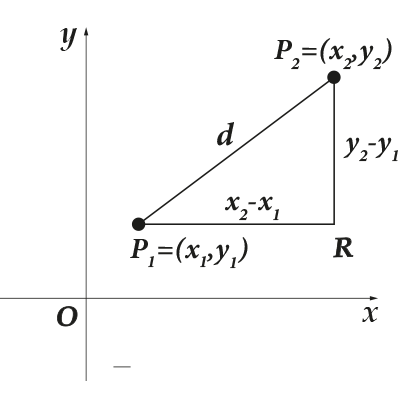
Ne yaptım? Öncelikle bağlandım noktalar ve bir ayrıca noktadan bir çizgi çizdi, eksene paralel ve bu noktadan eksene paralel bir çizgi çizdim. Bir noktada kesişerek dikkat çekici bir şekil mi oluşturdular? Onun nesi bu kadar özel? Evet, sen ve ben dik üçgen hakkında neredeyse her şeyi biliyoruz. Elbette Pisagor teoremi. Gerekli bölüm bu üçgenin hipotenüsüdür ve bölümler bacaklardır. Noktanın koordinatları nelerdir? Evet, resimden bulmak kolaydır: Parçalar eksenlere paralel olduğundan ve sırasıyla uzunluklarını bulmak kolaydır: Parçaların uzunluklarını sırasıyla ile belirtirsek, o zaman
Şimdi Pisagor teoremini kullanalım. Bacakların uzunluklarını biliyoruz, hipotenüsü bulacağız:
Dolayısıyla iki nokta arasındaki mesafe, koordinatlardan olan farkların karelerinin toplamının köküdür. Veya - iki nokta arasındaki mesafe, onları bağlayan parçanın uzunluğudur. Noktalar arasındaki mesafenin yöne bağlı olmadığını görmek kolaydır. Daha sonra:
Buradan üç sonuç çıkarıyoruz:
İki nokta arasındaki mesafeyi hesaplama konusunda biraz pratik yapalım:
Örneğin, eğer ve arasındaki mesafe şuna eşitse:
Veya başka bir yoldan gidelim: vektörün koordinatlarını bulun
Ve vektörün uzunluğunu bulun:
Gördüğünüz gibi aynı şey!
Şimdi biraz kendiniz pratik yapın:
Görev: Belirtilen noktalar arasındaki mesafeyi bulun:
Kontrol ediyoruz:
Kulağa biraz farklı gelse de, aynı formülü kullanan birkaç problem daha var:
1. Göz kapağı uzunluğunun karesini bulun.

2. Göz kapağı uzunluğunun karesini bulun

Sanırım onlarla zorluk çekmeden başa çıktın? Kontrol ediyoruz:
1. Bu da dikkat içindir) Vektörlerin koordinatlarını daha önce bulmuştuk: . O halde vektörün koordinatları vardır. Uzunluğunun karesi şuna eşit olacaktır:
2. Vektörün koordinatlarını bulun
O zaman uzunluğunun karesi
Karmaşık bir şey yok, değil mi? Basit aritmetik, başka bir şey değil.
Aşağıdaki problemler açık bir şekilde sınıflandırılamaz; bunlar daha çok genel bilgi ve basit resimler çizme yeteneği ile ilgilidir.
1. Noktayı apsis eksenine bağlayan kesimden gelen açının sinüsünü bulun.
 Ve
Ve
Burada nasıl ilerleyeceğiz? Eksen ile arasındaki açının sinüsünü bulmamız gerekiyor. Sinüs'ü nerede arayabiliriz? Bu doğru, içinde dik üçgen. Peki ne yapmamız gerekiyor? Bu üçgeni inşa edin!
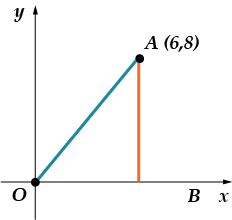
Noktanın koordinatları ve olduğundan, segment eşittir ve segmenttir. Açının sinüsünü bulmamız gerekiyor. Size sinüsün bir oran olduğunu hatırlatmama izin verin karşı bacak o zaman hipotenüse
Bizim için yapacak ne kaldı? Hipotenüsü bulun. Bunu iki şekilde yapabilirsiniz: Pisagor teoremini kullanarak (bacaklar bilinir!) veya iki nokta arasındaki mesafe formülünü kullanarak (aslında ilk yöntemle aynı şeydir!). Ben ikinci yola gideceğim:
Cevap:
Bir sonraki görev size daha da kolay görünecek. Noktanın koordinatlarında.
Görev 2. Per-pen-di-ku-lyar'ın ab-ciss eksenine indirildiği noktadan itibaren. Nai-di-te abs-cis-su os-no-va-niya per-pen-di-ku-la-ra.
Bir çizim yapalım:
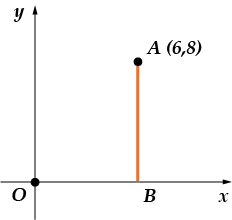
Bir dikmenin tabanı x eksenini (ekseni) kestiği noktadır, benim için bu bir noktadır. Şekil koordinatlara sahip olduğunu göstermektedir: . Apsisle yani “x” bileşeniyle ilgileniyoruz. O eşittir.
Cevap: .
Görev 3. Koşullarda önceki görev noktadan koordinat eksenlerine olan uzaklıkların toplamını bulun.
Bir noktadan eksenlere olan mesafenin ne olduğunu biliyorsanız, görev genellikle basittir. Bilirsin? Umarım, ama yine de hatırlatacağım:
Peki, hemen yukarıdaki çizimimde zaten böyle bir dik çizgi çizmiş miydim? Hangi eksendedir? Eksene. Peki uzunluğu ne kadardır? O eşittir. Şimdi eksene kendiniz dik bir çizgi çizin ve uzunluğunu bulun. Eşit olacak değil mi? O zaman toplamları eşittir.
Cevap: .
Görev 4. Görev 2 koşullarında noktanın koordinatını bulun, simetrik nokta apsis eksenine göre.
Simetrinin ne olduğu sizin için sezgisel olarak açık sanırım? Pek çok nesnede bu özellik var: pek çok bina, masa, uçak, pek çok geometrik şekiller: top, silindir, kare, eşkenar dörtgen vb. Kabaca söylemek gerekirse simetri şu şekilde anlaşılabilir: bir şekil iki (veya daha fazla) özdeş yarıdan oluşur. Bu simetriye eksenel simetri denir. O halde eksen nedir? Bu tam olarak şeklin göreceli olarak eşit yarıya "kesilebileceği" çizgidir (bu resimde simetri ekseni düzdür):

Şimdi görevimize geri dönelim. Eksene göre simetrik olan bir nokta aradığımızı biliyoruz. O halde bu eksen simetri eksenidir. Bu, eksenin parçayı iki eşit parçaya keseceği bir noktayı işaretlememiz gerektiği anlamına gelir. Böyle bir noktayı kendiniz işaretlemeye çalışın. Şimdi benim çözümümle karşılaştırın:
![]()
Sizin için de aynı şekilde mi sonuçlandı? İyi! Bulunan noktanın koordinatıyla ilgileniyoruz. Eşittir
Cevap:
Şimdi söyleyin bana, birkaç saniye düşündükten sonra, A noktasına ordinatına göre simetrik olan bir noktanın apsisi ne olur? Cevabınız nedir? Doğru cevap: .
İÇİNDE Genel dava kural şu şekilde yazılabilir:
Apsis eksenine göre bir noktaya simetrik bir noktanın koordinatları vardır:
Ordinat eksenine göre bir noktaya simetrik bir noktanın koordinatları vardır:
Eh, şimdi tamamen korkutucu görev: orijine göre noktaya simetrik olan bir noktanın koordinatlarını bulun. Önce kendin düşün, sonra çizimime bak!
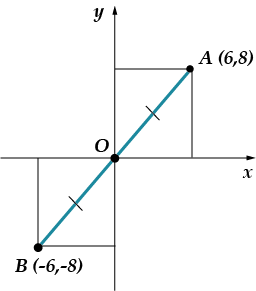
Cevap:
Şimdi paralelkenar problemi:
Görev 5: Noktalar ver-shi-na-mi pa-ral-le-lo-gram-ma olarak görünür. Bu noktada or-di'yi bulun.
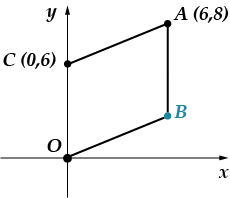
Bu sorunu iki şekilde çözebilirsiniz: mantık ve koordinat yöntemi. Önce koordinat yöntemini kullanacağım, sonra size bunu nasıl farklı şekilde çözebileceğinizi anlatacağım.
Noktanın apsisinin eşit olduğu oldukça açıktır. (noktadan apsis eksenine çizilen dik üzerinde yer alır). Ordinatı bulmamız gerekiyor. Şeklimizin paralelkenar olmasından yararlanalım, bu şu anlama geliyor. İki nokta arasındaki mesafe formülünü kullanarak doğru parçasının uzunluğunu bulalım:
Noktayı eksene bağlayan dikmeyi indiriyoruz. Kesişme noktasını harfle belirteceğim.
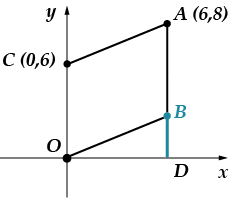
Segmentin uzunluğu eşittir. (bu noktayı tartıştığımız yerde sorunu kendiniz bulun), sonra Pisagor teoremini kullanarak parçanın uzunluğunu bulacağız:
Bir parçanın uzunluğu tam olarak ordinatıyla çakışır.
Cevap: .
Başka bir çözüm (Sadece bunu gösteren bir resim vereceğim)
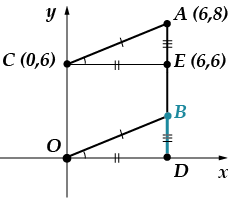
Çözüm ilerlemesi:
1. Davranış
2. Noktanın ve uzunluğun koordinatlarını bulun
3. Bunu kanıtlayın.
Bir diğeri bölüm uzunluğu sorunu:
Noktalar üçgenin üstünde görünür. Orta çizgisinin paralel uzunluğunu bulun.

Ne olduğunu hatırlıyor musun? orta hatüçgen? O zaman bu görev sizin için temeldir. Hatırlamıyorsan sana hatırlatayım: Üçgenin orta çizgisi, orta noktaları birleştiren çizgidir zıt taraflar. Tabana paralel ve yarısına eşittir.
Taban bir segmenttir. Uzunluğunu daha önce aramamız gerekiyordu, eşit. Daha sonra orta çizginin uzunluğu yarısı kadar büyük ve eşittir.
Cevap: .
Yorum Yap: Bu sorun, biraz sonra ele alacağımız başka bir şekilde çözülebilir.
Bu arada, işte size birkaç problem; bunlar üzerinde pratik yapın; çok basitler ama koordinat yöntemini kullanma konusunda daha iyi olmanıza yardımcı oluyorlar!
1. Noktalar tra-pe-tion'ların en üst noktasıdır. Orta çizgisinin uzunluğunu bulun.

2. Noktalar ve görünümler ver-shi-na-mi pa-ral-le-lo-gram-ma. Bu noktada or-di'yi bulun.

3. Noktayı birleştirerek kesimden itibaren uzunluğu bulun ve

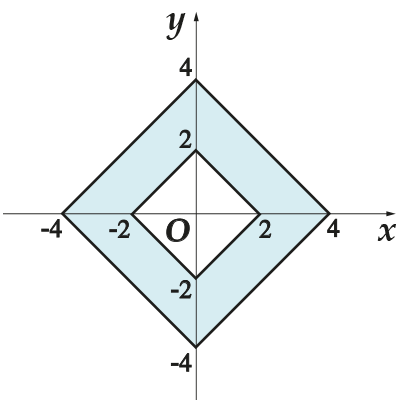
4. Koordinat düzleminde renkli şeklin arkasındaki alanı bulun.
5. Merkezi na-cha-le ko-or-di-nat'ta olan bir daire bu noktadan geçiyor. Onun yarıçapını bulun.
6. Çemberin-di-te ra-di-us'unu bulun, dik açı hakkında-san-noy-no-ka'yı tanımlayın, bir şeyin üst kısımlarının bir ko-veya -di-na-varlığı var, o kadar sorumlusunuz ki

Çözümler:
1. Bir yamuğun orta çizgisinin tabanlarının toplamının yarısına eşit olduğu bilinmektedir. Taban eşittir ve taban. Daha sonra
Cevap:
2. Bu problemi çözmenin en kolay yolu (paralelkenar kuralı) olduğunu not etmektir. Vektörlerin koordinatlarını hesaplamak zor değildir: . Vektörleri eklerken koordinatlar eklenir. Sonra koordinatları var. Vektörün orijini koordinatların olduğu nokta olduğundan nokta da bu koordinatlara sahiptir. Ordinatla ilgileniyoruz. O eşittir.
Cevap:
3. Hemen iki nokta arasındaki mesafe formülüne göre hareket ediyoruz:
Cevap:
4. Resme bakın ve gölgeli alanın hangi iki şeklin arasına sıkıştırıldığını söyleyin? İki kare arasına sıkıştırılmıştır. Daha sonra istenen şeklin alanı, büyük karenin alanından küçük olanın alanına eşittir. Taraf küçük kare noktaları birleştiren bir segmenttir ve uzunluğu
O zaman küçük karenin alanı
Aynısını büyük bir kare için yapıyoruz: kenarı noktaları birleştiren bir segmenttir ve uzunluğu
O halde büyük karenin alanı
İstenilen şeklin alanını aşağıdaki formülü kullanarak buluyoruz:
Cevap:
5. Eğer bir dairenin merkezi orijine sahipse ve bir noktadan geçiyorsa, yarıçapı tam olarak şu şekilde olacaktır: uzunluğa eşit segment (bir çizim yapın ve bunun neden açık olduğunu anlayacaksınız). Bu parçanın uzunluğunu bulalım:
Cevap:
6. Bir dikdörtgenin çevrelediği dairenin yarıçapının yarıya eşit onun köşegenleri. İki köşegenden herhangi birinin uzunluğunu bulalım (sonuçta dikdörtgende bunlar eşittir!)
Cevap:
Peki her şeyin üstesinden geldin mi? Bunu anlamak çok zor olmadı değil mi? Burada tek bir kural var - görsel bir resim oluşturabilmek ve içindeki tüm verileri basitçe "okuyabilmek".
Çok az şeyimiz kaldı. Aslında tartışmak istediğim iki nokta daha var.
Bu basit sorunu çözmeye çalışalım. İki puan verelim. Doğru parçasının orta noktasının koordinatlarını bulun. Bu sorunun çözümü şu şekildedir: Nokta istenen orta olsun, o zaman koordinatları vardır:
Yani: parçanın ortasının koordinatları = parçanın uçlarının karşılık gelen koordinatlarının aritmetik ortalaması.
Bu kural çok basittir ve genellikle öğrenciler için zorluk yaratmaz. Hangi problemlerde ve nasıl kullanıldığını görelim:
1. Kesimden-di-te veya-di-na-tu se-re-di-ny'yi bulun, noktayı bağlayın ve

2. Puanlar dünyanın zirvesi gibi görünüyor. Dia-go-na-ley'in per-re-se-che-niya'sını bul.

3. Çemberin merkezini bulun, dikdörtgen-no-ka hakkında-san-noy'u tanımlayın, bir şeyin üstleri co-or-di-na-you-sorumlu bir şekilde-ama var.

Çözümler:
1. İlk sorun tam bir klasiktir. Segmentin ortasını belirlemek için hemen ilerliyoruz. Koordinatları var. Ordinat eşittir.
Cevap:
2. Bu dörtgenin bir paralelkenar (hatta bir eşkenar dörtgen) olduğunu görmek kolaydır. Kenar uzunluklarını hesaplayıp birbirleriyle karşılaştırarak bunu kendiniz kanıtlayabilirsiniz. Paralelkenarlar hakkında ne biliyorum? Köşegenleri kesişme noktasına göre ikiye bölünmüştür! Evet! Peki köşegenlerin kesişme noktası nedir? Bu herhangi bir köşegenin ortasıdır! Özellikle köşegeni seçeceğim. O zaman noktanın koordinatları vardır. Noktanın ordinatı eşittir.
Cevap:
3. Dikdörtgenin çevrelediği dairenin merkezi neyle çakışmaktadır? Köşegenlerinin kesişme noktasına denk gelir. Dikdörtgenin köşegenleri hakkında ne biliyorsunuz? Eşittirler ve kesişme noktası onları ikiye böler. Görev bir öncekine indirildi. Örneğin köşegeni ele alalım. O zaman çevrel çemberin merkezi ise orta noktadır. Koordinatları arıyorum: Apsis eşittir.
Cevap:
Şimdi kendi başınıza biraz pratik yapın, kendinizi test edebilmeniz için her sorunun yanıtını vereceğim.
1. Çemberin yarıçapını bulun, üçgen açıyı tanımlayın-no-ka, bir şeyin üst kısımlarında bir co-or-di -no misters var

2. Çemberin merkezini bulun-di-te veya-di-on-noy'u, üstleri koordinatlara sahip olan üçgen-no-ka hakkında tanımlayın
3. Merkezi ab-cis eksenine değecek bir noktada olan bir çemberin yarıçapı ne olmalıdır?
4. Eksenin yeniden ayrıldığı noktayı ve kesme noktasını bulun, noktayı birleştirin ve

Yanıtlar:
Her şey başarılı mıydı? Bunu gerçekten umuyorum! Şimdi - son itiş. Şimdi özellikle dikkatli olun. Şimdi açıklayacağım materyal sadece konuyla doğrudan ilgili değil basit görevler B kısmındaki koordinat yöntemine göre değişir, ancak aynı zamanda C2 probleminin her yerinde bulunur.
Hangi sözlerimi henüz tutmadım? Vektörler üzerinde hangi işlemleri tanıtmaya söz verdiğimi ve hangilerini sonuçta tanıttığımı hatırlıyor musunuz? Hiçbir şeyi unutmadığıma emin misin? Unutmuş olmak! Vektör çarpımının ne anlama geldiğini açıklamayı unuttum.
Bir vektörü bir vektörle çarpmanın iki yolu vardır. Seçilen yönteme bağlı olarak farklı nitelikteki nesneler elde edeceğiz:
Çapraz çarpım oldukça akıllıca yapılmıştır. Bir sonraki makalede bunun nasıl yapılacağını ve neden gerekli olduğunu tartışacağız. Ve bunda skaler çarpıma odaklanacağız.
Bunu hesaplamamıza izin veren iki yol vardır:
Tahmin ettiğiniz gibi sonuç aynı olmalı! O halde önce ilk yönteme bakalım:
Koordinatlar aracılığıyla nokta çarpımı
Bul: - skaler çarpım için genel kabul görmüş gösterim
Hesaplama formülü aşağıdaki gibidir:
Yani skaler çarpım= vektör koordinatlarının çarpımlarının toplamı!
Örnek:
Bul-di-te
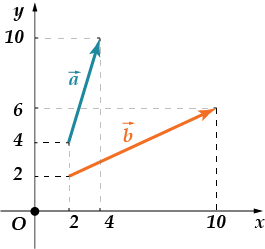
Çözüm:
Her bir vektörün koordinatlarını bulalım:
Skaler çarpımı aşağıdaki formülü kullanarak hesaplıyoruz:
Cevap:
Bakın kesinlikle karmaşık bir şey yok!
Peki, şimdi kendiniz deneyin:
· Yüzyılların skaler bir pro-iz-ve-de-nie'sini bulun ve
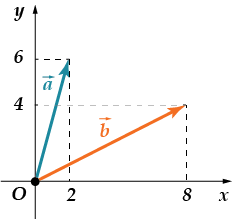
Becerebildin mi? Belki küçük bir yakalama fark ettiniz? Hadi kontrol edelim:
Vektör koordinatları aşağıdaki gibi Son görev! Cevap: .
Koordinat olana ek olarak, skaler çarpımı hesaplamanın başka bir yolu da vardır, yani vektörlerin uzunlukları ve aralarındaki açının kosinüsü aracılığıyla:
Ve vektörleri arasındaki açıyı belirtir.
Yani skaler çarpım, vektörlerin uzunlukları ile aralarındaki açının kosinüsünün çarpımına eşittir.
Madem ki çok daha basit olan birinci formüle sahibiz, en azından içinde kosinüs yok, bu ikinci formüle neden ihtiyacımız var? Ve birinci ve ikinci formüllerden vektörler arasındaki açıyı nasıl bulacağımızı çıkarabilmemiz için buna ihtiyaç var!
O zaman vektörün uzunluğunun formülünü hatırlayalım!
Daha sonra bu verileri skaler çarpım formülünde değiştirirsem şunu elde ederim:
Ama başka bir şekilde:
Peki sen ve ben ne elde ettik? Artık iki vektör arasındaki açıyı hesaplamamızı sağlayan bir formülümüz var! Bazen kısa olması açısından şu şekilde de yazılır:
Yani, vektörler arasındaki açıyı hesaplamak için kullanılan algoritma aşağıdaki gibidir:
- Koordinatlar aracılığıyla skaler çarpımı hesaplayın
- Vektörlerin uzunluklarını bulun ve çarpın
- 1. noktanın sonucunu 2. noktanın sonucuna bölün
Örneklerle pratik yapalım:
1. Göz kapakları ile arasındaki açıyı bulun. Cevabı grad-du-sah'ta verin.
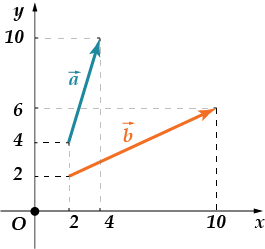
2. Önceki problemin koşullarında vektörler arasındaki kosinüsü bulun
Haydi şunu yapalım: İlk sorunu çözmenize yardım edeceğim ve ikincisini kendiniz yapmaya çalışın! Kabul etmek? O zaman başlayalım!
1. Bu vektörler bizim eski dostlarımızdır. Skaler çarpımlarını zaten hesaplamıştık ve eşitti. Koordinatları: , . Sonra uzunluklarını buluyoruz:
Daha sonra vektörler arasındaki kosinüsü ararız:
Açının kosinüsü nedir? Burası köşe.
Cevap:
Şimdi ikinci sorunu kendiniz çözün ve sonra karşılaştırın! Çok kısa bir çözüm sunacağım:
2. Koordinatları vardır, koordinatları vardır.
Vektörler arasındaki açı olsun ve sonra
Cevap:
B kısmındaki problemlerin doğrudan vektörler ve koordinat yöntemi ile ilgili olduğuna dikkat edilmelidir. sınav kağıdı oldukça nadir. Ancak C2 problemlerinin büyük çoğunluğu bir koordinat sistemi getirilerek kolayca çözülebilir. Dolayısıyla bu makaleyi, karmaşık sorunları çözmek için ihtiyaç duyacağımız oldukça akıllı yapılar yapacağımız temel olarak düşünebilirsiniz.
