విమానాల జతల ఖండన ద్వారా ఏర్పడిన డైహెడ్రల్ కోణాలను నిర్ణయించండి. సమస్య: ఒక విమానం ఒక రేఖను కలుస్తుంది

ఈ కథనం విమానాల మధ్య కోణం మరియు దానిని ఎలా కనుగొనాలి. మొదట, రెండు విమానాల మధ్య కోణం యొక్క నిర్వచనం ఇవ్వబడింది మరియు గ్రాఫికల్ ఇలస్ట్రేషన్ ఇవ్వబడింది. దీని తరువాత, కోఆర్డినేట్ పద్ధతిని ఉపయోగించి రెండు ఖండన విమానాల మధ్య కోణాన్ని కనుగొనే సూత్రం విశ్లేషించబడింది మరియు ఈ విమానాల యొక్క సాధారణ వెక్టర్స్ యొక్క తెలిసిన కోఆర్డినేట్‌లను ఉపయోగించి ఖండన విమానాల మధ్య కోణాన్ని లెక్కించడానికి మిమ్మల్ని అనుమతించే ఒక సూత్రం పొందబడింది. ముగింపులో ఇది చూపబడింది వివరణాత్మక పరిష్కారాలులక్షణ పనులు.

పేజీ నావిగేషన్.

విమానాల మధ్య కోణం - నిర్వచనం.

రెండు ఖండన విమానాల మధ్య కోణం యొక్క నిర్ణయాన్ని క్రమంగా చేరుకోవడానికి మాకు అనుమతించే వాదనలను అందజేద్దాం.

మాకు రెండు ఖండన విమానాలు మరియు . ఈ విమానాలు సరళ రేఖ వెంట కలుస్తాయి, దీనిని మేము c అక్షరంతో సూచిస్తాము. లైన్ c యొక్క పాయింట్ M గుండా మరియు c లైన్‌కి లంబంగా ఒక విమానాన్ని నిర్మిస్తాము. ఈ సందర్భంలో, విమానం విమానాలను కలుస్తుంది మరియు. విమానాలు కలిసే సరళ రేఖను a గానూ, విమానాలు కలిసే సరళ రేఖను b గానూ సూచిస్తాము. సహజంగానే, పంక్తులు a మరియు b పాయింట్ M వద్ద కలుస్తాయి.

ఖండన పంక్తుల a మరియు b మధ్య కోణం విమానం వెళుతున్న c లైన్‌లోని పాయింట్ M యొక్క స్థానంపై ఆధారపడి ఉండదని చూపడం సులభం.

లైన్ cకి లంబంగా మరియు విమానం నుండి భిన్నమైన విమానాన్ని నిర్మిస్తాము. విమానం విమానాలు మరియు సరళ రేఖల ద్వారా కలుస్తుంది, వీటిని మేము వరుసగా 1 మరియు బి 1గా సూచిస్తాము.

విమానాలను నిర్మించే పద్ధతి ప్రకారం, a మరియు b పంక్తులు c లైన్‌కు లంబంగా ఉంటాయి మరియు a 1 మరియు b 1 పంక్తులు c లైన్‌కి లంబంగా ఉంటాయి. a మరియు 1 పంక్తులు ఒకే విమానంలో ఉంటాయి మరియు c లైన్‌కి లంబంగా ఉంటాయి కాబట్టి, అవి సమాంతరంగా ఉంటాయి. అదేవిధంగా, b మరియు b 1 పంక్తులు ఒకే విమానంలో ఉంటాయి మరియు c లైన్‌కి లంబంగా ఉంటాయి, కాబట్టి అవి సమాంతరంగా ఉంటాయి. కాబట్టి మీరు చేయవచ్చు సమాంతర బదిలీవిమానం నుండి విమానం, దీనిలో సరళ రేఖ a 1 సరళ రేఖ aతో మరియు సరళ రేఖ b 1 సరళ రేఖతో సమానంగా ఉంటుంది. కాబట్టి, రెండు ఖండన రేఖల మధ్య కోణం a 1 మరియు b 1 కోణానికి సమానంఖండన పంక్తుల మధ్య a మరియు b.

ఇది ఖండన రేఖల మధ్య కోణం a మరియు b ఖండన విమానాలలో ఉంటుంది మరియు విమానం వెళ్ళే పాయింట్ M ఎంపికపై ఆధారపడి ఉండదని ఇది రుజువు చేస్తుంది. కాబట్టి, ఈ కోణాన్ని రెండు ఖండన విమానాల మధ్య కోణంగా తీసుకోవడం తార్కికం.

ఇప్పుడు మీరు రెండు ఖండన విమానాల మధ్య కోణం యొక్క నిర్వచనాన్ని వినిపించవచ్చు మరియు.

నిర్వచనం.

సరళ రేఖలో కలుస్తున్న రెండు విమానాల మధ్య కోణం మరియు- ఇది a మరియు b అనే రెండు ఖండన రేఖల మధ్య కోణం, దీనితో పాటు విమానాలు మరియు c లైన్‌కు లంబంగా ఉండే విమానంతో కలుస్తాయి.

రెండు విమానాల మధ్య కోణం యొక్క నిర్వచనం కొద్దిగా భిన్నంగా ఇవ్వబడుతుంది. విమానాలు మరియు కలుస్తున్న సరళ రేఖ c పై ఉంటే, M బిందువును గుర్తించి, దాని ద్వారా a మరియు b సరళ రేఖలను గీయండి, c సరళ రేఖకు లంబంగా మరియు సమతలంలో పడి మరియు వరుసగా, అప్పుడు సరళ రేఖల మధ్య కోణం a మరియు b అనేది విమానాల మధ్య కోణం మరియు. సాధారణంగా ఆచరణలో, విమానాల మధ్య కోణాన్ని పొందేందుకు ఇటువంటి నిర్మాణాలు నిర్వహిస్తారు.

ఖండన రేఖల మధ్య కోణం మించదు కాబట్టి, ఇది పేర్కొన్న నిర్వచనం నుండి అనుసరిస్తుంది డిగ్రీ కొలతరెండు ఖండన విమానాల మధ్య కోణం వ్యక్తీకరించబడింది వాస్తవ సంఖ్యవిరామం నుండి. ఈ సందర్భంలో, ఖండన విమానాలు అంటారు లంబంగా, వాటి మధ్య కోణం తొంభై డిగ్రీలు ఉంటే. సమాంతర విమానాల మధ్య కోణం అస్సలు నిర్ణయించబడదు లేదా సున్నాకి సమానంగా పరిగణించబడుతుంది.

రెండు ఖండన విమానాల మధ్య కోణాన్ని కనుగొనడం.

సాధారణంగా, రెండు ఖండన విమానాల మధ్య కోణాన్ని కనుగొన్నప్పుడు, మీరు మొదట ఖండన సరళ రేఖలను చూడటానికి అదనపు నిర్మాణాలను నిర్వహించాలి, దీని మధ్య కోణం కావలసిన కోణానికి సమానంగా ఉంటుంది, ఆపై సమానత్వ పరీక్షలు, సారూప్యతలను ఉపయోగించి అసలు డేటాతో ఈ కోణాన్ని కనెక్ట్ చేయండి. పరీక్షలు, కొసైన్ సిద్ధాంతం లేదా కోణం యొక్క సైన్, కొసైన్ మరియు టాంజెంట్ యొక్క నిర్వచనాలు. జ్యామితి కోర్సులో ఉన్నత పాఠశాలఇలాంటి సమస్యలు వస్తాయి.

ఉదాహరణగా, 2012 గణితంలో యూనిఫైడ్ స్టేట్ ఎగ్జామ్ నుండి సమస్య C2కి పరిష్కారాన్ని ఇద్దాం (పరిస్థితి ఉద్దేశపూర్వకంగా మార్చబడింది, కానీ ఇది పరిష్కారం యొక్క సూత్రాన్ని ప్రభావితం చేయదు). అందులో, మీరు రెండు ఖండన విమానాల మధ్య కోణాన్ని కనుగొనవలసి ఉంటుంది.

ఉదాహరణ.

పరిష్కారం.

మొదట, డ్రాయింగ్ చేద్దాం.

విమానాల మధ్య కోణాన్ని "చూడడానికి" అదనపు నిర్మాణాలను చేద్దాం.

ముందుగా, ABC మరియు BED 1 విమానాలు కలిసే సరళ రేఖను నిర్వచిద్దాం. పాయింట్ B వారి సాధారణ పాయింట్లలో ఒకటి. రెండవది కనుక్కోండి సాధారణ పాయింట్ఈ విమానాలు. DA మరియు D 1 E పంక్తులు ఒకే విమానం ADD 1లో ఉంటాయి మరియు అవి సమాంతరంగా ఉండవు మరియు అందువల్ల కలుస్తాయి. మరోవైపు, లైన్ DA విమానం ABCలో ఉంటుంది మరియు లైన్ D 1 E - విమానం BED 1లో ఉంటుంది, కాబట్టి, DA మరియు D 1 E పంక్తుల ఖండన స్థానం ఒక సాధారణ బిందువుగా ఉంటుంది. ABC విమానాలుమరియు BED 1. కాబట్టి, DA మరియు D 1 E పంక్తులను వాటి ఖండనకు కొనసాగిద్దాం, వాటి ఖండన బిందువును F అక్షరంతో సూచిస్తుంది. అప్పుడు BF అనేది ABC మరియు BED 1 విమానాలు కలిసే సరళ రేఖ.

ABC మరియు BED 1 విమానాలలో వరుసగా రెండు పంక్తులను నిర్మించడం మిగిలి ఉంది, BF రేఖపై ఒక పాయింట్ గుండా మరియు BF రేఖకు లంబంగా వెళుతుంది - ఈ పంక్తుల మధ్య కోణం, నిర్వచనం ప్రకారం, మధ్య కావలసిన కోణానికి సమానంగా ఉంటుంది. విమానాలు ABC మరియు BED 1. మనం చేద్దాం.

చుక్క A అనేది ABC విమానంలో పాయింట్ E యొక్క ప్రొజెక్షన్. పాయింట్ M వద్ద లంబ కోణంలో BF ఖండన రేఖను గీద్దాం. అప్పుడు సరళ రేఖ AM అనేది ABC విమానం మరియు మూడు లంబాల సిద్ధాంతం ద్వారా EM యొక్క సరళ రేఖ యొక్క ప్రొజెక్షన్.

అందువలన, ABC మరియు BED 1 విమానాల మధ్య అవసరమైన కోణం సమానంగా ఉంటుంది.

కుడి త్రిభుజం AEM నుండి ఈ కోణం యొక్క సైన్, కొసైన్ లేదా టాంజెంట్‌ను (అందువలన కోణం కూడా) గుర్తించవచ్చు, దాని రెండు భుజాల పొడవులు మనకు తెలిస్తే. షరతు నుండి పొడవు AEని కనుగొనడం సులభం: పాయింట్ E 4 నుండి 3 నిష్పత్తిలో AA 1ని విభజిస్తుంది, పాయింట్ A నుండి లెక్కించబడుతుంది మరియు AA 1 వైపు పొడవు 7, అప్పుడు AE = 4. AM నిడివిని కనుగొనండి.

దీన్ని చేయడానికి, పరిగణించండి కుడి త్రిభుజంలంబ కోణం Aతో ABF, ఇక్కడ AM ఎత్తు. షరతు ప్రకారం AB = 2. కుడి త్రిభుజాల DD 1 F మరియు AEF సారూప్యత నుండి AF వైపు పొడవును మనం కనుగొనవచ్చు:

పైథాగరియన్ సిద్ధాంతాన్ని ఉపయోగించి, మేము త్రిభుజం ABF నుండి కనుగొంటాము. మేము త్రిభుజం ABF వైశాల్యం ద్వారా AM పొడవును కనుగొంటాము: ఒక వైపు త్రిభుజం ABF వైశాల్యం సమానం , మరోవైపు , ఎక్కడ .

అందువలన, కుడి త్రిభుజం AEM నుండి మేము కలిగి ఉన్నాము .

అప్పుడు ABC మరియు BED 1 విమానాల మధ్య అవసరమైన కోణం సమానంగా ఉంటుంది (గమనించండి ).

సమాధానం:

కొన్ని సందర్భాల్లో, రెండు ఖండన విమానాల మధ్య కోణాన్ని కనుగొనడానికి, Oxyzని సెట్ చేయడం మరియు కోఆర్డినేట్ పద్ధతిని ఉపయోగించడం సౌకర్యంగా ఉంటుంది. అక్కడితో ఆపేద్దాం.

పనిని సెట్ చేద్దాం: రెండు ఖండన విమానాల మధ్య కోణాన్ని కనుగొనండి మరియు . కావలసిన కోణాన్ని ఇలా సూచిస్తాం.

ఇచ్చిన దీర్ఘచతురస్రాకార కోఆర్డినేట్ సిస్టమ్ ఆక్సిజ్‌లో ఖండన విమానాల యొక్క సాధారణ వెక్టర్స్ యొక్క కోఆర్డినేట్‌లు మనకు తెలుసు మరియు వాటిని కనుగొనే అవకాశం ఉందని మేము ఊహిస్తాము. వీలు విమానం యొక్క సాధారణ వెక్టర్, మరియు విమానం యొక్క సాధారణ వెక్టర్. ఖండన విమానాల మధ్య కోణాన్ని ఎలా కనుగొనాలో మరియు ఈ విమానాల యొక్క సాధారణ వెక్టర్స్ యొక్క కోఆర్డినేట్ల ద్వారా మేము చూపుతాము.

విమానాలు మరియు కలుస్తున్న సరళ రేఖను c గా సూచిస్తాము. లైన్ c పై పాయింట్ M ద్వారా మేము లైన్ cకి లంబంగా ఒక విమానం గీస్తాము. విమానం విమానాలను కలుస్తుంది మరియు వరుసగా a మరియు b రేఖల వెంట, పంక్తులు a మరియు b పాయింట్ M వద్ద కలుస్తాయి. నిర్వచనం ప్రకారం, ఖండన విమానాల మధ్య కోణం మరియు ఖండన పంక్తుల మధ్య కోణానికి సమానం a మరియు b.

మనం సాధారణ వెక్టర్స్ మరియు ప్లేన్‌లను మరియు ప్లేన్‌లోని పాయింట్ M నుండి ప్లాట్ చేద్దాం. ఈ సందర్భంలో, వెక్టార్ లైన్ a కి లంబంగా ఉండే రేఖపై ఉంటుంది మరియు వెక్టర్ b లైన్‌కి లంబంగా ఉండే రేఖపై ఉంటుంది. అందువలన, విమానంలో వెక్టర్ అనేది లైన్ a యొక్క సాధారణ వెక్టర్, ఇది లైన్ b యొక్క సాధారణ వెక్టర్.

ఖండన రేఖల మధ్య కోణాన్ని కనుగొనే వ్యాసంలో, సాధారణ వెక్టర్స్ యొక్క కోఆర్డినేట్‌లను ఉపయోగించి ఖండన రేఖల మధ్య కోణం యొక్క కొసైన్‌ను లెక్కించడానికి మాకు అనుమతించే సూత్రాన్ని మేము అందుకున్నాము. అందువలన, a మరియు b పంక్తుల మధ్య కోణం యొక్క కొసైన్, మరియు, తత్ఫలితంగా, ఖండన విమానాల మధ్య కోణం యొక్క కొసైన్మరియు సూత్రం ద్వారా కనుగొనబడింది, ఎక్కడ మరియు విమానాల యొక్క సాధారణ వెక్టర్స్ మరియు వరుసగా. అప్పుడు అది లెక్కించబడుతుంది .

కోఆర్డినేట్ పద్ధతిని ఉపయోగించి మునుపటి ఉదాహరణను పరిష్కరిద్దాం.

ఉదాహరణ.

డాన్ క్యూబాయిడ్ ABCDA 1 B 1 C 1 D 1, దీనిలో AB=2, AD=3, AA 1 =7 మరియు పాయింట్ E AA 1ని 4 నుండి 3 నిష్పత్తిలో విభజించి, పాయింట్ A నుండి లెక్కించబడుతుంది. ABC మరియు BED 1 విమానాల మధ్య కోణాన్ని కనుగొనండి.

పరిష్కారం.

ఒక శీర్షం వద్ద ఉన్న దీర్ఘచతురస్రాకార సమాంతర పైప్ యొక్క భుజాలు జత వైపు లంబంగా ఉన్నందున, పరిచయం చేయడం సౌకర్యంగా ఉంటుంది దీర్ఘచతురస్రాకార వ్యవస్థ Oxyzని ఇలా సమన్వయం చేస్తుంది: ప్రారంభాన్ని C శీర్షంతో సమలేఖనం చేయండి మరియు CD, CB మరియు CC 1 వైపులా వరుసగా Ox, Oy మరియు Oz సమన్వయ అక్షాలను నిర్దేశించండి.

ABC మరియు BED 1 విమానాల మధ్య కోణాన్ని ఫార్ములా ఉపయోగించి ఈ విమానాల యొక్క సాధారణ వెక్టర్స్ యొక్క కోఆర్డినేట్‌ల ద్వారా కనుగొనవచ్చు, ఇక్కడ మరియు వరుసగా ABC మరియు BED 1 విమానాల యొక్క సాధారణ వెక్టర్స్ ఉంటాయి. సాధారణ వెక్టర్స్ యొక్క కోఆర్డినేట్లను గుర్తించండి.

విమానాల మధ్య కోణం యొక్క కొలత పదునైన మూలలో, ఈ విమానాలలో పడి ఉన్న రెండు సరళ రేఖల ద్వారా ఏర్పడతాయి మరియు వాటి ఖండన రేఖకు లంబంగా గీసారు.

నిర్మాణ అల్గోరిథం

1. ఒక ఏకపక్ష బిందువు K నుండి, ఇవ్వబడిన ప్రతి సమతలానికి లంబాలు గీయబడతాయి.
2. స్థాయి రేఖ చుట్టూ తిరగడం ద్వారా, పాయింట్ K వద్ద శీర్షంతో కోణం γ° నిర్ణయించబడుతుంది.
3. γ° > 90° అందించిన ϕ° = 180 – γ° విమానాల మధ్య కోణాన్ని లెక్కించండి. γ° అయితే< 90°, то ∠ϕ° = ∠γ°.

α మరియు β విమానాలు జాడల ద్వారా ఇవ్వబడినప్పుడు బొమ్మ చూపిస్తుంది. అవసరమైన అన్ని నిర్మాణాలు అల్గోరిథం ప్రకారం నిర్వహించబడ్డాయి మరియు క్రింద వివరించబడ్డాయి.

పరిష్కారం

1. డ్రాయింగ్‌లోని ఏకపక్ష ప్రదేశంలో, పాయింట్ K అని గుర్తు పెట్టండి. దాని నుండి మేము లంబంగా m మరియు n, వరుసగా, α మరియు β విమానాలకు తగ్గిస్తాము. m మరియు n అంచనాల దిశ క్రింది విధంగా ఉంటుంది: m""⊥f 0α , m"⊥h 0α , n""⊥f 0β , n"⊥h 0β .
2. మేము పంక్తుల m మరియు n మధ్య ∠γ° వాస్తవ పరిమాణాన్ని నిర్ణయిస్తాము. దీన్ని చేయడానికి, ఫ్రంటల్ f చుట్టూ మేము ప్రొజెక్షన్ యొక్క ఫ్రంటల్ ప్లేన్‌కు సమాంతర స్థానానికి శీర్షం K తో కోణం యొక్క సమతలాన్ని తిప్పుతాము. పాయింట్ K యొక్క టర్నింగ్ వ్యాసార్థం R విలువకు సమానంఒక లంబ త్రిభుజం O""K""K 0 యొక్క హైపోటెన్యూస్, దీని వైపు K""K 0 = y K – y O.
3. కావలసిన కోణం ϕ° = ∠γ°, ఎందుకంటే ∠γ° తీవ్రమైనది.

సమాంతర మరియు ఖండన రేఖల ద్వారా అందించబడిన α మరియు β విమానాల మధ్య కోణం γ°ని కనుగొనడానికి అవసరమైన సమస్యకు దిగువ బొమ్మ పరిష్కారాన్ని చూపుతుంది.

పరిష్కారం

1. మేము క్షితిజ సమాంతరాలు h 1, h 2 మరియు ఫ్రంట్‌లు f 1, f 2, ప్రొజెక్షన్‌ల దిశను నిర్ణయిస్తాము. విమానాలకు చెందినవిα మరియు β, బాణాలచే సూచించబడిన క్రమంలో. స్క్వేర్‌పై ఏకపక్ష పాయింట్ K నుండి. α మరియు β మేము e మరియు k లంబాలను వదిలివేస్తాము. ఈ సందర్భంలో, e""⊥f"" 1 , e"⊥h" 1 మరియు k""⊥f"" 2 , k"⊥h" 2 .
2. మేము e మరియు k పంక్తుల మధ్య ∠γ°ని నిర్వచించాము. దీన్ని చేయడానికి, h 3 క్షితిజ సమాంతర రేఖను గీయండి మరియు దాని చుట్టూ మేము పాయింట్ K ను K 1 స్థానానికి తిప్పుతాము, దీనిలో △CKD క్షితిజ సమాంతర సమతలానికి సమాంతరంగా మారుతుంది మరియు దానిపై సహజ పరిమాణంలో ప్రతిబింబిస్తుంది - △C"K" 1 D ". భ్రమణ కేంద్రం O" యొక్క ప్రొజెక్షన్, K"O"కి లంబంగా h" 3కి గీసినదానిపై ఉంది. R వ్యాసార్థం O"K"K 0 అనే కుడి త్రిభుజం నుండి నిర్ణయించబడుతుంది, దీని వైపు K"K 0 = Z O - Z K.
3. కావలసిన విలువ యొక్క విలువ ∠ϕ° = ∠γ°, ఎందుకంటే కోణం γ° తీవ్రంగా ఉంటుంది.

కథనం విమానాల మధ్య కోణాన్ని కనుగొనడం గురించి మాట్లాడుతుంది. నిర్వచనం ఇచ్చిన తర్వాత, మేము గ్రాఫిక్ ఇలస్ట్రేషన్ ఇస్తాము మరియు పద్ధతిని ఉపయోగించి కోఆర్డినేట్‌లను కనుగొనే వివరణాత్మక పద్ధతిని పరిశీలిస్తాము. మేము ఖండన విమానాల కోసం ఒక సూత్రాన్ని పొందుతాము, ఇందులో సాధారణ వెక్టర్స్ యొక్క కోఆర్డినేట్‌లు ఉంటాయి.

Yandex.RTB R-A-339285-1

అంతరిక్షంలో విమానం మరియు రేఖ గురించి కథనాలలో గతంలో అధ్యయనం చేసిన డేటా మరియు భావనలను పదార్థం ఉపయోగిస్తుంది. మొదట, రెండు ఖండన విమానాల మధ్య కోణాన్ని నిర్ణయించడానికి ఒక నిర్దిష్ట విధానాన్ని కలిగి ఉండటానికి అనుమతించే తార్కికానికి వెళ్లడం అవసరం.

రెండు ఖండన విమానాలు γ 1 మరియు γ 2 ఇవ్వబడ్డాయి. వారి ఖండన c హోదాను తీసుకుంటుంది. χ విమానం యొక్క నిర్మాణం ఈ విమానాల ఖండనతో సంబంధం కలిగి ఉంటుంది. విమానం χ పాయింట్ M ద్వారా సరళ రేఖ c వలె వెళుతుంది. γ 1 మరియు γ 2 విమానాల ఖండన విమానం χ ఉపయోగించి చేయబడుతుంది. మేము లైన్ γ 1 మరియు χ ఖండన రేఖ యొక్క హోదాను పంక్తి a గా మరియు γ 2 మరియు χ లను కలిపే రేఖను లైన్ b గా తీసుకుంటాము. a మరియు b పంక్తుల ఖండన M అనే బిందువును ఇస్తుందని మేము కనుగొన్నాము.

పాయింట్ M యొక్క స్థానం ఖండన పంక్తుల a మరియు b మధ్య కోణాన్ని ప్రభావితం చేయదు మరియు పాయింట్ M లైన్ cలో ఉంది, దీని ద్వారా విమానం χ వెళుతుంది.

లైన్ cకి లంబంగా మరియు విమానం χ నుండి భిన్నమైన విమానం χ 1ని నిర్మించడం అవసరం. χ 1 సహాయంతో γ 1 మరియు γ 2 విమానాల ఖండన a 1 మరియు b 1 పంక్తుల హోదాను తీసుకుంటుంది.

χ మరియు χ 1 లను నిర్మించేటప్పుడు, a మరియు b పంక్తులు c పంక్తికి లంబంగా ఉంటాయి, అప్పుడు a 1, b 1 లైన్ cకి లంబంగా ఉంటాయి. c సరళ రేఖకు లంబంగా ఉన్న విమానం γ 1లో a మరియు a 1 సరళ రేఖలను కనుగొనడం, అప్పుడు వాటిని సమాంతరంగా పరిగణించవచ్చు. అదే విధంగా, γ 2 విమానంలో b మరియు b 1 యొక్క స్థానం c సరళ రేఖకు లంబంగా ఉండటం వాటి సమాంతరతను సూచిస్తుంది. దీనర్థం χ 1 నుండి χ విమానం యొక్క సమాంతర బదిలీని చేయడం అవసరం, ఇక్కడ మనకు a మరియు a 1, b మరియు b 1 అనే రెండు ఏకకాల సరళ రేఖలు లభిస్తాయి. ఖండన పంక్తుల a మరియు b 1 మధ్య కోణం a మరియు b ఖండన రేఖల కోణానికి సమానంగా ఉంటుందని మేము కనుగొన్నాము.

క్రింద ఉన్న బొమ్మను చూద్దాం.

ఖండన పంక్తుల a మరియు b మధ్య పాయింట్ M యొక్క స్థానం, అంటే ఖండన బిందువుపై ఆధారపడని కోణం ఉందని ఈ ప్రతిపాదన నిరూపించబడింది. ఈ పంక్తులు γ 1 మరియు γ 2 విమానాలలో ఉన్నాయి. వాస్తవానికి, ఫలిత కోణాన్ని రెండు ఖండన విమానాల మధ్య కోణంగా పరిగణించవచ్చు.

ఇప్పటికే ఉన్న ఖండన విమానాలు γ 1 మరియు γ 2 మధ్య కోణాన్ని నిర్ణయించడానికి ముందుకు వెళ్దాం.

నిర్వచనం 1

రెండు ఖండన విమానాల మధ్య కోణం γ 1 మరియు γ 2 a మరియు b పంక్తుల ఖండన ద్వారా ఏర్పడిన కోణం అని పిలుస్తారు, ఇక్కడ γ 1 మరియు γ 2 విమానాలు χ పంక్తికి లంబంగా ఉన్న విమానంతో కలుస్తాయి.

దిగువ బొమ్మను పరిగణించండి.

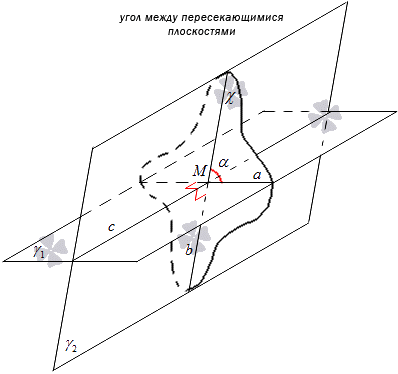
నిర్ణయాన్ని మరొక రూపంలో సమర్పించవచ్చు. γ 1 మరియు γ 2 విమానాలు కలుస్తున్నప్పుడు, c అంటే అవి కలిసే రేఖ, ఒక పాయింట్ Mను గుర్తించండి, దీని ద్వారా లైన్ c మరియు γ 1 మరియు γ 2 రేఖకు లంబంగా a మరియు b పంక్తులను గీయండి, ఆపై వాటి మధ్య కోణం a మరియు b పంక్తులు విమానాల మధ్య కోణంగా ఉంటాయి. ఆచరణలో, విమానాల మధ్య కోణాన్ని నిర్మించడానికి ఇది వర్తిస్తుంది.

ఖండన చేసినప్పుడు, విలువలో 90 డిగ్రీల కంటే తక్కువ కోణం ఏర్పడుతుంది, అంటే, కోణం యొక్క డిగ్రీ కొలత ఈ రకమైన (0, 90] విరామంలో చెల్లుబాటు అవుతుంది. అదే సమయంలో, ఈ విమానాలను లంబంగా పిలుస్తారు ఖండన వద్ద లంబ కోణం ఏర్పడుతుంది, సమాంతర విమానాల మధ్య కోణం సున్నాకి సమానంగా పరిగణించబడుతుంది.

ఖండన విమానాల మధ్య కోణాన్ని కనుగొనడానికి సాధారణ మార్గం అదనపు నిర్మాణాలను నిర్వహించడం. ఇది ఖచ్చితత్వంతో దాన్ని గుర్తించడంలో సహాయపడుతుంది మరియు త్రిభుజం, సైన్స్ మరియు కోసైన్‌ల సమానత్వం లేదా సారూప్యత సంకేతాలను ఉపయోగించి దీన్ని చేయవచ్చు.

నుండి ఒక ఉదాహరణను ఉపయోగించి సమస్యలను పరిష్కరించడాన్ని పరిశీలిద్దాం ఏకీకృత రాష్ట్ర పరీక్ష సమస్యలుబ్లాక్ C 2.

ఉదాహరణ 1

ఒక దీర్ఘచతురస్రాకార సమాంతర పైప్డ్ A B C D A 1 B 1 C 1 D 1, ఇక్కడ A B = 2, A D = 3, A A 1 = 7, పాయింట్ E 4: 3 నిష్పత్తిలో A A 1ని విభజిస్తుంది. A B C మరియు B E D 1 విమానాల మధ్య కోణాన్ని కనుగొనండి.

పరిష్కారం

స్పష్టత కోసం, డ్రాయింగ్ చేయడం అవసరం. మేము దానిని పొందుతాము

విమానాల మధ్య కోణంతో పనిచేయడం మరింత సౌకర్యవంతంగా చేయడానికి దృశ్యమాన ప్రాతినిధ్యం అవసరం.

A B C మరియు B E D 1 విమానాల ఖండన సంభవించే సరళ రేఖను మేము నిర్ణయిస్తాము. పాయింట్ B ఒక సాధారణ పాయింట్. ఖండన యొక్క మరొక సాధారణ పాయింట్ కనుగొనబడాలి. ఒకే విమానం A D D 1లో ఉన్న D A మరియు D 1 E సరళ రేఖలను పరిశీలిద్దాం. వాటి స్థానం సమాంతరతను సూచించదు;

అయితే, సరళరేఖ D A A B C విమానంలో మరియు D 1 E B E D 1లో ఉంది. దీని నుండి మనకు సరళ రేఖలు లభిస్తాయి D Aమరియు డి 1 ఇఒక సాధారణ ఖండన స్థానం కలిగి ఉంటుంది, ఇది A B C మరియు B E D 1 విమానాలకు సాధారణం. పంక్తుల ఖండన బిందువును సూచిస్తుంది D Aమరియు D 1 E అక్షరం F. దీని నుండి B F అనేది A B C మరియు B E D 1 విమానాలు కలిసే సరళ రేఖ అని మనం పొందుతాము.

క్రింద ఉన్న బొమ్మను చూద్దాం.

సమాధానాన్ని పొందడానికి, A B C మరియు B E D 1 విమానాలలో ఉన్న సరళ రేఖలను నిర్మించడం అవసరం, ఇది B F లైన్‌లో మరియు దానికి లంబంగా ఉన్న పాయింట్ గుండా వెళుతుంది. అప్పుడు ఈ సరళ రేఖల మధ్య ఫలిత కోణం A B C మరియు B E D 1 విమానాల మధ్య కావలసిన కోణంగా పరిగణించబడుతుంది.

దీని నుండి పాయింట్ A అనేది A B C ప్లేన్‌పై పాయింట్ E యొక్క ప్రొజెక్షన్ అని మనం చూడవచ్చు. M పాయింట్ వద్ద లంబ కోణంలో B F రేఖాంశ ఖండన రేఖను గీయడం అవసరం. ఇది సరళ రేఖ A M అనేది ప్రొజెక్షన్ అని చూడవచ్చు. A B C విమానంలో E M యొక్క సరళ రేఖ, A M ⊥ B F లంబంగా ఉన్న సిద్ధాంతం ఆధారంగా. దిగువ బొమ్మను పరిగణించండి.

∠ A M E అనేది A B C మరియు B E D 1 విమానాల ద్వారా ఏర్పడిన కావలసిన కోణం. ఫలిత త్రిభుజం A E M నుండి మనం కోణం యొక్క సైన్, కొసైన్ లేదా టాంజెంట్‌ను కనుగొనవచ్చు, ఆపై దాని రెండు భుజాలు తెలిసినట్లయితే మాత్రమే కోణాన్ని కనుగొనవచ్చు. షరతు ప్రకారం, A E పొడవు ఈ విధంగా కనుగొనబడింది: సరళ రేఖ A A 1 నిష్పత్తి 4: 3లో పాయింట్ E ద్వారా విభజించబడింది, అంటే సరళ రేఖ యొక్క మొత్తం పొడవు 7 భాగాలు, ఆపై A E = 4 భాగాలు. మేము A M ను కనుగొన్నాము.

A B F లంబకోణ త్రిభుజాన్ని పరిగణనలోకి తీసుకోవడం అవసరం. మనకు A M ఎత్తుతో లంబ కోణం A ఉంటుంది. A B = 2 పరిస్థితి నుండి, D D 1 F మరియు A E F త్రిభుజాల సారూప్యత ద్వారా A F పొడవును కనుగొనవచ్చు. మనకు A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

పైథాగరియన్ సిద్ధాంతాన్ని ఉపయోగించి A B F త్రిభుజం B F వైపు పొడవును కనుగొనడం అవసరం. మేము B F = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 అని పొందుతాము. A M వైపు పొడవు A B F త్రిభుజం ప్రాంతం ద్వారా కనుగొనబడుతుంది. ప్రాంతం S A B C = 1 2 · A B · A F మరియు S A B C = 1 2 · B F · A M రెండింటికి సమానంగా ఉంటుందని మేము కలిగి ఉన్నాము.

మనకు A M = A B A F B F = 2 4 2 5 = 4 5 5

అప్పుడు మనం A E M త్రిభుజం యొక్క కోణం యొక్క టాంజెంట్ యొక్క విలువను కనుగొనవచ్చు. మనకు లభిస్తుంది:

t g ∠ A M E = A E A M = 4 4 5 5 = 5

A B C మరియు B E D 1 విమానాల ఖండన ద్వారా పొందిన కావలసిన కోణం a r c t g 5కి సమానం, అప్పుడు సరళీకరణపై మేము r c t g 5 = a r c sin 30 6 = a r c cos 6 6ని పొందుతాము.

సమాధానం: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

ఖండన రేఖల మధ్య కోణాన్ని కనుగొనే కొన్ని సందర్భాలు ఉపయోగించి పేర్కొనబడ్డాయి సమన్వయ విమానం O x y z మరియు కోఆర్డినేట్ పద్ధతి. నిశితంగా పరిశీలిద్దాం.

ఖండన విమానాలు γ 1 మరియు γ 2 మధ్య కోణాన్ని కనుగొనాల్సిన అవసరం ఉన్న చోట సమస్య ఉంటే, మేము కోరుకున్న కోణాన్ని αగా సూచిస్తాము.

అప్పుడు ఇచ్చిన వ్యవస్థకోఆర్డినేట్‌లు మనకు ఖండన విమానాల γ 1 మరియు γ 2 యొక్క సాధారణ వెక్టర్‌ల కోఆర్డినేట్‌లను కలిగి ఉన్నాయని చూపిస్తుంది. అప్పుడు మేము n 1 → = n 1 x, n 1 y, n 1 z అనేది విమానం γ 1 యొక్క సాధారణ వెక్టర్, మరియు n 2 → = (n 2 x, n 2 y, n 2 z) - కోసం విమానం γ 2. పరిగణలోకి తీసుకుందాం వివరణాత్మక అన్వేషణవెక్టర్స్ యొక్క కోఆర్డినేట్‌ల వెంట ఈ విమానాల మధ్య ఉన్న కోణం.

γ 1 మరియు γ 2 విమానాలు c అక్షరంతో కలిసే సరళ రేఖను పేర్కొనడం అవసరం. c లైన్‌లో మనకు ఒక పాయింట్ M ఉంటుంది, దీని ద్వారా cకి లంబంగా χ విమానం గీస్తాము. a మరియు b రేఖల వెంట ఉన్న విమానం χ పాయింట్ M వద్ద γ 1 మరియు γ 2 విమానాలను కలుస్తుంది. ఖండన విమానాలు γ 1 మరియు γ 2 మధ్య కోణం వరుసగా ఈ విమానాలకు చెందిన a మరియు b ఖండన రేఖల కోణానికి సమానం అని నిర్వచనం నుండి ఇది అనుసరిస్తుంది.

χ విమానంలో మేము పాయింట్ M నుండి సాధారణ వెక్టర్లను ప్లాట్ చేస్తాము మరియు వాటిని n 1 → మరియు n 2 → లను సూచిస్తాము. వెక్టర్ n 1 → పంక్తి aకి లంబంగా ఉన్న పంక్తిపై ఉంది మరియు వెక్టర్ n 2 → లైన్ bకి లంబంగా ఉంటుంది. ఇక్కడ నుండి మేము దానిని పొందుతాము ఇచ్చిన విమానంχ పంక్తి n 1 →కి సమానమైన పంక్తి యొక్క సాధారణ వెక్టార్‌ను కలిగి ఉంటుంది మరియు పంక్తి b కోసం n 2 →కి సమానం. దిగువ బొమ్మను పరిగణించండి.

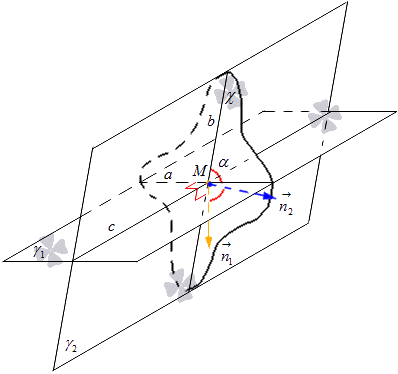
ఇక్కడ నుండి మనం ఒక సూత్రాన్ని పొందుతాము, దీని ద్వారా వెక్టర్స్ కోఆర్డినేట్‌లను ఉపయోగించి ఖండన రేఖల కోణం యొక్క సైన్‌ను లెక్కించవచ్చు. a మరియు b సరళ రేఖల మధ్య కోణం యొక్క కొసైన్, ఖండన విమానాల γ 1 మరియు γ 2 మధ్య ఉన్న కొసైన్‌తో సమానమని మేము కనుగొన్నాము, దీని నుండి ఉద్భవించింది cos సూత్రాలుα = cos n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n x 2 n 2 + n 2 z 2, ఇక్కడ మనకు n 1 → = (n 1 x, n 1 y, n 1 z) మరియు n 2 → = (n 2 x, n 2 y, n 2 z) అక్షాంశాలు సూచించిన విమానాల వెక్టర్స్.

ఖండన రేఖల మధ్య కోణం సూత్రాన్ని ఉపయోగించి లెక్కించబడుతుంది

α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + 2 n 2

ఉదాహరణ 2

షరతు ప్రకారం, సమాంతర పైప్డ్ A B C D A 1 B 1 C 1 D 1 ఇవ్వబడింది , ఇక్కడ A B = 2, A D = 3, A A 1 = 7, మరియు పాయింట్ E A A 1 4: 3 వైపును విభజిస్తుంది. A B C మరియు B E D 1 విమానాల మధ్య కోణాన్ని కనుగొనండి.

పరిష్కారం

పరిస్థితి నుండి దాని భుజాలు జత వైపు లంబంగా ఉన్నాయని స్పష్టమవుతుంది. దీనర్థం C పాయింట్ వద్ద శీర్షంతో O x y z కోఆర్డినేట్ సిస్టమ్‌ను పరిచయం చేయడం మరియు O x, O y, O z అక్షాలను సమన్వయం చేయడం అవసరం. సరైన వైపులా దిశను సెట్ చేయడం అవసరం. దిగువ బొమ్మను పరిగణించండి.

ఖండన విమానాలు ఎ బి సిమరియు బి ఇ డి 1α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n సూత్రం ద్వారా కనుగొనబడే కోణాన్ని రూపొందించండి 2 y 2 + n 2 z 2, దీనిలో n 1 → = (n 1 x, n 1 y, n 1 z) మరియు n 2 → = (n 2 x, n 2 y, n 2 z ) సాధారణ వెక్టర్స్ ఈ విమానాలు. కోఆర్డినేట్‌లను నిర్ణయించడం అవసరం. బొమ్మ నుండి మనకు అది కనిపిస్తుంది కోఆర్డినేట్ అక్షం O x y విమానం A B Cతో సమానంగా ఉంటుంది, దీని అర్థం సాధారణ వెక్టార్ k → యొక్క కోఆర్డినేట్‌లు n 1 → = k → = (0, 0, 1) విలువకు సమానం.

విమానం B E D 1 యొక్క సాధారణ వెక్టర్ తీసుకోబడుతుంది వెక్టర్ ఉత్పత్తి B E → మరియు B D 1 → , ఇక్కడ వాటి కోఆర్డినేట్‌లు కోఆర్డినేట్‌ల ద్వారా కనుగొనబడతాయి తీవ్రమైన పాయింట్లు B, E, D 1, ఇవి సమస్య యొక్క పరిస్థితుల ఆధారంగా నిర్ణయించబడతాయి.

మేము ఆ B (0, 3, 0), D 1 (2, 0, 7) పొందుతాము. ఎందుకంటే A E E A 1 = 4 3, A 2, 3, 0, A 1 2, 3, 7 పాయింట్ల కోఆర్డినేట్‌ల నుండి మనం E 2, 3, 4ని కనుగొంటాము. మేము B E → = (2 , 0 , 4) , B D 1 → = 2 , - 3 , 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 - 3 · 7 = 12 i → - 6 j → - 6 k → ⇔ n 2 → = (12 , - 6 , - 6)

ఆర్క్ కొసైన్ ద్వారా కోణాన్ని లెక్కించడానికి సూత్రంలో కనుగొనబడిన కోఆర్డినేట్‌లను ప్రత్యామ్నాయం చేయడం అవసరం. మాకు దొరికింది

α = a r c cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = a r c cos 6 6 6 = a r c cos 6 6

కోఆర్డినేట్ పద్ధతి ఇదే ఫలితాన్ని ఇస్తుంది.

సమాధానం: a r c cos 6 6 .

అంతిమ సమస్య విమానాల యొక్క ఇప్పటికే తెలిసిన సమీకరణాలతో ఖండన విమానాల మధ్య కోణాన్ని కనుగొనే లక్ష్యంతో పరిగణించబడుతుంది.

ఉదాహరణ 3

కోఆర్డినేట్ సిస్టమ్ O x y zలో నిర్వచించబడిన మరియు 2 x - 4 y + z + 1 = 0 మరియు 3 y - z సమీకరణాల ద్వారా ఇవ్వబడిన రెండు ఖండన రేఖల ద్వారా ఏర్పడిన కోణం యొక్క సైన్, కొసైన్ మరియు కోణం యొక్క విలువను లెక్కించండి. - 1 = 0.

పరిష్కారం

ఒక అంశాన్ని అధ్యయనం చేస్తున్నప్పుడు సాధారణ సమీకరణం A x + B y + C z + D = 0 రూపం యొక్క సరళ రేఖ A, B, C సాధారణ వెక్టర్ యొక్క కోఆర్డినేట్‌లకు సమానమైన గుణకాలు అని వెల్లడించింది. దీనర్థం n 1 → = 2, - 4, 1 మరియు n 2 → = 0, 3, - 1 అందించబడిన పంక్తుల యొక్క సాధారణ వెక్టర్స్.

విమానాల యొక్క సాధారణ వెక్టర్స్ యొక్క కోఆర్డినేట్‌లను ఖండన విమానాల యొక్క కావలసిన కోణాన్ని లెక్కించడానికి సూత్రంలోకి మార్చడం అవసరం. అప్పుడు మనకు అది వస్తుంది

α = a r c cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210

ఇక్కడ నుండి మనం కోణం యొక్క కొసైన్ తీసుకుంటుంది cos వీక్షణα = 13,210. అప్పుడు ఖండన రేఖల కోణం అస్పష్టంగా ఉండదు. లో ప్రత్యామ్నాయం చేస్తోంది త్రికోణమితి గుర్తింపు, కోణం యొక్క సైన్ విలువ వ్యక్తీకరణకు సమానంగా ఉంటుందని మేము కనుగొన్నాము. దానిని లెక్కించి కనుక్కుందాము

పాపం α = 1 - కాస్ 2 α = 1 - 13,210 = 41,210

సమాధానం: sin α = 41,210, cos α = 13,210, α = a r c cos 13,210 = a r c పాపం 41,210.

మీరు టెక్స్ట్‌లో లోపాన్ని గమనించినట్లయితే, దయచేసి దాన్ని హైలైట్ చేసి, Ctrl+Enter నొక్కండి

ఉద్యోగ రకం: 14
అంశం: విమానాల మధ్య కోణం

పరిస్థితి

డానా సరైన ప్రిజం ABCDA_1B_1C_1D_1, M మరియు N వరుసగా AB మరియు BC అంచుల మధ్య బిందువులు, పాయింట్ K అనేది MN యొక్క మధ్య బిందువు.

ఎ) KD_1 మరియు MN పంక్తులు లంబంగా ఉన్నాయని నిరూపించండి.

బి) MND_1 మరియు ABC విమానాల మధ్య కోణాన్ని కనుగొనండి AB=8, AA_1=6\sqrt 2.

పరిష్కారం చూపండి

పరిష్కారం

ఎ)\triangle DCN మరియు \triangle MADలో మేము కలిగి ఉన్నాము: \angle C=\angle A=90^(\circ), CN=AM=\frac12AB, CD=DA.

అందువల్ల రెండు కాళ్లపై \triangle DCN=\triangle MAD. అప్పుడు MD=DN, \triangle DMNసమద్విబాహులు. అంటే క మెడియ న్ డీకే కూడా ఓ ఎత్తు. కాబట్టి, DK \perp MN.

షరతు ద్వారా DD_1 \perp MND, D_1K - ఏటవాలు, KD - ప్రొజెక్షన్, DK \perp MN.

అందువల్ల, సిద్ధాంతం ద్వారా మూడు లంబంగా MN\perp D_1K.

బి)లో నిరూపించబడింది ఎ), DK \perp MN మరియు MN \perp D_1K, కానీ MN అనేది MND_1 మరియు ABC విమానాల ఖండన రేఖ, అంటే \angle DKD_1 - సరళ కోణం MND_1 మరియు ABC విమానాల మధ్య డైహెడ్రల్ కోణం.

పైథాగరియన్ సిద్ధాంతం ప్రకారం \ ట్రయాంగిల్ DAM లో DM= \sqrt (DA^2+AM^2)= \sqrt (64+16)= 4\చ.5, MN= \sqrt (MB^2+BN^2)= \sqrt (16+16)= 4\sqrt 2.కాబట్టి, పైథాగరియన్ సిద్ధాంతం ద్వారా \triangle DKMలో DK= \sqrt (DM^2-KM^2)= \sqrt (80-8)= 6\sqrt 2.ఆపై \triangle DKD_1లో, tg\angle DKD_1=\frac(DD_1)(DK)=\frac(6\sqrt 2)(6\sqrt 2)=1.

దీని అర్థం \angle DKD_1=45^(\circ).

సమాధానం

45^(\circ).

ఉద్యోగ రకం: 14
అంశం: విమానాల మధ్య కోణం

పరిస్థితి

కుడివైపున చతుర్భుజ ప్రిజం ABCDA_1B_1C_1D_1 బేస్ యొక్క భుజాలు 4, పక్క పక్కటెముకలు 6కి సమానం. పాయింట్ M అనేది అంచు CC_1 మధ్యలో ఉంటుంది, పాయింట్ N అనేది BB_1 అంచుపై గుర్తు పెట్టబడింది, అంటే BN:NB_1=1:2.

ఎ) AMN విమానం అంచు DD_1ని ఏ నిష్పత్తిలో విభజిస్తుంది?

బి) ABC మరియు AMN విమానాల మధ్య కోణాన్ని కనుగొనండి.

పరిష్కారం చూపండి

పరిష్కారం

ఎ)ప్లేన్ AMN పాయింట్ K వద్ద అంచు DD_1ని కలుస్తుంది, ఇది ఈ విమానం ద్వారా ఇవ్వబడిన ప్రిజం విభాగంలో నాల్గవ శీర్షం. క్రాస్ సెక్షన్ ఒక సమాంతర చతుర్భుజం ANMK ఎందుకంటే ఇచ్చిన ప్రిజం యొక్క వ్యతిరేక ముఖాలు సమాంతరంగా ఉంటాయి.

BN =\frac13BB_1=2. KL \ సమాంతర CD గీద్దాం, ఆపై ABN మరియు KLM త్రిభుజాలు సమానంగా ఉంటాయి, అంటే ML=BN=2, LC=MC-ML=3-2=1, KD=LC=1.అప్పుడు KD_1=6-1=5. ఇప్పుడు మీరు KD:KD_1=1:5 నిష్పత్తిని కనుగొనవచ్చు.

బి) F అనేది CD మరియు KM సరళ రేఖల ఖండన స్థానం. ABC మరియు AMN విమానాలు AF సరళ రేఖ వెంట కలుస్తాయి. కోణం \angle KHD =\alpha అనేది డైహెడ్రల్ కోణం యొక్క సరళ కోణం (HD\perp AF, తర్వాత మూడు లంబాల సిద్ధాంతానికి విలోమ సిద్ధాంతం ద్వారా, KH \perp AF), మరియు ఇది లంబ త్రిభుజం KHD యొక్క తీవ్రమైన కోణం, లెగ్ KD=1.

త్రిభుజాలు FKD మరియు FMC ఒకేలా ఉంటాయి (KD \parallel MC), కాబట్టి FD:FC=KD:MC, FD:(FD+4)=1:3 నిష్పత్తిని పరిష్కరిస్తే, మనకు FD=2 వస్తుంది. 2 మరియు 4 కాళ్లతో AFD (\angle D=90^(\circ)) కుడి త్రిభుజంలో, మేము హైపోటెన్యూస్‌ను గణిస్తాము AF=\sqrt (4^2+2^2)=2\sqrt 5, DH= AD\cdot FD:AF= \frac(4\cdot 2)(2\sqrt 5)= \frac4(\sqrt 5).

కుడి త్రిభుజం KHDలో మనం కనుగొంటాము tg \alpha =\frac(KD)(DH)=\frac(\sqrt 5)4,దీని అర్థం కావలసిన కోణం \alpha =arctg\frac(\sqrt 5)4.

సమాధానం

ఎ) 1:5;

బి) arctg\frac(\sqrt 5)4.

మూలం: "గణితం. యూనిఫైడ్ స్టేట్ ఎగ్జామ్ 2017 కోసం ప్రిపరేషన్. ప్రొఫైల్ స్థాయి" Ed. F. F. లైసెంకో, S. కులబుఖోవా.

ఉద్యోగ రకం: 14
అంశం: విమానాల మధ్య కోణం

పరిస్థితి

సాధారణ చతుర్భుజాకార పిరమిడ్ KMNPQ 6కి సమానమైన బేస్ సైడ్ MNPQ మరియు పక్క అంచుతో అందించబడింది 3\sqrt (26).

ఎ)పాయింట్ F అంచు MK మధ్యలో ఉంటే, వికర్ణ MPకి సమాంతరంగా లైన్ NF గుండా వెళుతున్న విమానంతో పిరమిడ్ యొక్క ఒక విభాగాన్ని నిర్మించండి.

బి)సెక్షన్ ప్లేన్ మరియు KMP ప్లేన్ మధ్య కోణాన్ని కనుగొనండి.

పరిష్కారం చూపండి

పరిష్కారం

ఎ) KO అనేది పిరమిడ్ యొక్క ఎత్తుగా ఉండనివ్వండి, F MK యొక్క మధ్య బిందువు; FE\ సమాంతర MP (PKM విమానంలో) . FE కాబట్టి మధ్య రేఖ\triangle PKM, తర్వాత FE=\frac(MP)2.

పిరమిడ్‌లోని ఒక విభాగాన్ని NF గుండా మరియు MPకి సమాంతరంగా, అంటే విమానం NFEతో నిర్మిస్తాం. L అనేది EF మరియు KO యొక్క ఖండన స్థానం. పాయింట్లు L మరియు N కావలసిన విభాగానికి చెందినవి మరియు KQN విమానంలో ఉన్నందున, LN మరియు KQ యొక్క ఖండనగా పొందిన పాయింట్ T, కావలసిన విభాగం మరియు అంచు KQ యొక్క ఖండన బిందువు కూడా. NETF అనేది అవసరమైన విభాగం.

బి) NFE మరియు MPK విమానాలు FE సరళ రేఖ వెంట కలుస్తాయి. దీనర్థం ఈ విమానాల మధ్య కోణం డైహెడ్రల్ కోణం OFEN యొక్క సరళ కోణానికి సమానం, దానిని నిర్మిస్తాం: LO\perpMP, MP\ సమాంతర FE,అందుచేత, LO\perpFE;\triangle NFE - ఐసోసెల్స్ (NE=NF సంబంధిత మధ్యస్థంగా సమాన త్రిభుజాలు KPN మరియు KMN ), NL దాని మధ్యస్థం (EL=LF, PO=OM నుండి, మరియు \triangle KEF \sim \triangle KPM) . అందువల్ల NL \perp FE మరియు \angle NLO కావాల్సినది.

ON=\frac12QN=\frac12MN\sqrt 2=3\sqrt 2.

\త్రిభుజం KON - దీర్ఘచతురస్రాకారం.

పైథాగరియన్ సిద్ధాంతం ప్రకారం లెగ్ KO సమానం KO=\sqrt (KN^2-ON^2).

OL = \frac12KO= \frac12\sqrt(KN^2-ON^2)= \frac12\sqrt (9\cdot 26-9\cdot 2)= \frac12\sqrt(9(26-2))= \frac32\sqrt (24)= \frac32\cdot 2\sqrt 6= 3\sqrt 6.

tg\angle NLO =\frac(ON)(OL)=\frac(3\sqrt 2)(3\sqrt 6)=\frac1(\sqrt 3),

\angle NLO=30^(\circ).

సమాధానం

మూలం: "గణితం. యూనిఫైడ్ స్టేట్ ఎగ్జామ్ 2017 కోసం ప్రిపరేషన్. ప్రొఫైల్ స్థాయి." Ed. F. F. లైసెంకో, S. కులబుఖోవా.

ఉద్యోగ రకం: 14
అంశం: విమానాల మధ్య కోణం

పరిస్థితి

సాధారణ త్రిభుజాకార ప్రిజం ABCA_(1)B_(1)C_(1) యొక్క అన్ని అంచులు 6కి సమానం. AC మరియు BB_(1) మరియు శీర్షం A_(1) అంచుల మధ్య బిందువుల ద్వారా కట్టింగ్ ప్లేన్ డ్రా చేయబడింది.

ఎ)అంచు BC 2:1 నిష్పత్తిలో కట్టింగ్ ప్లేన్ ద్వారా విభజించబడిందని నిరూపించండి, C శీర్షం నుండి లెక్కించబడుతుంది.

బి)కట్టింగ్ ప్లేన్ మరియు బేస్ ప్లేన్ మధ్య కోణాన్ని కనుగొనండి.

పరిష్కారం చూపండి

పరిష్కారం

ఎ) D మరియు E వరుసగా AC మరియు BB_(1) అంచుల మధ్య బిందువులుగా ఉండనివ్వండి.

AA_(1)C_(1) విమానంలో మేము A_(1)D సరళ రేఖను గీస్తాము, ఇది K పాయింట్ వద్ద CC_(1) సరళ రేఖను కలుస్తుంది, BB_(1)C_(1) - ఒక సరళ రేఖ KE, ఇది పాయింట్ F వద్ద అంచు BCని కలుస్తుంది. A_(1) మరియు E పాయింట్లను కనెక్ట్ చేయడం, విమానం AA_(1)B_(1), అలాగే D మరియు F, ABC విమానంలో పడుకోవడం, మేము విభాగాన్ని A_(1)EFDని పొందుతాము.

\bigtriangleup AA_(1)D=\bigtriangleup CDKలెగ్ వెంట AD=DC మరియు తీవ్రమైన కోణం.

\angle ADA_(1)=\angle CDK - నిలువుగా ఉండే వాటి వలె, అది AA_(1)=CK=6ని అనుసరిస్తుంది. \bigtriangleup CKF మరియు \bigtriangleup BFE రెండు కోణాల్లో సమానంగా ఉంటాయి \angle FBE=\angle KCF=90^\circ,\angle BFE=\angle CFK - నిలువుగా ఉండే వాటి వలె.

\frac(CK)(BE)=\frac(6)(3)=2,అంటే, సారూప్యత గుణకం 2, అంటే CF:FB=2:1.

బి) AH \perp DFని చేద్దాం. సెక్షన్ ప్లేన్ మరియు బేస్ ప్లేన్ మధ్య కోణం AHA_(1) కోణానికి సమానం. నిజానికి, సెగ్మెంట్ AH \perp DF (DF అనేది ఈ విమానాల ఖండన రేఖ) అనేది A_(1)H సెగ్మెంట్‌ని బేస్ ప్లేన్‌పై ప్రొజెక్షన్, కాబట్టి, మూడు లంబాల సిద్ధాంతం ప్రకారం, A_(1)H \perp DF. \angle AHA_(1)=arctg\frac(AA_(1))(AH). AA_(1)=6.

AHని కనుగొనండి. \angle ADH =\angle FDC (నిలువుగా ఉంటుంది).

\bigtriangleup DFCలో కొసైన్ సిద్ధాంతం ద్వారా:

DF^2=FC^2+DC^2- 2FC \cdot DC \cdot \cos 60^\circ,

DF^2=4^2+3^2-2 \cdot 4 \cdot 3 \cdot \frac(1)(2)=13.

FC^2=DF^2+DC^2- 2DF\cdot DC\cdot\cos\angle FDC,

4^2=13+9-2\sqrt(13) \cdot 3 \cdot \cos \angle FDC,

\cos \angle FDC=\frac(6)(2\sqrt(13) \cdot 3)=\frac(1)(\sqrt(13)).

ప్రాథమిక త్రికోణమితి గుర్తింపుకు అనుగుణంగా

\sin \angle FDC=\sqrt(1-\left (\frac(1)(\sqrt(13))\right)^2)=\frac(2\sqrt(3))(\sqrt(13)) .\bigtriangleup ADH నుండి మనం AHని కనుగొంటాము:

AH=AD \cdot \sin \angle ADH, (\angle FDC=\angle ADH). AH=3 \cdot \frac(2\sqrt(3))(\sqrt(13))=\frac(6\sqrt(13))(\sqrt(13)).

\angle AHA_(1)= arctg\frac(AA_(1))(AH)= arctg\frac(6 \cdot \sqrt(13))(6\sqrt(3))= arctg\frac(\sqrt(39))(3).

సమాధానం

arctg\frac(\sqrt(39))(3).

మూలం: "గణితం. యూనిఫైడ్ స్టేట్ ఎగ్జామ్ 2017 కోసం ప్రిపరేషన్. ప్రొఫైల్ స్థాయి." Ed. F. F. లైసెంకో, S. కులబుఖోవా.

ఉద్యోగ రకం: 14
అంశం: విమానాల మధ్య కోణం

పరిస్థితి

కుడి ప్రిజం ABCDA_(1)B_(1)C_(1)D_(1) యొక్క ఆధారం ఒక రాంబస్ గురు కోణం B 120^\circకి సమానం. ఈ ప్రిజం యొక్క అన్ని అంచులు 10కి సమానం. P మరియు K అనే పాయింట్లు వరుసగా CC_(1) మరియు CD అంచుల మధ్య బిందువులు.

ఎ) PK మరియు PB_(1) పంక్తులు లంబంగా ఉన్నాయని నిరూపించండి.

బి) PKB_(1) మరియు C_(1)B_(1)B విమానాల మధ్య కోణాన్ని కనుగొనండి.

పరిష్కారం చూపండి

పరిష్కారం

ఎ)మేము కోఆర్డినేట్ పద్ధతిని ఉపయోగిస్తాము. వెతుకుదాం స్కేలార్ ఉత్పత్తివెక్టర్స్ \vec(PK) మరియు \vec(PB_(1)), ఆపై ఈ వెక్టర్స్ మధ్య కోణం యొక్క కొసైన్. Oy అక్షాన్ని CD వెంట, Oz అక్షం CC_(1), మరియు Ox axis \perp CDని నిర్దేశిద్దాం. సి మూలం.

అప్పుడు C (0;0;0); C_(1)(0;0;10); P(0;0;5); K(0;5;0); B(BC \cos 30^\circ; BC\sin 30^\circ; 0),అంటే B(5\sqrt(3); 5;0), B_(1)(5\sqrt(3); 5;10).

వెక్టర్స్ యొక్క కోఆర్డినేట్లను కనుగొనండి: \vec(PK)=\(0;5;-5\); \vec(PB_(1))=\(5\sqrt(3); 5;5\).

\vec(PK) మరియు \vec(PB_(1)) మధ్య కోణం \alphaకి సమానంగా ఉండనివ్వండి.

మాకు దొరికింది \cos \alpha=\frac(\vec(PK) \cdot \vec(PB_(1)))(|\vec(PK)| \cdot |\vec(PB_(1))|)= \frac(0 \cdot 5\sqrt(3) + 5 \cdot 5-5 \cdot 5)(|\vec(PK)| \cdot |\vec(PB_(1))|)=0.

\cos \alpha =0, ​​అంటే \vec(PK) \perp \vec(PB_(1)) మరియు PK మరియు PB_(1) పంక్తులు లంబంగా ఉంటాయి.

బి)విమానాల మధ్య కోణం ఈ విమానాలకు లంబంగా ఉన్న సున్నా కాని వెక్టర్స్ మధ్య కోణానికి సమానంగా ఉంటుంది (లేదా, కోణం మందంగా ఉంటే, దాని ప్రక్కనే ఉన్న కోణం). ఇటువంటి వెక్టర్‌లను విమానాలకు సాధారణాలు అంటారు. వాటిని వెతుకుదాం.

\vec(n_(1))=\(x; y; z\) విమానం PKB_(1)కి లంబంగా ఉండనివ్వండి. వ్యవస్థను పరిష్కరించడం ద్వారా దాన్ని కనుగొనండి \begin(కేసులు) \vec(n_(1)) \perp \vec(PK), \\ \vec(n_(1)) \perp \vec(PB_(1)). \ ముగింపు (కేసులు)

\begin(కేసులు) \vec(n_(1)) \cdot \vec(PK)=0, \\ \vec(n_(1)) \cdot \vec(PB_(1))=0; \ ముగింపు (కేసులు)

\begin(కేసులు) 0x+5y-5z=0, \\ 5\sqrt(3)x+5y+5z=0; \ ముగింపు (కేసులు)

\begin(కేసులు)y=z, \\ x=\frac(-y-z)(\sqrt(3)). \ ముగింపు (కేసులు)

తీసుకుందాం y=1; z=1; x=\frac(-2)(\sqrt(3)), \vec(n_(1))=\ఎడమ \( \frac(-2)(\sqrt(3)); 1;1 \కుడి \).

\vec(n_(2))=\(x; y; z\) విమానం C_(1)B_(1)Bకి లంబంగా ఉండనివ్వండి. వ్యవస్థను పరిష్కరించడం ద్వారా దాన్ని కనుగొనండి \begin(కేసులు) \vec(n_(2)) \perp \vec(CC_(1)), \\ \vec(n_(2)) \perp \vec(CB). \ ముగింపు (కేసులు)

\vec(CC_(1))=\(0;0;10\), \vec(CB)=\(5\sqrt(3); 5; 0\).

\begin(కేసులు) \vec(n_(2)) \cdot \vec(CC_(1))=0, \\ \vec(n_(2)) \cdot \vec(CB)=0; \ ముగింపు (కేసులు)

\begin(కేసులు) 0x+0y+10z=0, \\ 5\sqrt(3)x+5y+0z=0; \ ముగింపు (కేసులు)

\begin(కేసులు)z=0, \\ y=-\sqrt(3)x. \ ముగింపు (కేసులు)

తీసుకుందాం x=1; y=-\sqrt(3); z=0, \vec(n_(2))=\(1; -\sqrt(3);0\).

కావలసిన కోణం \beta (ఇది మాడ్యులస్‌కు సమానం\vec(n_(1)) మరియు \vec(n_(2)) ) మధ్య కోణం యొక్క కొసైన్ ).

\cos \beta= \frac(|\vec(n_(1)) \cdot \vec(n_(2))|)(|\vec(n_(1))| \cdot |\vec(n_(2))|)= \frac(\left |-\dfrac(2)(\sqrt(3))\cdot 1+1 \cdot (-\sqrt(3))+1 \cdot 0 \right |)(\sqrt(\dfrac( 4)(3)+1+1) \cdot \sqrt(1+3+0))= \frac(\dfrac(5)(\sqrt(3)))(2\sqrt(\dfrac(10)(3)))= \frac(\sqrt(10))(4).

\cos \beta =\frac(\sqrt(10))(4), \beta=\arccos\frac(\sqrt(10))(4).

సమాధానం

\arccos\frac(\sqrt(10))(4)

మూలం: "గణితం. యూనిఫైడ్ స్టేట్ ఎగ్జామ్ 2017 కోసం ప్రిపరేషన్. ప్రొఫైల్ స్థాయి." Ed. F. F. లైసెంకో, S. కులబుఖోవా.

ABCD ఒక చతురస్రం మరియు పక్క ముఖాలు- సమాన దీర్ఘ చతురస్రాలు.

సెక్షన్ ప్లేన్ వికర్ణ ACకి సమాంతరంగా M మరియు D పాయింట్ల గుండా వెళుతుంది కాబట్టి, దానిని A_(1)AC ప్లేన్‌లో పాయింట్ M ద్వారా నిర్మించడానికి మేము ACకి సమాంతరంగా MN విభాగాన్ని గీస్తాము. మేము లైన్ మరియు విమానం యొక్క సమాంతరత ఆధారంగా AC \parallel (MDN)ని పొందుతాము.

విమానం MDN సమాంతర విమానాలు A_(1)AD మరియు B_(1)BC, ఆపై, ఆస్తి ద్వారా కలుస్తుంది సమాంతర విమానాలు, MDN విమానంతో A_(1)ADD_(1) మరియు B_(1)BCC_(1) ముఖాల ఖండన రేఖలు సమాంతరంగా ఉంటాయి.

సెగ్మెంట్ MDకి సమాంతరంగా సెగ్మెంట్ NE డ్రా చేద్దాం.

క్వాడ్రాంగిల్ DMEN అనేది అవసరమైన విభాగం.

బి)సెక్షన్ ప్లేన్ మరియు బేస్ ప్లేన్ మధ్య కోణాన్ని కనుగొనండి. పాయింట్ D గుండా వెళుతున్న p కొంత సరళ రేఖ వెంట బేస్ ప్లేన్‌ను సెక్షన్ ప్లేన్ కలుస్తుంది. AC \parallel MN, కాబట్టి, AC \parallel p (ఒక విమానం మరొక సమతలానికి సమాంతరంగా ఒక రేఖ గుండా వెళితే మరియు ఈ విమానాన్ని కలుస్తుంది, అప్పుడు విమానాల ఖండన రేఖ ఈ రేఖకు సమాంతరంగా ఉంటుంది). BD \perp AC చతురస్రం యొక్క వికర్ణంగా ఉంటుంది, అంటే BD \perp p. BD అనేది ABC విమానంలో ED యొక్క ప్రొజెక్షన్, తర్వాత మూడు లంబంగా ఉన్న ED \perp p సిద్ధాంతం ద్వారా, \angle EDB అనేది సెక్షన్ ప్లేన్ మరియు బేస్ ప్లేన్ మధ్య డైహెడ్రల్ కోణం యొక్క సరళ కోణం.

చతుర్భుజ DMEN రకాన్ని సెట్ చేయండి. MD \parallel EN, ME \parallel DNని పోలి ఉంటుంది, దీని అర్థం DMEN సమాంతర చతుర్భుజం, మరియు MD=DN (కుడి త్రిభుజాలు MAD మరియు NCD రెండు కాళ్లపై సమానంగా ఉంటాయి: AD=DC చతురస్రం వైపులాగా, AM=CN సమాంతర రేఖల మధ్య దూరాలు AC మరియు MN), కాబట్టి DMEN ఒక రాంబస్. అందువల్ల, F అనేది MN యొక్క మధ్య బిందువు.

షరతు ప్రకారం AM:MA_(1)=2:3, ఆపై AM=\frac(2)(5)AA_(1)=\frac(2)(5) \cdot 5\sqrt(6)=2\sqrt(6).

AMNC అనేది దీర్ఘచతురస్రం, F అనేది MN మధ్యలో, O అనేది AC మధ్యలో ఉంటుంది. అంటే, FO\ సమాంతర MA, FO\perp AC, FO=MA=2\sqrt(6).

చతురస్రం యొక్క వికర్ణం అని తెలుసుకోవడం a\sqrt(2),ఇక్కడ a అనేది చతురస్రం వైపు, మనకు లభిస్తుంది BD=4\sqrt(2). OD=\frac(1)(2)BD=\frac(1)(2) \cdot 4\sqrt(2)=2\sqrt(2).

లంబ త్రిభుజంలో FOD\nspace tg \angle FDO=\frac(FO)(OD)=\frac(2\sqrt(6))(2\sqrt(2))=\sqrt(3).కాబట్టి, \angle FDO=60^\circ.

\(\బ్లాక్ట్రియాంగిల్ రైట్\) డైహెడ్రల్ కోణం అనేది రెండు అర్ధ-విమానాలు మరియు సరళ రేఖ \(a\) ద్వారా ఏర్పడిన కోణం, ఇది వాటి సాధారణ సరిహద్దు.

\(\బ్లాక్ట్రియాంగిల్ రైట్\) \(\xi\) మరియు \(\pi\) విమానాల మధ్య కోణాన్ని కనుగొనడానికి, మీరు సరళ కోణాన్ని కనుగొనాలి (మరియు కారంగాలేదా నేరుగా) విమానాల ద్వారా ఏర్పడిన డైహెడ్రల్ కోణం \(\xi\) మరియు \(\pi\) :

దశ 1: వీలు \(\xi\cap\pi=a\) (విమానాల ఖండన రేఖ). విమానంలో \(\xi\) మేము గమనించండి ఏకపక్ష పాయింట్\(F\) మరియు \(FA\perp a\) ;

దశ 2: \(FG\perp \pi\) ;

దశ 3: TTP ప్రకారం (\(FG\) – లంబంగా, \(FA\) – ఏటవాలు, \(AG\) – ప్రొజెక్షన్) మేము కలిగి: \(AG\perp a\) ;

దశ 4: కోణాన్ని \(\ఆంగిల్ FAG\) విమానాలు \(\xi\) మరియు \(\pi\) ద్వారా ఏర్పడిన డైహెడ్రల్ కోణం యొక్క సరళ కోణం అంటారు.

త్రిభుజం \(AG\) కుడి-కోణంగా ఉందని గమనించండి.
ఈ విధంగా నిర్మించిన విమానం \(AFG\) \(\xi\) మరియు \(\pi\) రెండు విమానాలకు లంబంగా ఉంటుందని కూడా గమనించండి. కాబట్టి, మేము దానిని భిన్నంగా చెప్పవచ్చు: విమానాల మధ్య కోణం\(\xi\) మరియు \(\pi\) అనేది రెండు ఖండన రేఖలు \(c\in \xi\) మరియు \(b\in\pi\) మధ్య కోణం మరియు లంబంగా మరియు \(\xi\) ) , మరియు \(\pi\) .

టాస్క్ 1 #2875

టాస్క్ స్థాయి: యూనిఫైడ్ స్టేట్ ఎగ్జామ్ కంటే చాలా కష్టం

డానా చతుర్భుజ పిరమిడ్, అన్ని అంచులు సమానంగా ఉంటాయి మరియు ఆధారం ఒక చతురస్రం. \(6\cos \alpha\)ని కనుగొనండి, ఇక్కడ \(\alpha\) అనేది దాని ప్రక్క ప్రక్క ముఖాల మధ్య కోణం.

లెట్ \(SABCD\) – ఈ పిరమిడ్(\(S\) అనేది ఒక శీర్షం) దీని అంచులు \(a\) కు సమానంగా ఉంటాయి. పర్యవసానంగా, అన్ని వైపు ముఖాలు సమాన సమబాహు త్రిభుజాలుగా ఉంటాయి. ముఖాలు \(SAD\) మరియు \(SCD\) మధ్య కోణాన్ని కనుగొనండి.

\(CH\perp SD\) చేద్దాం. ఎందుకంటే \(\ట్రయాంగిల్ SAD=\ట్రయాంగిల్ SCD\), అప్పుడు \(AH\) కూడా \(\ట్రయాంగిల్ SAD\) యొక్క ఎత్తు అవుతుంది. కాబట్టి, నిర్వచనం ప్రకారం, \(\angle AHC=\alpha\) అనేది ముఖాల \(SAD\) మరియు \(SCD\) మధ్య డైహెడ్రల్ కోణం యొక్క సరళ కోణం.
ఆధారం చతురస్రం కాబట్టి, \(AC=a\sqrt2\) . \(CH=AH\) ఎత్తు అని కూడా గమనించండి సమబాహు త్రిభుజంవైపు \(a\) , కాబట్టి, \(CH=AH=\frac(\sqrt3)2a\) .
అప్పుడు, \(\ట్రయాంగిల్ AHC\) నుండి కొసైన్ సిద్ధాంతం ద్వారా : \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]

సమాధానం: -2

టాస్క్ 2 #2876

టాస్క్ స్థాయి: యూనిఫైడ్ స్టేట్ ఎగ్జామ్ కంటే చాలా కష్టం

విమానాలు \(\pi_1\) మరియు \(\pi_2\) కొసైన్ \(0.2\) కు సమానమైన కోణంలో కలుస్తాయి. విమానాలు \(\pi_2\) మరియు \(\pi_3\) లంబ కోణంలో కలుస్తాయి మరియు విమానాల ఖండన రేఖ \(\pi_1\) మరియు \(\pi_2\) యొక్క ఖండన రేఖకు సమాంతరంగా ఉంటుంది విమానాలు \(\pi_2\) మరియు \(\ pi_3\) . \(\pi_1\) మరియు \(\pi_3\) విమానాల మధ్య కోణం యొక్క సైన్‌ని కనుగొనండి.

\(\pi_1\) మరియు \(\pi_2\) యొక్క ఖండన రేఖను సరళ రేఖ \(a\), \(\pi_2\) మరియు \(\pi_3\) ఖండన రేఖ సరళంగా ఉండనివ్వండి లైన్ \(b\), మరియు ఖండన రేఖ \(\pi_3\) మరియు \(\pi_1\) – సరళ రేఖ \(c\) . \(a\parallel b\) , ఆ తర్వాత \(c\parallel a\parallel b\) (సిద్ధాంతపరమైన సూచన "జామెట్రీ ఇన్ స్పేస్" \(\rightarrow\) "స్టీరియోమెట్రీకి పరిచయం, సమాంతరత").

\(A\in a, B\in b\) పాయింట్లను గుర్తు చేద్దాం, తద్వారా \(AB\perp a, AB\perp b\) (ఇది \(a\parallel b\) నుండి సాధ్యమవుతుంది). \(C\in c\) అని గుర్తు చేద్దాం, తద్వారా \(BC\perp c\) , కాబట్టి, \(BC\perp b\) . ఆపై \(AC\perp c\) మరియు \(AC\perp a\) .
నిజానికి, \(AB\perp b, BC\perp b\) , అప్పుడు \(b\) విమానం \(ABC\) కు లంబంగా ఉంటుంది. \(c\parallel a\parallel b\), అప్పుడు పంక్తులు \(a\) మరియు \(c\) కూడా విమానం \(ABC\)కి లంబంగా ఉంటాయి మరియు అందువల్ల ఈ విమానం నుండి ఏదైనా రేఖకు, ప్రత్యేకించి , లైన్ \ (AC\) .

ఇది దాన్ని అనుసరిస్తుంది \(\angle BAC=\angle (\pi_1, \pi_2)\), \(\angle ABC=\angle (\pi_2, \pi_3)=90^\circ\), \(\angle BCA=\angle (\pi_3, \pi_1)\). ఇది \(\ట్రయాంగిల్ ABC\) దీర్ఘచతురస్రాకారం అని తేలింది, అంటే \[\sin \angle BCA=\cos \angle BAC=0.2.\]

సమాధానం: 0.2

టాస్క్ 3 #2877

టాస్క్ స్థాయి: యూనిఫైడ్ స్టేట్ ఎగ్జామ్ కంటే చాలా కష్టం

ఇవ్వబడిన సరళ రేఖలు \(a, b, c\) ఒక బిందువు వద్ద కలుస్తాయి మరియు వాటిలో ఏదైనా రెండింటి మధ్య కోణం \(60^\circ\)కి సమానంగా ఉంటుంది. \(\cos^(-1)\alpha\) , ఇక్కడ \(\alpha\) అనేది పంక్తులు \(a\) మరియు \(c\) మరియు పంక్తుల ద్వారా ఏర్పడిన విమానం మధ్య కోణం \( b\ ) మరియు \(c\) . మీ సమాధానాన్ని డిగ్రీలలో ఇవ్వండి.

పంక్తులు \(O\) పాయింట్ వద్ద కలుస్తాయి. వాటిలో ఏదైనా రెండింటి మధ్య కోణం \(60^\circ\)కి సమానం కాబట్టి, మూడు సరళ రేఖలు ఒకే సమతలంలో ఉండవు. \(a\) పంక్తిపై \(A\) పాయింట్‌ని గుర్తు పెట్టండి మరియు \(AB\perp b\) మరియు \(AC\perp c\) . అప్పుడు \(\ట్రయాంగిల్ AOB=\ట్రయాంగిల్ AOC\)హైపోటెన్యూస్ మరియు తీవ్రమైన కోణంతో పాటు దీర్ఘచతురస్రాకారంగా. కాబట్టి, \(OB=OC\) మరియు \(AB=AC\) .
\(AH\perp (BOC)\) చేద్దాం. అప్పుడు సిద్ధాంతం ద్వారా మూడు లంబంగా \(HC\perp c\) , \(HB\perp b\) . \(AB=AC\) నుండి , ఆపై \(\ట్రయాంగిల్ AHB=\ట్రయాంగిల్ AHC\)హైపోటెన్యూస్ మరియు లెగ్ వెంట దీర్ఘచతురస్రాకారంగా. కాబట్టి, \(HB=HC\) . దీని అర్థం \(OH\) ​​అనేది కోణం \(BOC\) (బిందువు \(H\) కోణం యొక్క భుజాల నుండి సమాన దూరంలో ఉన్నందున).

ఈ విధంగా మేము \(a\) మరియు \(c\) పంక్తులు మరియు \(b\) మరియు \(c రేఖల ద్వారా ఏర్పడిన విమానం ద్వారా ఏర్పడిన డైహెడ్రల్ కోణం యొక్క సరళ కోణాన్ని కూడా నిర్మించాము. \) . ఇది కోణం \(ACH\) .

ఈ కోణాన్ని కనుక్కోండి. మేము \(A\) పాయింట్‌ని ఏకపక్షంగా ఎంచుకున్నాము కాబట్టి, \(OA=2\) . ఆపై దీర్ఘచతురస్రాకారంలో \(\త్రిభుజం AOC\) : \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ]\(OH\) ​​ఒక ద్వైపాక్షికం కాబట్టి, \(\angle HOC=30^\circ\) , కాబట్టి, దీర్ఘచతురస్రాకారంలో \(\త్రిభుజం HOC\) : \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\]ఆపై దీర్ఘచతురస్రాకార \(\ట్రయాంగిల్ ACH\) నుండి : \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]

సమాధానం: 3

టాస్క్ 4 #2910

టాస్క్ స్థాయి: యూనిఫైడ్ స్టేట్ ఎగ్జామ్ కంటే చాలా కష్టం

\(\pi_1\) మరియు \(\pi_2\) విమానాలు \(l\) సరళ రేఖ వెంట కలుస్తాయి, దానిపై \(M\) మరియు \(N\) పాయింట్లు ఉంటాయి. విభాగాలు \(MA\) మరియు \(MB\) సరళ రేఖకు లంబంగా ఉంటాయి \(l\) మరియు విమానాలు వరుసగా \(\pi_1\) మరియు \(\pi_2\) మరియు \(MN = 15 \) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) . \(3\cos\alpha\) , ఇక్కడ \(\alpha\) అనేది విమానాల \(\pi_1\) మరియు \(\pi_2\) .

త్రిభుజం \(AMN\) కుడి-కోణం, \(AN^2 = AM^2 + MN^2\), ఎక్కడ నుండి \ త్రిభుజం \(BMN\) కుడి-కోణం, \(BN^2 = BM^2 + MN^2\), దీని నుండి \మేము త్రిభుజం కోసం కొసైన్ సిద్ధాంతాన్ని వ్రాస్తాము \(AMB\): \ అప్పుడు \ విమానాల మధ్య కోణం \(\alpha\) ఒక తీవ్రమైన కోణం, మరియు \(\angle AMB\) మొండిగా మారినందున, \(\cos\alpha=\dfrac5(12)\) . అప్పుడు \

సమాధానం: 1.25

టాస్క్ 5 #2911

టాస్క్ స్థాయి: యూనిఫైడ్ స్టేట్ ఎగ్జామ్ కంటే చాలా కష్టం

\(ABCDA_1B_1C_1D_1\) అనేది సమాంతర గొట్టం, \(ABCD\) అనేది సైడ్ \(a\) ఉన్న చతురస్రం, పాయింట్ \(M\) అనేది పాయింట్ \(A_1\) నుండి సమతలానికి పడిపోయిన లంబానికి ఆధారం \. ((ABCD)\) , అదనంగా, \(M\) అనేది చతురస్రం యొక్క వికర్ణాల ఖండన బిందువు \(ABCD\) . అని తెలిసింది \(A_1M = \dfrac(\sqrt(3))(2)a\). విమానాల మధ్య కోణాన్ని కనుగొనండి \((ABCD)\) మరియు \((AA_1B_1B)\) . మీ సమాధానాన్ని డిగ్రీలలో ఇవ్వండి.

చిత్రంలో చూపిన విధంగా \(MN\)ని \(AB\)కి లంబంగా నిర్మిస్తాం.

\(ABCD\) అనేది వైపు \(a\) మరియు \(MN\perp AB\) మరియు \(BC\perp AB\) , ఆపై \(MN\సమాంతర BC\) ఉన్న చతురస్రం. \(M\) అనేది చతురస్రం యొక్క వికర్ణాల ఖండన బిందువు కాబట్టి, \(M\) అనేది \(AC\) మధ్యలో ఉంటుంది కాబట్టి, \(MN\) అనేది మధ్య రేఖ మరియు \(MN =\frac12BC= \frac(1)(2)a\).
\(MN\) అనేది \(A_1N\) విమానంలో \((ABCD)\) యొక్క ప్రొజెక్షన్, మరియు \(MN\) \(AB\)కి లంబంగా ఉంటుంది, ఆపై, మూడు లంబాల సిద్ధాంతం ద్వారా, \ (A_1N\) \(AB \)కి లంబంగా ఉంటుంది మరియు \((ABCD)\) మరియు \((AA_1B_1B)\) విమానాల మధ్య కోణం \(\angle A_1NM\) .
\[\mathrm(tg)\, \angle A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\angle A_1NM = 60^(\circ)\]

సమాధానం: 60

టాస్క్ 6 #1854

టాస్క్ స్థాయి: యూనిఫైడ్ స్టేట్ ఎగ్జామ్ కంటే చాలా కష్టం

చతురస్రంలో \(ABCD\) : \(O\) – వికర్ణాల ఖండన స్థానం; \(S\) – చతురస్రం యొక్క సమతలంలో ఉండదు, \(SO \perp ABC\) . \(SO = 5\) మరియు \(AB = 10\) అయితే \(ASD\) మరియు \(ABC\) విమానాల మధ్య కోణాన్ని కనుగొనండి.

కుడి త్రిభుజాలు \(\ట్రయాంగిల్ SAO\) మరియు \(\త్రిభుజం SDO\) రెండు వైపులా సమానంగా ఉంటాయి మరియు వాటి మధ్య కోణం (\(SO \perp ABC\) \(\Rightarrow\) \(\angle SOA = \angle SOD = 90^\circ\); \(AO = DO\) , ఎందుకంటే \(O\) – స్క్వేర్ యొక్క వికర్ణాల ఖండన స్థానం, \(SO\) – సాధారణ వైపు) \(\Rightarrow\) \(AS = SD\) \(\Rightarrow\) \(\triangle ASD\) – isoscelles. \(K\) అనేది \(AD\) మధ్యలో ఉంటుంది, ఆపై \(SK\) అనేది త్రిభుజంలోని ఎత్తు \(\త్రిభుజం ASD\), మరియు \(OK\) అనేది త్రిభుజంలోని ఎత్తు \( AOD\) \(\ రైట్‌టారో\) విమానం \(SOK\) విమానాలకు లంబంగా ఉంటుంది \(ASD\) మరియు \(ABC\) \(\Rightarrow\) \(\angle SKO\) – కోరుకున్నదానికి సమానమైన సరళ కోణం డైహెడ్రల్ కోణం.

\(\త్రిభుజం SKO\) లో : \(OK = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\రైట్‌టారో\) \(\ట్రయాంగిల్ SOK\) – సమద్విబాహు త్రిభుజం \(\రైట్‌టారో\) \(\కోణం SKO = 45^\circ\) .

సమాధానం: 45

టాస్క్ 7 #1855

టాస్క్ స్థాయి: యూనిఫైడ్ స్టేట్ ఎగ్జామ్ కంటే చాలా కష్టం

చతురస్రంలో \(ABCD\) : \(O\) – వికర్ణాల ఖండన స్థానం; \(S\) – చతురస్రం యొక్క సమతలంలో ఉండదు, \(SO \perp ABC\) . \(SO = 5\) మరియు \(AB = 10\) అయితే \(ASD\) మరియు \(BSC\) విమానాల మధ్య కోణాన్ని కనుగొనండి.

కుడి త్రిభుజాలు \(\ట్రయాంగిల్ SAO\) , \(\ట్రయాంగిల్ SDO\) , \(\ట్రయాంగిల్ SOB\) మరియు \(\త్రిభుజం SOC\) రెండు వైపులా సమానంగా ఉంటాయి మరియు వాటి మధ్య కోణం (\(SO \perp ABC \) \(\కుడి బాణం\) \(\angle SOA = \angle SOD = \angle SOB = \angle SOC = 90^\circ\); \(AO = OD = OB = OC\), ఎందుకంటే \(O\) – చతురస్రం యొక్క వికర్ణాల ఖండన స్థానం, \(SO\) – సాధారణ వైపు) \(\రైట్‌టారో\) \(AS = DS = BS = CS\) \(\రైట్‌టారో\) \( \triangle ASD\) మరియు \(\ట్రయాంగిల్ BSC\) సమద్విబాహులు. \(K\) అనేది \(AD\) మధ్యలో ఉంటుంది, ఆపై \(SK\) అనేది త్రిభుజంలోని ఎత్తు \(\త్రిభుజం ASD\), మరియు \(OK\) అనేది త్రిభుజంలోని ఎత్తు \( AOD\) \(\ రైట్‌టారో\) విమానం \(SOK\) విమానం \(ASD\) కు లంబంగా ఉంటుంది. \(L\) అనేది \(BC\) మధ్యలో ఉంటుంది, ఆపై \(SL\) అనేది త్రిభుజంలోని ఎత్తు \(\ట్రయాంగిల్ BSC\), మరియు \(OL\) అనేది త్రిభుజంలోని ఎత్తు \( BOC\) \(\ రైట్‌టారో\) విమానం \(SOL\) (అకా ప్లేన్ \(SOK\)) విమానం \(BSC\) కు లంబంగా ఉంటుంది. ఈ విధంగా, మేము \(\ కోణం KSL\) అనేది కావలసిన డైహెడ్రల్ కోణానికి సమానమైన సరళ కోణం అని పొందుతాము.

\(KL = KO + OL = 2\cdot OL = AB = 10\)\(\Rightarrow\) \(OL = 5\) ; \(SK = SL\) – సమాన ఎత్తులు సమద్విబాహు త్రిభుజాలు, ఇది పైథాగరియన్ సిద్ధాంతాన్ని ఉపయోగించి కనుగొనవచ్చు: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). అని గమనించవచ్చు \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)\(\రైట్‌టారో\) త్రిభుజం కోసం \(\త్రిభుజం KSL\) విలోమ పైథాగరియన్ సిద్ధాంతం \(\రైట్‌టారో\) \(\ట్రయాంగిల్ KSL\) – కుడి త్రిభుజం \(\రైట్‌టారో\) \(\కోణం KSL = 90 ^\ సర్క్\) .

సమాధానం: 90

గణితంలో యూనిఫైడ్ స్టేట్ ఎగ్జామ్ తీసుకోవడానికి విద్యార్థులను సిద్ధం చేయడం, నియమం ప్రకారం, విమానాల మధ్య కోణాన్ని నిర్ణయించడానికి మిమ్మల్ని అనుమతించే ప్రాథమిక సూత్రాలను పునరావృతం చేయడంతో ప్రారంభమవుతుంది. జ్యామితి యొక్క ఈ విభాగం లోపల తగినంత వివరంగా కవర్ చేయబడినప్పటికీ పాఠశాల పాఠ్యాంశాలు, చాలా మంది గ్రాడ్యుయేట్లు ప్రాథమిక విషయాలను పునరావృతం చేయాలి. విమానాల మధ్య కోణాన్ని ఎలా కనుగొనాలో అర్థం చేసుకోవడం, హైస్కూల్ విద్యార్థులు సమస్యను పరిష్కరించేటప్పుడు సరైన సమాధానాన్ని త్వరగా లెక్కించగలుగుతారు మరియు ఏకీకృత రాష్ట్ర పరీక్షలో ఉత్తీర్ణత సాధించిన ఫలితాలపై మంచి స్కోర్‌లను పొందగలుగుతారు.

ప్రధాన సూక్ష్మ నైపుణ్యాలు

డైహెడ్రల్ కోణాన్ని ఎలా కనుగొనాలనే ప్రశ్న ఇబ్బందులను కలిగించదని నిర్ధారించుకోవడానికి, యూనిఫైడ్ స్టేట్ ఎగ్జామినేషన్ పనులను ఎదుర్కోవడంలో మీకు సహాయపడే పరిష్కార అల్గోరిథంను అనుసరించమని మేము సిఫార్సు చేస్తున్నాము.

మొదట మీరు విమానాలు కలిసే సరళ రేఖను నిర్ణయించాలి.

అప్పుడు మీరు ఈ రేఖపై ఒక బిందువును ఎంచుకోవాలి మరియు దానికి రెండు లంబాలను గీయాలి.

తరువాత ప్రక్రియ- కనుగొనడం త్రికోణమితి ఫంక్షన్లంబంగా ఏర్పడిన డైహెడ్రల్ కోణం. ఫలితంగా త్రిభుజం సహాయంతో దీన్ని చేయడానికి అత్యంత అనుకూలమైన మార్గం, దీనిలో కోణం ఒక భాగం.

సమాధానం కోణం యొక్క విలువ లేదా దాని త్రికోణమితి ఫంక్షన్.

ష్కోల్కోవోతో పరీక్ష పరీక్షకు సిద్ధమవడం మీ విజయానికి కీలకం

ముందు రోజు తరగతుల సమయంలో ఏకీకృత రాష్ట్ర పరీక్షలో ఉత్తీర్ణతచాలా మంది పాఠశాల పిల్లలు 2 విమానాల మధ్య కోణాన్ని లెక్కించడానికి అనుమతించే నిర్వచనాలు మరియు సూత్రాలను కనుగొనడంలో సమస్యను ఎదుర్కొంటున్నారు. పాఠశాల పాఠ్య పుస్తకంమీకు అవసరమైనప్పుడు ఇది ఎల్లప్పుడూ చేతిలో ఉండదు. మరియు కనుగొనేందుకు అవసరమైన సూత్రాలుమరియు ఇంటర్నెట్‌లో ఆన్‌లైన్‌లో విమానాల మధ్య కోణాన్ని కనుగొనడంతోపాటు వాటి సరైన ఉపయోగానికి ఉదాహరణలు, కొన్నిసార్లు దీనికి చాలా సమయం వెచ్చించాల్సి ఉంటుంది.

గణిత పోర్టల్ "ష్కోల్కోవో" అందిస్తుంది కొత్త విధానంరాష్ట్ర పరీక్ష కోసం సిద్ధం చేయడానికి. మా వెబ్‌సైట్‌లోని తరగతులు విద్యార్థులు తమకు తాముగా అత్యంత కష్టతరమైన విభాగాలను గుర్తించడంలో మరియు జ్ఞానంలో అంతరాలను పూరించడంలో సహాయపడతాయి.

మేము అవసరమైన అన్ని పదార్థాలను సిద్ధం చేసాము మరియు స్పష్టంగా సమర్పించాము. ప్రాథమిక నిర్వచనాలుమరియు సూత్రాలు "సైద్ధాంతిక సమాచారం" విభాగంలో ప్రదర్శించబడతాయి.

మెటీరియల్‌ని బాగా అర్థం చేసుకోవడానికి, తగిన వ్యాయామాలను అభ్యసించాలని కూడా మేము సూచిస్తున్నాము. పనుల యొక్క పెద్ద ఎంపిక వివిధ స్థాయిలలోసంక్లిష్టత, ఉదాహరణకు, "కేటలాగ్" విభాగంలో ప్రదర్శించబడుతుంది. అన్ని టాస్క్‌లు సరైన సమాధానాన్ని కనుగొనడానికి వివరణాత్మక అల్గారిథమ్‌ను కలిగి ఉంటాయి. వెబ్‌సైట్‌లోని వ్యాయామాల జాబితా నిరంతరం అనుబంధంగా మరియు నవీకరించబడుతుంది.

రెండు విమానాల మధ్య కోణాన్ని కనుగొనడం అవసరమయ్యే సమస్యలను పరిష్కరించడంలో అభ్యాసం చేస్తున్నప్పుడు, విద్యార్థులు ఏదైనా పనిని ఆన్‌లైన్‌లో “ఇష్టమైనవి”గా సేవ్ చేసే అవకాశం ఉంది. దీనికి ధన్యవాదాలు వారు అతని వద్దకు తిరిగి రాగలుగుతారు అవసరమైన మొత్తంసమయం మరియు దాని నిర్ణయం యొక్క పురోగతిని చర్చించండి పాఠశాల ఉపాధ్యాయుడులేదా ఒక శిక్షకుడు.