పిరమిడ్ భావన

నిర్వచనం 1

బహుభుజితో ఏర్పడిన రేఖాగణిత బొమ్మ మరియు ఈ బహుభుజి ఉన్న సమతలంలో లేని బిందువు, బహుభుజి యొక్క అన్ని శీర్షాలకు అనుసంధానించబడి, పిరమిడ్ అంటారు (Fig. 1).

పిరమిడ్ తయారు చేయబడిన బహుభుజిని పిరమిడ్ యొక్క ఆధారం అంటారు; ఫలితంగా ఏర్పడే త్రిభుజాలు, ఒక బిందువుతో అనుసంధానించబడినప్పుడు, పిరమిడ్ యొక్క ప్రక్క ముఖాలు, త్రిభుజాల భుజాలు పిరమిడ్ యొక్క భుజాలు మరియు బిందువు సాధారణం. అన్ని త్రిభుజాలకు పిరమిడ్ పైభాగం ఉంటుంది.

పిరమిడ్ల రకాలు

పిరమిడ్ యొక్క బేస్ వద్ద ఉన్న కోణాల సంఖ్యను బట్టి, దీనిని త్రిభుజాకార, చతుర్భుజాకార మరియు మొదలైనవి (Fig. 2) అని పిలుస్తారు.

మూర్తి 2.

పిరమిడ్ యొక్క మరొక రకం సాధారణ పిరమిడ్.

సాధారణ పిరమిడ్ యొక్క ఆస్తిని పరిచయం చేసి, నిరూపిద్దాం.

సిద్ధాంతం 1

సాధారణ పిరమిడ్ యొక్క అన్ని పార్శ్వ ముఖాలు ఒకదానికొకటి సమానంగా ఉండే సమద్విబాహు త్రిభుజాలు.

రుజువు.

$S$ ఎత్తు $h=SO$ శీర్షంతో సాధారణ $n-$gonal పిరమిడ్‌ను పరిగణించండి. బేస్ చుట్టూ ఒక వృత్తాన్ని గీయండి (Fig. 4).

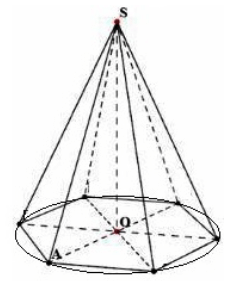
చిత్రం 4.

$SOA$ త్రిభుజాన్ని పరిగణించండి. పైథాగరియన్ సిద్ధాంతం ప్రకారం, మనకు లభిస్తుంది

సహజంగానే, ఏదైనా వైపు అంచు ఈ విధంగా నిర్వచించబడుతుంది. పర్యవసానంగా, అన్ని వైపు అంచులు ఒకదానికొకటి సమానంగా ఉంటాయి, అనగా, అన్ని వైపు ముఖాలు సమద్విబాహు త్రిభుజాలు. ఒకరికొకరు సమానమని నిరూపిద్దాం. ఆధారం సాధారణ బహుభుజి కాబట్టి, అన్ని వైపు ముఖాల స్థావరాలు ఒకదానికొకటి సమానంగా ఉంటాయి. పర్యవసానంగా, త్రిభుజాల సమానత్వం యొక్క III ప్రమాణం ప్రకారం అన్ని పార్శ్వ ముఖాలు సమానంగా ఉంటాయి.

సిద్ధాంతం నిరూపించబడింది.

సాధారణ పిరమిడ్ భావనకు సంబంధించిన క్రింది నిర్వచనాన్ని ఇప్పుడు పరిచయం చేద్దాం.

నిర్వచనం 3

సాధారణ పిరమిడ్ యొక్క అపోథెమ్ దాని వైపు ముఖం యొక్క ఎత్తు.

సహజంగానే, సిద్ధాంతం వన్ ద్వారా, అన్ని అపోథెమ్‌లు ఒకదానికొకటి సమానంగా ఉంటాయి.

సిద్ధాంతం 2

సాధారణ పిరమిడ్ యొక్క పార్శ్వ ఉపరితల వైశాల్యం బేస్ మరియు అపోథెమ్ యొక్క సెమీ చుట్టుకొలత యొక్క ఉత్పత్తిగా నిర్ణయించబడుతుంది.

రుజువు.

$n-$gonal పిరమిడ్ యొక్క ఆధారం వైపు $a$తో మరియు అపోథెమ్‌ని $d$తో సూచిస్తాము. అందువలన, వైపు ముఖం యొక్క ప్రాంతం సమానంగా ఉంటుంది

సిద్ధాంతం 1 ప్రకారం, అన్ని వైపులా సమానంగా ఉంటాయి కాబట్టి

సిద్ధాంతం నిరూపించబడింది.

మరొక రకమైన పిరమిడ్ కత్తిరించబడిన పిరమిడ్.

నిర్వచనం 4

ఒక సాధారణ పిరమిడ్ ద్వారా దాని స్థావరానికి సమాంతరంగా ఉన్న విమానం గీస్తే, ఈ విమానం మరియు బేస్ యొక్క విమానం మధ్య ఏర్పడిన బొమ్మను కత్తిరించబడిన పిరమిడ్ అంటారు (Fig. 5).

మూర్తి 5. కత్తిరించబడిన పిరమిడ్

కత్తిరించబడిన పిరమిడ్ యొక్క పార్శ్వ ముఖాలు ట్రాపెజాయిడ్లు.

సిద్ధాంతం 3

సాధారణ కత్తిరించబడిన పిరమిడ్ యొక్క పార్శ్వ ఉపరితల వైశాల్యం స్థావరాలు మరియు అపోథెమ్ యొక్క సెమీ-పెరిమీటర్ల మొత్తం యొక్క ఉత్పత్తిగా నిర్ణయించబడుతుంది.

రుజువు.

$n-$gonal పిరమిడ్ యొక్క స్థావరాల భుజాలను వరుసగా $a\ మరియు\ b$తో మరియు అపోథెమ్‌ను $d$తో సూచిస్తాము. అందువలన, వైపు ముఖం యొక్క ప్రాంతం సమానంగా ఉంటుంది

అన్ని వైపులా సమానంగా ఉంటాయి కాబట్టి

సిద్ధాంతం నిరూపించబడింది.

నమూనా పని

ఉదాహరణ 1

కత్తిరించబడిన త్రిభుజాకార పిరమిడ్ యొక్క పార్శ్వ ఉపరితలం యొక్క వైశాల్యాన్ని బేస్ సైడ్ 4 మరియు అపోథెమ్ 5తో సాధారణ పిరమిడ్ నుండి పొందినట్లయితే, పక్క ముఖాల మధ్యరేఖ గుండా వెళుతున్న విమానాన్ని కత్తిరించడం ద్వారా కనుగొనండి.

పరిష్కారం.

మధ్యరేఖ సిద్ధాంతాన్ని ఉపయోగించి, కత్తిరించబడిన పిరమిడ్ యొక్క పైభాగం $4\cdot \frac(1)(2)=2$కి సమానం మరియు అపోథెమ్ $5\cdot \frac(1)(2)కి సమానం అని మేము కనుగొన్నాము. =2.5$.

అప్పుడు, సిద్ధాంతం 3 ద్వారా, మనకు లభిస్తుంది

పిరమిడ్. కత్తిరించబడిన పిరమిడ్

పిరమిడ్బహుభుజి, దీని ముఖాలలో ఒకటి బహుభుజి ( బేస్ ), మరియు అన్ని ఇతర ముఖాలు సాధారణ శీర్షంతో త్రిభుజాలు ( పక్క ముఖాలు ) (Fig. 15). పిరమిడ్ అంటారు సరైన , దాని బేస్ ఒక సాధారణ బహుభుజి అయితే మరియు పిరమిడ్ యొక్క పైభాగం బేస్ మధ్యలోకి అంచనా వేయబడి ఉంటే (Fig. 16). అన్ని అంచులు సమానంగా ఉండే త్రిభుజాకార పిరమిడ్ అంటారు టెట్రాహెడ్రాన్ .

పార్శ్వ పక్కటెముకపిరమిడ్ అనేది బేస్‌కు చెందని ప్రక్క ముఖం వైపు ఎత్తు పిరమిడ్ అనేది దాని పైభాగం నుండి బేస్ యొక్క సమతలానికి దూరం. సాధారణ పిరమిడ్ యొక్క అన్ని పార్శ్వ అంచులు ఒకదానికొకటి సమానంగా ఉంటాయి, అన్ని పార్శ్వ ముఖాలు సమానమైన సమద్విబాహు త్రిభుజాలు. శీర్షం నుండి గీసిన సాధారణ పిరమిడ్ వైపు ముఖం యొక్క ఎత్తు అంటారు అపోథెమ్ . వికర్ణ విభాగం ఒకే ముఖానికి చెందని రెండు పార్శ్వ అంచుల గుండా వెళుతున్న విమానం ద్వారా పిరమిడ్ యొక్క విభాగం అంటారు.

పార్శ్వ ఉపరితల వైశాల్యంపిరమిడ్ అనేది అన్ని పార్శ్వ ముఖాల ప్రాంతాల మొత్తం. మొత్తం ఉపరితల వైశాల్యం అన్ని వైపు ముఖాలు మరియు ఆధారం యొక్క ప్రాంతాల మొత్తం అంటారు.

సిద్ధాంతాలు

1. పిరమిడ్‌లో అన్ని పార్శ్వ అంచులు బేస్ యొక్క సమతలానికి సమానంగా వంపుతిరిగి ఉంటే, అప్పుడు పిరమిడ్ పైభాగం బేస్ సమీపంలో చుట్టుముట్టబడిన వృత్తం మధ్యలో అంచనా వేయబడుతుంది.

2. పిరమిడ్ యొక్క అన్ని ప్రక్క అంచులు సమాన పొడవు కలిగి ఉంటే, అప్పుడు పిరమిడ్ యొక్క పైభాగం బేస్ సమీపంలో చుట్టుముట్టబడిన వృత్తం మధ్యలో అంచనా వేయబడుతుంది.

3. పిరమిడ్‌లోని అన్ని ముఖాలు బేస్ యొక్క సమతలానికి సమానంగా వంపుతిరిగి ఉంటే, అప్పుడు పిరమిడ్ పైభాగం బేస్‌లో చెక్కబడిన వృత్తం మధ్యలో అంచనా వేయబడుతుంది.

ఏకపక్ష పిరమిడ్ వాల్యూమ్‌ను లెక్కించడానికి, సరైన సూత్రం:

ఎక్కడ వి- వాల్యూమ్;

S బేస్- బేస్ ప్రాంతం;

హెచ్- పిరమిడ్ ఎత్తు.

సాధారణ పిరమిడ్ కోసం, కింది సూత్రాలు సరైనవి:

ఎక్కడ p- బేస్ చుట్టుకొలత;

h a- అపోథెమ్;

హెచ్- ఎత్తు;

S పూర్తి

S వైపు

S బేస్- బేస్ ప్రాంతం;

వి- సాధారణ పిరమిడ్ వాల్యూమ్.

కత్తిరించబడిన పిరమిడ్పిరమిడ్ యొక్క స్థావరానికి సమాంతరంగా బేస్ మరియు కట్టింగ్ ప్లేన్ మధ్య ఉన్న పిరమిడ్ యొక్క భాగాన్ని పిలుస్తారు (Fig. 17). సాధారణ కత్తిరించబడిన పిరమిడ్ బేస్ మరియు పిరమిడ్ యొక్క స్థావరానికి సమాంతరంగా ఉండే కట్టింగ్ ప్లేన్ మధ్య ఉండే సాధారణ పిరమిడ్ యొక్క భాగాన్ని అంటారు.

కారణాలుకత్తిరించబడిన పిరమిడ్ - ఇలాంటి బహుభుజాలు. పక్క ముఖాలు - ట్రాపెజాయిడ్స్. ఎత్తు కత్తిరించబడిన పిరమిడ్ దాని స్థావరాల మధ్య దూరం. వికర్ణ కత్తిరించబడిన పిరమిడ్ అనేది ఒకే ముఖంపై పడని దాని శీర్షాలను కలిపే ఒక విభాగం. వికర్ణ విభాగం ఒకే ముఖానికి చెందని రెండు పార్శ్వ అంచుల గుండా వెళుతున్న విమానం ద్వారా కత్తిరించబడిన పిరమిడ్ యొక్క విభాగం.

కత్తిరించబడిన పిరమిడ్ కోసం క్రింది సూత్రాలు చెల్లుతాయి:

(4)

ఎక్కడ ఎస్ 1 , ఎస్ 2 - ఎగువ మరియు దిగువ స్థావరాల ప్రాంతాలు;

S పూర్తి- మొత్తం ఉపరితల వైశాల్యం;

S వైపు- పార్శ్వ ఉపరితల వైశాల్యం;

హెచ్- ఎత్తు;

వి- కత్తిరించబడిన పిరమిడ్ వాల్యూమ్.

సాధారణ కత్తిరించబడిన పిరమిడ్ కోసం సూత్రం సరైనది:

ఎక్కడ p 1 , p 2 - స్థావరాల చుట్టుకొలతలు;

h a- సాధారణ కత్తిరించబడిన పిరమిడ్ యొక్క అపోథెమ్.

ఉదాహరణ 1.సాధారణ త్రిభుజాకార పిరమిడ్‌లో, బేస్ వద్ద డైహెడ్రల్ కోణం 60º. బేస్ యొక్క సమతలానికి వైపు అంచు యొక్క వంపు కోణం యొక్క టాంజెంట్‌ను కనుగొనండి.

పరిష్కారం.యొక్క డ్రాయింగ్ (Fig. 18) తయారు చేద్దాం.

పిరమిడ్ సక్రమంగా ఉంటుంది, అంటే బేస్ వద్ద ఒక సమబాహు త్రిభుజం ఉంటుంది మరియు అన్ని వైపు ముఖాలు సమానమైన సమద్విబాహు త్రిభుజాలుగా ఉంటాయి. బేస్ వద్ద ఉన్న డైహెడ్రల్ కోణం అనేది పిరమిడ్ యొక్క సైడ్ ఫేస్ బేస్ యొక్క సమతలానికి వంపు కోణం. సరళ కోణం కోణం aరెండు లంబాల మధ్య: మొదలైనవి. పిరమిడ్ యొక్క పైభాగం త్రిభుజం మధ్యలో అంచనా వేయబడింది (త్రిభుజం యొక్క వృత్తాకార కేంద్రం మరియు లిఖిత వృత్తం ABC) ప్రక్క అంచు యొక్క వంపు కోణం (ఉదాహరణకు ఎస్.బి.) అనేది అంచు మరియు బేస్ యొక్క విమానంలో దాని ప్రొజెక్షన్ మధ్య కోణం. పక్కటెముక కోసం ఎస్.బి.ఈ కోణం కోణం అవుతుంది SBD. టాంజెంట్‌ను కనుగొనడానికి మీరు కాళ్ళను తెలుసుకోవాలి SOమరియు O.B.. సెగ్మెంట్ యొక్క పొడవును తెలియజేయండి BD 3కి సమానం ఎ. చుక్క గురించిలైన్ సెగ్మెంట్ BDభాగాలుగా విభజించబడింది: మరియు నుండి మేము కనుగొంటాము SO: మేము కనుగొన్న దాని నుండి:

సమాధానం:

ఉదాహరణ 2.సాధారణ కత్తిరించబడిన చతుర్భుజాకార పిరమిడ్ దాని స్థావరాల యొక్క వికర్ణాలు సెం.మీ మరియు సెం.మీలకు సమానంగా ఉంటే మరియు దాని ఎత్తు 4 సెం.మీ ఉంటే దాని వాల్యూమ్‌ను కనుగొనండి.

పరిష్కారం.కత్తిరించబడిన పిరమిడ్ వాల్యూమ్‌ను కనుగొనడానికి, మేము ఫార్ములా (4)ని ఉపయోగిస్తాము. స్థావరాల వైశాల్యాన్ని కనుగొనడానికి, మీరు బేస్ చతురస్రాల భుజాలను కనుగొని, వాటి వికర్ణాలను తెలుసుకోవాలి. స్థావరాల భుజాలు వరుసగా 2 సెం.మీ మరియు 8 సెం.మీ.కి సమానంగా ఉంటాయి. దీని అర్థం స్థావరాల ప్రాంతాలు మరియు మొత్తం డేటాను సూత్రంలోకి మార్చడం, మేము కత్తిరించబడిన పిరమిడ్ యొక్క వాల్యూమ్‌ను గణిస్తాము:

సమాధానం: 112 సెం.మీ 3.

ఉదాహరణ 3.సాధారణ త్రిభుజాకార కత్తిరించబడిన పిరమిడ్ యొక్క పార్శ్వ ముఖం యొక్క వైశాల్యాన్ని కనుగొనండి, దీని స్థావరాల భుజాలు 10 సెం.మీ మరియు 4 సెం.మీ, మరియు పిరమిడ్ యొక్క ఎత్తు 2 సెం.మీ.

పరిష్కారం.యొక్క డ్రాయింగ్ (Fig. 19) తయారు చేద్దాం.

ఈ పిరమిడ్ యొక్క ప్రక్క ముఖం ఒక సమద్విబాహు ట్రాపెజాయిడ్. ట్రాపెజాయిడ్ యొక్క వైశాల్యాన్ని లెక్కించడానికి, మీరు బేస్ మరియు ఎత్తు తెలుసుకోవాలి. స్థావరాలు షరతు ప్రకారం ఇవ్వబడ్డాయి, ఎత్తు మాత్రమే తెలియదు. మేము ఆమెను ఎక్కడ నుండి కనుగొంటాము ఎ 1 ఇఒక బిందువు నుండి లంబంగా ఎ 1 దిగువ బేస్ యొక్క విమానంలో, ఎ 1 డి- నుండి లంబంగా ఎ 1 చొప్పున AC. ఎ 1 ఇ= 2 సెం.మీ., ఇది పిరమిడ్ యొక్క ఎత్తు కాబట్టి. కనుగొనేందుకు DEఎగువ వీక్షణను చూపించే అదనపు డ్రాయింగ్‌ను తయారు చేద్దాం (Fig. 20). చుక్క గురించి- ఎగువ మరియు దిగువ స్థావరాల కేంద్రాల ప్రొజెక్షన్. నుండి (Fig. 20 చూడండి) మరియు మరోవైపు అలాగే– వృత్తంలో వ్రాసిన వ్యాసార్థం మరియు ఓం- ఒక వృత్తంలో వ్రాసిన వ్యాసార్థం:

MK = DE.

నుండి పైథాగరియన్ సిద్ధాంతం ప్రకారం

వైపు ముఖం ప్రాంతం:

సమాధానం:

ఉదాహరణ 4.పిరమిడ్ యొక్క బేస్ వద్ద ఒక సమద్విబాహు ట్రాపెజాయిడ్ ఉంది, దీని స్థావరాలు ఎమరియు బి (a> బి) ప్రతి వైపు ముఖం పిరమిడ్ యొక్క బేస్ యొక్క సమతలానికి సమానమైన కోణాన్ని ఏర్పరుస్తుంది జె. పిరమిడ్ యొక్క మొత్తం ఉపరితల వైశాల్యాన్ని కనుగొనండి.

పరిష్కారం.యొక్క డ్రాయింగ్ (Fig. 21) తయారు చేద్దాం. పిరమిడ్ యొక్క మొత్తం ఉపరితల వైశాల్యం SABCDప్రాంతాల మొత్తానికి మరియు ట్రాపజోయిడ్ వైశాల్యానికి సమానం ఎ బి సి డి.

పిరమిడ్ యొక్క అన్ని ముఖాలు బేస్ యొక్క సమతలానికి సమానంగా వంగి ఉంటే, అప్పుడు శీర్షం బేస్‌లో చెక్కబడిన వృత్తం మధ్యలో అంచనా వేయబడుతుంది అనే ప్రకటనను ఉపయోగిస్తాము. చుక్క గురించి- శీర్ష ప్రొజెక్షన్ ఎస్పిరమిడ్ బేస్ వద్ద. త్రిభుజం SODత్రిభుజం యొక్క ఆర్తోగోనల్ ప్రొజెక్షన్ CSDబేస్ యొక్క విమానానికి. ప్లేన్ ఫిగర్ యొక్క ఆర్తోగోనల్ ప్రొజెక్షన్ యొక్క ప్రాంతంపై సిద్ధాంతాన్ని ఉపయోగించి, మేము పొందుతాము:

అలాగే దీని అర్థం అందువలన, ట్రాపెజాయిడ్ యొక్క ప్రాంతాన్ని కనుగొనడంలో సమస్య తగ్గించబడింది ఎ బి సి డి. ట్రాపెజాయిడ్ గీద్దాం ఎ బి సి డివిడిగా (Fig. 22). చుక్క గురించి- ట్రాపెజాయిడ్‌లో చెక్కబడిన వృత్తం మధ్యలో.

ఒక వృత్తాన్ని ట్రాపెజాయిడ్‌లో లిఖించవచ్చు కాబట్టి, లేదా పైథాగరియన్ సిద్ధాంతం నుండి మనకు

ఈ వీడియో ట్యుటోరియల్ వినియోగదారులకు పిరమిడ్ థీమ్ యొక్క ఆలోచనను పొందడానికి సహాయపడుతుంది. సరైన పిరమిడ్. ఈ పాఠంలో మనం పిరమిడ్ భావనతో పరిచయం పొందుతాము మరియు దానికి నిర్వచనం ఇస్తాము. సాధారణ పిరమిడ్ అంటే ఏమిటి మరియు దానిలో ఏ లక్షణాలు ఉన్నాయో పరిశీలిద్దాం. అప్పుడు మేము సాధారణ పిరమిడ్ యొక్క పార్శ్వ ఉపరితలం గురించి సిద్ధాంతాన్ని నిరూపిస్తాము.

ఈ పాఠంలో మనం పిరమిడ్ భావనతో పరిచయం పొందుతాము మరియు దానికి నిర్వచనం ఇస్తాము.

బహుభుజిని పరిగణించండి ఎ 1 ఎ 2...ఒక ఎన్, ఇది α విమానంలో ఉంటుంది మరియు పాయింట్ పి, ఇది α విమానంలో ఉండదు (Fig. 1). చుక్కలను కనెక్ట్ చేద్దాం పిశీర్షాలతో A 1, A 2, A 3, … ఒక ఎన్. మాకు దొరికింది nత్రిభుజాలు: A 1 A 2 R, A 2 A 3 Rమరియు అందువలన న.

నిర్వచనం. పాలీహెడ్రాన్ RA 1 A 2 ...A n, తో తయారు చేయబడినది n-చదరపు ఎ 1 ఎ 2...ఒక ఎన్మరియు nత్రిభుజాలు RA 1 A 2, RA 2 A 3 …RA n A n-1 అంటారు n- బొగ్గు పిరమిడ్. అన్నం. 1.

అన్నం. 1

చతుర్భుజ పిరమిడ్‌ను పరిగణించండి PABCD(Fig. 2).

ఆర్- పిరమిడ్ పైభాగం.

ఎ బి సి డి- పిరమిడ్ యొక్క ఆధారం.

RA- పక్క పక్కటెముక.

AB- బేస్ పక్కటెముక.

పాయింట్ నుండి ఆర్లంబంగా డ్రాప్ చేద్దాం RNబేస్ ప్లేన్‌కి ఎ బి సి డి. లంబంగా గీసినది పిరమిడ్ యొక్క ఎత్తు.

అన్నం. 2

పిరమిడ్ యొక్క పూర్తి ఉపరితలం పార్శ్వ ఉపరితలాన్ని కలిగి ఉంటుంది, అనగా, అన్ని పార్శ్వ ముఖాల వైశాల్యం మరియు బేస్ యొక్క ప్రాంతం:

S పూర్తి = S వైపు + S ప్రధాన

ఒక పిరమిడ్ సరైనది అయితే:

• దాని ఆధారం సాధారణ బహుభుజి;
• పిరమిడ్ పైభాగాన్ని బేస్ మధ్యలో కలుపుతున్న విభాగం దాని ఎత్తు.

సాధారణ చతుర్భుజ పిరమిడ్ ఉదాహరణను ఉపయోగించి వివరణ

సాధారణ చతుర్భుజ పిరమిడ్‌ను పరిగణించండి PABCD(Fig. 3).

ఆర్- పిరమిడ్ పైభాగం. పిరమిడ్ యొక్క ఆధారం ఎ బి సి డి- ఒక సాధారణ చతుర్భుజం, అంటే ఒక చతురస్రం. చుక్క గురించి, వికర్ణాల ఖండన బిందువు, చదరపు కేంద్రం. అంటే, ROపిరమిడ్ యొక్క ఎత్తు.

అన్నం. 3

వివరణ: సరైనది nఒక త్రిభుజంలో, లిఖించబడిన వృత్తం యొక్క కేంద్రం మరియు వృత్తం యొక్క కేంద్రం సమానంగా ఉంటాయి. ఈ కేంద్రాన్ని బహుభుజి కేంద్రం అంటారు. కొన్నిసార్లు వారు శీర్షం మధ్యలోకి అంచనా వేయబడిందని చెబుతారు.

దాని శీర్షం నుండి గీసిన సాధారణ పిరమిడ్ యొక్క పార్శ్వ ముఖం యొక్క ఎత్తు అంటారు అపోథెమ్మరియు నియమించబడినది h a.

1. సాధారణ పిరమిడ్ యొక్క అన్ని పార్శ్వ అంచులు సమానంగా ఉంటాయి;

2. పక్క ముఖాలు సమాన సమద్విబాహు త్రిభుజాలు.

మేము సాధారణ చతుర్భుజ పిరమిడ్ యొక్క ఉదాహరణను ఉపయోగించి ఈ లక్షణాల యొక్క రుజువును ఇస్తాము.

ఇచ్చిన: PABCD- సాధారణ చతుర్భుజ పిరమిడ్,

ఎ బి సి డి- చదరపు,

RO- పిరమిడ్ ఎత్తు.

నిరూపించండి:

1. RA = PB = RS = PD

2.∆ABP = ∆BCP =∆CDP =∆DAP అంజీర్ చూడండి. 4.

అన్నం. 4

రుజువు.

RO- పిరమిడ్ ఎత్తు. అంటే సూటిగా ROవిమానానికి లంబంగా ABC, అందువలన నేరుగా JSC, VO, SOమరియు DOఅందులో పడి ఉంది. కాబట్టి త్రిభుజాలు ROA, ROV, ROS, ROD- దీర్ఘచతురస్రాకార.

ఒక చతురస్రాన్ని పరిగణించండి ఎ బి సి డి. చతురస్రం యొక్క లక్షణాల నుండి అది అనుసరిస్తుంది AO = VO = CO = DO.

అప్పుడు కుడి త్రిభుజాలు ROA, ROV, ROS, RODకాలు RO- సాధారణ మరియు కాళ్ళు JSC, VO, SOమరియు DOసమానంగా ఉంటాయి, అంటే ఈ త్రిభుజాలు రెండు వైపులా సమానంగా ఉంటాయి. త్రిభుజాల సమానత్వం నుండి విభాగాల సమానత్వం అనుసరిస్తుంది, RA = PB = RS = PD.పాయింట్ 1 నిరూపించబడింది.

విభాగాలు ABమరియు సూర్యుడుఅవి ఒకే చతురస్రానికి భుజాలు కాబట్టి సమానంగా ఉంటాయి, RA = PB = RS. కాబట్టి త్రిభుజాలు AVRమరియు VSR -సమద్విబాహులు మరియు మూడు వైపులా సమానంగా ఉంటాయి.

ఇదే విధంగా మనం త్రిభుజాలను కనుగొంటాము ABP, VCP, CDP, DAPసమద్విబాహులు మరియు సమానమైనవి, పేరా 2లో నిరూపించాల్సిన అవసరం ఉంది.

సాధారణ పిరమిడ్ యొక్క పార్శ్వ ఉపరితలం యొక్క వైశాల్యం బేస్ మరియు అపోథెమ్ యొక్క చుట్టుకొలత యొక్క సగం ఉత్పత్తికి సమానం:

దీన్ని నిరూపించడానికి, సాధారణ త్రిభుజాకార పిరమిడ్‌ని ఎంచుకుందాం.

ఇచ్చిన: RAVS- సాధారణ త్రిభుజాకార పిరమిడ్.

AB = BC = AC.

RO- ఎత్తు.

నిరూపించండి: . అంజీర్ చూడండి. 5.

అన్నం. 5

రుజువు.

RAVS- సాధారణ త్రిభుజాకార పిరమిడ్. అంటే AB= AC = BC. వీలు గురించి- త్రిభుజం మధ్యలో ABC, అప్పుడు ROపిరమిడ్ యొక్క ఎత్తు. పిరమిడ్ యొక్క బేస్ వద్ద ఒక సమబాహు త్రిభుజం ఉంటుంది ABC. గమనించండి, అది .

త్రిభుజాలు RAV, RVS, RSA- సమాన సమద్విబాహు త్రిభుజాలు (ఆస్తి ద్వారా). త్రిభుజాకార పిరమిడ్ మూడు వైపుల ముఖాలను కలిగి ఉంటుంది: RAV, RVS, RSA. దీని అర్థం పిరమిడ్ యొక్క పార్శ్వ ఉపరితలం యొక్క వైశాల్యం:

S వైపు = 3S RAW

సిద్ధాంతం నిరూపించబడింది.

సాధారణ చతుర్భుజాకార పిరమిడ్ యొక్క బేస్ వద్ద వ్రాయబడిన వృత్తం యొక్క వ్యాసార్థం 3 మీ, పిరమిడ్ యొక్క ఎత్తు 4 మీ. పిరమిడ్ యొక్క పార్శ్వ ఉపరితలం యొక్క వైశాల్యాన్ని కనుగొనండి.

ఇచ్చిన: సాధారణ చతుర్భుజ పిరమిడ్ ఎ బి సి డి,

ఎ బి సి డి- చదరపు,

ఆర్= 3 మీ,

RO- పిరమిడ్ ఎత్తు,

RO= 4 మీ.

కనుగొనండి: S వైపు. అంజీర్ చూడండి. 6.

అన్నం. 6

పరిష్కారం.

నిరూపితమైన సిద్ధాంతం ప్రకారం, .

మొదట ఆధారం వైపు వెతుకుదాం AB. సాధారణ చతుర్భుజాకార పిరమిడ్ యొక్క బేస్ వద్ద వ్రాయబడిన వృత్తం యొక్క వ్యాసార్థం 3 మీ అని మనకు తెలుసు.

అప్పుడు, ఎం.

చదరపు చుట్టుకొలతను కనుగొనండి ఎ బి సి డి 6 మీటర్ల వైపుతో:

ఒక త్రిభుజాన్ని పరిగణించండి BCD. వీలు ఎం- వైపు మధ్యలో DC. ఎందుకంటే గురించి- మధ్య BD, ఆ (m)

త్రిభుజం DPC- ఐసోసెల్స్. ఎం- మధ్య DC. అంటే, RM- మధ్యస్థం, అందువలన త్రిభుజంలో ఎత్తు DPC. అప్పుడు RM- పిరమిడ్ యొక్క అపోథెమ్.

RO- పిరమిడ్ ఎత్తు. అప్పుడు, నేరుగా ROవిమానానికి లంబంగా ABC, అందువలన నేరుగా ఓం, అందులో పడి ఉంది. అపోథెమ్‌ని కనుగొనండి RMలంబ త్రిభుజం నుండి రొమ్.

ఇప్పుడు మనం పిరమిడ్ యొక్క పార్శ్వ ఉపరితలాన్ని కనుగొనవచ్చు:

సమాధానం: 60 m2.

సాధారణ త్రిభుజాకార పిరమిడ్ యొక్క ఆధారం చుట్టూ చుట్టుముట్టబడిన వృత్తం యొక్క వ్యాసార్థం m కి సమానం. పార్శ్వ ఉపరితల వైశాల్యం 18 m 2. అపోథెమ్ యొక్క పొడవును కనుగొనండి.

ఇచ్చిన: ABCP- సాధారణ త్రిభుజాకార పిరమిడ్,

AB = BC = SA,

ఆర్= m,

S వైపు = 18 m2.

కనుగొనండి: . అంజీర్ చూడండి. 7.

అన్నం. 7

పరిష్కారం.

లంబ త్రిభుజంలో ABCచుట్టుపక్కల వృత్తం యొక్క వ్యాసార్థం ఇవ్వబడింది. ఒక వైపు వెతుకుదాం ABఈ త్రిభుజం సైన్స్ నియమాన్ని ఉపయోగిస్తుంది.

సాధారణ త్రిభుజం (m) వైపు తెలుసుకోవడం, మేము దాని చుట్టుకొలతను కనుగొంటాము.

సాధారణ పిరమిడ్ యొక్క పార్శ్వ ఉపరితల వైశాల్యంపై సిద్ధాంతం ద్వారా, ఎక్కడ h a- పిరమిడ్ యొక్క అపోథెమ్. అప్పుడు:

సమాధానం: 4 మీ.

కాబట్టి, పిరమిడ్ అంటే ఏమిటి, సాధారణ పిరమిడ్ అంటే ఏమిటి మరియు సాధారణ పిరమిడ్ యొక్క పార్శ్వ ఉపరితలం గురించి మేము సిద్ధాంతాన్ని నిరూపించాము. తదుపరి పాఠంలో మనం కత్తిరించబడిన పిరమిడ్‌తో పరిచయం పొందుతాము.

గ్రంథ పట్టిక

1. జ్యామితి. తరగతులు 10-11: సాధారణ విద్యా సంస్థల విద్యార్థులకు పాఠ్య పుస్తకం (ప్రాథమిక మరియు ప్రత్యేక స్థాయిలు) / I. M. స్మిర్నోవా, V. A. స్మిర్నోవ్. - 5వ ఎడిషన్., రెవ. మరియు అదనపు - M.: Mnemosyne, 2008. - 288 p.: అనారోగ్యం.
2. జ్యామితి. తరగతులు 10-11: సాధారణ విద్యా సంస్థల కోసం పాఠ్యపుస్తకం / Sharygin I.F. - M.: బస్టర్డ్, 1999. - 208 pp.: ill.
3. జ్యామితి. గ్రేడ్ 10: గణితం /E యొక్క లోతైన మరియు ప్రత్యేక అధ్యయనంతో సాధారణ విద్యా సంస్థల కోసం పాఠ్య పుస్తకం. V. పోటోస్కువ్, L. I. జ్వాలిచ్. - 6వ ఎడిషన్, స్టీరియోటైప్. - M.: బస్టర్డ్, 008. - 233 p.: అనారోగ్యం.

1. ఇంటర్నెట్ పోర్టల్ "యాక్లాస్" ()
2. ఇంటర్నెట్ పోర్టల్ “పెడగోగికల్ ఆలోచనల పండుగ “సెప్టెంబర్ మొదటి” ()
3. ఇంటర్నెట్ పోర్టల్ “Slideshare.net” ()

ఇంటి పని

1. ఒక సాధారణ బహుభుజి క్రమరహిత పిరమిడ్‌కు ఆధారం కాగలదా?
2. సాధారణ పిరమిడ్ యొక్క విభజిత అంచులు లంబంగా ఉన్నాయని నిరూపించండి.
3. పిరమిడ్ యొక్క అపోథెమ్ దాని బేస్ వైపు సమానంగా ఉంటే, సాధారణ చతుర్భుజ పిరమిడ్ యొక్క బేస్ వైపున ఉన్న డైహెడ్రల్ కోణం యొక్క విలువను కనుగొనండి.
4. RAVS- సాధారణ త్రిభుజాకార పిరమిడ్. పిరమిడ్ యొక్క బేస్ వద్ద డైహెడ్రల్ కోణం యొక్క సరళ కోణాన్ని నిర్మించండి.

దీనిలో పక్క పక్కటెముకలలో ఒకటి బేస్‌కు లంబంగా ఉంటుంది.

ఈ సందర్భంలో, ఈ అంచు పిరమిడ్ యొక్క ఎత్తుగా ఉంటుంది.

పిరమిడ్ యొక్క లక్షణాలు.

1. అన్ని వైపు అంచులు ఒకే పరిమాణంలో ఉన్నప్పుడు, అప్పుడు:

• పిరమిడ్ యొక్క పునాదికి సమీపంలో ఉన్న వృత్తాన్ని వివరించడం సులభం, మరియు పిరమిడ్ యొక్క పైభాగం ఈ వృత్తం మధ్యలో అంచనా వేయబడుతుంది;
• పక్క పక్కటెముకలు బేస్ యొక్క విమానంతో సమాన కోణాలను ఏర్పరుస్తాయి;
• అంతేకాకుండా, వ్యతిరేకం కూడా నిజం, అనగా. పక్క పక్కటెముకలు బేస్ యొక్క సమతలంతో సమాన కోణాలను ఏర్పరుచుకున్నప్పుడు లేదా పిరమిడ్ యొక్క బేస్ చుట్టూ ఒక వృత్తాన్ని వర్ణించగలిగినప్పుడు మరియు పిరమిడ్ పైభాగం ఈ వృత్తం మధ్యలోకి అంచనా వేయబడినప్పుడు, అన్ని వైపు అంచులు పిరమిడ్ యొక్క పరిమాణం ఒకే విధంగా ఉంటుంది.

2. ప్రక్క ముఖాలు ఒకే విలువ యొక్క బేస్ యొక్క సమతలానికి వంపు కోణం కలిగి ఉన్నప్పుడు, అప్పుడు:

• పిరమిడ్ యొక్క పునాదికి సమీపంలో ఉన్న వృత్తాన్ని వివరించడం సులభం, మరియు పిరమిడ్ యొక్క పైభాగం ఈ వృత్తం మధ్యలో అంచనా వేయబడుతుంది;
• పక్క ముఖాల ఎత్తులు సమాన పొడవు;
• ప్రక్క ఉపరితలం యొక్క వైశాల్యం బేస్ చుట్టుకొలత మరియు ప్రక్క ముఖం యొక్క ఎత్తు యొక్క ½ ఉత్పత్తికి సమానం.

3. పిరమిడ్ యొక్క బేస్ వద్ద ఒక బహుభుజి ఉంటే, దాని చుట్టూ ఒక వృత్తాన్ని వర్ణించవచ్చు (అవసరమైన మరియు తగినంత పరిస్థితి) ఒక గోళాన్ని పిరమిడ్ చుట్టూ వివరించవచ్చు. గోళం యొక్క కేంద్రం వాటికి లంబంగా పిరమిడ్ అంచుల మధ్య గుండా వెళ్ళే విమానాల ఖండన బిందువుగా ఉంటుంది. ఈ సిద్ధాంతం నుండి మేము ఒక గోళాన్ని ఏదైనా త్రిభుజాకారంలో మరియు ఏదైనా సాధారణ పిరమిడ్ చుట్టూ వర్ణించవచ్చని నిర్ధారించాము;

4. పిరమిడ్ యొక్క అంతర్గత డైహెడ్రల్ కోణాల ద్విభాగ విమానాలు 1వ బిందువు వద్ద కలుస్తే (అవసరమైన మరియు తగినంత పరిస్థితి) ఒక గోళాన్ని పిరమిడ్‌లో లిఖించవచ్చు. ఈ పాయింట్ గోళానికి కేంద్రంగా మారుతుంది.

5. శంకువు పిరమిడ్‌లో వాటి శీర్షాలు ఏకీభవించినప్పుడు చెక్కబడి ఉంటుంది మరియు శంకువు యొక్క ఆధారం పిరమిడ్ పునాదిలో చెక్కబడి ఉంటుంది. ఈ సందర్భంలో, పిరమిడ్ యొక్క అపోథెమ్‌లు సమాన పరిమాణాలు (అవసరమైన మరియు తగినంత పరిస్థితి) కలిగి ఉంటే మాత్రమే పిరమిడ్‌లోకి కోన్‌ను అమర్చడం సాధ్యమవుతుంది;

6. శంకువు పిరమిడ్ సమీపంలో వర్ణించబడుతుంది, వాటి శీర్షాలు ఏకీభవిస్తే, పిరమిడ్ బేస్ సమీపంలో కోన్ యొక్క ఆధారం వివరించబడుతుంది. ఈ సందర్భంలో, పిరమిడ్ యొక్క అన్ని పార్శ్వ అంచులు ఒకే విలువలను కలిగి ఉంటే (అవసరమైన మరియు తగినంత పరిస్థితి) మాత్రమే పిరమిడ్ సమీపంలో ఉన్న కోన్‌ను వివరించడం సాధ్యమవుతుంది. ఈ శంకువులు మరియు పిరమిడ్ల ఎత్తులు ఒకే విధంగా ఉంటాయి.

7. ఒక సిలిండర్ పిరమిడ్‌లో చెక్కబడి ఉంటుంది, దాని బేస్‌లలో ఒకటి పిరమిడ్ విభాగంలో బేస్‌కు సమాంతరంగా ఉన్న విమానం ద్వారా చెక్కబడిన సర్కిల్‌తో సమానంగా ఉంటుంది మరియు రెండవ బేస్ పిరమిడ్ యొక్క స్థావరానికి చెందినది.

8. పిరమిడ్ పైభాగం దాని బేస్‌లలో ఒకదానికి చెందినప్పుడు పిరమిడ్ సమీపంలో వివరించబడుతుంది మరియు సిలిండర్ యొక్క రెండవ బేస్ పిరమిడ్ యొక్క బేస్ సమీపంలో వివరించబడుతుంది. ఈ సందర్భంలో, పిరమిడ్ యొక్క ఆధారం చెక్కబడిన బహుభుజి (అవసరమైన మరియు తగినంత పరిస్థితి) అయితే మాత్రమే పిరమిడ్ సమీపంలోని సిలిండర్‌ను వివరించడం సాధ్యమవుతుంది.

దీర్ఘచతురస్రాకార పిరమిడ్ యొక్క వాల్యూమ్ మరియు వైశాల్యాన్ని నిర్ణయించడానికి సూత్రాలు.

వి- పిరమిడ్ వాల్యూమ్,

ఎస్- పిరమిడ్ బేస్ యొక్క ప్రాంతం,

h- పిరమిడ్ ఎత్తు,

Sb- పిరమిడ్ యొక్క పార్శ్వ ఉపరితలం యొక్క ప్రాంతం,

a- అపోథెమ్ (అయోమయం చెందకూడదు α ) పిరమిడ్లు,

పి- పిరమిడ్ బేస్ చుట్టుకొలత,

n- పిరమిడ్ యొక్క బేస్ యొక్క భుజాల సంఖ్య,

బి- పిరమిడ్ వైపు అంచు పొడవు,

α - పిరమిడ్ పైభాగంలో ఫ్లాట్ కోణం.

ఇక్కడ మీరు పిరమిడ్‌లు మరియు సంబంధిత సూత్రాలు మరియు భావనల గురించి ప్రాథమిక సమాచారాన్ని కనుగొనవచ్చు. వీరంతా యూనిఫైడ్ స్టేట్ ఎగ్జామ్‌కు సన్నాహకంగా గణిత బోధకుడితో చదువుతారు.

ఒక విమానం, బహుభుజిని పరిగణించండి , అందులో అబద్ధం మరియు ఒక పాయింట్ S, దానిలో అబద్ధం కాదు. S ను బహుభుజి యొక్క అన్ని శీర్షాలకు కనెక్ట్ చేద్దాం. ఫలితంగా వచ్చే పాలిహెడ్రాన్‌ను పిరమిడ్ అంటారు. విభాగాలను సైడ్ రిబ్స్ అంటారు. బహుభుజిని బేస్ అని పిలుస్తారు మరియు పాయింట్ S అనేది పిరమిడ్ యొక్క పైభాగం. n సంఖ్యపై ఆధారపడి, పిరమిడ్‌ను త్రిభుజాకారం (n=3), చతుర్భుజం (n=4), పెంటగోనల్ (n=5) మరియు మొదలైనవి అంటారు. త్రిభుజాకార పిరమిడ్‌కు ప్రత్యామ్నాయ పేరు టెట్రాహెడ్రాన్. పిరమిడ్ యొక్క ఎత్తు అనేది దాని పైభాగం నుండి బేస్ యొక్క సమతలానికి లంబంగా అవరోహణ.

పిరమిడ్‌ను రెగ్యులర్ అని పిలుస్తారు ఒక సాధారణ బహుభుజి, మరియు పిరమిడ్ యొక్క ఎత్తు యొక్క ఆధారం (లంబంగా ఉన్న ఆధారం) దాని కేంద్రం.

గురువు యొక్క వ్యాఖ్య:
"రెగ్యులర్ పిరమిడ్" మరియు "రెగ్యులర్ టెట్రాహెడ్రాన్" భావనలను కంగారు పెట్టవద్దు. సాధారణ పిరమిడ్‌లో, పక్క అంచులు బేస్ అంచులకు తప్పనిసరిగా సమానంగా ఉండవు, కానీ సాధారణ టెట్రాహెడ్రాన్‌లో, మొత్తం 6 అంచులు సమానంగా ఉంటాయి. ఇది అతని నిర్వచనం. సమానత్వం బహుభుజి యొక్క కేంద్రం P సమానంగా ఉంటుందని నిరూపించడం సులభం బేస్ ఎత్తుతో, కాబట్టి సాధారణ టెట్రాహెడ్రాన్ ఒక సాధారణ పిరమిడ్.

అపోథెమ్ అంటే ఏమిటి?
పిరమిడ్ యొక్క అపోథెమ్ దాని వైపు ముఖం యొక్క ఎత్తు. పిరమిడ్ సక్రమంగా ఉంటే, దాని అన్ని అపోథెమ్‌లు సమానంగా ఉంటాయి. రివర్స్ నిజం కాదు.

తన పరిభాష గురించి ఒక గణిత బోధకుడు: పిరమిడ్‌లతో 80% పని రెండు రకాల త్రిభుజాల ద్వారా నిర్మించబడింది:
1) అపోథెమ్ SK మరియు ఎత్తు SPని కలిగి ఉంటుంది
2) పార్శ్వ అంచు SA మరియు దాని ప్రొజెక్షన్ PA కలిగి ఉంటుంది

ఈ త్రిభుజాల సూచనలను సరళీకృతం చేయడానికి, గణిత బోధకుడు వాటిలో మొదటిదానిని పిలవడం మరింత సౌకర్యవంతంగా ఉంటుంది. అపోథెమల్, మరియు రెండవది వ్యయమైన. దురదృష్టవశాత్తూ, మీరు ఏ పాఠ్యపుస్తకాలలోనూ ఈ పరిభాషను కనుగొనలేరు మరియు ఉపాధ్యాయుడు దీనిని ఏకపక్షంగా పరిచయం చేయాలి.

పిరమిడ్ వాల్యూమ్ కోసం ఫార్ములా:
1) , పిరమిడ్ యొక్క బేస్ ప్రాంతం ఎక్కడ ఉంది మరియు పిరమిడ్ యొక్క ఎత్తు
2) , లిఖించబడిన గోళం యొక్క వ్యాసార్థం ఎక్కడ ఉంది మరియు పిరమిడ్ యొక్క మొత్తం ఉపరితలం యొక్క వైశాల్యం.
3) , ఇక్కడ MN అనేది ఏదైనా రెండు క్రాసింగ్ అంచుల మధ్య దూరం మరియు మిగిలిన నాలుగు అంచుల మధ్య బిందువులచే ఏర్పడిన సమాంతర చతుర్భుజం యొక్క వైశాల్యం.

పిరమిడ్ ఎత్తు యొక్క పునాది యొక్క ఆస్తి:

పాయింట్ P (చిత్రాన్ని చూడండి) కింది షరతుల్లో ఒకదానిని నెరవేర్చినట్లయితే పిరమిడ్ యొక్క బేస్ వద్ద లిఖించబడిన వృత్తం మధ్యలో సమానంగా ఉంటుంది:
1) అన్ని అపోథీలు సమానం
2) అన్ని వైపు ముఖాలు సమానంగా బేస్కు వంపుతిరిగి ఉంటాయి
3) అన్ని అపోథెమ్‌లు పిరమిడ్ ఎత్తుకు సమానంగా ఉంటాయి
4) పిరమిడ్ యొక్క ఎత్తు అన్ని వైపుల ముఖాలకు సమానంగా వంపుతిరిగి ఉంటుంది

గణిత ఉపాధ్యాయుని వ్యాఖ్య: దయచేసి అన్ని పాయింట్లు ఒక సాధారణ ఆస్తి ద్వారా ఏకం చేయబడతాయని గమనించండి: ఒక మార్గం లేదా మరొకటి, పార్శ్వ ముఖాలు ప్రతిచోటా చేరి ఉంటాయి (అపోథెమ్స్ వాటి మూలకాలు). అందువల్ల, బోధకుడు తక్కువ ఖచ్చితమైన, కానీ నేర్చుకోవడం, సూత్రీకరణ కోసం మరింత సౌకర్యవంతంగా అందించగలడు: పాయింట్ P దాని పార్శ్వ ముఖాల గురించి ఏదైనా సమాన సమాచారం ఉన్నట్లయితే, లిఖిత వృత్తం యొక్క కేంద్రం, పిరమిడ్ యొక్క ఆధారంతో సమానంగా ఉంటుంది. దానిని నిరూపించడానికి, అన్ని అపోథెమ్ త్రిభుజాలు సమానంగా ఉన్నాయని చూపితే సరిపోతుంది.

మూడు షరతుల్లో ఒకటి నిజమైతే, పాయింట్ P పిరమిడ్ యొక్క బేస్ సమీపంలో చుట్టుముట్టబడిన వృత్తం యొక్క కేంద్రంతో సమానంగా ఉంటుంది:
1) అన్ని వైపు అంచులు సమానంగా ఉంటాయి
2) అన్ని వైపు పక్కటెముకలు బేస్కు సమానంగా వంపుతిరిగి ఉంటాయి
3) అన్ని వైపు పక్కటెముకలు సమానంగా ఎత్తుకు వంపుతిరిగి ఉంటాయి