Znalezienie współrzędnych wektora jest dość powszechnym warunkiem wielu problemów matematycznych. Możliwość znalezienia współrzędnych wektorowych pomoże Ci w innych, nie tylko złożone zadania z podobne tematy. W tym artykule przyjrzymy się wzorowi na znalezienie współrzędnych wektorowych i kilku problemom.
Znajdowanie współrzędnych wektora w płaszczyźnie
Co to jest samolot? Płaszczyzna jest uważana za przestrzeń dwuwymiarową, przestrzeń o dwóch wymiarach (wymiar x i wymiar y). Na przykład papier jest płaski. Powierzchnia stołu jest płaska. Każda figura nieobjętościowa (kwadrat, trójkąt, trapez) jest również płaszczyzną. Tak więc, jeśli w opisie problemu musisz znaleźć współrzędne wektora leżącego na płaszczyźnie, natychmiast pamiętamy o x i y. Możesz znaleźć współrzędne takiego wektora w następujący sposób: Współrzędne wektora AB = (xB - xA; yB - xA). Ze wzoru jasno wynika, że ze współrzędnych punkt końcowy musisz odjąć współrzędne punktu początkowego.
Przykład:
- Vector CD ma współrzędne początkowe (5; 6) i końcowe (7; 8).
- Znajdź współrzędne samego wektora.
- Korzystając z powyższego wzoru otrzymujemy następujące wyrażenie: CD = (7-5; 8-6) = (2; 2).
- Zatem współrzędne wektora CD = (2; 2).
- Odpowiednio współrzędna x jest równa dwa, współrzędna y również wynosi dwa.
Znajdowanie współrzędnych wektora w przestrzeni
Czym jest przestrzeń? Przestrzeń jest już wymiarem trójwymiarowym, w którym podane są 3 współrzędne: x, y, z. Jeśli chcesz znaleźć wektor leżący w przestrzeni, wzór praktycznie się nie zmienia. Dodawana jest tylko jedna współrzędna. Aby znaleźć wektor, należy odjąć współrzędne początku od współrzędnych końca. AB = (xB – xA; yB – yA; zB – zA)
Przykład:
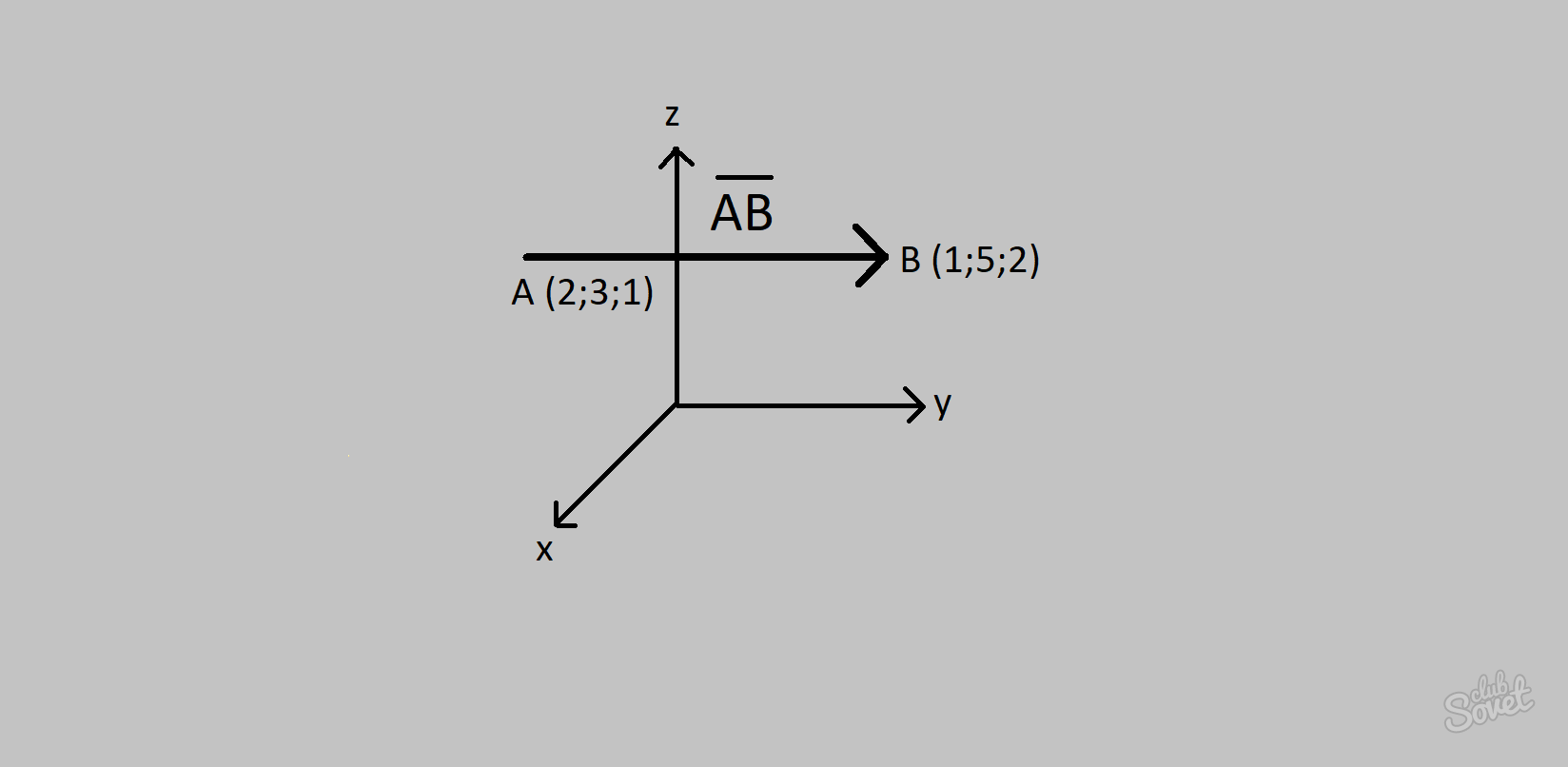
- Wektor DF ma początkowy (2; 3; 1) i końcowy (1; 5; 2).
- Stosując powyższy wzór otrzymujemy: Współrzędne wektora DF = (1-2; 5-3; 2-1) = (-1; 2; 1).
- Pamiętaj, że wartość współrzędnej może być ujemna, nie ma problemu.
Jak znaleźć współrzędne wektora online?
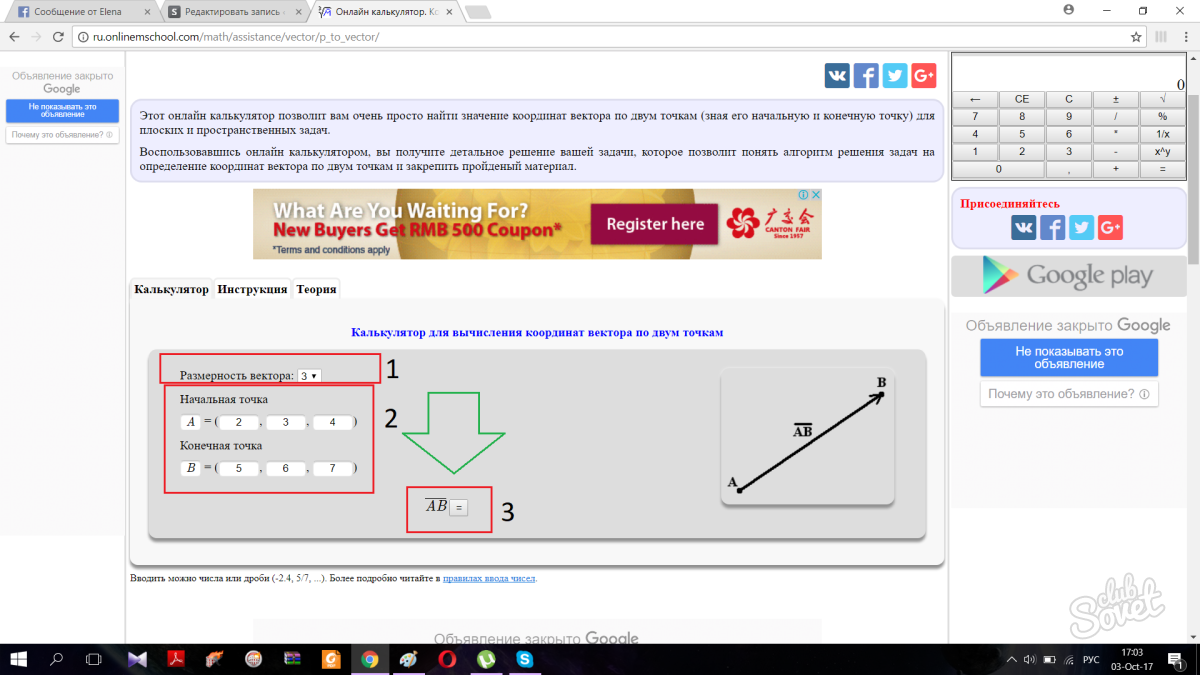
Jeśli z jakiegoś powodu nie chcesz samodzielnie znajdować współrzędnych, możesz skorzystać z kalkulatora online. Aby rozpocząć, wybierz wymiar wektorowy. Wymiar wektora odpowiada za jego wymiary. Wymiar 3 oznacza, że wektor znajduje się w przestrzeni, wymiar 2 oznacza, że znajduje się na płaszczyźnie. Następnie wpisz współrzędne punktów w odpowiednie pola, a program sam wyznaczy współrzędne wektora. Wszystko jest bardzo proste.
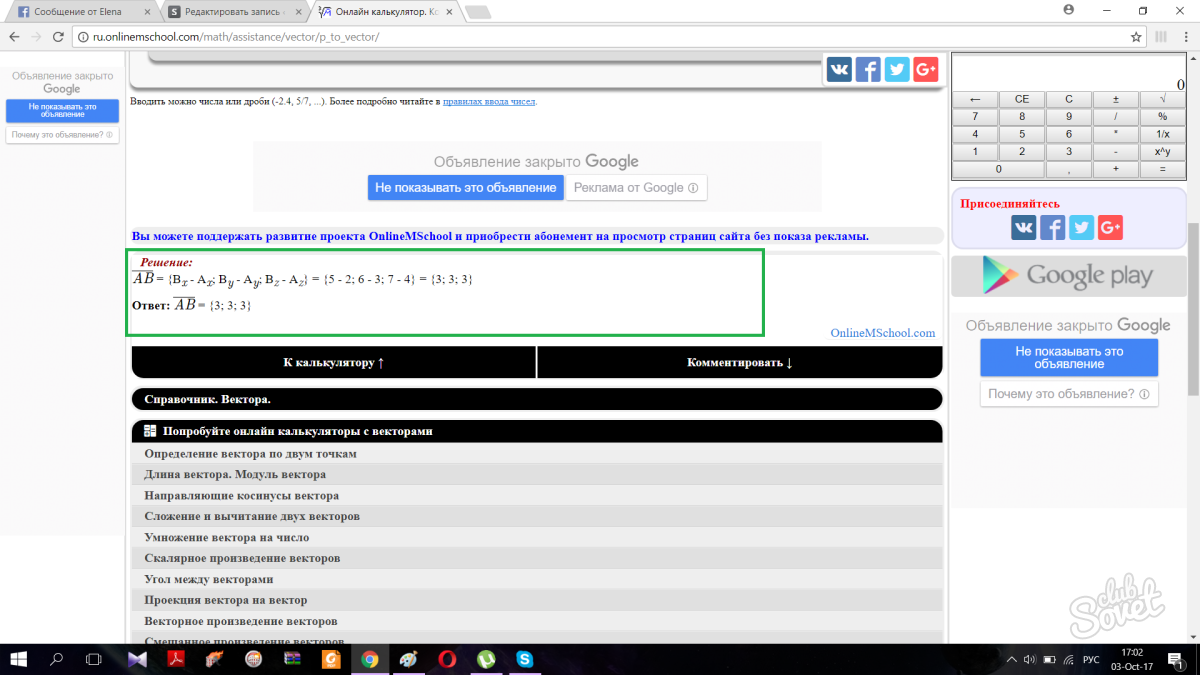
Po kliknięciu przycisku strona automatycznie przewinie się w dół i wyświetli poprawną odpowiedź wraz z krokami rozwiązania.
Zaleca się dobrze się uczyć ten temat, ponieważ pojęcie wektora występuje nie tylko w matematyce, ale także w fizyce. Studenci wydziału Technologie informacyjne Studiują także temat wektorów, ale na bardziej złożonym poziomie.
Jeżeli dane są dwa punkty płaszczyzny i, to wektor ma następujące współrzędne:
Jeżeli dane są dwa punkty w przestrzeni i, to wektor ma następujące współrzędne:
To jest, ze współrzędnych końca wektora musisz odjąć odpowiednie współrzędne początek wektora.
Ćwiczenia: Dla tych samych punktów zapisz wzory na znalezienie współrzędnych wektora. Wzory na końcu lekcji.
Przykład 1
Biorąc pod uwagę dwa punkty płaszczyzny i . Znajdź współrzędne wektora
Rozwiązanie: według odpowiedniego wzoru:
Alternatywnie można zastosować następujący wpis:
Estetycy zadecydują o tym:
Osobiście jestem przyzwyczajony do pierwszej wersji nagrania.
Odpowiedź:
Zgodnie z warunkiem nie było potrzeby budowania rysunku (co jest typowe dla zadań geometria analityczna), ale żeby wyjaśnić pewne kwestie manekinom, nie będę zbyt leniwy:
Zdecydowanie musisz zrozumieć różnica między współrzędnymi punktu i współrzędnymi wektorowymi:
Współrzędne punktu– są to współrzędne zwykłe w prostokątnym układzie współrzędnych. Postaw punkty płaszczyzna współrzędnych Myślę, że każdy może to zrobić od klasy 5-6. Każdy punkt ma ściśle określone miejsce na płaszczyźnie i nie można go nigdzie przenieść.
Współrzędne wektora jest jego rozwinięciem w zakresie podstawy, w w tym przypadku. Każdy wektor jest dowolny, zatem w razie potrzeby możemy go łatwo odsunąć od innego punktu płaszczyzny. Co ciekawe, w przypadku wektorów w ogóle nie trzeba budować osi, układ prostokątny współrzędnych, potrzebujesz jedynie podstawy, w tym przypadku ortonormalnej podstawy płaszczyzny.
Zapisy współrzędnych punktów i współrzędnych wektorów wydają się być podobne: , i znaczenie współrzędnych absolutnie różny i powinieneś być świadomy tej różnicy. Ta różnica dotyczy oczywiście także przestrzeni.
Szanowni Państwo, zapełnijmy ręce:
Przykład 2
a) Punkty i są przyznawane. Znajdź wektory i .
b) Punkty i są przyznawane. Znajdź wektory i .
c) Punkty i są przyznawane. Znajdź wektory i .
d) Przyznawane są punkty. Znajdź wektory.
Być może to wystarczy. To są przykłady niezależna decyzja, staraj się ich nie zaniedbywać, to się opłaci ;-). Nie ma potrzeby wykonywania rysunków. Rozwiązania i odpowiedzi na końcu lekcji.
Co jest ważne przy rozwiązywaniu problemów z geometrii analitycznej? Ważne jest, aby zachować DUŻĄ OSTROŻNOŚĆ, aby uniknąć mistrzowskiego błędu „dwa plus dwa równa się zero”. Od razu przepraszam, jeśli gdzieś popełniłem błąd =)
Jak znaleźć długość odcinka?
Długość, jak już wspomniano, jest oznaczona znakiem modułu.
Jeżeli dane są dwa punkty płaszczyzny i , to długość odcinka można obliczyć ze wzoru
Jeżeli dane są dwa punkty w przestrzeni i, to długość odcinka można obliczyć za pomocą wzoru
Notatka: Formuły pozostaną poprawne, jeśli zamienimy odpowiednie współrzędne: I , ale pierwsza opcja jest bardziej standardowa
Przykład 3
Rozwiązanie: według odpowiedniego wzoru:
Odpowiedź:
Dla jasności zrobię rysunek 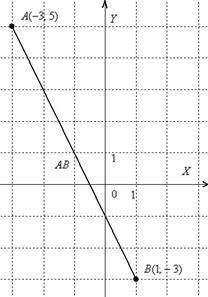
Odcinek - to nie jest wektor i oczywiście nie można go nigdzie przenieść. Dodatkowo, jeśli rysujesz w skali: 1 jednostka. = 1 cm (dwie komórki notesu), wówczas uzyskaną odpowiedź można sprawdzić zwykłą linijką, bezpośrednio mierząc długość odcinka.
Tak, rozwiązanie jest krótkie, ale jest w nim jeszcze kilka ważne punkty które chciałbym wyjaśnić:
Po pierwsze, w odpowiedzi podajemy wymiar: „jednostki”. Warunek nie mówi CO to jest, milimetry, centymetry, metry czy kilometry. Dlatego matematycznie poprawnym rozwiązaniem byłoby ogólne sformułowanie: „jednostki” - w skrócie „jednostki”.
Po drugie, powtórzmy materiał szkolny, co jest przydatne nie tylko dla rozważanego problemu:
Zwróć uwagę na ważny technika techniczna – usunięcie mnożnika spod pierwiastka. W wyniku obliczeń otrzymujemy wynik, a dobry styl matematyczny polega na usunięciu współczynnika spod pierwiastka (jeśli to możliwe). Bardziej szczegółowo proces wygląda następująco: . Oczywiście pozostawienie odpowiedzi bez zmian nie byłoby błędem - ale z pewnością byłoby mankamentem i poważnym argumentem za sprzeczeniem ze strony nauczyciela.
Oto inne typowe przypadki: 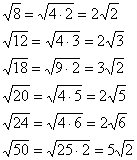
Często jest ich wystarczająco dużo u nasady duża liczba, Na przykład . Co zrobić w takich przypadkach? Korzystając z kalkulatora sprawdzamy, czy liczba jest podzielna przez 4: . Tak, został całkowicie podzielony, a więc: ![]() . A może liczbę można ponownie podzielić przez 4? . Zatem:
. A może liczbę można ponownie podzielić przez 4? . Zatem: ![]() . Ostatnia cyfra liczby jest nieparzysta, więc dzielenie przez 4 po raz trzeci oczywiście nie zadziała. Spróbujmy podzielić przez dziewięć: . W rezultacie:
. Ostatnia cyfra liczby jest nieparzysta, więc dzielenie przez 4 po raz trzeci oczywiście nie zadziała. Spróbujmy podzielić przez dziewięć: . W rezultacie:
Gotowy.
Wniosek: jeśli pod pierwiastkiem otrzymamy liczbę, której nie da się wydobyć w całości, to staramy się usunąć czynnik spod pierwiastka - za pomocą kalkulatora sprawdzamy, czy liczba jest podzielna przez: 4, 9, 16, 25, 36, 49 itd.
Podczas decyzji różne zadania korzenie są powszechne, zawsze staraj się wyciągać czynniki spod pierwiastka, aby uniknąć niższej oceny i niepotrzebnych problemów z finalizacją rozwiązań w oparciu o uwagi nauczyciela.
Powtórzmy także pierwiastki kwadratowe i inne potęgi:
Zasady działań ze stopniami w ogólna perspektywa może być znaleziony w podręcznik szkolny w algebrze, ale myślę, że z podanych przykładów wszystko lub prawie wszystko jest już jasne.
Zadanie samodzielnego rozwiązania segmentu w przestrzeni:
Przykład 4
Punkty i są przyznawane. Znajdź długość odcinka.
Rozwiązanie i odpowiedź znajdują się na końcu lekcji.
Jak znaleźć długość wektora?
Jeśli podany jest wektor płaski, jego długość oblicza się ze wzoru.
Jeśli podany jest wektor przestrzenny, jego długość oblicza się ze wzoru ![]() .
.
Wzory te (jak również wzory na długość odcinka) można łatwo wyprowadzić za pomocą dobrze znanego twierdzenia Pitagorasa.
Przykład 5
Punkty i są przyznawane. Znajdź długość wektora.
Wziąłem te same punkty, co w przykładzie 3.
Rozwiązanie: Najpierw znajdźmy wektor:
Korzystając ze wzoru obliczamy długość wektora:
Odpowiedź:
Nie zapomnij podać wymiaru – „jednostek”! Nawiasem mówiąc, czy zawsze konieczne jest obliczenie wartości przybliżonej (w w tym przykładzie 8.94), jeśli nie jest to wymagane w warunku? Z mojego punktu widzenia nie będzie to zbyteczne, brak przybliżonej wartości prowadzi do szukania nitów. Wskazane jest zaokrąglanie do 2-3 miejsc po przecinku.
Zróbmy rysunek do zadania:
Jaka jest podstawowa różnica w porównaniu z przykładem 3? Różnica jest taka, że tutaj mówimy o wektorze, a nie o segmencie. Wektor można przesunąć w dowolne miejsce na płaszczyźnie.
Jakie są podobieństwa między przykładem 3 i przykładem 5? Z geometrycznego punktu widzenia jest oczywiste, że długość odcinka jest równa długości wektora. Oczywiste jest również, że długość wektora będzie taka sama. W rezultacie: ![]() .
.
b) Biorąc pod uwagę wektory , , i . Znajdź ich długości.
Rozwiązania i odpowiedzi na końcu lekcji.
W tym artykule zaczniemy omawiać jedną „magiczną różdżkę”, która pozwoli Ci zredukować wiele problemów geometrycznych do prostej arytmetyki. Ten „kij” może znacznie ułatwić Ci życie, zwłaszcza gdy nie masz pewności co do budowania figury przestrzenne, sekcje itp. Wszystko to wymaga pewnej wyobraźni i umiejętności praktycznych. Metoda, którą zaczniemy tutaj rozważać, pozwoli ci prawie całkowicie abstrahować od dowolnego rodzaju konstrukcje geometryczne i rozumowanie. Metoda nazywa się „metoda współrzędnych”. W tym artykule rozważymy następujące pytania:
- Płaszczyzna współrzędnych
- Punkty i wektory na płaszczyźnie
- Konstruowanie wektora z dwóch punktów
- Długość wektora (odległość między dwoma punktami).
- Współrzędne środka odcinka
- Iloczyn skalarny wektorów
- Kąt między dwoma wektorami
Myślę, że już zgadłeś, dlaczego tak nazywa się metoda współrzędnych? Zgadza się, otrzymał taką nazwę, ponieważ nie współpracuje z obiekty geometryczne, a wraz z nimi charakterystyki numeryczne(współrzędne). A sama transformacja, która pozwala przejść od geometrii do algebry, polega na wprowadzeniu układu współrzędnych. Jeśli pierwotna figura była płaska, wówczas współrzędne są dwuwymiarowe, a jeśli figura jest trójwymiarowa, wówczas współrzędne są trójwymiarowe. W tym artykule rozważymy tylko przypadek dwuwymiarowy. Głównym celem artykułu jest nauczenie Cię, jak z nich korzystać podstawowe techniki metoda współrzędnych (czasami okazują się przydatne przy rozwiązywaniu problemów z planimetrii w Części B Unified State Examination). Kolejne dwie części tego tematu poświęcone są omówieniu metod rozwiązywania problemów C2 (zagadnienie stereometrii).
Od czego logiczne byłoby rozpoczęcie dyskusji na temat metody współrzędnych? Prawdopodobnie z koncepcji układu współrzędnych. Przypomnij sobie, kiedy spotkałeś ją po raz pierwszy. Wydaje mi się, że w 7 klasie, kiedy dowiedziałeś się o istnieniu funkcja liniowa, Na przykład. Przypomnę, że budowałeś to punkt po punkcie. Pamiętasz? Ty wybierz dowolna liczba, podstawiłem go do wzoru i obliczyłem w ten sposób. Na przykład, jeśli, to, jeśli, to itd. Co ostatecznie otrzymałeś? I otrzymałeś punkty ze współrzędnymi: i. Następnie narysowałeś „krzyż” (układ współrzędnych), wybrałeś na nim skalę (ile komórek będziesz miał jako segment jednostkowy) i zaznaczyłeś na nim uzyskane punkty, które następnie połączyłeś linią prostą; otrzymany wynik linia jest wykresem funkcji.
Jest tu kilka punktów, które należy wyjaśnić nieco bardziej szczegółowo:
1. Wybierasz pojedynczy segment ze względu na wygodę, aby wszystko ładnie i zwięźle zmieściło się na rysunku.
2. Przyjmuje się, że oś biegnie od lewej do prawej, a oś biegnie od dołu do góry
3. Przecinają się pod kątem prostym, a punkt ich przecięcia nazywany jest początkiem. Jest to oznaczone literą.
4. Pisząc współrzędne punktu, np. po lewej stronie w nawiasie podaje się współrzędne punktu wzdłuż osi, a po prawej stronie wzdłuż osi. W szczególności oznacza to po prostu, że w danym momencie
5. Aby ustawić dowolny punkt oś współrzędnych, należy podać jego współrzędne (2 cyfry)
6. Dla dowolnego punktu leżącego na osi
7. Dla dowolnego punktu leżącego na osi
8. Oś nazywana jest osią x
9. Oś nazywana jest osią y
Teraz zrobimy to z tobą Następny krok: Zaznaczmy dwa punkty. Połączmy te dwa punkty odcinkiem. I umieścimy strzałkę tak, jakbyśmy rysowali odcinek od punktu do punktu: to znaczy, że skierujemy nasz odcinek!

Pamiętasz, jak nazywa się inny segment kierunkowy? Zgadza się, nazywa się to wektorem!
Jeśli więc połączymy kropkę z kropką, i początek będzie punktem A, a końcem będzie punkt B, wtedy otrzymamy wektor. Ty też robiłeś tę konstrukcję w 8 klasie, pamiętasz?
Okazuje się, że wektory, podobnie jak punkty, można oznaczyć dwiema liczbami: liczby te nazywane są współrzędnymi wektorowymi. Pytanie: Czy sądzisz, że wystarczy znać współrzędne początku i końca wektora, aby znaleźć jego współrzędne? Okazuje się, że tak! Odbywa się to bardzo prosto:
Zatem, ponieważ w wektorze punkt jest początkiem, a punkt końcem, wektor ma następujące współrzędne:
Na przykład, jeśli, to współrzędne wektora
Teraz zróbmy odwrotnie, znajdź współrzędne wektora. Co musimy w tym celu zmienić? Tak, musisz zamienić początek i koniec: teraz początek wektora będzie w punkcie, a koniec będzie w punkcie. Następnie:
Przyjrzyj się uważnie, jaka jest różnica między wektorami a? Jedyną różnicą są znaki we współrzędnych. Są przeciwieństwami. Fakt ten jest zwykle zapisywany w ten sposób:
Czasami, jeśli nie jest wyraźnie określone, który punkt jest początkiem wektora, a który końcem, wówczas wektory są oznaczane przez więcej niż dwa wielkimi literami i jedną małą literą, na przykład: , itp.
Teraz trochę ćwiczyć siebie i znajdź współrzędne następujących wektorów:
Badanie:
Teraz rozwiąż nieco trudniejszy problem:
Wektor mający początek w punkcie ma współ-lub-di-na-ty. Znajdź punkty abs-cis-su.
Wszystko to samo jest dość prozaiczne: niech będą współrzędnymi punktu. Następnie
Skompilowałem system w oparciu o definicję współrzędnych wektorowych. Wtedy punkt ma współrzędne. Nas interesuje odcięta. Następnie
Odpowiedź:
Co jeszcze można zrobić z wektorami? Tak, prawie wszystko jest takie samo jak z zwykłe liczby(z tą różnicą, że nie możesz dzielić, ale możesz pomnożyć na dwa sposoby, z których jeden omówimy tutaj nieco później)
- Wektory można dodawać do siebie
- Wektory można od siebie odejmować
- Wektory można mnożyć (lub dzielić) przez dowolną liczbę niezerową
- Wektory można mnożyć przez siebie
Wszystkie te operacje mają bardzo wyraźną reprezentację geometryczną. Na przykład zasada trójkąta (lub równoległoboku) dotycząca dodawania i odejmowania:
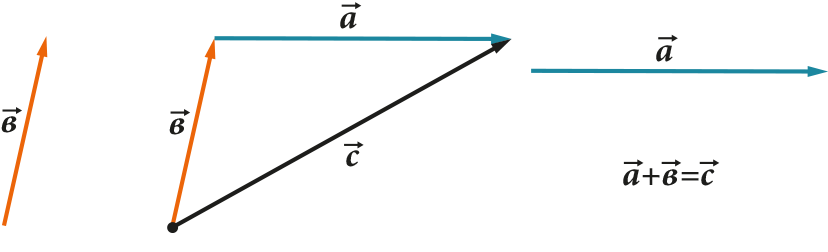
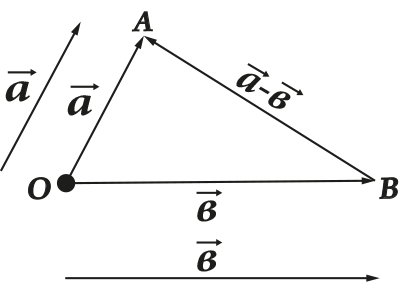
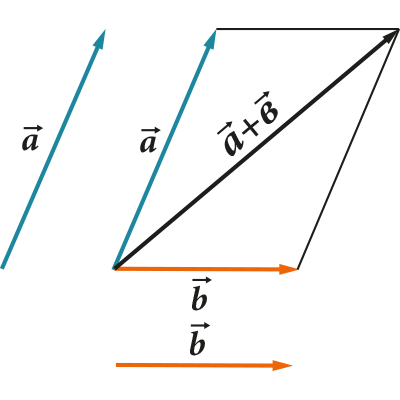
Wektor rozciąga się, kurczy lub zmienia kierunek po pomnożeniu lub podzieleniu przez liczbę:

Jednak tutaj będziemy zainteresowani pytaniem, co dzieje się ze współrzędnymi.
1. Dodając (odejmując) dwa wektory, dodajemy (odejmujemy) ich współrzędne element po elemencie. To jest:
2. Podczas mnożenia (dzielenia) wektora przez liczbę wszystkie jego współrzędne są mnożone (dzielone) przez tę liczbę:
Na przykład:
· Znajdź ilość co-or-din-nat stulecie-ra.
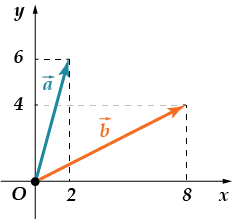
Najpierw znajdźmy współrzędne każdego z wektorów. Obydwa mają ten sam początek – punkt początkowy. Ich końcówki są inne. Następnie, . Teraz obliczmy współrzędne wektora, wtedy suma współrzędnych wynikowego wektora będzie równa.
Odpowiedź:
Teraz rozwiąż samodzielnie następujący problem:
· Znajdź sumę współrzędnych wektorowych
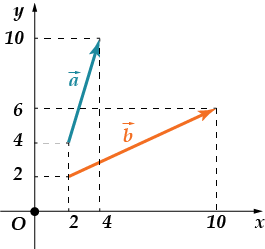
Sprawdzamy:
Rozważmy teraz następujący problem: mamy dwa punkty na płaszczyźnie współrzędnych. Jak znaleźć odległość między nimi? Niech będzie pierwszy punkt i drugi. Oznaczmy odległość między nimi przez. Dla przejrzystości zróbmy następujący rysunek:
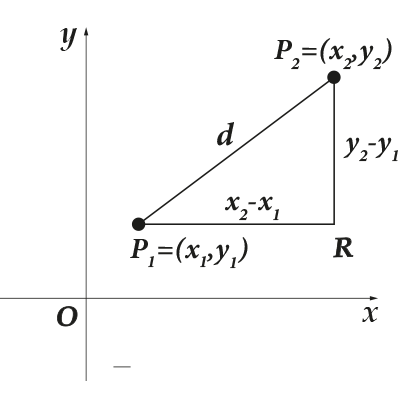
Co ja zrobiłem? Przede wszystkim podłączyłem kropki i, a również narysował linię od punktu, równolegle do osi, a od punktu narysowałem linię równoległą do osi. Czy przecięły się w jednym punkcie, tworząc niezwykłą figurę? Co jest w niej takiego wyjątkowego? Tak, ty i ja wiemy prawie wszystko o trójkącie prostokątnym. No cóż, na pewno twierdzenie Pitagorasa. Wymagany odcinek to przeciwprostokątna tego trójkąta, a segmenty to nogi. Jakie są współrzędne punktu? Tak, łatwo je znaleźć na obrazku: Ponieważ odcinki są równoległe do osi i odpowiednio ich długości są łatwe do znalezienia: jeśli oznaczymy długości odcinków odpowiednio przez, to
Skorzystajmy teraz z twierdzenia Pitagorasa. Znamy długości nóg, znajdziemy przeciwprostokątną:
Zatem odległość między dwoma punktami jest pierwiastkiem sumy kwadratów różnic ze współrzędnych. Lub - odległość między dwoma punktami to długość łączącego je odcinka. Łatwo zauważyć, że odległość między punktami nie zależy od kierunku. Następnie:
Stąd wyciągamy trzy wnioski:
Poćwiczmy trochę obliczanie odległości między dwoma punktami:
Na przykład, jeśli, to odległość między i jest równa
Albo pójdźmy inną drogą: znajdź współrzędne wektora
I znajdź długość wektora:
Jak widać, to samo!
Teraz poćwicz trochę sam:
Zadanie: znajdź odległość pomiędzy wskazanymi punktami:
Sprawdzamy:
Oto kilka kolejnych problemów wykorzystujących tę samą formułę, chociaż brzmią one nieco inaczej:
1. Znajdź kwadrat długości powieki.

2. Znajdź kwadrat długości powieki

Myślę, że poradziłeś sobie z nimi bez trudności? Sprawdzamy:
1. A to dla uważności) Współrzędne wektorów znaleźliśmy już wcześniej: . Wtedy wektor ma współrzędne. Kwadrat jego długości będzie równy:
2. Znajdź współrzędne wektora
Wtedy kwadrat jego długości wynosi
Nic skomplikowanego, prawda? Prosta arytmetyka, nic więcej.
Poniższych problemów nie można jednoznacznie sklasyfikować, dotyczą one raczej ogólnej erudycji i umiejętności rysowania prostych obrazów.
1. Znajdź sinus kąta odcięcia, łączącego punkt z osią odciętych.
 I
I
Jak będziemy tutaj postępować? Musimy znaleźć sinus kąta pomiędzy i osią. Gdzie możemy szukać sinusa? Zgadza się, w trójkąt prostokątny. Co więc musimy zrobić? Zbuduj ten trójkąt!
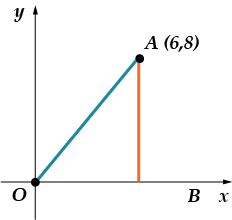
Ponieważ współrzędne punktu to i, to segment jest równy, i segment. Musimy znaleźć sinus kąta. Przypominam, że sinus jest stosunkiem Przeciwna strona następnie do przeciwprostokątnej
Co nam pozostało do zrobienia? Znajdź przeciwprostokątną. Można to zrobić na dwa sposoby: korzystając z twierdzenia Pitagorasa (nogi są znane!) lub korzystając ze wzoru na odległość między dwoma punktami (właściwie to samo, co w przypadku pierwszej metody!). Ja pójdę drugą drogą:
Odpowiedź:
Następne zadanie będzie Ci się wydawać jeszcze łatwiejsze. Znajduje się na współrzędnych punktu.
Zadanie 2. Od tego miejsca per-pen-di-ku-lyar jest opuszczany na oś odciętą. Nai-di-te abs-cis-su os-no-va-niya per-pen-di-ku-la-ra.
Zróbmy rysunek:
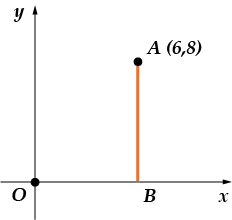
Podstawą prostopadłej jest punkt, w którym przecina ona oś x (oś), dla mnie jest to punkt. Z rysunku wynika, że ma on współrzędne: . Nas interesuje odcięta - czyli składnik „x”. Ona jest równa.
Odpowiedź: .
Zadanie 3. W warunkach poprzednie zadanie znajdź sumę odległości punktu od osi współrzędnych.
Zadanie jest na ogół elementarne, jeśli wiadomo, jaka jest odległość punktu od osi. Wiesz, że? Mam nadzieję, ale i tak przypominam:
Czy na powyższym rysunku narysowałem już jedną taką prostopadłą? Na której osi się znajduje? Do osi. A jaka jest w takim razie jego długość? Ona jest równa. Teraz samodzielnie narysuj prostopadłą do osi i znajdź jej długość. Będzie równo, prawda? Wtedy ich suma jest równa.
Odpowiedź: .
Zadanie 4. W warunkach zadania 2 znajdź rzędną punktu, punkt symetryczny względem osi odciętej.
Myślę, że intuicyjnie jest dla ciebie jasne, czym jest symetria? Wiele obiektów to ma: wiele budynków, stołów, samolotów, wiele figury geometryczne: kula, walec, kwadrat, romb itp. Z grubsza symetrię można rozumieć w następujący sposób: figura składa się z dwóch (lub więcej) identycznych połówek. Symetria ta nazywana jest symetrią osiową. Czym zatem jest oś? To jest dokładnie linia, wzdłuż której figurę można, mówiąc relatywnie, „przeciąć” na równe połowy (na tym zdjęciu oś symetrii jest prosta):

Wróćmy teraz do naszego zadania. Wiemy, że szukamy punktu, który jest symetryczny względem osi. Wtedy ta oś jest osią symetrii. Oznacza to, że musimy zaznaczyć taki punkt, aby oś przecięła odcinek na dwie równe części. Spróbuj sam oznaczyć taki punkt. Teraz porównaj z moim rozwiązaniem:
![]()
Czy u Ciebie zadziałało to w ten sam sposób? Cienki! Nas interesuje rzędna znalezionego punktu. To jest równe
Odpowiedź:
A teraz powiedz mi, po kilku sekundach zastanowienia, jaka będzie odcięta punktu symetrycznego do punktu A względem rzędnej? Jaka jest twoja odpowiedź? Poprawna odpowiedź: .
W przypadek ogólny regułę można zapisać w następujący sposób:
Punkt symetryczny do punktu względem osi odciętej ma współrzędne:
Punkt symetryczny do punktu względem osi rzędnych ma współrzędne:
Cóż, teraz jest to całkowicie przerażające zadanie: znajdź współrzędne punktu symetrycznego do punktu względem początku układu współrzędnych. Najpierw pomyśl sam, a potem spójrz na mój rysunek!
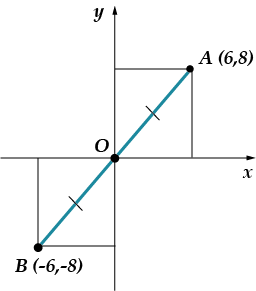
Odpowiedź:
Teraz problem z równoległobokiem:
Zadanie 5: Punkty pojawiają się ver-shi-na-mi paral-le-lo-gram-ma. Znajdź lub-di-na-tym punkcie.
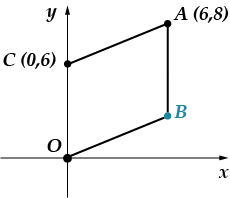
Problem ten można rozwiązać na dwa sposoby: logicznie i metodą współrzędnych. Najpierw użyję metody współrzędnych, a potem powiem, jak można to rozwiązać inaczej.
Jest całkiem jasne, że odcięta punktu jest równa. (leży na prostopadłej poprowadzonej od punktu do osi odciętej). Musimy znaleźć współrzędną. Skorzystajmy z faktu, że nasza figura jest równoległobokiem, to znaczy, że. Znajdźmy długość odcinka, korzystając ze wzoru na odległość między dwoma punktami:
Opuszczamy prostopadłą łączącą punkt z osią. Punkt przecięcia oznaczę literą.
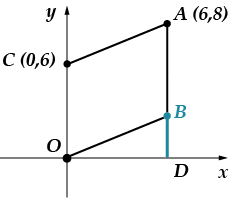
Długość odcinka jest równa. (sam znajdź problem, w którym omawialiśmy ten punkt), wówczas długość odcinka znajdziemy za pomocą twierdzenia Pitagorasa:
Długość odcinka pokrywa się dokładnie z jego rzędną.
Odpowiedź: .
Inne rozwiązanie (podam tylko zdjęcie ilustrujące to)
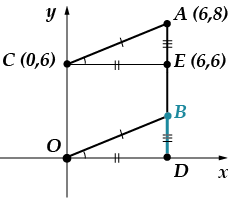
Postęp rozwiązania:
1. Postępowanie
2. Znajdź współrzędne punktu i długość
3. Udowodnij to.
Inny Problem z długością segmentu:
Punkty pojawiają się na górze trójkąta. Znajdź długość jego linii środkowej, równoległej.

Czy pamiętasz co to jest Środkowa linia trójkąt? W takim razie to zadanie jest dla Ciebie elementarne. Jeśli nie pamiętasz, to przypomnę: środkowa linia trójkąta to linia łącząca środki przeciwne strony. Jest równoległy do podstawy i równy jej połowie.
Podstawą jest segment. Musieliśmy wcześniej szukać jego długości, jest równa. Następnie długość linii środkowej jest o połowę mniejsza i równa.
Odpowiedź: .
Komentarz: problem ten można rozwiązać w inny sposób, do którego przejdziemy nieco później.
Tymczasem mam dla Ciebie kilka zadań, poćwicz nad nimi, są bardzo proste, ale pomagają Ci lepiej posługiwać się metodą współrzędnych!
1. Punkty znajdują się na górze tra-pecji. Znajdź długość jego linii środkowej.

2. Punkty i występy ver-shi-na-mi pa-ral-le-lo-gram-ma. Znajdź lub-di-na-tym punkcie.

3. Znajdź długość od cięcia, łącząc punkt i

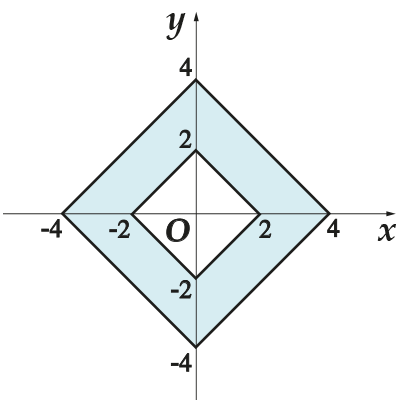
4. Znajdź obszar za kolorową figurą na płaszczyźnie współrzędnych.
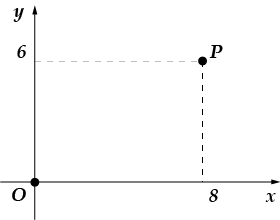
5. Przez ten punkt przechodzi okrąg o środku w na-cha-le ko-or-din-nat. Znajdź jej rad-di-nas.
6. Znajdź di-te ra-di-us koła, opisz-san-noy o kącie prostym-no-ka, wierzchołki czegoś mają współ-lub -di-na-jesteś tak odpowiedzialny

Rozwiązania:
1. Wiadomo, że linia środkowa trapezu jest równa połowie sumy jego podstaw. Podstawa jest równa i podstawa. Następnie
Odpowiedź:
2. Najprostszym sposobem rozwiązania tego problemu jest zanotowanie tego (reguła równoległoboku). Obliczanie współrzędnych wektorów nie jest trudne: . Podczas dodawania wektorów dodawane są współrzędne. Następnie ma współrzędne. Punkt ma również te współrzędne, ponieważ początkiem wektora jest punkt o współrzędnych. Nas interesuje rzędna. Ona jest równa.
Odpowiedź:
3. Od razu postępujemy zgodnie ze wzorem na odległość między dwoma punktami:
Odpowiedź:
4. Spójrz na ilustrację i powiedz mi, pomiędzy którymi dwiema postaciami „wciśnięty” jest zacieniony obszar? Jest wciśnięty pomiędzy dwa kwadraty. Następnie obszar pożądanej figury jest równy obszarowi dużego kwadratu minus obszar małego. Strona mały kwadrat jest odcinkiem łączącym punkty, a jego długość wynosi
Następnie obszar małego kwadratu wynosi
To samo robimy z dużym kwadratem: jego bok jest odcinkiem łączącym punkty, a jego długość
Następnie obszar dużego kwadratu wynosi
Obszar pożądanej figury znajdujemy za pomocą wzoru:
Odpowiedź:
5. Jeśli okrąg ma początek w środku i przechodzi przez punkt, to jego promień będzie dokładnie równy równa długości segment (zrób rysunek, a zrozumiesz, dlaczego jest to oczywiste). Znajdźmy długość tego odcinka:
Odpowiedź:
6. Wiadomo, że promień okręgu opisanego na prostokącie równy połowie jego przekątne. Znajdźmy długość dowolnej z dwóch przekątnych (w końcu w prostokącie są one równe!)
Odpowiedź:
No cóż, poradziłeś sobie ze wszystkim? Nie było zbyt trudno to rozgryźć, prawda? Zasada jest tu tylko jedna – umieć stworzyć obraz wizualny i po prostu „odczytać” z niego wszystkie dane.
Niewiele nam zostało. Są jeszcze dwie kwestie, które chciałbym omówić.
Spróbujmy rozwiązać ten prosty problem. Niech dwa punkty zostaną podane. Znajdź współrzędne środka odcinka. Rozwiązanie tego problemu jest następujące: niech punkt będzie pożądanym środkiem, wówczas będzie miał współrzędne:
To jest: współrzędne środka odcinka = średnia arytmetyczna odpowiednich współrzędnych końców odcinka.
Zasada ta jest bardzo prosta i zazwyczaj nie sprawia uczniom trudności. Zobaczmy, jakie problemy i jak się z niego korzysta:
1. Find-di-te or-di-na-tu se-re-di-ny from-cut, połącz punkt i

2. Punkty wydają się być na szczycie świata. Znajdź punkty di-te or-di-na-tu per-re-se-che-niya jego dia-go-na-ley.

3. Znajdź di-te abs-cis-su środek okręgu, opisz-san-noy o prostokątnym-nie-ka, wierzchołki czegoś mają współ-lub-di-na-ty tak-odpowiedzialnie-ale.

Rozwiązania:
1. Pierwszy problem jest po prostu klasyczny. Natychmiast przystępujemy do wyznaczania środka odcinka. Ma współrzędne. Rzędna jest równa.
Odpowiedź:
2. Łatwo zauważyć, że ten czworokąt jest równoległobokiem (nawet rombem!). Możesz to sam udowodnić, obliczając długości boków i porównując je ze sobą. Co wiem o równoległobokach? Jego przekątne są podzielone na pół w punkcie przecięcia! Tak! Jaki jest zatem punkt przecięcia przekątnych? To jest środek dowolnej przekątnej! Wybiorę w szczególności przekątną. Wtedy punkt ma współrzędne. Współrzędna punktu jest równa.
Odpowiedź:
3. Z czym pokrywa się środek okręgu opisanego na prostokącie? Pokrywa się z punktem przecięcia jego przekątnych. Co wiesz o przekątnych prostokąta? Są równe i punkt przecięcia dzieli je na pół. Zadanie zostało zredukowane do poprzedniego. Weźmy na przykład przekątną. Zatem jeśli jest środkiem okręgu opisanego, to jest jego środkiem. Szukam współrzędnych: Odcięta jest równa.
Odpowiedź:
Teraz poćwicz trochę sam, podam odpowiedzi na każde pytanie, abyś mógł się sprawdzić.
1. Find-di-te ra-di-us koła, opisz-san-noy o trójkącie-no-ka, wierzchołki czegoś mają co-or-di -no panowie

2. Znajdź di-te lub-di-on-ten środek koła, opisz-san-noy o trójkącie-no-ka, którego wierzchołki mają współrzędne
3. Jakiego rodzaju ra-di-u-sa powinien mieć okrąg ze środkiem w punkcie tak, aby dotykał osi odciętej?
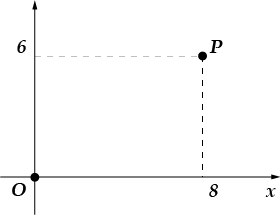
4. Znajdź-te lub-di-na-tym punkcie ponownego oddzielenia osi i od cięcia, połącz punkt i

Odpowiedzi:
Czy wszystko się udało? Naprawdę na to liczę! Teraz - ostatnie pchnięcie. Zachowaj teraz szczególną ostrożność. Materiał, który teraz wyjaśnię, jest bezpośrednio powiązany nie tylko z nim proste zadania do metody współrzędnych z części B, ale można ją również znaleźć wszędzie w zadaniu C2.
Której z moich obietnic jeszcze nie dotrzymałem? Pamiętacie, jakie operacje na wektorach obiecałem wprowadzić, a jakie ostatecznie wprowadziłem? Jesteś pewien, że o niczym nie zapomniałem? Zapomniałem! Zapomniałem wyjaśnić, co oznacza mnożenie wektorów.
Istnieją dwa sposoby pomnożenia wektora przez wektor. W zależności od wybranej metody otrzymamy obiekty o różnym charakterze:
Iloczyn krzyżowy jest wykonany całkiem sprytnie. O tym, jak to zrobić i dlaczego jest to potrzebne, porozmawiamy w następnym artykule. W tym przypadku skupimy się na iloczynie skalarnym.
Obliczamy to na dwa sposoby:
Jak się domyślasz, wynik powinien być taki sam! Przyjrzyjmy się więc najpierw pierwszej metodzie:
Iloczyn kropkowy za pomocą współrzędnych
Znajdź: - ogólnie przyjęty zapis iloczynu skalarnego
Wzór do obliczeń jest następujący:
To jest produkt skalarny= suma iloczynów współrzędnych wektorowych!
Przykład:
Znajdź-di-te
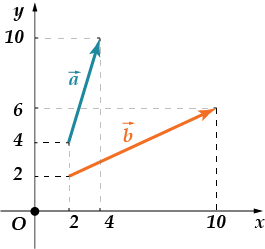
Rozwiązanie:
Znajdźmy współrzędne każdego z wektorów:
Iloczyn skalarny obliczamy korzystając ze wzoru:
Odpowiedź:
Widzisz, absolutnie nic skomplikowanego!
Cóż, teraz spróbuj sam:
· Znajdź skalarne pro-iz-ve-de-nie stuleci i
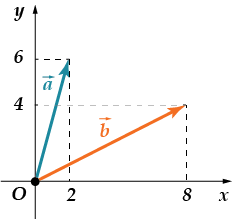
Czy udało Ci się? Może zauważyłeś mały haczyk? Sprawdźmy:
Współrzędne wektora jak w ostatnie zadanie! Odpowiedź: .
Oprócz współrzędnych istnieje inny sposób obliczenia iloczynu skalarnego, a mianowicie poprzez długości wektorów i cosinus kąta między nimi:
Oznacza kąt między wektorami i.
Oznacza to, że iloczyn skalarny jest równy iloczynowi długości wektorów i cosinusa kąta między nimi.
Po co nam ta druga formuła, skoro mamy pierwszą, która jest znacznie prostsza, to przynajmniej nie ma w niej cosinusów. I jest to potrzebne, abyśmy z pierwszego i drugiego wzoru mogli wywnioskować, jak znaleźć kąt między wektorami!
Niech zatem zapamiętamy wzór na długość wektora!
Następnie, jeśli podstawię te dane do wzoru na iloczyn skalarny, otrzymam:
Ale w inny sposób:
Więc co ty i ja dostaliśmy? Mamy teraz wzór, który pozwala nam obliczyć kąt między dwoma wektorami! Czasami dla zwięzłości zapisano to również w ten sposób:
Oznacza to, że algorytm obliczania kąta między wektorami jest następujący:
- Oblicz iloczyn skalarny za pomocą współrzędnych
- Znajdź długości wektorów i pomnóż je
- Wynik z punktu 1 podziel przez wynik z punktu 2
Poćwiczmy na przykładach:
1. Znajdź kąt między powiekami i. Podaj odpowiedź w grad-du-sah.
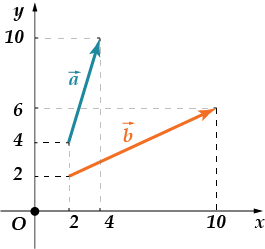
2. W warunkach poprzedniego zadania znajdź cosinus między wektorami
Zróbmy tak: pomogę Ci rozwiązać pierwszy problem, a drugi spróbuj zrobić sam! Zgadzać się? Zatem zaczynajmy!
1. Te wektory to nasi starzy przyjaciele. Obliczyliśmy już ich iloczyn skalarny i był równy. Ich współrzędne to: , . Następnie znajdujemy ich długości:
Następnie szukamy cosinusa między wektorami:
Jaki jest cosinus kąta? To jest róg.
Odpowiedź:
Cóż, teraz rozwiąż sam drugi problem, a następnie porównaj! Podam tylko bardzo krótkie rozwiązanie:
2. ma współrzędne, ma współrzędne.
Niech będzie kątem między wektorami i, a następnie
Odpowiedź:
Należy zauważyć, że problemy bezpośrednio na wektorach i metodzie współrzędnych w części B arkusz egzaminacyjny dość rzadkie. Jednak zdecydowaną większość problemów C2 można łatwo rozwiązać poprzez wprowadzenie układu współrzędnych. Można więc potraktować ten artykuł jako podstawę, na podstawie której wykonamy całkiem sprytne konstrukcje, które będą nam potrzebne do rozwiązania skomplikowanych problemów.
