Okrąg wpisany u podstawy piramidy. Rozwiązywanie problemów geometrycznych


Piramida. Poprawna piramida
Wielościany

Ten samouczek wideo pomoże użytkownikom zapoznać się z motywem Piramidy. Poprawna piramida. W tej lekcji zapoznamy się z pojęciem piramidy i podamy jej definicję. Zastanówmy się, czym jest zwykła piramida i jakie ma właściwości. Następnie udowodnimy twierdzenie o powierzchni bocznej zwykła piramida.


W tej lekcji zapoznamy się z pojęciem piramidy i podamy jej definicję.

Rozważ wielokąt A 1 A 2...Jakiś, która leży w płaszczyźnie α, oraz punkt P, która nie leży w płaszczyźnie α (rys. 1). Połączmy kropki P ze szczytami Za 1, Za 2, Za 3, … Jakiś. Dostajemy N trójkąty: A 1 A 2 R, A 2 A 3 R i tak dalej.

Definicja. Wielościan RA 1 A 2 ...A n, złożony z N-kwadrat A 1 A 2...Jakiś I N trójkąty RA 1 A 2, RA 2A 3 …RA n A n-1 nazywa się N-piramida węglowa. Ryż. 1.

Ryż. 1

Rozważmy czworokątną piramidę PABCD(ryc. 2).

R- szczyt piramidy.

ABCD- podstawa piramidy.

RA - boczne żebro.

AB- żebro podstawy.

Z punktu R opuśćmy prostopadłą RN do płaszczyzny bazowej ABCD. Wykreślona prostopadłość to wysokość piramidy.

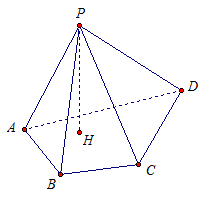
Ryż. 2

Pełna powierzchnia Piramida składa się z powierzchni bocznej, to znaczy obszaru wszystkich ścian bocznych i obszaru podstawy:

S pełny = S strona + S główny

Piramidę nazywamy prawidłową, jeśli:

  • jego fundament - regularny wielokąt;
  • odcinek łączący wierzchołek piramidy ze środkiem podstawy to jej wysokość.

Wyjaśnienie na przykładzie regularnej piramidy czworokątnej

Rozważmy regularną czworokątną piramidę PABCD(ryc. 3).

R- szczyt piramidy. Podstawa piramidy ABCD- regularny czworobok, czyli kwadrat. Kropka O, punkt przecięcia przekątnych, jest środkiem kwadratu. Oznacza, RO jest wysokością piramidy.

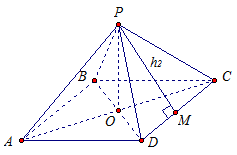
Ryż. 3

Wyjaśnienie: w poprawnym N W trójkącie środek okręgu wpisanego i środek okręgu opisanego pokrywają się. Środek ten nazywany jest środkiem wielokąta. Czasami mówią, że wierzchołek jest rzutowany na środek.

Nazywa się wysokość bocznej ściany regularnej piramidy narysowanej od jej wierzchołka apotem i jest wyznaczony h.

1. wszystkie boczne krawędzie regularnej piramidy są równe;

2. boczne twarze są przystającymi trójkątami równoramiennymi.

Dowód tych właściwości przedstawimy na przykładzie regularnej piramidy czworokątnej.

Dany: PABCD- regularna czworokątna piramida,

ABCD- kwadrat,

RO- wysokość piramidy.

Udowodnić:

1. RA = PB = RS = PD

2.∆ABP = ∆BCP =∆CDP =∆DAP Patrz rys. 4.

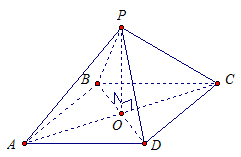
Ryż. 4

Dowód.

RO- wysokość piramidy. To znaczy prosto RO prostopadle do płaszczyzny ABC, a zatem bezpośredni JSC, VO, SO I DO leżąc w nim. Zatem trójkąty ROA, ROV, ROS, ROD- prostokątny.

Rozważmy kwadrat ABCD. Z własności kwadratu wynika, że AO = VO = CO = DO.

Następnie trójkąty prostokątne ROA, ROV, ROS, ROD noga RO- generał i nogi JSC, VO, SO I DO są równe, co oznacza, że ​​te trójkąty są równe z dwóch stron. Z równości trójkątów wynika równość odcinków, RA = PB = RS = PD. Punkt 1 został udowodniony.

Segmenty AB I Słońce są równe, ponieważ są bokami tego samego kwadratu, RA = PB = RS. Zatem trójkąty AVR I VSR - równoramienne i równe z trzech stron.

W podobny sposób znajdujemy trójkąty ABP, VCP, CDP, DAP są równoramienne i równe, jak wymaga tego udowodnienie w paragrafie 2.

Pole powierzchni bocznej regularnej piramidy jest równe połowie iloczynu obwodu podstawy i apothemu:

Aby to udowodnić, wybierzmy regularną piramidę trójkątną.

Dany: RAVY- regularna trójkątna piramida.

AB = BC = AC.

RO- wysokość.

Udowodnić: . Zobacz ryc. 5.

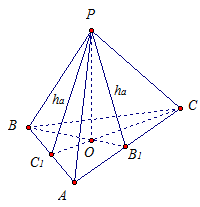
Ryż. 5

Dowód.

RAVY- regularna trójkątna piramida. To jest AB= AC = BC. Pozwalać O- środek trójkąta ABC, Następnie RO jest wysokością piramidy. U podstawy piramidy leży trójkąt równoboczny ABC. Zauważ, że .

Trójkąty RAV, RVS, RPA- równy trójkąty równoramienne(według własności). Trójkątna piramida ma trzy ściany boczne: RAV, RVS, RPA. Oznacza to, że pole powierzchni bocznej piramidy wynosi:

Strona S = 3S RAW

Twierdzenie zostało udowodnione.

Promień okręgu wpisanego w podstawę regularnej czworokątnej piramidy wynosi 3 m, wysokość piramidy wynosi 4 m. Znajdź pole powierzchni bocznej piramidy.

Dany: regularna czworokątna piramida ABCD,

ABCD- kwadrat,

R= 3 m,

RO- wysokość piramidy,

RO= 4 m.

Znajdować: Strona S. Zobacz ryc. 6.

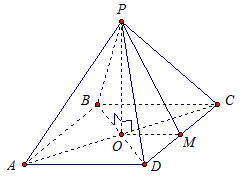
Ryż. 6

Rozwiązanie.

Zgodnie ze sprawdzonym twierdzeniem, .

Najpierw znajdźmy bok podstawy AB. Wiemy, że promień okręgu wpisanego w podstawę czworokątnej piramidy foremnej wynosi 3 m.

Następnie m.in.

Znajdź obwód kwadratu ABCD o boku 6 m:

Rozważmy trójkąt BCD. Pozwalać M- środek boku DC. Ponieważ O- środek BD, To (M).

Trójkąt DPC- równoramienne. M- środek DC. To jest, RM- mediana, a co za tym idzie wysokość w trójkącie DPC. Następnie RM- apotem piramidy.

RO- wysokość piramidy. Potem prosto RO prostopadle do płaszczyzny ABC, a zatem bezpośredni OM, leżąc w nim. Znajdźmy apotem RM z trójkąt prostokątny ROM.

Teraz możemy znaleźć powierzchnia boczna piramidy:

Odpowiedź: 60 m2.

Promień okręgu opisanego na podstawie regularnej trójkątnej piramidy jest równy m. Pole powierzchni bocznej wynosi 18 m 2. Znajdź długość apothemu.

Dany: ABCP- regularna trójkątna piramida,

AB = BC = SA,

R= m,

Strona S = 18 m2.

Znajdować: . Zobacz ryc. 7.

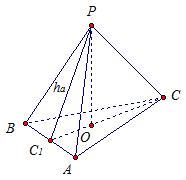
Ryż. 7

Rozwiązanie.

W trójkącie prostokątnym ABC Podany jest promień okręgu opisanego. Znajdźmy stronę AB ten trójkąt, korzystając z twierdzenia sinusów.

Znając bok regularnego trójkąta (m), znajdujemy jego obwód.

Według twierdzenia o powierzchni bocznej regularnej piramidy , Gdzie h- apotem piramidy. Następnie:

Odpowiedź: 4 m.

Przyjrzeliśmy się więc, czym jest piramida, czym jest regularna piramida i udowodniliśmy twierdzenie o powierzchni bocznej regularnej piramidy. W następnej lekcji zapoznamy się ze ściętą piramidą.

Bibliografia

  1. Geometria. Klasy 10-11: podręcznik dla uczniów instytucje edukacyjne(podstawowe i poziomy profilu) / I. M. Smirnova, V. A. Smirnov. - wyd. 5, wyd. i dodatkowe - M.: Mnemosyne, 2008. - 288 s.: il.
  2. Geometria. Klasa 10-11: Podręcznik do kształcenia ogólnego instytucje edukacyjne/ Sharygin I.F. - M.: Drop, 1999. - 208 s.: chory.
  3. Geometria. Klasa 10: Podręcznik dla instytucji kształcenia ogólnego z pogłębioną i specjalistyczne badanie matematyka /E. V. Potoskuev, L. I. Zvalich. - wyd. 6, stereotyp. - M.: Drop, 008. - 233 s.: chory.
  1. Portal internetowy „Yaklass” ()
  2. Portal internetowy „Festiwal pomysły pedagogiczne„Pierwszy września” ()
  3. Portal internetowy „Slideshare.net” ()

Praca domowa

  1. Czy wielokąt foremny może być podstawą nieregularnej piramidy?
  2. Udowodnić, że rozłączne krawędzie ostrosłupa foremnego są prostopadłe.
  3. Znajdź wartość kąt dwuścienny po stronie podstawy regularnej czworokątnej piramidy, jeśli apotem piramidy jest równy bokowi jej podstawy.
  4. RAVY- regularna trójkątna piramida. Zbudować kąt liniowy kąt dwuścienny u podstawy piramidy.

Chudaeva E.V., Miejska Instytucja Oświatowa „Insarskaya Liceum nr 1”, Insar, Republika Mordowii

ROZWIĄZYWANIE PROBLEMÓW GEOMETRYCZNYCH

(Przez Materiały do ​​​​egzaminu ujednoliconego stanu)

Zadanie nr 1

Zadanie nr 2

Zadanie nr 3

Zadanie nr 4. Oblicz objętość regularnej trójkątnej piramidy, której bok jest równy 6, a apotem piramidy jest równy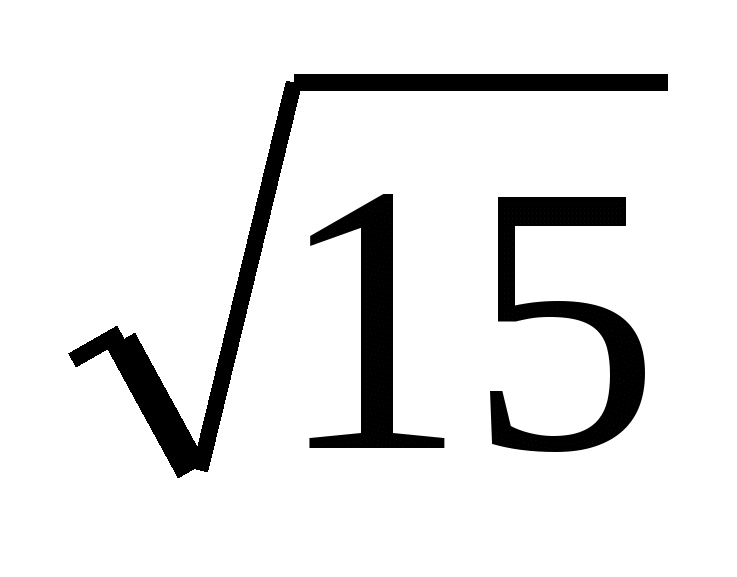

.

Problem nr 5. Oblicz objętość regularnej ostrosłupa trójkątnego, jeśli promień okręgu wpisanego u podstawy wynosi 2, a wysokość ostrosłupa foremnego wynosi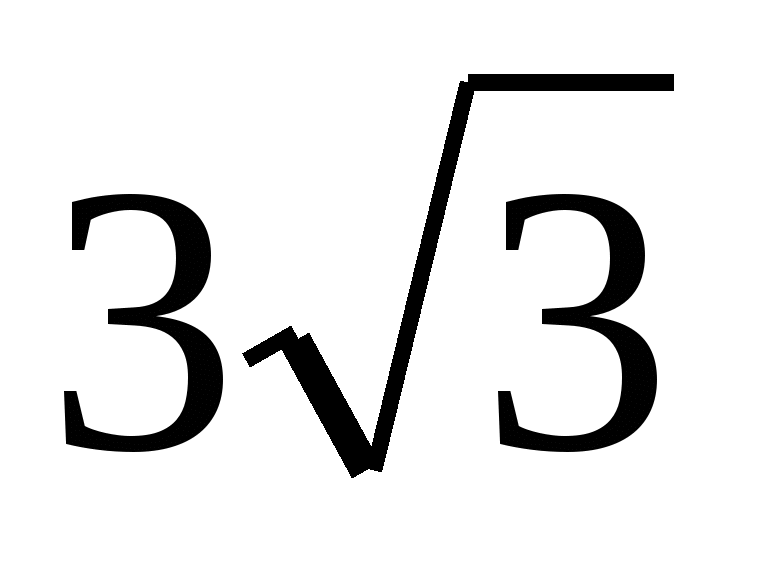

.

Problem nr 6. Oblicz pole powierzchni bocznej regularnej czworokątnej piramidy, jeśli jej krawędzie wynoszą 5, a promień okręgu opisanego wokół podstawy wynosi 3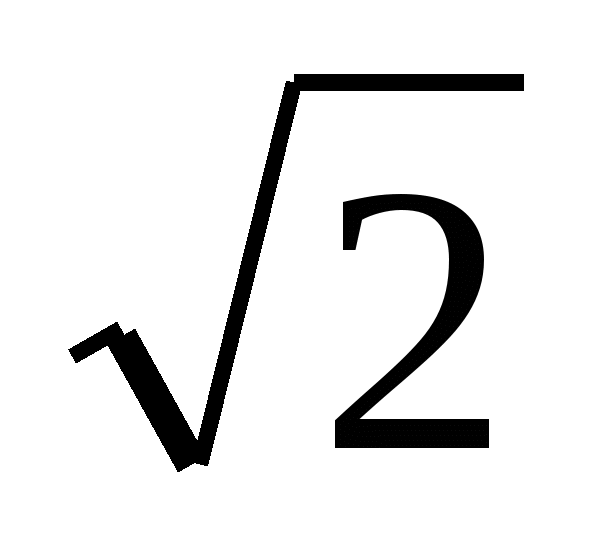

.

Problem nr 7

Problem nr 8

Problem nr 9. Po prawej sześciokątna piramida bok podstawy wynosi 2, a krawędź boczna wynosi 2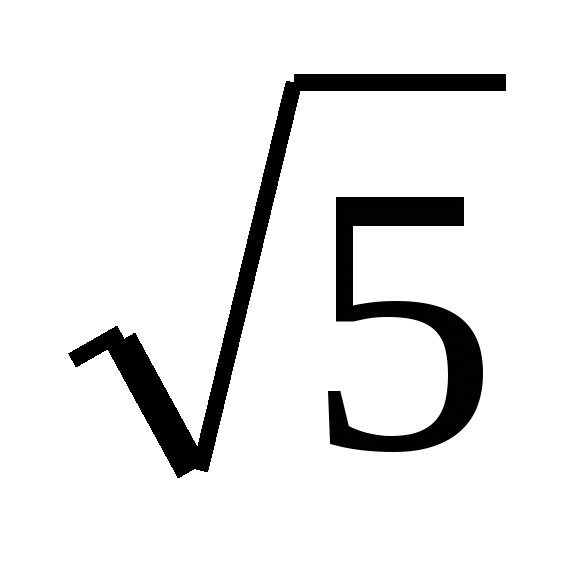

. Znajdź objętość piramidy.

Problem nr 10R spełnia równanie R 2 + R – 6 = 0. Znajdź objętość pryzmatu.

Zadanie nr 11. Blisko prawego trójkątny pryzmat cylinder jest opisany. Odległość osi cylindra od boku podstawy pryzmatu jest równa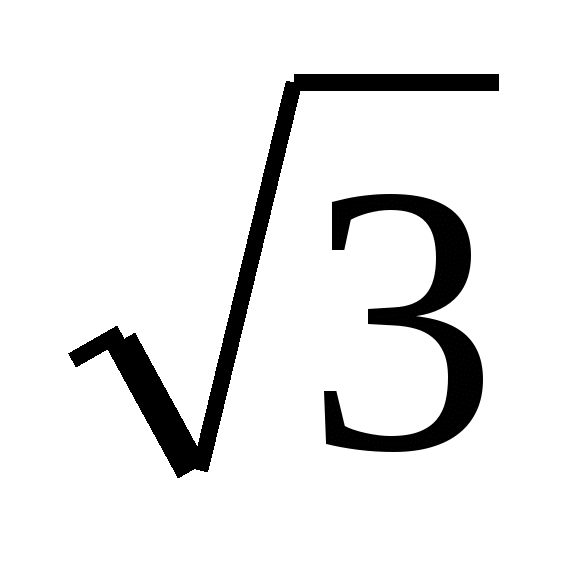

. Wysokość walca jest równa trzem jego promieniom. Znajdź objętość pryzmatu.

Zadanie nr 12

Zadanie nr 13

Zadanie nr 14. W regularny czworokątny pryzmat wpisano cylinder. Objętość walca wynosi 16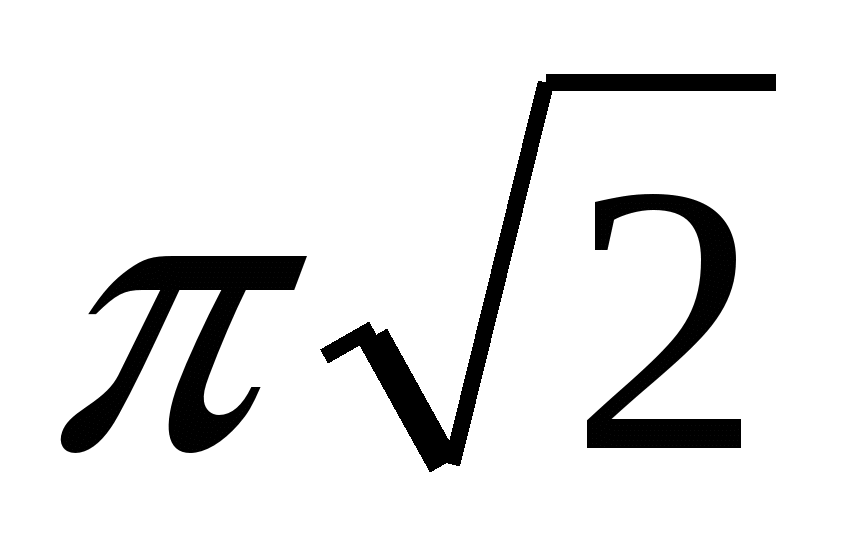

, a promień okręgu opisanego wokół podstawy pryzmatu jest równy

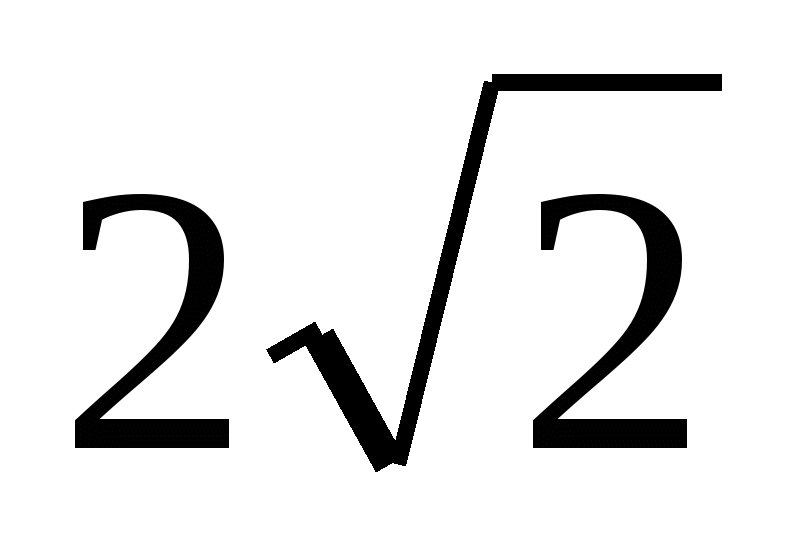. Znajdź przekątną pryzmatu.

Zadanie nr 15. W regularny sześciokątny pryzmat wpisano cylinder. Znajdź wysokość pryzmatu, jeśli jego pole wynosi 54, a promień walca wynosi 3.


Zadanie nr 16. Blisko prawego sześciokątny pryzmat cylinder jest opisany. Objętość walca wynosi 16 , wysokość cylindra wynosi 4. Znajdź objętość pryzmatu.

Zadanie nr 17. Walec opisano wokół regularnego sześciokątnego pryzmatu. Objętość cylindra wynosi 10 . Znajdź objętość walca wpisanego w ten sam pryzmat.

ROZWIĄZYWANIE PROBLEMÓW GEOMETRYCZNYCH

(na podstawie materiałów z egzaminu Unified State Exam)

Zadanie nr 1 . Oblicz objętość regularnej piramidy trójkątnej, jeśli promień okręgu opisanego na podstawie jest równy , a wysokość piramidy jest równa 4.

R 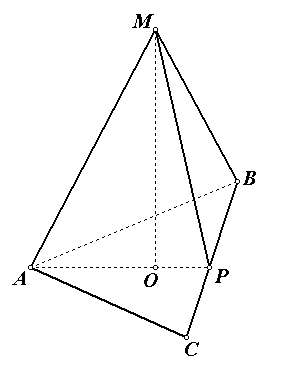decyzja.


.

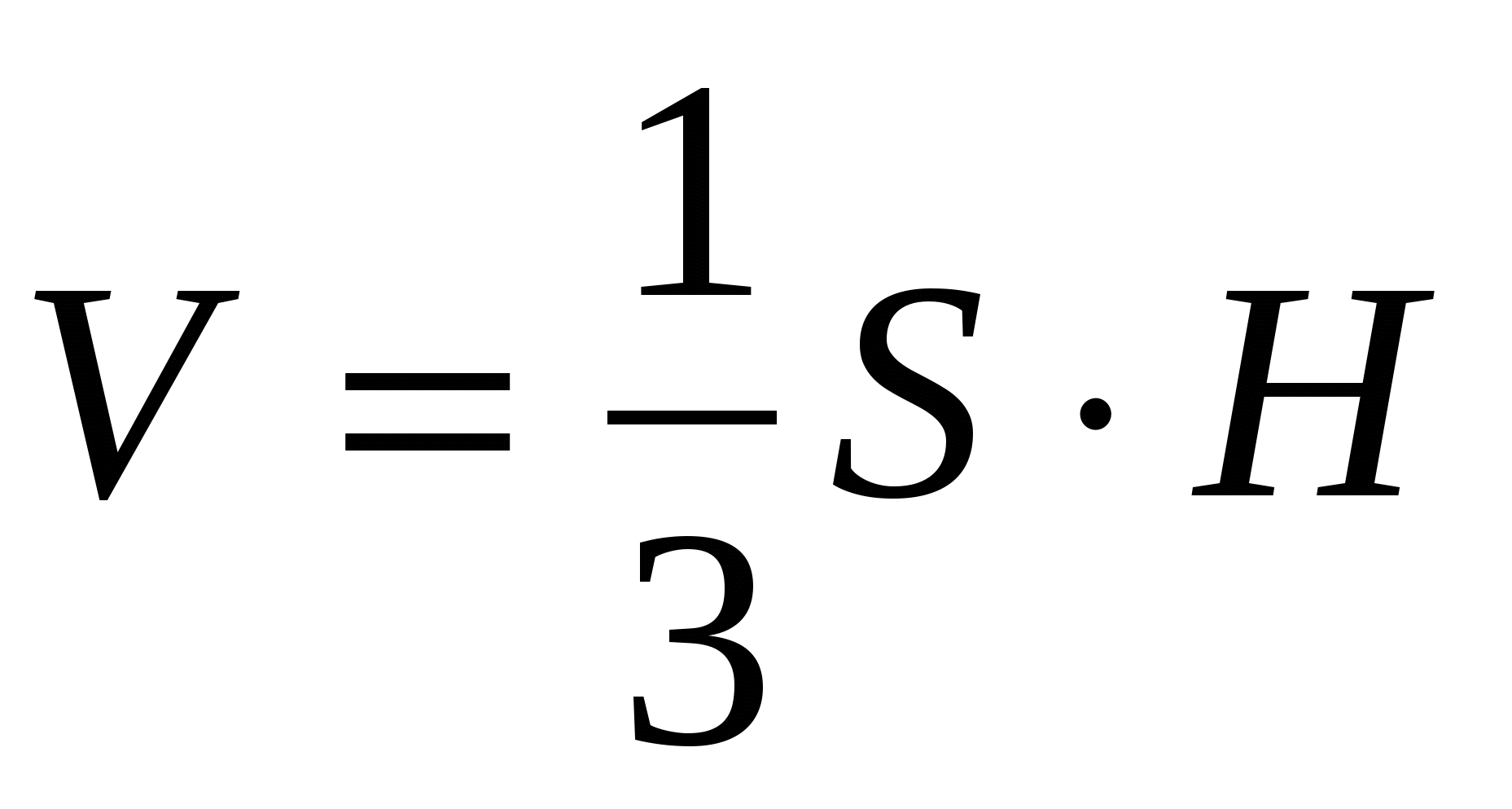1) znajdź bok podstawy regularnej piramidy, korzystając ze wzoru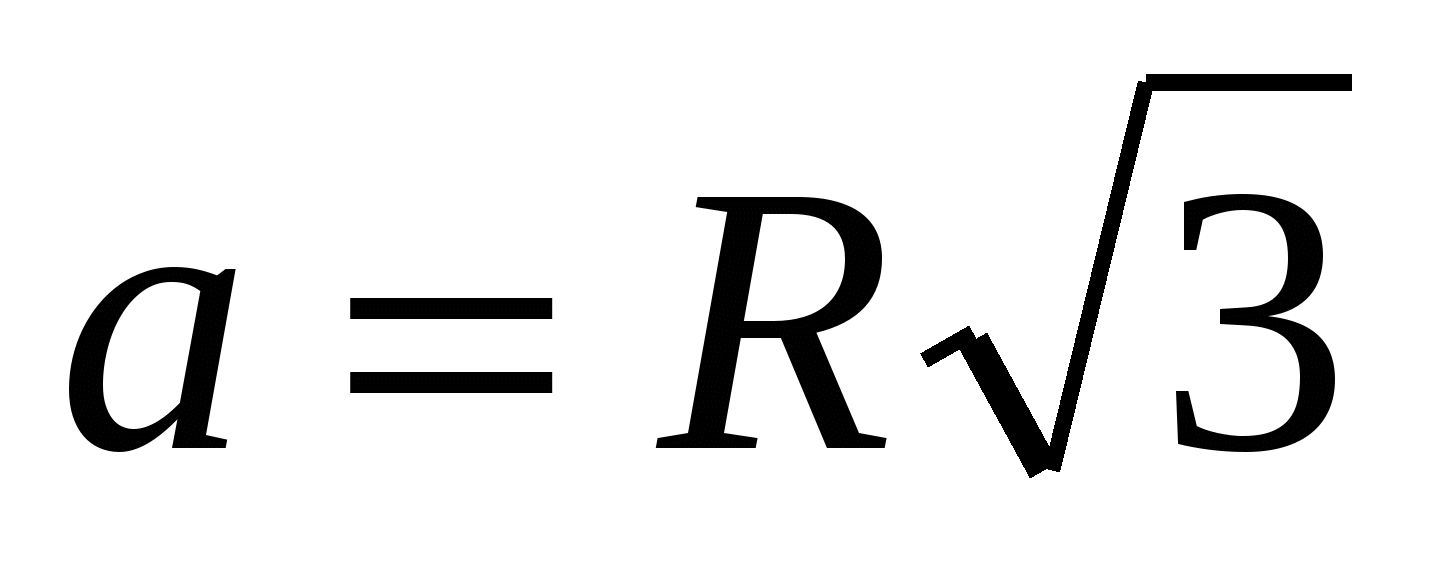

,

.

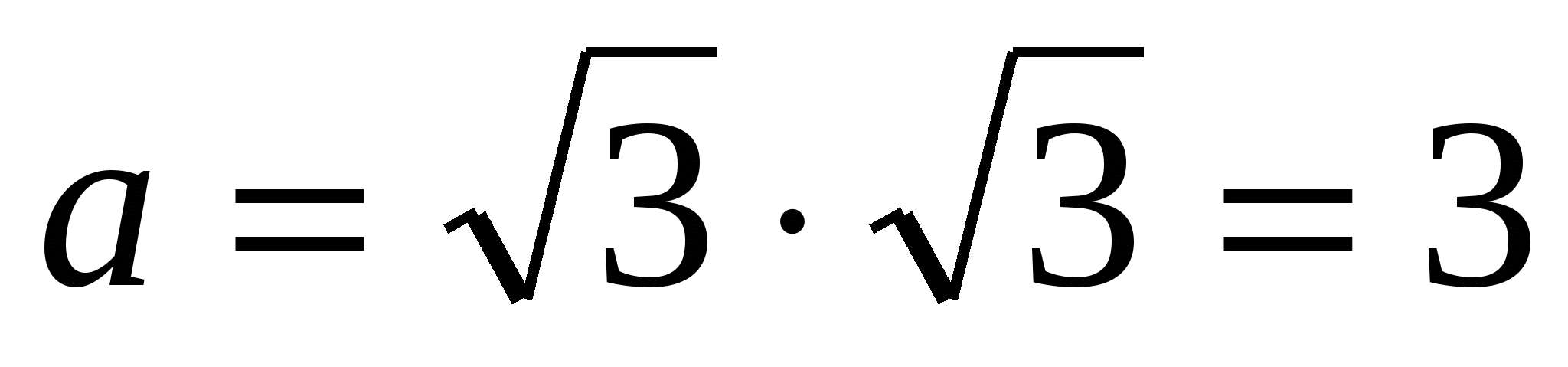2) znajdź obszar podstawy jako obszar regularnego trójkąta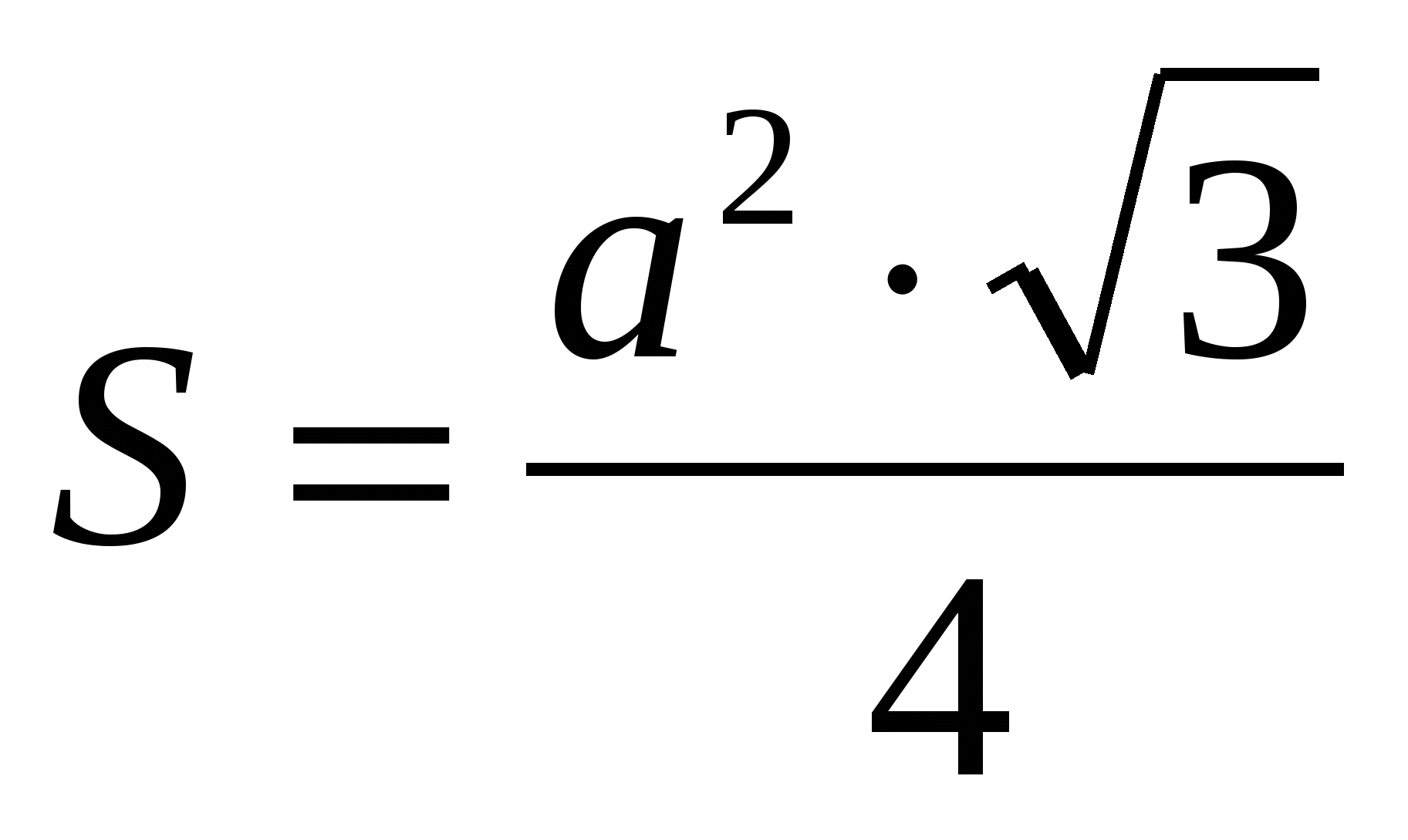

,

.

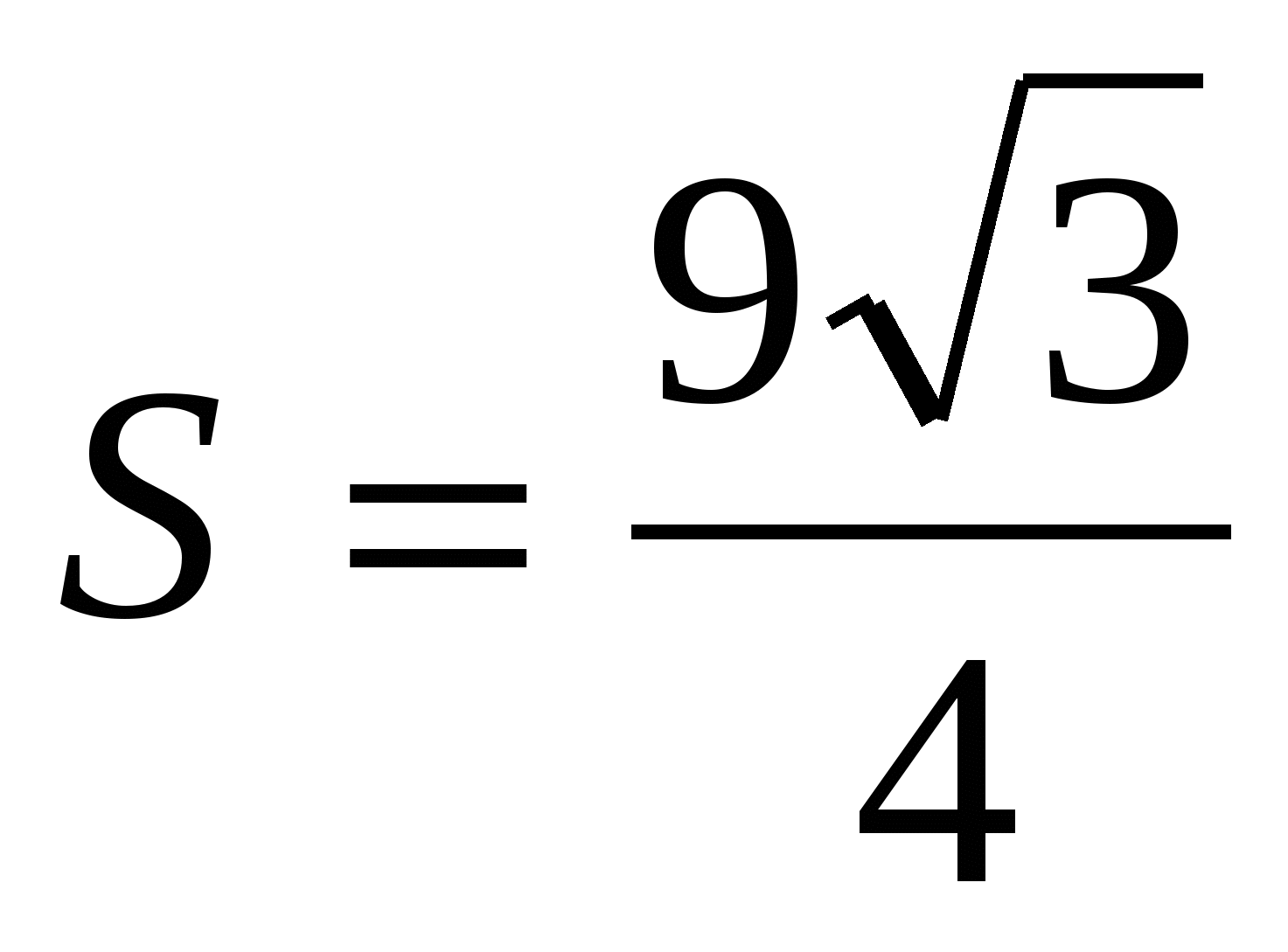3) obliczyć objętość piramidy


.

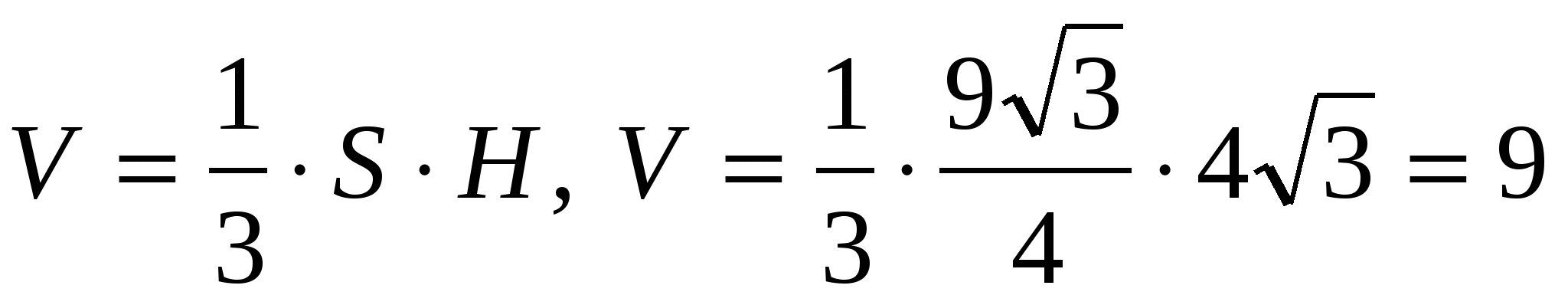Odpowiedź. 9

Zadanie nr 2 . Oblicz objętość regularnej piramidy trójkątnej, jeśli promień okręgu wpisanego w podstawę jest równy , a boczne krawędzie piramidy są równe 6.

Rozwiązanie.

1) promień okręgu wpisanego w trójkąt foremny jest 2 razy mniejszy od promienia okręgu opisanego na tym trójkącie, tj.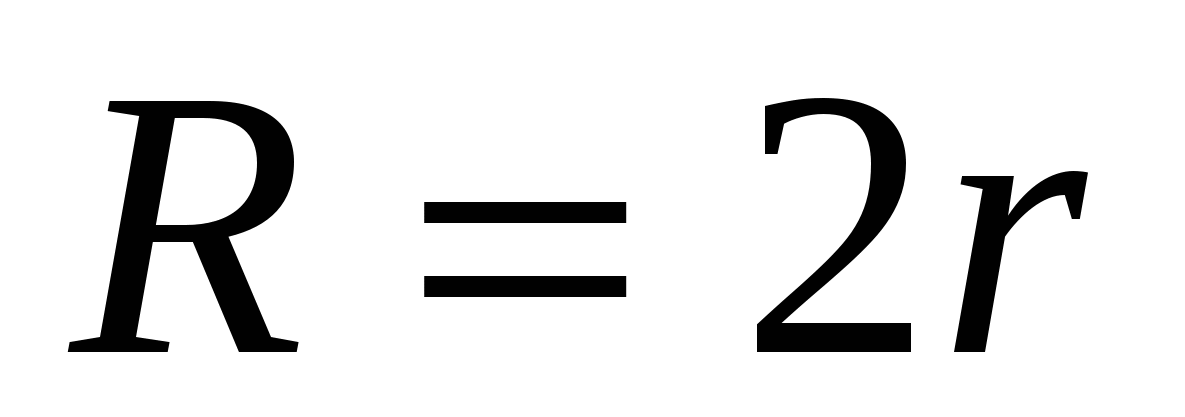

, Następnie

.



.



.

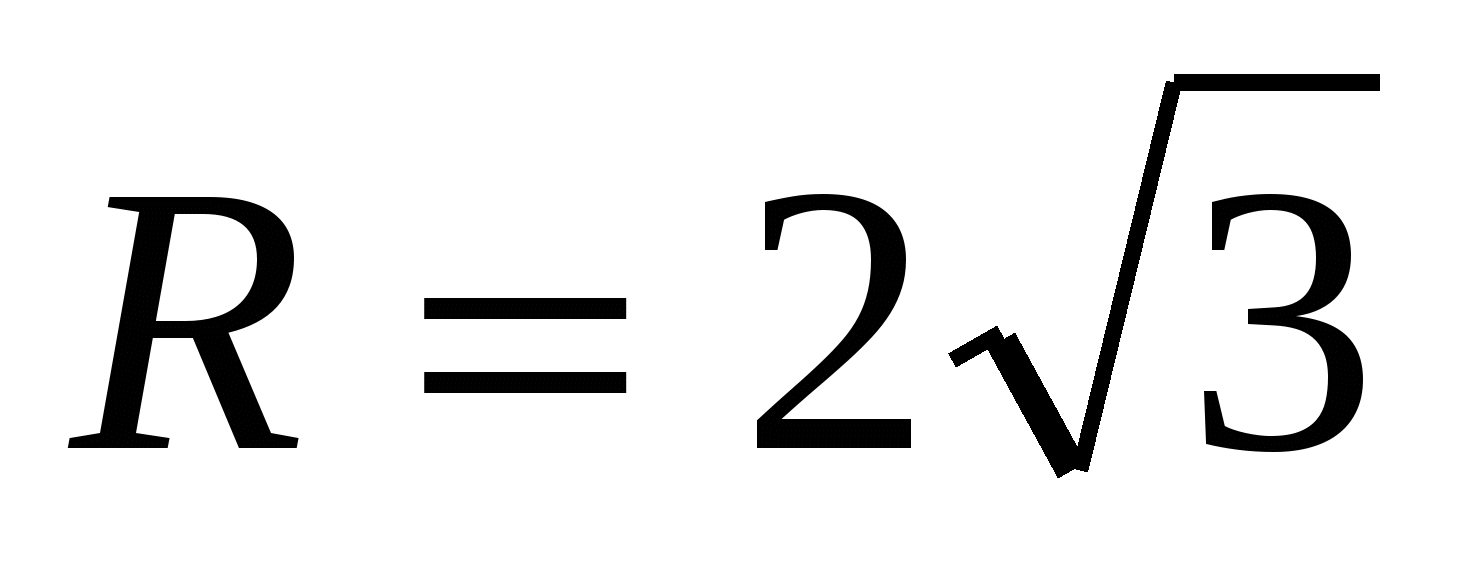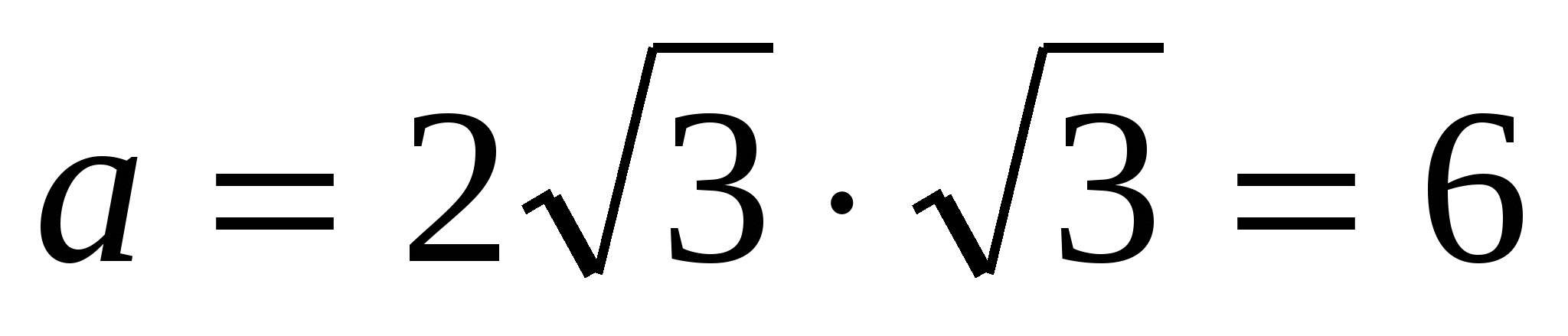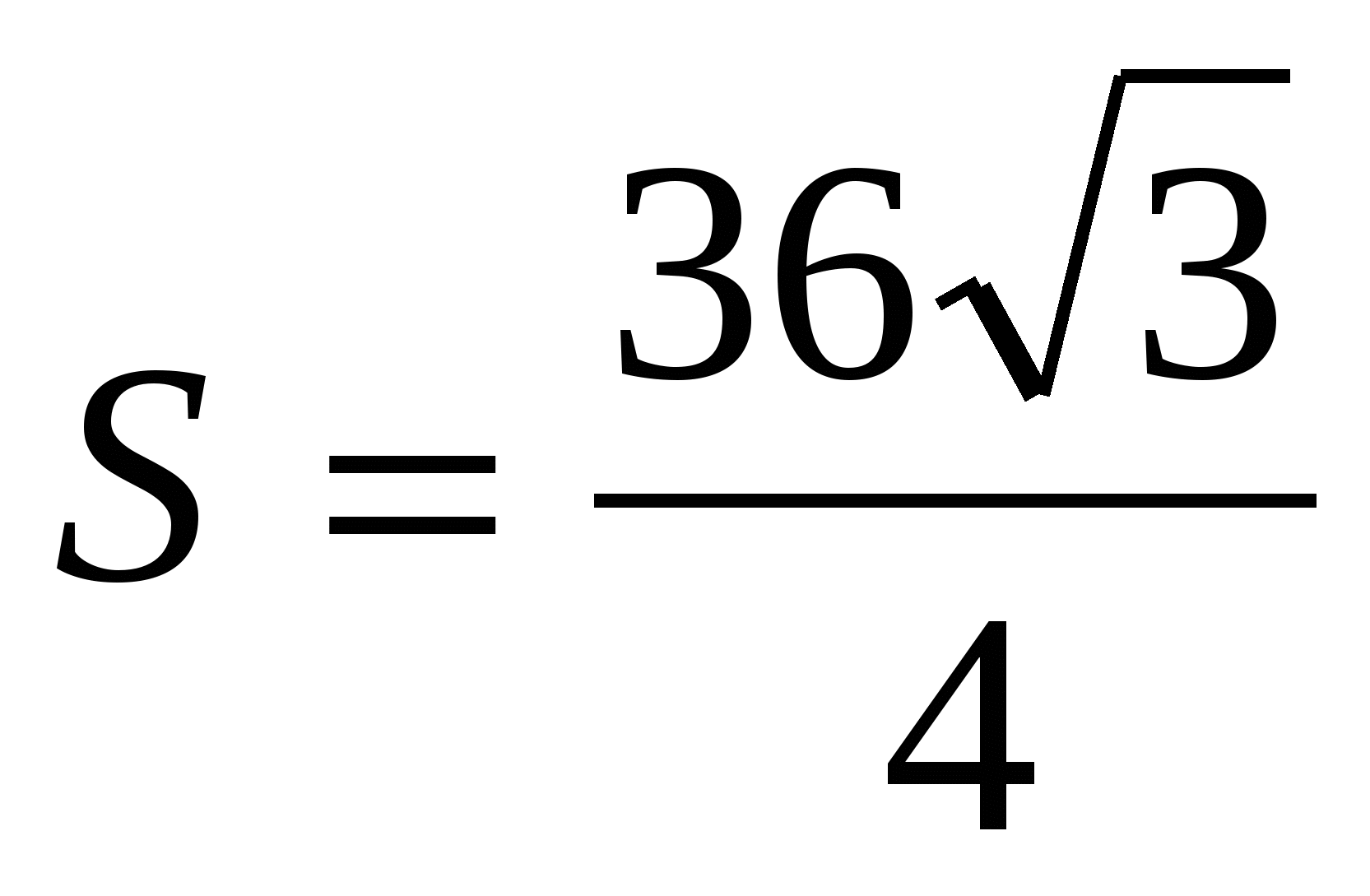4) z trójkąta prostokątnego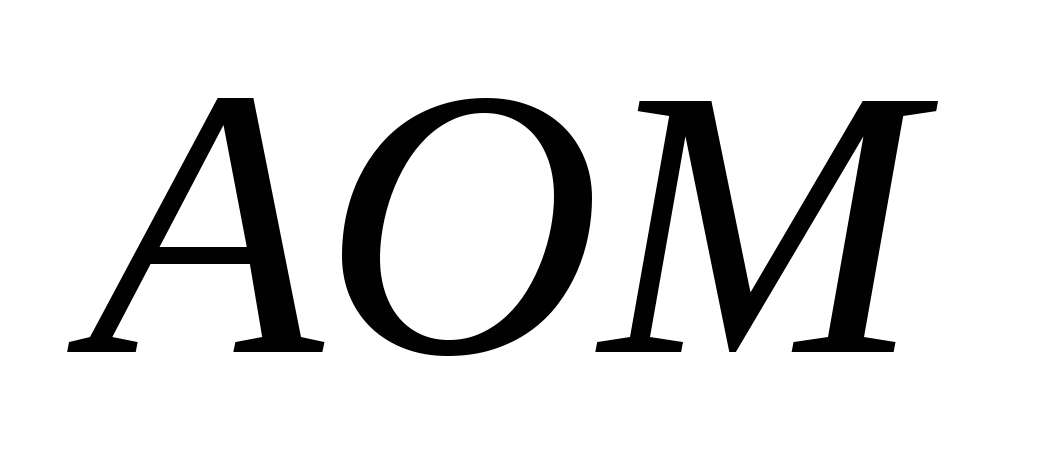

Korzystając z twierdzenia Pitagorasa, wyznaczamy wysokość piramidy:

, .

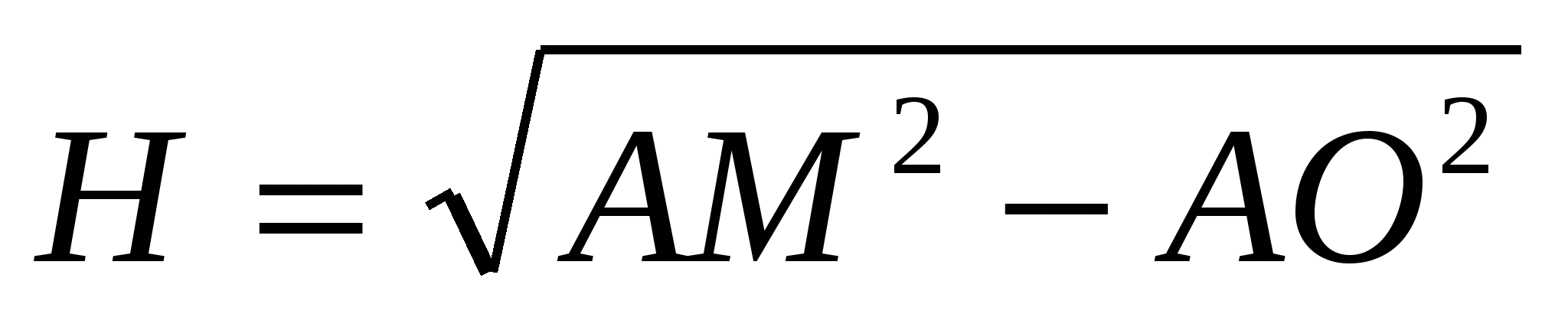5) obliczyć objętość piramidy


.

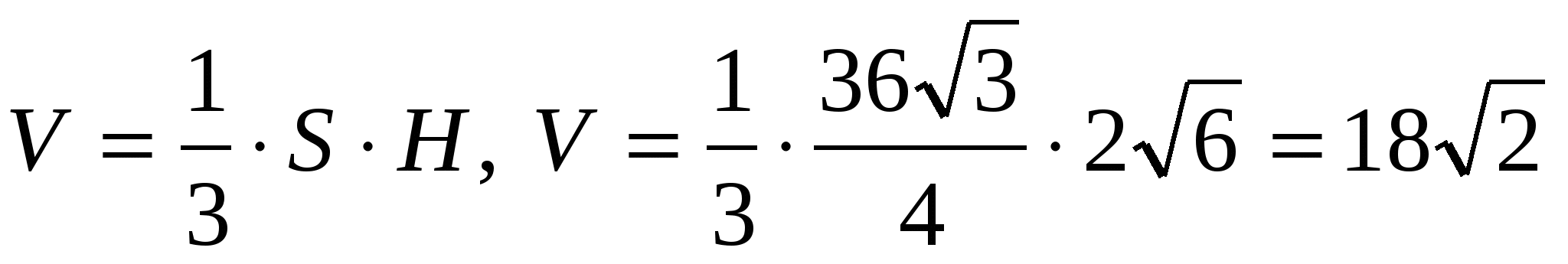Odpowiedź. 18.

Zadanie nr 3 . Oblicz pole powierzchni bocznej regularnej piramidy trójkątnej, jeśli promień okręgu opisanego w pobliżu podstawy jest równy , a wysokość piramidy jest równa 1.

R 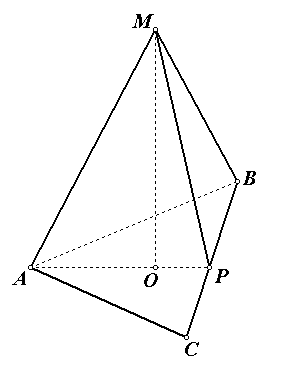decyzja.


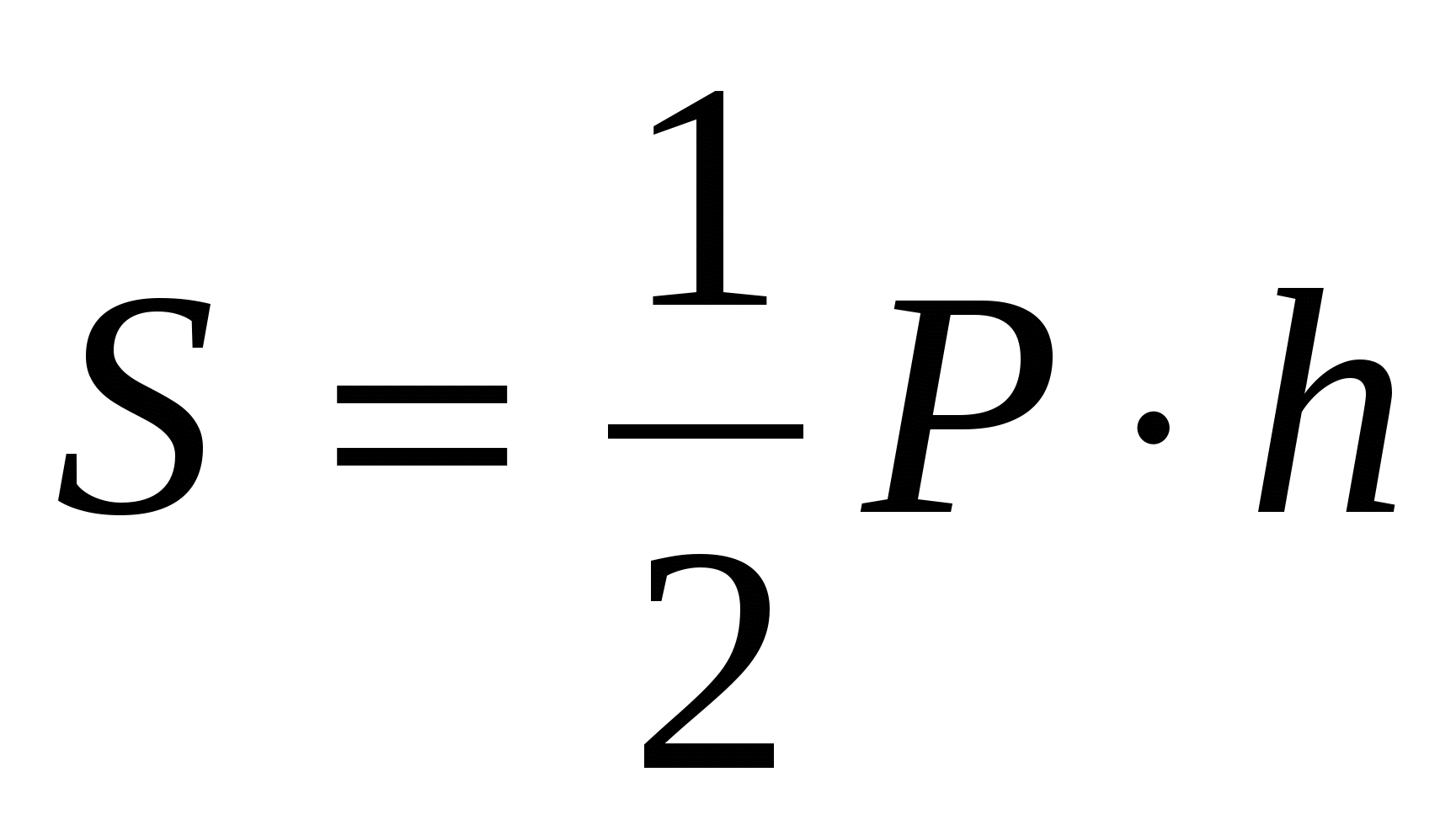
1) znajdź bok podstawy regularnej piramidy, korzystając ze wzoru , .

2) znajdź obwód podstawy P = 3· A,

P = 9.

3) promień okręgu wpisanego w trójkąt foremny jest 2 razy mniejszy od promienia okręgu opisanego na tym trójkącie, tj. , Następnie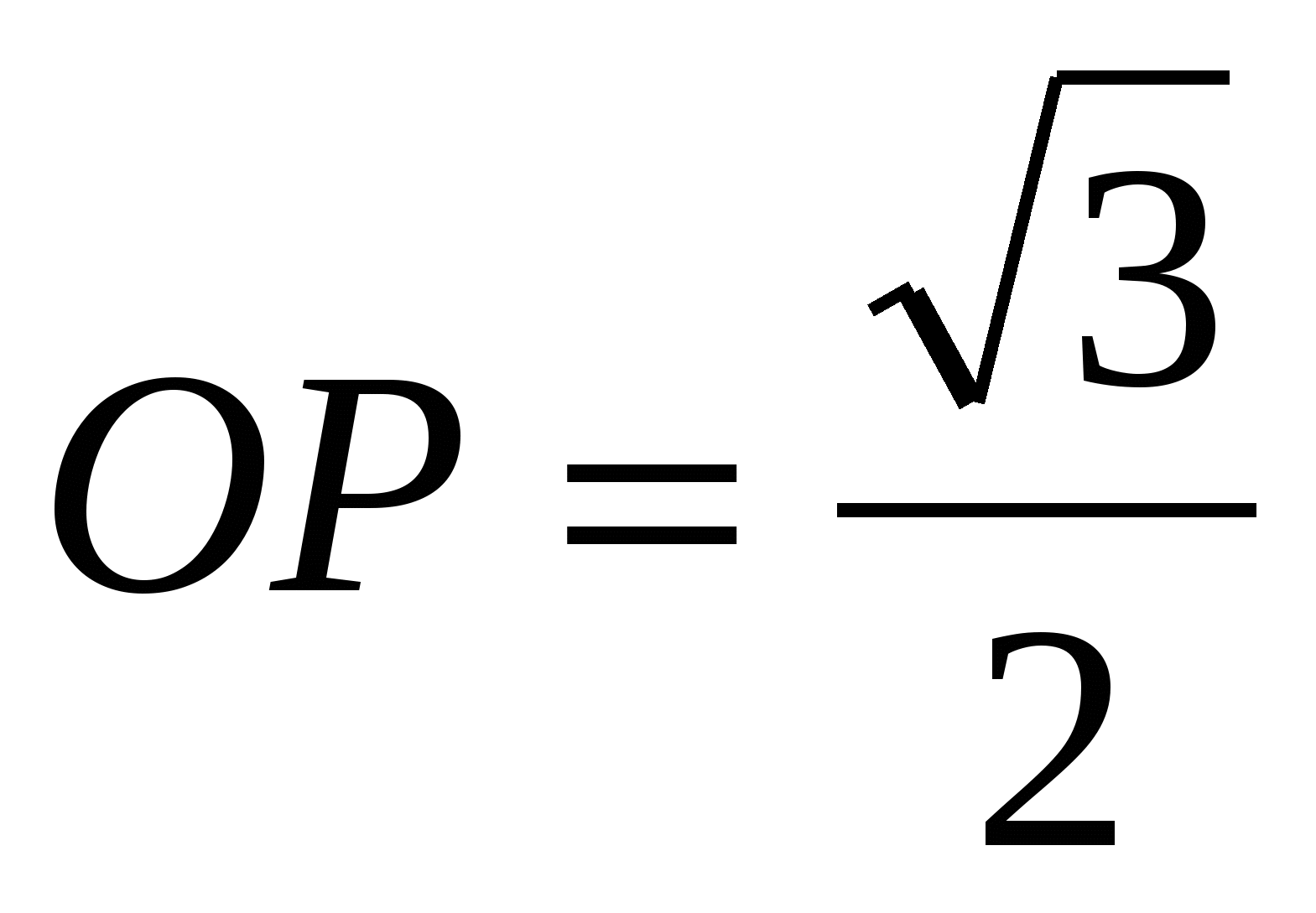

.

4) z trójkąta prostokątnegoMPA PAN :

,

PAN =

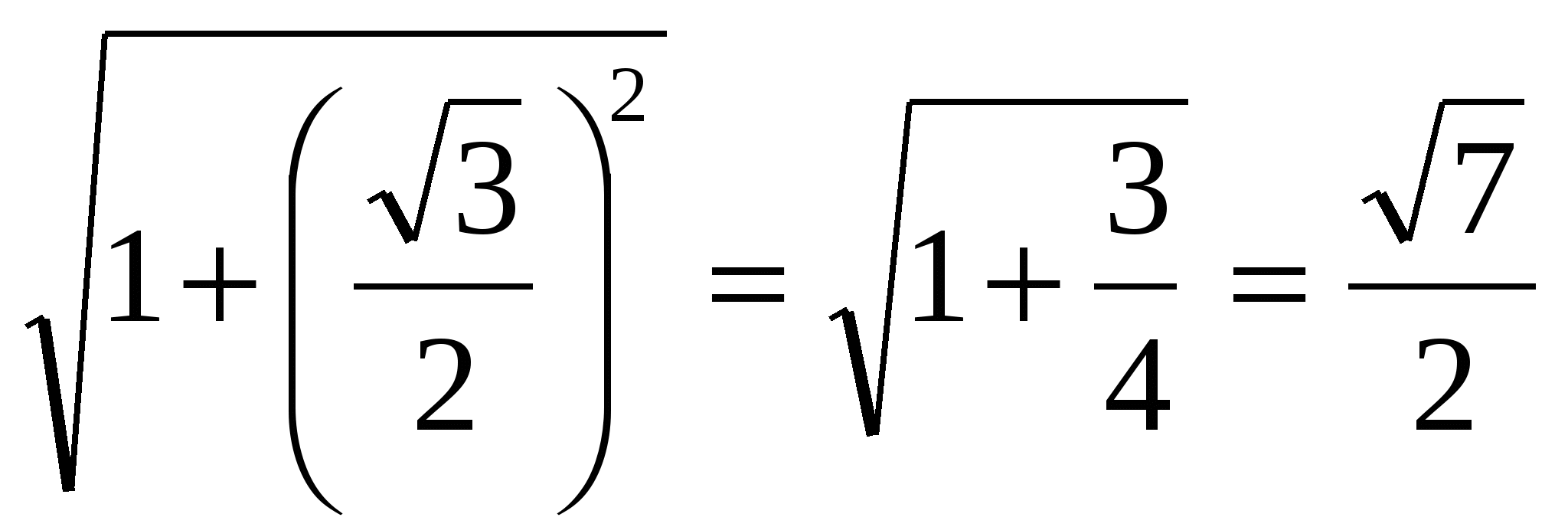
5) obliczyć pole powierzchni bocznej regularnej piramidy:

,

.

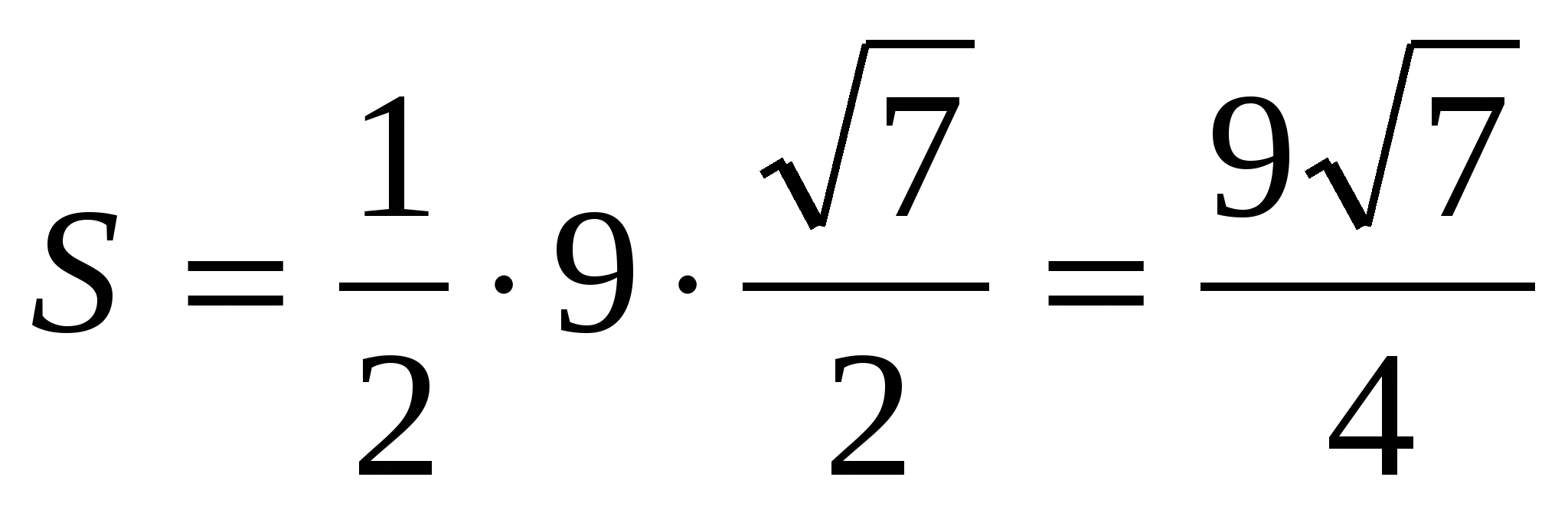Odpowiedź.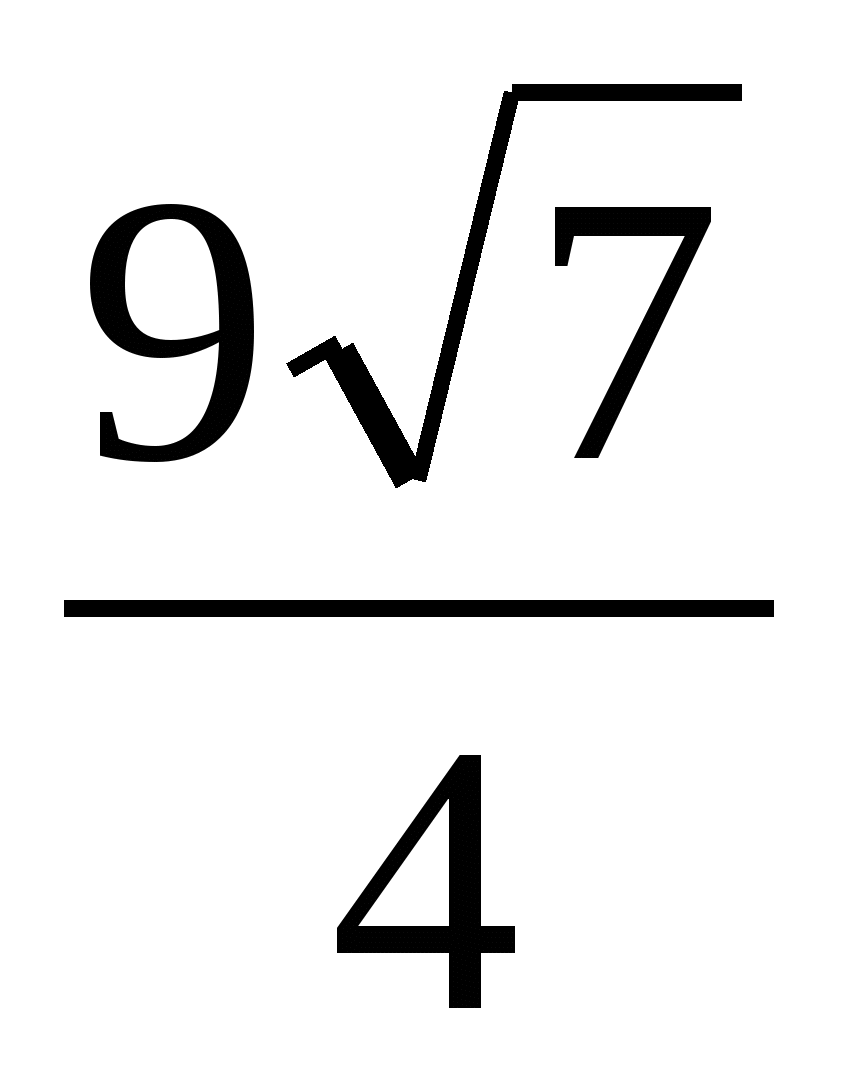

.

Zadanie nr 4 . Oblicz objętość regularnej piramidy trójkątnej, której bok podstawy wynosi 6, a apothem wynosi 6.

Rozwiązanie. ,

1) znajdź promień okręgu opisanego przy podstawie i wpisanego w podstawę: ,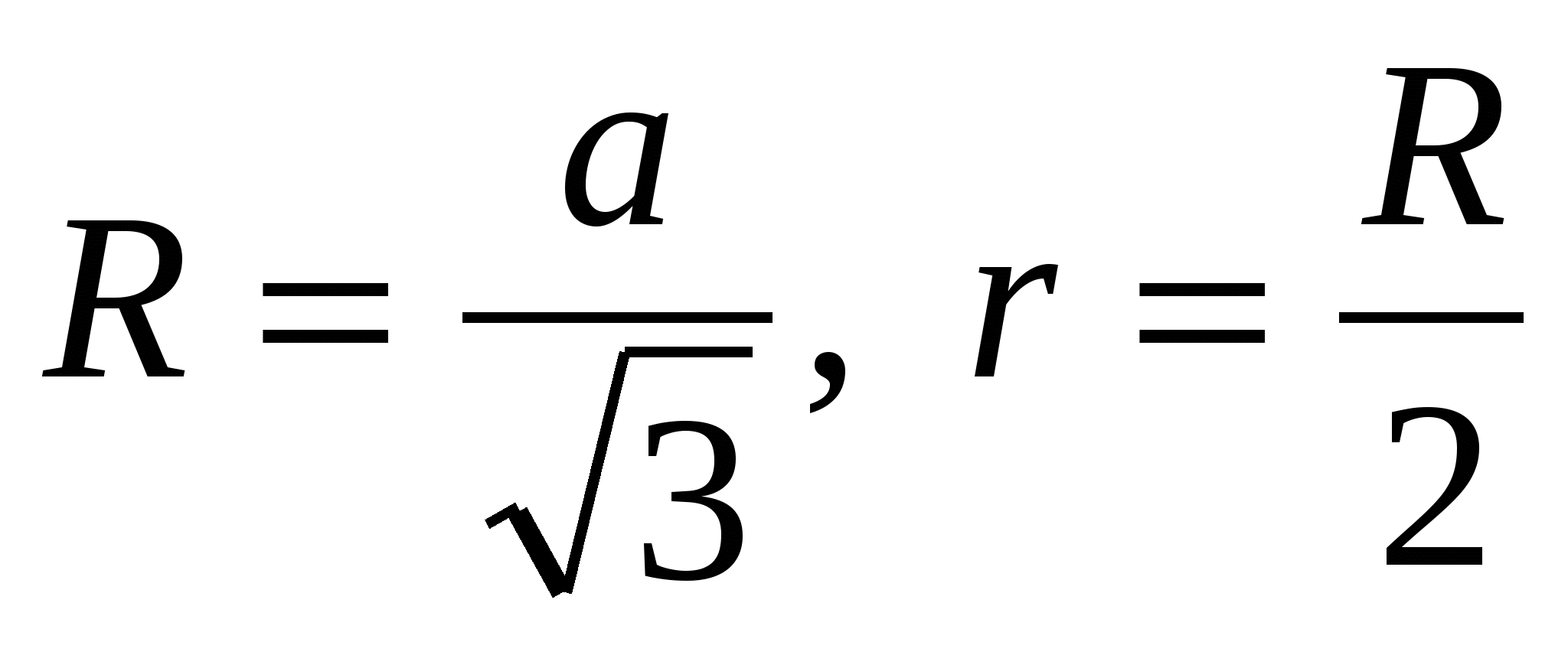

to jest

.

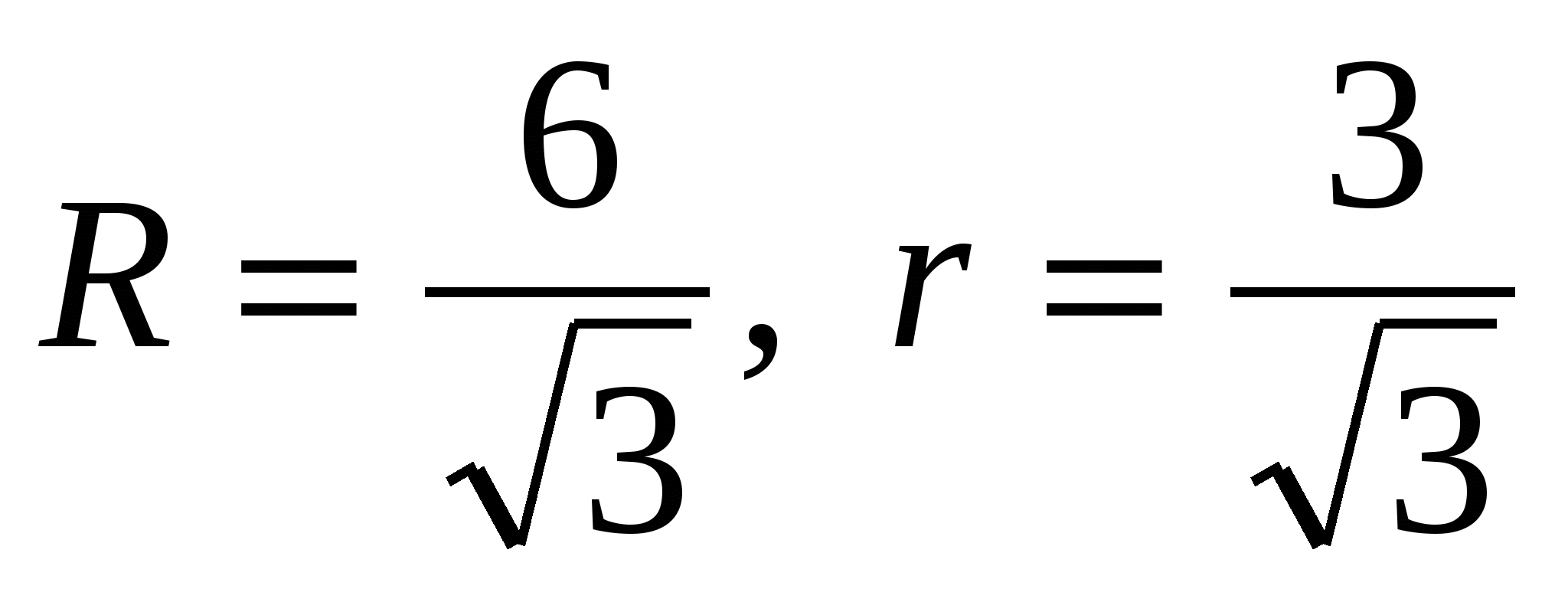2) znajdź pole podstawy jako pole regularnego trójkąta,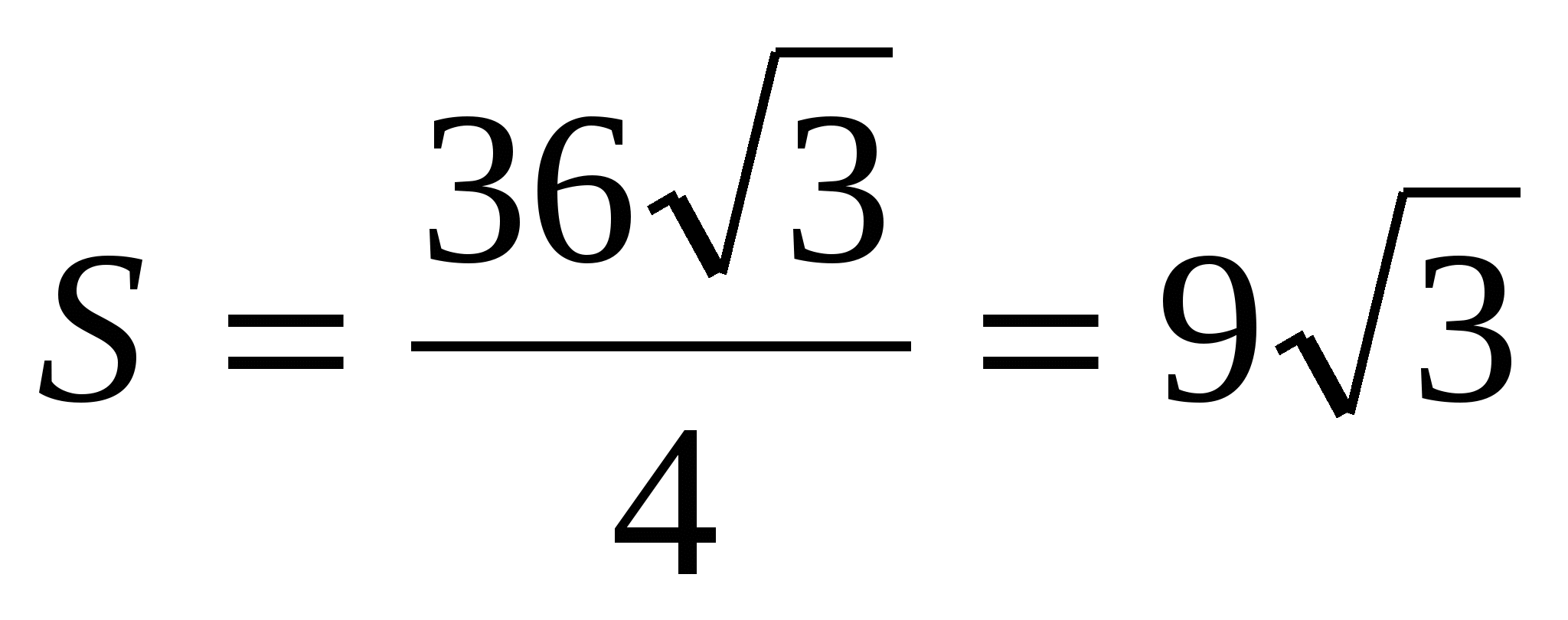

.

MPA Korzystając z twierdzenia Pitagorasa, znajdujemy wysokość:

, MO =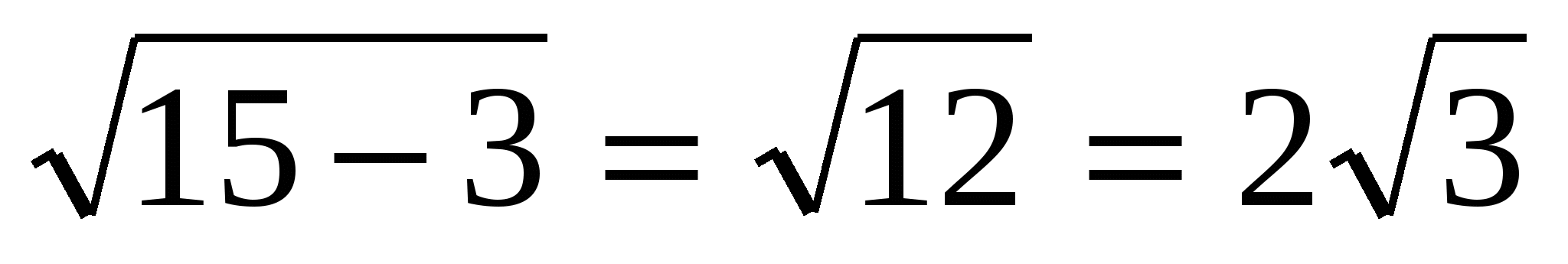

.



.

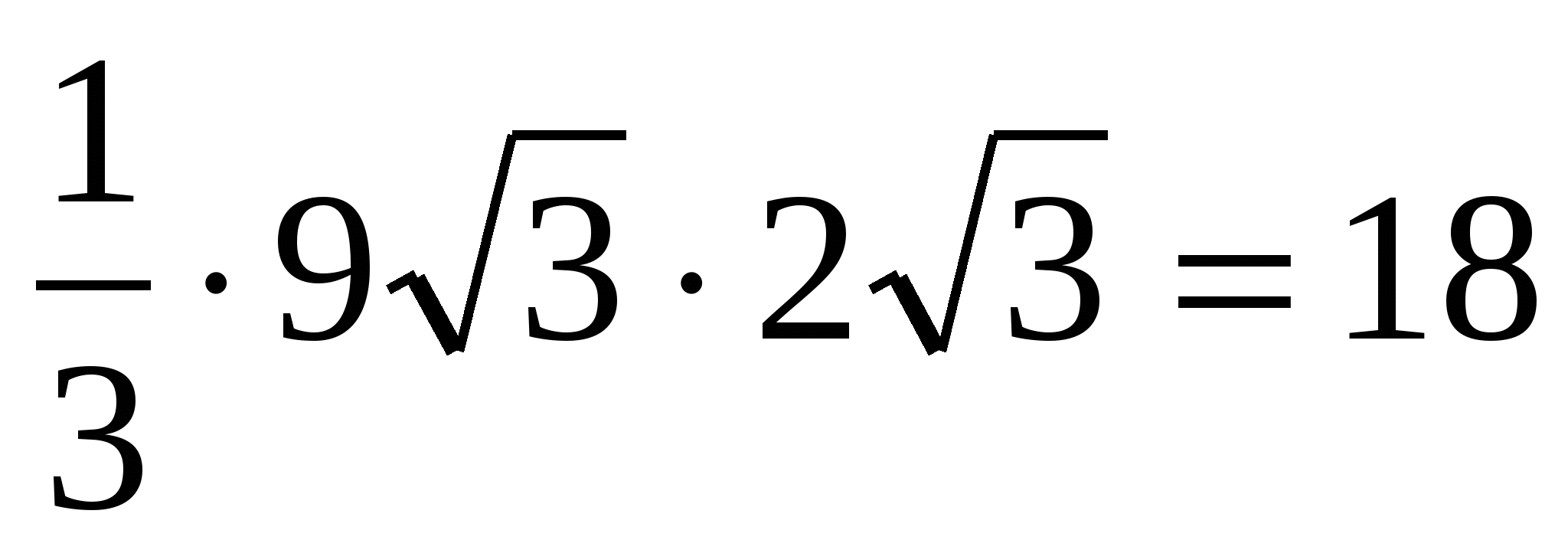Odpowiedź. 18.

Problem nr 5 . Oblicz objętość regularnej piramidy trójkątnej, jeśli promień okręgu wpisanego u podstawy wynosi 2, a wysokość regularnej piramidy wynosi .

Rozwiązanie.

1) promień okręgu wpisanego w trójkąt foremny jest 2 razy mniejszy od promienia okręgu opisanego na tym trójkącie, tj. , Następnie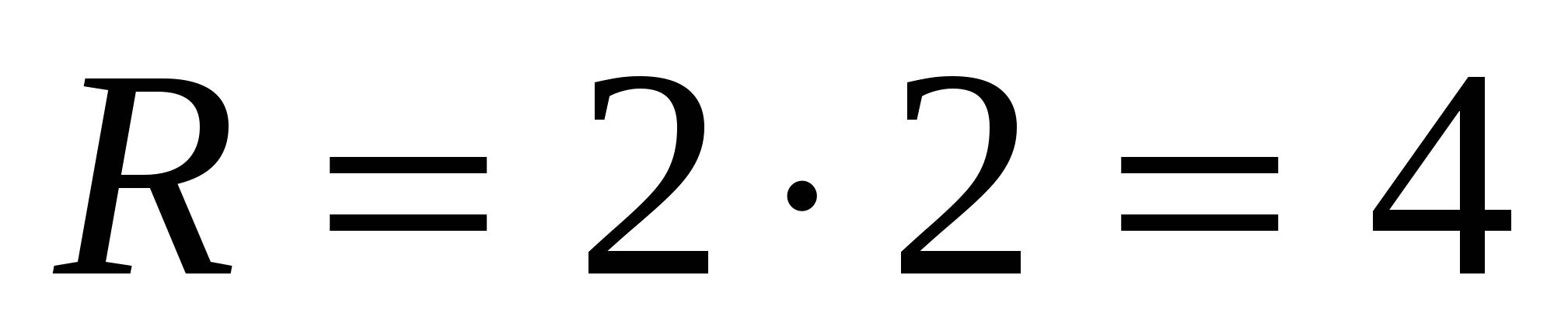

.

2) znajdź bok podstawy regularnej piramidy, korzystając ze wzoru,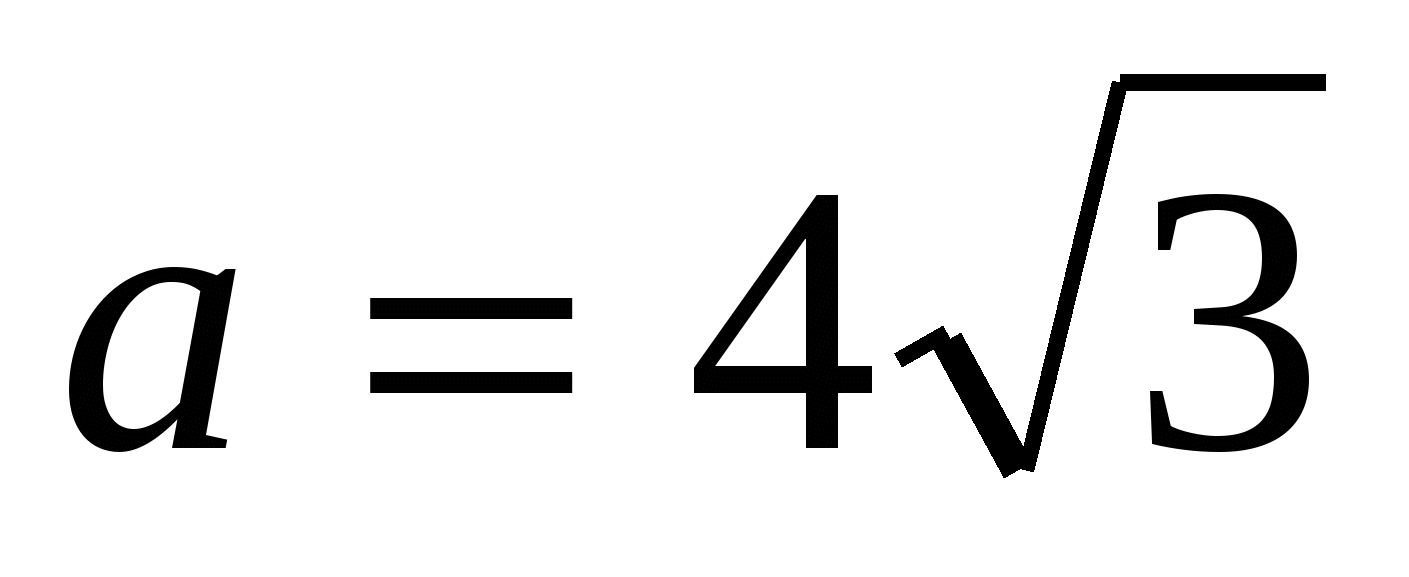

.

3) znajdź pole podstawy jako pole regularnego trójkąta,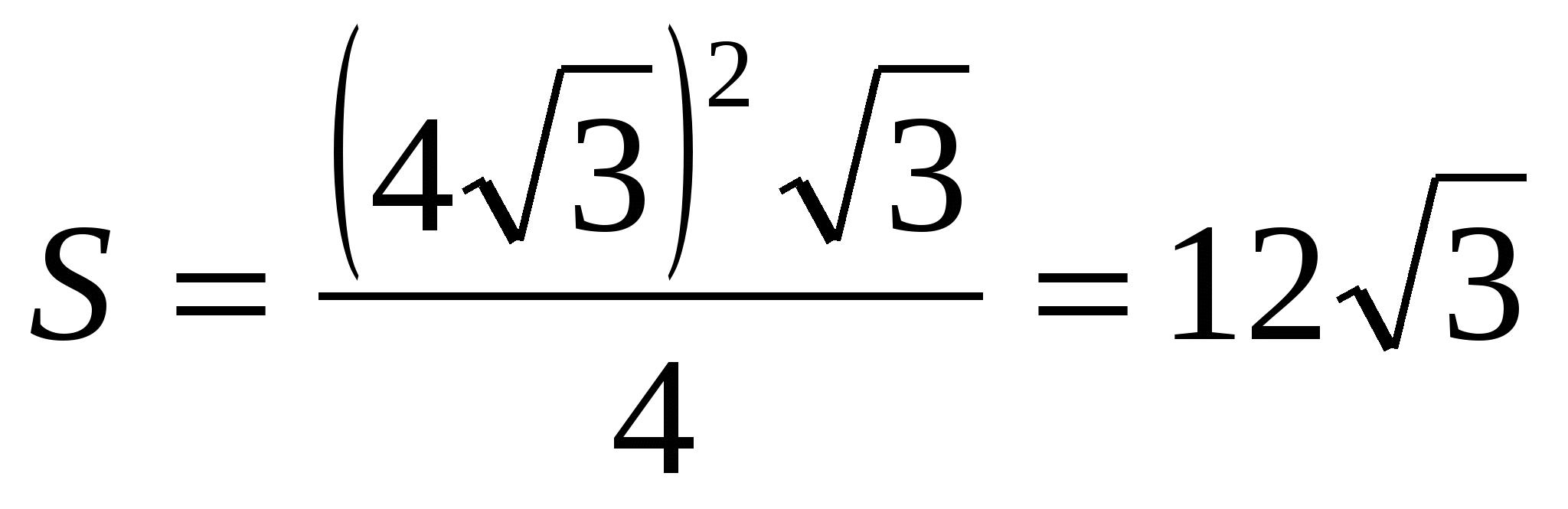

.

4) obliczyć objętość regularnej piramidy: =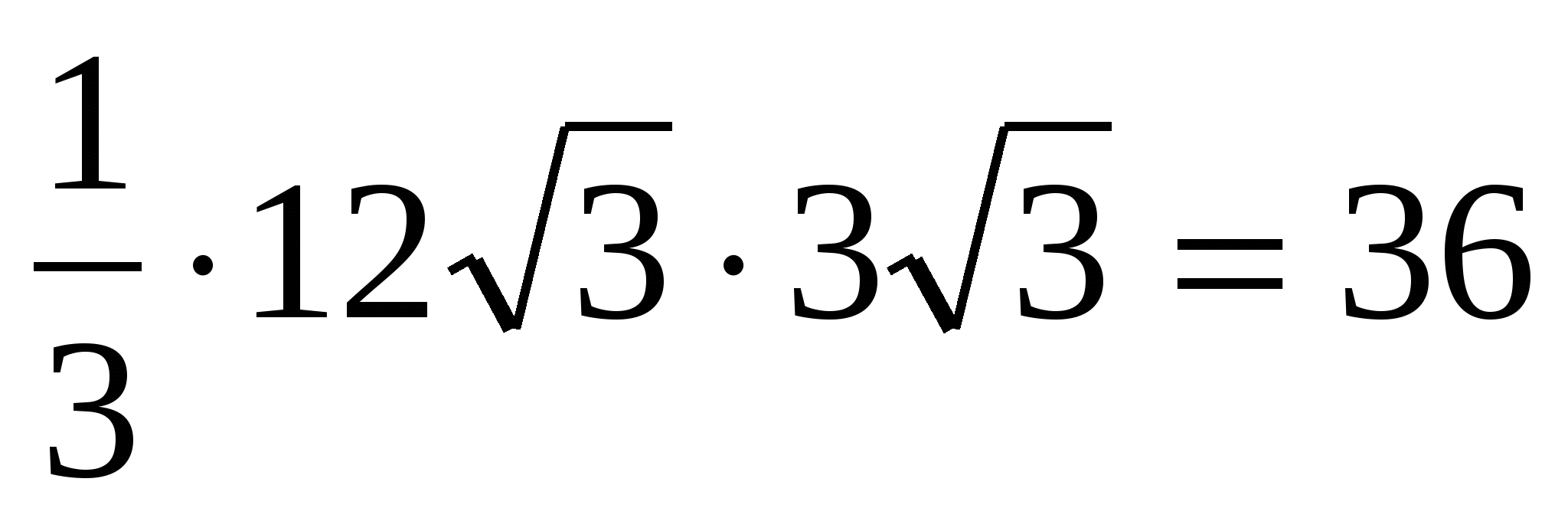

.

Odpowiedź. 36.

Problem nr 6 . Oblicz pole powierzchni bocznej regularnej czworokątnej piramidy, jeśli jej krawędzie wynoszą 5, a promień okręgu opisanego wokół podstawy wynosi 3.

R decyzja .

1) znajdź bok podstawy, korzystając ze wzoru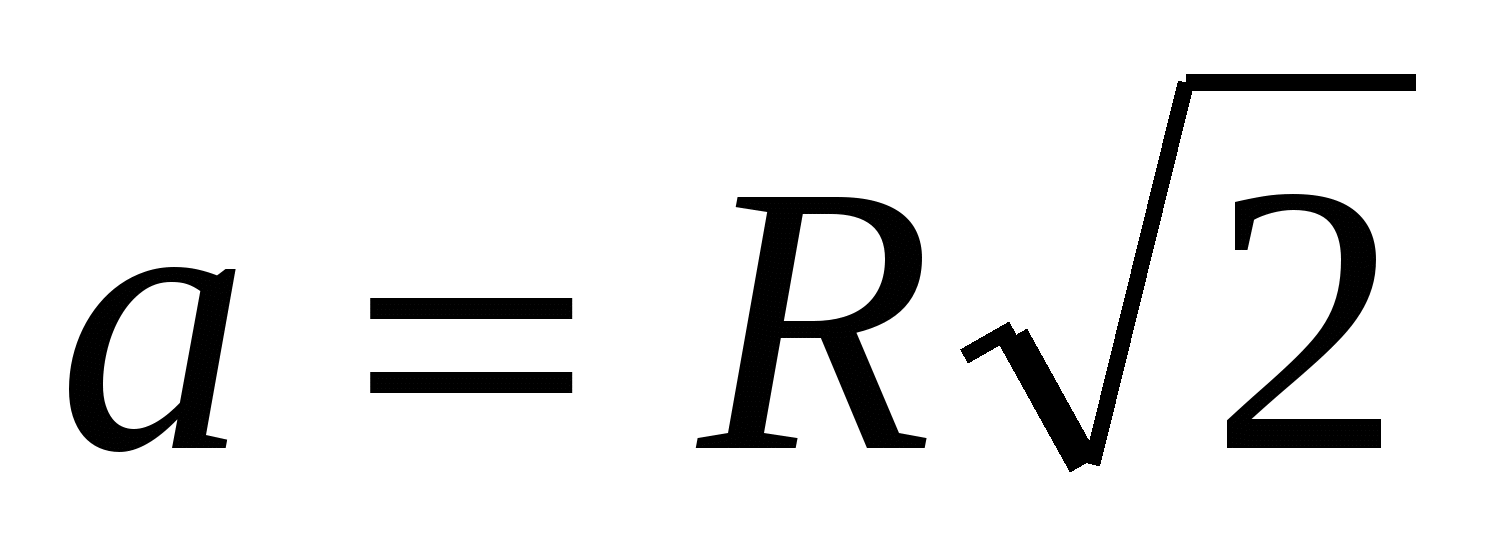

, tj.

.

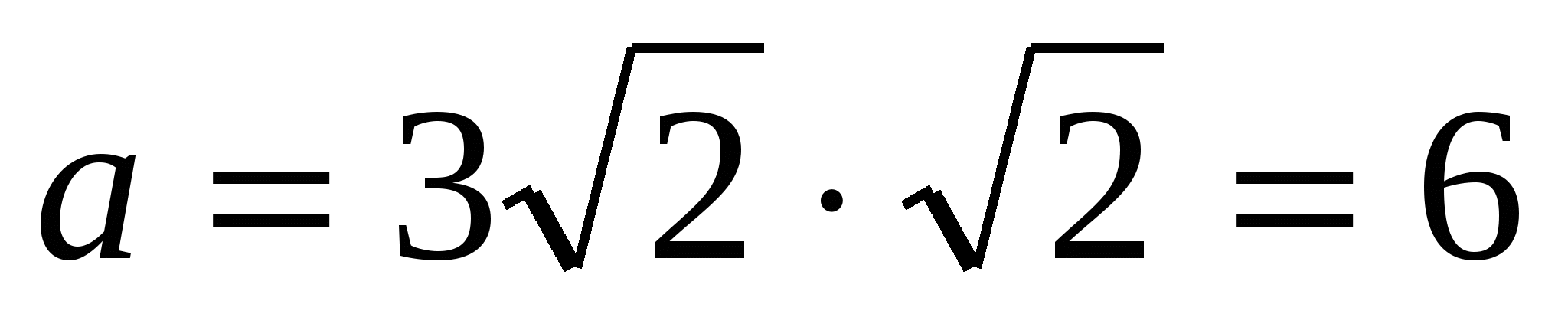2) znajdź obwód podstawy: R = 4A,

P = 24.

3) z trójkąta prostokątnegoM DR Korzystając z twierdzenia Pitagorasa, znajdujemy apotemPAN :

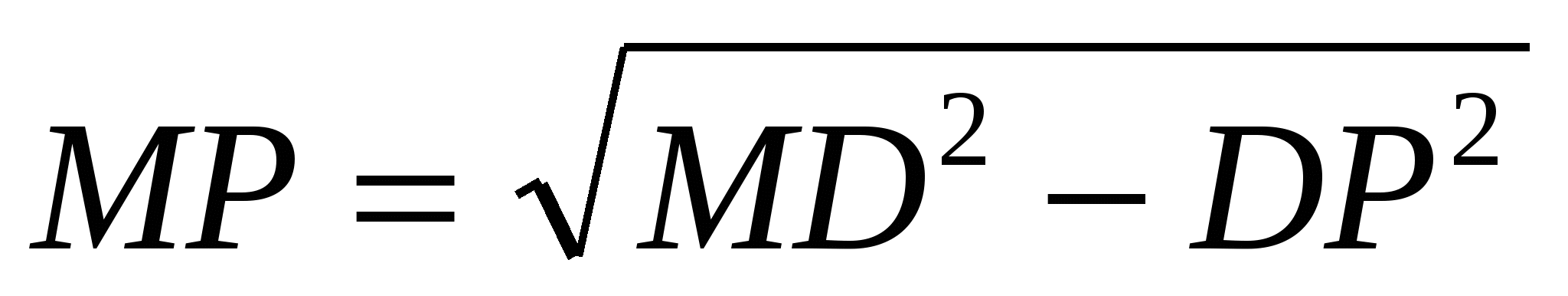, D.P. =

Następnie: PAN =

.

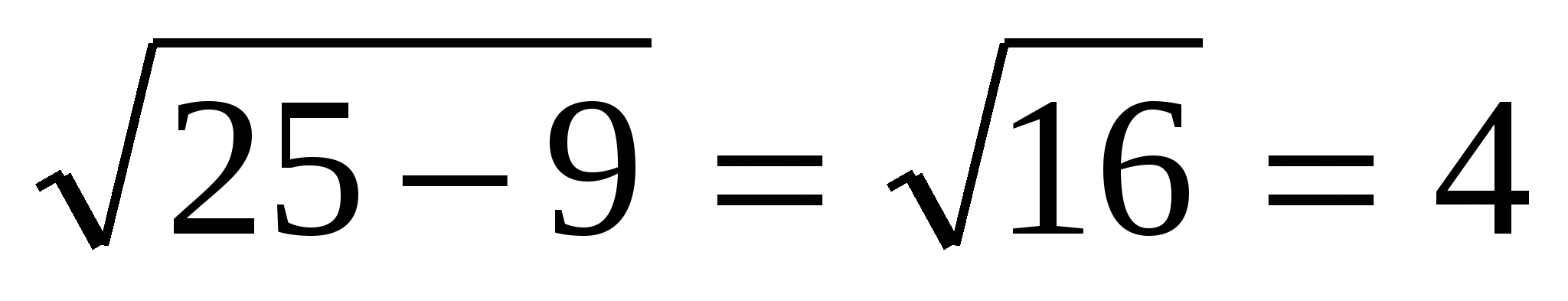4) obliczyć pole powierzchni bocznej piramidy: =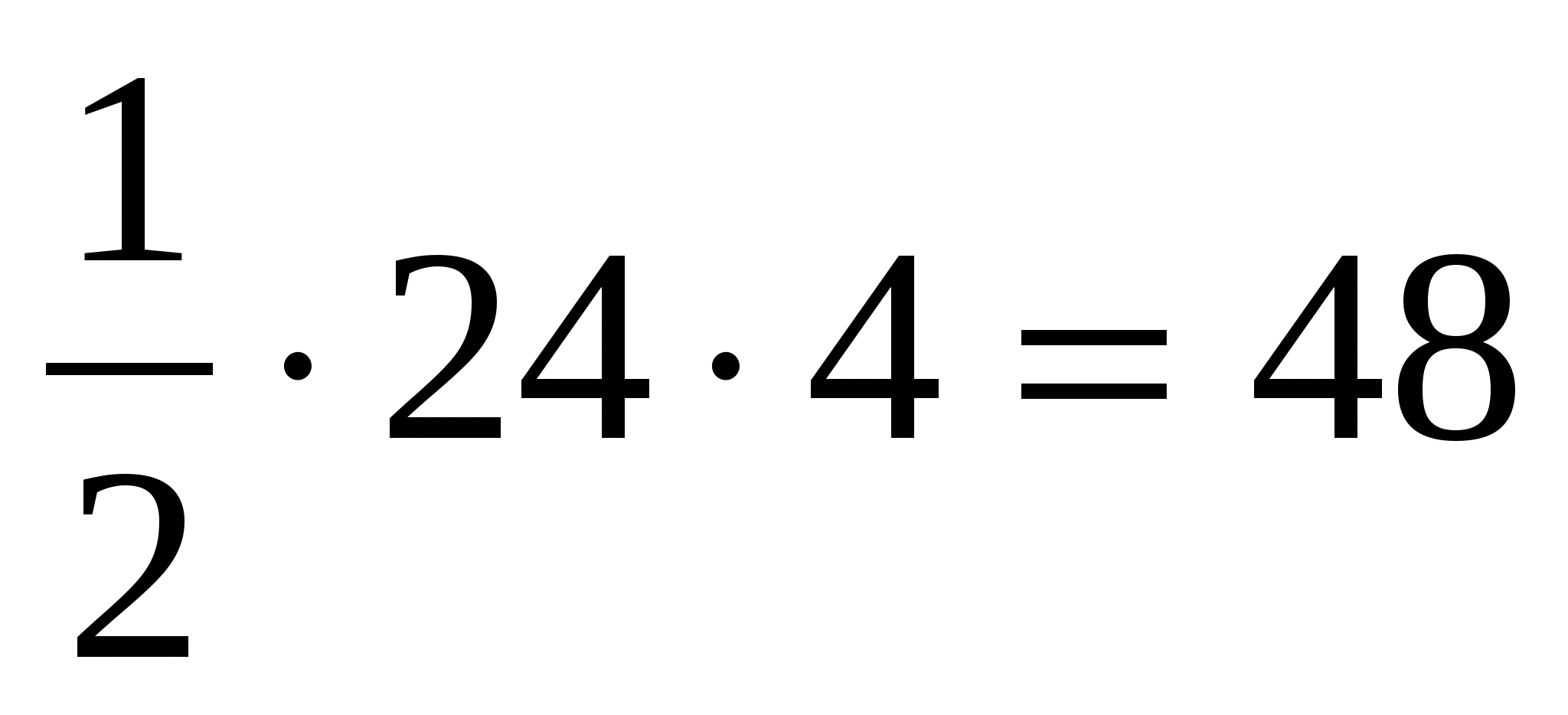

.

Odpowiedź. 48.

Problem nr 7 . Po prawej czworokątna piramida Pole powierzchni bocznej wynosi 16, a pole podstawy wynosi 4. Znajdź wysokość piramidy.


Rozwiązanie.

1) znajdź bok podstawy: ponieważ podstawą piramidy jest kwadrat o polu równym 4, to bok kwadratu wynosi 2, a jego obwód wynosi 8.

2) według warunku = 16 tj.


.

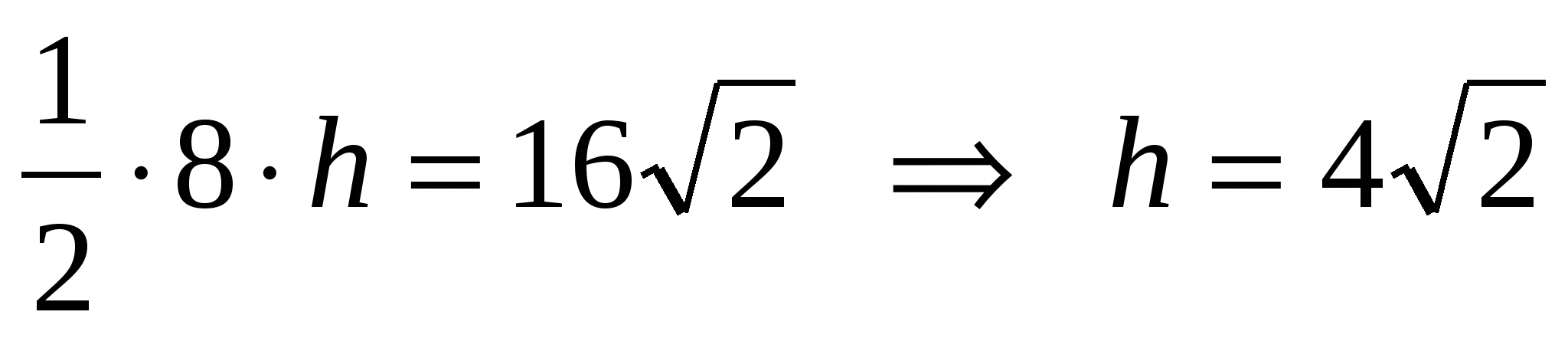3) z trójkąta prostokątnegoMPA Korzystając z twierdzenia Pitagorasa znajdujemy wysokość: , biorąc pod uwagę, że OP = 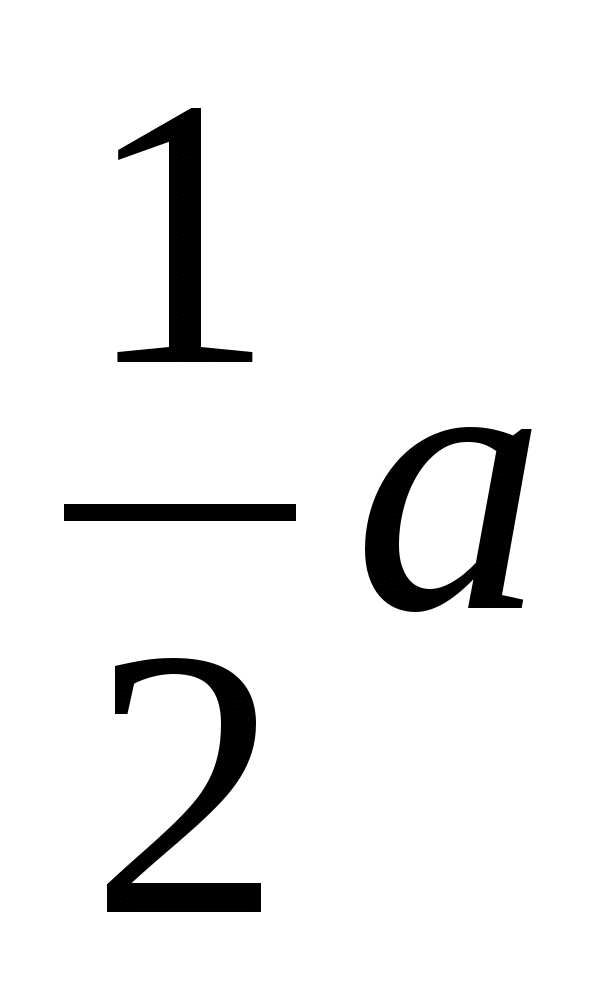= 1, otrzymujemy: MO =

.

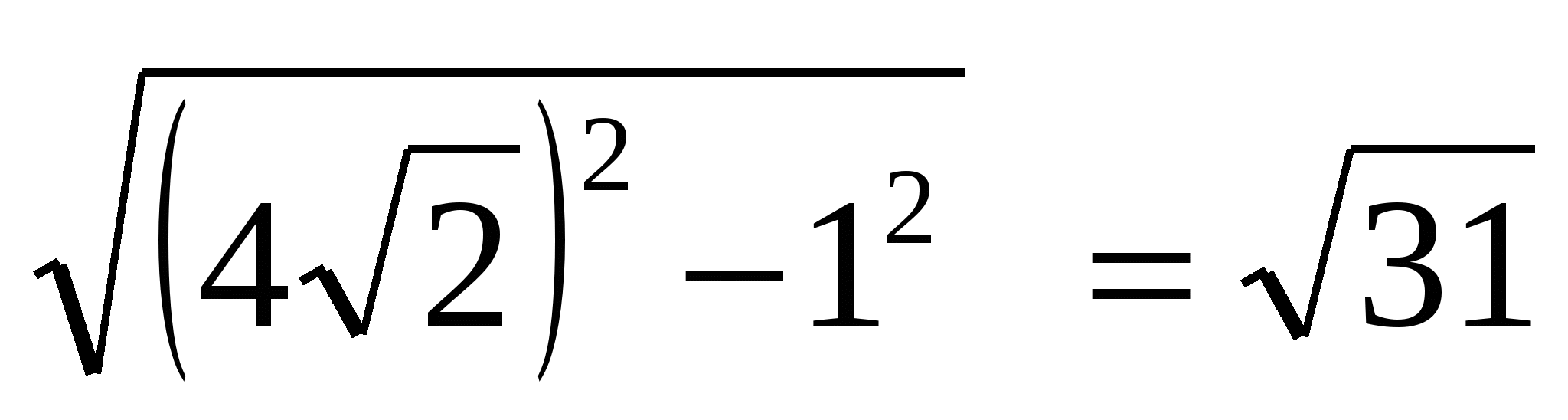Odpowiedź.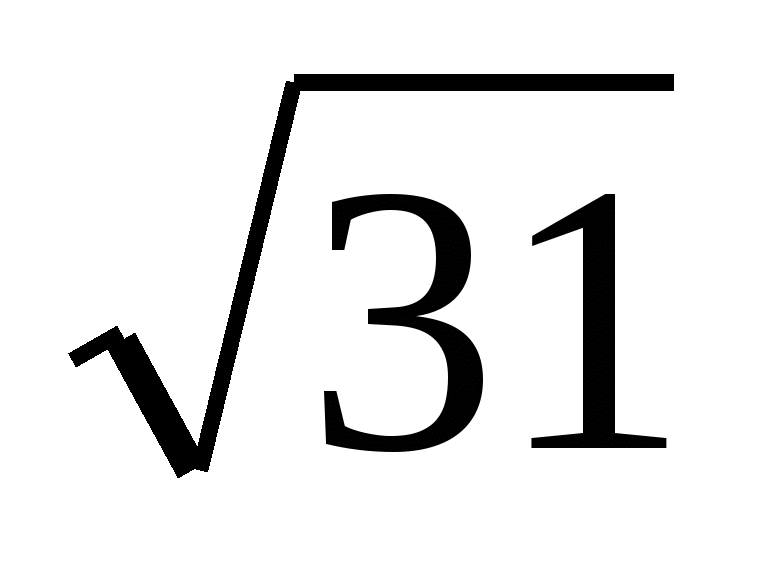

.



Problem nr 8. Oblicz objętość regularnej piramidy sześciokątnej, jeśli bok podstawy wynosi 4, a boczne krawędzie piramidy wynoszą 5.

Rozwiązanie.

1) bok podstawy sześciokąta foremnego jest równy promieniowi okręgu wokół niego opisanego, tj.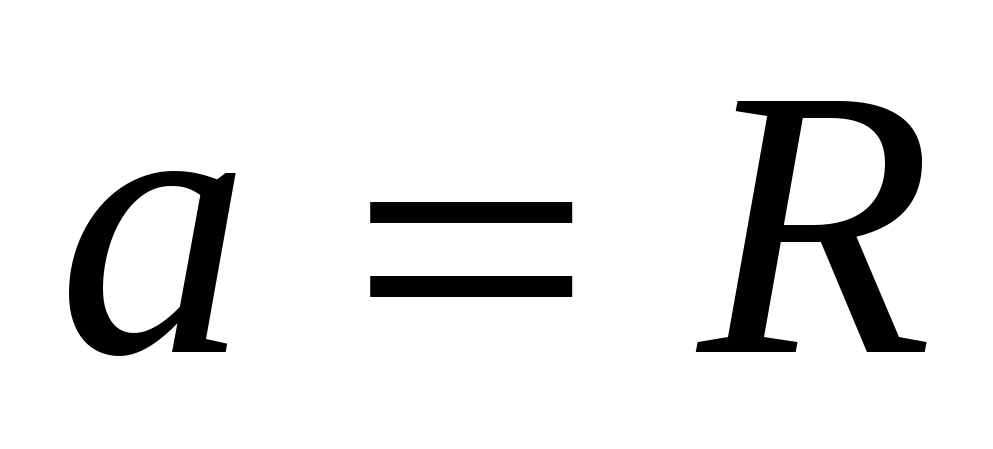

,

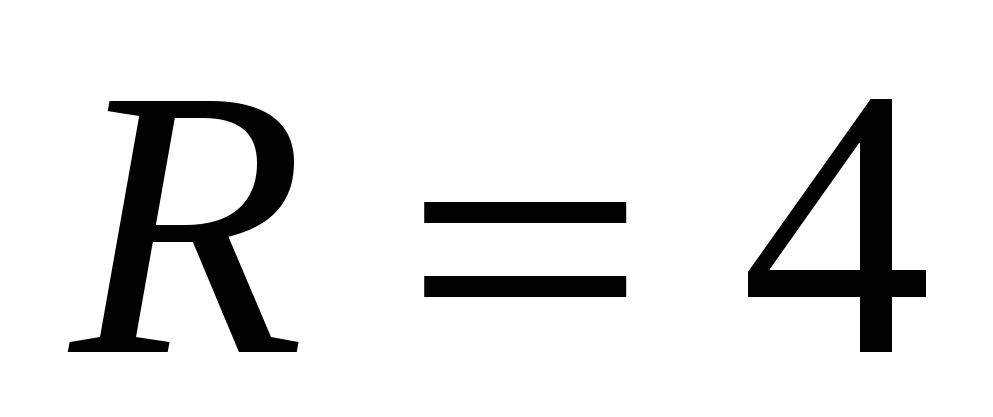
2) znajdź obszar regularnego sześciokąta za pomocą wzoru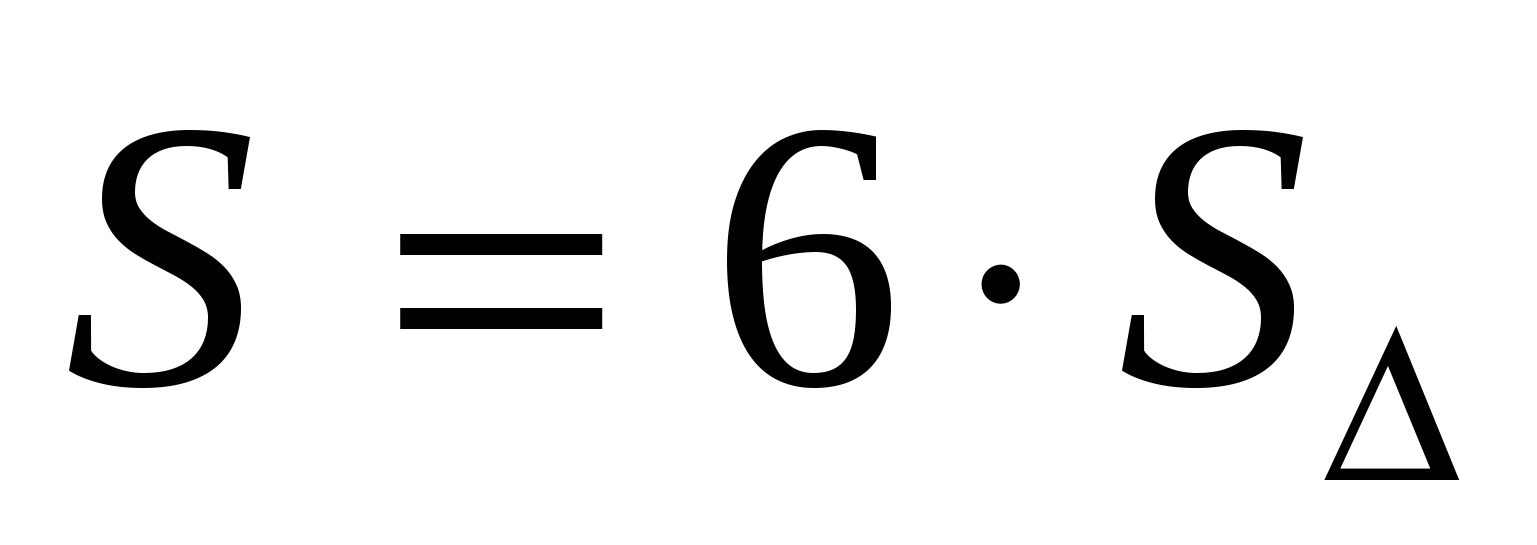

Lub

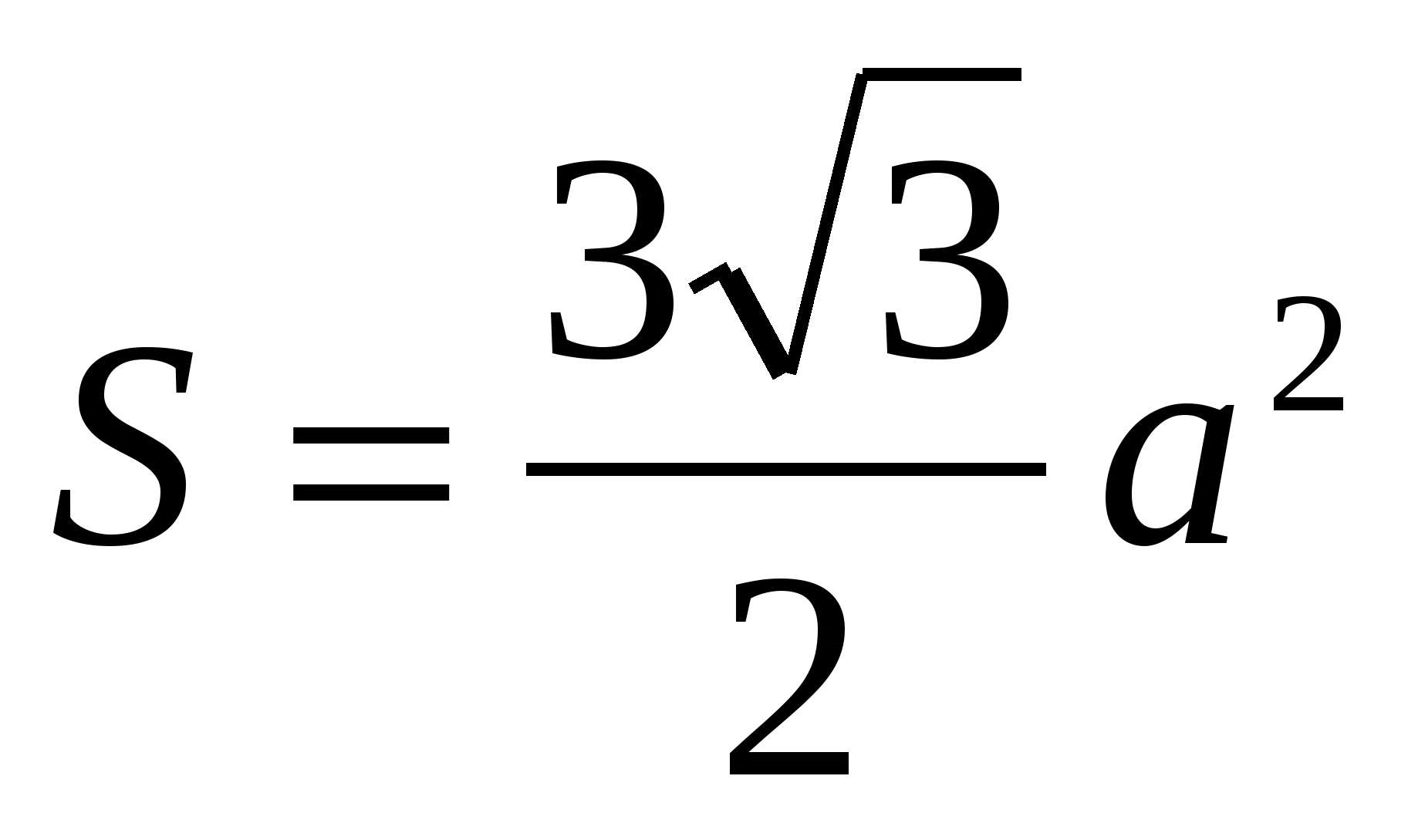= 24.

3) z trójkąta prostokątnegoMOU znajdźmy wysokość MO : .

4) obliczyć objętość piramidy: =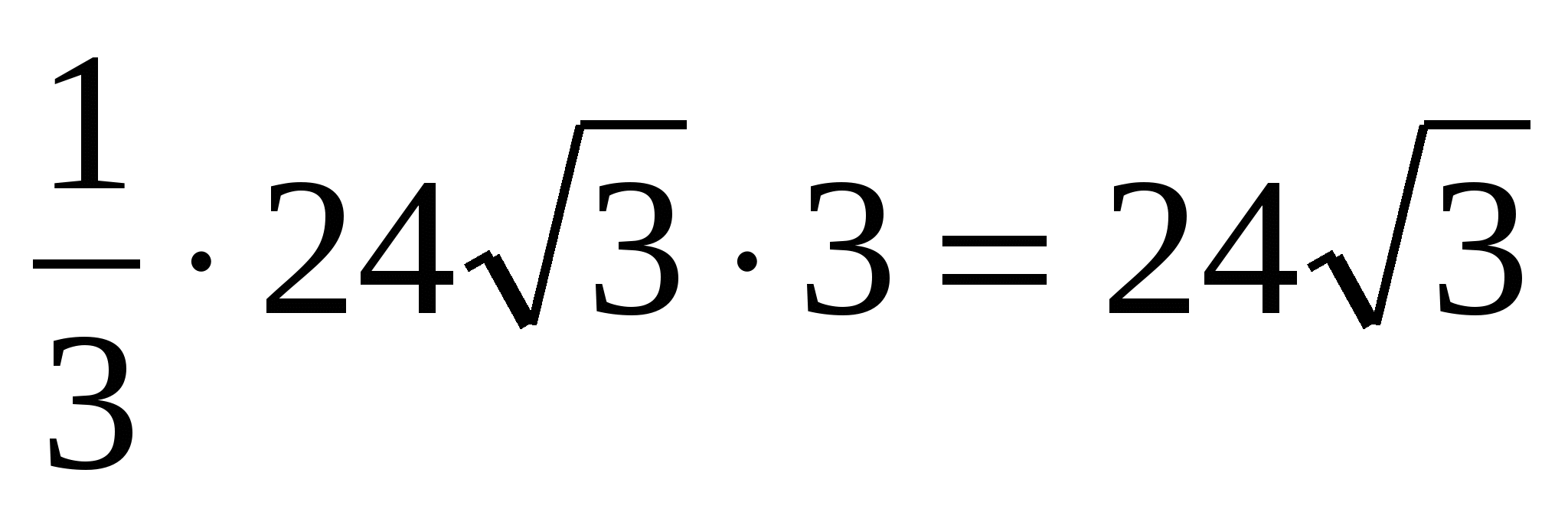

.

Odpowiedź. 24.

Problem nr 9 . W regularnej piramidzie sześciokątnej bok podstawy wynosi 2, a krawędź boczna wynosi 2. Znajdź objętość piramidy.


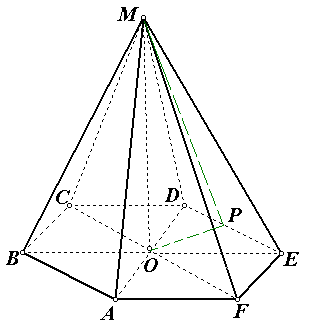
Rozwiązanie.

1) znajdź obszar regularnego sześciokąta za pomocą wzoru lub = 12.

2) z trójkąta prostokątnegoMOU znajdźmy wysokość MO, biorąc pod uwagę, że w zwykły sześciokąt : .

3) obliczyć objętość piramidy: =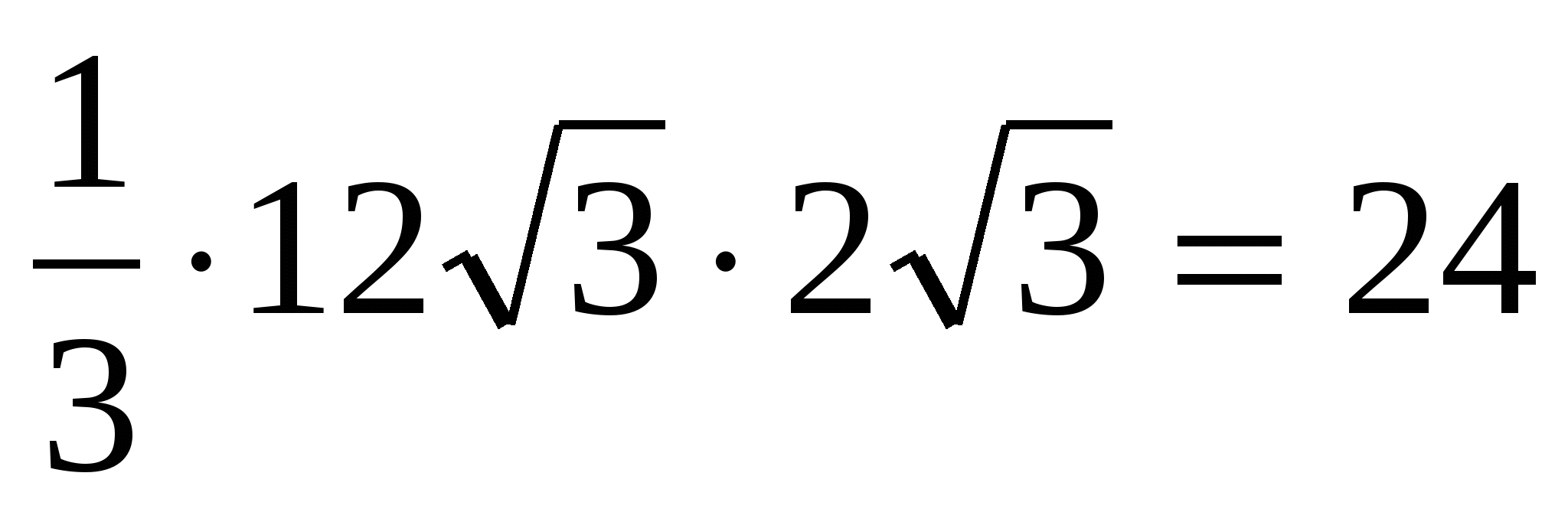

.

Odpowiedź: 24.

Problem nr 10 . Walec opisano wokół regularnego trójkątnego pryzmatu. Wysokość walca wynosi 5, a promień jego podstawy wynosiRspełnia równanieR 2 + R – 6 = 0. Znajdź objętość pryzmatu.

R 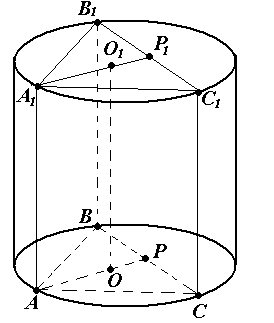decyzja. V = S · H

1) ponieważ pryzmat jest wpisany w cylinder, to wysokość pryzmatu jest równa wysokości walca, a podstawa pryzmatu jest wpisana w podstawę walca, N = 5.

2) według warunku R spełnia równanie R 2 + R – 6 = 0, rozwiązanie, które znajdujemy

R 1 = - 3, R 2 = 2, ponieważ promień jest wartością dodatnią, to -3 nie spełnia warunków problemu.

3) znajdź bok wpisanego trójkąta foremnego, korzystając ze wzoru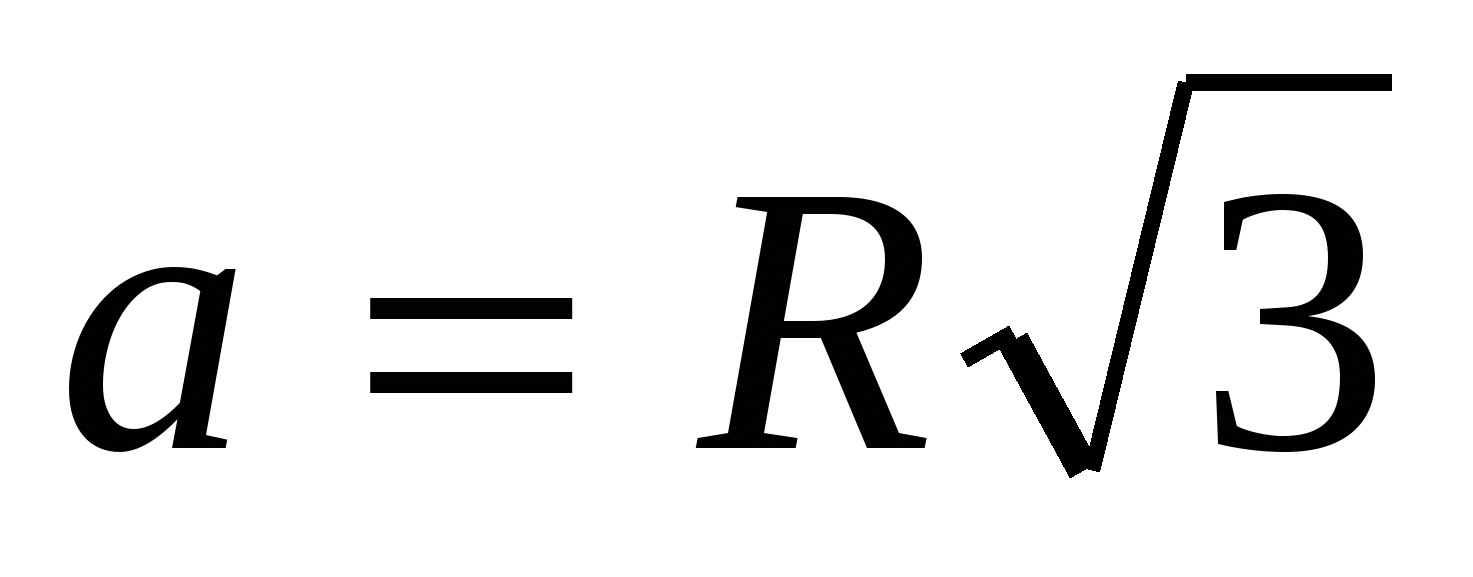

,

.

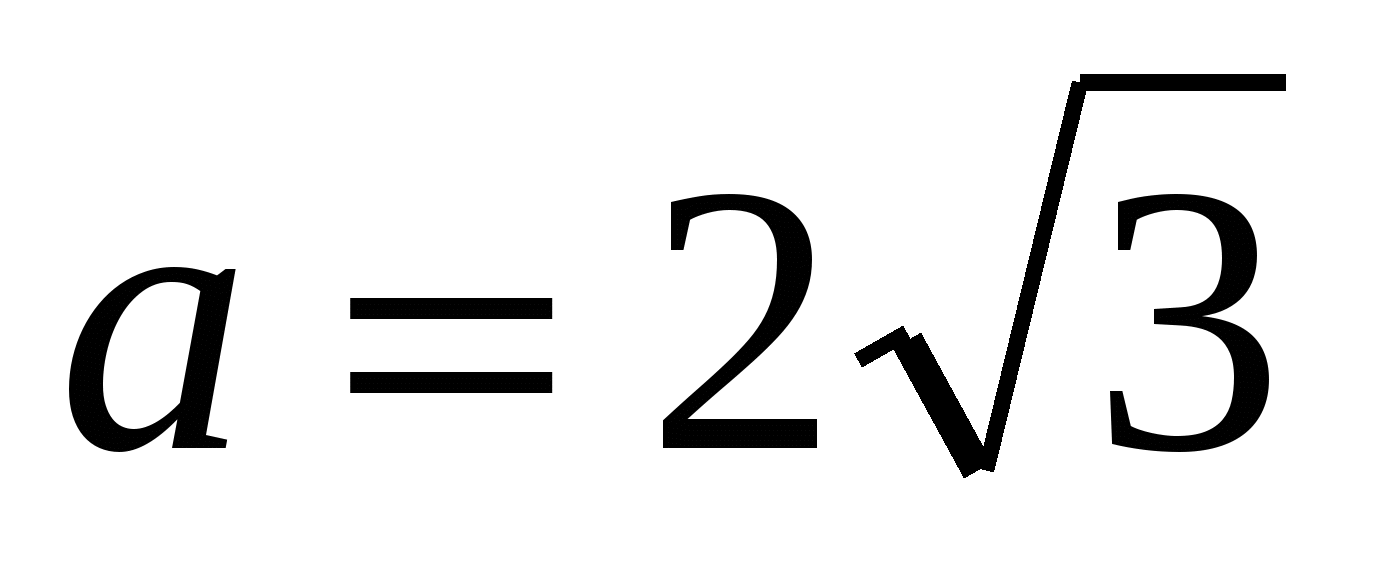4) znajdź obszar podstawy prawidłowy pryzmat, jako obszar regularnego trójkąta: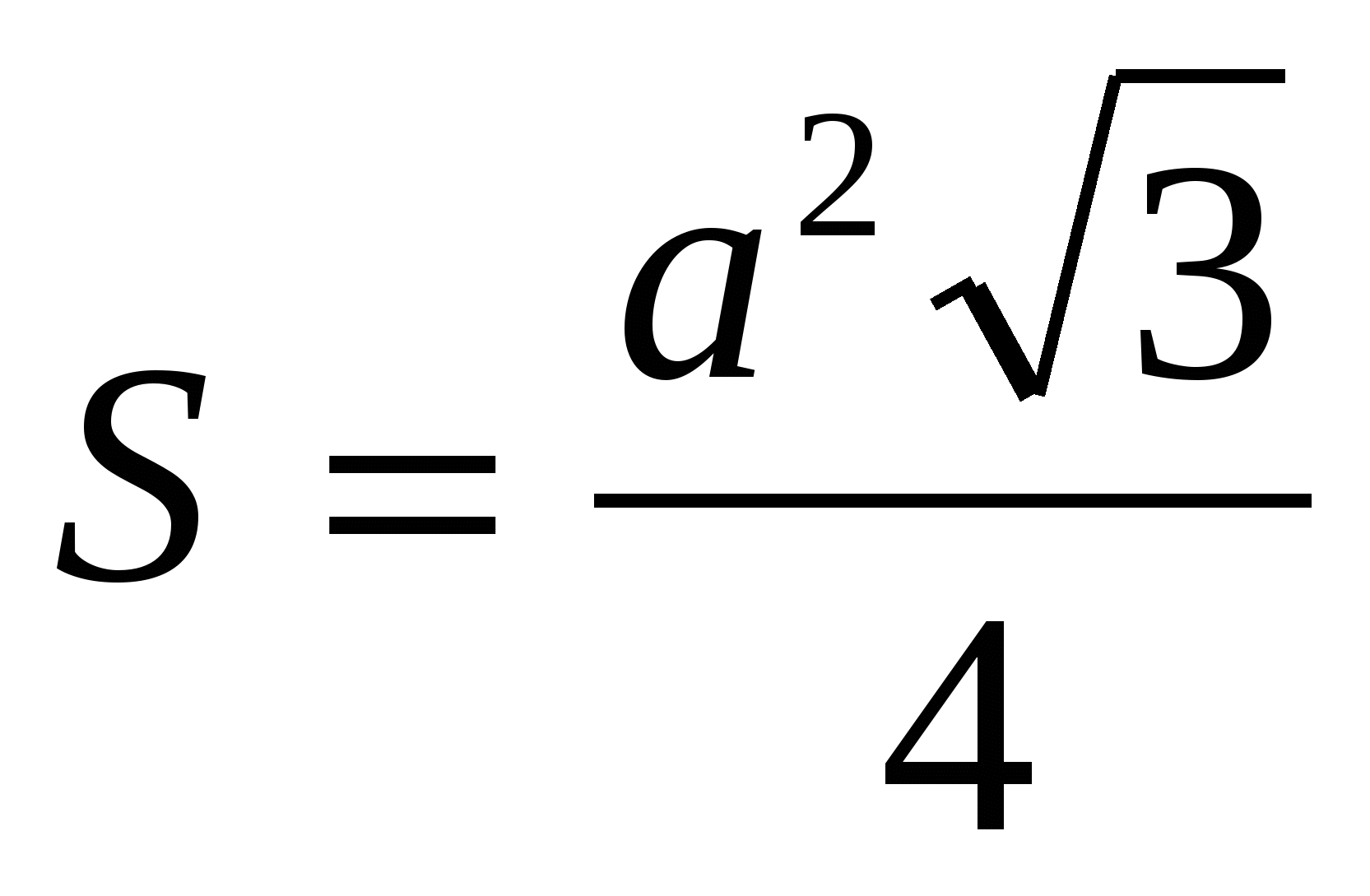

=


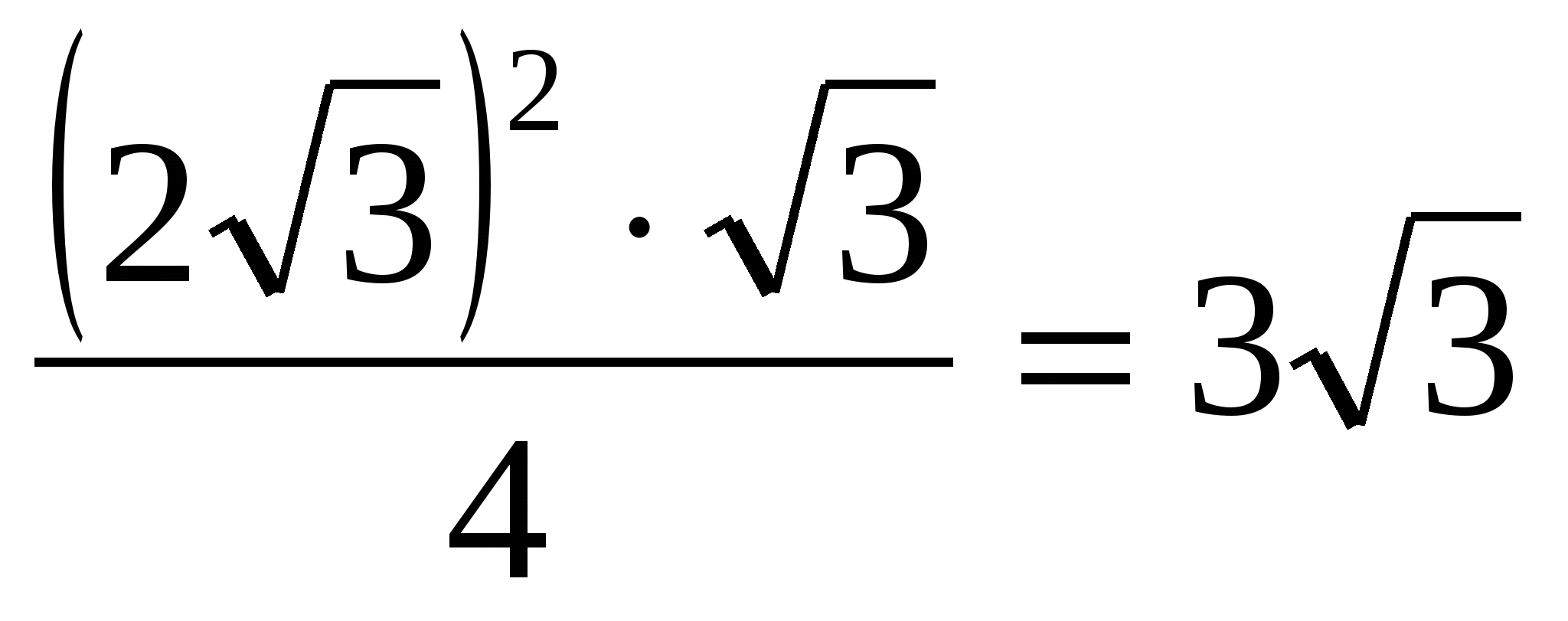
5) obliczyć objętość pryzmatu:V = S · H =

.

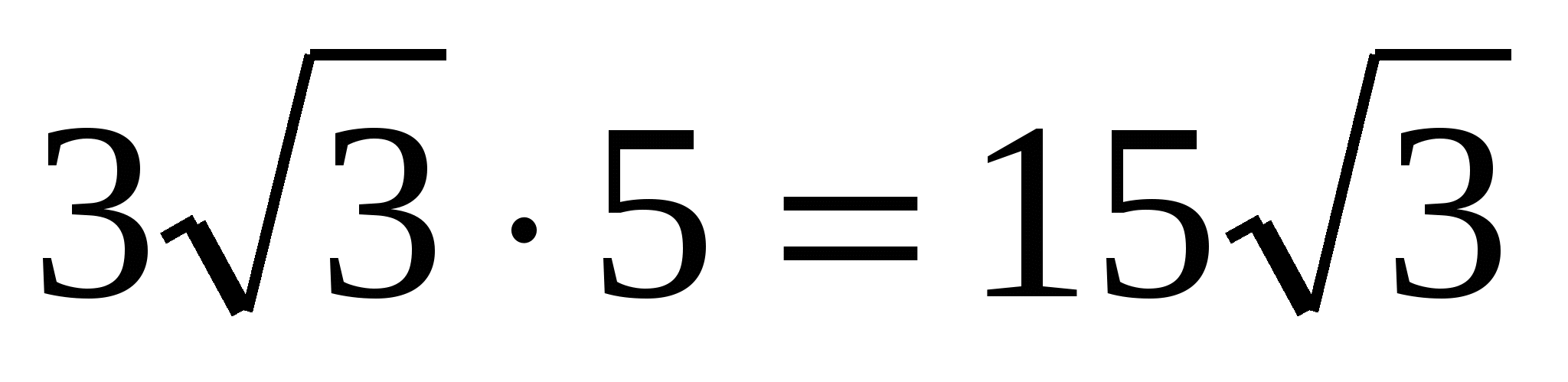Odpowiedź. 15.

Zadanie nr 11 . Walec opisano wokół regularnego trójkątnego pryzmatu. Odległość osi walca od boku podstawy pryzmatu jest równa . Wysokość walca jest równa trzem jego promieniom. Znajdź objętość pryzmatu.


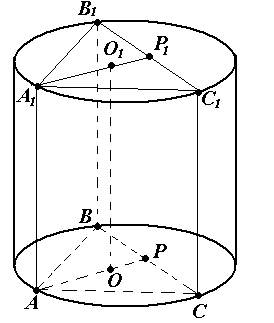
Rozwiązanie. V = S · H

1) Ponieważ pryzmat jest wpisany w cylinder, wysokość pryzmatu jest równa wysokości walca, a podstawa pryzmatu jest wpisana w podstawę walca, zgodnie z warunkiem N = 3 R..

2) Odległość między osią walca a bokiem podstawy pryzmatu jest równa promieniowi wpisanego trójkątaABC kręgi, tj.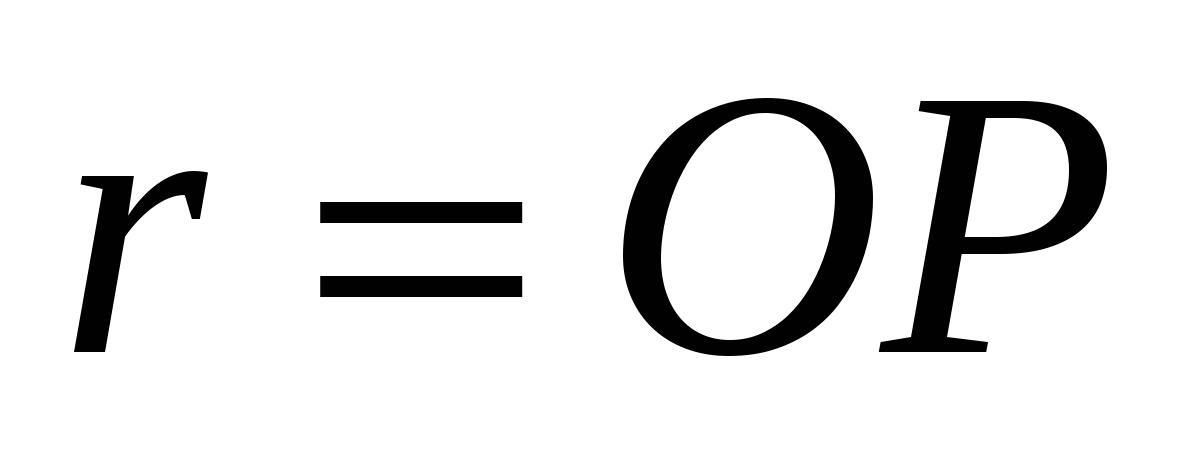

, i według warunku jest równa .

3) promień okręgu wpisanego w trójkąt foremny jest 2 razy mniejszy od promienia okręgu opisanego na tym trójkącie, tj. , Następnie .

4) znajdź bok wpisanego trójkąta foremnego, korzystając ze wzoru,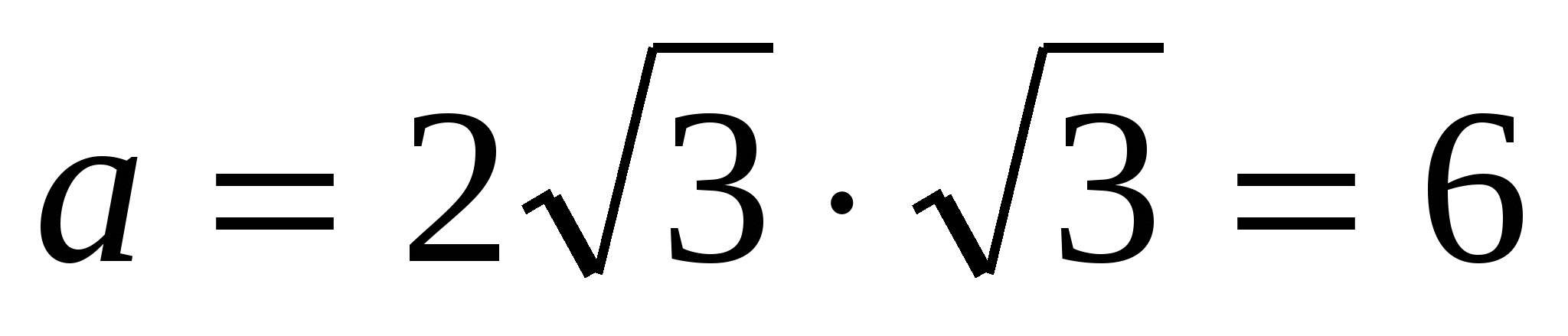

.

5) znajdź obszar podstawy regularnego pryzmatu, jako obszar regularnego trójkąta: =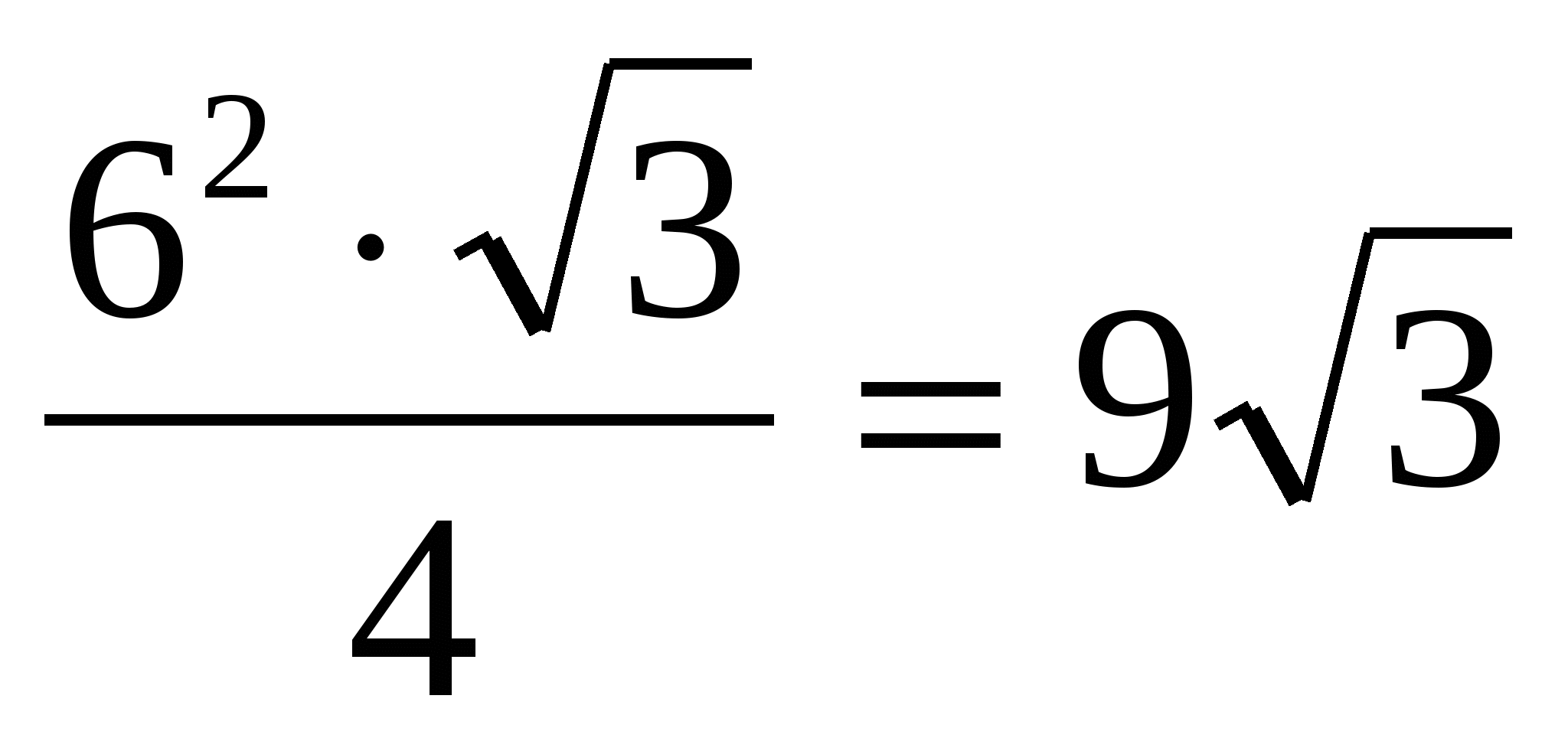

6) obliczyć objętość pryzmatu:V = S · H = S· 3 · R =

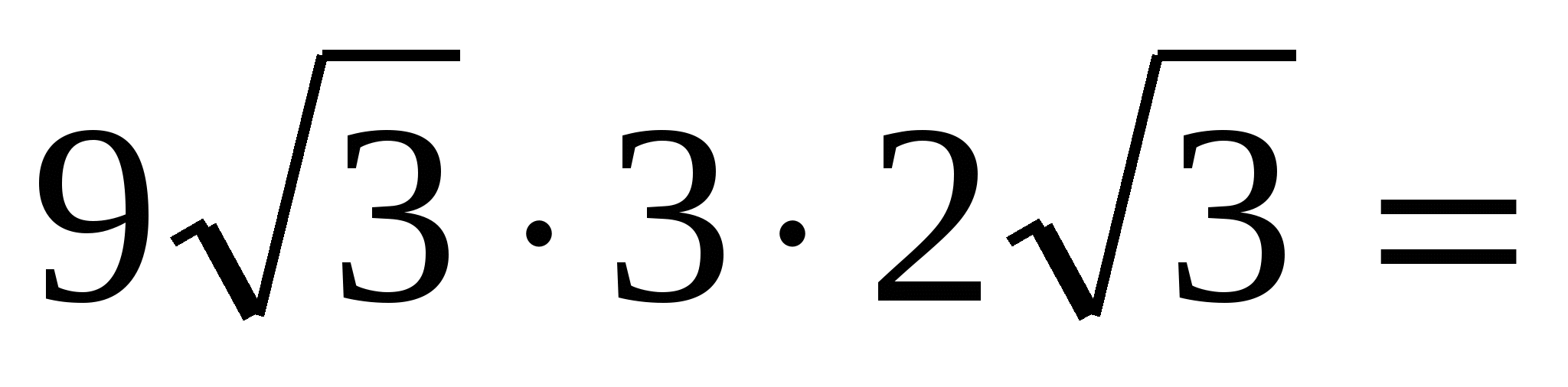162.

Odpowiedź. 162.

Zadanie nr 12. Walec opisano wokół regularnego trójkątnego pryzmatu. Pole powierzchni bocznej cylindra wynosi 16 . Znajdź objętość pryzmatu, jeśli bok jego podstawy wynosi 5.

Rozwiązanie. V = S · H

2) Znajdź obszar podstawy regularnego pryzmatu jako obszar regularnego trójkąta: =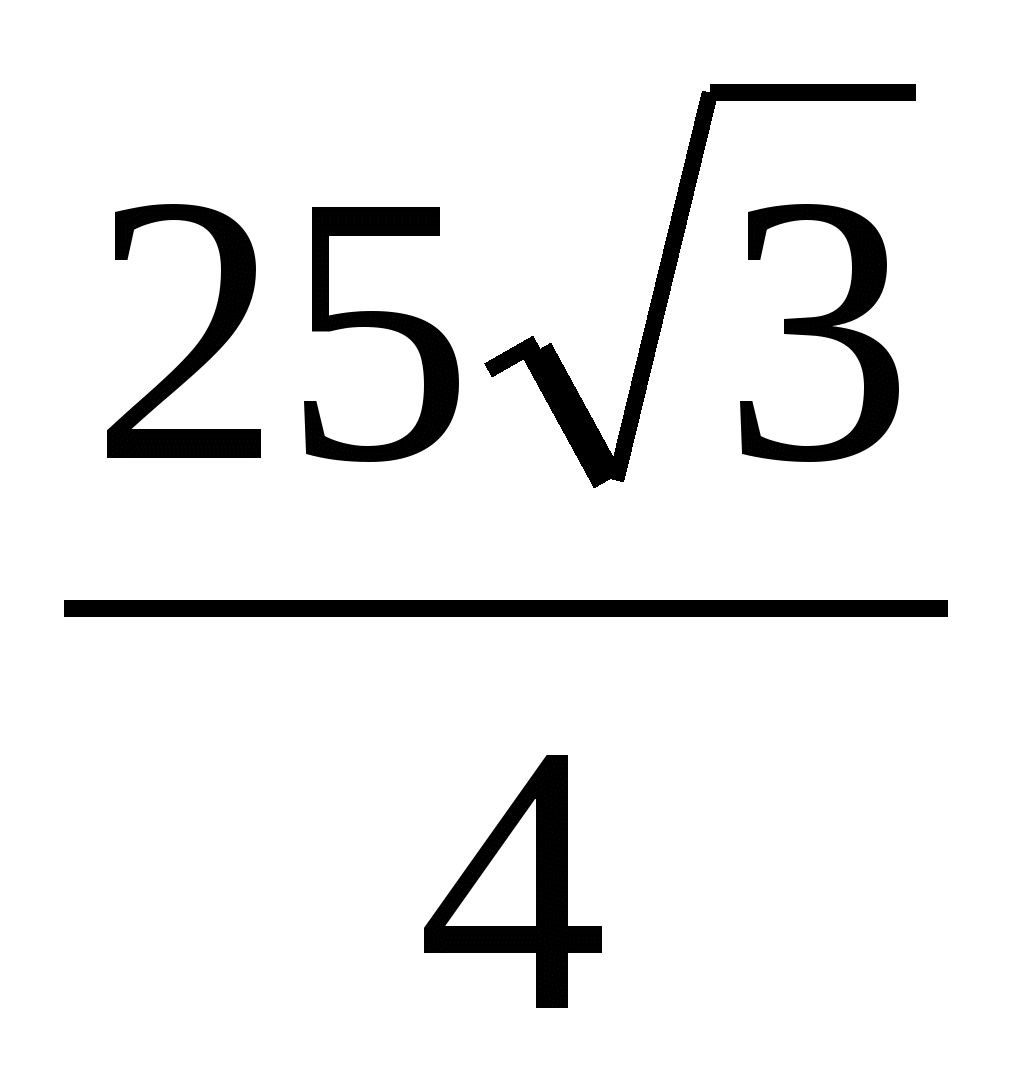

.

3) Zatem bok wpisanego trójkąta foremnego oblicza się ze wzoru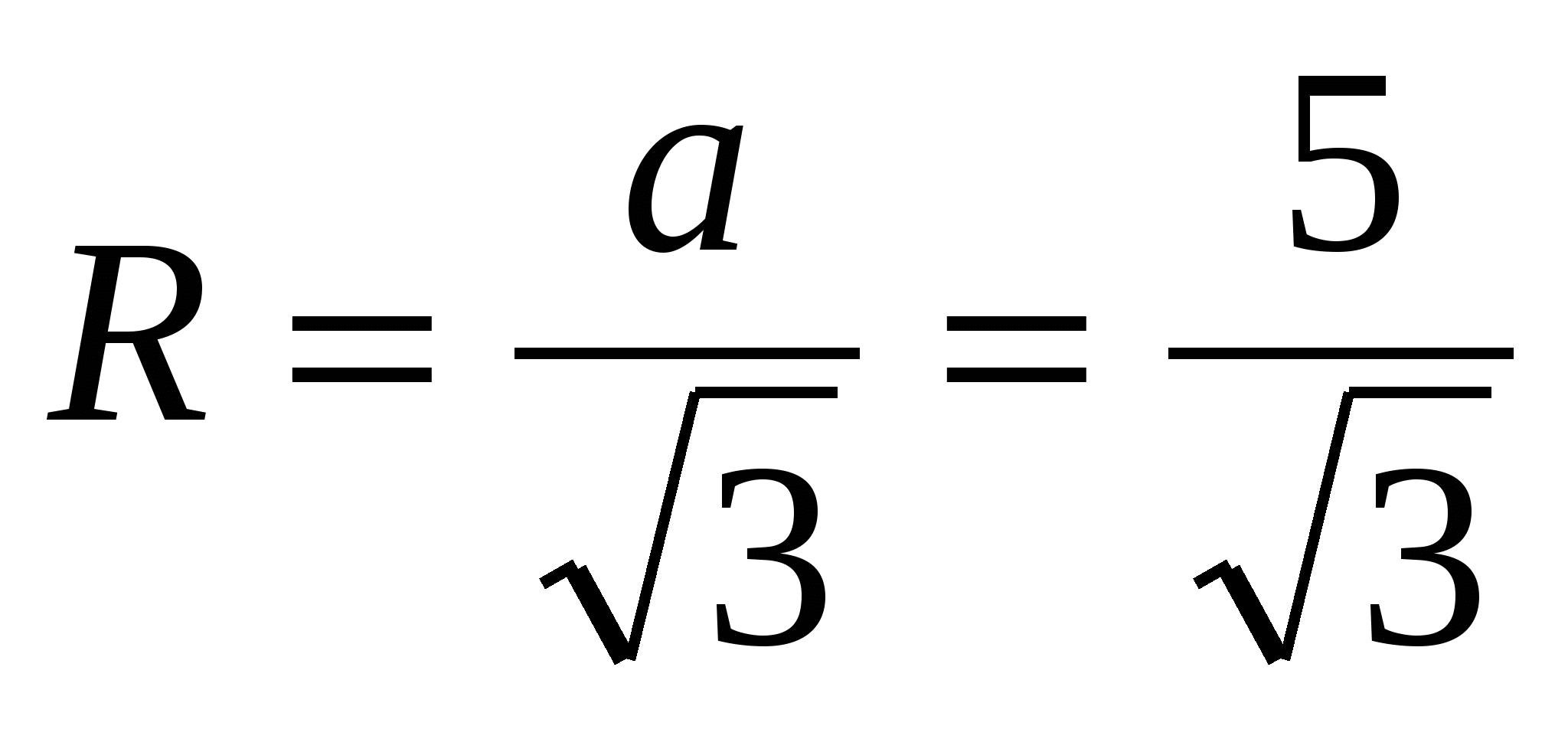

.

4) Zgodnie z warunkiem powierzchnia bocznej powierzchni cylindra wynosi 16· te.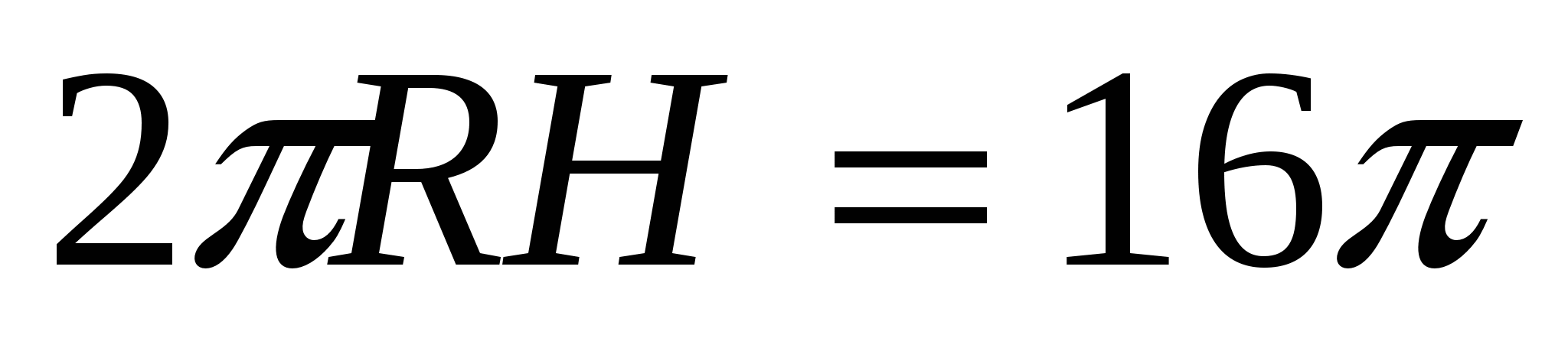

, GdzieN =

=

.

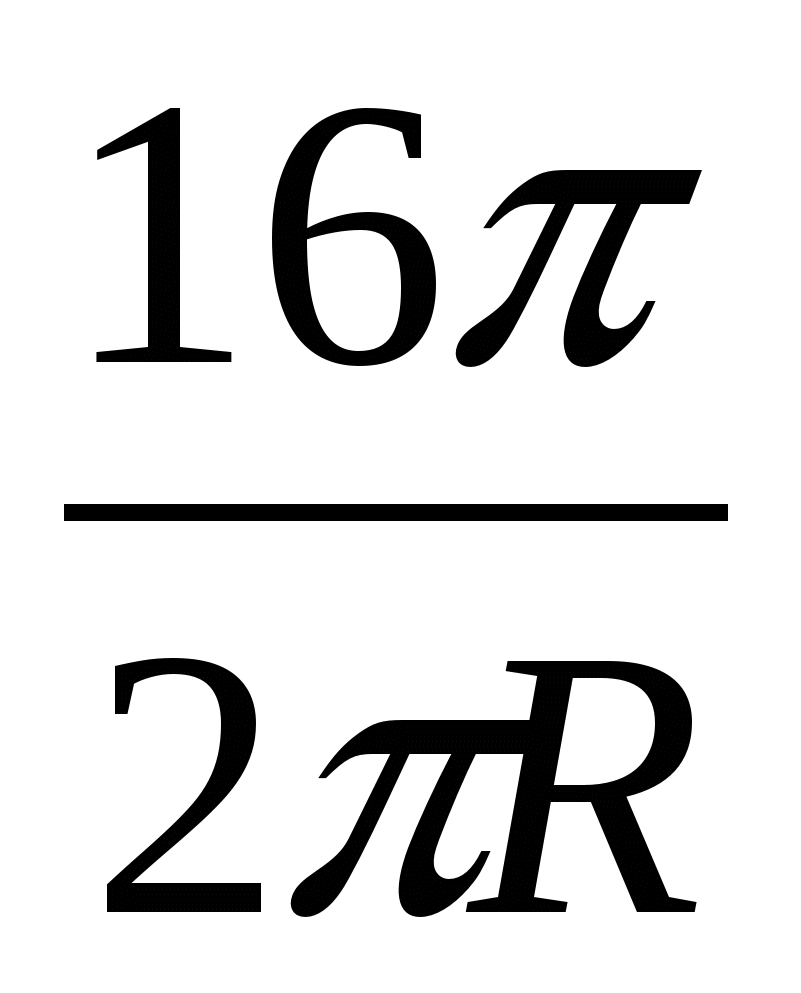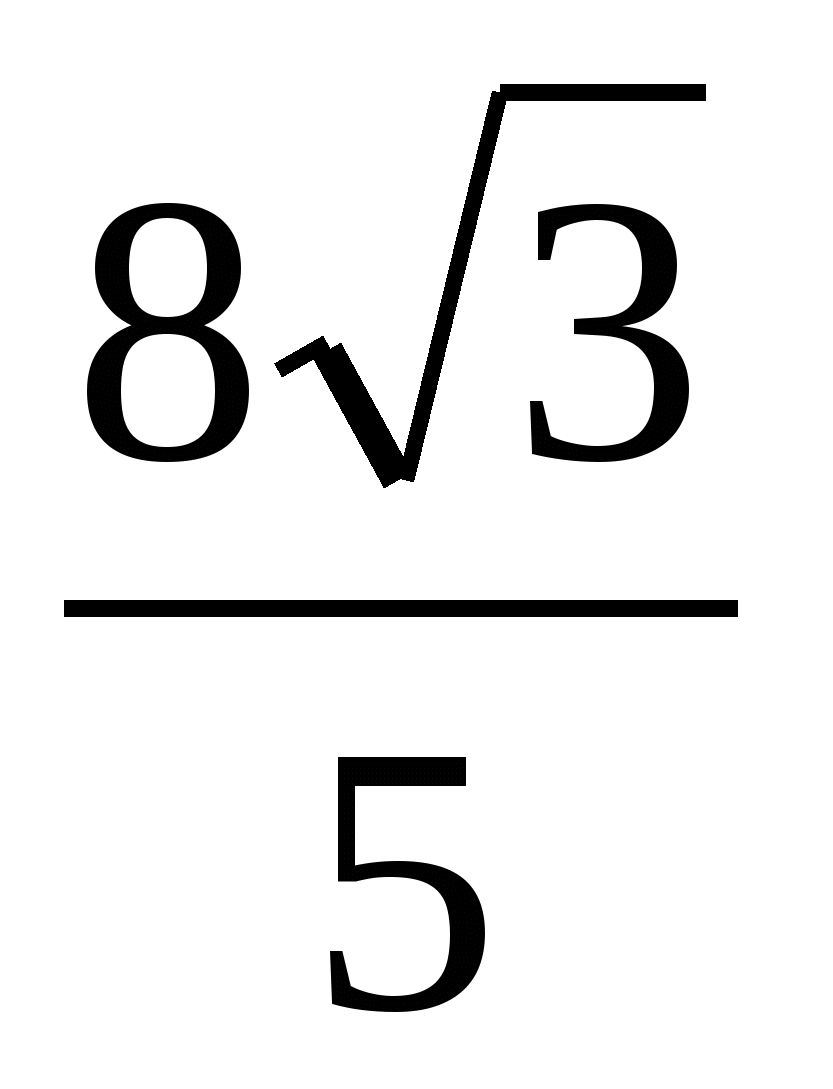5) Oblicz objętość pryzmatu:V = S · H = · = 30.

Odpowiedź. trzydzieści.

Zadanie nr 13. Blisko prawego czworokątny pryzmat Opisano walec, którego powierzchnia boczna wynosi 20. Znajdź powierzchnię boczną pryzmatu.

Rozwiązanie.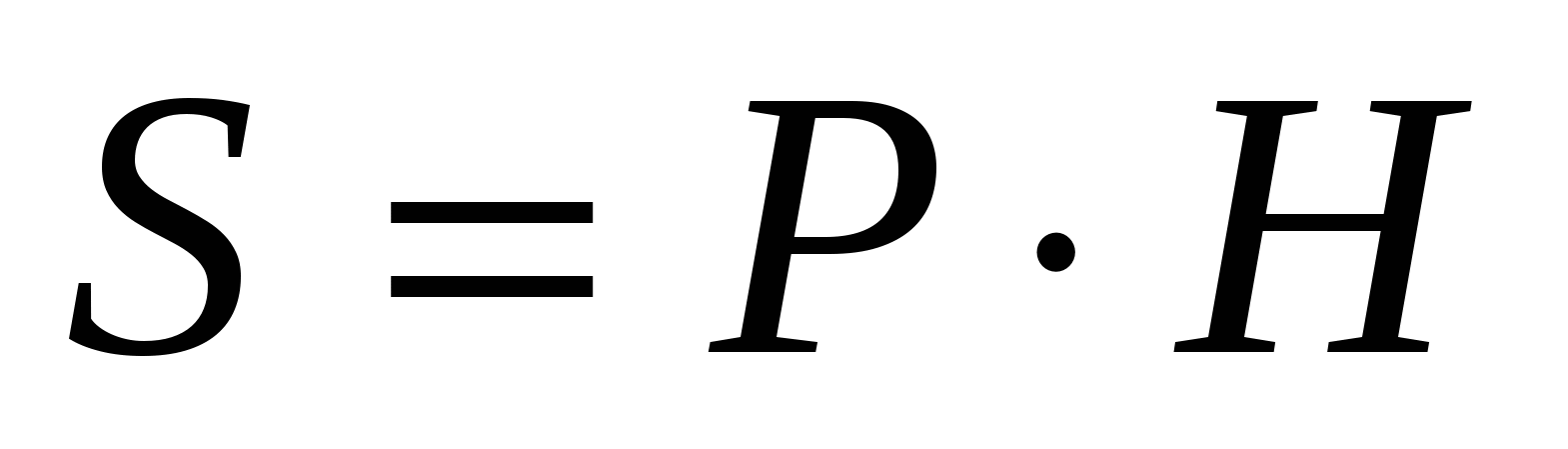

1) Ponieważ pryzmat jest wpisany w cylinder, wysokość pryzmatu jest równa wysokości cylindra, a podstawa pryzmatu jest wpisana w podstawę cylindra.

2) Zgodnie z warunkiem powierzchnia bocznej powierzchni cylindra wynosi 20, tj.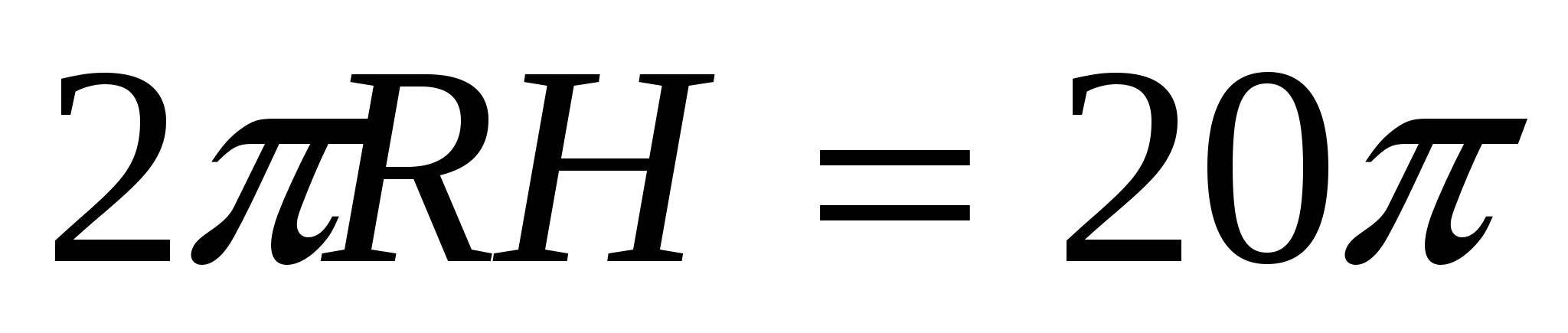

,

.

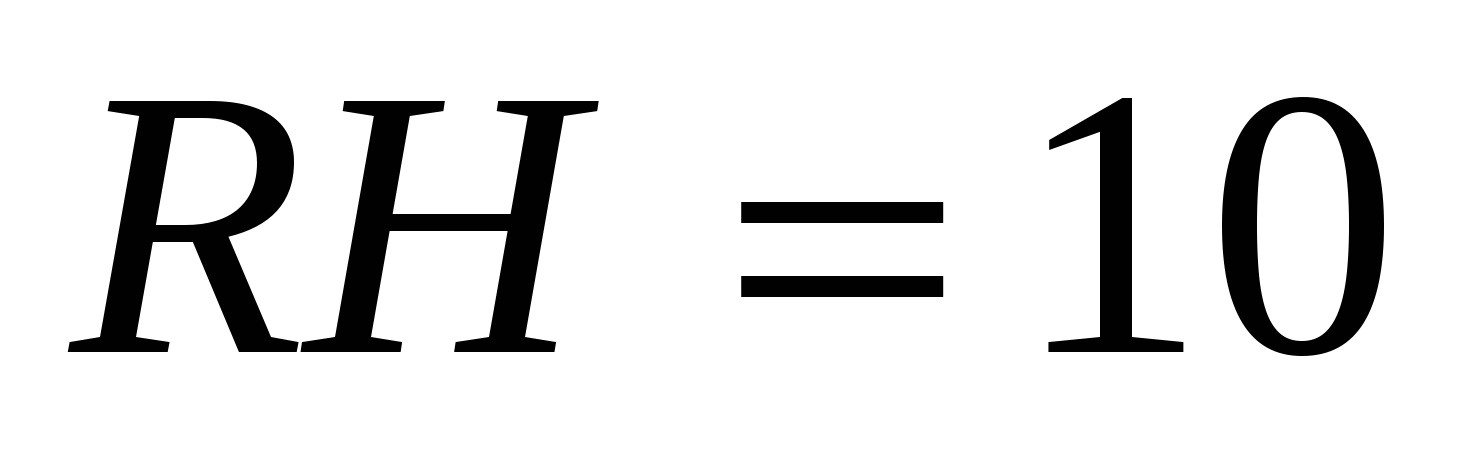3) ponieważ pryzmat jest regularny, to u jego podstawy znajduje się kwadrat z bokiem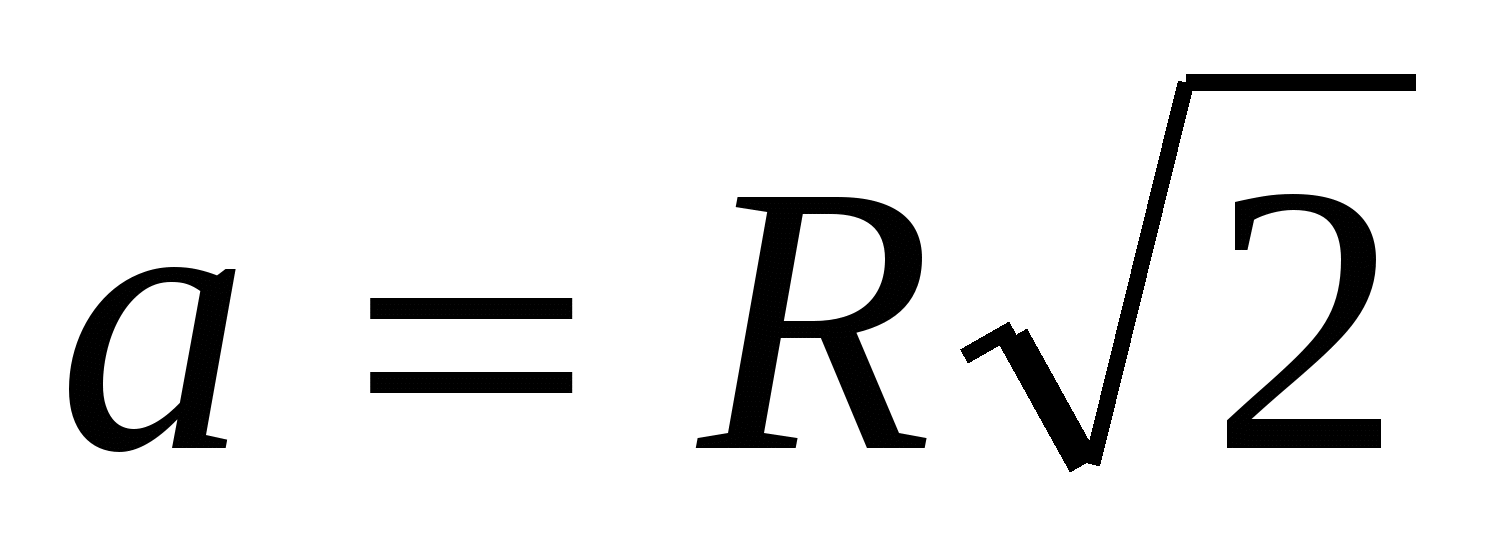

, to obwód podstawy jest równy

.

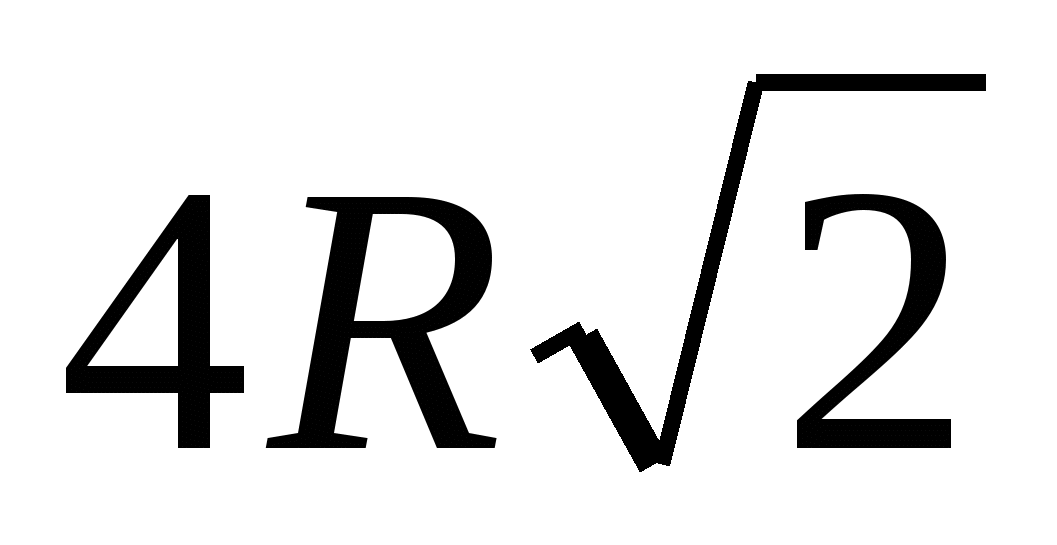4) obliczyć pole powierzchni bocznej pryzmatu = ., tj. – 36 a ·

.

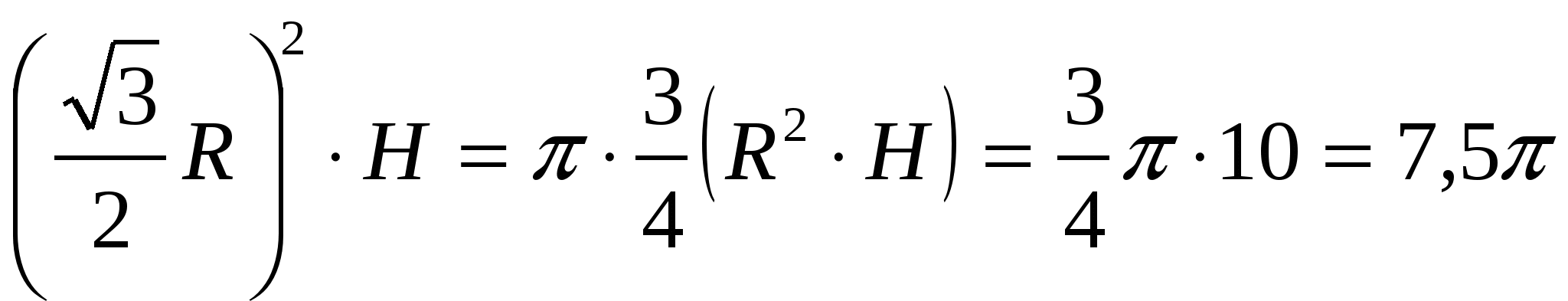Odpowiedź. 7,5  .

Chudaeva E.V., Miejska Instytucja Oświatowa „Insarskaya Liceum nr 1”, Insar, Republika Mordowii

ROZWIĄZYWANIE PROBLEMÓW GEOMETRYCZNYCH

(na podstawie materiałów z egzaminu Unified State Exam)

Zadanie nr 1

Zadanie nr 2

Zadanie nr 3

Zadanie nr 4

Problem nr 5

Problem nr 6

Problem nr 7

Problem nr 8

Problem nr 9

Problem nr 10R spełnia równanie R 2 + R – 6 = 0. Znajdź objętość pryzmatu.

Zadanie nr 11

Zadanie nr 12

Zadanie nr 13

Zadanie nr 14. W regularny czworokątny pryzmat wpisano cylinder. Objętość walca wynosi 16, a promień okręgu opisanego wokół podstawy graniastosłupa wynosi . Znajdź przekątną pryzmatu.

Zadanie nr 15. W regularny sześciokątny pryzmat wpisano cylinder. Znajdź wysokość pryzmatu, jeśli jego pole wynosi 54, a promień walca wynosi 3.


Zadanie nr 16. Walec opisano wokół regularnego sześciokątnego pryzmatu. Objętość walca wynosi 16 , wysokość cylindra wynosi 4. Znajdź objętość pryzmatu.

Zadanie nr 17. Walec opisano wokół regularnego sześciokątnego pryzmatu. Objętość cylindra wynosi 10 . Znajdź objętość walca wpisanego w ten sam pryzmat.

ROZWIĄZYWANIE PROBLEMÓW GEOMETRYCZNYCH

(na podstawie materiałów z egzaminu Unified State Exam)

Zadanie nr 1 . Oblicz objętość regularnej piramidy trójkątnej, jeśli promień okręgu opisanego na podstawie jest równy , a wysokość piramidy jest równa 4.

Rozwiązanie.

3) obliczyć objętość piramidy

Odpowiedź. 9

Zadanie nr 2 . Oblicz objętość regularnej piramidy trójkątnej, jeśli promień okręgu wpisanego w podstawę jest równy , a boczne krawędzie piramidy są równe 6.

Rozwiązanie.

4) z trójkąta prostokątnego korzystając z twierdzenia Pitagorasa znajdujemy wysokość piramidy: , .

5) obliczyć objętość piramidy

Odpowiedź. 18.

Zadanie nr 3 . Oblicz pole powierzchni bocznej regularnej piramidy trójkątnej, jeśli promień okręgu opisanego w pobliżu podstawy jest równy , a wysokość piramidy jest równa 1.

Rozwiązanie.

1) znajdź bok podstawy regularnej piramidy, korzystając ze wzoru , .

2) znajdź obwód podstawy P = 3· A,

P = 9.

4) z trójkąta prostokątnegoMPA PAN : ,

PAN =

5) obliczyć pole powierzchni bocznej regularnej piramidy:

Odpowiedź. .

Zadanie nr 4 . Oblicz objętość regularnej piramidy trójkątnej, której bok podstawy wynosi 6, a apothem wynosi 6.

Rozwiązanie. ,

1) znajdź promień okręgu opisanego przy podstawie i wpisanego w podstawę: , czyli .

2) znajdź pole podstawy jako pole regularnego trójkąta, .

MPA Korzystając z twierdzenia Pitagorasa, znajdujemy wysokość: , MO = .

Odpowiedź. 18.

Problem nr 5 . Oblicz objętość regularnej piramidy trójkątnej, jeśli promień okręgu wpisanego u podstawy wynosi 2, a wysokość regularnej piramidy wynosi .

Rozwiązanie.

1) promień okręgu wpisanego w trójkąt foremny jest 2 razy mniejszy od promienia okręgu opisanego na tym trójkącie, tj. , Następnie .

2) znajdź bok podstawy regularnej piramidy, korzystając ze wzoru , .

3) znajdź pole podstawy jako pole regularnego trójkąta, .

4) obliczyć objętość regularnej piramidy: = .

Odpowiedź. 36.

Problem nr 6 . Oblicz pole powierzchni bocznej regularnej czworokątnej piramidy, jeśli jej krawędzie wynoszą 5, a promień okręgu opisanego wokół podstawy wynosi 3.

Rozwiązanie .

1) znajdź bok podstawy za pomocą wzoru, tj. .

2) znajdź obwód podstawy: R = 4A,

P = 24.

3) z trójkąta prostokątnegoM DR Korzystając z twierdzenia Pitagorasa, znajdujemy apotemPAN : , D.P. =

Następnie: PAN = .

4) obliczyć pole powierzchni bocznej piramidy: = .

Odpowiedź. 48.

Problem nr 7 . W regularnej czworokątnej piramidzie pole powierzchni bocznej wynosi 16, a pole podstawy wynosi 4. Znajdź wysokość piramidy.

Rozwiązanie.

1) znajdź bok podstawy: ponieważ podstawą piramidy jest kwadrat o polu równym 4, to bok kwadratu wynosi 2, a jego obwód wynosi 8.

2) według warunku = 16 tj.

3) z trójkąta prostokątnegoMPA Korzystając z twierdzenia Pitagorasa znajdujemy wysokość: , biorąc pod uwagę, że OR = = 1, otrzymujemy: MO = .

Odpowiedź. .



Problem nr 8. Oblicz objętość regularnej piramidy sześciokątnej, jeśli bok podstawy wynosi 4, a boczne krawędzie piramidy wynoszą 5.

Rozwiązanie.

1) bok podstawy sześciokąta foremnego jest równy promieniowi okręgu wokół niego opisanego, tj. ,

2) znajdź obszar regularnego sześciokąta za pomocą wzoru lub = 24.

3) z trójkąta prostokątnegoMOU znajdźmy wysokość MO : .

4) obliczyć objętość piramidy: =.

Odpowiedź. 24.

Problem nr 9 . W regularnej piramidzie sześciokątnej bok podstawy wynosi 2, a krawędź boczna wynosi 2. Znajdź objętość piramidy.

Rozwiązanie.

1) znajdź obszar regularnego sześciokąta za pomocą wzoru lub = 12.

2) z trójkąta prostokątnegoMOU znajdźmy wysokość MO, biorąc pod uwagę, że w regularnym sześciokącie: .

3) obliczyć objętość piramidy: =.

Odpowiedź: 24.

Problem nr 10 . Walec opisano wokół regularnego trójkątnego pryzmatu. Wysokość walca wynosi 5, a promień jego podstawy wynosiRspełnia równanieR 2 + R – 6 = 0. Znajdź objętość pryzmatu.

Rozwiązanie. V = S · H

1) ponieważ pryzmat jest wpisany w cylinder, to wysokość pryzmatu jest równa wysokości walca, a podstawa pryzmatu jest wpisana w podstawę walca, N = 5.

2) według warunku R spełnia równanie R 2 + R – 6 = 0, rozwiązanie, które znajdujemy

R 1 = - 3, R 2 = 2, ponieważ promień jest wartością dodatnią, to -3 nie spełnia warunków problemu.

3) znajdź bok wpisanego trójkąta foremnego, korzystając ze wzoru , .

4) znajdź obszar podstawy regularnego pryzmatu, jako obszar regularnego trójkąta: =
5) obliczyć objętość pryzmatu:V = S · H = .

Odpowiedź. 15.

Zadanie nr 11 . Walec opisano wokół regularnego trójkątnego pryzmatu. Odległość osi walca od boku podstawy pryzmatu jest równa . Wysokość walca jest równa trzem jego promieniom. Znajdź objętość pryzmatu.

Rozwiązanie. V = S · H

1) Ponieważ pryzmat jest wpisany w cylinder, wysokość pryzmatu jest równa wysokości walca, a podstawa pryzmatu jest wpisana w podstawę walca, zgodnie z warunkiem N = 3 R..

2) Odległość między osią walca a bokiem podstawy pryzmatu jest równa promieniowi wpisanego trójkątaABC kręgi, tj. , i według warunku jest równa .

3) promień okręgu wpisanego w trójkąt foremny jest 2 razy mniejszy od promienia okręgu opisanego na tym trójkącie, tj. , Następnie .

4) znajdź bok wpisanego trójkąta foremnego, korzystając ze wzoru , .

5) znajdź obszar podstawy regularnego pryzmatu, jako obszar regularnego trójkąta: =

6) obliczyć objętość pryzmatu:V = S · H = S· 3 · R = 162.

Odpowiedź. 162.

Zadanie nr 12. Walec opisano wokół regularnego trójkątnego pryzmatu. Pole powierzchni bocznej cylindra wynosi 16 . Znajdź objętość pryzmatu, jeśli bok jego podstawy wynosi 5.

Rozwiązanie. V = S · H

2) Znajdź obszar podstawy regularnego pryzmatu jako obszar regularnego trójkąta: =.

3) Bok wpisanego trójkąta foremnego znajduje się według wzoru, a następnie .

4) Zgodnie z warunkiem powierzchnia bocznej powierzchni cylindra wynosi 16· czyli skąd N = = .

5) Oblicz objętość pryzmatu:V = S · H = · = 30.

Odpowiedź. trzydzieści.

Zadanie nr 13. Walec opisano wokół regularnego czworokątnego pryzmatu, którego powierzchnia boczna wynosi 20. Znajdź powierzchnię boczną pryzmatu.

Rozwiązanie.

1) Ponieważ pryzmat jest wpisany w cylinder, wysokość pryzmatu jest równa wysokości cylindra, a podstawa pryzmatu jest wpisana w podstawę cylindra.

2) Zgodnie z warunkiem powierzchnia bocznej powierzchni cylindra wynosi 20, tj. , .

3) ponieważ pryzmat jest regularny, to u jego podstawy leży kwadrat o boku , wówczas obwód podstawy jest równy .

4) obliczyć pole powierzchni bocznej pryzmatu = ., a promień walca wynosi 3. , wysokość walca wynosi 4. Znajdź objętość pryzmatu. .

5) zapisz wzór na obliczenie objętości walca wpisanego w pryzmat:V = S · H, te.:

V = = ·.

Odpowiedź. 7,5  .