កំណត់មុំ dihedral ដែលបង្កើតឡើងដោយចំនុចប្រសព្វនៃយន្តហោះគូ។ បញ្ហា៖ យន្តហោះកាត់ខ្សែបន្ទាត់

អត្ថបទនេះគឺអំពីមុំរវាងយន្តហោះ និងរបៀបស្វែងរកវា។ ទីមួយ និយមន័យនៃមុំរវាងយន្តហោះពីរត្រូវបានផ្តល់ឱ្យ ហើយគំនូរក្រាហ្វិកត្រូវបានផ្តល់ឱ្យ។ បន្ទាប់ពីនេះ គោលការណ៍នៃការស្វែងរកមុំរវាងយន្តហោះប្រសព្វគ្នាពីរដោយប្រើវិធីសាស្ត្រកូអរដោណេត្រូវបានវិភាគ ហើយរូបមន្តមួយត្រូវបានទទួលដែលអនុញ្ញាតឱ្យអ្នកគណនាមុំរវាងយន្តហោះប្រសព្វគ្នាដោយប្រើកូអរដោនេដែលគេស្គាល់នៃវ៉ិចទ័រធម្មតានៃយន្តហោះទាំងនេះ។ នៅក្នុងការសន្និដ្ឋានវាត្រូវបានបង្ហាញ ដំណោះស្រាយលម្អិតភារកិច្ចលក្ខណៈ។

ការរុករកទំព័រ។

មុំរវាងយន្តហោះ - និយមន័យ។

ចូរយើងបង្ហាញអំណះអំណាងដែលនឹងអនុញ្ញាតឱ្យយើងចូលទៅជិតបន្តិចម្តងៗនូវការកំណត់មុំរវាងយន្តហោះប្រសព្វគ្នាពីរ។

អនុញ្ញាតឱ្យយើងទទួលបានយន្តហោះប្រសព្វគ្នាពីរ និង . ប្លង់ទាំងនេះប្រសព្វគ្នាតាមបន្ទាត់ត្រង់មួយ ដែលយើងសម្គាល់ដោយអក្សរ គ។ ចូរបង្កើតយន្តហោះឆ្លងកាត់ចំណុច M នៃបន្ទាត់ c ហើយកាត់កែងទៅបន្ទាត់ c ។ ក្នុងករណីនេះយន្តហោះនឹងប្រសព្វគ្នារវាងយន្តហោះនិង។ ចូរយើងសម្គាល់បន្ទាត់ត្រង់ដែលយន្តហោះប្រសព្វគ្នាជា a និងបន្ទាត់ត្រង់ដែលយន្តហោះប្រសព្វគ្នាជា ខ។ ជាក់ស្តែង បន្ទាត់ a និង b ប្រសព្វគ្នានៅចំណុច M ។

វាងាយស្រួលក្នុងការបង្ហាញថាមុំរវាងបន្ទាត់ប្រសព្វ a និង b មិនអាស្រ័យលើទីតាំងនៃចំណុច M នៅលើបន្ទាត់ c ដែលយន្តហោះឆ្លងកាត់នោះទេ។

ចូរ​សង់​យន្តហោះ​កាត់​កែង​ទៅ​នឹង​បន្ទាត់ c និង​ខុស​ពី​យន្តហោះ។ យន្តហោះត្រូវបានប្រសព្វគ្នាដោយយន្តហោះ និងតាមបណ្តោយបន្ទាត់ត្រង់ ដែលយើងសម្គាល់ថាជា 1 និង b 1 រៀងគ្នា។

តាមវិធីសាស្រ្តនៃការសាងសង់ប្លង់ វាធ្វើតាមដែលបន្ទាត់ a និង b កាត់កែងទៅបន្ទាត់ c ហើយបន្ទាត់ a 1 និង b 1 គឺកាត់កែងទៅបន្ទាត់ c ។ ដោយសារបន្ទាត់ a និង 1 ស្ថិតនៅក្នុងប្លង់តែមួយ ហើយកាត់កែងទៅបន្ទាត់ c បន្ទាប់មកពួកវាស្របគ្នា។ ស្រដៀងគ្នានេះដែរ បន្ទាត់ b និង b 1 ស្ថិតនៅក្នុងប្លង់តែមួយ ហើយកាត់កែងទៅបន្ទាត់ c ដូច្នេះពួកវាគឺស្របគ្នា។ ដូច្នេះអ្នកអាចធ្វើបាន ការផ្ទេរប៉ារ៉ាឡែល plan to plane ដែលក្នុងនោះបន្ទាត់ត្រង់ a 1 ស្របគ្នាជាមួយបន្ទាត់ត្រង់ a និងបន្ទាត់ត្រង់ b ជាមួយបន្ទាត់ត្រង់ b 1 ។ ដូច្នេះមុំរវាងបន្ទាត់ប្រសព្វពីរ a 1 និង b 1 ស្មើនឹងមុំរវាងបន្ទាត់ប្រសព្វ a និង b ។

នេះបង្ហាញថាមុំរវាងបន្ទាត់ប្រសព្វ a និង b ស្ថិតនៅក្នុងយន្តហោះប្រសព្វគ្នា ហើយមិនអាស្រ័យលើជម្រើសនៃចំណុច M ដែលយន្តហោះឆ្លងកាត់នោះទេ។ ដូច្នេះ វាជាឡូជីខលក្នុងការយកមុំនេះជាមុំរវាងប្លង់ប្រសព្វគ្នាពីរ។

ឥឡូវនេះអ្នកអាចបញ្ចេញនិយមន័យនៃមុំរវាងយន្តហោះប្រសព្វគ្នាពីរ និង។

និយមន័យ។

មុំរវាងយន្តហោះពីរប្រសព្វគ្នាក្នុងបន្ទាត់ត្រង់មួយ និង- នេះគឺជាមុំរវាងបន្ទាត់ប្រសព្វគ្នាពីរ a និង b ដែលនៅតាមបណ្តោយយន្តហោះ ហើយប្រសព្វគ្នាជាមួយប្លង់កាត់កែងទៅនឹងបន្ទាត់ គ។

និយមន័យនៃមុំរវាងយន្តហោះពីរអាចត្រូវបានផ្តល់ឱ្យខុសគ្នាបន្តិចបន្តួច។ ប្រសិនបើនៅលើបន្ទាត់ត្រង់ c តាមបណ្តោយដែលយន្តហោះនិងប្រសព្វគ្នា សម្គាល់ចំណុច M ហើយគូរបន្ទាត់ត្រង់ a និង b កាត់វាកាត់កែងទៅបន្ទាត់ត្រង់ c ហើយដេកក្នុងយន្តហោះ ហើយរៀងគ្នា បន្ទាប់មកមុំរវាងបន្ទាត់ត្រង់ a និង b គឺជាមុំរវាងយន្តហោះ និង។ ជាធម្មតានៅក្នុងការអនុវត្តជាក់ស្តែង គ្រាន់តែសំណង់បែបនេះត្រូវបានអនុវត្តដើម្បីទទួលបានមុំរវាងយន្តហោះ។

ដោយសារមុំរវាងបន្ទាត់ប្រសព្វគ្នាមិនលើសពី វាធ្វើតាមនិយមន័យដែលបានបញ្ជាក់នោះ។ រង្វាស់ដឺក្រេមុំរវាងយន្តហោះប្រសព្វគ្នាពីរត្រូវបានបង្ហាញ ចំនួនពិតពីចន្លោះពេល។ ក្នុងករណីនេះយន្តហោះប្រសព្វត្រូវបានគេហៅថា កាត់កែងប្រសិនបើមុំរវាងពួកវាគឺកៅសិបដឺក្រេ។ មុំរវាងប្លង់ប៉ារ៉ាឡែលមិនត្រូវបានកំណត់ទាល់តែសោះ ឬចាត់ទុកថាស្មើសូន្យ។

ស្វែងរកមុំរវាងយន្តហោះប្រសព្វគ្នាពីរ។

ជាធម្មតា នៅពេលស្វែងរកមុំរវាងប្លង់ប្រសព្វគ្នាដំបូង អ្នកត្រូវតែធ្វើការសាងសង់បន្ថែម ដើម្បីមើលបន្ទាត់ត្រង់ប្រសព្វ មុំរវាងដែលស្មើនឹងមុំដែលចង់បាន ហើយបន្ទាប់មកទាក់ទងមុំនេះទៅនឹងទិន្នន័យដើមដោយប្រើតេស្តសមភាព ភាពស្រដៀងគ្នា។ តេស្ត ទ្រឹស្តីបទកូស៊ីនុស ឬនិយមន័យនៃស៊ីនុស កូស៊ីនុស និងតង់សង់នៃមុំ។ នៅក្នុងវគ្គសិក្សានៃធរណីមាត្រ វិទ្យាល័យបញ្ហាស្រដៀងគ្នាកើតឡើង។

ជាឧទាហរណ៍ សូមផ្តល់ដំណោះស្រាយចំពោះបញ្ហា C2 ពីការប្រឡងបង្រួបបង្រួមរដ្ឋក្នុងគណិតវិទ្យាសម្រាប់ឆ្នាំ 2012 (លក្ខខណ្ឌត្រូវបានផ្លាស់ប្តូរដោយចេតនា ប៉ុន្តែវាមិនប៉ះពាល់ដល់គោលការណ៍នៃដំណោះស្រាយទេ)។ នៅក្នុងវា អ្នកគ្រាន់តែត្រូវរកមុំរវាងយន្តហោះប្រសព្វគ្នាពីរ។

ឧទាហរណ៍។

ដំណោះស្រាយ។

ដំបូងយើងធ្វើគំនូរ។

ចូរយើងធ្វើការសាងសង់បន្ថែមដើម្បី "មើល" មុំរវាងយន្តហោះ។

ដំបូង យើងកំណត់បន្ទាត់ត្រង់មួយ ដែលយន្តហោះ ABC និង BED 1 ប្រសព្វគ្នា។ ចំណុច B គឺជាចំណុចរួមមួយរបស់ពួកគេ។ តោះស្វែងរកទីពីរ ចំណុចរួមយន្តហោះទាំងនេះ។ បន្ទាត់ DA និង D 1 E ស្ថិតនៅលើយន្តហោះដូចគ្នា ADD 1 ហើយពួកវាមិនស្របគ្នាទេ ដូច្នេះហើយប្រសព្វគ្នា។ ម្យ៉ាងវិញទៀត បន្ទាត់ DA ស្ថិតនៅក្នុងយន្តហោះ ABC ហើយបន្ទាត់ D 1 E - នៅក្នុងយន្តហោះ BED 1 ដូច្នេះចំនុចប្រសព្វនៃបន្ទាត់ DA និង D 1 E នឹងជាចំណុចរួម។ យន្តហោះ ABCនិង BED 1 ។ ដូច្នេះ ចូរយើងបន្តបន្ទាត់ DA និង D 1 E ទៅចំនុចប្រសព្វរបស់ពួកគេ ដោយសម្គាល់ចំណុចប្រសព្វរបស់ពួកគេជាមួយនឹងអក្សរ F ។ បន្ទាប់មក BF គឺជាបន្ទាត់ត្រង់ដែលយន្តហោះ ABC និង BED 1 ប្រសព្វគ្នា។

វានៅសល់ដើម្បីសាងសង់បន្ទាត់ពីរដែលស្ថិតនៅក្នុងយន្តហោះ ABC និង BED 1 រៀងគ្នាឆ្លងកាត់ចំណុចមួយនៅលើបន្ទាត់ BF និងកាត់កែងទៅបន្ទាត់ BF - មុំរវាងបន្ទាត់ទាំងនេះតាមនិយមន័យនឹងស្មើនឹងមុំដែលចង់បានរវាង យន្តហោះ ABC និង BED 1 ។ តោះធ្វើបែបនេះ។

ចំណុច A គឺជាការព្យាករនៃចំណុច E ទៅលើយន្តហោះ ABC ។ តោះគូរបន្ទាត់ត្រង់ប្រសព្វ BF នៅមុំខាងស្តាំត្រង់ចំនុច M ។ បន្ទាប់មក បន្ទាត់ត្រង់ AM គឺជាការព្យាករនៃបន្ទាត់ត្រង់ EM ទៅលើយន្តហោះ ABC ហើយតាមទ្រឹស្តីបទនៃកាត់កែងបី។

ដូច្នេះមុំដែលត្រូវការរវាងយន្តហោះ ABC និង BED 1 គឺស្មើនឹង .

យើងអាចកំណត់ស៊ីនុស កូស៊ីនុស ឬតង់ហ្សង់នៃមុំនេះ (ហើយដូច្នេះមុំខ្លួនវា) ពីត្រីកោណខាងស្តាំ AEM ប្រសិនបើយើងដឹងពីប្រវែងនៃជ្រុងទាំងពីររបស់វា។ តាមលក្ខខណ្ឌវាងាយស្រួលក្នុងការស្វែងរកប្រវែង AE: ចាប់តាំងពីចំនុច E បែងចែកចំហៀង AA 1 ក្នុងសមាមាត្រនៃ 4 ទៅ 3 ដោយរាប់ពីចំណុច A ហើយប្រវែងនៃចំហៀង AA 1 គឺ 7 បន្ទាប់មក AE = 4 ។ ចូររកប្រវែង AM ។

ដើម្បីធ្វើដូចនេះសូមពិចារណា ត្រីកោណកែង ABF ដែលមានមុំខាងស្តាំ A ដែល AM ជាកំពស់។ តាមលក្ខខណ្ឌ AB = 2 ។ យើងអាចរកឃើញប្រវែងនៃចំហៀង AF ពីភាពស្រដៀងគ្នានៃត្រីកោណកែង DD 1 F និង AEF៖

ដោយប្រើទ្រឹស្តីបទពីថាហ្គោរ យើងរកឃើញពីត្រីកោណ ABF ។ យើង​រក​ឃើញ​ប្រវែង AM តាម​តំបន់​ត្រីកោណ ABF ៖ នៅ​ម្ខាង​ផ្ទៃ​ត្រីកោណ ABF គឺ​ស្មើ , នៅម្ខាងទៀត។ កន្លែងណា .

ដូច្នេះពីត្រីកោណខាងស្តាំ AEM យើងមាន .

បន្ទាប់មកមុំដែលត្រូវការរវាងយន្តហោះ ABC និង BED 1 គឺស្មើគ្នា (ចំណាំថា ).

ចម្លើយ៖

ក្នុងករណីខ្លះ ដើម្បីស្វែងរកមុំរវាងយន្តហោះប្រសព្វគ្នាពីរ វាងាយស្រួលក្នុងការកំណត់ Oxyz ហើយប្រើវិធីសាស្ត្រកូអរដោនេ។ តោះឈប់នៅទីនោះ។

ចូរយើងកំណត់ភារកិច្ច៖ រកមុំរវាងយន្តហោះប្រសព្វគ្នាពីរ និង . ចូរយើងកំណត់មុំដែលចង់បានជា .

យើងនឹងសន្មត់ថានៅក្នុងប្រព័ន្ធសំរបសំរួលរាងចតុកោណ Oxyz យើងដឹងពីកូអរដោនេនៃវ៉ិចទ័រធម្មតានៃយន្តហោះប្រសព្វគ្នា ហើយឬមានឱកាសស្វែងរកពួកវា។ អនុញ្ញាតឱ្យ គឺជាវ៉ិចទ័រធម្មតានៃយន្តហោះ និង គឺជាវ៉ិចទ័រធម្មតានៃយន្តហោះ។ យើងនឹងបង្ហាញពីរបៀបស្វែងរកមុំរវាងយន្តហោះប្រសព្វគ្នា និងតាមរយៈកូអរដោនេនៃវ៉ិចទ័រធម្មតានៃយន្តហោះទាំងនេះ។

ចូរ​យើង​បង្ហាញ​ពី​បន្ទាត់​ត្រង់​ដែល​ប្លង់​និង​ប្រសព្វ​ជា គ។ តាមរយៈចំណុច M នៅលើបន្ទាត់ c យើងគូរប្លង់កាត់កែងទៅបន្ទាត់ c ។ យន្តហោះប្រសព្វគ្នារវាងយន្តហោះ និងតាមបណ្តោយបន្ទាត់ a និង b រៀងគ្នា បន្ទាត់ a និង b ប្រសព្វគ្នានៅចំណុច M ។ តាមនិយមន័យ មុំរវាងប្លង់ប្រសព្វ និងស្មើនឹងមុំរវាងបន្ទាត់ប្រសព្វ a និង ខ។

ចូរយើងគូររូបវ៉ិចទ័រ និងប្លង់ធម្មតា និងពីចំណុច M ក្នុងយន្តហោះ។ ក្នុងករណីនេះ វ៉ិចទ័រស្ថិតនៅលើបន្ទាត់ដែលកាត់កែងទៅបន្ទាត់ a ហើយវ៉ិចទ័រស្ថិតនៅលើបន្ទាត់ដែលកាត់កែងទៅបន្ទាត់ ខ។ ដូច្នេះក្នុងប្លង់ វ៉ិចទ័រគឺជាវ៉ិចទ័រធម្មតានៃបន្ទាត់ a គឺជាវ៉ិចទ័រធម្មតានៃបន្ទាត់ ខ។

នៅក្នុងអត្ថបទស្វែងរកមុំរវាងបន្ទាត់ប្រសព្វគ្នា យើងបានទទួលរូបមន្តដែលអនុញ្ញាតឱ្យអ្នកគណនាកូស៊ីនុសនៃមុំរវាងបន្ទាត់ប្រសព្វដោយប្រើកូអរដោនេនៃវ៉ិចទ័រធម្មតា។ ដូច្នេះកូស៊ីនុសនៃមុំរវាងបន្ទាត់ a និង b ហើយជាលទ្ធផល។ កូស៊ីនុសនៃមុំរវាងយន្តហោះប្រសព្វហើយត្រូវបានរកឃើញដោយរូបមន្ត កន្លែងណា និង គឺជាវ៉ិចទ័រធម្មតានៃយន្តហោះ និងរៀងៗខ្លួន។ បន្ទាប់មកវាត្រូវបានគណនាជា .

តោះដោះស្រាយឧទាហរណ៍មុនដោយប្រើវិធីសាស្ត្រកូអរដោណេ។

ឧទាហរណ៍។

ដាន់ គូប ABCDA 1 B 1 C 1 D 1 ដែលក្នុងនោះ AB=2, AD=3, AA 1=7 និងចំនុច E បែងចែកចំហៀង AA 1 ក្នុងសមាមាត្រនៃ 4 ទៅ 3 ដោយរាប់ចាប់ពីចំនុច A។ រកមុំរវាងយន្តហោះ ABC និង BED 1។

ដំណោះស្រាយ។

ដោយសារជ្រុងនៃរាងចតុកោណកែងប៉ារ៉ាឡែលភីបនៅចំនុចកំពូលមួយគឺកាត់កែងជាគូ វាងាយស្រួលក្នុងការណែនាំ ប្រព័ន្ធចតុកោណសំរបសំរួល Oxyz ដូចនេះ៖ តម្រឹមការចាប់ផ្តើមជាមួយ vertex C ហើយដឹកនាំអ័ក្សកូអរដោនេ Ox, Oy និង Oz តាមជ្រុង CD, CB និង CC 1 រៀងគ្នា។

មុំរវាងយន្តហោះ ABC និង BED 1 អាចត្រូវបានរកឃើញតាមរយៈកូអរដោណេនៃវ៉ិចទ័រធម្មតានៃយន្តហោះទាំងនេះដោយប្រើរូបមន្ត ដែលនិងជាវ៉ិចទ័រធម្មតារបស់យន្តហោះ ABC និង BED 1 រៀងគ្នា។ ចូរកំណត់កូអរដោនេនៃវ៉ិចទ័រធម្មតា។

រង្វាស់នៃមុំរវាងយន្តហោះគឺ មុំស្រួចបង្កើត​ឡើង​ដោយ​បន្ទាត់​ត្រង់​ពីរ​ដែល​ស្ថិត​នៅ​ក្នុង​យន្តហោះ​ទាំង​នេះ ហើយ​គូស​កាត់​កែង​ទៅ​នឹង​បន្ទាត់​នៃ​ចំណុច​ប្រសព្វ​របស់​ពួកគេ។

ក្បួនដោះស្រាយសំណង់

1. ពីចំណុចដែលបំពាន K កាត់កែងត្រូវបានគូរទៅប្លង់នីមួយៗដែលបានផ្តល់ឱ្យ។
2. ដោយការបង្វិលជុំវិញបន្ទាត់កម្រិត មុំ γ° ជាមួយចំនុចកំពូលនៅចំណុច K ត្រូវបានកំណត់។
3. គណនាមុំរវាងប្លង់ ϕ° = 180 – γ° ផ្តល់ថា γ° > 90° ។ ប្រសិនបើγ°< 90°, то ∠ϕ° = ∠γ°.

តួលេខបង្ហាញពីករណីនៅពេលដែលយន្តហោះ α និង β ត្រូវបានផ្តល់ឱ្យដោយដាន។ សំណង់ចាំបាច់ទាំងអស់ត្រូវបានអនុវត្តតាមក្បួនដោះស្រាយហើយត្រូវបានពិពណ៌នាខាងក្រោម។

ដំណោះស្រាយ

1. នៅកន្លែងដែលបំពានក្នុងគំនូរ សម្គាល់ចំណុច K. ពីវា យើងបន្ទាបកាត់កែង m និង n រៀងគ្នាទៅនឹងប្លង់ α និង β ។ ទិសដៅនៃការព្យាករ m និង n មានដូចខាងក្រោម៖ m""⊥f 0α, m"⊥h 0α, n""⊥f 0β, n"⊥h 0β ។
2. យើងកំណត់ទំហំពិត ∠γ° រវាងបន្ទាត់ m និង n ។ ដើម្បីធ្វើដូចនេះនៅជុំវិញផ្នែកខាងមុខ f យើងបង្វិលយន្តហោះនៃមុំជាមួយ vertex K ទៅទីតាំងមួយស្របទៅនឹងយន្តហោះខាងមុខនៃការព្យាករ។ កាំបង្វិល R នៃចំណុច K ស្មើនឹងតម្លៃអ៊ីប៉ូតេនុសនៃត្រីកោណខាងស្តាំ O""K""K 0 ដែលផ្នែកម្ខាងគឺ K""K 0 = y K - y O ។
3. មុំដែលចង់បានគឺ ϕ° = ∠γ° ចាប់តាំងពី ∠γ° គឺស្រួច។

រូបខាងក្រោមបង្ហាញពីដំណោះស្រាយចំពោះបញ្ហាដែលវាត្រូវបានទាមទារដើម្បីស្វែងរកមុំγ°រវាងយន្តហោះ α និង β ដែលផ្តល់ដោយបន្ទាត់ប៉ារ៉ាឡែល និងប្រសព្វរៀងៗខ្លួន។

ដំណោះស្រាយ

1. យើងកំណត់ទិសដៅនៃការព្យាករផ្តេក h 1, h 2 និងផ្នែកខាងមុខ f 1, f 2, ជាកម្មសិទ្ធិរបស់យន្តហោះα និង β តាមលំដាប់ដែលបង្ហាញដោយព្រួញ។ ពីចំណុចបំពាន K នៅលើការ៉េ។ α និង β យើងលុបកាត់កែង e និង k ។ ក្នុងករណីនេះ e ""⊥f"" 1 , e "⊥h" 1 និង k""⊥f"" 2 , k "⊥h" 2 ។
2. យើងកំណត់ ∠γ° រវាងបន្ទាត់ e និង k ។ ដើម្បីធ្វើដូចនេះគូរបន្ទាត់ផ្តេក h 3 ហើយនៅជុំវិញវាយើងបង្វិលចំណុច K ទៅទីតាំង K 1 ដែល △CKD នឹងក្លាយទៅជាស្របទៅនឹងយន្តហោះផ្តេក ហើយនឹងត្រូវបានឆ្លុះបញ្ចាំងលើវាតាមទំហំធម្មជាតិ - △C "K" 1 D "។ ការព្យាករនៃចំណុចកណ្តាលនៃការបង្វិល O" ស្ថិតនៅលើចំណុចទាញទៅ h" 3 កាត់កែងទៅ K "O" ។ កាំ R ត្រូវបានកំណត់ពីត្រីកោណខាងស្តាំ O"K"K 0 ដែលចំហៀង K"K 0 = Z O - Z K ។
3. តម្លៃនៃតម្លៃដែលចង់បានគឺ ∠ϕ° = ∠γ° ចាប់តាំងពីមុំ γ° គឺស្រួច។

អត្ថបទនិយាយអំពីការស្វែងរកមុំរវាងយន្តហោះ។ បន្ទាប់ពីផ្តល់និយមន័យ យើងនឹងផ្តល់រូបភាពក្រាហ្វិក និងពិចារណាវិធីសាស្រ្តលម្អិតនៃការស្វែងរកកូអរដោនេដោយប្រើវិធីសាស្ត្រ។ យើងទទួលបានរូបមន្តសម្រាប់ប្លង់ប្រសព្វ ដែលរួមបញ្ចូលកូអរដោនេនៃវ៉ិចទ័រធម្មតា។

Yandex.RTB R-A-339285-1

សម្ភារៈនឹងប្រើប្រាស់ទិន្នន័យ និងគំនិតដែលត្រូវបានសិក្សាពីមុននៅក្នុងអត្ថបទអំពីយន្តហោះ និងបន្ទាត់នៅក្នុងលំហ។ ជាដំបូង វាចាំបាច់ក្នុងការបន្តទៅការវែកញែកដែលអនុញ្ញាតឱ្យយើងមានវិធីសាស្រ្តជាក់លាក់មួយក្នុងការកំណត់មុំរវាងយន្តហោះប្រសព្វគ្នាពីរ។

យន្តហោះប្រសព្វពីរ γ 1 និង γ 2 ត្រូវបានផ្តល់ឱ្យ។ ចំនុចប្រសព្វរបស់ពួកគេនឹងយកការកំណត់គ។ ការសាងសង់យន្តហោះ χ ត្រូវបានផ្សារភ្ជាប់ជាមួយនឹងចំនុចប្រសព្វនៃយន្តហោះទាំងនេះ។ យន្តហោះ χ ឆ្លងកាត់ចំណុច M ជាបន្ទាត់ត្រង់ c ។ ចំនុចប្រសព្វនៃយន្តហោះ γ 1 និង γ 2 នឹងត្រូវបានធ្វើឡើងដោយប្រើយន្តហោះ χ ។ យើងយកការកំណត់បន្ទាត់ប្រសព្វ γ 1 និង χ ជាបន្ទាត់ a ហើយបន្ទាត់ប្រសព្វ γ 2 និង χ ជាបន្ទាត់ ខ។ យើងឃើញថាចំនុចប្រសព្វនៃបន្ទាត់ a និង b ផ្តល់ចំនុច M ។

ទីតាំងនៃចំណុច M មិនប៉ះពាល់ដល់មុំរវាងបន្ទាត់ប្រសព្វ a និង b ហើយចំនុច M ស្ថិតនៅលើបន្ទាត់ c ដែលយន្តហោះ χ ឆ្លងកាត់។

វាចាំបាច់ក្នុងការសាងសង់យន្តហោះ χ 1 កាត់កែងទៅនឹងបន្ទាត់ c និងខុសពីយន្តហោះ χ ។ ចំនុចប្រសព្វនៃយន្តហោះ γ 1 និង γ 2 ដោយមានជំនួយពី χ 1 នឹងយកការរចនាបន្ទាត់ a 1 និង b 1 ។

វាអាចត្រូវបានគេមើលឃើញថានៅពេលសាងសង់ χ និង χ 1 បន្ទាត់ a និង b កាត់កែងទៅបន្ទាត់ c បន្ទាប់មក a 1, b 1 មានទីតាំងនៅកាត់កែងទៅបន្ទាត់ c ។ ការស្វែងរកបន្ទាត់ត្រង់ a និង a 1 ក្នុងយន្តហោះ γ 1 ដោយកាត់កែងទៅបន្ទាត់ត្រង់ c បន្ទាប់មកពួកគេអាចចាត់ទុកថាស្របគ្នា។ ដូចគ្នាដែរ ទីតាំងនៃ b និង b 1 ក្នុងយន្តហោះ γ 2 ដែលកាត់កែងទៅនឹងបន្ទាត់ត្រង់ c បង្ហាញពីភាពស្របគ្នា។ នេះមានន័យថា ចាំបាច់ត្រូវធ្វើការផ្ទេរប៉ារ៉ាឡែលនៃយន្តហោះ χ 1 ទៅ χ ដែលយើងទទួលបានបន្ទាត់ត្រង់ពីរស្របគ្នា a និង a 1, b និង b 1 ។ យើងរកឃើញថាមុំរវាងបន្ទាត់ប្រសព្វ a និង b 1 គឺស្មើនឹងមុំនៃបន្ទាត់ប្រសព្វ a និង b ។

តោះមើលរូបខាងក្រោម។

សំណើនេះត្រូវបានបញ្ជាក់ដោយការពិតដែលថារវាងបន្ទាត់ប្រសព្វ a និង b មានមុំមួយដែលមិនអាស្រ័យលើទីតាំងនៃចំណុច M នោះគឺជាចំណុចប្រសព្វ។ ខ្សែទាំងនេះស្ថិតនៅក្នុងយន្តហោះ γ 1 និង γ 2 ។ តាមពិតមុំលទ្ធផលអាចត្រូវបានចាត់ទុកថាជាមុំរវាងយន្តហោះប្រសព្វគ្នាពីរ។

ចូរបន្តទៅការកំណត់មុំរវាងយន្តហោះប្រសព្វដែលមានស្រាប់ γ 1 និង γ 2 ។

និយមន័យ ១

មុំរវាងយន្តហោះប្រសព្វពីរ γ 1 និង γ 2ហៅថាមុំដែលបង្កើតឡើងដោយចំនុចប្រសព្វនៃបន្ទាត់ a និង b ដែលយន្តហោះ γ 1 និង γ 2 ប្រសព្វគ្នាជាមួយយន្តហោះ χ កាត់កែងទៅបន្ទាត់ គ។

ពិចារណារូបភាពខាងក្រោម។

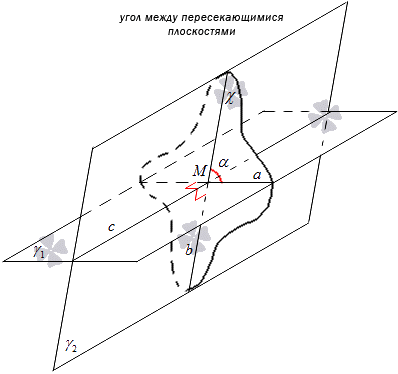
ការប្តេជ្ញាចិត្តអាចត្រូវបានដាក់ក្នុងទម្រង់មួយផ្សេងទៀត។ នៅពេលដែលយន្តហោះ γ 1 និង γ 2 ប្រសព្វគ្នា ដែល c ជាបន្ទាត់ដែលពួកគេប្រសព្វគ្នា សម្គាល់ចំណុច M ដែលគូសបន្ទាត់ a និង b កាត់កែងទៅបន្ទាត់ c ហើយដេកក្នុងយន្តហោះ γ 1 និង γ 2 បន្ទាប់មកមុំរវាង បន្ទាត់ a និង b នឹងជាមុំរវាងប្លង់។ នៅក្នុងការអនុវត្ត នេះគឺអាចអនុវត្តបានសម្រាប់ការសាងសង់មុំរវាងយន្តហោះ។

នៅពេលប្រសព្វគ្នា មុំមួយត្រូវបានបង្កើតឡើងដែលមានតម្លៃតិចជាង 90 ដឺក្រេ ពោលគឺរង្វាស់ដឺក្រេនៃមុំមានសុពលភាពនៅចន្លោះពេលនៃប្រភេទនេះ (0, 90]។ ក្នុងពេលជាមួយគ្នានោះ ប្លង់ទាំងនេះត្រូវបានគេហៅថាកាត់កែងប្រសិនបើ មុំខាងស្តាំត្រូវបានបង្កើតឡើងនៅចំនុចប្រសព្វ មុំរវាងប្លង់ប៉ារ៉ាឡែលត្រូវបានចាត់ទុកថាស្មើសូន្យ។

វិធីធម្មតាដើម្បីស្វែងរកមុំរវាងយន្តហោះប្រសព្វគ្នាគឺត្រូវអនុវត្តការសាងសង់បន្ថែម។ វាជួយកំណត់វាដោយភាពត្រឹមត្រូវ ហើយនេះអាចត្រូវបានធ្វើដោយប្រើសញ្ញានៃភាពស្មើគ្នា ឬភាពស្រដៀងគ្នានៃត្រីកោណ ស៊ីនុស និងកូស៊ីនុសនៃមុំមួយ។

ចូរយើងពិចារណាការដោះស្រាយបញ្ហាដោយប្រើឧទាហរណ៍ពី បញ្ហាប្រឡងរដ្ឋបង្រួបបង្រួមប្លុក C 2 ។

ឧទាហរណ៍ ១

ដែលបានផ្តល់ឱ្យចតុកោណ parallelepiped A B C D A 1 B 1 C 1 D 1 ដែលចំហៀង A B = 2, A D = 3, A A 1 = 7 ចំនុច E បែងចែកចំហៀង A A 1 ក្នុងសមាមាត្រ 4: 3 ។ រកមុំរវាងយន្តហោះ A B C និង B E D 1 ។

ដំណោះស្រាយ

សម្រាប់ភាពច្បាស់លាស់វាចាំបាច់ក្នុងការធ្វើគំនូរ។ យើងទទួលបាននោះ។

ការតំណាងដែលមើលឃើញគឺចាំបាច់ដើម្បីធ្វើឱ្យវាកាន់តែងាយស្រួលក្នុងការធ្វើការជាមួយមុំរវាងយន្តហោះ។

យើងកំណត់បន្ទាត់ត្រង់ដែលចំនុចប្រសព្វនៃយន្តហោះ A B C និង B E D 1 កើតឡើង។ ចំណុច B គឺជាចំណុចរួម។ ចំណុចរួមមួយទៀតនៃចំនុចប្រសព្វគួរតែត្រូវបានរកឃើញ។ ចូរយើងពិចារណាបន្ទាត់ត្រង់ D A និង D 1 E ដែលមានទីតាំងនៅក្នុងយន្តហោះដូចគ្នា A D D 1 ។ ទីតាំងរបស់ពួកគេមិនបង្ហាញពីភាពស្របគ្នាទេ វាមានន័យថាពួកគេមានចំនុចប្រសព្វ។

ទោះយ៉ាងណាក៏ដោយ បន្ទាត់ត្រង់ D A ស្ថិតនៅក្នុងយន្តហោះ A B C និង D 1 E ក្នុង B E D 1 ។ ពីនេះយើងទទួលបានបន្ទាត់ត្រង់ ឃនិង ឃ 1 អ៊ីមានចំណុចប្រសព្វទូទៅ ដែលជារឿងធម្មតាសម្រាប់យន្តហោះ A B C និង B E D 1 ។ ចង្អុលបង្ហាញចំណុចប្រសព្វនៃបន្ទាត់ ឃនិង D 1 E អក្សរ F ។ ពីនេះយើងទទួលបានថា B F គឺជាបន្ទាត់ត្រង់ដែលយន្តហោះ A B C និង B E D 1 ប្រសព្វគ្នា។

តោះមើលរូបខាងក្រោម។

ដើម្បីទទួលបានចំលើយ វាចាំបាច់ក្នុងការសង់បន្ទាត់ត្រង់ដែលមានទីតាំងនៅក្នុងយន្តហោះ A B C និង B E D 1 ឆ្លងកាត់ចំណុចដែលស្ថិតនៅលើបន្ទាត់ B F និងកាត់កែងទៅវា។ បន្ទាប់មកមុំលទ្ធផលរវាងបន្ទាត់ត្រង់ទាំងនេះត្រូវបានចាត់ទុកថាជាមុំដែលចង់បានរវាងយន្តហោះ A B C និង B E D 1 ។

ពីនេះយើងអាចឃើញថាចំនុច A គឺជាការព្យាករនៃចំនុច E ទៅលើយន្តហោះ A B C ។ វាចាំបាច់ក្នុងការគូសបន្ទាត់ត្រង់ប្រសព្វ B F នៅមុំខាងស្តាំត្រង់ចំនុច M ។ គេអាចឃើញថាបន្ទាត់ត្រង់ A M គឺជាការព្យាករ។ នៃបន្ទាត់ត្រង់ E M នៅលើយន្តហោះ A B C ដោយផ្អែកលើទ្រឹស្តីបទអំពីកាត់កែងទាំងនោះ A M ⊥ B F ។ ពិចារណារូបភាពខាងក្រោម។

∠ A M E គឺជាមុំដែលចង់បានដែលបង្កើតឡើងដោយយន្តហោះ A B C និង B E D 1 ។ ពីត្រីកោណលទ្ធផល A E M យើងអាចរកឃើញស៊ីនុស កូស៊ីនុស ឬតង់សង់នៃមុំ ហើយបន្ទាប់មកមុំដោយខ្លួនឯង លុះត្រាតែភាគីទាំងពីរដឹង។ តាមលក្ខខណ្ឌ យើងមានថាប្រវែង A E ត្រូវបានរកឃើញតាមវិធីនេះ៖ បន្ទាត់ត្រង់ A A 1 ត្រូវបានបែងចែកដោយចំនុច E ក្នុងសមាមាត្រ 4:3 ដែលមានន័យថាប្រវែងសរុបនៃបន្ទាត់ត្រង់គឺ 7 ផ្នែក បន្ទាប់មក A E = 4 ផ្នែក។ យើងរកឃើញ A M.

វាចាំបាច់ក្នុងការពិចារណាត្រីកោណកែង A B F ។ យើងមានមុំខាងស្តាំ A ជាមួយនឹងកម្ពស់ A M. ពីលក្ខខណ្ឌ A B = 2 បន្ទាប់មកយើងអាចរកប្រវែង A F ដោយភាពស្រដៀងគ្នានៃត្រីកោណ D D 1 F និង A E F ។ យើងទទួលបានថា A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

វាចាំបាច់ក្នុងការស្វែងរកប្រវែងចំហៀង B F នៃត្រីកោណ A B F ដោយប្រើទ្រឹស្តីបទពីតាហ្គោរ។ យើងទទួលបាន B F = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 ។ ប្រវែងនៃចំហៀង A M ត្រូវបានរកឃើញតាមរយៈតំបន់នៃត្រីកោណ A B F ។ យើង​មាន​ថា​ផ្ទៃ​អាច​ស្មើ​ទាំង S A B C = 1 2 · A B · A F និង S A B C = 1 2 · B F · A M ។

យើងទទួលបាន A M = A B A F B F = 2 4 2 5 = 4 5 5

បន្ទាប់មកយើងអាចរកតម្លៃតង់សង់នៃមុំនៃត្រីកោណ A E M. យើងទទួលបាន៖

t g ∠ A M E = A E A M = 4 4 5 5 = 5

មុំដែលចង់បានដែលទទួលបានដោយចំនុចប្រសព្វនៃយន្តហោះ A B C និង B E D 1 គឺស្មើនឹង a r c t g 5 បន្ទាប់មកតាមភាពសាមញ្ញយើងទទួលបាន r c t g 5 = a r c sin 30 6 = a r c cos 6 6 ។

ចម្លើយ៖ a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

ករណីខ្លះនៃការស្វែងរកមុំរវាងបន្ទាត់ប្រសព្វត្រូវបានបញ្ជាក់ដោយប្រើ សំរបសំរួលយន្តហោះ O x y z និងវិធីសាស្ត្រកូអរដោនេ។ ចូរយើងពិនិត្យមើលឱ្យកាន់តែច្បាស់។

ប្រសិនបើអ្នកត្រូវបានផ្តល់បញ្ហាដែលអ្នកត្រូវការរកមុំរវាងយន្តហោះប្រសព្វγ 1 និង γ 2 យើងសម្គាល់មុំដែលចង់បានជាα។

បន្ទាប់មក ប្រព័ន្ធដែលបានផ្តល់ឱ្យកូអរដោនេបង្ហាញថាយើងមានកូអរដោនេនៃវ៉ិចទ័រធម្មតានៃយន្តហោះប្រសព្វγ 1 និង γ 2 ។ បន្ទាប់មកយើងសម្គាល់ថា n 1 → = n 1 x, n 1 y, n 1 z គឺជាវ៉ិចទ័រធម្មតានៃយន្តហោះ γ 1, និង n 2 → = (n 2 x, n 2 y, n 2 z) - សម្រាប់ យន្តហោះ γ 2 ។ ចូរយើងពិចារណា ការរកឃើញលម្អិតមុំដែលស្ថិតនៅចន្លោះប្លង់ទាំងនេះតាមកូអរដោនេនៃវ៉ិចទ័រ។

វាចាំបាច់ក្នុងការកំណត់បន្ទាត់ត្រង់ដែលយន្តហោះ γ 1 និង γ 2 ប្រសព្វជាមួយអក្សរ គ។ នៅលើបន្ទាត់ c យើងមានចំនុច M ដែលយើងគូរប្លង់ χ កាត់កែងទៅ c ។ យន្តហោះ χ តាមបណ្តោយបន្ទាត់ a និង b ប្រសព្វគ្នារវាងយន្តហោះ γ 1 និង γ 2 នៅចំណុច M ។ ពីនិយមន័យវាដូចខាងក្រោមថាមុំរវាងយន្តហោះប្រសព្វγ 1 និង γ 2 គឺស្មើនឹងមុំនៃបន្ទាត់ប្រសព្វ a និង b ដែលជាកម្មសិទ្ធិរបស់យន្តហោះទាំងនេះរៀងគ្នា។

នៅក្នុងយន្តហោះ χ យើងគូរវ៉ិចទ័រធម្មតាពីចំនុច M ហើយសម្គាល់ពួកវា n 1 → និង n 2 → ។ វ៉ិចទ័រ n 1 → ស្ថិតនៅលើបន្ទាត់កាត់កែងទៅបន្ទាត់ a ហើយវ៉ិចទ័រ n 2 → មានទីតាំងនៅលើបន្ទាត់កាត់កែងទៅបន្ទាត់ b ។ ពីទីនេះយើងទទួលបានវា។ យន្តហោះដែលបានផ្តល់ឱ្យχ មានវ៉ិចទ័រធម្មតានៃបន្ទាត់ a ស្មើនឹង n 1 → និងសម្រាប់បន្ទាត់ b ស្មើ n 2 → ។ ពិចារណារូបភាពខាងក្រោម។

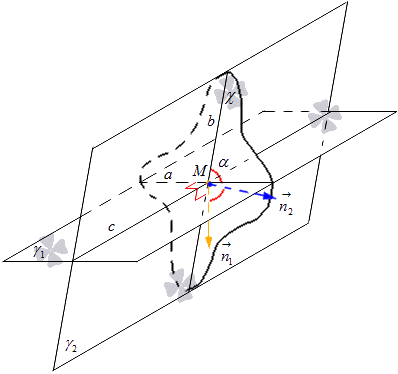
ពីទីនេះយើងទទួលបានរូបមន្តដែលយើងអាចគណនាស៊ីនុសនៃមុំនៃបន្ទាត់ប្រសព្វដោយប្រើកូអរដោនេនៃវ៉ិចទ័រ។ យើងបានរកឃើញថាកូស៊ីនុសនៃមុំរវាងបន្ទាត់ត្រង់ a និង b គឺដូចគ្នានឹងកូស៊ីនុសរវាងប្លង់ប្រសព្វ γ 1 និង γ 2 ដែលត្រូវបានចេញមកពី រូបមន្ត cosα = cos n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2 ដែលយើងមាននោះ n 1 → = (n 1 x, n 1 y, n 1 z) និង n 2 → = (n 2 x, n 2 y, n 2 z) គឺជាកូអរដោនេនៃ វ៉ិចទ័រនៃយន្តហោះដែលតំណាង។

មុំរវាងបន្ទាត់ប្រសព្វត្រូវបានគណនាដោយប្រើរូបមន្ត

α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2

ឧទាហរណ៍ ២

យោងតាមលក្ខខណ្ឌ ប៉ារ៉ាឡែលភីប A B C D A 1 B 1 C 1 D 1 ត្រូវបានផ្តល់ឱ្យ , ដែល A B = 2, A D = 3, A A 1 = 7, និងចំនុច E បែងចែកចំហៀង A A 1 4:3 ។ រកមុំរវាងយន្តហោះ A B C និង B E D 1 ។

ដំណោះស្រាយ

តាម​លក្ខខណ្ឌ​វា​ច្បាស់​ថា​ជ្រុង​របស់​វា​កាត់​កែង​ជា​គូ។ នេះមានន័យថា ចាំបាច់ត្រូវណែនាំប្រព័ន្ធកូអរដោណេ O x y z ជាមួយ vertex នៅចំណុច C និងកូអរដោនេអ័ក្ស O x, O y, O z ។ វាចាំបាច់ក្នុងការកំណត់ទិសដៅទៅភាគីសមស្រប។ ពិចារណារូបភាពខាងក្រោម។

យន្តហោះប្រសព្វ A B Cនិង B E D ១បង្កើតមុំដែលអាចរកឃើញដោយរូបមន្ត α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2 ដែលក្នុងនោះ n 1 → = (n 1 x, n 1 y, n 1 z) និង n 2 → = (n 2 x, n 2 y, n 2 z) គឺជាវ៉ិចទ័រធម្មតានៃ យន្តហោះទាំងនេះ។ វាចាំបាច់ដើម្បីកំណត់កូអរដោនេ។ តាមរូបភាពយើងឃើញ អ័ក្សសំរបសំរួល O x y ស្របគ្នានឹងប្លង់ A B C មានន័យថា កូអរដោនេនៃវ៉ិចទ័រធម្មតា k → ស្មើនឹងតម្លៃ n 1 → = k → = (0, 0, 1) ។

វ៉ិចទ័រធម្មតានៃយន្តហោះ B E D 1 ត្រូវបានយក ផលិតផលវ៉ិចទ័រ B E → និង B D 1 → ដែលកូអរដោនេរបស់ពួកគេត្រូវបានរកឃើញដោយកូអរដោនេ ចំណុចខ្លាំង B, E, D 1 ដែលត្រូវបានកំណត់ដោយផ្អែកលើលក្ខខណ្ឌនៃបញ្ហា។

យើងទទួលបាន B (0, 3, 0), D 1 (2, 0, 7) ។ ដោយសារតែ A E E A 1 = 4 3 ពីកូអរដោនេនៃចំនុច A 2, 3, 0, A 1 2, 3, 7 យើងរកឃើញ E 2, 3, 4 ។ យើងរកឃើញថា B E → = (2 , 0 , 4) , B D 1 → = 2 , − 3 , 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 − 3 7 = 12 · i → − 6 j → − 6 k → ⇔ n 2 → = (12 , - 6 , - 6)

វាចាំបាច់ក្នុងការជំនួសកូអរដោនេដែលបានរកឃើញទៅក្នុងរូបមន្តសម្រាប់គណនាមុំតាមរយៈអ័ក្សកូស៊ីនុស។ យើងទទួលបាន

α = a r c cos 0 12 + 0 ( − 6 ) + 1 ( − 6 ) 0 2 + 0 2 + 1 2 12 2 + ( − 6 ) 2 + ( − 6 ) 2 = a r c cos 6 6 6 = a r c cos 6 ៦

វិធីសាស្ត្រសម្របសម្រួលផ្តល់លទ្ធផលស្រដៀងគ្នា។

ចម្លើយ៖ a r c cos ៦ ៦.

បញ្ហាចុងក្រោយត្រូវបានពិចារណាជាមួយនឹងគោលដៅនៃការស្វែងរកមុំរវាងយន្តហោះប្រសព្វគ្នាដែលបានផ្តល់ឱ្យសមីការដែលគេស្គាល់ដែលមានស្រាប់នៃយន្តហោះ។

ឧទាហរណ៍ ៣

គណនាស៊ីនុស កូស៊ីនុសនៃមុំ និងតម្លៃនៃមុំដែលបង្កើតឡើងដោយបន្ទាត់ប្រសព្វគ្នាពីរ ដែលត្រូវបានកំណត់ក្នុងប្រព័ន្ធកូអរដោនេ O x y z និងផ្តល់ដោយសមីការ 2 x − 4 y + z + 1 = 0 និង 3 y - z - 1 = 0 ។

ដំណោះស្រាយ

នៅពេលសិក្សាប្រធានបទ សមីការទូទៅបន្ទាត់ត្រង់នៃទម្រង់ A x + B y + C z + D = 0 បានបង្ហាញថា A, B, C គឺជាមេគុណស្មើនឹងកូអរដោនេនៃវ៉ិចទ័រធម្មតា។ នេះមានន័យថា n 1 → = 2, − 4, 1 និង n 2 → = 0, 3, − 1 គឺជាវ៉ិចទ័រធម្មតានៃបន្ទាត់ដែលបានផ្តល់ឱ្យ។

វាចាំបាច់ក្នុងការជំនួសកូអរដោនេនៃវ៉ិចទ័រធម្មតានៃយន្តហោះទៅក្នុងរូបមន្តសម្រាប់គណនាមុំដែលចង់បាននៃយន្តហោះប្រសព្វគ្នា។ បន្ទាប់មកយើងទទួលបានវា។

α = a r c cos 2 0 + − 4 3 + 1 (− 1) 2 2 + − 4 2 + 1 2 = a r c cos 13 210

ពីទីនេះយើងមានដែលកូស៊ីនុសនៃមុំយក ទិដ្ឋភាព cosα = 13,210 ។ បន្ទាប់មកមុំនៃបន្ទាត់ប្រសព្វគ្នាមិនមានរាងមូលទេ។ ការជំនួសនៅក្នុង អត្តសញ្ញាណត្រីកោណមាត្រយើងរកឃើញថាតម្លៃនៃស៊ីនុសនៃមុំគឺស្មើនឹងកន្សោម។ ចូរ​យើង​គណនា​ហើយ​រក​ឃើញ

sin α = 1 - cos 2 α = 1 - 13,210 = 41,210

ចម្លើយ៖ sin α = 41,210, cos α = 13,210, α = a r c cos 13,210 = a r c sin 41,210 ។

ប្រសិនបើអ្នកសម្គាល់ឃើញកំហុសនៅក្នុងអត្ថបទ សូមរំលេចវា ហើយចុច Ctrl+Enter

ប្រភេទការងារ៖ ១៤
ប្រធានបទ៖ មុំរវាងយន្តហោះ

លក្ខខណ្ឌ

ដាណា prism ត្រឹមត្រូវ។ ABCDA_1B_1C_1D_1, M និង N គឺជាចំណុចកណ្តាលនៃគែម AB និង BC រៀងគ្នា ចំនុច K គឺជាចំណុចកណ្តាលនៃ MN ។

ក)បង្ហាញថាបន្ទាត់ KD_1 និង MN កាត់កែង។

ខ)ស្វែងរកមុំរវាងយន្តហោះ MND_1 និង ABC ប្រសិនបើ AB=8, AA_1=6\sqrt 2.

បង្ហាញដំណោះស្រាយ

ដំណោះស្រាយ

ក)នៅក្នុង \ ត្រីកោណ DCN និង \ ត្រីកោណ MAD យើងមាន៖ \angle C=\angle A=90^(\circ), CN=AM=\frac12AB, ស៊ីឌី=DA។

ដូច្នេះ \\ ត្រីកោណ DCN = \\ ត្រីកោណ MAD នៅលើជើងពីរ។ បន្ទាប់មក MD=DN, \ ត្រីកោណ DMN isosceles ។ នេះមានន័យថា DK មធ្យមក៏ជាកម្ពស់ផងដែរ។ ដូច្នេះ DK \perp MN ។

DD_1 \perp MND តាមលក្ខខណ្ឌ, D_1K - oblique, KD - ការព្យាករណ៍, DK \perp MN ។

ដូច្នេះ តាមទ្រឹស្តីបទអំពី កាត់កែងបី MN\perp D_1K ។

ខ)ដូចដែលបានបញ្ជាក់នៅក្នុង ក), DK \perp MN និង MN \perp D_1K ប៉ុន្តែ MN គឺជាបន្ទាត់ប្រសព្វនៃយន្តហោះ MND_1 និង ABC ដែលមានន័យថា \angle DKD_1 - មុំលីនេអ៊ែរមុំ dihedral រវាងយន្តហោះ MND_1 និង ABC ។

នៅក្នុង \ ត្រីកោណ DAM យោងតាមទ្រឹស្តីបទពីថាហ្គោរ DM= \sqrt (DA^2+AM^2)= \sqrt (64+16)= 4\sqrt 5, MN= \sqrt (MB^2+BN^2)= \sqrt (16+16)= ៤\ sqrt ២.ដូច្នេះនៅក្នុង \ ត្រីកោណ DKM ដោយទ្រឹស្តីបទពីថាហ្គោរ DK= \sqrt (DM^2-KM^2)= \sqrt (80-8)= 6\sqrt ២.បន្ទាប់មកនៅក្នុង \ ត្រីកោណ DKD_1, tg\angle DKD_1=\frac(DD_1)(DK)=\frac(6\sqrt 2)(6\sqrt 2)=1.

នេះមានន័យថា \angle DKD_1=45^(\circ)។

ចម្លើយ

៤៥ ^ (\ រង្វង់) ។

ប្រភេទការងារ៖ ១៤
ប្រធានបទ៖ មុំរវាងយន្តហោះ

លក្ខខណ្ឌ

នៅខាងស្ដាំ ព្រីសរាងបួនជ្រុង ABCDA_1B_1C_1D_1 ជ្រុងនៃមូលដ្ឋានគឺ 4, ឆ្អឹងជំនីរចំហៀងស្មើនឹង 6 ។ ចំណុច M គឺជាចំណុចកណ្តាលនៃគែម CC_1 ចំណុច N ត្រូវបានសម្គាល់នៅលើគែម BB_1 ដូចជា BN:NB_1=1:2 ។

ក)តើយន្តហោះ AMN បែងចែកគែម DD_1 ក្នុងសមាមាត្រអ្វី?

ខ)ស្វែងរកមុំរវាងយន្តហោះ ABC និង AMN ។

បង្ហាញដំណោះស្រាយ

ដំណោះស្រាយ

ក)យន្តហោះ AMN កាត់គែម DD_1 នៅចំណុច K ដែលជាចំនុចកំពូលទីបួននៃផ្នែកនៃព្រីសដែលបានផ្តល់ឱ្យដោយយន្តហោះនេះ។ ផ្នែកឈើឆ្កាងគឺជាប្រលេឡូក្រាម ANMK ពីព្រោះមុខទល់មុខនៃព្រីសដែលបានផ្តល់ឱ្យគឺស្របគ្នា។

BN =\frac13BB_1=2.ចូរគូរ KL \parallel CD បន្ទាប់មកត្រីកោណ ABN និង KLM គឺស្មើគ្នា ដែលមានន័យថា ML=BN=2, LC=MC-ML=3-2=1, KD=LC=1។បន្ទាប់មក KD_1=6-1=5 ។

ខ)ឥឡូវនេះ អ្នកអាចរកឃើញសមាមាត្រ KD:KD_1=1:5។

F គឺជាចំណុចប្រសព្វនៃបន្ទាត់ត្រង់ CD និង KM ។ យន្តហោះ ABC និង AMN ប្រសព្វគ្នាតាមបន្ទាត់ត្រង់ AF ។ មុំ \angle KHD = \ alpha គឺជាមុំលីនេអ៊ែរនៃមុំ dihedral (HD\perp AF បន្ទាប់មកដោយទ្រឹស្តីបទបញ្ច្រាសទៅទ្រឹស្តីបទនៃកាត់កែងបី KH \perp AF) និងជាមុំស្រួចនៃត្រីកោណខាងស្តាំ KHD, ជើង KD=1 ។ ត្រីកោណ FKD និង FMC គឺស្រដៀងគ្នា (KD \parallel MC) ដូច្នេះ FD:FC=KD:MC ដោះស្រាយសមាមាត្រ FD:(FD+4)=1:3 យើងទទួលបាន FD=2។ នៅក្នុងត្រីកោណកែង AFD (\angle D=90^(\circ)) ដែលមានជើង 2 និង 4 យើងគណនាអ៊ីប៉ូតេនុស AF=\sqrt (4^2+2^2)=2\sqrt 5, DH= AD\cdot FD:AF=

\\ frac (4 \\ cdot 2) (2 \\ sqrt 5) = \\ frac4 (\ sqrt 5) ។នៅក្នុងត្រីកោណកែង KHD យើងរកឃើញ tg \alpha = \\ frac(KD)(DH)=\frac(\sqrt 5)4,

ចម្លើយ

ក) 1:5;

ខ) នេះមានន័យថាមុំដែលចង់បាន

\alpha=arctg\frac(\sqrt ៥) ៤. arctg\frac(\sqrt ៥) ៤.ប្រភព៖ "គណិតវិទ្យា។ ការរៀបចំសម្រាប់ការប្រឡងបង្រួបបង្រួមរដ្ឋ 2017 ។

ប្រភេទការងារ៖ ១៤
ប្រធានបទ៖ មុំរវាងយន្តហោះ

លក្ខខណ្ឌ

កម្រិតប្រវត្តិរូប " អេដ។ F. F. Lysenko, S. Yu.

ក)សាងសង់ផ្នែកមួយនៃពីរ៉ាមីតជាមួយនឹងយន្តហោះឆ្លងកាត់បន្ទាត់ NF ស្របទៅនឹង MP អង្កត់ទ្រូង ប្រសិនបើចំណុច F ជាពាក់កណ្តាលនៃគែម MK ។

ខ)ស្វែងរកមុំរវាងប្លង់ផ្នែក និងយន្តហោះ KMP ។

បង្ហាញដំណោះស្រាយ

ដំណោះស្រាយ

ក)សូមឱ្យ KO ជាកម្ពស់នៃពីរ៉ាមីត, F ចំណុចកណ្តាលនៃ MK ; FE \parallel MP (នៅក្នុងយន្តហោះ PKM) ។ ចាប់តាំងពី FE គឺ បន្ទាត់កណ្តាល\ ត្រីកោណ PKM បន្ទាប់មក FE=\frac(MP) ២.

អនុញ្ញាតឱ្យយើងសាងសង់ផ្នែកមួយនៃពីរ៉ាមីតជាមួយនឹងយន្តហោះឆ្លងកាត់ NF និងស្របទៅនឹង MP នោះគឺយន្តហោះ NFE ។ L គឺជាចំនុចប្រសព្វនៃ EF និង KO ។ ដោយសារចំនុច L និង N ជាកម្មសិទ្ធិរបស់ផ្នែកដែលចង់បាន ហើយស្ថិតនៅក្នុងយន្តហោះ KQN បន្ទាប់មកចំនុច T ដែលទទួលបានជាចំនុចប្រសព្វនៃ LN និង KQ ក៏ជាចំនុចប្រសព្វនៃផ្នែកដែលចង់បាន និងគែម KQ ផងដែរ។ NETF គឺជាផ្នែកដែលត្រូវការ។

ខ)យន្តហោះ NFE និង MPK ប្រសព្វគ្នាតាមបណ្តោយបន្ទាត់ត្រង់ FE ។ នេះមានន័យថាមុំរវាងយន្តហោះទាំងនេះស្មើនឹងមុំលីនេអ៊ែរនៃមុំ dihedral OFEN ចូរយើងសាងសង់វា៖ LO\perpMP, MP\ប៉ារ៉ាឡែល FE,ហេតុនេះ LO\perpFE;\triangle NFE - isosceles (NE=NF ជាមេដ្យានដែលត្រូវគ្នា។ ត្រីកោណស្មើគ្នា KPN និង KMN ) NL គឺជាមធ្យមរបស់វា (EL=LF ចាប់តាំងពី PO=OM និង \\ ត្រីកោណ KEF \\ ស៊ីម \\ ត្រីកោណ KPM) ។ ដូច្នេះ NL \perp FE និង \angle NLO គឺជាអ្វីដែលចង់បាន។

ON=\frac12QN=\frac12MN\sqrt 2=3\sqrt 2.

\\ ត្រីកោណ KON - ចតុកោណ។

ជើង KO យោងតាមទ្រឹស្តីបទពីថាហ្គោរគឺស្មើនឹង KO=\sqrt (KN^2-ON^2) ។

OL= \frac12KO= \frac12\sqrt(KN^2-ON^2)= \frac12\sqrt (9\cdot 26-9\cdot 2) = \frac12\sqrt(9(26-2))= \\ frac32 \\ sqrt (24) = \frac32\cdot 2\sqrt 6= 3\sqrt ៦.

tg\angle NLO =\frac(ON)(OL)=\frac(3\sqrt 2)(3\sqrt 6)=\frac1(\sqrt 3),

\angle NLO=30^(\circ) ។

ចម្លើយ

ប្រភព៖ "គណិតវិទ្យា។ ការរៀបចំសម្រាប់ការប្រឡងបង្រួបបង្រួមរដ្ឋ 2017 ។ កម្រិតប្រវត្តិរូប។" អេដ។ F. F. Lysenko, S. Yu.

ប្រភេទការងារ៖ ១៤
ប្រធានបទ៖ មុំរវាងយន្តហោះ

លក្ខខណ្ឌ

គែមទាំងអស់នៃព្រីសត្រីកោណធម្មតា ABCA_(1)B_(1)C_(1) គឺស្មើនឹង 6។ យន្តហោះកាត់ត្រូវបានគូរតាមចំនុចកណ្តាលនៃគែម AC និង BB_(1) និង vertex A_(1) ។

ក)បង្ហាញថាគែម BC ត្រូវបានបែងចែកដោយប្លង់កាត់ក្នុងសមាមាត្រ 2: 1 ដោយរាប់ពីកំពូល C ។

ខ)រកមុំរវាងយន្តហោះកាត់ និងប្លង់គោល។

បង្ហាញដំណោះស្រាយ

ដំណោះស្រាយ

ក)អនុញ្ញាតឱ្យ D និង E ជាចំណុចកណ្តាលនៃគែម AC និង BB_(1) រៀងគ្នា។

នៅក្នុងយន្តហោះ AA_(1)C_(1) យើងគូរបន្ទាត់ត្រង់ A_(1)D ដែលកាត់បន្ទាត់ត្រង់ CC_(1) នៅចំណុច K ក្នុងយន្តហោះ BB_(1)C_(1) - បន្ទាត់ត្រង់ KE ដែលប្រសព្វគែម BC នៅចំណុច F ។ ចំណុចតភ្ជាប់ A_(1) និង E ដេកក្នុងយន្តហោះ AA_(1)B_(1) ក៏ដូចជា D និង F ដែលដេកក្នុងយន្តហោះ ABC យើងទទួលបានផ្នែក A_(1)EFD ។

\bigtriangleup AA_(1)D=\bigtriangleup CDKតាមជើង AD=DC និងមុំស្រួច។

\angle ADA_(1)=\angle CDK - ដូចជាបញ្ឈរ វាធ្វើតាមនោះ AA_(1)=CK=6។ \bigtriangleup CKF និង \bigtriangleup BFE គឺស្រដៀងគ្នានៅមុំពីរ\angle FBE=\angle KCF=90^\circ,

\angle BFE=\angle CFK - ដូចជាបញ្ឈរ។\frac(CK)(BE)=\frac(6)(3)=2,

ខ)នោះគឺមេគុណភាពស្រដៀងគ្នាគឺ 2 ដែលមានន័យថា CF:FB = 2: 1 ។ តោះអនុវត្ត AH \ perp DF ។មុំរវាងប្លង់ផ្នែក និងប្លង់គោលគឺស្មើនឹងមុំ AHA_(1)។

ជាការពិតផ្នែក AH \perp DF (DF គឺជាបន្ទាត់ប្រសព្វនៃយន្តហោះទាំងនេះ) គឺជាការព្យាករនៃផ្នែក A_(1)H ទៅលើយន្តហោះមូលដ្ឋាន ដូច្នេះយោងទៅតាមទ្រឹស្តីបទនៃកាត់កែងបី A_(1)H \ perp DF ។

\angle AHA_(1)=arctg\frac(AA_(1))(AH)។

AA_(1)=6. តោះស្វែងរក AH ។ \angle ADH = \angle FDC (ដូចគ្នាទៅនឹងបញ្ឈរ)។

តាមទ្រឹស្តីបទកូស៊ីនុសក្នុង \bigtriangleup DFC៖

DF^2=FC^2+DC^2- 2FC \cdot DC \cdot \cos 60^\circ,

DF^2=4^2+3^2-2 \\cdot 4 \\cdot 3 \\cdot \\frac(1)(2)=13។

FC^2=DF^2+DC^2-

2DF\cdot DC\cdot\cos\angle FDC,

4^2=13+9-2\sqrt(13) \cdot 3 \cdot \cos \angle FDC,\cos \angle FDC=\frac(6)(2\sqrt(13)\cdot 3)=\frac(1)(\sqrt(13))។

ដោយ​កូរ៉ូឡារី​ទៅ​អត្តសញ្ញាណ​ត្រីកោណមាត្រ​មូលដ្ឋាន \sin \angle FDC=\sqrt(1-\left (\frac(1)(\sqrt(13))\right)^2)=\frac(2\sqrt(3))(\sqrt(13)) .

ពី \bigtriangleup ADH យើងរកឃើញ AH: AH=AD \cdot \sin \angle ADH, (\angle FDC=\angle ADH)។ AH=3 \cdot \frac(2\sqrt(3))(\sqrt(13))=\frac(6\sqrt(13))(\sqrt(13))។ \angle AHA_(1)=

ចម្លើយ

arctg\frac(AA_(1))(AH)=

ប្រភព៖ "គណិតវិទ្យា។ ការរៀបចំសម្រាប់ការប្រឡងបង្រួបបង្រួមរដ្ឋ 2017 ។ កម្រិតប្រវត្តិរូប។" អេដ។ F. F. Lysenko, S. Yu.

ប្រភេទការងារ៖ ១៤
ប្រធានបទ៖ មុំរវាងយន្តហោះ

លក្ខខណ្ឌ

arctg\frac(6 \cdot \sqrt(13))(6\sqrt(3))= arctg\frac(\sqrt(39))(3)។ arctg\frac(\sqrt(39))(3)។

ក)មូលដ្ឋាននៃព្រីសខាងស្តាំ ABCDA_(1)B_(1)C_(1)D_(1) គឺជារូបចម្លាក់ដែលមាន

ខ)មុំ obtuse

បង្ហាញដំណោះស្រាយ

ដំណោះស្រាយ

ក) B ស្មើនឹង 120^\circ ។ គែមទាំងអស់នៃព្រីសនេះគឺស្មើនឹង 10 ។ ចំណុច P និង K គឺជាចំណុចកណ្តាលនៃគែម CC_(1) និង CD រៀងគ្នា។បង្ហាញថាបន្ទាត់ PK និង PB_(1) កាត់កែង។

រកមុំរវាងយន្តហោះ PKB_(1) និង C_(1)B_(1)B ។ យើងនឹងប្រើវិធីសាស្ត្រកូអរដោនេ។ ចូរយើងស្វែងរកផលិតផលចំនុច វ៉ិចទ័រ \vec(PK) និង \vec(PB_(1)) ហើយបន្ទាប់មកកូស៊ីនុសនៃមុំរវាងវ៉ិចទ័រទាំងនេះ។ តោះតម្រង់អ័ក្ស Oy តាម CD អ័ក្ស Oz តាម CC_(1) និង Ox axis \perp CD។ C គឺជាប្រភពដើម។ បន្ទាប់មក C (0;0;0);

C_(1)(0;0;10); P(0;0;5);

K(0;5;0);

B(BC \cos 30^\circ; BC\sin 30^\circ; 0), នោះគឺ B(5\sqrt(3); 5;0),

\cos \alpha =0 ដែលមានន័យថា \vec(PK) \perp \vec(PB_(1)) ហើយបន្ទាត់ PK និង PB_(1) គឺកាត់កែង។

ខ)មុំរវាងប្លង់គឺស្មើនឹងមុំរវាងវ៉ិចទ័រដែលមិនមែនជាសូន្យកាត់កែងទៅនឹងយន្តហោះទាំងនេះ (ឬប្រសិនបើមុំគឺ obtuse មុំនៅជាប់នឹងវា)។ វ៉ិចទ័របែបនេះត្រូវបានគេហៅថាធម្មតាទៅនឹងយន្តហោះ។ ចូរយើងស្វែងរកពួកគេ។

អនុញ្ញាតឱ្យ \vec(n_(1))=\(x; y; z\) កាត់កែងទៅនឹងយន្តហោះ PKB_(1)។ ចូរយើងស្វែងរកវាដោយការដោះស្រាយប្រព័ន្ធ

\begin(cases) \vec(n_(1)) \perp \vec(PK), \\ \vec(n_(1)) \perp \vec(PB_(1))។ \end(ករណី)

\begin(cases) \vec(n_(1)) \\cdot \vec(PK)=0, \\ \vec(n_(1)) \\cdot \vec(PB_(1))=0; \end(ករណី)

\begin(cases) 0x+5y-5z=0, \\ 5\sqrt(3)x+5y+5z=0; \end(ករណី)

\begin(cases)y=z, \\ x=\frac(-y-z)(\sqrt(3))។ \end(ករណី) តោះយក y=1; z=1; x=\frac(-2)(\sqrt(3)),

\vec(n_(1))=\left \(\frac(-2)(\sqrt(3));1;1\right\) អនុញ្ញាតឱ្យ \vec(n_(2))=\(x; y; z\) កាត់កែងទៅនឹងយន្តហោះ C_(1)B_(1)B ។

ចូរយើងស្វែងរកវាដោយការដោះស្រាយប្រព័ន្ធ

\begin(cases) \vec(n_(2)) \perp \vec(CC_(1)), \\ \vec(n_(2)) \perp \vec(CB)។ \end(ករណី)

\vec(CC_(1))=\(0;0;10\), \vec(CB)=\(5\sqrt(3); 5; 0\)។

\begin(cases) \vec(n_(2)) \cdot \vec(CC_(1))=0, \\ \vec(n_(2)) \cdot \vec(CB)=0; \end(ករណី)

\begin(cases)y=z, \\ x=\frac(-y-z)(\sqrt(3))។ \end(ករណី) \begin(cases) 0x+0y+10z=0, \\ 5\sqrt(3)x+5y+0z=0; \end(ករណី) \begin(cases)z=0, \\ y=-\sqrt(3)x ។ \end(ករណី)

x=1; y=-\sqrt(3); z=0, \vec(n_(2))=\(1; -\sqrt(3);0\)ចូរយើងស្វែងរកកូស៊ីនុសនៃមុំដែលចង់បាន \beta (វា

ស្មើនឹងម៉ូឌុល កូស៊ីនុសនៃមុំរវាង \vec(n_(1)) និង \vec(n_(2))) ។ \cos \beta= \frac(|\vec(n_(1)) \cdot \vec(n_(2))|)(|\vec(n_(1))|\cdot |\vec(n_(2))|)= \frac(\left |-\dfrac(2)(\sqrt(3))\cdot 1+1\cdot (-\sqrt(3))+1\cdot 0\right |)(\sqrt(\dfrac( 4)(3)+1+1) \\cdot \sqrt(1+3+0))=

\frac(\dfrac(5)(\sqrt(3)))(2\sqrt(\dfrac(10)(3))))= \frac(\sqrt(10))(4).

ចម្លើយ

\cos \beta = \frac(\sqrt(10))(4),

ប្រភព៖ "គណិតវិទ្យា។ ការរៀបចំសម្រាប់ការប្រឡងបង្រួបបង្រួមរដ្ឋ 2017 ។ កម្រិតប្រវត្តិរូប។" អេដ។ F. F. Lysenko, S. Yu.

\beta=\arccos\frac(\sqrt(10))(4). \arccos\frac(\sqrt(10))(4) ABCD គឺជាការ៉េនិង

មុខចំហៀង

- ចតុកោណកែងស្មើគ្នា។ ចាប់តាំងពីប្លង់ផ្នែកឆ្លងកាត់ចំណុច M និង D ស្របទៅនឹងអង្កត់ទ្រូង AC បន្ទាប់មកដើម្បីបង្កើតវានៅក្នុងយន្តហោះ A_(1) AC ដល់ចំណុច M យើងគូរផ្នែក MN ស្របទៅនឹង AC ។ យើងទទួលបាន AC \parallel (MDN) ដោយផ្អែកលើភាពស្របគ្នានៃបន្ទាត់ និងយន្តហោះ។យន្តហោះ MDN កាត់​យន្តហោះ​ប៉ារ៉ាឡែល A_(1)AD និង B_(1)BC បន្ទាប់មក​តាម​លក្ខណៈ​សម្បត្តិ

យន្តហោះស្របគ្នា។

បន្ទាត់ប្រសព្វនៃមុខ A_(1)ADD_(1) និង B_(1)BCC_(1) ជាមួយយន្តហោះ MDN គឺស្របគ្នា។

ខ)ចូររកមុំរវាងប្លង់ផ្នែក និងប្លង់គោល។ សូម​ឲ្យ​ប្លង់​ផ្នែក​កាត់​ប្លង់​គោល​តាម​បណ្តោយ​បន្ទាត់​ត្រង់​ខ្លះ p ឆ្លងកាត់​ចំណុច D ។ AC \parallel MN ដូច្នេះ AC \parallel p (ប្រសិនបើ​យន្តហោះ​ឆ្លងកាត់​បន្ទាត់​ស្រប​នឹង​យន្តហោះ​ផ្សេងទៀត ហើយ​ប្រសព្វ​យន្តហោះ​នេះ នោះ​បន្ទាត់​ប្រសព្វ​នៃ​យន្តហោះ​គឺ​ស្រប​នឹង​បន្ទាត់​នេះ)។ BD \perp AC ជាអង្កត់ទ្រូងនៃការ៉េ ដែលមានន័យថា BD \perp p ។

BD គឺជាការព្យាករនៃ ED ទៅលើយន្តហោះ ABC បន្ទាប់មកតាមទ្រឹស្តីបទនៃបន្ទាត់កាត់កែងបី ED \perp p ដូច្នេះ \angle EDB គឺជាមុំលីនេអ៊ែរនៃមុំ dihedral រវាងប្លង់ផ្នែក និងប្លង់គោល។

កំណត់ប្រភេទនៃ DMEN បួនជ្រុង។ MD \parallel EN ស្រដៀងនឹង ME \parallel DN ដែលមានន័យថា DMEN គឺជាប៉ារ៉ាឡែល ហើយចាប់តាំងពី MD=DN (ត្រីកោណខាងស្តាំ MAD និង NCD គឺស្មើគ្នានៅលើជើងពីរ៖ AD=DC ជាជ្រុងនៃការ៉េ AM=CN ជា ចម្ងាយរវាងបន្ទាត់ប៉ារ៉ាឡែល AC និង MN) ដូច្នេះ DMEN គឺជារូបចម្លាក់។ ដូច្នេះ F គឺជាចំណុចកណ្តាលនៃ MN ។ តាមលក្ខខណ្ឌ AM:MA_(1)=2:3 បន្ទាប់មក

AM=\frac(2)(5)AA_(1)=\frac(2)(5) \cdot 5\sqrt(6)=2\sqrt(6)។ AMNC គឺជាចតុកោណកែង F គឺពាក់កណ្តាលនៃ MN, O គឺជាពាក់កណ្តាលនៃ AC ។ មានន័យថា FO\ប៉ារ៉ាឡែល MA, FO\ perp AC,

FO=MA=2\sqrt(6)។ ដោយដឹងថាអង្កត់ទ្រូងនៃការ៉េគឺ a\sqrt(2), កន្លែងដែល a គឺជាផ្នែកម្ខាងនៃការ៉េយើងទទួលបាន BD=4\sqrt(2) ។

OD=\frac(1)(2)BD=\frac(1)(2)\cdot 4\sqrt(2)=2\sqrt(2)។ នៅក្នុងត្រីកោណកែង FOD\enspace tg \angle FDO=\frac(FO)(OD)=\frac(2\sqrt(6))(2\sqrt(2))=\sqrt(3)។

ដូច្នេះ \angle FDO=60^\circ ។

\(\blacktriangleright\) មុំ Dihedral គឺជាមុំមួយដែលបង្កើតឡើងដោយពាក់កណ្តាលប្លង់ពីរ និងបន្ទាត់ត្រង់ \(a\) ដែលជាព្រំដែនរួមរបស់ពួកគេ។ \(\blacktriangleright\) ដើម្បីស្វែងរកមុំរវាងប្លង់ \(\xi\) និង \(\pi\) អ្នកត្រូវស្វែងរកមុំលីនេអ៊ែរ (និងហឹរ ឬផ្ទាល់

) មុំ dihedral បង្កើតឡើងដោយយន្តហោះ \(\xi\) និង \(\pi\) : ជំហានទី 1: អនុញ្ញាតឱ្យ \(\xi\cap\pi=a\) (បន្ទាត់នៃចំនុចប្រសព្វនៃយន្តហោះ) ។ នៅក្នុងយន្តហោះ \(\xi\) យើងកត់សំគាល់ចំណុចបំពាន

\(F\) និងអនុវត្ត \(FA\perp a\);

ជំហានទី 2: អនុវត្ត \(FG\perp \pi\);

ជំហានទី 3: យោងតាម ​​TTP (\(FG\) - កាត់កែង, \(FA\) - oblique, \(AG\) - ការព្យាករណ៍) យើងមាន: \(AG\perp a\);

ជំហានទី 4៖ មុំ \(\angle FAG\) ត្រូវបានគេហៅថាមុំលីនេអ៊ែរនៃមុំ dihedral ដែលបង្កើតឡើងដោយយន្តហោះ \(\xi\) និង \(\pi\) ។
ចំណាំថាត្រីកោណ \(AG\) ជាមុំខាងស្តាំ។ ចំណាំផងដែរថាយន្តហោះ \(AFG\) ដែលត្រូវបានសាងសង់តាមរបៀបនេះគឺកាត់កែងទៅនឹងយន្តហោះទាំងពីរ \(\xi\) និង \(\pi\) ។ ដូច្នេះយើងអាចនិយាយខុសគ្នា៖\(\xi\) និង \(\pi\) គឺ​ជា​មុំ​រវាង​បន្ទាត់​ប្រសព្វ​គ្នា​ពីរ \(c\in \xi\) និង \(b\in\pi\) បង្កើត​ប្លង់​កាត់​កែង​ទៅ និង \(\xi\ ) និង \(\pi\) ។

កិច្ចការទី 1 #2875

កម្រិតកិច្ចការ៖ ពិបាកជាងការប្រឡងរដ្ឋបង្រួបបង្រួម

ដាណា ពីរ៉ាមីតរាងបួនជ្រុងគែមទាំងអស់ស្មើគ្នា ហើយមូលដ្ឋានគឺជាការ៉េ។ ស្វែងរក \(6\cos \alpha\) ដែល \(\alpha\) គឺជាមុំរវាងមុខចំហៀងរបស់វា។

អនុញ្ញាតឱ្យ \(SABCD\) - ពីរ៉ាមីតនេះ។(\(S\) គឺជាចំនុចកំពូល) ដែលគែមរបស់វាស្មើនឹង \(a\) ។ អាស្រ័យហេតុនេះ មុខចំហៀងទាំងអស់គឺជាត្រីកោណស្មើគ្នា។ ចូរយើងស្វែងរកមុំរវាងមុខ \(SAD\) និង \(SCD\) ។

តោះធ្វើ \(CH\perp SD\) ។ ដោយសារតែ \\(\ត្រីកោណ SAD=\ត្រីកោណ SCD\)បន្ទាប់មក \(AH\) ក៏នឹងជាកម្ពស់នៃ \(\ត្រីកោណ SAD\) ផងដែរ។ ដូច្នេះតាមនិយមន័យ \(\angle AHC=\alpha\) គឺជាមុំលីនេអ៊ែរនៃមុំ dihedral រវាងមុខ \(SAD\) និង \(SCD\) ។
ដោយសារមូលដ្ឋានគឺជាការ៉េ បន្ទាប់មក \(AC=a\sqrt2\) ។ សូមចំណាំផងដែរថា \(CH=AH\) គឺជាកម្ពស់ ត្រីកោណសមមូលជាមួយចំហៀង \(a\) ដូច្នេះ \(CH=AH=\frac(\sqrt3)2a\) ។
បន្ទាប់មកដោយទ្រឹស្តីបទកូស៊ីនុសពី \(\ត្រីកោណ AHC\)៖ \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]

ចម្លើយ៖ -២

កិច្ចការទី 2 #2876

កម្រិតកិច្ចការ៖ ពិបាកជាងការប្រឡងរដ្ឋបង្រួបបង្រួម

យន្តហោះ \(\pi_1\) និង \(\pi_2\) ប្រសព្វគ្នានៅមុំមួយដែលកូស៊ីនុសស្មើនឹង \(0.2\) ។ ប្លង់ \\(\pi_2\) និង \(\pi_3\) ប្រសព្វគ្នានៅមុំខាងស្តាំ ហើយបន្ទាត់នៃចំនុចប្រសព្វនៃយន្តហោះ \(\pi_1\) និង \(\pi_2\) គឺស្របទៅនឹងបន្ទាត់ប្រសព្វនៃ យន្តហោះ \(\pi_2\) និង \(\ pi_3\) ។ ស្វែងរកស៊ីនុសនៃមុំរវាងប្លង់ \(\pi_1\) និង \(\pi_3\) ។

សូមឱ្យបន្ទាត់ប្រសព្វនៃ \(\pi_1\) និង \(\pi_2\) ជាបន្ទាត់ត្រង់ \(a\) បន្ទាត់ប្រសព្វនៃ \(\pi_2\) និង \(\pi_3\) ជាបន្ទាត់ត្រង់ បន្ទាត់ \(b\) និងបន្ទាត់ប្រសព្វ \(\pi_3\) និង \(\pi_1\) – បន្ទាត់ត្រង់ \(c\) ។ ចាប់តាំងពី \(a\parallel b\) បន្ទាប់មក \(c\parallel a\parallel b\) (យោងទៅតាមទ្រឹស្តីបទពីផ្នែកនៃទ្រឹស្ដីយោង "ធរណីមាត្រក្នុងលំហ" \(\rightarrow\) "សេចក្តីផ្តើមចំពោះស្តេរ៉េអូមេទ្រី, ភាពស្របគ្នា”) ។

ចូរសម្គាល់ចំណុច \(A\in a, B\in b\) ដូច្នេះ \(AB\perp a, AB\perp b\) (វាអាចទៅរួចចាប់តាំងពី \(a\parallel b\))។ ចូរយើងសម្គាល់ \(C\in c\) ដូច្នេះ \(BC\perp c\) ដូច្នេះ \(BC\perp b\) ។ បន្ទាប់មក \(AC\perp c\) និង \(AC\perp a\) ។
ជាការពិត ចាប់តាំងពី \(AB\perp b, BC\perp b\) បន្ទាប់មក \(b\) គឺកាត់កែងទៅនឹងយន្តហោះ \(ABC\) ។ ចាប់តាំងពី \(c\parallel a\parallel b\) បន្ទាប់មកបន្ទាត់ \(a\) និង \(c\) ក៏កាត់កែងទៅនឹងយន្តហោះ \(ABC\) ហើយដូច្នេះចំពោះបន្ទាត់ណាមួយពីយន្តហោះនេះ ជាពិសេស , បន្ទាត់ \ (AC\) ។

វាធ្វើតាមនោះ។ \(\angle BAC=\angle (\pi_1, \pi_2)\), \(\angle ABC=\angle (\pi_2, \pi_3)=90^\circ\), \(\angle BCA=\angle (\pi_3, \pi_1)\). វាប្រែថា \(\ត្រីកោណ ABC\) មានរាងចតុកោណកែង ដែលមានន័យថា \[\sin \angle BCA=\cos \angle BAC=0.2.\]

ចម្លើយ៖ ០.២

កិច្ចការទី 3 #2877

កម្រិតកិច្ចការ៖ ពិបាកជាងការប្រឡងរដ្ឋបង្រួបបង្រួម

បានផ្តល់ឱ្យបន្ទាត់ត្រង់ \(a, b, c\) ប្រសព្វគ្នានៅចំណុចមួយ ហើយមុំរវាងពួកវាទាំងពីរគឺស្មើនឹង \(60^\circ\) ។ ស្វែងរក \(\cos^(-1)\alpha\) ដែល \(\alpha\) ជាមុំរវាងយន្តហោះដែលបង្កើតដោយបន្ទាត់ \(a\) និង \(c\) និង យន្តហោះដែលបង្កើតដោយបន្ទាត់ \( b\) និង \(c\) ។ ផ្តល់ចម្លើយរបស់អ្នកជាដឺក្រេ។

អនុញ្ញាតឱ្យបន្ទាត់ប្រសព្វគ្នានៅចំណុច \(O\) ។ ដោយសារមុំរវាងពួកវាទាំងពីរគឺស្មើនឹង \(60^\circ\) នោះបន្ទាត់ត្រង់ទាំងបីមិនអាចស្ថិតនៅក្នុងប្លង់តែមួយបានទេ។ ចូរយើងគូសចំនុច \(A\) នៅលើបន្ទាត់ \(a\) ហើយគូរ \(AB\perp b\) និង \(AC\perp c\) ។ បន្ទាប់មក \\ (\\ ត្រីកោណ AOB = \\ ត្រីកោណ AOC \\)ជាចតុកោណកែងតាមបណ្តោយអ៊ីប៉ូតេនុស និងមុំស្រួច។ ដូច្នេះ \(OB=OC\) និង \(AB=AC\) ។
តោះធ្វើ \(AH\perp (BOC)\) ។ បន្ទាប់មកដោយទ្រឹស្តីបទអំពីបីកាត់កែង \(HC\perp c\), \(HB\perp b\) ។ ចាប់តាំងពី \(AB=AC\) បន្ទាប់មក \\ (\\ ត្រីកោណ AHB = \\ ត្រីកោណ AHC \\)រាងចតុកោណកែងតាមបណ្តោយអ៊ីប៉ូតេនុស និងជើង។ ដូច្នេះ \(HB=HC\) ។ នេះមានន័យថា \(OH\) ​​គឺជាផ្នែកនៃមុំ \(BOC\) (ចាប់តាំងពីចំនុច \(H\) គឺស្មើគ្នាពីជ្រុងនៃមុំ)។

ចំណាំថាតាមវិធីនេះ យើងក៏បានសាងសង់មុំលីនេអ៊ែរនៃមុំ dihedral ដែលបង្កើតឡើងដោយយន្តហោះដែលបង្កើតឡើងដោយបន្ទាត់ \(a\) និង \(c\) និងប្លង់ដែលបង្កើតឡើងដោយបន្ទាត់ \(b\) និង \(c \\) ។ នេះគឺជាមុំ \(ACH\) ។

ចូរយើងស្វែងរកមុំនេះ។ ដោយសារយើងជ្រើសរើសចំណុច \(A\) តាមអំពើចិត្ត អនុញ្ញាតឱ្យយើងជ្រើសរើសវាដូច្នេះ \(OA=2\) ។ បន្ទាប់មកនៅក្នុងចតុកោណ \\ (\ ត្រីកោណ AOC)៖ \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ]ដោយសារ \(OH\) ​​​​ជា bisector នោះ \(\angle HOC=30^\circ\) ដូច្នេះ​ក្នុង​ចតុកោណ \(\ត្រីកោណ HOC\) : \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3)\]បន្ទាប់មកពីចតុកោណ \\ (\ ត្រីកោណ ACH ) : \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]

ចម្លើយ៖ ៣

កិច្ចការទី 4 # 2910

កម្រិតកិច្ចការ៖ ពិបាកជាងការប្រឡងរដ្ឋបង្រួបបង្រួម

ប្លង់ \(\pi_1\) និង \(\pi_2\) ប្រសព្វគ្នាតាមបន្ទាត់ត្រង់ \(l\) ដែលចំនុច \(M\) និង \(N\) ស្ថិតនៅ។ ចម្រៀក \(MA\) និង \(MB\) កាត់កែងទៅនឹងបន្ទាត់ត្រង់ \(l\) ហើយស្ថិតនៅលើយន្តហោះ \(\pi_1\) និង \(\pi_2\) រៀងគ្នា និង \(MN = 15 \) , \(AN = 39\), \(BN = 17\), \(AB = 40\) ។ ស្វែងរក \(3\cos\alpha\) ដែល \(\alpha\) ជាមុំរវាងប្លង់ \(\pi_1\) និង \(\pi_2\) ។

ត្រីកោណ \(AMN\) ជាមុំខាងស្តាំ \(AN^2 = AM^2 + MN^2\) មកពីណា \ ត្រីកោណ \(BMN\) មានរាងចតុកោណ \(BN^2 = BM^2 + MN^2\) ដែល \យើងសរសេរទ្រឹស្តីបទកូស៊ីនុសសម្រាប់ត្រីកោណ \(AMB\): \ បន្ទាប់មក \ ដោយសារមុំ \(\alpha\) រវាងប្លង់គឺជាមុំស្រួច ហើយ \(\angle AMB\) ប្រែទៅជា obtuse បន្ទាប់មក \(\cos\alpha=\dfrac5(12)\) ។ បន្ទាប់មក \

ចម្លើយ៖ ១.២៥

កិច្ចការទី 5 #2911

កម្រិតកិច្ចការ៖ ពិបាកជាងការប្រឡងរដ្ឋបង្រួបបង្រួម

\(ABCDA_1B_1C_1D_1\) គឺ​ជា​ប៉ារ៉ាឡែល​ពី​ចំណុច \(ABCD\) ជា​ការ៉េ​ដែល​មាន​ចំហៀង \(a\) ចំណុច \(M\) ជា​មូលដ្ឋាន​កាត់​កាត់​ពី​ចំណុច \(A_1\) ទៅ​កាន់​យន្តហោះ \ ((ABCD)\) លើសពីនេះទៀត \(M\) គឺជាចំនុចប្រសព្វនៃអង្កត់ទ្រូងនៃការ៉េ \(ABCD\) ។ វាត្រូវបានគេស្គាល់ថា \(A_1M = \dfrac(\sqrt(3))(2)a\). រកមុំរវាងយន្តហោះ \((ABCD)\) និង \((AA_1B_1B)\) ។ ផ្តល់ចម្លើយរបស់អ្នកជាដឺក្រេ។

ចូរយើងសង់ \(MN\) កាត់កែងទៅ \(AB\) ដូចបង្ហាញក្នុងរូប។

ដោយសារ \(ABCD\) គឺជាការ៉េដែលមានចំហៀង \(a\) និង \(MN\perp AB\) និង \(BC\perp AB\) បន្ទាប់មក \(MN\parallel BC\) ។ ដោយសារ \(M\) គឺជាចំណុចប្រសព្វនៃអង្កត់ទ្រូងនៃការ៉េ នោះ \(M\) គឺពាក់កណ្តាលនៃ \(AC\) ដូច្នេះ \(MN\) គឺជាបន្ទាត់កណ្តាល និង \(MN =\frac12BC=\frac(1)(2)a\).
\(MN\) គឺជាការព្យាករនៃ \(A_1N\) ទៅលើយន្តហោះ \((ABCD)\) ហើយ \(MN\) កាត់កែងទៅ \(AB\) បន្ទាប់មក តាមទ្រឹស្តីបទនៃ កាត់កែងបី \ (A_1N\) គឺកាត់កែងទៅនឹង \(AB \) និងមុំរវាងយន្តហោះ \((ABCD)\) និង \((AA_1B_1B)\) គឺ \(\angle A_1NM\) ។
\[\mathrm(tg)\, \angle A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\angle A_1NM = 60^(\circ)\]

ចម្លើយ៖ ៦០

កិច្ចការទី 6 # 1854

កម្រិតកិច្ចការ៖ ពិបាកជាងការប្រឡងរដ្ឋបង្រួបបង្រួម

នៅក្នុងការ៉េមួយ \(ABCD\) : \(O\) - ចំនុចប្រសព្វនៃអង្កត់ទ្រូង; \(S\) - មិនស្ថិតនៅក្នុងប្លង់នៃការ៉េទេ \(SO \perp ABC\) ។ រកមុំរវាងប្លង់ \(ASD\) និង \(ABC\) ប្រសិនបើ \(SO = 5\) និង \(AB = 10\) ។

ត្រីកោណកែង \\(\ត្រីកោណ SAO\) និង \(\ត្រីកោណ SDO\) គឺស្មើគ្នានៅជ្រុងពីរ និងមុំរវាងពួកវា (\(SO \perp ABC\) \(\Rightarrow\) \(\angle SOA = \angle SOD = 90^\circ\); \(AO = DO\) ពីព្រោះ \(O\) - ចំនុចប្រសព្វនៃអង្កត់ទ្រូងនៃការ៉េ \(SO\) - ផ្នែករួម) \(\Rightarrow\) \(AS = SD\) \(\Rightarrow\) \(\ត្រីកោណ ASD\) – isosceles ។ ចំណុច \(K\) គឺពាក់កណ្តាលនៃ \(AD\) បន្ទាប់មក \(SK\) គឺជាកំពស់ក្នុងត្រីកោណ \(\triangle ASD\) ហើយ \(OK\) ជាកំពស់ក្នុងត្រីកោណ \( AOD\) \(\Rightarrow\) យន្តហោះ \(SOK\) កាត់កែងទៅនឹងយន្តហោះ \(ASD\) និង \(ABC\) \(\Rightarrow\) \(\angle SKO\) - មុំលីនេអ៊ែរ ស្មើនឹងការចង់បាន មុំ dihedral ។

ក្នុង \(\ត្រីកោណ SKO\)៖ \(យល់ព្រម = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\Rightarrow\) \(\triangle SOK\) - isosceles ត្រីកោណកែង \(\Rightarrow\) \(\angle SKO = 45^\circ\) ។

ចម្លើយ៖ ៤៥

កិច្ចការទី 7 # 1855

កម្រិតកិច្ចការ៖ ពិបាកជាងការប្រឡងរដ្ឋបង្រួបបង្រួម

នៅក្នុងការ៉េមួយ \(ABCD\) : \(O\) - ចំនុចប្រសព្វនៃអង្កត់ទ្រូង; \(S\) - មិនស្ថិតនៅក្នុងប្លង់នៃការ៉េទេ \(SO \perp ABC\) ។ រកមុំរវាងយន្តហោះ \(ASD\) និង \(BSC\) ប្រសិនបើ \(SO = 5\) និង \(AB = 10\) ។

ត្រីកោណកែង \\(\ត្រីកោណ SAO\) , \(\ត្រីកោណ SDO\) , \(\ត្រីកោណ SOB\) និង \(\ត្រីកោណ SOC\) គឺស្មើគ្នាជាពីរជ្រុង និងមុំរវាងពួកវា (\(SO \perp ABC \\) \\ (\\ ព្រួញស្ដាំ \\) \(\angle SOA = \angle SOD = \angle SOB = \angle SOC = 90^\circ\); \(AO = OD = OB = OC\), ដោយសារតែ \(O\) - ចំនុចប្រសព្វនៃអង្កត់ទ្រូងនៃការ៉េ \(SO\) - ផ្នែកធម្មតា) \(\Rightarrow\) \(AS = DS = BS = CS\) \(\Rightarrow\) \( \triangle ASD\) និង \(\triangle BSC\) គឺជា isosceles ។ ចំណុច \(K\) គឺពាក់កណ្តាលនៃ \(AD\) បន្ទាប់មក \(SK\) គឺជាកំពស់ក្នុងត្រីកោណ \(\triangle ASD\) ហើយ \(OK\) ជាកំពស់ក្នុងត្រីកោណ \( AOD\) \(\ Rightarrow\) យន្តហោះ \(SOK\) គឺកាត់កែងទៅនឹងយន្តហោះ \(ASD\) ។ ចំណុច \(L\) គឺពាក់កណ្តាលនៃ \(BC\) បន្ទាប់មក \(SL\) គឺជាកំពស់ក្នុងត្រីកោណ \(\ត្រីកោណ BSC\) ហើយ \(OL\) ជាកំពស់ក្នុងត្រីកោណ \( BOC\) \(\rightarrow\) យន្តហោះ \(SOL\) (aka plane \(SOK\)) កាត់កែងទៅនឹងយន្តហោះ \(BSC\) ។ ដូច្នេះ យើងទទួលបាននោះ \(\angle KSL\) គឺជាមុំលីនេអ៊ែរ ស្មើនឹងមុំ dihedral ដែលចង់បាន។

\(KL = KO + OL = 2\cdot OL = AB = 10\)\\(\Rightarrow\) \\(OL = 5\); \(SK = SL\) - កម្ពស់ស្មើគ្នា ត្រីកោណ isoscelesដែលអាចត្រូវបានរកឃើញដោយប្រើទ្រឹស្តីបទពីថាហ្គ័រ៖ \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). វាអាចត្រូវបានកត់សម្គាល់ឃើញ \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)\(\Rightarrow\) សម្រាប់ត្រីកោណ \(\triangle KSL\) ទ្រឹស្ដីបទពីតាហ្គោរ ច្រាសកាន់ \(\Rightarrow\) \(\triangle KSL\) – ត្រីកោណស្តាំ \(\Rightarrow\) \(\angle KSL = 90 ^\ រង្វង់\) ។

ចម្លើយ៖ ៩០

ការរៀបចំសិស្សដើម្បីប្រលងជាប់ Unified State ក្នុងគណិតវិទ្យា ជាក្បួនចាប់ផ្តើមជាមួយនឹងការធ្វើឡើងវិញនូវរូបមន្តមូលដ្ឋាន រួមទាំងរូបមន្តដែលអនុញ្ញាតឱ្យអ្នកកំណត់មុំរវាងយន្តហោះ។ ទោះបីជាការពិតដែលថាផ្នែកនៃធរណីមាត្រនេះត្រូវបានគ្របដណ្តប់នៅក្នុងលម្អិតគ្រប់គ្រាន់នៅក្នុង កម្មវិធីសិក្សារបស់សាលានិស្សិតបញ្ចប់ការសិក្សាជាច្រើនត្រូវការសម្ភារៈមូលដ្ឋានឡើងវិញ។ ការយល់ដឹងពីរបៀបស្វែងរកមុំរវាងយន្តហោះ សិស្សវិទ្យាល័យនឹងអាចគណនាបានរហ័សនូវចម្លើយត្រឹមត្រូវនៅពេលដោះស្រាយបញ្ហា ហើយពឹងផ្អែកលើការទទួលបានពិន្ទុសមរម្យលើលទ្ធផលនៃការប្រឡងជាប់រដ្ឋបង្រួបបង្រួម។

nuances ចម្បង

ដើម្បីធានាថាសំណួរអំពីរបៀបស្វែងរកមុំ dihedral មិនបង្កឱ្យមានការលំបាក យើងសូមផ្តល់អនុសាសន៍ឱ្យធ្វើតាមក្បួនដោះស្រាយដំណោះស្រាយដែលនឹងជួយអ្នកដោះស្រាយជាមួយនឹងភារកិច្ចប្រឡងរដ្ឋបង្រួបបង្រួម។

ដំបូងអ្នកត្រូវកំណត់បន្ទាត់ត្រង់ដែលយន្តហោះប្រសព្វគ្នា។

បន្ទាប់មកអ្នកត្រូវជ្រើសរើសចំណុចមួយនៅលើបន្ទាត់នេះហើយគូរកាត់កែងពីរទៅវា។

ជំហានបន្ទាប់- ការស្វែងរក មុខងារត្រីកោណមាត្រមុំ dihedral បង្កើតឡើងដោយកាត់កែង។ មធ្យោបាយងាយស្រួលបំផុតដើម្បីធ្វើវាគឺដោយមានជំនួយពីត្រីកោណលទ្ធផលដែលមុំគឺជាផ្នែកមួយ។

ចម្លើយនឹងជាតម្លៃនៃមុំ ឬអនុគមន៍ត្រីកោណមាត្ររបស់វា។

ការរៀបចំសម្រាប់ការធ្វើតេស្តប្រឡងជាមួយ Shkolkovo គឺជាគន្លឹះនៃភាពជោគជ័យរបស់អ្នក។

ក្នុង​ថ្នាក់​រៀន​ថ្ងៃ​មុន។ ឆ្លងកាត់ការប្រឡងរដ្ឋឯកភាពសិស្សសាលាជាច្រើនប្រឈមមុខនឹងបញ្ហានៃការស្វែងរកនិយមន័យ និងរូបមន្តដែលអនុញ្ញាតឱ្យពួកគេគណនាមុំរវាងយន្តហោះ 2 ។ សៀវភៅសិក្សាសាលាវាមិនតែងតែមាននៅក្នុងដៃទេនៅពេលដែលអ្នកត្រូវការវា។ និងដើម្បីស្វែងរក រូបមន្តចាំបាច់និងឧទាហរណ៍នៃការប្រើប្រាស់ត្រឹមត្រូវរបស់ពួកគេ រួមទាំងការស្វែងរកមុំរវាងយន្តហោះនៅលើអ៊ីនធឺណិតតាមអ៊ីនធឺណិត ដែលជួនកាលត្រូវការពេលវេលាច្រើន។

វិបផតថលគណិតវិទ្យា "Shkolkovo" ផ្តល់ជូន វិធីសាស្រ្តថ្មី។ដើម្បីត្រៀមប្រឡងថ្នាក់រដ្ឋ។ ថ្នាក់រៀននៅលើគេហទំព័ររបស់យើងនឹងជួយសិស្សឱ្យស្គាល់ផ្នែកដែលពិបាកបំផុតសម្រាប់ខ្លួនគេ និងបំពេញចន្លោះនៃចំណេះដឹង។

យើងបានរៀបចំ និងបង្ហាញយ៉ាងច្បាស់នូវសម្ភារៈចាំបាច់ទាំងអស់។ និយមន័យមូលដ្ឋាននិងរូបមន្តត្រូវបានបង្ហាញនៅក្នុងផ្នែក "ព័ត៌មានទ្រឹស្តី" ។

ដើម្បីយល់កាន់តែច្បាស់អំពីសម្ភារៈ យើងក៏ស្នើឱ្យអនុវត្តលំហាត់សមស្របផងដែរ។ ជម្រើសដ៏ធំនៃភារកិច្ច កម្រិតខុសគ្នាជាឧទាហរណ៍ ភាពស្មុគស្មាញត្រូវបានបង្ហាញនៅក្នុងផ្នែក "កាតាឡុក"។ កិច្ចការទាំងអស់មានក្បួនដោះស្រាយលម្អិតសម្រាប់ការស្វែងរកចម្លើយត្រឹមត្រូវ។ បញ្ជីនៃលំហាត់នៅលើគេហទំព័រត្រូវបានបំពេញបន្ថែម និងធ្វើបច្ចុប្បន្នភាពជានិច្ច។

ខណៈពេលដែលកំពុងអនុវត្តការដោះស្រាយបញ្ហាដែលតម្រូវឱ្យស្វែងរកមុំរវាងយន្តហោះពីរ សិស្សមានឱកាសដើម្បីរក្សាទុកកិច្ចការណាមួយតាមអ៊ីនធឺណិតជា "ចំណូលចិត្ត"។ សូមអរគុណដល់ការនេះពួកគេនឹងអាចត្រលប់ទៅគាត់វិញ។ បរិមាណដែលត្រូវការពេលវេលា និងពិភាក្សាអំពីវឌ្ឍនភាពនៃការសម្រេចចិត្តរបស់ខ្លួនជាមួយ គ្រូបង្រៀនសាលាឬគ្រូបង្រៀន។