ដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងត្រូវបានគេប្រើជាញឹកញាប់ដើម្បីគណនាដែនកំណត់ដែលមានស៊ីនុស arcsine តង់សង់ អាកតង់ហ្សង់ និងលទ្ធផលមិនច្បាស់លាស់នៃសូន្យចែកនឹងសូន្យ។
រូបមន្ត
រូបមន្តសម្រាប់ដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងគឺ៖ $$ \lim_(\alpha\to 0) \frac(\sin\alpha)(\alpha) = 1$$
យើងកត់សំគាល់ថាសម្រាប់ $ \alpha\to 0$ យើងទទួលបាន $\sin\alpha\to 0$ ដូច្នេះយើងមានសូន្យនៅក្នុងភាគយក និងភាគបែង។ ដូច្នេះ រូបមន្តនៃដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងគឺត្រូវការដើម្បីបង្ហាញភាពមិនច្បាស់លាស់ $ \frac(0)(0) $ ។
ដើម្បីអនុវត្តរូបមន្ត លក្ខខណ្ឌពីរត្រូវតែបំពេញ៖
- កន្សោមដែលមាននៅក្នុងស៊ីនុស និងភាគបែងនៃប្រភាគគឺដូចគ្នា។
- កន្សោមនៅក្នុងស៊ីនុស និងភាគបែងនៃប្រភាគមានទំនោរទៅសូន្យ
យកចិត្តទុកដាក់! $ \lim_(x\to 0) \frac(\sin(2x^2+1))(2x^2+1) \neq 1$ ទោះបីជាកន្សោមនៅក្រោមស៊ីនុស និងក្នុងភាគបែងគឺដូចគ្នាក៏ដោយ ប៉ុន្តែ $2x ^2+1 = 1$ សម្រាប់ $x\ ទៅ 0$ ។ លក្ខខណ្ឌទីពីរមិនត្រូវបានបំពេញ ដូច្នេះអ្នកមិនអាចអនុវត្តរូបមន្តបានទេ!
ផលវិបាក
កម្រណាស់នៅក្នុងកិច្ចការដែលអ្នកអាចមើលឃើញដែនកំណត់ដ៏អស្ចារ្យដំបូងបង្អស់ ដែលអ្នកអាចសរសេរចម្លើយភ្លាមៗ។ នៅក្នុងការអនុវត្តអ្វីគ្រប់យ៉ាងមើលទៅមានភាពស្មុគស្មាញបន្តិចប៉ុន្តែសម្រាប់ករណីបែបនេះវានឹងមានប្រយោជន៍ក្នុងការដឹងពីផលវិបាកនៃដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង។ សូមអរគុណដល់ពួកគេ អ្នកអាចគណនាបានយ៉ាងឆាប់រហ័សនូវដែនកំណត់ដែលត្រូវការ។
$$ \lim_(\alpha\to 0) \frac(\alpha)(\sin\alpha) = 1$$
$$ \lim_(\alpha\to 0) \frac(\sin(a\alpha))(\sin(b\alpha))) = \frac(a)(b) $$
$$ \lim_(\alpha\to 0) \frac(tg\alpha)(\alpha) = 1$$
$$ \lim_(\alpha\to 0) \frac(\arcsin\alpha)(\alpha) = 1$$
$$ \lim_(\alpha\to 0) \frac(arctg\alpha)(\alpha) = 1$$
ឧទាហរណ៍នៃដំណោះស្រាយ
ចូរយើងពិចារណាដែនកំណត់ដ៏គួរឱ្យកត់សម្គាល់ទីមួយ ឧទាហរណ៍នៃដំណោះស្រាយរបស់វាសម្រាប់ការគណនាដែនកំណត់ដែលមានអនុគមន៍ត្រីកោណមាត្រ និងភាពមិនច្បាស់លាស់ $ \bigg[\frac(0)(0)\bigg] $
| ឧទាហរណ៍ ១ |
| គណនា $\lim_(x\to 0) \frac(\sin2x)(4x) $ |
| ដំណោះស្រាយ |
|
សូមក្រឡេកមើលដែនកំណត់ហើយសម្គាល់ថាវាមានស៊ីនុស។ បន្ទាប់មក យើងជំនួស $x = 0$ ទៅក្នុងភាគយក និងភាគបែង ហើយទទួលបានសូន្យមិនប្រាកដប្រជាចែកនឹងសូន្យ៖ $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \frac(0)(0 ) $$ មានសញ្ញាពីររួចហើយដែលយើងត្រូវអនុវត្តដែនកំណត់ដ៏អស្ចារ្យ ប៉ុន្តែមានចំនុចតូចមួយ៖ យើងមិនអាចអនុវត្តរូបមន្តភ្លាមៗបានទេ ដោយសារកន្សោមនៅក្រោមសញ្ញាស៊ីនុសខុសពីកន្សោមនៅក្នុងភាគបែង។ ហើយយើងត្រូវការឱ្យពួកគេស្មើគ្នា។ ដូច្នេះ ដោយមានជំនួយពីការបំប្លែងបឋមនៃភាគយក យើងនឹងប្រែក្លាយវាទៅជា $2x$។ ដើម្បីធ្វើដូចនេះយើងនឹងយកពីរចេញពីភាគបែងនៃប្រភាគជាកត្តាដាច់ដោយឡែក។ វាមើលទៅដូចនេះ៖ $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \lim_(x\to 0) \frac(\sin2x)(2\cdot 2x) = $$$$ = \frac(1)(2) \lim_(x\to 0) \frac(\sin2x)(2x) = \frac(1)(2)\cdot 1 = \frac(1)(2) $$ សូម ចំណាំថា នៅចុងបញ្ចប់ $\lim_(x\to 0) \frac(\sin2x)(2x) = 1$ ត្រូវបានទទួលតាមរូបមន្ត។ ប្រសិនបើអ្នកមិនអាចដោះស្រាយបញ្ហារបស់អ្នកបានទេ សូមផ្ញើវាមកពួកយើង។ យើងនឹងផ្តល់ដំណោះស្រាយលម្អិត។ អ្នកនឹងអាចមើលវឌ្ឍនភាពនៃការគណនា និងទទួលបានព័ត៌មាន។ នេះនឹងជួយអ្នកឱ្យទទួលបានចំណាត់ថ្នាក់របស់អ្នកពីគ្រូរបស់អ្នកទាន់ពេលវេលា! |
| ចម្លើយ |
| $$ \lim_(x\to 0) \frac(\sin2x)(4x) =\frac(1)(2)$$ |
| ឧទាហរណ៍ ២ |
| ស្វែងរក $\lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) $ |
| ដំណោះស្រាយ |
|
ដូចដែលតែងតែជាដំបូងអ្នកត្រូវដឹងពីប្រភេទនៃភាពមិនច្បាស់លាស់។ ប្រសិនបើវាជាសូន្យចែកនឹងសូន្យ នោះយើងយកចិត្តទុកដាក់ចំពោះវត្តមានរបស់ស៊ីនុស៖ $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = \frac(0) (0) = $$ ភាពមិនច្បាស់លាស់នេះអនុញ្ញាតឱ្យយើងប្រើរូបមន្តនៃដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង ប៉ុន្តែកន្សោមពីភាគបែងមិនស្មើនឹងអាគុយម៉ង់នៃស៊ីនុសទេ? ដូច្នេះរូបមន្តមិនអាចត្រូវបានគេអនុវត្តតាមពាក្យថាជាប្រធានទេ។ វាចាំបាច់ក្នុងការគុណនិងបែងចែកប្រភាគដោយអាគុយម៉ង់នៃស៊ីនុស៖ $$ = \lim_(x\to 0) \frac((x^3+2x)\sin(x^3+2x))((2x -x^4)(x^3+2x)) = $$ ឥឡូវយើងសរសេរលក្ខណសម្បត្តិនៃដែនកំណត់៖ $$ = \lim_(x\to 0) \frac((x^3+2x))(2x -x^4)\cdot \lim_(x\to 0) \frac(\sin(x^3+2x))((x^3+2x)) = $$ ដែនកំណត់ទីពីរសមនឹងរូបមន្តយ៉ាងពិតប្រាកដ និងស្មើ ទៅមួយ៖ $$ = \lim_(x\to 0) \frac(x^3+2x)(2x-x^4)\cdot 1 = \lim_(x\to 0) \frac(x^3+2x )(2x-x^4) = $$ ជំនួសម្តងទៀត $x = 0$ ទៅជាប្រភាគ ហើយយើងទទួលបានភាពមិនច្បាស់លាស់ $ \frac(0)(0) $ ។ ដើម្បីលុបបំបាត់វា វាគ្រប់គ្រាន់ក្នុងការយក $x$ ចេញពីតង្កៀប ហើយកាត់បន្ថយវាដោយ៖ $$ = \lim_(x\to 0) \frac(x(x^2+2))(x(2-x^ 3)) = \ lim_(x\to 0) \frac(x^2+2)(2-x^3)=$$$$=\frac(0^2+2)(2-0^3) = \frac(2)(2) = 1$$ |
| ចម្លើយ |
| $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = 1$$ |
| ឧទាហរណ៍ 4 |
| គណនា $\lim_(x\to0) \frac(\sin2x)(tg3x) $ |
| ដំណោះស្រាយ |
|
តោះចាប់ផ្តើមការគណនាជាមួយការជំនួស $x=0$ ។ ជាលទ្ធផល យើងទទួលបានភាពមិនច្បាស់លាស់ $\frac(0)(0)$។ ដែនកំណត់មានស៊ីនុស និងតង់ហ្សង់ ដែលបង្ហាញអំពីការអភិវឌ្ឍន៍ដែលអាចកើតមាននៃស្ថានភាពដោយប្រើរូបមន្តនៃដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង។ ចូរបំប្លែងភាគយក និងភាគបែងនៃប្រភាគទៅជារូបមន្ត និងលទ្ធផល៖ $$ \lim_(x\to0) \frac(\sin2x)(tg3x) = \frac(0)(0) = \lim_(x\to0) \frac(\frac(\sin2x)(2x)\cdot 2x )(\frac(tg3x)(3x)\cdot 3x) = $$ ឥឡូវនេះយើងឃើញថានៅក្នុងភាគយក និងភាគបែងមានកន្សោមដែលសមនឹងរូបមន្ត និងលទ្ធផល។ អាគុយម៉ង់ស៊ីនុស និងអាគុយម៉ង់តង់សង់គឺដូចគ្នាសម្រាប់ភាគបែងដែលត្រូវគ្នា $$ = \lim_(x\to0) \frac(1\cdot 2x)(1\cdot 3x) = \frac(2)(3)$$ |
| ចម្លើយ |
| $$ \lim_(x\to0) \frac(\sin2x)(tg2x) = \frac(2)(3) $$ |
អត្ថបទ៖ "ដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងឧទាហរណ៍នៃដំណោះស្រាយ" បាននិយាយអំពីករណីដែលវាត្រូវបានគេណែនាំឱ្យប្រើរូបមន្តនេះនិងផលវិបាករបស់វា។
ភស្តុតាង៖
ចូរយើងបង្ហាញទ្រឹស្តីបទដំបូងសម្រាប់ករណីនៃលំដាប់ 
យោងតាមរូបមន្តលេខពីររបស់ញូតុន៖
សន្មតថាយើងទទួលបាន
ពីសមភាពនេះ (1) វាធ្វើតាមថានៅពេលដែល n កើនឡើង ចំនួននៃពាក្យវិជ្ជមាននៅខាងស្តាំកើនឡើង។ លើសពីនេះទៀតនៅពេលដែល n កើនឡើងចំនួនថយចុះដូច្នេះតម្លៃ 
កំពុងកើនឡើង។ ដូច្នេះលំដាប់ 
ការកើនឡើង និង (2)* យើងបង្ហាញថាវាមានព្រំដែន។ ជំនួសវង់ក្រចកនីមួយៗនៅផ្នែកខាងស្តាំនៃសមភាពជាមួយមួយ ផ្នែកខាងស្តាំនឹងកើនឡើង ហើយយើងទទួលបានវិសមភាព
ចូរពង្រឹងវិសមភាពលទ្ធផល ជំនួស 3,4,5, ... ឈរនៅក្នុងភាគបែងនៃប្រភាគ ដោយលេខ 2៖ យើងរកឃើញផលបូកក្នុងតង្កៀបដោយប្រើរូបមន្តសម្រាប់ផលបូកនៃលក្ខខណ្ឌនៃដំណើរការធរណីមាត្រ៖ ដូច្នេះ 
(3)*
ដូច្នេះ លំដាប់ត្រូវបានកំណត់ពីខាងលើ ហើយវិសមភាព (២) និង (៣) ត្រូវបានពេញចិត្ត៖ 
ដូច្នេះដោយផ្អែកលើទ្រឹស្តីបទ Weierstrass (លក្ខណៈវិនិច្ឆ័យសម្រាប់ការបញ្ចូលគ្នានៃលំដាប់មួយ) លំដាប់។ 
monotonically កើនឡើង និងត្រូវបានកំណត់ ដែលមានន័យថាវាមានដែនកំណត់ តំណាងដោយអក្សរ e ។ ទាំងនោះ។ 
ដោយដឹងថាដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរគឺជាការពិតសម្រាប់តម្លៃធម្មជាតិនៃ x យើងបង្ហាញពីដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរសម្រាប់ x ពិតប្រាកដ នោះគឺយើងបង្ហាញថា 
. ចូរយើងពិចារណាករណីពីរ៖
1. សូមឲ្យតម្លៃនីមួយៗនៃ x ត្រូវបានរុំព័ទ្ធរវាងចំនួនគត់វិជ្ជមានពីរ៖ តើផ្នែកចំនួនគត់នៃ x នៅឯណា។ => =>
ប្រសិនបើ ដូច្នេះ យោងទៅតាមដែនកំណត់ 
យើងមាន
ដោយផ្អែកលើលក្ខណៈវិនិច្ឆ័យ (អំពីដែនកំណត់នៃមុខងារកម្រិតមធ្យម) នៃអត្ថិភាពនៃដែនកំណត់ 
2. អនុញ្ញាតឱ្យ។ ចូរធ្វើការជំនួស − x = t បន្ទាប់មក
ពីករណីទាំងពីរនេះវាធ្វើតាមនោះ។ 
សម្រាប់ x ពិតប្រាកដ។
ផលវិបាក៖
9 .) ការប្រៀបធៀបនៃភាពគ្មានទីបញ្ចប់។ ទ្រឹស្តីបទស្តីពីការជំនួស infinitesimals ជាមួយសមមូលក្នុងដែនកំណត់ និងទ្រឹស្តីបទនៅលើផ្នែកសំខាន់នៃ infinitesimals ។
អនុញ្ញាតឱ្យមុខងារ a( x) និង ខ( x) - ព្រឹក នៅ x ® x 0 .
និយមន័យ។
1) ក( x) ហៅ លំដាប់ខ្ពស់ជាងគ្មានកំណត់ ខ (x) ប្រសិនបើ
សរសេរចុះ៖ a( x) = o(b( x)) .
2) ក( x) និងខ( x)ត្រូវបានហៅ infinitesimals នៃលំដាប់ដូចគ្នា។, ប្រសិនបើ
កន្លែងណា CÎℝ និង គ¹ 0 .
សរសេរចុះ៖ a( x) = អូ(ខ( x)) .
3) ក( x) និងខ( x) ត្រូវបានហៅ សមមូល , ប្រសិនបើ
សរសេរចុះ៖ a( x) ~ ខ( x).
4) ក( x) ហៅថា infinitesimal នៃលំដាប់ k ទាក់ទង
ពិតជាគ្មានដែនកំណត់ខ( x),
ប្រសិនបើគ្មានដែនកំណត់ក( x)និង(ខ( x)) គ មានលំដាប់ដូចគ្នា, i.e. ប្រសិនបើ
កន្លែងណា CÎℝ និង គ¹ 0 .
ទ្រឹស្តីបទ 6 (នៅលើការជំនួស infinitesimals ជាមួយសមមូល) ។
អនុញ្ញាតឱ្យក( x), ខ( x), a 1 ( x), b 1 ( x)– ខ.ម. នៅ x ® x 0 . ប្រសិនបើក( x) ~ មួយ 1 ( x), ខ( x) ~ ខ ១ ( x),
នោះ។ 
ភស្តុតាង៖ អនុញ្ញាតឱ្យ ( x) ~ មួយ 1 ( x), ខ( x) ~ ខ ១ ( x), បន្ទាប់មក
ទ្រឹស្តីបទ 7 (អំពីផ្នែកសំខាន់នៃអថេរ) ។
អនុញ្ញាតឱ្យក( x)និងខ( x)– ខ.ម. នៅ x ® x 0 , និងខ( x)– ខ.ម. លំដាប់ខ្ពស់ជាងក( x).
= , a ចាប់តាំងពី b( x) - លំដាប់ខ្ពស់ជាង a( x) បន្ទាប់មក i.e. 
ពី វាច្បាស់ណាស់ថា a( x) + ខ( x) ~ ក ( x)
10) ការបន្តនៃអនុគមន៍នៅចំណុចមួយ (ជាភាសានៃ epsilon-delta ដែនកំណត់ធរណីមាត្រ) ការបន្តមួយចំហៀង។ ការបន្តនៅលើចន្លោះពេលនៅលើផ្នែកមួយ។ លក្ខណៈសម្បត្តិនៃមុខងារបន្ត។
1. និយមន័យជាមូលដ្ឋាន
អនុញ្ញាតឱ្យ f(x) ត្រូវបានកំណត់នៅក្នុងសង្កាត់មួយចំនួននៃចំណុច x 0 .
និយមន័យ ១. មុខងារ f(x) ហៅ បន្តនៅចំណុចមួយ។ x 0 ប្រសិនបើសមភាពគឺជាការពិត
កំណត់ចំណាំ.
1) ដោយគុណធម៌នៃទ្រឹស្តីបទ 5 §3 សមភាព (1) អាចត្រូវបានសរសេរជាទម្រង់
លក្ខខណ្ឌ (២) និយមន័យនៃការបន្តនៃមុខងារនៅចំណុចមួយក្នុងភាសានៃដែនកំណត់ម្ខាង.
២) សមភាព (១) ក៏អាចសរសេរជា៖
ពួកគេនិយាយថា៖ «ប្រសិនបើមុខងារបន្តនៅចំណុចមួយ។ x 0 បន្ទាប់មកសញ្ញានៃដែនកំណត់ និងមុខងារអាចត្រូវបានផ្លាស់ប្តូរ។"
និយមន័យ 2 (ជាភាសាអ៊ីឌី)។
មុខងារ f(x) ហៅ បន្តនៅចំណុចមួយ។ x 0 ប្រសិនបើ"e>0 $d>0 ដូច, អ្វី
ប្រសិនបើ xអូយូ( x 0 , ឃ) (ឧ. | x – x 0 | < d),
បន្ទាប់មក f(xអាយយូ( f(x 0), អ៊ី) (ឧ. | f(x) – f(x 0) | < e).
អនុញ្ញាតឱ្យ x, x 0 Î ឃ(f) (x 0 - ថេរ, x –បំពាន)
ចូរសម្គាល់: ឃ x= x–x 0 – ការបង្កើនអាគុយម៉ង់
ឃ f(x 0) = f(x) – f(x 0) – ការបង្កើនមុខងារនៅ pointx 0
និយមន័យ 3 (ធរណីមាត្រ) ។
មុខងារ f(x) លើ ហៅ បន្តនៅចំណុចមួយ។
x 0
ប្រសិនបើនៅចំណុចនេះ ការកើនឡើងគ្មានកំណត់នៅក្នុងអាគុយម៉ង់ត្រូវគ្នាទៅនឹងការកើនឡើងគ្មានកំណត់នៅក្នុងអនុគមន៍, i.e.
អនុញ្ញាតឱ្យមុខងារ f(x) ត្រូវបានកំណត់នៅលើចន្លោះពេល [ x 0 ; x 0 + ឃ) (នៅចន្លោះពេល ( x 0 - ឃ; x 0 ]).
និយមន័យ។ មុខងារ f(x) ហៅ បន្តនៅចំណុចមួយ។
x 0 នៅខាងស្ដាំ
(ឆ្វេង
), ប្រសិនបើសមភាពគឺជាការពិត
វាច្បាស់ណាស់។ f(x) គឺបន្តនៅចំណុច x 0 Û f(x) គឺបន្តនៅចំណុច x 0 ស្តាំនិងឆ្វេង។
និយមន័យ។ មុខងារ f(x) ហៅ បន្តសម្រាប់ចន្លោះពេល អ៊ី ( ក; ខ) ប្រសិនបើវាបន្តនៅគ្រប់ចំណុចនៃចន្លោះពេលនេះ។.
មុខងារ f(x) ត្រូវបានគេហៅថាបន្តនៅលើផ្នែក [ក; ខ] ប្រសិនបើវាបន្តនៅចន្លោះពេល (ក; ខ) និងមានការបន្តមួយផ្លូវត្រង់ចំណុចព្រំដែន(ឧ. បន្តនៅចំណុច កនៅខាងស្តាំនៅចំណុច ខ- ឆ្វេង) ។
11) ចំណុចបំបែក, ចំណាត់ថ្នាក់របស់ពួកគេ។
និយមន័យ។ ប្រសិនបើមុខងារ f(x) បានកំណត់នៅក្នុងសង្កាត់មួយចំនួននៃចំណុច x 0 , ប៉ុន្តែមិនបន្តនៅចំណុចនេះទេ។ f(x) ហៅថាមិនបន្តនៅចំណុច x 0 , និងចំណុចខ្លួនឯង x 0 ហៅថាចំណុចបំបែក មុខងារ f(x) .
កំណត់ចំណាំ.
1) f(x) អាចត្រូវបានកំណត់នៅក្នុងសង្កាត់ដែលមិនពេញលេញនៃចំណុច x 0 .
បន្ទាប់មកពិចារណាការបន្តផ្នែកម្ខាងដែលត្រូវគ្នានៃមុខងារ។
2) ពីនិយមន័យនៃចំណុចÞ x 0 គឺជាចំណុចបំបែកនៃមុខងារ f(x) ក្នុងករណីពីរ៖
ក) U( x 0 , ឃ) អូ ឃ(f) ប៉ុន្តែសម្រាប់ f(x) សមភាពមិនជាប់
ខ) U * ( x 0 , ឃ) អូ ឃ(f) .
សម្រាប់មុខងារបឋម មានតែករណី ខ) ដែលអាចធ្វើទៅបាន។
អនុញ្ញាតឱ្យ x 0 - ចំណុចបំបែកមុខងារ f(x) .
និយមន័យ។ ចំណុច x 0 ហៅ ចំណុចបំបែក ខ្ញុំ ប្រភេទ ប្រសិនបើមុខងារ f(x)មានដែនកំណត់កំណត់នៅខាងឆ្វេង និងស្តាំនៅចំណុចនេះ។.
ប្រសិនបើដែនកំណត់ទាំងនេះស្មើគ្នា នោះចំនុច x 0 ហៅ ចំណុចបំបែកដែលអាចដកចេញបាន។ , បើមិនដូច្នេះទេ - ចំណុចលោត .
និយមន័យ។ ចំណុច x 0 ហៅ ចំណុចបំបែក II ប្រភេទ ប្រសិនបើយ៉ាងហោចណាស់ដែនកំណត់ម្ខាងនៃអនុគមន៍ f(x)នៅចំណុចនេះគឺស្មើគ្នា¥ ឬមិនមាន.
12) លក្ខណៈសម្បត្តិនៃមុខងារបន្តនៅចន្លោះពេលមួយ (ទ្រឹស្តីបទនៃ Weierstrass (ដោយគ្មានភស្តុតាង) និង Cauchy
ទ្រឹស្តីបទរបស់ Weierstrass
អនុញ្ញាតឱ្យអនុគមន៍ f(x) បន្តនៅចន្លោះពេលបន្ទាប់មក
1) f(x) ត្រូវបានកំណត់ត្រឹម
2) f(x) យកតម្លៃតូចបំផុត និងធំបំផុតរបស់វានៅលើចន្លោះពេល
និយមន័យ៖ តម្លៃនៃអនុគមន៍ m=f ត្រូវបានគេហៅថាតូចបំផុត ប្រសិនបើ m≤f(x) សម្រាប់ x€ D(f) ណាមួយ។
តម្លៃនៃអនុគមន៍ m=f ត្រូវបានគេនិយាយថាធំជាងគេប្រសិនបើ m≥f(x) សម្រាប់ x € D(f) ណាមួយ។
មុខងារអាចយកតម្លៃតូចបំផុត/ធំបំផុតនៅចំណុចជាច្រើននៃផ្នែក។
f(x 3)=f(x 4)=អតិបរមា
ទ្រឹស្តីបទ Cauchy ។
អនុញ្ញាតឱ្យអនុគមន៍ f(x) បន្តនៅលើផ្នែក ហើយ x ជាលេខដែលមានរវាង f(a) និង f(b) បន្ទាប់មកយ៉ាងហោចណាស់មានចំនុចមួយ x 0 € ដូចនេះ f(x 0)= g
ឥឡូវនេះ ជាមួយនឹងព្រលឹងដ៏ស្ងប់ស្ងាត់ សូមបន្តពិចារណា ដែនកំណត់ដ៏អស្ចារ្យ.
មើលទៅដូចជា ។
ជំនួសឱ្យអថេរ x មុខងារផ្សេងៗអាចមានវត្តមាន រឿងសំខាន់គឺថាពួកគេមានទំនោរទៅ 0 ។
វាចាំបាច់ក្នុងការគណនាដែនកំណត់
ដូចដែលអ្នកអាចឃើញដែនកំណត់នេះគឺស្រដៀងទៅនឹងការកត់សម្គាល់ដំបូងប៉ុន្តែនេះមិនមែនជាការពិតទាំងស្រុងនោះទេ។ ជាទូទៅ ប្រសិនបើអ្នកសម្គាល់ឃើញអំពើបាបនៅក្នុងដែនកំណត់នោះ អ្នកគួរតែគិតភ្លាមៗអំពីថាតើវាអាចទៅរួចក្នុងការប្រើប្រាស់ដែនកំណត់ដ៏គួរឱ្យកត់សម្គាល់ដំបូង។
យោងតាមច្បាប់លេខ 1 របស់យើង យើងជំនួសសូន្យជំនួសឱ្យ x:
យើងទទួលបានភាពមិនប្រាកដប្រជា។
ឥឡូវនេះ ចូរយើងព្យាយាមរៀបចំដែនកំណត់ដ៏អស្ចារ្យដំបូងដោយខ្លួនយើង។ ដើម្បីធ្វើដូចនេះយើងធ្វើបន្សំសាមញ្ញមួយ៖
ដូច្នេះ យើងរៀបចំភាគយក និងភាគបែង ដើម្បីបន្លិច 7x ។ ឥឡូវនេះដែនកំណត់គួរឱ្យកត់សម្គាល់ដែលធ្លាប់ស្គាល់បានបង្ហាញខ្លួនរួចហើយ។ វាត្រូវបានណែនាំឱ្យគូសវាសនៅពេលសម្រេចចិត្ត៖
ចូរជំនួសដំណោះ ស្រាយទៅនឹងឧទាហរណ៍ដ៏គួរឱ្យកត់សម្គាល់ទីមួយ ហើយទទួលបាន៖
ធ្វើឱ្យប្រភាគសាមញ្ញ៖
ចម្លើយ៖ ៧/៣ ។
ដូចដែលអ្នកអាចឃើញអ្វីគ្រប់យ៉ាងគឺសាមញ្ញណាស់។
មើលទៅដូចជា 
ដែល e = 2.718281828... ជាចំនួនមិនសមហេតុផល។
មុខងារផ្សេងៗអាចមានវត្តមានជំនួសឱ្យអថេរ x រឿងសំខាន់គឺថាពួកគេមានទំនោរទៅ .
វាចាំបាច់ក្នុងការគណនាដែនកំណត់
នៅទីនេះយើងឃើញវត្តមាននៃសញ្ញាប័ត្រនៅក្រោមសញ្ញានៃដែនកំណត់ដែលមានន័យថាវាអាចប្រើដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរ។
ដូចរាល់ដង យើងនឹងប្រើច្បាប់លេខ 1 - ជំនួស x ជំនួសវិញដោយ៖
វាអាចត្រូវបានគេមើលឃើញថានៅ x មូលដ្ឋាននៃដឺក្រេគឺ , ហើយនិទស្សន្តគឺ 4x > , i.e. យើងទទួលបានភាពមិនច្បាស់លាស់នៃទម្រង់៖
ចូរយើងប្រើដែនកំណត់ដ៏អស្ចារ្យទីពីរដើម្បីបង្ហាញពីភាពមិនច្បាស់លាស់របស់យើង ប៉ុន្តែដំបូងយើងត្រូវរៀបចំវា។ ដូចដែលអ្នកអាចឃើញយើងត្រូវសម្រេចបាននូវវត្តមាននៅក្នុងសូចនាករដែលយើងលើកមូលដ្ឋានទៅថាមពល 3x ហើយក្នុងពេលតែមួយទៅនឹងថាមពល 1/3x ដូច្នេះការបញ្ចេញមតិមិនផ្លាស់ប្តូរ៖
កុំភ្លេចរំលេចដែនកំណត់ដ៏អស្ចារ្យរបស់យើង៖
នោះហើយជាអ្វីដែលពួកគេពិតជា ដែនកំណត់ដ៏អស្ចារ្យ!
ប្រសិនបើអ្នកនៅតែមានសំណួរអំពី ដែនកំណត់ដ៏អស្ចារ្យទីមួយ និងទីពីរបន្ទាប់មកមានអារម្មណ៍សេរីដើម្បីសួរពួកគេនៅក្នុងមតិយោបល់។
យើងនឹងឆ្លើយគ្រប់គ្នាតាមដែលអាចធ្វើទៅបាន។
អ្នកក៏អាចធ្វើការជាមួយគ្រូបង្រៀនលើប្រធានបទនេះផងដែរ។
យើងមានសេចក្តីសោមនស្សរីករាយក្នុងការផ្តល់ជូនអ្នកនូវសេវាកម្មជ្រើសរើសគ្រូដែលមានសមត្ថភាពនៅក្នុងទីក្រុងរបស់អ្នក។ ដៃគូរបស់យើងនឹងជ្រើសរើសគ្រូបង្រៀនដ៏ល្អសម្រាប់អ្នកយ៉ាងឆាប់រហ័សក្នុងលក្ខខណ្ឌអំណោយផល។
មិនមានព័ត៌មានគ្រប់គ្រាន់ទេ? - អ្នកអាច !
អ្នកអាចសរសេរការគណនាគណិតវិទ្យានៅក្នុង notepads ។ វាជាការរីករាយជាងក្នុងការសរសេរជាលក្ខណៈបុគ្គលនៅក្នុងសៀវភៅកត់ត្រាដែលមាននិមិត្តសញ្ញា (http://www.blocnot.ru) ។
មានដែនកំណត់គួរឱ្យកត់សម្គាល់មួយចំនួន ប៉ុន្តែភាពល្បីល្បាញបំផុតគឺដែនកំណត់គួរឱ្យកត់សម្គាល់ទីមួយ និងទីពីរ។ អ្វីដែលគួរឱ្យកត់សម្គាល់អំពីដែនកំណត់ទាំងនេះគឺថាពួកវាត្រូវបានគេប្រើយ៉ាងទូលំទូលាយហើយដោយមានជំនួយរបស់ពួកគេអ្នកអាចរកឃើញដែនកំណត់ផ្សេងទៀតដែលបានរកឃើញនៅក្នុងបញ្ហាជាច្រើន។ នេះជាអ្វីដែលយើងនឹងធ្វើនៅក្នុងផ្នែកជាក់ស្តែងនៃមេរៀននេះ។ ដើម្បីដោះស្រាយបញ្ហាដោយកាត់បន្ថយវាទៅដែនកំណត់គួរឱ្យកត់សម្គាល់ទីមួយ ឬទីពីរ មិនចាំបាច់បង្ហាញភាពមិនច្បាស់លាស់ដែលមាននៅក្នុងពួកគេទេ ព្រោះតម្លៃនៃដែនកំណត់ទាំងនេះត្រូវបានគណនាដោយអ្នកគណិតវិទូដ៏អស្ចារ្យជាយូរមកហើយ។
ដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងត្រូវបានគេហៅថាដែនកំណត់នៃសមាមាត្រនៃស៊ីនុសនៃធ្នូគ្មានដែនកំណត់ទៅនឹងធ្នូដូចគ្នា ដែលបង្ហាញជារង្វាស់រ៉ាដ្យង់៖
ចូរបន្តទៅការដោះស្រាយបញ្ហានៅដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង។ ចំណាំ៖ ប្រសិនបើមានអនុគមន៍ត្រីកោណមាត្រនៅក្រោមសញ្ញាកំណត់ នេះគឺជាសញ្ញាស្ទើរតែប្រាកដដែលថាកន្សោមនេះអាចត្រូវបានកាត់បន្ថយដល់ដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង។
ឧទាហរណ៍ ១.ស្វែងរកដែនកំណត់។
ដំណោះស្រាយ។ ជំនួសវិញ។ xសូន្យនាំទៅរកភាពមិនច្បាស់លាស់៖
.
ភាគបែងគឺស៊ីនុស ដូច្នេះកន្សោមអាចត្រូវបាននាំមកដល់កម្រិតគួរឱ្យកត់សម្គាល់ដំបូង។ តោះចាប់ផ្តើមការផ្លាស់ប្តូរ៖
.
ភាគបែងគឺជាស៊ីនុសនៃ X បី ប៉ុន្តែភាគយកមាន X តែមួយប៉ុណ្ណោះ ដែលមានន័យថា អ្នកត្រូវយក X បីនៅក្នុងភាគយក។ ដើម្បីអ្វី? ណែនាំ ៣ x = កនិងទទួលបានការបញ្ចេញមតិ។
ហើយយើងមកដល់ការបំរែបំរួលនៃកម្រិតដ៏គួរឲ្យកត់សម្គាល់ដំបូងគេ៖
ព្រោះវាមិនមានបញ្ហាថាអក្សរមួយណា (អថេរ) ក្នុងរូបមន្តនេះឈរជំនួស X។
យើងគុណ X ដោយបីហើយចែកភ្លាមៗ៖
.
ដោយអនុលោមតាមដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងដែលបានកត់សម្គាល់ យើងជំនួសកន្សោមប្រភាគ៖
ឥឡូវនេះយើងអាចដោះស្រាយដែនកំណត់នេះ៖
.
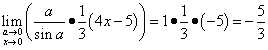ឧទាហរណ៍ ២.ស្វែងរកដែនកំណត់។
ដំណោះស្រាយ។ ការជំនួសដោយផ្ទាល់ម្តងទៀតនាំឱ្យមាន "សូន្យបែងចែកដោយសូន្យ" ភាពមិនប្រាកដប្រជា:
.
ដើម្បីទទួលបានដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង វាចាំបាច់ដែល x នៅក្រោមសញ្ញាស៊ីនុសនៅក្នុងភាគយក ហើយគ្រាន់តែ x ក្នុងភាគបែងមានមេគុណដូចគ្នា។ អនុញ្ញាតឱ្យមេគុណនេះស្មើនឹង 2។ ដើម្បីធ្វើដូច្នេះ ស្រមៃមើលមេគុណបច្ចុប្បន្នសម្រាប់ x ដូចខាងក្រោម ប្រតិបត្តិការជាមួយប្រភាគ យើងទទួលបាន៖
.
ឧទាហរណ៍ ៣.ស្វែងរកដែនកំណត់។
ដំណោះស្រាយ។ នៅពេលជំនួស យើងទទួលបានភាពមិនច្បាស់លាស់ម្តងទៀត "សូន្យចែកនឹងសូន្យ"៖
.
អ្នកប្រហែលជាយល់រួចហើយថាពីកន្សោមដើមអ្នកអាចទទួលបានដែនកំណត់ដ៏អស្ចារ្យដំបូងគុណនឹងដែនកំណត់ដ៏អស្ចារ្យដំបូង។ ដើម្បីធ្វើដូចនេះយើងបំបែកការេនៃ x ក្នុងភាគយក និងស៊ីនុសក្នុងភាគបែងទៅជាកត្តាដូចគ្នា ហើយដើម្បីទទួលបានមេគុណដូចគ្នាសម្រាប់ x និងស៊ីនុស យើងចែក x ក្នុងភាគយកដោយ 3 ហើយគុណនឹងភ្លាមៗ។ ដោយ 3. យើងទទួលបាន:
.
ឧទាហរណ៍ 4 ។ស្វែងរកដែនកំណត់។
ដំណោះស្រាយ។ ជាថ្មីម្តងទៀតយើងទទួលបានភាពមិនច្បាស់លាស់ "សូន្យចែកនឹងសូន្យ"៖
.
យើងអាចទទួលបានសមាមាត្រនៃដែនកំណត់គួរឱ្យកត់សម្គាល់ពីរដំបូង។ យើងបែងចែកទាំងភាគយក និងភាគបែងដោយ x ។ បន្ទាប់មក ដើម្បីឱ្យមេគុណសម្រាប់ស៊ីនុស និង xes ស្របគ្នា យើងគុណនឹង x ខាងលើដោយ 2 ហើយចែកភ្លាមៗដោយ 2 ហើយគុណនឹង x ទាបដោយ 3 ហើយចែកនឹង 3 ភ្លាមៗ។
ឧទាហរណ៍ 5 ។ស្វែងរកដែនកំណត់។
ដំណោះស្រាយ។ ហើយម្តងទៀតភាពមិនប្រាកដប្រជានៃ "សូន្យបែងចែកដោយសូន្យ"៖
យើងចងចាំពីត្រីកោណមាត្រថាតង់សង់គឺជាសមាមាត្រនៃស៊ីនុសទៅកូស៊ីនុស ហើយកូស៊ីនុសនៃសូន្យគឺស្មើនឹងមួយ។ យើងអនុវត្តការផ្លាស់ប្តូរ និងទទួលបាន៖
.
ឧទាហរណ៍ ៦.ស្វែងរកដែនកំណត់។
ដំណោះស្រាយ។ អនុគមន៍ត្រីកោណមាត្រនៅក្រោមសញ្ញានៃដែនកំណត់ម្តងទៀតបង្ហាញពីការប្រើប្រាស់ដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង។ យើងតំណាងឱ្យវាជាសមាមាត្រនៃស៊ីនុសទៅកូស៊ីនុស។
ពាក្យ "ដែនកំណត់គួរឱ្យកត់សម្គាល់" ត្រូវបានគេប្រើយ៉ាងទូលំទូលាយនៅក្នុងសៀវភៅសិក្សា និងជំនួយការបង្រៀន ដើម្បីសម្គាល់អត្តសញ្ញាណសំខាន់ៗដែលជួយយ៉ាងសំខាន់។ សម្រួលការងាររបស់អ្នក។លើការស្វែងរកដែនកំណត់។
ប៉ុន្តែទៅ អាចនាំមកដែនកំណត់របស់អ្នកចំពោះភាពគួរឱ្យកត់សម្គាល់ អ្នកត្រូវពិនិត្យមើលវាឱ្យបានល្អ ព្រោះពួកវាមិនត្រូវបានរកឃើញក្នុងទម្រង់ផ្ទាល់ទេ ប៉ុន្តែជាញឹកញាប់នៅក្នុងទម្រង់នៃផលវិបាក បំពាក់ដោយលក្ខខណ្ឌ និងកត្តាបន្ថែម។ ទោះជាយ៉ាងណាក៏ដោយទ្រឹស្តីដំបូងបន្ទាប់មកឧទាហរណ៍ហើយអ្នកនឹងទទួលបានជោគជ័យ!
ដែនកំណត់ដ៏អស្ចារ្យដំបូង
ចូលចិត្ត? បន្ថែមទៅចំណាំ
ដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូងត្រូវបានសរសេរដូចខាងក្រោម (ភាពមិនច្បាស់លាស់នៃទម្រង់ $0/0$):
$$ \lim\limits_(x\to 0)\frac(\sin x)(x)=1. $$
កូរ៉ូឡាពីដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង
$$ \lim\limits_(x\to 0)\frac(x)(\sin x)=1. $$ $$ \lim\limits_(x\to 0)\frac(\sin (ax))(\sin (bx))=\frac(a)(b)។ $$ $$ \lim\limits_(x\to 0)\frac(\tan x)(x)=1. $$ $$ \lim\limits_(x\to 0)\frac(\arcsin x)(x)=1. $$ $$ \lim\limits_(x\to 0)\frac(\arctan x)(x)=1. $$ $$ \lim\limits_(x\to 0)\frac(1-\cos x)(x^2/2)=1. $$ដំណោះស្រាយឧទាហរណ៍៖ ១ ដែនកំណត់ដ៏អស្ចារ្យ
ឧទាហរណ៍ ១. គណនាដែនកំណត់ $$\lim\limits_(x\to 0)\frac(\sin 3x)(8x).$$
ដំណោះស្រាយ។ជំហានដំបូងគឺតែងតែដូចគ្នា - យើងជំនួសតម្លៃដែនកំណត់ $x=0$ ទៅក្នុងមុខងារ ហើយទទួលបាន៖
$$\left[\frac(\sin 0)(0)\right] = \left[\frac(0)(0)\right].$$
យើងទទួលបានភាពមិនច្បាស់លាស់នៃទម្រង់ $\left[\frac(0)(0)\right]$ ដែលគួរតែត្រូវបានបង្ហាញ។ ប្រសិនបើអ្នកក្រឡេកមើលឱ្យជិត ដែនកំណត់ដើមគឺស្រដៀងនឹងការកត់សម្គាល់ដំបូងដែរ ប៉ុន្តែមិនដូចគ្នាទេ។ ភារកិច្ចរបស់យើងគឺធ្វើឱ្យមានភាពស្រដៀងគ្នា។ ចូរយើងបំប្លែងវាដូចនេះ - មើលកន្សោមក្រោមស៊ីនុស ធ្វើដូចគ្នាក្នុងភាគបែង (និយាយទាក់ទងគ្នា គុណ និងចែកដោយ $3x$) បន្ទាប់មកកាត់បន្ថយ និងសម្រួល៖
$$ \lim\limits_(x\to 0)\frac(\sin 3x)(8x) = \lim\limits_(x\to 0)\frac(\sin 3x)(3x)\frac(3x)(8x )=\lim\limits_(x\to 0)\frac(\sin (3x))(3x)\frac(3)(8)=\frac(3)(8)។ $$
ខាងលើគឺពិតជាដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង: $$ \lim\limits_(x\to 0)\frac(\sin (3x))(3x) = \lim\limits_(y\to 0)\frac(\sin ( y ))(y)=1, \\text(បានធ្វើការជំនួសតាមលក្ខខណ្ឌ) y=3x។ $$ ចម្លើយ៖ $3/8$.
ឧទាហរណ៍ ២. គណនាដែនកំណត់ $$\lim\limits_(x\to 0)\frac(1-\cos 3x)(\tan 2x\cdot \sin 4x))$$
ដំណោះស្រាយ។យើងជំនួសតម្លៃដែនកំណត់ $x=0$ ទៅក្នុងមុខងារ ហើយទទួលបាន៖
$$\left[\frac(1-\cos 0)(\tan 0\cdot \sin 0)\right] =\left[\frac(1-1)(0\cdot 0)\right]=\left [\frac(0)(0)\right].$$
យើងទទួលបានភាពមិនច្បាស់លាស់នៃទម្រង់ $\left[\frac(0)(0)\right]$ ។ ចូរបំប្លែងដែនកំណត់ដោយប្រើដែនកំណត់ដ៏អស្ចារ្យដំបូង (បីដង!) ក្នុងភាពសាមញ្ញ៖
$$\lim\limits_(x\to 0)\frac(1-\cos 3x)(\tan 2x\cdot \sin 4x) = \lim\limits_(x\to 0)\frac( 2\sin^2 (3x/2))(\sin 2x\cdot \sin 4x)\cdot \cos 2x = $$ $$ = 2\lim\limits_(x\to 0)\frac(\sin^2 (3x/2)) )((3x/2)^2) \\cdot \\frac(2x)(\sin 2x) \cdot \frac(4x)(\sin 4x)\cdot \frac((3x/2)^2)( 2x \ cdot 4x) \cdot \cos 2x = $$ $$ =2\lim\limits_(x\to 0) 1 \cdot 1 \cdot 1 \cdot \frac((9/4)x^2)( 8x^2 ) \cdot \cos 2x= 2 \cdot \frac(9)(32) \lim\limits_(x\to 0) \cos 2x=\frac(9)(16) ។ $$
ចម្លើយ៖ $9/16$.
ឧទាហរណ៍ ៣. ស្វែងរកដែនកំណត់ $$\lim\limits_(x\to 0)\frac(\sin (2x^3+3x))(5x-x^5))$$
ដំណោះស្រាយ។ចុះប្រសិនបើមានកន្សោមស្មុគស្មាញនៅក្រោមអនុគមន៍ត្រីកោណមាត្រ? វាមិនសំខាន់ទេ យើងបន្តតាមរបៀបដូចគ្នានៅទីនេះ។ ដំបូងយើងពិនិត្យមើលប្រភេទនៃភាពមិនច្បាស់លាស់ ជំនួស $x=0$ ក្នុងមុខងារ ហើយទទួលបាន៖
$$\left[\frac(\sin (0+0))(0-0)\right] = \left[\frac(0)(0)\right].$$
យើងទទួលបានភាពមិនច្បាស់លាស់នៃទម្រង់ $\left[\frac(0)(0)\right]$ ។ គុណ និងចែកដោយ $2x^3+3x$:
$$ \lim\limits_(x\to 0)\frac(\sin (2x^3+3x))(5x-x^5)=\lim\limits_(x\to 0)\frac(\sin (2x ^3+3x))((2x^3+3x)) \cdot \frac(2x^3+3x)(5x-x^5)=\lim\limits_(x\to 0) 1 \cdot \frac( 2x^3+3x)(5x-x^5)= \left[\frac(0)(0)\right] = $$
ជាថ្មីម្តងទៀត យើងទទួលបានភាពមិនច្បាស់លាស់ ប៉ុន្តែក្នុងករណីនេះ វាគ្រាន់តែជាប្រភាគប៉ុណ្ណោះ។ ចូរកាត់បន្ថយចំនួនភាគយក និងភាគបែងដោយ $x$៖
$$ = \lim\limits_(x\to 0) \frac(2x^2+3)(5-x^4)=\left[\frac(0+3)(5-0)\right] =\ frac(3)(5)។ $$
ចម្លើយ៖ $3/5$.
ដែនកំណត់ដ៏អស្ចារ្យទីពីរ
ដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរត្រូវបានសរសេរដូចខាងក្រោម (ភាពមិនច្បាស់លាស់នៃទម្រង់ $1^\infty$):
$$ \lim\limits_(x\to \infty) \left(1+\frac(1)(x)\right)^(x)=e, \quad \text(or) \quad \lim\limits_( x\ ទៅ 0) \left(1+x\right)^(1/x)=e. $$
ផលវិបាកនៃដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរ
$$ \lim\limits_(x\to \infty) \left(1+\frac(a)(x)\right)^(bx)=e^(ab)។ $$ $$ \lim\limits_(x\to 0)\frac(\ln (1+x))(x)=1. $$ $$ \lim\limits_(x\to 0)\frac(e^x -1)(x)=1. $$ $$ \lim\limits_(x\to 0)\frac(a^x-1)(x \ln a)=1, a>0, a \ne 1. $$ $$ \lim\limits_( x\to 0)\frac((1+x)^(a)-1)(ax)=1។ $$ឧទាហរណ៍នៃដំណោះស្រាយ៖ ២ ដែនកំណត់ដ៏អស្ចារ្យ
ឧទាហរណ៍ 4 ។ ស្វែងរកដែនកំណត់ $$\lim\limits_(x\to \infty)\left(1-\frac(2)(3x)\right)^(x+3).$$
ដំណោះស្រាយ។តោះពិនិត្យមើលប្រភេទនៃភាពមិនច្បាស់លាស់ ជំនួស $x=\infty$ ទៅក្នុងមុខងារ ហើយទទួលបាន៖
$$\left[\left(1-\frac(2)(\infty)\right)^(\infty)\right]=\left.$$
យើងទទួលបានភាពមិនច្បាស់លាស់នៃទម្រង់ $\left$ ។ ដែនកំណត់អាចត្រូវបានកាត់បន្ថយទៅជារឿងគួរឱ្យកត់សម្គាល់ទីពីរ។ តោះបម្លែង៖
$$ \lim\limits_(x\to \infty)\left(1-\frac(2)(3x)\right)^(x+3) = \lim\limits_(x\to \infty)\left( 1+\frac(1)((-3x/2))\right)^(\frac(-3x/2)(-3x/2)(x+3))=$$$$=\lim\limits_ (x\to \infty)\left(\left(1+\frac(1)((-3x/2)))\right)^((-3x/2))\right)^\frac(x+3 )(-៣x/២)=$$
កន្សោមក្នុងវង់ក្រចកគឺពិតជាដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរ $\lim\limits_(t\to \infty) \left(1+\frac(1)(t)\right)^(t)=e$, only $t= - 3x/2$ ដូច្នេះ
$$ = \lim\limits_(x\to \infty)\left(e\right)^\frac(x+3)(-3x/2)=\lim\limits_(x\to \infty)e^\ frac(1+3/x)(-3/2)=e^(-2/3)។ $$
ចម្លើយ៖$e^(-2/3)$ ។
ឧទាហរណ៍ 5 ។ ស្វែងរកដែនកំណត់ $$\lim\limits_(x\to \infty)\left(\frac(x^3+2x^2+1)(x^3+x-7)\right)^(x).$ $
ដំណោះស្រាយ។យើងជំនួស $x=\infty$ ទៅក្នុងមុខងារ ហើយទទួលបានភាពមិនច្បាស់លាស់នៃទម្រង់ $\left[\frac(\infty)(\infty)\right]$។ ហើយយើងត្រូវការ $\left$ ។ ដូច្នេះ ចូរចាប់ផ្តើមដោយការបំប្លែងកន្សោមក្នុងវង់ក្រចក៖
$$ \lim\limits_(x\to \infty)\left(\frac(x^3+2x^2+1)(x^3+x-7)\right)^(x) = \lim\limits_ (x\to \infty)\left(\frac(x^3+(x-7)-(x-7)+2x^2+1)(x^3+x-7)\right)^(x ) = \lim\limits_(x\to \infty)\left(\frac(((x^3+x-7)+(-x+7+2x^2+1))(x^3+x-7) )\right)^(x) = $$ $$ = \lim\limits_(x\to \infty)\left(1+\frac(2x^2-x+8)(x^3+x-7) \right)^(x) = \lim\limits_(x\to \infty)\left(\left(1+\frac(2x^2-x+8)(x^3+x-7)\right) ^(\frac(x^3+x-7)(2x^2-x+8))\right)^(x \frac(2x^2-x+8)(x^3+x-7))) =$$
កន្សោមក្នុងវង់ក្រចកគឺពិតជាដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរ $\lim\limits_(t\to \infty) \left(1+\frac(1)(t)\right)^(t)=e$, only $t= \frac(x^3+x-7)(2x^2-x+8) \to \infty$ ដូច្នេះ
$$ = \lim\limits_(x\to \infty)\left(e\right)^(x \frac(2x^2-x+8)(x^3+x-7))= \lim\limits_ (x\to \infty)e^(\frac(2x^2-x+8)(x^2+1-7/x))= \lim\limits_(x\to \infty)e^(\frac (2-1/x+8/x^2)(1+1/x^2-7/x^3))=e^(2)។ $$