Udsnit af geometriske figurer har forskellige former. Tværsnittet af et parallelepipedum er uvægerligt et rektangel eller kvadrat. Den har en række parametre, der kan detekteres ved hjælp af en analytisk metode.
Instruktioner
1. Det er muligt at tegne fire snit gennem parallelepipedet, som er firkanter eller rektangler. Hver den har to diagonale og to tværsnit. Som sædvanlig har de forskellige størrelser. Undtagelsen er terningen, hvor de er identiske. Før du konstruerer et udsnit af et parallelepipedum, skal du få en idé om, hvad denne figur repræsenterer. Der er to typer parallelepipeder - almindelige og rektangulære. I et almindeligt parallelepipedum er fladerne placeret i en vis vinkel i forhold til basen, mens de i en rektangulær er vinkelrette på den. Alle ansigter rektangulær parallelepipedum er rektangler eller firkanter. Det følger af dette, at en terning er særlig situation rektangulær parallelepipedum.
2. Hver sektion af et parallelepipedum har visse sammenstillinger. De vigtigste er areal, omkreds og længder af diagonaler. Hvis siderne af sektionen eller nogle af dens andre parametre er kendt fra disse problemer, er dette nok til at bestemme dens omkreds eller areal. Diagonalerne af sektionerne bestemmes også langs siderne. Den første af disse parametre er arealet af den diagonale sektion. For at bestemme arealet af den diagonale sektion er det nødvendigt at kende højden og siderne af bunden af parallelepipedet. Hvis længden og bredden af bunden af parallelepipedet er givet, så find diagonalen ved hjælp af Pythagoras sætning: d=?a^2+b^2. Efter at have fundet diagonalen og kender højden af parallelepipediet, beregner du kryds- tværsnitsareal af parallelepipedet: S=d*h.
3. Omkredsen af den diagonale sektion kan også beregnes ved hjælp af to værdier - basens diagonal og højden af parallelepipedummet. I dette tilfælde skal du først finde to diagonaler (øvre og nedre baser) ved hjælp af Pythagoras sætning, og derefter lægge dem sammen med det dobbelte af højden.
4. Hvis du tegner et fly, parallelt med ribbenene parallelepipedum, er det muligt at opnå et rektangulært snit, hvis sider er en af siderne af bunden af parallelepipedummet og højden. Find arealet af dette afsnit på følgende måde: S = a * h. Find omkredsen af dette afsnit på en lignende måde ved at bruge følgende formel: p = 2 * (a + h).
5. Det sidste tilfælde opstår, når sektionen løber parallelt med parallelepipedets to baser. Så er dens areal og omkreds lig med værdien af arealet og omkredsen af baserne, dvs.: S=a*b - tværsnitsareal; p=2*(a+b).
Inden man går videre til at finde højden af et parallelepipedum, er det nødvendigt at afklare, hvad en højde er, og hvad et parallelepipedum er. I geometri er højden en vinkelret fra toppen af en figur til dens base, eller et segment, der forbinder de øvre og nedre baser ved hjælp af den korteste metode. Et parallelepipedum er et polyeder, der har to parallelle og ens polygon som baser, hvis hjørner er forenet af segmenter. Parallepipedet er opbygget af seks parallelogrammer, parallelt i par og lig med hinanden.
Instruktioner
1. Der kan være tre højder i et parallelogram, afhængigt af figurens placering i rummet; ved at dreje parallelepipedet om på siden, bytter du dens baser og ansigter. De øvre og nedre parallelogrammer er uvægerligt baser. Hvis figurens laterale kanter er vinkelrette på baserne, så er parallelepipedet lige, og hver af dets kanter er en klar højde. Tilladt at måle.
2. For at få et lige parallelepipedum af samme størrelse fra et skråtstillet parallelepipedum skal du forlænge sidefladerne i én retning. Herefter skal du bygge vinkelret snit, fra hvis hjørner, afsæt længden af kanten af parallelepipedet, og i denne afstand konstruer et andet vinkelret snit. De to parallelogrammer, du har konstrueret, vil binde det nye parallelepipedum, som i areal er lig med det første. For fremtiden skal det bemærkes, at mængderne lige store figurer identisk.
3. Ofte stillede spørgsmål Vi møder højder i problemer. Vi får altid data, der gør det muligt for os at beregne det. Dette kan være volumenet, lineære dimensioner af parallelepipedet, længderne af dets diagonaler. Altså volumenet af parallelepipedet lig med produktet dens base ved dens højde, det vil sige ved at kende volumen og størrelsen af basen, er det let at finde ud af højden ved at dividere den første med den anden. Hvis du har at gøre med et rektangulært parallelepipedum, det vil sige en hvis base er et rektangel, kan de forsøge at komplicere din opgave på grund af dens særlige kvaliteter. Så i et rektangulært parallelepipedum, hvert kvadrat af sin diagonal lig med summen kvadrater af 3 dimensioner af et parallelepipedum. Hvis den "givne" for problemet med en rektangulær parallelepiped angiver længden af dens diagonal og længderne af siderne af basen, så er denne information nok til at finde ud af størrelsen på den ønskede højde.
Et parallelepipedum er et specialtilfælde af et prisme, hvor alle seks flader er parallellogrammer eller rektangler. Parallelepiped med rektangulære kanter også kaldet rektangulær. Et parallelepipedum har fire krydsende diagonaler. Hvis der er givet tre kanter a, b, c, kan du finde alle diagonalerne af et rektangulært parallelepipedum ved at udføre yderligere konstruktioner.
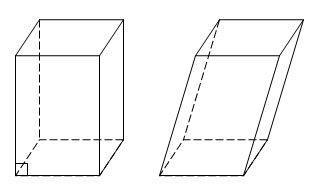
Instruktioner
1. Tegn et rektangulært parallelepipedum. Skriv de kendte data ned: tre kanter a, b, c. Konstruer først en diagonal m. For at bestemme det bruger vi kvaliteten af et rektangulært parallelepipedum, ifølge hvilket alle dets vinkler er rigtige.
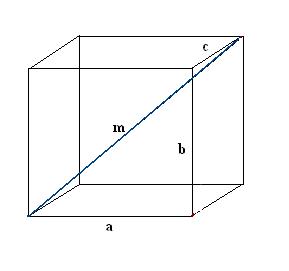
2.
Konstruer diagonalen n af en af sidefladerne på parallelepipedet. Udfør konstruktionen, så den ønskede kant, den ønskede diagonal af parallelepipedet og diagonalen af ansigtet tilsammen danner en retvinklet trekant a, n, m.
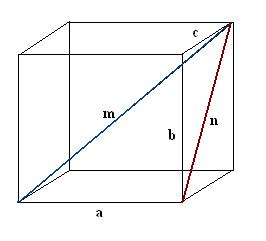
3. Find den konstruerede diagonal af ansigtet. Hun er hypotenusen af en anden retvinklet trekant b, c, n. Ifølge Pythagoras sætning er n² = c² + b². Beregn dette udtryk og tag kvadratroden af den resulterende værdi - dette vil være diagonalen af ansigt n.
4. Find diagonalen af parallelepipedummet m. For at gøre dette skal du i den retvinklede trekant a, n, m finde den ukendte hypotenuse: m² = n² + a². Erstat de kendte værdier, og beregn derefter kvadratroden. Det resulterende resultat vil være den første diagonal af parallelepipedummet m.
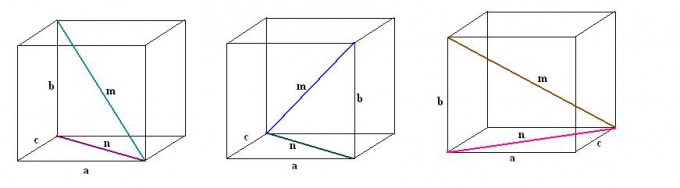
5. Tegn på samme måde alle de tre andre diagonaler af parallelepipedummet i trin. For dem alle skal du også udføre yderligere konstruktion af diagonaler af tilstødende ansigter. Ved at se på de rette trekanter, der er dannet, og anvende Pythagoras sætning, opdag værdierne af de resterende diagonaler af kuben.
Video om emnet
Mange rigtige genstande har en parallelepipedumsform. Eksempler er rummet og poolen. Dele med denne form er ikke ualmindelige i industrien. Af denne grund opstår ofte opgaven med at finde volumen af en given figur.
Instruktioner
1. Et parallelepipedum er et prisme, hvis basis er et parallelogram. Et parallelepipedum har ansigter - alle de planer, der dannes denne figur. Hver af dem har seks ansigter, og alle er parallellogrammer. Dens modsatte sider er lige store og parallelle med hinanden. Derudover har den diagonaler, der skærer hinanden i et punkt og halverer i det.
2. Der er 2 typer parallelepipedum. For den første er alle flader parallellogrammer, og for den anden er de rektangler. Den sidste kaldes et rektangulært parallelepipedum. Alle dens flader er rektangulære, og sidefladerne er vinkelrette på bunden. Hvis et rektangulært parallelepipedum har flader, hvis baser er kvadrater, så kaldes det en terning. I dette tilfælde er dens ansigter og kanter ens. En kant er en side af ethvert polyeder, som inkluderer et parallelepipedum.
3. For at finde volumen af et parallelepipedum skal du kende arealet af dets base og højde. Volumenet findes ud fra hvilket bestemt parallelepipedum, der optræder i problemets forhold. Et almindeligt parallelepipedum har et parallelogram i bunden, mens et rektangulært har et rektangel eller et kvadrat, som uvægerligt har rette vinkler. Hvis der er et parallelogram i bunden af et parallelepipedum, så findes dets volumen som følger: V = S * H, hvor S er arealet af basen, H er højden af parallelepipedummet. Højden af et parallelepipedum er normalt dens side rib. I bunden af et parallelepipedum kan der også være et parallelogram, der ikke er et rektangel. Fra forløbet af planimetri er det kendt, at arealet af et parallelogram er lig med: S = a*h, hvor h er højden af parallelogrammet, a er længden af basen, dvs. :V=a*hk*H
4. Hvis det andet tilfælde opstår, når bunden af parallelepipedet er et rektangel, beregnes volumenet ved hjælp af den samme formel, men arealet af basen findes på en lidt anden måde: V = S * H, S = a * b, hvor a og b er siderne, henholdsvis rektangel og parallelepipedum.V=a*b*H
5. For at finde rumfanget af en terning, bør man være styret af primitiv logiske metoder. Da alle terningens flader og kanter er lige store, og der ved bunden af terningen er en firkant, styret af formlerne angivet ovenfor, kan vi udlede følgende formel: V = a^3
I mange lærebøger er der opgaver relateret til konstruktionen af udsnit af forskellige geometriske figurer, herunder parallelepipeder. For at klare en sådan opgave bør du bevæbne dig med noget viden.
Du får brug for
- - papir;
- - pen;
- - lineal.
Instruktioner
1. Tegn et parallelepipedum på et stykke papir. Hvis dit problem siger, at parallelepipedet skal være rektangulært, så gør dets hjørner rigtige. Husk at modstående kanter skal være parallelle med hinanden. Navngiv dens hjørner, f.eks. S1, T1, T, R, P, R1, P1 (som vist på billedet).
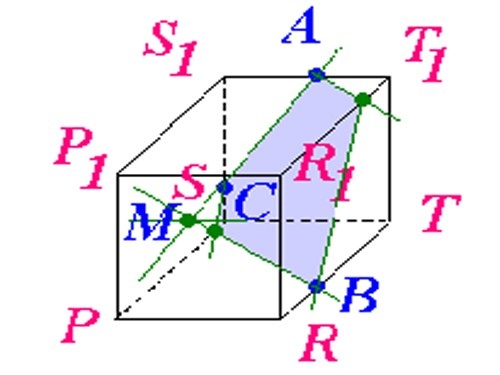
2. På kanten af SS1TT1 sæt 2 punkter: A og C, lad punkt A være på segmentet S1T1, og punkt C på segmentet S1S. Hvis dit problem ikke siger, hvor præcis disse punkter skal være, og afstanden fra hjørnerne ikke er angivet, skal du placere dem vilkårligt. Tegn en lige linje gennem punkterne A og C. Fortsæt denne linje, indtil den skærer linjestykket ST. Marker skæringsstedet, lad det være punkt M.
3. Placer et punkt på stykket RT, angiv det som punkt B. Tegn en ret linje gennem punkterne M og B. Angiv skæringspunktet for denne linje med kanten SP som punkt K.
4. Kombiner punkterne K og C. De skal ligge på samme flade PP1SS1. Tegn senere en ret linje gennem punkt B, parallelt med segmentet KS, fortsæt linjen, indtil den skærer kanten R1T1. Udpeg skæringspunktet som punkt E.
5. Kombiner punkterne A og E. Fremhæv senere den resulterende polygon ACKBE med en anden farve - dette vil være afsnittet bagved af dette parallelepipedum.
Bemærk!
Husk, at når du konstruerer en sektion af et parallelepipedum, må du kun forbinde de punkter, der ligger i samme plan; hvis de punkter, du har, ikke er tilstrækkelige til at konstruere sektionen, fuldend dem ved at forlænge segmenterne, indtil de skærer ansigtet hvor punktet er nødvendigt.
Nyttige råd
Hvert parallelepipedum kan have 4 sektioner: 2 diagonale og 2 tværgående. For større klarhed skal du vælge den resulterende polygon-sektion; til dette kan du blot skitsere den eller skygge den med en anden farve.
Tip 6: Sådan finder du længden af diagonalerne på et parallelepipedum
Et parallelepipedum er et prisme, hvis basis er et parallelogram. Parallelogrammerne, der udgør et parallelepipedum, kaldes dets flader, deres sider kaldes kanter, og parallelepipedets spidser kaldes parallellepipedets spidser.
Instruktioner
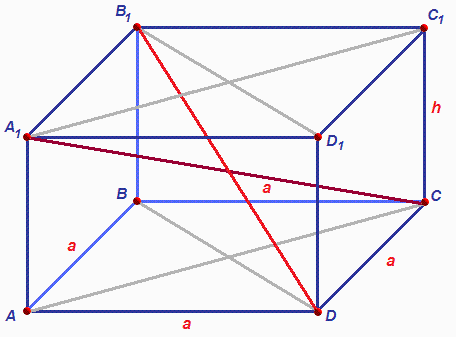
1. U parallelepipedum det er tilladt at konstruere fire krydsende diagonaler. Hvis de givne 3 kanter a, b og c er kendte, så find længderne diagonaler rektangulær parallelepipedum Det vil ikke være svært at udføre yderligere formationer.
2. Tegn først et rektangulært parallelepipedum. Underskriv alle de data, du kender, der skal være tre af dem: kanter a, b og c. Tegn den første diagonal m. For at konstruere det skal du bruge egenskaben af rektangulære parallelepipeder, ifølge hvilke alle vinkler af lignende figurer er rigtige.
3. Konstruer diagonalen n af en af fladerne parallelepipedum. Lav konstruktionen på en sådan måde, at den eller de berømte kant(er), den ukendte diagonal parallelepipedum og diagonalen af den tilstødende flade (n) dannede en retvinklet trekant a, n, m.
4. Se på den konstruerede diagonal af ansigtet (n). Det er hypotenusen af en anden retvinklet trekant b, c, n. Følg Pythagoras sætning, som siger, at kvadratet af hypotenusen er lig med summen af kvadraterne af benene (n? = c? + b?), find kvadratet af hypotenusen, og tag kvadratroden af den resulterende værdi - dette vil være længden af diagonalen af ansigtet n.
5. Find diagonalen af parallelepipedum m. For at finde dens værdi, i en retvinklet trekant a, n, m, beregne hypotenusen ved hjælp af den samme formel: m? = n? + a?. Beregn kvadratroden. Den opdagede total vil være den første diagonal af din parallelepipedum. Diagonal m.
6. Korrekt, tegn også alle de andre diagonaler i trin. parallelepipedum, for som alle udfører ekstra konstruktioner diagonaler tilstødende kanter. Brug Pythagoras sætning til at opdage værdierne af de resterende diagonaler givet parallelepipedum .
7. Der er en anden metode, der kan bruges til at bestemme længden af diagonalen. Ifølge en af egenskaberne ved et parallelogram er kvadratet af diagonalen lig med summen af kvadraterne på dens 3 sider. Heraf følger, at længden kan findes ved at tilføje sidernes kvadrater parallelepipedum og udtræk kvadratet fra den resulterende værdi.
Nyttige råd
Egenskaber ved et parallelepipedum: - et parallelepipedum er symmetrisk omkring midten af dets diagonal; - ethvert segment med ender, der tilhører overfladen af et parallelepipedum og går gennem midten af dets diagonal, er delt i to af det, især alle diagonaler af et parallelepipedum skærer hinanden i et punkt og er delt i to af det; - modsatte flader af en parallelepipedum parallele og lige; - kvadratet på diagonallængden af et rektangulært parallelepiped er lig med summen af kvadraterne af dets tre dimensioner.
Et parallelepipedum er en tredimensionel geometrisk figur med tre måledimensioner: længde, bredde og højde. De er alle involveret i at finde arealet af begge overflader parallelepipedum: fuld og side.
Instruktioner
1. Et parallelepipedum er et polyeder bygget på basis af et parallelogram. Den har seks ansigter, som også er disse todimensionelle former. Alt efter hvordan de er placeret i rummet, skelnes der mellem lige og skrå parallelepipedum. Denne forskel er udtrykt i ligheden mellem vinklen mellem basen og sidekanten på 90°.
2. Baseret på hvilket særligt tilfælde af et parallelogram basen tilhører, kan vi skelne mellem et rektangulært parallelepipedum og dets særligt almindelige sort - terningen. Disse former er især almindelige i Hverdagen og kaldes standard. De er iboende i husholdningsapparater, møbler, elektroniske enheder osv., såvel som i selve menneskelige boliger, hvis dimensioner er af væsentlig betydning for beboere og ejendomsmæglere.
3. Normalt tror man det firkant begge overflader parallelepipedum, side og fuld. Den første numeriske kollation repræsenterer det fælles område af dens ansigter, den anden er den samme værdi plus områderne af begge baser, dvs. summen af alle todimensionelle figurer, der udgør et parallelepipedum. Følgende formler bære navnet på de vigtigste sammen med volumen: Sb = P h, hvor P er omkredsen af basen, h er højden; Sp = Sb + 2 S, hvor So er firkant grunde.
4. Til specielle tilfælde, terning og figur med rektangulære baser, er formlerne forenklet. Nu er det ikke længere nødvendigt at bestemme højden, som er lig med længden af den lodrette kant, men firkant og omkredsen er meget lettere at opdage på grund af tilstedeværelsen af rette vinkler; kun længde og bredde er involveret i deres bestemmelse. Det viser sig, at for en rektangulær parallelepipedum:Sb = 2 c (a + b), hvor 2 (a + b) er dobbeltsummen af siderne af basen (perimeter), c er længden af sidekanten; Sp = Sb + 2 a b = 2 a c + 2 b c + 2 a b = 2 (a c + b c + a b).
5. Alle kanter af en terning har identiske længder, derfor: Sb = 4 a a = 4 a?; Sp = Sb + 2 a? = 6 a?.
Spørgsmålet vedrører analytisk geometri. Det løses ved hjælp af ligningerne for rumlige linjer og planer, repræsentationen af terningen og dens geometriske egenskaber, samt brug af vektoralgebra. Metoder til løsning af lineære ligningssystemer kan være nødvendige.
Instruktioner
1. Vælg disse opgaver, så de er omfattende, men ikke overflødige. Skærende fly? skal gives ved en generel ligning på formen Ax+By+Cz+D=0, som den bedste måde i overensstemmelse med hans vilkårlige valg. For at definere en terning er koordinaterne for 3 af dens hjørner absolut nok. Tag f.eks. punkterne M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3), ifølge figur 1. Denne figur illustrerer et tværsnit af en terning. Den skærer to sideribber og tre basisribber.
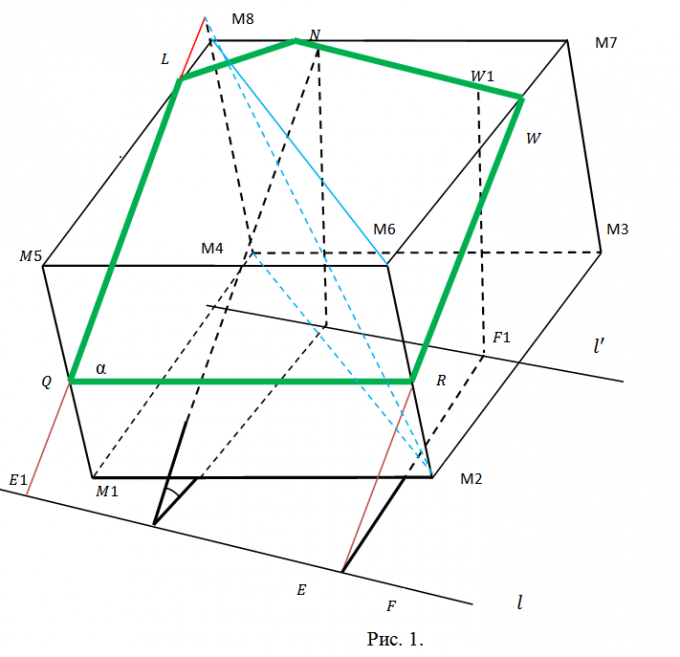
2. Beslut dig for en plan for det efterfølgende arbejde. Vi skal lede efter koordinaterne for punkterne Q, L, N, W, R hvor sektionen skærer terningens tilsvarende kanter. For at gøre dette skal du finde ligningerne for linjerne, der indeholder disse kanter, og se efter skæringspunkterne mellem kanterne og planet?. Senere vil dette blive fulgt ved at opdele femkanten QLNWR i trekanter (se fig. 2) og beregne arealet af dem alle ved hjælp af vektorproduktets egenskaber. Metoden er den samme hver gang. Derfor kan vi begrænse os til punkterne Q og L og arealet af trekanten?QLN.
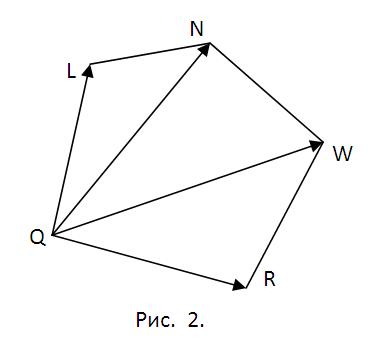
3. Retningsvektoren h for den rette linje, der indeholder kanten M1M5 (og punktet Q), findes som vektorproduktet M1M2=(x2-x1, y2-y1, z2-z1) og M2M3=(x3-x2, y3- y2, z3-z2), h=(ml, n1, p1)=. Den resulterende vektor er en guide for alle andre sidekanter. Find længden af kanten af terningen som f.eks. ?=?((x2-x1)^2+(y2-y1)^2+(z2-z1)^2). Hvis modulet af vektoren h |h|??, skal du erstatte det med det tilsvarende collineær vektor s=(m, n, p)=(h/|h|)?. Skriv nu ligningen for den lige linje, der indeholder M1M5 parametrisk (se fig. 3). Efter at have erstattet de tilsvarende udtryk i ligningen for skæreplanet, får du A(x1+mt)+B(y1+nt)+C(z1+pt)+D=0. Bestem t, indsæt det i ligningerne for M1M5 og skriv koordinaterne for punktet Q(qx, qy, qz) ned (fig. 3).
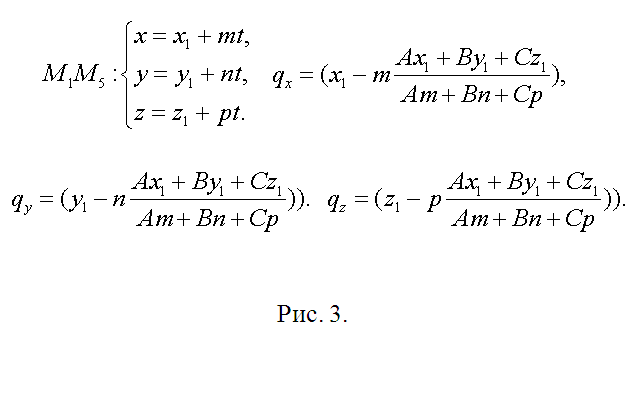
4. Tilsyneladende har punkt M5 koordinaterne M5(x1+m, y1+n, z1+p). Retningsvektoren for den rette linje, der indeholder kanten M5M8, falder sammen med M2M3=(x3-x2, y3-y2,z3-z2). Gentag derefter den foregående begrundelse vedrørende punktet L(lx, ly, lz) (se fig. 4). Alt, hvad der følger for N(nx, ny, nz) er en nøjagtig kopi af dette trin.
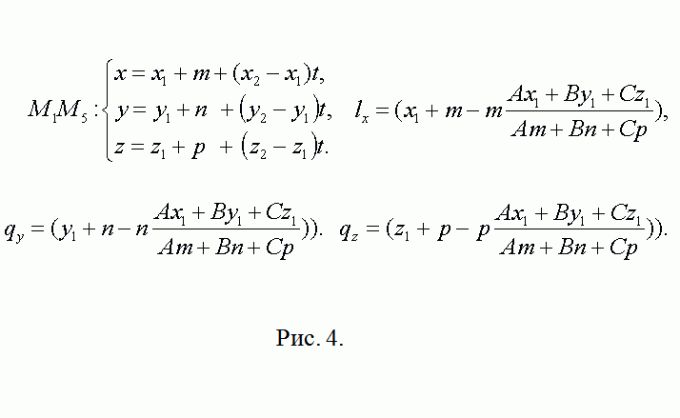
5. Skriv vektorerne QL=(lx-qx, ly-qy, lz-qz) og QN=(nx-qx, ny-qy, nz-qz). Den geometriske betydning af deres vektorprodukt er, at dets modul lig med areal parallelogram bygget på vektorer. Som følge heraf er området?QLN S1=(1/2)||. Følg den foreslåede metode og beregn arealerne af trekanterne ?QNW og ?QWR - S1 og S2. Vektor kunstværk Det er mere behageligt at finde alle med støtte fra determinantvektoren (se fig. 5). Skriv det endelige resultat S=S1+S2+S3 ned.
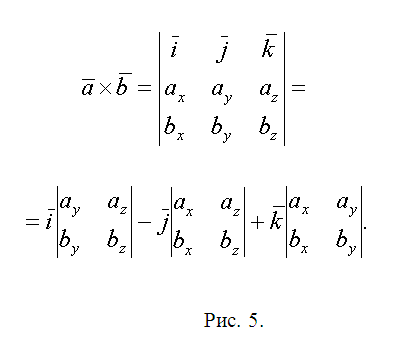
Tip 9: Sådan finder du det diagonale tværsnitsareal af et prisme
Et prisme er et polyeder med to parallelle baser og sideflader i form af et parallelogram og i antal, lig med tallet sider af basispolygonen.
Instruktioner
1. I et vilkårligt prisme er sideribberne placeret i en vinkel i forhold til bundens plan. Et særligt tilfælde er et lige prisme. I det sider ligge i planer vinkelret på baserne. I et lige prisme er sidefladerne rektangler, og sidekanterne er lig med prismets højde.
2. Den diagonale sektion af et prisme er en del af planet, der helt er indeholdt i polyederens indre rum. Den diagonale sektion kan begrænses af to sideribber geometrisk krop og diagonaler af baserne. Tilsyneladende er antallet af tilladte diagonalsnit bestemt af antallet af diagonaler i basispolygonen.
3. Eller grænserne for det diagonale snit kan være diagonalerne på sidefladerne og modsatte sider prisme baser. Det diagonale tværsnit af et rektangulært prisme har form som et rektangel. I det generelle tilfælde af et vilkårligt prisme er formen af diagonalsnittet et parallelogram.
4. I rektangulær prisme Arealet af diagonalsektionen S bestemmes af formlerne: S=d*Hhvor d er basens diagonal, H er prismets højde. Eller S=a*Dhvor a er den side af basen, der hører samtidig til snitplanet, D er diagonalen af sidefladen.
5. I et vilkårligt indirekte prisme er diagonalsektionen et parallelogram, hvis ene side er lig med prismets laterale kant, den anden er lig med basens diagonal. Eller siderne af diagonalsnittet kan være diagonalerne på sidefladerne og siderne af baserne mellem prismets spidser, hvorfra sidefladernes diagonaler er tegnet. Arealet af et parallelogram S bestemmes af formlen: S=d*hhvor d er diagonalen af prismets basis, h er højden af parallelogrammet - prismets diagonale snit. Eller S=a* hhvor a er siden af prismets basis, som også er grænsen for diagonalsnittet, h er højden af parallelogrammet.
6. For at bestemme højden af diagonalsnittet er det utilfredsstillende at kende prismets lineære dimensioner. Vi har brug for data om prismets hældning til basisplanet. Det efterfølgende problem kommer ned til en trinvis løsning af flere trekanter afhængigt af de indledende data om vinklerne mellem elementerne i prismet.
"Golden Section" - Formålet med undersøgelsen: At udlede verdens skønhedslov fra matematikkens synspunkt. Admiralitet. Vindue. Udført af 10. klasses elev Yulia Smetanina. Forbønskatedralen (St. Basil's Cathedral). Gyldent snit i arkitektur. I matematik er en proportion ligheden mellem to forhold: a:b = c:d. Egyptiske pyramider.
"Konstruktion af sektioner" - Sektioner udføres i samme skala som det billede, det vedrører. Funktioner ved at lave sektioner. Anvendelse af dimensioner. Udpegning af sektioner. Omridset af de udsatte sektioner udføres solid linje. Regler for at lave sektioner. Afsnit. Snit i tegningerne er opdelt i udvidede og overlejrede.
"Parallelepiped grade 10" - Vinklen er 60?. 3. Fire, hvis parallelepipedet er en terning. Vinklen er 60?. 3.Lige kvadrater, vinkler 90?. Islands spar-krystaller har en rhombohedron-form. Mulighed 2. Givet parallelepiped ABCDA1B1C1D1. Diagonaler af et parallelepipedum. Bevis at linjerne B1C og A1D er parallelle. 2. Parallepipedets diagonaler er lige store. Parallelepiped.
"Volumen af et parallelepiped" - Vi gør det samme nu. I Det gamle Babylon Enhederne for volumen var terninger. Lad os nu definere, hvad volumenheder er? Det betyder, ifølge reglen for beregning af volumen, at vi får: 3x3x3=27 (cm3). Opgave nr. 2. Find rumfanget af en terning, hvis kant er 3 cm. En volumenhed svarende til 1 dm3 kaldes en liter. Opgave nr. 1.
"Lektion rektangulært parallelepipedum" - Lektionsmål: Længde. Afspejling. Find arealet af bunden af det rektangulære parallelepipedum. Konstruer et rektangel givet længde(a) og højde (h). Scan. Kanter. Ribben. Idrætsminut. Algoritme til at konstruere et rektangulært parallelepipedum. Tre gange længden mindre højde, og bredden er 6 gange mindre end højden.
"Volumen af et rektangulært parallelepipedum" - T e s t. ( Geometrisk figur). 6. Alle flader af et parallelepipedum er rektangler. 3. Alle flader af en terning er firkanter. Svar til næste spørgsmål: Firkanter. Navngiv de kanter, der har toppunkt E. Forøg. Volumetrisk. Opgave 2: Dimensionerne af et rektangulært parallelepipedum er 3cm, 6cm og 6cm.
Med. 1
Lektionsbaserede udviklinger 11. klasse ved hjælp af lærebogen "Geometri" L. S. Atanasyan
LEKTION nr. 1. REKTANGULÆRT KOORDINATSYSTEM B RUM !:
primære mål : introducere begrebet et rektangulært koordinatsystem, lære at konstruere et punkt, kende dets koordinater og bestemme det. koordinater for et punkt konstrueret i et rektangulært koordinatsystem.
jeg . Mundtligt arbejde .
II indbygget i overensstemmelse med s. 42 lærebøger.
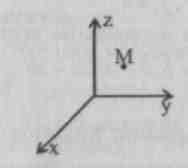Problemet er, om punktets position er indstillet M.
V plads? Ingen. Det er nødvendigt at konstruere projektioner af punktet M pr fly (Åh), (Oxz) (Ozy).
TIL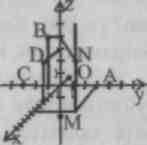 
test spørgsmål
Find punkternes koordinater ved hjælp af billedet A, B, C,D, M, N.
Tegn et koordinatsystem Oxyz og plot punkterne
Løsning af problemer: nr. 400 (mundtlig), 401 (mundtlig), 402.
Lektier: teori (paragraf 42), nr. 501.
LEKTION nr. 2. VEKTORKOORDINATER
primære mål : introducere begrebet vektorkoordinater
jeg . Forklaring af nyt materiale bygge i overensstemmelse med paragraf 43 i lærebogen.
II . Problemløsning : nr. 403, 404,407(a, b, g, i, j, l) 410, 408, 412.
III
. Lektier
: teori (punkt 13), gentagelse (punkt 38, 39), nr. 405, 407 (d, e, f, g, h), 409 (c, d, e, f, h, m), 411.
LEKTION nr. 3. FORHOLD MELLEM VEKTORKOORDINATER OG PUNKTKOORDINATER
Primært mål: bevise, at koordinaterne for ethvert punkt er lig med de tilsvarende koordinater for dets radiusvektor; lære at finde koordinaterne for en vektor, ved at kende koordinaterne for dens begyndelse og slutning.
jeg . Forklaring af nyt materiale bygge i overensstemmelse med paragraf 44 i lærebogen.
II. Problemløsning : nr. 416.417, 418 (a), 419.420.
III. Lektier : teori (punkt 44), nr. 418 (b, c), 421.
LEKTION nr. 4. DE ENKLE PROBLEMER I KOORDINATER
Primært mål: udled formler til at finde koordinaterne for midten af et segment, længden af en vektor ud fra dens koordinater og afstanden mellem to punkter.
Tjek lektier. nr. 421. Løs nr. 422.
III. Forklaring af nyt materiale bygge i overensstemmelse med paragraf 45 i lærebogen.
IV. Løsning af problemer: Nej. 424, 426, 427, 430.
V. Lektier: teori (punkt 45), nr. 425, 429, 431.
LEKTION nr. 5.6 VINKEL MELLEM VEKTORER
Primært mål: generaliser begrebet "vinkel mellem vektorer", lær dig at finde vinklen mellem vektorer i rummet.
Sh. Forklaring af nyt materiale konstruer i overensstemmelse med afsnit 46. Vis et eksempel på at finde vinkler mellem vektorer på stereometriske modeller (vær opmærksom på de vektorer, der ligger på krydsende rette linjer).
IV. Problemløsning № 442,507,508
V. Lektier: teori (klausul 46), nr. 441, til gentagelse - nr. 490, 491 (mundtlig), 492, 501.
№
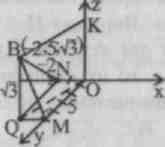501.
Find VM,BN, VH.
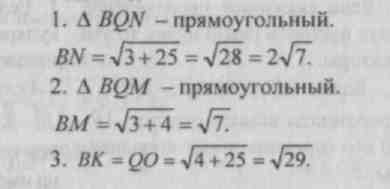Løsning.
Forklaring af nyt materiale.
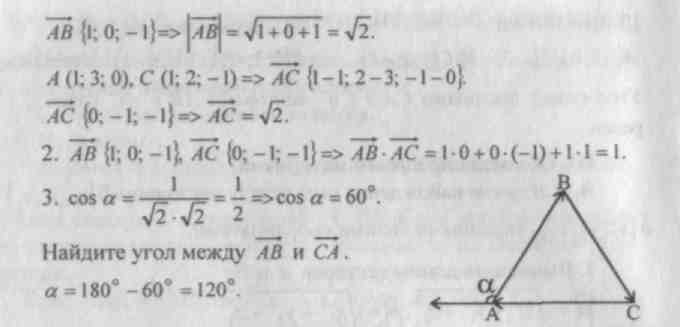
Lektier: teori (klausul 48), nr. 451, 453, 464 (b, c, d), 469 (b, c).
Diktat
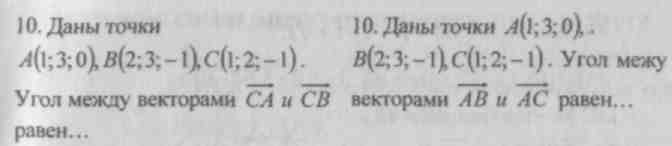
LEKTION nr. 7 SKALAR PRODUKT AF VEKTORER
Primært mål: udvikle evnen til at løse problemer med at finde en vinkel med vektorer, rette linjer, en ret linje og en plan.
jeg. Tjek hjemmearbejde ( ved bestyrelsen): nr. 451 (b, d), nr. 464 (c; d).
II. Problemløsning(ifølge færdige tegninger).
Algoritme til løsning af problemer:
Gå ind rektangulært system koordinere" 1
Skriv koordinaterne for alle punkter ned.
Brug en algoritme til at finde vinklen mellem rette linjer, mellem en ret linje og en plan.
III. Problemløsning.
(vektormetode)
III. (Vektorkoordinatmetode).
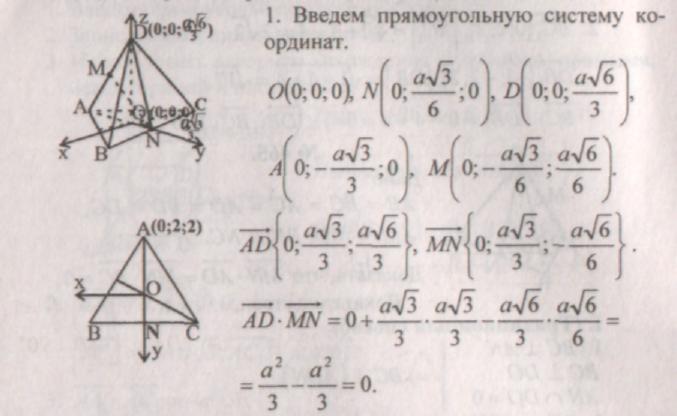
Lektier:№ 455, 457, 462.
LEKTION nr. 8 SKALAR PRODUKT AF VEKTORER
Primært mål: udvikle evnen til at finde vinkler mellem rette linjer, mellem en ret linje og en plan.
№ 455.
(Tegningen er udarbejdet på forhånd. Eleverne siger fra, eller nogen skriver svarene på tavlen). 
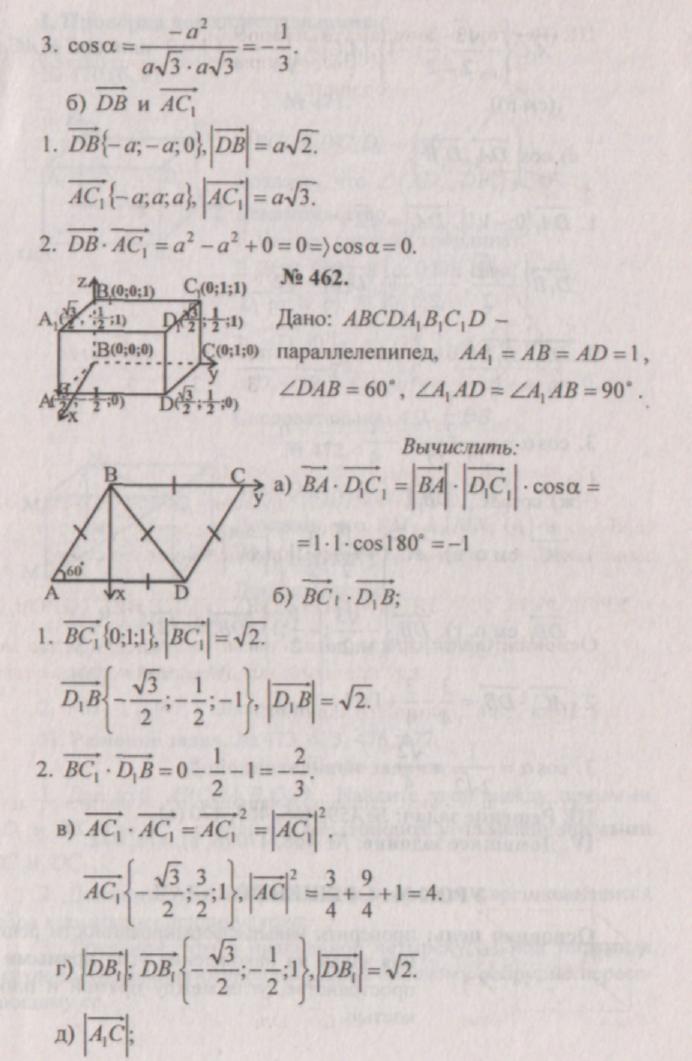
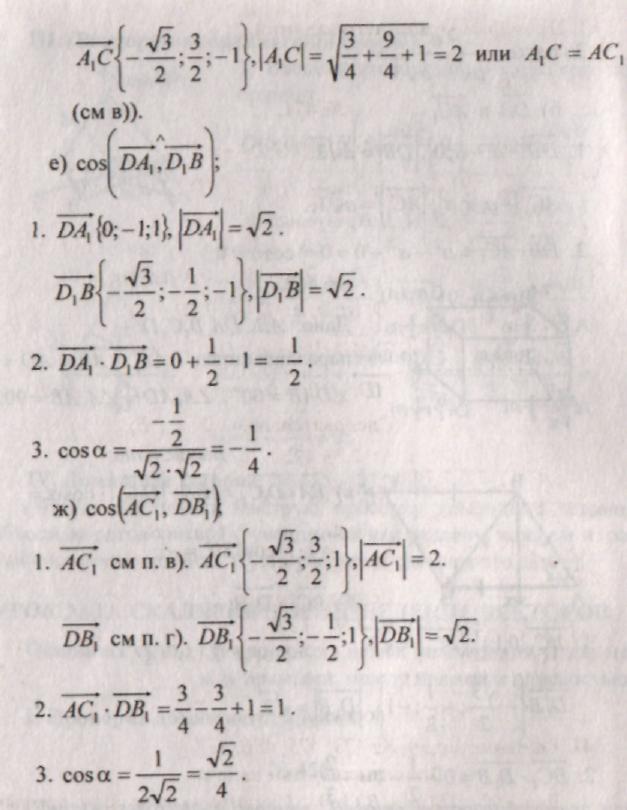
III. Problemløsning: nr. 459, 466, 467, 470 (a).
IV. Lektier: nr. 468, 470 (b, c), 471, 472.
LEKTION nr. 9 TEST nr. 1
Test til selvtest og korrektion af elevernes viden
|
Mulighed |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
jeg |
V |
G |
V |
b |
EN |
b |
G |
V |
|
II |
b |
EN |
V |
G |
V |
b |
G |
G |
|
Mulighed |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
jeg |
b |
G |
b |
V |
V |
G |
V |
b |
|
II |
b |
EN |
G |
V |
G |
EN |
V |
b |
LEKTION #10. CYLINDER
Primært mål: introducere begrebet en cylinder, elementer af en cylinder.
jeg. Forklaring af nyt materiale bygge efter planen:
1. Koncept cylindrisk overflade, cylinder.
Overveje forskellige varer omgivende miljø, hvilket giver en idé om cylinderen - en cirkulær blyant, et glas, en penny, en pande, et stykke rør osv. (De viste cylindre skal have forskellige forhold mellem højde og diameter.) Giv et billede af en cylinder, vis på tegningen - akse, højde, radius, generatorer, cylinderbaser.
2. Indtast begrebet aksial sektion af en cylinder, indstil dens egenskaber:
a) cylinderens aksiale snit er et rektangel;
b) to aksiale sektioner af cylinderen er ens med hinanden.
Introducer begrebet en ligesidet cylinder med et aksialt tværsnit
som er en firkant.
3. Betragt snittet af en firkant ved et plan
EN) parallel akse cylinder;
b) vinkelret på cylinderaksen.
4. Introducer begrebet et tangentplan for en cylinder som et plan, der går gennem cylinderens generatrix og vinkelret på det aksiale snit tegnet gennem denne generatrix. (En analogi med en tangent til en cirkel).
II. Problemløsning:№ 521, 522, 526, 529.
III. Lektier:№ 523, 525, 530.
LEKTION #11. CYLINDER
Primært mål: at formulere evnen til at løse problemer med at finde elementerne i en cylinder.
jeg. Tjek lektier(ved tavlen).
II. Mundtligt arbejde.
Identificer genstande i naturen, teknologien, arkitekturen og blandt genstandene omkring dig, der har en cylindrisk form.
Forklar hvad man kalder en cylinder, en cirkulær cylinder. Nævn dets hovedelementer og giv dem en definition.
Giv definitionen af en lige cylinder.
Hvor mange aksiale sektioner af cylinderen passerer gennem hver af dens generatrices?
Bestem typen af cylinderens aksiale snit. Begrund dit svar.
Kan den aksiale sektion af en cylinder være: a) et rektangel; b) kvadratisk; c) trapez?
Har cylinderen: a) et symmetricentrum; b) symmetriakse; c) symmetriplan? Angiv dem i hvert enkelt tilfælde. Hvor mange er der? Vises på modellen.
Lade AA 1 I 1 I Og MM1 N 1 N - to aksiale sektioner af cylinderen. Sammenlign deres områder.
En cylinder ruller langs et fly. Hvilken figur opnås, når dens akse bevæger sig?
Hvilket af følgende udsagn er sandt:
b) enhver sektion af en cylinder i et plan er en cirkel lig med omkredsen af basen;
c) et plan vinkelret på cylinderens akse skærer den i en cirkel, lige grundlag cylinder;
d) snittet af en cylinder for plan kan være en cirkel, et rektangel og en ellipse?
12. Formuler og bevis en sætning om snittet af en cylinder i et plan vinkelret på dens akse.
III. Problemløsning: nr. 527 (b), 532, 534.
IV. Lektier: nr. 527 (a), 531, 535.
LEKTION #12. KEGLE
Primært mål: kontrollere formuleringsniveauet for problemløsningsevnen til at finde elementerne i en cylinder. Introducer begreberne for en kegle og elementer i en kegle.
Selvstændigt arbejde (15 min).
Sektionen af cylinderen med et plan parallelt med aksen er en firkant, hvis areal er 20 dm. Find cylinderens aksiale tværsnitsareal, hvis dens diagonal er 10 dm.
Mulighed II
Cylinderens højde er 16 cm, bundens radius er 10 cm Cylinderen krydses af et plan parallelt med aksen, så tværsnittet er kvadratisk. Find afstanden fra cylinderaksen til dette afsnit.
Udviklingen af cylinderens laterale overflade er et rektangel, hvis diagonal, lig med 12l, danner en vinkel på 30° på den ene side. Find cylinderens samlede overfladeareal, hvis dens højde er lig med den korteste side af udviklingen.
1. Begreber for en kegle, dens elementer (top, akse, generatorer, base, sideflade kegle). Keglebillede
N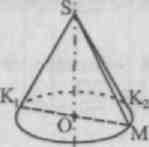 
i figuren tegner vi tangenter fra punktet S
til ellipsen, der repræsenterer keglens bund. Lad os betegne med TIL 1
Og TIL 2
berøringspunkter. En almindelig fejl er, at eleverne antager trekanten S.K. 1
K 2
for billedet af keglens aksiale snit. Dog akkorden TIL 1
TIL 2
går ikke gennem midten OM keglens bund. At konstruere et billede af et aksialt snit, der passerer gennem generatricen S.K. 1
det er nok at konstruere et billede af diameteren TIL 1
M og forbind det resulterende punkt M med top S
kegle S.K. 1
Og S.K. 2
- billeder af ekstreme generatorer, dvs. de adskiller de synlige generatorer (deres billeder fås ved at forbinde vilkårligt punkt buer TIL 1
MK 2
ellipse med toppunkt S) fra usynlig.
2. Overvej tværsnittet af en kegle med forskellige planer, og fremhæve to tilfælde:
Skæring fly gennem toppunktet af en kegle;
Skæreplanet er parallelt med keglens bund.
1(a). Hvis de skærer hinanden i to punkter, får vi i tværsnittet af keglen ligebenet trekant, hvis basis er et segment med ender i disse punkter. Fra aksialt snit. Det opnås, hvis skæringspunkterne, der overvejes, er enderne af diameteren af keglens bund. Blandt keglerne skiller en ligesidet sig ud (den aksiale sektion er ligesidet trekant). Hvis R er radius af dens base, så er generatrixen af en ligesidet kegle lig med 2 R .
1(b). Hvis de kun har én fælles punkt, så er det pågældende plan tangent til keglen.
Tangentplanet til en kegle kan defineres på forskellige måder.
Definition 1. Planet, der passerer gennem keglens generatrix, er vinkelret på det aksiale snit trukket gennem denne generatrix.
Definition 2. Et plan, der kun har én fælles generatrix med en kegle.
Fortolkningen af et plan tangent til en kegle og et plan tangent til en cylinder bør være den samme i den samme lærebog. Det skal bemærkes, at ved at acceptere et af forslagene 1 eller 2 in som definition, er det nødvendigt at gøre eleverne bekendt med den anden som en egenskab ved et tangentplan til en kegle.
1 (c). Ved at fortsætte vores overvejelse af planet, der passerer gennem keglens toppunkt, kommer vi til sagen: hvis planen og basens cirkel ikke har fælles punkter, så har det pågældende plan med keglen kun ét fælles punkt - keglens toppunkt.
2. Når man beviser sætningen om sektionen af en kegle med et plan parallelt med dens base (nr. 556), er det tilrådeligt at opnå følgende konklusioner:
1. Det afsnit, der overvejes, er en cirkel.
2. Udpeget af R Og r - henholdsvis radius af keglen og sektionen under overvejelse og gennem N Og h højden af den givne og afskårne kegle, får vi det, ,hvor k er lighedskoefficienten for de givne og afskårne kegler. Bevis det
Generaliser ved at løse opgave nr. 557.
Overvejelse af afsnittet, vinkelret på aksen kegle, tillader effektiv brug homotetisk metode svarende til tværsnit af pyramiden efter plan, parallelt med bunden. Efter at have etableret formen og placeringen af sektionen introduceres konceptet med en afkortet kegle.
Når man afbilder en keglestub, er det bekvemt først at tegne keglen, hvorfra den afkortede kegle er opnået.
Problemløsning: nr. 548 (a), 549.
Lektier: teori (s. 55, 56), nr. 547, 548 (b, c), 550.
LEKTION #13. KEGLE
Primært mål: introducere begrebet området af den laterale overflade af en kegle som området for dens udvikling.
jeg. Tjek lektier(ved tavlen).
II
Introducer begrebet lateral overfladeareal ved hjælp af udviklingen af en kegle.
Det samlede overfladeareal af en kegle.
Udled en formel til at beregne arealet af den laterale overflade af en afkortet kegle.
V. Lektier: nr. 560 (b, c), 561, 563, 568.
LEKTION nr. 14. KULLE OG BUD. Sfæreligning. RELATIV POSITION AF KUGLE OG FLY. TANGENT FLY TIL Sfæren. OMRÅDE AF Sfæren
Primært mål: gå ind begreber kugle og bold, udled kuglens ligning, overvej den relative position af kuglen og planet, definer tangentplanet til kuglen, skriv ned formlen til beregning af kuglens areal.
jeg. Forklaring af nyt materiale konstruere på en forelæsningsmåde i overensstemmelse med paragraf 58 - 62 i lærebogen.
For eksempler, brug problemer: nr. 575 til at forstå definitionerne af sfæren; nr. 576, 578 til beregning af kuglens ligning; nr. 586 til illustration relativ position kugler og fly; nr. 593 (a), 594 for at praktisere formlen for arealet af en kugle.
Problemløsning:
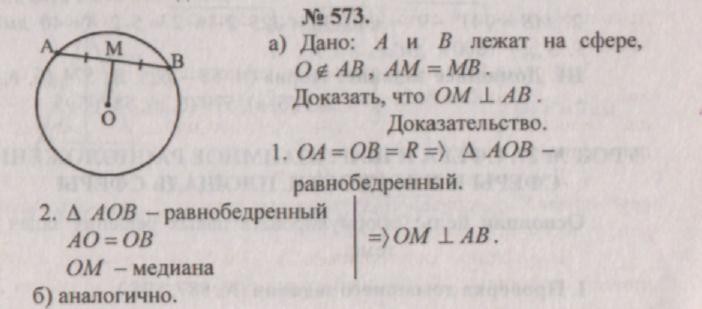
III. Lektier: teori (s. 58 - 62), nr. 574 (b, c, d).
577 (b, c), 579 (6, c), 587, 595.
LEKTION nr. 15. KULLE OG BOLD. RELATIV POSITION AF KUGLE OG FLY. OMRÅDE AF Sfæren
Primært mål: formulere evnen til at løse problemer om et emne.
Undersøgelse hjem opgaver (nr. 587, 595.)
Problemløsning
III. Hjemmearbejde: Nej. 582, 584, 585, 592, 597.
LEKTION nr. 16. FORBEREDELSE TIL TESTEN
Primært mål: gentage, systematisere, generalisere det undersøgte materiale.
jeg. Tjek lektier(ved tavlen): nr. 582, 584, 585.
II. Mundtligt arbejde- om spørgsmål til kapitel VI.
III. Problemløsning.
Lektion #17 Prøve № 2
LEKTION nr. 18. VOLUMEN AF ET REKTANGULÆRT PARALLELEPIPED
Primært mål: introducere begrebet kropsvolumen.
I. Forklaring af nyt materiale.
EN. Begrebet volumen af en krop introduceres i analogi med begrebet areal flad figur. Muligt sammen med elever udfylde anden halvdel borde.
Kontrolspørgsmål.
Hvad er volumen af en krop?
Hvad vil det sige at måle kropsvolumen?
4. Sådan får du 
enhed terning?
5. Enhedsterningen passer ind i den del af rummet, som oktaederet optager, 2 gange og 2 gange - den brøkdel af enhedsterningen, hvilket tal er karakteriseret V oktaeder?
B. Volumen af en terning lig med terning hans ribben. V= a 3 .
Udled formlen til beregning V terning, hvis dens diagonal er kendt
II. Problemløsning.
1. Det samlede overfladeareal af en terning er 6 m 2 . Find dens volumen. (1 m 3)
Terningens rumfang er 8 m. Find det samlede overfladeareal.
Hvis hver kant af en terning øges med 1 m, vil dens volumen stige 125 gange. Find kanten af terningen.
Tre terninger af bly har kanter på 3, 4 og 5 cm. De smeltes til én terning. Find hans ribben
Rumfanget af en terning er A. Find arealet af dens diagonal
III. To kroppe hvis volumener er lige store, kaldes lige store.
(Når du beviser følgende sætning, skal du bruge en model eller en tidligere udarbejdet tegning.)
Sætning. Et skrå prisme er lige stort som et lige prisme, hvis basis er vinkelret på den skrå sektion, og sidekanten er lig med sidekanten skrå prisme.
Kontrolspørgsmål.
Hvilke to legemer kaldes lige store?
To kroppe er lige store. Er de lige store?
De to kroppe er lige store. Er de ligeværdige?
LEKTION nr. 19. VOLUMEN AF ET REKTANGULÆRT PARALLELEPIPED
Primært mål: udvikle evnen til at løse problemer for at finde volumen af et parallelepipedum.
I. Mundtligt arbejde.
Hvad er volumen af en krop?
Hvad er rumfanget af en terning? En tiendedel af det?
Terningen er gennemskåret af to diagonale sektioner. Hvad er volumen af hver del?
I en terning med en kant på 2 cm diagonalt snit lavet. Hvad er volumen af hver af de resulterende dele?
Det samlede overfladeareal af kuben er 24 cm2. Hvad er rumfanget af en terning?
Terningens diagonal er EN. Find dens volumen.
Volumen af en terning V. Find dens diagonal.
Diagonalen på en terningsflade er 8. Hvad er terningens rumfang?
Rumfanget af det skrå prisme er 27 cm 3 . Hvad er størrelsen af en kant af en terning af samme størrelse?
Forklaring af nyt materiale.
Volumenet af et rektangulært parallelepipedum er lig med produktet af dets tre dimensioner. V = abc . Eller volumenet af et rektangulært parallelepipedum er lig med produktet af bundens areal og højden. V= S grundlæggende H
III. Problemløsning.
Lektier: teori (vol. 64), nr. 648.650.651.652
IV. Selvstændigt arbejde.
MULIGHED I
1. Volumenet af et rektangulært parallelepipedum er 96 cm, sidekanten er 8 cm. Hvad er arealet af basen?
Basen af et rektangulært parallelepipedum er en firkant med side EN. Sidefladens diagonal danner en vinkel α med bundens plan.
I et rektangulært parallelepipedum danner diagonalerne af tilstødende sideflader, der udgår fra det samme toppunkt, vinklerne α og β med fælles siderib udgår fra samme toppunkt. Sidekanten af parallelepipedet er lig med b . Find volumenet af parallelepipedet.
Volumenet af et rektangulært parallelepipedum er 100 cm 3, basisarealet er 25 cm 2. Find højden af parallelepipedummet.
I et rektangulært parallelepipedum er basen en firkant. Parallepipedets diagonal er d og danner en vinkel α med sidekanten generel begyndelse. Find volumenet af parallelepipedet.
LEKTION nr. 20. BIND AF ET DIREKTE PRISME
Primært mål: udled en formel til at beregne volumenet af et lige prisme.
I. Kontrol af lektier.
P. Forklaring af nyt materiale.
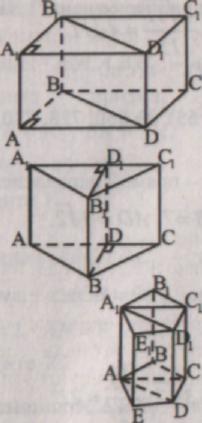
Grundlaget for et lige prisme er en retvinklet trekant. Dens volumen er lig med produktet af arealet af basen og højden.
Basen af et lige prisme - vilkårlig trekant. Dens volumen er lig med produktet af arealet af basen og højden.
Vilkårlig lige prisme. Bevis, at dens volumen er lig med produktet af arealet af basen og højden.
AT. Volumenet af et lige prisme er lig med produktet af arealet af basen og højden. 
Sh. Problemløsning.№ 659, 661, 662, 729.
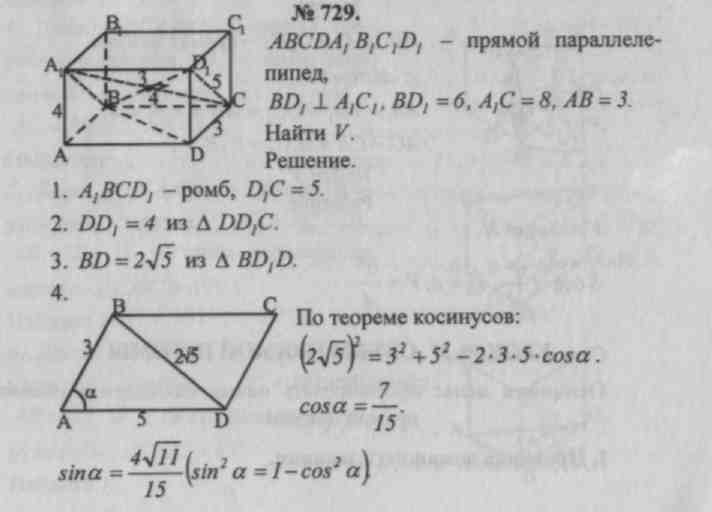
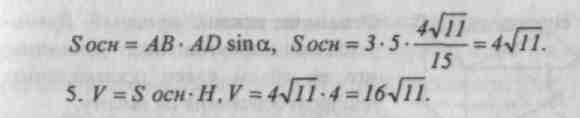
Lektier: teori (punkt 65), nr. 660, 728, 730, 731.
LEKTION nr. 21. CYLINDERVOLUMEN
Primært mål: udled en formel til at beregne volumenet af en cylinder.
jeg . Forklaring af det nye bygge i overensstemmelse med paragraf 66 i lærebogen.
II. Problemløsning. Ingen. 671, 672.
Sh. Hjemmearbejde: teori (punkt 66), nr. 666, 667, 668, 699, 670.
Yderligere opgaver.
En sektion af cylinderen med et plan parallelt med aksen afskærer en bue på 60° fra bundens omkreds. Tværsnitsarealet er S, og snittets diagonal danner en vinkel α med planet for cylinderens basis. Find cylinderens volumen.
En sektion af en cylinder i et plan parallelt med aksen afskærer en bue på 90° fra bundens omkreds. Tværsnitsarealet er S, og snittets diagonal danner en vinkel α med cylinderens generatrix. Find cylinderens volumen.
En terning er indskrevet i en cylinder. Rumfanget af terningen er F. Find cylinderens rumfang.
LEKTION nr. 22. BIND AF EN PYRAMID
Hovedmål: udvikle evnen til at finde volumen af en pyramide, hvis toppunkt er projiceret til midten indskrevet i bunden af en cirkel eller omskrevet omkring bunden af en cirkel.
I. Kontrol af lektier.
Fortsæt med sætningerne.
Hvis alle laterale kanter af pyramiden er ens, så projiceres toppunktet på basen i...
Hvis alle pyramidens apotemer er ens, så projiceres spidsen på basen i...
Jeg falder dihedrale vinkler når basen er ens, så projiceres toppunktet på basen i...
Hvis alle sideribberne er på linje med bundens plan lige store vinkler, så projiceres toppunktet på basen i...
Sh. Problemløsning.№ 691, 693, 695, 740.
IV. Lektier:№ 692, 694.
P. Diktat.
LEKTION nr. 23,24. FORBEREDELSE TIL TEST TEST TEST nr. 4
Primært mål: Tjek niveauet for udvikling af problemløsningsevner for at finde volumen af en cylinder, skrå prisme, pyramide og kegle.
LEKTION nr. 25 BIND AF KUGLEN OG DENS DELE
Hovedmål: udled formlen for rumfanget af en kugle og dens dele.
I. Forklaring af nyt materiale.
1. Volumen af en kugle med radius R lige med
For bevis, se punkt 71.
2. Et sfærisk segment er den del af kuglen, der er afskåret fra det af et plan (fig. a, c).
OM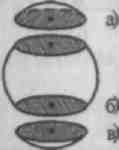 
bind kuglesegment bestemmes af formlen 
, hvor H er højden af det sfæriske segment
3. Det sfæriske lag er den del af bolden, der er placeret mellem to parallelle planer, der skærer bolden (fig. 323, b).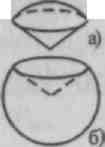 
4. En sfærisk sektor er et legeme, der er opnået fra et sfærisk segment og en kegle. Rumfanget af den sfæriske sektor bestemmes af formlen, hvor H er højden af det tilsvarende sfæriske segment
II. Problemløsning.
Opgave 1. Hvad er rumfanget af en sfærisk sektor, hvis radius af dens grundcirkel er 60 cm og kuglens radius er 75 cm?
Løsning. 1. Under bunden af sektoren i opgaven forstås som grundlag segment svarende til sektoren. Lade R - kuglens radius, r - radius af segmentbasen.
2. Vores opgave handler om at finde højden af dette segment: N – RO 1 . ELLER - kuglens radius vinkelret på bunden af segmentet.
3. Fra en retvinklet trekant O.O. l M(˂ M.O. 1 O= 90°) lad os finde: OO 1 = √OM 2 - O 1 M 2 = √75 2 +60 2 =40, derfor H = P.O. l = OP- O.O. l = R-00 ] =75-45 = 30.
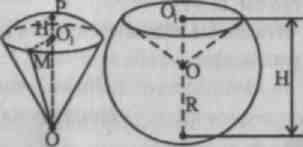
4. Volumen af den sfæriske sektor. =112500π
5. Bemærk. Problemet har to løsninger:
1) Den sfæriske sektor, som vi betragtede, kaldes konveks, og dens højde er lig med R – OO 1 , kaldes ikke-konveks.
Lad os finde dens volumen.
6. Overvej det andet tilfælde, hvor sektorhøjden N =R + O.O. 1 = 120, så det resulterende volumen vil være 4 gange større end det beregnede volumen: V = π45 10 4 cm 3
7. Det nødvendige volumen er således enten 112.500π cm eller 450.000π cm 3.
III. Hjemmelavet opgave: teori (s. 71, 72), nr. 710, 711, 717.
LEKTIE№ 26 . VOLUMEN AF KUGLEN OG DENS DELE
Primært mål: formulere evnen til at finde rumfanget af en kugle og dens dele.
I. Kontrol af lektier.
Sh. Problemløsning.
EN. 1. Den ydre diameter på en hul kugle er 18 cm, vægtykkelsen er 3 cm Find volumen af det materiale, som kuglen er lavet af.
[b84πcm 3.]
Diameteren på en blykugle er 30 cm Hvor mange bolde med en diameter på 3 cm kan man lave af dette bly?
Radierne af de tre kugler er 3, 4, 5 cm. Find radius af en kugle, hvis rumfang er lig med summen af deres rumfang,
Den største kugle er skåret ud af en terning. Hvor mange procent af materialet fjernes? [≈ 47,6 %]
Kuglesektorradius R, vinkel ind aksialt snit 120°. Find lydstyrken.
Bevis, at hvis radierne af tre kugler er i forholdet 1:2:3, så er rumfanget af den større kugle 3 gange mere end beløbet mængder af mindre kugler.
Højden af kuglesegmentet er 0,4 gange kuglens radius. Hvilken del er volumenet af dette segment fra volumenet af en cylinder med samme base og højde? 13\24
To lige bold arrangeret således, at midten af den ene ligger på overfladen af den anden. Hvordan hænger volumen af den samlede del af kuglerne sammen med volumen af hele kuglen?
Kuglens diameter, lig med 30 cm, fungerer som aksen for en cylinder, hvis basisradius er 12 cm. Find rumfanget af den del af bolden,
Hvilken figur har et større volumen: en kugle med en radius på 1 dm eller en regulær? trekantet prisme, hvor hver kant er lig med 2 dm? [Kuglens volumen er større.]
Et udsnit af en kugle i et plan vinkelret på dens radius deler radius i to. Find forholdet mellem rumfanget af kuglens dele.
Et udsnit af en kugle med et plan vinkelret på dens diameter deler diameteren i forholdet 1:2. Find forholdet mellem rumfanget af kuglens dele.
LEKTION nr. 27. OMRÅDE AF EN KULLE
Primært mål: udled en formel til at beregne overfladearealet af en bold.
jeg. Forklaring af nyt materiale bygge i overensstemmelse med paragraf 73 i lærebogen.
II. Problemløsning: nr. 722, 723, 724; til gentagelse - nr. 761, 762, 763.
III. Hjemmearbejde: kort.
LEKTION nr. 28. FORBEREDELSE TIL TESTEN
I. Spørgsmål til gennemgang af emnet.
Bolden og dens elementer.
Kuglens volumen og dens dele.
Revolutionslegemer og deres volumener.
Polyedre og deres volumener.
Boldens overfladeareal.
Overfladeareal af polyedre.
III. Problemløsning.
Rumfang af en kugle radius R lige med V. Find volumen af en kugle med radius: 2 R; 0,5R.
Overfladeareal almindelig tetraeder lig med kuglens overfladeareal. Find forholdet mellem rumfanget af tetraederet og kuglen.
Diameteren af en kugle med en radius på 12 cm er opdelt i 3 dele, hvis længde er i forholdet 3:3:2. Planer vinkelret på diameteren trækkes gennem delepunkterne. Find volumen af hver dannede dele af bolden.
5. Til den højre firkantet pyramide en bold er indskrevet, så pyramidens sideflader rører boldens overflade, og dens stor cirkel ligger i bunden af pyramiden. Sideflader pyramider hælder til basens plan i en vinkel EN, og kuglens rumfang er lig med V . Find pyramidens rumfang.
Hjemmeprøve
Mulighed 1
Kuglens rumfang er 400 cm3. En anden kugle er bygget på radius som på diameteren. Find volumen af den lille kugle.
3. Det diagonale snit af et rektangulært parallelepipedum indskrevet i en kugle er et kvadrat med areal S. Find kuglens rumfang.
4. Diameteren af en kugle med en radius på 12 cm er opdelt i 3 dele, hvis længder er i forholdet 1:3:4. Planer vinkelret på diameteren trækkes gennem delepunkterne. Find volumen af det resulterende sfæriske lag.
MO "Senkinskaya Secondary School"
Med. 1