Pyramide koncept
Definition 1
En geometrisk figur dannet af en polygon og et punkt, der ikke ligger i det plan, der indeholder denne polygon, forbundet med alle polygonens hjørner, kaldes en pyramide (fig. 1).
Polygonen, hvorfra pyramiden er lavet, kaldes bunden af pyramiden; de resulterende trekanter, når de er forbundet med et punkt, er pyramidens sideflader, siderne af trekanter er pyramidens sider, og punktet fælles til alle trekanter er toppen af pyramiden.
Typer af pyramider
Afhængigt af antallet af vinkler ved bunden af pyramiden kan den kaldes trekantet, firkantet og så videre (fig. 2).
Figur 2.
En anden type pyramide er den almindelige pyramide.
Lad os introducere og bevise egenskaben af en almindelig pyramide.
Sætning 1
Alle sideflader af en regulær pyramide er ligebenede trekanter, der er lig med hinanden.
Bevis.
Overvej en regulær $n-$gonal pyramide med toppunkt $S$ af højden $h=SO$. Lad os tegne en cirkel omkring basen (fig. 4).
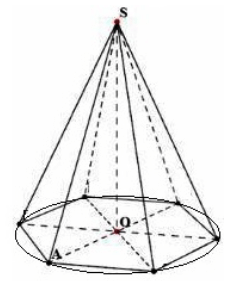
Figur 4.
Overvej trekanten $SOA$. Ifølge Pythagoras sætning får vi
Det er klart, at enhver sidekant vil blive defineret på denne måde. Følgelig er alle sidekanter lig med hinanden, det vil sige, at alle sideflader er ligebenede trekanter. Lad os bevise, at de er lige med hinanden. Da basen er en regulær polygon, er grundfladerne på alle sideflader lig med hinanden. Følgelig er alle sideflader ens i henhold til III-kriteriet om trekanters lighed.
Sætningen er bevist.
Lad os nu introducere følgende definition relateret til begrebet en regulær pyramide.
Definition 3
Apotemet for en almindelig pyramide er højden af dens sideflade.
Det er klart, at ved sætning 1 er alle apotemer lige hinanden.
Sætning 2
Det laterale overfladeareal af en regulær pyramide bestemmes som produktet af halvperimeteren af basen og apotemet.
Bevis.
Lad os betegne siden af bunden af $n-$gonalpyramiden med $a$ og apotemet med $d$. Derfor er arealet af sidefladen lig med
Da alle sider ifølge sætning 1 er lige, altså
Sætningen er bevist.
En anden type pyramide er en afkortet pyramide.
Definition 4
Hvis et plan parallelt med dets basis trækkes gennem en almindelig pyramide, så kaldes figuren dannet mellem dette plan og basens plan en afkortet pyramide (fig. 5).
Figur 5. Afkortet pyramide
Sidefladerne af den afkortede pyramide er trapezoider.
Sætning 3
Det laterale overfladeareal af en regulær afkortet pyramide bestemmes som produktet af summen af halvperimetrene af baserne og apotemet.
Bevis.
Lad os betegne siderne af bundene af $n-$gonalpyramiden med henholdsvis $a\ og\ b$, og apotemet med $d$. Derfor er arealet af sidefladen lig med
Da alle sider er lige, altså
Sætningen er bevist.
Prøveopgave
Eksempel 1
Find arealet af sidefladen af en afkortet trekantet pyramide, hvis den er opnået fra en regulær pyramide med basisside 4 og apotem 5 ved at afskære et plan, der går gennem midtlinjen af sidefladerne.
Løsning.
Ved at bruge midtlinjesætningen finder vi, at den øverste base af den afkortede pyramide er lig med $4\cdot \frac(1)(2)=2$, og apotemet er lig med $5\cdot \frac(1)(2) = 2,5 $.
Så får vi ved sætning 3
Pyramide. Afkortet pyramide
Pyramide er et polyeder, hvis flader er en polygon ( grundlag ), og alle andre flader er trekanter med et fælles toppunkt ( sideflader ) (Fig. 15). Pyramiden kaldes korrekt , hvis dens base er en regulær polygon, og toppen af pyramiden er projiceret ind i midten af basen (fig. 16). En trekantet pyramide med alle kanter lige kaldes tetraeder .
Sideribben af en pyramide er den side af sidefladen, der ikke hører til basen Højde pyramiden er afstanden fra dens top til bundens plan. Alle laterale kanter af en regulær pyramide er ens med hinanden, alle laterale flader er ens ligebenede trekanter. Højden af sidefladen af en regulær pyramide trukket fra toppunktet kaldes apotem . Diagonalt snit kaldes et udsnit af en pyramide af et plan, der går gennem to sidekanter, der ikke hører til den samme flade.
Sidefladeareal pyramide er summen af arealerne af alle sideflader. Samlet overfladeareal kaldes summen af arealerne af alle sidefladerne og grundfladen.
Sætninger
1. Hvis alle sidekanterne i en pyramide er lige skråtstillede til bundens plan, så projiceres toppen af pyramiden ind i midten af cirklen, der er omskrevet nær bunden.
2. Hvis alle sidekanterne af en pyramide har lige store længder, så projiceres toppen af pyramiden ind i midten af en cirkel, der er omskrevet nær bunden.
3. Hvis alle flader i en pyramide hælder lige meget til bundens plan, så projiceres toppen af pyramiden ind i midten af en cirkel, der er indskrevet i bunden.
For at beregne rumfanget af en vilkårlig pyramide er den korrekte formel:
Hvor V- volumen;
S base– basisareal;
H– pyramidens højde.
For en almindelig pyramide er følgende formler korrekte:
Hvor s– basisomkreds;
h a– apotem;
H- højde;
S fuld
S side
S base– basisareal;
V– volumen af en regulær pyramide.
Afkortet pyramide kaldet den del af pyramiden, der er indesluttet mellem bunden og et skæreplan parallelt med pyramidens bund (fig. 17). Regelmæssig afkortet pyramide kaldes den del af en regulær pyramide, der er indesluttet mellem bunden og et skærende plan parallelt med bunden af pyramiden.
Grunde afkortet pyramide - lignende polygoner. Sideflader – trapez. Højde af en afkortet pyramide er afstanden mellem dens baser. Diagonal en afkortet pyramide er et segment, der forbinder dets hjørner, som ikke ligger på samme flade. Diagonalt snit er et udsnit af en afkortet pyramide af et plan, der går gennem to sidekanter, der ikke hører til den samme flade.
For en afkortet pyramide er følgende formler gyldige:
(4)
Hvor S 1 , S 2 - områder af de øvre og nedre baser;
S fuld– samlet overfladeareal;
S side– lateral overfladeareal;
H- højde;
V– volumen af en afkortet pyramide.
For en regulær afkortet pyramide er formlen korrekt:
Hvor s 1 , s 2 - omkredse af baserne;
h a– apotem af en regulær afkortet pyramide.
Eksempel 1. I en regulær trekantet pyramide er den dihedriske vinkel ved bunden 60º. Find tangenten af hældningsvinklen af sidekanten til basens plan.
Løsning. Lad os lave en tegning (fig. 18).
 |
Pyramiden er regulær, hvilket betyder, at der ved bunden er en ligesidet trekant, og alle sidefladerne er lige store trekanter. Den dihedriske vinkel ved bunden er hældningsvinklen af pyramidens sideflade til bundens plan. Den lineære vinkel er vinklen -en mellem to perpendikulære: osv. Toppen af pyramiden projiceres i midten af trekanten (midten af den omskrevne cirkel og den indskrevne cirkel af trekanten ABC). Hældningsvinklen på sidekanten (f.eks S.B.) er vinklen mellem selve kanten og dens projektion på bundens plan. Til ribben S.B. denne vinkel vil være vinklen SBD. For at finde tangenten skal du kende benene SÅ Og O.B.. Lad længden af segmentet BD er lig med 3 EN. Prik OM linjestykke BD er opdelt i dele: og Fra finder vi SÅ: 
Fra vi finder: 
Svar:
Eksempel 2. Find rumfanget af en regulær afkortet firkantet pyramide, hvis diagonalerne på dens baser er lig med cm og cm, og dens højde er 4 cm.
Løsning. For at finde volumen af en afkortet pyramide bruger vi formel (4). For at finde arealet af baserne skal du finde siderne af basiskvadrene, kende deres diagonaler. Siderne af baserne er lig med henholdsvis 2 cm og 8 cm. Det betyder, at basenes areal og Substituerer alle data i formlen, beregner vi rumfanget af den afkortede pyramide:
Svar: 112 cm 3.
Eksempel 3. Find arealet af sidefladen af en almindelig trekantet afkortet pyramide, hvis sider er 10 cm og 4 cm, og pyramidens højde er 2 cm.
Løsning. Lad os lave en tegning (fig. 19).
Sidefladen af denne pyramide er en ligebenet trapez. For at beregne arealet af en trapez skal du kende basen og højden. Baserne er givet efter tilstanden, kun højden forbliver ukendt. Vi finder hende hvorfra EN 1 E vinkelret fra et punkt EN 1 på planet for den nederste base, EN 1 D– vinkelret fra EN 1 pr AC. EN 1 E= 2 cm, da dette er pyramidens højde. At finde DE Lad os lave en ekstra tegning, der viser topvisningen (fig. 20). Prik OM– projektion af midten af den øvre og nedre base. siden (se Fig. 20) og På den anden side Okay– radius indskrevet i cirklen og 
OM– radius indskrevet i en cirkel:
MK = DE.
Ifølge Pythagoras sætning fra
Sidefladeområde: 
Svar:
Eksempel 4. I bunden af pyramiden ligger en ligebenet trapez, hvis baser EN Og b (-en> b). Hver sideflade danner en vinkel svarende til pyramidens bundplan j. Find det samlede overfladeareal af pyramiden.
Løsning. Lad os lave en tegning (fig. 21). Samlet overfladeareal af pyramiden SABCD lig med summen af arealerne og arealet af trapez ABCD.
Lad os bruge det udsagn, at hvis alle pyramidens flader hælder lige meget til basens plan, så projiceres toppunktet ind i midten af cirklen, der er indskrevet i basen. Prik OM– vertex projektion S ved bunden af pyramiden. Trekant SOD er den ortogonale projektion af trekanten CSD til basens plan. Ved at bruge sætningen om arealet af den ortogonale projektion af en plan figur får vi:
Ligeledes betyder det 
Således blev problemet reduceret til at finde området af trapez ABCD. Lad os tegne en trapez ABCD separat (fig. 22). Prik OM– midten af en cirkel indskrevet i en trapez.
Da en cirkel kan indskrives i en trapezoid, så eller Fra Pythagoras sætning har vi
Denne videotutorial hjælper brugere med at få en idé om Pyramid-temaet. Korrekt pyramide. I denne lektion vil vi stifte bekendtskab med begrebet en pyramide og give det en definition. Lad os overveje, hvad en almindelig pyramide er, og hvilke egenskaber den har. Derefter beviser vi sætningen om sidefladen af en regulær pyramide.
I denne lektion vil vi stifte bekendtskab med begrebet en pyramide og give det en definition.
Overvej en polygon A 1 A 2...En n, som ligger i α-planet, og punktet P, som ikke ligger i α-planet (fig. 1). Lad os forbinde prikkerne P med toppe A 1, A 2, A 3, … En n. Vi får n trekanter: A 1 A 2 R, A 2 A 3 R og så videre.
Definition. Polyeder RA1A2 ...A n, består af n-firkant A 1 A 2...En n Og n trekanter RA 1 A 2, RA 2 A 3 …RA n A n-1 kaldes n-kulpyramide. Ris. 1.
Ris. 1
Overvej en firkantet pyramide PABCD(Fig. 2).
R- toppen af pyramiden.
ABCD- bunden af pyramiden.
RA- side rib.
AB- bund rib.
Fra punkt R lad os slippe vinkelret RN til basisplanet ABCD. Den tegnede vinkelrette er pyramidens højde.
Ris. 2
Den fulde overflade af pyramiden består af sidefladen, det vil sige arealet af alle sideflader og arealet af basen:
S fuld = S side + S hoved
En pyramide kaldes korrekt, hvis:
- dens base er en regulær polygon;
- segmentet, der forbinder toppen af pyramiden med midten af basen, er dens højde.
Forklaring ved hjælp af eksemplet med en regulær firkantet pyramide
Overvej en regulær firkantet pyramide PABCD(Fig. 3).
R- toppen af pyramiden. Basen af pyramiden ABCD- en regulær firkant, det vil sige en firkant. Prik OM, skæringspunktet for diagonalerne, er midten af kvadratet. Midler, RO er pyramidens højde.
Ris. 3
Forklaring: i den rigtige n I en trekant falder midten af den indskrevne cirkel og midten af den omskårne cirkel sammen. Dette center kaldes polygonens centrum. Nogle gange siger de, at toppunktet er projiceret ind i midten.
Højden af sidefladen af en regulær pyramide trukket fra dens toppunkt kaldes apotem og er udpeget h a.
1. alle sidekanter af en regulær pyramide er lige store;
2. Sidefladerne er lige store trekanter.
Vi vil give et bevis for disse egenskaber ved at bruge eksemplet med en regulær firkantet pyramide.
Givet: PABCD- almindelig firkantet pyramide,
ABCD- firkantet,
RO- pyramidens højde.
Bevise:
1. RA = PB = RS = PD
2.∆ABP = ∆BCP =∆CDP =∆DAP Se fig. 4.
Ris. 4
Bevis.
RO- pyramidens højde. Altså lige RO vinkelret på planet ABC, og derfor direkte JSC, VO, SO Og GØR ligger i den. Altså trekanter ROA, ROV, ROS, ROD- rektangulær.
Overvej en firkant ABCD. Af en firkants egenskaber følger det AO = VO = CO = GØR.
Så de rette trekanter ROA, ROV, ROS, ROD ben RO- generelt og ben JSC, VO, SO Og GØR er ens, hvilket betyder, at disse trekanter er ens på to sider. Fra trekanters lighed følger ligheden af segmenter, RA = PB = RS = PD. Punkt 1 er bevist.
Segmenter AB Og Sol er ens, fordi de er sider af samme firkant, RA = PB = RS. Altså trekanter AVR Og VSR - ligebenet og lige på tre sider.
På lignende måde finder vi, at trekanter ABP, VCP, CDP, DAP er ligebenede og lige, som det kræves bevist i stk.
Arealet af den laterale overflade af en regulær pyramide er lig med halvdelen af produktet af omkredsen af basen og apotemet:
For at bevise dette, lad os vælge en almindelig trekantet pyramide.
Givet: RAVS- almindelig trekantet pyramide.
AB = BC = AC.
RO- højde.
Bevise: 
. Se fig. 5.
Ris. 5
Bevis.
RAVS- almindelig trekantet pyramide. Det er AB= AC = BC. Lade OM- midten af trekanten ABC, Derefter RO er pyramidens højde. I bunden af pyramiden ligger en ligesidet trekant ABC. Læg mærke til det 
.
Trekanter RAV, RVS, RSA- ens ligebenede trekanter (efter egenskab). En trekantet pyramide har tre sideflader: RAV, RVS, RSA. Dette betyder, at arealet af pyramidens laterale overflade er:
S side = 3S RAW
Sætningen er bevist.
Radius af en cirkel indskrevet i bunden af en regulær firkantet pyramide er 3 m, pyramidens højde er 4 m. Find arealet af pyramidens sideflade.
Givet: regulær firkantet pyramide ABCD,
ABCD- firkantet,
r= 3 m,
RO- pyramidens højde,
RO= 4 m.
Find: S side. Se fig. 6.
Ris. 6
Løsning.
Ifølge den beviste sætning,.
Lad os først finde siden af basen AB. Vi ved, at radius af en cirkel indskrevet i bunden af en regulær firkantet pyramide er 3 m.
Så m.
Find kvadratets omkreds ABCD med en side på 6 m:
Overvej en trekant BCD. Lade M- midt på siden DC. Fordi OM- midten BD, At 
(m).
Trekant DPC- ligebenet. M- midten DC. Det er, RM- median, og derfor højden i trekanten DPC. Derefter RM- apotem af pyramiden.
RO- pyramidens højde. Så lige RO vinkelret på planet ABC, og derfor direkte OM, ligger i den. Lad os finde apotemet RM fra en retvinklet trekant Rom.
Nu kan vi finde pyramidens sideflade:
Svar: 60 m2.
Radius af cirklen, der er afgrænset omkring bunden af en regulær trekantet pyramide, er lig med m. Det laterale overfladeareal er 18 m 2. Find apotemets længde.
Givet: ABCP- almindelig trekantet pyramide,
AB = BC = SA,
R= m,
S side = 18 m2.
Find: . Se fig. 7.
Ris. 7
Løsning.
I en retvinklet trekant ABC Radius af den omskrevne cirkel er givet. Lad os finde en side AB denne trekant ved hjælp af sinusloven.
Når vi kender siden af en regulær trekant (m), finder vi dens omkreds.
Ved sætningen om det laterale overfladeareal af en regulær pyramide, hvor h a- apotem af pyramiden. Derefter:
Svar: 4 m.
Så vi så på, hvad en pyramide er, hvad en regulær pyramide er, og vi beviste sætningen om sidefladen af en regulær pyramide. I den næste lektion vil vi stifte bekendtskab med den afkortede pyramide.
Bibliografi
- Geometri. Klasse 10-11: lærebog for studerende på almene uddannelsesinstitutioner (grundlæggende og specialiserede niveauer) / I. M. Smirnova, V. A. Smirnov. - 5. udg., rev. og yderligere - M.: Mnemosyne, 2008. - 288 s.: ill.
- Geometri. 10-11 klassetrin: Lærebog for almene uddannelsesinstitutioner / Sharygin I.F. - M.: Bustard, 1999. - 208 s.: ill.
- Geometri. 10. klasse: Lærebog for almene uddannelsesinstitutioner med dybdegående og specialiserede studier i matematik /E. V. Potoskuev, L. I. Zvalich. - 6. udg., stereotype. - M.: Bustard, 008. - 233 s.: ill.
- Internetportal "Yaklass" ()
- Internetportal "Festival for pædagogiske ideer "Første september" ()
- Internetportal "Slideshare.net" ()
Lektier
- Kan en regulær polygon være bunden af en uregelmæssig pyramide?
- Bevis, at usammenhængende kanter af en regulær pyramide er vinkelrette.
- Find værdien af den dihedriske vinkel ved siden af bunden af en regulær firkantet pyramide, hvis pyramidens apotem er lig med siden af dens base.
- RAVS- almindelig trekantet pyramide. Konstruer den lineære vinkel af den dihedriske vinkel ved bunden af pyramiden.
I hvilken en af sideribberne er vinkelret på bunden.
I dette tilfælde vil denne kant være højden af pyramiden.
Egenskaber af pyramiden.
1. Når alle sidekanterne har samme størrelse, så:
- det er let at beskrive en cirkel nær bunden af pyramiden, og toppen af pyramiden vil blive projiceret ind i midten af denne cirkel;
- sideribberne danner lige store vinkler med basens plan;
- Desuden er det modsatte også tilfældet, dvs. når sideribberne danner lige store vinkler med bundens plan, eller når en cirkel kan beskrives omkring bunden af pyramiden, og toppen af pyramiden vil blive projiceret ind i midten af denne cirkel, betyder det, at alle sidekanterne af pyramiden har samme størrelse.
2. Når sidefladerne har en hældningsvinkel til bundens plan med samme værdi, så:
- det er let at beskrive en cirkel nær bunden af pyramiden, og toppen af pyramiden vil blive projiceret ind i midten af denne cirkel;
- højderne af sidefladerne er lige lange;
- arealet af sidefladen er lig med ½ produktet af bundens omkreds og højden af sidefladen.
3. En kugle kan beskrives omkring en pyramide, hvis der i bunden af pyramiden er en polygon, som en cirkel kan beskrives omkring (en nødvendig og tilstrækkelig betingelse). Kuglens centrum vil være skæringspunktet for de fly, der passerer gennem midten af pyramidens kanter vinkelret på dem. Ud fra denne sætning konkluderer vi, at en kugle kan beskrives både omkring enhver trekantet og omkring enhver regulær pyramide;
4. En kugle kan indskrives i en pyramide, hvis halveringsfladen af pyramidens indre dihedrale vinkler skærer hinanden i 1. punkt (en nødvendig og tilstrækkelig betingelse). Dette punkt bliver kuglens centrum.
5. Keglen vil blive indskrevet i pyramiden, når deres toppunkter falder sammen, og keglens bund vil være indskrevet i bunden af pyramiden. I dette tilfælde er det kun muligt at passe en kegle ind i en pyramide, hvis pyramidens apotemer har lige store størrelser (en nødvendig og tilstrækkelig betingelse);
6. Keglen vil blive beskrevet nær pyramiden, hvis deres toppunkter falder sammen, og keglens bund vil blive beskrevet nær pyramidens bund. I dette tilfælde er det kun muligt at beskrive en kegle nær en pyramide, hvis alle pyramidens sidekanter har de samme værdier (en nødvendig og tilstrækkelig betingelse). Højden af disse kegler og pyramider er de samme.
7. En cylinder vil blive indskrevet i en pyramide, hvis en af dens baser falder sammen med en cirkel, der er indskrevet i pyramidens snit af et plan parallelt med basen, og den anden base hører til pyramidens basis.
8. Cylinderen vil blive beskrevet nær pyramiden, når toppen af pyramiden tilhører en af dens baser, og cylinderens anden base vil blive beskrevet nær pyramidens bund. I dette tilfælde er det kun muligt at beskrive en cylinder nær en pyramide, hvis bunden af pyramiden er en indskrevet polygon (en nødvendig og tilstrækkelig betingelse).
Formler til bestemmelse af volumen og arealet af en rektangulær pyramide.
V- volumen af pyramiden,
S- område af bunden af pyramiden,
h- pyramidens højde,
Sb- område af pyramidens laterale overflade,
-en- apotem (ikke at forveksle med α ) pyramider,
P- omkredsen af bunden af pyramiden,
n- antallet af sider af bunden af pyramiden,
b- længden af pyramidens sidekant,
α - flad vinkel i toppen af pyramiden.
Her kan du finde grundlæggende information om pyramider og relaterede formler og begreber. Alle studeres med en matematikvejleder som forberedelse til Unified State Exam.
Overvej et plan, en polygon 
, der ligger i det og et punkt S, der ikke ligger i det. Lad os forbinde S med alle polygonens hjørner. Det resulterende polyeder kaldes en pyramide. Segmenterne kaldes sideribber. 
Polygonen kaldes basen, og punktet S er toppen af pyramiden. Afhængigt af tallet n kaldes pyramiden trekantet (n=3), firkantet (n=4), femkantet (n=5) og så videre. Et alternativt navn for en trekantet pyramide er tetraeder. Højden af en pyramide er den vinkelrette, der falder fra dens top til bundens plan. 
En pyramide kaldes regulær if en regulær polygon, og bunden af pyramidens højde (grundlaget for vinkelret) er dens centrum.
Underviserens kommentar:
Forveksle ikke begreberne "almindelig pyramide" og "regelmæssig tetraeder". I en regulær pyramide er sidekanterne ikke nødvendigvis lig med basens kanter, men i en regulær tetraeder er alle 6 kanter ens. Dette er hans definition. Det er let at bevise, at ligheden indebærer, at polygonens centrum P falder sammen med en grundhøjde, så et regulært tetraeder er en regulær pyramide.
Hvad er et apotem?
En pyramides apotem er højden af dens sideflade. Hvis pyramiden er regulær, så er alle dens apotemer ens. Det omvendte er ikke sandt. 
En matematiklærer om sin terminologi: 80 % af arbejdet med pyramider er bygget op gennem to typer trekanter:
1) Indeholder apotem SK og højde SP
2) Indeholder sidekanten SA og dens fremspring PA 
For at forenkle referencer til disse trekanter er det mere bekvemt for en matematikvejleder at ringe til den første af dem apotemal, og andet kyst. Desværre finder du ikke denne terminologi i nogen af lærebøgerne, og læreren skal introducere den ensidigt.
Formel for volumen af en pyramide:
1) 
, hvor er arealet af bunden af pyramiden, og er højden af pyramiden
2) , hvor er radius af den indskrevne kugle, og er arealet af den samlede overflade af pyramiden.
3) 
, hvor MN er afstanden mellem to krydsende kanter, og er arealet af parallelogrammet dannet af midtpunkterne af de fire resterende kanter.
Egenskab for bunden af højden af en pyramide:
Punkt P (se figur) falder sammen med midten af den indskrevne cirkel ved bunden af pyramiden, hvis en af følgende betingelser er opfyldt:
1) Alle apotemer er lige
2) Alle sideflader er lige skråtstillede i forhold til bunden
3) Alle apotemer er lige tilbøjelige til pyramidens højde
4) Pyramidens højde hælder lige meget til alle sideflader
Matematikvejleders kommentar: Bemærk venligst, at alle punkter er forenet af en fælles egenskab: på en eller anden måde er sideflader involveret overalt (apotemer er deres elementer). Derfor kan vejlederen tilbyde en mindre præcis, men mere praktisk for læring, formulering: punkt P falder sammen med midten af den indskrevne cirkel, bunden af pyramiden, hvis der er lige information om dens sideflader. For at bevise det er det nok at vise, at alle apotemtrekanter er lige store.
Punkt P falder sammen med midten af en cirkel, der er omskrevet nær bunden af pyramiden, hvis en af tre betingelser er sand:
1) Alle sidekanter er ens
2) Alle sideribber er lige skråtstillede til bunden
3) Alle sideribber er lige skråtstillede i forhold til højden