Efter segment kald en del af en ret linje, der består af alle punkter på denne linje, der er placeret mellem disse to punkter - de kaldes enderne af stykket.
Lad os se på det første eksempel. Lad et bestemt segment være defineret af to punkter i koordinatplanet. I I dette tilfælde vi kan finde dens længde ved at anvende Pythagoras sætning.
Så i koordinatsystemet tegner vi et segment med de givne koordinater for dets ender (x1; y1) Og (x2; y2) . På aksen x Og Y Tegn vinkelrette fra enderne af segmentet. Lad os markere med rødt de segmenter, der er projektioner fra det oprindelige segment på koordinataksen. Herefter overfører vi projektionssegmenterne parallelt med enderne af segmenterne. Vi får en trekant (rektangulær). Hypotenuse givet trekant segmentet AB selv bliver, og dets ben er de overførte fremspring.
Lad os beregne længden af disse fremskrivninger. Så ind på aksen Y projektionslængde er y2-y1 . og på aksen x projektionslængde er x2-x1 . Lad os anvende Pythagoras sætning: |AB|² = (y2 - y1)² + (x2 - x1)² . I dette tilfælde |AB| er længden af segmentet.
Hvis du bruger dette diagram for at beregne længden af et segment, så behøver du ikke engang at konstruere et segment. Lad os nu beregne længden af segmentet med koordinater (1;3) Og (2;5) . Ved at anvende Pythagoras sætning får vi: |AB|² = (2 - 1)² + (5 - 3)² = 1 + 4 = 5 . Det betyder, at længden af vores segment er lig med 5:1/2 .
Overvej følgende metode til at finde længden af et segment. For at gøre dette skal vi kende koordinaterne for to punkter i et eller andet system. Lad os overveje denne mulighed, ved hjælp af et todimensionalt kartesisk koordinatsystem.
Så i et todimensionalt koordinatsystem er koordinaterne givet ekstreme punkter segment. Hvis vi trækker lige linjer gennem disse punkter, skal de være vinkelrette på koordinataksen, så får vi retvinklet trekant. Det oprindelige segment vil være hypotenusen af den resulterende trekant. Benene i en trekant danner segmenter, deres længde er lig med projektionen af hypotenusen på koordinatakserne. Ud fra Pythagoras sætning konkluderer vi: for at finde længden af dette segment, skal du finde længderne af projektionerne på to koordinatakser.
Lad os finde projektionslængderne (X og Y) det originale segment på koordinatakser. Vi beregner dem ved at finde forskellen i koordinaterne af punkter langs en separat akse: X = X2-X1, Y = Y2-Y1 .
Beregn længden af segmentet EN . For at gøre dette skal du finde kvadratroden:
Hvis vores segment er placeret mellem punkter, hvis koordinater 2;4 Og 4;1 . så er dens længde tilsvarende lig med √((4-2)²+(1-4)²) = √13 ≈ 3,61 .
kommentarsystem KAKLEE
hvordan man beregner længden af et segment ved givne koordinater: Længde af et stykke Et stykke er en del af en ret linje, der består af alle punkter på denne linje, der er placeret mellem disse to punkter - de kaldes enderne af stykket. Lad os overveje
Der er tre hovedkoordinatsystemer, der bruges i geometri, teoretisk mekanik, andre grene af fysikken: kartesisk, polær og sfærisk. I disse koordinatsystemer har hvert punkt tre koordinater. Ved at kende koordinaterne for to punkter, kan du bestemme afstanden mellem disse to punkter.
Du får brug for
Kartesiske, polære og sfæriske koordinater for enderne af et segment
Udstationering af sponsor P&G Artikler om emnet "Sådan finder du længden af et segment ved hjælp af koordinater" Sådan finder du længden af et segment ved hjælp af punkter Sådan finder du længden af en side af en trekant ved hjælp af koordinater Sådan finder du længden af en vektor
Instruktioner
Overvej først et rektangulært kartesisk koordinatsystem. Positionen af et punkt i rummet i dette koordinatsystem bestemmes x,y koordinater og z. En radiusvektor tegnes fra origo til punktet. Projektionerne af denne radiusvektor på koordinatakserne vil være koordinaterne for dette punkt.
Lad dig nu have to punkter med koordinaterne henholdsvis x1,y1,z1 og x2,y2 og z2. Betegn med henholdsvis r1 og r2 radiusvektorerne for det første og andet punkt. Det er klart, at afstanden mellem disse to punkter vil være lig med størrelsen af vektoren r = r1-r2, hvor (r1-r2) er vektorforskellen.
Koordinaterne for vektoren r vil naturligvis være: x1-x2, y1-y2, z1-z2. Så vil størrelsen af vektoren r eller afstanden mellem to punkter være lig med: r = sqrt(((x1-x2)^2)+((y1-y2)^2)+((z1-z2)^2 )).
Betragt nu et polært koordinatsystem, hvor koordinaten for et punkt vil være givet af den radiale koordinat r (radiusvektor i XY-planet), vinkelkoordinaten? (vinklen mellem vektoren r og X-aksen) og z-koordinaten, svarende til z-koordinaten i Kartesisk system.
Polære koordinater for et punkt kan konverteres til kartesiske på følgende måde: x = r*cos?, y = r*sin?, z = z. Så vil afstanden mellem to punkter med koordinaterne r1, ?1 ,z1 og r2, ?2, z2 være lig med R = sqrt(((r1*cos?1-r2*cos?2)^2)+((r1) *sin? 1-r2*sin?2)^2)+((z1-z2)^2)) = sqrt((r1^2)+(r2^2)-2r1*r2(cos?1*cos? 2+sin ?1*sin?2)+((z1-z2)^2))
Overvej nu et sfærisk koordinatsystem. I den er positionen af et punkt angivet med tre koordinater r, ? Og?. r er afstanden fra udgangspunktet til punktet, ? Og? - henholdsvis azimuth og zenitvinkel. Hjørne? svarende til vinklen med samme betegnelse i polære system koordinater, ikke? - vinklen mellem radiusvektoren r og Z-aksen med 0
Lad os konvertere sfæriske koordinater til kartesiske: x = r*sin?*cos?, y = r*sin?*sin?*sin?, z = r*cos?. Afstanden mellem punkter med koordinaterne r1, ?1, ?1 og r2, ?2 og?2 vil være lig med R = sqrt(((r1*sin?1*cos?1-r2*sin?2*cos?2 )^2 )+((r1*sin?1*sin?1-r2*sin?2*sin?2)^2)+((r1*cos?1-r2*cos?2)^2)) = ((( r1*sin?1)^2)+((r2*sin?2)^2)-2r1*r2*sin?1*sin?2*(cos?1*cos?2+sin?1* sin?2 )+((r1*cos?1-r2*cos?2)^2))
Hvor simpeltAndre nyheder om emnet:
For at definere en vektor i rummet bruges et koordinatsystem. Det skal tages i betragtning, at det ud over længden (modulus) også er karakteriseret ved retning. Længden af vektoren kan simpelthen måles eller findes ved hjælp af formler. Du skal bruge - en lineal; - vinkelmåler Sponsoreret af P&G Articles
For at finde projektionen af en vektor eller et segment på koordinatakserne skal du sænke perpendikulære fra yderpunkterne til hver af akserne. Hvis koordinaterne for en vektor eller et segment er kendt, kan dets projektion på aksen beregnes. Det samme kan gøres, hvis længden af vektoren og vinklen mellem den og aksen er kendt. Til dig
Du kan bestemme afstanden mellem to punkter ved at måle længden af det segment, der er konstrueret mellem dem. Hvis punkternes koordinater er kendt, så kan afstanden beregnes vha matematiske formler. Du skal bruge - en lineal; - afstandsmåler; - vinkelmåler; - begrebet Cartesiske koordinater. Sponsor
Top af enhver flad eller volumetrisk geometrisk figur unikt bestemt af dets koordinater i rummet. På samme måde kan evt vilkårligt punkt i samme koordinatsystem, og dette gør det muligt at beregne afstanden mellem dette vilkårlige punkt og
En vektor er en størrelse karakteriseret ved sin numerisk værdi og retning. Med andre ord er en vektor et rettet segment. Positionen af vektor AB i rummet er specificeret af koordinaterne for begyndelsespunktet for vektor A og slutpunktet for vektor B. Lad os overveje, hvordan man bestemmer koordinaterne for midten af vektoren.
At vide rumlige koordinater Givet to punkter i ethvert system, kan du nemt bestemme længden af det lige linjesegment mellem dem. Nedenfor beskriver vi, hvordan man gør dette i forhold til todimensionelle og tredimensionelle kartesiske (rektangulære) koordinatsystemer. Sponsor af P&G-placering Artikler om emnet "Sådan finder du
For at bestemme afstanden fra et punkt til en linje skal du kende linjens ligninger og koordinaterne for punktet i det kartesiske koordinatsystem. Afstanden fra et punkt til en linje vil være vinkelret tegnet fra dette punkt til linjen. Du skal bruge koordinaterne for punktet og linjens ligning
Der er tre hovedkoordinatsystemer, der bruges i geometri, teoretisk mekanik og andre grene af fysikken: kartesisk, polær og sfærisk. I disse koordinatsystemer har hvert punkt tre koordinater. Ved at kende koordinaterne for to punkter, kan du bestemme afstanden mellem disse to punkter.
Du får brug for
- Kartesiske, polære og sfæriske koordinater for enderne af et segment
Instruktioner
Overvej først et rektangulært kartesisk koordinatsystem. Positionen af et punkt i rummet i dette koordinatsystem bestemmes koordinater x, y og z. En radiusvektor tegnes fra origo til punktet. Projektionerne af denne radiusvektor på koordinatakserne vil være koordinater dette punkt.
Antag at du nu har to point med koordinater henholdsvis x1,y1,z1 og x2,y2 og z2. Betegn med henholdsvis r1 og r2 radiusvektorerne for det første og andet punkt. Det er klart, at afstanden mellem disse to punkter vil være lig med størrelsen af vektoren r = r1-r2, hvor (r1-r2) er vektorforskellen.
Koordinaterne for vektoren r vil naturligvis være: x1-x2, y1-y2, z1-z2. Så vil størrelsen af vektoren r eller afstanden mellem to punkter være lig med: r = sqrt(((x1-x2)^2)+((y1-y2)^2)+((z1-z2)^2 )).
Betragt nu et polært koordinatsystem, hvor koordinaten for et punkt vil være givet af den radiale koordinat r (radiusvektor i XY-planet), vinkelkoordinaten? (vinklen mellem vektoren r og X-aksen) og z-koordinaten, svarende til z-koordinaten i det kartesiske system. Et punkts polære koordinater kan konverteres til kartesiske koordinater som følger: x = r*cos?, y = r*sin?, z = z. Derefter afstanden mellem to punkter med koordinater r1, ?1,z1 og r2, ?2, z2 vil være lig med R = sqrt(((r1*cos?1-r2*cos?2)^2)+((r1*sin?1-r2*sin ?2 )^2)+((z1-z2)^2)) = sqrt((r1^2)+(r2^2)-2r1*r2(cos?1*cos?2+sin?1*sin? 2) +((z1-z2)^2))
Overvej nu et sfærisk koordinatsystem. I den er punktets position angivet med tre koordinater r, ? Og?. r er afstanden fra udgangspunktet til punktet, ? Og? - henholdsvis azimuth og zenitvinkel. Hjørne? ligner en vinkel med samme betegnelse i det polære koordinatsystem, ikke? - vinklen mellem radiusvektoren r og Z-aksen, og koordinaterne r1, ?1, ?1 og r2, ?2 og ?2 vil være lig med R = sqrt(((r1*sin?1*cos?1 -r2*sin? 2*cos?2)^2)+((r1*sin?1*sin?1-r2*sin?2*sin?2)^2)+((r1*cos?1-r2 *cos?2) ^2)) = (((r1*sin?1)^2)+((r2*sin?2)^2)-2r1*r2*sin?1*sin?2*(cos? 1*cos?2 +sin?1*sin?2)+((r1*cos?1-r2*cos?2)^2))
Lad et segment være defineret af to punkter i koordinatplanet, så kan dets længde findes ved hjælp af Pythagoras sætning.
Instruktioner
Lad koordinaterne for enderne af segmentet (x1- y1) og (x2- y2) være givet. Tegn et linjestykke i koordinatsystemet.
Tegn vinkelrette fra enderne af segmentet på X- og Y-akserne. Segmenterne markeret med rødt på figuren er projektioner af det oprindelige segment på koordinatakserne.
Hvis du gør parallel overførsel, projektionssegmenter til enderne af segmenterne, får du en retvinklet trekant. Benene i denne trekant vil være de overførte projektioner, og hypotenusen vil være selve segmentet AB.
Projektionslængder er nemme at beregne. Længden af projektionen på Y-aksen vil være lig med y2-y1, og længden af projektionen på X-aksen vil være x2-x1. Derefter, ved Pythagoras sætning, |AB|²- = (y2 - y1)²- + (x2 - x1)²-, hvor |AB| - segmentets længde.
Efter at have præsenteret denne ordning for at finde længden af et segment i almindelig sag, er det let at beregne længden af et segment uden at konstruere et segment. Lad os beregne længden af segmentet, hvis endekoordinater er (1-3) og (2-5). Derefter |AB|²- = (2 - 1)²- + (5 - 3)²- = 1 + 4 = 5, så længden af det påkrævede segment er 5^1/2.
OBS, kun I DAG!
Alt interessant
Du kan bestemme afstanden mellem to punkter ved at måle længden af det segment, der er konstrueret mellem dem. Hvis punkternes koordinater er kendt, så kan afstanden beregnes ved hjælp af matematiske formler. Du skal bruge - lineal; - afstandsmåler; -...
En vektor kan opfattes som et ordnet par af punkter i rummet eller et rettet linjestykke. I skoleforløb analytisk geometri ofte overvejet forskellige opgaver at bestemme dens projektioner - på koordinatakser, på en ret linje, på et plan...
Hvert materielt objekt indtager sin plads i rummet. Koordinater fysisk krop- Det her numeriske karakteristika dens placering, bestemmer den relative position af objekter. Instruktioner 1 Angiv summen af koordinaterne for hvilke objekter du skal bruge...
I fysik og matematik er en vektor karakteriseret ved størrelse og retning og placeret i ortogonalt system koordinater, er det unikt angivet af et par punkter - start og slut. Afstanden mellem punkterne bestemmer størrelsen af vektoren og hældningsvinklen...
En vektor, som et rettet segment, afhænger ikke kun af absolut værdi(modul), som er lig med dens længde. En anden vigtig egenskab er vektorens retning. Det kan bestemmes både af koordinater og af vinklen mellem vektoren og koordinataksen...
En vektor er et segment, der ikke kun har en længde, men også en retning. Vektorer spiller stor rolle i matematik, men især i fysik, da fysik meget ofte beskæftiger sig med størrelser, der bekvemt er repræsenteret som vektorer. Derfor i…
Toppunktet af enhver flad eller tredimensionel geometrisk figur er unikt bestemt af dens koordinater i rummet. På samme måde kan ethvert vilkårligt punkt i det samme koordinatsystem bestemmes entydigt, og det gør det muligt...
En vektor er ikke kun karakteriseret ved dens absolutte længde, men også ved dens retning. Derfor, for at "fikse" det i rummet, bruger de forskellige systemer koordinater Det er ved at kende koordinaterne for en vektor, at du kan bestemme dens længde ved hjælp af...
For at definere en vektor i rummet bruges et koordinatsystem. Det skal tages i betragtning, at det ud over længden (modulus) også er karakteriseret ved retning. Længden af vektoren kan simpelthen måles eller findes ved hjælp af formler. Du får brug for-…
For at finde projektionen af en vektor eller et segment på koordinatakserne skal du sænke perpendikulære fra yderpunkterne til hver af akserne. Hvis koordinaterne for en vektor eller et segment er kendt, kan dets projektion på aksen beregnes. Det samme kan gøres, hvis du ved...
En vektor er en størrelse karakteriseret ved dens numeriske værdi og retning. Med andre ord er en vektor et rettet segment. Positionen af vektor AB i rummet er specificeret af koordinaterne for startpunktet for vektor A og slutpunktet for vektor B.…
Længden, som allerede nævnt, er angivet med modultegnet.
Hvis to punkter i flyet er givet og , så kan længden af segmentet beregnes ved hjælp af formlen
Hvis der er givet to punkter i rummet, så kan længden af segmentet beregnes ved hjælp af formlen
Bemærk: Formlerne forbliver korrekte, hvis de tilsvarende koordinater byttes om: Og , men den første mulighed er mere standard
Eksempel 3
Løsning: efter den tilsvarende formel:
Svar: 
For klarhedens skyld vil jeg lave en tegning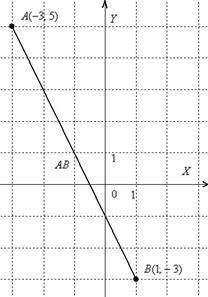 
Linjestykke - dette er ikke en vektor, og du kan selvfølgelig ikke flytte den nogen steder. Hvis du derudover tegner i målestok: 1 enhed. = 1 cm (to notesbogceller), så kan det resulterende svar kontrolleres med en almindelig lineal ved direkte at måle længden af segmentet.
Ja, løsningen er kort, men der er et par mere i den vigtige punkter som jeg gerne vil præcisere:
For det første sætter vi i svaret dimensionen: "enheder". Tilstanden siger ikke HVAD det er, millimeter, centimeter, meter eller kilometer. Derfor ville en matematisk korrekt løsning være den generelle formulering: "enheder" - forkortet som "enheder."
For det andet, lad os gentage skolemateriale, hvilket ikke kun er nyttigt for det betragtede problem:
Vær opmærksom på vigtig teknisk teknik
– fjerner multiplikatoren fra under roden. Som et resultat af beregningerne har vi et resultat, og god matematisk stil involverer at fjerne faktoren fra under roden (hvis det er muligt). Mere detaljeret ser processen sådan ud: 
. Det ville selvfølgelig ikke være en fejl at lade svaret være som det er – men det ville bestemt være en mangel og et tungtvejende argument for at skændes fra lærerens side.
Her er andre almindelige tilfælde: 
Ofte er der nok ved roden stort antal, For eksempel . Hvad skal man gøre i sådanne tilfælde? Ved hjælp af lommeregneren tjekker vi, om tallet er deleligt med 4: . Ja, det var helt opdelt, således: 
. Eller måske kan tallet divideres med 4 igen? . Dermed: 
. Det sidste ciffer i tallet er ulige, så at dividere med 4 for tredje gang vil naturligvis ikke fungere. Lad os prøve at dividere med ni: . Som resultat:
Parat.
Konklusion: hvis vi under roden får et tal, der ikke kan udtrækkes som en helhed, så forsøger vi at fjerne faktoren fra under roden - ved hjælp af en lommeregner tjekker vi om tallet er deleligt med: 4, 9, 16, 25, 36, 49 osv.
Under beslutningen forskellige opgaver rødder er almindelige, prøv altid at trække faktorer ud under roden for at undgå en lavere karakter og unødvendige problemer med at færdiggøre dine løsninger baseret på lærerens kommentarer.
Lad os også gentage kvadratrødder og andre kræfter: 
Regler for handlinger med grader i generel opfattelse kan findes i skole lærebog i algebra, men jeg tror ud fra eksemplerne, at alt eller næsten alt allerede er klart.
Opgave til selvstændig beslutning med et segment i rummet:
Eksempel 4
Point og gives. Find længden af segmentet.
Løsningen og svaret er i slutningen af lektionen.