Tegn grafer over stykkevis lineære funktioner på planet. Stykkevis funktion

Virkelige processer, der forekommer i naturen, kan beskrives ved hjælp af funktioner. Vi kan således skelne mellem to hovedtyper af processer, der er modsat hinanden – det er disse gradvist eller sammenhængende Og krampagtig(et eksempel ville være en bold, der falder og hopper). Men hvis der er diskontinuerlige processer, så er der særlige midler at beskrive dem. Til dette formål introduceres funktioner, der har diskontinuiteter og spring, det vil sige, i forskellige dele af tallinjen opfører funktionen sig efter forskellige love og i overensstemmelse hermed specificeres forskellige formler. Begreberne diskontinuitetspunkter og aftagelig diskontinuitet introduceres.

Du er helt sikkert allerede stødt på funktioner defineret af flere formler, afhængigt af værdierne af argumentet, for eksempel:

y = (x – 3, for x > -3;
(-(x – 3), ved x< -3.

Sådanne funktioner kaldes stykkevis eller stykvis angivet. Udsnit af tallinjen med forskellige formler opgaver, lad os kalde dem komponenter domæne. Foreningen af alle komponenter er definitionsdomænet for den stykkevise funktion. De punkter, der opdeler definitionsdomænet for en funktion i komponenter, kaldes grænsepunkter. Formler definerende stykvis funktion på hver komponent af definitionsdomænet kaldes indgående funktioner. Grafer af stykkevis givne funktioner opnås ved at kombinere dele af grafer konstrueret på hvert af partitionsintervallerne.

Øvelser.

Konstruer grafer af stykvise funktioner:

1) (-3, ved -4 ≤ x< 0,
f(x) = (0, for x = 0,
(1, ved 0< x ≤ 5.

Grafen for den første funktion er en ret linje, der går gennem punktet y = -3. Den udspringer af et punkt med koordinater (-4; -3), løber parallelt med x-aksen til et punkt med koordinater (0; -3). Grafen for den anden funktion er et punkt med koordinater (0; 0). Den tredje graf ligner den første - det er en lige linje, der går gennem punktet y = 1, men allerede i området fra 0 til 5 langs Ox-aksen.

Svar: Figur 1.

2) (3 hvis x ≤ -4,
f(x) = (|x 2 – 4|x| + 3|, hvis -4< x ≤ 4,
(3 – (x – 4) 2 hvis x > 4.

Lad os overveje hver funktion separat og bygge dens graf.

Så f(x) = 3 er en ret linje, parallelt med aksenÅh, men du behøver kun at afbilde det i området, hvor x ≤ -4.

Grafen for funktionen f(x) = |x 2 – 4|x| + 3| kan fås fra parablen y = x 2 – 4x + 3. Efter at have konstrueret sin graf, skal den del af figuren, der ligger over Ox-aksen, forblive uændret, og den del, der ligger under abscisse-aksen, skal vises symmetrisk i forhold til til okseaksen. Vis derefter symmetrisk den del af grafen, hvor
x ≥ 0 i forhold til Oy-aksen for negativ x. Vi forlader grafen opnået som et resultat af alle transformationer kun i området fra -4 til 4 langs abscisse-aksen.

Grafen for den tredje funktion er en parabel, hvis grene er rettet nedad, og toppunktet er i punktet med koordinaterne (4; 3). Vi afbilder tegningen kun i området, hvor x > 4.

Svar: Figur 2.

3) (8 – (x + 6) 2, hvis x ≤ -6,
f(x) = (|x 2 – 6|x| + 8|, hvis -6 ≤ x< 5,
(3 hvis x ≥ 5.

Opbygning af det foreslåede stykkevis givet funktion tilsvarende forrige punkt. Her er graferne for de to første funktioner hentet fra parablens transformationer, og grafen for den tredje er en ret linje parallel med Ox.

Svar: Figur 3.

4) Tegn grafen for funktionen y = x – |x| + (x – 1 – |x|/x) 2 .

Løsning. Omfanget af denne funktion er alt reelle tal, undtagen nul. Lad os udvide modulet. For at gøre dette skal du overveje to tilfælde:

1) For x > 0 får vi y = x – x + (x – 1 – 1) 2 = (x – 2) 2.

2) Ved x< 0 получим y = x + x + (x – 1 + 1) 2 = 2x + x 2 .

Vi har således en stykkevis defineret funktion:

y = ((x – 2) 2, for x > 0;
( x 2 + 2x, ved x< 0.

Graferne for begge funktioner er parabler, hvis grene er rettet opad.

Svar: Figur 4.

5) Tegn en graf for funktionen y = (x + |x|/x – 1) 2.

Løsning.

Det er let at se, at funktionens domæne er alle reelle tal undtagen nul. Efter at have udvidet modulet får vi en stykkevis given funktion:

1) For x > 0 får vi y = (x + 1 – 1) 2 = x 2 .

2) Ved x< 0 получим y = (x – 1 – 1) 2 = (x – 2) 2 .

Lad os omskrive det.

y = (x 2, for x > 0;
((x – 2) 2, ved x< 0.

Graferne for disse funktioner er parabler.

Svar: Figur 5.

6) Er der en funktion, hvis graf er koordinatplan Det har fælles punkt fra enhver lige linje?

Løsning.

Ja, det findes.

Et eksempel kunne være funktionen f(x) = x 3 . Faktisk skærer grafen for en kubisk parabel den lodrette linje x = a i punktet (a; a 3). Lad nu den rette linje være givet ved ligningen y = kx + b. Derefter ligningen
x 3 – kx – b = 0 har ægte rod x 0 (da et polynomium af ulige grader altid har mindst én reel rod). Følgelig skærer grafen for funktionen den rette linje y = kx + b, for eksempel i punktet (x 0; x 0 3).

blog.site, ved kopiering af materiale helt eller delvist kræves et link til den originale kilde.

7
Algebra-lektion i klasse 9A af lærer Mikitchuk Zh.N. Kommunal uddannelsesinstitution "Grundskole nr. 23"19/03/07Lektionens emne: "Stykvis definerede funktioner" Mål:

det angivne emne

talekultur

Som et resultat af at generalisere emnet bør eleverne ved godt:

forskellige funktioner

være i stand til:

bygge en graf af en stykkevis given funktion; læs diagrammet; definere en funktion analytisk ved hjælp af en graf.

Under timerne

I. Organisatorisk og psykologisk øjeblik. Lad os starte vores lektion med ordene fra D.K. Fadeev "Uanset hvilket problem du løser, i slutningen venter et lykkeligt øjeblik på dig - en glædelig følelse af succes, styrker troen på din styrke. Lad disse ord få reel bekræftelse i vores lektion. II. Tjek lektier. Lad os starte lektionen som sædvanligt med at kontrollere d/z - Gentag definitionen af en stykkevis funktion og planen for at studere funktioner 1). På bordet tegne graferne for stykvise funktioner, du har opfundet (fig. 1, 2, 3)2). Kort.№1. Arranger rækkefølgen for at studere funktioners egenskaber:

mindste værdi

nr. 2. Tegn skematisk graferne for funktionerne:

A) y = kx + b, k0; B) y = kx, k0;

B) y = , k0.

3).Mundtligt arbejde . - 2 minutter

Hvilken funktion kaldes stykkevis?En stykkevis funktion er en funktion defineret af forskellige formler med forskellige intervaller.

Hvilke funktioner består de stykvise funktioner vist i fig. 1, 2, 3 af? Hvilke andre funktionsnavne kender du? Hvad kaldes graferne for de tilsvarende funktioner? Er figuren vist i fig. 4 en graf for en funktion? Hvorfor?Svar: nej, fordi Ved definition af en funktion er hver værdi af den uafhængige variabel x forbundet med en enkelt værdi af den afhængige variabel y. 4) Selvkontrol - 3 min.Vælg de korrekte fra de foreslåede grafer og tilsvarende formler, der definerer funktionerne. Lav et velkendt ord ud fra bogstaverne i de svar, du modtager. Svar: GRAFIK Hvor i livet, i videnskaben, i hverdagen støder vi stadig på ordet GRAFIK? - Graf over massens afhængighed af volumen, - volumen på tryk; - vagtplan; - togplan; - grafer bruges til at præsentere forskellige oplysninger, for eksempel volumen industriel produktion V Saratov-regionen i perioden fra 1980 til 2002. Ved hjælp af denne graf kan du følge nedgangen og væksten i produktionen i de enkelte år - Fortæl hvilken funktionsgraf der repræsenterer denne information. Svar: stykkevis funktion.III. Budskab om emnet, formålet med lektionen. Lektionens emne:"Stykvis definerede funktioner" Mål:- ved at bruge eksemplet på en stykkevis given funktion, huske planen for at studere funktioner;

gentag trinene til at konstruere en stykkevis given funktion; anvende generaliseret viden ved løsning af ikke-standardiserede problemer.IV. Opdatering af tidligere erhvervet viden. Vi stødte først på konceptet med en funktion i 7. klasse, mens vi studerede lineær afhængighed. Fra et modelleringsperspektiv reelle processer, svarer denne afhængighed til ensartede processer Eksempel: Fodgængerbevægelse med konstant hastighed for tiden t. Formel: s =vt, graf – linjestykker, placeret i første kvartal.
Hovedemnet i 8. klasse er kvadratisk funktion, simulering af ensartet accelererede processer Eksempel: den formel du studerede i 9. klasse til bestemmelse af modstanden af en opvarmet lampe (R) ved konstant kraft(P) og skiftende spænding (U). FormelR =

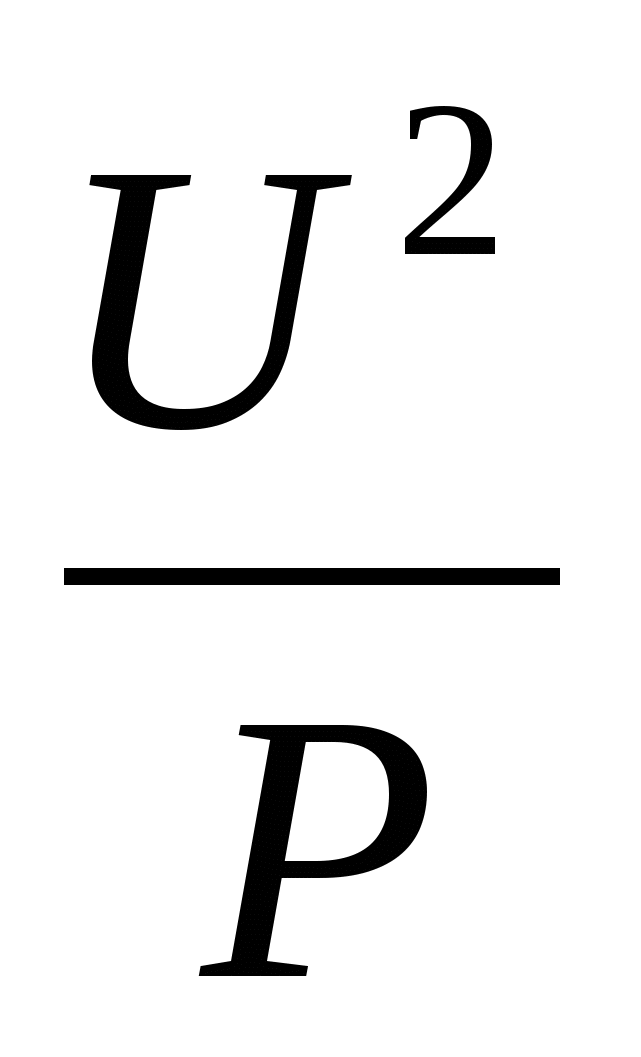, grafen er en gren af en parabel placeret i første kvartal.
Til 3 år vores viden om funktioner blev beriget, antallet af undersøgte funktioner voksede, og det sæt af opgaver til at løse, som vi måtte ty til grafer, blev udvidet. Nævn disse typer opgaver... - løsning af ligninger;- løsning af ligningssystemer;- løsning af uligheder;- undersøgelse af funktioners egenskaber.V. Forberedelse af eleverne til generaliseringsaktiviteter. Lad os huske en af opgavetyperne, nemlig at studere funktioners egenskaber eller læse en graf Lad os gå til lærebogen. Side 65 Fig. 20a fra nr. 250. Dyrke motion: læse grafen for funktionen. Proceduren for at studere funktionen ligger foran os. 1. definitionsdomæne – (-∞; +∞)2. lige, ulige – hverken lige eller ulige3. monotoni - øges [-3; +∞), falder[-5;-3], konstant (-∞; -5);4. begrænsethed – begrænset nedefra5. den største og mindste værdi af funktionen – y max = 0, y max – findes ikke;6. kontinuitet - kontinuerlig gennem hele definitionsområdet;7. Værdiområdet er konveks både ned og op (-∞; -5] og [-2; +∞).VI. Gengivelse af viden på et nyt niveau. Du ved, at opbygning og undersøgelse af grafer over stykkevis givne funktioner er gennemgået i anden del af algebraeksamen i funktionsafsnittet og bedømt med 4 og 6 point. Lad os gå til opgavesamlingen Side 119 - nr. 4.19-1. Løsning: 1).y = - x, - kvadratisk funktion, graf - parabel, forgrener sig (a = -1, a 0). x -2 -1 0 1 2 y -4 -1 0 1 4 2) y = 3x – 10, - lineær funktion, graf - ligeLad os lave en tabel med nogle værdierx 3

3 y 0-1 3) y= -3x -10, - lineær funktion, graf - ligeLad os lave en tabel med nogle værdier x -3 -3 y 0 -1 4) Lad os konstruere grafer over funktioner i ét koordinatsystem og udvælge dele af graferne med givne intervaller.
Lad os finde ud af grafen ved hvilke værdier af x værdierne af funktionen er ikke-negative. Svar: f(x)  0 ved x = 0 og ved

 3 VII.Arbejde med ikke-standardiserede opgaver. nr. 4.29-1), side 121. Løsning: 1) Lige linje (venstre) y = kx + b passerer gennem punkterne (-4;0) og (-2;2). Dette betyder -4 k + b = 0, -2 k + b = 2;

k = 1, b = 4, y = x+4. Svar: x +4, hvis x -2 y = hvis -2  x 3 kr 3 hvis x  3
VIII.Videnskontrol. Så lad os opsummere kort. Hvad gentog vi i lektionen Planlæg for at studere funktioner, trin til at konstruere en graf af en stykkevis funktion, specificering af en funktion analytisk. Lad os tjekke, hvordan du mestrer dette materiale. Test for "4" - "5", "3" I mulighed nr. U

2 1 -1 -1 1 X

D(f) = , konveks op og ned på , konveks op og ned på , falder på ________ Afgrænset af ____________ eksisterer slet ikke, højst =_____ Kontinuerlig gennem hele definitionsdomænet E(f) = ____________ Konveks begge ned og op ved hele definitionsområdet

Tilbage frem

Opmærksomhed! Forhåndsvisninger af dias er kun til informationsformål og repræsenterer muligvis ikke alle funktionerne i præsentationen. Hvis du er interesseret dette arbejde, download venligst den fulde version.

Lærebog: Algebra 8. klasse, redigeret af A. G. Mordkovich.

Lektionstype: Opdagelse af ny viden.

Mål:

for læreren mål er fastsat på hvert trin af lektionen;

for eleven:

Personlige mål:

Lær at klart, præcist, kompetent udtrykke dine tanker verbalt og skrivning, forstå betydningen af opgaven;
Lær at anvende erhvervet viden og færdigheder til at løse nye problemer;
Lær at kontrollere processen og resultaterne af dine aktiviteter;

Meta-fagmål:

I kognitiv aktivitet:

Udvikling logisk tænkning og tale, evnen til logisk at underbygge sine domme og udføre simple systematiseringer;
Lær at fremsætte hypoteser hvornår problemløsning, forstå behovet for at kontrollere dem;
Anvend viden i en standardsituation, lær at udføre opgaver selvstændigt;
Overfør viden til en ændret situation, se opgaven i sammenhæng med problemsituationen;

I informations- og kommunikationsaktiviteter:

Lær at føre en dialog, anerkend retten til en anden mening;

I reflekterende aktivitet:

Lær at forudse mulige konsekvenser dine handlinger;
Lær at eliminere årsagerne til vanskeligheder.

Fagmål:

Find ud af, hvad en stykkevis funktion er;
Lær at definere en stykkevis given funktion analytisk ud fra dens graf;

Under timerne

1. Selvbestemmelse pædagogiske aktiviteter

Formål med scenen:

inkludere elever i læringsaktiviteter;
bestemme indholdet af lektionen: vi fortsætter med at gentage emnet for numeriske funktioner.

Organisation pædagogisk proces på trin 1:

T: Hvad gjorde vi i tidligere lektioner?

D: Vi gentog emnet numeriske funktioner.

U: I dag vil vi fortsætte med at gentage emnet fra tidligere lektioner, og i dag skal vi finde ud af, hvilke nye ting vi kan lære i dette emne.

2. Opdatering af viden og registrering af vanskeligheder i aktiviteter

Formål med scenen:

opdatering pædagogisk indhold, nødvendigt og tilstrækkeligt for opfattelsen af nyt materiale: husk formlerne numeriske funktioner, deres egenskaber og konstruktionsmetoder;
opdatering mentale operationer, nødvendigt og tilstrækkeligt til opfattelsen af nyt materiale: sammenligning, analyse, generalisering;
registrere en individuel vanskelighed i en aktivitet, der viser det personligt betydeligt niveau utilstrækkelig eksisterende viden: specificering af en stykkevis given funktion analytisk, samt konstruering af dens graf.

Organisering af uddannelsesprocessen på trin 2:

T: Diasset viser fem numeriske funktioner. Bestem deres type.

1) fraktioneret-rationel;

2) kvadratisk;

3) irrationel;

4) funktion med modul;

5) beroligende.

T: Navngiv de formler, der svarer til dem.

3) ;

4) ;

U: Lad os diskutere, hvilken rolle hver koefficient spiller i disse formler?

D: Variablerne "l" og "m" er ansvarlige for at flytte graferne for disse funktioner henholdsvis venstre - højre og op - ned, koefficienten "k" i den første funktion bestemmer positionen af grenene af hyperbelen: k> 0 - grenene er i I- og III-kvarteret, k< 0 - во II и IV четвертях, а коэффициент “а” определяет направление ветвей параболы: а>0 - grene er rettet opad, og< 0 - вниз).

2. Slide 2

U: Definer analytisk de funktioner, hvis grafer er vist i figurerne. (i betragtning af at de flytter y=x2). Læreren skriver svarene ned på tavlen.

D: 1) );

2);

3. Slide 3

U: Definer analytisk de funktioner, hvis grafer er vist i figurerne. (med tanke på at de flytter). Læreren skriver svarene ned på tavlen.

4. Slide 4

U: Brug de tidligere resultater til at definere analytisk de funktioner, hvis grafer er vist i figurerne.

3. Identificering af årsager til vanskeligheder og opstilling af mål for aktiviteter

Formål med scenen:

organisere kommunikativ interaktion, hvorunder særegen ejendom en opgave, der forårsagede vanskeligheder i læringsaktiviteter;
blive enige om formålet og emnet for lektionen.

Organisering af uddannelsesprocessen på trin 3:

T: Hvad volder dig vanskeligheder?

D: Stykker af grafer vises på skærmen.

T: Hvad er formålet med vores lektion?

D: Lær at definere dele af funktioner analytisk.

T: Formuler emnet for lektionen. (Børn forsøger selv at formulere et emne. Læreren præciserer det. Emne: Stykkevis funktion.)

4. Konstruktion af et projekt for at komme ud af en vanskelighed

Formål med scenen:

organisere kommunikativ interaktion for at bygge en ny virkemåde, eliminering af årsagen til den identificerede vanskelighed;
rette op ny vej handlinger.

Organisering af uddannelsesprocessen på trin 4:

T: Lad os læse opgaven grundigt igennem igen. Hvilke resultater bliver bedt om at blive brugt som hjælp?

D: Tidligere, dvs. dem, der er skrevet på tavlen.

U: Måske er disse formler allerede svaret på denne opgave?

D: Nej, fordi disse formler definerer kvadratisk og rationel funktion, og diaset viser deres brikker.

U: Lad os diskutere, hvilke intervaller af x-aksen, der svarer til stykkerne af den første funktion?

U: Så ser den analytiske måde at specificere den første funktion på: if

T: Hvad skal der gøres for at udføre en lignende opgave?

D: Skriv formlen ned, og bestem, hvilke intervaller af abscisseaksen, der svarer til stykkerne af denne funktion.

5. Primær konsolidering i ekstern tale

Formål med scenen:

registrere det studerede undervisningsindhold i ekstern tale.

Organisering af uddannelsesprocessen på trin 5:

7. Inklusion i vidensystemet og gentagelse

Formål med scenen:

træne færdigheder i at bruge nyt indhold i sammenhæng med tidligere lært indhold.

Organisering af uddannelsesprocessen på trin 7:

U: Definer analytisk den funktion, hvis graf er vist i figuren.

8. Refleksion over aktiviteter i lektionen

Formål med scenen:

optage nyt indhold lært i lektionen;
evaluere dine egne aktiviteter i lektionen;
tak til dine klassekammerater, som hjalp med at få lektionsresultaterne;
registrere uløste vanskeligheder som retningslinier for fremtidige uddannelsesaktiviteter;
diskutere og skrive lektier ned.

Organisering af uddannelsesprocessen på trin 8:

T: Hvad lærte vi om i klassen i dag?

D: Med en stykkevis given funktion.

T: Hvilket arbejde har vi lært at udføre i dag?

D: Spørg denne type fungerer analytisk.

T: Ræk hånden op, hvem forstod emnet for dagens lektion? (Diskuter eventuelle problemer, der er opstået med de andre børn).

Lektier

nr. 21.12(a, c);
nr. 21.13(a, c);
№22.41;
№22.44.

Virkelige processer, der forekommer i naturen, kan beskrives ved hjælp af funktioner. Vi kan således skelne mellem to hovedtyper af processer, der er modsat hinanden – det er disse gradvist eller sammenhængende Og krampagtig(et eksempel ville være en bold, der falder og hopper). Men hvis der er diskontinuerlige processer, så er der specielle midler til at beskrive dem. Til dette formål introduceres funktioner, der har diskontinuiteter og spring, det vil sige, at i forskellige dele af tallinjen opfører funktionen sig efter forskellige love og derfor er specificeret af forskellige formler. Begreberne diskontinuitetspunkter og aftagelig diskontinuitet introduceres.

Du er helt sikkert allerede stødt på funktioner defineret af flere formler, afhængigt af værdierne af argumentet, for eksempel:

y = (x – 3, for x > -3;
(-(x – 3), ved x< -3.

Sådanne funktioner kaldes stykkevis eller stykvis angivet. Lad os kalde dele af tallinjen med forskellige formler til specificering komponenter domæne. Foreningen af alle komponenter er definitionsdomænet for den stykkevise funktion. De punkter, der opdeler definitionsdomænet for en funktion i komponenter, kaldes grænsepunkter. Formler, der definerer en stykkevis funktion på hver komponent af definitionsdomænet, kaldes indgående funktioner. Grafer af stykkevis givne funktioner opnås ved at kombinere dele af grafer konstrueret på hvert af partitionsintervallerne.

Øvelser.

Konstruer grafer af stykvise funktioner:

1) (-3, ved -4 ≤ x< 0,
f(x) = (0, for x = 0,
(1, ved 0< x ≤ 5.

Svar: Figur 1.

2) (3 hvis x ≤ -4,
f(x) = (|x 2 – 4|x| + 3|, hvis -4< x ≤ 4,
(3 – (x – 4) 2 hvis x > 4.

Lad os overveje hver funktion separat og bygge dens graf.

Så f(x) = 3 er en ret linje parallel med Ox-aksen, men den skal kun afbildes i området, hvor x ≤ -4.

Grafen for den tredje funktion er en parabel, hvis grene er rettet nedad, og toppunktet er i punktet med koordinaterne (4; 3). Vi afbilder tegningen kun i området, hvor x > 4.

Svar: Figur 2.

3) (8 – (x + 6) 2, hvis x ≤ -6,
f(x) = (|x 2 – 6|x| + 8|, hvis -6 ≤ x< 5,
(3 hvis x ≥ 5.

Konstruktionen af den foreslåede stykkevis givne funktion svarer til det foregående afsnit. Her er graferne for de to første funktioner hentet fra parablens transformationer, og grafen for den tredje er en ret linje parallel med Ox.

Svar: Figur 3.

4) Tegn grafen for funktionen y = x – |x| + (x – 1 – |x|/x) 2 .

Løsning. Domænet for denne funktion er alle reelle tal undtagen nul. Lad os udvide modulet. For at gøre dette skal du overveje to tilfælde:

1) For x > 0 får vi y = x – x + (x – 1 – 1) 2 = (x – 2) 2.

2) Ved x< 0 получим y = x + x + (x – 1 + 1) 2 = 2x + x 2 .

Vi har således en stykkevis defineret funktion:

y = ((x – 2) 2, for x > 0;
( x 2 + 2x, ved x< 0.

Graferne for begge funktioner er parabler, hvis grene er rettet opad.

Svar: Figur 4.

5) Tegn en graf for funktionen y = (x + |x|/x – 1) 2.

Løsning.

Det er let at se, at funktionens domæne er alle reelle tal undtagen nul. Efter at have udvidet modulet får vi en stykkevis given funktion:

1) For x > 0 får vi y = (x + 1 – 1) 2 = x 2 .

2) Ved x< 0 получим y = (x – 1 – 1) 2 = (x – 2) 2 .

Lad os omskrive det.

y = (x 2, for x > 0;
((x – 2) 2, ved x< 0.

Graferne for disse funktioner er parabler.

Svar: Figur 5.

6) Findes der en funktion, hvis graf på koordinatplanet har et fælles punkt med en ret linje?

Løsning.

Ja, det findes.

Et eksempel kunne være funktionen f(x) = x 3 . Faktisk skærer grafen for en kubisk parabel den lodrette linje x = a i punktet (a; a 3). Lad nu den rette linje være givet ved ligningen y = kx + b. Derefter ligningen
x 3 – kx – b = 0 har en reel rod x 0 (da et polynomium af ulige grader altid har mindst én reel rod). Følgelig skærer grafen for funktionen den rette linje y = kx + b, for eksempel i punktet (x 0; x 0 3).

hjemmeside, ved kopiering af materiale helt eller delvist kræves et link til kilden.

Analytisk funktionstildeling

Funktion %%y = f(x), x \i X%% er givet på en eksplicit analytisk måde, hvis der gives en formel, der angiver rækkefølgen matematiske operationer, som skal udføres med argumentet %%x%% for at få værdien %%f(x)%% af denne funktion.

Eksempel

%% y = 2 x^2 + 3x + 5, x \in \mathbb(R)%%;
%% y = \frac(1)(x - 5), x \neq 5%%;
%% y = \sqrt(x), x \geq 0%%.

Altså for eksempel i fysik med ensartet acceleration lige bevægelse et legemes hastighed bestemmes af formlen %%v = v_0 + a t%%, og formlen for forskydningen %%s%% af et legeme ved uniform accelereret bevægelse over tidsintervallet fra %%0%% til %%t%% skrives som: %% s = s_0 + v_0 t + \frac(a t^2)(2) %%.

Stykkevis definerede funktioner

Nogle gange kan den pågældende funktion specificeres med flere formler, der fungerer i forskellige dele af dens definitionsdomæne, hvor argumentet for funktionen ændres. For eksempel: $$ y = \begin(cases) x ^ 2,~ if~x< 0, \\ \sqrt{x},~ если~x \geq 0. \end{cases} $$

Funktioner af denne type kaldes nogle gange sammensatte eller stykvis angivet. Et eksempel på en sådan funktion er %%y = |x|%%

Funktion Domæne

Hvis en funktion er specificeret på en eksplicit analytisk måde ved hjælp af en formel, men definitionsdomænet for funktionen i form af mængden %%D%% ikke er angivet, vil vi med %%D%% altid mene mængden af værdier af argumentet %%x%% for hvilket denne formel har betydningen. Så for funktionen %%y = x^2%% er definitionsdomænet mængden %%D = \mathbb(R) = (-\infty, +\infty)%%, da argumentet %%x%% kan tage alle værdier på sig tallinje. Og for funktionen %%y = \frac(1)(\sqrt(1 - x^2))%% vil definitionsdomænet være værdisættet %%x%%, der opfylder uligheden %%1 - x^2 > 0%%, t.e. %%D = (-1, 1) %%.

Fordele ved eksplicit at specificere en funktion analytisk

Bemærk, at den eksplicitte analytiske metode til at specificere en funktion er ret kompakt (formlen fylder som regel lidt), er nem at reproducere (formlen er ikke svær at skrive) og er mest velegnet til at udføre matematiske operationer og transformationer på funktioner.

Nogle af disse operationer - algebraiske (addition, multiplikation osv.) - er velkendte fra skoleforløb matematik, andet (differentiering, integration) vil blive studeret i fremtiden. Denne metode er dog ikke altid klar, da karakteren af funktionens afhængighed af argumentet ikke altid er klar, og nogle gange kræves der besværlige beregninger for at finde funktionsværdierne (hvis de er nødvendige).

Implicit funktionstildeling

Funktion %%y = f(x)%% defineret på en implicit analytisk måde, hvis relationen $$F(x,y) = 0 er givet, ~~~~~~~~~~(1)$$ forbinder værdierne af funktionen %%y%% og argumentet %% x%%. Hvis du angiver argumentværdier, så for at finde værdien %%y%% svarende til en specifik værdi %%x%%, skal du løse ligningen %%(1)%% med hensyn til %%y%%, mens specifik betydning%%x%%.

Til givet værdi%%x%% ligningen %%(1)%% har muligvis ingen løsning eller mere end én løsning. I det første tilfælde indstillet værdi%%x%% hører ikke til omfanget af den implicit specificerede funktion, men i det andet tilfælde angiver den funktion med flere værdier, som har mere end én betydning for en given argumentværdi.

Bemærk, at hvis ligningen %%(1)%% eksplicit kan løses med hensyn til %%y = f(x)%%, så får vi den samme funktion, men allerede specificeret på en eksplicit analytisk måde. Så ligningen %%x + y^5 - 1 = 0%%

og ligheden %%y = \sqrt(1 - x)%% definerer den samme funktion.

Parametrisk funktionsspecifikation

Når afhængigheden af %%y%% af %%x%% ikke er angivet direkte, men i stedet angives afhængigheden af begge variable %%x%% og %%y%% af en tredje hjælpevariabel %%t%% i formen

$$ \begin(cases) x = \varphi(t),\\ y = \psi(t), \end(cases) ~~~t \in T \subseteq \mathbb(R), ~~~~~ ~~~~~(2) $$ hvad de taler om parametrisk metode til at specificere funktionen;

så kaldes hjælpevariablen %%t%% en parameter.

Hvis det er muligt at eliminere parameteren %%t%% fra ligningerne %%(2)%%, så kommer vi frem til en funktion defineret af den eksplicitte eller implicitte analytiske afhængighed af %%y%% af %%x%% . For eksempel fra relationerne $$ \begin(cases) x = 2 t + 5, \\ y = 4 t + 12, \end(cases), ~~~t \in \mathbb(R), $$ undtagen for %-parameteren %t%% får vi afhængigheden %%y = 2 x + 2%%, som definerer en ret linje i %%xOy%%-planet.

Grafisk metode

Eksempel grafisk opgave funktioner

Det viser ovenstående eksempler analytisk metode funktionstildeling svarer til dens grafisk billede , som kan betragtes som praktisk og visuel form funktionsbeskrivelser. Nogle gange brugt grafisk metode angivelse af en funktion, når afhængigheden af %%y%% af %%x%% er angivet af en linje på planet %%xOy%%. På trods af al klarheden mister den dog i nøjagtighed, da værdierne af argumentet og de tilsvarende funktionsværdier kun kan opnås fra grafen. Den resulterende fejl afhænger af skalaen og nøjagtigheden af måling af abscissen og ordinaten af individuelle punkter på grafen. Fremover vil vi kun tildele funktionsgrafen rollen som illustration af funktionens adfærd, og derfor vil vi begrænse os til at konstruere "skitser" af grafer, der afspejler funktionernes hovedtræk.

Tabelmetode

Bemærk tabelmetode funktionstildelinger, når nogle argumentværdier og tilsvarende funktionsværdier er inde i en bestemt rækkefølge er placeret i bordet. Sådan er de berømte borde bygget trigonometriske funktioner, logaritmetabeller osv. Forholdet mellem mængder målt ved eksperimentelle undersøgelser, observationer, tests.

Ulempen ved denne metode er, at det er umuligt direkte at bestemme funktionsværdier for argumentværdier, der ikke er inkluderet i tabellen. Hvis der er tillid til, at argumentværdierne, der ikke er præsenteret i tabellen, tilhører definitionsdomænet for den pågældende funktion, så kan de tilsvarende funktionsværdier beregnes tilnærmelsesvis ved hjælp af interpolation og ekstrapolation.

Eksempel

x	3	5.1	10	12.5
y	9	23	80	110

Algoritmiske og verbale metoder til at specificere funktioner

Funktionen kan indstilles algoritmisk(eller software) på en måde, der er meget brugt i computerberegninger.

Endelig kan det bemærkes beskrivende(eller verbal-) en måde at specificere en funktion på, når reglen for at matche funktionsværdierne med argumentværdierne er udtrykt i ord.

For eksempel, funktionen %%[x] = m~\forall (x \in )