Многогранники. Призма, параллелепипед, пирамида
Многогранник - это такое тело, поверхность которого состоит из конечного числа плоских многоугольников

Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности
Эти многоугольники называются гранями , их стороны – рёбрами, их вершины – вершинами многогранника. Отрезки, соединяющие две вершины и не лежащие на одной грани, называются диагоналями многогранника.
Призма – это многогранник, две грани которой ABCDE и A 1 B 1 C 1 D 1 E 1
( основания призмы ) – равные многоугольники с соответственно параллельными сторонами, а остальные грани (AA 1 B 1 B, BB 1 C 1 C и т.д.) - параллелограммы, плоскости которых параллельны прямой (AA 1 , или BB 1 , или CC 1 и т.д.). Параллелограммы AA 1 B 1 B, BB 1 C 1 C и т.д. называются боковыми гранями ; рёбра AA 1 , BB 1 , CC 1 и т.д. называются боковыми рёбрами.
Высота призмы – это любой перпендикуляр, опущенный из любой точки основания на плоскость другого основания.
В зависимости от формы многоугольника, лежащего в основании, призма может быть соответственно: треугольной, четырёхугольной, пятиугольной, шестиугольной и т.д.
Если боковые рёбра призмы перпендикулярны к плоскости основания, то такая призма называется прямой
; в противном случае – это наклонная призма
. На рисунке показаны прямая и наклонная призмы


Если в основании прямой призмы лежит правильный многоугольник , то такая призма также называется правильной .
Свойства призмы
1 о. Основания призмы являются равными многоугольниками.
2 о. Боковые грани призмы являются параллелограммами.
3 о. Боковые ребра призмы равны.
Параллелепипед - это призма, основания которой параллелограммы. Таким образом, параллелепипед имеет шесть граней и все они – параллелограммы. Противоположные грани попарно равны и параллельны. У параллелепипеда
четыре диагонали; они все пересекаются в одной точке и делятся в ней пополам.

Если четыре боковые грани параллелепипеда – прямоугольники, то он называется прямым
. Прямой параллелепипед, у которого все шесть граней – прямоугольники, называется прямоугольным
. Диагональ прямоугольного параллелепипеда d
и его рёбра a, b, c
связаны соотношением: d
2
= a
2 + b
2 + c
2 .

Прямоугольный параллелепипед, все грани которого квадраты, называется кубом
. В се рёбра куба равны.
се рёбра куба равны.
Свойства параллелепипеда
1 о. У параллелепипеда 8 вершин, 12 ребер и 6 граней.
2 о. Каждая грань параллелепипеда - параллелограмм.
3 о. Противолежащие грани параллелепипеда равны.
4 о. Параллельные ребра параллелепипеда равны.
Пирамида – это многогранник, у которого одна грань ( основание пирамиды ) – это произвольный многоугольник (ABCDE, рис.80), а остальные грани ( боковые грани ) – треугольники с общей вершиной S, называемой вершиной пирамиды .
Перпендикуляр SO, опущенный из вершины пирамиды на её основание, называется высотой пирамиды . В зависимости от формы многоугольника, лежащего в основании, пирамида может быть соответственно: треугольной, четырёхугольной, пятиугольной, шестиугольной и т.д. Треугольная пирамида является тетраэдром ( четырёхгранником ), четырёхугольная – пятигранником и т.д.
Пирамида называется правильной , если в основании лежит правильный многоугольник, а её высота падает в центр основания. Все боковые рёбра правильной пирамиды равны; все боковые грани – равнобедренные треугольники. Высота боковой грани (SF) называется апофемой правильной пирамиды.

Если провести сечение abcde , параллельное основанию ABCDE (рис.81) пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Параллельные грани ABCDE и abcde называются основаниями ; расстояние Oo между ними – высотой . Усечённая пирамида называется правильной , если пирамида, из которой она была получена – правильная . Все боковые грани правильной усечённой пирамиды – равные равнобочные трапеции. Высота Ff боковой грани
(рис.81) называется апофемой правильной усечённой пирамиды.
Свойства правильной пирамиды
1 о. Основание правильной пирамиды - правильный многоугольник.
2 о. Боковые грани правильной пирамиды - равнобедренные треугольники.
3 о. Боковые ребра правильной пирамиды равны.
Вариант 1.
1. К многогранникам относятся:
А) параллелепипед; В) цилиндр; С) конус; D ) шар
2. Если в основании призмы лежит квадрат, то она является:
А) неправильной призмой; В) правильной призмой; С) выпуклой призмой; Д) квадратной
3. Высота, длина, ширина прямоугольного параллелепипеда равны соответственно: 2 см, 3см, 1см. Найдите сумму длин всех ребер
A ) 6 ; B ) 20; C ) 12; D )24
4. Боковые ребра пирамиды равны 7 см, 12 см, 5 см. Одно из них перпендикулярно к основанию. Чему равна высота пирамиды?
A ) 7 ; B ) 12; C ) 5
5. Перпендикуляр, опущенный из вершины пирамиды на плоскость основания, называется:
А) медианой; В) осью; С) диагональю; D ) высотой.
6. Боковая поверхность призмы состоит из:
А) параллелограммов; В)окружностей; С) ромбов; Д) треугольников.
7. Сколько боковых граней имеет треугольная призма?
A )1 ; B ) 2; C ) 3; D ) много
8. Какое наименьшее число боковых граней может иметь пирамида?
A )1 ; B ) 2; C ) 3; D ) 4
9. Какие из представленных фигур называются конусом?
На рисунке изображен конус.
Найти:
10. Диаметр основания
A
) АВ;
B
)
SO
;
C
)
AO
;
D
)
SB
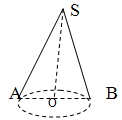
11. Образующую
A) SO; B) О B; C) AO; D) SB
12. Осевое сечение
A ) ASO ; B ) ASB ; C ) круг; D ) SBO
13. Радиус круга равен 2 см. Найдите его площадь
A ) 2; B )3 ; C ) 4 ; D ) 5
14. Высота цилиндра 3 см. Радиус основания 2 см. Найти длину образующей
A ) 3; B ) 2 ; C ) 1 ; D ) 5
15. Площадь большого круга шара 144 π см 2 . Найти радиус шара.
A ) ; B ) 14 ; C ) 72 ; D ) 12
Вариант 2.
К телам вращения относятся
А) цилиндр, B )параллелепипед; С) призма; D ) пирамида;
2 . Если боковые ребра призмы перпендикулярны основанию, то призма является:
А) наклонной; В)невыпуклой; С) прямой; Д) выпуклой.
3. Высота, длина, ширина прямоугольного параллелепипеда равны соответственно: 2 см, 4 см, 1см. Найдите сумму длин всех ребер
A ) 6 ; B ) 28; C ) 7; D )24
4. Боковые ребра пирамиды равны 3 см, 15 см, 5 см. Одно из них перпендикулярно к основанию. Чему равна высота пирамиды?
A ) 3 ; B ) 15; C ) 5
5. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется:
А) медианой; B ) апофемой; С) биссектрисой; D ) высотой.
6. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани называется:
А) диагональю; В) ребром; С) осью; D ) гранью
7. Какая фигура не может быть в основании призмы?
А) прямоугольник; В) квадрат; С) треугольник; D ) круг
8. Сколько оснований имеет правильная призма?
A ) 1; B ) 2; C ) 3; D )много
9. Какие из представленных фигур называются призмами?
На рисунке изображен конус.
Найти:
10. радиус основания
A
) АВ;
B
)
SO
;
C
)
AO
;
D
)
SB

11. Высоту
A) SO; B) О B; C) AO; D) SB
12. Осевое сечение
A ) ASO ; B ) ASB ; C ) круг; D ) SBO
13. Радиус круга равен 3 см. Найдите его площадь
A ) 6; B )7 ; C ) 8 ; D ) 9
14. Высота цилиндра 5 см. Радиус основания 4 см. Найти длину образующей
A ) 5; B ) 4 ; C ) 1 ; D ) 9
15. Площадь большого круга шара 9 π см 2 . Найти радиус шара.
A ) ; B ) 8 ; C ) 2 ; D ) 3
Вариант 1Вариант 2
1 ; 5
2 ; 6
Общий исторический обзор
Первые геометрические понятия возникли в доисторические времена. Разные формы материальных тел наблюдал человек в природе: формы растений и животных, гор и извилин рек, круга и серпа Луны и т. п. Однако человек не только пассивно наблюдал природу, но практически осваивал и использовал ее богатства. В процессе практической деятельности он накапливал геометрические сведения. Материальные потребности побуждали людей изготовлять орудия труда, обтесывать камни и строить жилища, лепить глиняную посуду и натягивать тетиву на лук. Конечно, десятки и сотни тысяч раз натягивали люди свои луки изготовляли разные предметы с прямыми ребрами и т. п., пока постепенно дошли до отвлеченного понятия прямой линии. Примерно то же можно сказать о других основных геометрических понятиях. Практическая деятельность человека служила основой длительного процесса выработки отвлеченных понятий, открытия простейших геометрических зависимостей и соотношений.
Начало геометрии было положено в древности при решении чисто практических задач. Со временем, когда накопилось большое количество геометрических фактов, у людей появилось потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств. Постепенно создавалась геометрическая наука. Примерно в VI - V вв. до н. э. в Древней Греции в геометрии начался новый этап развития, что объясняется высоким уровнем, которого достигла общественно-политическая и культурная жизнь в греческих государствах. Произведения, содержащие систематическое изложение геометрии, появились в Греции еще в V до н.э., но они были вытеснены “Началами” Евклида.
Геометрические знания примерно в объеме современного курса средней школы были изложены еще 2200 лет назад в “Началах” Евклида. Конечно, изложенная в “Началах” наука геометрия не могла быть создана одним ученым. Известно, что Евклид в своей работе опирался на труды десятков предшественников, среди которых были Фалес и Пифагор, Демокрит и Гиппократ, Архит, Теэтет, Евдокс и др. Ценой больших усилий, исходя из отдельных геометрических сведений, накопленных тысячелетиями в практической деятельности людей, эти великие ученые сумели на протяжении 3 - 4 столетий привести геометрическую науку к высокой ступени совершенства. Историческая заслуга Евклида состоит в том, что он, создавая свои “Начала”, объединил результаты своих предшественников, упорядочил и привел в одну систему основные геометрические знания того времени. На протяжении двух тысячелетий геометрия изучалась в том объеме, порядке и стиле, как она была изложена в “Началах” Евклида. Многие учебники элементарной геометрии во всем мире представляли (а многие и поныне представляют) собой лишь переработку книги Евклида. “Начала” на протяжении веков были настольной книгой величайших ученых.
В XVII в. Декарт благодаря методу координат сделал возможным изучение свойств геометрических фигур с помощью алгебры. С этого времени начала развиваться аналитическая геометрия. В XVII - XVIII вв. зарождается и разрабатывается дифференциальная геометрия, изучающая свойства фигур с помощью методов математического анализа. В XVIII- XIX вв. развитие военного дела и архитектуры привело к разработке методов точного изображения пространственных фигур на плоском чертеже, в связи с чем появляются начертательная геометрия, научные основы которой заложил французский математик Г. Монж, и проективная геометрия, основы которой были созданы в трудах французских математиков Д. Дезарга и Б. Паскаля (XVII в.). В ее создании важнейшую роль сыграл другой французский математик - Ж. В. Понселе (XIX в.).
Коренной перелом в геометрии впервые произвел в первой половине ХIХ в. великий русский математик Николай Иванович Лобачевский, который создал новую, неевклидову геометрию, называемую ныне геометрией Лобачевского.
Открытие Лобачевского было началом нового периода в развитии геометрии. За ним последовали новые открытия немецкого математика Б. Римана и др.
В настоящее время геометрия тесно переплетается со многими другими разделами математики. Одним из источников развития и образования новых понятий в геометрии, как и в других областях математики, являются современные задачи естествознания, физики и техники.
Первоначальное понятие о многогранниках.
Многогранники и их элементы.
Проблемы нам создают не те вещи,
которых мы не знаем, а те, о которых мы
ошибочно полагаем, что знаем.
В. Роджерс
| Определение. Многогранником называется тело, поверхность которого является объединением конечного числа многоугольников. В соответствии с общим определением выпуклого множества, многогранник является выпуклым, если вместе с любыми двумя своими точками он содержит соединяющий их отрезок. На рисунке показаны выпуклый и, соответственно, невыпуклый многогранники. | ||||
| Многоугольник, принадлежащий поверхности многогранника, называется его гранью, если он не содержится ни в каком другом многоугольнике, также принадлежащем поверхности многогранника. Стороны граней называются рёбрами многогранника, а вершины – вершинами многогранника. Отрезки, соединяющие вершины многогранника, не принадлежащие одной грани, называются диагоналями этого многогранника. | ||||
| Определение. Многогранник называется правильным, если все его грани – равные правильные многоугольники и из каждой его вершины выходит одинаковое число рёбер. | ||||
| Рёбра | ||||
| Тетраэдр | 4 | 4 | 6 | |
| 6 | 8 | 12 | ||
| 8 | 6 | 12 | ||
| Додекаэдр | 12 | 20 | 30 | |
| Икосаэдр | 20 | 12 | 30 | |
| Призма n-угольная | 2n | 3n | n+2 | |
| Пирамида n-угольная | n+1 | 2n | n+1 | |
| Теорема Эйлера. | Для числа граней Г, числа вершин В и числа рёбер Р любого выпуклого многогранника справедливо соотношение: |
|||
| Принцип Кавальери: | Если два тела могут быть расположены так, что любая плоскость, параллельная какой-нибудь данной плоскости и пересекающая оба тела, даёт в сечении с ними равновеликие фигуры, то объёмы таких тел равны. | |||
| Определение. Призма – многогранник, составленный из двух равных многоугольников A 1 A 2 …A n и B 1 B 2 …B n , расположенных в параллельных плоскостях, и n параллелограммов. | |
| Два равных многоугольника, лежащие в параллельных плоскостях, называются основаниями призмы (A 1 A 2 …A n и B 1 B 2 …B n). |
|
| Остальные грани призмы, являющиеся параллелограммами, называются её боковыми гранями (A n A 1 B 1 B n) |
|
| Рёбра, не лежащие в основании призмы, называются боковыми рёбрами (A 1 B 1 ; A 2 B 2 … A n B n) |
|
| Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы (h). |
|
| Диагональная плоскость – плоскость, проходящая через диагональ основания и боковое ребро призмы. | |
| Диагональное сечение – фигура, полученная при пересечении диагональной плоскости с поверхностью призмы. | |
| Перпендикулярное сечение – сечение призмы плоскостью, перпендикулярной её боковым рёбрам. | |
| В призму можно вписать сферу тогда и только тогда, если в перпендикулярное сечение призмы можно вписать окружность, диаметр которой равен высоте призмы. | |
| Если боковые рёбра призмы перпендикулярны к основаниям, то есть если основания служат нормальными сечениями боковой поверхности, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна её боковому ребру. Плоские углы основания являются плоскими углами двугранных углов между боковыми гранями. | |
| Прямая призма называется правильной, если её основания – правильные многоугольники. У такой призмы все боковые грани – равные многоугольники. В правильную призму можно вписать сферу тогда и только тогда, когда её высота равна диметру окружности, вписанной в основание. | |
| Площадь боковой поверхности призмы – это сумма площадей всех её боковых граней. | S бок =Р п */g/, где Р п – периметр перпендикулярного сечения, /g/ - длина бокового ребра |
| Площадь полной поверхности призмы – сумма площадей всех её граней | S полн =S бок +2S осн |
| Объём призмы. Объёмом геометрического тела называется величина части пространства, занимаемого этим телом. Доп. справка: в геометрии принято: · За единицу объёма принимают объём куба с ребром единичной длины. · Равные тела имеют равные объёмы · Объём объединения нескольких неперекрывающихся (т.е. не имеющих общих внутренних точек) тел равен сумме их объёмов · Если одно тело содержит другое, то объём первого тела не меньше объёма второго | |
| Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы. | S бок =P осн *h |
| Частным случаем призмы является параллелепипед – призма, основанием которой служат параллелограммы. | |
| Основные свойства параллелепипеда: | 1. Противоположные грани параллелепипеда попарно равны и параллельны. 2. Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам. 3. сумма квадратов всех диагоналей параллелепипеда равна сумме квадратов всех его рёбер. 4. квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений. |
| Если все грани параллелепипеда являются прямоугольниками, то параллелепипед называется прямоугольным. В нём все диагонали равны между собой. Если боковые рёбра параллелепипеда перпендикулярны основанию, то параллелепипед является прямым. Куб также является частным случаем призмы. Куб есть прямоугольный параллелепипед с равными рёбрами. | |
| Объём параллелепипеда | |
| Объём прямоугольного параллелепипеда | |
| Объём куба | |
| Диагональ прямоугольного параллелепипеда | d 2 =a 2 +b 2 +c 2 , где d – диагональ, a,b,c – рёбра |
Пирамида.
Слово «пирамида» в геометрию ввели греки, которые, как полагают, заимствовали его
у египтян, создавших самые знаменитые
пирамиды в мире. Другая теория выводит
этот термин из греческого слова «пирос»
(рожь) – считают, что греки выпекали хлебцы,
имевшие форму пирамиды.
| Определение. Пирамида – это многогранник, одна из граней которого – произвольный n – угольник A 1 A 2 …A n , а остальные грани – треугольники с общей вершиной. | |
| Этот n – угольник A 1 A 2 …A n называется основанием пирамиды. |
|
| Остальные (треугольные) грани называются боковыми гранями (A 2 PA 3 , …, A n PA 1) |
|
| Общая вершина всех боковых граней называется вершиной пирамиды (P). |
|
| Рёбра пирамиды, не принадлежащие основанию, называются её боковыми рёбрами (PA 1 , PA 2 , …, PA n) |
|
| Объединение боковых граней пирамиды называется её боковой поверхностью. |
|
| Перпендикуляр, проведённый из вершины пирамиды к плоскости основания, называется высотой пирамиды (РН). |
|
| Пирамида называется правильной, если её основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является её высотой. | |
| Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой этой пирамиды (РЕ). Все апофемы равны друг другу. |
|
| Если в основании пирамиды лежит n-угольник, то пирамида называется n-угольной. Треугольная пирамида называется тетраэдром. Тетраэдр называется правильным, если все его рёбра равны (т.о. все грани правильного тетраэдра – равные правильные треугольники). | |
| Некоторые свойства правильной пирамиды: · Все боковые рёбра равны между собой · Все боковые грани – равные равнобедренные треугольники · Все двугранные углы при основании равны · Все плоские углы при вершине равны · Все плоские при основании равны · Апофемы боковых граней одинаковы по длине · В любую правильную пирамиду можно вписать сферу |
|
| Площадью полной поверхности пирамиды называется сумма площадей всех её граней. | S полн =S бок +S осн |
| Площадь боковой поверхности пирамиды – сумма площадей её боковых граней. | |
| Площадь боковой грани | S бок.гр. =1/2*m*/g/, где m – апофема, /g/ - основание грани |
| Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. | S бок =1/2 * (P осн * m), где m – апофема, Р – периметр многоугольника основания. |
| Объём пирамиды. | V=(1/3)*S осн *h |
Усечённая пирамида.
| Определение. Усечённая пирамида – многогранник, гранями которого являются n-угольники A 1 A 2 …A n и B 1 B 2 …B n (нижнее и верхнее основания), расположенные в параллельных плоскостях, и n четырёхугольников A 1 A 2 B 2 B 1 , A 2 A 3 B 3 B 2 , …, A n A 1 B 1 B n . Усечённая пирамида является частным случаем пирамиды. | |
| Основания усечённой пирамиды – основание исходной пирамиды и многоугольник, полученный при пересечении её плоскостью (A 1 A 2 …A n и B 1 B 2 …B n). |
|
| Отрезки A 1 B 1 , A 2 B 2 , …, A n B n называются боковыми рёбрами усечённой пирамиды. |
|
| Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется высотой усечённой пирамиды (СН). |
|
| Боковые грани усечённой пирамиды – трапеции. |
|
| Усечённую пирамиду с основаниями A 1 A 2 …A n и B 1 B 2 …B n обозначают так: A 1 A 2 …A n B 1 B 2 …B n . |
|
| Усечённая пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания правильной усечённой пирамиды – правильные многоугольники, а боковые грани – равнобедренные трапеции. | |
| Высоты этих трапеций называются апофемами (КК 1) |
|
| Свойства усечённой пирамиды: | 1. Боковые рёбра и высота пирамиды разделятся секущей плоскостью на пропорциональные отрезки 2. В сечении получится многоугольник, подобный многоугольнику, ежащеему в основании 3. Площади сечения и основания будут относится между собой, как квадраты их расстояний от вершины пирамиды |
| Теорема. Если две пирамиды с равными высотами пересечь плоскостями, параллельными основаниям, на одинаковом расстоянии от вершины, то площади сечений будут пропорциональны площади оснований. |
|
| Площадь поверхности усечённой пирамиды | S=(1/2)*m*(P+P 1), где m – апофема |
| Теорема. Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему. | S бок =1/2*(Р в +Р н)* m, где m – апофема, Р в, Р н – периметр верхнего и нижнего оснований |
| Объём усечённой пирамиды: | V=(1/3)*h*(S 1 +√S 1 S 2 +S 2), где S 1 , S 2 – площади оснований. |
| Площадь боковой грани | S бок.гр. =1/2*m*(g+g 1), где m – апофема, g, g 1 – основания боковой грани |
Тетраэдр.
| Определение. Тетраэдр – поверхность, составленная из четырёх треугольников. Любая грань может быть принята за основание пирамиды. Тетраэдр является частным случаем пирамиды. | |
| Тетраэдр состоящий из треугольников ABC, DAB, DBC, DCA обозначается так: DABC |
|
| Треугольники, из которых состоит тетраэдр, называются гранями. |
|
| Стороны треугольников, из которых состоит тетраэдр, называются рёбрами. |
|
| Вершины треугольников, из которых состоит тетраэдр, называются вершинами тетраэдра. |
|
| Два ребра тетраэдра, не имеющие общих вершин, называются противоположными. |
|
| Иногда выделяют одну грань тетраэдра и называют её основанием, а три другие – боковыми гранями. |
|
| Медианы тетраэдра – отрезки, соединяющие его вершины с центроидами противоположных граней. | |
| Тетраэдр, все грани которого равны, называется равногранным. | |
| Свойства равногранного тетраэдра: | описанный параллелепипед равногранного тетраэдра – прямоугольный развёртка тетраэдра, полученная при разрезании его по трём сходящимся в одной вершине рёбрам, - треугольник у него имеются три оси симметрии все трёхгранные углы равны все медианы (тетраэдра) равны все высоты (тетраэдра) равны центры вписанной и описанной сфер и центроид совпадают радиусы описанных окружностей граней равны периметры граней равны площади граней равны |
| Тетраэдр, в вершине которого сходятся три взаимно перпендикулярных ребра, называется прямоугольным | Для него выполняется своего рода «теорема Пифагора»: S 2 =S 2 1 +S 2 2 +S 2 3 |
| Тетраэдр, составленный из четырёх равносторонних треугольников, называется правильным. | |
| Объём правильного тетраэдра. | V=(a 3 *√2)/12 |
| Радиус описанной сферы в правильном тетраэдре | |
| Высота правильного тетраэдра | |
| Площадь поверхности правильного тетраэдра | |
| Радиус вписанной окружности правильного тетраэдра |
Список используемой литературы
Стереометрия 10, А. Калинин, Д. Терешин, М.,1996 Геометрия 10 – 11, Л. Атанасян, М., 1994 Школьная шпаргалка, О. Бекетова, С. – Петербург, 1995 Математика в кармане, В. Герцев, М., 1996
с.1.31.38Прямой параллелепипедfigure.1.3 с.1.41.410Пирамидаfigure.1.4
с.2.72.737Прямой параллелепипедfigure.2.7 с.2.82.837Наклонный параллелепипедfigure.2.8
Министерство образования и науки Российской Федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ТАМБОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ Г.Р. ДЕРЖАВИНА»
Кафедра математического анализа
Пример курсовой
Дёмина Станислава Александровича
Научный руководитель
Зав. кафедрой зав.каф., д.ф.м.н.
Тамбов 2015
1.1.4 Пирамида . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.1.5 Усеченная Пирамида . . . . . . . . . . . . . . . . . . . . . 11
1.2 Свойства граней и диагоналей параллелепипеда . . . . . . . . . 12
1.2.1 Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1.2.2 Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
1.3 Свойства параллельных сечений в пирамиде . . . . . . . . . . . 16
1.3.1 Теоремы . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.3.2 Следствие . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
1.3.3 Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
1.3.4 Следствие . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
1.4 Боковая поверхность призмы и пирамиды . . . . . . . . . . . . . 21
1.4.1 Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
1.4.2 Следствие . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
1.4.3 Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
1.4.4 Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
2 ОБЪЕМ ПРИЗМЫ И ПИРАМИДЫ |
2.0.5 Основные допущения в объемах. . . . . . . . . . . . . . . 25
2.0.6 Единица объёма. . . . . . . . . . . . . . . . . . . . . . . . 26
2.1 Объем параллелепипеда. . . . . . . . . . . . . . . . . . . . . . . . 26
2.1.1 Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
2.1.2 Следствие. . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2.1.3 Лемма . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
2.1.4 Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
МНОГОГРАННИКИ
1.1 ПАРАЛЛЕЛЕПИПЕД И ПИРАМИДА
1.1.1 Многогранник
Многогранником называется тело, ограниченное плоскими многоугольниками. Общие стороны смежных многоугольников называются ребрами многогранника. Многоугольники, которые ограничивают многогранник, называются его гранями. Грани многогранника, сходящиеся в одной точке, образуют многогранный угол; вершины таких многогранных углов называются вершинами многогранника. Прямые, соединяющие две какие-нибудь вершины, не лежащие на одной грани, называются диагоналями многогранника. Мы будем рассматривать только выпуклые многогранники, т. е. такие, которые расположены по одну сторону от плоскости каждой из его граней. Наименьшее число граней в многограннике - четыре; такой многогранник получается от пересечения трехгранного угла какой-нибудь плоскостью.
1.1.2 Призма
Призмой называется многогранник, у которого две грани - равные многоугольники с соответственно параллельными сторонами, а все остальные грани - параллелограммы. Чтобы показать возможность существования такого многогранника, возьмем (рис. 1.1) какой-нибудь многоугольник ABCDE и через его вершины проведем ряд параллельных прямых, не лежащих в его плоскости. Взяв затем на одной из этих прямых произвольную точку A1 , проведем через нее плоскость, параллельную плоскости ABCDE через каждые две соседние параллельные прямые также проведем плоскости. Пересечение всех этих плоскостей определит многогранник ABCDEA1 B1 C1 D1 E1 , удовлетворяющий определению призмы. Действительно, параллельные плоскости ABCDE и A1 B1 C1 D1 пересекаются боковыми плоскостями по параллельным прямым; поэтому фигуры AA1 E1 E, EE1 D1 D и т.д. параллелограммы. С другой стороны, у многоугольников ABCDE и A1 B1 C1 D1 равны соответ-
ственно стороны (как противоположные стороны параллелограммов) и углы (как углы с параллельными и одинаково направленными сторонами); следовательно, эти многоугольники равны. Многоугольники ABCDE и A1 B1 C1 D1 , лежащие в параллельных плоскостях, называются основаниями призмы, перпендикуляр OO1 , опущенный из какой-нибудь точки одного основания на плоскость другого, называется высотой призмы. Параллелограммы AA1 B1 B и т. д. называются боковыми гранями призмы, а их стороны AA1 ; BB1 и т. д., соединяющие соответственные вершины оснований, боковыми ребрами. У призмы все боковые ребра равны как отрезки параллельных прямых, заключенные между параллельными плоскостями. Отрезок прямой, соединяющий какие-нибудь две вершины, не прилежащие к одной грани, называется диагональю призмы. Таков, например, отрезок AD1 (рис. 1.1). Плоскость, проведенная через какие-нибудь два боковых ребра, не прилежащих к одной боковой грани призмы (например, через ребра AA1 и CC1 рис. 1.1), называется диагональной плоскостью (на рисунке не показанной). Призма называется прямой или наклонной, смотря по тому, будут ли ее боковые ребра перпендикулярны или наклонны к основаниям. У прямой призмы боковые гранипрямоугольники. За высоту такой призмы можно принять боковое ребро. Прямая призма называется правильной, если ее основания - правильные многоугольники. У такой призмы все боковые грани - равные прямоугольники. Призмы бывают треугольные, четырехугольные и т.д., смотря по тому, что является основанием: треугольник, четырехугольники т. д.
set2D(3; 12; 2; 24); | ||||||||
p4 = tablePlot(6 22 );
p5 = tablePlot(2 4 );
;0 dash0 ); |
||||||||

dash0 ); | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
dash0 ); | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
dash0 ); | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
dash0 ); | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
; ;0 noAxes0 ); Рис. 1.1: Многоугольник 1.1.3 ПараллелепипедПараллелеп ипе дом называют призму, у которой основаниями служат параллелограммыназывают призму, у которой основаниями служат параллелограммы (рис. 1.2). Параллелепипеды, как и всякие призмы, могут быть прямые и наклонные. Прямой параллелепипед называется прямоугольным, если его основание прямоугольник (рис.1.3). Из этих определений следует: 1) у параллелепипеда все шесть граней параллелограммы;
2) у прямого параллелепипеда четыре боковые грани прямоугольники, а два основания параллелограммы; 3) у прямоугольного параллелепипеда все шесть граней прямоугольни- Три ребра прямоугольного параллелепипеда, сходящиеся к одной вершине, называются его измерениями: одно из них можно рассматривать как длину, другое как ширину, а третье как высоту. Прямоугольный параллелепипед, имеющий равные измерения, называет- ся кубом. У куба все грани – квадраты.
showPlots(;0 noAxes0 ); Рис. 1.2: Наклонный параллелепипед
Ход урока
Рефлективный анализ урока геометрии в 9 классе По теме «Параллелепипед. Призма. Пирамида.» Данный урок я провела в 9 классе. В классе присутствовало 13 учеников, из них 1 мальчик имеет оценку «отлично», 8 учеников – оценку «хорошо», 4 ученика – оценку «удовлетворительно». Класс со средними знаниями, но ученики в этом классе в основном являются практиками, им легче выполнить работу письменно, очень тяжело дается объяснение своих действий. Данный урок построен на изучении нового материала и первичном его закреплении и, поэтому я не ставила своей задачей суммативное оценивание учеников, а применила формативное оценивание. Основной целью данного урока, наравне с тем, чтобы сформировать у учащихся общее представление о многогранниках и его элементах, стала цель внедрение новой программы в практику, для того чтобы все ученики стали более активно работать на уроке, учиться вступать в диалог, добывать самостоятельно новые знания, самостоятельно стали оценивать не только себя, но и работу одноклассников. Для того, чтобы активизировать учащихся и подвести их к изучению нового материала, я провела актуализацию знаний, предложила ученикам в устной работе, ответить на «тонкие» и «толстые» вопросы. Я объяснила ребятам, какие вопросы называются «тонкими», а какие «толстыми», а затем ученики не только отвечали на мои вопросы, но и задавали свои, а так же оспаривали ответы одноклассников. На этом этапе урока применила прием критического мышления .
На каждом моем уроке ученик сидел на определенном месте и на всем протяжении урока они практически видели только меня. Анализируя данную ситуацию, меня очень заинтересовал метод групповой работы, так как на сегодняшний день существует достаточно доказательств, которые указывают на то, что диалог в классе занимает центральное место на уроке. Диалог может способствовать интеллектуальному развитию учеников и их результативности в обучении. Выготский утверждает и я с этим согласна, что развитие становится более эффективным в период, когда ученики работают в «зоне ближайшего развития» (ЗБР). ЗБР определяет навыки и способности, которые развивает ученик. На данном уроке я решила применить модули: критическое мышление, новые подходы в преподавании и обучении (диалогическое обучение), оценивание для обучения, применение ИКТ. Так как работа в группах подразумевает общение, то на всех этапах уроках наблюдалось диалоговое обучение . Но не все ребята выходили на открытый диалог, они смущались, закрывались, соглашались со всем, о чем говорили сильные ученицы на уроке, т.е. больше использовался кумулятивный тип беседы. Но меня удивило то, что некоторые учащиеся боялись высказаться, скорее всего к этой форме работы они не привыкли. Сначала каждая группа вела исследовательскую работу, используя интернет (ИКТ), для добывания информации по новой теме и прибегая к беседе, сходились на общем мнении и создавали постер.
При завершении практической и творческой работы, группа в течении трех минут показывала, защищала и делала анализ своего постера. Я наблюдала то, что каждый ученик в группе старался выступить и показать то, что он тоже принимал участие в добывании информации. Особенно меня удивило отношение всей группы к каждому участнику, сопереживание за выступление каждого. То есть я наблюдала тесное сотрудничество внутри каждой группы. Чего раньше не наблюдала.
Оценивал работу каждой группы независимый оценщик – Гончаренко Егор, выбранный, в начале урока путем нечаянной нехватки карточки. К своей работе он отнесся с большой ответственностью, хотя по натуре он ученик, который очень тяжело вникает в процесс обучения, но отвлекается по любому поводу. При оглашении баллов, он очень тщательно аргументировал уровень каждой работы, ни на шаг не отходя от критерий, разработанных ранее, и поэтому с его оцениванием согласились все дети. Я увидела этого ребенка с другой стороны – не вялым и ничего не успевающим, а ответственным и справедливым. Я думаю, после моих одобрений в его адрес, он в таком же темпе продолжит работу на всех уроках.
Так же учащихся заинтересовал приём «перепутанной логические цепи», где они находили соответствие между чертежами многоугольников и описанием их элементов. Эту работу я предложила выполнить сначала индивидуально, затем в парах, а потом в группе. И заметила, что эту работу более активно они выполняли в группах. Для себя сделала вывод: пополнять свою методическую копилку различными приёмами именно по работе в группах. Завершила урок рефлексией. Дети письменно отвечали на вопросы: «Как я сегодня работал?» и «Что нового я сегодня узнал?»
Теперь о недостатках: Не уложились по времени, возможно, повлияло то, что дети ещё не привыкли к подобному виду работы. На закрепление мало осталось времени. И одно задание из закрепления с последующей взаимопроверкой не было проведено. Вывод: В целом я достигла цели урока, хотя конечно не всё успела, что запланировала, надо точнее просчитывать время каждого этапа урока и ускорить темп работы. Поэтому, основной задачей я ставлю научить работать в группах и парах, а это требует определённого времени. В будущем планирую делать упор именно на диалогическое обучение, и стратегию критического мышления Приложение 1 Приложение 2 Задание Что такое параллелепипед? Как правильно начертить параллелепипед? Что является боковой поверхностью и полной поверхностью параллелепипеда? Как найти боковую поверхность и полную поверхность параллелепипеда? Задание Что такое призма? Как правильно начертить призму? Основные понятия: вершины, ребра, грани, основания. Что является боковой поверхностью и полной поверхностью призмы? Как найти боковую поверхность и полную поверхность призмы? Задание Что такое пирамида? Как правильно начертить пирамиду? Основные понятия: вершины, ребра, грани, основания. Что является боковой поверхностью и полной поверхностью пирамиды? Как найти боковую поверхность и полную поверхность пирамиды? Приложение 3 Около изображенных многогранников поставить числа, соответствующих высказываний. 1.Тетраэдр 2.Параллелепипед 3.Треугольная призма
5. Восемь вершин 6.Боковые грани – параллелограммы 7.Боковые грани – треугольники 8.Шесть граней
10.Боковые ребра параллельные 11.Можно провести диагональ боковой грани | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||














 9. Двенадцать ребер
9. Двенадцать ребер