Системою матеріальних точок називається така їх сукупність, у якій становище та рух кожної точки залежить від становища та руху всіх точок даної системи. Часто систему матеріальних точок називають механічною системою.
Центр мас системи матеріальних точок. Визначення радіусу-вектора центру мас. Властивості центру мас. Швидкість центру мас. Висновок рівняння руху центру мас. Закон збереження координати центру мас системи матеріальних точок.
тром мас (або центром інерції)
системи матеріальних точок називає-
ся уявна точка С, положення
якої характеризує розподіл
маси цієї системи Її радіус-вектор

Центр мас замкнутої системи або рухається прямолінійно і поступово, або залишається нерухомим.
Швидкість центру мас
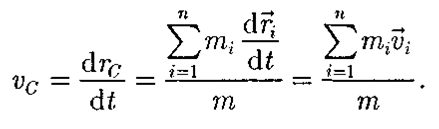
Для безперервного розподілу маси із щільністю r  . Якщо сили тяжіння, прикладені до кожної частки системи, спрямовані в одну сторону, Центр мас збігається з центром тяжіння. Але якщо не паралельні, Центр мас і центр тяжкості не збігаються.
. Якщо сили тяжіння, прикладені до кожної частки системи, спрямовані в одну сторону, Центр мас збігається з центром тяжіння. Але якщо не паралельні, Центр мас і центр тяжкості не збігаються.
Взявши похідну за часом від , отримаємо: 
тобто. повний імпульссистеми дорівнює творуїї маси на швидкість центру мас.
Підставляючи цей вислів до закону зміни повного імпульсу, знаходимо: 
Центр мас системи рухається як частка, в якій зосереджена вся маса системи і до якої прикладена результуюча зовнішніхсил.
При поступальномуруху всі крапки твердого тіларухаються так само, як і центр мас (за такими ж траєкторіями), тому для опису поступального рухудостатньо записати та вирішити рівняння руху центру мас.
Так як  , то центр мас замкнутої системиповинен зберігати стан спокою або рівномірного прямолінійного руху, тобто. = Const. Але при цьому вся система може обертатися, розлітатися, вибухати тощо. внаслідок дії внутрішніх сил
.
, то центр мас замкнутої системиповинен зберігати стан спокою або рівномірного прямолінійного руху, тобто. = Const. Але при цьому вся система може обертатися, розлітатися, вибухати тощо. внаслідок дії внутрішніх сил
.
Rс(t1) = Rc(t2) закон збереження координати центру мас
Робота потенційних (консервативних) сил на прикладі сили тяжіння. Визначення потенційних (консервативних) силових полів. Введення поняття потенційної енергіїчерез роботу сили. Зв'язок сили та потенційної енергії
Потенційна сила - сила, робота якої залежить тільки від початкового і кінцевого положення точки її застосування і не залежить ні від виду траєкторії, ні від закону руху цієї точки. Консервативні сили - такі сили, робота яких з будь-якої замкнутої траєкторії дорівнює 0.
Потенційне (консервативне) силове поле: Потенційним називається поле, робота якого при переході з однієї точки поля в іншу не залежить від форми траєкторії. Потенційними є поле сили тяжіння та електростатичне поле.
Введення поняття потенц. Енергії через роботу сил - Потенційна енергія - скалярна фізична величина, характеризує запас енергії якогось тіла (чи матеріальної точки), що у потенційному силовому полі, що йде придбання (зміна) кінетичної енергії тіла з допомогою роботи сил поля.
Зв'язок сили та потенційної енергії - Кожній точці потенційного полявідповідає деяке значення сили, що діє на тіло, і деяке значення потенційної енергії U. Отже, між силою та U має бути зв'язок, з іншого боку, dA = –dU,
Сукупність математичних точок, переміщення та становище яких заздалегідь обумовлено. (Напр. велосипед, Сонячна система).
Маса системи визначається як арифметична сумамас точок, що входять до системи.
ЦМС - точка, становище якої у просторі визначається з допомогою радіус – вектора.
2. Зовнішні та внутрішні сили системи матеріальної точки. Властивості внутрішніх сил.
Сили реакції зв'язку ділять на сили і реакції, що задаються.
Зовнішні сили (F e) – сили, що діють на тіла системи, що розглядається, з боку тіл, що не увійшли в розглянуту систему.
Внутрішні сили (F i) - сили, що взаємодіють між тілами в системі, що розглядається.
3. Робота внутрішніх сил матеріальної системи.
Сума робіт внутрішніх сил незмінної системи при кожному її переміщенні дорівнює нулю.
Нехай А та В – дві точки системи.
Р А і Р В – рівні за модулем і протилежні
напряму сили взаємодії між цими точками.
При русі точки А та В отримають елементарні переміщення ds A та ds B .
На переміщеннях ds A II і ds II, перпендикулярних до ліній дії сил, сили роботи не виробляють. Так як відстань між точками А і В незмінної системи при її русі змінюватися не може, то переміщення ds A I і ds I повинні бути рівні і спрямовані в одну сторону. Звідси слідує що.
4. Теорема про рух центру мас системи. Закон збереження руху центру мас.
Де c – точка центру мас
A c – прискорення центру мас
M – маса всієї системи
Закон збереження руху центру мас: Якщо сума, то має місце закон збереження руху центру мас.
=>
5. Диференціальне рівняння поступального руху твердого тіла.
Поступальне m*a c =∑F e i
a i =m i *V i у рух хутра системи
m i – маса i-ої точки
F e i - рівнодіюча всіх зовнішніх сил
Q i =m i *V i у руху i-ої точки
Складемо всі рівняння (1) для системи
…………
________
∑Q i =∑ (m i *V i)
Q=M*V c (3) у руху всієї системи
M*r c = ∑(m i * r i) (2)
Продиференціюємо рівняння (2) за часом:
M * v c = ∑ (m i * r i)
6. Теорема про зміну кількості руху матеріальної системи.
Диференційна форма
Інтегральна форма
де - кількість руху механічної системиу кінцевому та початковому положенні
Сума імпульсів у кінцевому та початковому положенні
7. Момент кількості руху твердого тіла, що обертається довкола нерухомої осі.
Проекція моменту кількості руху твердого тіла щодо будь-якого центру на будь-яку вісь z, що проходить через цей центр, називається моментом l z кількості руху тіла щодо цієї осі:
8. Теорема про зміну моменту кількості руху матеріальної системи.
(1) Якщо сума (1) = 0, то L0 = const L0x = const.
Похідна за часом від моменту l z кількості руху точки щодо якоїсь нерухомої осі z дорівнює моменту сили F, що діє на точку, відносно тієї ж осі.
Наслідок з (1): якщо момент сили, що діє на точку, щодо якоїсь осі протягом деякого часу дорівнює нулю, то момент кількості руху цієї точки щодо цієї осі весь цей час залишається постійним.
9. Поняття момент інерції тіла. Радіус інерції.
Моментом інерції твердого тіла щодо будь-якої осі z (осьовим моментом інерції) називається скалярна величина, рівна сумі, Складеної з творів маси m k кожної точки тіла на квадрат її відстані r k до цієї осі.
Момент інерції нескінченно тонкого кільця ( матеріального кола) щодо його осі обертання дорівнює добутку його маси на квадрат радіусу:
Момент інерції тіла щодо осі подати у вигляді добутку маси тіла на квадрат довжини деякого відрізка, що називається радіусом інерції тіла щодо відповідної осі:
Під радіусом інерції тіла щодо якоїсь осі можна розуміти радіус такого нескінченно тонкого кільця, в якому потрібно зосередити всю масу М тіла, щоб отримати момент інерції кільця, рівний моментуінерції тіла щодо цієї осі.
10. Момент інерції щодо паралельних осей(Теорема Гюйгенса - Штейна).
Момент інерції тіла щодо якоїсь осі дорівнює моментуінерції цього тіла щодо центральної осі, паралельної даної осі, складеному з добутком маси тіла на квадрат відстані між цими осями.
Теорема Гюйгенса – Штейна.
11. Осьові моменти інерції однорідних тіл: стрижень, порожнистий і суцільний циліндри, куля.
Момент інерції тонкого прямого стрижня постійного перерізу
Момент інерції однорідного прямого тонкого стрижня щодо центральної осі симетрії дорівнює 1/12 добутку маси стрижня на квадрат його довжини.
Момент інерції суцільного
круглого циліндра.
Момент інерції однорідного суцільного круглого циліндра щодо осі його обертання дорівнює половинідобутку маси циліндра на квадрат його радіусу.
Момент інерції порожнистого круглого циліндра.
Момент інерції однорідного порожнистого круглого циліндра щодо осі обертання дорівнює половині добутку маси циліндра на суму квадратів його зовнішнього і внутрішнього радіусів.
12. Динамічне рівняння обертання твердого тіла довкола нерухомої осі.
Добуток моменту інерції тіла щодо його осі обертання на кутове прискорення тіла дорівнює головному моменту всіх прикладених до тіла зовнішніх сил щодо тієї ж осі.
Рівняння (1) називається динамічним рівнянням обертального рухутверде тіло.
13. Теорема про зміну кінетичної енергії матеріальної системи.
Зміна кінетичної енергії механічної системи на деякому переміщенні дорівнює сумі робіт зовнішніх і внутрішніх сил, які діють матеріальні точки системи у цьому переміщенні.
Де Т - кінетична енергія в кінцевий момент часу
Т 0 - кінетична енергія в початковий моментчасу
∑А i е +∑А i j – сума робіт зовнішніх та внутрішніх сил
Умова: необхідне початкове та кінцеве положення.
14. Кінетична енергія матеріальної системи. Теорема Кеніга.
Механічна система – сукупність тіл, пов'язаних між собою різними зв'язками.
Положення та рух кожного з тіл взаємно обумовлено. Кінетична енергія механічної системи визначається як арифметична сума кінетичних енергій i-го тіла, що входить до системи.
Теорема Кеніга:
Кінетична енергія механічної системи дорівнює сумі кінетичної енергії центру мас системи, маса якого дорівнює масі всієї системи, і кінетичної енергії цієї системи в її відносному русіщодо центру мас.
15. Кінетична енергія твердого тіла при різних видахйого рухи.
Кінетична енергія тіла визначається залежно від того – який рух відбувається.
1) поступальний рух
2) обертальний рух
3) плоскопаралельний рух
16. Динамічне плоскопаралельний рух твердого тіла.
17. Принцип Даламбер для матеріальної точки.
Геометрична сума всіх прикладених до точки сил і сили інерції цієї точки дорівнює нулю. , де
18. Принцип Даламбер для матеріальної системи.
(i=1,2,…,n), де -равнодействующая сил, що задаються, прикладених до точки; -Рівнодіюча реакцій зв'язків, прикладених до цієї точки; -Сила інерції матеріальної точки.
Рівняння показує, що в будь-який момент часу геометрична сума рівнодіючої сил, що діє, рівнодіючої реакції зв'язків і сили інерції для кожної матеріальної точки невільної механічної системи дорівнює нулю.
19. Головний вектор та головний момент сил інерції абсолютно твердого тіла.
Поступальний рух
Головний вектор - головний момент, де J z - момент інерції тіла щодо осі обертання, ε - алгебраїчна величина кутового прискорення тіла.
20. Механічні зв'язки, утримуючі та неутримуючі зв'язки, стаціонарні та нестаціонарні, головні та неголовні.
Зв'язки – тіла, які обмежують свободу переміщення іншого тіла.
OA=l – гнучка нитка - рівняння жорсткого зв'язку
Класифікація зв'язків:
1) головні – зв'язки, рівняння яких не містять
диференціали координат.
2) неголовні – зв'язки, рівняння яких містять
диференціали координат.
Стаціонарні (рівняння яких не містять
параметр t.)
Нестаціонарні (рівняння яких містять
параметр t.)
Утримуючі (рівняння визначається
рівністю).
Неутримуючі (рівняння визначається нерівністю).
21. Можливі переміщення.
Можливе переміщення – переміщення тіла, що допускається накладеними на систему зв'язками.
Можливе переміщення точки прийнято позначати символом, на відміну її дійсного елементарного переміщення.
22. Елементарна робота сили на можливому переміщенні. Ідеальні зв'язки.
Ідеальними зв'язками називаються зв'язки, сума елементарних робіт реакцій яких на будь-яких можливих переміщення точок системи дорівнює нулю. До ідеальних зв'язків відносяться всі стаціонарні геометричні зв'язкибез тертя.
Гладка поверхня (реакція спрямована нормалі до поверхні, переміщення такого зв'язку можливе лише у дотичній площині, т. е. завжди перпендикулярно до напрямку реакції зв'язку і робота =0)
Нерухомий шарнір (точка застосування цієї реакції
зв'язку залишається нерухомим за будь-якого переміщення системи
та робота реакції дорівнює нулю).
Рухомий шарнір, що з'єднує два тіла (реакція R 1 і R 2
цих тіл один на одного рівні за модулем і спрямовані по одній
прямий в протилежні сторони, при будь-якому елементарному
переміщення точки застосування реакцій зв'язку сума їх
елементарних робіт дорівнює 0).
23. Принцип можливих переміщень. Принцип Лагранжа.
Для рівноваги системи з ідеальними зв'язкаминеобхідно і достатньо, щоб дорівнювала нулю сума елементарних робіт усіх доданих до неї активних сил на будь-якому можливому переміщенні системи з рівноваги.
Основне припущення: всі переміщення нескінченно малі (S, δφ).
Переміщення точок приймаються прямолінійними.
24. Принцип Даламбер - Лагранжа ( загальне рівняннядинамічної системи).
Сума елементарних робіт усіх активних чи заданих сил та сума елементарних робіт усіх сил інерції дорівнює нулю.
Загальне рівняння динаміки.
25. Узагальнена координата, швидкість та прискорення.
Незалежні величини, завданням яких однозначно визначається становище всіх точок механічної системи, називається узагальненими координатами цієї системи. Для голономних систем число незалежних узагальнених координат механічної системи дорівнює числу ступенів волі цієї системи.
Похідні від узагальнених координат за часом називають узагальненими швидкостями.
Похідні від узагальнених швидкостей за часом називають узагальненими прискореннями.
26. Узагальнені сили та способи їх обчислення.
Узагальненою силою, що відповідає узагальненій координаті, називають скалярну величину, що визначається ставленням елементарної роботи діючих силна переміщення механічної системи, викликаному елементарним збільшенням координати до величини цього збільшення.
Узагальнені сили поділяються на узагальнені зовнішні та внутрішні сили.
27. Умова рівноваги механічної системи у узагальнених координатах.
Для будь-якої системи сил умови рівноваги мають вигляд
Умови рівноваги консервативної системи сил мають вигляд
28. Рівняння Лагранжа ІІ роду.
(j=1, 2, …, s)
Ці рівняння є диференційне рівняннядругого порядку щодо узагальнених координат системи q1, q2, …, qs.
29. Рівняння Лагранжа II роду, що рухається в потенційному силовому полі.
Якщо матеріальна системапереміщається в потенційному силовому полі під дією лише сил поля (всі зв'язки накладені на систему ідеальні), то узагальнені сили можна визначити за формулою
Q i = - дП/дq i
Введемо на розгляд функцію L=Т-П (кінет. потенц.)
Ця функція називається функцією Лагранжа. Тоді підставляючи її в рівняння Лагранжа ІІ-го роду:
Систему sдиф. рівнянь зв. рівняннями Лагранжа 2-го роду. Ці рівняння представ. собою диф. рівняння другого порядку віднос. узагальнених коорд. системи, …, Інтегруючи ці рівняння та визначаючи за початком. Умовам постійні інтегрування, отримуємо sурав. рухи хутро. системи в узагальнених координатах:
30. Вільні коливанняодномасової системи з одним ступенем свободи.
Диференційне рівняння вільних коливань.
Період вільних коливань
Рівняння руху вантажу
Частота вільних коливань
31. Вимушені коливання.
За одночасної дії відновлюючої та обурюючої сил матеріальна точка робить складне коливальний рух, що є результатом накладення вільних і вимушених коливаньточки.
Вимушені коливання не залежать від початкових умовруху точки.
Рівняння вимушених коливань малої частоти.
Амплітуда коливань малої частоти
Рівняння вимушених коливань великої частоти
Амплітуда коливань великої частоти
Відношення амплітуди вимушених коливань А В до величини А 0 називається коефіцієнтом динамічності.
32. Коливання систем із двома і більше ступенями свободи. Вільні та власні коливання.
Коливання, відповідні зміни лише з узагальнених координат зв. Власними. Вільні коливання є результатом складання власних. Системи з одним ступенем свободи мають лише одну частоту коливання. Тому для них для них вільні та власні коливання збігаються. Система з двома ступенями свободи має дві частоти власних коливань. Аналогічно можна показати що система має n-ступенів свободи матиме n-частот своїх коливань, тобто. чисоступеней свободи дорівнює числу частот.
33. Явище удару у точках. Ударна сила та ударний імпульс.
Ударом називається явище у якому результаті взаємодії тіл їх швидкість змінюється на кінцеву величину за дуже малий проміжок часу. Як правило, явище удару супроводжується пластичною деформацією контактованих тіл, в результаті яких механічна енергія перетворюється на теплову. Тому при вирішенні задач про удар тіл не можна використовувати теорему про зміну кінетичної енергії. У цих випадках застосовується теорема про зміну кількості руху та моменту кол-ва руху, записуючи в інтегральній формі.
Явище удару- явище, у якому за мізерно проміжок часу швидкості точок тіла змінюються на кінцеву величину(удар м'яча об стіну тощо.)
Кінцева зміна кол-ва руху тб. тіла за мізерно малий час удару відбувається тому, що модулі сил, які розвиваються при ударі дуже великі, внаслідок чого імпульси цих сил за час удару є кінцевими величинами. Такі сили називають. - Миттєвими чи ударними.
1) дією негайних сил за час удару можна знехтувати.
2) переміщ. матер. крапки за час удару можна не враховувати.
3) результат дії ударної сили на матер. точку виражається кінцевою зміною за час удару вектора швидкості, що визначається рівнянням – b
34. Теорема про зміну кількості руху матеріальної точки під час удару.
Зміна кількості руху механічної системи за час удару дорівнює геометричній сумівсіх зовнішніх ударних імпульсів, доданих до точок системи.
(1)
Рівняння висловлює теорему про зміну кол-ва рух хутро. системи при ударі:
Зміна кол-ва рух хутро. системи за час удару До= геометричній сумі всіх зовнішніх ударних імпульсів Sдоданих до системи.
Кількість рух. можна виразити через масу всієї системи mта швидкості центру мас системи та за формулами
Підставимо дані рівняння (1) і отримаємо це рівняння визначає зміну швидкості центру мас при ударі.
За відсутності зовнішніх ударних імпульсів маємо:
При дії на хутро. систему лише внутрішніх ударних імпульсів у рух системи не змінюється.
сторінка 1
Якби ми не віднімали, а складали рівняння (6.1), у нас вийшов би просто закон збереження імпульсу
Його можна переписати суто формально як закон сталості у часі
деякої швидкості Vc:
Перейдемо до системи відліку, що рухається зі швидкістю (6.4). Швидкості
частинок 1 і 2 при цьому перетворюються наступним чином:
тобто в новій системі відліку вони виражаються через швидкість відносного
руху. Зв'яжемо швидкість Vc з радіусом-вектором деякої точки rз:
Зазначимо, що визначення (6.6) збігається з відомим з шкільного курсу
фізики поняття центру тяжіння. Для доказу перенесемо початок
координат у точку rс. Тоді, абсолютно аналогічно (6.5), отримаємо
Таким чином,
(Центр тяжкості визначається рівністю творів маси на «плечо»). Але визначення (6.4) і (6.6) більш коректні та універсальніші, оскільки без будь-яких проблем узагальнюються на будь-яке число матеріальних точок, а отже, і на
макроскопічні тіла. Точку С у механіці – і взагалі у фізиці – прийнято називати
центром мас чи центром інерції системи матеріальних точок.
Нехай у деякій інерційної системикоординат положення взаємодіючих матеріальних точок з масами m 1 , m 2 ... m N задаються в кожний момент часу t за допомогою радіусів-векторів r 1 (t), r 2 (t), ... r N(t)
(Див. рис. 6.3 а). Тоді центром мас системи матеріальних точок, що розглядається, називається така точка, радіус-вектор якої R r 1 (t), r 2 (t), ... r N (t) матеріальних точок за
Підкреслимо, що в загальному випадкустановище центру мас не збігається з
положенням якоїсь із матеріальних точок системи (див. рис. 6.3 б),
хоча іноді таке може статися.

Мал. 6.3 центром мас системи матеріальних точок називається така точка, радіус-вектор якої R c(t) виражається через радіуси-вектори r 1 (t), r 2 (t), ... r N (t) матеріальних точок
Продиференціюємо за часом ліву та праву частини рівності (6.7).
Похідна радіуса-вектора є за визначенням швидкість, так
що в результаті ми отримуємо
де Vc - швидкість центру мас, v 1, v 2, ... v N - швидкості матеріальних точок. Величина m 1 v 1 (6.8) - імпульс першої матеріальної точки, m 2 V 2 - імпульс другої точки і
і т.д. Отже, у фігурних дужках висловлювання (6.8) стоїть сума імпульсів аналізованої системи матеріальних точок, т. е. імпульс Р всієї системи. Отже, рівність (6.8) можна переписати як
Р = (m 1 + m 2 + …. + m N) V c. (6.9)
У системі відліку, де центр мас спочиває,
Якщо нас не цікавить відносний рух матеріальних точок, а цікавить рух системи як цілого, то всю систему можна розглядати як одну матеріальну точку, що рухається зі швидкістю Vc і має імпульс Р. Згадаємо, що маса матеріальної точки є, за визначенням, коефіцієнт пропорційності між імпульсом та швидкістю. Тому коефіцієнт пропорційності, що стоїть у рівності (6.9), укладений у фігурні дужки, є маса М розглянутої системи:
М = m 1 + m 2 + …. + m N , (6.10)
т. е. маса системи матеріальних точок дорівнює сумі мас цих точок. Співвідношення (6.10), згідно з яким маса складного тіладорівнює сумі мас його частин, здається нам звичним та очевидним. Однак, як ми ще переконаємося, у релятивістській механіці (тобто у загальному випадку) ситуація буде зовсім іншою. У граничному випадку ньютонової механіки рівність (6.10) є окремий випадокпевного
фізичного закону- Закону збереження маси.
За відсутності зовнішніх сил, т. е. для замкнутої системи, сума імпульсів всіх тіл системи залежить від часу; тоді з (6.9) випливає важлива властивість руху центру мас замкнутої системи матеріальних точок:
тобто. центр мас замкнутої системи матеріальних точок нерухомий або
рухається рівномірно та прямолінійнохоча кожна з матеріальних точок може здійснювати складний рух. Наведене вище твердження називають іноді теоремою руху центру мас.
Ми зараз доведемо таку важливу властивість кінетичної енергії:
кінетична енергія Т системи матеріальних точок дорівнює сумі кінетичної енергії всієї маси системи, подумки зосередженої в її центрі мас і що рухається разом з ним, і кінетичної енергії Т" тієї ж системи в її відносному русі по відношенню до системи відліку, що рухається разом із центром мас:
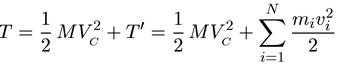
де М = m 1 + m 2 + ... + m N. Vc - швидкість центру мас у вихідній системі відліку, v i - швидкість i-ої матеріальної точки щодо системи відліку, що рухається разом з точкою С. Таку систему зазвичай називають "системою центру мас", "системою центру інерції" або просто "ц-системою" . (Систему відліку, в якій поставлено завдання, якщо ця система не збігається з ц-системою, називається лабораторною системою відліку або л-системою).
Для доказу отримаємо спочатку більш загальне співвідношення, що пов'язує кінетичну енергію у двох системах відліку (див. рис. 6.4). Для координат і швидкостей точок у старій системі Ri, Vi і в новій системі ri, vi запишемо перетворення Галілея:
де R - радіус-вектор переходу зі старої системи до нової, а V -відповідно, швидкість руху нової системи щодо старої.
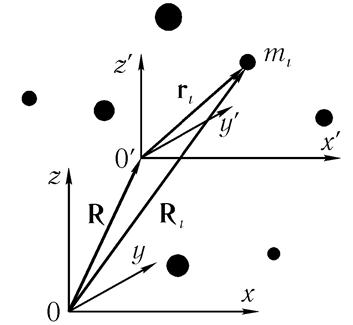
Мал. 6.4 зв'язок координат у двох системах відліку
Тоді кінетичну енергію в старій системі відліку можна уявити у вигляді
 (6.12)
(6.12)
Праву частину (6.12) можна подати у вигляді трьох сум:
де Р – повний імпульс системи матеріальних точок у новій системі відліку. Співвідношення (6.13) прийнято називати теоремою Кеніга. Якщо ж нова системазбігається з ц-системою, то сумарний імпульс у ній дорівнює нулю, V = Vc, отже, має місце співвідношення (6.11).
На закінчення цього параграфа відзначимо два важливі властивості, які з визначення центру мас. По-перше, частинки в (6.7) можна об'єднувати в будь-які групи, наприклад:
Звідси, як легко зрозуміти, слід, що центр мас будь-якої системи макроскопічних тіл може бути знайдений як центр мас системи матеріальних точок, припущення, що маса кожного тіла зосереджена у його власному центрі мас.
І по-друге, від підсумовування (6.7) неважко перейти до інтегрування,
якщо ми обчислюємо положення центру мас тіла з безперервним розподілом густини речовини ρ(т):

