Å finne koordinatene til en vektor er en ganske vanlig betingelse for mange problemer i matematikk. Evnen til å finne vektorkoordinater vil hjelpe deg i andre, mer komplekse oppgaver med lignende emner. I denne artikkelen skal vi se på formelen for å finne vektorkoordinater og flere problemer.
Finne koordinatene til en vektor i et plan
Hva er et fly? Et plan anses å være et todimensjonalt rom, et rom med to dimensjoner (x-dimensjonen og y-dimensjonen). For eksempel er papir flatt. Overflaten på bordet er flat. Enhver ikke-volumetrisk figur (kvadrat, trekant, trapes) er også et plan. Derfor, hvis du i problemformuleringen trenger å finne koordinatene til en vektor som ligger på et plan, husker vi umiddelbart om x og y. Du kan finne koordinatene til en slik vektor på følgende måte: AB vektorkoordinater = (xB - xA; yB - xA). Fra formelen er det klart at fra koordinatene sluttpunkt du må trekke fra koordinatene til utgangspunktet.
Eksempel:
- Vektor-CD har innledende (5; 6) og siste (7; 8) koordinater.
- Finn koordinatene til selve vektoren.
- Ved å bruke formelen ovenfor får vi følgende uttrykk: CD = (7-5; 8-6) = (2; 2).
- Dermed er koordinatene til CD-vektoren = (2; 2).
- Følgelig er x-koordinaten lik to, y-koordinaten er også to.
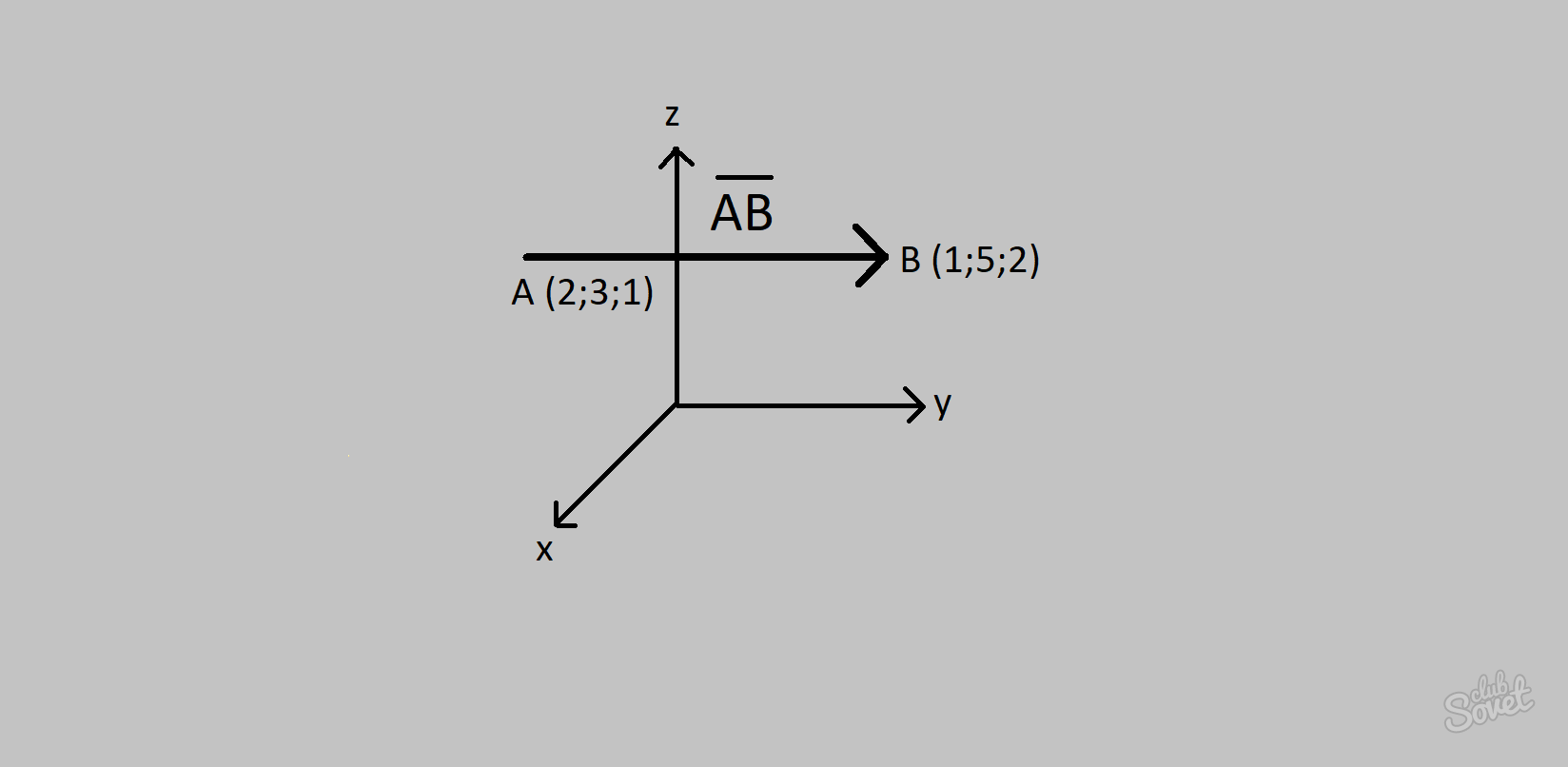
Finne koordinatene til en vektor i rommet
Hva er plass? Rommet er allerede en tredimensjonal dimensjon, hvor 3 koordinater er gitt: x, y, z. Hvis du trenger å finne en vektor som ligger i rommet, endres formelen praktisk talt ikke. Bare én koordinat legges til. For å finne en vektor må du trekke startkoordinatene fra sluttkoordinatene. AB = (xB - xA; yB - yA; zB - zA)
Eksempel:
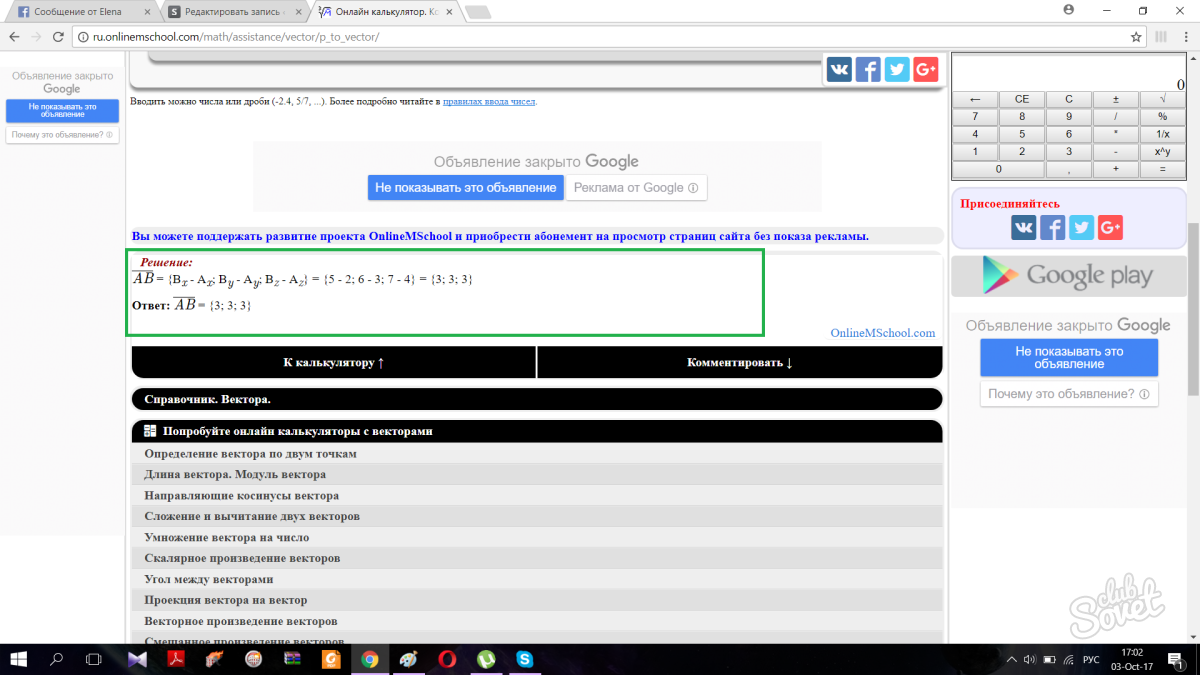
- Vektor DF har initial (2; 3; 1) og siste (1; 5; 2).
- Ved å bruke formelen ovenfor får vi: Vektorkoordinater DF = (1-2; 5-3; 2-1) = (-1; 2; 1).
- Husk at koordinatverdien kan være negativ, det er ikke noe problem.
Hvordan finne vektorkoordinater på nettet?
Hvis du av en eller annen grunn ikke vil finne koordinatene selv, kan du bruke en online kalkulator. For å begynne, velg vektordimensjonen. Dimensjonen til en vektor er ansvarlig for dens dimensjoner. Dimensjon 3 betyr at vektoren er i rommet, dimensjon 2 betyr at den er på planet. Deretter setter du inn koordinatene til punktene i de aktuelle feltene, og programmet vil bestemme koordinatene til selve vektoren for deg. Alt er veldig enkelt.
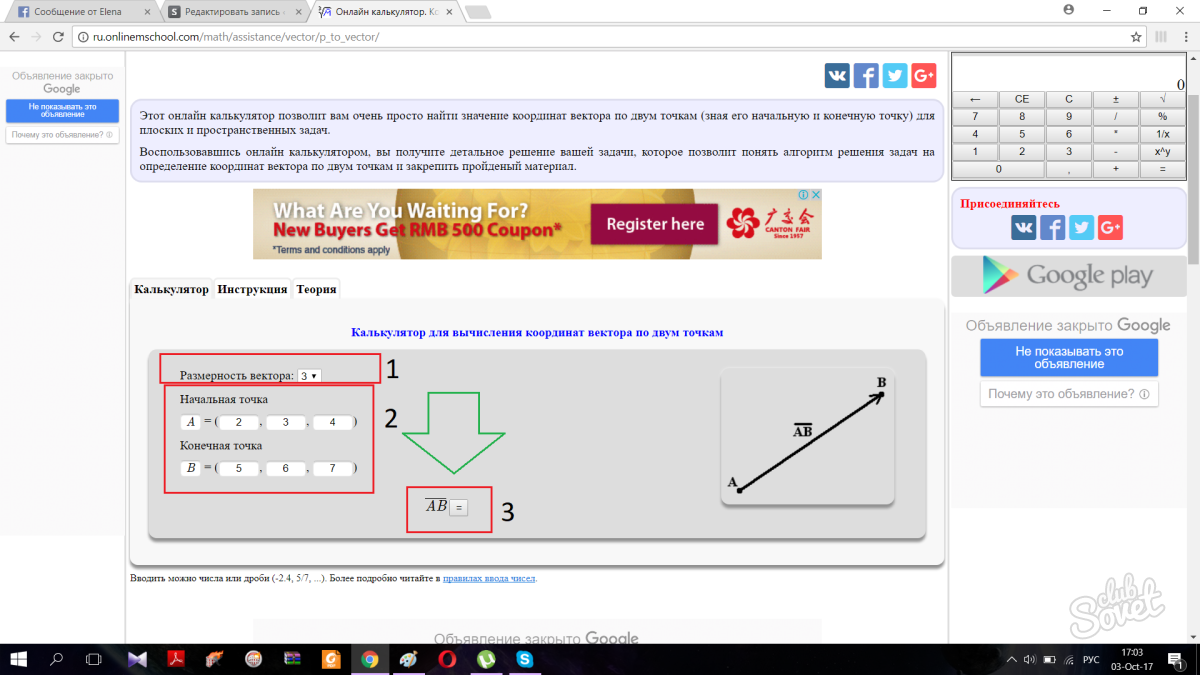
Ved å klikke på knappen vil siden automatisk rulle ned og gi deg riktig svar sammen med løsningstrinnene.
Det anbefales å studere godt dette emnet, fordi konseptet med en vektor finnes ikke bare i matematikk, men også i fysikk. Fakultetsstudenter Informasjonsteknologier De studerer også temaet vektorer, men på et mer komplekst nivå.
Hvis to punkter på planet og er gitt, har vektoren følgende koordinater:
Hvis to punkter i rommet og er gitt, har vektoren følgende koordinater:
Det er, fra koordinatene til enden av vektoren du må trekke fra de tilsvarende koordinatene begynnelsen av vektoren.
Trening: For de samme punktene, skriv ned formlene for å finne koordinatene til vektoren. Formler på slutten av leksjonen.
Eksempel 1
Gitt to punkter av flyet og . Finn vektorkoordinater
Løsning: i henhold til den tilsvarende formelen:
Alternativt kan følgende oppføring brukes:
Esteter avgjør dette:
Personlig er jeg vant til den første versjonen av innspillingen.
Svar:
I henhold til betingelsen var det ikke nødvendig å bygge en tegning (som er typisk for oppgaver analytisk geometri), men for å avklare noen punkter for dummies, vil jeg ikke være for lat:
Du må definitivt forstå forskjellen mellom punktkoordinater og vektorkoordinater:
Punktkoordinater– dette er vanlige koordinater i et rektangulært koordinatsystem. Sett poeng på koordinatplan Jeg tror alle kan gjøre det fra 5.-6. klasse. Hvert punkt har en streng plass på flyet, og de kan ikke flyttes hvor som helst.
Koordinatene til vektoren er dens utvidelse når det gjelder grunnlaget, i i dette tilfellet. Enhver vektor er gratis, så om nødvendig kan vi enkelt flytte den bort fra et annet punkt i planet. Det er interessant at for vektorer trenger du ikke å bygge akser i det hele tatt, rektangulært system koordinater, trenger du bare en basis, i dette tilfellet en ortonormal basis av planet.
Registreringene av koordinater til punkter og koordinater til vektorer ser ut til å være like: , og betydningen av koordinater absolutt annerledes, og du bør være godt klar over denne forskjellen. Denne forskjellen gjelder selvfølgelig også plass.
Mine damer og herrer, la oss fylle hendene våre:
Eksempel 2
a) Poeng og gis. Finn vektorer og .
b) Poeng og gis. Finn vektorer og .
c) Poeng og gis. Finn vektorer og .
d) Poeng gis. Finn vektorer.
Kanskje det er nok. Dette er eksempler på uavhengig avgjørelse, prøv å ikke forsømme dem, det vil lønne seg ;-). Det er ikke nødvendig å lage tegninger. Løsninger og svar på slutten av leksjonen.
Hva er viktig når man løser analytiske geometriproblemer? Det er viktig å være EKSTREMT FORSIKTIG for å unngå å gjøre den mesterlige feilen "to pluss to er lik null". Jeg beklager med en gang hvis jeg har gjort en feil et sted =)
Hvordan finne lengden på et segment?
Lengden, som allerede nevnt, er indikert med modultegnet.
Hvis to punkter på planet er gitt og , kan lengden på segmentet beregnes ved hjelp av formelen
Hvis to punkter i rommet og er gitt, kan lengden på segmentet beregnes ved hjelp av formelen
Merk: Formlene forblir korrekte hvis de tilsvarende koordinatene byttes: Og , men det første alternativet er mer standard
Eksempel 3
Løsning: i henhold til den tilsvarende formelen:
Svar:
For klarhetens skyld vil jeg lage en tegning 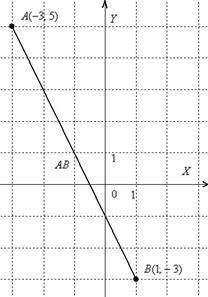
Linjestykke - dette er ikke en vektor, og du kan selvfølgelig ikke flytte den hvor som helst. I tillegg, hvis du tegner i målestokk: 1 enhet. = 1 cm (to notatbokceller), så kan det resulterende svaret kontrolleres med en vanlig linjal ved direkte å måle lengden på segmentet.
Ja, løsningen er kort, men det er et par flere i den viktige poeng som jeg ønsker å presisere:
For det første setter vi i svaret dimensjonen: "enheter". Tilstanden sier ikke HVA det er, millimeter, centimeter, meter eller kilometer. Derfor vil en matematisk korrekt løsning være den generelle formuleringen: "enheter" - forkortet som "enheter."
For det andre, la oss gjenta skolemateriell, som ikke bare er nyttig for problemet som vurderes:
Følg med på viktig teknisk teknikk – fjerne multiplikatoren fra under roten. Som et resultat av beregningene har vi et resultat og god matematisk stil innebærer å fjerne faktoren fra under roten (hvis mulig). Mer detaljert ser prosessen slik ut: . Å la svaret være slik det er, ville selvsagt ikke være en feil – men det ville absolutt være en mangel og et tungtveiende argument for å krangle fra lærerens side.
Her er andre vanlige tilfeller: 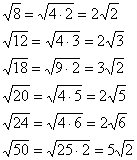
Ofte er det nok ved roten stort antall, For eksempel . Hva skal man gjøre i slike tilfeller? Ved hjelp av kalkulatoren sjekker vi om tallet er delelig med 4: . Ja, det var helt delt, slik: ![]() . Eller kanskje tallet kan deles på 4 igjen? . Dermed:
. Eller kanskje tallet kan deles på 4 igjen? . Dermed: ![]() . Det siste sifferet i tallet er oddetall, så å dele med 4 for tredje gang vil åpenbart ikke fungere. La oss prøve å dele på ni: . Som et resultat:
. Det siste sifferet i tallet er oddetall, så å dele med 4 for tredje gang vil åpenbart ikke fungere. La oss prøve å dele på ni: . Som et resultat:
Klar.
Konklusjon: hvis vi under roten får et tall som ikke kan trekkes ut som en helhet, så prøver vi å fjerne faktoren fra under roten - ved hjelp av en kalkulator sjekker vi om tallet er delelig med: 4, 9, 16, 25, 36, 49 osv.
Under avgjørelsen ulike oppgaver røtter er vanlige, prøv alltid å trekke ut faktorer fra under roten for å unngå lavere karakter og unødvendige problemer med å sluttføre løsningene dine basert på lærerens kommentarer.
La oss også gjenta kvadratrøtter og andre krefter:
Regler for handlinger med grader i generelt syn finnes i skole lærebok i algebra, men jeg tror fra eksemplene gitt, alt eller nesten alt er allerede klart.
Oppgave for uavhengig løsning med et segment i rommet:
Eksempel 4
Poeng og gis. Finn lengden på segmentet.
Løsningen og svaret er på slutten av leksjonen.
Hvordan finne lengden på en vektor?
Hvis en planvektor er gitt, beregnes lengden ved hjelp av formelen.
Hvis en romvektor er gitt, beregnes lengden ved hjelp av formelen ![]() .
.
Disse formlene (så vel som formlene for lengden på et segment) er lett utledet ved å bruke det velkjente Pythagoras teoremet.
Eksempel 5
Poeng og gis. Finn lengden på vektoren.
Jeg tok de samme punktene som i eksempel 3.
Løsning: Først, la oss finne vektoren:
Ved hjelp av formelen beregner vi lengden på vektoren:
Svar:
Ikke glem å angi dimensjonen - "enheter"! Forresten, er det alltid nødvendig å beregne en omtrentlig verdi (i i dette eksemplet 8.94), hvis dette ikke er påkrevd i tilstanden? Fra mitt synspunkt vil det ikke være overflødig; mangelen på en omtrentlig verdi fører til nit-plukking. Det anbefales å runde av til 2-3 desimaler.
La oss lage en tegning for oppgaven:
Hva er den grunnleggende forskjellen fra eksempel 3? Forskjellen er at her snakker vi om en vektor, ikke et segment. Vektoren kan flyttes til et hvilket som helst punkt i planet.
Hva er likhetene mellom eksempel 3 og eksempel 5? Det er geometrisk åpenbart at lengden på segmentet er lik lengden på vektoren. Det er også åpenbart at vektorlengden vil være den samme. Som et resultat: ![]() .
.
b) Gitt vektorene , , og . Finn lengdene deres.
Løsninger og svar på slutten av leksjonen.
I denne artikkelen vil vi begynne å diskutere en "tryllestav" som lar deg redusere mange geometriproblemer til enkel aritmetikk. Denne "pinnen" kan gjøre livet ditt mye enklere, spesielt når du føler deg usikker på å bygge romlige figurer, seksjoner osv. Alt dette krever en viss fantasi og praktiske ferdigheter. Metoden som vi vil begynne å vurdere her vil tillate deg å nesten fullstendig abstrahere fra alle slags geometriske konstruksjoner og resonnement. Metoden kalles "koordinatmetode". I denne artikkelen vil vi vurdere følgende spørsmål:
- Koordinat fly
- Punkter og vektorer på planet
- Konstruere en vektor fra to punkter
- Vektorlengde (avstand mellom to punkter).
- Koordinater til midten av segmentet
- Punktprodukt av vektorer
- Vinkel mellom to vektorer
Jeg tror du allerede har gjettet hvorfor koordinatmetoden kalles det? Det er riktig, det fikk det navnet fordi det ikke fungerer med geometriske objekter, og med dem numeriske egenskaper(koordinater). Og selve transformasjonen, som lar oss gå fra geometri til algebra, består i å introdusere et koordinatsystem. Hvis den opprinnelige figuren var flat, er koordinatene todimensjonale, og hvis figuren er tredimensjonale, så er koordinatene tredimensjonale. I denne artikkelen vil vi kun vurdere det todimensjonale tilfellet. Og hovedmålet med artikkelen er å lære deg hvordan du bruker noen grunnleggende teknikker koordinatmetode (de viser seg noen ganger å være nyttige når man løser problemer med planimetri i del B av Unified State Examination). De neste to delene om dette emnet er viet en diskusjon av metoder for å løse problemer C2 (problemet med stereometri).
Hvor ville det være logisk å begynne å diskutere koordinatmetoden? Sannsynligvis fra konseptet med et koordinatsystem. Husk når du møtte henne første gang. Det virker for meg som i 7. klasse, da du lærte om eksistensen lineær funksjon, For eksempel. La meg minne deg på at du bygget det punkt for punkt. Husker du? Du velger vilkårlig nummer, erstattet det i formelen og beregnet det på denne måten. For eksempel hvis, da, hvis, da osv. Hva fikk du til slutt? Og du fikk poeng med koordinater: og. Deretter tegnet du et "kryss" (koordinatsystem), valgte en skala på det (hvor mange celler du vil ha som et enhetssegment) og markerte punktene du fikk på det, som du deretter koblet sammen med en rett linje linje er grafen til funksjonen.
Det er noen punkter her som bør forklares litt mer detaljert:
1. Du velger et enkelt segment av bekvemmelighetshensyn, slik at alt passer vakkert og kompakt inn i tegningen.
2. Det er akseptert at aksen går fra venstre til høyre, og aksen går fra bunn til topp
3. De skjærer hverandre i rette vinkler, og skjæringspunktet kalles origo. Det er angitt med en bokstav.
4. Når du skriver koordinatene til et punkt, for eksempel, til venstre i parentes er det koordinaten til punktet langs aksen, og til høyre langs aksen. Spesielt betyr det ganske enkelt at på punktet
5. For å sette et hvilket som helst punkt på koordinataksen, må du angi koordinatene (2 tall)
6. For ethvert punkt som ligger på aksen,
7. For ethvert punkt som ligger på aksen,
8. Aksen kalles x-aksen
9. Aksen kalles y-aksen
La oss nå gjøre det med deg neste steg: La oss markere to punkter. La oss koble disse to punktene med et segment. Og vi setter pilen som om vi tegnet et segment fra punkt til punkt: det vil si at vi gjør segmentet vårt rettet!

Husker du hva et annet retningssegment kalles? Det er riktig, det kalles en vektor!
Så hvis vi kobler prikk til prikk, og begynnelsen vil være punkt A, og slutten vil være punkt B, da får vi en vektor. Du gjorde også denne konstruksjonen i 8. klasse, husker du?
Det viser seg at vektorer, som punkter, kan betegnes med to tall: disse tallene kalles vektorkoordinater. Spørsmål: Tror du det er nok for oss å vite koordinatene til begynnelsen og slutten av en vektor for å finne dens koordinater? Det viser seg at ja! Og dette gjøres veldig enkelt:
Siden i en vektor punktet er begynnelsen og punktet er slutten, har vektoren følgende koordinater:
For eksempel hvis, så koordinatene til vektoren
La oss nå gjøre det motsatte, finne koordinatene til vektoren. Hva må vi endre for dette? Ja, du må bytte begynnelsen og slutten: nå vil begynnelsen av vektoren være på punktet, og slutten vil være på punktet. Deretter:
Se nøye, hva er forskjellen mellom vektorer og? Deres eneste forskjell er tegnene i koordinatene. De er motsetninger. Dette faktum er vanligvis skrevet slik:
Noen ganger, hvis det ikke er spesifikt oppgitt hvilket punkt som er begynnelsen av vektoren og hvilket som er slutten, er vektorer merket med mer enn to med store bokstaver, og en liten bokstav, for eksempel: , etc.
Nå litt øve på selv og finn koordinatene til følgende vektorer:
Undersøkelse:
Løs nå et litt vanskeligere problem:
En vektor med et startpunkt i et punkt har en co-eller-di-na-du. Finn abs-cis-su-punktene.
Det samme er ganske prosaisk: La være koordinatene til punktet. Deretter
Jeg kompilerte systemet basert på definisjonen av hva vektorkoordinater er. Da har punktet koordinater. Vi er interessert i abscissen. Deretter
Svar:
Hva annet kan du gjøre med vektorer? Ja, nesten alt er det samme som med vanlige tall(bortsett fra at du ikke kan dele, men du kan multiplisere på to måter, hvorav den ene skal diskuteres her litt senere)
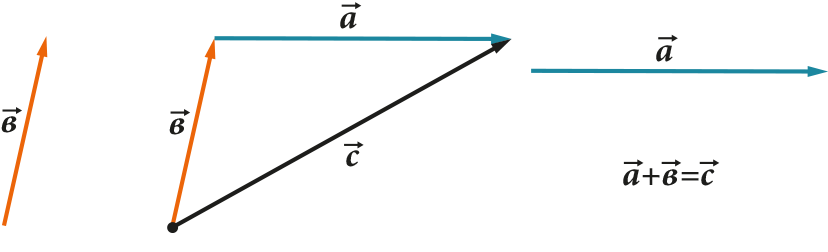
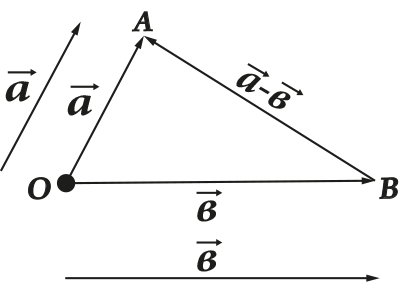
- Vektorer kan legges til hverandre
- Vektorer kan trekkes fra hverandre
- Vektorer kan multipliseres (eller divideres) med et vilkårlig tall som ikke er null
- Vektorer kan multipliseres med hverandre
Alle disse operasjonene har en veldig tydelig geometrisk representasjon. For eksempel, trekanten (eller parallellogram) regelen for addisjon og subtraksjon:
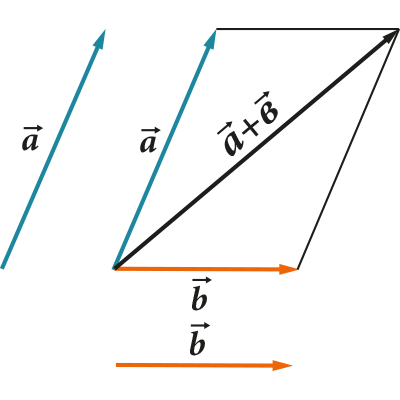
En vektor strekker seg eller trekker seg sammen eller endrer retning når den multipliseres eller divideres med et tall:

Men her vil vi være interessert i spørsmålet om hva som skjer med koordinatene.
1. Når vi adderer (subtraherer) to vektorer, legger vi til (subtraherer) deres koordinater element for element. Det er:
2. Når du multipliserer (deler) en vektor med et tall, blir alle dens koordinater multiplisert (delt) med dette tallet:
For eksempel:
· Finn mengden co-or-di-nat århundre-til-ra.
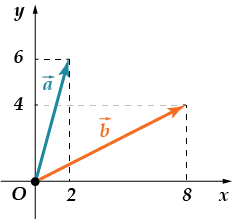
La oss først finne koordinatene til hver av vektorene. De har begge samme opphav - opprinnelsespunktet. Endene deres er forskjellige. Deretter, . La oss nå beregne koordinatene til vektoren. Da er summen av koordinatene til den resulterende vektoren lik.
Svar:
Løs nå følgende problem selv:
· Finn summen av vektorkoordinater
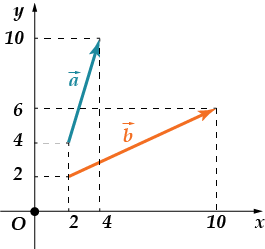
Vi sjekker:
La oss nå vurdere følgende problem: vi har to punkter på koordinatplanet. Hvordan finne avstanden mellom dem? La det første punktet være, og det andre. La oss angi avstanden mellom dem med. La oss lage følgende tegning for klarhet:
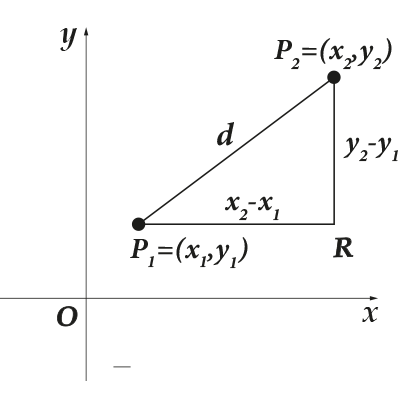
Hva jeg har gjort? Først og fremst koblet jeg meg prikker og,a trakk også en linje fra punktet, parallelt med aksen, og fra punktet tegnet jeg en linje parallelt med aksen. Skjærte de seg på et punkt og dannet en bemerkelsesverdig figur? Hva er så spesielt med henne? Ja, du og jeg vet nesten alt om den rette trekanten. Vel, Pythagoras teorem helt sikkert. Det nødvendige segmentet er hypotenusen til denne trekanten, og segmentene er bena. Hva er koordinatene til punktet? Ja, de er lette å finne fra bildet: Siden segmentene er parallelle med aksene og henholdsvis lengdene deres er enkle å finne: hvis vi betegner lengdene til segmentene med hhv.
La oss nå bruke Pythagoras teorem. Vi vet lengden på bena, vi finner hypotenusen:
Dermed er avstanden mellom to punkter roten av summen av kvadrerte forskjeller fra koordinatene. Eller - avstanden mellom to punkter er lengden på segmentet som forbinder dem. Det er lett å se at avstanden mellom punktene ikke er avhengig av retningen. Deretter:
Herfra trekker vi tre konklusjoner:
La oss øve litt på å beregne avstanden mellom to punkter:
For eksempel hvis, så er avstanden mellom og lik
Eller la oss gå en annen vei: finn koordinatene til vektoren
Og finn lengden på vektoren:
Som du kan se, er det det samme!
Nå skal du trene litt selv:
Oppgave: Finn avstanden mellom de angitte punktene:
Vi sjekker:
Her er et par flere problemer med samme formel, selv om de høres litt annerledes ut:
1. Finn kvadratet av lengden på øyelokket.

2. Finn kvadratet på øyelokkets lengde

Jeg tror du taklet dem uten problemer? Vi sjekker:
1. Og dette er for oppmerksomhet) Vi har allerede funnet koordinatene til vektorene tidligere: . Da har vektoren koordinater. Kvadraten på lengden vil være lik:
2. Finn koordinatene til vektoren
Da er kvadratet av lengden
Ikke noe komplisert, ikke sant? Enkel aritmetikk, ikke noe mer.
Følgende problemer kan ikke klassifiseres entydig de handler mer om generell lærdom og evnen til å tegne enkle bilder.
1. Finn sinusen til vinkelen fra kuttet, koble punktet, med abscisseaksen.
 Og
Og
Hvordan skal vi gå frem her? Vi må finne sinusen til vinkelen mellom og aksen. Hvor kan vi se etter sinus? Det stemmer, i høyre trekant. Så hva må vi gjøre? Bygg denne trekanten!
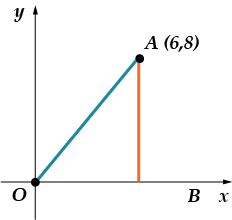
Siden koordinatene til punktet er og, er segmentet lik, og segmentet. Vi må finne sinusen til vinkelen. La meg minne deg på at sinus er et forhold motsatt ben til hypotenusen, da
Hva har vi igjen å gjøre? Finn hypotenusen. Du kan gjøre dette på to måter: ved å bruke Pythagoras teorem (bena er kjent!) eller ved å bruke formelen for avstanden mellom to punkter (faktisk det samme som den første metoden!). Jeg går den andre veien:
Svar:
Den neste oppgaven vil virke enda enklere for deg. Hun er på koordinatene til punktet.
Oppgave 2. Fra punktet senkes per-pen-di-ku-lyaren ned på ab-ciss-aksen. Nai-di-te abs-cis-su os-no-va-niya per-pen-di-ku-la-ra.
La oss lage en tegning:
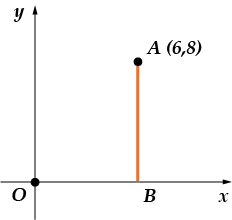
Grunnlaget til en perpendikulær er punktet der den skjærer x-aksen (aksen), for meg er dette et punkt. Figuren viser at den har koordinater: . Vi er interessert i abscissen - det vil si "x" -komponenten. Hun er likestilt.
Svar: .
Oppgave 3. I forhold forrige oppgave finn summen av avstandene fra punktet til koordinataksene.
Oppgaven er generelt elementær hvis du vet hva avstanden fra et punkt til aksene er. Du vet? Jeg håper, men minner deg likevel:
Så, på tegningen min rett ovenfor, har jeg allerede tegnet en slik vinkelrett? Hvilken akse er den på? Til aksen. Og hva er lengden da? Hun er likestilt. Tegn nå en vinkelrett på aksen selv og finn lengden. Det blir likt, ikke sant? Da er summen deres lik.
Svar: .
Oppgave 4. I betingelsene for oppgave 2, finn ordinaten til punktet, symmetrisk punkt i forhold til abscisseaksen.
Jeg tror det er intuitivt klart for deg hva symmetri er? Mange gjenstander har det: mange bygninger, bord, fly, mange geometriske figurer: kule, sylinder, firkant, rombe osv. Grovt sett kan symmetri forstås slik: en figur består av to (eller flere) like halvdeler. Denne symmetrien kalles aksial symmetri. Hva er da en akse? Dette er nøyaktig linjen langs hvilken figuren relativt sett kan "skjæres" i like halvdeler (i dette bildet er symmetriaksen rett):

La oss nå gå tilbake til oppgaven vår. Vi vet at vi ser etter et punkt som er symmetrisk om aksen. Da er denne aksen symmetriaksen. Dette betyr at vi må markere et punkt slik at aksen kutter segmentet i to like deler. Prøv å markere et slikt punkt selv. Sammenlign nå med min løsning:
![]()
Fungerte det på samme måte for deg? Fint! Vi er interessert i ordinaten til det funnet punktet. Det er likt
Svar:
Fortell meg nå, etter å ha tenkt noen sekunder, hva vil abscissen til et punkt som er symmetrisk til punkt A i forhold til ordinaten? Hva er svaret ditt? Korrekt svar: .
I generell sak regelen kan skrives slik:
Et punkt som er symmetrisk til et punkt i forhold til abscisseaksen har koordinatene:
Et punkt som er symmetrisk til et punkt i forhold til ordinataksen har koordinater:
Vel, nå er det helt skummelt oppgave: finn koordinatene til et punkt symmetrisk til punktet i forhold til origo. Du tenker først selv, og så ser du på tegningen min!
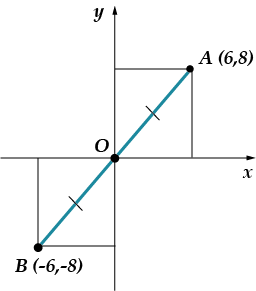
Svar:
Nå parallellogram problem:
Oppgave 5: Punktene vises ver-shi-na-mi pa-ral-le-lo-gram-ma. Finn eller-di-på-det punktet.
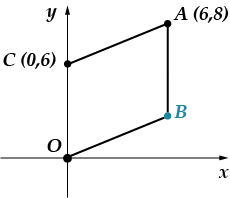
Du kan løse dette problemet på to måter: logikk og koordinatmetoden. Jeg bruker først koordinatmetoden, og så skal jeg fortelle deg hvordan du kan løse det annerledes.
Det er helt klart at abscissen til punktet er lik. (den ligger på vinkelrett tegnet fra punktet til abscisseaksen). Vi må finne ordinaten. La oss dra nytte av det faktum at vår figur er et parallellogram, dette betyr det. La oss finne lengden på segmentet ved å bruke formelen for avstanden mellom to punkter:
Vi senker vinkelrett som forbinder punktet med aksen. Jeg vil angi skjæringspunktet med en bokstav.
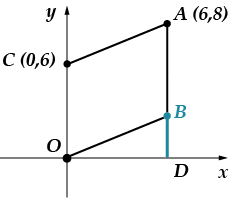
Lengden på segmentet er lik. (finn oppgaven selv der vi diskuterte dette punktet), så vil vi finne lengden på segmentet ved å bruke Pythagoras teorem:
Lengden på et segment sammenfaller nøyaktig med ordinaten.
Svar: .
En annen løsning (jeg skal bare gi et bilde som illustrerer det)
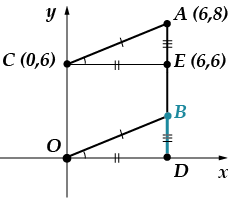
Løsningsfremgang:
1. Oppførsel
2. Finn punktkoordinatene og lengden
3. Bevis det.
En annen problem med segmentlengde:
Punktene vises på toppen av trekantene. Finn lengden på midtlinjen, parallell.

Husker du hva det er midtlinje triangel? Da er denne oppgaven elementær for deg. Hvis du ikke husker, så minner jeg deg på: midtlinjen i en trekant er linjen som forbinder midtpunktene motsatte sider. Den er parallell med basen og lik halvparten av den.
Basen er et segment. Vi måtte se etter lengden tidligere, den er lik. Da er lengden på midtlinjen halvparten så stor og lik.
Svar: .
Kommentar: dette problemet kan løses på en annen måte, som vi kommer til litt senere.
I mellomtiden, her er noen problemer for deg, øv deg på dem, de er veldig enkle, men de hjelper deg å bli bedre til å bruke koordinatmetoden!
1. Punktene er toppen av tra-pe-sjonene. Finn lengden på midtlinjen.

2. Poeng og utseende ver-shi-na-mi pa-ral-le-lo-gram-ma. Finn eller-di-på-det punktet.

3. Finn lengden fra kuttet, koble punktet og

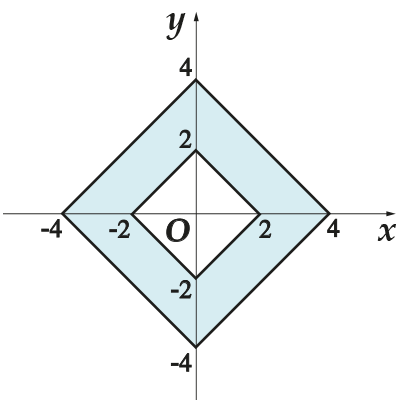
4. Finn området bak den fargede figuren på koordinatplanet.
5. En sirkel med sentrum i na-cha-le ko-or-di-nat går gjennom punktet. Finn hennes ra-di-us.
6. Finn-di-te ra-di-us av sirkelen, beskriv-san-noy om den rette vinkelen-no-ka, toppen av noe har en med-eller -di-na-du er så ansvarlig

Løsninger:
1. Det er kjent at midtlinjen til en trapes er lik halvparten av summen av dens baser. Basen er lik, og basen. Deretter
Svar:
2. Den enkleste måten å løse dette problemet på er å merke seg det (parallelogramregelen). Å beregne koordinatene til vektorer er ikke vanskelig: . Når vektorer legges til, legges koordinatene til. Da har den koordinater. Punktet har også disse koordinatene, siden opprinnelsen til vektoren er punktet med koordinatene. Vi er interessert i ordinaten. Hun er likestilt.
Svar:
3. Vi handler umiddelbart i henhold til formelen for avstanden mellom to punkter:
Svar:
4. Se på bildet og fortell meg hvilke to figurer det skraverte området er "klemt" mellom? Den er klemt mellom to firkanter. Da er arealet til den ønskede figuren lik arealet til den store firkanten minus arealet til den lille. Side liten firkant er et segment som forbinder punkter og lengden er
Da er arealet av den lille firkanten
Vi gjør det samme med en stor firkant: siden er et segment som forbinder punktene og lengden er
Da er arealet av det store torget
Vi finner arealet til ønsket figur ved å bruke formelen:
Svar:
5. Hvis en sirkel har origo som senter og går gjennom et punkt, vil radiusen være nøyaktig lik lengde segment (lag en tegning og du vil forstå hvorfor dette er åpenbart). La oss finne lengden på dette segmentet:
Svar:
6. Det er kjent at radiusen til en sirkel omskrevet rundt et rektangel lik halvparten dens diagonaler. La oss finne lengden på en av de to diagonalene (tross alt, i et rektangel er de like!)
Svar:
Vel, taklet du alt? Det var ikke veldig vanskelig å finne ut av det, var det? Det er bare én regel her - kunne lage et visuelt bilde og ganske enkelt "lese" alle dataene fra det.
Vi har veldig lite igjen. Det er bokstavelig talt to punkter til som jeg ønsker å diskutere.
La oss prøve å løse dette enkle problemet. La to poeng og gis. Finn koordinatene til midtpunktet av segmentet. Løsningen på dette problemet er som følger: la punktet være det ønskede midten, så har det koordinater:
Det er: koordinater til midten av segmentet = det aritmetiske gjennomsnittet av de tilsvarende koordinatene til endene av segmentet.
Denne regelen er veldig enkel og forårsaker vanligvis ikke vanskeligheter for elevene. La oss se i hvilke problemer og hvordan det brukes:
1. Finn-di-te eller-di-na-tu se-re-di-ny fra-cut, koble-punktet og

2. Poengene ser ut til å være toppen av verden. Finn-di-te eller-di-na-tu poeng per-re-se-che-niya av hans dia-go-na-ley.

3. Finn-di-te abs-cis-su sentrum av sirkelen, beskriv-san-noy om rektangulære-no-ka, toppen av noe har co-eller-di-na-du så-ansvarlig-men.

Løsninger:
1. Det første problemet er rett og slett en klassiker. Vi fortsetter umiddelbart for å bestemme midten av segmentet. Den har koordinater. Ordinaten er lik.
Svar:
2. Det er lett å se at denne firkanten er et parallellogram (til og med en rombe!). Du kan bevise dette selv ved å beregne lengdene på sidene og sammenligne dem med hverandre. Hva vet jeg om parallellogrammer? Diagonalene er delt i to av skjæringspunktet! Ja! Så hva er skjæringspunktet mellom diagonalene? Dette er midten av noen av diagonalene! Jeg vil spesielt velge diagonalen. Da har punktet koordinater Ordinaten til punktet er lik.
Svar:
3. Hva sammenfaller midten av sirkelen som er omskrevet om rektangelet? Det faller sammen med skjæringspunktet mellom diagonalene. Hva vet du om diagonalene til et rektangel? De er like og skjæringspunktet deler dem i to. Oppgaven ble redusert til den forrige. La oss ta for eksempel diagonalen. Så hvis er sentrum av den omskrevne sirkelen, så er midtpunktet. Jeg leter etter koordinater: Abscissen er lik.
Svar:
Nå skal du øve litt på egen hånd, jeg vil bare gi svarene på hvert problem slik at du kan teste deg selv.
1. Finn-di-te ra-di-us av sirkelen, beskriv-san-noy om tri-angle-no-ka, toppen av noe har en co-eller-di -no misters

2. Finn-di-te eller-di-på-det sentrum av sirkelen, beskriv-san-noy om trekanten-no-ka, hvis topper har koordinater
3. Hva slags ra-di-u-sa skal det være en sirkel med senter i et punkt slik at den berører ab-ciss-aksen?
4. Finn-di-de eller-di-på-det punktet for re-se-sesjon av aksen og fra-skjæring, koble-punktet og

Svar:
Var alt vellykket? Jeg håper virkelig på det! Nå - siste push. Vær spesielt forsiktig. Materialet som jeg nå skal forklare er direkte relatert ikke bare til enkle oppgaver til koordinatmetoden fra del B, men finnes også overalt i oppgave C2.
Hvilke av løftene mine har jeg ennå ikke holdt? Husker du hvilke operasjoner på vektorer jeg lovet å introdusere og hvilke jeg til slutt introduserte? Er du sikker på at jeg ikke har glemt noe? Glemte! Jeg glemte å forklare hva vektormultiplikasjon betyr.
Det er to måter å multiplisere en vektor med en vektor. Avhengig av den valgte metoden vil vi få gjenstander av forskjellig natur:
Kryssproduktet er gjort ganske smart. Vi vil diskutere hvordan du gjør det og hvorfor det er nødvendig i neste artikkel. Og i denne vil vi fokusere på det skalære produktet.
Det er to måter som lar oss beregne det:
Som du gjettet, bør resultatet være det samme! Så la oss først se på den første metoden:
Prikk produkt via koordinater
Finn: - generelt akseptert notasjon for skalarprodukt
Formelen for beregning er som følger:
Det er skalært produkt= summen av produkter av vektorkoordinater!
Eksempel:
Finn-di-te
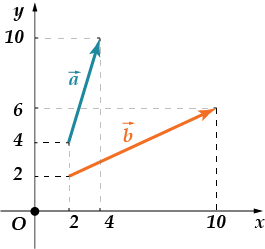
Løsning:
La oss finne koordinatene til hver av vektorene:
Vi beregner skalarproduktet ved å bruke formelen:
Svar:
Se, absolutt ikke noe komplisert!
Vel, prøv det selv:
· Finn en skalar pro-iz-ve-de-nie av århundrer og
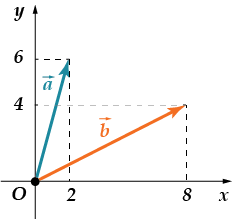
Klarte du deg? Kanskje du la merke til en liten hake? La oss sjekke:
Vektorkoordinater som i forrige oppgave! Svar: .
I tillegg til koordinaten, er det en annen måte å beregne skalarproduktet på, nemlig gjennom lengdene på vektorene og cosinus til vinkelen mellom dem:
Angir vinkelen mellom vektorene og.
Det vil si at skalarproduktet er lik produktet av lengdene til vektorene og cosinus til vinkelen mellom dem.
Hvorfor trenger vi denne andre formelen, hvis vi har den første, som er mye enklere, er det i det minste ingen cosinus i den. Og det er nødvendig slik at du og jeg fra den første og andre formelen kan utlede hvordan du finner vinkelen mellom vektorer!
La Så husk formelen for lengden på vektoren!
Så hvis jeg erstatter disse dataene i skalarproduktformelen, får jeg:
Men på en annen måte:
Så hva fikk du og jeg? Vi har nå en formel for å beregne vinkelen mellom to vektorer! Noen ganger er det også skrevet slik for korthets skyld:
Det vil si at algoritmen for å beregne vinkelen mellom vektorer er som følger:
- Beregn skalarproduktet gjennom koordinater
- Finn lengdene på vektorene og gang dem
- Del resultatet av punkt 1 med resultatet av punkt 2
La oss øve med eksempler:
1. Finn vinkelen mellom øyelokkene og. Gi svaret i grad-du-sah.
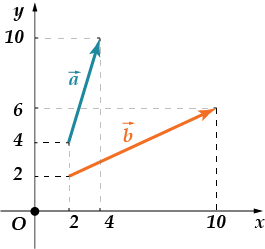
2. I betingelsene i forrige oppgave, finn cosinus mellom vektorene
La oss gjøre dette: Jeg skal hjelpe deg med å løse det første problemet, og prøve å gjøre det andre selv! Bli enige? Så la oss begynne!
1. Disse vektorene er våre gamle venner. Vi har allerede beregnet deres skalarprodukt, og det var likt. Koordinatene deres er: , . Så finner vi lengdene deres:
Deretter ser vi etter cosinus mellom vektorene:
Hva er cosinus til vinkelen? Dette er hjørnet.
Svar:
Vel, løs nå det andre problemet selv, og sammenlign! Jeg vil gi en veldig kort løsning:
2. har koordinater, har koordinater.
La være vinkelen mellom vektorene og, da
Svar:
Det skal bemerkes at problemene direkte på vektorer og koordinatmetoden i del B eksamensoppgave ganske sjelden. De aller fleste C2-problemene kan imidlertid enkelt løses ved å innføre et koordinatsystem. Så du kan vurdere denne artikkelen som grunnlaget som vi vil lage ganske smarte konstruksjoner som vi trenger for å løse komplekse problemer.
