Математика. Теоретска механика

Најдете неопределен интеграл(збир на антидеривати или „антидеривати“) значи да се врати функцијата од познат дериват на оваа функција. Обновен сет на антидеривати Ф(x) + СО за функција ѓ(x) ја зема предвид константата на интеграција В. Според брзината на движење материјална точка(дериват) може да се врати законот за движење на оваа точка (антидериватив); според забрзувањето на движењето на точката - нејзината брзина и законот на движење. Како што можете да видите, интеграцијата е широко поле за активностите на Шерлок Холмс од физиката. И во економијата, многу концепти се претставени преку функции и нивните деривати, и затоа, на пример, можно е да се врати обемот на производи произведени во соодветното време користејќи ја продуктивноста на трудот во одреден момент во времето (дериват).

Пронаоѓањето на неопределен интеграл бара прилично мал број основни формули за интеграција. Но, процесот на негово пронаоѓање е многу потежок од само примена на овие формули. Целата сложеност не се однесува на интеграцијата, туку на доведување на интеграбилниот израз во форма што овозможува да се најде неопределен интеграл користејќи ги основните формули споменати погоре. Ова значи дека за да започнете со практиката на интеграција, треба да го активирате она што сте го научиле средно школовештини за трансформација на изразување.

Ќе научиме да наоѓаме интеграли користејќи својства и табела на неопределени интегралиод лекција за основните поими на оваа тема (се отвора во нов прозорец).

Постојат неколку методи за пронаоѓање на интегралот, од кои метод на замена на променливаИ метод на интеграција со делови- задолжителен џентлменски комплет за сите кои успешно положиле виша математика. Сепак, покорисно и попријатно е да се започне со совладување на интеграцијата користејќи го методот на проширување, заснован на следните две теореми за својствата на неопределен интеграл, што ги повторуваме овде за погодност.

Теорема 3.Постојан множителво интеграндот може да се извади како знак на неопределен интеграл, т.е.

Теорема 4.Неопределен интеграл на алгебарски збир конечен бројфункциите се еднакви алгебарски збирнеопределени интеграли на овие функции, т.е.

(2)

Дополнително, следново правило може да биде корисно при интеграцијата: ако изразот на интеграндот содржи константен фактор, тогаш изразот на антидериватот се множи со инверзната на константниот фактор, т.е.

(3)

Бидејќи оваа лекција е воведна лекција за решавање на проблемите за интеграција, важно е да се забележат две работи кои или веќе почетна фаза, или малку подоцна може да ве изненадат. Изненадувањето се должи на фактот што интеграцијата е инверзна операција на диференцијацијата и неопределениот интеграл со право може да се нарече „антидериватив“.

Првото нешто што не треба да ве изненади при интегрирањето.Во табелата со интеграли има формули кои немаат аналози меѓу формулите за деривативни табели . Ова се следните формули:

Сепак, можете да бидете сигурни дека дериватите на изразите на десните страни на овие формули се совпаѓаат со соодветните интегранти.

Втората работа што не треба да изненадува при интегрирањето. Иако изводот на која било елементарна функција е исто така елементарна функција, неопределени интеграли на некои елементарни функции веќе не се елементарни функции . Примери за такви интеграли може да бидат следниве:

За да се развијат техники за интеграција, ќе бидат корисни следните вештини: намалување на дропки, делење полином во броителот на дропка со моном во именителот (да се добие збир на неопределени интеграли), претворање на корените во моќи, множење на моном со полином, подигање на моќ. Овие вештини се потребни за трансформации на интеградот, што треба да резултира со збир од интегралите присутни во табелата со интеграли.

Наоѓање на неопределени интеграли заедно

Пример 1.Најдете го неопределен интеграл

Решение. Во именителот на интеграндот гледаме полином во кој x е квадрат. Ова е речиси сигурен знак дека можете да го примените интегралот на табелата 21 (со резултат на арктангенс). Го вадиме факторот два од именителот (постои такво својство на интегралот - константниот фактор може да се извади надвор од знакот на интегралот; тој беше споменат погоре како теорема 3). Резултатот од сето ова:

Сега именителот е збир на квадрати, што значи дека можеме да го примениме споменатиот табеларен интеграл. Конечно го добиваме одговорот:

Пример 2.Најдете го неопределен интеграл

Решение. Повторно ја применуваме теоремата 3 - својството на интегралот, врз основа на кое константниот фактор може да се извади од знакот на интегралот:

Ја применуваме формулата 7 од табелата со интеграли (променлива до моќност) на функцијата интегранд:

Ги намалуваме добиените дропки и го имаме конечниот одговор:

Пример 3.Најдете го неопределен интеграл

Решение. Применувајќи ја прво теорема 4, а потоа теорема 3 на својствата, го наоѓаме овој интеграл како збир од три интеграли:

Сите три добиени интеграли се табеларни. Ја користиме формулата (7) од табелата со интеграли за n = 1/2, n= 2 и n= 1/5, а потоа

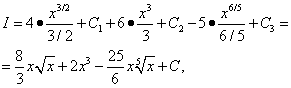
ги комбинира сите три произволни константи кои беа воведени кога наоѓање на триинтеграли. Затоа, во слични ситуации, треба да се воведе само една произволна константа на интеграција.

Пример 4.Најдете го неопределен интеграл

Решение. Кога именителот на интеграндот содржи моном, можеме да го поделиме броителот со именителот член по член. Оригиналниот интеграл се претвори во збир од два интеграли:

За да го примениме интегралот на табелата, ги трансформираме корените во моќи и еве го конечниот одговор:

Продолжуваме заедно да наоѓаме неопределени интеграли

Пример 7.Најдете го неопределен интеграл

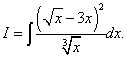
Решение. Ако го трансформираме интеграндот со квадратирање на биномот и делење на броителот со именителот член по член, тогаш оригиналниот интеграл станува збир од три интеграли.

Дали е можно да се подведе нелинеарна функција под диференцијалниот знак? Да, ако интеграндот е производ на два фактора: едниот фактор е сложена функција на некоја нелинеарна функција, а другиот фактор е изводот на оваа нелинеарна функција. Ајде да погледнеме што е кажано со примери.

Најдете неопределени интеграли.

Пример 1. ∫(2x + 1) (x 2 + x + 2) 5 dx = ∫(x 2 + x + 2) 5 d (x 2 + x + 2) =(x²+x+2) 6 : 6 + C.

Што претставува овој интегранд? Работа функција за напојувањеод (x 2 + x + 2) и множителот (2x + 1), кој е еднаков на дериватот на основата на моќта: (x 2 + x + 2)" = 2x + 1.

Ова ни овозможи да ставиме (2x + 1) под диференцијалниот знак:

∫u 5 du=u 6 : 6+ C. (Формула 1). )

Испитување. (F (x)+ C)" =((x²+x+2) 6 : 6 + C)'=1/6 6 (x 2 + x + 2) 5 (x 2 + x + 2)" =

=(x 2 + x + 2) 5 · (2x + 1) = (2x + 1) (x 2 + x + 2) 5 = f (x).

Пример 2.∫(3x 2 – 2x + 3)(x 3 - x 2 + 3x + 1) 5 dx = ∫(x 3 – x 2 + 3x + 1) 5 d (x 3 – x 2 + 3x + 1) =

=(x³- x²+3x+1) 6 : 6+C

И како овој пример се разликува од примерот 1? Ништо! Истата петта моќност со основата (x 3 – x 2 + 3x + 1) се множи со триномот (3x 2 – 2x + 3), кој е извод на основата на моќноста: (x 3 – x 2 + 3x + 1)" = 3x 2 – 2x + 3. Оваа основа на степенот ја доведовме под диференцијалниот знак, од кој вредноста на интеграндот не се промени, а потоа ја применивме истата формула 1). Интеграли)

Пример 3.

Овде дериватот на (2x 3 – 3x) ќе даде (6x 2 – 3), а кај нас

има (12x 2 – 6), односно изразот во 2 пати поголем, што значи ставаме (2x 3 – 3x) под диференцијалниот знак и ставаме фактор пред интегралот 2 . Да ја примениме формулата 2) (лист ).

Еве што се случува:

Ајде да провериме, имајќи предвид дека:

Примери. Најдете неопределени интеграли.

1. ∫(6x+5) 3 dx. Како ќе одлучиме? Гледајќи го листот и резонираме нешто вака: интеграндот претставува степен, а имаме формула за интегралот на степенот (формула 1) ), но во него основата на степенот uи променливата за интеграција исто така u.

И имаме променлива за интеграција X, и основата на степенот (6x+5). Да направиме промена на интеграциската променлива: наместо dx пишуваме d (6x+5). Што се смени? Бидејќи она што доаѓа по диференцијалниот знак d е стандардно диференцирано,

тогаш d (6x+5)=6dx, т.е. при замена на променливата x со променливата (6x+5), функцијата интегранд се зголемила 6 пати, па пред знакот интегрален го ставаме факторот 1/6. Овие аргументи може да се напишат вака:

Така, овој пример го решивме со воведување на нова променлива (променливата x беше заменета со променливата 6x+5). Каде ја напиша новата променлива (6x+5)? Под диференцијалниот знак. Затоа, овој методчесто се нарекува воведување нова променлива метод (или начин ) сумирање(нова променлива ) под диференцијалниот знак.

Во вториот пример, прво добивме диплома со негативен индикатор, а потоа се става под диференцијалниот знак (7x-2) и се користи формулата за интегрален степен 1) (Интеграли ).

Да го погледнеме примерот на решението 3.

На интегралот му претходи коефициент 1/5. Зошто? Бидејќи d (5x-2) = 5dx, тогаш, со замена на функцијата u = 5x-2 под диференцијалниот знак, го зголемивме интеграндот за 5 пати, така што вредноста даден изразне се промени - беше неопходно да се подели со 5, т.е. помножете се со 1/5. Следно, формулата беше искористена 2) (Интеграли) .

Сите наједноставни интегрални формули ќе изгледаат вака:

∫f (x) dx=F (x)+C, и еднаквоста мора да биде исполнета:

(F (x)+C)"=f (x).

Формулите за интеграција може да се добијат со превртување на соодветните формули за диференцијација.

Навистина,

Експонент nможе да биде фракционо. Честопати треба да го пронајдете неопределениот интеграл на функцијата y=√x. Да го пресметаме интегралот на функцијата f (x)=√x со помош на формулата 1) .

Да го напишеме овој пример како формула 2) .

Бидејќи (x+C)"=1, тогаш ∫dx=x+C.

3) ∫dx=x+C.

Заменувајќи го 1/x² со x -2, го пресметуваме интегралот од 1/x².

Можете ли да го добиете овој одговор со контактирање позната формуладиференцијација:

Да го напишеме нашето размислување во форма на формула 4).

Помножувајќи ги двете страни на добиената еднаквост со 2, ја добиваме формулата 5).

Ајде да ги најдеме интегралите на главните тригонометриски функции, знаејќи ги нивните деривати: (sinx)"=cosx; (cosx)"=-sinx; (tgx)"=1/cos²x; (ctgx)"=-1/sin²x. Ги добиваме формулите за интеграција 6) — 9).

6) ∫cosxdx=sinx+C;

7) ∫sinxdx=-cosx+C;

По проучувањето на показната и логаритамски функции, да додадеме уште неколку формули.

Основните својства не се определен интеграл.

Јас.Изводот на неопределен интеграл е еднаков на интеграндот .

(∫f (x) dx)"=f (x).

II.Диференцијалот на неопределен интеграл е еднаков на интеграндот.

d∫f (x) dx=f (x) dx.

III.Неопределен интеграл на диференцијал (дериват) на некоја функција еднаков на збиротоваа функција и произволна константа C.

∫dF (x)=F (x)+Cили ∫F"(x) dx=F (x)+C.

Ве молиме запомнете: во I, II и III својствазнаците на диференцијалот и интегралниот (интегрален и диференцијален) се „јадат“ еден со друг!

IV.Константниот фактор на интеграндот може да се извади од интегралниот знак.

∫kf (x) dx=k ∫f (x) dx,Каде к - постојана, не е еднакво на нула.

В.Интегралот на алгебарскиот збир на функции е еднаков на алгебарскиот збир на интегралите на овие функции.

∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx.

VI.Ако F (x) е антидериват на f (x), и кИ бсе константни вредности и к≠0, тогаш (1/k)·F (kx+b) е антидериват за f (kx+b). Навистина, според правилото за пресметување на дериватот комплексна функцијание имаме:

Можете да напишете:

За секој математичка операцијаима спротивен ефект. За дејството на диференцијација (пронаоѓање деривати на функции) постои и обратно дејство- интеграција. Преку интеграцијата се наоѓа (реконструира) функција од нејзиниот даден извод или диференцијал. Пронајдената функција се нарекува антидериват.

Дефиниција.Диференцијабилна функција F(x)се нарекува антидериват на функцијата f(x)на даден интервал, ако за сите Xод овој интервал важи следнава еднаквост: F′(x)=f (x).

Примери. Најдете антидеривати за функциите: 1) f (x)=2x; 2) f (x)=3cos3x.

1) Бидејќи (x²)′=2x, тогаш, по дефиниција, функцијата F (x)=x² ќе биде антидериват на функцијата f (x)=2x.

2) (sin3x)′=3cos3x. Ако означиме f (x)=3cos3x и F (x)=sin3x, тогаш, по дефиниција за антидериват, имаме: F′(x)=f (x), и затоа, F (x)=sin3x е антидериват за f ( x)=3cos3x.

Забележете дека (sin3x +5 )′= 3cos3x, и (sin3x -8,2 )′= 3cos3x, ... В општ погледможе да се напише: (sin3x +C)′= 3cos3x, Каде СО- некоја константна вредност. Овие примери укажуваат на двосмисленоста на дејството на интеграцијата, за разлика од дејството на диференцијација, кога која било диференцијабилна функција има еден извод.

Дефиниција.Доколку функцијата F(x)е антидериват на функцијата f(x)на одреден интервал, тогаш множеството на сите антидеривати на оваа функција има форма:

F(x)+C, каде што C е кој било реален број.

Множеството од сите антидеривати F (x)+C на функцијата f (x) на разгледуваниот интервал се нарекува неопределен интеграл и се означува со симболот ∫ (интегрален знак). Напиши: ∫f (x) dx=F (x)+C.

Изразување ∫f(x)dxпрочитајте: „интегрален ef од x до de x“.

f(x)dx- интегрален израз,

f(x)- интегранд функција,

Xе интеграциската променлива.

F(x)- антидериват на функција f(x),

СО- некоја константна вредност.

Сега разгледаните примери може да се напишат на следниов начин:

1) ∫ 2xdx=x²+C. 2) ∫ 3cos3xdx=sin3x+C.

Што значи знакот г?

d-диференцијален знак - има двојна цел: прво, овој знак го одделува интеграндот од интеграциската променлива; второ, сè што доаѓа по овој знак стандардно се диференцира и се множи со интеграндот.

Примери. Најдете ги интегралите: 3) ∫ 2 pxdx; 4) ∫ 2 pxdp.

3) По иконата за диференцијал гтрошоците XX, А Р

∫ 2хрdx=рх²+С. Споредете со пример 1).

Ајде да направиме проверка. F′(x)=(px²+C)′=p·(x²)′+C′=p·2x=2px=f (x).

4) По иконата за диференцијал гтрошоците Р. Ова значи дека интеграциската променлива Р, и мултипликаторот Xтреба да се смета за некоја константна вредност.

∫ 2хрд=р²х+С. Споредете со примери 1) И 3).

Ајде да направиме проверка. F′(p)=(p²x+C)′=x·(p²)′+C′=x·2p=2px=f (p).

Страница 1 од 1 1

Интегрална пресметка.

Антидеривативна функција.

Дефиниција: Се повикува функцијата F(x). антидеривативна функцијаФункција f(x) на отсечката ако еднаквоста е вистина во која било точка од оваа отсечка:

Треба да се забележи дека може да има бесконечен број на антидеривати за истата функција. Тие ќе се разликуваат едни од други по некој константен број.

F 1 (x) = F 2 (x) + C.

Неопределен интеграл.

Дефиниција: Неопределен интеграл functionf(x) е збир на антидеривативни функции кои се дефинирани со релацијата:

Напиши:

Услов за постоење на неопределен интеграл на одредена отсечка е континуитетот на функцијата на оваа отсечка.

Својства:

Пример:

Наоѓањето на вредноста на неопределениот интеграл главно се поврзува со пронаоѓањето на антидериватот на функцијата. За некои функции ова е доста тешка задача. Подолу ќе ги разгледаме методите за наоѓање неопределени интеграли за главните класи на функции - рационални, ирационални, тригонометриски, експоненцијални итн.

За погодност, вредностите на неопределените интеграли на повеќето елементарни функции се собираат во посебни табели на интеграли, кои понекогаш се прилично обемни. Тие вклучуваат различни најчесто користени комбинации на функции. Но, повеќето формули претставени во овие табели се меѓусебни последици, па подолу ви претставуваме табела со основни интеграли, со чија помош можете да ги добиете вредностите на неопределени интеграли од различни функции.

Интегрален	Значење	Интегрален	Значење

	lnsinx+ В



	ln

Методи на интеграција.

Да разгледаме три главни методи на интеграција.

Директна интеграција.

Методот на директна интеграција се заснова на претпоставката дека можно значењеантидеривативна функција со понатамошна верификација на оваа вредност со диференцијација. Во принцип, забележуваме дека диференцијацијата е моќна алатка за проверка на резултатите од интеграцијата.

Ајде да ја разгледаме примената на овој метод користејќи пример:

Треба да ја најдеме вредноста на интегралот . Врз основа на добро познатата формула за диференцијација
можеме да заклучиме дека бараниот интеграл е еднаков на
, каде што C е некој константен број. Меѓутоа, од друга страна
. Така, конечно можеме да заклучиме:

Забележете дека, за разлика од диференцијацијата, каде што се користеа јасни техники и методи за пронаоѓање на изводот, правила за пронаоѓање на изводот и, конечно, дефиниција на изводот, таквите методи не се достапни за интеграција. Ако при наоѓањето на дериватот користевме, така да се каже, конструктивни методи, кои врз основа на одредени правила доведоа до резултат, тогаш при наоѓањето на антидериватот треба да се потпреме главно на знаењето за табелите на деривати и антидеривати.

Што се однесува до методот на директна интеграција, тој е применлив само за некои многу ограничени класи на функции. Има многу малку функции за кои можете веднаш да најдете антидериват. Затоа, во повеќето случаи, се користат методите опишани подолу.

Начин на замена (замена на променливи).

Теорема: Ако треба да го пронајдете интегралот
, но тешко е да се најде антидериватот, па со помош на замената x =  (t) и dx =  (t) dt излегува:

Доказ : Да ја разликуваме предложената еднаквост:

Според својството бр. 2 од неопределениот интеграл дискутиран погоре:

ѓ(x) dx = ѓ[  (т)]  (т) dt

која имајќи ја предвид воведената нотација е почетната претпоставка. Теоремата е докажана.

Пример.Најдете го неопределен интеграл
.

Ајде да направиме замена т = синкс, dt = cosxdt.

Пример.

Замена
Добиваме:

Подолу ќе разгледаме други примери за користење на методот на замена за различни типови на функции.

Интеграција по делови.

Методот се заснова на добро познатата формула за дериват на производ:

(uv)=uv+vu

каде uиv се некои функции на x.

Во диференцијална форма: d(uv) =udv+vdu

Интегрирајќи, добиваме:
, и во согласност со горенаведените својства на неопределен интеграл:

или
;

Добивме формула за интеграција по делови, која ни овозможува да ги најдеме интегралите на многу елементарни функции.

Пример.

Како што можете да видите, доследната примена на формулата за интеграција по делови ви овозможува постепено да ја поедноставите функцијата и да го доведете интегралот до табеларен.

Пример.

Може да се види дека како резултат на повеќекратна примена на интеграција по делови, функцијата не може да се поедностави во табеларна форма. Сепак, последниот добиен интеграл не се разликува од оригиналниот. Затоа, го поместуваме на левата страна на еднаквоста.

Така, интегралот беше пронајден без воопшто да се користат табели на интеграли.

Пред детално да ги разгледаме методите за интегрирање на различни класи на функции, даваме уште неколку примери за наоѓање неопределени интеграли со нивно намалување на табеларни.

Пример.

Интеграција на елементарни дропки.

Дефиниција: ОсновноСледниве четири типа на дропки се нарекуваат:

Јас.
III.

II.
IV.

m, n- цели броеви(m2,n2) и b 2 – 4ac<0.

Првите два вида интеграли на елементарни дропки може едноставно да се доведат до табелите со замена на t=ax+b.

Да го разгледаме методот на интегрирање на елементарни дропки од типот III.

Интегралот на дропка од типот III може да се претстави како:

Овде, во општа форма, е прикажано намалувањето на фракциониот интеграл од тип III на два табеларни интеграли.

Ајде да ја разгледаме примената на горната формула користејќи примери.

Пример.

Општо земено, ако триномот ax 2 +bx+c го има изразот b 2 – 4ac>0, тогаш дропката, по дефиниција, не е елементарна, но сепак може да се интегрира на начин наведен погоре.

Пример.

Сега да ги разгледаме методите за интегрирање на едноставни дропки од типот IV.

Прво, да разгледаме посебен случај со M = 0, N = 1.

Потоа интегралот на формата
може да се претстави во форма со избирање на целосниот квадрат во именителот
. Да ја направиме следната трансформација:

Вториот интеграл вклучен во оваа еднаквост ќе го земеме по делови.

Да означиме:

За оригиналниот интеграл добиваме:

Резултирачката формула се нарекува повторливи.Ако го примените n-1 пати, добивате табеларен интеграл
.

Сега да се вратиме на интегралот на елементарна дропка од типот IV во општиот случај.

Во добиената еднаквост, првиот интеграл со помош на замена т = u 2 + ссведена на табеларно , а формулата за повторување дискутирана погоре се применува на вториот интеграл.

И покрај очигледната сложеност на интегрирање на елементарна дропка од тип IV, во пракса е прилично лесно да се користи за дропки со мал степен n, а универзалноста и општоста на пристапот овозможува многу едноставна имплементација на овој метод на компјутер.

Пример:

Интеграција на рационални функции.

Интегрирање на рационални дропки.

За да се интегрира рационална дропка потребно е да се разложи на елементарни дропки.

Теорема: Ако
- правилна рационална дропка, чиј именител P(x) е претставен како производ на линеарни и квадратни фактори (забележете дека секој полином со реални коефициенти може да се претстави во оваа форма: П(x) = (x - а)  …(x - б)  (x 2 + px + q)  …(x 2 + rx + с)  ), тогаш оваа дропка може да се разложи на елементарни според следнава шема:

каде што A i , B i , M i , N i , R i , S i се некои постојани величини.

Кога интегрираат рационални дропки, тие прибегнуваат кон разложување на првобитната дропка во елементарни. За да се најдат величините A i , B i , M i , N i , R i , S i , т.н. метод на неизвесни коефициенти, чија суштина е дека за два полиноми да бидат идентично еднакви, потребно е и доволно коефициентите на исти сили на x да бидат еднакви.

Ајде да ја разгледаме употребата на овој метод користејќи конкретен пример.

Пример.

Со намалување на заеднички именител и изедначување на соодветните броители, добиваме:

Пример.

Бидејќи Ако фракцијата е неправилна, прво мора да го изберете целиот нејзин дел:

6x 5 – 8x 4 – 25x 3 + 20x 2 – 76x– 7 3x 3 – 4x 2 – 17x+ 6

6x 5 – 8x 4 – 34x 3 + 12x 2 2x 2 + 3

9x 3 + 8x 2 – 76x - 7

9x 3 – 12x 2 – 51x +18

20x 2 – 25x – 25

Да го факторизираме именителот на добиената дропка. Може да се види дека при x = 3 именителот на дропката се претвора во нула. Потоа:

3x 3 – 4x 2 – 17x+ 6x- 3

3x 3 – 9x 2 3x 2 + 5x- 2

Така 3x 3 – 4x 2 – 17x+ 6 = (x– 3)(3x 2 + 5x– 2) = (x– 3)(x+ 2)(3x– 1). Потоа:

За да се избегне отварање загради, групирање и решавање на систем од равенки (кој во некои случаи може да испадне доста голем) при наоѓање на неизвесни коефициенти, т.н. метод произволни вредности . Суштината на методот е дека неколку (според бројот на неодредени коефициенти) произволни вредности на x се заменети во горенаведениот израз. За да се поедностават пресметките, вообичаено е да се земат како произволни вредности точките во кои именителот на дропот е еднаков на нула, т.е. во нашиот случај – 3, -2, 1/3. Добиваме:

Конечно добиваме:

Пример.

Да ги најдеме неодредените коефициенти:

Тогаш вредноста на дадениот интеграл:

Интеграција на некои тригонометрии

функции.

Може да има бесконечен број интеграли од тригонометриските функции. Повеќето од овие интеграли воопшто не можат да се пресметаат аналитички, па да разгледаме некои главни типовифункции кои секогаш можат да се интегрираат.

Интеграл на формата
.

Овде R е ознаката на некоја рационална функција на променливите sinx и cosx.

Интегралите од овој тип се пресметуваат со помош на замена
. Оваа замена ви овозможува да конвертирате тригонометриска функција во рационална.

Потоа

Така:

Трансформацијата опишана погоре се нарекува универзална тригонометриска замена.

Пример.

Несомнената предност на оваа замена е што со нејзина помош секогаш можете да трансформирате тригонометриска функција во рационална и да го пресметате соодветниот интеграл. Недостатоците го вклучуваат фактот дека трансформацијата може да резултира со прилично сложена рационална функција, чија интеграција ќе потрае многу време и напор.

Меѓутоа, ако е невозможно да се примени порационална замена на променливата, овој метод е единствениот ефективен.

Пример.

Интеграл на формата
Ако

функцијаРcosx.

И покрај можноста за пресметување на таков интеграл со помош на универзалната тригонометриска замена, порационално е да се користи замена т = синкс.

Функција
може да содржи cosx само во парни сили, и затоа може да се претвори во рационална функција во однос на sinx.

Пример.

Општо земено, за да се примени овој метод, неопходна е само необичноста на функцијата во однос на косинусот, а степенот на синусот вклучен во функцијата може да биде кој било, и цел број и фракционо.

Интеграл на формата
Ако

функцијаРе чудно во однос насинкс.

По аналогија со случајот разгледан погоре, замената е направена т = cosx.

Пример.

Интеграл на формата

функцијаРдури и релативносинксИcosx.

За да ја трансформирате функцијата R во рационална, користете ја замената

t = tgx.

Пример.

Интеграл на производот на синусите и косинусите

разни аргументи.

Во зависност од видот на работата, ќе се примени една од трите формули:

Пример.

Понекогаш при интегрирање на тригонометриски функции е погодно да се користат добро познати тригонометриски формули за да се намали редоследот на функциите.

Пример.

Понекогаш се користат некои нестандардни техники.

Пример.

Интеграција на некои ирационални функции.

Не сите ирационална функцијаможе да има интеграл изразен со елементарни функции. За да го пронајдете интегралот на ирационална функција, треба да користите замена што ќе ви овозможи да ја трансформирате функцијата во рационална, чиј интеграл секогаш може да се најде, како што е секогаш познато.

Ајде да погледнеме неколку техники за интегрирање на различни видови ирационални функции.

Интеграл на формата
Кадеn- природен број.

Користење на замена
функцијата е рационализирана.

Пример.

Ако составот на ирационална функција вклучува корени од различни степени, тогаш како нова променлива рационално е да се земе коренот на степен еднаков на најмалиот заеднички множител на степените на корените вклучени во изразот.

Ајде да го илустрираме ова со пример.

Пример.

Интеграција на биномни диференцијали.

Дефиниција: Биномен диференцијалнаречен израз

x м (а + bx n ) стр dx

Каде м, n, И стр– рационални броеви.

Како што беше докажано од академик П.Л. Чебишев. (1821-1894), интегралот на биномниот диференцијал може да се изрази во смисла на елементарни функции само во следните три случаи:

Ако Ре цел број, тогаш интегралот се рационализира со помош на замената

, каде што  е заедничкиот именител мИ n.

Функцијата F(x) се нарекува антидериват за функцијата f(x) на интервалот (a; b) ако f(x) за сите x (a; б) еднаквоста F (x) = f(x). 2

Теорема 1. Ако F(x) е антидериват за f(x) на (a; b), тогаш F(x) + C, каде што C е број, исто така е антидериват за f(x) на (a; б). Доказ: (F + C) = F + C = f + 0 = f 3

Да докажеме две помошни теореми: Ако функцијата g(x) е константна на (a; b), тогаш g (x) = 0. Ако g (x) = 0 за сите x (a; b), тогаш g( x) = C на (а; б). 4

Теорема 2. Ако F(x) е антидериват за f(x) на интервалот (a; b), а G(x) е друг антидериват за f(x) на (a; b), тогаш G = F + C, каде што C е број. 5

Множеството од сите антидеривати за функцијата f(x) на интервалот (a; b) се нарекува неопределен интеграл и се означува со интегралот f(x)dx. dx Пресметување на неопределен интеграл на дадена функцијанаречена интеграција 6

Ако функцијата f(x) е континуирана, а функцијата (t) има континуиран извод (t), тогаш важи формулата: f((t)) (t) dt = f(x) dx, каде што x = ( т). 8

Нека u(x) и v(x) се диференцијабилни функции на некој интервал. Тогаш (uv) = u v + v u Ова имплицира (uv) dx = (u v + v u)dx = = u v dx + v u dx или uv dx = uv – u v dx. 10

Ова имплицира формула наречена формула за интеграција по делови: интеграција по делови u(x)dv(x) = u(x) v(x) – v(x)du(x) 11

Дефинитивен интеграл на функција во интервал е границата до која се стреми интегралната сума за време на овој процес, доколку постои граница: 13

Бројот a се нарекува долна граница на интеграција, а бројот b се нарекува горна граница на интеграција.На слика 2 заоблен трапезистакнати со засенчување. Областа S на овој трапез е одредена со формулата 14

Нека функцијата f(t) е дефинирана и континуирана на некој интервал што содржи точка a. Тогаш на секој број x од овој интервал може да му се додели број, со што ќе се дефинира функцијата I(x) на интервалот, која се нарекува дефинитивен интеграл со променлива горна граница 17

Извод на определен интеграл во однос на горната границаво точката x е еднаква на вредноста на интеграндот во точката x. 18

Нека функцијата y = f(x) е дефинирана и континуирана на полу-бесконечен интервал)