ಪಾಠದ ಪಠ್ಯ ಪ್ರತಿಲೇಖನ:
ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿನ ಒಂದು ಬಿಂದುವಿನ ಮೂಲಕ ಮೂರು ಜೋಡಿಯಾಗಿ ಲಂಬವಾಗಿರುವ ರೇಖೆಗಳನ್ನು ಎಳೆದರೆ, ಪ್ರತಿಯೊಂದರಲ್ಲೂ ಒಂದು ದಿಕ್ಕು ಮತ್ತು ಘಟಕ ವಿಭಾಗವನ್ನು ಆಯ್ಕೆ ಮಾಡಿದರೆ, ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಆಯತಾಕಾರದ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸಲಾಗಿದೆ ಎಂದು ಅವರು ಹೇಳುತ್ತಾರೆ.
ಅವುಗಳ ಮೇಲೆ ಆಯ್ಕೆಮಾಡಿದ ನಿರ್ದೇಶನಗಳೊಂದಿಗೆ ನೇರ ರೇಖೆಗಳನ್ನು ನಿರ್ದೇಶಾಂಕ ಅಕ್ಷಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಈ ಕೆಳಗಿನಂತೆ ಗೊತ್ತುಪಡಿಸಲಾಗಿದೆ: ಆಕ್ಸ್, ಓಯ್, ಓಝ್, ಅವುಗಳ ಸ್ವಂತ ಹೆಸರುಗಳನ್ನು ಹೊಂದಿವೆ: ಅಬ್ಸಿಸ್ಸಾ ಅಕ್ಷ, ಆರ್ಡಿನೇಟ್ ಅಕ್ಷ ಮತ್ತು ಅನ್ವಯಿಸುವ ಅಕ್ಷ, ಮತ್ತು ಅವುಗಳ ಸಾಮಾನ್ಯ ಬಿಂದು- ನಿರ್ದೇಶಾಂಕಗಳ ಮೂಲ. ಇದನ್ನು ಸಾಮಾನ್ಯವಾಗಿ O ಅಕ್ಷರದಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ.
ಸಂಪೂರ್ಣ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯನ್ನು Oxyz ಎಂದು ಗೊತ್ತುಪಡಿಸಲಾಗಿದೆ.
Ox ಮತ್ತು Oy, Oy ಮತ್ತು Oz, Oz ಮತ್ತು Ox ಎಂಬ ನಿರ್ದೇಶಾಂಕ ಅಕ್ಷಗಳ ಮೂಲಕ ವಿಮಾನಗಳನ್ನು ಚಿತ್ರಿಸಿದರೆ, ಅಂತಹ ವಿಮಾನಗಳನ್ನು ನಿರ್ದೇಶಾಂಕ ವಿಮಾನಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಅನುಕ್ರಮವಾಗಿ Oxy, Oyz, Ozx ಎಂದು ಸೂಚಿಸಲಾಗುತ್ತದೆ.
ಪಾಯಿಂಟ್ O ಪ್ರತಿಯೊಂದು ನಿರ್ದೇಶಾಂಕ ಅಕ್ಷಗಳನ್ನು ಎರಡು ಕಿರಣಗಳಾಗಿ ವಿಭಜಿಸುತ್ತದೆ. ಅಕ್ಷದ ದಿಕ್ಕಿನೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾಗುವ ಕಿರಣವನ್ನು ಧನಾತ್ಮಕ ಅರೆ-ಅಕ್ಷ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಮತ್ತು ಇತರ ಕಿರಣವನ್ನು ಋಣಾತ್ಮಕ ಅರೆ-ಅಕ್ಷ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
ಆಯತಾಕಾರದ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ, ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಪ್ರತಿ ಪಾಯಿಂಟ್ M ಟ್ರಿಪಲ್ ಸಂಖ್ಯೆಗಳೊಂದಿಗೆ ಸಂಬಂಧಿಸಿದೆ, ಅದನ್ನು ಅದರ ನಿರ್ದೇಶಾಂಕಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಸಮತಲದ ಮೇಲಿನ ಬಿಂದುಗಳ ನಿರ್ದೇಶಾಂಕಗಳಂತೆಯೇ ಅವುಗಳನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ.
ಅದನ್ನು ಹೇಗೆ ಮಾಡಲಾಗುತ್ತದೆ ಎಂದು ನೋಡೋಣ.
ಪಾಯಿಂಟ್ ಎಂ ಮೂಲಕ ಮೂರು ವಿಮಾನಗಳನ್ನು ಸೆಳೆಯೋಣ, ಅಕ್ಷಗಳಿಗೆ ಲಂಬವಾಗಿನಿರ್ದೇಶಾಂಕಗಳು, ಮತ್ತು M₁, M₂ ಮತ್ತು M₃ ಈ ವಿಮಾನಗಳ ಛೇದಕ ಬಿಂದುಗಳನ್ನು ಅನುಕ್ರಮವಾಗಿ, ಅಬ್ಸಿಸ್ಸಾ, ಆರ್ಡಿನೇಟ್ ಮತ್ತು ಅನ್ವಯಿಸು ಅಕ್ಷಗಳೊಂದಿಗೆ ಸೂಚಿಸುತ್ತವೆ.
ಪಾಯಿಂಟ್ M ನ ಮೊದಲ ನಿರ್ದೇಶಾಂಕವನ್ನು (ಇದನ್ನು ಅಬ್ಸಿಸ್ಸಾ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಸಾಮಾನ್ಯವಾಗಿ x ಅಕ್ಷರದಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ) ಈ ಕೆಳಗಿನಂತೆ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ: x = OM₁, M₁ ಧನಾತ್ಮಕ ಅರೆ-ಅಕ್ಷದ ಬಿಂದುವಾಗಿದ್ದರೆ;
x= - OM₁, M₁ ಋಣಾತ್ಮಕ ಅರೆ-ಅಕ್ಷದ ಬಿಂದುವಾಗಿದ್ದರೆ; x =0 M₁ ಬಿಂದು O ಯೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾದರೆ.
ಅದೇ ರೀತಿ, M₂ ಬಿಂದುವನ್ನು ಬಳಸಿ, M ಬಿಂದುವಿನಲ್ಲಿ ಎರಡನೇ ನಿರ್ದೇಶಾಂಕ (ಆರ್ಡಿನೇಟ್) ಅನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ,
ಮತ್ತು M₃ ಬಿಂದುವನ್ನು ಬಳಸುವುದು - M ಬಿಂದುವಿನ ಮೂರನೇ ನಿರ್ದೇಶಾಂಕ (ಅನ್ವಯಿಸಿ) z.
ಪಾಯಿಂಟ್ M (x; y; z) ನ ಪದನಾಮದ ನಂತರ ಪಾಯಿಂಟ್ M ನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಆವರಣಗಳಲ್ಲಿ ಬರೆಯಲಾಗುತ್ತದೆ.
ಅಬ್ಸಿಸ್ಸಾವನ್ನು ಮೊದಲು ಸೂಚಿಸಲಾಗುತ್ತದೆ, ಆರ್ಡಿನೇಟ್ ಎರಡನೆಯದು ಮತ್ತು ಅರ್ಜಿಯು ಮೂರನೆಯದು ಎಂದು ನೆನಪಿಡಿ.
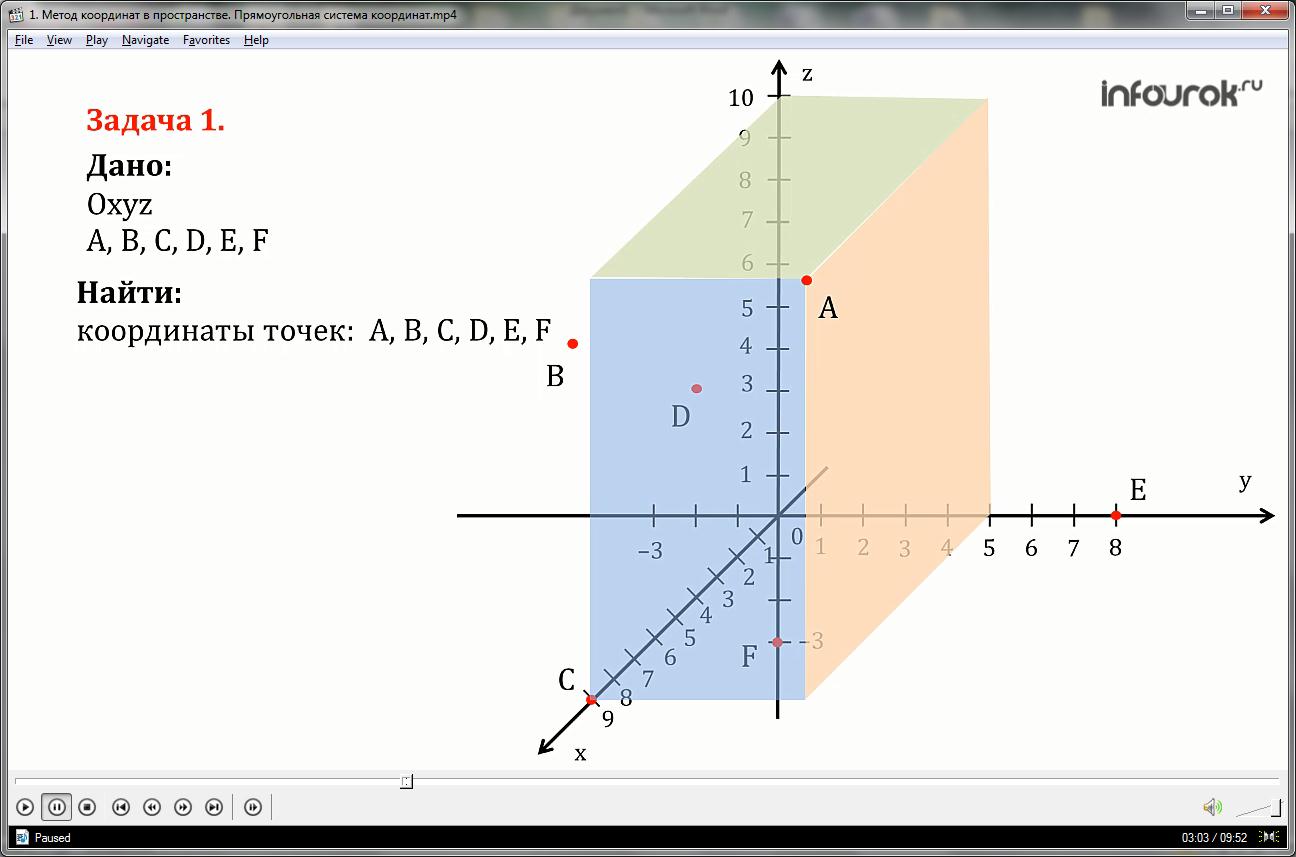
ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವ ಎ, ಬಿ, ಸಿ, ಡಿ, ಇ, ಎಫ್ ಬಿಂದುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ.
ನಿರ್ದೇಶಾಂಕ ಅಕ್ಷಗಳಿಗೆ ಲಂಬವಾಗಿರುವ ಪಾಯಿಂಟ್ A ಮೂಲಕ ಮೂರು ವಿಮಾನಗಳನ್ನು ಸೆಳೆಯೋಣ, ನಂತರ ಈ ಸಮತಲಗಳ ಛೇದನದ ಬಿಂದುಗಳು ಕ್ರಮವಾಗಿ ಅಬ್ಸಿಸ್ಸಾ, ಆರ್ಡಿನೇಟ್ ಮತ್ತು ಅನ್ವಯಿಸುವ ಅಕ್ಷಗಳು, ಪಾಯಿಂಟ್ A ನ ನಿರ್ದೇಶಾಂಕಗಳಾಗಿರುತ್ತದೆ. ಪಾಯಿಂಟ್ A ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ: abscissa = 9, ಆರ್ಡಿನೇಟ್ = 5, ಅರ್ಜಿ = 10 ಮತ್ತು ಇದನ್ನು ಈ ರೀತಿ ಬರೆಯಲಾಗಿದೆ: ಎ (9; 5; 10).
ಕೆಳಗಿನ ಬಿಂದುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಇದೇ ರೀತಿ ಬರೆಯಲಾಗಿದೆ:
ಪಾಯಿಂಟ್ B ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ: abscissa = 4, ಆರ್ಡಿನೇಟ್ = -3, ಅನ್ವಯಿಸು = 6
ಪಾಯಿಂಟ್ C ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ: abscissa = 9, ಆರ್ಡಿನೇಟ್ = 0, ಅನ್ವಯಿಸು = 0
ಬಿಂದುವು D ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ: abscissa = 4, ಆರ್ಡಿನೇಟ್ = 0, ಅನ್ವಯಿಸು = 5
ಪಾಯಿಂಟ್ E ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ: abscissa = 0, ಆರ್ಡಿನೇಟ್ = 8, ಅನ್ವಯಿಸು = 0
ಪಾಯಿಂಟ್ ಎಫ್ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ: abscissa = 0, ಆರ್ಡಿನೇಟ್ = 0, ಅನ್ವಯಿಸು = -3
ಒಂದು ಬಿಂದು M (x; y; z) ನಿರ್ದೇಶಾಂಕ ಅಕ್ಷದ ಮೇಲೆ ನಿರ್ದೇಶಾಂಕ ಸಮತಲದಲ್ಲಿ ಇದ್ದರೆ, ಅದರ ಕೆಲವು ನಿರ್ದೇಶಾಂಕಗಳು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
MЄОху (ಪಾಯಿಂಟ್ M ಆಕ್ಸಿ ಪ್ಲೇನ್ಗೆ ಸೇರಿದ್ದರೆ), ಆಗ ಪಾಯಿಂಟ್ M ನ ಅನ್ವಯವು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ: z=0.
ಹಾಗೆಯೇ, МЄОхz (ಪಾಯಿಂಟ್ M Oxz ಸಮತಲಕ್ಕೆ ಸೇರಿದ್ದರೆ), ನಂತರ y = 0, ಮತ್ತು МЄОуz (ಪಾಯಿಂಟ್ M Oyz ಸಮತಲಕ್ಕೆ ಸೇರಿದ್ದರೆ), ನಂತರ x = 0.
МЄОх (ಪಾಯಿಂಟ್ M ಅಬ್ಸಿಸ್ಸಾ ಅಕ್ಷದ ಮೇಲೆ ಇದ್ದರೆ), ಪಾಯಿಂಟ್ M ನ ಆರ್ಡಿನೇಟ್ ಮತ್ತು ಅನ್ವಯಿಸುವಿಕೆಯು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ: y=o ಮತ್ತು z=0. ನಮ್ಮ ಉದಾಹರಣೆಯಲ್ಲಿ, ಇದು ಪಾಯಿಂಟ್ ಸಿ ಆಗಿದೆ.
МЄОу (ಪಾಯಿಂಟ್ M ಆರ್ಡಿನೇಟ್ ಮೇಲೆ ಇರುತ್ತದೆ), ನಂತರ x=0 ಮತ್ತು z=0. ನಮ್ಮ ಉದಾಹರಣೆಯಲ್ಲಿ, ಇದು ಪಾಯಿಂಟ್ ಇ.
МЄОz (ಪಾಯಿಂಟ್ M ಅಪ್ಲಿಕೇಶನ್ ಅಕ್ಷದ ಮೇಲೆ ಇರುತ್ತದೆ), ನಂತರ x = 0 ಮತ್ತು y = 0. ನಮ್ಮ ಉದಾಹರಣೆಯಲ್ಲಿ, ಇದು ಪಾಯಿಂಟ್ F ಆಗಿದೆ.
ಪಾಯಿಂಟ್ M ನ ಎಲ್ಲಾ ಮೂರು ನಿರ್ದೇಶಾಂಕಗಳು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿದ್ದರೆ, ಇದರರ್ಥ M=O (0; 0; 0) ನಿರ್ದೇಶಾಂಕಗಳ ಮೂಲವಾಗಿದೆ.
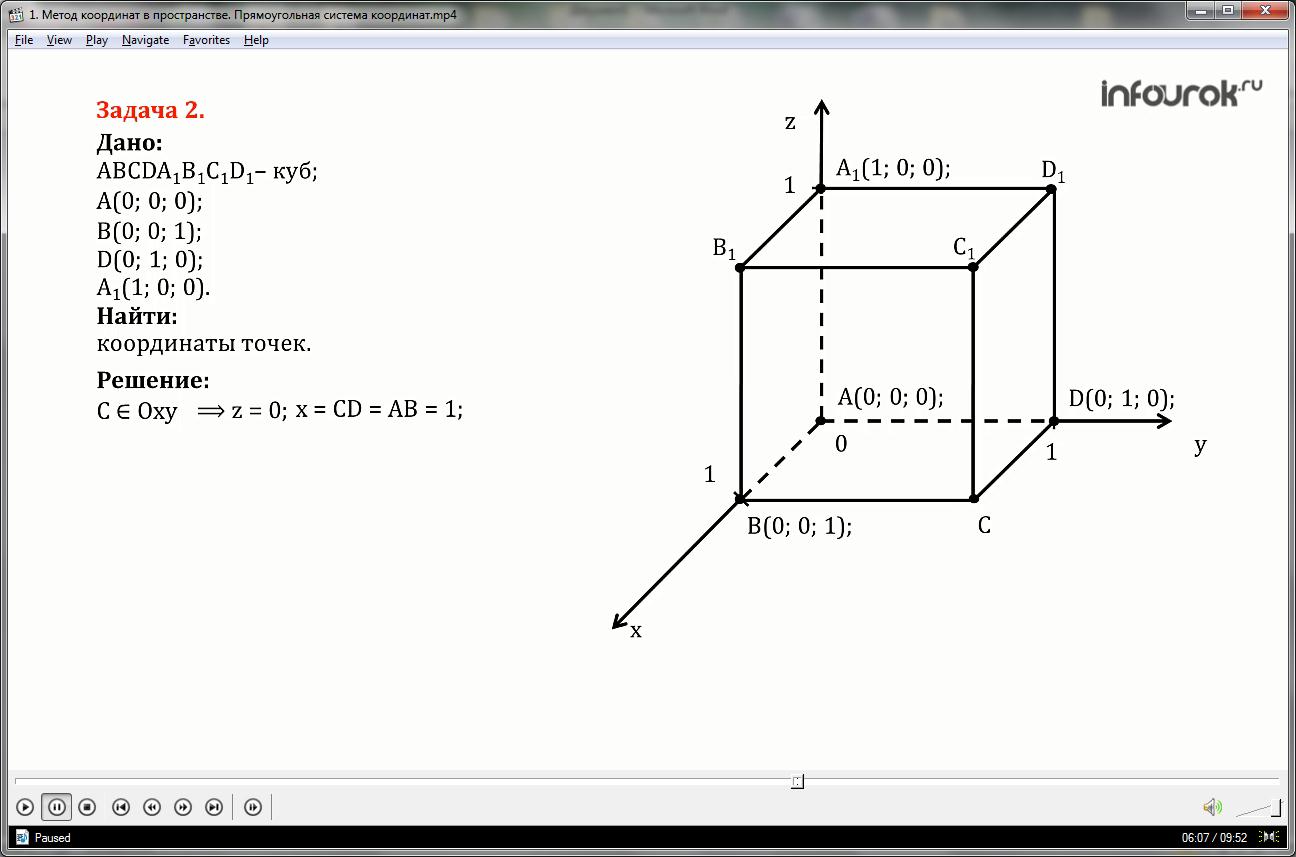
ಘನ ABCDA 1 B 1 C 1 D 1: A(0; 0; 0) ನ ನಾಲ್ಕು ಶೃಂಗಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ನೀಡಲಾಗಿದೆ; ಬಿ(0; 0; 1); ಡಿ(0; 1; 0); A 1 (1; 0; 0). ಘನದ ಉಳಿದ ಶೃಂಗಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹುಡುಕಿ.
ಆಕೃತಿಯು ಘನವಾಗಿರುವುದರಿಂದ, ಎಲ್ಲಾ ಬದಿಗಳು ಒಂದಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಎಲ್ಲಾ ಮುಖಗಳು ಚೌಕಗಳಾಗಿವೆ.
ಪಾಯಿಂಟ್ ಸಿ ಆಕ್ಸಿ ಪ್ಲೇನ್ಗೆ ಸೇರಿದೆ, ಅಂದರೆ, ಅದರ z ನಿರ್ದೇಶಾಂಕವು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, x ನಿರ್ದೇಶಾಂಕವು ಸೈಡ್ ಸಿಡಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಮತ್ತು ಎಬಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ ಅದು ಒಂದಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ, ನಿರ್ದೇಶಾಂಕ Y ಬದಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಘನ CB ನ, ಅಂದರೆ ಅದು AD ಗೆ ಸಮ ಮತ್ತು ಒಂದಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ.
ಅಂತೆಯೇ, ಪಾಯಿಂಟ್ B 1 Oxz ಸಮತಲಕ್ಕೆ ಸೇರಿದೆ, ಅಂದರೆ, ಅದರ y ನಿರ್ದೇಶಾಂಕವು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, x ನಿರ್ದೇಶಾಂಕವು ಬದಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, x ನಿರ್ದೇಶಾಂಕವು A1B1 ಬದಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಮತ್ತು AB ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಒಂದು, z ನಿರ್ದೇಶಾಂಕವು ಘನ B B1 ನ ಬದಿಗೆ ಸಮನಾಗಿರುತ್ತದೆ, ಅಂದರೆ AA1 ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಮತ್ತು ಒಂದಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ.
ಪಾಯಿಂಟ್ D 1 Oyz ಸಮತಲಕ್ಕೆ ಸೇರಿದೆ, ಅಂದರೆ, ಅದರ x ನಿರ್ದೇಶಾಂಕವು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, y ನಿರ್ದೇಶಾಂಕವು A 1 D 1 ಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಮತ್ತು AD ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ ಅದು ಒಂದಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ, z ನಿರ್ದೇಶಾಂಕವು ಸಮಾನವಾಗಿರುತ್ತದೆ ಘನ A 1 B 1 ನ ಬದಿಗೆ, ಅಂದರೆ ಅದು AB ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಮತ್ತು ಒಂದಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ.
ಪಾಯಿಂಟ್ C 1 ಯಾವುದೇ ಸಮತಲಕ್ಕೆ ಸೇರಿಲ್ಲ, ಅಂದರೆ, ಎಲ್ಲಾ ನಿರ್ದೇಶಾಂಕಗಳು ಶೂನ್ಯದಿಂದ ಭಿನ್ನವಾಗಿರುತ್ತವೆ, x ನಿರ್ದೇಶಾಂಕವು C 1 D 1 ಬದಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಮತ್ತು AB ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ ಅದು ಒಂದಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ, ನಿರ್ದೇಶಾಂಕ y ಘನ B 1 C 1 ನ ಬದಿಗೆ ಸಮನಾಗಿರುತ್ತದೆ, ಅಂದರೆ ಅದು AD ಗೆ ಸಮನಾಗಿರುತ್ತದೆ ಮತ್ತು ಒಂದಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ ಮತ್ತು z ನಿರ್ದೇಶಾಂಕವು CC 1 ಬದಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ AA 1 ಮತ್ತು ಒಂದಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
Oxy, Oxz, Oyz ಮತ್ತು ನಿರ್ದೇಶಾಂಕ ಅಕ್ಷಗಳು Ox, Oy, Oz ನಿರ್ದೇಶಾಂಕ ವಿಮಾನಗಳ ಮೇಲೆ ಪಾಯಿಂಟ್ C(; ;) ನ ಪ್ರಕ್ಷೇಪಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹುಡುಕಿ.
1) ಆಕ್ಸಿ ಪ್ಲೇನ್ಗೆ ಲಂಬವಾಗಿ ಬಿಡಿ - ಇದು CN, Oxz ಪ್ಲೇನ್ಗೆ - CL ಮತ್ತು Oyz ಪ್ಲೇನ್ಗೆ - ಲೈನ್ CR ಗೆ.
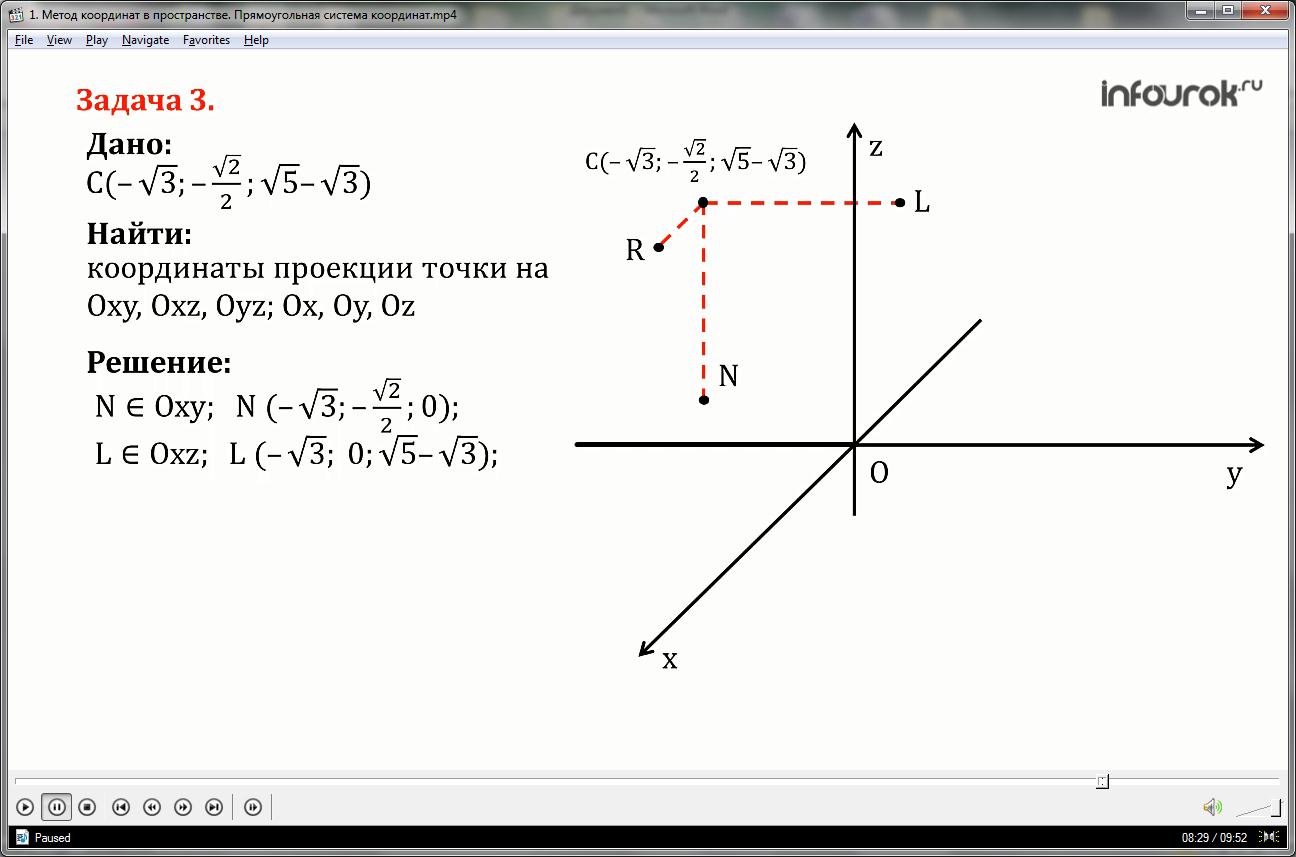
ಹೀಗಾಗಿ, ಆಕ್ಸಿ ಪ್ಲೇನ್ಗೆ ಬಿಂದು C ಯ ಪ್ರಕ್ಷೇಪಣವು ಪಾಯಿಂಟ್ N ಆಗಿರುತ್ತದೆ ಮತ್ತು ಇದು ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ x ಸಮನಾದ ಮೈನಸ್ ರೂಟ್ ಮೂರು, y ಸಮನಾದ ಮೈನಸ್ ರೂಟ್ ಎರಡರಿಂದ ಎರಡು, z ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
Oxz ಸಮತಲದ ಮೇಲೆ C ಬಿಂದುವಿನ ಪ್ರಕ್ಷೇಪಣವು ಪಾಯಿಂಟ್ L ಆಗಿದೆ ಮತ್ತು ಇದು ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ x ಮೂರು ಮೈನಸ್ ರೂಟ್ಗೆ ಸಮನಾಗಿರುತ್ತದೆ, i ಶೂನ್ಯಕ್ಕೆ ಸಮ, z ಮೂಲಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆಐದರಿಂದ ಮೂರರ ಮೂಲವನ್ನು ಕಳೆಯಿರಿ.
Oyz ಸಮತಲಕ್ಕೆ C ಬಿಂದುವಿನ ಪ್ರಕ್ಷೇಪಣವು ಪಾಯಿಂಟ್ R ಆಗಿದೆ ಮತ್ತು ಇದು ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ x ಶೂನ್ಯಕ್ಕೆ ಸಮ, y ಎರಡು ಮೈನಸ್ ರೂಟ್ಗೆ ಸಮನಾಗಿರುತ್ತದೆ, z ಎಂಬುದು ಮೂರರ ಐದು ಮೈನಸ್ ಮೂಲಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
2) ಬಿಂದುವಿನಿಂದ N ನಾವು ಆಕ್ಸ್ ಅಕ್ಷಕ್ಕೆ ಲಂಬವಾಗಿ ಸೆಳೆಯುತ್ತೇವೆ - ನೇರ ರೇಖೆ NK, ಮತ್ತು Oy - ನೇರ ರೇಖೆ NG, ಮತ್ತು Oz ಅಕ್ಷಕ್ಕೆ ನಾವು R ಬಿಂದುವಿನಿಂದ ಲಂಬವಾಗಿ ಸೆಳೆಯುತ್ತೇವೆ - ಇದು ನೇರ ರೇಖೆ RP ಆಗಿದೆ.
ಆಕ್ಸ್ ಅಕ್ಷದ ಮೇಲೆ ಬಿಂದು C ಯ ಪ್ರಕ್ಷೇಪಣ - ಪಾಯಿಂಟ್ K ನ ನಿರ್ದೇಶಾಂಕಗಳು x ಅನ್ನು ಮೈನಸ್ ಮೂರರ ಮೂಲಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ ಮತ್ತು y ಮತ್ತು z ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
Oy ಅಕ್ಷದ ಮೇಲೆ C ಬಿಂದುವಿನ ಪ್ರಕ್ಷೇಪಣ - ಪಾಯಿಂಟ್ G ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾದ x ಮತ್ತು z ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ, i ಎರಡರಿಂದ ಎರಡು ಮೂಲವನ್ನು ಮೈನಸ್ ಮಾಡಲು ಸಮಾನವಾಗಿರುತ್ತದೆ.
Oz ಅಕ್ಷದ ಮೇಲೆ ಪಾಯಿಂಟ್ C ನ ಪ್ರಕ್ಷೇಪಣ - ಪಾಯಿಂಟ್ P ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾದ x ಮತ್ತು y ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ, z ಸಮಾನ ಮೂಲಐದರಿಂದ ಮೂರರ ಮೂಲವನ್ನು ಕಳೆಯಿರಿ.
ಶಿಕ್ಷಣ ಸಚಿವಾಲಯ ರಷ್ಯ ಒಕ್ಕೂಟ
ಪುರಸಭೆ ಶೈಕ್ಷಣಿಕ ಸಂಸ್ಥೆ"ಸರಾಸರಿ ಮಾಧ್ಯಮಿಕ ಶಾಲೆಸಂಖ್ಯೆ 18"
ಅಮೂರ್ತ
ಜ್ಯಾಮಿತಿಯಿಂದ
ವಿಷಯ: ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ನಿರ್ದೇಶಾಂಕಗಳ ವಿಧಾನ
11 ನೇ ತರಗತಿಯ ವಿದ್ಯಾರ್ಥಿ "ಸಿ" ಪೂರ್ಣಗೊಳಿಸಿದ್ದಾರೆ
ಮೆಲ್ನಿಕ್ ರೋಮನ್
ಮೇಲ್ವಿಚಾರಕ
ಗಣಿತ ಶಿಕ್ಷಕ ಬಕ್ಷೀವಾ I.K.
ಬೈಸ್ಕ್ - 2008
ವಿಷಯ
ಪರಿಚಯ……………………………………………………………..… 3.
ಅಧ್ಯಾಯ 1.
ಸಮನ್ವಯ ವಿಧಾನ: ಅಭಿವೃದ್ಧಿಯ ಇತಿಹಾಸ ………………………………………… 4
ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಒಂದು ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳು…………………………………………5
ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಅಂಕಿಗಳನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುವುದು …………………………………………………… 8
ಅಧ್ಯಾಯ 2.
ನಿರ್ದೇಶಾಂಕ ವಾಹಕಗಳಾಗಿ ವೆಕ್ಟರ್ನ ವಿಭಜನೆ. ನಿರ್ದೇಶಾಂಕಗಳು
ವೆಕ್ಟರ್ ………………………………………………………………………………… ..10
ರೇಖೀಯ ಕಾರ್ಯಾಚರಣೆಗಳುನಿರ್ದೇಶಾಂಕಗಳಲ್ಲಿ ವಾಹಕಗಳ ಮೇಲೆ ………………………………12
ನಿರ್ದೇಶಾಂಕಗಳಲ್ಲಿ ಎರಡು ವೆಕ್ಟರ್ಗಳ ಕೋಲಿನಿಯರಿಟಿಯ ಸ್ಥಿತಿ ……..13
ನಿರ್ದೇಶಾಂಕಗಳಲ್ಲಿನ ಸರಳವಾದ ಸಮಸ್ಯೆಗಳು ………………………………………….14
ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನವಾಹಕಗಳು ಮತ್ತು ಅವುಗಳ ನಿರ್ದೇಶಾಂಕಗಳ ಮೂಲಕ ವೆಕ್ಟರ್ಗಳ ನಡುವಿನ ಕೋನವನ್ನು ಲೆಕ್ಕಹಾಕುವುದು ………………………………………………………… 15
ನೇರ ರೇಖೆಗಳು ಮತ್ತು ಸಮತಲಗಳ ನಡುವಿನ ಕೋನಗಳ ಲೆಕ್ಕಾಚಾರ ………………………….16
4. ಅಧ್ಯಾಯ 3.
4.1. ಅಪ್ಲಿಕೇಶನ್ ಸಮನ್ವಯ ವಿಧಾನಸ್ಟೀರಿಯೊಮೆಟ್ರಿಕ್ ಅನ್ನು ಪರಿಹರಿಸಲು
ಕಾರ್ಯಗಳು ………………………………………………………..…………….. 19
ತೀರ್ಮಾನ. …………………………………………………………………..26
ಗ್ರಂಥಸೂಚಿ…………………………………………………… 27
ಪರಿಚಯ
ನನ್ನ ಕೆಲಸದ ವಿಷಯವೆಂದರೆ "ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ನಿರ್ದೇಶಾಂಕಗಳ ವಿಧಾನ." ಈ ವಿಷಯಯಾವುದೇ ಪದವೀಧರರಿಗೆ ಇಂದು ಪ್ರಸ್ತುತವಾಗಿದೆ ಪ್ರೌಢಶಾಲೆಏಕೆಂದರೆ:
ಕೆಲಸದ ಗುರಿ: ಈ ವಿಷಯದ ಬಗ್ಗೆ ಜ್ಞಾನವನ್ನು ವ್ಯವಸ್ಥಿತಗೊಳಿಸಿ ಮತ್ತು ಅಪ್ಲಿಕೇಶನ್ ಅನ್ನು ಪರಿಗಣಿಸಿ ಈ ವಿಧಾನವಿವಿಧ ಸ್ಟೀರಿಯೊಮೆಟ್ರಿಕ್ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸುವಾಗ.
ಗುರಿಯನ್ನು ಸಾಧಿಸಲು, ಈ ಕೆಳಗಿನವುಗಳನ್ನು ಹೊಂದಿಸಲಾಗಿದೆ ಕಾರ್ಯಗಳು:
ಅನೇಕ ಪರೀಕ್ಷೆಗಳನ್ನು ಅನುಮತಿಸುತ್ತದೆ ಜ್ಯಾಮಿತೀಯ ಸಮಸ್ಯೆಗಳುವಿಶ್ಲೇಷಣಾತ್ಮಕವಾಗಿ ಪರಿಹರಿಸಿ, ಇದು ಜ್ಯಾಮಿತಿಯ ಕಡಿಮೆ ಜ್ಞಾನದ ಅಗತ್ಯವಿರುತ್ತದೆ ಮತ್ತು ಮರಣದಂಡನೆಯ ಸಮಯವನ್ನು ಗಮನಾರ್ಹವಾಗಿ ಕಡಿಮೆ ಮಾಡುತ್ತದೆ;
ಈ ವಿಧಾನವು ವಿಶ್ಲೇಷಣಾತ್ಮಕ ಜ್ಯಾಮಿತಿಗೆ ಆಧಾರವಾಗಿದೆ, ಇದನ್ನು ಉನ್ನತ ಗಣಿತದ ಕೋರ್ಸ್ನಲ್ಲಿ ಅಧ್ಯಯನ ಮಾಡಲಾಗುತ್ತದೆ.
ವಿಷಯದ ಬಗ್ಗೆ ಸೈದ್ಧಾಂತಿಕ ವಸ್ತುಗಳನ್ನು ಅಧ್ಯಯನ ಮಾಡಿ;
ಅಧ್ಯಯನ ಮಾಡಿದ ವಸ್ತುವನ್ನು ವ್ಯವಸ್ಥಿತಗೊಳಿಸಿ ಮತ್ತು ಸಾರಾಂಶಗೊಳಿಸಿ;
ವಿಧಾನವನ್ನು ಬಳಸುವ ವೈಶಿಷ್ಟ್ಯಗಳನ್ನು ಗುರುತಿಸಿ;
ಸ್ಟೀರಿಯೊಮೆಟ್ರಿಕ್ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸಲು ನಿರ್ದೇಶಾಂಕ ವಿಧಾನದ ಅನ್ವಯವನ್ನು ಪರಿಗಣಿಸಿ;
ಸ್ಟಿರಿಯೊಮೆಟ್ರಿಕ್ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸಲು ಇತರ ವಿಧಾನಗಳೊಂದಿಗೆ ನಿರ್ದೇಶಾಂಕ ವಿಧಾನದ ಅಪ್ಲಿಕೇಶನ್ ಅನ್ನು ಹೋಲಿಕೆ ಮಾಡಿ.
ಬಳಸಿದ ವಿಧಾನಗಳು :
ವಿಶ್ಲೇಷಣೆ ಮತ್ತು ಸಂಶ್ಲೇಷಣೆಯ ವಿಧಾನ,
ಹೋಲಿಕೆ ವಿಧಾನ.
ಅಧ್ಯಾಯ 1
1. ಸಮನ್ವಯ ವಿಧಾನ: ಅಭಿವೃದ್ಧಿಯ ಇತಿಹಾಸ.
ನಿರ್ದೇಶಾಂಕ ವಿಧಾನವು ಸಂಖ್ಯೆಗಳು ಅಥವಾ ಇತರ ಚಿಹ್ನೆಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಒಂದು ಬಿಂದು ಅಥವಾ ದೇಹದ ಸ್ಥಾನವನ್ನು ನಿರ್ಧರಿಸುವ ಒಂದು ಮಾರ್ಗವಾಗಿದೆ.
ಬಿಂದುವಿನ ಸ್ಥಾನವನ್ನು ನಿರ್ಧರಿಸಲು ಬಳಸುವ ಸಂಖ್ಯೆಗಳನ್ನು ಪಾಯಿಂಟ್ ನಿರ್ದೇಶಾಂಕಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
ನಮಗೆ ಚಿರಪರಿಚಿತ ಭೌಗೋಳಿಕ ನಿರ್ದೇಶಾಂಕಗಳುಭೂಮಿಯ ಮೇಲ್ಮೈಯಲ್ಲಿ ಒಂದು ಬಿಂದುವಿನ ಸ್ಥಾನವನ್ನು ನಿರ್ಧರಿಸಿ - ಪ್ರತಿ ಬಿಂದು ಭೂಮಿಯ ಮೇಲ್ಮೈಎರಡು ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ: ಅಕ್ಷಾಂಶ ಮತ್ತು ರೇಖಾಂಶ.
ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಒಂದು ಬಿಂದುವಿನ ಸ್ಥಾನವನ್ನು ನಿರ್ಧರಿಸಲು, ಮೂರು ಸಂಖ್ಯೆಗಳು ಅಗತ್ಯವಿದೆ. ಉದಾಹರಣೆಗೆ, ಉಪಗ್ರಹದ ಸ್ಥಾನವನ್ನು ನಿರ್ಧರಿಸಲು, ನೀವು ಭೂಮಿಯ ಮೇಲ್ಮೈಗಿಂತ ಅದರ ಎತ್ತರವನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸಬಹುದು, ಹಾಗೆಯೇ ಅದು ಇರುವ ಬಿಂದುವಿನ ಅಕ್ಷಾಂಶ ಮತ್ತು ರೇಖಾಂಶವನ್ನು ಸೂಚಿಸಬಹುದು.
ನಿರ್ದೇಶಾಂಕ ವಿಧಾನವನ್ನು ಬಳಸಿಕೊಂಡು, ನೀವು ಬಹುತೇಕ ಸಂಪೂರ್ಣ ಶಾಲಾ ರೇಖಾಗಣಿತ ಕೋರ್ಸ್ ಅನ್ನು ಒಂದೇ ರೇಖಾಚಿತ್ರವಿಲ್ಲದೆ ಪ್ರಸ್ತುತಪಡಿಸಬಹುದು, ಕೇವಲ ಸಂಖ್ಯೆಗಳನ್ನು ಬಳಸಿ ಮತ್ತು ಬೀಜಗಣಿತದ ಕಾರ್ಯಾಚರಣೆಗಳು. ಉದಾಹರಣೆಗೆ, ವೃತ್ತವನ್ನು ಸಮೀಕರಣವನ್ನು ಪೂರೈಸುವ ಬಿಂದುಗಳ ಸೆಟ್ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಬಹುದು ಮತ್ತು ಸರಳ ರೇಖೆಯನ್ನು ಸಮೀಕರಣವನ್ನು ಪೂರೈಸುವ ಬಿಂದುಗಳ ಸೆಟ್ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಬಹುದು.  . ಹೀಗಾಗಿ, ಈ ವಿಧಾನದ ಸಹಾಯದಿಂದ ತೋರಿಕೆಯಲ್ಲಿ ಸಂಪೂರ್ಣವಾಗಿ ಒಟ್ಟಿಗೆ ಸಂಪರ್ಕಿಸಲು ಸಾಧ್ಯವಾಯಿತು ವಿವಿಧ ವಿಜ್ಞಾನಗಳುಬೀಜಗಣಿತ ಮತ್ತು ಜ್ಯಾಮಿತಿ. ಈ ಸಂಪರ್ಕವು ಮೂಲಭೂತವಾಗಿ, ಗಣಿತಶಾಸ್ತ್ರದಲ್ಲಿ ಒಂದು ಕ್ರಾಂತಿಯಾಗಿದೆ. ಇದು ಗಣಿತವನ್ನು ಏಕೀಕೃತ ವಿಜ್ಞಾನವಾಗಿ ಮರುಸ್ಥಾಪಿಸಿತು.
. ಹೀಗಾಗಿ, ಈ ವಿಧಾನದ ಸಹಾಯದಿಂದ ತೋರಿಕೆಯಲ್ಲಿ ಸಂಪೂರ್ಣವಾಗಿ ಒಟ್ಟಿಗೆ ಸಂಪರ್ಕಿಸಲು ಸಾಧ್ಯವಾಯಿತು ವಿವಿಧ ವಿಜ್ಞಾನಗಳುಬೀಜಗಣಿತ ಮತ್ತು ಜ್ಯಾಮಿತಿ. ಈ ಸಂಪರ್ಕವು ಮೂಲಭೂತವಾಗಿ, ಗಣಿತಶಾಸ್ತ್ರದಲ್ಲಿ ಒಂದು ಕ್ರಾಂತಿಯಾಗಿದೆ. ಇದು ಗಣಿತವನ್ನು ಏಕೀಕೃತ ವಿಜ್ಞಾನವಾಗಿ ಮರುಸ್ಥಾಪಿಸಿತು.
ನಿರ್ದೇಶಾಂಕ ವಿಧಾನದ ಸೃಷ್ಟಿಕರ್ತರನ್ನು ಫ್ರೆಂಚ್ ತತ್ವಜ್ಞಾನಿ ಮತ್ತು ಗಣಿತಜ್ಞ ರೆನೆ ಡೆಸ್ಕಾರ್ಟೆಸ್ (1596-1650) ಎಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ, ಅವರು 1637 ರಲ್ಲಿ ಪ್ರಕಟವಾದ ಡೆಸ್ಕಾರ್ಟೆಸ್ನ ದೊಡ್ಡ ತಾತ್ವಿಕ ಗ್ರಂಥದ ಕೊನೆಯ ಭಾಗದಲ್ಲಿ, ಜ್ಯಾಮಿತೀಯ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸಲು ನಿರ್ದೇಶಾಂಕ ವಿಧಾನ ಮತ್ತು ಅದರ ಅನ್ವಯವನ್ನು ವಿವರಿಸಿದರು.
ಡೆಸ್ಕಾರ್ಟೆಸ್ ಅವರ ಆಲೋಚನೆಗಳ ಬೆಳವಣಿಗೆಯು ಗಣಿತಶಾಸ್ತ್ರದ ವಿಶೇಷ ಶಾಖೆಯ ಹೊರಹೊಮ್ಮುವಿಕೆಗೆ ಕಾರಣವಾಯಿತು, ಇದನ್ನು ಈಗ ವಿಶ್ಲೇಷಣಾತ್ಮಕ ರೇಖಾಗಣಿತ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
ಈ ಹೆಸರು ಸ್ವತಃ ಸಿದ್ಧಾಂತದ ಮೂಲ ಕಲ್ಪನೆಯನ್ನು ವ್ಯಕ್ತಪಡಿಸುತ್ತದೆ. ವಿಶ್ಲೇಷಣಾತ್ಮಕ ಜ್ಯಾಮಿತಿಯು ಗಣಿತಶಾಸ್ತ್ರದ ಭಾಗವಾಗಿದ್ದು, ಜ್ಯಾಮಿತೀಯ ಸಮಸ್ಯೆಗಳನ್ನು ವಿಶ್ಲೇಷಣಾತ್ಮಕವಾಗಿ (ಅಂದರೆ ಬೀಜಗಣಿತವಾಗಿ) ಪರಿಹರಿಸುತ್ತದೆ.
ಡೆಸ್ಕಾರ್ಟೆಸ್ ಜೊತೆಗೆ, ವಿಶ್ಲೇಷಣಾತ್ಮಕ ರೇಖಾಗಣಿತದ ಸ್ಥಾಪಕ ಗಮನಾರ್ಹ ಫ್ರೆಂಚ್ ಗಣಿತಜ್ಞ P. ಫೆರ್ಮಾಟ್. ನಿರ್ದೇಶಾಂಕ ವಿಧಾನವನ್ನು ಬಳಸಿಕೊಂಡು, ಫೆರ್ಮಾಟ್ ನೇರ ರೇಖೆಗಳು ಮತ್ತು ಎರಡನೇ ಕ್ರಮಾಂಕದ ವಕ್ರಾಕೃತಿಗಳನ್ನು ಅಧ್ಯಯನ ಮಾಡಿದರು. ಮೂರು ಆಯಾಮದ ಜಾಗದಲ್ಲಿ ವಿಶ್ಲೇಷಣಾತ್ಮಕ ರೇಖಾಗಣಿತದ ಅಧ್ಯಯನವು 18 ನೇ ಶತಮಾನದಲ್ಲಿ A. ಕ್ಲೈರಾಟ್ ಅವರಿಂದ ಗಮನಾರ್ಹವಾಗಿ ಮುಂದುವರೆದಿದೆ. ಸಮತಲದಲ್ಲಿ ಮತ್ತು ಒಳಗೆ ಸ್ಪಷ್ಟವಾಗಿ ಮತ್ತು ಸ್ಥಿರವಾಗಿ ವಿಶ್ಲೇಷಣಾತ್ಮಕ ರೇಖಾಗಣಿತ ಮೂರು ಆಯಾಮದ ಜಾಗ L. ಯೂಲರ್ ಅವರು 1748 ರಲ್ಲಿ ಪಠ್ಯಪುಸ್ತಕದಲ್ಲಿ "ಇಂಟ್ರೊಡಕ್ಷನ್ ಟು ದಿ ಅನಾಲಿಸಿಸ್ ಆಫ್ ಇನ್ಫಿನೈಟ್ಸ್" ನಲ್ಲಿ ವಿವರಿಸಿದ್ದಾರೆ.
IN XIXಶತಮಾನದಲ್ಲಿ, ಜ್ಯಾಮಿತಿಯ ಅಭಿವೃದ್ಧಿಯಲ್ಲಿ ಮತ್ತೊಂದು ಹಂತವನ್ನು ತೆಗೆದುಕೊಳ್ಳಲಾಗಿದೆ - ಬಹುಆಯಾಮದ ಸ್ಥಳಗಳನ್ನು ಅಧ್ಯಯನ ಮಾಡಲಾಯಿತು. ಸಿದ್ಧಾಂತದ ಸೃಷ್ಟಿಕರ್ತರಿಗೆ ಮುಖ್ಯ ಕಲ್ಪನೆಯು ಡೆಸ್ಕಾರ್ಟೆಸ್ನ "ಜ್ಯಾಮಿತಿ" ಯೊಂದಿಗೆ ಸಾದೃಶ್ಯವಾಗಿದೆ. ವಿಮಾನದಲ್ಲಿ ಅವರ ಪಾಯಿಂಟ್ ಒಂದು ಜೋಡಿ ಸಂಖ್ಯೆಗಳು 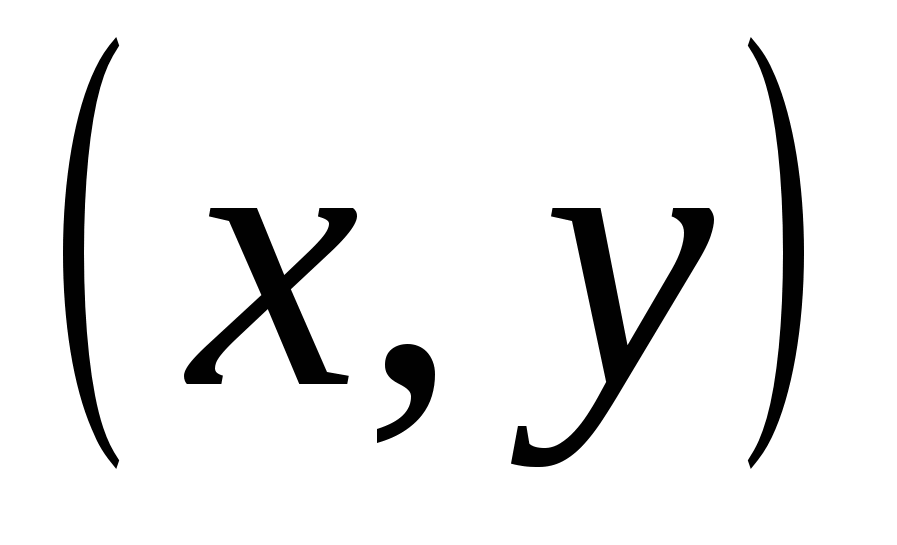 , ಮೂರು ಆಯಾಮದ ಜಾಗದಲ್ಲಿ ಒಂದು ಬಿಂದು - ಸಂಖ್ಯೆಗಳ ಟ್ರಿಪಲ್
, ಮೂರು ಆಯಾಮದ ಜಾಗದಲ್ಲಿ ಒಂದು ಬಿಂದು - ಸಂಖ್ಯೆಗಳ ಟ್ರಿಪಲ್ 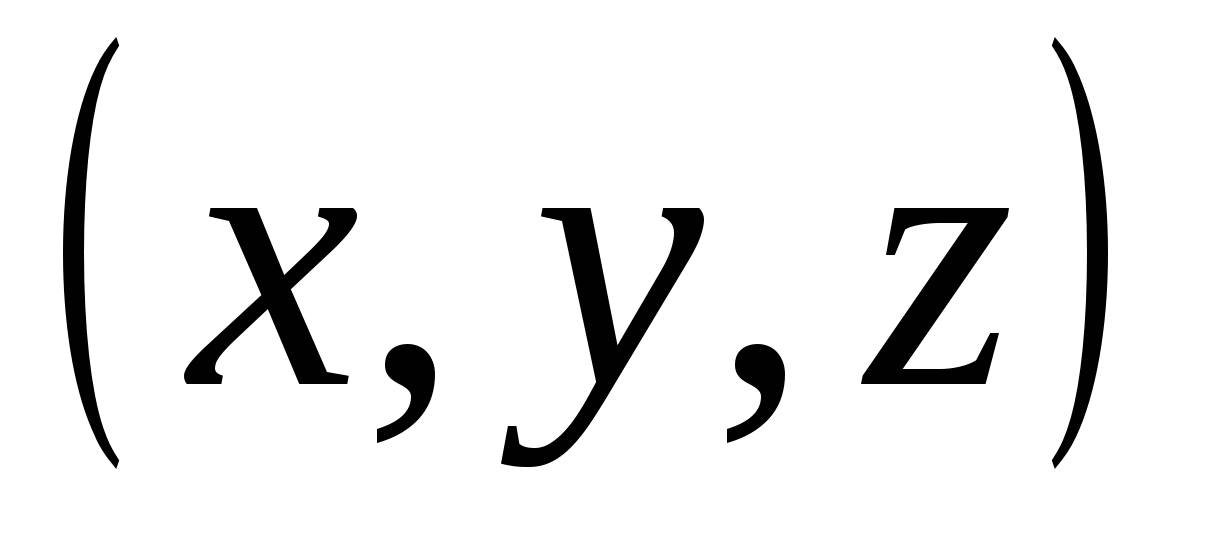 ; ವಿ ಹೊಸ ಸಿದ್ಧಾಂತನಾಲ್ಕು ಆಯಾಮದ ಜಾಗದಲ್ಲಿ ಒಂದು ಬಿಂದುವು ಸಂಖ್ಯೆಗಳ ನಾಲ್ಕು ಪಟ್ಟು
; ವಿ ಹೊಸ ಸಿದ್ಧಾಂತನಾಲ್ಕು ಆಯಾಮದ ಜಾಗದಲ್ಲಿ ಒಂದು ಬಿಂದುವು ಸಂಖ್ಯೆಗಳ ನಾಲ್ಕು ಪಟ್ಟು 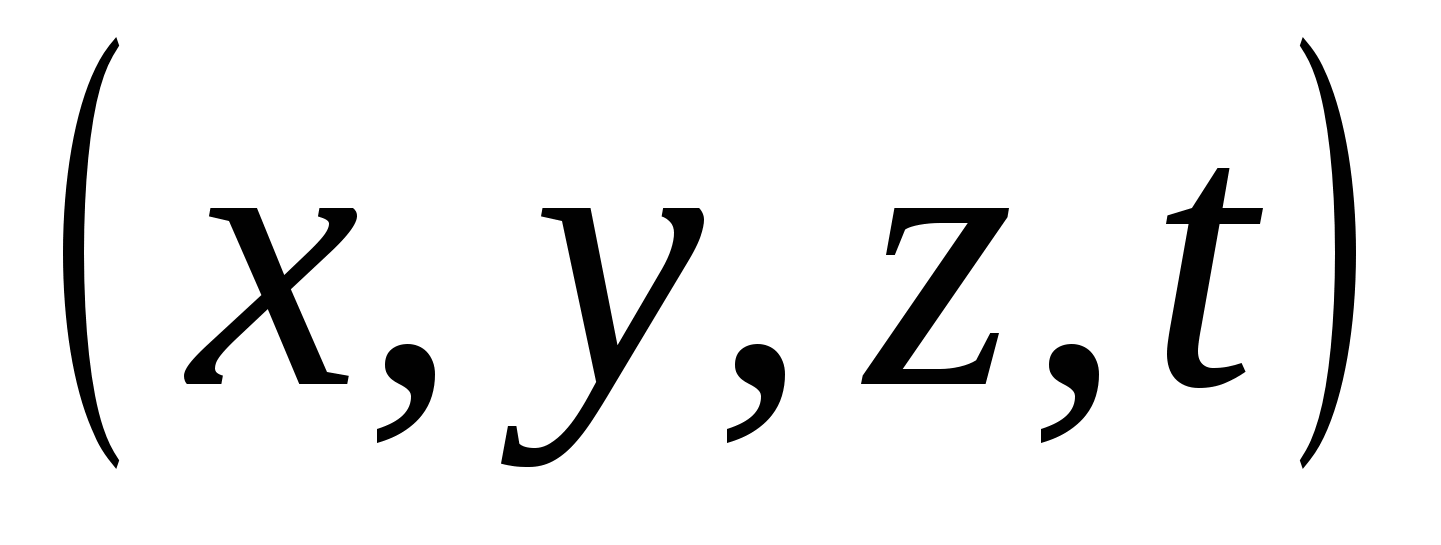 . ಡೆಸ್ಕಾರ್ಟೆಸ್ನಲ್ಲಿ
. ಡೆಸ್ಕಾರ್ಟೆಸ್ನಲ್ಲಿ 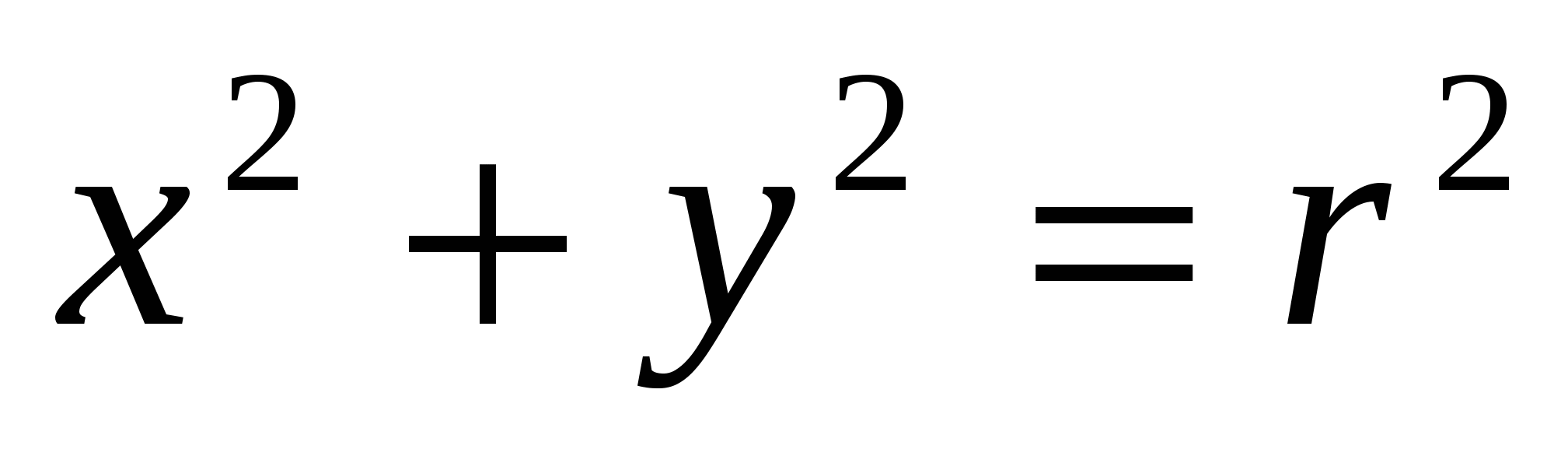 - ಸಮತಲದಲ್ಲಿ ವೃತ್ತದ ಸಮೀಕರಣ,
- ಸಮತಲದಲ್ಲಿ ವೃತ್ತದ ಸಮೀಕರಣ,  - ಮೂರು ಆಯಾಮದ ಜಾಗದಲ್ಲಿ ಚೆಂಡಿನ ಮೇಲ್ಮೈಯ ಸಮೀಕರಣ; ಹೊಸ ಸಿದ್ಧಾಂತದಲ್ಲಿ
- ಮೂರು ಆಯಾಮದ ಜಾಗದಲ್ಲಿ ಚೆಂಡಿನ ಮೇಲ್ಮೈಯ ಸಮೀಕರಣ; ಹೊಸ ಸಿದ್ಧಾಂತದಲ್ಲಿ 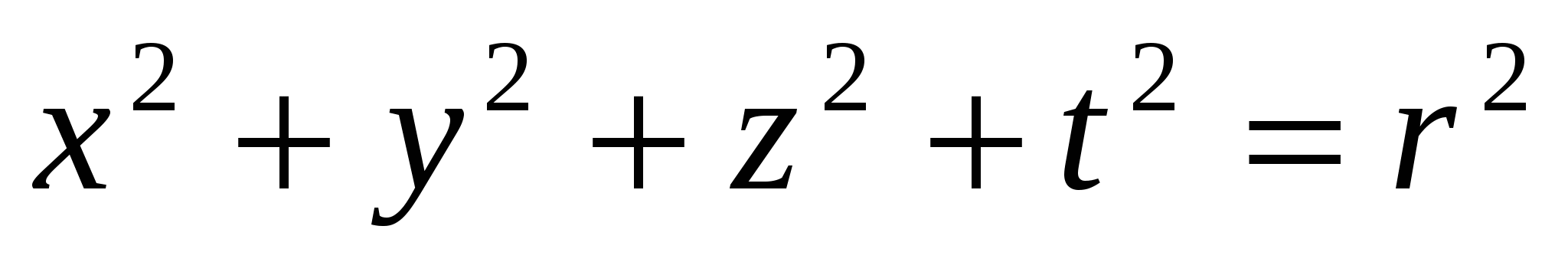 ನಾಲ್ಕು ಆಯಾಮದ ಜಾಗದಲ್ಲಿ ಗೋಳದ ಮೇಲ್ಮೈ. ಅದೇ ರೀತಿ ರಲ್ಲಿಎನ್
-
ಆಯಾಮದ ಜ್ಯಾಮಿತಿಯು ಸಮತಲಗಳು, ನೇರ ರೇಖೆಗಳು, ಬಿಂದುಗಳ ನಡುವಿನ ಅಂತರಗಳು, ನೇರ ರೇಖೆಗಳ ನಡುವಿನ ಕೋನಗಳು ಇತ್ಯಾದಿಗಳನ್ನು ಪರಿಗಣಿಸುತ್ತದೆ.
ನಾಲ್ಕು ಆಯಾಮದ ಜಾಗದಲ್ಲಿ ಗೋಳದ ಮೇಲ್ಮೈ. ಅದೇ ರೀತಿ ರಲ್ಲಿಎನ್
-
ಆಯಾಮದ ಜ್ಯಾಮಿತಿಯು ಸಮತಲಗಳು, ನೇರ ರೇಖೆಗಳು, ಬಿಂದುಗಳ ನಡುವಿನ ಅಂತರಗಳು, ನೇರ ರೇಖೆಗಳ ನಡುವಿನ ಕೋನಗಳು ಇತ್ಯಾದಿಗಳನ್ನು ಪರಿಗಣಿಸುತ್ತದೆ.
ಬಹುಆಯಾಮದ ರೇಖಾಗಣಿತದ ಕಲ್ಪನೆಗಳು ಕೊನೆಯಲ್ಲಿ ಗಣಿತಶಾಸ್ತ್ರದಲ್ಲಿ ದೃಢವಾಗಿ ಸ್ಥಾಪಿತವಾದವುXIXಶತಮಾನಗಳು, ಮತ್ತು ಅತ್ಯಂತ ಆರಂಭದಲ್ಲಿXXಶತಮಾನಗಳಿಂದ, ಅವರು ಅಪ್ಲಿಕೇಶನ್ ಅನ್ನು ಕಂಡುಕೊಂಡಿದ್ದಾರೆ ವಿಶೇಷ ಸಿದ್ಧಾಂತಸಾಪೇಕ್ಷತೆ, ಎಲ್ಲಿ ಮೂರು ಪ್ರಾದೇಶಿಕ ನಿರ್ದೇಶಾಂಕಗಳುನಾಲ್ಕನೆಯದನ್ನು ಸೇರಿಸಲಾಗಿದೆ - ಸಮಯ. ಹೀಗಾಗಿ, ನಂತರದ ಪೀಳಿಗೆಯ ವಿಜ್ಞಾನಿಗಳು ಅಭಿವೃದ್ಧಿಪಡಿಸಿದ ಡೆಸ್ಕಾರ್ಟೆಸ್ನ ಜ್ಯಾಮಿತಿಯ ಕಲ್ಪನೆಗಳು ಆಧುನಿಕ ವಿಜ್ಞಾನದ ಆಧಾರದ ಮೇಲೆ ನೆಲೆಗೊಂಡಿವೆ.
2. ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಒಂದು ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳು .
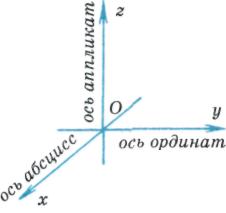 ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಒಂದು ಬಿಂದುವಿನ ಮೂಲಕ ಮೂರು ಜೋಡಿಯಾಗಿ ಲಂಬವಾಗಿರುವ ರೇಖೆಗಳನ್ನು ಎಳೆದರೆ ಆಯತಾಕಾರದ (ಕಾರ್ಟೀಸಿಯನ್) ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯನ್ನು ನೀಡಲಾಗುತ್ತದೆ, ಅವುಗಳಲ್ಲಿ ಪ್ರತಿಯೊಂದಕ್ಕೂ ಒಂದು ದಿಕ್ಕನ್ನು ಆಯ್ಕೆ ಮಾಡಲಾಗುತ್ತದೆ ಮತ್ತು ವಿಭಾಗಗಳಿಗೆ ಅಳತೆಯ ಘಟಕವನ್ನು ಆಯ್ಕೆ ಮಾಡಲಾಗುತ್ತದೆ. ಕ್ರಮವಾಗಿ ನಿರ್ದೇಶಾಂಕ ಅಕ್ಷಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವ ವಿಮಾನಗಳು
ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಒಂದು ಬಿಂದುವಿನ ಮೂಲಕ ಮೂರು ಜೋಡಿಯಾಗಿ ಲಂಬವಾಗಿರುವ ರೇಖೆಗಳನ್ನು ಎಳೆದರೆ ಆಯತಾಕಾರದ (ಕಾರ್ಟೀಸಿಯನ್) ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯನ್ನು ನೀಡಲಾಗುತ್ತದೆ, ಅವುಗಳಲ್ಲಿ ಪ್ರತಿಯೊಂದಕ್ಕೂ ಒಂದು ದಿಕ್ಕನ್ನು ಆಯ್ಕೆ ಮಾಡಲಾಗುತ್ತದೆ ಮತ್ತು ವಿಭಾಗಗಳಿಗೆ ಅಳತೆಯ ಘಟಕವನ್ನು ಆಯ್ಕೆ ಮಾಡಲಾಗುತ್ತದೆ. ಕ್ರಮವಾಗಿ ನಿರ್ದೇಶಾಂಕ ಅಕ್ಷಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವ ವಿಮಾನಗಳು 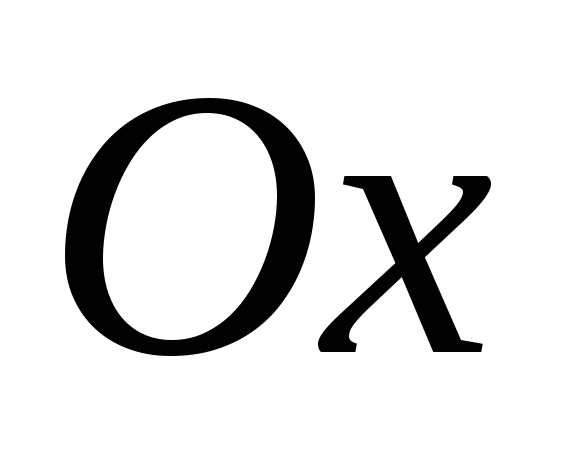 ಮತ್ತು
ಮತ್ತು 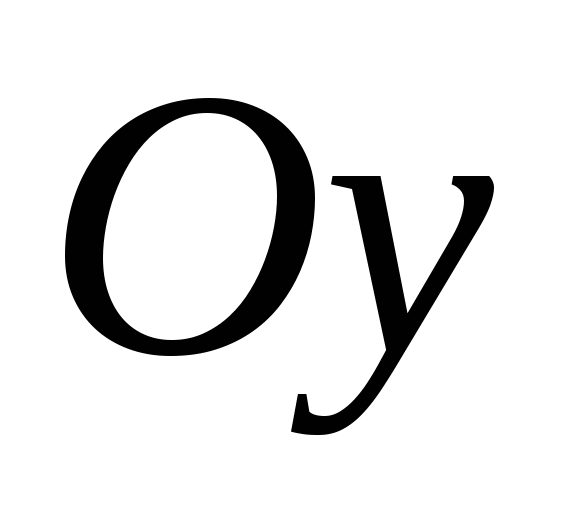 ,
, 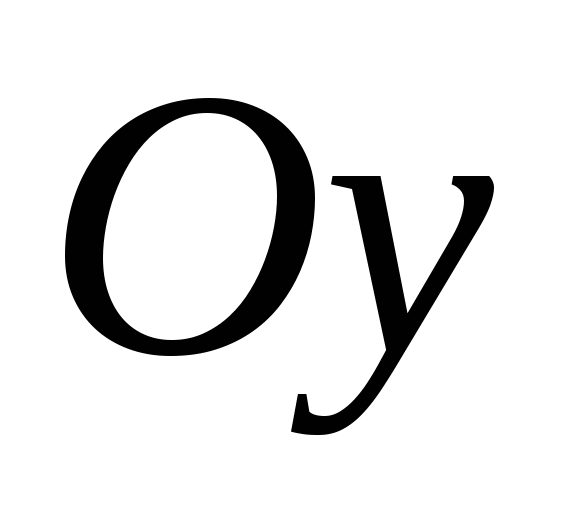 ಮತ್ತು
ಮತ್ತು  ,
,  ಮತ್ತು
ಮತ್ತು 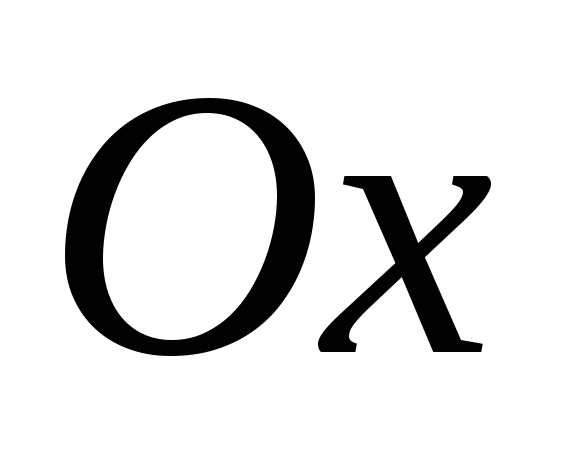 , ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆಸಮನ್ವಯ ವಿಮಾನಗಳು
ಮತ್ತು ಗೊತ್ತುಪಡಿಸಲಾಗಿದೆ
, ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆಸಮನ್ವಯ ವಿಮಾನಗಳು
ಮತ್ತು ಗೊತ್ತುಪಡಿಸಲಾಗಿದೆ 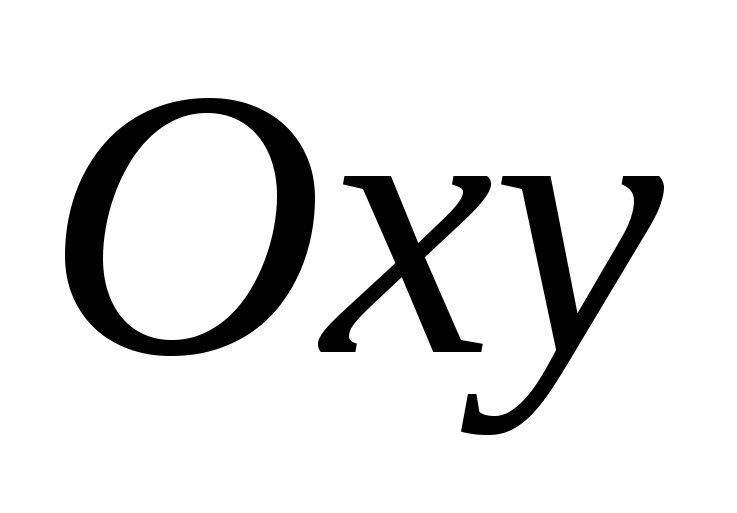 ,
, 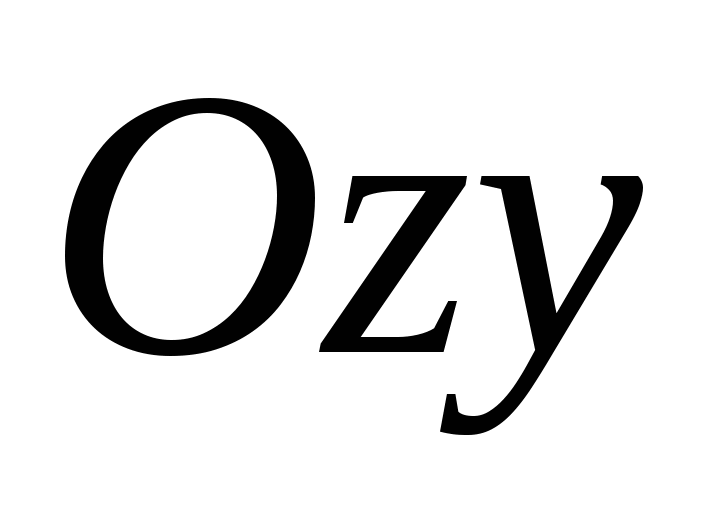 ,
,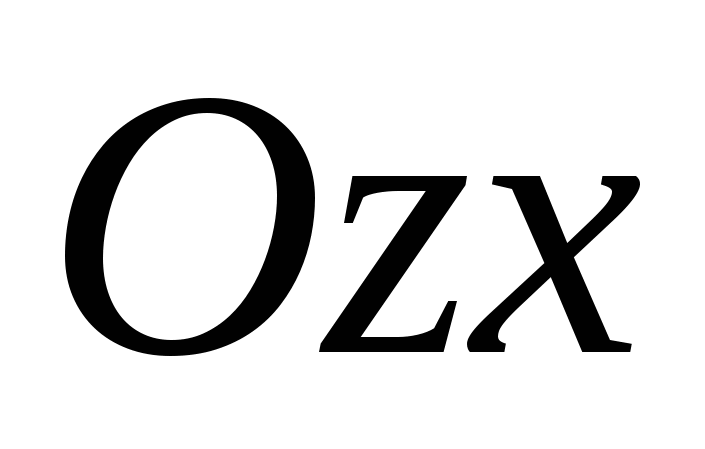 .
.
TO  ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿನ ಒಂದು ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳು ನಿರ್ದೇಶಾಂಕ ಅಕ್ಷಗಳ ಮೇಲೆ ಈ ಬಿಂದುವಿನ ಪ್ರಕ್ಷೇಪಗಳ ನಿರ್ದೇಶಾಂಕಗಳಾಗಿವೆ.
ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿನ ಒಂದು ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳು ನಿರ್ದೇಶಾಂಕ ಅಕ್ಷಗಳ ಮೇಲೆ ಈ ಬಿಂದುವಿನ ಪ್ರಕ್ಷೇಪಗಳ ನಿರ್ದೇಶಾಂಕಗಳಾಗಿವೆ.
ಪಾಯಿಂಟ್ ಕಕ್ಷೆಗಳು: 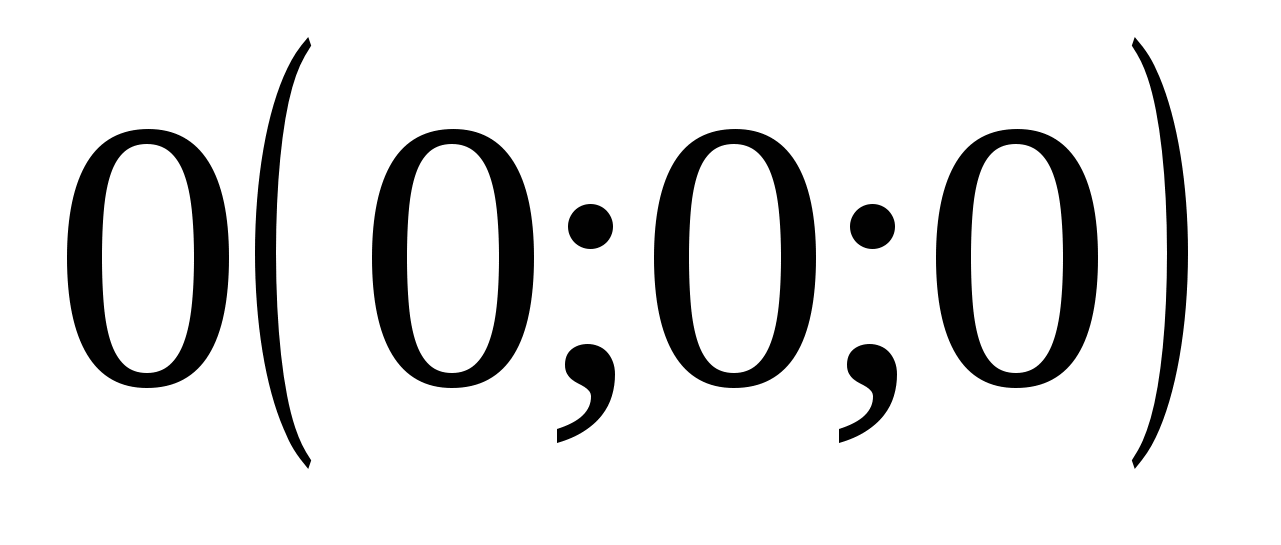 ,
, 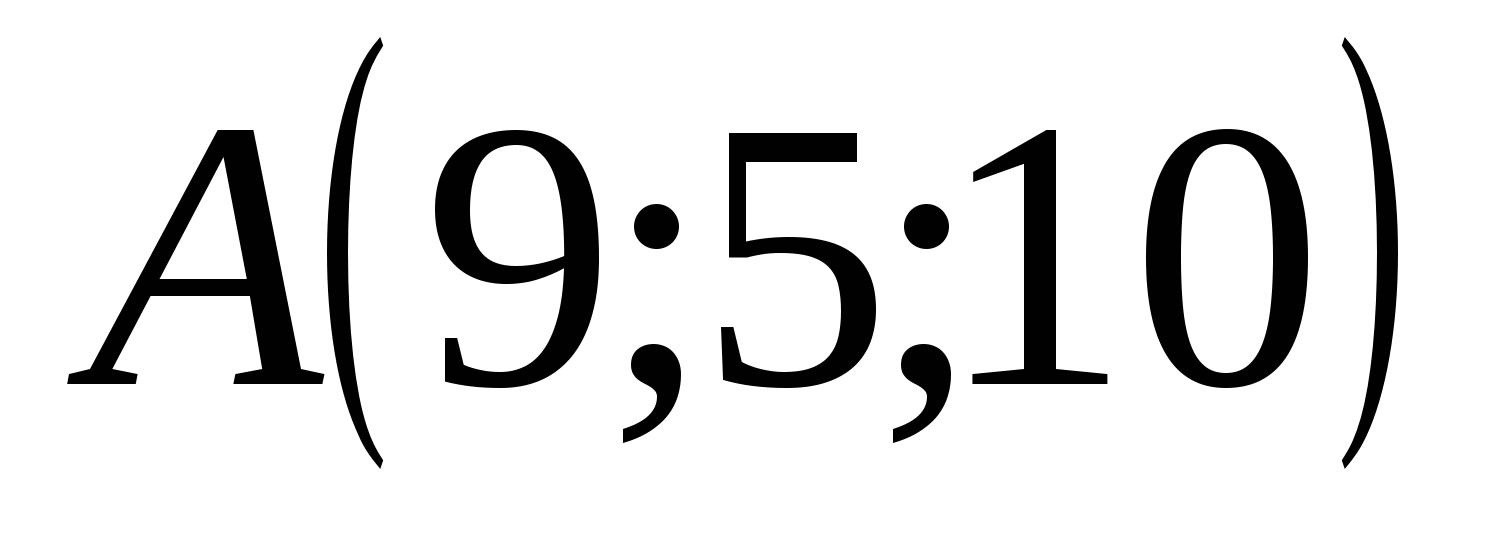 ,
, 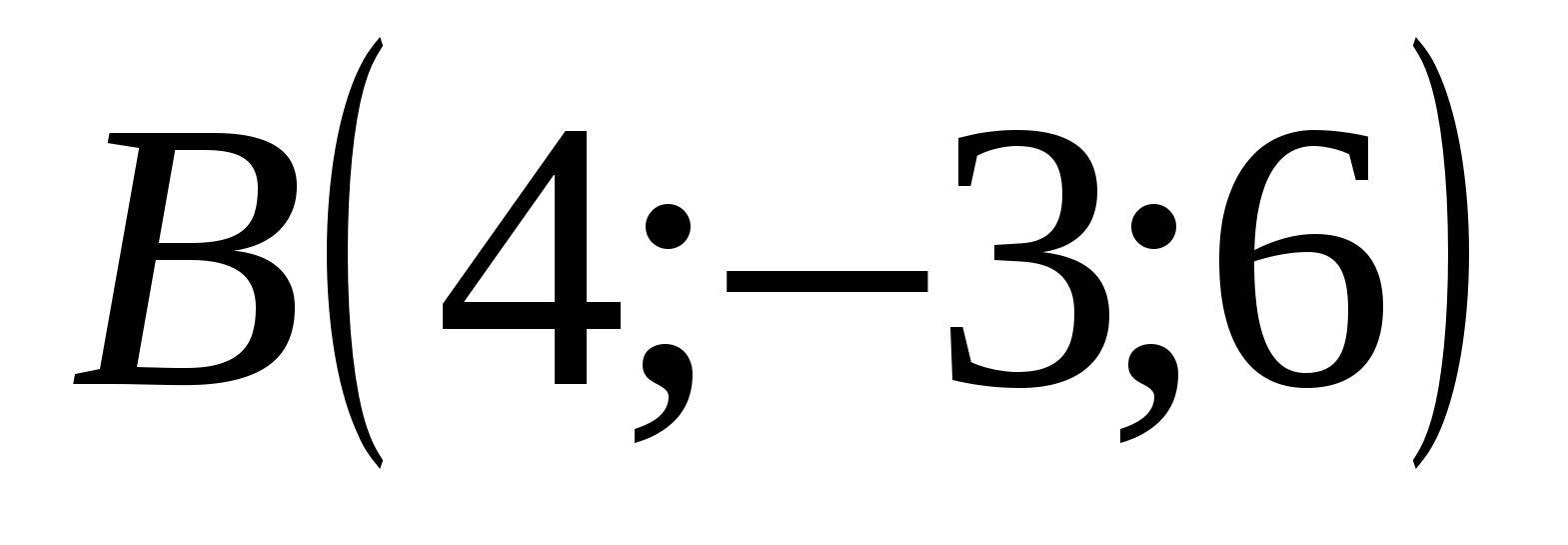 ,
, 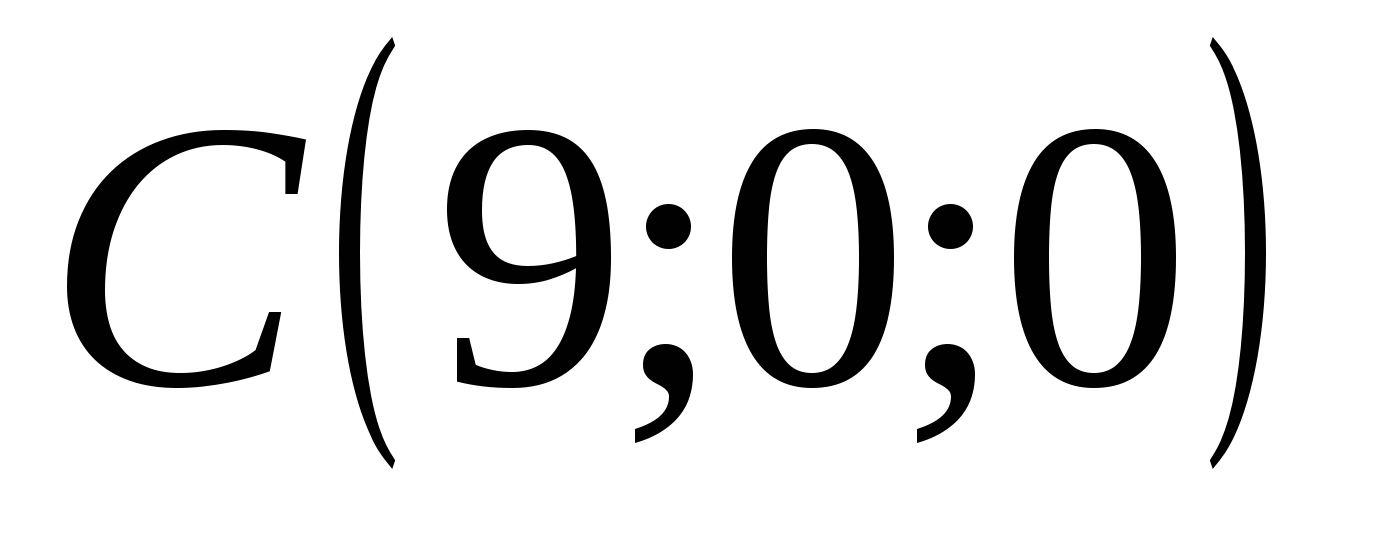 ,
, 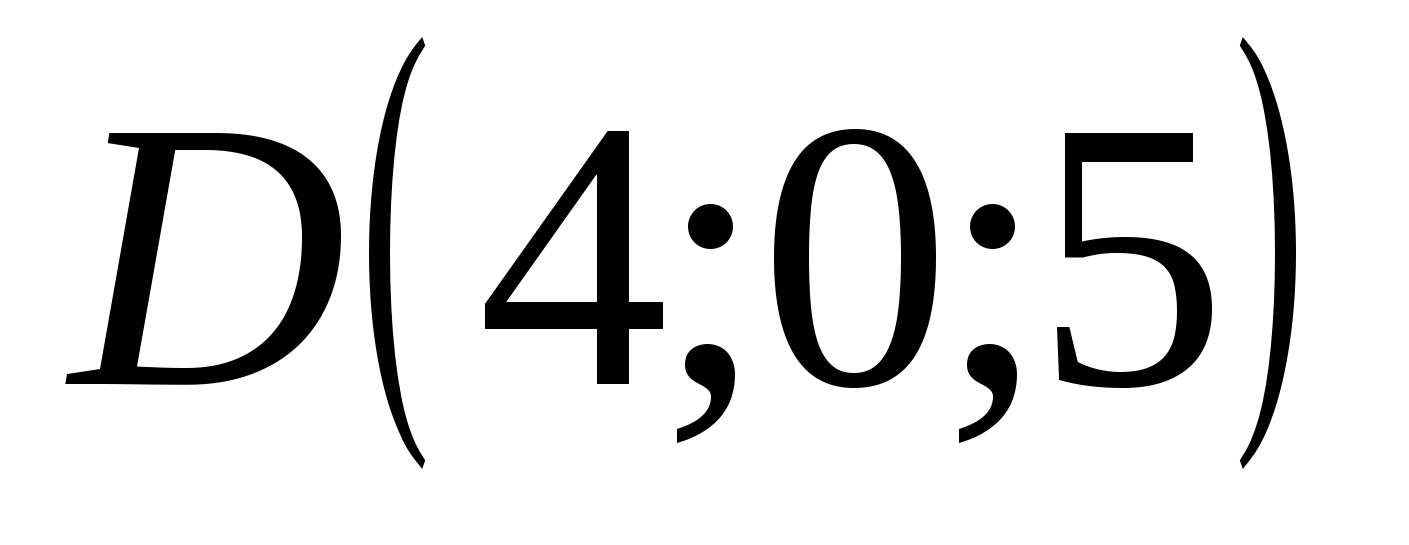 ,
, 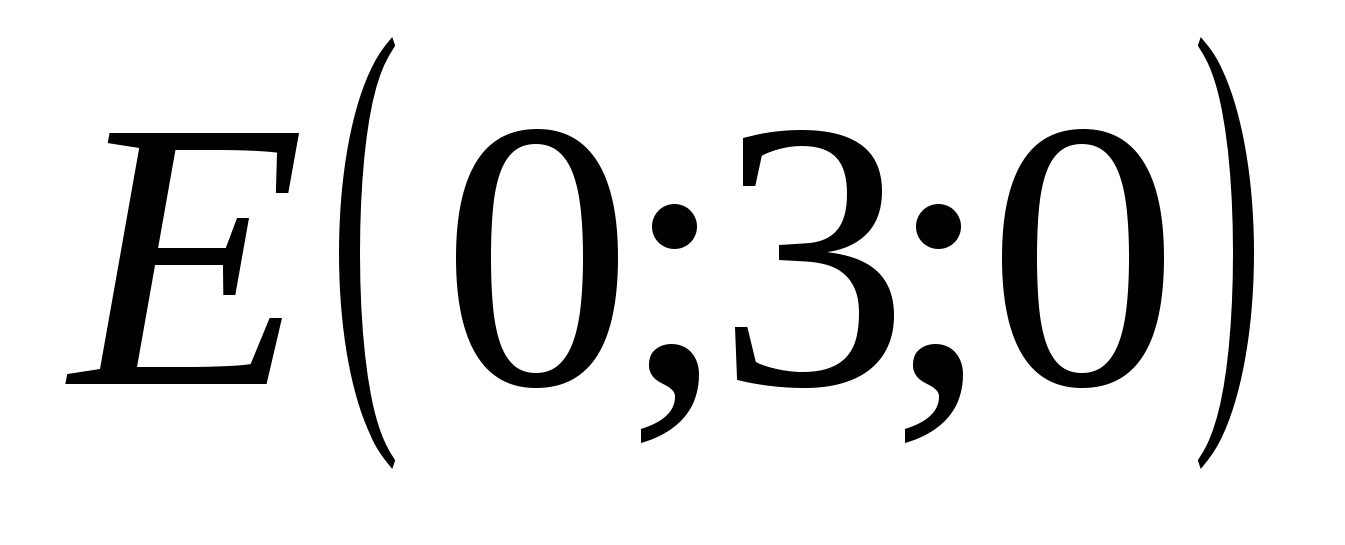 ,
, 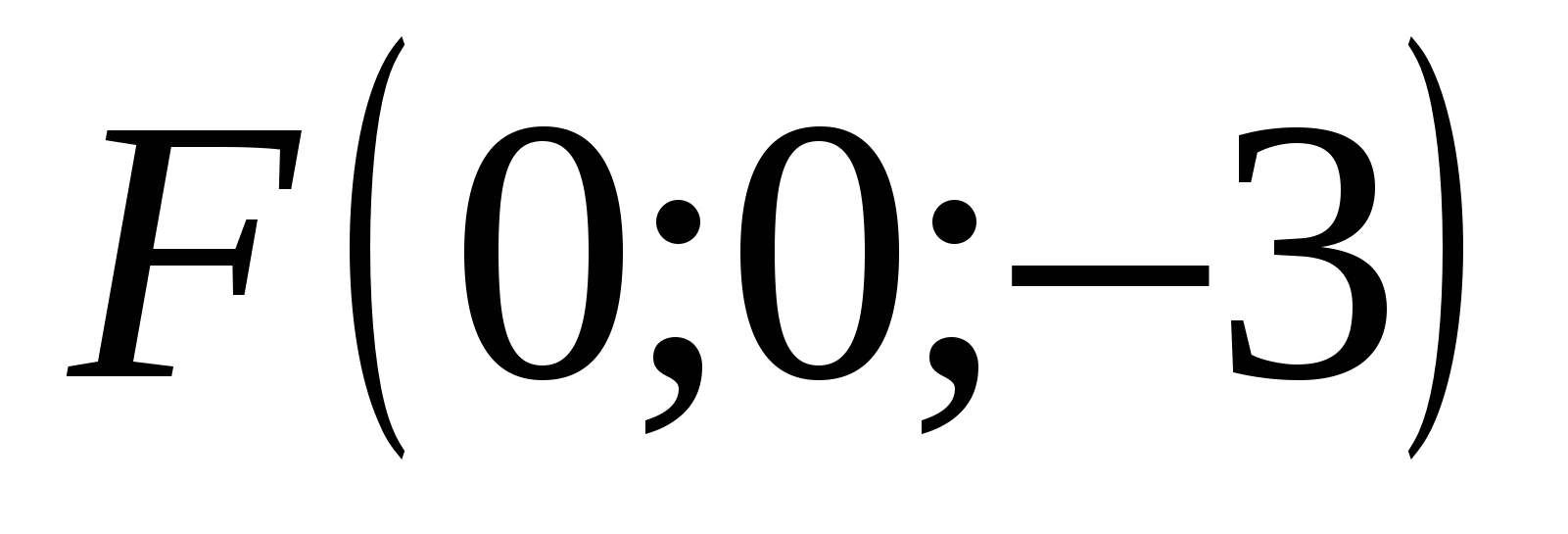 .
.
ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ, ಹೊರತುಪಡಿಸಿ ಸಮನ್ವಯ ಅಕ್ಷಗಳು, ಸಮನ್ವಯ ವಿಮಾನಗಳನ್ನು ಸಹ ಪರಿಗಣಿಸಲು ಅನುಕೂಲಕರವಾಗಿದೆ, ಅಂದರೆ. ಯಾವುದೇ ಎರಡು ಅಕ್ಷಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವ ವಿಮಾನಗಳು. ಅಂತಹ ಮೂರು ವಿಮಾನಗಳಿವೆ:
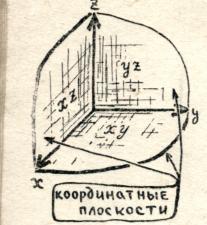
ವಿಮಾನ ![]() (ಅಕ್ಷಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವುದು
(ಅಕ್ಷಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವುದು  ಮತ್ತು
ಮತ್ತು 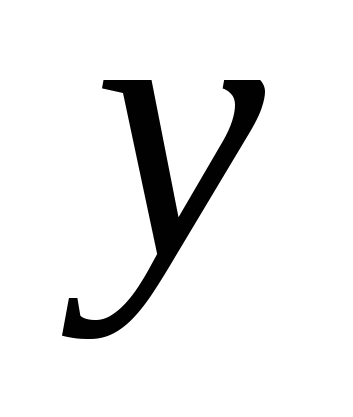 ) - ರೂಪದ ಬಿಂದುಗಳ ಸೆಟ್
) - ರೂಪದ ಬಿಂದುಗಳ ಸೆಟ್  , ಎಲ್ಲಿ
, ಎಲ್ಲಿ  ಮತ್ತು
ಮತ್ತು 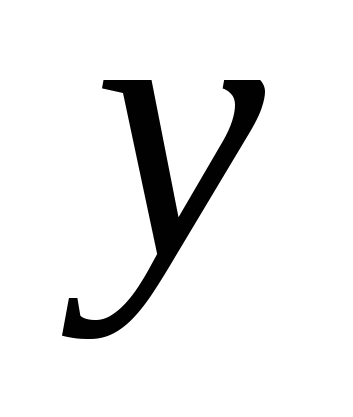 - ಯಾವುದೇ ಸಂಖ್ಯೆಗಳು;
- ಯಾವುದೇ ಸಂಖ್ಯೆಗಳು;
ವಿಮಾನ 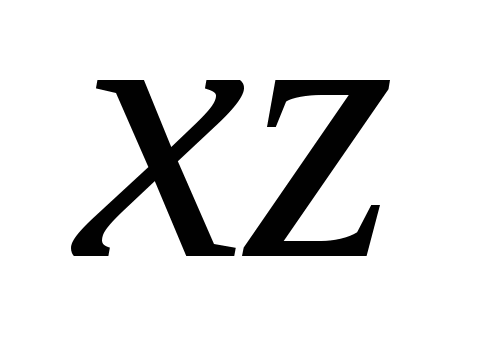 (ಅಕ್ಷಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವುದು
(ಅಕ್ಷಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವುದು  ಮತ್ತು
ಮತ್ತು  ) - ರೂಪದ ಬಿಂದುಗಳ ಸೆಟ್
) - ರೂಪದ ಬಿಂದುಗಳ ಸೆಟ್ 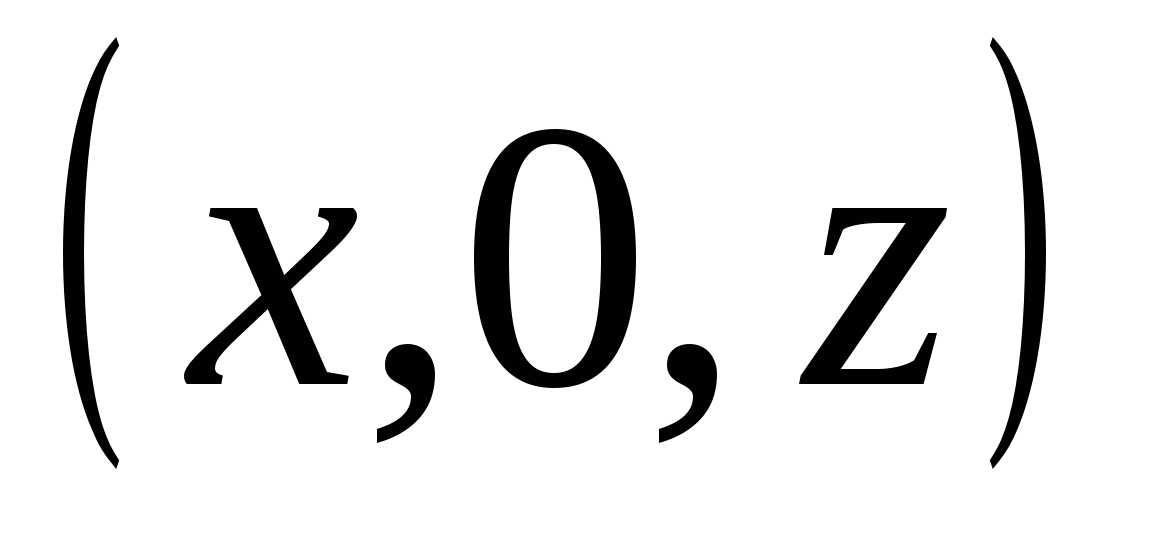 , ಎಲ್ಲಿ
, ಎಲ್ಲಿ  ಮತ್ತು
ಮತ್ತು  - ಯಾವುದೇ ಸಂಖ್ಯೆಗಳು;
- ಯಾವುದೇ ಸಂಖ್ಯೆಗಳು;
ವಿಮಾನ  (ಅಕ್ಷಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವುದು
(ಅಕ್ಷಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವುದು 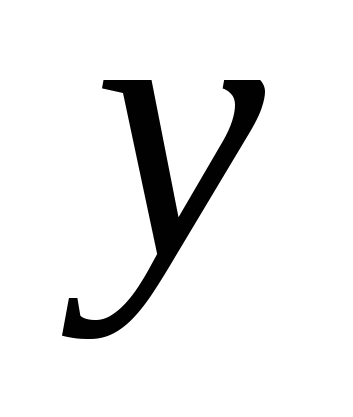 ಮತ್ತು
ಮತ್ತು  ) - ರೂಪದ ಬಿಂದುಗಳ ಸೆಟ್
) - ರೂಪದ ಬಿಂದುಗಳ ಸೆಟ್ 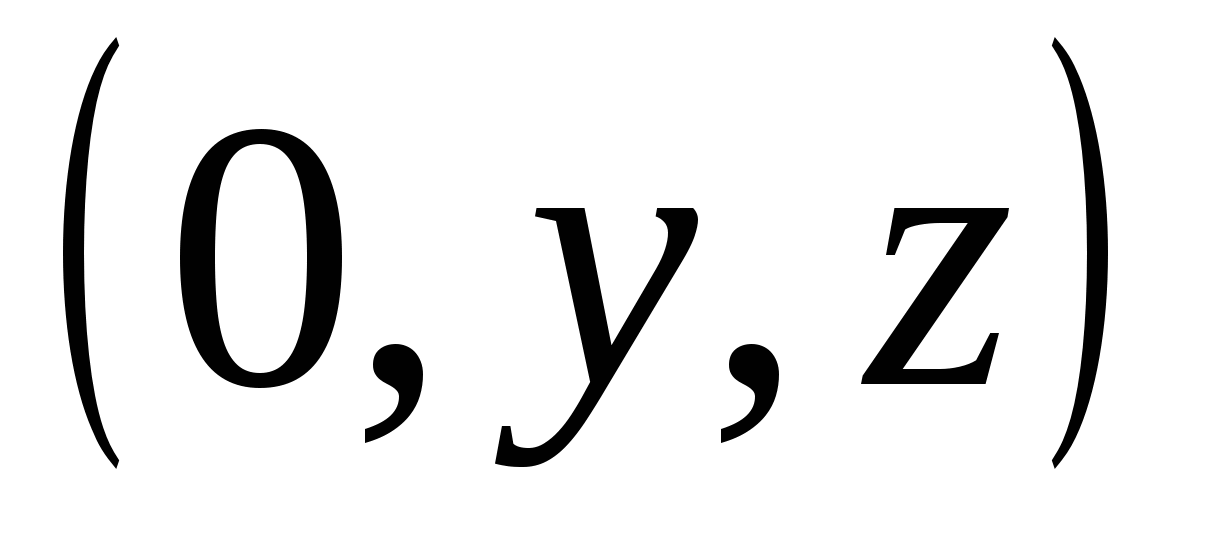 , ಎಲ್ಲಿ
, ಎಲ್ಲಿ 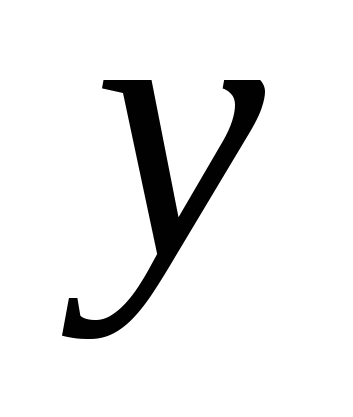 ಮತ್ತು
ಮತ್ತು  - ಯಾವುದೇ ಸಂಖ್ಯೆಗಳು.
- ಯಾವುದೇ ಸಂಖ್ಯೆಗಳು.
ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಎಂ ಬಿಂದುವಿಗೆ ನೀವು ಮೂರು ಸಂಖ್ಯೆಗಳನ್ನು ಕಾಣಬಹುದು 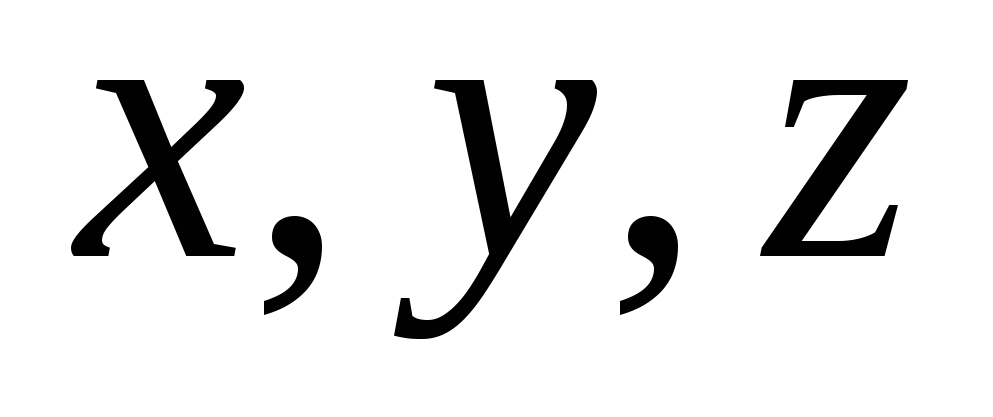 , ಇದು ಅದರ ನಿರ್ದೇಶಾಂಕಗಳಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ.
, ಇದು ಅದರ ನಿರ್ದೇಶಾಂಕಗಳಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ.
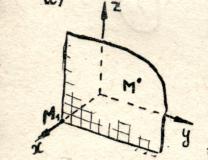 ಮೊದಲ ಸಂಖ್ಯೆಯನ್ನು ಕಂಡುಹಿಡಿಯಲು
ಮೊದಲ ಸಂಖ್ಯೆಯನ್ನು ಕಂಡುಹಿಡಿಯಲು  , ಎಂ ಬಿಂದುವಿಗೆ ಸಮಾನಾಂತರವಾಗಿ ಸಮತಲವನ್ನು ಸೆಳೆಯೋಣ ಸಮನ್ವಯ ಸಮತಲ
, ಎಂ ಬಿಂದುವಿಗೆ ಸಮಾನಾಂತರವಾಗಿ ಸಮತಲವನ್ನು ಸೆಳೆಯೋಣ ಸಮನ್ವಯ ಸಮತಲ  (ಅಕ್ಷಕ್ಕೆ ಲಂಬವಾಗಿX).ಅಕ್ಷದೊಂದಿಗೆ ಈ ಸಮತಲದ ಛೇದನದ ಬಿಂದು
(ಅಕ್ಷಕ್ಕೆ ಲಂಬವಾಗಿX).ಅಕ್ಷದೊಂದಿಗೆ ಈ ಸಮತಲದ ಛೇದನದ ಬಿಂದು  (ಪಾಯಿಂಟ್ ಎಂ 1
) ಈ ಅಕ್ಷದ ಮೇಲೆ ನಿರ್ದೇಶಾಂಕವನ್ನು ಹೊಂದಿದೆ
(ಪಾಯಿಂಟ್ ಎಂ 1
) ಈ ಅಕ್ಷದ ಮೇಲೆ ನಿರ್ದೇಶಾಂಕವನ್ನು ಹೊಂದಿದೆ  .ಇದು ಸಂಖ್ಯೆ
.ಇದು ಸಂಖ್ಯೆ  - ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕ ಎಂ 1
ಅಕ್ಷದ ಮೇಲೆ
- ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕ ಎಂ 1
ಅಕ್ಷದ ಮೇಲೆ  - ಕರೆಯಲಾಗುತ್ತದೆಅಬ್ಸಿಸ್ಸಾಅಂಕಗಳು ಎಂ.
- ಕರೆಯಲಾಗುತ್ತದೆಅಬ್ಸಿಸ್ಸಾಅಂಕಗಳು ಎಂ.
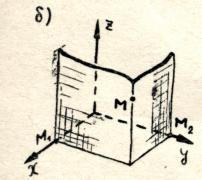 ಎರಡನೇ ನಿರ್ದೇಶಾಂಕವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ಪಾಯಿಂಟ್ M ಮೂಲಕ ಸಮತಲವನ್ನು ಎಳೆಯಿರಿ ವಿಮಾನಕ್ಕೆ ಸಮಾನಾಂತರವಾಗಿ
ಎರಡನೇ ನಿರ್ದೇಶಾಂಕವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ಪಾಯಿಂಟ್ M ಮೂಲಕ ಸಮತಲವನ್ನು ಎಳೆಯಿರಿ ವಿಮಾನಕ್ಕೆ ಸಮಾನಾಂತರವಾಗಿ 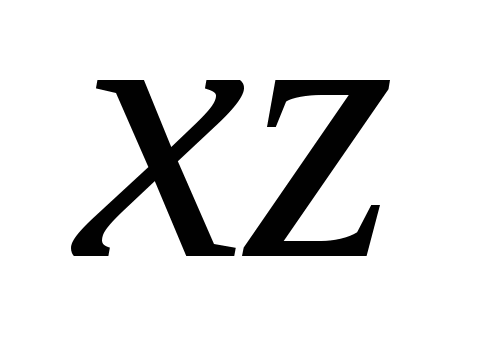 (ಅಕ್ಷಕ್ಕೆ ಲಂಬವಾಗಿವೈ), ಅಕ್ಷದಲ್ಲಿ ಕಂಡುಬರುತ್ತದೆ ವೈಪಾಯಿಂಟ್ ಎಂ 2. ಸಂಖ್ಯೆ ವೈ- ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕ ಎಂಪ್ರತಿ ಅಕ್ಷಕ್ಕೆ 2 ವೈ- ಕರೆಯಲಾಗುತ್ತದೆ ಆರ್ಡಿನೇಟ್ಅಂಕಗಳು ಎಂ.
(ಅಕ್ಷಕ್ಕೆ ಲಂಬವಾಗಿವೈ), ಅಕ್ಷದಲ್ಲಿ ಕಂಡುಬರುತ್ತದೆ ವೈಪಾಯಿಂಟ್ ಎಂ 2. ಸಂಖ್ಯೆ ವೈ- ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕ ಎಂಪ್ರತಿ ಅಕ್ಷಕ್ಕೆ 2 ವೈ- ಕರೆಯಲಾಗುತ್ತದೆ ಆರ್ಡಿನೇಟ್ಅಂಕಗಳು ಎಂ.
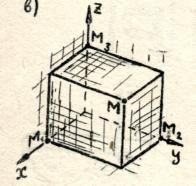 ಇದೇ ರೀತಿಯ ನಿರ್ಮಾಣಗಳನ್ನು ಕೈಗೊಳ್ಳುವ ಮೂಲಕ ಪಾಯಿಂಟ್ M ನ ಮೂರನೇ ನಿರ್ದೇಶಾಂಕವನ್ನು ನಾವು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ, ಆದರೆ z ಅಕ್ಷಕ್ಕೆ ಲಂಬವಾಗಿರುತ್ತದೆ. ಫಲಿತಾಂಶದ ಸಂಖ್ಯೆ z ಅನ್ನು ಕರೆಯೋಣ ಅನ್ವಯಿಸುಅಂಕಗಳು ಎಂ.
ಇದೇ ರೀತಿಯ ನಿರ್ಮಾಣಗಳನ್ನು ಕೈಗೊಳ್ಳುವ ಮೂಲಕ ಪಾಯಿಂಟ್ M ನ ಮೂರನೇ ನಿರ್ದೇಶಾಂಕವನ್ನು ನಾವು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ, ಆದರೆ z ಅಕ್ಷಕ್ಕೆ ಲಂಬವಾಗಿರುತ್ತದೆ. ಫಲಿತಾಂಶದ ಸಂಖ್ಯೆ z ಅನ್ನು ಕರೆಯೋಣ ಅನ್ವಯಿಸುಅಂಕಗಳು ಎಂ.
3. ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಅಂಕಿಗಳನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುವುದು.
ಸಮತಲದಲ್ಲಿರುವಂತೆಯೇ, ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿನ ನಿರ್ದೇಶಾಂಕಗಳು ಸಂಖ್ಯೆಗಳನ್ನು ಬಳಸಿಕೊಂಡು ನಿರ್ದಿಷ್ಟಪಡಿಸಲು ಸಾಧ್ಯವಾಗಿಸುತ್ತದೆ ಮತ್ತು ಸಂಖ್ಯಾತ್ಮಕ ಅನುಪಾತಗಳುಬಿಂದುಗಳು ಮಾತ್ರವಲ್ಲ, ರೇಖೆಗಳು, ಮೇಲ್ಮೈಗಳು ಮತ್ತು ಇತರ ಬಿಂದುಗಳ ಸೆಟ್. ಉದಾಹರಣೆಗೆ, ನಾವು ಕೇವಲ ಎರಡು ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸಿದರೆ ಮತ್ತು ಮೂರನೆಯದನ್ನು ಅನಿಯಂತ್ರಿತವೆಂದು ಪರಿಗಣಿಸಿದರೆ ಯಾವ ಅಂಕಗಳನ್ನು ಪಡೆಯಲಾಗುತ್ತದೆ ಎಂದು ನೋಡೋಣ.
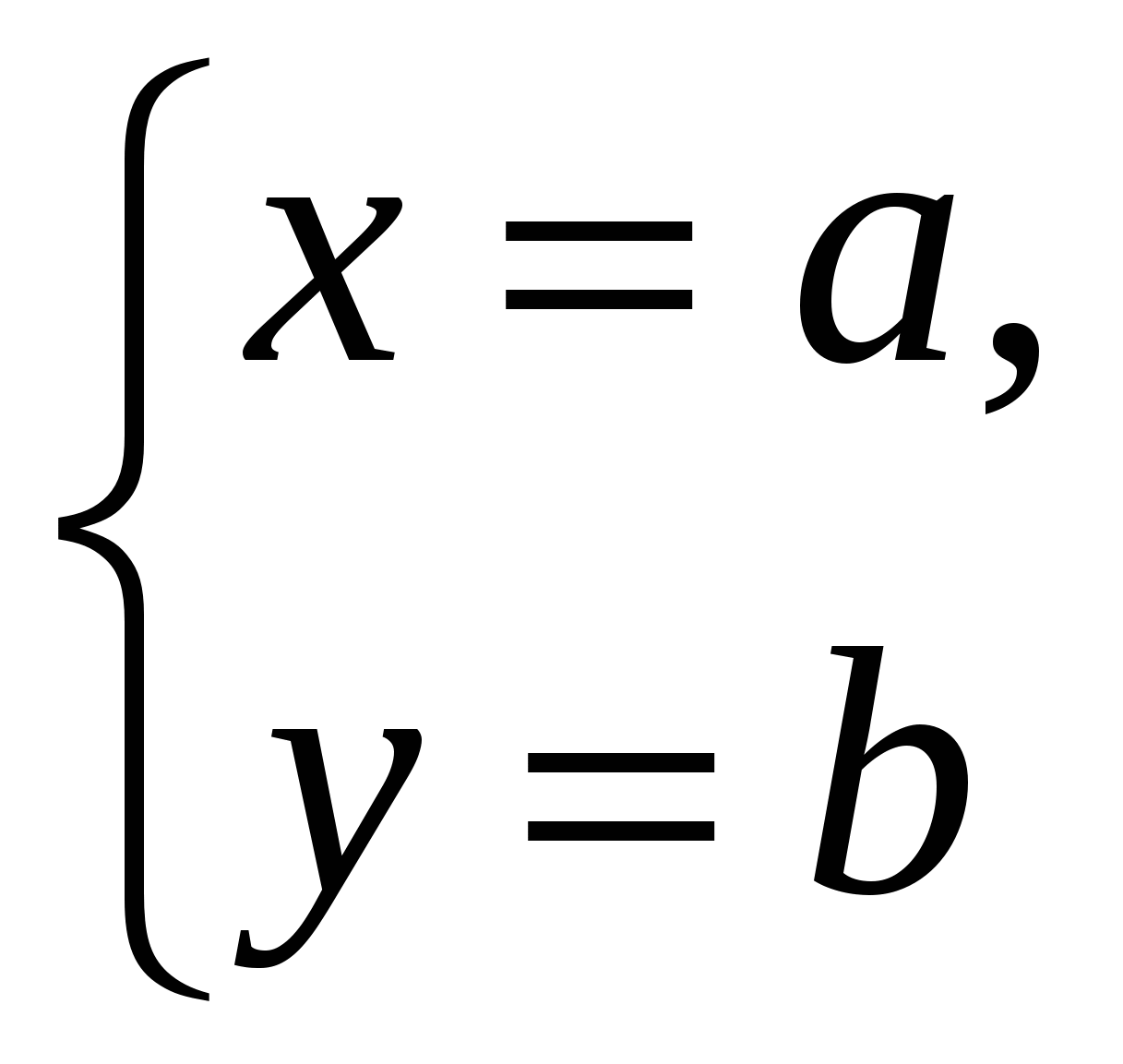
(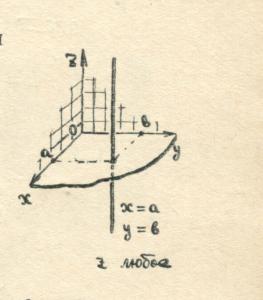 ಉದಾಹರಣೆಗೆ,
ಉದಾಹರಣೆಗೆ, 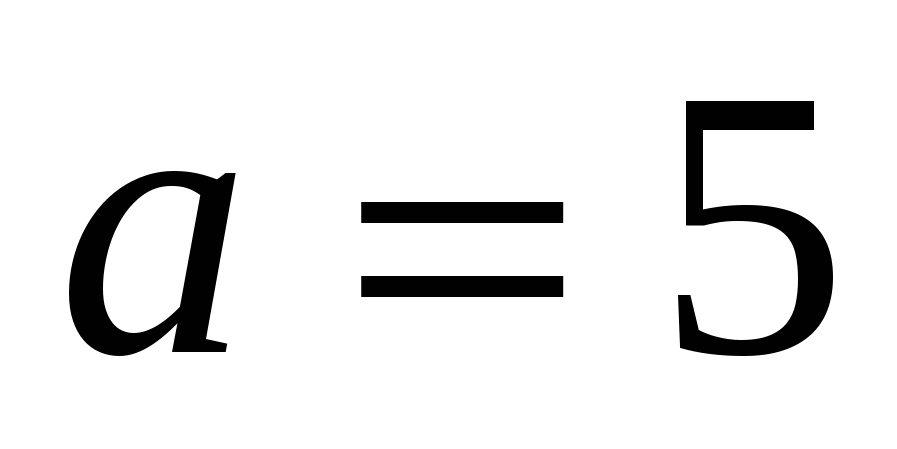
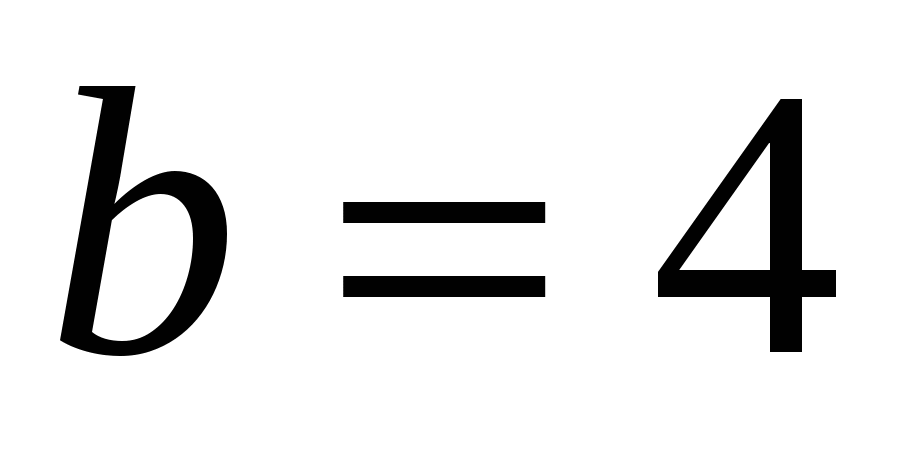 ), ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ನೇರ ರೇಖೆಯನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಿ, ಅಕ್ಷಕ್ಕೆ ಸಮಾನಾಂತರವಾಗಿ
), ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ನೇರ ರೇಖೆಯನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಿ, ಅಕ್ಷಕ್ಕೆ ಸಮಾನಾಂತರವಾಗಿ  .
.
ಅಂತಹ ಸಾಲಿನಲ್ಲಿರುವ ಎಲ್ಲಾ ಬಿಂದುಗಳು ಒಂದೇ ಅಬ್ಸಿಸ್ಸಾ ಮತ್ತು ಅದೇ ಆರ್ಡಿನೇಟ್ ಅನ್ನು ಹೊಂದಿರುತ್ತವೆ. ಸಮನ್ವಯಗೊಳಿಸು  ಯಾವುದೇ ಮೌಲ್ಯವನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು.
ಯಾವುದೇ ಮೌಲ್ಯವನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು.
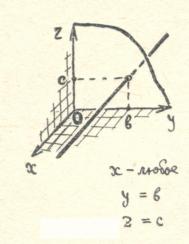


ನೀವು ಹೇಗೆ ಹೊಂದಿಸಬಹುದು ಎಂಬುದನ್ನು ತೋರಿಸುವ ಕೆಲವು ಉದಾಹರಣೆಗಳನ್ನು ನೋಡೋಣ
ಜಾಗ ವಿವಿಧ ಸೆಟ್ಗಳುಸಮೀಕರಣಗಳು ಮತ್ತು ನಿರ್ದೇಶಾಂಕಗಳ ನಡುವಿನ ಇತರ ಸಂಬಂಧಗಳನ್ನು ಬಳಸುವುದು.
1) ಸಮೀಕರಣವನ್ನು ಪರಿಗಣಿಸಿ.
ಬಿಂದುವಿನ ಅಂತರದಿಂದ 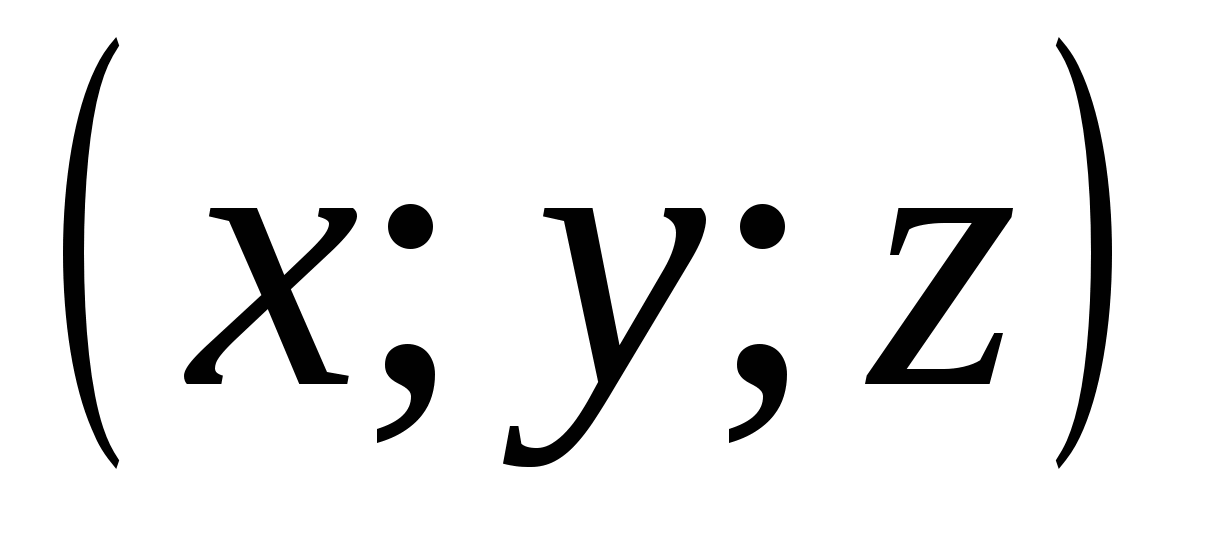 ಮೂಲದಿಂದ ಅಭಿವ್ಯಕ್ತಿಯಿಂದ ನೀಡಲಾಗಿದೆ
ಮೂಲದಿಂದ ಅಭಿವ್ಯಕ್ತಿಯಿಂದ ನೀಡಲಾಗಿದೆ 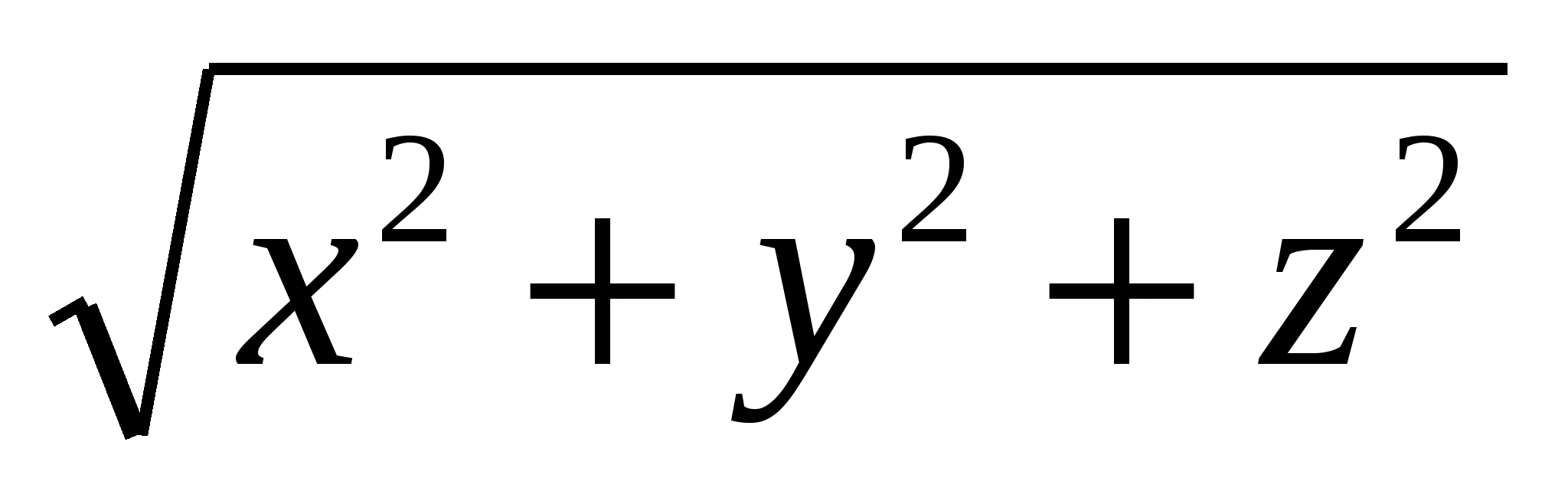 , ನಂತರ ಜ್ಯಾಮಿತೀಯ ಭಾಷೆಗೆ ಸಂಬಂಧವನ್ನು ಅನುವಾದಿಸಲಾಗಿದೆ ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗುತ್ತದೆ
, ನಂತರ ಜ್ಯಾಮಿತೀಯ ಭಾಷೆಗೆ ಸಂಬಂಧವನ್ನು ಅನುವಾದಿಸಲಾಗಿದೆ ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗುತ್ತದೆ 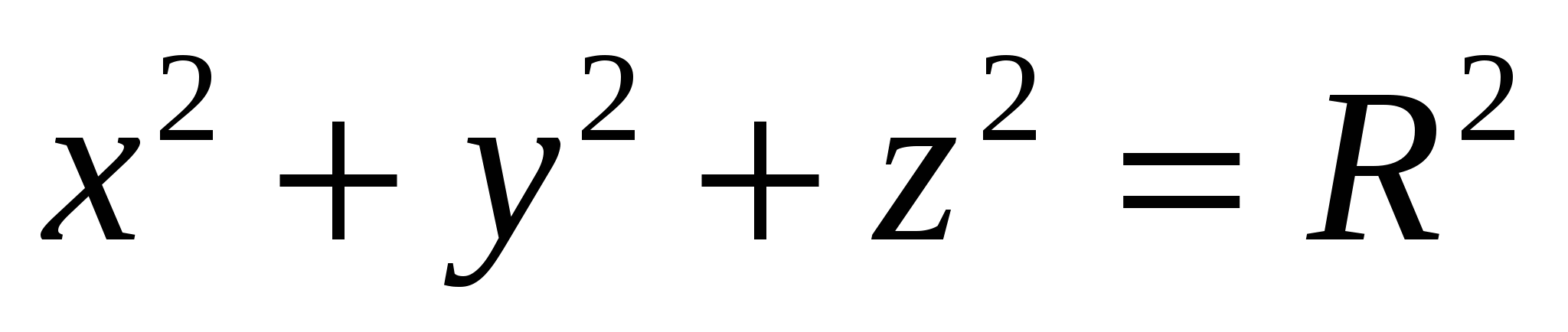 ನಿರ್ದೇಶಾಂಕಗಳೊಂದಿಗೆ ಬಿಂದು ಎಂದರ್ಥ
ನಿರ್ದೇಶಾಂಕಗಳೊಂದಿಗೆ ಬಿಂದು ಎಂದರ್ಥ 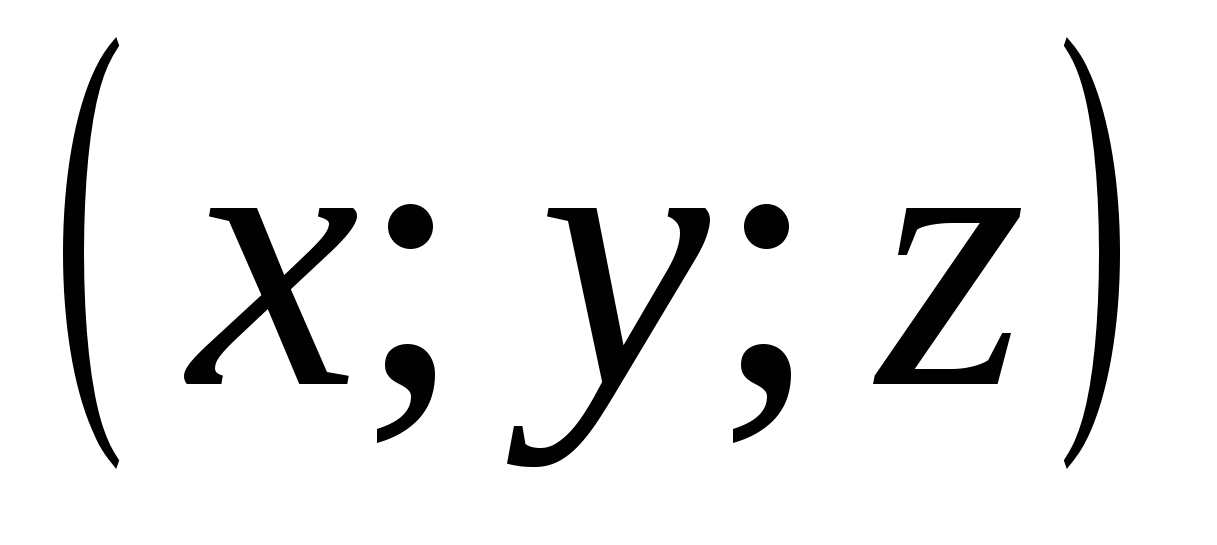 , ದೂರದಲ್ಲಿದೆಆರ್
ಮೂಲದಿಂದ. ಇದರರ್ಥ ಸಂಬಂಧವು ಹೊಂದಿರುವ ಎಲ್ಲಾ ಬಿಂದುಗಳ ಸೆಟ್
, ದೂರದಲ್ಲಿದೆಆರ್
ಮೂಲದಿಂದ. ಇದರರ್ಥ ಸಂಬಂಧವು ಹೊಂದಿರುವ ಎಲ್ಲಾ ಬಿಂದುಗಳ ಸೆಟ್ 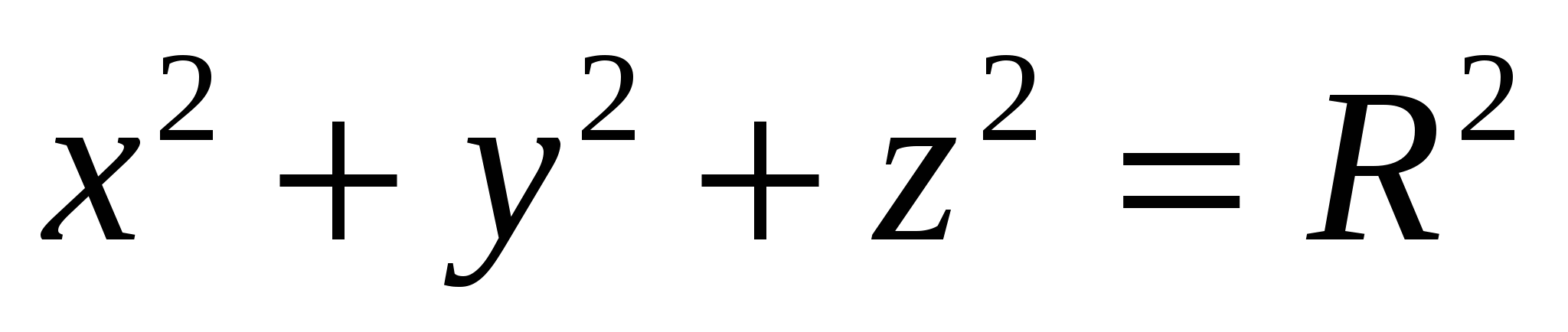 , ಚೆಂಡಿನ ಮೇಲ್ಮೈ - ಮೂಲ ಮತ್ತು ತ್ರಿಜ್ಯದಲ್ಲಿ ಕೇಂದ್ರವನ್ನು ಹೊಂದಿರುವ ಗೋಳಆರ್
.
, ಚೆಂಡಿನ ಮೇಲ್ಮೈ - ಮೂಲ ಮತ್ತು ತ್ರಿಜ್ಯದಲ್ಲಿ ಕೇಂದ್ರವನ್ನು ಹೊಂದಿರುವ ಗೋಳಆರ್
.
2) ಸಂಬಂಧವನ್ನು ತೃಪ್ತಿಪಡಿಸುವ ನಿರ್ದೇಶಾಂಕಗಳು ಎಲ್ಲಿವೆ ಎಂಬುದನ್ನು ನಾವು ಪರಿಗಣಿಸೋಣ  .
.
ಈ ಸಂಬಂಧವು ಬಿಂದುವಿನ ಅಂತರವನ್ನು ಸೂಚಿಸುತ್ತದೆ 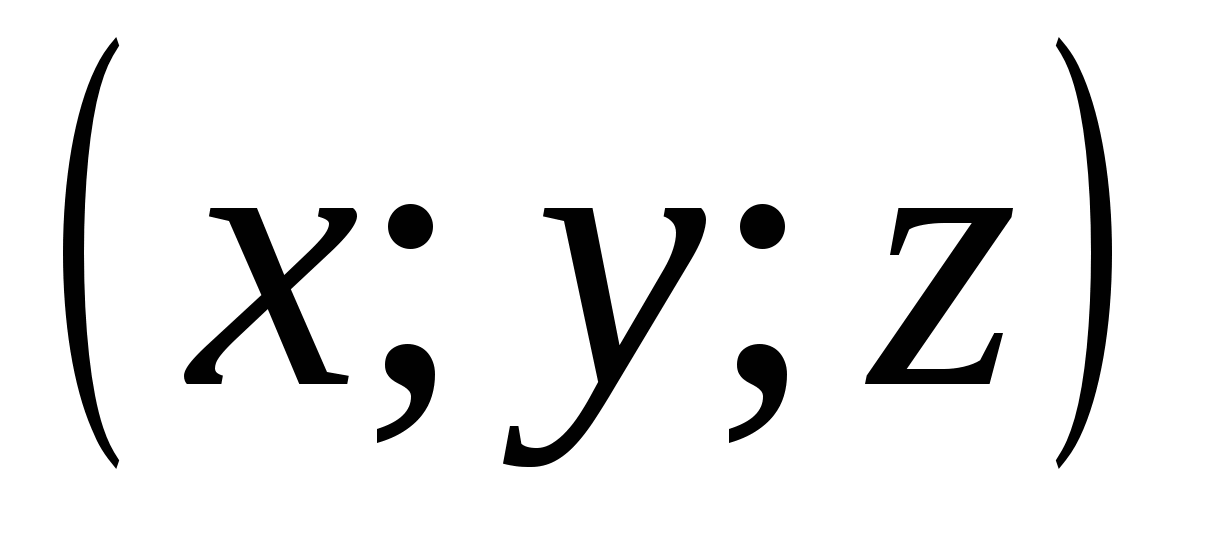 ನಿರ್ದೇಶಾಂಕಗಳ ಮೂಲವು ಒಂದಕ್ಕಿಂತ ಕಡಿಮೆಯಿರುತ್ತದೆ, ನಂತರ ಅಗತ್ಯವಿರುವ ಸೆಟ್ ಚೆಂಡಿನೊಳಗೆ ಇರುವ ಬಿಂದುಗಳ ಗುಂಪಾಗಿದ್ದು, ನಿರ್ದೇಶಾಂಕಗಳ ಮೂಲದಲ್ಲಿ ಕೇಂದ್ರವನ್ನು ಮತ್ತು ಒಂದಕ್ಕೆ ಸಮಾನವಾದ ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿರುತ್ತದೆ.
ನಿರ್ದೇಶಾಂಕಗಳ ಮೂಲವು ಒಂದಕ್ಕಿಂತ ಕಡಿಮೆಯಿರುತ್ತದೆ, ನಂತರ ಅಗತ್ಯವಿರುವ ಸೆಟ್ ಚೆಂಡಿನೊಳಗೆ ಇರುವ ಬಿಂದುಗಳ ಗುಂಪಾಗಿದ್ದು, ನಿರ್ದೇಶಾಂಕಗಳ ಮೂಲದಲ್ಲಿ ಕೇಂದ್ರವನ್ನು ಮತ್ತು ಒಂದಕ್ಕೆ ಸಮಾನವಾದ ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿರುತ್ತದೆ.
ಅಧ್ಯಾಯ 2
1. ನಿರ್ದೇಶಾಂಕ ವಾಹಕಗಳಾಗಿ ವೆಕ್ಟರ್ನ ವಿಭಜನೆ. ವೆಕ್ಟರ್ ನಿರ್ದೇಶಾಂಕಗಳು.
ಜಾಗದ ಆಧಾರವು ಕೋಪ್ಲಾನಾರ್ ಅಲ್ಲದ ವಾಹಕಗಳ ಯಾವುದೇ ಆದೇಶದ ಟ್ರಿಪಲ್ ಆಗಿದೆ 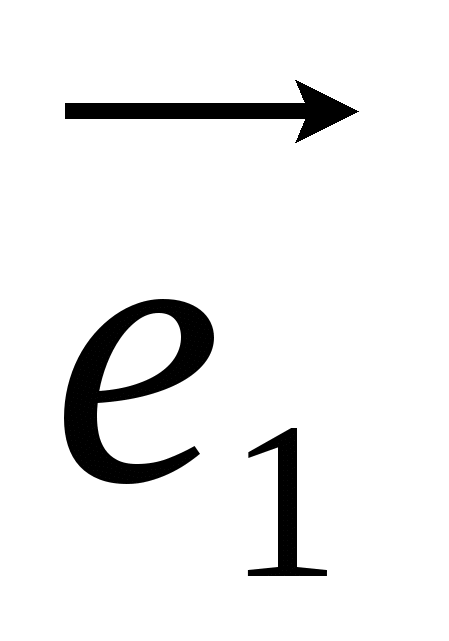 ,
, 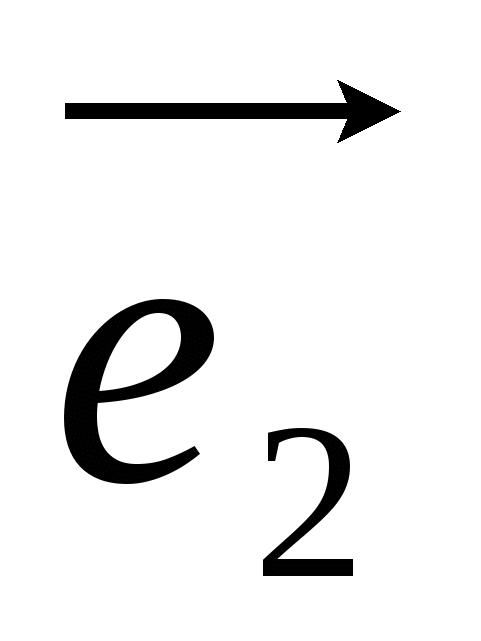 ,
, 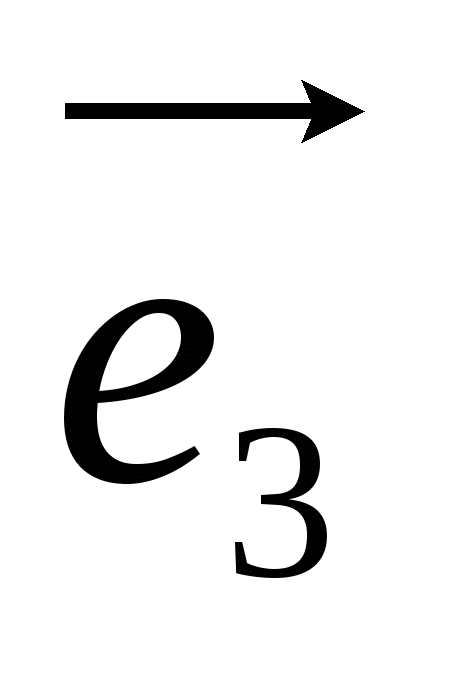 , ಚಿಹ್ನೆಯಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ
, ಚಿಹ್ನೆಯಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ 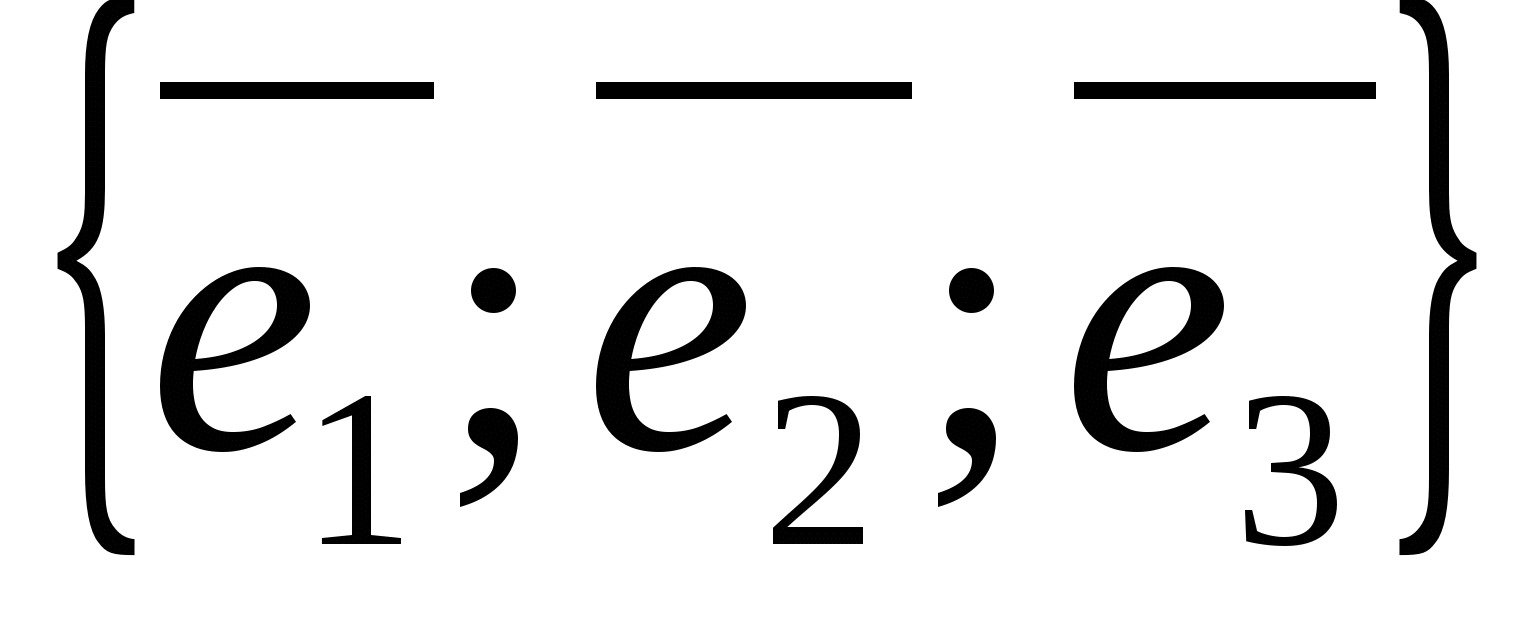 .
.
ವಿಶೇಷ ಪ್ರಕರಣವು ಆಯತಾಕಾರದ ಆರ್ಥೋನಾರ್ಮಲ್ ಆಧಾರವಾಗಿದೆ 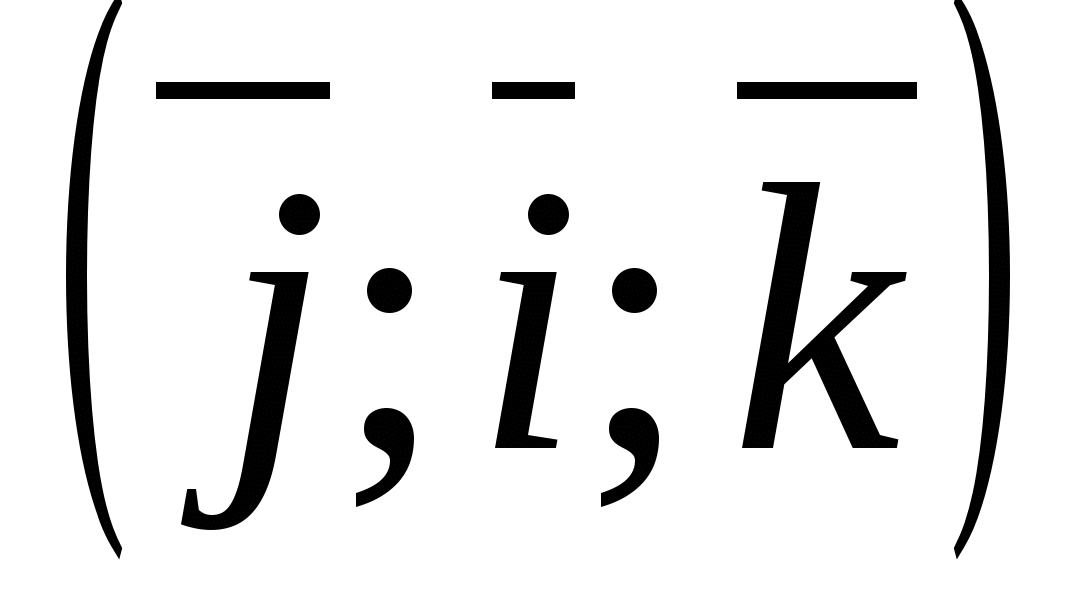 , ಎಲ್ಲಿ
, ಎಲ್ಲಿ 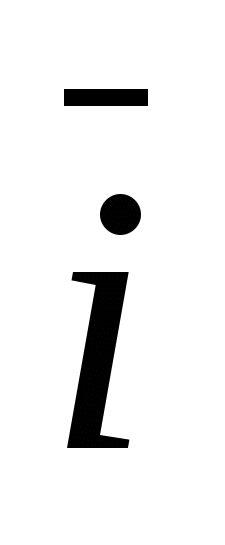 - x-ಅಕ್ಷದ ಘಟಕ ವೆಕ್ಟರ್, ಮೂಲಕ -
- x-ಅಕ್ಷದ ಘಟಕ ವೆಕ್ಟರ್, ಮೂಲಕ -  ಆರ್ಡಿನೇಟ್ ಅಕ್ಷದ ಘಟಕ ವೆಕ್ಟರ್ ಮತ್ತು ಮೂಲಕ
ಆರ್ಡಿನೇಟ್ ಅಕ್ಷದ ಘಟಕ ವೆಕ್ಟರ್ ಮತ್ತು ಮೂಲಕ 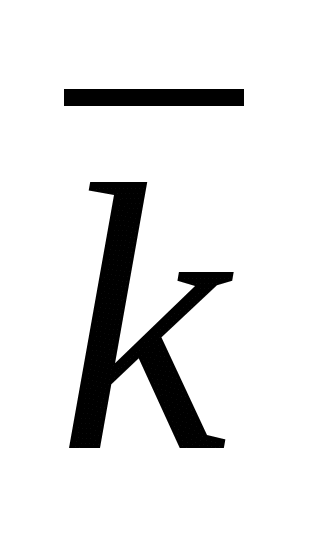 - ಘಟಕ ವೆಕ್ಟರ್ಅಕ್ಷದ ಅನ್ವಯ, ಅಂದರೆ.
- ಘಟಕ ವೆಕ್ಟರ್ಅಕ್ಷದ ಅನ್ವಯ, ಅಂದರೆ. 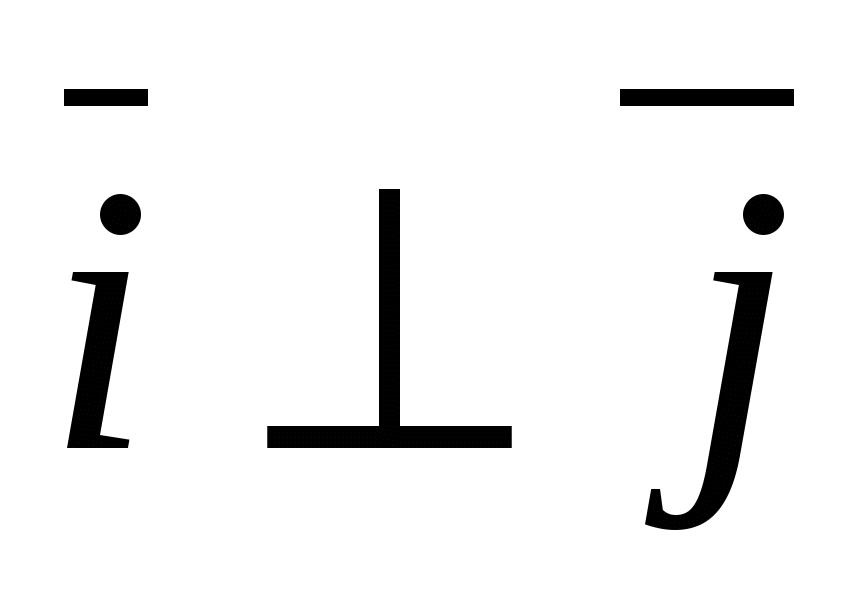 ,
, 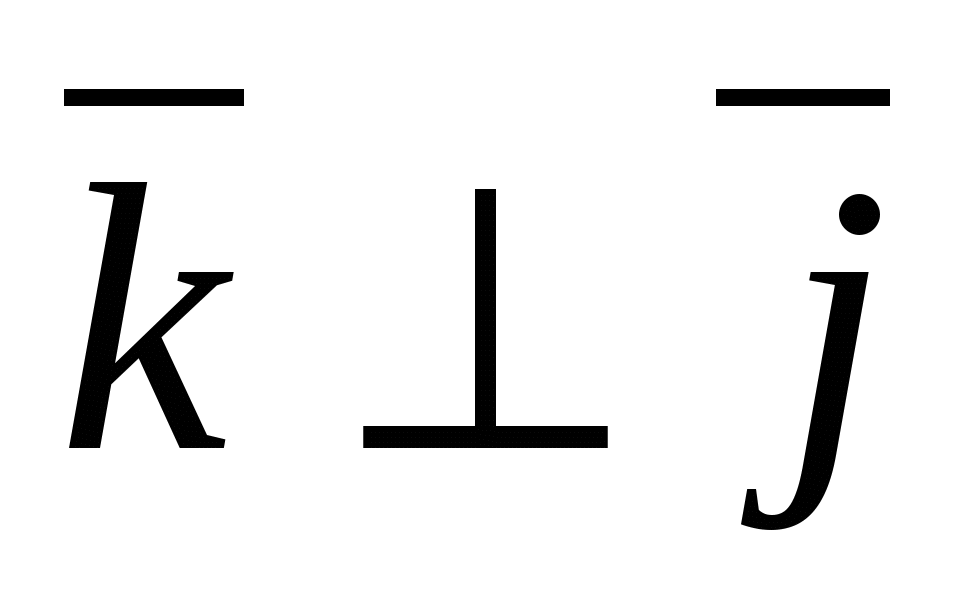 ,
, 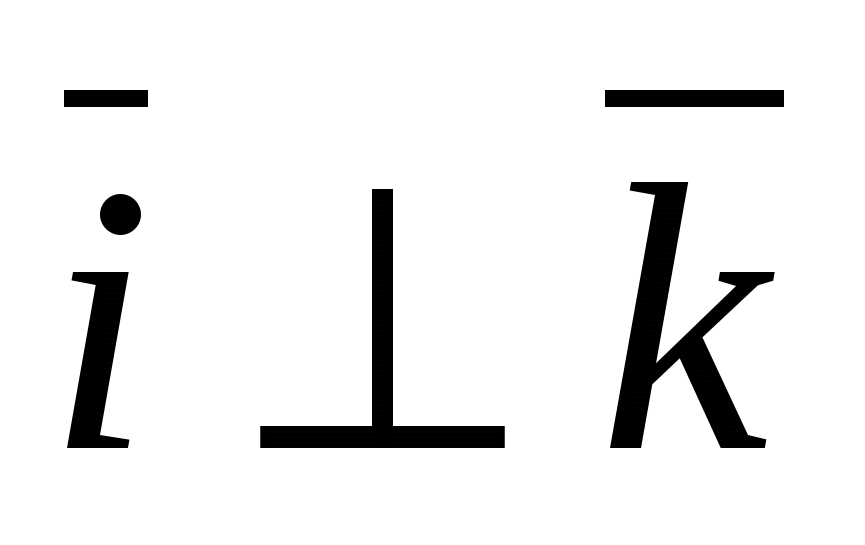 ,
,  .
.
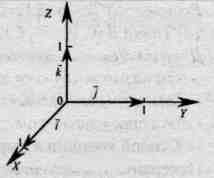
ಈ ಆಧಾರ 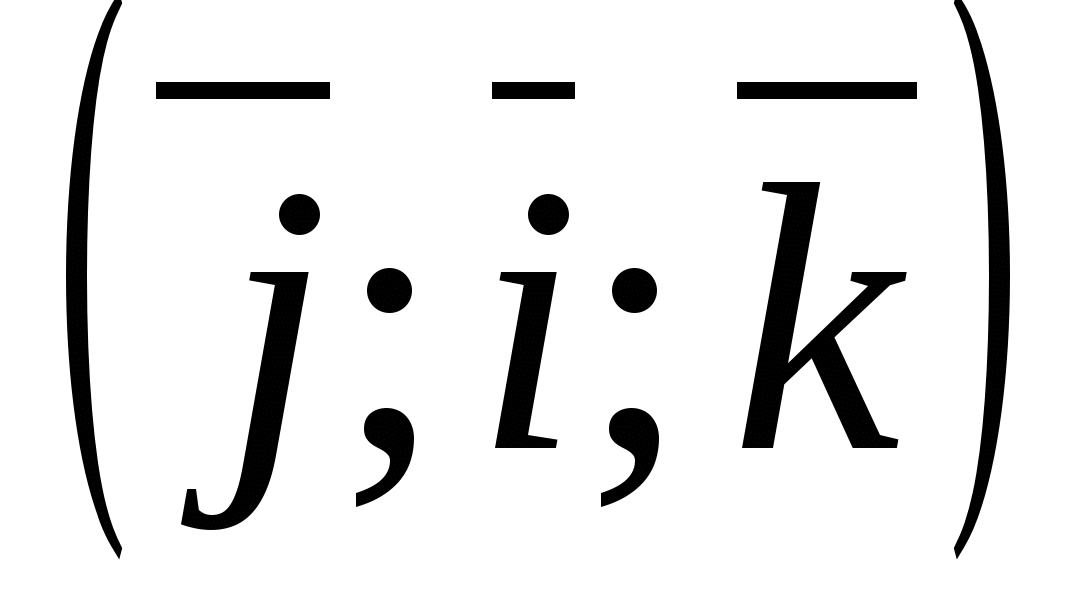 ಮತ್ತು ಕೌಂಟ್ಡೌನ್ ಆರಂಭಬಗ್ಗೆ ಒಂದು ಆಯತಾಕಾರದ ಕಾರ್ಟೇಶಿಯನ್ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯನ್ನು ವಿವರಿಸಿ
ಮತ್ತು ಕೌಂಟ್ಡೌನ್ ಆರಂಭಬಗ್ಗೆ ಒಂದು ಆಯತಾಕಾರದ ಕಾರ್ಟೇಶಿಯನ್ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯನ್ನು ವಿವರಿಸಿ  ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ.
ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ.
ಪ್ರಮೇಯ 1
ಯಾವುದೇ ಬಾಹ್ಯಾಕಾಶ ವೆಕ್ಟರ್
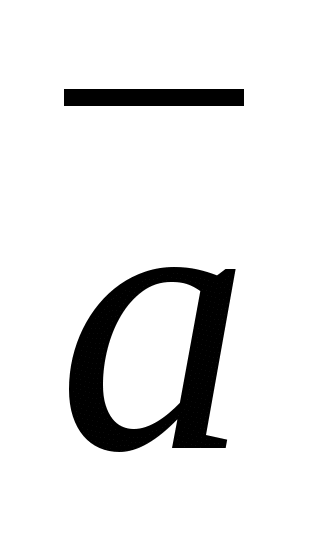 ನಿರ್ದೇಶಾಂಕ ವಾಹಕಗಳಾಗಿ ವಿಸ್ತರಿಸಬಹುದು, ಅಂದರೆ. ರೂಪದಲ್ಲಿ ಪ್ರಸ್ತುತ -
ನಿರ್ದೇಶಾಂಕ ವಾಹಕಗಳಾಗಿ ವಿಸ್ತರಿಸಬಹುದು, ಅಂದರೆ. ರೂಪದಲ್ಲಿ ಪ್ರಸ್ತುತ -
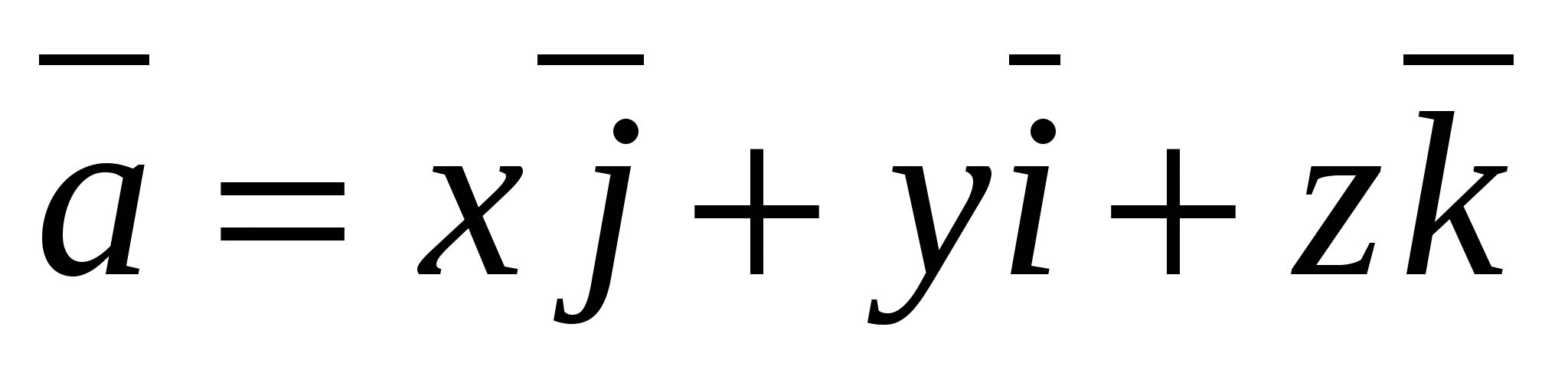 ,
,
ಮತ್ತು ವಿಸ್ತರಣೆ ಗುಣಾಂಕಗಳು 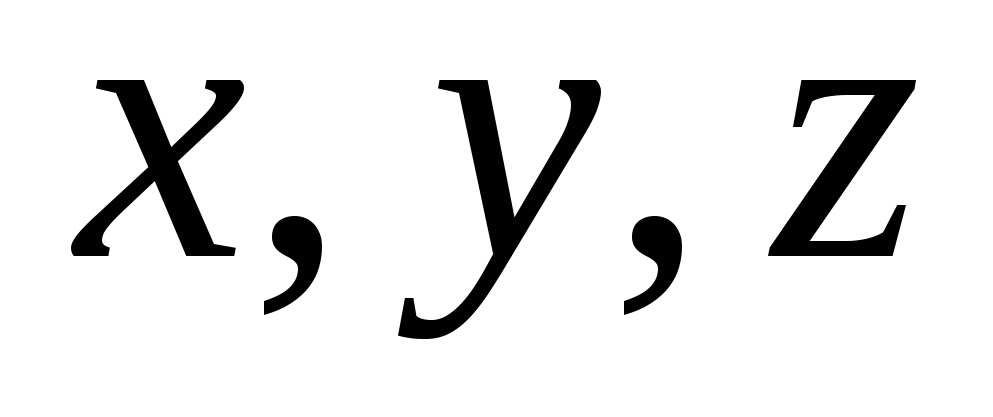 ವಿಶಿಷ್ಟ ರೀತಿಯಲ್ಲಿ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ.
ವಿಶಿಷ್ಟ ರೀತಿಯಲ್ಲಿ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ.
ಎಚ್ 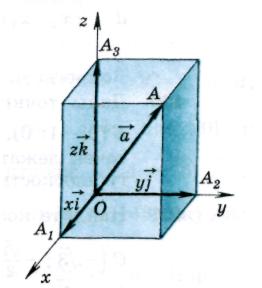 ಇಸ್ಲಾ
ಇಸ್ಲಾ 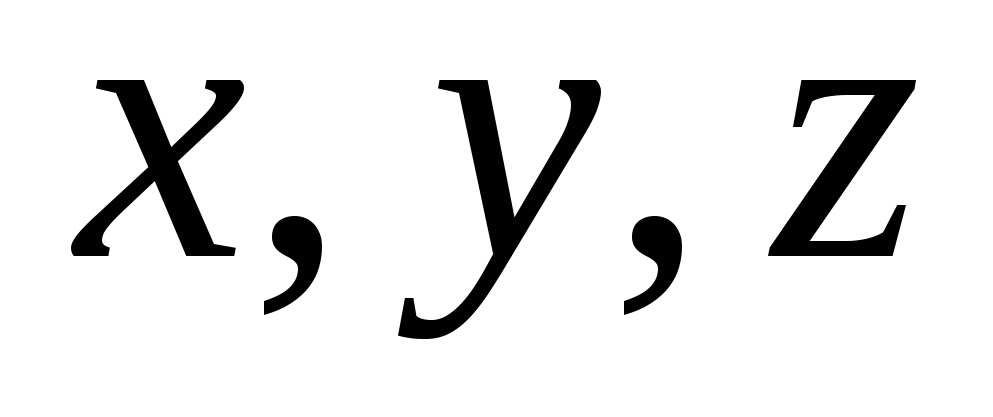 ವೆಕ್ಟರ್ ನಿರ್ದೇಶಾಂಕಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ
ವೆಕ್ಟರ್ ನಿರ್ದೇಶಾಂಕಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ 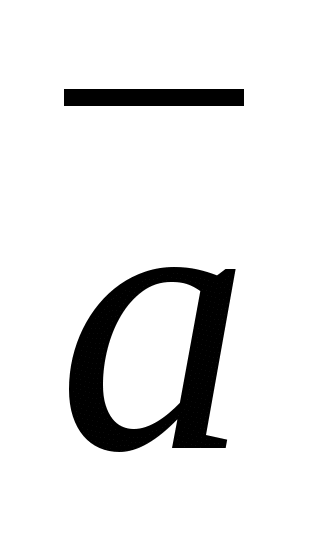 , ಅಂದರೆ
, ಅಂದರೆ 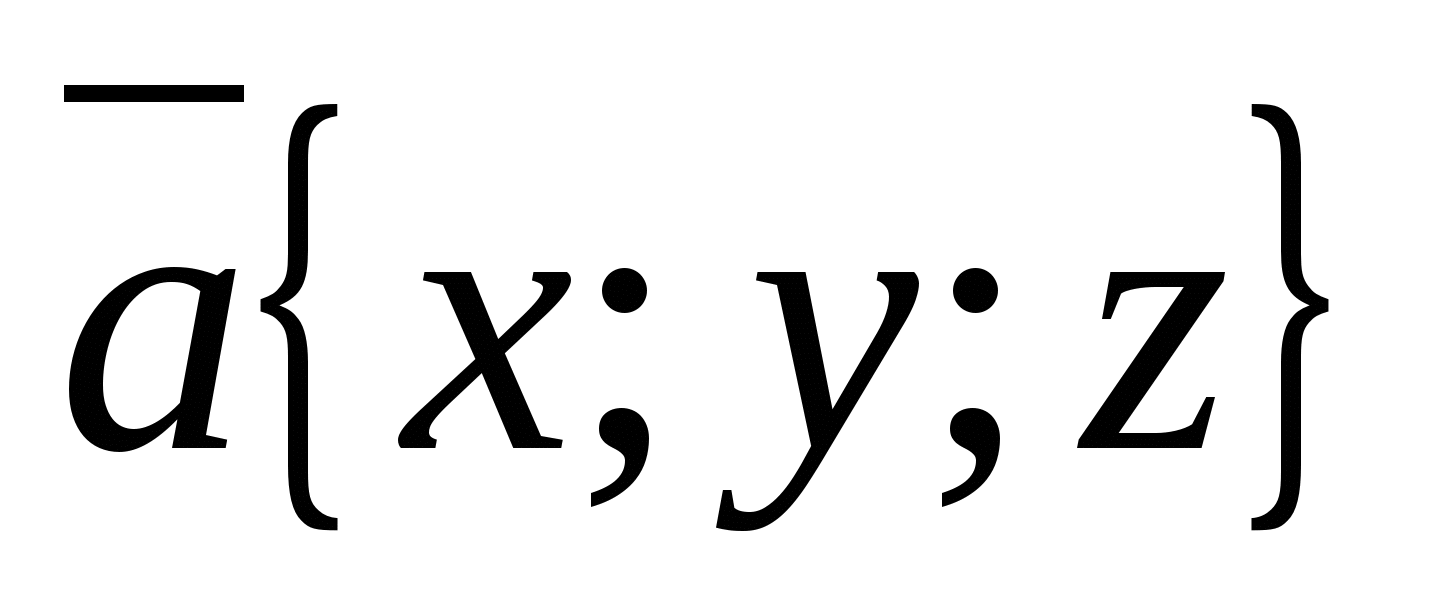 . ಶೂನ್ಯ ವೆಕ್ಟರ್ ಅನ್ನು ಹೀಗೆ ಪ್ರತಿನಿಧಿಸಬಹುದು
. ಶೂನ್ಯ ವೆಕ್ಟರ್ ಅನ್ನು ಹೀಗೆ ಪ್ರತಿನಿಧಿಸಬಹುದು 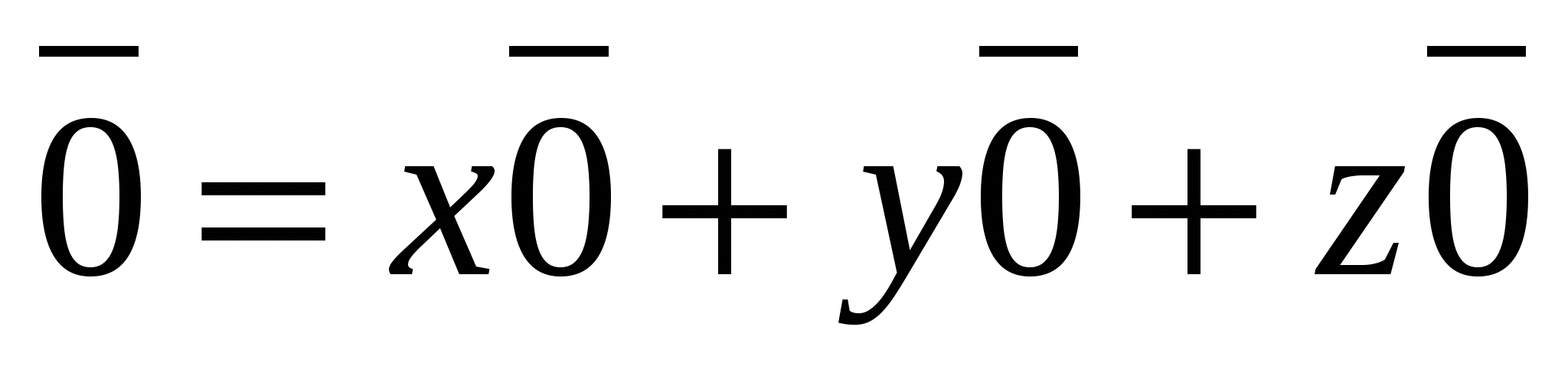 , ನಂತರ ಶೂನ್ಯ ವೆಕ್ಟರ್ನ ಎಲ್ಲಾ ನಿರ್ದೇಶಾಂಕಗಳು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ,
, ನಂತರ ಶೂನ್ಯ ವೆಕ್ಟರ್ನ ಎಲ್ಲಾ ನಿರ್ದೇಶಾಂಕಗಳು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, 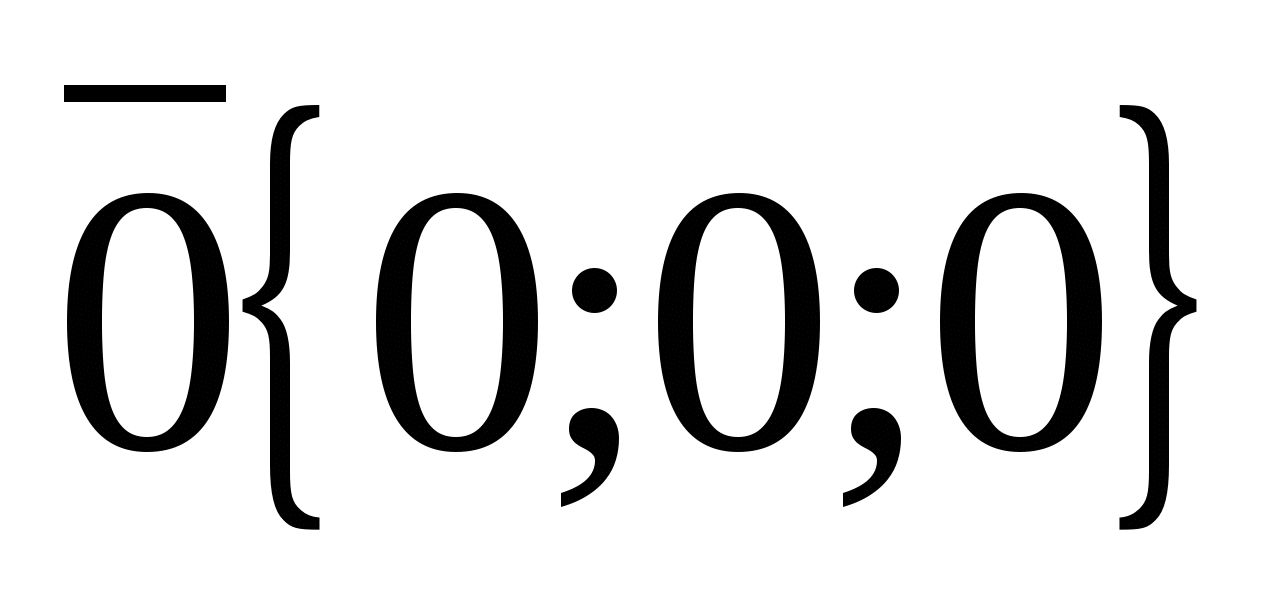 .
.
2. ನಿರ್ದೇಶಾಂಕಗಳಲ್ಲಿನ ವಾಹಕಗಳ ಮೇಲೆ ರೇಖೀಯ ಕಾರ್ಯಾಚರಣೆಗಳು.
ನಿಯಮ 1.
ಸಮಾನರ ನಿರ್ದೇಶಾಂಕಗಳು
ವಾಹಕಗಳು ಕ್ರಮವಾಗಿ ಸಮಾನವಾಗಿರುತ್ತವೆ,
ಆ. ವಾಹಕಗಳಾಗಿದ್ದರೆ 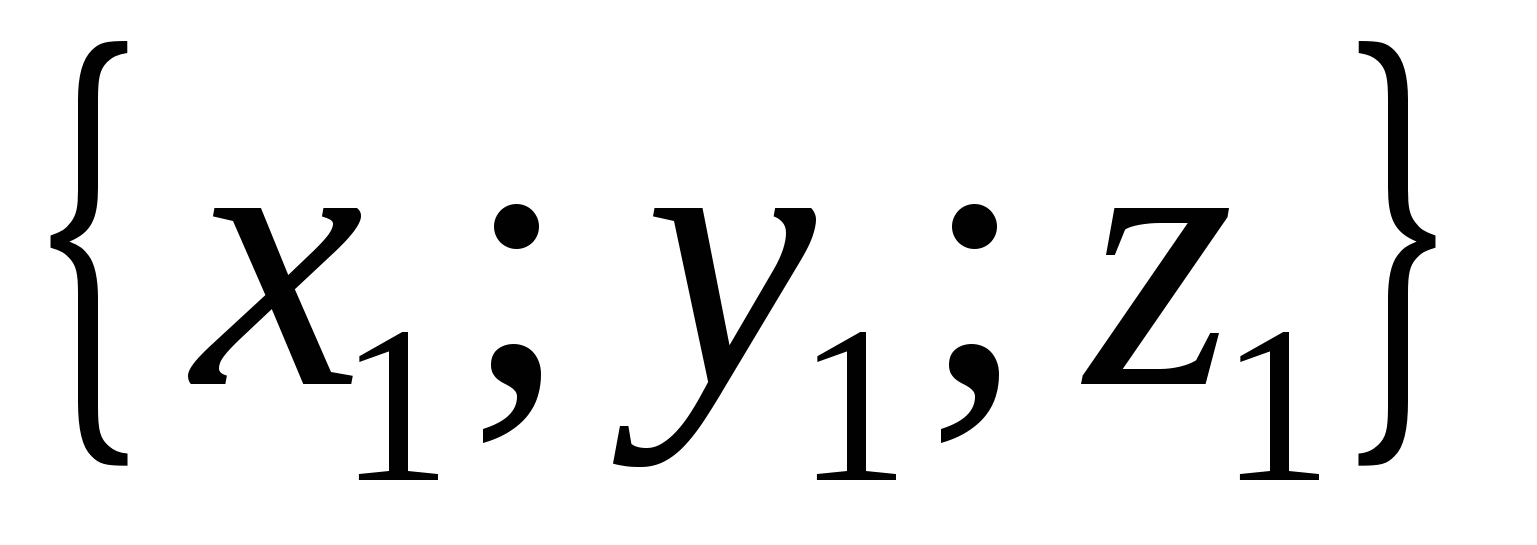 ಮತ್ತು
ಮತ್ತು 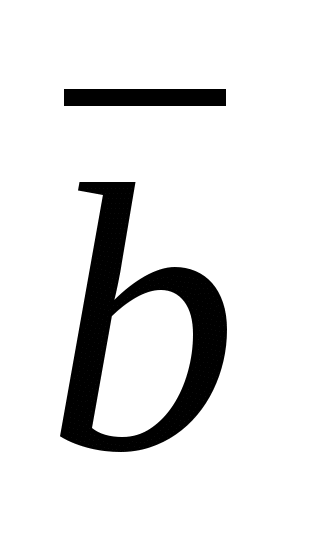
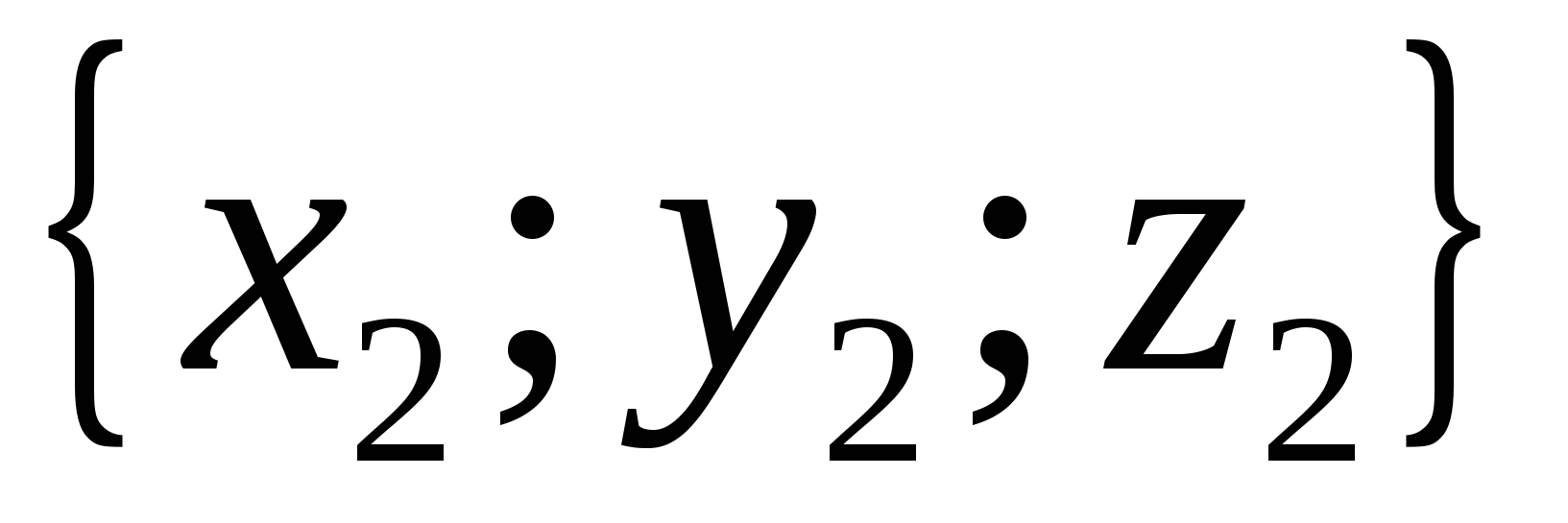 ನಂತರ ಸಮಾನವಾಗಿರುತ್ತದೆ
ನಂತರ ಸಮಾನವಾಗಿರುತ್ತದೆ 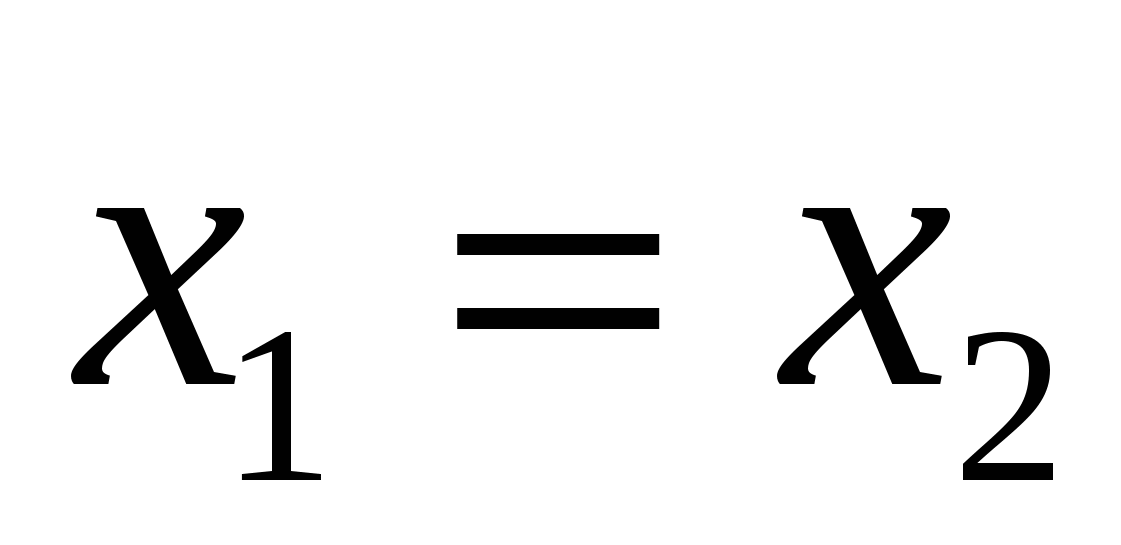 ,
,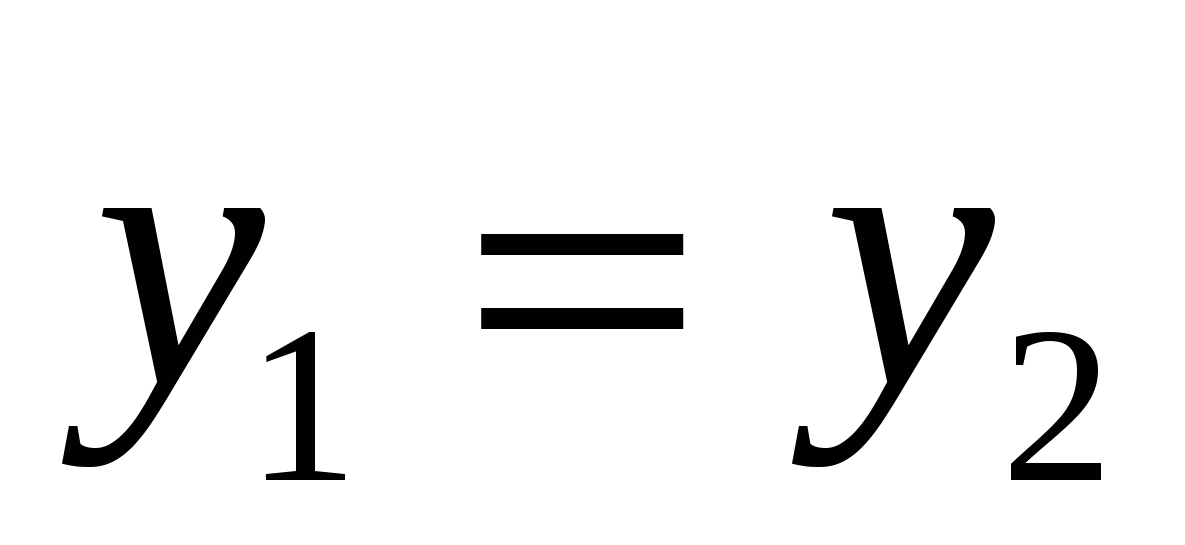 ಮತ್ತು
ಮತ್ತು 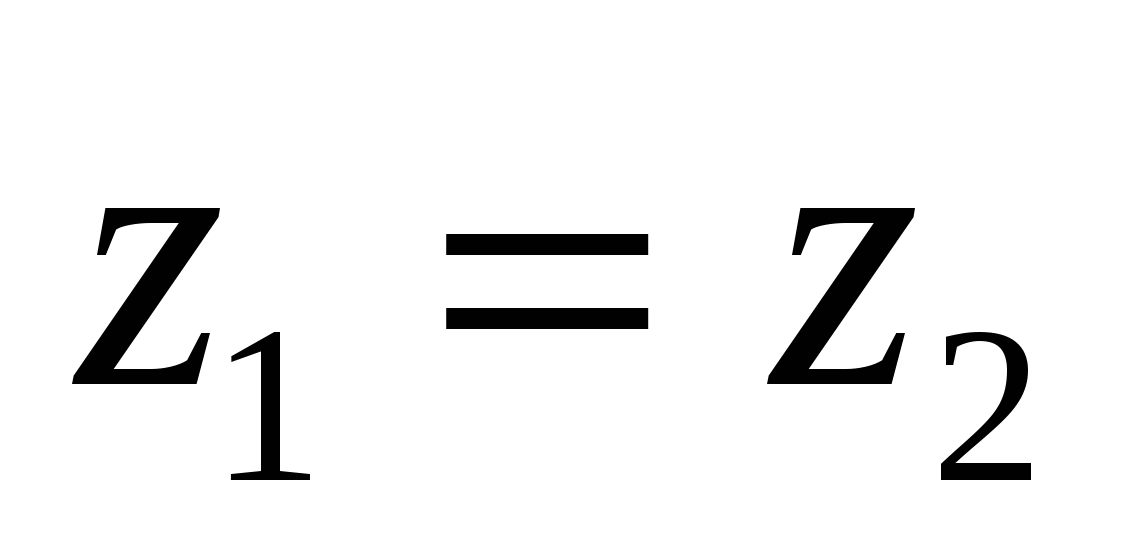 .
.
ನಿಯಮ 2.
ಎರಡು ಅಥವಾ ಹೆಚ್ಚಿನ ವೆಕ್ಟರ್ಗಳ ಮೊತ್ತದ ಪ್ರತಿಯೊಂದು ನಿರ್ದೇಶಾಂಕವು ಈ ವೆಕ್ಟರ್ಗಳ ಅನುಗುಣವಾದ ನಿರ್ದೇಶಾಂಕಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ವೇಳೆ 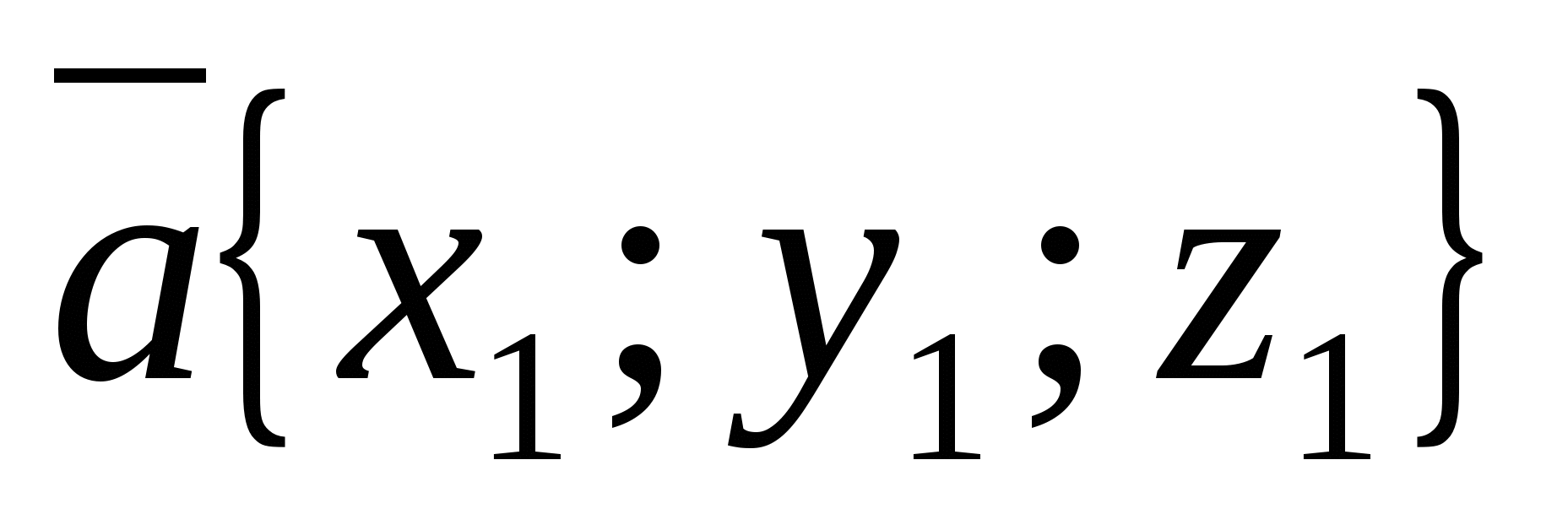 ಮತ್ತು
ಮತ್ತು 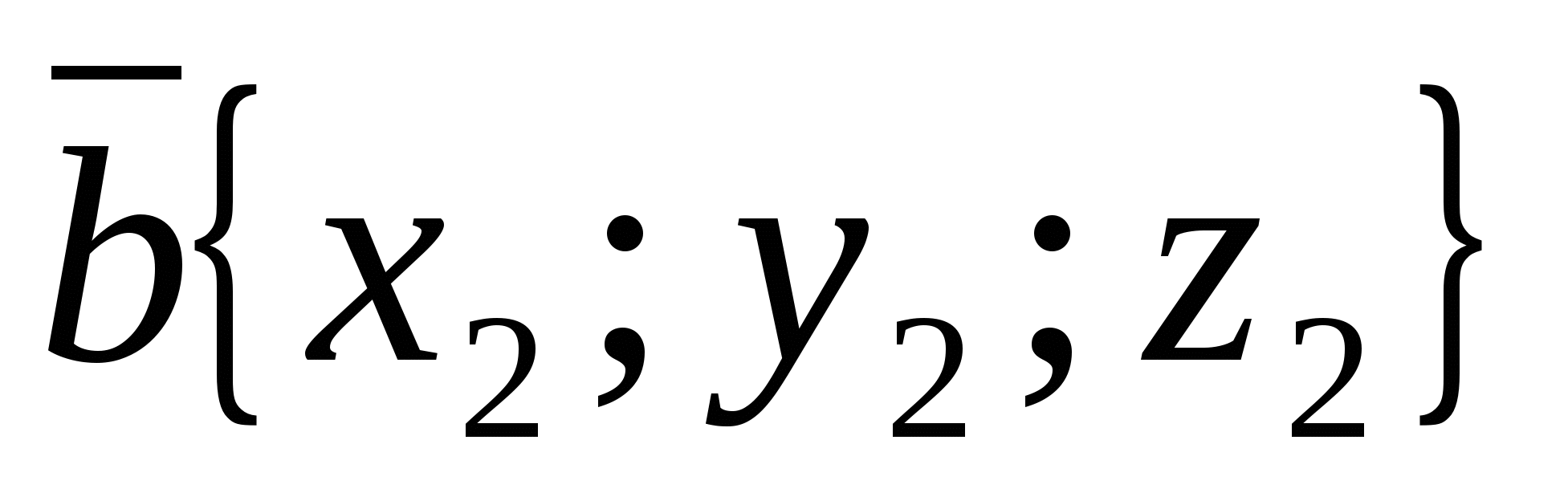 -ಕೊಟ್ಟಿರುವ ವೆಕ್ಟರ್, ನಂತರ ವೆಕ್ಟರ್
-ಕೊಟ್ಟಿರುವ ವೆಕ್ಟರ್, ನಂತರ ವೆಕ್ಟರ್ 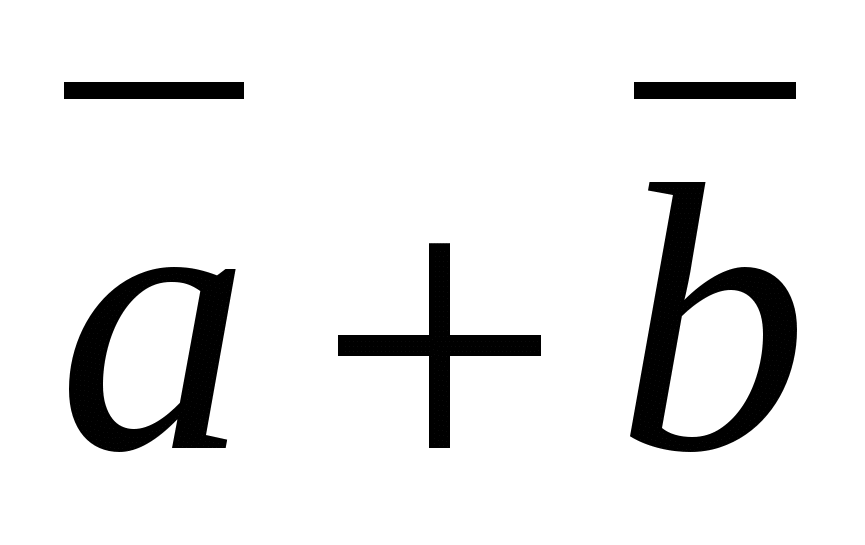 ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ.
ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ.
ನಿಯಮ 3.
ಎರಡು ವೆಕ್ಟರ್ಗಳ ವ್ಯತ್ಯಾಸದ ಪ್ರತಿಯೊಂದು ನಿರ್ದೇಶಾಂಕವು ಈ ವೆಕ್ಟರ್ಗಳ ಅನುಗುಣವಾದ ನಿರ್ದೇಶಾಂಕಗಳ ವ್ಯತ್ಯಾಸಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ವೇಳೆ 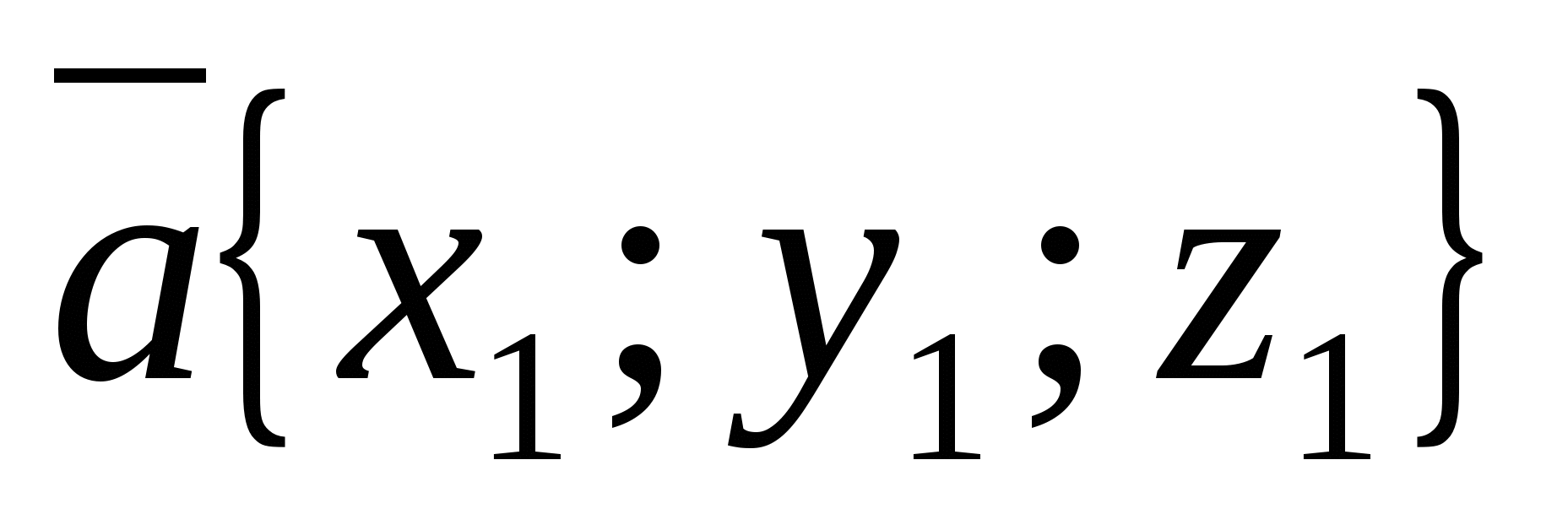 ಮತ್ತು
ಮತ್ತು 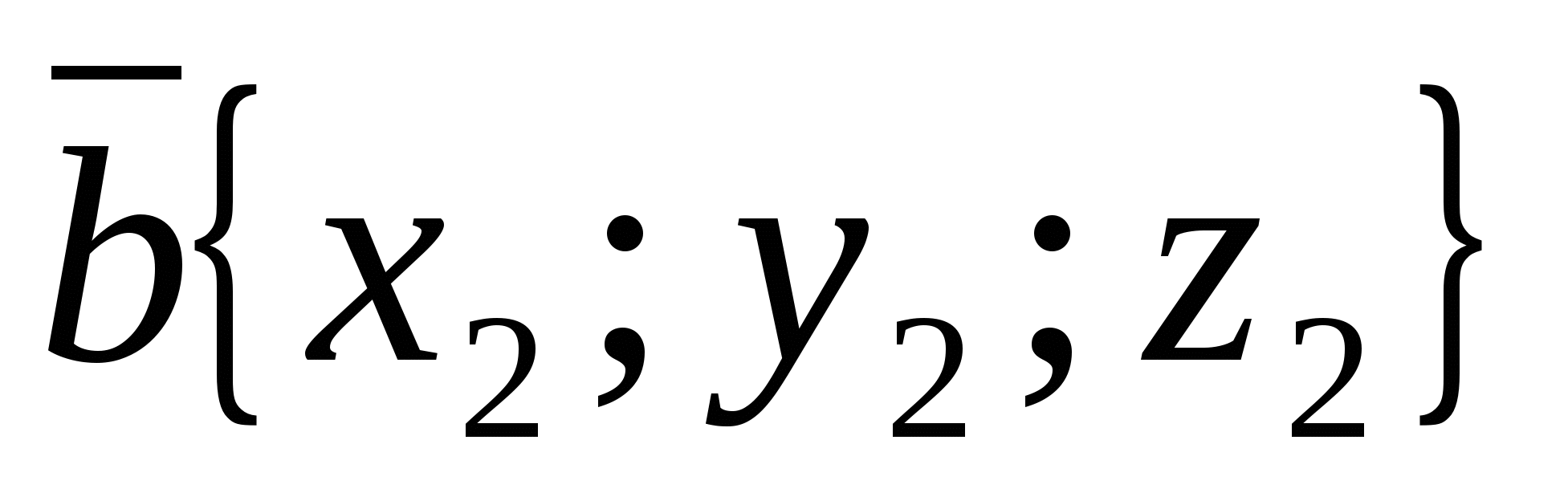 -ಕೊಟ್ಟಿರುವ ವೆಕ್ಟರ್, ನಂತರ ವೆಕ್ಟರ್
-ಕೊಟ್ಟಿರುವ ವೆಕ್ಟರ್, ನಂತರ ವೆಕ್ಟರ್ 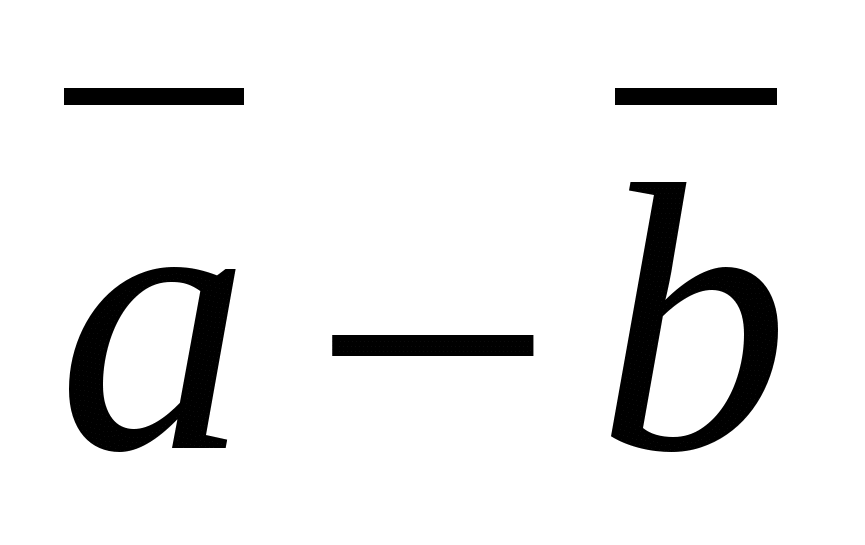 ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ
ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ
ನಿಯಮ 4.
ವೆಕ್ಟರ್ ಮತ್ತು ಸಂಖ್ಯೆಯ ಉತ್ಪನ್ನದ ಪ್ರತಿಯೊಂದು ನಿರ್ದೇಶಾಂಕವು ವೆಕ್ಟರ್ ಮತ್ತು ಈ ಸಂಖ್ಯೆಯ ಅನುಗುಣವಾದ ನಿರ್ದೇಶಾಂಕಗಳ ಉತ್ಪನ್ನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ವೇಳೆ 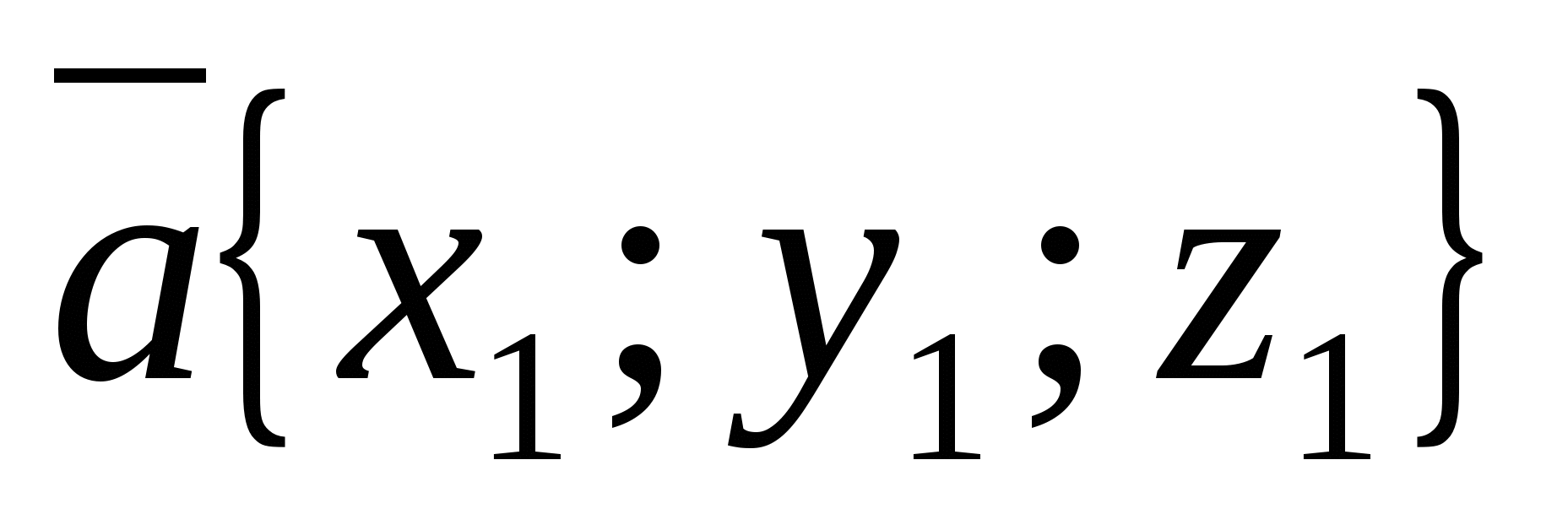 - ಕೊಟ್ಟಿರುವ ವೆಕ್ಟರ್,
- ಕೊಟ್ಟಿರುವ ವೆಕ್ಟರ್, ![]() - ನೀಡಿದ ಸಂಖ್ಯೆ, ನಂತರ ವೆಕ್ಟರ್
- ನೀಡಿದ ಸಂಖ್ಯೆ, ನಂತರ ವೆಕ್ಟರ್ 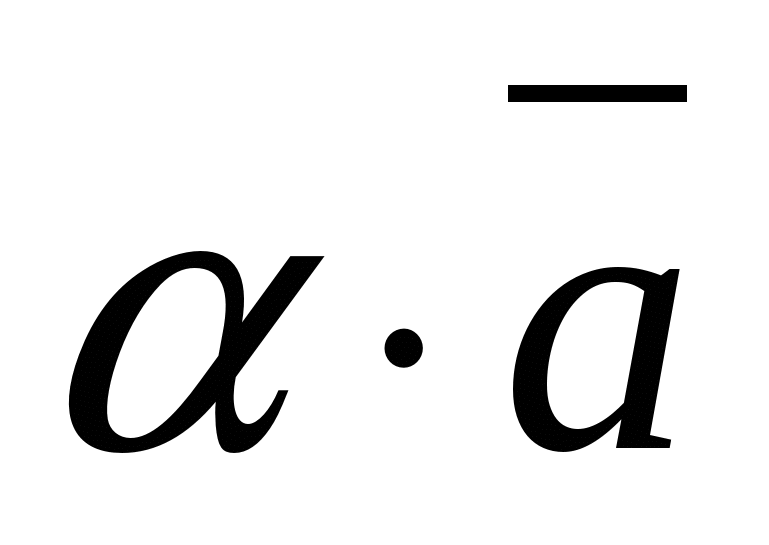 ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ.
ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ. 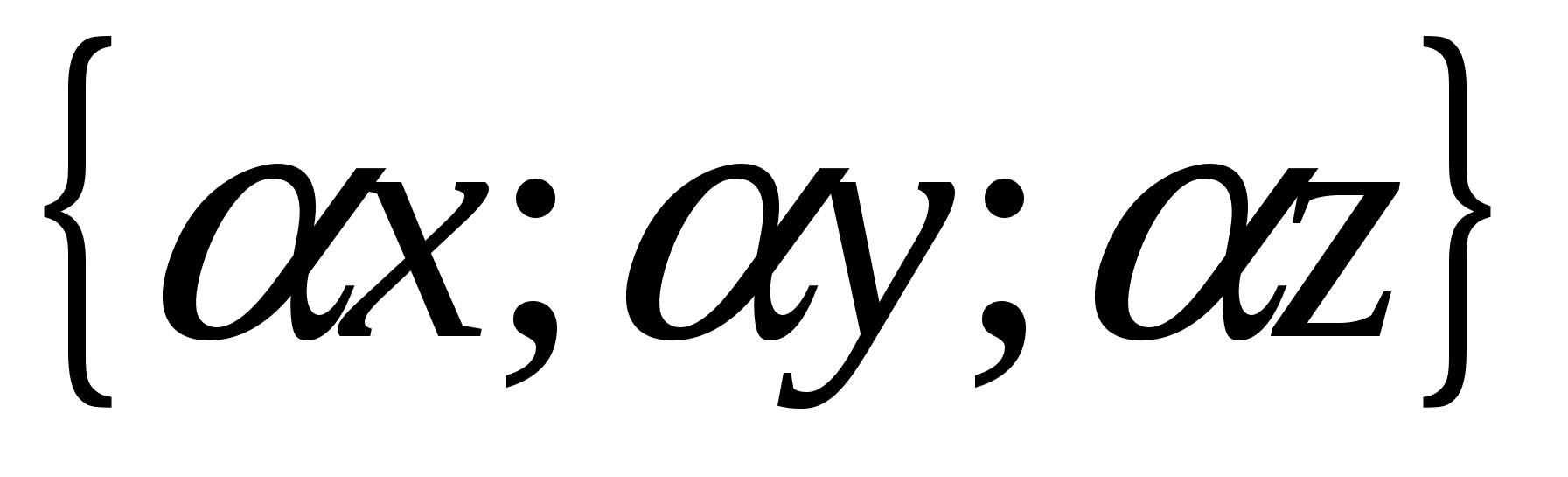 .
.
ಉದಾಹರಣೆ.
ವೆಕ್ಟರ್ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹುಡುಕಿ 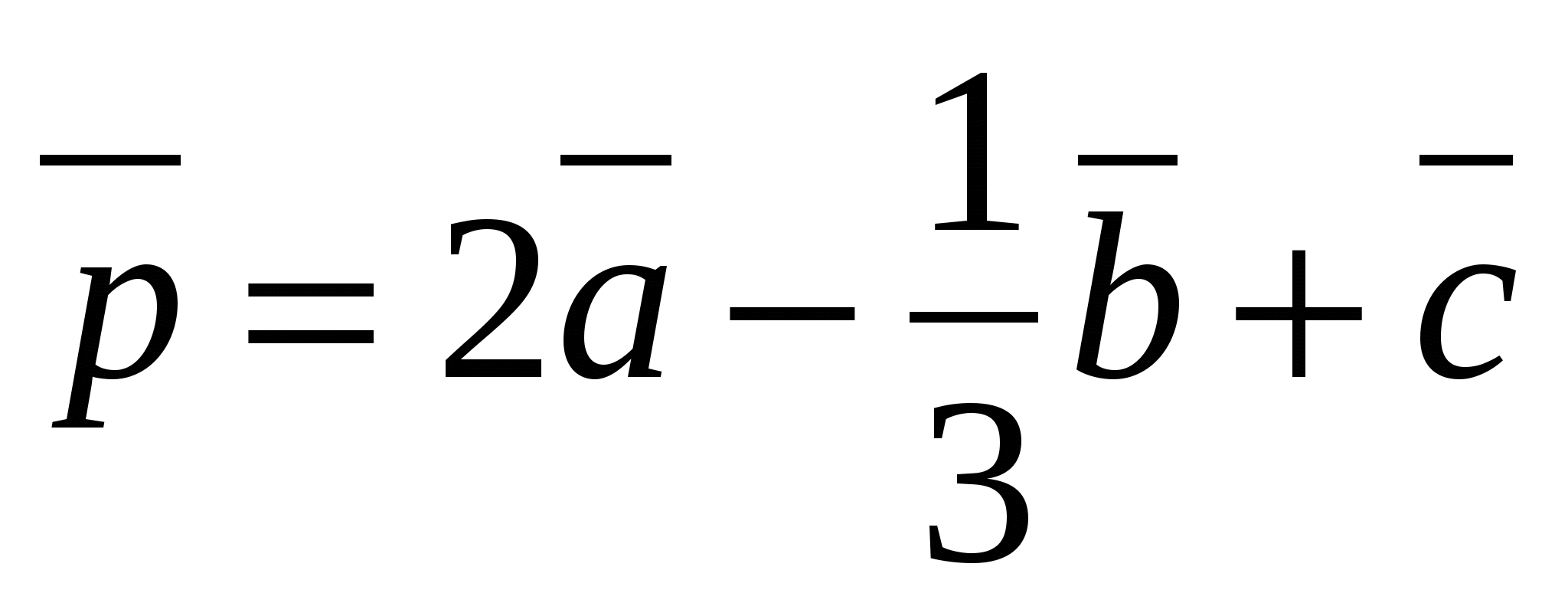 , ವೇಳೆ
, ವೇಳೆ 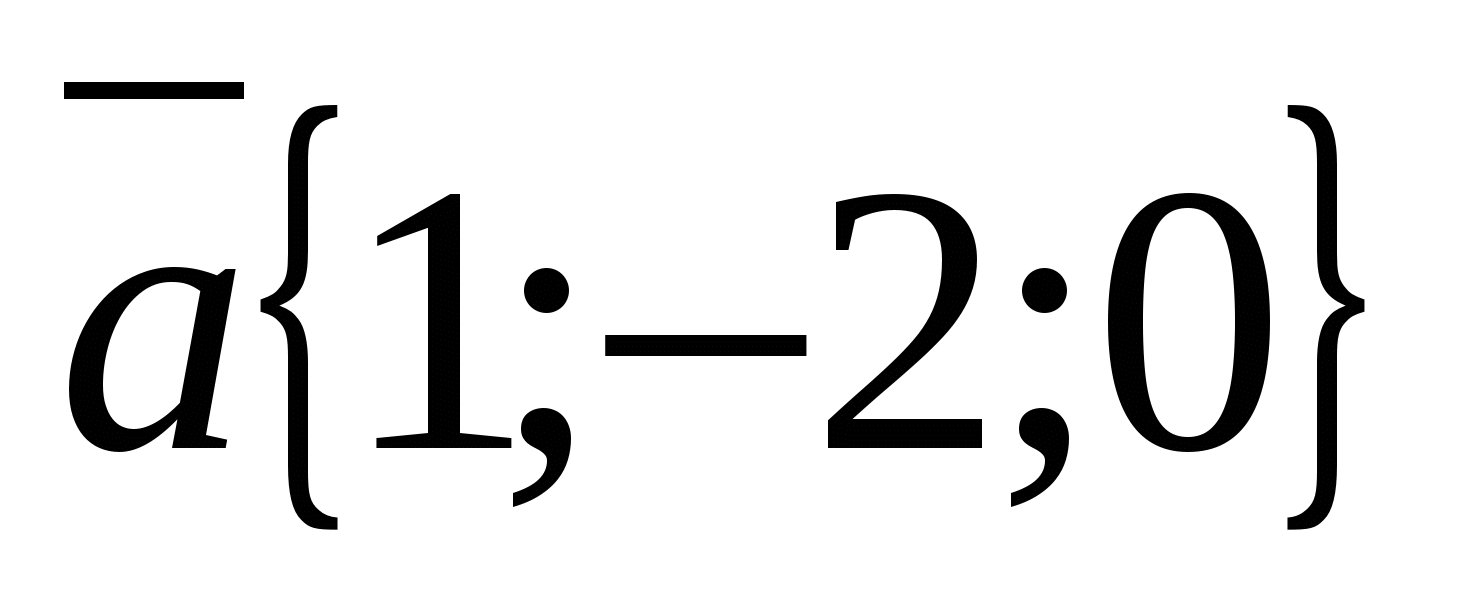 ,
, 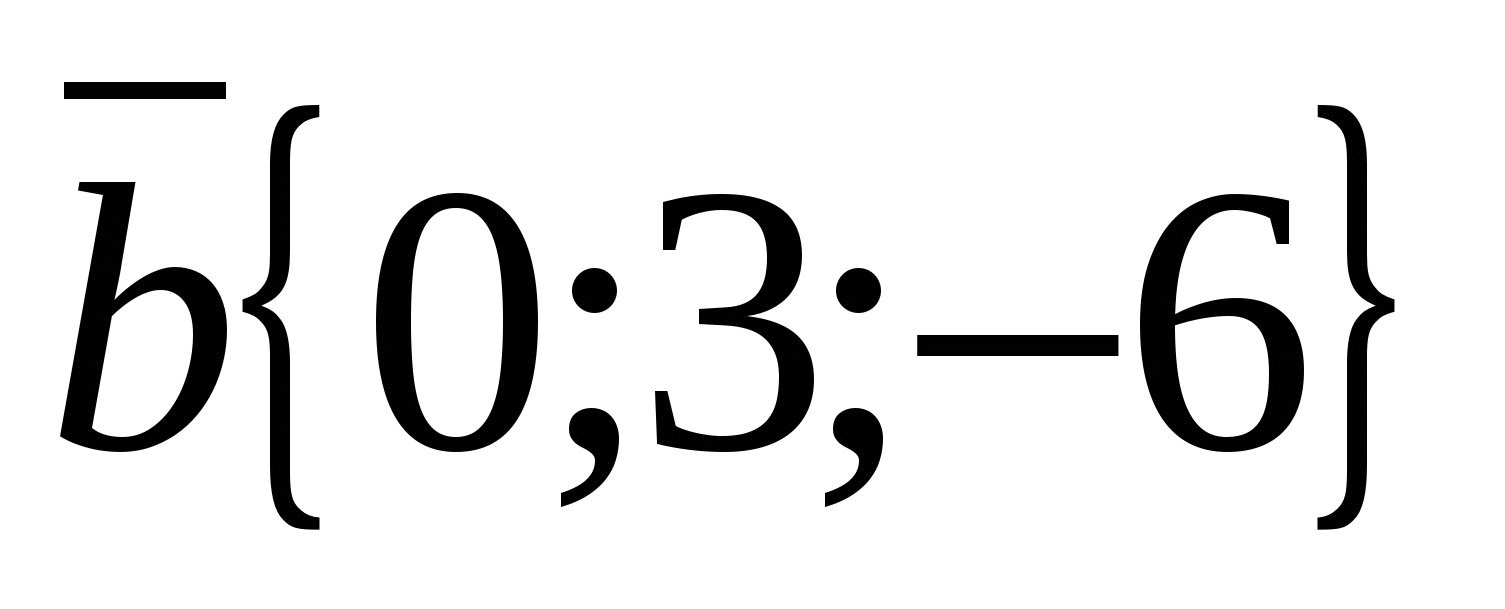 ,
, 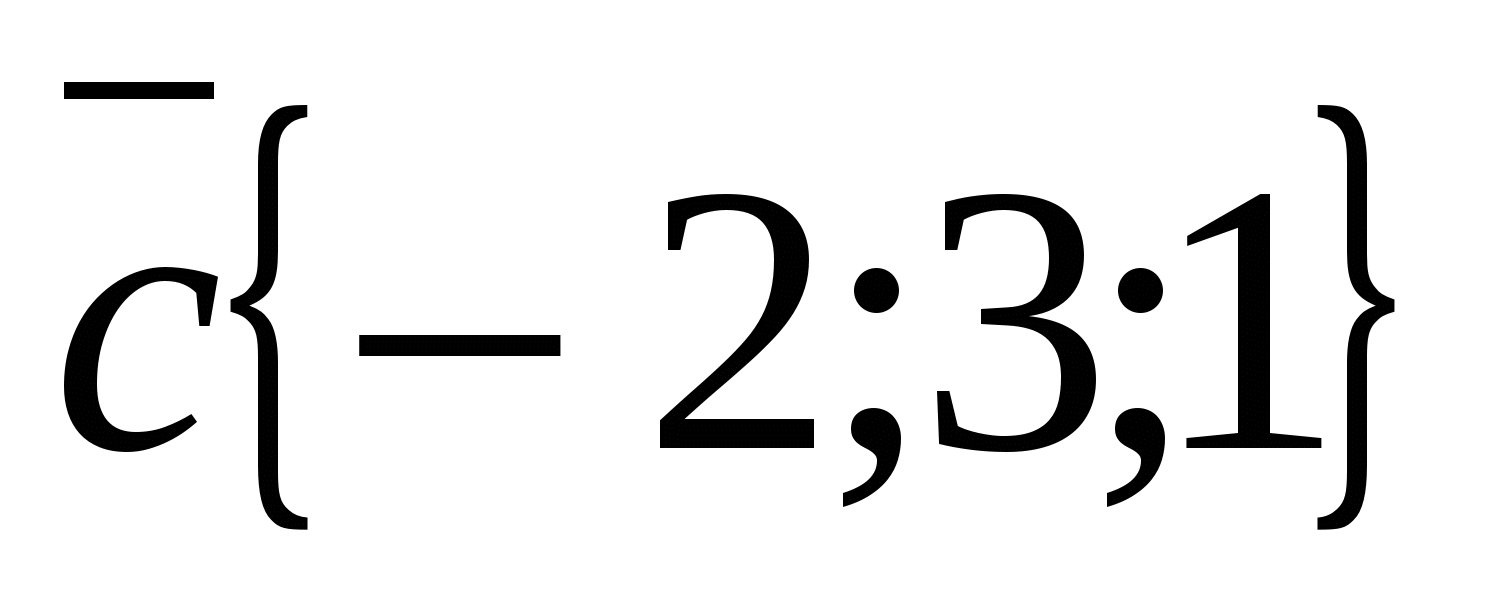 .
.
ಪರಿಹಾರ.
ವೆಕ್ಟರ್ 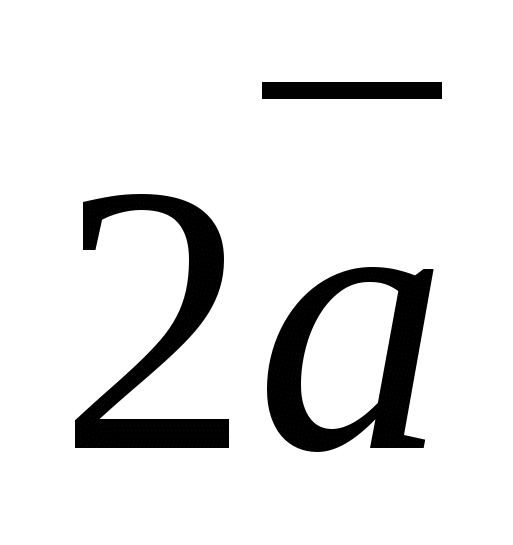 ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ
ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ 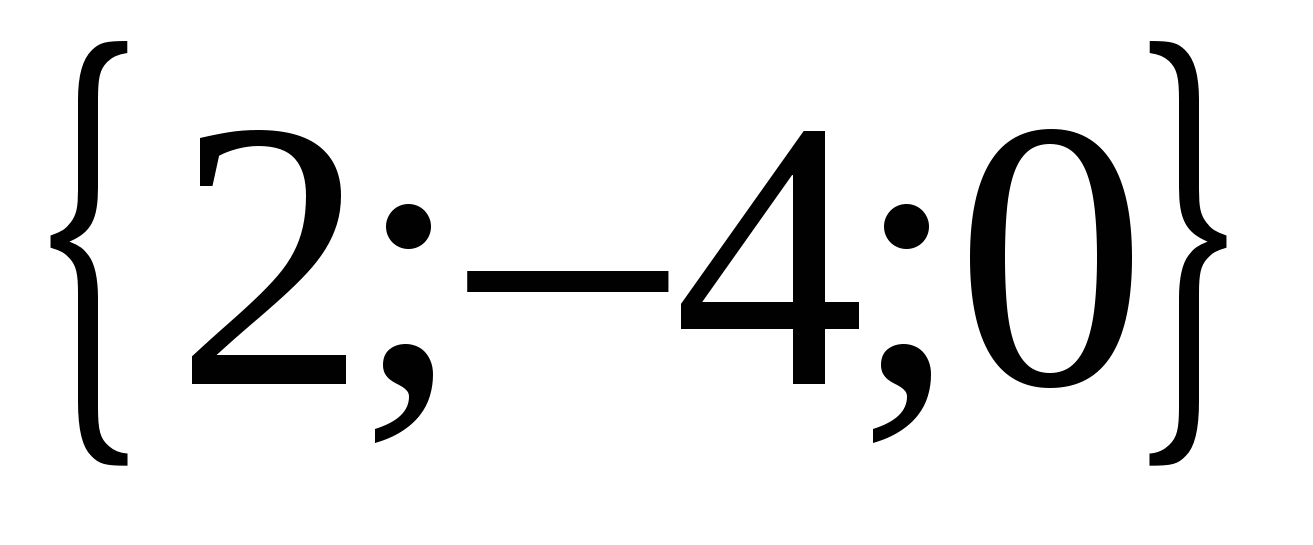 , ಮತ್ತು ವೆಕ್ಟರ್
, ಮತ್ತು ವೆಕ್ಟರ್  - ನಿರ್ದೇಶಾಂಕಗಳು
- ನಿರ್ದೇಶಾಂಕಗಳು 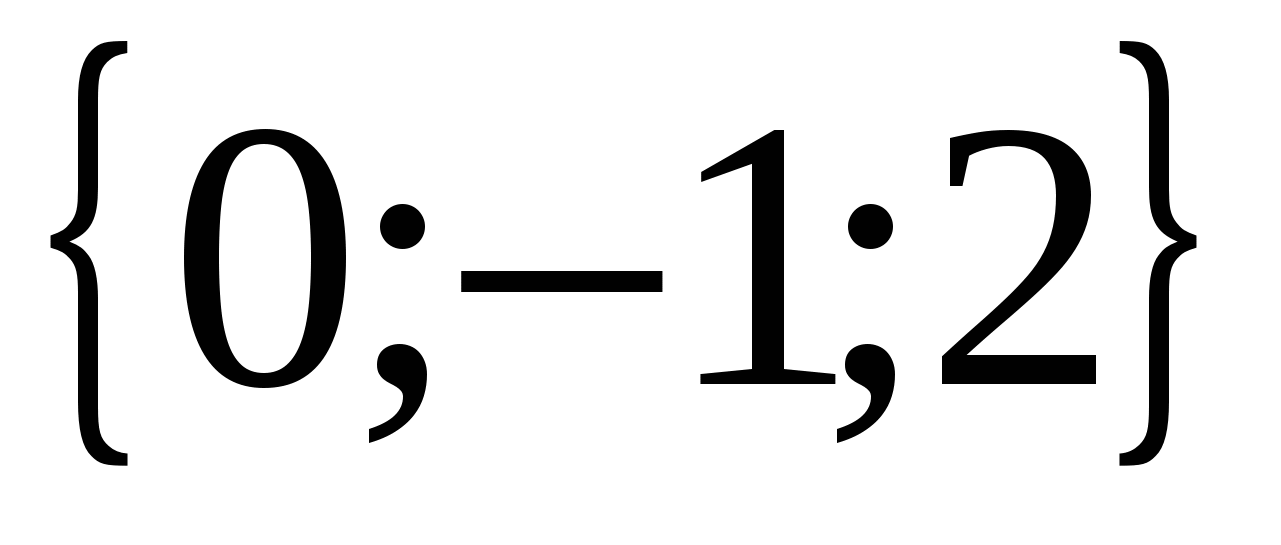 .
.
ಏಕೆಂದರೆ 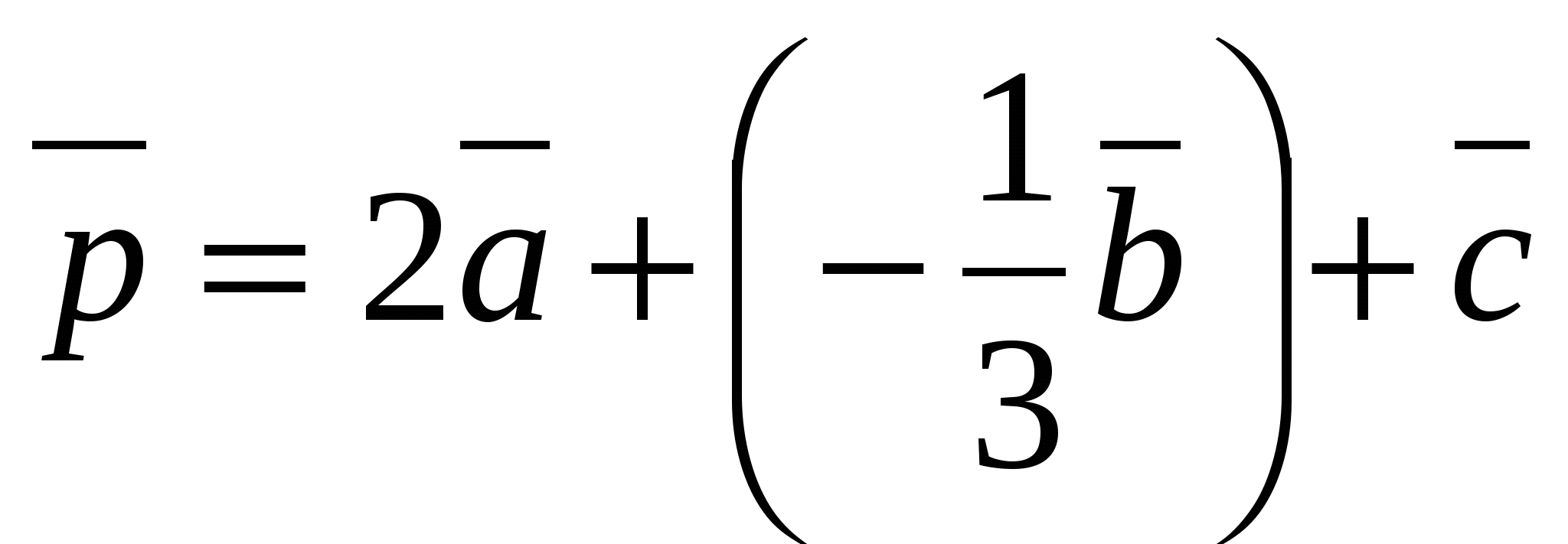 , ನಂತರ ಅದರ ನಿರ್ದೇಶಾಂಕಗಳು
, ನಂತರ ಅದರ ನಿರ್ದೇಶಾಂಕಗಳು  ಹೀಗೆ ಲೆಕ್ಕ ಹಾಕಬಹುದು:
ಹೀಗೆ ಲೆಕ್ಕ ಹಾಕಬಹುದು:  ,
, 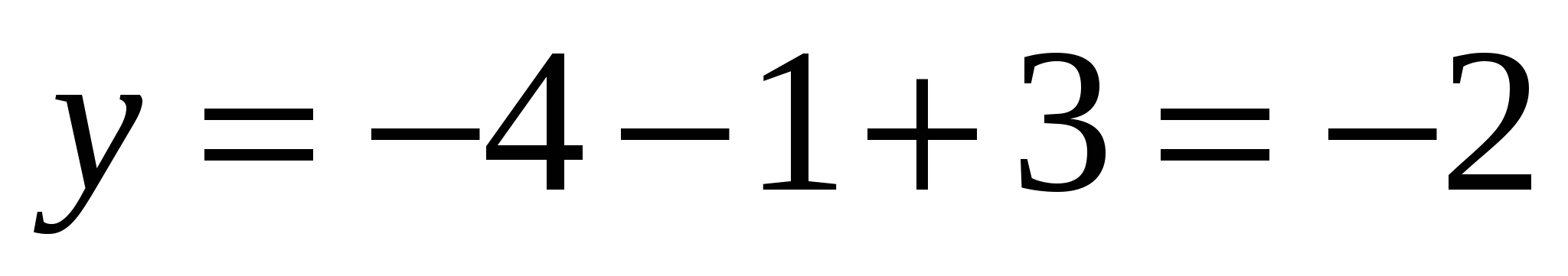 ,
, 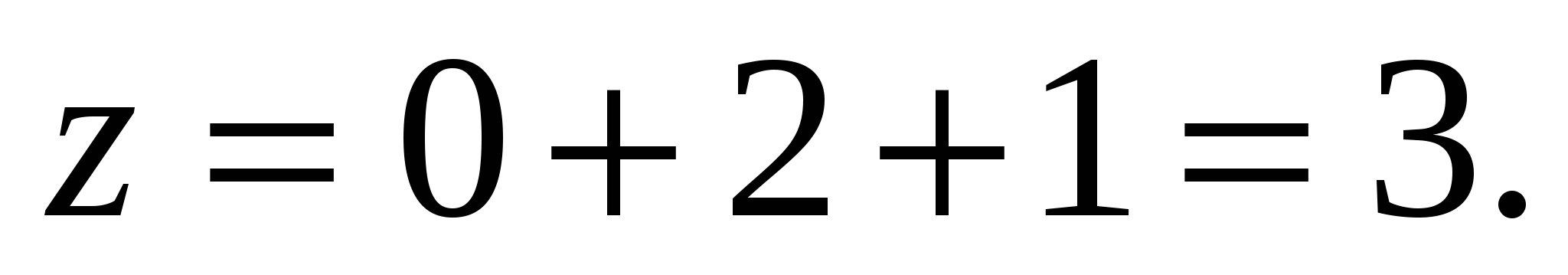 ಆದ್ದರಿಂದ ಇದು ವೆಕ್ಟರ್ ಆಗಿದೆ
ಆದ್ದರಿಂದ ಇದು ವೆಕ್ಟರ್ ಆಗಿದೆ 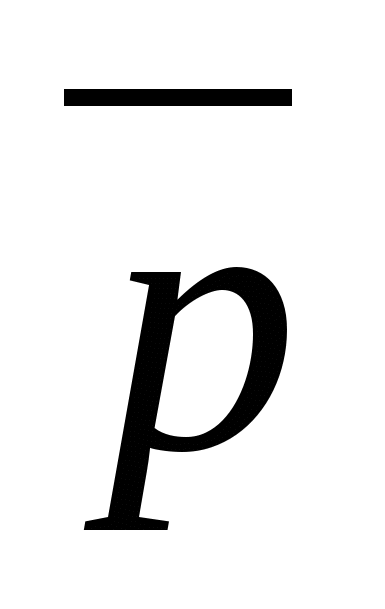 ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ
ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ 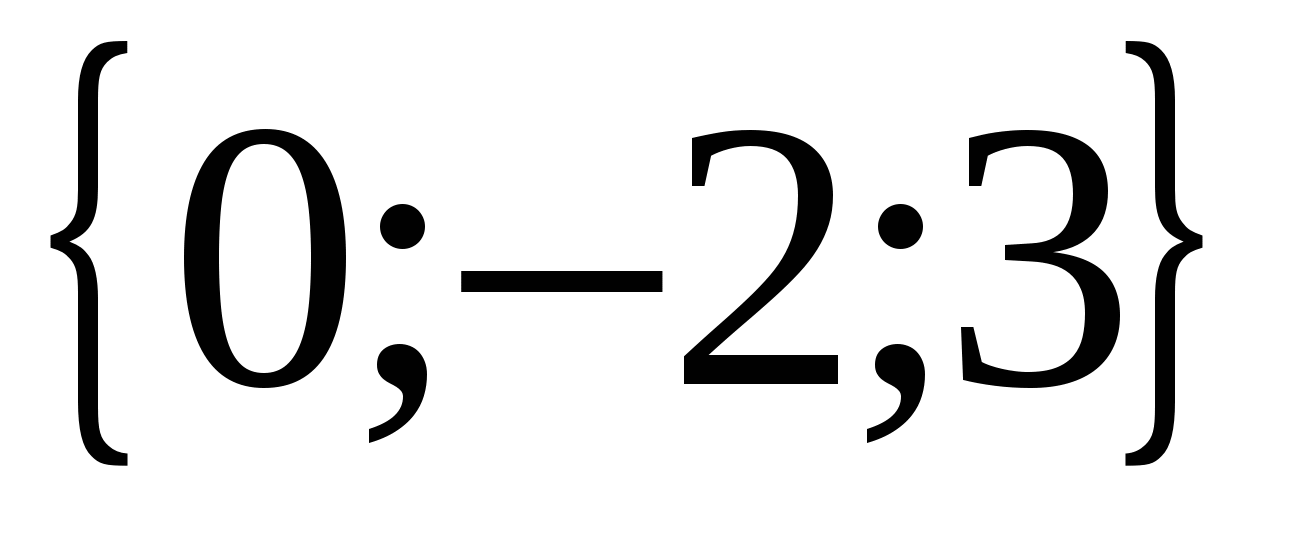 .
.
3. ವೆಕ್ಟರ್ ನಿರ್ದೇಶಾಂಕಗಳು ಮತ್ತು ಬಿಂದು ನಿರ್ದೇಶಾಂಕಗಳ ನಡುವಿನ ಸಂಬಂಧ.
ವ್ಯಾಖ್ಯಾನ.
ಒಂದು ನಿರ್ದಿಷ್ಟ ಬಿಂದುವಿನ ಅಂತ್ಯವು ಹೊಂದಿಕೆಯಾಗುವ ವೆಕ್ಟರ್ ಮತ್ತು ಅದರ ಪ್ರಾರಂಭವು ನಿರ್ದೇಶಾಂಕಗಳ ಮೂಲದೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾಗುತ್ತದೆ, ಇದನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ತ್ರಿಜ್ಯ ವೆಕ್ಟರ್ಈ ಹಂತ.
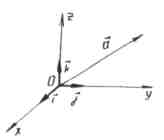
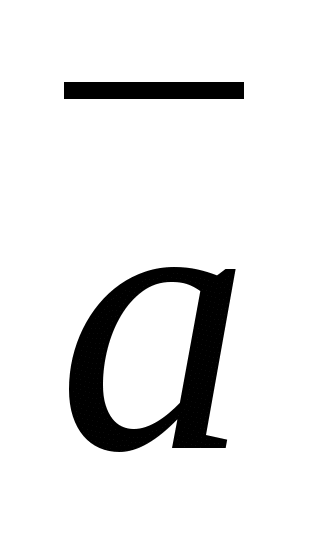
 - ತ್ರಿಜ್ಯ ವೆಕ್ಟರ್
- ತ್ರಿಜ್ಯ ವೆಕ್ಟರ್
 ,
,
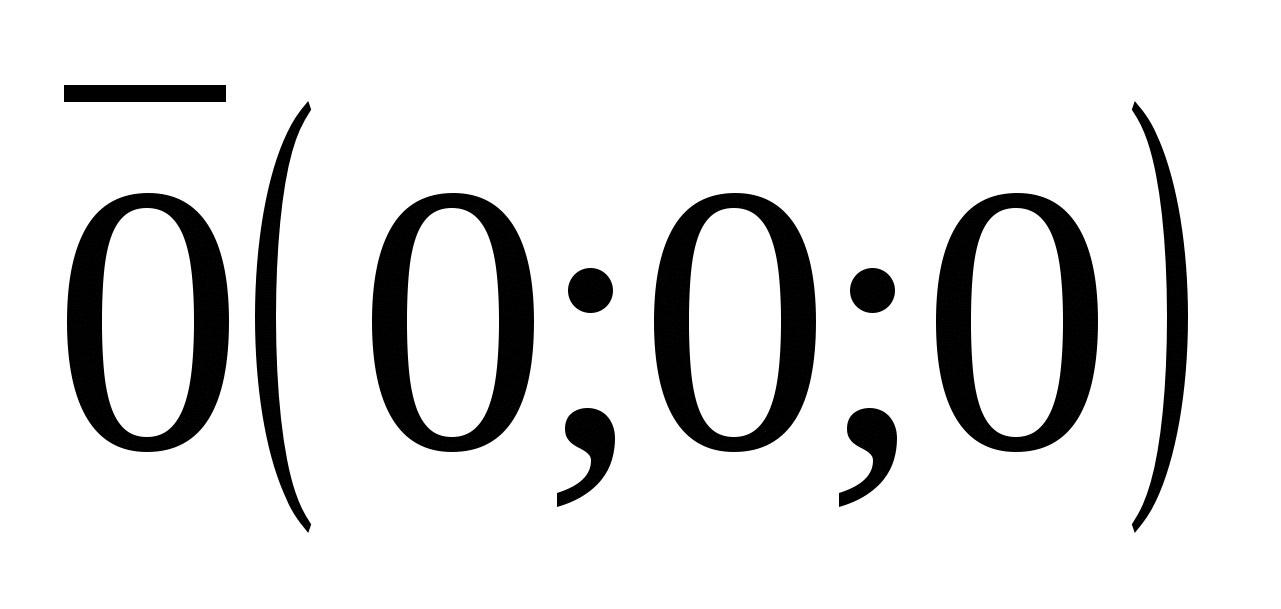 ;
;
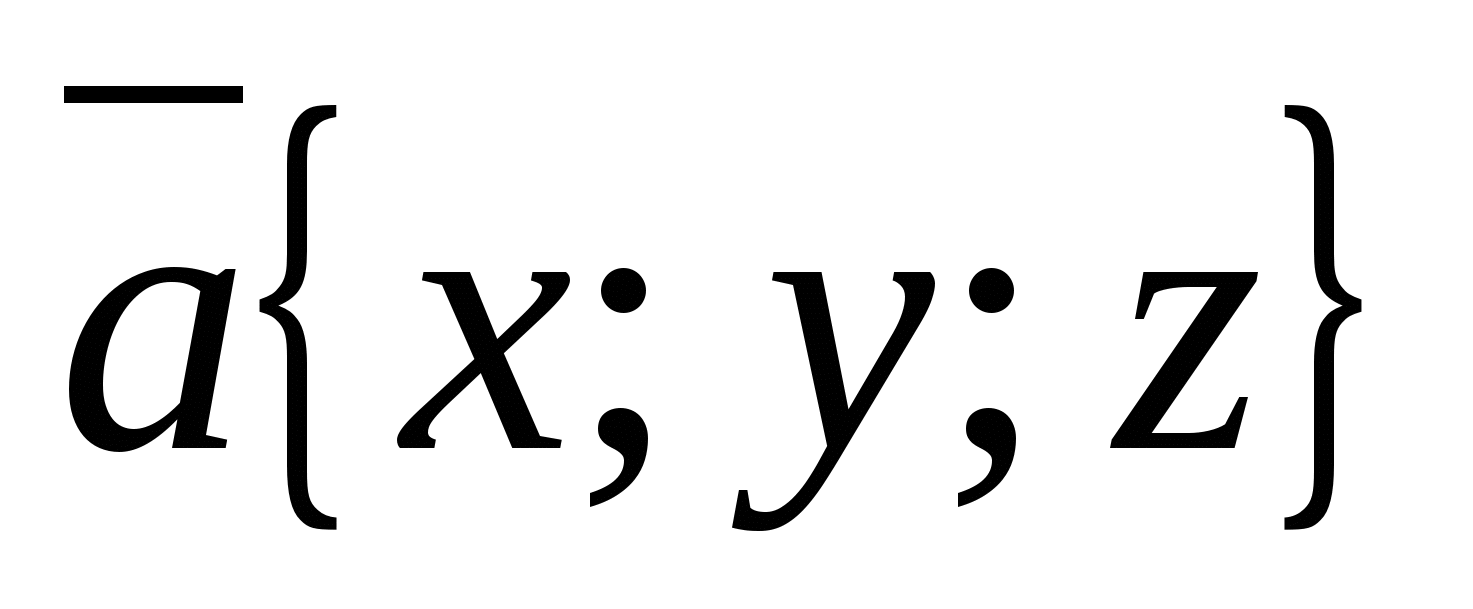
ನಿಯಮ 5.
ಯಾವುದೇ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳು ಅದರ ತ್ರಿಜ್ಯದ ವೆಕ್ಟರ್ನ ಅನುಗುಣವಾದ ನಿರ್ದೇಶಾಂಕಗಳಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ,.

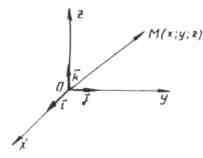
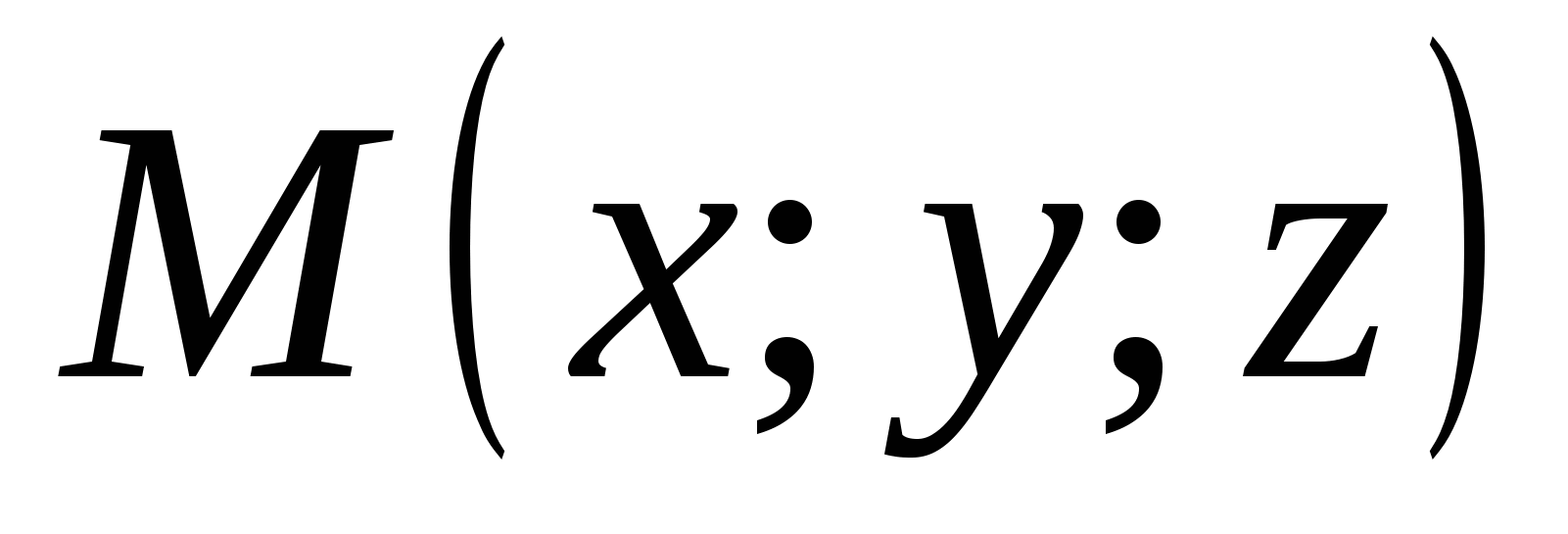
ನಿಯಮ 6.
ಪ್ರತಿಯೊಂದು ವೆಕ್ಟರ್ ನಿರ್ದೇಶಾಂಕವು ಅದರ ಅಂತ್ಯ ಮತ್ತು ಪ್ರಾರಂಭದ ಅನುಗುಣವಾದ ನಿರ್ದೇಶಾಂಕಗಳ ನಡುವಿನ ವ್ಯತ್ಯಾಸಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
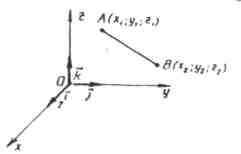 .
.
4. ನಿರ್ದೇಶಾಂಕಗಳಲ್ಲಿ ಎರಡು ವೆಕ್ಟರ್ಗಳ ಕೋಲಿನಿಯರಿಟಿಯ ಸ್ಥಿತಿ.
ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಅವಕಾಶ ಮಾಡಿಕೊಡಿ  ಎರಡು ವಾಹಕಗಳಿಗೆ ಅವುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ನೀಡಲಾಗಿದೆ
ಎರಡು ವಾಹಕಗಳಿಗೆ ಅವುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ನೀಡಲಾಗಿದೆ  ಮತ್ತು
ಮತ್ತು 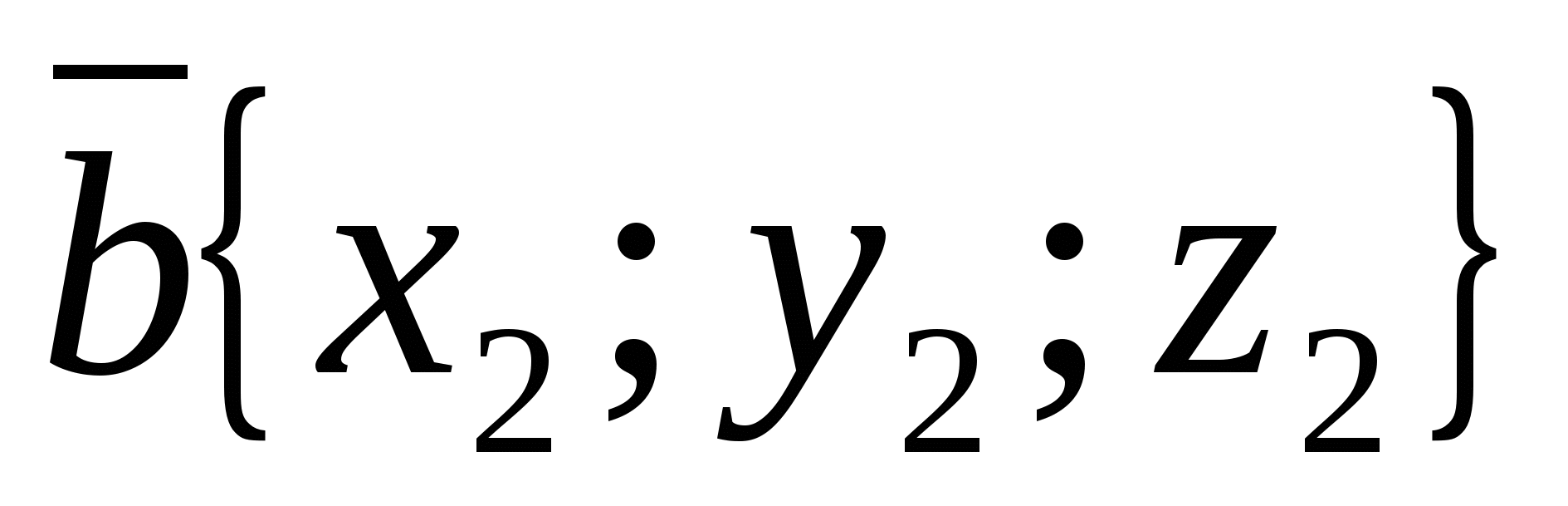 .
.
ನಿಯಮ 7.
ವಾಹಕಗಳು
 ಮತ್ತು
ಮತ್ತು 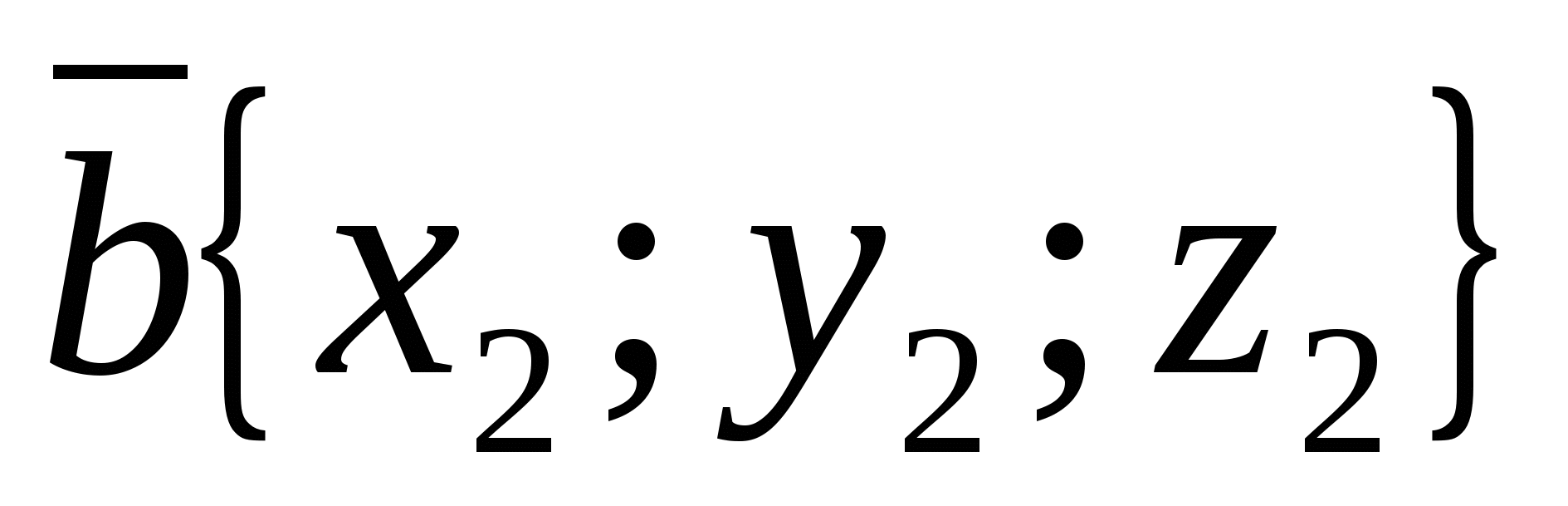 ಅವುಗಳ ಅನುಗುಣವಾದ ನಿರ್ದೇಶಾಂಕಗಳು ಅನುಪಾತದಲ್ಲಿದ್ದರೆ ಮಾತ್ರ ಕೋಲಿನಿಯರ್,
ಅವುಗಳ ಅನುಗುಣವಾದ ನಿರ್ದೇಶಾಂಕಗಳು ಅನುಪಾತದಲ್ಲಿದ್ದರೆ ಮಾತ್ರ ಕೋಲಿನಿಯರ್, 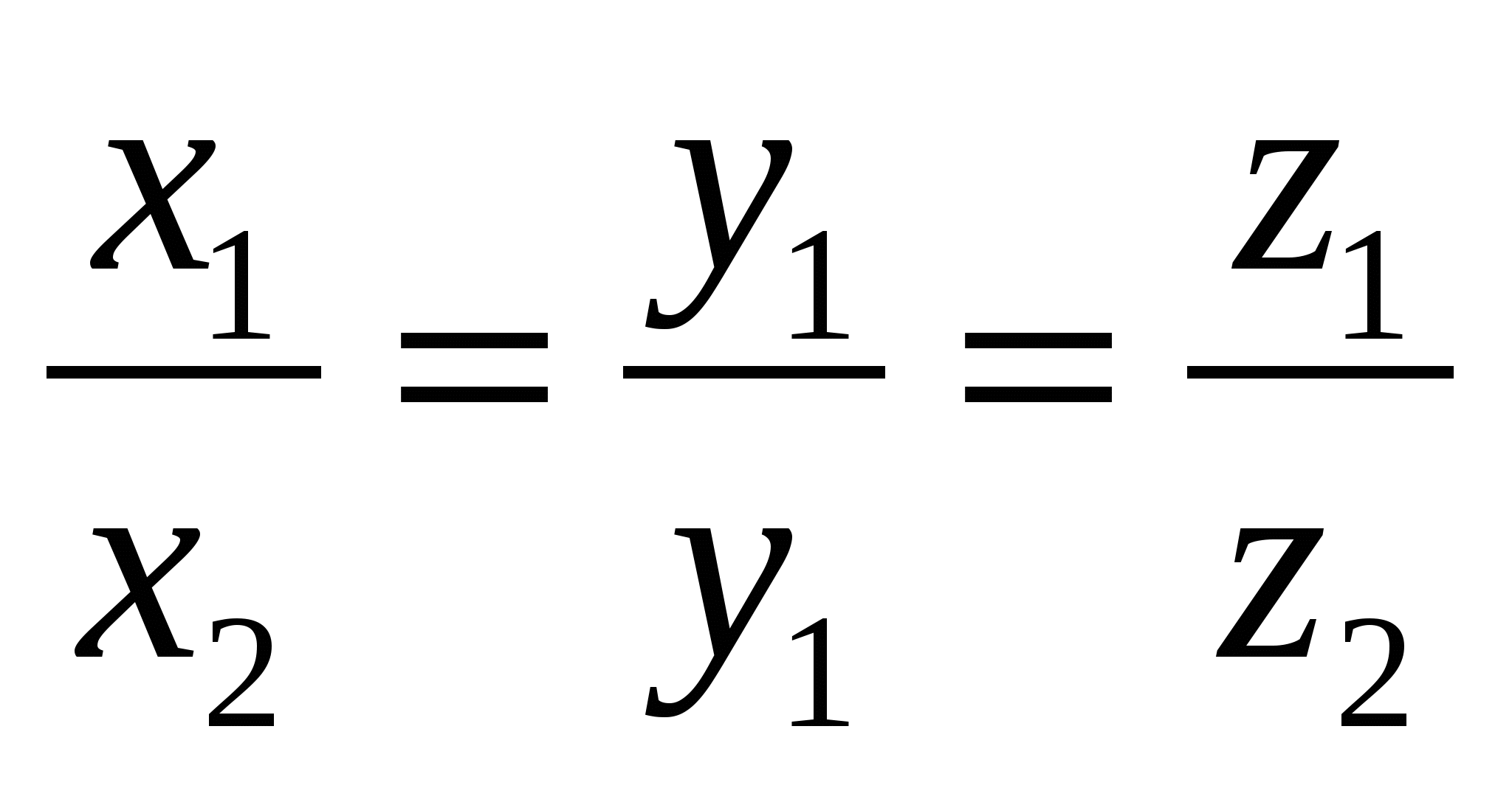 .
.
ಉದಾಹರಣೆ.
a) ವಾಹಕಗಳನ್ನು ಪರಿಗಣಿಸಿ 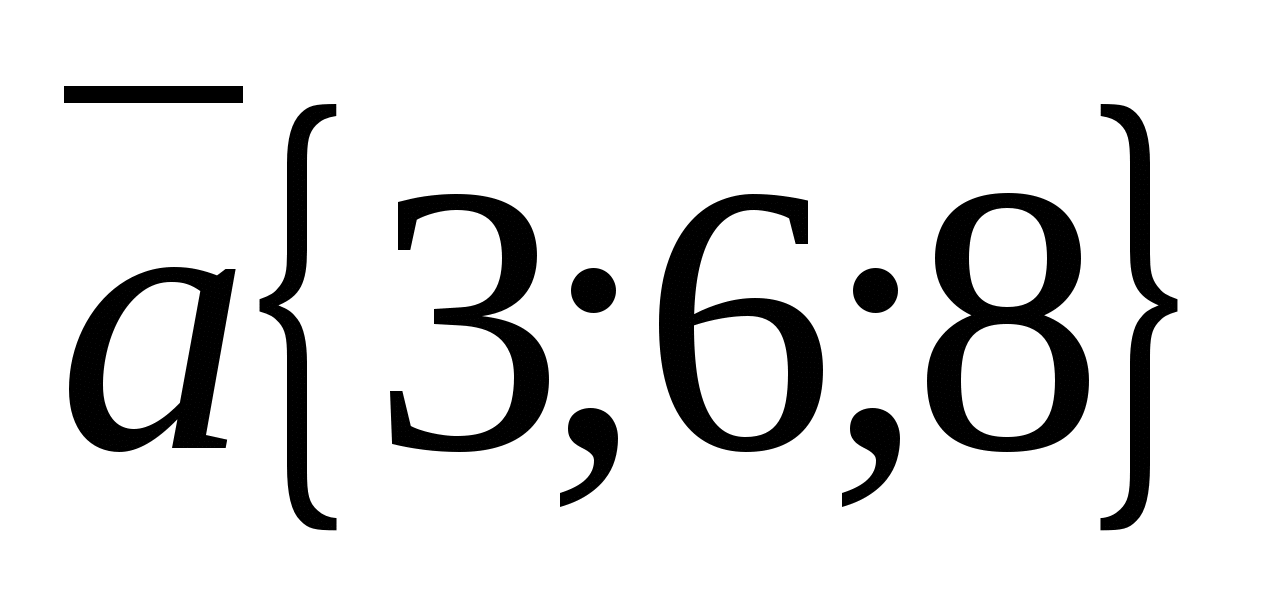 ಮತ್ತು
ಮತ್ತು 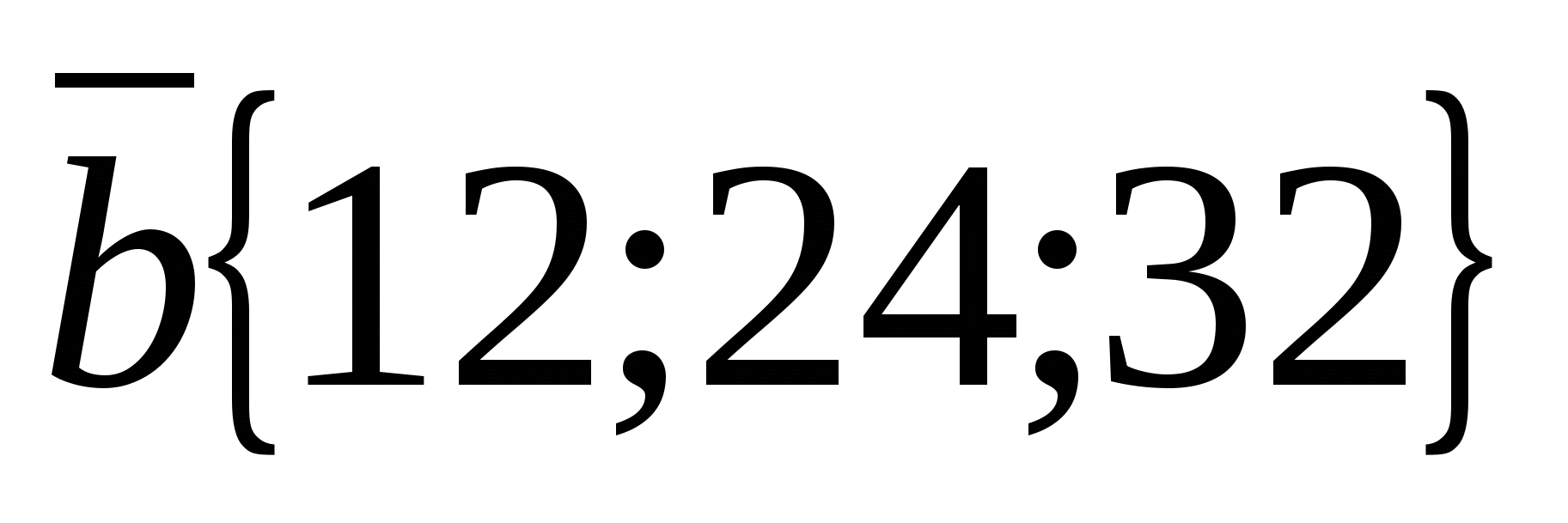 .
.
ವೆಕ್ಟರ್ ನಿರ್ದೇಶಾಂಕಗಳು 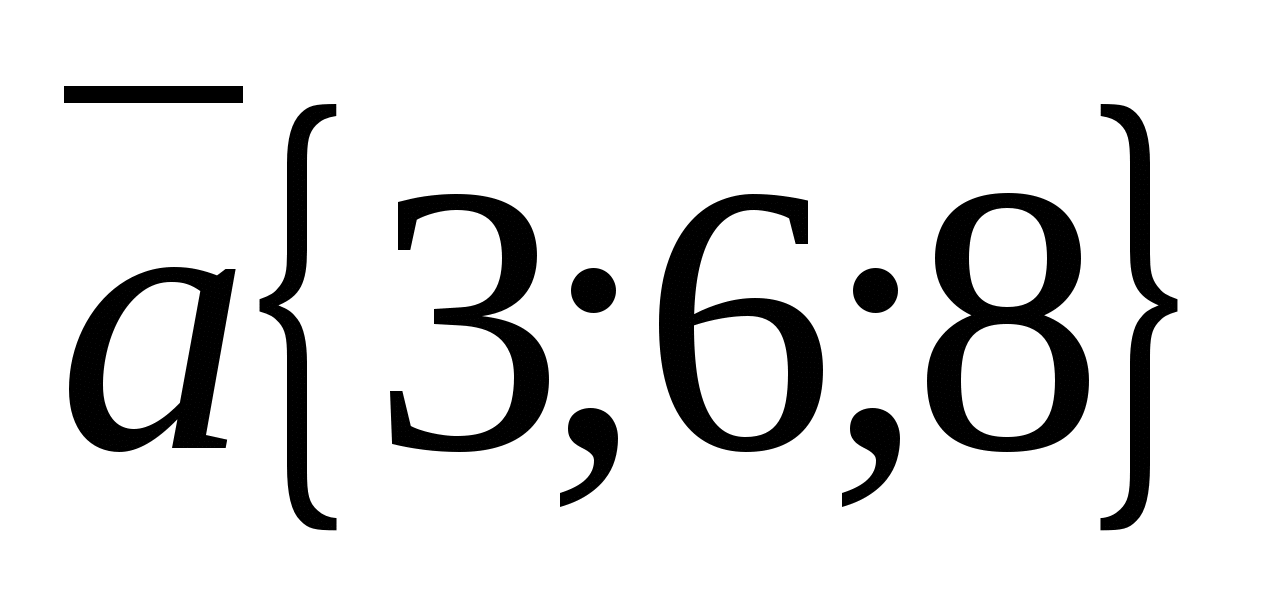 ಅನುಗುಣವಾದ ವೆಕ್ಟರ್ ನಿರ್ದೇಶಾಂಕಗಳಿಗೆ ಅನುಪಾತದಲ್ಲಿರುತ್ತವೆ
ಅನುಗುಣವಾದ ವೆಕ್ಟರ್ ನಿರ್ದೇಶಾಂಕಗಳಿಗೆ ಅನುಪಾತದಲ್ಲಿರುತ್ತವೆ 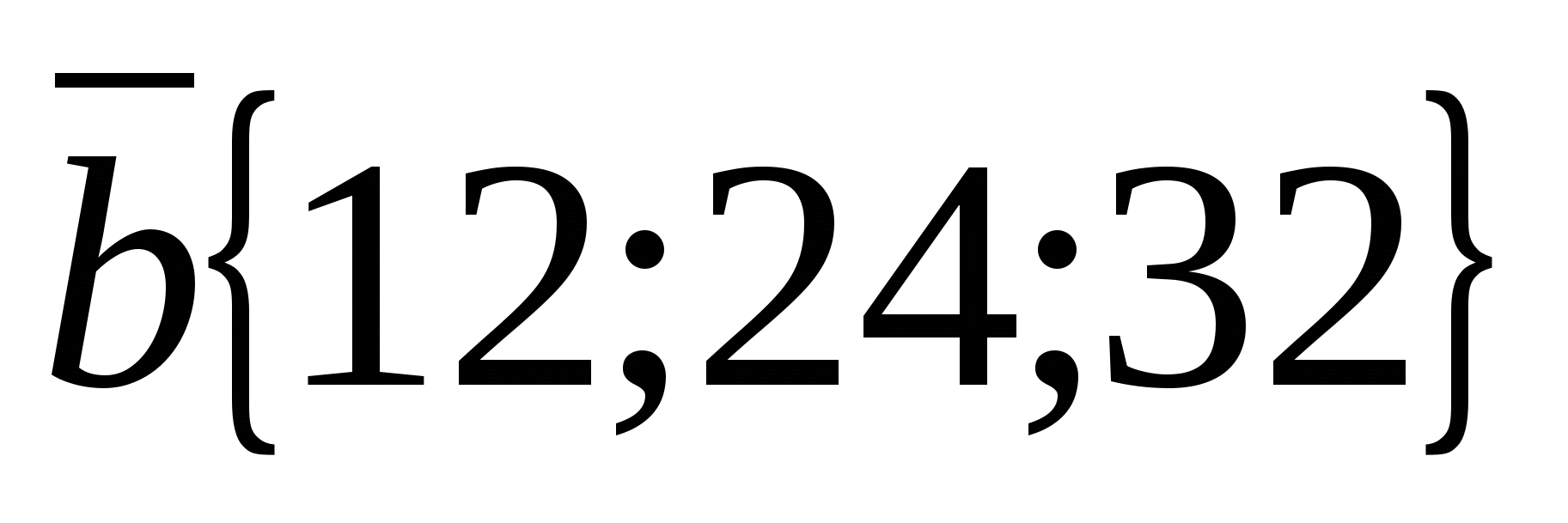 :
: 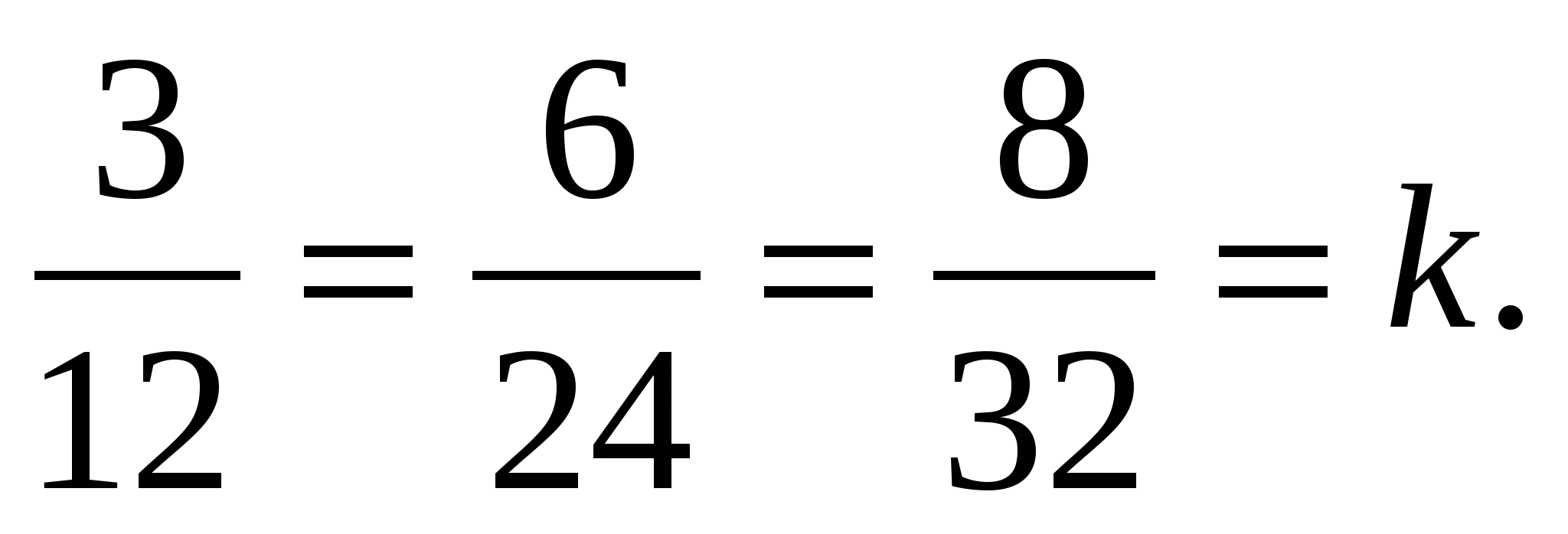 ಅದಕ್ಕೇ
ಅದಕ್ಕೇ 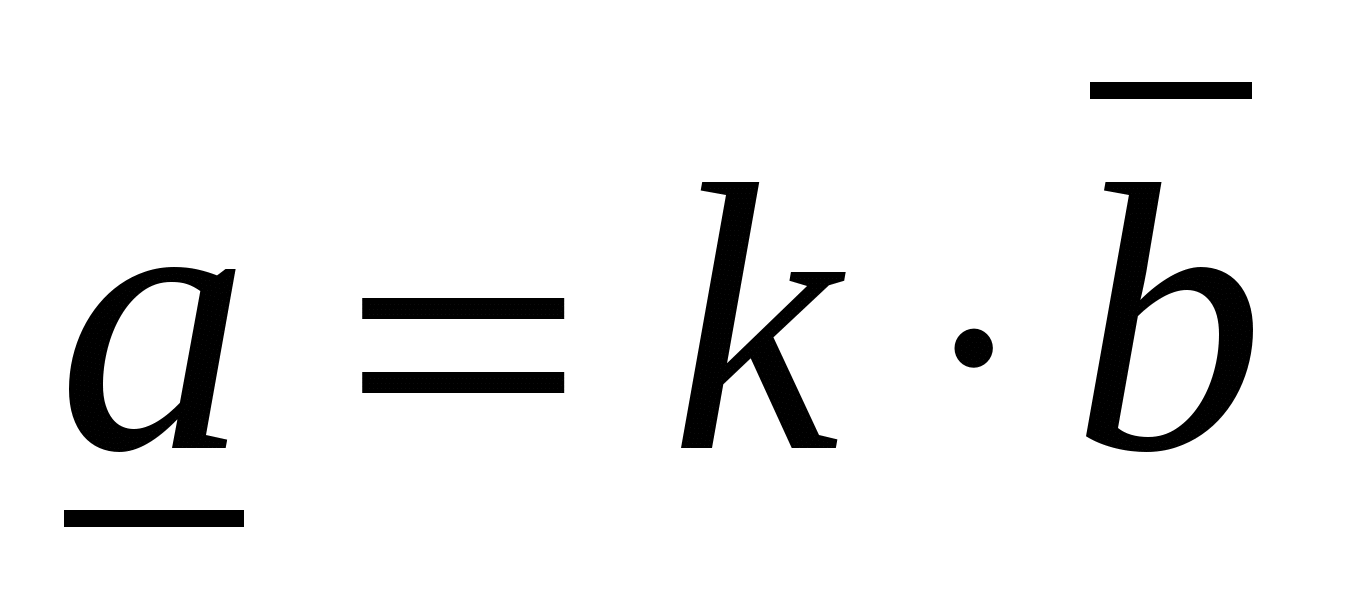 , ಮತ್ತು ಆದ್ದರಿಂದ ವಾಹಕಗಳು ಕಾಲಿನಿಯರ್ ಆಗಿರುತ್ತವೆ.
, ಮತ್ತು ಆದ್ದರಿಂದ ವಾಹಕಗಳು ಕಾಲಿನಿಯರ್ ಆಗಿರುತ್ತವೆ.
ಬಿ) ವಾಹಕಗಳನ್ನು ಪರಿಗಣಿಸಿ 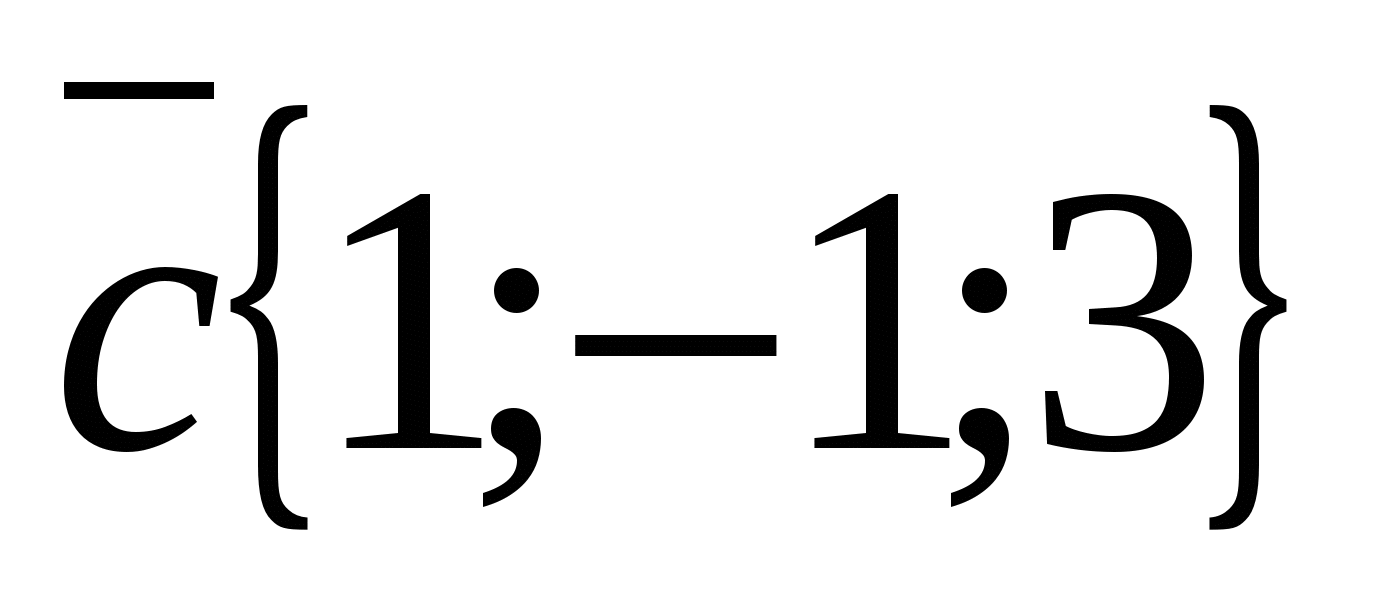 ಮತ್ತು
ಮತ್ತು 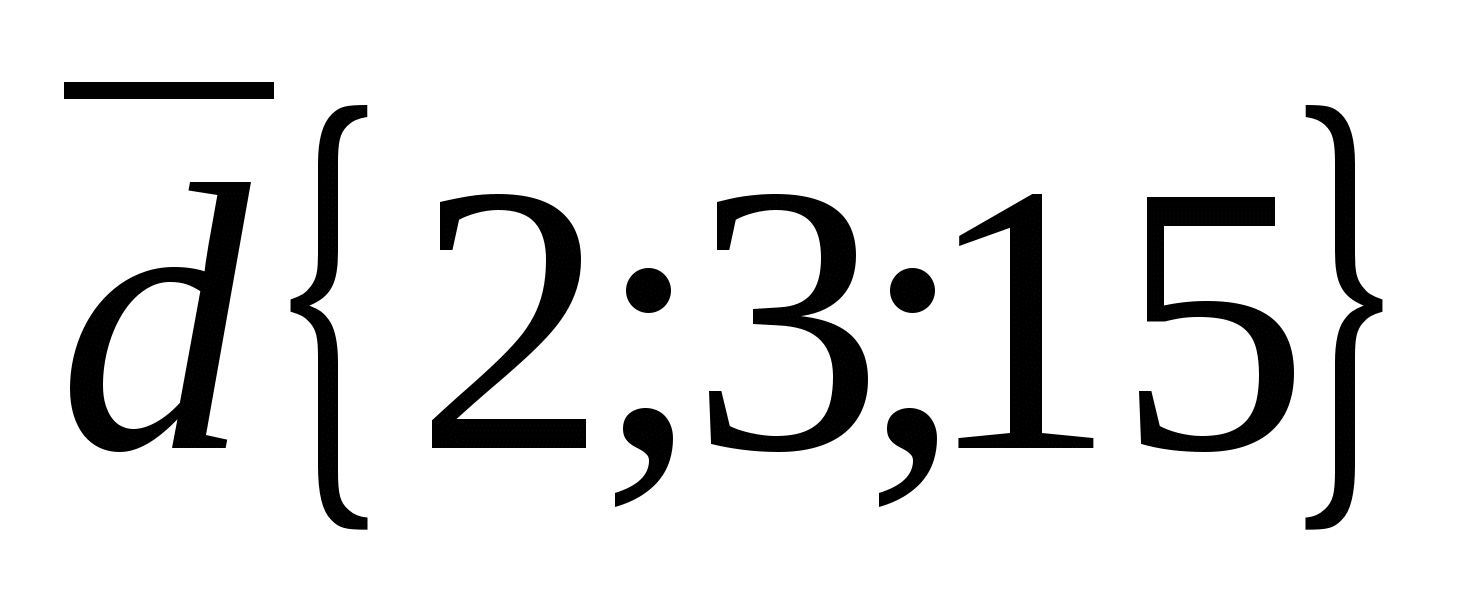 .
.
ವೆಕ್ಟರ್ ನಿರ್ದೇಶಾಂಕಗಳು 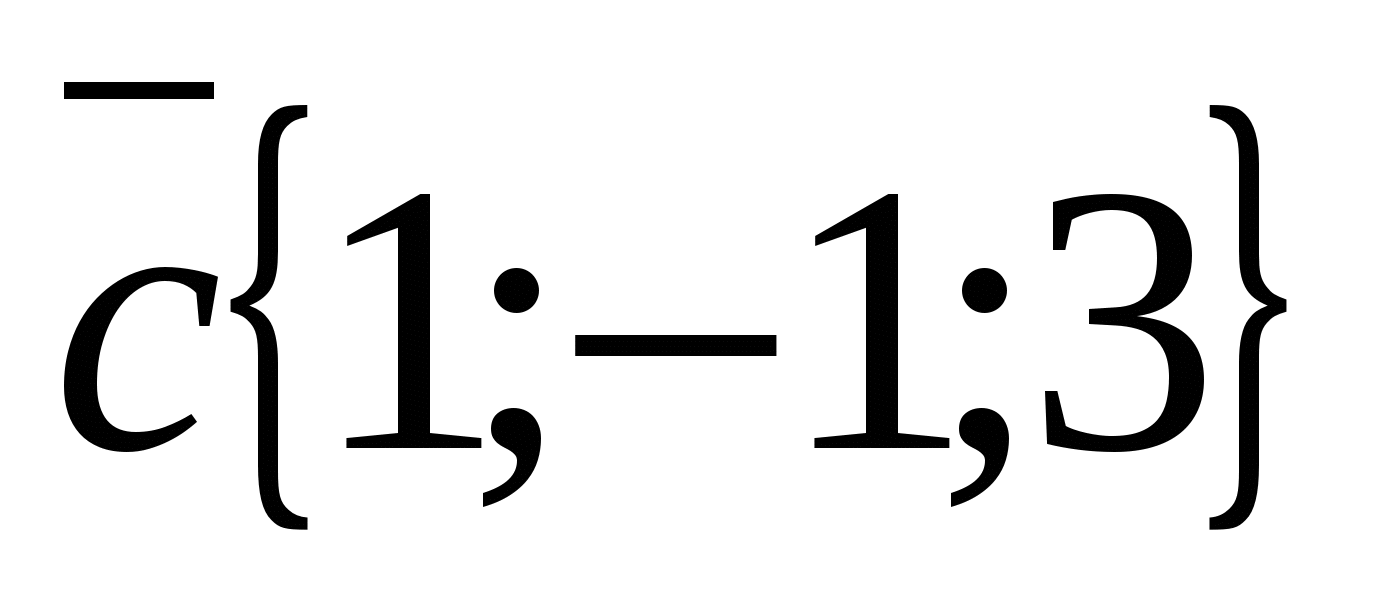 ಅನುಗುಣವಾದ ವೆಕ್ಟರ್ ನಿರ್ದೇಶಾಂಕಗಳಿಗೆ ಅನುಪಾತದಲ್ಲಿರುವುದಿಲ್ಲ
ಅನುಗುಣವಾದ ವೆಕ್ಟರ್ ನಿರ್ದೇಶಾಂಕಗಳಿಗೆ ಅನುಪಾತದಲ್ಲಿರುವುದಿಲ್ಲ 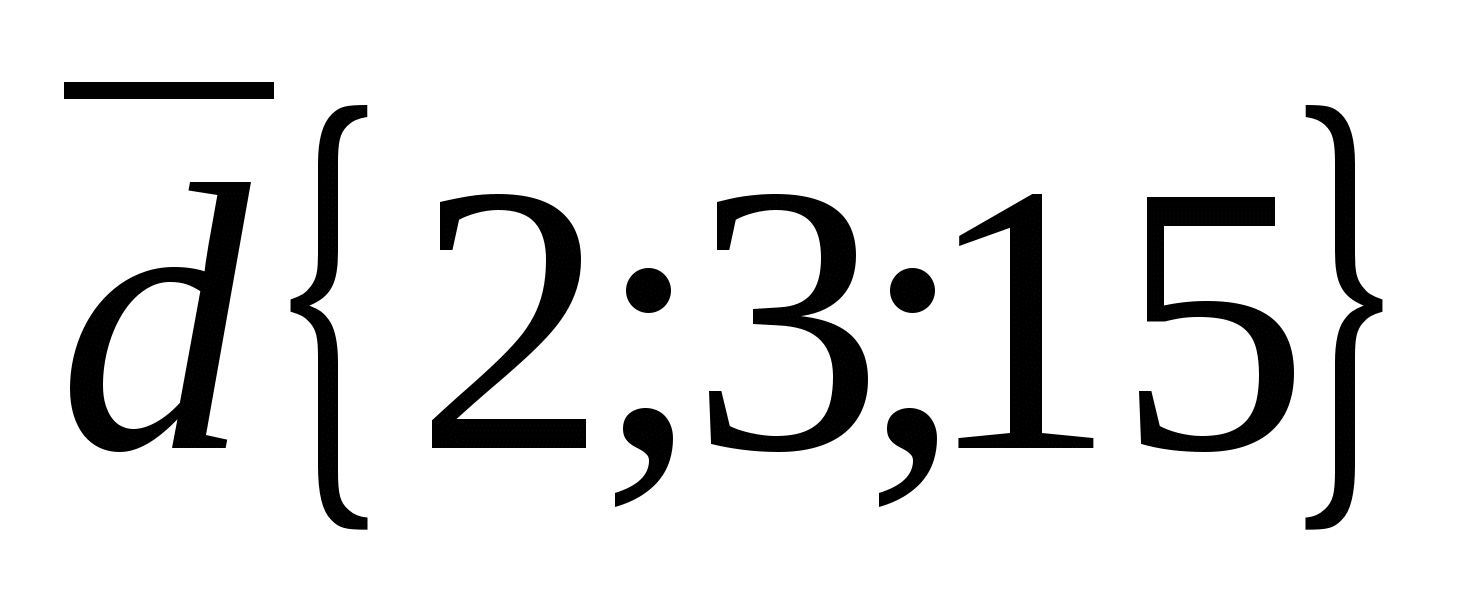 , ಉದಾಹರಣೆಗೆ
, ಉದಾಹರಣೆಗೆ 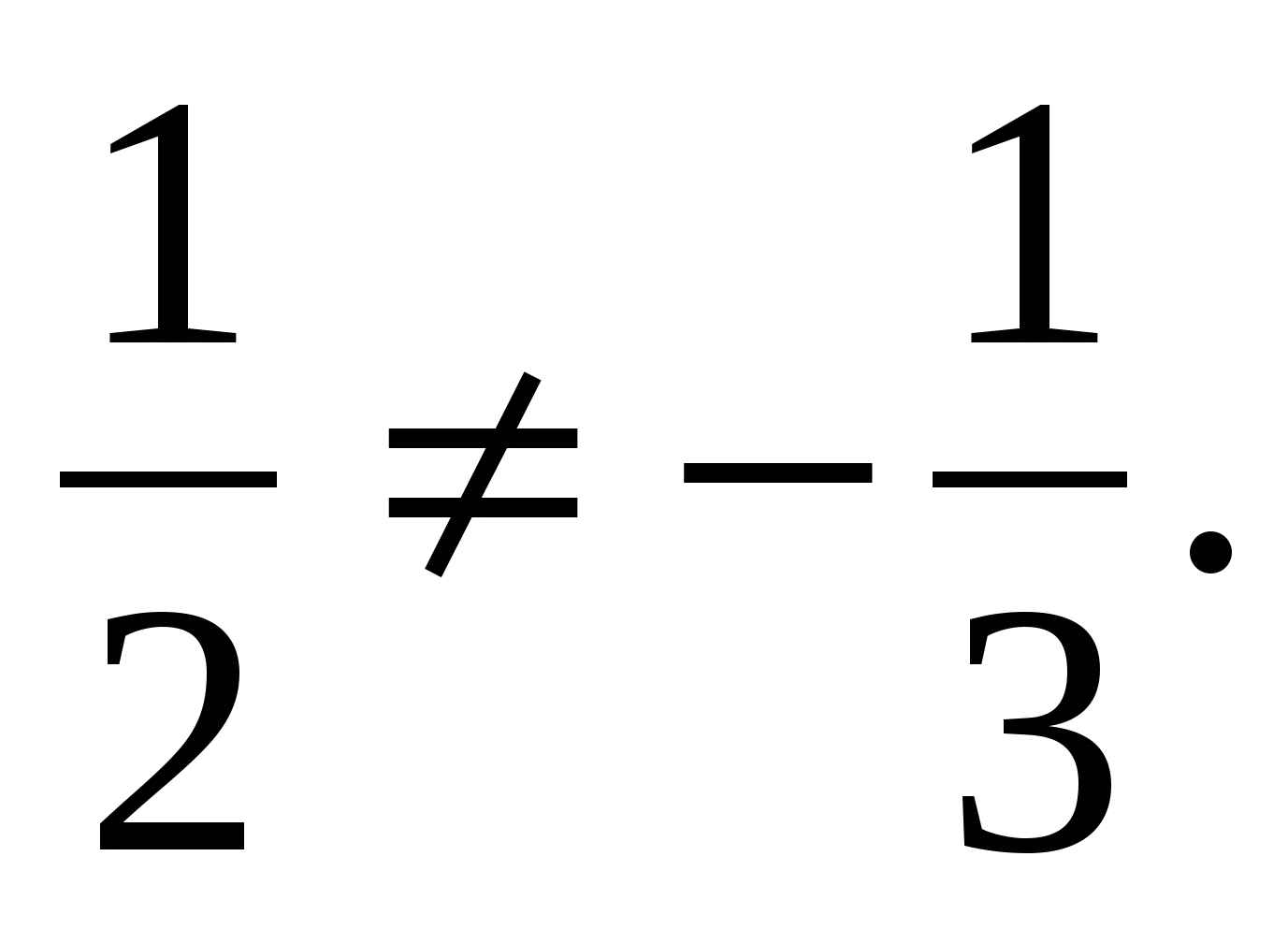 ಇದರರ್ಥ ವೆಕ್ಟರ್ಗಳು ಕಾಲಿನಿಯರ್ ಅಲ್ಲ.
ಇದರರ್ಥ ವೆಕ್ಟರ್ಗಳು ಕಾಲಿನಿಯರ್ ಅಲ್ಲ.
5. ನಿರ್ದೇಶಾಂಕಗಳಲ್ಲಿನ ಸರಳ ಸಮಸ್ಯೆಗಳು.
ಕಾರ್ಯ 1.
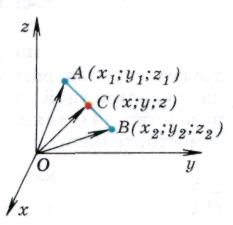 ಒಂದು ವಿಭಾಗದ ಮಧ್ಯದ ಪ್ರತಿಯೊಂದು ನಿರ್ದೇಶಾಂಕವು ಅದರ ತುದಿಗಳ ಅನುಗುಣವಾದ ನಿರ್ದೇಶಾಂಕಗಳ ಅರ್ಧದಷ್ಟು ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
ಒಂದು ವಿಭಾಗದ ಮಧ್ಯದ ಪ್ರತಿಯೊಂದು ನಿರ್ದೇಶಾಂಕವು ಅದರ ತುದಿಗಳ ಅನುಗುಣವಾದ ನಿರ್ದೇಶಾಂಕಗಳ ಅರ್ಧದಷ್ಟು ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
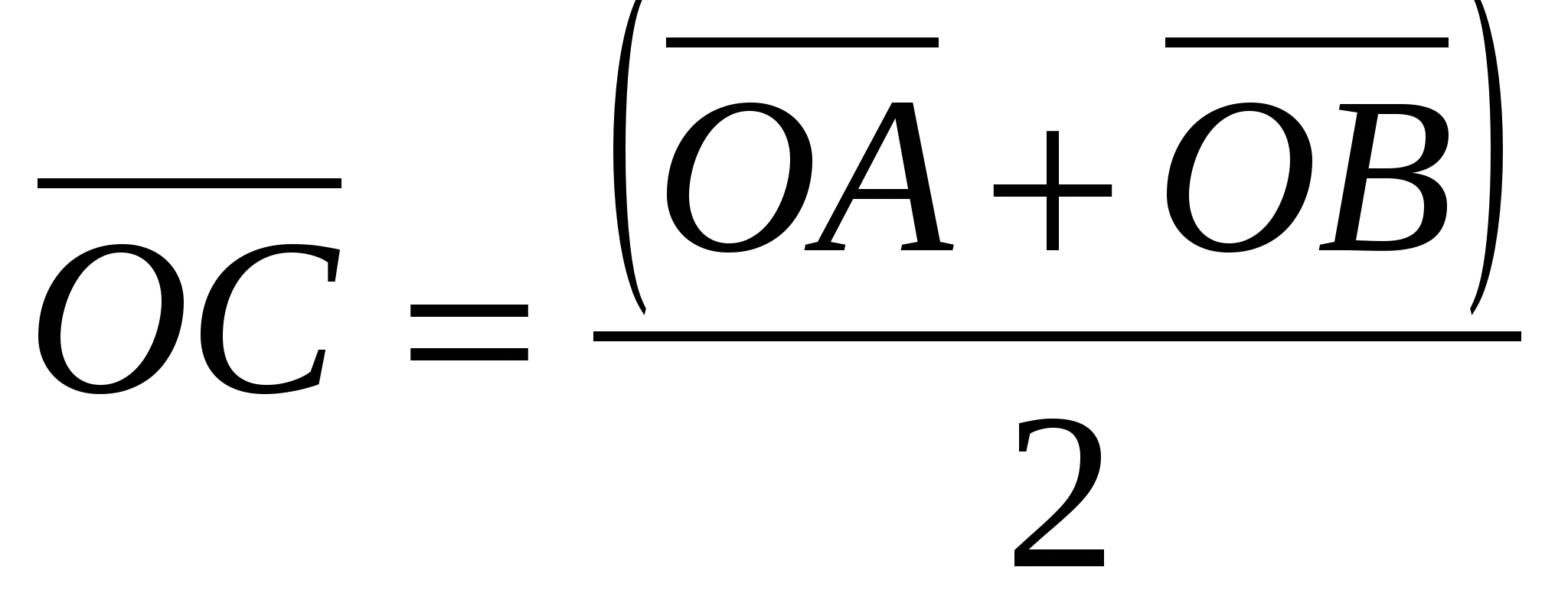 , ಎಲ್ಲಿ
, ಎಲ್ಲಿ 
 ,
, 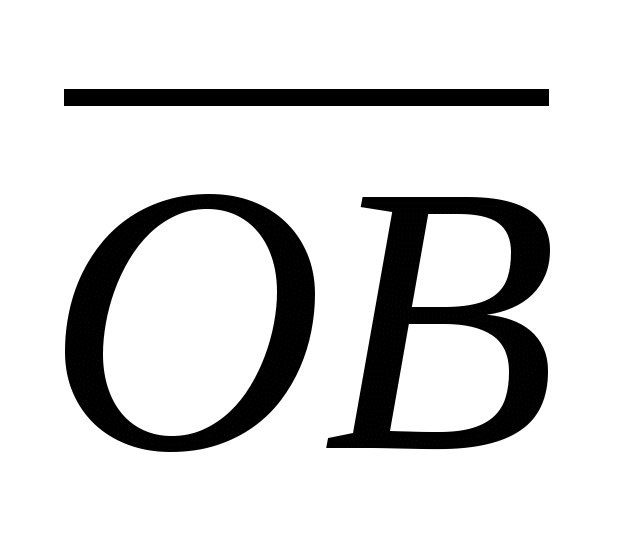
 ಮತ್ತು
ಮತ್ತು 
 .
.
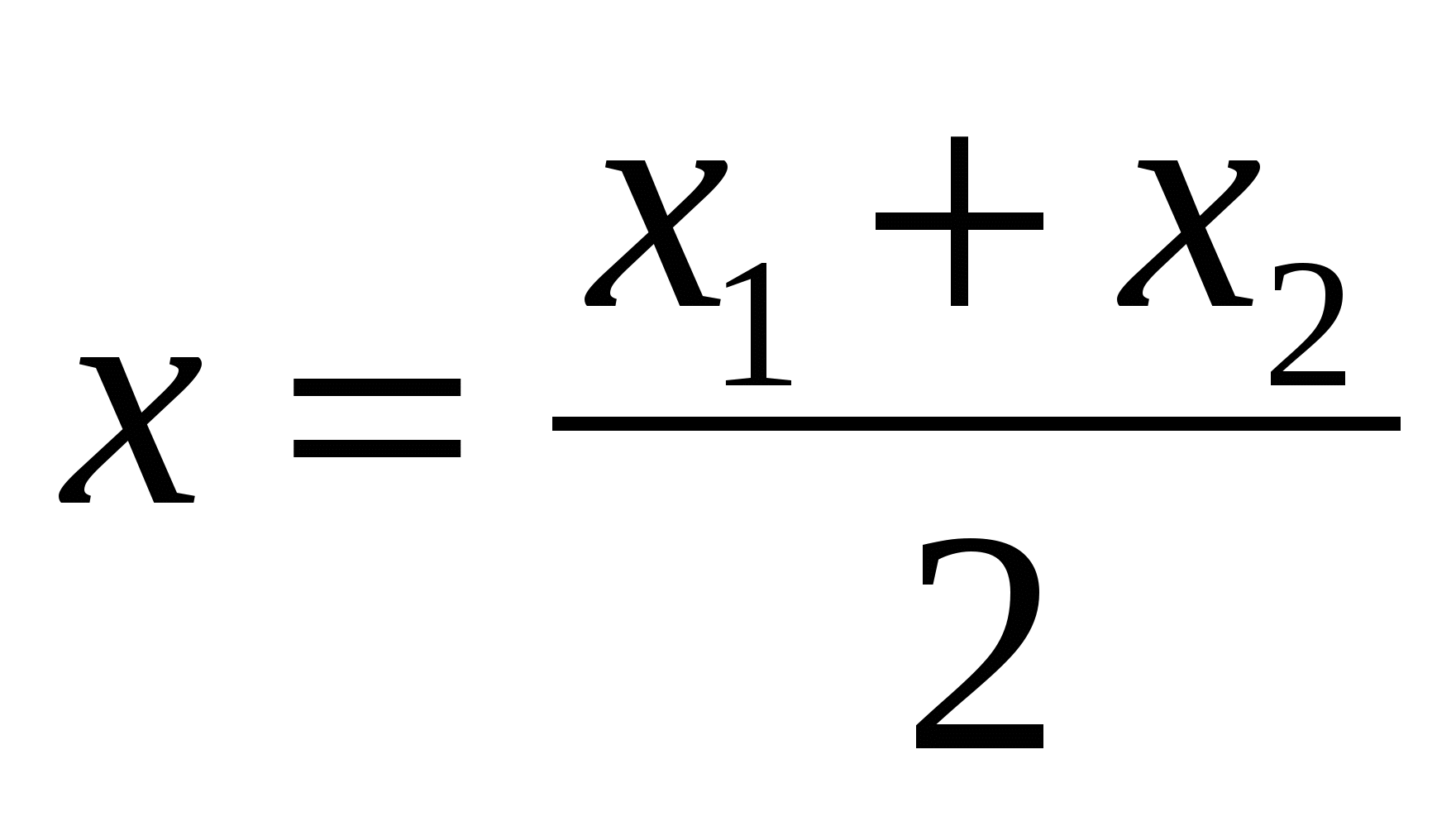 ,
,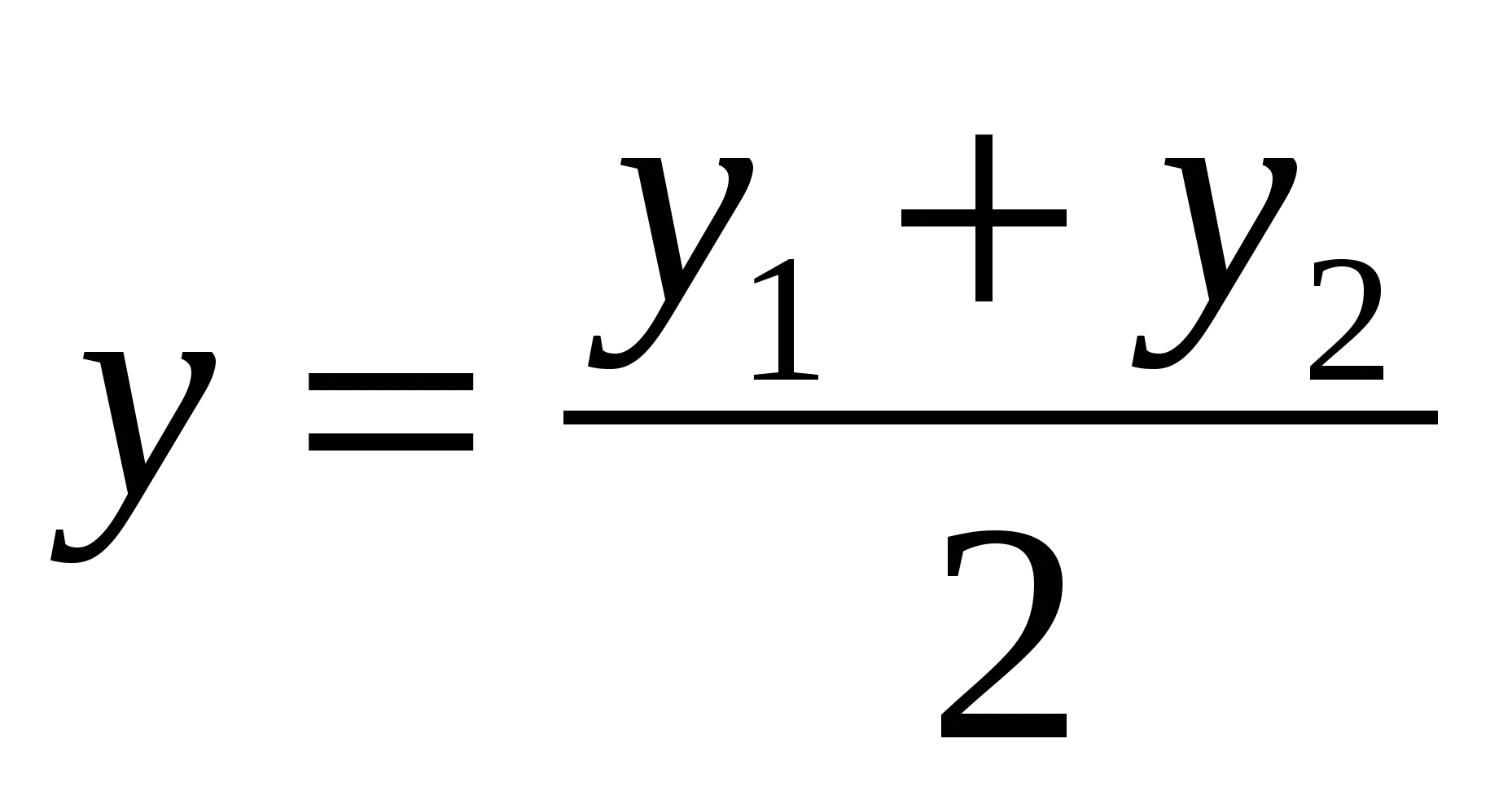 ,
, 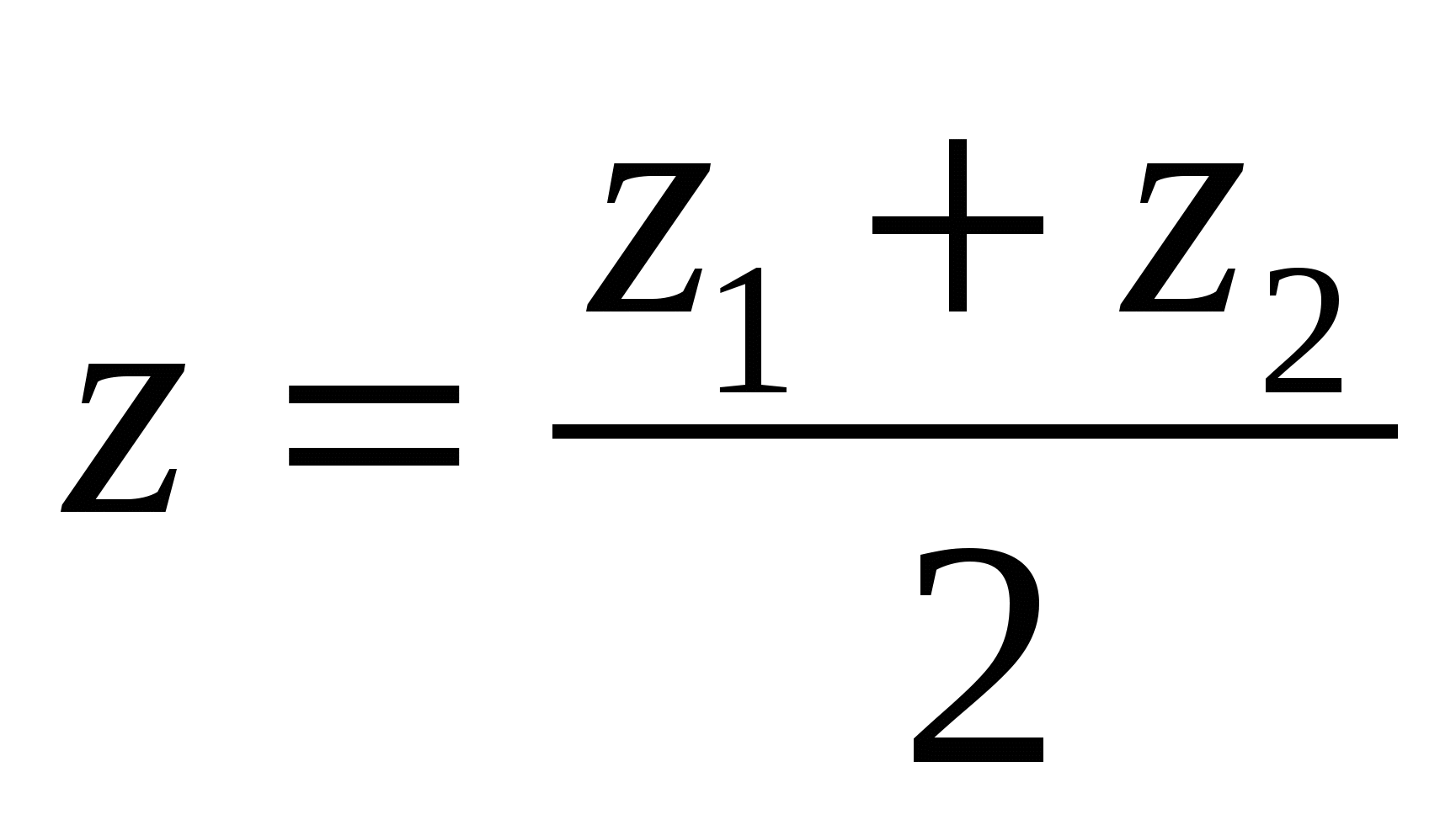 ,
,
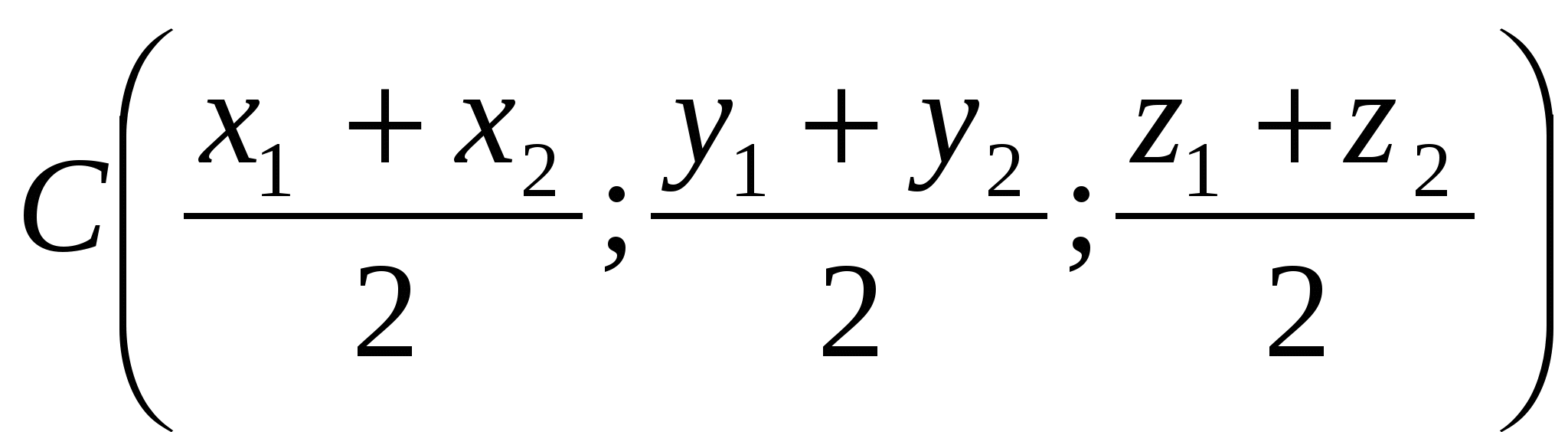
ಬೌ) ಅದರ ನಿರ್ದೇಶಾಂಕಗಳಿಂದ ವೆಕ್ಟರ್ನ ಉದ್ದದ ಲೆಕ್ಕಾಚಾರ.
ವೆಕ್ಟರ್ ಅನ್ನು ಪರಿಗಣಿಸಿ 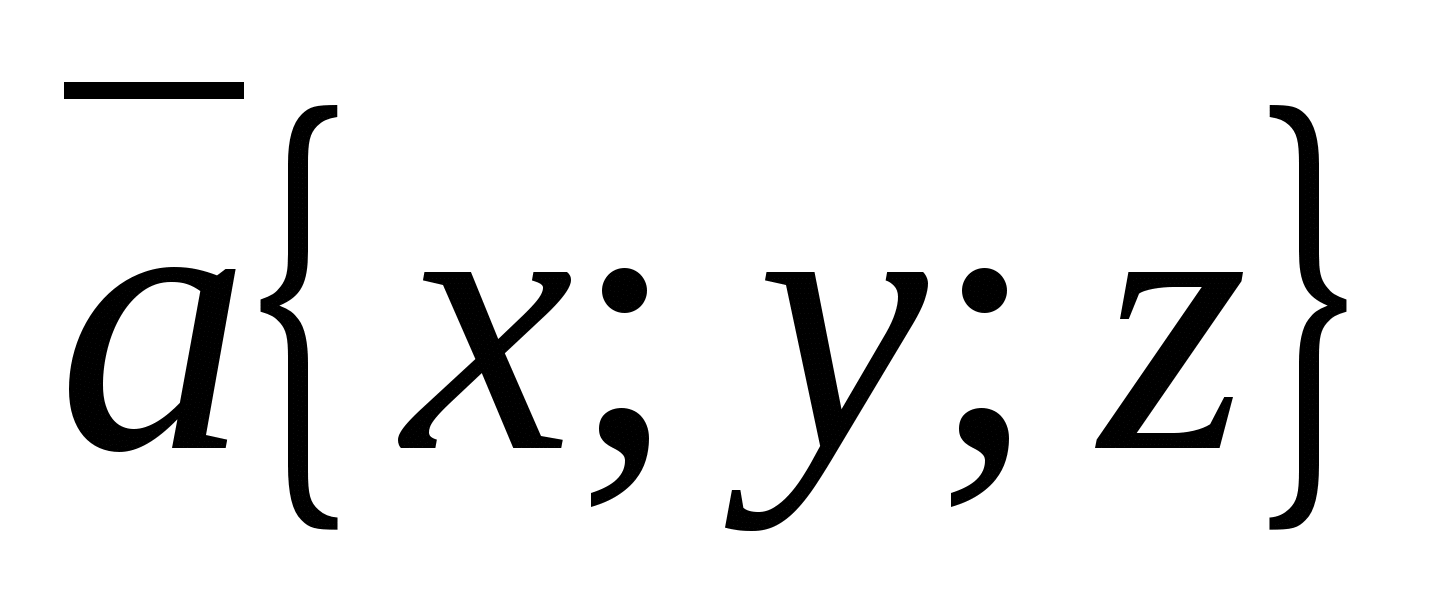 ,
,
ವೆಕ್ಟರ್ ಉದ್ದವನ್ನು ಸೂತ್ರದಿಂದ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ
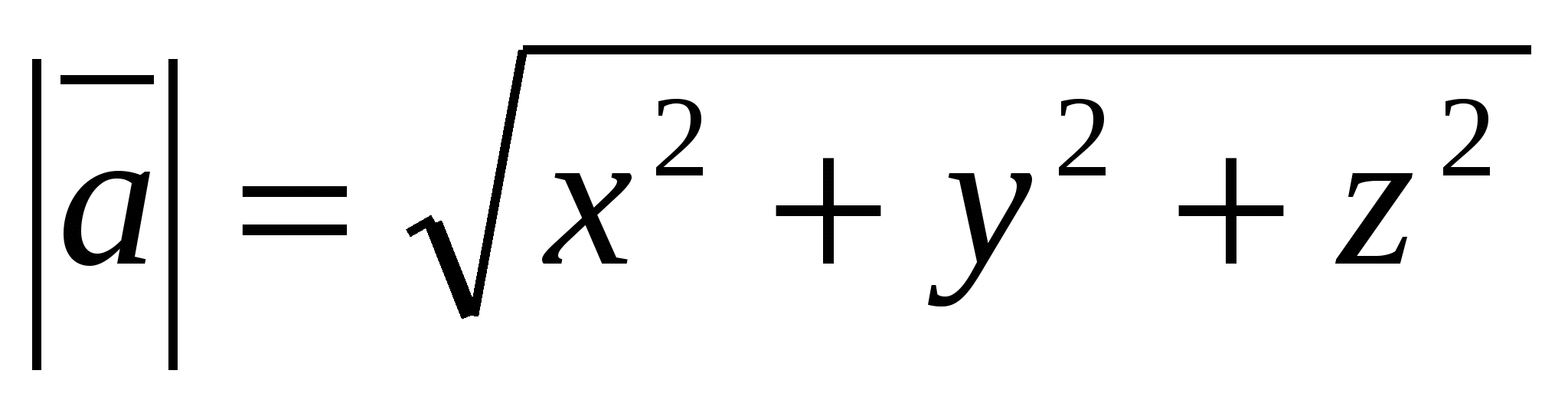 .
.
ಏಕೆಂದರೆ  =
=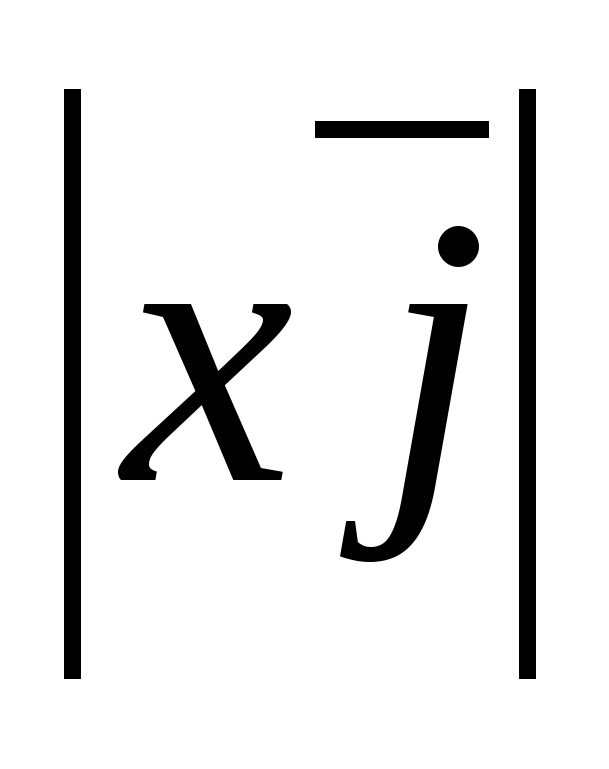 =
=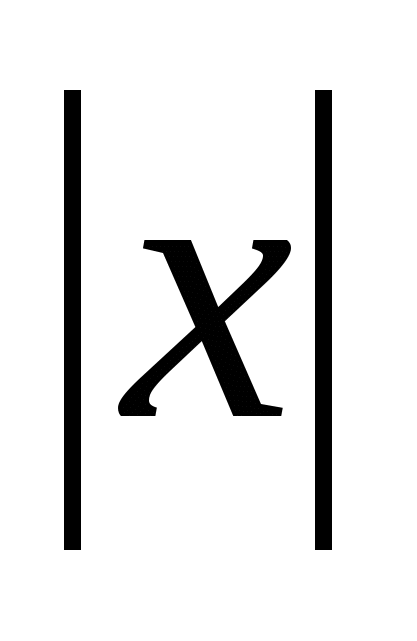 ,
,
 =
= =
=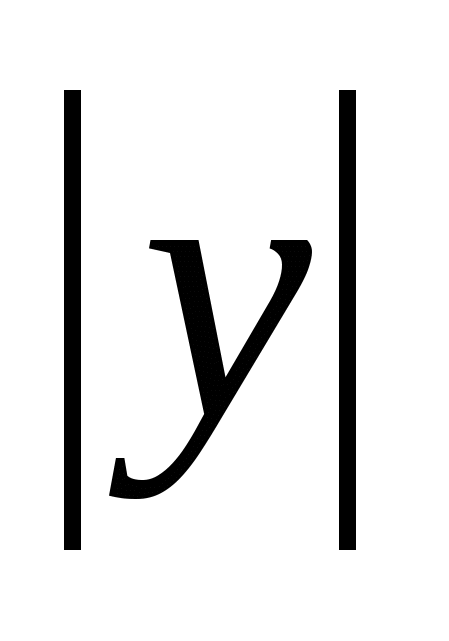 ,
,
 =
= =
= , ಮತ್ತು
, ಮತ್ತು 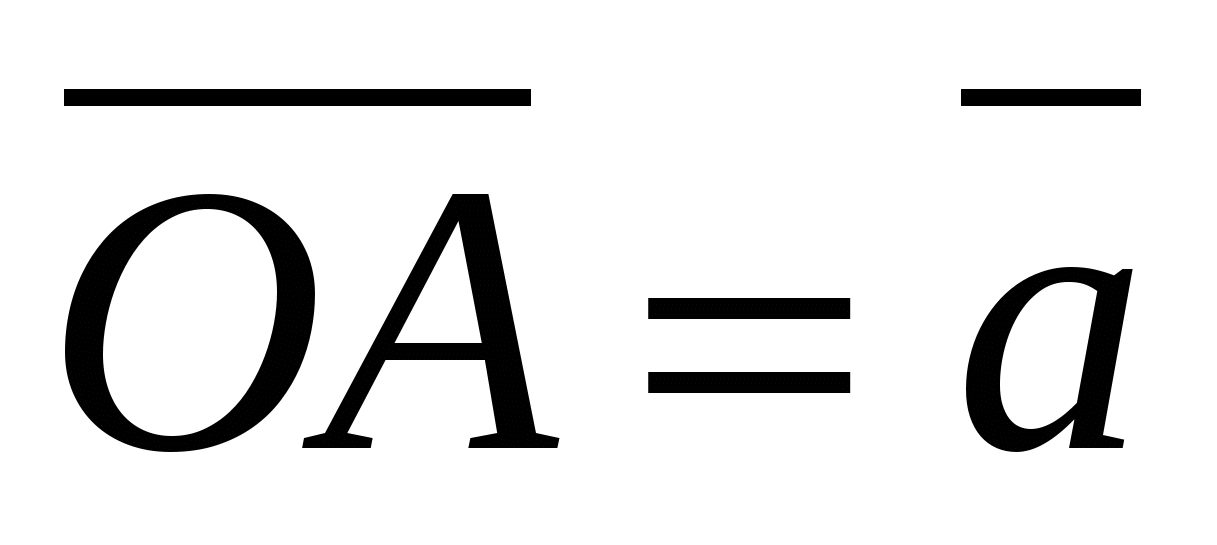 , ನಂತರ ಸಮಾನತೆಯಿಂದ
, ನಂತರ ಸಮಾನತೆಯಿಂದ 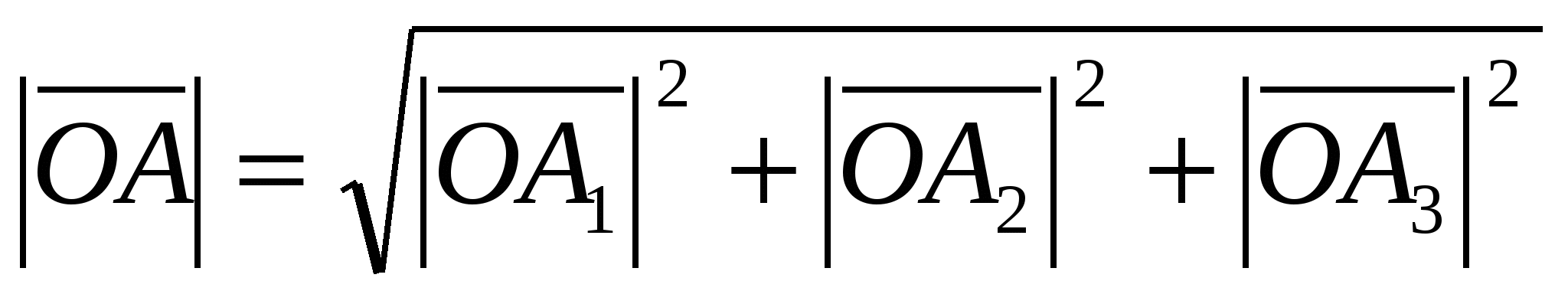 ನಾವು ಸೂತ್ರವನ್ನು ಪಡೆಯುತ್ತೇವೆ: .
ನಾವು ಸೂತ್ರವನ್ನು ಪಡೆಯುತ್ತೇವೆ: .
ವಿ) ಎರಡು ಬಿಂದುಗಳ ನಡುವಿನ ಅಂತರ.
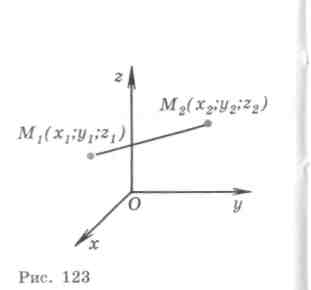 ಎರಡನ್ನು ಪರಿಗಣಿಸೋಣ ಅನಿಯಂತ್ರಿತ ಅಂಕಗಳು: ಪಾಯಿಂಟ್
ಎರಡನ್ನು ಪರಿಗಣಿಸೋಣ ಅನಿಯಂತ್ರಿತ ಅಂಕಗಳು: ಪಾಯಿಂಟ್  ಮತ್ತು ಅವಧಿ
ಮತ್ತು ಅವಧಿ 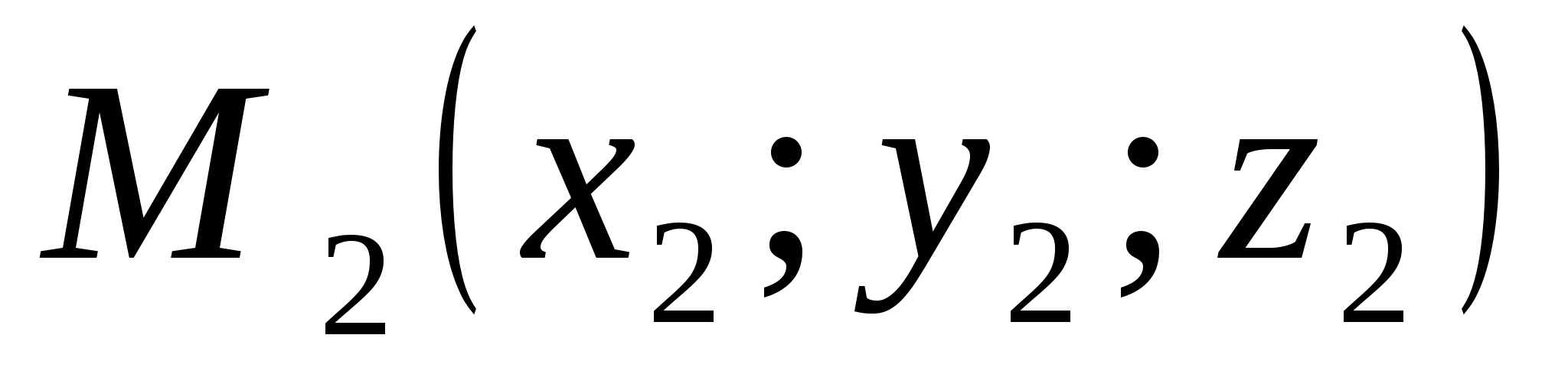 . ದೂರವನ್ನು ವ್ಯಕ್ತಪಡಿಸೋಣಡಿ
ಬಿಂದುಗಳ ನಡುವೆ
. ದೂರವನ್ನು ವ್ಯಕ್ತಪಡಿಸೋಣಡಿ
ಬಿಂದುಗಳ ನಡುವೆ 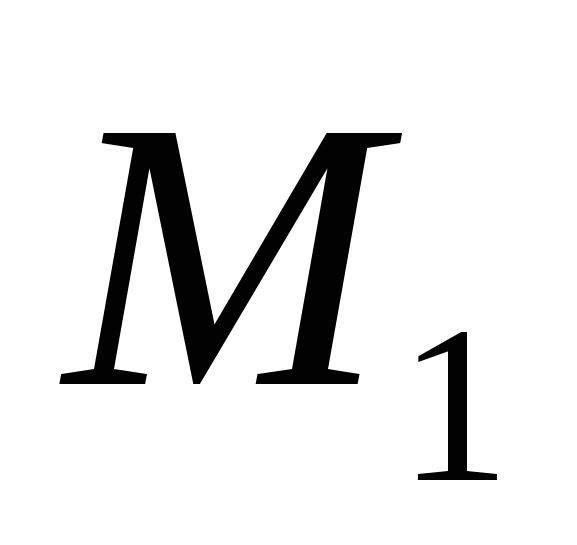 ಮತ್ತು
ಮತ್ತು 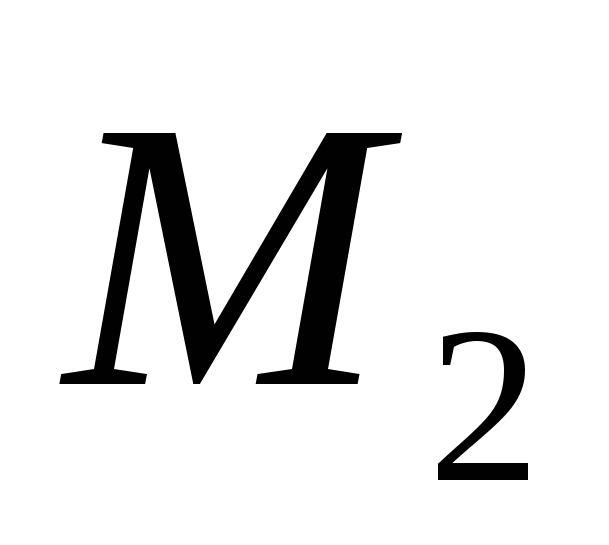 ಅವರ ನಿರ್ದೇಶಾಂಕಗಳ ಮೂಲಕ.
ಅವರ ನಿರ್ದೇಶಾಂಕಗಳ ಮೂಲಕ.
ಅಲ್ಲಿ ವೆಕ್ಟರ್ ಅನ್ನು ಪರಿಗಣಿಸಿ .
ಆದರೆ 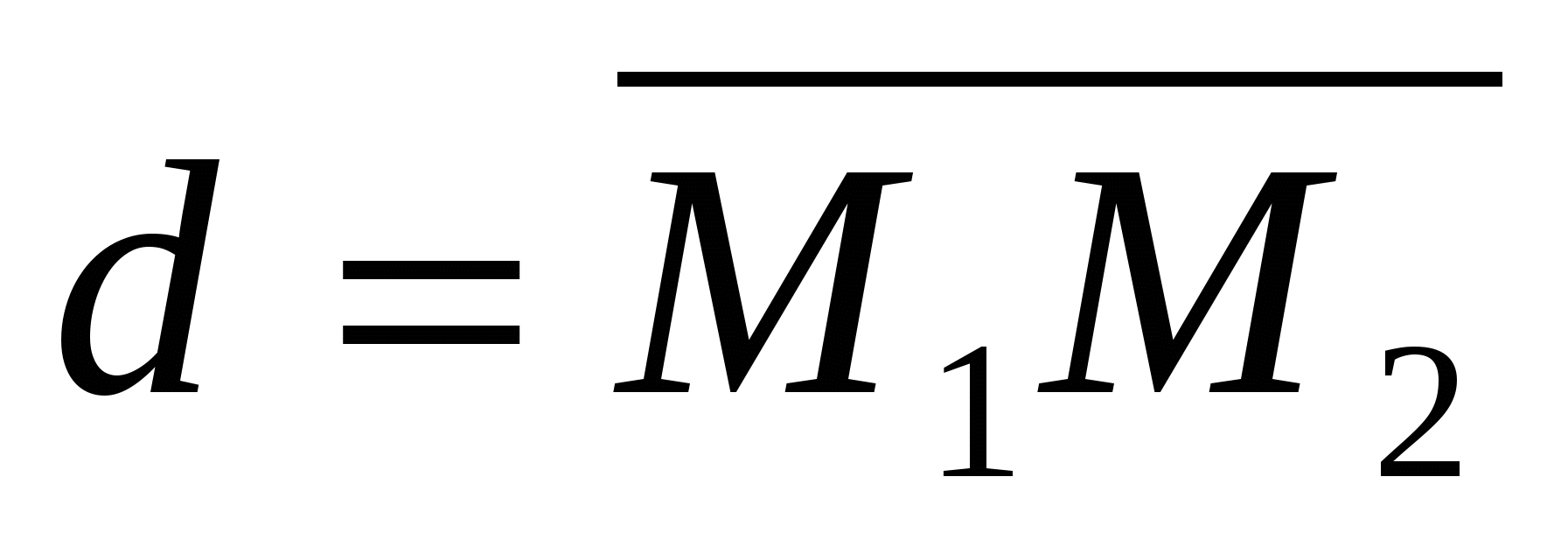 . ಹೀಗಾಗಿ,ಬಿಂದುಗಳ ನಡುವಿನ ಅಂತರ
. ಹೀಗಾಗಿ,ಬಿಂದುಗಳ ನಡುವಿನ ಅಂತರ 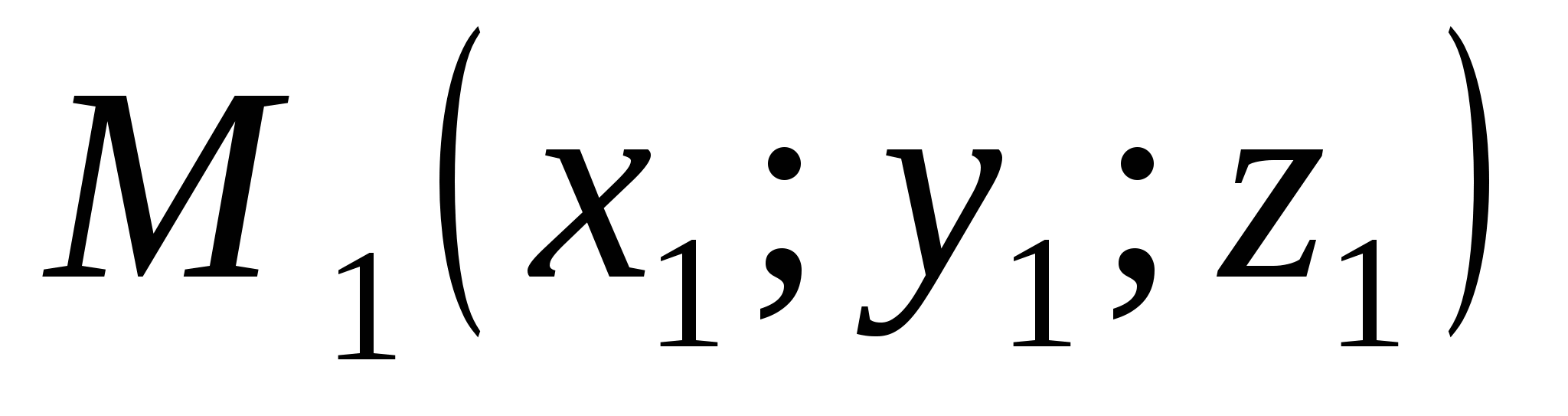 ಮತ್ತು
ಮತ್ತು 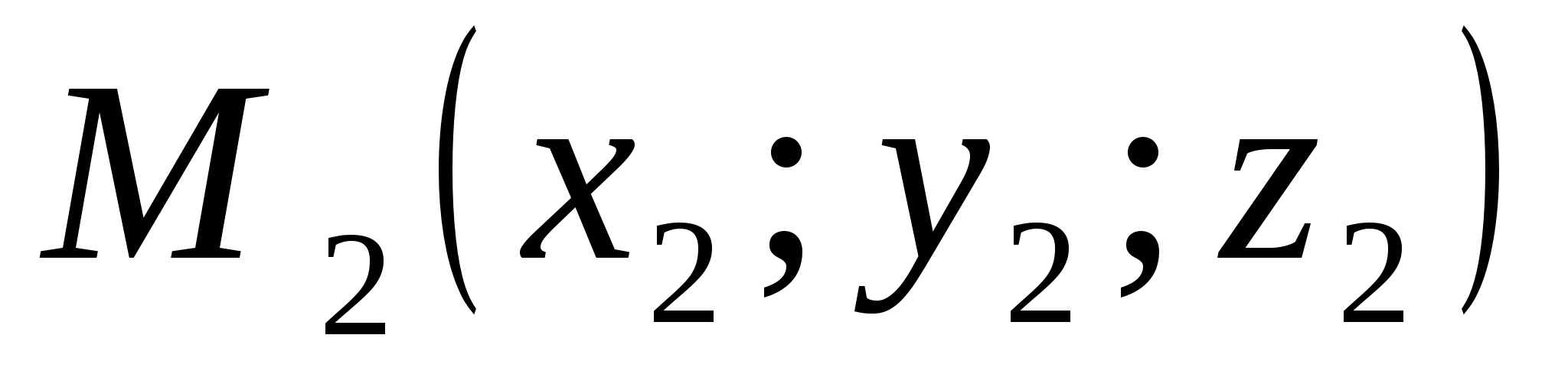
ಸೂತ್ರದ ಮೂಲಕ ಲೆಕ್ಕಹಾಕಲಾಗಿದೆ .
6. ವೆಕ್ಟರ್ಗಳ ಡಾಟ್ ಉತ್ಪನ್ನ ಮತ್ತು ಅವುಗಳ ನಿರ್ದೇಶಾಂಕಗಳ ಮೂಲಕ ವೆಕ್ಟರ್ಗಳ ನಡುವಿನ ಕೋನದ ಲೆಕ್ಕಾಚಾರ.
1) ವೆಕ್ಟರ್ಗಳ ಡಾಟ್ ಉತ್ಪನ್ನ
ಎರಡು ವೆಕ್ಟರ್ಗಳ ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನವು ಅವುಗಳ ಉದ್ದಗಳ ಉತ್ಪನ್ನವಾಗಿದೆ ಮತ್ತು ಅವುಗಳ ನಡುವಿನ ಕೋನದ ಕೊಸೈನ್ ಆಗಿದೆ.
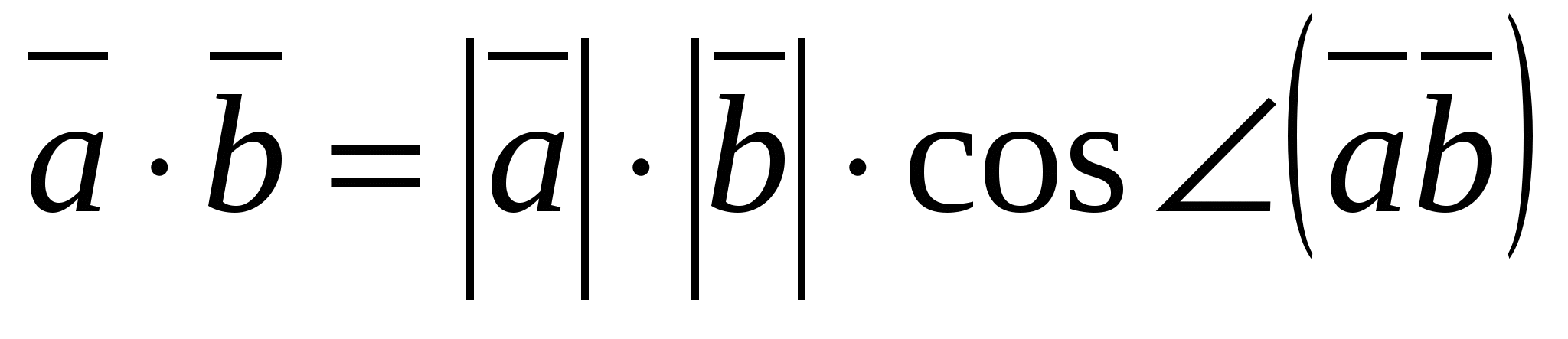
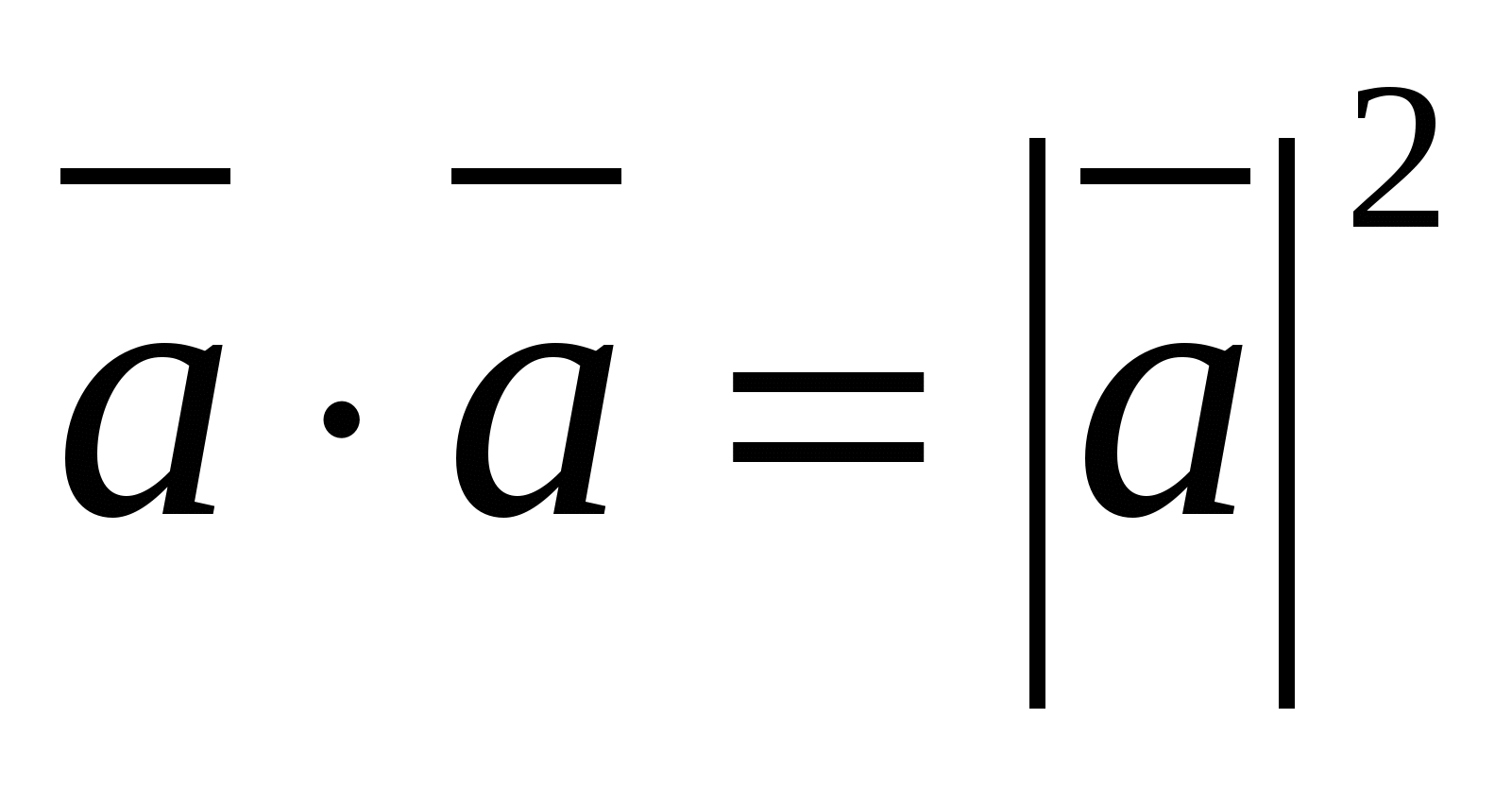
ಆ.
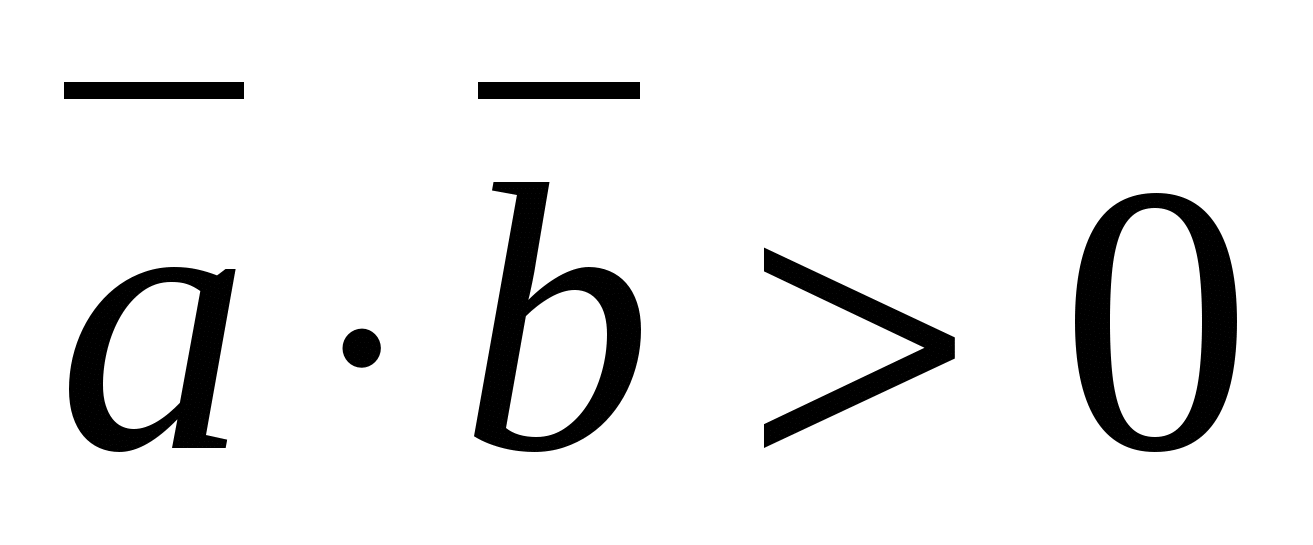

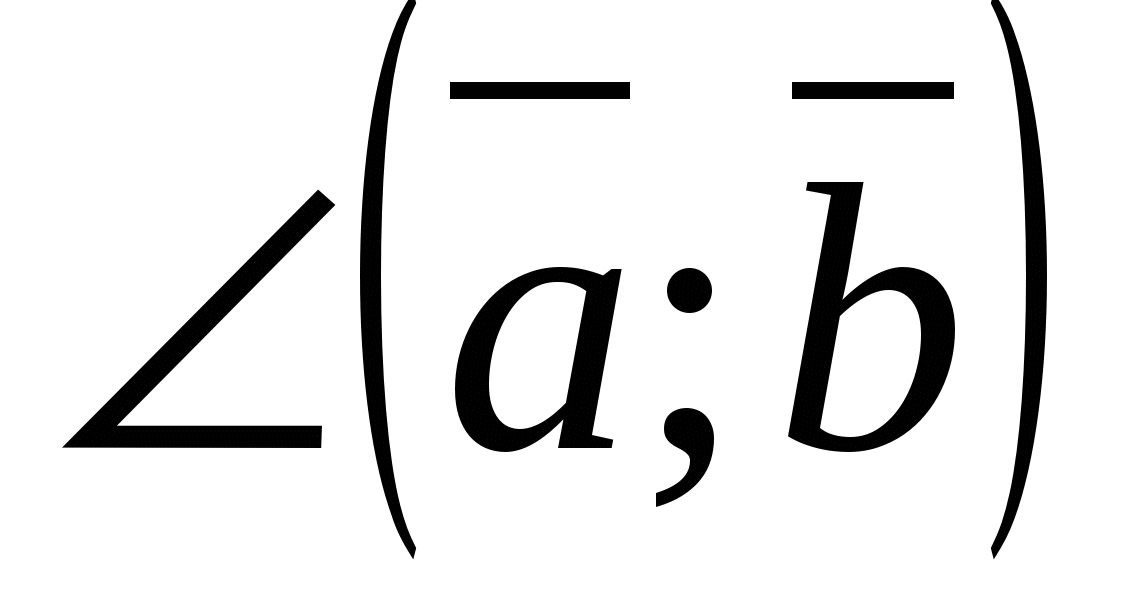 - ಮಸಾಲೆಯುಕ್ತ.
- ಮಸಾಲೆಯುಕ್ತ.
ಶೂನ್ಯ ವಾಹಕಗಳ ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನವು ಋಣಾತ್ಮಕವಾಗಿರುತ್ತದೆ ಮತ್ತು ವೆಕ್ಟರ್ಗಳ ನಡುವಿನ ಕೋನವು ಮೊಂಡಾಗಿದ್ದರೆ ಮಾತ್ರ,
ಆ.
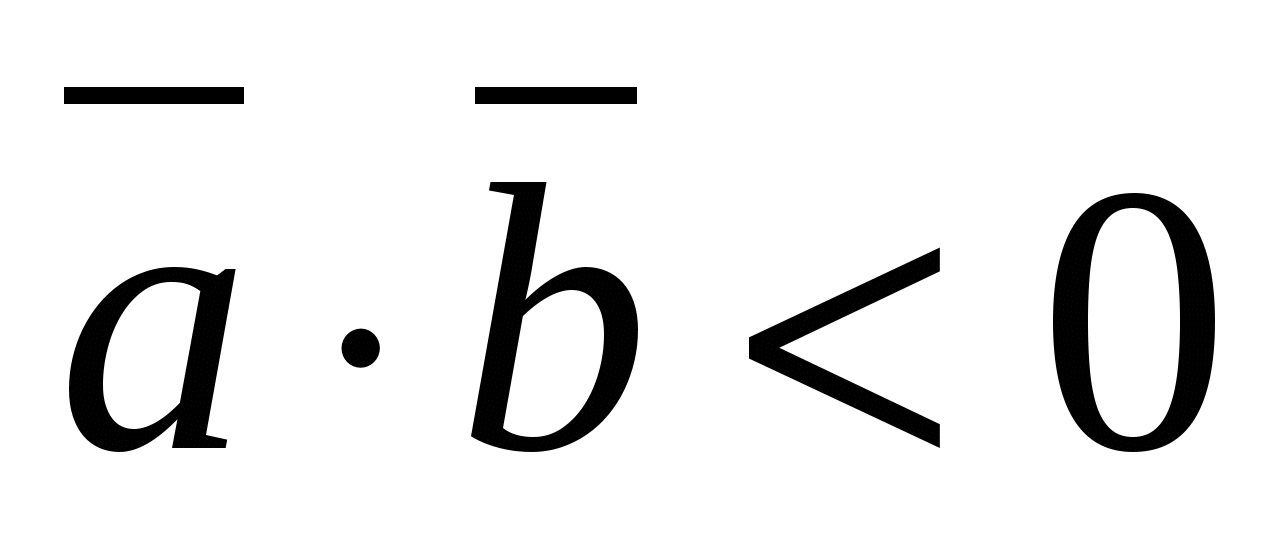

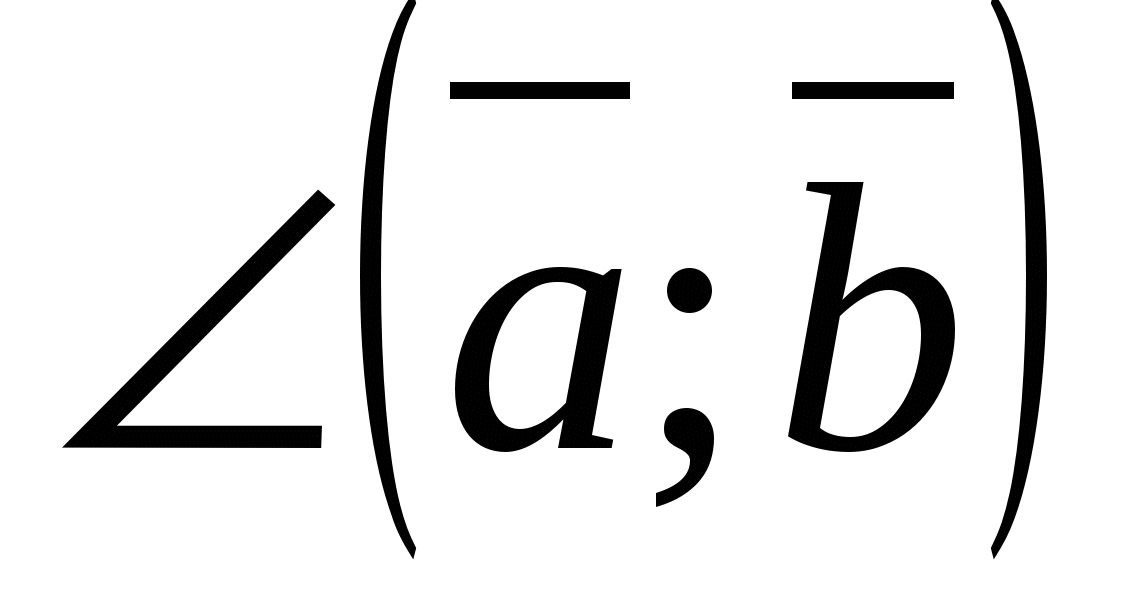 - ಮೊಂಡಾದ.
- ಮೊಂಡಾದ.
ಯಾವುದೇ ವಾಹಕಗಳಿಗೆ, 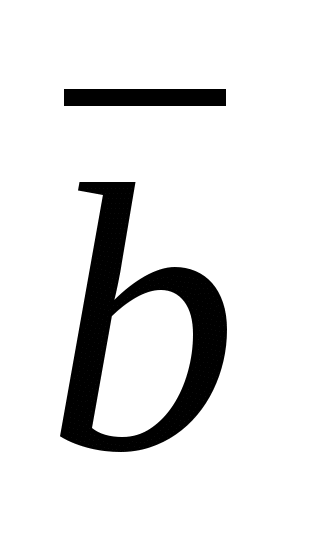 ,
, 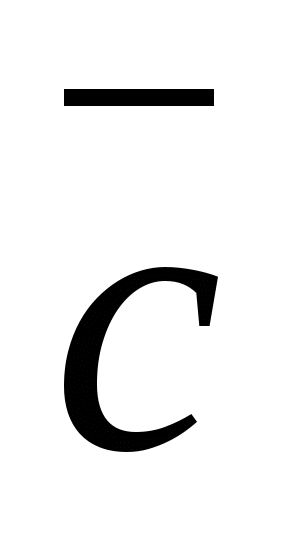 , ಮತ್ತು ಯಾವುದೇ ಸಂಖ್ಯೆಕೆ
ಸಮಾನತೆಗಳು ಮಾನ್ಯವಾಗಿವೆ:
, ಮತ್ತು ಯಾವುದೇ ಸಂಖ್ಯೆಕೆ
ಸಮಾನತೆಗಳು ಮಾನ್ಯವಾಗಿವೆ:
1. 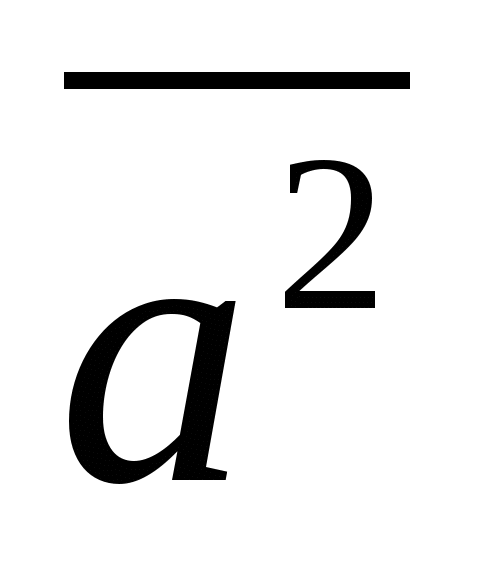
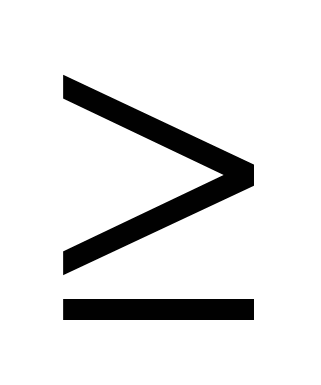 0, ಮತ್ತು
0, ಮತ್ತು 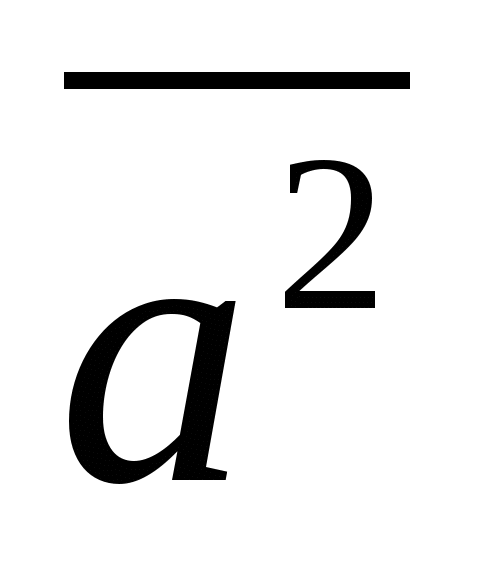 >0 ನಲ್ಲಿ
>0 ನಲ್ಲಿ 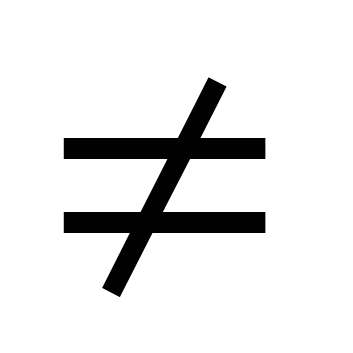 0.
0.
2. 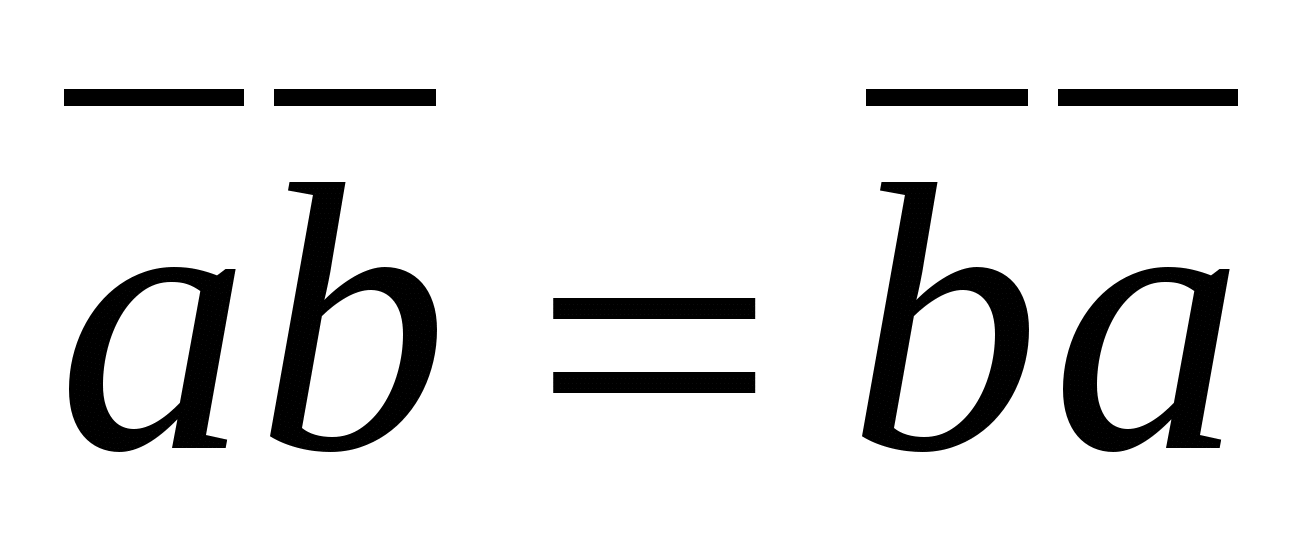 (ವರ್ಗಾವಣೆ ಕಾನೂನು).
(ವರ್ಗಾವಣೆ ಕಾನೂನು).
3.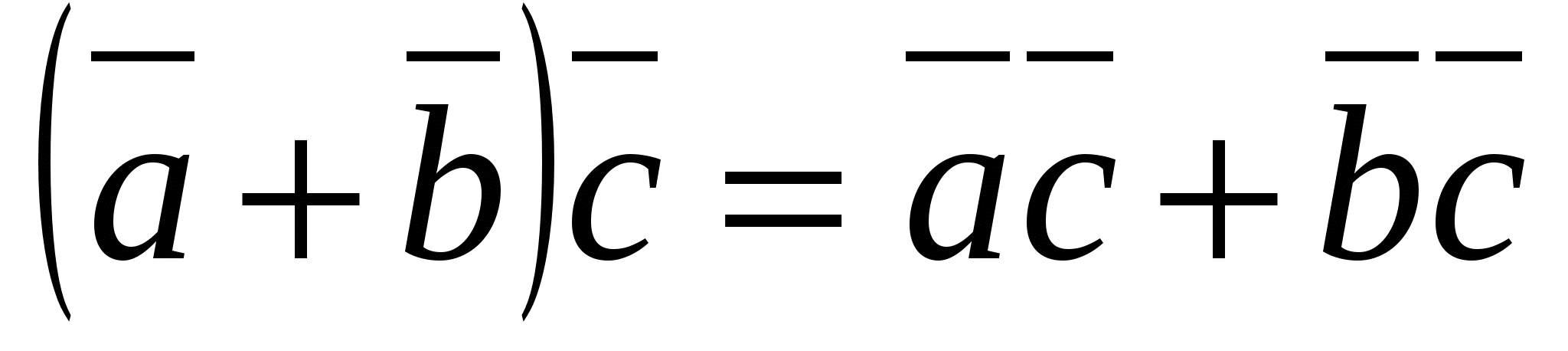 (ವಿತರಣಾ ಕಾನೂನು).
(ವಿತರಣಾ ಕಾನೂನು).
4. 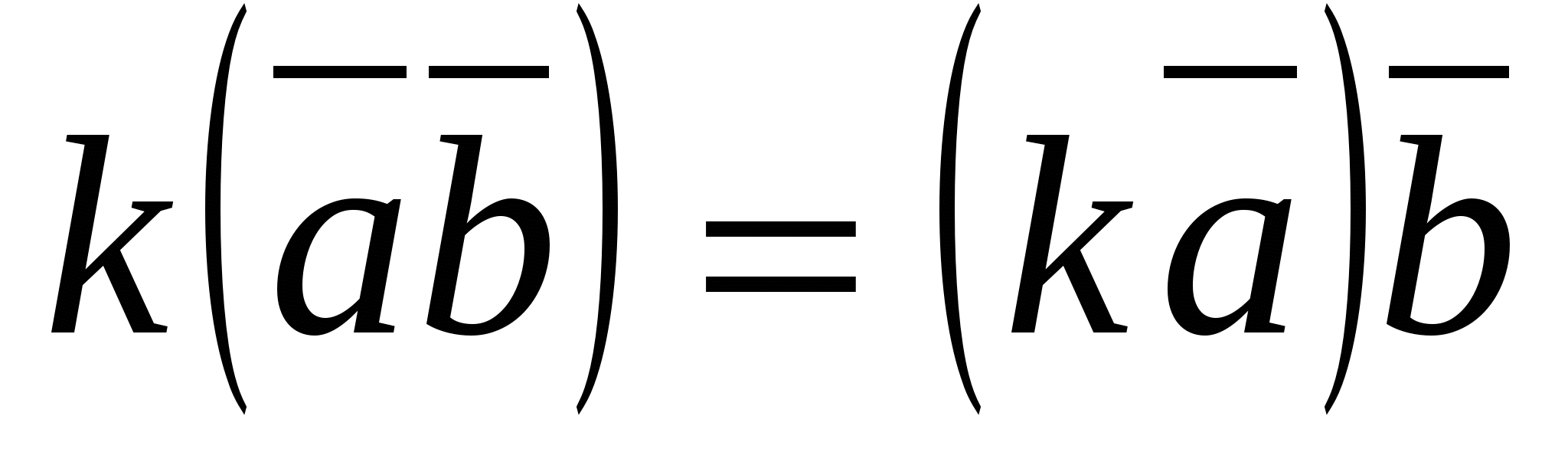 (ಸಂಯೋಜಿತ ಕಾನೂನು).
(ಸಂಯೋಜಿತ ಕಾನೂನು).
2) ಅವುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಬಳಸಿಕೊಂಡು ವಾಹಕಗಳ ನಡುವಿನ ಕೋನದ ಲೆಕ್ಕಾಚಾರ.
ಕೋನದ ಕೊಸೈನ್  ಶೂನ್ಯವಲ್ಲದ ವಾಹಕಗಳ ನಡುವೆ
ಶೂನ್ಯವಲ್ಲದ ವಾಹಕಗಳ ನಡುವೆ 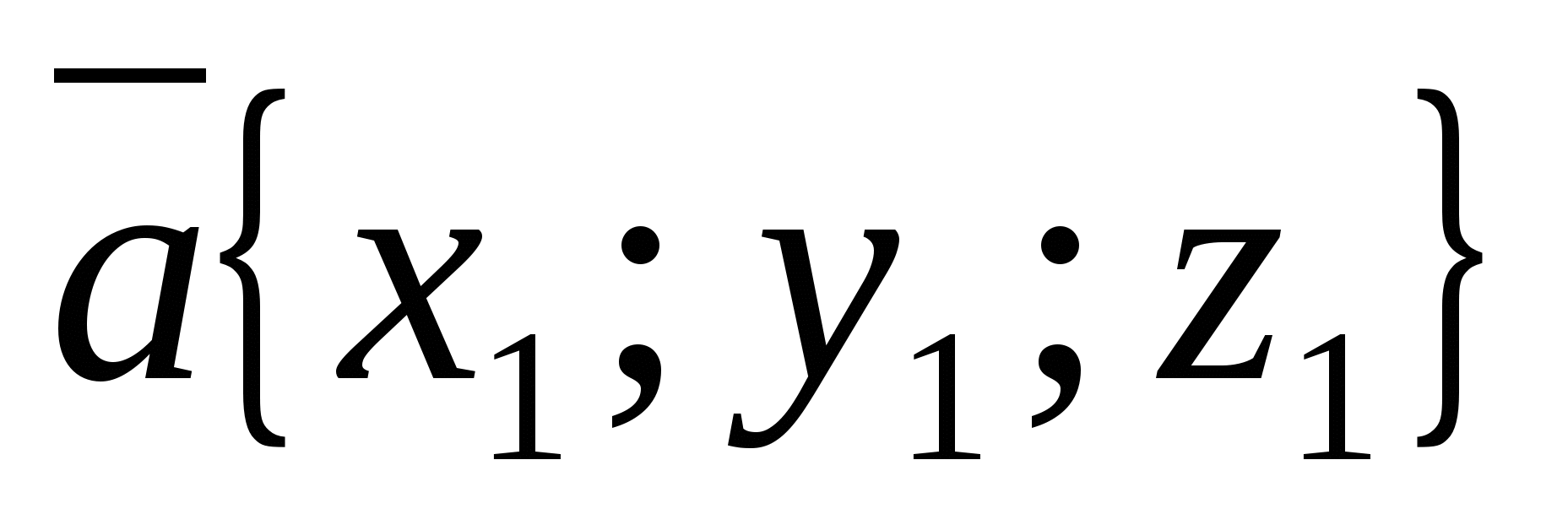 ಮತ್ತು
ಮತ್ತು 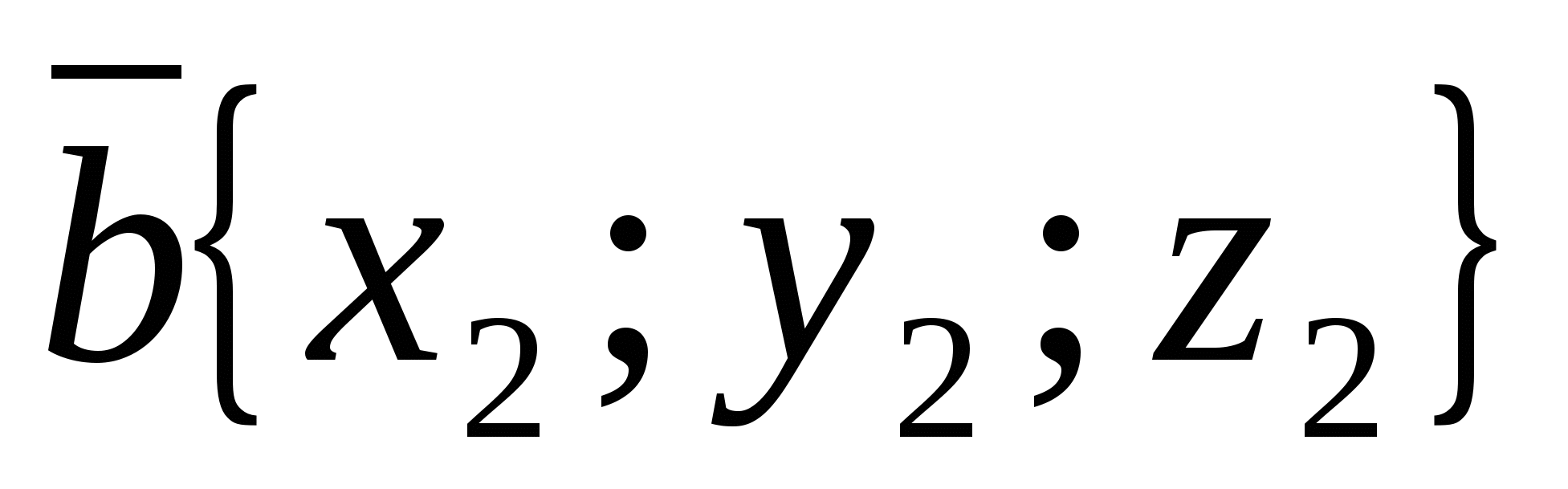 ಸೂತ್ರದ ಮೂಲಕ ಲೆಕ್ಕಹಾಕಲಾಗಿದೆ
ಸೂತ್ರದ ಮೂಲಕ ಲೆಕ್ಕಹಾಕಲಾಗಿದೆ
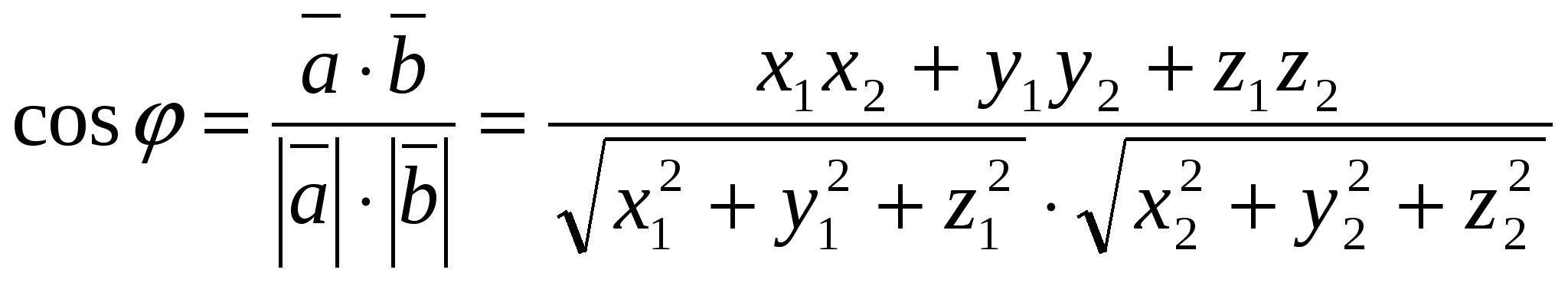 ,
,
ಎಲ್ಲಿ 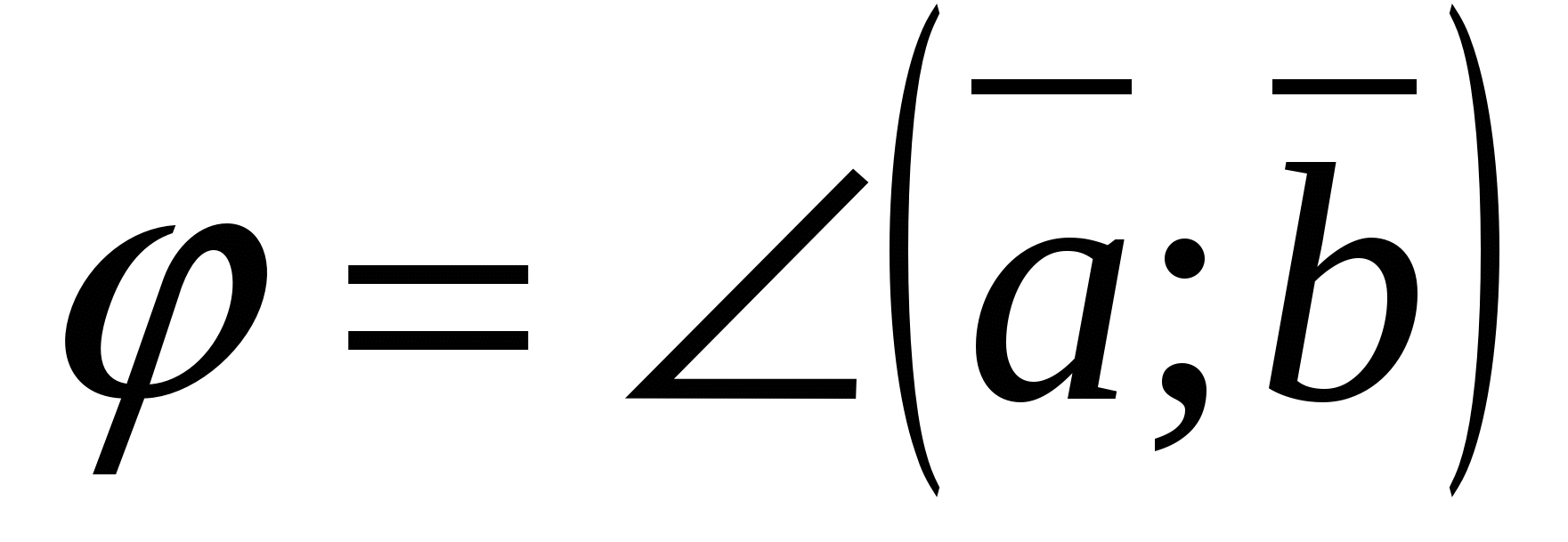
7. ನೇರ ರೇಖೆಗಳು ಮತ್ತು ವಿಮಾನಗಳ ನಡುವಿನ ಕೋನಗಳ ಲೆಕ್ಕಾಚಾರ.
1) ನೇರ ರೇಖೆಗಳ ನಡುವಿನ ಕೋನ.
ಈ ಸಮಸ್ಯೆಯನ್ನು ಪರಿಹರಿಸಲು, ನಾವು ನೇರ ರೇಖೆಯ ನಿರ್ದೇಶನ ವೆಕ್ಟರ್ ಪರಿಕಲ್ಪನೆಯನ್ನು ಪರಿಚಯಿಸುತ್ತೇವೆ.
ವ್ಯಾಖ್ಯಾನ.
ಶೂನ್ಯ ಸದಿಶವನ್ನು ಒಂದು ರೇಖೆಯ ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಅದು ಒಂದು ಸಾಲಿನಲ್ಲಿ a ಅಥವಾ a ಗೆ ಸಮಾನಾಂತರವಾಗಿರುವ ರೇಖೆಯಲ್ಲಿದ್ದರೆ.
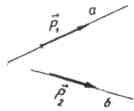 ಉದಾಹರಣೆ
ಉದಾಹರಣೆ
ವಾಹಕಗಳು 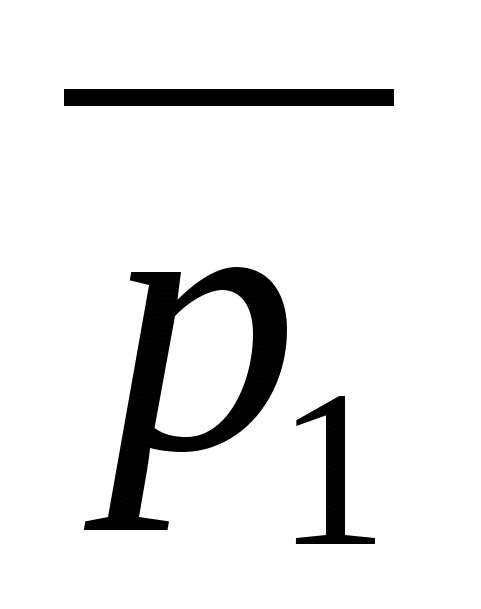 ಮತ್ತು
ಮತ್ತು  ನೇರ ಮಾರ್ಗದರ್ಶಿಗಳುಎ
ಮತ್ತು ಬಿ
, ಕ್ರಮವಾಗಿ.
ನೇರ ಮಾರ್ಗದರ್ಶಿಗಳುಎ
ಮತ್ತು ಬಿ
, ಕ್ರಮವಾಗಿ.
ವ್ಯಾಖ್ಯಾನ.
ರೇಖೆಗಳ ನಡುವಿನ ಕೋನವು ಈ ರೇಖೆಗಳ ದಿಕ್ಕಿನ ವಾಹಕಗಳ ನಡುವಿನ ಕೋನವಾಗಿದೆ.
ನೇರ ರೇಖೆಗಳ ನಡುವಿನ ಕೋನಎ
ಮತ್ತು ಬಿ
ಕೋನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆನೇರ ರೇಖೆಗಳ ದಿಕ್ಕಿನ ವಾಹಕಗಳ ನಡುವೆ, 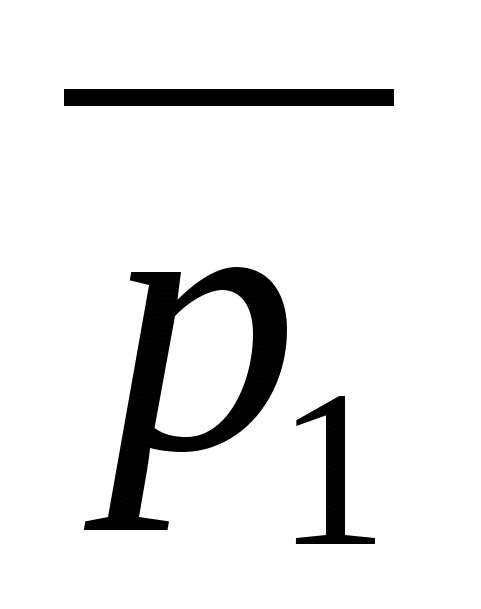 ಮತ್ತು
ಮತ್ತು 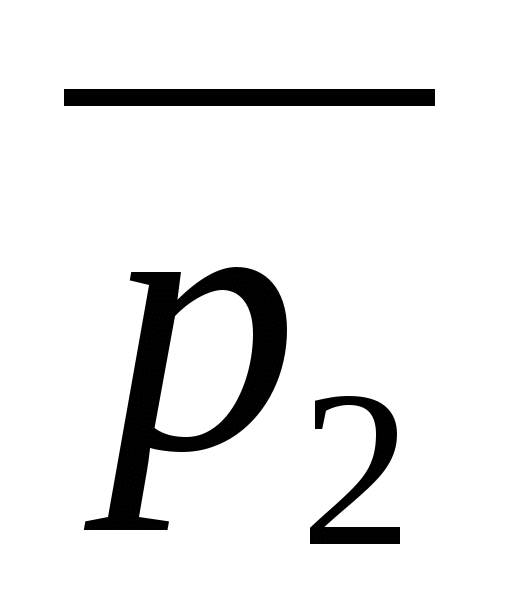 .
.
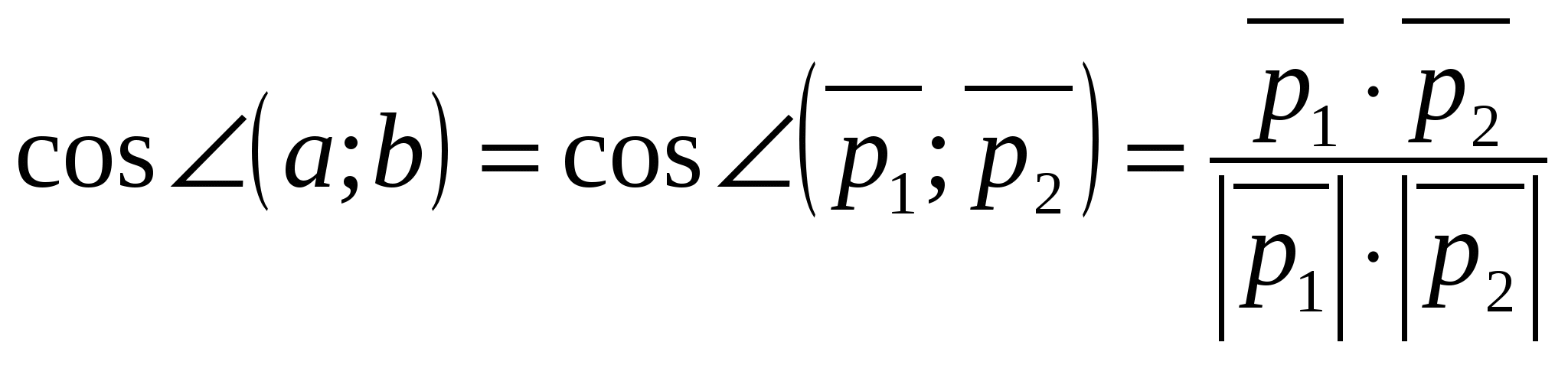 .
.
2) ನೇರ ರೇಖೆ ಮತ್ತು ಸಮತಲದ ನಡುವಿನ ಕೋನ.
ವ್ಯಾಖ್ಯಾನ.
ಒಂದು ರೇಖೆ ಮತ್ತು ಸಮತಲದ ನಡುವಿನ ಕೋನವು ನಿರ್ದಿಷ್ಟ ರೇಖೆಯ ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ಮತ್ತು ಶೂನ್ಯವಲ್ಲದ ವೆಕ್ಟರ್ ನಡುವಿನ ಕೋನವಾಗಿದೆ ಸಮತಲಕ್ಕೆ ಲಂಬವಾಗಿ(ಸಾಮಾನ್ಯ).
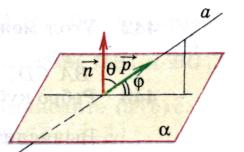
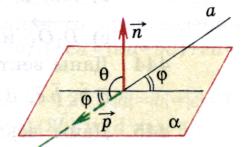
ಅವಕಾಶ 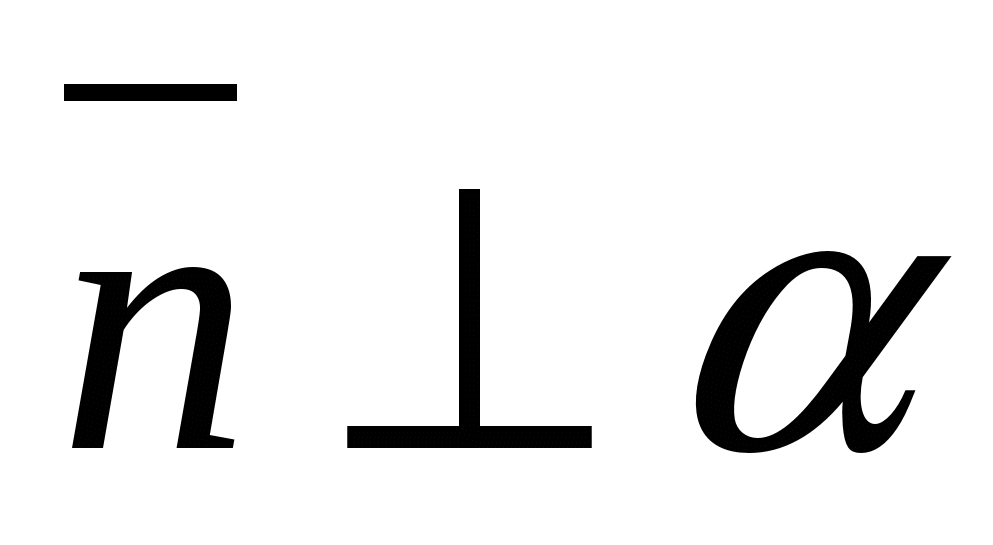 , (
, (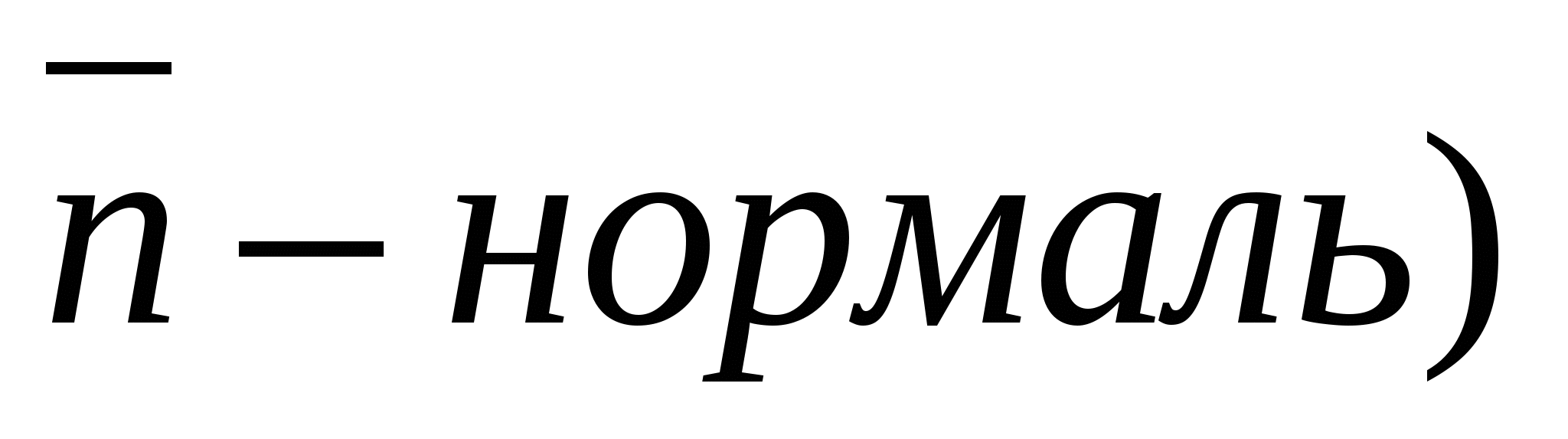
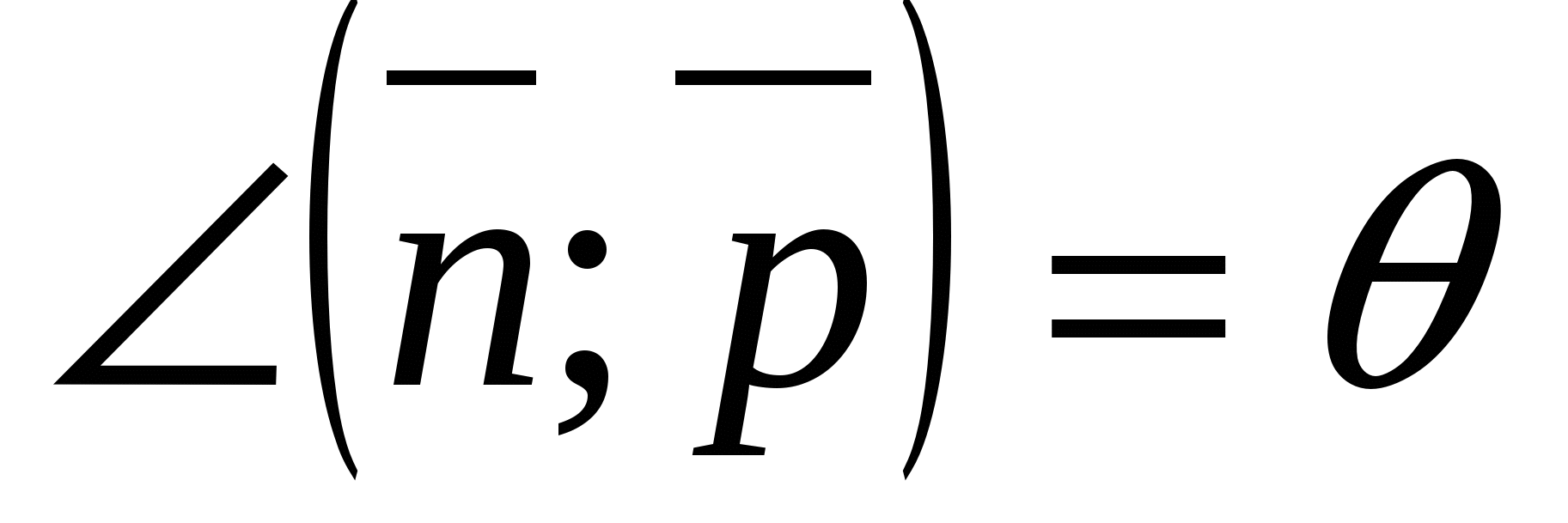 , ಎ
, ಎ 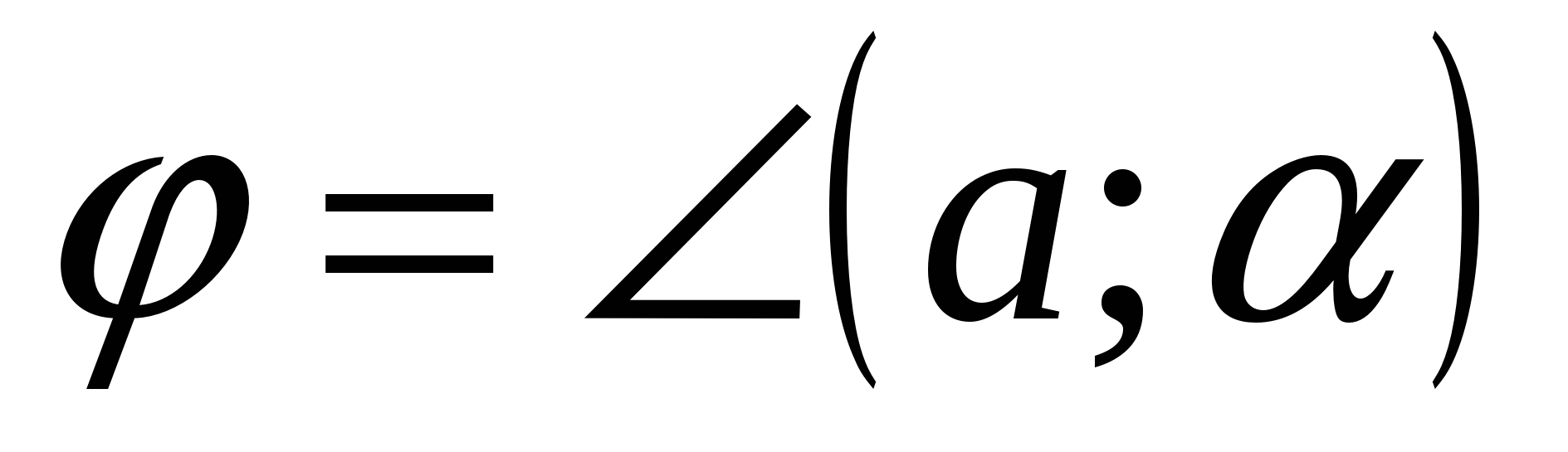 - ಬಯಸಿದ ಕೋನ (
- ಬಯಸಿದ ಕೋನ ( 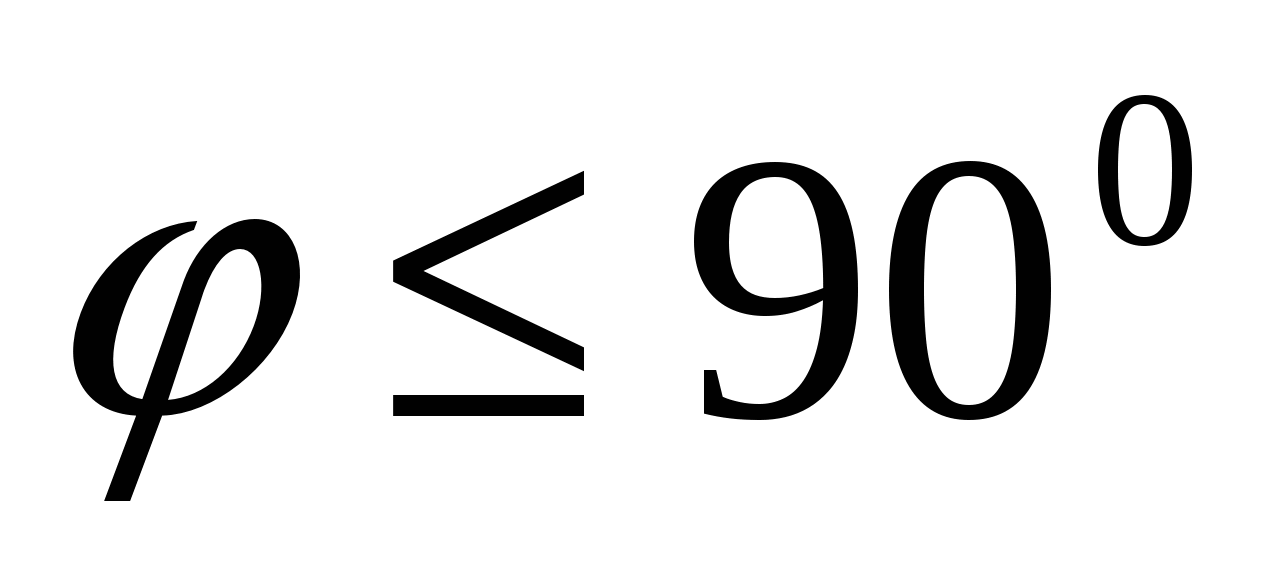 ).
).
ನಂತರ

ಅರ್ಥ  .
.
ಅಧ್ಯಾಯ 3.
ಸ್ಟೀರಿಯೊಮೆಟ್ರಿಕ್ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸಲು ನಿರ್ದೇಶಾಂಕ ವಿಧಾನದ ಅಪ್ಲಿಕೇಶನ್.
ಸಮಸ್ಯೆ.1
MABC ಪಿರಮಿಡ್ನ ತಳಭಾಗದಲ್ಲಿದೆ ಬಲ ತ್ರಿಕೋನಎಬಿಸಿ. 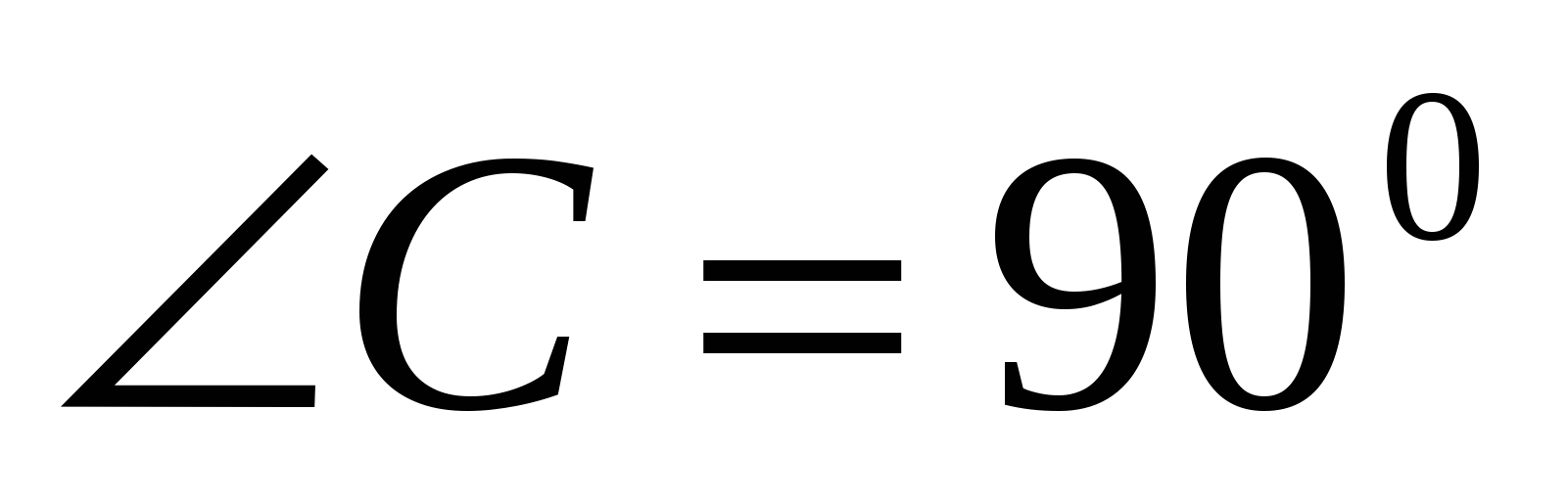 ,
ಎ.ಸಿ.=3,
ಬಿ.ಸಿ.=5. ಎಡ್ಜ್ AM AC ಗೆ ಲಂಬವಾಗಿರುತ್ತದೆ, AM=4,
,
ಎ.ಸಿ.=3,
ಬಿ.ಸಿ.=5. ಎಡ್ಜ್ AM AC ಗೆ ಲಂಬವಾಗಿರುತ್ತದೆ, AM=4, 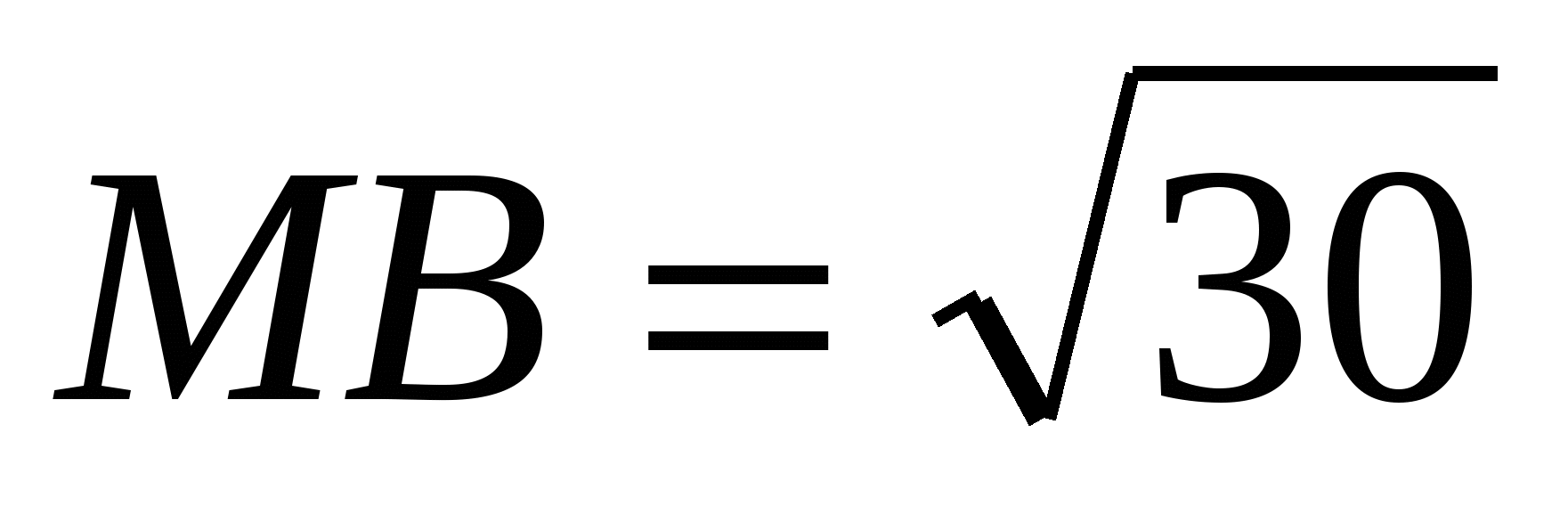 . ಪಿರಮಿಡ್ನ ಪರಿಮಾಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
. ಪಿರಮಿಡ್ನ ಪರಿಮಾಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಆರ್ 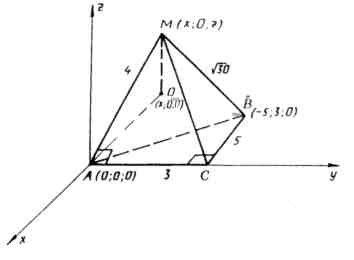 ನಿರ್ಧಾರ.
ನಿರ್ಧಾರ.
1) ಬಿಂದುವಿನ ಮೂಲದೊಂದಿಗೆ ಆಯತಾಕಾರದ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯನ್ನು ನಾವು ಪರಿಚಯಿಸೋಣ  . ಅಕ್ಷರೇಖೆ
. ಅಕ್ಷರೇಖೆ 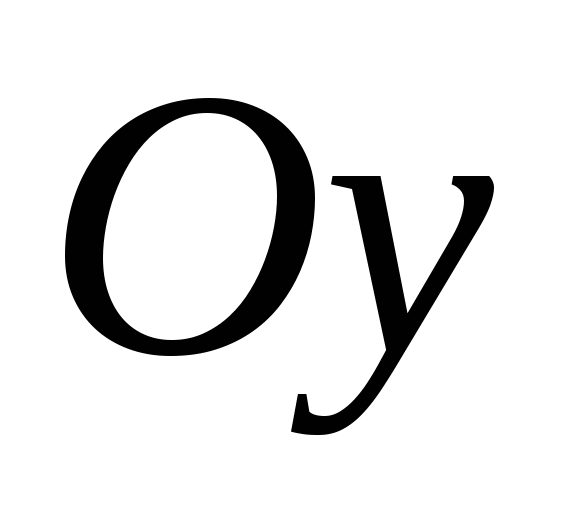 ಅಂಚಿನಲ್ಲಿ ನಿರ್ದೇಶಿಸೋಣಎಸಿ, ಮತ್ತು ವಿಮಾನ ಓಹ್
ವೈ
ಪಿರಮಿಡ್ನ ತಳದಲ್ಲಿಎಬಿಸಿ.
ಅಂಚಿನಲ್ಲಿ ನಿರ್ದೇಶಿಸೋಣಎಸಿ, ಮತ್ತು ವಿಮಾನ ಓಹ್
ವೈ
ಪಿರಮಿಡ್ನ ತಳದಲ್ಲಿಎಬಿಸಿ.
ಈ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ: 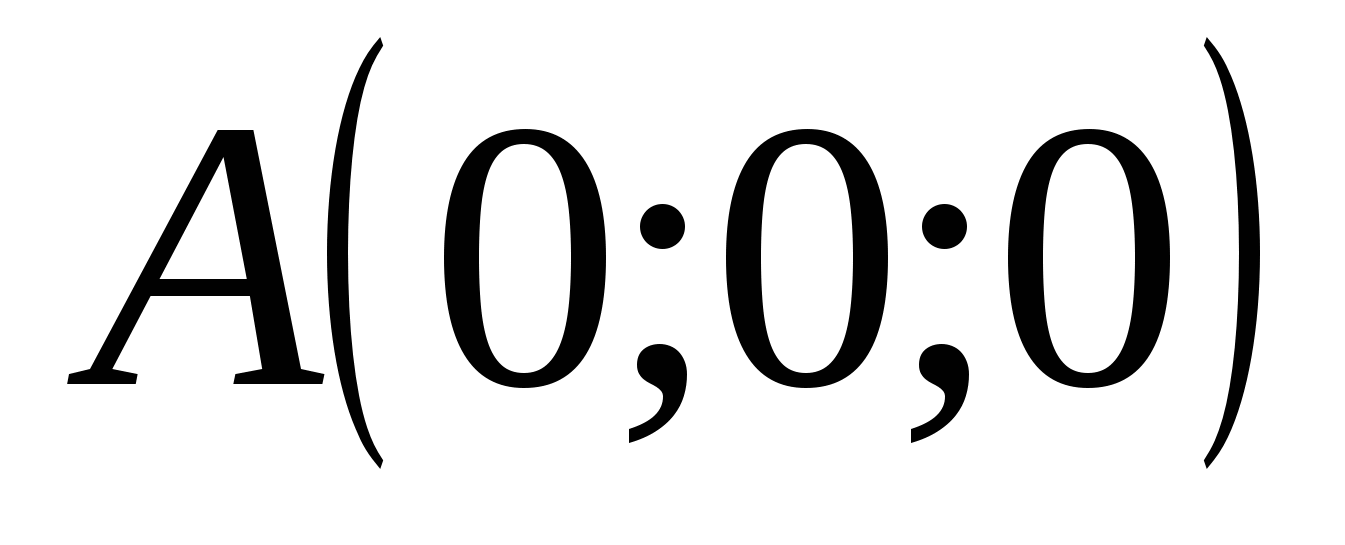 ,
, 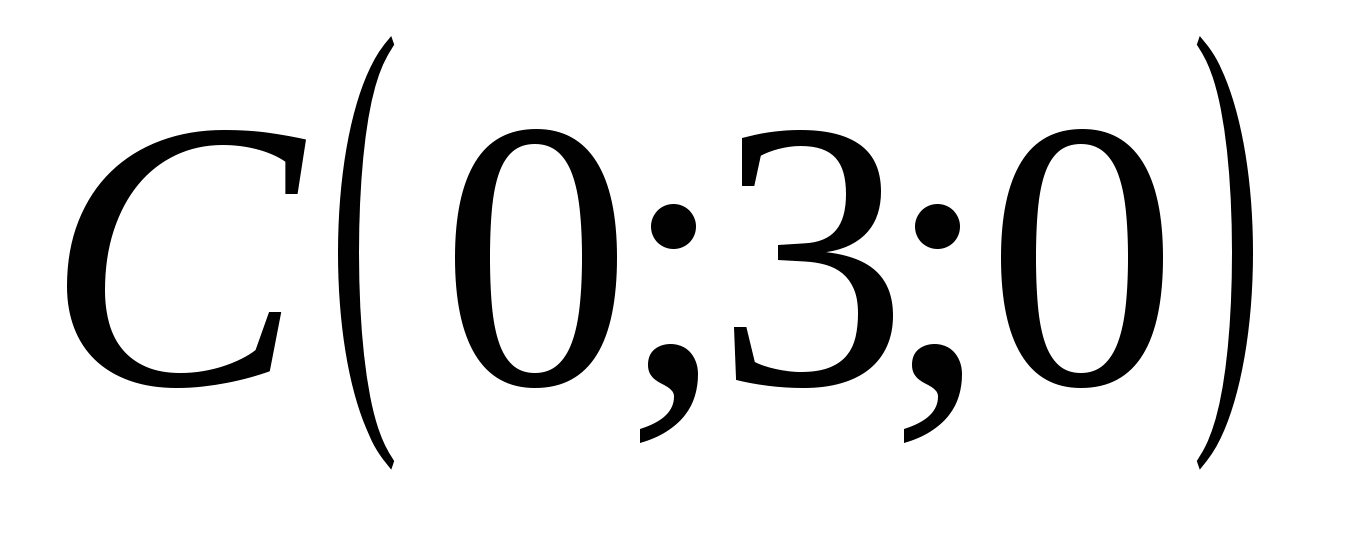 ,
, 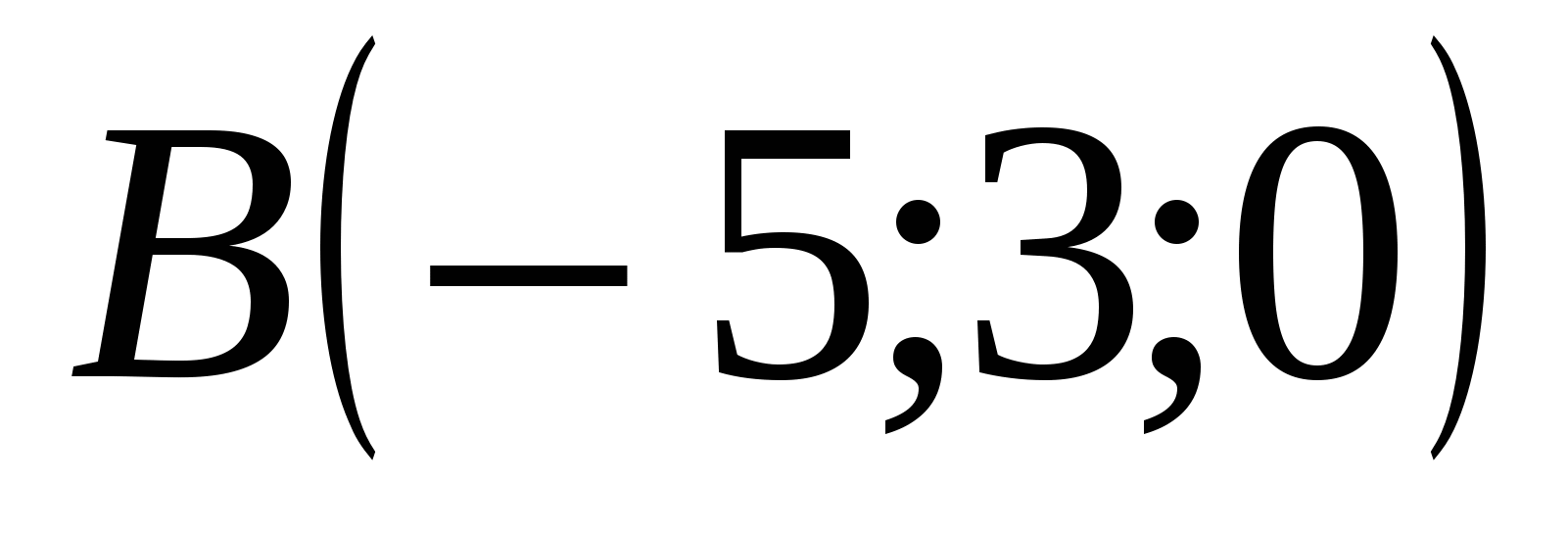 . ಷರತ್ತಿನಿಂದ
. ಷರತ್ತಿನಿಂದ 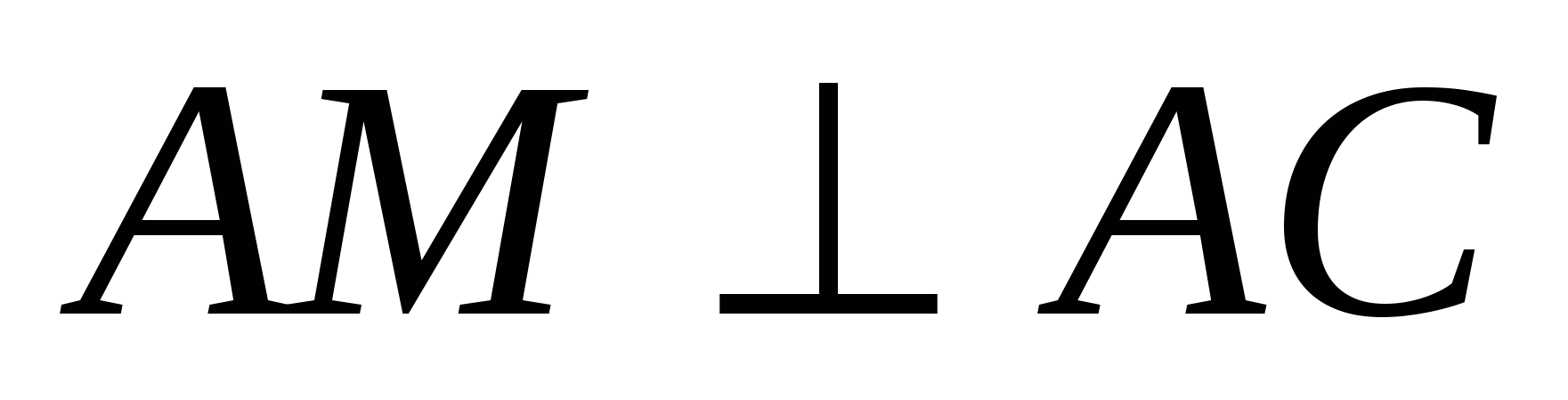 , ನಂತರ ಪಾಯಿಂಟ್ M ಸಮತಲದಲ್ಲಿದೆxz
ಮತ್ತು ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ
, ನಂತರ ಪಾಯಿಂಟ್ M ಸಮತಲದಲ್ಲಿದೆxz
ಮತ್ತು ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ
 .
.
2) 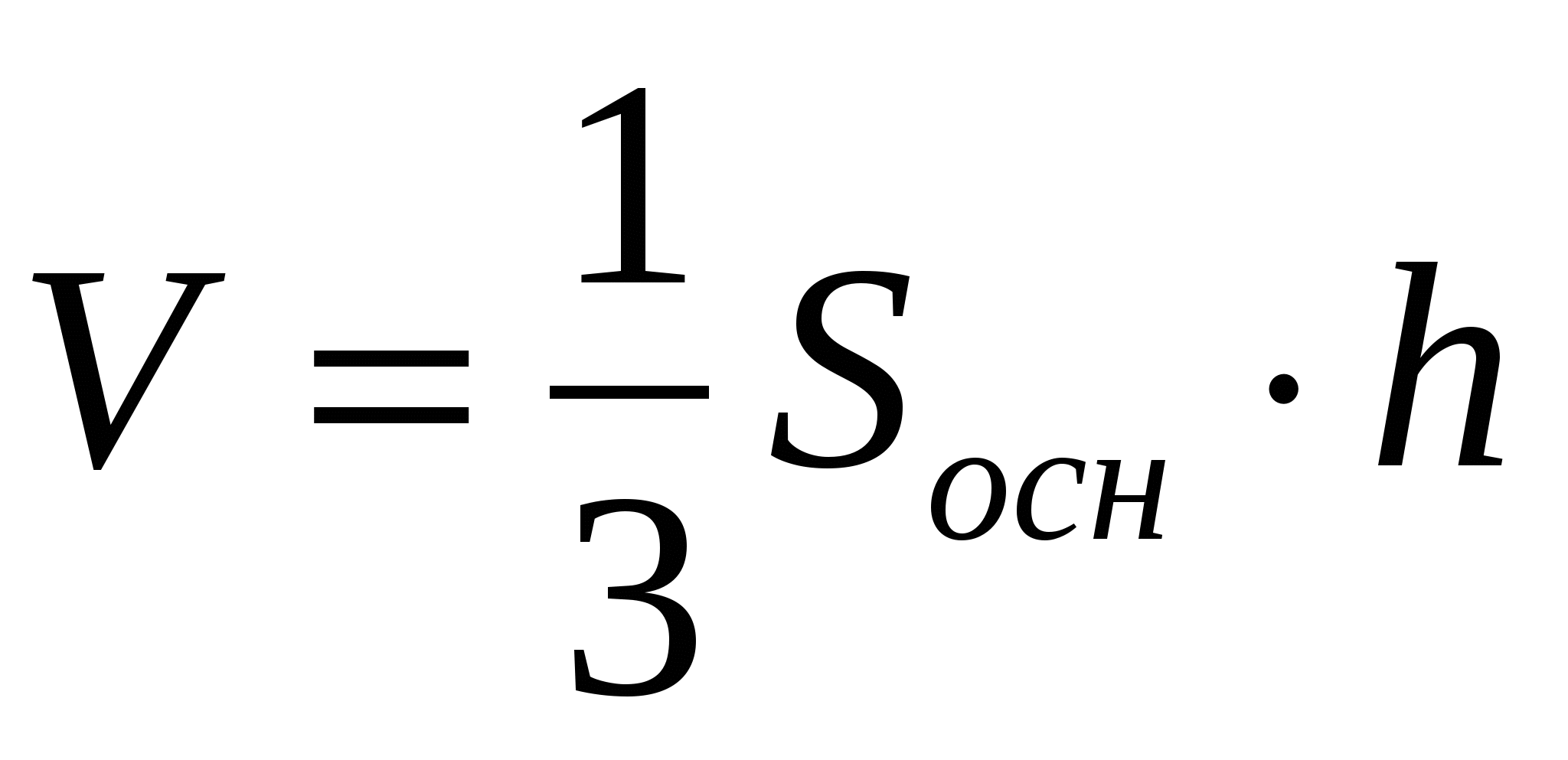 ,
, 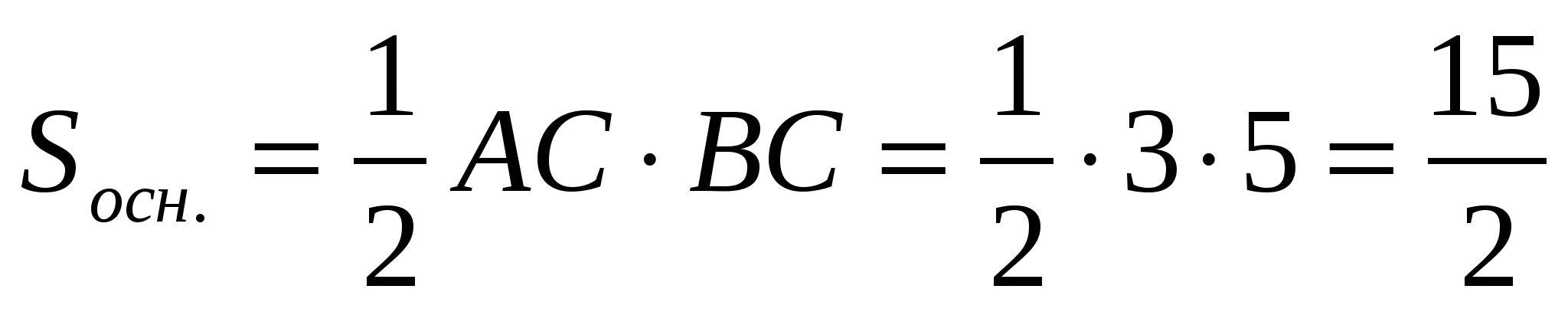 .
.
ಪಿರಮಿಡ್ನ ಎತ್ತರವನ್ನು ಕಂಡುಹಿಡಿಯೋಣ. ಹಂತದಿಂದ ಬಿಡೋಣಎಂಲಂಬವಾಗಿರುವ ಎಂ
ಡಿ
ವಿಮಾನಕ್ಕೆ (ಎಬಿಸಿ),
ನಂತರ  , ಏಕೆಂದರೆ
, ಏಕೆಂದರೆ 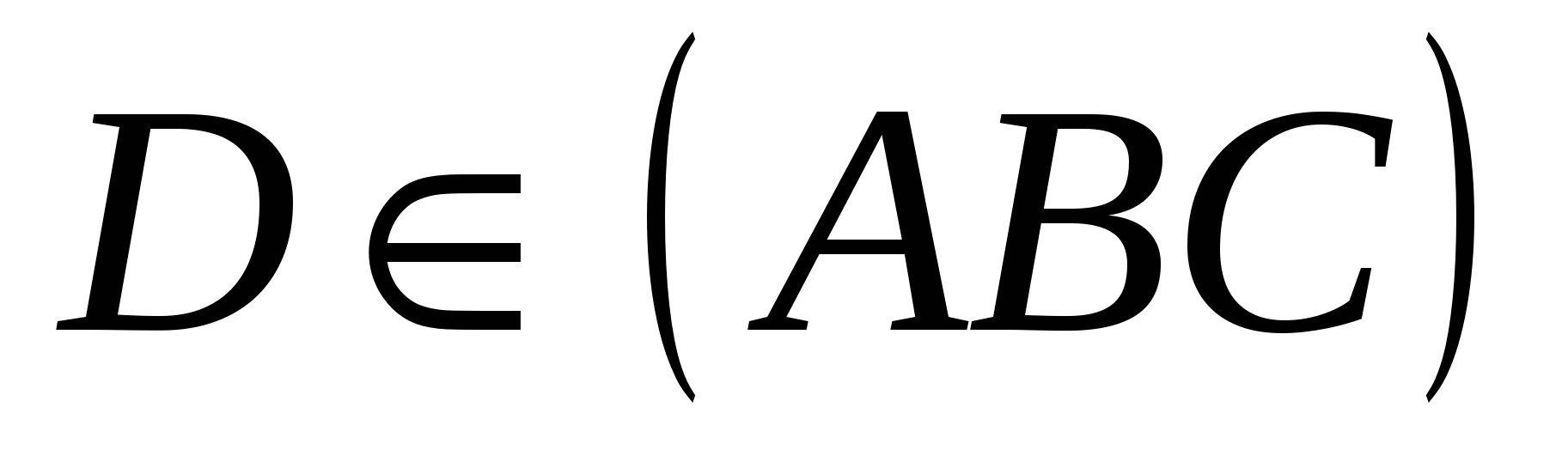 . ಆದ್ದರಿಂದ,
. ಆದ್ದರಿಂದ,  ಮತ್ತು ಬಿಂದುಗಳ ನಡುವಿನ ಅಂತರಎಂಮತ್ತು ಡಿಸಮನಾಗಿರುತ್ತದೆ, ಏಕೆಂದರೆ
ಮತ್ತು ಬಿಂದುಗಳ ನಡುವಿನ ಅಂತರಎಂಮತ್ತು ಡಿಸಮನಾಗಿರುತ್ತದೆ, ಏಕೆಂದರೆ 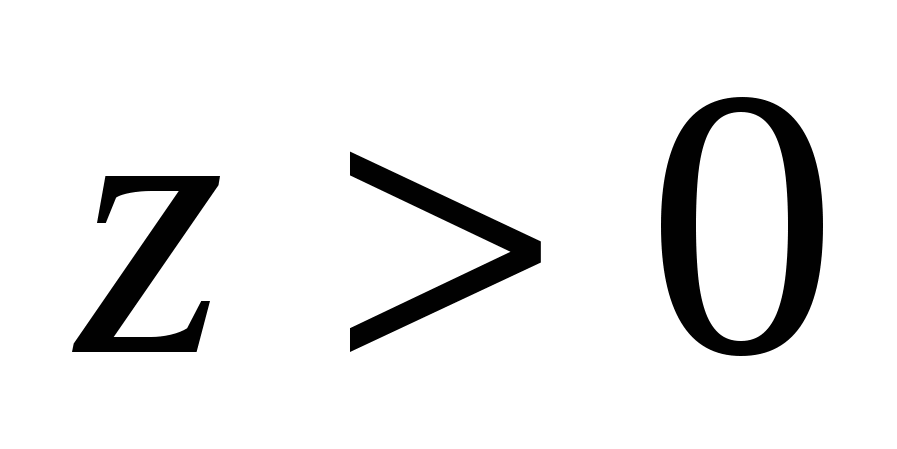 .
.
ನಿರ್ದೇಶಾಂಕ ಮೌಲ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯೋಣz
ಹೊಂದಿರುವ ಬಿಂದುಗಳ ನಡುವಿನ ಅಂತರವನ್ನು ಬಳಸುವುದು ನಿರ್ದೇಶಾಂಕ ನೀಡಲಾಗಿದೆ: 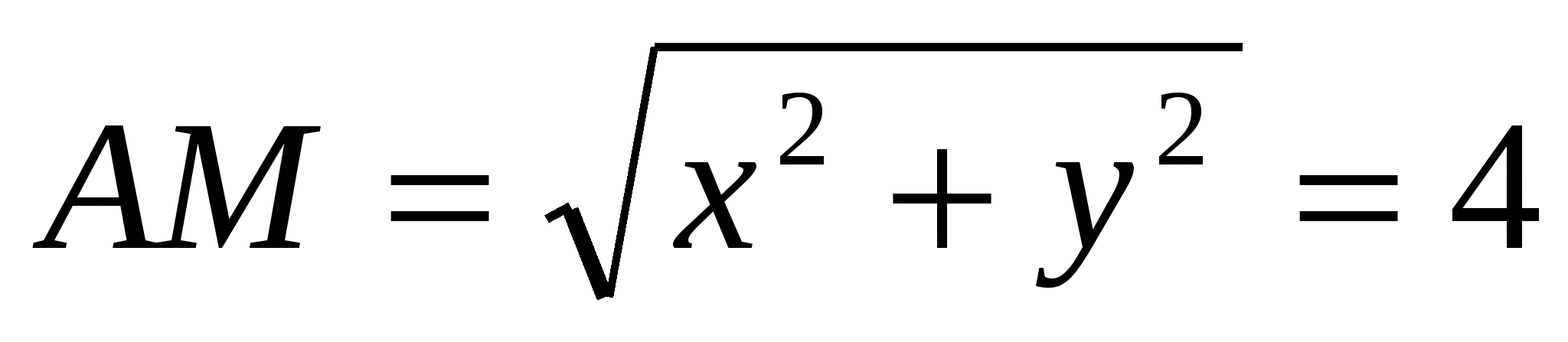 ,
,  . , ಅಂದರೆ
. , ಅಂದರೆ 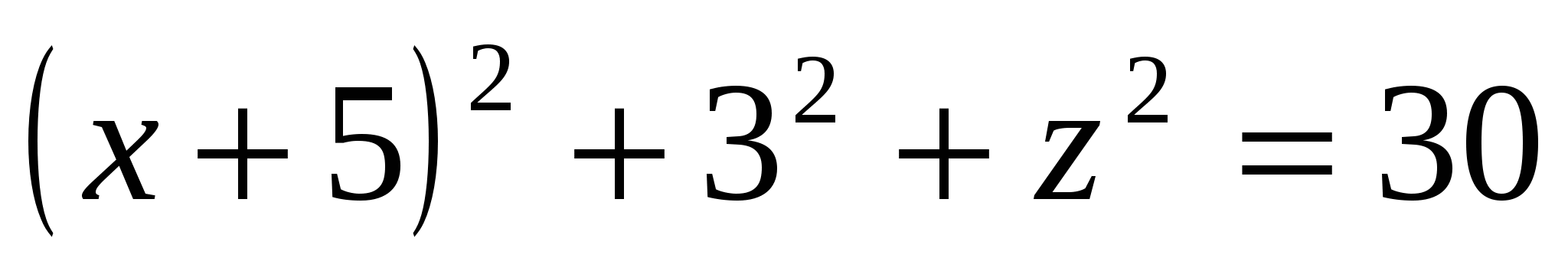 .
.
ನಾವು ಹೊಂದಿದ್ದೇವೆ: 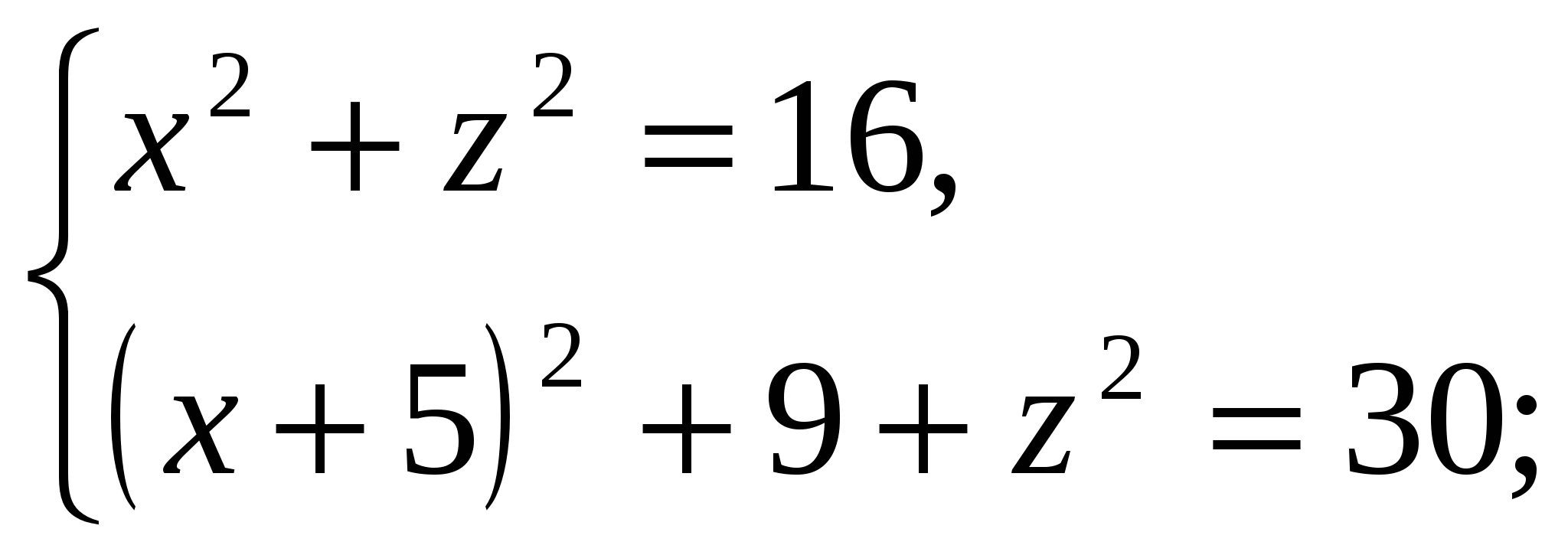
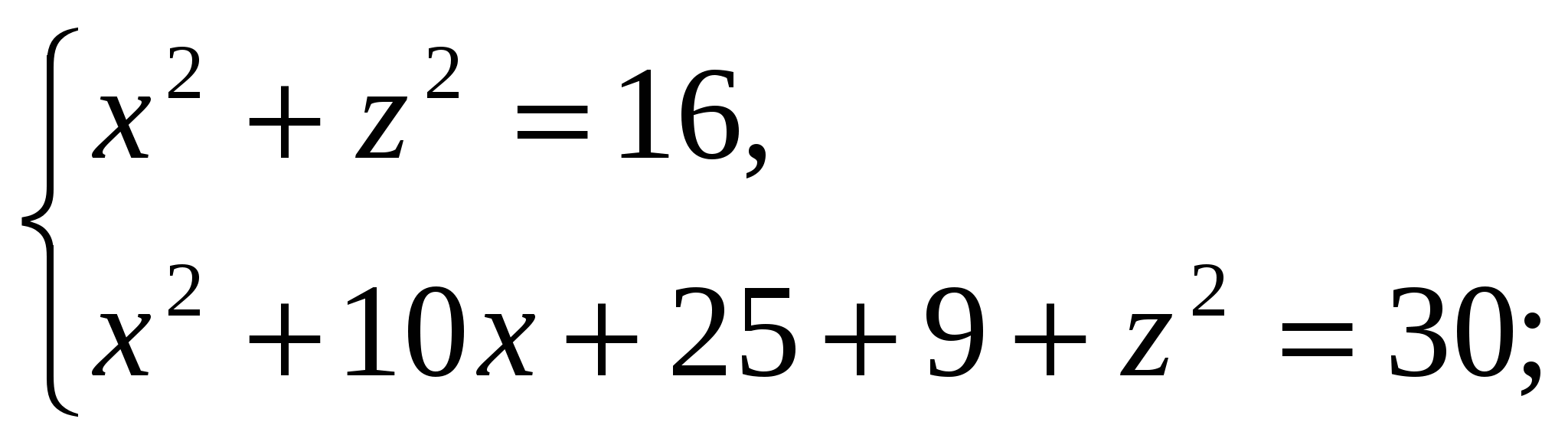
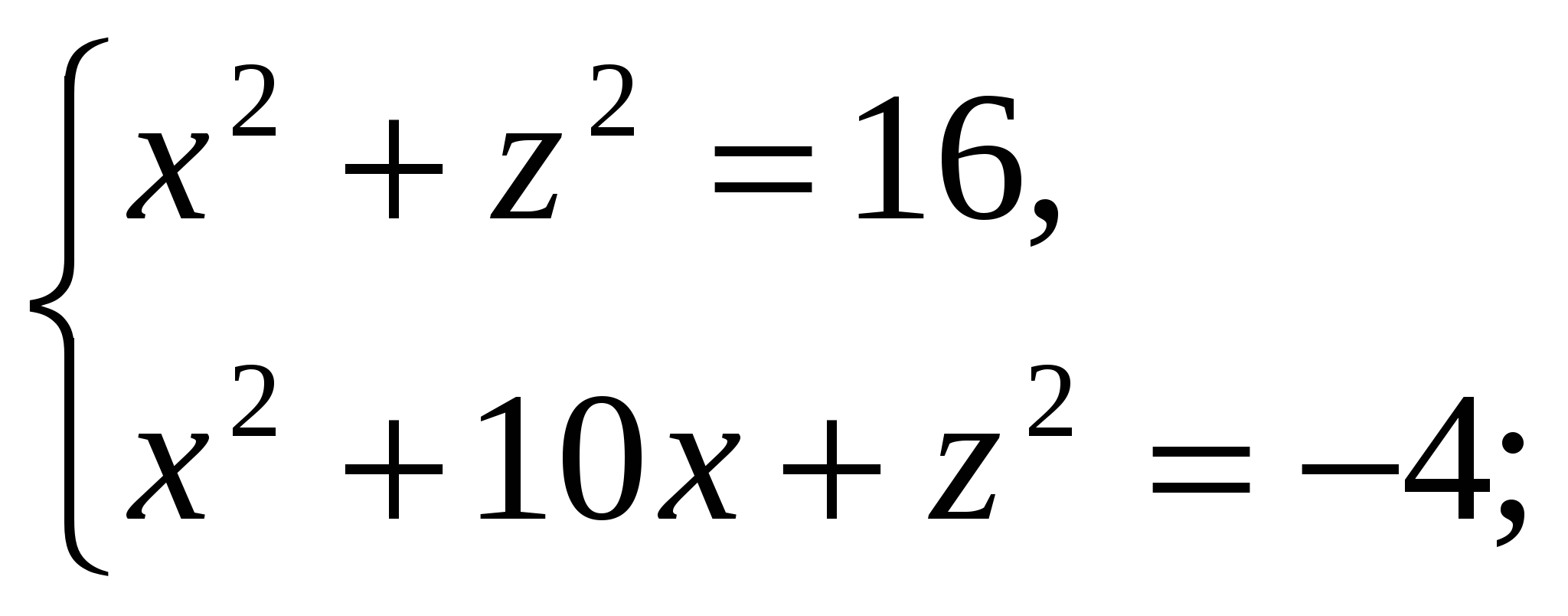
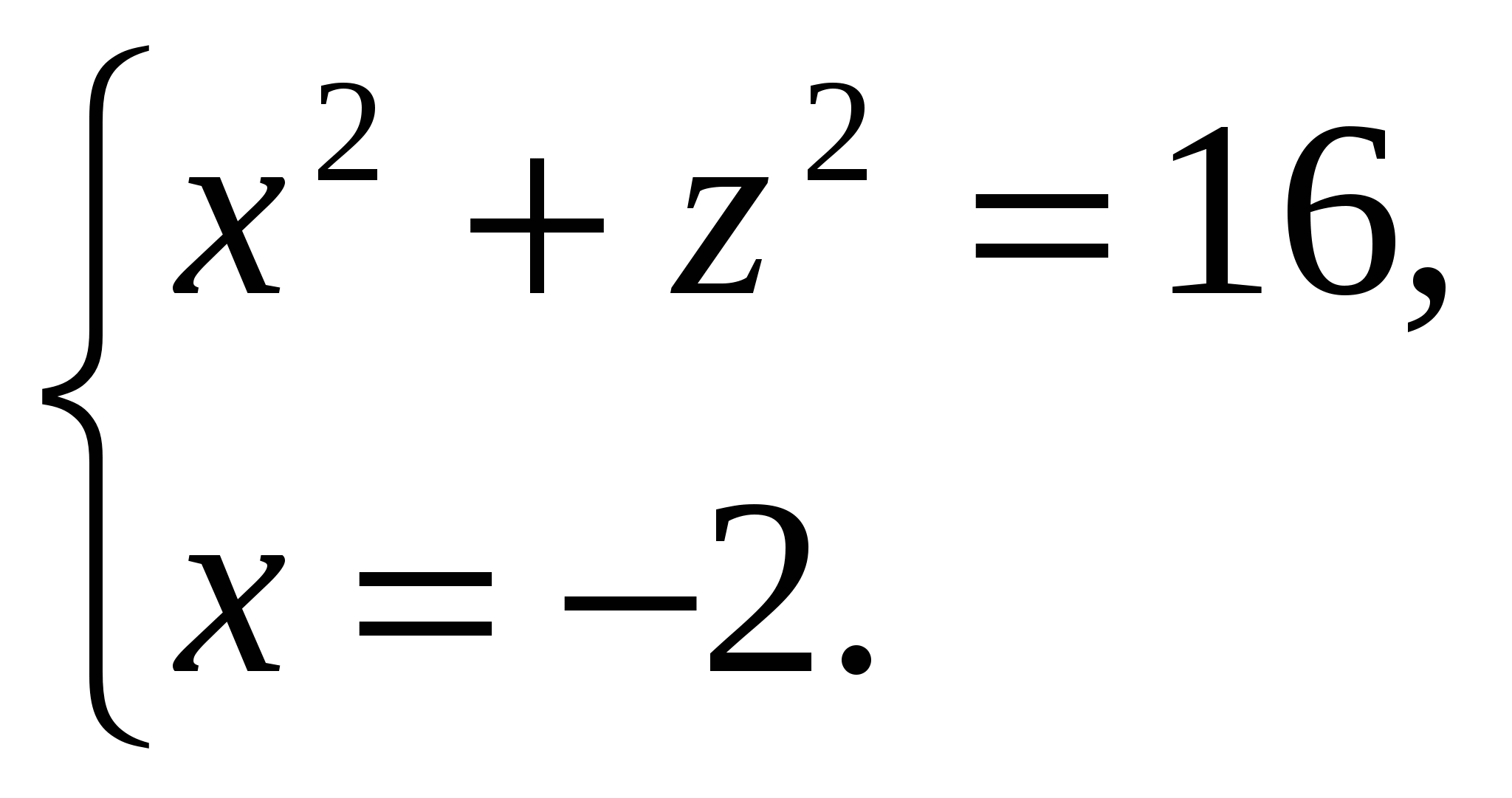
ಏಕೆಂದರೆ 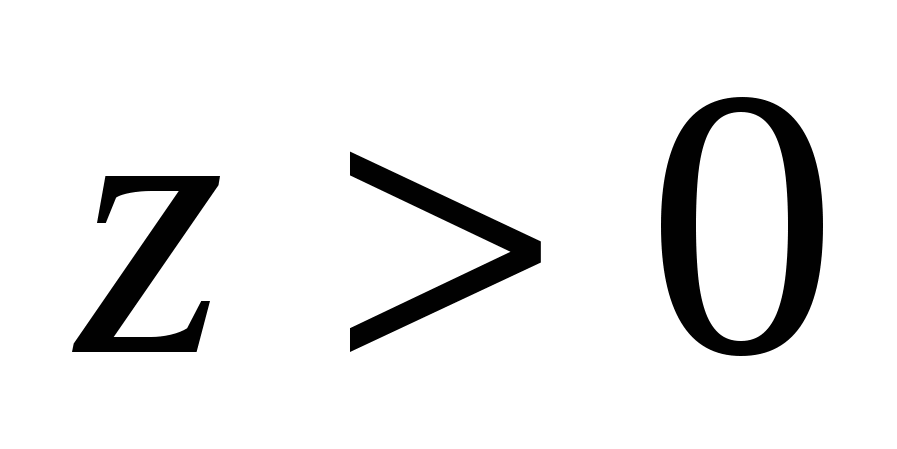 , ನಂತರ ಪಿರಮಿಡ್ನ ಎತ್ತರವು ಸಮಾನವಾಗಿರುತ್ತದೆ
, ನಂತರ ಪಿರಮಿಡ್ನ ಎತ್ತರವು ಸಮಾನವಾಗಿರುತ್ತದೆ 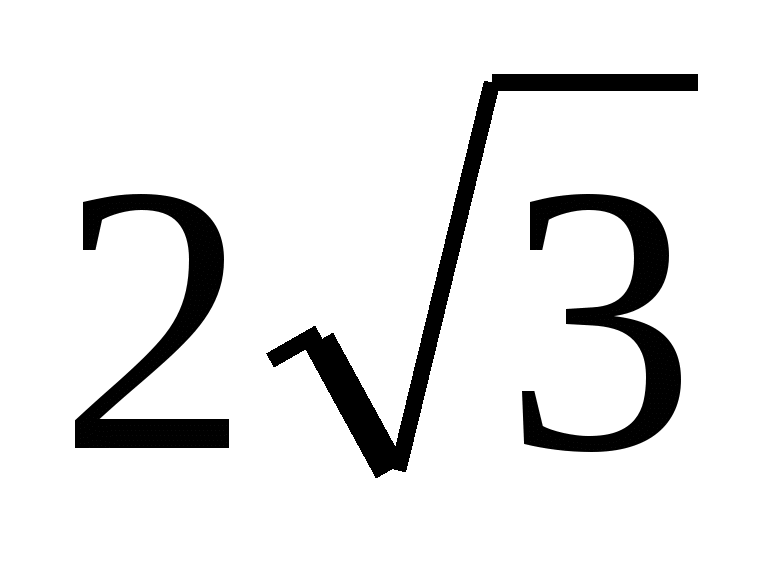 . ಆದ್ದರಿಂದ
. ಆದ್ದರಿಂದ 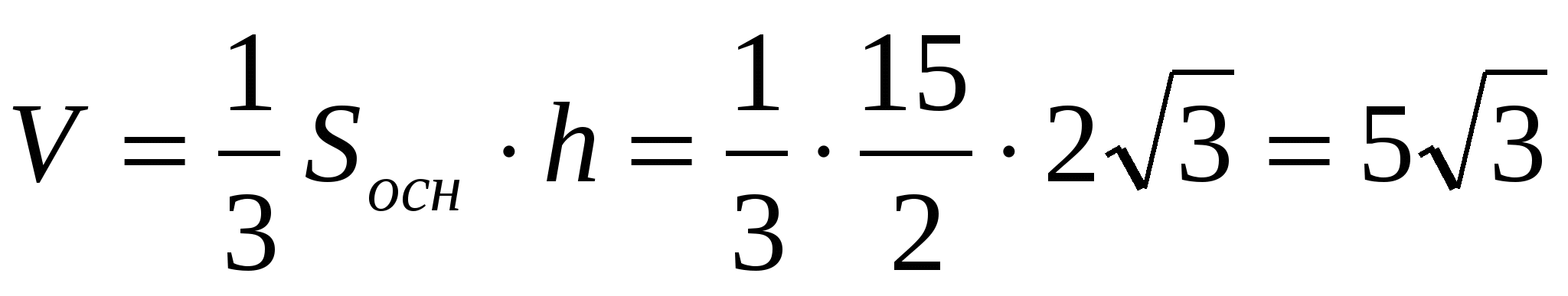 .
.
ಉತ್ತರ: 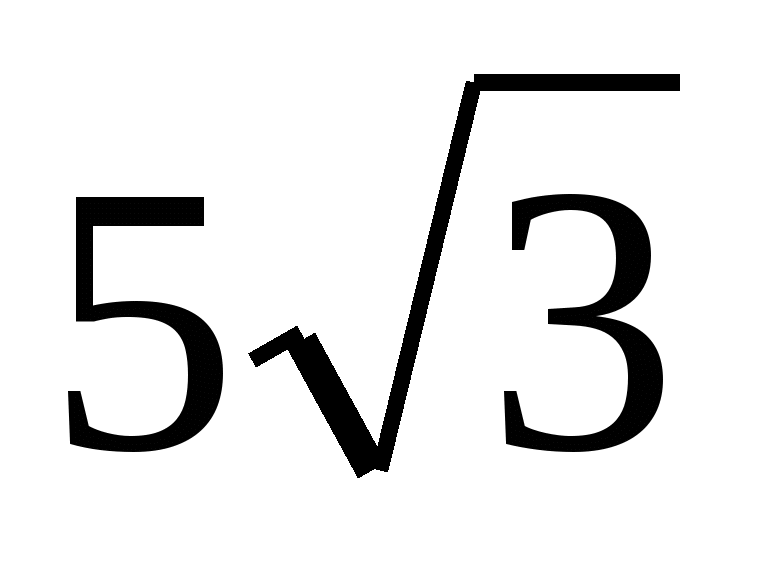 .
.
ಸಮಸ್ಯೆ.2.
ಒಂದು ಆಯತಾಕಾರದ ಸಮಾನಾಂತರದಲ್ಲಿ 
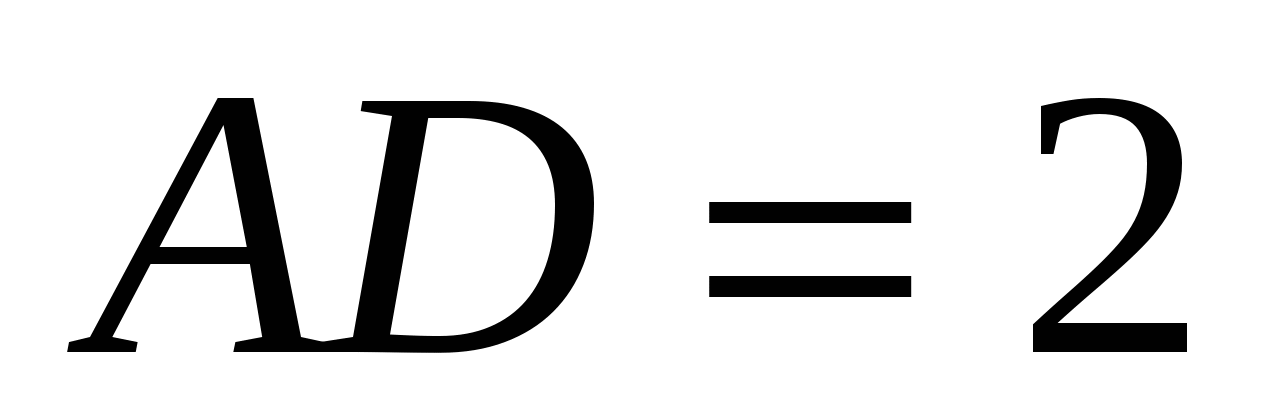 ,
, 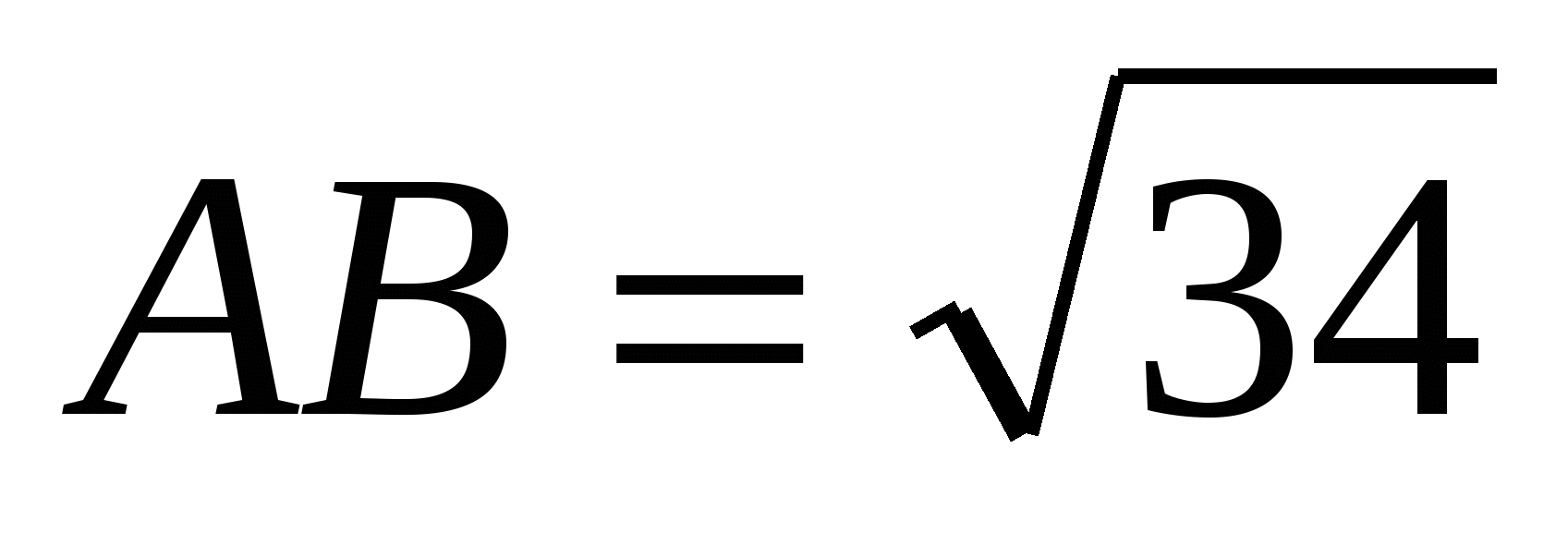 ,
,  . ಹುಡುಕಿ:
ನೇರ ರೇಖೆಗಳ ನಡುವಿನ ಕೋನ
. ಹುಡುಕಿ:
ನೇರ ರೇಖೆಗಳ ನಡುವಿನ ಕೋನ  ಮತ್ತು
ಮತ್ತು  .
.
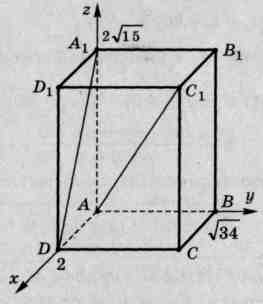 ಪರಿಹಾರ.
ಪರಿಹಾರ.
1) ಬಿಂದುವಿನಲ್ಲಿ ಮೂಲದೊಂದಿಗೆ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯನ್ನು ಪರಿಚಯಿಸೋಣ 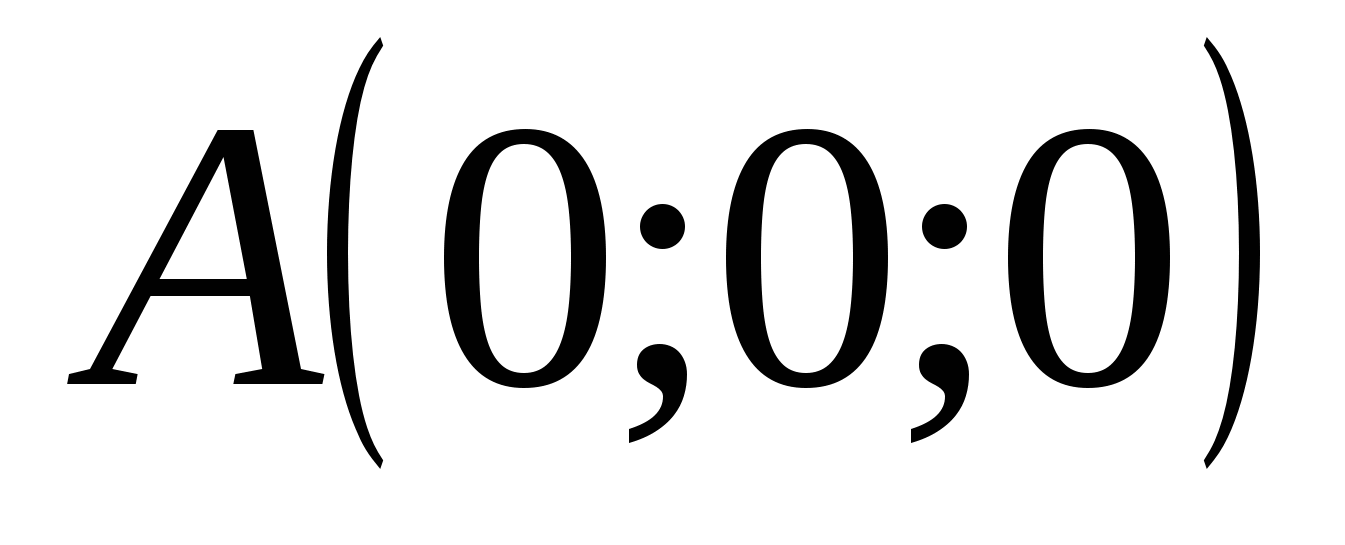 . ಅಚ್ಚುಗಳು
. ಅಚ್ಚುಗಳು 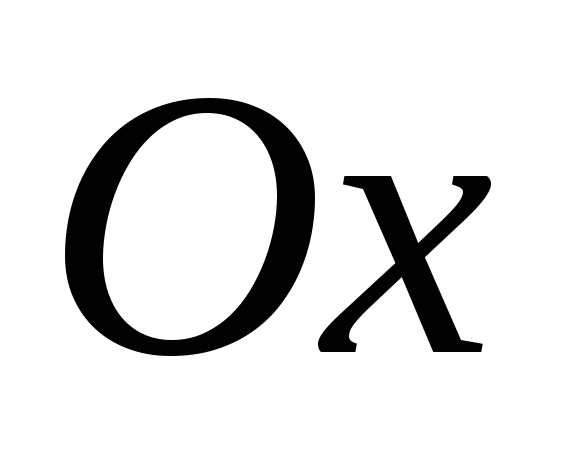 ,
,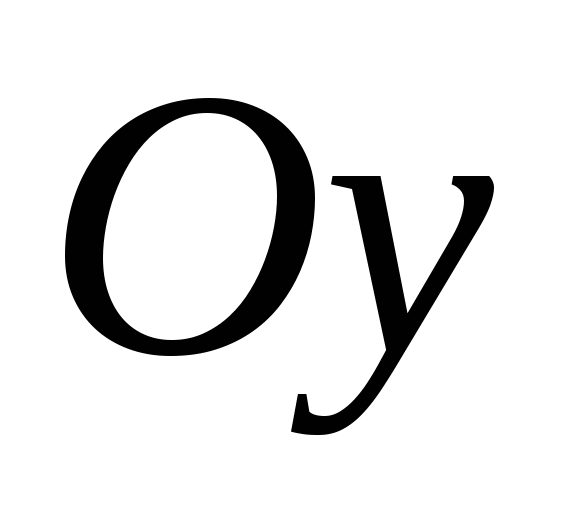 ಮತ್ತು
ಮತ್ತು  ಪಕ್ಕೆಲುಬುಗಳ ಉದ್ದಕ್ಕೂ ನಿರ್ದೇಶಿಸೋಣ
ಪಕ್ಕೆಲುಬುಗಳ ಉದ್ದಕ್ಕೂ ನಿರ್ದೇಶಿಸೋಣ  ,
, 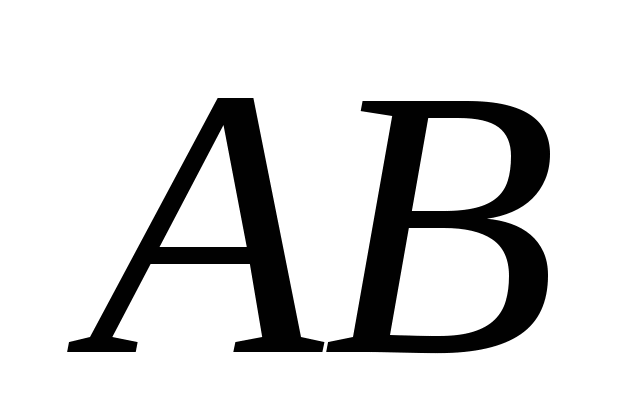 ಮತ್ತು
ಮತ್ತು 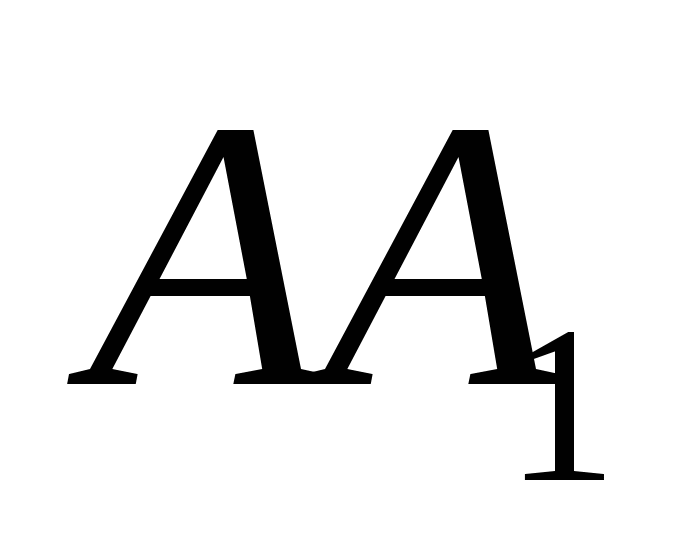 ಕ್ರಮವಾಗಿ. ನೇರ ರೇಖೆಗಳ ನಡುವಿನ ಕೋನವು ಬದಲಾಗುವುದರಿಂದ
ಕ್ರಮವಾಗಿ. ನೇರ ರೇಖೆಗಳ ನಡುವಿನ ಕೋನವು ಬದಲಾಗುವುದರಿಂದ 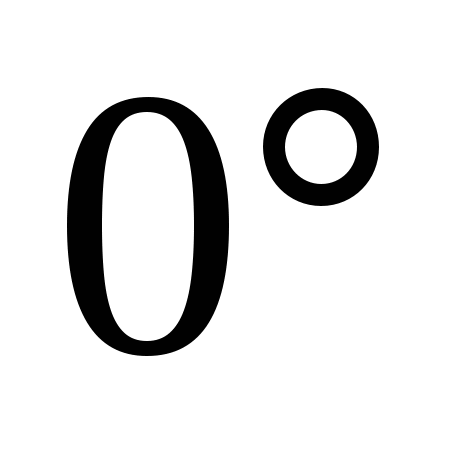 ಮೊದಲು
ಮೊದಲು  , ಮತ್ತು ವಾಹಕಗಳ ನಡುವಿನ ಕೋನ
, ಮತ್ತು ವಾಹಕಗಳ ನಡುವಿನ ಕೋನ 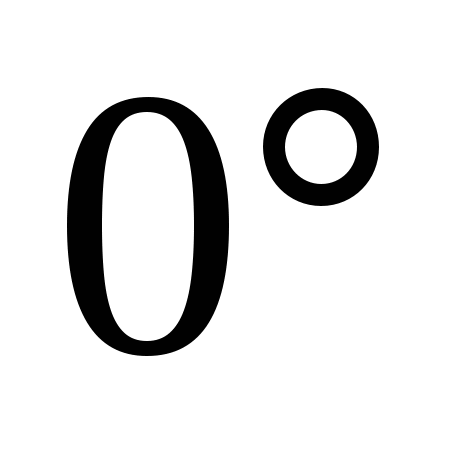 ಮೊದಲು
ಮೊದಲು 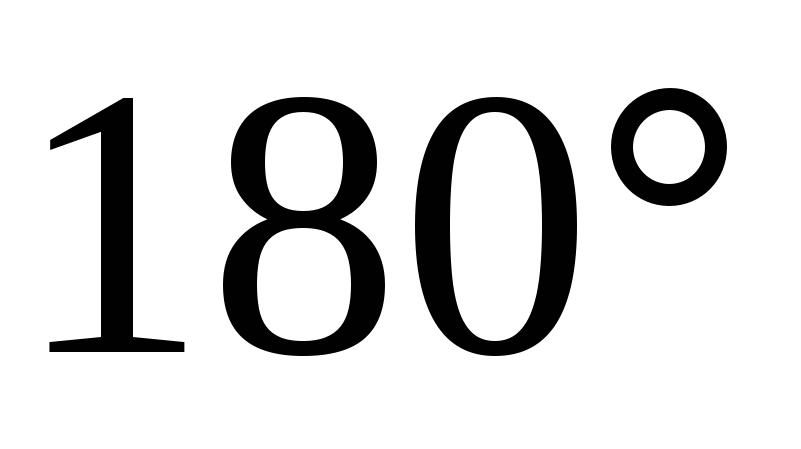 , ನಂತರ ರೇಖೆಗಳ ನಡುವಿನ ಕೋನ
, ನಂತರ ರೇಖೆಗಳ ನಡುವಿನ ಕೋನ  ಮತ್ತು
ಮತ್ತು  ವಾಹಕಗಳ ನಡುವಿನ ಕೋನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ
ವಾಹಕಗಳ ನಡುವಿನ ಕೋನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ 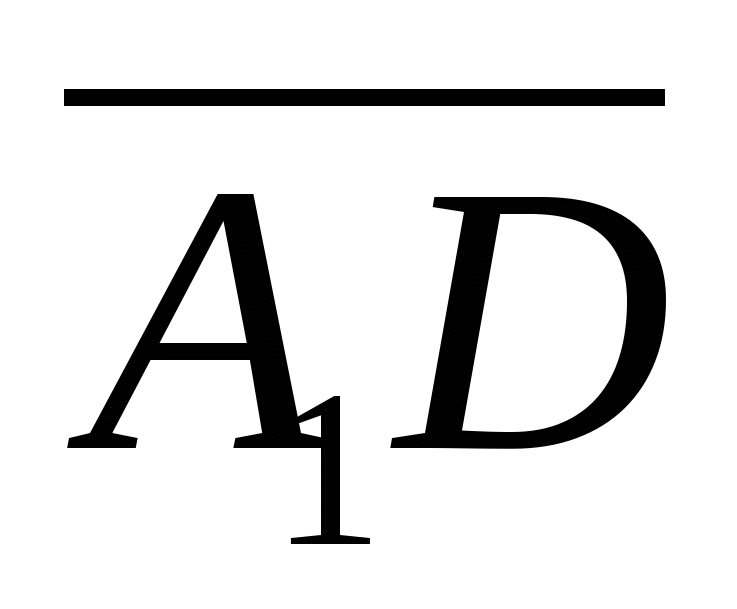 ಮತ್ತು
ಮತ್ತು 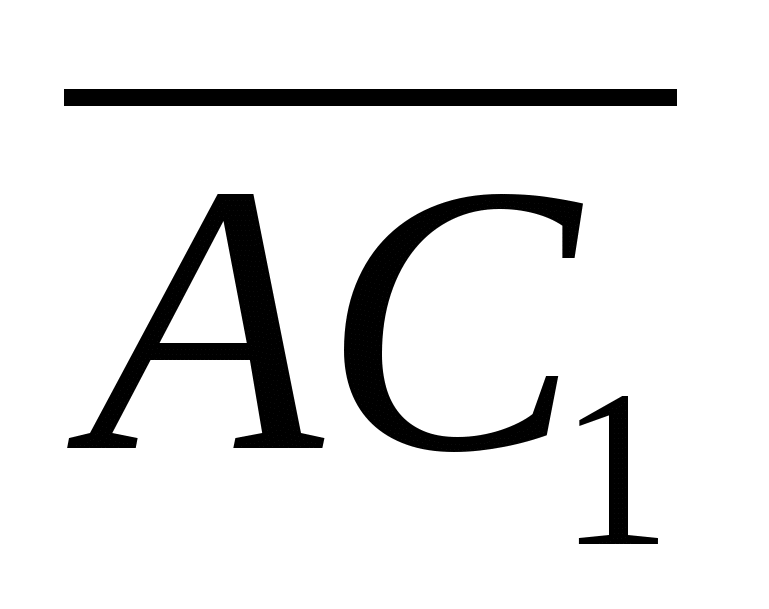 , ಅದು ತೀವ್ರವಾಗಿದ್ದರೆ, ಅಥವಾ ಅದರ ಪಕ್ಕದಲ್ಲಿ, ವಾಹಕಗಳ ನಡುವಿನ ಕೋನವು ಮಂದವಾಗಿದ್ದರೆ.
, ಅದು ತೀವ್ರವಾಗಿದ್ದರೆ, ಅಥವಾ ಅದರ ಪಕ್ಕದಲ್ಲಿ, ವಾಹಕಗಳ ನಡುವಿನ ಕೋನವು ಮಂದವಾಗಿದ್ದರೆ.
ಹೀಗಾಗಿ,
2) ವಾಹಕಗಳ ನಡುವಿನ ಕೋನವನ್ನು ಲೆಕ್ಕಹಾಕಿ 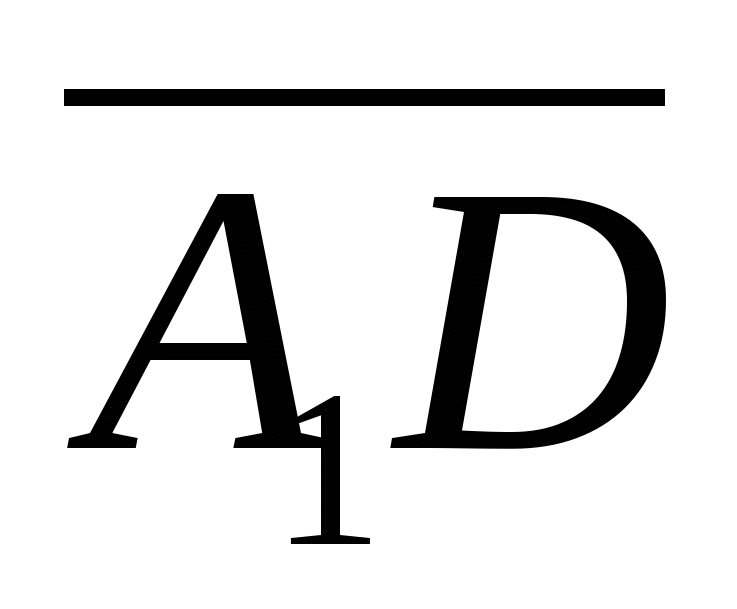 ಮತ್ತು
ಮತ್ತು 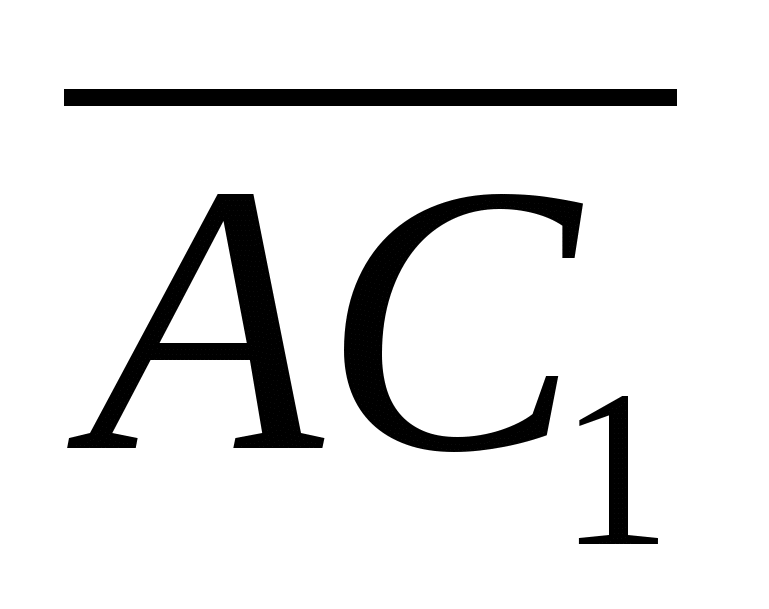 .
.
ಬಿಂದುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಬಳಸಿಕೊಂಡು ವಾಹಕಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹುಡುಕಿ 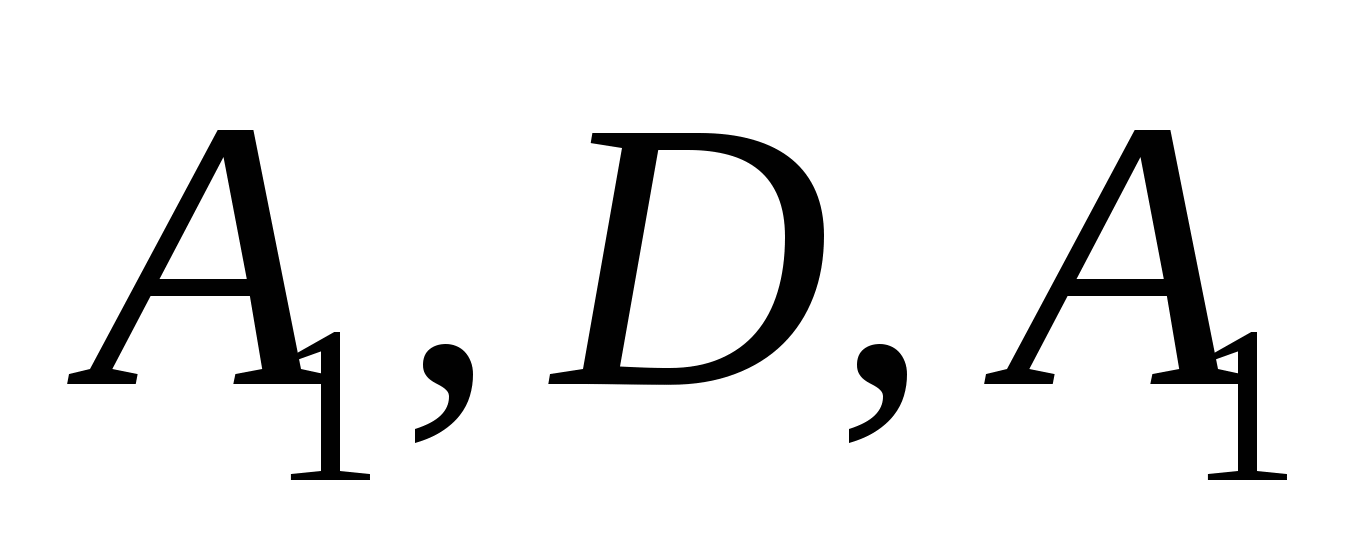 ಮತ್ತು
ಮತ್ತು  :
:
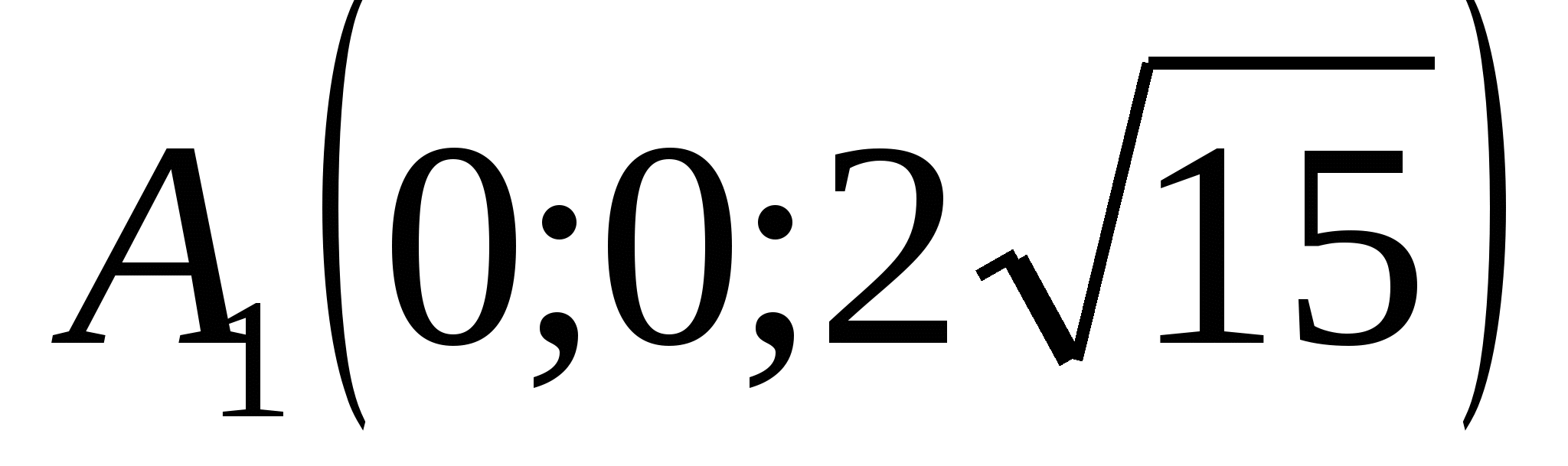 ,
, 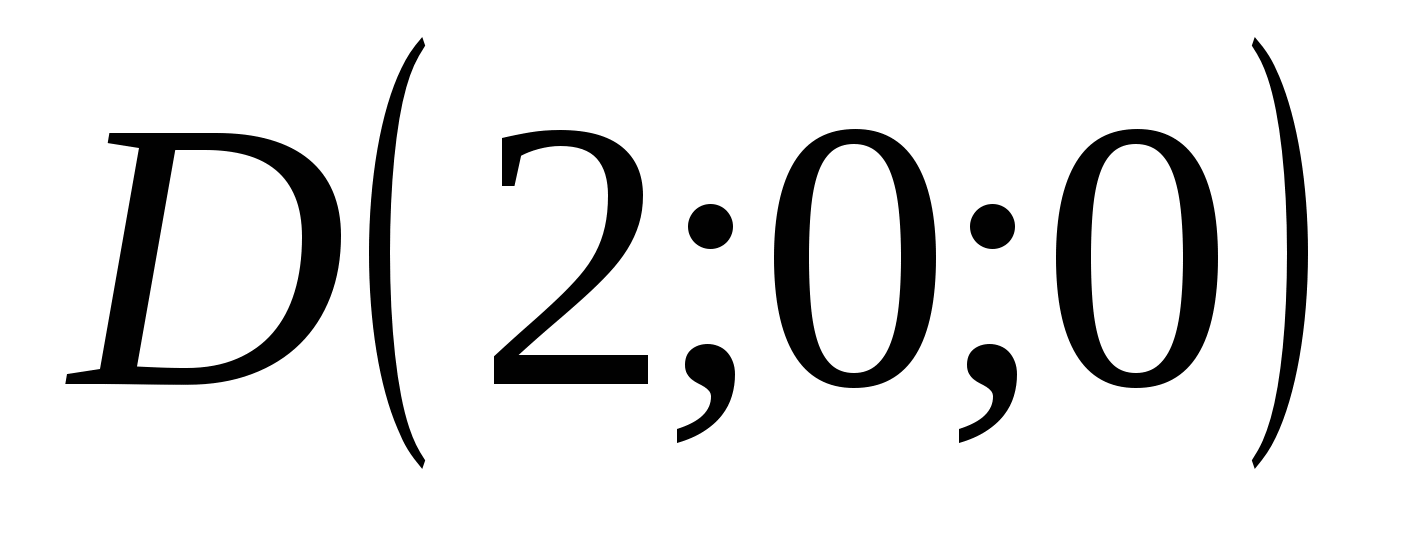 ,
,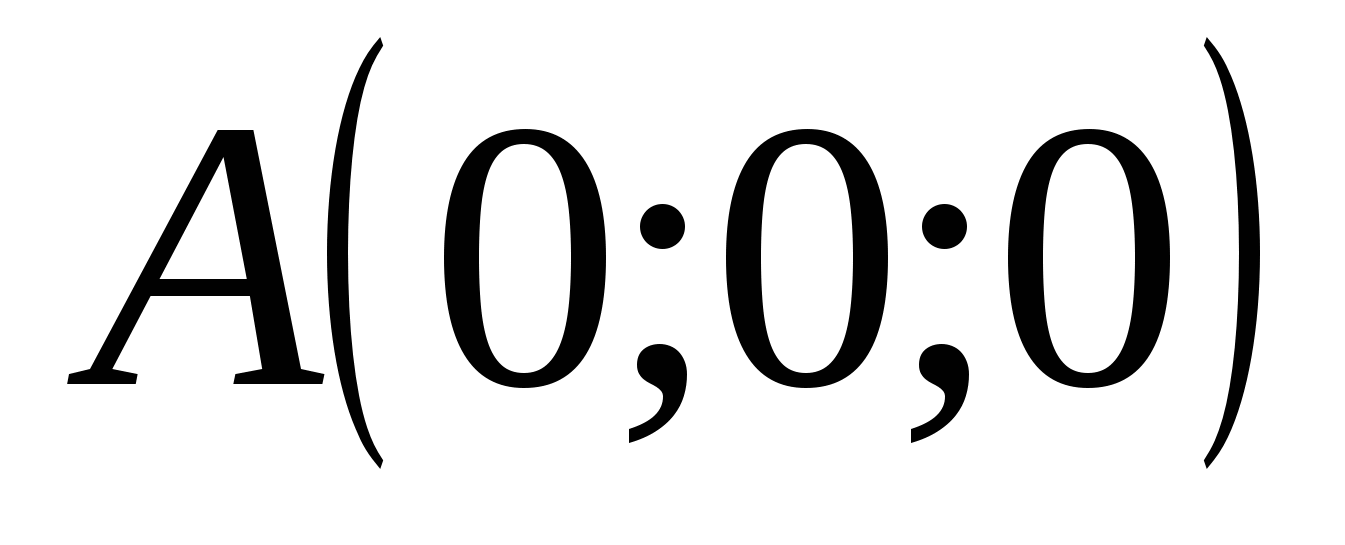 ,
,  .
.
ನಂತರ ವಾಹಕಗಳ ನಿರ್ದೇಶಾಂಕಗಳು 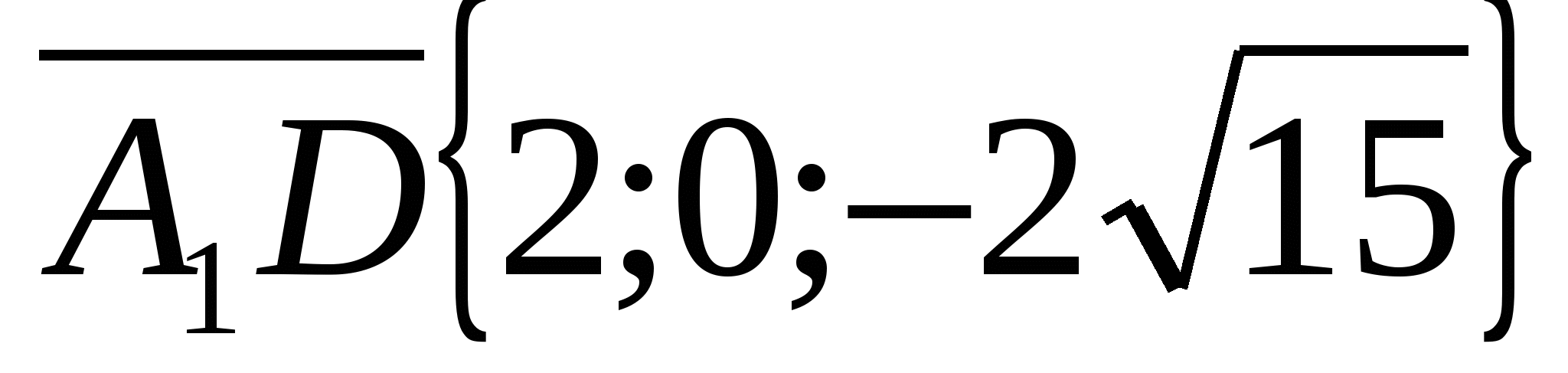 ಮತ್ತು
ಮತ್ತು 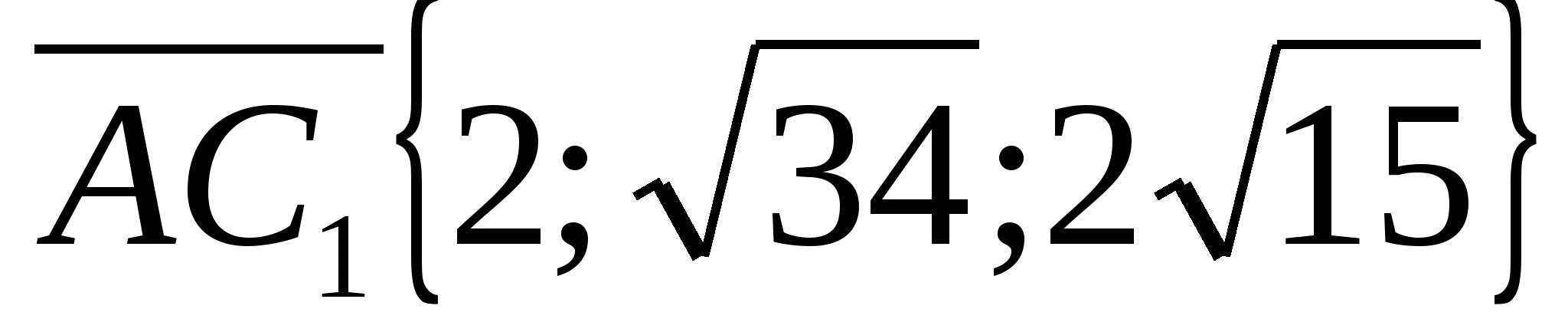 .
.
=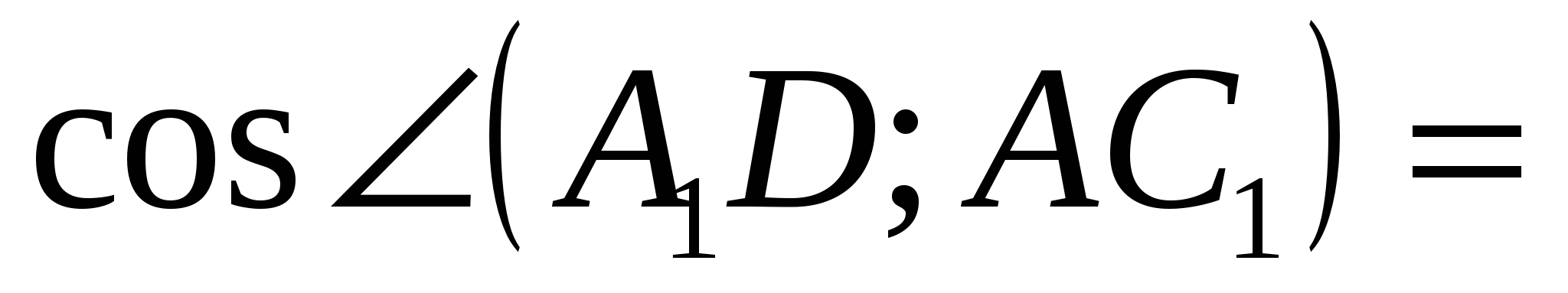
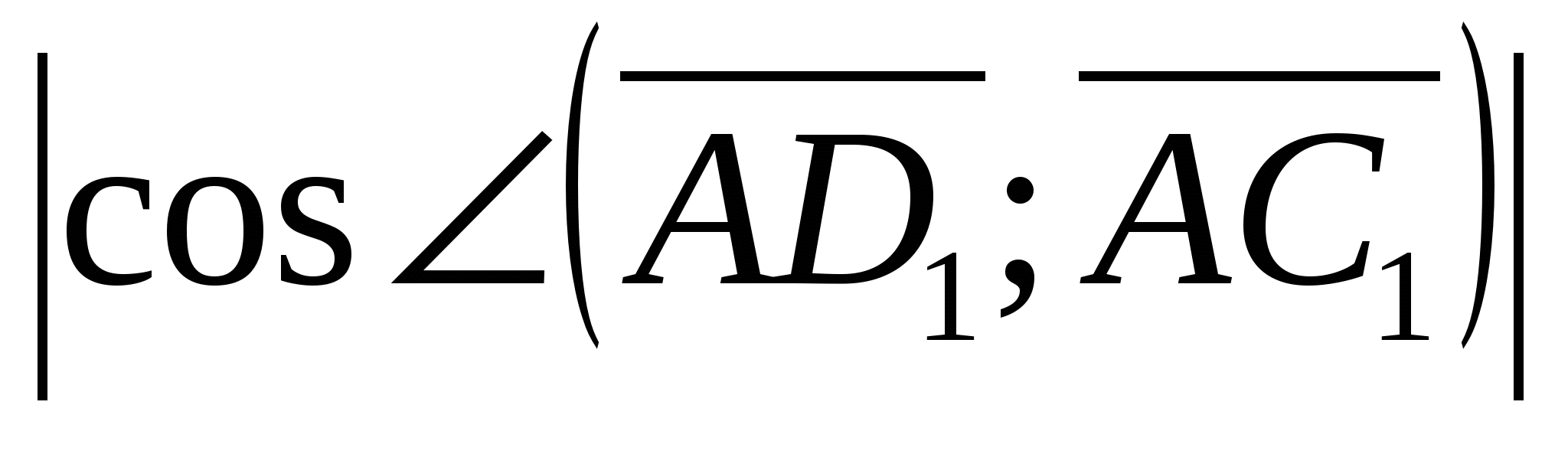 =
= =
=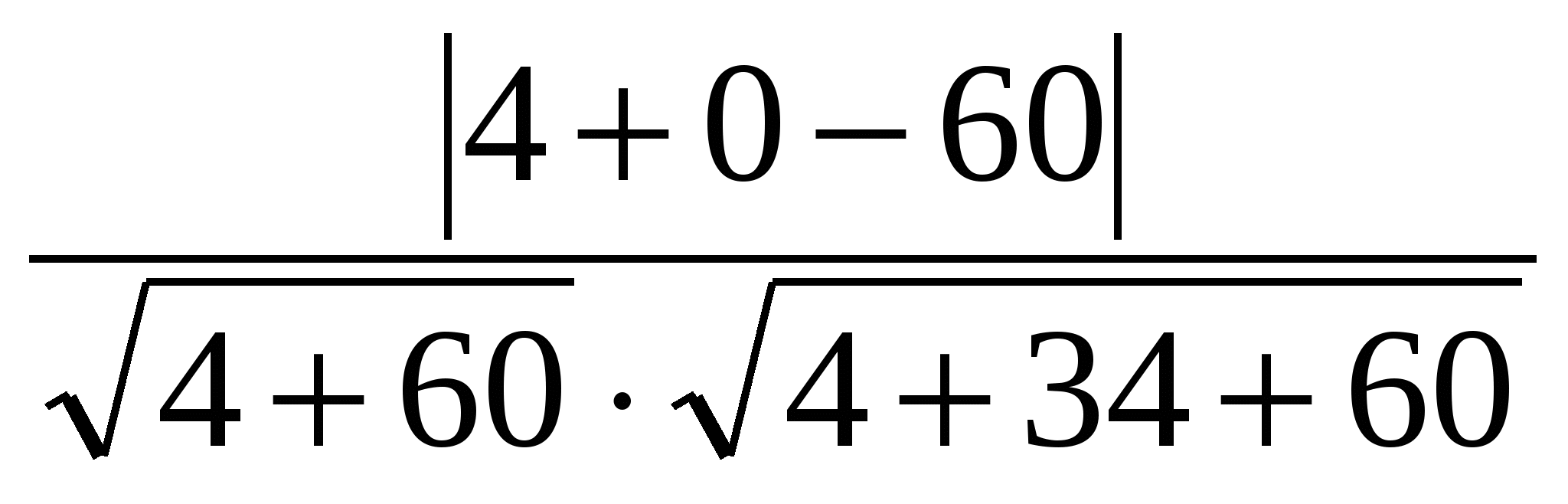
=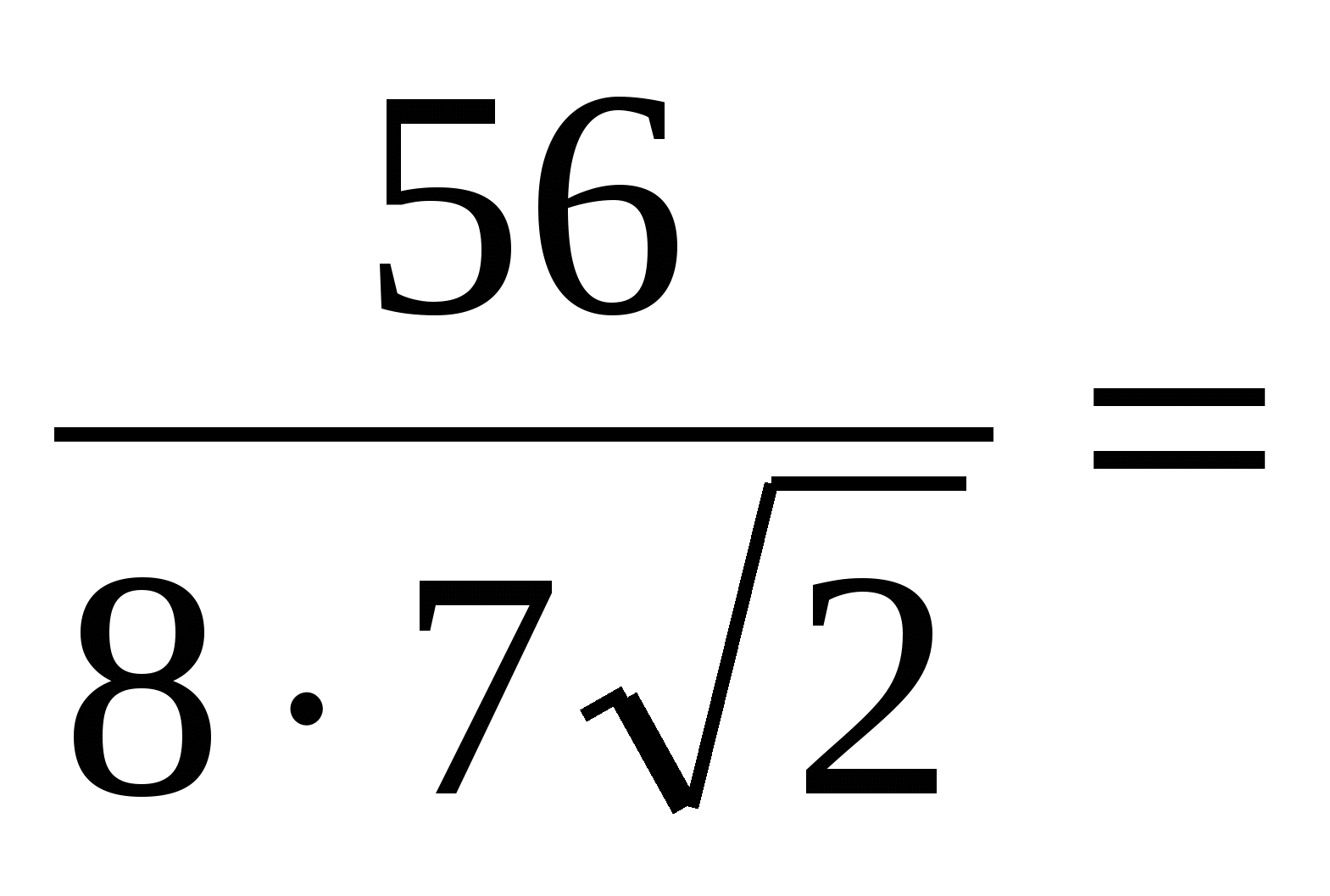
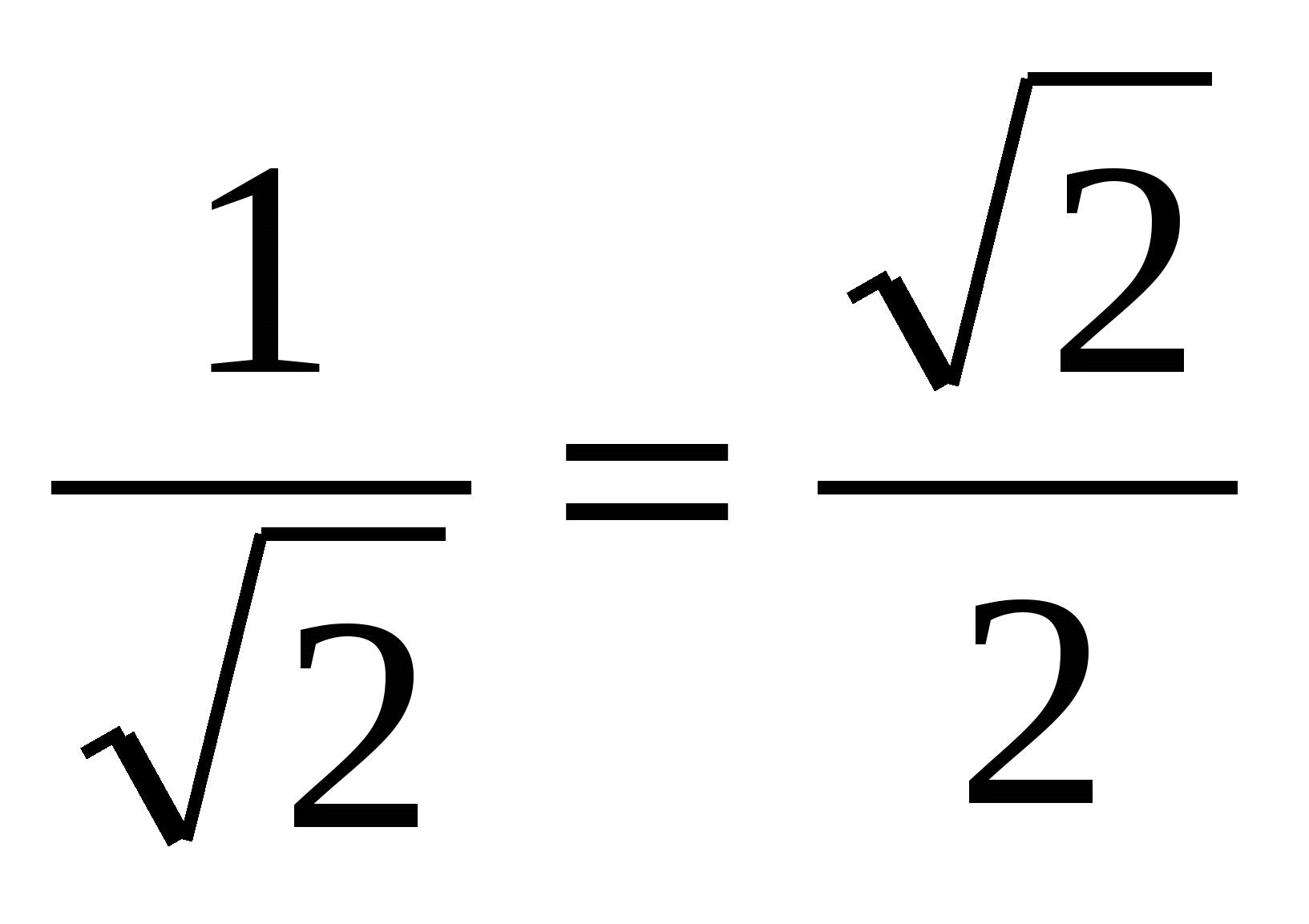 .
.
ಆದ್ದರಿಂದ, 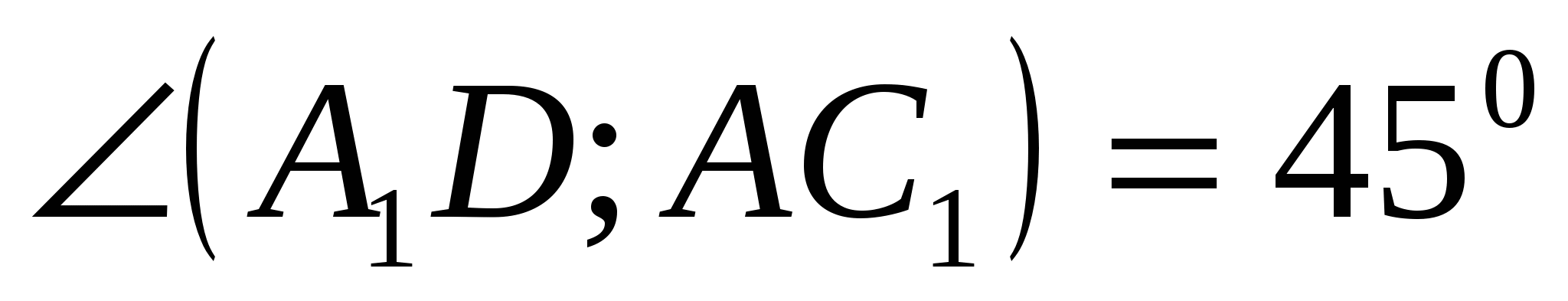
ಉತ್ತರ:
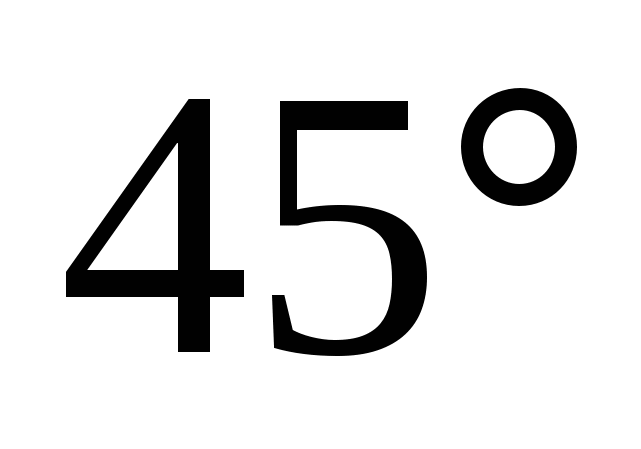 .
.
ಕಾರ್ಯ 3.
ಡಾನ್ ಘನಾಕೃತಿಯ  . ನೇರ ರೇಖೆಯ ನಡುವಿನ ಕೋನವನ್ನು ಹುಡುಕಿ
. ನೇರ ರೇಖೆಯ ನಡುವಿನ ಕೋನವನ್ನು ಹುಡುಕಿ 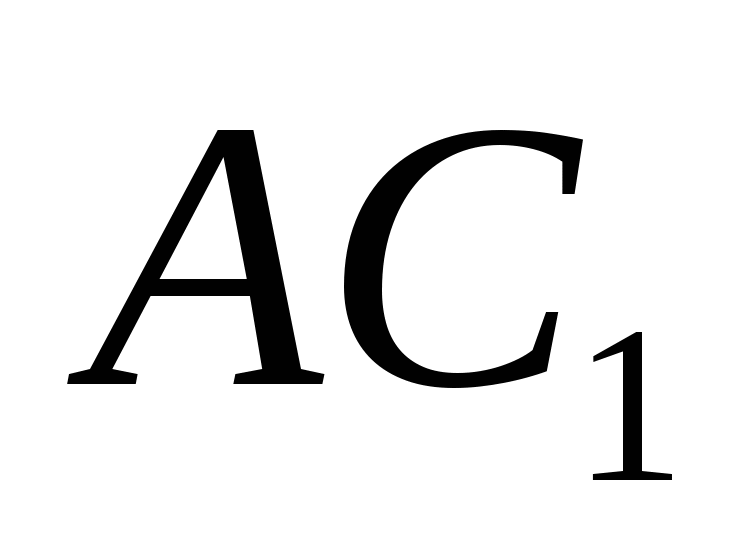 ಮತ್ತು ಬೇಸ್ನ ವಿಮಾನ
ಮತ್ತು ಬೇಸ್ನ ವಿಮಾನ  .
.
ಪರಿಹಾರ.
1 ) ನೇರ ರೇಖೆಯ ನಡುವಿನ ಕೋನ
) ನೇರ ರೇಖೆಯ ನಡುವಿನ ಕೋನ 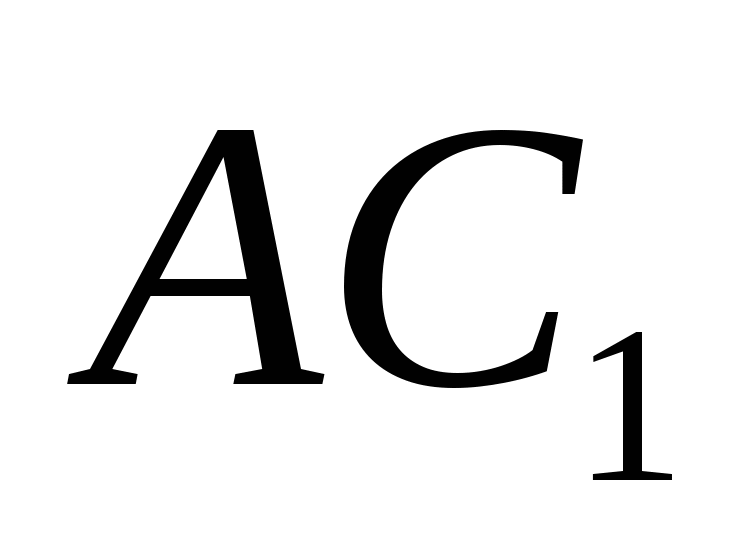 ಮತ್ತು ವಿಮಾನಎಬಿ
1
ಜೊತೆಗೆ- ಇದು
ನೇರ ರೇಖೆಯ ನಡುವಿನ ಕೋನ ಮತ್ತು ಸಮತಲದ ಮೇಲೆ ಅದರ ಪ್ರಕ್ಷೇಪಣ. ಸಾಮಾನ್ಯ ನಡುವಿನ ಕೋನ
ಮತ್ತು ವಿಮಾನಎಬಿ
1
ಜೊತೆಗೆ- ಇದು
ನೇರ ರೇಖೆಯ ನಡುವಿನ ಕೋನ ಮತ್ತು ಸಮತಲದ ಮೇಲೆ ಅದರ ಪ್ರಕ್ಷೇಪಣ. ಸಾಮಾನ್ಯ ನಡುವಿನ ಕೋನ 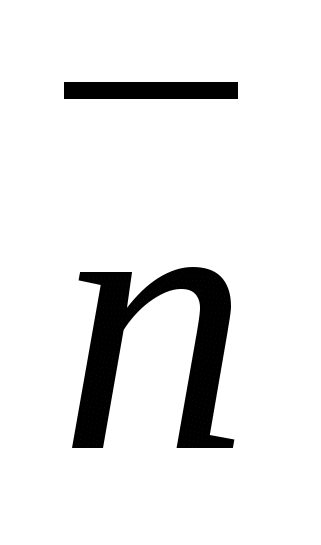 ಸಮತಲ ಮತ್ತು ನೇರ ರೇಖೆಗೆ
ಸಮತಲ ಮತ್ತು ನೇರ ರೇಖೆಗೆ 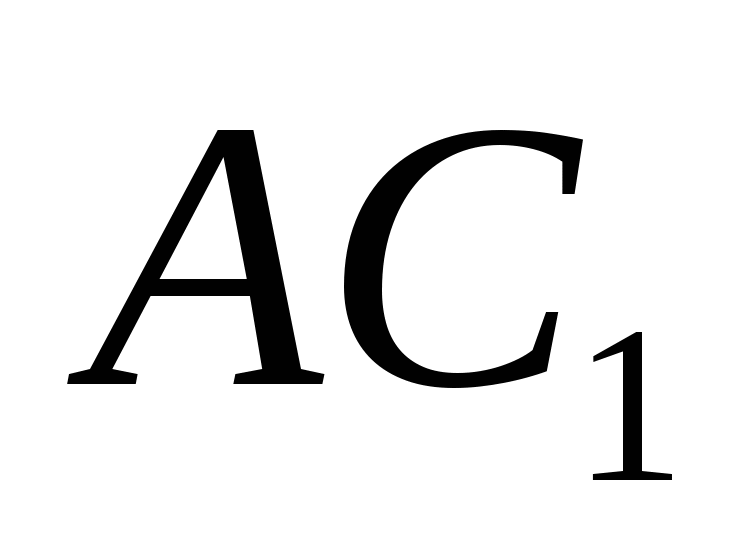 90 ಕ್ಕೆ ಪೂರಕವಾಗಿದೆ 0, ಆದ್ದರಿಂದ.
90 ಕ್ಕೆ ಪೂರಕವಾಗಿದೆ 0, ಆದ್ದರಿಂದ.
ಆದ್ದರಿಂದ, ನೇರ ರೇಖೆಯ ನಡುವಿನ ಕೋನವನ್ನು ಕಂಡುಹಿಡಿಯಲು 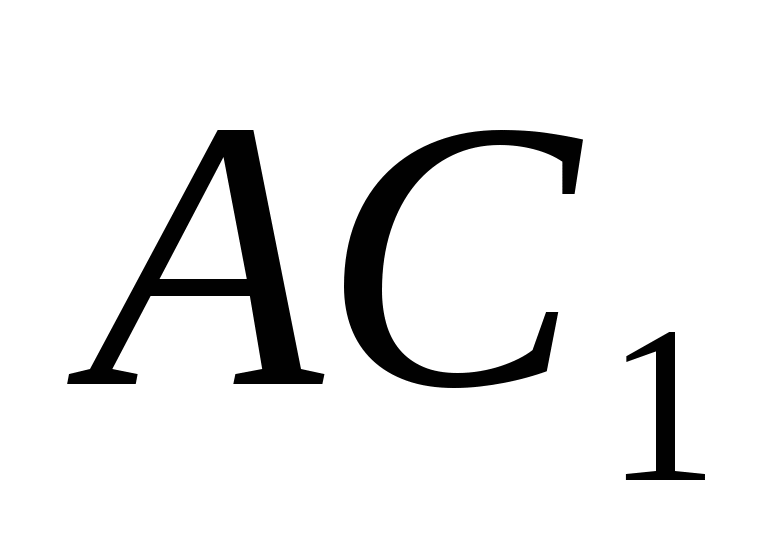 ಮತ್ತು ವಿಮಾನ (
ಮತ್ತು ವಿಮಾನ (  ), ನೀವು ನೇರ ರೇಖೆಯ ನಡುವಿನ ಕೋನವನ್ನು ಕಂಡುಹಿಡಿಯಬೇಕು
), ನೀವು ನೇರ ರೇಖೆಯ ನಡುವಿನ ಕೋನವನ್ನು ಕಂಡುಹಿಡಿಯಬೇಕು 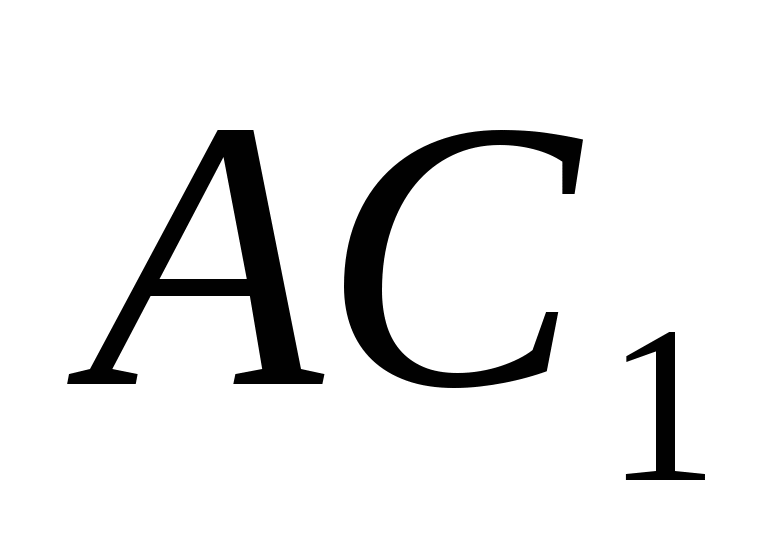 ಮತ್ತು ಸಾಮಾನ್ಯ
ಮತ್ತು ಸಾಮಾನ್ಯ 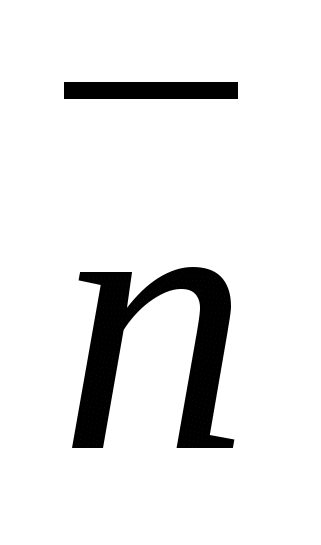 ವಿಮಾನಕ್ಕೆ (
ವಿಮಾನಕ್ಕೆ (  )
.
)
.
2 ) ನಾವು ಬಿಂದುವಿನಲ್ಲಿ ಮೂಲದೊಂದಿಗೆ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯನ್ನು ಪರಿಚಯಿಸೋಣ
) ನಾವು ಬಿಂದುವಿನಲ್ಲಿ ಮೂಲದೊಂದಿಗೆ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯನ್ನು ಪರಿಚಯಿಸೋಣ 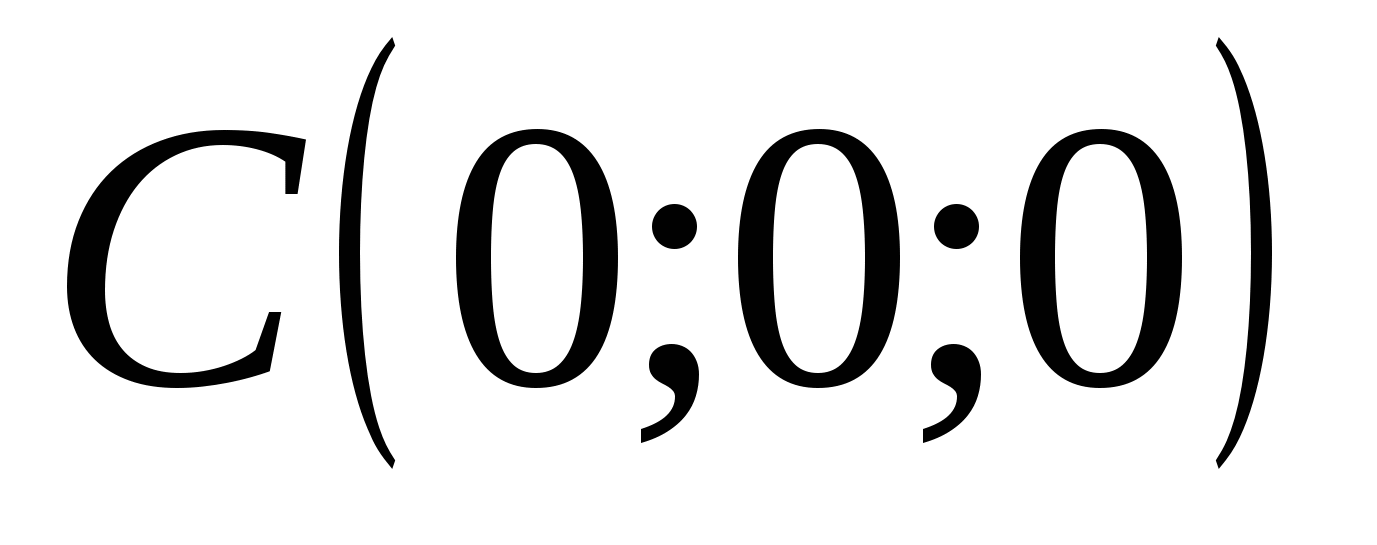 . ಅಚ್ಚುಗಳು
. ಅಚ್ಚುಗಳು 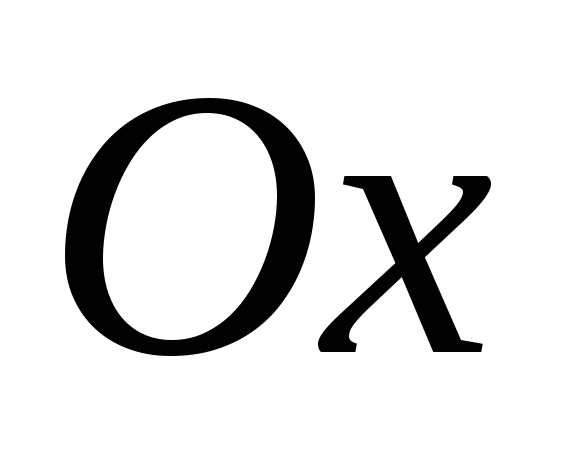 ,
,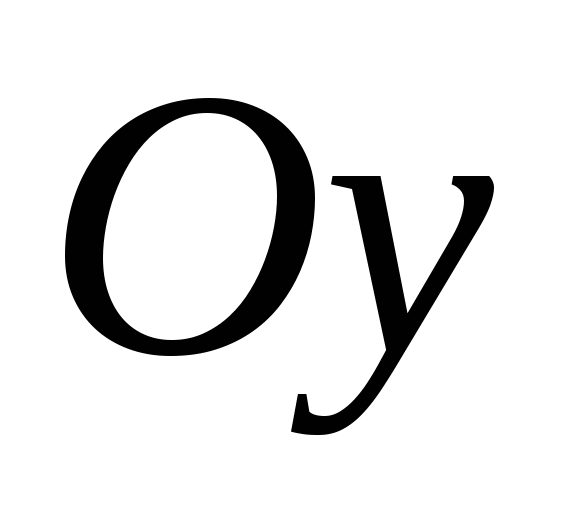 ಮತ್ತು
ಮತ್ತು  ಪಕ್ಕೆಲುಬುಗಳ ಉದ್ದಕ್ಕೂ ನಿರ್ದೇಶಿಸೋಣ
ಪಕ್ಕೆಲುಬುಗಳ ಉದ್ದಕ್ಕೂ ನಿರ್ದೇಶಿಸೋಣ  ,
, 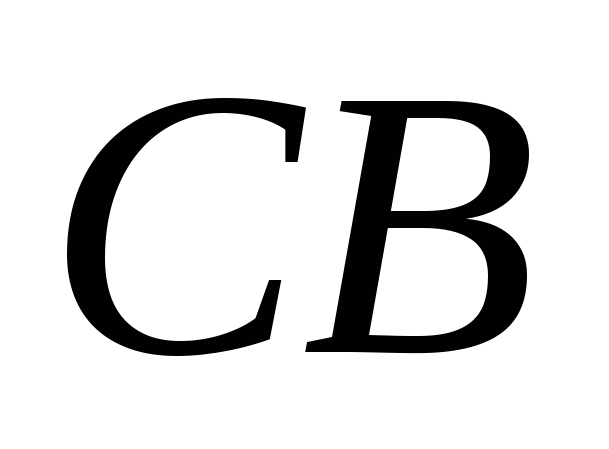 ಮತ್ತು
ಮತ್ತು 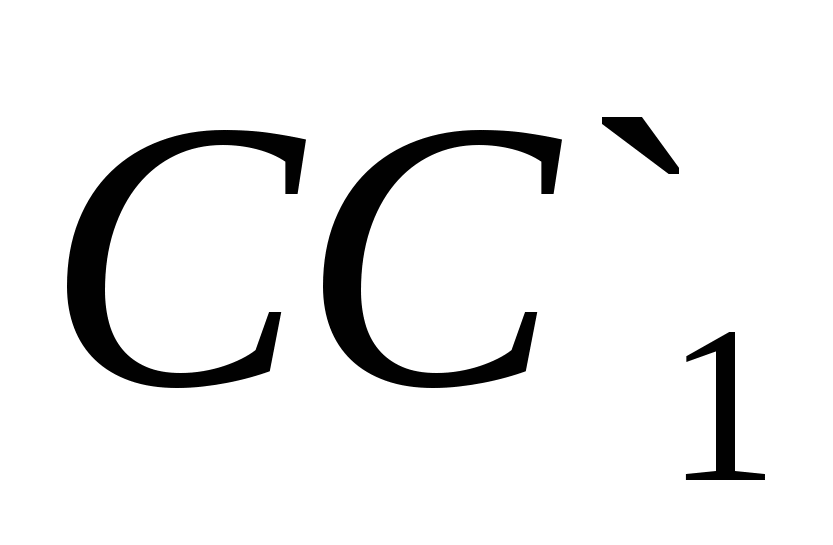 ಕ್ರಮವಾಗಿ.
ಕ್ರಮವಾಗಿ.
ಪಾಯಿಂಟ್ ಕಕ್ಷೆಗಳು:
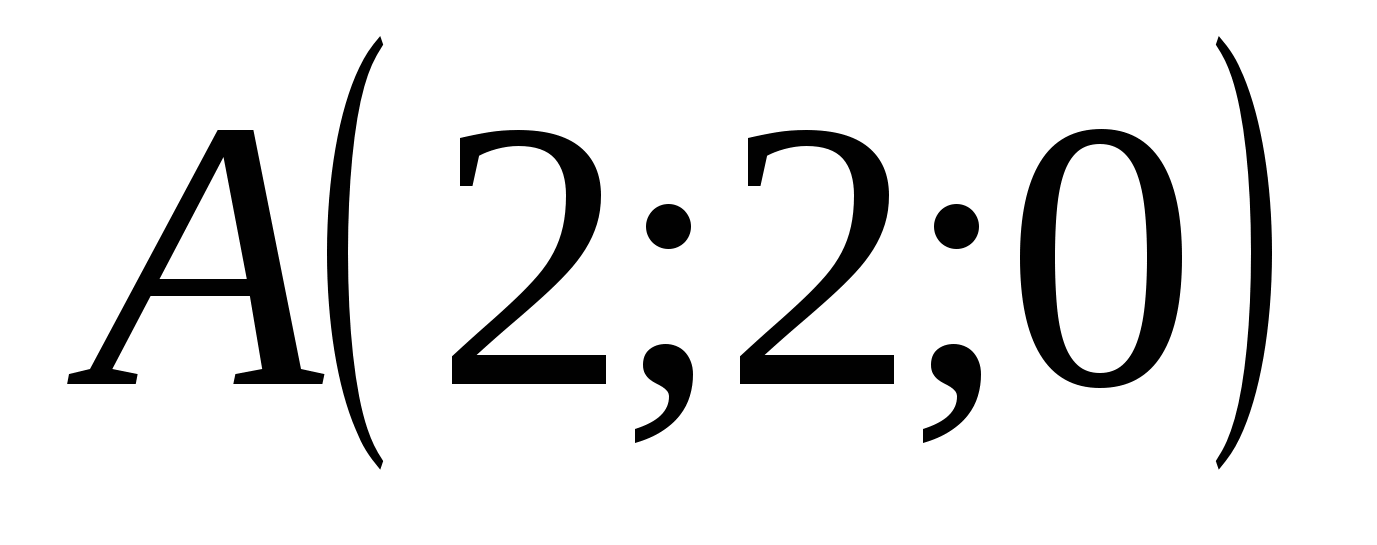 ,
, 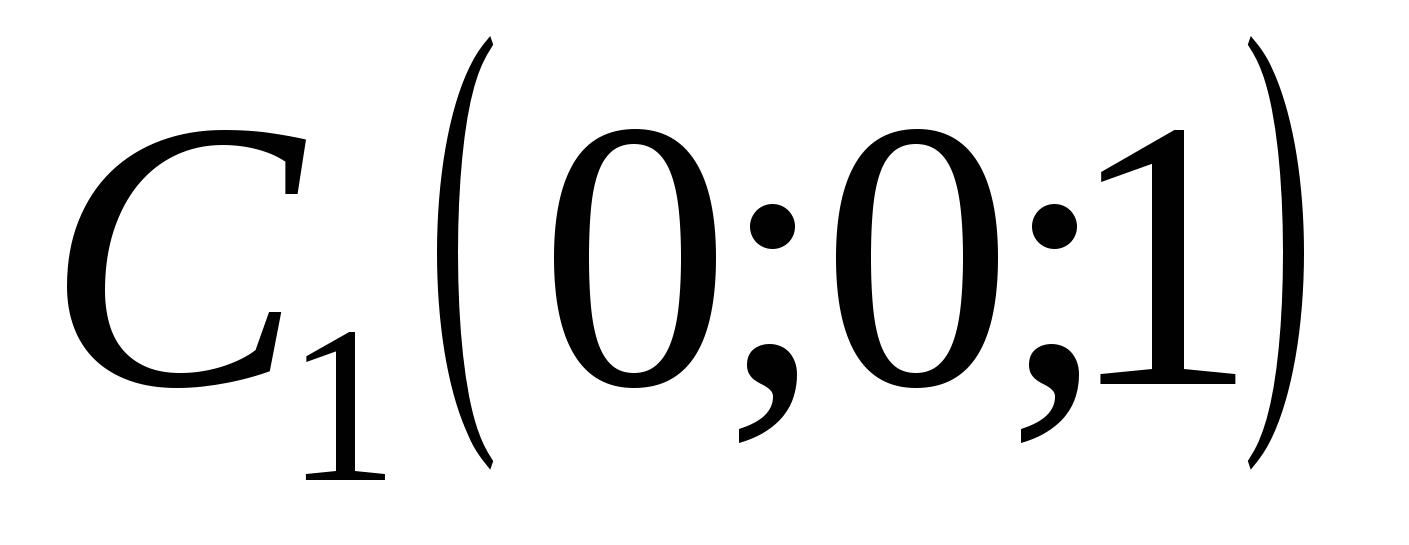 ,
, 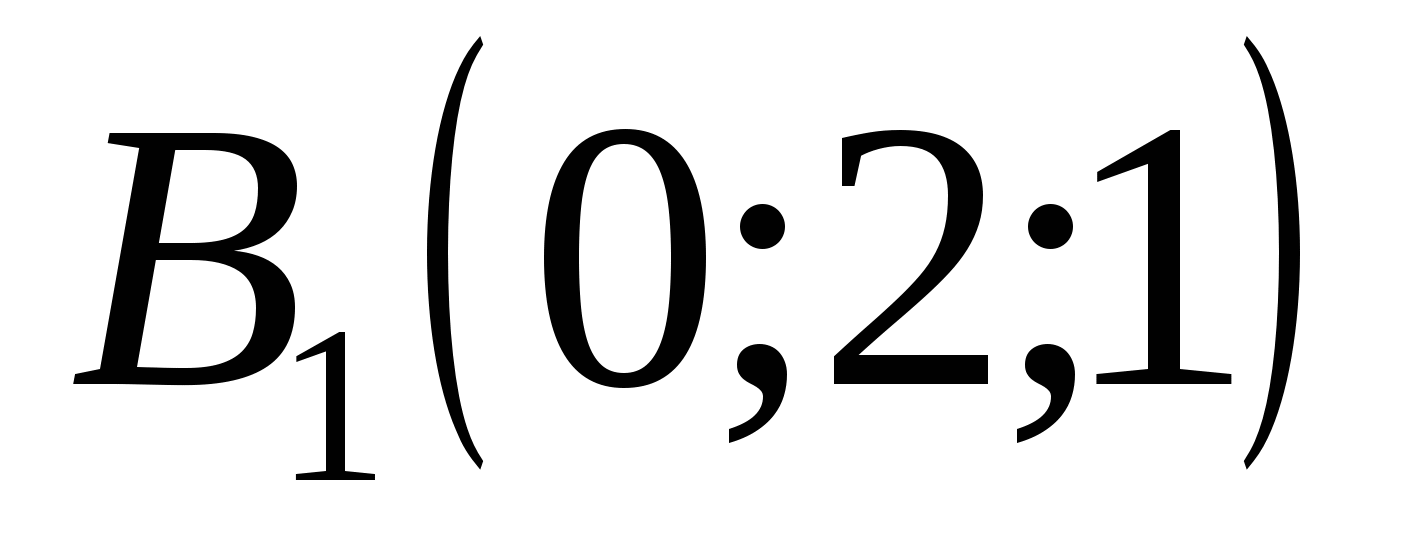 ,
,
ಎ 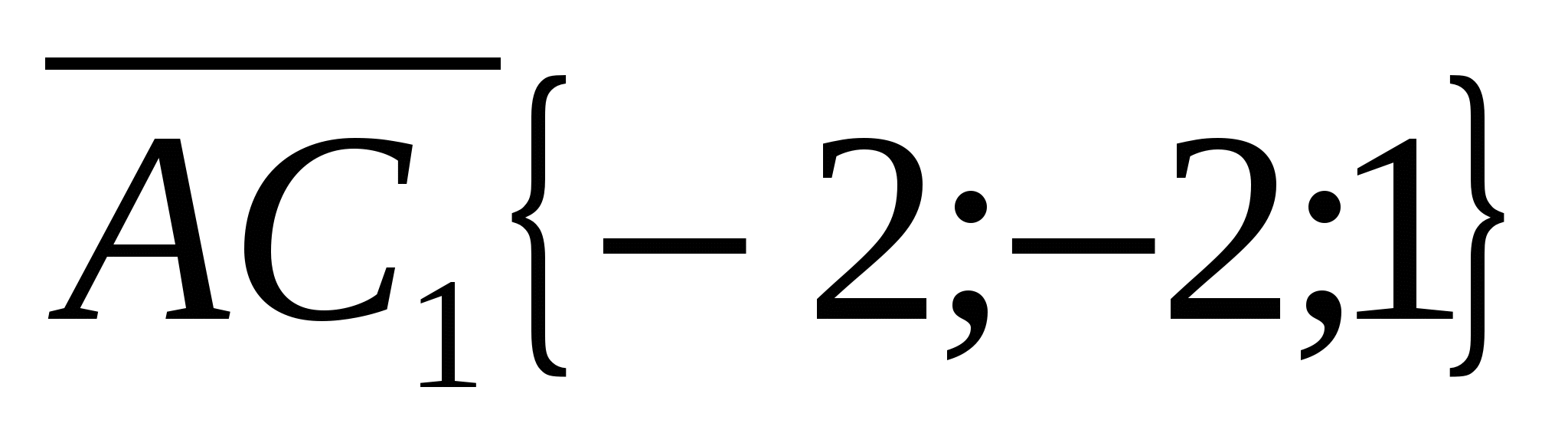 .
.
3) ಸಾಮಾನ್ಯ ಸಮತಲದ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹುಡುಕಿ (  ) ನಾವು ಸಮತಲದ ಸಮೀಕರಣವನ್ನು ಬರೆಯೋಣ (
) ನಾವು ಸಮತಲದ ಸಮೀಕರಣವನ್ನು ಬರೆಯೋಣ (  ), ಬಿಂದುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಬದಲಿಸುವುದುಎ
,
ಬಿ
1
ಮತ್ತು ಜೊತೆಗೆವಿ
ಸಮತಲ ಸಮೀಕರಣ
.
), ಬಿಂದುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಬದಲಿಸುವುದುಎ
,
ಬಿ
1
ಮತ್ತು ಜೊತೆಗೆವಿ
ಸಮತಲ ಸಮೀಕರಣ
.
ನಾವು ರೇಖೀಯ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಯನ್ನು ಪಡೆಯುತ್ತೇವೆ:
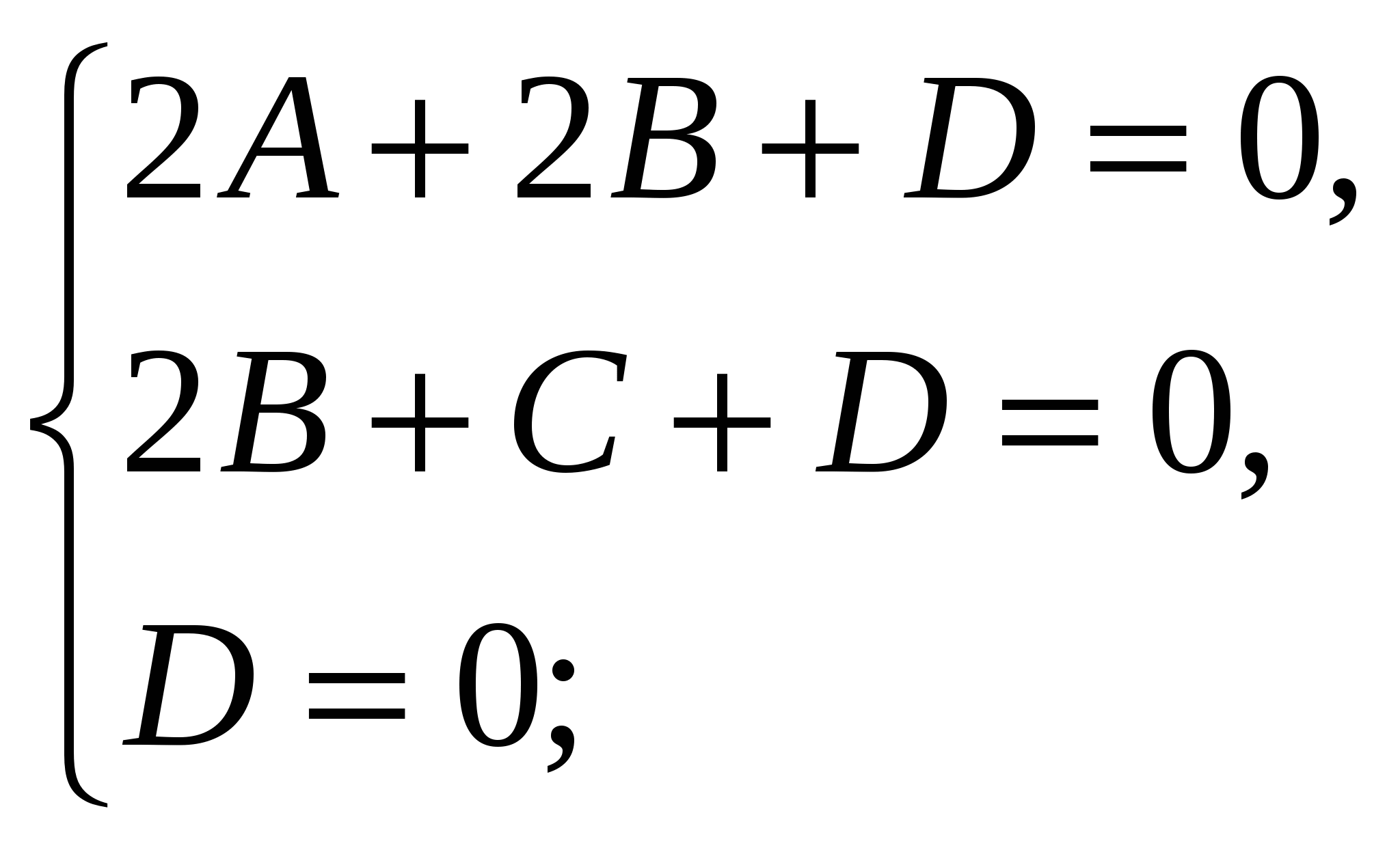
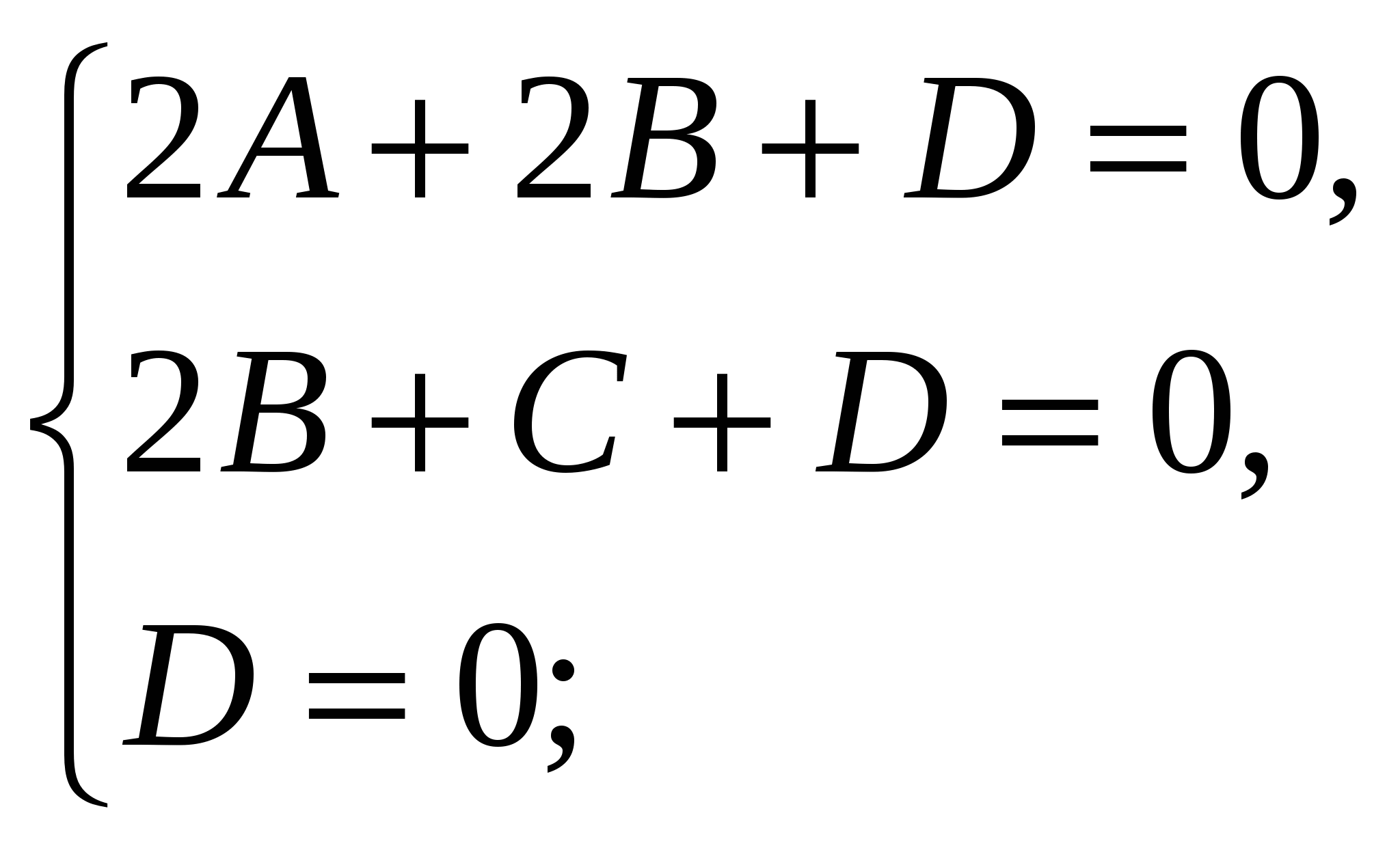
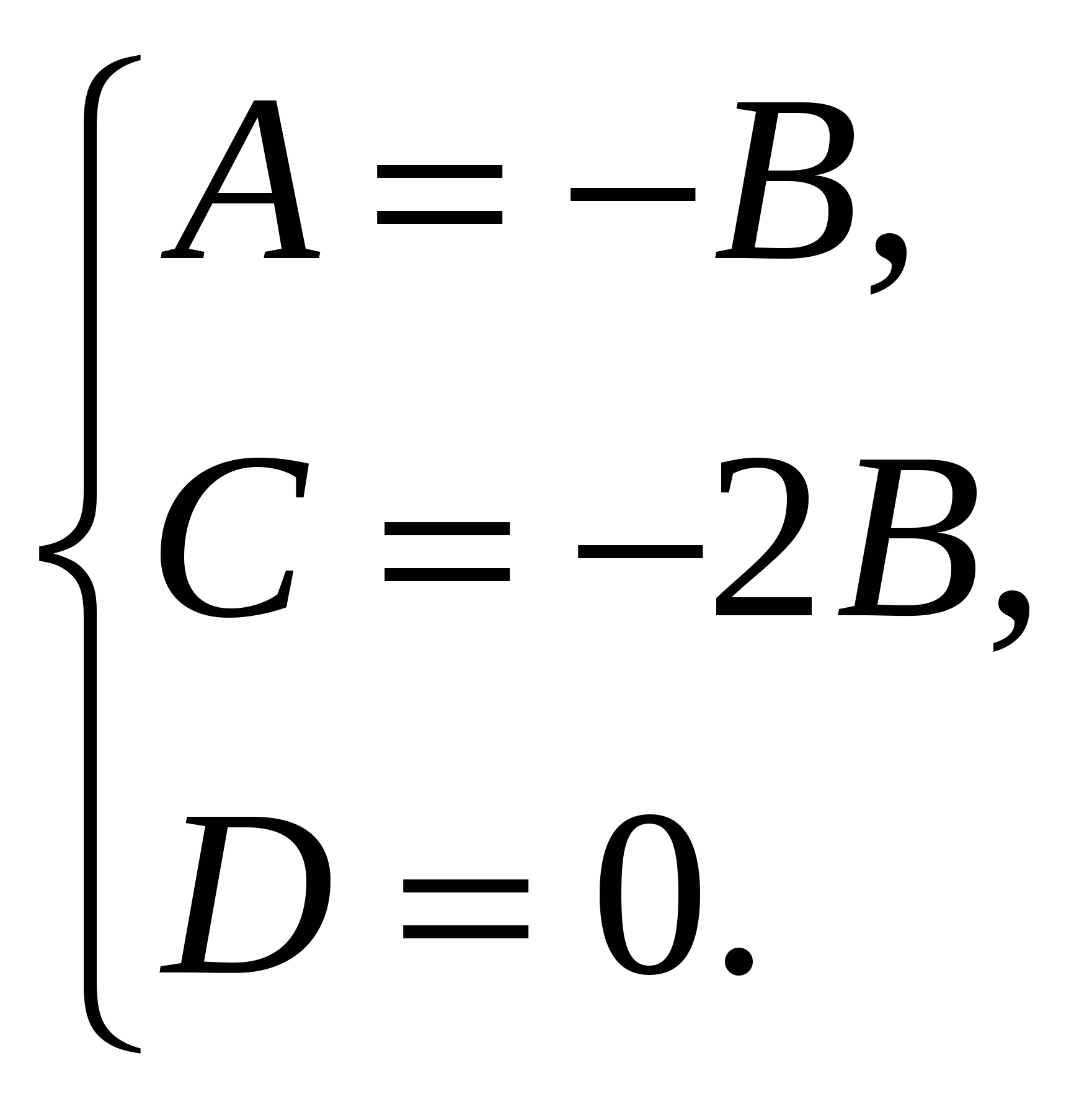
ಆದ್ದರಿಂದ, ಸಮತಲದ ಸಮೀಕರಣ (  ) ರೂಪವನ್ನು ಹೊಂದಿದೆ , ಅಥವಾ
) ರೂಪವನ್ನು ಹೊಂದಿದೆ , ಅಥವಾ  , ಮತ್ತು ಸಾಮಾನ್ಯ ವೆಕ್ಟರ್ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ
, ಮತ್ತು ಸಾಮಾನ್ಯ ವೆಕ್ಟರ್ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿದೆ 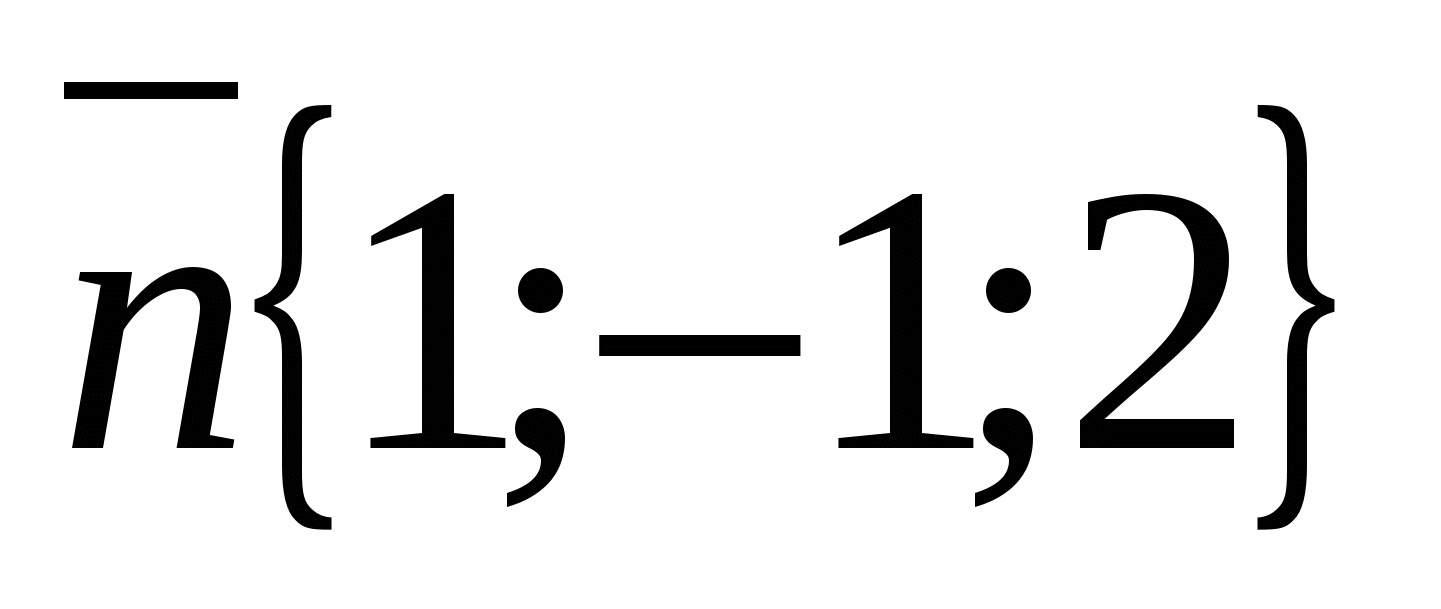 .
.
ಅರ್ಥ
ಮತ್ತು 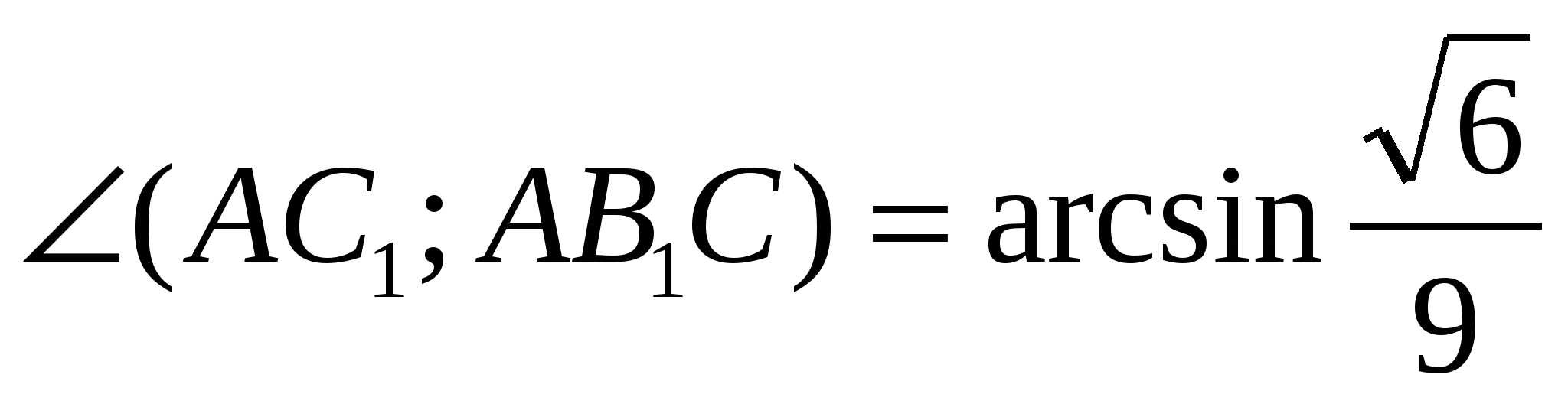 .
.
ಉತ್ತರ:
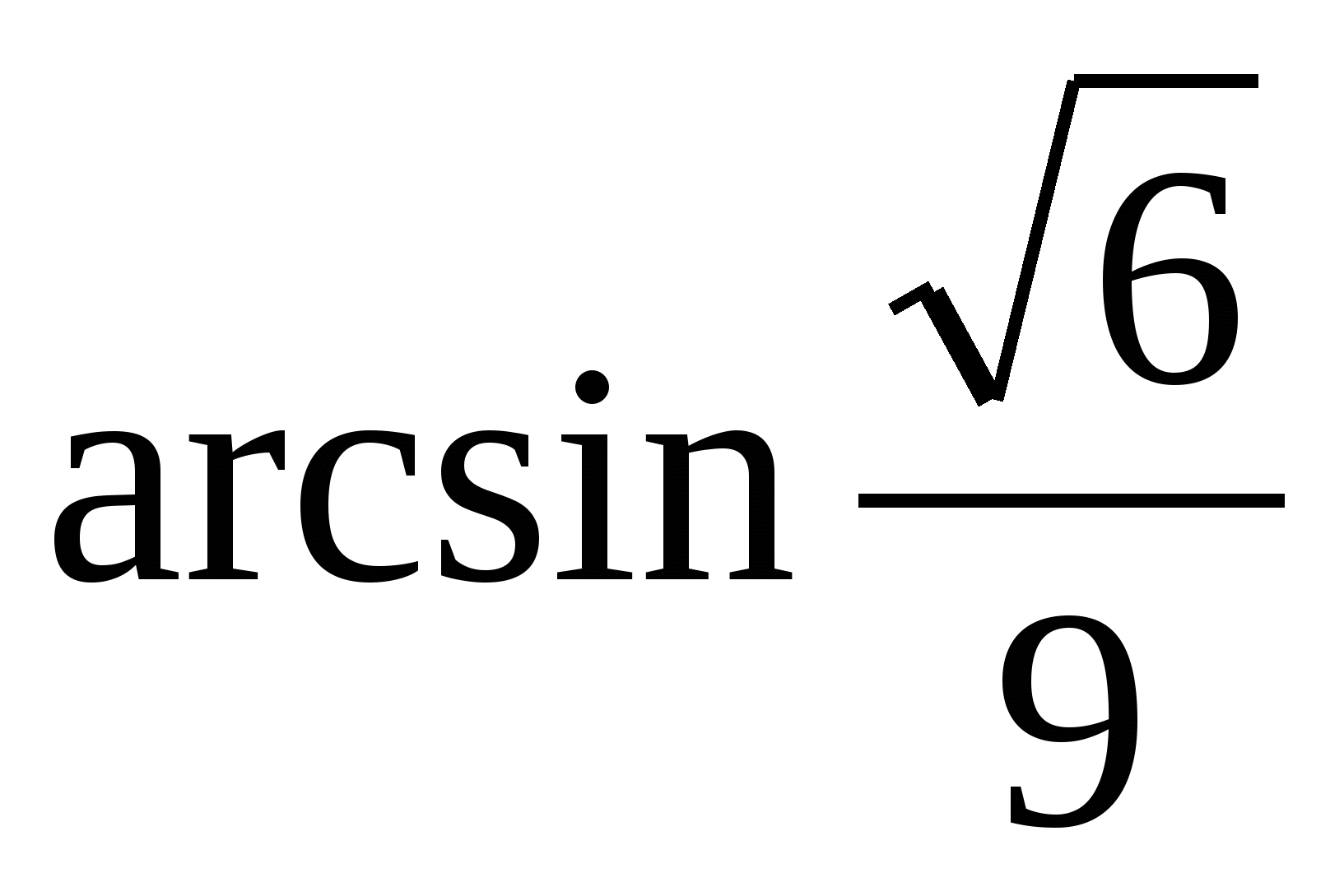 .
.
ಸಮಸ್ಯೆಯನ್ನು ಎರಡು ರೀತಿಯಲ್ಲಿ ಪರಿಹರಿಸುವುದನ್ನು ಪರಿಗಣಿಸೋಣ.
ಕಾರ್ಯ 4. ವಿಧಾನ 1: ಜ್ಯಾಮಿತೀಯ.
ಪಕ್ಕೆಲುಬುಗಳ ಮೇಲೆ 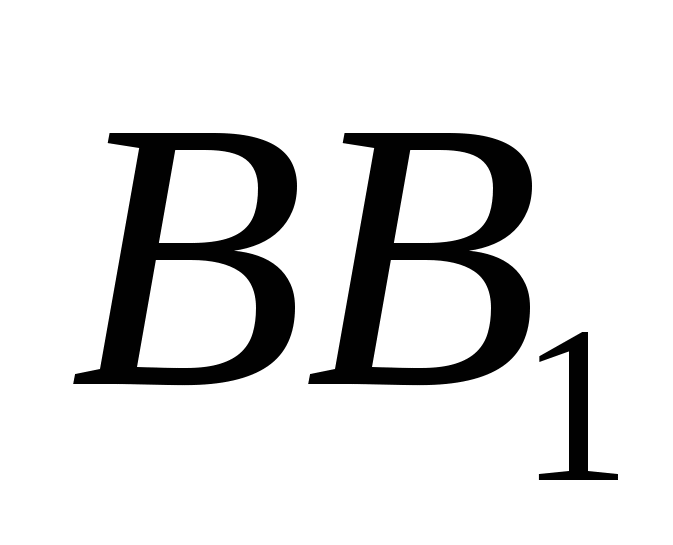 ,
,  ಮತ್ತು. . ನೇರವಾಗಿ ಹೋಗೋಣ - ಮಧ್ಯಮ ಸಾಲುತ್ರಿಕೋನ ಮತ್ತು, ಅಂದರೆ. ಮತ್ತು,
ಮತ್ತು. . ನೇರವಾಗಿ ಹೋಗೋಣ - ಮಧ್ಯಮ ಸಾಲುತ್ರಿಕೋನ ಮತ್ತು, ಅಂದರೆ. ಮತ್ತು,
ಅಧ್ಯಯನ ಮಾಡಿದ ಸೈದ್ಧಾಂತಿಕ ವಸ್ತುವನ್ನು ವ್ಯವಸ್ಥಿತಗೊಳಿಸಲಾಗಿದೆ.
ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸಲು ವಿಧಾನವನ್ನು ಬಳಸುವಾಗ, ವಿಧಾನದ ಕೆಳಗಿನ ವೈಶಿಷ್ಟ್ಯಗಳನ್ನು ಗುರುತಿಸಲಾಗಿದೆ:
ಕೌಶಲ್ಯ ಸರಿಯಾದ ಆಡಳಿತಸಮನ್ವಯ ವ್ಯವಸ್ಥೆಗಳು,
ಪಾಯಿಂಟ್ ನಿರ್ದೇಶಾಂಕಗಳ ಸರಿಯಾದ ನಿರ್ಣಯ,
ವಿಧಾನದ ವಿಶ್ಲೇಷಣಾತ್ಮಕ ಉಪಕರಣದ ಜ್ಞಾನ.
ವಿಧಾನದ ಅನ್ವಯವನ್ನು ಪರಿಹಾರವೆಂದು ಪರಿಗಣಿಸಲಾಗಿದೆ ವಿವಿಧ ರೀತಿಯಕಾರ್ಯಗಳು, ಮತ್ತು ಇತರ ವಿಧಾನಗಳೊಂದಿಗೆ ಹೋಲಿಸಿದರೆ.
ಕೆಲಸ ಮಾಡುವಾಗ ನಾನು ಕೆಲವು ತೊಂದರೆಗಳನ್ನು ಎದುರಿಸಿದೆ:
ಗುರಿ ಮತ್ತು ಉದ್ದೇಶಗಳನ್ನು ಹೊಂದಿಸುವಾಗ;
ಸಾಕಷ್ಟು ಪರಿಮಾಣ ಸೈದ್ಧಾಂತಿಕ ವಸ್ತುಶಾಲೆಯ ಪಠ್ಯಪುಸ್ತಕದಲ್ಲಿ;
ವಿಧಾನವನ್ನು ಬಳಸುವ ವಿಶಿಷ್ಟತೆಗಳನ್ನು ಗುರುತಿಸುವಾಗ,
ಅಮೂರ್ತದ ಪ್ರಸ್ತುತಿಗಾಗಿ ವಸ್ತುಗಳನ್ನು ಆಯ್ಕೆಮಾಡುವಾಗ.
ಗ್ರಂಥಸೂಚಿ.
ಎಲ್ S. ಅಟನಾಸ್ಯನ್, V. F. ಬುಟುಜೋವ್, S. B. ಕಡೋಮ್ಟ್ಸೆವ್, L. S. ಕಿಸೆಲೆವಾ, E. G. ಪೊಜ್ನ್ಯಾಕ್. ಜ್ಯಾಮಿತಿ, 10-11.M., ಶಿಕ್ಷಣ, 2003.
ವಿ.ಎನ್.ಲಿಟ್ವಿನೆಂಕೊ. ಕಾರ್ಯಾಗಾರ ಪ್ರಾಥಮಿಕ ಗಣಿತ. ಸ್ಟೀರಿಯೊಮೆಟ್ರಿ: ಟ್ಯುಟೋರಿಯಲ್.-ಎಂ.: ವರ್ಬಮ್-ಎಂ, 2000.
ಅವರು.ಗೆಲ್ಫಾಂಡ್, E.G. ಗ್ಲಾಗೊಲೆವಾ, A.A. ಕಿರಿಲೋವ್.ಸಮನ್ವಯ ವಿಧಾನ - ಎಂ.: ನೌಕಾ, 1968.
S.G. ಗ್ರಿಗೊರಿವ್.ವೆಕ್ಟರ್ ಬೀಜಗಣಿತ ಮತ್ತು ವಿಶ್ಲೇಷಣಾತ್ಮಕ ಜ್ಯಾಮಿತಿ. ಉನ್ನತ ಗಣಿತಶಾಸ್ತ್ರದ ಪಠ್ಯಪುಸ್ತಕ.-ಎಂ.: ಮಾಹಿತಿ ಮತ್ತು ಅನುಷ್ಠಾನ ಕೇಂದ್ರ "ಮಾರ್ಕೆಟಿಂಗ್", 2000.
I. ಇವನೋವಾ, Z. ಇಲ್ಚೆಂಕೋವಾ.ಅಪ್ಲಿಕೇಶನ್ ನಿರ್ದೇಶಾಂಕ ವೆಕ್ಟರ್ಸ್ಟೀರಿಯೊಮೆಟ್ರಿಕ್ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸಲು.//ಗಣಿತಶಾಸ್ತ್ರ, 2007, ಸಂ. 2.
A.V. ಡೊರೊಫೀವ್.ಡೆಸ್ಕಾರ್ಟೆಸ್ ಮತ್ತು ಅವನ ರೇಖಾಗಣಿತ.//ಗಣಿತಶಾಸ್ತ್ರ, 1992, ಸಂಖ್ಯೆ. 4.
