ಶಿಕ್ಷಣ ಸಂಸ್ಥೆ "ಬೆಲರೂಸಿಯನ್ ರಾಜ್ಯ
ಕೃಷಿ ಅಕಾಡೆಮಿ"
ಉನ್ನತ ಗಣಿತಶಾಸ್ತ್ರ ವಿಭಾಗ
ಮಾರ್ಗಸೂಚಿಗಳು
ಪತ್ರವ್ಯವಹಾರ ಶಿಕ್ಷಣಕ್ಕಾಗಿ (NISPO) ಅಕೌಂಟಿಂಗ್ ವಿಭಾಗದ ವಿದ್ಯಾರ್ಥಿಗಳಿಂದ "ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ಸ್" ವಿಷಯವನ್ನು ಅಧ್ಯಯನ ಮಾಡಲು
ಗೋರ್ಕಿ, 2013
ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರ
ಡಿಸ್ಕ್ರೀಟ್ ಮತ್ತು ನಿರಂತರ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರ
ಸಂಭವನೀಯತೆ ಸಿದ್ಧಾಂತದಲ್ಲಿನ ಮುಖ್ಯ ಪರಿಕಲ್ಪನೆಗಳಲ್ಲಿ ಒಂದು ಪರಿಕಲ್ಪನೆಯಾಗಿದೆ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ . ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಪರೀಕ್ಷೆಯ ಪರಿಣಾಮವಾಗಿ, ಅದರ ಹಲವು ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳಲ್ಲಿ ಒಂದನ್ನು ಮಾತ್ರ ತೆಗೆದುಕೊಳ್ಳುವ ಪ್ರಮಾಣವಾಗಿದೆ, ಮತ್ತು ಯಾವುದು ಮುಂಚಿತವಾಗಿ ತಿಳಿದಿಲ್ಲ.
ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳಿವೆ ಪ್ರತ್ಯೇಕ ಮತ್ತು ನಿರಂತರ . ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ (DRV) ಒಂದು ಯಾದೃಚ್ಛಿಕ ವೇರಿಯೇಬಲ್ ಆಗಿದ್ದು ಅದು ಪರಸ್ಪರ ಪ್ರತ್ಯೇಕವಾಗಿರುವ ಸೀಮಿತ ಸಂಖ್ಯೆಯ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು, ಅಂದರೆ. ಈ ಪ್ರಮಾಣದ ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳನ್ನು ಮರು ಲೆಕ್ಕಾಚಾರ ಮಾಡಬಹುದಾದರೆ. ನಿರಂತರ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ (CNV) ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಆಗಿದೆ, ಎಲ್ಲಾ ಸಂಭಾವ್ಯ ಮೌಲ್ಯಗಳು ಸಂಖ್ಯಾ ರೇಖೆಯ ನಿರ್ದಿಷ್ಟ ಮಧ್ಯಂತರವನ್ನು ಸಂಪೂರ್ಣವಾಗಿ ತುಂಬುತ್ತವೆ.
ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳನ್ನು ಲ್ಯಾಟಿನ್ ವರ್ಣಮಾಲೆಯ X, Y, Z, ಇತ್ಯಾದಿಗಳ ದೊಡ್ಡ ಅಕ್ಷರಗಳಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ. ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳನ್ನು ಅನುಗುಣವಾದ ಸಣ್ಣ ಅಕ್ಷರಗಳಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ.
ರೆಕಾರ್ಡ್ ಮಾಡಿ 
ಅಂದರೆ "ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಸಂಭವನೀಯತೆ X 0.28 ಕ್ಕೆ ಸಮಾನವಾದ 5 ರ ಮೌಲ್ಯವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ.
ಉದಾಹರಣೆ 1 . ದಾಳಗಳನ್ನು ಒಮ್ಮೆ ಎಸೆಯಲಾಗುತ್ತದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, 1 ರಿಂದ 6 ರವರೆಗಿನ ಸಂಖ್ಯೆಗಳು ಕಾಣಿಸಿಕೊಳ್ಳಬಹುದು, ಇದು ಬಿಂದುಗಳ ಸಂಖ್ಯೆಯನ್ನು ಸೂಚಿಸುತ್ತದೆ. ನಾವು ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ಸೂಚಿಸೋಣ X=(ಸುತ್ತಿಕೊಂಡ ಅಂಕಗಳ ಸಂಖ್ಯೆ). ಪರೀಕ್ಷೆಯ ಪರಿಣಾಮವಾಗಿ ಈ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಆರು ಮೌಲ್ಯಗಳಲ್ಲಿ ಒಂದನ್ನು ಮಾತ್ರ ತೆಗೆದುಕೊಳ್ಳಬಹುದು: 1, 2, 3, 4, 5 ಅಥವಾ 6. ಆದ್ದರಿಂದ, ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ X DSV ಇದೆ.
ಉದಾಹರಣೆ 2 . ಕಲ್ಲನ್ನು ಎಸೆದಾಗ ಅದು ನಿರ್ದಿಷ್ಟ ದೂರವನ್ನು ಕ್ರಮಿಸುತ್ತದೆ. ನಾವು ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ಸೂಚಿಸೋಣ X=(ಕಲ್ಲಿನ ಹಾರಾಟದ ದೂರ). ಈ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯೇಬಲ್ ನಿರ್ದಿಷ್ಟ ಮಧ್ಯಂತರದಿಂದ ಯಾವುದೇ, ಆದರೆ ಒಂದೇ ಒಂದು ಮೌಲ್ಯವನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು. ಆದ್ದರಿಂದ, ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ X NSV ಇದೆ.
ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವಿತರಣಾ ಕಾನೂನು
ಪ್ರತ್ಯೇಕವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ಅದು ತೆಗೆದುಕೊಳ್ಳಬಹುದಾದ ಮೌಲ್ಯಗಳು ಮತ್ತು ಈ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುವ ಸಂಭವನೀಯತೆಗಳಿಂದ ನಿರೂಪಿಸಲಾಗಿದೆ. ಪ್ರತ್ಯೇಕವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳು ಮತ್ತು ಅವುಗಳ ಅನುಗುಣವಾದ ಸಂಭವನೀಯತೆಗಳ ನಡುವಿನ ಪತ್ರವ್ಯವಹಾರವನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ವಿತರಣೆಯ ಕಾನೂನು .
ಸಾಧ್ಯವಿರುವ ಎಲ್ಲಾ ಮೌಲ್ಯಗಳು ತಿಳಿದಿದ್ದರೆ 
ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ Xಮತ್ತು ಸಂಭವನೀಯತೆಗಳು 
ಈ ಮೌಲ್ಯಗಳ ನೋಟ, ನಂತರ DSV ವಿತರಣೆಯ ಕಾನೂನು ಎಂದು ನಂಬಲಾಗಿದೆ Xತಿಳಿದಿದೆ ಮತ್ತು ಟೇಬಲ್ ರೂಪದಲ್ಲಿ ಬರೆಯಬಹುದು:
|
|
|
|
|
|
|||
|
|
|
|
|
|
ಆಯತಾಕಾರದ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಬಿಂದುಗಳನ್ನು ಚಿತ್ರಿಸಿದರೆ DSV ವಿತರಣಾ ಕಾನೂನನ್ನು ಚಿತ್ರಾತ್ಮಕವಾಗಿ ಚಿತ್ರಿಸಬಹುದು 
,
,
…,
ಮತ್ತು ಅವುಗಳನ್ನು ನೇರ ರೇಖೆಯ ಭಾಗಗಳೊಂದಿಗೆ ಸಂಪರ್ಕಪಡಿಸಿ. ಪರಿಣಾಮವಾಗಿ ಆಕೃತಿಯನ್ನು ವಿತರಣಾ ಬಹುಭುಜಾಕೃತಿ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
ಉದಾಹರಣೆ 3 . ಸ್ವಚ್ಛಗೊಳಿಸಲು ಉದ್ದೇಶಿಸಿರುವ ಧಾನ್ಯವು 10% ಕಳೆಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಯಾದೃಚ್ಛಿಕವಾಗಿ 4 ಧಾನ್ಯಗಳನ್ನು ಆಯ್ಕೆ ಮಾಡಲಾಗಿದೆ. ನಾವು ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ಸೂಚಿಸೋಣ X=(ಆಯ್ದ ನಾಲ್ಕು ಕಳೆಗಳ ಸಂಖ್ಯೆ). DSV ವಿತರಣಾ ಕಾನೂನನ್ನು ನಿರ್ಮಿಸಿ Xಮತ್ತು ವಿತರಣೆ ಬಹುಭುಜಾಕೃತಿ.
ಪರಿಹಾರ . ಉದಾಹರಣೆ ಪರಿಸ್ಥಿತಿಗಳ ಪ್ರಕಾರ. ನಂತರ:
DSV X ನ ವಿತರಣಾ ಕಾನೂನನ್ನು ಟೇಬಲ್ ರೂಪದಲ್ಲಿ ಬರೆಯೋಣ ಮತ್ತು ವಿತರಣಾ ಬಹುಭುಜಾಕೃತಿಯನ್ನು ನಿರ್ಮಿಸೋಣ:
|
|
ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ನಿರೀಕ್ಷೆ
ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಪ್ರಮುಖ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಅದರ ಗುಣಲಕ್ಷಣಗಳಿಂದ ವಿವರಿಸಲಾಗಿದೆ. ಈ ಗುಣಲಕ್ಷಣಗಳಲ್ಲಿ ಒಂದಾಗಿದೆ ನಿರೀಕ್ಷಿತ ಮೌಲ್ಯ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್.
DSV ವಿತರಣೆ ಕಾನೂನು ತಿಳಿದಿರಲಿ X:
|
|
|
|
|
|
|||
|
|
|
|
|
|
ಗಣಿತದ ನಿರೀಕ್ಷೆ
ಡಿಎಸ್ವಿ Xಈ ಪ್ರಮಾಣ ಮತ್ತು ಅನುಗುಣವಾದ ಸಂಭವನೀಯತೆಯ ಪ್ರತಿ ಮೌಲ್ಯದ ಉತ್ಪನ್ನಗಳ ಮೊತ್ತವಾಗಿದೆ: 
.
ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಗಣಿತದ ನಿರೀಕ್ಷೆಯು ಅದರ ಎಲ್ಲಾ ಮೌಲ್ಯಗಳ ಅಂಕಗಣಿತದ ಸರಾಸರಿಗೆ ಸರಿಸುಮಾರು ಸಮಾನವಾಗಿರುತ್ತದೆ. ಆದ್ದರಿಂದ, ಪ್ರಾಯೋಗಿಕ ಸಮಸ್ಯೆಗಳಲ್ಲಿ, ಈ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಸರಾಸರಿ ಮೌಲ್ಯವನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಗಣಿತದ ನಿರೀಕ್ಷೆಯಂತೆ ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ.
ಉದಾಹರಣೆ 8 . ಶೂಟರ್ 4, 8, 9 ಮತ್ತು 10 ಅಂಕಗಳನ್ನು 0.1, 0.45, 0.3 ಮತ್ತು 0.15 ರ ಸಂಭವನೀಯತೆಗಳೊಂದಿಗೆ ಗಳಿಸುತ್ತಾನೆ. ಒಂದು ಹೊಡೆತದಿಂದ ಅಂಕಗಳ ಸಂಖ್ಯೆಯ ಗಣಿತದ ನಿರೀಕ್ಷೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಪರಿಹಾರ . ನಾವು ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ಸೂಚಿಸೋಣ X=(ಸ್ಕೋರ್ ಮಾಡಿದ ಅಂಕಗಳ ಸಂಖ್ಯೆ). ನಂತರ . ಹೀಗಾಗಿ, ಒಂದು ಹೊಡೆತದಿಂದ ಗಳಿಸಿದ ಸರಾಸರಿ ಅಂಕಗಳ ಸಂಖ್ಯೆ 8.2, ಮತ್ತು 10 ಹೊಡೆತಗಳೊಂದಿಗೆ - 82.
ಮುಖ್ಯ ಗುಣಲಕ್ಷಣಗಳು ಗಣಿತದ ನಿರೀಕ್ಷೆಗಳೆಂದರೆ:
.
.
, ಎಲ್ಲಿ 
,
.
.
, ಎಲ್ಲಿ Xಮತ್ತು ವೈಸ್ವತಂತ್ರ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳಾಗಿವೆ.
ವ್ಯತ್ಯಾಸ 
ಎಂದು ಕರೆದರು ವಿಚಲನ
ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ Xಅದರ ಗಣಿತದ ನಿರೀಕ್ಷೆಯಿಂದ. ಈ ವ್ಯತ್ಯಾಸವು ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಆಗಿದೆ ಮತ್ತು ಅದರ ಗಣಿತದ ನಿರೀಕ್ಷೆಯು ಶೂನ್ಯವಾಗಿರುತ್ತದೆ, ಅಂದರೆ. 
.
ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವ್ಯತ್ಯಾಸ
ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ನಿರೂಪಿಸಲು, ಗಣಿತದ ನಿರೀಕ್ಷೆಯ ಜೊತೆಗೆ, ನಾವು ಸಹ ಬಳಸುತ್ತೇವೆ ಪ್ರಸರಣ , ಇದು ಗಣಿತದ ನಿರೀಕ್ಷೆಯ ಸುತ್ತ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಮೌಲ್ಯಗಳ ಪ್ರಸರಣವನ್ನು (ಹರಡುವಿಕೆ) ಅಂದಾಜು ಮಾಡಲು ಸಾಧ್ಯವಾಗಿಸುತ್ತದೆ. ಸಮಾನವಾದ ಗಣಿತದ ನಿರೀಕ್ಷೆಗಳೊಂದಿಗೆ ಎರಡು ಏಕರೂಪದ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳನ್ನು ಹೋಲಿಸಿದಾಗ, "ಅತ್ಯುತ್ತಮ" ಮೌಲ್ಯವನ್ನು ಕಡಿಮೆ ಹರಡುವಿಕೆ ಎಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ, ಅಂದರೆ. ಕಡಿಮೆ ಪ್ರಸರಣ.
ವ್ಯತ್ಯಾಸ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ Xಅದರ ಗಣಿತದ ನಿರೀಕ್ಷೆಯಿಂದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವರ್ಗ ವಿಚಲನದ ಗಣಿತದ ನಿರೀಕ್ಷೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ: .
ಪ್ರಾಯೋಗಿಕ ಸಮಸ್ಯೆಗಳಲ್ಲಿ, ವ್ಯತ್ಯಾಸವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಸಮಾನವಾದ ಸೂತ್ರವನ್ನು ಬಳಸಲಾಗುತ್ತದೆ.
ಪ್ರಸರಣದ ಮುಖ್ಯ ಗುಣಲಕ್ಷಣಗಳು:
.
Xಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯ ಕಾನೂನಿನಿಂದ ನೀಡಲಾಗಿದೆ: ನಂತರ ಅದರ ಪ್ರಮಾಣಿತ ವಿಚಲನವು ... 0.80 ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ
ಪರಿಹಾರ:
ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ X ನ ಪ್ರಮಾಣಿತ ವಿಚಲನವನ್ನು ಹೀಗೆ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ 
, ಅಲ್ಲಿ ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವ್ಯತ್ಯಾಸವನ್ನು ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ಲೆಕ್ಕಾಚಾರ ಮಾಡಬಹುದು ನಂತರ , ಮತ್ತು 
ಪರಿಹಾರ:
ಎ(ಯಾದೃಚ್ಛಿಕವಾಗಿ ಚಿತ್ರಿಸಿದ ಚೆಂಡು ಕಪ್ಪು) ನಾವು ಒಟ್ಟು ಸಂಭವನೀಯತೆಯ ಸೂತ್ರವನ್ನು ಅನ್ವಯಿಸುತ್ತೇವೆ: ಬಿಳಿ ಚೆಂಡನ್ನು ಮೊದಲ ಚಿತಾಭಸ್ಮದಿಂದ ಎರಡನೇ ಚಿತಾಗಾರಕ್ಕೆ ವರ್ಗಾಯಿಸುವ ಸಂಭವನೀಯತೆ ಇಲ್ಲಿದೆ; - ಕಪ್ಪು ಚೆಂಡನ್ನು ಮೊದಲ ಚಿತಾಭಸ್ಮದಿಂದ ಎರಡನೇ ಚಿತಾಭಸ್ಮಕ್ಕೆ ವರ್ಗಾಯಿಸುವ ಸಂಭವನೀಯತೆ; - ಬಿಳಿ ಚೆಂಡನ್ನು ಮೊದಲ ಚಿತಾಭಸ್ಮದಿಂದ ಎರಡನೆಯದಕ್ಕೆ ಸರಿಸಿದರೆ ಡ್ರಾ ಬಾಲ್ ಕಪ್ಪು ಎಂದು ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆ; - ಕಪ್ಪು ಚೆಂಡನ್ನು ಮೊದಲ ಚಿತಾಭಸ್ಮದಿಂದ ಎರಡನೆಯದಕ್ಕೆ ಸರಿಸಿದರೆ ಡ್ರಾ ಬಾಲ್ ಕಪ್ಪು ಎಂದು ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆ.
ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ X ಅನ್ನು ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯ ನಿಯಮದಿಂದ ನೀಡಲಾಗಿದೆ: ನಂತರ ಸಂಭವನೀಯತೆ 
ಸಮಾನ...
ಪರಿಹಾರ:
ಪ್ರತ್ಯೇಕವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವ್ಯತ್ಯಾಸವನ್ನು ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ಲೆಕ್ಕಹಾಕಬಹುದು. ನಂತರ
ಅಥವಾ . ಕೊನೆಯ ಸಮೀಕರಣವನ್ನು ಪರಿಹರಿಸುವುದು, ನಾವು ಎರಡು ಬೇರುಗಳನ್ನು ಪಡೆಯುತ್ತೇವೆ ಮತ್ತು
ವಿಷಯ: ಸಂಭವನೀಯತೆಯ ನಿರ್ಣಯ
12 ಭಾಗಗಳ ಬ್ಯಾಚ್‌ನಲ್ಲಿ, 5 ದೋಷಯುಕ್ತ ಭಾಗಗಳಿವೆ. ಮೂರು ಭಾಗಗಳನ್ನು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಆಯ್ಕೆ ಮಾಡಲಾಗಿದೆ. ನಂತರ ಆಯ್ಕೆಮಾಡಿದ ಭಾಗಗಳಲ್ಲಿ ಯಾವುದೇ ಸೂಕ್ತ ಭಾಗಗಳಿಲ್ಲದ ಸಂಭವನೀಯತೆಯು ಸಮಾನವಾಗಿರುತ್ತದೆ...
ಪರಿಹಾರ:
ಈವೆಂಟ್ ಎ ಅನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು (ಆಯ್ಕೆ ಮಾಡಿದ ಭಾಗಗಳಲ್ಲಿ ಯಾವುದೇ ಸೂಕ್ತ ಭಾಗಗಳಿಲ್ಲ), ನಾವು ಅಲ್ಲಿ ಸೂತ್ರವನ್ನು ಬಳಸುತ್ತೇವೆ ಎನ್ ಮೀ– ಈವೆಂಟ್ A ಸಂಭವಿಸುವುದಕ್ಕೆ ಅನುಕೂಲಕರವಾದ ಪ್ರಾಥಮಿಕ ಫಲಿತಾಂಶಗಳ ಸಂಖ್ಯೆ. ನಮ್ಮ ಸಂದರ್ಭದಲ್ಲಿ, ಸಂಭವನೀಯ ಪ್ರಾಥಮಿಕ ಫಲಿತಾಂಶಗಳ ಒಟ್ಟು ಸಂಖ್ಯೆಯು ಲಭ್ಯವಿರುವ 12 ರಿಂದ ಮೂರು ವಿವರಗಳನ್ನು ಹೊರತೆಗೆಯುವ ವಿಧಾನಗಳ ಸಂಖ್ಯೆಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ.
ಮತ್ತು ಅನುಕೂಲಕರ ಫಲಿತಾಂಶಗಳ ಒಟ್ಟು ಸಂಖ್ಯೆಯು ಐದರಿಂದ ಮೂರು ದೋಷಯುಕ್ತ ಭಾಗಗಳನ್ನು ಹೊರತೆಗೆಯುವ ವಿಧಾನಗಳ ಸಂಖ್ಯೆಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ. 
ಬ್ಯಾಂಕ್ ಎಲ್ಲಾ ಸಾಲಗಳಲ್ಲಿ 44% ಅನ್ನು ಕಾನೂನು ಘಟಕಗಳಿಗೆ ಮತ್ತು 56% ವ್ಯಕ್ತಿಗಳಿಗೆ ನೀಡುತ್ತದೆ. ಕಾನೂನು ಘಟಕವು ಸಮಯಕ್ಕೆ ಸಾಲವನ್ನು ಮರುಪಾವತಿಸುವುದಿಲ್ಲ ಎಂಬ ಸಂಭವನೀಯತೆ 0.2 ಆಗಿದೆ; ಮತ್ತು ಒಬ್ಬ ವ್ಯಕ್ತಿಗೆ ಈ ಸಂಭವನೀಯತೆ 0.1 ಆಗಿದೆ. ನಂತರ ಮುಂದಿನ ಸಾಲವನ್ನು ಸಮಯಕ್ಕೆ ಮರುಪಾವತಿ ಮಾಡುವ ಸಂಭವನೀಯತೆ ...
| 0,856 |
ಪರಿಹಾರ:
ಘಟನೆಯ ಸಂಭವನೀಯತೆಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಎ(ನೀಡಿದ ಸಾಲವನ್ನು ಸಮಯಕ್ಕೆ ಮರುಪಾವತಿಸಲಾಗುವುದು) ಒಟ್ಟು ಸಂಭವನೀಯತೆಯ ಸೂತ್ರವನ್ನು ಅನ್ವಯಿಸಿ: . ಕಾನೂನು ಘಟಕಕ್ಕೆ ಸಾಲವನ್ನು ನೀಡಿದ ಸಂಭವನೀಯತೆ ಇಲ್ಲಿದೆ; - ಒಬ್ಬ ವ್ಯಕ್ತಿಗೆ ಸಾಲವನ್ನು ನೀಡಿದ ಸಂಭವನೀಯತೆ; - ಕಾನೂನು ಘಟಕಕ್ಕೆ ನೀಡಿದರೆ ಸಾಲವನ್ನು ಸಮಯಕ್ಕೆ ಮರುಪಾವತಿ ಮಾಡುವ ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆ; - ಸಾಲವನ್ನು ಒಬ್ಬ ವ್ಯಕ್ತಿಗೆ ನೀಡಿದರೆ ಅದನ್ನು ಸಮಯಕ್ಕೆ ಮರುಪಾವತಿ ಮಾಡುವ ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆ. ನಂತರ 
ವಿಷಯ: ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯ ನಿಯಮಗಳು
ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ X ಗಾಗಿ 
| 0,655 |
ವಿಷಯ: ಸಂಭವನೀಯತೆಯ ನಿರ್ಣಯ
ಡೈ ಅನ್ನು ಎರಡು ಬಾರಿ ಸುತ್ತಿಕೊಳ್ಳಲಾಗುತ್ತದೆ. ನಂತರ ಸುತ್ತಿಕೊಂಡ ಬಿಂದುಗಳ ಮೊತ್ತವು ಒಂಬತ್ತಕ್ಕಿಂತ ಕಡಿಮೆಯಿಲ್ಲದ ಸಂಭವನೀಯತೆ ...
ಪರಿಹಾರ:
ಈವೆಂಟ್ ಅನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು (ರೋಲ್ ಮಾಡಿದ ಅಂಕಗಳ ಮೊತ್ತವು ಕನಿಷ್ಠ ಒಂಬತ್ತು ಆಗಿರುತ್ತದೆ), ನಾವು ಸೂತ್ರವನ್ನು ಬಳಸುತ್ತೇವೆ , ಅಲ್ಲಿ ಪರೀಕ್ಷೆಯ ಸಂಭವನೀಯ ಪ್ರಾಥಮಿಕ ಫಲಿತಾಂಶಗಳ ಒಟ್ಟು ಸಂಖ್ಯೆ, ಮತ್ತು ಮೀ- ಘಟನೆಯ ಸಂಭವಕ್ಕೆ ಅನುಕೂಲಕರವಾದ ಪ್ರಾಥಮಿಕ ಫಲಿತಾಂಶಗಳ ಸಂಖ್ಯೆ ಎ. ನಮ್ಮ ಸಂದರ್ಭದಲ್ಲಿ ಅದು ಸಾಧ್ಯ 
ಪ್ರಾಥಮಿಕ ಪರೀಕ್ಷಾ ಫಲಿತಾಂಶಗಳು, ಇವುಗಳಲ್ಲಿ ಅನುಕೂಲಕರವಾದ ರೂಪದ ಫಲಿತಾಂಶಗಳು , , , , , , ಮತ್ತು , ಅಂದರೆ. ಆದ್ದರಿಂದ, 
ವಿಷಯ: ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯ ನಿಯಮಗಳು
ಸಂಭವನೀಯತೆ ವಿತರಣೆ ಕಾರ್ಯವು ರೂಪವನ್ನು ಹೊಂದಿದೆ: 
ನಂತರ ನಿಯತಾಂಕದ ಮೌಲ್ಯವು ಇದಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ ...
| 0,7 | |||
| 0,85 | |||
| 0,6 |
ಪರಿಹಾರ:
ಎ-ಪ್ರಿಯರಿ 
. ಆದ್ದರಿಂದ, ಮತ್ತು . ಈ ಷರತ್ತುಗಳನ್ನು ತೃಪ್ತಿಪಡಿಸಲಾಗಿದೆ, ಉದಾಹರಣೆಗೆ, ಮೌಲ್ಯದಿಂದ
ವಿಷಯ: ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಸಂಖ್ಯಾತ್ಮಕ ಗುಣಲಕ್ಷಣಗಳು
ನಿರಂತರವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯೇಬಲ್ ಅನ್ನು ಸಂಭವನೀಯತೆ ವಿತರಣಾ ಕಾರ್ಯದಿಂದ ನಿರ್ದಿಷ್ಟಪಡಿಸಲಾಗಿದೆ: 
ನಂತರ ಅದರ ವ್ಯತ್ಯಾಸವೆಂದರೆ ...
ಪರಿಹಾರ:
ಈ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಮಧ್ಯಂತರದಲ್ಲಿ ಏಕರೂಪವಾಗಿ ವಿತರಿಸಲ್ಪಡುತ್ತದೆ. ನಂತರ ಅದರ ವ್ಯತ್ಯಾಸವನ್ನು ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ಲೆಕ್ಕ ಹಾಕಬಹುದು 
. ಅದು 
ವಿಷಯ: ಒಟ್ಟು ಸಂಭವನೀಯತೆ. ಬೇಯಸ್ ಸೂತ್ರಗಳು
ಮೊದಲ ಪಾತ್ರೆಯಲ್ಲಿ 6 ಕಪ್ಪು ಚೆಂಡುಗಳು ಮತ್ತು 4 ಬಿಳಿ ಚೆಂಡುಗಳಿವೆ. ಎರಡನೇ ಪಾತ್ರೆಯಲ್ಲಿ 2 ಬಿಳಿ ಮತ್ತು 8 ಕಪ್ಪು ಚೆಂಡುಗಳಿವೆ. ಒಂದು ಚೆಂಡನ್ನು ಯಾದೃಚ್ಛಿಕ ಚಿತಾಭಸ್ಮದಿಂದ ತೆಗೆದುಕೊಳ್ಳಲಾಗಿದೆ, ಅದು ಬಿಳಿ ಬಣ್ಣಕ್ಕೆ ತಿರುಗಿತು. ನಂತರ ಈ ಚೆಂಡನ್ನು ಮೊದಲ ಚಿತಾಭಸ್ಮದಿಂದ ಎಳೆದ ಸಂಭವನೀಯತೆ ...
ಪರಿಹಾರ:
ಎ(ಯಾದೃಚ್ಛಿಕವಾಗಿ ಚಿತ್ರಿಸಿದ ಚೆಂಡು ಬಿಳಿಯಾಗಿರುತ್ತದೆ) ಒಟ್ಟು ಸಂಭವನೀಯತೆಯ ಸೂತ್ರದ ಪ್ರಕಾರ: . ಮೊದಲ ಚಿತಾಭಸ್ಮದಿಂದ ಚೆಂಡನ್ನು ಎಳೆಯುವ ಸಂಭವನೀಯತೆ ಇಲ್ಲಿದೆ; ಎರಡನೇ ಚಿತಾಭಸ್ಮದಿಂದ ಚೆಂಡನ್ನು ಎಳೆಯುವ ಸಂಭವನೀಯತೆ; - ಮೊದಲ ಚಿತಾಭಸ್ಮದಿಂದ ಎಳೆದರೆ ಎಳೆದ ಚೆಂಡು ಬಿಳಿಯಾಗಿರುತ್ತದೆ ಎಂಬ ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆ; ಎರಡನೇ ಚಿತಾಭಸ್ಮದಿಂದ ಎಳೆದರೆ ಎಳೆದ ಚೆಂಡು ಬಿಳಿಯಾಗಿರುತ್ತದೆ ಎಂಬ ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆಯಾಗಿದೆ.
ನಂತರ 
.
ಬೇಯ್ಸ್ ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ಈ ಚೆಂಡನ್ನು ಮೊದಲ ಚಿತಾಭಸ್ಮದಿಂದ ಎಳೆಯಲಾದ ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆಯನ್ನು ಈಗ ಲೆಕ್ಕಾಚಾರ ಮಾಡೋಣ: 
ವಿಷಯ: ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಸಂಖ್ಯಾತ್ಮಕ ಗುಣಲಕ್ಷಣಗಳು
ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ Xಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯ ಕಾನೂನಿನಿಂದ ನೀಡಲಾಗಿದೆ: 
ನಂತರ ಅದರ ವ್ಯತ್ಯಾಸವೆಂದರೆ ...
| 7,56 | |||
| 3,2 | |||
| 3,36 | |||
| 6,0 |
ಪರಿಹಾರ:
ಪ್ರತ್ಯೇಕವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವ್ಯತ್ಯಾಸವನ್ನು ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ಲೆಕ್ಕಹಾಕಬಹುದು
ವಿಷಯ: ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯ ನಿಯಮಗಳು
ಪರಿಹಾರ:
ಎ-ಪ್ರಿಯರಿ . ನಂತರ
a) ನಲ್ಲಿ,
ಬಿ) ನಲ್ಲಿ,
ಸಿ) ನಲ್ಲಿ,
d) ನಲ್ಲಿ,
d) ನಲ್ಲಿ, .
ಆದ್ದರಿಂದ,
ವಿಷಯ: ಸಂಭವನೀಯತೆಯ ನಿರ್ಣಯ
ತ್ರಿಜ್ಯ 4 ರ ವೃತ್ತದೊಳಗೆ ಒಂದು ಬಿಂದುವನ್ನು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಎಸೆಯಲಾಗುತ್ತದೆ. ನಂತರ ಬಿಂದುವು ವೃತ್ತದಲ್ಲಿ ಕೆತ್ತಲಾದ ಚೌಕದ ಹೊರಗೆ ಇರುವ ಸಂಭವನೀಯತೆ ...
ವಿಷಯ: ಸಂಭವನೀಯತೆಯ ನಿರ್ಣಯ
12 ಭಾಗಗಳ ಬ್ಯಾಚ್‌ನಲ್ಲಿ, 5 ದೋಷಯುಕ್ತ ಭಾಗಗಳಿವೆ. ಮೂರು ಭಾಗಗಳನ್ನು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಆಯ್ಕೆ ಮಾಡಲಾಗಿದೆ. ನಂತರ ಆಯ್ಕೆಮಾಡಿದ ಭಾಗಗಳಲ್ಲಿ ಯಾವುದೇ ದೋಷಯುಕ್ತ ಭಾಗಗಳಿಲ್ಲದ ಸಂಭವನೀಯತೆಯು ಸಮಾನವಾಗಿರುತ್ತದೆ...
ಪರಿಹಾರ:
ಈವೆಂಟ್ ಅನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು (ಆಯ್ದ ಭಾಗಗಳಲ್ಲಿ ಯಾವುದೇ ದೋಷಯುಕ್ತ ಭಾಗಗಳಿಲ್ಲ), ನಾವು ಸೂತ್ರವನ್ನು ಬಳಸುತ್ತೇವೆ, ಅಲ್ಲಿ ಎನ್ಸಂಭವನೀಯ ಪ್ರಾಥಮಿಕ ಪರೀಕ್ಷಾ ಫಲಿತಾಂಶಗಳ ಒಟ್ಟು ಸಂಖ್ಯೆ, ಮತ್ತು ಮೀ- ಘಟನೆಯ ಸಂಭವಕ್ಕೆ ಅನುಕೂಲಕರವಾದ ಪ್ರಾಥಮಿಕ ಫಲಿತಾಂಶಗಳ ಸಂಖ್ಯೆ. ನಮ್ಮ ಸಂದರ್ಭದಲ್ಲಿ, ಸಂಭವನೀಯ ಪ್ರಾಥಮಿಕ ಫಲಿತಾಂಶಗಳ ಒಟ್ಟು ಸಂಖ್ಯೆಯು ಲಭ್ಯವಿರುವ 12 ರಿಂದ ಮೂರು ವಿವರಗಳನ್ನು ಹೊರತೆಗೆಯುವ ವಿಧಾನಗಳ ಸಂಖ್ಯೆಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ. ಮತ್ತು ಅನುಕೂಲಕರ ಫಲಿತಾಂಶಗಳ ಒಟ್ಟು ಸಂಖ್ಯೆಯು ಮೂರು ದೋಷರಹಿತ ಭಾಗಗಳನ್ನು ಏಳರಿಂದ ಹೊರತೆಗೆಯುವ ವಿಧಾನಗಳ ಸಂಖ್ಯೆಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ. ಆದ್ದರಿಂದ, 
ವಿಷಯ: ಒಟ್ಟು ಸಂಭವನೀಯತೆ. ಬೇಯಸ್ ಸೂತ್ರಗಳು
| 0,57 | |||
| 0,43 | |||
| 0,55 | |||
| 0,53 |
ಪರಿಹಾರ:
ಘಟನೆಯ ಸಂಭವನೀಯತೆಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಎ
ನಂತರ 
ವಿಷಯ: ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯ ನಿಯಮಗಳು
ಸಂಭವನೀಯ ವಿತರಣಾ ಕಾನೂನಿನಿಂದ ಪ್ರತ್ಯೇಕವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸಲಾಗಿದೆ:
ನಂತರ ಸಂಭವನೀಯತೆ 
ಸಮಾನ...
ಪರಿಹಾರ:
ಸೂತ್ರವನ್ನು ಬಳಸೋಣ 
. ನಂತರ 
ವಿಷಯ: ಒಟ್ಟು ಸಂಭವನೀಯತೆ. ಬೇಯಸ್ ಸೂತ್ರಗಳು
| 0,875 | |||
| 0,125 | |||
| 0,105 | |||
| 0,375 |
ಪರಿಹಾರ:
ಈವೆಂಟ್ನ ಸಂಭವನೀಯತೆಯನ್ನು ಮೊದಲು ಲೆಕ್ಕಾಚಾರ ಮಾಡೋಣ ಎ 
.
.
ವಿಷಯ: ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಸಂಖ್ಯಾತ್ಮಕ ಗುಣಲಕ್ಷಣಗಳು
ಆಗ ಅದರ ಗಣಿತದ ನಿರೀಕ್ಷೆ...
ಪರಿಹಾರ:
ಸೂತ್ರವನ್ನು ಬಳಸೋಣ . ನಂತರ .
ವಿಷಯ: ಸಂಭವನೀಯತೆಯ ನಿರ್ಣಯ
ಪರಿಹಾರ:
ವಿಷಯ: ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಸಂಖ್ಯಾತ್ಮಕ ಗುಣಲಕ್ಷಣಗಳು
ನಿರಂತರವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯ ಸಾಂದ್ರತೆಯಿಂದ ನಿರ್ದಿಷ್ಟಪಡಿಸಲಾಗುತ್ತದೆ 
. ನಂತರ ಗಣಿತದ ನಿರೀಕ್ಷೆ ಎಮತ್ತು ಈ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯೇಬಲ್ನ ಪ್ರಮಾಣಿತ ವಿಚಲನವು ಸಮಾನವಾಗಿರುತ್ತದೆ ...
 |
|||
 |
|||
 |
|||
 |
ಪರಿಹಾರ:
ಸಾಮಾನ್ಯವಾಗಿ ವಿತರಿಸಲಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಸಂಭವನೀಯತೆಯ ವಿತರಣೆ ಸಾಂದ್ರತೆಯು ರೂಪವನ್ನು ಹೊಂದಿದೆ 
, ಎಲ್ಲಿ ,. ಅದಕ್ಕೇ .
ವಿಷಯ: ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯ ನಿಯಮಗಳು
ಸಂಭವನೀಯ ವಿತರಣಾ ಕಾನೂನಿನಿಂದ ಪ್ರತ್ಯೇಕವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸಲಾಗಿದೆ:
ನಂತರ ಮೌಲ್ಯಗಳು ಎಮತ್ತು ಬಿಸಮಾನವಾಗಿರಬಹುದು...
 |
|||
 |
|||
 |
|||
 |
ಪರಿಹಾರ:
ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳ ಸಂಭವನೀಯತೆಗಳ ಮೊತ್ತವು 1 ಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ನಂತರ . ಉತ್ತರವು ಈ ಸ್ಥಿತಿಯನ್ನು ಪೂರೈಸುತ್ತದೆ: .
ವಿಷಯ: ಸಂಭವನೀಯತೆಯ ನಿರ್ಣಯ
ತ್ರಿಜ್ಯ 5 ರ ಸಣ್ಣ ವೃತ್ತವನ್ನು 8 ತ್ರಿಜ್ಯದ ವೃತ್ತದಲ್ಲಿ ಇರಿಸಲಾಗುತ್ತದೆ. ನಂತರ ದೊಡ್ಡ ವೃತ್ತಕ್ಕೆ ಯಾದೃಚ್ಛಿಕವಾಗಿ ಎಸೆಯಲ್ಪಟ್ಟ ಒಂದು ಬಿಂದುವು ಚಿಕ್ಕ ವೃತ್ತಕ್ಕೆ ಬೀಳುವ ಸಂಭವನೀಯತೆ ...
ಪರಿಹಾರ:
ಅಪೇಕ್ಷಿತ ಘಟನೆಯ ಸಂಭವನೀಯತೆಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು, ನಾವು ಸೂತ್ರವನ್ನು ಬಳಸುತ್ತೇವೆ , ಅಲ್ಲಿ ಸಣ್ಣ ವೃತ್ತದ ಪ್ರದೇಶ ಮತ್ತು ದೊಡ್ಡ ವೃತ್ತದ ಪ್ರದೇಶವಾಗಿದೆ. ಆದ್ದರಿಂದ, .
ವಿಷಯ: ಒಟ್ಟು ಸಂಭವನೀಯತೆ. ಬೇಯಸ್ ಸೂತ್ರಗಳು
ಮೊದಲ ಪಾತ್ರೆಯಲ್ಲಿ 3 ಕಪ್ಪು ಚೆಂಡುಗಳು ಮತ್ತು 7 ಬಿಳಿ ಚೆಂಡುಗಳಿವೆ. ಎರಡನೇ ಪಾತ್ರೆಯಲ್ಲಿ 4 ಬಿಳಿ ಚೆಂಡುಗಳು ಮತ್ತು 5 ಕಪ್ಪು ಚೆಂಡುಗಳಿವೆ. ಒಂದು ಚೆಂಡನ್ನು ಮೊದಲ ಚಿತಾಗಾರದಿಂದ ಎರಡನೇ ಪಾತ್ರೆಗೆ ವರ್ಗಾಯಿಸಲಾಯಿತು. ನಂತರ ಎರಡನೇ ಕಲಶದಿಂದ ಯಾದೃಚ್ಛಿಕವಾಗಿ ಎಳೆಯುವ ಚೆಂಡು ಬಿಳಿಯಾಗುವ ಸಂಭವನೀಯತೆ...
| 0,47 | |||
| 0,55 | |||
| 0,35 | |||
| 0,50 |
ಪರಿಹಾರ:
ಘಟನೆಯ ಸಂಭವನೀಯತೆಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಎ(ಯಾದೃಚ್ಛಿಕವಾಗಿ ಚಿತ್ರಿಸಿದ ಚೆಂಡು ಬಿಳಿಯಾಗಿರುತ್ತದೆ) ಒಟ್ಟು ಸಂಭವನೀಯತೆಯ ಸೂತ್ರವನ್ನು ಅನ್ವಯಿಸಿ: . ಬಿಳಿ ಚೆಂಡನ್ನು ಮೊದಲ ಚಿತಾಗಾರದಿಂದ ಎರಡನೇ ಚಿತಾಗಾರಕ್ಕೆ ವರ್ಗಾಯಿಸಿದ ಸಂಭವನೀಯತೆ ಇಲ್ಲಿದೆ; - ಕಪ್ಪು ಚೆಂಡನ್ನು ಮೊದಲ ಚಿತಾಭಸ್ಮದಿಂದ ಎರಡನೇ ಚಿತಾಭಸ್ಮಕ್ಕೆ ವರ್ಗಾಯಿಸುವ ಸಂಭವನೀಯತೆ; - ಬಿಳಿ ಚೆಂಡನ್ನು ಮೊದಲ ಚಿತಾಭಸ್ಮದಿಂದ ಎರಡನೆಯದಕ್ಕೆ ಸ್ಥಳಾಂತರಿಸಿದರೆ ಡ್ರಾ ಬಾಲ್ ಬಿಳಿಯಾಗಿರುತ್ತದೆ ಎಂಬ ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆ; - ಕಪ್ಪು ಚೆಂಡನ್ನು ಮೊದಲ ಚಿತಾಗಾರದಿಂದ ಎರಡನೆಯದಕ್ಕೆ ಸರಿಸಿದರೆ ಡ್ರಾ ಬಾಲ್ ಬಿಳಿಯಾಗಿರುತ್ತದೆ ಎಂಬ ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆ.
ನಂತರ 
ವಿಷಯ: ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯ ನಿಯಮಗಳು
ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ಗಾಗಿ:
ಸಂಭವನೀಯತೆ ವಿತರಣೆ ಕಾರ್ಯವು ರೂಪವನ್ನು ಹೊಂದಿದೆ:
ನಂತರ ನಿಯತಾಂಕದ ಮೌಲ್ಯವು ಇದಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ ...
| 0,7 | |||
| 0,85 | |||
| 0,6 |
TASK N 10 ದೋಷವನ್ನು ವರದಿ ಮಾಡಿದೆ
ವಿಷಯ: ಒಟ್ಟು ಸಂಭವನೀಯತೆ. ಬೇಯಸ್ ಸೂತ್ರಗಳು
ಬ್ಯಾಂಕ್ ಎಲ್ಲಾ ಸಾಲಗಳಲ್ಲಿ 70% ಅನ್ನು ಕಾನೂನು ಘಟಕಗಳಿಗೆ ಮತ್ತು 30% ವ್ಯಕ್ತಿಗಳಿಗೆ ನೀಡುತ್ತದೆ. ಕಾನೂನು ಘಟಕವು ಸಮಯಕ್ಕೆ ಸಾಲವನ್ನು ಮರುಪಾವತಿಸುವುದಿಲ್ಲ ಎಂಬ ಸಂಭವನೀಯತೆ 0.15 ಆಗಿದೆ; ಮತ್ತು ಒಬ್ಬ ವ್ಯಕ್ತಿಗೆ ಈ ಸಂಭವನೀಯತೆ 0.05 ಆಗಿದೆ. ಸಾಲ ಮರುಪಾವತಿಯಾಗಿಲ್ಲ ಎಂಬ ಸಂದೇಶ ಬಂದಿದೆ. ನಂತರ ಕಾನೂನು ಘಟಕವು ಈ ಸಾಲವನ್ನು ಮರುಪಾವತಿ ಮಾಡದಿರುವ ಸಂಭವನೀಯತೆ...
| 0,875 | |||
| 0,125 | |||
| 0,105 | |||
| 0,375 |
ಪರಿಹಾರ:
ಈವೆಂಟ್ನ ಸಂಭವನೀಯತೆಯನ್ನು ಮೊದಲು ಲೆಕ್ಕಾಚಾರ ಮಾಡೋಣ ಎ(ನೀಡಿದ ಸಾಲವನ್ನು ಸಮಯಕ್ಕೆ ಮರುಪಾವತಿಸಲಾಗುವುದಿಲ್ಲ) ಒಟ್ಟು ಸಂಭವನೀಯತೆಯ ಸೂತ್ರದ ಪ್ರಕಾರ: ಕಾನೂನು ಘಟಕಕ್ಕೆ ಸಾಲವನ್ನು ನೀಡಿದ ಸಂಭವನೀಯತೆ ಇಲ್ಲಿದೆ; - ಒಬ್ಬ ವ್ಯಕ್ತಿಗೆ ಸಾಲವನ್ನು ನೀಡಿದ ಸಂಭವನೀಯತೆ; - ಕಾನೂನು ಘಟಕಕ್ಕೆ ನೀಡಿದರೆ ಸಾಲವನ್ನು ಸಮಯಕ್ಕೆ ಮರುಪಾವತಿಸಲಾಗುವುದಿಲ್ಲ ಎಂಬ ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆ; - ಒಬ್ಬ ವ್ಯಕ್ತಿಗೆ ಸಾಲವನ್ನು ನೀಡಿದರೆ ಸಾಲವನ್ನು ಸಮಯಕ್ಕೆ ಮರುಪಾವತಿಸಲಾಗುವುದಿಲ್ಲ ಎಂಬ ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆ. ನಂತರ .
ಬೇಯೆಸ್ ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ಕಾನೂನು ಘಟಕದಿಂದ ಈ ಸಾಲವನ್ನು ಮರುಪಾವತಿ ಮಾಡಲಾಗಿಲ್ಲ ಎಂಬ ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆಯನ್ನು ಈಗ ಲೆಕ್ಕಾಚಾರ ಮಾಡೋಣ: .
TASK N 11 ದೋಷವನ್ನು ವರದಿ ಮಾಡಿದೆ
ವಿಷಯ: ಸಂಭವನೀಯತೆಯ ನಿರ್ಣಯ
12 ಭಾಗಗಳ ಬ್ಯಾಚ್‌ನಲ್ಲಿ, 5 ದೋಷಯುಕ್ತ ಭಾಗಗಳಿವೆ. ಮೂರು ಭಾಗಗಳನ್ನು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಆಯ್ಕೆ ಮಾಡಲಾಗಿದೆ. ನಂತರ ಆಯ್ಕೆಮಾಡಿದ ಭಾಗಗಳಲ್ಲಿ ಯಾವುದೇ ಸೂಕ್ತ ಭಾಗಗಳಿಲ್ಲದ ಸಂಭವನೀಯತೆಯು ಸಮಾನವಾಗಿರುತ್ತದೆ...
ಪರಿಹಾರ:
ಈವೆಂಟ್ ಅನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು (ಆಯ್ದ ಭಾಗಗಳಲ್ಲಿ ಯಾವುದೇ ಸೂಕ್ತ ಭಾಗಗಳಿಲ್ಲ), ನಾವು ಸೂತ್ರವನ್ನು ಬಳಸುತ್ತೇವೆ, ಅಲ್ಲಿ ಎನ್ಸಂಭವನೀಯ ಪ್ರಾಥಮಿಕ ಪರೀಕ್ಷಾ ಫಲಿತಾಂಶಗಳ ಒಟ್ಟು ಸಂಖ್ಯೆ, ಮತ್ತು ಮೀ- ಘಟನೆಯ ಸಂಭವಕ್ಕೆ ಅನುಕೂಲಕರವಾದ ಪ್ರಾಥಮಿಕ ಫಲಿತಾಂಶಗಳ ಸಂಖ್ಯೆ. ನಮ್ಮ ಸಂದರ್ಭದಲ್ಲಿ, ಸಂಭವನೀಯ ಪ್ರಾಥಮಿಕ ಫಲಿತಾಂಶಗಳ ಒಟ್ಟು ಸಂಖ್ಯೆಯು ಲಭ್ಯವಿರುವ 12 ರಿಂದ ಮೂರು ವಿವರಗಳನ್ನು ಹೊರತೆಗೆಯುವ ವಿಧಾನಗಳ ಸಂಖ್ಯೆಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ. ಮತ್ತು ಅನುಕೂಲಕರ ಫಲಿತಾಂಶಗಳ ಒಟ್ಟು ಸಂಖ್ಯೆಯು ಐದರಿಂದ ಮೂರು ದೋಷಯುಕ್ತ ಭಾಗಗಳನ್ನು ಹೊರತೆಗೆಯುವ ವಿಧಾನಗಳ ಸಂಖ್ಯೆಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ. ಆದ್ದರಿಂದ,
TASK N 12 ದೋಷವನ್ನು ವರದಿ ಮಾಡಿದೆ
ವಿಷಯ: ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಸಂಖ್ಯಾತ್ಮಕ ಗುಣಲಕ್ಷಣಗಳು
ನಿರಂತರವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯೇಬಲ್ ಅನ್ನು ಸಂಭವನೀಯ ವಿತರಣಾ ಸಾಂದ್ರತೆಯಿಂದ ನಿರ್ದಿಷ್ಟಪಡಿಸಲಾಗಿದೆ: 
ನಂತರ ಅದರ ವ್ಯತ್ಯಾಸವೆಂದರೆ ...
ಪರಿಹಾರ:
ನಿರಂತರ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವ್ಯತ್ಯಾಸವನ್ನು ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ಲೆಕ್ಕಹಾಕಬಹುದು
ನಂತರ 
ವಿಷಯ: ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯ ನಿಯಮಗಳು
ಸಂಭವನೀಯ ವಿತರಣಾ ಕಾನೂನಿನಿಂದ ಪ್ರತ್ಯೇಕವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸಲಾಗಿದೆ:
ನಂತರ ಅದರ ಸಂಭವನೀಯತೆ ವಿತರಣೆ ಕಾರ್ಯವು ರೂಪವನ್ನು ಹೊಂದಿದೆ...
| |
|||
 |
|||
 |
|||
 |
ಪರಿಹಾರ:
ಎ-ಪ್ರಿಯರಿ . ನಂತರ
a) ನಲ್ಲಿ,
ಬಿ) ನಲ್ಲಿ,
ಸಿ) ನಲ್ಲಿ,
d) ನಲ್ಲಿ,
d) ನಲ್ಲಿ, .
ಆದ್ದರಿಂದ, 
ವಿಷಯ: ಒಟ್ಟು ಸಂಭವನೀಯತೆ. ಬೇಯಸ್ ಸೂತ್ರಗಳು
5 ಬಿಳಿ ಮತ್ತು 5 ಕಪ್ಪು ಚೆಂಡುಗಳನ್ನು ಹೊಂದಿರುವ ಮೂರು ಕಲಶಗಳಿವೆ, ಮತ್ತು 6 ಬಿಳಿ ಮತ್ತು 4 ಕಪ್ಪು ಚೆಂಡುಗಳನ್ನು ಹೊಂದಿರುವ ಏಳು ಕಲಶಗಳಿವೆ. ಒಂದು ಚೆಂಡನ್ನು ಯಾದೃಚ್ಛಿಕ ಚಿತಾಭಸ್ಮದಿಂದ ಎಳೆಯಲಾಗುತ್ತದೆ. ಆಗ ಈ ಚೆಂಡು ಬಿಳಿಯಾಗಿರುವ ಸಂಭವನೀಯತೆ...
| 0,57 | |||
| 0,43 | |||
| 0,55 | |||
| 0,53 |
ಪರಿಹಾರ:
ಘಟನೆಯ ಸಂಭವನೀಯತೆಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಎ(ಯಾದೃಚ್ಛಿಕವಾಗಿ ಚಿತ್ರಿಸಿದ ಚೆಂಡು ಬಿಳಿಯಾಗಿರುತ್ತದೆ) ಒಟ್ಟು ಸಂಭವನೀಯತೆಯ ಸೂತ್ರವನ್ನು ಅನ್ವಯಿಸಿ: . ಚೆಂಡನ್ನು ಮೊದಲ ಸರಣಿಯ ಉರ್ನ್‌ಗಳಿಂದ ಎಳೆಯುವ ಸಂಭವನೀಯತೆ ಇಲ್ಲಿದೆ; - ಚೆಂಡನ್ನು ಎರಡನೇ ಸರಣಿಯ ಚಿತಾಭಸ್ಮದಿಂದ ಎಳೆಯುವ ಸಂಭವನೀಯತೆ; - ಮೊದಲ ಸರಣಿಯ ಚಿತಾಭಸ್ಮದಿಂದ ಎಳೆಯಲ್ಪಟ್ಟರೆ ಡ್ರಾ ಬಾಲ್ ಬಿಳಿಯಾಗಿರುತ್ತದೆ ಎಂಬ ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆ; - ಎರಡನೇ ಸರಣಿಯ ಚಿತಾಭಸ್ಮದಿಂದ ಎಳೆಯಲ್ಪಟ್ಟ ಚೆಂಡನ್ನು ಬಿಳಿಯಾಗಿರುತ್ತದೆ ಎಂಬ ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆ.
ನಂತರ .
ವಿಷಯ: ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯ ನಿಯಮಗಳು
ಸಂಭವನೀಯ ವಿತರಣಾ ಕಾನೂನಿನಿಂದ ಪ್ರತ್ಯೇಕವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸಲಾಗಿದೆ:
ನಂತರ ಸಂಭವನೀಯತೆ ಸಮಾನ...
ವಿಷಯ: ಸಂಭವನೀಯತೆಯ ನಿರ್ಣಯ
ಡೈ ಅನ್ನು ಎರಡು ಬಾರಿ ಸುತ್ತಿಕೊಳ್ಳಲಾಗುತ್ತದೆ. ಆಗ ಡ್ರಾ ಮಾಡಿದ ಬಿಂದುಗಳ ಮೊತ್ತ ಹತ್ತು ಆಗುವ ಸಂಭವನೀಯತೆ...
ವ್ಯಾಖ್ಯಾನ 2.3. X ನಿಂದ ಸೂಚಿಸಲಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯೇಬಲ್ ಅನ್ನು ಡಿಸ್ಕ್ರೀಟ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಅದು ಸೀಮಿತ ಅಥವಾ ಎಣಿಕೆ ಮಾಡಬಹುದಾದ ಮೌಲ್ಯಗಳ ಗುಂಪನ್ನು ತೆಗೆದುಕೊಂಡರೆ, ಅಂದರೆ. ಸೆಟ್ - ಸೀಮಿತ ಅಥವಾ ಎಣಿಸಬಹುದಾದ ಸೆಟ್.
ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಉದಾಹರಣೆಗಳನ್ನು ಪರಿಗಣಿಸೋಣ.
1.
ಎರಡು ನಾಣ್ಯಗಳನ್ನು ಒಮ್ಮೆ ಎಸೆಯಲಾಗುತ್ತದೆ. ಈ ಪ್ರಯೋಗದಲ್ಲಿನ ಲಾಂಛನಗಳ ಸಂಖ್ಯೆಯು ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಆಗಿದೆ X. ಇದರ ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳು 0,1,2, ಅಂದರೆ. 
- ಒಂದು ಸೀಮಿತ ಸೆಟ್.
2. ನಿರ್ದಿಷ್ಟ ಸಮಯದೊಳಗೆ ಆಂಬ್ಯುಲೆನ್ಸ್ ಕರೆಗಳ ಸಂಖ್ಯೆಯನ್ನು ದಾಖಲಿಸಲಾಗುತ್ತದೆ. ಯಾದೃಚ್ಛಿಕ ಮೌಲ್ಯ X- ಕರೆಗಳ ಸಂಖ್ಯೆ. ಇದರ ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳು 0, 1, 2, 3, ..., ಅಂದರೆ. =(0,1,2,3,...) ಎಣಿಸಬಹುದಾದ ಸೆಟ್ ಆಗಿದೆ.
3. ಗುಂಪಿನಲ್ಲಿ 25 ವಿದ್ಯಾರ್ಥಿಗಳಿದ್ದಾರೆ. ಒಂದು ನಿರ್ದಿಷ್ಟ ದಿನದಂದು, ತರಗತಿಗೆ ಬಂದ ವಿದ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆಯನ್ನು ದಾಖಲಿಸಲಾಗುತ್ತದೆ - ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ X. ಇದರ ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳು: 0, 1, 2, 3, ...,25 ಅಂದರೆ. =(0, 1, 2, 3, ..., 25).
ಉದಾಹರಣೆ 3 ರಲ್ಲಿ ಎಲ್ಲಾ 25 ಜನರು ತರಗತಿಗಳನ್ನು ತಪ್ಪಿಸಿಕೊಳ್ಳಬಾರದು, ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ Xಈ ಮೌಲ್ಯವನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು. ಇದರರ್ಥ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಮೌಲ್ಯಗಳು ವಿಭಿನ್ನ ಸಂಭವನೀಯತೆಗಳನ್ನು ಹೊಂದಿವೆ.
ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಗಣಿತದ ಮಾದರಿಯನ್ನು ಪರಿಗಣಿಸೋಣ.
ಯಾದೃಚ್ಛಿಕ ಪ್ರಯೋಗವನ್ನು ನಡೆಸಲಿ, ಇದು ಪ್ರಾಥಮಿಕ ಘಟನೆಗಳ ಸೀಮಿತ ಅಥವಾ ಎಣಿಕೆ ಮಾಡಬಹುದಾದ ಜಾಗಕ್ಕೆ ಅನುರೂಪವಾಗಿದೆ. ಈ ಜಾಗದ ಮ್ಯಾಪಿಂಗ್ ಅನ್ನು ನೈಜ ಸಂಖ್ಯೆಗಳ ಸೆಟ್‌ಗೆ ಪರಿಗಣಿಸೋಣ, ಅಂದರೆ, ಪ್ರತಿ ಪ್ರಾಥಮಿಕ ಘಟನೆಗೆ ನಿರ್ದಿಷ್ಟ ನೈಜ ಸಂಖ್ಯೆಯನ್ನು ನಿಯೋಜಿಸೋಣ , . ಸಂಖ್ಯೆಗಳ ಸೆಟ್ ಸೀಮಿತವಾಗಿರಬಹುದು ಅಥವಾ ಎಣಿಕೆ ಮಾಡಬಹುದು, ಅಂದರೆ. 
ಅಥವಾ
ಒಂದು-ಬಿಂದು ಸೇರಿದಂತೆ ಯಾವುದೇ ಉಪವಿಭಾಗವನ್ನು ಒಳಗೊಂಡಿರುವ ಉಪವಿಭಾಗಗಳ ವ್ಯವಸ್ಥೆಯು ಸಂಖ್ಯಾತ್ಮಕ ಗುಂಪಿನ (-ಸೀಮಿತ ಅಥವಾ ಎಣಿಸಬಹುದಾದ) -ಬೀಜಗಣಿತವನ್ನು ರೂಪಿಸುತ್ತದೆ.
ಯಾವುದೇ ಪ್ರಾಥಮಿಕ ಘಟನೆಯು ಕೆಲವು ಸಂಭವನೀಯತೆಗಳೊಂದಿಗೆ ಸಂಬಂಧಿಸಿದೆ p i(ಸೀಮಿತ ಎಲ್ಲದರ ಸಂದರ್ಭದಲ್ಲಿ), ಮತ್ತು , ನಂತರ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಪ್ರತಿಯೊಂದು ಮೌಲ್ಯವನ್ನು ನಿರ್ದಿಷ್ಟ ಸಂಭವನೀಯತೆಯೊಂದಿಗೆ ಸಂಯೋಜಿಸಬಹುದು p i, ಅಂದರೆ .
ಅವಕಾಶ Xಅನಿಯಂತ್ರಿತ ನೈಜ ಸಂಖ್ಯೆಯಾಗಿದೆ. ಸೂಚಿಸೋಣ R X (x)ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಆಗಿರುವ ಸಂಭವನೀಯತೆ Xಗೆ ಸಮಾನವಾದ ಮೌಲ್ಯವನ್ನು ತೆಗೆದುಕೊಂಡಿತು X, ಅಂದರೆ P X (x)=P(X=x). ನಂತರ ಕಾರ್ಯ R X (x)ಆ ಮೌಲ್ಯಗಳಿಗೆ ಮಾತ್ರ ಧನಾತ್ಮಕ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು X, ಇದು ಸೀಮಿತ ಅಥವಾ ಎಣಿಸಬಹುದಾದ ಸೆಟ್‌ಗೆ ಸೇರಿದೆ 
, ಮತ್ತು ಎಲ್ಲಾ ಇತರ ಮೌಲ್ಯಗಳಿಗೆ ಈ ಮೌಲ್ಯದ ಸಂಭವನೀಯತೆ P X (x) = 0.
ಆದ್ದರಿಂದ, ನಾವು ಮೌಲ್ಯಗಳ ಗುಂಪನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಿದ್ದೇವೆ, -ಬೀಜಗಣಿತವನ್ನು ಯಾವುದೇ ಉಪವಿಭಾಗಗಳ ವ್ಯವಸ್ಥೆಯಾಗಿ ಮತ್ತು ಪ್ರತಿ ಘಟನೆಗೆ ( X = x) ಸಂಭವನೀಯತೆಯನ್ನು ಹೋಲಿಸಲಾಗಿದೆ ಯಾವುದಕ್ಕೂ, ಅಂದರೆ. ಸಂಭವನೀಯ ಸ್ಥಳವನ್ನು ನಿರ್ಮಿಸಲಾಗಿದೆ.
ಉದಾಹರಣೆಗೆ, ಸಮ್ಮಿತೀಯ ನಾಣ್ಯವನ್ನು ಎರಡು ಬಾರಿ ಎಸೆಯುವುದನ್ನು ಒಳಗೊಂಡಿರುವ ಪ್ರಯೋಗದ ಪ್ರಾಥಮಿಕ ಘಟನೆಗಳ ಸ್ಥಳವು ನಾಲ್ಕು ಪ್ರಾಥಮಿಕ ಘಟನೆಗಳನ್ನು ಒಳಗೊಂಡಿದೆ: , ಅಲ್ಲಿ
ನಾಣ್ಯವನ್ನು ಎರಡು ಬಾರಿ ಎಸೆದಾಗ, ಎರಡು ಬಾಲಗಳು ಕಾಣಿಸಿಕೊಂಡವು; ನಾಣ್ಯವನ್ನು ಎರಡು ಬಾರಿ ಎಸೆದಾಗ, ಎರಡು ಕೋಟುಗಳು ಬಿದ್ದವು;
ನಾಣ್ಯದ ಮೊದಲ ಟಾಸ್‌ನಲ್ಲಿ, ಹ್ಯಾಶ್ ಬಂದಿತು, ಮತ್ತು ಎರಡನೆಯದರಲ್ಲಿ, ಕೋಟ್ ಆಫ್ ಆರ್ಮ್ಸ್;
ನಾಣ್ಯದ ಮೊದಲ ಟಾಸ್‌ನಲ್ಲಿ, ಕೋಟ್ ಆಫ್ ಆರ್ಮ್ಸ್ ಬಂದಿತು, ಮತ್ತು ಎರಡನೆಯದರಲ್ಲಿ, ಹ್ಯಾಶ್ ಮಾರ್ಕ್.
ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ಅನುಮತಿಸಿ X- ಗ್ರ್ಯಾಟಿಂಗ್ ಡ್ರಾಪ್‌ಔಟ್‌ಗಳ ಸಂಖ್ಯೆ. ಇದನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ ಮತ್ತು ಅದರ ಮೌಲ್ಯಗಳ ಸೆಟ್ 
. ಏಕ-ಬಿಂದು ಸೇರಿದಂತೆ ಎಲ್ಲಾ ಸಂಭಾವ್ಯ ಉಪವಿಭಾಗಗಳು ಬೀಜಗಣಿತವನ್ನು ರೂಪಿಸುತ್ತವೆ, ಅಂದರೆ. =(Ø, (1), (2), (0,1), (0,2), (1,2), (0,1,2)).
ಘಟನೆಯ ಸಂಭವನೀಯತೆ ( X=x i}, і = 1,2,3, ಅದರ ಮೂಲಮಾದರಿಯ ಘಟನೆಯ ಸಂಭವಿಸುವಿಕೆಯ ಸಂಭವನೀಯತೆ ಎಂದು ನಾವು ವ್ಯಾಖ್ಯಾನಿಸುತ್ತೇವೆ:
ಆದ್ದರಿಂದ, ಪ್ರಾಥಮಿಕ ಘಟನೆಗಳ ಮೇಲೆ ( X = xi) ಸಂಖ್ಯಾತ್ಮಕ ಕಾರ್ಯವನ್ನು ಹೊಂದಿಸಿ ಆರ್ ಎಕ್ಸ್, ಆದ್ದರಿಂದ 
.
ವ್ಯಾಖ್ಯಾನ 2.4. ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯೇಬಲ್ನ ವಿತರಣೆಯ ನಿಯಮವು ಜೋಡಿ ಸಂಖ್ಯೆಗಳ ಒಂದು ಗುಂಪಾಗಿದೆ (x i, р i), ಇಲ್ಲಿ x i ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳು ಮತ್ತು р i ಎಂಬುದು ಈ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುವ ಸಂಭವನೀಯತೆಗಳು, ಮತ್ತು .
ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯೇಬಲ್ನ ವಿತರಣಾ ನಿಯಮವನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸುವ ಸರಳ ರೂಪವು ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳನ್ನು ಮತ್ತು ಅನುಗುಣವಾದ ಸಂಭವನೀಯತೆಗಳನ್ನು ಪಟ್ಟಿ ಮಾಡುವ ಕೋಷ್ಟಕವಾಗಿದೆ:
| … | … | ||||
| … | … |
ಅಂತಹ ಕೋಷ್ಟಕವನ್ನು ವಿತರಣಾ ಸರಣಿ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ವಿತರಣಾ ಸರಣಿಯನ್ನು ಹೆಚ್ಚು ದೃಷ್ಟಿಗೋಚರವಾಗಿ ನೀಡಲು, ಅದನ್ನು ಸಚಿತ್ರವಾಗಿ ಚಿತ್ರಿಸಲಾಗಿದೆ: ಅಕ್ಷದ ಮೇಲೆ ಓಹ್ಚುಕ್ಕೆಗಳು x iಮತ್ತು ಅವುಗಳಿಂದ ಉದ್ದದ ಲಂಬಗಳನ್ನು ಎಳೆಯಿರಿ p i. ಪರಿಣಾಮವಾಗಿ ಅಂಕಗಳನ್ನು ಸಂಪರ್ಕಿಸಲಾಗಿದೆ ಮತ್ತು ಬಹುಭುಜಾಕೃತಿಯನ್ನು ಪಡೆಯಲಾಗುತ್ತದೆ, ಇದು ವಿತರಣಾ ಕಾನೂನಿನ ರೂಪಗಳಲ್ಲಿ ಒಂದಾಗಿದೆ (ಚಿತ್ರ 2.1).
ಹೀಗಾಗಿ, ಪ್ರತ್ಯೇಕವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸಲು, ನೀವು ಅದರ ಮೌಲ್ಯಗಳು ಮತ್ತು ಅನುಗುಣವಾದ ಸಂಭವನೀಯತೆಗಳನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸಬೇಕು.
ಉದಾಹರಣೆ 2.2.ಪ್ರತಿ ಬಾರಿ ಸಂಭವನೀಯತೆಯೊಂದಿಗೆ ನಾಣ್ಯವನ್ನು ಸೇರಿಸಿದಾಗ ಯಂತ್ರದ ನಗದು ಸ್ಲಾಟ್ ಅನ್ನು ಪ್ರಚೋದಿಸಲಾಗುತ್ತದೆ ಆರ್. ಒಮ್ಮೆ ಅದನ್ನು ಪ್ರಚೋದಿಸಿದರೆ, ನಾಣ್ಯಗಳು ಕೆಳಗೆ ಬರುವುದಿಲ್ಲ. ಅವಕಾಶ X- ಯಂತ್ರದ ನಗದು ಸ್ಲಾಟ್ ಅನ್ನು ಪ್ರಚೋದಿಸುವ ಮೊದಲು ಸೇರಿಸಬೇಕಾದ ನಾಣ್ಯಗಳ ಸಂಖ್ಯೆ. ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ವಿತರಣೆಯ ಸರಣಿಯನ್ನು ನಿರ್ಮಿಸಿ X.
ಪರಿಹಾರ.ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳು X: x 1 = 1, x 2 = 2,..., x k = k, ...ಈ ಮೌಲ್ಯಗಳ ಸಂಭವನೀಯತೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ: ಪು 1- ಹಣ ಸ್ವೀಕರಿಸುವವರು ಮೊದಲ ಬಾರಿಗೆ ಅದನ್ನು ಕಡಿಮೆ ಮಾಡಿದಾಗ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಸಂಭವನೀಯತೆ, ಮತ್ತು p 1 = p; ಪು 2 -ಎರಡು ಪ್ರಯತ್ನಗಳನ್ನು ಮಾಡುವ ಸಂಭವನೀಯತೆ. ಇದನ್ನು ಮಾಡಲು, ಇದು ಅವಶ್ಯಕ: 1) ಹಣ ಸ್ವೀಕರಿಸುವವರು ಮೊದಲ ಪ್ರಯತ್ನದಲ್ಲಿ ಕೆಲಸ ಮಾಡುವುದಿಲ್ಲ; 2) ಎರಡನೇ ಪ್ರಯತ್ನದಲ್ಲಿ ಅದು ಕೆಲಸ ಮಾಡಿದೆ. ಈ ಘಟನೆಯ ಸಂಭವನೀಯತೆ (1–р) ಆರ್. ಅಂತೆಯೇ 
ಮತ್ತು ಇತ್ಯಾದಿ, 
. ವಿತರಣಾ ಶ್ರೇಣಿ Xರೂಪವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ
| 1 | 2 | 3 | … | ಗೆ | … | |
| ಆರ್ | qp | q 2 ಪು | q r -1 p |
ಸಂಭವನೀಯತೆಗಳನ್ನು ಗಮನಿಸಿ ಆರ್ ಕೆಛೇದದೊಂದಿಗೆ ಜ್ಯಾಮಿತೀಯ ಪ್ರಗತಿಯನ್ನು ರೂಪಿಸಿ: 1–p=q, q<1, ಆದ್ದರಿಂದ ಈ ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಜ್ಯಾಮಿತೀಯ.
ಗಣಿತದ ಮಾದರಿಯನ್ನು ನಿರ್ಮಿಸಲಾಗಿದೆ ಎಂದು ನಾವು ಊಹಿಸೋಣ 
ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಮೂಲಕ ವಿವರಿಸಿದ ಪ್ರಯೋಗ X, ಮತ್ತು ಅನಿಯಂತ್ರಿತ ಘಟನೆಗಳ ಸಂಭವಿಸುವಿಕೆಯ ಸಂಭವನೀಯತೆಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವುದನ್ನು ಪರಿಗಣಿಸಿ.
ಅನಿಯಂತ್ರಿತ ಘಟನೆಯು ಸೀಮಿತ ಅಥವಾ ಎಣಿಕೆ ಮಾಡಬಹುದಾದ ಮೌಲ್ಯಗಳ ಗುಂಪನ್ನು ಹೊಂದಿರಲಿ x i: A= {x 1, x 2,..., x i, ....ಈವೆಂಟ್ ಎರೂಪದ ಹೊಂದಾಣಿಕೆಯಾಗದ ಘಟನೆಗಳ ಒಕ್ಕೂಟವಾಗಿ ಪ್ರತಿನಿಧಿಸಬಹುದು: ನಂತರ, ಕೊಲ್ಮೊಗೊರೊವ್ ಅವರ ಮೂಲತತ್ವ 3 ಅನ್ನು ಬಳಸಿ , ನಾವು ಪಡೆಯುತ್ತೇವೆ
ನಾವು ಘಟನೆಗಳ ಸಂಭವಿಸುವಿಕೆಯ ಸಂಭವನೀಯತೆಗಳನ್ನು ಅವುಗಳ ಮೂಲಮಾದರಿಯ ಘಟನೆಗಳ ಸಂಭವಿಸುವಿಕೆಯ ಸಂಭವನೀಯತೆಗಳಿಗೆ ಸಮನಾಗಿರುತ್ತದೆ ಎಂದು ನಿರ್ಧರಿಸಿದ್ದೇವೆ. ಇದರರ್ಥ ಯಾವುದೇ ಘಟನೆಯ ಸಂಭವನೀಯತೆ 
, , ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ಲೆಕ್ಕಾಚಾರ ಮಾಡಬಹುದು, ಏಕೆಂದರೆ ಈ ಘಟನೆಯನ್ನು ಘಟನೆಗಳ ಒಕ್ಕೂಟದ ರೂಪದಲ್ಲಿ ಪ್ರತಿನಿಧಿಸಬಹುದು, ಅಲ್ಲಿ .
ನಂತರ ವಿತರಣೆ ಕಾರ್ಯ F(x) = Р(–<Х<х) ಸೂತ್ರದಿಂದ ಕಂಡುಹಿಡಿಯಲಾಗುತ್ತದೆ. ಇದು ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವಿತರಣಾ ಕಾರ್ಯವನ್ನು ಅನುಸರಿಸುತ್ತದೆ Xನಿರಂತರವಾಗಿದೆ ಮತ್ತು ಜಿಗಿತಗಳಲ್ಲಿ ಹೆಚ್ಚಾಗುತ್ತದೆ, ಅಂದರೆ ಇದು ಒಂದು ಹಂತದ ಕಾರ್ಯವಾಗಿದೆ (ಚಿತ್ರ 2.2):
ಸೆಟ್ ಸೀಮಿತವಾಗಿದ್ದರೆ, ಸೂತ್ರದಲ್ಲಿನ ಪದಗಳ ಸಂಖ್ಯೆ ಸೀಮಿತವಾಗಿರುತ್ತದೆ, ಆದರೆ ಅದನ್ನು ಎಣಿಕೆ ಮಾಡಬಹುದಾದರೆ, ಪದಗಳ ಸಂಖ್ಯೆಯನ್ನು ಎಣಿಸಬಹುದು.
ಉದಾಹರಣೆ 2.3.ತಾಂತ್ರಿಕ ಸಾಧನವು ಪರಸ್ಪರ ಸ್ವತಂತ್ರವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಎರಡು ಅಂಶಗಳನ್ನು ಒಳಗೊಂಡಿದೆ. T ಸಮಯದಲ್ಲಿ ಮೊದಲ ಅಂಶದ ವೈಫಲ್ಯದ ಸಂಭವನೀಯತೆ 0.2, ಮತ್ತು ಎರಡನೇ ಅಂಶದ ವೈಫಲ್ಯದ ಸಂಭವನೀಯತೆ 0.1 ಆಗಿದೆ. ಯಾದೃಚ್ಛಿಕ ಮೌಲ್ಯ X T ಸಮಯದಲ್ಲಿ ವಿಫಲವಾದ ಅಂಶಗಳ ಸಂಖ್ಯೆ. ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವಿತರಣಾ ಕಾರ್ಯವನ್ನು ಹುಡುಕಿ ಮತ್ತು ಅದರ ಗ್ರಾಫ್ ಅನ್ನು ರೂಪಿಸಿ.
ಪರಿಹಾರ.ತಾಂತ್ರಿಕ ಸಾಧನದ ಎರಡು ಅಂಶಗಳ ವಿಶ್ವಾಸಾರ್ಹತೆಯನ್ನು ಅಧ್ಯಯನ ಮಾಡುವ ಪ್ರಯೋಗದ ಪ್ರಾಥಮಿಕ ಘಟನೆಗಳ ಸ್ಥಳವನ್ನು ನಾಲ್ಕು ಪ್ರಾಥಮಿಕ ಘಟನೆಗಳಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ , , , : – ಎರಡೂ ಅಂಶಗಳು ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತವೆ; - ಮೊದಲ ಅಂಶವು ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತಿದೆ, ಎರಡನೆಯದು ದೋಷಯುಕ್ತವಾಗಿದೆ; - ಮೊದಲ ಅಂಶವು ದೋಷಯುಕ್ತವಾಗಿದೆ, ಎರಡನೆಯದು ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತಿದೆ; - ಎರಡೂ ಅಂಶಗಳು ದೋಷಯುಕ್ತವಾಗಿವೆ. ಪ್ರತಿಯೊಂದು ಪ್ರಾಥಮಿಕ ಘಟನೆಗಳನ್ನು ಸ್ಥಳಗಳ ಪ್ರಾಥಮಿಕ ಘಟನೆಗಳ ಮೂಲಕ ವ್ಯಕ್ತಪಡಿಸಬಹುದು 
ಮತ್ತು 
, ಅಲ್ಲಿ - ಮೊದಲ ಅಂಶವು ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ; - ಮೊದಲ ಅಂಶ ವಿಫಲವಾಗಿದೆ; - ಎರಡನೇ ಅಂಶವು ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತಿದೆ; - ಎರಡನೇ ಅಂಶ ವಿಫಲವಾಗಿದೆ. ನಂತರ, ಮತ್ತು ತಾಂತ್ರಿಕ ಸಾಧನದ ಅಂಶಗಳು ಪರಸ್ಪರ ಸ್ವತಂತ್ರವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುವುದರಿಂದ, ನಂತರ
8. ಪ್ರತ್ಯೇಕವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಮೌಲ್ಯಗಳು ಮಧ್ಯಂತರಕ್ಕೆ ಸೇರಿರುವ ಸಂಭವನೀಯತೆ ಏನು?
ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯೇಬಲ್ ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತದೆ, ಅದು ಕೆಲವು ಸಂಭವನೀಯತೆಗಳೊಂದಿಗೆ ವೈಯಕ್ತಿಕ, ಪ್ರತ್ಯೇಕ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು.
ಉದಾಹರಣೆ 1.ಮೂರು ನಾಣ್ಯ ಟಾಸ್‌ಗಳಲ್ಲಿ ಕೋಟ್ ಆಫ್ ಆರ್ಮ್ಸ್ ಎಷ್ಟು ಬಾರಿ ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತದೆ. ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳು: 0, 1, 2, 3, ಅವುಗಳ ಸಂಭವನೀಯತೆಗಳು ಕ್ರಮವಾಗಿ ಸಮಾನವಾಗಿರುತ್ತದೆ:
P(0) = ; Р(1) = ; Р(2) = ; Р(3) = .
ಉದಾಹರಣೆ 2.ಐದು ಅಂಶಗಳನ್ನು ಒಳಗೊಂಡಿರುವ ಸಾಧನದಲ್ಲಿ ವಿಫಲವಾದ ಅಂಶಗಳ ಸಂಖ್ಯೆ. ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳು: 0, 1, 2, 3, 4, 5; ಅವುಗಳ ಸಂಭವನೀಯತೆಗಳು ಪ್ರತಿ ಅಂಶದ ವಿಶ್ವಾಸಾರ್ಹತೆಯನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ.
ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ Xವಿತರಣಾ ಸರಣಿ ಅಥವಾ ವಿತರಣಾ ಕಾರ್ಯ (ಅವಿಭಾಜ್ಯ ವಿತರಣಾ ಕಾನೂನು) ಮೂಲಕ ನೀಡಬಹುದು.
ವಿತರಣೆಯ ಸಮೀಪದಲ್ಲಿದೆ ಎಲ್ಲಾ ಸಂಭಾವ್ಯ ಮೌಲ್ಯಗಳ ಸೆಟ್ ಆಗಿದೆ Xiಮತ್ತು ಅವುಗಳ ಅನುಗುಣವಾದ ಸಂಭವನೀಯತೆಗಳು ಆರ್ನಾನು = ಪಿ(X = xi), ಇದನ್ನು ಟೇಬಲ್ ಆಗಿ ಸೂಚಿಸಬಹುದು:
| x i | x n |
|||
| p i | ಆರ್ ಎನ್ |
ಅದೇ ಸಮಯದಲ್ಲಿ, ಸಂಭವನೀಯತೆಗಳು ಆರ್iಸ್ಥಿತಿಯನ್ನು ಪೂರೈಸಲು
ಆರ್i= 1 ಏಕೆಂದರೆ 
ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳ ಸಂಖ್ಯೆ ಎಲ್ಲಿದೆ ಎನ್ಸೀಮಿತ ಅಥವಾ ಅನಂತವಾಗಿರಬಹುದು.
ವಿತರಣಾ ಸರಣಿಯ ಚಿತ್ರಾತ್ಮಕ ಪ್ರಾತಿನಿಧ್ಯ ವಿತರಣಾ ಬಹುಭುಜಾಕೃತಿ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ . ಅದನ್ನು ನಿರ್ಮಿಸಲು, ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳು ( Xi) x-ಅಕ್ಷದ ಉದ್ದಕ್ಕೂ ಮತ್ತು ಸಂಭವನೀಯತೆಗಳನ್ನು ರೂಪಿಸಲಾಗಿದೆ ಆರ್i- ಆರ್ಡಿನೇಟ್ ಅಕ್ಷದ ಉದ್ದಕ್ಕೂ; ಅಂಕಗಳು ಎiನಿರ್ದೇಶಾಂಕಗಳೊಂದಿಗೆ ( Xನಾನು, ಆರ್i) ಮುರಿದ ರೇಖೆಗಳಿಂದ ಸಂಪರ್ಕಿಸಲಾಗಿದೆ.
ವಿತರಣಾ ಕಾರ್ಯ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ Xಕಾರ್ಯ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಎಫ್(X), ಬಿಂದುವಿನಲ್ಲಿ ಅವರ ಮೌಲ್ಯ Xಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಸಂಭವನೀಯತೆಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ Xಈ ಮೌಲ್ಯಕ್ಕಿಂತ ಕಡಿಮೆ ಇರುತ್ತದೆ X, ಅದು
F(x) = P(X< х).
ಕಾರ್ಯ ಎಫ್(X) ಫಾರ್ ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ಸೂತ್ರದ ಮೂಲಕ ಲೆಕ್ಕಹಾಕಲಾಗಿದೆ
ಎಫ್(X) = ಆರ್i , (1.10.1)
ಅಲ್ಲಿ ಸಂಕಲನವನ್ನು ಎಲ್ಲಾ ಮೌಲ್ಯಗಳ ಮೇಲೆ ನಡೆಸಲಾಗುತ್ತದೆ i, ಯಾವುದಕ್ಕಾಗಿ Xi< х.
ಉದಾಹರಣೆ 3. 100 ಉತ್ಪನ್ನಗಳನ್ನು ಒಳಗೊಂಡಿರುವ ಬ್ಯಾಚ್‌ನಿಂದ, ಅದರಲ್ಲಿ 10 ದೋಷಪೂರಿತವಾಗಿದೆ, ಅವುಗಳ ಗುಣಮಟ್ಟವನ್ನು ಪರಿಶೀಲಿಸಲು ಐದು ಉತ್ಪನ್ನಗಳನ್ನು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಆಯ್ಕೆ ಮಾಡಲಾಗುತ್ತದೆ. ಯಾದೃಚ್ಛಿಕ ಸಂಖ್ಯೆಯ ವಿತರಣೆಗಳ ಸರಣಿಯನ್ನು ನಿರ್ಮಿಸಿ Xಮಾದರಿಯಲ್ಲಿ ಒಳಗೊಂಡಿರುವ ದೋಷಯುಕ್ತ ಉತ್ಪನ್ನಗಳು.
ಪರಿಹಾರ. ಮಾದರಿಯಲ್ಲಿ ದೋಷಯುಕ್ತ ಉತ್ಪನ್ನಗಳ ಸಂಖ್ಯೆಯು 0 ರಿಂದ 5 ರವರೆಗಿನ ಯಾವುದೇ ಪೂರ್ಣಾಂಕವಾಗಿರಬಹುದು, ನಂತರ ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳು Xiಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ Xಸಮಾನವಾಗಿವೆ:
x 1 = 0, x 2 = 1, x 3 = 2, x 4 = 3, x 5 = 4, x 6 = 5.
ಸಂಭವನೀಯತೆ ಆರ್(ಎಕ್ಸ್ = ಕೆ) ಮಾದರಿಯು ನಿಖರವಾಗಿ ಒಳಗೊಂಡಿದೆ ಕೆ(ಕೆ = 0, 1, 2, 3, 4, 5) ದೋಷಯುಕ್ತ ಉತ್ಪನ್ನಗಳು, ಸಮಾನವಾಗಿರುತ್ತದೆ
P (X = k) = .
0.001 ನಿಖರತೆಯೊಂದಿಗೆ ಈ ಸೂತ್ರವನ್ನು ಬಳಸುವ ಲೆಕ್ಕಾಚಾರಗಳ ಪರಿಣಾಮವಾಗಿ, ನಾವು ಪಡೆಯುತ್ತೇವೆ:
ಆರ್ 1 = ಪಿ(X = 0) @ 0,583;ಆರ್ 2 = ಪಿ(X = 1) @ 0,340;ಆರ್ 3 = ಪಿ(X = 2) @ 0,070;
ಆರ್ 4 = ಪಿ(X = 3) @ 0,007;ಆರ್ 5 = ಪಿ(X= 4) @ 0;ಆರ್ 6 = ಪಿ(X = 5) @ 0.
ಪರಿಶೀಲಿಸಲು ಸಮಾನತೆಯನ್ನು ಬಳಸುವುದು ಆರ್ಕೆ=1, ಲೆಕ್ಕಾಚಾರಗಳು ಮತ್ತು ಪೂರ್ಣಾಂಕವನ್ನು ಸರಿಯಾಗಿ ಮಾಡಲಾಗಿದೆಯೆ ಎಂದು ನಾವು ಖಚಿತಪಡಿಸಿಕೊಳ್ಳುತ್ತೇವೆ (ಟೇಬಲ್ ನೋಡಿ).
| x i | ||||||
| p i |
ಉದಾಹರಣೆ 4.ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವಿತರಣಾ ಸರಣಿಯನ್ನು ನೀಡಲಾಗಿದೆ X :
| x i | |||||
| p i |
ಸಂಭವನೀಯತೆ ವಿತರಣೆ ಕಾರ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ ಎಫ್(X) ಈ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯೇಬಲ್ ಮತ್ತು ಅದನ್ನು ನಿರ್ಮಿಸಿ.
ಪರಿಹಾರ. ಒಂದು ವೇಳೆ Xನಂತರ £ 10 ಎಫ್(X)= ಪಿ(X<X) = 0;
10 ಆಗಿದ್ದರೆ<Xನಂತರ £ 20 ಎಫ್(X)= ಪಿ(X<X) = 0,2 ;
20 ಆಗಿದ್ದರೆ<Xನಂತರ £ 30 ಎಫ್(X)= ಪಿ(X<X) = 0,2 + 0,3 = 0,5 ;
30 ಆಗಿದ್ದರೆ<Xನಂತರ £ 40 ಎಫ್(X)= ಪಿ(X<X) = 0,2 + 0,3 + 0,35 = 0,85 ;
40 ಆಗಿದ್ದರೆ<Xನಂತರ £ 50 ಎಫ್(X)= ಪಿ(X<X) = 0,2 + 0,3 + 0,35 + 0,1=0,95 ;
ಒಂದು ವೇಳೆ X> 50, ನಂತರ ಎಫ್(X)= ಪಿ(X<X) = 0,2 + 0,3 + 0,35 + 0,1 + 0,05 = 1.
ಸಂಭವನೀಯತೆ ಸಿದ್ಧಾಂತದ ಅನ್ವಯಗಳಲ್ಲಿ, ಪ್ರಯೋಗದ ಪರಿಮಾಣಾತ್ಮಕ ಗುಣಲಕ್ಷಣಗಳು ಪ್ರಾಥಮಿಕ ಪ್ರಾಮುಖ್ಯತೆಯನ್ನು ಹೊಂದಿವೆ. ಪರಿಮಾಣಾತ್ಮಕವಾಗಿ ನಿರ್ಧರಿಸಬಹುದಾದ ಪ್ರಮಾಣ ಮತ್ತು ಪ್ರಯೋಗದ ಪರಿಣಾಮವಾಗಿ, ಪ್ರಕರಣವನ್ನು ಅವಲಂಬಿಸಿ ವಿಭಿನ್ನ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್.
ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಉದಾಹರಣೆಗಳು:
1. ಒಂದು ಡೈನ ಹತ್ತು ಎಸೆತಗಳಲ್ಲಿ ಸಮ ಸಂಖ್ಯೆಯ ಬಿಂದುಗಳು ಎಷ್ಟು ಬಾರಿ ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತವೆ.
2. ಸರಣಿ ಹೊಡೆತಗಳನ್ನು ಹಾರಿಸುವ ಶೂಟರ್‌ನಿಂದ ಗುರಿಯ ಮೇಲೆ ಹಿಟ್‌ಗಳ ಸಂಖ್ಯೆ.
3. ಸ್ಫೋಟಗೊಳ್ಳುವ ಶೆಲ್ನ ತುಣುಕುಗಳ ಸಂಖ್ಯೆ.
ನೀಡಲಾದ ಪ್ರತಿಯೊಂದು ಉದಾಹರಣೆಗಳಲ್ಲಿ, ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಪ್ರತ್ಯೇಕ ಮೌಲ್ಯಗಳನ್ನು ಮಾತ್ರ ತೆಗೆದುಕೊಳ್ಳಬಹುದು, ಅಂದರೆ, ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಗಳ ಸರಣಿಯನ್ನು ಬಳಸಿಕೊಂಡು ಸಂಖ್ಯೆ ಮಾಡಬಹುದಾದ ಮೌಲ್ಯಗಳು.
ಅಂತಹ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್, ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳನ್ನು ಪ್ರತ್ಯೇಕ ಪ್ರತ್ಯೇಕ ಸಂಖ್ಯೆಗಳು, ಈ ವೇರಿಯಬಲ್ ಕೆಲವು ಸಂಭವನೀಯತೆಗಳೊಂದಿಗೆ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ, ಇದನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಪ್ರತ್ಯೇಕವಾದ.
ಪ್ರತ್ಯೇಕವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳ ಸಂಖ್ಯೆಯು ಸೀಮಿತ ಅಥವಾ ಅನಂತವಾಗಿರಬಹುದು (ಎಣಿಕೆ ಮಾಡಬಹುದಾದ).
ವಿತರಣೆಯ ಕಾನೂನುಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅದರ ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳು ಮತ್ತು ಅವುಗಳ ಅನುಗುಣವಾದ ಸಂಭವನೀಯತೆಗಳ ಪಟ್ಟಿಯಾಗಿದೆ. ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯೇಬಲ್ನ ವಿತರಣಾ ನಿಯಮವನ್ನು ಟೇಬಲ್ ರೂಪದಲ್ಲಿ (ಸಂಭಾವ್ಯ ವಿತರಣಾ ಸರಣಿ), ವಿಶ್ಲೇಷಣಾತ್ಮಕವಾಗಿ ಮತ್ತು ಸಚಿತ್ರವಾಗಿ (ಸಂಭವ ವಿತರಣಾ ಬಹುಭುಜಾಕೃತಿ) ನಿರ್ದಿಷ್ಟಪಡಿಸಬಹುದು.
ಪ್ರಯೋಗವನ್ನು ನಡೆಸುವಾಗ, "ಸರಾಸರಿ" ಅಧ್ಯಯನದ ಮೌಲ್ಯವನ್ನು ಮೌಲ್ಯಮಾಪನ ಮಾಡುವುದು ಅಗತ್ಯವಾಗಿರುತ್ತದೆ. ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಸರಾಸರಿ ಮೌಲ್ಯದ ಪಾತ್ರವನ್ನು ಎಂಬ ಸಂಖ್ಯಾತ್ಮಕ ಗುಣಲಕ್ಷಣದಿಂದ ಆಡಲಾಗುತ್ತದೆ ಗಣಿತದ ನಿರೀಕ್ಷೆ,ಇದು ಸೂತ್ರದಿಂದ ನಿರ್ಧರಿಸಲ್ಪಡುತ್ತದೆ
ಎಲ್ಲಿ X 1 , X 2 ,.. , X ಎನ್- ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಮೌಲ್ಯಗಳು X, ಎ ಪ 1 ,ಪ 2 , ... , ಪ ಎನ್- ಈ ಮೌಲ್ಯಗಳ ಸಂಭವನೀಯತೆಗಳು (ಗಮನಿಸಿ ಪ 1 + ಪ 2 +…+ ಪ ಎನ್ = 1).
ಉದಾಹರಣೆ. ಗುರಿಯಲ್ಲಿ ಶೂಟಿಂಗ್ ನಡೆಸಲಾಗುತ್ತದೆ (ಚಿತ್ರ 11).
I ನಲ್ಲಿನ ಹಿಟ್ ಮೂರು ಅಂಕಗಳನ್ನು ನೀಡುತ್ತದೆ, II ರಲ್ಲಿ - ಎರಡು ಅಂಕಗಳು, III ರಲ್ಲಿ - ಒಂದು ಪಾಯಿಂಟ್. ಒಬ್ಬ ಶೂಟರ್ ಒಂದು ಹೊಡೆತದಲ್ಲಿ ಗಳಿಸಿದ ಅಂಕಗಳ ಸಂಖ್ಯೆಯು ರೂಪದ ವಿತರಣಾ ನಿಯಮವನ್ನು ಹೊಂದಿದೆ
ಶೂಟರ್‌ಗಳ ಕೌಶಲ್ಯವನ್ನು ಹೋಲಿಸಲು, ಗಳಿಸಿದ ಅಂಕಗಳ ಸರಾಸರಿ ಮೌಲ್ಯಗಳನ್ನು ಹೋಲಿಸಲು ಸಾಕು, ಅಂದರೆ. ಗಣಿತದ ನಿರೀಕ್ಷೆಗಳು ಎಂ(X) ಮತ್ತು ಎಂ(ವೈ):
ಎಂ(X) = 1 0,4 + 2 0,2 + 3 0,4 = 2,0,
ಎಂ(ವೈ) = 1 0,2 + 2 0,5 + 3 0,3 = 2,1.
ಎರಡನೇ ಶೂಟರ್ ಸರಾಸರಿ ಸ್ವಲ್ಪ ಹೆಚ್ಚಿನ ಸಂಖ್ಯೆಯ ಅಂಕಗಳನ್ನು ನೀಡುತ್ತದೆ, ಅಂದರೆ. ಪದೇ ಪದೇ ಹಾರಿಸಿದಾಗ ಅದು ಉತ್ತಮ ಫಲಿತಾಂಶವನ್ನು ನೀಡುತ್ತದೆ.
ಗಣಿತದ ನಿರೀಕ್ಷೆಯ ಗುಣಲಕ್ಷಣಗಳನ್ನು ನಾವು ಗಮನಿಸೋಣ:
1. ಸ್ಥಿರ ಮೌಲ್ಯದ ಗಣಿತದ ನಿರೀಕ್ಷೆಯು ಸ್ಥಿರತೆಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:
ಎಂ(ಸಿ) = ಸಿ.
2. ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಮೊತ್ತದ ಗಣಿತದ ನಿರೀಕ್ಷೆಯು ಪದಗಳ ಗಣಿತದ ನಿರೀಕ್ಷೆಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ:
ಎಂ =(X 1 + X 2 +…+ X ಎನ್)= ಎಂ(X 1)+ ಎಂ(X 2)+…+ ಎಂ(X ಎನ್).
3. ಪರಸ್ಪರ ಸ್ವತಂತ್ರ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಉತ್ಪನ್ನದ ಗಣಿತದ ನಿರೀಕ್ಷೆಯು ಅಂಶಗಳ ಗಣಿತದ ನಿರೀಕ್ಷೆಗಳ ಉತ್ಪನ್ನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ
ಎಂ(X 1 X 2 … X ಎನ್) = ಎಂ(X 1)ಎಂ(X 2)… ಎಂ(X ಎನ್).
4. ದ್ವಿಪದ ವಿತರಣೆಯ ಗಣಿತದ ನಿರಾಕರಣೆಯು ಪ್ರಯೋಗಗಳ ಸಂಖ್ಯೆ ಮತ್ತು ಒಂದು ಪ್ರಯೋಗದಲ್ಲಿ ಸಂಭವಿಸುವ ಘಟನೆಯ ಸಂಭವನೀಯತೆಯ ಉತ್ಪನ್ನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ (ಕಾರ್ಯ 4.6).
ಎಂ(X) = pr.
ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ "ಸರಾಸರಿಯಲ್ಲಿ" ಅದರ ಗಣಿತದ ನಿರೀಕ್ಷೆಯಿಂದ ಹೇಗೆ ವಿಪಥಗೊಳ್ಳುತ್ತದೆ ಎಂಬುದನ್ನು ನಿರ್ಣಯಿಸಲು, ಅಂದರೆ. ಸಂಭವನೀಯತೆ ಸಿದ್ಧಾಂತದಲ್ಲಿ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಮೌಲ್ಯಗಳ ಹರಡುವಿಕೆಯನ್ನು ನಿರೂಪಿಸಲು, ಪ್ರಸರಣದ ಪರಿಕಲ್ಪನೆಯನ್ನು ಬಳಸಲಾಗುತ್ತದೆ.
ವ್ಯತ್ಯಾಸಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ Xವರ್ಗ ವಿಚಲನದ ಗಣಿತದ ನಿರೀಕ್ಷೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ:
ಡಿ(X) = ಎಂ[(X - ಎಂ(X)) 2 ].
ಪ್ರಸರಣವು ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಪ್ರಸರಣದ ಸಂಖ್ಯಾತ್ಮಕ ಲಕ್ಷಣವಾಗಿದೆ. ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಪ್ರಸರಣವು ಚಿಕ್ಕದಾಗಿದೆ, ಅದರ ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳು ಗಣಿತದ ನಿರೀಕ್ಷೆಯ ಸುತ್ತ ಹೆಚ್ಚು ನಿಕಟವಾಗಿ ನೆಲೆಗೊಂಡಿವೆ ಎಂದು ವ್ಯಾಖ್ಯಾನದಿಂದ ಸ್ಪಷ್ಟವಾಗುತ್ತದೆ, ಅಂದರೆ, ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಮೌಲ್ಯಗಳು ಅದರ ಗಣಿತದ ನಿರೀಕ್ಷೆಯಿಂದ ನಿರೂಪಿಸಲ್ಪಡುತ್ತವೆ. .
ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ವ್ಯತ್ಯಾಸವನ್ನು ಲೆಕ್ಕಹಾಕಬಹುದು ಎಂದು ವ್ಯಾಖ್ಯಾನದಿಂದ ಅದು ಅನುಸರಿಸುತ್ತದೆ
.
ಮತ್ತೊಂದು ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ವ್ಯತ್ಯಾಸವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಅನುಕೂಲಕರವಾಗಿದೆ:
ಡಿ(X) = ಎಂ(X 2) - (ಎಂ(X)) 2 .
ಪ್ರಸರಣವು ಈ ಕೆಳಗಿನ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿದೆ:
1. ಸ್ಥಿರಾಂಕದ ವ್ಯತ್ಯಾಸವು ಶೂನ್ಯವಾಗಿರುತ್ತದೆ:
ಡಿ(ಸಿ) = 0.
2. ಸ್ಥಿರವಾದ ಅಂಶವನ್ನು ವರ್ಗೀಕರಿಸುವ ಮೂಲಕ ಪ್ರಸರಣ ಚಿಹ್ನೆಯಿಂದ ಹೊರತೆಗೆಯಬಹುದು:
ಡಿ(CX) = ಸಿ 2 ಡಿ(X).
3. ಸ್ವತಂತ್ರ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಮೊತ್ತದ ವ್ಯತ್ಯಾಸವು ಪದಗಳ ವ್ಯತ್ಯಾಸದ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:
ಡಿ(X 1 + X 2 + X 3 +…+ X ಎನ್)= ಡಿ(X 1)+ ಡಿ(X 2)+…+ ಡಿ(X ಎನ್)
4. ದ್ವಿಪದ ವಿತರಣೆಯ ವ್ಯತ್ಯಾಸವು ಪ್ರಯೋಗಗಳ ಸಂಖ್ಯೆಯ ಉತ್ಪನ್ನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಮತ್ತು ಒಂದು ಪ್ರಯೋಗದಲ್ಲಿ ಈವೆಂಟ್ ಸಂಭವಿಸುವ ಮತ್ತು ಸಂಭವಿಸದಿರುವ ಸಂಭವನೀಯತೆ:
ಡಿ(X) = npq.
ಸಂಭವನೀಯತೆ ಸಿದ್ಧಾಂತದಲ್ಲಿ, ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವ್ಯತ್ಯಾಸದ ವರ್ಗಮೂಲಕ್ಕೆ ಸಮಾನವಾದ ಸಂಖ್ಯಾತ್ಮಕ ಗುಣಲಕ್ಷಣವನ್ನು ಹೆಚ್ಚಾಗಿ ಬಳಸಲಾಗುತ್ತದೆ. ಈ ಸಂಖ್ಯಾತ್ಮಕ ಲಕ್ಷಣವನ್ನು ಸರಾಸರಿ ಚದರ ವಿಚಲನ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಇದನ್ನು ಚಿಹ್ನೆಯಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ
.
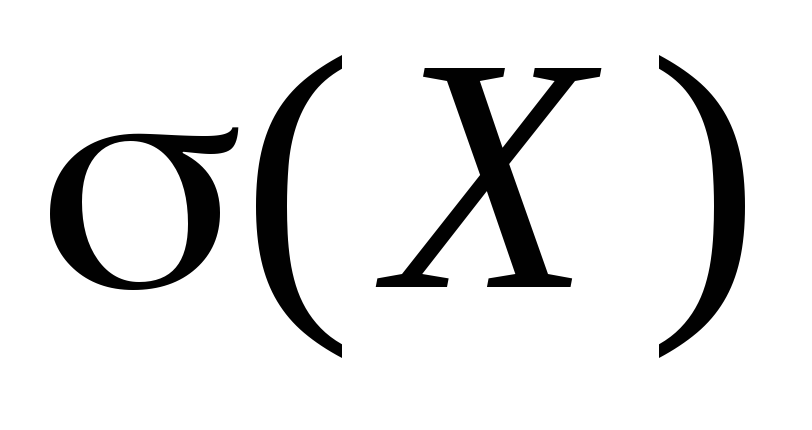ಇದು ಅದರ ಸರಾಸರಿ ಮೌಲ್ಯದಿಂದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವಿಚಲನದ ಅಂದಾಜು ಗಾತ್ರವನ್ನು ನಿರೂಪಿಸುತ್ತದೆ ಮತ್ತು ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನಂತೆಯೇ ಅದೇ ಆಯಾಮವನ್ನು ಹೊಂದಿರುತ್ತದೆ.
4.1. ಗುರಿಕಾರನು ಗುರಿಯತ್ತ ಮೂರು ಗುಂಡುಗಳನ್ನು ಹಾರಿಸುತ್ತಾನೆ. ಪ್ರತಿ ಹೊಡೆತದಿಂದ ಗುರಿಯನ್ನು ಹೊಡೆಯುವ ಸಂಭವನೀಯತೆ 0.3 ಆಗಿದೆ.
ಹಿಟ್‌ಗಳ ಸಂಖ್ಯೆಗಾಗಿ ವಿತರಣಾ ಸರಣಿಯನ್ನು ನಿರ್ಮಿಸಿ.
ಪರಿಹಾರ. ಹಿಟ್‌ಗಳ ಸಂಖ್ಯೆಯು ಪ್ರತ್ಯೇಕವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಆಗಿದೆ X. ಪ್ರತಿ ಮೌಲ್ಯ X ಎನ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ Xಒಂದು ನಿರ್ದಿಷ್ಟ ಸಂಭವನೀಯತೆಗೆ ಅನುರೂಪವಾಗಿದೆ ಪ ಎನ್ .
ಈ ಸಂದರ್ಭದಲ್ಲಿ ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವಿತರಣಾ ಕಾನೂನನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸಬಹುದು ವಿತರಣೆಯ ಹತ್ತಿರ.
ಈ ಸಮಸ್ಯೆಯಲ್ಲಿ X 0, 1, 2, 3 ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ. ಬರ್ನೌಲಿಯ ಸೂತ್ರದ ಪ್ರಕಾರ
,
ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಸಂಭವನೀಯ ಮೌಲ್ಯಗಳ ಸಂಭವನೀಯತೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:
ಆರ್ 3 (0) = (0,7) 3 = 0,343,
ಆರ್ 3 (1)
=
0,3(0,7) 2
= 0,441,
ಆರ್ 3 (2)
=
(0,3) 2 0,7
= 0,189,
ಆರ್ 3 (3) = (0,3) 3 = 0,027.
ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಮೌಲ್ಯಗಳನ್ನು ಜೋಡಿಸುವ ಮೂಲಕ Xಹೆಚ್ಚುತ್ತಿರುವ ಕ್ರಮದಲ್ಲಿ, ನಾವು ವಿತರಣಾ ಸರಣಿಯನ್ನು ಪಡೆಯುತ್ತೇವೆ:
|
X ಎನ್ | ||||
ಮೊತ್ತವನ್ನು ಗಮನಿಸಿ
ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಸಂಭವನೀಯತೆ ಎಂದರ್ಥ Xಸಂಭವನೀಯ ಮೌಲ್ಯಗಳಿಂದ ಕನಿಷ್ಠ ಒಂದು ಮೌಲ್ಯವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ, ಮತ್ತು ಈ ಘಟನೆಯು ವಿಶ್ವಾಸಾರ್ಹವಾಗಿದೆ, ಆದ್ದರಿಂದ
.
4.2 .1 ರಿಂದ 4 ರವರೆಗಿನ ಸಂಖ್ಯೆಗಳೊಂದಿಗೆ ಪಾತ್ರೆಯಲ್ಲಿ ನಾಲ್ಕು ಚೆಂಡುಗಳಿವೆ. ಎರಡು ಚೆಂಡುಗಳನ್ನು ಹೊರತೆಗೆಯಲಾಗುತ್ತದೆ. ಯಾದೃಚ್ಛಿಕ ಮೌಲ್ಯ X- ಚೆಂಡು ಸಂಖ್ಯೆಗಳ ಮೊತ್ತ. ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವಿತರಣಾ ಸರಣಿಯನ್ನು ನಿರ್ಮಿಸಿ X.
ಪರಿಹಾರ.ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಮೌಲ್ಯಗಳು X 3, 4, 5, 6, 7. ಅನುಗುಣವಾದ ಸಂಭವನೀಯತೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ. ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಮೌಲ್ಯ 3 Xಆಯ್ಕೆಮಾಡಿದ ಚೆಂಡುಗಳಲ್ಲಿ ಒಂದಕ್ಕೆ 1 ಸಂಖ್ಯೆ ಮತ್ತು ಇತರ 2 ಅನ್ನು ಹೊಂದಿರುವಾಗ ಮಾತ್ರ ಸ್ವೀಕರಿಸಬಹುದು. ಸಂಭವನೀಯ ಪರೀಕ್ಷಾ ಫಲಿತಾಂಶಗಳ ಸಂಖ್ಯೆಯು ನಾಲ್ಕು (ಬಾಲ್ಗಳ ಸಂಭವನೀಯ ಜೋಡಿಗಳ ಸಂಖ್ಯೆ) ಎರಡು ಸಂಯೋಜನೆಗಳ ಸಂಖ್ಯೆಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
ನಾವು ಪಡೆಯುವ ಶಾಸ್ತ್ರೀಯ ಸಂಭವನೀಯತೆಯ ಸೂತ್ರವನ್ನು ಬಳಸಿ
ಅಂತೆಯೇ,
ಆರ್(X= 4) =ಆರ್(X= 6) =ಆರ್(X= 7) = 1/6.
ಮೊತ್ತ 5 ಎರಡು ಸಂದರ್ಭಗಳಲ್ಲಿ ಕಾಣಿಸಿಕೊಳ್ಳಬಹುದು: 1 + 4 ಮತ್ತು 2 + 3, ಆದ್ದರಿಂದ
.
Xರೂಪವನ್ನು ಹೊಂದಿದೆ:
ವಿತರಣಾ ಕಾರ್ಯವನ್ನು ಹುಡುಕಿ ಎಫ್(X) ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ Xಮತ್ತು ಅದನ್ನು ರೂಪಿಸಿ. ಗೆ ಲೆಕ್ಕಾಚಾರ Xಅದರ ಗಣಿತದ ನಿರೀಕ್ಷೆ ಮತ್ತು ವ್ಯತ್ಯಾಸ.
ಪರಿಹಾರ. ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವಿತರಣಾ ನಿಯಮವನ್ನು ವಿತರಣಾ ಕಾರ್ಯದಿಂದ ನಿರ್ದಿಷ್ಟಪಡಿಸಬಹುದು
ಎಫ್(X) =ಪಿ(X X).
ವಿತರಣಾ ಕಾರ್ಯ ಎಫ್(X) ಇದು ಸಂಪೂರ್ಣ ಸಂಖ್ಯೆಯ ಸಾಲಿನಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾದ ಕಡಿಮೆಯಾಗದ, ಎಡ-ನಿರಂತರ ಕಾರ್ಯವಾಗಿದೆ.
ಎಫ್ (- )= 0,ಎಫ್ (+ )= 1.
ಪ್ರತ್ಯೇಕವಾದ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ಗಾಗಿ, ಈ ಕಾರ್ಯವನ್ನು ಸೂತ್ರದಿಂದ ವ್ಯಕ್ತಪಡಿಸಲಾಗುತ್ತದೆ
.
ಆದ್ದರಿಂದ ಈ ಸಂದರ್ಭದಲ್ಲಿ
ವಿತರಣಾ ಕಾರ್ಯದ ಗ್ರಾಫ್ ಎಫ್(X) ಒಂದು ಹಂತದ ಸಾಲು (ಚಿತ್ರ 12)
|
ಎಫ್(X) | ||||||
ನಿರೀಕ್ಷಿತ ಮೌಲ್ಯಎಂ(X) ಮೌಲ್ಯಗಳ ತೂಕದ ಅಂಕಗಣಿತದ ಸರಾಸರಿಯಾಗಿದೆ X 1 , X 2 ,……X ಎನ್ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ Xಮಾಪಕಗಳೊಂದಿಗೆ ρ 1, ρ 2, …… , ρ ಎನ್ ಮತ್ತು ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಸರಾಸರಿ ಮೌಲ್ಯ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ X. ಸೂತ್ರದ ಪ್ರಕಾರ
ಎಂ(X)= x 1 ρ 1 + x 2 ρ 2 +……+ x ಎನ್ ρ ಎನ್
ಎಂ(X) = 3·0.14+5·0.2+7·0.49+11·0.17 = 6.72.
ಪ್ರಸರಣಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಮೌಲ್ಯಗಳ ಪ್ರಸರಣದ ಮಟ್ಟವನ್ನು ಅದರ ಸರಾಸರಿ ಮೌಲ್ಯದಿಂದ ನಿರೂಪಿಸುತ್ತದೆ ಮತ್ತು ಸೂಚಿಸಲಾಗುತ್ತದೆ ಡಿ(X):
ಡಿ(X)=ಎಂ[(ಹೆಚ್.ಎಂ(X)) 2 ]= ಎಂ(X 2) –[ಎಂ(X)] 2 .
ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ಗಾಗಿ, ವ್ಯತ್ಯಾಸವು ರೂಪವನ್ನು ಹೊಂದಿರುತ್ತದೆ
ಅಥವಾ ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ಲೆಕ್ಕ ಹಾಕಬಹುದು
ಸಮಸ್ಯೆಯ ಸಂಖ್ಯಾತ್ಮಕ ಡೇಟಾವನ್ನು ಸೂತ್ರಕ್ಕೆ ಬದಲಿಸಿ, ನಾವು ಪಡೆಯುತ್ತೇವೆ:
ಎಂ(X 2) = 3 2 ∙ 0,14+5 2 ∙ 0,2+7 2 ∙ 0,49+11 2 ∙ 0,17 = 50,84
ಡಿ(X) = 50,84-6,72 2 = 5,6816.
4.4. ಎರಡು ದಾಳಗಳನ್ನು ಒಂದೇ ಸಮಯದಲ್ಲಿ ಎರಡು ಬಾರಿ ಸುತ್ತಿಕೊಳ್ಳಲಾಗುತ್ತದೆ. ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ವಿತರಣೆಯ ದ್ವಿಪದ ನಿಯಮವನ್ನು ಬರೆಯಿರಿ X- ಎರಡು ಡೈಸ್‌ಗಳಲ್ಲಿ ಸಮ ಒಟ್ಟು ಸಂಖ್ಯೆಯ ಬಿಂದುಗಳ ಸಂಭವಿಸುವಿಕೆಯ ಸಂಖ್ಯೆ.
ಪರಿಹಾರ. ನಾವು ಯಾದೃಚ್ಛಿಕ ಘಟನೆಯನ್ನು ಪರಿಚಯಿಸೋಣ
ಎ= (ಒಂದು ಎಸೆತದೊಂದಿಗೆ ಎರಡು ದಾಳಗಳು ಒಟ್ಟು ಸಮ ಸಂಖ್ಯೆಯ ಅಂಕಗಳಿಗೆ ಕಾರಣವಾಯಿತು).
ಸಂಭವನೀಯತೆಯ ಶಾಸ್ತ್ರೀಯ ವ್ಯಾಖ್ಯಾನವನ್ನು ಬಳಸಿಕೊಂಡು ನಾವು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ
ಆರ್(ಎ)=
,
ಎಲ್ಲಿ ಎನ್ - ಸಂಭವನೀಯ ಪರೀಕ್ಷಾ ಫಲಿತಾಂಶಗಳ ಸಂಖ್ಯೆಯನ್ನು ನಿಯಮದ ಪ್ರಕಾರ ಕಂಡುಹಿಡಿಯಲಾಗುತ್ತದೆ
ಗುಣಾಕಾರ:
ಎನ್ = 6∙6 =36,
ಮೀ - ಈವೆಂಟ್ ಅನ್ನು ಬೆಂಬಲಿಸುವ ಜನರ ಸಂಖ್ಯೆ ಎಫಲಿತಾಂಶಗಳು - ಸಮಾನ
ಮೀ= 3∙6=18.
ಹೀಗಾಗಿ, ಒಂದು ಪ್ರಯೋಗದಲ್ಲಿ ಯಶಸ್ಸಿನ ಸಂಭವನೀಯತೆ
ρ = ಪಿ(ಎ)= 1/2.
ಬರ್ನೌಲ್ಲಿ ಪರೀಕ್ಷಾ ಯೋಜನೆಯನ್ನು ಬಳಸಿಕೊಂಡು ಸಮಸ್ಯೆಯನ್ನು ಪರಿಹರಿಸಲಾಗುತ್ತದೆ. ಇಲ್ಲಿ ಒಂದು ಸವಾಲು ಎರಡು ದಾಳಗಳನ್ನು ಒಮ್ಮೆ ಉರುಳಿಸುತ್ತದೆ. ಅಂತಹ ಪರೀಕ್ಷೆಗಳ ಸಂಖ್ಯೆ ಎನ್ = 2. ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ Xಸಂಭವನೀಯತೆಗಳೊಂದಿಗೆ 0, 1, 2 ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ
ಆರ್ 2 (0)
=
,ಆರ್ 2 (1)
=
∙
,ಆರ್ 2 (2)
=
ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಅಗತ್ಯವಿರುವ ದ್ವಿಪದ ವಿತರಣೆ Xವಿತರಣಾ ಸರಣಿಯಾಗಿ ಪ್ರತಿನಿಧಿಸಬಹುದು:
|
X ಎನ್ | |||
|
ρ ಎನ್ |
4.5 . ಆರು ಭಾಗಗಳ ಬ್ಯಾಚ್‌ನಲ್ಲಿ ನಾಲ್ಕು ಪ್ರಮಾಣಿತ ಭಾಗಗಳಿವೆ. ಮೂರು ಭಾಗಗಳನ್ನು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಆಯ್ಕೆ ಮಾಡಲಾಗಿದೆ. ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯನ್ನು ನಿರ್ಮಿಸಿ X- ಆಯ್ಕೆಮಾಡಿದವರಲ್ಲಿ ಪ್ರಮಾಣಿತ ಭಾಗಗಳ ಸಂಖ್ಯೆ ಮತ್ತು ಅದರ ಗಣಿತದ ನಿರೀಕ್ಷೆಯನ್ನು ಕಂಡುಕೊಳ್ಳಿ.
ಪರಿಹಾರ.ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಮೌಲ್ಯಗಳು X 0,1,2,3 ಸಂಖ್ಯೆಗಳು. ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿದೆ ಆರ್(X=0)=0, ಏಕೆಂದರೆ ಕೇವಲ ಎರಡು ಪ್ರಮಾಣಿತವಲ್ಲದ ಭಾಗಗಳಿವೆ.
ಆರ್(X=1) =
=1/5,
ಆರ್(X= 2) =
= 3/5,
ಆರ್(X=3) =
= 1/5.
ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವಿತರಣಾ ಕಾನೂನು Xಅದನ್ನು ವಿತರಣಾ ಸರಣಿಯ ರೂಪದಲ್ಲಿ ಪ್ರಸ್ತುತಪಡಿಸೋಣ:
|
X ಎನ್ | ||||
|
ρ ಎನ್ |
ನಿರೀಕ್ಷಿತ ಮೌಲ್ಯ
ಎಂ(X)=1 ∙ 1/5+2 ∙ 3/5+3 ∙ 1/5=2.
4.6 . ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಗಣಿತದ ನಿರೀಕ್ಷೆಯನ್ನು ಸಾಬೀತುಪಡಿಸಿ X- ಘಟನೆಯ ಘಟನೆಗಳ ಸಂಖ್ಯೆ ಎವಿ ಎನ್ಸ್ವತಂತ್ರ ಪ್ರಯೋಗಗಳು, ಪ್ರತಿಯೊಂದರಲ್ಲೂ ಈವೆಂಟ್ ಸಂಭವಿಸುವ ಸಂಭವನೀಯತೆಯು ಸಮಾನವಾಗಿರುತ್ತದೆ ρ - ಒಂದು ಪ್ರಯೋಗದಲ್ಲಿ ಈವೆಂಟ್ ಸಂಭವಿಸುವ ಸಂಭವನೀಯತೆಯ ಮೂಲಕ ಪ್ರಯೋಗಗಳ ಸಂಖ್ಯೆಯ ಉತ್ಪನ್ನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ, ದ್ವಿಪದ ವಿತರಣೆಯ ಗಣಿತದ ನಿರೀಕ್ಷೆಯನ್ನು ಸಾಬೀತುಪಡಿಸಲು
ಎಂ(X) =ಎನ್ . ρ ,
ಮತ್ತು ಪ್ರಸರಣ
ಡಿ(X) =ಎನ್.ಪಿ. .
ಪರಿಹಾರ.ಯಾದೃಚ್ಛಿಕ ಮೌಲ್ಯ X 0, 1, 2..., ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು ಎನ್. ಸಂಭವನೀಯತೆ ಆರ್(X= ಕೆ) ಬರ್ನೌಲಿಯ ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ಕಂಡುಬರುತ್ತದೆ:
ಆರ್(X=k)= ಆರ್ ಎನ್(ಕೆ)= 
ρ
ಗೆ
(1-ρ
) n-ಗೆ
ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವಿತರಣಾ ಸರಣಿ Xರೂಪವನ್ನು ಹೊಂದಿದೆ:
|
X ಎನ್ | |||||
|
ρ ಎನ್ |
q ಎನ್ |
|
|
|
ρq n- 1
ρq n- 2
ρ
ಎನ್ಎಲ್ಲಿ q= 1- ρ .
ಗಣಿತದ ನಿರೀಕ್ಷೆಗಾಗಿ ನಾವು ಅಭಿವ್ಯಕ್ತಿ ಹೊಂದಿದ್ದೇವೆ:
ಎಂ(X)=
ρq ಎನ್ -
1
+2
ρ
2
q ಎನ್ -
2
+…+.ಎನ್
ρ
ಎನ್
ಒಂದು ಪರೀಕ್ಷೆಯ ಸಂದರ್ಭದಲ್ಲಿ, ಅಂದರೆ, ಜೊತೆ n= 1 ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ಗಾಗಿ X 1 - ಈವೆಂಟ್ನ ಘಟನೆಗಳ ಸಂಖ್ಯೆ ಎ- ವಿತರಣಾ ಸರಣಿಯು ರೂಪವನ್ನು ಹೊಂದಿದೆ:
|
X ಎನ್ | ||
|
ρ ಎನ್ |
ಎಂ(X 1)= 0∙ q + 1 ∙ ಪ = ಪ
ಡಿ(X 1) = ಪ – ಪ 2 = ಪ(1- ಪ) = pq.
ಒಂದು ವೇಳೆ X k - ಈವೆಂಟ್ನ ಘಟನೆಗಳ ಸಂಖ್ಯೆ ಎಯಾವ ಪರೀಕ್ಷೆಯಲ್ಲಿ, ನಂತರ ಆರ್(X ಗೆ)= ρ ಮತ್ತು
X=X 1 +X 2 +….+X ಎನ್ .
ಇಲ್ಲಿಂದ ನಾವು ಪಡೆಯುತ್ತೇವೆ
ಎಂ(X)=ಎಂ(X 1 )+ಎಂ(X 2)+ … +ಎಂ(X ಎನ್)= nρ,
ಡಿ(X)=ಡಿ(X 1)+ಡಿ(X 2)+ ... +ಡಿ(X ಎನ್)=npq.
4.7. ಗುಣಮಟ್ಟ ನಿಯಂತ್ರಣ ವಿಭಾಗವು ಗುಣಮಟ್ಟಕ್ಕಾಗಿ ಉತ್ಪನ್ನಗಳನ್ನು ಪರಿಶೀಲಿಸುತ್ತದೆ. ಉತ್ಪನ್ನವು ಪ್ರಮಾಣಿತವಾಗಿರುವ ಸಂಭವನೀಯತೆ 0.9 ಆಗಿದೆ. ಪ್ರತಿ ಬ್ಯಾಚ್ 5 ಉತ್ಪನ್ನಗಳನ್ನು ಒಳಗೊಂಡಿದೆ. ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಗಣಿತದ ನಿರೀಕ್ಷೆಯನ್ನು ಹುಡುಕಿ X- ಬ್ಯಾಚ್‌ಗಳ ಸಂಖ್ಯೆ, ಪ್ರತಿಯೊಂದೂ 4 ಪ್ರಮಾಣಿತ ಉತ್ಪನ್ನಗಳನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ - 50 ಬ್ಯಾಚ್‌ಗಳು ತಪಾಸಣೆಗೆ ಒಳಪಟ್ಟಿದ್ದರೆ.
ಪರಿಹಾರ. ಯಾದೃಚ್ಛಿಕವಾಗಿ ಆಯ್ಕೆಮಾಡಿದ ಪ್ರತಿ ಬ್ಯಾಚ್‌ನಲ್ಲಿ 4 ಪ್ರಮಾಣಿತ ಉತ್ಪನ್ನಗಳಿರುವ ಸಂಭವನೀಯತೆ ಸ್ಥಿರವಾಗಿರುತ್ತದೆ; ಅದನ್ನು ಸೂಚಿಸೋಣ ρ .ನಂತರ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಗಣಿತದ ನಿರೀಕ್ಷೆ Xಸಮನಾಗಿರುತ್ತದೆ ಎಂ(X)= 50∙ρ.
ಸಂಭವನೀಯತೆಯನ್ನು ಕಂಡುಹಿಡಿಯೋಣ ρ ಬರ್ನೌಲಿಯ ಸೂತ್ರದ ಪ್ರಕಾರ:
ρ=ಪಿ 5 (4)=
= 0,94∙0,1=0,32.
ಎಂ(X)= 50∙0,32=16.
4.8 . ಮೂರು ದಾಳಗಳನ್ನು ಎಸೆಯಲಾಗುತ್ತದೆ. ಕೈಬಿಡಲಾದ ಬಿಂದುಗಳ ಮೊತ್ತದ ಗಣಿತದ ನಿರೀಕ್ಷೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಪರಿಹಾರ.ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವಿತರಣೆಯನ್ನು ನೀವು ಕಾಣಬಹುದು X- ಕೈಬಿಡಲಾದ ಬಿಂದುಗಳ ಮೊತ್ತ ಮತ್ತು ನಂತರ ಅದರ ಗಣಿತದ ನಿರೀಕ್ಷೆ. ಆದಾಗ್ಯೂ, ಈ ಮಾರ್ಗವು ತುಂಬಾ ತೊಡಕಾಗಿದೆ. ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ಪ್ರತಿನಿಧಿಸುವ ಮತ್ತೊಂದು ತಂತ್ರವನ್ನು ಬಳಸುವುದು ಸುಲಭವಾಗಿದೆ X, ಹಲವಾರು ಸರಳವಾದ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಮೊತ್ತದ ರೂಪದಲ್ಲಿ ಗಣಿತದ ನಿರೀಕ್ಷೆಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಬೇಕಾಗಿದೆ, ಅದರ ಗಣಿತದ ನಿರೀಕ್ಷೆಯು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಸುಲಭವಾಗಿದೆ. ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಆಗಿದ್ದರೆ X iಸುತ್ತಿಕೊಂಡ ಬಿಂದುಗಳ ಸಂಖ್ಯೆ i- ನೇ ಮೂಳೆಗಳು ( i= 1, 2, 3), ನಂತರ ಬಿಂದುಗಳ ಮೊತ್ತ Xರೂಪದಲ್ಲಿ ವ್ಯಕ್ತಪಡಿಸಲಾಗುವುದು
X = X 1 + ಎಕ್ಸ್ 2 + ಎಕ್ಸ್ 3 .
ಮೂಲ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಗಣಿತದ ನಿರೀಕ್ಷೆಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು, ಗಣಿತದ ನಿರೀಕ್ಷೆಯ ಆಸ್ತಿಯನ್ನು ಬಳಸುವುದು ಮಾತ್ರ ಉಳಿದಿದೆ
ಎಂ(X 1 + ಎಕ್ಸ್ 2 + ಎಕ್ಸ್ 3 )= ಎಂ(X 1 )+ ಎಂ(X 2)+ ಎಂ(X 3 ).
ಎಂಬುದು ಸ್ಪಷ್ಟ
ಆರ್(X i = ಕೆ)= 1/6, TO= 1, 2, 3, 4, 5, 6, i= 1, 2, 3.
ಆದ್ದರಿಂದ, ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಗಣಿತದ ನಿರೀಕ್ಷೆ X iತೋರುತ್ತಿದೆ
ಎಂ(X i) = 1/6∙1 + 1/6∙2 +1/6∙3 + 1/6∙4 + 1/6∙5 + 1/6∙6 = 7/2,
ಎಂ(X) = 3∙7/2 = 10,5.
4.9. ಪರೀಕ್ಷೆಯ ಸಮಯದಲ್ಲಿ ವಿಫಲವಾದ ಸಾಧನಗಳ ಸಂಖ್ಯೆಯ ಗಣಿತದ ನಿರೀಕ್ಷೆಯನ್ನು ನಿರ್ಧರಿಸಿ:
ಎ) ಎಲ್ಲಾ ಸಾಧನಗಳಿಗೆ ವೈಫಲ್ಯದ ಸಂಭವನೀಯತೆ ಒಂದೇ ಆಗಿರುತ್ತದೆ ಆರ್, ಮತ್ತು ಪರೀಕ್ಷೆಯಲ್ಲಿರುವ ಸಾಧನಗಳ ಸಂಖ್ಯೆಯು ಸಮಾನವಾಗಿರುತ್ತದೆ ಎನ್;
ಬಿ) ವೈಫಲ್ಯದ ಸಂಭವನೀಯತೆ i – ಸಾಧನವು ಸಮಾನವಾಗಿರುತ್ತದೆ ಪ i , i= 1, 2, … , ಎನ್.
ಪರಿಹಾರ.ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ಅನುಮತಿಸಿ Xನಂತರ ವಿಫಲವಾದ ಸಾಧನಗಳ ಸಂಖ್ಯೆ
X = X 1 + ಎಕ್ಸ್ 2 +… + X ಎನ್ ,
X i
=
ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿದೆ
ಆರ್(X i = 1)= ಆರ್ i , ಆರ್(X i = 0)= 1– ಆರ್ i ,i= 1, 2, … ,ಎನ್.
ಎಂ(X i)= 1∙ಆರ್ i + 0∙(1-ಆರ್ i)=ಪಿ i ,
ಎಂ(X)=ಎಂ(X 1)+ಎಂ(X 2)+… +ಎಂ(X ಎನ್)=ಪಿ 1 +ಪಿ 2 +… + ಪಿ ಎನ್ .
"a" ಸಂದರ್ಭದಲ್ಲಿ ಸಾಧನದ ವೈಫಲ್ಯದ ಸಂಭವನೀಯತೆಯು ಒಂದೇ ಆಗಿರುತ್ತದೆ, ಅಂದರೆ
ಆರ್ i =ಪು,i= 1, 2, … ,ಎನ್.
ಎಂ(X)= ಎನ್.ಪಿ..
ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ನಾವು ಗಮನಿಸಿದರೆ ಈ ಉತ್ತರವನ್ನು ತಕ್ಷಣವೇ ಪಡೆಯಬಹುದು Xನಿಯತಾಂಕಗಳೊಂದಿಗೆ ದ್ವಿಪದ ವಿತರಣೆಯನ್ನು ಹೊಂದಿದೆ ( ಎನ್, ಪ).
4.10. ಎರಡು ದಾಳಗಳನ್ನು ಏಕಕಾಲದಲ್ಲಿ ಎರಡು ಬಾರಿ ಎಸೆಯಲಾಗುತ್ತದೆ. ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ವಿತರಣೆಯ ದ್ವಿಪದ ನಿಯಮವನ್ನು ಬರೆಯಿರಿ X -ಎರಡು ಡೈಸ್‌ಗಳ ಮೇಲೆ ಸಮ ಸಂಖ್ಯೆಯ ಬಿಂದುಗಳ ರೋಲ್‌ಗಳ ಸಂಖ್ಯೆ.
ಪರಿಹಾರ. ಅವಕಾಶ
ಎ=(ಮೊದಲ ಡೈನಲ್ಲಿ ಸಮ ಸಂಖ್ಯೆಯನ್ನು ರೋಲಿಂಗ್ ಮಾಡುವುದು)
ಬಿ =(ಎರಡನೇ ದಾಳದಲ್ಲಿ ಸಮ ಸಂಖ್ಯೆಯನ್ನು ರೋಲಿಂಗ್ ಮಾಡುವುದು).
ಒಂದೇ ಎಸೆತದಲ್ಲಿ ಎರಡೂ ಡೈಸ್‌ಗಳಲ್ಲಿ ಸಮ ಸಂಖ್ಯೆಯನ್ನು ಪಡೆಯುವುದು ಉತ್ಪನ್ನದಿಂದ ವ್ಯಕ್ತವಾಗುತ್ತದೆ ಎಬಿ.ನಂತರ
ಆರ್
(ಎಬಿ)
= ಆರ್(ಎ)∙ಆರ್(IN)
=
.
ಎರಡು ದಾಳಗಳ ಎರಡನೇ ಎಸೆತದ ಫಲಿತಾಂಶವು ಮೊದಲನೆಯದನ್ನು ಅವಲಂಬಿಸಿರುವುದಿಲ್ಲ, ಆದ್ದರಿಂದ ಬರ್ನೌಲಿಯ ಸೂತ್ರವು ಯಾವಾಗ ಅನ್ವಯಿಸುತ್ತದೆ
ಎನ್ = 2,p = 1/4, q = 1– ಪು = 3/4.
ಯಾದೃಚ್ಛಿಕ ಮೌಲ್ಯ X 0, 1, 2 ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು , ಬರ್ನೌಲಿಯ ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ಸಂಭವನೀಯತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದು:
ಆರ್(X= 0)= ಪಿ 2 (0) = q 2 = 9/16,
ಆರ್(X= 1)= ಪಿ 2
(1)= ಸಿ 
,ಆರ್∙q
=
6/16,
ಆರ್(X= 2)= ಪಿ 2
(2)= ಸಿ 
,
ಆರ್ 2
=
1/16.
ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ವಿತರಣಾ ಸರಣಿ X:
4.11. ಸಾಧನವು ಹೆಚ್ಚಿನ ಸಂಖ್ಯೆಯ ಸ್ವತಂತ್ರವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಅಂಶಗಳನ್ನು ಒಳಗೊಂಡಿದೆ, ಕಾಲಾನಂತರದಲ್ಲಿ ಪ್ರತಿ ಅಂಶದ ವೈಫಲ್ಯದ ಒಂದೇ ಸಣ್ಣ ಸಂಭವನೀಯತೆಯೊಂದಿಗೆ ಟಿ. ಕಾಲಾನಂತರದಲ್ಲಿ ನಿರಾಕರಣೆಗಳ ಸರಾಸರಿ ಸಂಖ್ಯೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ ಟಿಅಂಶಗಳು, ಈ ಸಮಯದಲ್ಲಿ ಕನಿಷ್ಠ ಒಂದು ಅಂಶವು ವಿಫಲಗೊಳ್ಳುವ ಸಂಭವನೀಯತೆಯು 0.98 ಆಗಿದ್ದರೆ.
ಪರಿಹಾರ. ಕಾಲಾನಂತರದಲ್ಲಿ ನಿರಾಕರಿಸಿದ ಜನರ ಸಂಖ್ಯೆ ಟಿಅಂಶಗಳು - ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ X, ಇದು ಪಾಯ್ಸನ್ ಕಾನೂನಿನ ಪ್ರಕಾರ ವಿತರಿಸಲ್ಪಡುತ್ತದೆ, ಅಂಶಗಳ ಸಂಖ್ಯೆಯು ದೊಡ್ಡದಾಗಿರುವುದರಿಂದ, ಅಂಶಗಳು ಸ್ವತಂತ್ರವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತವೆ ಮತ್ತು ಪ್ರತಿ ಅಂಶದ ವೈಫಲ್ಯದ ಸಂಭವನೀಯತೆಯು ಚಿಕ್ಕದಾಗಿದೆ. ಈವೆಂಟ್ನ ಘಟನೆಗಳ ಸರಾಸರಿ ಸಂಖ್ಯೆ ಎನ್ಪರೀಕ್ಷೆಗಳು ಸಮಾನವಾಗಿರುತ್ತದೆ
ಎಂ(X) = ಎನ್.ಪಿ..
ವೈಫಲ್ಯದ ಸಂಭವನೀಯತೆಯಿಂದ TOನಿಂದ ಅಂಶಗಳು ಎನ್ಸೂತ್ರದಿಂದ ವ್ಯಕ್ತಪಡಿಸಲಾಗಿದೆ
ಆರ್ ಎನ್
(TO)
,
ಅಲ್ಲಿ = ಎನ್.ಪಿ., ನಂತರ ಒಂದು ಅಂಶವು ಸಮಯದಲ್ಲಿ ವಿಫಲಗೊಳ್ಳದ ಸಂಭವನೀಯತೆ ಟಿ ನಾವು ಪಡೆಯುತ್ತೇವೆ ಕೆ = 0:
ಆರ್ ಎನ್ (0)= ಇ - .
ಆದ್ದರಿಂದ, ವಿರುದ್ಧ ಘಟನೆಯ ಸಂಭವನೀಯತೆ ಸಮಯದಲ್ಲಿದೆ ಟಿ ಕನಿಷ್ಠ ಒಂದು ಅಂಶ ವಿಫಲಗೊಳ್ಳುತ್ತದೆ - 1 ಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ - ಇ - ಸಮಸ್ಯೆಯ ಪರಿಸ್ಥಿತಿಗಳ ಪ್ರಕಾರ, ಈ ಸಂಭವನೀಯತೆ 0.98 ಆಗಿದೆ. Eq ನಿಂದ.
1 - ಇ - = 0,98,
ಇ - = 1 – 0,98 = 0,02,
ಇಲ್ಲಿಂದ = -ಎಲ್ಎನ್ 0,02 4.
ಆದ್ದರಿಂದ, ಸಮಯದಲ್ಲಿ ಟಿಸಾಧನದ ಕಾರ್ಯಾಚರಣೆ, ಸರಾಸರಿ 4 ಅಂಶಗಳು ವಿಫಲಗೊಳ್ಳುತ್ತವೆ.
4.12 . "ಎರಡು" ಬರುವವರೆಗೆ ದಾಳಗಳನ್ನು ಸುತ್ತಿಕೊಳ್ಳಲಾಗುತ್ತದೆ. ಥ್ರೋಗಳ ಸರಾಸರಿ ಸಂಖ್ಯೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಪರಿಹಾರ. ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ಪರಿಚಯಿಸೋಣ X- ನಮಗೆ ಆಸಕ್ತಿಯ ಘಟನೆ ಸಂಭವಿಸುವವರೆಗೆ ನಡೆಸಬೇಕಾದ ಪರೀಕ್ಷೆಗಳ ಸಂಖ್ಯೆ. ಸಂಭವನೀಯತೆ X= 1 ಡೈಸ್ನ ಒಂದು ಎಸೆತದ ಸಮಯದಲ್ಲಿ "ಎರಡು" ಕಾಣಿಸಿಕೊಳ್ಳುವ ಸಂಭವನೀಯತೆಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ.
ಆರ್(X= 1) = 1/6.
ಈವೆಂಟ್ X= 2 ಎಂದರೆ ಮೊದಲ ಪರೀಕ್ಷೆಯಲ್ಲಿ "ಎರಡು" ಬರಲಿಲ್ಲ, ಆದರೆ ಎರಡನೆಯದರಲ್ಲಿ ಅದು ಬಂದಿತು. ಘಟನೆಯ ಸಂಭವನೀಯತೆ X= 2 ಸ್ವತಂತ್ರ ಘಟನೆಗಳ ಸಂಭವನೀಯತೆಯನ್ನು ಗುಣಿಸುವ ನಿಯಮದಿಂದ ಕಂಡುಹಿಡಿಯಲಾಗುತ್ತದೆ:
ಆರ್(X= 2) = (5/6)∙(1/6)
ಅಂತೆಯೇ,
ಆರ್(X= 3) = (5/6) 2 ∙1/6, ಆರ್(X= 4) = (5/6) 2 ∙1/6
ಇತ್ಯಾದಿ ನಾವು ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಗಳ ಸರಣಿಯನ್ನು ಪಡೆಯುತ್ತೇವೆ:
|
(5/6) ಗೆ ∙1/6 |
ಥ್ರೋಗಳ ಸರಾಸರಿ ಸಂಖ್ಯೆ (ಪ್ರಯೋಗಗಳು) ಗಣಿತದ ನಿರೀಕ್ಷೆಯಾಗಿದೆ
ಎಂ(X) = 1∙1/6 + 2∙5/6∙1/6 + 3∙(5/6) 2 ∙1/6 + … + TO (5/6) TO -1 ∙1/6 + … =
1/6∙(1+2∙5/6 +3∙(5/6) 2 + … + TO (5/6) TO -1 + …)
ಸರಣಿಯ ಮೊತ್ತವನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:
TOಜಿ
TO -1
= (
ಜಿ TO)
ಜಿ
.
ಆದ್ದರಿಂದ,
ಎಂ(X) = (1/6) (1/ (1 – 5/6) 2 = 6.
ಹೀಗಾಗಿ, "ಎರಡು" ಬರುವವರೆಗೆ ನೀವು ಡೈಸ್ನ ಸರಾಸರಿ 6 ಎಸೆತಗಳನ್ನು ಮಾಡಬೇಕಾಗುತ್ತದೆ.
4.13. ಈವೆಂಟ್ ಸಂಭವಿಸುವ ಅದೇ ಸಂಭವನೀಯತೆಯೊಂದಿಗೆ ಸ್ವತಂತ್ರ ಪರೀಕ್ಷೆಗಳನ್ನು ನಡೆಸಲಾಗುತ್ತದೆ ಎಪ್ರತಿ ಪರೀಕ್ಷೆಯಲ್ಲಿ. ಈವೆಂಟ್ ಸಂಭವಿಸುವ ಸಂಭವನೀಯತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ ಎ, ಮೂರು ಸ್ವತಂತ್ರ ಪ್ರಯೋಗಗಳಲ್ಲಿ ಘಟನೆಯ ಸಂಭವಿಸುವಿಕೆಯ ಸಂಖ್ಯೆಯ ವ್ಯತ್ಯಾಸವು 0.63 ಆಗಿದ್ದರೆ .
ಪರಿಹಾರ.ಮೂರು ಪ್ರಯೋಗಗಳಲ್ಲಿ ಘಟನೆಯ ಸಂಭವಿಸುವಿಕೆಯ ಸಂಖ್ಯೆಯು ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಆಗಿದೆ X, ದ್ವಿಪದ ಕಾನೂನಿನ ಪ್ರಕಾರ ವಿತರಿಸಲಾಗಿದೆ. ಸ್ವತಂತ್ರ ಪ್ರಯೋಗಗಳಲ್ಲಿ ಈವೆಂಟ್ನ ಸಂಭವಿಸುವಿಕೆಯ ಸಂಖ್ಯೆಯ ವ್ಯತ್ಯಾಸವು (ಪ್ರತಿ ಪ್ರಯೋಗದಲ್ಲಿ ಈವೆಂಟ್ ಸಂಭವಿಸುವ ಅದೇ ಸಂಭವನೀಯತೆಯೊಂದಿಗೆ) ಈವೆಂಟ್ನ ಸಂಭವಿಸುವ ಮತ್ತು ಸಂಭವಿಸದಿರುವ ಸಂಭವನೀಯತೆಗಳ ಮೂಲಕ ಪ್ರಯೋಗಗಳ ಸಂಖ್ಯೆಯ ಉತ್ಪನ್ನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. (ಸಮಸ್ಯೆ 4.6)
ಡಿ(X) = npq.
ಷರತ್ತಿನ ಪ್ರಕಾರ ಎನ್ = 3, ಡಿ(X) = 0.63, ಆದ್ದರಿಂದ ನೀವು ಮಾಡಬಹುದು ಆರ್ಸಮೀಕರಣದಿಂದ ಕಂಡುಹಿಡಿಯಿರಿ
0,63 = 3∙ಆರ್(1-ಆರ್),
ಇದು ಎರಡು ಪರಿಹಾರಗಳನ್ನು ಹೊಂದಿದೆ ಆರ್ 1 = 0.7 ಮತ್ತು ಆರ್ 2 = 0,3.