Määrake kahetahulised nurgad, mis moodustuvad tasandipaaride lõikumisel. Ülesanne: tasapind lõikub sirgega

See artikkel räägib tasapindadevahelisest nurgast ja selle leidmisest. Esiteks on toodud kahe tasandi vahelise nurga määratlus ja graafiline illustratsioon. Pärast seda analüüsiti koordinaatide meetodil kahe risuva tasandi vahelise nurga leidmise põhimõtet ja saadi valem, mis võimaldab arvutada ristuvate tasandite vahelise nurga, kasutades nende tasandite normaalvektorite teadaolevaid koordinaate. Kokkuvõtteks on näidatud üksikasjalikud lahendused iseloomulikud ülesanded.

Leheküljel navigeerimine.

Tasapindadevaheline nurk – määratlus.

Esitagem argumendid, mis võimaldavad meil järk-järgult läheneda kahe lõikuva tasandi vahelise nurga määramisele.

Olgu meile antud kaks ristuvat lennukit ja . Need tasandid lõikuvad mööda sirgjoont, mida tähistame tähega c. Ehitame tasapinna, mis läbib sirge c punkti M ja on risti sirgega c. Sel juhul ristub lennuk tasapindadega ja. Tähistame sirgjoont, mida mööda tasandid ristuvad, kui a ja sirget, mida mööda tasapinnad ristuvad, kui b. Ilmselt ristuvad sirged a ja b punktis M.

Lihtne on näidata, et nurk lõikuvate sirgete a ja b vahel ei sõltu punkti M asukohast sirgel c, mida tasand läbib.

Ehitame sirgega c risti oleva ja tasapinnast erineva tasapinna. Tasapinda lõikuvad tasapinnad ja piki sirgeid, mida tähistame vastavalt kui a 1 ja b 1.

Tasapindade konstrueerimise meetodist järeldub, et sirged a ja b on risti sirgega c ning sirged a 1 ja b 1 on risti sirgega c. Kuna sirged a ja a 1 asuvad samal tasapinnal ja on sirgega c risti, siis on nad paralleelsed. Sarnaselt asuvad sirged b ja b 1 samal tasapinnal ja on sirgega c risti, seega on nad paralleelsed. Nii et saate teha paralleelne ülekanne tasapind tasapinnale, milles sirge a 1 ühtib sirgega a ja sirge b sirgega b 1. Seetõttu on kahe ristuva sirge vaheline nurk a 1 ja b 1 võrdne nurgaga ristuvate sirgete a ja b vahel.

See tõestab, et nurk ristuvate sirgete a ja b vahel, mis asuvad ristuvatel tasapindadel, ei sõltu punkti M valikust, mida tasand läbib. Seetõttu on loogiline võtta seda nurka kahe lõikuva tasandi vahelise nurgana.

Nüüd saate hääletada kahe ristuva tasandi vahelise nurga määratlust ja.

Definitsioon.

Nurk kahe tasandi vahel, mis ristuvad sirgjoonel ja- see on nurk kahe ristuva sirge a ja b vahel, mida mööda tasandid ja lõikuvad tasapinnaga, mis on risti sirgega c.

Kahe tasapinna vahelise nurga määratluse võib anda veidi erinevalt. Kui sirgele c, mida mööda tasapinnad ja lõikuvad, tähistada punkt M ja tõmmata läbi selle sirgjoonega c risti olevad sirgjooned a ja b, mis paiknevad vastavalt tasapindades ja, siis sirgjoonte vaheline nurk a ja b on tasapindade ja vaheline nurk. Tavaliselt tehakse praktikas just selliseid konstruktsioone, et saada tasapindadevaheline nurk.

Kuna ristuvate joonte vaheline nurk ei ületa , tuleneb definitsioonist, et kraadi mõõt väljendatakse kahe lõikuva tasandi vaheline nurk tegelik arv intervallist . Sel juhul nimetatakse lõikuvaid tasapindu risti, kui nendevaheline nurk on üheksakümmend kraadi. Paralleelsete tasapindade vahelist nurka kas ei määrata üldse või loetakse võrdseks nulliga.

Kahe ristuva tasandi vahelise nurga leidmine.

Tavaliselt tuleb kahe ristuva tasandi vahelise nurga leidmisel esmalt teostada täiendavad konstruktsioonid, et näha ristuvaid sirgeid, mille vaheline nurk on võrdne soovitud nurgaga ning seejärel ühendada see nurk algandmetega, kasutades võrdusteste, sarnasust. testid, koosinusteoreem või nurga siinuse, koosinuse ja tangensi definitsioonid. Geomeetria käigus Keskkool tekivad sarnased probleemid.

Toome näitena 2012. aasta matemaatika ühtse riigieksami ülesande C2 lahendus (tingimust muudeti tahtlikult, kuid see ei mõjuta lahenduse põhimõtet). Selles tuli lihtsalt leida nurk kahe ristuva tasandi vahel.

Näide.

Lahendus.

Esiteks teeme joonise.

Teeme täiendavaid konstruktsioone, et “näha” tasapindade vahelist nurka.

Esmalt defineerime sirge, mida mööda tasandid ABC ja BED 1 lõikuvad. Punkt B on üks nende ühistest punktidest. Otsime teise üles ühine punkt need lennukid. Sirged DA ja D 1 E asuvad samal tasapinnal ADD 1 ja nad ei ole paralleelsed ning seetõttu lõikuvad. Teisest küljest asub sirge DA tasapinnal ABC ja sirge D 1 E - tasapinnal BED 1, seetõttu on sirgete DA ja D 1 E lõikepunkt ühine punkt ABC lennukid ja VOODI 1. Niisiis, jätkame sirgeid DA ja D 1 E nende ristumiskohani, tähistades nende ristumispunkti tähega F. Siis BF on sirge, mida mööda tasandid ABC ja BED 1 lõikuvad.

Jääb konstrueerida kaks sirget, mis asuvad vastavalt tasanditel ABC ja BED 1, mis läbivad sirge BF ühte punkti ja on risti sirgega BF - nende joonte vaheline nurk on definitsiooni järgi võrdne soovitud nurgaga lennukid ABC ja BED 1. Teeme seda.

Punkt A on punkti E projektsioon tasapinnale ABC. Joonistame sirge, mis lõikab punktis M täisnurga all sirget BF. Siis on sirge AM sirge EM projektsioon tasapinnale ABC ja seda kolme risti teoreemi järgi.

Seega on tasandite ABC ja BED 1 vaheline nõutav nurk võrdne .

Selle nurga (ja seega ka nurga enda) siinuse, koosinuse või puutuja saame määrata täisnurksest kolmnurgast AEM, kui teame selle kahe külje pikkused. Tingimusest on lihtne leida pikkust AE: kuna punkt E jagab külje AA 1 punktist A lugedes suhtega 4:3 ja külje AA 1 pikkus on 7, siis AE = 4. Leiame pikkuse AM.

Selleks kaaluge täisnurkne kolmnurk ABF täisnurgaga A, kus AM on kõrgus. Tingimuse järgi AB = 2. Külje AF pikkuse leiame täisnurksete kolmnurkade DD 1 F ja AEF sarnasusest:

Pythagorase teoreemi kasutades leiame kolmnurgast ABF. Leiame pikkuse AM läbi kolmnurga ABF pindala: ühel küljel on kolmnurga ABF pindala võrdne , teisel pool , kus .

Seega on meil täisnurksest kolmnurgast AEM .

Siis on nõutav nurk tasapindade ABC ja BED 1 vahel võrdne (pange tähele, et ).

Vastus:

Mõnel juhul on kahe lõikuva tasandi vahelise nurga leidmiseks mugav määrata Oxyz ja kasutada koordinaatide meetodit. Lõpetame seal.

Paneme ülesandeks: leida nurk kahe ristuva tasandi ja . Tähistame soovitud nurka kui .

Eeldame, et antud ristkülikukujulises koordinaatsüsteemis Oxyz on meil teada ristuvate tasandite normaalvektorite koordinaadid ja või on võimalus need leida. Lase on tasapinna normaalvektor ja on tasapinna normaalvektor. Näitame, kuidas leida nurk lõikuvate tasandite vahel ja nende tasandite normaalvektorite koordinaatide kaudu.

Tähistame sirgjoont, mida mööda tasapinnad ja ristuvad, kui c. Läbi punkti M sirgel c joonestame tasapinna, mis on risti sirgega c. Tasapind lõikub tasapindadega ja piki sirgeid a ja b ristuvad sirged a ja b punktis M. Definitsiooni järgi on nurk ristuvate tasapindade vahel ja võrdne lõikuvate sirgete a ja b vahelise nurgaga.

Joonistame normaalvektorid ja tasandid ning punktist M tasapinnal. Sel juhul asub vektor sirgel, mis on risti sirgega a, ja vektor sirgel, mis on risti sirgega b. Seega tasapinnal on vektor sirge a normaalvektor, on sirge b normaalvektor.

Lõikuvate sirgete vahelise nurga leidmise artiklis saime valemi, mis võimaldab arvutada ristuvate sirgete vahelise nurga koosinuse normaalvektorite koordinaatide abil. Seega on sirgete a ja b vahelise nurga koosinus ja sellest tulenevalt ristuvate tasandite vahelise nurga koosinus ja leitakse valemiga, kus Ja on tasandite normaalvektorid ja vastavalt. Seejärel arvutatakse see järgmiselt .

Lahendame eelmise näite koordinaatide meetodil.

Näide.

Dan risttahukas ABCDA 1 B 1 C 1 D 1, milles AB=2, AD=3, AA 1 =7 ja punkt E jagab külje AA 1 vahekorras 4:3, lugedes punktist A. Leidke nurk tasapindade ABC ja BED 1 vahel.

Lahendus.

Kuna ristkülikukujulise rööptahuka küljed ühes tipus on paarikaupa risti, on mugav sisse viia ristkülikukujuline süsteem koordineerib Oxyz nii: joonda algus tipuga C ning suuna koordinaatteljed Ox, Oy ja Oz vastavalt mööda külgi CD, CB ja CC 1.

Tasapindade ABC ja BED 1 vahelise nurga saab leida nende tasandite normaalvektorite koordinaatide kaudu, kasutades valemit , kus ja on vastavalt tasandite ABC ja BED 1 normaalvektorid. Määrame normaalvektorite koordinaadid.

Tasapindadevahelise nurga mõõt on terav nurk, mis on moodustatud kahest sirgjoonest, mis asuvad neil tasapindadel ja on tõmmatud risti nende ristumisjoonega.

Ehitusalgoritm

1. Suvalisest punktist K tõmmatakse igale antud tasapinnale ristid.
2. Ümber nivoojoone pöörates määratakse nurk γ° tipuga K punktis K.
3. Arvutage tasapindade vaheline nurk ϕ° = 180 – γ° eeldusel, et γ° > 90°. Kui γ°< 90°, то ∠ϕ° = ∠γ°.

Joonisel on kujutatud juhtum, kui tasandid α ja β on antud jälgedega. Kõik vajalikud konstruktsioonid viidi läbi vastavalt algoritmile ja neid kirjeldatakse allpool.

Lahendus

1. Joonisel suvalises kohas märgi punkt K. Sellest langetame ristid m ja n vastavalt tasanditele α ja β. Projektsioonide m ja n suund on järgmine: m""⊥f 0α , m"⊥h 0α , n""⊥f 0β , n"⊥h 0β .
2. Määrame joonte m ja n vahel tegeliku suuruse ∠γ°. Selleks pöörame ümber frontaalse f nurga tasandi tipuga K asendisse, mis on paralleelne projektsiooni esitasandiga. Punkti K pöörderaadius R võrdne väärtusega täisnurkse kolmnurga hüpotenuus O""K""K 0, mille külg on K""K 0 = y K – y O.
3. Soovitud nurk on ϕ° = ∠γ°, kuna ∠γ° on terav.

Alloleval joonisel on toodud lahendus ülesandele, mille puhul on vaja leida nurk γ° tasapindade α ja β vahel, mis on antud vastavalt paralleelsete ja ristuvate joontega.

Lahendus

1. Määrame horisontaalide h 1, h 2 ja frontide f 1, f 2 projektsiooni suuna, lennukitele kuuluvα ja β nooltega näidatud järjekorras. Ruudu suvalisest punktist K. α ja β jätame ristid e ja k välja. Sel juhul e""⊥f"" 1 , e"⊥h" 1 ja k""⊥f""" 2 , k"⊥h" 2 .
2. Määratleme ∠γ° joonte e ja k vahel. Selleks tõmmake horisontaaljoon h 3 ja selle ümber pöörame punkti K asendisse K 1, kus △CKD muutub horisontaaltasandiga paralleelseks ja peegeldub sellel loomulikus suuruses - △C"K" 1 D ". Pöörlemiskeskme projektsioon O" asub joonega h" 3 risti K"O". Raadius R määratakse täisnurksest kolmnurgast O"K"K 0, mille külg K"K 0 = Z O – Z K.
3. Soovitud väärtuse väärtus on ∠ϕ° = ∠γ°, kuna nurk γ° on terav.

Artiklis räägitakse tasapindadevahelise nurga leidmisest. Pärast definitsiooni andmist anname graafilise illustratsiooni ja kaalume üksikasjalikku meetodit koordinaatide leidmiseks meetodi abil. Saame ristumistasandite valemi, mis sisaldab normaalvektorite koordinaate.

Yandex.RTB R-A-339285-1

Materjalis kasutatakse andmeid ja mõisteid, mida on varem uuritud artiklites, mis käsitlevad tasapinda ja joont ruumis. Esiteks on vaja liikuda edasi arutluskäigu juurde, mis võimaldab meil teatud lähenemisviisi kahe risuva tasandi vahelise nurga määramiseks.

Antud on kaks lõikuvat tasandit γ 1 ja γ 2. Nende ristmik saab tähise c. χ tasandi ehitus on seotud nende tasandite lõikepunktiga. Tasand χ läbib punkti M sirgjoonena c. Tasapindade γ 1 ja γ 2 lõikepunkt tehakse tasapinna χ abil. γ 1 ja χ lõikuvat sirget võtame sirgeks a ning joont, mis ristub γ 2 ja χ, sirgeks b. Leiame, et sirgete a ja b lõikepunkt annab punkti M.

Punkti M asukoht ei mõjuta nurka ristuvate sirgete a ja b vahel ning punkt M asub sirgel c, mida läbib tasapind χ.

Vaja on konstrueerida tasapind χ 1, mis on risti sirgega c ja erineb tasapinnast χ. Tasapindade γ 1 ja γ 2 lõikepunkt χ 1 abil saab sirgeid a 1 ja b 1.

Näha on, et χ ja χ 1 konstrueerimisel on sirged a ja b risti sirgega c, siis a 1, b 1 paiknevad risti sirgega c. Leides tasapinnal γ 1 sirgjooned a ja a 1, mis on risti sirgega c, siis võib neid lugeda paralleelseks. Samamoodi näitab b ja b 1 asukoht γ 2 tasapinnal risti sirgjoonega c nende paralleelsust. See tähendab, et on vaja teha tasapinna χ 1 paralleelne ülekanne χ-le, kus saame kaks kokkulangevat sirget a ja a 1, b ja b 1. Leiame, et nurk ristuvate sirgete a ja b 1 vahel on võrdne ristuvate sirgete a ja b nurgaga.

Vaatame allolevat joonist.

Seda väidet tõestab asjaolu, et lõikuvate sirgete a ja b vahel on nurk, mis ei sõltu punkti M asukohast, see tähendab lõikepunktist. Need jooned asuvad tasapindadel γ 1 ja γ 2. Tegelikult võib saadud nurka pidada kahe lõikuva tasandi vaheliseks nurgaks.

Liigume edasi olemasolevate ristuvate tasandite γ 1 ja γ 2 vahelise nurga määramise juurde.

Definitsioon 1

Nurk kahe lõikuva tasandi γ 1 ja γ 2 vahel nimetatakse nurka, mille moodustab sirgete a ja b lõikepunkt, kus tasapinnad γ 1 ja γ 2 lõikuvad sirgega c risti oleva tasandiga χ.

Mõelge allolevale joonisele.

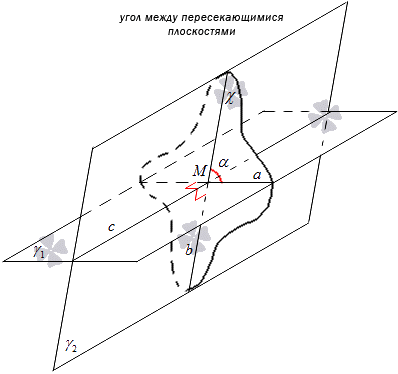
Otsuse võib esitada muus vormis. Kui tasapinnad γ 1 ja γ 2 lõikuvad, kus c on sirge, millel need lõikuvad, märkige punkt M, mille kaudu tõmmatakse sirge c risti olevad jooned a ja b, mis asuvad tasapindadel γ 1 ja γ 2, siis nurk nende vahel. sirged a ja b on tasapindade vaheline nurk. Praktikas on see rakendatav tasapindadevahelise nurga konstrueerimiseks.

Lõikumisel moodustub nurk, mille väärtus on väiksem kui 90 kraadi ehk nurga kraadimõõt kehtib seda tüüpi intervallil (0, 90]. Samas nimetatakse neid tasapindu risti, kui ristumiskohas moodustub täisnurk Paralleelsete tasandite vaheline nurk loetakse võrdseks nulliga.

Tavaline viis ristuvate tasandite vahelise nurga leidmiseks on teha lisakonstruktsioone. See aitab seda täpselt määrata ja seda saab teha kolmnurga võrdsuse või sarnasuse märkide, siinuste ja nurga koosinuste abil.

Vaatleme probleemide lahendamist näite abil Ühtse riigieksami probleemid plokk C 2.

Näide 1

Antud on ristkülikukujuline rööptahukas A B C D A 1 B 1 C 1 D 1, kus külg A B = 2, A D = 3, A A 1 = 7, punkt E jagab külje A A 1 suhtega 4:3. Leidke nurk tasapindade A B C ja B E D 1 vahel.

Lahendus

Selguse huvides on vaja teha joonis. Me saame sellest aru

Visuaalne esitus on vajalik, et muuta tasapindadevahelise nurgaga töötamine mugavamaks.

Määrame sirge, mida mööda toimub tasandite A B C ja B E D 1 ristumiskoht. Punkt B on ühine punkt. Tuleks leida veel üks ühine ristumispunkt. Vaatleme sirgeid D A ja D 1 E, mis asuvad samal tasapinnal A D D 1. Nende asukoht ei näita paralleelsust, see tähendab, et neil on ühine lõikepunkt.

Kuid sirge D A asub tasapinnal A B C ja D 1 E tasapinnal B E D 1. Sellest saame, et sirged jooned D A Ja D 1 E neil on ühine lõikepunkt, mis on ühine tasapindadele A B C ja B E D 1. Näitab joonte lõikepunkti D A ja D 1 E täht F. Sellest saame, et B F on sirge, mida mööda tasandid A B C ja B E D 1 lõikuvad.

Vaatame allolevat joonist.

Vastuse saamiseks on vaja konstrueerida sirgjooned, mis asuvad tasanditel A B C ja B E D 1, mis läbivad punkti, mis asub sirgel B F ja on sellega risti. Seejärel peetakse nende sirgjoonte vahelist nurka soovitud nurgaks tasapindade A B C ja B E D 1 vahel.

Sellest näeme, et punkt A on punkti E projektsioon tasapinnale A B C. Vajalik on tõmmata sirge, mis lõikub sirge B F täisnurga all punktis M. On näha, et sirge A M on projektsioon. sirge E M tasapinnale A B C, tuginedes teoreemile nende ristide A M ⊥ B F kohta. Mõelge allolevale pildile.

∠ A M E on soovitud nurk, mille moodustavad tasapinnad A B C ja B E D 1. Saadud kolmnurgast A E M leiame nurga siinuse, koosinuse või puutuja ja seejärel nurga enda, kui on teada selle kaks külge. Tingimusel saame, et pikkus A E leitakse nii: sirge A A 1 jagatakse punktiga E vahekorras 4:3, mis tähendab, et sirge kogupikkus on 7 osa, siis A E = 4 osa. Leiame A M.

Tuleb arvestada täisnurkse kolmnurgaga A B F. Meil on täisnurk A kõrgusega A M. Tingimusest A B = 2, siis leiame pikkuse A F kolmnurkade D D 1 F ja A E F sarnasuse järgi. Saame, et A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

Kolmnurga A B F külje B F pikkus on vaja leida Pythagorase teoreemi abil. Saame, et B F  = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . Külje A M pikkus leitakse läbi kolmnurga A B F ala. Meil on, et pindala võib olla võrdne nii S A B C = 1 2 · A B · A F kui ka S A B C = 1 2 · B F · A M .

Saame, et A M = A B A F B F = 2 4 2 5 = 4 5 5

Siis leiame kolmnurga A E M nurga puutuja väärtuse. Saame:

t g ∠ A M E = A E A M = 4 4 5 5 = 5

Tasapindade A B C ja B E D 1 lõikel saadud soovitud nurk võrdub a r c t g 5, siis saame lihtsustamisel a r c t g 5 = a r c sin 30 6 = a r c cos 6 6.

Vastus: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

Mõned lõikuvate joonte vahelise nurga leidmise juhtumid on täpsustatud kasutades koordinaattasand O x y z ja koordinaatide meetod. Vaatame lähemalt.

Kui on antud ülesanne, kus on vaja leida nurk lõikuvate tasapindade γ 1 ja γ 2 vahel, tähistame soovitud nurga α-ga.

Siis antud süsteem koordinaadid näitab, et meil on ristuvate tasandite γ 1 ja γ 2 normaalvektorite koordinaadid. Seejärel märgime, et n 1 → = n 1 x, n 1 y, n 1 z on tasandi γ 1 normaalvektor ja n 2 → = (n 2 x, n 2 y, n 2 z) - tasapind γ 2. Mõelgem üksikasjalik leid nurk, mis paikneb nende tasandite vahel piki vektorite koordinaate.

On vaja määrata sirgjoon, mida mööda tasapinnad γ 1 ja γ 2 lõikuvad tähega c. Sirgel c on punkt M, mille kaudu joonistame tasandi χ, mis on risti c-ga. Tasapind χ piki sirgeid a ja b lõikub tasapindadega γ 1 ja γ 2 punktis M. definitsioonist järeldub, et nurk lõikuvate tasandite γ 1 ja γ 2 vahel on võrdne nendele tasapindadele kuuluvate vastavalt ristuvate sirgete a ja b nurgaga.

Tasapinnale χ joonistame normaalvektorid punktist M ja tähistame neid n 1 → ja n 2 → . Vektor n 1 → asub sirgega a risti asetseval sirgel ja vektor n 2 → paikneb sirgega b. Siit saame selle antud lennukχ joone a normaalvektor on võrdne n 1 → ja sirge b korral n 2 →. Mõelge allolevale joonisele.

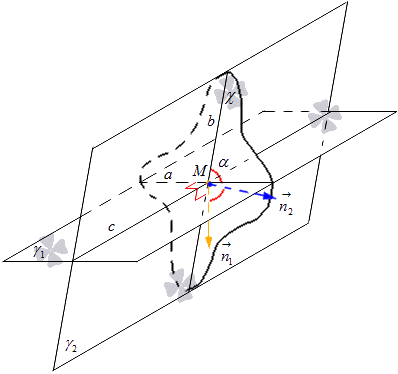
Siit saame valemi, mille abil saame vektorite koordinaatide abil arvutada ristuvate sirgete nurga siinuse. Leidsime, et sirgete a ja b vahelise nurga koosinus on sama, mis lõikuvate tasandite γ 1 ja γ 2 vaheline koosinus, mis on tuletatud cos valemidα = cos n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 y n 2 a + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 a 2 + n 2 z 2, kus meil on, et n 1 → = (n 1 x, n 1 y, n 1 z) ja n 2 → = (n 2 x, n 2 y, n 2 z) on koordinaadid kujutatud tasandite vektorid.

Ristumisjoonte vaheline nurk arvutatakse valemi abil

α = a rc cos n 1 x n 2 x + n 1 a n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2

Näide 2

Tingimuse järgi on antud rööptahukas A B C D A 1 B 1 C 1 D 1 , kus A B = 2, A D = 3, A A 1 = 7 ja punkt E jagab külje A A 1 4:3. Leidke nurk tasapindade A B C ja B E D 1 vahel.

Lahendus

Tingimusest on selge, et selle küljed on paarikaupa risti. See tähendab, et on vaja kasutusele võtta koordinaatsüsteem O x y z, mille tipp on punktis C ja koordinaatteljed O x, O y, O z. Vajalik on määrata suund vastavatele külgedele. Mõelge allolevale joonisele.

Lõikuvad lennukid A B C Ja B E D 1 moodustavad nurga, mille saab leida valemiga α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2, milles n 1 → = (n 1 x, n 1 y, n 1 z) ja n 2 → = (n 2 x, n 2 y, n 2 z ) on normaalvektorid need lennukid. On vaja määrata koordinaadid. Jooniselt näeme seda koordinaatide telg O x y langeb kokku tasapinnaga A B C, mis tähendab, et normaalvektori k → koordinaadid on võrdsed väärtusega n 1 → = k → = (0, 0, 1).

Võetakse tasapinna B E D 1 normaalvektor vektorprodukt B E → ja B D 1 → , kus nende koordinaadid leitakse koordinaatide järgi äärmuslikud punktid B, E, D 1, mis määratakse ülesande tingimustest lähtuvalt.

Saame, et B (0, 3, 0), D 1 (2, 0, 7). Kuna A E E A 1 = 4 3, siis punktide A 2, 3, 0, A 1 2, 3, 7 koordinaatidest leiame E 2, 3, 4. Leiame, et B E → = (2, 0, 4), B D 1 → = 2, - 3, 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 - 3 7 = 12 · i → - 6 j → - 6 k → ⇔ n 2 → = (12 , - 6 , - 6)

Leitud koordinaadid on vaja asendada kaarekoosinuse läbiva nurga arvutamise valemiga. Saame

α = a rc cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = a r c cos 6 6 6 = a r c cos 6 6

Koordinaatide meetod annab sarnase tulemuse.

Vastus: a r c cos 6 6 .

Lõpuülesannet käsitletakse eesmärgiga leida nurk ristuvate tasandite vahel olemasolevate teadaolevate tasandite võrranditega.

Näide 3

Arvutage nurga siinus, koosinus ja nurga väärtus, mille moodustavad kaks ristuvat sirget, mis on defineeritud koordinaatsüsteemis O x y z ja antud võrranditega 2 x - 4 y + z + 1 = 0 ja 3 y - z - 1 = 0.

Lahendus

Teemat uurides üldvõrrand sirgjoon kujul A x + B y + C z + D = 0 näitas, et A, B, C on koefitsiendid, mis on võrdsed normaalvektori koordinaatidega. See tähendab, et n 1 → = 2, - 4, 1 ja n 2 → = 0, 3, - 1 on antud sirgete normaalvektorid.

Tasapindade normaalvektorite koordinaadid on vaja asendada ristuvate tasandite soovitud nurga arvutamise valemis. Siis me saame selle

α = a r c cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210

Siit saame teada, et nurga koosinus võtab cos vaadeα = 13 210. Siis ei ole ristuvate sirgete nurk nüri. Asendamine sisse trigonomeetriline identiteet, leiame, et nurga siinuse väärtus on võrdne avaldisega. Arvutame ja leiame selle

sin α = 1 - cos 2 α = 1 - 13 210 = 41 210

Vastus: sin α = 41 210, cos α = 13 210, α = a r c cos 13 210 = a r c sin 41 210.

Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter

Töö tüüp: 14
Teema: Tasapindadevaheline nurk

Seisund

Dana õige prisma ABCDA_1B_1C_1D_1, M ja N on vastavalt servade AB ja BC keskpunktid, punkt K on MN keskpunkt.

A) Tõesta, et sirged KD_1 ja MN on risti.

b) Leidke nurk tasapindade MND_1 ja ABC vahel, kui AB=8, AA_1=6\sqrt 2.

Näita lahendust

Lahendus

A)\triangle DCN ja \triangle MAD puhul on meil: \angle C=\angle A=90^(\circ), CN=AM=\frac12AB, CD=DA.

Seega \kolmnurk DCN=\kolmnurk MAD kahel jalal. Siis MD=DN, \kolmnurk DMN võrdhaarne. See tähendab, et DK mediaan on ka kõrgus. Seetõttu DK \perp MN.

DD_1 \perp MND tingimuse järgi, D_1K - kaldus, KD - projektsioon, DK \perp MN.

Seega teoreemi järgi umbes kolm risti MN\perp D_1K.

b) Nagu tõestati aastal A), DK \perp MN ja MN \perp D_1K, kuid MN on tasandite MND_1 ja ABC lõikejoon, mis tähendab \nurka DKD_1 - lineaarne nurk kahetahuline nurk tasapindade MND_1 ja ABC vahel.

\kolmnurgas DAM Pythagorase teoreemi järgi DM= \sqrt (DA^2+AM^2)= \sqrt (64+16)= 4\ruut 5, MN= \sqrt (MB^2+BN^2)= \sqrt (16+16)= 4\sqrt 2. Seetõttu \kolmnurgas DKM Pythagorase teoreemi järgi DK= \sqrt (DM^2-KM^2)= \sqrt (80-8)= 6\sqrt 2. Seejärel \kolmnurgas DKD_1, tg\angle DKD_1=\frac(DD_1)(DK)=\frac(6\sqrt 2)(6\sqrt 2)=1.

See tähendab \angle DKD_1=45^(\circ).

Vastus

45^(\circ).

Töö tüüp: 14
Teema: Tasapindadevaheline nurk

Seisund

Paremal nelinurkne prisma ABCDA_1B_1C_1D_1 aluse küljed on 4, külgmised ribid on võrdsed 6-ga. Punkt M on serva CC_1 keskpunkt, punkt N on märgitud servale BB_1 nii, et BN:NB_1=1:2.

A) Millises vahekorras jagab AMN-tasand serva DD_1?

b) Leidke nurk tasapindade ABC ja AMN vahel.

Näita lahendust

Lahendus

A) Tasapind AMN lõikub servaga DD_1 punktis K, mis on antud prisma lõike neljas tipp sellel tasandil. Ristlõige on rööpkülik ANMK, kuna antud prisma vastasküljed on paralleelsed.

BN =\frac13BB_1=2. Joonistame KL \paralleel CD, siis kolmnurgad ABN ja KLM on võrdsed, mis tähendab ML=BN=2, LC=MC-ML=3-2=1, KD=LC=1. Siis KD_1=6-1=5. Nüüd leiate suhte KD:KD_1=1:5.

b) F on sirgete CD ja KM lõikepunkt. Tasapinnad ABC ja AMN lõikuvad piki sirget AF. Nurk \angle KHD =\alpha on kahetahulise nurga lineaarnurk (HD\perp AF, siis teoreemi järgi kolme risti teoreemiga KH \perp AF) ja see on täisnurkse kolmnurga KHD teravnurk, jalg KD=1.

Kolmnurgad FKD ja FMC on sarnased (KD \parallel MC), mistõttu FD:FC=KD:MC, lahendades suhte FD:(FD+4)=1:3, saame FD=2. Täisnurkses kolmnurgas AFD (\angle D=90^(\circ)) jalgadega 2 ja 4 arvutame hüpotenuusi AF=\sqrt (4^2+2^2)=2\sqrt 5, DH= AD\cdot FD:AF= \frac(4\cdot 2)(2\sqrt 5)= \frac4(\sqrt 5).

Leiame täisnurkses kolmnurgas KHD tg \alpha =\frac(KD)(DH)=\frac(\sqrt 5)4, see tähendab soovitud nurka \alpha =arctg\frac(\sqrt 5)4.

Vastus

A) 1:5;

b) arctg\frac(\sqrt 5)4.

Allikas: “Matemaatika. Ettevalmistus 2017. aasta ühtseks riigieksamiks. Profiili tase" Ed. F. F. Lõssenko, S. Yu. Kulabukhova.

Töö tüüp: 14
Teema: Tasapindadevaheline nurk

Seisund

Antud on tavaline nelinurkne püramiid KMNPQ, mille aluse külg MNPQ on 6 ja külgserv 3\sqrt (26).

A) Koostage püramiidi lõik, mille tasapind läbib sirget NF paralleelselt diagonaaliga MP, kui punkt F on serva MK keskpunkt.

b) Leidke nurk lõiketasandi ja KMP tasandi vahel.

Näita lahendust

Lahendus

A) Olgu KO püramiidi kõrgus, F MK keskpunkt ; FE \parallel MP (PKM tasapinnas) . Kuna FE on keskmine joon\kolmnurk PKM, siis FE=\frac(MP)2.

Ehitame püramiidi lõigu, mille tasapind läbib NF ja on paralleelne MP-ga, st tasapinnaga NFE. L on EF ja KO ristumispunkt. Kuna punktid L ja N kuuluvad soovitud lõiku ja asuvad tasapinnal KQN, siis LN ja KQ lõikepunktina saadud punkt T on ühtlasi ka soovitud lõigu ja serva KQ lõikepunkt. NETF on vajalik jaotis.

b) Tasapinnad NFE ja MPK ristuvad piki sirget FE. See tähendab, et nende tasandite vaheline nurk on võrdne kahetahulise nurga OFEN lineaarnurgaga, konstrueerime selle: LO\perpMP, MP\parallel FE, seega, LO\perpFE;\kolmnurk NFE - võrdhaarne (NE=NF vastavate mediaanidena võrdsed kolmnurgad KPN ja KMN ), NL on selle mediaan (EL=LF, kuna PO=OM ja \kolmnurk KEF \sim \kolmnurk KPM) . Seega on soovitud NL \perp FE ja \angle NLO.

ON=\frac12QN=\frac12MN\sqrt 2=3\sqrt 2.

\kolmnurk KON – ristkülikukujuline.

Jalg KO on Pythagorase teoreemi järgi võrdne KO=\sqrt (KN^2-ON^2).

OL= \frac12KO= \frac12\sqrt(KN^2-ON^2)= \frac12\sqrt (9\cdot 26-9\cdot 2)= \frac12\sqrt(9(26-2))= \frac32\sqrt (24)= \frac32\cdot 2\sqrt 6= 3\ruut 6.

tg\angle NLO =\frac(ON)(OL)=\frac(3\sqrt 2)(3\sqrt 6)=\frac1(\sqrt 3),

\angle NLO=30^(\circ).

Vastus

Allikas: “Matemaatika. Ettevalmistus 2017. aasta ühtseks riigieksamiks. Profiili tase." Ed. F. F. Lõssenko, S. Yu. Kulabukhova.

Töö tüüp: 14
Teema: Tasapindadevaheline nurk

Seisund

Korrapärase kolmnurkse prisma ABCA_(1)B_(1)C_(1) kõik servad on võrdsed 6-ga. Läbi servade AC ja BB_(1) keskpunktide ning tipu A_(1) tõmmatakse lõiketasand.

A) Tõesta, et serv BC jagatakse lõiketasandiga vahekorras 2:1, lugedes tipust C.

b) Leidke lõiketasapinna ja alustasandi vaheline nurk.

Näita lahendust

Lahendus

A) Olgu D ja E vastavalt servade AC ja BB_(1) keskpunktid.

Tasapinnal AA_(1)C_(1) joonistame sirge A_(1)D, mis lõikab sirget CC_(1) punktis K, tasapinnal BB_(1)C_(1) - sirge KE, mis lõikab serva BC punktis F . Ühendades punktid A_(1) ja E, mis asuvad tasapinnal AA_(1)B_(1), samuti D ja F, mis asuvad tasapinnal ABC, saame lõigu A_(1)EFD.

\bigtriangleup AA_(1)D=\bigtriangleup CDK piki jalga AD=DC ja teravnurk.

\angle ADA_(1)=\angle CDK – nagu vertikaalsed, järeldub, et AA_(1)=CK=6. \bigtriangleup CKF ja \bigtriangleup BFE on kahe nurga all sarnased \angle FBE=\angle KCF=90^\circ,\angle BFE=\angle CFK - nagu vertikaalsed.

\frac(CK)(BE)=\frac(6)(3)=2, see tähendab, et sarnasuse koefitsient on 2, mis tähendab, et CF:FB=2:1.

b) Teeme läbi AH \perp DF. Nurk lõiketasandi ja alustasandi vahel on võrdne nurgaga AHA_(1). Tõepoolest, lõik AH \perp DF (DF on nende tasandite lõikejoon) on lõigu A_(1)H projektsioon põhitasandile, seetõttu on kolme risti teoreemi kohaselt A_(1)H \perp DF. \angle AHA_(1)=arctg\frac(AA_(1))(AH). AA_(1)=6.

Leiame AH. \angle ADH =\angle FDC (sama mis vertikaalne).

Koosinusteoreemiga \bigtriangleup DFC-s:

DF^2=FC^2+DC^2- 2FC \cdot DC \cdot \cos 60^\circ,

DF^2=4^2+3^2-2 \cdot 4 \cdot 3 \cdot \frac(1)(2)=13.

FC^2=DF^2+DC^2- 2DF\cdot DC\cdot\cos\angle FDC,

4^2=13+9-2\sqrt(13) \cdot 3 \cdot \cos \angle FDC,

\cos \angle FDC=\frac(6)(2\sqrt(13) \cdot 3)=\frac(1)(\sqrt(13)).

Põhilise trigonomeetrilise identiteedi tulemusena

\sin \angle FDC=\sqrt(1-\left (\frac(1)(\sqrt(13))\right)^2)=\frac(2\sqrt(3))(\sqrt(13)) .\bigtriangleup ADH-st leiame AH:

AH=AD \cdot \sin \angle ADH, (\angle FDC=\angle ADH). AH=3 \cdot \frac(2\sqrt(3))(\sqrt(13))=\frac(6\sqrt(13))(\sqrt(13)).

\nurk AHA_(1)= arctg\frac(AA_(1))(AH)= arctg\frac(6 \cdot \sqrt(13))(6\sqrt(3))= arctg\frac(\sqrt(39))(3).

Vastus

arctg\frac(\sqrt(39))(3).

Allikas: “Matemaatika. Ettevalmistus 2017. aasta ühtseks riigieksamiks. Profiili tase." Ed. F. F. Lõssenko, S. Yu. Kulabukhova.

Töö tüüp: 14
Teema: Tasapindadevaheline nurk

Seisund

Täisprisma ABCDA_(1)B_(1)C_(1)D_(1) alus on romb nürinurk B võrdne 120^\circ. Selle prisma kõik servad on võrdsed 10-ga. Punktid P ja K on vastavalt servade CC_(1) ja CD keskpunktid.

A) Tõesta, et sirged PK ja PB_(1) on risti.

b) Leidke nurk tasapindade PKB_(1) ja C_(1)B_(1)B vahel.

Näita lahendust

Lahendus

A) Kasutame koordinaatide meetodit. Otsime üles skalaarkorrutis vektorid \vec(PK) ja \vec(PB_(1)) ning seejärel nende vektorite vahelise nurga koosinus. Suuname Oy telje mööda CD-d, Oz-telge mööda CC_(1) ja Ox-telge \perp CD-d. C on päritolu.

Seejärel C (0;0;0); C_(1)(0;0;10); P(0;0;5); K(0;5;0); B(BC \cos 30^\circ; BC\sin 30^\circ; 0), see on B(5\sqrt(3); 5;0), B_(1)(5\sqrt(3); 5;10).

Leiame vektorite koordinaadid: \vec(PK)=\(0;5;-5\); \vec(PB_(1))=\(5\sqrt(3); 5;5\).

Olgu nurk \vec(PK) ja \vec(PB_(1)) vahel võrdne \alphaga.

Saame \cos \alpha=\frac(\vec(PK) \cdot \vec(PB_(1)))(|\vec(PK)| \cdot |\vec(PB_(1))|)= \frac(0 \cdot 5\sqrt(3) + 5 \cdot 5-5 \cdot 5)(|\vec(PK)| \cdot |\vec(PB_(1))|)=0.

\cos \alpha =0, ​​mis tähendab \vec(PK) \perp \vec(PB_(1)) ja jooned PK ja PB_(1) on risti.

b) Tasapindadevaheline nurk võrdub nende tasanditega risti olevate nullist erineva vektorite vahelise nurgaga (või kui nurk on nüri, siis sellega külgneva nurgaga). Selliseid vektoreid nimetatakse tasandite normaalseteks. Otsime nad üles.

Olgu \vec(n_(1))=\(x; y; z\) tasandiga PKB_(1) risti. Leiame selle süsteemi lahendades \begin(cases) \vec(n_(1)) \perp \vec(PK), \\ \vec(n_(1)) \perp \vec(PB_(1)). \end(juhtumid)

\begin(cases) \vec(n_(1)) \cdot \vec(PK)=0, \\ \vec(n_(1)) \cdot \vec(PB_(1))=0; \end(juhtumid)

\begin(cases) 0x+5y-5z=0, \\ 5\sqrt(3)x+5y+5z=0; \end(juhtumid)

\begin(cases)y=z, \\ x=\frac(-y-z)(\sqrt(3)). \end(juhtumid)

Võtame y = 1; z = 1; x=\frac(-2)(\sqrt(3)), \vec(n_(1))=\left \( \frac(-2)(\sqrt(3)); 1;1 \right \).

Olgu \vec(n_(2))=\(x; y; z\) risti tasapinnaga C_(1)B_(1)B. Leiame selle süsteemi lahendades \begin(cases) \vec(n_(2)) \perp \vec(CC_(1)), \\ \vec(n_(2)) \perp \vec(CB). \end(juhtumid)

\vec(CC_(1))=\(0;0;10\), \vec(CB)=\(5\sqrt(3); 5; 0\).

\begin(cases) \vec(n_(2)) \cdot \vec(CC_(1))=0, \\ \vec(n_(2)) \cdot \vec(CB)=0; \end(juhtumid)

\begin(cases) 0x+0y+10z=0, \\ 5\sqrt(3)x+5y+0z=0; \end(juhtumid)

\begin(cases)z=0, \\ y=-\sqrt(3)x. \end(juhtumid)

Võtame x=1; y=-\sqrt(3); z=0, \vec(n_(2))=\(1; -\sqrt(3);0\).

Leiame soovitud nurga koosinuse \beta (it võrdne mooduliga\vec(n_(1)) ja \vec(n_(2)) vahelise nurga koosinus).

\cos \beta= \frac(|\vec(n_(1)) \cdot \vec(n_(2))|)(|\vec(n_(1))| \cdot |\vec(n_(2))|)= \frac(\left |-\dfrac(2)(\sqrt(3))\cdot 1+1 \cdot (-\sqrt(3))+1 \cdot 0 \right |)(\sqrt(\dfrac( 4)(3)+1+1) \cdot \sqrt(1+3+0))= \frac(\dfrac(5)(\sqrt(3)))(2\sqrt(\dfrac(10)(3)))= \frac(\sqrt(10))(4).

\cos \beta =\frac(\sqrt(10))(4), \beta=\arccos\frac(\sqrt(10))(4).

Vastus

\arccos\frac(\sqrt(10))(4)

Allikas: “Matemaatika. Ettevalmistus 2017. aasta ühtseks riigieksamiks. Profiili tase." Ed. F. F. Lõssenko, S. Yu. Kulabukhova.

ABCD on ruut ja külgmised näod- võrdsed ristkülikud.

Kuna lõiketasand läbib punkte M ja D paralleelselt diagonaaliga AC, siis selle konstrueerimiseks tasapinnal A_(1)AC läbi punkti M joonistame lõigu MN paralleelselt AC-ga. AC \parallel (MDN) saame sirge ja tasandi paralleelsuse põhjal.

Tasand MDN lõikub paralleeltasanditega A_(1)AD ja B_(1)BC, siis omaduse järgi paralleelsed tasapinnad, on tahkude A_(1)ADD_(1) ja B_(1)BCC_(1) lõikejooned MDN-tasandiga paralleelsed.

Joonistame lõigu NE paralleelselt lõiguga MD.

Nelinurkne DMEN on vajalik sektsioon.

b) Leiame lõiketasandi ja alustasandi vahelise nurga. Olgu lõiketasapind lõikunud põhitasapinnaga mööda mingit punkti D läbivat sirget p. AC \parallel MN, seega AC \parallel p (kui tasapind läbib teise tasapinnaga paralleelset sirget ja lõikub selle tasandiga, siis tasandite lõikejoon on paralleelne selle sirgega). BD \perp AC ruudu diagonaalidena, mis tähendab BD \perp p. BD on ED projektsioon tasapinnale ABC, siis kolme risti ED \perp p teoreemi järgi on \angle EDB kahetahulise nurga lineaarnurk lõiketasandi ja alustasandi vahel.

Määrake nelinurga DMEN tüüp. MD \parallel EN, sarnane ME \parallel DN, mis tähendab, et DMEN on rööpkülik ja kuna MD=DN (täisnurksed kolmnurgad MAD ja NCD on kahel jalal võrdsed: AD=DC on ruudu küljed, AM=CN kui paralleelsirgete AC ja MN vahemaad), seetõttu on DMEN romb. Seega on F MN keskpunkt.

Tingimuse järgi AM:MA_(1)=2:3, siis AM=\frac(2)(5)AA_(1)=\frac(2)(5) \cdot 5\sqrt(6)=2\sqrt(6).

AMNC on ristkülik, F on MN keskpunkt, O on AC keskpunkt. Tähendab, FO\parallel MA, FO\perp AC, FO=MA=2\sqrt(6).

Teades, et ruudu diagonaal on a\sqrt(2), kus a on ruudu külg, saame BD=4\sqrt(2). OD=\frac(1)(2)BD=\frac(1)(2) \cdot 4\sqrt(2)=2\sqrt(2).

Täisnurkses kolmnurgas FOD\enspace tg \angle FDO=\frac(FO)(OD)=\frac(2\sqrt(6))(2\sqrt(2))=\sqrt(3). Seetõttu \angle FDO=60^\circ.

\(\blacktriangleright\) Dihedraalnurk on nurk, mille moodustavad kaks pooltasapinda ja sirgjoon \(a\), mis on nende ühine piir.

\(\blacktriangleright\) Tasapindade \(\xi\) ja \(\pi\) vahelise nurga leidmiseks peate leidma lineaarnurga (ja vürtsikas või otse) kahetahuline nurk, mille moodustavad tasapinnad \(\xi\) ja \(\pi\) :

1. samm: olgu \(\xi\cap\pi=a\) (tasapindade lõikejoon). Tasapinnal \(\xi\) märgime suvaline punkt\(F\) ja teostada \(FA\perp a\) ;

2. samm: teostage \(FG\perp \pi\) ;

3. samm: TTP järgi (\(FG\) – risti, \(FA\) – kaldu, \(AG\) – projektsioon) on meil: \(AG\perp a\) ;

4. samm: nurka \(\angle FAG\) nimetatakse tasapindade \(\xi\) ja \(\pi\) moodustatud kahetahulise nurga lineaarnurgaks.

Pange tähele, et kolmnurk \(AG\) on täisnurkne.
Pange tähele ka seda, et sel viisil konstrueeritud tasand \(AFG\) on risti mõlema tasapinnaga \(\xi\) ja \(\pi\) . Seetõttu võime seda öelda erinevalt: tasapindadevaheline nurk\(\xi\) ja \(\pi\) on nurk kahe ristuva sirge \(c\in \xi\) ja \(b\in\pi\) vahel, mis moodustavad tasandiga risti ja \(\xi\ ) ja \(\pi\) .

Ülesanne 1 #2875

Ülesande tase: keerulisem kui ühtne riigieksam

Dana nelinurkne püramiid, mille kõik servad on võrdsed ja alus on ruut. Leidke \(6\cos \alpha\) , kus \(\alpha\) on selle külgnevate külgpindade vaheline nurk.

Olgu \(SABCD\) – see püramiid(\(S\) on tipp), mille servad on võrdsed \(a\) . Järelikult on kõik külgpinnad võrdsed võrdkülgsed kolmnurgad. Leiame tahkude \(SAD\) ja \(SCD\) vahelise nurga.

Teeme \(CH\perp SD\) . Sest \(\kolmnurk SAD=\kolmnurk SCD\), siis on \(AH\) ka \(\triangle SAD\) kõrgus. Seetõttu on definitsiooni järgi \(\angle AHC=\alpha\) kahetahulise nurga lineaarnurk tahkude \(SAD\) ja \(SCD\) vahel.
Kuna alus on ruut, siis \(AC=a\sqrt2\) . Pange tähele ka seda, et \(CH=AH\) on kõrgus Võrdkülgne kolmnurk küljega \(a\) , seega \(CH=AH=\frac(\sqrt3)2a\) .
Seejärel koosinusteoreemiga \(\kolmnurk AHC\): \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]

Vastus: -2

Ülesanne 2 #2876

Ülesande tase: keerulisem kui ühtne riigieksam

Tasapinnad \(\pi_1\) ja \(\pi_2\) lõikuvad nurga all, mille koosinus on võrdne \(0,2\). Tasapinnad \(\pi_2\) ja \(\pi_3\) lõikuvad täisnurga all ning tasandite \(\pi_1\) ja \(\pi_2\) lõikejoon on paralleelne tasandite lõikejoonega. tasapinnad \(\pi_2\) ja \(\ pi_3\) . Leidke tasandite \(\pi_1\) ja \(\pi_3\) vahelise nurga siinus.

Olgu \(\pi_1\) ja \(\pi_2\) lõikejoon sirge \(a\), \(\pi_2\) ja \(\pi_3\) lõikejoon sirge joon \(b\) ning lõikejoon \(\pi_3\) ja \(\pi_1\) – sirge \(c\) . Kuna \(a\parallel b\) , siis \(c\parallel a\parallel b\) (vastavalt teoreemile teoreetilise viite jaotisest "Geomeetria ruumis" \(\rightarrow\) "Sissejuhatus stereomeetriasse, paralleelsus”).

Märgistame punktid \(A\in a, B\in b\) nii, et \(AB\perp a, AB\perp b\) (see on võimalik, kuna \(a\paralleel b\) ). Märgistame \(C\in c\) nii, et \(BC\perp c\) , seega \(BC\perp b\) . Seejärel \(AC\perp c\) ja \(AC\perp a\) .
Tõepoolest, kuna \(AB\perp b, BC\perp b\) , siis \(b\) on risti tasapinnaga \(ABC\) . Kuna \(c\parallel a\parallel b\), siis sirged \(a\) ja \(c\) on samuti risti tasapinnaga \(ABC\) ja seega mis tahes sirgega sellelt tasapinnalt, eriti , rida \ (AC\) .

Sellest järeldub \(\angle BAC=\angle (\pi_1, \pi_2)\), \(\angle ABC=\angle (\pi_2, \pi_3)=90^\circ\), \(\angle BCA=\angle (\pi_3, \pi_1)\). Selgub, et \(\kolmnurk ABC\) on ristkülikukujuline, mis tähendab \[\sin \angle BCA=\cos \angle BAC=0.2.\]

Vastus: 0,2

Ülesanne 3 #2877

Ülesande tase: keerulisem kui ühtne riigieksam

Antud sirged \(a, b, c\), mis lõikuvad ühes punktis ja nurk nende kahe vahel on võrdne \(60^\circ\) . Leidke \(\cos^(-1)\alpha\) , kus \(\alpha\) on nurk joonte \(a\) ja \(c\) moodustatud tasandi ning joonte \( b\ ) ja \(c\) . Esitage oma vastus kraadides.

Olgu sirged ristuvad punktis \(O\) . Kuna nende kahe vaheline nurk on võrdne \(60^\circ\), ei saa kõik kolm sirget asuda samal tasapinnal. Märgime reale \(a\) punkti \(A\) ja joonistame \(AB\perp b\) ja \(AC\perp c\) . Siis \(\kolmnurk AOB=\kolmnurk AOC\) ristkülikukujulisena piki hüpotenuusi ja teravnurka. Seetõttu \(OB=OC\) ja \(AB=AC\) .
Teeme \(AH\perp (BOC)\) . Siis teoreemi järgi umbes kolm risti \(HC\perp c\) , \(HB\perp b\) . Kuna \(AB=AC\) , siis \(\kolmnurk AHB=\kolmnurk AHC\) ristkülikukujulisena piki hüpotenuusi ja jalga. Seetõttu \(HB=HC\) . See tähendab, et \(OH\) ​​on nurga \(BOC\) poolitaja (kuna punkt \(H) on nurga külgedest võrdsel kaugusel).

Pange tähele, et sel viisil konstrueerisime ka joonte \(a\) ja \(c\) moodustatud tasapinnaga moodustatud kahetahulise nurga lineaarnurga ning joonte \(b\) ja \(c) moodustatud tasapinna \) . See on nurk \(ACH\) .

Leiame selle nurga. Kuna valisime punkti \(A\) suvaliselt, siis valime selle nii, et \(OA=2\) . Seejärel ristkülikukujuliselt \(\kolmnurk AOC\): \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ] Kuna \(OH\) ​​​​on poolitaja, siis \(\angle HOC=30^\circ\) ristkülikukujulises \(\kolmnurgas HOC\): \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\] Seejärel ristkülikukujulisest \(\kolmnurgast ACH\): \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]

Vastus: 3

Ülesanne 4 #2910

Ülesande tase: keerulisem kui ühtne riigieksam

Tasapinnad \(\pi_1\) ja \(\pi_2\) lõikuvad piki sirget \(l\), millel asuvad punktid \(M\) ja \(N\). Lõigud \(MA\) ja \(MB\) on risti sirgjoonega \(l\) ja asuvad vastavalt tasapindadel \(\pi_1\) ja \(\pi_2\) ning \(MN = 15) \) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) . Leidke \(3\cos\alpha\) , kus \(\alpha\) on nurk tasapindade \(\pi_1\) ja \(\pi_2\) vahel.

Kolmnurk \(AMN\) on täisnurkne, \(AN^2 = AM^2 + MN^2\), kust \ Kolmnurk \(BMN\) on täisnurkne, \(BN^2 = BM^2 + MN^2\), millest \Kirjutame kolmnurga \(AMB\) koosinusteoreemi: \ Siis \ Kuna tasapindadevaheline nurk \(\alpha\) on teravnurk ja \(\angle AMB\) osutus nüriks, siis \(\cos\alpha=\dfrac5(12)\) . Siis \

Vastus: 1.25

Ülesanne 5 #2911

Ülesande tase: keerulisem kui ühtne riigieksam

\(ABCDA_1B_1C_1D_1\) on rööptahukas, \(ABCD\) on ruut küljega \(a\), punkt \(M\) on punktist \(A_1\) tasapinnale langetatud risti alus. ((ABCD)\) , lisaks on \(M\) ruudu \(ABCD\) diagonaalide lõikepunkt. On teada, et \(A_1M = \dfrac(\sqrt(3))(2)a\). Leidke nurk tasapindade \((ABCD)\) ja \((AA_1B_1B)\) vahel. Esitage oma vastus kraadides.

Ehitame \(MN\) risti \(AB\)-ga, nagu on näidatud joonisel.

Kuna \(ABCD\) on ruut küljega \(a\) ja \(MN\perp AB\) ja \(BC\perp AB\) , siis \(MN\paralleel BC\) . Kuna \(M\) on ruudu diagonaalide lõikepunkt, siis \(M\) on \(AC\) keskpunkt, seega on \(MN\) keskjoon ja \(MN =\frac12BC= \frac(1)(2)a\).
\(MN\) on \(A_1N\) projektsioon tasapinnale \((ABCD)\) ja \(MN\) on risti \(AB\), siis kolme risti teoreemi järgi \ (A_1N\) on risti nurgaga \(AB \) ning tasapindade \((ABCD)\) ja \((AA_1B_1B)\) vaheline nurk on \(\nurk A_1NM\) .
\[\mathrm(tg)\, \angle A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\angle A_1NM = 60^(\circ)\]

Vastus: 60

Ülesanne 6 #1854

Ülesande tase: keerulisem kui ühtne riigieksam

Ruudus \(ABCD\) : \(O\) – diagonaalide lõikepunkt; \(S\) – ei asu ruudu tasapinnal, \(SO \perp ABC\) . Leidke nurk tasapindade \(ASD\) ja \(ABC\) vahel, kui \(SO = 5\) ja \(AB = 10\) .

Täisnurksed kolmnurgad \(\kolmnurk SAO\) ja \(\kolmnurk SDO\) on kahes küljes võrdsed ja nendevaheline nurk (\(SO \perp ABC\) \(\Rightarrow\) \(\angle SOA = \angle SOD = 90^\circ\); \(AO = DO\) , sest \(O\) – ruudu diagonaalide lõikepunkt, \(SO\) – ühine pool) \(\Paremnool\) \(AS = SD\) \(\Paremnool\) \(\kolmnurk ASD\) – võrdhaarne. Punkt \(K\) on \(AD\) keskpunkt, siis \(SK\) on kolmnurga \(\kolmnurk ASD\) kõrgus ja \(OK\) on kolmnurga kõrgus \( AOD\) \(\ Paremnool\) tasapind \(SOK\) on risti tasapindadega \(ASD\) ja \(ABC\) \(\Rightarrow\) \(\angle SKO\) – lineaarnurk, mis võrdub soovitud kahetahuline nurk.

In \(\kolmnurk SKO\): \(OK = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\Rightarrow\) \(\kolmnurk SOK\) – võrdhaarne täisnurkne kolmnurk \(\Rightarrow\) \(\angle SKO = 45^\circ\) .

Vastus: 45

Ülesanne 7 #1855

Ülesande tase: keerulisem kui ühtne riigieksam

Ruudus \(ABCD\) : \(O\) – diagonaalide lõikepunkt; \(S\) – ei asu ruudu tasapinnal, \(SO \perp ABC\) . Leidke nurk tasapindade \(ASD\) ja \(BSC\) vahel, kui \(SO = 5\) ja \(AB = 10\) .

Täisnurksed kolmnurgad \(\kolmnurk SAO\) , \(\kolmnurk SDO\) , \(\kolmnurk SOB\) ja \(\kolmnurk SOC\) on kahes küljes võrdsed ja nendevaheline nurk (\(SO \perp ABC) \) \(\Paremnool\) \(\angle SOA = \angle SOD = \angle SOB = \angle SOC = 90^\circ\); \(AO = OD = OB = OC\), sest \(O\) – ruudu diagonaalide lõikepunkt, \(SO\) – ühine külg) \(\Paremnool\) \(AS = DS = BS = CS\) \(\Paremnool\) \( \kolmnurk ASD\) ja \(\kolmnurk BSC\) on võrdhaarsed. Punkt \(K\) on \(AD\) keskpunkt, siis \(SK\) on kolmnurga \(\kolmnurk ASD\) kõrgus ja \(OK\) on kolmnurga kõrgus \( AOD\) \(\ Paremnool\) tasand \(SOK\) on risti tasapinnaga \(ASD\) . Punkt \(L\) on \(BC\) keskpunkt, siis \(SL\) on kolmnurga \(\kolmnurk BSC\) kõrgus ja \(OL\) on kolmnurga kõrgus \( BOC\) \(\ Paremnool\) tasapind \(SOL\) (teise nimega tasapind \(SOK\)) on risti tasapinnaga \(BSC\) . Seega saame, et \(\angle KSL\) on lineaarnurk, mis võrdub soovitud kahetahulise nurgaga.

\(KL = KO + OL = 2\cdot OL = AB = 10\)\(\Paremnool\) \(OL = 5\) ; \(SK = SL\) – võrdsed kõrgused võrdhaarsed kolmnurgad, mille võib leida Pythagorase teoreemi abil: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). Võib märgata, et \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)\(\Paremnool\) kolmnurga \(\kolmnurk KSL\) Pythagorase pöördteoreem kehtib \(\Rightarrow\) \(\kolmnurk KSL\) – täisnurkne kolmnurk \(\Rightarrow\) \(\angle KSL = 90 ^\ ring\) .

Vastus: 90

Õpilaste ettevalmistamine matemaatika ühtse riigieksami sooritamiseks algab reeglina põhivalemite kordamisega, sealhulgas nende, mis võimaldavad teil määrata tasapindadevahelise nurga. Hoolimata asjaolust, et see geomeetria osa on sees piisavalt üksikasjalikult käsitletud kooli õppekava, peavad paljud lõpetajad põhimaterjali kordama. Mõistes tasapindade vahelise nurga leidmist, saavad keskkooliõpilased ülesande lahendamisel kiiresti õige vastuse välja arvutada ja loota ühtse riigieksami sooritamise tulemuste kohta korralike hinnete saamisele.

Peamised nüansid

Tagamaks, et kahetahulise nurga leidmise küsimus ei tekitaks raskusi, soovitame järgida lahendusalgoritmi, mis aitab teil ühtse riigieksami ülesannetega toime tulla.

Kõigepealt peate määrama sirge, mida mööda tasapinnad ristuvad.

Seejärel peate sellel joonel valima punkti ja tõmbama sellele kaks risti.

Järgmine samm- leidmine trigonomeetriline funktsioon perpendikulaaride moodustatud kahetahuline nurk. Kõige mugavam on seda teha saadud kolmnurga abil, mille osaks on nurk.

Vastuseks on nurga väärtus või selle trigonomeetriline funktsioon.

Shkolkovoga eksamitestiks valmistumine on teie edu võti

Eelmisel päeval tundide ajal ühtse riigieksami sooritamine Paljud koolilapsed seisavad silmitsi definitsioonide ja valemite leidmise probleemiga, mis võimaldavad neil arvutada kahe tasapinna vahelise nurga. Kooliõpik See ei ole alati käepärast täpselt siis, kui seda vajate. Ja leida vajalikud valemid ja näiteid nende õigest kasutamisest, sealhulgas Internetist lennukitevahelise nurga leidmiseks, mis nõuab mõnikord palju aega.

Matemaatikaportaal "Shkolkovo" pakub uus lähenemine valmistuda riigieksamiks. Meie veebisaidi tunnid aitavad õpilastel tuvastada enda jaoks kõige raskemad lõigud ja täita teadmistes lünki.

Oleme koostanud ja selgelt esitanud kogu vajaliku materjali. Põhimõisted ja valemid on esitatud jaotises "Teoreetiline teave".

Materjali paremaks mõistmiseks soovitame harjutada ka vastavaid harjutusi. Suur valik ülesandeid erineval määral keerukus on näiteks esitatud jaotises "Kataloog". Kõik ülesanded sisaldavad üksikasjalikku algoritmi õige vastuse leidmiseks. Kodulehel olev harjutuste nimekiri täieneb ja täieneb pidevalt.

Kahe tasapinna vahelise nurga leidmist nõudvate ülesannete lahendamist harjutades on õpilastel võimalus salvestada kõik ülesanded veebis lemmikutena. Tänu sellele saavad nad tema juurde tagasi pöörduda nõutav summa aega ja arutage temaga oma otsuse edenemist kooli õpetaja või juhendaja.