Sistem maddi noktalar her bir noktanın konumunun ve hareketinin, belirli bir sistemdeki tüm noktaların konumuna ve hareketine bağlı olduğu bir dizi denir. Maddi noktalardan oluşan bir sisteme genellikle mekanik sistem denir.
Maddi noktalar sisteminin kütle merkezi. Kütle merkezinin yarıçap vektörünün belirlenmesi. Kütle merkezinin özellikleri. Kütle merkezinin hızı. Kütle merkezinin hareket denkleminin türetilmesi. Maddi noktalar sisteminin kütle merkezinin koordinatlarının korunumu yasası.
kütle merkezi (veya eylemsizlik merkezi)
maddi nokta sistemleri denir
Xia sanal noktası C, konum
dağılımı karakterize eden
bu sistemin kütlesi. Yarıçapı vektörü

Kapalı bir sistemin kütle merkezi ya doğrusal ve düzgün bir şekilde hareket eder ya da sabit kalır.
Kütle hızının merkezi
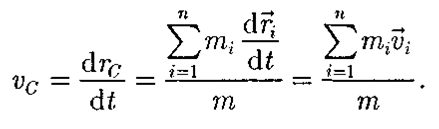
Yoğunluğu r olan sürekli bir kütle dağılımı için  . Sistemin her bir parçacığına uygulanan yerçekimi kuvvetleri yönlendirilirse Tek Yön o zaman kütle merkezi ağırlık merkeziyle çakışır. Ama eğer paralel değil ise kütle merkezi ile ağırlık merkezi çakışmaz.
. Sistemin her bir parçacığına uygulanan yerçekimi kuvvetleri yönlendirilirse Tek Yön o zaman kütle merkezi ağırlık merkeziyle çakışır. Ama eğer paralel değil ise kütle merkezi ile ağırlık merkezi çakışmaz.
zamana göre türevini alırsak şunu elde ederiz: 
onlar. tam dürtü sistemler ürüne eşit kütlesi, kütle merkezinin hızına bağlıdır.
Bu ifadeyi toplam momentumdaki değişim yasasında yerine koyarsak şunu buluruz: 
Sistemin kütle merkezi, sistemin tüm kütlesinin yoğunlaştığı ve ortaya çıkan kütlenin kendisine uygulandığı bir parçacık gibi hareket eder. harici kuvvet
Şu tarihte: ilerici tüm noktaları hareket ettir sağlam kütle merkeziyle aynı şekilde hareket eder (aynı yörüngeler boyunca), dolayısıyla ileri hareket Kütle merkezinin hareket denklemini yazıp çözmek yeterlidir.
Çünkü  , sonra kütle merkezi kapalı sistem dinlenme veya üniforma durumunu korumalıdır doğrusal hareket yani =sabit. Ancak aynı zamanda tüm sistem dönebilir, uçabilir, patlayabilir vb. eylem sonucu iç kuvvetler
.
, sonra kütle merkezi kapalı sistem dinlenme veya üniforma durumunu korumalıdır doğrusal hareket yani =sabit. Ancak aynı zamanda tüm sistem dönebilir, uçabilir, patlayabilir vb. eylem sonucu iç kuvvetler
.
Rс(t1) = Rc(t2) kütle merkezi koordinatlarının korunumu yasası
Örnek olarak yerçekimi kullanılarak potansiyel (korunumlu) kuvvetlerin çalışması. Potansiyel (korunumlu) kuvvet alanlarının belirlenmesi. Konseptin tanıtımı potansiyel enerji kuvvet çalışması yoluyla. Kuvvet ve potansiyel enerji arasındaki ilişki
Potansiyel kuvvet, işi yalnızca uygulandığı noktanın başlangıç ve son konumuna bağlı olan ve ne yörünge türüne ne de bu noktanın hareket yasasına bağlı olmayan bir kuvvettir. Korunumlu kuvvetler, herhangi bir kapalı yol boyunca işi 0'a eşit olan kuvvetlerdir.
Potansiyel (korunumlu) kuvvet alanı: Potansiyel, alanın bir noktasından diğerine hareket ederken işi yörüngenin şekline bağlı olmayan bir alandır. Potansiyel alanlar yerçekimi alanı ve elektrostatik alandır.
Potansiyel kavramının tanıtılması. Kuvvetlerin çalışması yoluyla enerji - Potansiyel enerji - skaler fiziksel miktar, alan kuvvetlerinin çalışması nedeniyle vücudun kinetik enerjisini elde etmek (değiştirmek) için kullanılan, potansiyel bir kuvvet alanında bulunan belirli bir cismin (veya maddi noktanın) enerji rezervini karakterize eder.
Kuvvet ve potansiyel enerji arasındaki ilişki - Her nokta potansiyel alan cisme etki eden kuvvetin belirli bir değerine ve U potansiyel enerjisinin belirli bir değerine karşılık gelir. Bu da kuvvet ile U arasında bir bağlantı olması gerektiği anlamına gelir, diğer taraftan dA = –dU,
Hareketi ve konumu önceden belirlenmiş bir dizi matematiksel nokta (örneğin bisiklet, Güneş sistemi).
Sistemin kütlesi şu şekilde tanımlanır: aritmetik toplam Sisteme dahil edilen nokta kütleleri.
CMS, uzaydaki konumu yarıçap vektörü kullanılarak belirlenen bir noktadır.
2. Maddi bir noktanın sisteminin dış ve iç kuvvetleri. İç kuvvetlerin özellikleri.
Bağ reaksiyon kuvvetleri belirtilen ve reaksiyon kuvvetlerine bölünmüştür.
Dış kuvvetler (F e), söz konusu sistemin gövdelerine, söz konusu sisteme dahil olmayan gövdelerden etki eden kuvvetlerdir.
İç kuvvetler (Fi), söz konusu sistemdeki cisimler arasında etkileşime giren kuvvetlerdir.
3. Malzeme sisteminin iç kuvvetlerinin işi.
Değişmeyen bir sistemin iç kuvvetlerinin herhangi bir hareket için yaptığı işin toplamı sıfıra eşittir.
A ve B sistemin iki noktası olsun.
RA ve R B – modül olarak eşit ve zıt
bu noktalar arasındaki etkileşim kuvvetinin yönü.
Hareket ederken, A ve B noktaları ds A ve ds B temel hareketlerini alacaktır.
Kuvvetlerin etki çizgisine dik olan ds A II ve ds B II hareketlerinde kuvvetler iş üretmez. Değişmez bir sistemin A ve B noktaları arasındaki mesafe hareketi sırasında değişemeyeceğinden ds A I ve ds B I hareketlerinin eşit ve aynı yönde olması gerekir. Bunu takip ediyor.
4. Sistemin kütle merkezinin hareketine ilişkin teorem. Kütle merkezinin hareketinin korunumu kanunu.
c kütle noktasının merkezi nerede
A c – kütle merkezinin ivmesi
M – tüm sistemin kütlesi
Kütle merkezinin hareket korunumu kanunu: Toplam ise kütle merkezinin hareket korunumu kanunu geçerlidir.
=>
5. Katı bir cismin öteleme hareketinin diferansiyel denklemi.
Öteleme m*a c =∑F e i
a i =m i *V i mekanik sistemin hareket sayısı
m i – i'inci noktanın kütlesi
F e i - hepsinin sonucu dış kuvvetler
Q i =m i *V i i'inci noktanın hareket sayısı
Sistem için tüm denklemleri (1) toplayalım
…………
________
∑Q ben =∑ (m ben *V ben)
Q=M*V c (3) tüm sistemin hareket miktarı
M*r c = ∑(m ben * r ben) (2)
Denklemin (2) zamana göre türevini alalım:
M*v c =∑(m i * r ben)
6. Maddi bir sistemin momentumundaki değişime ilişkin teorem.
Diferansiyel form
İntegral formu
hareket miktarı nerede mekanik sistem son ve başlangıç konumunda
Son ve başlangıç pozisyonundaki darbelerin toplamı
7. Sabit bir eksen etrafında dönen katı bir cismin momentum momenti.
Katı bir cismin herhangi bir merkeze göre açısal momentumunun, bu merkezden geçen herhangi bir z eksenine izdüşümüne, cismin bu eksene göre açısal momentumu lz denir:
8. Bir maddi sistemin açısal momentumundaki değişime ilişkin teorem.
(1) Toplam (1)=0 ise L 0 =sabit L 0 x =sabit.
Bir noktanın herhangi bir sabit z eksenine göre momentumunun lz momentinin zamana göre türevi, aynı eksene göre noktaya etki eden F kuvvetinin momentine eşittir.
(1)'den çıkan sonuç: Bir noktaya etki eden kuvvetin momenti bir süre herhangi bir eksene göreli ise sıfıra eşit ise belirli bir noktanın bu eksene göre açısal momentumu tüm bu süre boyunca sabit kalır.
9. Bir cismin eylemsizlik momenti kavramı. Atalet yarıçapı.
Katı bir cismin herhangi bir z eksenine göre atalet momenti (eksenel atalet momenti) skaler bir büyüklüktür, toplamına eşit, vücudun her noktasının m k kütlesinin, belirli bir eksene olan r k mesafesinin karesi ile çarpımından oluşur.
Sonsuz ince bir halkanın eylemsizlik momenti ( malzeme çemberi) dönme eksenine göre kütlesinin çarpımının yarıçapının karesine eşittir:
Bir cismin bir eksene göre atalet momenti, cismin kütlesinin, karşılık gelen eksene göre cismin atalet yarıçapı olarak adlandırılan belirli bir parçanın uzunluğunun karesi ile çarpımı olarak temsil edilir:
Bir cismin herhangi bir eksene göre atalet yarıçapından, halkanın atalet momentini elde etmek için cismin tüm M kütlesini yoğunlaştırmanın gerekli olduğu böylesine sonsuz ince bir halkanın yarıçapını anlayabiliriz, ana eşit Vücudun bu eksene göre ataleti.
10. Göreceli eylemsizlik momenti paralel eksenler(Huygens-Stein teoremi).
Bir cismin herhangi bir eksene göre atalet momenti ana eşit bu cismin göreceli eylemsizliği merkezi eksen Belirli bir eksene paralel olan, vücut kütlesinin çarpımına ve bu eksenler arasındaki mesafenin karesine eklenir.
Huygens-Stein teoremi.
11. Homojen cisimlerin eksenel atalet momentleri: çubuk, içi boş ve katı silindirler, top.
Sabit kesitli ince düz bir çubuğun eylemsizlik momenti
Homojen düz ince bir çubuğun merkezi simetri eksenine göre atalet momenti, çubuğun kütlesinin uzunluğunun karesine göre çarpımının 1/12'sine eşittir.
Katının eylemsizlik momenti
yuvarlak silindir.
Homojen katı dairesel bir silindirin dönme eksenine göre atalet momenti yarıya eşit silindirin kütlesi ile yarıçapının karesinin çarpımı.
İçi boş dairesel bir silindirin eylemsizlik momenti.
Homojen içi boş yuvarlak bir silindirin dönme eksenine göre atalet momenti, silindirin kütlesinin dış ve iç yarıçaplarının karelerinin toplamı ile çarpımının yarısına eşittir.
12. Katı bir cismin sabit bir eksen etrafında dönmesinin dinamik denklemi.
Bir cismin dönme eksenine göre atalet momenti ile cismin açısal ivmesinin çarpımı, aynı eksene göre cisme uygulanan tüm dış kuvvetlerin asal momentine eşittir.
Denklem (1) dinamik denklem olarak adlandırılır dönme hareketi sağlam gövde.
13. Bir maddi sistemin kinetik enerjisindeki değişime ilişkin teorem.
Belirli bir yer değiştirmede mekanik bir sistemin kinetik enerjisindeki değişim, bu yer değiştirmede sistemin maddi noktalarına etki eden dış ve iç kuvvetlerin çalışmalarının toplamına eşittir.
T zamanın son anında kinetik enerjidir
T 0 - kinetik enerji başlangıç anı zaman
∑А i e +∑А i j – dış ve iç kuvvetlerin çalışmalarının toplamı
Koşul: Başlangıç ve bitiş konumları gerekli.
14. Maddi bir sistemin kinetik enerjisi. Koenig teoremi.
Mekanik sistem, çeşitli bağlantılarla birbirine bağlanan bir dizi gövdedir.
Her bedenin pozisyonları ve hareketleri karşılıklı olarak belirlenir. Mekanik bir sistemin kinetik enerjisi, sisteme dahil olan i'inci cismin kinetik enerjilerinin aritmetik toplamı olarak tanımlanır.
Koenig teoremi:
Mekanik bir sistemin kinetik enerjisi, kütlesi tüm sistemin kütlesine eşit olan sistemin kütle merkezinin kinetik enerjisinin ve bu sistemin kinetik enerjisinin toplamına eşittir. bağıl hareket kütle merkezine göre.
15. Katı bir cismin kinetik enerjisi farklı türler onun hareketleri.
Bir vücudun kinetik enerjisi, ne tür bir hareketin yapıldığına bağlı olarak belirlenir.
1) ileri hareket
2) dönme hareketi
3) düzlem paralel hareket
16. Katı bir cismin dinamik düzlemsel paralel hareketi.
17. Maddi bir nokta için D'Alembert ilkesi.
Bir noktaya uygulanan tüm kuvvetlerin geometrik toplamı ve bu noktanın eylemsizlik kuvveti sıfıra eşittir. , Nerede
18. Maddi bir sistem için D'Alembert ilkesi.
(i=1,2,…,n), noktaya uygulanan belirtilen kuvvetlerin bileşkesi; -bu noktaya uygulanan bağların reaksiyonlarının sonucu; -maddi bir noktanın eylemsizlik kuvveti.
Denklem, herhangi bir anda, belirtilen kuvvetlerin bileşkesinin, bağlantıların bileşke reaksiyonunun ve özgür olmayan bir mekanik sistemin her maddi noktası için eylemsizlik kuvvetinin geometrik toplamının sıfıra eşit olduğunu gösterir.
19. Kesinlikle katı bir cismin ana vektörü ve ana eylemsizlik momenti.
İleri hareket
Ana vektör ana momenttir; burada Jz, vücudun dönme eksenine göre atalet momentidir, ε, vücudun açısal ivmesinin cebirsel değeridir.
20. Mekanik bağlantılar, tutucu ve tutucu olmayan bağlantılar, sabit ve sabit olmayan, kafalı ve kafasız.
Bağlantılar başka bir cismin hareket özgürlüğünü kısıtlayan cisimlerdir.
OA=l – esnek diş – sert bağlantı denklemi
Bağlantıların sınıflandırılması:
1) kafa – denklemleri içermeyen bağlantılar
koordinat diferansiyelleri.
2) baş olmayanlar – denklemleri aşağıdakileri içeren bağlantılar
koordinat diferansiyelleri.
Durağan (denklemleri içermeyen
parametre t.)
Durağan olmayan (denklemleri içeren
parametre t.)
Tutma (denklem belirlenir
eşitlik).
Tutmayan (denklem eşitsizlikle belirlenir).
21. Olası hareketler.
Olası hareket, sisteme dayatılan bağlantıların izin verdiği bedenin hareketidir.
Bir noktanın olası hareketi, onun gerçek temel hareketinin aksine, genellikle bir sembolle gösterilir.
22. Olası yer değiştirmede temel kuvvet işi. İdeal bağlantılar.
İdeal bağlantılar, sistemdeki olası herhangi bir nokta yer değiştirmesi için temel reaksiyonların toplamı sıfıra eşit olan bağlantılardır. İdeal bağlantılar tüm sabit bağlantıları içerir geometrik bağlantılar sürtünme olmadan.
Pürüzsüz yüzey (reaksiyon yüzeye dik olarak yönlendirilir, böyle bir bağın hareketi yalnızca teğet düzlemde mümkündür, yani her zaman bağ reaksiyonunun yönüne diktir ve iş = 0)
Sabit menteşe (bunun reaksiyonunun uygulama noktası)
sistem ne kadar hareket ederse etsin bağlantı hareketsiz kalır
ve reaksiyonun işi sıfırdır).
İki gövdeyi birbirine bağlayan hareketli bir menteşe (reaksiyon R 1 ve R 2)
bu cisimler büyüklük olarak birbirine eşittir ve bir yöne yönlendirilir
doğrudan zıt taraflar, herhangi bir ilkokul için
bu bağlantının reaksiyonlarının uygulama noktasını hareket ettirerek bunların toplamı
temel çalışma 0'dır).
23. Olası hareketler ilkesi. Lagrange ilkesi.
Sistemi dengelemek için ideal bağlantılar Sistemin denge konumundan olası herhangi bir yer değiştirmesi için kendisine uygulanan tüm aktif kuvvetlerin temel işlerinin toplamının sıfıra eşit olması gerekli ve yeterlidir.
Temel varsayım: tüm yer değiştirmeler sonsuz küçüktür (δS, δφ).
Noktaların hareketlerinin doğrusal olduğu varsayılmaktadır.
24. D'Alembert – Lagrange ilkesi ( genel denklem dinamik sistem).
Tüm aktif veya belirli kuvvetlerin temel işlerinin toplamı ve tüm eylemsizlik kuvvetlerinin temel işlerinin toplamı sıfırdır.
Dinamiğin genel denklemi.
25. Genelleştirilmiş koordinat, hız ve ivme.
Spesifikasyonu bir mekanik sistemin tüm noktalarının konumunu benzersiz bir şekilde belirleyen bağımsız niceliklere, bu sistemin genelleştirilmiş koordinatları denir. Holonomik sistemler için, bir mekanik sistemin bağımsız genelleştirilmiş koordinatlarının sayısı, bu sistemin serbestlik derecesinin sayısına eşittir.
Genelleştirilmiş koordinatların zaman türevlerine genelleştirilmiş hızlar denir.
Genelleştirilmiş hızların zaman türevlerine genelleştirilmiş ivmeler denir.
26. Genelleştirilmiş kuvvetler ve bunların hesaplanması için yöntemler.
Genelleştirilmiş koordinata karşılık gelen genelleştirilmiş kuvvete denir skaler miktar, ilişki tarafından tanımlanan temel çalışma aktif kuvvetler Koordinatın bu artışın büyüklüğüne göre temel bir artışının neden olduğu mekanik bir sistemin hareketi üzerinde.
Genelleştirilmiş kuvvetler genelleştirilmiş dış ve iç kuvvetlere bölünmüştür.
27. Genelleştirilmiş koordinatlarda mekanik bir sistem için denge koşulu.
Herhangi bir kuvvet sistemi için denge koşulları şu şekildedir:
Muhafazakar bir kuvvetler sistemi için denge koşulları şu şekildedir:
28. İkinci türden Lagrange denklemi.
(j=1, 2, …, s)
Bu denklemler diferansiyel denklemler q 1, q 2, ..., q s sisteminin genelleştirilmiş koordinatlarına göre ikinci derece.
29. Potansiyel bir kuvvet alanında hareket eden ikinci türden Lagrange denklemi.
Eğer malzeme sistemi yalnızca alan kuvvetlerinin etkisi altında potansiyel bir kuvvet alanında hareket eder (sisteme uygulanan tüm bağlantılar idealdir), daha sonra genelleştirilmiş kuvvetler formülle belirlenebilir
Q ben = - dP/dq i
L=T-P (kinetik potansiyel) fonksiyonunu dikkate alalım.
Bu fonksiyona Lagrange fonksiyonu denir. Daha sonra bunu ikinci türden Lagrange denkleminde yerine koyarsak:
sistem S fark Denklemler denir 2. tür Lagrange denklemleri. Bu denklemler sunulmuştur. bir farktır. ikinci dereceden bağıl denklemler. genelleştirilmiş koordinatlar sistemler, ..., Bu denklemlerin integrali alınarak başlangıca göre belirlenmesi. Sürekli entegrasyonun koşulları, şunu elde ederiz: S eşdeğer. kürk hareketleri genelleştirilmiş koordinatlardaki sistemler:
30. Serbest titreşimler Tek serbestlik dereceli tek kütleli sistem.
Serbest titreşimlerin diferansiyel denklemi.
Serbest salınım süresi
Kargo hareketi denklemi
Serbest titreşim frekansı
31. Zorlanmış titreşimler.
Geri getirici ve bozucu kuvvetlerin eş zamanlı etkisi ile maddi bir nokta karmaşık bir işlemi gerçekleştirir. salınım hareketi serbest ve süperpozisyonunun bir sonucudur. zorunlu salınımlar puan.
Zorlanmış salınımlar şunlara bağlı değildir: başlangıç koşulları nokta hareketi.
Düşük frekanslı zorlanmış salınımların denklemi.
Düşük frekanslı salınım genliği
Yüksek frekanslı zorlanmış salınımların denklemi
Yüksek frekanslı salınım genliği
Zorunlu salınımların A B genliğinin A 0 değerine oranı η'ya dinamizm katsayısı denir.
32. İki veya daha fazla serbestlik derecesine sahip sistemlerin salınımları. Serbest ve doğal titreşimler.
Genelleştirilmiş koordinatlardan yalnızca birindeki değişikliğe karşılık gelen salınımlara denir. Sahip olmak. Serbest titreşimler kendilerinin eklenmesinin sonucudur. Bir serbestlik derecesine sahip sistemler yalnızca bir titreşim frekansına sahiptir. Bu nedenle onlar için serbest ve doğal titreşimler örtüşür. İki serbestlik dereceli sistemin iki frekansı vardır doğal titreşimler. Benzer şekilde, n serbestlik derecesine sahip bir sistemin n frekansta doğal salınımlara sahip olacağı gösterilebilir; Serbestlik derecesi sayısı frekans sayısına eşittir.
33. Noktalarda çarpma olgusu. Darbe kuvveti ve darbe dürtüsü.
Çarpma, cisimlerin etkileşimi sonucunda hızlarının çok kısa bir süre içinde sınırlı miktarda değiştiği bir olgudur. Kural olarak, darbe olgusuna, temas eden cisimlerin plastik deformasyonu eşlik eder, bunun sonucunda mekanik enerji termal enerjiye dönüştürülür. Bu nedenle cisimlerin etkisiyle ilgili problemleri çözerken kinetik enerjideki değişim teoremini kullanamazsınız. Bu durumlarda, momentum ve açısal momentumdaki değişime ilişkin integral formda yazılan teorem uygulanır.
Çarpma olgusu, ihmal edilebilecek kadar küçük bir zaman periyodunda, vücut üzerindeki noktaların hızlarının sonlu miktarda değiştiği (bir topun duvara çarpması vb.)
TV hareketlerinin sayısında son değişiklik. Çarpma sırasında gelişen kuvvetlerin büyüklükleri çok büyük olduğundan, çarpma sırasında bu kuvvetlerin darbeleri sonlu değerler olduğundan ihmal edilebilecek kadar kısa bir çarpma süresinde bir gövde meydana gelir. Bu tür kuvvetlere denir. - anında veya şok.
1) Çarpma sırasında anlık olmayan kuvvetlerin etkisi ihmal edilebilir.
2) hareket et önemli. Çarpma sırasındaki noktalar göz ardı edilebilir.
3) malzeme üzerindeki darbe kuvvetinin sonucu. nokta, hız vektörünün etkisi sırasındaki sonlu değişimle ifade edilir ve aşağıdaki denklemle belirlenir: B
34. Çarpma anında maddi bir noktanın momentumundaki değişime ilişkin teorem.
Çarpma sırasında mekanik sistemin momentumundaki değişim şuna eşittir: geometrik toplam hepsi harici şok darbeleri, sistemin noktalarına uygulanır.
(1)
Denklem kürkün hareket sayısındaki değişime ilişkin teoremi ifade etmektedir. darbe sistemleri:
Kürk hareketlerinin sayısını değiştirme. çarpma sırasındaki sistemler İLE= tüm dış şok darbelerinin geometrik toplamı S sisteme bağlı.
Hareket sayısı tüm sistemin kütlesi cinsinden ifade edilebilir M ve sistemin kütle merkezinin hızı ve formüllere göre
Bu denklemleri (1)'de yerine koyalım ve çarpma anında kütle merkezinin hızındaki değişimi belirleyen bu denklemi elde edelim.
Harici şok darbelerinin yokluğunda elimizde:
Kürk üzerinde hareket ederken. Sistem yalnızca iç şok darbelerinden oluşur, sistemin hareket miktarı değişmez.
sayfa 1
Çıkarmasak da denklemleri (6.1) ekleseydik, basitçe momentumun korunumu yasasını elde ederdik
Zamandaki sabitlik yasası olarak tamamen resmi olarak yeniden yazılabilir.
biraz hız Vc:
Hızla (6.4) hareket eden bir referans sistemine geçelim. Hızlar
parçacıklar 1 ve 2 dönüştürülür aşağıdaki gibi:
yani yeni referans çerçevesinde göreceli hız aracılığıyla ifade edilirler.
hareketler. Vc hızını belirli bir noktanın yarıçap vektörüyle ilişkilendirelim. Rİle:
Tanım (6.6)'nın yukarıdan bilinen tanımla örtüştüğüne dikkat edin. okul kursu
Fizikte ağırlık merkezi kavramı. Bunu kanıtlamak için hadi başlangıca taşıyalım
noktaya koordinatlar Rİle. Daha sonra (6.5)’e tamamen benzer şekilde şunu elde ederiz:
Böylece,
(ağırlık merkezi, kütle ve “omuz” çarpımlarının eşitliği ile belirlenir). Ancak (6.4) ve (6.6) numaralı tanımlar daha doğru ve daha evrenseldir, çünkü herhangi bir sayıda maddi noktaya sorunsuz bir şekilde genelleştirilebilirler ve dolayısıyla
makroskobik cisimler. Mekanikte ve genel olarak fizikte C noktasına genellikle C noktası denir.
maddi noktalardan oluşan bir sistemin kütle merkezi veya eylemsizlik merkezi.
Biraz içeri girsin eylemsizlik sistemi kütleleri m 1, m 2, ... m N olan etkileşim halindeki malzeme noktalarının konum koordinatları, yarıçap vektörleri kullanılarak t zamanının her anında belirtilir. R 1(t), R 2 (t), ... R N(t)
(bkz. Şekil 6.3 a). O halde, dikkate alınan maddi noktalar sisteminin kütle merkezi, yarıçap vektörü olan bir noktadır. R R 1(t), R 2 (t), ... R N (t) malzeme noktalarına göre
Şunu vurgulayalım genel durum kütle merkezinin konumu ile çakışmıyor
sistemin maddi noktalarından herhangi birinin konumu (bkz. Şekil 6.3 b),
ancak bazen bu gerçekleşebilir.

Pirinç. Şekil 6.3'te, maddi noktalar sisteminin kütle merkezi, yarıçap vektörü olan bir noktadır. R c(t) yarıçap vektörleri cinsinden ifade edilir R 1(t), R 2 (t), ... R N(t) malzeme noktası
Eşitliğin (6.7) sol ve sağ taraflarını zamana göre ayıralım.
Yarıçap vektörünün zamana göre türevi tanım gereği hızdır, dolayısıyla
sonuç olarak ne elde ediyoruz
burada Vc kütle merkezinin hızıdır, v 1, v 2,... v N maddi noktaların hızlarıdır. (6.8)'deki m 1 v 1 miktarı birinci maddi noktanın momentumudur, m 2 V 2 ikinci noktanın momentumudur ve
vesaire. Dolayısıyla, (6.8) ifadesinin süslü parantezleri içinde, söz konusu maddi noktalar sisteminin darbelerinin toplamı, yani tüm sistemin darbesi P bulunur. Sonuç olarak, eşitlik (6.8) şu şekilde yeniden yazılabilir:
P = (m 1 + m 2 + .... + m N )V c. (6.9)
Kütle merkezinin hareketsiz olduğu bir referans çerçevesinde,
Eğer maddi noktaların bağıl hareketleriyle değil de sistemin bir bütün olarak hareketiyle ilgileniyorsak, o zaman tüm sistem Vc hızıyla hareket eden ve P momentumuna sahip tek bir maddesel nokta olarak düşünülebilir. Kütlenin şunu hatırlayın: Maddi bir noktanın değeri, tanımı gereği, itme ve hız arasındaki orantı katsayısıdır. Bu nedenle, süslü parantez içine alınmış eşitlikteki orantılılık katsayısı (6.9), söz konusu sistemin kütlesi M'dir:
M = m1 + m2 + …. +m N , (6.10)
yani maddi noktalar sisteminin kütlesi bu noktaların kütlelerinin toplamına eşittir. İlişki (6.10), buna göre kütle karmaşık vücut parçalarının kütlelerinin toplamına eşit olan şey bize tanıdık ve açık görünüyor. Ancak daha sonra göreceğimiz gibi göreli mekanikte (yani daha genel durumda) durum tamamen farklı olacaktır. Newton mekaniğinin sınırlayıcı durumunda eşitlik (6.10) şu şekildedir: özel durum kesin
fizik kanunu- kütlenin korunumu yasası.
Dış kuvvetlerin yokluğunda, yani kapalı bir sistem için, sistemin tüm cisimlerinin darbelerinin toplamı zamana bağlı değildir; daha sonra (6.9)'dan kapalı bir maddi noktalar sisteminin kütle merkezinin hareketinin önemli bir özelliği gelir:
yani. Maddi noktalardan oluşan kapalı bir sistemin kütle merkezi hareketsizdir veya
düzgün ve doğrusal olarak hareket eder Her ne kadar maddi noktaların her biri performans gösterse de karmaşık hareket. Yukarıdaki ifadeye bazen kütle merkezinin hareketine ilişkin teorem denir.
Şimdi kinetik enerjinin aşağıdaki önemli özelliğini kanıtlayacağız:
bir maddi noktalar sisteminin kinetik enerjisi T, zihinsel olarak kütle merkezinde yoğunlaşan ve onunla birlikte hareket eden sistemin tüm kütlesinin kinetik enerjisinin ve aynı sistemin kinetik enerjisinin T'nin toplamına eşittir. Kütle merkeziyle birlikte hareket eden referans sistemine göre bağıl hareket:
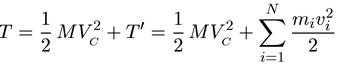
burada M = m 1 + m 2 + ... + m N. Vc, orijinal referans çerçevesindeki kütle merkezinin hızıdır, v i, i. maddesel noktanın C noktasıyla birlikte hareket eden referans çerçevesine göre hızıdır. Böyle bir sisteme genellikle “kütle merkezi sistemi” adı verilir. , “atalet merkezi sistemi” veya kısaca “c-sistemi”. (Sorunun ortaya çıktığı referans sistemi, eğer bu sistem c-sistemi ile örtüşmüyorsa genellikle laboratuvar referans sistemi veya l-sistemi olarak adlandırılır).
Bunu kanıtlamak için öncelikle iki referans sistemindeki kinetik enerjiyi birbirine bağlayan daha genel bir ilişki elde ederiz (bkz. Şekil 6.4). Eski sistemdeki Ri, Vi ve yeni sistemdeki ri, vi'deki noktaların koordinatları ve hızları için Galile dönüşümlerini yazıyoruz:
burada R, eski sistemden yenisine geçişin yarıçap vektörüdür ve V buna göre yeni sistemin eskisine göre hareket hızıdır.
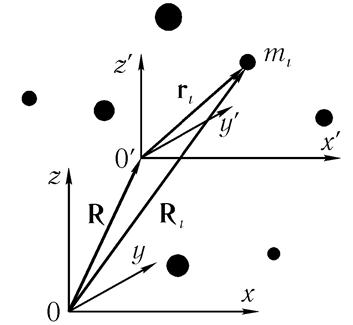
Pirinç. 6.4 İki referans sisteminde koordinatların bağlantısı
Daha sonra eski referans çerçevesindeki kinetik enerji şu şekilde temsil edilebilir:
 (6.12)
(6.12)
(6.12) denkleminin sağ tarafı üç toplamla gösterilebilir:
burada P, yeni referans çerçevesindeki malzeme noktaları sisteminin toplam momentumudur. İlişki (6.13) genellikle Koenig teoremi olarak adlandırılır. Eğer yeni sistem q-sistemiyle çakışıyorsa, o zaman içindeki toplam momentum sıfırdır, V = Vc, bu da (6.11) ilişkisinin geçerli olduğu anlamına gelir.
Bu bölümü sonuçlandırmak için iki tanesine dikkat edelim. önemli özellikler kütle merkezinin tanımından kaynaklanmaktadır. İlk olarak (6.7)'deki parçacıklar herhangi bir grupta birleştirilebilir, örneğin:
Buradan, anlaşılması kolay olduğu gibi, makroskobik cisimlerden oluşan herhangi bir sistemin kütle merkezinin, her cismin kütlesinin kendi içinde yoğunlaştığı varsayımı altında, maddi noktalardan oluşan bir sistemin kütle merkezi olarak bulunabileceği sonucu çıkar. kendi kütle merkezi.
İkincisi, (6.7)'deki toplamdan integrale geçmek kolaydır,
Madde yoğunluğunun sürekli dağılımı ρ(t) olan bir cismin kütle merkezinin konumunu hesaplarsak:

