Mis on trigonomeetrilise funktsiooni väärtus. Trigonomeetrilised funktsioonid

TRIGONOMEETRILISTE FUNKTSIOONIDE VÄÄRTUSTE TABEL

Trigonomeetriliste funktsioonide väärtuste tabel on koostatud nurkade 0, 30, 45, 60, 90, 180, 270 ja 360 kraadi ja vastavate nurkade väärtuste jaoks vradiaanides. Trigonomeetrilistest funktsioonidest on tabelis ära toodud siinus, koosinus, puutuja, kootangens, sekant ja kosekants. Lahenduse mugavuse huvides kooli näited trigonomeetriliste funktsioonide väärtused tabelis on kirjutatud murdosa kujul, säilitades numbrite ruutjuure eraldamise märgid, mis aitab sageli kompleksi vähendada. matemaatilised avaldised. Puutuja ja kotangensi puhul ei saa mõne nurga väärtusi määrata. Selliste nurkade puutuja ja kotangensi väärtuste jaoks on trigonomeetriliste funktsioonide väärtuste tabelis kriips. Üldtunnustatud seisukoht on, et selliste nurkade puutuja ja kotangens on võrdne lõpmatusega. Eraldi lehel on valemid trigonomeetriliste funktsioonide vähendamiseks.

Trigonomeetrilise siinusfunktsiooni väärtuste tabel näitab järgmiste nurkade väärtusi: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 in kraadi mõõt, mis radiaannurga mõõtmisel vastab sin 0 pi, sin pi/6, sin pi/4, sin pi/3, sin pi/2, sin pi, sin 3 pi/2, sin 2 pi. Kooli siinuste tabel.

Trigonomeetrilise koosinusfunktsiooni jaoks on tabelis näidatud järgmiste nurkade väärtused: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 kraadides, mis vastab cos 0 pi , cos pi 6, cos pi 4, cos pi 3, cos pi 2, cos pi, cos 3 pi korda 2, cos 2 pi nurkade radiaanis. Kooli koosinuste tabel.

Trigonomeetrilise puutuja funktsiooni trigonomeetriline tabel annab väärtused järgmiste nurkade jaoks: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 kraadides, mis vastab tg 0 pi, tg pi/6, tg pi/4, tg pi/3, tg pi, tg 2 pi nurkade radiaanis. Trigonomeetriliste puutujafunktsioonide järgmisi väärtusi ei määratleta tan 90, tan 270, tan pi/2, tan 3 pi/2 ja neid loetakse võrdseks lõpmatusega.

Trigonomeetrilises tabelis oleva trigonomeetrilise funktsiooni kotangensi jaoks on antud järgmiste nurkade väärtused: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 kraadimõõtes, mis vastab ctg pi/6, ctg pi/4 , ctg pi/3, tg pi/ 2, tan 3 pi/2 nurkade radiaanis. Trigonomeetriliste kotangentsete funktsioonide järgmisi väärtusi ei määratleta ctg 0, ctg 180, ctg 360, ctg 0 pi, ctg pi, ctg 2 pi ja neid peetakse võrdseks lõpmatusega.

Trigonomeetriliste funktsioonide sekant ja kosekant väärtused on antud samade nurkade jaoks kraadides ja radiaanides nagu siinus, koosinus, puutuja, kotangens.

Mittestandardsete nurkade trigonomeetriliste funktsioonide väärtuste tabel näitab siinuse, koosinuse, puutuja ja kotangensi väärtusi nurkade jaoks kraadides 15, 18, 22,5, 36, 54, 67,5 72 kraadi ja radiaanides pi/12 , pi/10, pi/ 8, pi/5, 3pi/8, 2pi/5 radiaani. Trigonomeetriliste funktsioonide väärtused on väljendatud murdude ja ruutjuurtena, et koolinäidetes oleks murdude vähendamine lihtsam.

Veel kolm trigonomeetria koletist. Esimene on puutuja 1,5 poolteist kraadi ehk pi jagatuna 120-ga. Teine on pi koosinus jagatud 240-ga, pi/240. Pikim on pi koosinus jagatud 17-ga, pi/17.

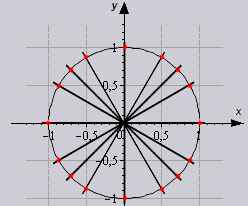
Funktsioonide siinus ja koosinus väärtuste trigonomeetriline ring kujutab visuaalselt siinuse ja koosinuse märke sõltuvalt nurga suurusest. Eriti blondide puhul on koosinusväärtused segaduse vähendamiseks rohelise kriipsuga alla joonitud. Kraadide teisendamine radiaanideks on samuti väga selgelt esitatud, kui radiaane väljendatakse pi-ga.

See trigonomeetriline tabel esitab siinuse, koosinuse, puutuja ja kotangensi väärtused nurkade 0 null kuni 90 üheksakümmend kraadi jaoks ühekraadise intervalliga. Esimese neljakümne viie kraadi puhul tuleks vaadata trigonomeetriliste funktsioonide nimetusi tabeli ülaosas. Esimene veerg sisaldab kraadi, siinuste, koosinuste, puutujate ja kotangentide väärtused on kirjutatud järgmisesse nelja veergu.

Nurkade puhul nelikümmend viis kraadi kuni üheksakümmend kraadi on trigonomeetriliste funktsioonide nimed kirjutatud tabeli allossa. Viimases veerus on kraadid, koosinuste, siinuste, kotangentide ja puutujate väärtused on kirjutatud eelmisse nelja veergu. Peaksite olema ettevaatlik, kuna trigonomeetriliste funktsioonide nimed trigonomeetrilise tabeli allosas erinevad tabeli ülaosas olevatest nimedest. Siinused ja koosinused on vahetatud, nagu puutuja ja kotangens. See on tingitud trigonomeetriliste funktsioonide väärtuste sümmeetriast.

Trigonomeetriliste funktsioonide märgid on näidatud ülaltoodud joonisel. Sine on positiivsed väärtused 0 kuni 180 kraadi või 0 kuni pi. Negatiivsed väärtused siinus on 180 kuni 360 kraadi või pi kuni 2 pi. Koosinusväärtused on positiivsed vahemikus 0 kuni 90 ja 270 kuni 360 kraadi või 0 kuni 1/2 pi ja 3/2 kuni 2 pi. Tangensil ja kotangensil on positiivsed väärtused 0 kuni 90 kraadi ja 180 kuni 270 kraadi, mis vastavad väärtustele 0 kuni 1/2 pi ja pi kuni 3/2 pi. Puutuja ja kotangensi negatiivsed väärtused on 90 kuni 180 kraadi ja 270 kuni 360 kraadi või 1/2 pi kuni pi ja 3/2 pi kuni 2 pi. Trigonomeetriliste funktsioonide märkide määramisel nurkade jaoks, mis on suuremad kui 360 kraadi või 2 pi, peaksite kasutama nende funktsioonide perioodilisuse omadusi.

Trigonomeetrilised funktsioonid siinus, puutuja ja kotangens on paaritu funktsioonid. Nende funktsioonide väärtused negatiivsete nurkade jaoks on negatiivsed. Koosinus on ühtlane trigonomeetriline funktsioon – negatiivse nurga koosinusväärtus on positiivne. Trigonomeetriliste funktsioonide korrutamisel ja jagamisel tuleb järgida märgireegleid.

1. Trigonomeetrilise siinusfunktsiooni väärtuste tabel näitab järgmiste nurkade väärtusi

   Dokument

   Eraldi lehel on redutseerimisvalemid trigonomeetrilinefunktsioonid. IN laudväärtusedSesttrigonomeetrilinefunktsioonidsinusantudväärtusedSestjärgnevnurgad: patt 0, patt 30, patt 45 ...

2. Kavandatav matemaatiline aparaat on n-mõõtmeliste hüperkompleksarvude kompleksarvutuse täielik analoog mis tahes vabadusastmega n ja on mõeldud mittelineaarsete arvude matemaatiliseks modelleerimiseks.

   Dokument

   ... funktsioonid võrdub funktsioonid Pildid. Sellest teoreemist peaks, Mida Sest leides koordinaadid U, V, piisab arvutamisest funktsiooni... geomeetria; polünaar funktsioonid(kahemõõtmelise mitmemõõtmelised analoogid trigonomeetrilinefunktsioonid), nende omadused, tabelid ja rakendus; ...

3. Artiklis mõistame täielikult, kuidas see välja näeb laud trigonomeetrilised väärtused, siinus, koosinus, puutuja ja kotangens. Vaatleme trigonomeetriliste funktsioonide põhitähendust 0,30,45,60,90,...,360 kraadise nurga all. Ja vaatame, kuidas neid tabeleid trigonomeetriliste funktsioonide väärtuste arvutamisel kasutada.
   Kõigepealt vaatame koosinuse, siinuse, puutuja ja kotangensi tabel nurga all 0, 30, 45, 60, 90,... kraadi. Nende suuruste määratlus võimaldab meil määrata 0 ja 90 kraadi nurkade funktsioonide väärtuse:

   sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, kotangent alates 00 on määratlemata
   sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, puutuja alates 90 0 on ebakindel

   Kui võtad täisnurksed kolmnurgad mille nurgad on 30 kuni 90 kraadi. Saame:

   sin 30 0 = 1/2, cos 30 0 = √3/2, tan 30 0 = √3/3, cos 30 0 = √3
   sin 45 0 = √ 2/2, cos 45 0 = √ 2/2, tan 45 0 = 1, cos 45 0 = 1
   sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 = √3, võrevoodi 60 0 = √3/3

   Esitame kõik saadud väärtused kujul trigonomeetriline tabel:

   Siinuste, koosinuste, puutujate ja kotangentide tabel!

   Kui kasutame vähendamise valemit, suureneb meie tabel, lisades väärtused nurkade jaoks kuni 360 kraadi. See näeb välja selline:

   

   Samuti saab perioodilisuse omadustest lähtuvalt tabelit suurendada, kui asendame nurgad 0 0 +360 0 *z .... 330 0 +360 0 *z-ga, milles z on täisarv. Selles tabelis on võimalik arvutada kõigi nurkade väärtused, vastavad punktidühes ringis.

   

   Vaatame, kuidas tabelit lahenduses kasutada.
   Kõik on väga lihtne. Kuna vajalik väärtus asub meile vajalike lahtrite ristumispunktis. Näiteks võtke 60-kraadise nurga koefitsient, tabelis näeb see välja järgmine:

   

   Trigonomeetriliste funktsioonide põhiväärtuste lõpptabelis jätkame samamoodi. Kuid selles tabelis on võimalik teada saada, kui suur on puutuja 1020 kraadise nurga all, see = -√3 Kontrollime 1020 0 = 300 0 +360 0 *2. Leiame selle tabeli abil.

   

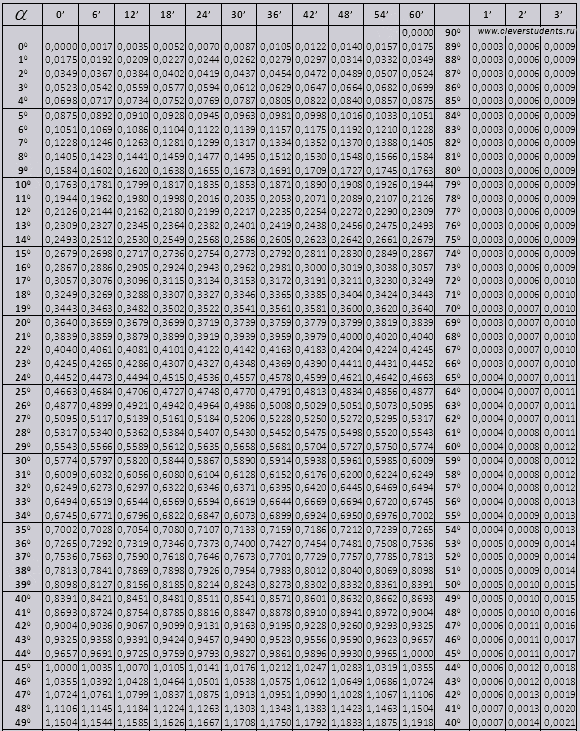
   Bradis laud. Siinuse, koosinuse, puutuja ja kotangensi jaoks.

   Bradise tabelid on jagatud mitmeks osaks, mis koosnevad koosinuse ja siinuse, puutuja ja kotangensi tabelitest - mis on jagatud kaheks osaks (kuni 90 kraadi nurkade tg ja väikeste nurkade ctg).

   Siinus ja koosinus

   
   
   

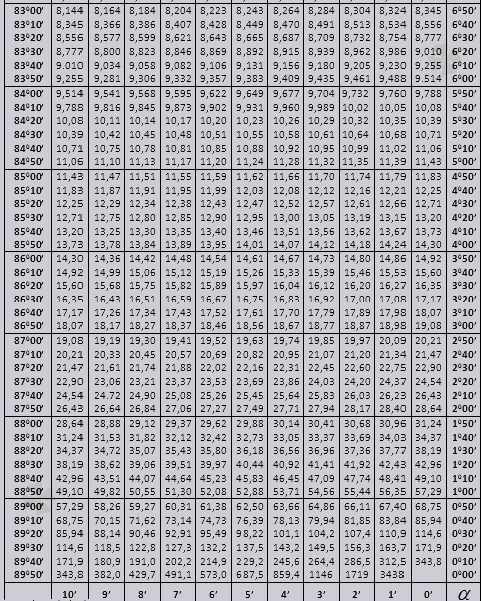
   tg nurk alates 00-st, mis lõpeb 760-ga, ctg-nurgaga, mis algab 140-ga ja lõpeb 900-ga.

   
   
   

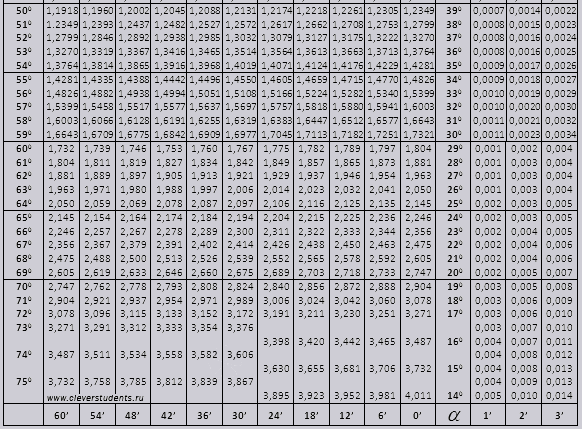
   tg kuni 900 ja väikeste nurkade ctg.

   
   

   Mõelgem välja, kuidas kasutada ülesannete lahendamisel Bradise tabeleid.

   Leiame tähise sin (tähistus vasakpoolses servas veerus) 42 minutit (tähistus on ülemisel real). Ristmiku järgi otsime tähist, see = 0,3040.
   
   Minutiväärtused on näidatud kuueminutilise intervalliga, mida teha, kui meile vajalik väärtus jääb täpselt sellesse intervalli. Võtame 44 minutit, aga tabelis on ainult 42. Võtame aluseks 42 ja kasutame lisaveerge parem pool, võtke 2. parandus ja lisage 0,3040 + 0,0006, saame 0,3046.
   
   Sin 47 minutiga võtame aluseks 48 minutit ja lahutame sellest 1 paranduse, st 0,3057 - 0,0003 = 0,3054
   
   Cos-i arvutamisel töötame sarnaselt patuga, ainult et võtame aluseks tabeli alumise rea. TO näide cos 20 0 = 0.9397
   
   Tg nurga väärtused kuni 90 0 ja väikese nurga cot on õiged ja neis pole parandusi. Näiteks leidke tg 78 0 37 min = 4,967
   
   
   ja ctg 20 0 13 min = 25,83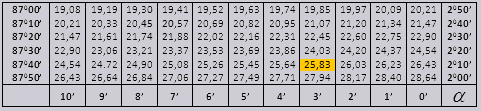
   
   

   Noh, vaatasime peamisi trigonomeetrilised tabelid. Loodame, et see teave oli teile väga kasulik. Kui teil on tabelite kohta küsimusi, kirjutage need kindlasti kommentaaridesse!

   Märkus. Seinakaitserauad on kaitserauad seinte kaitsmiseks. Järgige linki raamita seinakaitserauad (http://www.spi-polymer.ru/otboyniki/) ja uurige lisateavet.

   Viiendal sajandil eKr sõnastas Vana-Kreeka filosoof Zenon Eleast oma kuulsad apooriad, millest kuulsaim on "Achilleuse ja kilpkonna" apooria. See kõlab järgmiselt:

   Oletame, et Achilleus jookseb kümme korda kiiremini kui kilpkonn ja on sellest tuhat sammu maas. Aja jooksul, mis kulub Achilleuse läbimiseks, roomab kilpkonn sada sammu samas suunas. Kui Achilleus jookseb sada sammu, roomab kilpkonn veel kümme sammu jne. Protsess jätkub lõpmatuseni, Achilleus ei jõua kilpkonnale kunagi järele.

   See arutluskäik sai loogiliseks šokiks kõigile järgnevatele põlvkondadele. Aristoteles, Diogenes, Kant, Hegel, Hilbert... Nad kõik pidasid ühel või teisel viisil Zenoni apooriat. Šokk oli nii tugev, et " ...arutelud jätkuvad tänaseni, et jõuda ühisele arvamusele paradokside olemuse üle teadusringkond siiani pole see võimalik olnud... olime kaasatud teema uurimisse matemaatiline analüüs, hulgateooria, uued füüsikalised ja filosoofilised lähenemised; ükski neist ei saanud probleemi üldtunnustatud lahenduseks..."[Wikipedia, "Zeno's Aporia". Kõik saavad aru, et neid lollitatakse, aga keegi ei saa aru, milles pettus seisneb.

   Matemaatilisest vaatenurgast näitas Zenon oma apooriates selgelt üleminekut kvantiteedilt . See üleminek eeldab rakendust püsivate asemel. Nii palju kui ma aru saan, matemaatiline aparaat Muutuvate mõõtühikute kasutamine pole kas veel välja töötatud või pole seda Zenoni apooria puhul rakendatud. Meie tavapärase loogika rakendamine viib meid lõksu. Me rakendame mõtlemise inertsi tõttu vastastikusele väärtusele konstantseid ajaühikuid. KOOS füüsiline punkt Perspektiivist tundub, et aeg aeglustub, kuni see täielikult peatub hetkel, mil Achilleus jõuab kilpkonnale järele. Kui aeg peatub, ei suuda Achilleus enam kilpkonnast üle joosta.

   Kui pöörame oma tavapärase loogika ümber, loksub kõik paika. Achilleus jookseb kaasa püsikiirus. Tema tee iga järgmine lõik on kümme korda lühem kui eelmine. Sellest tulenevalt on selle ületamiseks kulunud aeg kümme korda väiksem kui eelmisel. Kui rakendame selles olukorras "lõpmatuse" mõistet, siis oleks õige öelda: "Achilleus jõuab kilpkonnale lõpmatult kiiresti järele."

   Kuidas seda loogilist lõksu vältida? Püsi sees konstantsed ühikud aja mõõtmised ja ärge minge vastastikustele suurustele. Zenoni keeles näeb see välja järgmine:

   Aja jooksul, mis kulub Achilleuse tuhande sammu jooksmiseks, roomab kilpkonn sada sammu samas suunas. Järgmise ajaintervalli jaoks võrdne esimesega, Achilleus jookseb veel tuhat sammu ja kilpkonn roomab sada sammu. Nüüd on Achilleus kilpkonnast kaheksasada sammu ees.

   See lähenemine kirjeldab adekvaatselt tegelikkust ilma loogiliste paradoksideta. Aga ei ole täielik lahendus Probleemid. Einsteini väide valguse kiiruse vastupandamatusest on väga sarnane Zenoni apooriaga "Achilleus ja kilpkonn". Seda probleemi tuleb veel uurida, ümber mõelda ja lahendada. Ja lahendust tuleb otsida mitte lõpmata suurtes arvudes, vaid mõõtühikutes.

   Veel üks Zenoni huvitav apooria räägib lendavast noolest:

   Lendav nool on liikumatu, kuna ta on igal ajahetkel puhkeolekus ja kuna ta on igal ajahetkel puhkab, siis on ta alati puhkeolekus.

   Selles apoorias ületatakse loogiline paradoks väga lihtsalt - piisab, kui selgitada, et igal ajahetkel on lendav nool paigal erinevates ruumipunktides, mis tegelikult on liikumine. Siin tuleb märkida veel üks punkt. Ühe maanteel oleva auto foto järgi on võimatu kindlaks teha ei selle liikumise fakti ega kaugust selleni. Et teha kindlaks, kas auto liigub, vajate kahte samast punktist tehtud fotot erinevad hetked aega, kuid nende järgi ei saa kaugust määrata. Auto kauguse määramiseks vajate kahte fotot, mis on tehtud erinevad punktid ruumi ühel ajahetkel, kuid nende järgi on võimatu kindlaks teha liikumise fakti (loomulikult on arvutusteks siiski vaja lisaandmeid, abiks on trigonomeetria). Mida ma tahan välja tuua Erilist tähelepanu, on see, et kaks punkti ajas ja kaks punkti ruumis on erinevad asjad, mida ei tohiks segi ajada, sest need pakuvad erinevaid uurimisvõimalusi.

   Kolmapäeval, 4. juulil 2018

   Vikipeedias on väga hästi kirjeldatud komplekti ja multikomplekti erinevusi. Vaatame.

   Nagu näete, "komplektis ei saa olla kahte identset elementi", kuid kui komplektis on identsed elemendid, nimetatakse sellist komplekti "multiseks". Mõistlikud olendid ei mõista kunagi sellist absurdset loogikat. See on tase rääkivad papagoid ja treenitud ahvid, kellel puudub mõistus sõnast "täiesti". Matemaatikud tegutsevad tavaliste koolitajatena, kuulutades meile oma absurdseid ideid.

   Kunagi olid silla ehitanud insenerid silda katsetades silla all paadis. Kui sild kokku kukkus, suri keskpärane insener oma loomingu rusude all. Kui sild koormusele vastu pidas, ehitas andekas insener teisi sildu.

   Pole tähtis, kuidas matemaatikud peituvad fraasi "krutke mind, ma olen majas" või õigemini "matemaatikaõpingud" taha. abstraktsed mõisted", on üks nabanöör, mis seob neid lahutamatult reaalsusega. See nabanöör on raha. Rakenda matemaatiline teooria seab matemaatikutele endile.

   Õppisime väga hästi matemaatikat ja nüüd istume kassa taga ja anname palka välja. Nii et matemaatik tuleb meie juurde oma raha pärast. Loeme talle kogu summa välja ja laotame oma lauale erinevatesse hunnikutesse, millesse paneme sama nimiväärtusega arveid. Seejärel võtame igast virnast ühe arve ja anname selle matemaatikule." matemaatiline komplekt palgad." Selgitame matemaatikule, et allesjäänud arved saab ta kätte alles siis, kui ta tõestab, et ilma identsete elementideta hulk ei võrdu identsete elementidega hulgaga. Siit algab lõbus.

   Esiteks hakkab tööle saadikute loogika: "Seda võib teistele rakendada, aga mulle mitte!" Siis hakkavad nad meile kinnitama, et sama nimiväärtusega vekslitel on erinevad arvenumbrid, mis tähendab, et neid ei saa pidada samadeks elementideks. Olgu, loeme palgad müntidesse – müntidel pole numbreid. Siin hakkab matemaatik meeletult füüsikat meenutama: see on erinevatel müntidel erinevad kogused muda, kristallstruktuur ja aatomite paigutus igas mündis on ainulaadne...

   Ja nüüd on mul kõige rohkem huvi Küsi: kus on joon, millest kaugemal muutuvad multihulga elemendid hulga elementideks ja vastupidi? Sellist joont pole olemas – kõike otsustavad šamaanid, teadus ei ole siin lähedalgi valetamisele.

   Vaata siia. Valime välja sama alaga jalgpallistaadionid. Väljade pindalad on samad – see tähendab, et meil on multikomplekt. Aga kui vaadata nende samade staadioninimesid, siis saame neid palju, sest nimed on erinevad. Nagu näete, on sama elementide komplekt nii hulk kui ka multikomplekt. Kumb on õige? Ja siin tõmbab matemaatik-šamaan-teramees varrukast trumpide ässa ja hakkab meile rääkima kas komplektist või multikomplektist. Igal juhul veenab ta meid, et tal on õigus.

   Et mõista, kuidas tänapäeva šamaanid hulgateooriaga opereerivad, sidudes selle reaalsusega, piisab, kui vastata ühele küsimusele: mille poolest erinevad ühe hulga elemendid teise hulga elementidest? Ma näitan teile, ilma igasuguse "mõeldava mitte ühe tervikuna" või "ei ole mõeldav ühtse tervikuna".

   Pühapäev, 18. märts 2018

   Arvu numbrite summa on šamaanide tants tamburiiniga, millel pole matemaatikaga mingit pistmist. Jah, matemaatikatundides õpetatakse meid leidma arvu numbrite summat ja seda kasutama, aga seepärast ongi nad šamaanid, et õpetada järeltulijatele nende oskusi ja tarkust, muidu surevad šamaanid lihtsalt välja.

   Kas vajate tõestust? Avage Wikipedia ja proovige leida leht "Arvu numbrite summa". Teda pole olemas. Matemaatikas pole valemit, mille abil saaks leida mis tahes arvu numbrite summa. Lõppude lõpuks on numbrid graafilised sümbolid, mille abil kirjutame numbreid ja matemaatika keeles kõlab ülesanne nii: "Leia suvalist arvu esindavate graafiliste sümbolite summa." Matemaatikud ei suuda seda ülesannet lahendada, kuid šamaanid saavad sellega hõlpsasti hakkama.

   Mõelgem välja, mida ja kuidas me arvude summa leidmiseks teeme antud number. Ja nii, olgu meil number 12345. Mida tuleb teha, et leida selle arvu numbrite summa? Vaatleme kõiki samme järjekorras.

   1. Kirjutage number paberile. Mida me oleme teinud? Oleme teisendanud numbri graafiliseks numbrisümboliks. See ei ole matemaatiline tehe.

   2. Lõikasime ühe saadud pildi mitmeks üksikuid numbreid sisaldavaks pildiks. Pildi lõikamine ei ole matemaatiline tehe.

   3. Teisendage üksikud graafilised sümbolid numbriteks. See ei ole matemaatiline tehe.

   4. Lisage saadud numbrid. Nüüd on see matemaatika.

   Arvu 12345 numbrite summa on 15. Need on šamaanide õpetatavad “lõikamis- ja õmbluskursused”, mida matemaatikud kasutavad. Kuid see pole veel kõik.

   Matemaatilisest seisukohast pole vahet, millisesse arvusüsteemi me arvu kirjutame. Niisiis, sisse erinevad süsteemid Arvutuses on sama arvu numbrite summa erinev. Matemaatikas märgitakse numbrisüsteem numbrist paremal oleva alaindeksina. KOOS suur hulk 12345 Ma ei taha oma pead petta, vaatame numbrit 26 artiklist . Kirjutame selle arvu kahend-, kaheksand-, kümnend- ja kuueteistkümnendsüsteemis. Me ei vaata iga sammu mikroskoobi all, me oleme seda juba teinud. Vaatame tulemust.

   Nagu näete, on erinevates numbrisüsteemides sama numbri numbrite summa erinev. Sellel tulemusel pole matemaatikaga mingit pistmist. See on sama, kui määraksite ristküliku pindala meetrites ja sentimeetrites, saaksite täiesti erinevad tulemused.

   Null näeb kõigis numbrisüsteemides välja ühesugune ja sellel pole numbrite summat. See on veel üks argument selle kasuks, et. Küsimus matemaatikutele: kuidas on matemaatikas määratud midagi, mis ei ole arv? Mis, matemaatikute jaoks ei eksisteeri midagi peale numbrite? Ma võin seda lubada šamaanidele, kuid mitte teadlastele. Tegelikkus ei seisne ainult numbrites.

   Saadud tulemust tuleks pidada tõestuseks, et arvusüsteemid on arvude mõõtühikud. Lõppude lõpuks ei saa me numbreid võrrelda erinevad üksused mõõdud. Kui samad toimingud sama suuruse erinevate mõõtühikutega annavad pärast nende võrdlemist erinevaid tulemusi, siis pole sellel matemaatikaga mingit pistmist.

   Mis on tõeline matemaatika? See on siis, kui tulemus matemaatiline tehe ei sõltu numbri suurusest, kasutatavast mõõtühikust ja sellest, kes toimingu sooritab.
   

   Silt uksel Ta avab ukse ja ütleb:

   Oh! Kas see pole mitte naiste tualett?
   - Noor naine! See on laboratoorium hingede indefiilse pühaduse uurimiseks nende taevasse tõusmise ajal! Halo peal ja nool üles. Mis tualett veel?

   Naine... Halo peal ja nool alla on isased.

   Kui selline disainikunstiteos vilksatab teie silme ees mitu korda päevas,

   Siis pole üllatav, et äkki leiate oma autost kummalise ikooni:

   Mina isiklikult pingutan selle nimel, et kakaval inimesel oleks näha miinus nelja kraadi (üks pilt) (mitmest pildist koosnev kompositsioon: miinusmärk, number neli, kraadide tähistus). Ja ma ei arva, et see tüdruk on loll, ei füüsikaga kursis. Tal on lihtsalt taju stereotüüp graafilised pildid. Ja matemaatikud õpetavad meile seda kogu aeg. Siin on näide.

   1A ei ole "miinus neli kraadi" ega "üks a". See on "kakav mees" või number "kakskümmend kuus" kuueteistkümnendsüsteemis. Need inimesed, kes pidevalt selles numbrisüsteemis töötavad, tajuvad numbrit ja tähte automaatselt ühe graafilise sümbolina.