ГЛАВА ТРЕТА

ПОЛИЕДРИ

II ОБЕМ ПРИЗМА И ПИРАМИДА

82. Основни предпоставки в томове.Количеството заето място геометрично тяло, се нарича обем на това тяло.

Поставяме задачата - да намерим израз за това количество под формата на определено число, което измерва това количество. При това ще се ръководим от следното отправни точки:

1) Равни телаимат равни обеми.

2) Обемът на тялото(например всеки паралелепипед, показан на фиг. 87), състоящ се от части(P и Q), равно на суматаобеми от тези части.

Две тела с еднакъв обем се наричат ​​еднакви по размер.

83. Единица за обем.При измерване на обеми единицата обем се приема за обем на куб, в който всеки ръб е равен на линейна единица. Така се използват кубични метри (m3), кубични сантиметри (cm3) и т.н.

Обем на паралелепипед

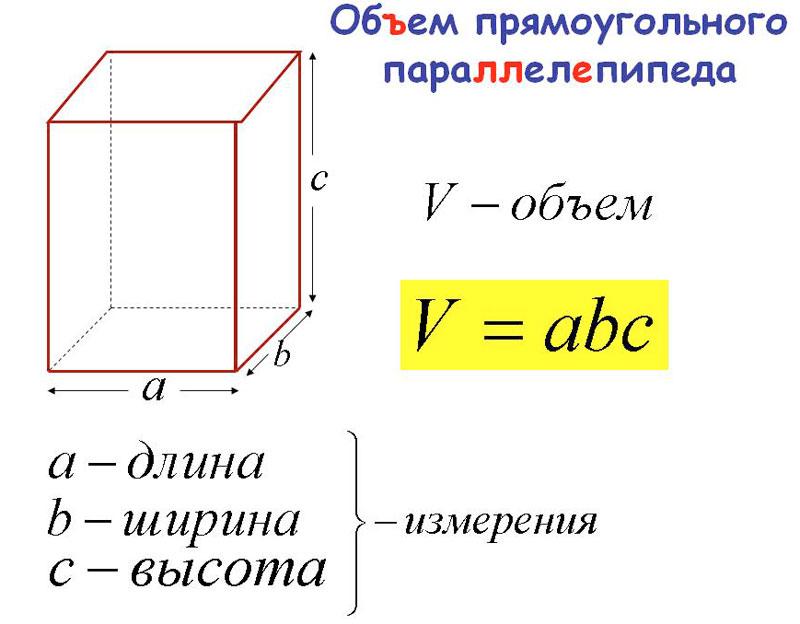
84. Теорема.Обем на правоъгълен паралелепипед равно на произведениетонеговите три измерения.

В това кратки изразиТази теорема трябва да се разбира по следния начин: числото, изразяващо обема на правоъгълен паралелепипед в кубична единица, е равно на произведението на числа, изразяващи неговите три измерения в съответната линейна единица, тоест в единица, която е ръб на куб, чийто обем се приема за кубична единица. Така че, ако Xе число, изразяващо обема на правоъгълен паралелепипед в кубически сантиметри, И а, бИ с-числа, изразяващи трите му измерения в линейни сантиметри, тогава теоремата гласи, че x = abc.

В доказателството ще разгледаме специално следните три случая:

1) Измерванията са изразени цели числа.

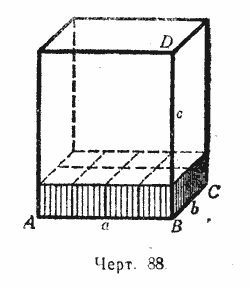
Нека, например, измерванията са (фиг. 88): AB = А, слънце = bи BD = c,
Къде а, бИ с- някои цели числа (например, както е показано на нашия чертеж: А = 4, b= 2 и с= 5). Тогава основата на паралелепипеда съдържа абтакива квадрати, всеки от които представлява съответния квадратна единица. Всеки от тези квадрати очевидно може да побере една кубична единица. След това получавате слой (показан на чертежа), състоящ се от абкубични единици. Тъй като височината на този слой е равна на една линейна единица, а височината на целия паралелепипед съдържа стакива единици, тогава можем да поставим вътре в паралелепипеда стакива слоеве. Следователно обемът на този паралелепипед е равен на абвкубични единици.

2) Измерванията са изразени дробни числа . Нека размерите на паралелепипеда са:

м / п , стр / р , r / s

. (някои от тези дроби може да са равни на цяло число). Намаляване на дробите до същия знаменател, ще имаме:

mqs / nqs , pns / nqs , rnq / nqs

Да вземем 1 / nqsделът на линейна единица за нова (спомагателна) единица за дължина. Тогава в тази нова мерна единица на този паралелепипед те ще бъдат изразени в цели числа, а именно: mqs, pnsИ rnq, и следователно според доказаното (в случай 1) обемът на паралелепипеда е равен на произведението ( mqs) (pns) (rnq), ако измерим този обем с нова кубична единица, съответстваща на нова линейна единица. Една кубична единица, съответстваща на предишната линейна единица, съдържа ( nqs) 3 ; това означава, че новата кубична единица е 1/( nqs) 3 бивши. Следователно обемът на паралелепипеда, изразен в предишните единици, е равен на:

3) Измерванията са изразени ирационални числа. Нека този паралелепипед (фиг. 89), който за краткост обозначаваме с една буква Q, има размерите:

AB = α; AC = β; AD = γ,

където всички числа α, β и γ или само някои от тях са ирационални.

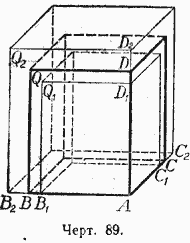
Всяко от числата α, β и γ може да бъде представено като безкрайност десетичен знак. Нека вземем приблизителните стойности на тези дроби с пв десетични знаци, първо с дефицит и след това с излишък. Стойностите с недостатък ще бъдат обозначени с α п , β п , γ п, стойности с излишък α" п , β" п , γ" п. Нека положим върху ръба AB, започвайки от точка A, две отсечки AB 1 = α пи AB 2 = α" п.
На ръба AC от същата точка A нанасяме отсечките AC 1 = β пи AC 2 = β" па на ръба AD от същата точка-отсечка AD 1 = γ пи AD 2 = γ" п.

В този случай ще имаме:

AB 1< АВ < АВ 2 ; АС 1 < АС < АС 2 ; AD 1 < AD < AD 2 .

Нека сега построим два спомагателни паралелепипеда; единият (да го наречем Q 1) с измервания AB 1, AC 1 и AD 1, а другият (да го наречем Q 2) с измервания AB 2, AC 2 и AD 2. Паралелепипедът Q 1 ще се побере изцяло в паралелепипеда Q, а паралелепипедът Q 2 ще съдържа паралелепипеда Q вътре в него.

От доказаното (в случай 2) ще имаме:

обем Q 1 = α п β п γ п (1)

обем Q 2 = α" п β" п γ" п (2)

Нека дефинираме обема Q 1< объёма Q 2 .

Нека сега започнем да увеличаваме броя п. Това означава, че вземаме приблизителни стойности на числата α, β, γ все по-големи и в по-голяма степенточност.

Нека видим как се променят обемите на паралелепипедите Q 1 и Q 2.

С неограничено увеличение побем Q 1 очевидно нараства поради равенство (1) с безкрайно нарастване пима за своя граница границата на продукта (α п β п γ п). Обемът Q 2 очевидно намалява и поради равенството (2) има границата на произведението (α" п β" п γ" п). Но от алгебрата е известно, че и двата продукта
α п β п γ пи α" п β" п γ" пс неограничено увеличение пимат обща граница, която е продуктът ирационални числа αβγ.

Приемаме тази граница като мярка за обема на паралелепипеда Q: обем Q = αβγ.

Може да се докаже, че така определеният обем отговаря на условията, установени за обем (§ 82). Всъщност с това определение за обем равни паралелепипеди, очевидно имат равни обеми. Следователно първото условие (§ 82) е изпълнено. Нека го разбием сега този паралелепипед Q с равнина, успоредна на основата му, на две: Q 1 и Q 2 (фиг. 90).

Тогава ще имаме:

обем Q = AB AC AD,
обем Q 1 = AB AA 1 AD,
том Q 2 = A 1 B 1 A 1 C A 1 D 1.

Добавяйки последните две равенства член по член и отбелязвайки, че A 1 B 1 = AB и A 1 D 1 = AD, получаваме:

обем Q 1 + обем Q 2 = AB AA 1 AD + AB A 1 C AD = AB AD (AA 1 + A 1 C) = AB AD AC, от тук получаваме:

обем Q 1 + обем Q 2 = обем Q.

Следователно второто условие на § 82 също е изпълнено, ако паралелепипедът е сгънат от две части, получени чрез разрязването му с равнина, успоредна на едно от лицата.

85. Следствие.Нека размерите на правоъгълен паралелепипед, които служат като страни на основата му, са изразени с числа АИ b, а третото измерение (височината) е число с. След това, обозначавайки неговия обем в съответните кубични единици с буквата V, можем да напишем:

V= абв.

Тъй като работата абизразява площта на основата, тогава можем да кажем това Обемът на правоъгълен паралелепипед е равен на произведението на площта на основата и височината .

Коментирайте.Съотношение на две кубични единици различни именаравно на третата степен на отношението на тези линейни единици, които служат като ръбове за тези кубични единици. Да, отношение кубичен метърна кубичен дециметър е равно на 10 3, т.е. 1000. Следователно, например, ако имаме куб с дължина на ръба Алинейни единици и друг куб с ръб с дължина 3 Алинейни единици, то отношението на техните обеми ще бъде равно на 3 3, т.е. 27, което ясно се вижда от чертеж 91.

86. Лема. Наклонената призма е равна по размер на права призма, чиято основа е равна на перпендикулярното сечение на наклонената призма, а височината е равна на нейния страничен ръб.

Нека е дадена наклонената призма ABCDEA 1 B 1 C 1 D 1 E 1 (фиг. 92).

Нека продължим всичко странични ребраИ странични лицав една посока.

Нека вземем малко предимство в продължението произволна точкаАи ние ще ви преведем през него перпендикулярно сечение abcde. След това, оставяйки настрана ааа 1 = AA 1, нека начертаем А 1 перпендикулярно сечение а 1 b 1 c 1 d 1 д 1. Тъй като равнините на двете сечения са успоредни, тогава bb 1 = ss 1 =дд 1 = тя 1 = аа 1 = AA 1 (§17). В резултат на това полиедърът а 1 d, за която сеченията, които сме начертали, са взети за основа, е права призма, която се обсъжда в теоремата.

Нека докажем, че тази наклонена призма е равна по размер на тази права линия. За да направим това, нека първо се уверим, че полиедрите а D и а 1 D 1 са равни. Причините им abcdeИ а 1 b 1 c 1 d 1 д 1 са равни като основите на призма а 1 d; от друга страна, добавяйки към двете страни на равенството A 1 A = А 1 Апо същата отсечка A 1 А, получаваме: АА = А 1 A 1; като това b B = b 1 в 1, с C = с 1 C 1 и т.н. Нека сега си представим, че полиедърът а D е вградено в полиедър а 1 D 1, така че основите им да съвпадат; тогава страничните ребра, перпендикулярни на основите и съответно равни, също ще съвпадат; следователно полиедър а D ще бъде съвместим с полиедъра а 1 D 1; Това означава, че тези тела са равни. Сега отбележете, че ако към права призма а 1 dдобавете полиедър а D и до наклонена призма A 1 D добавете полиедър а 1 D 1 равно а D, тогава получаваме същия полиедър а 1 D. От това следва, че две призми A 1 D и а 1 dеднакви по големина.

87. Теорема. Обемът на паралелепипед е равен на произведението на площта на основата и височината.

По-рано доказахме тази теорема за правоъгълен паралелепипед, сега ще я докажем за прав паралелепипед, а след това за наклонен.

1). Нека (фиг. 93) AC 1 е прав паралелепипед, тоест такъв, чиято основа ABCD е някакъв вид успоредник, а всички странични стени са правоъгълници.

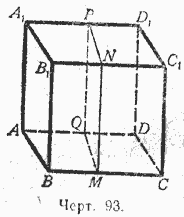
Нека вземем страничната повърхност AA 1 B 1 B като основа; тогава паралелепипедът ще бъде
наклонен. Гледайки го като специален случайнаклонена призма, въз основа на лемата от предишния параграф, можем да твърдим, че този паралелепипед е равен по размер на прав паралелепипед, чиято основа е перпендикулярно сечение MNPQ и чиято височина е BC. Четириъгълникът MNPQ е правоъгълник, защото ъглите му служат линейни ъглидиректен двустенни ъгли; следователно прав паралелепипед с основа правоъгълник MNPQ трябва да е правоъгълен и следователно обемът му е равен на продукт от тринеговите измервания, за които могат да се вземат сегментите MN, MQ и BC. по този начин

обем AC 1 = MN MQ BC = MN (MQ BC).

Но продуктът MQ BC изразява площта на успоредник ABCD, следователно

обем ACX = (площ ABCD) MN = (площ ABCD) BB 1.

2) Нека (фиг. 94) AC 1 е наклонен паралелепипед.

Тя е равна по размер на права линия, чиято основа е перпендикулярното сечение MNPQ (т.е. перпендикулярно на ръбовете AD, BC, ...), а височината е ръбът BC. Но, според доказани доказателства, обемът прав паралелепипедравно на произведението на площта на основата и височината; означава,

обем AC 1 = (площ MNPQ) BC.

Ако RS е височината на сечението MNPQ, тогава площта MNPQ = MQ RS, следователно

обем AC 1 = MQ RS BC = (BC MQ) RS.

Продуктът BC MQ изразява лицето на успоредника ABCD; следователно, обем AC 1 = (площ ABCOD) RS.

Сега остава да докажем, че отсечката RS представлява височината на паралелепипеда. Наистина, сечението MNPQ, перпендикулярно на ръбовете BC, B 1 C 1, .. . , трябва да са перпендикулярни на лицата ABCD, BB 1 C 1 C, .... минаващи през тези ръбове (§ 43). Следователно, ако построим перпендикуляр на равнината ABCD от точка S, тогава той трябва да лежи изцяло в равнината MNPQ (§ 44) и следователно трябва да се слее с правата RS, която лежи в тази равнина и е перпендикулярна на MQ . Това означава, че отсечката SR е височината на паралелепипеда. По този начин обемът и наклонен паралелепипедравна на произведението на площта на основата и височината.

Последица.Ако V, B и H са числа, изразяващи в съответните единици обема, основната площ и височината на паралелепипеда, тогава можем да запишем.

Формули за обем

Обеми прости тела. Правоъгълен паралелепипед, цилиндър, пирамида, конус, сфера, паралелепипед.

Обем и повърхнини на правилни тела.

Общата информация за обемите и повърхнините на правилните тела е дадена в таблицата.

Име на фигурата	Площ и обем на фигура S	Име на фигурата	Площ и обем на фигура S
Правоъгълен паралелепипед		Цилиндър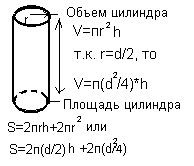
Сфера		паралелепипед

Пример 1. Изчисляване на обема на правоъгълен резервоар.

Резервоарът за вода има формата на правоъгълен паралелепипед с дължина 1 m, ширина 65 cm и височина 30 cm. Определете обема на резервоара в m 3, cm 3, литри

Обемът на правоъгълен паралелепипед е l*b*h

а) V резервоар = 1 * 0,65 * 03 = 0,195 m 3

б) 1 m 315000 mm 2 =315000/100=3150 cm 2

1 m 3 =10 6 cm 3, което означава 0,195 m 3 =0,195*10 6 =195000 cm 3

в) 1 литър = 1000 cm 3, което означава 195 000 cm 3 = 195 l

Пример 2. Изчисляване на обема и повърхността на трапецовидна призма.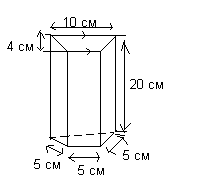

Изчислете обема и обща площповърхността на призмата, показана на фиг.

Тялото, показано на фиг. - Това е трапецовидна призма.

Тъй като обем = площ напречно сечение* височина, тогава

V=1/2*(10+5)*4*20=30*20=600 cm 3

Тъй като площта на повърхността се изчислява чрез събиране на сумата от площите на два трапеца и сумата от площите на четири правоъгълника, тогава

S=(2*30)+3(5*20)+(10*20)=560 cm 2

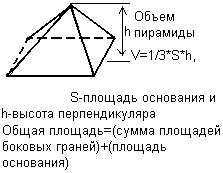
Пример 3: Изчисляване на обем и обща повърхност правилна пирамида.

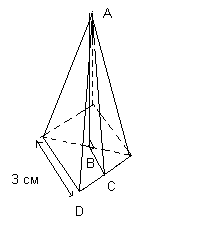
Определете обема и общата повърхност на правилна пирамида с квадратна основа, показана на фигурата, ако нейната височина е 15 cm.

Тъй като обемът на пирамидата = 1/3 (основна площ) * височина, тогава

V=1/3*(5*5)*15=125 см 3

Общата повърхност включва площ квадратна основаи площта на четири равни триъгълника.

Площта на триъгълника ADE=1/2*основа*(височина на страната).

Височината на AC лицето може да се намери с помощта на Питагоровата теорема от триъгълник ABC, където AB=15 cm, BC=1/2*3=1,5 cm и AC 2 =AB 2 +BC 2 =225+2,25=227,25

Следователно площта на триъгълника ADE

S ADE =1/2*3*15,07=22,605 cm 2

Общата площ на пирамидата е S=(3*3)+4*22.605=99.42 cm 2.

Пример 4. Изчисляване на обема и общата повърхност на конус.

Определете обема и общата повърхност на конус с радиус 4 cm и височина 10 cm.

Обем на конуса V=1/3πr 2 h =1/3*π4 2 *10=167.5cm 3

Общата повърхност е равна на сумата от площта конична повърхности основна площ, т.е. S=πrl+πr 2

Фигурата показва, че дължината на образуващата l може да бъде намерена с помощта на Питагоровата теорема.

l 2 =10 2 +4 2 =116 cm

Следователно общата повърхност е

S=π*4*10.8)+(π*4 2 =185.89 cm 2

Пример 5. Изчисляване на обема и общата повърхност на призмата.

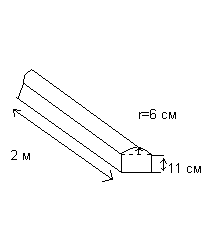
На фиг. показан дървен профил. Да намерим: а) обема му в m3

б) общата му повърхност

Профилът е призма, чието напречно сечение се състои от правоъгълник и полукръг. Тъй като радиусът на полукръга е 6 cm, диаметърът е 12 cm.

Тогава размерите на правоъгълника са 12*11 см

Площ на напречното сечение S. =(11*12)+1/2* π 6 2 =188,52 cm 2

Тъй като обемът на дървена част е равен на произведението на площта на напречното сечение и дължината, тогава

а) V=188,52*200=37704 cm 3 =37704 cm 3 /10 6 = 0,037704 m 3

b) Общата площ включва два края (всяка площ е 188,52 cm 2), три правоъгълника и извита повърхност (която е полуцилиндър). Следователно общата повърхност

S=(2*188.52)+2*(11*200)+(12*200)+1/2*(2π*6*200)=377.04+4400+2400+3768=10945.04 cm 2 =1.094504 m2.

Пример 6. Изчисляване на обема и общата повърхност на сложен котел.

Котелът се състои от цилиндрична секция с дължина 9 m и диаметър 5 m, към единия край на която е прикрепена полусферична секция с диаметър 5 m, а към другия край конична секция с височина 3 m и диаметър на основата 5 m. Изчислете обема на котела и общата му повърхност.

V полукълбо P =2/3*πr 3 =2/3*π*2.5 3 =10.42 π m 3

V цилиндър Q = π r 2 h=π*2,5 2 *9=56,25 π m 3

V конус R =1/3 π r 2 =1/3*π*2,5 2 *3=6,25π m 3

Общ обем на котела V= 10,42 π m 3 +56,25 π m 3 +6,25π m 3 =72,92π=228,97 m 3

S полукълба P. =2*(πr 2)=2*π*2,5 2 =12,5π m 2

S страна повърхност на цилиндъра Q. =2πrh=2*π*2.5*9=45π m 2 (тъй като този цилиндър е тръба без основи)

Дължината на образуващата на конуса l се изчислява с помощта на Питагоровата теорема от триъгълник ABC;

l=(3 2 +2,5 2) 1/2 =3,9 m.

S конус R. =πrl=π*2,5*3,9=9,75 π m 2

Обща площ на котела

S= 12.5π+45π+9.75 π=67.25π=211.2 m2

всички добър ден! Казвам се Иван и съм баща на ученик, който не е много добър по математика. Наскоро сина ми получи задача - да намери обема на паралелепипед и след като побърника малко и не успя да реши задачата, той се обърна към мен. Училищни знанияНе беше останало много в паметта ми и затова трябваше да взема учебниците, да ги препрочитам и след това да обяснявам материала, който съм учил, на сина си. Със сигурност моят опит ще бъде полезен за други родители и затова написах тази статия, която предоставя подробна информация за решаване на проблеми в обема на това геометрична фигура.

Малко теория

Преди да ви кажа как всъщност да намерите обема и площта на паралелепипед и използвайки каква формула, нека си припомним заедно какво е това. Тази геометрична фигура има три еквивалентни интерпретации:

1. Паралелепипедът е многостен с 6 лица, чиято особеност е, че всяко от тях е успоредник.
2. Терминът включва също шестоъгълник с 3 чифта лица, които ще бъдат успоредни едно на друго.
3. Призма, базирана на успоредник, се нарича още паралелепипед.

Най-често е необходимо да се изчисли обемът на паралелепипедите на няколко различни видове. Всеки случай има своя собствена формула и собствено решение и по-долу ще обясня подробно как се решава типични задачичрез изчисляване на обемите на различни видове от тази геометрична фигура.

Да преминем към практиката

Как да решим задачата за намиране на обема на правоъгълен паралелепипед? Особеността на този тип фигура е, че всяко от лицата й е правоъгълник. Ако искате да разберете как изглежда правоъгълен паралелепипед, погледнете най-обикновената кутия за обувки.

За да решим проблема, първо търсим стойностите на двете страни на основата на фигурата. Партиите имат перпендикулярно разположениеедна спрямо друга и се намират по формулата: P-AxB, където A е дължината, а B е ширината. След това откриваме още един ключов параметър, а именно намираме височината. И след това преминаваме към изчисляване на обема, в който ще работи следната формула: V = PxH, тоест, за да получите обема, трябва да умножите основната площ по височината. Как да намерите височината - тук си струва да разгледате учебник по геометрия и да напишете формула за намиране на ръба на фигура.

За да намерим обема на прав паралелепипед, нека да разгледаме как изглежда тази конкретна фигура. Неговите странични лица са правоъгълници, перпендикулярни на основата, и следователно обемът ще бъде изчислен идентичен на задачата по-горе, но трябва само да вземете предвид, че височината няма да бъде ръбът на фигурата, а сегмент, свързващ лицата, противоположни на една друга и перпендикулярни на основата. Основата тук е успоредник и следователно формулата ще бъде малко по-сложна: P=AxBxsin(a). A, B са дължината и ширината на основата, а "a" е ъгълът, който ще образуват при пресичане.

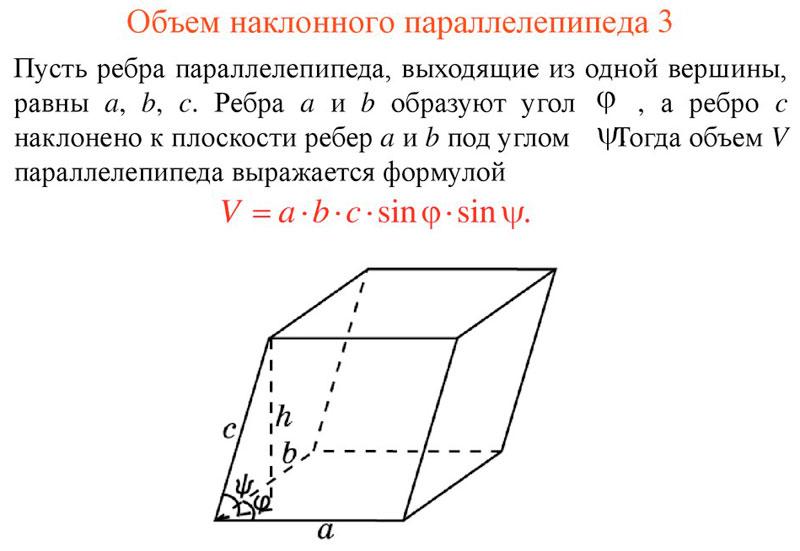
Обем на паралелепипед

Нека да разберем обема на наклонен тип фигура. Лицата на този тип фигура не са перпендикулярни на нейната основа и следователно изчисленията трябва да започнат с намиране на височината. Умножаваме височината по площта на основата и получаваме обема, тоест нашата формула изглежда така както следва: V=PxN.

Остава да разберете как да изчислите обема на фигура, чиито страни са квадратни. Тази фигура по-често се нарича куб, но в същото време е паралелепипед, всяко лице на което е квадрат. Следователно всичките му ръбове ще бъдат равни един на друг. Формулата за изчисляване на обема ще бъде възможно най-проста: трябва да измерите ребрата и да повишите резултата от изчисленията до 3-та степен.

Така се намира обемът на такава интересна геометрична фигура като паралелепипед. Надявам се, че краткият лист за измама, който написах, ще бъде добра помощ за ученици и родители при решаването на задачи по геометрия и вашият ученик няма да напише нито един тест с лоша оценка!