Tìm đạo hàm của một hàm lượng giác. Bài đại số và bắt đầu giải tích “đạo hàm hàm lượng giác”

Để tìm đạo hàm của hàm lượng giác cần sử dụng bảng dẫn xuất, cụ thể là đạo hàm 6-13.

Khi bạn tìm thấy đạo hàm nguyên tố hàm lượng giác Để tránh những lỗi thường gặp, bạn nên chú ý những điểm sau:

  • trong một biểu thức hàm, một trong các thuật ngữ thường sin, cosin hoặc hàm lượng giác khác không phải từ đối số của hàm, mà từ số (hằng số), do đó đạo hàm của số hạng này bằng 0;
  • hầu như luôn luôn bạn cần đơn giản hóa biểu thức thu được do lấy vi phân và để làm được điều này, bạn cần tự tin sử dụng kiến ​​​​thức về các phép tính với phân số;
  • để đơn giản hóa biểu thức bạn hầu như luôn cần biết nhận thức lượng giác, ví dụ, công thức góc đôi và công thức tính sự thống nhất là tổng bình phương của sin và cos.

Ví dụ 1. Tìm đạo hàm của một hàm số

Giải pháp. Hãy nói với đạo hàm cosin mọi thứ đều rõ ràng, nhiều người bắt đầu nghiên cứu các công cụ phái sinh sẽ nói. Thế còn đạo hàm của sin mười hai chia cho pi? Trả lời: đếm bằng 0! Ở đây, sin (xét cho cùng là một hàm!) là một cái bẫy, vì đối số không phải là biến X hay bất kỳ biến nào khác mà chỉ là một số. Nghĩa là sin của số này cũng là một số. Và đạo hàm của một số (hằng số), như chúng ta biết từ bảng đạo hàm, bằng 0. Vì vậy, chúng ta chỉ để lại sin âm của X và tìm đạo hàm của nó, không quên dấu:

.

Ví dụ 2. Tìm đạo hàm của một hàm số

.

Giải pháp. Thuật ngữ thứ hai tương tự như thuật ngữ đầu tiên trong ví dụ trước. Nghĩa là nó là một số và đạo hàm của số đó bằng 0. Ta tìm đạo hàm của số hạng thứ hai là đạo hàm của thương:

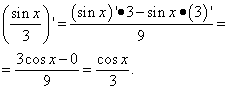
Ví dụ 3. Tìm đạo hàm của một hàm số

Giải pháp. Đây là một vấn đề khác: ở đây trong số hạng đầu tiên không có hàm arcsine hoặc hàm lượng giác nào khác, nhưng có x, có nghĩa là nó là hàm của x. Do đó, chúng tôi phân biệt nó như một thuật ngữ trong tổng các hàm:

Ở đây cần có kỹ năng thực hiện các phép tính với phân số, cụ thể là loại bỏ cấu trúc ba tầng của phân số.

Ví dụ 4. Tìm đạo hàm của một hàm số

.

Giải pháp. Ở đây chữ "phi" đóng vai trò tương tự như "x" trong các trường hợp trước (và trong hầu hết các trường hợp khác, nhưng không phải tất cả) - biến độc lập. Vì vậy, khi tìm đạo hàm của tích các hàm số, chúng ta sẽ không vội khai báo đạo hàm của căn “phi” bằng 0. Vì thế:

Nhưng giải pháp không kết thúc ở đó. Vì các thuật ngữ tương tự được đặt trong hai dấu ngoặc đơn nên chúng ta vẫn phải chuyển đổi (đơn giản hóa) biểu thức. Do đó, chúng ta nhân các dấu ngoặc với các thừa số đằng sau chúng, sau đó đưa các số hạng về mẫu số chung và thực hiện các phép biến đổi cơ bản khác:

Ví dụ 5. Tìm đạo hàm của một hàm số

Giải pháp. Trong ví dụ này, chúng ta sẽ cần biết thực tế là có một hàm lượng giác như vậy - cát tuyến - và các công thức của nó thông qua cosine. Hãy phân biệt:

Ví dụ 6. Tìm đạo hàm của một hàm số

.

Giải pháp. Trong ví dụ này, chúng ta sẽ phải nhớ công thức góc nhân đôi ở trường. Nhưng trước tiên hãy phân biệt:

,

(đây là công thức góc đôi)

Từ quá trình hình học và toán học, học sinh đã quen với việc khái niệm đạo hàm được truyền đạt cho các em thông qua diện tích của hình, vi phân, giới hạn của hàm số và giới hạn. Chúng ta hãy thử xem xét khái niệm đạo hàm từ một góc độ khác và xác định cách liên kết các hàm đạo hàm và hàm lượng giác.

Vì vậy, hãy xem xét một số đường cong tùy ý được mô tả bởi hàm trừu tượng y = f(x).

Hãy tưởng tượng rằng lịch trình là bản đồ của một tuyến du lịch. Gia số ∆x (delta x) trong hình là một khoảng cách nhất định của đường đi và ∆y là sự thay đổi độ cao của đường đi so với mực nước biển.
Khi đó, tỷ lệ ∆x/∆y sẽ mô tả độ phức tạp của tuyến đường trên mỗi đoạn của tuyến đường. Sau khi học được giá trị này, bạn có thể tự tin nói liệu đường đi lên/xuống dốc có dốc hay không, liệu bạn có cần thiết bị leo núi hay không và liệu khách du lịch có cần một phương tiện nhất định hay không. rèn luyện thể chất. Nhưng chỉ báo này sẽ chỉ có giá trị cho một khoảng cách nhỏ∆x.

Nếu người tổ chức chuyến đi lấy các giá trị ban đầu và điểm cuối các đường đi, tức là ∆x – sẽ là bằng chiều dài tuyến đường, nó sẽ không thể có được dữ liệu khách quan về mức độ khó khăn của chuyến đi. Do đó, cần phải xây dựng một biểu đồ khác mô tả tốc độ và “chất lượng” của những thay đổi trên đường đi, hay nói cách khác là xác định tỷ lệ ∆x/∆y cho mỗi “mét” của tuyến đường.

Biểu đồ này sẽ là một dẫn xuất trực quan của một đường dẫn cụ thể và sẽ mô tả một cách khách quan những thay đổi của nó tại mỗi khoảng thời gian quan tâm. Rất dễ dàng để xác minh điều này; giá trị ∆x/∆y không gì khác hơn là một vi phân được lấy cho ý nghĩa cụ thể x và y. Chúng ta hãy áp dụng phép vi phân không phải cho các tọa độ cụ thể mà cho toàn bộ hàm:

Hàm đạo hàm và hàm lượng giác

Các hàm lượng giác gắn bó chặt chẽ với đạo hàm. Điều này có thể được hiểu từ hình vẽ sau. Trong hình trục tọa độ hàm số Y = f (x) được hiển thị - đường cong màu xanh.

K(x0; f(x0)) – điểm tùy ý, x0 + ∆x là khoảng tăng dọc theo trục OX và f (x0 + ∆x) là khoảng tăng dọc theo trục OY tại một điểm L nhất định.

Vẽ đường thẳng đi qua các điểm K và L rồi dựng tam giác vuông KLN. Nếu bạn nhẩm di chuyển đoạn LN dọc theo đồ thị Y = f(x) thì điểm L và N sẽ có xu hướng về các giá trị K(x0; f(x0)). Hãy gọi điểm này là điểm bắt đầu có điều kiện của biểu đồ - giới hạn, nhưng nếu hàm là vô hạn, ít nhất là trên một trong các khoảng, thì xu hướng này cũng sẽ là vô hạn và giá trị giới hạn của nó gần bằng 0.

Bản chất của xu hướng này có thể được mô tả bằng một tiếp tuyến với điểm đã chọn y = kx + b hoặc bằng đồ thị đạo hàm của hàm ban đầu dy - đường thẳng màu xanh lá cây.

Nhưng lượng giác ở đâu đây?! Mọi chuyện rất đơn giản, hãy xét tam giác vuông KLN. Giá trị vi phân của một điểm K cụ thể là tiếp tuyến của góc α hoặc ∠K:

Bằng cách này, chúng ta có thể mô tả ý nghĩa hình học của đạo hàm và mối quan hệ của nó với các hàm lượng giác.

Công thức đạo hàm của hàm lượng giác

Các phép biến đổi sin, cosin, tiếp tuyến, cotang khi xác định đạo hàm phải thuộc lòng.

Hai công thức cuối cùng không phải là lỗi, vấn đề là có sự khác biệt giữa việc xác định đạo hàm của một đối số đơn giản và một hàm có cùng khả năng.

Hãy xem xét bảng so sánh với các công thức tính đạo hàm của sin, cosin, tang và cotang:

Các công thức cũng được rút ra cho các dẫn xuất của arcsine, arccosine, arctangent và arccotangent, mặc dù chúng cực kỳ hiếm khi được sử dụng:

Điều đáng chú ý là các công thức trên rõ ràng là không đủ để giải quyết thành công nhiệm vụ điển hình Kỳ thi Thống nhất Nhà nước, những gì sẽ được chứng minh khi giải quyết ví dụ cụ thể tìm đạo hàm của một biểu thức lượng giác.

Bài tập: Cần tìm đạo hàm của hàm số và tìm giá trị của nó cho π/4:

Giải pháp: Để tìm y’ cần nhớ lại các công thức cơ bản để chuyển hàm số ban đầu thành đạo hàm, cụ thể là.

Chủ thể:"Đạo hàm của hàm lượng giác".
Loại bài học- Bài học củng cố kiến ​​thức.
Hình thức bài học- Bài học tích hợp
Vị trí của bài học trong hệ thống bài học của phần này- bài học chung.
Các mục tiêu được đặt ra một cách toàn diện:

  • giáo dục: biết quy tắc lấy vi phân, có khả năng áp dụng các quy tắc tính đạo hàm khi giải phương trình, bất phương trình; cải thiện môn học, bao gồm tính toán, kỹ năng và khả năng; kỹ năng máy tính;
  • đang phát triển: phát triển các kỹ năng trí tuệ, logic và lợi ích nhận thức;
  • giáo dục: rèn luyện khả năng thích ứng điều kiện hiện đạiđào tạo.

Phương pháp:

  • sinh sản và năng suất;
  • thực tế và bằng lời nói;
  • làm việc độc lập;
  • học tập theo chương trình, T.S.O.;
  • sự kết hợp của mặt trước, nhóm và công việc cá nhân;
  • học tập khác biệt;
  • quy nạp-suy diễn.

Các hình thức kiểm soát:

TIẾN ĐỘ BÀI HỌC

TÔI. Thời điểm tổ chức

II. Cập nhật kiến ​​thức tham khảo

a) Truyền đạt mục tiêu, mục đích:

  • biết quy tắc lấy vi phân, có khả năng áp dụng các quy tắc tính đạo hàm khi giải các bài toán, phương trình, bất phương trình;
  • cải thiện môn học, bao gồm tính toán, kỹ năng và khả năng; kỹ năng máy tính;
  • phát triển các kỹ năng trí tuệ và logic và lợi ích nhận thức;
  • trau dồi khả năng thích ứng với điều kiện học tập hiện đại.

b) Lặp lại tài liệu giáo dục

Quy tắc tính đạo hàm (lặp lại công thức trên máy tính có âm thanh). doc.7.

  1. Đạo hàm của sin là gì?
  2. Đạo hàm của cosin là gì?
  3. Đạo hàm của tiếp tuyến là gì?
  4. Đạo hàm của cotang là gì?

III. Công việc truyền miệng

Tìm đạo hàm.

Tùy chọn 1.

Tùy chọn 2.

Tại = 2X + 5.

Tại = 2X – 5.

Tại= 4cos X.

Tại= 3sin X.

Tại= tg X+ctg X.

Tại= tg X-ctg X.

Tại= tội lỗi 3 X.

Tại= cos 4 X.

Tùy chọn trả lời.

– 4sin X

– 3cos X

1/cos 2 X+ 1/sin 2 X

1/cos 2 X–1/sin 2 X

1/sin 2 X–1/cos 2 X

– 4sin4 X

– 3cos3 X

Trao đổi sổ ghi chép. Trong thẻ chẩn đoán, hãy đánh dấu các nhiệm vụ đã hoàn thành đúng bằng dấu + và các nhiệm vụ đã hoàn thành sai bằng dấu -.

IV. Giải phương trình bằng đạo hàm

– Làm thế nào để tìm được điểm mà đạo hàm bằng 0?

Để tìm các điểm tại đó đạo hàm chức năng này bằng 0, bạn cần:

- xác định bản chất của chức năng,
- tìm diện tích định nghĩa hàm,
– tìm đạo hàm của hàm này,
– giải phương trình f "(x) = 0,
- chọn câu trả lời đúng.

Nhiệm vụ 1.

Được cho: Tại = X–tội lỗi x.
Tìm thấy: những điểm tại đó đạo hàm bằng 0.
Giải pháp. Hàm được xác định và khả vi trên tập hợp tất cả các số thực, vì hàm được xác định và khả vi trên tập hợp tất cả các số thực g(x) = x Và t(x) = – tội lỗi x.
Sử dụng quy tắc phân biệt, chúng tôi nhận được f "(x) = (x–tội lỗi x)" = (x)" – (tội lỗi x)" = 1 – cos x.
Nếu như f "(x) = 0 thì 1 – cos x = 0.
vì x= 1/; hãy loại bỏ sự vô tỉ trong mẫu số, chúng ta sẽ có cos x = /2.
Theo công thức t= ± arccos Một+ 2n, n Z, ta được: X= ± arccos /2 + 2n, n Z.
Trả lời: x = ± /4 + 2n, n Z.

V. Giải phương trình bằng thuật toán

Tìm tại điểm nào đạo hàm biến mất.

f(x) = tội lỗi x+vì x

f(x) = tội lỗi 2 x – x

f(x) = 2x+cos(4 x – )

Học sinh có thể chọn một trong ba ví dụ. Ví dụ đầu tiên được đánh giá " 3 ", thứ hai - " 4 ", thứ ba -" 5 " Giải pháp trong sổ ghi chép, sau đó kiểm tra lẫn nhau. Một học sinh quyết định trên bảng. Nếu lời giải sai thì học sinh cần quay lại thuật toán và thử giải lại.

Điều khiển được lập trình.

Tùy chọn 1

Tùy chọn 2

y = 2X 3

y = 3X 2

y = 1/4 X 4 + 2X 2 – 7

y = 1/2 X 4 + 4X + 5

y = X 3 + 4X 2 – 3X.
Giải phương trình y " = 0

y = 2X 3 – 9X 2 + 12X + 7.
Giải phương trình y " = 0.

y= tội lỗi 2 X– cos 3 X.

y= cos 2 X– tội lỗi 3 X.

y= tg X–ctg( X + /4).

y=ctg X+tg( X – /4).

y= tội lỗi 2 X.

y= cos 2 X.

Tùy chọn trả lời.

Khi rút ra công thức đầu tiên của bảng, chúng ta sẽ tiến hành định nghĩa hàm đạo hàm tại một điểm. Chúng ta hãy đi đâu x- bất kì số thực, nghĩa là, x– bất kỳ số nào từ miền định nghĩa của hàm số. Chúng ta hãy viết giới hạn của tỷ số giữa độ tăng của hàm và độ tăng của đối số tại:

Cần lưu ý rằng dưới dấu giới hạn, biểu thức thu được không phải là độ bất định của 0 chia cho 0, vì tử số không chứa giá trị vô cùng nhỏ mà chính xác là bằng 0. Nói cách khác, số gia của hàm hằng luôn bằng 0.

Như vậy, đạo hàm của hàm hằngbằng 0 trong toàn bộ miền định nghĩa.

Đạo hàm của hàm công suất.

Công thức đạo hàm chức năng điện trông giống như , trong đó số mũ P- bất kỳ số thực nào

Trước tiên chúng ta hãy chứng minh công thức tính số mũ tự nhiên, nghĩa là, với p = 1, 2, 3, …

Chúng ta sẽ sử dụng định nghĩa đạo hàm. Chúng ta hãy viết giới hạn của tỷ số giữa độ tăng của hàm lũy thừa và độ tăng của đối số:

Để đơn giản hóa biểu thức ở tử số, chúng ta chuyển sang công thức nhị thức Newton:

Kể từ đây,

Điều này chứng tỏ công thức đạo hàm của hàm lũy thừa đối với số mũ tự nhiên.

Đạo hàm của hàm số mũ.

Chúng tôi trình bày đạo hàm của công thức đạo hàm dựa trên định nghĩa:

Chúng ta đã đến chỗ không chắc chắn. Để mở rộng nó, chúng tôi giới thiệu một biến mới và tại . Sau đó . Trong lần chuyển đổi trước, chúng tôi đã sử dụng công thức chuyển đổi sang cơ số logarit mới.

Hãy thay thế vào giới hạn ban đầu:

Nếu chúng ta nhớ lại giới hạn đáng chú ý thứ hai, chúng ta sẽ đi đến công thức đạo hàm của hàm số mũ:

Đạo hàm của hàm logarit.

Hãy chứng minh công thức đạo hàm của hàm logarit với mọi x từ miền định nghĩa và tất cả các giá trị hợp lệ của cơ sở Một logarit Theo định nghĩa đạo hàm ta có:

Như bạn đã nhận thấy, trong quá trình chứng minh, các phép biến đổi được thực hiện bằng cách sử dụng các tính chất của logarit. Bình đẳng đúng do giới hạn đáng chú ý thứ hai.

Đạo hàm của hàm lượng giác.

Để rút ra công thức đạo hàm của hàm lượng giác, chúng ta sẽ phải nhớ lại một số công thức lượng giác, cũng như giới hạn đáng chú ý đầu tiên.

Theo định nghĩa đạo hàm của hàm sin ta có .

Hãy sử dụng công thức hiệu của hàm sin:

Vẫn còn phải chuyển sang giới hạn đáng chú ý đầu tiên:

Do đó, đạo hàm của hàm tội lỗi x có vì x.

Công thức đạo hàm của cosin được chứng minh theo cách tương tự.

Do đó, đạo hàm của hàm vì x có –sin x.

Chúng ta sẽ rút ra các công thức cho bảng đạo hàm của tiếp tuyến và cotang bằng cách sử dụng các quy tắc vi phân đã được chứng minh (đạo hàm của một phân số).

Đạo hàm của hàm hyperbol.

Quy tắc đạo hàm và công thức đạo hàm của hàm số mũ từ bảng đạo hàm cho phép chúng ta suy ra công thức đạo hàm của sin hyperbol, cosin, tang và cotang.

Đạo hàm của hàm nghịch đảo.

Để tránh nhầm lẫn trong khi trình bày, chúng ta hãy biểu thị trong chỉ số dưới đối số của hàm mà vi phân được thực hiện, nghĩa là nó là đạo hàm của hàm f(x) Qua x.

Bây giờ chúng ta hãy xây dựng quy tắc tìm đạo hàm hàm nghịch đảo.

Hãy để các chức năng y = f(x) Và x = g(y) nghịch đảo lẫn nhau, được xác định trên các khoảng và tương ứng. Nếu tại một điểm có đạo hàm hữu hạn khác 0 của hàm f(x), thì tại điểm có đạo hàm hữu hạn của hàm nghịch đảo g(y), Và . Trong một bài viết khác .

Quy tắc này có thể được sửa đổi lại cho bất kỳ x từ khoảng , sau đó chúng tôi nhận được .

Hãy kiểm tra tính hợp lệ của các công thức này.

Hãy tìm hàm nghịch đảo của logarit tự nhiên (Đây y là một hàm và x- lý lẽ). Giải phương trình này cho x, chúng tôi nhận được (ở đây x là một hàm và y– lập luận của cô ấy). Đó là, và các hàm nghịch đảo lẫn nhau.

Từ bảng đạo hàm ta thấy rằng Và .

Hãy đảm bảo rằng các công thức tìm đạo hàm của hàm nghịch đảo dẫn chúng ta đến kết quả tương tự:

Trình bày các đạo hàm của hàm lượng giác nghịch đảo và đạo hàm của các công thức của chúng. Biểu thức cho các đạo hàm bậc cao hơn cũng được đưa ra. Liên kết đến các trang có nhiều hơn báo cáo chi tiết công thức đầu ra.

Đầu tiên, chúng ta rút ra công thức đạo hàm của arcsine. Cho phép
y = arcsin x.
Vì arcsine là hàm nghịch đảo của sin nên
.
Ở đây y là hàm của x.
.
Đạo hàm theo biến x:
.
Chúng tôi áp dụng:
.

Vì vậy, chúng tôi đã tìm thấy:
.
Và công thức trước có dạng:
.
.

Từ đây
.
Bằng cách này, bạn có thể thu được công thức đạo hàm của cung cosin. Tuy nhiên, sẽ dễ dàng hơn khi sử dụng công thức liên quan đến hàm lượng giác nghịch đảo:
.

Sau đó Một mô tả chi tiết hơn được trình bày trên trang “Dẫn xuất các dẫn xuất của arcsine và arccosine”. Ở đó nó được đưa rađạo hàm của đạo hàm theo hai cách

- đã thảo luận ở trên và theo công thức tính đạo hàm của hàm nghịch đảo.

Đạo hàm của arctangent và arccotangent

Theo cách tương tự, chúng ta sẽ tìm được đạo hàm của arctang và arctangent.
y = Cho phép.
arctan x
.
Arctangent là hàm nghịch đảo của tiếp tuyến:
.
Đạo hàm theo biến x:
.
Chúng tôi áp dụng:
.

Chúng ta áp dụng công thức tính đạo hàm của hàm phức:
.

Đạo hàm của cung cotang:

Theo cách tương tự, chúng ta sẽ tìm được đạo hàm của arctang và arctangent.
.
Dẫn xuất arcsin
.
Chúng ta đã tìm được đạo hàm bậc nhất của arcsine:
;
.
Bằng cách lấy vi phân, ta tìm được đạo hàm bậc hai:
.
Nó cũng có thể được viết dưới dạng sau: Từ đây chúng ta có được phương trình vi phân
.

, được thỏa mãn bởi đạo hàm arcsine bậc một và bậc hai:

Bằng cách vi phân phương trình này, chúng ta có thể tìm được đạo hàm bậc cao hơn.

Đạo hàm của arcsine bậc n Đạo hàm của arcsine cấp n có:
,
lượt xem tiếp theo
;
.
đâu là đa thức bậc .

Nó được xác định bởi các công thức:
.

Đây .

Đa thức thỏa mãn phương trình vi phân:
.
Đạo hàm của arccosine bậc n
.

Đạo hàm của cung cosin được lấy từ đạo hàm của cung sin bằng công thức lượng giác:

Do đó, đạo hàm của các hàm này chỉ khác nhau về dấu:
.

Đạo hàm của arctang

.
Cho phép . Chúng ta đã tìm được đạo hàm của cotang cung bậc một:

Hãy chia phân số thành dạng đơn giản nhất:

.

Đây là đơn vị tưởng tượng, .
.

Chúng ta vi phân một lần và đưa phân số về mẫu số chung:

Thay vào , ta được:
;
.

Đạo hàm của arctan bậc n

Do đó, đạo hàm của arctang cấp n có thể được biểu diễn theo nhiều cách:
.
Đạo hàm của arc cotang
.

Hãy để nó như vậy ngay bây giờ.
.

Ta áp dụng công thức nối các hàm lượng giác nghịch đảo:
Khi đó đạo hàm cấp n của tiếp tuyến cung chỉ khác dấu với đạo hàm của tiếp tuyến cung: Thay vào , ta tìm được: Văn học đã qua sử dụng: