Å finne en ubestemt integral (et sett med antiderivater eller "antiderivater") betyr å rekonstruere en funksjon fra den kjente deriverte av denne funksjonen. Restaurert sett med antiderivater F(x) + MED for funksjon f(x) tar hensyn til integrasjonskonstanten C. Ved bevegelseshastighet materiell poeng(derivert) bevegelsesloven til dette punktet (antiderivativ) kan gjenopprettes; i henhold til akselerasjonen av et punkts bevegelse - dets hastighet og bevegelsesloven. Som du kan se, er integrering et bredt felt for aktivitetene til fysikkens Sherlock Holmeses. Og i økonomi er mange konsepter representert gjennom funksjoner og deres derivater, og derfor er det for eksempel mulig å gjenopprette volumet av produkter produsert på tilsvarende tidspunkt ved å bruke arbeidsproduktivitet på et bestemt tidspunkt (derivat).
Å finne en ubestemt integral krever et ganske lite antall grunnleggende integrasjonsformler. Men prosessen med å finne det er mye vanskeligere enn bare å bruke disse formlene. All kompleksiteten er ikke knyttet til integrasjon, men til å bringe det integrerbare uttrykket til en form som gjør det mulig å finne det ubestemte integralet ved hjelp av grunnformlene nevnt ovenfor. Dette betyr at for å begynne praksisen med integrering, må du aktivere det du har lært i videregående skole ferdigheter for å transformere uttrykk.
Vi skal lære å finne integraler ved hjelp av egenskaper og tabell over ubestemte integraler fra en leksjon om de grunnleggende begrepene i dette emnet (åpnes i et nytt vindu).
Det finnes flere metoder for å finne integralet, hvorav variabel erstatningsmetode Og integrasjon etter deler metode- et obligatorisk herresett for alle som har bestått høyere matematikk. Det er imidlertid mer nyttig og morsomt å begynne å mestre integrasjon ved hjelp av dekomponeringsmetoden, basert på følgende to teoremer om egenskaper ubestemt integral, som vi gjentar her for enkelhets skyld.
Teorem 3.Konstant multiplikator i integranden kan tas ut som tegnet på det ubestemte integralet, dvs.
Teorem 4. Ubestemt integral av en algebraisk sum endelig antall funksjoner er like algebraisk sum ubestemte integraler av disse funksjonene, dvs.
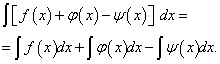 (2)
(2)
I tillegg kan følgende regel være nyttig i integrasjon: hvis uttrykket av integranden inneholder en konstant faktor, multipliseres uttrykket av antideriverten med inversen av konstantfaktoren, dvs.
![]() (3)
(3)
Siden denne leksjonen er en introduksjon til løsning av integreringsproblemer, er det viktig å merke seg to ting som enten allerede det første stadiet, eller litt senere kan de overraske deg. Overraskelsen skyldes det faktum at integrasjon er den inverse operasjonen av differensiering og det ubestemte integralet med rette kan kalles "antiderivatet".
Det første du ikke bør bli overrasket over når du integrerer. I tabellen over integraler det er formler som ikke har noen analoger blant de deriverte tabellformlene . Dette er følgende formler:
![]()
![]()
Du kan imidlertid sørge for at de deriverte av uttrykkene på høyresiden av disse formlene faller sammen med de tilsvarende integrandene.
Den andre tingen som ikke burde være overraskende ved integrering. Selv om den deriverte av enhver elementær funksjon også er en elementær funksjon, ubestemte integraler av noen elementære funksjoner er ikke lenger elementære funksjoner . Eksempler på slike integraler kan være følgende:
![]()
![]()
![]()
For å utvikle integrasjonsteknikker vil følgende ferdigheter være nyttige: å redusere brøker, dele et polynom i telleren av en brøk med et monom i nevneren (for å få summen av ubestemte integraler), konvertere røtter til potenser, multiplisere et monom med en polynom, heve til en potens. Disse ferdighetene er nødvendige for transformasjoner av integranden, som skal resultere i summen av integralene som er tilstede i tabellen over integraler.
Å finne ubestemte integraler sammen
Eksempel 1. Finn det ubestemte integralet
![]() .
.
Løsning. Vi ser i nevneren til integranden et polynom der x er kvadratisk. Dette er et nesten sikkert tegn på at du kan bruke tabellintegral 21 (med en arctangent som resultat). Vi tar ut faktor-to fra nevneren (det er en slik egenskap ved integralet - konstantfaktoren kan tas ut utover fortegnet til integralet; den ble nevnt ovenfor som setning 3). Resultatet av alt dette:
Nå er nevneren summen av kvadrater, som betyr at vi kan bruke den nevnte tabellintegralen. Til slutt får vi svaret:
![]() .
.
Eksempel 2. Finn det ubestemte integralet
Løsning. Vi bruker igjen teorem 3 - egenskapen til integralet, på grunnlag av hvilken den konstante faktoren kan tas ut av tegnet til integralet:
Vi bruker formel 7 fra tabellen over integraler (variabel til en potens) på integrandfunksjonen:
![]() .
.
Vi reduserer de resulterende brøkene og vi har det endelige svaret:
Eksempel 3. Finn det ubestemte integralet
![]()
Løsning. Ved å bruke først teorem 4 og deretter teorem 3 på egenskaper, finner vi dette integralet som summen av tre integraler:
Alle tre oppnådde integraler er tabellformede. Vi bruker formel (7) fra tabellen over integraler for n = 1/2, n= 2 og n= 1/5, og deretter

![]()
kombinerer alle tre vilkårlige konstanter som ble introdusert når finne tre integraler. I lignende situasjoner bør derfor bare én vilkårlig integrasjonskonstant introduseres.
Eksempel 4. Finn det ubestemte integralet
Løsning. Når nevneren til integranden inneholder en monomial, kan vi dele telleren med nevneren ledd for ledd. Det opprinnelige integralet ble til summen av to integraler:
![]() .
.
For å bruke tabellintegralen transformerer vi røttene til potenser og her er det endelige svaret:

Vi fortsetter å finne ubestemte integraler sammen
Eksempel 7. Finn det ubestemte integralet
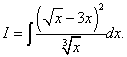
Løsning. Hvis vi transformerer integranden ved å kvadrere binomialet og dele telleren med nevneren ledd for ledd, så blir det opprinnelige integralet summen av tre integraler.
Antiderivativ funksjon og ubestemt integral
Fakta 1. Integrasjon er den inverse virkningen av differensiering, nemlig å gjenopprette en funksjon fra den kjente deriverte av denne funksjonen. Funksjonen er dermed gjenopprettet F(x) er kalt antiderivat for funksjon f(x).
Definisjon 1. Funksjon F(x f(x) på et eller annet intervall X, hvis for alle verdier x fra dette intervallet holder likheten F "(x)=f(x), det er denne funksjonen f(x) er et derivat av antiderivative funksjon F(x). .
For eksempel funksjonen F(x) = synd x er et antiderivat av funksjonen f(x) = cos x på hele talllinjen, siden for enhver verdi av x (synd x)" = (cos x) .
Definisjon 2. Ubestemt integral av en funksjon f(x) er settet med alle antiderivatene. I dette tilfellet brukes notasjonen
∫
f(x)dx
,hvor er skiltet ∫ kalt integrertegnet, funksjonen f(x) – integrand funksjon, og f(x)dx – integrert uttrykk.
Således, hvis F(x) – noe antiderivat for f(x), Det
∫
f(x)dx = F(x) +C
Hvor C - vilkårlig konstant (konstant).
For å forstå betydningen av settet med antiderivater av en funksjon som et ubestemt integral, er følgende analogi passende. La det være en dør (tradisjonell tredør). Dens funksjon er å "være en dør." Hva er døren laget av? Laget av tre. Dette betyr at settet med antiderivater av integranden til funksjonen "å være en dør", det vil si dens ubestemte integral, er funksjonen "å være et tre + C", der C er en konstant, som i denne sammenheng kan angi for eksempel typen tre. Akkurat som en dør er laget av tre ved hjelp av noen verktøy, er en avledet av en funksjon "laget" fra en antiderivatfunksjon ved å bruke formler vi lærte mens vi studerte den deriverte .
Da er funksjonstabellen til vanlige gjenstander og deres tilsvarende antiderivater ("å være en dør" - "å være et tre", "å være en skje" - "å være metall", etc.) lik tabellen over grunnleggende ubestemte integraler, som vil bli gitt nedenfor. Tabellen med ubestemte integraler viser vanlige funksjoner med en indikasjon på antiderivatene som disse funksjonene er "laget" fra. I en del av problemene med å finne det ubestemte integralet, er det gitt integrander som kan integreres direkte uten mye anstrengelse, det vil si ved å bruke tabellen over ubestemte integraler. I mer komplekse problemer må integranden først transformeres slik at tabellintegraler kan brukes.
Fakta 2. Når vi gjenoppretter en funksjon som en antiderivert, må vi ta hensyn til en vilkårlig konstant (konstant) C, og for ikke å skrive en liste over antiderivater med forskjellige konstanter fra 1 til uendelig, må du skrive et sett med antiderivater med en vilkårlig konstant C, for eksempel slik: 5 x³+C. Så en vilkårlig konstant (konstant) er inkludert i uttrykket av antiderivatet, siden antiderivatet kan være en funksjon, for eksempel 5 x³+4 eller 5 x³+3 og når differensiert, 4 eller 3, eller en hvilken som helst annen konstant går til null.
La oss stille integreringsproblemet: for denne funksjonen f(x) finne en slik funksjon F(x), hvis derivat lik f(x).
Eksempel 1. Finn settet med antiderivater av en funksjon
Løsning. For denne funksjonen er antiderivatet funksjonen
Funksjon F(x) kalles et antiderivat for funksjonen f(x), hvis derivatet F(x) er lik f(x), eller, som er det samme, differensial F(x) er lik f(x) dx, dvs.
![]() (2)
(2)
Derfor er funksjonen et antiderivat av funksjonen. Det er imidlertid ikke det eneste antiderivatet for . De fungerer også som funksjoner
Hvor MED– vilkårlig konstant. Dette kan verifiseres ved differensiering.
Så hvis det er ett antiderivat for en funksjon, så er det det for det uendelig sett antiderivater som avviker med en konstant term. Alle antiderivater for en funksjon er skrevet i skjemaet ovenfor. Dette følger av følgende teorem.
Teorem (formell faktaerklæring 2). Hvis F(x) – antiderivat for funksjonen f(x) på et eller annet intervall X, deretter et hvilket som helst annet antiderivat for f(x) på samme intervall kan representeres i skjemaet F(x) + C, Hvor MED– vilkårlig konstant.
I det neste eksemplet går vi til tabellen over integraler, som vil bli gitt i avsnitt 3, etter egenskapene til det ubestemte integralet. Vi gjør dette før vi leser hele tabellen slik at essensen av ovenstående er tydelig. Og etter tabellen og eiendommene vil vi bruke dem i sin helhet under integreringen.
Eksempel 2. Finn sett med antideriverte funksjoner:
Løsning. Vi finner sett med antideriverte funksjoner som disse funksjonene er "laget" fra. Når du nevner formler fra tabellen over integraler, for nå er det bare å akseptere at det er slike formler der, og vi vil studere selve tabellen over ubestemte integraler litt lenger.
1) Bruk av formel (7) fra tabellen over integraler for n= 3, får vi
![]()
2) Ved å bruke formel (10) fra tabellen over integraler for n= 1/3, vi har
3) Siden
deretter i henhold til formel (7) med n= -1/4 finner vi
![]()
Det er ikke selve funksjonen som er skrevet under integrertegnet f, og dets produkt ved differensialen dx. Dette gjøres først og fremst for å indikere hvilken variabel antiderivatet søkes etter. For eksempel,
![]() ,
,
![]() ;
;
her i begge tilfeller er integranden lik , men dens ubestemte integraler i tilfellene som vurderes viser seg å være forskjellige. I det første tilfellet betraktes denne funksjonen som en funksjon av variabelen x, og i den andre - som en funksjon av z .
Prosessen med å finne det ubestemte integralet til en funksjon kalles å integrere den funksjonen.
Geometrisk betydning av det ubestemte integralet
Anta at vi må finne en kurve y=F(x) og vi vet allerede at tangenten til hellingsvinkelen til tangenten i hvert punkt er gitt funksjon f(x) abscisse av dette punktet.
I følge geometrisk sans derivert, tangent til tangentvinkelen i et gitt punkt på kurven y=F(x) lik verdien av derivatet F"(x). Så vi må finne en slik funksjon F(x), for hvilket F"(x)=f(x). Funksjon som kreves i oppgaven F(x) er et antiderivat av f(x). Betingelsene for problemet tilfredsstilles ikke av en kurve, men av en familie av kurver. y=F(x)- en av disse kurvene, og en hvilken som helst annen kurve kan fås fra den parallell overføring langs aksen Oy.
La oss kalle grafen til antiderivertefunksjonen til f(x) integrert kurve. Hvis F"(x)=f(x), deretter grafen til funksjonen y=F(x) det er en integralkurve.
Fakta 3. Det ubestemte integralet er geometrisk representert av familien av alle integralkurver , som på bildet nedenfor. Avstanden til hver kurve fra opprinnelsen til koordinatene bestemmes av en vilkårlig integrasjonskonstant C.

Egenskaper til det ubestemte integralet
Fakta 4. Teorem 1. Den deriverte av et ubestemt integral er lik integranden, og dens differensial er lik integranden.
Fakta 5. Teorem 2. Ubestemt integral av differensialen til en funksjon f(x) lik funksjon f(x) opp til en konstant term , dvs.
![]() (3)
(3)
Teoremer 1 og 2 viser at differensiering og integrasjon er gjensidig inverse operasjoner.
Fakta 6. Teorem 3. Konstantfaktoren i integranden kan tas ut av fortegnet til det ubestemte integralet , dvs.
Løsning trigonometriske ulikheter ved bruk av enhetssirkel
Når du løser trigonometriske ulikheter i formen, hvor --- en av trigonometriske funksjoner, er det praktisk å bruke den trigonometriske sirkelen for å tydeligst presentere løsningene på ulikheten og skrive ned svaret. Hovedmetoden for å løse trigonometriske ulikheter er å redusere dem til de enkleste typeulikhetene. La oss se på et eksempel på hvordan man løser slike ulikheter.
Eksempel Løs ulikheten.
Løsning. La oss tegne en trigonometrisk sirkel og merke på den punktene som ordinaten er overlegen for.


For å løse denne ulikheten vil det være. Det er også klart at hvis et visst tall avviker fra et hvilket som helst tall fra det spesifiserte intervallet med, vil det heller ikke være mindre. Derfor trenger du bare å legge til løsninger i endene av det funnet segmentet. Til slutt finner vi at alle vil være en løsning på den opprinnelige ulikheten.


For å løse ulikheter med tangent og cotangens er konseptet med en linje med tangenter og cotangens nyttig. Dette er de rette linjene og henholdsvis (i figur (1) og (2)), vedrørende trigonometrisk sirkel.

Det er lett å se at hvis vi konstruerer en stråle med opprinnelsen ved koordinatenes opprinnelse, og danner en vinkel med den positive retningen til abscisseaksen, så vil lengden av segmentet fra punktet til skjæringspunktet for denne strålen med tangentlinjen er nøyaktig lik tangenten til vinkelen som denne strålen lager med abscisseaksen. En lignende observasjon forekommer for cotangens.
Eksempel Løs ulikheten.




Løsning. La oss betegne, da vil ulikheten ta den enkleste formen: . La oss vurdere et lengdeintervall lik den minste positive perioden (LPP) til tangenten. På dette segmentet, ved å bruke tangentlinjen, fastslår vi det. La oss nå huske hva som må legges til siden NPP fungerer. Så, . Tilbake til variabelen, vi får det

Det er praktisk å løse ulikheter med inverse trigonometriske funksjoner ved å bruke grafer av inverse trigonometriske funksjoner. La oss vise hvordan dette gjøres med et eksempel.
Løse trigonometriske ulikheter grafisk
Merk at hvis --- periodisk funksjon, så for å løse ulikheten er det nødvendig å finne løsningene på et segment hvis lengde er lik funksjonens periode. Alle løsninger på den opprinnelige ulikheten vil bestå av de funnet verdiene, så vel som alle de som skiller seg fra de funnet av et heltall av perioder av funksjonen
La oss vurdere løsningen på ulikhet ().
Siden har ulikheten ingen løsninger. Hvis, så settet med løsninger på ulikheten --- en haug med alle reelle tall.
La være. Sinusfunksjonen har den minste positiv periode, så ulikheten kan løses først på et lengdesegment, f.eks. Vi bygger grafer over funksjoner og ().

På segmentet øker sinusfunksjonen, og ligningen, der, har én rot. På segmentet avtar sinusfunksjonen, og ligningen har en rot. På numerisk intervall Grafen til funksjonen er plassert over grafen til funksjonen. Derfor, for alle fra intervallet) holder ulikheten if. På grunn av periodisiteten til sinusfunksjonen er alle løsninger på ulikheten gitt av ulikheter på formen: .
Vi vil løse ulikheter med tangent ved hjelp av enhetssirkelen.
Algoritme for å løse ulikheter med tangent:
- tegne om klisjeen vist i figuren ovenfor;
- på tangentlinjen markerer vi $a$ og tegner en rett linje fra origo til dette punktet;
- skjæringspunktet for denne linjen med halvsirkelen vil være skyggelagt hvis ulikheten ikke er streng og ikke skyggelagt hvis den er streng;
- området vil være plassert under linjen og opp til sirkelen hvis ulikheten inneholder tegnet "$>$", og under linjen og opp til sirkelen hvis ulikheten inneholder tegnet "$<$”;
- for å finne skjæringspunktet er det nok å finne arctangensen $a$, dvs. $x_(1)=(\rm arctg) a$;
- som svar blir det resulterende intervallet skrevet ut, og lagt til $+ \pi n$ til endene.
Eksempler på å løse ulikheter ved hjelp av en algoritme.
Eksempel 1: Løs ulikhet:
$(\rm tg)(x) \leq 1.$
Dermed vil løsningen ha formen:
$x \in \left(-\frac(\pi)(2) + \pi n; \frac(\pi)(4) + \pi n\right], \ n \in Z.$
Viktig! Peker $-\frac(\pi)(2)$ og $\frac(\pi)(2)$ ved tangenten alltid (uavhengig av ulikhetstegnet) revet ut!
Eksempel 2: Løs ulikhet:
$(\rm tg)(x) > – \sqrt(3).$
Vi markerer punktet $- \sqrt(3)$ på tangentlinjen og tegner en rett linje fra origo til denne. Skjæringspunktet mellom denne linjen og halvsirkelen vil ikke være skyggelagt, siden ulikheten er streng. Området vil ligge over den rette linjen og opp til sirkelen, siden ulikhetstegnet er $>$. la oss finne skjæringspunktet:
$x_(1) = (\rm arctg)(\left(-\sqrt(3)\right)) = -\frac(\pi)(3).$
$t \in \left(-\frac(\pi)(3) + \pi n; \frac(\pi)(2) + \pi n\right).$
La oss gå tilbake til den opprinnelige variabelen:
$\left(2x-\frac(\pi)(3)\right) \in \left(-\frac(\pi)(3) + \pi n; \frac(\pi)(2) + \pi n\høyre).$
Sistnevnte tilsvarer systemet med ulikheter
$\left\(\begin(array)(c) 2x-\frac(\pi)(3) > -\frac(\pi)(3) + \pi n, \\ 2x-\frac(\pi) (3)< \frac{\pi}{2}+\pi n, \end{array} \right.$
har løst som vi får svaret. Egentlig,
$\left\(\begin(array)(c) 2x > \pi n, \\ 2x< \frac{5 \pi}{6} + \pi n, \end{array} \right.$
$\left\(\begin(array)(c) x > \frac(\pi n)(2), \\ x< \frac{5\pi}{12}+\frac{\pi n}{2}. \end{array} \right. $
Og til slutt får vi:
$x \i \venstre(\frac(\pi n)(2); \frac(5\pi)(12) + \frac(\pi n)(2)\høyre), \n \i Z.$
Ulikheter er relasjoner av formen a › b, der a og b er uttrykk som inneholder minst én variabel. Ulikheter kan være strenge - ‹, › og ikke-strenge - ≥, ≤.
Trigonometriske ulikheter er uttrykk for formen: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, der F(x) er representert ved en eller flere trigonometriske funksjoner .
Et eksempel på den enkleste trigonometriske ulikheten er: sin x ‹ 1/2. Bestemme seg for lignende oppgaver akseptert grafisk, er det utviklet to metoder for dette.
Metode 1 - Løse ulikheter ved å tegne en funksjon grafisk
For å finne et intervall som tilfredsstiller betingelsene for ulikhet sin x ‹ 1/2, må du utføre følgende trinn:
- På koordinataksen konstruer en sinusformet y = sin x.
- Tegn en graf på samme akse numerisk argument ulikheter, dvs. en rett linje som går gjennom punktet ½ av ordinaten OY.
- Marker skjæringspunktene til de to grafene.
- Skyggelegg segmentet som er løsningen på eksempelet.
Når det er strenge skilt i et uttrykk, er ikke skjæringspunktene løsninger. Siden den minste positive perioden til en sinusoid er 2π, skriver vi svaret som følger:
![]()
Hvis fortegnene til uttrykket ikke er strenge, må løsningsintervallet omsluttes firkantede parenteser— . Svaret på problemet kan også skrives som følgende ulikhet: ![]()
Metode 2 - Løse trigonometriske ulikheter ved hjelp av enhetssirkelen
Lignende problemer kan enkelt løses ved hjelp av en trigonometrisk sirkel. Algoritmen for å finne svar er veldig enkel:
- Først må du tegne en enhetssirkel.
- Deretter må du merke deg verdien av buefunksjonen til argumentet til høyre side av ulikheten på sirkelbuen.
- Det er nødvendig å tegne en rett linje som går gjennom verdien av buefunksjonen parallelt med abscisseaksen (OX).
- Etter det gjenstår det bare å velge sirkelbuen, som er settet med løsninger på den trigonometriske ulikheten.
- Skriv ned svaret i ønsket skjema.
La oss se på trinnene i løsningen ved å bruke et eksempel ulikheter synd x › 1/2. Punktene α og β er markert på sirkelen - verdier
![]()
Punktene på buen plassert over α og β er intervallet for å løse den gitte ulikheten.

Hvis du trenger å løse et eksempel for cos, vil svarbuen være plassert symmetrisk til OX-aksen, ikke OY. Du kan vurdere forskjellen mellom løsningsintervallene for sin og cos i diagrammene under i teksten.

Grafiske løsninger for tangent- og cotangente ulikheter vil avvike fra både sinus og cosinus. Dette er på grunn av egenskapene til funksjoner.

Arktangens og arccotangent er tangenter til en trigonometrisk sirkel, og minimumsperioden for begge funksjoner er π. For raskt og riktig å bruke den andre metoden, må du huske på hvilken akse synd verdier, cos, tg og ctg.
Tangenttangenten går parallelt med OY-aksen. Hvis vi plotter verdien av arctan a på enhetssirkelen, vil det andre nødvendige punktet være plassert i diagonalkvartalet. Vinkler
De er bruddpunkter for funksjonen, siden grafen har en tendens til dem, men aldri når dem.

Når det gjelder cotangens, løper tangenten parallelt med OX-aksen, og funksjonen avbrytes i punktene π og 2π.

Komplekse trigonometriske ulikheter
Hvis argumentet til ulikhetsfunksjonen ikke bare er representert av en variabel, men av et helt uttrykk som inneholder en ukjent, så snakker vi allerede om kompleks ulikhet. Prosessen og prosedyren for å løse det er noe forskjellig fra metodene beskrevet ovenfor. Anta at vi må finne en løsning på følgende ulikhet:

Den grafiske løsningen innebærer å konstruere en vanlig sinusformet y = sin x ved å bruke vilkårlig valgte verdier av x. La oss beregne en tabell med koordinater for kontrollpunktene til grafen:

Resultatet skal være en vakker kurve.
For å gjøre det lettere å finne en løsning, la oss erstatte kompleks argumentasjon funksjoner

