Kursus video "Dapatkan A" merangkumi semua topik yang diperlukan untuk berjaya lulus Peperiksaan Negeri Bersepadu dalam matematik untuk 60-65 mata. Sepenuhnya semua masalah 1-13 Profil Peperiksaan Negeri Bersepadu matematik. Juga sesuai untuk lulus Peperiksaan Asas Negeri Bersepadu dalam matematik. Jika anda ingin lulus Peperiksaan Negeri Bersepadu dengan 90-100 mata, anda perlu menyelesaikan bahagian 1 dalam 30 minit dan tanpa kesilapan!
Kursus persediaan untuk Peperiksaan Negeri Bersepadu untuk gred 10-11, dan juga untuk guru. Semua yang anda perlukan untuk menyelesaikan Bahagian 1 Peperiksaan Negeri Bersepadu dalam matematik (12 masalah pertama) dan Masalah 13 (trigonometri). Dan ini adalah lebih daripada 70 mata pada Peperiksaan Negeri Bersepadu, dan pelajar 100 mata mahupun pelajar kemanusiaan tidak boleh melakukannya tanpanya.
Semua teori yang diperlukan. Cara cepat penyelesaian, perangkap dan rahsia Peperiksaan Negeri Bersepadu. Semua tugas semasa bahagian 1 dari Bank Tugas FIPI telah dianalisis. Kursus ini mematuhi sepenuhnya keperluan Peperiksaan Negeri Bersepadu 2018.
Kursus ini mengandungi 5 topik besar, 2.5 jam setiap satu. Setiap topik diberikan dari awal, ringkas dan jelas.
Beratus-ratus tugas Peperiksaan Negeri Bersatu. Masalah perkataan dan teori kebarangkalian. Algoritma yang mudah dan mudah diingati untuk menyelesaikan masalah. Geometri. teori, bahan rujukan, analisis semua jenis tugas Peperiksaan Negeri Bersepadu. Stereometri. Penyelesaian rumit, helaian cheat berguna, pembangunan imaginasi spatial. Trigonometri dari awal kepada masalah 13. Memahami bukannya menjejalkan. Penjelasan visual konsep yang kompleks. Algebra. Akar, kuasa dan logaritma, fungsi dan terbitan. Asas untuk penyelesaian tugasan yang kompleks 2 bahagian Peperiksaan Negeri Bersepadu.
Objektif pelajaran:
- Memperkenalkan konsep satah selari.
- Pertimbangkan dan buktikan teorem yang menyatakan tanda keselarian satah dan sifat satah selari.
- Jejaki aplikasi teorem ini dalam menyelesaikan masalah.
Rancangan pengajaran (tulis di papan tulis):
I. Persediaan kerja lisan.
II. Pembelajaran bahan baharu:
1. Kedudukan relatif dua satah di angkasa.
2. Penentuan satah selari.
3. Tanda satah selari.
4. Sifat satah selari.
III. Ringkasan pelajaran.
IV. Kerja rumah.
SEMASA KELAS
I. Kerja lisan
Saya ingin memulakan pelajaran dengan petikan dari surat falsafah Chaadaev:
“Dari mana datangnya kuasa ajaib analisis dalam matematik ini? Hakikatnya ialah minda di sini bertindak dengan tunduk sepenuhnya kepada peraturan ini.”
Kita akan melihat ketaatan kepada peraturan ini dalam tugasan seterusnya. Untuk mempelajari bahan baharu, anda perlu mengulang beberapa soalan. Untuk melakukan ini, anda perlu mewujudkan pernyataan yang mengikuti daripada pernyataan ini dan mewajarkan jawapan anda:
II. Mempelajari bahan baharu
1. Bagaimanakah dua satah boleh terletak di angkasa lepas? Apakah set titik kepunyaan kedua-dua satah?
Jawapan:
a) bertepatan (maka kita akan berurusan dengan satu kapal terbang, ia tidak memuaskan);
b) bersilang, ;
c) tidak bersilang ( perkara biasa sama sekali tidak).
2. Definisi: Jika dua satah tidak bersilang, maka ia dipanggil selari
3. Jawatan:
4. Berikan contoh satah selari daripada persekitaran
5. Bagaimana untuk mengetahui sama ada mana-mana dua satah di angkasa adalah selari?
Jawapan:
Anda boleh menggunakan definisi, tetapi ini tidak sesuai, kerana Ia tidak selalu mungkin untuk mewujudkan persimpangan pesawat. Oleh itu, adalah perlu untuk mempertimbangkan syarat yang mencukupi untuk menegaskan bahawa pesawat adalah selari.
6. Mari kita pertimbangkan situasi:
b) jika 
?
c) jika 
?
Mengapa jawapan dalam a) dan b) "tidak selalu", tetapi dalam c) "ya"? (Garis bersilang mentakrifkan satah dengan cara yang unik, yang bermaksud ia ditakrifkan secara unik!)
Situasi 3 ialah tanda keselarian dua satah.
7. Teorem: Jika dua garis bersilang bagi satu satah masing-masing selari dengan dua garis satah lain, maka satah ini adalah selari.
Diberi:
Buktikan:
Bukti:
(Pelajar menggunakan sebutan untuk lukisan itu.)
1. Nota: . Begitu juga:
2. Biarkan: .
3. Kami mempunyai: Begitu juga:
4. Kami memperoleh: melalui M terdapat percanggahan dengan aksiom planimetri.
5. Jadi: tidak betul, bermakna, dsb.
8. Selesaikan No 51 (Murid menggunakan simbol pada lukisan).
Diberi:
Buktikan:
Bukti:
1 cara
1. Mari kita bina 
2 cara
Masuk melalui melalui .
9. Mari kita pertimbangkan dua sifat satah selari:
Teorem: Jika dua satah selari bersilang dengan satu pertiga, maka garis persilangannya adalah selari.
(Pelajar sendiri menyiapkan binaan dan menandakannya pada lukisan).
Diberi:
Dalam pelajaran ini kita akan mentakrifkan satah selari dan mengimbas kembali aksiom mengenai persilangan dua satah. Seterusnya, kami akan membuktikan teorem - tanda selari satah dan, bergantung padanya, kami akan menyelesaikan beberapa masalah pada selari satah.
Topik: Keselarian garis dan satah
Pelajaran: Satah Selari
Dalam pelajaran ini kita akan mentakrifkan satah selari dan mengingat aksiom mengenai persilangan dua satah.
Definisi. Dua satah dipanggil selari jika tidak bersilang.
Jawatan: .
Ilustrasi satah selari(Rajah 1.)
1. Apakah satah yang dipanggil selari?
2. Bolehkah satah yang melalui garisan tidak selari selari?
3. Apa yang boleh jadi susunan bersama dua garis lurus, setiap satunya terletak pada salah satu daripada dua satah selari yang berbeza?
4. Geometri. Darjah 10-11: buku teks untuk pelajar institusi pendidikan(asas dan tahap profil) / I. M. Smirnova, V. A. Smirnov. - Edisi ke-5, diperbetulkan dan dikembangkan - M.: Mnemosyne, 2008. - 288 ms: ill.
Tugasan 1, 2, 5 ms 29
Hubungan selari satah, sifat dan aplikasinya dipertimbangkan.
Perwakilan visual lokasi kedua-duanya
pesawat memberikan pemodelan menggunakan satah permukaan dinding bersebelahan, siling dan lantai bilik, katil dua tingkat, dua helaian kertas yang diikat
ahli silap mata, dsb. (Gamb. 242–244).
Walaupun ada set tak terhingga pilihan untuk susunan relatif pelbagai satah, untuk mewujudkan dan mencirikan ukuran sudut dan jarak yang akan digunakan pada masa hadapan, kita akan mula-mula menumpukan pada mereka yang klasifikasi (serta garis lurus dengan satah) adalah berdasarkan bilangan titik persamaan mereka.
1. Dua pesawat mempunyai sekurang-kurangnya tiga biasa mata yang tidak terletak pada baris yang sama. Pesawat sedemikian bertepatan (aksiom C 2, §7).
2. Titik sepunya dua satah terletak pada satu garis lurus, iaitu garis persilangan satah ini (aksiom C 3, §7). Pesawat sedemikian bersilang.
3. Kedua-dua pesawat tidak mempunyai titik sepunya.
DALAM dalam kes ini mereka dipanggil selari-
Dua satah dipanggil selari jika mereka tidak mempunyai titik sepunya.
Keselarian satah ditunjukkan oleh tanda ||: α || β.
Seperti biasa, ketika memperkenalkan konsep geometri timbul-
Tiada masalah dengan kewujudan mereka. Kewujudan persilangan-
Pesawat Xia adalah ciri ciri ruang,
dan kami telah menggunakan ini berkali-kali. Kurang jelas adalah
Kewujudan satah selari didedahkan. Tidak ada
meragui bahawa, sebagai contoh, satah graf bertentangan
Kubus adalah selari, iaitu, mereka tidak bersilang. Tetapi secara langsung
Sesungguhnya, mengikut definisi, ini tidak boleh ditubuhkan. Untuk penyelesaian
pemahaman soalan yang dikemukakan, serta isu-isu lain yang berkaitan dengan
keselarian satah, perlu ada tanda selari.
Untuk mencari tanda, adalah dinasihatkan untuk mempertimbangkan pesawat,
"anyaman" daripada garis lurus. Adalah jelas bahawa setiap garis lurus adalah salah satu daripada
satah selari mesti selari dengan yang lain.
DALAM sebaliknya pesawat akan mempunyai titik yang sama. Cukup
Adakah satah β betul-betul selari dengan garis lurus α yang sama
supaya satah α dan β adalah selari? betul-betul
tetapi, tidak (justify this!). Pengalaman praktikal menunjukkan bahawa
dua garis bersilang itu sudah memadai. Untuk mengamankan
pada tiang terdapat platform yang selari dengan tanah, letak sahaja
pada dua rasuk yang dipasang pada tiang, selari |
||
duniawi (Rajah 245). Ada banyak lagi |
||
contoh penggunaan teknik peruntukan ini |
||
keselarian permukaan rata sebenar |
||
objek (cuba ini!). |
||
Pertimbangan di atas membolehkan kita merumuskan |
||
tuliskan pernyataan berikut. |
||
(tanda satah selari). |
||
bersilang garis lurus satu satah |
||
Jika satah itu selari dengan satah kedua, maka satah ini selari.
Biarkan garis bersilang a dan b bagi satah α selari dengan satah β. Mari kita buktikan bahawa satah α dan β adalah selari dengan percanggahan. Untuk melakukan ini, mari kita andaikan bahawa satah α dan β bersilang sepanjang garis lurus
t (Gamb. 246). Garis a dan b tidak boleh bersilang garis mengikut keadaan. Walau bagaimanapun, kemudian dalam satah α dua garis lurus dilukis melalui satu titik yang tidak bersilang dengan garis lurus, iaitu selari dengannya. Ini adalah percanggahan
dan melengkapkan bukti teorem.
Tanda selari satah digunakan apabila meletakkan struktur rata secara mendatar (papak konkrit, lantai, cakera peranti goniometer, dll.) menggunakan dua aras yang diletakkan dalam satah struktur pada garis lurus yang bersilang. Berdasarkan ciri ini, adalah mungkin untuk membina satah selari dengan yang ini.
Masalah 1. Melalui satu titik yang terletak di luar satah tertentu, lukis satah selari dengan satah yang diberi.
Biarkan satah β dan satu titik M di luar satah diberi (Rajah 247, a). Mari kita lukis melalui titik M dua garis bersilang a dan b, selari dengan satah β. Untuk melakukan ini, anda perlu mengambil dua garis lurus c dan d bersilang dalam satah β (Rajah 247, b). Kemudian melalui titik M lukis garis a dan b selari dengan garis c dan d, masing-masing.
tetapi (Rajah 247, c).
Garisan bersilang a dan b selari dengan satah β, berdasarkan keselarian garis dan satah (Teorem 1 §11). Mereka secara unik menentukan satah α. Mengikut kriteria yang terbukti, α || β.
Contoh 1. Diberi kubus ABCDA 1 B 1 C 1 D 1 , titik M , N , P ialah titik tengah bagi tepi BC , B 1 C 1 , A 1 D 1 , masing-masing. Tetapkan kedudukan relatif pesawat: 1) ABB 1 dan PNM; 2) NMA dan A 1 C 1 C ; 3)A 1 NM
dan PC 1 C; 4) MAD 1 dan DB 1 C.
1) Satah ABB 1 dan РNM (Rajah 248) adalah selari, berdasarkan keselarian satah (Teorem 1). Memang, garis РN dan NM bersilang dan selari dengan satah ABB 1, berdasarkan keselarian garis dan satah (Teorem 1 §11), kerana segmen РN dan NM menghubungkan titik tengah. sisi bertentangan segi empat sama, jadi ia selari dengan sisi segi empat sama:
РN ||A 1 B 1 ,NM ||В 1 B.
2) Satah NMA dan A 1 C 1 C bersilang di sepanjang garis lurus AA 1 (Gamb. 249). Sesungguhnya, garis AA 1 dan CC 1 adalah selari, berdasarkan keselarian garisan (AA 1 ||ВB 1,ВB 1 ||СC 1). Oleh itu, garis lurus AA 1 terletak pada satah A 1 C 1 C. Kepunyaan garis lurus AA 1 kepada satah NMA adalah wajar.
3) Satah A 1 NM dan РС 1 C (Rajah 250) adalah selari, berdasarkan keselarian satah. Sesungguhnya, NM ||С 1 C . Oleh itu, garis lurus NM adalah selari dengan satah PC 1 C. Segmen PC 1 dan A 1 N juga selari, kerana segiempat PC 1 NA 1 ialah segiempat selari (A 1 P ||NC 1, A 1 P = NC 1). Oleh itu, garis A 1 N adalah selari dengan satah PC 1 C. Garisan A 1 N dan NM bersilang.
4) Pesawat MAD 1 dan DB 1 C bersilang (Gamb. 251). Walaupun garis persimpangan mereka tidak mudah dibina, tidak sukar untuk menunjukkan satu titik garisan ini. Memang, garis A 1 D dan B 1 C adalah selari, kerana segiempat A 1 B 1 CD ialah segiempat selari (A 1 B 1 = AB = CD , A 1 B 1 || AB , AB || CD ). Oleh itu, garisan A 1 D tergolong dalam satah DB 1 C. Garisan A 1 D dan AD 1 bersilang pada satu titik yang sama dengan satah MAD 1 dan DB 1 C.
Tanda selari satah yang diberi |
||
kadangkala ia lebih senang digunakan dalam keadaan yang sedikit berbeza |
||
1′ (tanda satah selari). |
||
Jika dua garis bersilang bagi satu satah masing-masing selari dengan dua garis satah lain, maka satah ini adalah selari.
Dengan menggunakan kriteria keselarian garis dan satah (Teorem 1 §11), adalah mudah untuk menentukan bahawa keadaan Teorem 1 mengikuti daripada syarat Teorem 1. Penggunaan songsang teorem kepada kriteria selari sesuatu garis dan satah (Teorem 2 §11) melengkapkan justifikasi untuk kesetaraan syarat Teorem 1 dan 1 '.
Sememangnya, timbul persoalan tentang keunikan binaan yang diberikan dalam Masalah 1. Oleh kerana kami perlu menggunakan sifat ini lebih daripada sekali, kami akan menyerlahkannya sebagai teorem yang berasingan. Namun, mari kita lihat kenyataan lain dahulu.
Teorem 2 (tentang persilangan dua satah selari dengan satu pertiga).
Jika dua satah selari bersilang dengan satah ketiga, maka garis persilangan satah itu adalah selari.
Biarkan satah selari α, β dan satah γ yang bersilang diberi (Rajah 252). Mari kita nyatakan garis persimpangan
melalui a dan b. Garis-garis ini terletak pada satah γ dan tidak bersilang, kerana satah α dan β tidak mempunyai titik sepunya. Oleh itu, secara langsung
a dan b adalah selari.
Teorem 3 (mengenai kewujudan dan keunikan satah yang selari dengan yang ini).
Melalui satu titik yang terletak di luar satah tertentu, seseorang boleh melukis satu satah selari dengan satah yang diberi.
Pembinaan pesawat sebegini telah dijalankan dalam masalah 1. Kami akan membuktikan keunikan pembinaan itu dengan percanggahan. Mari kita andaikan bahawa dua satah berbeza α dan γ dilukis melalui titik M, pa-
satah selari β (Rajah 253), dan garis lurus t ialah garis persilangan mereka. Mari kita lukis satah δ melalui titik M, bersilang dengan garis itu
m dan satah β (bagaimana ini boleh dilakukan?). Mari kita nyatakan dengan a dan b
garis persilangan satah δ dengan satah α dan γ, dan melalui c - garis persilangan satah δ dan β (Rajah 253). Mengikut Teorem 2,a ||c
dan b ||s. Iaitu, dalam satah δ melalui
dua garis lurus selari dengan garis lurus melalui titik M. Percanggahan menunjukkan bahawa andaian itu tidak betul.
Hubungan selari satah mempunyai beberapa sifat yang mempunyai analog dalam planimetri.
Teorem 4 (pada segmen garis selari antara satah selari).
Segmen garis selari yang dipotong oleh satah selari adalah sama antara satu sama lain.
Biarkan dua satah selari α dan β dan segmen diberi AB
dan CD garis lurus selari a dan d, dipotong oleh satah ini (Rajah 254, a). Mari kita lukis satah γ melalui garis lurus a dan d (Rajah 254, b). Ia bersilang dengan satah α dan β sepanjang garis lurus AC dan BD, yang, menurut Teorem 2, adalah selari. Oleh itu, segiempat ABCD ialah segi empat selari; sisi bertentangan AC dan BD adalah sama.
Daripada harta di atas ia mengikuti bahawa jika kita merancang dari semua titik pesawat
pada satu sisi kapal terbang garis selari sama panjang, maka hujung segmen ini membentuk dua satah selari. Di atas harta inilah pembinaan paip selari menggunakan pemendapan segmen adalah berdasarkan (Rajah 255).
Teorem 5 (mengenai transitiviti hubungan selari satah).
Jika setiap dua satah selari dengan satu pertiga, maka kedua-dua satah itu selari antara satu sama lain.
Biarkan satah α dan β selari dengan satah γ. Mari kita anggap itu
α dan β tidak selari. Kemudian satah α dan β mempunyai titik sepunya, dan melalui titik ini terdapat dua satah berbeza selari dengan satah γ, yang bercanggah dengan Teorem 3. Oleh itu, satah α dan β tidak mempunyai titik sepunya, iaitu, ia selari .
Teorem 5 ialah satu lagi tanda keselarian satah. Ia digunakan secara meluas dalam kedua-dua geometri dan aktiviti amali. Sebagai contoh, dalam bangunan bertingkat, keselarian lantai dan satah siling pada setiap tingkat menjamin keselarian mereka pada tingkat yang berbeza.
Masalah 2. Buktikan bahawa jika garis lurus bersilang dengan satah α, maka ia juga memotong setiap satah selari dengan satah α.
Biarkan satah α dan β selari, dan garis lurus a memotong satah α pada titik A. Mari kita buktikan bahawa ia juga bersilang dengan pesawat
β. Mari kita anggap bahawa ini tidak berlaku. Maka garis lurus a adalah selari dengan satah β. Mari kita lukis satah γ melalui garis lurus dan titik sewenang-wenangnya satah β (Rajah 256).
Satah ini memotong satah selari α dan β sepanjang garis lurus b ialah. bersama-
mengikut Teorem 2, b || c, iaitu, dalam satah γ, dua garis a dan b melalui titik A, selari dengan garis c . Percanggahan ini membuktikan kenyataan tersebut.
Cuba buktikan sendiri bahawa jika satah α bersilang dengan satah β, maka ia juga bersilang setiap satah selari dengan satah β.
Contoh 2. Dalam tetrahedron ABCD, titik K, F, E ialah titik tengah tepi DA, DC, DB, aM dan P - pusat jisim muka ABD dan ВСD, masing-masing.
1) Tetapkan kedudukan relatif pesawat KEF dan ABC;
DEF dan ABC.
2) Membina garisan persilangan pesawat AFB dan KEC.
3) Cari luas keratan rentas tetrahedron dengan satah selari dengan satah ABD dan melalui titik P jika semua tepi tetrahedron adalah sama.
Mari bina lukisan yang memenuhi syarat (Rajah 257, a). 1) Satah KEF dan ABC adalah selari, berdasarkan keselarian satah (Teorem 1'): garis bersilang KE dan KF satah KEF adalah selari dengan garis bersilang AB dan AC satah ABC (garis tengah bagi yang sepadan
segi tiga sedia ada).
Satah DEF dan ABC bersilang di sepanjang garis lurus BC, kerana garis lurus BC kepunyaan kedua-dua satah, dan ia tidak boleh bertepatan - titik A, B, C, D tidak terletak dalam satah yang sama.
2) Satah AFB bersilang dengan satah KEC sepanjang garis lurus yang mengandungi titik P, kerana garis CE dan BF yang terletak dalam satah ini berada dalam satah BCD dan bersilang di titik P. Satu lagi titik ialah titik persilangan Q bagi garis lurus AF dan CK dalam satah ACD (Rajah 257, b). Jelas sekali, titik ini ialah pusat jisim muka ACD. Persimpangan yang diperlukan ialah garis PQ.
3) Bina bahagian yang dinyatakan dalam keadaan, menggunakan tanda selari satah. Mari kita lukis garisan melalui titik P dan Q selari dengan garisan DB dan DA, masing-masing (Rajah 257, c). Garis-garis ini bersilang dengan CD segmen pada titik L. Yang terakhir mengikuti dari sifat pusat jisim segitiga - ia membahagikan median segitiga dalam nisbah 2: 1, mengira dari puncak. Ia kekal untuk menggunakan teorem Thales. Oleh itu, pesawat PLQ dan BDA adalah selari. Bahagian yang diperlukan ialah segi tiga LSN.
Secara pembinaan, segi tiga BCD dan SCL adalah serupa dengan pekali persamaan CE CP =3 2. Oleh itu LS =3 2 BD . Serupa dengan yang ditubuhkan
kesamaan berikut ditambah: LN =3 2 AD,NS =3 2 AB. Ia berikutan bahawa segi tiga LSN dan ABD adalah serupa dengan pekali persamaan 3 2. Mengikut sifat-sifat kawasan segi tiga yang serupa,
S LNS =4 9 S ABD . Ia kekal untuk mencari kawasan segitiga ABD. Oleh-
kerana, mengikut keadaan, semua tepi tetrahedron adalah sama dengan a, maka S ABD =4 3 a 2.
Luas yang diperlukan ialah 3 1 3 a 2 .
Adalah wajar untuk ambil perhatian bahawa jawapan hanya bergantung pada kawasan muka ABD. Oleh itu, kesamaan semua tepi hanyalah satu cara untuk mencari kawasan ini. Oleh itu, tugasan ini boleh digeneralisasikan dengan ketara.
Jawab. 1)KEF ||ABC ; 3)3 1 3 a 2 .
Soalan ujian
1. Adakah benar dua satah selari jika setiap garis yang terletak dalam satu satah selari dengan satah yang satu lagi?
2. Satah α dan β adalah selari. Adakah terdapat garis condong yang terletak pada pesawat ini?
3. Dua sisi segitiga adalah selari dengan beberapa satah. Adakah sisi ketiga segi tiga selari dengan satah ini?
4. Dua sisi segi empat selari adalah selari dengan satah tertentu. Adakah benar bahawa satah segi empat selari adalah selari dengan satah yang diberi?
5. Bolehkah segmen dua garis lurus yang dipotong oleh satah selari tidak sama?
6. Bolehkah keratan rentas kubus itu trapezoid sama kaki? Bolehkah keratan rentas kubus itu pentagon biasa? Adakah benar bahawa dua satah selari dengan garis yang sama adalah selari antara satu sama lain?
Garis persilangan satah α dan β dengan satah γ adalah selari antara satu sama lain. Adakah satah α dan β selari?
Bolehkah tiga muka kubus selari dengan satah yang sama?
Latihan grafik
1. Rajah 258 menunjukkan kubus ABCDA 1 B 1 C 1 D 1, titik M, N, K, L, P ialah titik tengah bagi tepi yang sepadan. Isi jadual mengikut contoh yang diberikan dengan memilih lokasi yang diperlukan satah α dan β.
bersama
lokasi
α || β α = β
α × β α || β α = β
A1 B1 C1 | D 1 KP |
||
dan ADC | dan BB1 D | dan MNP | dan BMN |
B 1 KP | A1 DC1 | A1 C1 C |
|
dan PLN | dan DMN | dan AB1 C | dan MKP |
2. Dalam Rajah. 259 menunjukkan sebuah tetrahedron ABCD, titik K, F, M, N, Q ialah titik tengah bagi tepi yang sepadan. Sila jelaskan:
1) satah yang melalui titik K selari dengan satah ABC;
2) satah yang melalui garis BD selari dengan satah MNQ.
3. Tentukan apakah bahagian rajah oleh satah yang melalui tiga titik yang diberi yang ditunjukkan dalam rajah itu.
kah 260, a)–e) dan 261, a)–d).
4. Bina lukisan berdasarkan data yang diberi.
1) Daripada bucu segi empat selari ABCD yang terletak dalam salah satu daripada dua satah selari, garis selari dilukis yang bersilang dengan satah kedua pada titik A 1 , B 1 , C 1 , D 1 , masing-masing.
2) Segitiga A 1 B 1 C 1 ialah unjuran segitiga ABC pada satah α yang selari dengannya. Titik M ialah tengah matahari, M 1 ialah unjuran titik M ke atas satah α.
207. Dalam kubus ABCDA 1 B 1 C 1 D 1 titik O, O 1 ialah pusat muka ABCD dan A 1 B 1 C 1 D 1, masing-masing, M ialah tengah tepi AB.
1°) Tentukan kedudukan relatif satah MO 1 O
dan ADD 1, ABD 1 dan CO 1 C 1.
2°) Bina titik persilangan satah DCC 1 dan garis lurus MO 1 dan garis persilangan satah MCC 1 dan A 1 D 1 C 1.
3) Cari luas keratan rentas kubus dengan satah yang selari dengan satah AD 1 C 1 dan melalui titik O 1 jika tepi kubus itu sama dengan a.
208. Dalam tetrahedron ABCD, titik K, L, P ialah pusat jisim muka ABD, BDC, ABC, masing-masing, dan aM ialah tengah tepi AD.
1°) Tentukan kedudukan relatif satah ACD
dan KLP ;
2°) Bina titik persilangan satah ABC dan garis ML dan garis persilangan satah MKL dan ABC.
3) Cari luas keratan rentas tetrahedron dengan satah yang melalui titik K, L dan M selari dengan garis lurus AD, jika semua tepi tetrahedron adalah sama.
209. Diberi kubus ABCDA 1 B 1 C 1 D 1 . Titik L, M, M 1 ialah titik tengah bagi tepi AB, AD dan A 1 D 1, masing-masing.
1°) Tentukan kedudukan relatif bagi satah B 1 D 1 D
dan LMM1.
2) Bina satah melalui titik M selari dengan satah ACC 1.
3) Bina bahagian kubus dengan satah melalui titik M 1 selari dengan satah CDD 1.
4) Tentukan kedudukan relatif satah MA 1 B 1
dan CDM1.
5) Bina satah melalui garis C 1 D 1 selari dengan satah CDM 1.
210. Dalam piramid segi empat biasa SABCD, semua sisi adalah sama antara satu sama lain. Titik L, M dan N ialah titik tengah bagi tepi AS, BS, CS, masing-masing.
1°) Tentukan kedudukan relatif bagi: garis lurus LM dan BC; garis lurus LN dan satah ABD; pesawat LMN dan BDC.
2°) Buktikan bahawa segi tiga ABC dan LMN adalah serupa.
3) Bina bahagian piramid menggunakan satah AMN; kapal terbang LMN; kapal terbangLBC.
4*) Manakah antara bahagian piramid yang melalui bucu S mempunyai luas terbesar?
Keselarian garis dan satah
Dalam tetrahedron SABC semua muka adalah segi tiga sekata. Titik L, M dan N ialah titik tengah bagi tepi AS, BS, CS, masing-masing. 1°) Tentukan kedudukan relatif bagi garis lurus LM dan BC. 2°) Tentukan kedudukan relatif bagi garis lurus LN dan satah ABC.
3) Buktikan bahawa segi tiga LMN dan ABC adalah serupa.
Daripada bucu segi empat selari ABCD terletak di salah satu daripada |
|||
dua satah selari, dilukis secara berpasangan selari |
|||
garis lurus linear yang bersilang dengan satah kedua yang sepadan |
|||
khususnya pada titik A 1, B 1, C 1, D 1. | |||
1°) Buktikan bahawa sisi empat A 1 B 1 C 1 D 1 adalah selari |
|||
2°) Buktikan bahawa segiempat selari ABCD dan A 1 B 1 C 1 D 1 |
|||
adalah sama antara satu sama lain. | |||
3°) Tentukan kedudukan relatif bagi satah ABC 1 |
|||
dan DD1 C1. | |||
4) Lukis satah 1 melalui tengah segmen AA jadi |
|||
supaya ia bersilang garis-garis ini pada titik-titik yang |
|||
bucu segi empat selari sama dengan segi empat selari |
|||
mu ABCD. | |||
Diberi dua satah selari dan satu titik O, bukan kepunyaan |
|||
menekan mana-mana pesawat ini dan tidak berbaring di antara |
|||
mereka. Dari titik O | tiga sinar dilukis bersilang dengan satah |
||
tulang, masing-masing, pada titik A, B, C dan A 1, B 1, C 1 dan tidak berbohong |
|||
terbaring dalam pesawat yang sama. | |||
1°) Tentukan kedudukan relatif bagi satah ini |
|||
dan satah yang melalui titik tengah segmen AA 1, BB 1, CC 1. |
|||
2) Cari perimeter segi tiga A 1 B 1 C 1 ifOA = m, |
|||
AA 1 = n, AB = c, AC = b, BC = a. | |||
Segitiga A 1 B 1 C 1 ialah unjuran bagi segi tiga ABC |
|||
ke atas satah α selari dengannya. Titik M - pertengahan ratus |
|||
rons BC ;M 1 - unjuran titik M | ke atas satah α. Titik N |
||
membahagi sisi AB | dalam nisbah 1:2. | satah M 1 MN dan lurus |
|
1) Bina titik persilangan N 1 |
|||
saya A 1 B 1 . | |||
2) Tentukan bentuk segiempat M 1 N 1 NM. |
|||
M terletak di luar satah trapezoid ABCB dari tapak- |
|||
mi AD | dan B.C. Bina garis persilangan satah: |
||
1°) ABM dan CDM; | 2) CBM dan ADM. |
||
Bina satu bahagian kubus iaitu: 1°) segi tiga sama sisi; 2) pentagon.
217. Bina bahagian tetrahedron iaitu segi empat selari.
218°. Buktikan bahawa muka bertentangan dengan paip selari adalah selari.
219. Buktikan bahawa set semua garisan yang melalui titik ini dan selari dengan satah tertentu, membentuk satah selari dengan satah yang diberi.
220. Diberi empat titik A, B, C, D, tidak terletak dalam satah yang sama. Buktikan bahawa setiap satah selari dengan garis AB dan CD bersilang dengan garis AC, AD, BD, BC pada bucu segiempat selari.
221. Buktikan bahawa satah dan garis yang bukan milik satah ini adalah selari antara satu sama lain jika kedua-duanya selari dengan satah yang sama.
222. Melalui titik O persilangan pepenjuru kubus ABCDA 1 B 1 C 1 D 1 sebuah satah dilukis selari dengan muka ABCD. Satah ini bersilang tepi BB 1 dan CC 1 pada titik M dan N, masing-masing. Buktikan bahawa sudut MON ialah sudut tegak.
223. Buktikan bahawa dua satah selari antara satu sama lain jika dan hanya jika setiap garis lurus yang bersilang dengan salah satu satah juga bersilang dengan yang kedua.
224*. Dalam piramid segi tiga SABC, melalui segmen AD dan CE, dengan D ialah titik tengah SB, dan E ialah titik tengah SA, lukis bahagian piramid selari antara satu sama lain.
225. Cari tempat geometri:
1) titik tengah semua segmen dengan hujung pada dua data satah selari; 2*) titik tengah segmen dengan hujung pada dua garis bersilang yang diberikan.
226*. Sisi AB bagi segi tiga ABC terletak pada satah α adalah selari dengan satah β. Segitiga sama 1 B 1 C 1 ialah unjuran selari segi tiga ABC kepada satah β;AB = 5,BC = 6,AC = 9.
1) Nyatakan kedudukan relatif garis lurus AB dan A 1 B 1,
BC dan B1 C1, A1 C1 dan AC.
2) Cari luas segi tiga A 1 B 1 C 1.
227*. Diberi dua garis bersilang. Nyatakan set semua titik dalam ruang yang melaluinya satu garisan boleh dilukis bersilang setiap dua garisan yang diberi.
Definisi asas
Kedua-dua pesawat itu dipanggil
adalah selari,
jika mereka tidak mempunyai mata yang sama.
Kenyataan utama
Tanda selari - Jika dua garis lurus bersilang bagi satu satah satah masing-masing selari dengan dua garis lurus satah kedua, maka satah ini
tulang adalah selari.
Teorem bersilang Jika dua satah bersilang selari dua satah tidak selari bersilang dengan satah ketiga, maka garis-garis persilangan ketiga satah itu
mereka selari.
a α,b α,a ×b ,c β,d β,a ||c ,b ||d α || β
α || β, a = γ∩α,b = γ∩βa ||b
M α
β: α || β,M β
Bersedia untuk bertema
untuk penilaian mengenai topik "Paralelisme garis dan satah"
Tugas mengawal diri
1. Empat mata tidak tergolong dalam satah yang sama. Bolehkah beberapa daripada mereka berbaring pada garis lurus yang sama?
2. Bolehkah tiga satah berbeza mempunyai dua titik persamaan?
3. Bolehkah dua garisan condong selari dengan garis ketiga pada masa yang sama?
4. Adakah benar itu lurus a dan b tidak selari jika tiada garis c selari dengan a dan b?
5. Bolehkah mereka segmen yang sama mempunyai unjuran yang tidak sama rata?
6. Bolehkah sinar menjadi unjuran selari bagi garis?
7. Bolehkah segi empat sama menjadi imej kubus?
8. Adakah benar melalui titik tertentu dalam ruang hanya satu satah boleh dilukis selari dengan garis tertentu?
9. Adakah selalu mungkin untuk melukis garis melalui titik tertentu selari dengan dua satah tertentu yang tidak mengandungi titik ini?
10. Adakah mungkin untuk melukis satah selari melalui dua garis bersilang?
Jawapan kepada tugas untuk mengawal diri
Sampel ujian
Dua segi empat selari ABCD dan ABC 1 D 1 terletak pada satah yang berbeza.
1°) Tentukan kedudukan relatif bagi garis lurus CD dan C 1 D 1.
2°) Tentukan kedudukan relatif bagi garis lurus C 1 D 1 dan satah
3°) Bina garis persilangan satah DD 1 C 1 dan СС 1.
4°) Tentukan kedudukan relatif satah ADD 1 dan BCC 1.
5) Melalui titik M, membahagi segmen AB dalam nisbah 2:1, mengira dari titik A, lukis satah α selari dengan satah C 1 BC. 6) Bina titik persilangan garis lurus AC dengan satah α dan cari nisbah di mana titik ini membahagi segmen AC.
Keselarian garis dan satah |
|||
Kedudukan relatif garisan dalam ruang |
|||
Jadual 21 |
|||
Bilangan mata biasa | |||
Sekurang-kurangnya dua | |||
berbohong dalam satu | jangan berbohong pada satu |
||
kapal terbang | kapal terbang |
||
Kedudukan relatif garis lurus dan satah di angkasa
Jadual 22 |
||||
Bilangan mata biasa | ||||
Sekurang-kurangnya dua | tiada |
|||
a terletak pada α | dan bersilang α | dan i α - selari |
(a α) | (a × α) | ny (a || α) |
Susunan kapal terbang di angkasa bersama |
||
Jadual 23 |
||
Bilangan mata biasa | ||
Sekurang-kurangnya tiga | Sekurang-kurangnya satu, tetapi | tiada |
tidak berbaring | tiada titik persamaan, tiada le- |
|
satu garis lurus | menekan pada satu garis lurus | |
trigonometri
Anda telah pun berurusan dengan fungsi trigonometri dalam pelajaran geometri. Sehingga kini, aplikasi mereka hanya terhad kepada menyelesaikan segi tiga, iaitu, kita bercakap tentang mencari beberapa unsur segitiga daripada yang lain. Daripada sejarah matematik diketahui bahawa kemunculan trigonometri dikaitkan dengan ukuran panjang dan sudut. Walau bagaimanapun, kini sfera
dia aplikasi adalah lebih luas berbanding zaman dahulu.
Perkataan "trigonometri" berasal dari bahasa Yunani τριγωνον
(trigonon) – segi tiga dan µετρεω (metreo) – ukur, ukur-
saya menyalak. Secara harfiah ia bermaksud mengukur segi tiga.
DALAM Bab ini mensistemkan bahan yang telah anda ketahui daripada kursus geometri, dan meneruskan kajian fungsi trigonometri dan aplikasi mereka untuk mencirikan proses kelompok, khususnya pergerakan putaran, proses berayun dan sebagainya.
Kebanyakan aplikasi trigonometri berkaitan secara khusus dengan proses berkala, iaitu proses yang berulang pada selang masa yang tetap. Matahari terbit dan terbenam, perubahan musim, putaran roda - ini adalah contoh paling mudah bagi proses sedemikian. mekanikal dan getaran elektromagnet juga merupakan contoh penting proses berkala. Oleh itu, kajian proses berkala adalah tugas yang penting. Dan peranan matematik dalam penyelesaiannya adalah penentu.
bersiap sedia untuk mempelajari topik "Fungsi trigonometri"
Adalah dinasihatkan untuk mula mempelajari topik "Fungsi Trigonometri" dengan menyemak definisi dan sifat fungsi trigonometri sudut segi tiga dan aplikasinya untuk menyelesaikan kedua-dua segi tiga tegak dan sewenang-wenangnya.
Sinus, kosinus, tangen, kotangen sudut segi empat tepat
segi tiga
Jadual 24
Sinus bagi sudut akut ialah nisbah kaki bertentangan kepada hipotenus:
sin α = a c .
Kosinus bagi sudut lancip ialah nisbah kaki bersebelahan kepada hipotenus:
cosα = b c .
Tangen sudut lancip ialah nisbah sisi bertentangan dengan sisi bersebelahan:
tg α =a b .
Kotangen bagi sudut lancip ialah nisbah sisi bersebelahan dengan sisi bertentangan:
ctgα = a b .
Sinus, kosinus, tangen, kotangen sudut dari 0° hingga 180°
Jadual 25
sin α = R y ; cosα = R x ;
tg α = x y ; cotgα = x y.
(X;di) - koordinat titik A terletak pada separuh bulatan atas, α - sudut yang dibentuk oleh jejari OA bulatan dengan paksi X.
Nilai sinus, kosinus, tangen, kotangen
beberapa sudut
Jadual 26
Sudut t
0° | 90° | 180° |
||||||||||
dosa t | ||||||||||||
cos t | ||||||||||||
tg t | ||||||||||||
ctg t | ||||||||||||
Fungsi trigonometri |
Menyelesaikan segi tiga sewenang-wenangnya
Jadual 27
Teorem sinus
Sisi segitiga adalah berkadar dengan sinus sudut bertentangan:
dosa aα = dosa bβ = dosa cγ .
Teorem kosinus
Kuadrat sisi arbitrari segitiga adalah sama dengan hasil tambah kuasa dua dua sisi yang lain tanpa dua kali hasil darab sisi ini dengan kosinus sudut di antara mereka:
c2 = a2 + b2 − 2 ab cos γ ,b2 = a2 + c2 − 2 ac cos β , a2 = b2 + c2 − 2 bc cos α .
Luas segi tiga adalah sama dengan separuh hasil darab dua sisinya dan sinus sudut di antara mereka:
S=1 2 abdosaγ = 1 2 acdosaβ = 1 2 bcdosaα .
Identiti asas trigonometri
Jadual 28 |
||||||||||||||||
0 ° ≤ α ≤ 180° | dosa 2 α + cos 2 α = 1 |
|||||||||||||||
0 ° ≤ α ≤ 180°, α ≠ 90° | ||||||||||||||||
1 +tgα = cos2 α |
||||||||||||||||
0 ° < α < 180° | 1 + ctg 2 α = | |||||||||||||||
dosa 2 α |
||||||||||||||||
Diberi segitiga ABC,DENGAN= 90°, matahari=3 ,AB= 2. Apakah yang sama dengan |
||||||||||||||||
DALAM ? | B. 45 °. | DALAM. 60 °. | ||||||||||||||
A. 30 °. | ||||||||||||||||
G. Tidak mustahil untuk mengira tanpa alat pengiraan. |
||||||||||||||||
Diberi segitiga | ABC , DENGAN | matahari= 3, | DALAM= 60°. Apa yang sama dengan |
|||||||||||||
AB ? | ||||||||||||||||
A. 3 | B. 6. | 3 . |
||||||||||||||
Menurut pihak-pihak ini segi tiga tepat cari |
||||||||||||||||
kosinus sudut yang lebih kecil: A= 3,b= 4,c | ||||||||||||||||
A. 0,8. | ||||||||||||||||
Manakah antara nilai yang diberikan tidak boleh mengambil kecondongan- |
||||||||||||||||
tiada sudut akut? | ||||||||||||||||
7 − 1 | 7 2 | |||||||||||||||
A. | ||||||||||||||||
5. Bandingkan jumlah sinus sudut tajam segi tiga tegak sewenang-wenang (kami menandakannya denganA) dengan satu.
< 1. B.A= 1.
> 1. G. Tidak mustahil untuk dibandingkan. Susun nombor dalam tertib menaik: A= dosa 30°, b= cos 30°,
= tg 30°.
<
b<c.B.a<c<b Fungsi trigonometri Untuk sudut akut yang manakah sinus kurang daripada kosinus? Untuk semua. Untuk yang lebih kecil 45°. Untuk 45° besar. G. Bukan untuk sesiapa. Apakah cos sama dengan? α, jika α ialah sudut lancip bagi segi tiga segi empat tepat segi empat sama dan dosaα = 12
.
Panjang bayang-bayang pokok ialah 15 m Sinaran Matahari membentuk sudut 30° dengan permukaan bumi. Berapakah anggaran ketinggian? pokok? Pilih hasil yang paling tepat. B. 13 m. DALAM. 7m. Apakah nilai ungkapan tersebut 1 −
x2
di X= – 0,8? B. –0,6. G.≈ 1,34. Daripada formula a2
+b2
=4
ekspres b< 0 черезa. A.b=4
−a2
. B.b=a2
−4
. b= −a2
− 4
. b= −4
−a2
. titik A terletak pada suku ketiga pada jarak 3 dari paksi X Dan pada jarak 10
dari asal. Apakah koordinat punya pasal A?
B.(−1; 3). DALAM.(−1; −3). G.(−3; −1). mata seterusnya kepunyaan bulatan x 2+
y 2 =
1? B.(0,5; 0,5). . G. 15.
Nyatakan koordinat titik tersebutA, berbaring pada bulatan jejari 1 (lihat rajah). (−1; 0).B.(1; 0). (0; − 1). G.(0; 1).A.DALAM.
Keselarian satah. Jika dua garis bersilang bagi satu satah masing-masing selari dengan dua garis bersilang bagi satah lain, maka satah ini adalah selari.
Bukti. biarlah a Dan b- data pesawat, a 1 Dan a 2– garis lurus dalam satah a, bersilang di titik A, b 1 Dan
b 2 sepadan, garis selari dengan mereka dalam satah b. Mari kita andaikan bahawa pesawat a Dan b tidak selari, iaitu, ia bersilang sepanjang beberapa garis lurus Dengan. Lurus A 1 adalah selari dengan garis b 1, yang bermaksud ia selari dengan pesawat itu sendiri b(tanda selari antara garis dan satah). Lurus A 2 adalah selari dengan garis b 2, ini bermakna ia selari dengan pesawat itu sendiri b(tanda selari antara garis dan satah). Lurus Dengan kepunyaan kapal terbang a, yang bermaksud sekurang-kurangnya satu daripada garis lurus a 1 atau a 2 memotong garisan dengan, iaitu, ia mempunyai persamaan dengannya. Tetapi lurus Dengan juga milik kapal terbang b, yang bermaksud melintasi garisan dengan, lurus a 1 atau a 2 bersilang dengan kapal terbang b, yang tidak boleh, kerana ia lurus a 1 Dan a 2 selari dengan kapal terbang b. Ia berikutan daripada ini bahawa pesawat a Dan b jangan bersilang, iaitu selari.
Teorem 1
. Jika dua satah selari bersilang dalam pertiga, maka garis lurus persilangan adalah selari. 
Bukti. biarlah a Dan b- satah selari, dan g
- kapal terbang yang memotong mereka. kapal terbang a bersilang dengan kapal terbang g
dalam garis lurus A. kapal terbang b bersilang dengan kapal terbang g dalam garis lurus b. Garisan persimpangan A Dan b berbaring dalam satah yang sama g
dan oleh itu boleh sama ada garis bersilang atau selari. Tetapi, kepunyaan dua satah selari, mereka tidak boleh mempunyai titik sepunya. Oleh itu mereka selari.
Teorem 2.
Segmen garis selari yang tertutup di antara dua satah selari adalah sama.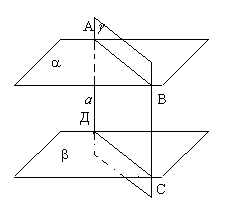 
Bukti. biarlah a Dan b- satah selari, dan A
Dan b- garis selari yang bersilang. Melalui garis lurus A Dan b kami akan menjalankan kapal terbang g
(garisan ini selari, yang bermaksud tentukan satah, dan hanya satu). kapal terbang a bersilang dengan kapal terbang g
dalam garis lurus AB .
kapal terbang b bersilang dengan kapal terbang g sepanjang garis lurus SD Mengikut teorem sebelumnya, garis lurus Dengan selari dengan garisan d. Langsung A,b, AB
Dan
SD milik kapal terbang g Sisi empat yang dibatasi oleh garis-garis ini ialah segi empat selari (sisi bertentangannya selari). Dan kerana ini ialah segi empat selari, maka sisi bertentangannya adalah sama, iaitu, AD = BC