"Sektioner af et parallelepipedum" - Opgave: konstruer et snit gennem kanten af et parallelepipedum og punkt K. Opgave: konstruer et snit, der går gennem punkterne M, N, K. M ? (ABB'A') N ? (ABCD) K ? CC'. Rektangel CKK'C' - afsnit ABCDA'B'C'D'. Rektangel ADKN - afsnit ABCDA’B’C’D’. 1. introduktion lærere – 3 min 2. Aktivering af elevernes viden.
"Proportioner af det gyldne snit" - "Golden Pentagon". Universets harmoni er baseret på tal. Udendørs lufttemperatur. Spiralorkaner og galakser. Gamle templer. "Gyldent rektangel". At bevare jorden betyder at bevare de gyldne proportioner. For eksempel er forholdet mellem land og vand på Jordens overflade i det gyldne snit.
"Volumen af et prisme" - Hvordan finder man volumenet af et lige prisme? Studie af sætningen om rumfanget af et prisme. Løsningen af problemet. Holder højden trekant ABC. Begrebet et prisme. Opgave. Område S af bunden af det oprindelige prisme. Lektionens mål. Spørgsmål. Grundlæggende trin til at bevise den direkte prismesætning? Volumen af det originale prisme lig med produktet S·h.
"Golden Ratio" - Vindue. Basil Kirke. Det gyldne snit i naturen. Det gyldne snit er en proportion. Parthenon. Egyptiske pyramider. I matematik er en proportion ligheden mellem to forhold: a:b = c:d. Formålet med undersøgelsen: At udlede verdens skønhedslov fra matematikkens synspunkt. Sankt Petersborg. Forbønskatedralen (St. Basil's Cathedral).
“Prisme 10. klasse” - Direkte. Korrekt. Prisme. Sp.p = Sside + 2Sbase Geometri. Et prisme er et polyeder, hvis flader er i parallelle planer. Side = Base + h For et lige prisme: Sp.p = Pbas. h + 2Sbas. Tilbøjelig. Formler til at finde område. Typer af prismer. Brug af prismer i hverdagen. Anvendelse af prisme i arkitektur.
“Arealbegrebet” - Geometri meritsystem i 8. klasse. Brug af multi-level undervisningsteknologi i klasseværelset. De grundlæggende principper for multi-level teknologi er: Materialet om emnet er blevet mestret, stemningen er høj. Emne: "Talls lighed" nr. 3 (a). Emne: “Polygoner” nr. 1 (1 time). Tematisk planlægning tests.
Instruktioner
Metoden til at beregne tværsnitsarealet afhænger også af de data, der allerede er tilgængelige i opgaven. Derudover er løsningen bestemt af, hvad der ligger i bunden af prismet. Hvis du skal finde det diagonale tværsnit af et prisme, skal du finde længden af diagonalen, som er lig med roden af summen (grundlaget for siderne i kvadratet). For eksempel, hvis basen af siderne i et rektangel er henholdsvis 3 cm og 4 cm, er længden af diagonalen lig med roden af (4x4 + 3x3) = 5 cm Find det diagonale tværsnitsareal ved hjælp af formel: gange diagonalen af basen med højden.
Hvis der er en trekant i bunden af prismet, for at beregne tværsnitsarealet af prismet, skal du bruge formlen: 1/2 af trekantens basis ganget med højden.
Hvis der er en cirkel ved bunden, skal du finde prismets tværsnitsareal ved at gange tallet "pi" med radius af den givne figur i en firkant.
Skelne følgende typer prismer er regelmæssige og lige. Hvis du skal finde et afsnit korrekt prisme, skal du kun kende længden af en af polygonens sider, for ved bunden er der en firkant med alle sider lige store. Find diagonalen af et kvadrat, som er lig med produktet af dets side og roden af to. Efter dette, multiplicerer du diagonalen og højden, får du tværsnitsarealet af et almindeligt prisme.
Et prisme har sine egne egenskaber. Således beregnes arealet af den laterale overflade af et vilkårligt prisme ved formlen, hvor er omkredsen vinkelret snit, - længden af sideribben. I dette tilfælde er det vinkelrette afsnit vinkelret på alle prismets laterale kanter, og dets vinkler er lineære vinkler dihedrale vinkler med tilsvarende sideribber. Et vinkelret snit er også vinkelret på alle sideflader.
Aksial er en sektion, der passerer gennem aksen geometrisk krop, dannet ved rotation af en bestemt geometrisk figur. En cylinder fås ved at dreje et rektangel rundt om en af dens sider, og det bestemmer mange af dens egenskaber. Generatorerne af dette geometriske legeme er parallelle og lig med hinanden, hvilket er meget vigtigt for at bestemme dets parametre aksialt snit, inklusive diagonaler.
Du får brug for
- - cylinder med specificerede parametre;
- - papir;
- - blyant;
- - lineal;
- - kompas;
- - Pythagoras sætning;
- - sætninger for sinus og cosinus.
Instruktioner
Konstruer en cylinder iht givne forhold. For at tegne det skal du kende basisradius og højde. I opgaven med at bestemme diagonalen kan andre forhold dog specificeres - for eksempel vinklen mellem diagonalen og generatricen eller diameteren af basen. I dette tilfælde, når du opretter en tegning, skal du bruge den størrelse, der er givet til dig. Tag resten tilfældigt og angiv, hvad der præcist er givet dig. Mærk skæringspunkterne for aksen og baserne som O og O."
Tegn det aksiale snit. Det er et rektangel, hvis to sider er basernes diametre, og de to andre er generatrices. Da generatorerne også er vinkelrette på baserne, er de også højderne af et givet geometrisk legeme. Mærk det resulterende rektangel ABCD. Tegn diagonaler AC og BD. Husk egenskaberne for diagonalerne i et rektangel. De er ens med hinanden og er delt i to i skæringspunktet.
Overvej trekant ADC. Det er rektangulært, fordi CD-generatrisen er vinkelret på basen. Det ene ben repræsenterer basens diameter, det andet - generatricen. Diagonalen er hypotenusen. Husk, hvordan længden af hypotenusen af evt retvinklet trekant. Det er lig med kvadratroden af summen af kvadraterne på benene. Det vil sige i I dette tilfælde d=√4r2+h2, hvor d er diagonalen, r er basens radius, og h er cylinderens højde.
Hvis cylinderens højde ikke er angivet i problemet, men vinklen på diagonalen af den aksiale sektion med basen eller generatricen er angivet, skal du bruge sætningen for sinus eller cosinus. Husk hvad data betyder trigonometriske funktioner. Dette er et forhold mellem modsat eller tilstødende givet vinkel ben til hypotenusen, hvilket er det du skal finde. Lad os sige, at du får højden og vinklen CAD mellem diagonalen og diameteren af basen. I dette tilfælde skal du bruge sinusloven, da vinkel CAD er modsat generatricen. Find hypotenusen d ved hjælp af formlen d=h/sinCAD. Hvis du får en radius og samme vinkel, så brug cosinussætningen. I dette tilfælde d=2r/cos CAD.
Fortsæt efter samme princip i tilfælde, hvor vinklen ACD mellem diagonalen og generatricen er specificeret. I dette tilfælde bruges sinussætningen, når radius er givet, og cosinussætningen, når højden er kendt.
Video om emnet
Det gyldne snit er en proportion, der er blevet betragtet som den mest perfekte og harmoniske siden oldtiden. Det danner grundlaget for mange gamle strukturer, fra statuer til templer, og er meget almindeligt i naturen. Samtidig er denne andel udtrykt ved overraskende elegante matematiske konstruktioner.
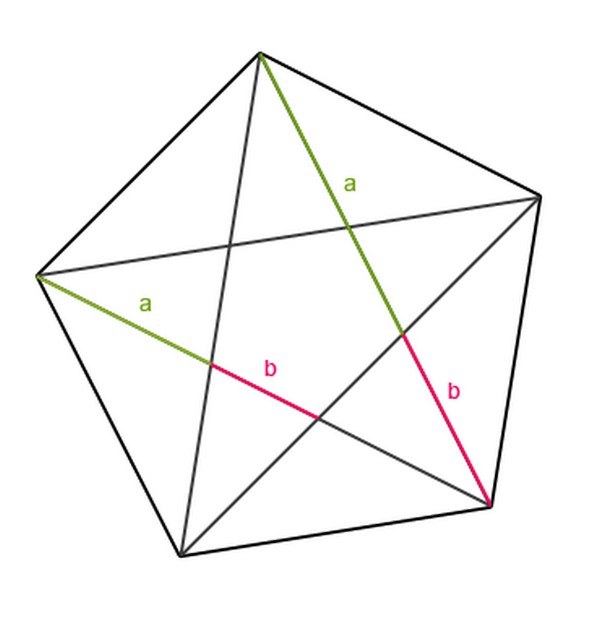
Instruktioner
Det gyldne snit bestemmes på følgende måde: dette er en opdeling af et segment i to dele, således at den mindre del er relateret til den større på samme måde som mest af- til hele segmentet.
Hvis længden af hele segmentet tages som 1, og længden af den større del som x, så vil den ønskede andel blive udtrykt ved ligningen:
(1 - x)/x = x/1.
Ved at gange begge sider af forholdet med x og overføre vilkårene får vi en andengradsligning:
x^2 + x - 1 = 0.
Ligningen har to rigtige rødder, hvoraf vi naturligvis kun interesserer os for den positive. Det er lig med (√5 - 1)/2, hvilket er omtrent lig med 0,618. Dette tal udtrykker gyldne snit. I matematik er det oftest betegnet med bogstavet φ.
Tallet φ har en række bemærkelsesværdige matematiske egenskaber. For eksempel, selv fra den oprindelige ligning er det klart, at 1/φ = φ + 1. Faktisk er 1/(0,618) = 1,618.
En anden måde at beregne det gyldne snit på er at bruge uendelig brøkdel. Med udgangspunkt i et hvilket som helst vilkårligt x kan du sekventielt konstruere en brøk:
x
1/(x + 1)
1/(1/(x+1) + 1)
1/(1/(1/(x+1) + 1) +1)
For at gøre beregningerne nemmere kan denne brøk repræsenteres som en iterativ procedure til beregning Næste skridt du skal tilføje en til resultatet af det foregående trin og dividere en med det resulterende tal. Med andre ord:
x0 = x
x(n + 1) = 1/(xn + 1).
Denne proces konvergerer, og dens grænse er φ + 1.
Hvis vi erstatter beregningen af den gensidige værdi med at udtrække kvadrat rod, det vil sige udfør en iterativ cyklus:
x0 = x
x(n + 1) = √(xn + 1),
så forbliver resultatet uændret: uanset det oprindeligt valgte x, konvergerer iterationerne til værdien φ + 1.
Det kaldes et polyeder, hvis to flader (baser) ligger i parallelle planer, og alle kanterne uden for disse flader er parallelle med hinanden. De andre flader af prismet end baserne kaldes sideflader, og deres kanter kaldes laterale ribben .
Alle sideribber er lig med hinanden som parallelle linjer, begrænset til to parallelle planer. Alle sideflader af prismet er parallellogrammer. De tilsvarende sider af prismets baser er lige store og parallelle. Derfor indeholder baserne lige mange polygoner.Prisme overflade består af to baser og en sideflade.Prisme højde kaldes et segment, der er en fælles vinkelret på de planer, som prismets grundflader ligger i.Prismets højde er lig med afstanden mellem basernes planer.Sektionen af et prisme af et plan trukket gennem to sidekanter, der ikke hører til den samme flade, kaldes diagonalt snit prismer .
Direkte prisme Et prisme kaldes et prisme, hvis sideribber er vinkelrette på bundens plan, kaldes skrå.Med det rigtige prisme kaldet et højre prisme, hvis basis er en regulær polygon.Et prisme, hvis basis er et parallelogram, kaldes parallelepipedum .
Lade l - side rib; P - base omkreds; S base - basisareal H - højde; P sektion - vinkelret sektion omkreds; S tværsnit – vinkelret snitareal; S b - lateral overfladeareal; V - volumen; S pp er prismets samlede overfladeareal.Vilkårlig prisme:
S b = P sektion ·l, V = S base ·H, V = S sektion ·lLige prisme:S pp = S b + 2S base, S b = PH, V = S base HProblemløsningEksempel 1.Det laterale overfladeareal er korrekt trekantet prisme lig med arealet af basen. Beregn længden af sidekanten, hvis siden af basen er 7 cm.Løsning .Vi finder arealet af bunden af prismet ved hjælp af formlen: 
Af betingelse er disse områder ens, dvs.Svar : .Eksempel 2.Find det samlede overfladeareal af et regulært trekantet prisme, hvis basisside er 6 cm og højden er 10 cm.Løsning .Arealet af bunden af prismet findes ved formlen: Svar :Eksempel 3.Basen af et lige prisme er ligebenet trekant, hvor højden trukket til bunden er 8 cm, er prismets højde 12 cm. Find fuld overflade prismer, hvis sidekant hvad trekantens basis indeholder er kvadratet.Løsning . 
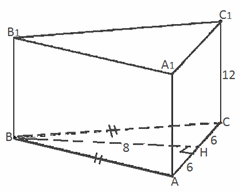Prismets overfladeareal vil være lig med summen af arealerne af baserne og summen af arealerne af sidefladerne, dvs.S = 2S ABC + S A1C1CA + 2S ABB1A1 .
Da sidefladen, der indeholder trekantens basis, er en firkant, er trekantens basis også 12 cm (basisdelen af trekanten er også en side af ansigtet).Svar: 480 cm 2.Eksempel 4.Grundlaget for et lige prisme er en trekant med sider på 5 og 3 cm og en vinkel på 120 grader mellem dem. Det største areal af sidefladerne er 35 cm 2, find arealet af sidefladen.Løsning .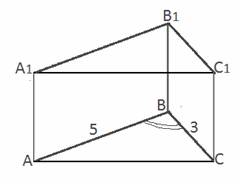 
Ifølge cosinussætningen: a 2 = b 2 + c 2 - 2bc cosAC 2 = AB 2 + BC 2 - 2 AB BC cos120AC 2 = 25 + 9 - 2 5 3 cos120AC 2 = 34 - 30 ·(-0,5)AC 2 = 49, AC = 7 cm.Hver af siderne på sidefladen er et rektangel med en højde lige høj prismer. Således sidefladen af prismet største område ligger på den side af basen, hvis sidelængde er størst.Det vil sige, at den største af sidefladerne har en længde på 7 cm.Så er prismets højde 35/7 = 5 cm.S b = 5 5 + 3 5 + 7 5 = 75 cm 2Svar: 75 cm 2.Eksempel 5.Til højre firkantet prisme grundarealet er 144 cm 2 og højden er 14 cm Find prismets diagonal og det samlede overfladeareal.Løsning . 
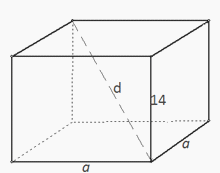Sbas = a 2 = 144, a = 12 cm.d 2 = a 2 + a 2 + c 2 = 144 + 144 + 196 = 484, d = 22 cm. S pp = 2S hoved + 4S b. S pp = 2 144 + 4 12 14 = 288 + 336 = 624 cm 2.Svar: diagonal 22 cm, samlet overflade 624 cm 2.Eksempel 6.Bestem den samlede overflade af et regulært firkantet prisme, hvis dets diagonal er 5 cm og diagonalen på dens sideflade er 4 cm.Løsning . 
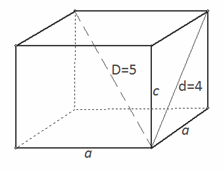Ifølge Pythagoras sætning:d 2 = a 2 + c 2 , D 2 = a 2 + a 2 + c 2 = 2a 2 + c 2.
Vi får to ligninger med to ubekendte:16 = a 2 + c 2, 25 = 2a 2 + c 2.Træk den første fra den anden ligning: a 2 = 9, a = 3. Derefter
92. På den rigtige måde trekantet pyramide ABCD (med toppunkt D) er basissiden 2 og sidekanten er 4. Find pyramidens tværsnitsareal ved planet KLM, hvor K, L, M er midtpunkterne på kanterne AB, BC og cd, hhv.
93. I et regulært trekantet prisme ABCA1 B1 C1 er sidekanten 4, og siden af basen er 6. Find prismets tværsnitsareal ved at flyet går gennem punkterne A, B og midten af kanten B1 C1.
95. Kanten på terningen ABCDA1 B1 C1 D1 er lig med 4. Find terningens tværsnitsareal ved at flyet går gennem toppunktet D1 og midtpunkterne på kanterne AD og CD.
96. Kanten på terningen ABCDA1 B1 C1 D1 er lig med 4. Punkt E er midten af kanten A1 D1. Find terningens tværsnitsareal ved ACE-plan.
97. I et regulært firkantet prisme ABCDA1 B1 C1 D1 er siden af basen 1 og højden er 2. Punkt M er midten af kanten AA1. Find prismets tværsnitsareal ved planet
BMD1.
3 s
98.V rektangulær parallelepipedum ABCDA1 B1 C1 D1 kanter er kendt: AB = 3, AD = 3, AA1 = 5. Punkt M er placeret på kant AA1, således at AM = 4. a) Find tværsnitsarealet af parallelepipedummet ved plan BMD1. b) Find vinklen mellem planerne BMD1 og ABC (tip: brug arealsætning ortogonal projektion polygon).