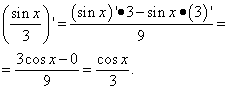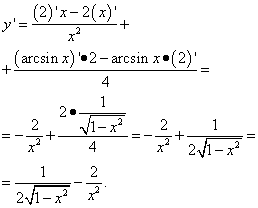المشتقات الجزئية للدوال المثلثية أمثلة على الحلول. اشتقاق مشتقات ظل التمام وظل التمام

أوجد المشتقة.

الخيار 1.

الخيار 2.

في = 2X + 5.

في = 2X – 5.

في= 4cos X.

في= 3 خطيئة X.

في= تيراغرام X+ctg X.

في= تيراغرام X-ctg X.

في= الخطيئة 3 X.

في= كوس 4 X.

خيارات الإجابة.

- 4الخطيئة X

- 3كوس X

1/كوس 2 X+ 1/الخطيئة 2 X

1/كوس 2 X–1/الخطيئة 2 X

1/الخطيئة 2 X-1/كوس 2 X

- 4الخطيئة4 X

- 3cos3 X

و(س) = خطيئة س+كوس س

و(س) = الخطيئة 2 س – س

و(س) = 2س+كوس(4 س – )

الخيار 1

الخيار 2

ذ = 2X 3

ذ = 3X 2

ذ = 1/4 X 4 + 2X 2 – 7

ذ = 1/2 X 4 + 4X + 5

ذ = X 3 + 4X 2 – 3X.
حل المعادلة ذ " = 0

ذ = 2X 3 – 9X 2 + 12X + 7.
حل المعادلة ذ " = 0.

ذ= الخطيئة 2 X- كوس 3 X.

ذ= كوس 2 X- الخطيئة 3 X.

ذ= تيراغرام X–ctg( X + /4).

ذ=ctg X+ تيراغرام( X – /4).

ذ= الخطيئة 2 X.

ذ= كوس 2 X.

خيارات الإجابة.

من سياق الهندسة والرياضيات، اعتاد تلاميذ المدارس على حقيقة أن مفهوم المشتق يتم نقله إليهم من خلال مساحة الشكل، والتفاضلات، وحدود الوظائف، وكذلك الحدود. دعونا نحاول أن ننظر إلى مفهوم المشتقة من زاوية مختلفة، ونحدد كيف يمكن ربط الدوال المشتقة والدوال المثلثية.

لذلك، دعونا نفكر في بعض المنحنيات التعسفية الموصوفة بواسطة الدالة المجردة y = f(x).

لنتخيل أن الجدول الزمني عبارة عن خريطة لطريق سياحي. الزيادة ∆x (دلتا x) في الشكل هي مسافة معينة من المسار، و∆y هو التغير في ارتفاع المسار فوق مستوى سطح البحر.
ثم يتبين أن النسبة ∆x/∆y ستميز مدى تعقيد المسار في كل جزء من المسار. بعد أن تعلمت هذه القيمة، يمكنك أن تقول بثقة ما إذا كان الصعود/الهبوط شديد الانحدار، وما إذا كنت ستحتاج إلى معدات التسلق وما إذا كان السائحون بحاجة إلى معدات معينة التدريب البدني. لكن هذا المؤشر سيكون صالحا لواحد فقط فجوة صغيرة∆س.

إذا أخذ منظم الرحلة القيم الأولية و نقاط النهايةالمسارات، أي ∆x – سوف تكون يساوي الطولالطريق، فلن يتمكن من الحصول على بيانات موضوعية حول درجة صعوبة الرحلة. لذلك، من الضروري إنشاء رسم بياني آخر يصف سرعة و"جودة" التغييرات في المسار، وبعبارة أخرى، تحديد النسبة ∆x/∆y لكل "متر" من المسار.

سيكون هذا الرسم البياني مشتقًا مرئيًا لمسار معين وسيصف بشكل موضوعي التغييرات التي تطرأ عليه عند كل فترة زمنية من الاهتمام. من السهل جدًا التحقق من ذلك؛ فالقيمة ∆x/∆y ليست أكثر من مجرد تفاضل معنى محددس و ص. دعونا نطبق التمايز ليس على إحداثيات محددة، ولكن على الوظيفة ككل:

الدوال المشتقة والمثلثية

ترتبط الدوال المثلثية ارتباطًا وثيقًا بالمشتقات. ويمكن فهم ذلك من الرسم التالي. في الصورة محور الإحداثياتتظهر الدالة Y = f (x) - المنحنى الأزرق.

ك (x0؛ و (x0)) – نقطة تعسفية، x0 + ∆x هي الزيادة على طول محور OX، و f (x0 + ∆x) هي الزيادة على طول محور OY عند نقطة معينة L.

لنرسم خطًا مستقيمًا عبر النقطتين K وL ونبنيه المثلث الأيمنكلن. إذا قمت بتحريك المقطع LN عقليًا على طول الرسم البياني Y = f (x)، فستميل النقطتان L و N إلى القيم K (x0؛ f (x0)). دعنا نسمي هذه النقطة البداية الشرطية للرسم البياني - الحد؛ إذا كانت الدالة لا نهائية، على الأقل في إحدى الفواصل الزمنية، فسيكون هذا الاتجاه أيضًا لا نهائيًا، وتكون قيمته الحدية قريبة من 0.

يمكن وصف طبيعة هذا الاتجاه من خلال مماس للنقطة المحددة y = kx + b أو من خلال رسم بياني لمشتق الدالة الأصلية dy - الخط المستقيم الأخضر.

ولكن أين علم المثلثات هنا؟! كل شيء بسيط للغاية، فكر في المثلث القائم KLN. القيمة التفاضلية لنقطة معينة K هي ظل الزاوية α أو ∠K:

وبهذه الطريقة يمكننا وصف المعنى الهندسي للمشتقة وعلاقتها بالدوال المثلثية.

الصيغ المشتقة للدوال المثلثية

يجب حفظ تحويلات الجيب وجيب التمام والظل وظل التمام عند تحديد المشتق.

الصيغتان الأخيرتان ليستا خطأ، النقطة المهمة هي أن هناك فرقًا بين تعريف مشتق وسيطة بسيطة ودالة بنفس الصفة.

دعونا نفكر جدول المقارنةمع صيغ لمشتقات الجيوب الأنفية وجيب التمام والظل وظل التمام:

تم أيضًا اشتقاق الصيغ لمشتقات أركسين وأركوسين وظل قوسي وظل قوسي، على الرغم من أنها نادرًا ما تستخدم:

تجدر الإشارة إلى أن الصيغ المذكورة أعلاه ليست كافية بشكل واضح للتوصل إلى حل ناجح المهام النموذجيةامتحان الدولة الموحد ما سيتم توضيحه عند الحل مثال ملموسالبحث عن مشتقة التعبير المثلثي.

يمارس: من الضروري إيجاد مشتقة الدالة وإيجاد قيمتها لـ π/4:

حل: للعثور على y’ من الضروري أن نتذكر الصيغ الأساسية لتحويل الدالة الأصلية إلى مشتق، وهي.

يتم عرض مشتقات الدوال المثلثية العكسية واشتقاق صيغها. يتم أيضًا إعطاء تعبيرات للمشتقات ذات الترتيب الأعلى. روابط لصفحات بها المزيد بيان مفصلصيغ الإخراج.

أولًا، نشتق صيغة مشتقة أركسين. يترك
ص= أرسين x.
بما أن arcsine هي الدالة العكسية للجيب، إذن
.
هنا y دالة لـ x.
.
التفاضل بالنسبة للمتغير x:
.
نحن نطبق:
.

لذلك وجدنا:
.
لأنه إذن .
ثم
.

والصيغة السابقة تأخذ الشكل:
.
.
.

من هنا بهذه الطريقة بالضبط، يمكنك الحصول على صيغة مشتقة قوس جيب التمام. ومع ذلك، فمن الأسهل استخدام صيغة تتعلق بالدوال المثلثية العكسية:ثم

ويرد وصف أكثر تفصيلاً في صفحة "اشتقاق مشتقات أركسين وأركوسين". هناك يتم إعطاؤه

اشتقاق المشتقات بطريقتين

- تمت مناقشته أعلاه ووفقًا لصيغة مشتقة الدالة العكسية.
ص= اشتقاق مشتقات ظل التمام و ظل التمام.
وبنفس الطريقة سنوجد مشتقات ظل التمام وظل التمام.
.
يترك
.
أركانتان x
.
نحن نطبق:
.

مشتق من ظل التمام القوسي:
.

مشتقات أركسين

- تمت مناقشته أعلاه ووفقًا لصيغة مشتقة الدالة العكسية.
.
لقد وجدنا بالفعل مشتق من الدرجة الأولى من arcsine:
.
وبالاشتقاق نجد المشتقة من الدرجة الثانية:
;
.
ويمكن كتابتها أيضًا بالشكل التالي:
.
من هنا نحصل المعادلة التفاضلية، والتي يتم استيفاءها بواسطة مشتقات arcsine من الرتبة الأولى والثانية:
.

ومن خلال اشتقاق هذه المعادلة، يمكننا إيجاد مشتقات ذات رتبة أعلى.

مشتق من arcsine من الترتيب n

مشتق قوس جيب التمام من الرتبة n له العرض التالي:
,
حيث هو كثير الحدود من الدرجة.
;
.
يتم تحديده بواسطة الصيغ:

هنا .
.

كثير الحدود يفي بالمعادلة التفاضلية:

مشتق من arccosine من الرتبة n
.
يتم الحصول على مشتقات قوس جيب التمام من مشتقات جيب التمام باستخدام الصيغة المثلثية:
.

ولذلك تختلف مشتقات هذه الدوال في الإشارة فقط:

مشتقات قوس الظل
.

يترك . لقد وجدنا مشتقة ظل التمام القوسي من الدرجة الأولى:

.
دعونا نقسم الكسر إلى أبسط صورة:

هنا الوحدة التخيلية .

.

نحن نفرق مرة واحدة ونصل الكسر إلى قاسم مشترك:
.

بالتعويض نحصل على:

مشتقة ظل الزاوية من الرتبة n
;
.

وبالتالي، يمكن تمثيل مشتق ظل الزاوية من الرتبة n بعدة طرق:

مشتقات ظل التمام القوسي
.
فليكن الآن.
.

دعونا نطبق الصيغة التي تربط الدوال المثلثية العكسية:
.

ثم يختلف المشتق من الدرجة n لظل القوس فقط في الإشارة عن مشتق قوس الظل:
وبالتعويض نجد: الأدب المستخدم:ن.م. غونتر، آر.أو. كوزمين، مجموعة من المشاكل على

الرياضيات العليا ، "لان"، 2003. للعثور على مشتقة من دالة مثلثيةبحاجة لاستخدام

جدول المشتقات وهي المشتقات 6-13. عندما تجد

• مشتقات الدوال المثلثية البسيطة لتجنب الأخطاء الشائعة، عليك الانتباه إلى النقاط التالية:في تعبير دالة، يكون أحد المصطلحات غالبًا
• جيب التمام، جيب التمام أو وظيفة مثلثية أخرى
• ليس من وسيطة الدالة، بل من الرقم (الثابت)، وبالتالي فإن مشتقة هذا الحد تساوي صفرًا؛ تحتاج دائمًا تقريبًا إلى تبسيط التعبير الذي تم الحصول عليه نتيجة للتمايز، ولهذا تحتاج إلى استخدام المعرفة بالعمليات مع الكسور بثقة؛لتبسيط التعبير الذي تحتاج دائمًا إلى معرفته الهويات المثلثية، على سبيل المثال، الصيغة

زاوية مزدوجةوصيغة الوحدة كمجموع مربعات الجيب وجيب التمام.

مثال 1. أوجد مشتقة الدالةحل. دعنا نقول مع مشتق جيب التماماثني عشر مقسوما على بي؟ الجواب: عد يساوي الصفر! هنا الجيب (دالة في النهاية!) هو فخ، لأن الوسيطة ليست المتغير X أو أي متغير آخر، ولكنها مجرد رقم. وهذا يعني أن جيب هذا الرقم هو أيضًا رقم. ومشتقة العدد (الثابت)، كما نعلم من جدول المشتقات، تساوي صفرًا. لذلك، نترك فقط جيب X الناقص ونجد مشتقته، دون أن ننسى الإشارة:

.

مثال 2.وصيغة الوحدة كمجموع مربعات الجيب وجيب التمام.

.

حل. الحد الثاني هو نفس حالة الحد الأول في المثال السابق. أي أنه عدد، ومشتقة العدد هي صفر. نجد مشتقة الحد الثاني كمشتقة حاصل القسمة:

مثال 3.وصيغة الوحدة كمجموع مربعات الجيب وجيب التمام.

حل. هذه مشكلة أخرى: هنا في الحد الأول لا يوجد قوس جيب الجيب أو أي دالة مثلثية أخرى، ولكن هناك x، مما يعني أنها دالة لـ x. ولذلك نفرقه كمصطلح في مجموع الوظائف:

هنا كانت هناك حاجة إلى مهارات في العمليات مع الكسور، أي في القضاء على هيكل الكسر المكون من ثلاثة طوابق.

مثال 4.وصيغة الوحدة كمجموع مربعات الجيب وجيب التمام.

.

حل. هنا يلعب الحرف "phi" نفس الدور الذي يلعبه "x" في الحالات السابقة (وفي معظم الحالات الأخرى، ولكن ليس كلها) - المتغير المستقل. لذلك، عندما نبحث عن مشتقة حاصل ضرب الدوال، لن نتسرع في إعلان أن مشتقة جذر "phi" تساوي صفرًا. لذا:

لكن الحل لا ينتهي عند هذا الحد. وبما أن المصطلحات المتشابهة مجمعة بين قوسين، فلا يزال يتعين علينا تحويل (تبسيط) التعبير. ولذلك، فإننا نضرب الأقواس في العوامل التي تقف وراءها، ثم نأتي بالحدود إلى قاسم مشترك ونقوم بإجراء تحويلات أولية أخرى:

مثال 5.وصيغة الوحدة كمجموع مربعات الجيب وجيب التمام.

حل. في هذا المثال، سنحتاج إلى معرفة حقيقة وجود مثل هذه الدالة المثلثية - القاطع - وصيغها من خلال جيب التمام. دعونا نفرق:

مثال 6.وصيغة الوحدة كمجموع مربعات الجيب وجيب التمام.

.

حل. في هذا المثال، سيطلب منا أن نتذكر صيغة ضعف الزاوية من المدرسة. ولكن أولا دعونا نفرق:

,

(هذه هي صيغة الزاوية المزدوجة)