Mnożenie liczb całkowitych o różnych znakach. Mnożenie

Teraz zajmijmy się mnożenie i dzielenie.

Powiedzmy, że musimy pomnożyć +3 przez -4. Jak to zrobić?

Rozważmy taki przypadek. Trzy osoby popadły w długi, a każda z nich miała 4 dolary długu. Jaki jest całkowity dług? Aby go znaleźć, należy zsumować wszystkie trzy długi: 4 dolary + 4 dolary + 4 dolary = 12 dolarów. Zdecydowaliśmy, że dodanie trzech liczb 4 jest oznaczone jako 3x4. Od w w tym przypadku mówimy o długu, przed cyfrą 4 znajduje się znak „-”. Wiemy, że całkowity dług wynosi 12 dolarów, więc naszym problemem jest teraz 3x(-4)=-12.

Ten sam wynik otrzymamy, jeśli zgodnie z zadaniem każda z czterech osób będzie miała dług w wysokości 3 dolarów. Innymi słowy, (+4)x(-3)=-12. A ponieważ kolejność czynników nie ma znaczenia, otrzymujemy (-4)x(+3)=-12 i (+4)x(-3)=-12.

Podsumujmy wyniki. Gdy pomnożysz jedną liczbę dodatnią i jedną liczbę ujemną, wynikiem zawsze będzie liczba ujemna. Wartość liczbowa odpowiedzi będzie taka sama jak w przypadku liczb dodatnich. Produkt (+4)x(+3)=+12. Obecność znaku „-” wpływa tylko na znak, ale nie wpływa na wartość liczbową.

Jak pomnożyć dwie liczby ujemne?

Niestety bardzo trudno jest znaleźć odpowiedni przykład z życia wzięty na ten temat. Łatwo jest sobie wyobrazić dług na 3 czy 4 dolary, ale zupełnie nie można sobie wyobrazić -4 czy -3 osób, które popadły w długi.

Być może pójdziemy inną drogą. Przy mnożeniu, gdy zmienia się znak jednego z czynników, zmienia się znak iloczynu. Jeśli zmienimy znaki obu czynników, musimy zmienić dwukrotnie znak pracy, najpierw od dodatniego do ujemnego, a następnie odwrotnie, od ujemnego do dodatniego, to znaczy produkt będzie miał początkowy znak.

Dlatego jest całkiem logiczne, choć trochę dziwne, że (-3) x (-4) = +12.

Stanowisko znaku po pomnożeniu zmienia się to w następujący sposób:

liczba dodatnia x liczba dodatnia = liczba dodatnia;
liczba ujemna x liczba dodatnia = liczba ujemna;
liczba dodatnia x liczba ujemna = liczba ujemna;
liczba ujemna x liczba ujemna = liczba dodatnia.

Innymi słowy, mnożenie dwóch liczb przez identyczne znaki, otrzymujemy liczbę dodatnią. Mnożenie dwóch liczb przez różne znaki, otrzymujemy liczbę ujemną.

Ta sama zasada dotyczy działania przeciwnego do mnożenia - dla.

Możesz to łatwo sprawdzić, uruchamiając odwrotne operacje mnożenia. W każdym z powyższych przykładów, jeśli pomnożysz iloraz przez dzielnik, otrzymasz dywidendę i upewnisz się, że ma ten sam znak, na przykład (-3)x(-4)=(+12).

Jako że zbliża się zima, czas pomyśleć o tym, w co zmienić żelazne podkowy, aby nie poślizgnąć się na lodzie i czuć się na nim pewnie. zimowe drogi. Możesz na przykład kupić opony Yokohama na stronie internetowej: mvo.ru lub kilku innych, najważniejsze jest to, że są wysokiej jakości, więcej informacji i cen można znaleźć na stronie Mvo.ru.

W tym artykule zajmiemy się mnożenie liczb o różnych znakach. Tutaj najpierw sformułowamy zasadę mnożenia liczb dodatnich i ujemnych, uzasadnimy ją, a następnie rozważymy zastosowanie tej reguły przy rozwiązywaniu przykładów.

Nawigacja strony.

Zasada mnożenia liczb o różnych znakach

Mnożenie liczby dodatniej przez liczbę ujemną, a także liczby ujemnej przez liczbę dodatnią, przeprowadza się w następujący sposób: zasada mnożenia liczb o różnych znakach: aby pomnożyć liczby o różnych znakach, należy pomnożyć i umieścić znak minus przed otrzymanym iloczynem.

Zapiszmy tę regułę w formie listu. Dla każdej dodatniej liczby rzeczywistej a i dowolnej ujemnej liczby rzeczywistej −b równość a·(−b)=−(|a|·|b|) , a także dla liczby ujemnej −a i liczby dodatniej b równość (−a)·b=−(|a|·|b|) .

Zasada mnożenia liczb o różnych znakach jest w pełni zgodna właściwości operacji na liczbach rzeczywistych. Rzeczywiście na ich podstawie łatwo wykazać, że dla liczb rzeczywistych i dodatnich a i b istnieje łańcuch równości postaci a·(−b)+a·b=a·((−b)+b)=a·0=0, co dowodzi, że a·(−b) i a·b są liczby przeciwne, co implikuje równość a·(−b)=−(a·b) . Z tego wynika ważność omawianej reguły mnożenia.

Należy zauważyć, że podana zasada mnożenia liczb o różnych znakach obowiązuje w obu przypadkach liczby rzeczywiste, zarówno dla liczb wymiernych, jak i dla liczb całkowitych. Wynika to z faktu, że operacje na liczbach wymiernych i całkowitych mają te same własności, które zostały użyte w powyższym dowodzie.

Oczywiste jest, że mnożenie liczb o różnych znakach zgodnie z otrzymaną regułą sprowadza się do mnożenia liczb dodatnich.

Pozostaje tylko rozważyć przykłady zastosowania zdemontowanej reguły mnożenia przy mnożeniu liczb o różnych znakach.

Przykłady mnożenia liczb o różnych znakach

Przyjrzyjmy się kilku rozwiązaniom przykłady mnożenia liczb przez różne znaki. Zacznijmy prosty przypadek, aby skupić się na etapach reguł, a nie na złożoności obliczeniowej.

Przykład.

Pomnóż liczbę ujemną −4 przez liczbę dodatnią 5.

Rozwiązanie.

Zgodnie z zasadą mnożenia liczb o różnych znakach, najpierw musimy pomnożyć wartości bezwzględne pierwotnych czynników. Moduł -4 wynosi 4, a moduł 5 wynosi 5, a pomnożenie liczb naturalnych 4 i 5 daje 20. Na koniec pozostaje postawić znak minus przed wynikową liczbą, mamy -20. To kończy mnożenie.

W skrócie rozwiązanie można zapisać w następujący sposób: (−4)·5=−(4,5)=−20.

Odpowiedź:

(−4)·5=−20.

Podczas mnożenia liczby ułamkowe z różnymi znakami musisz umieć mnożyć ułamki zwykłe, mnożyć ułamki dziesiętne i ich kombinacje z liczbami naturalnymi i mieszanymi.

Przykład.

Mnoży liczby o różnych znakach 0, (2) i .

Rozwiązanie.

Zamieniając okresowy ułamek dziesiętny na ułamek zwykły, a także zamieniając liczbę mieszaną na ułamek niewłaściwy, z iloczynu pierwotnego dojdziemy do produktu zwykłe ułamki z różnymi znakami formy. Iloczyn ten, zgodnie z zasadą mnożenia liczb o różnych znakach, jest równy . Pozostaje tylko pomnożyć ułamki zwykłe w nawiasach .

Cele Lekcji:

Edukacyjny:

formułowanie zasad mnożenia liczb o tych samych i różnych znakach;
doskonalenie i doskonalenie umiejętności mnożenia liczb o różnych znakach.

Edukacyjny:

rozwój operacje umysłowe: porównanie, uogólnienie, analiza, analogia;
rozwój umiejętności niezależna praca;
poszerzanie horyzontów uczniów.

Edukacyjny:

wspieranie kultury prowadzenia dokumentacji;
edukacja odpowiedzialności, uwagi;
rozwijanie zainteresowania tematem.

Typ lekcji: nauka nowego materiału.

Sprzęt: komputer, rzutnik multimedialny, karty do gry „Walka Matematyczna”, testy, karty wiedzy.

Plakaty na ścianach:

Wiedza jest najwspanialszym z dóbr. Każdy o to zabiega, ale nie przychodzi to samo.
Al-Biruni
We wszystkim chcę dotrzeć do samej istoty...
B. Pasternaka

Plan lekcji

Moment organizacyjny (1 min).
wstęp nauczyciele (3 min).
Praca ustna(10 minut).
Prezentacja materiału (15 min).
Łańcuch matematyczny (5 min).
Praca domowa(2 minuty).
Próba (6 minut).
Podsumowanie lekcji (3 min).

Podczas zajęć

I. Moment organizacyjny

gotowość uczniów do zajęć.

II. Mowa inauguracyjna nauczyciela

Kochani, spotkaliśmy się dzisiaj z Wami nie na próżno, ale w celu owocnej pracy: zdobywania wiedzy.

Odkąd istnieje wszechświat,
Nie ma człowieka, który nie potrzebuje wiedzy.
Niezależnie od tego, jaki język i wiek wybierzemy,
Człowiek od zawsze dążył do wiedzy...
Rudaki

Na zajęciach będziemy się uczyć nowy materiał, skonsoliduj to, pracuj samodzielnie, oceniaj siebie i swoich towarzyszy. Każdy ma na biurku kartę wiedzy, w której nasza lekcja podzielona jest na etapy. Punkty, które zdobyłeś różne etapy sam wpiszesz lekcję na tę kartę. A na koniec lekcji podsumujemy. Umieść te karty w widocznym miejscu.

III. Praca ustna (w formie gry „Walka Matematyczna”)

Chłopaki, zanim zaczniemy nowy temat, powtórzmy to, czego nauczyliśmy się wcześniej. Każdy ma na biurku kartkę papieru z grą „Mathematical Combat”. Kolumny pionowe i poziome zawierają liczby, które należy dodać. Liczby te zaznaczono kropkami. Odpowiedzi napiszemy w tych komórkach w polu, w którym znajdują się kropki.

Do zakończenia trzy minuty. Rozpoczęliśmy pracę.

Teraz wymieniliśmy się pracami z sąsiadką z biurka i sprawdzamy je między sobą. Jeśli uważasz, że odpowiedź jest błędna, przekreśl ją ostrożnie i wpisz obok właściwą. Sprawdźmy.

Sprawdźmy teraz odpowiedzi na ekranie ( Na ekranie wyświetlane są prawidłowe odpowiedzi).

Za poprawnie rozwiązane

5 zadań otrzymuje 5 punktów;
4 zadania – 4 punkty;
3 zadania – 3 punkty;
2 zadania – 2 punkty;
1 zadanie – 1 punkt.

Dobrze zrobiony. Odłożyli wszystko na bok. Kochani, wpiszmy do naszych kart wiedzy liczbę punktów zdobytych w „Bitwie matematycznej” ( Aneks 1).

IV. Prezentacja materiału

Otwórz skoroszyty. Zapisz numer, świetna robota.

Jakie znasz działania na liczbach dodatnich i ujemnych?
Jak dodać dwie liczby ujemne?
Jak dodać dwie liczby o różnych znakach?
Jak odejmować liczby o różnych znakach?
Zawsze używasz słowa „moduł”. Jaki jest moduł liczby? A?

Temat dzisiejszej lekcji jest również związany z działaniem liczb o różnych znakach. Ale był ukryty w anagramie, w którym musisz zamienić litery i uzyskać znajome słowo. Spróbujmy to rozgryźć.

ENOZHEUMNI

Zapisujemy temat lekcji: „Mnożenie”.

Cel naszej lekcji: zapoznanie się z mnożeniem dodatnich i liczby ujemne i sformułować zasady mnożenia liczb o tych samych i różnych znakach.

Cała uwaga skierowana na tablicę. Przed tobą tabela z zadaniami, przy rozwiązywaniu których sformułujemy zasady mnożenia liczb dodatnich i ujemnych.

2*3 = 6°C;
–2*3 = –6°С;
–2*(–3) = 6°С;
2*(–3) = –6°С;

1. Temperatura powietrza wzrasta o 2°C co godzinę. Teraz termometr pokazuje 0°C ( Załącznik 2– Termometr) (slajd 1 na komputerze).

Ile otrzymałeś?(6 ° Z).
Ktoś napisze rozwiązanie na tablicy, a my wszyscy jesteśmy w zeszytach.
Spójrzmy na termometr, czy otrzymaliśmy poprawną odpowiedź? (slajd 2 na komputerze).

2. Temperatura powietrza spada o 2°C co godzinę. Termometr pokazuje teraz 0°C (slajd 3 na komputerze). Jaką temperaturę powietrza pokaże termometr po 3 godzinach?

Ile otrzymałeś?(–6 ° Z).
Odpowiednie rozwiązanie zapisujemy na tablicy i w zeszytach. Analogia do zadania 1.
.(slajd 4 na komputerze).

3. Temperatura powietrza spada o 2°C co godzinę. Termometr pokazuje teraz 0°C (slajd 5 na komputerze).

Ile otrzymałeś?(6 ° Z).
Odpowiednie rozwiązanie zapisujemy na tablicy i w zeszytach. Analogia do zadań 1 i 2.
Porównajmy wynik z odczytem termometru.(slajd 6 na komputerze).

4. Temperatura powietrza wzrasta o 2°C co godzinę. Termometr pokazuje teraz 0°C (slajd 7 na komputerze). Jaką temperaturę powietrza wskazywał termometr 3 godziny temu?

Ile otrzymałeś?(–6 ° Z).
Odpowiednie rozwiązanie zapisujemy na tablicy i w zeszytach. Analogia do zadań 1-3.
Porównajmy wynik z odczytem termometru.(slajd 8 na komputerze).

Spójrz na swoje wyniki. Mnożąc liczby o tych samych znakach (przykłady 1 i 3), pod jakim znakiem otrzymałeś odpowiedź? (pozytywny).

Cienki. Ale w przykładzie 3 oba czynniki są negatywne, a odpowiedź jest pozytywna. Który koncepcja matematyczna pozwala przejść od liczb ujemnych do dodatnich? (moduł).

Zasada uwagi: Aby pomnożyć dwie liczby o tych samych znakach, należy pomnożyć ich wartości bezwzględne i przed wynikiem umieścić znak plus. (powtarzają się 2 osoby).

Wróćmy do przykładu 3. Jakie są moduły (–2) i (–3)? Pomnóżmy te moduły. Ile otrzymałeś? Z jakim znakiem?

Mnożąc liczby o różnych znakach (przykłady 2 i 4), pod jakim znakiem otrzymałeś odpowiedź? (negatywny).

Sformułuj własne zasady mnożenia liczb o różnych znakach.

Reguła: Mnożąc liczby o różnych znakach, należy pomnożyć ich moduły i umieścić znak minus przed wynikiem. (powtarzają się 2 osoby).

Wróćmy do przykładów nr 2 i nr 4. Jakie są wielkości ich czynników? Pomnóżmy te moduły. Ile otrzymałeś? Jaki znak powinien zostać podany w rezultacie?

Korzystając z tych dwóch zasad, możesz także mnożyć ułamki zwykłe: dziesiętny, mieszany, zwykły.

Na tablicy przed tobą znajduje się kilka przykładów. Trzy zdecydujemy wspólnie ze mną, a resztę sami. Zwróć uwagę na nagranie i projekt.

Dobrze zrobiony. Otwórzmy podręczniki i zaznaczmy zasady, których należy się nauczyć na następną lekcję (str. 190, §7 (pkt. 35)). Znajomość tych zasad pomoże Ci w przyszłości szybko opanować dzielenie liczb dodatnich i ujemnych.

V. Łańcuch matematyczny

A teraz Dunno chce sprawdzić, jak nauczyłeś się nowego materiału i zada Ci kilka pytań. Musimy zapisać rozwiązanie i odpowiedzi w zeszytach ( Dodatek 3– Łańcuch matematyczny).

Prezentacja komputerowa
Cześć chłopaki. Widzę, że jesteś bardzo mądry i dociekliwy, dlatego chcę zadać Ci kilka pytań. Zachowaj ostrożność, szczególnie w przypadku znaków.
Moje pierwsze pytanie brzmi: pomnóż (–3) przez (–13).
Pytanie drugie: pomnóż to, co dostałeś w pierwszym zadaniu przez (–0,1).
Pytanie trzecie: pomnóż wynik drugiego zadania przez (–2).
Pytanie czwarte: pomnóż (-1/3) przez wynik trzeciego zadania.
I ostatnie, piąte pytanie: oblicz temperaturę zamarzania rtęci, mnożąc wynik czwartego zadania przez 15.
Dziękuję za pracę. Życzę Ci sukcesu.

Kochani sprawdźmy jak wykonaliśmy zadania. Wszyscy wstali.

Ile dostałeś w pierwszym zadaniu?

Ci, którzy mają inną odpowiedź, siadają, a ci, którzy siadają, dajemy sobie 0 punktów za łańcuch matematyczny na karcie zapisu wiedzy. Reszta nic nie wkłada.

Ile dostałeś w drugim zadaniu?

Jeśli masz inną odpowiedź, usiądź i dodaj 1 punkt do swojej karty wiedzy za łańcuch matematyczny.

Ile dostałeś w trzecim zadaniu?

Jeśli masz inną odpowiedź, usiądź i dodaj 2 punkty do swojej karty wiedzy za łańcuch matematyczny.

Ile dostałeś w czwartym zadaniu?

Jeśli masz inną odpowiedź, usiądź i dodaj 3 punkty do swojej karty rekordu wiedzy za łańcuch matematyczny.

Ile dostałeś w piątym zadaniu?

Jeśli masz inną odpowiedź, usiądź i dodaj 4 punkty do swojej karty wiedzy za łańcuch matematyczny. Pozostali chłopcy rozwiązali poprawnie wszystkie 5 zadań. Usiądź, przyznaj sobie 5 punktów za łańcuch matematyczny na karcie zapisu wiedzy.

Jaka jest temperatura zamarzania rtęci?(–39 °C).

VI. Praca domowa

§7 (klauzula 35, s. 190), nr 1121 – podręcznik: Matematyka. Klasa 6: [N.Ya.Vilenkin i inni]

Zadanie kreatywne: Napisz zadanie dotyczące mnożenia liczb dodatnich i ujemnych.

VII. Test

Przejdźmy dalej Następny etap lekcja: zdawanie testu ( Dodatek 4).

Musisz rozwiązać zadania i zakreślić liczbę prawidłowej odpowiedzi. Za pierwsze dwa poprawnie wykonane zadania otrzymasz 1 punkt, za zadanie 3 - 2 punkty, za zadanie 4 - 3 punkty. Rozpoczęliśmy pracę.

Δ –1 punkt;
o –2 punkty;
–3 punkty.

Zapiszmy teraz liczby prawidłowych odpowiedzi w tabeli pod testem. Sprawdźmy wyniki. Powinieneś otrzymać numer 1418 w pustych komórkach (piszę na tablicy). Osoba, która go otrzymała, umieszcza 7 punktów na karcie wiedzy. Ci, którzy popełnili błędy, wpisują na kartę wiedzy liczbę punktów zdobytych wyłącznie za poprawnie wykonane zadania.

Wielka Wielka Wojna trwała dokładnie 1418 dni. Wojna Ojczyźniana, zwycięstwo, za które naród rosyjski zapłacił wysoką cenę. A 9 maja 2010 roku będziemy obchodzić 65. rocznicę zwycięstwa nad hitlerowskimi Niemcami.

VIII. Podsumowanie lekcji

Teraz obliczmy łączną liczbę punktów zdobytych za lekcję i wpiszmy wyniki do karty zapisu wiedzy uczniów. Następnie rozdajemy te karty.

15 – 17 punktów – ocena „5”;
10 – 14 punktów – ocena „4”;
mniej niż 10 punktów – ocena „3”.

Podnieście ręce, którzy otrzymali „5”, „4”, „3”.

Jaki temat dzisiaj poruszaliśmy?
Jak pomnożyć liczby o tych samych znakach; z różnymi znakami?

Tak więc nasza lekcja dobiegła końca. Chcę PODZIĘKOWAĆ za Twoją pracę podczas tej lekcji.

Ta lekcja dotyczy mnożenia i dzielenia. liczby wymierne.

Treść lekcji

Mnożenie liczb wymiernych

Zasady mnożenia liczb całkowitych dotyczą także liczb wymiernych. Innymi słowy, aby pomnożyć liczby wymierne, trzeba to umieć

Trzeba także znać podstawowe prawa mnożenia, takie jak: prawo przemienności mnożenia, prawo łączenia mnożenia, prawo rozdzielności mnożenia i mnożenia przez zero.

Przykład 1. Znajdź wartość wyrażenia

Jest to mnożenie liczb wymiernych o różnych znakach. Aby pomnożyć liczby wymierne o różnych znakach, należy pomnożyć ich moduły i postawić minus przed wynikową odpowiedzią.

Aby wyraźnie zobaczyć, że mamy do czynienia z liczbami o różnych znakach, każdą liczbę wymierną ujęliśmy w nawiasy kwadratowe wraz z jej znakami

Moduł liczby jest równy , a moduł liczby jest równy . Mnożenie powstałych modułów jako ułamki dodatnie, otrzymaliśmy odpowiedź, ale przed odpowiedzią postawiliśmy minus, jak wymagała od nas zasada. Aby zapewnić ten minus przed odpowiedzią, w nawiasie wykonano mnożenie modułów, poprzedzone minusem.

Krótkie rozwiązanie wygląda następująco:

Przykład 2. Znajdź wartość wyrażenia

Przykład 3. Znajdź wartość wyrażenia

Jest to mnożenie ujemnych liczb wymiernych. Aby pomnożyć ujemne liczby wymierne, należy pomnożyć ich moduły i umieścić plus przed wynikową odpowiedzią

Rozwiązanie dla ten przykład można krótko napisać:

Przykład 4. Znajdź wartość wyrażenia

Rozwiązanie tego przykładu można krótko zapisać:

Przykład 5. Znajdź wartość wyrażenia

Jest to mnożenie liczb wymiernych o różnych znakach. Pomnóżmy moduły tych liczb i postawmy minus przed wynikową odpowiedzią

Krótkie rozwiązanie będzie wyglądać znacznie prościej:

Przykład 6. Znajdź wartość wyrażenia

Zamieńmy liczbę mieszaną na ułamek niewłaściwy. Przepiszmy resztę tak, jak jest

Otrzymaliśmy mnożenie liczb wymiernych o różnych znakach. Pomnóżmy moduły tych liczb i postawmy minus przed wynikową odpowiedzią. Wpis z modułami można pominąć, aby nie zaśmiecać wyrażenia

Rozwiązanie tego przykładu można krótko napisać

Przykład 7. Znajdź wartość wyrażenia

Jest to mnożenie liczb wymiernych o różnych znakach. Pomnóżmy moduły tych liczb i postawmy minus przed wynikową odpowiedzią

Początkowo odpowiedź okazała się ułamkiem niewłaściwym, ale podkreśliliśmy w niej całą część. zauważ to cała część został oddzielony od modułu frakcji. Otrzymaną liczbę mieszaną ujęto w nawiasy poprzedzone znakiem minus. Ma to na celu zapewnienie spełnienia wymogu reguły. A zasada wymagała, aby otrzymaną odpowiedź poprzedzić minusem.

Rozwiązanie tego przykładu można krótko zapisać:

Przykład 8. Znajdź wartość wyrażenia

Najpierw pomnóżmy i pomnóżmy wynikową liczbę przez pozostałą liczbę 5. Pomińmy wpis z modułami, żeby nie zaśmiecać wyrażenia.

Odpowiedź: wartość wyrażenia równa się -2.

Przykład 9. Znajdź znaczenie wyrażenia:

Przetłumaczmy liczby mieszane do ułamków niewłaściwych:

Otrzymaliśmy mnożenie ujemnych liczb wymiernych. Pomnóżmy moduły tych liczb i postawmy plus przed wynikową odpowiedzią. Wpis z modułami można pominąć, aby nie zaśmiecać wyrażenia

Przykład 10. Znajdź wartość wyrażenia

Wyrażenie składa się z kilku czynników. Według prawo kombinacyjne mnożenie, jeśli wyrażenie składa się z kilku czynników, wówczas iloczyn nie będzie zależał od kolejności operacji. To pozwala nam obliczyć to wyrażenie w dowolnej kolejności.

Nie wymyślajmy koła na nowo, ale obliczmy to wyrażenie od lewej do prawej, w kolejności czynników. Pomińmy wpis z modułami, żeby nie zaśmiecać wyrażenia

Trzecia akcja:

Czwarta akcja:

Odpowiedź: wartość wyrażenia wynosi

Przykład 11. Znajdź wartość wyrażenia

Pamiętajmy o prawie mnożenia przez zero. Prawo to stanowi, że iloczyn jest równy zeru, jeśli co najmniej jeden z czynników równy zeru.

W naszym przykładzie jeden z czynników jest równy zero, więc nie tracąc czasu odpowiadamy, że wartość wyrażenia jest równa zero:

Przykład 12. Znajdź wartość wyrażenia

Iloczyn jest równy zero, jeśli przynajmniej jeden z czynników jest równy zero.

W naszym przykładzie jeden z czynników jest równy zero, więc nie tracąc czasu odpowiadamy, że wartość wyrażenia równa się zeru:

Przykład 13. Znajdź wartość wyrażenia

Możesz zastosować kolejność działań i najpierw obliczyć wyrażenie w nawiasach, a wynikową odpowiedź pomnożyć przez ułamek.

Możesz także skorzystać z rozdzielnego prawa mnożenia - pomnóż każdy wyraz sumy przez ułamek i dodaj otrzymane wyniki. Będziemy korzystać z tej metody.

Zgodnie z kolejnością działań, jeśli wyrażenie zawiera dodawanie i mnożenie, najpierw należy wykonać mnożenie. Dlatego w powstałym nowym wyrażeniu umieśćmy w nawiasach te parametry, które należy pomnożyć. W ten sposób możemy wyraźnie zobaczyć, które działania wykonać wcześniej, a które później:

Trzecia akcja:

Odpowiedź: wartość wyrażenia równa się

Rozwiązanie tego przykładu można zapisać znacznie krócej. Będzie to wyglądać tak:

Oczywiste jest, że ten przykład można rozwiązać nawet w umyśle. Dlatego powinieneś rozwinąć umiejętność analizowania wyrażeń przed ich rozwiązaniem. Prawdopodobnie da się to rozwiązać mentalnie i zaoszczędzić mnóstwo czasu i nerwów. A na sprawdzianach i egzaminach, jak wiadomo, czas jest bardzo cenny.

Przykład 14. Znajdź wartość wyrażenia −4,2 × 3,2

Jest to mnożenie liczb wymiernych o różnych znakach. Pomnóżmy moduły tych liczb i postawmy minus przed wynikową odpowiedzią

Zwróć uwagę, jak pomnożono moduły liczb wymiernych. W tym przypadku do pomnożenia modułów liczb wymiernych potrzebne było .

Przykład 15. Znajdź wartość wyrażenia −0,15 × 4

Jest to mnożenie liczb wymiernych o różnych znakach. Pomnóżmy moduły tych liczb i postawmy minus przed wynikową odpowiedzią

Zwróć uwagę, jak pomnożono moduły liczb wymiernych. W tym przypadku, aby pomnożyć moduły liczb wymiernych, trzeba było to umieć.

Przykład 16. Znajdź wartość wyrażenia −4,2 × (−7,5)

Jest to mnożenie ujemnych liczb wymiernych. Pomnóżmy moduły tych liczb i postawmy plus przed wynikową odpowiedzią

Podział liczb wymiernych

Zasady dzielenia liczb całkowitych dotyczą także liczb wymiernych. Innymi słowy, aby móc dzielić liczby wymierne, trzeba to umieć

W przeciwnym razie stosuje się te same metody dzielenia ułamków zwykłych i dziesiętnych. Aby podzielić ułamek zwykły przez inny ułamek, należy pomnożyć pierwszy ułamek przez odwrotność drugiego ułamka.

I dzielić dziesiętny na inny ułamek dziesiętny, należy przesunąć przecinek w dzielnej i dzielniku w prawo o tyle cyfr, ile jest po przecinku w dzielniku, a następnie wykonać dzielenie jak zwykłą liczbę.

Przykład 1. Znajdź znaczenie wyrażenia:

Jest to dzielenie liczb wymiernych o różnych znakach. Aby obliczyć takie wyrażenie, należy pomnożyć pierwszy ułamek przez odwrotność drugiego.

Zatem pomnóżmy pierwszy ułamek przez odwrotność drugiego.

Otrzymaliśmy mnożenie liczb wymiernych o różnych znakach. Wiemy już, jak obliczyć takie wyrażenia. Aby to zrobić, musisz pomnożyć moduły tych liczb wymiernych i postawić minus przed wynikową odpowiedzią.

Dokończmy ten przykład do końca. Wpis z modułami można pominąć, aby nie zaśmiecać wyrażenia

Zatem wartość wyrażenia wynosi

Szczegółowe rozwiązanie wygląda następująco:

Krótkie rozwiązanie wyglądałoby tak:

Przykład 2. Znajdź wartość wyrażenia

Jest to dzielenie liczb wymiernych o różnych znakach. Aby obliczyć to wyrażenie, należy pomnożyć pierwszy ułamek przez odwrotność drugiego.

Odwrotnością drugiego ułamka jest ułamek . Pomnóżmy przez to pierwszy ułamek:

Krótkie rozwiązanie wyglądałoby tak:

Przykład 3. Znajdź wartość wyrażenia

Jest to dzielenie ujemnych liczb wymiernych. Aby obliczyć to wyrażenie, musisz ponownie pomnożyć pierwszy ułamek przez odwrotność drugiego.

Odwrotnością drugiego ułamka jest ułamek . Pomnóżmy przez to pierwszy ułamek:

Otrzymaliśmy mnożenie ujemnych liczb wymiernych. Jak to się oblicza podobne wyrażenie już wiemy. Musisz pomnożyć moduły liczb wymiernych i umieścić plus przed wynikową odpowiedzią.

Zakończmy ten przykład do końca. Możesz pominąć wpis z modułami, aby nie zaśmiecać wyrażenia:

Przykład 4. Znajdź wartość wyrażenia

Aby obliczyć to wyrażenie, musisz pomnożyć pierwszą liczbę −3 przez ułamek, ułamek odwrotny.

Odwrotnością ułamka jest ułamek . Pomnóż przez nią pierwszą liczbę −3

Przykład 6. Znajdź wartość wyrażenia

Aby obliczyć to wyrażenie, musisz pomnożyć pierwszy ułamek przez liczbę odwrotność liczby 4.

Odwrotnością liczby 4 jest ułamek. Pomnóż przez to pierwszy ułamek

Przykład 5. Znajdź wartość wyrażenia

Aby obliczyć to wyrażenie, należy pomnożyć pierwszy ułamek przez odwrotność −3

Odwrotność -3 jest ułamkiem. Pomnóżmy przez to pierwszy ułamek:

Przykład 6. Znajdź wartość wyrażenia -14,4: 1,8

Jest to dzielenie liczb wymiernych o różnych znakach. Aby obliczyć to wyrażenie, należy podzielić moduł dywidendy przez moduł dzielnika i postawić minus przed wynikową odpowiedzią.

Zwróć uwagę, jak moduł dzielnej został podzielony przez moduł dzielnika. W tym przypadku, żeby zrobić to poprawnie, trzeba było umieć.

Jeśli nie chcesz bawić się z ułamkami dziesiętnymi (a to się często zdarza), to przelicz te liczby mieszane na ułamki niewłaściwe, a następnie wykonaj dzielenie.

Obliczmy w ten sposób poprzednie wyrażenie −14,4: 1,8. Zamieńmy ułamki dziesiętne na liczby mieszane:

Zamieńmy teraz powstałe liczby mieszane na ułamki niewłaściwe:

Teraz możesz dzielić bezpośrednio, czyli dzielić ułamek przez ułamek. Aby to zrobić, musisz pomnożyć pierwszy ułamek przez odwrotny ułamek drugiego:

Przykład 7. Znajdź wartość wyrażenia

Zamieńmy ułamek dziesiętny −2,06 na ułamek niewłaściwy i pomnóżmy ten ułamek przez odwrotność drugiego ułamka:

Ułamki wielopiętrowe

Często można spotkać się z wyrażeniem, w którym dzielenie ułamków zapisuje się za pomocą linii ułamkowej. Na przykład wyrażenie można zapisać w następujący sposób:

Jaka jest różnica między wyrażeniami i ? Naprawdę nie ma różnicy. Te dwa wyrażenia mają to samo znaczenie i możemy postawić między nimi znak równości:

W pierwszym przypadku znakiem podziału jest dwukropek, a wyrażenie zapisywane jest w jednym wierszu. W drugim przypadku dzielenie ułamków zapisuje się za pomocą linii ułamkowej. Rezultatem jest ułamek, na który ludzie zgadzają się zadzwonić wielopiętrowy.

W przypadku takich wyrażeń wielopiętrowych należy zastosować te same zasady dzielenia ułamków zwykłych. Pierwszy ułamek należy pomnożyć przez odwrotność drugiego.

Użyj w roztworze podobne frakcje niezwykle niewygodne, dlatego można je zapisać w zrozumiałej formie, używając dwukropka zamiast ukośnika jako znaku podziału.

Na przykład napiszmy ułamek wielopiętrowy w zrozumiałej formie. Aby to zrobić, musisz najpierw dowiedzieć się, gdzie jest pierwszy ułamek, a gdzie drugi, ponieważ nie zawsze można to zrobić poprawnie. Ułamki wielopoziomowe mają kilka linii ułamkowych, które mogą być mylące. Główna linia ułamkowa oddzielająca pierwszy ułamek od drugiego jest zwykle dłuższa od pozostałych.

Po określeniu głównej linii ułamkowej możesz łatwo zrozumieć, gdzie jest pierwszy ułamek, a gdzie drugi:

Przykład 2.

Znajdujemy główną linię ułamkową (jest najdłuższa) i widzimy, że liczba całkowita −3 jest dzielona przez ułamek zwykły

A gdybyśmy za główną (tą krótszą) przyjęli błędnie drugą linię ułamkową, to okazałoby się, że dzielimy ułamek przez liczbę całkowitą 5. W tym przypadku, nawet jeśli to wyrażenie zostanie poprawnie obliczone, to problem zostanie rozwiązany niepoprawnie, ponieważ dywidenda w tym przypadku jest liczbą -3, a dzielnikiem jest ułamek .

Przykład 3. Zapiszmy ułamek wielopoziomowy w zrozumiałej formie

Znajdujemy główną linię ułamkową (jest najdłuższa) i widzimy, że ułamek jest dzielony przez liczbę całkowitą 2

A gdybyśmy za wiodącą (tą krótszą) przyjęli błędnie pierwszą linię ułamkową, to okazałoby się, że dzielimy liczbę całkowitą -5 przez ułamek.W tym przypadku, nawet jeśli to wyrażenie zostanie poprawnie obliczone, problem zostanie rozwiązany niepoprawnie, ponieważ dywidenda w tym przypadku ułamek wynosi , a dzielnik jest liczbą całkowitą 2.

Pomimo tego, że ułamki wielopoziomowe są niewygodne w obsłudze, spotkamy się z nimi bardzo często, szczególnie podczas studiowania matematyki wyższej.

Naturalnie, to wymaga Dodatkowy czas i miejsce. Dlatego możesz użyć więcej szybka metoda. Ta metoda jest wygodna, a wynik pozwala uzyskać gotowe wyrażenie, w którym pierwszy ułamek został już pomnożony przez odwrotność ułamka drugiego.

Ta metoda jest implementowana w następujący sposób:

Jeśli na przykład ułamek jest czteropiętrowy, numer znajdujący się na pierwszym piętrze zostaje podniesiony na najwyższe piętro. A figura znajdująca się na drugim piętrze zostaje podniesiona na trzecie piętro. Otrzymane liczby należy połączyć znakami mnożenia (×)

W rezultacie omijając zapis pośredni, otrzymujemy nowe wyrażenie, w którym pierwszy ułamek został już pomnożony przez odwrotność ułamka drugiego. Wygoda i tyle!

Aby uniknąć błędów podczas używania Ta metoda możesz kierować się następującą zasadą:

Od pierwszego do czwartego. Od drugiego do trzeciego.

W regule mówimy o o podłogach. Postać z pierwszego piętra należy przenieść na czwarte piętro. A figurę z drugiego piętra należy przenieść na trzecie piętro.

Spróbujmy obliczyć ułamek wielopiętrowy, korzystając z powyższej reguły.

Podnosimy więc numer znajdujący się na pierwszym piętrze na czwarte piętro i podnosimy numer znajdujący się na drugim piętrze na trzecie piętro

W rezultacie omijając zapis pośredni, otrzymujemy nowe wyrażenie, w którym pierwszy ułamek został już pomnożony przez odwrotność ułamka drugiego. Następnie możesz wykorzystać swoją istniejącą wiedzę:

Spróbujmy obliczyć ułamek wielopoziomowy, korzystając z nowego schematu.

Są tylko pierwsze, drugie i czwarte piętro. Nie ma trzeciego piętra. Ale nie odchodzimy od podstawowego schematu: podnosimy figurę z pierwszego piętra na czwarte piętro. A ponieważ nie ma trzeciego piętra, numer znajdujący się na drugim piętrze pozostawiamy bez zmian

W rezultacie, pomijając zapis pośredni, otrzymaliśmy nowe wyrażenie, w którym pierwsza liczba -3 została już pomnożona przez odwrotność ułamka drugiej. Następnie możesz wykorzystać swoją istniejącą wiedzę:

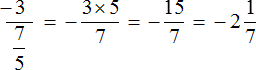
Spróbujmy obliczyć ułamek wielopiętrowy, korzystając z nowego schematu.

Są tylko drugie, trzecie i czwarte piętro. Nie ma pierwszego piętra. Ponieważ nie ma pierwszego piętra, nie ma co wchodzić na czwarte piętro, ale możemy podnieść figurę z drugiego piętra na trzecie:

W rezultacie, omijając zapis pośredni, otrzymaliśmy nowe wyrażenie, w którym pierwszy ułamek został już pomnożony przez odwrotność dzielnika. Następnie możesz wykorzystać swoją istniejącą wiedzę:

Używanie zmiennych

Jeśli wyrażenie jest złożone i wydaje Ci się, że będzie Cię to dezorientowało w procesie rozwiązywania problemu, wówczas część wyrażenia można umieścić w zmiennej i następnie pracować z tą zmienną.

Matematycy często to robią. Trudne zadanie podziel je na łatwiejsze podzadania i rozwiąż je. Następnie rozwiązane podzadania są zbierane w jedną całość. Ten proces twórczy a tego uczy się latami poprzez ciężki trening.

Użycie zmiennych jest uzasadnione w przypadku pracy z ułamkami wielopoziomowymi. Na przykład:

Znajdź wartość wyrażenia

Zatem w liczniku i mianowniku znajduje się wyrażenie ułamkowe wyrażenia ułamkowe. Innymi słowy, znów mamy do czynienia z ułamkiem wielopiętrowym, którego tak bardzo nie lubimy.

Wyrażenie w liczniku można wpisać do zmiennej o dowolnej nazwie, np.:

Jednak w matematyce w takim przypadku zwyczajowo nazywa się zmienne wielkimi literami łacińskimi. Nie łammy tej tradycji, a pierwsze wyrażenie oznaczmy dużą Litera łacińska A

A wyrażenie w mianowniku można oznaczyć wielką literą B

Teraz nasze oryginalne wyrażenie ma postać . Oznacza to, że dokonaliśmy wymiany wyrażenie numeryczne na literę, po uprzednim wpisaniu licznika i mianownika do zmiennych A i B.

Teraz możemy oddzielnie obliczyć wartość zmiennej A i wartość zmiennej B. Gotowe wartości wprowadzimy.

Znajdźmy wartość zmiennej A

Znajdźmy wartość zmiennej B

Podstawmy teraz ich wartości do wyrażenia głównego zamiast zmiennych A i B:

Otrzymaliśmy ułamek wielopiętrowy, w którym możemy zastosować schemat „od pierwszego do czwartego, od drugiego do trzeciego”, czyli podnieść numer znajdujący się na pierwszym piętrze na czwarte piętro i podnieść numer znajdujący się na drugim piętrze na trzecim piętrze. Dalsze obliczenia nie będą trudne:

Zatem wartość wyrażenia wynosi -1.

Oczywiście, że rozważaliśmy najprostszy przykład, ale naszym celem było nauczenie się, jak możemy używać zmiennych, aby sobie ułatwić i zminimalizować błędy.

Należy również zauważyć, że rozwiązanie tego przykładu można zapisać bez użycia zmiennych. To będzie wyglądać

To rozwiązanie jest szybsze i krótsze i w tym przypadku rozsądniej jest zapisać to w ten sposób, ale jeśli wyrażenie okaże się złożone, składające się z kilku parametrów, nawiasów, pierwiastków i potęg, wówczas wskazane jest obliczenie go w kilku etapach, wprowadzając część swoich wyrażeń do zmiennych.

Czy podobała Ci się lekcja?
Dołączć do naszego Nowa grupa VKontakte i zacznij otrzymywać powiadomienia o nowych lekcjach