ស្វែងរកដេរីវេនៃអនុគមន៍ត្រីកោណមាត្រ។ មេរៀនពិជគណិត និងការចាប់ផ្តើមនៃការវិភាគ "ដេរីវេនៃអនុគមន៍ត្រីកោណមាត្រ"

ដើម្បីស្វែងរក ដេរីវេនៃអនុគមន៍ត្រីកោណមាត្រ ត្រូវការប្រើ តារាងនៃនិស្សន្ទវត្ថុពោលគឺនិស្សន្ទវត្ថុ ៦-១៣។

នៅពេលអ្នករកឃើញ និស្សន្ទវត្ថុបឋម អនុគមន៍ត្រីកោណមាត្រ ដើម្បីជៀសវាងកំហុសទូទៅ អ្នកគួរតែយកចិត្តទុកដាក់លើចំណុចខាងក្រោម៖

• នៅក្នុងកន្សោមមុខងារ ពាក្យមួយក្នុងចំនោមពាក្យគឺជាញឹកញាប់ ស៊ីនុស កូស៊ីនុស ឬអនុគមន៍ត្រីកោណមាត្រផ្សេងទៀត។មិនមែនមកពីអាគុយម៉ង់នៃអនុគមន៍ទេ ប៉ុន្តែមកពីចំនួន (ថេរ) ដូច្នេះដេរីវេនៃពាក្យនេះគឺស្មើនឹងសូន្យ។
• ស្ទើរតែជានិច្ចកាល អ្នកត្រូវសម្រួលការបញ្ចេញមតិដែលទទួលបានជាលទ្ធផលនៃភាពខុសគ្នា ហើយសម្រាប់រឿងនេះ អ្នកត្រូវប្រើចំណេះដឹងនៃប្រតិបត្តិការដោយទំនុកចិត្តជាមួយប្រភាគ។
• ដើម្បីសម្រួលការបញ្ចេញមតិដែលអ្នកស្ទើរតែតែងតែត្រូវដឹង អត្តសញ្ញាណត្រីកោណមាត្រឧទាហរណ៍រូបមន្ត មុំទ្វេនិងរូបមន្តសម្រាប់ឯកភាពជាផលបូកនៃការ៉េនៃស៊ីនុស និងកូស៊ីនុស។

ឧទាហរណ៍ ១.ស្វែងរកដេរីវេនៃមុខងារ

ដំណោះស្រាយ។ ចូរនិយាយជាមួយ ដេរីវេនៃកូស៊ីនុសអ្វីគ្រប់យ៉ាងគឺច្បាស់លាស់ មនុស្សជាច្រើនដែលចាប់ផ្តើមសិក្សានិស្សន្ទវត្ថុនឹងនិយាយ។ អំពី​អ្វី ដេរីវេនៃស៊ីនុសដប់ពីរចែកដោយ pi? ចម្លើយ៖ រាប់ ស្មើនឹងសូន្យ! នៅទីនេះ ស៊ីនុស (មុខងារមួយបន្ទាប់ពីទាំងអស់!) គឺជាអន្ទាក់ ពីព្រោះអាគុយម៉ង់មិនមែនជាអថេរ X ឬអថេរផ្សេងទៀតទេ ប៉ុន្តែគ្រាន់តែជាលេខប៉ុណ្ណោះ។ នោះគឺស៊ីនុសនៃលេខនេះក៏ជាលេខផងដែរ។ ហើយដេរីវេនៃលេខ (ថេរ) ដូចដែលយើងដឹងពីតារាងនៃនិស្សន្ទវត្ថុគឺស្មើនឹងសូន្យ។ ដូច្នេះ យើងទុកតែស៊ីនុសដកនៃ X ហើយស្វែងរកដេរីវេរបស់វា ដោយមិនភ្លេចអំពីសញ្ញា៖

.

ឧទាហរណ៍ ២.ស្វែងរកដេរីវេនៃមុខងារ

.

ដំណោះស្រាយ។ ពាក្យ​ទីពីរ​គឺ​ជា​ករណី​ដូច​គ្នា​នឹង​ពាក្យ​ទី​មួយ​ក្នុង​ឧទាហរណ៍​មុន។ នោះគឺវាជាលេខ ហើយដេរីវេនៃលេខគឺសូន្យ។ យើងរកឃើញដេរីវេនៃពាក្យទីពីរជាដេរីវេនៃកូតា៖

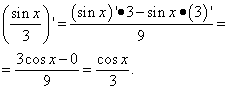
ឧទាហរណ៍ ៣.ស្វែងរកដេរីវេនៃមុខងារ

ដំណោះស្រាយ។ នេះគឺជាបញ្ហាមួយទៀត៖ នៅទីនេះក្នុងពាក្យទីមួយមិនមាន arcsine ឬអនុគមន៍ត្រីកោណមាត្រផ្សេងទៀតទេ ប៉ុន្តែមាន x ដែលមានន័យថាវាជាអនុគមន៍ x ។ ដូច្នេះ យើងបែងចែកវាជាពាក្យក្នុងផលបូកនៃមុខងារ៖

នៅទីនេះ ជំនាញក្នុងប្រតិបត្តិការជាមួយប្រភាគត្រូវបានទាមទារ ពោលគឺក្នុងការលុបបំបាត់រចនាសម្ព័ន្ធបីជាន់នៃប្រភាគ។

ឧទាហរណ៍ 4 ។ស្វែងរកដេរីវេនៃមុខងារ

.

ដំណោះស្រាយ។ នៅទីនេះអក្សរ "phi" ដើរតួនាទីដូចគ្នានឹង "x" នៅក្នុងករណីមុន (និងភាគច្រើនផ្សេងទៀតប៉ុន្តែមិនមែនទាំងអស់) - អថេរឯករាជ្យ។ ដូច្នេះហើយ នៅពេលយើងស្វែងរកដេរីវេនៃផលិតផលនៃមុខងារ យើងនឹងមិនប្រញាប់ប្រញាល់ប្រកាសពីដេរីវេនៃឫសនៃ "phi" ស្មើនឹងសូន្យនោះទេ។ ដូច្នេះ៖

ប៉ុន្តែដំណោះស្រាយមិនបញ្ចប់នៅទីនោះទេ។ ដោយសារពាក្យស្រដៀងគ្នាត្រូវបានប្រមូលក្នុងតង្កៀបពីរ យើងនៅតែតម្រូវឱ្យបំប្លែង (សម្រួល) កន្សោម។ ដូច្នេះ យើងគុណតង្កៀបដោយកត្តានៅពីក្រោយពួកវា ហើយបន្ទាប់មកយើងនាំយកលក្ខខណ្ឌទៅជាភាគបែងរួម ហើយអនុវត្តការបំប្លែងបឋមផ្សេងទៀត៖

ឧទាហរណ៍ 5 ។ស្វែងរកដេរីវេនៃមុខងារ

ដំណោះស្រាយ។ ក្នុងឧទាហរណ៍នេះ យើងនឹងត្រូវដឹងពីការពិតដែលថាមានអនុគមន៍ត្រីកោណមាត្របែបនេះ - សេកាន - និងរូបមន្តរបស់វាតាមរយៈកូស៊ីនុស។ ចូរយើងបែងចែក៖

ឧទាហរណ៍ ៦.ស្វែងរកដេរីវេនៃមុខងារ

.

ដំណោះស្រាយ។ ក្នុងឧទាហរណ៍នេះ យើងនឹងតម្រូវឱ្យចងចាំរូបមន្តមុំទ្វេពីសាលា។ ប៉ុន្តែ​ជា​ដំបូង​យើង​កំណត់​ភាព​ខុស​គ្នា​:

,

(នេះជារូបមន្តមុំទ្វេ)

ពីវគ្គសិក្សានៃធរណីមាត្រ និងគណិតវិទ្យា សិស្សសាលាត្រូវបានទម្លាប់ធ្វើការកត់សំគាល់លើការពិតដែលថាគំនិតនៃដេរីវេមួយត្រូវបានបញ្ជូនទៅពួកគេតាមរយៈផ្ទៃនៃតួលេខ ឌីផេរ៉ង់ស្យែល ដែនកំណត់នៃមុខងារ ក៏ដូចជាដែនកំណត់។ ចូរយើងព្យាយាមមើលគោលគំនិតនៃដេរីវេពីមុំផ្សេងគ្នា ហើយកំណត់ពីរបៀបដែលអនុគមន៍ដេរីវេទីវ និងត្រីកោណមាត្រអាចភ្ជាប់គ្នាបាន។

ដូច្នេះ សូម​យើង​ពិចារណា​ខ្សែ​កោង​តាម​អំពើ​ចិត្ត​មួយ​ចំនួន​ដែល​ត្រូវ​បាន​ពិពណ៌នា​ដោយ​អនុគមន៍​អរូបី y = f(x) ។

ចូរយើងស្រមៃថាកាលវិភាគគឺជាផែនទីនៃផ្លូវទេសចរណ៍។ ការកើនឡើង ∆x (ដីសណ្ត x) ក្នុងរូបគឺជាចម្ងាយជាក់លាក់នៃផ្លូវ ហើយ ∆y គឺជាការផ្លាស់ប្តូរកម្ពស់ផ្លូវខាងលើកម្រិតទឹកសមុទ្រ។
បន្ទាប់មកវាបង្ហាញថាសមាមាត្រ ∆x/∆y នឹងកំណត់លក្ខណៈស្មុគស្មាញនៃផ្លូវនៅលើផ្នែកនីមួយៗនៃផ្លូវ។ ដោយបានសិក្សាពីតម្លៃនេះ អ្នកអាចនិយាយដោយទំនុកចិត្តថាតើការឡើង/ចុះគឺចោត ឬយ៉ាងណា ថាតើអ្នកនឹងត្រូវការឧបករណ៍សម្រាប់ឡើងភ្នំ និងថាតើអ្នកទេសចរត្រូវការជាក់លាក់ដែរឬទេ។ ការបណ្តុះបណ្តាលរាងកាយ. ប៉ុន្តែសូចនាករនេះនឹងមានសុពលភាពសម្រាប់តែមួយប៉ុណ្ណោះ។ គម្លាតតូច∆x

ប្រសិនបើអ្នករៀបចំដំណើរកម្សាន្តយកតម្លៃសម្រាប់ដំបូងនិង ចំណុចបញ្ចប់ផ្លូវ នោះគឺ ∆x – នឹងជា ស្មើនឹងប្រវែងផ្លូវ វានឹងមិនអាចទទួលបានទិន្នន័យគោលបំណងអំពីកម្រិតនៃការលំបាកនៃការធ្វើដំណើរនោះទេ។ ដូច្នេះហើយ ចាំបាច់ត្រូវសាងសង់ក្រាហ្វមួយទៀតដែលនឹងកំណត់លក្ខណៈល្បឿន និង "គុណភាព" នៃការផ្លាស់ប្តូរក្នុងផ្លូវ ឬម្យ៉ាងទៀត កំណត់សមាមាត្រ ∆x/∆y សម្រាប់ "ម៉ែត្រ" នីមួយៗនៃផ្លូវ។

ក្រាហ្វនេះនឹងក្លាយជាដេរីវេដែលមើលឃើញសម្រាប់ផ្លូវជាក់លាក់មួយ ហើយនឹងពណ៌នាអំពីការផ្លាស់ប្តូររបស់វានៅចន្លោះចំណាប់អារម្មណ៍នីមួយៗ។ វាងាយស្រួលណាស់ក្នុងការផ្ទៀងផ្ទាត់នេះ តម្លៃ ∆x/∆y គឺគ្មានអ្វីក្រៅពីឌីផេរ៉ង់ស្យែលដែលបានយកនោះទេ។ អត្ថន័យជាក់លាក់ x និង y ។ អនុញ្ញាតឱ្យយើងអនុវត្តភាពខុសគ្នាមិនមែនចំពោះកូអរដោនេជាក់លាក់ទេ ប៉ុន្តែចំពោះមុខងារទាំងមូល៖

អនុគមន៍ដេរីវេ និងត្រីកោណមាត្រ

អនុគមន៍​ត្រីកោណមាត្រ​ត្រូវ​បាន​ភ្ជាប់​ដោយ​និស្សន្ទវត្ថុ។ នេះអាចយល់បានពីគំនូរខាងក្រោម។ នៅលើរូបភាព អ័ក្សសំរបសំរួលមុខងារ Y = f (x) ត្រូវបានបង្ហាញ - ខ្សែកោងពណ៌ខៀវ។

K (x0; f (x0)) - ចំណុចបំពាន, x0 + ∆x គឺជាចំនួនបន្ថែមតាមអ័ក្ស OX ហើយ f (x0 + ∆x) គឺជាការកើនឡើងតាមអ័ក្ស OY នៅចំណុចជាក់លាក់ L ។

ចូរគូរបន្ទាត់ត្រង់កាត់ចំនុច K និង L ហើយសង់ ត្រីកោណកែង KLN ប្រសិនបើអ្នករំកិលផ្នែក LN ទៅតាមក្រាហ្វ Y = f (x) នោះចំនុច L និង N នឹងមានទំនោរទៅរកតម្លៃ K (x0; f (x0)) ។ ចូរហៅចំណុចនេះថាការចាប់ផ្តើមតាមលក្ខខណ្ឌនៃក្រាហ្វ - ដែនកំណត់ ប្រសិនបើមុខងារគឺគ្មានកំណត់ យ៉ាងហោចណាស់នៅចន្លោះពេលណាមួយ ទំនោរនេះក៏នឹងគ្មានដែនកំណត់ ហើយតម្លៃកំណត់របស់វាគឺជិតដល់ 0 ។

ធម្មជាតិនៃទំនោរនេះអាចត្រូវបានពិពណ៌នាដោយតង់សង់ទៅចំណុចដែលបានជ្រើសរើស y = kx + b ឬដោយក្រាហ្វនៃដេរីវេនៃអនុគមន៍ដើម dy - បន្ទាត់ត្រង់ពណ៌បៃតង។

ប៉ុន្តែតើត្រីកោណមាត្រនៅទីនេះនៅឯណា? អ្វីគ្រប់យ៉ាងគឺសាមញ្ញណាស់, ពិចារណាត្រីកោណខាងស្តាំ KLN ។ តម្លៃឌីផេរ៉ង់ស្យែលសម្រាប់ចំណុចជាក់លាក់ K គឺជាតង់សង់នៃមុំ α ឬ ∠K៖

តាមវិធីនេះ យើងអាចពិពណ៌នាអំពីអត្ថន័យធរណីមាត្រនៃដេរីវេ និងទំនាក់ទំនងរបស់វាជាមួយនឹងអនុគមន៍ត្រីកោណមាត្រ។

រូបមន្តដេរីវេសម្រាប់អនុគមន៍ត្រីកោណមាត្រ

ការបំប្លែងស៊ីនុស កូស៊ីនុស តង់ហ្សង់ និងកូតង់សង់ នៅពេលកំណត់និស្សន្ទវត្ថុត្រូវតែទន្ទេញចាំ។

រូបមន្តពីរចុងក្រោយមិនមែនជាកំហុសទេ ចំនុចនោះគឺថាមានភាពខុសគ្នារវាងការកំណត់ដេរីវេនៃអាគុយម៉ង់សាមញ្ញ និងមុខងារក្នុងសមត្ថភាពដូចគ្នា។

ចូរយើងពិចារណា តារាងប្រៀបធៀបជាមួយនឹងរូបមន្តសម្រាប់ដេរីវេនៃ sinus, cosine, tangent និង cotangent៖

រូបមន្តក៏ត្រូវបានយកមកសម្រាប់ដេរីវេនៃ arcsine, arccosine, arctangent និង arccotangent ទោះបីជាពួកវាត្រូវបានគេប្រើកម្រណាស់៖

វាគួរឱ្យកត់សម្គាល់ថារូបមន្តខាងលើគឺច្បាស់ណាស់មិនគ្រប់គ្រាន់សម្រាប់ដំណោះស្រាយដែលទទួលបានជោគជ័យនោះទេ។ ភារកិច្ចធម្មតា។ការប្រឡងរដ្ឋបង្រួបបង្រួម, អ្វីដែលនឹងត្រូវបានបង្ហាញនៅពេលដោះស្រាយ ឧទាហរណ៍ជាក់ស្តែងស្វែងរកដេរីវេនៃកន្សោមត្រីកោណមាត្រ។

លំហាត់ប្រាណ៖ ចាំបាច់ត្រូវស្វែងរកដេរីវេនៃអនុគមន៍ និងស្វែងរកតម្លៃរបស់វាសម្រាប់ π/4៖

ដំណោះស្រាយ៖ ដើម្បីស្វែងរក y' វាចាំបាច់ក្នុងការរំលឹកឡើងវិញនូវរូបមន្តមូលដ្ឋានសម្រាប់បំប្លែងអនុគមន៍ដើមទៅជាដេរីវេ ពោលគឺ។

ប្រធានបទ៖"ដេរីវេនៃអនុគមន៍ត្រីកោណមាត្រ"។
ប្រភេទមេរៀន- មេរៀនក្នុងការបង្រួបបង្រួមចំណេះដឹង។
ទម្រង់មេរៀន- មេរៀនរួមបញ្ចូលគ្នា។
ទីកន្លែងនៃមេរៀននៅក្នុងប្រព័ន្ធមេរៀនសម្រាប់ផ្នែកនេះ។- មេរៀនទូទៅ។
គោលដៅត្រូវបានកំណត់យ៉ាងទូលំទូលាយ៖

• អប់រំ៖ដឹងពីច្បាប់នៃភាពខុសគ្នា អាចអនុវត្តច្បាប់សម្រាប់គណនានិស្សន្ទវត្ថុនៅពេលដោះស្រាយសមីការ និងវិសមភាព។ កែលម្អមុខវិជ្ជា រួមទាំងការគណនា ជំនាញ និងសមត្ថភាព។ ជំនាញ​កុំព្យូទ័រ;
• អភិវឌ្ឍន៍៖ការអភិវឌ្ឍជំនាញបញ្ញា និងតក្កវិជ្ជា និងផលប្រយោជន៍នៃការយល់ដឹង;
• អប់រំ៖បណ្តុះការសម្របខ្លួនទៅនឹង លក្ខខណ្ឌទំនើបការបណ្តុះបណ្តាល។

វិធីសាស្រ្ត៖

• បន្តពូជនិងផលិតភាព;
• ជាក់ស្តែងនិងពាក្យសំដី;
• ការងារឯករាជ្យ;
• ការរៀនតាមកម្មវិធី T.S.O.;
• ការរួមបញ្ចូលគ្នានៃផ្នែកខាងមុខ, ក្រុមនិង ការងារបុគ្គល;
• ការរៀនសូត្រខុសគ្នា;
• អាំងឌុចទិត-ដក។

ទម្រង់នៃការគ្រប់គ្រង៖

• ការស្ទង់មតិផ្ទាល់មាត់,
• ការគ្រប់គ្រងកម្មវិធី,
• ការងារឯករាជ្យ,
• កិច្ចការបុគ្គលលើ​កុំ​ព្យូ​រ​ទ័​រ,
• ការពិនិត្យដោយមិត្តភ័ក្តិដោយប្រើកាតវិនិច្ឆ័យរបស់សិស្ស។

ក្នុងអំឡុងពេលថ្នាក់

ខ្ញុំ ពេលវេលារៀបចំ

II. ការធ្វើបច្ចុប្បន្នភាពចំណេះដឹងយោង

ក) ទំនាក់ទំនងគោលដៅ និងគោលបំណង៖

• ដឹងពីច្បាប់នៃភាពខុសគ្នា អាចអនុវត្តច្បាប់សម្រាប់គណនានិស្សន្ទវត្ថុនៅពេលដោះស្រាយបញ្ហា សមីការ និងវិសមភាព។
• កែលម្អមុខវិជ្ជា រួមទាំងការគណនា ជំនាញ និងសមត្ថភាព។ ជំនាញ​កុំព្យូទ័រ;
• អភិវឌ្ឍជំនាញបញ្ញា និងតក្កវិជ្ជា និង ផលប្រយោជន៍ការយល់ដឹង;
• បណ្តុះការសម្របខ្លួនទៅនឹងលក្ខខណ្ឌសិក្សាទំនើប។

ខ) ពាក្យដដែលៗនៃសម្ភារៈអប់រំ

ច្បាប់សម្រាប់គណនានិស្សន្ទវត្ថុ (ពាក្យដដែលៗនៃរូបមន្តនៅលើកុំព្យូទ័រដែលមានសំឡេង)។ ឯកសារ ៧.

1. តើអ្វីជាដេរីវេនៃស៊ីនុស?
2. តើអ្វីជាដេរីវេនៃកូស៊ីនុស?
3. តើអ្វីជាដេរីវេនៃតង់សង់?
4. តើអ្វីជាដេរីវេនៃកូតង់សង់?

III. ការងារមាត់

ស្វែងរកដេរីវេ។
ជម្រើសទី 1 ។		ជម្រើសទី 2 ។
នៅ = 2X + 5.		នៅ = 2X – 5.
នៅ= 4 កូស X.		នៅ= ៣ បាប X.
នៅ= tg X+ctg X.		នៅ= tg X-ctg X.
នៅ= បាប ៣ X.		នៅ= cos 4 X.
ជម្រើសចម្លើយ។
	– ៤ បាប X		- ៣ កូស X
1/cos 2 X+ ១/ បាប ២ X	1/cos 2 X– ១/ បាប ២ X	១/ បាប ២ X-1/cos 2 X
	– បាប ៤ X		- ៣ កូស ៣ X

ប្តូរសៀវភៅកត់ត្រា។ នៅក្នុងកាតវិនិច្ឆ័យ សម្គាល់កិច្ចការដែលបានបញ្ចប់ដោយត្រឹមត្រូវដោយប្រើសញ្ញា + ហើយកិច្ចការដែលបានបញ្ចប់មិនត្រឹមត្រូវដោយសញ្ញា – ។

IV. ការដោះស្រាយសមីការដោយប្រើដេរីវេ

- តើធ្វើដូចម្តេចដើម្បីរកចំណុចដែលដេរីវេគឺសូន្យ?

ដើម្បីស្វែងរកចំណុចដែលដេរីវេ មុខងារនេះ។ស្មើនឹងសូន្យ អ្នកត្រូវការ៖

- កំណត់លក្ខណៈនៃមុខងារ
- ស្វែងរកតំបន់ និយមន័យមុខងារ,
- ស្វែងរកដេរីវេនៃមុខងារនេះ
- ដោះស្រាយសមីការ f "(x) = 0,
- ជ្រើសរើស​ចម្លើយ​ដែល​ត្រឹមត្រូវ។

កិច្ចការ 1 ។

បានផ្តល់ឱ្យ៖ នៅ = X- អំពើបាប x.
ស្វែងរក៖ចំណុចដែលនិស្សន្ទវត្ថុគឺសូន្យ។
ដំណោះស្រាយ។អនុគមន៍ត្រូវបានកំណត់ និងអាចខុសគ្នានៅលើសំណុំនៃចំនួនពិតទាំងអស់ ចាប់តាំងពីអនុគមន៍ត្រូវបានកំណត់ និងអាចខុសគ្នានៅលើសំណុំនៃចំនួនពិតទាំងអស់ g(x) = xនិង t(x) = - អំពើបាប x.
ដោយប្រើច្បាប់នៃភាពខុសគ្នាយើងទទួលបាន f "(x) = (x- អំពើបាប x)" = (x)" - (អំពើបាប x)" = 1 – cos x.
ប្រសិនបើ f "(x) = 0 បន្ទាប់មក 1 – cos x = 0.
cos x= 1/; ចូរយើងកម្ចាត់ភាពមិនសមហេតុផលនៅក្នុងភាគបែង យើងទទួលបាន cos x = /2.
យោងតាមរូបមន្ត t= ± arccos ក+ 2n, n Z យើងទទួលបាន៖ X= ± arccos /2 + 2n, n Z ។
ចម្លើយ៖ x = ± /4 + 2n, n Z ។

V. ការដោះស្រាយសមីការដោយប្រើក្បួនដោះស្រាយ

ស្វែងរកចំណុចណាដែលនិស្សន្ទវត្ថុបាត់។

f(x) = បាប x+ កូស x

f(x) = បាប ២ x – x

f(x) = 2x+cos(4 x – )

សិស្ស​អាច​ជ្រើសរើស​ឧទាហរណ៍​ណា​មួយ​ក្នុង​ចំណោម​ឧទាហរណ៍​បី។ ឧទាហរណ៍ទីមួយត្រូវបានវាយតម្លៃ " 3 ", ទីពីរ -" 4 ", ទីបី -" 5 " ដំណោះស្រាយក្នុងសៀវភៅកត់ត្រា អមដោយការត្រួតពិនិត្យគ្នាទៅវិញទៅមក។ សិស្សម្នាក់សម្រេចចិត្តនៅក្រុមប្រឹក្សាភិបាល។ ប្រសិនបើដំណោះស្រាយប្រែទៅជាមិនត្រឹមត្រូវ នោះសិស្សត្រូវត្រឡប់ទៅរកក្បួនដោះស្រាយ ហើយព្យាយាមដោះស្រាយម្តងទៀត។

ការគ្រប់គ្រងតាមកម្មវិធី។

ជម្រើសទី 1		ជម្រើសទី 2
y = 2X 3		y = 3X 2
y = 1/4 X 4 + 2X 2 – 7		y = 1/2 X 4 + 4X + 5
y = X 3 + 4X 2 – 3X. ដោះស្រាយសមីការ y " = 0		y = 2X 3 – 9X 2 + 12X + 7. ដោះស្រាយសមីការ y " = 0.
y= បាប ២ X– ខូស ៣ X.		y= cos 2 X- បាប ៣ X.
y= tg X-ctg( X + /4).		y=ctg X+ tg( X – /4).
y= បាប ២ X.		y= cos 2 X.
ជម្រើសចម្លើយ។
នៅពេលទាញយករូបមន្តដំបូងនៃតារាង យើងនឹងបន្តពីនិយមន័យនៃអនុគមន៍ដេរីវេនៅចំណុចមួយ។ តោះទៅណា x- ណាមួយ។ ចំនួនពិតនោះគឺ x- លេខណាមួយពីដែននៃនិយមន័យនៃអនុគមន៍។ អនុញ្ញាតឱ្យយើងសរសេរដែនកំណត់នៃសមាមាត្រនៃការកើនឡើងនៃអនុគមន៍ទៅនឹងការកើនឡើងនៃអាគុយម៉ង់នៅ: វាគួរតែត្រូវបានកត់សម្គាល់ថានៅក្រោមសញ្ញាកំណត់កន្សោមត្រូវបានទទួលដែលមិនមែនជាភាពមិនច្បាស់លាស់នៃសូន្យដែលបែងចែកដោយសូន្យចាប់តាំងពីភាគយកមិនមានតម្លៃមិនកំណត់ប៉ុន្តែពិតប្រាកដសូន្យ។ ម្យ៉ាងវិញទៀត ការបង្កើនមុខងារថេរគឺតែងតែសូន្យ។ ដូច្នេះ ដេរីវេនៃមុខងារថេរគឺស្មើនឹងសូន្យទូទាំងដែនទាំងមូលនៃនិយមន័យ. ដេរីវេនៃមុខងារថាមពល។ រូបមន្តដេរីវេ មុខងារថាមពលមើល​ទៅ​ដូច​ជា ដែលជាកន្លែងដែលនិទស្សន្ត ទំ- ចំនួនពិតណាមួយ។ ទីមួយ ចូរយើងបង្ហាញរូបមន្តសម្រាប់និទស្សន្តធម្មជាតិ នោះគឺសម្រាប់ p = 1, 2, 3, … យើងនឹងប្រើនិយមន័យនៃដេរីវេ។ អនុញ្ញាតឱ្យយើងសរសេរដែនកំណត់នៃសមាមាត្រនៃការកើនឡើងនៃអនុគមន៍ថាមពលមួយទៅនឹងការកើនឡើងនៃអាគុយម៉ង់: ដើម្បី​សម្រួល​កន្សោម​ក្នុង​លេខ​ភាគ យើង​ងាក​ទៅ​រូបមន្ត​លេខ​ពីរ​របស់​ញូតុន៖ អាស្រ័យហេតុនេះ នេះបង្ហាញពីរូបមន្តសម្រាប់ដេរីវេនៃអនុគមន៍ថាមពលសម្រាប់និទស្សន្តធម្មជាតិ។ ដេរីវេនៃអនុគមន៍អិចស្ប៉ូណង់ស្យែល។ យើង​បង្ហាញ​ពី​ការ​បង្កើត​រូបមន្ត​ដេរីវេ​ដោយ​ផ្អែក​លើ​និយមន័យ៖ យើងបានមកដល់ភាពមិនប្រាកដប្រជា។ ដើម្បីពង្រីកវា យើងណែនាំអថេរថ្មី ហើយនៅ . បន្ទាប់មក។ នៅក្នុងការផ្លាស់ប្តូរចុងក្រោយ យើងបានប្រើរូបមន្តសម្រាប់ការផ្លាស់ប្តូរទៅមូលដ្ឋានលោការីតថ្មី។ ចូរជំនួសដែនកំណត់ដើម៖ ប្រសិនបើយើងរំលឹកឡើងវិញនូវដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរ យើងមកដល់រូបមន្តសម្រាប់ដេរីវេនៃអនុគមន៍អិចស្ប៉ូណង់ស្យែល៖ ដេរីវេនៃអនុគមន៍លោការីត។ ចូរយើងបង្ហាញរូបមន្តសម្រាប់ដេរីវេនៃអនុគមន៍លោការីតសម្រាប់ទាំងអស់គ្នា xពីដែននៃនិយមន័យ និងតម្លៃត្រឹមត្រូវទាំងអស់នៃមូលដ្ឋាន កលោការីត តាមនិយមន័យនៃដេរីវេយើងមានៈ ដូចដែលអ្នកបានកត់សម្គាល់ ក្នុងអំឡុងពេលភស្តុតាង ការបំប្លែងត្រូវបានអនុវត្តដោយប្រើលក្ខណៈសម្បត្តិនៃលោការីត។ សមភាព គឺពិតដោយសារតែដែនកំណត់គួរឱ្យកត់សម្គាល់ទីពីរ។ ដេរីវេនៃអនុគមន៍ត្រីកោណមាត្រ។ ដើម្បីទាញយករូបមន្តសម្រាប់ដេរីវេនៃអនុគមន៍ត្រីកោណមាត្រ យើងនឹងត្រូវរំលឹកឡើងវិញនូវរូបមន្តត្រីកោណមាត្រមួយចំនួន ក៏ដូចជាដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង។ តាមនិយមន័យនៃដេរីវេសម្រាប់មុខងារស៊ីនុសដែលយើងមាន . ចូរយើងប្រើភាពខុសគ្នានៃរូបមន្តស៊ីនុស៖ វានៅសល់ដើម្បីងាកទៅរកដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង: ដូច្នេះ ដេរីវេនៃមុខងារ sin xមាន cos x. រូបមន្ត​សម្រាប់​ដេរីវេនៃ​កូស៊ីនុស​ត្រូវ​បាន​បង្ហាញ​ឱ្យ​ឃើញ​តាម​វិធី​ដូច​គ្នា។ ដូច្នេះ ដេរីវេនៃមុខងារ cos xមាន - sin x. យើងនឹងទាញយករូបមន្តសម្រាប់តារាងនៃនិស្សន្ទវត្ថុសម្រាប់តង់សង់ និងកូតង់សង់ ដោយប្រើប្រាស់ច្បាប់នៃភាពខុសគ្នាដែលបានបញ្ជាក់ (ដេរីវេនៃប្រភាគ)។ ដេរីវេនៃអនុគមន៍អ៊ីពែរបូល។ ច្បាប់នៃភាពខុសគ្នា និងរូបមន្តសម្រាប់ដេរីវេនៃអនុគមន៍អិចស្ប៉ូណង់ស្យែលពីតារាងនៃដេរីវេទីវ័រអនុញ្ញាតឱ្យយើងទាញយករូបមន្តសម្រាប់ដេរីវេនៃស៊ីនុស កូស៊ីនុស តង់ហ្សង់ និងអ៊ីពែបូលិក។ ដេរីវេនៃមុខងារបញ្ច្រាស។ ដើម្បីជៀសវាងការភាន់ច្រលំកំឡុងពេលធ្វើបទបង្ហាញ សូមបញ្ជាក់នៅក្នុង subscript នូវអាគុយម៉ង់នៃអនុគមន៍ដែលភាពខុសគ្នាត្រូវបានអនុវត្ត នោះគឺជាដេរីវេនៃអនុគមន៍ f(x)ដោយ x. ឥឡូវ​យើង​បង្កើត​ឡើង ច្បាប់សម្រាប់ការស្វែងរកដេរីវេ មុខងារបញ្ច្រាស. អនុញ្ញាតឱ្យមុខងារ y = f(x)និង x = g(y)បញ្ច្រាសទៅវិញទៅមក កំណត់នៅលើចន្លោះពេល និងរៀងៗខ្លួន។ ប្រសិនបើនៅចំណុចមួយមានដេរីវេមិនសូន្យនៃអនុគមន៍ f(x)បន្ទាប់មកនៅចំណុចមានដេរីវេកំណត់នៃអនុគមន៍ច្រាស g(y), និង . នៅក្នុងប្រកាសមួយទៀត . ច្បាប់នេះអាចត្រូវបានកែទម្រង់សម្រាប់ណាមួយ។ xពីចន្លោះពេលបន្ទាប់មកយើងទទួលបាន . តោះពិនិត្យមើលសុពលភាពនៃរូបមន្តទាំងនេះ។ ចូរយើងស្វែងរកអនុគមន៍បញ្ច្រាសសម្រាប់លោការីតធម្មជាតិ (នៅទីនេះ yគឺជាមុខងារ និង x- អាគុយម៉ង់) ។ ដោយបានដោះស្រាយសមីការនេះសម្រាប់ xយើងទទួលបាន (នៅទីនេះ xគឺជាមុខងារ និង y- អំណះអំណាងរបស់នាង) ។ នោះគឺ និងមុខងារបញ្ច្រាសទៅវិញទៅមក។ ពីតារាងនៃនិស្សន្ទវត្ថុយើងឃើញនោះ។ និង . ចូរប្រាកដថារូបមន្តសម្រាប់ការស្វែងរកដេរីវេនៃអនុគមន៍បញ្ច្រាសនាំយើងទៅរកលទ្ធផលដូចគ្នា៖ ដេរីវេនៃអនុគមន៍ត្រីកោណមាត្រច្រាស និងដេរីវេនៃរូបមន្តរបស់ពួកគេត្រូវបានបង្ហាញ។ កន្សោមសម្រាប់និស្សន្ទវត្ថុលំដាប់ខ្ពស់ជាងក៏ត្រូវបានផ្តល់ឱ្យផងដែរ។ តំណភ្ជាប់ទៅទំព័រដែលមានច្រើនទៀត សេចក្តីថ្លែងការណ៍លម្អិតរូបមន្តលទ្ធផល។ ដំបូងយើងទាញយករូបមន្តសម្រាប់ដេរីវេនៃ Arcsine ។ អនុញ្ញាតឱ្យ y= arcsin x. ចាប់តាំងពី arcsine គឺជាមុខងារបញ្ច្រាសនៃស៊ីនុស . នៅទីនេះ y គឺជាមុខងារនៃ x ។ បែងចែកដោយគោរពតាមអថេរ x៖ . យើងដាក់ពាក្យ៖ . ដូច្នេះយើងបានរកឃើញ៖ . ដោយសារតែបន្ទាប់មក។ បន្ទាប់មក . ហើយរូបមន្តមុនយកទម្រង់៖ . ពី​ទីនេះ . តាមវិធីនេះ អ្នកអាចទទួលបានរូបមន្តសម្រាប់ដេរីវេនៃកូស៊ីនុសធ្នូ។ ទោះយ៉ាងណាក៏ដោយ វាកាន់តែងាយស្រួលប្រើរូបមន្តដែលទាក់ទងនឹងអនុគមន៍ត្រីកោណមាត្របញ្ច្រាស៖ . បន្ទាប់មក . ការពិពណ៌នាលម្អិតបន្ថែមទៀតត្រូវបានបង្ហាញនៅលើទំព័រ "ការទាញយកនៃដេរីវេនៃ arcsine និង arccosine" ។ នៅទីនោះវាត្រូវបានផ្តល់ឱ្យ ដេរីវេនៃដេរីវេតាមពីរវិធី- បានពិភាក្សាខាងលើ និងយោងតាមរូបមន្តសម្រាប់ដេរីវេនៃអនុគមន៍បញ្ច្រាស។ ដេរីវេនៃដេរីវេនៃ arctangent និង arccotangent ដូចគ្នានេះដែរ យើងនឹងរកឃើញដេរីវេនៃ arctangent និង arccotangent។ អនុញ្ញាតឱ្យ y= អាកតាន x. Arctangent គឺជាមុខងារបញ្ច្រាសនៃតង់សង់៖ . បែងចែកដោយគោរពតាមអថេរ x៖ . យើងអនុវត្តរូបមន្តសម្រាប់ដេរីវេនៃមុខងារស្មុគស្មាញ៖ . ដូច្នេះយើងបានរកឃើញ៖ . ដេរីវេនៃកូតង់សង់ធ្នូ៖ . និស្សន្ទវត្ថុ Arcsine អនុញ្ញាតឱ្យ . យើង​បាន​រក​ឃើញ​និស្សន្ទវត្ថុ​លំដាប់​ទី​មួយ​នៃ​អាកស៊ីន​រួច​ហើយ៖ . តាមរយៈការបែងចែក យើងរកឃើញដេរីវេនៃលំដាប់ទីពីរ៖ ; . វាក៏អាចត្រូវបានសរសេរក្នុងទម្រង់ដូចខាងក្រោមៈ . ពីទីនេះយើងទទួលបាន សមីការឌីផេរ៉ង់ស្យែលដែលត្រូវបានពេញចិត្តដោយដេរីវេនៃ Arcsine នៃការបញ្ជាទិញទីមួយ និងទីពីរ៖ . តាមរយៈភាពខុសគ្នានៃសមីការនេះ យើងអាចរកឃើញនិស្សន្ទវត្ថុលំដាប់ខ្ពស់ជាង។ ដេរីវេនៃ arcsine នៃលំដាប់ទី n ដេរីវេនៃ arcsine នៃលំដាប់ n មាន ទិដ្ឋភាពបន្ទាប់: , តើពហុនាមនៃសញ្ញាបត្រនៅឯណា។ វាត្រូវបានកំណត់ដោយរូបមន្ត៖ ; . នៅទីនេះ ពហុធា បំពេញសមីការឌីផេរ៉ង់ស្យែល៖ . ដេរីវេនៃ arccosine នៃលំដាប់ទី n និស្សន្ទវត្ថុ​សម្រាប់​កូស៊ីនុស​ធ្នូ គឺ​ទទួល​បាន​ពី​ដេរីវេ​សម្រាប់​ស៊ីនុស​ធ្នូ ដោយ​ប្រើ​រូបមន្ត​ត្រីកោណមាត្រ៖ . ដូច្នេះ ដេរីវេនៃមុខងារទាំងនេះខុសគ្នាតែក្នុងសញ្ញាប៉ុណ្ណោះ៖ . ដេរីវេនៃអាកតង់សង់ អនុញ្ញាតឱ្យ។ . យើងបានរកឃើញដេរីវេនៃកូតង់សង់ធ្នូនៃលំដាប់ទីមួយ៖ . ចូរបំបែកប្រភាគទៅជាទម្រង់សាមញ្ញបំផុតរបស់វា៖ នេះគឺជាឯកតាស្រមើលស្រមៃ។ . យើងបែងចែកម្តង ហើយយកប្រភាគទៅជាភាគបែងធម្មតា៖ . ការជំនួសយើងទទួលបាន៖ ដេរីវេនៃ Arctangent នៃលំដាប់ទី n ; . ដូច្នេះ ដេរីវេនៃ Arctangent លំដាប់ទី 3 អាចត្រូវបានតំណាងតាមវិធីជាច្រើន៖ ដេរីវេនៃកូតង់សង់ធ្នូ . សូមឱ្យវាក្លាយជាឥឡូវនេះ។ តោះអនុវត្តរូបមន្តតភ្ជាប់អនុគមន៍ត្រីកោណមាត្របញ្ច្រាស៖ . បន្ទាប់មក ដេរីវេនៃតង់សង់ធ្នូ ខុសគ្នាតែក្នុងសញ្ញាពីដេរីវេនៃតង់សង់ធ្នូប៉ុណ្ណោះ៖ . ការជំនួសយើងរកឃើញ៖ ឯកសារយោង៖ N.M. Gunter, R.O. Kuzmin, ការប្រមូលបញ្ហានៅលើគណិតវិទ្យាខ្ពស់ជាង