Неопределеният интеграл на функцията f x се нарича. Математика

Първопроизводна функция и неопределен интеграл

Факт 1. Интегрирането е действие, обратно на диференцирането, а именно възстановяване на функция от известната производна на тази функция. Така функцията се възстановява Е(х) се нарича антипроизводноза функция f(х).

Определение 1. Функция Е(х f(х) на някакъв интервал X, ако за всички стойности хот този интервал равенството е в сила Е "(х)=f(х), т.е тази функция f(х) е производно на противопроизводна функция Е(х). .

Например функцията Е(х) = грях х е антипроизводна на функцията f(х) = cos х на цялата числова линия, тъй като за всяка стойност на x (грях х)" = (cos х) .

Определение 2. Неопределен интеграл на функция f(х) е множеството от всички свои първоизводни. В този случай се използва нотацията

∫

f(х)dx

къде е табелата ∫ наречен интегрален знак, функцията f(х) – интегрална функция, и f(х)dx – интегранд израз.

По този начин, ако Е(х) – някакво противопроизводно за f(х), Това

∫

f(х)dx = Е(х) +В

Къде В - произволна константа (константа).

За да се разбере значението на множеството от първоизводни на функция като неопределен интеграл, е подходяща следната аналогия. Нека има врата (традиционна дървена врата). Неговата функция е да „бъде врата“. От какво е направена вратата? Изработена от дърво. Това означава, че наборът от първоизводни на интегранта на функцията „да бъде врата“, тоест нейният неопределен интеграл, е функцията „да бъде дърво + C“, където C е константа, която в този контекст може означават например вида дърво. Точно както една врата е направена от дърво с помощта на някои инструменти, производна на функция е „направена“ от антипроизводна функция с помощта на формули, които научихме, докато изучавахме производната .

След това таблицата на функциите на общите обекти и съответните им антипроизводни („да бъде врата“ - „да бъде дърво“, „да бъде лъжица“ - „да бъде метал“ и т.н.) е подобна на таблицата на основните неопределени интеграли, които ще бъдат дадени по-долу. Таблицата с неопределени интеграли изброява общи функции, посочвайки антипроизводните, от които тези функции са „направени“. В част от задачите за намиране на неопределен интеграл са дадени интегранти, които могат да се интегрират директно без много усилия, тоест с помощта на таблицата на неопределените интеграли. При по-сложни задачи интегралната функция трябва първо да се трансформира, за да могат да се използват таблични интеграли.

Факт 2. Когато възстановяваме функция като антипроизводна, трябва да вземем предвид произволна константа (константа) В, и за да не пишете списък от първоизводни с различни константи от 1 до безкрайност, трябва да напишете набор от първоизводни с произволна константа В, например така: 5 х³+C. И така, произволна константа (константа) е включена в израза на антипроизводното, тъй като антипроизводното може да бъде функция, например 5 х³+4 или 5 х³+3 и когато се диференцира, 4 или 3, или всяка друга константа отива на нула.

Нека поставим проблема за интегриране: за тази функция f(х) намери такава функция Е(х), чиято производнаравно на f(х).

Пример 1.Намерете множеството от първоизводни на функция

Решение. За тази функция антипроизводната е функцията

функция Е(х) се нарича първоизводна за функцията f(х), ако производната Е(х) е равно на f(х), или, което е същото, диференциал Е(х) е равно f(х) dx, т.е.

(2)

Следователно функцията е антипроизводна на функцията. Това обаче не е единственото антипроизводно на . Те също служат като функции

Къде СЪС– произволна константа. Това може да се провери чрез диференциране.

По този начин, ако има една антипроизводна за функция, тогава за нея има безкрайно множествоантипроизводни, които се различават с постоянен член. Всички първоизводни за функция се записват в горната форма. Това следва от следната теорема.

Теорема (официално изложение на факт 2).Ако Е(х) – първоизводна за функцията f(х) на някакъв интервал X, след това всяка друга антипроизводна за f(х) на същия интервал могат да бъдат представени във формата Е(х) + В, Къде СЪС– произволна константа.

В следващия пример се обръщаме към таблицата с интеграли, която ще бъде дадена в параграф 3, след свойствата на неопределения интеграл. Правим това преди да прочетем цялата таблица, за да е ясна същността на горното. И след таблицата и свойствата ще ги използваме изцяло по време на интеграцията.

Пример 2.Намерете набори от първоизводни функции:

Решение. Ние намираме набори от антипроизводни функции, от които тези функции са „направени“. Когато споменавате формули от таблицата на интегралите, засега просто приемете, че има такива формули там, а самата таблица на неопределените интеграли ще проучим малко по-нататък.

1) Прилагайки формула (7) от таблицата на интегралите за п= 3, получаваме

2) Използвайки формула (10) от таблицата на интегралите за п= 1/3, имаме

3) Тъй като

след това съгласно формула (7) с п= -1/4 намираме

Не самата функция е записана под знака интеграл f, и неговото произведение от диференциала dx. Това се прави основно, за да се посочи по коя променлива се търси антипроизводната. например,

, ;

тук и в двата случая подинтегралната функция е равна на , но нейните неопределени интеграли в разглежданите случаи се оказват различни. В първия случай тази функция се разглежда като функция на променливата х, а във втория - като функция на z .

Процесът на намиране на неопределен интеграл на функция се нарича интегриране на тази функция.

Геометричен смисъл на неопределения интеграл

Да предположим, че трябва да намерим крива y=F(x)и вече знаем, че тангенсът на ъгъла на наклона на допирателната във всяка точка е дадена функция f(x)абсцисата на тази точка.

Според геометричен смисълпроизводна, тангенс на допирателния ъгъл в дадена точка на кривата y=F(x)равна на стойността на производната F"(x). Така че трябва да намерим такава функция F(x), за което F"(x)=f(x). Функция, необходима в задачата F(x)е антипроизводно на f(x). Условията на задачата се удовлетворяват не от една крива, а от семейство криви. y=F(x)- една от тези криви и всяка друга крива може да бъде получена от нея паралелен трансферпо оста Ой.

Нека наречем графиката на първоизводната функция на f(x)интегрална крива. Ако F"(x)=f(x), след това графиката на функцията y=F(x)има интегрална крива.

Факт 3. Неопределеният интеграл е геометрично представен от семейството на всички интегрални криви , както е на снимката по-долу. Разстоянието на всяка крива от началото на координатите се определя от произволна константа на интегриране В.

Свойства на неопределения интеграл

Факт 4. Теорема 1. Производната на неопределен интеграл е равна на интегранта, а неговият диференциал е равен на интегранта.

Факт 5. Теорема 2. Неопределен интеграл от диференциала на функция f(х) равно на функция f(х) до постоянен срок , т.е.

(3)

Теореми 1 и 2 показват, че диференцирането и интегрирането са взаимно обратни операции.

Факт 6. Теорема 3. Постоянен множителв интегралната функция може да се извади като знак на неопределения интеграл , т.е.

1. Антипроизводно. Неопределен интеграл. Свойства на неопределения интеграл. Таблица на интегралите. Замяна на променливи. Интеграция по части.

Определение.Извиква се функцията F(x). антипроизводноот функцията f(x) върху отсечката, ако във всички точки на тази отсечка е изпълнено равенството F`(x) = f(x).

(-cos x )` = sin x

(1 -cos x)` = sin x

Функция f(x) непрекъсната функцияна сегмента.

Теорема . Ако функция F 1 (x) b F2 (x) -две първоизводни на функцията f(x) върху отсечката , то разликата между тях е равна на постоянно число.

доказателство

Е 1`(x)= f(x) (1)

Е 2`(x)= f(x), тогава F 1`(x)- Ф 2`(x)= Конст.

φ(x) = F 1 - Ф 2

φ`(x) = F 1 ` -Ф 2 ` = 0

Тези. да отбележим:

Е 1 (x)-F 2 (x) = φ(x) (2)

Тогава въз основа на равенства (1) ще бъде:

Е 1`(x)- Ф 2 ` (x) = f(x) - f(x) = 0 или φ` (x) = ` = 0 за всяка стойност на x в сегмента. Но от равенството φ` (x) = 0 следва, че φ(x) е константа.

Наистина, нека приложим теоремата на Лагранж към функцията φ(x), която очевидно е непрекъсната и диференцируема на интервала. Каквато и да е точката x на сегмента, ние имаме по силата на теоремата на Лагранж.

φ (x) - φ (a) = φ` (x) (x-a), където a< x< х.

Тъй като φ` (x) = 0, тогава φ (x) - φ (a) = 0 или φ (x) = φ (a) (3)

По този начин функцията φ(x) във всяка точка x от сегмента запазва стойностите на φ(a), което означава, че функцията φ(x) е постоянна на сегмента. Означавайки константата φ(a) с C, от равенства (2), (3) получаваме:

Е 1 (x)-F 2 (x) = C

Определение.Ако функцията F (x) е антипроизводна за f (x), тогава изразът F (x) + C се нарича неопределен интегрална функцията f (x) и се означава със символа ∫ f (x) dx. Така, по дефиниция,

∫ f (x) dx = F (x) + C, Ако F(x) = f(x).

В този случай се извиква функцията f (x). интегрална функция, f (x) dx - интегрант, знак ∫ - интегрален знак.

От това определение следват следните свойства:
1. Производната на неопределения интеграл е равна на интегранта, т.е. Ако F`(x) = f(x), тогава и

(∫f (x) dx)` = (F (x) + C)` = f (x) (4)

Последното равенство трябва да се приеме в смисъл, че производната на всяка първоизводна е равна на интегранта.

2. Диференциалът на неопределения интеграл е равен на интегранта

d (∫ f (x) dx) = f (x) dx (5)

Това се получава въз основа на формула (4)

3. Неопределеният интеграл на диференциала на някаква функция е равен на тази функция плюс произволна константа

∫ dF (x) = F (x) + C

Валидността на последното равенство може лесно да се провери чрез диференциране (диференциалите на двете страни на равенството са равни на dFx)

Таблица на неопределените интеграли.

10.

11.

12.

13.

14.

Линейни свойства.

Интегрирането е линейна операция.

1. ∫ dx =∫ f 1(x)dx+∫ f 2(x)dx

∫ a f (x) dx = a ∫ f (x) dx

∫ f (x) dx = F (x) + C

2. ∫ f (x+c) dx = F (x+c) + C

3. Заместване. 1-ви начин за изчисляване на неопределени интеграли.

x = φ (t), тогава ∫ f (φ (t)) φ` (t) dt = F (x) + C = ∫ f (x) dx

x = φ (t) dx dt = φ`

Интеграция по части.

Нека uИ v- две диференцируеми функции на x. Тогава, както е известно, диференциалът на продукта uv изчислено от:

следната формула

d(uv) = udv + vdu

От тук, интегрирайки, получаваме:∫uv =∫udv+

vdu∫или∫udv+

udv = uv - Последната формула се наричаформула за интегриране по части. Тази формула най-често се прилага заинтегриране на изрази∫ , което може да бъде представено като произведение на два фактора u и dv, така че функцията v да може да бъде намерена от нейния диференциал dv и интегралът да може да бъде изчислен∫ v du заедно представляват задача, по-проста от директното изчисляване на интеграла

u dv. ∫Пример. x sin x dx = ∫∫ - x cos x +

cos x dx = -x cos x + sin x + C защото = v, uдв dx = sin x И = dx, vду

= - cos x. Е(х) + СЪС за функция f(хНамирането на неопределен интеграл (набор от антипроизводни или „антипроизводни“) означава реконструиране на функция от известната производна на тази функция. Възстановен набор от антипроизводни В) отчита константата на интегриране . По скорост на движениематериална точка

Намирането на неопределен интеграл изисква сравнително малък брой основни формули за интегриране. Но процесът на намирането му е много по-труден от простото прилагане на тези формули. Цялата сложност не е свързана с интегрирането, а с привеждането на интегрируемия израз във форма, която прави възможно намирането на неопределения интеграл с помощта на основните формули, споменати по-горе. Това означава, че за да започнете практиката на интеграция, трябва да активирате това, което сте научили гимназияумения за трансформация на израза.

Ще се научим да намираме интеграли с помощта на свойства и таблица на неопределените интегралиот урок за основните понятия на тази тема (отваря се в нов прозорец).

Има няколко метода за намиране на интеграла, от които метод за заместване на променливиИ метод на интегриране по части- задължителен джентълменски комплект за всички успешно преминали висша математика. Въпреки това е по-полезно и приятно да започнете да усвоявате интегрирането с помощта на метода на разширение, базиран на следните две теореми за свойствата на неопределения интеграл, които повтаряме тук за удобство.

Теорема 3.Постоянният множител в интегранта може да бъде изваден от знака на неопределения интеграл, т.е.

Теорема 4.Неопределен интеграл на алгебрична сума крайно числофункциите са равни алгебрична суманеопределени интеграли на тези функции, т.е.

(2)

В допълнение, следното правило може да бъде полезно при интегрирането: ако изразът на интегранта съдържа постоянен множител, тогава изразът на антипроизводното се умножава по обратния на постоянния множител, т.е.

(3)

Тъй като този урок е въведение в решаването на интеграционни проблеми, важно е да се отбележат две неща, които или вече начален етап, или малко по-късно може да ви изненадат. Изненадата се дължи на факта, че интегрирането е обратна операция на диференцирането и неопределеният интеграл с право може да се нарече „антипроизводна“.

Първото нещо, от което не трябва да се изненадвате при интегрирането.В таблицата на интегралите има формули, които нямат аналози сред производните таблични формули . Това са следните формули:

Можете обаче да се уверите, че производните на изразите от дясната страна на тези формули съвпадат със съответните интегранти.

Второто нещо, което не трябва да бъде изненадващо при интегрирането. Въпреки че производната на всяка елементарна функция също е елементарна функция, вече не са неопределени интеграли на някои елементарни функции елементарни функции . Примери за такива интеграли могат да бъдат следните:

За развиване на техники за интегриране ще бъдат полезни следните умения: намаляване на дроби, деление на полином в числителя на дроб на моном в знаменателя (за получаване на сумата от неопределени интеграли), преобразуване на корени в степени, умножение на моном по a полином, повдигане на степен. Тези умения са необходими за преобразуване на интегралната функция, което трябва да доведе до сумата от интегралите, присъстващи в таблицата с интеграли.

Намиране на неопределени интеграли заедно

Пример 1.Намерете неопределения интеграл

Решение. Виждаме в знаменателя на интегранта полином, в който х е на квадрат. Това е почти сигурен знак, че можете да приложите табличен интеграл 21 (с арктангенс като резултат). Изваждаме множител-две от знаменателя (има такова свойство на интеграла - постоянният множител може да бъде изнесен отвъд знака на интеграла; споменато е по-горе като теорема 3). Резултатът от всичко това:

Сега знаменателят е сумата от квадрати, което означава, че можем да приложим споменатия табличен интеграл. Накрая получаваме отговора:

Пример 2.Намерете неопределения интеграл

Решение. Отново прилагаме теорема 3 - свойството на интеграла, въз основа на което постоянният множител може да бъде изваден от знака на интеграла:

Прилагаме формула 7 от таблицата на интегралите (променлива на степен) към функцията интегранд:

Редуцираме получените дроби и имаме крайния отговор:

Пример 3.Намерете неопределения интеграл

Решение. Прилагайки първо теорема 4 и след това теорема 3 за свойствата, намираме този интеграл като сбор от три интеграла:

И трите получени интеграла са таблични. Използваме формула (7) от таблицата на интегралите за п = 1/2, п= 2 и п= 1/5 и след това

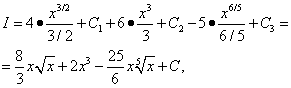
комбинира и трите произволни константи, които са въведени, когато намиране на триинтеграли. Следователно в подобни ситуации трябва да се въведе само една произволна интеграционна константа.

Пример 4.Намерете неопределения интеграл

Решение. Когато знаменателят на интегранта съдържа моном, можем да разделим числителя на знаменателя член по член. Първоначалният интеграл се превърна в сбор от два интеграла:

За да приложим табличния интеграл, трансформираме корените в степени и ето окончателния отговор:

Продължаваме да намираме неопределени интеграли заедно

Пример 7.Намерете неопределения интеграл

Решение. Ако преобразуваме интегралната функция чрез повдигане на квадрат на бинома и разделяне на числителя на знаменателя член по член, тогава първоначалният интеграл става сбор от три интеграла.

Възможно ли е да се включи нелинейна функция под диференциалния знак? Да, ако подинтегралната функция е произведение на два фактора: единият фактор е комплексна функция на някаква нелинейна функция, а другият фактор е производната на тази нелинейна функция. Нека разгледаме казаното с примери.

Намерете неопределени интеграли.

Пример 1. ∫(2x + 1)(x 2 + x + 2) 5 dx = ∫(x 2 + x + 2) 5 d (x 2 + x + 2) =(x²+x+2) 6 : 6 + С.

Какво представлява този интегранд? работа степенна функцияот (x 2 + x + 2) и множителя (2x + 1), който е равен на производната на основата на степента: (x 2 + x + 2)" = 2x + 1.

Това ни позволи да поставим (2x + 1) под диференциалния знак:

∫u 5 du=u 6 : 6+ С. (Формула 1). )

преглед. (F (x)+ C)" =((x²+x+2) 6 : 6 + C)′=1/6 6 (x 2 + x + 2) 5 (x 2 + x + 2)" =

=(x 2 + x + 2) 5 · (2x + 1) = (2x + 1)(x 2 + x + 2) 5 = f (x).

Пример 2.∫(3x 2 – 2x + 3)(x 3 - x 2 + 3x + 1) 5 dx = ∫(x 3 – x 2 + 3x + 1) 5 d (x 3 – x 2 + 3x + 1) =

=(x³- x²+3x+1) 6 : 6+С

И как този пример се различава от пример 1? Нищо! Същата пета степен с основата (x 3 – x 2 + 3x + 1) се умножава по тричлена (3x 2 – 2x + 3), който е производната на основата на степента: (x 3 – x 2 + 3x + 1)" = 3x 2 – 2x + 3. Поставихме тази основа на степента под диференциалния знак, от който стойността на интегранта не се промени, и след това приложихме същата формула 1 (). Интеграли)

Пример 3.

Тук производната на (2x 3 – 3x) ще даде (6x 2 – 3), а при нас

има (12x 2 – 6), тоест изразът в 2 пъти по-голямо, което означава, че поставяме (2x 3 – 3x) под диференциалния знак и поставяме фактор пред интеграла 2 . Нека приложим формулата 2) (лист ).

Ето какво се случва:

Нека проверим, като вземем предвид, че:

Примери. Намерете неопределени интеграли.

1. ∫(6x+5) 3 dx. Как ще решим? Гледане на листа и ние разсъждаваме нещо подобно: интегралната функция представлява степен и имаме формула за интеграла на степента (формула 1) ), но в него основата на степента защото= sin x интеграционна променливасъщото u.

И имаме интегрираща променлива X, и основата на степента (6x+5). Нека направим промяна в променливата за интегриране: вместо dx пишем d (6x+5). Какво се промени? Тъй като това, което идва след диференциалния знак d, по подразбиране е диференцирано,

тогава d (6x+5)=6dx, т.е. при замяната на променливата x с променливата (6x+5), функцията интегранд се увеличи 6 пъти, така че поставихме фактора 1/6 пред знака за интеграл. Тези аргументи могат да бъдат записани така:

И така, решихме този пример, като въведохме нова променлива (променливата x беше заменена с променливата 6x+5). Къде записахте новата променлива (6x+5)? Под диференциалния знак. Ето защо, този методчесто се нарича въвеждане на нова променлива метод (или начин ) обобщаване(нова променлива ) под диференциалния знак.

Във втория пример първо получихме степен с отрицателен показател, и след това го постави под знака за разлика (7x-2) и използва формулата за интеграл на степента 1) (Интеграли ).

Нека да разгледаме примерното решение 3.

Интегралът се предшества от коефициент 1/5. защо Тъй като d (5x-2) = 5dx, тогава чрез заместване на функцията u = 5x-2 под диференциалния знак, ние увеличихме интегранта с 5 пъти, следователно, така че стойността даден изразне се е променило - трябваше да се раздели на 5, т.е. умножете по 1/5. След това беше използвана формулата 2) (интеграли) .

Всички най-прости интегрални формули ще изглеждат така:

∫f (x) dx=F (x)+Cи трябва да е спазено равенството:

(F (x)+C)"=f (x).

Формулите за интегриране могат да бъдат получени чрез обръщане на съответните формули за диференциране.

наистина

експонента пможе да бъде дробна. Често трябва да намерите неопределения интеграл на функцията y=√x. Нека изчислим интеграла на функцията f (x)=√x с помощта на формулата 1) .

Нека напишем този пример като формула 2) .

Тъй като (x+C)"=1, тогава ∫dx=x+C.

3) ∫dx=x+C.

Заменяйки 1/x² с x -2, изчисляваме интеграла от 1/x².

Можете ли да получите този отговор, като се свържете известна формуладиференциация:

Нека напишем нашето разсъждение под формата на формула 4).

Умножавайки двете страни на полученото равенство по 2, получаваме формулата 5).

Да намерим интегралите на главните тригонометрични функции, знаейки техните производни: (sinx)"=cosx; (cosx)"=-sinx; (tgx)"=1/cos²x; (ctgx)"=-1/sin²x. Получаваме формулите за интегриране 6) — 9).

6) ∫cosxdx=sinx+C;

7) ∫sinxdx=-cosx+C;

След изучаване на демонстративните и логаритмични функции, нека добавим още няколко формули.

Основни свойства на неопределения интеграл.

азПроизводната на неопределения интеграл е равна на интегранта .

(∫f (x) dx)"=f (x).

II.Диференциалът на неопределения интеграл е равен на интегранта.

d∫f (x) dx=f (x) dx.

III. Неопределен интегралот диференциала (производната) на някаква функция равно на сумататази функция и произволна константа C.

∫dF (x)=F (x)+Cили ∫F"(x) dx=F (x)+C.

Моля, обърнете внимание: в I, II и III имотизнаците на диференциала и интеграла (интеграл и диференциал) се “изяждат” взаимно!

IV.Постоянният множител на подинтегралната функция може да бъде изваден от интегралния знак.

∫kf (x) dx=k ∫f (x) dx,Къде к - постоянен, не е равно на нула.

V.Интегралът на алгебрична сума от функции е равен на алгебричната сума на интегралите на тези функции.

∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx.

VI.Ако F (x) е антипроизводна на f (x), и к= sin x bса постоянни стойности и к≠0, тогава (1/k)·F (kx+b) е първоизводна за f (kx+b). Наистина, според правилото за изчисляване на производната сложна функцияимаме:

Можете да напишете:

За всички математическа операцияима обратен ефект. За действието диференциране (намиране на производни на функции) също има обратно действие— интеграция. Чрез интегриране функцията се намира (реконструира) от дадената й производна или диференциал. Намерената функция се извиква антипроизводно.

Определение.Диференцируема функция F(x)се нарича първоизводна на функцията f(x)на даден интервал, ако за всички Xот този интервал е в сила следното равенство: F′(x)=f (x).

Примери. Намерете първоизводни за функциите: 1) f (x)=2x; 2) f (x)=3cos3x.

1) Тъй като (x²)′=2x, тогава по дефиниция функцията F (x)=x² ще бъде антипроизводна на функцията f (x)=2x.

2) (sin3x)′=3cos3x. Ако означим f (x)=3cos3x и F (x)=sin3x, тогава по дефиниция на антипроизводна имаме: F′(x)=f (x) и следователно F (x)=sin3x е антипроизводно за f ( x)=3cos3x.

Имайте предвид, че (sin3x +5 )′= 3cos3x, и (sin3x -8,2 )′= 3cos3x, ... В общ изгледможе да се напише: (sin3x +C)′= 3cos3x, Къде СЪС- някаква постоянна стойност. Тези примери показват неяснотата на действието на интегриране, за разлика от действието на диференциране, когато всяка диференцируема функция има една производна.

Определение.Ако функцията F(x)е антипроизводна на функцията f(x)на определен интервал, тогава наборът от всички антипроизводни на тази функция има формата:

F(x)+C, където C е всяко реално число.

Множеството от всички първоизводни F (x) + C на функцията f (x) на разглеждания интервал се нарича неопределен интеграл и се обозначава със символа ∫ (интегрален знак). Запишете: ∫f (x) dx=F (x)+C.

Изразяване ∫f(x)dxпрочетете: „интеграл ef от x до de x.“

f(x)dx- интегрален израз,

f(x)- интегрална функция,

Xе интеграционната променлива.

F(x)- първоизводна на функция f(x),

СЪС- някаква постоянна стойност.

Сега разгледаните примери могат да бъдат записани по следния начин:

1) ∫ 2xdx=x²+C. 2) ∫ 3cos3xdx=sin3x+C.

Какво означава знакът d?

г—диференциален знак - има двойна цел: първо, този знак разделя интегранта от интегралната променлива; второ, всичко, което идва след този знак, се диференцира по подразбиране и се умножава по интегранта.

Примери. Намерете интегралите: 3) ∫ 2pxdx; 4) ∫ 2pxdp.

3) След диференциалната икона dразходи XX, А r

∫ 2хрdx=рх²+С. Сравнете с примера 1).

Да направим проверка. F′(x)=(px²+C)′=p·(x²)′+C′=p·2x=2px=f (x).

4) След диференциалната икона dразходи r. Това означава, че интеграционната променлива r, и множителя Xтрябва да се счита за някаква постоянна стойност.

∫ 2хрдр=р²х+С. Сравнете с примери 1) И 3).

Да направим проверка. F′(p)=(p²x+C)′=x·(p²)′+C′=x·2p=2px=f (p).

Страница 1 от 1 1

Интегрално смятане.

Антипроизводна функция.

определение: Извиква се функцията F(x). противопроизводна функцияфункция f(x) върху сегмента, ако равенството е вярно във всяка точка на този сегмент:

Трябва да се отбележи, че може да има безкрайно много антипроизводни за една и съща функция. Те ще се различават един от друг с някакво постоянно число.

F 1 (x) = F 2 (x) + C.

Неопределен интеграл.

определение: Неопределен интеграл functionf(x) е набор от първоизводни функции, които са определени от релацията:

Запишете:

Условието за съществуването на неопределен интеграл върху определен сегмент е непрекъснатостта на функцията върху този сегмент.

Свойства:

Пример:

Намирането на стойността на неопределения интеграл е свързано главно с намирането на първоизводната на функцията. За някои функции това е доста трудна задача. По-долу ще разгледаме методите за намиране на неопределени интеграли за основните класове функции - рационални, ирационални, тригонометрични, експоненциални и др.

За удобство стойностите на неопределените интеграли на повечето елементарни функции се събират в специални таблици с интеграли, които понякога са доста обемни. Те включват различни често използвани комбинации от функции. Но повечето от формулите, представени в тези таблици, са следствия една от друга, така че по-долу представяме таблица с основни интеграли, с помощта на които можете да получите стойностите на неопределени интеграли на различни функции.

Интеграл	Значение	Интеграл	Значение

	lnsinx+ C



	вътре

Интеграционни методи.

Нека разгледаме три основни метода на интеграция.

Директна интеграция.

Методът на пряка интеграция се основава на предположението, че възможно значениеантипроизводна функция с допълнителна проверка на тази стойност чрез диференциране. Като цяло отбелязваме, че диференциацията е мощен инструмент за проверка на резултатите от интеграцията.

Нека да разгледаме приложението на този метод, използвайки пример:

Трябва да намерим стойността на интеграла . Въз основа на добре познатата формула за диференциация
можем да заключим, че търсеният интеграл е равен на
, където C е някакво постоянно число. Въпреки това, от друга страна
. Така най-накрая можем да заключим:

Обърнете внимание, че за разлика от диференциацията, където са използвани ясни техники и методи за намиране на производната, правила за намиране на производната и накрая дефиницията на производната, такива методи не са достъпни за интегриране. Ако при намирането на производната използвахме, така да се каже, конструктивни методи, които въз основа на определени правила доведоха до резултата, тогава при намирането на първоизводната трябва да разчитаме главно на познаването на таблици с производни и първоизводни.

Що се отнася до метода на директна интеграция, той е приложим само за някои много ограничени класове функции. Има много малко функции, за които веднага можете да намерите антипроизводно. Ето защо в повечето случаи се използват описаните по-долу методи.

Метод на заместване (заместване на променливи).

Теорема: Ако трябва да намерите интеграла
, но е трудно да се намери първоизводната, тогава с помощта на замяната x =  (t) и dx =  (t) dt се оказва:

Доказателство : Нека разграничим предложеното равенство:

Съгласно свойство № 2 на неопределения интеграл, разгледан по-горе:

f(х) dx = f[  (t)]  (t) дт

което, като се има предвид въведеното означение, е изходното предположение. Теоремата е доказана.

u dv.Намерете неопределения интеграл
.

Да направим замяна t = sinx, дт = cosxdt.

u dv.

Замяна
Получаваме:

По-долу ще разгледаме други примери за използване на метода на заместване за различни видове функции.

Интеграция по части.

Методът се основава на добре известната формула за производна на продукт:

(uv)=uv+vu

където uиv са някои функции на x.

В диференциална форма: d(uv) =udv+vdu

Интегрирайки, получаваме:
, и в съответствие с горните свойства на неопределения интеграл:

или
;

Получихме формула за интегриране по части, която ни позволява да намерим интегралите на много елементарни функции.

u dv.

Както можете да видите, последователното прилагане на формулата за интегриране по части ви позволява постепенно да опростите функцията и да доведете интеграла до табличен.

u dv.

Вижда се, че в резултат на многократно прилагане на интегриране по части, функцията не може да бъде опростена до таблична форма. Последният получен интеграл обаче не се различава от оригиналния. Затова го преместваме в лявата страна на равенството.

По този начин интегралът беше намерен без изобщо да се използват таблици с интеграли.

Преди да разгледаме подробно методите за интегриране на различни класове функции, ние даваме още няколко примера за намиране на неопределени интеграли чрез свеждането им до таблични.

u dv.

Интегриране на елементарни дроби.

определение: ЕлементарноСледните четири вида фракции се наричат:

аз
III.

II.
IV.

m,n– естествени числа(m2,n2) и b 2 – 4ac<0.

Първите два вида интеграли на елементарни дроби могат съвсем просто да бъдат приведени в таблици чрез заместване на t=ax+b.

Нека разгледаме метода за интегриране на елементарни дроби от тип III.

Интегралът на дроб от тип III може да бъде представен като:

Тук в общ вид е показано редуцирането на дробен интеграл от тип III до два таблични интеграла.

Нека да разгледаме приложението на горната формула с примери.

u dv.

Най-общо казано, ако тричленът ax 2 +bx+c има израза b 2 – 4ac>0, тогава дробта по дефиниция не е елементарна, но въпреки това може да бъде интегрирана по посочения по-горе начин.

Пример.

u dv.

Нека сега разгледаме методите за интегриране на прости дроби от тип IV.

Първо, нека разгледаме специален случай с M = 0, N = 1.

След това интегралът на формата
могат да бъдат представени във формуляра чрез избиране на пълния квадрат в знаменателя
. Нека направим следната трансформация:

Вторият интеграл, включен в това равенство, ще вземем по части.

Да обозначим:

За първоначалния интеграл получаваме:

Получената формула се нарича рецидивиращ.Ако го приложите n-1 пъти, получавате табличен интеграл
.

Нека сега се върнем към интеграла на елементарна дроб от IV тип в общия случай.

В полученото равенство, първият интеграл с помощта на заместването t = защото 2 + sсведени до таблични и формулата за рекурентност, обсъдена по-горе, се прилага към втория интеграл.

Въпреки привидната сложност на интегрирането на елементарна дроб от тип IV, на практика е доста лесно да се използва за дроби с малка степен п, а универсалността и обобщеността на подхода прави възможна много проста реализация на този метод на компютър.

Пример:

Интегриране на рационални функции.

Интегриране на рационални дроби.

За да се интегрира една рационална дроб, е необходимо тя да се разложи на елементарни дроби.

Теорема: Ако
- правилна рационална дроб, чийто знаменател P(x) е представен като произведение на линейни и квадратни множители (имайте предвид, че всеки полином с реални коефициенти може да бъде представен в следната форма: П(х) = (х - а)  …(х - b)  (х 2 + px + р)  …(х 2 + rx + s)  ), тогава тази фракция може да се разложи на елементарни по следната схема:

където A i ,B i ,M i ,N i ,R i ,S i са някои постоянни величини.

Когато интегрират рационални дроби, те прибягват до разлагане на първоначалната дроб на елементарни. За намиране на величините A i , B i , M i , N i , R i , S i се използват т.нар. метод на несигурни коефициенти, чиято същност е, че за да бъдат идентично равни два полинома е необходимо и достатъчно коефициентите при едни и същи степени на x да са равни.

Нека разгледаме използването на този метод, използвайки конкретен пример.

u dv.

Привеждайки до общ знаменател и приравнявайки съответните числители, получаваме:

u dv.

защото Ако дробта е неправилна, първо трябва да изберете цялата й част:

6x 5 – 8x 4 – 25x 3 + 20x 2 – 76x– 7 3x 3 – 4x 2 – 17x+ 6

6x 5 – 8x 4 – 34x 3 + 12x 2 2x 2 + 3

9x 3 + 8x 2 – 76x - 7

9x 3 – 12x 2 – 51x +18

20x 2 – 25x – 25

Нека разложим на множители знаменателя на получената дроб. Вижда се, че при x = 3 знаменателят на дробта става нула. След това:

3x 3 – 4x 2 – 17x+ 6x- 3

3x 3 – 9x 2 3x 2 + 5x- 2

Така 3x 3 – 4x 2 – 17x+ 6 = (x– 3)(3x 2 + 5x– 2) = (x– 3)(x+ 2)(3x– 1). След това:

За да се избегне отварянето на скоби, групирането и решаването на система от уравнения (която в някои случаи може да се окаже доста голяма) при намиране на несигурни коефициенти, т.нар. метод произволни стойности . Същността на метода е, че няколко (според броя на неопределените коефициенти) произволни стойности на x се заместват в горния израз. За да се опростят изчисленията, обичайно е да се вземат като произволни стойности точки, при които знаменателят на фракцията е равен на нула, т.е. в нашия случай – 3, -2, 1/3. Получаваме:

Накрая получаваме:

u dv.

Нека намерим неопределените коефициенти:

Тогава стойността на дадения интеграл:

Интегриране на някои тригонометрии

функции.

Може да има безкраен брой интеграли от тригонометрични функции. Повечето от тези интеграли изобщо не могат да бъдат изчислени аналитично, така че нека разгледаме някои основни видовефункции, които винаги могат да бъдат интегрирани.

Интеграл на формата
.

Тук R е обозначението на някаква рационална функция на променливите sinx и cosx.

Интегралите от този тип се изчисляват чрез заместване
. Това заместване ви позволява да преобразувате тригонометрична функция в рационална.

Тогава

Така:

Описаната по-горе трансформация се нарича универсално тригонометрично заместване.

u dv.

Безспорното предимство на това заместване е, че с негова помощ винаги можете да трансформирате тригонометрична функция в рационална и да изчислите съответния интеграл. Недостатъците включват факта, че трансформацията може да доведе до доста сложна рационална функция, чието интегриране ще отнеме много време и усилия.

Ако обаче е невъзможно да се приложи по-рационална замяна на променливата, този метод е единственият ефективен.

u dv.

Интеграл на формата
Ако

функцияРcosx.

Въпреки възможността за изчисляване на такъв интеграл с помощта на универсалното тригонометрично заместване, по-рационално е да се използва заместването t = sinx.

функция
може да съдържа cosx само в четни степени и следователно може да се преобразува в рационална функция по отношение на sinx.

u dv.

Най-общо казано, за да се приложи този метод, е необходима само нечетността на функцията спрямо косинуса, а степента на синуса, включена във функцията, може да бъде произволна, както цяло число, така и дробна.

Интеграл на формата
Ако

функцияРе странно спрямоsinx.

По аналогия с разгледания по-горе случай се извършва замяната t = cosx.

u dv.

Интеграл на формата

функцияРдори относителноsinxИcosx.

За да трансформирате функцията R в рационална, използвайте заместването

t = tgx.

u dv.

Интеграл на произведението от синуси и косинуси

различни аргументи.

В зависимост от вида на работата ще се прилага една от трите формули:

u dv.

Понякога при интегриране на тригонометрични функции е удобно да се използват добре известни тригонометрични формули, за да се намали редът на функциите.

u dv.

Понякога се използват някои нестандартни техники.

u dv.

Интегриране на някои ирационални функции.

Не всеки ирационална функцияможе да има интеграл, изразен чрез елементарни функции. За да намерите интеграла на ирационална функция, трябва да използвате заместване, което ще ви позволи да трансформирате функцията в рационална, чийто интеграл винаги може да бъде намерен, както винаги е известно.

Нека да разгледаме някои техники за интегриране на различни видове ирационални функции.

Интеграл на формата
Къдеп- естествено число.

Използване на заместване
функцията е рационализирана.

u dv.

Ако съставът на ирационална функция включва корени от различни степени, тогава като нова променлива е рационално да се вземе корен от степен, равна на най-малкото общо кратно на степените на корените, включени в израза.

Нека илюстрираме това с пример.

u dv.

Интегриране на биномни диференциали.

определение: Биномен диференциалнаречен израз

х м (а + bx п ) стр dx

Къде м, п, И стр– рационални числа.

Както беше доказано от академик П. Л. Чебишев. (1821-1894), интегралът на биномен диференциал може да бъде изразен чрез елементарни функции само в следните три случая:

Ако rе цяло число, тогава интегралът се рационализира с помощта на заместването

, където  е общият знаменател мИ п.