Định nghĩa góc đa diện. Góc đa diện Góc đa diện là một hình tương tự về mặt không gian của đa giác

Định nghĩa.

Chúng ta hãy lấy một số góc (Hình 37): ASB, BSC, CSD, nằm cạnh nhau tuần tự, nằm trong cùng một mặt phẳng xung quanh đỉnh chung S. Chúng ta hãy quay mặt phẳng của góc ASB quanh cạnh chung SB sao cho mặt phẳng này tạo thành một phần góc nhị diện với mặt phẳng BSC. Sau đó, không làm thay đổi góc nhị diện thu được, chúng ta xoay nó quanh đường thẳng SC sao cho mặt phẳng BSC tạo một góc nhị diện nhất định với mặt phẳng CSD. Hãy tiếp tục vòng quay tuần tự này xung quanh mỗi cạnh chung. Nếu cạnh cuối SF trùng với cạnh SA thứ nhất thì tạo thành một hình (Hình 38), hình này được gọi là góc đa diện . Các góc ASB, BSC,... được gọi là góc phẳng hoặc các cạnh , các cạnh SA, SB, ... được gọi là xương sườn , và đỉnh chung S-đứng đầu

góc đa diện. Mỗi cạnh cũng là một cạnh của một góc nhị diện nhất định; do đó, trong một góc đa diện có số góc nhị diện và số góc phẳng bằng số cạnh của nó. Số nhỏ nhất có ba mặt trong một góc đa diện; góc này được gọi là hình tam giác

. Có thể có các góc tứ diện, ngũ giác, v.v.

Một góc đa diện được biểu thị bằng một chữ cái S đặt ở đỉnh hoặc bằng một loạt chữ cái SABCDE, trong đó chữ cái đầu tiên biểu thị đỉnh và các chữ cái còn lại - các cạnh theo thứ tự vị trí của chúng.

Một góc đa diện được gọi là lồi nếu nó nằm hoàn toàn trên một cạnh của mặt phẳng mỗi mặt của nó và được kéo dài vô tận. Ví dụ, đây là góc thể hiện trong hình 38. Ngược lại, góc trong hình 39 không thể được gọi là lồi vì nó nằm ở cả hai phía của cạnh ASB hoặc cạnh BCC. Nếu chúng ta cắt tất cả các mặt của một góc đa diện với một mặt phẳng thì một đa giác sẽ được hình thành trong phần ( abcde

). Trong một góc đa diện lồi, đa giác này cũng lồi. Chúng ta sẽ chỉ xét lồi.

góc đa diện Định lý.

Trong một góc tam diện, mỗi góc phẳng nhỏ hơn tổng hai góc phẳng còn lại.

Gọi góc lớn nhất trong góc tam diện SABC (Hình 40) là góc ASC.

Trên góc này, chúng ta vẽ góc ASD, bằng góc ASB, rồi vẽ một đường thẳng AC cắt SD tại điểm D. Hãy vẽ SB = SD. Bằng cách kết nối B với A và C, chúng ta nhận được \(\Delta\)ABC, trong đó< АВ + ВС.

Hai tam giác ASD và ASB bằng nhau vì chúng có một góc bằng nhau các cạnh bằng nhau: do đó AD = AB. Do đó, nếu trong bất đẳng thức dẫn xuất, chúng ta loại bỏ các số hạng bằng nhau AD và AB, thì chúng ta thu được DC< ВС.

Bây giờ chúng ta nhận thấy rằng trong các tam giác SCD và SCB, hai cạnh của cái này bằng hai cạnh của cái kia, nhưng cạnh thứ ba không bằng nhau; trong trường hợp này, góc lớn hơn nằm đối diện với cạnh lớn hơn của các cạnh này; Có nghĩa,

∠CSD< ∠ CSВ.

Bằng cách cộng góc ASD vào vế trái của bất đẳng thức này và góc ASB bằng nó vào vế phải, chúng ta thu được bất đẳng thức cần chứng minh:

∠ASC< ∠ CSB + ∠ ASB.

Chúng ta đã chứng minh rằng ngay cả góc phẳng lớn nhất cũng nhỏ hơn tổng của hai góc còn lại. Điều này có nghĩa là định lý đã được chứng minh.

Kết quả. Trừ cả hai vế của bất đẳng thức cuối cùng bằng góc ASB hoặc góc CSB; chúng tôi nhận được:

∠ASC - ∠ASB< ∠ CSB;

∠ASC - ∠CSB< ∠ ASB.

Xét các bất đẳng thức này từ phải qua trái và xét góc ASC lớn nhất trong ba góc lớn hơn hiệu của hai góc còn lại nên ta đi đến kết luận rằng trong một góc tam diện, mỗi góc trong mặt phẳng lớn hơn hiệu của hai góc còn lại.

góc đa diện Trong một góc đa diện lồi, tổng các góc phẳng nhỏ hơn 4d (360°) .

Hãy cắt các mặt (Hình 41) của góc lồi SABCDE với một mặt phẳng nào đó; từ đây chúng ta có được một mặt cắt lồi N-gon ABCDE.

Áp dụng định lý đã được chứng minh trước đó cho mỗi góc tam diện có đỉnh tại các điểm A, B, C, D và E, chúng ta pacholym:

∠ABC< ∠ABS + ∠SВC, ∠BCD < ∠BCS + ∠SCD и т. д.

Chúng ta hãy cộng tất cả các bất đẳng thức này theo từng số hạng. Khi đó ở vế trái ta được tổng các góc của đa giác ABCDE, bằng 2 dn - 4d , và bên phải - tổng các góc của các tam giác ABS, SBC, v.v., ngoại trừ các góc nằm ở đỉnh S. Biểu thị tổng các góc cuối này bằng chữ cái X , sau khi cộng ta được:

2dn - 4d < 2dn - x .

Vì trong sự khác biệt 2 dn - 4d và 2 dn - x các số bị trừ bằng nhau thì để hiệu thứ nhất nhỏ hơn số thứ hai thì cần phải có số trừ 4 d nhiều hơn số tiền được khấu trừ X ; điều đó có nghĩa là 4 d > X , tức là X < 4d .

Các trường hợp đơn giản nhất về sự bằng nhau của các góc tam diện

Định lý. Các góc tam giác bằng nhau nếu chúng có:

1) dọc theo một góc nhị diện nằm giữa hai góc phẳng tương ứng bằng nhau và cách đều nhau, hoặc

2) dọc theo một góc phẳng bằng nhau nằm giữa hai góc nhị diện tương ứng bằng nhau và cách đều nhau.

1) Cho S và S 1 là hai góc tam giác (Hình 42), trong đó ∠ASB = ∠A 1 S 1 B 1, ∠ASC = ∠A 1 S 1 C 1 (và các giá trị này góc bằng nhau nằm giống hệt nhau) và góc nhị diện AS bằng góc nhị diện A 1 S 1 .

Ta ghép góc S 1 vào góc S sao cho các điểm S 1 và S, các đường thẳng S 1 A 1 và SA và các mặt phẳng A 1 S 1 B 1 và ASB trùng nhau. Khi đó cạnh S 1 B 1 sẽ đi dọc theo SB (do các góc A 1 S 1 B 1 và ASB bằng nhau), mặt phẳng A 1 S 1 C 1 sẽ đi dọc theo ASC (do sự bằng nhau của các góc nhị diện ) và cạnh S 1 C 1 sẽ đi dọc theo cạnh SC (do các góc A 1 S 1 C 1 và ASC bằng nhau). Do đó, các góc tam diện sẽ trùng với tất cả các cạnh của chúng, tức là. họ sẽ bằng nhau.

2) Dấu hiệu thứ hai, giống như dấu hiệu đầu tiên, được chứng minh bằng cách nhúng.

Các góc đa diện đối xứng

Như đã biết, góc đứng bằng nhau khi nói về các góc tạo bởi đường thẳng hoặc mặt phẳng. Hãy xem liệu tuyên bố này có đúng khi xét đến các góc đa diện hay không.

Chúng ta hãy tiếp tục (Hình 43) tất cả các cạnh của góc SABCDE nằm ngoài đỉnh S, khi đó một góc đa diện khác SA 1 B 1 C 1 D 1 E 1 được hình thành, có thể gọi là thẳng đứng so với góc thứ nhất Dễ dàng nhận thấy cả hai góc lần lượt có góc phẳng và góc nhị diện bằng nhau nhưng đều nằm trong thứ tự ngược lại. Thật vậy, nếu chúng ta tưởng tượng một người quan sát nhìn từ bên ngoài một góc đa diện ở đỉnh của nó, thì các cạnh SA, SB, SC, SD, SE đối với anh ta dường như sẽ nằm theo hướng ngược chiều kim đồng hồ, trong khi nhìn vào góc SA 1 B 1 C 1 D 1 E 1, người ta thấy các cạnh SA 1, SB 1, ..., nằm theo chiều kim đồng hồ.

Các góc đa diện có các góc phẳng và góc nhị diện tương ứng bằng nhau nhưng nằm theo thứ tự ngược lại, thường không thể kết hợp được khi lồng nhau; điều đó có nghĩa là chúng không bằng nhau. Những góc như vậy gọi là đối xứng(so với đỉnh S). Tính đối xứng của các hình trong không gian sẽ được thảo luận chi tiết hơn dưới đây.

Vật liệu khác

Xét ba tia a, b, c cùng xuất phát từ một điểm và không nằm trong cùng một mặt phẳng. Góc tam giác (abc) là hình được tạo thành từ ba góc phẳng (ab), (bc) và (ac) (Hình 2). đỉnh chung của một góc phẳng gọi là đỉnh của một góc tam diện. Các góc nhị diện tạo bởi các mặt của một góc tam diện được gọi là các góc nhị diện của một góc tam diện.

Khái niệm góc đa diện được định nghĩa tương tự (Hình 3).

đa diện

Trong phép đo lập thể, các hình trong không gian gọi là vật thể được nghiên cứu. Về mặt trực quan, một vật thể (hình học) phải được hình dung như một phần của không gian bị chiếm giữ. cơ thể vật lý và bị giới hạn bởi bề mặt.

Khối đa diện là một khối có bề mặt bao gồm số hữu hạnđa giác phẳng (Hình 4). Một khối đa diện được gọi là lồi nếu nó nằm trên một cạnh của mặt phẳng của mọi đa giác phẳng trên bề mặt của nó. Phần chung mặt phẳng như vậy và bề mặt của khối đa diện lồi được gọi là một mặt. Các mặt của khối đa diện lồi đều phẳng đa giác lồi. Các cạnh của các mặt được gọi là các cạnh của khối đa diện và các đỉnh được gọi là các đỉnh của khối đa diện.

Hãy để chúng tôi giải thích điều này bằng ví dụ về một khối lập phương quen thuộc (Hình 5). Có một khối lập phương đa diện lồi. Bề mặt của nó gồm có sáu hình vuông: ABCD, BEFC, .... Đây là các mặt của nó. Các cạnh của hình lập phương là các cạnh của các hình vuông: AB, BC, BE,.... Các đỉnh của hình lập phương là các đỉnh của các hình vuông: A, B, C, D, E, .... Hình lập phương có sáu mặt, mười hai cạnh và tám đỉnh.

Đối với các khối đa diện đơn giản nhất - lăng kính và hình chóp, sẽ là đối tượng chính của nghiên cứu của chúng tôi - chúng tôi sẽ đưa ra các định nghĩa về bản chất, không sử dụng khái niệm vật thể. Chúng sẽ được định nghĩa là các hình hình học biểu thị tất cả các điểm trong không gian thuộc về chúng. Ý tưởng cơ thể hình học và bề mặt của nó ở trường hợp chung sẽ được trao sau.

Góc đa diện

phần không gian được giới hạn bởi một khối đa diện bề mặt hình nón, hướng của nó là một đa giác phẳng không có giao điểm. Các mặt của bề mặt này được gọi là các mặt của bức tranh khảm, và mặt trên được gọi là đỉnh của bức tranh khảm. M.u. được gọi là đều nếu tất cả các góc thẳng và tất cả các góc nhị diện của nó bằng nhau. Meroy M.u. là diện tích được giới hạn bởi đa giác cầu có được nhờ giao điểm của các mặt của đa giác, một hình cầu có bán kính bằng một, và có tâm ở đỉnh M. y. Xem thêm Góc đặc.

To lớn bách khoa toàn thư Liên Xô. - M.: Bách khoa toàn thư Liên Xô. 1969-1978 .

Xem "góc đa diện" là gì trong các từ điển khác:

Xem góc vững chắc ... To lớn Từ điển bách khoa

Xem góc vững chắc. * * * GÓC ĐA PHƯƠNG GÓC ĐA PHƯƠNG, xem Góc khối (xem GÓC RẮN) ... Từ điển bách khoa

Phần không gian được giới hạn bởi một hốc của hình nón đa diện. bề mặt hướng tới một nhóm đa giác phẳng không có giao điểm. Các mặt của bề mặt này được gọi là. các cạnh của M.u., đỉnh của đỉnh M.u. Góc đa diện được gọi là Chính xác... Bách khoa toàn thư toán học

Xem góc đặc... Khoa học tự nhiên. Từ điển bách khoa

góc đa diện- toán học. Một phần không gian được giới hạn bởi nhiều mặt phẳng đi qua một điểm (đỉnh của một góc)... Từ điển của nhiều biểu thức

ĐA NĂNG, nhiều mặt, nhiều mặt (sách). 1. Có nhiều mặt hoặc nhiều mặt. Đá nhiều mặt. Góc đa diện (một phần không gian được giới hạn bởi một số mặt phẳng cắt nhau tại một điểm; mat.). 2. chuyển... ... Từ điển Ushakova

- (thảm.). Nếu vẽ các đường thẳng OA và 0B từ điểm O trên một mặt phẳng cho trước thì chúng ta thu được góc AOB (Hình 1). Tệ thật. 1. Điểm 0 được gọi đỉnh của góc và các đường thẳng OA, 0B là các cạnh của góc. Giả sử có hai góc ΒΟΑ và Β 1 Ο 1 Α 1. Hãy đặt chúng sao cho... ...

Thuật ngữ này có ý nghĩa khác, xem Góc (ý nghĩa). Góc ∠ Kích thước ° Đơn vị SI Radian ... Wikipedia

Phẳng, hình hình học, được hình thành bởi hai tia (cạnh của chữ U.) phát ra từ một điểm (đỉnh của chữ U.). Mọi U., có một đỉnh ở tâm O của một đường tròn nào đó (tâm U.), xác định trên đường tròn một cung AB, giới hạn bởi... ... Bách khoa toàn thư vĩ đại của Liên Xô

GÓC ĐA PHƯƠNG

Một góc đa diện là hình dạng không gian tương tự của một đa giác. Hãy nhớ lại rằng đa giác trên một mặt phẳng là một hình được tạo bởi một đường đứt nét khép kín đơn giản và vùng bên trong bị giới hạn bởi nó. Chúng ta sẽ coi một tia trong không gian là một điểm tương tự của một điểm trên mặt phẳng và một góc phẳng trong không gian là một điểm tương tự của một đoạn trên mặt phẳng. Khi đó, dạng tương tự của một đường đứt nét khép kín đơn giản trên mặt phẳng là một bề mặt được hình thành bởi một tập hợp hữu hạn các góc phẳngMỘT 1 SA 2 , MỘT 2 SA 3 , …, MỘT -1 SA n, Một SA 1 có một đỉnh chungS (Hình 1), trong đó các góc lân cận không có điểm chung, ngoại trừ các điểm của tia chung và các góc không liền kề không có điểm chung điểm chung, ngoại trừ đỉnh chung. Hình được tạo bởi bề mặt biểu thị và một trong hai phần không gian bị giới hạn bởi bề mặt đó được gọi là với mặt phẳng BSC. Sau đó, không làm thay đổi góc nhị diện thu được, chúng ta xoay nó quanh đường thẳng SC sao cho mặt phẳng BSC tạo một góc nhị diện nhất định với mặt phẳng CSD. Hãy tiếp tục vòng quay tuần tự này xung quanh mỗi cạnh chung. Nếu cạnh cuối SF trùng với cạnh SA thứ nhất thì tạo thành một hình (Hình 38), hình này được gọi là. Đỉnh chungSgọi điện , và đỉnh chung S- góc đa diện. TiaSA 1 , …, SA nđược gọi là xương sườn góc đa diện và các góc của mặt phẳngMỘT 1 SA 2 , MỘT 2 SA 3 , …, MỘT -1 SA n, Một SA 1 – hoặc góc đa diện. Một góc đa diện được biểu thị bằng các chữ cáiSA 1 … MỘT, chỉ ra đỉnh và các điểm trên các cạnh của nó. Tùy thuộc vào số lượng mặt, các góc đa diện được gọi là tam diện, tứ diện, ngũ diện (Hình 2), v.v.

Một góc đa diện được gọi là lồi, nếu nó là một hình lồi, tức là cùng với hai điểm bất kỳ của nó cũng chứa điểm nối chúngđoạn Trong Hình 2, các góc tam giác và tứ diện đều lồi, nhưng góc ngũ giác thì không.
Hãy xem xét một số tính chất của hình tam giác và các tính chất tương tự của các góc tam diện.
Bất động sản 1(Bất đẳng thức tam giác). Mỗi cạnh của một tam giác nhỏ hơn tổng hai cạnh còn lại của nó.
Tính chất tương tự của góc tam diện là tính chất sau.
Bất động sản 1". Mỗi góc phẳng của một góc tam diện nhỏ hơn tổng hai góc phẳng còn lại của nó.
Bằng chứng. Xét một góc tam giác SABC . Gọi góc phẳng lớn nhất của nó là góc A.S.C.. Khi đó bất đẳng thức giữ nguyên

ASB ASC< ASC + BSC ;BSC ASC< ASC + ASB .

Do đó, còn lại việc chứng minh bất đẳng thức ASC< A.S.B.+ BSC.
Hãy đặt nó ở rìa A.S.C. góc A.S.D., bình đẳng A.S.B. , và thời kỳ B chúng ta hãy chọn sao cho SB = SD(Hình 3). Khi đó các hình tam giác A.S.B. Và A.S.D. bằng nhau (ở hai cạnh và góc giữa chúng) và do đó, AB = AD. Hãy sử dụng bất đẳng thức tam giác A.C.< AB + BC . Trừ từ cả hai phần của nó AD = AB, ta thu được bất đẳng thức DC< BC. Trong hình tam giác DSC Và BSC một bên là chung ( S.C.), SD = SB Và DC< BC. Trong trường hợp này, chống lại mặt lớn hơn nằm một góc lớn hơn và do đó, DSC< BSC . Cộng vào cả hai vế của bất đẳng thức này góc A.S.D. , bình đẳng A.S.B., ta thu được bất đẳng thức cần thiết ASC< A.S.B.+ BSC.

Hệ quả 1.Tổng các góc phẳng của một góc tam diện nhỏ hơn 360° .
Bằng chứng. Cho phép SABC- một góc tam giác nhất định. Xét một góc tam giác có đỉnh MỘT, được hình thành bởi các cạnh ABS, ACS và góc BAC. Do tính chất đã được chứng minh nên bất đẳng thức đúng BAC< BAS+ CAS. Tương tự với các góc tam giác có đỉnh B Và VỚI có những bất đẳng thức: ABC< ABS+ CBS, ACB< ACS+ BCS. Cộng các bất đẳng thức này và tính đến tổng các góc của một tam giác ABC bằng 180° , chúng ta nhận được 180 ° < BAS+CAS+ ABS+CBS+BCS+ ACS= 180 ° - ASB+ 180° - BSC+ 180° - A.S.C.. Kể từ đây, ASB+BSC+ASC< 360 ° .
Hệ quả 2.Tổng các góc phẳng của một góc đa diện lồi nhỏ hơn 360.
Chứng minh tương tự như phần trước.
Hệ quả 3.Tổng các góc nhị diện của một góc tam diện lớn hơn 180° .
Bằng chứng. Cho phép SABC- góc tam giác. Hãy chọn một số điểm P bên trong nó và thả vuông góc từ nó PA 1 , P.B. 1 , máy tính 1 ở cạnh (Hình 4).

Góc phẳng B 1 máy tính 1 , MỘT 1 máy tính 1 , MỘT 1 P.B. 1 bổ sung các góc nhị diện tương ứng với các cạnh SA, SB, SC lên tới 180° . Do đó tổng các góc nhị diện này là 540° - ( B 1 máy tính 1 +A 1 máy tính 1 + MỘT 1 P.B. 1 ). Xét rằng tổng các góc phẳng của một hình tam giác với một đỉnh P góc nhỏ hơn 360° , ta thấy tổng các góc nhị diện của góc tam diện ban đầu lớn hơn 180° .
Tài sản 2.Các đường phân giác của một tam giác cắt nhau tại một điểm.
Thuộc tính 2". Các mặt phẳng phân giác của các góc nhị diện của một góc tam diện cắt nhau dọc theo một đường thẳng.
Chứng minh tương tự như trường hợp máy bay. Cụ thể là hãy SABC- góc tam giác. Mặt phẳng phân giác của một góc nhị diện SA là GMT của góc cách đều các mặt của nó A.S.C. Và A.S.B.. Tương tự, mặt phẳng phân giác của một góc nhị diện S.B. là GMT của góc cách đều các mặt của nó B.S.A. Và BSC . Đường giao nhau của chúng VÌ THẾ sẽ cách đều tất cả các mặt của góc tam diện và do đó, mặt phẳng phân giác của góc nhị diện sẽ đi qua nó S.C. .
Tài sản 3.Các đường trung trực của các cạnh của một tam giác cắt nhau tại một điểm.
Thuộc tính 3".Các mặt phẳng đi qua các đường phân giác của các mặt của một góc tam diện và vuông góc với các mặt này thì cắt nhau dọc theo một đường thẳng.
Chứng minh tương tự như chứng minh tính chất trước.
Tài sản 4.Các đường trung tuyến của một tam giác cắt nhau tại một điểm.
Tài sản 4".Các mặt phẳng đi qua các cạnh của một góc tam diện và các đường phân giác của các mặt đối diện cắt nhau dọc theo một đường thẳng.
Bằng chứng. Xét một góc tam giác SABC,SA=SB=SC(Hình 5). Khi đó các đường phân giác SA 1 , S.B. 1 , S.C. 1 góc BSC, ASC, ASB là đường trung bình của các tam giác tương ứng. Đó là lý do tại sao A.A. 1 , BB 1 , CC 1 - Đường trung bình của tam giác ABC. Cho phép ồ- giao điểm của chúng. Thẳng VÌ THẾ nằm trong cả ba mặt phẳng đang xét và do đó là đường giao nhau của chúng.

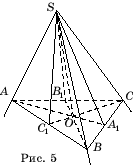
Tài sản 5.Các đường cao của tam giác cắt nhau tại một điểm.
Thuộc tính 5". Các mặt phẳng đi qua các cạnh của một góc tam diện và vuông góc với các mặt đối diện thì cắt nhau dọc theo một đường thẳng.
Bằng chứng. Xét một góc tam giác có đỉnh S và xương sườn a, b, c. Hãy biểu thị Một 1 , b 1 , c 1 – các đường giao nhau của các mặt với các mặt phẳng đi qua các cạnh tương ứng và vuông góc với các mặt này (Hình 6). Hãy sửa điểm C trên rìa c và thả vuông góc từ nó CA 1 Và C.B. 1 trên đường thẳng Một 1 và b 1 . Hãy biểu thị MỘT Và B giao điểm đường CA 1 và C.B. 1 với những đường thẳng Một Và b. Sau đó SA 1 là một hình chiếu A.A. 1 đến bờ vực BSC. Bởi vì BC vuông góc SA 1 , thì nó vuông góc và A.A. 1 . Tương tự như vậy, A.C. vuông góc BB 1 . Như vậy, A.A. 1 và BB 1 là các đường cao của tam giác ABC. Cho phép ồ- giao điểm của chúng. Máy bay đi qua đường Một Và Một 1 , b Và b 1 vuông góc với mặt phẳng ABC và do đó, đường giao nhau của chúng VÌ THẾ vuông góc ABC. Có nghĩa, VÌ THẾ vuông góc AB. Ở phía bên kia, CO vuông góc AB. Do đó mặt phẳng đi qua cạnh c Và VÌ THẾ sẽ vuông góc với mặt đối diện.
Tính chất 6 (định lý sin). Trong một hình tam giác ABC với các bên a, b, c theo đó, sự bình đẳng xảy ra Một : tội lỗi A = b: tội lỗi B=c: tội lỗi C.
Tài sản 6".Đặt a, b, g - góc phẳng của một góc tam diện, a, b, c- các góc nhị diện đối diện với chúng. Sau đó tội lỗi a : tội lỗi Một= tội lỗi b : tội lỗi b= sin g : tội lỗi c.
Bằng chứng. Cho phép SABC- góc tam giác. Hãy thả từ điểm C vuông góc CC 1 lên máy bay A.S.B. và vuông góc CA 1 trên rìa SA(Hình 7). Khi đó góc CA 1 C 1 sẽ góc tuyến tính góc nhị diện Một. Đó là lý do tại sao CC 1 = CA 1 tội lỗi Một = S.C. tội lỗi tội lỗi Một. Tương tự nó được chỉ ra rằng CC 1 = CB 1 tội lỗi b = SC tội lỗi một tội lỗi b. Do đó, tội bình đẳng tội lỗi một = tội lỗi một tội lỗi b và do đó, tội lỗi bình đẳng một: tội lỗi Một= tội lỗi b : tội lỗi b. Bằng cách tương tự, người ta chứng minh rằng đẳng thức có tội b: tội lỗi b= sin g : tội lỗi c.

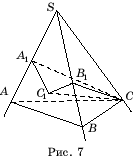
Tài sản 7.Nếu ở tứ giác lồi Nếu bạn có thể nội tiếp một đường tròn thì tổng các cạnh đối diện bằng nhau.
Tài sản 7". Nếu một hình cầu có thể nội tiếp được một góc tứ diện lồi thì tổng các góc phẳng đối diện sẽ bằng nhau.

Văn học
1. Hadamard J. Hình học cơ bản. Phần II. Lập thể. – M.: Uchpedgiz, 1938.
2. Perepelkin D.I. Tốt hình học cơ bản. Phần II. Hình học trong không gian. – M.-L.: Gostekhizdat, 1949.
3. Bách khoa toàn thư toán tiểu học. Quyển IV. Hình học. - M.; 1963.
4. Smirnova I.M. Trong thế giới đa diện. – M.: Giáo dục, 1995.

BẢNG BẢN VĂN BẢN CỦA BÀI HỌC:

Trong phép đo phẳng, một trong những đối tượng nghiên cứu là góc.

Góc là một hình hình học gồm một điểm - đỉnh của góc và hai tia phát ra từ điểm này.

Hai góc, một cạnh chung và hai cạnh kia là phần tiếp theo của nhau, được gọi là kề nhau trong phép đo mặt phẳng.

La bàn có thể được coi là mô hình của một góc phẳng.

Chúng ta hãy nhắc lại khái niệm về góc nhị diện.

Đây là hình được tạo bởi đường thẳng a và hai nửa mặt phẳng c biên giới chung Và, không thuộc cùng một mặt phẳng trong hình học được gọi là góc lưỡng diện. Nửa mặt phẳng là các mặt của một góc nhị diện. Đường thẳng a là cạnh của một góc nhị diện.

Mái nhà thể hiện rõ góc nhị diện.

Nhưng mái nhà ở hình hai được làm theo dạng hình được tạo thành từ sáu góc phẳng có một đỉnh chung sao cho các góc đều lấy nhau. theo một thứ tự nhất định và mỗi cặp góc kề bù, kể cả góc đầu tiên và góc cuối cùng, có mặt chung. Hình dạng mái nhà này được gọi là gì?

Trong hình học, một hình được tạo thành từ các góc

Và các góc tạo nên góc này được gọi là góc phẳng. Các cạnh của góc phẳng được gọi là các cạnh của một góc đa diện. Điểm O gọi là đỉnh của góc.

Ví dụ về các góc đa diện có thể được tìm thấy trong tứ diện và hình bình hành.

Các mặt của tứ diện DBA, ABC, DBC tạo thành các góc đa diện BADC. Thông thường nó được gọi là góc tam diện.

Trong một hình bình hành, các mặt AA1D1D, ABCD, AA1B1B tạo thành các góc tam diện AA1DB.

Vâng, mái nhà được làm theo hình lục giác. Nó bao gồm sáu góc phẳng.

Một số tính chất đúng của góc đa diện. Hãy để chúng tôi xây dựng chúng và chứng minh chúng. Ở đây nói rằng tuyên bố

Đầu tiên, đối với bất kỳ góc đa diện lồi nào đều có một mặt phẳng cắt tất cả các cạnh của nó.

Để chứng minh, hãy xét góc đa diện OA1A2 A3…An.

Theo điều kiện, nó lồi. Một góc được gọi là lồi nếu nó nằm trên một cạnh của mặt phẳng và mỗi góc phẳng của nó.

Vì theo điều kiện góc này lồi nên các điểm O, A1, A2, A3, An nằm trên một cạnh của mặt phẳng OA1A2

Hãy thực hiện đường giữa KM của tam giác OA1A2 và chọn từ các cạnh OA3, OA4, OAn cạnh tạo thành góc nhị diện nhỏ nhất với mặt phẳng OKM. Gọi đây là cạnh OAi.(оа tổng)

Ta xét nửa mặt phẳng α với ranh giới CM, chia góc nhị diện OKMAi thành hai góc nhị diện. Mọi đỉnh từ A đến An đều nằm trên một phía của mặt phẳng α và điểm O ở phía bên kia. Do đó, mặt phẳng α cắt tất cả các cạnh của góc đa diện. Tuyên bố đã được chứng minh.

Các góc đa diện lồi có một tính chất quan trọng khác.

Tổng các góc phẳng của một góc đa diện lồi nhỏ hơn 360°.

Xét một góc đa diện lồi có đỉnh tại điểm O. Theo khẳng định đã được chứng minh, có một mặt phẳng cắt tất cả các cạnh của nó.

Chúng ta hãy vẽ một mặt phẳng α như vậy, để nó cắt các cạnh của góc tại các điểm A1, A2, A3, v.v. trên An.

Mặt phẳng α tính từ vùng ngoài của góc phẳng sẽ cắt tam giác. Tổng các góc là 180°. Chúng ta thu được rằng tổng của tất cả các góc phẳng từ A1OA2 đến AnOA1 bằng biểu thức, chúng ta biến đổi biểu thức này, sắp xếp lại các số hạng, chúng ta nhận được

TRONG biểu hiện này các tổng được chỉ ra trong ngoặc là tổng các góc phẳng của một góc tam diện và như đã biết chúng lớn hơn góc phẳng thứ ba.

Bất đẳng thức này có thể được viết cho tất cả các góc tam diện tạo thành một góc đa diện cho trước.

Do đó, chúng ta thu được sự tiếp tục của đẳng thức sau

Đáp án chứng tỏ tổng các góc phẳng của một góc đa diện lồi nhỏ hơn 360 độ.