ความต่อเนื่องของฟังก์ชันในตัวอย่างช่วงเวลา ความต่อเนื่องของฟังก์ชัน ณ จุดหนึ่งและตามช่วงเวลา

คำนิยาม- ถ้าฟังก์ชั่น ฉ(x) ถูกกำหนดไว้ในช่วงเวลา [ ก, ข] มีความต่อเนื่องในแต่ละจุดของช่วงเวลา ( ก, ข) ณ จุดนั้น กต่อเนื่องไปทางขวา ณ จุดนั้น ขต่อเนื่องกันทางซ้าย แล้วเราบอกว่าฟังก์ชัน ฉ(x) อย่างต่อเนื่องในส่วนนี้ [ก, ข].

กล่าวอีกนัยหนึ่งคือฟังก์ชัน ฉ(x) ต่อเนื่องในช่วงเวลา [ ก, ข] หากตรงตามเงื่อนไขสามประการ:

1) "x 0 Î( ก, ข): ฉ(x) = ฉ(x 0);

2) ฉ(x) = ฉ(ก);

3) ฉ(x) = ฉ(ข).

สำหรับฟังก์ชันที่ต่อเนื่องในช่วงเวลาหนึ่ง เราจะพิจารณาคุณสมบัติบางอย่างซึ่งเรากำหนดในรูปแบบของทฤษฎีบทต่อไปนี้ โดยไม่ต้องทำการพิสูจน์

ทฤษฎีบท 1- ถ้าฟังก์ชั่น ฉ(x) ต่อเนื่องในช่วงเวลา [ ก, ข] จากนั้นจะถึงค่าต่ำสุดและสูงสุดในส่วนนี้

ทฤษฎีบทนี้ระบุว่า (รูปที่ 1.15) ว่าในส่วน [ ก, ข] มีจุดดังกล่าว x 1 นั่น ฉ(x 1) ปอนด์ ฉ(x) สำหรับใดๆ xจาก [ ก, ข] และนั่นคือประเด็น x 2 (x 2 โอ[ ก, ข]) ดังนั้น " xÎ[ ก, ข] (ฉ(x 2)³ ฉ(x)).

ความหมาย ฉ(x 1) ใหญ่ที่สุดสำหรับฟังก์ชันที่กำหนดใน [ ก, ข], ก ฉ(x 2) – เล็กที่สุด เรามาแสดงว่า: ฉ(x 1) = ม, ฉ(x 2) =ม- ตั้งแต่ ฉ(x) ความไม่เท่าเทียมกันถือ: " xÎ[ ก, ข] ม£ ฉ(x) £ มจากนั้นเราจะได้ข้อพิสูจน์ต่อไปนี้จากทฤษฎีบทที่ 1

ผลที่ตามมา- ถ้าฟังก์ชั่น ฉ(x) ต่อเนื่องกันในช่วงเวลาหนึ่ง จากนั้นจึงถูกผูกไว้ในช่วงเวลานี้

ทฤษฎีบท 2- ถ้าฟังก์ชั่น ฉ(x) ต่อเนื่องในช่วงเวลา [ ก,ข] และที่ส่วนท้ายของส่วนจะใช้ค่าของเครื่องหมายต่าง ๆ จากนั้นจะมีจุดภายในดังกล่าว x 0 ส่วน [ ก, ข] ซึ่งฟังก์ชันเปลี่ยนเป็น 0 เช่น - x 0 Î ( ก, ข) (ฉ(x 0) = 0).

ทฤษฎีบทนี้ระบุว่ากราฟของฟังก์ชัน ย = ฉ(x) ต่อเนื่องในช่วงเวลา [ ก, ข] ตัดกับแกน วัวอย่างน้อยหนึ่งครั้งหากค่า ฉ(ก) และ ฉ(ข) มี สัญญาณตรงกันข้าม- ดังนั้น (รูปที่ 1.16) ฉ(ก) > 0, ฉ(ข) < 0 и функция ฉ(x) กลายเป็น 0 ที่จุด x 1 , x 2 , x 3 .

ทฤษฎีบท 3- ให้ฟังก์ชัน ฉ(x) ต่อเนื่องในช่วงเวลา [ ก, ข], ฉ(ก) = ก, ฉ(ข) = บีและ ก¹ บี- (รูปที่ 1.17) แล้วสำหรับเลขอะไรก็ตาม คล้อมรอบระหว่างตัวเลข กและ บีมีจุดภายในเช่นนั้น x 0 ส่วน [ ก, ข], อะไร ฉ(x 0) = ค.

ผลที่ตามมา- ถ้าฟังก์ชั่น ฉ(x) ต่อเนื่องในช่วงเวลา [ ก, ข], ม – ค่าที่น้อยที่สุด ฉ(x), ม – มูลค่าสูงสุดฟังก์ชั่น ฉ(x) บนส่วน [ ก, ข] จากนั้นฟังก์ชันจะรับค่าใดๆ (อย่างน้อยหนึ่งครั้ง) ม, สรุประหว่าง มและ มและดังนั้นส่วน [ ม. ม] คือเซตของค่าฟังก์ชันทั้งหมด ฉ(x) บนส่วน [ ก, ข].

โปรดทราบว่าหากฟังก์ชันต่อเนื่องในช่วงเวลา ( ก, ข) หรือมีอยู่ในส่วน [ ก, ข] จุดความไม่ต่อเนื่อง จากนั้นทฤษฎีบท 1, 2, 3 สำหรับฟังก์ชันดังกล่าวจะไม่เป็นจริง

โดยสรุป ให้พิจารณาทฤษฎีบทเกี่ยวกับการมีอยู่ของฟังก์ชันผกผัน

ขอให้เราระลึกว่าตามช่วง เราหมายถึงส่วนหรือช่วง หรือช่วงครึ่ง ช่วง มีจำกัดหรืออนันต์

ทฤษฎีบท 4- อนุญาต ฉ(x) ต่อเนื่องกันตามช่วงเวลา เอ็กซ์เพิ่มขึ้น (หรือลดลง) โดย เอ็กซ์และมีค่าต่างๆ มากมาย ย- แล้วสำหรับฟังก์ชั่น ย = ฉ(x) มีฟังก์ชันผกผัน x= เจ(ย) กำหนดไว้ในช่วงเวลา ยต่อเนื่องและเพิ่มขึ้น (หรือลดลง) โดย ยที่มีหลายความหมาย เอ็กซ์.

ความคิดเห็น- ให้ฟังก์ชัน x= เจ(ย) คือค่าผกผันของฟังก์ชัน ฉ(x- เนื่องจากอาร์กิวเมนต์มักจะเขียนแทนด้วย xและฟังก์ชันผ่าน ยแล้วเราจะเขียน ฟังก์ชันผกผันเช่น ย=เจ(x).

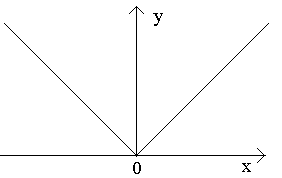
ตัวอย่างที่ 1- การทำงาน ย = x 2 (รูปที่ 1.8, a) บนชุด เอ็กซ์= ก, ข[ และมีความต่อเนื่องในทุกจุดของช่วงเวลานี้ แล้วเรียกว่าต่อเนื่องในช่วงเวลา ] ก, ข- แนวคิดเรื่องความต่อเนื่องของฟังก์ชันในช่วงเวลาของรูปแบบ ]- ∞ ถูกกำหนดในทำนองเดียวกัน ข[ , ]ก, + [ . ให้ฟังก์ชั่นตอนนี้ ย = ฉ(x) กำหนดไว้ในช่วงเวลา [ ก, ข- ความแตกต่างระหว่างช่วงเวลาและเซ็กเมนต์: จุดขอบเขตของช่วงเวลาจะไม่รวมอยู่ในช่วงเวลา แต่จุดขอบเขตของเซ็กเมนต์จะรวมอยู่ในเซ็กเมนต์ ในที่นี้เราควรพูดถึงสิ่งที่เรียกว่าความต่อเนื่องด้านเดียว: ณ จุดนั้น กเหลืออยู่ในส่วน [ ก, ข] เราทำได้แค่เข้าใกล้จากทางขวาและตรงจุดเท่านั้น ข- ทางซ้ายเท่านั้น ฟังก์ชันนี้เรียกว่าต่อเนื่องในช่วงเวลา [ ก, ข] ถ้ามันต่อเนื่องกันทั้งหมด จุดภายในของส่วนนี้ต่อเนื่องกันทางด้านขวา ณ จุดนั้น กและปล่อยให้ต่อเนื่องตรงจุดนั้น ข.

ตัวอย่างของฟังก์ชันต่อเนื่องอาจเป็นฟังก์ชันพื้นฐานใดๆ ก็ได้ แต่ละ ฟังก์ชั่นเบื้องต้นมีความต่อเนื่องตามช่วงที่กำหนดไว้ ตัวอย่างเช่น ฟังก์ชัน และ ต่อเนื่องในช่วงเวลาใดๆ [ ก, ข] ฟังก์ชันจะต่อเนื่องในช่วงเวลา [ 0 , ข] ฟังก์ชันจะต่อเนื่องกับส่วนใดๆ ที่ไม่มีจุด ก = 2 .

ตัวอย่างที่ 4ตรวจสอบฟังก์ชันเพื่อความต่อเนื่อง

สารละลาย. เรามาตรวจสอบเงื่อนไขกันก่อน ฟังก์ชั่นไม่ได้ถูกกำหนดไว้ที่จุด - 3 และ 3 เงื่อนไขอย่างน้อยหนึ่งเงื่อนไขสำหรับความต่อเนื่องของฟังก์ชันตลอดเส้นจำนวนทั้งหมดไม่เป็นที่พอใจ นั่นเป็นเหตุผล ฟังก์ชั่นนี้มีความต่อเนื่องเป็นระยะ

.

ตัวอย่างที่ 5กำหนดว่าพารามิเตอร์มีค่าเท่าใด กอย่างต่อเนื่องตลอด ขอบเขตของคำจำกัดความการทำงาน

สารละลาย.

ลองหาลิมิตทางขวามือได้ที่:

.

แน่นอนว่าคุณค่า ณ จุดนั้น x= 2 ควรเท่ากัน ขวาน :

ก = 1,5 .

ตัวอย่างที่ 6กำหนดว่าค่าพารามิเตอร์ใด กและ ขอย่างต่อเนื่องตลอด ขอบเขตของคำจำกัดความการทำงาน

สารละลาย.
มาหาขีดจำกัดด้านซ้ายของฟังก์ชัน ณ จุดนั้น:

.

ดังนั้นค่า ณ จุดต้องเป็น 1:

ลองหาฟังก์ชันทางซ้ายตรงจุด:

แน่นอนว่าค่าของฟังก์ชัน ณ จุดหนึ่งๆ ควรเท่ากับ:

คำตอบ: ฟังก์ชันจะต่อเนื่องตลอดขอบเขตคำจำกัดความทั้งหมดเมื่อ ก = 1; ข = -3 .

คุณสมบัติพื้นฐานของฟังก์ชันต่อเนื่อง

คณิตศาสตร์มาถึงแนวคิดเรื่องฟังก์ชันต่อเนื่องโดยการศึกษากฎการเคลื่อนที่ต่างๆ พื้นที่และเวลาไม่มีที่สิ้นสุด และการพึ่งพาอาศัยกัน เช่น เส้นทาง สจากเวลา ทีที่แสดงออกมาตามกฎหมาย ส = ฉ(ที) , ให้ตัวอย่างการต่อเนื่อง ฟังก์ชั่น ฉ(ที- อุณหภูมิของน้ำร้อนยังเปลี่ยนแปลงอย่างต่อเนื่องและเป็นฟังก์ชันต่อเนื่องของเวลาด้วย: ต = ฉ(ที) .

ใน การวิเคราะห์ทางคณิตศาสตร์คุณสมบัติบางอย่างได้รับการพิสูจน์แล้ว ฟังก์ชั่นต่อเนื่อง- ให้เรานำเสนอคุณสมบัติที่สำคัญที่สุดเหล่านี้

1. หากฟังก์ชันต่อเนื่องในช่วงเวลาหนึ่งจะใช้ค่าของสัญญาณที่แตกต่างกันที่จุดสิ้นสุดของช่วงเวลา จากนั้น ณ จุดใดจุดหนึ่งของช่วงเวลานี้จะใช้ค่านั้น เท่ากับศูนย์- ในข้อความที่เป็นทางการมากขึ้น คุณสมบัตินี้ถูกกำหนดไว้ในทฤษฎีบทที่เรียกว่าทฤษฎีบทโบลซาโน-คอชีบทแรก

2. ฟังก์ชั่น ฉ(x) ต่อเนื่องในช่วงเวลา [ ก, ข] รับค่ากลางทั้งหมดระหว่างค่าที่จุดสิ้นสุดนั่นคือระหว่าง ฉ(ก) และ ฉ(ข- ในข้อความที่เป็นทางการมากขึ้น คุณสมบัตินี้ถูกกำหนดไว้ในทฤษฎีบทที่เรียกว่าทฤษฎีบทโบลซาโน-คอชีบทที่สอง

ความต่อเนื่องของฟังก์ชันในช่วงเวลาหนึ่ง

ชื่อพารามิเตอร์	ความหมาย
หัวข้อบทความ:	ความต่อเนื่องของฟังก์ชันในช่วงเวลาหนึ่ง
รูบริก (หมวดหมู่เฉพาะเรื่อง)	คณิตศาสตร์

คำนิยาม.โดยปกติฟังก์ชันจะเรียกว่าต่อเนื่องในช่วงเวลาหนึ่ง หากฟังก์ชันต่อเนื่องที่ทุกจุดของช่วงเวลานี้

หากกำหนดฟังก์ชันเมื่อใด เอ็กซ์=กและในนั้น ฉ(เอ็กซ์) = ฉ(ก),

แล้วพวกเขาก็พูดอย่างนั้น ฉ(เอ็กซ์) ณ จุดนั้น และต่อเนื่องกันทางด้านขวา- ในทำนองเดียวกันหาก ฉ(เอ็กซ์) = ฉ(ข) แล้วพวกเขาก็พูดแบบนั้นตรงจุด ขฟังก์ชั่นนี้ ทิ้งไว้อย่างต่อเนื่อง.

คำนิยาม.โดยปกติแล้วฟังก์ชันจะเรียกว่าต่อเนื่องในช่วงเวลา [ ก, ข] หากมีความต่อเนื่องกันในแต่ละจุด (ณ จุด กต่อเนื่องไปทางขวา ณ จุดนั้น ข– ต่อเนื่องกันทางซ้าย)

มูลค่าสูงสุดฟังก์ชั่น ที่ = ฉ(x) บนส่วน [ ก, ข ฉ(x 1) นั่น ฉ(x) £ ฉ(x 1) สำหรับทุกคน เอ็กซ์ Î [ ก, ข].

ค่าต่ำสุดฟังก์ชั่น ที่ = ฉ(x) บนส่วน [ ก, ข] เป็นเรื่องปกติที่จะเรียกสิ่งนี้ว่าความหมาย ฉ(x 2) นั่น ฉ(x) ³ ฉ(x 2) สำหรับทุกคน เอ็กซ์ Î [ ก, ข].

ฟังก์ชันที่ต่อเนื่องในช่วงเวลาหนึ่งจะมีจำนวนหนึ่ง คุณสมบัติที่สำคัญซึ่งแสดงได้ด้วยทฤษฎีบทต่อไปนี้

ทฤษฎีบท 3.3.1ฟังก์ชันต่อเนื่องในช่วงเวลา [ ก, ข] ถึงค่าต่ำสุดของมัน มและคุณค่าสูงสุด มนั่นคือมีจุดดังกล่าว x 1 และ x 2 ส่วนนี้นั่นเอง ฉ(x 1) = ม, ฉ(x 2) = ม.

ทฤษฎีบทนี้มีความหมายทางเรขาคณิตอย่างง่าย (ดูรูปที่ 2)

ทฤษฎีบท 3.3.2ถ้าฟังก์ชั่น ที่ = ฉ(x) ต่อเนื่องในช่วงเวลา [ ก, ข] และที่จุดสิ้นสุดจะมีค่าไม่เท่ากัน ฉ(ก) = ก, ฉ(ข) = B, A ¹ B ดังนั้นไม่ว่าตัวเลข C จะอยู่ระหว่าง A และ B ก็จะมีจุดหนึ่ง กับ Î [ ก, ข] ดังนั้น ฉ(กับ) = ส.

ความหมายทางเรขาคณิตทฤษฎีบทแสดงไว้ในรูปที่ 3 เส้นตรงใดๆ ที่= C โดยที่ A< C < B (или A >C > B) ตัดกราฟของฟังก์ชัน ที่ = ฉ(x).

ผลที่ตามมาหากฟังก์ชันต่อเนื่องบนเซ็กเมนต์และรับค่าของเครื่องหมายต่าง ๆ ที่ส่วนท้าย แสดงว่าในส่วนนี้จะมีอย่างน้อยหนึ่งจุดที่ฟังก์ชันหายไป

ความหมายทางเรขาคณิตของผลลัพธ์ที่ได้แสดงไว้ในรูปที่ 4

คำถามเพื่อการควบคุมตนเอง

1. ฟังก์ชันใดที่มักเรียกว่าต่อเนื่อง ณ จุดหนึ่ง

2. ให้คำจำกัดความที่เทียบเท่ากันในแง่ของการเพิ่มฟังก์ชันและอาร์กิวเมนต์

3. สิ่งที่สามารถพูดเกี่ยวกับผลรวม, ผลต่าง, ผลคูณและผลหารของฟังก์ชันต่อเนื่องสองฟังก์ชัน?

4. สำหรับค่าใดของการโต้แย้งที่เป็นเหตุผลทั้งหมดและ ฟังก์ชันเศษส่วน-ตรรกยะต่อเนื่อง?

5. เมื่อใดที่ฟังก์ชันเชิงซ้อนจะต่อเนื่องกัน ณ จุดหนึ่ง?

6. โดยทั่วไปเรียกว่าจุดพักของฟังก์ชันอะไร?

7. จุดใดที่เรียกว่าจุดไม่ต่อเนื่องของประเภทแรก?

8. ปริมาณใดที่มักเรียกว่าฟังก์ชันกระโดด?

9. อธิบายแนวคิดของ "จุดไม่ต่อเนื่องแบบถอดได้" ยกตัวอย่าง.

10. จุดใดที่เรียกว่าจุดไม่ต่อเนื่องประเภทที่สอง? ยกตัวอย่าง.

11. อธิบายแนวคิด: "ความต่อเนื่องในช่วงเวลาหนึ่ง", "ความต่อเนื่องทางด้านขวา", "ความต่อเนื่องทางด้านซ้าย", "ความต่อเนื่องบนส่วน"

12. กำหนดค่าฟังก์ชันที่ใหญ่ที่สุดและเล็กที่สุด

13. กำหนดทฤษฎีบทเกี่ยวกับความสัมพันธ์ระหว่างความต่อเนื่องของเซ็กเมนต์กับค่าที่ใหญ่ที่สุดและเล็กที่สุดของฟังก์ชัน อธิบายด้วยภาพวาด

14. กำหนดทฤษฎีบทเกี่ยวกับความสัมพันธ์ระหว่างความต่อเนื่องของฟังก์ชันในช่วงเวลาหนึ่งและช่วงของค่าฟังก์ชัน แสดงความหมายทางเรขาคณิตในรูป

15. ให้ข้อพิสูจน์กับทฤษฎีบทข้างต้นและการตีความทางเรขาคณิต

การบรรยายครั้งที่ 4

หัวข้อการบรรยาย: อนุพันธ์ของฟังก์ชัน

โครงร่างการบรรยาย:แนวคิดเรื่องอนุพันธ์ เรขาคณิตและ ความหมายทางกายภาพ- กฎพื้นฐานของการสร้างความแตกต่าง อนุพันธ์ ฟังก์ชั่นที่ซับซ้อน- แอปพลิเคชั่นบางตัวเป็นอนุพันธ์

4.1. แนวคิดเรื่องอนุพันธ์ ความหมายทางเรขาคณิต และทางกายภาพ

พิจารณาฟังก์ชัน ที่ = ฉ(x) ระบุในช่วงเวลา ] ก, ข- อนุญาต เอ็กซ์Î ] ก, ข[ และ เอ็กซ์ Î ] ก, ข[ แล้วเพิ่มฟังก์ชันที่จุดนั้น เอ็กซ์ 0 แสดงโดยสูตร D ที่ = ฉ(x 0+ด เอ็กซ์) – ฉ(x 0).

คำนิยาม. ฟังก์ชันอนุพันธ์ y = ฉ(x) ณ จุดนั้น เอ็กซ์ 0 โดยปกติเรียกว่าขีดจำกัดของอัตราส่วนของการเพิ่มขึ้นของฟังก์ชันนี้ต่อการเพิ่มขึ้นของอาร์กิวเมนต์ เมื่อค่าหลังมีแนวโน้มเป็นศูนย์:

ฉ'(x 0) = หรือ คุณ"(x 0) =.

ความหมายทางเรขาคณิตของอนุพันธ์: อนุพันธ์ของฟังก์ชันที่กำหนด ณ จุดหนึ่งจะเท่ากับแทนเจนต์ของมุมระหว่างแกน Ox และแทนเจนต์กับกราฟของฟังก์ชันนี้ที่ จุดที่สอดคล้องกัน(ดูรูปที่ 1):

ฉ"(x 0) = ตาล ก.

คุณสมบัติของหน้าที่ต่อเนื่องในการสัมภาษณ์

ให้เราพิจารณาคุณสมบัติบางอย่างของฟังก์ชันต่อเนื่องในช่วงเวลาหนึ่ง เรานำเสนอคุณสมบัติเหล่านี้โดยไม่มีข้อพิสูจน์

การทำงาน ย = ฉ(x)เรียกว่า อย่างต่อเนื่องในส่วนนี้ [ก, ข] หากต่อเนื่องกันที่จุดภายในทั้งหมดของส่วนนี้และที่จุดสิ้นสุด นั่นคือ ที่จุด กและ ขต่อเนื่องกันทางขวาและซ้ายตามลำดับ

ทฤษฎีบท 1ฟังก์ชันต่อเนื่องในช่วงเวลา [ ก, ข] อย่างน้อยที่สุดจุดหนึ่งของกลุ่มนี้ก็ได้ค่าสูงสุดและอย่างน้อยที่สุดก็มีจุดหนึ่งที่น้อยที่สุด

ทฤษฎีบทระบุว่าถ้าเป็นฟังก์ชัน ย = ฉ(x)มีความต่อเนื่องในช่วงเวลา [ ก, ข] แล้วมีอย่างน้อยหนึ่งจุด x1 Î [ ก, ข] เพื่อให้ค่าของฟังก์ชัน ฉ(x)ณ จุดนี้จะเป็นค่าที่ใหญ่ที่สุดในกลุ่มนี้: ฉ(x 1) ≥ ฉ(x)- ในทำนองเดียวกันก็มีประเด็นดังกล่าว x2ซึ่งค่าฟังก์ชันจะน้อยที่สุดจากค่าทั้งหมดในกลุ่ม: ฉ(x 1) ≤ ฉ(x).

เห็นได้ชัดว่าอาจมีจุดดังกล่าวอยู่หลายประการ เช่น รูปที่แสดงว่าฟังก์ชัน ฉ(x)รับค่าน้อยที่สุดที่จุดสองจุด x2และ x 2 ".

ความคิดเห็น- ข้อความของทฤษฎีบทอาจไม่ถูกต้องได้หากเราพิจารณาค่าของฟังก์ชันในช่วงเวลา ( ก, ข- แท้จริงแล้วถ้าเราพิจารณาถึงฟังก์ชัน ย = xบน (0, 2) จากนั้นจะต่อเนื่องในช่วงเวลานี้ แต่ไปไม่ถึงค่าที่ใหญ่ที่สุดหรือเล็กที่สุดในนั้น: ถึงค่าเหล่านี้เมื่อสิ้นสุดช่วงเวลา แต่จุดสิ้นสุดไม่เข้ากัน ไปยังโดเมนของเรา

นอกจากนี้ ทฤษฎีบทนี้จะไม่เป็นจริงสำหรับฟังก์ชันที่ไม่ต่อเนื่อง ยกตัวอย่าง.

ผลที่ตามมาถ้าฟังก์ชั่น ฉ(x)ต่อเนื่องบน [ ก, ข] จากนั้นจะถูกจำกัดไว้ในส่วนนี้

ทฤษฎีบท 2ให้ฟังก์ชัน ย = ฉ(x)มีความต่อเนื่องในช่วงเวลา [ ก, ข] และที่ส่วนท้ายของส่วนนี้จะใช้ค่าของเครื่องหมายต่าง ๆ จากนั้นจะมีจุดภายในส่วนอย่างน้อยหนึ่งจุด x = คซึ่งฟังก์ชันจะเป็นศูนย์: ฉ(ค)= 0 โดยที่< C< b

ทฤษฎีบทนี้มีความหมายทางเรขาคณิตอย่างง่าย: ถ้าจุดของกราฟของฟังก์ชันต่อเนื่อง ย = ฉ(x)สอดคล้องกับส่วนท้ายของส่วน [ ก, ข] นอนอยู่ข้างๆ ด้านที่แตกต่างกันจากแกน วัวจากนั้นกราฟนี้จะตัดแกนอย่างน้อยที่จุดหนึ่งของส่วน วัว- ฟังก์ชันที่ไม่ต่อเนื่องอาจไม่มีคุณสมบัตินี้

ทฤษฎีบทนี้ยอมรับลักษณะทั่วไปต่อไปนี้

ทฤษฎีบท 3 (ทฤษฎีบทค่ากลาง)ให้ฟังก์ชัน ย = ฉ(x)มีความต่อเนื่องในช่วงเวลา [ ก, ข] และ ฉ(ก) = ก, ฉ(ข) = บี- แล้วสำหรับเลขอะไรก็ตาม ค, สรุประหว่าง กและ บีมีจุดดังกล่าวอยู่ในส่วนนี้ คÎ [ ก, ข], อะไร ฉ(ค) = ค.

ทฤษฎีบทนี้มีความชัดเจนทางเรขาคณิต พิจารณากราฟของฟังก์ชัน ย = ฉ(x)- อนุญาต ฉ(ก) = ก, ฉ(ข) = บี- แล้วเส้นตรงใดๆ ย = ค, ที่ไหน ค– หมายเลขใด ๆ ระหว่าง กและ บีจะตัดกราฟของฟังก์ชันอย่างน้อยที่จุดหนึ่ง แอบซิสซาของจุดตัดกันจะเป็นค่านั้น x = คซึ่ง ฉ(ค) = ค.

ดังนั้น ฟังก์ชันต่อเนื่องที่ย้ายจากค่าหนึ่งไปอีกค่าหนึ่ง จำเป็นต้องผ่านค่ากลางทั้งหมด โดยเฉพาะอย่างยิ่ง:

ผลที่ตามมาถ้าฟังก์ชั่น ย = ฉ(x)มีความต่อเนื่องในช่วงเวลาหนึ่งและรับค่าที่ใหญ่ที่สุดและน้อยที่สุด จากนั้นในช่วงเวลานี้จะใช้เวลาอย่างน้อยหนึ่งครั้งค่าใดๆ ที่อยู่ระหว่างค่าที่เล็กที่สุดและใหญ่ที่สุด

อนุพันธ์และการประยุกต์ คำจำกัดความของอนุพันธ์

ให้เรามีฟังก์ชั่นบางอย่าง y=ฉ(x)กำหนดไว้เป็นช่วงๆ สำหรับแต่ละค่าอาร์กิวเมนต์ xจากช่วงเวลานี้ฟังก์ชัน y=ฉ(x)มีความหมายบางอย่าง

พิจารณาค่าอาร์กิวเมนต์สองค่า: เริ่มต้น x 0 และใหม่ x.

ความแตกต่าง x–x 0 เรียกว่า โดยการเพิ่มอาร์กิวเมนต์ xตรงจุด x 0 และแสดงแทน ∆x- ดังนั้น, ∆x = x – x 0 (การเพิ่มอาร์กิวเมนต์อาจเป็นค่าบวกหรือลบก็ได้) จากความเท่าเทียมกันนี้เป็นไปตามนั้น x=x 0 +∆x, เช่น. ความหมายดั้งเดิมตัวแปรได้รับการเพิ่มขึ้นบ้าง แล้วถ้าถึงจุดนั้น xค่าฟังก์ชัน 0 คือ ฉ(x 0 ), แล้วเข้า จุดใหม่ xฟังก์ชันจะรับค่า ฉ(x) = ฉ(x 0 +∆x).

ความแตกต่าง ใช่ 0 = ฉ(x) – ฉ(x 0 ) เรียกว่า เพิ่มฟังก์ชัน ย = ฉ(x)ตรงจุด x 0 และระบุด้วยสัญลักษณ์ ∆y- ดังนั้น,

Δy = ฉ(x) – ฉ(x 0 ) = ฉ(x 0 +Δx) - ฉ(x 0 ) .

(1)

โดยปกติแล้วค่าเริ่มต้นของอาร์กิวเมนต์ x 0 ถือว่าคงที่และเป็นค่าใหม่ x- ตัวแปร. แล้ว ย 0 = ฉ(x 0 ) ปรากฎว่าคงที่และ ย = ฉ(x)- ตัวแปร. เพิ่มขึ้น ∆yและ ∆xจะเป็นตัวแปรด้วยและสูตร (1) แสดงว่า ดีเป็นฟังก์ชันของตัวแปร ∆x.

มาสร้างอัตราส่วนของการเพิ่มขึ้นของฟังก์ชันต่อการเพิ่มขึ้นของอาร์กิวเมนต์กัน

ให้เราหาลิมิตของอัตราส่วนนี้กันที่ ∆x→0. หากมีขีดจำกัดนี้ เรียกว่าอนุพันธ์ของฟังก์ชันนี้ ฉ(x)ตรงจุด x 0 และแสดงถึง ฉ "(x 0) ดังนั้น,

อนุพันธ์ฟังก์ชั่นนี้ ย = ฉ(x)ตรงจุด x 0 เรียกว่าขีดจำกัดของอัตราส่วนการเพิ่มฟังก์ชัน Δ ยถึงการเพิ่มอาร์กิวเมนต์ Δ xเมื่ออันหลังมีแนวโน้มเป็นศูนย์โดยพลการ

โปรดทราบว่าสำหรับฟังก์ชันเดียวกันอนุพันธ์ใน จุดต่างๆ xสามารถรับค่าที่แตกต่างกันได้ เช่น อนุพันธ์ถือได้ว่าเป็นฟังก์ชันของการโต้แย้ง x- ฟังก์ชันนี้ถูกกำหนดไว้ ฉ "(x)

อนุพันธ์จะแสดงด้วยสัญลักษณ์ ฉ "(เอ็กซ์),ย ", . ความหมายเฉพาะอนุพันธ์ที่ x = กแสดงโดย ฉ "(ก) หรือ ย "- x=ก.

การดำเนินการหาอนุพันธ์ของฟังก์ชัน ฉ(x)เรียกว่าดิฟเฟอเรนติเอตของฟังก์ชันนี้

หากต้องการค้นหาอนุพันธ์โดยตรงตามคำจำกัดความ คุณสามารถใช้สิ่งต่อไปนี้: หลักการง่ายๆ:

ตัวอย่าง.

ความรู้สึกทางกลของอนุพันธ์

เป็นที่ทราบกันดีจากฟิสิกส์ว่ากฎ การเคลื่อนไหวสม่ำเสมอดูเหมือน ส = โวลต์ เสื้อ, ที่ไหน ส– เส้นทางเดินทางไปสู่ช่วงเวลาแห่งกาลเวลา ที, โวลต์– ความเร็วของการเคลื่อนที่สม่ำเสมอ

แต่เพราะว่า การเคลื่อนไหวส่วนใหญ่ที่เกิดขึ้นในธรรมชาตินั้นไม่สม่ำเสมอ โดยทั่วไปแล้วจะเป็นความเร็ว และด้วยเหตุนี้จึงรวมถึงระยะทางด้วย สจะขึ้นอยู่กับเวลา ที, เช่น. จะเป็นฟังก์ชันของเวลา

ดังนั้นให้จุดวัตถุเคลื่อนที่เป็นเส้นตรงไปในทิศทางเดียวตามกฎหมาย ส=ส(ท)

เรามาทำเครื่องหมายจุดหนึ่งของเวลากัน ที 0 . ณ จุดนี้ได้ผ่านเส้นทางไปแล้ว s=s(ต 0 ). เรามากำหนดความเร็วกัน โวลต์ชี้วัตถุ ณ ขณะหนึ่ง ที 0 .

เมื่อต้องการทำเช่นนี้ เรามาพิจารณาจุดอื่นของเวลากัน ที 0 + Δ ที- สอดคล้องกับเส้นทางการเดินทาง =s(ท 0 + Δ ที- จากนั้นในช่วงเวลาหนึ่ง Δ ทีจุดนั้นเคลื่อนที่ไปตามเส้นทาง Δs =s(ท 0 + Δ เสื้อ)–เซนต์).

ลองพิจารณาทัศนคติ เรียกว่าความเร็วเฉลี่ยในช่วงเวลา Δ ที- ความเร็วเฉลี่ยไม่สามารถระบุความเร็วการเคลื่อนที่ของจุดใดจุดหนึ่งในขณะนั้นได้อย่างแม่นยำ ที 0 (เนื่องจากการเคลื่อนไหวไม่สม่ำเสมอ) เพื่อแสดงความเร็วที่แท้จริงนี้ได้อย่างแม่นยำยิ่งขึ้นโดยใช้ ความเร็วเฉลี่ยคุณต้องใช้เวลาให้สั้นลง Δ ที.

ดังนั้นความเร็วในการเคลื่อนที่เข้า ช่วงเวลานี้เวลา ที 0 (ความเร็วทันที) คือขีดจำกัดของความเร็วเฉลี่ยในช่วงเวลาจาก ที 0 ถึง ที 0 +Δ ทีเมื่อ ∆ ที→0:

,

เหล่านั้น. ความเร็วไม่สม่ำเสมอนี่คืออนุพันธ์ของระยะทางที่เดินทางเทียบกับเวลา

ความหมายทางเรขาคณิตของอนุพันธ์

ก่อนอื่นให้เราแนะนำคำจำกัดความของเส้นสัมผัสเส้นโค้งที่จุดที่กำหนดก่อน

ขอให้เรามีเส้นโค้งและจุดคงที่บนมัน ม 0(ดูรูป) พิจารณาอีกประเด็นหนึ่ง มเส้นโค้งนี้แล้ววาดเส้นตัด ม 0 ม- ถ้าตรงประเด็น มเริ่มเคลื่อนตัวไปตามโค้งและจุด ม 0ยังคงนิ่งอยู่ จากนั้นซีแคนต์จะเปลี่ยนตำแหน่ง ถ้าด้วยการประมาณจุดอย่างไม่จำกัด มตามทางโค้งจนถึงจุดหนึ่ง ม 0ด้านใดด้านหนึ่งเส้นตัดมีแนวโน้มที่จะครอบครองตำแหน่งของเส้นตรงเส้นหนึ่ง ม 0 ตแล้วตรงไป ม 0 ตเรียกว่าแทนเจนต์กับเส้นโค้ง ณ จุดที่กำหนด ม 0.

ที่., แทนเจนต์สู่เส้นโค้ง ณ จุดที่กำหนด ม 0เรียกว่าตำแหน่งลิมิตของซีแคนต์ ม 0 มเมื่อชี้ มโน้มตัวไปตามโค้งจนถึงจุดหนึ่ง ม 0.

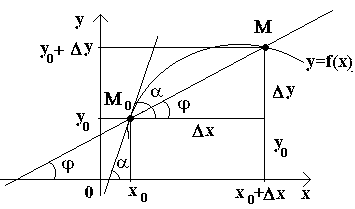
ให้เราพิจารณาฟังก์ชันต่อเนื่องกัน y=ฉ(x)และเส้นโค้งที่สอดคล้องกับฟังก์ชันนี้ ในระดับหนึ่งค่า เอ็กซ์ฟังก์ชัน 0 รับค่า y 0 =ฉ(x 0)ค่านิยมเหล่านี้ x 0 และ ย 0 บนเส้นโค้งสอดคล้องกับจุด ม 0 (x 0 ; ปี 0)ให้เราโต้แย้งกัน x 0เพิ่มขึ้น ∆ เอ็กซ์- ค่าใหม่ของอาร์กิวเมนต์สอดคล้องกับค่าที่เพิ่มขึ้นของฟังก์ชัน ย 0 +Δ y=ฉ(x 0 –Δ เอ็กซ์)- เราได้รับประเด็น ม(x 0+Δ x; ใช่ 0+Δ ใช่)ลองวาดซีแคนต์กัน ม 0 มและแสดงด้วย φ มุมที่เกิดจากเส้นตัดที่มีทิศทางบวกของแกน วัว- เรามาสร้างความสัมพันธ์กันและสังเกตว่า

ถ้าตอนนี้ Δ x→0 จากนั้นเนื่องจากความต่อเนื่องของฟังก์ชัน Δ ที่→0 และด้วยเหตุนี้จุด มเคลื่อนที่ไปตามเส้นโค้งเข้าหาจุดโดยไม่มีขีดจำกัด ม 0- จากนั้นซีแคนต์ ม 0 มมักจะเข้ารับตำแหน่งแทนเจนต์กับเส้นโค้งที่จุดนั้น ม 0และมุม φ→α ที่ Δ x→0 โดยที่ α แสดงถึงมุมระหว่างทิศทางแทนเจนต์กับทิศทางบวกของแกน วัว- เนื่องจากฟังก์ชัน tan φ ขึ้นอยู่กับ φ อย่างต่อเนื่องสำหรับ φ≠π/2 ดังนั้นสำหรับ φ→α tan φ → tan α ดังนั้น ความชันของแทนเจนต์จะเป็น:

เหล่านั้น. ฉ "(x)= ทีจี แอลฟา

ดังนั้นในทางเรขาคณิต ใช่ "(x 0)แสดงถึงความชันของเส้นสัมผัสกันกับกราฟของฟังก์ชันนี้ ณ จุดนั้น x 0, เช่น. ที่ มูลค่าที่กำหนดการโต้แย้ง xอนุพันธ์จะเท่ากับแทนเจนต์ของมุมที่เกิดจากแทนเจนต์กับกราฟของฟังก์ชัน ฉ(x)ในจุดที่เหมาะสม ม 0 (x; ย)โดยมีทิศทางแกนบวก วัว.

ตัวอย่าง.หา ความลาดชันสัมผัสกับเส้นโค้ง ย = x 2 ณ จุด ม(-1; 1).

เราได้เห็นแล้วว่า ( x 2)" = 2เอ็กซ์- แต่สัมประสิทธิ์เชิงมุมของเส้นสัมผัสเส้นโค้งคือ tan α = ย"| x=-1 = – 2.

ความแตกต่างของฟังก์ชัน ความต่อเนื่องของฟังก์ชันที่แตกต่าง

การทำงาน y=ฉ(x)เรียกว่า หาความแตกต่างได้ในบางจุด x 0 ถ้ามันมีอนุพันธ์ที่แน่นอน ณ จุดนี้ เช่น ถ้าความสัมพันธ์มีขอบเขตจำกัดและมีขอบเขตจำกัด

หากฟังก์ชันสามารถหาอนุพันธ์ได้ในแต่ละจุดของเซกเมนต์หนึ่ง [ ก; ข] หรือช่วงเวลา ( ก; ข) แล้วพวกเขาก็บอกว่าเธอ หาความแตกต่างได้บนส่วน [ ก; ข] หรือตามลำดับในช่วง ( ก; ข).

ทฤษฎีบทต่อไปนี้ถูกต้อง โดยสร้างการเชื่อมโยงระหว่างฟังก์ชันหาอนุพันธ์และฟังก์ชันต่อเนื่อง

ทฤษฎีบท.ถ้าฟังก์ชั่น y=ฉ(x)แยกแยะได้ในบางจุด x 0แล้วมันก็ต่อเนื่อง ณ จุดนี้

ดังนั้น จากความสามารถในการหาอนุพันธ์ของฟังก์ชัน ความต่อเนื่องของฟังก์ชันจะตามมา

การพิสูจน์- ถ้า , ที่

,

โดยที่ α เป็นปริมาณที่น้อยมาก เช่น ปริมาณที่มีแนวโน้มเป็นศูนย์เป็นΔ x→0. แต่แล้ว

Δ ย=ฉ "(x 0) Δ x+αΔ x=> Δ ย→0 ที่ Δ x→0 เช่น ฉ(x) – ฉ(x 0)→0 ณ x→x 0 ซึ่งหมายความว่าฟังก์ชัน ฉ(x)อย่างต่อเนื่อง ณ จุดหนึ่ง x 0 . Q.E.D.

ดังนั้นฟังก์ชันนี้จึงไม่สามารถมีอนุพันธ์ที่จุดไม่ต่อเนื่องได้ ตรงกันข้ามไม่เป็นความจริง: มีฟังก์ชันต่อเนื่องที่ไม่สามารถหาอนุพันธ์ได้ในบางจุด (นั่นคือ ไม่มีอนุพันธ์ที่จุดเหล่านี้)

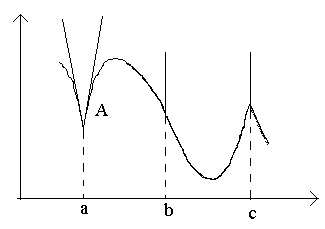
พิจารณาประเด็นต่างๆ ในรูป ก ข ค

ตรงจุด กที่ ∆ x→ อัตราส่วน 0 ไม่มีขีดจำกัด (เนื่องจากขีดจำกัดด้านเดียวแตกต่างกันสำหรับ Δ x→0–0 และ Δ x→0+0) ตรงจุด กกราฟไม่มีเส้นสัมผัสกันที่กำหนดไว้ แต่มีเส้นสัมผัสทางเดียวที่แตกต่างกันสองเส้นที่มีความชัน ถึง 1 และ ถึง 2. จุดประเภทนี้เรียกว่าจุดมุม

ตรงจุด ขที่ ∆ x→0 ความสัมพันธ์จะมีเครื่องหมายคงที่ไม่มีกำหนด ขนาดใหญ่- ฟังก์ชันนี้มีอนุพันธ์ไม่สิ้นสุด ณ จุดนี้กราฟจะมีเส้นสัมผัสแนวตั้ง ประเภทจุด – “จุดเปลี่ยนเว้า” ของแทนเจนต์แนวตั้ง

ตรงจุด คอนุพันธ์ด้านเดียวเป็นสัญญาณที่แตกต่างกันในปริมาณมากอย่างไม่สิ้นสุด ณ จุดนี้ กราฟมีเส้นสัมผัสแนวตั้งสองเส้นที่ผสานกัน ประเภท – “จุดกลับ” พร้อมแทนเจนต์แนวตั้ง – กรณีพิเศษจุดมุม