ค้นหาอนุพันธ์ของฟังก์ชันตรีโกณมิติ บทเรียนพีชคณิตและจุดเริ่มต้นของการวิเคราะห์ "อนุพันธ์ของฟังก์ชันตรีโกณมิติ"

การค้นหา อนุพันธ์ของฟังก์ชันตรีโกณมิติ จำเป็นต้องใช้ ตารางอนุพันธ์คืออนุพันธ์ 6-13

เมื่อคุณพบ อนุพันธ์เฉพาะ ฟังก์ชันตรีโกณมิติ เพื่อหลีกเลี่ยงข้อผิดพลาดทั่วไป คุณควรใส่ใจกับประเด็นต่อไปนี้:

• ในนิพจน์ฟังก์ชัน คำใดคำหนึ่งมักจะเป็น ไซน์ โคไซน์ หรือฟังก์ชันตรีโกณมิติอื่นๆไม่ได้มาจากอาร์กิวเมนต์ของฟังก์ชัน แต่มาจากตัวเลข (ค่าคงที่) ดังนั้นอนุพันธ์ของเทอมนี้จึงเท่ากับศูนย์
• เกือบทุกครั้งคุณจะต้องทำให้นิพจน์ที่ได้รับจากการหาอนุพันธ์ง่ายขึ้นและด้วยเหตุนี้คุณจึงจำเป็นต้องใช้ความรู้เกี่ยวกับการปฏิบัติการกับเศษส่วนอย่างมั่นใจ
• เพื่อลดความซับซ้อนของนิพจน์ที่คุณจำเป็นต้องรู้เกือบตลอดเวลา อัตลักษณ์ตรีโกณมิติตัวอย่างเช่น สูตร มุมคู่และสูตรความสามัคคีเป็นผลรวมของกำลังสองของไซน์และโคไซน์

ตัวอย่างที่ 1ค้นหาอนุพันธ์ของฟังก์ชัน

สารละลาย. เอาเป็นว่ากับ อนุพันธ์ของโคไซน์ทุกอย่างชัดเจน หลายคนที่เริ่มศึกษาอนุพันธ์จะพูดว่า แล้วไง อนุพันธ์ของไซน์สิบสองหารด้วยพายเหรอ? คำตอบ: นับ เท่ากับศูนย์- ที่นี่ไซน์ (ฟังก์ชัน!) เป็นกับดัก เนื่องจากอาร์กิวเมนต์ไม่ใช่ตัวแปร X หรือตัวแปรอื่นใด แต่เป็นเพียงตัวเลข นั่นคือไซน์ของจำนวนนี้ก็เป็นตัวเลขเช่นกัน และอนุพันธ์ของตัวเลข (ค่าคงที่) อย่างที่เรารู้จากตารางอนุพันธ์นั้นมีค่าเท่ากับศูนย์ ดังนั้นเราจึงเหลือเพียงลบไซน์ของ X แล้วหาอนุพันธ์ของมันโดยไม่ลืมเครื่องหมาย:

.

ตัวอย่างที่ 2ค้นหาอนุพันธ์ของฟังก์ชัน

.

สารละลาย. เทอมที่สองเป็นกรณีเดียวกับเทอมแรกในตัวอย่างก่อนหน้า นั่นคือมันคือตัวเลข และอนุพันธ์ของตัวเลขคือศูนย์ เราพบว่าอนุพันธ์ของเทอมที่สองเป็นอนุพันธ์ของผลหาร:

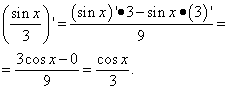
ตัวอย่างที่ 3ค้นหาอนุพันธ์ของฟังก์ชัน

สารละลาย. นี่เป็นอีกปัญหาหนึ่ง: ในเทอมแรกไม่มีอาร์คไซน์หรือฟังก์ชันตรีโกณมิติอื่นๆ แต่มี x ซึ่งหมายความว่ามันคือฟังก์ชันของ x ดังนั้นเราจึงแยกความแตกต่างออกเป็นคำในผลรวมของฟังก์ชัน:

ในที่นี้จำเป็นต้องมีทักษะในการดำเนินการกับเศษส่วน กล่าวคือ ในการกำจัดโครงสร้างเศษส่วนสามชั้น

ตัวอย่างที่ 4ค้นหาอนุพันธ์ของฟังก์ชัน

.

สารละลาย. ในที่นี้ตัวอักษร "phi" มีบทบาทเหมือนกับ "x" ในกรณีก่อนหน้านี้ (และในกรณีอื่นๆ ส่วนใหญ่ แต่ไม่ใช่ทั้งหมด) ซึ่งเป็นตัวแปรอิสระ ดังนั้น เมื่อเรามองหาอนุพันธ์ของผลคูณของฟังก์ชัน เราจะไม่เร่งรีบที่จะประกาศอนุพันธ์ของรากของ “phi” ให้เท่ากับศูนย์ ดังนั้น:

แต่การแก้ปัญหาไม่ได้จบเพียงแค่นั้น เนื่องจากคำศัพท์ที่คล้ายกันถูกรวบรวมไว้ในวงเล็บสองวงเล็บ เราจึงยังคงต้องแปลง (ลดความซับซ้อน) นิพจน์ ดังนั้นเราจึงคูณวงเล็บด้วยปัจจัยที่อยู่ข้างหลัง แล้วนำพจน์มาเป็นตัวส่วนร่วมและทำการแปลงเบื้องต้นอื่นๆ:

ตัวอย่างที่ 5ค้นหาอนุพันธ์ของฟังก์ชัน

สารละลาย. ในตัวอย่างนี้ เราจะต้องรู้ข้อเท็จจริงที่ว่ามีฟังก์ชันตรีโกณมิติ - ซีแคนต์ - และสูตรของมันผ่านโคไซน์ มาแยกแยะกัน:

ตัวอย่างที่ 6ค้นหาอนุพันธ์ของฟังก์ชัน

.

สารละลาย. ในตัวอย่างนี้ เราจะต้องจำสูตรมุมคู่จากโรงเรียน แต่ก่อนอื่นมาแยกความแตกต่าง:

,

(นี่คือสูตรมุมคู่)

จากหลักสูตรเรขาคณิตและคณิตศาสตร์เด็กนักเรียนจะคุ้นเคยกับความจริงที่ว่าแนวคิดของอนุพันธ์นั้นถูกถ่ายทอดให้พวกเขาผ่านพื้นที่ของรูป, ส่วนต่าง, ขีด จำกัด ของฟังก์ชันรวมถึงขีด จำกัด ลองมาดูแนวคิดเรื่องอนุพันธ์จากมุมที่ต่างออกไป แล้วพิจารณาว่าฟังก์ชันอนุพันธ์และฟังก์ชันตรีโกณมิติสามารถเชื่อมโยงกันได้อย่างไร

ลองพิจารณาเส้นโค้งใดๆ ก็ได้ซึ่งอธิบายโดยฟังก์ชันนามธรรม y = f(x)

ลองจินตนาการว่าตารางเวลาเป็นแผนที่เส้นทางท่องเที่ยว การเพิ่มขึ้น ∆x (เดลต้า x) ในรูปคือระยะทางที่แน่นอนของเส้นทาง และ ∆y คือการเปลี่ยนแปลงความสูงของเส้นทางเหนือระดับน้ำทะเล
จากนั้นปรากฎว่าอัตราส่วน ∆x/∆y จะเป็นตัวกำหนดลักษณะความซับซ้อนของเส้นทางในแต่ละส่วนของเส้นทาง เมื่อเรียนรู้คุณค่านี้แล้ว คุณจะบอกได้อย่างมั่นใจว่าทางขึ้น/ลงชันหรือไม่ คุณจะต้องใช้อุปกรณ์ปีนเขาหรือไม่ และนักท่องเที่ยวต้องการอุปกรณ์บางอย่างหรือไม่ การฝึกทางกายภาพ- แต่ตัวบ่งชี้นี้จะใช้ได้เพียงตัวเดียวเท่านั้น ช่องว่างเล็ก ๆ∆x.

หากผู้จัดทริปนำค่าเริ่มต้นและ จุดสิ้นสุดเส้นทาง นั่นคือ ∆x – จะเป็น เท่ากับความยาวเส้นทางนั้นจะไม่สามารถรับข้อมูลวัตถุประสงค์เกี่ยวกับระดับความยากของการเดินทางได้ ดังนั้นจึงจำเป็นต้องสร้างกราฟอีกอันหนึ่งที่จะระบุลักษณะความเร็วและ “คุณภาพ” ของการเปลี่ยนแปลงในเส้นทาง หรืออีกนัยหนึ่งคือกำหนดอัตราส่วน ∆x/∆y สำหรับแต่ละ “เมตร” ของเส้นทาง

กราฟนี้จะเป็นอนุพันธ์เชิงภาพสำหรับเส้นทางเฉพาะ และจะอธิบายการเปลี่ยนแปลงในแต่ละช่วงเวลาที่สนใจอย่างเป็นกลาง มันง่ายมากที่จะตรวจสอบสิ่งนี้ ค่า ∆x/∆y นั้นไม่มีอะไรมากไปกว่าค่าดิฟเฟอเรนเชียล ความหมายเฉพาะ x และ y ให้เราใช้การสร้างความแตกต่างไม่ใช่กับพิกัดเฉพาะ แต่กับฟังก์ชันโดยรวม:

ฟังก์ชันอนุพันธ์และตรีโกณมิติ

ฟังก์ชันตรีโกณมิติเชื่อมโยงกับอนุพันธ์อย่างแยกไม่ออก สามารถเข้าใจได้จากรูปวาดต่อไปนี้ บนภาพ แกนพิกัดฟังก์ชั่น Y = f (x) ปรากฏขึ้น - เส้นโค้งสีน้ำเงิน

เค (x0; ฉ (x0)) – จุดใดก็ได้, x0 + ∆x คือส่วนเพิ่มตามแกน OX และ f (x0 + ∆x) คือส่วนเพิ่มตามแกน OY ที่จุด L

ลองวาดเส้นตรงผ่านจุด K และ L แล้วสร้าง สามเหลี่ยมมุมฉากเคแอลเอ็น หากคุณย้ายส่วน LN ทางจิตใจไปตามกราฟ Y = f (x) จากนั้นจุด L และ N จะมีแนวโน้มไปที่ค่า K (x0; f (x0)) ลองเรียกจุดนี้ว่าจุดเริ่มต้นแบบมีเงื่อนไขของกราฟ - ขีด จำกัด หากฟังก์ชันไม่มีที่สิ้นสุดอย่างน้อยในช่วงใดช่วงหนึ่งแนวโน้มนี้จะไม่มีที่สิ้นสุดเช่นกันและค่าจำกัดของมันใกล้กับ 0

ลักษณะของแนวโน้มนี้สามารถอธิบายได้ด้วยเส้นสัมผัสของจุดที่เลือก y = kx + b หรือโดยกราฟของอนุพันธ์ของฟังก์ชันดั้งเดิม dy - เส้นตรงสีเขียว

แต่ตรีโกณมิติที่นี่อยู่ที่ไหน! ทุกอย่างง่ายมาก ลองพิจารณาสามเหลี่ยมมุมฉาก KLN ค่าดิฟเฟอเรนเชียลสำหรับจุดเฉพาะ K คือแทนเจนต์ของมุม α หรือ ∠K:

ด้วยวิธีนี้ เราสามารถอธิบายความหมายทางเรขาคณิตของอนุพันธ์และความสัมพันธ์กับฟังก์ชันตรีโกณมิติได้

สูตรอนุพันธ์สำหรับฟังก์ชันตรีโกณมิติ

จะต้องจดจำการเปลี่ยนแปลงของไซน์, โคไซน์, แทนเจนต์และโคแทนเจนต์เมื่อพิจารณาหาอนุพันธ์

สองสูตรสุดท้ายไม่ใช่ข้อผิดพลาด ประเด็นก็คือ มีความแตกต่างระหว่างการกำหนดอนุพันธ์ของอาร์กิวเมนต์อย่างง่ายกับฟังก์ชันที่มีความสามารถเท่ากัน

ลองพิจารณาดู ตารางเปรียบเทียบด้วยสูตรอนุพันธ์ของไซนัส โคไซน์ แทนเจนต์ และโคแทนเจนต์:

สูตรยังได้มาจากอนุพันธ์ของอาร์คไซน์ อาร์คโคซีน อาร์กแทนเจนต์ และอาร์กโคแทนเจนต์ แม้ว่าจะไม่ค่อยมีการใช้มากนัก:

เป็นที่น่าสังเกตว่าสูตรข้างต้นไม่เพียงพอสำหรับการแก้ปัญหาที่ประสบความสำเร็จอย่างชัดเจน งานทั่วไปการสอบ Unified State สิ่งที่จะแสดงเมื่อแก้โจทย์ ตัวอย่างที่เป็นรูปธรรมค้นหาอนุพันธ์ของนิพจน์ตรีโกณมิติ

ออกกำลังกาย: จำเป็นต้องค้นหาอนุพันธ์ของฟังก์ชันและหาค่าของฟังก์ชันสำหรับ π/4:

สารละลาย: ในการค้นหา y’ จำเป็นต้องจำสูตรพื้นฐานสำหรับการแปลงฟังก์ชันดั้งเดิมเป็นอนุพันธ์ กล่าวคือ

เรื่อง:"อนุพันธ์ของฟังก์ชันตรีโกณมิติ"
ประเภทบทเรียน– บทเรียนในการบูรณาการความรู้
แบบฟอร์มบทเรียน– บทเรียนบูรณาการ
สถานที่เรียนในระบบบทเรียนสำหรับส่วนนี้- บทเรียนทั่วไป
มีการกำหนดเป้าหมายไว้อย่างครอบคลุม:

• เกี่ยวกับการศึกษา:รู้กฎของความแตกต่าง สามารถใช้กฎในการคำนวณอนุพันธ์ในการแก้สมการและอสมการได้ ปรับปรุงวิชา รวมถึงการคำนวณ ทักษะและความสามารถ ความถนัดทางด้านคอมพิวเตอร์;
• การพัฒนา:การพัฒนาทักษะทางปัญญาและตรรกะและความสนใจทางปัญญา
• เกี่ยวกับการศึกษา:ปลูกฝังความสามารถในการปรับตัวกับ สภาพที่ทันสมัยการฝึกอบรม.

วิธีการ:

• การสืบพันธุ์และการผลิต;
• การปฏิบัติและวาจา
• งานอิสระ
• การเรียนรู้แบบโปรแกรม ส.ส.;
• การรวมกันของหน้าผากกลุ่มและ งานของแต่ละบุคคล;
• การเรียนรู้ที่แตกต่าง;
• อุปนัยนิรนัย

รูปแบบการควบคุม:

• การสำรวจช่องปาก
• การควบคุมโปรแกรม,
• งานอิสระ,
• การมอบหมายงานส่วนบุคคลบนคอมพิวเตอร์,
• การทบทวนโดยผู้ทรงคุณวุฒิโดยใช้บัตรวินิจฉัยของนักเรียน

ระหว่างชั้นเรียน

ฉัน. เวลาจัดงาน

ครั้งที่สอง การอัพเดตความรู้อ้างอิง

ก) การสื่อสารเป้าหมายและวัตถุประสงค์:

• รู้กฎของความแตกต่าง สามารถใช้กฎในการคำนวณอนุพันธ์ในการแก้โจทย์ปัญหาสมการและอสมการได้
• ปรับปรุงวิชา รวมถึงการคำนวณ ทักษะและความสามารถ ความถนัดทางด้านคอมพิวเตอร์;
• พัฒนาทักษะทางปัญญาและตรรกะและ ความสนใจทางปัญญา;
• ปลูกฝังความสามารถในการปรับตัวให้เข้ากับสภาพการเรียนรู้สมัยใหม่

b) การทำซ้ำสื่อการศึกษา

กฎการคำนวณอนุพันธ์ (การทำซ้ำสูตรบนคอมพิวเตอร์พร้อมเสียง) เอกสาร 7.

1. อนุพันธ์ของไซน์คืออะไร?
2. อนุพันธ์ของโคไซน์คืออะไร?
3. อนุพันธ์ของแทนเจนต์คืออะไร?
4. อนุพันธ์ของโคแทนเจนต์คืออะไร?

สาม. งานช่องปาก

หาอนุพันธ์.
ตัวเลือกที่ 1.		ตัวเลือกที่ 2
ที่ = 2เอ็กซ์ + 5.		ที่ = 2เอ็กซ์ – 5.
ที่= 4คอส เอ็กซ์.		ที่= 3ซิน เอ็กซ์.
ที่= ทีจี เอ็กซ์+กะรัต เอ็กซ์.		ที่= ทีจี เอ็กซ์-ctg เอ็กซ์.
ที่= บาป 3 เอ็กซ์.		ที่= คอส 4 เอ็กซ์.
ตัวเลือกคำตอบ
	– 4ซิน เอ็กซ์		– 3คอส เอ็กซ์
1/คอส 2 เอ็กซ์+ 1/บาป 2 เอ็กซ์	1/คอส 2 เอ็กซ์–1/บาป 2 เอ็กซ์	1/บาป 2 เอ็กซ์–1/คอส 2 เอ็กซ์
	– 4ซิน4 เอ็กซ์		– 3cos3 เอ็กซ์

แลกเปลี่ยนสมุดบันทึก ในการ์ดวินิจฉัย ทำเครื่องหมายงานที่เสร็จสมบูรณ์อย่างถูกต้องด้วยเครื่องหมาย + และงานที่เสร็จสมบูรณ์ไม่ถูกต้องด้วยเครื่องหมาย –

IV. การแก้สมการโดยใช้อนุพันธ์

– จะหาจุดที่อนุพันธ์เป็นศูนย์ได้อย่างไร?

เพื่อหาจุดที่เป็นอนุพันธ์ ฟังก์ชั่นนี้เท่ากับศูนย์ คุณต้องการ:

– กำหนดลักษณะของฟังก์ชัน
– ค้นหาพื้นที่ คำจำกัดความของฟังก์ชัน,
– ค้นหาอนุพันธ์ของฟังก์ชันนี้
– แก้สมการ ฉ "(x) = 0,
- เลือกคำตอบที่ถูกต้อง.

ภารกิจที่ 1

ที่ให้ไว้: ที่ = เอ็กซ์-บาป x.
หา:จุดที่อนุพันธ์เป็นศูนย์
สารละลาย.ฟังก์ชันถูกกำหนดและสามารถหาอนุพันธ์ได้บนเซตของจำนวนจริงทั้งหมด เนื่องจากฟังก์ชันถูกกำหนดและสามารถหาอนุพันธ์ได้บนเซตของจำนวนจริงทั้งหมด ก(x) = xและ ที(x) = – บาป x.
เราได้รับกฎการแยกความแตกต่าง ฉ "(x) = (x-บาป x)" = (x)" – (บาป x)" = 1 – cos x.
ถ้า ฉ "(x) = 0 จากนั้น 1 – cos x = 0.
เพราะ x= 1/; ลองกำจัดความไม่ลงตัวในตัวส่วนออก เราจะได้ cos x = /2.
ตามสูตรครับ ที= ±ส่วนโค้ง ก+ 2n, n Z เราได้: เอ็กซ์= ± อาร์คคอส /2 + 2n, n Z
คำตอบ: x = ± /4 + 2n, n Z

V. การแก้สมการโดยใช้อัลกอริทึม

ค้นหาจุดที่อนุพันธ์หายไป

ฉ(x) = บาป x+คอส x

ฉ(x) = บาป 2 x – x

ฉ(x) = 2x+คอส(4 x – )

นักเรียนสามารถเลือกตัวอย่างใดก็ได้จากสามตัวอย่าง ตัวอย่างแรกได้รับการจัดอันดับ " 3 ", ที่สอง - " 4 ", ที่สาม - " 5 - วิธีแก้ปัญหาในโน้ตบุ๊กตามด้วยการตรวจสอบร่วมกัน นักเรียนคนหนึ่งตัดสินใจที่กระดาน หากวิธีแก้ปัญหาไม่ถูกต้อง นักเรียนจะต้องกลับไปที่อัลกอริทึมแล้วลองแก้ไขอีกครั้ง

การควบคุมโปรแกรม

ตัวเลือกที่ 1		ตัวเลือกที่ 2
ย = 2เอ็กซ์ 3		ย = 3เอ็กซ์ 2
ย = 1/4 เอ็กซ์ 4 + 2เอ็กซ์ 2 – 7		ย = 1/2 เอ็กซ์ 4 + 4เอ็กซ์ + 5
ย = เอ็กซ์ 3 + 4เอ็กซ์ 2 – 3เอ็กซ์. แก้สมการ ย " = 0		ย = 2เอ็กซ์ 3 – 9เอ็กซ์ 2 + 12เอ็กซ์ + 7. แก้สมการ ย " = 0.
ย= บาป 2 เอ็กซ์– คอส 3 เอ็กซ์.		ย= คอส 2 เอ็กซ์– บาป 3 เอ็กซ์.
ย= ทีจี เอ็กซ์–ctg( เอ็กซ์ + /4).		ย=กะทิ เอ็กซ์+ ทีจี( เอ็กซ์ – /4).
ย= บาป 2 เอ็กซ์.		ย= คอส 2 เอ็กซ์.
ตัวเลือกคำตอบ
เมื่อได้สูตรแรกของตาราง เราจะเริ่มจากคำจำกัดความของฟังก์ชันอนุพันธ์ ณ จุดหนึ่ง เอาล่ะเอาที่ไหน. x- ใดๆ เบอร์จริง, นั่นคือ, x– จำนวนใดๆ จากโดเมนนิยามของฟังก์ชัน ให้เราเขียนขีด จำกัด ของอัตราส่วนของการเพิ่มขึ้นของฟังก์ชันต่อการเพิ่มขึ้นของอาร์กิวเมนต์ที่ : ควรสังเกตว่าภายใต้เครื่องหมายขีด จำกัด จะได้นิพจน์ซึ่งไม่ใช่ความไม่แน่นอนของศูนย์หารด้วยศูนย์เนื่องจากตัวเศษไม่มีค่าน้อยที่สุด แต่เป็นศูนย์อย่างแม่นยำ กล่าวอีกนัยหนึ่ง การเพิ่มขึ้นของฟังก์ชันคงที่จะเป็นศูนย์เสมอ ดังนั้น, อนุพันธ์ของฟังก์ชันคงที่เท่ากับศูนย์ตลอดขอบเขตคำจำกัดความทั้งหมด. อนุพันธ์ของฟังก์ชันยกกำลัง สูตรอนุพันธ์ ฟังก์ชั่นพลังงานดูเหมือน โดยที่เลขชี้กำลัง พี- จำนวนจริงใดๆ ก่อนอื่นให้เราพิสูจน์สูตรของเลขชี้กำลังธรรมชาติ นั่นก็คือ สำหรับ พี = 1, 2, 3, … เราจะใช้คำจำกัดความของอนุพันธ์ ให้เราเขียนขีด จำกัด ของอัตราส่วนของการเพิ่มขึ้นของฟังก์ชันกำลังต่อการเพิ่มขึ้นของอาร์กิวเมนต์: เพื่อให้นิพจน์ในตัวเศษง่ายขึ้น เราจะใช้สูตรทวินามของนิวตัน: เพราะฉะนั้น, สิ่งนี้พิสูจน์สูตรสำหรับอนุพันธ์ของฟังก์ชันกำลังของเลขชี้กำลังธรรมชาติ อนุพันธ์ของฟังก์ชันเลขชี้กำลัง เรานำเสนอที่มาของสูตรอนุพันธ์ตามคำจำกัดความ: เรามาถึงความไม่แน่นอนแล้ว เพื่อขยายมัน เราแนะนำตัวแปรใหม่และที่ . แล้ว . ในการเปลี่ยนผ่านครั้งล่าสุด เราใช้สูตรในการเปลี่ยนไปใช้ฐานลอการิทึมใหม่ แทนที่ด้วยขีดจำกัดเดิม: หากเรานึกถึงขีดจำกัดอันน่าทึ่งอันที่สอง เราจะได้สูตรอนุพันธ์ของฟังก์ชันเลขชี้กำลัง: อนุพันธ์ของฟังก์ชันลอการิทึม ขอให้เราพิสูจน์สูตรเพื่อหาอนุพันธ์ของฟังก์ชันลอการิทึมสำหรับทุกคน xจากขอบเขตของคำจำกัดความและค่าฐานที่ถูกต้องทั้งหมด กลอการิทึม ตามคำจำกัดความของอนุพันธ์เรามี: ดังที่คุณสังเกตเห็น ในระหว่างการพิสูจน์ การแปลงได้ดำเนินการโดยใช้คุณสมบัติของลอการิทึม ความเท่าเทียมกัน เป็นจริงเนื่องจากขีดจำกัดที่น่าทึ่งประการที่สอง อนุพันธ์ของฟังก์ชันตรีโกณมิติ เพื่อให้ได้สูตรอนุพันธ์ของฟังก์ชันตรีโกณมิติ เราจะต้องจำสูตรตรีโกณมิติบางสูตร รวมถึงขีดจำกัดแรกที่น่าทึ่งด้วย ตามนิยามของอนุพันธ์ของฟังก์ชันไซน์ที่เรามี . ลองใช้สูตรผลต่างของไซน์: ยังคงต้องหันไปสู่ขีดจำกัดแรกที่น่าทึ่ง: ดังนั้นอนุพันธ์ของฟังก์ชัน บาป xมี เพราะ x. สูตรสำหรับอนุพันธ์ของโคไซน์ได้รับการพิสูจน์ด้วยวิธีเดียวกันทุกประการ ดังนั้นอนุพันธ์ของฟังก์ชัน เพราะ xมี –บาป x. เราจะได้สูตรสำหรับตารางอนุพันธ์สำหรับแทนเจนต์และโคแทนเจนต์โดยใช้กฎการหาอนุพันธ์ที่ได้รับการพิสูจน์แล้ว (อนุพันธ์ของเศษส่วน) อนุพันธ์ของฟังก์ชันไฮเปอร์โบลิก กฎของการสร้างความแตกต่างและสูตรสำหรับอนุพันธ์ของฟังก์ชันเลขชี้กำลังจากตารางอนุพันธ์ทำให้เราสามารถหาสูตรสำหรับอนุพันธ์ของไซน์ไฮเปอร์โบลิก, โคไซน์, แทนเจนต์และโคแทนเจนต์ อนุพันธ์ของฟังก์ชันผกผัน เพื่อหลีกเลี่ยงความสับสนระหว่างการนำเสนอ ให้เราแสดงตัวห้อยอาร์กิวเมนต์ของฟังก์ชันที่ใช้สร้างความแตกต่าง นั่นคือ มันเป็นอนุพันธ์ของฟังก์ชัน ฉ(x)โดย x. ตอนนี้เรามากำหนดกัน กฎการหาอนุพันธ์ ฟังก์ชันผกผัน. ปล่อยให้ฟังก์ชั่น ย = ฉ(x)และ x = ก(ย)ผกผันซึ่งกันและกัน กำหนดตามช่วงเวลาและตามลำดับ ถ้า ณ จุดหนึ่ง มีอนุพันธ์จำกัดที่ไม่เป็นศูนย์ของฟังก์ชัน ฉ(x)จากนั้น ณ จุดนั้นจะมีอนุพันธ์จำกัดของฟังก์ชันผกผัน ก(ย), และ - ในอีกโพสต์หนึ่ง . กฎนี้สามารถกำหนดรูปแบบใหม่ได้ xจากช่วงเวลา แล้วเราจะได้ . มาตรวจสอบความถูกต้องของสูตรเหล่านี้กัน ลองหาฟังก์ชันผกผันของลอการิทึมธรรมชาติกัน (ที่นี่ ยเป็นฟังก์ชัน และ x- การโต้แย้ง). เมื่อแก้สมการนี้แล้ว xเราได้รับ (ที่นี่ xเป็นฟังก์ชัน และ ย– ข้อโต้แย้งของเธอ) นั่นคือ, และฟังก์ชันผกผันซึ่งกันและกัน จากตารางอนุพันธ์เราจะเห็นว่า และ . ตรวจสอบให้แน่ใจว่าสูตรในการค้นหาอนุพันธ์ของฟังก์ชันผกผันทำให้เราได้ผลลัพธ์เดียวกัน: นำเสนออนุพันธ์ของฟังก์ชันตรีโกณมิติผกผันและที่มาของสูตร นอกจากนี้ยังมีการแสดงนิพจน์สำหรับอนุพันธ์ลำดับที่สูงกว่าด้วย ลิงค์ไปยังหน้าที่มีมากขึ้น คำชี้แจงโดยละเอียดสูตรผลลัพธ์ ขั้นแรก เราได้สูตรสำหรับอนุพันธ์อาร์กไซน์ อนุญาต ย= อาร์คซิน x. เนื่องจากอาร์กไซน์เป็นฟังก์ชันผกผันของไซน์ . โดยที่ y คือฟังก์ชันของ x แยกความแตกต่างด้วยความเคารพกับตัวแปร x: . เราใช้: . ดังนั้นเราจึงพบว่า: . เพราะว่าแล้ว. แล้ว . และสูตรก่อนหน้าจะอยู่ในรูปแบบ: - . จากที่นี่ . ด้วยวิธีนี้ คุณจะได้สูตรสำหรับอนุพันธ์ของอาร์คโคไซน์ อย่างไรก็ตาม การใช้สูตรที่เกี่ยวข้องกับฟังก์ชันตรีโกณมิติผกผันจะง่ายกว่า: . แล้ว คำอธิบายโดยละเอียดเพิ่มเติมแสดงอยู่ในหน้า “การได้มาของอนุพันธ์ของอาร์คไซน์และอาร์กโคไซน์” มีให้ที่มาของอนุพันธ์ในสองวิธี - กล่าวถึงข้างต้นและตามสูตรอนุพันธ์ของฟังก์ชันผกผัน ที่มาของอนุพันธ์ของอาร์กแทนเจนต์และอาร์กโคแทนเจนต์ ในทำนองเดียวกัน เราจะหาอนุพันธ์ของอาร์กแทนเจนต์และอาร์กโคแทนเจนต์ ย= อนุญาต. อาร์คแทน เอ็กซ์ . อาร์กแทนเจนต์เป็นฟังก์ชันผกผันของแทนเจนต์: . แยกความแตกต่างด้วยความเคารพกับตัวแปร x: . ดังนั้นเราจึงพบว่า: . เราใช้สูตรสำหรับอนุพันธ์ของฟังก์ชันที่ซับซ้อน: . อนุพันธ์ของอาร์คโคแทนเจนต์: ในทำนองเดียวกัน เราจะหาอนุพันธ์ของอาร์กแทนเจนต์และอาร์กโคแทนเจนต์ . อนุพันธ์อาร์คไซน์ . เราได้พบอนุพันธ์อันดับหนึ่งของอาร์คไซน์แล้ว: ; . โดยการแยกความแตกต่าง เราจะพบอนุพันธ์อันดับสอง: . นอกจากนี้ยังสามารถเขียนในรูปแบบต่อไปนี้: จากที่นี่เราได้รับสมการเชิงอนุพันธ์ . ซึ่งพอใจกับอนุพันธ์อาร์คไซน์ของลำดับที่หนึ่งและที่สอง: การแยกสมการนี้ทำให้เราสามารถหาอนุพันธ์ลำดับที่สูงกว่าได้ อนุพันธ์ของอาร์คไซน์ลำดับที่ n อนุพันธ์ของอาร์คไซน์ของลำดับ n มี: , มุมมองถัดไป ; . พหุนามของดีกรีอยู่ที่ไหน . ถูกกำหนดโดยสูตร: ที่นี่ . . พหุนามเป็นไปตามสมการเชิงอนุพันธ์: อนุพันธ์ของอาร์คโคไซน์ลำดับที่ n . อนุพันธ์อาร์กโคไซน์ได้มาจากอนุพันธ์อาร์กไซน์โดยใช้สูตรตรีโกณมิติ: . ดังนั้นอนุพันธ์ของฟังก์ชันเหล่านี้จึงแตกต่างกันเพียงเครื่องหมาย: อนุพันธ์ของอาร์กแทนเจนต์ . อนุญาต . เราพบอนุพันธ์ของอาร์คโคแทนเจนต์ของลำดับแรก: . แบ่งเศษส่วนให้อยู่ในรูปแบบที่ง่ายที่สุด: นี่คือหน่วยจินตภาพ, . เราแยกความแตกต่างเพียงครั้งเดียวและนำเศษส่วนมาเป็นตัวส่วนร่วม: . การทดแทน เราได้รับ: อนุพันธ์ของอาร์กแทนเจนต์ลำดับที่ n ; . ดังนั้นอนุพันธ์ของอาร์กแทนเจนต์ของลำดับที่ n สามารถแสดงได้หลายวิธี: อนุพันธ์ของอาร์คโคแทนเจนต์ . ปล่อยให้มันเป็นตอนนี้ ลองใช้สูตรเชื่อมต่อฟังก์ชันตรีโกณมิติผกผัน: . จากนั้นอนุพันธ์ลำดับที่ n ของส่วนโค้งแทนเจนต์จะแตกต่างกันเฉพาะสัญญาณจากอนุพันธ์ของส่วนโค้งแทนเจนต์: . การทดแทน เราพบว่า: อ้างอิง: น.เอ็ม. กันเตอร์, อาร์.โอ. Kuzmin การรวบรวมปัญหาบนคณิตศาสตร์ที่สูงขึ้น