Намирането на координатите на вектор е доста често срещано условие за много задачи в математиката. Способността да намерите векторни координати ще ви помогне в други, повече сложни задачис подобни теми. В тази статия ще разгледаме формулата за намиране на векторни координати и няколко задачи.
Намиране на координатите на вектор в равнина
Какво е самолет? Равнината се счита за двумерно пространство, пространство с две измерения (измерението x и измерението y). Например хартията е плоска. Повърхността на масата е плоска. Всяка необемна фигура (квадрат, триъгълник, трапец) също е равнина. По този начин, ако в изявлението на проблема трябва да намерите координатите на вектор, който лежи на равнина, веднага си спомняме за x и y. Можете да намерите координатите на такъв вектор както следва: векторни координати AB = (xB - xA; yB - xA). От формулата става ясно, че от координатите крайна точкатрябва да извадите координатите на началната точка.
Пример:
- Вектор CD има начална (5; 6) и крайна (7; 8) координати.
- Намерете координатите на самия вектор.
- Използвайки горната формула, получаваме следния израз: CD = (7-5; 8-6) = (2; 2).
- Така координатите на вектора CD = (2; 2).
- Съответно координатата x е равна на две, координатата y също е две.
Намиране на координатите на вектор в пространството
Какво е пространство? Пространството вече е триизмерно измерение, където са дадени 3 координати: x, y, z. Ако трябва да намерите вектор, който лежи в пространството, формулата практически не се променя. Добавя се само една координата. За да намерите вектор, трябва да извадите координатите на началото от крайните координати. AB = (xB - xA; yB - yA; zB - zA)
Пример:
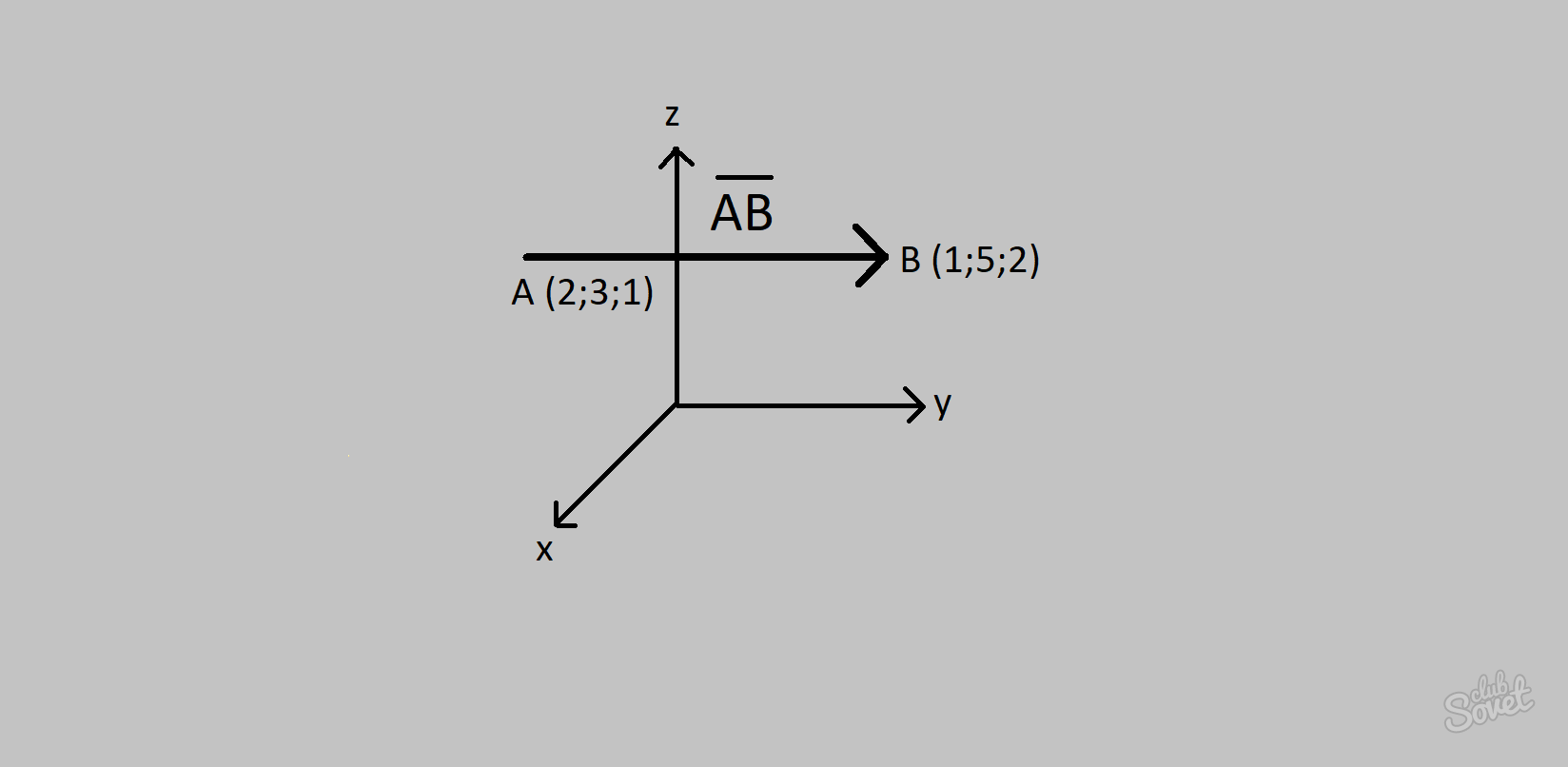
- Вектор DF има начален (2; 3; 1) и краен (1; 5; 2).
- Прилагайки горната формула, получаваме: Векторни координати DF = (1-2; 5-3; 2-1) = (-1; 2; 1).
- Не забравяйте, че координатната стойност може да бъде отрицателна, няма проблем.
Как да намеря векторни координати онлайн?
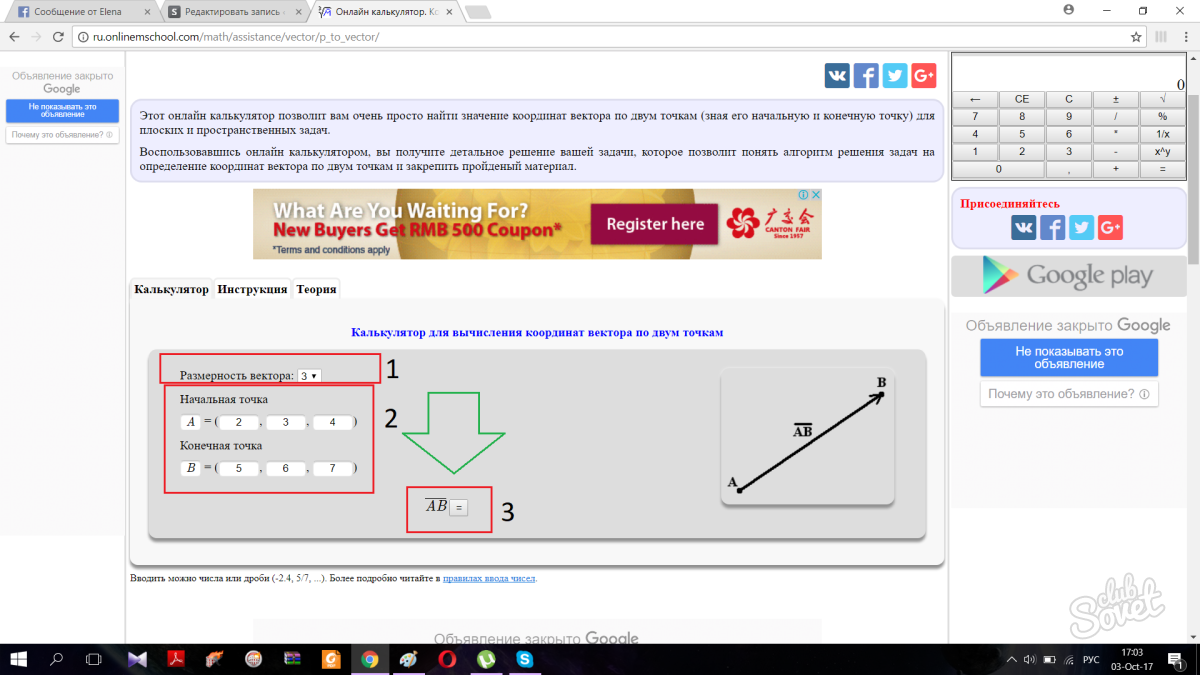
Ако по някаква причина не искате сами да намерите координатите, можете да използвате онлайн калкулатор. За да започнете, изберете векторното измерение. Размерността на вектора отговаря за неговите размери. Размерност 3 означава, че векторът е в пространството, размерност 2 означава, че е в равнината. След това въведете координатите на точките в съответните полета и програмата ще определи за вас координатите на самия вектор. Много е просто.
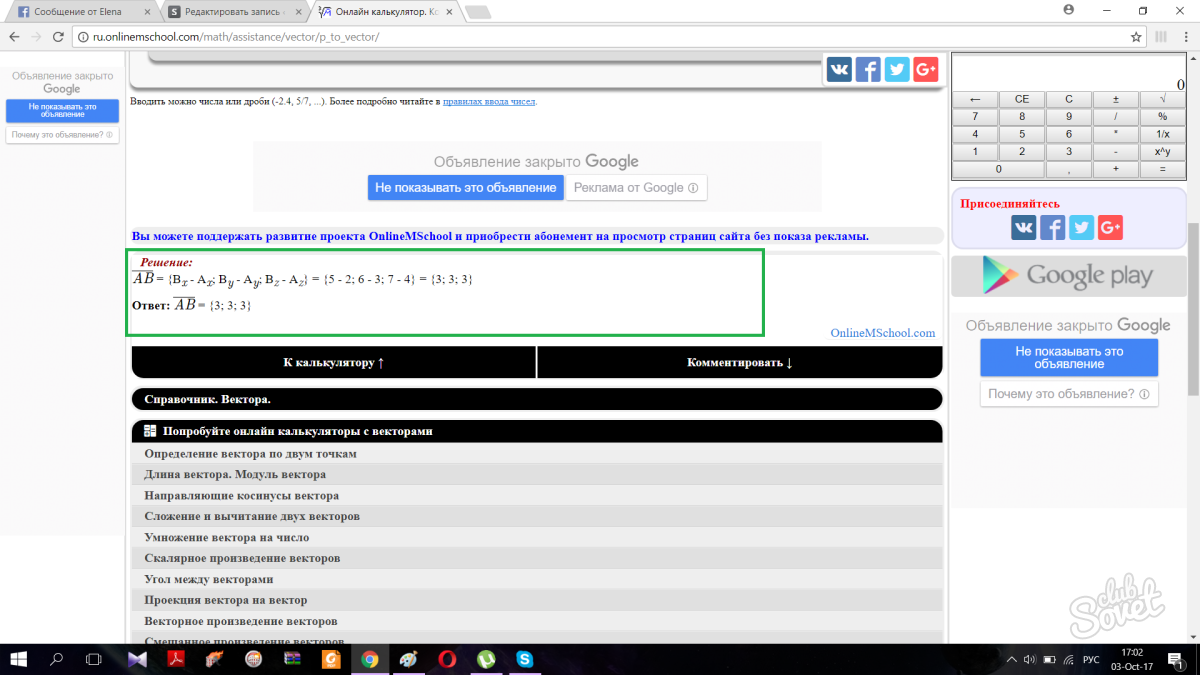
Като щракнете върху бутона, страницата автоматично ще се превърти надолу и ще ви даде правилния отговор заедно със стъпките за решение.
Препоръчва се да се учи добре тази тема, защото концепцията за вектор се среща не само в математиката, но и във физиката. Студенти от факултета Информационни технологииТе също изучават темата за векторите, но на по-сложно ниво.
Ако са дадени две точки от равнината и , тогава векторът има следните координати:
Ако са дадени две точки в пространството и , тогава векторът има следните координати:
т.е. от координатите на края на векторатрябва да извадите съответните координати началото на вектора.
Упражнение:За същите точки запишете формулите за намиране на координатите на вектора. Формули в края на урока.
Пример 1
Дадени са две точки от равнината и . Намерете векторни координати
Решение:по съответната формула:
Като алтернатива може да се използва следният запис:
Естетите ще решат това:
Лично аз съм свикнал с първия вариант на записа.
отговор:
Според условието не е необходимо да се изгражда чертеж (което е типично за задачите аналитична геометрия), но за да изясня някои точки за манекени, няма да бъда твърде мързелив:
Определено трябва да разберете разлика между координатите на точката и векторните координати:
Координати на точки– това са обикновени координати в правоъгълна координатна система. Поставете точки координатна равнинаМисля, че всеки може от 5-6 клас. Всяка точка има строго определено място в равнината и не може да бъде преместена никъде.
Координатите на векторае разширяването му по отношение на основата, в в този случай. Всеки вектор е свободен, така че ако е необходимо, можем лесно да го отдалечим от друга точка в равнината. Интересно е, че за векторите изобщо не е нужно да изграждате оси, правоъгълна системакоординати, трябва ви само основа, в този случай ортонормална основа на равнината.
Записите на координати на точки и координати на вектори изглеждат подобни: , и значение на координатитеабсолютно различни, и трябва да сте добре запознати с тази разлика. Тази разлика, разбира се, важи и за пространството.
Дами и господа, нека напълним ръцете си:
Пример 2
а) Дадени са точки и . Намерете вектори и .
б) Дадени са точки и . Намерете вектори и .
в) Дадени са точки и . Намерете вектори и .
г) Дават се точки. Намерете вектори.
Може би това е достатъчно. Това са примери за независимо решение, опитайте се да не ги пренебрегвате, ще ви се отплати ;-). Няма нужда да правите чертежи. Решения и отговори в края на урока.
Какво е важно при решаването на задачи по аналитична геометрия?Важно е да бъдете ИЗКЛЮЧИТЕЛНО ВНИМАТЕЛНИ, за да избегнете майсторската грешка „две плюс две е равно на нула“. Веднага се извинявам, ако съм сбъркал някъде =)
Как да намерим дължината на сегмент?
Дължината, както вече беше отбелязано, се обозначава със знака за модул.
Ако са дадени две точки от равнината и , тогава дължината на сегмента може да се изчисли с помощта на формулата
Ако са дадени две точки в пространството и , тогава дължината на сегмента може да се изчисли с помощта на формулата
Забележка: Формулите ще останат правилни, ако съответните координати се разменят: И , но първият вариант е по-стандартен
Пример 3
Решение:по съответната формула:
отговор:
За по-голяма яснота ще направя чертеж 
сегмент – това не е вектор, и, разбира се, не можете да го преместите никъде. Освен това, ако рисувате в мащаб: 1 единица. = 1 см (две клетки от тетрадка), тогава полученият отговор може да се провери с обикновена линийка чрез директно измерване на дължината на отсечката.
Да, решението е кратко, но в него има още няколко важни точкикоето бих искал да изясня:
Първо, в отговора поставяме измерението: „единици“. В условието не пише КАКВО е, милиметри, сантиметри, метри или километри. Следователно, математически правилното решение би било общата формулировка: „единици“ - съкратено като „единици“.
Второ, нека повторим училищен материал, което е полезно не само за разглеждания проблем:
Моля, обърнете внимание важно техническа техника – премахване на множителя изпод корена. В резултат на изчисленията имаме резултат и добрият математически стил включва премахване на фактора под корена (ако е възможно). По-подробно процесът изглежда така: . Разбира се, да оставим отговора такъв, какъвто е, няма да е грешка - но със сигурност би било недостатък и сериозен аргумент за заяждане от страна на учителя.
Ето и други често срещани случаи: 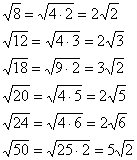
Често има достатъчно в основата голям брой, Например. Какво да правим в такива случаи? С помощта на калкулатора проверяваме дали числото се дели на 4: . Да, беше напълно разделено, така че: ![]() . Или може би числото отново може да се раздели на 4? . Така:
. Или може би числото отново може да се раздели на 4? . Така: ![]() . Последната цифра на числото е нечетна, така че разделянето на 4 за трети път очевидно няма да работи. Нека се опитаме да разделим на девет: . В резултат на това:
. Последната цифра на числото е нечетна, така че разделянето на 4 за трети път очевидно няма да работи. Нека се опитаме да разделим на девет: . В резултат на това:
Готови.
Заключение:ако под корена получим число, което не може да бъде извлечено като цяло, тогава се опитваме да премахнем фактора от под корена - с помощта на калкулатор проверяваме дали числото се дели на: 4, 9, 16, 25, 36, 49 и др.
По време на решението различни задачикорените са често срещани, винаги се опитвайте да извличате фактори от корена, за да избегнете по-ниска оценка и ненужни проблеми с финализирането на вашите решения въз основа на коментарите на учителя.
Нека също повторим корени на квадрат и други степени:
Правила за действия със степени в общ изгледможе да се намери в училищен учебникпо алгебра, но мисля, че от дадените примери вече всичко или почти всичко е ясно.
Задача за самостоятелно решение с отсечка в пространството:
Пример 4
Дават се точки и . Намерете дължината на отсечката.
Решението и отговорът са в края на урока.
Как да намерим дължината на вектор?
Ако е даден плосък вектор, тогава неговата дължина се изчислява по формулата.
Ако е даден пространствен вектор, тогава неговата дължина се изчислява по формулата ![]() .
.
Тези формули (както и формулите за дължината на отсечка) се извеждат лесно с помощта на добре известната Питагорова теорема.
Пример 5
Дават се точки и . Намерете дължината на вектора.
Взех същите точки като в Пример 3.
Решение:Първо, нека намерим вектора:
Използвайки формулата, изчисляваме дължината на вектора:
отговор:
Не забравяйте да посочите размерността – „единици“! Между другото, винаги ли е необходимо да се изчислява приблизителна стойност (в в този пример 8.94), ако това не се изисква в условието? От моя гледна точка няма да е излишно; липсата на приблизителна стойност води до придирчивост. Препоръчително е да закръглите до 2-3 знака след десетичната запетая.
Нека направим чертеж към задачата:
Каква е основната разлика от пример 3? Разликата е, че тук говорим за вектор, а не за сегмент. Векторът може да бъде преместен във всяка точка в равнината.
Какви са приликите между Пример 3 и Пример 5? Геометрично очевидно е, че дължината на сегмента е равна на дължината на вектора. Също така е очевидно, че дължината на вектора ще бъде същата. В резултат на това: ![]() .
.
б) Дадени са векторите , , и . Намерете техните дължини.
Решения и отговори в края на урока.
В тази статия ще започнем да обсъждаме една „вълшебна пръчка“, която ще ви позволи да намалите много геометрични проблеми до проста аритметика. Тази „пръчка“ може да направи живота ви много по-лесен, особено когато се чувствате несигурни относно строителството пространствени фигури, раздели и т.н. Всичко това изисква известно въображение и практически умения. Методът, който ще започнем да разглеждаме тук, ще ви позволи почти напълно да се абстрахирате от всякакъв вид геометрични конструкциии разсъждение. Методът се нарича "координативен метод". В тази статия ще разгледаме следните въпроси:
- Координатна равнина
- Точки и вектори на равнината
- Построяване на вектор от две точки
- Дължина на вектора (разстояние между две точки).
- Координати на средата на сегмента
- Точково произведение на вектори
- Ъгъл между два вектора
Мисля, че вече се досетихте защо координатният метод се нарича така? Точно така, получи това име, защото не работи с геометрични обекти, и с тях числови характеристики(координати). А самата трансформация, която ни позволява да преминем от геометрия към алгебра, се състои във въвеждането на координатна система. Ако оригиналната фигура е плоска, тогава координатите са двуизмерни, а ако фигурата е триизмерна, тогава координатите са триизмерни. В тази статия ще разгледаме само двумерния случай. И основната цел на статията е да ви научи как да използвате някои основни техникикоординатен метод (те понякога се оказват полезни при решаване на задачи по планиметрия в част Б на Единния държавен изпит). Следващите два раздела по тази тема са посветени на обсъждане на методите за решаване на задачи C2 (проблемът на стереометрията).
Къде би било логично да започнем обсъждането на метода на координатите? Вероятно от концепцията за координатна система. Спомнете си кога я срещнахте за първи път. Струва ми се, че в 7 клас, когато научихте за съществуването линейна функция, Например. Нека ви напомня, че го изградихте точка по точка. помниш ли Вие избрахте произволно число, го замести във формулата и го изчисли по този начин. Например ако, тогава, ако, тогава и т.н. Какво получихте в крайна сметка? И получихте точки с координати: и. След това нарисувате „кръст“ (координатна система), избирате върху него мащаб (колко клетки ще имате като единичен сегмент) и отбелязвате точките, които сте получили върху него, които след това свързвате с права линия; линия е графиката на функцията.
Тук има няколко точки, които трябва да ви бъдат обяснени малко по-подробно:
1. Избирате един сегмент от съображения за удобство, така че всичко да пасне красиво и компактно в чертежа
2. Прието е оста да върви отляво надясно, а оста да върви отдолу нагоре
3. Те се пресичат под прав ъгъл, а точката на тяхното пресичане се нарича начало. Обозначава се с буква.
4. При изписване на координатите на точка, например, отляво в скоби има координатата на точката по оста, а отдясно по оста. По-специално, това просто означава, че в точката
5. За да зададете всяка точка на координатна ос, трябва да посочите координатите му (2 числа)
6. За всяка точка, лежаща на оста,
7. За всяка точка, лежаща на оста,
8. Оста се нарича ос x
9. Оста се нарича у-ос
Сега нека го направим с вас следващата стъпка: Нека отбележим две точки. Нека свържем тези две точки с отсечка. И ще поставим стрелката, сякаш рисуваме сегмент от точка до точка: тоест ще направим нашия сегмент насочен!

Помните ли как се нарича друг насочен сегмент? Точно така, нарича се вектор!
Така че, ако свържем точка с точка, и началото ще бъде точка А, а краят ще бъде точка Б,тогава получаваме вектор. Вие също сте правили тази конструкция в 8 клас, помните ли?
Оказва се, че векторите, подобно на точките, могат да бъдат обозначени с две числа: тези числа се наричат векторни координати. Въпрос: Смятате ли, че е достатъчно да знаем координатите на началото и края на един вектор, за да намерим неговите координати? Оказва се, че да! И това се прави много просто:
Така, тъй като във вектор точката е началото, а краят е краят, векторът има следните координати:
Например, ако, тогава координатите на вектора
Сега нека направим обратното, да намерим координатите на вектора. Какво трябва да променим за това? Да, трябва да размените началото и края: сега началото на вектора ще бъде в точката, а краят ще бъде в точката. След това:
Погледнете внимателно, каква е разликата между векторите и? Единствената им разлика са знаците в координатите. Те са противоположности. Този факт обикновено се записва така:
Понякога, ако не е конкретно посочено коя точка е началото на вектора и коя е краят, тогава векторите се означават с повече от две с главни буквии една малка буква, например: и т.н.
Сега малко практикасебе си и намерете координатите на следните вектори:
преглед:
Сега решете един малко по-сложен проблем:
Вектор с начало в точка има ко-или-ди-на-ти. Намерете точките abs-cis-su.
Всичко това е доста прозаично: Нека са координатите на точката. Тогава
Компилирах системата въз основа на дефиницията какво представляват векторните координати. Тогава точката има координати. Интересуваме се от абсцисата. Тогава
отговор:
Какво друго можете да правите с вектори? Да, почти всичко е същото като с обикновени числа(освен че не можете да разделяте, но можете да умножавате по два начина, единият от които ще обсъдим тук малко по-късно)
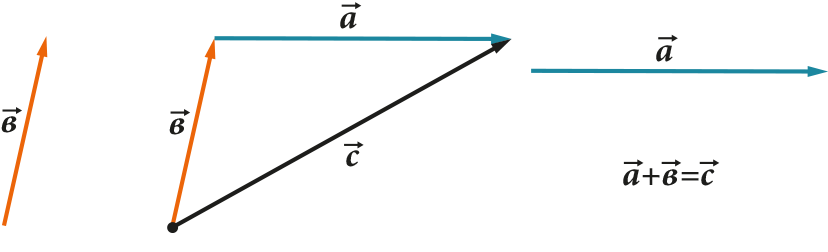
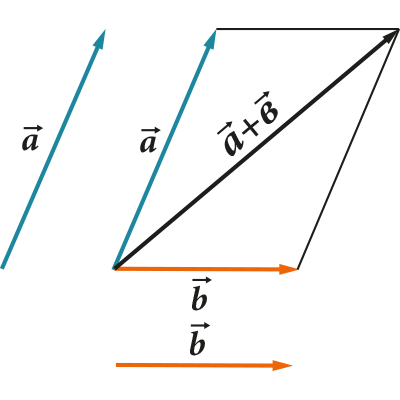
- Векторите могат да се добавят един към друг
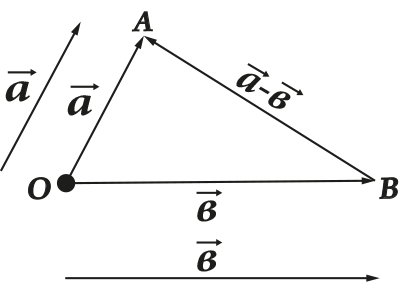
- Векторите могат да се изваждат един от друг
- Векторите могат да бъдат умножени (или разделени) по произволно различно от нула число
- Векторите могат да се умножават един по друг
Всички тези операции имат много ясно геометрично представяне. Например правилото на триъгълника (или успоредника) за събиране и изваждане:
Векторът се разтяга, свива или променя посоката си, когато се умножи или раздели на число:

Тук обаче ще ни интересува въпросът какво се случва с координатите.
1. Когато събираме (изваждаме) два вектора, добавяме (изваждаме) техните координати елемент по елемент. това е:
2. При умножаване (разделяне) на вектор с число, всичките му координати се умножават (разделят) на това число:
Например:
· Намерете количеството ко-или-ди-нат век към ра.
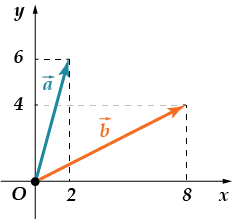
Нека първо намерим координатите на всеки от векторите. И двете имат един и същ произход - началната точка. Краищата им са различни. Тогава, . Сега нека изчислим координатите на вектора. Тогава сумата от координатите на получения вектор е равна.
отговор:
Сега решете сами следния проблем:
· Намерете сумата от векторни координати
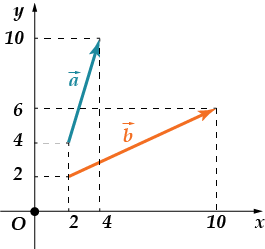
Ние проверяваме:
Нека сега разгледаме следната задача: имаме две точки на координатната равнина. Как да намерим разстоянието между тях? Нека първата точка е и втората. Нека означим разстоянието между тях с. Нека направим следния чертеж за по-голяма яснота:
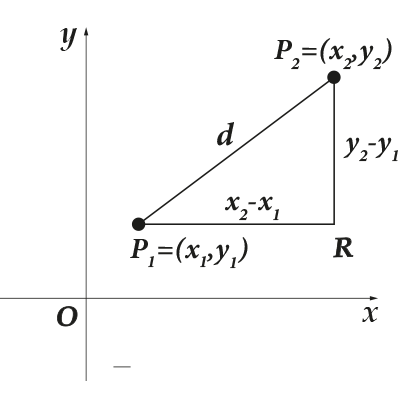
какво направих Първо се свързах точки и, асъщо начерта линия от точката, успоредна на оста, и от точката начертах права, успоредна на оста. Дали са се пресичали в точка, образувайки забележителна фигура? Какво е толкова специално за нея? Да, вие и аз знаем почти всичко за правоъгълния триъгълник. Е, Питагоровата теорема със сигурност. Търсеният сегмент е хипотенузата на този триъгълник, а сегментите са краката. Какви са координатите на точката? Да, лесно се намират от картинката: Тъй като отсечките са успоредни на осите и съответно дължините им се намират лесно: ако означим дължините на отсечките съответно с, то
Сега нека използваме Питагоровата теорема. Знаем дължините на краката, ще намерим хипотенузата:
По този начин разстоянието между две точки е корен от сумата на квадратите на разликите от координатите. Или - разстоянието между две точки е дължината на отсечката, която ги свързва.
Лесно се вижда, че разстоянието между точките не зависи от посоката. След това:
Оттук правим три извода:
Нека се упражним малко за изчисляване на разстоянието между две точки:
Например, ако, тогава разстоянието между и е равно на
Или да отидем по друг начин: да намерим координатите на вектора
И намерете дължината на вектора:
Както можете да видите, това е едно и също!
Сега упражнете малко себе си:
Задача: намерете разстоянието между посочените точки:
Ние проверяваме:
Ето още няколко задачи, използващи същата формула, въпреки че звучат малко по-различно:

1. Намерете квадрата на дължината на клепача.

2. Намерете квадрата на дължината на клепача
1. И това е за внимание) Вече намерихме координатите на векторите по-рано: . Тогава векторът има координати. Квадратът на неговата дължина ще бъде равен на:
2. Намерете координатите на вектора
Тогава квадратът на неговата дължина е
Нищо сложно, нали? Проста аритметика, нищо повече.
Следващите проблеми не могат да бъдат класифицирани еднозначно;
1. Намерете синуса на ъгъла от разреза, свързващ точката с абсцисната ос.
 И
И
Как ще процедираме тук? Трябва да намерим синуса на ъгъла между и оста. Къде можем да търсим синус? Точно така, в правоъгълен триъгълник. И така, какво трябва да направим? Изградете този триъгълник!
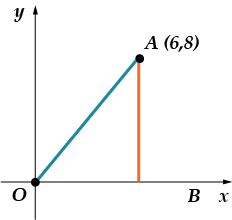
Тъй като координатите на точката са и, тогава отсечката е равна на и отсечката. Трябва да намерим синуса на ъгъла. Нека ви напомня, че синус е отношение срещуположния краккъм хипотенузата, тогава
Какво ни остава да правим? Намерете хипотенузата. Можете да направите това по два начина: като използвате Питагоровата теорема (краката са известни!) или като използвате формулата за разстоянието между две точки (всъщност, същото като първия метод!). Ще тръгна по втория път:
отговор:
Следващата задача ще ви се стори още по-лесна. Тя е на координатите на точката.
Задача 2.От точката per-pen-di-ku-lyar се спуска върху оста на ab-ciss. Nai-di-te abs-cis-su os-no-va-niya per-pen-di-ku-la-ra.
Да направим чертеж:
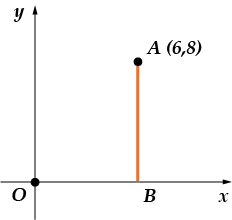
Основата на перпендикуляра е точката, в която той пресича оста x (ос), за мен това е точка. Фигурата показва, че има координати: . Интересуваме се от абсцисата - тоест компонентът "x". Тя е равна.
отговор: .
Задача 3.В условия предишна задачанамерете сумата от разстоянията от точката до координатните оси.
Задачата като цяло е елементарна, ако знаеш какво е разстоянието от точка до осите. знаеш ли Надявам се, но все пак ще ви напомня:
И така, в моя чертеж точно по-горе, начертах ли вече един такъв перпендикуляр? На коя ос е? Към оста. И каква е дължината му тогава? Тя е равна. Сега сами начертайте перпендикуляр на оста и намерете дължината му. Ще бъде равно, нали? Тогава сборът им е равен.
отговор: .
Задача 4.В условията на задача 2 намерете ординатата на точката, симетрична точкаспрямо абсцисната ос.
Мисля, че интуитивно ви е ясно какво е симетрия? Много обекти го имат: много сгради, маси, самолети, много геометрични форми: топка, цилиндър, квадрат, ромб и др. Грубо казано, симетрията може да се разбира по следния начин: една фигура се състои от две (или повече) еднакви половини. Тази симетрия се нарича аксиална симетрия. Какво тогава е ос? Това е точно линията, по която фигурата може, условно казано, да бъде "разрязана" на равни половини (на тази снимка оста на симетрия е права):

Сега да се върнем към нашата задача. Знаем, че търсим точка, която е симетрична спрямо оста. Тогава тази ос е оста на симетрия. Това означава, че трябва да отбележим точка, така че оста да разрязва сегмента на две равни части. Опитайте се сами да маркирате такава точка. Сега сравнете с моето решение:
![]()
По същия начин ли се получи и при вас? Добре! Интересува ни ординатата на намерената точка. То е равно
отговор:
Сега ми кажете, след като помислих няколко секунди, каква ще бъде абсцисата на точка, симетрична на точка А спрямо ординатната ос? какъв е вашият отговор Правилен отговор:.
IN общ случайправилото може да се напише така:
Точка, симетрична на точка спрямо абсцисната ос, има координатите:
Точка, симетрична на точка спрямо ординатната ос, има координати:
Е, сега е напълно страшно задача: намерете координатите на точка, симетрична на точката спрямо началото. Вие първо помислете за себе си, а след това погледнете моята рисунка!
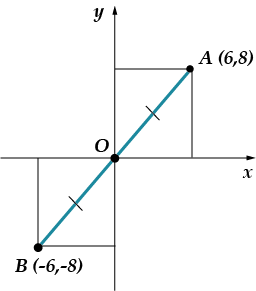
отговор:
Сега задача с успоредник:
Задача 5: Точките се появяват ver-shi-na-mi pa-ral-le-lo-gram-ma. Намерете или-ди-на-тази точка.
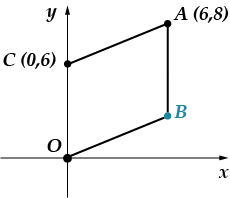
Можете да решите този проблем по два начина: логически и координатен метод. Първо ще използвам метода на координатите и след това ще ви кажа как можете да го решите по различен начин.
Съвсем ясно е, че абсцисата на точката е равна. (лежи върху перпендикуляра, прекаран от точката към абсцисната ос). Трябва да намерим ординатата. Нека се възползваме от факта, че нашата фигура е успоредник, това означава, че. Нека намерим дължината на отсечката, използвайки формулата за разстоянието между две точки:
Спускаме перпендикуляра, свързващ точката с оста. Ще обознача пресечната точка с буква.
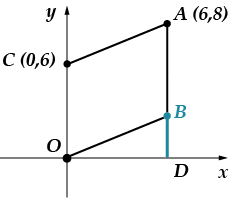
Дължината на отсечката е равна. (намерете проблема сами там, където обсъждахме тази точка), тогава ще намерим дължината на сегмента, използвайки Питагоровата теорема:
Дължината на сегмента съвпада точно с неговата ордината.
отговор: .
Друго решение (просто ще дам снимка, която го илюстрира)
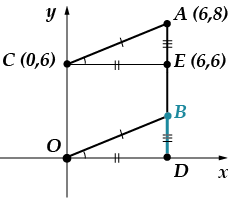
Напредък на решението:
1. Поведение
2. Намерете координатите на точката и дължината
3. Докажете това.
Още един проблем с дължината на сегмента:
Точките се появяват на върха на триъгълника. Намерете дължината на средната му линия, успоредна.

Помните ли какво е средна линиятриъгълник? Тогава тази задача е елементарна за вас. Ако не помните, тогава ще ви напомня: средната линия на триъгълник е линията, която свързва средните точки противоположни страни. Тя е успоредна на основата и равна на половината от нея.
Основата е сегмент. Трябваше да търсим дължината му по-рано, тя е равна. Тогава дължината на средната линия е наполовина по-голяма и равна.
отговор: .
Коментар: този проблем може да бъде решен по друг начин, който ще разгледаме малко по-късно.
Междувременно, ето няколко задачи за вас, практикувайте с тях, те са много прости, но ви помагат да станете по-добри в използването на метода на координатите!
1. Точките са върха на тра-пе-циите. Намерете дължината на средната му линия.

2. Точки и изяви ver-shi-na-mi pa-ral-le-lo-gram-ma. Намерете или-ди-на-тази точка.

3. Намерете дължината от разреза, свързвайки точката и

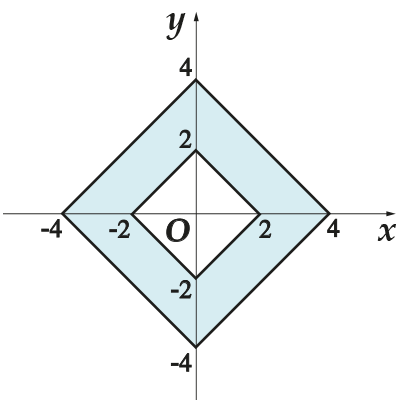
4. Намерете площта зад оцветената фигура на координатната равнина.
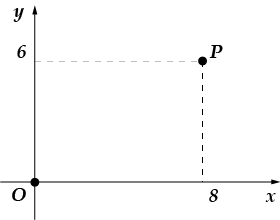
5. През точката минава кръг с център на-ча-ле ко-ор-ди-нат. Намерете я ra-di-us.
6. Намерете-di-te ra-di-us на кръга, опишете-san-noy за правия ъгъл-no-ka, върховете на нещо имат ко-или -di-na-ти си толкова отговорен

Решения:
1. Известно е, че средната линия на трапец е равна на половината от сбора на неговите основи. Основата е равна, а основата. Тогава
отговор:
2. Най-лесният начин да решите тази задача е да отбележите това (правилото на успоредника). Изчисляването на координатите на векторите не е трудно: . При добавяне на вектори се добавят координатите. Тогава има координати. Точката също има тези координати, тъй като началото на вектора е точката с координатите. Интересуваме се от ординатата. Тя е равна.
отговор:
3. Веднага действаме по формулата за разстоянието между две точки:
отговор:
4. Погледнете снимката и ми кажете между кои две фигури е „притисната“ защрихованата област? Той е притиснат между два квадрата. Тогава площта на желаната фигура е равна на площта на големия квадрат минус площта на малкия. отстрани малък квадрате сегмент, свързващ точки и дължината му е
Тогава площта на малкия квадрат е
Правим същото с голям квадрат: страната му е сегмент, свързващ точките, а дължината му е
Тогава площта на големия квадрат е
Намираме площта на желаната фигура по формулата:
отговор:
5. Ако една окръжност има началото като център и минава през точка, тогава нейният радиус ще бъде точно равен на дължинатасегмент (направете чертеж и ще разберете защо това е очевидно). Нека намерим дължината на този сегмент:
отговор:
6. Известно е, че радиусът на окръжност, описана около правоъгълник равен на половинатанеговите диагонали. Нека намерим дължината на всеки от двата диагонала (все пак в правоъгълник те са равни!)
отговор:
Е, справихте ли се с всичко? Не беше много трудно да го разбера, нали? Тук има само едно правило - можете да направите визуална картина и просто да „четете“ всички данни от нея.
Остава ни много малко. Има буквално още две точки, които бих искал да обсъдя.
Нека се опитаме да разрешим този прост проблем. Нека две точки и да бъдат дадени. Намерете координатите на средата на отсечката. Решението на този проблем е следното: нека точката е желаната среда, тогава тя има координати:
това е: координати на средата на сегмента = средноаритметичната стойност на съответните координати на краищата на сегмента.
Това правило е много просто и обикновено не създава затруднения на учениците. Нека да видим при какви проблеми и как се използва:
1. Find-di-te or-di-na-tu se-re-di-ny from-cut, connect-the-point и

2. Точките изглеждат върховете на света. Find-di-te or-di-na-tu точки per-re-se-che-niya на неговия dia-go-na-ley.

3. Намерете-di-te abs-cis-su център на кръга, опишете-san-noy за правоъгълната-no-ka, върховете на нещо имат co-or-di-na-you толкова-отговорно-но.

Решения:
1. Първият проблем е просто класически. Пристъпваме веднага към определяне на средата на сегмента. Има си координати. Ординатата е равна.
отговор:
2. Лесно се вижда, че този четириъгълник е успоредник (дори ромб!). Можете сами да докажете това, като изчислите дължините на страните и ги сравните една с друга. Какво знам за успоредниците? Диагоналите му са разделени наполовина от пресечната точка! да! И така, каква е пресечната точка на диагоналите? Това е средата на някой от диагоналите! Ще избера по-специално диагонала. Тогава точката има координати. Ординатата на точката е равна на.
отговор:
3. С какво съвпада центърът на окръжността, описана около правоъгълника? Тя съвпада с пресечната точка на неговите диагонали. Какво знаете за диагоналите на правоъгълник? Те са равни и точката на пресичане ги дели наполовина. Задачата беше намалена до предишната. Да вземем например диагонала. Тогава, ако е центърът на описаната окръжност, тогава е средната точка. Търся координати: Абсцисата е равна.
отговор:
Сега упражнявайте малко сами, аз просто ще дам отговорите на всеки проблем, за да можете да се тествате.
1. Намерете-di-te ra-di-us на кръга, опишете-san-noy за триъгълника-no-ka, върховете на нещо имат co-or-di -on-you

2. Намерете-ди-те или-ди-на-този център на кръга, опишете-сан-ной за триъгълника-но-ка, чиито върхове имат координати
3. Какъв вид ра-ди-у-са трябва да има кръг с център в точка, така че да съответства на аб-цисната ос?
4. Намерете-ди-тези или-ди-на-тази точка на пренасочване на оста и от изрязване, свързване на точката и

Отговори:
Всичко успешно ли беше? Силно се надявам! Сега - последния тласък. Сега бъдете особено внимателни. Материалът, който сега ще обясня е пряко свързан не само с прости задачикъм координатния метод от част B, но се среща и навсякъде в задача C2.
Кое от обещанията си все още не съм спазил? Помните ли какви операции върху вектори обещах да въведа и кои в крайна сметка въведох? Сигурен ли си, че не съм забравил нищо? забравих! Забравих да обясня какво означава векторно умножение.
Има два начина за умножаване на вектор по вектор. В зависимост от избрания метод ще получим обекти от различно естество:
Кръстосаното произведение е направено доста умно. Ще обсъдим как да го направим и защо е необходимо в следващата статия. И в този ще се съсредоточим върху скаларното произведение.
Има два начина, които ни позволяват да го изчислим:
Както се досещате, резултатът трябва да е същият! Така че нека първо да разгледаме първия метод:
Точково произведение чрез координати
Намерете: - общоприета нотация за скаларно произведение
Формулата за изчисление е следната:
това е точков продукт= сбор от произведенията на векторните координати!
Пример:
Намери-ди-те
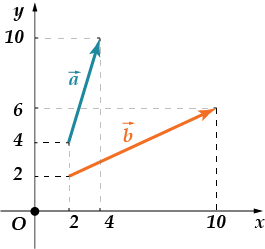
Решение:
Нека намерим координатите на всеки от векторите:
Изчисляваме скаларното произведение по формулата:
отговор:
Вижте, абсолютно нищо сложно!
Е, сега опитайте сами:
· Намерете скаларен про-из-ве-де-ние от векове и
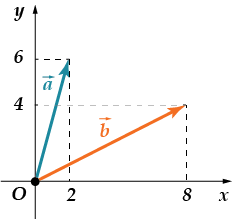
успяхте ли Може би сте забелязали малка уловка? Да проверим:
Векторни координати като в последна задача! Отговор: .
В допълнение към координатния, има и друг начин за изчисляване на скаларния продукт, а именно чрез дължините на векторите и косинуса на ъгъла между тях:
Означава ъгъла между векторите и.
Тоест скаларното произведение е равно на произведението от дължините на векторите и косинуса на ъгъла между тях.
Защо ни трябва тази втора формула, ако имаме първата, която е много по-проста, поне в нея няма косинуси. И това е необходимо, за да можем от първата и втората формула вие и аз да изведем как да намерим ъгъла между векторите!
Нека Тогава си спомнете формулата за дължината на вектора!
След това, ако заместя тези данни във формулата за скаларно произведение, получавам:
Но от друга страна:
И така, какво получихме ти и аз? Вече имаме формула, която ни позволява да изчислим ъгъла между два вектора! Понякога се пише и така за краткост:
Тоест алгоритъмът за изчисляване на ъгъла между векторите е следният:
- Изчислете скаларното произведение чрез координати
- Намерете дължините на векторите и ги умножете
- Разделете резултата от точка 1 на резултата от точка 2
Нека практикуваме с примери:
1. Намерете ъгъла между клепачите и. Дайте отговора на град-ду-сах.
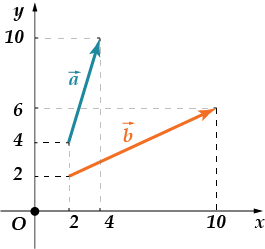
2. В условията на предишната задача намерете косинуса между векторите
Нека направим това: аз ще ви помогна да решите първия проблем и се опитайте да направите втория сам! Съгласни ли сте? Тогава да започваме!
1. Тези вектори са наши стари приятели. Вече изчислихме тяхното скаларно произведение и беше равно. Техните координати са: , . След това намираме техните дължини:
След това търсим косинуса между векторите:
Колко е косинусът на ъгъла? Това е ъгълът.
отговор:
Е, сега решете втората задача сами и след това сравнете! Ще дам само едно много кратко решение:
2. има координати, има координати.
Нека е ъгълът между векторите и, тогава
отговор:
Трябва да се отбележи, че задачите директно върху векторите и координатния метод в част Б изпитна работадоста рядко. Въпреки това, по-голямата част от проблемите на C2 могат лесно да бъдат решени чрез въвеждане на координатна система. Така че можете да считате тази статия за основата, на базата на която ще направим доста умни конструкции, които ще ни трябват за решаване на сложни проблеми.
