Правоъгълна (други имена - плоска, двуизмерна) координатна система, кръстена на френския учен Декарт (1596-1650) " Декартова системакоординати в равнината” се образува от пресичането в равнината под прав ъгъл (перпендикуляр) на две числови оси, така че положителната полуос на едната е насочена надясно (ос x или абсцисната ос), а втората е насочена нагоре (у-ос или ординатна ос).
Пресечната точка на осите съвпада с нулевата точка на всяка от тях и се нарича начало на координатите.
За всяка от осите се избира произволен мащаб (отсечка с една дължина). Всяка точка от равнината съответства на една двойка числа, наречени координати на тази точка от равнината. Обратно, всяка подредена двойка числа съответства на една точка от равнината, за която тези числа са координати.
Първата координата на точка се нарича абциса на тази точка, а втората координата се нарича ордината.
Цялата координатна равнина е разделена на 4 квадранта (четвърти). Квадрантите са разположени от първия до четвъртия обратно на часовниковата стрелка (виж фигурата).
За да определите координатите на точка, трябва да намерите нейното разстояние до абсцисата и ординатната ос. Тъй като разстоянието (най-късото) се определя от перпендикуляра, тогава от точката два перпендикуляра (спомагателни линии на координатната равнина) се спускат върху оста, така че точката на тяхното пресичане е местоположението дадена точкав координатната равнина. Точките на пресичане на перпендикуляри с оси се наричат проекции на точката върху координатните оси.
Първият квадрант е ограничен от положителните полуоси на абсцисата и ординатата. Следователно координатите на точките в тази четвърт на равнината ще бъдат положителни
(знаци "+" и
Например точка M (2; 4) на фигурата по-горе.
Вторият квадрант е ограничен от отрицателната ос x и положителната ос y. Следователно координатите на точките по абсцисната ос ще бъдат отрицателни (знак "-"), а по ординатната ос те ще бъдат положителни (знак "+").
Например точка C (-4; 1) на фигурата по-горе.
Третият квадрант е ограничен от отрицателната ос x и отрицателната ос y. Следователно координатите на точките по абсцисната и ординатната ос ще бъдат отрицателни (знаци „-“ и „-“).
Например точка D (-6; -2) на фигурата по-горе.
Четвъртият квадрант е ограничен от положителната ос x и отрицателната ос y. Следователно координатите на точките по абсцисната ос ще бъдат положителни (знакът "+"). и по ординатната ос - отрицателен (знак "-").
Например точка R (3; -3) на фигурата по-горе.
Конструиране на точка с нейните зададени координати
ще намерим първата координата на точката по оста x и ще начертаем спомагателна права през нея - перпендикуляр;
намираме втората координата на точката на ординатната ос и начертаваме спомагателна линия през нея - перпендикуляр;
точката на пресичане на два перпендикуляра (спомагателни линии) ще съответства на точката с дадените координати.
основно професионално образование
"Професионално училище № 5" Белгород
Обобщение на урока
по математика на тема:
Правоъгълна системакоординати в пространството
за ученици от 11 клас
учител по информатика и математика
ГОУ НПО ПУ №5
Белгород 2010 г
Тема на урока
: Правоъгълна координатна система в пространството. Векторни координати
Цели на урока: - развива логически и пространствен мислене
Въвеждане на концепцията за координатна система в пространството, векторни координати
Литература: Геометрия 10-11 клас Л. С. Атанасян, М.: Образование, 2006 г.
По време на часовете:
орг. Момент
Обяснение на нов материал
Ако през точка в пространството се начертаят три по двойки перпендикулярни прави, на всяка от тях се избере посока (посочена със стрелка) и се избере мерната единица за сегменти, тогава се казва, че правоъгълна координатна системав пространството (фиг. 121). Наричат се прави линии с избрани върху тях посоки координатни оси, и техния обща точка - произход. Обикновено се обозначава с буквата O. Координатните оси се означават по следния начин: Ox, Oy, Oz - и имат имена: абсцисна ос, ординатна ос, апликативна ос. Цялата координатна система е обозначена като Oxyz. Равнините, минаващи съответно през координатните оси Ox и Oy, Oy и Oz, Oz и Ox, се наричат координатни равнинии се обозначават Oxy, Oyz, Ozx.
Точка O разделя всяка от координатните оси на два лъча. Лъч, чиято посока съвпада с посоката на оста, се нарича положителна полуос, а другата греда отрицателна полуос.
IN 
в правоъгълна координатна система всяка точка M от пространството е свързана с тройка числа, които се наричат нейни координати. Те се определят подобно на координатите на точки в равнината. Нека начертаем три равнини през точка M, перпендикулярни на координатните оси, и означим с M 1, M 2 и M 3 точките на пресичане на тези равнини съответно с абсцисната, ординатната и апликативната ос (фиг. 122). Първата координата на точка М (нарича се абсцисатаи обикновено се обозначава с буквата x) се определя, както следва: x = OM 1, ако M 1 е точката на положителната полуос; x = - OM 1, ако M 1 е точката на отрицателната полуос; x = 0, ако M 1 съвпада с точка O. По същия начин, използвайки точка M 2 втората координата ( ордината) y точка M и с помощта на точка M 3 третата координата ( прилагам) z точка M. Координатите на точка M се записват в скоби след обозначението на точката: M (x; y; z), като абсцисата е посочена на първо място, ординатата е посочена на второ място, а приложението е посочено на трето място. Фигура 123 показва шест точки A (9; 5; 10), B (4; -3; 6), C (9; 0; 0), E (4; 0; 5), E (0; 3; 0 ) , F (0; 0; -3).
д 
ако точка M (x; y; z) лежи върху координатна равнинаили на координатната ос, то някои от координатите му са равни на нула. Така че, ако M € Oxy, тогава приложението на точката M е равно на нула: z = 0. По същия начин, ако M с Oxz, тогава y = 0 и ако M € Oyz, тогава x = 0. Ако M € Ox , тогава ординатата и апликата на точката M са равни на нула: y = 0 и z = 0 (например в точка C на фигура 123). Ако M € Oy, тогава x = 0 и z = 0; ако M€ Oz, тогава x = 0 и y = 0. И трите координати на началото са равни на нула: 0 (0; 0; 0).
Векторни координати
З 
Нека дефинираме правоъгълна координатна система Oxyz в пространството. На всяка от положителните полуоси нанасяме от началото на координатите единичен вектор
, т.е. вектор, чиято дължина е равна на единица. азединичен вектор на оста x, през й- единичен вектор на ординатната ос и през кединичен вектор на приложната ос (фиг. 124). Нека наречем вектори i, j, k координатни вектори. Очевидно тези вектори не са компланарни. Ето защо всеки вектораи може да се разложи на координатни вектори, т.е., представя го във формата
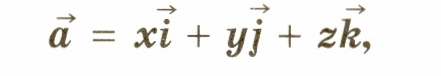
и коефициентите на разширение x, y,zсе определят по уникален начин.
ДА СЕ 
коефициентите x, y и z при разлагането на вектор a в координатни вектори се наричат векторни координатиав тази координатна система. Координатите на вектора a ще запишем във къдрави скоби след обозначението на вектора: a (x; y; z). Фигура 125 показва кубоид, имащи следните размери: OA 1 = 2, OA 2 = 2, OA 3 =4. Координатите на векторите, показани на тази фигура, са: a (2; 2; 4), b(2; 2; -1), A 3 A (2; 2; 0), i(1; 0; 0), j (0; 1; 0), k(0; 0; 1).
Тъй като нулевият вектор може да бъде представен като 0 = oi+ oj+ 0k, тогава всички координати на нулевия вектор са равни на нула. Освен това, координати равни векторисъответно равни, т.е. ако векторите a(x 1, y 1, z 1) и b(x 2, y 2, z 2) са равни, тогава x 1 = x 2, y 1 = y 2 и z 1 = z 2 ( обясни защо).
Нека помислим правила, които позволяват да се използват координатите на тези вектори, за да се намерят координатите на тяхната сума и разлика, както и координатите на продукта даден векторза този номер.
1 0 . Всяка координата на сумата от два или повече вектора е равна на сумата от съответните координати на тези вектори.С други думи, ако a (x 1, y 1, z 1) и b(x 2, y 2, z 2) са дадени вектори, тогава векторът a + b има координати (x 1 + x 2, y 1 + y 2 , z 1 + z 2 ).
2 0 . Всяка координата на разликата на два вектора е равна на разликата на съответните координати на тези вектори. С други думи, ако a (x 1, y 1, z 1) и b(x 2 y 2; z 2) са дадени вектори, тогава векторът a- b има координати (x 1 - x 2, y 1 – y 2, z 1 - z 2 ).
3 ОТНОСНО. Всяка координата на произведението на вектор и число е равна на произведението на съответната координата на вектора и това число. С други думи, ако a(x;y;x) -
За да определим позицията на точка в пространството, ще използваме декартова система правоъгълни координати(фиг. 2).
Декартовата правоъгълна координатна система в пространството се образува от три взаимно перпендикулярни координатни оси OX, OY, OZ. Координатните оси се пресичат в точка O, която се нарича начало, на всяка ос е избрана положителна посока, обозначена със стрелки, и мерна единица за сегментите на осите. Мерните единици обикновено (не непременно) са еднакви за всички оси. Оста OX се нарича абсцисна ос (или просто абциса), оста OY е ординатната ос, а оста OZ е приложимата ос.
Положението на точка А в пространството се определя от три координати x, y и z. Координатата x е равна на дължината на сегмента OB, координатата y е дължината на сегмента OC, координатата z е дължината на сегмента OD в избраните мерни единици. Отсечките OB, OC и OD се определят от равнини, начертани от точка, успоредна съответно на равнините YOZ, XOZ и XOY.
Координатата x се нарича абсцисата на точка A, координатата y се нарича ордината на точка A, а координатата z се нарича апликация на точка A.
Символично се изписва така:
или свържете координатен запис към конкретна точка с помощта на индекс:
x A, y A, z A,
Всяка ос се разглежда като числова линия, т.е. има положителна посока и точките, лежащи на отрицателния лъч, са присвоени отрицателни стойностикоординати (разстоянието се взема със знак минус). Тоест, ако например точка B лежи не както на фигурата - върху лъча OX, а върху неговото продължение в обратна странаот точка O (на отрицателната част на оста OX), тогава абсцисата x на точка A ще бъде отрицателна (минус разстоянието OB). По същия начин и за другите две оси.
Координатните оси OX, OY, OZ, показани на фиг. 2, образуват дясна координатна система. Това означава, че ако погледнете равнината YOZ по положителната посока на оста OX, тогава движението на оста OY към оста OZ ще бъде по посока на часовниковата стрелка. Тази ситуация може да се опише с помощта на правилото на гимлет: ако гимлетът (винт с дясна резба) се завърти в посока от оста OY към оста OZ, тогава той ще се движи по положителната посока на оста OX.
Вектори с единична дължина, насочени по дължина координатни оси, се наричат координатни единични вектори. Те обикновено се обозначават като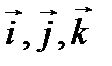 
(фиг. 3). Там е и обозначението 
Единичните вектори формират основата на координатната система.
В случай на дясна координатна система, валидно следните формулис вектор работиортов:
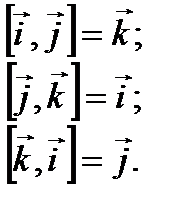
Правоъгълна координатна система в пространството е взаимно тройна перпендикулярни оси, пресичащи се в една точка O, наречена начало.
Координатните оси обикновено се обозначават с букви и се наричат съответно абсцисната ос, ординатната ос, приложната ос или ос Oy, ос (фиг. 33).
Единичните вектори на координатните оси Ox, Oy, Oz се означават съответно или. Ще използваме основно последното обозначение.
Има дясна и лява координатна система.
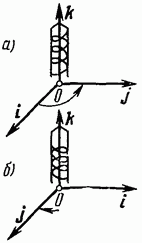
Координатната система се нарича права, ако се вижда, че от края на третия орт до завоя от първия орт към втория орт се случва обратно на часовниковата стрелка (фиг. 34, а).
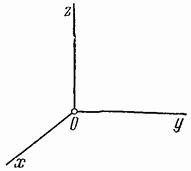
Координатната система се нарича лява, ако от края на третия орт въртенето от първия орт към втория орт се вижда като настъпващо по посока на часовниковата стрелка (фиг. 34, b).
По този начин, ако завиете винта в посока на вектора k, като го завъртите, тогава в случай на дясна система резбата трябва да е дясна, а в случай на лява система - наляво -ръчен (фиг. 35).
Много разпоредби на векторната алгебра не зависят от това дали използваме дясна или лява координатна система. Понякога обаче това обстоятелство има значение. По-нататък винаги ще използваме дясната координатна система, както е обичайно във физиката.