Четырехугольная пирамида

Решая задачу C2 методом координат, многие ученики сталкиваются с одной и той же проблемой. Они не могут рассчитать координаты точек , входящих в формулу скалярного произведения. Наибольшие трудности вызывают пирамиды . И если точки основания считаются более-менее нормально, то вершины - настоящий ад.

Сегодня мы займемся правильной четырехугольной пирамидой. Есть еще треугольная пирамида (она же - тетраэдр ). Это более сложная конструкция, поэтому ей будет посвящен отдельный урок.

Для начала вспомним определение:

Определение

Правильная пирамида - это такая пирамида, у которой:

В основании лежит правильный многоугольник: треугольник, квадрат и т.д.;
Высота, проведенная к основанию, проходит через его центр.

В частности, основанием четырехугольной пирамиды является квадрат . Прямо как у Хеопса, только чуть поменьше.

Ниже приведены расчеты для пирамиды, у которой все ребра равны 1. Если в вашей задаче это не так, выкладки не меняются - просто числа будут другими.

Вершины четырехугольной пирамиды

Итак, пусть дана правильная четырехугольная пирамида SABCD , где S - вершина, основание ABCD - квадрат. Все ребра равны 1. Требуется ввести систему координат и найти координаты всех точек. Имеем:

Вводим систему координат с началом в точке A :

Ось OX направлена параллельно ребру AB ;
Ось OY - параллельно AD . Поскольку ABCD - квадрат, AB ⊥ AD ;
Наконец, ось OZ направим вверх, перпендикулярно плоскости ABCD .

Теперь считаем координаты. Дополнительное построение: SH - высота, проведенная к основанию. Для удобства вынесем основание пирамиды на отдельный рисунок. Поскольку точки A , B , C и D лежат в плоскости OXY , их координата z = 0. Имеем:

A = (0; 0; 0) - совпадает с началом координат;
B = (1; 0; 0) - шаг на 1 по оси OX от начала координат;
C = (1; 1; 0) - шаг на 1 по оси OX и на 1 по оси OY ;
D = (0; 1; 0) - шаг только по оси OY .
H = (0,5; 0,5; 0) - центр квадрата, середина отрезка AC .

Осталось найти координаты точки S . Заметим, что координаты x и y точек S и H совпадают, поскольку они лежат на прямой, параллельной оси OZ . Осталось найти координату z для точки S .

Рассмотрим треугольники ASH и ABH :

AS = AB = 1 по условию;
Угол AHS = AHB = 90°, поскольку SH - высота, а AH ⊥ HB как диагонали квадрата;
Сторона AH - общая.

Следовательно, прямоугольные треугольники ASH и ABH равны по одному катету и гипотенузе. Значит, SH = BH = 0,5 · BD . Но BD - диагональ квадрата со стороной 1. Поэтому имеем:

Итого координаты точки S :

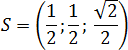
В заключение, выпишем координаты всех вершин правильной прямоугольной пирамиды:

Что делать, когда ребра разные

А что, если боковые ребра пирамиды не равны ребрам основания? В этом случае рассмотрим треугольник AHS :

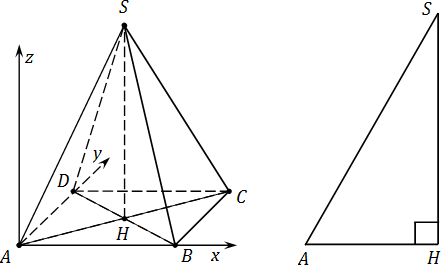
Треугольник AHS - прямоугольный , причем гипотенуза AS - это одновременно и боковое ребро исходной пирамиды SABCD . Катет AH легко считается: AH = 0,5 · AC . Оставшийся катет SH найдем по теореме Пифагора . Это и будет координата z для точки S .

Задание.

В основании четырехугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 4 и BC = 6. Длины боковых ребер пирамиды SA = 3, SB = 5, SD = 3√5.

а) Докажите, что SA – высота пирамиды.

б) Найдите расстояние от вершины А до плоскости SBС.

Решение:

а) Докажите, что SA – высота пирамиды.

Рассмотрим треугольник SAB. По теореме, обратной теореме Пифагора (Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный), стороны этого треугольника удовлетворяют равенству:

SB 2 = SA 2 + AB 2

Следовательно, треугольник SAB – прямоугольный,

Рассмотрим треугольник SAD. По теореме, обратной теореме Пифагора, стороны этого треугольника удовлетворяют равенству:

SD 2 = AD 2 + SA 2

Следовательно, треугольник SAD – прямоугольный,

Значит, SA – высота пирамиды.

б) Найдите расстояние от вершины А до плоскости SBС.

Расстоянием от точки до плоскости называется перпендикуляр, проведенный от точки до данной плоскости.

1 способ:

SA перпендикулярна плоскости ABC, SB – наклонная к плоскости ABC, АВ – проекция наклонной SB на плоскость ABC. Тока В – основание наклонной, через точку В проходит прямая ВС перпендикулярно проекции АВ (ABCD – прямоугольник), тогда по теореме о трех перпендикулярах прямая ВС перпендикулярна наклонной SB.

Прямая ВС перпендикулярна двум пересекающимся прямым АВ и SB, лежащим в плоскости ASB, следовательно ВС перпендикулярна плоскости ASB. ВС лежит в плоскости SBС, значит, плоскости ASB и SBС перпендикулярны. Следовательно, расстоянием от точки А до плоскости SBС будет являться перпендикуляр АК (высота прямоугольного треугольника ∆ ASB).

Задание.

В основании четырехугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = √11 и BC = 2√3. Длины боковых ребер пирамиды SA = 5, SB = 6, SD = √37.

а) Докажите, что SA – высота пирамиды.

б) Найдите угол между прямой SC и плоскостью ASB.

Решение:

а) Докажите, что SA – высота пирамиды.

SB 2 = SA 2 + AB 2

Следовательно, треугольник SAB – прямоугольный,

SD 2 = AD 2 + SA 2

Следовательно, треугольник SAD – прямоугольный,

Значит, SA – высота пирамиды.

б) Найдите угол между прямой SC и плоскостью ASB.

Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.

Прямая ВС перпендикулярна двум пересекающимся прямым АВ и SB, лежащим в плоскости ASB, следовательно ВС перпендикулярна плоскости ASB.

Проекцией SС на плоскость ASB будет прямая SB. Таким образом, угол между прямой SС и плоскостью ASB является угол между прямой SС и ее проекцией SB на эту плоскость, т. е ∠BSC.

Рассмотрим прямоугольный треугольник BSC:

Ответ: 30 ˚

Понравилось? Нажмите

Задание 14. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 8 и ВС = 6. Длины боковых рёбер пирамиды SA = √21, SB = √85 , SD = √57.

а) Докажите, что SA - высота пирамиды.

б) Найдите угол между прямыми SC и BD.

Решение.

а) Рассмотрим треугольник SAB. Из значения его сторон следует, что

Следовательно, SB – гипотенуза и угол SAB – прямой.

Аналогично для треугольника SAD:

получаем, что SD – гипотенуза и угол SAD – прямой. В результате получаем, что при и , следует (по признаку перпендикулярности прямой и плоскости), и следовательно, SA – высота пирамиды.

б) Угол между прямыми SC и BD – это угол между двумя скрещивающимися прямыми, который соответствует углу между прямыми NO и OD (см. рисунок). Так как прямая и точка O делит прямую AC пополам, то и точка N будет делить AS пополам. Следовательно, ON – это средняя линия треугольника ASC и равна

Вычислим диагональ AC из прямоугольного треугольника ACD.